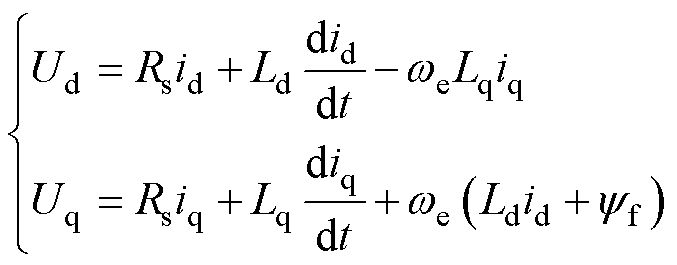 (1)
(1)
摘要 永磁同步电机(PMSM)无传感器控制系统中,观测器的设计至关重要,其精确性与稳定性直接影响系统性能。此外,如何有效适应突变负载引起的波动,提升系统运行的可靠性,是无传感器控制的一大难点。为此,该文首先在新坐标系下建立了永磁同步电机的数学模型,利用扩展卡尔曼滤波(EKF)算法来精确估计电机状态,提升控制精度的同时确保可靠运行。然后,分析了在电机稳定运行时和突变负载后的电流谐波变化,在线性自抗扰控制的基础上,引入二阶振荡函数,提出一种改进的惯性自抗扰控制(IADRC)技术,旨在削弱电流谐波的干扰。最后,利用奈奎斯特稳定判据证明了系统的稳定性,并通过仿真和实验证明了该方法的有效性和优越性。
关键词:永磁同步电机 惯性自抗扰控制 扩展卡尔曼滤波器 电流谐波 新坐标系
近年来,在电动航空领域中电动垂直起降(electric Vertical Take-Off and Landing, eVTOL)航空器迅速发展,对于电推进系统的要求不仅限于提供高效和可靠的动力输出,还需要动力系统有着精准和灵敏的控制能力。随着飞行器的应用领域不断扩大,对推进系统的性能要求日益严苛。在这种背景下,开发出优秀的控制算法对于最大化挖掘永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)的潜力至关重要。通过这些先进的控制技术,可以有效降低能耗,增加飞行持久力,且有助于降低维护成本,从而推动电动航空的进一步发 展[1-5]。
在电机控制领域,转子位置的获取是保证其转速精确的关键,常规条件下是利用位置传感器来实现对转子位置的检测,但存在对空间的占用、成本的提高与复杂工况下的可靠性等诸多问题。故无传感器控制算法得到更加广泛的应用。根据原理的不同,无传感器控制分为两种:基于基波数学模型的状态观测法和基于高频信号的状态分析法。对此,国内外学者进行了大量的研究。文献[6]提出了一种基于有效反电动势的全阶滑模观测器,该观测器具有二阶低通滤波的特性,可滤除反电动势中含有的高频噪声,具有高鲁棒性和高转矩输出的特点。文献[7]介绍了一种极坐标多信号通量观测器(Polar Coordinate Multi-signal Flux Observer, PCMFO),通过整合多个子观测器同步估计转子位置和磁通量,从而代替了传统的估计步骤。文献[8]描述了一种基于梯度下降的非线性位置观测器,利用黄金分割搜索优化步长,有效减少位置估计误差。文献[9]提出一种改进的双四路滤波器锁相环,以减小产生的位置误差,提高了系统的稳态精度。文献[10]提出了一种基于高频注入的角度自调整在线抑制方法,通过估计反电动势增量,有效减小位置误差。文献[11]介绍了一种结合开关PI控制的模型参考自适应系统观测器下的模糊逻辑控制器,通过电压补偿和双闭环控制提升控制精度和动态性能。文献[12]介绍了一种三阶自适应级联线性扩张状态观测器(Adaptive Cascaded Linear Expanded State Observer, ACLESO),用以替代传统锁相环(Phase-Locked Loop, PLL),降低噪声敏感性并确保速度、相位和扰动估计的准确性。文献[13]介绍了一种级联扩张状态观测器与自适应非奇异快速终端滑模控制器的综合控制策略,优化了系统的动态性能、稳态精度和鲁棒性。文献[14]提出一种负载变化下无传感器脉动抑制策略和转矩电流相位补偿方法,保证了电磁转矩和负载实时匹配。文献[15]提出了一种融合电气模型和机械模型的无传感器电机驱动方案,通过扩展卡尔曼滤波和信号注入技术在重载和低速条件下改善位置和速度估计,实现高效的伺服控制。
其中,滑模观测器(Sliding Mode Observer, SMO)以其优秀的鲁棒性受到重视,但是存在估计转速抖动以及相位滞后等问题。模型参考自适应(Model Reference Adaptive System, MRAS)方法利用自适应控制策略,调整参数匹配参考模型,从而实现对电机状态的精确估计,但是其存在对环境变化敏感等问题。神经网络算法在提升控制系统精度和稳定性方面有效,但由于其对芯片算力要求高,实际应用还不普及。相比之下,扩展卡尔曼滤波(Extended Kalman Filter, EKF)展现出独特优势,其既能保证对电机状态的精确估计,又能有效减少干扰和抑制系统噪声,具有高鲁棒性的优点,相比神经网络算法,其对计算资源的需求显著减少[16]。但是,当控制系统面临突变负载的问题时,EKF的残差矩阵不再满足自相关的高斯白噪声分布,这将会导致EKF对状态变量的跟踪性能下降,从而产生谐波[17]。
因此,为有效抑制永磁同步电机中的各种谐波扰动,文献[18]分析了霍尔位置误差对电流谐波和转矩脉动的影响,并提出了一种基于谐波分解复系数滤波器的锁相环结构来有效过滤谐波并精确估计转子位置。文献[19]提出一种基于离散时间重复控制的电流环线性自抗扰(Active Disturbance Rejection Control, ADRC)策略,来重复控制补偿交流扰动,以扩张观测器(Extend State Observer, ESO)抑制直流扰动,显著降低了系统的电流谐波。文献[20]根据粒子群(Particle Swarm Optimization, PSO)算法对转移概率和随机增益两种随机参数进行快速寻优,抑制了电流谐波与声振响应。文献[21]提出了一种准谐振自抗扰控制算法,通过并联准谐振环节与扩张状态观测器结合,同时估计了直流与交流扰动,有效抑制了系统的电流谐波。文献[22]提出了一种基于自适应线性神经元算法的低频补偿策略,有效降低了脉冲宽度调制(Pulse Width Modulation, PWM)噪声和偶数载波倍数附近的谐波。文献[23]分析了5次谐波对容错控制的影响,并提出了基于估计旋转坐标变换的容错控制策略,改善故障后的控制性能。文献[24]结合改进的复矢量控制器和虚拟阻抗,提出了有源阻尼方法,有效抑制了系统谐波。文献[25]针对Vienna整流器电流过零点畸变问题,提出了一种新型调制策略,最大程度地减少了电流畸变并保证了直流侧中点电压平衡。文献[26]提出一种基于滑模扰动观测器的开环电流控制策略,设计了滑模扰动观测器进行扰动观测,解决了传统开环控制易受参数扰动影响的问题,优化了系统的模拟精度与准确性。文献[27]提出一种新型的非对称空间矢量PWM(Space Vector PWM, SVPWM)的方法,通过优化开关频率和矢量阶数,提升了系统抑制谐波的性能。文献[28]针对三电平中点钳位(Neutral- Point-Clamped, NPC)型三相逆变器在特定次谐波消除脉宽调制(Selected Harmonic Elimi- nation PWM, SHEPWM)中的中点电位偏移,有效降低了开关损耗。文献[29]通过使用方波和调制波的部分差值作为微调量,优化了逆变器在功率不平衡条件下的性能,提高了高功率模块的工作能力。
为了精确获取转子位置并解决EKF在突变负载下谐波加剧的问题,本文首先建立了在新坐标系下的永磁同步电机数学模型并利用EKF进行无传感器控制。然后,针对EKF观测器突变负载后所造成的扰动,在谐波方面进行了分析,提出了一种惯性自抗扰控制(Inertial Active Disturbance Rejection Control, IADRC)方法。最后,通过仿真和实验验证了该控制策略的可行性和有效性。
PMSM的dq轴定子电压数学模型是在旋转坐标系下对电机性能进行分析的方法。该模型将电机的定子电压、电流以及磁通量等参数转换到同步旋转的dq坐标系中。
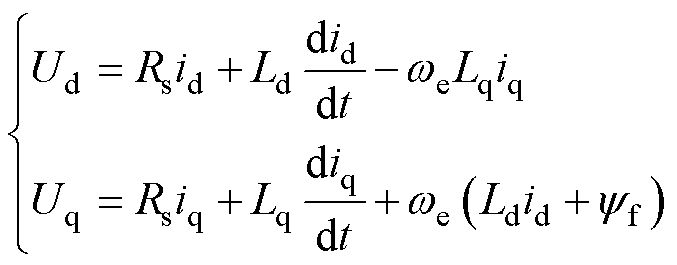 (1)
(1)
式中,id和iq分别为d、q轴下的定子电流;Ud和Uq分别为d、q轴下的定子电压;Ld和Lq分别为d、q轴下的电感;we为电角速度;Rs为定子电阻;yf为永磁体磁链。
为解决在低速状态下无传感器观测受到低信噪比的影响,以及高速状态下电机电磁噪声对观测准确性的干扰,使得基于传统数学模型下的算法无法准确预测转子位置的问题。新坐标系下的PMSM数学模型将定子的电感和磁通分解为基波驱动频率(相对低频)和高频两个分量。
PMSM矢量控制下的三种坐标系如图1所示,在这种坐标系下,正交dq坐标系以任意瞬间角速度旋转,旋转后被定义为新的估计旋转坐标系gd,得到新的定子电压数学模型为
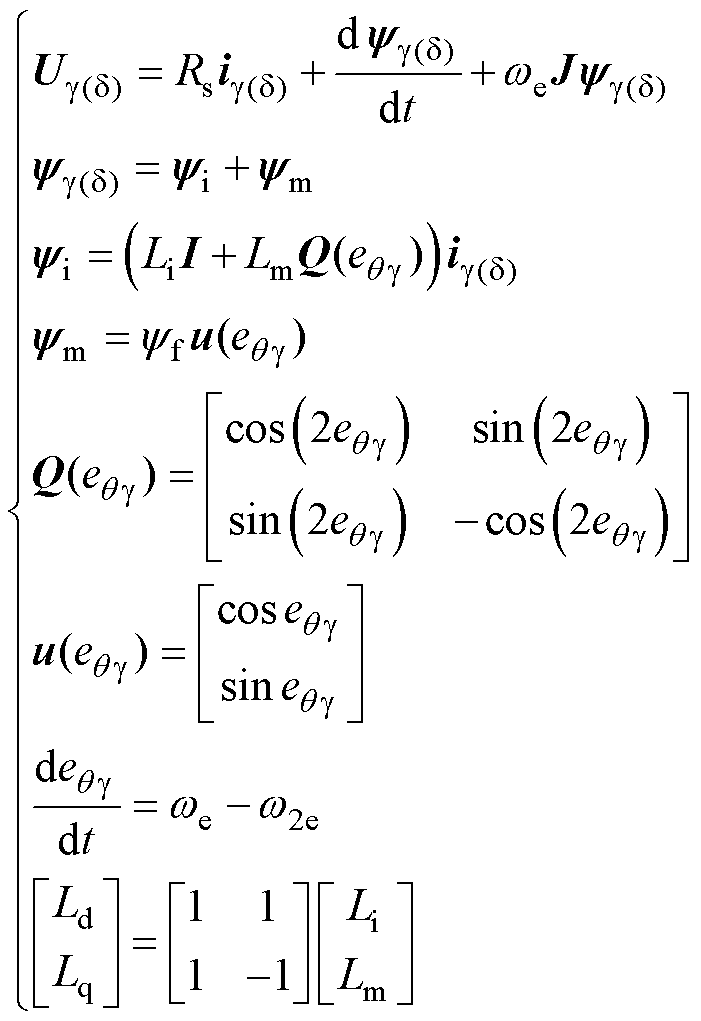 (2)
(2)
其中
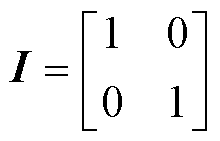 (3)
(3)
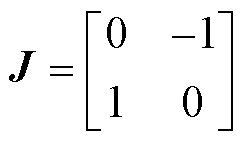 (4)
(4)
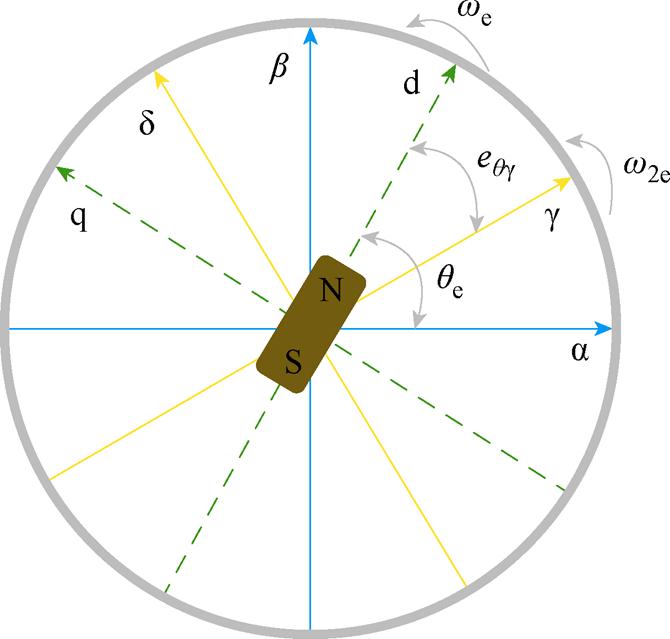
图1 电机各坐标系变化关系
Fig.1 The relationship between the coordinate systems of the motor
式中,Ug(d)=[Ud Uq]T和ig(d)=[id iq]T分别为定子电压、电流;yg(d)为定子磁通;yi和ym分别为基频磁通和高频磁通;Li和Lm分别为基频电感和高频电感;w2e为ab 到gd 坐标系的电角速度;eqg 为dq到gd坐标系下的位置误差角。
根据式(2),当坐标系上估计轴gd与旋转轴dq重合时,假设角度满足eqg≈0,deqg/dt=0。
首先,对PMSM定子磁通yg(d)求导得
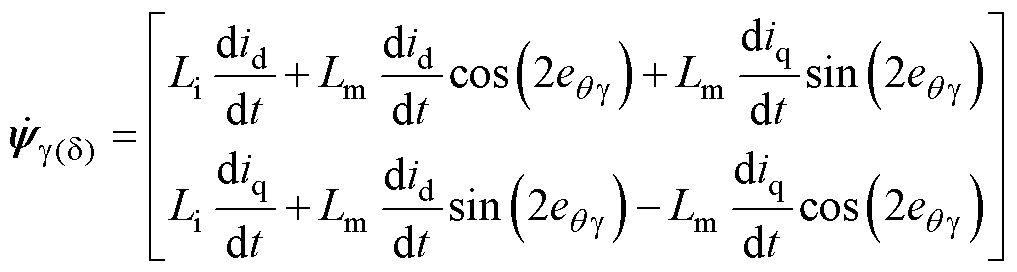 (5)
(5)
将式(5)用矩阵形式表示为
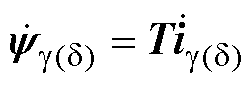 (6)
(6)
式中,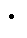 为对该值求导;T为转换矩阵。
为对该值求导;T为转换矩阵。
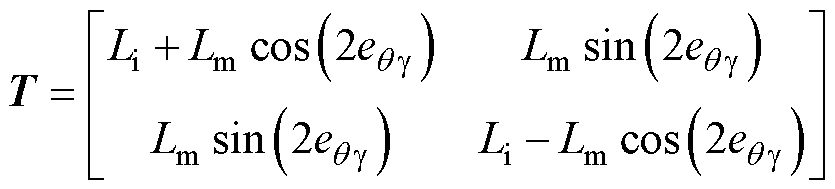 (7)
(7)
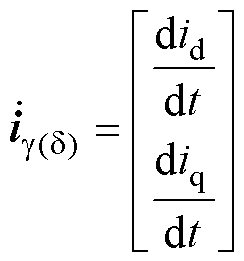 (8)
(8)
建立新的gd 轴数学模型为
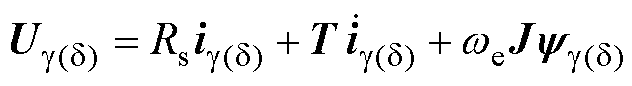 (9)
(9)
将永磁同步电机的定子电压方程转换为电流状态方程,有

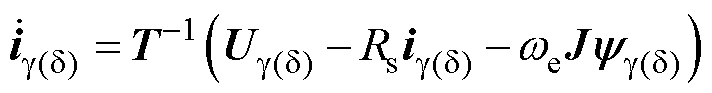 (10)
(10)
引入一个n×n的零元素矩阵,表示为0n×n。因此,建立基于扩展卡尔曼滤波的状态空间表达式为
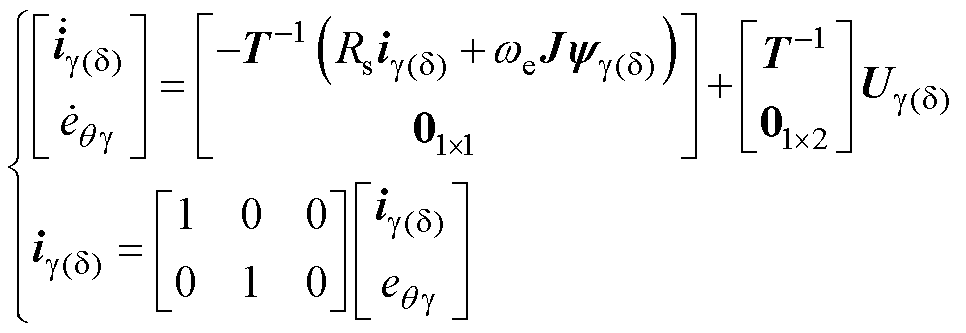 (11)
(11)
其中
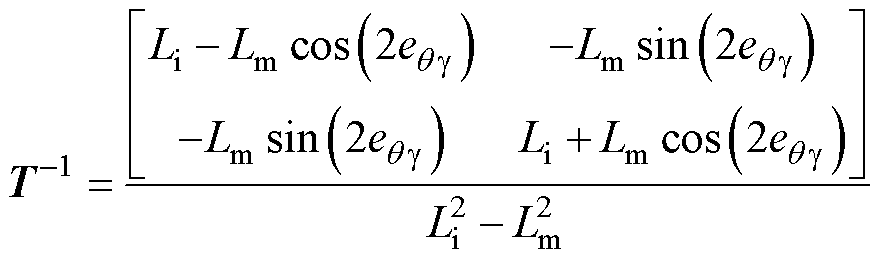 (12)
(12)
式(11)的非线性状态空间表达式可简写为
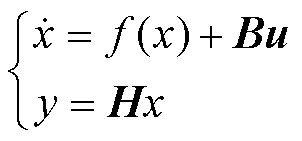 (13)
(13)
在此基础上建立扩展卡尔曼滤波观测器,进行离散化建模,有
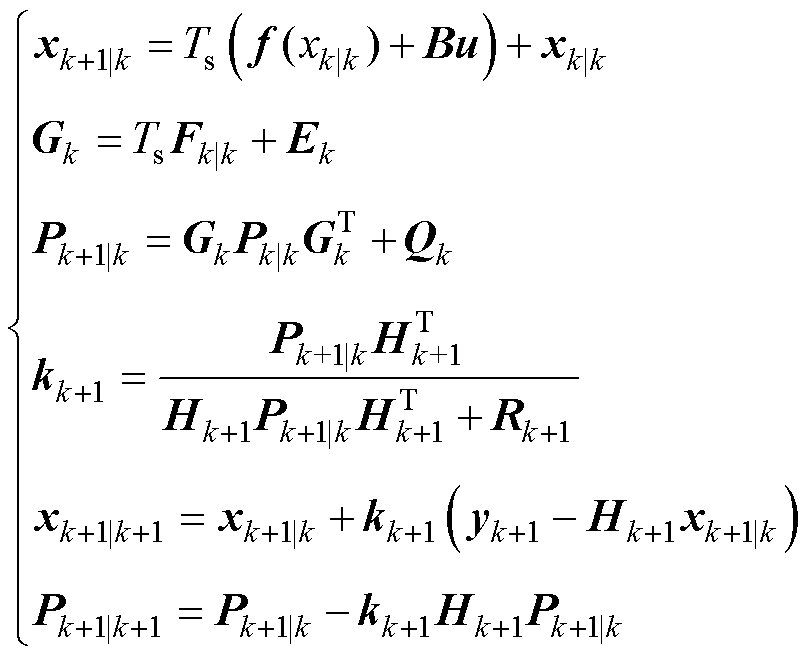 (14)
(14)
式中,Ts为离散采样时间;Fk|k为非线性函数f(xk)的一阶泰勒展开;Ek为单位矩阵;Gk为滤波增益矩阵;Qk和Rk+1分别为系统噪声和测量噪声方差的协方差矩阵;kk+1为下一时刻的卡尔曼增益矩阵;Pk+1|k和Pk+1|k+1分别为初始时刻和下一时刻的状态误差协方差矩阵,初始值设为P0;xk+1|k和xk+1|k+1分别为初始时刻和下一时刻的状态向量,初始值设为x0。
Fk|k、Qk、Rk、P0、x0的表达式为
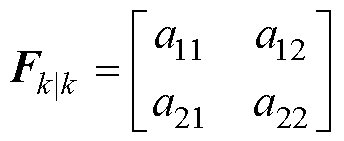 (15)
(15)
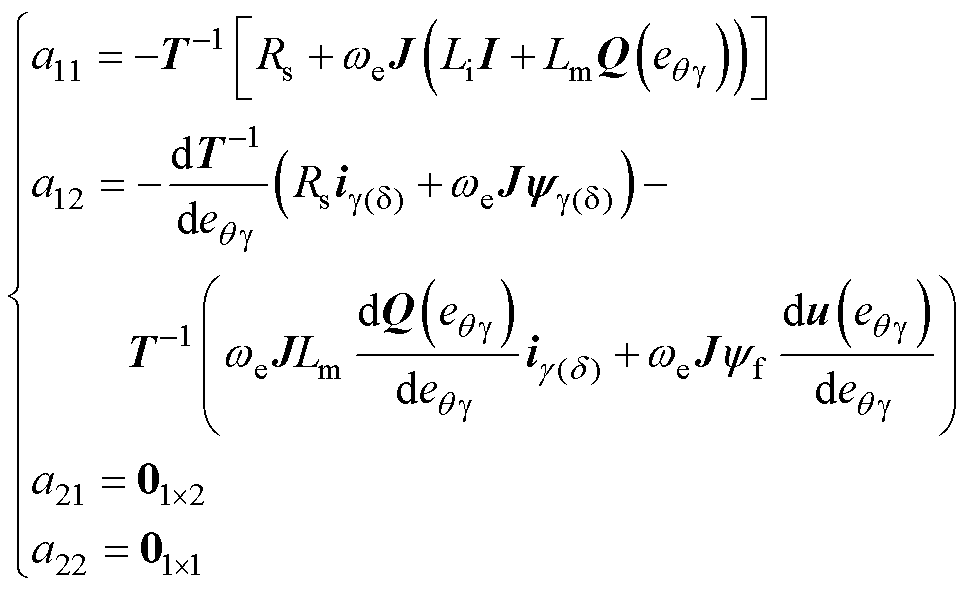 (16)
(16)
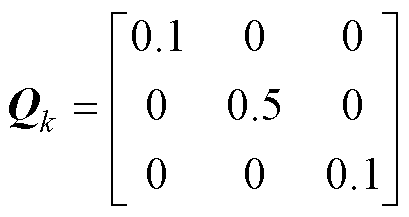 (17)
(17)
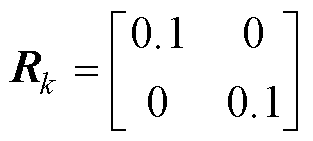 (18)
(18)

 (19)
(19)
 (20)
(20)
在EKF的估计中,将P0设为对角矩阵,表示初始状态误差。不同的P0值会对算法的初始状态产生一定的影响,但当收敛时P0的影响消失。x0表示状态变量的初值,值得注意的是,因为本状态空间表达式是基于deqg/dt=0推导出来的,为保证eqg不为零,需要在每次电机运行的时候,赋予eqg一个合适的初值。
eqg越大,即初始条件下,旋转坐标系与估计旋转坐标系的夹角越大,相对通过EKF估算得出之后的状态变量eqg所包含的高频误差干扰越大,eqg越小,即初始条件旋转坐标系与估计旋转坐标系的夹角越小,相对于通过EKF估算得出之后的状态变量eqg所包含的高频干扰也越小,但是数值过小,通过EKF预测的状态变量越小,起动时响应时间变大。因此,综合考虑上述情况与实际环境,调整范围为(0, 1),本文取值为0.1。
Qk是表示系统噪声和模型误差的时变矩阵,其由两个分量组成:一是常数对角矩阵;另一个是时变矩阵。矩阵内的时变元素比常数矩阵元素小两个数量级。因此,Qk可以近似为一个常数对角矩阵。
Rk+1与测量噪声有关,EKF的增益与Rk+1的元素成反比,元素的增加意味着更大的测量噪声,降低了测量数据的可信度。Rk+1的非对角元素比对角元素小一个数量级,因此,Rk+1被设为对角矩阵。
扩展卡尔曼滤波算法原理如图2所示。
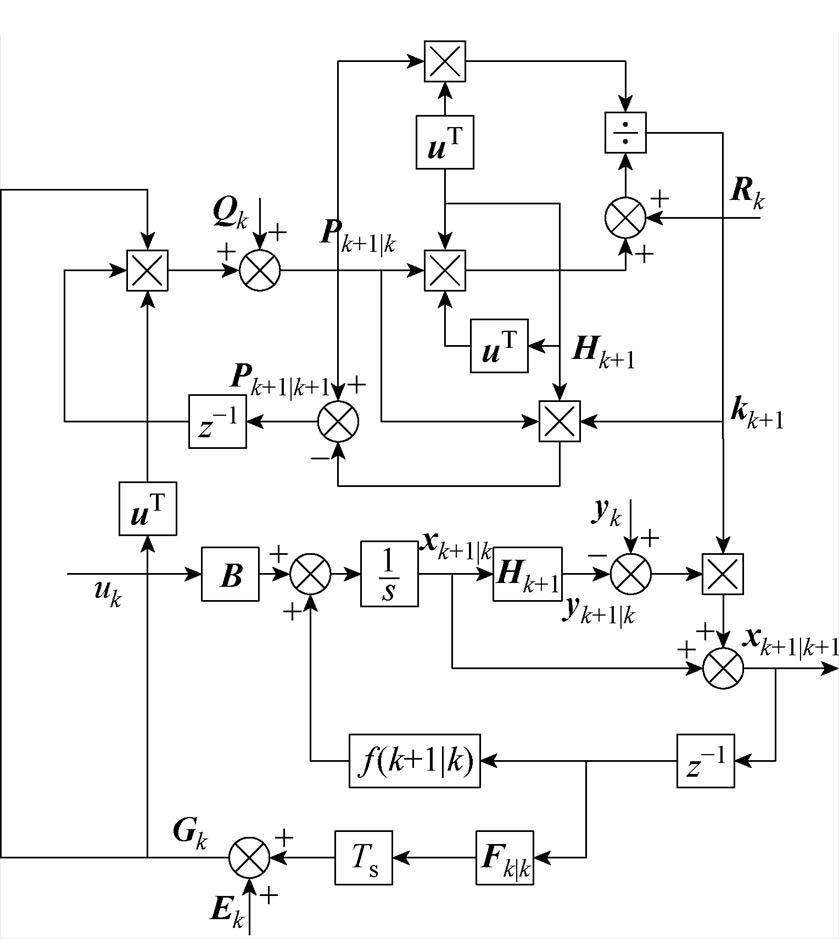
图2 基于新数学模型的扩展卡尔曼滤波原理
Fig.2 Schematic diagram of extended Kalman filter based on the new mathematical model
式(16)中
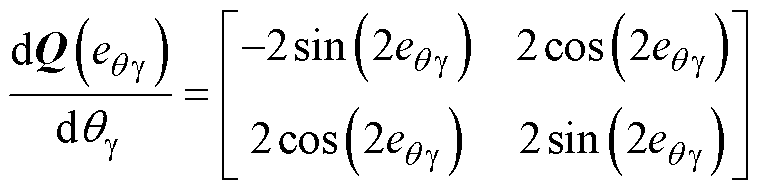 (21)
(21)
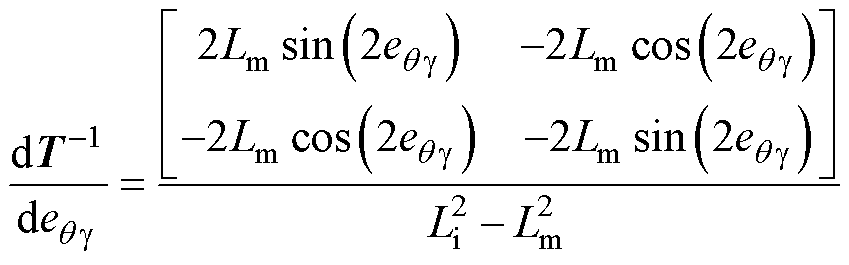 (22)
(22)
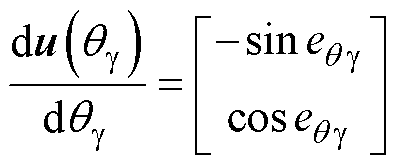 (23)
(23)
锁相环的原理如图3所示。输入eqg作为PLL的估计误差,通过适当地调节参数使得转子位置的估计值收敛到实际值。
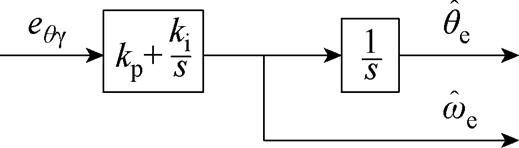
图3 PLL原理
Fig.3 PLL schematic
如果满足以下条件,则估计的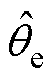 和
和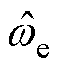 接近实际值
接近实际值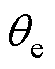 和
和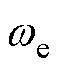 。条件为
。条件为
 (24)
(24)
采用一种多项式形式H(s),该多项式满足赫尔维茨稳定性准则,有
 (25)
(25)
符合渐近稳定性质,有
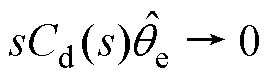 (26)
(26)
永磁同步电机无传感器控制在转子位置速度的检测方法中,多数都是通过检测基波反电动势weyf cosqe和weyf sinqe来获得转子位置的信息,这种基波激励的方法虽实施简单,但在低速和中高速范围中we的不断变化导致反电动势难以有效检测,多只适用于中高速运行。
传统的非线性磁链观测器通过观测系统的非线性模型,忽略了电角速度we的影响,估计状态磁链yf sinqe和yf cosqe。因此,在低、中、高速范围都有着优秀的性能和效果。
新坐标系下扩展卡尔曼滤波算法的原理,即通过EKF对非线性系统的高精度估算性能,在系统模型下检测出电角度误差eqg,忽略weyf的影响,相比非线性磁链观测器降低了对磁链参数的敏感性要求。
搭建仿真环境,保持其他参数不变,验证新坐标系下EKF观测器的性能,并选择传统的非线性磁链观测器作比较,如图4所示,A是基于新坐标系下的EKF观测器,B代表传统的非线性磁链观测器。电机带额定负载起动。
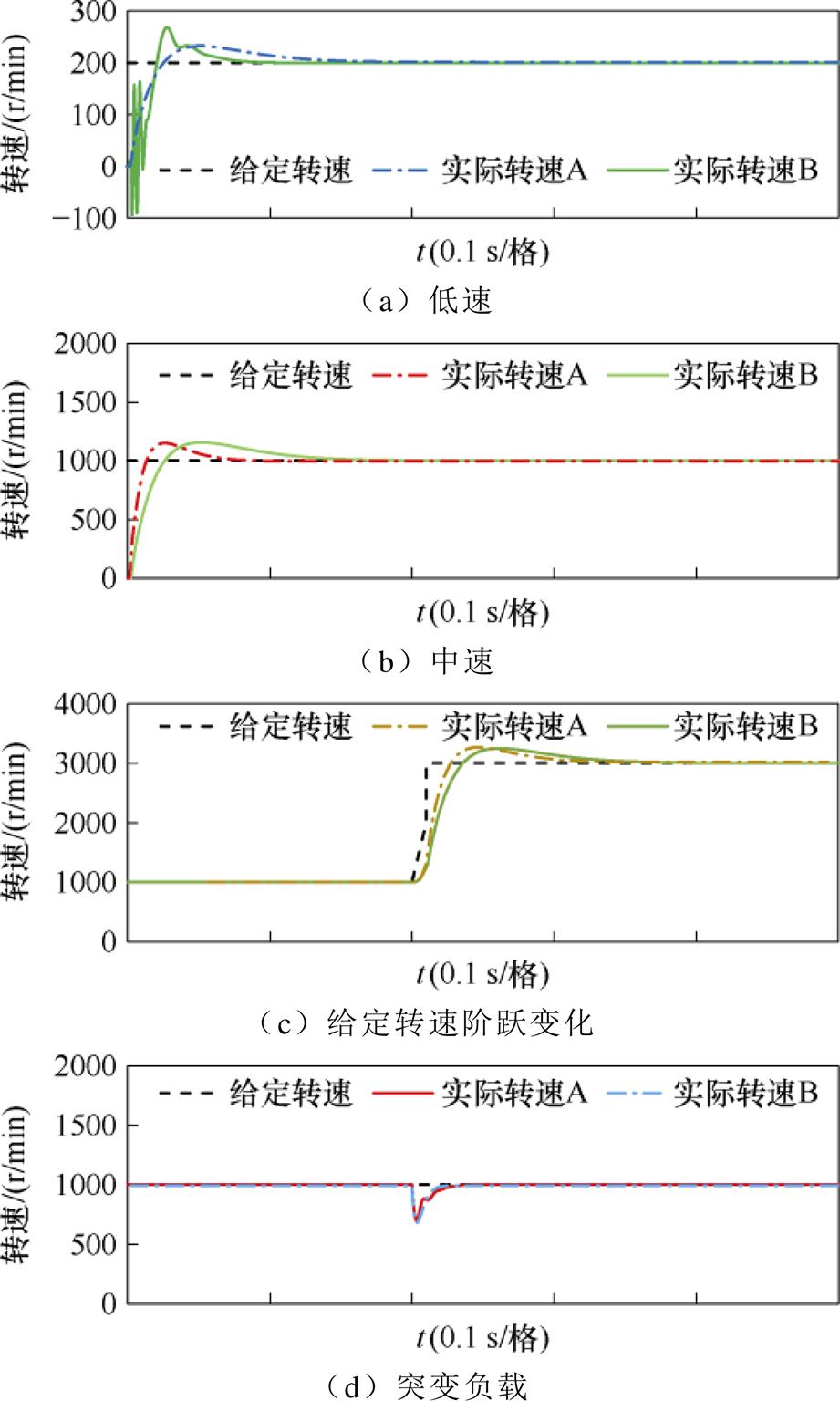
图4 不同观测器实际转速对比
Fig.4 Comparison of the actual rotational speed of different observers
图4展示了电机的实际转速波形,包括在低速和中速下带额定负载的起动波形、从1 000 r/min到3 000 r/min的给定转速阶跃变化波形和突变负载条件下的波形。通过对比这些不同条件下的转速波形,分析两种观测器的性能。
图5展示了低速(200 r/min)起动的位置误差波形,结合图4a进行分析可见,在低速带载起动下,尽管转速B能够成功起动,其初始转速波形却呈现出显著的振荡现象。相对而言,转速A在相同条件下的起动过程更为平稳,表明其在低速带载起动时具有更优的动态性能和控制稳定性。
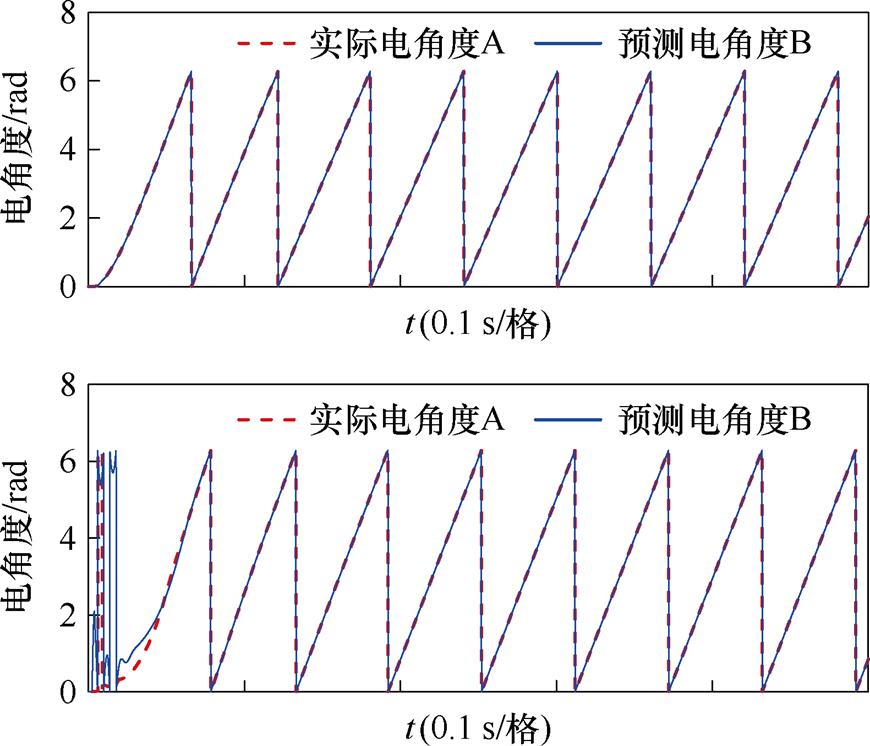
图5 不同观测器初始位置对比波形
Fig.5 Comparison of waveforms at the initial positions of different observers
由图4b和图4c可知,在中速(1 000 r/min)带载起动条件下,以及转速阶跃到高速(3 000 r/min)时,转速A相比转速B,有着更优秀的动态响应性能和转速追踪能力。
同时从图4d中可以看出,两种观测器在面对负载扰动情况下,抗干扰能力几乎相同。但是实际转速A在经过每次负载扰动时,转速波形出现了更为明显的抖动。这是因为卡尔曼滤波在处理突变负载情况时,误差协方差函数不满足互不相关的条件,进而影响到之后一段时间内的电流波形,使得电流谐波含量增大。
图6为电机不同转速区间的转速误差放大图,从图中可以看出,随着给定转速的增加,实际转速误差在不断变大,但是相比之下,转速A精度更高,符合扩展卡尔曼滤波高精度的前提。
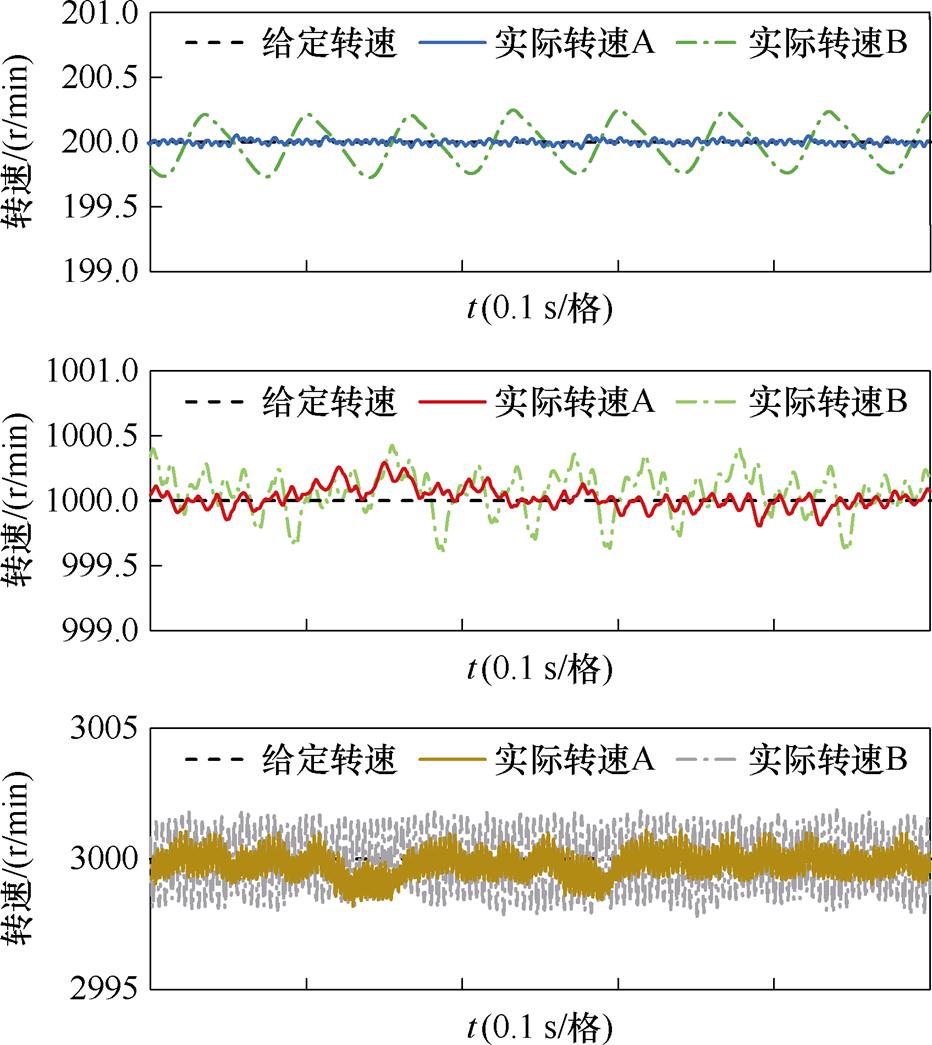
图6 不同观测器实际转速误差对比
Fig.6 Comparison of actual speed errors of different observers
永磁同步电机控制系统在运行时,电流谐波扰动主要可分为周期性扰动和非周期性扰动。
电机稳定运行时,磁链谐波和死区效应是影响电流谐波的主要因素,它们会导致以6倍基频为周期的电压误差谐波,从而在相电流中产生显著的5次和7次谐波分量[19]。
考虑磁链和电压谐波扰动的相电流ia、ib、ic为
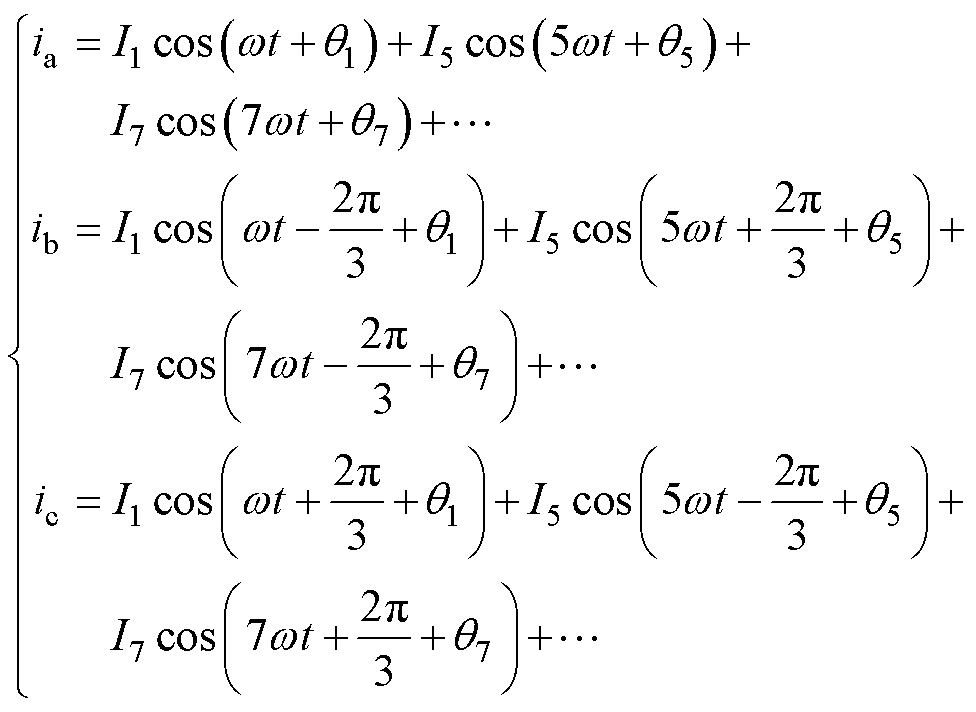 (27)
(27)
式中,I1为三相电流1次基波幅值;I5和I7分别为三相电流5次和7次谐波的幅值;q1为三相电流1次基波相位;q5和q7分别为三相电流5次和7次的相位。
对式(27)进行坐标旋转变化,得到dq轴电 流为
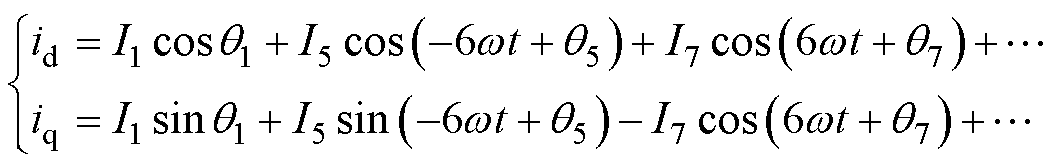 (28)
(28)
由式(28)可知,在周期扰动中,三相电流的5、7次谐波最终导致dq轴电流出现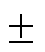 6次谐波。
6次谐波。
搭建仿真环境,给定转速在1 000 r/min满载运行,电流环采用PI控制器,进行快速傅里叶分析(Fast Fourier Transistor, FFT),如图7所示,基本频率为83.3Hz,最终得出与上述一致的结果。图中,基波占比100%,表明基波电流在电机正常运行中起主导作用。而2~10次谐波中,5、7次谐波含量较多,满足上述分析。
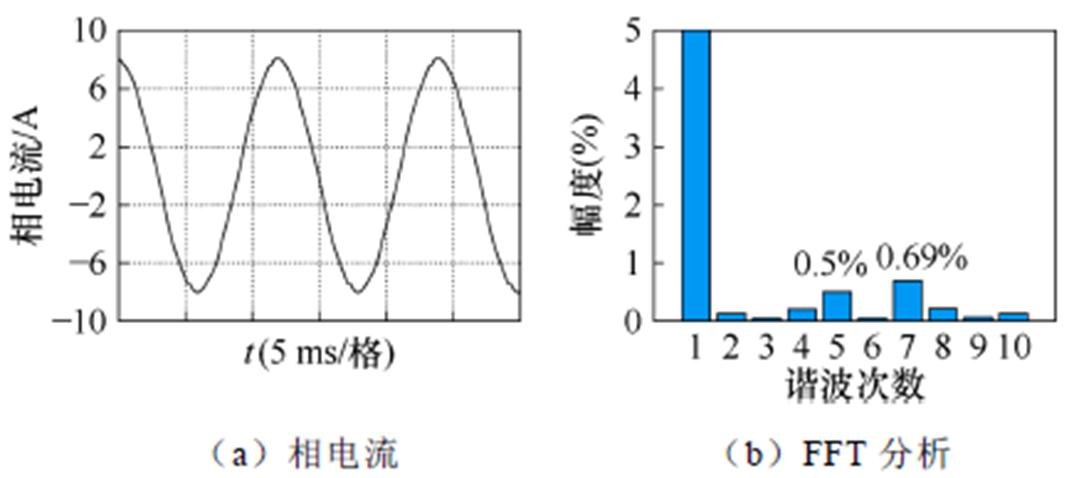
图7 满载高速运行谐波分析
Fig.7 Harmonic analysis of high-speed operation at full load
造成电流谐波的非周期性扰动的原因主要包括:负载突变引起的扰动、电阻电感引起的参数失配、控制算法的不合理性等。
而扩展卡尔曼滤波算法在处理负载阶跃变化时,所造成的波动会更加明显,取给定转速在1 000 r/min下突加2/3额定负载之后一段时间的三相电流进行仿真验证。
将基于新坐标系下的EKF和传统非线性磁链观测对比,电流环采用PI控制器。
传统非线性磁链、新坐标系EKF突加负载之后运行谐波分析分别如图8、图9所示。基波频率为83.3 Hz,包括周期性5、7次扰动谐波在内,突变负载后的三相电流在一段时间内各种谐波扰动含量都明显增大,同时EKF相比传统非线性磁链观测器所造成的三相谐波含量更高,这些都属于非周期性谐波扰动。
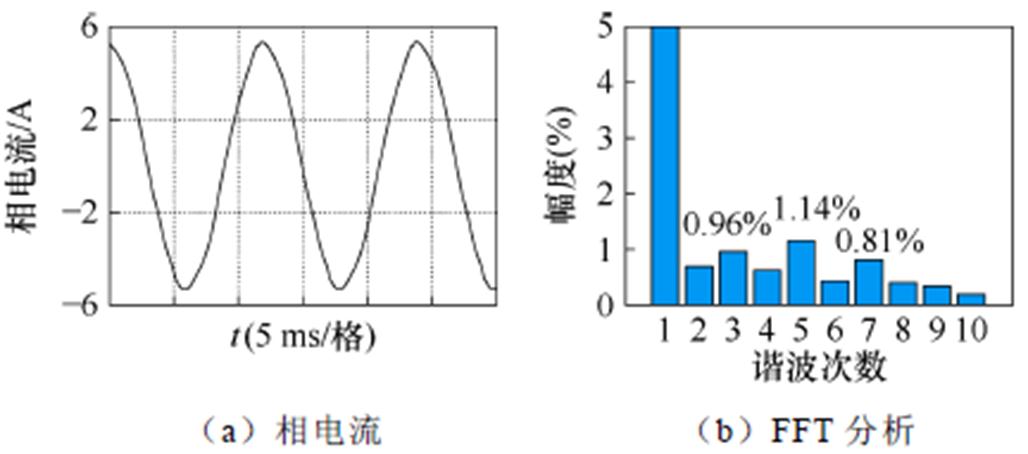
图8 传统非线性磁链突加负载之后运行谐波分析
Fig.8 Harmonic analysis is run after loading of traditional nonlinear magnetic sponzes
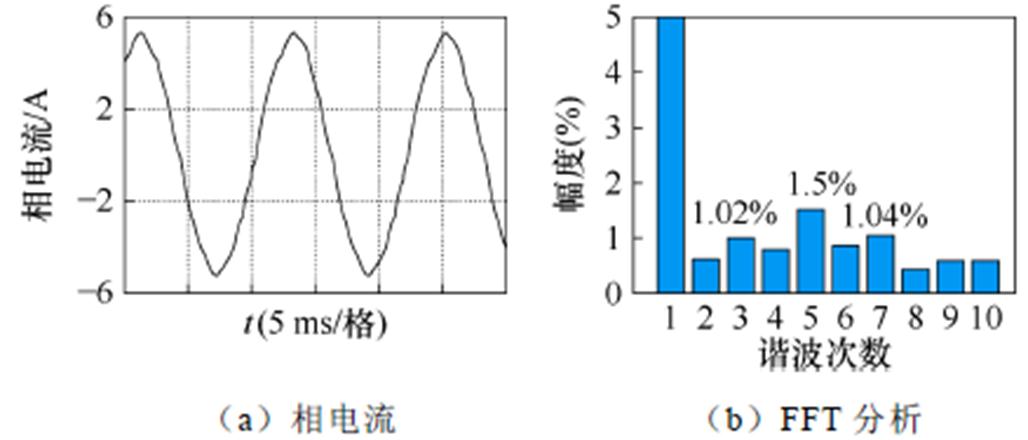
图9 新坐标系EKF突加负载之后运行谐波分析
Fig.9 Harmonic analysis is run after the EKF load is abruptly loaded in the new coordinate system
扩展卡尔曼滤波算法由于突变负载之后将导致三相系统不平衡,3次谐波的含量比其余谐波增加的更多。
3次谐波三相电流的大小和相位均相同,将造成电机三相不平衡。而当电机处于三相不平衡运行时,静止坐标系下的定子电压、电流均会包含正序和负序分量,有
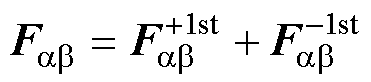 (29)
(29)
式中,Fab 为电压或电流矢量;上标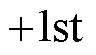 和
和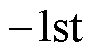 分别指代正序和负序分量。将ab 坐标系变换到dq坐标系,有
分别指代正序和负序分量。将ab 坐标系变换到dq坐标系,有
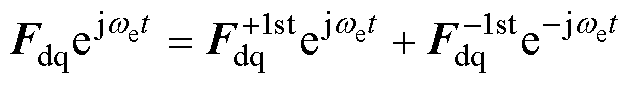 (30)
(30)
整理得
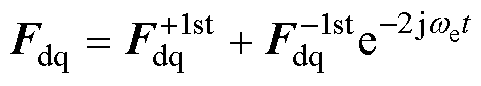 (31)
(31)
由三相不平衡引起的负序分量在dq坐标系下表现为-2次谐波。
因此,在做到滤除非周期谐波的同时,对3、5、7次谐波进行再次滤波,可以有效地解决负载变化下扩展卡尔曼滤波加剧谐波干扰的问题。
自抗扰控制技术(Active Disturbance Rejection Control, ADRC)是一种将传统PI控制结合现代控制的基本理念:即利用反馈来纠正误差,与现代控制理论的主要成就相结合的方法。这种技术主要由三个组成部分构成:跟踪微分器(Tracking Differentiator, TD),用于优化控制命令的动态响应;误差反馈控制律(State Error Feedback, SEF),通过反馈机制来调整误差;扩张状态观测器(ESO),能够估计系统的非周期性扰动。
本文提出IADRC技术,在ESO上做出了改进,即改进的ESO(Improved ESO, IESO)分别用来滤除上述新坐标系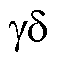 下的周期性扰动和非周期性扰动。
下的周期性扰动和非周期性扰动。
IESO是IADRC系统核心,根据式(10)可知,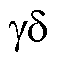 坐标系下的电流方程为
坐标系下的电流方程为
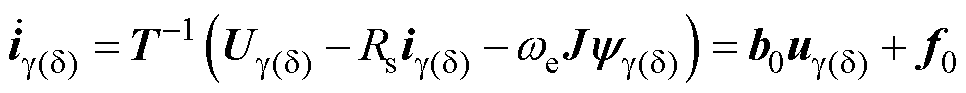 (32)
(32)
其中

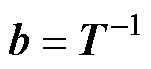
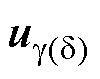 =
=
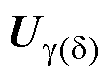
式中,f0为扰动。
以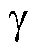 轴为例,设置状态变量x1和x2,x1=ig,x2=f,则有
轴为例,设置状态变量x1和x2,x1=ig,x2=f,则有
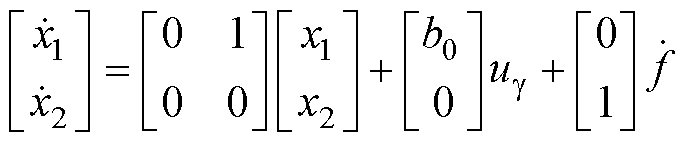 (33)
(33)
式中,ig为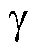 轴电流分量;ug为
轴电流分量;ug为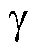 轴电压分量;b0为矩阵b的
轴电压分量;b0为矩阵b的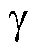 轴分量;f为
轴分量;f为 轴扰动f0分量。
轴扰动f0分量。
对式(33)搭建传统的线性扩张观测器(Liner Extended State Observer, LESO),有
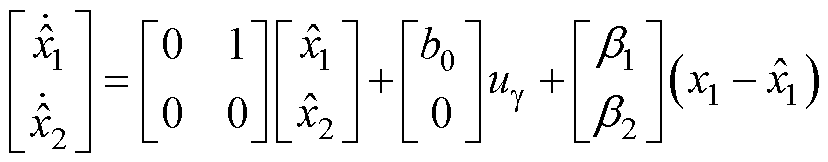 (34)
(34)
传统的LESO结构如图10所示,根据极点配置原则 和
和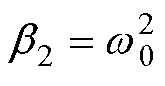 ,即可保证状态变量
,即可保证状态变量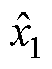 收敛于
收敛于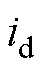 ,
, 收敛于
收敛于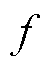 。
。
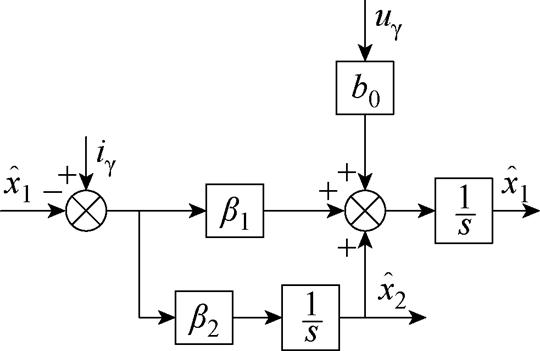
图10 传统LESO结构
Fig.10 Diagram of the traditional LESO structure
其中,基于扰动部分的公式为
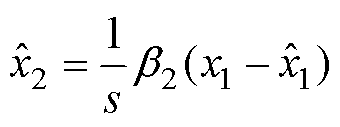 (35)
(35)
在频域上分析, 相当于一个低通滤波器,截止频率与
相当于一个低通滤波器,截止频率与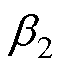 有关,因此可以有效地抑制非周期性的谐波扰动。但是当某些谐波含量较高时,以图9b的FFT分析为例,3、5、7次谐波含量较多,较小的
有关,因此可以有效地抑制非周期性的谐波扰动。但是当某些谐波含量较高时,以图9b的FFT分析为例,3、5、7次谐波含量较多,较小的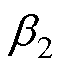 不能完全抑制所有的谐波扰动,较大的
不能完全抑制所有的谐波扰动,较大的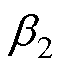 会放大截止频率以内的谐波扰动,从而受到严重的高频噪声干扰。合适的
会放大截止频率以内的谐波扰动,从而受到严重的高频噪声干扰。合适的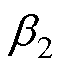 又往往因为某一次项的谐波含量较高,而无法完全抑制该项谐波。
又往往因为某一次项的谐波含量较高,而无法完全抑制该项谐波。
针对新坐标系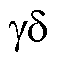 轴电流的-2、
轴电流的-2、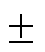 6次谐波进行抑制,本文引入了一个二阶振荡环节控制器,其传递函数为
6次谐波进行抑制,本文引入了一个二阶振荡环节控制器,其传递函数为
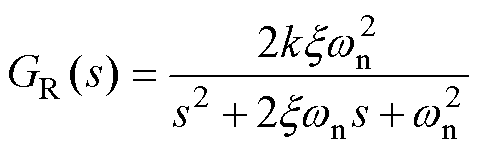 (36)
(36)
式中,x 为阻尼系数,且0<x <1;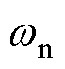 为谐振频率;k为增益系数。
为谐振频率;k为增益系数。
对不同参数下的函数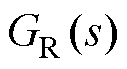 进行伯德图分析。如图11所示,不同频率
进行伯德图分析。如图11所示,不同频率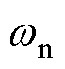 在幅值附近增益接近或等于1,从
在幅值附近增益接近或等于1,从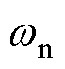 向两侧偏离时,幅值变为负数,对应的增益接近0。随着频率
向两侧偏离时,幅值变为负数,对应的增益接近0。随着频率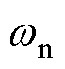 的增加,会使得系统在更高的频率下保持有效响应,但同时会增加振动幅度。
的增加,会使得系统在更高的频率下保持有效响应,但同时会增加振动幅度。
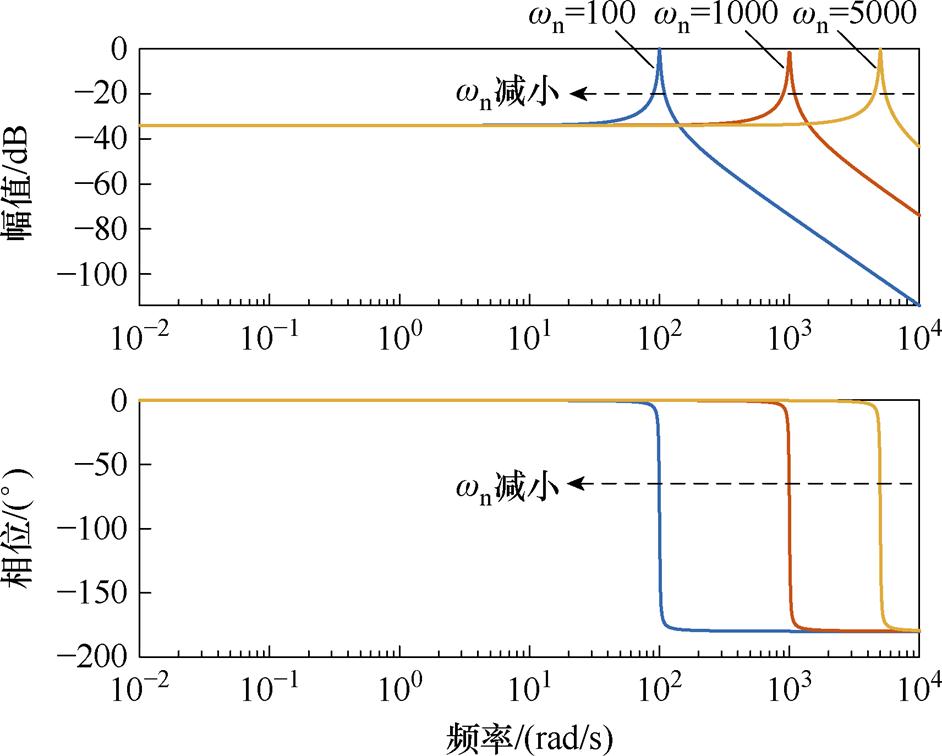
图11 不同参数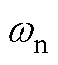 下的GR(s)伯德图
下的GR(s)伯德图
Fig.11 Bode's diagram with different parameters 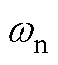
图12所示为不同参数 下的GR(s)伯德图。
下的GR(s)伯德图。 的减小会降低谐振频率
的减小会降低谐振频率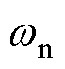 两侧的幅值增益,从而能够有效地筛选出特定频率,但同时会减小系统的带宽。
两侧的幅值增益,从而能够有效地筛选出特定频率,但同时会减小系统的带宽。
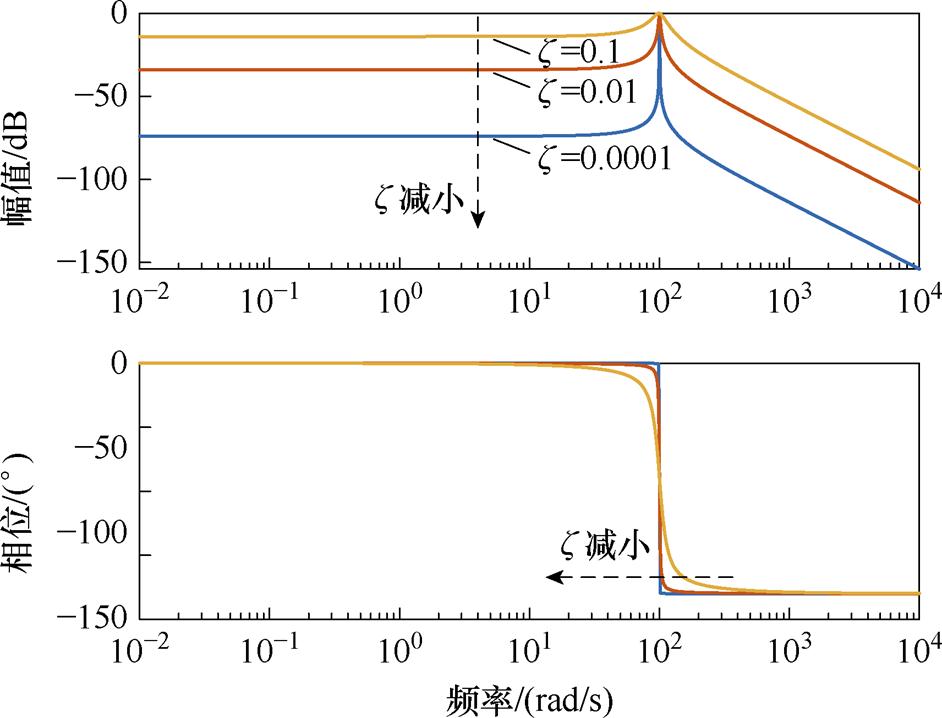
图12 不同参数x 下的GR(s)伯德图
Fig.12 Bode's diagram with different parameters x
图13所示为不同增益k下的伯德图。随着增益k的增大而提高信号的放大能力,但是过高的增益k可能导致高频噪声的放大,这将对系统性能产生负面影响。
对系统动态性能综合考虑,设计参数k =10,x =0.01,有效得出所需的特定频率谐波。
因此,本文在LESO的基础上提出了IESO,结构如图14所示。基本扩展状态观测器包含一个积分,它在零频率处具有无限增益。这个特性使得ESO能够估计并抑制直流扰动,而引入二阶振荡函数是利用其在特定频率谐波的抑制能力。
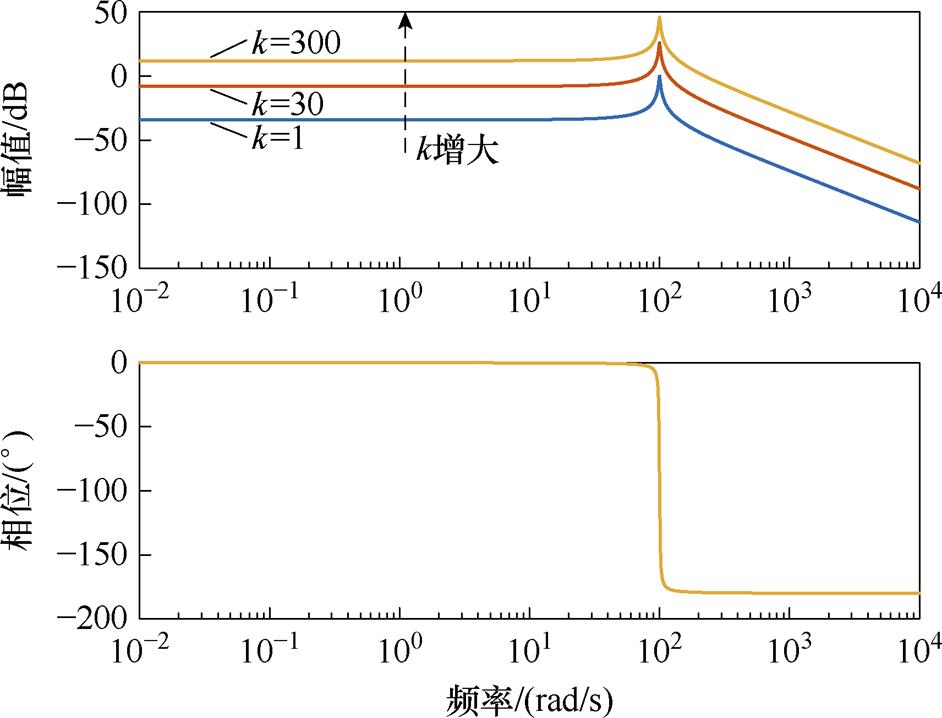
图13 不同参数k下的GR(s)伯德图
Fig.13 GR(s) Bode's diagram with different parameters k
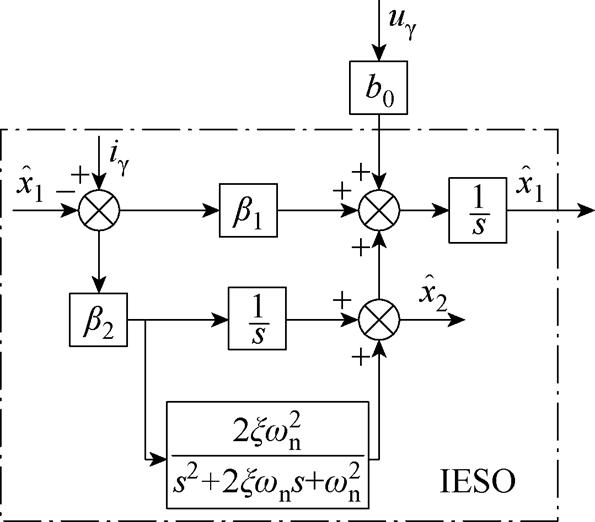
图14 IESO结构
Fig.14 IESO structure diagram
电流内环需要具备优异的谐波抑制和抗扰动能力,设计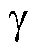 轴电流环如图15所示,
轴电流环如图15所示,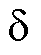 轴电流环结构与之相同。
轴电流环结构与之相同。

图15 IADRC结构
Fig.15 IADRC structure diagram
 为电机简化模型,其中,L为电机相电感,R为电机相电阻。设计IADRC控制器,kp为控制器增益。
为电机简化模型,其中,L为电机相电感,R为电机相电阻。设计IADRC控制器,kp为控制器增益。
观测器数学模型为
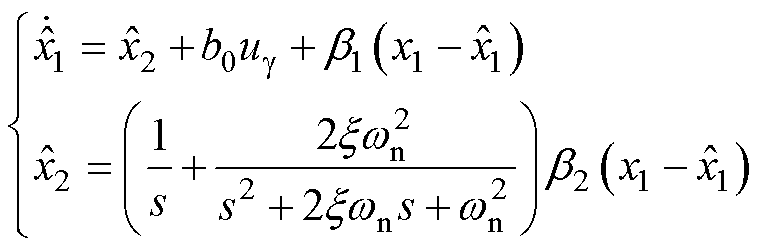 (37)
(37)
线性误差反馈控制率为
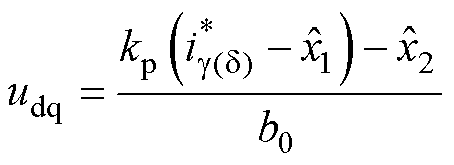 (38)
(38)
对图15进行等效变换,推导得到IADRC结构等效框图如图16所示。
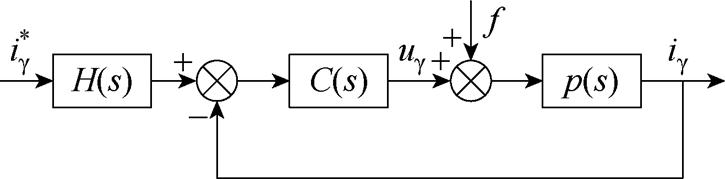
图16 IADRC结构等效框图
Fig.16 Equivalent block diagram of IADRC structure
各个环节的传递函数表示为
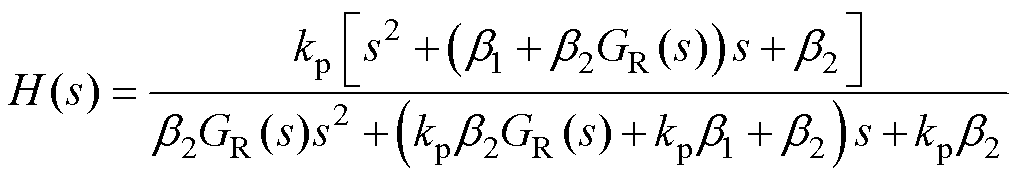 (39)
(39)
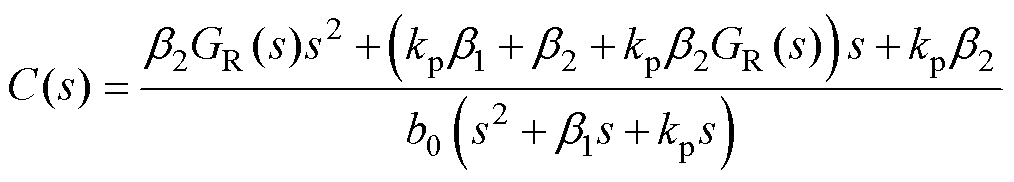 (40)
(40)
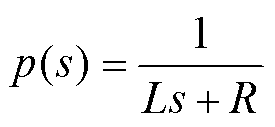 (41)
(41)
进而得到整个系统的传递函数为

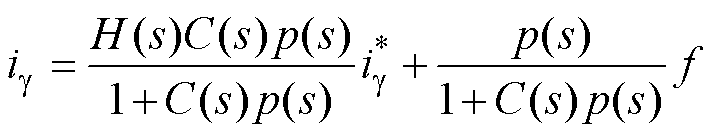 (42)
(42)
令
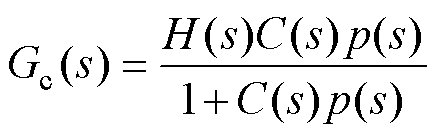 (43)
(43)
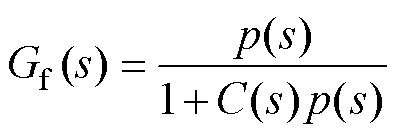 (44)
(44)
在不考虑系统的输入情况下,系统输出ig与扰动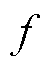 的关系就是Gf (s),对其进行伯德图的绘制,并与传统LADRC(即当GR(s)=0时)进行对比。
的关系就是Gf (s),对其进行伯德图的绘制,并与传统LADRC(即当GR(s)=0时)进行对比。
参数w0决定了系统抑制扰动的能力,w0越大抑制能力越强,但w0受采样噪声限制不能太大。
参数kp决定了系统响应对误差的敏感度,kp过大会导致系统反应过度引起振荡,kp过小会导致电机对负载变化的适应性差,无法快速达到设定的性能要求。
根据实际情况进行综合考虑,设计合适的参数kp=200,w0=8 000 Hz。Gf(s)伯德图如图17所示,基频wn=173.33 rad/s,基频附近幅值下降,意味着系统输出对扰动输入有着明显的抑制作用。因此,当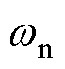 =
=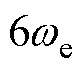 、
、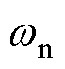 =
=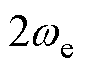 ,即可以有效抑制
,即可以有效抑制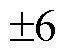 次谐波和-2次谐波。
次谐波和-2次谐波。
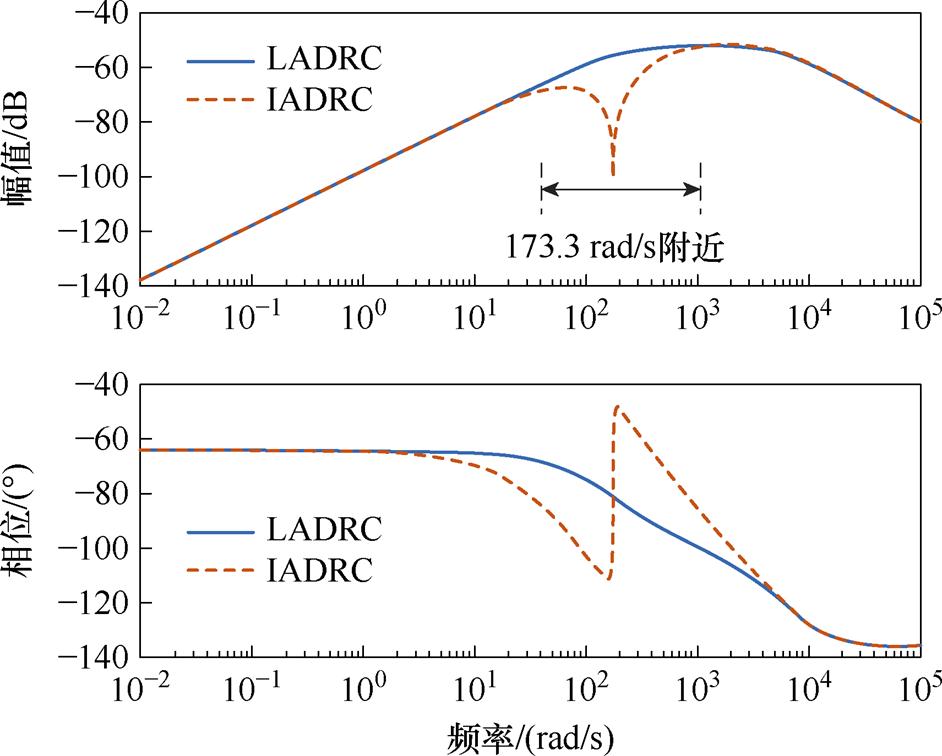
图17 Gf (s)伯德图
Fig.17 Gf (s) Bode's diagram
对开环系统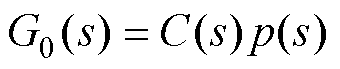 进行奈奎斯特图证明系统的稳定性。根据奈奎斯特稳定判据,反馈控制系统稳定的充分必要条件是半闭合曲线不穿过(-1, j0) 点,并且逆时针包围临界点 (-1, j0) 点的圈数R0等于开环传递函数的正实部极点数P。Z表示系统闭环右半平面极点个数为0,N+表示正穿越的次数和(从上向下穿越),N-表示负穿越的次数和(从下向上穿越),满足P=Z-R0=Z-2(N+-N-)=0,表示系统稳定。
进行奈奎斯特图证明系统的稳定性。根据奈奎斯特稳定判据,反馈控制系统稳定的充分必要条件是半闭合曲线不穿过(-1, j0) 点,并且逆时针包围临界点 (-1, j0) 点的圈数R0等于开环传递函数的正实部极点数P。Z表示系统闭环右半平面极点个数为0,N+表示正穿越的次数和(从上向下穿越),N-表示负穿越的次数和(从下向上穿越),满足P=Z-R0=Z-2(N+-N-)=0,表示系统稳定。
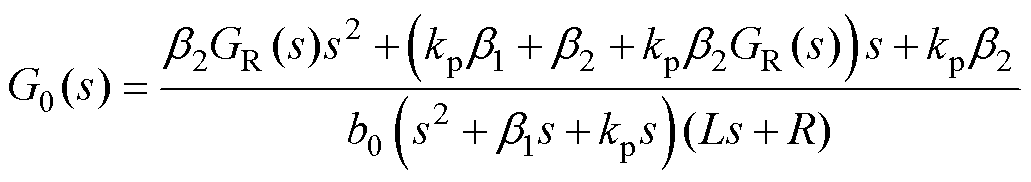 (45)
(45)
当b1>0,kp>0时,式(45)中s2+b1s+kps可知存在两个负值极点。已知电机L>0,R>0, 必有一个负值极点。所以开环传递函数的正实部极点数P=0。
必有一个负值极点。所以开环传递函数的正实部极点数P=0。
G0(s)奈奎斯特图如图18所示,可知穿越 (-1, j0) 点正穿越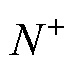 为1次,负穿越
为1次,负穿越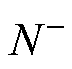 为1次,因此R=0,满足
为1次,因此R=0,满足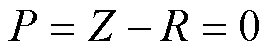 ,说明系统是稳定的。
,说明系统是稳定的。
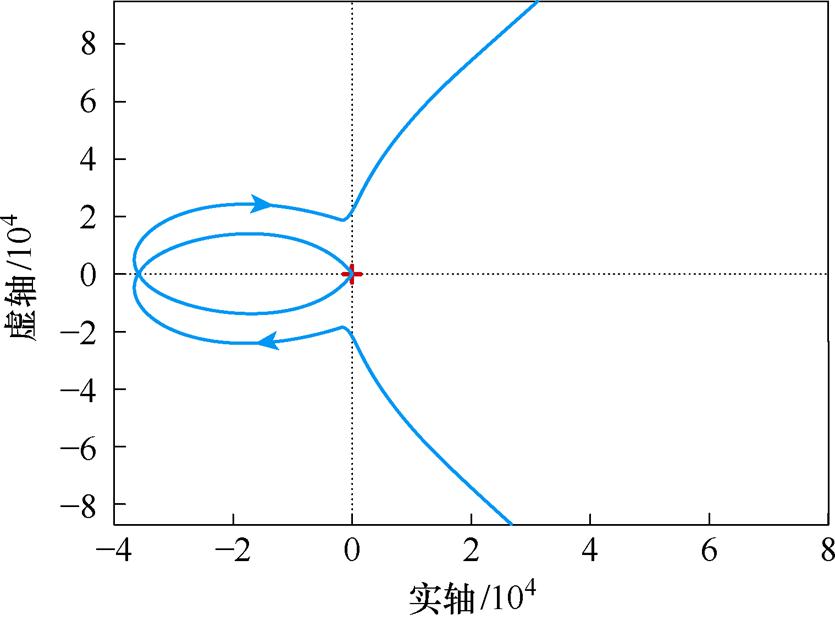
图18 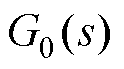 奈奎斯特图
奈奎斯特图
Fig.18  Nyquist diagram
Nyquist diagram
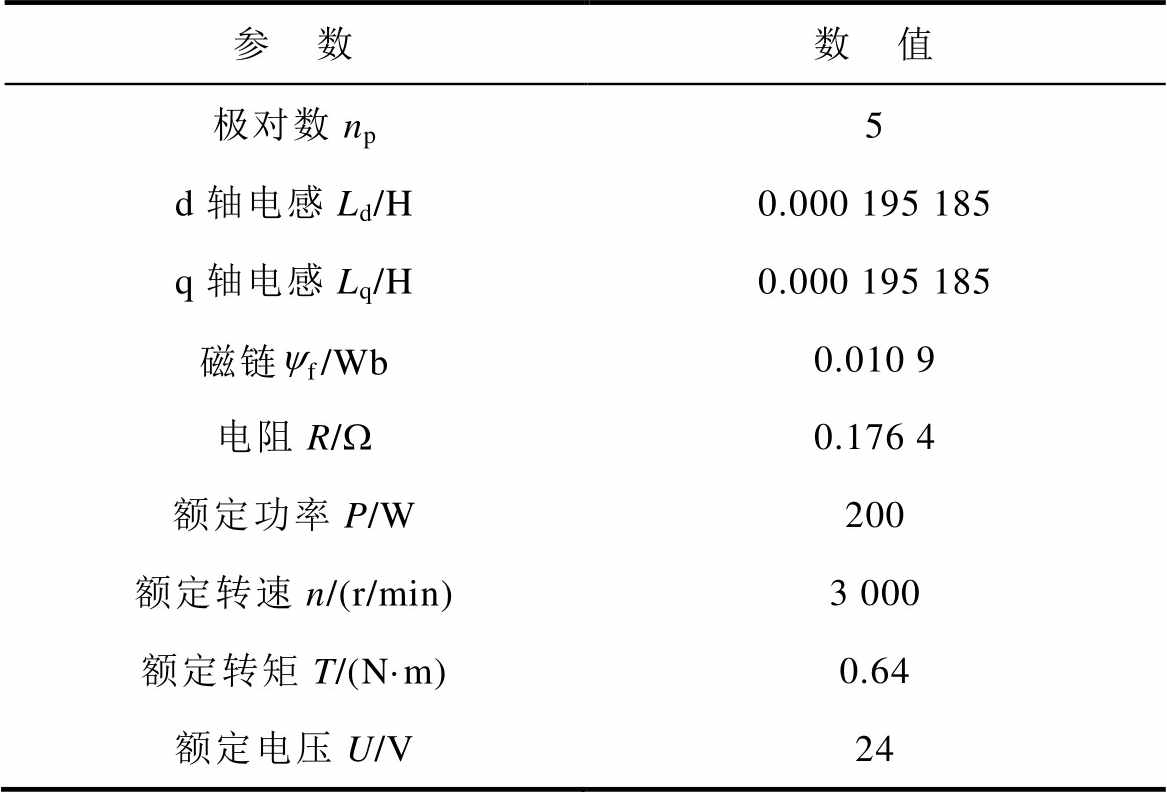
搭建仿真环境,验证IADRC的滤波效果。电机参数见表1,开关频率为10 kHz,死区时间为2 ms。
表1 电机参数
Tab.1 Motor parameters
参 数数 值 极对数np5 d轴电感Ld/H0.000 195 185 q轴电感Lq/H0.000 195 185 磁链yf/Wb0.010 9 电阻R/W0.176 4 额定功率P/W200 额定转速n/(r/min)3 000 额定转矩T/(N·m)0.64 额定电压U/V24
取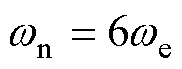 来自适应滤除
来自适应滤除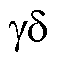 轴
轴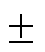 6次谐波,同时当处理突变负载时,取
6次谐波,同时当处理突变负载时,取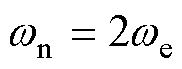 来自适应滤除
来自适应滤除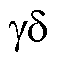 轴的
轴的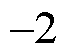 次谐波。
次谐波。
基于新坐标系的EKF无感算法,总体结构如图19所示。进行以下仿真,转速给定1 000 r/min,基频为83.3 Hz,IADRC的参数:w0=8 000 Hz,k=10,kp=200,锁相环参数:kp=212.1,ki=22 500。
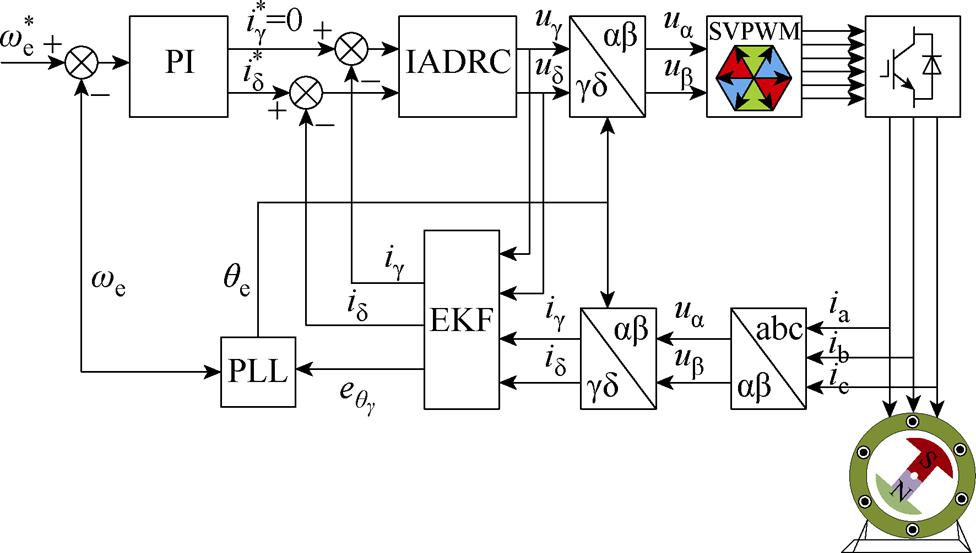
图19 控制系统总体结构
Fig.19 Overall structure of the control system
将PI控制器、LADRC控制器和IADRC控制器进行对比,如图20所示,对LADRC控制器和IADRC控制器满载稳定运行的三相电流进行FFT分析,并与图7对比。如图20所示,通过LADRC的滤波处理,有效减少了低次谐波,但同时却不能完全抑制某项值较高的次数谐波(5、7次谐波),而IADRC的引入,很好地抑制了需要抑制的特定谐波。
突加负载之后运行分析如图21所示,为在1.5 s时突加2/3额定负载后的相电流分析,将LADRC控制器和IADRC控制器滤波效果对比,并与图9进行比较。LADRC的抗干扰能力很好地抑制了低次谐波,同时IADRC在LADRC的基础上进一步抑制了特定的谐波。

图20 满载稳定转速运行分析
Fig.20 Analysis of stable speed operation at full load
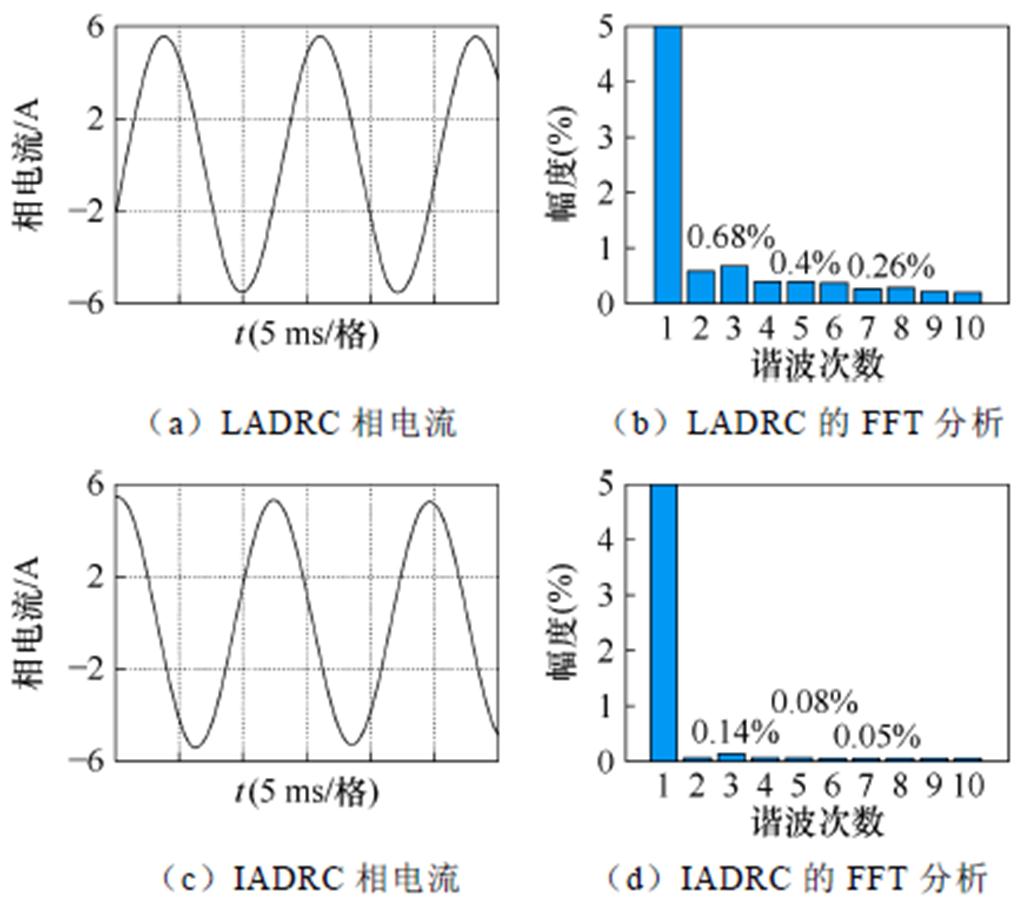
图21 突加负载之后运行分析
Fig.21 Running the analysis after a sudden load
实验参数:IADRC参数与上述仿真参数一致。电流环PI参数kp=wcL,ki=wcRs。这里wc为电流环带宽,设为800 Hz。转速环PI参数设置为kp=Jwc2/ (1.5npyf),ki=wc2kp。其中,wc2为转速环带宽,设为30 Hz。锁相环PLL参数kp=1.414wc3,ki=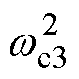 。其中,wc3为锁相环带宽,设为800 Hz。
。其中,wc3为锁相环带宽,设为800 Hz。
主控芯片采用STM32f407,驱动芯片采用IR2110STRPBF,开关频率为10 kHz,死区时间为2 ms,实验平台如图22所示。

图22 实验平台
Fig.22 Experimental platform
实验首先验证了基于新坐标系下的EKF算法性能,包括对给定转速的追踪性能、转速误差精度、低速起动位置误差、算法的低速带负载能力以及算法的带载起动能力。
之后验证了在扩展卡尔曼滤波算法的基础上,IADRC对稳定转速下满载谐波的抑制效果、突变额定负载之后谐波的抑制效果以及对突变负载之后的转速影响。
如图23所示为转速追踪性能与误差精度,在每过一段时间内给定转速增加1 000 r/min,基于新坐标系下的EKF无感控制算法转速精度能保持在5 r/min之内。在高速范围内,转速在0.1 s左右达到给定转速,没有出现明显的转速滞后现象,转速追踪性能表现出色。
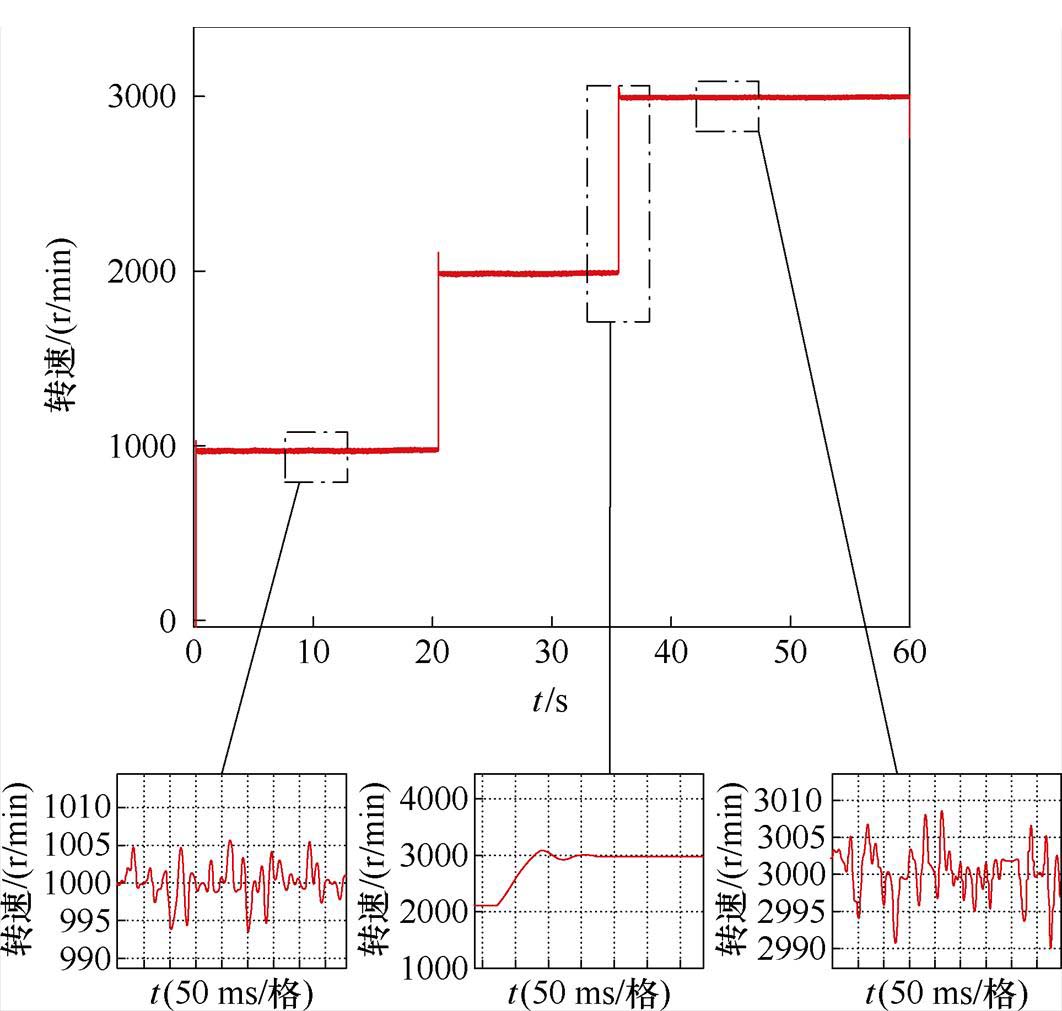
图23 转速追踪性能与误差精度
Fig.23 Rotation speed tracking performance and error accuracy
图24所示为低速200 r/min的初始位置角误差,算法在低速起动时位置角能够精准地跟随给定值,位置误差在0.04~0.05 rad之间,起动时位置曲线平滑,不存在堵转等现象。
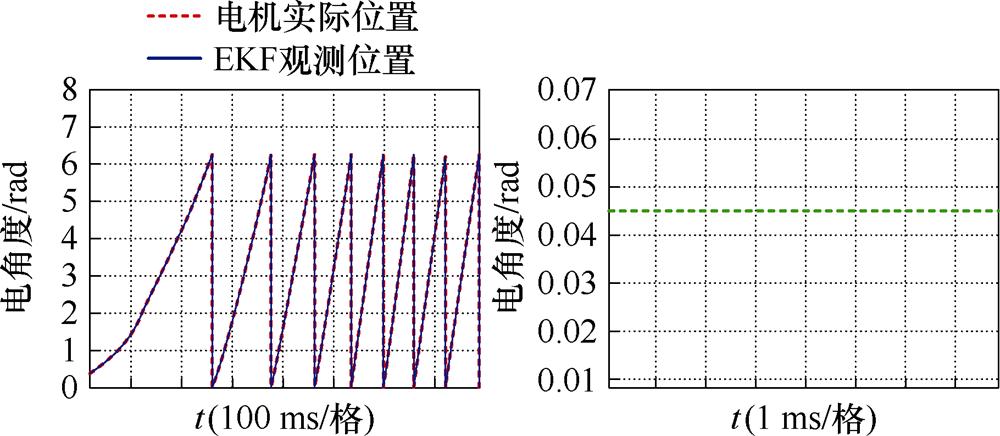
图24 初始位置角误差
Fig.24 Initial position angular waveforms
图25所示为带额定负载500 r/min起动波形,从图中可以看出,带额定负载起动,转速的响应曲线平滑,时间约为0.3 s,带载下的实际转速误差在6 r/min左右。
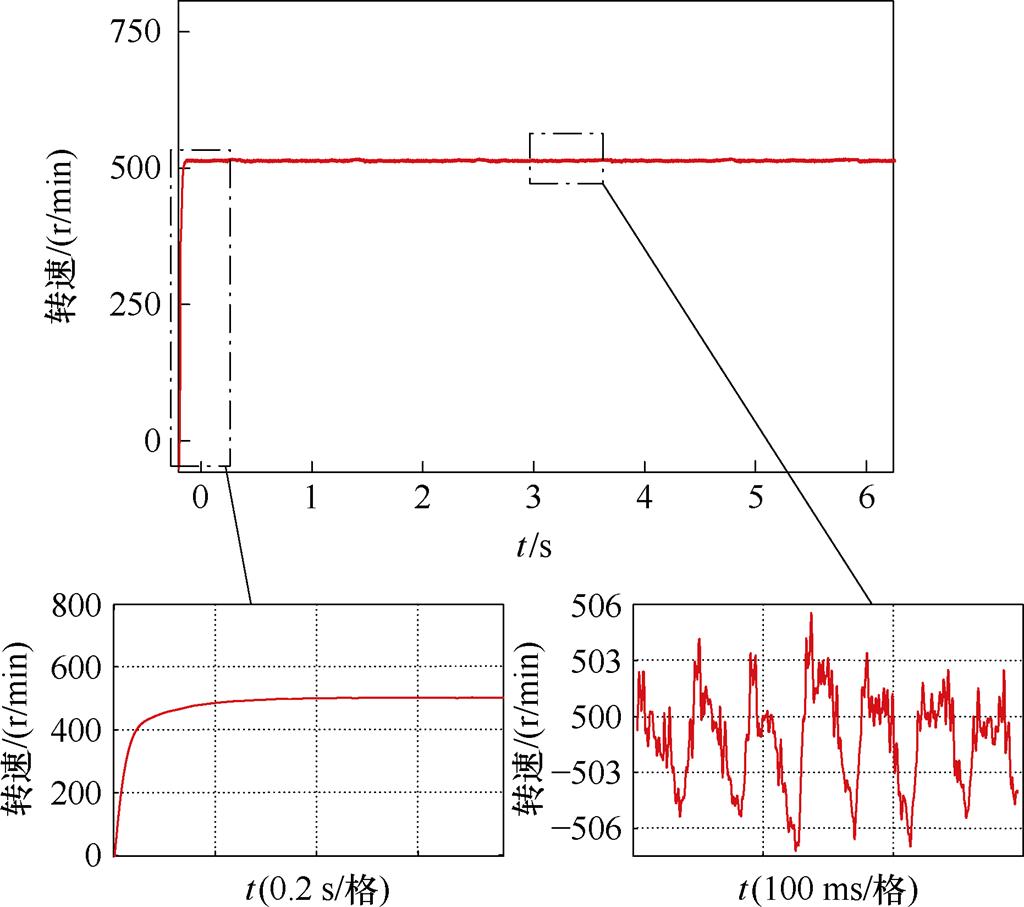
图25 带额定负载起动转速
Fig.25 Starting speed diagram with rated load
PI低速带载三相电流波形如图26所示,为给定转速200 r/min的三相电流波形,逐步加入1/10的额定转矩负载,最高加载到150%的额定转矩,三相电流达到了电机的瞬时最大电流15 A。新型EKF无感算法在低速范围的转矩带载能力满足实验电机的最大承受电流。
在中速范围内,给定转速1 000 r/min的额定负载运行。如图27所示,基频为83.3 Hz,LADRC相比PI起到了对低次谐波的抑制作用,5次谐波含量相比PI降低了50.5%,7次谐波含量相比PI降低了77.4%。IADRC算法在LADRC算法的基础上,起到了对特定谐波的更进一步抑制,5次谐波含量相比LADRC降低了41.3%,7次谐波含量相比LADRC降低了49.4%。

图26 PI低速带载三相电流波形
Fig.26 PI low-speed loaded three-phase current waveforms

图27 满载稳定转速运行分析
Fig.27 Analysis of stable speed operation at full load
进行突变额定负载之后的三相电流对比分析,如图28所示,基频为83.3 Hz。LADRC的5次谐波含量相比PI降低了70.5%,7次谐波含量相比PI降低了79.1%,3次谐波含量相比PI降低了54.8%。同时IADRC对5次谐波的抑制相比LADRC下降了44%,对7次谐波的抑制相比LADRC下降了13%,对3次谐波的抑制相比LADRC下降了88%,抑制与理论结果一致。
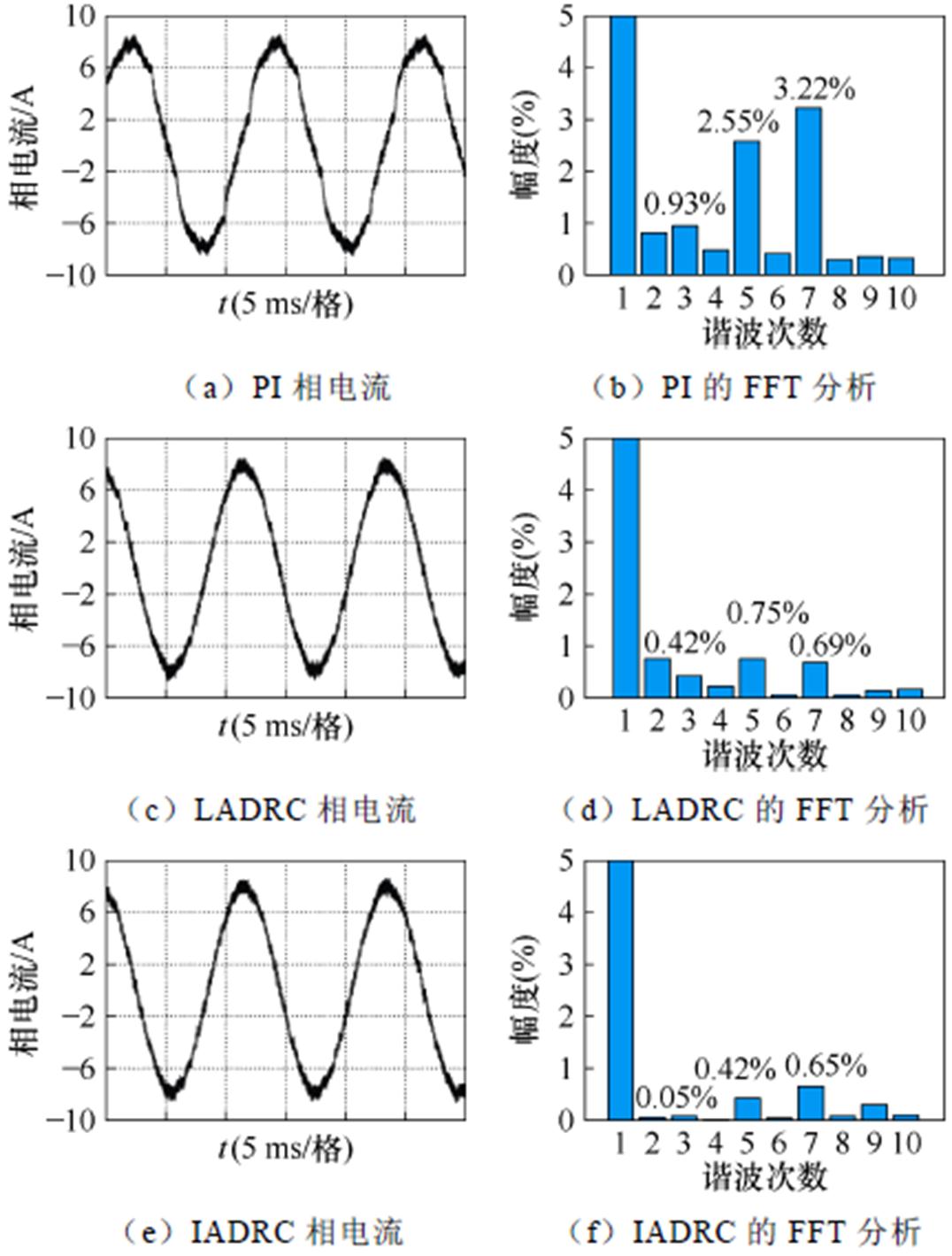
图28 突加负载之后运行分析
Fig.28 Running the analysis after a sudden load
突加负载转速误差对比如图29所示,进一步证明了控制策略的有效性。在未受突变负载干扰时,采用PI控制系统的转速误差约为5 r/min。面对突变负载干扰时,该误差增至约9 r/min。而采用LADRC控制策略,在相同条件下,未受扰动时转速误差降至约2 r/min,受扰动时增至约4 r/min。同时,IADRC控制相比LADRC虽然在转速误差方面未见显著减少,但是其转速曲线的波动性更平缓,对于维持转速稳定性起到积极作用。

图29 突加负载转速误差对比
Fig.29 Comparison of speed error of sudden load
综上分析,新坐标系下的EKF算法结合IADRC的策略不仅有着较高的转速追踪性能和精度,同时也提高了电机在不同运行条件下的适应性和稳定性。这种控制策略的优势在于能够有效应对突变负载和电流谐波下的挑战。
本文首先提出了基于新坐标系下的数学模型,并推导出基于新坐标系下的EKF无传感器控制算法。分析得出了EKF在面对突变负载时,会严重加剧谐波的产生,于是提出了IADRC算法来抑制谐波的诞生,并通过频域分析说明了算法的有效性。
1)新型无感算法有着高精度转速的同时,也拥有着低速高转矩的特性和优秀的高转速追踪能力。
2)通过改变传统LADRC的传递函数,从而影响整个系统,通过Bode图分析整个系统的频域模型。与PI控制、LADRC对比分析,IADRC在低通滤波的基础上,能够再次抑制频谱上的3、5、7次谐波。
3)IADRC搭配新型EKF的组合控制策略,不仅能够很好地抑制谐波,同时有着良好的控制效果。
参考文献
[1] 王科雷, 周洲, 马悦文, 等. 垂直起降固定翼无人机技术发展及趋势分析[J]. 航空工程进展, 2022, 13(5): 1-13.
Wang Kelei, Zhou Zhou, Ma Yuewen, et al. Development and trend analysis of vertical takeoff and landing fixed wing UAV[J]. Advances in Aeronautical Science and Engineering, 2022, 13(5): 1-13.
[2] 陈鹏, 陈洋, 王威. 无人机声学定位技术综述[J]. 华南理工大学学报(自然科学版), 2022, 50(12): 109-123.
Chen Peng, Chen Yang, Wang Wei. Review for UAV acoustic positioning[J]. Journal of South China University of Technology (Natural Science Edition), 2022, 50(12): 109-123.
[3] Zheng Chunlei, Yan Yiping, Liu Yang. Prospects of eVTOL and modular flying cars in China urban settings[J]. Journal of Intelligent and Connected Vehicles, 2023, 6(4): 187-189.
[4] Wu Pengcheng, Yang Xuxi, Wei Peng, et al. Safety assured online guidance with airborne separation for urban air mobility operations in uncertain envi- ronments[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(10): 19413-19427.
[5] 张洪. eVTOL的性能特征、关键技术与发展瓶颈探究[J]. 空运商务, 2022(10): 55-60.
Zhang Hong. Investigation of Performance Characte- ristics, key technologies, and development bottlenecks of eVTOLs[J]. Air Transport Business, 2022(10): 55-60.
[6] 张兴, 郭磊磊, 杨淑英, 等. 永磁同步发电机无速度传感器控制[J]. 中国电机工程学报, 2014, 34(21): 3440-3447.
Zhang Xing, Guo Leilei, Yang Shuying, et al. Speed sensorless control of permanent magnet synchronous generators[J]. Proceedings of the CSEE, 2014, 34(21): 3440-3447.
[7] Ge Yang, Song Weizhang, Yang Yang, et al. A polar- coordinate-multisignal-flux-observer-based PMSM non-PLL sensorless control[J]. IEEE Transactions on Power Electronics, 2023, 38(9): 10579-10583.
[8] Yan Hao, Wang Wenjie, Xu Yongxiang, et al. Position sensorless control for PMSM drives with single current sensor[J]. IEEE Transactions on Industrial Electronics, 2023, 70(1): 178-188.
[9] Wu Lijian, Lü Zekai, Chen Zekai, et al. An enhanced sensorless control scheme for PMSM drives con- sidering self-inductance asymmetry[J]. CES Transa- ctions on Electrical Machines and Systems, 2022, 6(4): 384-392.
[10] Bi Guangdong, Zhang Guoqiang, Wang Qiwei, et al. High-frequency injection angle self-adjustment based online position error suppression method for sensorless PMSM drives[J]. IEEE Transactions on Power Electronics, 2023, 38(2): 1412-1417.
[11] Liu Zhaohua, Nie Jie, Wei Hualiang, et al. Switched PI control based MRAS for sensorless control of PMSM drives using fuzzy-logic-controller[J]. IEEE Open Journal of Power Electronics, 2053, 3: 368-381.
[12] Chen Lijun, Liu Dongliang, Sun Liming, et al. Sensorless control of permanent magnet synchronous motor based on adaptive enhanced extended state observer[J]. International Journal of Circuit Theory and Applications, 2024, DOI: 10.1002/cta.3983.
[13] Chen Lijun, Liu Dongliang, Zhu Minchen, et al. Non-cascaded sensorless control of SPMSM based on cascaded extended state observer[J]. IEEE Access, 2024, 12: 24488-24499.
[14] 杨凯, 李孺涵, 罗成, 等. 负载变化下无传感器感应电机主动零频穿越及脉动抑制策略[J]. 电工技术学报, 2023, 38(18): 4910-4920.
Yang Kai, Li Ruhan, Luo Cheng, et al. Proactive low-frequency ride-through method and its ripple reduction for sensorless induction motor drives under load variations[J]. Transactions of China Electro- technical Society, 2023, 38(18): 4910-4920.
[15] Qian Linfang, Sun Le, Wang Kuan, et al. Fusion of position estimation techniques for a swing servo by a permanent-magnet synchronous machine[J]. IEEE Transactions on Industrial Electronics, 2023, 70(7): 6551-6562.
[16] Bendjedia B, Chouireb S. Comparative study between sensorless vector control of PMSM drives based on MRAS, SMO and EKF observers[C]//2023 Inter- national Conference on Advances in Electronics, Control and Communication Systems (ICAECCS), BLIDA, Algeria, 2023: 1-6.
[17] Wang Chongwu, He Yuyao, Li Hong. The study on the PMSM sensorless control using the sub-optimal fading extend Kalman filter[C]//2013 IEEE 10th International Conference on Power Electronics and Drive Systems (PEDS), Kitakyushu, Japan, 2013: 294-297.
[18] Xin Zhuangzhuang, Wang Jiajun, Zhao Hongjiang. Rotor position estimation using harmonic- decomposition complex-coefficient filter-based PLL for PMSM with switch Hall-effect sensors[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2024, 12(2): 2249-2259.
[19] Tian Minghe, Wang Bo, Yu Yong, et al. Discrete-time repetitive control-based ADRC for current loop disturbances suppression of PMSM drives[J]. IEEE Transactions on Industrial Informatics, 2022, 18(5): 3138-3149.
[20] 陈勇, 邱子桢, 马凯, 等. 基于Markov链随机脉宽调制的永磁同步电机高频边带谐波与声振响应抑制[J]. 电机与控制学报, 2023, 27(9): 109-118.
Chen Yong, Qiu Zizhen, Ma Kai, et al. Investigation into Markov-chain random modulation for suppression high-frequency sideband vibro-acoustics in permanent magnet synchronous motor[J]. Electric Machines and Control, 2023, 27(9): 109-118.
[21] 许家群, 王天琪, 贾普凡. 永磁同步电机准谐振自抗扰电流谐波抑制[J].中国电机工程学报, 2023, 43(6): 2450-2459.
Xu Jiaqun, Wang Tianqi, Jia Pufan. Quasi-resonant anti-disturbance harmonic suppression of permanent magnet synchronous motors[J]. Proceedings of the Chinese Society for Electrical Engineering, 2023, 43(6): 2450-2459.
[22] Xu Yongxiang, Zhang Wentao, Huang Yingliang, et al. Multisector three-phase PMSM drive system with low-frequency and high-frequency PWM noise[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(2): 1639-1648.
[23] Zhang Zhifeng, Wu Yue, Su Hequn, et al. Research on open-circuit fault tolerant control of six-phase permanent magnet synchronous machine based on fifth harmonic current injection[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(3): 306-314.
[24] Lü Zekai, Wu Lijian. Current control scheme for LC- equipped PMSM drive considering decoupling and resonance suppression in synchronous complex-vector frame[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(2): 2061-2073.
[25] 姜卫东, 胡业波, 张庆岩, 等. 基于调制波分解的Vienna整流器的调制方法[J]. 电工技术学报, 2023, 38(16): 4339-4352.
Jiang Weidong, Hu Yebo, Zhang Qingyan, et al. Modulation method of Vienna rectifier based on modulation wave decomposition[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4339- 4352.
[26] 王泽尚, 孙立清, 王志福, 等. 基于扰动补偿的电机模拟器电流控制策略[J]. 电工技术学报, 2023,
38(22): 5987-5998.
Wang Zeshang, Sun Liqing, Wang Zhifu, et al. Current control strategy of electric motor emulator based on disturbance compensation[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 5987-5998.
[27] Yang Yang, Song Weizhang, Ge Yang, et al. A Markov chain random asymmetrical SVPWM method to suppress high-frequency harmonics of output current in an IMC-PMSM system[J]. IEEE Transa- ctions on Power Electronics, 2024, 39(1): 135-148.
[28] 董志强, 王琛琛, 周明磊, 等. 基于SHEPWM的三电平三相逆变器中点电位主动平衡控制策略[J]. 电工技术学报, 2024, 39(4): 1147-1158.
Dong Zhiqiang, Wang Chenchen, Zhou Minglei, et al. Active neutral-point voltage balance control strategy for three-level three-phase inverter under SHEPWM[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1147-1158.
[29] 樊启高, 卢禹卓, 毕恺韬, 等. 基于倍频采样的两相交错并联三电平双向直流变换器功率均衡解耦控制策略[J]. 电工技术学报, 2022, 37(14): 3654-3664.
Fan Qigao, Lu Yuzhuo, Bi Kaitao, et al. Decoupled power-balancing control strategy for two-phase interleaved parallel bidirectional DC converter based on frequency-doubling sampling[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3654- 3664.
Abstract Regarding the sensorless control system of permanent magnet synchronous motors (PMSM), this paper combines extended Kalman filtering (EKF) and improved inertial active disturbance rejection control (IADRC). By establishing a mathematical model under the new coordinate system and applying the EKF algorithm, the state of the motor is accurately estimated, thus ensuring the accuracy and stability of the control system. Aiming at the current harmonic disturbance caused by the sudden load change, this paper introduces the second-order oscillation function to optimize the traditional linear active disturbance rejection control and proposes an improved IADRC strategy, which significantly attenuates the harmonic disturbances and strengthens the system's immunity to disturbances.
According to the traditional mathematical model of the PMSM motor under the 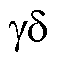 -axis, the mathematical model of the PMSM motor under the estimated rotational coordinate system
-axis, the mathematical model of the PMSM motor under the estimated rotational coordinate system 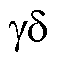 is constructed, and the angle
is constructed, and the angle 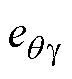 between the dq-axis and the
between the dq-axis and the 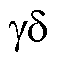 -axis is directly estimated, eliminating the influence of the other observers. After that, through the mutual validation of simulation and the mathematical model, the second-order oscillating function is connected in parallel to suppress current harmonics. The 3rd, 5th, and 7th periodic harmonics with high harmonic contents are suppressed. Its effectiveness and stability are proved by Bode's plot and the Nyquist curve plot, respectively.
-axis is directly estimated, eliminating the influence of the other observers. After that, through the mutual validation of simulation and the mathematical model, the second-order oscillating function is connected in parallel to suppress current harmonics. The 3rd, 5th, and 7th periodic harmonics with high harmonic contents are suppressed. Its effectiveness and stability are proved by Bode's plot and the Nyquist curve plot, respectively.
The EKF's direct estimation method of error angle 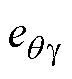 in
in 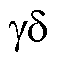 coordinate system is verified Through simulation and experiment, speed step, sudden load addition, and starting with rated load. Meanwhile, compared with the traditional PI control and LADRC control, IADRC plays a role in suppressing the low harmonics when the motor is running stably at 1 000 r/min with rated load. The 5th and 7th harmonic contents are reduced by 50.5% and 77.4% compared to PI. The IADRC algorithm based on the LADRC algorithm can suppress specific harmonics, with a 41.3% reduction in 5th harmonic content compared to the LADRC and a 49.4% reduction in 7th harmonic content compared to the PI. Comparative analysis of the three-phase currents after a sudden change in the rated load shows that compared to PI, the 5th harmonic content of the LADRC is reduced by 70.5%, the 7th harmonic content is reduced by 79.1%, and the 3rd harmonic content is reduced by 54.8%. Meanwhile, compared to LADRC, the 5th harmonic decreases by 44%, the 7th harmonic decreases by 13%, and the 3rd harmonic decreases by 88%.
coordinate system is verified Through simulation and experiment, speed step, sudden load addition, and starting with rated load. Meanwhile, compared with the traditional PI control and LADRC control, IADRC plays a role in suppressing the low harmonics when the motor is running stably at 1 000 r/min with rated load. The 5th and 7th harmonic contents are reduced by 50.5% and 77.4% compared to PI. The IADRC algorithm based on the LADRC algorithm can suppress specific harmonics, with a 41.3% reduction in 5th harmonic content compared to the LADRC and a 49.4% reduction in 7th harmonic content compared to the PI. Comparative analysis of the three-phase currents after a sudden change in the rated load shows that compared to PI, the 5th harmonic content of the LADRC is reduced by 70.5%, the 7th harmonic content is reduced by 79.1%, and the 3rd harmonic content is reduced by 54.8%. Meanwhile, compared to LADRC, the 5th harmonic decreases by 44%, the 7th harmonic decreases by 13%, and the 3rd harmonic decreases by 88%.
Keywords:Permanent magnet synchronous motor, inertial active disturbance rejection control, extended Kalman filter, current harmonics, a new coordinate system
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.240590
国家自然科学基金资助项目(52477185)。
收稿日期 2024-04-18
改稿日期 2024-07-01
刘栋良 男,1977年生,教授,博士生导师,研究方向为电机及其控制、新能源及电力电子/电动汽车驱动系统、电动航空驱动系统、电动船舶推进系统。
E-mail: LiuDL@hdu.edu.cn
赵金洋 男,1999年生,硕士研究生,研究方向为电动航空驱动系统。
E-mail: 1224603950@qq.com(通信作者)
(编辑 崔文静)