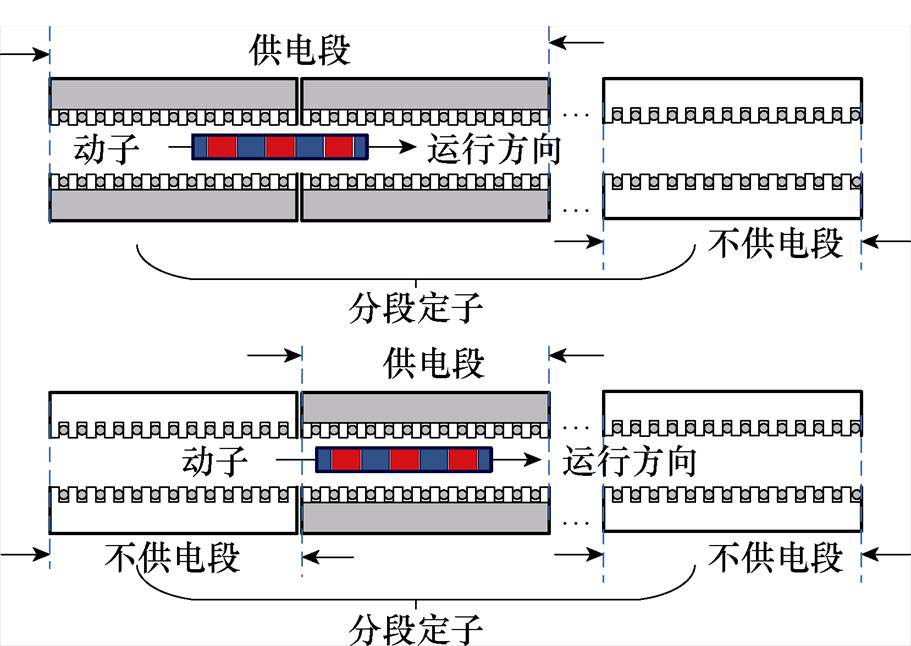
图1 分段直线电机结构
Fig.1 Structure diagram of the segmented linear motor
摘要 针对分段供电永磁直线同步电机（PMLSM）在运行过程中易受外部扰动、参数变化等因素的影响，该文提出了一种新型滑模控制器与终端滑模扰动观测器（TSMDO）相结合的速度控制策略。首先，分析了传统滑模控制器存在收敛速度和抖振程度相互矛盾的问题。其次，设计了一种新型的滑模趋近律，使得所提滑模速度控制（SMSC）加快了系统的收敛速度、抑制了滑模的抖振、保证了电机速度跟踪的动态性能。然后，为了提升电机速度跟踪的稳态性能，基于终端滑模理论设计了TSMDO，该观测器可以对外部扰动、参数变化等不确定性因素进行观测并补偿。最后，通过与PI控制、传统SMSC的对比实验，验证了所提控制策略的有效性。实验结果表明，所提控制策略不仅提高了分段供电PMLSM速度跟踪的动态和稳态性能，而且减小了加速度波动。
关键词：永磁直线同步电机 加速度波动 滑模速度控制 终端滑模扰动观测器
直线电机没有中间传动装置，直接带动载荷作直线运动，因此广泛应用于物流运输、磁悬浮交通、电磁推进和军事等领域。永磁直线同步电机（Permanent Magnet Linear Synchronous Motor, PMLSM）由于动子侧采用永磁体励磁，具有效率高、推力密度大、动态响应快等优势[1-2]，主要适用于具有长行程、高速和高加速度特点的大功率电磁推进装置中。
在相同的加速度下，载荷的目标速度越高，PMLSM所需的定子轨道就越长。此时，直线电机通常采用定子分段供电的结构[3]，如图1所示。采用这种结构，逆变器便无需向整个定子轨道供电，仅需向与动子耦合的定子段供电，从而节省了逆变器的容量，提高了电压利用率[4]。然而，采用该分段结构带来了边端效应[5]，且在安装过程中难以保证每一段定子的气隙相等，因此动子在运行过程中会受到法向力的影响。法向力导致的扰动与负载力、定位力、摩擦力等外部扰动一同给电机的速度控制带来了挑战。此外，载荷通常是在短时间内被加速至目标速度，因而电磁推进装置通常运行在大电流、高加速度的工况下，电机参数容易发生改变[6-7]，这意味着速度控制系统需具备一定的参数鲁棒性。
图1 分段直线电机结构
Fig.1 Structure diagram of the segmented linear motor
现有的文献中已经对多种直线电机速度控制的方法做出了研究，如自适应PI控制[8]、模型预测控制（Model Predictive Control, MPC）[9-11]、滑模控制（Sliding Mode Control, SMC）[12-16]、自抗扰控制（Active Disturbance Rejection Control, ADRC）[17]等。在这些控制方法中，SMC因其对参数变化的鲁棒性和对扰动的不敏感性而受到更多的关注。由于负载转矩的变化，电机的速度会发生振荡，对此文献[18]设计了一种基于滑模理论的永磁同步电机速度控制器，该控制器抑制了振荡，实现了参数失配时速度的鲁棒控制。文献[19]提出了一种基于自适应滑模趋近律的快速终端滑模速度控制（Sliding Mode Speed Control, SMSC）方法，以提高跟踪精度。通过设计一种扩展滑模扰动观测器（Extend Sliding Mode Disturbance Observer, ESMDO）来估计内部和外部扰动，增强了系统的抗扰动能力。徐伟等学者设计了一种基于快速终端滑模控制理论的扩展状态观测器来估计电机系统的总扰动，提高了系统对前馈补偿后负载力扰动的鲁棒性[20]。然而，SMC的鲁棒性是通过使用较大的开关增益来实现的。因此，在SMC中会出现抖振问题，这是系统性能恶化的主要原因。为了解决抖振问题，SMC趋近律中的符号函数被饱和函数或Sigmoid函数取代[21-22]，但滑模的快速收敛性难以保证。文献[23]通过引入低通滤波器来消除高频信号，将相位滞后引入控制系统。文献[24]设计了一种基于积分项控制律的二阶终端滑模控制器，通过使用非线性控制增益，抑制了感应电机控制系统的抖振。文献[25]提出了一种负载转矩观测器，该观测器利用趋近律的导数，通过高阶滑模的理论消除了抖振问题。文献[26]提出了一种新型非奇异快速积分终端滑模控制策略，该策略利用自适应控制算法来估计集总不确定性并减少 抖振。
电磁推进装置对加速度有着较高的要求，负载力、定位力、摩擦力、法向力等外部扰动和参数变化不可忽视。由于PMLSM没有中间传动装置，这些扰动将直接作用于电机驱动系统。本文通过设计具有新型趋近律的滑模控制器来保证速度的快速收敛性并抑制抖振，设计终端滑模扰动观测器（Terminal extend Sliding Mode Disturbance Observer, TSMDO）观测并补偿包含在控制器输出中的扰动量。通过这种方法，既保证了电机控制系统速度跟踪的动态和稳态性能，又降低了加速度波动。最后在一台分段供电PMLSM上进行了对比实验验证。
考虑到dq轴系下PMLSM的数学模型，推力的方程为
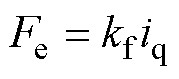（1）
其中
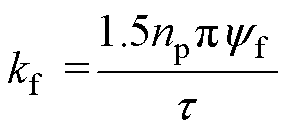
式中，Fe为电机的电磁推力；kf为推力系数；iq为电机的q轴电流；t 为极距；np为极对数；yf为永磁体磁链。
根据牛顿第二定律，并结合上述推力方程，电机的机械运动模型表示为
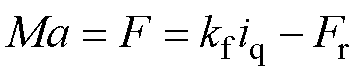（2）
式中，M为动子与载荷的总质量；a为动子的加速度；F为电机系统实际输出的推力；Fr为负载力、定位力、摩擦力、法向力等不同外部扰动的合力。进一步考虑电机在运行过程中参数发生的变化，根据式（2）可以推导得到
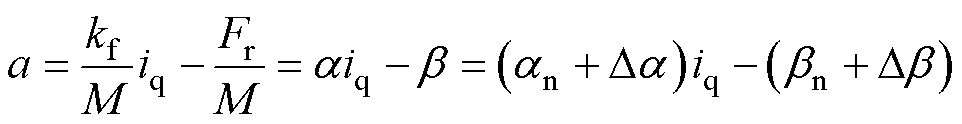（3）
其中
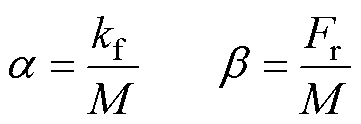
式中，Da 和Db 分别为电机参数变化的影响；带有下标“n”的参数表示电机参数的标称值。最终，可以获得PMLSM的运动数学模型为
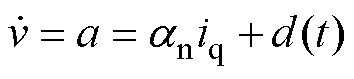（4）
其中
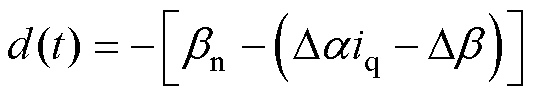
式中，v为动子的运动速度；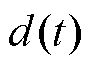
为电机速度控制系统的总扰动，包括负载力、定位力、摩擦力、法向力和参数变化所致的扰动。
由式（4）可知，电机的加速度受到d(t)的影响。根据F=Ma，加速度的波动将导致系统输出推力的波动。为了保证电磁驱动系统具有良好的加速性能，d(t)需要得到相关处理。
基于SMC的速度控制系统如图2所示。图中，Mn和kfn分别为动子及载荷的质量和电磁推力系数的标称值；vref和vm分别为速度给定值和测量值，C(s)为电流环传递函数。
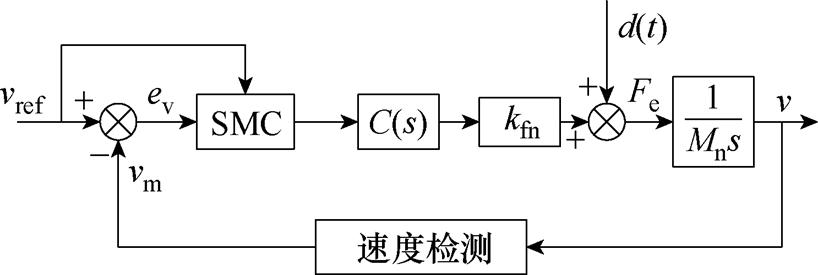
图2 滑模速度控制结构框图
Fig.2 Block diagram of SMSC
假设两个状态变量x1和x2，并满足
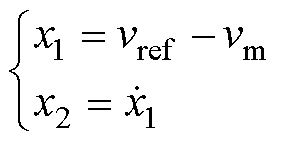（5）
若速度的测量足够准确，则v=vm。将式（4）代入式（5），可得
（6）
为了提高系统状态变量的收敛速度并减少滑模跟踪误差，这里引入了积分滑模[27-28]，得到积分滑模面为
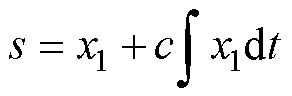（7）
式中，s为滑模面；c为可以调节的滑模面参数。假定令滑模面满足s=0，根据式（5）和式（7）可以推导得到
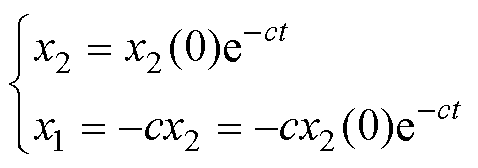（8）
根据式（7）和式（8）可知，如果状态变量x1到达滑模面（s＝0, t→∞)，系统状态变量最终将收敛到0。调整c可以改变收敛速度。该系统的相平面坐标如图3所示，其中c的大小表示滑模面函数的斜率。c的值越大，状态变量沿着滑模面收敛到坐标原点的速率就越快。
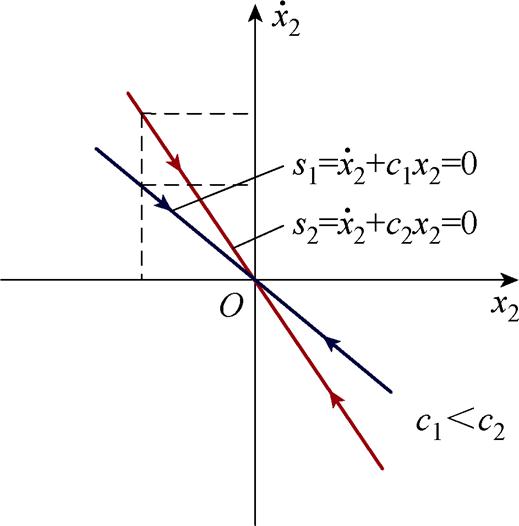
图3 滑模面
Fig.3 Sliding mode surface
进一步地，为了追求较快的收敛速度，可设计滑模趋近律为指数趋近律[29]，有
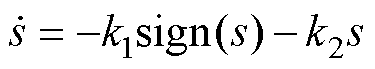（9）
式中，k1和k2为可调滑模增益。将式（9）代入李雅普诺夫方程V=0.5s2，可得
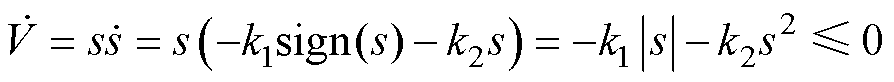（10）
若可调参数满足：k1＞0，k2＞0，可得滑模控制器是稳定的。
根据式（6）、式（7）、式（9）可得到滑模速度控制器方程为
（11）
式中，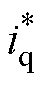
为滑模控制器的输出参考电流值。从式（11）中可以得到，总扰动部分d(t)包含在控制器方程的输出中，这将影响速度控制系统的速度精度。同时，控制器的输出中也包含着开关项k1sign(s)，这是引起滑模控制器抖振现象的根源，且k1的大小直接决定了抖振的程度。求取式（9）从0～t的积分，有
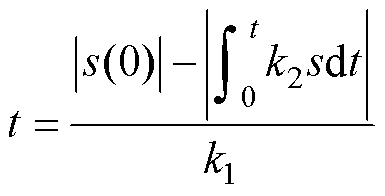（12）
根据式（12）不难发现，k1的取值越大可以减小收敛时间t。然而，根据式（11），k1增大会加剧系统的抖振现象，因此传统滑模控制器存在抖振抑制和收敛速度之间的矛盾。
本节针对传统滑模控制器存在抖振抑制和收敛速度之间矛盾的问题，设计了基于新型滑模趋近律的滑模速度控制器。并且，针对滑模控制器输出中包含的总扰动d(t)，设计了终端滑模扰动观测器，观测并补偿扰动的影响。
当系统的状态变量远离滑模面时，所设计的滑模趋近律能够保证变量以较快的速度趋近于滑模面；当系统的状态变量逐渐逼近滑模面时，所设计的滑模趋近律能够减小变量趋近于滑模面的速度，达到削弱抖振的目的。
基于式（9）且满足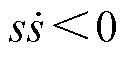
，设计新型的滑模趋近律，并采用饱和函数代替符号函数，有
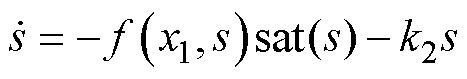（13）
式中，开关增益不再是常数，设计自适应函数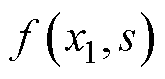
为
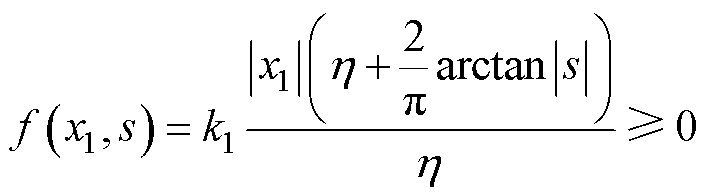（14）
式中，h 为可调参数。自适应增益函数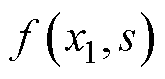的参数满足：k1＞0，0＜h＜1。
由式（14）不难得到，当状态变量x1的值较大，即距离滑模面s=0较远时，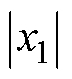
与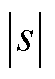
取值都较大，此时自适应增益函数满足
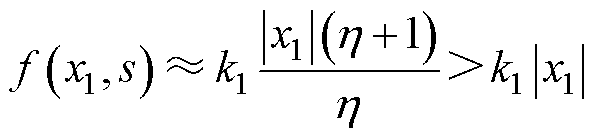（15）
可见，由于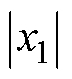的值较大，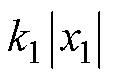
大于传统滑模趋近律式（9）的固定增益k1。因此，滑模控制具有更快的收敛速度。
当状态变量x1的值较小，即靠近滑模面s=0时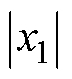，与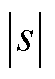取值都较小，此时自适应增益函数满足
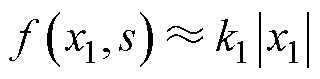（16）
可见，自适应增益函数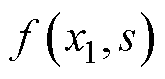也随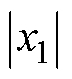的减小而减小。因此，随着x1不断逼近滑模面s=0，自适应增益函数取值将小于传统滑模趋近律式（9）的固定增益k1，减小了抖振。
根据V=0.5s2、式（10）、式（13）可推导得到
（17）
即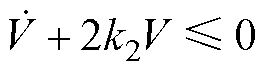
。引入函数S(t)＞0，不难得到
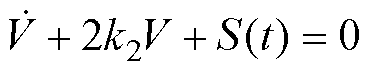（18）
进一步地，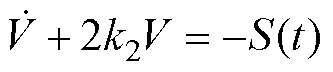
，解得
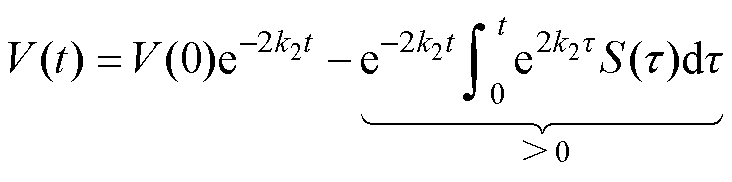（19）
即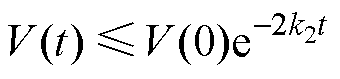
。将V=0.5s2代入可得
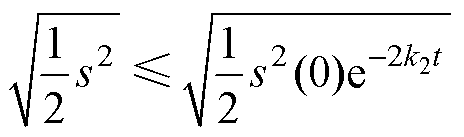（20）
即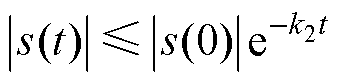
。因此，该滑模控制器满足指数渐近稳定，k2影响收敛速率的大小。
同理，如式（11）可得基于新型滑模趋近律的滑模速度控制器方程为
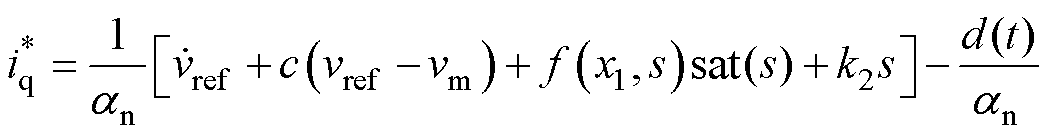（21）
至此，基于自适应滑模增益的新型滑模控制器已经设计完毕。
下面通过仿真对比传统滑模控制和本小节所提滑模控制的抖振程度和趋近时间。式（21）中存在总扰动d(t)，这里将集总扰动d(t)替换为上界l，满足|d(t)|≤l，则得控制器输入为
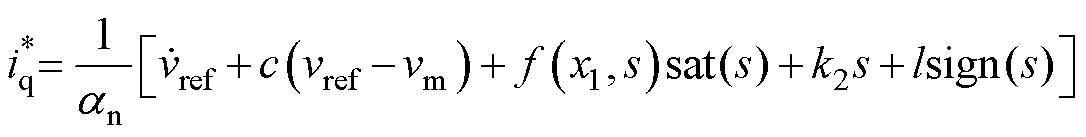（22）
假设存在一个系统，有
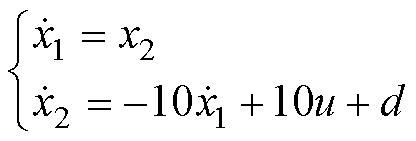（23）
式中，(x1, x2)为系统的状态，取初始状态(x1(0), x2(0))= (-2, -2)；u为系统的输入量；d为系统的扰动量。设计的滑模面为：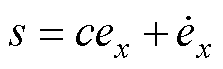
，令状态误差ex=xref -x1，其中，xref为速度误差状态变量给定值，且xref =sin(2t)。
首先分析在无扰动，即d(t)=0的情况。根据前述分析，可知传统滑模控制器方程为：
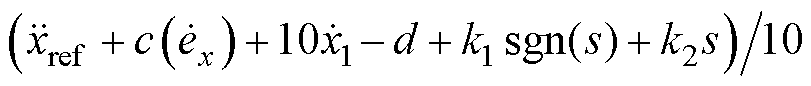，其中c=10，k1=40，k2=40；自适应滑模控制器方程为： 
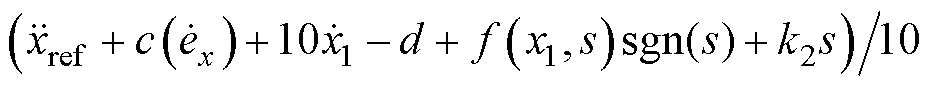，其中h=0.5。仿真结果如图4a、图4c、图4e、图4g所示。
其次分析存在扰动d(t)=6sin(4pt)，在控制器方程中，扰动d(t)由lsign(s)补偿且l为扰动的上界，满足|d(t)|≤l，这里取l=6，则传统滑模控制器方程为：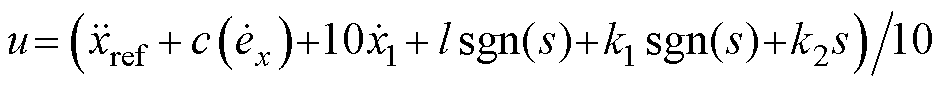
；自适应滑模控制器方程为：
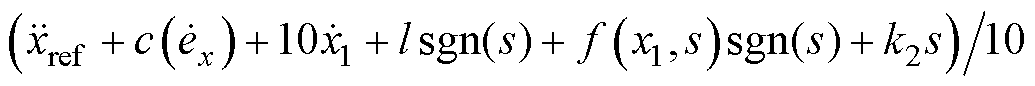。仿真结果如图4b、图4d、图4f、图4h所示。
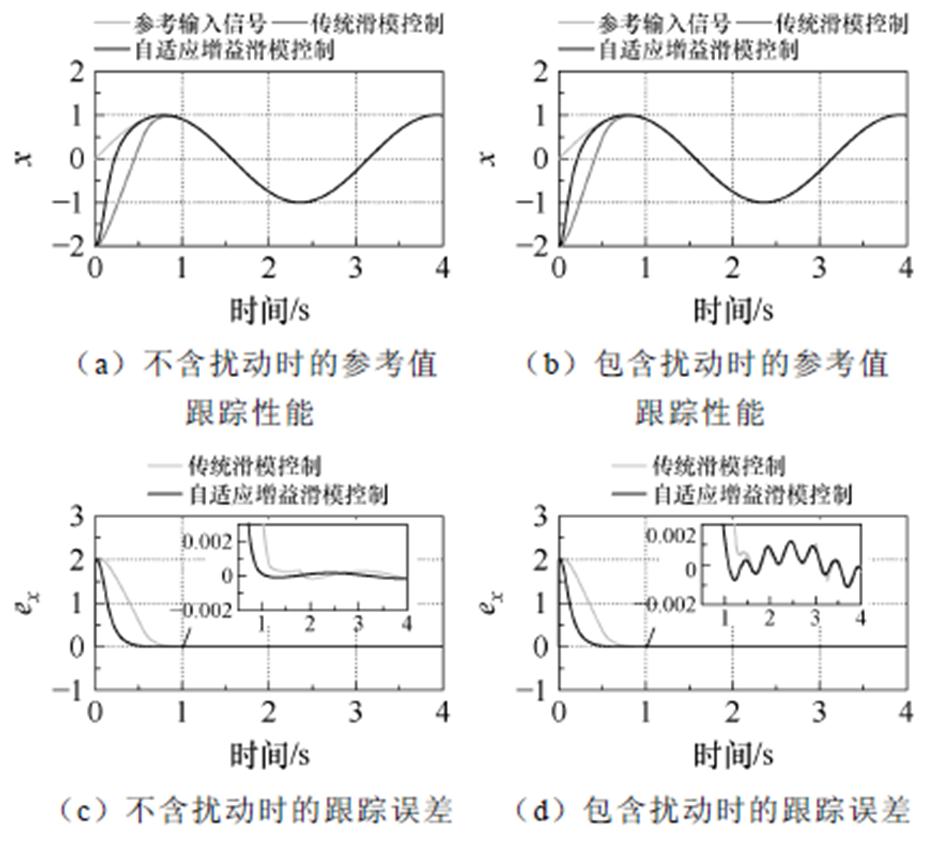
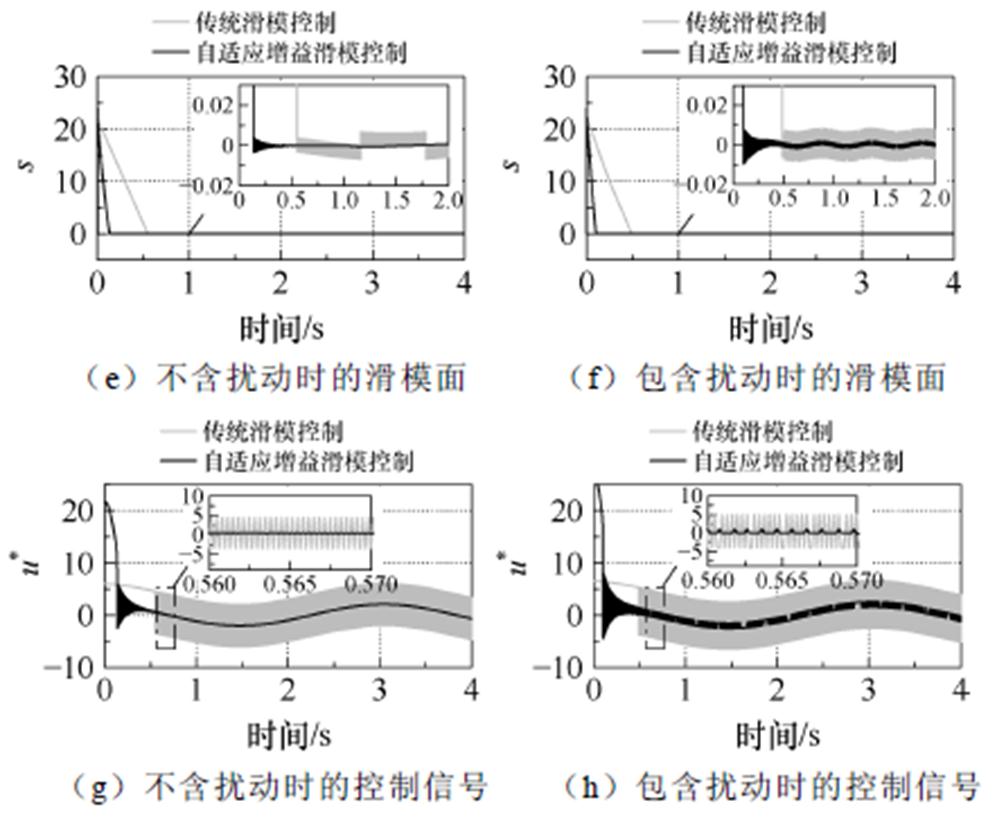
图4 传统滑模控制和新型滑模控制的性能对比
Fig.4 Performance comparison between traditional sliding mode control and adaptive sliding mode control
图4a、图4c、图4e、图4g中给出了无扰动时传统滑模控制和新型滑模控制的仿真结果。与传统滑模控制相比，自适应增益使得新型滑模控制可以实现更快的跟踪性能并减少抖振。图4b、图4d、图4f、图4h给出了传统滑模控制和新型滑模控制在扰动下的仿真结果对比，自适应增益使得滑模控制在保证较小抖振的同时仍然实现了更快的跟踪性能。因此表明，基于自适应增益的新型滑模控制可以减少抖振并获得比传统滑模控制更短的到达时间。
在式（11）、式（21）中存在总扰动d(t)的影响，如果不能抑制d(t)，则会降低控制性能。3.1节提到d(t)由lsign(s)补偿，造成抖振的大小与上界l有关，然而在实际应用中，d(t)无法准确测量，因此难以确定l的取值。虽然可使用误差控制和实验等方法来选择l，但这些方法耗时长、鲁棒性差。因此，本小节提出了在线估计d(t)的方法。
由于总扰动d(t)具有非线性和时变的特征，基于终端滑模理论设计了一种TSMDO来估计总扰动d(t)。由于在电机系统模型中，d(t)是有界的，因此在式（4）的基础上，可以将d(t)扩展为一个新的状态变量，有
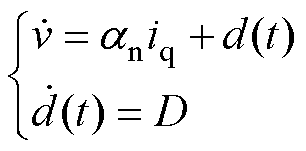（24）
式中，D为扰动d(t)的微分值。引入中间变量F，可设计TSMDO为
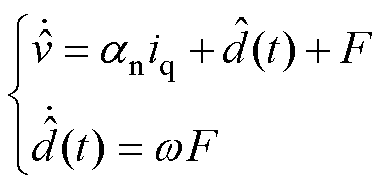（25）
式中，w 为可调参数。式（25）减去式（24）可得
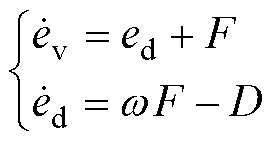（26）
式中，ev和ed分别为速度误差和扰动误差。设计的积分滑模面和趋近律分别为
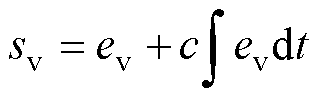（27）
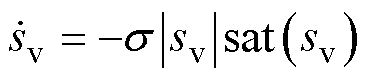（28）
式中，s 为观测器的可调参数。根据式（26）～式（28）可得
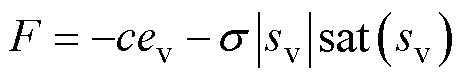（29）
根据李雅普诺夫函数V=0.5s2可得
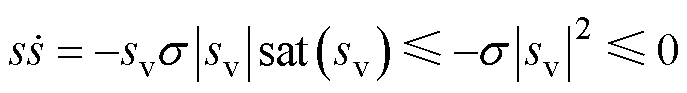（30）
不难知道，只要s＞0即可保证观测器稳定。若速度状态变量到达滑模面时可知ev=0，此时由式（26）可得
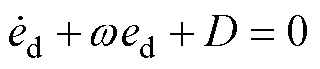（31）
解得
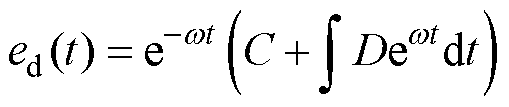
式中，C为常数。当w＞0时，ed收敛至零，w 决定ed收敛速度。
对式（24）和式（31）进行拉普拉斯变换，S为复变量，可得
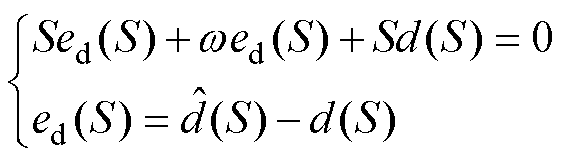（32）
式中，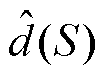
为扰动的观测值。不难得到
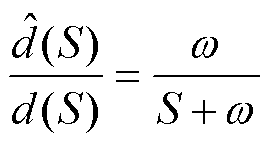（33）
由式（33）可知，观测器对于总扰动的观测可以等效为一阶低通滤波器，w 等效为滤波器的截止频率，抖振能够得到抑制。
实验平台为一台具有分段定子的PMLSM，来验证所提控制策略，如图5所示。该PMLSM由两个逆变器通过开关并联供电，如图6所示。奇数分段定子由逆变器1供电，而偶数分段定子由逆变器2供电，只有与动子相耦合的定子段才通电。该电机的参数见表1。
图5 PMLSM实验平台
Fig.5 Experimental platform of PMLSM
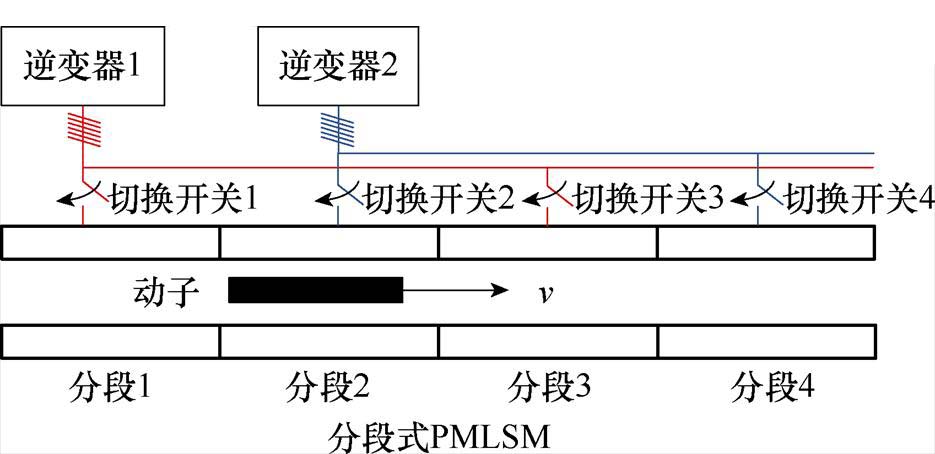
图6 供电方式
Fig.6 Power supply mode
表1 电机参数
Tab.1 Motor parameters
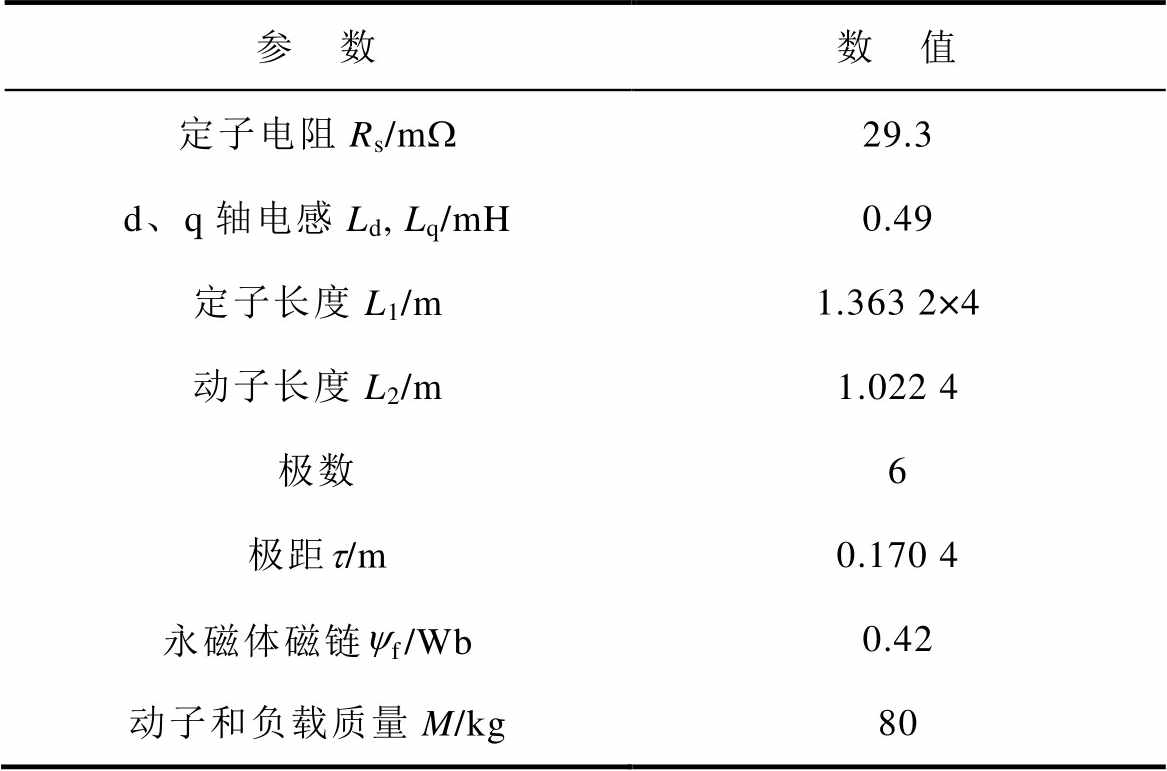
参 数数 值 定子电阻Rs/mW29.3 d、q轴电感Ld, Lq/mH0.49 定子长度L1/m1.363 2×4 动子长度L2/m1.022 4 极数6 极距t/m0.170 4 永磁体磁链yf/Wb0.42 动子和负载质量M/kg80
在实验过程中，电机首先经历0.4 s的匀加速过程，然后匀速运动0.2 s，最大运行速度为5 m/s。两个逆变器的开关频率为6 kHz，采样频率为6 kHz，控制周期为166.67 ms。由于直线电机的推力难以直接测量，本文采用加速度信号间接反映电机的推力。
在实验中，对PI控制、传统SMSC和所提新型的SMSC进行了对比实验。速度控制框图如图7 所示。
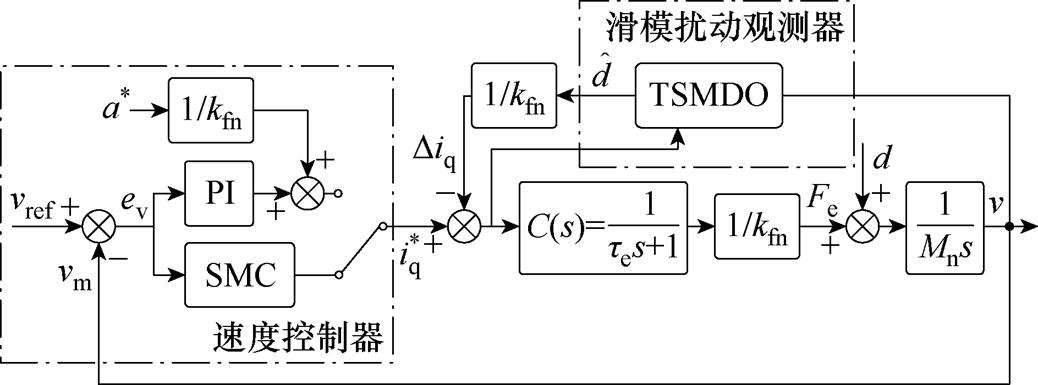
图7 速度控制框图
Fig.7 Block diagram of speed control
首先在速度控制中测试了PI控制器。为了提高控制系统的抗干扰能力，将速度回路设计为典型的Ⅱ型系统。PI控制器的可调参数kp、ki[30]为
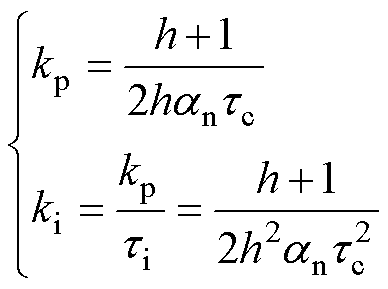（34）
式中，h为控制器的带宽；tc为电流环的时间常数，tc=3.33×10-3 s；ti为控制器等效时间常数。图8～图10分别表示h=3、h=5、h=8时的速度跟踪情况、速度误差、加速度和q轴电流的情况。
比较图8～图10可知，随着h的增大，速度跟随给定值的响应越来越快，速度误差由0.2 m/s减小到0.14 m/s，误差减小得不多。且由图10可见，动子加速完毕，在进入匀速运行段时，速度出现了明显的过调量。
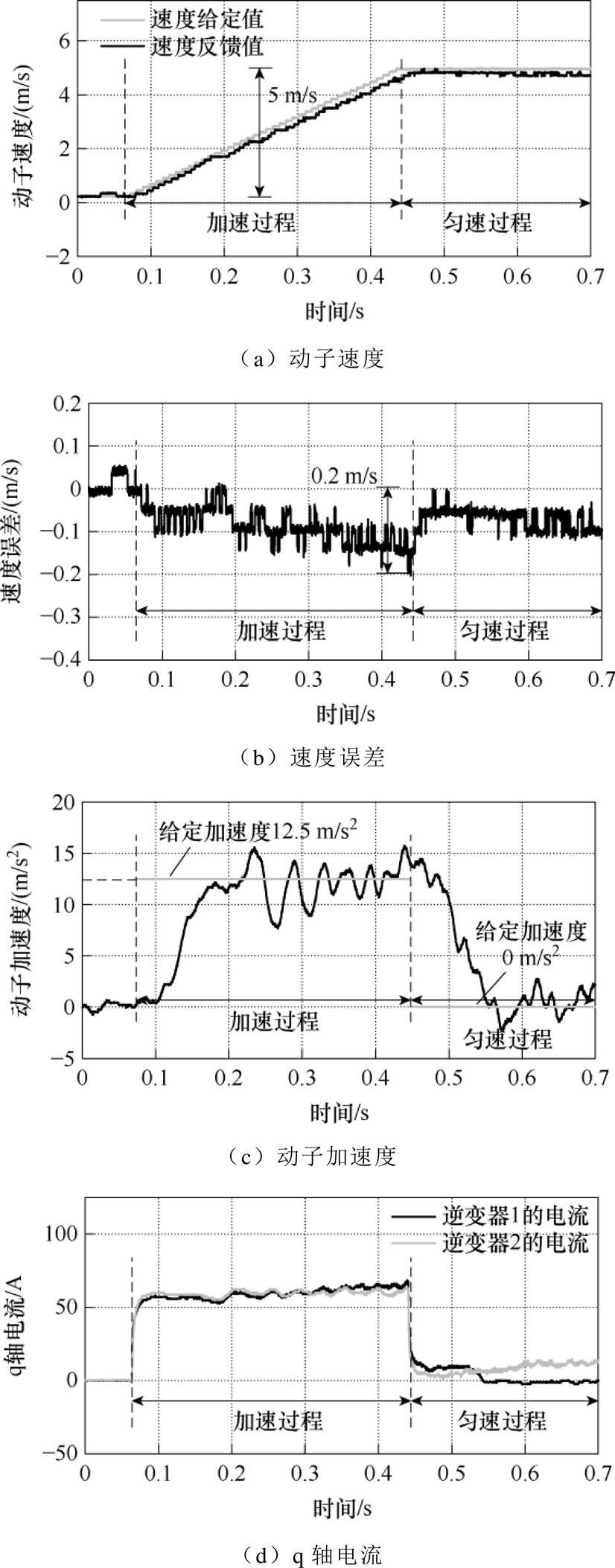
图8 PI控制器且h=3时的控制效果
Fig.8 Control performance of PI controller with h=3
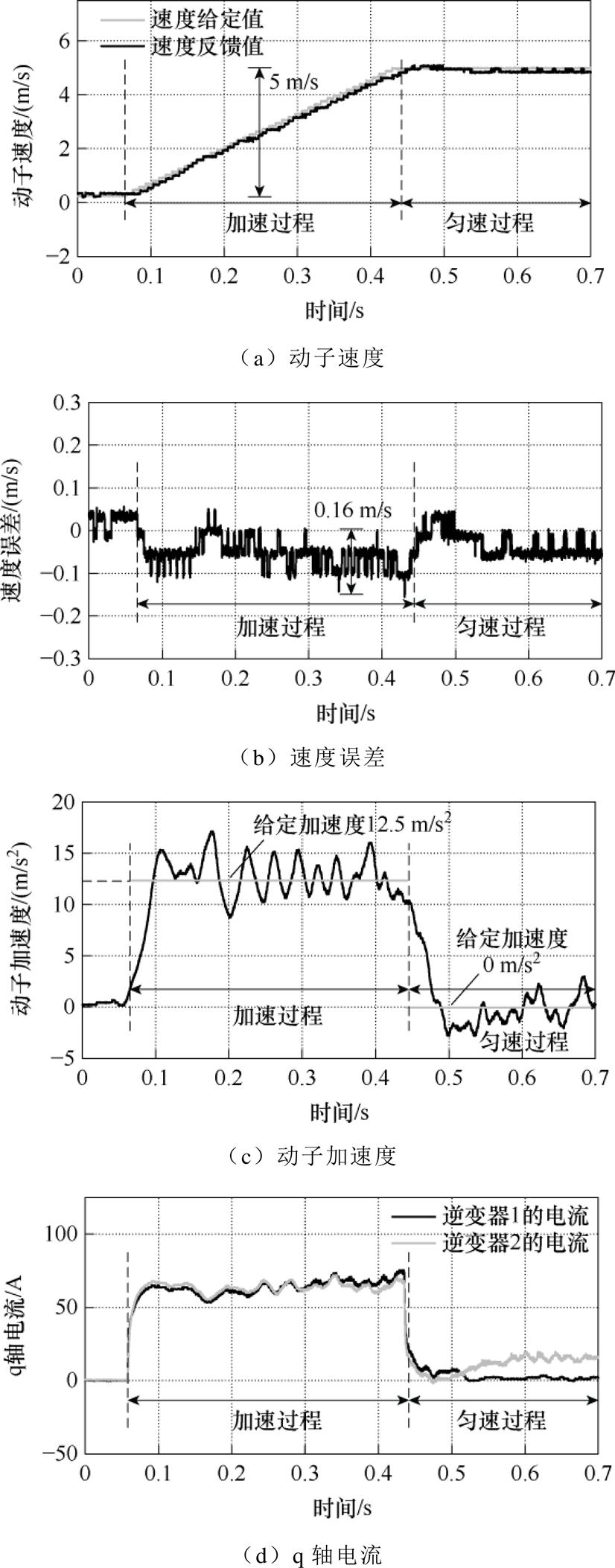
图9 PI控制器且h=5时的控制效果
Fig.9 Control performance of PI controller with h=5
图10 PI控制器且h=8时的控制效果
Fig.10 Control performance of PI controller with h=8
此外，在PI控制器下，图8～图10的加速度波动和q轴电流波动也随着h的增大而明显增大。其中，最大加速度波动分别为3、3.5、4.7 m/s2。
图11、图12分别给出了传统滑模速度控制和新型滑模速度控制下的动子速度跟踪波形、速度误差、加速度和q轴电流波形。滑模控制器的参数设计见表2。
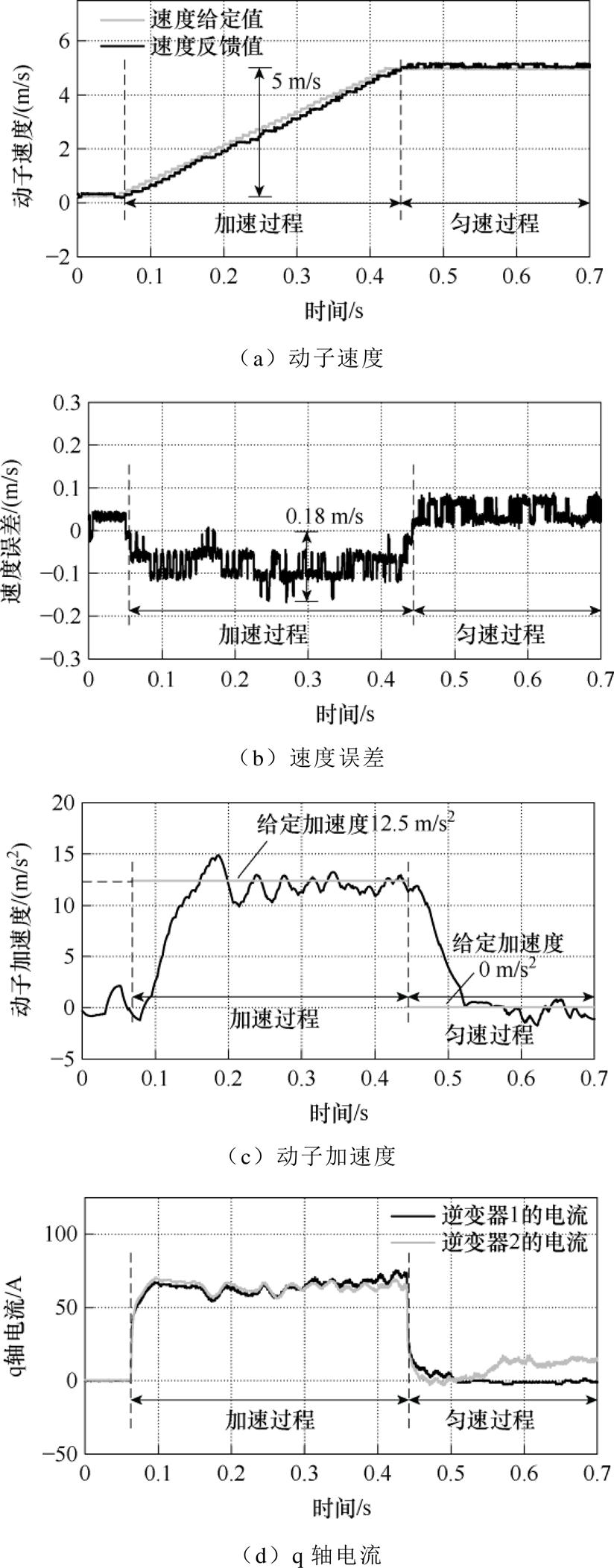
图11 传统滑模控制器的控制效果
Fig.11 Control performance of conventional sliding mode controller
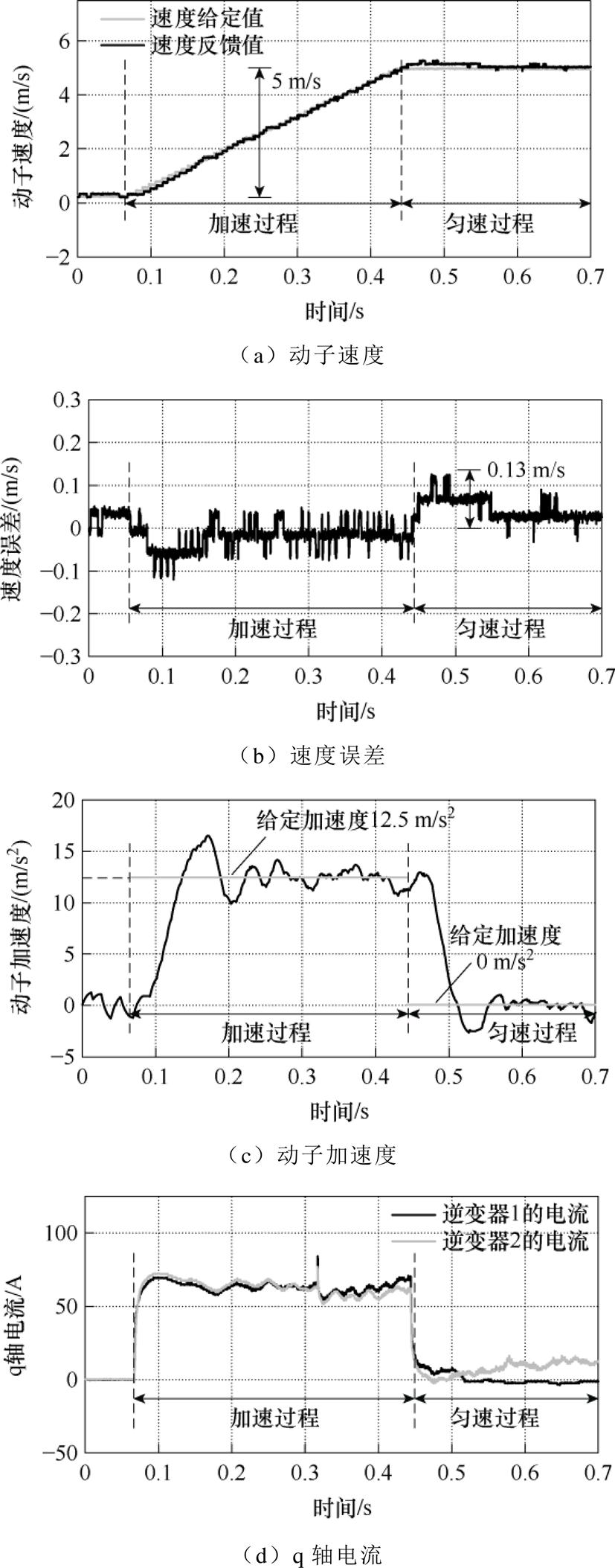
图12 新型滑模控制器的控制效果
Fig.12 Control performance of novel sliding mode controller
从图8a、图8b和图11a、图11b中可知，PI控制和传统滑模速度控制下，动子在加速过程中速度误差分别为0.2 m/s和0.18 m/s，速度的跟踪性能相差不大，然而在滑模速度控制下，动子在匀速段的跟踪性能要优于PI控制器。同时从图8c和图11c中可知，滑模控制的加速度波动小于PI控制器。PI控制器虽然可以通过增大h来保证与滑模控制器相同的匀速跟踪性能，但是不难发现，其加速度波动和q轴电流波动越来越大。从图10a、图10b和图12a、图12b中可知，在PI控制和新型滑模速度控制时，加速过程中的速度误差分别为0.14 m/s和0.13 m/s，两者速度的跟踪响应基本相同，而后者速度的过调量更小。同样地，从图10c、图10d和图12c、图12d中可知，新型滑模控制的加速度波动和q轴电流波动小于PI控制器。对比滑模速度控制和PI控制可知，滑模速度控制拥有更佳的速度收敛能力、加速度波动和q轴电流波动的抑制能力。
表2 两种滑模速度控制的参数
Tab.2 Parameters of two sliding mode speed control
参 数传统SMSC新型SMSC c55 k10.10.1 k2100100 h—0.001
从图11a、图11b和图12a、图12b可知，相同的参数，在匀速性能相差不大的情况下，两者的速度误差分别为0.18 m/s和0.13 m/s，新型滑模速度控制在新型滑模趋近律的作用下，拥有比传统趋近律更快的跟踪速度，动态响应更好。但是从图11c、图11d和图12c、图12d可知，加速段时加速度的波动和q轴电流波动依旧明显。为了抑制加速度波动，这里加入了所设计的TSMDO，观测器的参数设计为w=100，s=500。
带有TSMDO的控制效果如图13所示。从图12a、图12b和图13a、图13b可知，加入TSMDO后，速度跟踪误差减小为0.11 m/s，速度的动态跟踪性能得到改善。从图12c、图12d和图13c、图13d中可知，加速度的波动和q轴电流波动也明显减小。需要说明的是，观测器对于总扰动的观测可以等效为一阶低通滤波器，传递函数并不等于1，也意味着扰动观测值与真实的扰动不完全一致。因此，将扰动的观测值作为前馈进行补偿，仍然会存在扰动的影响，即加速度波动依然存在。所提方法能够削弱扰动的影响，但无法做到完全消除。
最后，通过调整参数，使得三种方法达到稳态，即在匀速段速度跟踪情况一致的前提下，三者的实验性能指标对比见表3。
图13 带有TSMDO的控制效果
Fig.13 Control performance with TSMDO
表3 三种速度控制策略的性能指标对比
Tab.3 Comparison of the performance of three speed control strategies
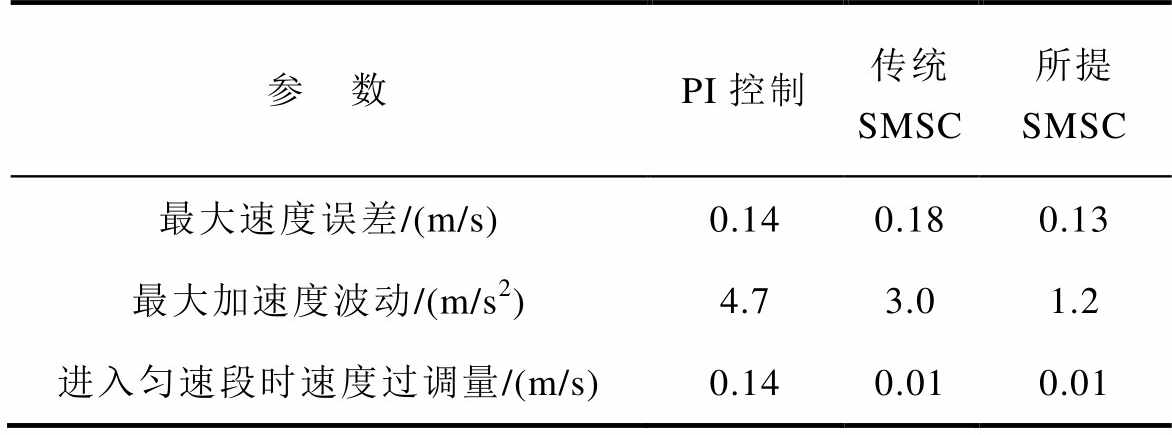
参 数PI控制传统 SMSC所提 SMSC 最大速度误差/(m/s)0.140.180.13 最大加速度波动/(m/s2)4.73.01.2 进入匀速段时速度过调量/(m/s)0.140.010.01
由表3可见，本文所提控制策略具有最佳的性能。至此，实验结果证明了所提新型滑模速度控制策略的有效性。
针对分段供电的PMLSM在运行过程中受到的负载力、定位力、摩擦力、法向力、参数变化导致的扰动的影响，使得电机速度控制的动态和稳态性能减弱，本文设计了基于新型滑模趋近律的SMSC，并在此基础上通过设计TSMDO观测滑模控制器输出中的总扰动，抑制扰动的影响。通过实验对比分析，得到主要结论如下：
1）相比于PI控制和传统的滑模控制，所提新型滑模控制策略由于其趋近律的自适应增益函数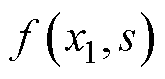会自适应调整滑模增益，因而具有更快的收敛速度，同时能够削弱抖振，保证较好的速度跟踪性能。
2）通过终端滑模理论设计的TSMDO，很好地抑制了SMSC输出中的总扰动d(t)，提高了系统的扰动抑制性能，减小了加速度波动，保证了电机输出平稳的推力。
参考文献
[1] 蒋钱, 卢琴芬, 李焱鑫. 双三相永磁直线同步电机的推力波动及抑制[J]. 电工技术学报, 2021, 36(5): 883-892.
Jiang Qian, Lu Qinfen, Li Yanxin. Thrust ripple and depression method of dual three-phase permanent magnet linear synchronous motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 883-892.
[2] 张康, 王丽梅. 基于反馈线性化的永磁直线同步电机自适应动态滑模控制[J]. 电工技术学报, 2021, 36(19): 4016-4024.
Zhang Kang, Wang Limei. Adaptive dynamic sliding mode control of permanent magnet linear syn- chronous motor based on feedback linearization[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4016-4024.
[3] 张明元, 马伟明, 何娜. 长初级直线电动机分段供电技术综述[J]. 中国电机工程学报, 2013, 33(27): 96-104.
Zhang Mingyuan, Ma Weiming, He Na. Application of block feeding methods in long primary linear motors[J]. Proceedings of the CSEE, 2013, 33(27): 96-104.
[4] 张明元, 马伟明, 徐兴华, 等. 一种考虑电流过零的直线电机分段供电策略[J]. 海军工程大学学报, 2019, 31(4): 11-16.
Zhang Mingyuan, Ma Weiming, Xu Xinghua, et al. A block feeding strategy for linear motor considering switching at current-crossing point[J]. Journal of Naval University of Engineering, 2019, 31(4): 11-16.
[5] 马名中, 马伟明, 范慧丽, 等. 长初级直线感应电机分段供电切换暂态过程[J]. 电机与控制学报, 2015, 19(9): 1-7.
Ma Mingzhong, Ma Weiming, Fan Huili, et al. Switch transient process of section powered long-primary linear induction motor[J]. Electric Machines and Control, 2015, 19(9): 1-7.
[6] 郭科宇, 李耀华, 史黎明, 等. 电枢分段供电永磁直线同步电机的非线性数学模型[J]. 电工技术学报, 2021, 36(6): 1126-1137.
Guo Keyu, Li Yaohua, Shi Liming, et al. Non-linear mathematic model of a segmented powered permanent magnet linear synchronous machine[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1126- 1137.
[7] Guo Keyu, Li Yaohua, Shi Liming, et al. A phase- domain model of dual three-phase segmented powered linear PMSM for hardware-assisted real-time simu- lation[J]. IEEE Transactions on Industry Applications, 2022, 58(4): 4511-4521.
[8] Jung J W, Leu V Q, Do T D, et al. Adaptive PID speed control design for permanent magnet syn- chronous motor drives[J]. IEEE Transactions on Power Electronics, 2015, 30(2): 900-908.
[9] 周世炯, 李耀华, 史黎明, 等. 分段式双三相永磁直线同步电机的无模型电流预测控制[J]. 电工技术学报, 2024, 39(4): 996-1009, 1021.
Zhou Shijiong, Li Yaohua, Shi Liming, et al. Model-free predictive current control of segmented dual three-phase permanent magnet linear syn- chronous motor[J]. Transactions of China Electro- technical Society, 2024, 39(4): 996-1009, 1021.
[10] 王政, 温从剑, 朱辰雨, 等. 位置伺服永磁电机鲁棒性无差拍预测转速控制[J]. 电工技术学报, 2023, 38(19): 5176-5184.
Wang Zheng, Wen Congjian, Zhu Chenyu, et al. Deadbeat predictive control for position servo permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5176-5184.
[11] 魏尧, 柯栋梁, 黄东晓, 等. 基于时间序列的永磁同步电机连续控制集无模型预测电流控制[J]. 电工技术学报, 2023, 38(22): 6027-6038.
Wei Yao, Ke Dongliang, Huang Dongxiao, et al. A continuous-control-set type model-free predictive current control based on time-series for permanent magnet synchronous motor drives[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6027- 6038.
[12] Zhang Yanqing, Yin Zhonggang, Li Wei, et al. Adaptive sliding-mode-based speed control in finite control set model predictive torque control for induction motors[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 8076-8087.
[13] 黄依婷, 沈建新, 王云冲, 等. 基于递推最小二乘法观测器的永磁同步伺服电机变参数滑模控制[J]. 中国电机工程学报, 2022, 42(18): 6835-6846.
Huang Yiting, Shen Jianxin, Wang Yunchong, et al. Variable parameter sliding mode control of permanent magnet synchronous servo machine based on recursive least square observer[J]. Proceedings of the CSEE, 2022, 42(18): 6835-6846.
[14] 郭昕, 黄守道, 彭昱, 等. 基于改进型双幂次趋近律与全局快速终端滑模观测器的IPMSM调速系统滑模控制[J]. 电工技术学报, 2023, 38(1): 190-203.
Guo Xin, Huang Shoudao, Peng Yu, et al. Sliding mode control of IPMSM speed regulation system based on an improved double power reaching law and global fast terminal sliding mode observer[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 190-203.
[15] 付东学, 赵希梅. 永磁直线同步电机自适应非奇异快速终端滑模控制[J]. 电工技术学报, 2020, 35(4): 717-723.
Fu Dongxue, Zhao Ximei. Adaptive nonsingular fast terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 717-723.
[16] Wang Yaoqiang, Feng Yutao, Zhang Xiaoguang, et al. A new reaching law for antidisturbance sliding-mode control of PMSM speed regulation system[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4117-4126.
[17] Zuo Yuefei, Mei Jie, Jiang Chaoqiang, et al. Linear active disturbance rejection controllers for PMSM speed regulation system considering the speed filter[J]. IEEE Transactions on Power Electronics, 2021, 36(12): 14579-14592.
[18] Yeam T I, Lee D C. Design of sliding-mode speed controller with active damping control for single- inverter dual-PMSM drive systems[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(5): 5794-5801.
[19] Junejo A K, Xu Wei, Mu Chaoxu, et al. Adaptive speed control of PMSM drive system based a new sliding-mode reaching law[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 12110-12121.
[20] Xu Wei, Junejo A K, Liu Yi, et al. An efficient antidisturbance sliding-mode speed control method for PMSM drive systems[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6879-6891.
[21] Chi Song, Zhang Zheng, Xu Longya. Sliding-mode sensorless control of direct-drive PM synchronous motors for washing machine applications[J]. IEEE Transactions on Industry Applications, 2009, 45(2): 582-590.
[22] Cao Xueqian, Ge Qiongxuan, Zhu Jinquan, et al. Periodic traction force fluctuations suppression strategy of maglev train based on flux linkage observation and harmonic current injection[J]. IEEE Transactions on Transportation Electrification, 2023, 9(2): 3434-3451.
[23] Kang K L, Kim J M, Hwang K B, et al. Sensorless control of PMSM in high speed range with iterative sliding mode observer[C]//Nineteenth Annual IEEE Applied Power Electronics Conference and Expo- sition, Anaheim, CA, USA, 2004: 1111-1116.
[24] Wang Bo, Wang Tianqing, Yu Yong, et al. Second- order terminal sliding-mode speed controller for induction motor drives with nonlinear control gain[J]. IEEE Transactions on Industrial Electronics, 2023, 70(11): 10923-10934.
[25] Wang Bo, Luo Cheng, Yu Yong, et al. Anti- disturbance speed control for induction machine drives using high-order fast terminal sliding-mode load torque observer[J]. IEEE Transactions on Power Electronics, 2018, 33(9): 7927-7937.
[26] Fu Dongxue, Zhao Ximei. A novel robust adaptive nonsingular fast integral terminal sliding mode controller for permanent magnet linear synchronous motors[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(2): 1672- 1683.
[27] 李政, 胡广大, 崔家瑞, 等. 永磁同步电机调速系统的积分型滑模变结构控制[J]. 中国电机工程学报, 2014, 34(3): 431-437.
Li Zheng, Hu Guangda, Cui Jiarui, et al. Sliding-mode variable structure control with integral action for permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2014, 34(3): 431-437.
[28] 曹学谦, 葛琼璇, 朱进权, 等. 基于积分滑模的高速磁悬浮列车牵引控制策略[J]. 电工技术学报, 2022, 37(14): 3598-3607.
Cao Xueqian, Ge Qiongxuan, Zhu Jinquan, et al. Traction-system research of high-speed maglev train based on integral sliding mode control[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(14): 3598-3607.
[29] 陈闯, 王勃, 于泳, 等. 基于改进指数趋近律的感应电机滑模转速观测器研究[J]. 电工技术学报, 2020, 35(增刊1): 155-163.
Chen Chuang, Wang Bo, Yu Yong, et al. Research on sliding mode speed observer of induction motor based on improved exponential reaching law[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(S1): 155-163.
[30] 陈伯时. 电力拖动自动控制系统: 运动控制系统[M]. 3版. 北京: 机械工业出版社, 2003.
Abstract Permanent magnet linear synchronous motors with section power supply are affected by disturbances like load force, detent force, and friction force. In the field of electromagnetic drive, the stator track is long. Linear motors usually adopt a segmented structure to save inverter capacity. However, it is difficult to ensure that the air gap of each segmented stator is equal during installation. Therefore, the mover is affected by the normal force. In addition, the load is usually accelerated to the target speed in a short time, so electromagnetic drive devices are usually operated under high current and high acceleration conditions, where the motor parameters are prone to change. Due to the lack of intermediate transmission devices in PMLSMs, these disturbances will directly affect the motor drive system and are included in the output of the controller. An SMSC with a novel convergence law is designed to ensure the fast convergence of speed and suppress the chattering. The designed TSMDO observes the disturbance output to ensure the disturbance suppression performance. Then, the acceleration fluctuations are reduced, and the thrust fluctuations are suppressed in the motor output.
Firstly, a mechanical motion model of PMLSM is established based on Newton's second law. It takes the disturbances as the lumped disturbance d(t) caused by load force, detent force, friction force, normal force, and parameter variation. Secondly, the shortcomings of conventional sliding mode control are analyzed, and a new adaptive sliding mode approaching law is proposed. The designed sliding mode approaching law ensures that variables can approach the sliding mode surface at a fast speed. As the state variables of the system gradually approach the sliding mode surface, the designed sliding mode approaching law can reduce the speed to weaken chattering. Then, due to the presence of d(t) in the output of the sliding mode speed controller, the TSMDO is designed to compensate for it. This observer is equivalent to a first-order low-pass filter. Finally, the proposed SMSC strategy is compared with PI control and conventional SMSC.
The experiments show that the PI controller can improve the dynamic tracking performance of speed by increasing h. However, this increases the acceleration fluctuation. At the same time, there is a noticeable overshoot when the rotor enters the constant speed range. The conventional SMSC has better dynamic tracking performance than PI control, resulting in small acceleration fluctuations. However, due to the fixed sliding mode gain, the increasing sliding mode gain increases the overshoot. The proposed SMSC has a faster tracking speed and better dynamic response than the conventional approaching law because of the new sliding mode approaching law. The proposed SMSC can adaptively change its gain when the speed state changes, ensuring good speed-tracking performance and reducing overshoot. The designed TSMDO effectively reduces the impact of thrust disturbances, acceleration fluctuations, and thrust fluctuations.
The main conclusions are as follows. (1) The proposed new sliding mode approaching law has a fast convergence speed due to the adaptive gain function f(x1, s) for adaptively adjusting the sliding mode gain. It can weaken chattering, ensuring speed dynamic tracking performance and convergence speed. (2) The designed TSMDO has a small chattering phenomenon. The introduction of TSMDO effectively suppresses the total disturbance d(t) in the SMSC output, reduces acceleration fluctuations, and ensures stable thrust output of the motor.
Keywords：Permanent magnet linear synchronous motors, acceleration fluctuations, sliding mode speed control, terminal sliding mode disturbance observer
中图分类号：TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.L11001
电磁驱动高速科学研究与试验设施关键技术及验证资助项目（E139320101）。
收稿日期 2024-07-04
改稿日期 2024-08-16
周世炯 男，1995年生，博士研究生，研究方向为大功率电力电子变换技术与直线电机驱动控制。
E-mail: shijiongz@mail.iee.ac.cn
史黎明 男，1964年生，研究员，博士生导师，研究方向为特种电机设计和驱动控制、无线电能传输技术等。
E-mail: limings@mail.iee.ac.cn（通信作者）
（编辑 崔文静）