 (1)
(1)
摘要 针对采用单电流传感器的永磁同步电机在低调制区与扇区边界区的重构死区问题,该文提出一种将改进的正三角形脉宽调制法与测量相位后移调制法结合的混合脉宽调制策略,在有效实现死区内电流重构的同时,突破传统正三角形脉宽调制无法单独实现电机中高转速运行的局限性。同时针对单电流传感器分时采样所导致的重构误差问题以及补偿过程过于复杂的问题,提出一种新的特殊点电流采样策略,通过固定电流传感器两次采样时刻与采样间隔,使传统的两步电流补偿简化为一步电流补偿,在提高电流重构准确性的同时简化了控制算法,显著提升了电机的控制性能。
关键词:永磁同步电机 单电流传感器 重构死区 混合脉宽调制 电流补偿
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)凭借其高功率密度、高效率和高可靠性等优势被广泛应用于工业生产等领域[1-6]。实时准确的三相电流反馈是交流驱动系统控制的关键,相较于传统的多电流传感器的驱动控制,使用单电流传感器实现三相电流的重构可以在降低成本的同时提高复杂工况下的电机系统的可靠性[7]。因此,如何在PMSM控制系统中使用单电流传感器进行电流的稳定准确采样成为国内外研究的重要课题之一。单电流传感器技术主要是通过移除传统的三相电压逆变器交流侧的电流传感器,只在直流侧安装一个电流传感器,在每个控制周期的其中两个有效电压矢量处对直流母线电流进行采样,从而实现三相电流的重构。然而,由于电流传感器物理条件的限制和开关周期内电流变化的不确定性,直接使用单电流传感器会不可避免地带来两个问题,即重构死区与重构误差问题。国内外许多学者对消除重构死区的方法进行了相关研究,主要有脉冲宽度调制(Pulse Width Modulation, PWM)移相法[8-10]、矢量脉冲插入法[11-14]、多个有效电压矢量合成取代零电压矢量法[15-17]、观测器法[18-20]等控制策略。
文献[8-10]提出将相位移动应用于逆变器开关管的开关状态上,当参考电压uref位于重构死区时,通过平移PWM输出开关信号,使有效电压矢量的作用时间满足最小采样时间Tmin的要求,但是这种方法可能会出现移相后仍然无法消除死区的情况,还需要进行二次移相。区别于移相法的PWM调整方式,文献[11-13]提出的矢量脉冲插入法是在每个开关周期结束之后插入三个满足最小采样时间的短测量脉冲构成一个首尾相接的矢量三角形,在每个插入短矢量处进行采样,完成三相电流重构。该方法的优势在于三相电流的可靠重构不受逆变器输出电压矢量的限制,可以固定三次采样时刻,但是测量脉冲的插入造成了开关次数的增加,开关损耗也大大增加,而且插入矢量会使整个开关周期变长,影响整个算法的作用区域。文献[16-17]提出将互补的有效电压矢量替代零电压矢量,保持逆变器输出电压矢量的大小和方向不变,实现在低调制死区的稳定电流重构。文献[18]提出将龙伯格观测器与单电流传感器相结合,在估计电机转子位置的同时实现三相电流的重构。
电流重构误差问题是由于单电流传感器与PWM信号结合进行两次采样的时刻难以确定,从而导致产生两类采样误差[21]。文献[22-23]中提出固定其中一个采样时刻以简化算法,但两个采样时刻的间隔没有固定,电流补偿算法仍然具有一定的复杂性。文献[24]提出将两次采样时间的间隔固定为最小采样时间,但采样时刻又变得随机。
本文提出一种基于单电流传感器的混合脉宽调制方法,能够有效解决电机运行在低调制区和扇区边界区的重构死区问题,接着采用一种新的特殊点电流采样策略,能够在固定两次采样时刻的同时,固定采样间隔为最小采样时间Tmin,从而消除第二类分时采样误差,只需一步补偿即可消除电流重构误差,简化补偿步骤。
PMSM的定子电压方程可以表示为
 (1)
(1)
式中,Rs为定子电阻;ud、uq、id和iq分别为d、q轴电压和电流;Ld和Lq分别为d、q轴电感;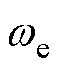 为电角速度;
为电角速度;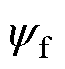 为永磁磁链。
为永磁磁链。
PMSM驱动多采用三相全桥逆变拓扑结构。采用该驱动方式时,直流母线中含有绕组各相的电流信息,考虑到电流传感器的耐压水平[24],本文将单电流传感器安装在靠近负极的直流母线侧。所采用的PMSM拓扑结构如图1所示。
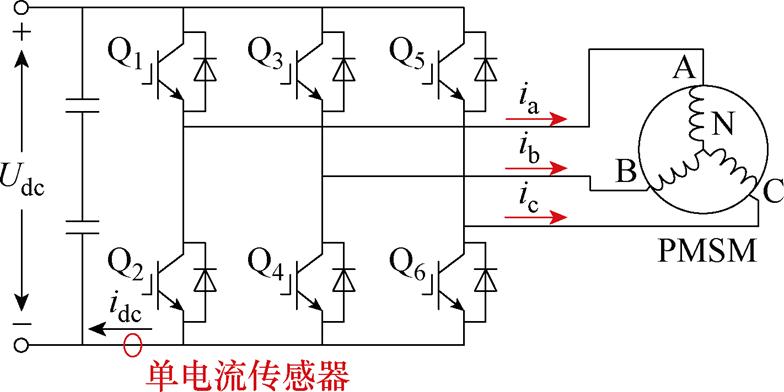
图1 直流母线采样的PMSM拓扑结构
Fig.1 PMSM topology structure for DC bus sampling
在空间矢量脉宽调制(Space Vector Pulse Width Modulation, SVPWM)控制方式下,通过控制逆变器的六个开关管的开通和关断,将电压矢量分为六个有效电压矢量和两个零矢量。不同开关状态下直流母线电流与相电流的对应关系见表1。其中,逆变器的开关状态由SaSbSc表示,S=1和S=0表示开关管上桥臂是、否处于导通状态。根据表1,直流母线电流传感器可以测得两相定子电流,剩余一相电流则根据基尔霍夫电流定律计算得到。
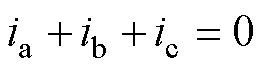 (2)
(2)
表1 不同开关状态下相电流与直流母线电流的关系
Tab.1 The relationship between phase current and DC bus current under different switching states

SaSbSc000, 111100110010011001101 ViV0, V7V1V2V3V4V5V6 idc0ia-icib-iaic-ib
在理想情况下,模拟数字转换器(Analog to Digital Converter, ADC)可以在瞬间完成对电流的采样,然而在实际条件下,由于死区时间、开关器件的延时导通与关断时间、ADC的电流信号转换时间的存在,使得电流传感器如果想要采集稳定可靠的电流信息至少需要一段时间,即最小采样时间Tmin。只有当开关周期内相关有效电压矢量的持续作用时间大于等于Tmin才能获得对应准确的相电流信息。
例如,当参考电压矢量uref落入第一扇区的低调制重构死区时,有效电压矢量V1、V2的持续时间很短以至于不能满足最小采样时间的要求,因此无法采集到准确的相电流信息。同理,当uref刚从第六扇区跨越到第一扇区时,由于V2的作用时间很短,同样不能满足Tmin的要求,会进入扇区边界处的重构死区。在其他扇区也存在相同的死区问题。整个重构死区的分布如图2中的红蓝颜色所示。
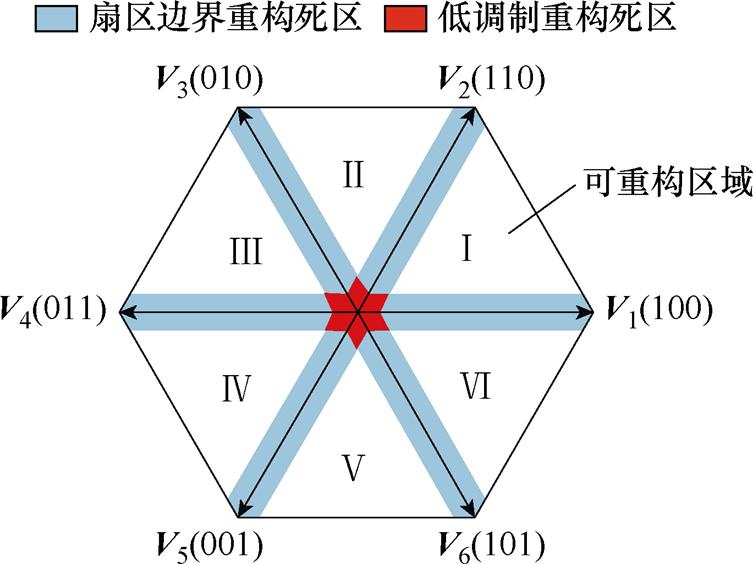
图2 电流重构死区
Fig.2 The current reconstruction dead zone
在传统SVPWM算法中采用单电流传感器进行采样的时刻通常为t1和t2,可以分别采样到A相电流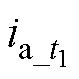 和C相电流
和C相电流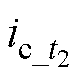 ,如图3所示。B相重构电流
,如图3所示。B相重构电流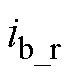 则是通过
则是通过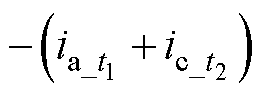 得到,
得到,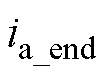 、
、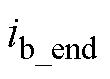 和
和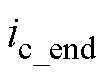 是开关周期结束后的准确三相电流。
是开关周期结束后的准确三相电流。
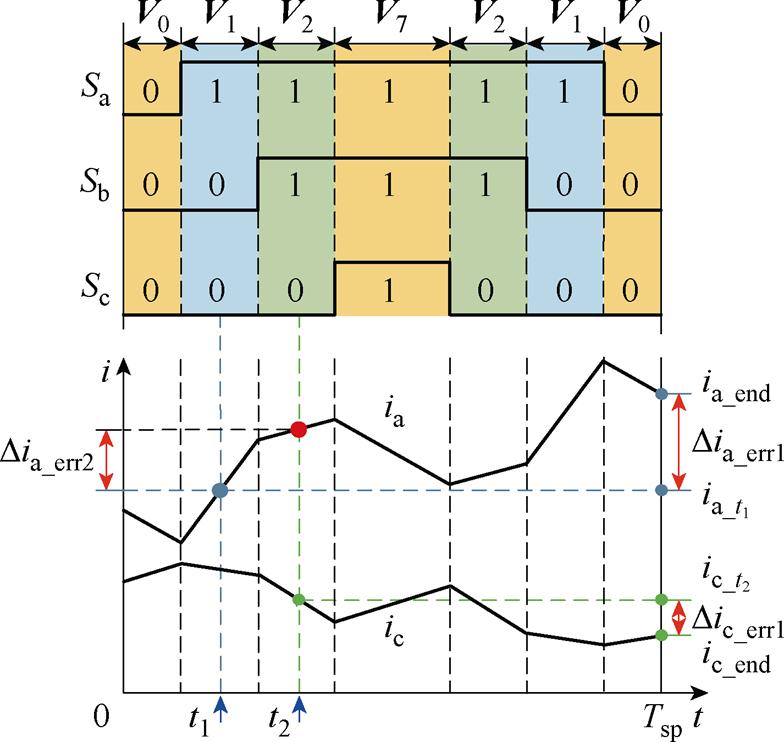
图3 传统的电流采样方法和电流重构误差
Fig.3 Conventional sampling method and reconstruction error
由于三相电流在一个开关周期内的时刻变化,因此会出现两类分时采样误差。第一类电流误差是由于传统SVPWM周期末的电压矢量为零矢量,无法在Tsp时刻采集到相电流信息,此类误差出现在采样时刻与开关周期结束Tsp之间,记为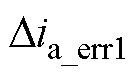 和
和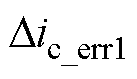 。第二类电流误差是由于无法在某一时刻同时进行两相电流采样,因此t2时刻的A相电流是t1时刻采样到的A相电流近似代替的,将在这两个采样时刻采样得到的电流误差记为
。第二类电流误差是由于无法在某一时刻同时进行两相电流采样,因此t2时刻的A相电流是t1时刻采样到的A相电流近似代替的,将在这两个采样时刻采样得到的电流误差记为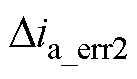 。以
。以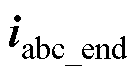 为参考,电流重构误差
为参考,电流重构误差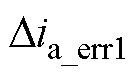 、
、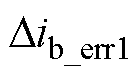 、
、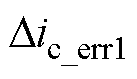 和
和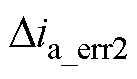 可以表示为
可以表示为
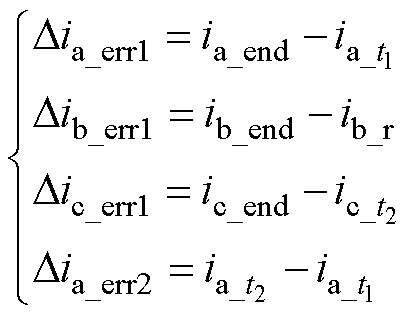 (3)
(3)
其中,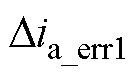 、
、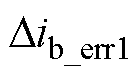 和
和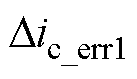 的关系满足
的关系满足
 (4)
(4)
经过对两类采样误差的分析,针对两次采样时刻的选择,如果尽可能地缩小两次采样之间的时间间隔和采样时刻与开关周期末的时间间隔,就能够在即使后续不进行重构电流补偿的情况下也能保证较高的电流重构准确性。
为了解决使用单电流传感器产生的重构死区问题,有学者提出了正三角形脉宽调制(Regular Triangle Pulse Width Modulation, RTPWM)算法[14]。RTPWM算法是只通过V1(100)、V3(010)、V5(001)三个有效电压矢量进行参考电压矢量uref的合成,在每个有效电压的中间时刻进行电流采样。原理如图4所示,由于传统RTPWM算法中不包含零矢量,三个电压矢量相互牵制约束,使得实际可以适用RTPWM算法的有效工作区域只有图4中电压矢量六边形的灰色区域,而且采样时刻跟随uref的变化而无法固定,不利于相电流的采集,增大了电流重构的难度。
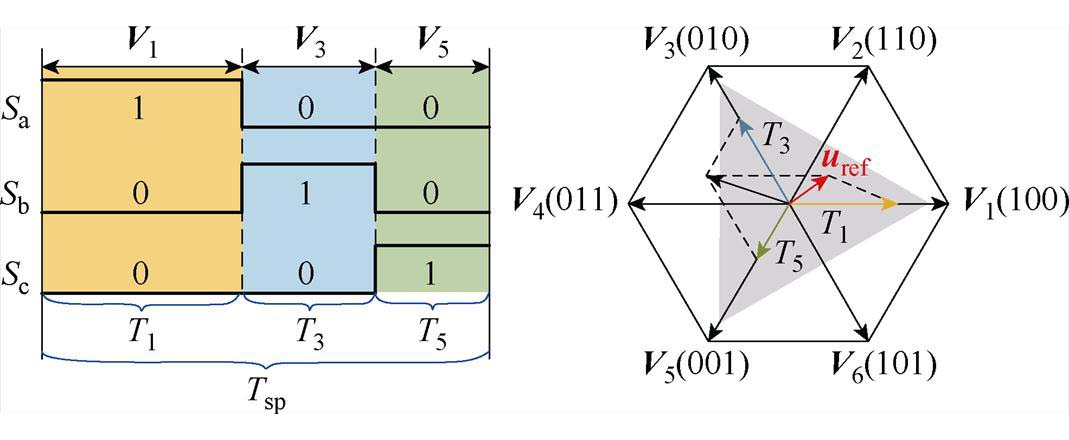
图4 传统RTPWM算法参考电压矢量合成
Fig.4 Reference voltage vector synthesis diagram of conventional RTPWM algorithm
改进的RTPWM(Improved RTPWM, IRTPWM)算法是在传统RTPWM算法的基础上,通过固定三个矢量中对合成uref影响最小的矢量的作用时间为最小采样时间Tmin,计算出另两个有效矢量的作用时间。本文将作用时间固定为Tmin的矢量定义为最优测量矢量,另两个矢量中满足最小采样时间Tmin的矢量定义为次优测量矢量,第三个矢量定义为中间电压矢量。
按照中间—次优—最优的矢量作用顺序排列有效电压矢量进行PWM发波,另外,将零矢量集中放在开关周期的始端进行周期之间的过渡,从而降低电流谐波含量。以第三扇区和第四扇区为例,此时V1的作用影响最小,将V1的作用时间T1固定为Tmin,T3、T5分别为V3、V5的作用时间,代入式(5)、式(6)解得三个有效电压矢量与零矢量的作用时间满足式(7)。
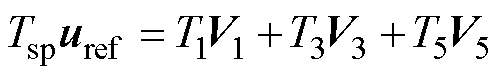 (5)
(5)
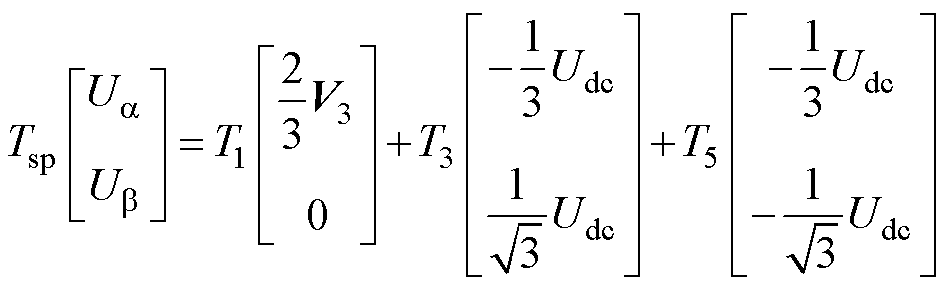 (6)
(6)
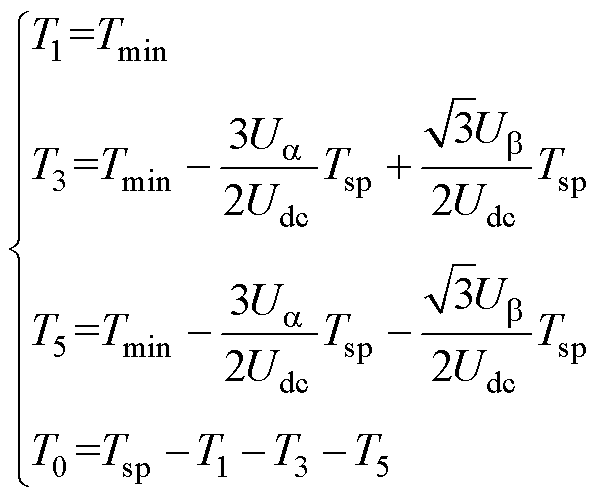 (7)
(7)
式中,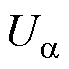 、
、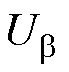 为uref在a、b 轴的分量;Udc为直流电源电压。
为uref在a、b 轴的分量;Udc为直流电源电压。
由于uref位于第三、四扇区,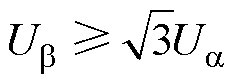 ,因此T3≥Tmin,T5<Tmin,T1和T3满足最小采样时间,定义V1为最优测量矢量,V3为次优测量矢量,V5为中间电压矢量,采用V0-V5-V3-V1的作用顺序,改进后的IRTPWM波形如图5所示。表2给出了其他 4个扇区的有效电压矢量与所定义矢量的对应关系。
,因此T3≥Tmin,T5<Tmin,T1和T3满足最小采样时间,定义V1为最优测量矢量,V3为次优测量矢量,V5为中间电压矢量,采用V0-V5-V3-V1的作用顺序,改进后的IRTPWM波形如图5所示。表2给出了其他 4个扇区的有效电压矢量与所定义矢量的对应关系。
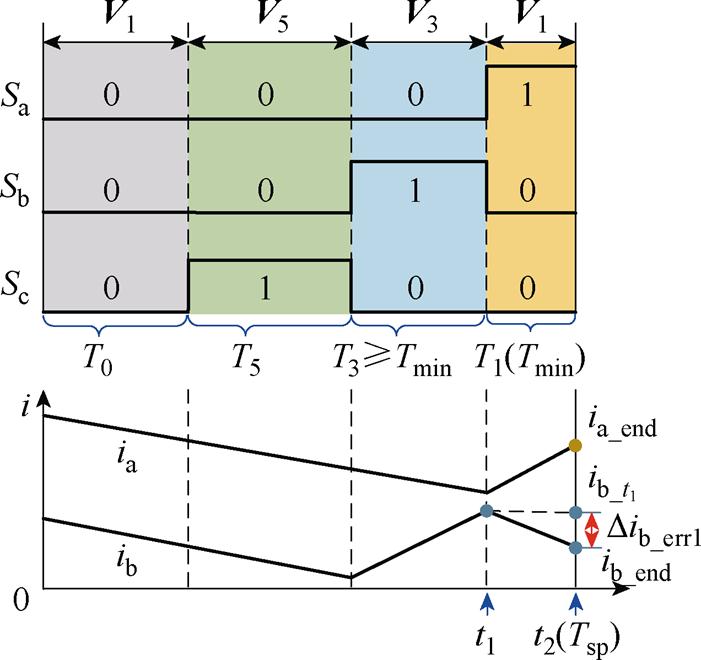
图5 第三、四扇区IRTPWM波形与两特殊点采样方法
Fig.5 The third and fourth sectors IRTPWM waveform with two special point sampling method
表2 不同扇区下有效电压矢量与定义矢量的关系
Tab.2 The relationship between the effective voltage vector and the defined vector for different sectors

扇区SⅠ ⅡⅢ ⅣⅤ Ⅵ 最优测量矢量V5(001)V1(100)V3(010) 次优测量矢量V3(010)V3(010)V1(100) 中间电压矢量V1(100)V5(001)V5(001)
由1.3节分析,为了缩小开关周期内采样点与周期末的时间差,本文将传统的在电压矢量的中间时刻采样改进为在电压矢量的下降沿时刻采样。具体地,在使用IRTPWM算法的第三、四扇区,分别在最优测量矢量V1作用的起始时刻与结束时刻,即Tsp-Tmin与Tsp时刻进行两次电流采样,由于电流的拖尾效应,可以分别得到ib和ia,然后通过式(2)得到ic。
由于在IRTPWM算法中对三个有效电压矢量进行了重新计算和排序,而且相较传统RTPWM算法增加了零矢量作用时间的限制,根据式(7)得出在第三、四扇区内采用改进RTPWM算法的工作区域。
同理根据表2,得到在其他4个扇区的改进RTPWM算法的工作区域,如图6左侧蓝色部分所示。为了简化IRTPWM算法与后续算法切换的判断条件,本文选择牺牲一部分工作区域,将改进RTPWM算法工作区域的内切圆作为IRTPWM算法的实际有效工作区域。假设Tsp=100 ms,Tmin=15 ms,可以计算出IRTPWM的最大参考电压矢量的幅值约为0.183Udc,约占传统SVPWM最大参考电压幅值的31.8%,完全能够包含低调制死区,可以实现电机在低调制区的三相电流重构。
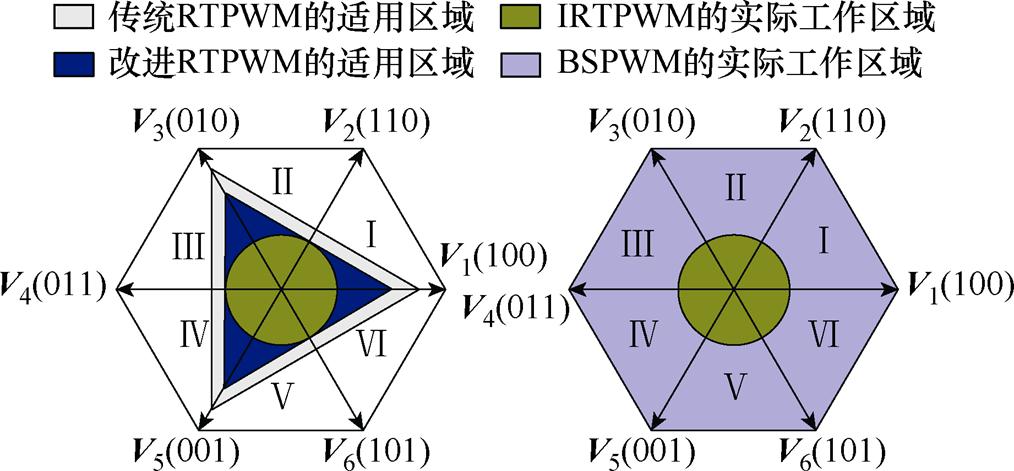
图6 IRTPWM法与测量相位后移调制法的有效区域
Fig.6 The effective regions of IRTPWM method and BSPWM method
为了解决IRTPWM的工作区域外的扇区边界重构死区问题,基于移相法提出后移相位构成测量区域的脉宽调制(Backward Shift phase Pulse Width Modulation, BSPWM)算法。
BSPWM算法具体是将三相开关PWM信号中占空比最大的开关状态向后移动到开关周期的末端,将占空比第二大的开关状态向后移动到距离开关周期末端Tmin的位置,将占空比最小的开关状态向后移动到距离开关周期末端2Tmin的位置。
以第一扇区为例,将a管的开通时刻与关断时刻均向后延迟T0/2,使关断时刻与Tsp时刻对齐;将b管的开通时刻和关断时刻均向后延迟(T0+T1)/2-Tmin,使关断时刻与Tsp-Tmin对齐;将c管的开通时刻和关断时刻均向后延迟(T0+T1+T2)/2-Tmin,使c管的关断时刻与Tsp-2Tmin对齐。BSPWM算法在第一扇区的PWM波如图7所示。分别在Tsp-Tmin和Tsp处进行两次电流采样,分别采集到-ic和ia,通过式(2)得到ib。
为了实现电机的宽速域稳定运行,需要将两种算法进行稳定快速的切换,本文所采用的切换方法是对参考电压uref的幅值进行判断,当uref不超过IRTPWM工作区域圆的半径时,即位于IRTPWM算法的实际工作区域时,系统采用IRTPWM算法,位于电压矢量六边形的其余区域时则采用BSPWM算法。

图7 第一扇区BSPWM波形与两特殊点采样方法
Fig.7 The first sector BSPWM waveforms with two special point sampling method
IRTPWM算法将作用时间为Tmin的最优测量矢量置于周期末段;提出的BSPWM算法也通过平移相位使待测有效电压矢量位于周期末段。对此提出特殊点电流采样策略,即在Tsp-Tmin和Tsp两个固定的特殊采样时刻进行母线电流的采集,使采样时刻距离周期末最近,同时将两次采样间隔固定为Tmin,从而消除第二类分时采样误差,最小化第一类分时采样误差。后续只需补偿第一类采样误差,从而达到简化电流补偿步骤的目的。
第一类采样误差数值的具体计算过程如下。首先,将式(1)的永磁同步电机电压方程转换为
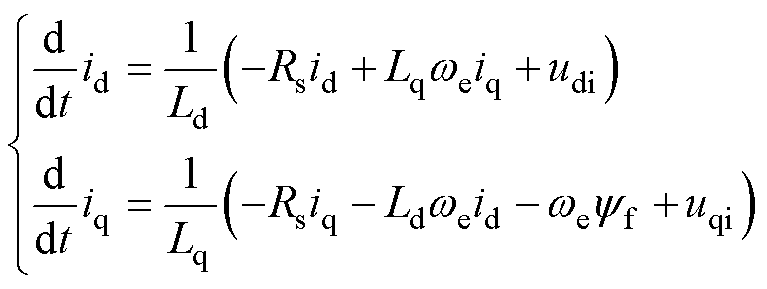 (8)
(8)
其中
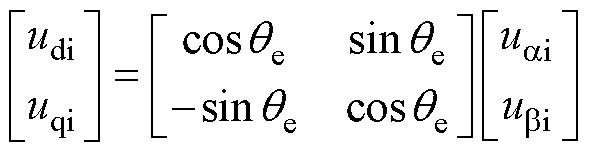 (9)
(9)
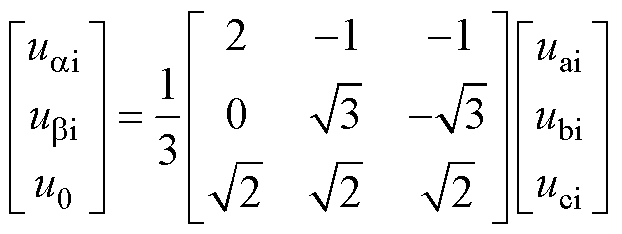 (10)
(10)
式中,udi和uqi为在两次采样间隔Tmin过程中所施加电压矢量的d、q轴电压分量;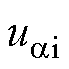 、
、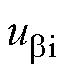 分别为a、b 轴电压分量;qe为电机位置角。
分别为a、b 轴电压分量;qe为电机位置角。
根据式(8)~式(10),可以获得三相电流在采样间隔内的变化率,将变化率与Tmin相乘即可获得三相电流的补偿值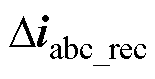 。
。
以uref位于BSPWM算法区域的第一扇区为例,从图7可以看出,由于在Tsp时刻对A相电流进行采样,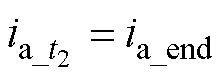 ,所以A相电流不需要补偿,只需要对C相电流补偿
,所以A相电流不需要补偿,只需要对C相电流补偿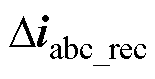 的对应部分,补偿后的重构电流
的对应部分,补偿后的重构电流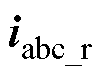 满足
满足
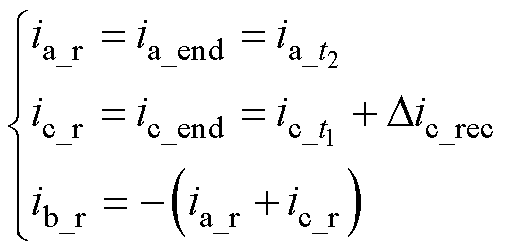 (11)
(11)
为了验证所提算法的有效性与可行性,在Matlab/ Simulink平台上进行了仿真验证,搭建的仿真模型的控制原理框图如图8所示,逆变器母线侧直流电压Udc设置为450 V,控制周期Tsp设置为100 ms,最小采样时间Tmin设置为15 ms。永磁同步电机的具体参数见表3。
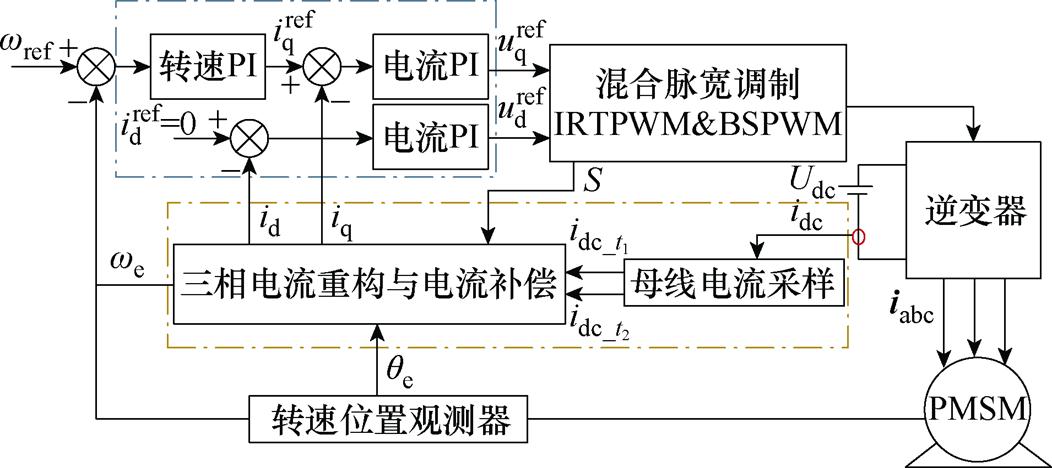
图8 混合脉宽调制控制系统原理框图
Fig.8 Block diagram of the mixed pules width modulation control system
图9给出了电机运行在四种不同稳态工况下的实际A相电流与重构A相电流的波形,以及通过计算二者的差值得出的相对应的重构电流误差波形。四种工况中,工况a和b为电机工作在IRTPWM算法的工作区域,工况c和d为电机工作在BSPWM算法的工作区域。
观察波形可以看出,无论是实际电流还是重构电流都有着很好的正弦性,而且经过一步补偿后重构稳态电流误差都保持在0.05 A左右,约为相电流幅值的3.6%,符合对稳态工况下电流重构误差的预期。
表3 永磁同步电机系统参数
Tab.3 The parameters of the PMSM
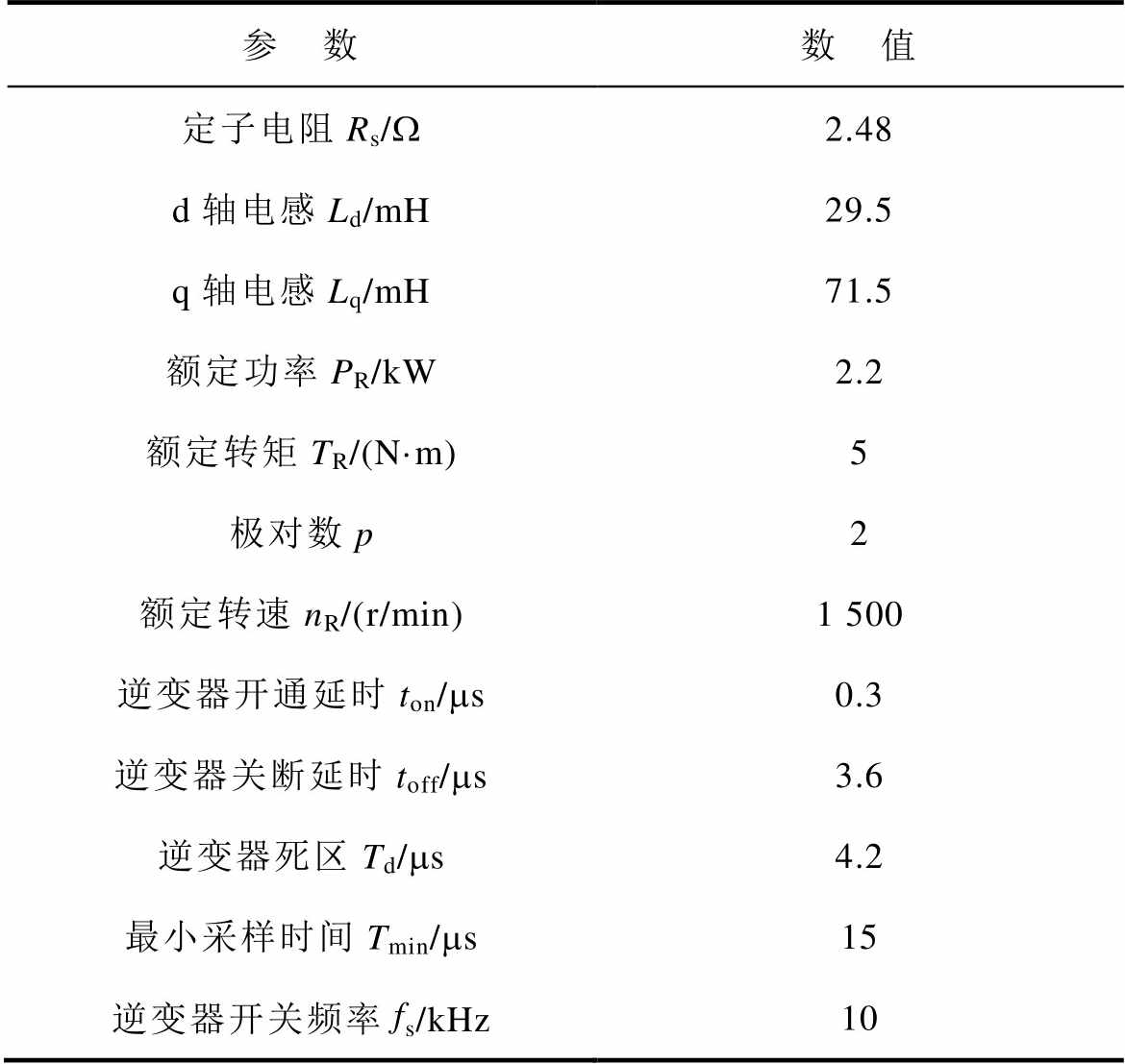
参 数数 值 定子电阻Rs/W2.48 d轴电感Ld/mH29.5 q轴电感Lq/mH71.5 额定功率PR/kW2.2 额定转矩TR/(N·m)5 极对数p2 额定转速nR/(r/min)1 500 逆变器开通延时ton/ms0.3 逆变器关断延时toff/ms3.6 逆变器死区Td/ms4.2 最小采样时间Tmin/ms15 逆变器开关频率fs/kHz10
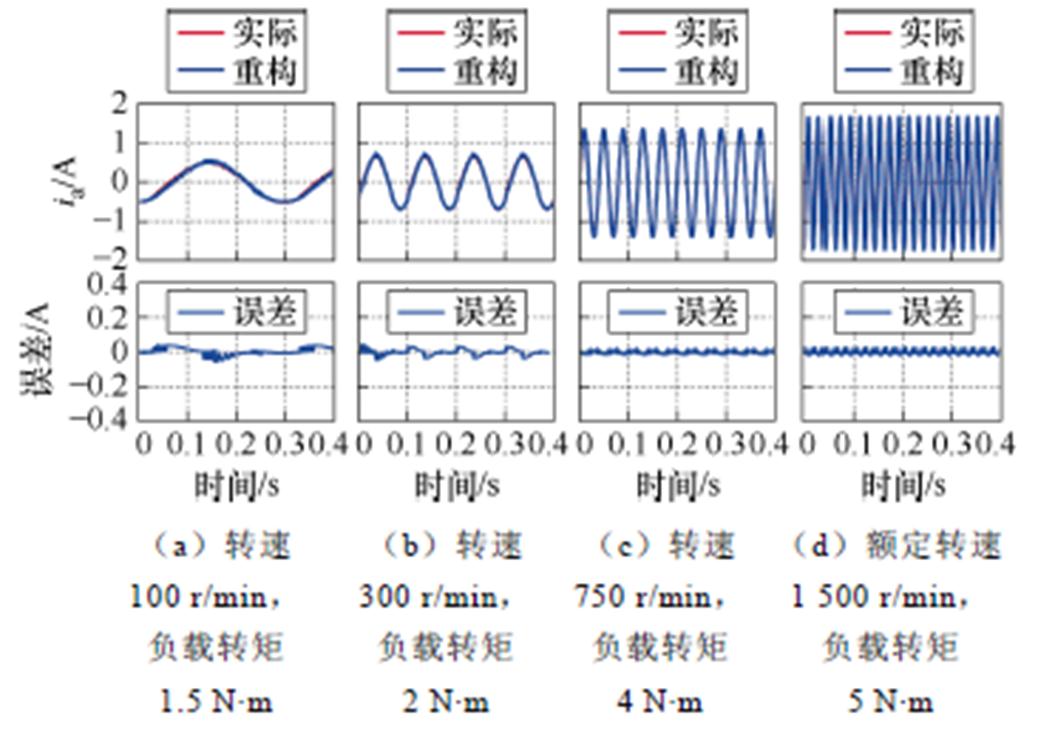
图9 运行于稳态工况下相电流重构仿真结果
Fig.9 Simulation results of phase current reconstruction running under steady-state conditions
图10的仿真结果展示的是电机运行在固定负载转矩为2 N·m,转速突增减(100 r/min—300 r/min— 100 r/min);固定转速为300r/min,负载转矩突增减(2 N·m—5 N·m—2 N·m)两个动态工况下的电流重构波形。此时落于IRTPWM的工作区域内,电机运行IRTPWM算法。A相电流与d、q轴重构电流的动态跟踪效果良好,误差较小。
图11的仿真结果展示的是电机运行在固定负载转矩为4 N·m,转速突增减(750 r/min—1 000 r/min— 750 r/min);固定转速为750 r/min,负载转矩突增减(2 N·m—5 N·m—2 N·m)两个动态工况下的电流重构波形。此时落于BSPWM的工作区域内,电机运行BSPWM算法。A相电流与d、q轴重构电流的动态跟踪效果良好,误差较小。

图10 采用IRTPWM算法动态工况下电流重构仿真结果
Fig.10 Simulation results of current reconstruction using IRTPWM under dynamic conditions
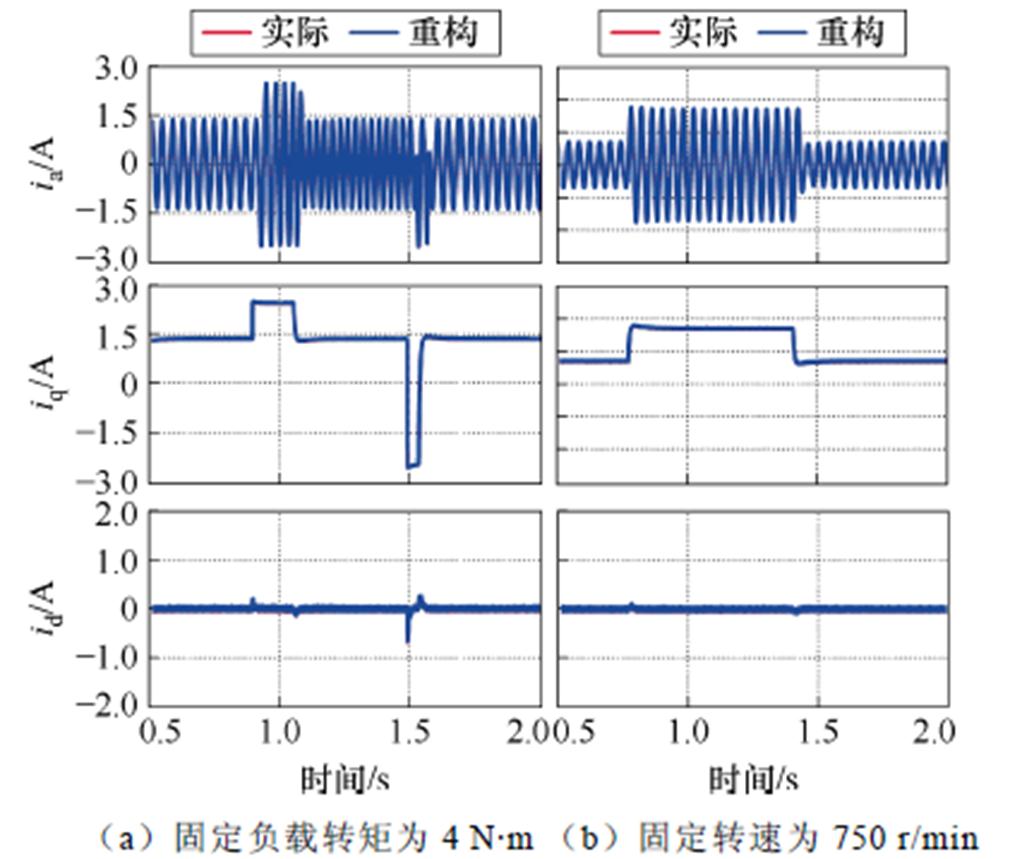
图11 采用BSPWM算法动态工况下电流重构仿真结果
Fig.11 Simulation results of current reconstruction using BSPWM under dynamic conditions
通过仿真验证可以看出,无论是在稳态工况还是动态工况下,电流的重构误差都在0.07 A以内,可以满足使用单电流传感器对电流的稳定准确采样要求,而且电流误差波形呈周期性变化,与相电流的周期性特征相符合。因此得出结论,仿真结果验证了所提方法的有效性与可行性。
为了进一步检验所提方法的有效性和准确性,搭建基于单电流传感器的电机实验平台进行相关实验的验证。实验平台硬件装置如图12所示,由PC端通过仿真器与DSPF28335控制板相连,控制由直流调压电源供电的功率板,连接PMSM带动磁粉制动器负载运行,电机的实时转速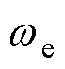 与位置角
与位置角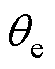 通过电机端部的增量式编码器捕获参与闭环控制,实验数据通过串行通信上传。
通过电机端部的增量式编码器捕获参与闭环控制,实验数据通过串行通信上传。

图12 硬件平台实物示意图
Fig.12 Physical schematic diagram of hardware platform
为了能够更好地观测实验数据,除了安装在直流母线端的单电流传感器,在逆变器的交流侧额外安装了两个电流传感器用来直接测量ABC三相的实际电流,但参与电流闭环控制的只有母线电流传感器通过重构得到的三相电流,传感器均采用基于巨磁阻的电流传感器,响应时间小于550 ns。在实验过程中,平台所设置的参数与仿真保持一致,见表3。
两种传统的脉宽调制与采样方法与各自改进后的方案在不同的稳态条件下运行的实验结果如图13~图16所示。实际电流表示两相电流传感器所测得的电流。

图13 在0.5 N·m负载下,300 r/min的稳态性能实验结果
Fig.13 Experimental results of steady-state performances at 300 r/min under 0.5 N·m load
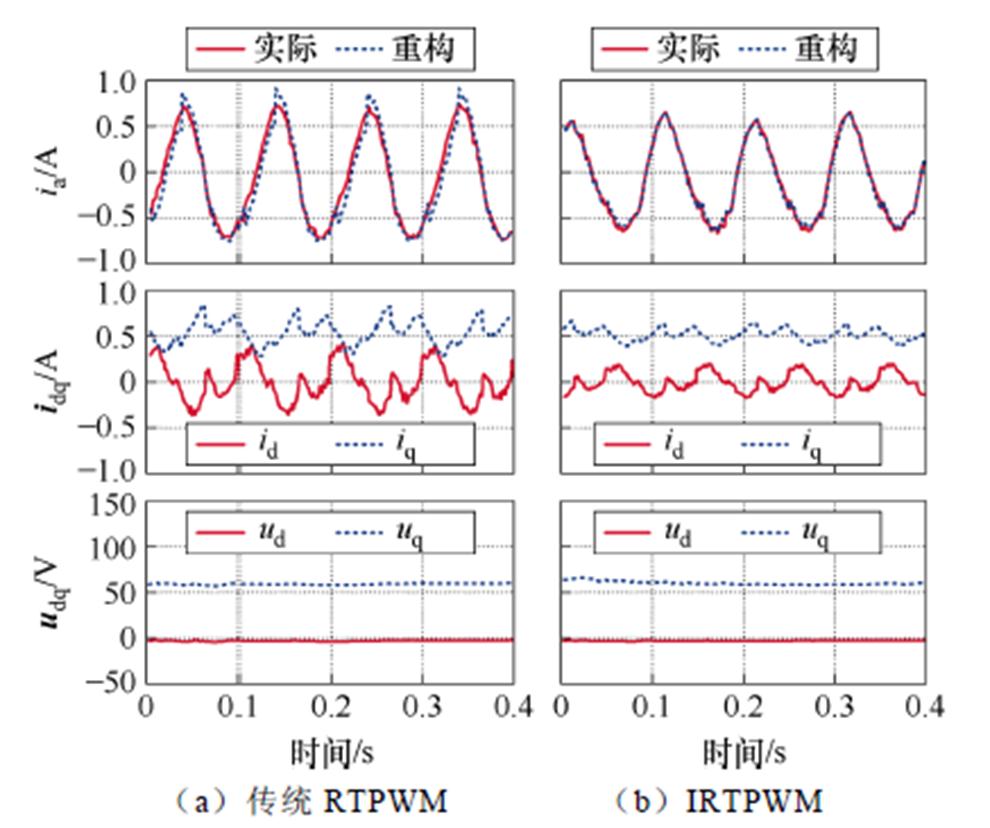
图14 在2 N·m负载下,300 r/min的稳态性能实验结果
Fig.14 Experimental results of steady-state performances at 300 r/min under 2 N·m load
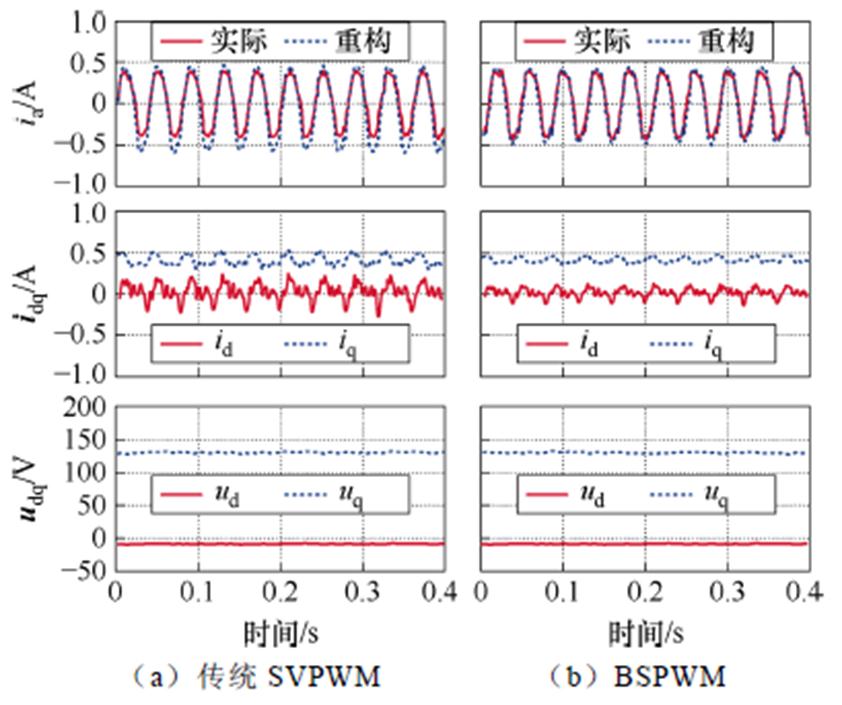
图15 在1 N·m负载下,750 r/min的稳态性能实验结果
Fig.15 Experimental results of steady-state performances at 750 r/min under 1 N·m load
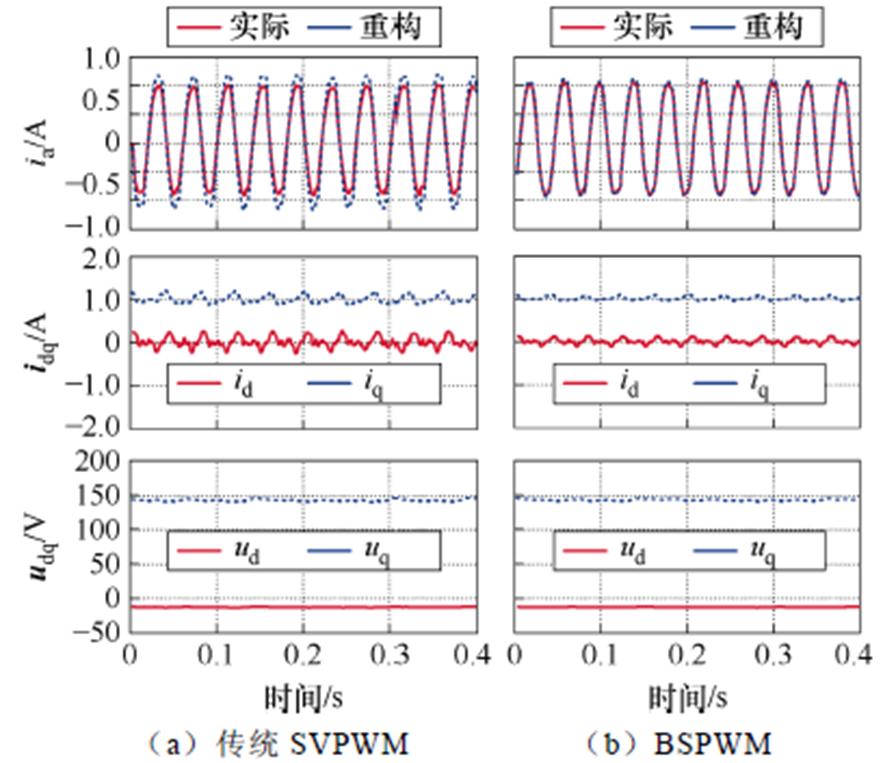
图16 在3 N·m负载下,750 r/min的稳态性能实验结果
Fig.16 Experimental results of steady-state performances at 750 r/min under 3 N·m load
从图13和图14可以看出,传统RTPWM算法在负载较小的工况下,重构电流发生了较大程度上的失真,随着负载转矩的增大,重构电流的失真有了很大程度上的改善,但是在两种不同负载转矩情况下,重构相电流都无法较好地跟踪实际相电流的变化,重构电流误差较大。而改进后的IRTPWM算法使得A相重构电流在负载转矩较低的工况下仍然保持着较好的正弦性,而且在两种不同负载转矩的情况下,重构相电流都能很好地跟踪实际相电流的变化,重构电流误差很小,稳定在0.1 A左右。
相较采用移相法解决电流重构死区的传统SVPWM算法,BSPWM算法也有着更好的重构电流跟踪性能,对比实验结果如图15和图16所示。无论是较大或较小的负载,BSPWM算法都能使A相电流的重构误差保持在0.15 A左右,约为相电流幅值的9%,可以满足对误差的要求。
此外,分别用标准差(Standard Deviation, SD)和快速傅里叶变换(Fast Fourier Transform, FFT)分析对重构电流误差和A相电流进行了定量分析。SD的计算定义为
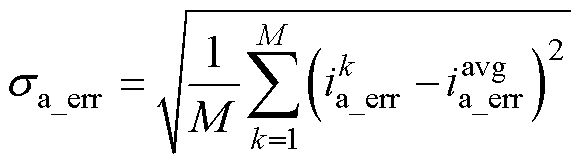 (12)
(12)
式中,M为采样点个数;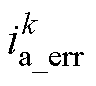 为第k次采样时刻的A相电流重构误差;
为第k次采样时刻的A相电流重构误差;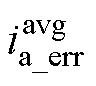 为A相电流重构误差的平均值;
为A相电流重构误差的平均值;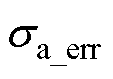 值越小,证明重构电流的跟踪精度越高,控制性能越好,具体结果见表4,A相重构电流THD比较结果如图17所示。
值越小,证明重构电流的跟踪精度越高,控制性能越好,具体结果见表4,A相重构电流THD比较结果如图17所示。
表4 采用两种方法的稳态实验数据
Tab.4 Steady state experimental data of two methods
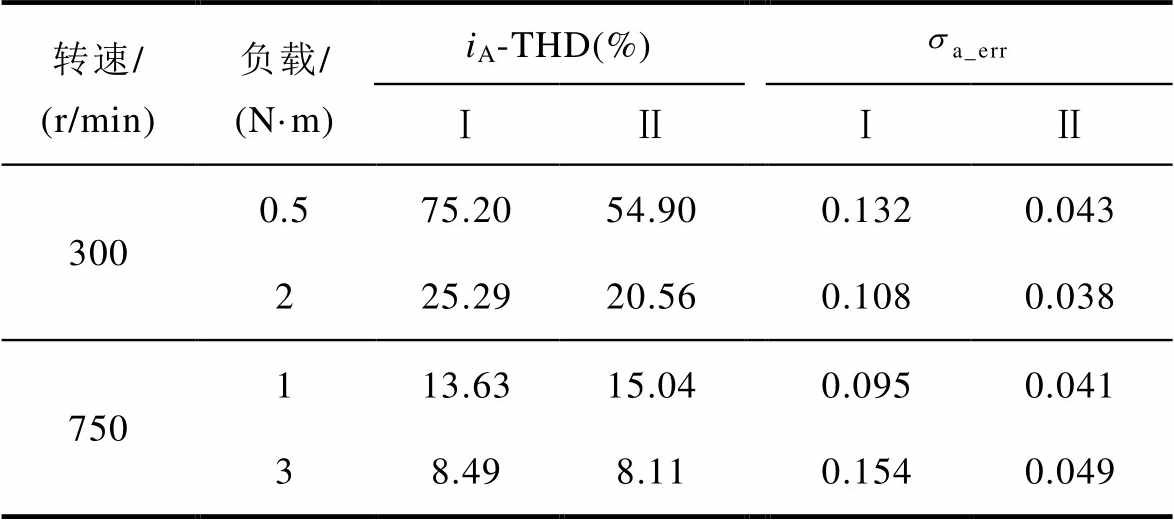
转速/ (r/min)负载/ (N·m)iA-THD(%) ⅠⅡⅠⅡ 3000.575.2054.900.1320.043 225.2920.560.1080.038 750113.6315.040.0950.041 38.498.110.1540.049
注:Ⅰ和Ⅱ分别表示传统脉宽调制与采样方案和改进后的脉宽调制与采样方案。
从表4中可以看出,在IRTPWM算法的工作区域(工况300 r/min,0.5 N·m和2 N·m)中,与传统RTPWM算法相比,优化效果明显,THD平均降低约22.85%,在同等情况下,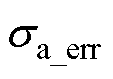 平均降低约66.11%。在BSPWM算法的工作区域(工况750 r/min,1 N·m和3 N·m)中,与传统SVPWM算法相比,
平均降低约66.11%。在BSPWM算法的工作区域(工况750 r/min,1 N·m和3 N·m)中,与传统SVPWM算法相比,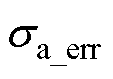 平均降低约62.51%,但THD优化效果不明显,基本与传统方法持平。实验结果验证了提出的方法在各自的线性调制区内的有效性与准确性。
平均降低约62.51%,但THD优化效果不明显,基本与传统方法持平。实验结果验证了提出的方法在各自的线性调制区内的有效性与准确性。
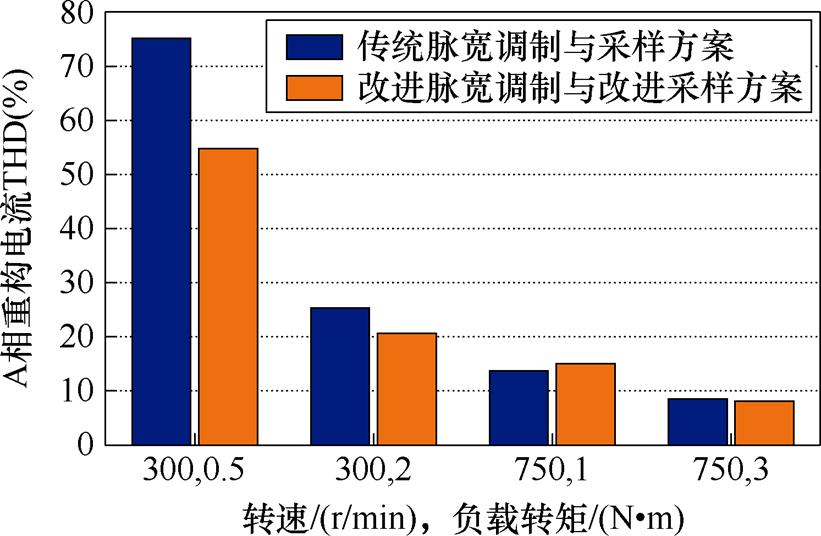
图17 A相重构电流THD比较结果
Fig.17 THD comparison results of reconstructed current
改进的脉宽调制与传统的脉宽调制方法虽然采用不同的采样点进行采样,但是最终都通过电流补偿将采样的最终电流对齐到了Tsp时刻,通过实验数据分析,改进后固定特殊点采样方案具有更高的准确性,究其原因,是由于电机运行过程中可能会出现参数失配问题,使得根据式(8)进行电流补偿会出现一定的补偿值不准确的问题,因此只有将采样时刻尽可能靠近Tsp才能从根本上提高重构电流准确性。
为了进一步验证电机运行在动态工况下所提方法进行电流重构的准确性,分别进行了以下实验,包括电机的负载转矩突增减实现算法的切换和电机的转速突增减实现算法的切换。实验结果如图18~图21所示,其中,图18、图19具体展现的是切换前后已经到达稳态的实验结果,图20、图21则具体展现了切换瞬间变量的变化情况。
图18为电机运行在固定负载转矩为2 N·m,转速在300 r/min和600 r/min之间切换的动态工况下的相电流重构实验结果,图19为电机运行在固定转速为400 r/min,负载转矩在1 N·m和3 N·m之间切换的动态工况下的相电流重构实验结果。从相电流波形和重构电流误差波形可以看出,无论是IRTPWM算法切换到BSPWM算法,还是从BSPWM算法切换到IRTPWM算法,电流重构误差均维持在较低水平。
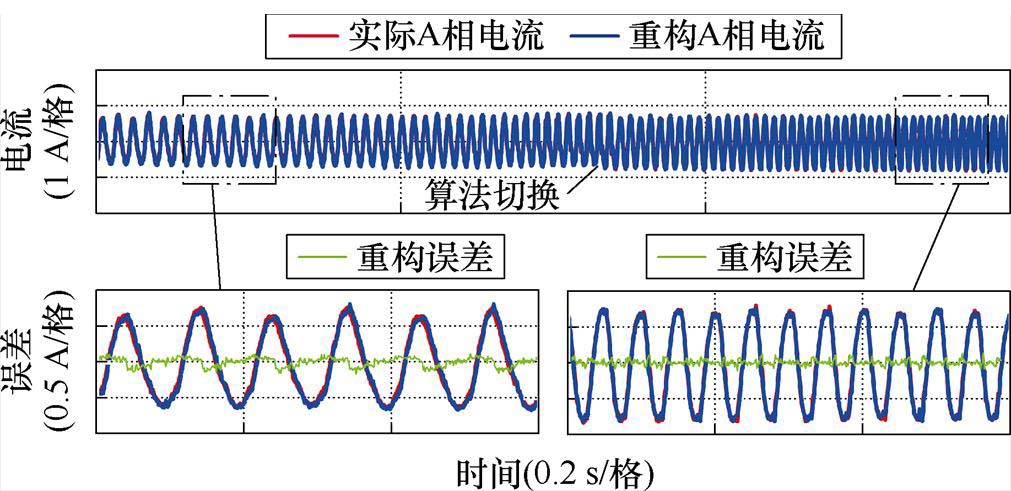
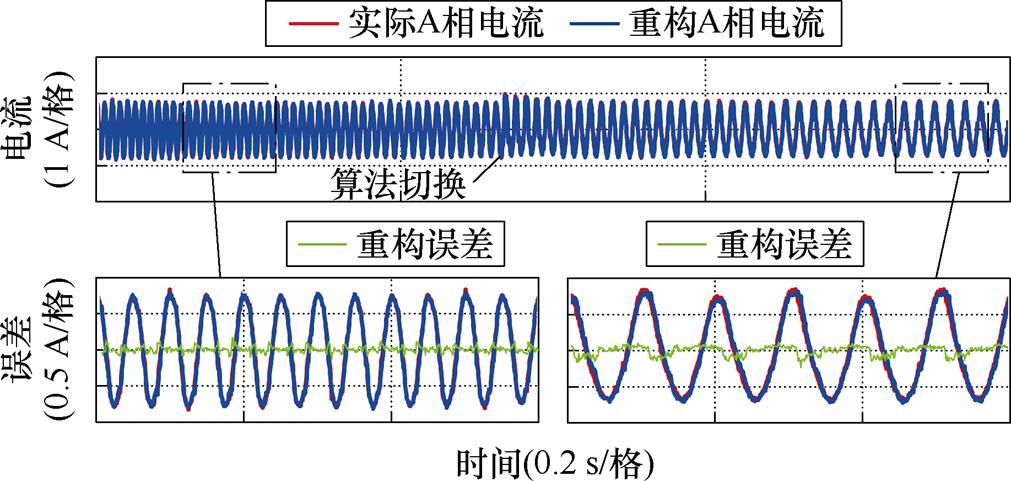
图18 电机转速突增减实现算法切换前后相电流重构的实验结果
Fig.18 Experimental results of phase current reconstruction during algorithm switching for sudden increase or decrease in motor speed
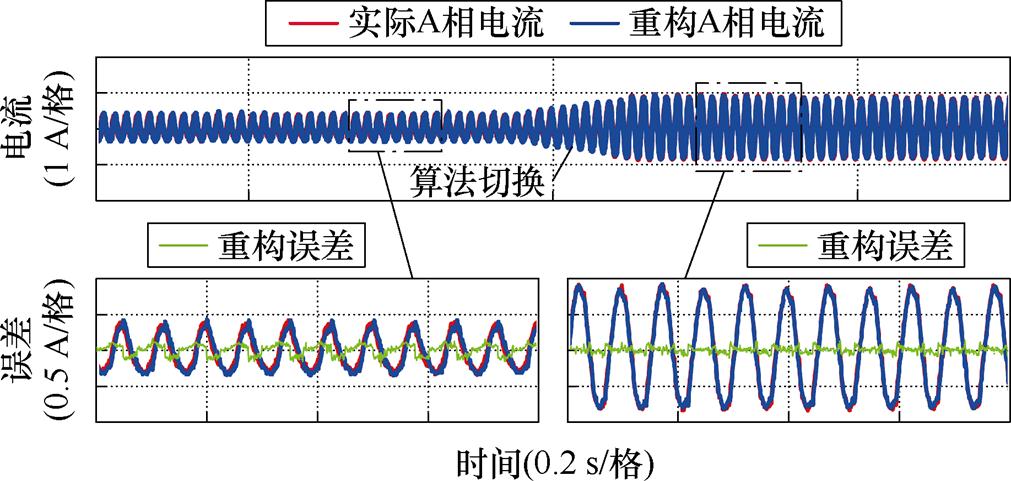

图19 负载转矩突增减实现算法切换前后相电流重构的实验结果
Fig.19 Experimental results of phase current reconstruction during algorithm switching for sudden increase or decrease in load torque
为了验证算法切换瞬间的动态性能,设计实验观察算法切换瞬间的电机转速以及电流波形如图20和图21所示。图20为转速突变时的算法切换瞬间,可以看出,转速的变化没有受到算法切换的影响,保持原有的变化斜率,d、q轴重构电流和d、q轴实际电流能够保持良好的动态过渡,验证了其在算法过渡瞬间良好的动态稳定性。虽然从图20中可以看出,在BSPWM算法区域中的d、q轴电流的跟踪性能略差于IRTPWM算法的d、q轴电流跟踪性能,但对电机控制系统影响较小,误差可以近似忽略。A相重构电流则在切换瞬间很好地跟踪了实际电流,没有受到扰动影响。

图20 电机转速突增减算法切换瞬间实验结果
Fig.20 Experimental results of algorithm switching moment for sudden increase or decrease in motor speed

图21 负载转矩突增减算法切换瞬间实验结果
Fig.21 Experimental results of algorithm switching moment for sudden increase or decrease in load torque
图21为转矩突变时的算法切换瞬间,转速会有较小程度的变化,但很快在PI控制器的调节下回到参考转速。d、q轴重构电流与A相重构电流也都符合预期,较好地跟踪了实际电流。实验结果证实了提出的混合脉宽调制方法在动态工况下的有效性与重构的准确性。
为了验证电机运行在极低转速和额定转速时所提方法的性能。分别让电机运行在极低转速为100 r/min,负载转矩为1.5 N·m的工况和额定转速为1 500 r/min,负载转矩为5 N·m的工况下,得到重构电流与实际电流的比较波形如图22所示。由实验结果可以看出,无论电机在低速还是额定转速运行时,电流重构误差均稳定在较低水平,验证了所提方法在宽速域范围内电流重构的有效性与准确性。
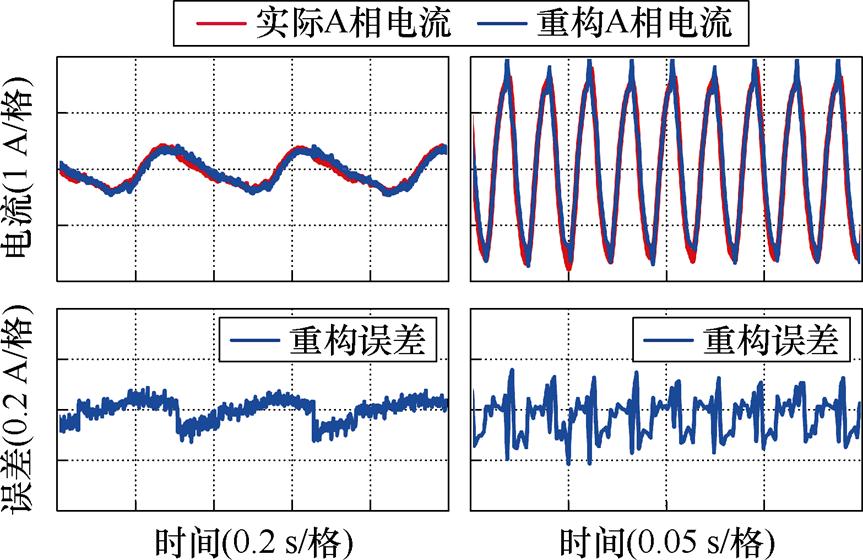
图22 运行于低速和额定转速的相电流重构实验结果
Fig.22 Experimental results of phase current reconstruction running at low speed and rated speed
针对基于单电流传感器技术的永磁同步电机控制系统在低调制区和扇区边界的重构死区问题,本文提出将两种脉冲宽度调制方法进行混合调制的技术,在解决死区问题的同时,突破了传统三矢量脉宽调制无法单独实现更高转速运行的局限性。同时针对传统采样策略中由于采样时刻不固定而导致的重构电流补偿算法过于复杂的问题,提出两次特殊点电流采样方案,在固定了两次采样时刻的同时,将两次采样的间隔时间也固定为最小间隔时间Tmin,消除了第二类分时采样误差,从而将传统的两步电流补偿策略缩小为一步电流补偿,简化了电流补偿过程,提高了电流重构的精度。然而,本文所提出的混合脉冲宽度调制方法目前只适用于电压矢量构成的正六边形区域,无法实现过调制区域的三相电流重构,针对过调制区域外的控制算法以及更加准确的采样补偿策略是未来研究的重点方向。
参考文献
[1] 郑长明, 董萱萱, 肖子语, 等. 基于虚拟电阻有源阻尼的LC滤波型永磁同步电机系统预测电流控制[J]. 电工技术学报, 2023, 38(22): 6059-6069.
Zheng Changming, Dong Xuanxuan, Xiao Ziyu, et al. Virtual resistance active damping based predictive current control of LC-filtered permanent magnet synchronous motor system[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6059-6069.
[2] Prabhakaran K K, Karthikeyan A. Electromagnetic torque-based model reference adaptive system speed estimator for sensorless surface mount permanent magnet synchronous motor drive[J]. IEEE Transa- ctions on Industrial Electronics, 2020, 67(7): 5936- 5947.
[3] 陈荣, 翟凯淼, 舒胡平. 永磁同步电机双矢量固定开关频率模型预测控制研究[J]. 电工技术学报, 2023, 38(14): 3812-3823.
Chen Rong, Zhai Kaimiao, Shu Huping. Predictive control of dual vector fixed switching frequency model for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3812-3823.
[4] 肖海峰, 许宇豪, 李文真, 等. 五相永磁同步电机串级模型预测电流控制[J]. 电气技术, 2023, 24(8): 1-11, 21.
Xiao Haifeng, Xu Yuhao, Li Wenzhen, et al. Model predictive current control based on series cost function for five-phase permanent magnet syn- chronous machines[J]. Electrical Engineering, 2023, 24(8): 1-11, 21.
[5] 张玉霖, 卢涛, 菅志军, 等. 基于滑模观测器无位置控制的PWM整流技术[J]. 微电机, 2023, 56(11): 45-48.
Zhang Yulin, Lu Tao, Jian Zhijun, et al. PWM rectification technology based on sliding mode observer sensorless control[J]. Micromotors, 2023, 56(11): 45-48.
[6] 程勇, 李思卿, 李森豪. 永磁同步电机干扰观测复合滑模控制技术[J]. 电机与控制应用, 2023, 50(3): 39-46, 64.
Cheng Yong, Li Siqing, Li Senhao. Compound sliding mode control technology of permanent magnet synchronous motor based on disturbance obser- vation[J]. Electric Machines & Control Application, 2023, 50(3): 39-46, 64.
[7] Song Yuge, Lu Jiadong, Hu Yihua, et al. Expanding limit of minimum sampling time using auxiliary vectors for PMSM drives with single DC-link current sensor[J]. IEEE Transactions on Industrial Electronics, 2023, 70(4): 3437-3448.
[8] Gu Yikun, Ni Fenglei, Yang Dapeng, et al. Switching- state phase shift method for three-phase-current reconstruction with a single DC-link current sensor[J]. IEEE Transactions on Industrial Electronics, 2011, 58(11): 5186-5194.
[9] Lai Y S, Lin Yongkai, Chen C W. New hybrid pulse- width modulation technique to reduce current distortion and extend current reconstruction range for three-phase inverter using only DC-link sensor[J]. IEEE Transactions on Power Electronics, 2012, 28(3): 1331-1337.
[10] 黄政, 陈永军, 刘湃, 等. 基于单电流传感器的永磁同步电机高速控制技术[J]. 微电机, 2022, 55(1): 48-54.
Huang Zheng, Chen Yongjun, Liu Pai, et al. Per- manent magnetic synchronous motor high speed control technique based on single current sensor[J]. Micromotors, 2022, 55(1): 48-54.
[11] 王文杰, 闫浩, 邹继斌, 等. 基于混合脉宽调制技术的永磁同步电机过调制区域相电流重构策略[J]. 中国电机工程学报, 2021, 41(17): 6050-6060.
Wang Wenjie, Yan Hao, Zou Jibin, et al. Phase current reconstruction strategy of PMSM under overmodulation mode based on a hybrid space vector pulse width modulation technique[J]. Proceedings of the CSEE, 2021, 41(17): 6050-6060.
[12] Kim H, Jahns T M. Current control for AC motor drives using a single DC-link current sensor and measurement voltage vectors[J]. IEEE Transactions on Industry Applications, 2006, 42(6): 1539-1547.
[13] 孙孝哲, 张祯滨, 韩明昊, 等. 双有源全桥变换器无电流传感器鲁棒预测控制[J]. 电工技术学报, 2024, 39(10): 3093-3104, 3140.
Sun Xiaozhe, Zhang Zhenbin, Han Minghao, et al. An enhanced current sensorless predictive control for dual active bridge converter[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3093-3104, 3140.
[14] 卢伟. 基于单电流传感器的PMSM宽运行范围相电流重构算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
Lu Wei. Research on phase current reconstruction algorithm of PMSM with wide operating range based on single current sensor[D]. Harbin: Harbin Institute of Technology, 2018.
[15] Shen Yongpeng, Wang Qiancheng, Liu Dongqi, et al. A mixed SVPWM technique for three-phase current reconstruction with single DC negative rail current sensor[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 5357-5372.
[16] Dusmez S, Qin Ling, Akin B. A new SVPWM technique for DC negative rail current sensing at low speeds[J]. IEEE Transactions on Industrial Elec- tronics, 2015, 62(2): 826-831.
[17] 申永鹏, 武克轩, 吴成中, 等. 互补非零矢量单传感器相电流重构策略[J]. 电工技术学报, 2023, 38(8): 2126-2135.
Shen Yongpeng, Wu Kexuan, Wu Chengzhong, et al. Complementary non-zero vector current reconstru- ction strategy with single sensor[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2126- 2135.
[18] Saritha B, Janakiraman P A. Sinusoidal three-phase current reconstruction and control using a DC-link current sensor and a curve-fitting observer[J]. IEEE Transactions on Industrial Electronics, 2007, 54(5): 2657-2664.
[19] Hafez B, Abdel-Khalik A S, Massoud A M, et al. Single-sensor-based three-phase permanent-magnet synchronous motor drive system with luenberger observers for motor line current reconstruction[J]. IEEE Transactions on Industry Applications, 2014, 50(4): 2602-2613.
[20] 王菁, 颜建虎, 季国东, 等. 一种基于双位置观测器的永磁同步电机低速无位置传感器控制方法[J]. 电工技术学报, 2023, 38(2): 375-386.
Wang Jing, Yan Jianhu, Ji Guodong, et al. A sensorless control method for permanent magnet syn- chronous machine based on dual position observers at low speed[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 375-386.
[21] Lu Jiadong, Hu Yihua, Liu Jinglin. Analysis and compensation of sampling errors in TPFS IPMSM drives with single current sensor[J]. IEEE Transa- ctions on Industrial Electronics, 2019, 66(5): 3852- 3855.
[22] Tian Lisi, Guo Xin, Liu Liwei, et al. Variable vector model predictive control for permanent magnet synchronous motors using a single DC-link current sensor[J]. IEEE Transactions on Power Electronics, 2024, 39(5): 5310-5319.
[23] 黄科元, 伍瑞泽, 黄守道, 等. 单电阻采样的永磁同步电动机相电流重构策略[J]. 电力系统及其自动化学报, 2018, 30(9): 114-120.
Huang Keyuan, Wu Ruize, Huang Shoudao, et al. Phase current reconstruction strategy for PMSM using one-shunt current sampling[J]. Proceedings of the CSU-EPSA, 2018, 30(9): 114-120.
[24] Tian Lisi, Wang Zaixiang, Yu Qiang, et al. Current reconstruction by one-step compensation for per- manent magnet synchronous motor with fixed sampling interval in position sensorless control[J]. IEEE Transactions on Industrial Electronics, 2023, 70(1): 200-210.
Abstract Permanent magnet synchronous motors are widely used in industrial production and other fields due to their advantages of high power density, high reliability, and high efficiency. Real-time and accurate three-phase current feedback is the key to AC drive system control. Compared with the traditional multi-current sensor drive control, using a single current sensor to achieve three-phase current reconstruction can reduce costs and improve the reliability of the motor system under complex working conditions. Combined with the improved IRTPWM algorithm and the BSPWM algorithm, this paper forms a hybrid pulse width modulation algorithm to solve the low-key brake dead zone and the reconstructed dead zone at the sector boundary. Then, an improved two-point sampling strategy is adopted to eliminate the second type of time-sharing sampling error and simplify the current compensation step, which fixes the sampling time of the two samples and the sampling spacing as the minimum sampling time.
Based on the traditional RTPWM algorithm, the improved IRTPWM algorithm calculates the action time of the other two effective voltage vectors. The action time of the vector is fixed with the least influence on the synthetic reference voltage vector among the three vectors, and the three effective voltage vectors and zero vectors are recorded. It collects the phase current at the beginning and end of the optimal measurement vector.
The traditional RTPWM algorithm cannot achieve medium and high-speed operation alone. The measurement phase backward shift modulation method (BSPWM) is proposed to eliminate the dead zone of current reconstruction by combining the measurement phase backward shift modulation method and the IRTPWM algorithm outside the working area of the IRTPWM algorithm. The mixed pulse width modulation algorithm can complete the current acquisition twice at two fixed particular sampling points, and the first type of time-sharing sampling error only needs to be compensated. Therefore, the current compensation steps of the traditional mixed pulse width modulation algorithm are reduced from four steps to two steps, and the computing burden of the processing unit is reduced.
The simulation and experimental results show that the error between the reconstruction and the actual current is tiny, which proves that the proposed current reconstruction has high accuracy in both steady-state and transient states. Under the dynamic working conditions of fixed load torque of 2 N·m with the rotation speed of 300 r/min and 600 r/min back and forth and fixed speed of 400 r/min with load torque switching back and forth between 1 N·m and 3 N·m, the motor speed, q-axis current, and three-phase current do not cause great disturbance due to the switching of the algorithm.
The following conclusions can be drawn. (1) The combination of the IRTPWM algorithm and BSPWM algorithm effectively eliminates the influence of the dead zone of current reconstruction. (2) The IRTPWM algorithm has higher current reconstruction accuracy and lower current harmonic value than the traditional RTPWM, and the BSPWM algorithm has higher current reconstruction accuracy than the traditional phase-shifting method. (3) The improved two-point sampling strategy can reduce the number of current compensations and current reconstruction errors, simplifying the experimental algorithm and improving the control performance of PMSM.
Keywords:Permanent magnet synchronous motor, single current sensor, reconstruction dead zone, mixed pulse width modulation, current compensation
中图分类号:TM341
DOI: 10.19595/j.cnki.1000-6753.tces.240519
国家自然科学基金面上资助项目(62373363, 62373359)。
收稿日期 2024-04-01
改稿日期 2024-07-18
田里思 男,1985年生,教授,硕士生导师,研究方向为电力电子与电力传动。
E-mail: tianlisi@cumt.edu.cn(通信作者)
宗耐龙 男,2000年生,硕士研究生,研究方向为永磁同步电机驱动控制系统。
E-mail: TS22230201P31@cumt.edu.cn
(编辑 崔文静)