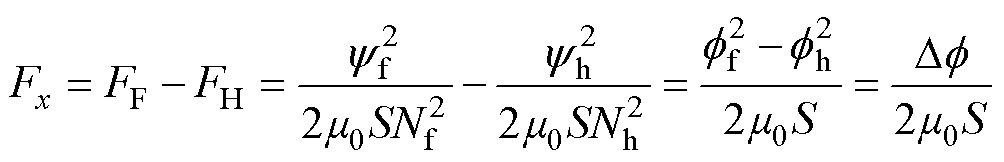 (1)
(1)
摘要 双稳态永磁操动机构分合闸线圈共用磁路,导致分合闸气隙磁通相互耦合,难以灵活控制永磁开关的动作特性,制约着开关的性能。针对这一问题,该文引入有限集模型预测控制,设计了双稳态永磁操作机构分合闸气隙磁通的解耦控制方法。首先,通过理论分析得出影响操动机构矢量磁力变化的本质参量“分合闸气隙的磁通平方差”;其次,设计磁通预测模型,对下一时刻分合闸气隙磁通进行预测;然后,将分合闸气隙磁通及机构驱动电路视作整体,构建开关状态集与代价函数;最后,在多个控制周期的滚动优化过程中,使分合闸气隙磁通快速趋近于各自参考值,实现解耦控制。通过仿真与实验,证实了该方法在显著降低双稳态永磁操作机构操作功的同时,能够有效提高机构的响应速度与控制灵活性。
关键词:双稳态永磁操动机构 永磁开关 有限集模型预测控制 解耦控制
双稳态永磁操动机构(Bi-stable Permanent Magnet Actuator, BPMA)将电磁机构与永磁体相结合,进行电磁操作、永磁锁扣,常用于中低压接触器及断路器,提高了双稳态永磁开关的操动可靠 性[1-3]。但是,在双稳态永磁操动机构动作过程中,永磁的锁扣作用将阻碍分合闸操作,导致铁心响应速度慢,始动电流大[4]。同时,由于分合闸线圈共用磁路,导致分合闸气隙磁链相互耦合,始终在动铁心上产生两个相互反向的作用力,这进一步阻碍机构的动作,导致难以直接控制其动作特性,限制了永磁开关性能的提升[5-6]。
针对上述问题,国内外已有大量学者对BPMA展开了研究:文献[7]设计了一种在动铁心分闸端带短路环的永磁机构,减少了分闸动作的响应时间;文献[8]设计了一种磁路分离的双稳态永磁机构,削弱了动作开始时的永磁保持力以及动作过程中永磁体对动作特性的影响;文献[9]设计了一种带分闸辅助线圈的新型单稳态永磁机构,减少了永磁的用量及分闸末速度。上述文献通过对永磁操动机构本体进行优化设计,有效地提高了机构的动作性能,但也加剧了机构的复杂度,设计困难。在控制层面:文献[10]设计了一种双稳态永磁机构的驱动拓扑,采用滞环方式对线圈电流进行控制,降低了在宽电压运行时断路器动作的分散性;文献[11]设计了一种带辅助电容的驱动电路,在合、分闸线圈上同时施加相反方向的电流来削弱永磁保持力,提高动作响应速度;文献[12]采用模糊算法实时调节线圈电流和位移,对给定参考曲线进行跟踪,提高断路器的动作一致性。总结目前双稳态永磁操动机构的控制方案,大多以线圈电流闭环控制为核心,没有考虑到气隙间磁力的耦合,难以对BPMA操动过程中的磁力进行直接控制,这种方式仅能使BPMA从一个稳态转换到另一个稳态,而无法精确控制转换过程,导致BPMA动态性能不理想,制约BPMA开关的性能。
在BPMA操动过程中,由于分、合闸线圈共用磁路,任意线圈产生的磁链均会贯穿分、合闸气隙,永磁体则根据分、合闸气隙的动态磁阻,自动分配永磁链,上下气隙中的电磁链及永磁链使动铁心始终受到两个反相磁力的耦合作用;随着动铁心的运动及线圈电流的变化,磁路快速饱和,电磁链与永磁链相互影响,加剧了分合闸气隙中磁链非线性耦合的复杂度。上述原因导致永磁开关的动作特性难以控制,因此,想要灵活控制永磁开关的动作特性,则需同时控制分、合闸气隙磁链,进而同时控制指向分合闸位置的磁力,通过快速削弱指向非励磁线圈的磁力,以及快速增加指向励磁线圈的磁力实现解耦控制。
上述控制过程属于非线性、多目标、强耦合的系统,在电力电子领域亦存在类似系统,有限集模型预测控制(Finite Control Set-Model Predictive Control, FCS-MPC)常用于解决该类问题[13-16]。FCS-MPC的核心思想为:利用电子开关状态离散化的特点搭建离散化预测模型,设计系统开关状态集合,通过枚举集合中不同的开关状态,得到系统不同的未来值,再经代价函数的在线寻优确定最优开关状态,作用于下一控制周期,经过多个周期的滚动优化,最终实现多目标优化控制[17-19]。
本文首先通过理论分析,得出BPMA动铁心的矢量磁力取决于“合、分闸气隙的磁通平方差”,对该磁通平方差进行准确控制即可实现BPMA的动态控制;然后引入FCS-MPC方法,根据驱动电路拓扑、电压状态矢量及气隙磁通分配方式,设计BPMA气隙磁通解耦控制策略,实现分、合闸气隙磁通的独立控制,进而实现对该磁通平方差的直接控制;最后通过仿真与实验,验证了该方法的有效性,在显著降低BPMA操作功的同时,能够有效提高机构的响应速度及控制灵活性。
BPMA合分闸线圈共用磁路,各线圈通正向电流时磁通路径如图1所示,根据“磁阻力”产生原理,穿过分闸气隙的磁通ff产生指向分闸方向的磁力FF,穿过合闸气隙的磁通fh产生指向合闸方向的磁力FH。FF与FH始终反向,忽略漏磁,动铁心所受总磁力Fx可表示为
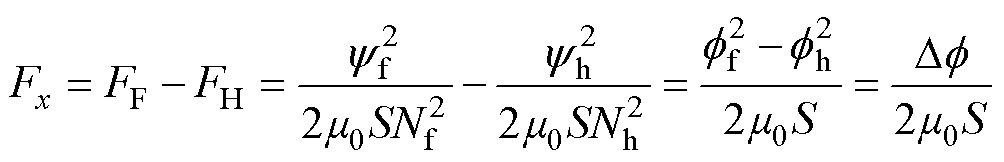 (1)
(1)
式中,yh为穿过合闸气隙磁链;yf为穿过分闸气隙磁链;m0为真空磁导率;S为磁路横截面积;Nh为合闸线圈匝数;Nf为分闸线圈匝数;Df 为定义的分、合闸气隙磁通平方差。可以看出,矢量磁力取决于磁通平方差,即Fx∝Df。因此,要对BPMA操动过程的总磁力进行动态控制仅需实时控制Df 即可。
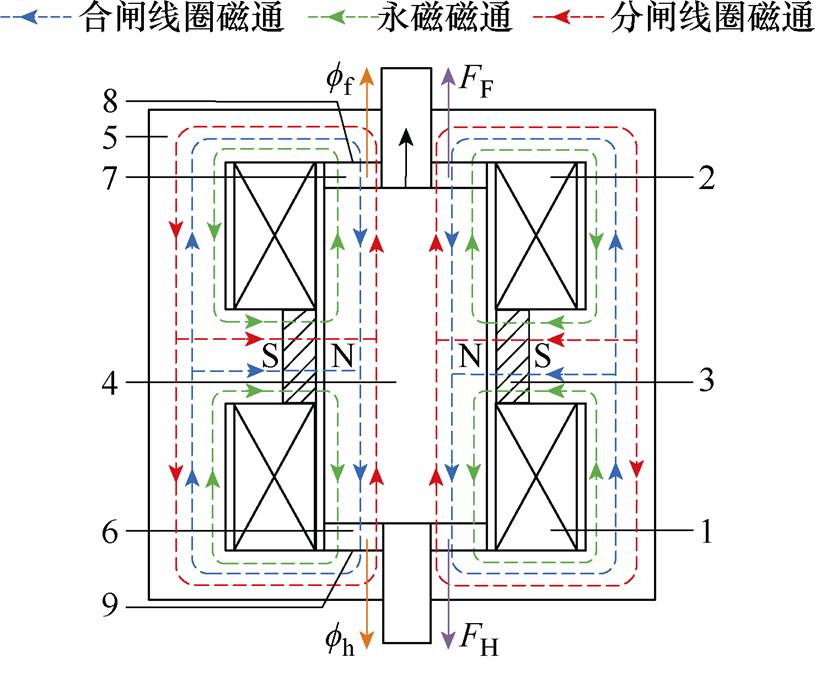
图1 BPMA操动原理
Fig.1 Operation principle of BPMA
1—合闸线圈 2—分闸线圈 3—永磁体 4—动铁心 5—静铁心 6—合闸气隙 7—分闸气隙 8—分闸稳态位置 9—合闸稳态位置
以此为目标,设计图2所示控制原理:首先设计分、合闸气隙磁通观测器,根据线圈电压、电流信号实时观测ff、fh;然后构建气隙磁通解耦控制器,以ffref、fhref作为分、合闸气隙磁通参考值,以ff、fh作为反馈值,通过控制策略输出驱动信号,控制驱动电路状态,使ff、fh分别跟踪ffref、fhref,进而独立控制ff、fh,实现气隙磁通的解耦,为Df的精确控制创造条件。
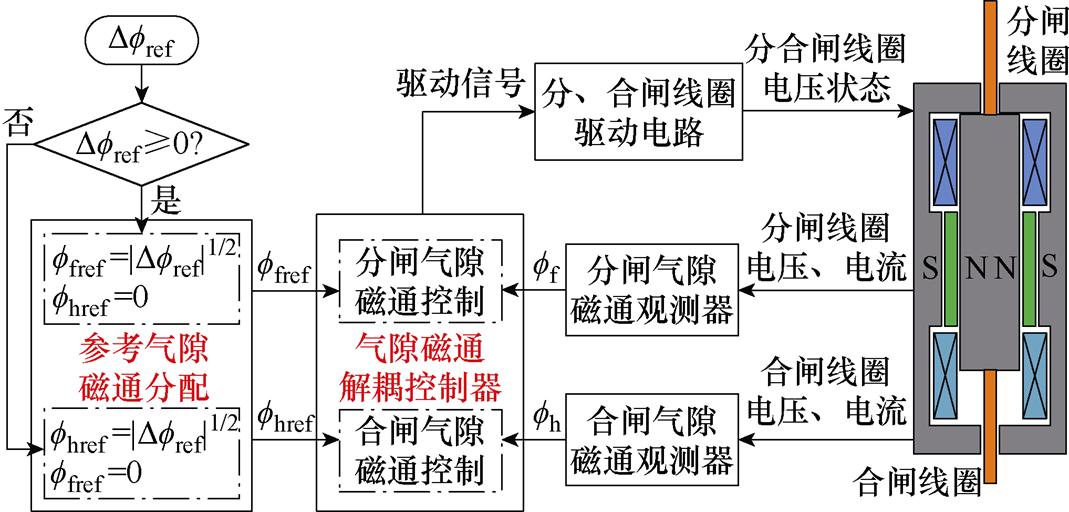
图2 BPMA解耦控制原理
Fig.2 Decoupling control principle of BPMA
在此基础上,设计分、合闸气隙磁通的分配方法,便于根据参考磁通平方差Dfref的幅值和方向生成ffref及fhref:当Dfref≥0时,令ffref=|Dfref|1/2,fhref=0;当Dfref<0时,令ffref=0,fhref=|Dfref|1/2。
通过这一分配方式,一方面确保Dfref为所需矢量值;另一方面使非必要气隙磁通参考值为0,可避免非必要的气隙励磁导致分、合闸气隙磁力在动铁心上相互抵消,造成内耗。因此,仅需控制另一气隙磁通的大小,即可灵活控制Df,进而控制矢量磁力Fx,提高磁力操动效率,实现BPMA的高性能动态控制。
线圈驱动电路如图3所示,线圈驱动均采用全桥拓扑。UDC为直流输入电压,S1~S8为开关管,构成桥臂B1~B4,通过对开关管的控制,可使分、合闸线圈的电压状态uf、uh在+UDC、0、-UDC间跳变。

图3 线圈驱动电路
Fig.3 Drive circuit of the coils
分、合闸线圈气隙磁通表示为
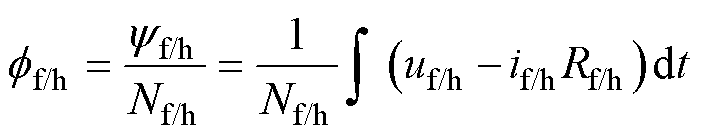 (2)
(2)
式中,if/h为分/合闸线圈电流;Rf/h为分/合闸线圈电阻。可知,当线圈电压为+UDC时,气隙磁通快速增加;当线圈电压为0时,气隙磁通缓慢减小;当线圈电压为-UDC时,气隙磁通快速减小。
按照永磁机构分、合闸线圈分别通正向电流时的作用效果来定义磁通方向,即:分闸气隙磁通向上为正,合闸气隙磁通向下为正,分、合闸线圈同时通正向电流时,两个气隙磁通相差180°。由于分、合闸线圈共用磁路,任一线圈的电压状态均会影响两个气隙磁通,如图4所示,总结不同线圈电压状态对分、合闸气隙磁通的作用效果可知,分、合闸线圈不同的电压状态组合会共同影响分、合闸气隙磁通的变化方向及变化速度,进而影响磁通方差的大小和方向。综上所述,仅需综合控制分、合闸线圈的电压状态即可有效控制Df 这一决定BPMA动态特性的本质参量。组合线圈的不同电压状态,可得矢量见表1。表中,ff/h(uh) 为uh电压状态对分/合闸气隙磁通的影响;ff/h(uf) 为uf电压状态对分/合闸气隙磁通的影响。

图4 电压状态对气隙磁通的影响
Fig.4 Effect of voltage state on air gap flux
表1 电压状态矢量
Tab.1 Voltage state vectors

状态nuhff/h(uh)ufff/h(uf) 100 20-UDC 30+UDC 4-UDC0 5-UDC-UDC 6-UDC+UDC 7+UDC0 8+UDC-UDC 9+UDC+UDC
双线圈同时励磁及动铁心运动均会加剧磁路非线性耦合的复杂度,若对每个线圈采用独立的PWM控制,则难以实现分、合闸气隙磁通的解耦[20]。本文引入FCS-MPC方法,将分、合闸气隙磁通及驱动电路视作整体来构建代价函数,以表1作为有限控制集,结合磁通预测模型遍历表1的电压状态,通过代价函数的最小化,寻找最优电压状态,作用于下一控制周期。在多个周期的滚动优化过程中,分、合闸气隙磁通快速趋近于各自参考值,实现解耦控制。
磁通难以直接测量,需构建观测器来间接得到分、合闸气隙磁通的当前状态。式(2)可改写成式(3)所示离散形式。
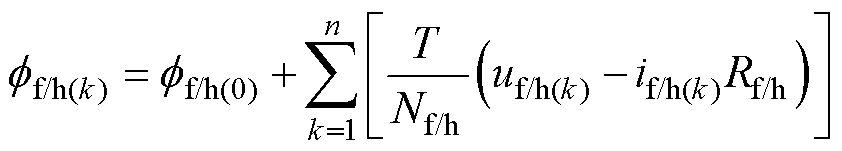 (3)
(3)
式中,T为离散系统的控制周期。根据式(3),仅需采集当前控制周期的分/合闸线圈电压uf/h(k)、分/合闸线圈电流if/h(k),即可观测分/合闸气隙的磁通ff/h(k)。
进一步建立磁通预测模型,式(2)改写成微分形式后进行欧拉离散,可得
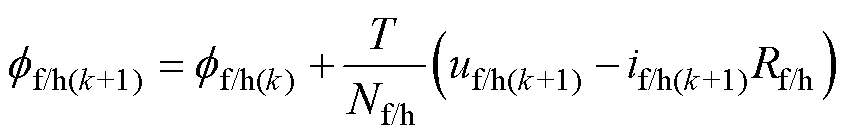 (4)
(4)
式中,ff/h(k+1)为预测的第k+1周期的分/合闸气隙磁通;ff/h(k)为观测的当前第k周期的分/合闸气隙磁通;uf/h(k+1)为第k+1周期施加在线圈上的电压状态,if/h(k+1)为第k+1周期的线圈电流。
由于线圈所在磁路为强感性,控制周期T极小,所以式(4)中的ih/f(k+1)可用ih/f(k)代替,式(4)可改为
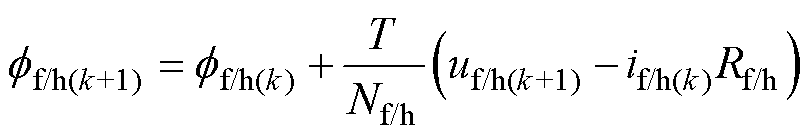 (5)
(5)
式(3)与式(5)结合,可构建图5所示气隙磁通的观测及预测模型:首先采集当前控制周期的uf/h(k)、if/h(k),根据式(3)计算得到当前分/合闸气隙磁通ff/h(k),完成磁通观测;然后以观测磁通ff/h(k)、采样电流if/h(k)作为输入,遍历表1中的电压状态用作uf/h(k+1),根据式(5)即可预测下一控制周期中所有可能的分/合闸气隙磁通ff/h(k+1),完成磁通预测。

图5 气隙磁通的观测及预测模型
Fig.5 Air gap flux observation and prediction model
代价函数的设计原则为:在其最小化过程中,分/合闸气隙磁通的预测值应分别趋近于各自参考值,因此可用代价函数为
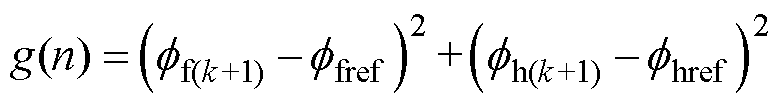 (6)
(6)
式中,g(n)为代入表1中电压状态n进行磁通预测时代价函数的输出;ff(k+1)为分闸气隙磁通预测值;fh(k+1)为合闸气隙磁通预测值;fhref为合闸气隙磁通参考值;ffref为分闸气隙磁通参考值。
在第k个控制周期中,遍历表1得g(1)~g(9),选取最小值gmin对应的电压状态,并转换为开关管驱动信号,用于在第k+1周期中控制驱动电路。在代价函数最小化过程中,分/合闸气隙磁通逐渐趋近于各自参考值,实现气隙磁通的解耦控制。
FCS-MPC整体原理如图6所示。由传感器采集分合闸线圈电压、电流信号uh(k)、ih(k)、uf(k)、if(k),输入图5所示分、合闸气隙磁通观测及预测模型,结合电压状态矢量表1,预测分、合闸气隙磁通fh(k+1)与ff(k+1)。Dfref按照图2分配方法,得到分、合闸气隙磁通参考值ffref、fhref,将分、合闸预测磁通及参考磁通输入代价函数式(6),进行遍历计算,寻找最小代价函数值gmin,再通过表1映射出gmin对应S1~S8的最优开关状态,在下一控制周期中驱动对应开关管,完成FCS-MPC气隙磁通的解耦控制。
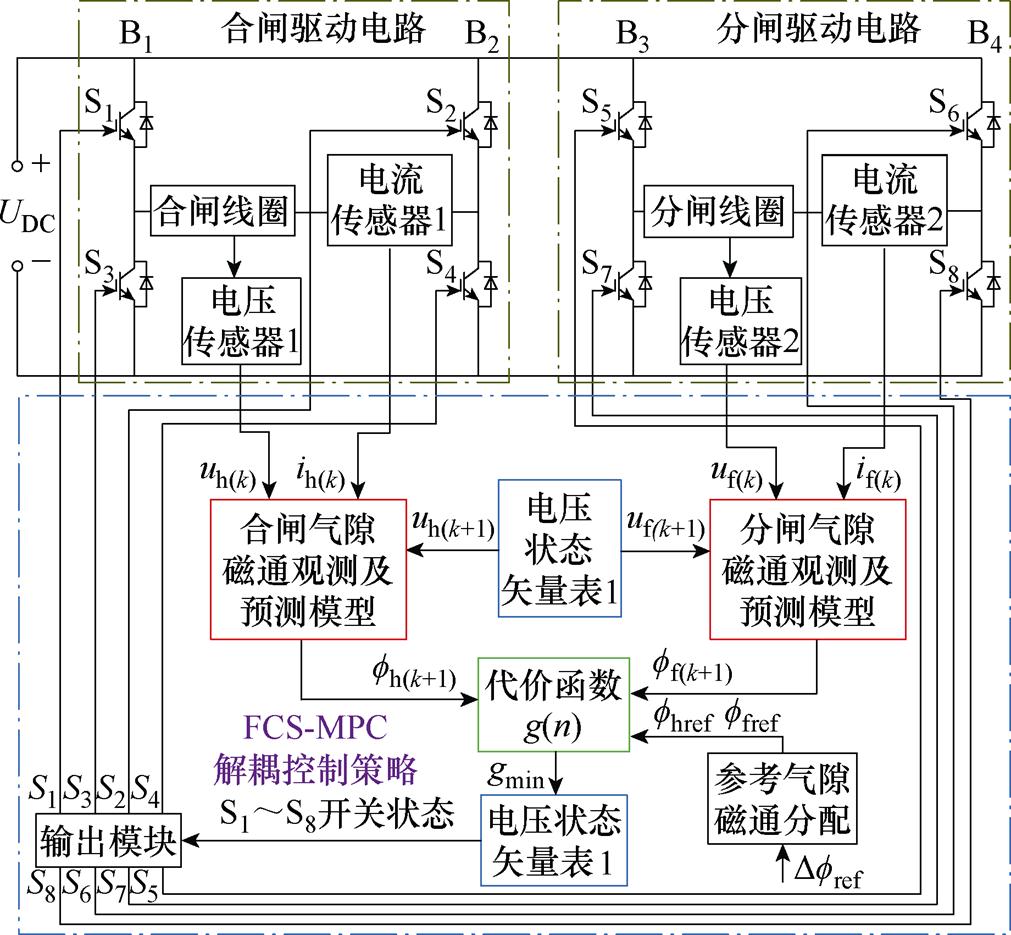
图6 FCS-MPC整体原理
Fig.6 The overall principle of FCS-MPC
根据图6原理,采用Multisim和LabVIEW构建联合仿真系统[21]:在Multisim中构建线圈驱动电路子模型及“磁路的电路等效模型”;在LabVIEW中构建FCS-MPC解耦策略子模型,同时构建BPMA动态仿真子模型。各子模型按图7所示连接。由BPMA动态仿真子模型输出分、合闸线圈电感Lf、Lh,互感M,分、合闸永磁磁动势Epmf、Epmh,配合FCS-MPC解耦策略子模型输出的驱动信号S1~S8,一同输入到线圈驱动电路子模型及磁路的电路等效模型中,更新BPMA磁路状态并控制驱动电路;将驱动电路中的分、合闸线圈电压uf、uh,分、合闸线圈电流if、ih输入到FCS-MPC解耦策略子模型,用以更新驱动信号,同时将uf、uh输入BPMA动态仿真子模型,激励动态模型运动。各子模型在每个仿真步长中交换数据,最终完成硬件控制电路、软件控制策略、BPMA本体之间逐点闭环的联合仿真。
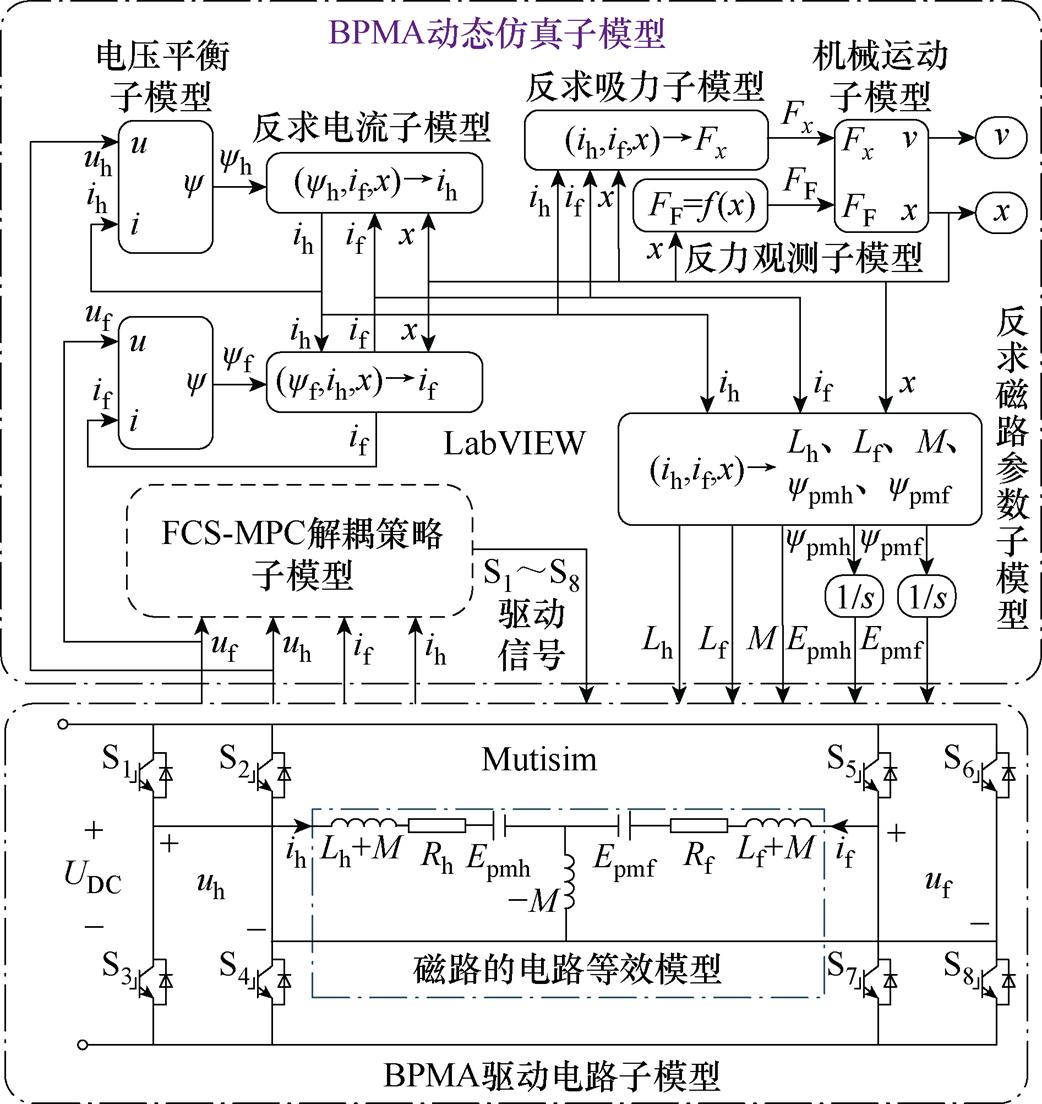
图7 BPMA联合仿真系统
Fig.7 Co-simulation system of the BPMA
对合闸过程进行仿真,设定Dfref=-0.000 15 Wb2,UDC=400 V,Dfref被分配为参考值fhref、ffref,FCS- MPC控制周期T设为50 ms,为避免线圈过电流,在控制策略中加入并行的逐周期限流程序,将线圈电流限制为±50 A,仿真波形如图8所示。图中,Tt为施加励磁到动铁心开始运动的触动时间,Tm为铁心开始运动到运动结束的动作时间,Ta为从励磁到运动结束的总时间。
(1)t0时刻,开始对线圈励磁,经控制策略作用后输出电压uh、uf施加到线圈;合闸线圈电流ih与合闸气隙磁通fh开始上升,分闸线圈电流if与分闸气隙磁通ff开始下降,使fh、ff快速趋近于各自的参考值,该阶段动铁心磁力快速下降,使机构从分闸保持状态快速进入合闸操作过程。
(2)t1时刻,ff降至参考值0,此后动态维持在零值,避免分闸气隙产生阻碍动铁心合闸的磁力;t2时刻,ih达到限流值后动态恒定,随着动铁心位移x的增加,fh继续增大,至t3时刻fh达到参考值,之后维持动态恒定,此时Df 也达到参考值Dfref,ih开始退出限流状态;然后随着x的增加,ih及if根据控制策略自动调整,将Df 动态维持在参考值;t4时刻,动铁心运动到合闸稳态位置,速度v降为0,运动结束。t1~t4时段,动铁心仅在fh的磁力作用下运动。
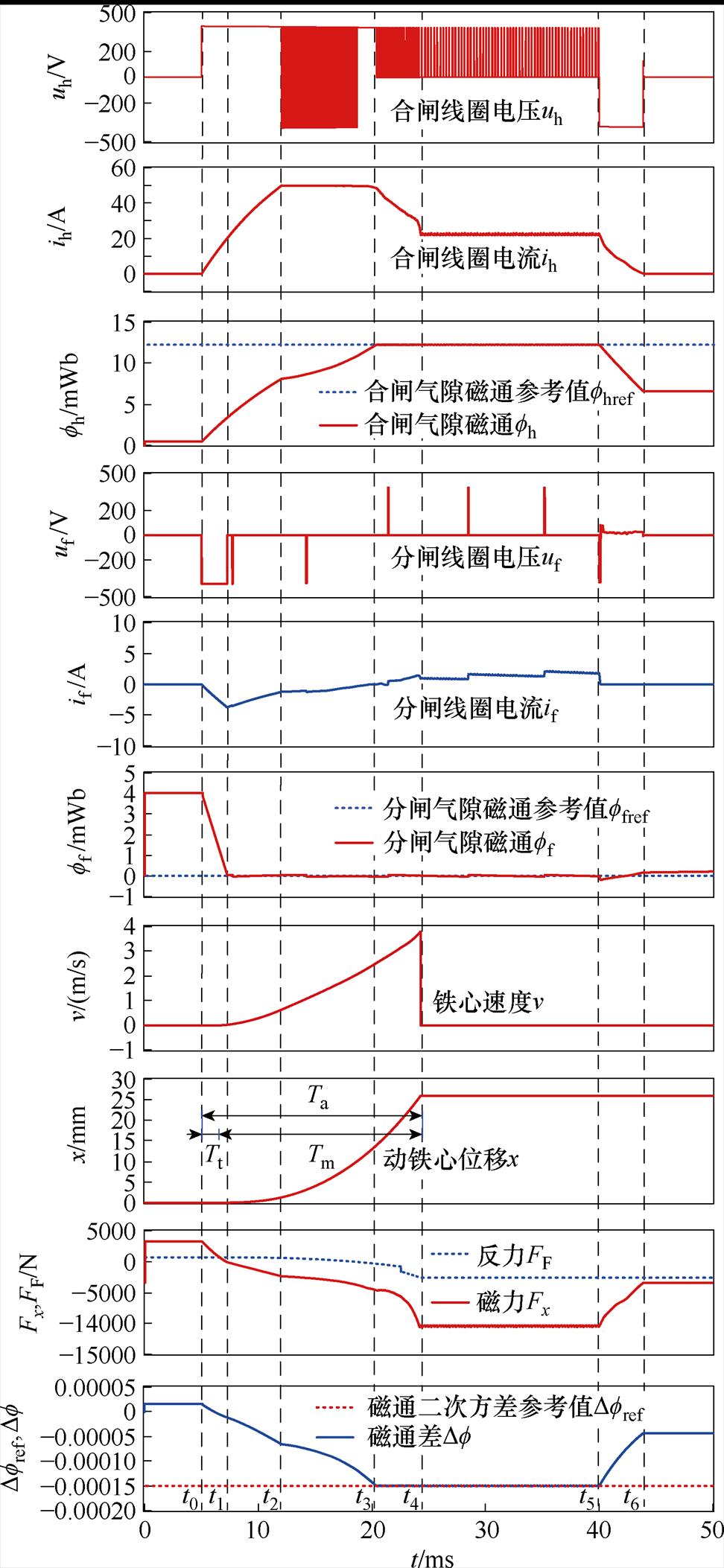
图8 FCS-MPC解耦仿真
Fig.8 Simulation of FCS-MPC decoupling control
(3)t4~t5时段,为保证机构可靠合闸,继续维持Df=Dfref;t5时刻,关闭驱动电路开关管,由于线圈为阻感负载,残余的ih通过开关管S2、S3的体二极管续流,使uh为-UDC,fh快速减小,机构快速退磁;至t6时刻,线圈电流衰减到0,退磁完毕,之后机构仅依靠永磁进行合闸状态保持。
对比不同Dfref下的线圈电流及铁心位移,如图9所示。
根据式(7)计算动作过程的操作功WQ为
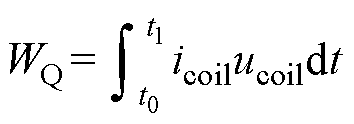 (7)
(7)
式中,ucoil为线圈电压;icoil为线圈电流;t0为励磁起始时间;t1为电流衰减至0的时间。总结图9可得表2,表中,yhref为穿过合闸气隙磁链参考值。可知,随着Dfref绝对值的增大,动作时间逐渐缩短,动作功耗逐渐增大。因此,可通过调节Dfref来控制动铁心的运动速度,但需权衡操作功。
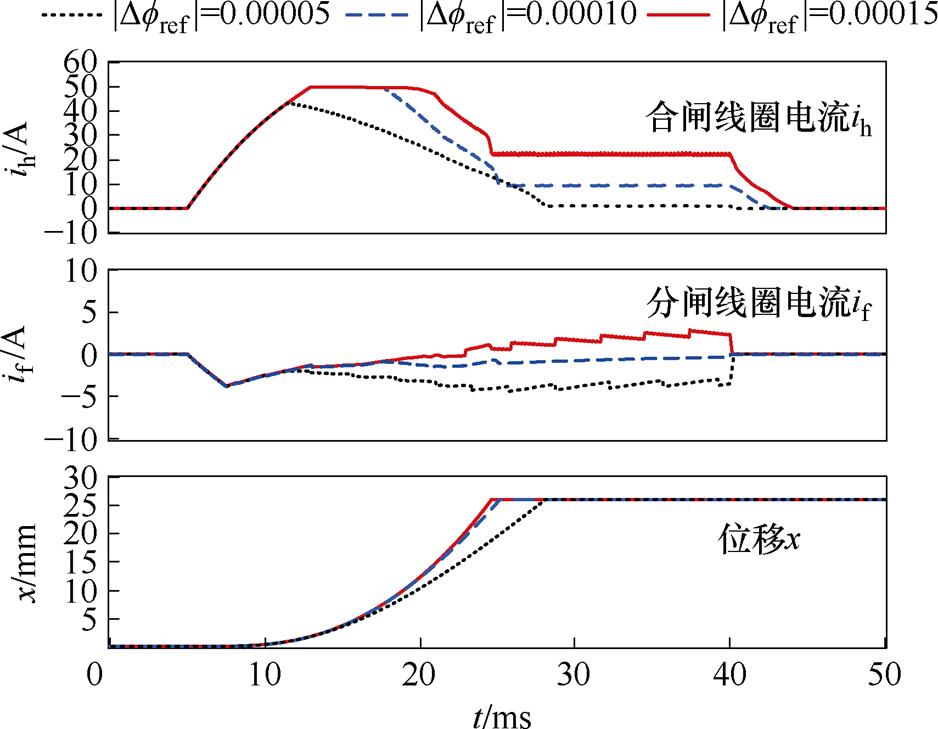
图9 电流和位移仿真对比
Fig.9 Simulation comparison of current and displacement
表2 不同Dfref的动作特性
Tab.2 Simulation action characteristics of different Dfref
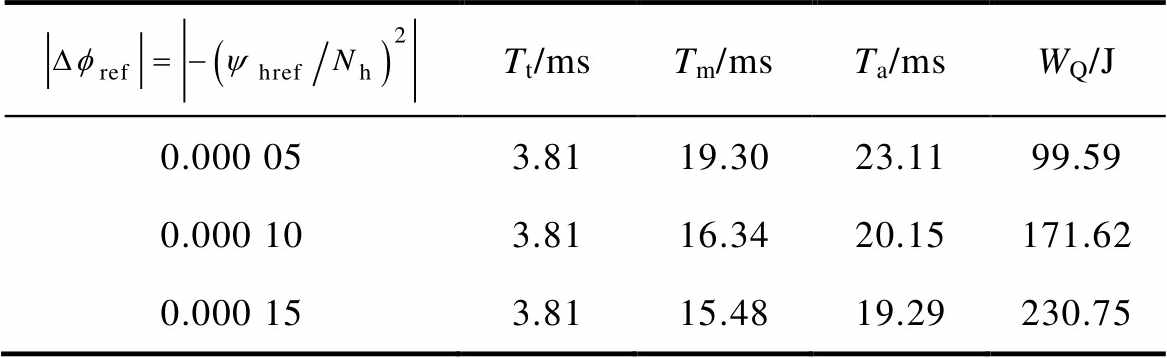
Tt/msTm/msTa/msWQ/J 0.000 053.8119.3023.1199.59 0.000 103.8116.3420.15171.62 0.000 153.8115.4819.29230.75
目前,常采用电流闭环方式对双稳态永磁断路器线圈进行励磁控制,同样将电流限制在50 A,其合闸过程仿真波形如图10所示。t0时刻对线圈进行励磁控制,t1时刻电流被限制在幅值处,t1~t2阶段由于运动反电动势电流略有下降,但随着铁心闭合,电流重新上升至幅值,t2时刻线圈停止励磁,至t3时刻电流衰减至0。电流闭环控制下的合闸过程仅对合闸线圈进行励磁控制,分闸线圈仅通过共用磁路感应出电压uf,且由于uf小于电源电压,分闸驱动电路开关管未导通,故分闸电流if始终为0。
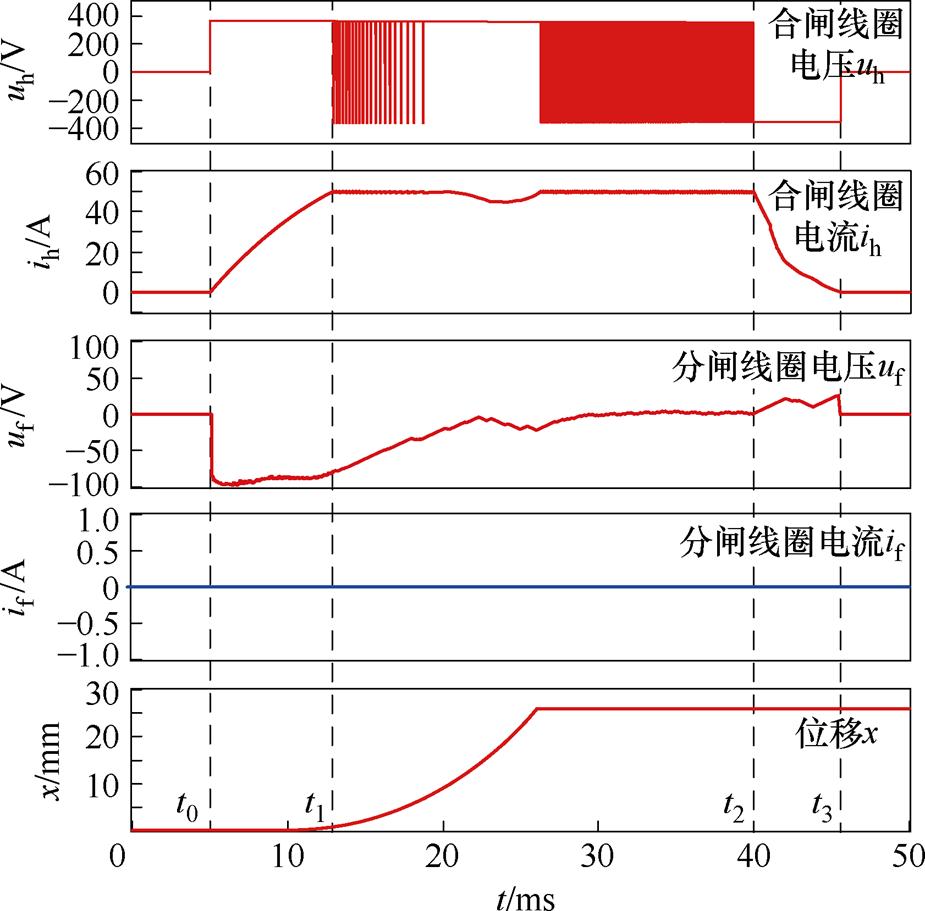
图10 电流控制仿真波形
Fig.10 Simulation waveforms of current control
对比图8解耦控制与图10电流闭环控制的动铁心位移及线圈电流,如图11所示。
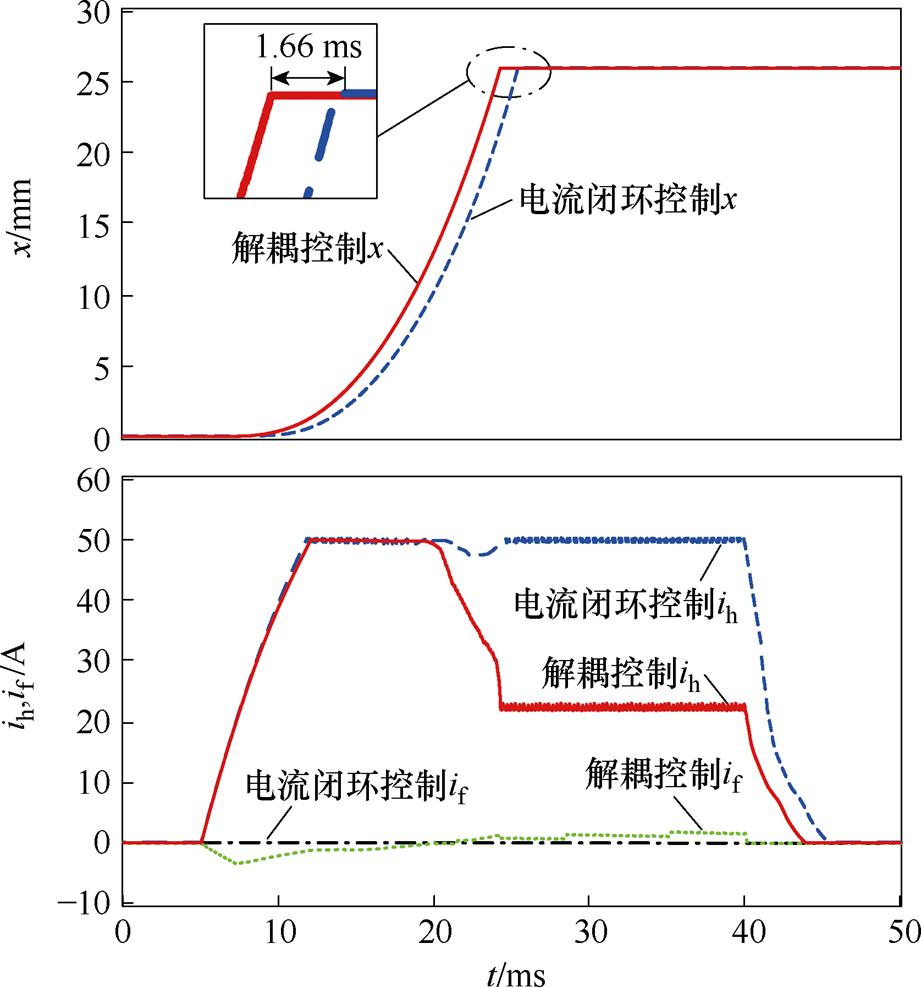
图11 电流闭环与解耦控制仿真对比
Fig.11 Comparison of current closed-loop and decoupling control simulation
总结图11可得表3数据,可知,气隙解耦控制能够根据动铁心行程,自动调整线圈电流,避免电流闭环控制时为可靠动作而长时间大电流运行的情况,有利于降低操作功;在相同电流限制值下,气隙解耦控制能够实现更快的动铁心响应。因此,磁通解耦控制能够独立控制分、合闸气隙磁通,提高BPMA控制灵活性,同时可以用更小的操作功获得更快的动作响应,有利于提升开关的控制及保护性能。
表3 不同策略仿真的动作特性与能量功耗
Tab.3 Simulation action characteristics and energy consumption of different Strategies

控制方法Tt/msTm/msTa/msWQ/J 磁通解耦3.8115.4819.29230.75 电流闭环4.7116.2420.95358.47
实验现场如图12所示,以NI sbRIO-9627单板控制器为核心,主要包括:模拟输入输出(AI/O),数字输入输出(DI/O),板载FPGA。由电压、电流传感器采集线圈电压、电流信号,通过AI接口输入控制器,在FPGA中运行FCS-MPC策略,通过DO接口输出驱动信号,控制驱动电路。由直线位移传感器测量动铁心位移,控制器内部计算的磁通通过AO接口输出,并将这些信号接入示波器。控制对象采用VSmK 12 kV/1 250 A双稳态永磁真空断路器。

图12 实验现场
Fig.12 Experimental site
气隙磁通解耦实验波形如图13所示,UDC= 400 V,Dfref=0.000 05 Wb2,断路器工作在分闸过程,控制周期T=50 ms,线圈电流限制值为±50 A,励磁时间为35 ms。

图13 气隙磁通解耦实验波形
Fig.13 Experimental waveforms of flux decoupling
对比不同磁通平方差参考值下的电流与位移实验波形如图14所示。

图14 不同Dfref电流与位移实验对比
Fig.14 Experimental comparison of current and displacement for different Dfref
图13中,t0~t1时段,分闸线圈电流if快速上升,合闸线圈电流ih快速下降,共同削减合闸位置的永磁保持力,t1时刻if到达限制值后在逐周期限流作用下维持动态恒定;随着动铁心向分闸位置运动,ff逐渐上升,fh快速下降,t2时刻fh下降到参考值0维持动态恒定,避免合闸气隙产生阻碍动铁心分闸的磁力,t3时刻ff上升至参考值后维持动态恒定,此时,Df 达到Dfref,之后随着分闸气隙的减小,if自动降低;t4时刻,动铁心到达分闸稳态位置,为保证可靠分闸,ff、fh动态维持在参考值;t5时刻,关闭励磁,操动机构开始快速退磁,至t6时刻,分合闸线圈电流衰减到0,分闸过程结束,之后仅依靠永磁体稳定保持分闸状态。
根据图以14及式(7)可得不同Dfref实验动作特性,见表4。
表4 不同Dfref实验动作特性
Tab.4 Experimental action characteristics of different Dfref
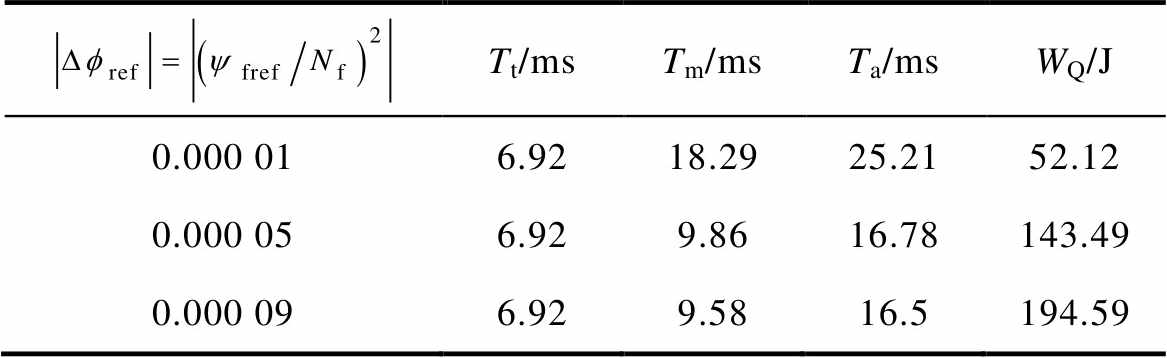
Tt/msTm/msTa/msWQ/J 0.000 016.9218.2925.2152.12 0.000 056.929.8616.78143.49 0.000 096.929.5816.5194.59
实验波形变化规律与仿真一致,随着参考值Dfref绝对值的增加,铁心动作时间缩短,同时操作功增加,证实了FCS-MPC解耦策略对双稳态永磁操动机构动作控制的实际有效性。
电流闭环控制实验波形如图15所示。t0时刻对分闸线圈进行励磁,t1时刻电流快速上升至幅值50 A后保持动态恒定,t2时刻关闭线圈励磁,t3时刻,线圈电流衰减至0。
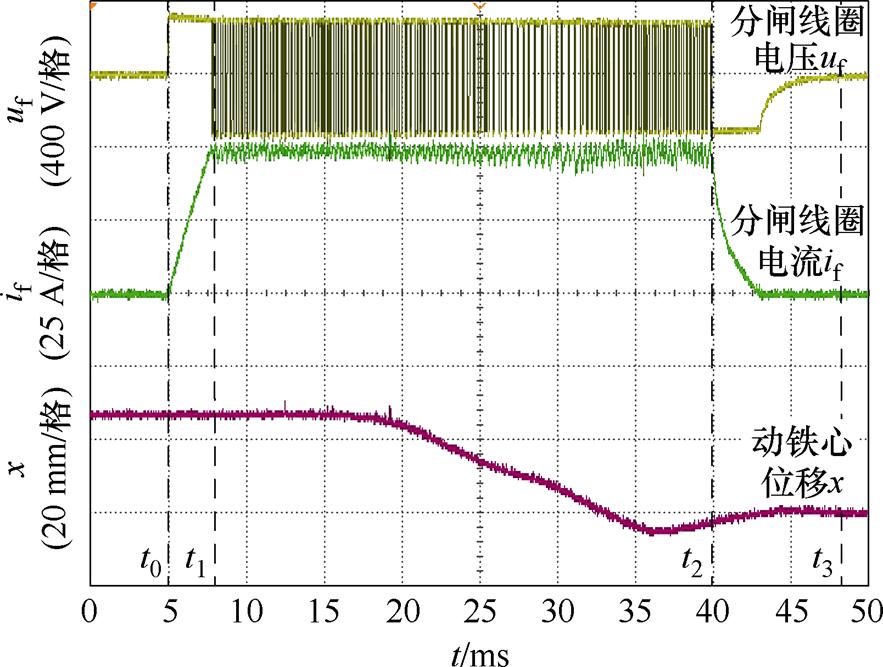
图15 电流控制实验波形
Fig.15 Experimental waveforms of current control
对比图13解耦控制与图15电流闭环控制的位移与电流波形如图16所示。

图16 电流控制实验波形
Fig.16 Experimental waveforms of current control
总结图16可得表5数据,同样可以看出:气隙磁通解耦控制能够使BPMA以更小的操作功获得更快的动作响应,节能的同时提高永磁开关的分合闸性能。
表5 不同策略实验动作特性与操作功
Tab.5 Experimental action characteristics and energy consumption of different strategies
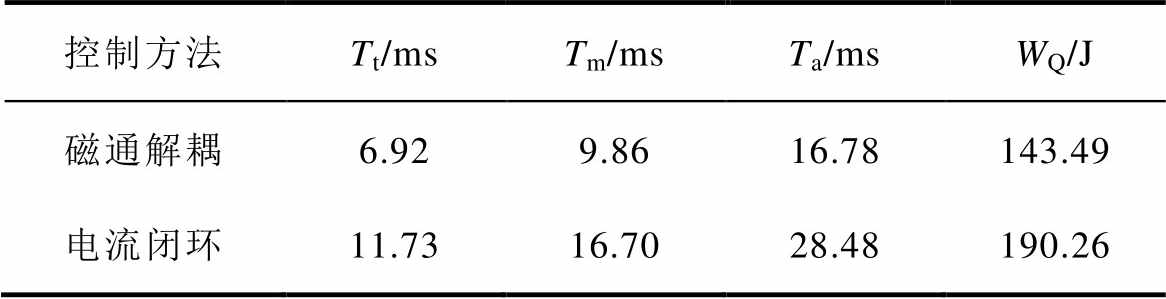
控制方法Tt/msTm/msTa/msWQ/J 磁通解耦6.929.8616.78143.49 电流闭环11.7316.7028.48190.26
相对电流闭环控制,解耦控制需要更多的计算资源,需要使用DSP或FPGA芯片,整体硬件成本较高。同时由于提高了分闸速度,分闸过程中对框架的冲击力增大,可能需要设计更有效的缓冲机构。
本文提出了BPMA分合闸气隙磁通解耦控制策略,经理论推导、仿真分析与实验验证得到以下 结论:
1)动铁心所受矢量磁力取决于分合闸气隙的“磁通平方差”,因此要进行BPMA的动态控制,仅需实时控制这一矢量磁通方差即可。
2)根据矢量磁通方差分配参考值时,始终令非必要气隙磁通的参考值为0,这一分配方式避免了分、合闸气隙磁力在动铁心上相互抵消,提高磁力的操动效率。
3)采用FCS-MPC方法,能够将分闸气隙磁通、合闸气隙磁通、驱动电路视作整体来统一约束,进行非线性、多目标控制,使分/合闸气隙磁通趋近于各自的参考值,实现解耦控制。
参考文献
[1] 程显, 袁晓东, 葛国伟, 等. 真空开关高动作稳定性的永磁操动机构控制系统[J]. 电工技术学报, 2021, 36(21): 4617-4626.
Cheng Xian, Yuan Xiaodong, Ge Guowei, et al. Permanent magnet mechanism control system with high operation stability of vacuum switch[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4617-4626.
[2] 李斌, 郭凤仪, 王智勇, 等. 双稳态永磁机构优化设计及智能控制器[J]. 电工技术学报, 2013, 28(10): 83-89.
Li Bin, Guo Fengyi, Wang Zhiyong, et al. Bi-state PMA optimization design and intelligent controller[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 83-89.
[3] 杨东文, 曾次玲, 谷丰强, 等. 配永磁机构真空断路器操动时间分散性的预测模型与影响因素研究[J]. 电力系统保护与控制, 2023, 51(5): 180-187.
Yang Dongwen, Zeng Ciling, Gu Fengqiang, et al. Influencing factor and forecasting model for the time dispersion of the operating mechanism of a vacuum circuit breaker with permanent magnetic actuator[J]. Power System Protection and Control, 2023, 51(5): 180-187.
[4] 谭东现, 李岩, 牟坚, 等. 动态式双稳态永磁机构的研究[J]. 高压电器, 2007, 43(3): 229-231.
Tan Dongxian, Li Yan, Mou Jian, et al. Research of novel dynamic bi-static permanent magnetic actuator[J]. High Voltage Apparatus, 2007, 43(3): 229-231.
[5] Wang Zhenxing, Sun Liqiong, He Sainan, et al. A permanent magnetic actuator for 126 kV vacuum circuit breakers[J]. IEEE Transactions on Magnetics, 2014, 50(3): 8200507.
[6] 谭东现, 崔寒, 李岩, 等. 双稳态永磁操动机构在40.5 kV户内真空断路器上的应用[J]. 高压电器, 2005, 41(2): 110-112.
Tan Dongxian, Cui Han, Li Yan, et al. Application of bi-stable permanent magnetic actuator for 40.5 kV indoor vacuum circuit breaker[J]. High Voltage Apparatus, 2005, 41(2): 110-112.
[7] 朱学贵, 王毅. 为提高分闸能力的永磁操动机构的研究与设计[J]. 中国电机工程学报, 2006, 26(7): 163-167.
Zhu Xuegui, Wang Yi. Research and design of permanent magnet actuator for higher opening capability[J]. Proceedings of the CSEE, 2006, 26(7): 163-167.
[8] 孙丽琼, 王振兴, 何塞楠, 等. 126kV真空断路器分离磁路式永磁操动机构[J]. 电工技术学报, 2015, 30(20): 49-56.
Sun Liqiong, Wang Zhenxing, He Sainan, et al. A permanent magnetic actuator with separated magnetic circuit for 126kV vacuum circuit breakers[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 49-56.
[9] Jiang Jiaming, Lin Heyun, Fang Shuhua. Optimization design of a permanent magnet actuator for 126-kV vacuum circuit breaker[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 0600105.
[10] 吕锦柏, 王毅, 谢将剑, 等. 基于线圈电流的永磁真空断路器控制方法[J]. 高电压技术, 2013, 39(4): 860-868.
Lü Jinbo, Wang Yi, Xie Jiangjian, et al. Control method for permanent magnetic vacuum circuit breaker based on coil current[J]. High Voltage Engineering, 2013, 39(4): 860-868.
[11] Fang Shuhua, Liu Qingdong, Lin Heyun, et al. A novel flux-weakening control strategy for permanent- magnet actuator of vacuum circuit breaker[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2275-2283.
[12] Dong Enyuan, Qin Taotao, Wang Yongxing, et al. Experimental research on speed control of vacuum breaker[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 2594-2601.
[13] 肖蕙蕙, 魏苏东, 郭强, 等. 优化开关序列的PWM整流器模型预测控制策略[J]. 电工技术学报, 2022, 37(14): 3665-3675, 3700.
Xiao Huihui, Wei Sudong, Guo Qiang, et al. Model predictive control strategy for PWM rectifier with optimized switching sequence[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3665- 3675, 3700.
[14] 张树林, 康劲松, 盛业哲. 一种无权重系数的三电平NPC逆变器低共模电压FCS-MPC算法[J]. 中国电机工程学报, 2023, 43(19): 7614-7625.
Zhang Shulin, Kang Jinsong, Sheng Yezhe. A low common mode voltage FCS-MPC scheme for three- level NPC inverter without weighting factor[J]. Proceedings of the CSEE, 2023, 43(19): 7614-7625.
[15] 张珍睿, 刘彦呈, 陈九霖, 等. 永磁同步电机幅值控制集模型预测控制策略[J]. 电工技术学报, 2022, 37(23): 6126-6134.
Zhang Zhenrui, Liu Yancheng, Chen Jiulin, et al. Amplitude control set model predictive control strategy for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 6126-6134.
[16] 陈卓易, 屈稳太, 邱建琪. 一种开关频率可控的有限集模型预测控制[J]. 电工技术学报, 2022, 37(16): 4134-4142.
Chen Zhuoyi, Qu Wentai, Qiu Jianqi. A switching- frequency-controlled finite-control-set model predictive control method[J]. Transactions of China Electro- technical Society, 2022, 37(16): 4134-4142.
[17] 宋琳, 聂子玲, 叶伟伟, 等. 基于前馈解耦控制的有源中点钳位五电平模型预测控制[J]. 电工技术学报, 2023, 38(7): 1910-1920.
Song Lin, Nie Ziling, Ye Weiwei, et al. Research on model predictive control of ANPC-5L permanent magnet synchronous motor based on feedforward decoupling[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1910-1920.
[18] 颜黎明, 郭鑫, 徐玺声, 等. 基于新型解析权重因子配置的感应电机模型预测转矩控制[J]. 电工技术学报, 2023, 38(20): 5421-5433.
Yan Liming, Guo Xin, Xu Xisheng, et al. Model predictive torque control of induction machine drives using novel analytic weighting factor assignment[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5421-5433.
[19] 柳志飞, 杜贵平, 杜发达. 有限集模型预测控制在电力电子系统中的研究现状和发展趋势[J]. 电工技术学报, 2017, 32(22): 58-69.
Liu Zhifei, Du Guiping, Du Fada. Research status and development trend of finite control set model predictive control in power electronics[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(22): 58-69.
[20] Kouro S, Cortes P, Vargas R, et al. Model predictive control-a simple and powerful method to control power converters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 1826-1838.
[21] Tang Longfei, Luan Shixu. Cosimulation of bistable permanent magnet circuit breakers[J]. IEEE Transa- ctions on Industrial Electronics, 2024, 71(3): 2800- 2809.
Abstract A Bi-stable permanent magnet actuator (BPMA) shares the same magnetic circuit as the breaking and closing coils, and the magnetic flux generated by any coil passes through the breaking and closing air gaps. The permanent magnet automatically distributes the permanent magnetic flux according to the dynamic reluctance of the air gaps. The electromagnetic flux and permanent magnetic flux in the upper and lower air gaps always cause the moving iron core to be coupled by two opposite magnetic forces. As the motion of the moving iron core and the change of coil current, the magnetic circuit quickly saturates, and the electromagnetic flux and permanent magnetic flux interact, exacerbating the complexity of nonlinear coupling in the breaking and closing air gaps. To flexibly control the action characteristics of permanent magnet switches, it is necessary to simultaneously control the air gap flux and the magnetic force pointing to the breaking and closing positions. Therefore, this paper proposes an air gap flux decoupling control method based on finite control set-model predictive control (FCS-MPC). Decoupling control can be achieved by rapidly weakening the magnetic force pointing to the non-excited coil and rapidly increasing the magnetic force pointing to the excited coil.
Firstly, according to the operating principle of BPMA, the vector magnetic force acting on the moving iron core depends on the “magnetic flux squared difference” of the breaking and closing air gaps. Therefore, only controlling this vector magnetic flux square difference in real-time can dynamically control BPMA. Secondly, a predictive model of the breaking and closing air gap magnetic flux is designed through discretization of the voltage balance equation, which can predict the magnetic flux at the next moment based on the voltage and current values collected at the current moment. Thirdly, the breaking and closing air gap magnetic flux and the mechanism drive circuit are regarded as a whole. A set of switching states is constructed through the excitation intensity analysis under different switching states. Predictive magnetic flux is obtained by traversing all switching state combinations. Finally, a decoupling control cost function is designed, the predictive magnetic flux under different switching combinations is input into the cost function, and the optimal control is selected for the next control period. In rolling optimization over multiple control periods, the breaking and closing air gap magnetic flux quickly approaches their respective reference values, achieving decoupling control.
A co-simulation platform for intelligent control is designed based on LabVIEW and Multisim, and hardware testing circuits are constructed. The simulation and experimental waveforms show that this proposed scheme can effectively control the breaking and closing air gap flux. As a result, the non-excited air gap flux to zero is quickly reduced, approaching the set reference value of the excited air gap flux and effectively weakening the coupling between the air gaps. Compared with the traditional current closed-loop control scheme, the proposed control scheme reduces the energy loss during the entire action process and improves the response and action time of the core action.
Keywords:Bi-stable permanent magnet actuator (BPMA), permanent magnet switches, finite control set-model predictive control (FCS-MPC), decoupling control
中图分类号:TM561
DOI: 10.19595/j.cnki.1000-6753.tces.240379
福建省自然科学基金(2021J01634)和国家自然科学基金(52277136)资助项目。
收稿日期 2024-03-08
改稿日期 2024-04-08
汤龙飞 男,1987年生,教授,硕士生导师,研究方向为智能电器及其在线监测。
E-mail: tlftel@fzu.edu.cn(通信作者)
陈明俊 男,1997年生,硕士研究生,研究方向为电器及其智能化技术。
E-mail: 884222475@qq.com
(编辑 崔文静)