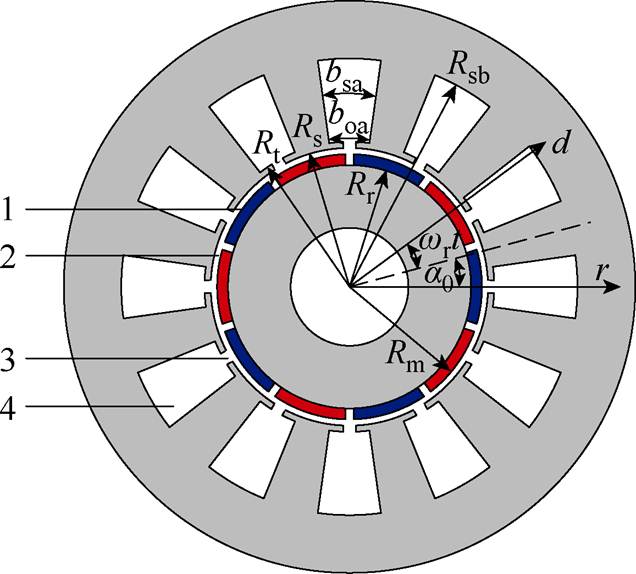
图1 电机模型和子域示意图
Fig.1 Machine model and four sub-regions
摘要 永磁同步电机退磁故障会降低电机的输出性能和负载能力,严重影响电机的使用寿命。建立准确的故障电机解析模型,进行快速电磁性能分析,获得故障情况下的电流、转矩等运行数据,有利于对退磁故障进行早期预测和诊断。该文针对永磁同步电机局部退磁故障,引入一个表示退磁区域空间角度的参数,推导了剩余磁化强度径向分量和切向分量的傅里叶系数,从而建立了永磁体局部退磁情况下的电机解析模型。在此基础上,针对实际应用中控制系统的电路接口,提出一种以磁链作为中间变量、由电压源逆变器驱动的解析模型,并将该模型应用到矢量控制系统中实现联合仿真,计算了电机的定子磁链、电流和转矩,经Ansys/Simplorer时步有限元模型和实验验证了该模型的准确性和有效性。相较于时步有限元法,该文提出的解析模型-控制电路联合仿真大幅缩短了计算时间,提高了运算效率。
关键词:永磁同步电机 退磁故障 解析建模
永磁同步电机具有结构紧凑、功率密度高、效率高等优点,广泛应用于机器人、航空航天、电动汽车、高端制造装备和国防军工等领域[1-3]。但由于电机运行过程可能受到高温、过载、过电流和机械振动等因素的影响,使得永磁材料发生不可逆退磁,导致电机出现均匀或局部退磁故障。退磁故障出现后会降低电机的输出性能和承载能力,严重影响电机的运行性能和使用寿命[4-6]。由于电机出现故障时,电流信号中一定包含了故障信息,目前基于电流信号对各类电气故障进行诊断的方法成为了研究热点[7-11]。因而针对退磁故障,建立准确的故障电机解析模型,进行快速电磁性能分析,获得不同退磁区域及不同运行工况下故障电机的电流、转矩等运行数据,可以为早期预测和诊断电机的退磁故障提供有力的支持。
目前,常用的退磁故障建模方法有数值法、磁路法和解析法三种。数值法一般通过直接修改永磁体材料的剩磁、矫顽力[12]或减少永磁体的体积[13]等方式来建立电机的退磁故障模型。磁路法一般通过改变电机磁路模型中退磁永磁体处的磁动势[14]或者等效磁通、磁阻[15]等方式来搭建电机的退磁模型。解析法模拟永磁体退磁故障的方法目前有等效电流和等效剩磁两种。等效电流的建模方法是通过将永磁体的退磁等效为永磁体表面的面电流来模拟退磁故障,如在正常永磁体的等效面电流之外增加一对或数对退磁等效电流来搭建永磁体的退磁模型等[16]。等效剩磁的方法是通过直接降低永磁体剩磁或磁化强度的方波幅值来模拟退磁,如将每极永磁体的剩余磁化强度整体乘以一个“退磁系数”来模拟径向充磁电机的局部退磁等[17-19],但这种方法仅考虑了每一极的永磁体剩余磁化强度整体幅值上的降低,从而将永磁体的局部退磁等效为整体永磁磁链的减少,没有考虑退磁区域空间角度的区别。事实上在工程实际中,永磁体发生局部退磁时不仅会出现整体永磁磁链的减少,而且随着退磁区域所占空间角度的改变,对应的剩余磁化强度径向分量和切向分量的傅里叶系数也会发生改变,从而导致气隙圆周上永磁体剩余磁化强度波形的畸变。因此,这种乘以常数系数的方法未考虑局部退磁区域的空间位置角对剩余磁化强度波形的影响,与实际情况不符。
此外,完整的电机控制系统由电机、外部控制电路、控制策略三部分构成,为了准确分析退磁情况下电机的运行性能,需要协同三个部分进行仿真,通常的做法有以下三种:①控制电路+简单电机模型仿真,将电机简化为相电阻、电感、磁链等参数的集合,通过直接设置这些参数来构建电机模型,具有计算速度快的优点,但忽视了电机内部结构,无法准确仿真局部退磁情况,只适用于部分标准化电机;②控制电路+时步有限元电机模型联合仿真,通常将电机电路方程与基于有限元法的磁场矩阵联立进行场路耦合模型的搭建[20],这种方法具有精度高、收敛可靠等优点,但基于有限元法的磁场计算需要大量的计算资源和时间;③控制电路+电机解析模型联合仿真,这种方法将解析模型与外电路联合,在考虑电机内部结构的基础上大幅缩短了运行时间,有利于进行实时计算。
本文以表贴式永磁同步电机为例,提出一种通过改变永磁体局部退磁区域的空间位置角从而改变其剩余磁化强度的解析建模方法。引入一个表示退磁区域空间位置角的参数——“退磁程度D”,通过改变D进而改变剩余磁化强度径向分量和切向分量的傅里叶系数,模拟永磁体局部退磁后剩余磁化强度大小和波形的改变,相较于直接将永磁体局部退磁等效为总体剩磁下降的方法更准确。在此基础上,以电机三相磁链为中间变量,建立了电压源激励下的退磁故障解析模型,并与控制电路相结合建立了系统仿真模型,计算了退磁故障下的磁链、电流和转矩等性能。此外,将计算结果与传统场路耦合时步有限元仿真结果及样机实测结果分别进行了对比,验证了本文所提出的退磁故障解析模型及其与控制电路联合仿真模型的准确性,且本文提出的控制电路与解析模型联合的仿真大大节省了运算时间,提高了运算效率。
本文在以下假设的基础上建立解析模型:①永磁材料退磁曲线为直线;②铁磁材料磁导率为无限;③忽略铁磁材料电导效应和涡流效应;④忽略电机端部效应。将电机的磁场求解域分为如图1所示的四个区域。

图1 电机模型和子域示意图
Fig.1 Machine model and four sub-regions
1—永磁体区域 2—气隙区域 3—定子槽口区域 4—定子槽区域
对应的矢量磁位轴向分量分别表示为Az1、Az2、Az3、Az4。图1中,Rr、Rm、Rs、Rt和Rsb分别为电机转子外半径、永磁体外半径、定子内半径、槽顶半径和槽底半径;boa和bsa分别为槽口和槽的机械角度;r为定子静止二维极坐标系的径向坐标轴;d为转子二维旋转极坐标系的径向坐标轴。永磁电机的转子初始位置角设为a0,在电机转速为wr的情况下,t时刻电机转子坐标系与定子坐标系的夹角为wt=wrt+a0。
对电机各子域,矢量磁位满足方程如下:
在气隙区域2和槽口区域3的矢量磁位满足拉普拉斯方程
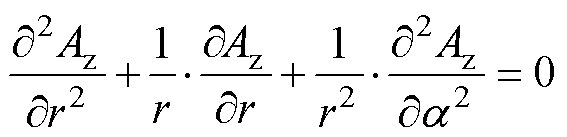 (1)
(1)
在槽区域4的矢量磁位满足泊松方程
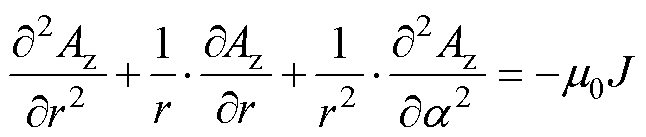 (2)
(2)
永磁体区域1的矢量磁位满足泊松方程
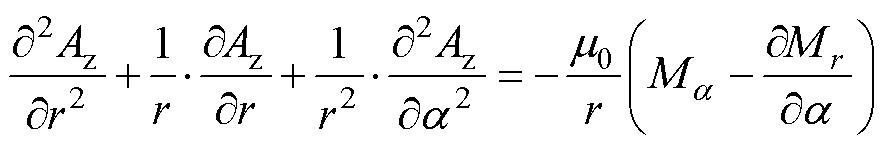 (3)
(3)
式中,J为绕组电流密度;r为二维极坐标系中径向坐标;m0为真空磁导率;a 为切向坐标;M为剩余磁化强度,沿径向和切向分解为Mr和Ma。
本文以局部退磁情况为例进行分析,首先引入退磁程度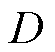 (
(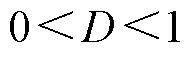 ),如图2所示,表示退磁区域所占的空间角度与一个极弧所占空间角度的比,即
),如图2所示,表示退磁区域所占的空间角度与一个极弧所占空间角度的比,即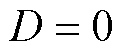 代表正常永磁体,
代表正常永磁体,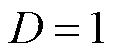 代表完全退磁,之后推导
代表完全退磁,之后推导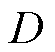 区域发生退磁后的剩余磁化强度表达式。在退磁故障发生后,气隙子域、槽口子域和槽子域不发生变化,仅永磁体子域的永磁体剩余磁化强度即式(3)中Mr和Ma改变。
区域发生退磁后的剩余磁化强度表达式。在退磁故障发生后,气隙子域、槽口子域和槽子域不发生变化,仅永磁体子域的永磁体剩余磁化强度即式(3)中Mr和Ma改变。
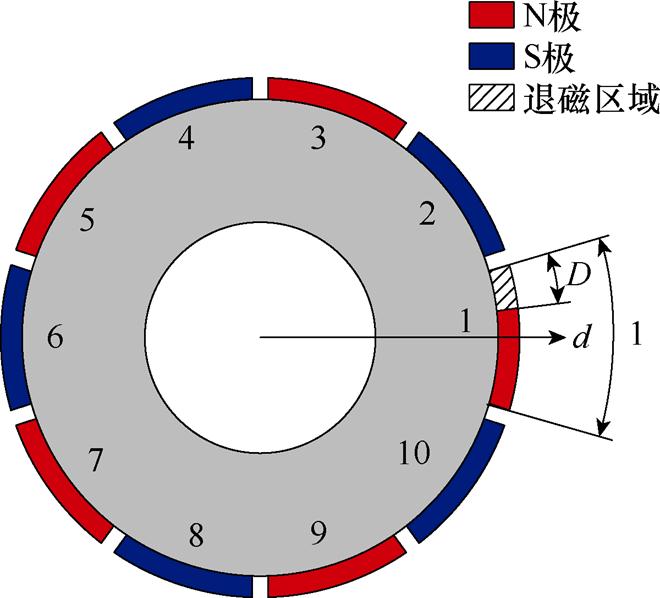
图2 局部退磁程度示意图
Fig.2 Model and magnets with partial demagnetization
设发生退磁的永磁体编号为i,i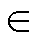 {1,2,…,2p},p为极对数,如图2所示。
{1,2,…,2p},p为极对数,如图2所示。
局部退磁后的剩余磁化强度可以看成由正常永磁体剩余磁化强度与所有局部退磁的永磁体所产生的影响叠加得到[21],即
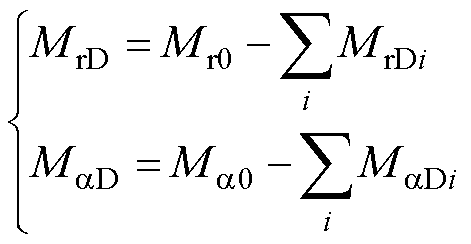 (4)
(4)
式中,Mr0和Ma0分别为永磁体正常情况下的剩余磁化强度径向和切向分量;MrDi和MaDi分别为第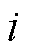 个永磁体发生局部退磁后的剩余磁化强度径向分量和切向分量,以平行充磁为例可以表示为
个永磁体发生局部退磁后的剩余磁化强度径向分量和切向分量,以平行充磁为例可以表示为
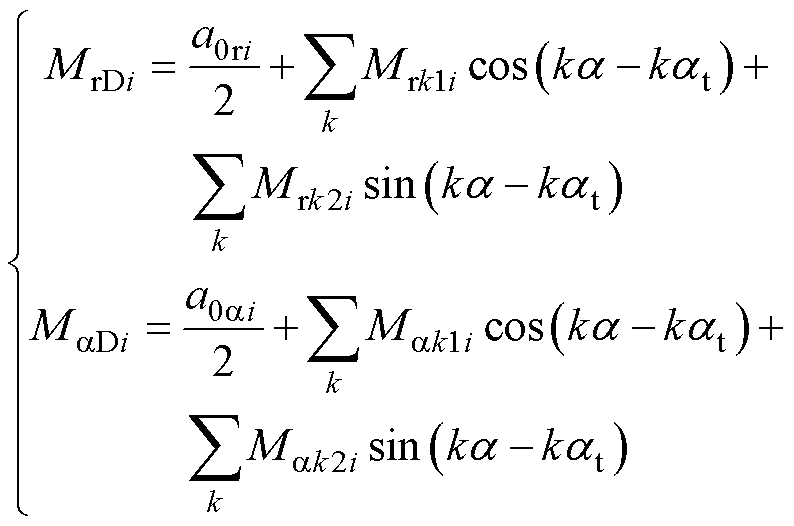 (5)
(5)
其中
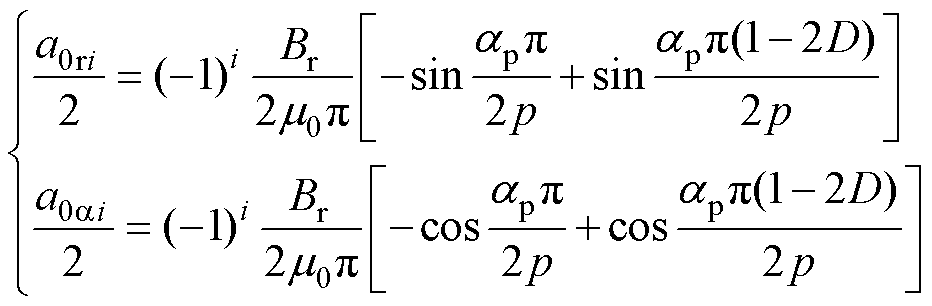 (6)
(6)
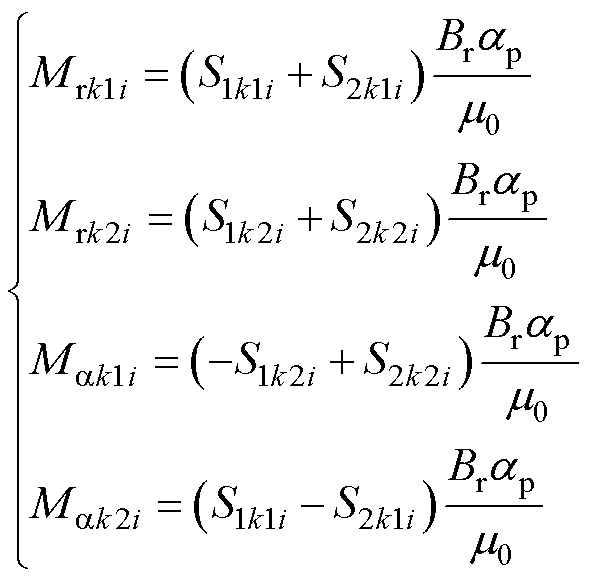 (7)
(7)
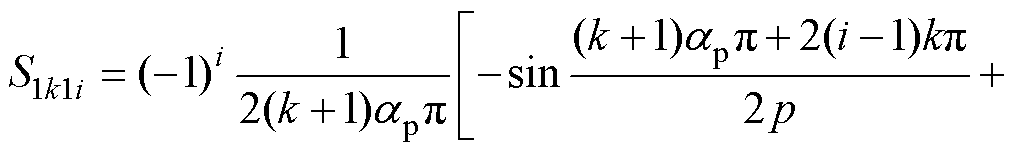
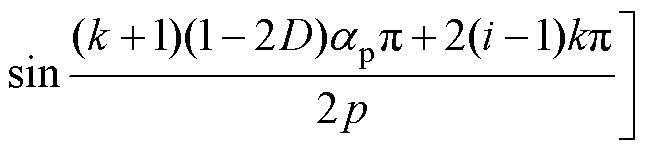 (8)
(8)
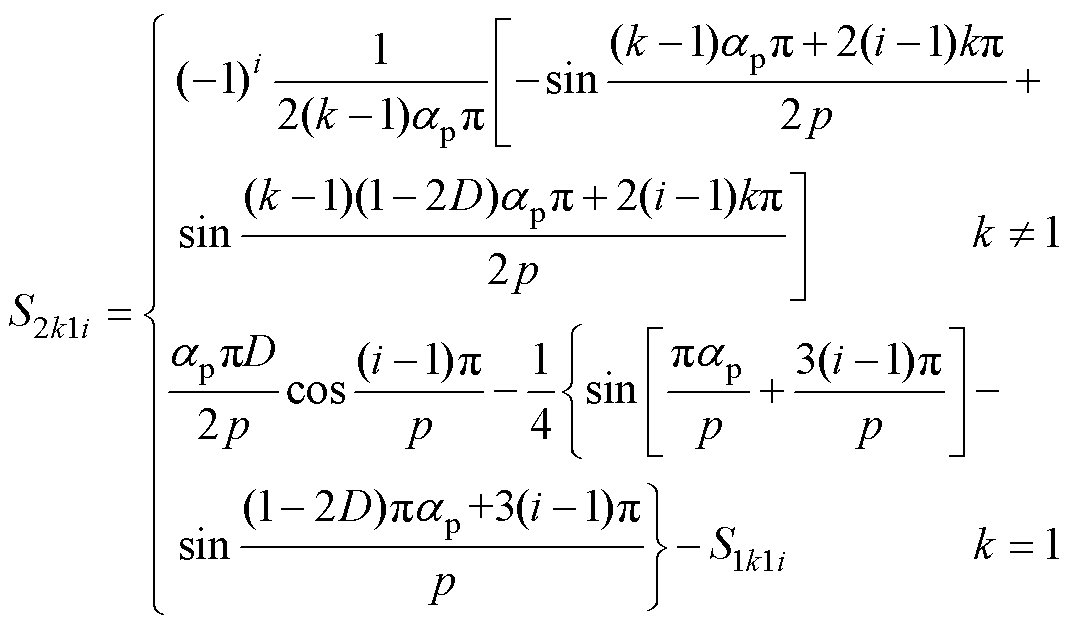 (9)
(9)
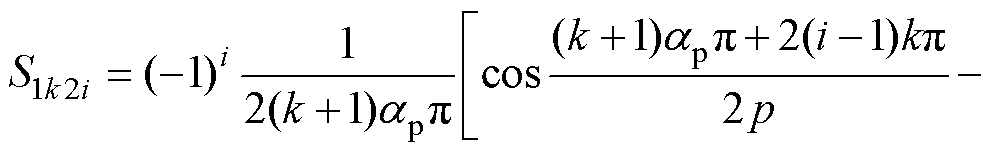
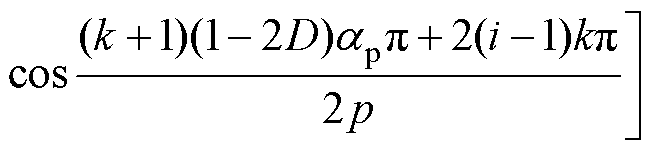 (10)
(10)
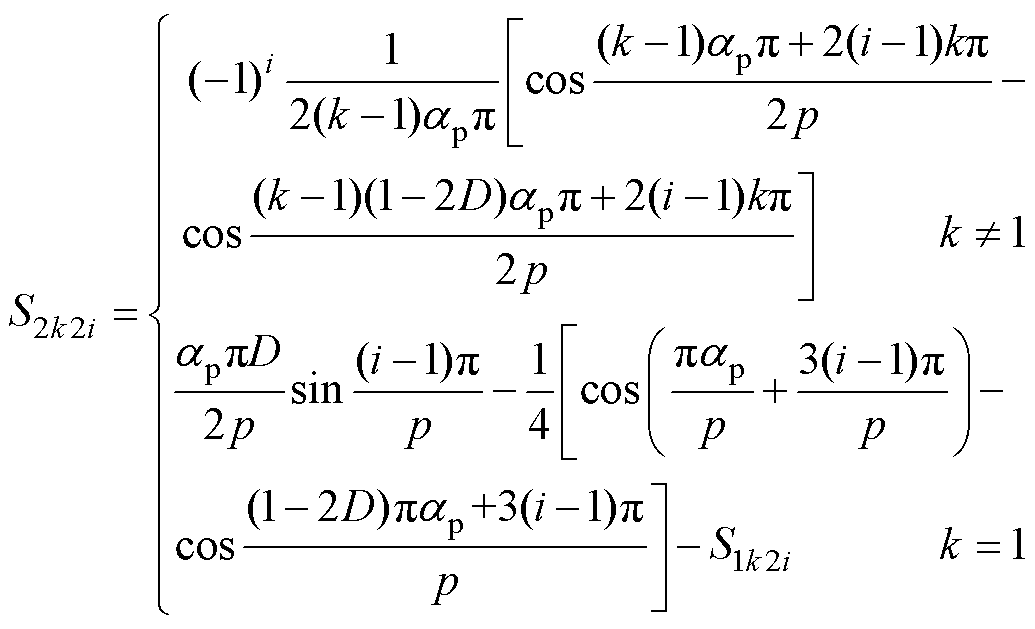 (11)
(11)
由以上推导过程可见,本文提出的“退磁程度D”实质上是一个空间位置角的概念,表示了退磁区域所占的空间角度与一个极弧所占空间角度的比。D的取值不同,不仅会导致剩余磁化强度幅值上的变化,而且会引起局部退磁产生的永磁体剩余磁化强度的傅里叶系数径向和切向分量均不同,从而导致合成后的剩余磁化强度在波形上也是不同的,故本文的建模方法同时体现了退磁区域的空间位置角对剩余磁化强度大小和波形的影响。相较于文献[17-19]中将退磁的永磁体单极(无论退磁区域所占有的空间角度大小)的剩磁整体乘以一个常数系数继而等效为总体磁链下降的方法,本文提出的退磁建模方法更符合工程实际情况。
对于电机的定子三相电压有
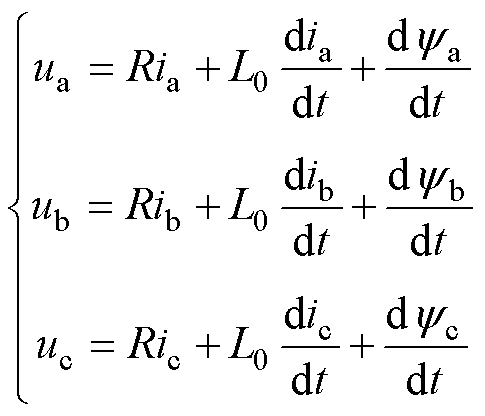 (12)
(12)
式中,R为相电阻;L0为绕组端部漏感;ya、yb、yc为定子三相磁链;ia、ib、ic为定子三相电流。
对式(12)进行前向欧拉离散,统一形式后有
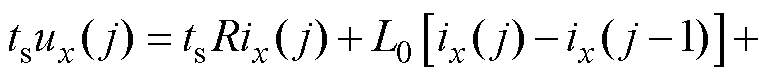
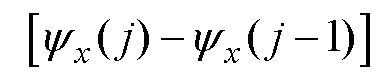 (13)
(13)
式中,x=a, b, c,分别为定子绕组的A相、B相和C相;ts为时间步长;j为循环的次数。
以双层集中绕组的三相永磁电机为例,电机三相磁链可由各相绕组占据的定子槽中的矢量磁位积分求得[22],即
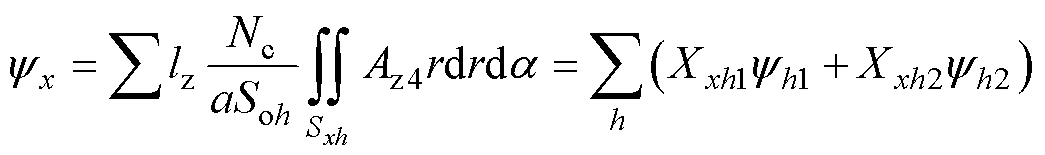 (14)
(14)
式中,lz为电机轴向长度;Nc为定子绕组每槽导体数;a为并联支路数;Soh为第h个槽的面积;Xxh1和Xxh2分别为第h槽左侧和右侧绕组中x相电流参考方向,取值1表示正,-1表示负,0表示该相无电流;yh1和yh2分别为第h槽左侧和右侧绕组的磁链值,有
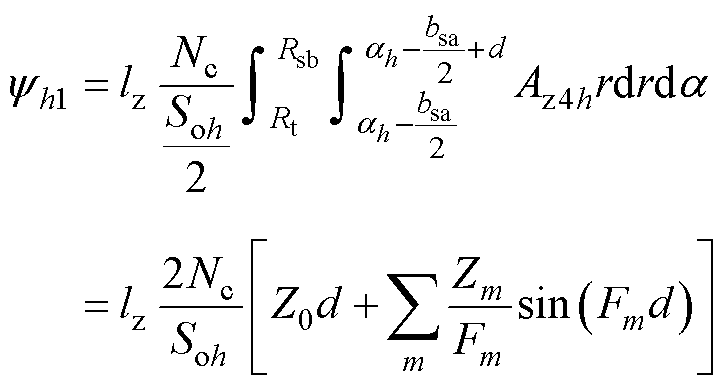 (15)
(15)
同理有yh2的值为
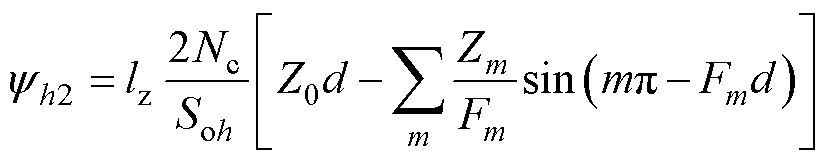 (16)
(16)
其中

式中,d为第h个槽中左侧绕组占据的弧度;ah为第h个槽的中心位置角;m为槽区域傅里叶分解的谐波次数。
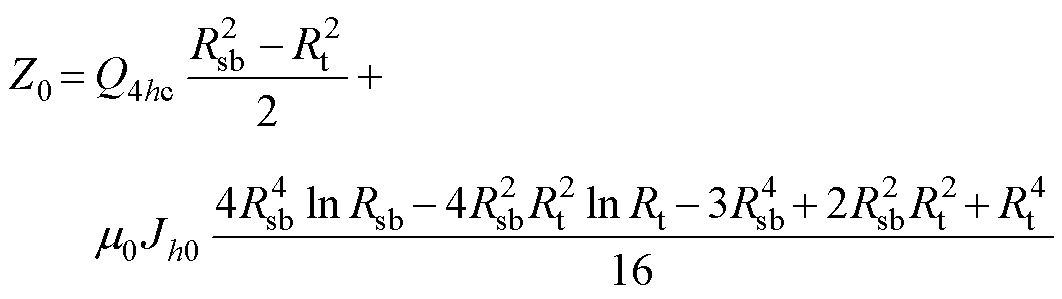 (17)
(17)
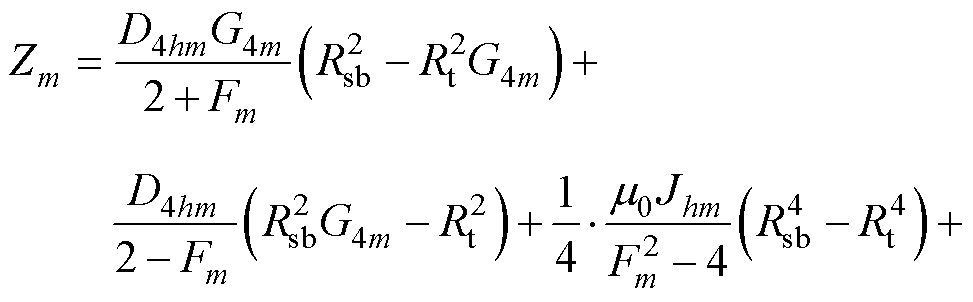
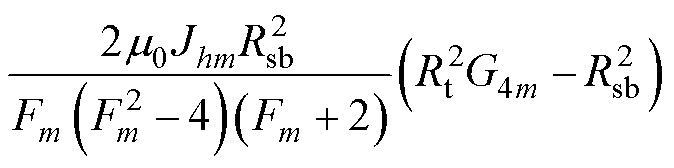 (18)
(18)
其中
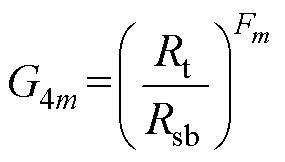

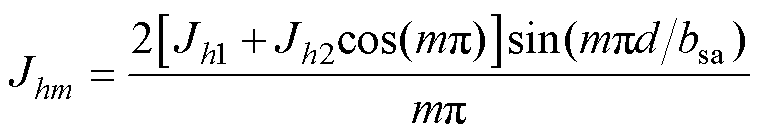
式中,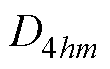 为待定系数;Jh1和Jh2分别为第h个槽内左侧和右侧电流密度。
为待定系数;Jh1和Jh2分别为第h个槽内左侧和右侧电流密度。
Q4hc的值为
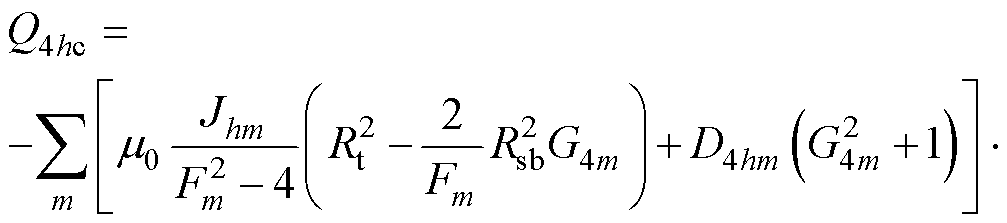
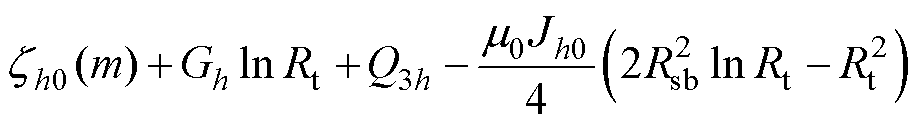 (19)
(19)
其中
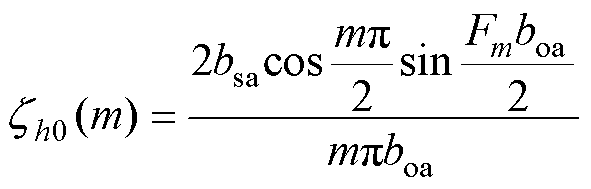 (20)
(20)
对电流密度Jh1和Jh2有
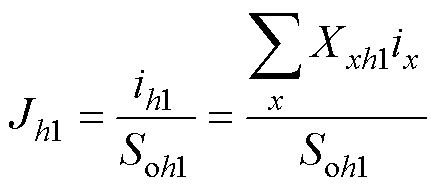 (21)
(21)
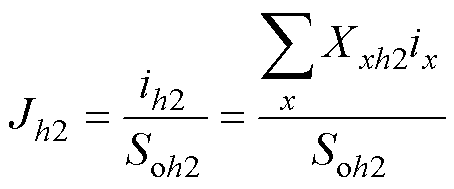 (22)
(22)
式中,Gh和Q3h为待定系数;ih1和ih2分别为第h槽左侧和右侧绕组中的电流;Soh1和Soh2分别为第h槽左侧和右侧绕组的面积。
联立式(14)~式(22)可求得三相磁链yx关于三相电流ix的表达式。通过将式(13)中的三相磁链yx( j)转化为三相电流ix( j)的表达式,可以得到电机三相电压ux( j)与电流ix( j)、前一时刻三相磁链yx( j-1)、电流ix( j-1)之间的关系[23]。
在此基础上,子域法槽区域中矢量磁位的方程即式(3)中绕组的电流密度变量可由式(21)、式(22)转化为电机三相电流,进而再转化为三相电压,以电压作为激励进行整个解析模型的求解,在槽区域的矢量磁位满足泊松方程
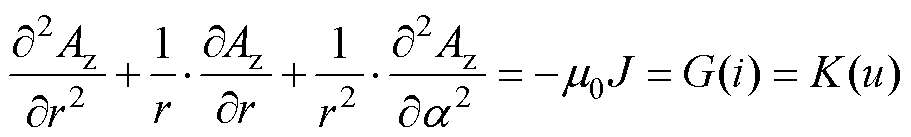 (23)
(23)
在替换后,气隙子域、槽口子域和永磁体子域不发生变化,仅槽子域改变。通过磁链和电流值的不断迭代计算,可以得到以电压作为激励的电机的性能。整个电压源激励电机解析模型的求解过程如图3所示。图3中,jmax为最大循环次数,t为仿真时间,tend为结束时间,FI为判断迭代稳定的函数,D 为判断迭代稳定的阈值。在正常情况下,FI为本电周期与前一电周期磁链方均根的差值,在局部退磁情况下为本机械周期与前一机械周期磁链方均根的差值。当运行结果误差小于阈值时视为迭代稳定,迭代稳定后仿真运行至设置的结束时间时整个程序结束,否则判断其是否达到最大仿真步长,若达到则终止运行防止死循环,若未达到,继续进行仿真。
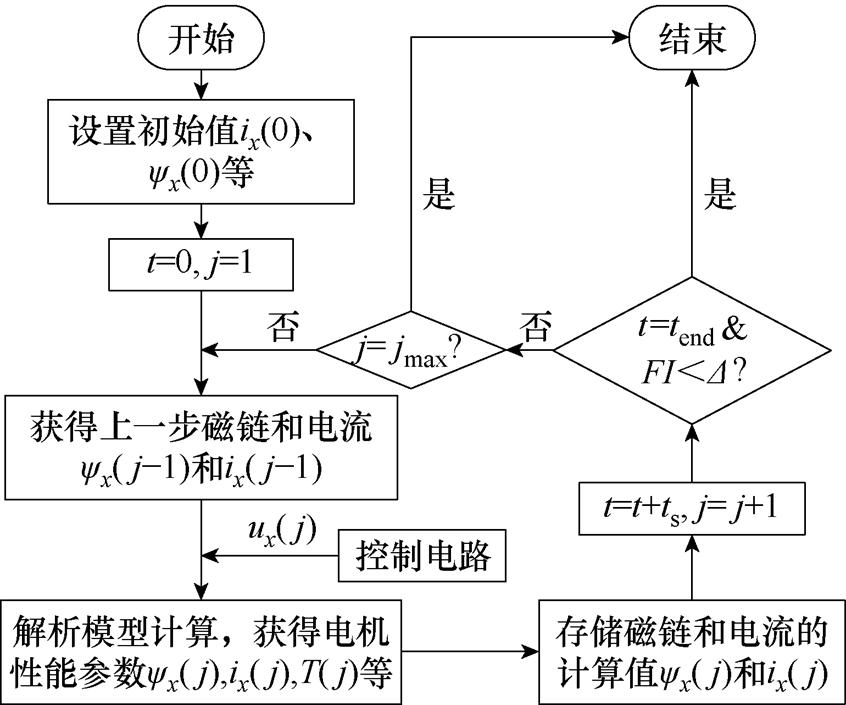
图3 求解流程
Fig.3 Block diagram of the proposed model
各子域间的边界条件为不同子域分界面处矢量磁位和切向磁场强度的连续,即
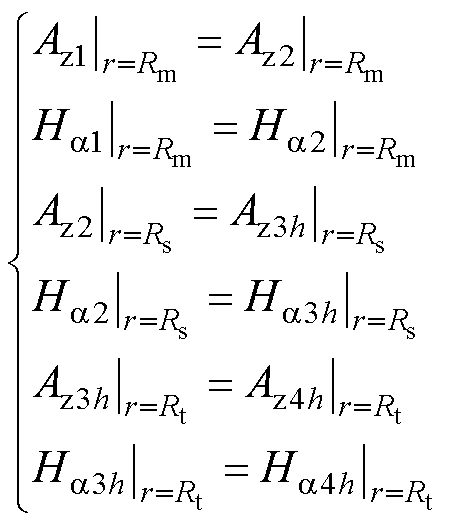 (24)
(24)
联立各个子域的方程,即可求得各待定系数的值,进而得到各磁场子域中矢量磁位的表达式,从而可以计算出电机运行时的各类参数如磁链和转矩等性能参数。
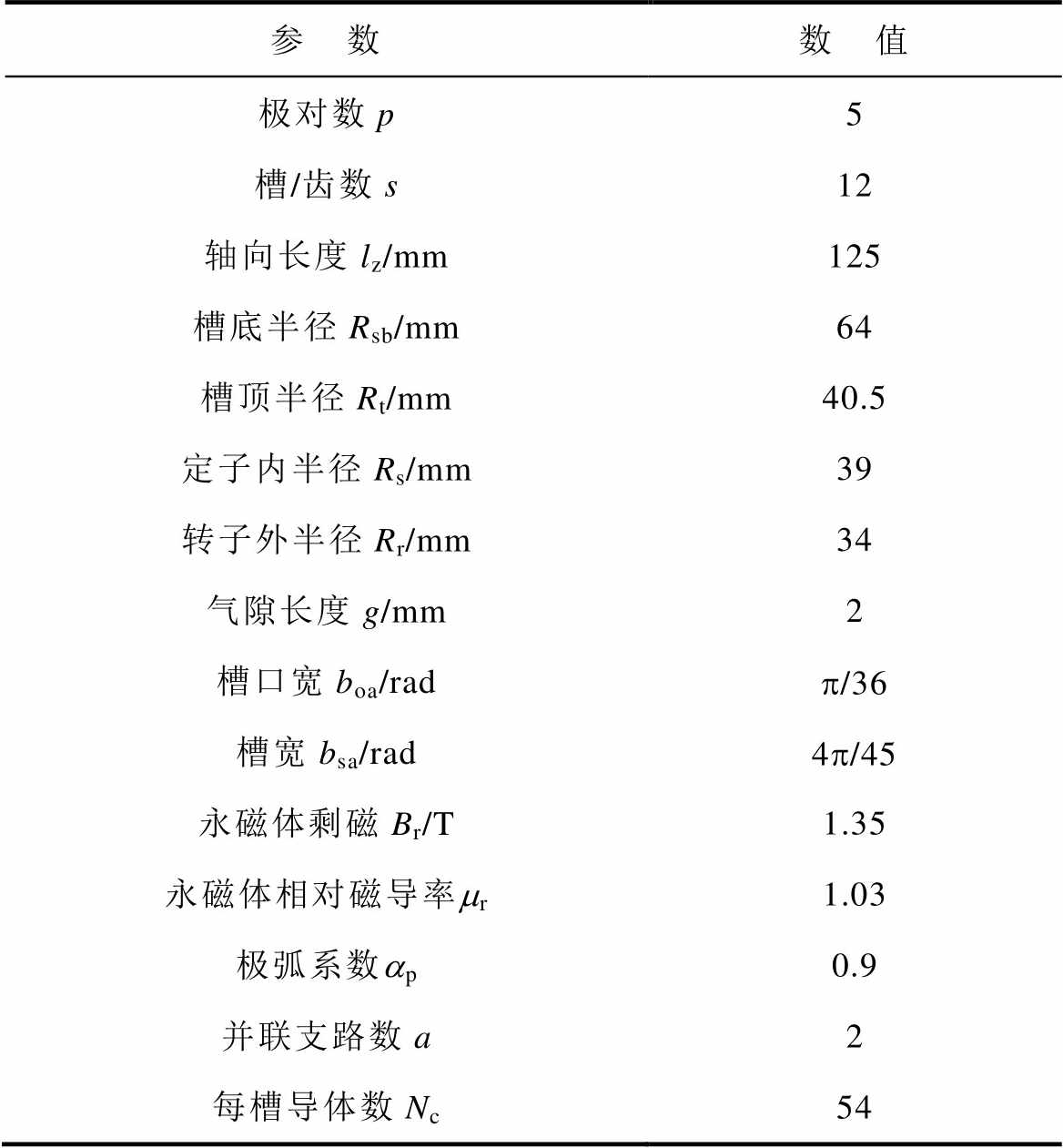
为了验证上述模型的正确性,以一台10极12槽永磁体平行充磁电机为样机,电机参数见表1。
表1 永磁电机的主要参数
Tab.1 Main parameters of permanent magnet motor
参 数数 值 极对数p5 槽/齿数s12 轴向长度lz/mm125 槽底半径Rsb/mm64 槽顶半径Rt/mm40.5 定子内半径Rs/mm39 转子外半径Rr/mm34 气隙长度g/mm2 槽口宽boa/radp/36 槽宽bsa/rad4p/45 永磁体剩磁Br/T1.35 永磁体相对磁导率mr1.03 极弧系数ap0.9 并联支路数a2 每槽导体数Nc54
采用Ansys/Simplorer建立了传统场路耦合有限元模型,并与本文提出的基于Matlab/Simulink建立的控制电路-解析模型联合仿真作对比,仿真模型示意框图如图4所示。

图4 仿真模型示意框图
Fig.4 Block diagram of simulation model
比较正常情况和局部退磁情况下的电机性能,局部退磁情况以一极永磁体退磁程度1/3(D=1/3)为例。控制电路均采用id=0矢量控制策略,仿真条件均为载波频率10 kHz,时间步长2 ms,直流母线电压Udc=350 V,电机转速nref=2 000 r/min,直交轴电流给定值id=0、iq=9 A。电机稳态时,解析模型-控制电路联合仿真和时步有限元模型在正常和局部退磁情况下求得的电机定子磁链如图5所示。局部退磁情况下,正常的磁体附近的磁场仍保持不变,发生退磁的永磁体产生的磁场下降,导致磁场分布不均匀,在磁链和电流中引入谐波。
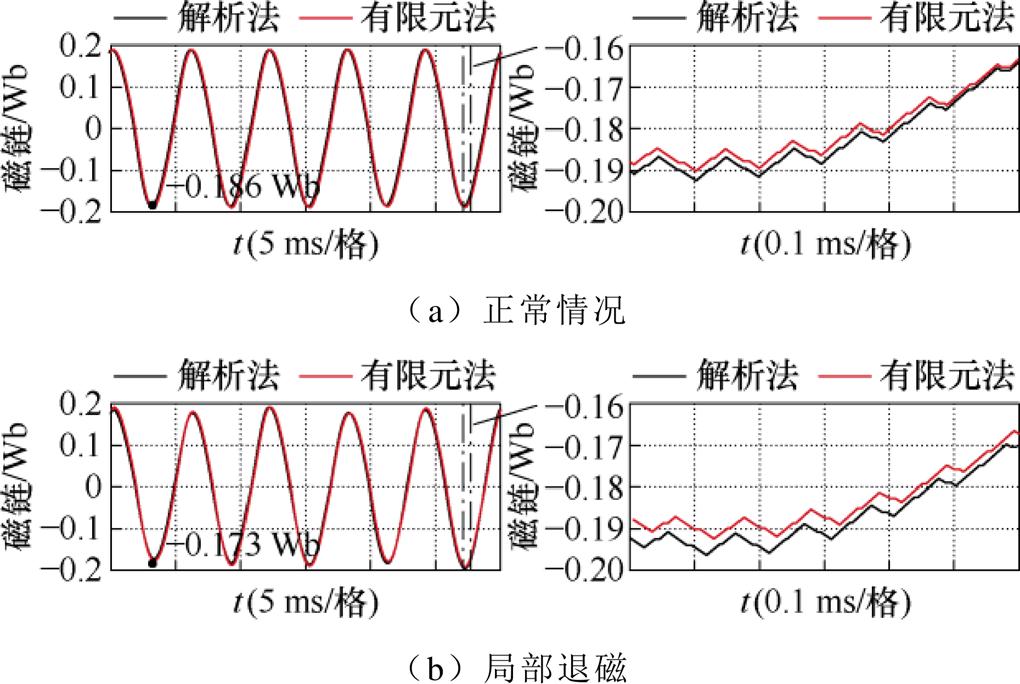
图5 磁链对比
Fig.5 Flux linkage comparison
两种模型在两种情况下求得的电机定子电流如图6所示。以一个机械周期为例进行两种模型计算的电机A相电流谐波分析,其谐波频谱如图7所示。
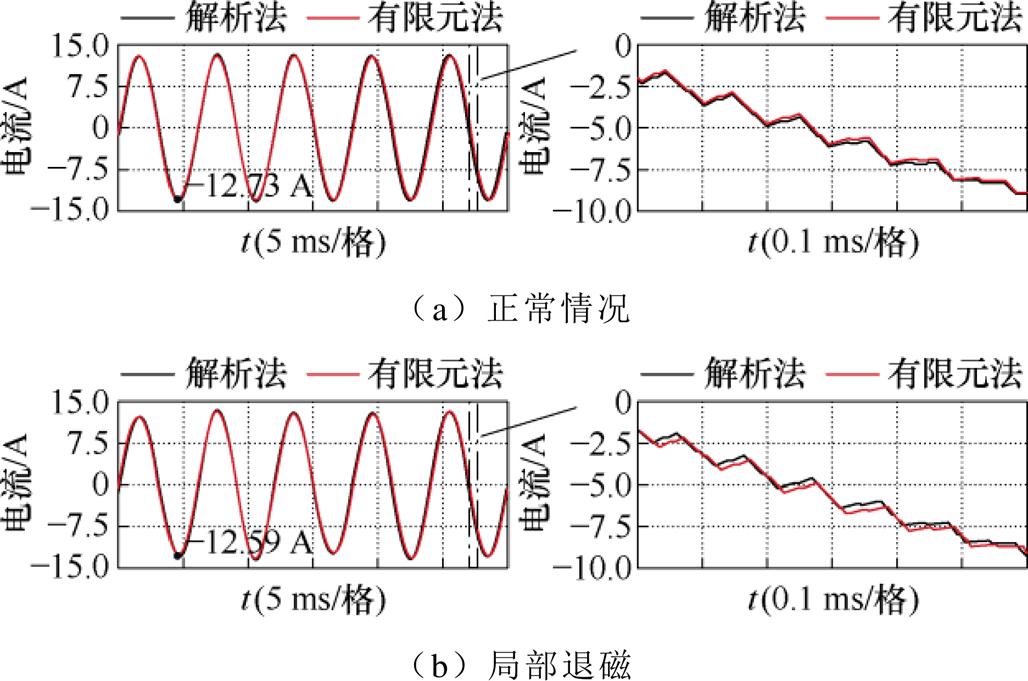
图6 电流对比
Fig.6 Current comparison
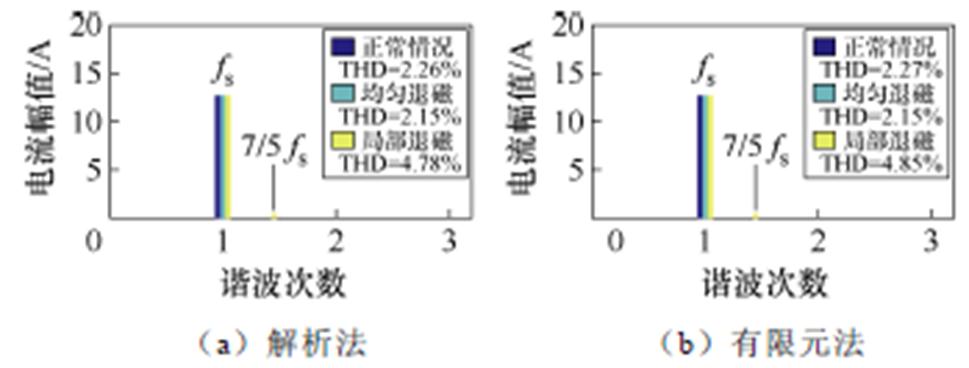
图7 电机电流谐波频谱(fs=166.67 Hz)
Fig.7 Harmonics in the current relative to fundamental at fs=166.67 Hz
局部退磁情况下除了基波与3次谐波还会在空载反电动势中引入基频附近的故障特征谐波,致使反电动势发生畸变,其频率为
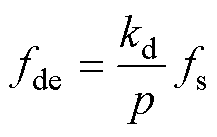 (25)
(25)
式中,fde为退磁故障频率;fs为电源频率;kd为正整数。
由于样机的极槽配合(p=5, s=12),反电动势中频率为2/5次电源频率及其整数倍(kd=2, 4, 6,…)的故障特征谐波被抑制[24]。因为电机绕组为星形联结,3次谐波无法在星形联结绕组中流通,正常电机相电流中几乎只存在基波分量,且局部退磁情况kd=3和其整数倍(kd=3, 6, 9,…)的谐波消失。通过对相电流谐波的分析,局部退磁会使定子电流中出现7/5次谐波,与理论分析吻合。各次谐波占比最大相对误差为0.256 5%,解析模型与有限元模型计算结果吻合。
图8显示了两种模型在额定电流下的电磁转矩。
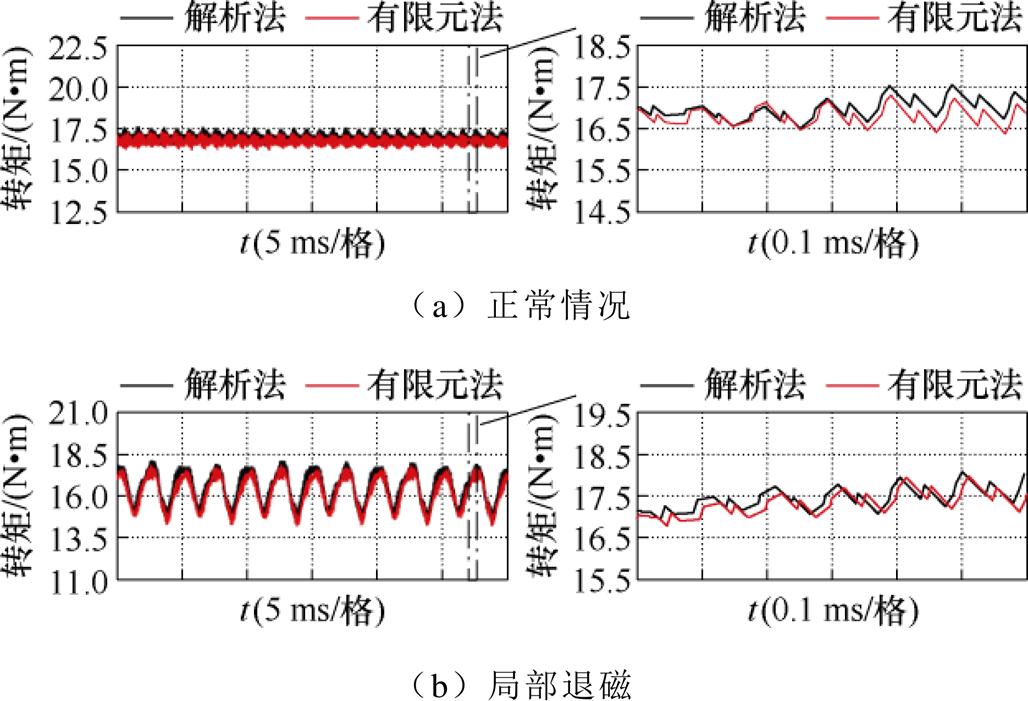
图8 转矩对比
Fig.8 Torque comparison
由图8可以看出,局部退磁的电磁转矩平均值较正常情况下降约2.5%,由于局部退磁的影响,转子对称性发生变化,转矩周期增大,磁场谐波增加,进而转矩脉动增大。
解析模型-控制电路联合仿真和时步有限元模型求得的磁链有效值、电流有效值和电磁转矩的平均值以及两者之间的误差见表2。误差为
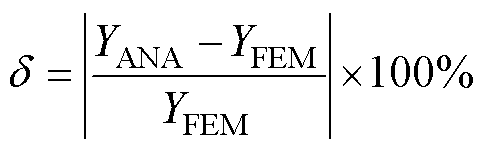 (26)
(26)
式中,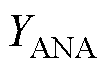 为解析模型的样机性能计算结果;
为解析模型的样机性能计算结果;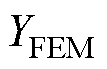 为时步有限元模型的样机性能计算结果。
为时步有限元模型的样机性能计算结果。
从表2可以看出,两种模型计算的定子磁链、定子电流和电磁转矩相对误差在正常情况下分别为0.997 7%、0.184 0%、和1.023 9%,局部退磁(D=1/3)时分别为0.231 7%、0.320 3%、0.945 2%。有限元法的结果略小于解析法的结果,原因是解析法未考虑饱和的影响。由计算结果可见,解析模型-控制电路联合仿真和时步有限元模型的计算结果基本吻合,验证了本文所建立的退磁故障解析模型-控制电路联合仿真的准确性。
表2 负载性能计算结果和误差对比
Tab.2 Comparison of load performance calculation results and errors
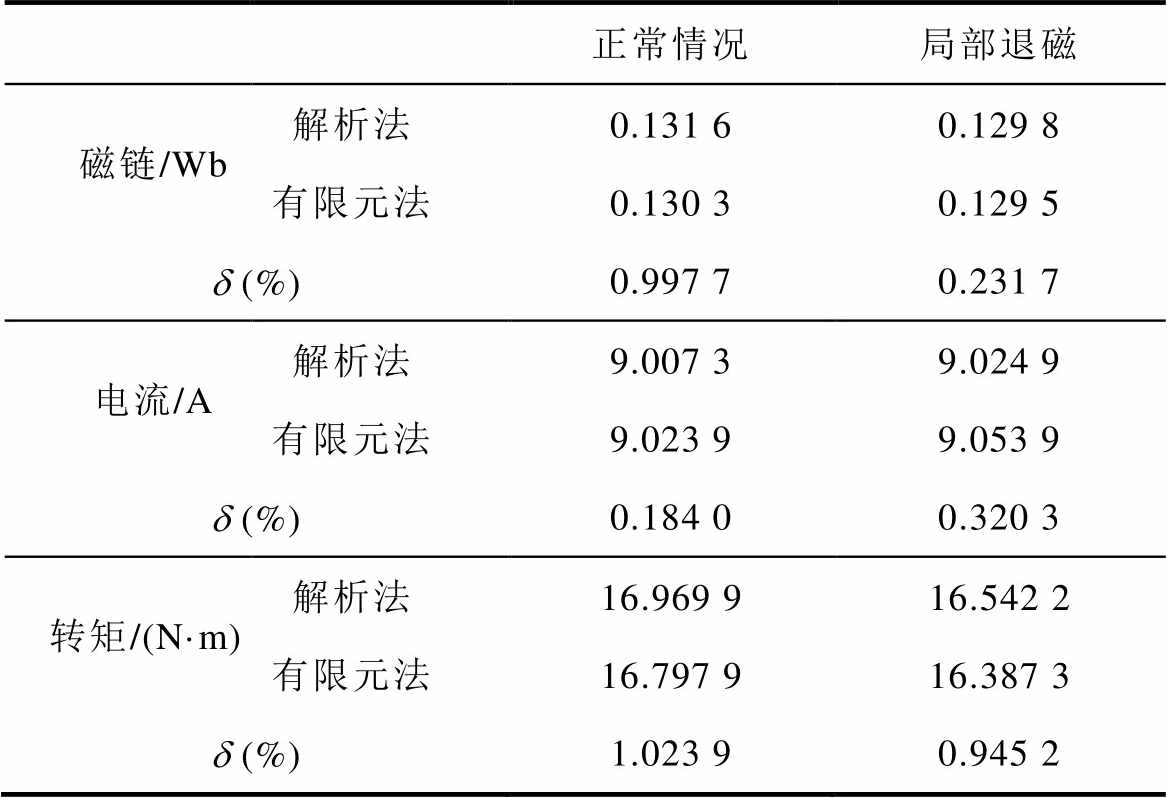
正常情况局部退磁 磁链/Wb解析法0.131 60.129 8 有限元法0.130 30.129 5 d (%)0.997 70.231 7 电流/A解析法9.007 39.024 9 有限元法9.023 99.053 9 d (%)0.184 00.320 3 转矩/(N·m)解析法16.969 916.542 2 有限元法16.797 916.387 3 d (%)1.023 90.945 2
在相同的仿真平台(i7-10700中央处理器@2.90 GHz)上进行计算,额定负载下解析模型-控制电路联合仿真与时步有限元模型在仿真步长为2 ms时计算一个电周期所需的时间见表3。
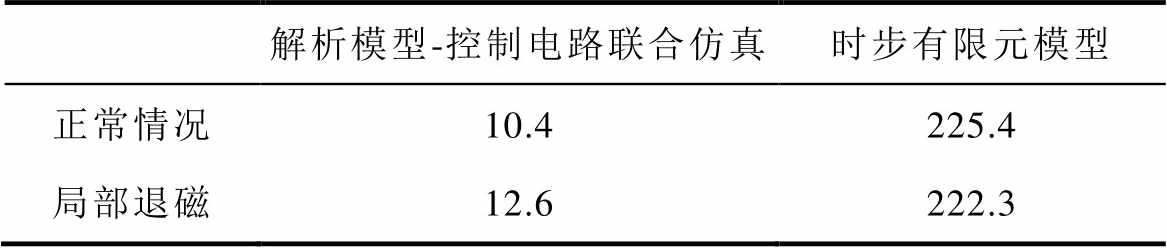
表3 计算时间对比
Tab.3 Computation time comparison (单位: min)
解析模型-控制电路联合仿真时步有限元模型 正常情况10.4225.4 局部退磁12.6222.3
从表3中可以看出,解析模型-控制电路联合仿真计算所需的时间大幅降低,约为时步有限元模型计算时间的1/20。因此,提供相同数量的样本数据的条件下,本文提出的方法可以比传统时步有限元方法节省约20倍的运算时间。
为了进一步验证所提出的解析模型-控制电路联合仿真的有效性,根据表1中的电机参数,制作了正常和局部退磁的10极12槽永磁同步电机样机。局部退磁情况一极永磁体中1/3替换为不充磁永磁体,故障样机定转子实物如图9所示。

图9 样机定转子实物
Fig.9 The stator and rotor of the prototype motor
样机测试实验基于ACS580-C24-09A8通用电机驱动器和测功机建立实验平台,平台实物照片如图10所示。其中测功机与被测电机通过联轴器连接,在上位机界面控制测功机。当电机稳定运行在转速n=2 000 r/min,负载转矩TL=15 N·m时,通过示波器采集样机的三相电流波形如图11a所示。在正常情况下的电机相电流主要由基波构成。局部退磁情况下磁场分布不均匀,在相电流中引入谐波,发生明显畸变,总谐波畸变率增加。以一个机械周期为例进行电机A相电流谐波分析,其谐波频谱如图11b所示。

图10 实验平台
Fig.10 Experimental platform
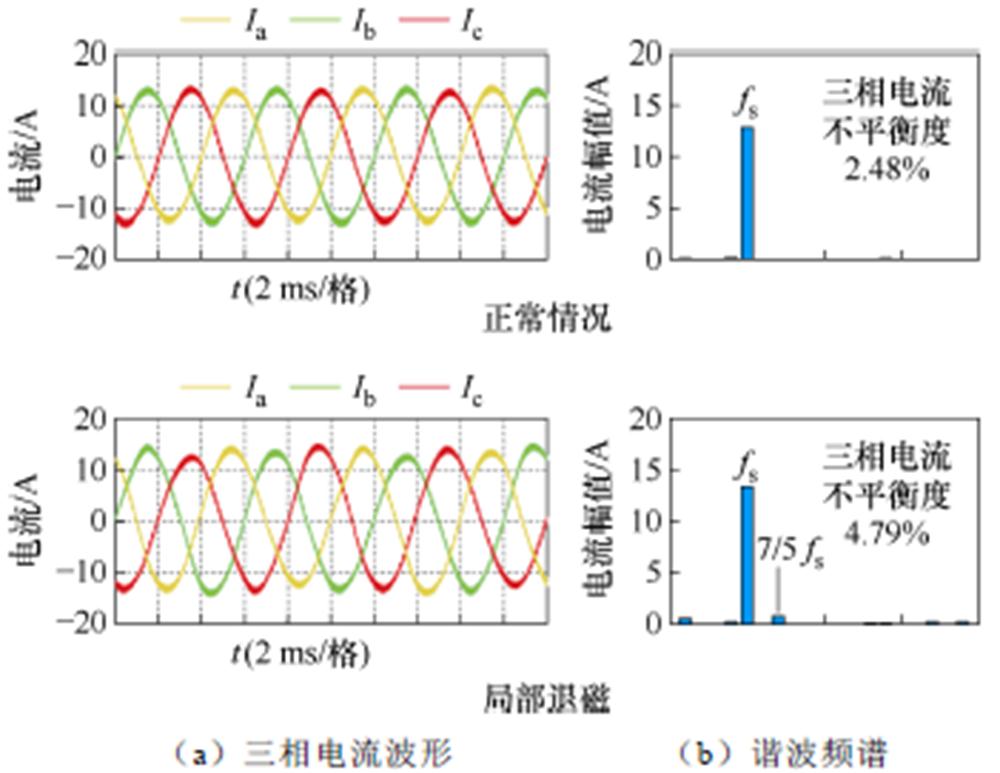
图11 三相电流波形及其频谱
Fig.11 Three-phase current and its spectrum
三台样机的一个机械周期的A相电流实验测试值、解析模型-控制电路联合仿真计算值和时步有限元模型的计算值对比如图12所示,可以看出,实测值与仿真值吻合良好。
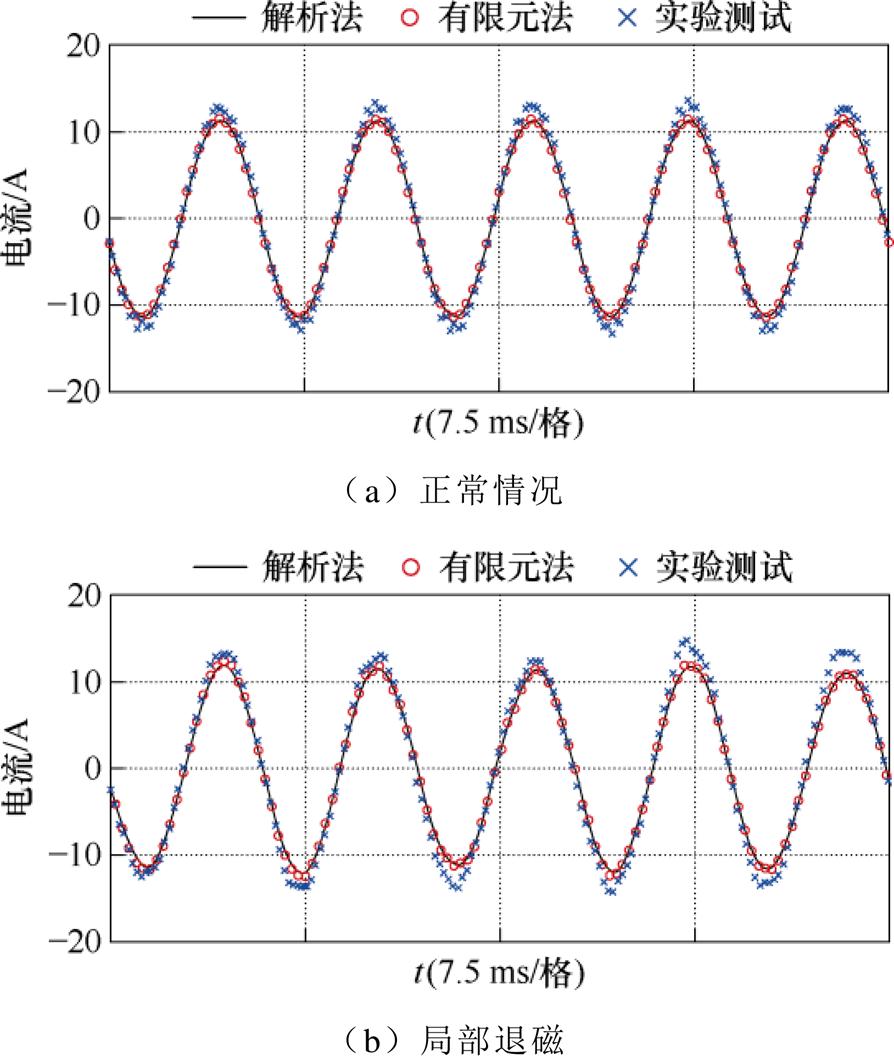
图12 电流对比
Fig.12 Current comparison
两台样机三种方法的相电流有效值见表4。以有限元法的计算结果为基准,两台电机解析法相电流有效值的误差分别为0.9%和1.3%,实验测量的相电流有效值的误差分别为12.6%和14.6%。产生相同转矩时实验测试的相电流偏大的原因可能有实验所测转矩为电磁转矩减去机械损耗转矩的差值,实际电机产生的电磁转矩大于所测输出转矩的值,所需的电流偏大;额定运行时永磁体温度上升,剩磁降低,达到相同转矩所需电流偏大;此外用于永磁体材料和铁心材料生产时的批次性误差、样机生产时的机械公差及人工测量时的偶然性误差也会导致误差的存在。
表4 电流有效值对比
Tab.4 Comparison of root mean square of current (单位: A)
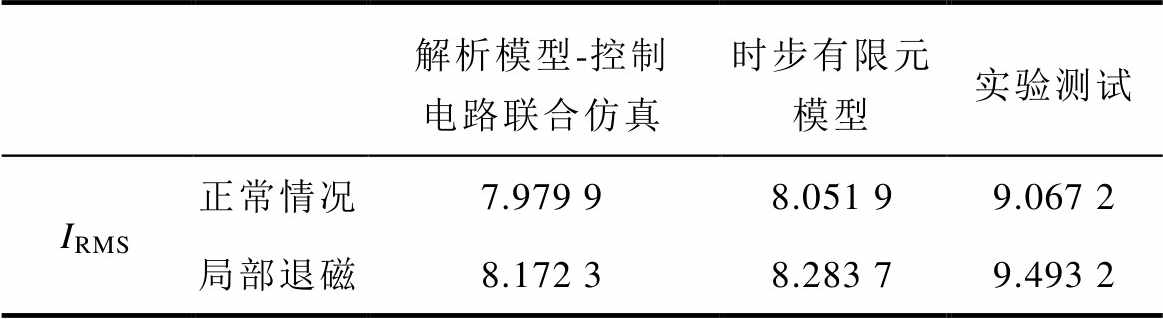
解析模型-控制电路联合仿真时步有限元模型实验测试 IRMS正常情况7.979 98.051 99.067 2 局部退磁8.172 38.283 79.493 2
以一个机械周期为例进行三种方法局部退磁情况下电机相电流谐波分析,其谐波频谱如图13所示。
表5显示了局部退磁情况下电机利用解析模型-控制电路联合仿真与时步有限元模型求得的相电流经过快速傅里叶变换(Fast Fourier Transform, FFT)后得到的各次谐波成分对比。通过对相电流谐波的分析,局部退磁使定子电流中出现7/5次谐波,与理论分析及仿真结果一致,验证了解析模型-控制电路联合仿真结果的准确性。
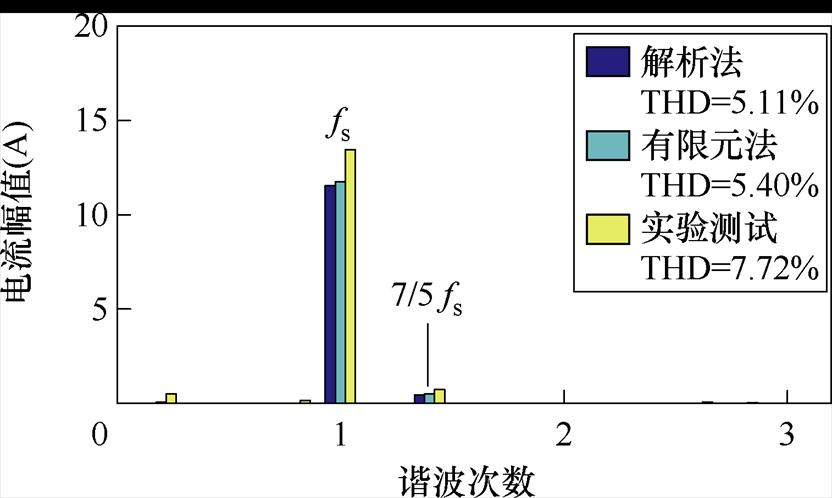
图13 电机A相电流谐波频谱(fs=166.67 Hz)
Fig.13 Harmonics in the A phase current relative to fundamental at fs=166.67 Hz
表5 电流谐波成分对比
Tab.5 Comparison of harmonic components of current
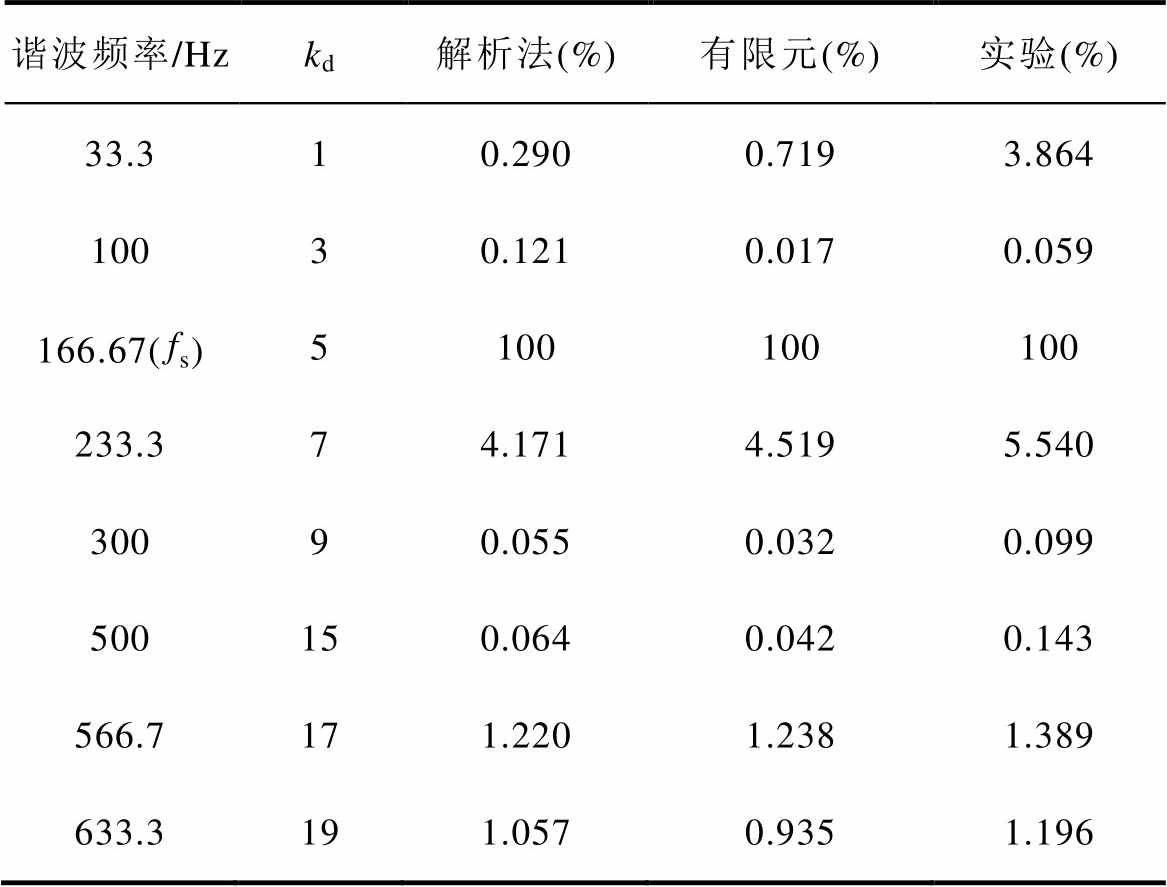
谐波频率/Hzkd解析法(%)有限元(%)实验(%) 33.310.2900.7193.864 10030.1210.0170.059 166.67( fs)5100100100 233.374.1714.5195.540 30090.0550.0320.099 500150.0640.0420.143 566.7171.2201.2381.389 633.3191.0570.9351.196
本文在子域法解析模型的基础上,提出一种通过改变永磁体局部退磁区域的剩余磁化强度来模拟退磁故障的解析建模方法。此外,以磁链为中间变量,将电机内部磁场与外部电源电压相耦合,建立了永磁同步电机退磁故障解析模型与控制电路的联合仿真模型,实现了对样机局部退磁情况下的运行性能的快速仿真。主要结论如下:
1)引入一个表示永磁体局部退磁区域空间位置角的参数D,通过推导D与永磁体剩余磁化强度径向和切向傅里叶系数的关系,推导了局部退磁区域对剩余磁化强度大小和波形的影响,从而建立了永磁体局部退磁情况下的电机解析模型。
2)基于上述解析模型,建立了永磁同步电机退磁故障解析模型与电压源控制电路的联合仿真模型,仿真了10极12槽表贴式样机在正常和局部退磁(D=1/3)情况下的负载性能,并建立了时步有限元模型进行了对比。结果显示,两种模型计算的定子磁链、定子电流和电磁转矩的相对误差在正常情况和局部退磁(D=1/3)情况均小于1.5%,表明本文所建立的故障解析-控制电路联合仿真模型与时步有限元模型计算结果基本吻合,但所需的计算时间仅为后者的1/20,大大提高了运算效率。
3)制作了故障样机,搭建了实验平台,实测了样机在相同控制策略下的电流波形并进行了频谱分析,局部退磁使定子电流中出现7/5次谐波,与仿真结果一致,验证了本文所建立的故障解析模型-控制电路联合仿真结果的准确性。
参考文献
[1] 章恒亮, 花为. 分布式驱动系统用轮毂电机及其技术综述[J]. 中国电机工程学报, 2024, 44(7): 2871- 2886.
Zhang Hengliang, Hua Wei. Overview of in-wheel traction machine and its key techniques for distributed-driving system[J]. Proceedings of the CSEE, 2024, 44(7): 2871-2886.
[2] 张丙楠, 杜博超, 赵天旭, 等. 舰船电力推进电机研究现状与发展综述[J]. 中国电机工程学报, 2022, 42(20): 7608-7623.
Zhang Bingnan, Du Bochao, Zhao Tianxu, et al. Overview of research status and development of ship electric propulsion motors[J]. Proceedings of the CSEE, 2022, 42(20): 7608-7623.
[3] 陈少先, 丁树业, 申淑锋, 等. 船舶用表贴式永磁同步电机的电磁振动分析与抑制[J]. 电工技术学报, 2023, 38(5): 1275-1286, 1298.
Chen Shaoxian, Ding Shuye, Shen Shufeng, et al. Analysis and suppression of electromagnetic vibration of surface mounted permanent magnet synchronous motor for ships[J]. Transactions of China Electro- technical Society, 2023, 38(5): 1275-1286, 1298.
[4] 崔刚, 熊斌, 黄康杰, 等. 电动汽车用永磁电机的失磁空间分布特性及影响因素[J]. 电工技术学报, 2023, 38(22): 5959-5974.
Cui Gang, Xiong Bin, Huang Kangjie, et al. Spatial distribution characteristics and influencing factors of demagnetization of permanent magnet motor for electric vehicle[J]. Transactions of China Electro- technical Society, 2023, 38(22): 5959-5974.
[5] 谢颖, 姜佳宁, 蔡蔚, 等. 表贴式高速永磁同步电机失磁故障及磁体选区渗重稀土研究[J]. 电机与控制学报, 2024, 28(2): 44-53.
Xie Ying, Jiang Jianing, Cai Wei, et al. Demag- netization failure of surface mount high speed permanent magnet synchronous motor and local infiltration of heavy rare earth[J]. Electric Machines and Control, 2024, 28(2): 44-53.
[6] 张丹, 赵吉文, 董菲, 等. 基于概率神经网络算法的永磁同步直线电机局部退磁故障诊断研究[J]. 中国电机工程学报, 2019, 39(1): 296-306, 344.
Zhang Dan, Zhao Jiwen, Dong Fei, et al. Partial demagnetization fault diagnosis research of per- manent magnet synchronous motors based on the PNN algorithm[J]. Proceedings of the CSEE, 2019, 39(1): 296-306, 344.
[7] 张建军, 岳啸鸣, 赵克斌, 等. 一起330MW汽轮发电机转子绕组短路故障分析及处理[J]. 电气技术, 2023, 24(3): 69-72.
Zhang Jianjun, Yue Xiaoming, Zhao Kebin, et al. Analysis and treatment of a 330MW turbine-generator rotor winding short circuit fault[J]. Electrical Engin- eering, 2023, 24(3): 69-72.
[8] 许小伟, 李随, 杨炎, 等. 基于数值计算的电机耦合故障特征提取[J]. 智能计算机与应用, 2021, 11(10): 43-49, 54.
Xu Xiaowei, Li Sui, Yang Yan, et al. Motor coupling fault feature extraction based on numerical calcu- lation[J]. Intelligent Computer and Applications, 2021, 11(10): 43-49, 54.
[9] 邱建琪, 沈佳晨, 史涔溦, 等. 基于残差卷积网络的多传感器融合永磁同步电机故障诊断[J]. 电机与控制学报, 2024, 28(7): 24-33, 42.
Qiu Jianqi, Shen Jiachen, Shi Cenwei, et al. Fault diagnosis of multi-sensor fusion permanent magnet synchronous motor based on residual convolutional neural network[J]. Electric Machines and Control, 2024, 28(7): 24-33, 42.
[10] 黄建, 尹佐生, 王天乙, 等. 基于容错齿磁通的五相永磁电机匝间短路故障诊断[J]. 电工技术学报, 2023, 38(14): 3733-3744.
Huang Jian, Yin Zuosheng, Wang Tianyi, et al. Diagnosis of inter-turn short-circuit fault for five- phase permanent magnet machine based on fault- tolerant tooth flux[J]. Transactions of China Electro- technical Society, 2023, 38(14): 3733-3744.
[11] 高彩霞, 苗壮, 陈昊, 等. 基于线圈子单元的永磁同步电机健康与定子绕组短路故障数学模型[J]. 电工技术学报, 2023, 38(4): 957-969.
Gao Caixia, Miao Zhuang, Chen Hao, et al. A mathematical model based on coil sub-element for permanent magnet synchronous motor with health and stator winding short-circuit fault[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 957- 969.
[12] Zeng Chong, Huang Song, Lei Jiayin, et al. Online rotor fault diagnosis of permanent magnet syn- chronous motors based on stator tooth flux[J]. IEEE Transactions on Industry Applications, 2021, 57(3): 2366-2377.
[13] Ullah Z, Lee S T, Hur J. A torque angle-based fault detection and identification technique for IPMSM[J]. IEEE Transactions on Industry Applications, 2020, 56(1): 170-182.
[14] Usman A, Rajpurohit B S. Modeling and classification of stator inter-turn fault and demagnetization effects in BLDC motor using rotor back-EMF and radial magnetic flux analysis[J]. IEEE Access, 2020, 8: 118030-118049.
[15] Xu Qi, Liu Xuyang, Miao Wenchao, et al. Online detecting magnet defect fault in PMSG with magnetic sensing[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2775-2786.
[16] Li Zhaokai, Huang Xiaoyan, Yu Yelong, et al. Nonlinear analytical modelling for surface-mounted permanent magnet motors with magnet defect fault[J]. IEEE Transactions on Energy Conversion, 2022, 37(3): 1955-1964.
[17] De Bisschop J, Sergeant P, Dupré L. Demagnetization fault detection in axial flux PM machines by using sensing coils and an analytical model[J]. IEEE Transactions on Magnetics, 2017, 53(6): 8203404- 8203407.
[18] De Bisschop J, Sergeant P, Hemeida A, et al. Analytical model for combined study of magnet demagnetization and eccentricity defects in axial flux permanent magnet synchronous machines[J]. IEEE Transactions on Magnetics, 2017, 53(9): 8107712.
[19] Verkroost L, De Bisschop J, Vansompel H, et al. Active demagnetization fault compensation for axial flux permanent-magnet synchronous machines using an analytical inverse model[J]. IEEE Transactions on Energy Conversion, 2020, 35(2): 591-599.
[20] Quintal-Palomo R E, Flota-Bañuelos M, Bassam A, et al. Post-fault demagnetization of a PMSG under field oriented control operation[J]. IEEE Access, 2021, 9: 53838-53848.
[21] Shi Cenwei, Peng Lin, Zhang Zhen, et al. Analytical modeling and analysis of permanent-magnet motor with demagnetization fault[J]. Sensors (Basel, Switzerland), 2022, 22(23): 9440.
[22] Wu L J, Zhu Z Q, Staton D, et al. Analytical prediction of electromagnetic performance of surface- mounted PM machines based on subdomain model accounting for tooth-tips[J]. IET Electric Power Applications, 2011, 5(7): 597-609.
[23] Zheng Bining, Zhang Zhen, Yan Dong, et al. A direct field-circuit coupled analytical modelling method for permanent magnet motor operation performance analysis[J]. IET Electric Power Applications, 2023, 17(2): 149-160.
[24] Zafarani M, Goktas T, Akin B. A comprehensive analysis of magnet defect faults in permanent magnet synchronous motors[C]//2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 2015: 2779-2783.
Abstract The demagnetization fault of permanent magnet synchronous motors (PMSM) reduces output performance and load capacity, seriously affecting the motor’s service life. Establishing an accurate fault motor analytical model, conducting rapid electromagnetic performance analysis, and obtaining operational data such as current and torque under fault conditions are beneficial for early prediction and diagnosis of demagnetization faults.
A parameter D is introduced for the partial demagnetization fault of the surface-mounted PMSM prototype, representing the spatial angle of the demagnetized region, defined as the ratio of the spatial angle occupied by the demagnetized region to that of one pole arc. The radial and tangential component equations of the residual magnetization Fourier coefficients as a function of parameter D are derived, which reflect the influence of the spatial angle of the demagnetized region on the magnitude and the waveform of the residual magnetization. An analytical model of PMSM under partial demagnetization is established.
In addition, regarding the control system’s circuit interface in practical applications, an analytical model of demagnetization faults in a PMSM driven by a voltage source inverter with magnetic flux linkage as the intermediate variable is established. This model is applied to the vector control circuit. Thus, a co-simulation model combining the analytical model and the control circuit is created.
The load performance of the prototype is calculated under normal conditions and partial demagnetization using the co-simulation model. Compared with the simulation results from the Ansys/Simplorer time-stepping finite element method and the measured results from the prototype on the experimental platform, the conclusions are as follows. (1) The proposed partial demagnetization analytical model reflects the influence of the demagnetized region on the magnitude and the waveform of the residual magnetization. This model is more consistent with actual conditions than the method of equating partial demagnetization to an overall reduction in magnetic flux linkage. (2) The calculation results of the co-simulation model are in good agreement with the time-stepping finite element simulation results, with the relative errors for the stator flux linkage, stator current, and electromagnetic torque less than 1.5% under normal and partial demagnetization conditions. Furthermore, the computation time of the co-simulation model is only 1/20 that of the finite element model, which greatly improves the operation efficiency. (3) The current waveforms of the prototype under the same control strategy are measured on the experimental platform and subjected to spectral analysis. The results are consistent with the co-simulation results, which validate the accuracy of the co-simulation model, combining the analytical model and the control circuit.
Keywords:Permanent magnet synchronous motor, demagnetization fault, analytical modeling
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.240646
国家重点研发计划(2022YFB2502603)和浙江省自然科学基金(LQ22E070008)资助项目。
收稿日期 2024-04-24
改稿日期 2024-07-26
史涔溦 女,1970年生,副教授,研究方向为永磁电机设计与控制。
E-mail: singing@zju.edu.cn
史婷娜 女,1969年生,教授,博士生导师,研究方向为电机系统及其控制。
E-mail: tnshi@zju.edu.cn(通信作者)
(编辑 崔文静)