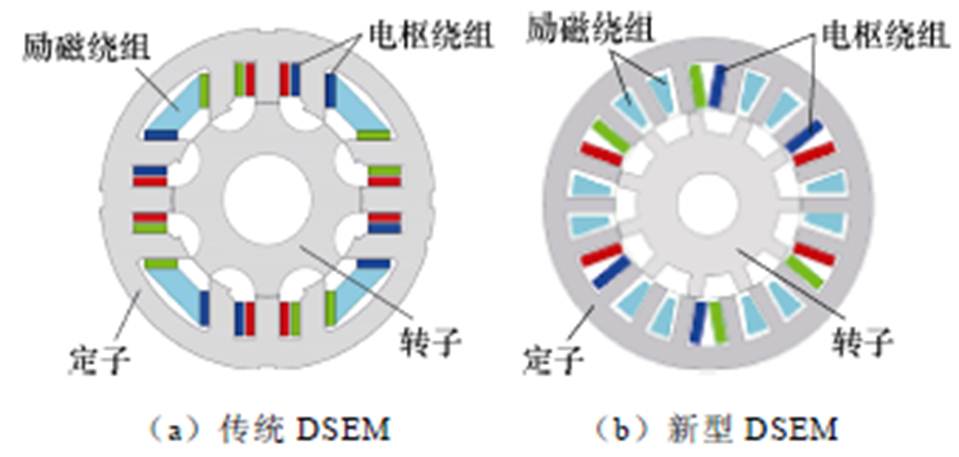
图1 DSEM的拓扑结构
Fig.1 Topology of DSEM
摘要 电励磁双凸极电机（DSEM）具有结构简单、制造成本低、可靠性高等优点，在电动汽车、航空航天等领域具有较好的应用前景，然而由于其转矩脉动较大、转矩密度不高，一定程度上限制了其发展应用。为了提高转矩性能，该文提出一种新型DSEM的拓扑结构，通过改变绕组连接形式和定转子极数配合，提高电机的转矩密度，并降低转矩脉动。分析了新型双凸极电机的工作机理，详细阐述了新型双凸极电机的定转子极数配合方法与电枢绕组形式，在此基础上根据磁场调制机理分析了定转子极数与磁场谐波及电磁转矩之间的联系，研究了不同转子极数对电机电磁性能的影响。最后，制作了一台新型18/11极双凸极电机样机，实验验证了理论分析的正确性和新型双凸极电机拓扑结构的优越性。
关键词：电励磁双凸极电机 磁场调制机理 极数配合 电磁转矩
电励磁双凸极电机（Doubly Salient Electric- excited Motor, DSEM）是在开关磁阻电机的定子上加入励磁绕组的一种双凸极结构电机，不但继承了开关磁阻电机转子上无绕组、转子结构简单、便于散热、转子转动惯量低、动态响应速度快的优点，并且在功率密度和效率上得到了提升，有研究表明，DSEM还具有功率密度高、容错性能好、控制灵活等优点，因此自问世以来一直受到国内外学者和研究机构的广泛关注，并在航空航天、风力发电、电动汽车驱动等领域得到初步应用[1-5]。
为了进一步提高双凸极电机的转矩密度，降低转矩脉动，国内外专家学者对其开展了定子结构、定/转子极数配合、转子极宽、转子槽型、励磁形式、控制技术等因素对电机性能影响的深入研究，并提出了多种改进方案。文献[6]提出了3N/4N极的电励磁双凸极发电机，详细分析了其功率密度、电压纹波和功率等变量，通过24/32极DSEM样机实验验证了其在低速发电场合的良好运行特性。文献[7]研究了用于增程式电动汽车车载系统的电励磁双凸极发电机，提出了三相12/8极和四相16/12极DSEM，通过对两种方案进行分析，选择了适合宽转速范围的12/8极DSEM的方案，并得到了实际装车应用。文献[8]设计了12/8极双定子结构DSEM，其两个定子沿轴向并列，两个转子错开差7.5°机械角，使电枢绕组相位错开60°电角度，两个定子轴向上对齐且间隔一段距离以实现电磁隔离，电机各相更为均衡，能有效地降低起动过程的转矩脉动。文献[9-10]为了解决传统多相DSEM存在的各相电感不对称与定位转矩问题，建立了多相DSEM普遍使用的定子极数、转子极数和定转子极弧系数等结构参数的约束公式，提出了一种新型短距励磁绕组绕制与布置方式，并提出了电感对称的四相、五相和六相双凸极电机拓扑结构。文献[11]提出了一种定子极为p 型结构的12/7极双凸极电机，相比传统的E型定子铁心双凸极电机，消除了磁路不对称，相绕组感应电动势呈现较高的正弦度，气隙磁场调制理论和有限元分析及实验均表明该电机具有较高的转矩密度，且相比12/8极E型铁心双凸极电机，12/7极p 型定子铁心双凸极电机的转矩脉动显著减小。文献[12-13]提出了一种定子不等极距的双向磁链12/7极永磁和混合励磁双凸极电机，通过改变电枢绕组绕制方式，使得电枢绕组磁链呈双极性变化，增大了电机的转矩密度，通过在定子上增加励磁绕组，提高电机的调磁能力。文献[14-15]根据磁场调制机理分析了不同定转子极数对双凸极变磁阻电机电磁性能和励磁绕组感应电动势纹波的影响。另外，为了降低电机的转矩脉动，双凸极电机控制技术得到不断改进，例如：文献[16]提出了基于换相提前角度与参考电流增益系数优化的转矩脉动补偿控制；文献[17]提出了基于电流变化特征的转矩闭环控制策略；文献[18-19]提出了改进型直接瞬时转矩控制，多正弦电流叠加控制；文献[20-21]分析了正弦供电双凸极同步磁阻电机的电枢电感各次谐波对输出转矩的贡献，推导了输出转矩的傅里叶级数展开计算公式，为进一步研究转矩脉动抑制策略提供了理论指导；文献[22]针对磁场调制双凸极磁阻电机提出了新型瞬时电磁转矩建模与电流分配策略，在不牺牲输出转矩和系统效率的情况下显著降低了转矩脉动。
虽然近年来有关双凸极电机的研究已经取得了诸多成果，然而相比于常规永磁同步电机，其转矩密度不够高、转矩脉动较大、振动噪声显著等问题依然是制约其发展和应用的主要原因[23-24]。为了进一步增大电机的转矩密度，本文通过改变励磁绕组和电枢绕组位置及绕制方式，提出了一种新型DSEM，不但实现了电机反电动势正弦化及电枢绕组磁链双极性变化，还具有较低的转矩脉动和较高的转矩密度。本文详细阐述了DSEM的定转子极数配合方法与电枢绕组形式，并根据磁场调制机理分析了定转子极数与磁场谐波及转矩谐波之间的联系，研究了不同转子极数对电机电磁性能的影响；在此基础上，制作了一台新型18/11极双凸极电机样机，实验验证了理论分析的正确性。
图1a所示为某传统三相12/8极DSEM的拓扑结构，定转子铁心均由凸极结构的硅钢片叠压而成；相绕组由跨距为1的4个集中式线圈串联而成，三相绕组依次排列；励磁绕组由跨距为3的4个集中式线圈串联而成，为了增大励磁绕组位置空间，定子凸极采用平行齿结构。通过对该电机电磁特性的分析可知，电机绕组磁链为单极性磁链，转矩密度不够高，且电机反电动势波形接近方波，需要采用方波驱动，存在转矩脉动大的缺点。
图1 DSEM的拓扑结构
Fig.1 Topology of DSEM
为了提高双凸极电机的转矩密度，降低转矩脉动，本文提出了如图1b所示的一种新型18/11DSEM，集中式励磁绕组由跨距为1的6个励磁线圈构成，相邻励磁线圈之间间隔两个定子齿；集中式电枢线圈跨励磁线圈及其两侧各一个定子凸极缠绕，三相电枢线圈依次排列，同相电枢线圈相互串联构成相绕组。
新型DSEM的工作原理如图2所示。设电机转子凸极与A相某电枢线圈A1所跨定子中间凸极PAM对齐位置为初始位置。在转子处于0°位置时，转子凸极逐渐滑出B1线圈所跨定子右侧凸极PBR，并逐渐滑入C1线圈所跨定子左侧凸极PCL，根据最小磁阻原理，A1线圈所跨励磁线圈通直流电流产生的励磁磁通FFA分别流经B1与C1线圈对应定子凸极PBR与PCL，并分别经气隙、转子凸极形成闭合回路，其磁路如图2a所示，此时A1线圈磁链达到正向最大值。当转子转到90°位置时，转子凸极完全滑出定子凸极PAM，励磁磁路如图2b所示，FFA一部分流经两侧相邻凸极而形成漏磁回路，另一部分流经定子凸极PCL，且B1线圈对应励磁磁通FFB一部分流经A1线圈所跨左侧凸极PAL，此时A1线圈合成磁链为零。当转子转到180°位置时，励磁磁路如图2c所示，FFA经相邻两侧凸极闭合而形成漏磁回路；FFB分别经B相定子中间凸极PBM、定子轭部、PAL、气隙、转子凸极和轭部形成主磁路；C1线圈对应励磁磁通FFC分别经C相中间定子凸极PCM、定子轭部、A相右侧凸极PAR、气隙、转子凸极和轭部形成主磁路，此时A1线圈磁链达到反向最大值。当转子转到270°位置时，励磁磁路如图2d所示，FFA一部分流经两侧相邻凸极而形成漏磁回路，另一部分流经定子凸极PBR，且FFC一部分流经PAR，此时A1线圈合成磁链为零。
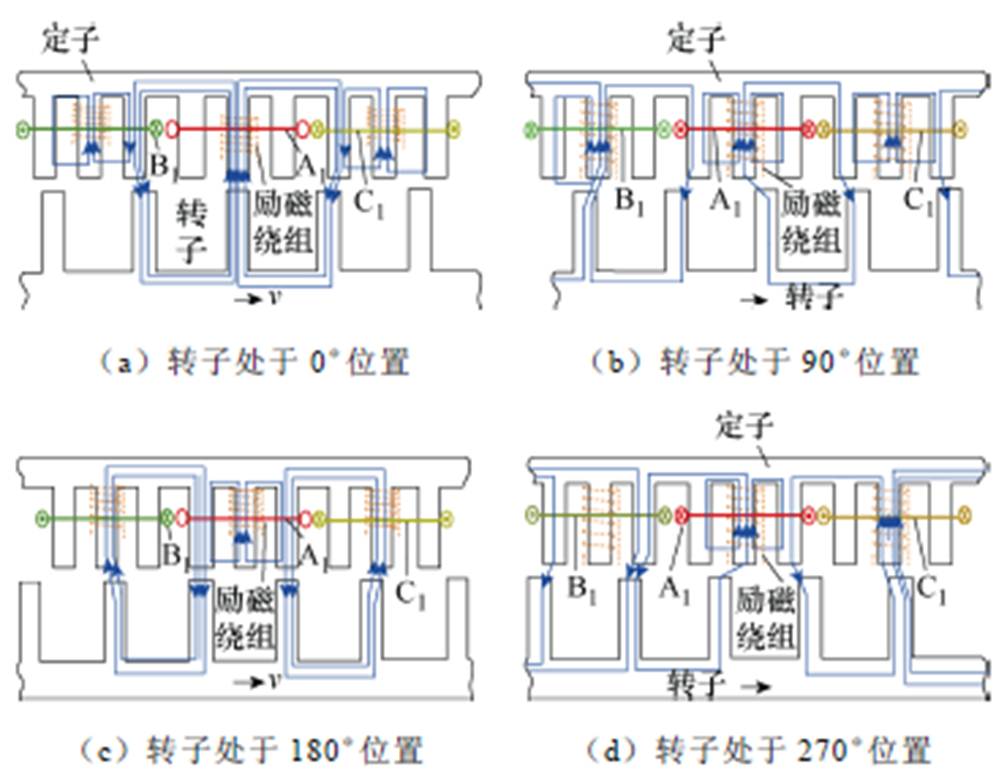
图2 新型DSEM的工作原理
Fig.2 Working principle of the new DSEM
以某新型18/11DSEM为例，图3所示为有限元仿真所得组成A相绕组的线圈A1、A2及三相电枢绕组A、B、C的空载磁链波形。可见，电枢线圈磁链呈双极性变化，三相线圈磁链和反电动势对称性好，且具有较高的正弦度。
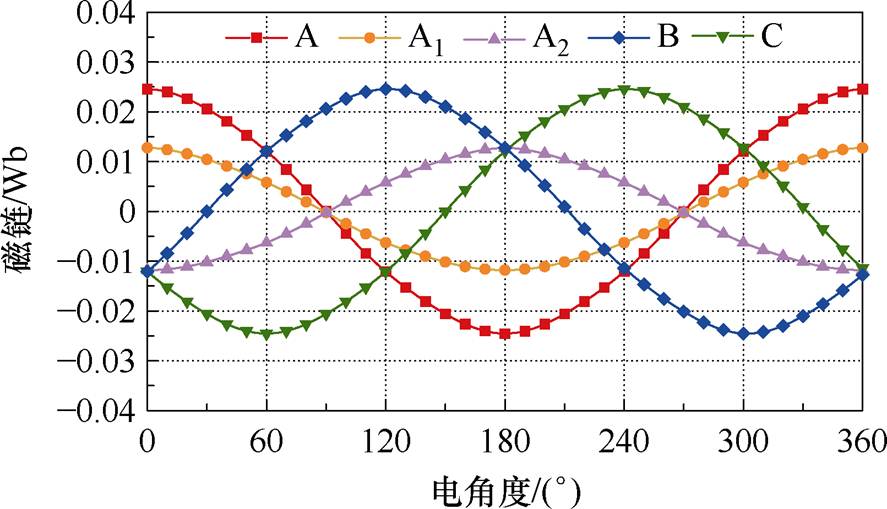
图3 线圈A1、A2及三相绕组的空载磁链
Fig.3 No-load flux linkage of A1, A2, A, B and C
根据新型DSEM的拓扑结构，每个相绕组的电枢线圈跨三个定子凸极缠绕，因此定子极数Ns为
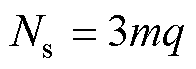（1）
式中，m为电机相数；q为大于0的任意自然数。
根据新型DSEM的工作原理，电机转子极数取极限时的定转子配合如图4所示，转子极数Nr的取值范围满足
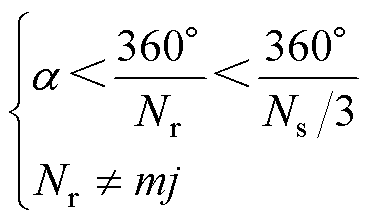（2）
式中，j为大于0的任意自然数；a 为电枢线圈所跨定子极的极距角，令D为定子凸极均匀分布时与不均匀分布时所对应极距角之差，则a 取值范围为
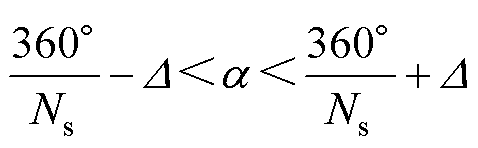（3）
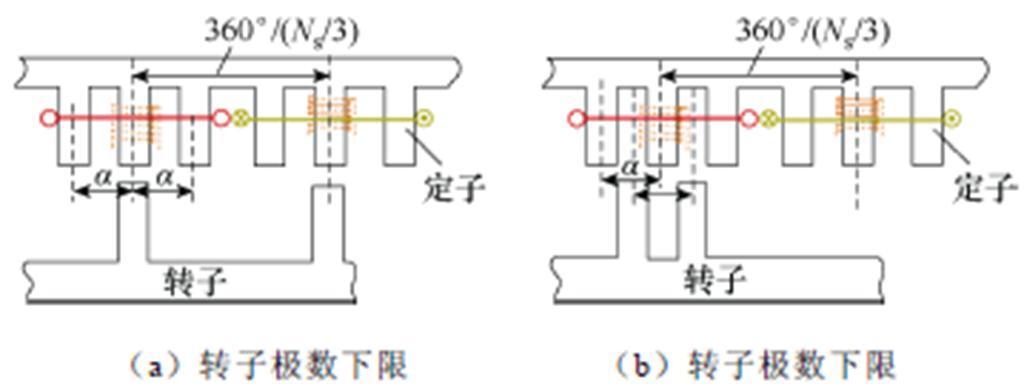
图4 电机定转子极数配合示意图
Fig.4 Stator/rotor pole number matching diagram
由式（2）、式（3）可得，定转子极数满足
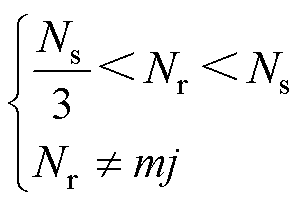（4）
根据新型DSEM的拓扑结构，单相电枢线圈数量na可表示为
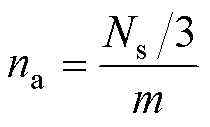（5）
相邻两个电枢线圈间的电角度差Dqe1为
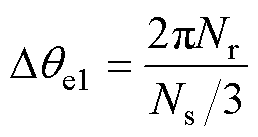（6）
同一相的两电枢线圈间的电角度差Dqe2为
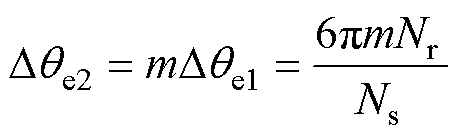（7）
当电机相数为3，且定子极数为18时，Dqe2= pNr。因此，不同转子极数电机的定子槽电动势星形图如图5所示。
图5 不同转子极数电机的定子槽电动势星形图
Fig.5 Star diagram of stator slot electromotive force for motors with different rotor poles
A相绕组两电枢线圈A1和A2在任意时刻t的反电动势eA1和eA2为
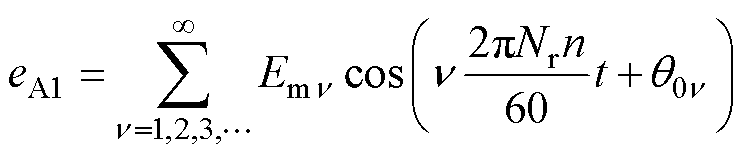（8）
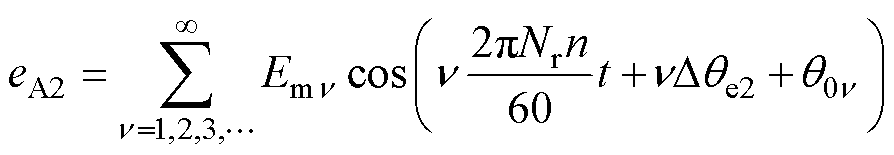（9）
式中，Emn 为n 次谐波槽电动势的幅值；q0n 为n 次谐波槽电动势的初始相位；n为电机转速（r/min）。
当转子极数为偶数时，每相绕组两电枢线圈槽电动势相位相同，正向串联，A相绕组电动势eA为
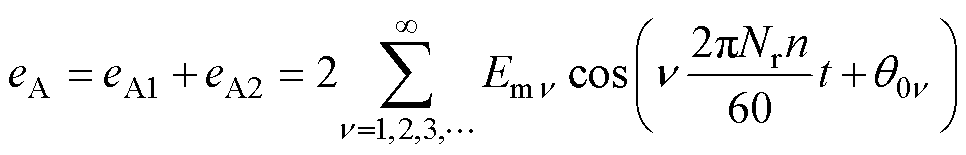（10）
当转子极数为奇数时，每相绕组两电枢线圈槽电动势相位相反，电枢线圈反向串联，A相绕组反电动势eA可表示为
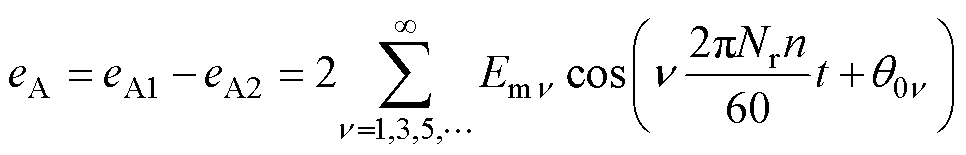（11）
可见，转子极数为奇数时，相绕组反电动势只含有奇数次谐波；当转子极数为偶数时，相绕组反电动势既含有奇数次谐波又含有偶数次谐波。
假设转子表面光滑，考虑定子极槽影响，新型DSEM电励磁绕组产生的空载气隙磁动势Fsf如图6所示，图中，d为同一线圈所跨定子凸极极距，w为定子凸极宽度的一半，Ff为磁动势最大值。根据磁通连续性定理和磁路欧姆定律可得，当同一电枢线圈所跨定子三个凸极宽度相同时，两侧定子凸极处所对应气隙磁动势幅值是中间定子凸极处气隙磁动势的一半，气隙磁动势Fsf的周期为2p/(Ns/3)，傅里叶级数展开形式为
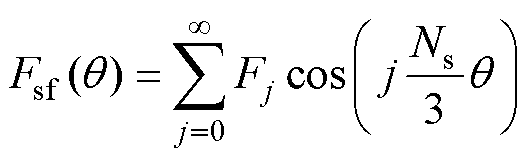（12）
式中，q 为定子凸极位置角。j次傅里叶系数Fj为
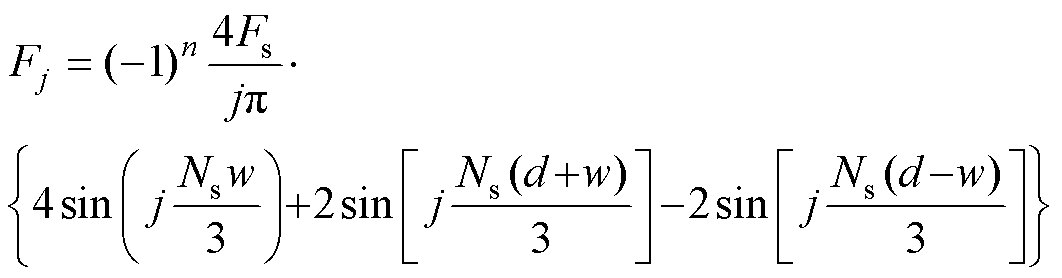（13）
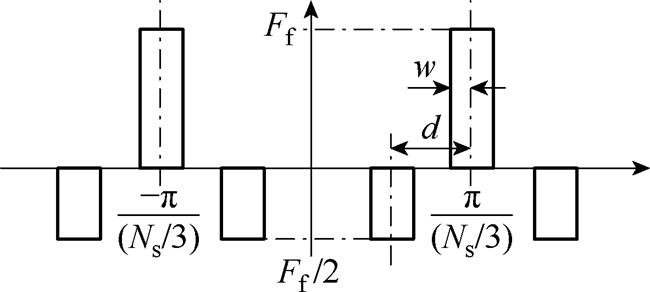
图6 空载气隙磁动势
Fig.6 Magnetomotive force of field winding
转子侧气隙磁导可表示为
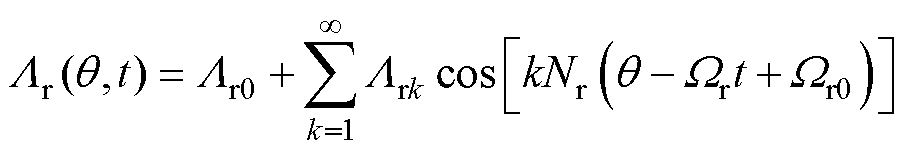（14）
式中，Lr0、Lrk分别为气隙磁导直流分量、k次谐波分量的傅里叶系数；k为气隙磁导谐波次数；Wr、Wr0分别为转子机械角速度及其初始值。
因此，电励磁磁动势产生的气隙磁通密度Bsf为
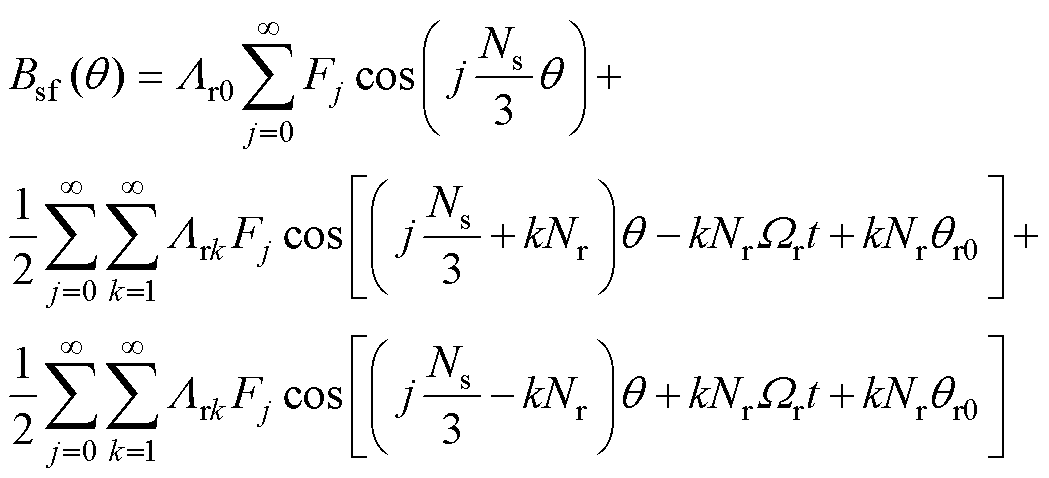（15）
当Ns=18时，空载气隙磁通密度谐波特性见表1。
相绕组磁动势与电枢线圈的串联极性有关，当转子极数为偶数时，极性相同的电枢线圈相串联，A相绕组电流iA产生的磁动势FsA为图7所示的偶谐函数，周期为2p/(Ns/3m)，傅里叶级数展开式为
表1 电励磁磁动势产生的气隙磁通密度谐波
Tab.1 Flux densityharmonics due to electromotive force
谐波次数谐波转速 6j0 6j+kNrkNrWr/(6j+kNr) 6j-kNr-kNrWr/(6j-kNr)
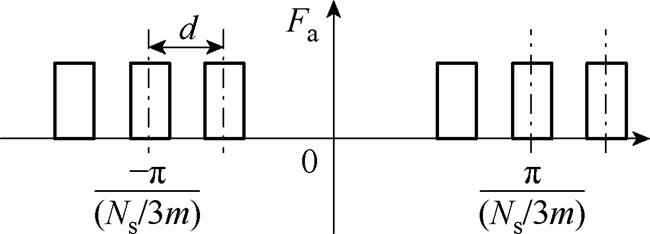
图7 相同极性电枢线圈串联时的相绕组磁动势
Fig.7 Phase winding magnetomotive force for armature coils with the same polarity connected in series
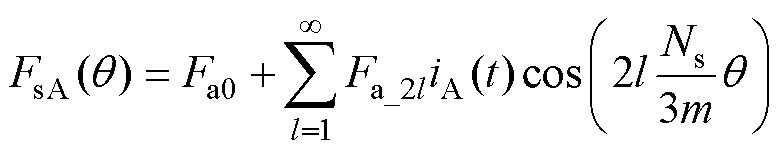（16）
式中，Fa0和Fal分别为直流分量和2l次谐波幅值。
三相对称绕组通入幅值为Im、角频率为we的三相对称电流iA、iB、iC，表达式为
（17）
令Ns=18，当且仅当
时，三相合成电枢反应磁动势Fsa非零，其表达式为
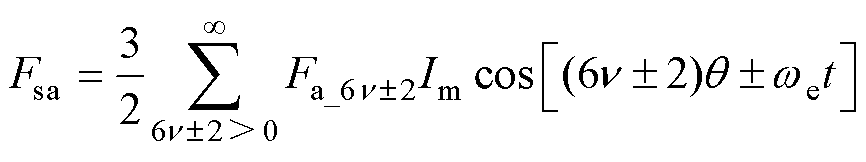（18）
式中，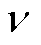
为任意正整数；Fa_6n±2为6n±2次傅里叶系数。
电枢反应磁动势Fsa产生的气隙磁通密度Bsa为
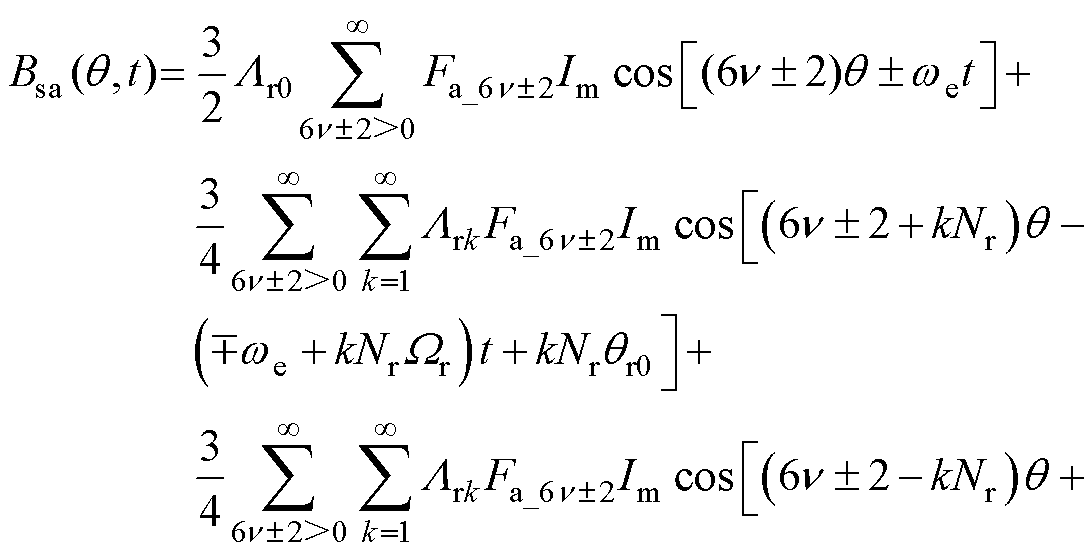
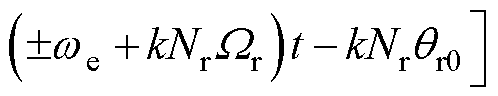（19）
电机电枢磁场气隙磁通密度谐波见表2，当Nr为非3的倍数之偶数时，电枢磁场中包含所有6j±kNr次谐波（j≥0，k≥1）。根据磁场调制理论，当空载气隙磁通密度与电枢反应磁通密度频次相同且转速相等时，两者相互作用能够产生恒定转矩，推导可得恒定转矩产生条件。
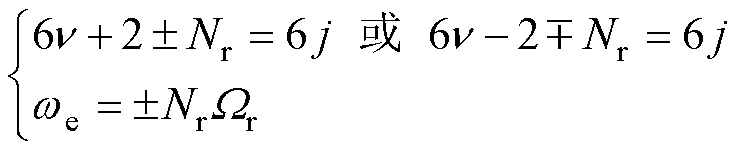（20）
表2 偶数转子极电枢磁场气隙磁通密度谐波特性
Tab.2 Armature reaction flux density harmonics for DSEM with even rotor poles
谐波次数谐波转速 6ν±2we/(6ν±2) 6ν+2±Nr+(k1)Nr(kNrWr-we)/(6ν+2+kNr) 6ν+2±Nr-(k±1)Nr-(kNrWr+we)/(6ν+2-kNr) 6ν-2Nr+(k±1)Nr(kNrWr+we)/(6ν-2+kNr) 6ν-2Nr-(k1)Nr-(kNrWr-we)/(6ν-2-kNr)
对于不同的偶数转子极DSEM，式（20）可表示为
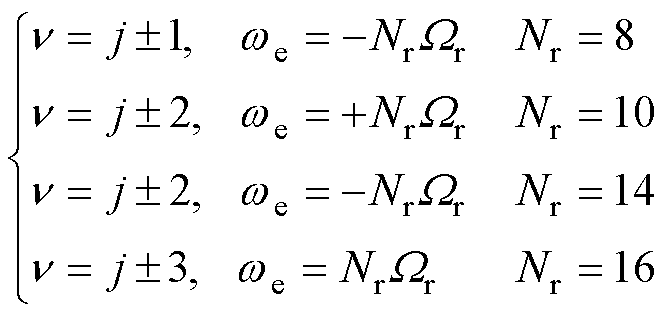（21）
可见，为了产生恒定转矩，转子极数为6k+2的DSEM与转子极数为6k+4的DSEM相序相反。
当极性相反的电枢线圈相串联时，磁动势为如图8所示的奇谐函数，其周期为2p/(Ns/6m)，傅里叶级数形式为
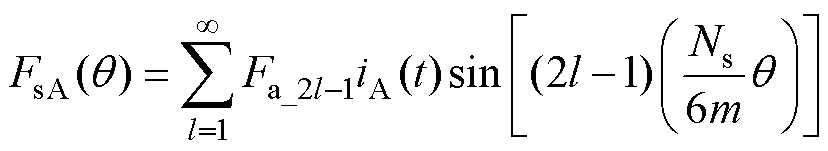（22）
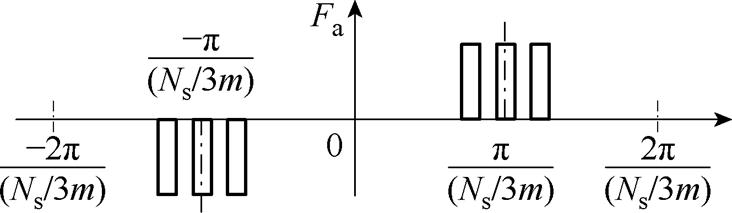
图8 相反极性电枢线圈串联时的相绕组磁动势
Fig.8 Phase winding magnetomotive force for armature coils with the contrary polarity connected in series
令Ns=18，当且仅当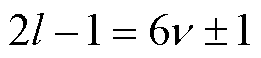
时，三相合成电枢反应磁动势非零，合成磁动势Fsa表达式为
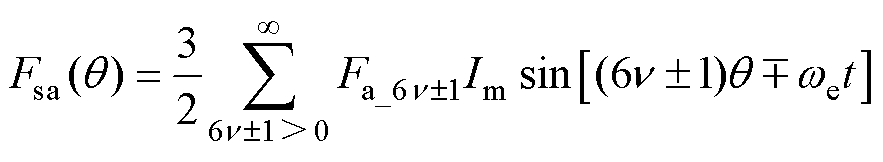（23）
电枢反应磁动势Fsa产生的气隙磁通密度Bsa为
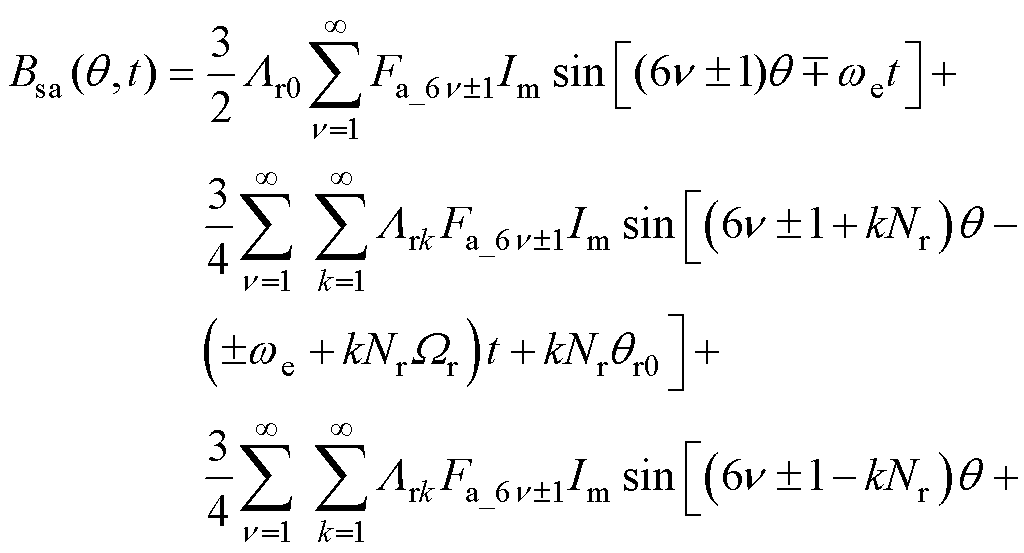
（24）
因此，电机电枢磁场气隙磁通密度谐波特性见表3，当Nr为非3的倍数之奇数时，电枢磁场中包含所有6j±kNr次谐波。根据磁场调制理论，恒定转矩产生条件为
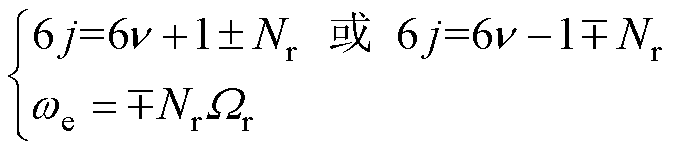（25）
表3 奇数转子极电枢反应磁动势气隙磁通密度谐波特性
Tab.3 Armature reaction flux density harmonics for DSEM with odd rotor poles
谐波次数谐波转速 6ν±1±we/(6ν±1) 6ν+1±Nr+(k1)Nr(kNrWr+we)/(6ν+1+kNr) 6ν+1±Nr-(k±1)Nr-(kNrWr-we)/(6ν+1-kNr) 6ν-1Nr+(k±1)Nr(kNrWr-we)/(6ν-1+kNr) 6ν-1Nr-(k1)Nr-(kNrWr+we)/(6ν-1-kNr)
对于不同的奇数转子极DSEM，式（25）可表示为
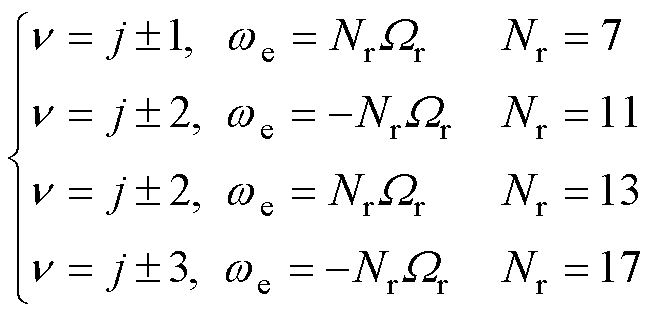（26）
可见，为了产生恒定转矩，转子极数为6k+1的DSEM与转子极数为6k+5的DSEM电机相序相反。
以18/10极和18/11极新型DSEM为例，有限元分析可得空载气隙磁通密度及电枢磁场气隙磁通密度沿着转子圆周分布波形及其谐波分析如图9a～图9d所示，分析可知图中气隙磁通密度谐波次数与表1～表3的理论分析相吻合；18/10极DSEM的空载磁场和电枢磁场气隙磁通密度中所含较高的2、4、6、12、14、16等偶数次空间谐波相互作用产生恒定转矩；18/11极DSEM的空载磁场和电枢磁场气隙磁通密度中所含较高的1、5、6、12、17等奇数次空间谐波相互作用产生恒定转矩。图9e所示为根据麦克斯韦应力张量公式计算所得气隙磁通密度谐波对平均转矩贡献占比，验证了以上气隙磁通密度谐波理论分析的可靠性。
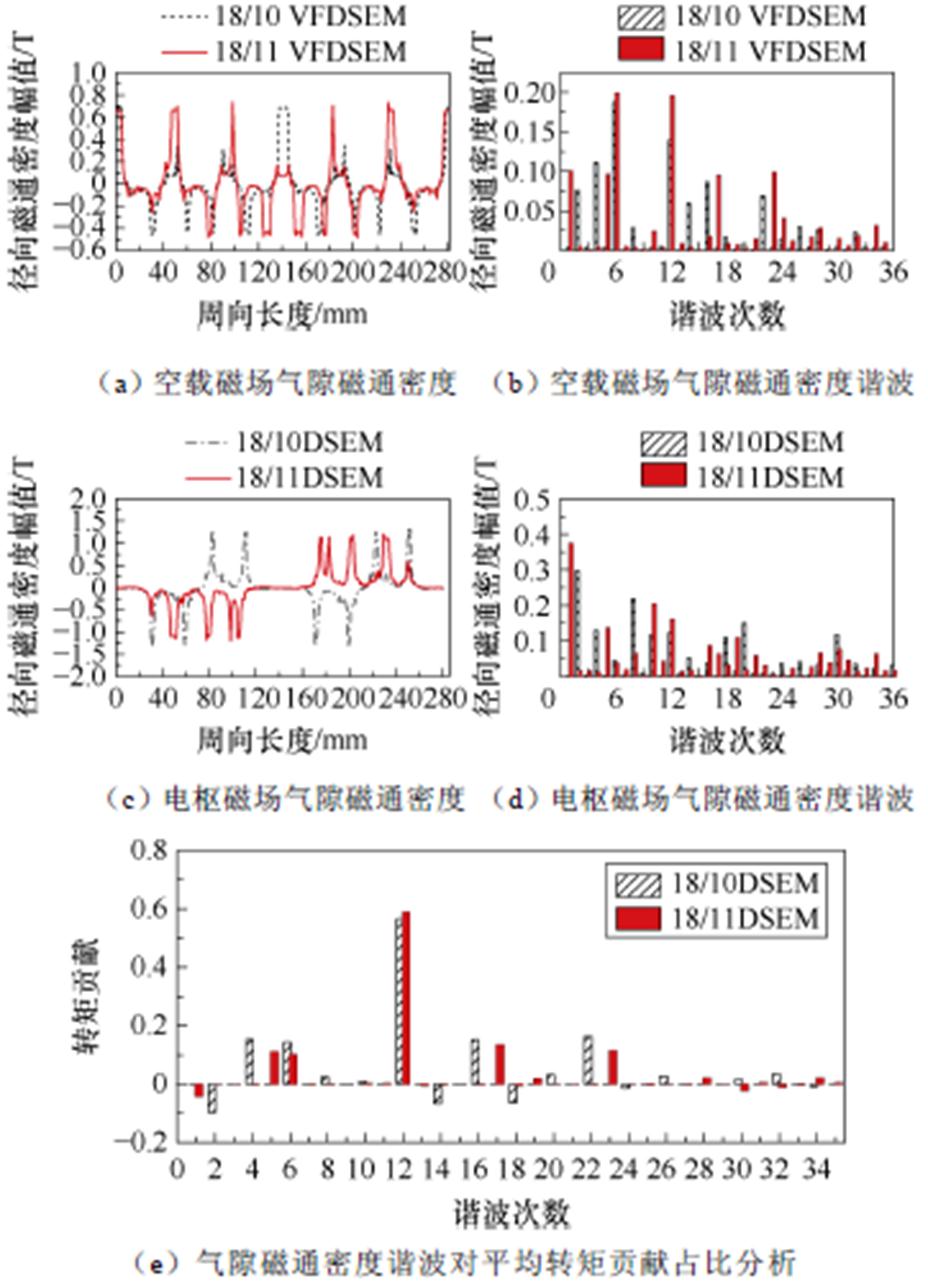
图9 新型DSEM气隙磁通密度分析
Fig.9 Analysis of air-gap flux density of mew DSEM
为了对不同转子极数电机的电磁性能进行对比，本文对相同外形尺寸下转子极数为7、8、10、11、13、14、16、17的DSEM电磁性能进行了有限元分析，电机绕组的电流密度和填充系数分别为4.5 A/mm2和65%，定转子极宽相等，且等于电枢绕组跨绕凸极间距的一半时，如图10所示，初始位置A相所跨绕的两侧凸极与转子凸极均对齐，漏磁最小，磁通利用率最高，此时定转子凸极宽b 满足
图10 定转子极宽设计原则示意图
Fig.10 Diagram of rotor extreme width design principle
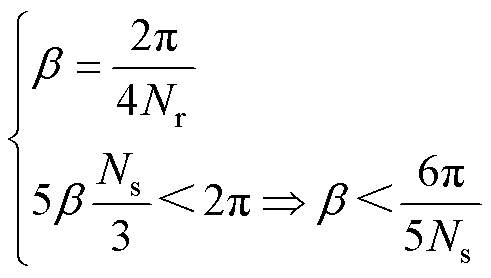（27）
当Nr=7时式（27）不成立，不失一般性，选取定转子凸极均匀分布的方式，即b=10°。基于以上设计原则可得不同转子极数的电机参数见表4。
表4 不同转子极数电机参数
Tab.4 Parameters with different rotor poles
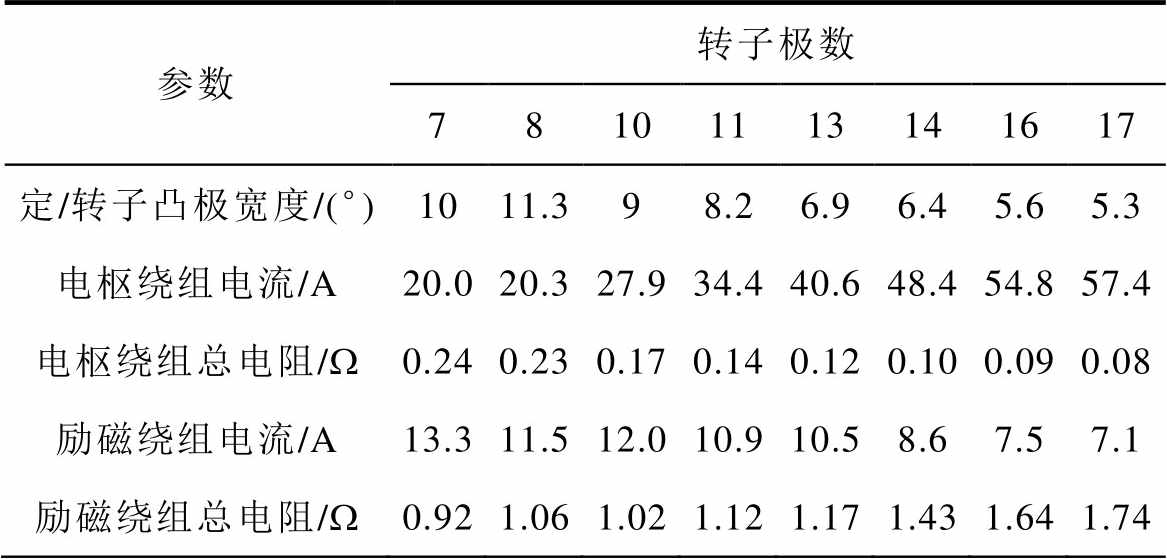
参数转子极数 78101113141617 定/转子凸极宽度/(°)1011.398.26.96.45.65.3 电枢绕组电流/A20.020.327.934.440.648.454.857.4 电枢绕组总电阻/W0.240.230.170.140.120.100.090.08 励磁绕组电流/A13.311.512.010.910.58.67.57.1 励磁绕组总电阻/W0.921.061.021.121.171.431.641.74
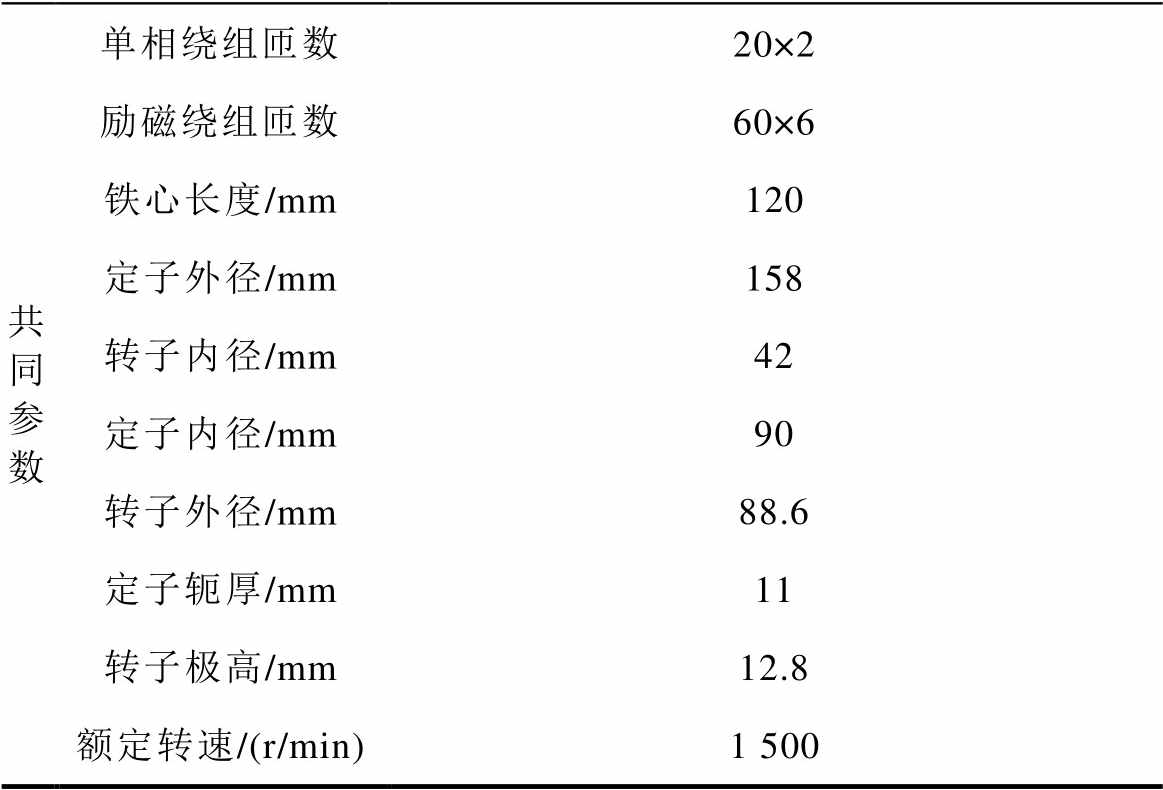
共同参数单相绕组匝数20×2 励磁绕组匝数60×6 铁心长度/mm120 定子外径/mm158 转子内径/mm42 定子内径/mm90 转子外径/mm88.6 定子轭厚/mm11 转子极高/mm12.8 额定转速/(r/min)1 500
图11和图12所示分别为不同转子极数电机的空载磁链和空载反电动势（Electromotive Force, EMF）的波形及谐波组成。由图可见，新型DSEM的磁链与反电动势波形具有较高的正弦度。Nr=17时的相绕组磁链和反电动势均最小；当Nr＞8时，相绕组磁链随着转子极数增大逐渐减小；当Nr＞10时，相绕组空载反电动势随着转子极数增大逐渐减小。分析其原因，在相同槽满率和电流密度条件下，励磁绕组安匝数随着转子极数的增大而减小，且转子极数越高，则基波频率越高，虽然磁链幅值显著降低，相绕组空载反电动势幅值受到频率增加的影响而下降缓慢。当转子极数为偶数时，相绕组磁链与空载反电动势中含有偶数次谐波，当转子极数为奇数时，相绕组磁链与空载反电动势中不含有偶数次谐波，与式（11）和式（12）的理论分析结果一致。对比可见，当转子极数取8和10时的空载反电动势基波幅值最大，分析其原因，当转子极数接近定子极数的1/2时，漏磁通最小，磁通利用率最高，考虑到偶数转子极下含有偶次谐波反电动势，当转子极数取11时能够获得较大的基波幅值，且谐波含量较少。
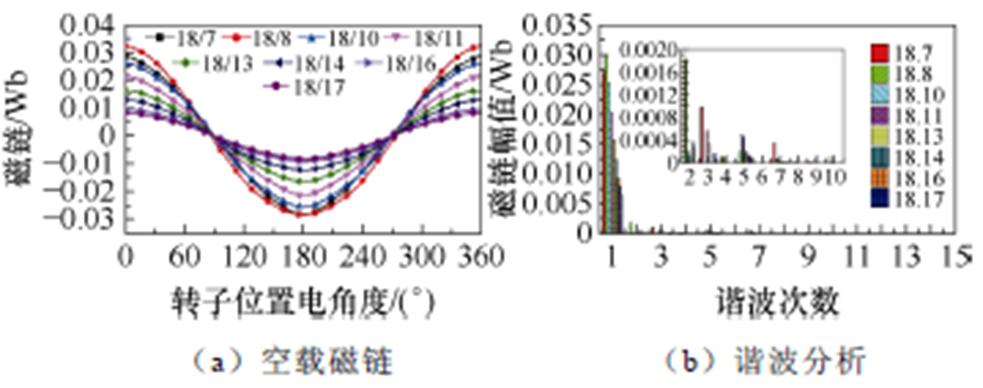
图11 空载磁链与谐波分析
Fig.11 No-load flux linkage waveforms and FFT
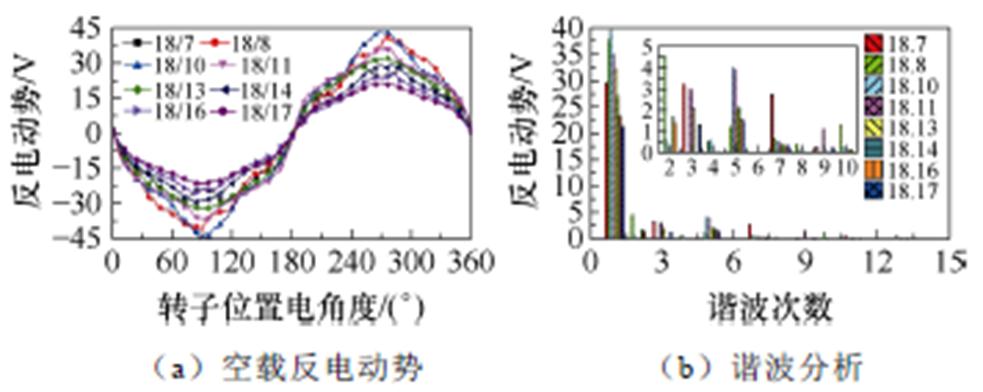
图12 空载反电动势与谐波分析
Fig.12 No-load EMF waveforms and harmonics
根据电机的工作原理，电机输出转矩包括定位转矩和电磁转矩两部分，其中定位转矩是指电机在只加励磁电流不加电枢电流时，由于电机定转子的齿槽效应形成的转矩，电磁转矩是电枢磁场与励磁磁场相互作用形成的转矩，电机输出转矩表达式为
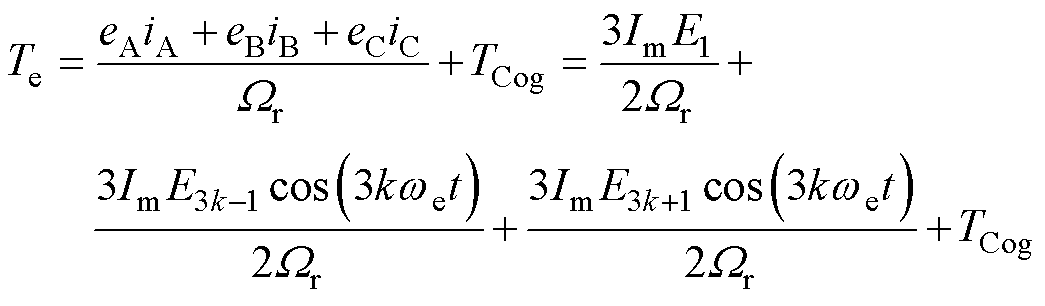（28）
式中，ep为p相绕组反电动势（p=A, B, C）；Ej为j次谐波反电动势幅值；TCog为齿槽转矩。可见，电磁转矩中的谐波转矩脉动主要由3k±1次反电动势谐波引入，对于偶数极转子的电机，由于存在2、8、10次等反电动势谐波，其转矩脉动较大。
图13所示为不同转子极数电机齿槽转矩波形、额定转矩波形及转矩特性对比柱状图。可见，偶数转子极电机转矩脉动很大，而奇数转子极电机转矩脉动明显减小；当转子极数为11或13时，电机输出转矩较大，转矩脉动较小，这是因为相绕组基波反电动势较大，5次谐波反电动势含量较少。
图13 不同转子极数DSEM的转矩特性
Fig.13 Torque features with odd rotor-pole number
图14所示为不同转子极数电机在满载状态下的铁心损耗和绕组铜耗结果。其中，绕组铜耗为电枢绕组损耗与励磁绕组损耗之和，忽略趋肤效应和邻近效应的影响，绕组铜耗pCu计算公式为
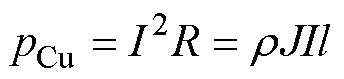（29）
式中，R、r、J、I、l分别为绕组的电阻、电阻率、电流密度、电流和总长度。
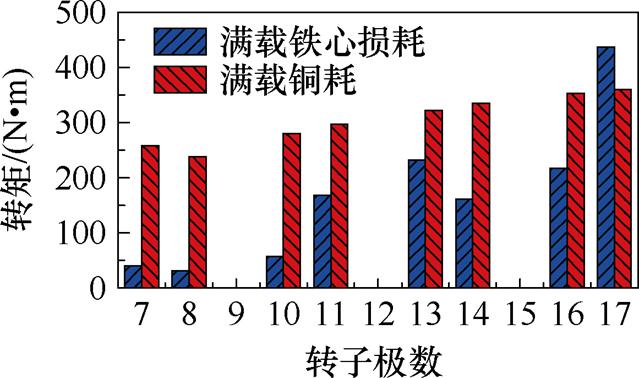
图14 不同转子极数电机铁心损耗和绕组铜耗
Fig.14 Core loss and copper loss with different rotor poles
由图14可见，在电流密度与槽满率恒定情况下，转子极数变化时，随着定子齿宽变窄，绕组铜耗略有增加趋势。铁心损耗随转子极数变化显著，这是由于不同转子极数对电机铁心磁通密度影响较大；对比可见，转子极数为偶数时的铁心损耗略低于转子极数为奇数时的损耗；转子极数为16和17时，铁心损耗最大，分析其原因，转子极数越多，电机铁心磁通密度交变频率越高，铁心损耗也越大。
对新型18/11DSEM的部分参数进行多目标优化并制作实验样机，表5所示为电机优化后的部分参数，将样机与永磁同步电机连接进行对拖实验，实验样机及实验平台如图15所示。
表5 多目标优化后样机部分参数
Tab.5 Partial parameters after objective optimization
参 数数 值 跨绕中间凸极宽度/(°)3.53 跨绕两侧凸极宽度/(°)8.15 单相绕组匝数50 转子凸极宽度/(°)11.14 中间与两侧凸极间距/(°)17.17 励磁绕组匝数70
图15 新型18/11DSEM样机与驱动实验平台
Fig.15 Experimental platform of new 18/11-DSEM prototype and motor drive experimental platform
当励磁电流为7 A，电机转速为1 500 r/min时，仿真与实验所得电机的空载电动势波形及其谐波分析结果如图16所示，可见仿真与实验波形及基波含量相近，3次和5次谐波含量较高，但由于电机加工误差的存在，样机反电动势中的谐波含量较高。
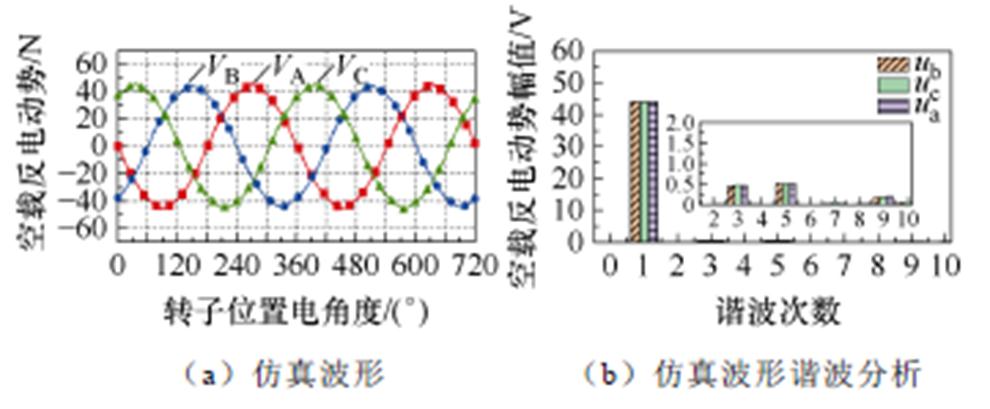
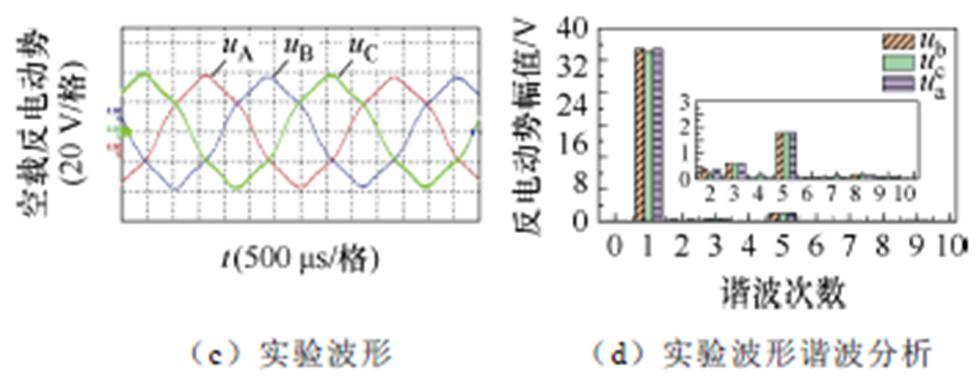
图16 空载反电动势的仿真与实验波形及其谐波分析
Fig.16 Simulated and experimental EMFs waveforms and its harmonics
实验检测电机转速为1 500 r/min时，励磁电流从1～8 A的相绕组空载反电动势，可得空载反电动势幅值的实验值与有限元计算值的对比结果如图17所示，可见，实验样机空载反电动势实验结果略低于仿真结果，这是由电机加工误差造成的，而绕组反电动势变化规律与仿真相近似，即：随着电机励磁电流增大，反电动势随励磁电流增大近似线性增大。
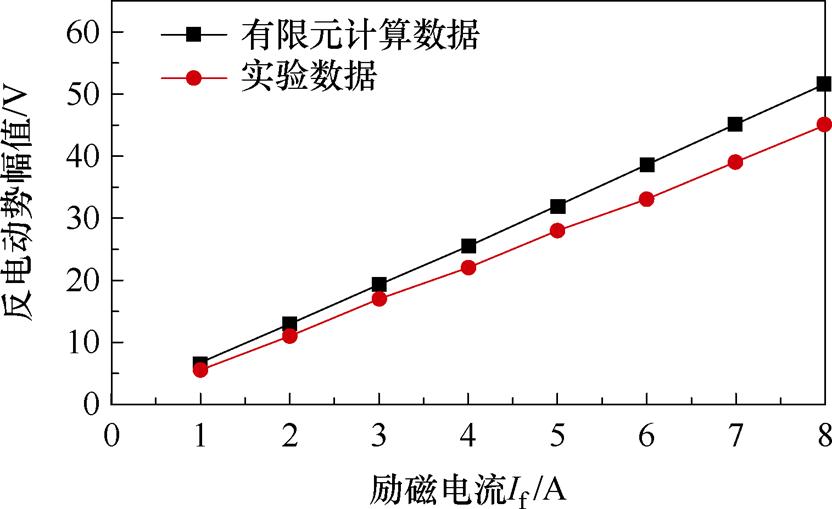
图17 绕组空载反电动势幅值变化曲线
Fig.17 Magnitude of no-load EMF versus field current
负载状态下，伺服电动机与整流桥及功率电阻相连，驱动控制器提供三相正弦电枢电流。当励磁电流为7 A时，电机的实验与仿真转矩结果如图18所示，其中图18a为不同电枢电流下电磁转矩的实验与仿真对比结果波形；图18b为电磁转矩的仿真波形；图18c为相电流16 A对应的电磁转矩实验波形；可见实验与有限元计算结果相近，受到转速波动、样机加工误差及测量误差等因素影响，转矩的实验波形有明显畸变。
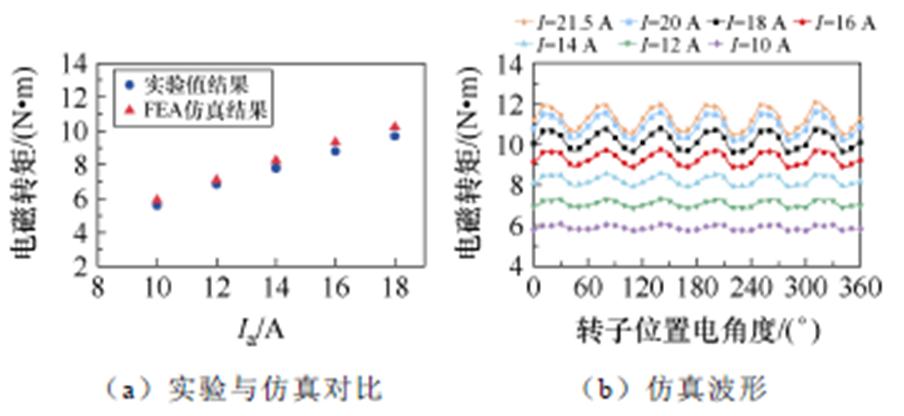
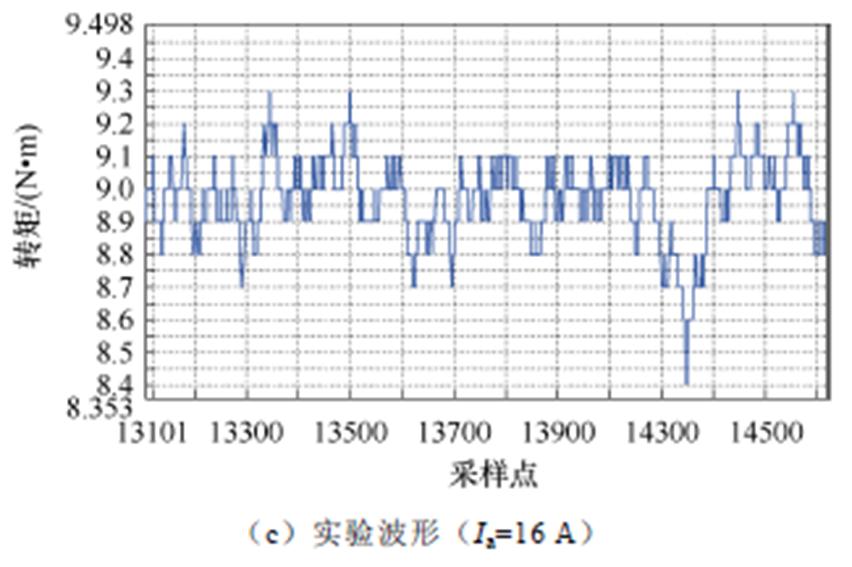
图18 实验转矩与仿真转矩对比
Fig.18 Comparison of tested torque and simulated torque
本文提出了新型DSEM的拓扑结构，并基于磁场调制理论分析了电机转子极数对电机绕组磁链、反电动势、转矩特性及损耗特性的影响，得出结论如下：
1）新型DSEM通过调整励磁绕组与电枢绕组的绕制方式，实现了电枢磁链双极性变化，反电动势具有较高的正弦度。
2）奇数转子极数电机与偶数转子极数电机的气隙磁通密度谐波产生恒定转矩的条件不同，分别见式（21）和式（26）。
3）转子极数为偶数时，电机反电动势存在较多的偶数次谐波，电机齿槽转矩大，转矩脉动也大；转子极数为奇数时，极性相反的电枢线圈相串联，电机反电动势中偶数次谐波相互抵消，谐波含量少，电机齿槽转矩较小，转矩脉动也较小。
4）对于定子极数为18的新型DSEM，当转子极数取11或13时，电机性能最优。
参考文献
[1] Fan Ying, Chau K T. Design, modeling, and analysis of a brushless doubly fed doubly salient machine for electric vehicles[J]. IEEE Transactions on Industry Applications, 2008, 44(3): 727-734.
[2] 赵耀, 沈翀, 李东东, 等. 极端条件下基于特征层面信号融合的电励磁双凸极电机匝间短路故障诊断[J]. 电工技术学报, 2023, 38(10): 2661-2674.
Zhao Yao, Shen Chong, Li Dongdong, et al. Inter-turn short circuit diagnosis of wound-field doubly salient machine based on multi-signal fusion on feature level under extreme conditions[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2661-2674.
[3] 朱德明, 周楠, 张卓然, 等. 直驱式多转子极电励磁双凸极风力发电机[J]. 电工技术学报, 2009, 24(12): 32-37, 56.
Zhu Deming, Zhou Nan, Zhang Zhuoran, et al. A multiple rotor poles doubly salient electromagnetic generator for direct driven wind turbine[J]. Transa- ctions of China Electrotechnical Society, 2009, 24(12): 32-37, 56.
[4] 沈燚明, 卢琴芬. 初级励磁型永磁直线电机研究现状与展望[J]. 电工技术学报, 2021, 36(11): 2325- 2343.
Shen Yiming, Lu Qinfen. Overview of permanent magnet linear machines with primary excitation[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2325-2343.
[5] 赵耀, 陆佳煜, 李东东, 等. 基于机电信号融合的电励磁双凸极电机绕组匝间短路故障诊断[J]. 电工技术学报, 2023, 38(1): 204-219.
Zhao Yao, Lu Jiayu, Li Dongdong, et al. A fault diagnosis strategy for winding inter-turn short-circuit fault in doubly salient electro-magnetic machine based on mechanical and electrical signal fusion[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 204-219.
[6] Du Yi, Shi Xiaoli, Xiao Feng, et al. Equivalent magnetic circuit analysis of doubly salient PM machine with Π-shaped stator iron core segments[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(4): 5201505.
[7] Wang Yu, Zhang Zhuoran, Yu Li, et al. Investigation of a variable-speed operating doubly salient brushless generator for automobile on-board generation appli- cation[J]. IEEE Transactions on Magnetics, 2015, 51(11): 8700604.
[8] Wei Jiadan, Zhang Taojing, Shi Liwei, et al. Dual- stator doubly salient electromagnetic motor driving system utilizing a nine-switch converter[J]. IEEE Transactions on Industry Applications, 2019, 55(2): 1550-1560.
[9] Shi Liwei, Zhou Bo. Armature reaction analysis of a new four-phase fault-tolerant doubly salient wound- field generator[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(7): 0612005.
[10] 史立伟, 周波, 魏佳丹, 等. 多相电励磁双凸极发电机的极数和极弧系数研究[J]. 中国电机工程学报, 2015, 35(7): 1782-1789.
Shi Liwei, Zhou Bo, Wei Jiadan, et al. Study on pole number and pole arc coefficients of multiphase wound-field doubly salient generators[J]. Proceedings of the CSEE, 2015, 35(7): 1782-1789.
[11] Du Yi, Zhang Chao, Zhu Xiaoyong, et al. Principle and analysis of doubly salient PM motor with Π- shaped stator iron core segments[J]. IEEE Transa- ctions on Industrial Electronics, 2019, 66(3): 1962- 1972.
[12] He Mingjie, Xu Wei, Zhu Jianguo, et al. A novel hybrid excited doubly salient machine with asymmetric stator poles[J]. IEEE Transactions on Industry Applications, 2019, 55(5): 4723-4732.
[13] Xu Wei, He Mingjie, Ye Caiyong. Novel syn- chronous machine with permanent magnet in stator yoke[C]//2015 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Shanghai, China, 2015: 44-45.
[14] Wang Wenting, Wang Yuankui, Ma Enlin, et al. Optimal designs of wound field switched flux machines with different DC windings configu- rations[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(4): 359-367.
[15] Sun Xiaoyong, Zhu Z Q, Cai S, et al. Influence of stator slot and rotor pole number combination on field winding induced voltage ripple in hybrid excitation switched flux machine[J]. IEEE Transactions on Energy Conversion, 2021, 36(2): 1245-1261.
[16] Zhang Lingmin, Wang Shuanghong. Torque ripple compensation control with optimized advanced angle for doubly salient electro-magnetic machine[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-5.
[17] Xiong Lei, Ge Hongjuan, Zhou Bo, et al. A torque closed-loop control strategy for torque ripple redu- ction based on current variation characteristic[C]// 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 2020: 1152-1157.
[18] 陈旭, 张卓然, 于立, 等. 基于改进型准比例谐振控制的电励磁双凸极电机电流谐波抑制方法[J]. 电工技术学报, 2023, 38(14): 3836-3848, 3861.
Chen Xu, Zhang Zhuoran, Yu Li, et al. Current harmonic suppression method of doubly salient electro-magnetic machine based on improved quasi proportional resonant control[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3836- 3848, 3861.
[19] Yang Yan, Wang Qin, Hu Yinfeng, et al. Multiple sine-wave superposition drive for the doubly salient motor based on Fourier linearization modeling[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 4419-4430.
[20] Zhang K, Li G J, Zhu Z Q, et al. Investigation on contribution of inductance harmonics to torque production in multiphase doubly salient synchronous reluctance machines[J]. IEEE Transactions on Mag- netics, 2019, 55(4): 8101110.
[21] Li G J, Zhang K, Zhu Z Q, et al. Comparative studies of torque performance improvement for different doubly salient synchronous reluctance machines by current harmonic injection[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 1094-1104.
[22] Yu Zhiyue, Gan Chun, Ni Kai, et al. Instantaneous torque modeling and torque ripple reduction strategy for flux modulated doubly-salient reluctance motor drives[J]. IEEE Transactions on Industrial Electronics, 2022, 69(10): 9838-9848.
[23] 付兴贺, 江政龙, 吕鸿飞, 等. 电励磁同步电机无刷励磁与转矩密度提升技术发展综述[J]. 电工技术学报, 2022, 37(7): 1689-1702.
Fu Xinghe, Jiang Zhenglong, Lü hongfei, et al. Review on the development of brushless excitation and torque density enhancement technology for elec- trically excited synchronous motor[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1689- 1702.
[24] Wu Hao, Zhao Wenliang, Li Zheng, et al. Torque improvement of spoke-type permanent magnet motor with auxiliary stator using harmonic current control strategy[J]. CES Transactions on Electrical Machines and Systems, 2023, 7(2): 210-217.
Abstract The doubly salient electric-excited motor has many advantages such as a simple structure, low manufacturing cost and high reliability, making it a good candidate for applications in electric vehicles, aerospace, and other fields. However, its large torque ripple and low torque density limit its development and applications. This paper proposes a new topology structure for the doubly salient electromagnetic machine (DSEM).
The topology structure and working mechanism of the proposed DSEM are analyzed in detail. The combination of stator poles and rotor poles is elaborated, and the winding method of armature windings is described with the influence on the harmonics of EMF. The relationship between the pole-combination and harmonics of the magnetic field, together with the output torque, is investigated according to the magnetic field modulation mechanism, and the air-gap flux density harmonics of 18/10 and 18/11 DSEMs are obtained by finite element analysis. The influence of pole combination on motor characteristics is analyzed by finite element analysis, including the no-load electromagnetic performance, the torque features, and the loss characters, which shows the superiority of the DSEM with odd-number rotor poles. Finally, a prototype of the new 18/11 DSEM is manufactured and tested.
The results show that due to the new winding method, the flux in armature windings changes bipolar, resulting in high sinusoidal flux linkages and, thus, a high sinusoidal EMF. The DSEM with odd-number rotor poles has more effective space magnetic harmonics than that with even-number rotor poles, almost with odd orders, resulting in higher output torque. Besides, due to the offset of even-order time-harmonics, the DSEM with odd-number rotor poles has higher sinusoidal EMFs and lower torque ripples. In addition, different rotor poles show different characteristics, as seen from the simulation results.
The following conclusions can be drawn. (1) By adjusting the winding method of the field winding and the armature winding, the new type of DSEM realizes the bipolar change of the armature flux, and the back EMF has a high sinusoidal degree. (2) As can be seen from equations (21) and (26), the effective harmonics’ frequency of air-gap flux density in the odd-rotor pole motor is different from that in the even-rotor pole motor, resulting in different torque harmonics. (3) If the number of rotor poles is even, there are more even order harmonics in the motor back EMF, and the cogging torque and torque ripple are also large; if odd, the armature coils with opposite polarity are connected in series, and the even harmonics in the motor back EMF cancel each other, resulting in smaller harmonic content, cogging torque, and torque ripples. (4) The motor performance is optimal for the proposed DSEM with 18 stator poles when the rotor pole number is 11 or 13.
Keywords：Doubly salient electro-magnetic machine, magnetic field modulation mechanism, polar combination, electromagnetic torque
中图分类号：TM303
DOI: 10.19595/j.cnki.1000-6753.tces.240603
国家自然科学基金项目（52177063）和河南省科技攻关项目（222102320074）资助。
收稿日期 2024-04-19
改稿日期 2024-08-20
贾宛英 女，1982年生，硕士生导师，研究方向为特种电机与驱动技术。
E-mail: 2019044@zzuli.edu.cn
王明杰 男，1982年生，硕士生导师，研究方向为直线电机与驱动技术。
E-mail: mjwang@zzuli.edu.cn（通信作者）
（编辑 崔文静）