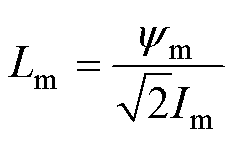 (1)
(1)
摘要 励磁电感作为稳态等效电路中励磁支路的主要参数,其准确求解对于潜水感应电机的电磁性能分析和驱动系统设计十分重要。该文提出一种基于主、漏磁路的层微元法计算不同转差下的励磁电感:主磁路计算得到感应电动势随励磁电流的变化曲线作为目标函数,漏磁路计算用于构建稳态等效电路中定子端电压表达式作为约束条件,利用约束条件在目标函数上确定励磁电感。在主、漏磁路的分析中,采用薄层微元等效理论积分,有效考虑齿槽结构、磁饱和等影响因素。以一台湿式潜水感应电机为例,分别采用提出的层微元法和传统磁链法进行励磁电感的解析计算,并进一步求解等效电路的稳态输出,通过样机试验以及齿磁路饱和情况下的有限元仿真验证方法的准确性。结果表明,层微元法比磁链法在齿磁路饱和时更有效地考虑铁心段的磁压降分布,励磁电感的计算更为准确,从而得出的等效电路稳态输出更接近有限元仿真结果。所提方法建立设计参数与励磁电感的直接联系,为潜水感应电机及其他各类电机的初始设计优化提供便利。
关键词:励磁电感 磁饱和 潜水感应电机 层微元法
感应电机广泛应用于诸多工业领域,如与潜水泵相连组成潜水电泵进行深井抽排水[1-2]。等效电路及其构成参数是进行电机本体设计和驱动系统设计的重要工具[3-4]。电路参数的准确求解对电机电磁性能分析和驱动模型建立十分重要,特别是表征电机内部主磁场分布的励磁电感参数。
近年来,以有限元法为主的数值分析手段在电机设计领域得以广泛应用,国内外学者利用有限元分析结果定解等效电路参数,包括励磁电感。文献[5]对一个极距下的径向气隙磁通密度进行积分计算主磁链,将定子电流视为磁化电流,利用二者之比计算励磁电感,这种方法仅适用于空载情况下的参数计算。为计及带载时的转子反应,文献[6]基于空载和堵转的仿真结果计算定转子耦合电路的复折算系数,进而快速识别不同转差下的励磁电感。文献[7]将瞬态场中的定转子电流根据矢量关系合成励磁电流,然后利用磁储能计算励磁电感。这两种方法均涉及多段相互关联的有限元仿真,且瞬态场的计算时间较长,特别是三维有限元分析[7]。因此,为降低时间成本,多采用时谐场、静磁场求解器进行仿真计算。其中,冻结磁导率法是对电磁场计算结果进行后处理的主流方法。这种方法既可以在空载仿真中再现带载时铁心饱和情况,直接计算励磁电感[8-9],也可以精确计算定转子漏磁参数后反推励磁电感[10]。此外,文献[11]提取电磁场计算结果后建立定转子自互感矩阵,借助Clarke变换从矩阵中分离励磁电感。
由上述分析可知,有限元法可获得精确的电磁场分布结果来定解等效电路参数,但这种方法并未实现电路参数与设计参数的直接联系,不利于电机的初始设计优化。解析法是快速分析各类设计参数对电机性能影响的有效方法。传统的解析计算利用基本公式和经验系数直接计算励磁电感[12-13],这种方法往往由于忽略铁心饱和、齿槽效应、转子运动等因素的影响,计算结果存在一定的误差。
为提高解析计算的准确度,文献[14]将实际铁磁材料的硅钢磁化曲线采用多段折线进行拟合,建立铁心磁导率和气隙磁场的关系函数来计算直线感应电机的励磁电感。文献[15]利用二维柱面坐标系建立气隙电感的表达式,使之能同时计及磁饱和、齿槽效应、定子斜槽等因素的影响。系数修正是在励磁电感计算中考虑磁饱和的常用手段:预设饱和系数值进行迭代计算,将预设值和计算值的误差作为收敛判据确定最终系数,以此修正不饱和情况下的励磁电感值[16-17]。此外,也有很多学者利用分布磁路的迭代计算结果直接得到不同转差下的励磁电感[18-20]。这些方法能有效考虑齿槽效应、磁饱和等因素的影响。但也存在如下问题:①用简单的长宽参数代替实际的槽形,使得铁心各段磁路的分析不够准确,容易忽略局部饱和位置;②励磁电感的计算涉及多段磁路和电路的非线性迭代,且不同转差下的参数计算均需要重复该迭代过程。
因此,为更精确地考虑齿槽结构和磁饱和问题,降低解析计算的复杂程度。本文提出了一种基于主、漏磁路的层微元法计算不同转差下的励磁电感:主磁路计算得到感应电动势随励磁电流的变化曲线作为目标函数,漏磁路计算用于构建稳态等效电路中定子端电压表达式作为约束条件,最后利用约束条件在目标函数上定解励磁电感。与前述解析法相比,这种方法具有如下优点:①在主、漏磁路的分析中,采用薄层微元等效理论积分,对齿槽结构、磁饱和等影响因素的考虑更为准确;②不同转差下励磁电感的定解不涉及饱和系数修正或非线性迭代过程,计算量显著减少。本文以一台湿式潜水感应电机为例进行励磁电感的解析计算,并进一步求解等效电路的稳态输出,通过样机试验以及磁饱和情况下的有限元仿真验证提出方法的有效性,并与传统磁链法的计算结果进行比较。
磁链法是电感计算的常用方法。在交流电路中,若介质磁导率不随磁场强度大小而变化,则电路中的电感可由交链电路的总磁链与电路中通过电流的比值得到。对于感应电机而言,励磁电流建立空间磁动势,产生穿过气隙的磁链连接定子和转子,进而构成回路。励磁电感为
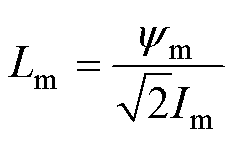 (1)
(1)
式中,Lm为励磁电感;Im为励磁电流的有效值;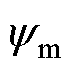 为励磁电流产生的主磁链的幅值,有
为励磁电流产生的主磁链的幅值,有
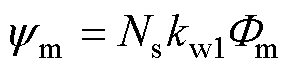 (2)
(2)
式中,Ns为绕组的每相串联匝数;kw1为基波绕组系数;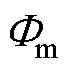 为每极基波磁通的幅值,有
为每极基波磁通的幅值,有
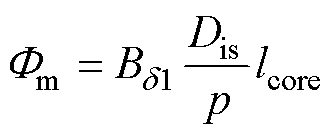 (3)
(3)
式中,Dis为定子内径;p为极对数;lcore为铁心长度;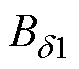 为气隙基波磁通密度的幅值,其大小取决于气隙基波磁动势,有
为气隙基波磁通密度的幅值,其大小取决于气隙基波磁动势,有
 (4)
(4)
式中,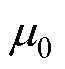 为真空磁导率;KCrs为计及定转子双边开槽的等效气隙系数[21];
为真空磁导率;KCrs为计及定转子双边开槽的等效气隙系数[21];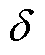 为气隙的实际长度;Fm为气隙基波磁动势的幅值,对于多相交流绕组而言,其值为
为气隙的实际长度;Fm为气隙基波磁动势的幅值,对于多相交流绕组而言,其值为
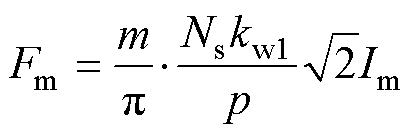 (5)
(5)
式中,m为相数。联立式(1)~式(5),可以得到磁链法下的励磁电感表达式为
 (6)
(6)
由式(6)可以看出,磁链法计算出的励磁电感,其大小主要取决于绕组结构和主磁路长度。此外,从推导流程中可以看出,磁链法认为交流绕组产生的空间磁动势全部作用于气隙,不计磁力线实际穿过定转子铁心产生的磁压降。因此,磁链法计算励磁电感时不考虑磁路饱和的影响。
本文提出一种基于主、漏磁路的层微元法计算感应电机的励磁电感,求解流程如图1所示,可将求解步骤划分为如下四个部分:
(1)主磁路计算。设定气隙磁通密度的变化范围,计算不同气隙磁通密度下的每极磁压降,分别将二者换算成感应电动势与励磁电流,得到目标函数 曲线。

图1 励磁电感解析计算的求解流程
Fig.1 Flow chart of the analytical calculation of the magnetizing inductance
(2)漏磁路计算。分析定子槽漏磁和转子导条的电流分布,计算定转子槽漏感及转子交流电阻。
(3)将步骤(2)中得到的参数与直接求解的定子电阻、定转子谐波及端部漏感结合,利用稳态等效电路构建定子端电压表达式作为约束条件。
(4)将目标函数曲线中的每一组感应电动势及励磁电流值代入步骤(3)构建的约束条件中,定解使得结果等于额定相电压的点,该点纵横坐标之比即为励磁电抗,进而得出励磁电感。
电路参数和磁压降的精确求解理论上涉及定积分运算。本文采用数值方法等效理论积分,微元法将连续函数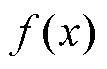 在定区间[x1, x2]上的积分转化为k个宽度均为
在定区间[x1, x2]上的积分转化为k个宽度均为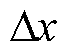 的矩形面积之和,矩形等分的个数越多,计算结果越接近真实积分,有
的矩形面积之和,矩形等分的个数越多,计算结果越接近真实积分,有
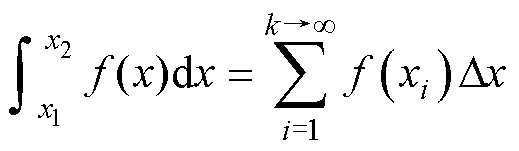 (7)
(7)
因此,层微元法的计算流程如图2所示,在主、漏磁路的计算中采用层微元法,将定转子的齿、槽以及轭部结构分别划分成若干等厚的薄层,视每个薄层中媒介的磁导率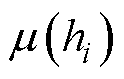 和电导率
和电导率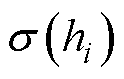 均为定值,磁力线的走向垂直于薄层分界面。这样不规则、非线性的磁路电路就被转化为若干规则、线性的磁路电路的累加运算,从而在磁压降及漏感的计算中能更准确地考虑实际的齿槽结构和铁磁材料的非线性属性。
均为定值,磁力线的走向垂直于薄层分界面。这样不规则、非线性的磁路电路就被转化为若干规则、线性的磁路电路的累加运算,从而在磁压降及漏感的计算中能更准确地考虑实际的齿槽结构和铁磁材料的非线性属性。
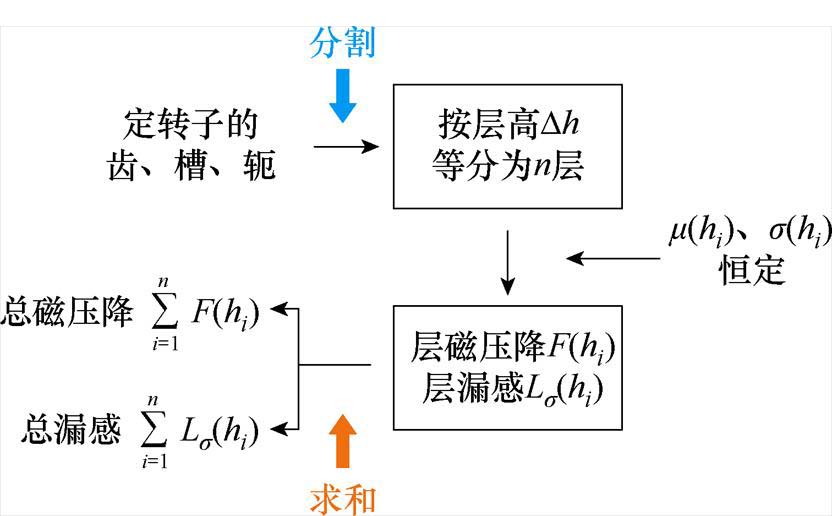
图2 层微元法的计算流程
Fig.2 Flow chart of the elementary layer method
本文以一台380 V,132 kW的湿式潜水感应电机为例进行励磁电感的解析计算。电机的有关尺寸参数见表1。
表1 潜水感应电机的参数
Tab.1 Parameters of the submersible induction machine
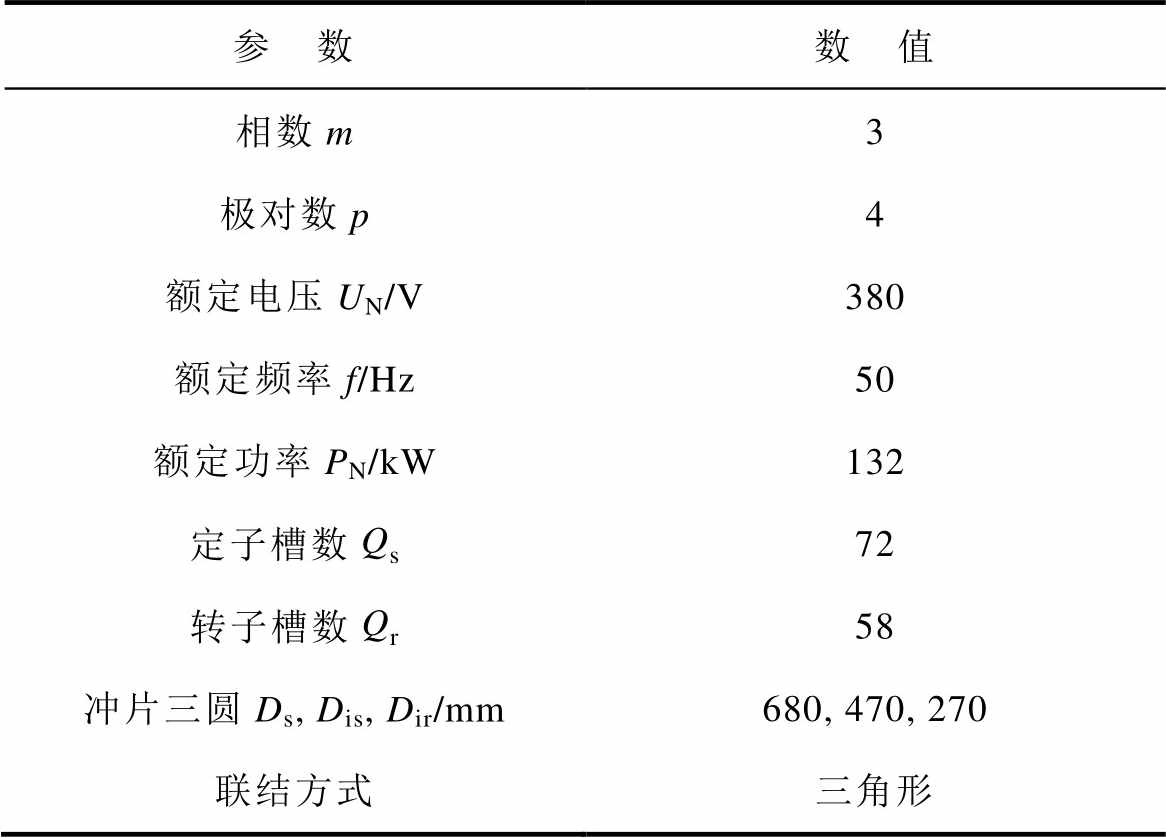
参 数数 值 相数m3 极对数p4 额定电压UN/V380 额定频率f/Hz50 额定功率PN/kW132 定子槽数Qs72 转子槽数Qr58 冲片三圆Ds, Dis, Dir/mm680, 470, 270 联结方式三角形
励磁电流产生磁链,穿过气隙进入定转子铁心,若考虑磁路饱和,则磁链在定转子铁心各段中均产生磁压降。一个完整的主磁路回路包含一对轴对称的磁极路径,考虑对称性,采用层微元法对单个磁极路径的磁压降进行分析,包括齿、轭及气隙三个部分。
首先分析齿部磁压降,以定子齿为例,磁力线由气隙进入定子铁心时,大部分从齿顶穿入,也有小部分由于饱和进入槽中。图3为定子齿的磁力线分布。
如图3所示,利用层微元法计算定子齿部的磁压降时,将定子齿和槽按同样的层高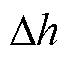 等分成n层,则齿和槽的薄层分界面位于同一高度。第k层的总磁通量包括穿过第k层的齿磁通和槽磁通两部分,考虑铁心叠片间的气隙磁通,有
等分成n层,则齿和槽的薄层分界面位于同一高度。第k层的总磁通量包括穿过第k层的齿磁通和槽磁通两部分,考虑铁心叠片间的气隙磁通,有

图3 定子齿的磁力线分布
Fig.3 Flux lines distribution in the stator teeth
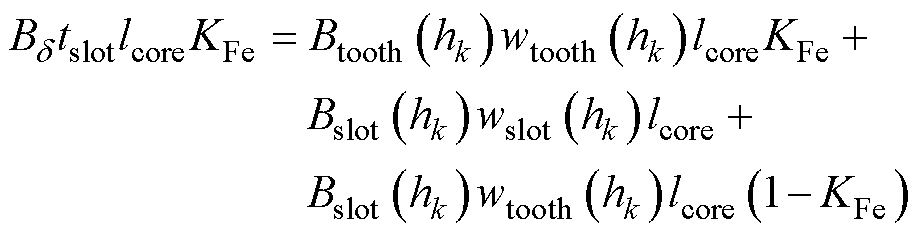 (8)
(8)
式中,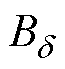 为气隙磁通密度的幅值;tslot为齿距,长度等于齿顶宽与槽开口之和;KFe为铁心的叠片系数;
为气隙磁通密度的幅值;tslot为齿距,长度等于齿顶宽与槽开口之和;KFe为铁心的叠片系数;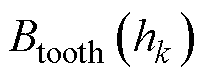 和
和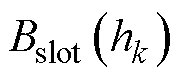 分别为第k层的齿磁通密度和槽磁通密度幅值;
分别为第k层的齿磁通密度和槽磁通密度幅值; 和
和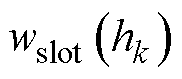 分别为第k层的齿宽和槽宽。第k层的齿槽分界面上无传导电流,且齿槽为均匀介质,因此可视同一层高的齿磁场强度
分别为第k层的齿宽和槽宽。第k层的齿槽分界面上无传导电流,且齿槽为均匀介质,因此可视同一层高的齿磁场强度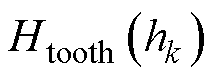 和槽磁场强度
和槽磁场强度 相同,从而由式(8)进一步推导
相同,从而由式(8)进一步推导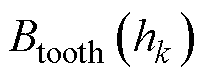 和
和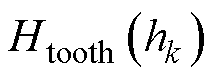 的关系为
的关系为
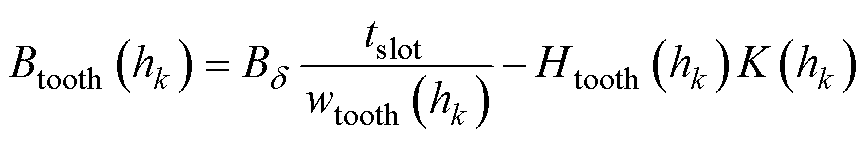 (9)
(9)
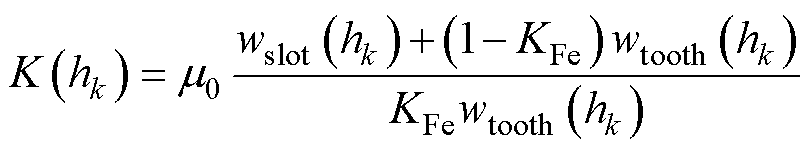 (10)
(10)
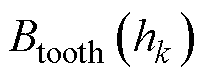 与
与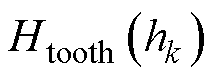 除了满足式(9)和式(10)的关系外,还应当位于铁心材料的磁化曲线上。将上述两式视作Btooth(h)关于Htooth(h)线性函数,其与磁化曲线的交点即为第k层的磁通密度与磁场强度。这样从底部到顶部,根据上述方法逐层求得不同高度的磁场强度后,再将所求的薄层磁压降累加求和,即可得到整个齿部的磁压降Ftooth为
除了满足式(9)和式(10)的关系外,还应当位于铁心材料的磁化曲线上。将上述两式视作Btooth(h)关于Htooth(h)线性函数,其与磁化曲线的交点即为第k层的磁通密度与磁场强度。这样从底部到顶部,根据上述方法逐层求得不同高度的磁场强度后,再将所求的薄层磁压降累加求和,即可得到整个齿部的磁压降Ftooth为
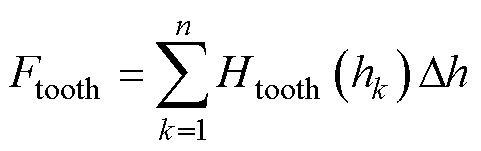 (11)
(11)
图4为定子不同层的齿宽、槽宽及该层齿部磁场强度的柱状分布,等分层数为50,定子槽形为开口平行槽。可以看出,从底层到顶层,除槽楔位置外槽宽不变,齿宽增加,齿部磁场强度相应减小,槽楔附近处齿宽最窄,磁场强度最大,磁通密度最高,电机运行中局部饱和点也往往出现在此处。转子也采用同样的方法计算齿磁压降。
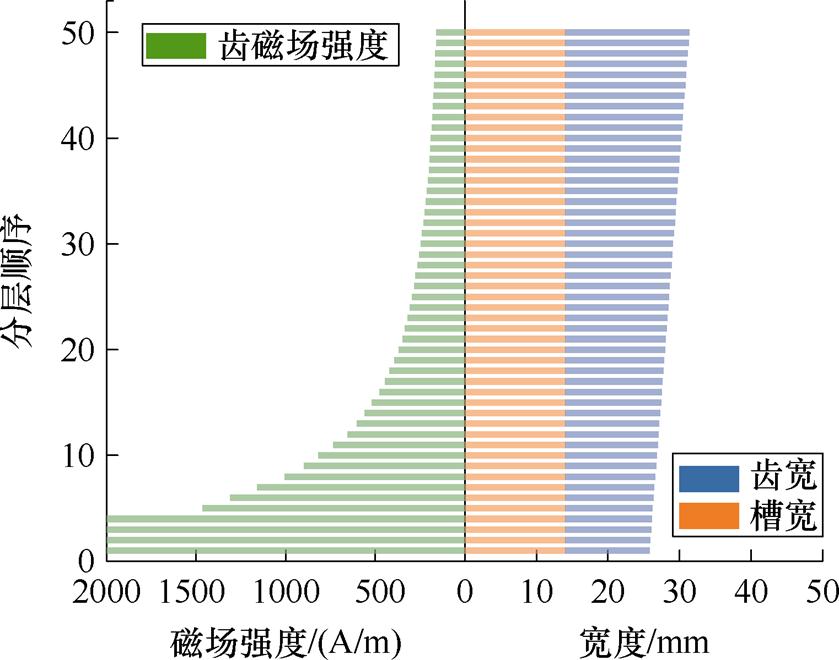
图4 不同层的齿宽、槽宽及齿磁场强度
Fig.4 Tooth width, slot width, and corresponding magnetic field strength of different layers
电机的气隙可视作磁导率恒定的媒介,其磁压降可由气隙参数直接求得,同样利用等效气隙系数KCrs考虑定转子双边开槽对气隙磁压降的影响[21]。
轭部的磁力线走向与齿部不同,定子轭的磁力线分布如图5所示,磁力线沿圆周向分散进入电机轭部,使得沿圆周向每一段轭磁路的磁力线分布不均匀。在相邻两对磁极回路的分界面处轭部磁场强度为0,记此位置的电角度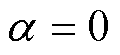 ;在一对磁极回路的轴中心线处磁场强度最大,则此位置的电角度
;在一对磁极回路的轴中心线处磁场强度最大,则此位置的电角度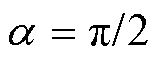 。从图5中轭部磁力线的分布可以看出:随着电角度的逐渐增大,磁力线逐段密集,从而磁场强度沿圆周向逐段增大。
。从图5中轭部磁力线的分布可以看出:随着电角度的逐渐增大,磁力线逐段密集,从而磁场强度沿圆周向逐段增大。
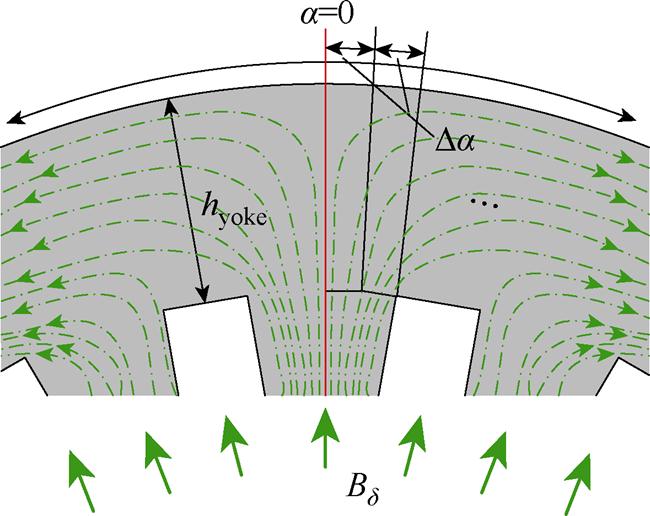
图5 定子轭的磁力线分布
Fig.5 Flux lines distribution in the stator yoke
同样采用层微元法计算轭部磁压降:将一极下的轭磁路按电角度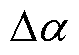 等分为n层,预设气隙磁场为正弦分布,在2.2节求得气隙基波磁通密度幅值
等分为n层,预设气隙磁场为正弦分布,在2.2节求得气隙基波磁通密度幅值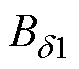 后,重新按
后,重新按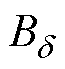 和
和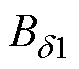 的比例对轭部磁压降进行修正。
的比例对轭部磁压降进行修正。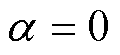 处齿磁通密度最大,轭磁通密度为0,则气隙磁通密度为余弦函数,第k段轭磁路的磁通密度
处齿磁通密度最大,轭磁通密度为0,则气隙磁通密度为余弦函数,第k段轭磁路的磁通密度 与气隙磁通密度的关系为
与气隙磁通密度的关系为
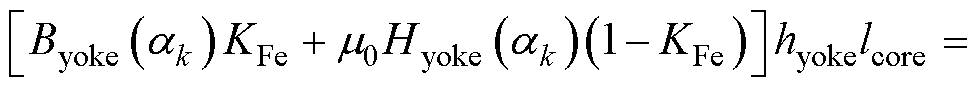
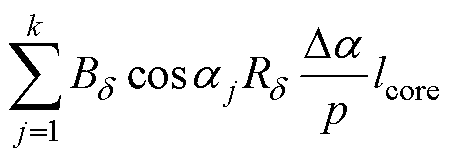 (12)
(12)
式中,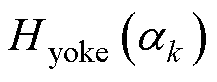 为第k段轭磁路的磁场强度;
为第k段轭磁路的磁场强度; 为轭部高度;
为轭部高度;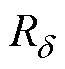 为气隙半径。轭磁路的磁通密度和磁场强度同样满足磁化曲线的关系。将式(12)视为
为气隙半径。轭磁路的磁通密度和磁场强度同样满足磁化曲线的关系。将式(12)视为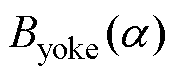 随
随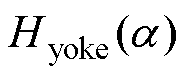 变化的线性函数,其与磁化曲线的交点即为对应于该层的轭部磁通密度及磁场强度。从
变化的线性函数,其与磁化曲线的交点即为对应于该层的轭部磁通密度及磁场强度。从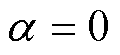 到
到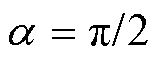 逐段叠加,就可以得到一个极距的轭部磁压降值为
逐段叠加,就可以得到一个极距的轭部磁压降值为
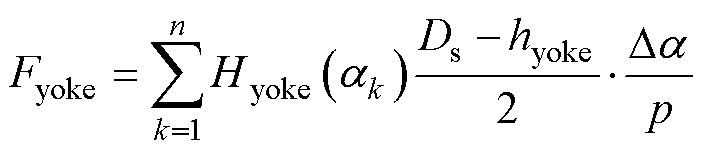 (13)
(13)
式中,Ds为定子外径。转子轭部磁压降也采用该方法计算,最后将一极下的主磁路各段磁压降进行累加求和,包括定转子齿、轭及气隙部分的磁压降,即可得到气隙磁通密度幅值为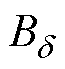 时的每极磁压降幅值Fsum。
时的每极磁压降幅值Fsum。
受铁心饱和、绕组分布、定转子双边开槽等因素的影响,气隙磁通密度中含有谐波分量。定解励磁电感所需的感应电动势为基波磁链的产物,因此需要计算对应于气隙磁通密度幅值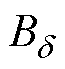 的气隙基波磁通密度幅值
的气隙基波磁通密度幅值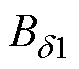 ,定解过程如图6所示。
,定解过程如图6所示。
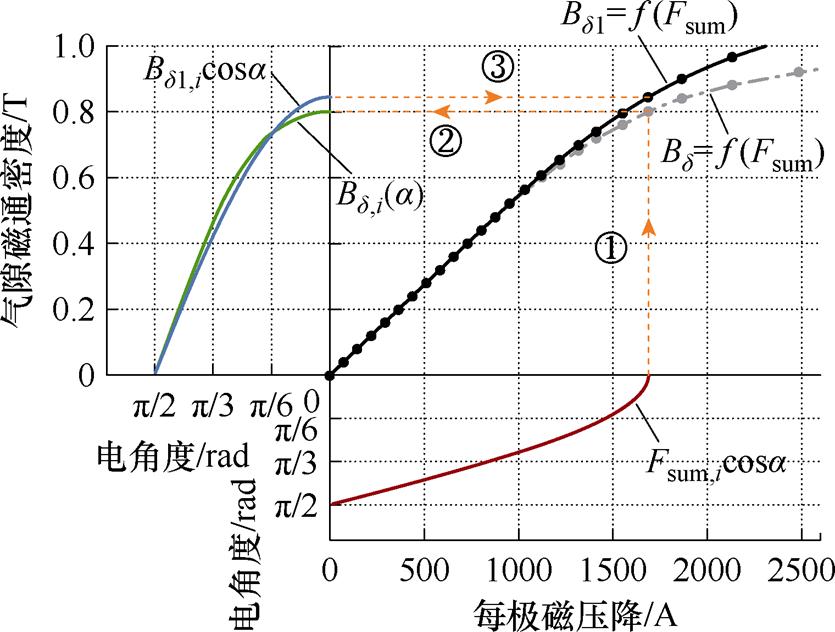
图6 气隙基波磁通密度的定解过程
Fig.6 Determination of the fundamental air-gap flux density
主要求解流程如下:
(1)在0~1 T的区间内设定一系列气隙磁通密度幅值等分点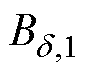 ~
~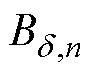 ,根据2.1节过程计算各点对应的每极磁压降值
,根据2.1节过程计算各点对应的每极磁压降值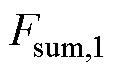 ~
~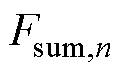 ,并绘制成曲线
,并绘制成曲线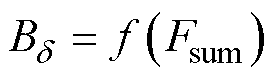 ,如图6中灰色曲线所示。
,如图6中灰色曲线所示。
(2)记灰色曲线上第i点的坐标为(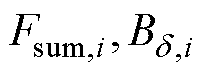 ),将
),将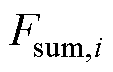 记为幅值,在[
记为幅值,在[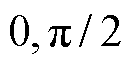 ]的电角度区间内设置等分点
]的电角度区间内设置等分点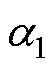 ~
~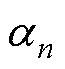 ,利用余弦表达式计算不同电角度下的每极磁压降
,利用余弦表达式计算不同电角度下的每极磁压降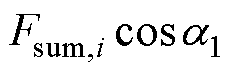 ~
~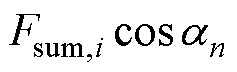 ,并绘制曲线
,并绘制曲线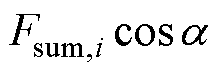 ,如图6中红色曲线所示。
,如图6中红色曲线所示。
(3)以灰色曲线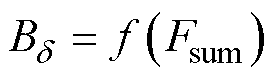 为映射关系,计算不同电角度
为映射关系,计算不同电角度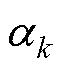 下每极磁压降
下每极磁压降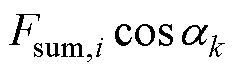 对应的气隙磁通密度幅值
对应的气隙磁通密度幅值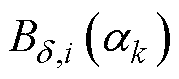 ,得到气隙磁通密度的1/4个电周期波形
,得到气隙磁通密度的1/4个电周期波形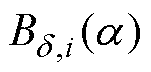 ,映射过程为图6中①、②,映射结果如图6中绿色曲线所示。
,映射过程为图6中①、②,映射结果如图6中绿色曲线所示。
(4)根据偶函数的傅里叶级数性质,计算气隙基波磁通密度幅值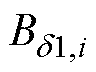 ,绘制成曲线
,绘制成曲线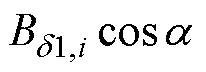 ,如图6中蓝色曲线所示,
,如图6中蓝色曲线所示,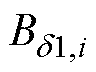 的计算表达式为
的计算表达式为
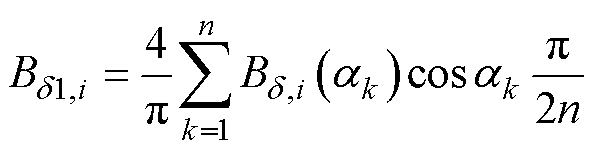 (14)
(14)
(5)对步骤(1)中灰色曲线上每点重复步骤(2)~步骤(4),得到每一个气隙磁通密度幅值点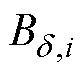 对应的基波磁通密度幅值
对应的基波磁通密度幅值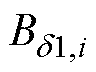 。然后以
。然后以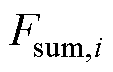 为横坐标,
为横坐标,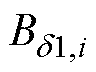 为纵坐标,对应过程为图6中③,绘制曲线
为纵坐标,对应过程为图6中③,绘制曲线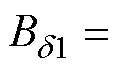
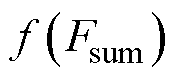 ,如图6中黑色曲线所示,该曲线即为目标函数。
,如图6中黑色曲线所示,该曲线即为目标函数。
构建定子端电压约束条件的等效电路参数,包括电阻和漏感。湿式潜水电机的定子绕组采用复合绝缘的散嵌线,导线截面积小且绝缘层较厚,因此不考虑导体间相互作用的邻近效应,直接计算其直流电阻。此外,气隙漏感与绕组谐波有关,不深入铁心内部,端部漏感取决于端部的几何尺寸,离铁心较远。二者均不涉及铁心饱和问题,可以直接利用设计参数求解[22]。而槽漏感与电机的齿槽结构密切相关,因此采用层微元法进行分析计算。
本文研究的潜水电机定子槽型为开口平行槽,绕组结构为双层短距分布。双层短距绕组的定子槽如图7所示,将整个定子槽等分成若干层:含有下层绕组的为m1层,含有上层绕组的为m2层,槽楔以及槽开口为m3层,厚度均为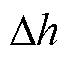 。
。
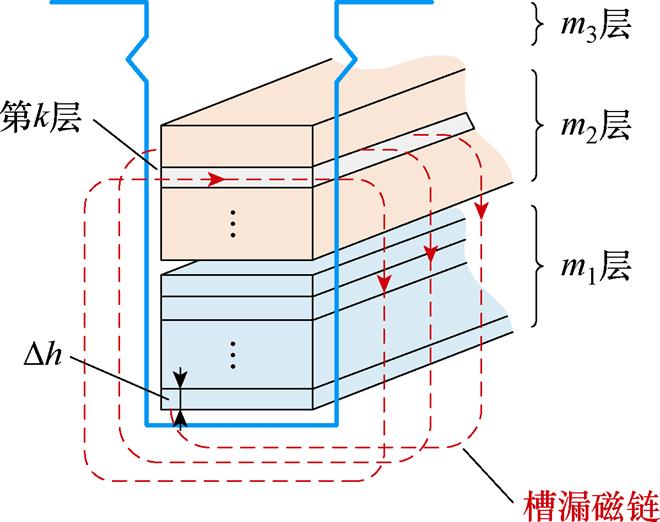
图7 双层短距绕组的定子槽
Fig.7 Stator slot of a double layer short-pitched winding
双层绕组的槽漏感组成为
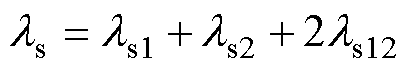 (15)
(15)
式中,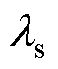 为一个定子槽的总漏感;
为一个定子槽的总漏感;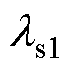 为下层自感;
为下层自感;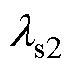 为上层自感;
为上层自感;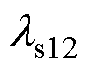 为上下层互感。
为上下层互感。
以图7中定子槽自下而上第k层的位置及其漏磁链路径为例,不计槽绝缘以及层间绝缘,假设槽内下层及上层绕组的总面积分别为A1和A2,总电流均为1 A,总匝数均为1且导体均匀分布,则第k层槽中下层绕组电流产生的自感磁链对应的自感为
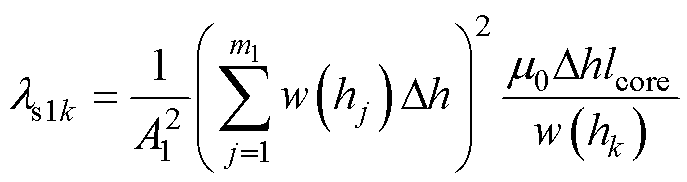 (16)
(16)
式中,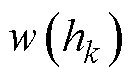 为第k层槽宽,由于整个下层绕组均在第k层中产生了自感磁链,因此累加上限为m1。
为第k层槽宽,由于整个下层绕组均在第k层中产生了自感磁链,因此累加上限为m1。
第k层槽中上层绕组电流产生的自感磁链对应的自感为
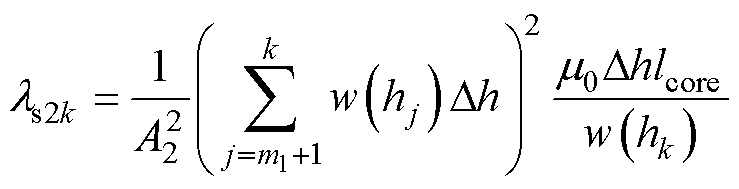 (17)
(17)
第k层槽中由上、下层绕组电流相互作用产生的互感磁链对应的互感为
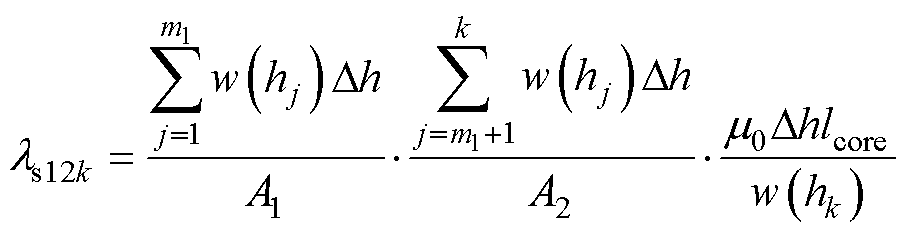 (18)
(18)
薄层所处的位置不同,计算时累加的上下限也有所调整。最后将所有薄层自感和互感的值分别累加,即可得到一个槽的上、下层自感和层间互感分别为
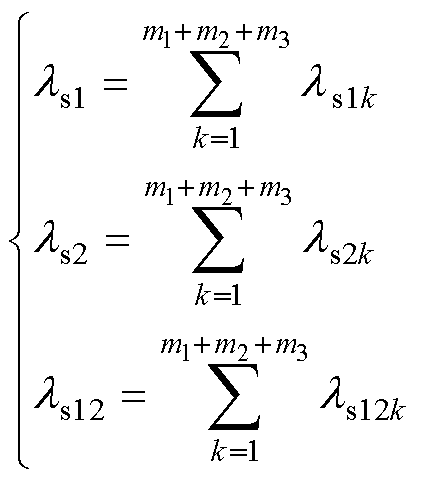 (19)
(19)
单槽漏感计算后,再根据整个绕组的空间分布计算定子的相槽漏感,图8为三相双层短距绕组在一对极下的相带分布示意图,从图中可以看出,上下层绕组分布规律相同,彼此错开q1个槽。记每极每相槽数为q,则整个定子绕组中上下层电流一致的每一相槽数为2p(q-q1),上下层电流不同的每一相槽数为2pq1,后者上下层电流的极性也相反。
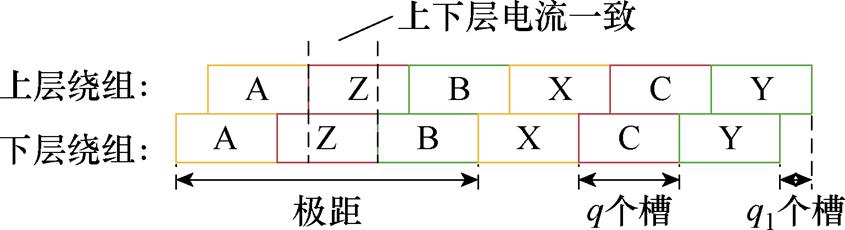
图8 三相双层短距绕组的相带分布
Fig.8 Phase zone distribution of a three-phase doule layer short-pitched winding
基于式(15)~式(19)的单位电流、单位匝数的槽漏感计算过程,以及双层短距绕组的空间分布,计算单相中所有槽的上下层自感以及层间互感并叠加,最后利用式(15)进行同类项合并,得到定子相槽漏感Lsslot的表达式为
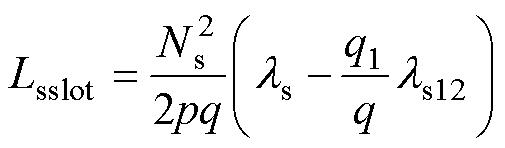 (20)
(20)
图9为层微元法计算出的定子槽漏感值随槽等分层数的变化曲线。从图中可以看出,槽的等分层数越多,定子槽漏感的计算结果越稳定,越趋于理论积分,符合微元法的思想。此外,层微元法对漏磁路进行逐层分析,相较于采用单一长宽代替实际槽型的漏感计算而言,其准确性显著提高。
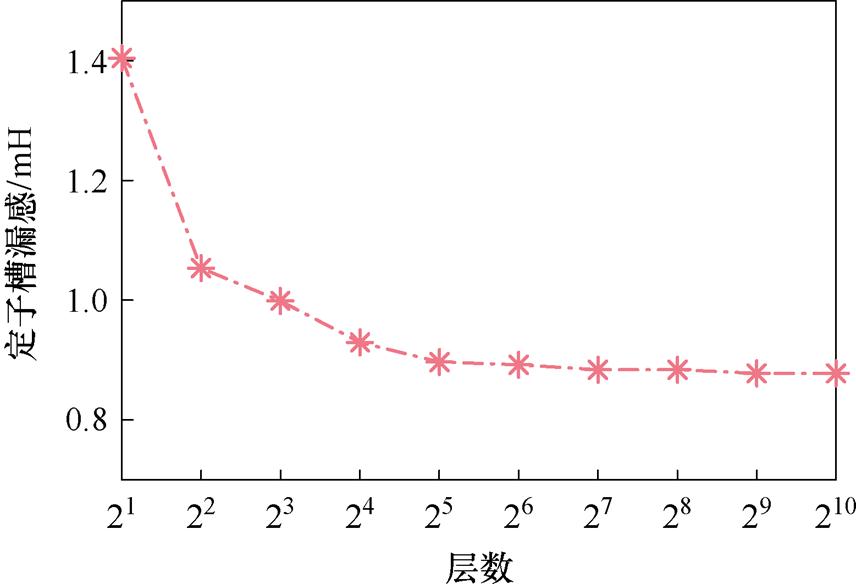
图9 等分层数不同时的定子槽漏感值
Fig.9 Stator slot leakage inductance with different numbers of equal-divided layers
本文所研究的湿式潜水感应电机,定子为开口平行槽、转子为半闭口平行槽,对于开口或半闭口槽而言,由于气隙的磁导率远大于铁心,漏磁力线经过槽口气隙时已产生较大的磁压降损失,因此齿顶受槽漏磁的影响较小,其磁场强度主要取决于主磁路的磁压降分布。而对于采用闭口槽或磁性槽楔的电机而言,计算槽漏感时采用闭口槽卡式系数将其等效成开口槽,可有效考虑磁桥位置处的饱和以及边缘效应的影响[23]。
潜水感应电机的转子结构为笼型,内置成型的转子导条。交变的气隙磁场切割转子导条产生感应涡流,使得导条沿横截面方向的电流分布不均,因此,转子侧交流电阻及漏感参数的计算与直流情况时不同,需要考虑电流非均匀分布的影响。
同样采用层微元法计算转子侧的交流电阻及漏感参数。图10左侧为潜水感应电机转子槽及其内部放置的实心导条。将导条从底部到顶部等分成n层,每层的高度均为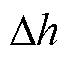 。
。
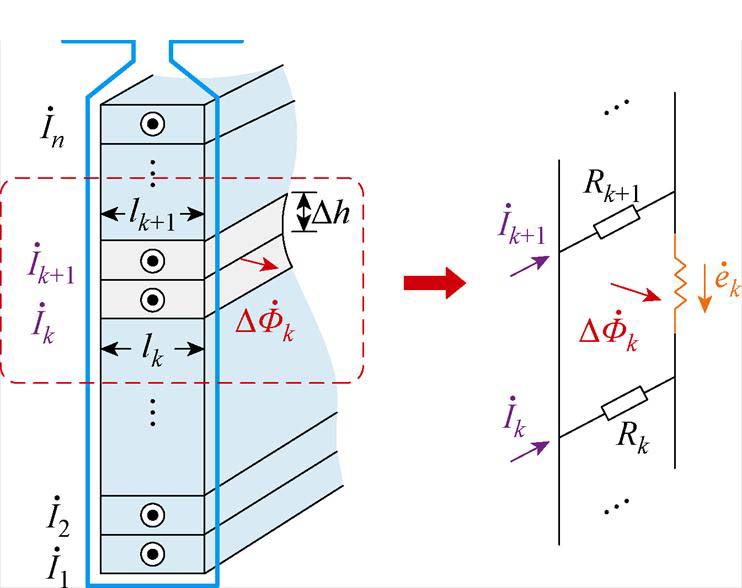
图10 转子导条分层及第k、k+1层等效电路
Fig.10 Layer-divided rotor bar and the equivalent circuit of the k th and k+1 th layer
交变磁通在转子导条层间产生感应电动势,继而产生感应涡流,使得上下层的电流不一致。图10左侧红色虚线框内为第k层与第k+1层导条,交变磁通在层间产生感应电动势,进而构成闭合回路,如图10右侧所示。回路电压方程为
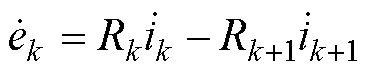 (21)
(21)
式中,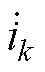 、
、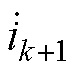 分别为第k层与第k+1层导体的电流相量;Rk、Rk+1分别为第k层与第k+1层导体的电阻,视每一薄层内电流为均匀分布,则上下层电阻为直流电阻,与各自的导体宽度成反比。
分别为第k层与第k+1层导体的电流相量;Rk、Rk+1分别为第k层与第k+1层导体的电阻,视每一薄层内电流为均匀分布,则上下层电阻为直流电阻,与各自的导体宽度成反比。
感应电动势相量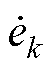 可计算为
可计算为
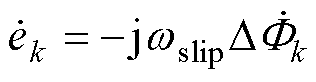 (22)
(22)
式中,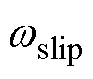 为转子的转差角频率;
为转子的转差角频率;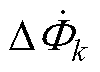 为第k个子回路中的交变磁通相量,有
为第k个子回路中的交变磁通相量,有
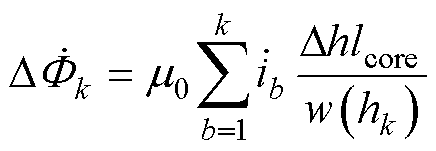 (23)
(23)
联立式(21)~式(23),结合直流电阻的计算公式,可得第k层与第k+1层电流的关系为
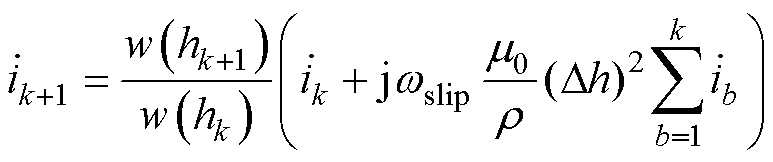 (24)
(24)
式中,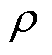 为导体的电阻率。利用式(24),从导体的底层开始,逐层求解各层电流,从而得到各层电流与导条总电流的大小与相位关系。
为导体的电阻率。利用式(24),从导体的底层开始,逐层求解各层电流,从而得到各层电流与导条总电流的大小与相位关系。
图11为单根转子导条在不同转差下的各层电流与总电流的相量图,底层电流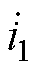 的幅值均为1 A,相位均为1 rad,导条等分层数均为15。从图中可以看出,转差接近于0时,各层电流的大小和相位几乎相同,无趋肤效应;转差越高,各层电流的差异越明显,交直流参数的区别越大。
的幅值均为1 A,相位均为1 rad,导条等分层数均为15。从图中可以看出,转差接近于0时,各层电流的大小和相位几乎相同,无趋肤效应;转差越高,各层电流的差异越明显,交直流参数的区别越大。
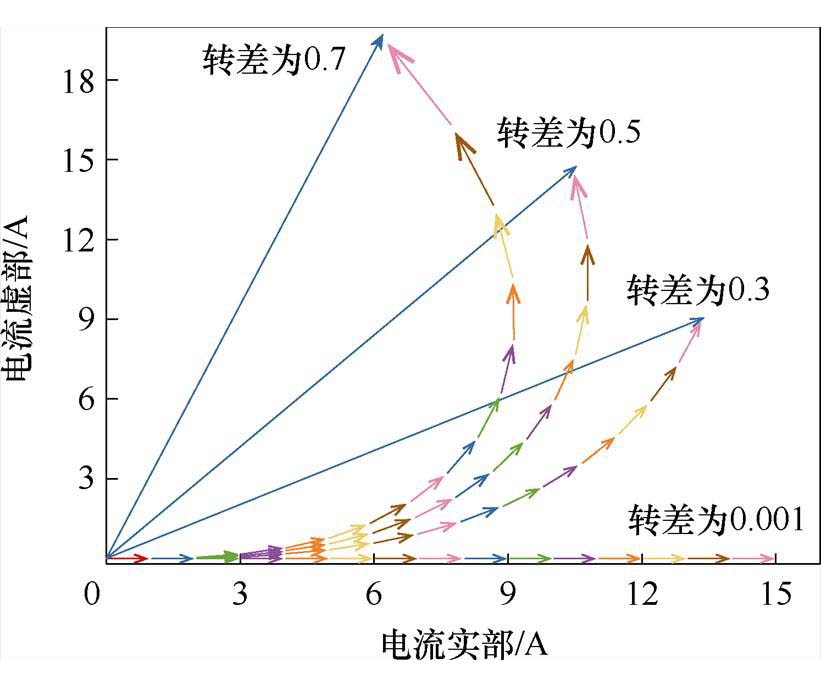
图11 不同转差下转子导条的总电流和各层电流
Fig.11 Total and layer currents of the rotor bar under different slip
计及端部电阻,转子侧的相电阻为
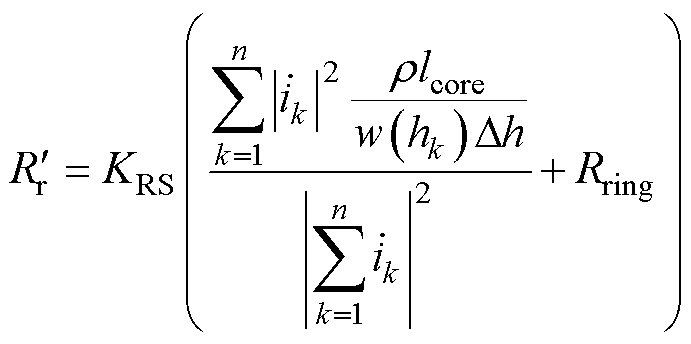 (25)
(25)
式中,KRS为转子侧参数归算到定子侧的比例系数;Rring为相邻两根导条之间的两段端环等效电阻,可由转子参数和端部尺寸直接求得[21]。
转子槽漏感的计算同样考虑上述电流不均匀分布的影响,忽略导条与转子槽的间隙,将导条顶部和槽开口之间的气隙部分再同样按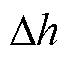 的高度等分为n1层,利用磁储能计算折算后的转子侧槽漏感
的高度等分为n1层,利用磁储能计算折算后的转子侧槽漏感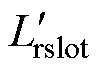 的表达式为
的表达式为
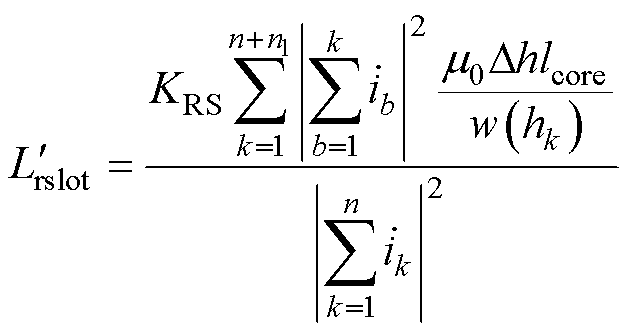 (26)
(26)
图12给出不同转差下的转子电阻和槽漏感值,并与直流情况下的参数值对比,从图中可以看出,随着转差的上升,转子的交流电阻增大,交流槽漏感减小。转子侧的气隙漏感与端部漏感与定子侧类似,由设计参数直接求解[22]。
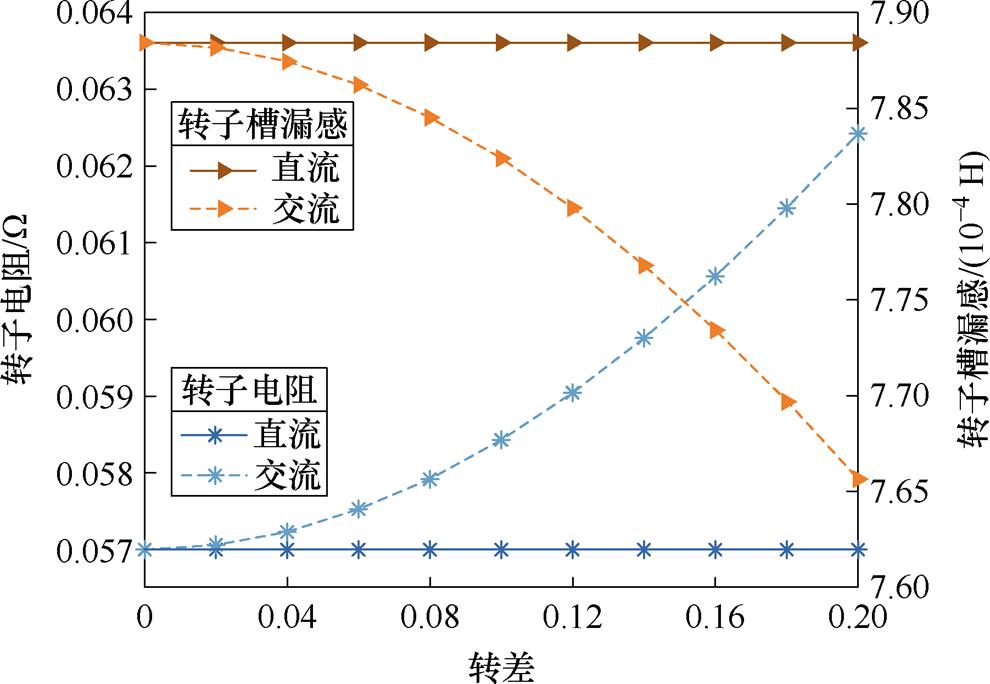
图12 不同转差下转子电阻与槽漏感
Fig.12 Resistance and slot leakage inductance of the rotor under different slip
由上述分析可知,转差不同,转子侧的参数相应发生变化,因此,构建不同转差下的定子端电压约束条件应当采用不同转差下的等效电路参数。
第2节主磁路的计算最终得到气隙基波磁通密度幅值随每极磁压降幅值的变化曲线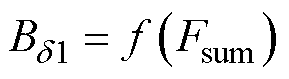 ,交变的气隙基波磁通产生基波感应电动势,其有效值Em为
,交变的气隙基波磁通产生基波感应电动势,其有效值Em为
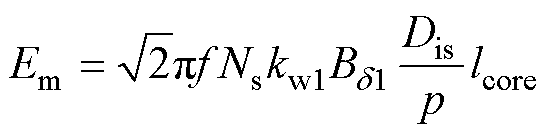 (27)
(27)
式中,f为频率。
励磁电流产生气隙磁链,进而在主磁路的各段产生磁压降,励磁电流有效值Im与每极磁压降幅值Fsum的关系同式(5),重新写为
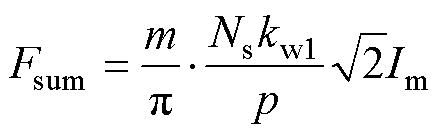 (28)
(28)
利用式(27)和式(28),将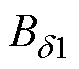 换算为Em,Fsum换算为Im,即可得到感应电动势有效值随励磁电流有效值的变化曲线Em=g(Im),作为励磁电感定解的目标函数。
换算为Em,Fsum换算为Im,即可得到感应电动势有效值随励磁电流有效值的变化曲线Em=g(Im),作为励磁电感定解的目标函数。
根据第3节漏磁路参数计算出的定转子槽漏感、转子电阻,结合由设计参数直接求解的定子电阻、定转子谐波及端部漏感,可以构建如图13所示的参数可调的稳态等效电路。图中,Rs为定子电阻;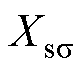 为定子漏抗;
为定子漏抗;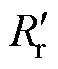 为折算后的转子电阻;
为折算后的转子电阻;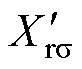 为折算后的转子漏抗;s为转差率;
为折算后的转子漏抗;s为转差率;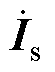 、
、 、
、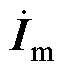 分别为定子、转子及励磁电流;
分别为定子、转子及励磁电流;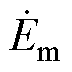 为感应电动势;Us为定子相电压幅值;UphN为额定相电压幅值。
为感应电动势;Us为定子相电压幅值;UphN为额定相电压幅值。
由于铁耗电流远小于磁化电流,可视励磁支路为纯感性支路,励磁电感的位置代入目标函数Em= g(Im)。转子转速不同,气隙磁场切割导条的转差频率不同,导条中感应涡流的分布也不同,因此转子侧参数为可调值,计算某一转差下的励磁电感时代入该转差下对应的转子侧参数。
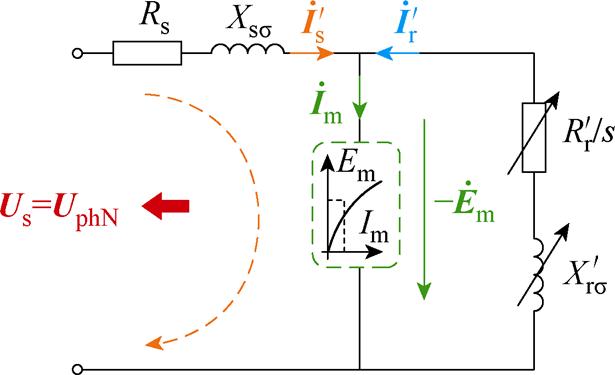
图13 参数可调的稳态等效电路
Fig.13 Steady-state equivalent circuit with adjustable parameters
励磁电感的定解过程可看作从目标函数曲线中找出满足上述稳态等效电路中定子端电压约束条件的点。将任意一组 (Im, Em) 代入某一转差下的稳态等效电路,设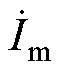 的初相位为0,则定子侧相电压
的初相位为0,则定子侧相电压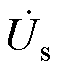 为
为
 (29)
(29)
式中,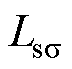 为定子漏感;
为定子漏感;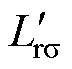 为折算后的转子漏感。已知定子额定相电压UphN为给定设计参数,因此,只有一组 (Im, Em) 值代入式(29)中满足
为折算后的转子漏感。已知定子额定相电压UphN为给定设计参数,因此,只有一组 (Im, Em) 值代入式(29)中满足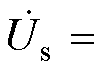
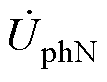 。该组 (Im, Em) 即为稳态电路解,并进一步求得励磁电感。
。该组 (Im, Em) 即为稳态电路解,并进一步求得励磁电感。
上述励磁电感的定解过程如图14所示,黑色曲线为感应电动势有效值随励磁电流有效值的变化曲线Em=g(Im)。不同转差下等效电路的参数不同,代入 (Im, Em) 计算定子端电压时会得到不同的曲线。额定相电压(UN=UphN=380 V)作为约束条件用黑色虚线表示,定子端电压曲线与黑色虚线的交点,在Em=g(Im)上的投影点为能满足该转差下稳态等效电路关系的 (Im, Em),如图14中放大部分所示,继而能求出该转差下的励磁电感。
图14中,在Em=g(Im)上与定子端电压曲线同色标记的星形点为满足稳态等效电路关系的最终解。可以看出:转差越大,交点的位置越高,励磁电感值越小。因为,此时磁力线经过更多的饱和路径,需要更大的励磁电流,符合电机的运行情况。
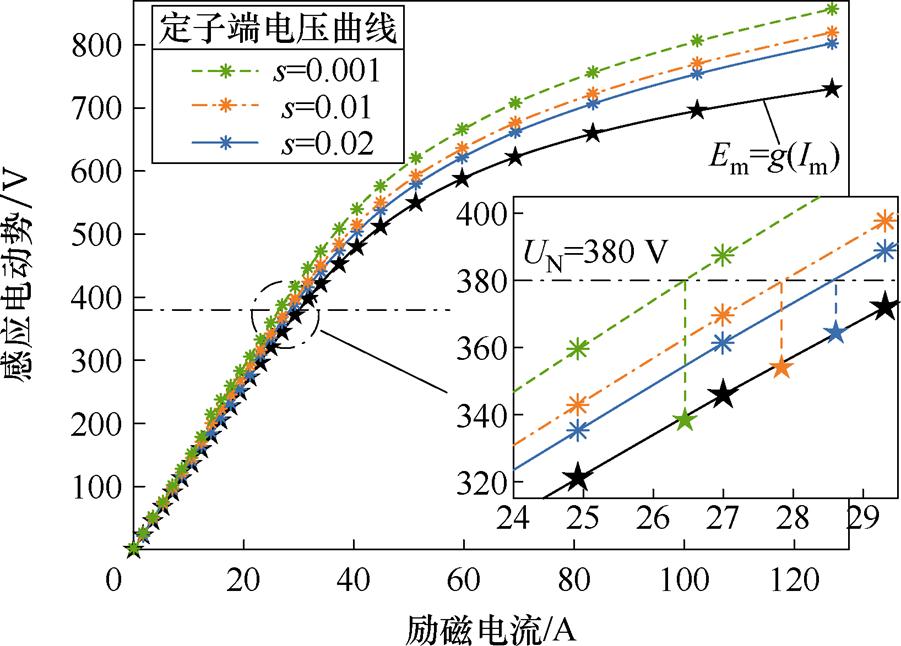
图14 励磁电感定解过程
Fig.14 Determination of the magnetizing inductance
励磁电感作为稳态等效电路中励磁支路的主要参数,其准确性通过电机的稳态输出加以验证。潜水感应电机通过控制所带泵负载的流量和扬程来调节其工作点的位置,样机、数据监测系统、试验井如图15所示。分别采用提出的层微元法和传统磁链法进行励磁电感的解析计算,进一步利用第3节计算的参数构建等效电路,并求解稳态输出。

图15 潜水感应电机及其试验平台
Fig.15 Submersible induction machine and testing platform
图16将采用层微元法和磁链法得出的电机输入功率和定子电流与负载试验进行比较。从图中可以看出,两种解析方法与样机的试验结果均比较接近。原因分析如下:潜水感应电机正常运行的工作区间在额定点附近且略低于额定点。电机各参数以额定点为技术要求进行设计,冲片尺寸、槽形等参数都留有一定饱和裕量,在样机试验的运行区间内饱和程度较轻,因此磁链法也能对励磁电感进行较为准确的计算,从而稳态输出的结果也相近。
图17给出试验电机利用层微元法进行磁路计算时的分段和总磁压降曲线,进一步验证上述分析:在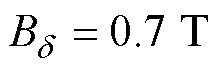 之前,定转子齿部和轭部的磁压降曲线均远小于气隙磁压降曲线,可近似认为气隙磁压降等于每极磁压降,气隙磁通密度幅值近似等于气隙基波磁通密度幅值(图中标注
之前,定转子齿部和轭部的磁压降曲线均远小于气隙磁压降曲线,可近似认为气隙磁压降等于每极磁压降,气隙磁通密度幅值近似等于气隙基波磁通密度幅值(图中标注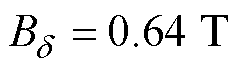 时,
时,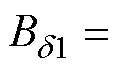
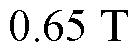 ),符合磁链法的假设条件。因此,磁链法和本文提出的层微元法在该情况下均能准确计算励磁电感,从而稳态等效电路的输出结果与负载试验接近。
),符合磁链法的假设条件。因此,磁链法和本文提出的层微元法在该情况下均能准确计算励磁电感,从而稳态等效电路的输出结果与负载试验接近。
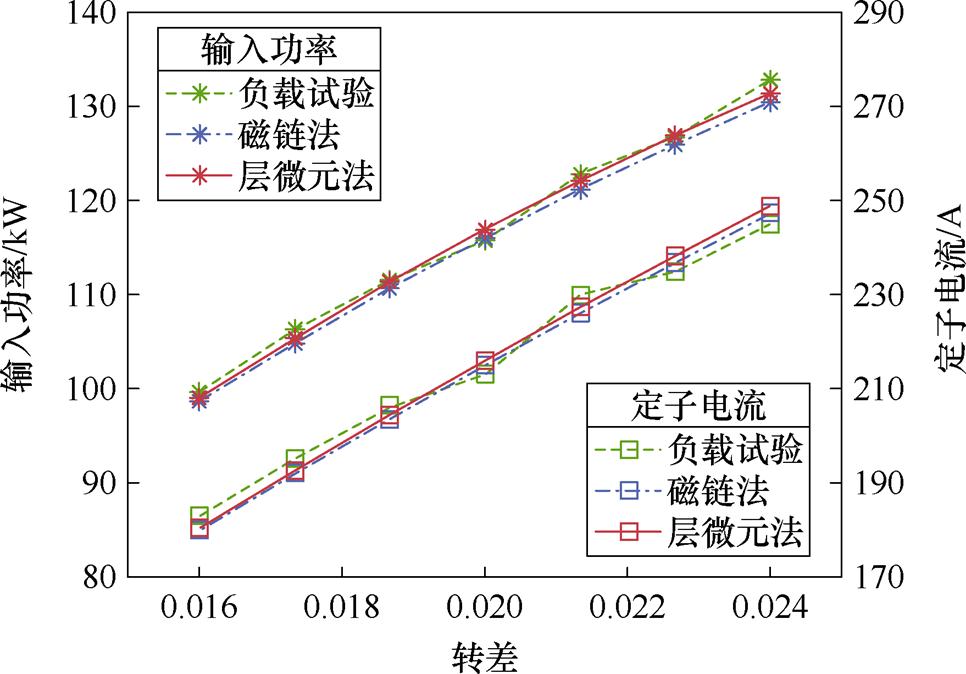
图16 不同转差下的输入功率和定子电流
Fig.16 Input power and stator current under different slip
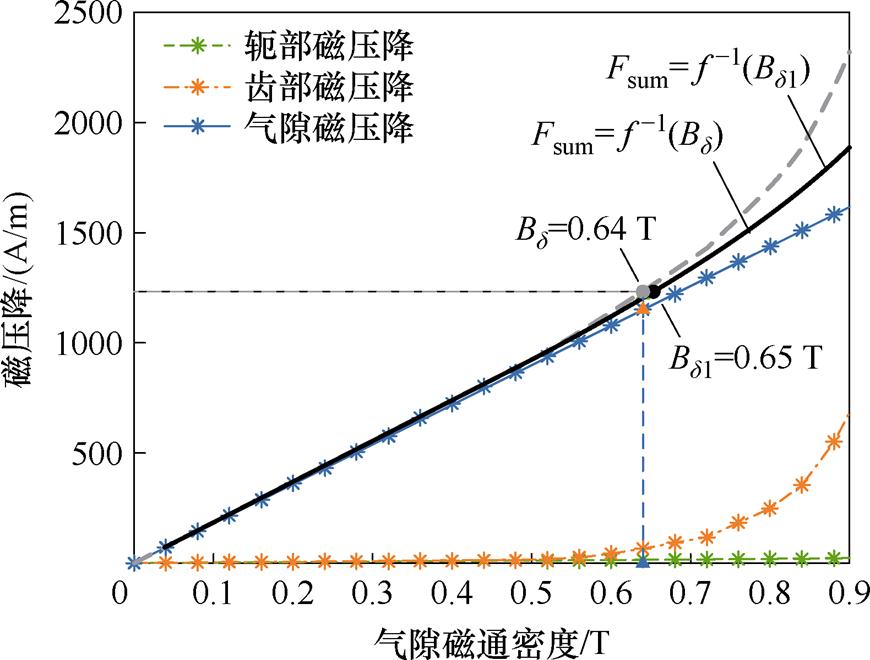
图17 不同气隙磁通密度下的分段和总磁压降
Fig.17 Divided and total magnetic voltage drops under different air-gap flux density
电机设计中,槽宽、槽高等参数选取不当,容易导致铁心出现局部饱和,使得励磁电感值发生变化,从而改变稳态输出。本节考察槽过宽导致定子齿部磁路饱和时,层微元法计算结果的准确性,并同样与磁链法进行比较,将尺寸调整后电机二维有限元模型的仿真结果作为标准值。为与5.1节负载试验的验证分析形成对照,两种解析法和有限元仿真的电机转差区间与5.1节相同。
定子槽形修改如图18所示,为保持定子电阻阻值以及气隙磁压降恒定,修改前后槽面积S1和槽开口b1均不变,从而槽内绕组的整体分布不变。定子内径不变的情况下,槽宽增大,齿宽相应减小,运行中容易出现齿磁路饱和;与此同时,槽面积不变的情况下,槽宽增大,槽高相应减小,漏磁链路径相应发生变化,因此,磁链法和层微元法的稳态等效电路中均对定子漏感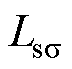 做修正。
做修正。
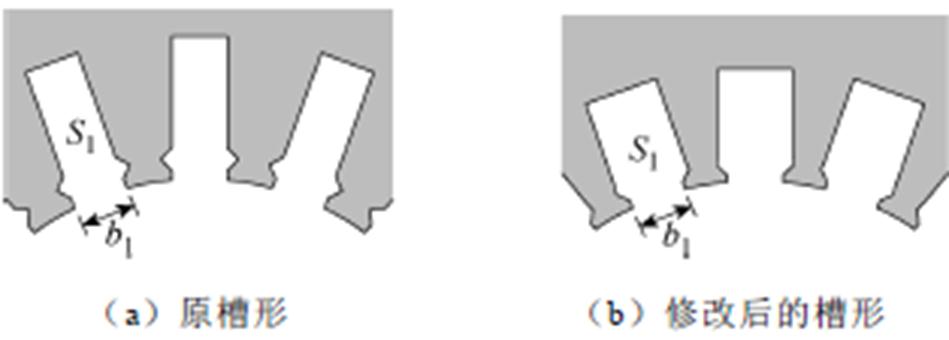
图18 定子槽形修改
Fig.18 Modification on the shape of the stator slot
图19为定子槽形修改后,不同转差下的输入功率、定子电流以及功率因数的变化曲线。将磁链法和层微元法的稳态等效电路计算结果与二维有限元仿真结果进行对比可以看出,有限元法(绿色曲线)和层微元法(红色曲线)在不同转差下的定子电流、输入功率的计算结果基本一致,二者的对应曲线也基本重合。此外,二者的功率因数变化曲线基本一致,层微元法的计算结果同有限元法存在不超过0.5%的误差(以有限元法为基准值)。但就磁链法的计算结果而言,磁链法计算出的输入功率和定子电流均低于有限元法,且随着转差逐渐升高,以转差s=0.024时的结果为例,输入功率与有限元法计算结果相差4.4 kW,定子电流相差6.7 A,功率因数相差约0.02,远高于层微元法的计算误差。

图19 不同转差下的输入功率、定子电流和功率因数(定子槽形修改)
Fig.19 Input power, stator current and power factor under different slip (stator slot shape modified)
原因分析如下:定子槽形修改保持槽开口b1不变,则在式(6)中,等效气隙系数KCrs保持不变,且式中的其他参数均不受槽形尺寸的影响,对磁链法而言,励磁电感的计算值并未发生变化,不能考虑由于尺寸修改导致的定子齿磁路饱和对等效电路参数的影响。因此,磁链法计算出的定子电流为不饱和值,小于磁饱和的实际结果。对于功率因数而言,实际饱和情况消耗更多的无功功率用以建立气隙磁场,因此磁链法计算得出的功率因数由于未考虑饱和而偏高。
图20给出修改定子槽形后,利用层微元法计算励磁电感时的分段与总磁压降的变化曲线,进一步验证上述分析:与图17相比可以看出,定子槽形变化使得齿部的饱和程度增加,齿部磁压降曲线在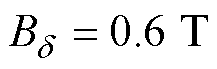 之后陡增,使得每极磁压降大于气隙磁压降,从而气隙磁通密度幅值与气隙基波磁通密度幅值存在较大差距(图中标注
之后陡增,使得每极磁压降大于气隙磁压降,从而气隙磁通密度幅值与气隙基波磁通密度幅值存在较大差距(图中标注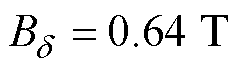 时,
时,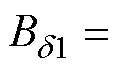
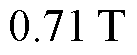 ),磁链法的假设在该情况下不能成立,因此计算结果存在较大误差。
),磁链法的假设在该情况下不能成立,因此计算结果存在较大误差。
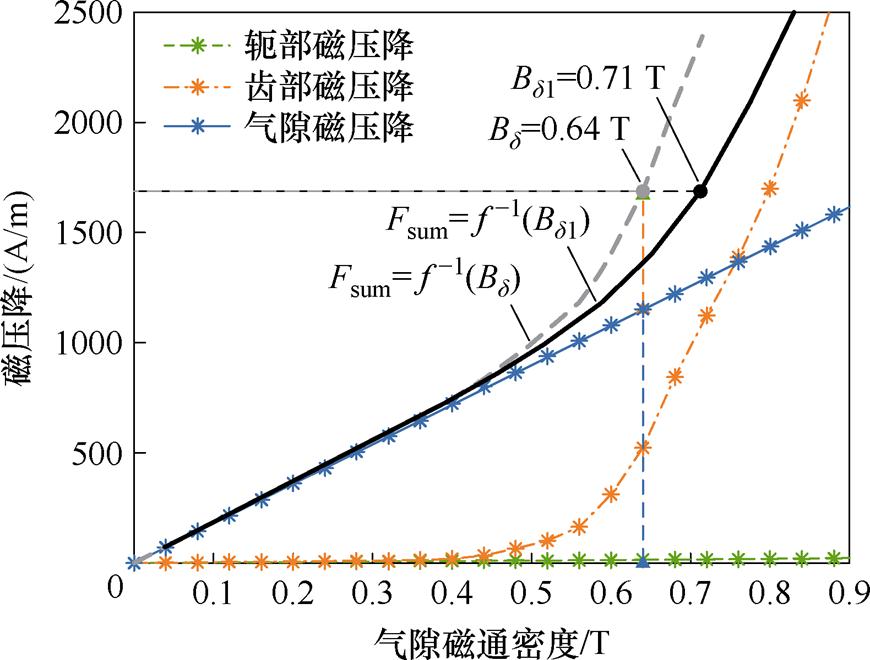
图20 不同气隙磁通密度下的分段和总磁压降(定子槽形修改)
Fig.20 Divided and total magnetic voltage drops under different air-gap flux density (stator slot shape modified)
本文针对电感计算常用的磁链法不能有效考虑磁饱和的问题,提出一种基于主、漏磁路的层微元法对潜水感应电机的励磁电感进行解析计算:主磁路计算得到感应电动势随励磁电流的变化曲线作为目标函数,漏磁路计算用于构建稳态等效电路中定子端电压表达式作为约束条件,目标函数上满足约束条件的点,其纵横坐标之比即为励磁电抗,继而得出励磁电感值。在主、漏磁路的分析中,采用薄层微元等效理论积分,有效考虑齿槽结构和铁磁材料的非线性属性。利用潜水感应电机的负载试验和定子齿磁路饱和情况下的有限元仿真验证所提方法的有效性,并与磁链法的计算结果进行对比,得出的结论如下:
1)当由于槽型修改导致定子齿磁路出现饱和时,在与负载试验相同的转差区间内,层微元法计算得出的定子电流、输入功率曲线同有限元分析基本重合,功率因数的变化曲线也基本一致,以有限元法为基准值时,误差不超过0.5%,说明层微元法能有效考虑由于尺寸参数不当导致的磁路饱和对电机稳态输出的影响。
2)磁链法计算励磁电感时,由于不考虑磁力线穿过定转子铁心产生的磁压降损失,在定子齿磁路饱和前后励磁电感值不发生变化,因此其稳态等效电路的计算结果中,输入功率和定子电流值均低于有限元法,且随着转差升高误差逐渐增大,在负载试验的转差区间内,输入功率最高可相差4.4 kW,定子电流相差6.7 A,远高于层微元法的计算误差。
综上所述,本文提出的基于主、漏磁路的层微元法在进行励磁电感的解析计算时能有效考虑磁路饱和,建立励磁电感与尺寸参数的直接联系,为潜水感应电机及其他各类电机的初始设计优化提供便利。
参考文献
[1] Li Jiaxin, Di Chong, Bao Xiaohua. Efficiency improvement for submersible motors by optimizing the ratio of diameter to shaft length[J]. IEEE Transa- ctions on Magnetics, 2022, 58(2): 8200806.
[2] 鲍晓华, 吕强, 王汉丰. 基于齿部磁场分析的大型潜水电机气隙偏心故障研究[J]. 电工技术学报, 2016, 31(8): 90-95.
Bao Xiaohua, Lü Qiang, Wang Hanfeng. Study on air-gap eccentricity fault in large submersible motors with tooth magnetic field analysis[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 90-95.
[3] 葛健, 徐伟, 刘毅, 等. 考虑端部效应的同心笼次级直线双馈电机等效电路[J]. 电工技术学报, 2022, 37(19): 4957-4968.
Ge Jian, Xu Wei, Liu Yi, et al. Equivalent circuit for nested-loop secondary linear doubly-fed machine considering end effect[J]. Transactions of China Electrotechnical Society, 2022, 37(19): 4957-4968.
[4] 杨凯, 李孺涵, 罗成, 等. 负载变化下无传感器感应电机主动零频穿越及脉动抑制策略[J]. 电工技术学报, 2023, 38(18): 4910-4920.
Yang Kai, Li Ruhan, Luo Cheng, et al. Proactive low-frequency ride-through method and its ripple reduction for sensorless induction motor drives under load variations[J]. Transactions of China Electro- technical Society, 2023, 38(18): 4910-4920.
[5] Rezaeealam B. Calculation of magnetizing and leakage inductances of induction machine using finite element method[J]. Electrical Engineering, 2021, 103(1): 315-323.
[6] Marfoli A, Papini L, Bolognesi P, et al. Analysis of induction machine: comparison of modelling tech- niques[C]//2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 2017: 1-7.
[7] Matsushita M, Ishibashi F, Mizuno S. Calculation of magnetizing inductance and magnetizing current of squirrel cage induction motor[C]//2016 19th Inter- national Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 2016: 1-5.
[8] 凌在汛, 周理兵, 张毅, 等. 屏蔽感应电机等效电路参数的有限元计算法[J]. 电工技术学报, 2016, 31(22): 28-34.
Ling Zaixun, Zhou Libing, Zhang Yi, et al. Para- meters calculation of canned solid-rotor induction motor by finite element analysis[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 28-34.
[9] 凌在汛, 周理兵, 张毅, 等. 笼型实心转子屏蔽感应电机电磁场及参数研究(四): 等效电路参数有限元计算法及验证[J]. 电工技术学报, 2018, 33(21): 4987-4997.
Ling Zaixun, Zhou Libing, Zhang Yi, et al. Para- meters determination and electromagnetic field analysis of canned solid-rotor induction motor (4): equivalent parameters calculation by finite element method and its verification[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4987-4997.
[10] 燕婧文, 狄冲, 鲍晓华, 等. 基于二维有限元法的感应电机T型等效电路参数的分析与计算[J]. 中国电机工程学报, 2021, 41(增刊1): 294-302.
Yan Jingwen, Di Chong, Bao Xiaohua, et al. Analysis and calculation of T-type equivalent circuit para- meters of induction motor based on two-dimensional finite element method[J]. Proceedings of the CSEE, 2021, 41(S1): 294-302.
[11] Wang Yan, Yang Jiaqiang, Deng Rongfeng, et al. Parameters estimation for multiphase induction machine with concentrated windings through finite element method[J]. IET Electric Power Applications, 2020, 14(10): 1807-1817.
[12] 刘光军, 王雪帆, 熊飞. 绕线转子无刷双馈电机‘P’型等效电路[J]. 中国电机工程学报, 2016, 36(20): 5632-5638.
Liu Guangjun, Wang Xuefan, Xiong Fei. A ‘P’-type equivalent circuit of wound rotor brushless doubly- fed machines[J]. Proceedings of the CSEE, 2016, 36(20): 5632-5638.
[13] 朱熙, 范瑜, 吕刚, 等. 单边盘式感应电机的数学模型与转矩分析[J]. 中国电机工程学报, 2010, 30(24): 69-74.
Zhu Xi, Fan Yu, Lü Gang, et al. Modeling and torque analysis of a disc induction motor[J]. Proceedings of the CSEE, 2010, 30(24): 69-74.
[14] 张育兴, 马名中, 马伟明, 等. 双定子直线感应电机饱和特性分析[J]. 中国电机工程学报, 2012, 32(36): 102-108.
Zhang Yuxing, Ma Mingzhong, Ma Weiming, et al. Analysis of saturation characteristics of double-stator linear induction motors[J]. Proceedings of the CSEE, 2012, 32(36): 102-108.
[15] 欧阳斌, 刘德志, 翟小飞, 等. 斜槽电机中绕组电感参数的解析计算方法[J]. 中国电机工程学报, 2011, 31(15): 69-74.
Ouyang Bin, Liu Dezhi, Zhai Xiaofei, et al. Analytical calculation of inductances of windings in electrical machines with slot skew[J]. Proceedings of the CSEE, 2011, 31(15): 69-74.
[16] Roshandel E, Mahmoudi A, Kahourzade S, et al. Saturation consideration in modeling of the induction machine using subdomain technique to predict perfor- mance[J]. IEEE Transactions on Industry Appli- cations, 2022, 58(1): 261-272.
[17] 黄子果, 王善铭, 倪守辉. 光滑实心转子异步电机等效电路参数的二维计算方法[J]. 中国电机工程学报, 2016, 36(9): 2505-2512.
Huang Ziguo, Wang Shanming, Ni Shouhui. 2D calculation methods of equivalent-circuit parameters in smooth solid rotor induction machines[J]. Pro- ceedings of the CSEE, 2016, 36(9): 2505-2512.
[18] Wang Dong, Wu Xinzhen, Chen Junquan, et al. A distributed magnetic circuit approach to analysis of multiphase induction machines with nonsinusoidal supply[J]. IEEE Transactions on Energy Conversion, 2015, 30(2): 522-532.
[19] Ansari M N, Dalal A, Kumar P, et al. Analytical method for accurate determination of nonlinear magnetization curve of induction motor[C]//2015 Annual IEEE India Conference (INDICON), New Delhi, India, 2015: 1-6.
[20] 王东, 吴新振, 马伟明, 等. 非正弦供电十五相感应电机磁路计算方法[J]. 中国电机工程学报, 2009, 29(12): 58-64.
Wang Dong, Wu Xinzhen, Ma Weiming, et al. Mag- netic circuit calculation of fifteen-phase induction motor with non-sinusoidal supply[J]. Proceedings of the CSEE, 2009, 29(12): 58-64.
[21] Pyrhönen J, Jokinen T, Hrabovcová V. Design of rotating electrical machines[M]. Chichester: John Wiley & Sons Ltd, 2014.
[22] 陈世坤. 电机设计[M]. 北京: 机械工业出版社, 2000.
[23] 鲍晓华, 梁娜, 方勇, 等. 考虑边缘效应和磁饱和影响的闭口槽潜水电机卡特系数计算新方法[J]. 电工技术学报, 2015, 30(12): 220-227.
Bao Xiaohua, Liang Na, Fang Yong, et al. Novel method of evaluation of Carter factor for closed slot submersible motor including fringing effect and magnetic saturation[J]. Transactions of China Electro- technical Society, 2015, 30(12): 220-227.
Abstract The equivalent circuit is valuable for designing an induction machine and its driving system, and its parameters are essential for analyzing the electromagnetic performance and establishing the driving model, especially the magnetizing inductance that characterizes the main flux distribution in the machine. The finite element analysis can precisely determine the magnetizing inductance. However, it is unsuitable for the initial design stage when the design parameters need frequent adjustment. Traditional analytical calculations like the flux linkage method neglect the influence factors, such as core saturation, tooth-slot effect, and rotor movement in the actual operation, causing accuracy issues. The improved analytical calculation method can significantly enhance the accuracy. However, the magnetic circuit in each core segment still needs to be more accurate, and the local saturation points are easily ignored. Besides, the solving process contains nonlinear iterations of multi-segment of the magnetic circuit, which has repeating calculations under different slips.
This paper proposes an elementary layer method based on the main and leakage magnetic circuits to calculate the magnetizing inductance. Firstly, the magnetic voltage drop of each pole of the main magnetic circuit under different air-gap flux densities is calculated, and the magnetic voltage drop and the air-gap flux density are converted into the electromotive force and the magnetizing current to obtain the objective function. Secondly, the distribution of the leakage flux in the stator slot and the current induced in the rotor bar is analyzed to calculate the slot leakage inductance of the stator and rotor, together with the rotor AC resistance. The stator terminal voltage expression is constructed as the constraint condition. Finally, each set of the electromotive force and the magnetizing current on the objective function are substituted into the constraint condition to make the results equal to the rated phase voltage of the stator. The ratio of the set is the value of the magnetizing reactance, and therefore, the magnetizing inductance is obtained. In the main and leakage flux circuits, the irregular and nonlinear magnetic and electric circuits are regularized and linearized using the thin layer elements to substitute theoretical integral. Hence, the tooth-slot structure and the nonlinear material properties can be considered more accurately when calculating the magnetic voltage drop and leakage inductance.
A wet submersible induction machine is an example of the analytical calculation of the magnetizing inductance using the proposed elementary layer method and the traditional flux leakage method. Besides, the steady-state outputs of the equivalent circuit are obtained. The prototype test and the finite element simulation under the magnetic saturation of the stator teeth are conducted. The results show that the elementary layer method considers the distribution of the magnetic voltage drop in the core segment, which is more effective than the flux linkage method when the tooth magnetic circuit is saturated. Therefore, the calculation of the magnetizing inductance is more accurate, and in the steady-state outputs of the equivalent circuit, the stator current, input power, and power factor curves are consistent with the finite element analysis. The error is less than 0.5% when the finite element results are used as the reference. The proposed method links the design parameters and the magnetizing inductance, providing convenience for the initial design and optimization of the submersible induction machine and other types of machines.
Keywords:Magnetizing inductance, magnetic saturation, submersible induction machine, elementary layer method
中图分类号:TM346+.2
DOI: 10.19595/j.cnki.1000-6753.tces.240640
国家自然科学基金(51977055)和安徽省科技重大专项(201903a05020042)资助项目。
收稿日期 2024-04-24
改稿日期 2024-07-02
鲍晓华 男,1972年生,教授,博士生导师,研究方向为电机设计理论和技术、电机电磁场理论分析及计算、大型电机及高速电机的可靠性技术。
E-mail: baoxh@hfut.edu.cn(通信作者)
刘 婕 女,1999年生,硕士研究生,研究方向为电机电磁场分析和优化设计。
E-mail: 2020110351@mail.hfut.edu.cn
(编辑 崔文静)