基于有源整流的无线电能传输系统双边LCL零电压软开关控制策略
李 争1,2 于治昊1 高世豪1 唐明磊1 孙鹤旭1
(1. 河北科技大学电气工程学院 石家庄 050018 2. 燕山大学电气工程学院 秦皇岛 066004)
摘要 在无线电能传输(WPT)系统中,为了实现精确的电压调节和系统的高效率运行,同时避免增加额外的DC-DC变换电路和谐振元件,该文提出一种双边LCL移相控制策略。该策略通过调节逆变器和有源整流器(AR)的内外移相角,实现恒压输出和所有开关管的零电压开通。通过对系统的功率损耗进行分析,得出系统最大效率运行时变流器内移相角之间的约束条件。基于此约束条件,进一步确定了实现零电压软开关(ZVS)的最小外移相角,从而实现了系统的高效率运行。此外,引入功率角作为中间变量,利用压控振荡器(VCO)实现AR的频率同步,从而使系统控制更加简便,同时提高了控制精度。最后,搭建了一台50 W的实验样机,验证了理论的有效性;根据实验结果,在耦合系数k=0.31的情况下,系统的传输效率可达93.8%。
关键词:无线电能传输 移相控制 有源整流 零电压软开关
0 引言
无线电能传输(Wireless Power Transfer, WPT)技术,通过磁场耦合的方式传输电能,而无需任何物理接触。因其方便、安全、维护成本低等优点,受到越来越多的关注。目前,已推广到电动汽车[1-3]、植入式医疗[4-5]、消费电子[6-7]等诸多领域。
实际中许多用电设备都要求其供电电源具有恒压特性[8-10],即供电电压不受负载和其他参数变化的影响。因此,电压的准确调节对负载的安全稳定运行至关重要。而WPT系统的传输效率会受到负载变化的影响。当负载发生变化时,系统不能始终工作在最大效率点,导致系统的传输效率较低[11-12]。同时,为了减小电能传输过程中的开关损耗,需要所有的MOSFET尽可能地实现零电压软开关(Zero Voltage Switching, ZVS)。
为了实现上述目标,文献[11-21]中已经提出了许多控制方案。一般来说,这些控制方案可以分为三类:辅助DC-DC变换器控制、变谐振网络控制和有源整流器(Active Rectifier, AR)控制。
对于辅助DC-DC变换器控制,文献[11]采用了一种解耦控制策略,通过在系统的前后端添加辅助DC-DC变换器,实现了恒压输出和阻抗匹配。文献[13]提出双端附加DC-DC变换器控制方法,可同时实现电流/电压调节、ZVS和阻抗匹配。在此系统中,由于选择逆变器的工作频率作为谐振网络的谐振频率,在忽略系统寄生参数的情况下,也保证了逆变器的ZVS运行。为了减少DC-DC变换器的使用,文献[14]提出了一种通过调整逆变器的移相角和DC-DC变换器的次级占空比来实现阻抗匹配和电流/电压控制的方法。在传统的附加DC-DC变换器和简单控制下,输出电压可能会不稳定。为此,文献[15]利用基于超局部模型的智能反馈控制器来稳定整流电路后端升降压转换器的电压响应。然而,上述控制策略均需要额外的DC-DC变换器,这不仅增加了系统的复杂性还产生了额外的功率损耗。因此,为了避免使用DC-DC变换器,文献[16]通过变谐振网络实现蓄电池的恒流/恒压充电以及零相位特性。文献[17]利用不同补偿拓扑的恒压/恒流特性进行拓扑切换,以实现系统恒压/恒流输出。文献[18]通过调整一次侧的串联和并联补偿电容,以维持输出电压恒定。但上述变谐振网络的控制策略均未实现ZVS。为此,文献[19]通过实时跟踪和调整开关管的导通角,使开关管在零电压状态下实现ZVS,减少了开关损耗。此外,该方法还引入动态补偿电容,保证系统始终工作在最佳状态,提高了系统的稳定性和可靠性。需注意的是,不管是辅助DC-DC变换器控制还是变谐振网络控制,都需要附加额外的元件,增加了系统的成本和复杂性。
为了更好地利用逆变器和AR,不增加额外的DC-DC变换器和电感/电容阵列,文献[20]提出了一种双边移相控制策略,通过控制逆变器和AR的移相角( 和
和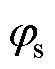 ),同时实现阻抗匹配和效率优化。文献[21]提出了一种带有辅助测量线圈的AR控制方法,利用检测接收端电流的过零信号实现AR同步,引入辅助线圈测量接收侧的非谐振度,并根据计算出的AR移相角的补偿值进行调谐。然而,在上述两种控制策略中,逆变器和AR都不能实现ZVS,这会极大地恶化WPT系统的安全运行,特别是在大功率的应用场合。文献[2]采用变频移相控制策略,调整逆变器的频率和移相角,实现了逆变器的ZVS和恒压/恒流充电。进一步地,文献[3]提出了一种变角移相控制策略,通过调节逆变器与AR之间的外移相角实现了逆变器和AR的ZVS,调节AR的内移相角以实现精确的电压控制。这种方法虽然能实现WPT系统的ZVS运行,但仅限于简单的串联-串联(Series-Series, S-S)型补偿拓扑。
),同时实现阻抗匹配和效率优化。文献[21]提出了一种带有辅助测量线圈的AR控制方法,利用检测接收端电流的过零信号实现AR同步,引入辅助线圈测量接收侧的非谐振度,并根据计算出的AR移相角的补偿值进行调谐。然而,在上述两种控制策略中,逆变器和AR都不能实现ZVS,这会极大地恶化WPT系统的安全运行,特别是在大功率的应用场合。文献[2]采用变频移相控制策略,调整逆变器的频率和移相角,实现了逆变器的ZVS和恒压/恒流充电。进一步地,文献[3]提出了一种变角移相控制策略,通过调节逆变器与AR之间的外移相角实现了逆变器和AR的ZVS,调节AR的内移相角以实现精确的电压控制。这种方法虽然能实现WPT系统的ZVS运行,但仅限于简单的串联-串联(Series-Series, S-S)型补偿拓扑。
为此,本文提出了一种不附加任何DC-DC变换器和变谐振网络结构的双边LCL移相控制策略,可同时实现负载的恒压输出、ZVS以及最大效率追踪。本设计在满足最大效率条件的基础上,确定了实现ZVS的最小移相角,实现了所有MOSFET的ZVS运行,有效地降低了功率损耗。此外,引入功率角,通过压控振荡器(Voltage-Controlled Oscillator, VCO)实现频率同步,提高了控制精度,有助于进一步提高系统效率。
1 系统模型分析
1.1 主电路拓扑与基本控制方法
为了提高系统效率,需使得WPT系统中的变流器实现ZVS。然而,仅依靠自适应谐振的移相控制来实现ZVS,无法确保系统效率的最大化。因此,同时实现ZVS和最大化效率传输显得尤为重要。本文通过调节AR的内移相角和两个变流器之间的外移相角来实现上述控制目标,并利用逆变器的相移来实现负载的恒压输出。
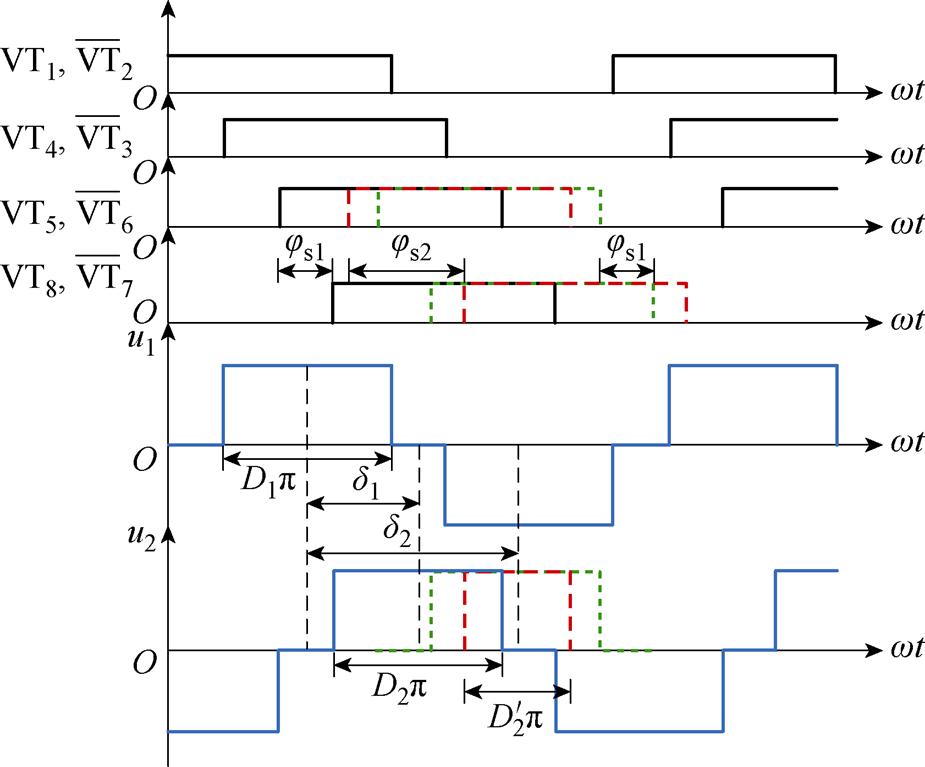
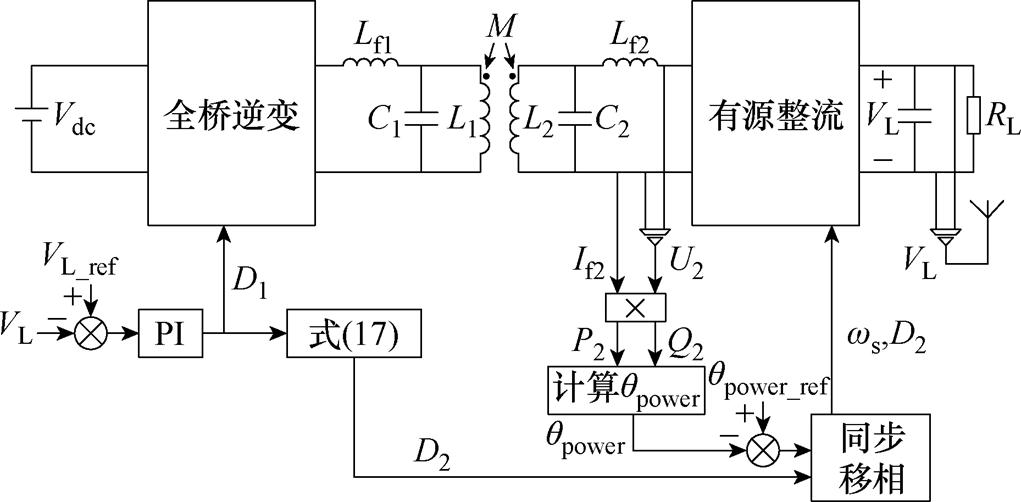
LCL-LCL型主电路拓扑如图1所示,L1和L2分别为一次、二次线圈电感;M为互感;Lf1和Lf2分别为一次、二次侧补偿电感;C1、C2、Rf1、Rf2和R1、R2分别为一次、二次侧的补偿电容、补偿电感的等效内阻和线圈的等效内阻;Cd1和Cd2为稳压电容;RL为负载电阻;Vdc为直流电源电压;VL为系统输出电压;IL为系统输出电流;u1为逆变器的输出电压;u2为AR的输入电压;i1和i2分别为流经L1和L2的电流;if1和if2分别为流经Lf1和Lf2的电流。WPT系统由高频逆变电路、LCL-LCL拓扑网络以及AR电路组成。全桥逆变电路(由开关管VT1~VT4组成)将直流电压Vdc逆变为高频交流电压u1,经LCL补偿网络传输到一次线圈电感L1,电流i1在线圈中产生高频交变磁场。根据电磁感应定律,一次线圈的交变磁场在二次线圈电感L2中产生交流电压u2,再经补偿网络和AR电路(由开关管VT5~VT8组成)输出直流电压VL给负载RL供电。D1、D2分别为u1、u2的电压占空比,d 为u1与u2之间的相位差。
1.2 等效电路分析
在WPT补偿网络中,通常使用基波等效模型进行分析[22-23]。交流等效电路如图2所示,图中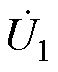 为逆变器的输出电压基波分量;
为逆变器的输出电压基波分量;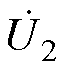 为AR的输入电压基波分量;
为AR的输入电压基波分量;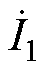 和
和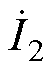 分别为电感L1和L2上的基波电流;
分别为电感L1和L2上的基波电流;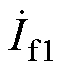 和
和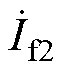 分别为电感Lf1、Lf2上的电流基波分量;Req为负载等效电阻,Req=8RL/p2。
分别为电感Lf1、Lf2上的电流基波分量;Req为负载等效电阻,Req=8RL/p2。
为了简化分析,将系统的工作频率w设置为谐振频率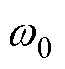 ,则有
,则有
忽略系统的寄生参数,变流器的驱动信号和电压波形如图3所示,其中开关管VT1、VT2(VT3、VT4)互补导通,VT5、VT6(VT7、VT8)互补导通,逆变器输出电压u1的脉冲宽度为D1p,AR的输入电压u2的脉冲宽度为D2p(D1、D2∈[0, 1]),逆变器和AR的内移相角可分别表示为(1-D1)p、(1-D2)p,d 为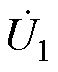 与
与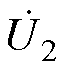 之间的相位差,同时也为外移相角。
之间的相位差,同时也为外移相角。
则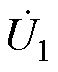 、
、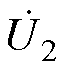 可分别表示为
可分别表示为
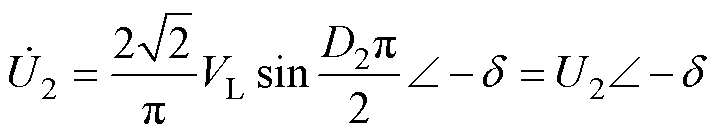 (3)
(3)
式中,U1和U2分别为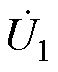 和
和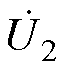 的模。
的模。
在图2交流等效电路中,忽略线圈内阻R1、R2和补偿电感的等效电阻Rf1、Rf2,并列写KVL方程为
输出的有功功率P2和无功功率Q2分别为
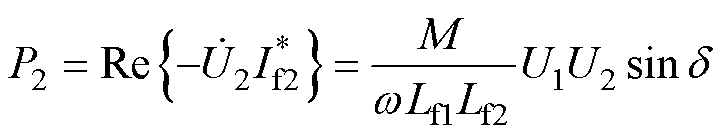 (5)
(5)
式中,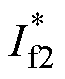 为
为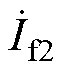 的共轭。从式(5)、式(6)可以看出,通过调节d,可以使无功功率降至最低。当d= 90°时,有功功率最大,无功功率为0。因此,应尽可能使WPT系统工作在d=90°附近,以获得最大传输效率。
的共轭。从式(5)、式(6)可以看出,通过调节d,可以使无功功率降至最低。当d= 90°时,有功功率最大,无功功率为0。因此,应尽可能使WPT系统工作在d=90°附近,以获得最大传输效率。
为简化计算,忽略AR的功率损耗,系统的输出功率Pout可以表示为
式(5)可改写为
 (8)
(8)
式中,If2为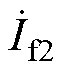 的模。结合式(3)、式(7)和式(8)解得
的模。结合式(3)、式(7)和式(8)解得
则系统的电压增益Gvvsys为
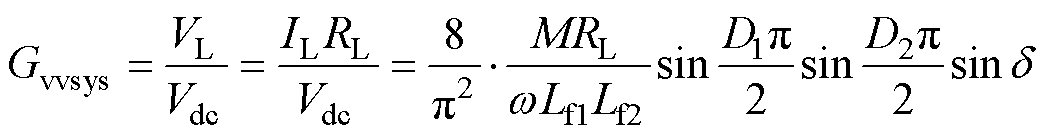 (10)
(10)
根据式(10)可知,负载的变化会导致电压增益Gvvsys也发生变化。在这种情况下,如果d 已知,可以通过调节D1和D2,适当调节系统的Gvvsys。当输入电压Vdc恒定不变时,可以调节Gvvsys,使输出电压恒定。
本文采用控制变量法研究负载变化对电压增益Gvvsys的影响,选取表1所示的系统参数进行研究,令d=90°,根据式(10)得出Gvvsys随D1、D2的变化情况,如图4a所示,在相同移相条件下,负载越大,Gvvsys越大。进一步地,为了更直观地显示d与Gvvsys的关系,D1、D2均设置为1,如图4b所示(其中d 的变化范围将在第2节中分析得出,此处设置为0.5p~p)。从图4中可以看出,在d 保持不变的情况下,Gvvsys随负载阻抗的增大而逐渐增大。此外,确定了Gvvsys便可以获得d 允许的变化范围。一般来说,d 的变化范围越大,越容易实现ZVS。
1.3 最大效率分析
WPT系统的电路损耗主要包括线圈损耗、补偿电感损耗以及功率开关器件的导通损耗和开关损耗。当WPT系统所有开关器件都实现ZVS时,开关损耗可以忽略不计,因此在本节忽略开关损耗。总损耗可用欧姆损耗来表示,由于系统参数对称,假设Lf1=Lf2=Lf,Rf1=Rf2=Rf,R1=R2=R。
表1 系统参数
Tab.1 System parameter
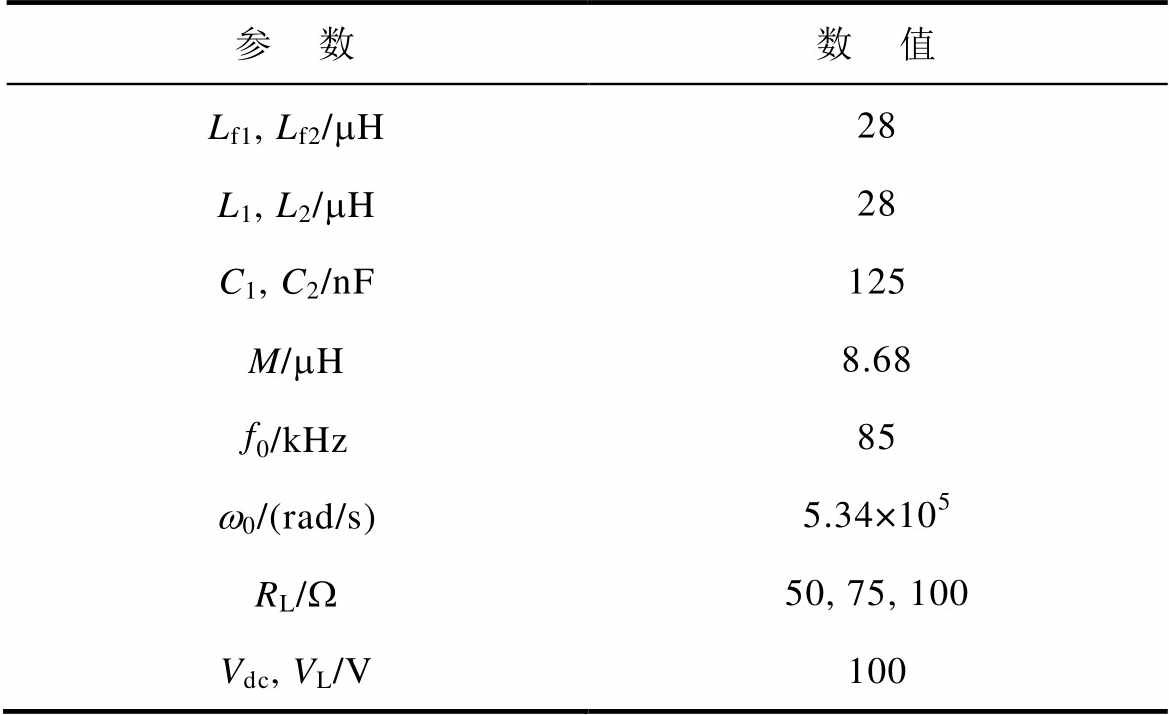
参 数数 值 Lf1, Lf2/mH28 L1, L2/mH28 C1, C2/nF125 M/mH8.68 f0/kHz85 w0/(rad/s)5.34×105 RL/W50, 75, 100 Vdc, VL/V100
根据图2所示的交流等效电路,总损耗PLoss可以表示为
式中,If1、If2、I1和I2分别为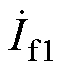 、
、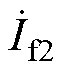 、
、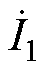 和
和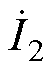 的模。
的模。
效率h 可以近似计算为
将式(5)和式(11)代入式(12)化简得
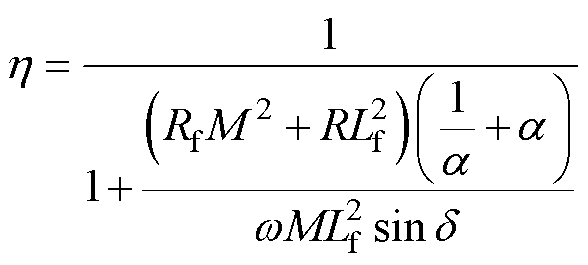 (13)
(13)
式中,a 为一次、二次交流电压之比,即
由式(13)可知,当WPT系统参数确定时,通过调节a 可以获得系统的最大效率。为确定实现最大效率的条件,令
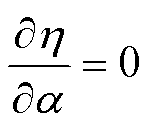 (15)
(15)
可得
由式(2)、式(3)、式(14)和式(16)得出
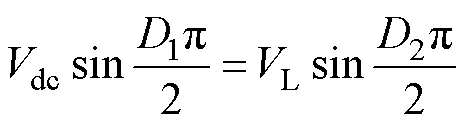 (17)
(17)
根据式(17)确定D1与D2的约束关系。然后代入式(10),可以求得D1和D2。
此时的最大效率为
根据式(13)可得交流电压比与传输效率之间的关系,交流电压比对传输效率的影响如图5所示。当d=90°、a=1时,系统的传输效率最大。随着a 与d 的偏移,效率逐渐降低,且偏移越大效率越低。
2 ZVS的实现
如果仅控制外移相角d=90°,系统的ZVS工作范围较窄,功率开关可能会硬开通,造成较大的开关损耗。在本节中,d 没有设置为90°,而是作为附加的控制变量,以产生实现ZVS的超前电流。第1节所用到的基波等效模型虽然有足够的精度,但由于全桥输出电流中含有高次谐波,在确定ZVS范围时存在不可忽略的误差,因此为了确定功率开关的ZVS范围,建立了基于谐波的等效模型,如图6所示。图中,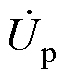 为考虑谐波时的逆变器输出电压相量,
为考虑谐波时的逆变器输出电压相量,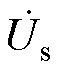 为考虑谐波的AR输入电压相量;
为考虑谐波的AR输入电压相量;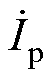 和
和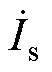 分别为考虑谐波的电感L1和L2电流;
分别为考虑谐波的电感L1和L2电流;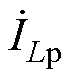 和
和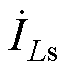 分别为考虑谐波的电感Lf1和Lf2电流。
分别为考虑谐波的电感Lf1和Lf2电流。
图6中,选择方波电压作为激励电压,并忽略Rf1、Rf2、R1和R2,选择系统最大效率所对应的d= 90°作为基准量,实现ZVS,而补偿量为Dd,有
此处的相移补偿角Dd∈[-90°, 90°]。
在谐波等效模型中,系统的阶数很高,很难进行计算。但由于Lf1、C1和Lf2、C2具有滤波功能,线圈电流中谐波含量很少,近似为正弦波。因此可以用基波等效模型代替精确模型计算线圈电流。
根据式(4)解得电流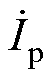 和
和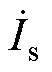 的时域表达式ip(t)和is(t)分别为
的时域表达式ip(t)和is(t)分别为
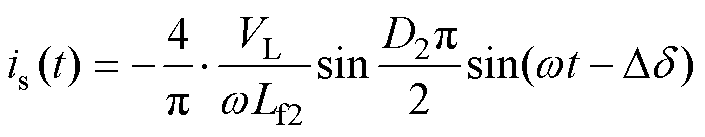 (21)
(21)
从而得到一次侧补偿电容电压的时域表达式uC1(t)为
同理可得,二次侧补偿电容电压的时域表达式uC2(t)为
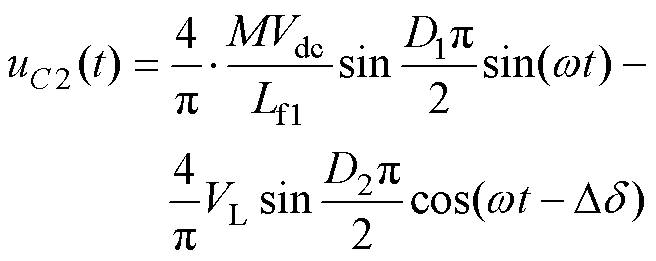 (23)
(23)
将图6进一步简化得到如图7所示的谐波简化模型,列写时域的KVL方程为
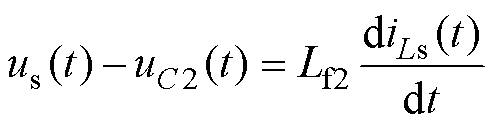 (25)
(25)
式中,up(t)、us(t)、iLp(t)和iLs(t)分别为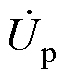 、
、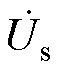 、
、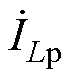 和
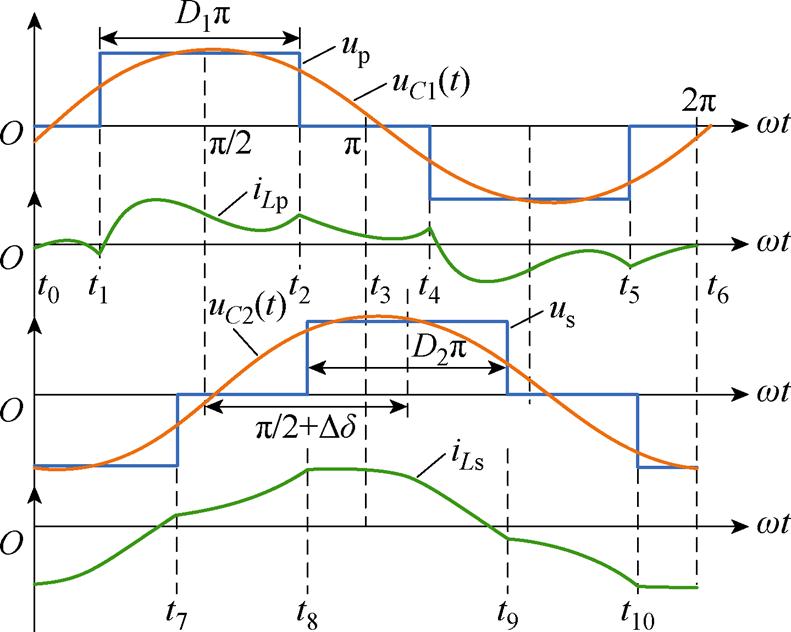
和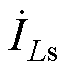 在时域下的表达式。通过对式(24)、式(25)积分,可以推导出一次和二次全桥输入和输出电流的表达式。图8显示了简化电路模型后的谐振网络输入和输出电压电流波形,选择t0(t0=0) 为波形的起点。由于波形是对称的,故只对前半个周期进行分析,后半个周期类似。
在时域下的表达式。通过对式(24)、式(25)积分,可以推导出一次和二次全桥输入和输出电流的表达式。图8显示了简化电路模型后的谐振网络输入和输出电压电流波形,选择t0(t0=0) 为波形的起点。由于波形是对称的,故只对前半个周期进行分析,后半个周期类似。
由图8可以看出
对式(24)积分,可得
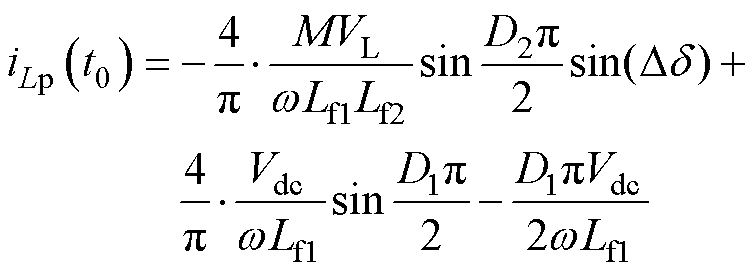 (27)
(27)
在确定波形的初值之后,通过获取波形上任一点的相位信息,便可以计算相应的电流值。因此可以求得iLp(t1)和iLp(t2)以及iLs(t0)和iLs(t7)分别为
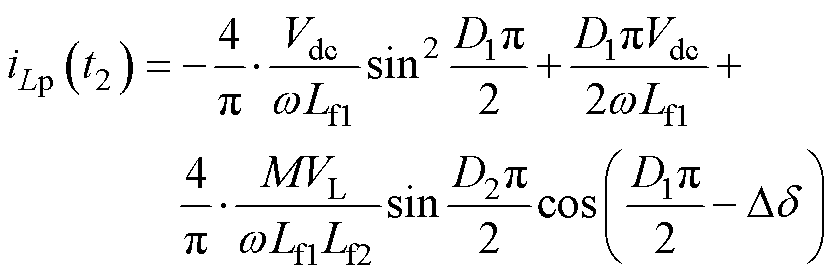 (29)
(29)
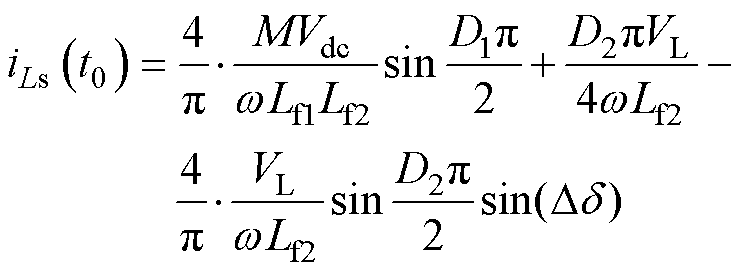 (30)
(30)
基于波形的对称性,要实现逆变器的ZVS,需满足iLp(t1)<0且iLp(t2)>0。由式(28)和式(29)不难得出,iLp(t1)+iLp(t2)>0,因此,只需满足iLp(t1)<0即可。同理,当iLs(t7)>0且iLs(t8)>0时,AR可以实现ZVS,而iLs(t7)<iLs(t8),所以只需满足iLs(t7)>0即可。综上所述,要实现所有MOSFET的ZVS,须满足条件
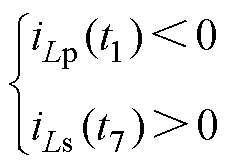 (32)
(32)
通过对iLp(t1)=0和iLs(t7)=0进行求解,可以确定在整个功率范围内,同时保持最小无功功率和实现ZVS所需的最小补偿角Dd。然而,在实际应用中,由于功率开关漏源之间存在一个并联的寄生电容,为了实现ZVS,需要足够的死区时间来输出电流,以确保在导通反并联二极管之前将并联电容的电压放电到零。放电电流的大小可以通过并联电容器来计算。在放电电流为idead的情况下,MOSFET实现ZVS的临界补偿角可以分别推导为
式中,Coss为MOSFET的结电容;td为死区时间;Up和Us分别为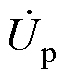 和
和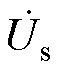 的模。所选择的MOSFET型号为IRFR/U120NPbF,根据数据手册得到Coss= 92 pF。为避免桥臂击穿和实现功率开关的ZVS,设置死区时间为353 ns,结合Up=100 V,Us=100 V,式(33)化简为
的模。所选择的MOSFET型号为IRFR/U120NPbF,根据数据手册得到Coss= 92 pF。为避免桥臂击穿和实现功率开关的ZVS,设置死区时间为353 ns,结合Up=100 V,Us=100 V,式(33)化简为
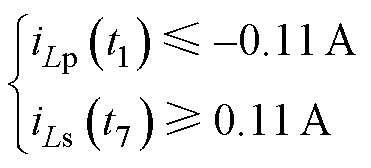 (34)
(34)
对式(34)进行计算,分别得出补偿角为Dd1(满足逆变器实现ZVS的补偿角)和Dd2(满足AR实现ZVS的补偿角)。所得出的临界补偿角可能为负,这意味着系统即使在没有进行补偿的情况下也可以实现ZVS。因此,在无功功率最小的情况下,一次侧和二次侧所有开关管实现ZVS的最佳补偿角Ddopt可以推导为
3 控制策略
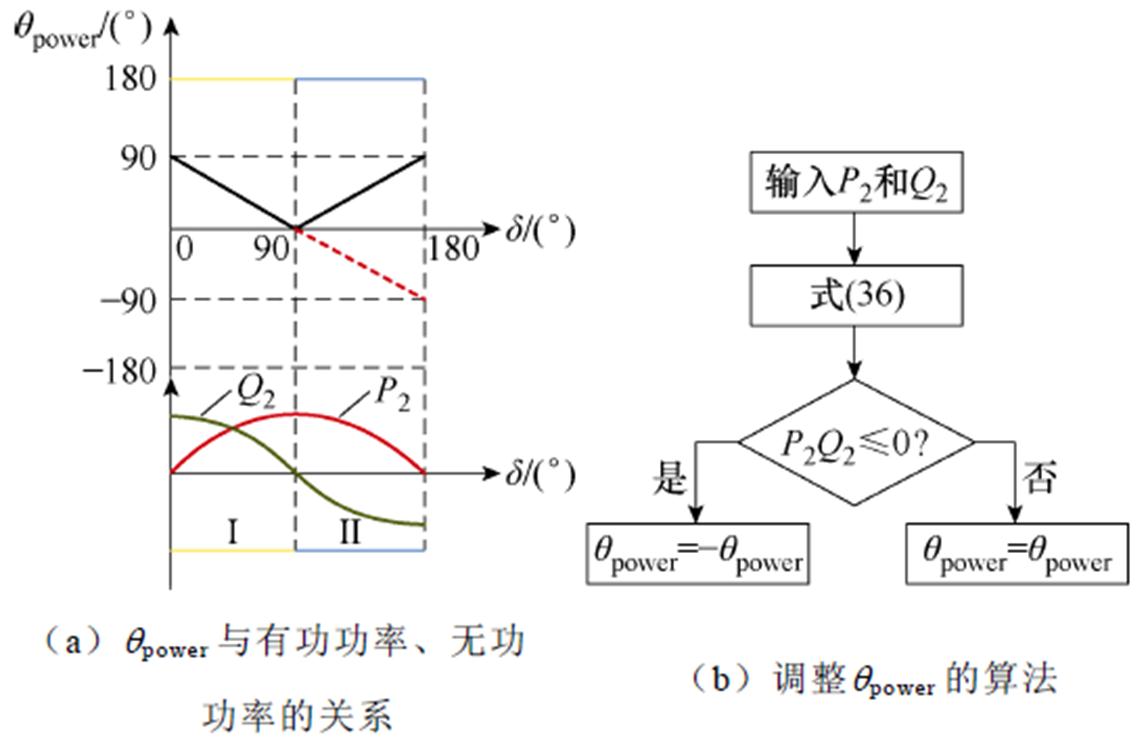
在二极管整流电路中,当接收端电流过零时,二极管通过偏压自然切换,而对于AR电路而言,一次、二次侧变流器必须以相同频率运行,以便功率从线圈的一次侧传输至二次侧。如果两个变流器在不同频率下工作,则输出功率将发生振荡,从而导致实际传输功率为零。因此,为了保证有效的功率传输,需要将MOSFET的驱动信号与接收端的电流进行同步。与文献[21]中所提到的附加测量线圈的同步方法不同,本文引入功率角qpower作为中间变量,由于d 与qpower之间有如式(36)所示的关系,因此可以通过控制qpower间接控制d从而实现频率 同步。
式中,d∈[0°, 180°];qpower∈[0°, 90°]。
系统控制框图如图9所示,主要针对逆变器和AR电路进行控制。一方面,根据式(17)可以确定系统最大效率传输时D1与D2的约束条件,基于此约束条件,同时调节D1和D2以实现恒压输出,由于在整个调压过程中,内移相角始终符合式(17)的约束,因此,系统能够维持最大的传输效率;另一方面,控制器首先对AR的输入电压和电流进行采样,采样后的数据经过乘法器、低通滤波器以及偏移电路处理得到平均功率,再按照式(36)计算获得功率角qpower,最后输入到AR控制器进行同步控制。图9中的ws为AR的开关频率,VL_ref与qpower_ref均为参考值。
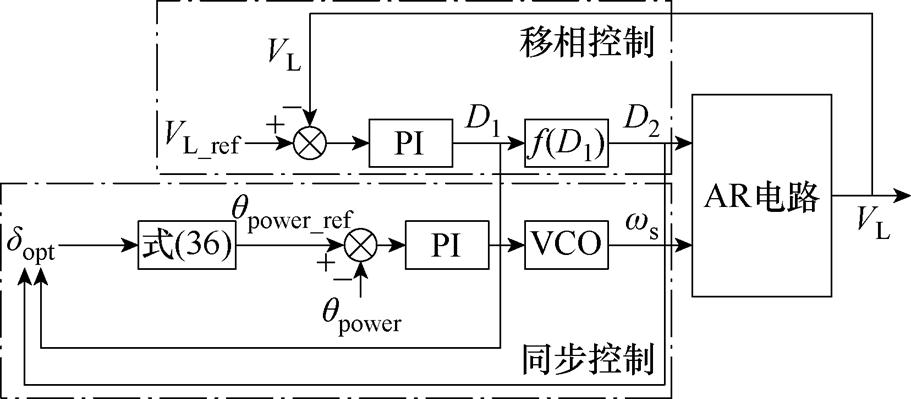
AR控制框图如图10所示。在同步控制模式下,根据式(34)、式(35)计算得到最佳的外移相角dopt,进而通过式(36)得到qpower_ref。接着,利用VCO锁定逆变器的频率。将得到的功率角qpower与qpower_ref进行比较,并通过PI控制器反馈误差。相应地,利用VCO得到了与逆变器相同的频率。由恒压调节和最大效率追踪得到的D2进行移相控制。
为了更直观地显示AR的调节过程,图11中展示了驱动信号以及对应的变流器输出电压波形。控制器通过调整AR每个支路控制信号的延迟来控制qpower。同时,使用VCO调整控制信号的频率与谐振频率匹配。在这个过程中,输出电压脉冲宽度不发生变化(外移相角由d1到d2)。根据D2调整AR的内移相角(内移相角由js1到js2,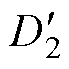 为调整之后的u2占空比),同时保持d2恒定。
为调整之后的u2占空比),同时保持d2恒定。
然而,为了实时控制所需的输出电压,调节D1和D2,也会导致qpower相应地变化,故调压过程与同步过程是高度耦合的。为了实现所有开关管的ZVS,使WPT系统稳定地运行,必须独立控制qpower。根据式(10),优先确定d 之后,结合最大效率约束条件,就可以得到D1和D2。因此,本文提出了一种简单解耦控制,将电压的调节时间设置为相对长于AR的控制时间,以减小电压调节对同步控制的影响。
此外,上述提到的同步控制方法对得到的qpower和d 之间的关系敏感,如图12a实线所示,qpower关于d=90°对称,当d∈[90°, 180°]时,由于对称性,qpower的计算结果将与d∈[0°, 90°]的一致。因此,可以按照图12b的算法将d∈[90°, 180°]的部分对应到qpower的负半周,如图12a虚线所示,以实现qpower和d 之间一一对应的关系,降低二者之间的敏感度。
4 仿真与实验验证
4.1 仿真验证
为了验证理论的有效性,在Matlab/Simulink中搭建了系统仿真模型,相关参数设置见表1。图13显示了在同步控制下驱动信号的移相情况。逆变器的输出电压和AR的输入电压在图13中用虚线标出。从图中可以看出,AR的工作频率始终等于逆变器的频率,并且为实现变流器的ZVS,对d 进行了补偿。此外,为实现恒压输出,AR的电压脉冲宽度也发生了变化。因此,本文所提到的同步控制策略可以在跟踪逆变器基准频率的同时实现移相调节。
补偿网络的输入输出电压电流波形如图14所示。图14a中,当只进行恒压控制和最大效率追踪,即相移补偿角Dd=0°时,输出电压恒定为100 V,负载为100 W。可以看到,逆变器和AR均只能实现一半开关管的ZVS。这会在MOSFET上产生较大的功率损耗和电压尖峰,损坏MOSFET。
根据所提出的相移补偿控制策略,测试了负载为50 W 和100 W 时的系统运行情况。如图14b、图14c所示,随着负载变化,D1、D2和补偿角Dd 也作出相应的调整,使所有的MOSFET实现ZVS。在相同负载情况下,负载增大时,D1和D2逐渐变小,而Dd逐渐变大,这是因为重载时,输出电流较小,而MOSFET的寄生电容较大,因此需要较大的补偿角才能产生较大的电感电流,从而使MOSFET的输出电容充分放电。
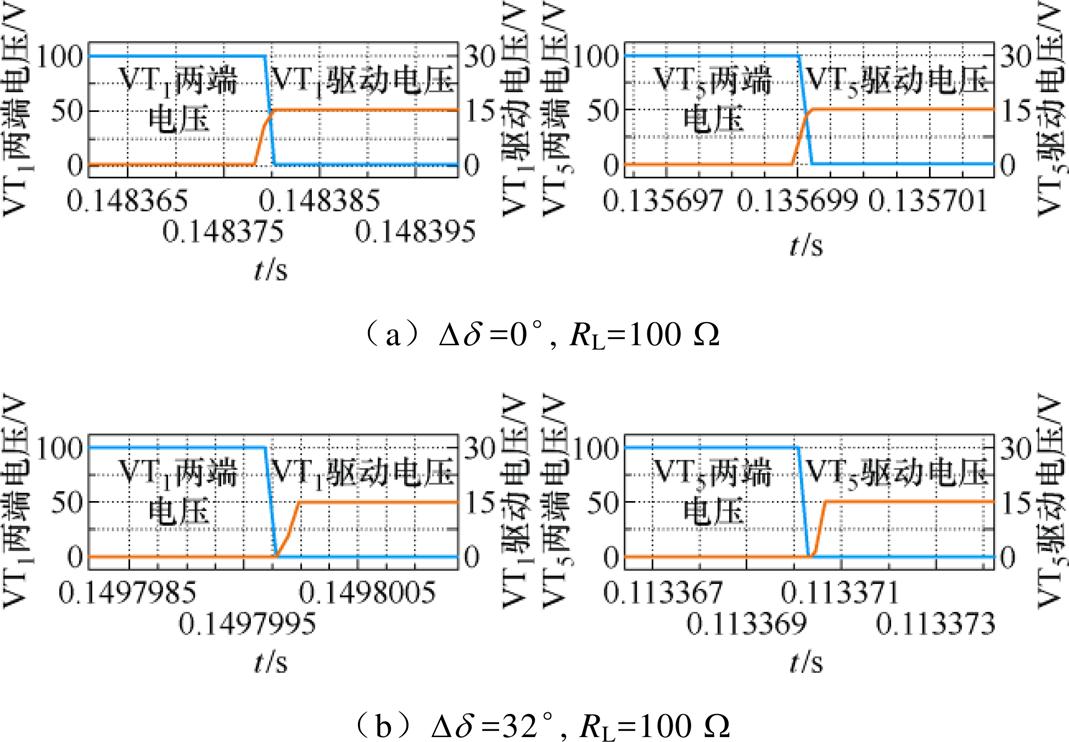
在RL=100 W 时,测得一次、二次侧开关管的工作状态如图15所示。可以看出,在没有补偿的系统中,VT1和VT5不能实现ZVS;而在加入补偿角的系统中,VT1和VT5均工作在ZVS状态,这样可显著减小电磁干扰和额外的开关损耗。
4.2 实验验证
为了验证仿真的准确性,搭建了如图16所示的实验平台。系统输入电压由直流电源提供,负载由电池和电阻组成,负载电池用于稳定输出电压,负载电阻则用于验证系统的恒压特性。变流器所采用的MOSFET的型号为IRFR/U120NPbF,采用EG2104S芯片驱动开关管。实验时将发射线圈与接收线圈上下正对放置,具体的实验参数见表2。
表2 实际参数
Tab.2 Actual parameter
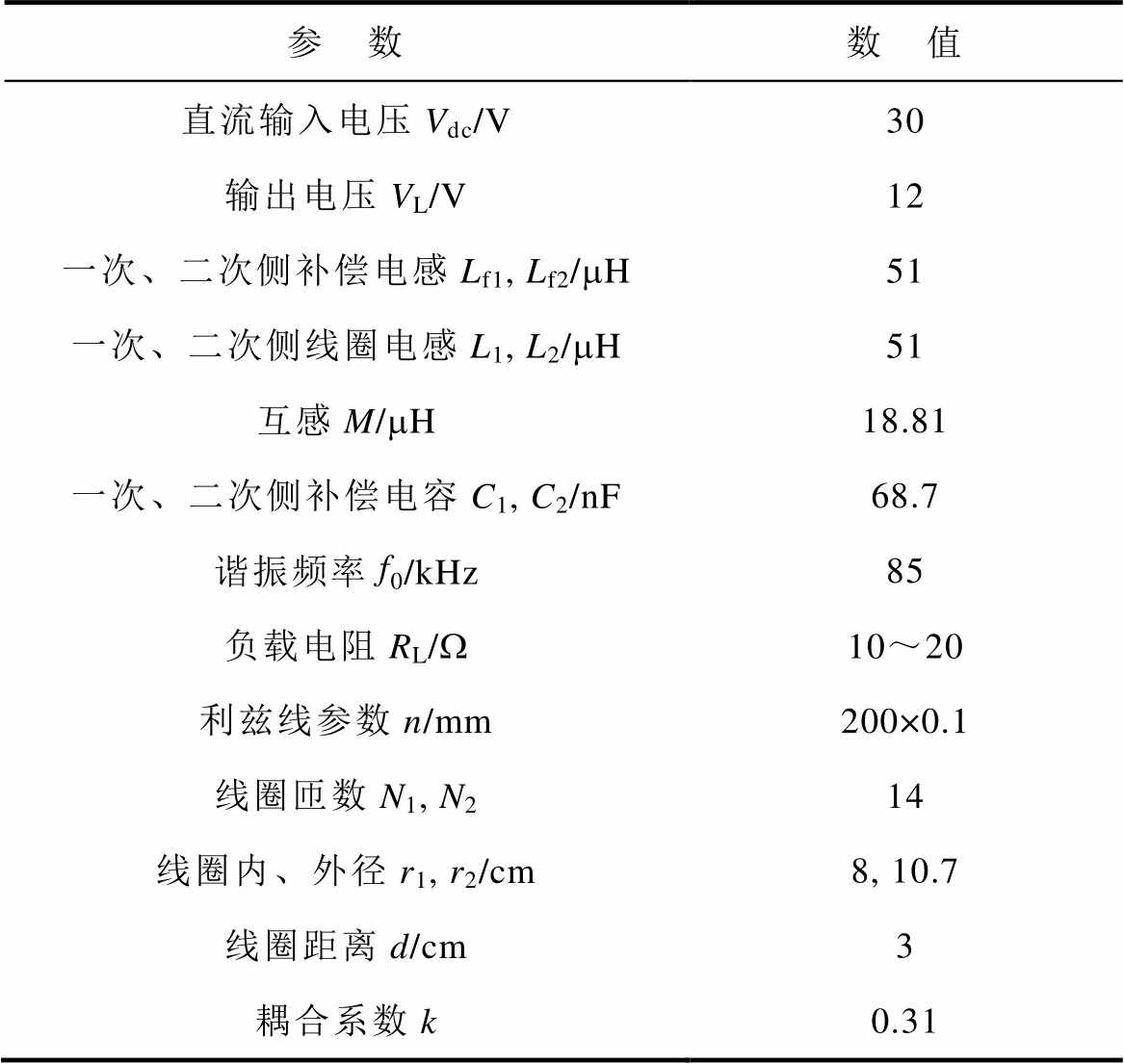
参 数数 值 直流输入电压Vdc/V30 输出电压VL/V12 一次、二次侧补偿电感Lf1, Lf2/mH51 一次、二次侧线圈电感L1, L2/mH51 互感M/mH18.81 一次、二次侧补偿电容C1, C2/nF68.7 谐振频率f0/kHz85 负载电阻RL/W10~20 利兹线参数n/mm200×0.1 线圈匝数N1, N214 线圈内、外径r1, r2/cm8, 10.7 线圈距离d/cm3 耦合系数k0.31
为验证本文所提出的控制策略的有效性,首先调节负载电阻使系统满载运行。同步控制下的输入输出电压变化情况如图17所示。如图17a所示,输入和输出电压频率相同并且均没有移相。接着,调节负载阻值为15 W,此时的电压波形如图17b所示,逆变器和AR产生了内移相角,同时AR依旧能够跟踪逆变器的开关频率。这意味着系统实现了恒压输出和频率同步。
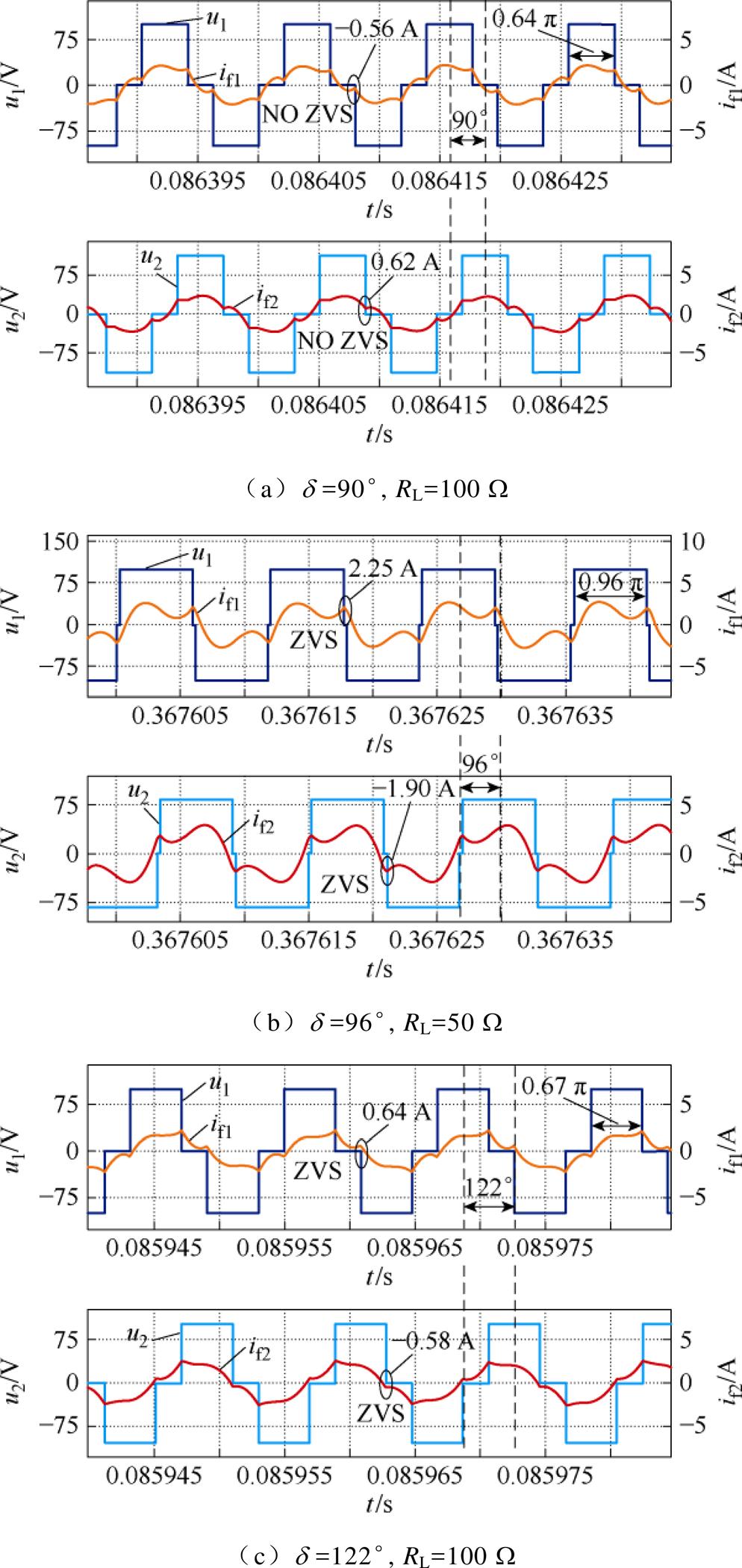
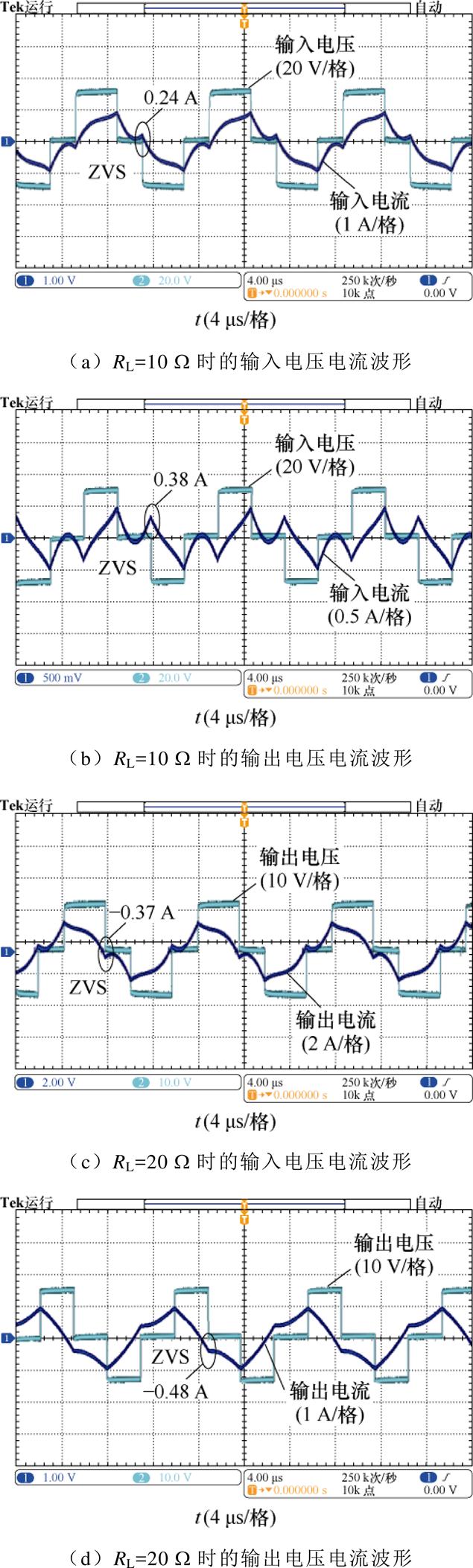
图18a~图18d分别展示了负载为10 W 和20 W 时的谐振网络输入电压、电流(up, iLp)和输出电压、电流(us, iLs)的波形。可以看出,us保持恒定,iLp和iLs始终在允许的范围内。可见,在同步控制下所有MOSFET均实现了ZVS。
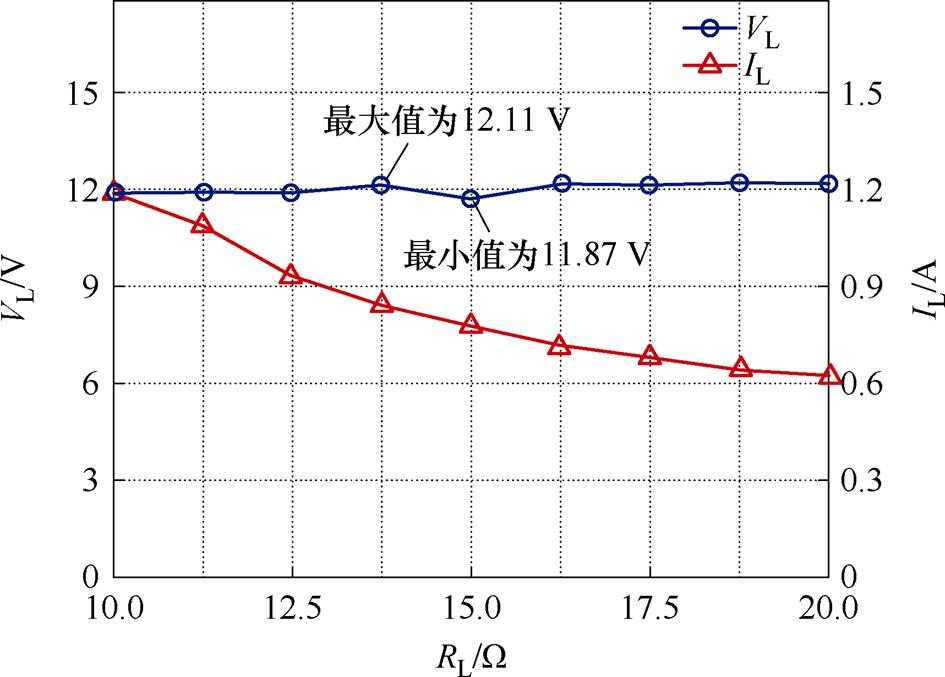
RL=15 W 时的负载输出电压电流如图19所示,控制器自动调节D1、D2,实现了负载的恒压输出。为显示恒压调节的整个过程,调节滑动变阻器,使负载从10 W 增加到20 W,记录稳态时的电压电流数值,如图20所示。在负载电压允许的变化范围内,可以看作恒压输出。
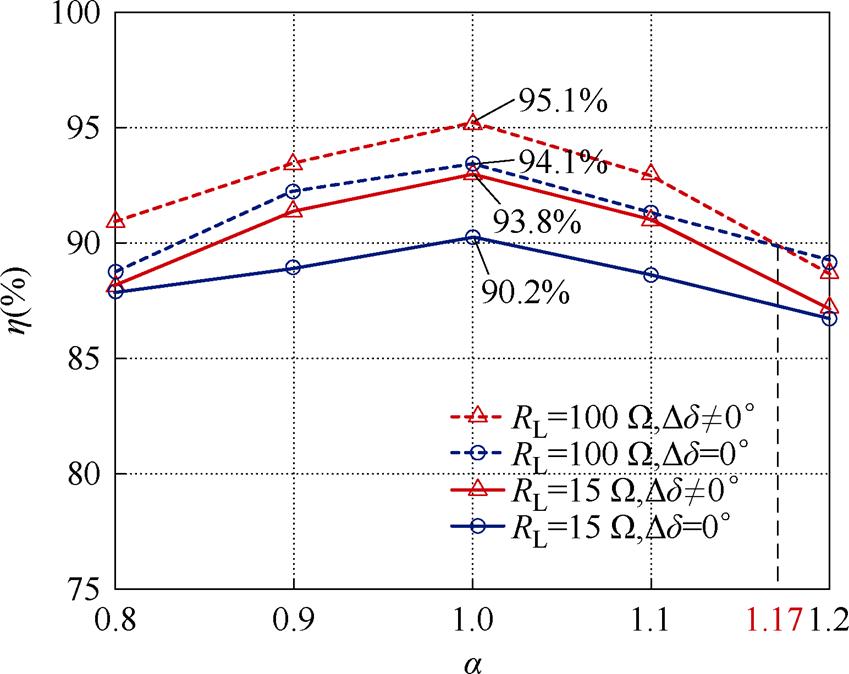
调整逆变器和AR的移相角改变a,得到了如图21所示的效率随交流电压比变化曲线。图中虚线表示仿真中RL=100 W 的效率曲线,实线表示实验中RL=15 W 的效率曲线。
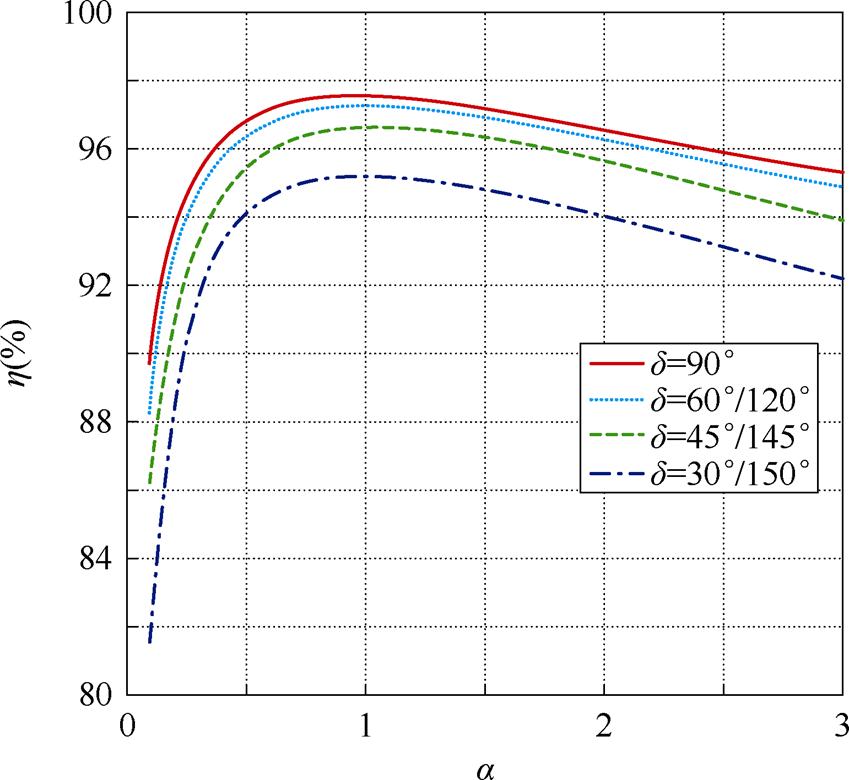
从图21中可以看出,最大效率均出现在a=1处,这与之前的分析一致。此外,Dd≠0°(有补偿角)的效率一般大于Dd=0°(无补偿角)的效率。但在a=1.2时,Dd≠0°时的效率小于Dd=0°时的效率。这是因为此时的相移补偿角过大,导致输出的有功功率减小量大于未损失的开关损耗,使得系统整体的效率低于无补偿角时的效率。因此,在保证系统高效率的前提下,实现ZVS是十分必要的。
5 结论
本文以LCL-LCL型补偿网络为例,提出了双边移相控制策略。利用逆变器移相实现恒压输出,AR移相实现最大效率追踪和变流器的ZVS。具体结论如下:
1)基于基波等效模型,分析了系统的恒压特性以及实现最大效率传输时D1和D2的约束条件;在忽略开关损耗的前提下,d=90°时,有功功率最大,无功功率为0。
2)基于谐波的时域模型,得出了电感电流的时域表达式。考虑波形的对称性,对电感电流约束条件进行了简化。最终,利用简化后的约束条件,得到了满足系统ZVS的最小外移相角dopt。
3)为了快速跟踪d的变化,引入功率角qpower作为中间变量,将d的变化等效为qpower的变化。利用VCO进行一次、二次侧的频率同步,在简化同步控制的同时提高了系统的控制精度。
在本文的控制策略下,系统在满足最大效率的同时实现了与负载无关的恒压输出和所有MOSFET的ZVS。实验结果表明,在耦合系数k=0.31的情况下,a=1时系统的传输效率最高,最高效率达93.8%。
参考文献
[1] 田勇, 冯华逸, 田劲东, 等. 电动汽车动态无线充电系统输出电流模型预测控制[J]. 电工技术学报, 2023, 38(9): 2310-2322, 2447.
Tian Yong, Feng Huayi, Tian Jindong, et al. Model predictive control for output current of electric vehicle dynamic wireless charging systems[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2310- 2322, 2447.
[2] Jiang Yongbin, Wang Laili, Wang Yue, et al. Analysis, design, and implementation of WPT system for EV’s battery charging based on optimal operation frequ- ency range[J]. IEEE Transactions on Power Elec- tronics, 2019, 34(7): 6890-6905.
[3] Jiang Yongbin, Wang Laili, Fang Jingyang, et al. A high-efficiency ZVS wireless power transfer system for electric vehicle charging with variable angle phase shift control[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 2356-2372.
[4] 陈伟华, 刘宗旺, 李政兴, 等. 谐振式无线供能心脏起搏器多线圈无功屏蔽研究[J]. 电工技术学报, 2022, 37(11): 2673-2685.
Chen Weihua, Liu Zongwang, Li Zhengxing, et al. Research on multi coil reactive shielding of resonant wireless energy supply cardiac pacemaker[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(11): 2673-2685.
[5] 李砚玲, 蒋旭应, 应杨江, 等. 感应无线供电系统的线圈自定位方法研究[J]. 中国电机工程学报, 2023, 43(11): 4367-4377.
Li Yanling, Jiang Xuying, Ying Yangjiang, et al. Research on coil self-positioning method for indu- ctive wireless power supply system[J]. Proceedings of the CSEE, 2023, 43(11): 4367-4377.
[6] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568.
Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[7] Zhang Yiming, Chen Shuxin, Li Xin, et al. Design methodology of free-positioning nonoverlapping wireless charging for consumer electronics based on antiparallel windings[J]. IEEE Transactions on Industrial Electronics, 2022, 69(1): 825-834.
[8] Yang Lin, Ren Li, Shi Yanyan, et al. Analysis and design of an S/S/P-compensated three-coil structure WPT system with constant current and constant voltage output[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(3): 2487-2500.
[9] Yuan Hao, Wang Chunfang, Xia Dongwei. Research on input-parallel single-switch WPT system with load-independent constant voltage output[J]. IEEE Transactions on Transportation Electrification, 2023, 9(1): 1888-1896.
[10] 姚若玉, 曲小慧, 郁继栋, 等. 自适应电池充电曲线的三线圈电池无线充电器[J]. 电力系统自动化, 2022, 46(7): 170-177.
Yao Ruoyu, Qu Xiaohui, Yu Jidong, et al. Three-coil wireless battery charger with self-adaptation to battery charging curve[J]. Automation of Electric Power Systems, 2022, 46(7): 170-177.
[11] 黄文聪, 饶天彪, 蒋煊焱, 等. 无线电能传输系统最大效率追踪及恒压输出复合控制方法[J]. 电工技术学报, 2024, 39(12): 3589-3601, 3615.
Huang Wencong, Rao Tianbiao, Jiang Xuanyan, et al. Maximum efficiency tracking and constant voltage output compound control method for wireless power transfer system[J]. Transactions of China Electro- technical Society, 2024, 39(12): 3589-3601, 3615.
[12] 赵进国, 赵晋斌, 张俊伟, 等. 无线电能传输系统中有源阻抗匹配网络断续电流模式最大效率跟踪研究[J]. 电工技术学报, 2022, 37(1): 24-35.
Zhao Jinguo, Zhao Jinbin, Zhang Junwei, et al. Maximum efficiency tracking study of active impedance matching network discontinous current mode in wireless power transfer system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(1): 24-35.
[13] Li Hongchang, Li Jie, Wang Kangping, et al. A maximum efficiency point tracking control scheme for wireless power transfer systems using magnetic resonant coupling[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3998-4008.
[14] Yang Yun, Zhong Wenxing, Kiratipongvoot S, et al. Dynamic improvement of series-series compensated wireless power transfer systems using discrete sliding mode control[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 6351-6360.
[15] Gheisarnejad M, Farsizadeh H, Tavana M R, et al. A novel deep learning controller for DC-DC Buck-Boost converters in wireless power transfer feeding CPLs[J]. IEEE Transactions on Industrial Electronics, 2021, 68(7): 6379-6384.
[16] 杨云虎, 贾维娜, 梁大壮, 等. LCC-LCC/S自切换恒流-恒压复合型无线电能传输系统[J]. 电工技术学报, 2023, 38(18): 4823-4837, 4852.
Yang Yunhu, Jia Weina, Liang Dazhuang, et al. A self-switching wireless power transfer system based on hybrid topology of LCC-LCC/S with constant current and constant voltage[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 4823-4837, 4852.
[17] Li Zheng, Xie Bo, Zhu Yiding, et al. Wireless charging constant power output system based on LCC/S-S self-switching[J]. IEEE Access, 2022, 10: 86435-86444.
[18] Li Weijie, Diao Lijun, Mei Weiyao, et al. Optimized resonant network design for high energy transfer efficiency of the WPT system[J]. Electronics, 2023, 12(9): 1984.
[19] 李争, 唐明磊, 解波, 等. 无线电能传输零电压开关角跟踪和动态电容补偿矩阵复合控制策略[J]. 电工技术学报, 2024, 39(12): 3602-3615.
Li Zheng, Tang Minglei, Xie Bo, et al. Composite control strategy of zero voltage switch angle tracking and dynamic capacitance compensation matrix for wireless power transfer[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3602-3615.
[20] Jiang Yongbin, Wang Laili, Wang Yue, et al. Phase- locked loop combined with chained trigger mode used for impedance matching in wireless high power transfer[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 4272-4285.
[21] Mai Ruikun, Liu Yeran, Li Yong, et al. An active- rectifier-based maximum efficiency tracking method using an additional measurement coil for wireless power transfer[J]. IEEE Transactions on Power Electronics, 2018, 33(1): 716-728.
[22] 郭星, 刘利强, 齐咏生, 等. 基于LCL-LCL/S混合自切换谐振式无线充电系统[J]. 电工技术学报, 2022, 37(10): 2422-2434.
Guo Xing, Liu Liqiang, Qi Yongsheng, et al. Hybrid self-switching resonant wireless charging system based on LCL-LCL/S[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2422-2434.
[23] Gupta R, Samanta S. A novel parameter tuning for LCL-LCL WPT with combined CC/CV charging and improved harmonic performance[J]. IEEE Transa- ctions on Industrial Electronics, 2024, 99: 1-11.
Two-Sided LCL Zero Voltage Switching Control Strategy Based on Active Rectifier for Wireless Power Transfer System
Li Zheng1,2 Yu Zhihao1 Gao Shihao1 Tang Minglei1 Sun Hexu1
(1. School of Electrical Engineering Hebei University of Science and Technology Shijiazhuang 050018 China 2. School of Electrical Engineering Yanshan University Qinhuangdao 066004 China)
Abstract In wireless power transfer (WPT) systems, achieving accurate voltage regulation and efficient operation are critical. Current research achieves constant voltage output and zero voltage switch (ZVS) with additional DC-DC converters and variable resonant networks. However, these approaches increase system losses and costs. Therefore, this paper proposes a two-sided LCL phase-shifting control strategy. The internal phase shift angle of the inverter and active rectifier (AR) is used to achieve constant voltage output and maximum efficiency tracking, and the external phase shift angle between the two converters achieves ZVS of all switching tubes. By analyzing the power loss, the constraint condition between the internal phase shift angle is obtained. The minimum external phase shift angle dopt of ZVS is further determined, and the system’s high efficiency is realized. In addition, the power angle qpower is introduced as the intermediate variable, and the frequency synchronization of the primary and secondary sides is realized using the voltage-controlled oscillator (VCO).
Firstly, utilizing the fundamental wave equivalent model, the constant voltage characteristics of the system and the constraint conditions of the inverter output voltage and AR input voltage pulse-width ratio D1 and D2 are analyzed. The results show that transmission efficiency peaks when the AC voltage ratio a =1. With load variations, achieving constant voltage output and maximum efficiency tracking is feasible by adjusting D1 and D2. Secondly, based on the time-domain harmonics model, the derivation and simplification of the time-domain expression of inductance current are conducted. The simplified model is then analyzed to determine the external phase shift angle d. By comparing d of the inverter and AR, the dopt is obtained. Thirdly, the overall control strategy is introduced. The constant voltage output is achieved by adjusting D1 and D2. The introduction of qpower as an intermediate variable establishes the relationship between d and qpower, enabling indirect control of d through the regulation of qpower. Subsequently, the frequency synchronization of the primary and secondary sides is realized using a VCO, effectively solving the synchronization challenge associated with an active rectifier.
Finally, system simulations and experiments were conducted. The experimental results show that the system can achieve ZVS for all MOSFETs and maintain a constant voltage output regardless of load variations. Moreover, the proposed synchronous control strategy can effectively track the switching frequency of the inverter and precisely adjust the required dopt. As D1 and D2 consistently adhere to the maximum efficiency constraints during system adjustments, the system also achieves maximum efficiency tracking. When the coupling coefficient k is 0.31, the transmission efficiency of the system is the highest, and the maximum efficiency is 93.8%.
Keywords:Wireless power transfer (WPT), phase-shifting control, active rectifier (AR), zero voltage switching (ZVS)
中图分类号:TM724
DOI: 10.19595/j.cnki.1000-6753.tces.240557
国家自然科学基金(51877070, U20A20198)和河北省自然科学基金(E2024208079, E2021208008)资助项目。
收稿日期 2024-04-08
改稿日期 2024-07-18
作者简介
李 争 男,1980年生,博士,教授,博士生导师,研究方向为功率变换与新能源技术。
E-mail: Lzhfgd@163.com(通信作者)
于治昊 男,2001年生,硕士研究生,研究方向为无线电能传输。
E-mail: yzh2001@stu.hebust.edu.cn
(编辑 陈 诚)
 和
和 ),同时实现阻抗匹配和效率优化。文献[21]提出了一种带有辅助测量线圈的AR控制方法,利用检测接收端电流的过零信号实现AR同步,引入辅助线圈测量接收侧的非谐振度,并根据计算出的AR移相角的补偿值进行调谐。然而,在上述两种控制策略中,逆变器和AR都不能实现ZVS,这会极大地恶化WPT系统的安全运行,特别是在大功率的应用场合。文献[2]采用变频移相控制策略,调整逆变器的频率和移相角,实现了逆变器的ZVS和恒压/恒流充电。进一步地,文献[3]提出了一种变角移相控制策略,通过调节逆变器与AR之间的外移相角实现了逆变器和AR的ZVS,调节AR的内移相角以实现精确的电压控制。这种方法虽然能实现WPT系统的ZVS运行,但仅限于简单的串联-串联(Series-Series, S-S)型补偿拓扑。
),同时实现阻抗匹配和效率优化。文献[21]提出了一种带有辅助测量线圈的AR控制方法,利用检测接收端电流的过零信号实现AR同步,引入辅助线圈测量接收侧的非谐振度,并根据计算出的AR移相角的补偿值进行调谐。然而,在上述两种控制策略中,逆变器和AR都不能实现ZVS,这会极大地恶化WPT系统的安全运行,特别是在大功率的应用场合。文献[2]采用变频移相控制策略,调整逆变器的频率和移相角,实现了逆变器的ZVS和恒压/恒流充电。进一步地,文献[3]提出了一种变角移相控制策略,通过调节逆变器与AR之间的外移相角实现了逆变器和AR的ZVS,调节AR的内移相角以实现精确的电压控制。这种方法虽然能实现WPT系统的ZVS运行,但仅限于简单的串联-串联(Series-Series, S-S)型补偿拓扑。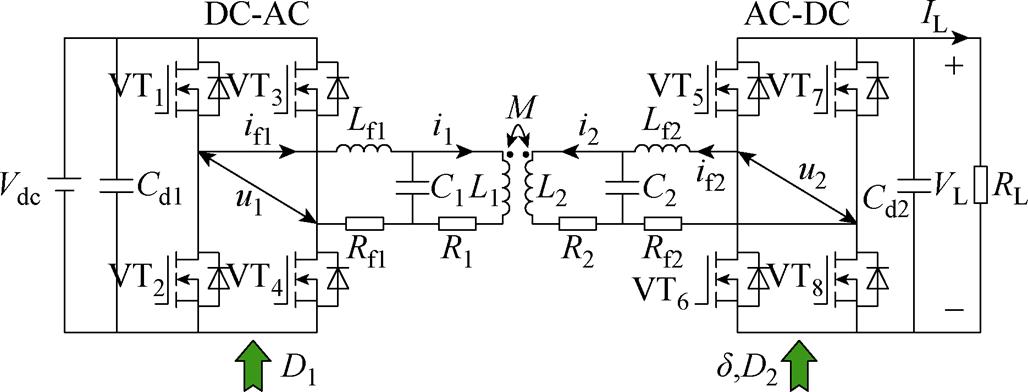
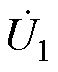 为逆变器的输出电压基波分量;
为逆变器的输出电压基波分量;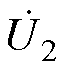 为AR的输入电压基波分量;
为AR的输入电压基波分量;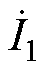 和
和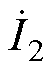 分别为电感L
分别为电感L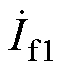 和
和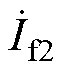 分别为电感L
分别为电感L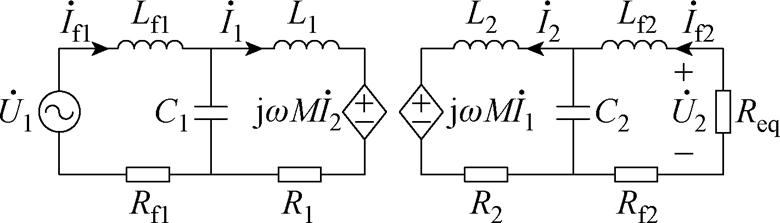
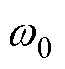 ,则有
,则有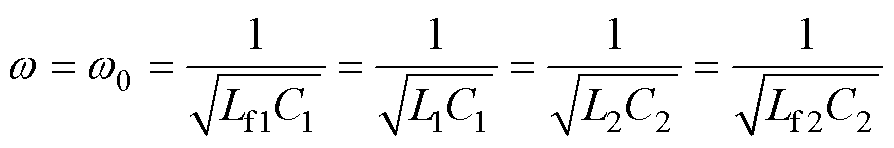 (1)
(1)

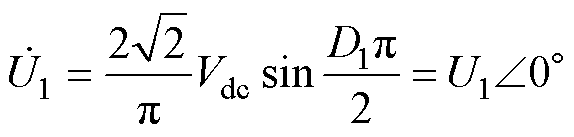 (2)
(2)
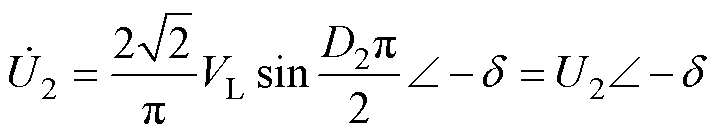 (3)
(3)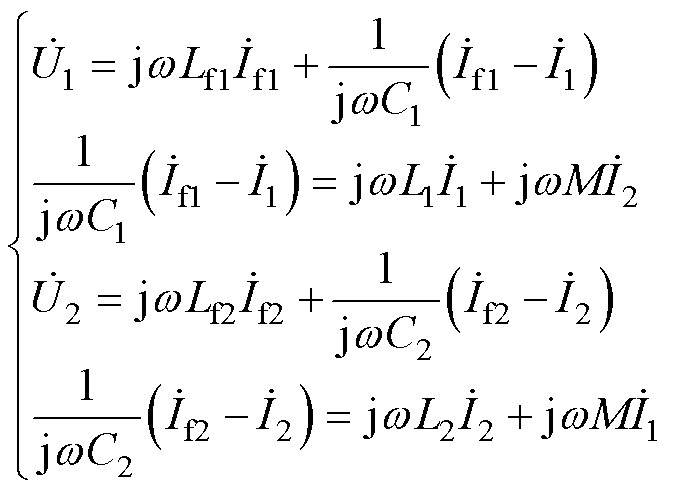 (4)
(4)
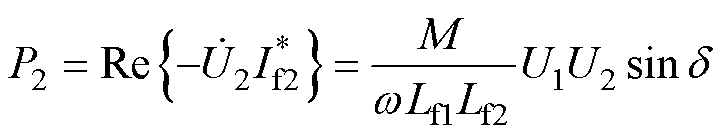 (5)
(5)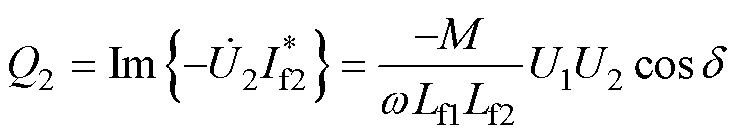 (6)
(6)
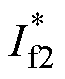 为
为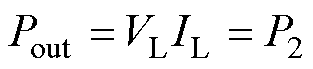 (7)
(7)
 (8)
(8)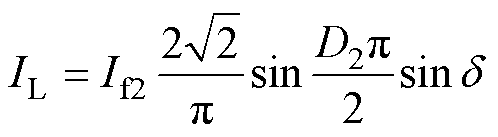 (9)
(9)
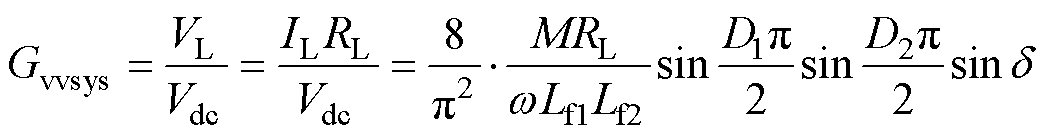 (10)
(10)

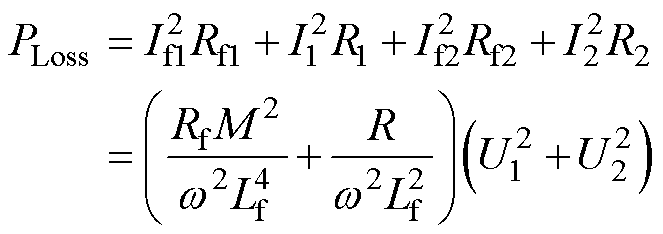 (11)
(11)
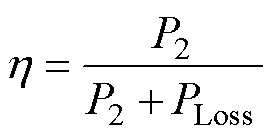 (12)
(12)
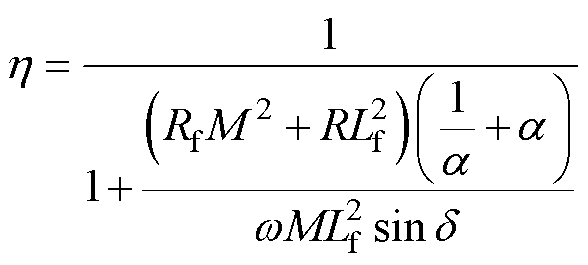 (13)
(13)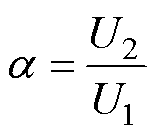 (14)
(14)
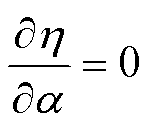 (15)
(15) (16)
(16)
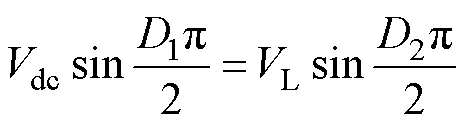 (17)
(17)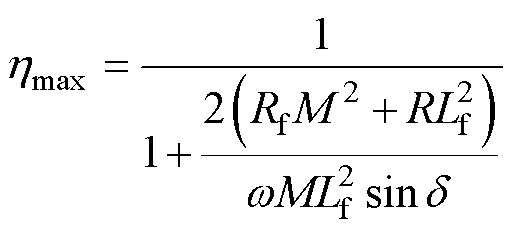 (18)
(18)
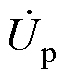 为考虑谐波时的逆变器输出电压相量,
为考虑谐波时的逆变器输出电压相量,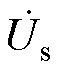 为考虑谐波的AR输入电压相量;
为考虑谐波的AR输入电压相量;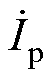 和
和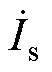 分别为考虑谐波的电感L
分别为考虑谐波的电感L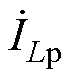 和
和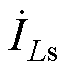 分别为考虑谐波的电感L
分别为考虑谐波的电感L
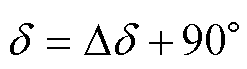 (19)
(19)
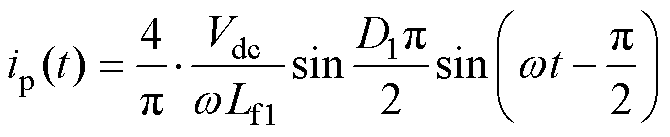 (20)
(20)
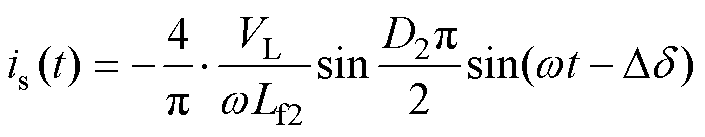 (21)
(21)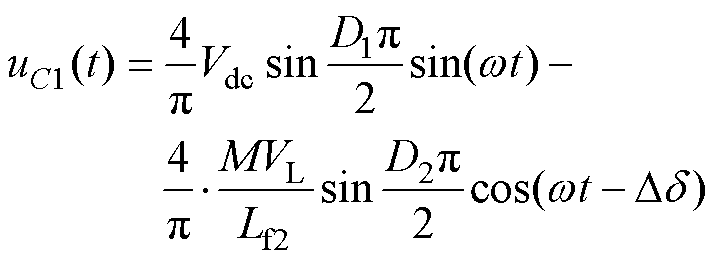 (22)
(22)
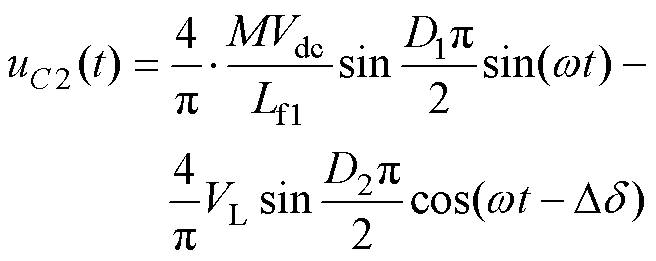 (23)
(23)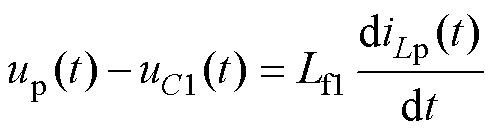 (24)
(24)
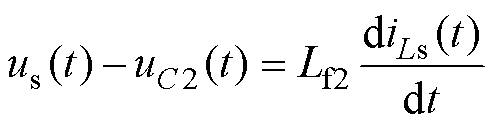 (25)
(25)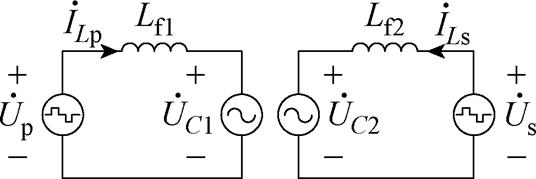
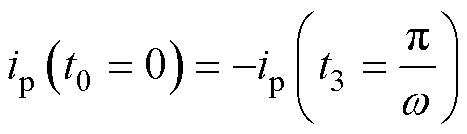 (26)
(26)
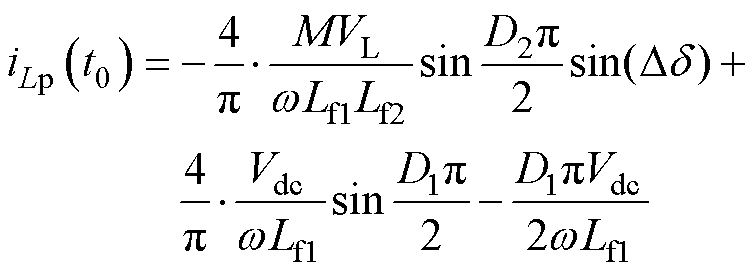 (27)
(27)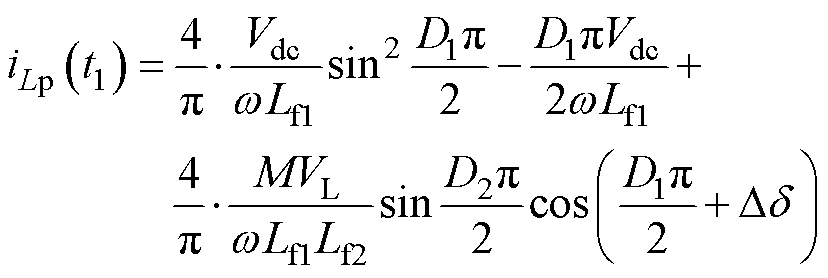 (28)
(28)
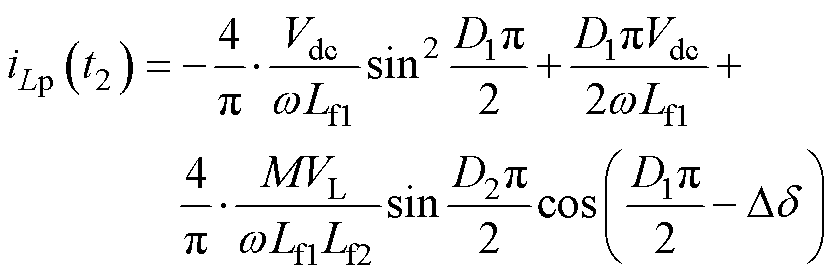 (29)
(29)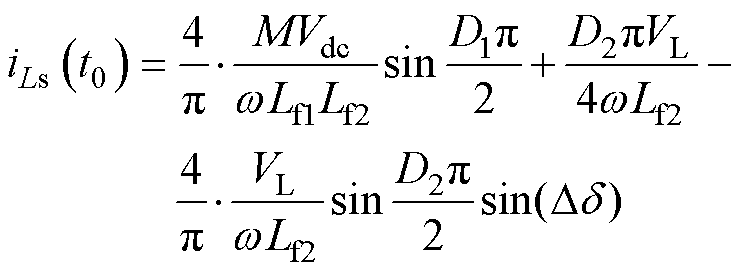 (30)
(30)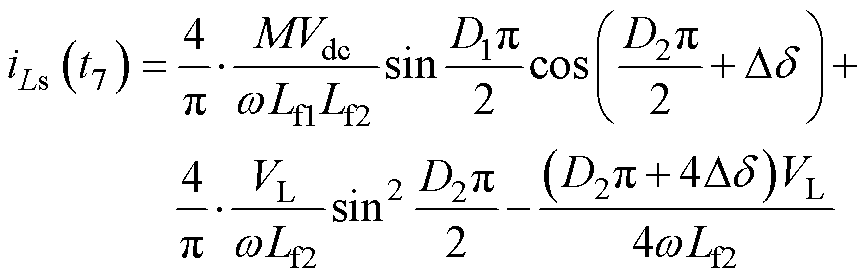 (31)
(31)
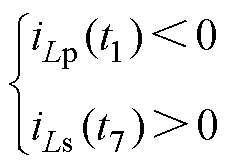 (32)
(32)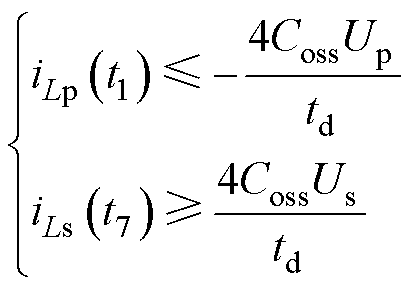 (33)
(33)
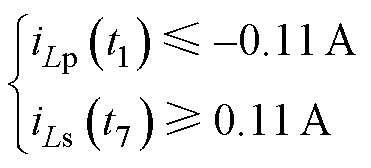 (34)
(34)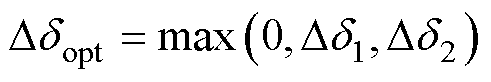 (35)
(35)
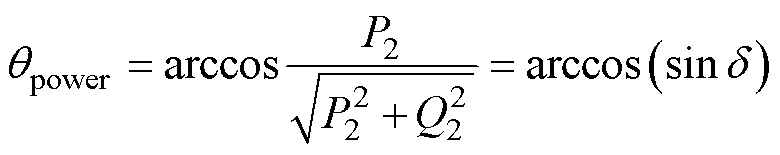 (36)
(36)
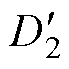 为调整之后的u
为调整之后的u