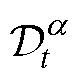可表示为摘要 分数阶元件作为分数阶电路的基本单元，其构建和实现方法是研究分数阶电路系统的基础。然而，目前单组件分数阶元件未见商业应用，分数阶元件仍以多元件的集成方式为主。与单组件分数阶元件相比，分数阶元件的多组件实现方法在构成元件种类、数量和参数选择方面更加灵活，且分数阶元件的阶数和阻抗系数可以调节，具有更强的实用性。为了能够根据具体应用需求选择合适的多组件分数阶元件，该文在总结现有大部分多组件分数阶元件构造方法的基础上，按照构成器件种类将其构造方法分为基于无源元件、基于运算放大器和基于电力电子变换器三类，重点介绍一些典型构造方法的工作原理，并对这些构造方法进行分析和比较。最后，该文探讨了多组件分数阶元件在电网功率补偿场合的应用，为拓展多组件分数阶元件的应用提供了参考。
关键词：分数阶电路 分数阶电容 分数阶电感 逆变器
分数阶微积分固有的微分及积分阶数的灵活性，使其成为捕捉实际系统动态行为的强大工 具[1-2]。近年来，分数阶微积分理论已经被成功地应用在控制系统、电路系统、模型辨识等领域[3]。
在控制系统领域，由于分数阶PDm控制器和PIlDm控制器[4]的积分阶次l和微分阶次m可调，使得永磁同步电机[5-6]、DC-DC变换器[7]等控制对象的稳定性和动态响应性能得到显著提升。在电路系统领域，分数阶元件（Fractional-Order Element, FOE）主要包括分数阶电容（Fractional-Order Capacitor, FOC）及分数阶电感（Fractional-Order Inductor, FOI）[8]，其阻抗或导纳特性表现出分数阶行为。研究发现，由于分数阶元件具有记忆特性、遗传特 性[9]和负阻特性等与整数阶元件不同的特性，采用分数阶元件描述电路的动态行为更加精确[10-12]。在模型辨识方面，当超级电容器采用分数阶元件的电路模型进行等效时[13]，相较于整数阶元件等效电路模型，模型的精度更高且模型所需的元件数量更少，在不同温度和电压下都具有出色的适应性[14-15]。因此，越来越多的研究将整数阶电路系统拓展至分数阶电路系统[16-18]，以探索分数阶元件给电路系统带来的独有优势。
分数阶元件作为分数阶电路系统的最基本单 元[8]，其构建和实现是研究分数阶电路系统的基础。目前分数阶元件的构造方法主要分为两种：单组件构造方法和多组件构造方法[19]。单组件构造方法采用不同分形结构的电极表面积、不同电介质材料等来构造分数阶元件[20-22]。然而，一旦封装完成，单组件分数阶元件的阶数和阻抗值固定。另外，由于缺乏既定且得到广泛认可的构造准则，单组件分数阶元件的发展受到很大的制约，目前尚未见到成功的商业应用[23]。多组件分数阶元件由电阻、电容等无源元件以及运算放大器、电力电子变换器等有源器件构成。多组件分数阶元件在构成元件的种类、数量和参数上可选择的范围更广，使得其构造相比单组件分数阶元件更具灵活性。同时，多组件分数阶元件不仅可以实现任意阶数下的分数阶元件，而且可以在不改变整体电路结构的情况下，仅通过改变控制电路参数就能调节阶数大小。虽然多组件分数阶元件的构造方法更加灵活，但采用不同构造方法得到的多组件分数阶元件特性不同，且不具备普遍适用性。为此，本文在总结现有大部分多组件分数阶元件构造方法的基础上，对多组件分数阶元件的功率、阶数变化范围等进行了分析与对比，为根据不同的应用场景选择多组件分数阶元件的构造方法提供参考。
本文首先介绍了分数阶元件的基本特性；其次分类阐述了多组件分数阶元件的构造原理，并对几种典型的多组件分数阶元件的构造方法进行了分析和比较；最后探讨了分数阶元件在电气工程领域的典型应用。
分数阶微积分是数学分析的一个分支，它将微分和积分的概念扩展到非整数阶。与传统整数阶微积分只涉及整数幂的微分和积分不同，分数阶微积分使用分数导数和分数积分进行计算。
由于缺乏一致且广泛接受的定义，分数阶微积分学的早期发展较为缓慢。随着分数阶理论的完善，根据Grünwald和Letnikov的定义整合成的GL（Grünwald-Letnikov）定义以及根据Liouville和Riemann的定义统一成的RL（Riemann-Liouville）定义在分数阶微积分学领域被广泛认可和使用[24]。
一个统一的分数阶微分、积分的算子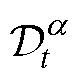可表示为
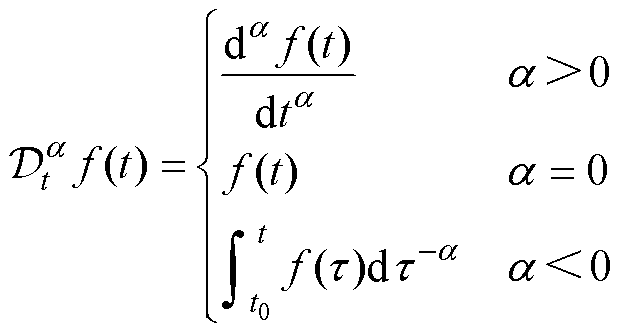（1）
式中，a 为阶数；t为自变量；t0为该变量的初始时刻的值。
Cauchy积分公式可在复分析领域中将复函数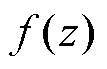
的高阶导数问题转换为封闭曲线的积分问题，已知Cauchy迭代积分公式的整数阶导数表达式为
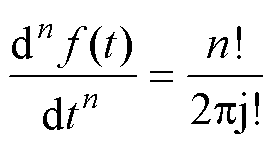
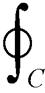
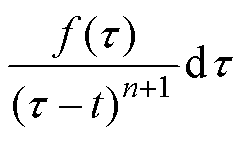（2）
式中，C为光滑的封闭曲线，在所属区域内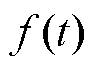
为单值解析函数。
当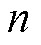
被非整数a 替代时，将t=a 点处出现的孤立奇点移除，并将阶乘替换为Gamma函数，即可将式（1）拓展为分数阶Cauchy迭代积分公式，有
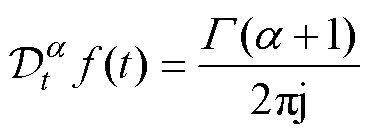
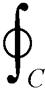
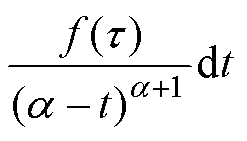（3）
式中，阶次g 可为任意正实数；Gamma函数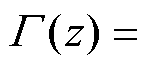
。
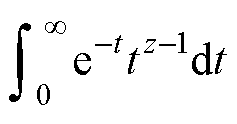利用式（3）可以推得常用三角函数的分数阶微分公式为
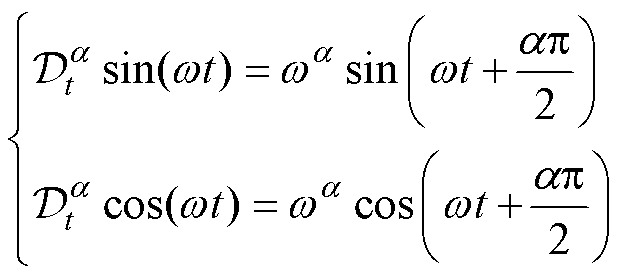（4）
式中，w 为角频率。
分数阶电容和电感的符号与整数阶电容和电感的符号不同，分数阶元件的电气符号如图1所示。
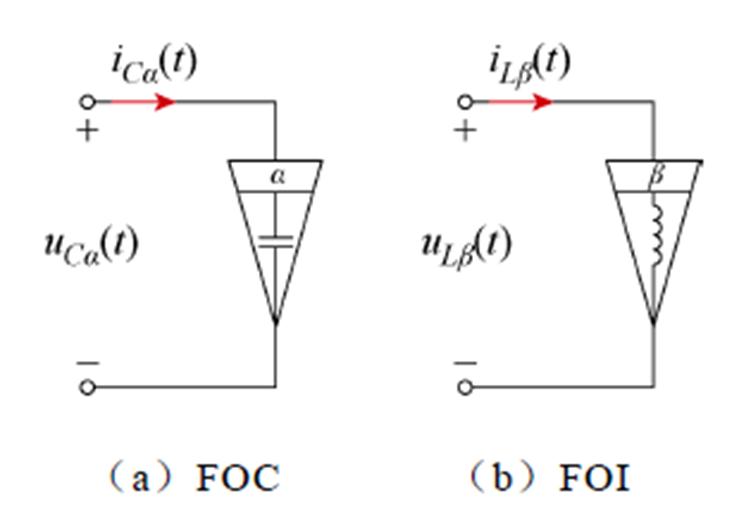
图1 分数阶元件的电气符号
Fig.1 Electrical symbols of FOC, FOI
分数阶元件与整数阶元件的区别在于引入了阶数a 和b [25]，分数阶电容FOC与分数阶电感FOI的伏安特性分别为
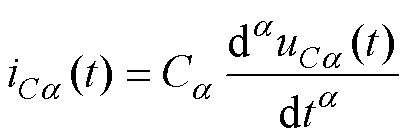（5）
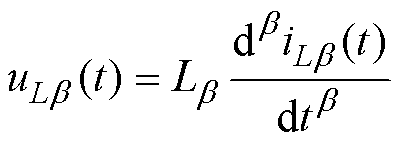（6）
式中，a 为FOC的阶数；b 为FOI的阶数；uCa (t)、iCa (t)分别为FOC的电压和电流；uLb (t)、iLb (t)分别为FOI的电压和电流；Ca和Lb分别为FOC的伪电容值和FOI的伪电感值，单位分别为F/s1-a和H/s1-b；其中阶数需满足0＜a, b＜2。
由分数阶微积分基本定义可得
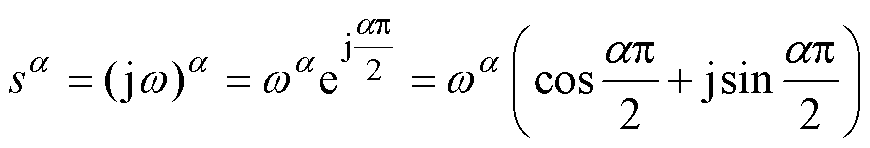（7）
式中，s=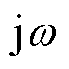
。
结合式（7）对式（5）和式（6）进行拉氏变换，可以得到FOC和FOI的阻抗值ZCa (jw)和ZLb (jw)分别为
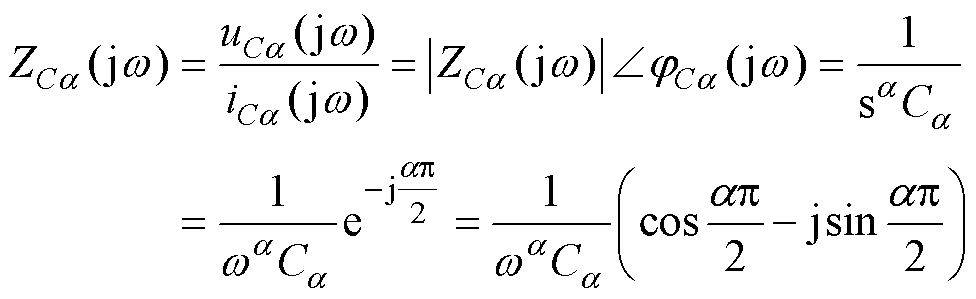（8）
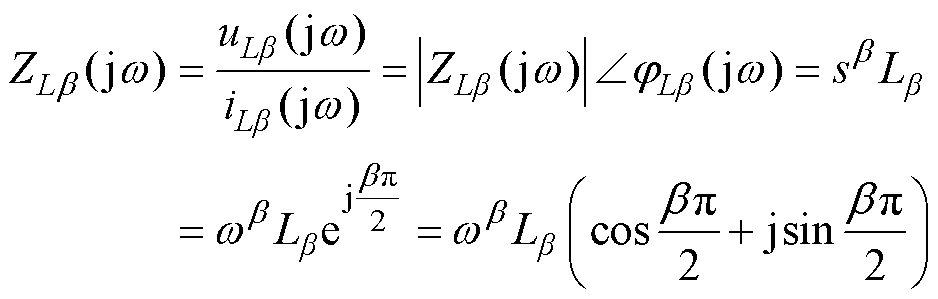（9）
在频域中，FOC和FOI的阻抗模分别由|ZCa(jw)|= 1/(waCa)、|ZLb (jw)|=wbLb 给出。两者阻抗的相位分别由jCa (jw)=-ap/2、jLb (jw)= bp/2给出。FOC、FOI的对数幅频特性曲线的斜率分别为-20a dB/dec及20b dB/dec。
图2给出了传统整数阶电路元件与分数阶元件FOE的特性。从图2可见阶数对分数阶元件特性的影响，阶数不仅决定了阻抗-频率特性中的斜率大小，而且决定了电压与电流的相位超前滞后关系。为了表征FOE的频率依赖性，定义了两个量[26]：①恒定相位区域（Constant Phase Zone, CPZ）为jCa、jLb 或 (a, b ) 保持恒定的频率范围，如图2相位频域特性中FOI、FOC相位保持相对恒定的范围fL～fH；②相角偏差（Phase Angle Deviation, PAD）表示CPZ内与相位恒定值的最大偏差，即图2中，fL～fH范围内FOI、FOC实际相位与理想相位的最大偏差角度。
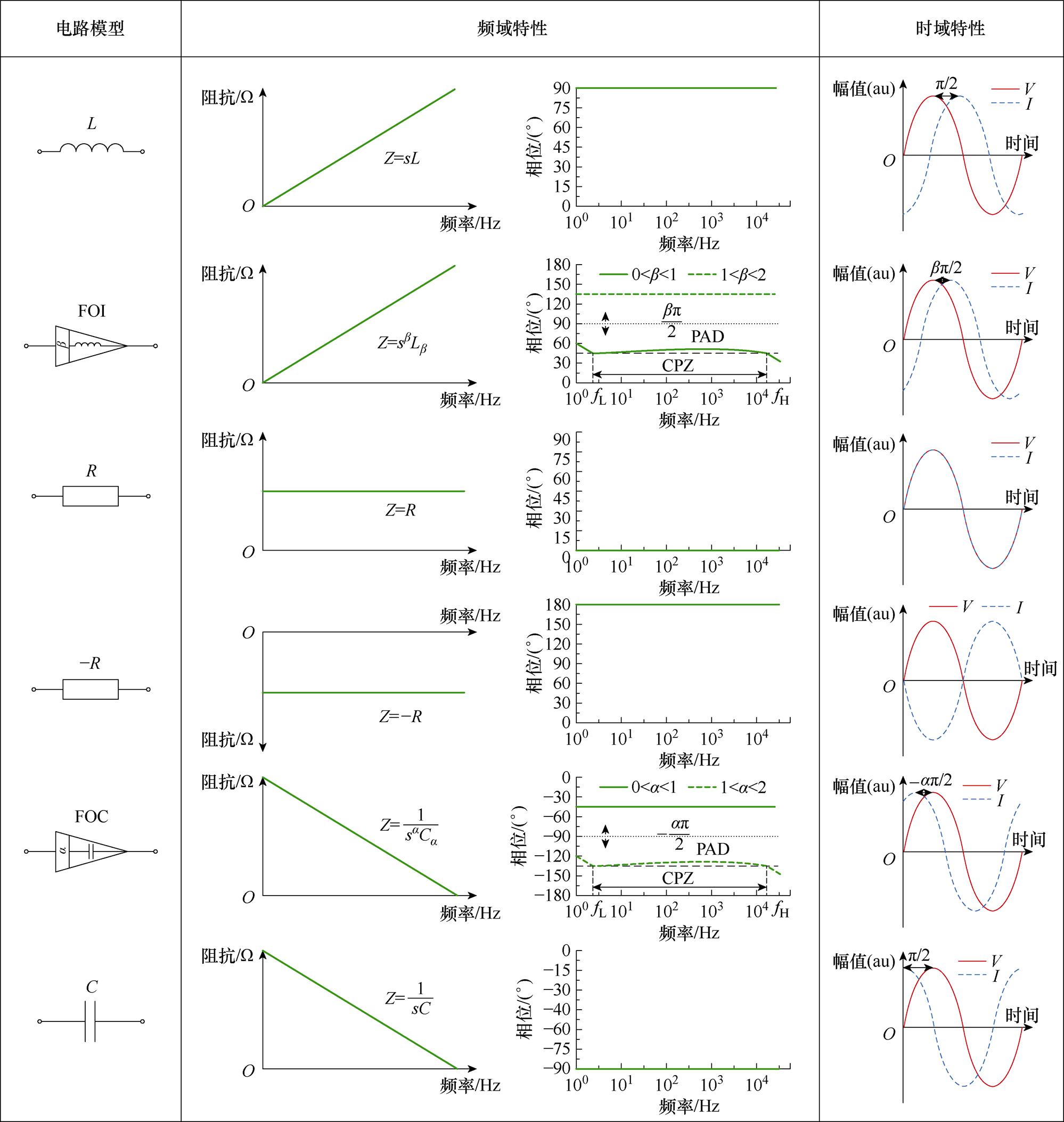
图2 理想电容、电感与分数阶电容、分数阶电感的特性
Fig.2 Characteristics of ideal capacitor, ideal inductor, fractional-order capacitor, and fractional-order inductor
由式（8）和式（9）可见，当0＜a, b＜1时，FOE表现为正电阻与整数阶元件的串联，需要消耗有功功率；当1＜a, b＜2时，FOE表现为负电阻与整数阶元件的串联，能够释放有功功率。设分数阶电容及电感两端电压的有效值分别为UCa及ULb，它们的复功率分别为
（10）
式中，PCa, PLb 分别为FOC及FOI的有功功率；QCa, QLb 分别为FOC及FOI的无功功率。
式（10）表明，分数阶元件的有功功率和无功功率的比值由阶数a 和b 唯一确定。
与单组件分数阶元件相比，多组件分数阶元件在构成元件种类、数量和参数等方面的选择范围更广，因此构造方法形式多样。多组件分数阶元件构造方法分类如图3所示，本文按照构成元器件的类型，将多组件分数阶元件的构造方法分为基于无源元件、基于运算放大器和基于电力电子变换器三类，下面重点介绍图中一些典型构造方法的工作原理。
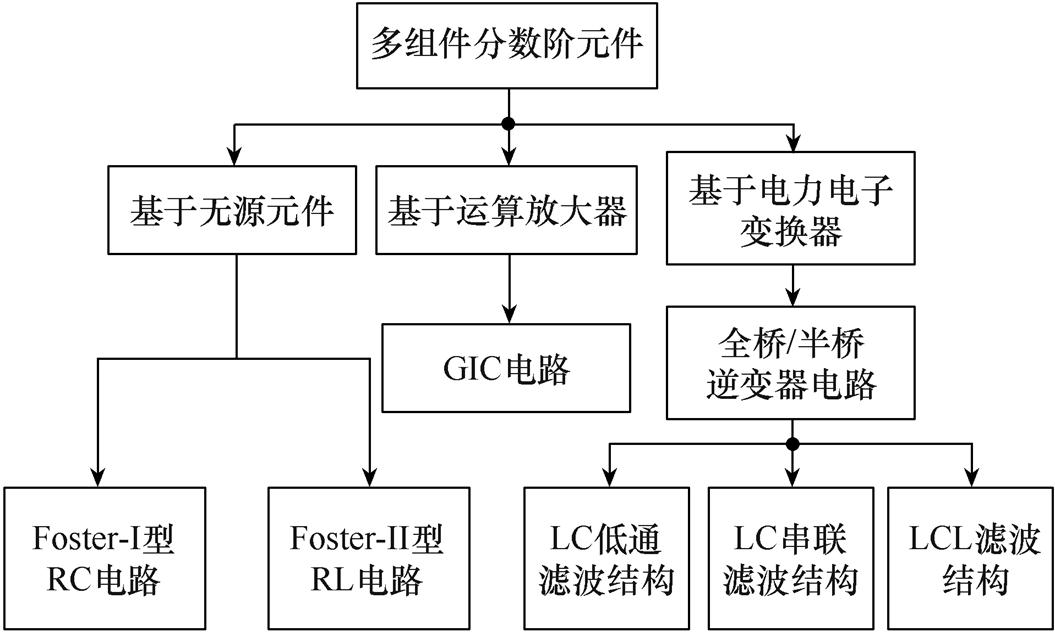
图3 多组件分数阶元件构造方法分类
Fig.3 Classification of construction methods for multi-component fractional order elements
基于无源元件的多组件分数阶元件在构造时仅使用电阻和电容、电感等无源元件，由于由电阻、电容和电感构成的无源网络无法释放能量，故基于无源元件只能构成0＜a, b＜1的FOE。
2.1.1 基于Foster Ⅰ型RC阶梯电路的分数阶电容
利用网络综合方法，通过选择适当取值的电阻和电容元件构建特定的阶梯结构电路，可以近似实现恒相位区域CPZ内的恒相角（Constant Phase Angle, CPA）特性以及如式（8）所示的阻抗特性，从而准确地实现分数阶电容。目前，采用RC网络实现分数阶电容的方法主要有Foster方法、Cauer方法及Valsa方法[27]。其中基于Foster Ⅰ型RC阶梯电路的分数阶电容如图4所示，由N+2个RC并联单元与一个额外的电阻串联而成，其中N为并联单元数。
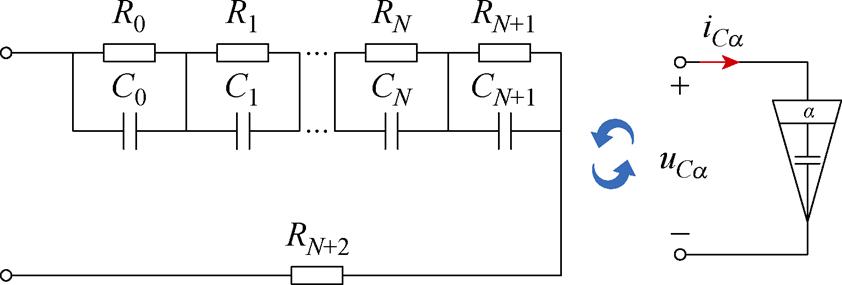
图4 基于Foster Ⅰ型RC阶梯电路的分数阶电容
Fig.4 FOC based on Foster Ⅰ RC ladder circuit
给定基电阻值R和基电容值C，则梯形网络的RC并联单元中电阻Ri（i=1, 2,…, N）的取值与基电阻R呈等比级数关系，Ri=miR；电容Ci的取值与基电容C也呈等比级数关系，Ci=niC。比值m、n与需实现的分数阶电容的阶数a 满足
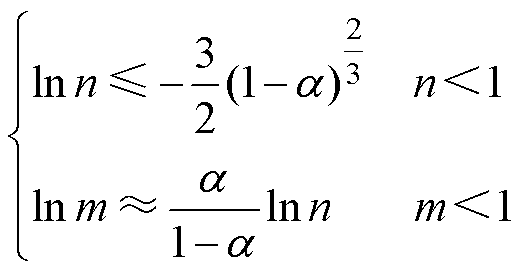（11）
RC并联单元中R0、C0取值应满足
（12）
RC并联单元中的RN+1、CN+1取值应满足
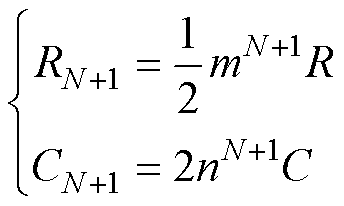（13）
第N+2个串联电阻RN+2取值应满足
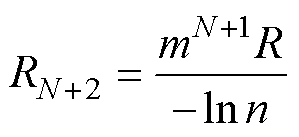（14）
设fB为构造的分数阶电容CPZ的频率下界，则电路时间常数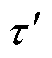
=RC的选取应满足
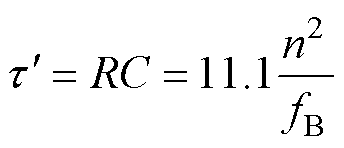（15）
设fT为CPZ的频率上界，则梯形网络中RC并联单元数N的选取应满足
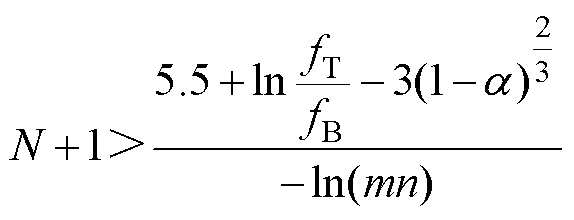（16）
得到的Foster Ⅰ型RC阶梯电路的频域阻抗为
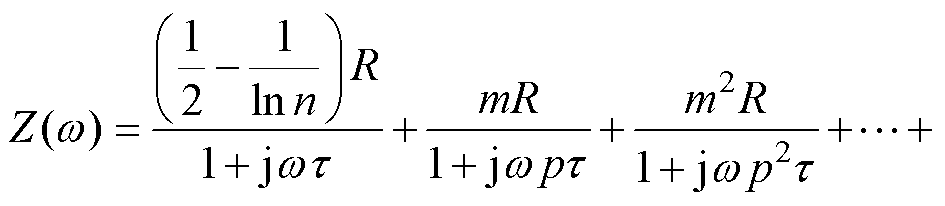
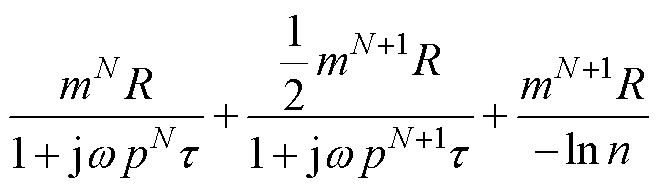（17）
其中
p=mn
给定所需要FOC的伪电容值Ca及阶数a，并设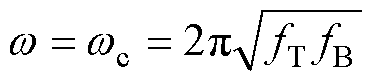
，由Z(w) =1/(waCa)可以得到R的大小，图4中其他元件参数可由式（11）～式（16）得到。
由式（16）可知，采用Foster Ⅰ型RC阶梯电路构造的分数阶电容的恒定相位区域CPZ（fT-fB）与RC并联单元数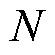
也即网络复杂性密切相关。若要扩大分数阶电容的恒定相位区域，则必须增加网络中使用元件的数量，元件数量增加的同时将导致电路体积的增大，在硬件实现时冗长的传输线有可能产生寄生效应，尤其是在高频情况下。
2.1.2 基于Foster Ⅱ型GL阶梯电路的分数阶电感
由式（8）及式（9）可知，分数阶电感的阻抗与分数阶电容的导纳在频域上具有相似的形式，可以将分数阶电感的阻抗传递函数视为分数阶电容的阻抗传递函数的倒数形式。因此，利用对偶原理，可以在2.1.1节分数阶电容的基础上，得到基于Foster Ⅱ型GL阶梯电路的分数阶电感，如图5所示。
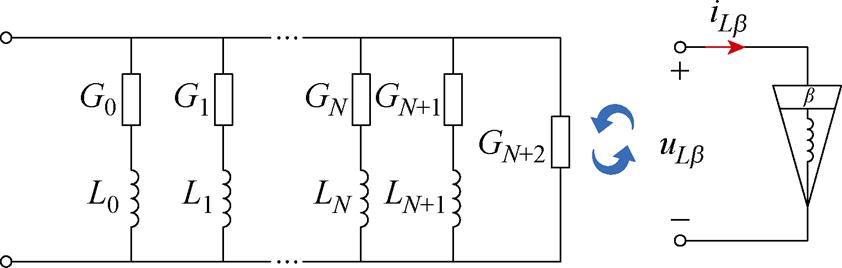
图5 基于Foster Ⅱ型GL阶梯电路的分数阶电感
Fig.5 FOI based on Foster Ⅱ GL ladder circuit
已知图4所示Foster Ⅰ型RC阶梯电路的导纳传递函数为
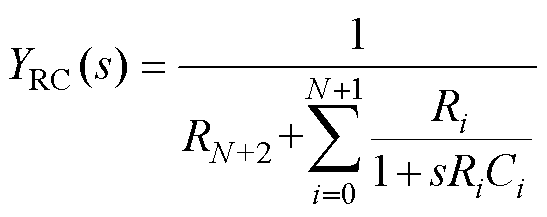（18）
可得图5所示Foster Ⅱ型GL阶梯电路的阻抗传递函数为
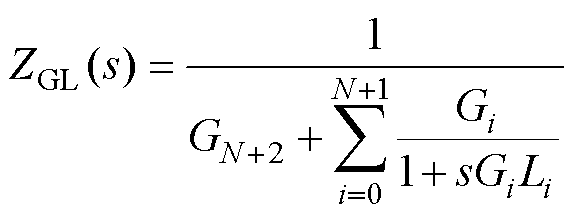（19）
对比式（18）、式（19）可知，Foster Ⅰ型RC阶梯电路的导纳传递函数与Foster Ⅱ型GL阶梯电路的阻抗传递函数具有相似的表达形式。因此，若基于Foster Ⅱ型GL阶梯电路的分数阶电感的阻抗在数值上等于基于Foster Ⅰ型RC阶梯电路的分数阶电容的导纳，即sbLb =saCa，只需令GL阶梯电路中与RC阶梯电路各参数取值满足Gi=Ri，Li=Ci。
与2.1.1节所述的设计步骤相同，在得到阶数为a、伪电容值为Ca的Foster Ⅰ型RC阶梯电路的基础上，将Foster Ⅱ型GL阶梯电路中的电导、电感取值分别等于FOC电路中的电阻、电容取值，即Gi=Ri、Li=Ci，便能够得到阶数b=a，伪电感值Lb =Ca的FOI等效电路。
为方便分析，可将FOC与FOI的阻抗特性统一为
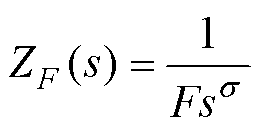（20）
式中，F为要构造的FOE的阻抗系数，单位为1/(Wss)，F＞0；s 为FOE的阶数，-2＜s ＜2；|ZF|为FOE的等效阻抗值，|ZF|=1/(Fws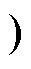
。
基于运算放大器的多组件分数阶元件主要由电阻、电容等无源元件以及运算放大器构成。在基于无源元件的多组件分数阶元件的基础上，加入由运算放大器构成的广义阻抗变换器（Generalized Impedance Converter, GIC）等有源电路，可以实现-2＜s ＜2的FOE。
由式（11）可知，Foster Ⅰ型RC阶梯电路只能实现阶数0＜a＜1的FOC，以该FOC为基础，加入如图6所示的由运算放大器构成的GIC电路，可以得到其余阶数的FOE[23]。
图6所示GIC电路的阻抗定义为
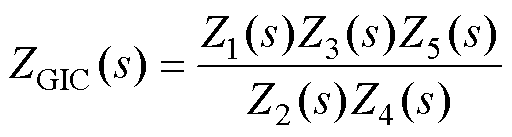（21）
若要得到阶数1＜s＜2的分数阶元件，可令Z1、Z2和Z4分别为电阻R1、R2和R4，Z3为电容C3，Z5为图4获得的FOC，即Z5(s)=1/(Casa)，0＜a＜1。此时，图6所示的GIC电路得到的分数阶元件的阻抗系数F和阶数s 分别为
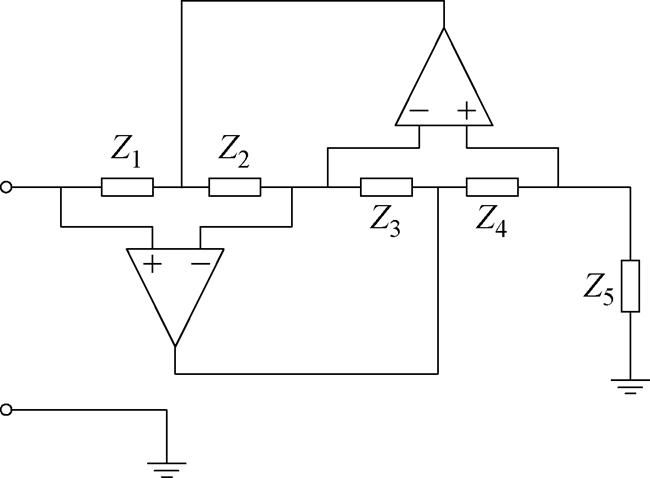
图6 基于运算放大器的GIC电路
Fig.6 GIC circuit based on operational amplifiers
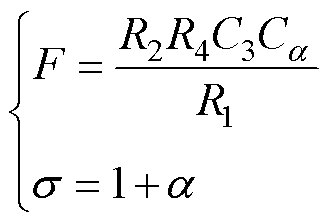（22）
由式（22）可知，所得到的分数阶元件阶数为1＜s＜2。
若令图6所示的GIC电路中的Z4为FOC，其余元件为电阻，则该GIC电路等效得到的分数阶元件阻抗系数F和阶数s 分别为
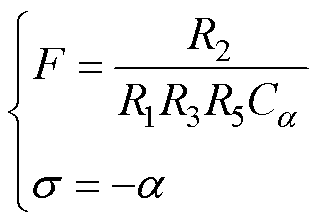（23）
由式（23）可知，所得到的分数阶元件阶数为-1＜s＜0。
进一步地，将Z2替换为电容C2，此时GIC电路对应的分数阶元件阻抗系数F和阶数s 分别为
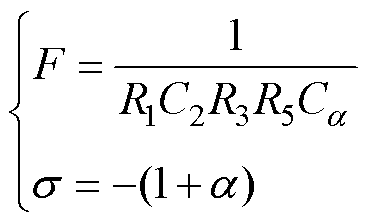（24）
由式（24）可知，所得到的分数阶元件阶数为-2＜s＜-1。
由上述分析可见，利用GIC电路及RC阶梯电路可以得到任意阶数的分数阶元件。
虽然基于运算放大器可构造出阶数大于1的分数阶元件，但其功率及电压受运算放大器的影响，相比之下，基于电力电子变换器（如全桥或半桥逆变器）构造的分数阶元件能够工作在高电压、大电流、大功率的场景下[28]。
基于电力电子变换器的多组件分数阶元件结构如图7所示。
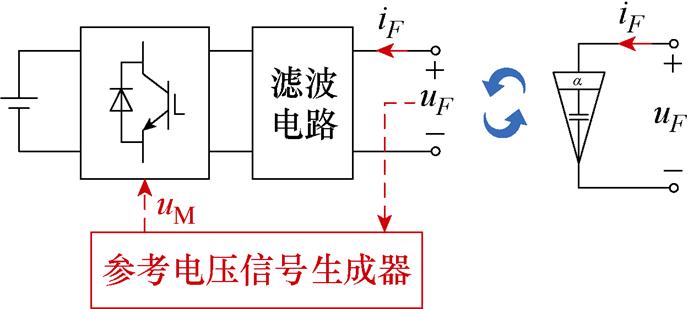
图7 基于电力电子变换器的多组件分数阶元件
Fig.7 Multi-component FOE based on power converter
设元件端口电压为uF，流入端口的电流为iF。参考式（20），如果控制逆变器的输出电压，使上述电流和电压满足
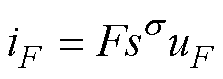（25）
则该电路可以等效为一个分数阶元件FOE。
通常逆变器输出端接滤波电路以滤除高次谐波分量，下面根据逆变器采用的滤波电路结构，对基于电力电子变换器的多组件分数阶元件构造方法进行分类介绍[28-29]。
2.3.1 LC低通滤波结构
采用LC低通滤波结构的多组件分数阶元件如图8所示。
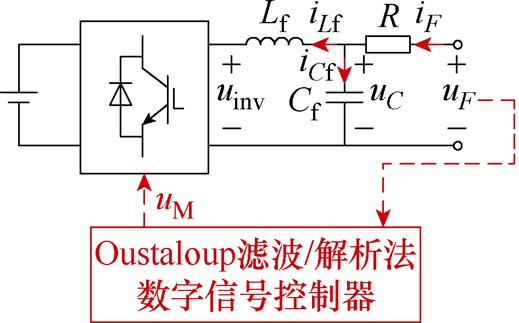
图8 采用LC低通滤波的多组件分数阶元件
Fig.8 Multi-component FOE with LC low-pass filter
逆变器的输出侧连接LC低通滤波器[30]，滤波器输出端与电阻R串联，因此输入电流可表示为
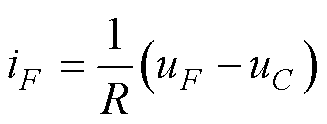（26）
联立式（25）和式（26），可推得滤波电容输出电压uC为
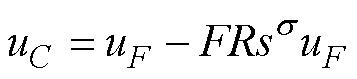（27）
合理选择LC低通滤波器的参数，电容电压uC可等效为逆变器输出电压uinv的基波分量。由式（27）可知，控制逆变器输出电压的关键在于对采样得到的端口输入电压uF进行分数阶求导运算。实现分数阶求导的方法之一是采用Oustaloup滤波近似[31-32]，即
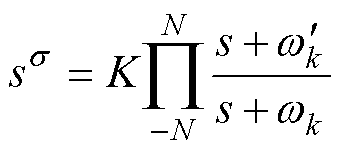（28）
其中
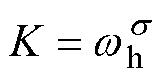
式中，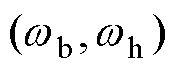
为拟合的角频率区间。滤波器的阶数为
。
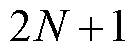使用Oustaloup滤波等效法的分数阶元件的恒定相位区域CPZ取决于对滤波器拟合频率段上、下限值wh、wb的选取，只需要增大wb、wh之间的区间，就能够扩大Oustaloup滤波拟合的频率段从而增大CPZ。然而Oustaloup滤波器在频率响应中，在频率段端点附近时对分数阶系统相频特性的拟合效果并不理想，这将造成频率段端点附近拟合的PAD较大[30-31]。
另一种生成逆变器参考信号的方法是采用解析法对LC低通滤波结构多组件FOE电路进行建模，根据电路关系得到输出电压uinv的参考值，使端口电压uF与流入端口的电流iF满足式（25）。
基于式（25），利用基尔霍夫电压和电流定律，图8中基于LC低通滤波的分数阶元件可以描述为
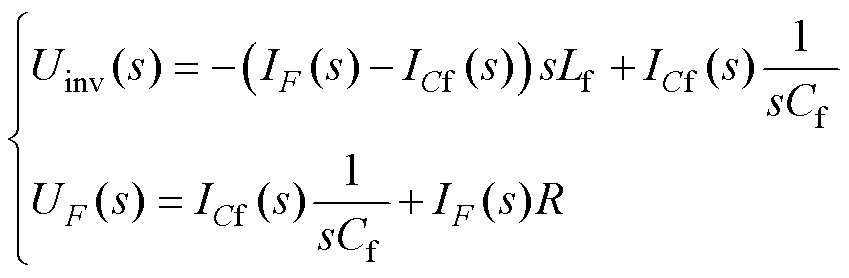（29）
求解可得满足式（25）的逆变器输出电压频域表示方式为
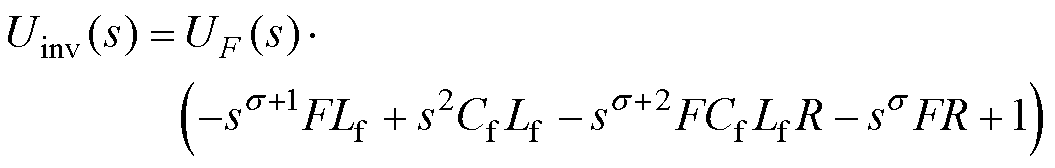（30）
设uF(t)=UFsin(w t)，令Ka=1/|ZF|=wsF，K1=R，K2=w Cf，K3=wLf，K4=sin(sp/2)，K5=cos(sp/2)，利用式（7）可以将式（30）转换至时域，表达式为
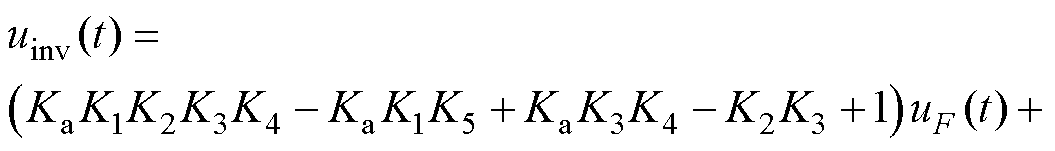
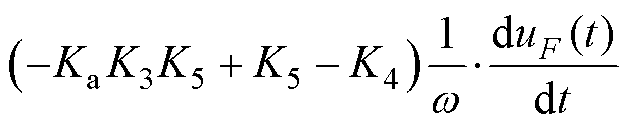（31）
由式（30）可见，采用解析法建立的多组件FOE模型考虑了滤波电感Lf、滤波电容Cf的大小，因此得到的FOE电路模型更加精确，在工作频率下可以获得更小的相位偏差，对相位的拟合效果将更好。
2.3.2 LC串联滤波结构
采用LC串联谐振滤波结构的分数阶元件如图9所示，其中Zr=Rr+sLr+1/(sCr)为LC串联滤波器的阻抗，Rr为Zr的寄生电阻。
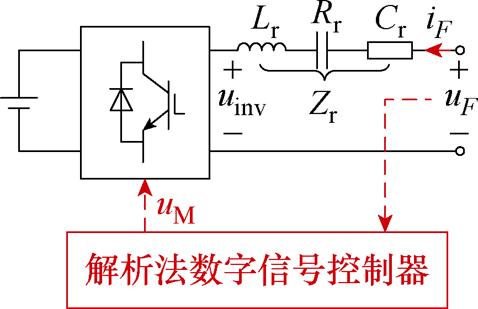
图9 采用LC串联滤波的多组件分数阶元件
Fig.9 Multi-component FOE with LC series filter
利用解析法，得到图9端口电流的表达式为
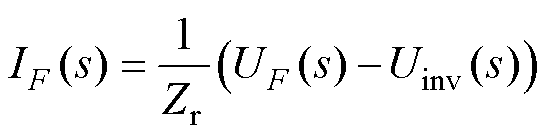（32）
设uF(t)=UFsin(w t)，令Ka=1/|ZF|=wsF，K1=Rr，K2=w Cr，K3=wLr，K4=sin(sp/2)，K5=cos(sp/2)，可得端口电压电流关系满足式（25）时所需的逆变器输出电压时域表示方式为
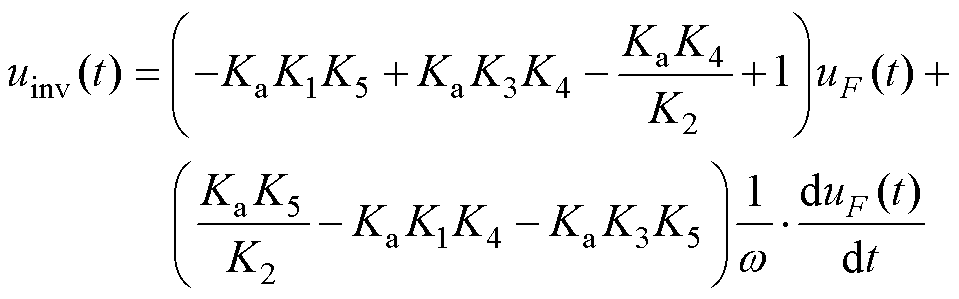（33）
串联谐振滤波器的谐振频率wr与阻尼系数z 分别定义为
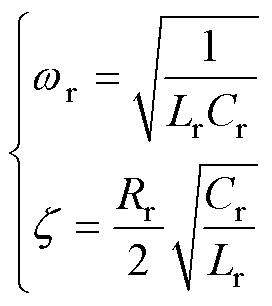（34）
设串联谐振滤波器内阻Rr=0.2 W 不变，采用不同的z 取值，得到串联谐振滤波器频率响应特性伯德图和传递函数冲激响应分别如图10、图11所示。从图10可见，阻尼系数z 对串联谐振滤波器带宽的影响较大，当阻尼系数较小时，串联谐振滤波器的选择性较好。但从图11可见，系统响应速度会因为z 的减小而相应变慢。比较串联谐振滤波器在工频50 Hz和高频1 000 Hz下的性能可以发现，在工频下串联谐振滤波器参数的选择难以同时满足系统的选择性和动态性能要求，在高频下易于同时满足系统的选择性和动态性能要求。因此，采用LC串联滤波结构的多组件分数阶元件更适用于高频场合。
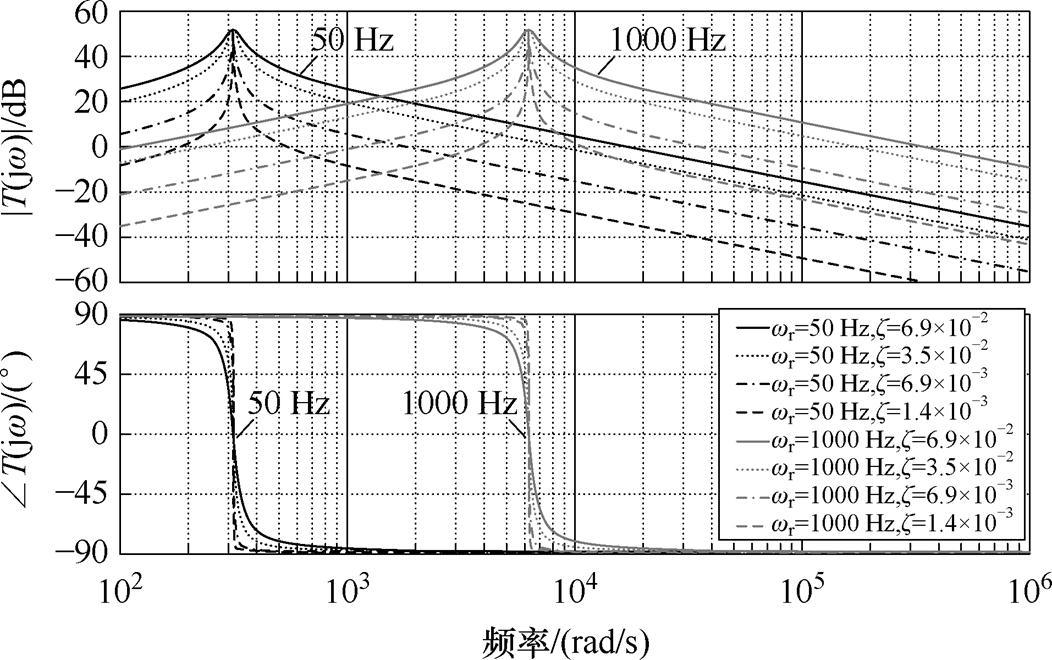
图10 不同z 取值下串联滤波器频率响应特性
Fig.10 Frequency response characteristics of series resonant filter under different damping coefficients
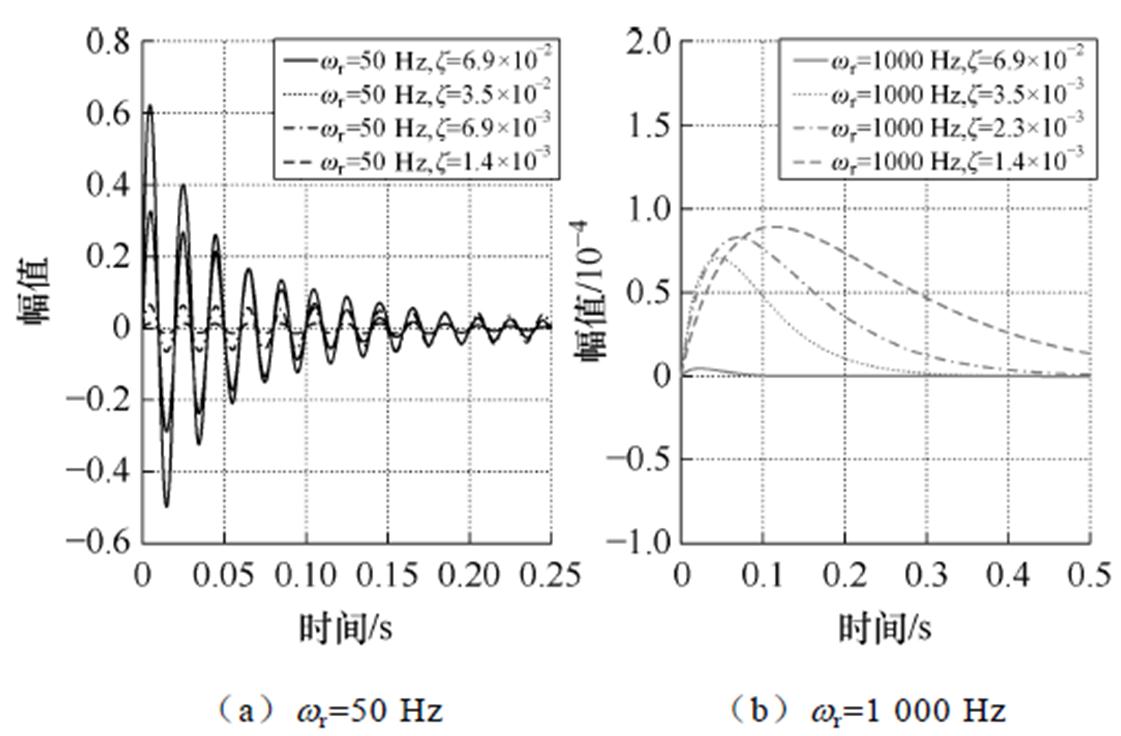
图11 不同z 取值下串联滤波器传递函数冲激响应
Fig.11 Impulse response of transfer function of series resonant filter under different damping coefficients
2.3.3 LCL滤波结构
将图8中的电阻R替换为电感L，得到采用LCL滤波结构的分数阶元件如图12所示。
由图12可见，逆变器的输出侧连接LCL滤波 器[33-34]，此时滤波电容电压UC(s)与端口电压UF(s)满足
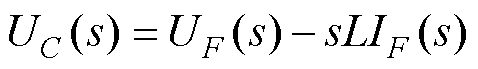（35）
结合式（25），可得UC(s)的表达式为
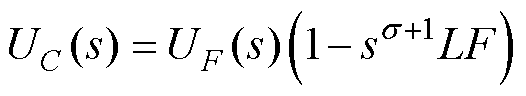（36）
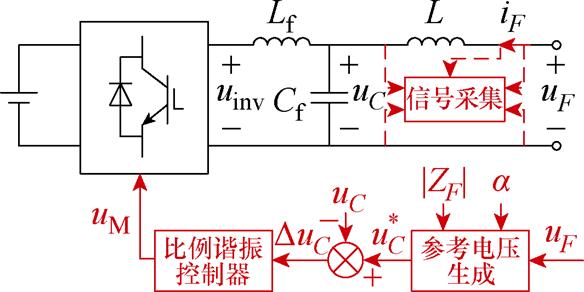
图12 采用LCL滤波的多组件分数阶元件
Fig.12 Multi-component FOE with LCL filter
设uF(t)=UFsin(w t)，令Ka=1/|ZF|=wsF，K1=wL，K2=sin(sp/2)，K3=cos(sp/2)，利用式（7）可得
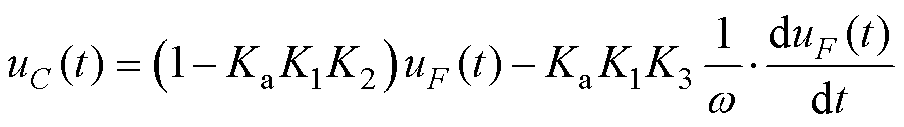（37）
已知LCL滤波器的谐振频率为
（38）
为使输入电流谐波幅值最小，通常选取LCL滤波器的电感比值Lf/L=1，滤波电容Cf取值也可以适当增大以节约电感磁心材料。为避免LCL滤波器的谐振峰值出现在低频或高频段[35]，谐振频率应该大于电网频率的5倍、小于开关频率的1/2。
由于比例谐振（Proportional Resonant, PR）控制器在谐振频率处有无穷大增益，对谐波的抑制能力十分强，能够实现对固定频率正弦参考信号的无静差跟踪控制[36-37]，故可用在数字信号控制器中，提高对谐波的抑制能力。
上述三种多组件分数阶元件构造方法的对比见表1，各构造方法的特点总结如下：
（1）基于无源元件的多组件分数阶元件通常需要借助合适的数学近似方法在期望的带宽内逼近包含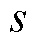
的分数阶次幂项的传递函数，继而使用RLC无源元件搭建符合该传递函数的具有分数阶阻抗特性的电路网络。为了达到较低的相位误差，需要增加阶数，使用大量的元件，致使整个电路结构复杂，且高阶传递函数的近似通常需要冗杂的计算过程。当计算得到的无源元件参数取值无法选用标准的市售无源元件时，用最接近的标准参数替代解析参数会造成分数阶元件的PAD偏差增加。此外，若需要改变FOE的阶数或阻抗系数，整个电路的元件都需要更换，因此该方法适用于FOE阶数和阻抗系数固定的场合。若对FOE相位拟合精度要求较高时，该构造方法仅适用于中低频场景。
表1 多组件分数阶元件的比较
Tab.1 Comparison among multi-component fractional-order elements
实现方法功率范围阶数范围频率范围控制方法相位偏差阶数和阻抗范围 基于无源元件Foster Ⅰ型RC阶梯电路取决于无源元件0～1fT～fB无与网络复杂性阶数N相关不可调 Foster Ⅱ型GL阶梯电路-1～0 基于运算放大器GIC电路取决于运算放大器-2～2fT～fB无小不可调 基于电力电子变换器LC低通滤波1～1 000 W-2～2与滤波器的截止频率有关Oustaloup滤波等效较大可通过改变控制参数调节 解析法较小 LC串联滤波解析法较小 LCL滤波解析法+比例谐振控制较小
（2）基于运算放大器的多组件分数阶元件可以实现阶数范围为-2～2的FOE。然而运算放大器的有限开环增益和增益不稳定性等非理想特性往往会造成所得到的FOE性能偏离其理想特性。因此，如何利用其他有源器件如跨导放大器（Operational Transconductance Amplifier, OTA）、电流反馈运算放大器（Current Feedback Operational Amplifier, CFOA）等构造FOE是一个值得继续探索的方向。
（3）基于电力电子变换器的多组件分数阶元件的功率等级取决于逆变器，且其阶数和阻抗可以通过改变控制参数调节，适用范围广。然而，滤波器的不同结构会影响分数阶元件的工作性能。因此，探索不同滤波结构在多组件分数阶元件上的应用，以及对滤波器进行参数优化成为基于电力电子变换器的FOE的一个发展方向。
对基于各种构造方法的多组件分数阶元件的特点进行总结，根据具体应用需求选择多组件分数阶元件的流程如图13所示。
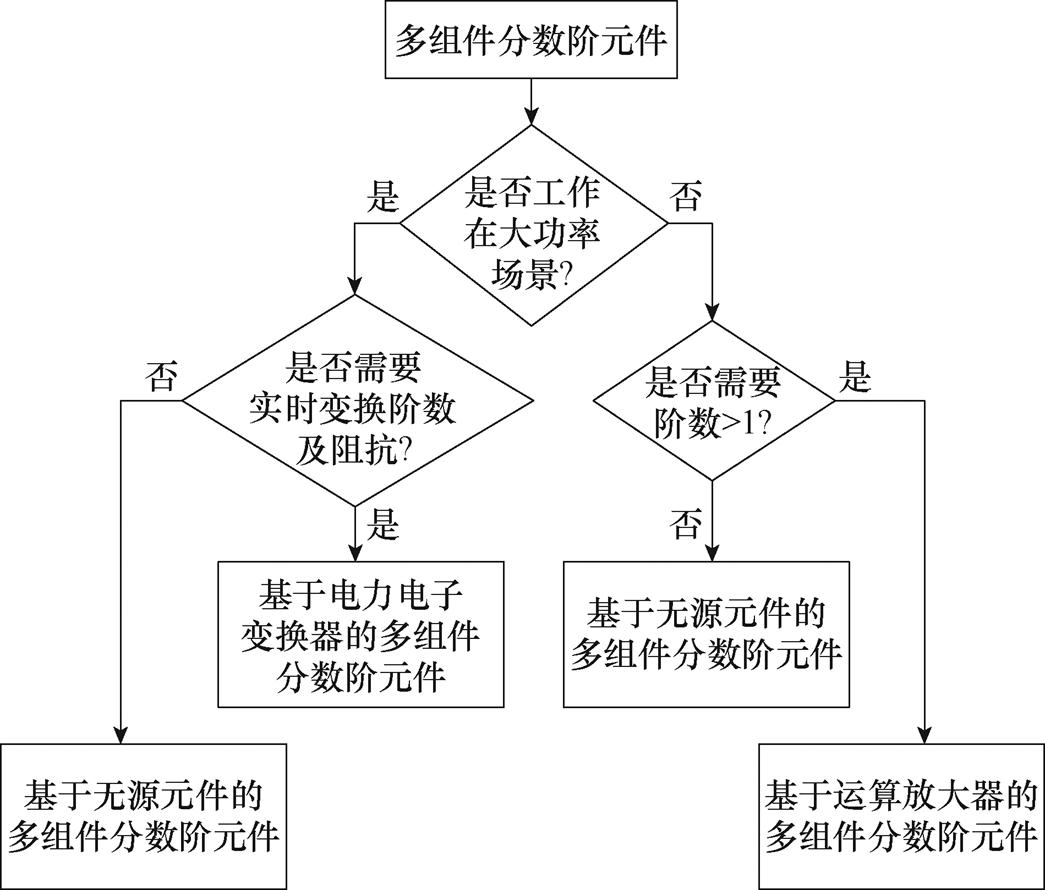
图13 多组件分数阶元件构造方法选择
Fig.13 Multi-component fractional order element construction method selection
将多组件分数阶元件的分数阶特性应用至实际系统中，不仅有助于提升系统性能，而且有利于发现新的系统特性。目前，多组件分数阶元件的记忆特性、负阻特性及阻抗变换特性等已使其在电气工程领域中的无线电能传输、电能质量改善等场合得到了成功应用[38-43]，该部分将重点探讨多组件分数阶元件在电网功率补偿场景下的成功应用。
分数阶元件特有的分数阶特性使其在电网功率补偿领域得到了应用。电气弹簧（Electrical Springs, ES）是一种可快速实现需求侧响应的电力电子装 置[44-45]，一种典型的三相整数阶电气弹簧拓扑如图14所示[46]，其中三相逆变器的输出通过隔离变压器与非关键负载（Noncritical Load, NCL）串联，再与关键负载（Critical Load, CL）并联。该三相电气弹簧的工作原理为通过调节各相输出电压ues*，*=A, B, C，改变非关键负载的电压大小，使非关键负载的功率跟随发电量波动，从而将可再生能源发电系统带来的功率波动实时转移到非关键负载上，使对电压变化敏感的关键负载保持电压恒定。然而，由于非关键负载所能承受的电压波动范围是有限的，且非关键负载的数量和功率也是有限的，故电气弹簧的应用受非关键负载的限制[47-48]。
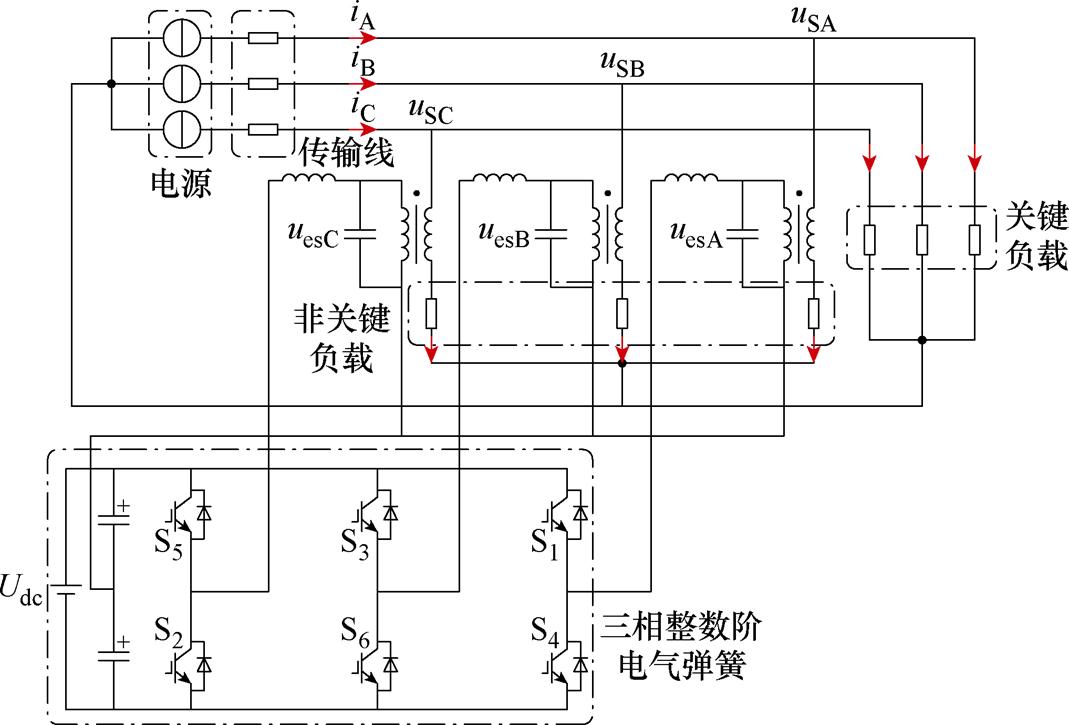
图14 三相整数阶电气弹簧拓扑
Fig.14 Topology of three-phase integer-order ES
为了解决上述问题，提出具有可同时实现有功功率和无功功率补偿的分数阶电气弹簧[48]，一种三相分数阶电气弹簧如图15所示，其中三相分数阶电容元件由三相逆变器和LC串联滤波器构成，经变压器与关键负载并联。
由式（10）可知，三相分数阶ES中每相有功功率P*a及无功功率Q*a的定义分别为
图15 三相分数阶电气弹簧拓扑
Fig.15 Topology of three-phase fractional-order ES
（39）
式中，US*为电网电压的有效值。
因此，三相分数阶电气弹簧通过控制每相等效分数阶电容的阶数以及伪电容大小，调节P*a、Q*a满足式（40），可在三相负载不对称的条件下，实现稳定负载电压、提高功率因数及平衡功率的作用。
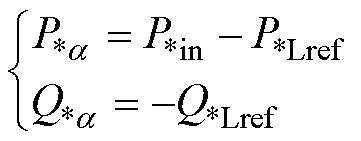（40）
式中，P*in为电网有功功率；P*Lref、Q*Lref分别为关键负载的额定有功功率和额定无功功率。
为了验证三相分数阶电气弹簧的性能，本文在RT-Box平台上开展了硬件在环实验验证，相关实验参数见表2。
图16展示了三相分数阶ES的实验结果，其中可再生能源发电系统以10 s为周期向电网注入波动的功率。
（1）0～10 s期间，三相分数阶ES未被激活，故可再生能源波动功率将导致电网电压波动。
（2）10～20 s期间，三相分数阶ES投入运行。三相分数阶ES投入后，当P*in＞P*Lref时，*相等效分数阶电容将控制阶数a*＜1，使其消耗有功功率；当P*in＜P*Lref时，*相等效分数阶电容将控制阶数a*＞1，使其释放有功功率，同时控制等效容值Ca*使式（40）成立。
表2 三相分数阶ES的实验参数
Tab.2 Parameters of three-phase fractional-order ES
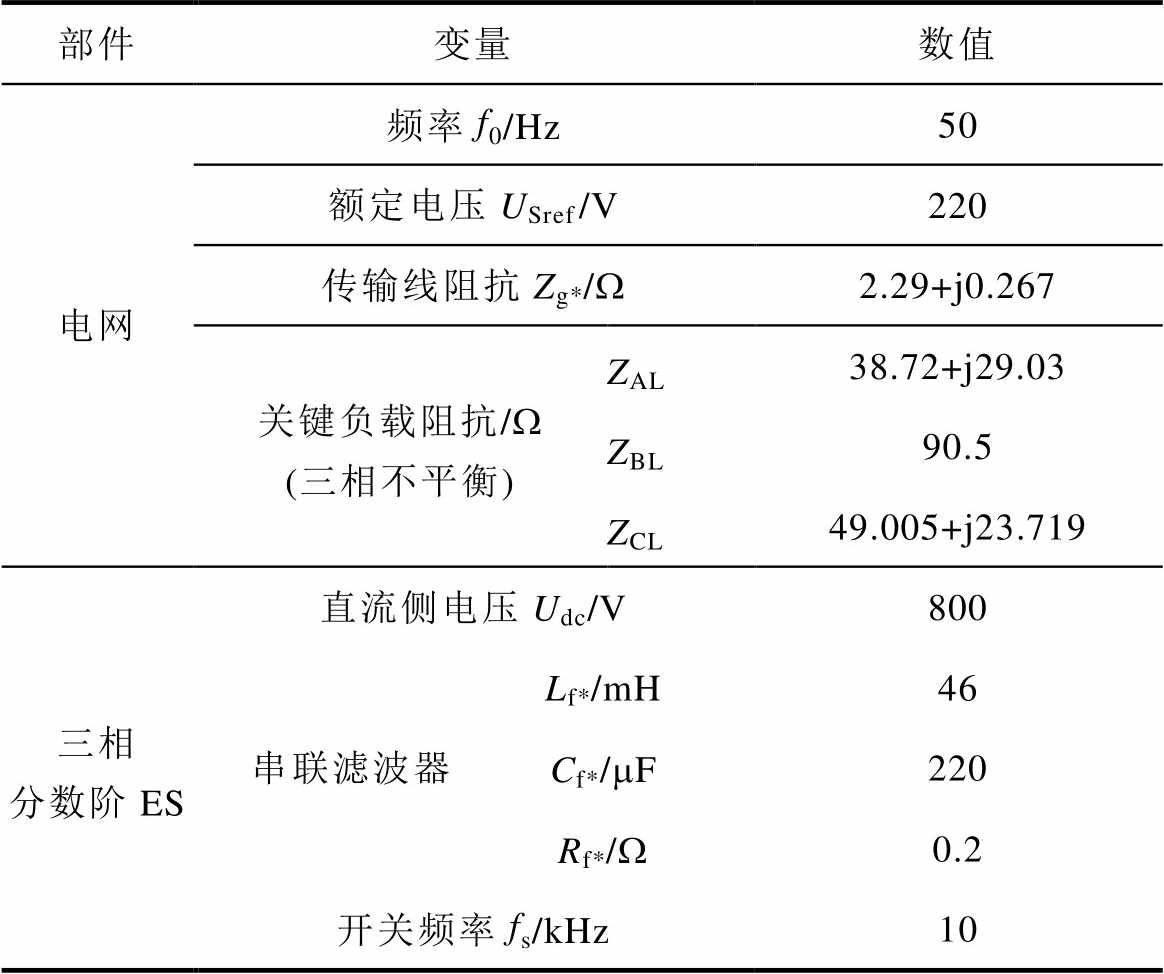
部件变量数值 电网频率f0/Hz50 额定电压USref/V220 传输线阻抗Zg*/W2.29+j0.267 关键负载阻抗/W (三相不平衡)ZAL38.72+j29.03 ZBL90.5 ZCL49.005+j23.719 三相分数阶ES直流侧电压Udc/V800 串联滤波器Lf*/mH46 Cf*/mF220 Rf*/W0.2 开关频率fs/kHz10
注：* =A, B, C。
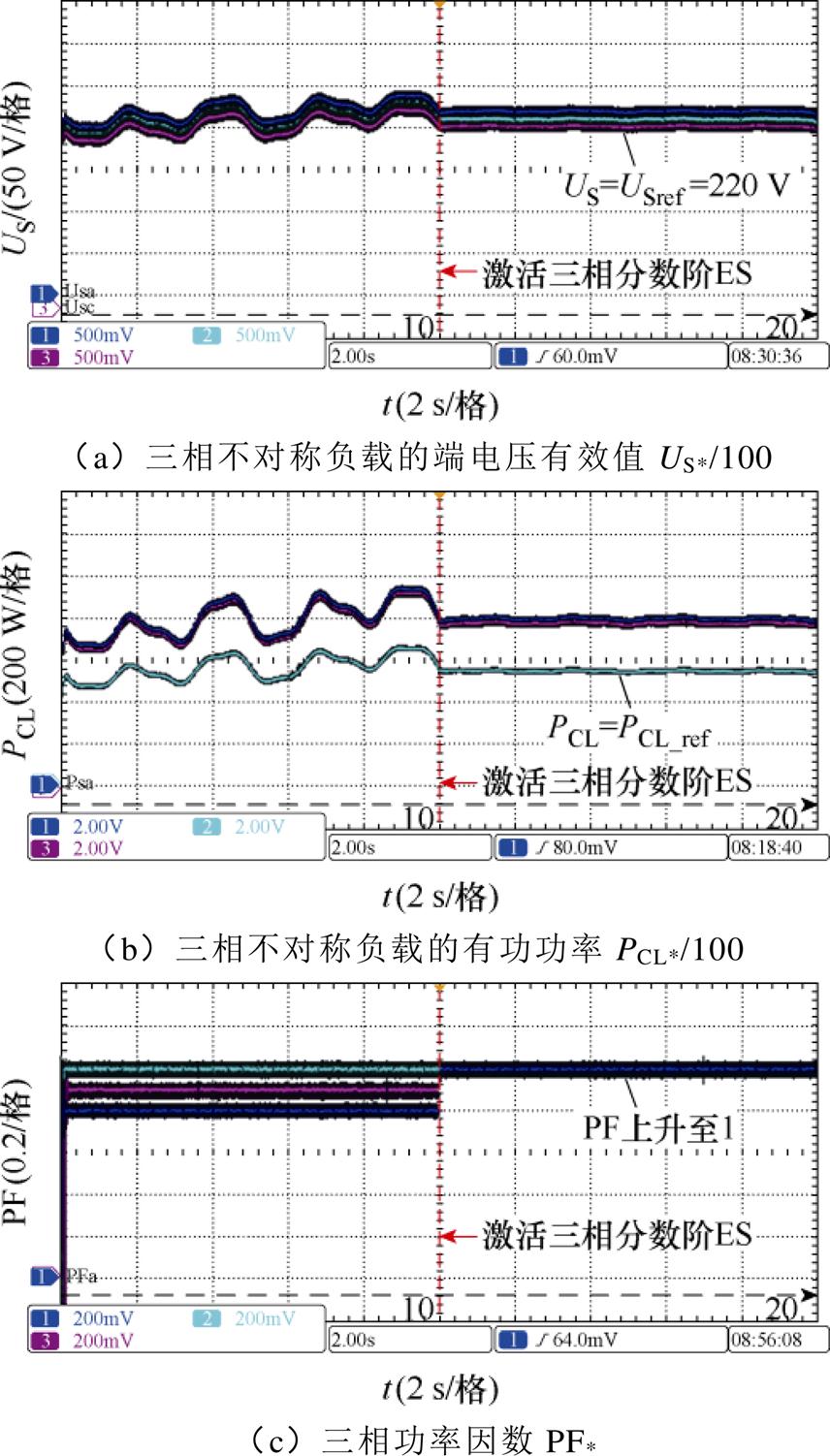
图16 三相负载不对称情况下三相分数阶ES实验波形
Fig.16 Experimental waveforms of three-phase fractional-order ES under three-phase asymmetric load conditions
从图16a可见，当三相分数阶ES投入后，关键负载的端电压有效值均保持在额定值；从图16b可见，虽然三相负载不平衡，但A、C相负载的有功功率均为800 W，而B相负载功率为534 W；从图16c可见，各相分数阶电容释放的无功功率补偿了关键负载消耗的无功功率，使三相系统功率因数上升至1。因此，实验结果验证了三相分数阶ES在稳定负载端电压、改善电网功率因数以及减缓三相功率不平衡现象方面的显著作用。
在越来越多的研究将整数阶电路系统拓展至分数阶电路系统的现实背景下，分数阶元件是研究分数阶电路系统的基础。针对目前单组件分数阶元件难以构造且阶数、阻抗固定的缺点，本文对构造上更具可实现性和灵活性的多组件分数阶元件的构造方法进行梳理，总结和归纳了几种典型多组件分数阶元件的电路模型和实现方法，并对其性能进行了比较。多组件分数阶元件已被证明能够有效提升实际系统的性能，本文工作为未来分数阶元件在电气工程领域的应用提供了参考。
参考文献
[1] Impedance spectroscopy: theory, experiment, and applications[M]. Third Edition. Hoboken, NJ: Wiley, 2018.
[2] Gabano J D, Poinot T, Kanoun H. Identification of a thermal system using continuous linear parameter- varying fractional modelling[J]. IET Control Theory & Applications, 2011, 5(7): 889-899.
[3] Elwakil A S. Fractional-order circuits and systems: an emerging interdisciplinary research area[J]. IEEE Circuits and Systems Magazine, 2010, 10(4): 40-50.
[4] Podlubny I. Fractional-order systems and PI/sup/spl lambda//D/sup/splmu//-controllers[J]. IEEE Transa- ctions on Automatic Control, 1999, 44(1): 208-214.
[5] 王瑞萍, 皮佑国. 基于分数阶PI速度控制器的永磁同步电动机控制[J]. 电工技术学报, 2012, 27(11): 69-75.
Wang Ruiping, Pi Youguo. Fractional-order PI speed controller for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 69-75.
[6] 赵鑫宇, 王丽梅. 永磁直线同步电机自适应分数阶终端滑模控制[J]. 电工技术学报, 2023, 38(20): 5434-5443.
Zhao Xinyu, Wang Limei. Adaptive fractional-order terminal sliding mode control for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5434-5443.
[7] 张晓超, 李虹, 苏文哲, 等. DC-DC变换器分数阶PIl控制与稳定性分析研究[J]. 电工电能新技术, 2019, 38(5): 21-31.
Zhang Xiaochao, Li Hong, Su Wenzhe, et al. Study on fractional-order PIl control and stability analysis of DC-DC converter[J]. Advanced Technology of Elec- trical Engineering and Energy, 2019, 38(5): 21-31.
[8] Mijat N, Jurisic D, Moschytz G S. Analog modeling of fractional-order elements: a classical circuit theory approach[J]. IEEE Access, 2021, 9: 110309-110331.
[9] Baleanu D, Golmankhaneh A K, Golmankhaneh A K, et al. Newtonian law with memory[J]. Nonlinear Dynamics, 2010, 60(1): 81-86.
[10] Piotrowska E, Rogowski K. Time-domain analysis of fractional electrical circuit containing two ladder elements[J]. Electronics, 2021, 10(4): 475.
[11] 王辉, 严欢, 张晓滨, 等. 基于分数阶的锂电池SOC和SOH联合在线估计[J/OL]. 电源学报, 2024: 1-14. (2024-01-11). https://kns.cnki.net/kcms/detail/ 12.1420.tm.20240110.1721.002.html.
Wang Hui, Yan Huan, Zhang Xiaobin, et al. Joint online estimation of SOC and SOH for lithium batteries based on fractional order models[J/OL]. Journal of Power Supply, 2024: 1-14. (2024-01-11). https://kns.cnki.net/kcms/detail/12.1420.tm.20240110.1721.002.html.
[12] 赵靖英, 胡劲, 张雪辉, 等. 基于锂电池模型和分数阶理论的SOC-SOH联合估计[J]. 电工技术学报, 2023, 38(17): 4551-4563.
Zhao Jingying, Hu Jin, Zhang Xuehui, et al. Joint estimation of the SOC-SOH based on lithium battery model and fractional order theory[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4551- 4563.
[13] Zhang Lei, Hu Xiaosong, Wang Zhenpo, et al. Fractional-order modeling and state-of-charge esti- mation for ultracapacitors[J]. Journal of Power Sources, 2016, 314: 28-34.
[14] 邓巧, 丘东元, 顾文超, 等. 超级电容器分数阶模型的分频段参数辨识方法[J]. 储能科学与技术, 2022, 11(10): 3371-3380.
Deng Qiao, Qiu Dongyuan, Gu Wenchao, et al. Parameter-identification method for fractional-order models of supercapacitors based on frequency-band division[J]. Energy Storage Science and Technology, 2022, 11(10): 3371-3380.
[15] 余波, 梁锐, 蒲亦非, 等. 超级电容器恒流充电的时域分数阶电路模型[J]. 电工技术学报, 2019, 34(17): 3533-3541.
Yu Bo, Liang Rui, Pu Yifei, et al. Time-domain fractional circuit model for constant current charging of supercapacitor[J]. Transactions of China Electro- technical Society, 2019, 34(17): 3533-3541.
[16] Xie Fan, Yang Zhiqiang, Yang Chen, et al. Constru- ction and experimental realization of the fractional- order transformer by oustaloup rational approxi- mation method[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2023, 70(4): 1550-1554.
[17] Wei Zhihao, Zhang Bo, Jiang Yanwei. Analysis and modeling of fractional-order Buck converter based on Riemann-liouville derivative[J]. IEEE Access, 2019, 7: 162768-162777.
[18] Fang Shucheng, Wang Xiaogang. Modeling and analysis method of fractional-order Buck-Boost converter[J]. International Journal of Circuit Theory and Applications, 2020, 48(9): 1493-1510.
[19] Adhikary A, Khanra M, Pal J, et al. Realization of fractional order elements[J]. INAE Letters, 2017, 2(2): 41-47.
[20] Sivarama Krishna M, Das S, Biswas K, et al. Fabrication of a fractional order capacitor with desired specifications: a study on process identi- fication and characterization[J]. IEEE Transactions on Electronic Devices, 2011, 58(11): 4067-4073.
[21] Samavati H, Hajimiri A, Shahani A R, et al. Fractal capacitors[J]. IEEE Journal of Solid-State Circuits, 1998, 33(12): 2035-2041.
[22] Mohapatra A S, Sarkar S, Biswas K. Fabricating solid state fractional capacitor in the frequency range of mHz to kHz[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2021, 11(11): 2035-2038.
[23] Adhikary A, Sen P, Sen S, et al. Design and performance study of dynamic fractors in any of the four quadrants[J]. Circuits, Systems, and Signal Processing, 2016, 35(6): 1909-1932.
[24] Podlubny I. Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications[M]. Elsevier, 1998.
[25] José Francisco G A, Juan R G, Manuel G C, et al. Fractional RC and LC electrical circuits[J]. Ingeniería, Investigacióny Tecnología, 2014, 15(2): 311-319.
[26] Zhang Li, Kartci A, Elwakil A, et al. Fractional-order inductor: design, simulation, and implementation[J]. IEEE Access, 2021, 9: 73695-73702.
[27] Kartci A, Agambayev A, Farhat M, et al. Synthesis and optimization of fractional-order elements using a genetic algorithm[J]. IEEE Access, 2019, 7: 80233- 80246.
[28] Jiang Yanwei, Zhang Bo. High-power fractional-order capacitor with 1＜a＜2 based on power converter[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 3157-3164.
[29] 卢曰海, 丘东元, 张波, 等. 大功率分数阶电感的电路实现[J]. 电源学报, 2018, 16(5): 147-152, 166.
Lu Yuehai, Qiu Dongyuan, Zhang Bo, et al. Circuit realization of high-power fractional inductor[J]. Journal of Power Supply, 2018, 16(5): 147-152, 166.
[30] 尹政, 胡存刚, 芮涛, 等. LC滤波型电压源逆变器无模型预测电压控制策略[J]. 电工技术学报, 2023, 38(14): 3723-3732.
Yin Zheng, Hu Cungang, Rui Tao, et al. Model-free predictive voltage control strategy for LC-filtered voltage source inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3723-3732.
[31] Oustaloup A, Levron F, Mathieu B, et al. Frequency- band complex noninteger differentiator: characteri- zation and synthesis[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2000, 47(1): 25-39.
[32] 柴秀慧, 曹晗, 张波, 等. Boost变换器全分数阶化系统分析与控制性能研究[J]. 电源学报, 2019, 17(6): 27-33.
Chai Xiuhui, Cao Han, Zhang Bo, et al. Research on analysis and control performance of full fractional- order boost converter system[J]. Journal of Power Supply, 2019, 17(6): 27-33.
[33] 沈姝衡, 方天治, 章益凡. 高带宽数字控制LCL型并网逆变器及其提高并网系统鲁棒性的谐振抑制技术研究[J]. 电工技术学报, 2022, 37(21): 5548- 5561.
Shen Shuheng, Fang Tianzhi, Zhang Yifan. A high- bandwidth digital-control LCL-type grid-tied inverter and resonance-suppressing technique for improving the robustness of grid-connected system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(21): 5548-5561.
[34] 张洪亮, 张子成, 陈杰, 等. 自适应三次谐波注入的回接型LCL光伏逆变器共模谐振电流抑制方法[J]. 电工技术学报, 2023, 38(1): 220-233.
Zhang Hongliang, Zhang Zicheng, Chen Jie, et al. Common-mode resonant current suppression for back-connected LCL photovoltaic inverter using adaptive third harmonic injection[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 220-233.
[35] 刘飞, 查晓明, 段善旭. 三相并网逆变器LCL滤波器的参数设计与研究[J]. 电工技术学报, 2010, 25(3): 110-116.
Liu Fei, Zha Xiaoming, Duan Shanxu. Design and research on parameter of LCL filter in three-phase grid-connected inverter[J]. Transactions of China Electrotechnical Society, 2010, 25(3): 110-116.
[36] 刘波, 杨旭, 孔繁麟, 等. 三相光伏并网逆变器控制策略[J]. 电工技术学报, 2012, 27(8): 64-70.
Liu Bo, Yang Xu, Kong Fanlin, et al. Control strategy study for three phase photovoltaic grid-connected inverters[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 64-70.
[37] 刘鹏飞, 卓菡. 带LCL滤波的并网逆变器的比例谐振控制[J]. 电气技术, 2013(1): 59-61.
Liu Pengfei, Zhuo Han. Proportional-resonant control of a grid connected inverter with LCL filter[J]. Electrical Engineering, 2013(1): 59-61.
[38] 张波, 荣超, 江彦伟, 等. 分数阶无线电能传输机理的提出及研究进展[J]. 电力系统自动化, 2022, 46(4): 197-207.
Zhang Bo, Rong Chao, Jiang Yanwei, et al. Proposal process and research progress of fractional-order wireless power transfer mechanism[J]. Automation of Electric Power Systems, 2022, 46(4): 197-207.
[39] 疏许健, 张波. 降低整数阶无线电能传输谐振频率的分数阶方法[J]. 电工技术学报, 2017, 32(18): 83-89.
Shu Xujian, Zhang Bo. A fractional-order method to reduce the resonant frequency of integer-order wireless power transmission system[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 83-89.
[40] Jiang Yanwei, Zhang Bo. A fractional-order wireless power transfer system insensitive to resonant frequ- ency[J]. IEEE Transactions on Power Electronics, 2020, 35(5): 5496-5505.
[41] Rong Chao, Zhang Bo, Jiang Yanwei, et al. A misalignment-tolerant fractional-order wireless charging system with constant current or voltage output[J]. IEEE Transactions on Power Electronics, 2022, 37(9): 11356-11368.
[42] Zhang Jingyu, He Liangzong, Lin Zhile. Fractional- order-based low-order harmonic current suppression method considering asymmetrical capacitor para- meters[J]. IEEE Transactions on Power Electronics, 2023, 38(3): 3775-3784.
[43] 林智乐, 张靖雨, 何良宗. 基于分数阶电容的多个低次电流谐波抑制方法[J]. 中国电机工程学报, 2022, 42(24): 8921-8932.
Lin Zhiyue, Zhang Jingyu, He Liangzong. Method of multiple low-order harmonic currents suppression based on fractional-order capacitor[J]. Proceedings of the CSEE, 2022, 42(24): 8921-8932.
[44] Hui S Y, Lee C K, Wu F F. Electric springs-a new smart grid technology[J]. IEEE Transactions on Smart Grid, 2012, 3(3): 1552-1561.
[45] Lee C K, Liu Heng, Tan S C, et al. Electric spring and smart load: technology, system-level impact, and opportunities[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(6): 6524-6544.
[46] Yan Shuo, Tan S C, Lee C K, et al. Electric springs for reducing power imbalance in three-phase power systems[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3601-3609.
[47] 贾何飞, 何英杰, 蔡雨希, 等. 电气弹簧双环解耦控制及有效运行范围研究[J]. 电工技术学报, 2020, 35(15): 3314-3326.
Jia Hefei, He Yingjie, Cai Yuxi, et al. Research of the electric spring about dual-loop decoupling control and effective operation range[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3314-3326.
[48] Ke Mingbin, Qiu Dongyuan, Zhang Bo, et al. An electric spring without noncritical load based on fractional-order components[J]. IEEE Journal of Emerging and Selected Topics in Industrial Elec- tronics, 2022, 3(3): 519-526.
Abstract Fractional-order elements (FOEs) serve as fundamental components in fractional-order circuits, forming the cornerstone of research into fractional-order circuit systems. Unlike single-component counterparts, the multi-component method offers greater flexibility in selecting constituent elements, enabling the adjustment of order and impedance coefficients for enhanced practicality. This paper provides a comprehensive overview of prevailing construction methods to facilitate the selection of appropriate multi-component FOEs for specific application needs. These methods are classified into three categories based on the type of constituent devices: passive devices, operational amplifiers, and power electronic converters.
In the construction method based on passive devices, two approaches involving Foster RLC ladder circuits are discussed. Passive RLC networks are used to create circuits that match the impedance characteristics of the transfer function. Reducing phase error requires increasing the order and using numerous components, leading to complex structures and cumbersome calculations. When standard off-the-shelf components cannot be used, replacing analytical parameters with standard ones increases the phase angle deviation. Adjusting the FOE order or impedance coefficients requires replacing all circuit components. This method is most suitable for fixed FOE order and impedance coefficients, which are effective in medium to low-frequency scenarios.
Next, the paper introduces the construction method based on operational amplifiers. The method of constructing FOEs based on generalized impedance converter (GIC) circuits can realize FOEs with orders varying from -2 to 2. However, the limited open-loop gain and gain instability of operational amplifiers often result in significant deviations of the obtained FOE performance from its ideal characteristics. Therefore, exploring how to use other active devices, such as operational transconductance amplifiers (OTA) and current feedback operational amplifiers (CFOA), to construct FOEs is an exploration direction. GIC circuits offer great integration and functionality, making them suitable for applications where precise impedance and phase characteristics are crucial.
The construction method based on power electronic converters is also discussed in detail.Multi-component FOEs based on power electronic converters have wide applications because their power level depends on the inverter, and their order and impedance can be adjusted by changing the control parameters. However, different structures of filters affect the operating performance of fractional-order elements. Therefore, exploring the application of different filter structures on multi-component FOEs and optimizing the parameters of the filters become the direction of development for power electronic converter-based FOEs. Power electronic converters provide the advantage of handling higher power levels and dynamic adaptability. The ability to digitally control the fractional order and impedance in real-time makes these elements highly versatile.
Lastly, this paper proposes a three-phase fractional-order electrical spring (TPFES). TPFES controls the order of the equivalent fractional-order capacitance of each phase and the pseudo-capacitance. The effect of stabilizing the load voltage is realized, the power factor is improved, and the power is balanced. The application in grid power compensation demonstrates that multi-component FOEs can effectively enhance the performance of practical circuit systems. This work provides a reference for future applications of fractional order components in electrical engineering.
Keywords：Fractional-order circuit, fractional-order capacitor, fractional-order inductor, inverter
中图分类号：TM502
DOI: 10.19595/j.cnki.1000-6753.tces.240580
国家自然科学基金资助项目（52277177, 52077085）。
收稿日期 2024-04-12
改稿日期 2024-06-19
王佳豪 男，2001年生，硕士研究生，研究方向为分数阶元件在电力系统中的应用。
E-mail: 201930134272@mail.scut.edu.cn
丘东元 女，1972年生，教授，博士生导师，研究方向为电力电子变换器拓扑构造与设计、无线电能传输机理及应用等。
E-mail: epdyqiu@scut.edu.cn（通信作者）
（编辑 陈 诚）