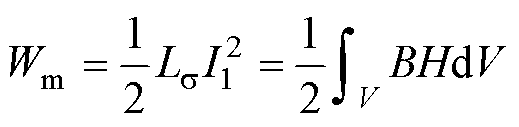 (1)
(1)
摘要 高频变压器的漏感作为电力电子变换器中的重要参数,对改善隔离型DC-DC变换器的运行模式和功率传输特性具有重要的意义。与圆导线相比,利兹线能够有效地减少高频磁性元件中的涡流损耗。然而,利兹线绕组的复杂结构给高频变压器漏感预测带来了严峻的挑战。一方面,磁心窗口各区域的磁场能量难以准确提取;另一方面,利兹线的多股和扭转结构难以准确表征。因此,该文基于镜像原理和网格化处理,精确提取磁心窗口不同区域的磁场能量。通过引入相对复数磁导率实现了多股利兹线的均匀化建模,揭示了宽频范围内磁场能量的衰减规律,提出坐标变换方法对利兹线的扭转结构进行表征,建立了计及利兹线扭转特征和频变特性的高频变压器漏感预测模型。最后,针对两种不同利兹线绕组的变压器模型,从计算精度和效率两方面进行了详细的实验研究和对比分析。结果表明,所提计算方法的最大偏差不超过4%,计算时间约为20 s,验证了该方法的准确性和高效性。
关键词:高频变压器 漏感 镜像法 利兹线绕组 频变特性
随着开关器件的发展和新型磁性材料在电力电子领域的广泛应用,电力电子装置高频化成为必然的发展趋势。电力电子变压器将电力电子技术与传统变压器相结合,在不影响设备运行的情况下实现变压器的高频化,有效地提升了变压器的功率密度和效率[1-3]。高频变压器作为电力电子变压器的重要磁性元件,在整个电路中起到电气隔离、电力传输与调节等作用[4-5]。其中,在隔离型DC-DC变换器中,高频变压器的漏感参数严重影响了变换器的工作性能。一方面,漏感过大将导致开关关断瞬间产生较大的尖峰电压,易造成过电压击穿[6];另一方面,漏感直接影响输入、输出直流母线之间的功率传输效率。因此,准确评估高频变压器的漏感参数对于电力电子变换器的设计具有重要的意义。
迄今为止,国内外学者围绕高频变压器漏感的精确预测开展了诸多研究,主要可归纳为两类:解析法和数值法。在现有的解析法中,一维Dowell模型[7]因其公式简单、计算速度快的优势被广泛应用在具有铜箔绕组或圆导线绕组的高频变压器漏感预测[8-13]中。该模型假设绕组的高度与磁心窗口的高度相等且磁心的磁导率为无穷大,此时磁心窗口中仅存在沿绕组高度方向呈一维分布的磁场。然而,在高频变压器设计中,为了满足绝缘要求,需要在磁心和绕组末端之间留有一定的距离(绕组高度小于窗口高度),此时在绕组的端部将产生显著的二维磁场分量,即端部效应。磁心窗口内的磁场分布不再严格满足上述假设,导致一维模型对漏感的预测误差增加。此外,利兹线被广泛应用于高频变压器中以减少涡流损耗,但却鲜有文献对利兹线绕组的高频变压器漏感进行研究。文献[14]采用面积等效方法计算中频变压器的漏感,该方法基于等效前后直流电阻不变的原则,将利兹线绕组等效为铜箔绕组后利用Dowell模型计算漏感参数。然而,该方法忽略了利兹线填充因子的影响,导致漏感的估计值偏低。文献[15]基于Tourkhani模型[16]提出了一种考虑利兹线填充因子和高频效应的漏感解析计算方法。但是,忽略了绕组层间不规则区域的漏磁能量,同样导致漏感值被低估。
数值法因其具有较高的计算精度以及较好的通用性等优势,似乎更适合解决上述问题。其中,有限元法(Finite Element Method, FEM)作为一种典型的数值计算方法,经常被研究人员用于详细分析变压器的漏感特性或验证漏感解析模型的正确 性[17-20]。然而,对于分析利兹线绕组,有限元法却面临着严峻的挑战。利兹线是由成百上千根较细的股线绞合而成的,导致其有限元模型的建立较为困难。随着频率的升高,需要更细的网格划分以保证计算精度,从而严重地增加了计算时间和成本。尽管二维有限元模型在一定程度上能够减少计算成本,但是面对结构复杂的利兹线绕组模型,建模及计算时间仍难以接受。除此之外,现有的漏感评估方法均未考虑利兹线的扭转结构对变压器漏感的 影响。
为了解决上述问题,本文首先提出了一种利兹线的均匀化等效模型,以提升建模的灵活性和计算的高效性。其次,基于镜像原理提取磁心窗口内的二维磁场能量,解决端部效应的影响。通过在镜像法中引入网格化处理,精确提取绕组中不同位置的内部和外部磁场,并提出坐标变换方法对利兹线的扭转结构进行表征。最后,根据磁场能量随频率变化的规律,建立计及利兹线扭转特性和高频效应的变压器漏感预测模型。为了验证所提出方法的精确性,设计并制作了两台不同的利兹线高频变压器样机。结果表明,本文所提出的漏感计算方法具有较好的准确性和高效性,并能够适用于高频变压器的优化设计。
目前,大部分的高频变压器漏感研究主要基于能量法。当二次绕组短路时,一次和二次绕组的磁动势相互抵消,只留下磁心窗口中的磁场能量。此时,变压器的漏感Lσ和磁心窗口中的总磁场能量Wm之间的关系描述为
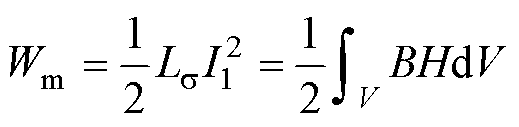 (1)
(1)
式中,I1为一次电流的有效值;B为所求区域的磁感应强度;H为磁场强度;V为磁心窗口的体积。
经典的一维Dowell漏感模型广泛应用于铜箔或圆导线绕组的高频变压器漏感评估,该模型以安培定理表征电流和磁场之间的基本关系。假设铜箔绕组与磁心窗口等高且磁心材料的磁导率为无限大,等高绕组之间存在纯垂直方向漏磁通。在此条件下,磁心窗口的磁场分布如图1所示,磁心窗口不同位置的磁场能量表达式如下所示。
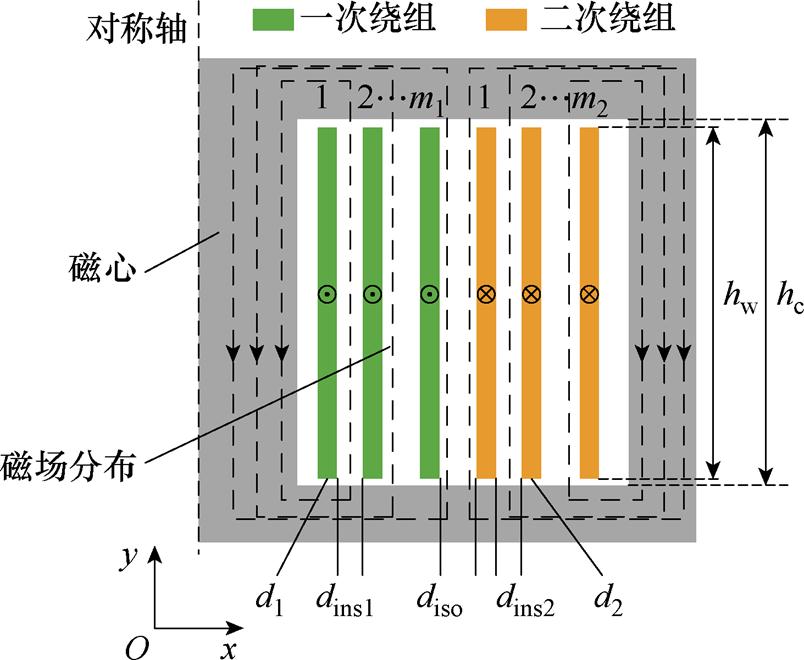
图1 一维Dowell漏感模型
Fig.1 1-D Dowell leakage inductance model
一次绕组和二次绕组之间的主绝缘距离diso中储存的能量可表示为
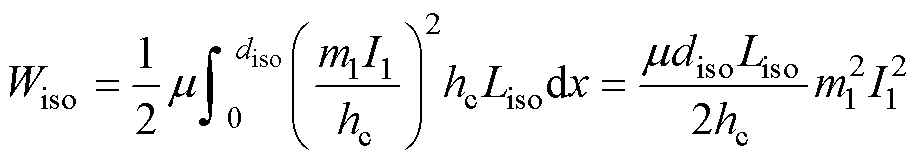 (2)
(2)
式中,hc、m1分别为磁心窗口的高度、一次绕组的层数;Liso为主绝缘区域的平均路径长度;m 为所求区域材料的磁导率。
一次绕组或二次绕组层间储存的能量为
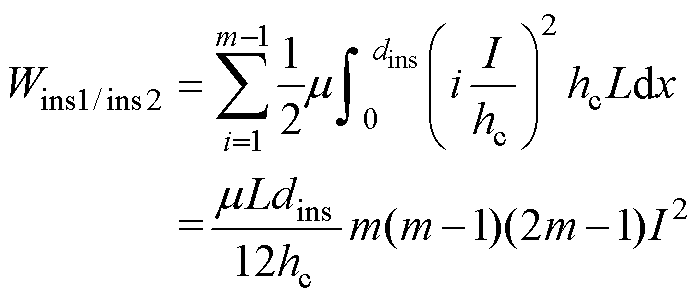 (3)
(3)
式中,dins、L、m和I分别为一次或二次绕组的层间绝缘距离、平均路径长度、层数和电流。
一次或二次侧铜箔绕组中储存的能量可表示为
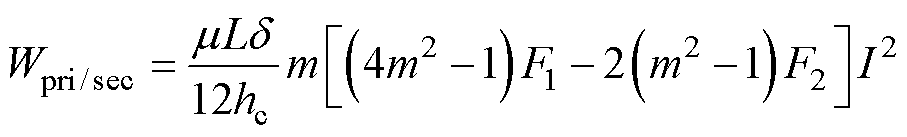 (4)
(4)
其中
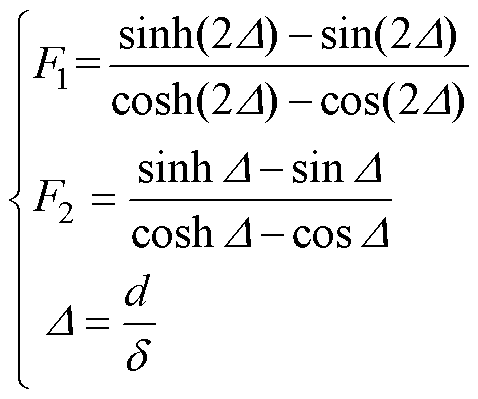 (5)
(5)
式中,d为一次或二次侧铜箔绕组的厚度;d 为趋肤深度。最后,对磁心窗口中的所有磁场能量求和,即可得到漏感与总磁场能量之间的关系式为
 (6)
(6)
该漏感解析方法能够简单且快速地评估具有铜箔或圆导线绕组的高频变压器漏感。然而,在高频和大容量变压器中,绕组末端与磁心之间必须留有特定的距离以满足绝缘要求。此时,磁心窗口内的磁场存在沿x方向的分量,不再满足一维假设,如图2所示,从而导致该模型对漏感的评估出现误差。
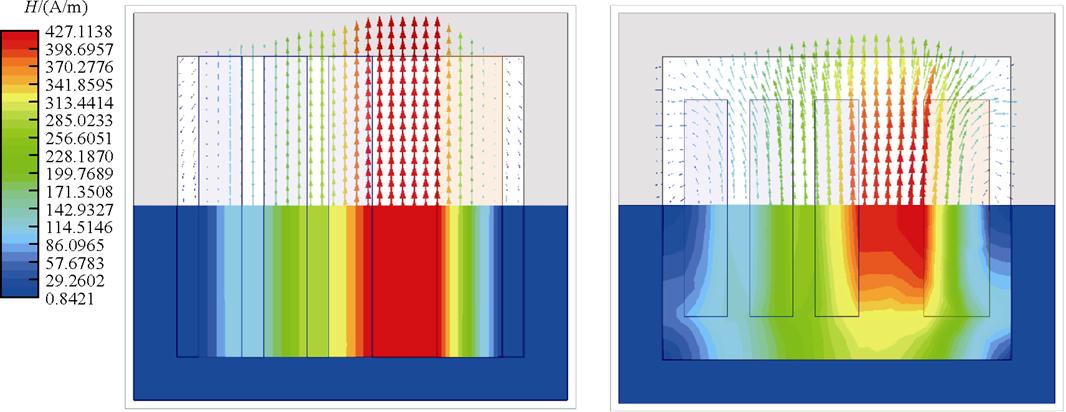
图2 端部效应对磁场分布的影响
Fig.2 Influence of edge effect on the distribution of magnetic field
不同于铜箔和圆导线,利兹线是一种由多根相互绝缘且外部并联的细圆导线绞合或编织而成的复合导体,其基本结构如图3所示。
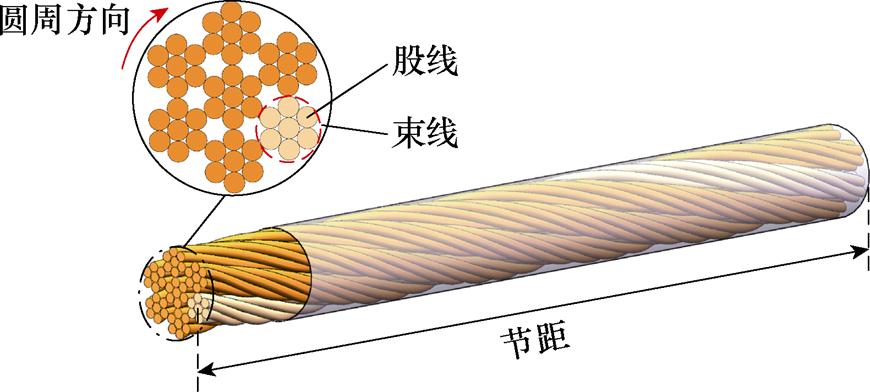
图3 利兹线的基本结构
Fig.3 Basic structure of the Litz wire
股线是带有绝缘漆的细圆导线,是构造利兹线的最基本单元。束线是由股线绞合而成的更高一级的结构。节距则是股线或束线绞合一周后的轴向长度。在理想绞合过程中,每根股线都能够同时沿径向和圆周方向变换位置并绞合在一起,然而,这种结构在真实利兹线中几乎很难实现。在实际情况下,大部分的股线仅能够沿圆周方向扭转,而位于中心的股线则保持位置不变。高频条件下,与实心圆导线相比,利兹线的特殊结构能够在一定程度上削弱导体中产生的涡流损耗。
在高频变压器的优化设计过程中,变压器的结构需要随决策变量的改变而快速更新,绕组的结构和排布也同时发生变化。然而,利兹线的复杂结构,无论是几何模型的建立还是仿真分析都很难在短时间内完成。为了解决这一问题,提出了一种利兹线的均匀化等效模型,该模型的等效过程如图4所示。首先,将具有扭转结构的利兹线等效为股线相互平行的平行导线,然后,再将平行导线均匀化处理等效为实心圆导线。由于求解顺序与等效过程完全相反,因此优先考虑利兹线的均匀化处理。
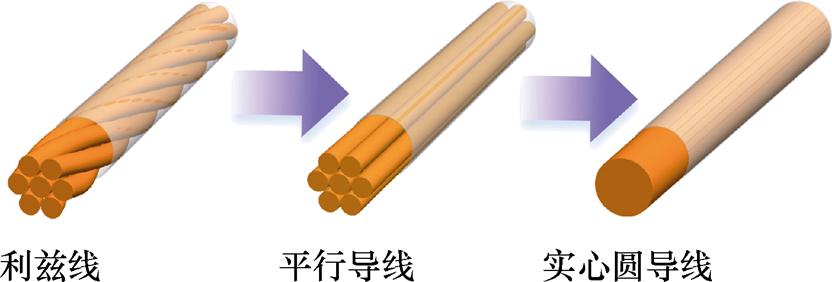
图4 利兹线均匀化的等效过程
Fig.4 Equivalent process for Litz-wire homogenization
当一根带有均匀电流密度的圆导线被放入垂直其轴线方向的时谐磁场中时,沿导线方向会产生相反方向的涡流。反磁场引起的涡流减少了通过圆导线的磁通,因此导体在磁场作用下的行为类似于一块有损耗的铁磁材料[21]。圆导线表现出来的宏观磁导率低于其实际磁导率。为了描述圆导线的这一特性,引入了相对复数磁导率,有
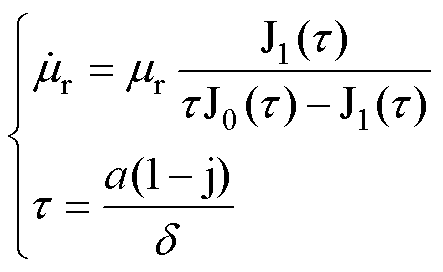 (7)
(7)
式中,mr和a分别为圆导线的相对磁导率和半径;j为虚数单位;Jn为n阶贝塞尔函数,n=0, 1。利兹线可以被认为是由空气和大量铜导线组成的复合导体,其均匀化的相对复数磁导率可以由Ollendorff公式[22]计 算得
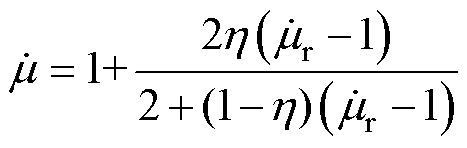 (8)
(8)
式中,h 为利兹线的填充系数。通过引入相对复数磁导率,可以在不需要考虑股线细节的情况下,将利兹线等效为均匀的实心圆导线,并通过静磁场近似表征其高频效应(相对复数磁导率适用条件为时谐场,这里将低频时谐磁场用静磁场作近似处理)。其中,相对复数磁导率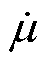 的实部可以表征利兹线中储存的磁场能量随频率的变化,而虚部与利兹线的邻近效应相关。当利兹线的填充系数为0.554,股线直径为0.1 mm时,相对复数磁导率的实部和虚部随频率变化的趋势如图5所示。随着频率的增加,利兹线中的磁场能量逐渐衰减,而邻近效应相关部分逐渐增加。
的实部可以表征利兹线中储存的磁场能量随频率的变化,而虚部与利兹线的邻近效应相关。当利兹线的填充系数为0.554,股线直径为0.1 mm时,相对复数磁导率的实部和虚部随频率变化的趋势如图5所示。随着频率的增加,利兹线中的磁场能量逐渐衰减,而邻近效应相关部分逐渐增加。
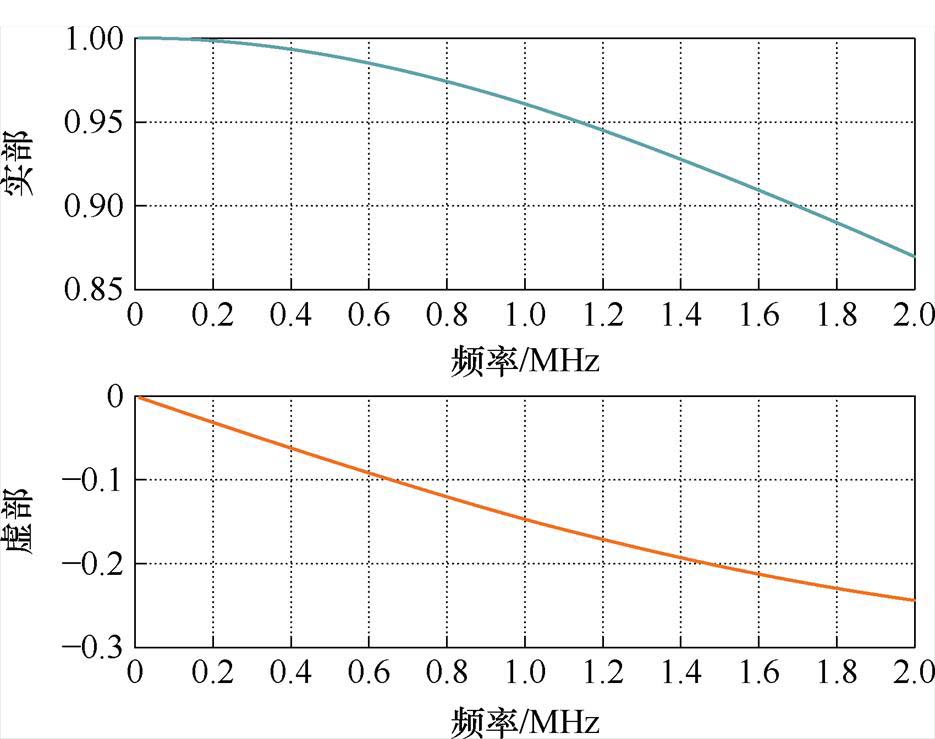
图5 相对复数磁导率随频率的变化趋势
Fig.5 Trend of relative complex permeability with frequency
为了分析高频效应对利兹线绕组中磁场能量的影响,建立了高频变压器磁心窗口的二维有限元仿真模型,如图6所示。其中,利兹线模型是由60根直径为0.2 mm的股线组成,一次和二次绕组均为两层,每层5匝。图6a中表明,频率为1 MHz时,利兹线导体内部的磁场能量要明显小于静磁场(0 Hz)时的能量。利用二维有限元模型提取不同频率下的磁心窗口中心线上的磁场强度,如图6b所示。
随着频率的升高,利兹线绕组中产生的涡流效应加剧,导致其内部的磁场强度显著降低。由于磁场能量的大小与磁场强度呈正相关性,因此高频条件下利兹线中磁场分布的趋势与能量分布的趋势相似。随着频率的增加,利兹线绕组中的磁场能量逐渐衰减,这与图5中相对复数磁导率实部描述的磁场能量频变特性相符。

图6 频率对利兹线中能量及磁场的影响
Fig.6 Effect of frequency on energy and magnetic fields in the Litz wire
基于上述分析,可以将高频变压器的磁心窗口划分为绕组区域和绝缘区域两部分。在绝缘区域,由于没有电流流通,可认为该区域内的磁场几乎不受高频效应的影响,磁场能量保持恒定,而绕组区域磁场能量的频变特性可以用相对复数磁导率的实部表征。因此,变压器磁心窗口中与频率相关的总磁场能量可以表示为
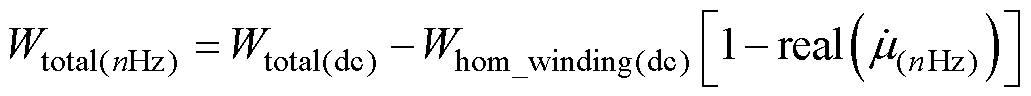 (9)
(9)
式中,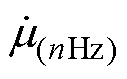 为任意频率下的相对复数磁导率;Wtotal(nHz)为变压器磁心窗口中任意频率下的总磁场能量;Wtotal(dc)为磁心窗口中静磁场下的总磁场能量;Whom_winding(dc)为静磁场下均匀化利兹线绕组中的磁场能量。下面只需要在静磁场下分别计算出变压器磁心窗口中的总磁场能量Wtotal(dc)和均匀化利兹线绕组中的磁场能量Whom_winding(dc),便可计算出高频变压器的总漏感值。
为任意频率下的相对复数磁导率;Wtotal(nHz)为变压器磁心窗口中任意频率下的总磁场能量;Wtotal(dc)为磁心窗口中静磁场下的总磁场能量;Whom_winding(dc)为静磁场下均匀化利兹线绕组中的磁场能量。下面只需要在静磁场下分别计算出变压器磁心窗口中的总磁场能量Wtotal(dc)和均匀化利兹线绕组中的磁场能量Whom_winding(dc),便可计算出高频变压器的总漏感值。
本文在解决当前漏感预测局限性的同时,力求所提出的漏感模型能够适用于高频变压器的优化设计环节。与有限元法相比,镜像法可以在Matlab中实现所有的计算处理,包括绕组不同位置的磁场提取及利兹线扭转结构表征,省去了有限元法针对不同结构变压器的复杂建模过程,并且更容易集成到高频变压器的优化程序中。因此,采用镜像法计算磁心窗口中不同区域的磁场能量。
镜像法作为一种求解边值问题的间接方法,其实质是在所求场域外引入假想的镜像导体,用镜像电流等效替代介质表面的磁化电流。对于变压器而言,磁心窗口内任意位置的磁场都是由原导体产生的原磁场与镜像导体产生的镜像磁场的叠加。镜像法中原导体和镜像导体的排布如图7所示。
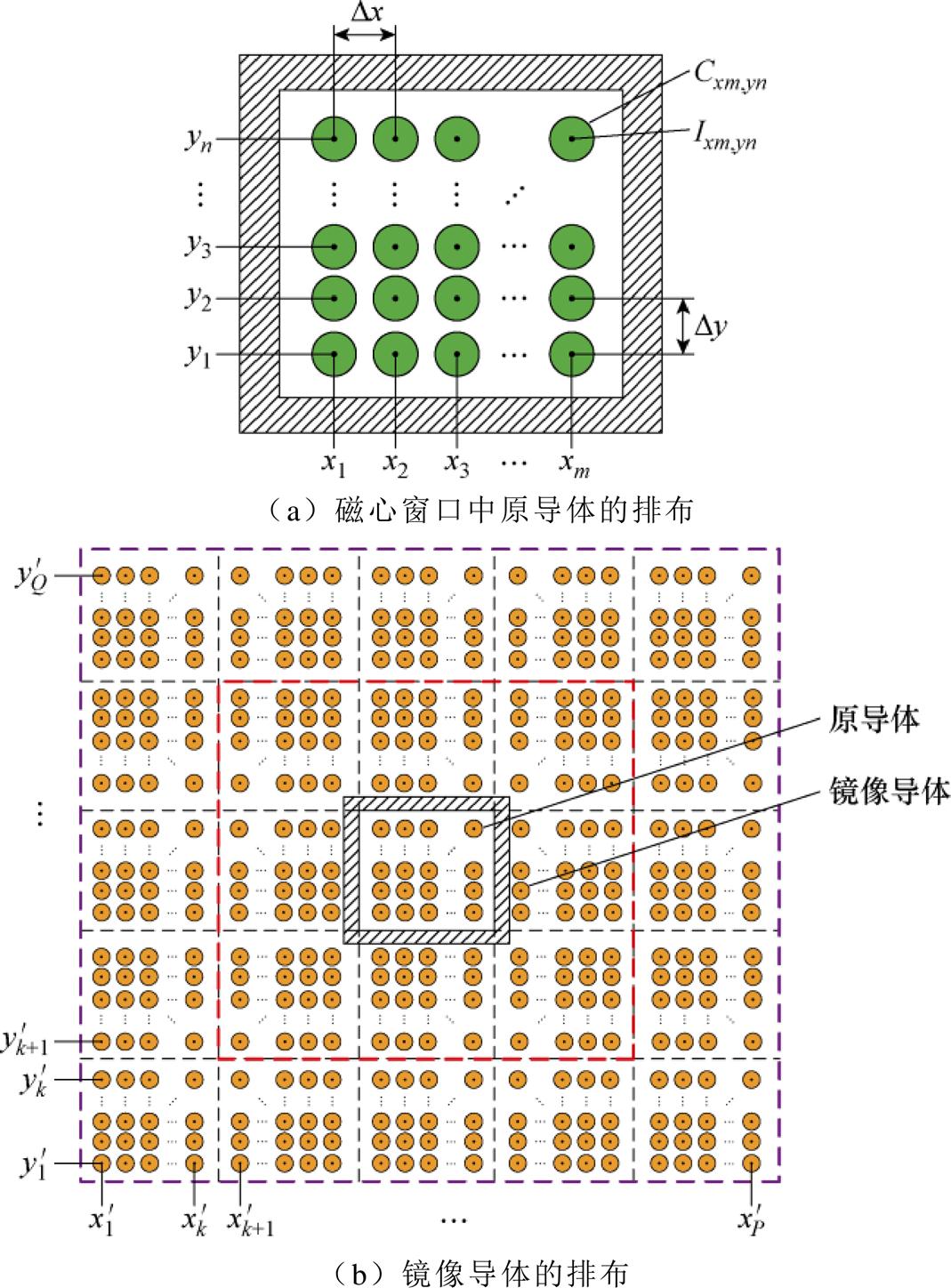
图7 镜像法中原导体和镜像导体的排布
Fig.7 Arrangement of the original and mirror conductors in the method of images
对于图7所示的四边界问题,在计算镜像导体产生的磁场时,需要将镜像导体中的电流乘以对应的权重因子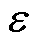 ,有
,有
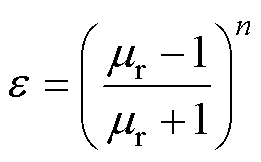 (10)
(10)
式中,mr为磁心的相对磁导率;n为被乘以权重因子的镜像导体所在的镜像层数,红色虚线区域镜像导体所在的镜像层数n=1,紫色与红色虚线之间导体所在的镜像层数n=2。在图7a所示的绕组排布中,磁心窗口内任意位置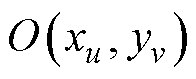 的原磁场是来自于磁心窗口内所有导体
的原磁场是来自于磁心窗口内所有导体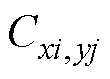 中流过电流
中流过电流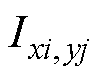 叠加作用的结果,原磁场x和y方向的分量分别为
叠加作用的结果,原磁场x和y方向的分量分别为
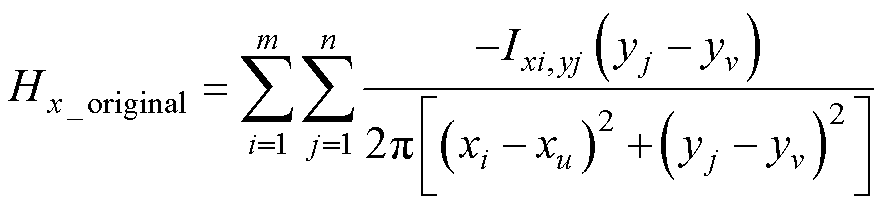 (11)
(11)
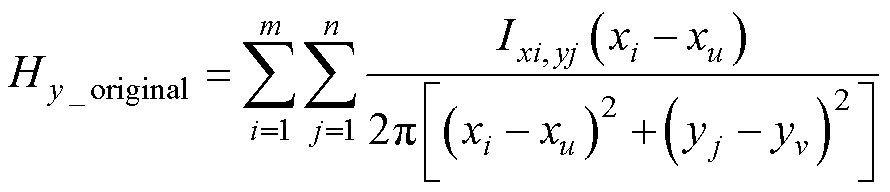 (12)
(12)
式中,n和m分别为图7a中对应原导体的总行数和总列数;xi和yj为第i行、第j列原导体中心的坐标值;xu和yv为磁心窗口中任意位置坐标值。
如图7b所示的镜像导体排布中,磁心窗口中任意位置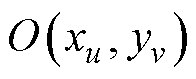 的镜像磁场是来自于磁心窗口外镜像导体
的镜像磁场是来自于磁心窗口外镜像导体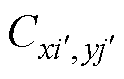 中流过电流
中流过电流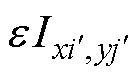 叠加作用的结果,镜像磁场x和y方向的分量分别为
叠加作用的结果,镜像磁场x和y方向的分量分别为
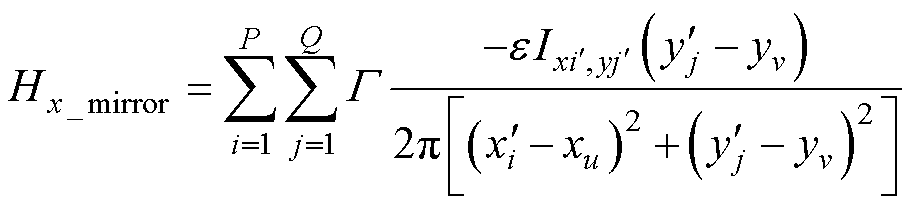 (13)
(13)
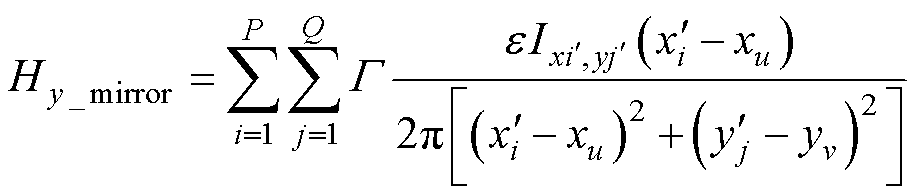 (14)
(14)
其中
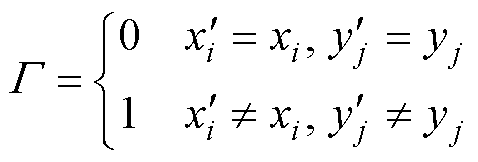 (15)
(15)
式中,P和Q分别为镜像导体的总行数和总列数;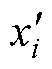 和
和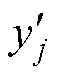 为镜像导体中心的坐标值。
为镜像导体中心的坐标值。
基于式(11)~式(14),可以得到磁心窗口中任意位置的磁场强度为
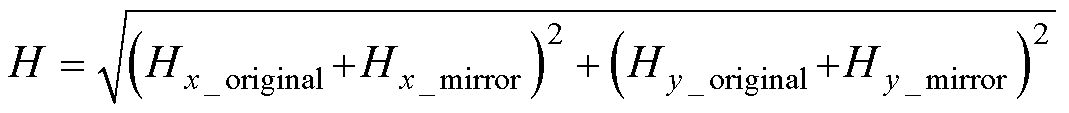 (16)
(16)
为了验证磁场计算的准确性,利用镜像法和二维有限元法分别计算一个带有14匝绕组的变压器模型,对比结果如图8所示。两种方法得到的窗口区域磁场分布基本一致,且在绕组末端都存在显著的二维磁场分布(端部效应)。为了进一步验证镜像法的准确性,分别用两种方法提取导体相同位置(导体中心)的磁场强度值。相同点位磁场值对比如图9所示。从图9中可以看出,两种方法计算相同位置磁场强度的结果几乎完全一致,证明了该方法分析二维静磁场的可行性。

图8 两种不同方法的磁场分布对比
Fig.8 Comparison of magnetic field distribution of two different methods
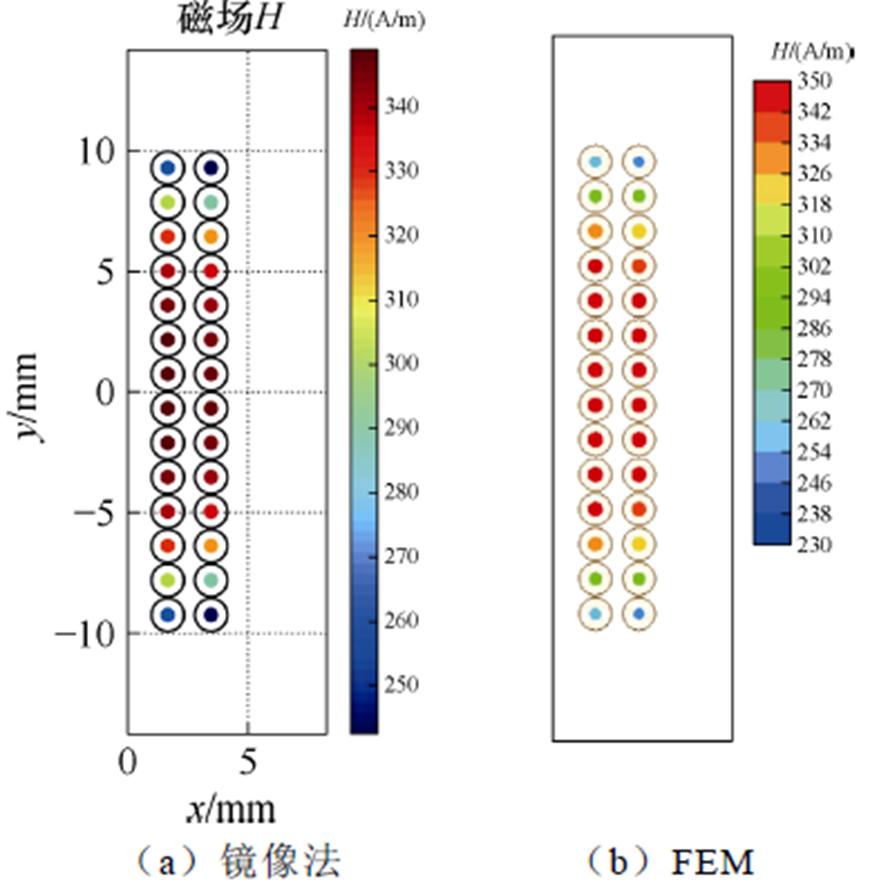
图9 相同点位磁场值对比
Fig.9 Comparison of magnetic field at the same locations
在计算磁心窗口的总磁场能量之前,需要先求出窗口内导体之间的电感矩阵。值得注意,这里的电感指的是在恒定磁场中,基于磁链与电流的比值定义的静态电感[23]。假设一个无限长直线电流带有沿z轴流动的电流Ic,则距离该长直线电流为r的任意一点的矢量磁位可以表示为
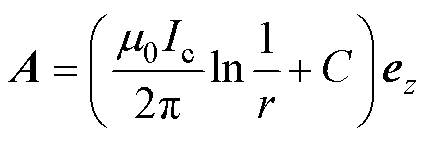 (17)
(17)
式中,ez为z轴的正向单位矢量;m0为真空磁导率;C为一个与矢量磁位参考点有关的常数,对于一个净电流为零的多导体系统,C=0[24]。磁心窗口中所有导体组成的矢量磁位矩阵为
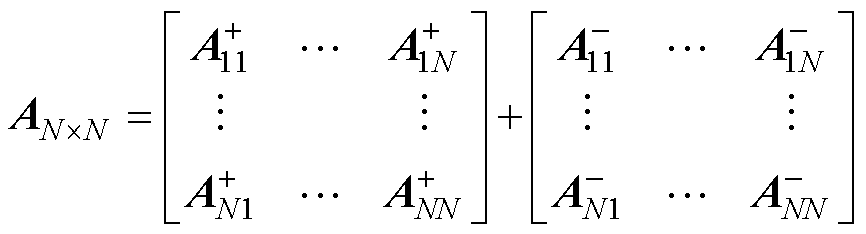 (18)
(18)
式中,N为磁心窗口中所有导体的数目;A+为磁心窗口内原导体之间的矢量磁位;A-为所有镜像导体对原导体的贡献之和;Aij为导体i在导体j处产生的矢量磁位。矢量磁位矩阵AN×N中的每个元素Aij可以根据能量法计算出其相应的互感为
 (19)
(19)
式中,rij为导体i与导体j圆心之间的距离;Sj和Jj分别为导体j的面积和电流密度;Ii和Ij分别为导体i和导体j中的电流。自感为
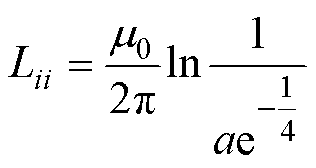 (20)
(20)
式中,e为自然对数。综上,电感矩阵可以表示为
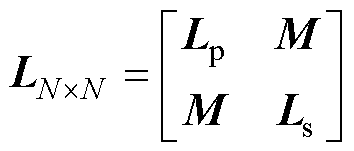 (21)
(21)
式中,Lp和Ls分别为一、二次侧导体的自感矩阵;M为一、二次侧导体间的互感矩阵。最终,磁心窗口中的总磁场能量可以表示为
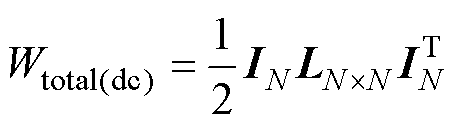 (22)
(22)
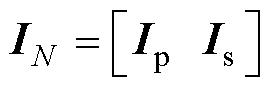 (23)
(23)
式中,Ip和Is分别为一次和二次绕组中电流值组成的行向量;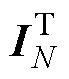 为向量IN的转置。
为向量IN的转置。
为了验证其有效性,采用该方法和二维有限元法分别提取了一、二次侧均为15匝绕组变压器模型的电感矩阵,如图10所示,两种方法提取的电感矩阵分布基本一致且对应元素的数值差异较小。

图10 不同方法计算的电感矩阵对比
Fig.10 Comparison of inductance matrices calculated by different methods
利兹线中的总磁场是由内部磁场和外部磁场叠加而成。由于均匀化模型是以股线之间相互平行为前提,因此并没有考虑其扭转结构对外部磁场的影响。受物体相对运动的启发,本文提出坐标变换法分析利兹线的扭转特性,将外部磁场的扭转代替利兹线自身的扭转,如图11所示。坐标变换之前,需要对均匀化的利兹线导体进行离散化处理,一方面是为了在导体不同区域实现坐标变换;另一方面是为了方便后续磁场强度的积分处理。
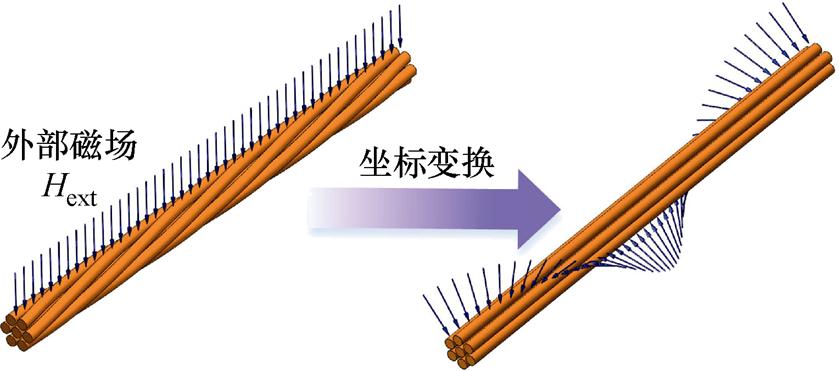
图11 外部磁场的坐标变换法
Fig.11 Coordinate transformation method for external magnetic fields
首先,利用镜像法提取各节点的磁场强度及其x和y方向的磁场分量。然后计算均匀化利兹线任意节点的内部磁场强度,有
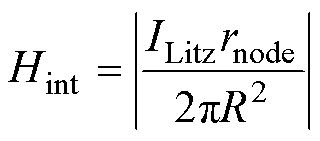 (24)
(24)
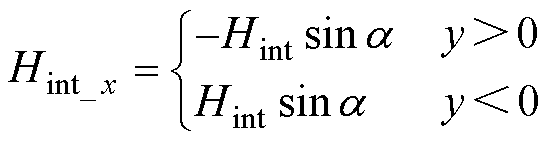 (25)
(25)
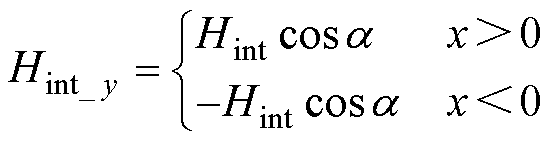 (26)
(26)
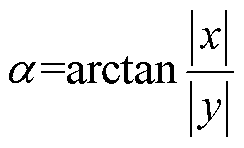 (27)
(27)
式中,x和y分别为节点在局部坐标系中的横坐标值与纵坐标值;a 为节点处磁场与横坐标轴的夹角;ILitz为流过利兹线导体的电流;rnode为利兹线导体中心到任意节点的距离;R为利兹线的半径。导体中任意节点的外部磁场x和y方向的分量为
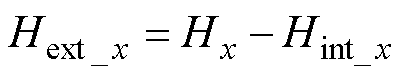 (28)
(28)
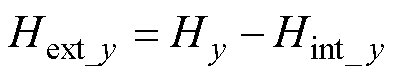 (29)
(29)
式中,Hx和Hy可由式(10)~式(15)计算得到。导体边缘的节点实施坐标变换后,外部磁场分量的表达式为
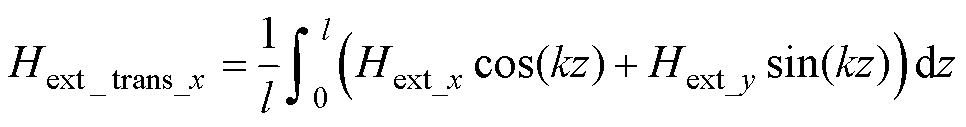 (30)
(30)
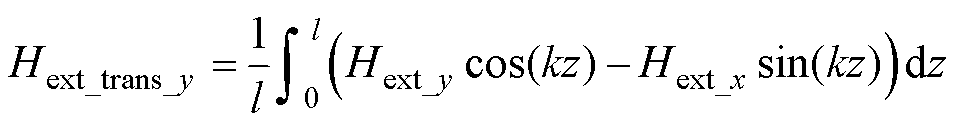 (31)
(31)
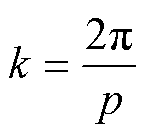 (32)
(32)
式中,p为利兹线的扭转节距;l为利兹线的长度。根据式(25)、式(26)、式(30)和式(31)可以计算出导体边缘节点的磁场强度,即
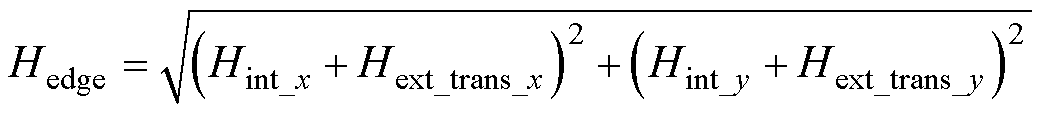 (33)
(33)
图12中描述了坐标变换前(红色箭头)和坐标变换后(绿色箭头)导体中每个节点磁场强度的大小(箭头长度)和方向(箭头指向)。坐标变换前,导体边缘具有显著的外部磁场分量。坐标变换后,导体边缘的外部磁场几乎被完全抵消,只剩下内部磁场和极少的外部磁场分量。
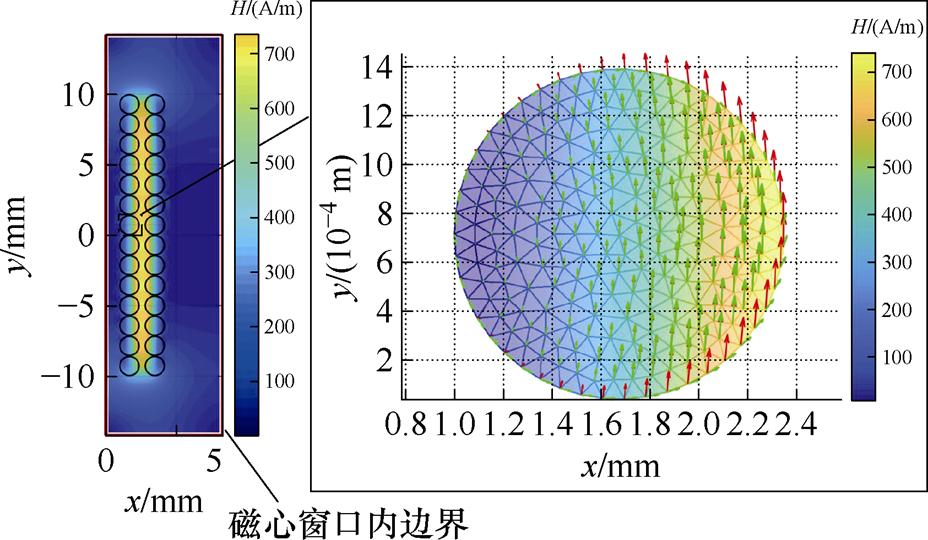
图12 坐标变换前后导体的磁场分布
Fig.12 Magnetic field distribution of the conductor before and after the coordinate transformation
最后,在每个导体的面积上对所有节点的磁场强度进行积分,再将所有导体的积分结果求和,从而得到均匀化利兹线绕组中的磁场能量为
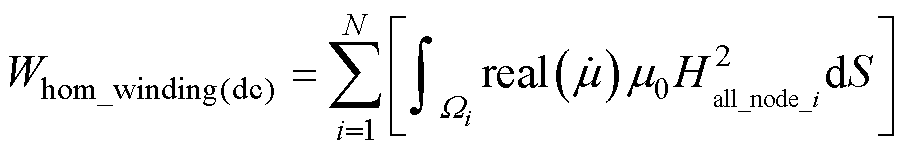 (34)
(34)
式中,Hall_node_i为第i个导体中所有节点的磁场强度;Wi为第i个导体的被积区域。将式(22)和式(34)代入式(9)并结合式(1),即可得到计及利兹线扭转特征和高频效应的变压器漏感表达式为
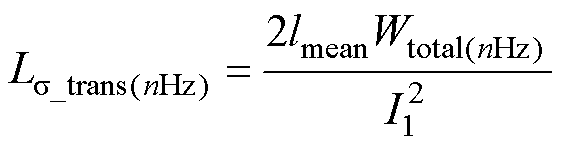 (35)
(35)
式中,lmean为整个绕组区域的平均路径长度。
为了验证所提出高频变压器漏感计算方法的正确性和可靠性,使用两种不同型号的利兹线制作两台高频变压器样机进行实验验证,如图13所示。其中,利兹线绕组的结构参数见表1,高频变压器样机的结构参数见表2。选用Ferroxcube 3F36铁氧体作为两台高频变压器样机的磁心。采用Keysight E4990A高精度阻抗分析仪测量两个变压器的漏感曲线,测量平台如图14所示。

图13 高频变压器样机
Fig.13 High-frequency transformer prototypes
表1 两种不同利兹线的结构参数
Tab.1 Structural parameters of two different Litz wires
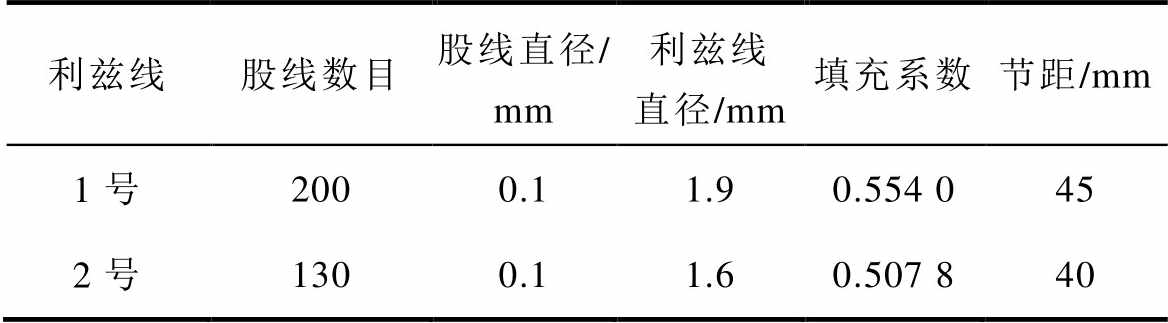
利兹线股线数目股线直径/ mm利兹线直径/mm填充系数节距/mm 1号2000.11.90.554 045 2号1300.11.60.507 840
表2 两个变压器样机的结构参数
Tab.2 Structural parameters of two different transformer prototypes
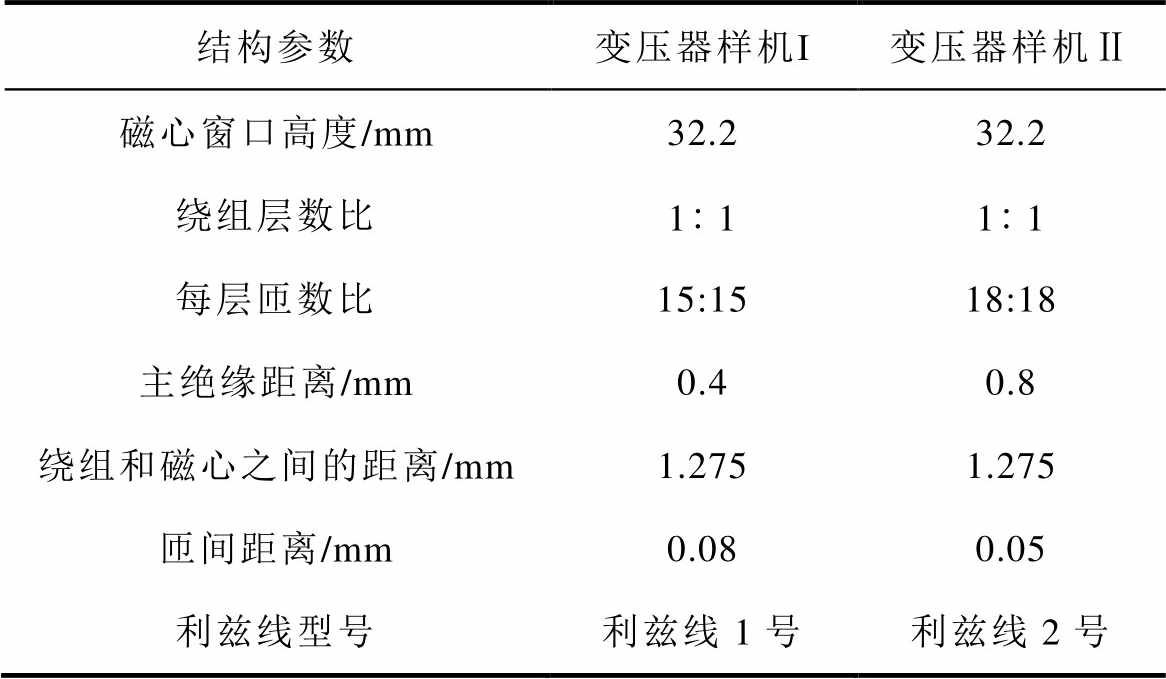
结构参数变压器样机Ⅰ变压器样机Ⅱ 磁心窗口高度/mm32.232.2 绕组层数比1111 每层匝数比15:1518:18 主绝缘距离/mm0.40.8 绕组和磁心之间的距离/mm1.2751.275 匝间距离/mm0.080.05 利兹线型号利兹线1号利兹线2号
此外,将本文提出的漏感计算方法(坐标变换前和坐标变换后)与面积等效法[14]、Zhang Ke等的方法[15]以及样机的测量结果进行比较,所得到的漏感测量曲线如图15、图16所示。通过引入平均无符号偏差(Average Unsigned Deviation, AUD)和最大无符号偏差(maximum Unsigned Deviation, UDmax)两个因子来评估不同方法在整个频率范围内的计算精度,其表达式为

图14 变压器漏感测量平台
Fig.14 Measurement platform for the leakage inductance of the transformer
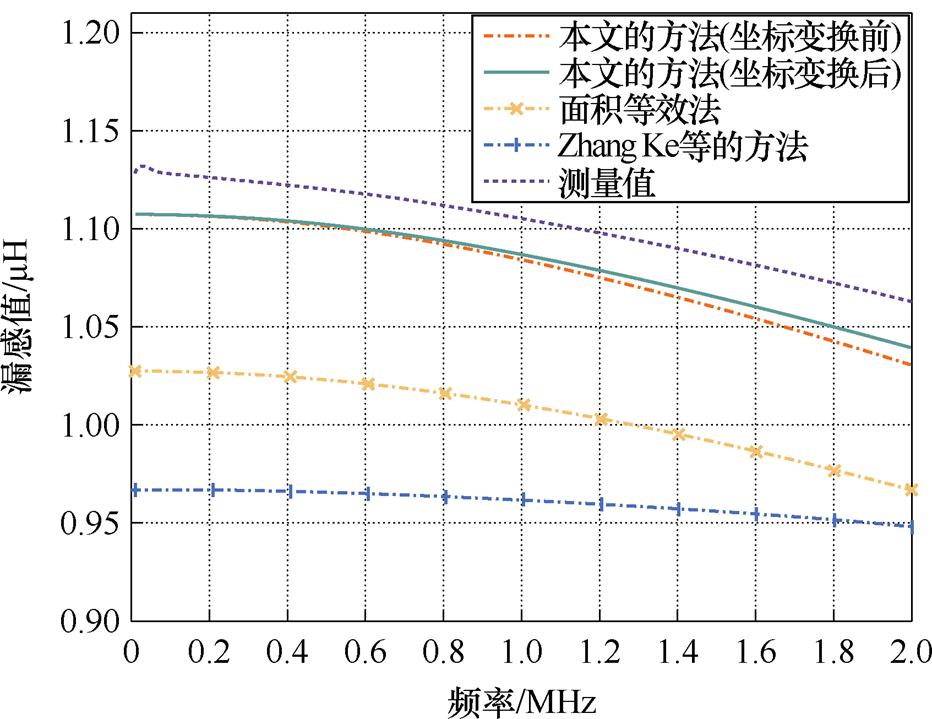
图15 变压器样机Ⅰ(15匝)漏感测量结果与计算结果对比
Fig.15 Comparison of measurement results and calculation results of leakage inductance for transformer prototype Ⅰ (15)

图16 变压器样机Ⅱ(18匝)漏感测量结果与计算结果对比
Fig.16 Comparison of measurement results and calculation results of leakage inductance for transformer prototype Ⅱ (18)
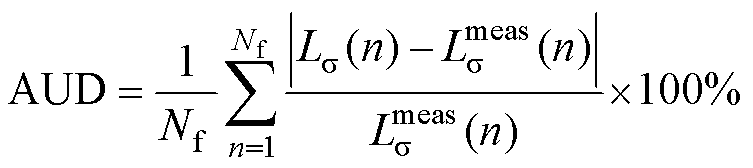 (36)
(36)
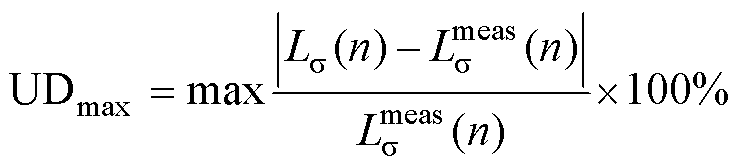 (37)
(37)
式中,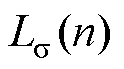 和
和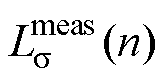 分别为在第n个频率点漏感的计算值和测量值;Nf为测量频率点的数目。不同计算方法的评估结果见表3。
分别为在第n个频率点漏感的计算值和测量值;Nf为测量频率点的数目。不同计算方法的评估结果见表3。
表3 不同方法的计算偏差
Tab.3 Calculation deviations of different methods (%)
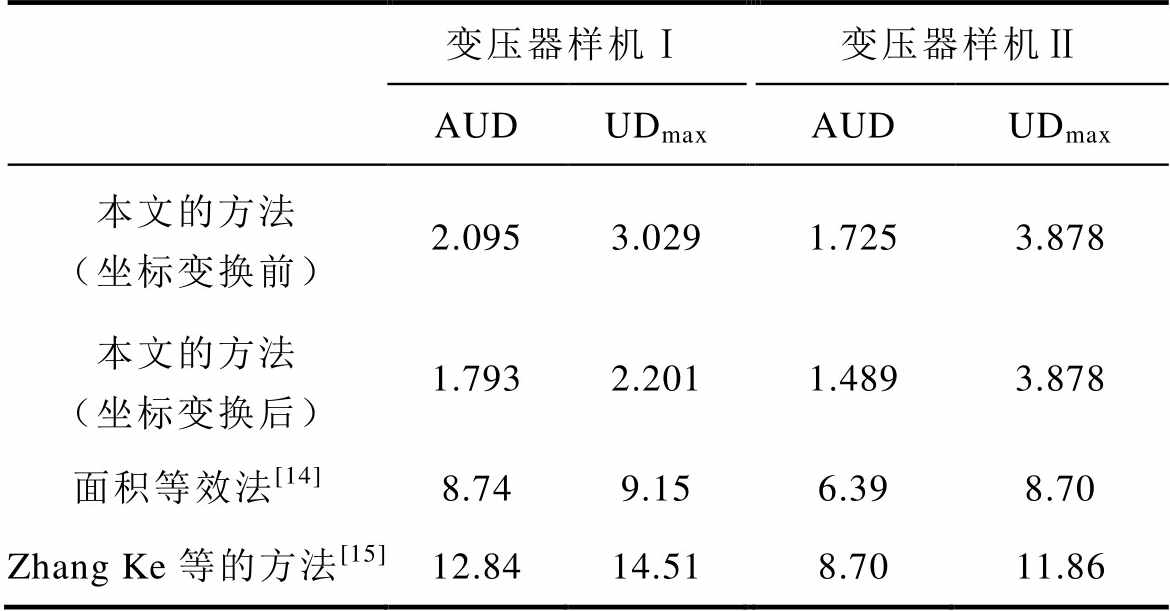
变压器样机Ⅰ变压器样机Ⅱ AUDUDmaxAUDUDmax 本文的方法(坐标变换前)2.0953.0291.7253.878 本文的方法(坐标变换后)1.7932.2011.4893.878 面积等效法[14]8.749.156.398.70 Zhang Ke等的方法[15]12.8414.518.7011.86
变压器样机Ⅰ、样机Ⅱ的测量和计算结果表明,随着频率的升高,高频变压器的漏感呈减小的趋势。这主要归因于高频条件下利兹线绕组中显著的趋肤效应和邻近效应导致绕组中磁场能量的衰减。从图15中可知,本文提出的方法、面积等效法和Zhang Ke等的方法都能够反映出漏感随频率衰减的变化趋势,但是本文所提出的方法与测量曲线吻合度更高,在考虑利兹线扭转结构后(坐标变换后)计算结果的趋势几乎与测量曲线一致。由于利兹线的扭转结构能够抵消一部分外部磁场,导致坐标变换后绕组内部储存的磁场能量要小于坐标变换前储存的能量,因此在同一频率下衰减的磁场能量更少。频率在1~2 MHz范围时,利兹线绕组中的邻近效应占主导,随着频率的增加邻近效应的作用更加明显,利兹线的扭转结构在有效抵消一部分邻近损耗的同时,能够抑制绕组中磁场能量的衰减。从图16中也可以得到相似的结论。
面积等效法将利兹线绕组等效为铜箔绕组后,基于一维磁场假设求解漏感参数,并且没有考虑利兹线填充因子的影响。尽管该方法存在一定的计算误差,但10%以内的计算偏差尚可接受。Zhang Ke等的方法在计算外部磁场时,同样认为外部磁场沿一维分布,并且忽略了绕组周围不规则区域的磁场能量,这也是造成漏感值被低估的主要原因。本文提出的方法基于镜像原理,准确表征磁心窗口区域的二维磁场分布,在考虑漏感高频效应的同时分析了利兹线扭转结构对漏感的影响。变压器样机Ⅰ的平均无符号偏差仅为1.793%,计算时间仅为16.693 s;变压器样机Ⅱ的平均无符号偏差仅为1.489%,计算时间仅为20.136 s。两台样机计算结果的最大无符号偏差均未超过4%,计算精度优于上述两种现有方法,计算时间完全满足高频变压器优化设计的高效性要求。
高频变压器的漏感是影响电力电子变换器传输特性及可靠运行的一个重要参数,对于变换器的设计具有重要的意义。本文针对利兹线绕组的高频变压器漏感预测方法开展研究,得到以下结论:
1)为了避免利兹线绕组的复杂建模以及减少漏感参数的计算时间,通过引入相对复数磁导率建立计及利兹线绞合结构的均匀化等效模型。分析了利兹线中磁场能量随频率的变化规律,随着频率的增加,利兹线中储存的磁场能量逐渐减少。
2)基于镜像原理提取磁心窗口区域的磁场能量,解决了现有方法依赖一维磁场假设,难以准确考虑绕组端部效应的局限性;将网格化处理引入镜像法中,提出坐标变换方法对利兹线的扭转结构进行表征,利兹线的扭转结构在一定程度上能够抵消一部分外部磁场,减少导体中储存的磁场能量。
3)设计并制作了两台不同结构的高频变压器样机,将测量结果与本文的方法、现有的两种漏感计算方法进行对比分析。结果表明,本文提出的方法在整个测量频率范围内的平均偏差仅为1.793%和1.489%,计算时间仅为16.693 s和20.136 s,实现了高频利兹线变压器漏感的精确和高效预测。
参考文献
[1] 陈润田, 李楚杉, 姚文熙, 等. 基于等效励磁电感的SiC串联器件型中压双有源桥变换器的软开关技术[J]. 电工技术学报, 2024, 39(12): 3732-3745.
Chen Runtian, Li Chushan, Yao Wenxi, et al. Soft- switching technique for medium voltage dual active bridge converter with series-connected SiC devices based on equivalent magnetizing inductance[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3732-3745.
[2] 胡钰杰, 李子欣, 罗龙, 等. 串联谐振间接矩阵型电力电子变压器高频电流特性分析及开关频率设计[J]. 电工技术学报, 2022, 37(6): 1442-1454.
Hu Yujie, Li Zixin, Luo Long, et al. Characteristic analysis of high-frequency-link current of series resonant indirect matrix type power electronics transformer and switching frequency design[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1442-1454.
[3] 蔡瑶, 卢志刚, 潘尧, 等. 计及多重差异的交直流混合多能微网多时间尺度优化调度[J]. 电工技术学报, 2024, 39(11): 3392-3410.
Cai Yao, Lu Zhigang, Pan Yao, et al. Multi-time-scale optimal scheduling of AC-DC hybrid multi-energy microgrid considering multiple differences[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3392-3410.
[4] 赵志刚, 白若南, 陈天缘, 等. 基于智能优化算法的高频变压器电磁结构优化设计[J]. 电工技术学报, 2024, 39(17): 5610-5625.
Zhao Zhigang, Bai Ruonan, Chen Tianyuan et al. Optimization design of electromagnetic structure of high frequency transformer based on intelligent optimization algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5610-5625.
[5] 汪涛, 骆仁松, 文继峰, 等. 基于辅助绕组的高频变压器绕组损耗测量方法[J]. 电工技术学报, 2022, 37(10): 2622-2630, 2655.
Wang Tao, Luo Rensong, Wen Jifeng, et al. A measurement method of winding loss for high- frequency transformer based on auxiliary winding[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2622-2630, 2655.
[6] Yin Hao, Lai Jidong, Ren Sheng, et al. An accurate calculation method of leakage inductance of high- frequency transformer with Litz wire winding considering irregular region[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(6): 7441-7451.
[7] Dowell P L. Effects of eddy currents in transformer windings[J]. Proceedings of the Institution of Electrical Engineers, 1966, 113(8): 1387.
[8] 律方成, 郭云翔, 李鹏. 大功率中频变压器漏感计算及其校正方法[J]. 高电压技术, 2016, 42(6): 1702- 1707.
Lü Fangcheng, Guo Yunxiang, Li Peng. Calculation and correction method for leakage inductance of high-power medium-frequency transformer[J]. High Voltage Engineering, 2016, 42(6): 1702-1707.
[9] 尹浩, 苏建徽, 赖纪东, 等. 中频圆导线变压器漏感的精确解析计算[J]. 电工技术学报, 2021, 36(15): 3211-3220.
Yin Hao, Su Jianhui, Lai Jidong, et al. Accurate analytical calculation of leakage inductance of round conductor transformer under the medium frequency[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3211-3220.
[10] Chen Bin. Analysis of effect of winding interleaving on leakage inductance and winding loss of high frequency transformers[J]. Journal of Electrical Engineering & Technology, 2019, 14(3): 1211- 1221.
[11] Wu Y H, Shigematsu K, Omoto Y, et al. An investigation and proposal for accurate leakage inductance modeling based on dowell model[C]//2022 International Power Electronics Conference (IPEC- Himeji 2022-ECCE Asia), Himeji, Japan, 2022: 1964- 1969.
[12] Ouyang Ziwei, Zhang Jun, Hurley W G. Calculation of leakage inductance for high-frequency trans- formers[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5769-5775.
[13] Bahmani M A, Thiringer T. Accurate evaluation of leakage inductance in high-frequency transformers using an improved frequency-dependent expression[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5738-5745.
[14] Mogorovic M, Dujic D. Medium frequency trans- former leakage inductance modeling and experimental verification[C]//2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 2017: 419-424.
[15] Zhang Ke, Chen Wu, Cao Xiaopeng, et al. Accurate calculation and sensitivity analysis of leakage inductance of high-frequency transformer with Litz wire winding[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 3951-3962.
[16] Tourkhani F, Viarouge P. Accurate analytical model of winding losses in round Litz wire windings[J]. IEEE Transactions on Magnetics, 2001, 37(1): 538- 543.
[17] 刘星亮, 邱祁, 王若宇, 等. 基于有限元仿真的高频高压变压器分段绕组漏感设计方法[J]. 高电压技术, 2020, 46(2): 610-617.
Liu Xingliang, Qiu Qi, Wang Ruoyu, et al. Design method for leakage inductance of high-frequency high-voltage transformer with winding segmented based on finite element simulation[J]. High Voltage Engineering, 2020, 46(2): 610-617.
[18] Li Xinyang, Huang Weican, Cui Bin, et al. Inductance characteristics of the high-frequency transformer in dual active bridge converters[C]//2019 22nd Inter- national Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-5.
[19] Shen Zhan, Wang Huai. Parasitics of orthocyclic windings in inductors and transformers[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 1994-2008.
[20] Hoke A F, Sullivan C R. An improved two- dimensional numerical modeling method for E-core transformers[C]//Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 2002: 151-157.
[21] Igarashi H. Semi-analytical approach for finite-element analysis of multi-turn coil considering skin and proximity effects[J]. IEEE Transactions on Magnetics, 2017, 53(1): 7400107.
[22] Ollendorff F. Magnetostatik der massekerne[J]. Archiv Für Elektrotechnik, 1931, 25(6): 436-447.
[23] 张惠娟, 杨文荣, 李玲玲. 工程电磁场与电磁波基础[M]. 北京: 机械工程出版社, 2010.
[24] Eslamian M, Vahidi B. New methods for computation of the inductance matrix of transformer windings for very fast transients studies[J]. IEEE Transactions on Power Delivery, 2012, 27(4): 2326-2333.
Abstract As an important parameter in power electronic converters, the leakage inductance of high-frequency transformers is of great significance in improving the operating mode and power transmission characteristics of isolated DC-DC converters. Compared with the solid round wire, the Litz wire can reduce eddy current losses in high-frequency magnetic components. However, the complicated structure of the Litz-wire windings poses a serious challenge to predicting leakage inductance in high-frequency transformers. On the one hand, it is difficult to precisely extract the magnetic field energy in various regions of the core window. On the other hand, it is hard to accurately characterize the multi-stranded and twisting structures of the Litz wires. Therefore, this paper presents a fast calculation method of leakage inductance in the high-frequency transformer with Litz-wire winding.
Firstly, a homogenized equivalent process for Litz wire is proposed to enhance the flexibility of modeling and the efficiency of computation. The magnetic field energy variation with frequency inside the Litz-wire conductors are analyzed. Then, the 2-D magnetic field energy inside the core window is extracted based on the method of images to eliminate the impact of the edge effect. The internal and external magnetic fields at different locations in the winding are accurately characterized by introducing the meshing into the method of images, and a coordinate transformation method is proposed to consider the twisting structure of the Litz wires. Finally, two high-frequency transformer prototypes with different structures are designed and fabricated. Compared with the measurement results and two existing methods, the accuracy and efficiency of the proposed approach are verified.
The following conclusions can be drawn. (1) A homogenized equivalent model of the Litz-wire twisting structure is developed by introducing the relative complex permeability, which simplifies the model building and reduces the computational cost. The variation of the magnetic field energy in the Litz wires with frequency is analyzed, and the magnetic field energy stored in the Litz wires gradually decreases with the frequency increase. (2) The meshing process is introduced into the method of images, and the coordinate transformation method is proposed to characterize the twisting structure of the Litz wire. It can counteract a part of the external magnetic field and reduce the magnetic field energy in the conductors. (3) Considering the twisting characteristics of the Litz wire and the high-frequency effect, a leakage inductance prediction model is developed based on the magnetic field energy variation with frequency. (4) The accuracy and efficiency of the proposed method are verified compared with the measurement and the current two analytical methods. The maximum error does not exceed 4% throughout the measurement frequency range, and the calculation time is about 20 seconds. Moreover, the proposed method can be effectively applied to fast iterative calculations in the optimal design of high-frequency transformers.
Keywords:High-frequency transformer, leakage inductance, the method of images, Litz-wire windings, frequency-dependent characteristic
中图分类号:TM433
DOI: 10.19595/j.cnki.1000-6753.tces.240527
国家自然科学基金项目(52077053, 52377008)和中央引导地方科技发展基金项目(226Z1601G)资助。
收稿日期 2024-04-02
改稿日期 2024-05-08
陈天缘 男,1992年生,博士研究生,研究方向为高频磁性元件的优化设计、工程电磁场数值仿真及应用。
E-mail: 202011401005@stu.hebut.edu.cn
赵志刚 男,1981年生,教授,博士生导师,研究方向为电工磁材料磁性能模拟与工程电磁场数值仿真及应用。
E-mail: zhaozhigang@hebut.edu.cn(通信作者)
(编辑 崔文静)