为拉普拉斯算子，
、
、
分别为火电机组出力、电池储能系统出力、负荷扰动，
、
分别为火电机组再热汽轮机、调速器传递函数，
为储能电池的传递函数，
为火电机组出力系数，M为电网惯性系数，D为系统阻尼系数，
为电网频率偏差。摘要 由于传统的电池储能系统控制策略抑制电网频率恶化效果较差，进而限制了电池储能系统参与一次调频时的性能。因此，该文提出基于电池储能系统的综合自适应一次调频策略。首先，为了减少电网频率偏差，将趋势控制策略和惯性与下垂控制策略相结合，抑制电网频率恶化；其次，自适应控制储能系统出力系数，趋势系数随着电网频率加速度自适应变化，惯性系数随着电网频率变化率自适应变化，下垂系数随着电网频率偏差自适应变化，提高储能系统的自适应能力；再次，为了防止储能电池过充过放，提高荷电状态（SOC）估算精度，提出多元自适应估算SOC方法，减少SOC估算误差；最后，通过仿真实验验证了所提控制策略的有效性。该研究成果可为储能系统参与一次调频方面的研究提供有益参考。
关键词：一次调频 惯性与下垂控制策略 趋势控制策略 自适应 荷电状态（SOC）估算
在“碳达峰、碳中和”背景下，可再生能源接入电网的比例不断增加，导致新型电力系统的惯性较低[1-5]。随着“十四五”新型储能发展实施方案的发布，储能系统参与一次调频得到全面发展。由于储能电池具有快速性、灵活性等特点，电网的稳定性得到了提高[6-11]。
基于荷电状态（State of Charge, SOC）的惯性与下垂控制策略可以防止储能电池过充过放，储能电池工作在最佳状态有助于发挥储能系统参与一次调频时的更高性能。文献[12]使用惯性与下垂相互切换方法参与一次调频，抑制电网频率恶化。文献[13]提出考虑SOC的变K法惯性与下垂综合控制策略，该方法防止了储能电池过充过放。文献[14]将惯性与下垂系数呈现logistic曲线变化，平滑储能电池出力，并且有较好的调频效果。文献[15]在电网频率恶化阶段使用惯性与下垂控制，在电网频率恢复阶段使用下垂控制，防止了惯性阻碍频率恢复。文献[16]在文献[15]基础上提出了负惯性控制策略，负惯性使电网频率恢复更快。文献[17-18]通过模糊控制方法确定惯性与下垂系数，模糊控制可以考虑多种条件对储能电池出力进行控制，但是该方法具有较强的主观性。以上文献没有考虑SOC估算精度，储能电池存在过充过放的风险。
目前，电池SOC估算方法有安时积分法[19]、开路电压法[20]、内阻法[21]、神经网络法[22]及卡尔曼滤波法[23]。安时积分法随着外界条件的变化，估算误差越来越大；开路电压法需要将储能电池静置测量；内阻法不适用于SOC实时估算；神经网络法需要大量的数据进行训练；卡尔曼滤波法只需要进行公式迭代，并进行修正，估算误差较小。文献[24]在卡尔曼滤波的基础上利用Preisach模型滤除电流与端电压噪声；文献[25]采样PID进行SOC估算补偿；文献[26]利用监督式学习算法对数据进行处理，但是没有考虑卡尔曼滤波迭代初期误差较大的问题。
本文提出基于电池储能系统的自适应一次调频策略。首先，将趋势控制策略和惯性与下垂控制策略相结合，定义了电池储能系统趋势出力与电网频率加速度，并解释了电网频率加速度、频率变化率、频率偏差三者之间的关系；然后，对电池储能系统出力系数进行自适应控制，根据电网频率加速度、电网频率变化率、电网频率偏差自适应确定趋势系数、惯性系数、下垂系数，提高储能系统的自适应能力，进而提高储能系统参与一次调频时的性能；最后，为了防止储能电池过充过放，提高SOC估算精度，提出了多元自适应估算SOC方法，有效地减少了SOC估算误差。在阶跃负荷扰动和连续负荷扰动情况下，通过Simulink仿真模型验证所提控制策略的有效性。
本文储能系统由锂电池组成，并使用综合自适应控制策略参与一次调频，建立相应模型如图1所示[18]。图中为拉普拉斯算子，、、分别为火电机组出力、电池储能系统出力、负荷扰动，、分别为火电机组再热汽轮机、调速器传递函数，为储能电池的传递函数，为火电机组出力系数，M为电网惯性系数，D为系统阻尼系数，为电网频率偏差。
图1 一次调频模型
Fig.1 Primary frequency control model
火电机组调速器传递函数
为
（1）
式中，
为火电机组调速器时间常数。
火电机组再热汽轮机传递函数
为
（2）
式中，
为汽轮机再热器增益；
为再热器时间常数；
为汽轮机时间常数。
储能电池的传递函数
为
（3）
式中，
为储能系统中锂电池响应时间常数。
当该模型出现负荷波动时，储能系统配合火电机组参与一次调频，根据电池储能系统响应速度快的特点，可以有效地降低电网频率偏差。
目前，储能系统参与一次调频普遍使用惯性与下垂控制策略，电网频率变化率与惯性出力有关，惯性出力越大，电网频率变化率越小；惯性出力越小，则相反。因此，惯性控制可以抑制电网频率变化率。电网频率偏差与下垂出力有关，下垂出力越大，电网频率偏差越小；相反，下垂出力越小，则电网频率偏差越大，下垂控制可以减小电网频率偏差。为了提高储能系统参与一次调频时的性能，本文在惯性与下垂控制策略基础上增加补偿项，提出了下垂、惯性、趋势相结合的控制策略，即
（4）
式中，
、
分别为电池储能系统惯性、下垂系数；
为频率变化率；
为补偿项。
本文将补偿项命名为电池储能系统趋势出力。当电网频率下降（上升）时，趋势控制策略使储能电池放电（充电），进而抑制电网频率恶化，其表达式为
（5）
式中，
为趋势系数；
为频率加速度。
该控制策略是在惯性与下垂的基础上增加了一项与电网频率变化率有关的有功功率值，电网频率变化率的变化速度（又称频率加速度）影响着储能系统趋势出力。频率加速度越大，趋势出力越大；相反，频率加速度越小，则趋势出力越小。电网频率加速度、频率变化率、频率偏差之间的关系如图2所示，电网频率偏差的斜率为电网频率变化率，电网频率变化率的斜率为电网频率加速度。
根据图2所示，
阶段为正惯性阶段，电网频率变化率与频率偏差均为负，所以惯性系数与下垂系数同号；
和
阶段为负惯性阶段，为了防止惯性出力抑制电网频率恢复，惯性系数与下垂系数应为异号；和阶段为负趋势阶段，频率加速度与频率偏差互为异号，为了防止电池储能系统趋势出力加大频率偏差，趋势系数与下垂系数应为异号；阶段为正趋势阶段，频率加速度与频率偏差均为负，所以趋势系数与下垂系数符号相同。
图2 频率偏差、频率变化率、频率加速度的关系
Fig.2 The relation of frequency deviation, frequency change rate and frequency acceleration
许多文献中储能系统出力系数（趋势、惯性、下垂系数）固定不变，只在放电状态下SOC在0.4～0.2之间，或充电状态下SOC在0.6～0.8之间时，呈现S形变化，自适应调节能力较差。因此，本文对电池储能系统出力系数进行自适应控制。
2.2.1 自适应确定趋势系数
趋势系数为
（6）
式中，
为趋势固定系数；
为趋势自适应项；
、
分别为充、放电约束系数。
趋势自适应项为
（7）
式中，
为趋势自适应系数。
趋势出力随着频率加速度自适应变化。趋势出力是由电网频率发生变化开始，到电网频率稳态阶段结束。该过程中趋势控制策略可以减缓电网频率偏差恶化速度，加快电网频率恢复速度，减小电网频率偏差。
2.2.2 自适应确定惯性系数
惯性系数为
（8）
式中，
为惯性固定系数；
为惯性自适应项。
惯性自适应项为
（9）
式中，
为惯性自适应系数。
惯性出力随着频率变化率自适应变化。当电网频率变化率增加时，电网频率将会有较快的恶化速度，惯性系数自适应变大来增加惯性出力，减缓电网频率恶化速度。
2.2.3 自适应确定下垂系数
下垂系数为
（10）
式中，
为下垂固定系数；
为下垂自适应项。
下垂自适应项为
（11）
式中，
为下垂自适应系数。
下垂出力随着频率偏差自适应变化。当电网频率偏差增大时，下垂系数自适应变大来增加下垂出力，减少电网频率偏差，有利于电网的稳定运行。
2.2.4 SOC约束系数
为了防止储能电池过充过放，储能系统出力应根据SOC进行约束。logistic曲线呈现S形变化，具有较强的自适应性，充、放电约束系数通过logistic曲线进行确定，可以平滑储能系统出力。
充、放电约束系数、分别为
（12）
（13）
式中，
为系数初始值；n为函数的变化趋势；
为荷电状态。电池储能系统的充、放电约束系数呈现S形变化，其中n取值不宜过大或过小，n取值过大，S形曲线变化较快；n取值过小，S形曲线变化较慢，自适应性较差。
本文方法提高了储能系统的出力，储能电池的SOC消耗较大。因此，本文对常规的SOC区域划分进行了调整，适当增加了储能电池正常充放电范围，但为了防止储能电池过充过放，减缓储能电池衰老速度，其停止充放电的SOC阈值则不变。区域规划如图3所示，考虑了电网频率调节的紧急程度。在放电状态下，SOC＞0.3时为安全区，安全区内储能系统出力不受SOC约束；0.2≤SOC≤0.3时为警戒区，警戒区内储能系统出力根据SOC呈现S形变化，平滑储能电池出力；SOC＜0.2时为危险区，危险区内储能系统停止出力。在充电状态下，SOC＜0.7为安全区；0.7≤SOC≤0.8时为警戒区；SOC＞0.8为危险区。充电状态下的安全区、警戒区、危险区所执行的功能与放电状态下安全区、警戒区、危险区所执行的功能一致。当电网频率偏差小于储能系统调频死区时，储能系统不动作。电网频率偏差数值超过0.2 Hz时为紧急区，紧急区中储能系统应该以最大功率参与一次调频，优先保证电网频率的恢复。
图3 区域规划
Fig.3 Regional planning
提高SOC估算精度是防止储能电池过充过放的关键。储能电池参与一次调频时，一般使用安时积分法估算SOC，但随着温度和电流的变化，SOC的估算误差逐渐增大，会导致储能电池过充过放，增加储能电池的出力深度，并减少其使用寿命。卡尔曼滤波法通过多次迭代不断修正误差，SOC估算精度较高，但是迭代初期SOC估算精度较低。由于本文提出的趋势控制增加了储能电池SOC的压力，储能电池会消耗较多的电量，增加了过充过放的风险，将会加快储能电池的老化速度。因此，本文提出了多元自适应估算SOC方法，提高了SOC估算精度，防止储能电池过充过放。
目前，电池等效模型有很多种，其中RC等效模型不仅结构简单，而且能够反映电池的静、动态特性。图4为储能电池等效模型，本文采用二阶RC等效电路模型。图4中
、
、
、
分别为电池开路电压、电化学极化电压、浓度差极化电压、端电压，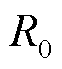
、
、
分别为电池内阻、电化学极化电阻、浓度差极化电阻，
、
分别为电化学极化电容、浓度差极化电容，
为工作电流。
图4 RC等效电路
Fig.4 RC equivalent circuit
端电压为
（14）
工作电流为
（15）
其中，电化学极化电阻与电容、浓度差极化电阻与电容随着温度、电流变化而变化。文献[25]对电化学极化电阻与电容、浓度差极化电阻与电容的数值，以及开路电压与SOC的关系已有研究。
安时积分法估算SOC为
（16）
式中，
为安时积分法估算的SOC；
为SOC初始值；
为电池效率；
为SOC额定值。
由于储能电池的健康状态（State of Health，SOH）的不同，电池电量不能达到额定值，因此，本文利用SOH进行电量修正。
SOH表达式为
（17）
式中，
为电池的SOH；
为SOC最大值。
将SOC额定值与SOH相乘，安时积分法估算的SOC数值更准确，即
（18）
由于卡尔曼滤波法适用于线性系统，SOC估算则是非线性系统，卡尔曼滤波法不适用于估算SOC。无迹卡尔曼滤波法中无损变化可以将非线性系统用于线性体系中，估算SOC结果的准确度更高。
首先，确定状态方程和观测方程为
（19）
（20）
（21）
（22）
式中，
为系统噪声。
其次，通过状态方程的均值与其协方差矩阵确定采样点集，预测k+1时刻状态方程为
（23）
式中，
为k时刻的状态X；
为k时刻预测k+1时刻的状态X。
然后，通过预测k+1时刻的状态方程均值与其协方差矩阵，使用无损变换得到新的采样点集，预测k+1时刻的观测方程为
（24）
最后，通过预测k+1时刻的观测方程均值与其协方差矩阵确定卡尔曼增益矩阵，更新状态方程与其协方差。
根据这两种方法的特点，修正SOC权重为
（25）
（26）
（27）
式中，
为卡尔曼滤波法估算的SOC；
、
分别为安时积分法、卡尔曼滤波法的权重；
为安时积分法估算SOC对应的电压与端电压差值；
为卡尔曼滤波法估算SOC后的对应电压与端电压差值；
在负荷扰动出现后开始计时。
当与异号时，与同号，可以减少SOC估算误差；当与同号时，与异号，可以防止权重分配导致估算误差增大的现象，提高估算精度。
本文使用开路电压法确定SOC初始值，通过安时积分法与卡尔曼滤波法相结合自适应估算SOC。由于安时积分法初始精度较高，而卡尔曼滤波初始精度较低，本文先以安时积分法为主，逐渐过渡到以卡尔曼滤波法为主。
本文基于电池储能系统的综合自适应一次调频策略包括自适应控制趋势出力、自适应控制惯性出力、自适应控制下垂出力、自适应估算SOC。本文控制策略根据电网频率加速度自适应控制趋势出力，电网频率变化率自适应控制惯性出力，电网频率偏差自适应控制下垂出力，提高储能系统的自适应性。通过自适应修正安时积分法与卡尔曼滤波法的权重来估算SOC，提高SOC估算精度，进而防止储能电池过充过放。根据对本文方法的原理分析，电池储能系统参与一次调频流程如图5所示。
首先，使用多元自适应估算SOC方法对SOC进行实时估算。通过时间的推移，自适应修正SOC权重，形成先以安时积分法为主，逐渐过渡到以卡尔曼滤波法为主的控制策略，有效地减小最大误差和平均误差。
然后，将趋势控制策略和惯性与下垂控制策略相结合。趋势控制根据频率加速度确定出力大小、惯性控制根据频率变化率确定出力大小，下垂控制根据频率偏差确定出力大小，有效地提高了储能系统的自适应性，进而提高了储能系统参与一次调频时的性能。
最后，根据SOC约束储能系统出力。针对SOC不同区域执行的不同功能对电池储能系统出力进行约束，安全区不受SOC约束、警戒区出力呈现S形变化、危险区停止工作、紧急区以最大功率参与一次调频，防止了储能系统过充过放。
图5 储能系统参与一次调频流程
Fig.5 Hybrid energy storage system participates in primary frequency control flow chart
本文火电机组选取1 000 MW（调频功率上限设为60 MW[27]），储能电池选取30 MW/10 MW·h（额定容量选取较小，方便观察SOC变化和估算误差[15]）。火电机组一次调频死区为0.033 Hz，储能电池参与一次调频死区为0.6倍火电机组一次调频死区[18]。通过Matalb中的Simulink搭建仿真模型来验证本文方法的有效性，如图6所示[13]，仿真运行前，负荷没有功率变化量。电网频率为50 Hz，本文其他参数见表1[14]。
图6 仿真模型
Fig.6 Simulation model
表1 仿真参数
Tab.1 Simulation parameter
参数数值 FHP(pu)0.5 TRH/s10 TCH/s0.3 Tg/s0.08 Kg20 D1 M10 TE/s0.1 P00.01 n15
电池储能系统参与一次调频的实际时间不超过60 s。本文在阶跃负荷扰动中，一次调频时间设为 60 s，负荷扰动在10 s时增加60 MW，其中负荷扰动、火电机组出力波动、储能电池出力波动如图7所示。阶跃扰动评价指标见表2。
图7 阶跃扰动各机组出力
Fig.7 Step disturbance of each unit output
本文使用无储能、变K法[12]、自适应法[14]与本文方法进行比较。变K法是在惯性与下垂控制策略的基础上，储能电池出力系数根据SOC呈现线性变化。放电时，出力系数从SOC为0.8开始线性衰减，到SOC为0.2时停止出力，充电与其相反。自适应法是在惯性与下垂控制策略的基础上，储能电池出力系数呈现S形变化，放电时，SOC在0.8～0.4之间为最大出力系数，SOC在0.4～0.2之间呈现S形衰减，SOC为0.2时停止出力，充电与其相反。阶跃扰动时电网频率偏差变化情况对比如图8所示。
表2 阶跃扰动评价指标
Tab.2 Step disturbance evaluation index
方法最大频率偏差/Hz稳态频率偏差/Hz 无储能-0.096-0.063 变K法-0.082-0.058 自适应法-0.067-0.053 本文方法-0.061-0.049
图8 阶跃扰动电网频率偏差
Fig.8 Step disturbance grid frequency deviation
根据图8和表2可知，无储能方法中电网最大频率偏差为-0.096 Hz，稳态频率偏差为-0.063 Hz，对比方法中，无储能电网频率偏差最大，说明电池储能系统可以很好地改善一次调频效果。变K法中电网最大频率偏差为-0.082 Hz，稳态频率偏差为 -0.058 Hz，自适应法中电网最大频率偏差为 -0.067 Hz，稳态频率偏差为-0.053 Hz，自适应法比变K法频率偏差小，因为变K法出力系数在SOC等于0.5时，出力系数小于最大出力系数，而自适应法SOC在0.5时出力系数为最大系数，所以自适应法的出力系数比变K法出力系数大，储能电池出力也就大，电网频率偏差就小。本文方法电网最大频率偏差、稳态频率偏差均最小，分别为-0.061 Hz、-0.049 Hz，本文方法储能电池出力根据电网频率加速度、电网频率变化率、电网频率偏差自适应确定，并且本文方法在惯性与下垂的基础上增加了趋势出力，其出力是这几种方法中最大的，一次调频效果最佳，与自适应法相比，最大频率偏差与稳态频率偏差分别减小了9%和8%。
图9a为加入趋势控制前后电网频率偏差对比，由此可知该控制策略可以减缓电网频率偏差恶化速度，加快电网频率恢复速度，减小电网最大频率偏差。图9b为自适应确定出力系数前后电网频率偏差对比，该控制策略可以减小电网最大频率偏差与电网稳态频率偏差。因此，本文方法将两者优点相结合，全方面提升了储能系统性能。
图9 改进前后对比
Fig.9 Comparison before and after improvement
阶跃负荷响应下安时积分法、卡尔曼滤波法、神经网络法[22]、本文方法的SOC估算如图10所示，SOC估算误差如图11所示，SOC误差见表3。
图10 SOC估算
Fig.10 SOC estimation
根据图10、图11、表3可知，随着时间推移，安时积分法估算误差逐渐增加，最大误差为0.42%，平均误差为0.21%。卡尔曼滤波法初期SOC估算误差较大，随着迭代次数的增加，卡尔曼滤波法估算误差逐渐减小，最大误差为0.88%，平均误差为0.13%。神经网络法在初期估算SOC较准确，最大误差为0.13%，平均误差为0.04%，但神经网络需要大量的数据进行训练，而且在未训练过的数据上的泛化能力容易受到限制。本文方法最大误差为0.09%，平均误差为0.01%，本文方法不断地自适应修正权重来确定SOC，进而提高了估算精度，并且计算方便、过程简单、实用性强。
图11 SOC估算误差
Fig.11 SOC estimation error
表3 SOC误差
Tab.3 SOC error
方法最大误差(%)平均误差(%) 安时积分法0.420.21 卡尔曼滤波法0.880.13 神经网络法0.130.04 本文方法0.090.01
在短时连续负荷扰动10 min中，储能电池的SOC初始值为0.5，其中负荷扰动、火电机组出力波动、储能电池出力波动如图12所示，电网频率偏差如图13所示，SOC变化如图14所示，评价指标见表4。
图12 短时间扰动各机组出力
Fig.12 Short time to disturb the output of each unit
图13 短时间扰动电网频率偏差
Fig.13 Short time disturbance of the power grid frequency deviation
图14 SOC变化
Fig.14 Change in SOC
表4 短时间扰动评价指标
Tab.4 Short time disturbance evaluation index
方法频率偏差/HzSOC 平均值峰间值平均值峰间值 无储能0.0480.197—— 变K法0.0440.1700.4900.021 自适应法0.0410.1400.4820.037 本文方法0.0380.1260.4740.052
根据图13、图14和表4可知，无储能方法的电网平均频率偏差为0.048 Hz，峰间值为0.197 Hz，对比方法中，无储能电网频率偏差最大。变K法的电网平均频率偏差为0.044 Hz，峰间值为0.170 Hz，SOC平均值为0.490，峰间值为0.021，变K法频率偏差较大，SOC消耗最小。自适应法的电网平均频率偏差为0.041 Hz，峰间值为0.140 Hz，SOC平均值为0.482，峰间值为0.037，电网频率偏差与SOC变化居中。本文方法电网频率偏差为0.038 Hz，峰间值为0.126 Hz，SOC平均值为0.474，峰间值0.052，本文方法电网频率偏差与峰间值最小，与自适应法相比，平均频率偏差和频率峰间值分别减小了7%、10%，一次调频效果最好，但SOC变化最大，这是因为趋势出力增加了电池储能系统出力，所以消耗的SOC较多。
在长时连续负荷扰动30 min中，负荷扰动、火电机组出力波动、储能电池出力波动如图15所示。长时间扰动电网频率偏差如图16所示，其评价指标见表5。根据图16和表5可知，无储能方法的电网平均频率偏差为0.044 Hz，峰间值为0.205 Hz。变K法的电网平均频率偏差为0.041 Hz，峰间值为0.172 Hz。自适应法的电网平均频率偏差为0.038 Hz，峰间值为0.140 Hz。本文方法电网频率偏差与峰间值最小，分别为0.035 Hz、0.126 Hz，一次调频效果最好，与自适应法相比，平均频率偏差和频率峰间值分别减小了8%、10%。
图15 长时间扰动各机组出力
Fig.15 Disturb the output of each unit for a long time
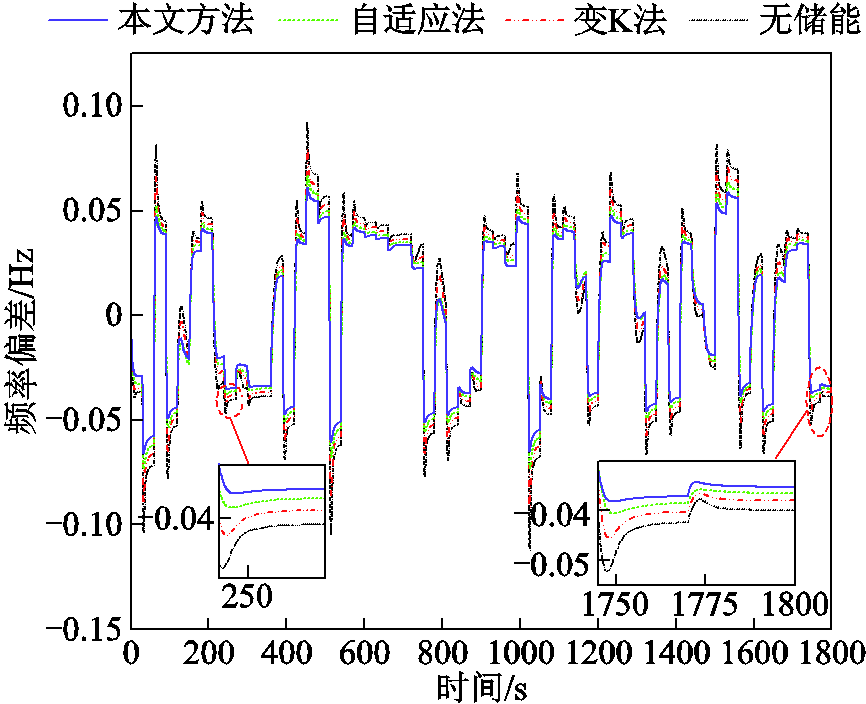
图16 长时间扰动电网频率偏差
Fig.16 Disturbance frequency deviation of power grid for a long time
表5 长时间扰动评价指标
Tab.5 Long time disturbance evaluation index
方法平均频率偏差/Hz频率峰间值/Hz 无储能0.0440.205 变K法0.0410.172 自适应法0.0380.140 本文方法0.0350.126
本文将趋势控制策略和惯性与下垂控制策略相结合，并通过修正SOC权重来提高SOC估算精度，提出了基于电池储能系统的综合自适应一次调频策略，得出以下结论：
1）趋势控制策略减缓了电网的频率恶化速度，加快了电网频率的恢复速度，减小了电网最大频率偏差。自适应确定出力系数有效地减小了电网的最大、稳态频率偏差。本文结合两者优点，储能系统性能得到全面提高。
2）提出多元自适应估算SOC方法，先以安时积分法为主，逐渐过渡到以卡尔曼滤波法为主。与安时积分法、卡尔曼滤波法、神经网络法比较，本文方法效果最佳，SOC估算最大误差为0.09%，平均误差为0.01%。
3）基于电池储能系统的综合自适应一次调频策略与自适应法相比，在阶跃负荷扰动下，最大频率偏差与稳态频率偏差分别减小了9%和8%。在短时连续负荷扰动下，平均频率偏差和频率峰间值分别减小了7%、10%。长时连续负荷扰动下，平均频率偏差和频率峰间值分别减小了8%、10%。
针对SOC估算问题，未来将对权重分配的控制策略进行重点研究。
参考文献
[1] 张怡静, 李智, 时艳强, 等. 基于储能惯量支撑的受端电网频率优化控制方法[J]. 电工技术学报, 2024, 39(11): 3556-3568. Zhang Yijing, Li Zhi, Shi Yanqiang, et al. Optimal frequency control method of receiving power grid based on energy storage inertia support[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3556-3568.
[2] 鲁宗相, 李佳明, 乔颖, 等. 新能源场站快速频率支撑能力评估研究现状与技术展望[J]. 电力系统自动化, 2024, 48(10): 1-19. Lu Zongxiang, Li Jiaming, Qiao Ying, et al. Research status and technology prospects of fast frequency support capability assessment for renewable energy stations[J]. Automation of Electric Power Systems, 2024, 48(10): 1-19.
[3] 张祥宇, 胡剑峰, 付媛, 等. 风储联合系统的虚拟惯量需求与协同支撑[J]. 电工技术学报, 2024, 39(3): 672-685. Zhang Xiangyu, Hu Jianfeng, Fu Yuan, et al. Virtual inertia demand and collaborative support of wind power and energy storage system[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 672-685.
[4] 刘凡, 李凤婷, 张高航, 等. 计及循环寿命和运营策略的风电汇集区域储能电站优化配置[J]. 电力系统保护与控制, 2023, 51(8): 127-139. Liu Fan, Li Fengting, Zhang Gaohang, et al. Optimal configuration of storage power stations in a wind power gathering area considering cycle life and operation strategy[J]. Power System Protection and Control, 2023, 51(8): 127-139.
[5] 刘小龙, 李欣然, 孟娅, 等. 离网状态储能/燃气机分层协调频率控制策略[J]. 电工技术学报, 2023, 38(17): 4800-4810. Liu Xiaolong, Li Xinran, Meng Ya, et al. Hierarchical coordination frequency control strategy of battery energy storage/gas turbine under off-grid state[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4800-4810.
[6] 陈勃旭, 崔炜, 陈宇, 等. 分布储能直流微电网中多储能荷电均衡控制策略[J]. 电力系统保护与控制, 2023, 51(24): 111-120. Chen Boxu, Cui Wei, Chen Yu, et al. Charge balance control strategy for multiple energy storage in a distributed energy storage DC microgrid[J]. Power System Protection and Control, 2023, 51(24): 111-120.
[7] 杨德健, 王鑫, 严干贵, 等. 计及调频死区的柔性风储联合频率控制策略[J]. 电工技术学报, 2023, 38(17): 4646-4656. Yang Dejian, Wang Xin, Yan Gangui, et al. Flexible frequency regulation scheme of DFIG embed battery energy storage system considering deadbands[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4646-4656.
[8] 张崇, 李博, 李笑宇, 等. 基于虚拟同步机控制参数自适应调节的储能系统调频方法[J]. 发电技术, 2024, 45(4): 772-780. Zhang Chong, Li Bo, Li Xiaoyu, et al. A frequency regulation method of energy storage system based on adaptive adjustment of virtual synchronous generator control parameters[J]. Power Generation Technology, 2024, 45(4): 772-780.
[9] 鄢仁武, 姜雪儿. 变调节因子的不同容量锂电池储能系统能量控制策略[J]. 电气技术, 2024, 25(2): 21-30. Yan Renwu, Jiang Xue’er. Energy control strategies for lithium battery energy storage systems with different capacities based on variable regulating factors[J]. Electrical Engineering, 2024, 25(2): 21-30.
[10] 梁继业, 袁至, 王维庆, 等. 基于储能系统多重约束的一次调频策略[J]. 高电压技术, 2024, 50(6): 2478-2489. Liang Jiye, Yuan Zhi, Wang Weiqing, et al. Primary frequency control strategy based on multiple constraint of energy storage system[J]. High Voltage Engineering, 2024, 50(6): 2478-2489.
[11] 杜锡力, 李笑竹, 陈来军, 等. 面向多场景调节需求的集中式共享储能鲁棒优化配置[J]. 电工技术学报, 2022, 37(23): 5911-5921. Du Xili, Li Xiaozhu, Chen Laijun, et al. Robust and optimized configuration of centralized shared energy storage for multi-scenario regulation demand[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5911-5921.
[12] 邓霞, 孙威, 肖海伟. 储能电池参与一次调频的综合控制方法[J]. 高电压技术, 2018, 44(4): 1157-1165. Deng Xia, Sun Wei, Xiao Haiwei. Integrated control strategy of battery energy storage system in primary frequency regulation[J]. High Voltage Engineering, 2018, 44(4): 1157-1165.
[13] 赵熙临, 张大恒, 桂玥, 等. 考虑荷电状态约束的储能参与电网一次调频综合控制策略[J]. 现代电力, 2022, 39(1): 95-103. Zhao Xilin, Zhang Daheng, Gui Yue, et al. An integrated control strategy for energy storage participating in primary frequency regulation considering state of charge constraint[J]. Modern Electric Power, 2022, 39(1): 95-103.
[14] 李军徽, 高卓, 应鸿, 等. 基于动态下垂系数与SOC基点的储能一次调频控制策略[J]. 电力系统保护与控制, 2021, 49(5): 1-10. Li Junhui, Gao Zhuo, Ying Hong, et al. Primary frequency regulation control strategy of energy storage based on dynamic droop coefficient and SOC reference[J]. Power System Protection and Control, 2021, 49(5): 1-10.
[15] 刘英培, 田仕杰, 梁海平, 等. 考虑SOC的电池储能系统一次调频策略研究[J]. 电力系统保护与控制, 2022, 50(13): 107-118. Liu Yingpei, Tian Shijie, Liang Haiping, et al. Control strategy of a battery energy storage system considering SOC in primary frequency regulation of power grid[J]. Power System Protection and Control, 2022, 50(13): 107-118.
[16] 李军徽, 高卓, 李翠萍, 等. 基于动态任务系数的储能辅助风电一次调频控制策略[J]. 电力系统自动化, 2021, 45(19): 52-59. Li Junhui, Gao Zhuo, Li Cuiping, et al. Control strategy for dynamic task coefficient based primary frequency regulation of wind power assisted by energy storage[J]. Automation of Electric Power Systems, 2021, 45(19): 52-59.
[17] 李培强, 丰云鹤, 李欣然, 等. 考虑超短期负荷预测的储能电池参与电网一次调频控制策略[J]. 电力系统自动化, 2019, 43(19): 87-93, 148. Li Peiqiang, Feng Yunhe, Li Xinran, et al. Control strategy for energy storage battery participating in primary frequency regulation of power grid considering ultra-short-term load forecasting[J]. Automation of Electric Power Systems, 2019, 43(19): 87-93, 148.
[18] 王育飞, 杨铭诚, 薛花, 等. 计及SOC的电池储能系统一次调频自适应综合控制策略[J]. 电力自动化设备, 2021, 41(10): 192-198, 219. Wang Yufei, Yang Mingcheng, Xue Hua, et al. Self-adaptive integrated control strategy of battery energy storage system considering SOC for primary frequency regulation[J]. Electric Power Automation Equipment, 2021, 41(10): 192-198, 219.
[19] 罗勇, 祁朋伟, 黄欢, 等. 基于容量修正的安时积分SOC估算方法研究[J]. 汽车工程, 2020, 42(5): 681-687. Luo Yong, Qi Pengwei, Huang Huan, et al. Study on battery SOC estimation by ampere-hourIntegral method with capacity correction[J]. Automotive Engineering, 2020, 42(5): 681-687.
[20] 王子毅, 朱承治, 周杨林, 等. 基于动态可重构电池网络的OCV-SOC在线估计[J]. 中国电机工程学报, 2022, 42(8): 2919-2928. Wang Ziyi, Zhu Chengzhi, Zhou Yanglin, et al. OCV-SOC estimation based on dynamic reconfigurable battery network[J]. Proceedings of the CSEE, 2022, 42(8): 2919-2928.
[21] 潘海鸿, 张沫, 王惠民, 等. 基于多影响因素建立锂离子电池充电内阻的动态模型[J]. 电工技术学报, 2021, 36(10): 2199-2206. Pan Haihong, Zhang Mo, Wang Huimin, et al. Establishing a dynamic model of lithium-ion battery charging internal resistance based on multiple factors[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2199-2206.
[22] 刘康, 康龙云, 岳睿, 等. 基于门控循环单元编解码器的锂离子电池荷电状态估计[J]. 电网技术, 2024, 48(5): 2161-2169. Liu Kang, Kang Longyun, Yue Rui, et al. Lithium-ion battery state of charge estimation based on gated recurrent unit encoder-decoder[J]. Power System Technology, 2024, 48(5): 2161-2169.
[23] 徐保荣, 王兴成, 张齐, 等. 自适应扩展卡尔曼滤波电池荷电状态估算方法[J]. 哈尔滨工业大学学报, 2021, 53(7): 92-98. Xu Baorong, Wang Xingcheng, Zhang Qi, et al. Adaptive extended Kalman filter for estimating the charging state of battery[J]. Journal of Harbin Institute of Technology, 2021, 53(7): 92-98.
[24] 刘征宇, 黎盼春, 朱诚诚, 等. 基于组合模型的锂电池参数辨识和电池荷电状态在线联合估计[J]. 中国机械工程, 2020, 31(10): 1162-1168. Liu Zhengyu, Li Panchun, Zhu Chengcheng, et al. Lithium battery parameter identification and SOC online joint estimation based on combined model[J]. China Mechanical Engineering, 2020, 31(10): 1162-1168.
[25] 周娟, 林加顺, 吴乃豪, 等. 一种联合PID控制与扩展卡尔曼滤波的磷酸铁锂电池荷电状态估算方法[J]. 电网技术, 2023, 47(4): 1623-1631. Zhou Juan, Lin Jiashun, Wu Naihao, et al. State of charge estimation for LiFeO4 battery combining PID control and extended Kalman filter[J]. Power System Technology, 2023, 47(4): 1623-1631.
[26] 刘兴涛, 李坤, 武骥, 等. 基于EKF-SVM算法的动力电池SOC估计[J]. 汽车工程, 2020, 42(11): 1522-1528, 1544. Liu Xingtao, Li Kun, Wu Ji, et al. State of charge estimation for traction battery based on EKF-SVM algorithm[J]. Automotive Engineering, 2020, 42(11): 1522-1528, 1544.
[27] 国家市场监督管理总局, 国家标准化管理委员会. 火力发电机组一次调频试验及性能验收导则: GB/T 30370—2022[S]. 北京: 中国标准出版社, 2022.
Abstract The primary frequency control of thermal power units has low energy efficiency and negative impact on the environment. The energy storage battery has the characteristic of fast response speed, but the control strategy of the energy storage system only considers the state of charge (SOC) near the minimum value in the discharge state, or the adaptive control when SOC is near the maximum value in the charging state, which has poor adaptability and does not consider the SOC estimation accuracy. As a result, the control strategy of the energy storage system has poor effect on inhibiting the deterioration of the power grid frequency, and then limits the performance of the energy storage system when it participates in the primary frequency control. To solve this problem, this paper proposes a comprehensive adaptive primary frequency control strategy based on battery energy storage system.
Firstly, the trend control strategy and the inertia and sag control strategy are combined to define the trend output of the battery energy storage system and the frequency acceleration of the power grid, and explain the relationship among the frequency acceleration, frequency change rate and frequency deviation of the power grid. Secondly, the output coefficient of the battery energy storage system is adaptive control, and the trend coefficient is determined according to the frequency acceleration of the power grid, the inertia coefficient is determined according to the frequency change rate of the power grid, and the sag coefficient is determined according to the frequency deviation of the power grid, so as to improve the adaptive ability of the energy storage system. Finally, in order to prevent the energy storage battery from overcharging and over discharging and improve the SOC estimation accuracy, a multi-element adaptive SOC estimation method is proposed.
Simulation results show that in the step load disturbance, the maximum frequency deviation and steady-state frequency deviation of the proposed method are the smallest, which are -0.061 Hz and -0.049 Hz respectively. Compared with the adaptive method, the maximum frequency deviation and steady-state frequency deviation are reduced by 20.7% and 40.0% respectively. SOC has the highest accuracy, with a maximum error of 0.09% and an average error of 0.01%. In the short-time continuous load disturbance, the grid frequency deviation of the proposed method is 0.038 Hz, the peak-to-peak value is 0.126 Hz, the average SOC is 0.474, the peak-to-peak value is 0.052, and the grid frequency deviation is the smallest, and the SOC fluctuation is large. In the case of long-term continuous load disturbance, the frequency deviation and peak-to-peak value of the proposed method are 0.035 Hz and 0.126 Hz respectively, and the single frequency control effect is the best. Compared with the adaptive method, the average frequency difference deviation and frequency peak-to-peak value are reduced by 50.0% and 21.5% respectively.
The following conclusions are drawn: (1) The trend control strategy can slow down the frequency deterioration, speed up the frequency recovery and reduce the maximum frequency deviation of the power grid. (2) Adaptive determination of output coefficient effectively reduces the maximum steady-state frequency deviation of the power grid and improves the adaptability of the energy storage system. (3) The multi-component adaptive humic acid SOC method is mainly based on ampere-hour integration method, and gradually transitions to Kalman filter method, which effectively reduces the maximum and average estimation errors.
keywords：Primary frequency control, inertia and sag control strategy, trend control strategy, self-adaptation, state of charge (SOC) estimation
DOI: 10.19595/j.cnki.1000-6753.tces.240456
中图分类号：TM614
新疆维吾尔自治区重大科技专项（2022A01004-1）和国家自然科学基金（52067020）资助项目。
收稿日期 2024-03-22
改稿日期 2024-07-24
梁继业 男，1999年生，硕士研究生，研究方向为储能技术应用。E-mail：2267599319@qq.com
袁 至 男，1984年生，副教授，博士生导师，研究方向为可再生能源发电与并网控制。E-mail：yzisthecure@163.com（通信作者）
（编辑 赫 蕾）