 (1)
(1)
摘要 为了快速获得各种工况下油浸式电力变压器绕组的温度分布与热点,该文提出了一种基于本征正交分解(POD)与克里金代理模型(KSM)相结合的快速计算方法。首先,基于POD降阶方法对变压器温度场的离散方程组进行降阶,得到降阶模态系数矩阵;其次,根据不同变压器工况对绕组温度场的影响程度选取重要工况参数,通过拉丁超立方采样形成工况参数矩阵即样本空间;然后,基于KSM方法构建样本空间与对应模态系数的代理模型,跳过对全阶模型的复杂非线性计算,以绕组工况为输入得到模态系数,结合模态高效重构温度场;最后,为验证该方法的有效性及与现有方法相比的优越性,分别用该方法与现有方法对110 kV油浸式变压器绕组八分区仿真模型与绕组温升实验测量数据进行对比分析。算例表明,该文所提方法对于相关测试工况的计算偏差更低,计算精度更高,且计算效率有较大幅度的提升,充分表明了该方法的有效性与优越性。该文所提变压器稳态温度场计算方法可为变压器数字化运维提供技术支撑。
关键词:油浸式电力变压器 温度场 本征正交分解 克里金代理模型
油浸式电力变压器作为输配电网中的关键一次设备,其运行可靠性直接影响电能的安全稳定供应。然而,由于内部传感器的安装有限等因素,难以实现相关部件的全场监测。建立高保真的数字化仿真模型并进行快速模拟计算为这一问题提供了有效的解决方案,也是变压器数字化运维的必然要求。
油浸式电力变压器绕组的温度与热点是变压器状态监测的重要指标,一般通过直接测量[1-3]、数值计算[4-6]和代理模型[7-10]的方式获得。直接测量法包括热电偶测量、光纤传感测量等,将传感器直接安装在绕组表面以实时获取绕组某一工况下的温度数值。该方法需要深入变压器内部布置传感器,且布置数量与位置均有限制,无法获得绕组全场的温度分布与热点。数值计算法是目前使用较为广泛的方法,也是当下学术界的研究热点,包括有限元法[11-12]、有限体积法[13-14]等。然而,对于产品级油浸式电力变压器而言,由于其结构呈空间多尺度特点,温度场仿真模型剖分得到的离散网格数量巨大,其温度场计算的自由度达上千万,导致离散方程的阶数过大,消耗计算资源巨大且求解时间过慢。针对此问题,文献[15]将本征正交分解(Proper Orthogonal Decomposition, POD)降阶技术和混合有限元法相结合计算绕组流-热耦合问题;文献[16]将GPU并行计算与混合有限元法相结合计算二维变压器流-热耦合问题;文献[17]结合POD和离散经验插值方法降低稳态流-热耦合控制方程的阶数,并改善其中的非线性项,极大地提高了计算效率。
尽管对于降阶算法以及并行计算的研究已经较为成熟,但现有降阶技术仍然由于数据存储的缺陷难以满足数字化运维的快速性要求。随着近些年计算机技术的越发成熟,神经网络[18-19]、深度学习[20]等代理模型的方法逐渐被学者应用于变压器温度预测问题中。代理模型法基于数据驱动来拟合输入参数与输出结果之间的映射关系,以方便运算的近似模型代替复杂的原始模型。由于代理模型并不关心其内部的计算过程,因此也被称为黑箱模型。但是,此类算法生成代理模型需要大量的数据样本,成本高,而且需要对数据进行预处理,操作繁琐。
响应面法(Response Surface Methodology, RSM)通过响应面函数拟合输入量与输出量的隐藏物理关系,可以解决复杂的非线性问题,其本质上也可以理解为代理模型。不同的RSM之间的区别在于选取不同的响应面函数构建多项表达式,包括多项式[21]、径向基函数[22]、克里金函数[23-25]、支持向量机函数[26]等。文献[27]将POD与包含线性表达式的径向基函数(Radial Basis Function including Linear Polynomial, RBFLP)响应面法相结合,构建了POD模态系数与其对应温度结果的响应面模型,输入绕组工况得到模态系数,结合模态重构绕组的温度场,但是计算结果仍然存在较大的误差。
因此,为了进一步提高计算精度、提升计算效率,本文在POD降阶方法的基础上,以克里金函数作为载体,将二者结合构建变压器工况参数与模态系数间的代理模型,实现各种工况下油浸式变压器绕组温度场的快速准确计算。结合具体算例从软件仿真和实验平台两方面对该方法的有效性进行验证,同时与现有方法进行对比,表明本文方法的优越性。
根据文献[6],油浸式电力变压器绕组稳态温度场的控制方程经离散后形成的有限元方程组为
 (1)
(1)
式中,K为温度场控制方程的刚度矩阵;t为需要求解的温度向量;F为右端项;n为方程自由度数量。
对于产品级油浸式电力变压器,由于结构呈空间多尺度特点,温度场仿真模型剖分得到的离散网格数量巨大,其温度场计算的自由度达上千万。本文拟通过降阶方法来减少计算时间。
POD可以利用已有的数据样本,通过特征向量分解,得到一组正交特征向量和相应的特征值,根据特征值大小,将特征向量按降序排列,以选取少量的最优模态近似物理模型,从而降低模型阶数,加快求解速度。为了降低式(1)的阶数,采用基于POD的降阶方法,其原理如图1所示。

图1 POD方法原理
Fig.1 Principle of POD method
图1中,T称为快照矩阵(snapshot),表示s种工况下,该全阶物理模型p个单元节点的温度矩阵,即
 (2)
(2)
式中, 为第s种工况下,模型的第p个节点的温度。
为第s种工况下,模型的第p个节点的温度。
对矩阵T进行奇异值分解,表示为
 (3)
(3)
式中,U、V分别为左、右正交矩阵,二者为快照矩阵的标准正交基底;Σ为奇异值矩阵,是一个由快照矩阵的特征值组成的对角矩阵,对角线上的特征值按照降序由大到小排列,且前后数值差异较大,因此需要根据式(4)选择满足条件的前d个特征值。
 (4)
(4)
式中,σi为第i个特征值对应的特征向量;m为特征值总数量。除此之外,满足条件的前d个特征值需要远大于后面若干个奇异值,同时,基于前d个特征值重构的物理场与全阶模型的误差应尽可能小。因此,温度向量t可近似表示为
 (5)
(5)
式中,带下标d的量表示由前d个特征值重构之后的对应物理量;α为降阶模态系数矩阵。
将式(5)代入式(1),则原方程可表示为
 (6)
(6)
经奇异值分解得到模态系数之后,建立与工况对应的代理模型。输入测试工况,通过该代理模型快速得到模态系数α,再与模态U线性加权,从而重构绕组温度场。
克里金代理模型(Kriging Surrogate Model, KSM)通过克里金函数描述输入与输出之间的变量关系,其一般表达式为
 (7)
(7)
式中,x为输入,即样本工况;y为输出,即对应的模态系数矩阵;G(x, β)为回归项;β为回归参数; 为非参数项,表征插值误差的随机过程。可以选取回归函数g(x)来表示回归项,常用的回归函数见表1。
为非参数项,表征插值误差的随机过程。可以选取回归函数g(x)来表示回归项,常用的回归函数见表1。
表1 常用的回归函数
Tab.1 Common used regression functions

阶数函数表达式 零阶 一阶,,…, 二阶,,…,,,,…,,,,…,,…,
因此,可以将回归项G(x, β)表达为回归函数g(x)与其对应系数β的线性组合,即
 (8)
(8)
式(7)中的z(x)为非参数项,表征插值误差服从正态分布的随机过程,z(x)~N(0, σ2),即服从均值为0、方差为σ2、协方差非零的随机正态分布。其中,协方差表示为
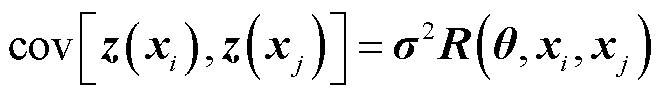 (9)
(9)
式中,xi与xj为样本空间的两个样本点;R(θ,xi, xj)为相关函数,表示这两个点的相对位置;θ为相关参数。常见的相关函数包括线性函数、指数函数、高斯函数和球形函数等。由于流-热耦合离散过程中非线性很强,因此本文选用高斯函数作为相关函数,对非线性环节的拟合效果更好,其表达式为
 (10)
(10)
式中,q=1,2,…,s,s为快照矩阵的列数。综上所述,求解该响应模型的关键就是确定回归系数β与方差σ2,采用极大似然估计法计算这两个参数,计算式为

式中,L(θ, xi, xj)为似然函数;N为样本点数量;本文中,Y即快照矩阵T。分别对式(11)中β和σ2取偏导数并令其等于0,可得
 (12)
(12)
式中, 和
和 分别为对
分别为对 和
和 取偏导数。
取偏导数。
因此,KSM具体的函数表达式为
 (13)
(13)
式中,r(x)=[R(θ, x1, x) … R(θ, xN, x)]T,表示待预测点与样本点之间的相关性。
本文将绕组工况作为输入,其对应的模态系数就是KSM的输出,即实现了不形成有限元刚度矩阵且不需要求解离散方程就可以得到模态系数矩阵,从而可以结合模态UT快速重构温度场。
综上所述,基于POD-KSM的绕组稳态温度场的计算流程为:
(1)确定样本空间并通过采样获得样本工况集合P={p1, p2,…, ps}。
(2)计算不同工况下全阶模型的温度场结果,从而构建绕组温度场的快照数据库。
(3)对快照矩阵T进行奇异值分解,得到模态系数矩阵α与模态UT。
(4)构造模态系数矩阵α与样本工况集P的KSM代理模型。
(5)输入测试工况Ptest,由代理模型获得对应模态系数αtest为
 (14)
(14)
(6)结合POD模态重构温度场为
 (15)
(15)
为了验证本文提出的POD-KSM降阶计算方法的有效性,以110 kV油浸式电力变压器八分区绕组模型为研究对象,其主要结构部件包括线饼、挡板、绝缘纸、油道及油箱壁,结构参数见表2,据此建立二维几何模型如图2所示。
表2 结构参数
Tab.2 Structural parameters

结构部件参数数值/mm 整体高度1 125.5 宽度155.5 线饼高度10.8 宽度138.0 挡板厚度1.5 宽度145.5 绝缘纸厚度0.7 水平油道线饼与线饼间距离6.0 线饼与挡板间距离3.0 竖直油道内侧宽度8.0 外侧宽度10.0

图2 绕组八分区二维模型
Fig.2 Two dimensional eight zone model of winding
由图2可见,在横向上,每个线饼由30匝扁铜导线缠绕组成,导线表面附着绝缘纸;在纵向上,挡板将模型分隔为8个分区,分区1~3各包含7个线饼,剩余分区各包含9个线饼。正常工作时,油流从最下方入口流入,流经油道与发热的绕组接触以后,受热浮力的作用,经纵向油道与横向油道流动至出口。
将模型导入Fluent仿真软件,根据表3设置模型的物性参数,其中变压器油的相关参数非线性较强,随温度T的变化而变化,故将其设置为以温度为自变量的函数。模型的边界条件包括:①变压器工作的环境温度为26.85℃;②根据入口流量换算得到入口油流速度v0和入口油温Tinlet;③出口设置为压力边界条件,大小为0,方向为竖直向上;④将挡板和油箱壁设置为无滑移壁面、绝热边界条件;⑤将绕组与油流交界处设置为无滑移壁面。
表3 物性参数
Tab.3 Physical parameters

对象参数数值 变压器油密度/(kg/m3)1 098.72-0.712T 比热容/[J/(kg·K)]807.163+3.28T 动力黏度/(Pa·s)0.084 6-4×10-4T+5×10-7T2 导热系数/[W/(m·K)]0.150 9-7.101×10-5T 铜导线密度/(kg/m3)8 900 比热容/[J/(kg·K)]381 导热系数/[W/(m·K)]387.6 绝缘油纸密度/(kg/m3)980 比热容/[J/(kg·K)]2 000 导热系数/[W/(m·K)]0.25 挡板密度/(kg/m3)700 比热容/[J/(kg·K)]2 310 导热系数/[W/(m·K)]0.17
根据文献[4],设置绕组温度场热源为
 (16)
(16)
式中,ST0为初始温度T0下的绕组损耗密度,本文取227 kW/m3;μ为导体的温度系数。对模型进行有限元剖分,由于油道和线饼、油道和挡板边界间的速度变化,以及线匝与绝缘纸边界间的温度变化梯度大,因此边界层的剖分需更精细,非边界区域网格尺寸为0.5 mm,模型节点共2 022 370个,该网格已经过独立性验证。
在油浸式电力变压器的实际运行过程中,入口油速、油温和绕组功率会明显地影响绕组热点温度,如图3所示。因此选取这3个变量作为POD-KSM降阶模型构建的样本空间。
根据POD-KSM降阶模型构建流程,第一步就是在样本空间通过采样方法获得样本工况的数据集合。为提高代理模型的计算精度,所采取的样本工况集合应能充分表达样本空间的数据特征,本文采用基于分层抽样思想的拉丁超立方采样方法获取样本矩阵。以图3横坐标刻度范围为影响区间,样本空间维数为3,选取100个采样点,通过拉丁超立方采样方法生成样本矩阵组成样本空间,如图4所示。

图3 绕组热点温度影响因素分析
Fig.3 Analysis of factors affecting the temperature of winding hotspots

图4 样本空间
Fig.4 Sample space
采用仿真软件Fluent计算得到100组不同工况下绕组的稳态温升结果。对结果进行批量处理形成快照矩阵T,对快照矩阵进行奇异值分解得到模态UT以及模态系数矩阵α,并根据式(4)衡量各模态重要程度,选择最优的模态数量满足系统需求。模态选择判断依据如图5所示。


图5 模态选择
Fig.5 Modal selection
由图5可见,当选取前10阶模态时,模态对系统的重要程度达99.9%以上,且前10阶模态奇异值远大于后若干奇异值。图5c直观地表征了选取前30阶模态时所重构物理场的效果,可见选取阶数低的模态会导致误差很大。因此,本文选取前10阶模态为基组成降阶子空间,结合由代理模型预测的模态系数,由式(15)重构得到某一工况下的绕组温度场,如图6所示。对应的绕组工况为:入口油速为0.124 5 m/s,入口油温为28.74℃,绕组功率为36.26 kW。

图6 POD温度场重构
Fig.6 POD temperature field reconstruction
通过计算100组训练集,得到模态系数与其对应工况结果的代理模型。为检验该模型的有效性,在样本空间内重新采集数据,另选50组工况作为测试组,测试降阶模型与全阶模型的误差。定义平均绝对误差EMAE和相对误差Erelative分别为
 (17)
(17)
 (18)
(18)
式中,TR为降阶模型计算结果;TF为全阶模型计算结果;Nnode为温度场节点总数。
计算50组测试点结果的平均绝对误差和相对误差,结果如图7所示。

图7 各测试点计算误差
Fig.7 Calculation error of each test point
由图7可见,在50个测试工况中,降阶模型的误差最大值出现在工况入口流速为0.094 6 m/s、入口油温为18.38℃、绕组功率为56.61 kW时,其最大平均绝对误差为1.19℃,最大相对误差为2.79%,说明本文所提POD-KSM降阶算法具有较高的计算精度。
为说明本文方法的优越性,针对前文选取的50组测试集,分别用本文方法与文献[27]的POD-RBFLP方法,对上述算例进行计算分析,二者的平均绝对误差与相对误差对比结果如图8所示。
由图8可得,对于选取的同一组测试工况,POD-KSM降阶模型得到的结果精度更高,最大相对误差为2.79%,而POD-RBFLP的最大相对误差为4.51%;前者的最大平均绝对误差为1.19℃,而后者的最大平均绝对误差为2.38℃。由此可说明,本文所提POD-KSM降阶算法比POD-RBFLP方法具有更高的计算精度。

图8 相同测试工况下本文方法与POD-RBFLP方法的计算误差
Fig.8 Calculation error of the proposed method and POD-RBFLP method under the same testing conditions
另外,在计算效率方面,使用同一台配置为13th Gen Intel(R) Core(TM) i9-13900K、RAM 128 GB的计算机,对比这两种算法在相同测试工况下的计算功率,结果见表4。表4中,预处理时间包括通过商业仿真软件获得原始不同工况下的数据集时间、导入Matlab通过编程生成POD模态的时间以及生成代理模型的时间,计算时间则是指计算50组测试工况的时间。
表4 计算效率对比
Tab.4 Calculation efficiency comparison

模型预处理时间/s计算时间/s 全阶模型68 273.12 POD-RBFLP5 099.290.902 POD-KSM5 097.290.3
结果表明,本文所提方法可将计算效率提升至全阶模型的13.39倍。若不考虑预处理时间,计算某一工况对应的结果仅需要0.006 s,相比于POD-RBFLP而言,效率提升将近67%,表明本文方法具有更高的计算效率。
为验证本文方法的工程应用价值,基于110 kV油浸式电力变压器绕组温升实验平台进行测试。实验装置如图9所示。温升实验平台由空心饼式无感绕组、器身绝缘、片式散热器、风扇、油泵、流量计、热电偶等组成。绕组功率通过精密功率测量仪获得,型号为日本YOKOGAWA WT3000。温度测量仪器为铜-康铜热电偶,安装位置为从上至下第12、20、30、38号线饼,水平方向从左至右第1、4、7、10、13、16、19、22、25、28、30个线匝。实验工况为强迫油循环,在油箱入口布置热电偶以测得入口油流温度。

图9 实验装置
Fig.9 Experimental device
设计实验工况为:入口油流速度为0.114 m/s,入口油温为55.21℃,绕组功率为38.378 9 kW。热电偶每10 s采集一次温度,当顶层油温变化率小于1 ℃/h时,视为绕组温升达到稳态,记录热电偶温度值。同时,将工况参数作为POD-KSM方法和POD-RBFLP方法的输入,代入代理模型得到温度结果,分别计算与实验记录结果的绝对误差,结果如图10所示。

图10 相同实验工况下本文方法与POD-RBFLP方法的绝对误差
Fig.10 The absolute error of the proposed method and the POD-RBFLP method under the same experimental conditions
从图10可以看出,在该实验工况下,POD-KSM方法与实验结果的绝对误差均小于POD-RBFLP方法,进一步表明本文方法具有较高的计算精度。同时,单次工况计算时间为0.01 s,可以满足实际工程实时预测的需求。相较于现有方法,本文所提方法的计算精度与计算效率有较大幅度提升。通过110 kV油浸式变压器绕组温升实验平台,验证了POD-KSM降阶模型的工程应用价值。
为了实现变压器绕组温度场的快速计算,本文将POD降阶模型与克里金代理模型相结合,提出一种基于POD-KSM的降阶方法;结合110 kV油浸式变压器绕组的仿真模型与实验平台验证该方法的有效性,同时与现有方法进行对比,验证了POD-KSM方法在计算精度和计算效率方面的优越性。主要结论如下:
1)本文所提方法将POD降阶方法与克里金代理模型结合,克里金函数通过构建协方差函数来描述数据点之间的相关性,能够准确地预测未知点的数据值。由于该方法主要考虑数据点的空间分布,因此在处理高维数据时性能较好。
2)对于绕组温度场计算,POD-KSM的计算结果与全阶模型的软件仿真结果基本吻合;对于选取的50组测试工况,最大平均绝对误差为1.19℃,最大相对误差为2.79%;与POD-RBFLP方法相比,在同样的50组测试工况下,POD-RBFLP方法的最大平均绝对误差为2.38℃,最大相对误差为4.51%;同时,结合温升实验数据进行对比,本文所提方法的计算误差更小。由此可见,本文所提方法具有较高的计算精度且优于现有方法。
3)在计算效率方面,使用相同配置的计算机对本文所提方法与POD-RBFLP方法进行对比。结果表明,本文所提方法可将计算效率提升至全阶模型的13.39倍;若不考虑预处理时间,计算某一工况对应的结果仅需要0.006 s,相比于POD-RBFLP而言,效率提升将近67%,充分说明了本文所提方法的高效性。
综上所述,本文所提POD-KSM降阶方法能够有效地计算油浸式电力变压器绕组的稳态温度场,且计算精度与计算效率均优于现有方法。在实际工程应用时,可结合变压器绕组的历史仿真数据建立POD-KSM降阶模型,实现绕组稳态温度场的高保真实时计算,为变压器的数字化运维提供技术支撑。
参考文献
[1] Liu Yunpeng, Li Xinye, Li Huan, et al. Experimental and numerical investigation of the internal temperature of an oil-immersed power transformer with DOFS[J]. Applied Sciences, 2020, 10(16): 5718.
[2] 刘云鹏, 李欢, 高树国, 等. 分布式光纤传感在大型变压器温度和绕组变形监测中的应用研究[J]. 中国电机工程学报, 2022, 42(16): 6126-6135. Liu Yunpeng, Li Huan, Gao Shuguo, et al. Research on application of distributed optical fiber sensing in monitoring of temperature and winding deformation of large transformer[J]. Proceedings of the CSEE, 2022, 42(16): 6126-6135.
[3] 刘云鹏, 黎晏霖, 李欢, 等. 基于布里渊光时域峰值边沿分析的变压器绕组局部热点检测[J]. 电工技术学报, 2024, 39(11): 3486-3498. Liu Yunpeng, Li Yanlin, Li Huan, et al. Local hot spot detection of transformer windings based on Brillouin optical time domain peak edge analysis[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3486-3498.
[4] 刘刚, 胡万君, 郝世缘, 等. 油浸式变压器绕组瞬态温升降阶快速计算方法[J]. 电工技术学报, 2024, 39(3): 643-657. Liu Gang, Hu Wanjun, Hao Shiyuan, et al. Reduced order calculation method of steady temperature rise of oil immersed power transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 643-657.
[5] 刘刚, 郝世缘, 胡万君, 等. 基于子循环自适应串行交错时间匹配算法的油浸式变压器绕组瞬态温升计算[J]. 电工技术学报, 2024, 39(4): 1185-1197. Liu Gang, Hao Shiyuan, Hu Wanjun, et al. Transient temperature rise calculation of oil immersed transformer winding based on sub cyclic adaptive staggered time matching algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1185-1197.
[6] 刘刚, 靳艳娇, 马永强, 等. 油浸式变压器流体场和温度场的数值分析[J]. 变压器, 2017, 54(5): 22-26. Liu Gang, Jin Yanjiao, Ma Yongqiang, et al. Numerical analysis of fluid field and temperature field of oil-immersed transformer[J]. Transformer, 2017, 54(5): 22-26.
[7] 刘云鹏, 高艺倩, 刘刚, 等. 基于U-net神经网络的油浸式变压器绕组流-热耦合快速计算[J]. 中国电机工程学报, 2024, 44(7): 2897-2909. Liu Yunpeng, Gao Yiqian, Liu Gang, et al. Fast calculation of flow-thermal coupling model of oil-immersed transformer windings based on U-net neural network[J]. Proceedings of the CSEE, 2024, 44(7): 2897-2909.
[8] 骆小满, 阮江军, 邓永清, 等. 基于多物理场计算和模糊神经网络算法的变压器热点温度反演[J]. 高电压技术, 2020, 46(3): 860-866. Luo Xiaoman, Ruan Jiangjun, Deng Yongqing, et al. Transformer hot-spot temperature inversion based on multi-physics calculation and fuzzy neural network algorithm[J]. High Voltage Engineering, 2020, 46(3): 860-866.
[9] 张宇娇, 赵志涛, 徐斌, 等. 基于U-net卷积神经网络的电磁场快速计算方法[J]. 电工技术学报, 2024, 39(9): 2730-2742. Zhang Yujiao, Zhao Zhitao, Xu Bin, et al. Fast calculation method of electromagnetic field based on U-net convolutional neural network[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2730-2742.
[10] 钟振鑫, 董玉玺, 张作刚, 等. 用于变压器温度预测的基于物理场数据增强的深度网络[J]. 高压电器, 2023, 59(8): 108-114. Zhong Zhenxin, Dong Yuxi, Zhang Zuogang, et al. Deep network based on physical data enhancement for temperature prediction of transformer[J]. High Voltage Apparatus, 2023, 59(8): 108-114.
[11] 刘刚, 王晓晗, 马永强, 等. 基于控制体—迎风有限元法的变压器绕组二维流体场—温度场耦合计算方法研究[J]. 高压电器, 2021, 57(6): 1-9. Liu Gang, Wang Xiaohan, Ma Yongqiang, et al. Study on coupled calculation method of two dimensional fluid and temperature field of transformer winding based on control volume-upstream FEM[J]. High Voltage Apparatus, 2021, 57(6): 1-9.
[12] 廖才波, 阮江军, 刘超, 等. 油浸式变压器三维电磁-流体-温度场耦合分析方法[J]. 电力自动化设备, 2015, 35(9): 150-155. Liao Caibo, Ruan Jiangjun, Liu Chao, et al. Comprehensive analysis of 3-D electromagnetic-fluid-thermal fields of oil-immersed transformer[J]. Electric Power Automation Equipment, 2015, 35(9): 150-155.
[13] 武卫革, 杜振斌, 刘刚, 等. 大型油浸式变压器绕组温度场仿真及验证[J]. 华北电力大学学报(自然科学版), 2020, 47(6): 68-74. Wu Weige, Du Zhenbin, Liu Gang, et al. Simulation and verification of winding temperature field for large oil immersed transformer[J]. Journal of North China Electric Power University (Natural Science Edition), 2020, 47(6): 68-74.
[14] 杜飞, 田镇熊, 刘宏磊, 等. 采用有限体积法的自然对流换热拓扑优化数值方法[J]. 西安交通大学学报, 2024, 58(8): 103-113. Du Fei, Tian Zhenxiong, Liu Honglei, et al. A numerical method for topology optimization of natural convection heat transfer based on finite volume method[J]. Journal of Xi’an Jiaotong University, 2024, 58(8): 103-113.
[15] 刘刚, 荣世昌, 武卫革, 等. 基于混合有限元法和降阶技术的油浸式变压器绕组2维瞬态流-热耦合场分析[J]. 高电压技术, 2022, 48(5): 1695-1704. Liu Gang, Rong Shichang, Wu Weige, et al. Two-dimensional transient flow-thermal coupling field analysis of oil-immersed transformer windings based on hybrid finite element method and reduced-order technology[J]. High Voltage Engineering, 2022, 48(5): 1695-1704.
[16] 刘刚, 靳立鹏, 胡万君, 等. 基于混合有限元法的油浸式变压器稳态流-热耦合场并行计算方法[J]. 高电压技术, 2024, 50(5): 2259-2269. Liu Gang, Jin Lipeng, Hu Wanjun, et al. Parallel calculation method for steady-state fluid-thermal coupling field of oil-immersed transformer based on hybrid finite element method[J]. High Voltage Engineering, 2024, 50(5): 2259-2269.
[17] 胡万君, 刘刚, 朱章宸, 等. 油浸式电力变压器绕组稳态温升降阶计算方法研究[J]. 中国电机工程学报, 2023, 43(16): 6505-6516. Hu Wanjun, Liu Gang, Zhu Zhangchen, et al. Reduced order calculation method of steady temperature rise of oil immersed power transformer[J]. Proceedings of the CSEE, 2023, 43(16): 6505-6516.
[18] 刘云鹏, 高艺倩, 刘刚, 等. 基于U-net神经网络的35 kV油浸式变压器绕组温度快速计算[J]. 高电压技术, 2024, 50(6): 2716-2725. Liu Yunpeng, Gao Yiqian, Liu Gang, et al. Fast calculation of 35 kV oil-immersed transformer winding temperature based on U-net neural network[J]. High Voltage Engineering, 2024, 50(6): 2716-2725.
[19] 任宏宇, 余瑶怡, 杜雄, 等. 基于优化长短期记忆神经网络的IGBT寿命预测模型[J]. 电工技术学报, 2024, 39(4): 1074-1086. Ren Hongyu, Yu Yaoyi, Du Xiong, et al. IGBT lifetime prediction model based on optimized long short-term memory neural network[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1074-1086.
[20] 马裕超, 汪欣, 钱勇, 等. 基于双传声器和深度学习的变压器状态识别[J]. 电力信息与通信技术, 2024, 22(2): 54-60. Ma Yuchao, Wang Xin, Qian Yong, et al. Transformer status recognition based on dual microphones and deep learning[J]. Electric Power Information and Communication Technology, 2024, 22(2): 54-60.
[21] 张重远, 刘迪程, 高成龙, 等. 基于Twin Builder的110 kV油浸式变压器3维磁场降阶模型及损耗分析[J]. 高电压技术, 2024, 50(3): 941-951.Zhang Zhongyuan, Liu Dicheng, Gao Chenglong, et al. Three-dimensional magnetic field model order reduction and loss analysis of 110 kV oil-immersed transformer based on Twin Builder[J]. High Voltage Engineering, 2024, 50(3): 941-951.
[22] Sideratos G, Hatziargyriou N D. A distributed memory RBF-based model for variable generation forecasting [J]. International Journal of Electrical Power & Energy Systems, 2020, 120: 106041.
[23] Revulagadda A P, Rana R, Suresh B, et al. A multiobjective optimization of 3D-slot jet configuration for enhancement of film cooling in an annular combustor liner[J]. International Journal of Heat and Mass Transfer, 2024, 218: 124745.
[24] Kasdorf S, Harmon J J, Notaroš B M. Kriging methodology for uncertainty quantification in computational electromagnetics[J]. IEEE Open Journal of Antennas and Propagation, 2024, 5(2): 474-486.
[25] 戴成昊, 许文天, 彭佳宁, 等. 基于Kriging代理模型的车轮多边形识别方法研究[J/OL]. 铁道标准设计, 2024: 1-11[2024-03-06]. https://doi.org/10.13238/ j.issn.1004-2954.202309280002. Dai Chenghao, Xu Wentian, Peng Jianing, et al. Research on wheel polygon recognition method based on Kriging proxy model[J/OL]. Railway Standard Design, 2024: 1-11[2024-03-06]. https://doi.org/10. 13238/j.issn.1004-2954.202309280002.
[26] 范贤浩, 刘捷丰, 张镱议, 等. 融合频域介电谱及支持向量机的变压器油浸纸绝缘老化状态评估[J]. 电工技术学报, 2021, 36(10): 2161-2168. Fan Xianhao, Liu Jiefeng, Zhang Yiyi, et al. Aging evaluation of transformer oil-immersed insulation combining frequency domain spectroscopy and support vector machine[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2161-2168.
[27] 刘刚, 胡万君, 郝世缘, 等. 面向数字孪生模型应用的油浸式变压器绕组温度POD-RBFLP降阶计算方法[J]. 中国电机工程学报, 2024, 44(11): 4566-4578. Liu Gang, Hu Wanjun, Hao Shiyuan, et al. Research on reduced order method of temperature rise of oil-immersed power transformer winding based on POD-RBFLP for digital twin model[J]. Proceedings of the CSEE, 2024, 44(11): 4566-4578.
[28] 谢裕清. 油浸式电力变压器流场及温度场耦合有限元方法研究[D]. 北京: 华北电力大学, 2017. Xie Yuqing. Study on coupled finite element method of flow field and temperature field of oil-immersed power transformer[D]. Beijing: North China Electric Power University, 2017.
Abstract In order to quickly obtain the temperature distribution and hot spots of the windings of oil immersed power transformers under various operating conditions, this paper proposes a fast calculation method based on the combination of the proper orthogonal decomposition (POD) and Kriging surrogate model (KSM). Firstly, based on the POD reduction method, the discrete equation system of the transformer temperature field was reduced. Through eigenvector decomposition, a set of orthogonal eigenvectors and corresponding eigenvalues were obtained, and these eigenvectors were arranged in descending order according to the size of the eigenvalues. A small number of optimal modes were selected to approximate the full order model, thereby reducing the model order and accelerating the solution speed; Secondly, analyzed the factors affecting the hot spot temperature of transformer windings, determined important operating parameters, and formed an operating parameter matrix or sample space through Latin hypercube sampling; Then, taking the operating parameters as input and modal coefficients as output, 50 sets are taken as the training set in the sample space. Based on the KSM method, a surrogate model was constructed for the sample space and corresponding modal coefficients. Equ.(14) in the text is the specific function expression of the surrogate model. This method uses the Kriging function to describe the correlation between data points by constructing a covariance function, which can accurately predict the data values of unknown points. Faced with the temperature field problem of windings under new operating conditions, the corresponding POD modal coefficients can be obtained through a surrogate model, and the full field data can be quickly obtained through modal reconstruction, bypassing the complex nonlinear calculation of the full order model and achieving rapid calculation of transformer winding temperature. Finally, to verify the effectiveness of the method, an eight zone numerical heat transfer model for the winding of a 110 kV oil immersed transformer was established, and the algorithm was compared with the calculation results of the simulation software Fluent. The results show that for the selected 50 test conditions, the maximum average absolute error is 1.19℃ and the maximum relative error is 2.79%. In terms of computational efficiency, the method proposed in this paper improves the computational efficiency to 13.39 times that of the full order model. If preprocessing time is not considered, it only takes 0.006 seconds to calculate the corresponding results for a certain condition. To verify the engineering application value of the method proposed in this paper, a temperature rise experimental platform based on product level oil immersed transformer winding structure was constructed. The temperature rise of the winding under certain operating conditions was measured and recorded, and the algorithm calculation results were compared with the experimental results. The calculation errors were all within an acceptable range, verifying the engineering application value of the POD-KSM reduced order model. At the same time, to demonstrate the superiority of the proposed method compared to existing methods, error analysis was conducted on the simulation and experimental results. The results showed that the proposed method outperformed existing methods in terms of computational accuracy and efficiency. The calculation method for steady-state temperature field of transformers proposed in this article can provide technical support for digital operation and maintenance of transformers.
keywords:Oil immersed power transformer, temperature field, proper orthogonal decomposition, Kriging surrogate model
DOI: 10.19595/j.cnki.1000-6753.tces.240544
中图分类号:TM411
国家自然科学基金联合基金(U23B20135)和河北省“三三三人才工程”(C20231116)资助项目。
收稿日期 2024-04-08
改稿日期 2024-05-19
张志宇 男,2000年生,硕士研究生,研究方向为变压器多物理场仿真及降阶计算。E-mail:faculty0627@163.com
刘 刚 男,1985年生,副教授,硕士生导师,研究方向为电气设备多物理场建模及仿真、电力系统时域仿真和电磁场理论及其应用。E-mail:liugang_em@163.com(通信作者)
(编辑 李 冰)