的变化特征。通过分析发现，随着负载变化，E类逆变器的输入直流电流I与输出电流幅值Im的比值β和E类逆变器ZVS状态具有强相关性。并进一步发现β会影响维持ZVS状态下负载R的变化范围。在此基础上，本文提出一种以负载R变化范围作为设计目标，通过选取合适的参数设计E类逆变器参数的方案，并搭建了一台输入电压为40 V、开关频率为500 kHz、额定功率为20 W、额定负载为40 Ω、负载变化范围为±20%的实验样机，验证了本文理论的正确性，样机效率达85.6%。摘要 针对E类逆变器在可变负载条件下难以维持开关管零电压开通（ZVS）状态而导致开关损耗及开关管结温过高等问题，该文提出一种可以适应动态负载变换范围的参数设计方案。该文基于E类逆变器功率及电压平衡关系对其电压波形特征进行分析，揭示了输入直流电流I与输出电流幅值Im的比值β与电压波形对负载敏感度的关系。基于此，提出一种在动态负载变化范围内维持开关管ZVS的设计方案，并搭建了一台开关频率为500 kHz、输入电压为40 V、额定功率为20 W、额定负载为40 Ω、负载变化范围为±20%的实验样机，验证了理论推导和设计方案的可行性，实现了E类逆变器在负载变化范围内均能实现ZVS软开关状态，且逆变器峰值效率达到了85.6%。
关键词：E类逆变器 开关损耗 动态负载 零电压开通
E类逆变器作为一种经典的谐振型逆变器，其主体由单个开关管、并联电容及一个串联谐振电路构成，整体结构简单[1-5]。由于采用谐振结构，其开关管可以工作在零电压开通（Zero Voltage Switching, ZVS）状态，这能极大地降低开关损耗，提高系统效率[6-8]。同时，其单管结构可避免桥式逆变器直通问题，使电路在高频情况下更可靠[9-10]。由于其极低的开关损耗，在1975年E类逆变器被首次提出时，就在3.9 MHz、26 W的情况下实现了96%的效率[3]。
目前，E类逆变器被广泛应用于DC-DC变换器、无线电能传输系统及通信设备等领域[11-14]。尤其随着个人消费电子产品、智能家居及便携式医疗等设备的兴起，对高功率密度及高效稳定设备的需求也日益增加[15-18]。在多数应用场景中，负载往往会发生一定范围的变化[19-20]。然而，E类逆变器的工作状态对负载变化十分敏感，易随着负载变化而难以维持ZVS状态[21-22]，从而增加系统损耗。针对该问题，目前已有多位学者展开研究。文献[9]提出一种带电容切换补偿网络的新型E类逆变器拓扑，通过对补偿网络的电容切换，可提高负载范围并实现恒流恒压输出。文献[21]提出了一种双路E类逆变器，利用耦合电感抑制偶次谐波电流，同时降低了逆变器对负载的敏感度。文献[22]通过切换额外并联电容器，以此在负载变化时保持ZVS，但由于增加额外的并联电容器，会增加电路的复杂性从而增加损耗。文献[23]通过在开关管两端并联额外的可调饱和电抗器来提高负载变化范围，但该方法电路复杂，容易造成额外损耗。
本文提出一种可以适应动态负载变换范围的E类逆变器参数设计方案。基于电压及功率平衡，对E类逆变器工作过程进行分析，并充分利用MOSFET体二极管续流作用，扩大了E类逆变器ZVS的可行域。同时研究了负载变化条件下，开关管电压波形的变化特征。通过分析发现，随着负载变化，E类逆变器的输入直流电流I与输出电流幅值Im的比值β和E类逆变器ZVS状态具有强相关性。并进一步发现β会影响维持ZVS状态下负载R的变化范围。在此基础上，本文提出一种以负载R变化范围作为设计目标，通过选取合适的参数设计E类逆变器参数的方案，并搭建了一台输入电压为40 V、开关频率为500 kHz、额定功率为20 W、额定负载为40 Ω、负载变化范围为±20%的实验样机，验证了本文理论的正确性，样机效率达85.6%。
为了简化分析过程，进行如下假设：①开关管占空比为50%且可以瞬间通断；②忽略开关管的导通电阻；③并联电容C1为线性；④扼流电感Lf足够大（Lf =7R/f），可忽略其交流分量且忽略自身直流电阻；⑤串联谐振品质因数Q足够大（Q≥10），输出电流波形近似为理想正弦；⑥负载R包括串联谐振的寄生电阻。
图1为E类逆变器等效电路模型，其中
为理想电压源，Lf为扼流电感，C1为开关管并联电容，C0和L分别为串联电容和串联电感，R为负载。E类逆变器工作状态如图2所示。当MOSFET导通时，并联电容C1被短路，其电压为0，且电路中C0-L-R进行谐振。当MOSFET关断时is为0，并联电容C1上两端电压逐渐上升，且电路中C1-C0-L-R形成谐振回路。当C1上两端电压谐振至0时，MOSFET导通，即可实现ZVS状态。
图1 E类逆变器基础电路模型
Fig.1 Basic circuit model of Class E inverter
图2 E类逆变器工作状态
Fig.2 Working status of Class E inverter
ZVS电压波形如图3所示。当0＜θ≤π时，MOSFET断开，并联电容C1上产生电压。图3a中绘制了三种常见的E类逆变器ZVS电压波形。
图3 ZVS电压波形
Fig.3 ZVS voltage waveforms
该波形在π时刻以电压为0作为约束条件，但当负载R变动时，该条件难以维持，从而脱离ZVS状态。而由于MOSFET体二极管的存在，使得当vs＜0时，可经体二极管迅速释放，实现ZVS状态[24]，如图3b所示。
当MOSFET关断时（0＜θ≤π），并联电容C1上电流
为
（1）
式中，φ为E类逆变器的相位。
此时MOSFET上电压波形与并联电容C1上电压相等，由此可得
（2）
将电压波形的零点记为α，即
并代入式（1），可得
（3）
假设E类逆变器功率损耗为零，则输入功率等于输出功率，可得
（4）
将式（3）、式（4）联立并化简可得
（5）
（6）
将式（5）、式（6）代入式（2）、式（4），化简可得
（7）
（8）
由式（5）、式（6）、式（8）可知，若Vdc和R确定，I、Im及P由β决定，即与过零点α和相位φ有关。由于扼流电感Lf在一个周期内的电压降落为零，且只在开关管关断的半个周期有值，因此可得
（9）
将式（7）代入式（9）进行化简得到
（10）
将式（10）代入式（7），化简得到为
（11）
根据文献[25]，E类逆变器需要额外的电抗X，其开关管电压波形才能实现ZVS软开关状态，因此需要建立电抗X的表达式进行求解。而由于C0-L0谐振时，其上电压压降为零，所以并联电容C1上的积分与电抗X和负载R上的电压积分应相等。因此可以推导出
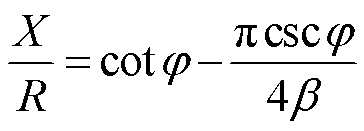（12）
由式（10）～式（12）将E类逆变器的电压、并联电容C1、电抗X与负载R建立等式关系。同时根据式（10）、式（12）可以看出，在角频率ω、并联电容C1和电抗X不变的情况下，R的变动会导致α和φ变化，因此将R、α和φ都作为变量，此时关系如式（13）所示。
（13）
通过对式（13）进行求解，可以得到满足一定角频率ω、电容C1、电抗X的负载R、过零点α和相位φ的解集。为了判断解集是否满足ZVS条件，首先需要找出符合ZVS条件的可行域。由于MOSFET体二极管的续流作用，在电压为负时可通过体二极管续流实现ZVS[24]。同时，由并联电容C1和电抗X需大于零，可得可行域约束条件为
（14）
结合式（13）、式（14）及ZVS约束条件可得ZVS可行域如图4所示。图中蓝色下三角形曲线为C1=0 F，红色曲线φmax和黑色虚线φmin分别由式（14）绘制，灰色区域为ZVS可行域。从图4可以看出，随着过零点α增大，可行域内相位φ的端点值逐渐减小，而当
时φ的范围为(-90°, 0°)，对应于图4中橙黄色上三角形直线。同时当曲线φmax趋近于180°时，其极限为φopt（约为-32.48°）。
图4 ZVS可行域
Fig.4 ZVS feasible region
为了进一步分析ZVS可行域上状态点的特性，将β作为参数变量对状态点进行分析。当β处于φmax极限φopt（约为-32.48°）时，β约为0.537。因此为了分析不同参数β与负载R之间的关系，在图4中分别绘制了β为0.5、0.4、0.3的曲线，并对这三条β曲线上的状态点进行分析。
为了分析可行域内不同参数β情况下状态点与负载R变动范围之间的关系，具体步骤如下：
1）选定β曲线上一个点，定义为初始状态点，得到α和φ，并设定一个初始的额定负载Req。
2）代入式（10）和式（12）得到一组C1、X。
3）将C1、X代入式（13），求得所有α、φ和R的解集。
4）将α、φ和R的解集代入式（14），则可得到满足ZVS状态的负载R变化范围。
分析中频率f =500 kHz，直流电压源Vdc=20 V，额定负载Req = 40 Ω。同时，在β为0.5、0.4、0.3的曲线上分别取50个初始状态点进行遍历。图5为在ZVS可行域以及不同β取值情况下，50个初始状态点的α与求解得到的最大负载Rmax之间的关系，并将Rmax标幺化为Rmax/Req。
从图5可以看出，当β为0.5、0.4、0.3时，最大负载Rmax最大可取到额定负载Req的130%、180%、250%，且随着β不断减小，最大负载Rmax增大的范围越显著。当过零点α=180°时，最大负载Rmax=Req，无法增大。而随着α不断减小，Rmax也随之增大。当α到130°左右时，Rmax开始急剧下降。为了进一步分析β与负载特性之间的关系，从β=0.5的曲线上取3个初始状态点进行具体分析，参数见表1。
图5 不同β条件下α与Rmax变化关系
Fig.5 The relationship between α and Rmax for different β
表1 不同过零点α所对应参数
Tab.1 Parameters for different zero crossing points α
βα/(°)φ/(°)C1/nFX/ΩReq/ΩRmax/Ω 0.5126136.8151.2-24.90-28.46-32.670.580.831.1463.0658.0654.0240404048.653.048.5
将表1中参数代入式（10）和式（12）可得到两个相交曲面，相交部分即为α、φ和R的公共解，如图6所示。图6中淡蓝色曲面由式（10）绘制，淡红色（含虚线）曲面由式（12）绘制，黑色交线部分为公共解。为了更好地分析公共解中负载α、φ和R之间的变化关系，对图6采用俯视，得到负载变化特性曲线如图7所示。
图6 相交曲面与公共解
Fig.6 Intersection curve and common solution
由图7可以看出，图中有两条斜线，黑色斜线与φmin重合，其为负载R=0的解，实际上R只能趋于0；红色长虚线为φmax，因此满足ZVS状态的区域为黑色斜线φmin与红色虚线φmax相夹区域。同时，图7上标记了R为0 Ω、40 Ω、Rmax的状态点，其中X代表过零点α，Y代表相位φ，Z代表负载R。可以看出，初始状态点（Req=40 Ω）会随着R变化而在黑色斜线（公共解）上移动。当负载R减小时，状态点会往φmin方向移动；当负载R增大时，状态点会往φmax方向移动；随着初始状态点的α减小，其黑色移动轨迹变得越来越平缓。
图7 负载变化特性曲线
Fig.7 Load variation characteristic curve
为了验证图7中状态点在黑色轨迹上的电压是否都在ZVS状态，绘制了图7中各状态点的理论电压，如图8所示，分别展示了β=0.5下过零点α为126°、136.8°、151.2°在不同负载R的电压。同时，表2记录了图8中各状态点在不同负载R下的电压峰值VSM。从表2可以看出，在负载范围30～70 Ω内，各状态点VSM在30 Ω时达到最大值，并逐渐减小。在该过程中，α为126°、136.8°、151.2°所对应的电压波形峰值分别约为118.8～95.2 V、102.1～78.2 V、89.4～67.1 V。可以看出，在同一负载R下，α越小，其VSM越高。且从图8可以看出，当负载R达到最大负载Rmax时，都达到极限软开关状态；此时若R再增大，则脱离软开关状态。
图8 开关管电压波形
Fig.8 Voltage waveforms of switching transistor
表2 不同状态点在不同负载下电压峰值VSM
Tab.2 Peak voltage waveform VSM at different operating points under different load conditions
VSM/V 30 Ω40 ΩRmax60 Ω70 Ω 126118.8113.7108.4101.895.2 136.8102.196.688.784.178.2 151.289.483.578.671.667.1
对开关管上电压波形峰值进行进一步分析。式（15）、式（16）是E类逆变器开关管上的峰值电压VSM和峰值电流ISM的表达式。同时，根据VSM和ISM可以得到系统输出功率能力Cp，如式（17）所示。
（15）
（16）
（17）
式中，
。
图9绘制了不同β下初始点的VSM/Vdc、ISMR/Vdc以及Cp趋势。从图9a可以看出，在同一β下，峰值电压VSM随着过零点α减小而不断增大。当α＞130°时，VSM相对较低，且VSM/Vdc变化相对平缓；而当α＜130°时，VSM开始急剧上升，且β越小，VSM/Vdc上升越快。这不仅对MOSFET的耐压能力提出更高要求，同时过高的峰值电压也会增加电路的不稳定性。对于峰值电流ISM，其随着β增大而增大，且只与β大小相关。因此，在选择状态点参数时，只要确定其β值，ISM即可确定。对于输出功率能力Cp，为了保证E类逆变器的输出能力，其应保持一个相对较大的值。从图9c可以看出，不同β下的Cp均在过零点α=180°达到最大值，分别约为0.097、0.087及0.072。且在同一α下，随着β增大，Cp增大；然后随着α不停地衰减，其Cp也不停地衰减，直至趋近于0。因此，在选择状态点参数时，其过零点α不应过小。
图9 不同初始点特性波形
Fig.9 Characteristic waveforms at different initial points
图9分析了不同初始点的VSM、ISM和Cp关系。但随着负载R变化，状态点会在轨迹上移动，从而使α、φ及β都会发生变化，此时VSM、ISM和Cp也会随之变化。为了分析不同初始点在负载R变动情况下的特性，图10绘制了在β=0.5时，不同初始点的VSM、ISM和Cp与负载R变化的关系。由于当初始点α＜130°时，VSM会急剧上升对电路造成影响，且其输出功率Cp也较低，故不适合于电路设计。因此选取7组α＞130°的初始点进行分析，且初始额定负载Req取40 Ω，并将此时状态下的VSM和ISM作为归一化的基准值，归一化后的峰值电压、峰值电流记为
、
。
在β=0.5时，不同初始点的、、Cp与负载R的变化关系如图10所示。从图10a可以看出，负载R越大时，越小，负载R与成反比。其意味着当负载R减小时，MOSFET上的峰值电压会上升，需要在开关管选取时留有一定裕度。同时，随着α越小，变化率更快，因此需要留有更大的裕度。从图10b可以看出，负载R与近似为二次函数关系，且随着初始点的α越小，其顶点峰值越小。但其整体幅值变化相对平缓，在负载范围10～50 Ω内，变化范围仅在1.06～0.90(pu)。因此，在动态负载下，E类逆变器开关管对耐流要求不高。
图10 动态负载变化特性曲线
Fig.10 Dynamic load variation characteristics curves
从图10c可以看出，负载R与输出功率Cp成正比。当负载R达到Rmax时，不同初始点的Cp都能达到0.1附近。但随着负载范围变大，其Cp明显下降。例如，在负载为40 Ω时，各曲线上的Cp分别为0.097、0.095、0.092、0.089、0.084、0.078、0.071，其值随着初始点α的减小而逐渐减小。由此，为了得到一个较好的动态特性，E类逆变器需要选择耐压能力相对较好的开关管，且其初始状态点α的选择不宜过小。
基于上述理论分析提出一种E类逆变器的设计方案。假设给定其直流电源电压Vdc为40 V，额定负载Req为40 Ω，负载变动范围为±20%（32～48 Ω），开关频率f取500 kHz（f取其他值时，负载变化范围依旧成立），额定功率P为20 W。
由式（8）可以确定β的值为
b=0.5负载变动情况见表3。根据表3可以看到，当初始点为α=151.2°、φ=-32.67°时，其负载变动可以达到±20%。将Vdc及Req代入表3，可以计算出峰值电压VSM、峰值电流ISM。
表3 β=0.5负载变动情况
Tab.3 Load variation under the region factor β=0.5
变动范围初始点/(°)RVSM/VdcISMR/VdcCp ±10%α=162φ=-35.300.9Req3.851.540.083 Req3.681.500.091 1.1Req3.531.460.098 ±20%α=151.2φ=-32.670.8Req4.331.230.071 Req3.981.500.084 1.2Req3.651.700.098 ±30%α=136.8φ=-28.460.7Req5.431.520.053 Req4.741.500.070 1.3Req4.051.400.091
当R=Req=40 Ω时：
，
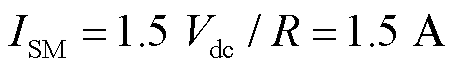；当R=0.8Req=32 Ω时：
，
；当R=1.2Req=48 Ω时：
，
。
由此可知，在负载32～48 Ω变化范围内，峰值电压VSM变化范围为146～173.2 V，峰值电流ISM变化范围为1.42～1.54 A。因此，开关管至少需要200 V耐压以及2 A耐流。再将α=151.2°、φ= -32.67°代入式（11）、式（13），得到并联电容C1和电抗X分别为
开关管型号为IRF740，根据数据手册可以查到其Coss=160 pF，Crss=17 pF。根据文献[25]，并联电容C1需减去MOSFET的输出电容Cout，输出电容Cout计算公式如式（18）所示。
（18）
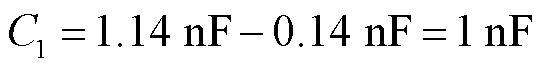（19）
而串联电容C0、串联电感L以及扼流电感Lf为
根据上述计算结果，本文采用LTspice仿真软件并导入了IRF740的Spice模型进行仿真，仿真实验参数见表4。图11绘制了在负载R为32、40、 48 Ω时，MOSFET上的仿真电压波形及电流波形。
表4 实验参数
Tab.4 Experimental parameters
参数数值 仿真实验 开关频率f/kHz500500 直流输入电压Vdc/V4040 扼流电感Lf/μH并联电容C0/nF串联电容C1/nF串联电感L/μH55510.9212755610.92128
从图11a可以看出，当负载R=32 Ω时，其峰值电压VSM=169.6 V，比理论值173.2 V低约3.6 V（误差约为-2.08%）；当负载R=40 Ω时，其VSM=161.5 V，比理论值159.2 V高约2.3 V（误差约为1.44%）；当负载R=48 Ω时，此时接近ZVS软开关极限，其VSM=153.7 V，比理论值146 V高约7.7 V（误差约为5.27%）。同时，由仿真结果可以看出，在这三种负载条件下，MOSFET上电压波形都满足ZVS软开关状态。
图11 仿真波形
Fig.11 Simulated waveforms
从图11b可以看出，当负载R=32 Ω时，其峰值电流ISM=1.51 A，比理论值1.54 A低约0.03 A（误差约为-1.95%）；当负载R=40 Ω时，其ISM=1.46 A，比理论值1.5 A低约0.04 A（误差约为-2.67%）；当负载R=48 Ω时，其ISM=1.37 A，比理论值1.42 A低约0.05 A（误差约为-3.52%）。由此可以看出，在这三种负载条件下，MOSFET上电流波形峰值变化不大。
为了验证上述参数设计的有效性，搭建了一台试验样机，如图12所示，实验参数见表4。同时，在负载R为32、40、48、60 Ω时，对MOSFET上的电压波形进行测量，如图13所示。从图13可以看出，当R=32 Ω时，VSM实验值为167 V，比理论值173.2 V低6.2 V（约为-3.58%）；R=40 Ω时，VSM实验值为158 V比理论值159.2 V低1.2 V（约为-0.75%）；R=48 Ω时，VSM实验值为148 V，比理论值146 V高2 V（约为1.37%），且此时处于临界ZVS软状态，系统效率达到峰值为85.6%；当负载 R=60 Ω，E类逆变器处于硬开关状态。同时，由实验结果可以看出，在上述参数设计下，E类逆变器可在负载R变动范围为32～48 Ω时，都处于ZVS软开关状态。
图12 实验样机
Fig.12 Experimental prototype
图13 实验波形对比
Fig.13 Comparison of experimental waveforms
系统在运行状态中的损耗分布如图14所示，其中扼流电感损耗采用实验测量电流的二次方乘以其内阻所得，通态损耗为实验测量开关管电流有效值的二次方乘以通态电阻所得。由图14可知，扼流电感损耗占比最大，其次分别是驱动损耗、通态损耗及其他损耗。这是因为在较大负载R情况下，E类逆变器需要较大感值电感作为扼流电感，从而增大了电感内阻，导致系统损耗上升。所以，尽可能地提高系统频率，减小电感感值和器件体积是提高电路效率的关键。
图14 损耗分布
Fig.14 Loss distribution
E类逆变器特性比较见表5。由表5可知，相较于现有宽负载范围下E类逆变器电路ZVS方案，所提的参数设计方案可在不增加额外电路及控制回路的情况下，在宽负载范围下，实现ZVS状态。这不仅降低了系统的复杂性，而且提高了系统的稳定性。
表5 E类逆变器特性比较
Tab.5 Performance comparison of Class E inverter
方法额外电路系统复杂度系统稳定性 切换补偿网络[9]需要中等较可靠 耦合电感[21]并联电容支路[22]饱和电抗器调谐[23]本文所提设计方案需要需要需要不需要复杂中等中等简单较可靠较可靠较可靠可靠
本文在理论分析与仿真的基础上提出一种适用于较宽负载变化范围的E类逆变器参数设计方案。通过一台500 kHz的实验样机，验证了所提出方案的可行性与自由度，所得结论如下：
1）通过对ZVS状态下E类逆变器工作状态进行分析，发现利用MOSFET体二极管特性可以扩大ZVS可行域范围。并发现E类逆变器的β越小，其负载R的变化范围越宽。
2）通过选取合适的参数β可以使E类逆变器在一定负载变化范围下保持ZVS状态。同时本文根据E类逆变器峰值电压VSM、电流ISM以及输出功率能力Cp与参数之间的关系，给出了基于负载变动范围作为参数的设计方案。
3）通过对负载变动±20%范围的设计方案进行仿真与实验，验证了上述理论分析的准确性，以及本文所提出的设计方案的可行性。样机的实验结果与理论计算结果基本相符，且整机的峰值效率达到了85.6%。
参考文献
[1] 管乐诗, 刘畅, 王懿杰, 等. 宽负载范围超高频功率变换技术: 谐振参数设计与匹配网络构建[J]. 电工技术学报, 2022, 37(24): 6170-6182. Guan Yueshi, Liu Chang, Wang Yijie, et al. Wide load range very high frequency power conversion technology: resonant parameter design and matching network construction[J]. Transactions of China Electro-technical Society, 2022, 37(24): 6170-6182.
[2] Sensui T, Koizumi H. Load-independent Class E zero-voltage-switching parallel resonant inverter[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 12805-12818.
[3] Sokal N O, Sokal A D. Class E-a new class of high-efficiency tuned single-ended switching power amplifiers[J]. IEEE Journal of Solid-State Circuits, 1975, 10(3): 168-176.
[4] 张俊伟, 赵晋斌. 基于支路振荡法E类逆变器软开关实现研究[J]. 电力系统保护与控制, 2021, 49(1): 133-140. Zhang Junwei, Zhao Jinbin. Research on soft switch implementation of an E-type inverter based on the branch oscillation method[J]. Power System Protection and Control, 2021, 49(1): 133-140.
[5] Zhang Shu, Wang Chen, Yue Fengfa, et al. A 500-kHz ZVS Class-E type DC-DC converter with two anti-series mosfets topology[J]. IEEE Transactions on Power Electronics, 2023, 38(9): 10810-10820.
[6] 李争, 唐明磊, 解波, 等. 无线电能传输零电压开关角跟踪和动态电容补偿矩阵复合控制策略[J]. 电工技术学报, 2024, 39(12): 3602-3615. Li Zheng, Tang Minglei, Xie Bo, et al. Composite control strategy of zero voltage switch angle tracking and dynamic capacitance compensation matrix for wireless power transfer[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3602-3615.
[7] 孙瑄瑨, 荣德生, 王宁. 具有谐振软开关的高增益耦合电感组合Boost-Zeta变换器[J]. 电工技术学报, 2024, 39(6): 1830-1842. Sun Xuanjin, Rong Desheng, Wang Ning. High step-up integrated boost-zeta converter with coupled inductor and resonant soft-switching[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1830-1842.
[8] 张婷婷, 赵晋斌, 邓平, 等. 基于Boost-class E变换器的高升压比S.E.L驱动电源设计与研究[J]. 电气传动, 2022, 52(13): 35-40. Zhang Tingting, Zhao Jinbin, Deng Ping, et al. Design and research of high voltage ratio driving power on S.E.L based on boost-Class E converter[J]. Electric Drive, 2022, 52(13): 35-40.
[9] 李厚基, 刘明, 杨煜志, 等. 基于E类逆变电路的宽负载范围软开关无线充电补偿网络研究[J]. 中国电机工程学报, 2022, 42(20): 7375-7387. Li Houji, Liu Ming, Yang Yuzhi, et al. Research on wide load range soft switching wireless charging compensation network based on Class E inverter circuit[J]. Proceedings of the CSEE, 2022, 42(20): 7375-7387.
[10] Yue Rui, Wang Chunfang, Li Houji, et al. Constant-voltage and constant-current output using P-CLCL compensation circuit for single-switch inductive power transfer[J]. IEEE Transactions on Power Electronics, 2021, 36(5): 5181-5190.
[11] An Xin, Yan Xin, Morath H, et al. A 60-GHz 8.4-dBm output power OOK-capable VCO based on a feedback Class-E amplifier[J]. IEEE Microwave and Wireless Technology Letters, 2023, 33(3): 283-286.
[12] Sekiya H, Tokano K, Zhu Wenqi, et al. Design procedure of load-independent Class-E WPT systems and its application in robot arm[J]. IEEE Transactions on Industrial Electronics, 2023, 70(10): 10014-10023.
[13] Zhang Junwei, Zhao Jinbin, Mao Ling, et al. ZVS operation of Class-E inverter based on secondary side zero compensation switching at variable coupling coefficient in WPT[J]. IEEE Transactions on Industry Applications, 2022, 58(1): 1022-1031.
[14] 李江南, 李锐华, 胡波. 一种单发射多接收磁耦合式多频谐振无线电能传输方法[J]. 电气技术, 2023, 24(11): 1-9, 27. Li Jiangnan, Li Ruihua, Hu Bo. A single-transmitter-multiple-receiver magnetic coupling multi-frequency resonant wireless power transfer method[J]. Electrical Engineering, 2023, 24(11): 1-9, 27.
[15] 唐丁源, 周玮, 黄亮, 等. 具有恒压输出特性的电场耦合式动态无线电能传输技术[J]. 电工技术学报, 2023, 38(20): 5385-5397. Tang Dingyuan, Zhou Wei, Huang Liang, et al. Dynamic electric-filed coupled wireless power transfer system with constant voltage output characteristics[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5385-5397.
[16] 李振杰, 霍玉昇, 何家房, 等. 兼具强抗偏移性与功率可控性的可重构无线充电系统研究[J]. 电源学报, 2023, 21(6): 24-34. Li Zhenjie, Huo Yusheng, He Jiafang, et al. Research on reconfigurable wireless charging system with strong anti-misalignment capability and power controllability[J]. Journal of Power Supply, 2023, 21(6): 24-34.
[17] 管乐诗, 程怡, 施震宇, 等. 一种10 MHz高频DC-DC功率变换器及其同步整流技术[J]. 电工技术学报, 2023, 38(18): 5029-5038. Guan Yueshi, Cheng Yi, Shi Zhenyu, et al. A 10 MHz high frequency DC-DC power converter and its synchronous rectification technology[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 5029-5038.
[18] 廖志贤, 李彬彬, 索之闻, 等. 磁集成三端口电力电子变压器的改进控制方法[J]. 电力系统自动化, 2023, 47(11): 133-143. Liao Zhixian, Li Binbin, Suo Zhiwen, et al. Improved control method for three-port power electronic trans-former based on magnetic integration[J]. Automation of Electric Power Systems, 2023, 47(11): 133-143.
[19] 麻秀范, 刘子豪, 王颖, 等. 考虑通信负载迁移及储能动态备电的5G基站光伏消纳能力研究[J]. 电工技术学报, 2023, 38(21): 5832-5845, 5922. Ma Xiufan, Liu Zihao, Wang Ying, et al. Research on photovoltaic absorption capacity of 5G base station considering communication load migration and energy storage dynamic backup[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5832-5845, 5922.
[20] Suetsugu T, Kazimierczuk M K. Design procedure of class-E amplifier for off-nominal operation at 50% duty ratio[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2006, 53(7): 1468-1476.
[21] 黄晓生, 陈为, 陈庆彬. 用于WPT的双路E类逆变器功率合成拓扑及其电感耦合集成[J]. 中国电机工程学报, 2015, 35(21): 5577-5584. Huang Xiaosheng, Chen Wei, Chen Qingbin. Topology of the power combination with dual class E inverters and magnetics integration of coupled inductors for WPT applications[J]. Proceedings of the CSEE, 2015, 35(21): 5577-5584.
[22] Huang Liang, Hu A P. Power flow control of capacitive power transfer by soft switching of extra capacitors in Class E converter[C]//2018 IEEE 4th Southern Power Electronics Conference (SPEC), Singapore, 2018: 1-5.
[23] Aldhaher S, Luk P C K, Whidborne J F. Tuning class E inverters applied in inductive links using saturable reactors[J]. IEEE Transactions on Power Electronics, 2014, 29(6): 2969-2978.
[24] He Liangzong, Guo Dong. Compound voltage clamped class-E converter with ZVS and flexible power transfer for WPT system[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 7123-7133.
[25] Ayachit A, Corti F, Reatti A, et al. Zero-voltage switching operation of transformer Class-E inverter at any coupling coefficient[J]. IEEE Transactions on Industrial Electronics, 2019, 66(3): 1809-1819.
Abstract The Class E inverter stands out due to its simple structure and application of resonant inverter technology, allowing it to operate stably in a zero voltage switching (ZVS) state. This characteristic significantly reduces switching losses, improves overall system efficiency, and effectively mitigates common penetration risks, making the circuit more reliable in high-frequency operating environments. However, maintaining the ZVS state of the Class E inverter under variable load conditions poses significant challenges, leading to considerable losses and imposing serious limitations on its application scenarios. Therefore, reducing the load sensitivity of Class E inverters is a key issue. This paper fully utilizes the continuous conduction characteristics of the MOSFET body diode to expand the feasible ZVS operating area of the Class E inverter. In-depth analysis shows that the ratio β between the input DC current I and the amplitude of the output current Im of the Class E inverter is significantly correlated with the range of load variation under ZVS conditions. This insight has led to the proposal of a parameter design scheme for the Class E inverter that can adapt to the range of dynamic load variations.
First, this paper analyzes the operating process of the Class E inverter based on voltage and power balance and establishes a mathematical model. Subsequently, the body diode of the MOSFET is utilized to expand the feasible ZVS operating area of the Class E inverter. Building on this, the paper analyzes the characteristics of the switch voltage waveform changing with load variations. The analysis demonstrates that the value of parameter β significantly impacts the trajectory of the operating point of the Class E inverter within the ZVS feasible region. Subsequently, the paper conducts a comparative analysis of the peak voltage, peak current, and output power capabilities at different operating points. Finally, based on the results of the aforementioned analysis, this paper proposes a design scheme for the parameters of the Class E inverter that can accommodate a dynamic range of load variations.
Based on the theoretical analysis presented above, this paper builds an experimental prototype with a rated load of 40 Ω and a load variation range of ±20%. When the load resistance is 32 Ω, 40 Ω, and 48 Ω, the theoretical peak voltages are 173.2 V, 159.2 V, and 146 V, respectively. The simulation results are 169.6 V, 161.5 V, and 153.7 V, respectively, while the experimental results are 167 V, 158 V, and 148 V, with errors of approximately -3.58%, -0.75%, and 1.37%. At the same time, the peak efficiency of the experimental prototype is 85.6%. These results validate the feasibility of the proposed parameter design scheme and demonstrate that the approach suggested in this paper can expand the load variation range while reducing switching losses under ZVS conditions in Class E inverters, thereby improving system efficiency.
The following conclusions can be drawn from the simulation and experimental analysis: (1) Utilizing the body diode characteristics of osfet can expand the feasible range of ZVS. It has been found that the smaller the ratio β, the broader the range of load variations it can accommodate. (2) By selecting suitable parameter β, the Class E inverter can maintain ZVS operation within a certain range of load variations. Meanwhile, this paper provides a design scheme that meets the load variation range. (3) Simulating and experimentally validating the proposed design scheme within a ±20% range of load variations demonstrates the feasibility of the scheme, and the peak efficiency of the entire system reached 85.6%.
Keywords：Class E inverter, switch loss, variable load, zero voltage switching (ZVS)
上海市自然科学基金资助项目（21ZR1425300）。
收稿日期 2024-04-08
改稿日期 2024-10-04
DOI: 10.19595/j.cnki.1000-6753.tces.240551
中图分类号：TM464
毛 玲 女，1981年生，副教授，研究方向为电动汽车有序充电、动力电池建模、状态估计及梯次利用、电动汽车与电网的互动等。E-mail：maoling2290@shep.edu.cn
赵晋斌 男，1972年生，教授，博士生导师，研究方向为电力电子电路、装置和系统、智能和模块化控制电力电子电路等。E-mail：zhaojinbin@shiep.edu.cn（通信作者）
（编辑 赫 蕾）