 与
与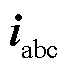 分别为工频侧三相电压和三相电流,
分别为工频侧三相电压和三相电流,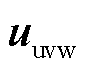 与
与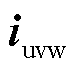 分别为低频侧三相电压和三相电流,
分别为低频侧三相电压和三相电流,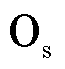 和
和 分别为工频侧中性点与低频侧中性点,
分别为工频侧中性点与低频侧中性点,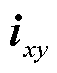 为桥臂xy的桥臂电流,
为桥臂xy的桥臂电流,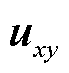 为桥臂xy的输出桥臂电压(x=a, b, c; y=u, v, w)。
为桥臂xy的输出桥臂电压(x=a, b, c; y=u, v, w)。摘要 低频输电是一种兼具传统交直流输电技术优势的新型输电技术,在海上风电送出、城市电网柔性互联等场景具有良好的应用前景。当柔性低频输电系统低频线路不对称故障时,模块化多电平矩阵变换器(M3C)通常采用故障控制策略实现相应的控制目标,使得故障电流的特征受到影响,进而影响线路保护的性能。该文首先分析了M3C电容电压不均衡原因,针对电容电压均衡控制限制M3C负序电流自由度问题,采用一种基于环流控制的电容电压均衡策略,实现了M3C电容电压均衡控制与负序电流控制相互解耦;其次,基于电流差动保护动作特性,提出一种基于控保协同的柔性低频输电系统保护性能提升方案。该方案以提升电流差动保护的性能为目标,综合M3C故障控制策略确定负序电流控制方案,并结合M3C桥臂过电流问题选取负序电流参考值;最后,在PSCAD/EMTDC中搭建了相应的柔性低频输电系统仿真模型,通过大量的仿真实验,验证了所提方案的可行性和有效性。
关键词:柔性低频输电系统 模块化多电平矩阵变换器 负序电流控制 电容电压均衡 电流差动保护
低频输电技术通过降低输电频率的方法,降低输电线路阻抗与电缆充电功率,以此提高输电线路输送容量,延长电能输送距离,是一种兼顾经济效益和技术优势的新型输电技术,具有良好的发展前景与应用空间[1-3]。低频输电作为一种新型输电方式,兼具传统工频交流输电与高压直流输电的优势[4-6]。相较于高压直流输电,柔性低频输电仍然采用交流电形式输送电能,保留了交流输电灵活变压、电流过零开断等特点,避免了直流输电中面临的故障电流难开断、直流不易变压等问题[7-9];相较于传统工频交流输电,在直流和工频之间选择合适的输电频率,有效地提高了线路的输电能力,减少了线路电抗对于功率传输的影响,改善了传统工频交流输电中输送容量易受长距离输电线路容升效应限制的问题[10]。
目前,已经开展了有关柔性低频输电系统的拓扑结构、经济性分析、稳定性分析以及大功率变频器等多方面研究[11-18]。变频器作为变换系统频率、传输系统能量的关键设备,影响着整个低频输电系统的运行,是低频输电技术研究的重点之一。模块化多电平矩阵变换器(Modular Multilevel Matrix Converter, M3C)因其具有灵活可控、无中间直流环节以及成本相对更低等优势,是目前被认为最适用于低频输电系统的大功率变频器[19-21]。目前已开展了有关M3C控制策略的研究。在稳态运行时,文献[22]将M3C视为3个子换流器并联结构,实现了工频侧与低频侧的独立控制。文献[23]通过建立子换流器的差模-共模数学模型,并将桥臂电容电压进行双αβ0变换,实现了M3C三个部分的稳定控制。在故障运行时,文献[24]通过选取不同的控制目标,控制M3C所提供的正负序电流,实现了系统侧消除有功/无功功率波动的需求;文献[25]通过负序控制消除子模块有功功率不平衡的方式,实现了在不对称故障下M3C的电容电压均衡;文献[26]通过控制M3C采用抑制负序电流为零的方法限制故障电流大小,避免M3C存在过电流的风险。
上述文献均采用负序电流控制实现一定的控制目标,但并未考虑负序电流对于线路保护性能的影响。目前有关负序电流对于线路保护的影响在基于模块化多电平变换器(Modular Multilevel Converter, MMC)的柔性直流输电系统中开展了一些研究。文献[27]指出MMC采用不同控制模式时所提供的线路电流有所变化,影响了线路距离保护的动作性能。文献[28]指出当交流系统两侧换流器均采用负序电流抑制控制策略时,以电流量构成的交流保护可能会出现拒动现象,因此需要为交流线路提供一定的负序电流。文献[29]分析了海上风电交流系统中MMC一侧为线路提供负序电流时,将使得线路两侧电流产生一定的相位差,进而影响距离保护、电流差动保护以及零序保护的动作性能。类比于上述问题,在柔性低频输电系统中负序电流的大小也将对线路保护的可靠性产生一定的影响。然而目前对于柔性低频输电系统的线路保护研究相对较少,尚未开展负序电流控制对线路保护性能影响的理论分析研究。
鉴于上述问题,本文以柔性低频输电系统为研究对象,提出一种基于控保协同的柔性低频输电系统电流差动保护性能提升方案。首先,分析了不对称故障下M3C电容电压不均衡原因,指出通过M3C负序电流控制实现电容电压均衡限制了M3C负序电流的自由度,并采用一种基于环流控制的电容电压均衡策略,实现了M3C电容电压均衡控制与负序电流控制相互解耦;其次,基于电流差动保护的动作特性,分析了负序电流大小对线路电流差动保护影响,以提升电流差动保护的性能为目标,综合M3C故障控制策略确定负序电流控制方案,并结合M3C桥臂过电流问题选取负序电流参考值。最后,在PSCAD/EMTDC中搭建相应的柔性低频输电系统仿真模型,对所提方案的可行性、可靠性以及负序电流参考值选取的合理性进行仿真验证。
柔性低频输电系统结构如图1所示。送端工频系统通过PQ站送出低频电能,经过低频线路将电能输送到线路对端,VF站将低频电能转换为工频电能传输给受端工频系统。
M3C的电路拓扑如图2所示,一共包含九条桥臂,每条桥臂均由一个桥臂电感L和N个级联子模块构成,其中子模块为基于IGBT的全桥功率模块。由图2可知,工频系统和低频系统通过M3C相互连接,其中 与
与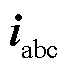 分别为工频侧三相电压和三相电流,
分别为工频侧三相电压和三相电流,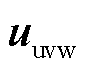 与
与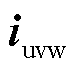 分别为低频侧三相电压和三相电流,
分别为低频侧三相电压和三相电流,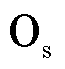 和
和 分别为工频侧中性点与低频侧中性点,
分别为工频侧中性点与低频侧中性点,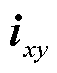 为桥臂xy的桥臂电流,
为桥臂xy的桥臂电流,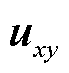 为桥臂xy的输出桥臂电压(x=a, b, c; y=u, v, w)。
为桥臂xy的输出桥臂电压(x=a, b, c; y=u, v, w)。
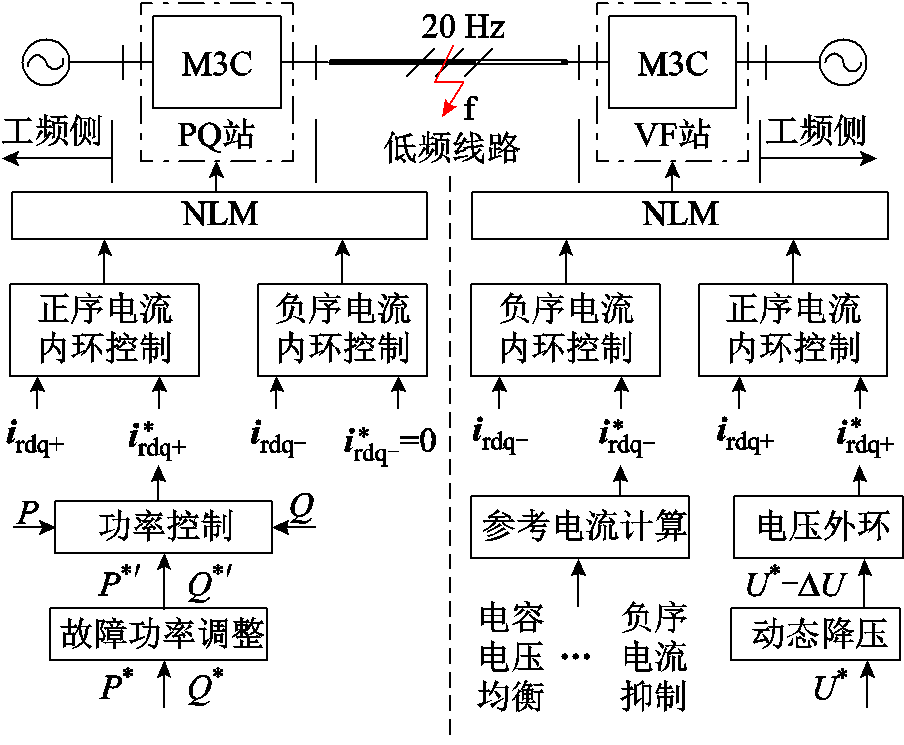
图1 柔性低频输电系统拓扑及低频侧故障控制框图
Fig.1 Flexible low frequency transmission system topology and low-frequency side fault control block diagram transmission system
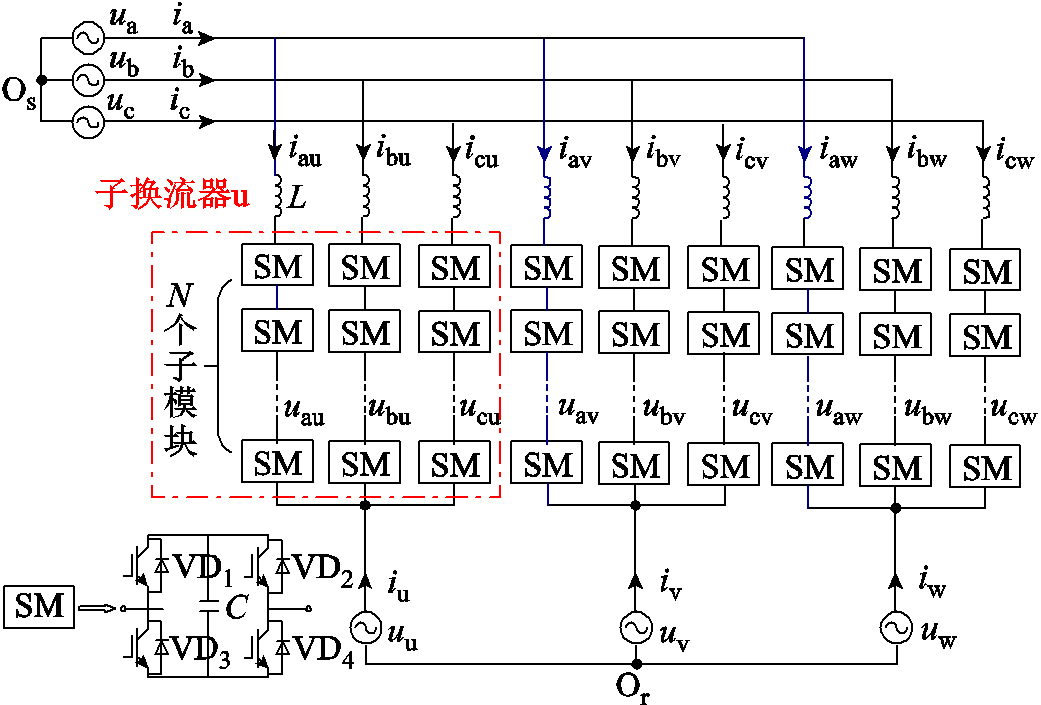
图2 M3C电路拓扑
Fig.2 Circuit topology of the M3C
图2中,工/低频侧每相均连接了三个桥臂支路,以低频侧u相为例,共连接了au、bu、cu三个桥臂支路,可将三个桥臂支路共同定义为子换流器u,因此M3C从低频侧可视为子换流器uvw的并联,在工频侧可视为子换流器abc的并联。
根据基尔霍夫电压定律及图2中M3C桥臂与两侧系统的电路关系,列写整个M3C的矩阵式电路方程为
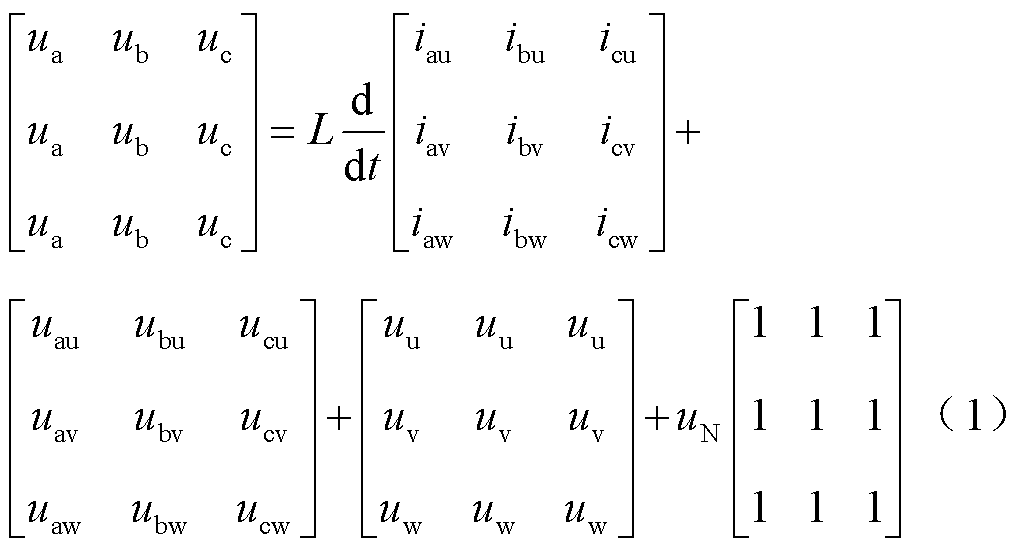
式中,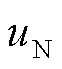 为工频侧中性点
为工频侧中性点 与低频侧中性点
与低频侧中性点 之间的电压差。
之间的电压差。
由式(1)分析可知,每个桥臂支路的电压和电流均包含工频侧与低频侧两种频率分量。为了实现工频侧与低频侧的独立控制,需要对两种频率的电气分量进行解耦。本文采用双αβ0变换实现工频侧与低频侧的电气分量解耦[16,23-24,30]。将矩阵式电路方程式进行双αβ0变换,根据双αβ0变换的计算过程,对各电气量解耦后方程为
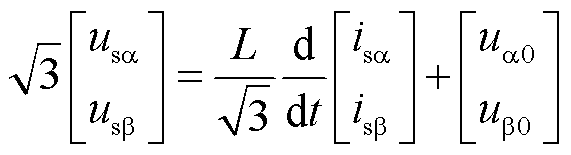 (2)
(2)
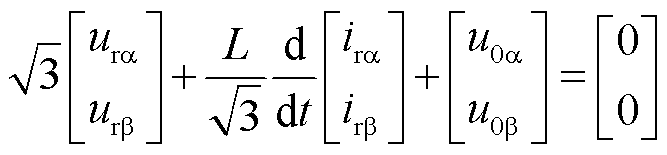 (3)
(3)
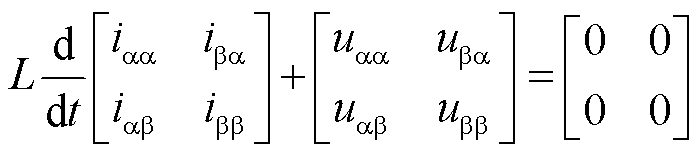 (4)
(4)
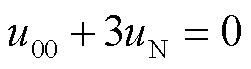 (5)
(5)
式中,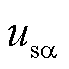 、
、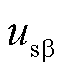 与
与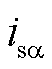 、
、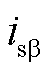 分别为工频侧电压和电流的
分别为工频侧电压和电流的 分量;
分量;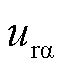 、
、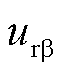 与
与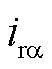 、
、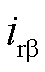 分别为低频侧电压和电流的
分别为低频侧电压和电流的 分量;
分量;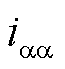 、
、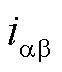 、
、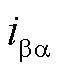 、
、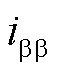 与工/低频侧电流无关,仅在M3C内部流通,表示循环电流;
与工/低频侧电流无关,仅在M3C内部流通,表示循环电流;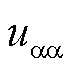 、
、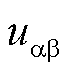 、
、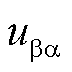 、
、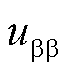 为子换流器内电压波动;
为子换流器内电压波动;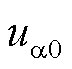 、
、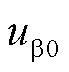 、
、 、
、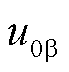 为子换流器间电压波动;
为子换流器间电压波动; 为桥臂电压总和,若忽略电感上的压降,共模电压为0。
为桥臂电压总和,若忽略电感上的压降,共模电压为0。
式(2)~式(4)共同构成了M3C在双 坐标系下的解耦模型,实现了工频侧、低频侧以及环流部分的解耦,便于对各部分进行独立控制以实现M3C的稳定运行。
坐标系下的解耦模型,实现了工频侧、低频侧以及环流部分的解耦,便于对各部分进行独立控制以实现M3C的稳定运行。
M3C工频侧接入工频系统,线路电压由工频系统提供,稳态时工频侧外环采用定电容电压/定无功功率控制。柔性低频输电系统线路两端均连接电力电子设备,需要主动构建线路电压,PQ站M3C稳态时一般采用定功率控制,VF站M3C低频侧外环采用定交流电压控制构建线路电压,控制框图详见附录附图1和附图2。
在低频线路发生不对称故障时, M3C低频侧转换为故障控制策略。本文VF站M3C低频侧故障控制框图如图3所示,其中负序控制电流参考值由抑制负序电流、实现M3C电容电压均衡等相应控制目标决定[24-26]。
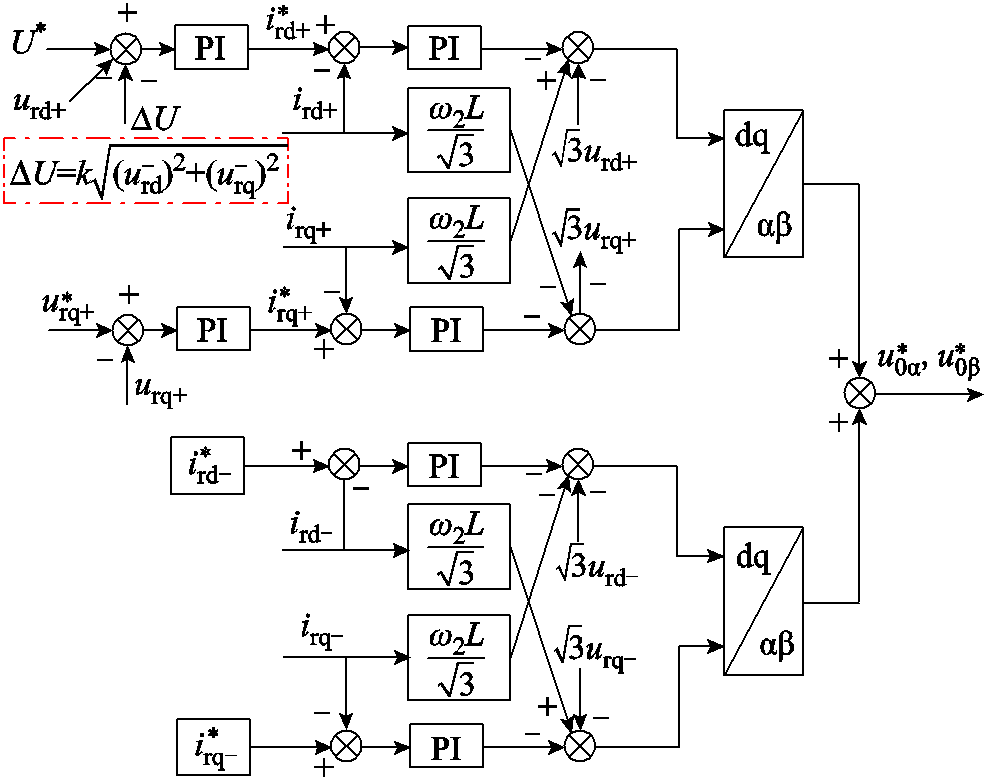
图3 M3C低频侧不对称故障控制框图
Fig.3 Asymmetric fault control block diagram of the M3C low frequency side
M3C作为柔性低频输电系统中连接工/低频系统的关键设备,通过桥臂中子模块电容充放电过程实现两侧系统的能量交换,其中桥臂电容电压可表示为[25]
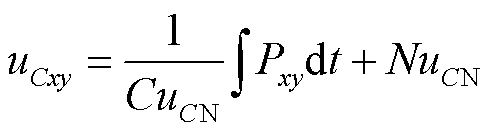 (6)
(6)
式中,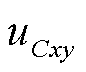 为桥臂
为桥臂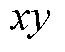 的总电容电压;
的总电容电压;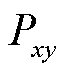 为流经桥臂
为流经桥臂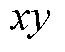 的有功功率;
的有功功率;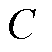 为桥臂电容值的总和;
为桥臂电容值的总和;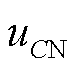 为桥臂电容电压额定值;N为桥臂中所包含子模块数量。
为桥臂电容电压额定值;N为桥臂中所包含子模块数量。
由式(6)可知,桥臂有功功率中直流分量能够使得桥臂电容电压偏移,影响桥臂电容电压的大小。在低频侧不对称故障工况下,根据工频侧、低频侧三相电压电流,计算得到低频侧发生不对称故障情况下每个桥臂的有功功率,并提取其中的直流分量,可得M3C桥臂有功功率直流分量表达式如式(7)~式(10),详细推导过程参见附录第2节。
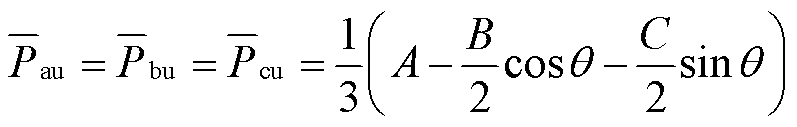 (7)
(7)
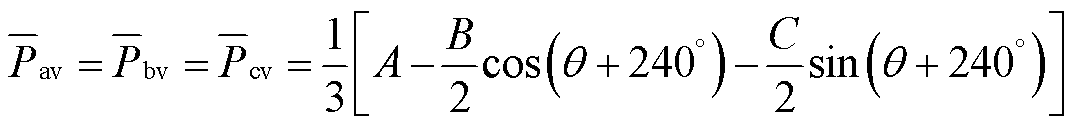 (8)
(8)
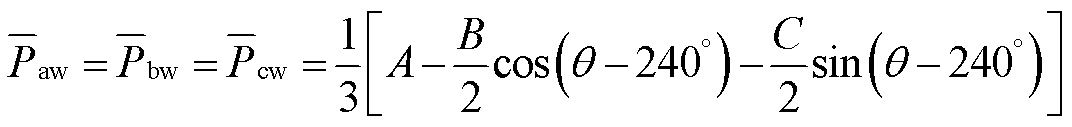 (9)
(9)
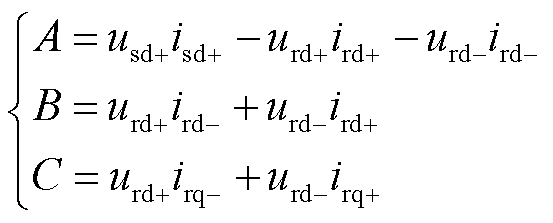 (10)
(10)
式中,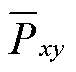 为桥臂
为桥臂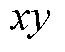 的有功功率直流分量;
的有功功率直流分量;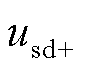 、
、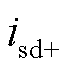 分别为工频侧电压电流的正序d轴分量;
分别为工频侧电压电流的正序d轴分量;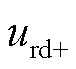 、
、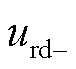 分别为低频侧电压的正负序d轴分量;
分别为低频侧电压的正负序d轴分量;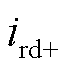 、
、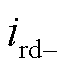 、
、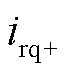 、
、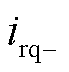 分别为低频侧电流的dq轴正负序分量;
分别为低频侧电流的dq轴正负序分量;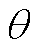 为低频侧正负序分量的夹角。
为低频侧正负序分量的夹角。
根据式(7)~式(10)可知,低频侧负序分量将对桥臂有功功率直流分量产生影响,进而对M3C桥臂电容电压产生影响。根据式(6)列写 M3C的9个桥臂电容电压直流分量与桥臂有功功率直流分量关系为
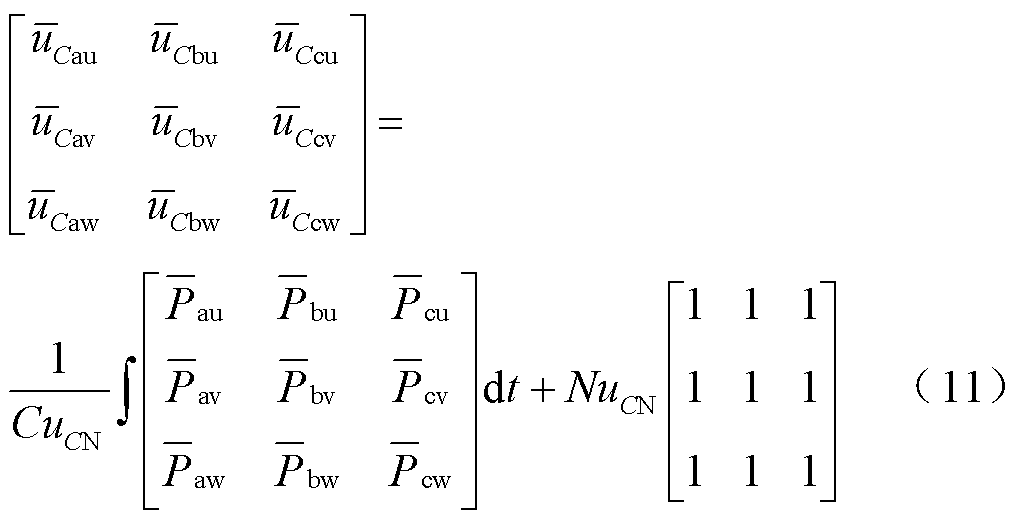
对式(11)进行基于等功率的双αβ0变换,变换过程详见附录第2节。将式(7)~式(10)代入并省略其中为零的分量,得到低频侧子换流器间电容电压不均衡分量与有功功率不平衡分量的关系为
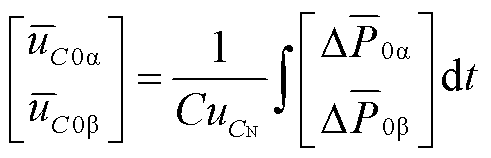 (12)
(12)
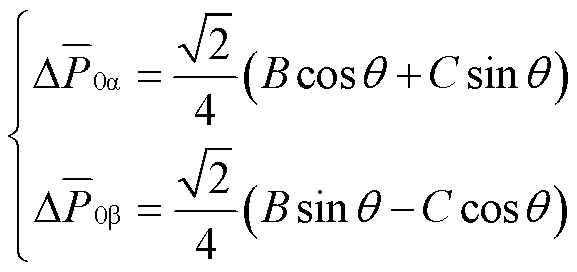 (13)
(13)
式中,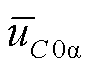 、
、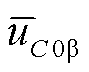 为低频侧子换流器间电容电压不均衡直流分量;
为低频侧子换流器间电容电压不均衡直流分量;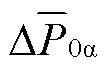 、
、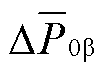 为由低频侧不对称故障引起的子换流器间有功功率不平衡直流分量。
为由低频侧不对称故障引起的子换流器间有功功率不平衡直流分量。
根据式(12)、式(13)可知,在稳态时不存在由低频侧不对称故障引起的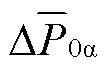 、
、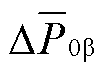 分量,此时
分量,此时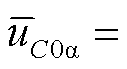
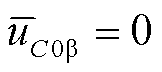 ,不存在子换流器间电容电压不均衡问题。在低频侧发生不对称故障时,
,不存在子换流器间电容电压不均衡问题。在低频侧发生不对称故障时,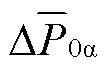 、
、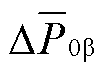 分量不为零,此时
分量不为零,此时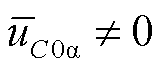 、
、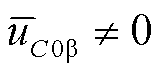 ,导致M3C子换流器间电容电压不均衡。为了实现低频侧不对称故障期间的电容电压均衡,可采用负序电流控制实现,即通过调控负序电流的大小使得
,导致M3C子换流器间电容电压不均衡。为了实现低频侧不对称故障期间的电容电压均衡,可采用负序电流控制实现,即通过调控负序电流的大小使得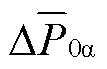 、
、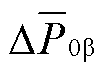 为零[25]。但该方案限制了负序电流控制的自由度,即无法实现M3C电容电压均衡与低频侧负序电流的解耦控制。因此,该方案可能引起线路过电压、保护灵敏性不足等问题。
为零[25]。但该方案限制了负序电流控制的自由度,即无法实现M3C电容电压均衡与低频侧负序电流的解耦控制。因此,该方案可能引起线路过电压、保护灵敏性不足等问题。
鉴于上述问题,为了实现M3C电容电压均衡控制与低频侧负序电流控制相互解耦,本文基于课题组前期研究成果,提出并采用一种基于环流控制的电容电压均衡策略[30],其基本实现思路如下。
低频侧发生不对称故障时,低频侧子换流器间存在有功功率不平衡直流分量,根据低频侧子换流器有功功率输入输出关系,并从三相静止坐标系基于等功率变换为两相静止坐标系,有
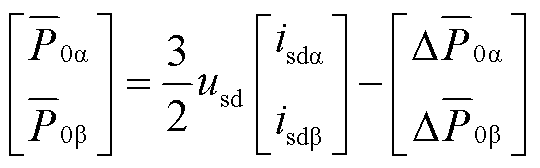 (14)
(14)
式中,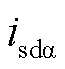 、
、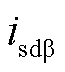 为分别工频dq轴下的桥臂电流环流分量;
为分别工频dq轴下的桥臂电流环流分量;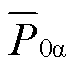 、
、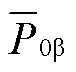 为低频侧子换流器间有功功率不平衡直流分量。
为低频侧子换流器间有功功率不平衡直流分量。
根据式(14)可知,在稳态时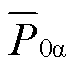 与
与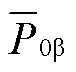 为零,此时子换流器间不存在有功功率不平衡,因此不存在相应的电容电压不均衡问题。但在低频侧不对称故障时,由不对称故障引起的有功功率不平衡直流分量将导致
为零,此时子换流器间不存在有功功率不平衡,因此不存在相应的电容电压不均衡问题。但在低频侧不对称故障时,由不对称故障引起的有功功率不平衡直流分量将导致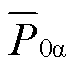 与
与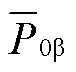 不为零。为实现控制
不为零。为实现控制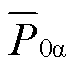 与
与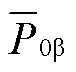 为0的目标,消除不对称故障带来的功率不平衡,可引入电流补偿分量,具体数值可由式(15)确定。
为0的目标,消除不对称故障带来的功率不平衡,可引入电流补偿分量,具体数值可由式(15)确定。
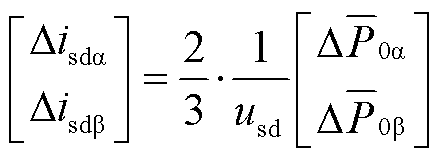 (15)
(15)
式中,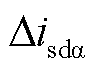 、
、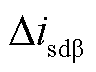 分别为引入的工频d、q轴下桥臂电流环流补偿分量。
分别为引入的工频d、q轴下桥臂电流环流补偿分量。
通过将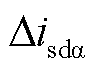 、
、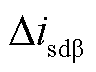 加入M3C环流控制中,能够消除子换流器间有功功率不平衡直流分量,进而实现低频侧不对称故障期间M3C的电容电压均衡,保障M3C的安全稳定运行。同时该方案基于M3C内部环流控制,与系统侧控制相互解耦,不依赖M3C负序电流控制,使得M3C能够灵活调控负序电流大小,为后续分析及提升柔性低频输电系统电流差动保护性能奠定基础。
加入M3C环流控制中,能够消除子换流器间有功功率不平衡直流分量,进而实现低频侧不对称故障期间M3C的电容电压均衡,保障M3C的安全稳定运行。同时该方案基于M3C内部环流控制,与系统侧控制相互解耦,不依赖M3C负序电流控制,使得M3C能够灵活调控负序电流大小,为后续分析及提升柔性低频输电系统电流差动保护性能奠定基础。
由图1可知,柔性低频输电系统为双端电力电子型电源系统,低频线路不对称故障期间PQ站与VF站M3C均采用故障控制策略。对于PQ站M3C,不对称故障时正序环采用动态功率控制[31-32],负序环采用负序电流抑制策略[33],即抑制PQ站负序电流为0。对于VF站M3C,不对称故障时正序环采用动态降压控制[26],负序电流控制通过改变负序电流参考值大小满足不同的控制需求。
以低频线路u相发生单相接地故障为例,根据图1建立相应的不对称故障复合序网图如图4所示。
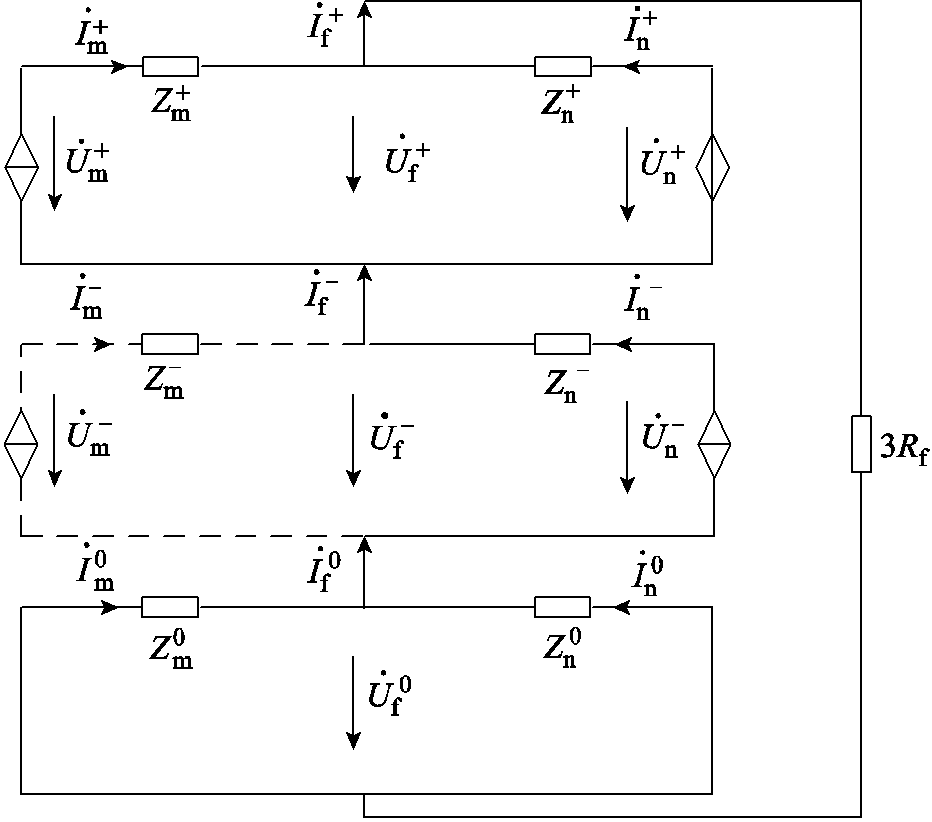
图4 单相接地故障复合序网图
Fig.4 Composite sequence network diagram for single phase-to-ground faults
图4中,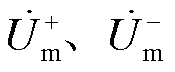 和
和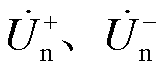 分别为PQ站与VF站正、负序电压分量;
分别为PQ站与VF站正、负序电压分量;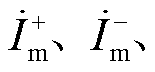
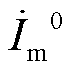 和
和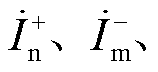
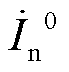 分别为PQ站与VF站正、负、零序电流分量;
分别为PQ站与VF站正、负、零序电流分量;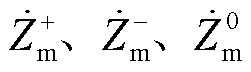 和
和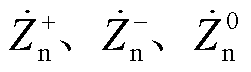 分别为PQ站与VF站线路阻抗等效正、负、零序分量;
分别为PQ站与VF站线路阻抗等效正、负、零序分量;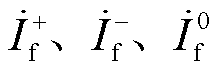 为故障点正、负、零序电流分量;
为故障点正、负、零序电流分量;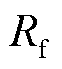 为过渡电阻。
为过渡电阻。
结合故障边界条件,可以得到低频输电线路两侧u相故障电流表达式,推导过程详见附录第3节。
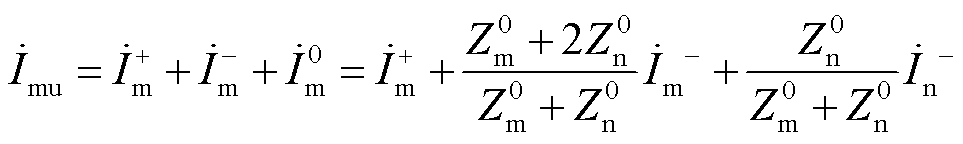 (16)
(16)
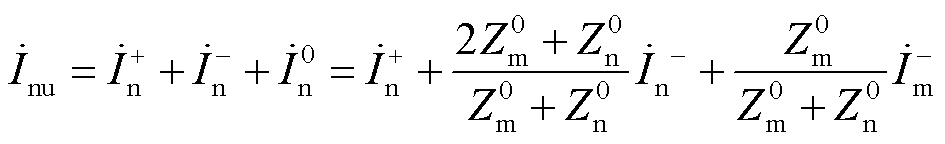 (17)
(17)
基于比例制动特性,可得电流差动保护的动作方程为
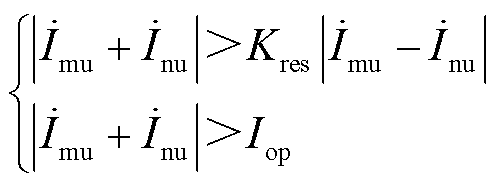 (18)
(18)
式中,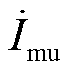 与
与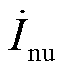 分别为低频线路PQ站与VF站的u相短路电流;
分别为低频线路PQ站与VF站的u相短路电流;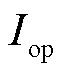 为最小动作电流;
为最小动作电流;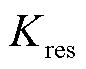 为比例制动系数整定值,本文取为0.85。
为比例制动系数整定值,本文取为0.85。
令动作量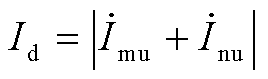 ,制动量
,制动量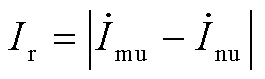 ,可得实际比例制动系数为
,可得实际比例制动系数为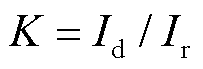 。结合式(18)电流差动保护动作方程可知,当满足
。结合式(18)电流差动保护动作方程可知,当满足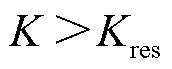 时,电流差动保护能够正确动作,因此可将K作为判断差动保护能否动作的依据。实际比例制动系数K的具体计算式为
时,电流差动保护能够正确动作,因此可将K作为判断差动保护能否动作的依据。实际比例制动系数K的具体计算式为
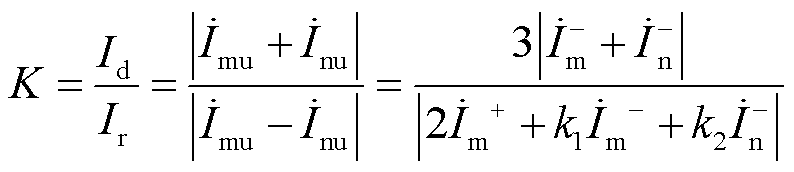 (19)
(19)
其中
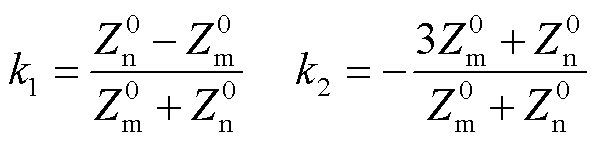
根据式(19)分析可知,单相接地故障时电流差动保护动作量仅由低频线路两侧负序电流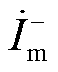 和
和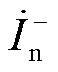 决定,而制动量还包含PQ站正序电流
决定,而制动量还包含PQ站正序电流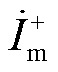 。由于低频线路两侧换流器在不对称故障期间均采用故障控制策略,使得低频线路故障特征相较于传统电力系统存在较大差异,可能导致动作量远小于制动量,使得比例制动系数较小,不能满足
。由于低频线路两侧换流器在不对称故障期间均采用故障控制策略,使得低频线路故障特征相较于传统电力系统存在较大差异,可能导致动作量远小于制动量,使得比例制动系数较小,不能满足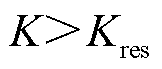 ,电流差动保护存在拒动现象。同时由于动作量与制动量均含有两侧负序电流
,电流差动保护存在拒动现象。同时由于动作量与制动量均含有两侧负序电流 和
和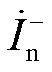 ,因此理论上能够通过两侧负序电流控制影响动作量与制动量的大小关系,使得比例制动系数在低频线路任意故障情况均能满足
,因此理论上能够通过两侧负序电流控制影响动作量与制动量的大小关系,使得比例制动系数在低频线路任意故障情况均能满足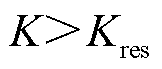 ,保证电流差动保护正确动作。
,保证电流差动保护正确动作。
目前有关柔性低频输电系统中M3C负序电流控制尚未考虑对于线路电流差动保护的影响,同时理论上能够通过调控线路负序电流大小改变动作量与制动量的大小关系,进而提升电流差动保护的性能。因此本文基于控保协同的思路,以提升电流差动保护性能为目标,结合M3C故障控制策略选取负序电流参考值。
由上述分析得到式(19)单相接地故障时比例制动系数表达式,对低频输电系统M3C负序电流参考值选取进行讨论。
(1)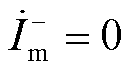 、
、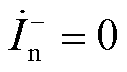 ,比例制动系数表示为
,比例制动系数表示为
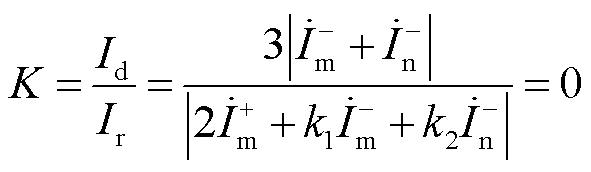 (20)
(20)
此时理论上动作量与比例制动系数为0,显然不能满足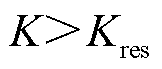 ,保护拒动。同时,低频线路两侧均采用负序电流抑制策略时,存在线路过电压风险,因此本文不采用该方案。
,保护拒动。同时,低频线路两侧均采用负序电流抑制策略时,存在线路过电压风险,因此本文不采用该方案。
(2)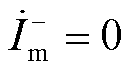 、
、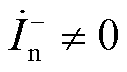 ,比例制动系数表示为
,比例制动系数表示为
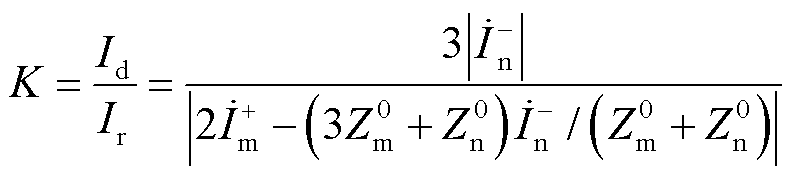 (21)
(21)
此时动作量与制动量所包含负序电流分量仅为VF站负序电流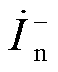 ,VF站M3C采用不同的负序电流参考值时将影响动作量与制动量的大小关系,进而影响电流差动保护的动作特性。因此选择恰当的负序电流控制参考值能够提升电流差动保护的动作性能。为了灵活调整M3C负序电流大小,本文第2节采用基于环流控制的电容电压均衡策略,实现了M3C负序电流控制与电容电压均衡控制相互解耦,为提升电流差动保护的动作性能奠定了基础。
,VF站M3C采用不同的负序电流参考值时将影响动作量与制动量的大小关系,进而影响电流差动保护的动作特性。因此选择恰当的负序电流控制参考值能够提升电流差动保护的动作性能。为了灵活调整M3C负序电流大小,本文第2节采用基于环流控制的电容电压均衡策略,实现了M3C负序电流控制与电容电压均衡控制相互解耦,为提升电流差动保护的动作性能奠定了基础。
根据式(18)所示差动保护动作特性方程,选取比例制动系数整定值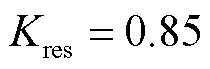 ,对VF站M3C负序电流大小以及线路故障位置采用数值遍历的方式进行计算,得到VF站M3C负序电流、故障位置、比例制动系数三者关系如图5所示。
,对VF站M3C负序电流大小以及线路故障位置采用数值遍历的方式进行计算,得到VF站M3C负序电流、故障位置、比例制动系数三者关系如图5所示。
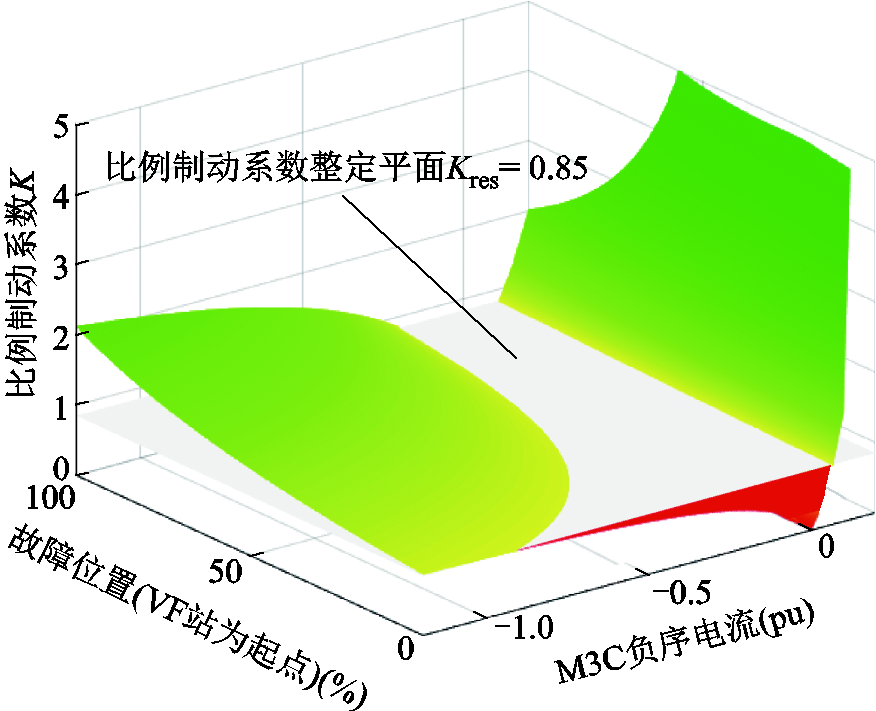
图5 VF站M3C负序电流、故障位置、比例制动系数关系
Fig.5 M3C negative sequence current of VF station, fault location, proportional restraint factor relationship diagram
以低频线路中点单相接地故障为例,选取图5中一组切面,得到VF站M3C负序电流大小与比例制动系数关系如图6所示。
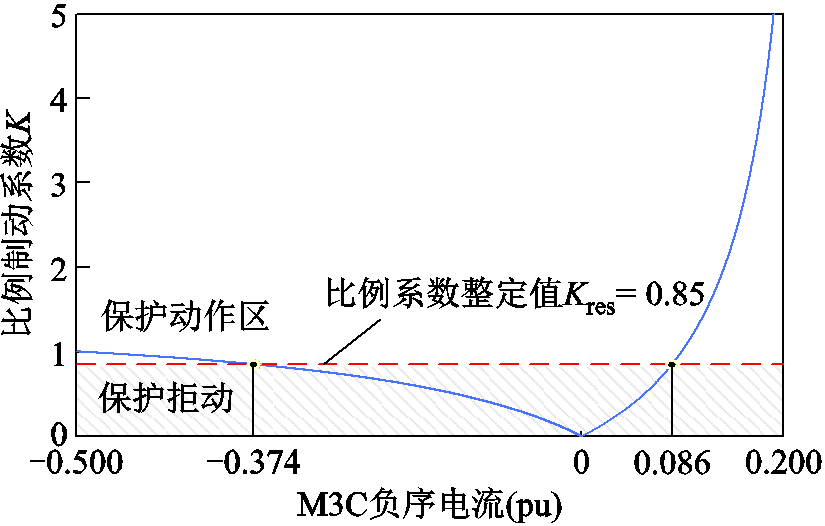
图6 比例制动系数与VF站M3C负序电流关系(低频线路中点单相接地故障)
Fig.6 Restraint coefficient and M3C negative sequence current of station VF relationship diagram (single-phase ground fault at midpoint of low-frequency line)
两相相间故障与两相接地故障所需VF站M3C负序电流大小分析过程见附录第3节。同样采取数值遍历的方式进行计算,可得满足低频线路电流差动保护性能所需负序电流见表1。
表1 基于电流差动保护性能所需负序电流
Tab.1 Based on the magnitude of negative sequence current required for current differential protection performance
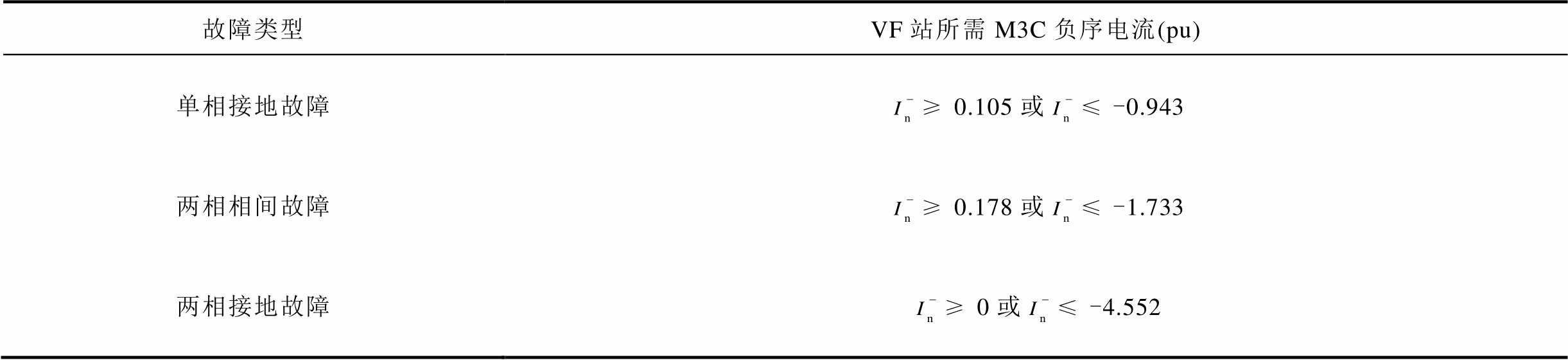
故障类型VF站所需M3C负序电流(pu) 单相接地故障0.105或-0.943 两相相间故障0.178或-1.733 两相接地故障0或-4.552
根据上述分析,综合考虑不同故障类型与故障位置,能够满足电流差动保护性能的VF站M3C负序电流参考值取值范围为
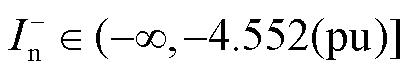 或
或
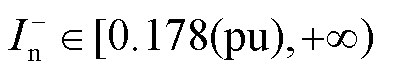 (22)
(22)
另一方面,M3C为柔性低频输电系统的关键变频设备,由于本身基于电力电子器件构成,桥臂耐受过电流能力有限,因此为了保障M3C的安全稳定运行,应当控制M3C桥臂电流在安全范围内。为保证在不对称故障期间M3C的桥臂安全,将M3C故障电流幅值限制为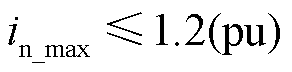 ,根据计算可得M3C负序电流参考值范围为
,根据计算可得M3C负序电流参考值范围为
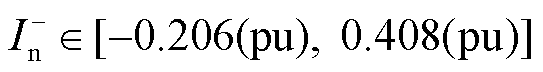 (23)
(23)
VF站M3C负序电流取值范围如图7所示,负序电流参考值应在式(22)与式(23)范围内选取,取值范围为
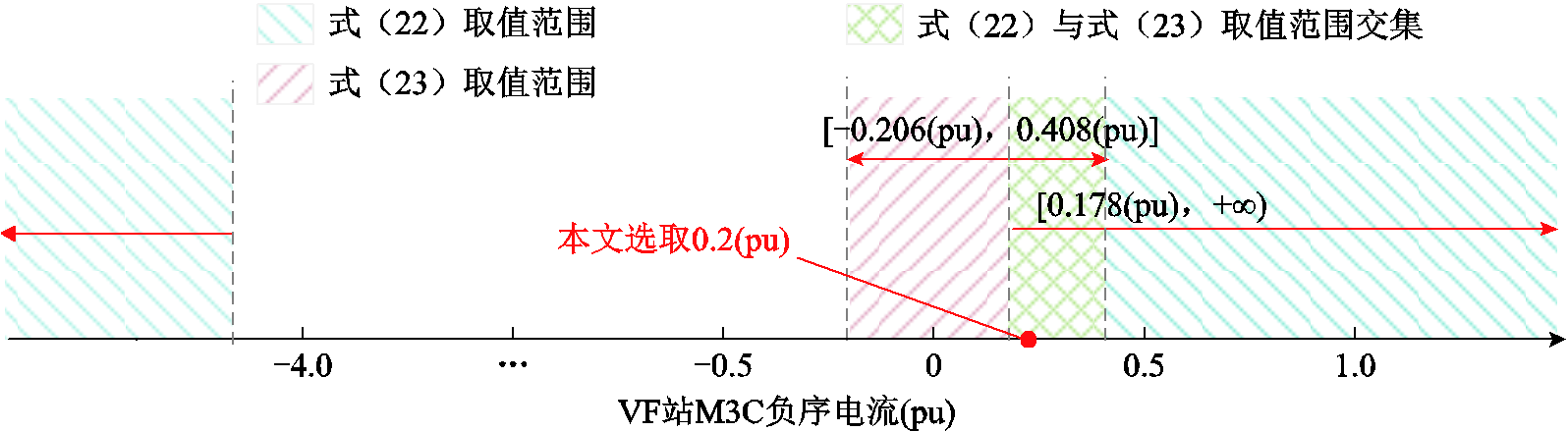
图7 VF站M3C负序电流取值范围示意图
Fig.7 Schematic diagram of the negative sequence current range of VF station M3C
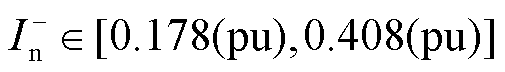 (24)
(24)
因此综合电流差动保护性能与M3C桥臂电流大小,并为电流差动保护保留一定的裕度,本文VF站M3C负序电流参考值选取为
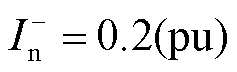 (25)
(25)
基于PSCAD/EMTDC仿真系统搭建如附图6所示的柔性低频输电系统仿真模型,仿真参数见附表1。M3C两侧通过变压器连接至线路,变压器在M3C侧为三角形联结,线路侧为星形联结。变压器可降低M3C接入的电压等级,减少桥臂子模块数量,同时能够保证输电线路电压等级。
为验证本文所采用控制策略的有效性,以及在本文控制策略下电流差动保护的可靠性,在低频线路设置不同类型的故障,仿真以0 s为故障起始时刻。
图8为低频线路中点u相接地故障时VF站M3C电容电压均衡与环流分量情况对比。由图8a、图8b可知,在采用传统控制策略[22]时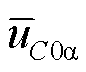 、
、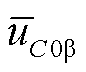 的直流分量在故障稳态时无法维持在0,此时M3C内部存在电容电压不均衡问题;在采用本文的环流控制策略时,
的直流分量在故障稳态时无法维持在0,此时M3C内部存在电容电压不均衡问题;在采用本文的环流控制策略时,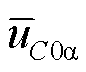 、
、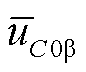 的直流分量在故障稳态时能够维持在0附近,实现了不对称故障期间M3C的电容电压均衡。对比图8c~图8f可知,在0.15 s电容电压相对稳定后,采用本文控制电容电压均衡策略时M3C内部环流分量未出现明显增大。
的直流分量在故障稳态时能够维持在0附近,实现了不对称故障期间M3C的电容电压均衡。对比图8c~图8f可知,在0.15 s电容电压相对稳定后,采用本文控制电容电压均衡策略时M3C内部环流分量未出现明显增大。
图9为以VF站为低频线路首端,vw两相接地故障时不同负序电流参考值下M3C侧电流幅值对比。由图9a可知,在大于式(24)边界值时v相故障电流幅值将超过M3C故障电流限值,M3C存在
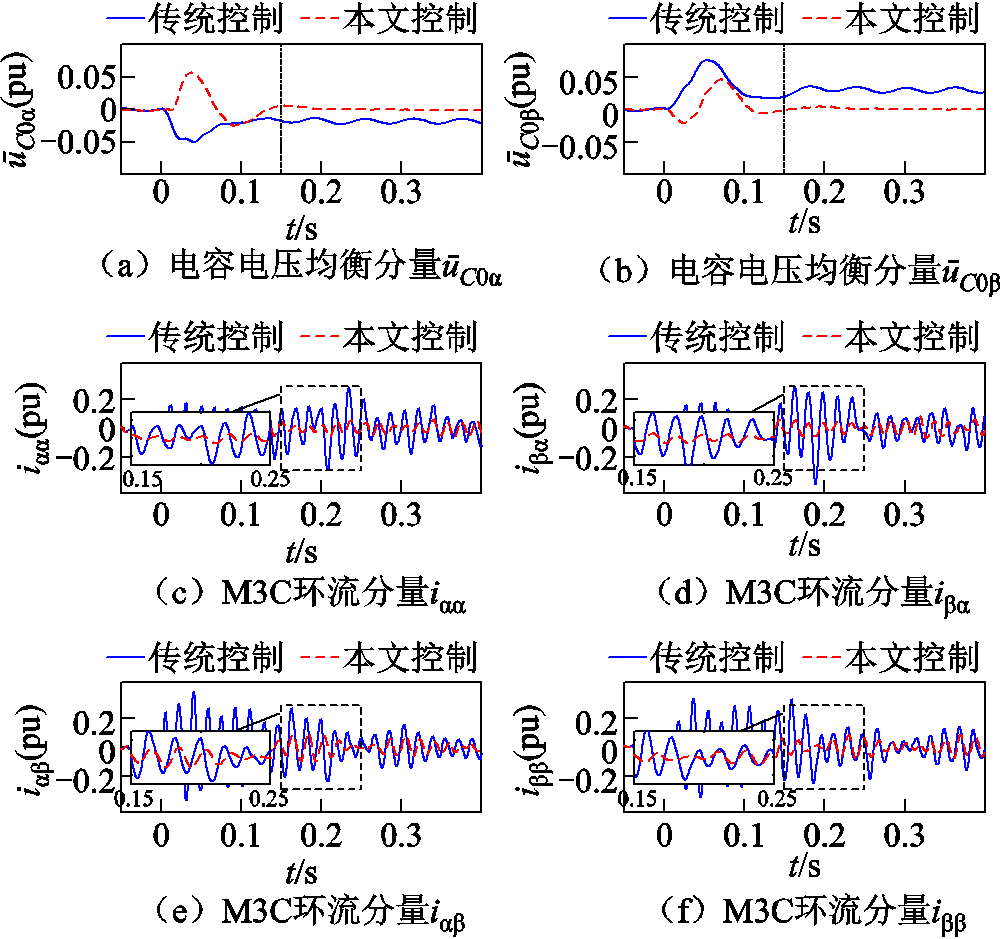
图8 低频线路中点u相接地故障时VF站M3C电容电压均衡与环流分量
Fig.8 Capacitor voltage balance circulating current of M3C of station VF at low frequency line midpoint u-phase ground faults
过电流风险;在负序电流选取边界值时,根据图9b可知,最大故障电流稳态时基本在M3C故障电流限值;而对于本文选取负序电流参考值,在不对称故障期间根据图9c可知,三相电流幅值均低于M3C的故障电流限值,避免了M3C的过电流问题。
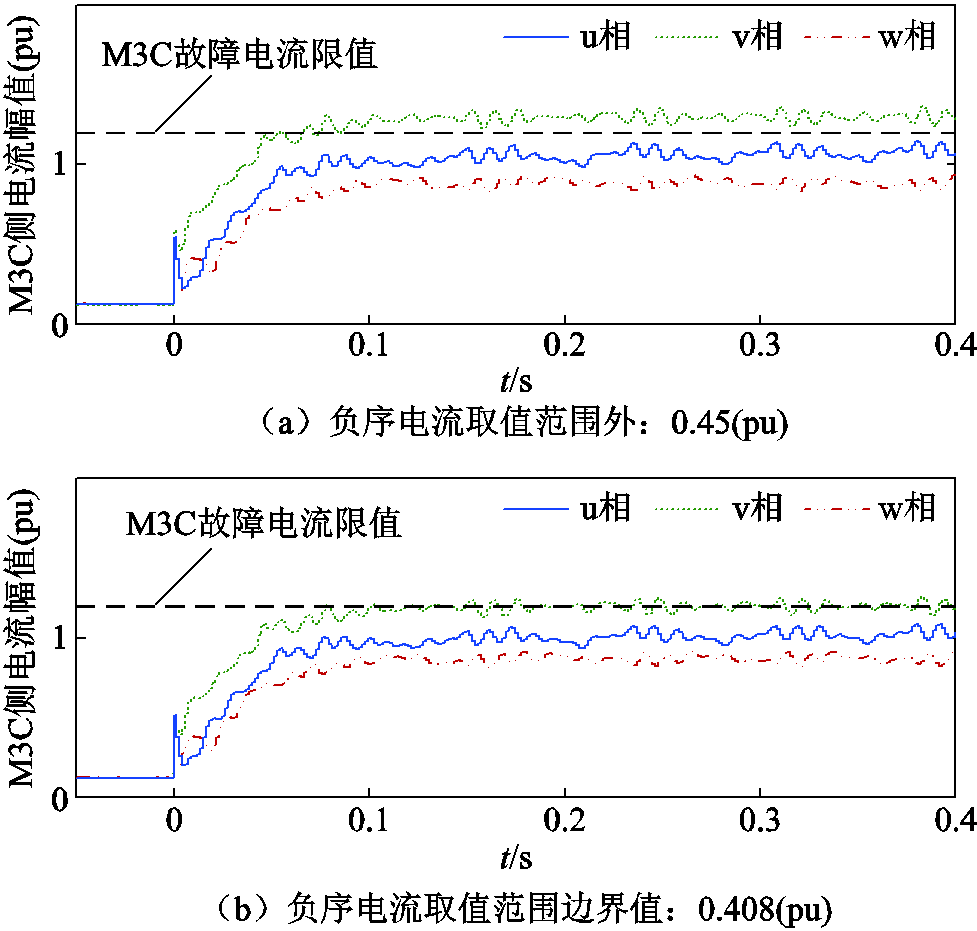
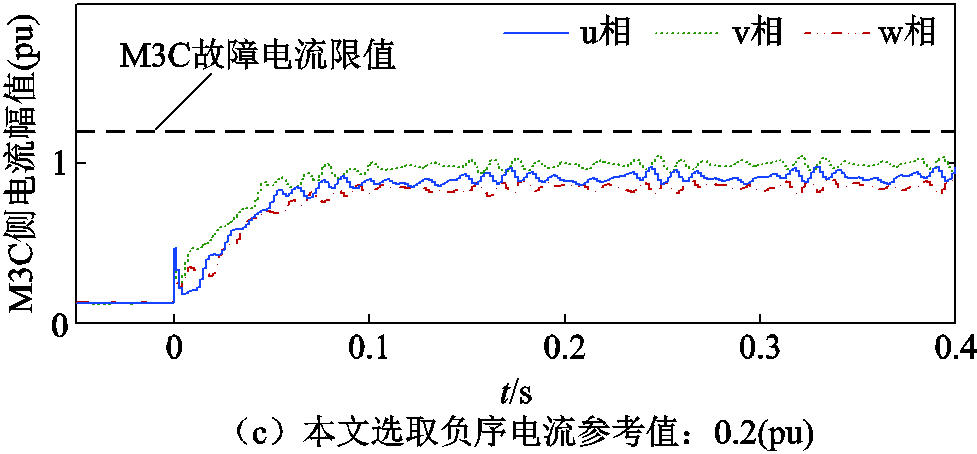
图9 VF站不同负序电流参考值下低频线路首端vw相接地故障电流幅值
Fig.9 Fault current magnitude at different negative sequence current magnitudes of VF station during a ground fault on the vw phase at the head of the low-frequency line
图10为低频线路中点u相接地故障时,VF站采用不同负序电流参考值下的动作电流与制动电流。根据图10a可知,VF站采用抑制负序电流策略时,动作电流基本为0,与3.2节理论分析内容相符;VF站采用本文负序电流参考值时,线路中负序电流不为0,此时动作电流明显大于制动电流。

图10 VF站不同负序电流参考值低频线路中点u相接地故障时动作电流与制动电流
Fig.10 Operating current and restraining current at different negative sequence current magnitudes of VF station at low frequency line midpoint u-phase ground faults
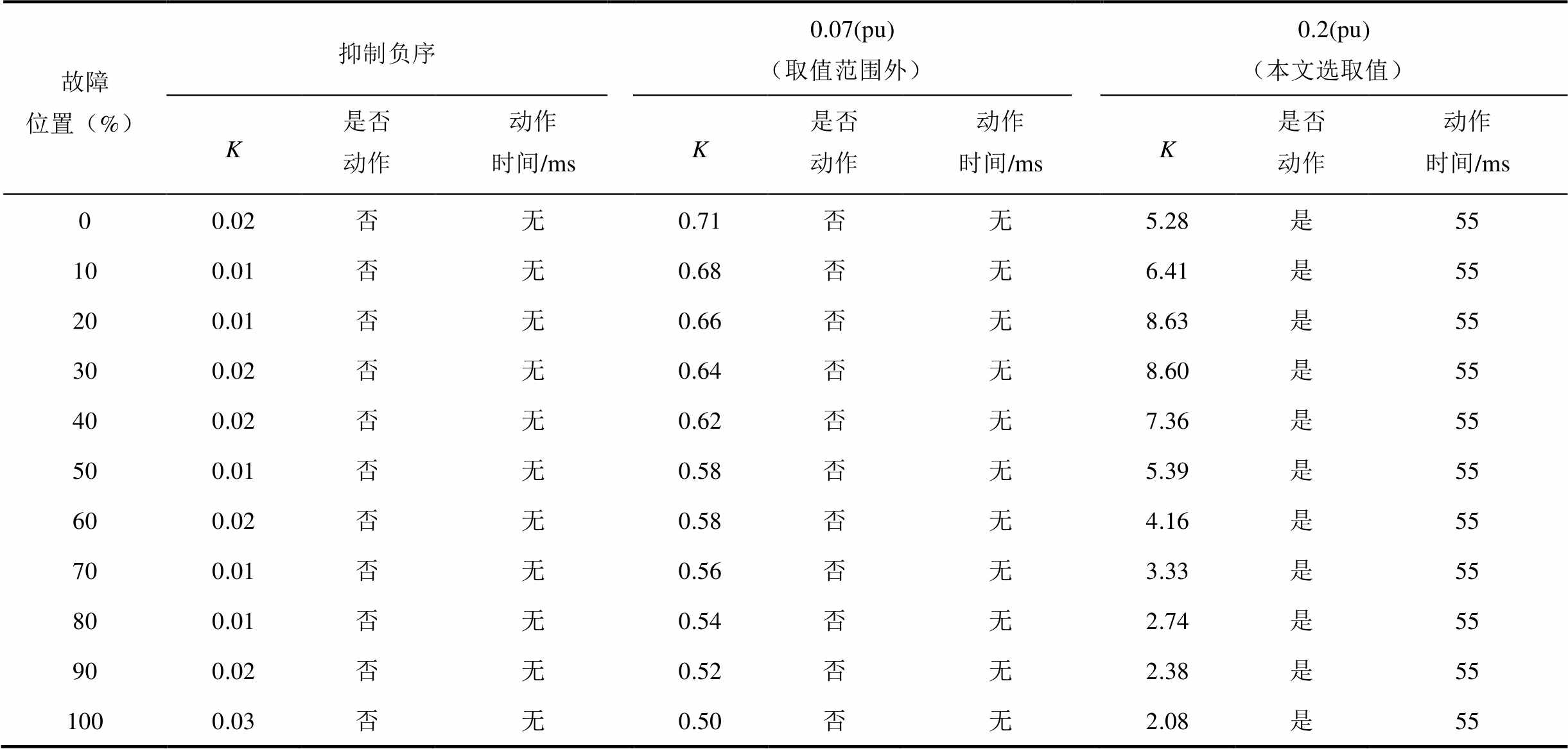
不同故障位置与VF站M3C的负序电流取值下单相接地故障电流差动保护制动系数对比及动作情况见表2。分析表2可知在抑制负序电流为0时,在所有故障位置(故障点与VF站之间的距离占线路全长的百分比)发生单相接地故障比例制动系数基本为0,电流差动保护拒动,与前述理论分析吻合。在负序电流取值为0.07(pu)时,K<0.85,电流差动保护依然拒动,而在本文选取的负序电流取值0.2(pu)时,在任意故障位置电流差动保护均能够正确动作。
表2 不同故障位置与VF站M3C负序电流下单相接地故障电流差动保护制动系数对比及动作情况
Tab.2 Comparison of restraint coefficients and actions of single-phase ground fault current differential protection under different fault locations and negative sequence currents of station VF
故障位置(%)抑制负序0.07(pu)(取值范围外)0.2(pu)(本文选取值) K是否动作动作时间/msK是否动作动作时间/msK是否动作动作时间/ms 00.02否无0.71否无5.28是55 100.01否无0.68否无6.41是55 200.01否无0.66否无8.63是55 300.02否无0.64否无8.60是55 400.02否无0.62否无7.36是55 500.01否无0.58否无5.39是55 600.02否无0.58否无4.16是55 700.01否无0.56否无3.33是55 800.01否无0.54否无2.74是55 900.02否无0.52否无2.38是55 1000.03否无0.50否无2.08是55
不同故障位置与不同VF站M3C负序电流取值下相间故障电流差动保护制动系数对比及动作情况见表3。同理分析表3在所有故障位置发生两相相间故障时,在抑制负序电流为0时比例制动系数基本为0,电流差动保护拒动,与前述理论分析吻合。而在负序电流取值为0.15(pu)时,比例制动系数仍小于0.85,电流差动保护依然拒动,而在本文选取的负序电流取值0.2(pu)时,在所有故障位置电流差动保护均能够正确动作。
表3 不同故障位置与不同VF站M3C负序电流取值下相间故障电流差动保护制动系数对比及动作情况
Tab.3 Comparison of restraint coefficients and actions of phase-to-phase fault current differential protection under different fault locations and negative sequence currents of station VF
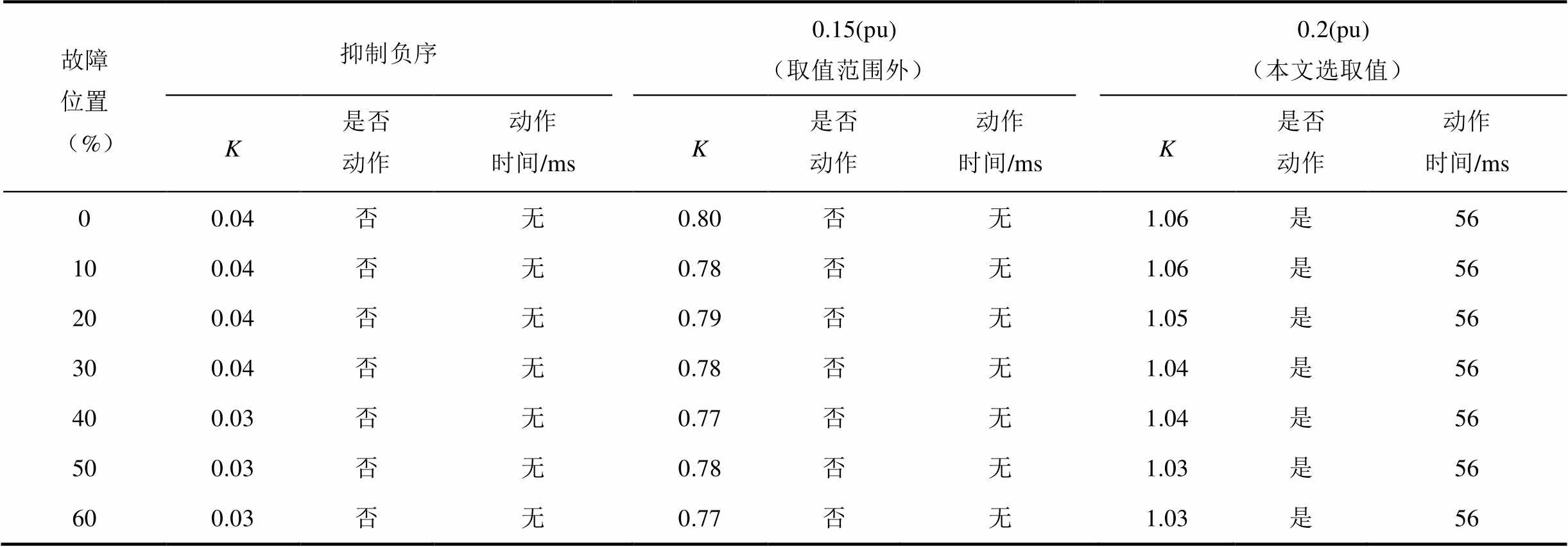
故障位置 (%)抑制负序0.15(pu)(取值范围外)0.2(pu)(本文选取值) K是否动作动作时间/msK是否动作动作时间/msK是否动作动作时间/ms 00.04否无0.80否无1.06是56 100.04否无0.78否无1.06是56 200.04否无0.79否无1.05是56 300.04否无0.78否无1.04是56 400.03否无0.77否无1.04是56 500.03否无0.78否无1.03是56 600.03否无0.77否无1.03是56
(续)
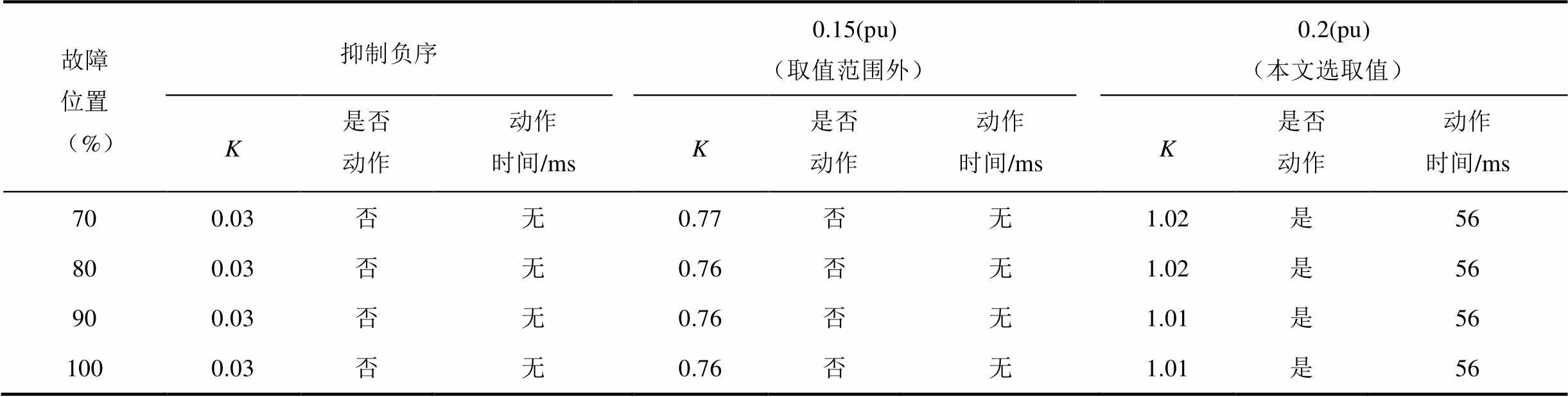
故障位置 (%)抑制负序0.15(pu)(取值范围外)0.2(pu)(本文选取值) K是否动作动作时间/msK是否动作动作时间/msK是否动作动作时间/ms 700.03否无0.77否无1.02是56 800.03否无0.76否无1.02是56 900.03否无0.76否无1.01是56 1000.03否无0.76否无1.01是56
不同故障位置与不同VF站M3C负序电流取值下两相接地故障电流差动保护制动系数对比及动作情况见表4。根据表4可分析在所有故障位置发生两相接地故障时,与单相接地故障、两相相间故障不同的是在抑制负序电流为0、本文选取的负序电流取值0.2(pu)以及负序电流选取范围内电流差动保护均能正确动作,与本文理论分析相符。
表4 不同故障位置与不同VF站M3C负序电流取值下两相接地故障电流差动保护制动系数对比及动作情况
Tab.4 Comparison of restraint coefficients and actions of two-phase ground fault current differential protection under different fault locations and negative sequence currents of station VF
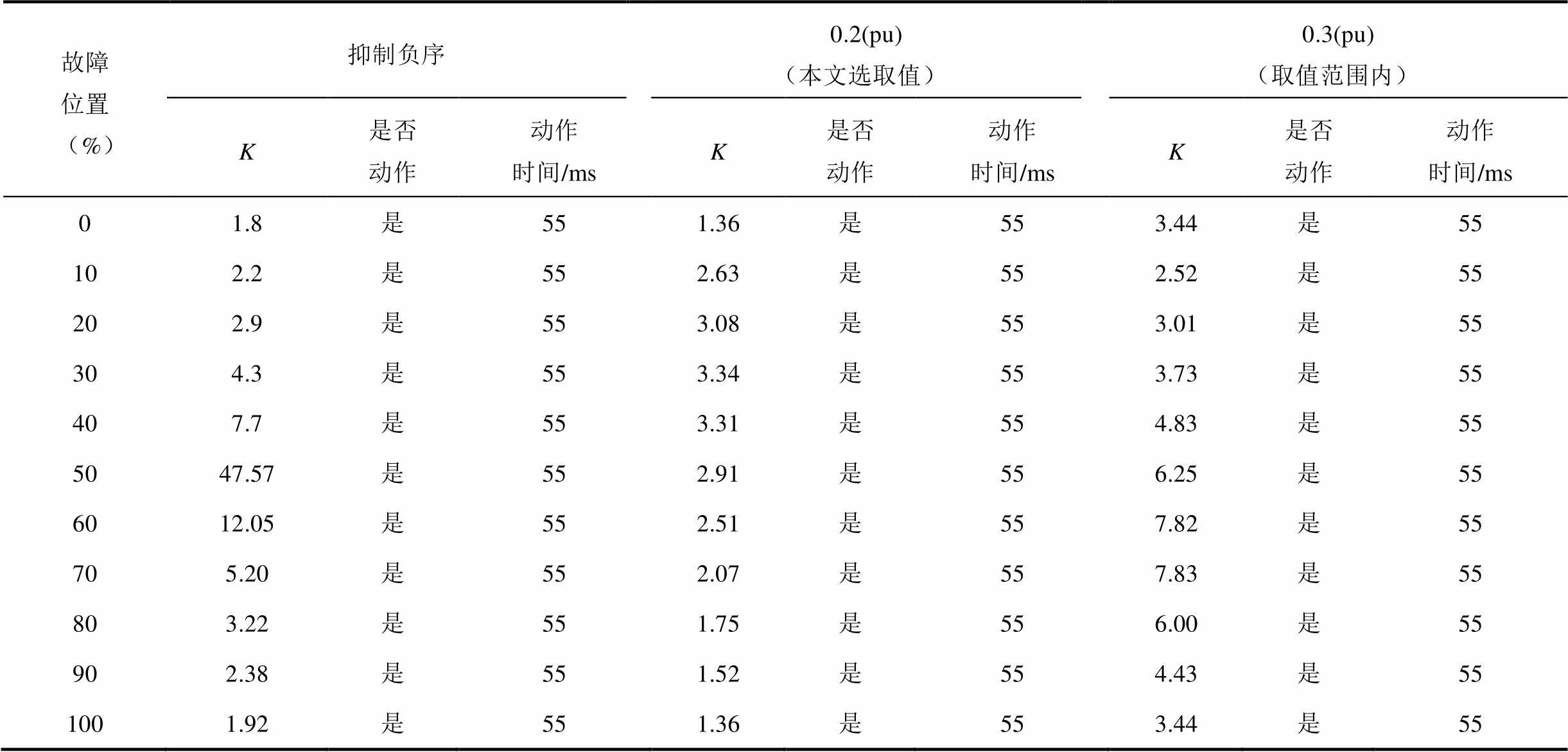
故障位置 (%)抑制负序0.2(pu)(本文选取值)0.3(pu)(取值范围内) K是否动作动作时间/msK是否动作动作时间/msK是否动作动作时间/ms 01.8是551.36是553.44是55 102.2是552.63是552.52是55 202.9是553.08是553.01是55 304.3是553.34是553.73是55 407.7是553.31是554.83是55 5047.57是552.91是556.25是55 6012.05是552.51是557.82是55 705.20是552.07是557.83是55 803.22是551.75是556.00是55 902.38是551.52是554.43是55 1001.92是551.36是553.44是55
表5为低频线路中点发生经不同过渡电阻的不对称故障,采用本文选取的负序电流参考值时比例制动系数情况,其他故障位置仿真结果见附表2。根据表5及附表2可知,在不同过渡电阻情况下比例制动系数均能够达到整定值0.85以上,电流差动保护能够正确动作,验证了本文方法所选取的负序电流参考值具有合理性。
表5 线路中点故障时不同过渡电阻电流差动保护制动系数对比及动作情况
Tab.5 Comparison of restraint coefficients and actions of different transition resistor current differential protection during line midpoint faults
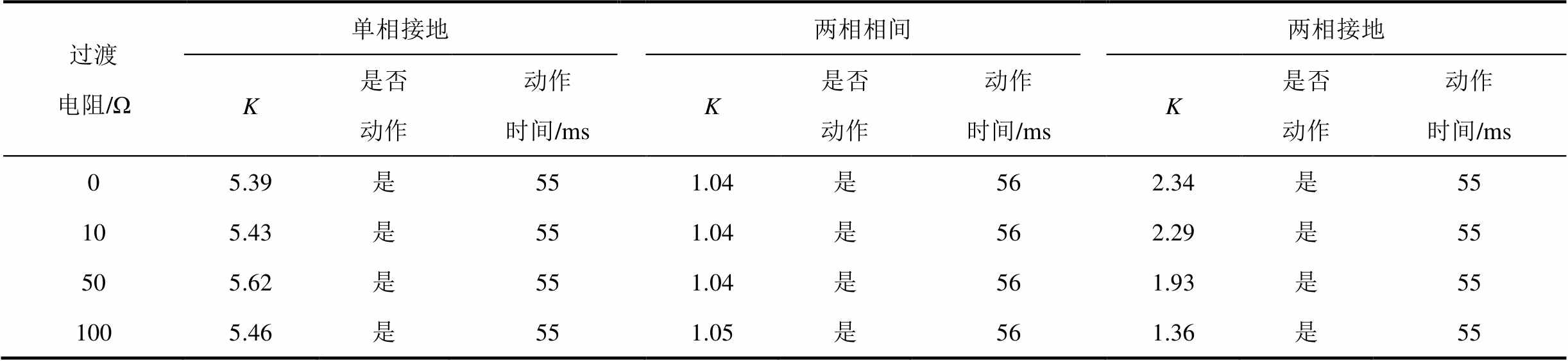
过渡电阻/Ω单相接地两相相间两相接地 K是否动作动作时间/msK是否动作动作时间/msK是否动作动作时间/ms 05.39是551.04是562.34是55 105.43是551.04是562.29是55 505.62是551.04是561.93是55 1005.46是551.05是561.36是55
本文提出了一种基于控保协同的柔性低频输电系统保护性能提升方案,结论如下:
1)本文分析了M3C负序电流控制实现电容电压均衡存在的问题,并采用一种基于环流控制的电容电压均衡策略,实现了M3C电容电压均衡控制与负序电流控制的相互解耦,为后续研究工作奠定了基础。
2)基于电流差动保护的动作特性,本文理论分析了负序电流大小对于电流差动保护动作性能的影响,指出能够通过调控线路负序电流改变动作量与制动量的大小关系,进而影响电流差动保护性能。
3)基于控保协同思想,本文以提升电流差动保护性能为目标,经过计算并综合M3C桥臂过电流问题,确定了VF站M3C负序电流参考值,保障了电流差动保护的动作性能。
柔性低频输电系统两侧均为电力电子器件,M3C采用控制策略对各种保护方案均有一定的影响。本文主要针对提升线路电流差动保护性能展开分析讨论,分析其他多种保护在柔性低频输电系统的适应性与改进措施将作为下一步研究内容。
附 录
1. M3C稳态控制结构框图
M3C工频侧控制框图、低频侧控制框图如附图1、附图2所示。电容电压均衡控制框图如附图3所示。
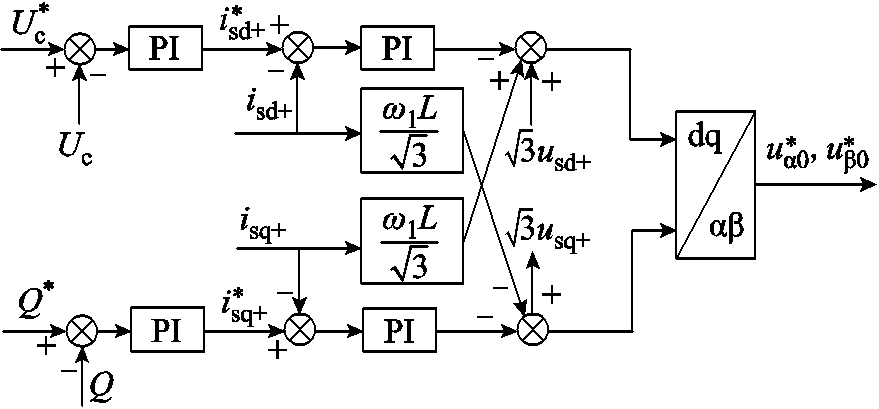
附图1 工频侧控制框图
App.Fig.1 Control block diagram of power frequency side
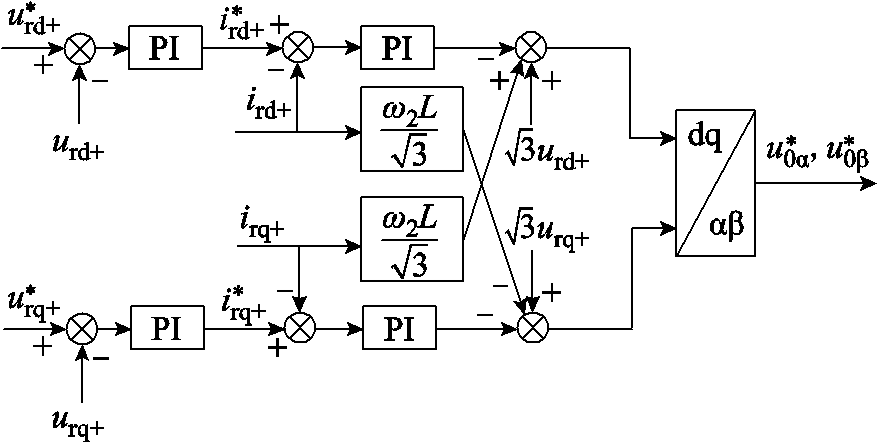
附图2 低频侧控制框图
App.Fig.2 Control block diagram of low frequency side
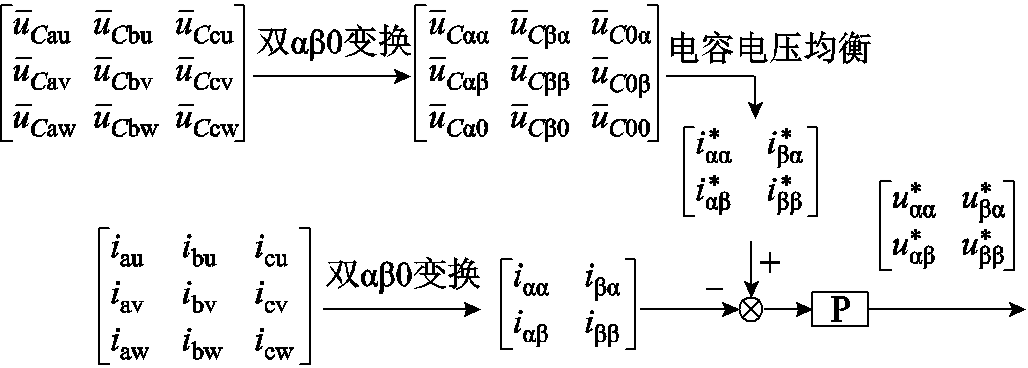
附图3 电容电压均衡控制框图
App.Fig.3 Control block diagram of capacitor voltage balance
2. M3C桥臂有功功率不平衡分量计算过程
在低频侧不对称故障情况下,低频侧电压可表示为
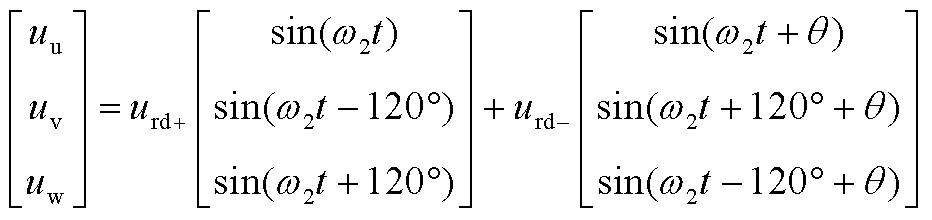 (A1)
(A1)
式中, 、
、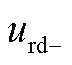 分别为低频侧电压的正、负序d轴分量;
分别为低频侧电压的正、负序d轴分量;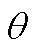 为正负序分量的夹角;w2为低频系统角速度。
为正负序分量的夹角;w2为低频系统角速度。
工频侧电压可表示为
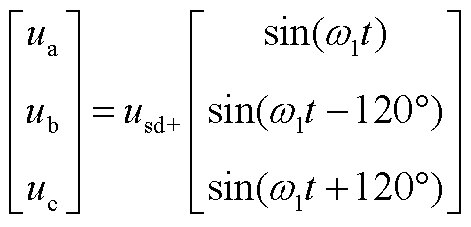 (A2)
(A2)
式中,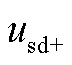 为工频侧电压的正序d轴分量;w1为工频系统角速度。
为工频侧电压的正序d轴分量;w1为工频系统角速度。
低频侧电流可表示为
 (A3)
(A3)
式中,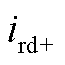 、
、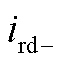
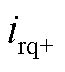 、
、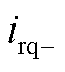 分别为低频侧电流的正、负序dq轴分量。
分别为低频侧电流的正、负序dq轴分量。
工频侧电流可表示为
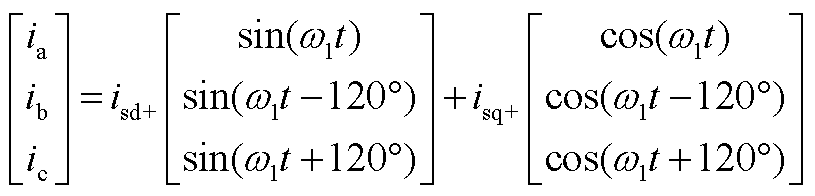 (A4)
(A4)
式中,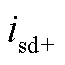 、
、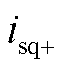 分别为工频频侧电流的正序dq轴分量。
分别为工频频侧电流的正序dq轴分量。
M3C桥臂(以桥臂au为例)有功功率计算式为
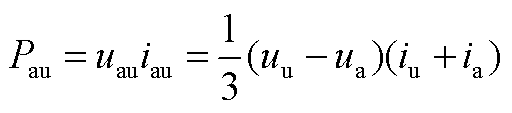 (A5)
(A5)
根据式(A1)~式(A5)计算得到M3C所有桥臂有功功率表达式如式(A6)~式(A9),并提取直流分量。
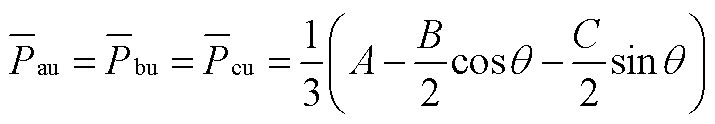 (A6)
(A6)
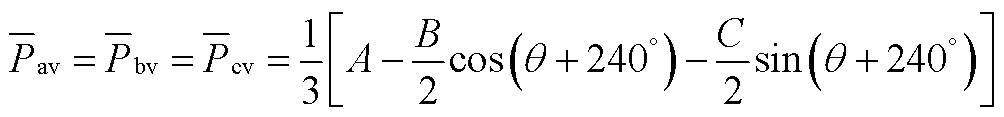 (A7)
(A7)
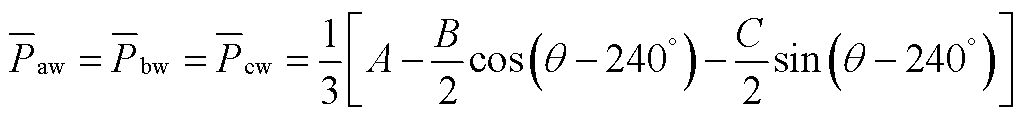 (A8)
(A8)
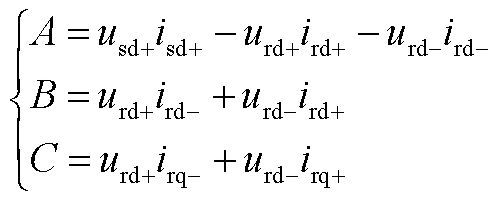 (A9)
(A9)
对式(11)进行基于等功率的双αβ0变换,变换过程如下。
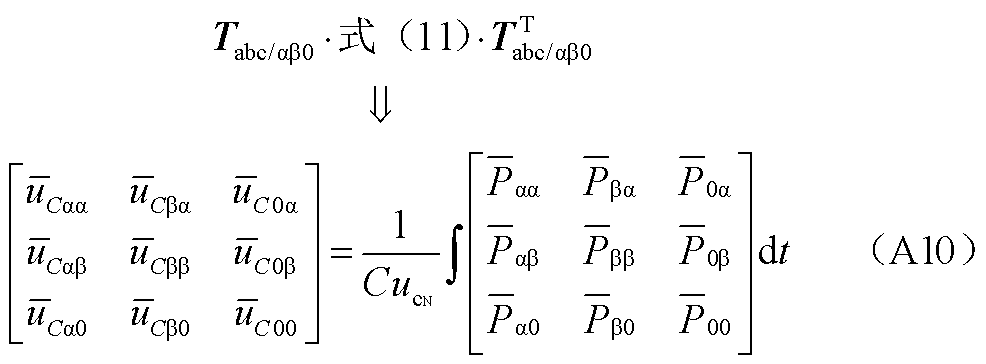
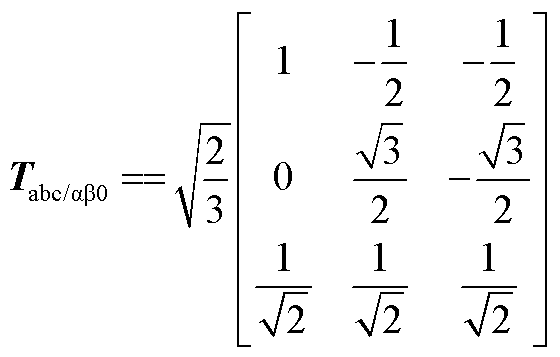 (A11)
(A11)
3. VF站M3C所需负序电流大小推导过程
对于单相接地故障,低频输电线路两侧u相故障电流表达式为
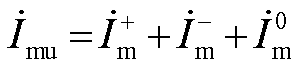 (A12)
(A12)
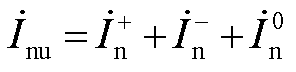 (A13)
(A13)
结合图4单相接地故障复合序网图,此时故障边界条件为
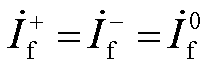 (A14)
(A14)
将式(A14)分别代入式(A12)、式(A13)可得

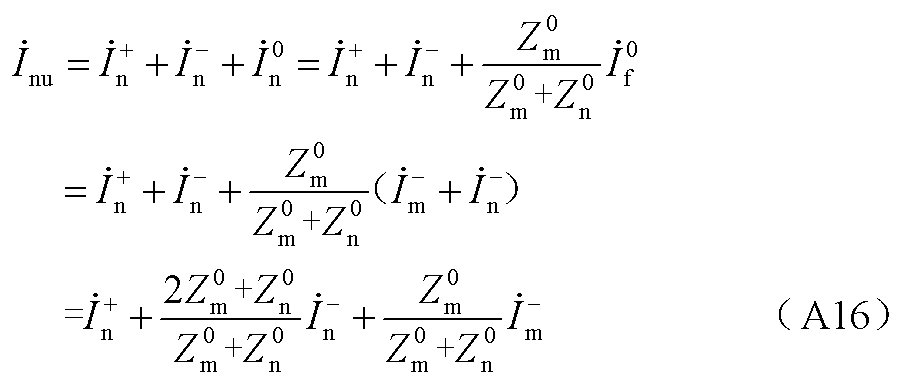
对于两相相间故障,本文以v相为例并结合附图4两相相间故障复合序网图,低频输电系统线路两侧v相故障电流表达式为
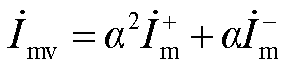 (A17)
(A17)
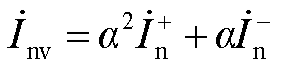 (A18)
(A18)
式中,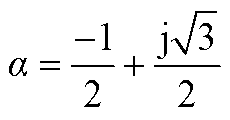 。
。
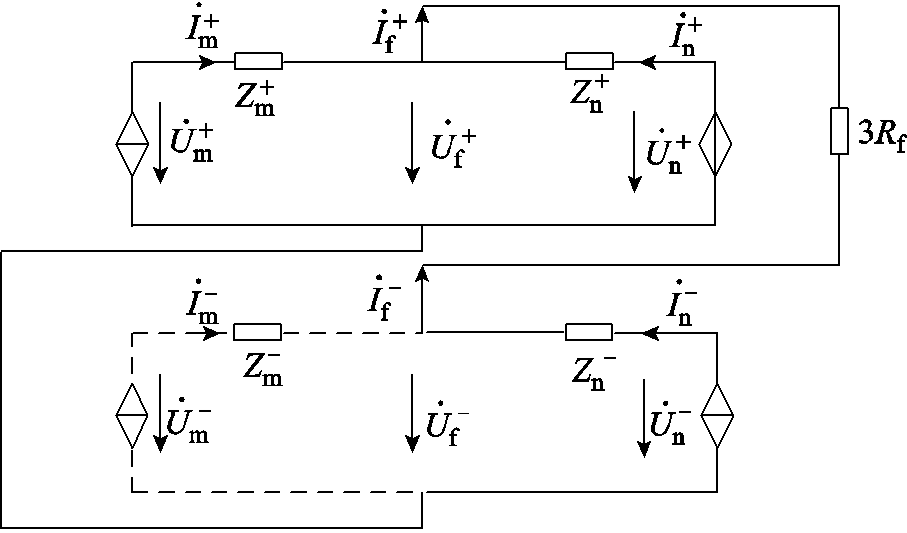
附图4 两相相间故障复合序网图
App.Fig.4 Composite sequence network diagram for two phase-to-phase faults
结合附图4两相相间故障复合序网图,此时故障边界条件为
 (A19)
(A19)
结合故障控制策略与边界条件,此时比例制动系数表达式为
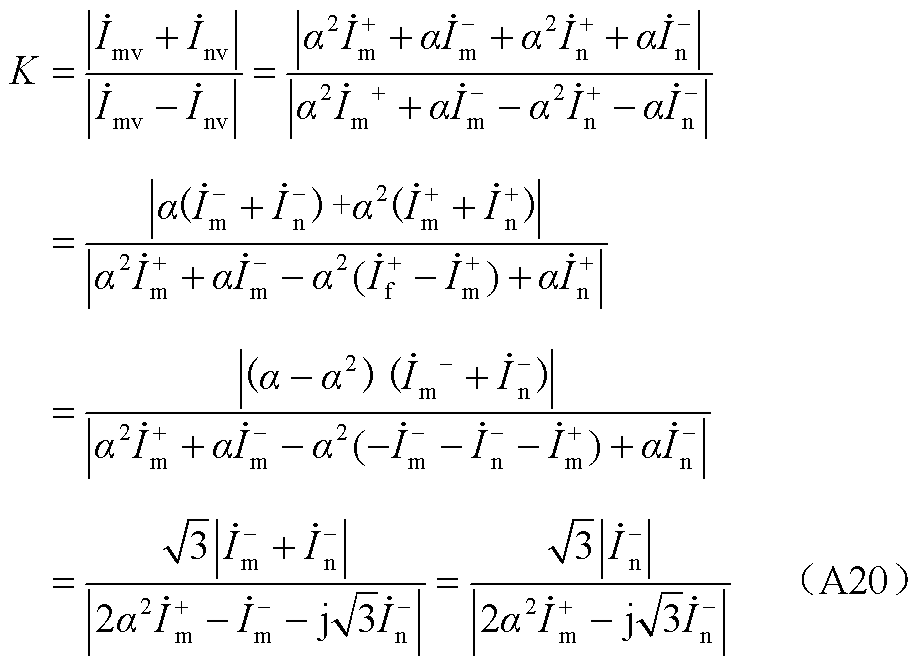
此时制动系数主要由VF站M3C负序电流大小决定,同理选取比例制动系数整定值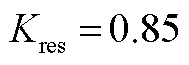 ,计算可得满足低频线路两相相间故障下电流差动保护动作性能所需VF站M3C负序电流为
,计算可得满足低频线路两相相间故障下电流差动保护动作性能所需VF站M3C负序电流为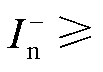 0.178(pu)或
0.178(pu)或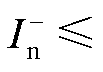 -1.733(pu)。
-1.733(pu)。
对于两相接地故障,本文以v相为例并结合附图5两相接地故障复合序网图,得低频输电系统线路两侧v相故障电流表达式为
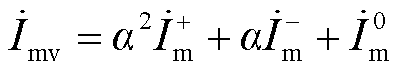 (A21)
(A21)
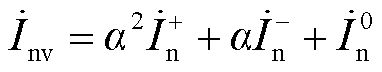 (A22)
(A22)
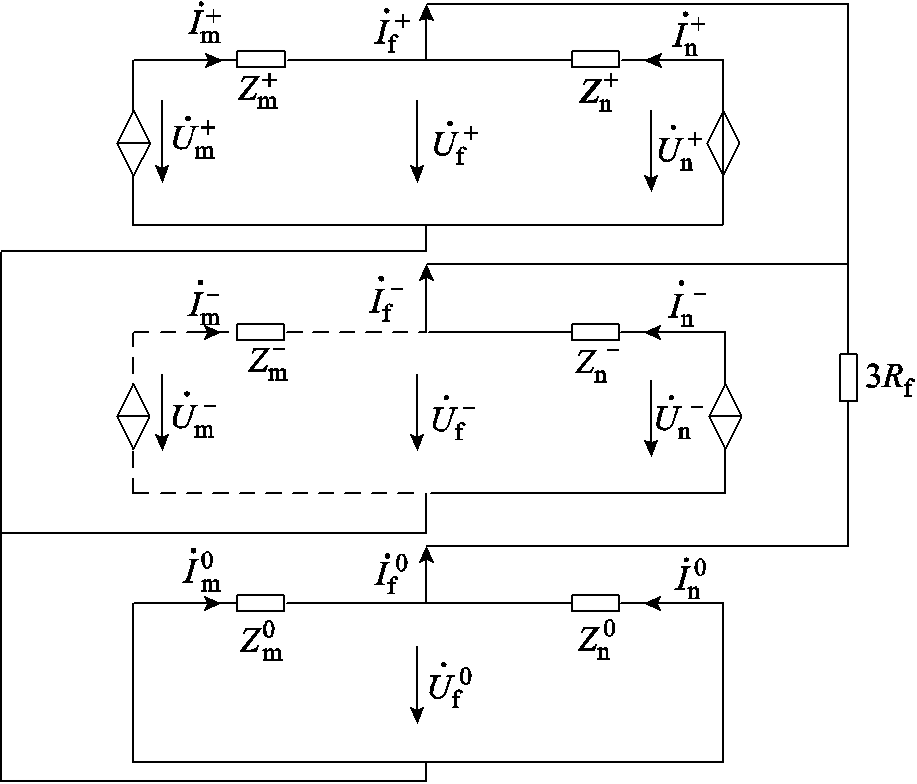
附图5 两相接地故障复合序网图
App.Fig.5 Composite sequence network diagram for two phase-to-ground faults
结合附图5两相接地故障复合序网图,此时故障边界条件为
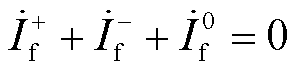 (A23)
(A23)
结合故障控制策略与边界条件,此时比例制动系数表达式为
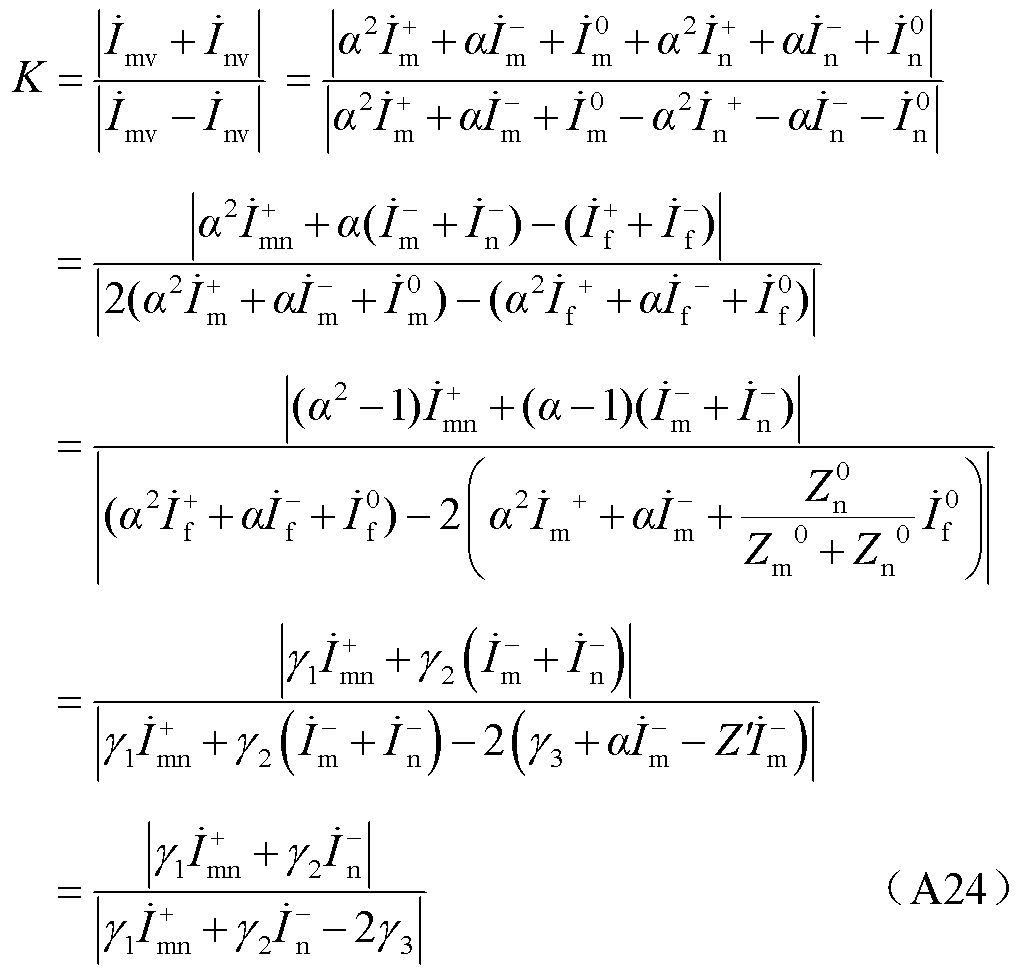
式中,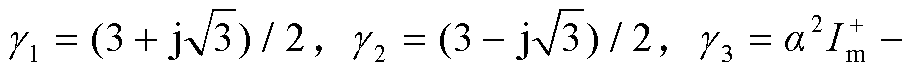
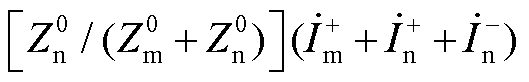 ,
,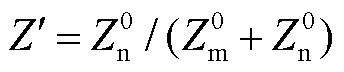 ,
,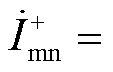
 。
。
与其余两种故障情况不同,此时比例制动系数分子项包含正序电流分量,比例制动系数K不完全由VF站M3C负序电流决定,需要结合具体情况进行分析。在本文所采用的控制策略以及系统结构、参数下,根据计算VF站M3C负序电流取值为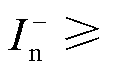 0或
0或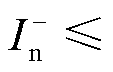 -4.552(pu)。
-4.552(pu)。
4. 仿真系统结构
柔性低频输电系统仿真结构如附图6所示。

附图6 柔性低频输电系统仿真结构
App.Fig.6 Simulation structure of flexible low frequency transmission system
5. 仿真系统参数
仿真参数见附表1。
附表1 仿真参数
App.Tab.1 Simulation parameters

参数数值 M3C容量/(MV·A)330 工频侧频率/Hz50 低频侧频率/Hz20 工频侧电压/kV220 低频侧电压/kV220
(续)

参数数值 桥臂电感/mH15.3 子模块电容/mF8.4 子模块个数/个108 子模块电容电压额定值/kV1.6 变压器额定容量/(MV·A)330 变压器短路电压(%)1 变压器电压比(kV/kV)220 kV/81.7 kV 变压器连接组别YnD 低频线路长度/km100 线路电阻/(W·km-1)0.053 线路电感/(mH·km-1)1.081 线路电容/(mF·km-1)0.013 2
6. 不同故障位置及过渡电阻下仿真结果
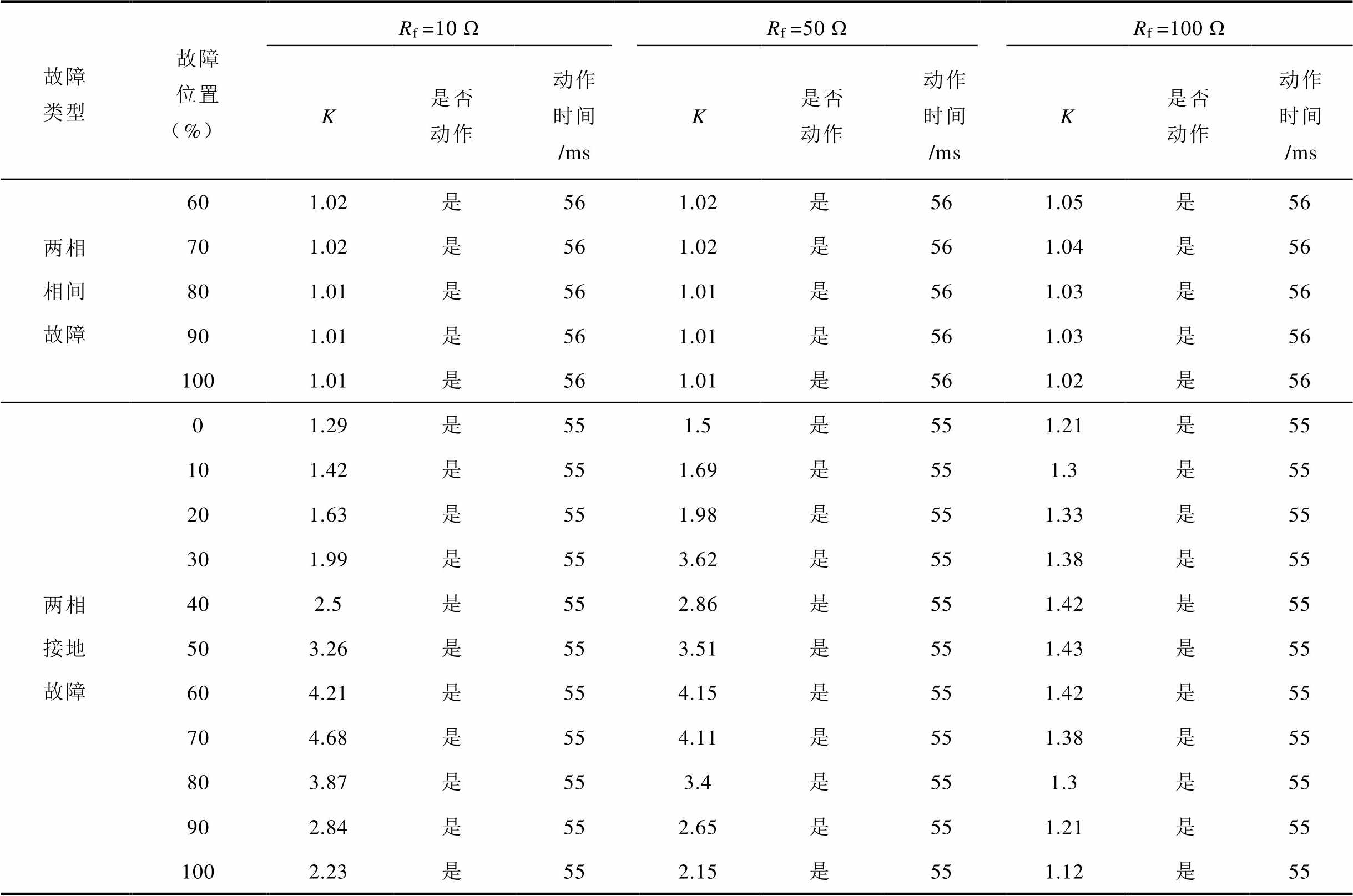
不同故障位置及过渡电阻下不对称故障电流差动保护制动系数对比及动作情况见附表2。
附表2 不同故障位置及过渡电阻下不对称故障电流差动保护制动系数对比及动作情况
App.Tab.2 Comparison of restraint coefficients and actions of differential protection against asymmetric fault currents with different fault locations and transition resistances
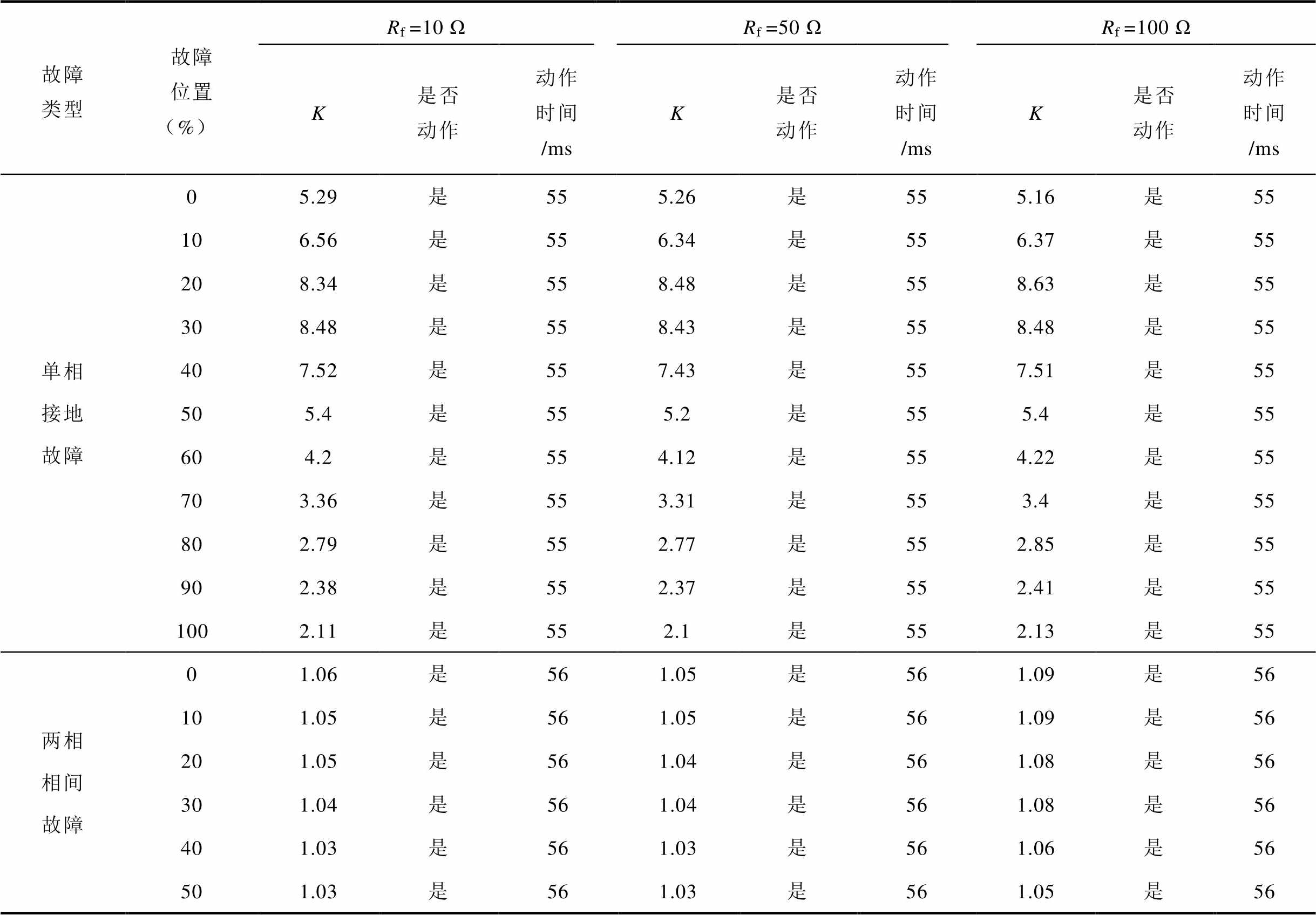
故障类型故障位置(%)Rf =10 ΩRf =50 ΩRf =100 Ω K是否动作动作时间 /msK是否动作动作时间 /msK是否动作动作时间 /ms 单相接地故障05.29是555.26是555.16是55 106.56是556.34是556.37是55 208.34是558.48是558.63是55 308.48是558.43是558.48是55 407.52是557.43是557.51是55 505.4是555.2是555.4是55 604.2是554.12是554.22是55 703.36是553.31是553.4是55 802.79是552.77是552.85是55 902.38是552.37是552.41是55 1002.11是552.1是552.13是55 两相相间故障01.06是561.05是561.09是56 101.05是561.05是561.09是56 201.05是561.04是561.08是56 301.04是561.04是561.08是56 401.03是561.03是561.06是56 501.03是561.03是561.05是56
(续)
故障类型故障位置(%)Rf =10 ΩRf =50 ΩRf =100 Ω K是否动作动作时间 /msK是否动作动作时间 /msK是否动作动作时间 /ms 两相相间故障601.02是561.02是561.05是56 701.02是561.02是561.04是56 801.01是561.01是561.03是56 901.01是561.01是561.03是56 1001.01是561.01是561.02是56 两相接地故障01.29是551.5是551.21是55 101.42是551.69是551.3是55 201.63是551.98是551.33是55 301.99是553.62是551.38是55 402.5是552.86是551.42是55 503.26是553.51是551.43是55 604.21是554.15是551.42是55 704.68是554.11是551.38是55 803.87是553.4是551.3是55 902.84是552.65是551.21是55 1002.23是552.15是551.12是55
参考文献
[1] 王锡凡, 王秀丽, 滕予非. 分频输电系统及其应用[J]. 中国电机工程学报, 2012, 32(13): 1-6, 184. Wang Xifan, Wang Xiuli, Teng Yufei. Fractional frequency transmission system and its applications[J]. Proceedings of the CSEE, 2012, 32(13): 1-6, 184.
[2] 黄明煌, 王秀丽, 刘沈全, 等. 分频输电应用于深远海风电并网的技术经济性分析[J]. 电力系统自动化, 2019, 43(5): 167-174. Huang Minghuang, Wang Xiuli, Liu Shenquan, et al. Technical and economic analysis on fractional frequency transmission system for integration of long-distance offshore wind farm[J]. Automation of Electric Power Systems, 2019, 43(5): 167-174.
[3] 李钢, 田杰, 王仙荣, 等. 远海风电送出技术应用现状及发展趋势[J]. 供用电, 2022, 39(11): 2-10. Li Gang, Tian Jie, Wang Xianrong, et al. Application status and development trend of offshore wind power transmission technology[J]. Distribution & Utilization, 2022, 39(11): 2-10.
[4] 赵国亮, 陈维江, 邓占锋, 等. 柔性低频交流输电关键技术及应用[J]. 电力系统自动化, 2022, 46(15): 1-10. Zhao Guoliang, Chen Weijiang, Deng Zhanfeng, et al. Key technologies and application of flexible low-frequency AC transmission[J]. Automation of Electric Power Systems, 2022, 46(15): 1-10.
[5] 林进钿, 倪晓军, 裘鹏. 柔性低频交流输电技术研究综述[J]. 浙江电力, 2021, 40(10): 42-50. Lin Jintian, Ni Xiaojun, Qiu Peng. Review of flexible low-frequency AC transmission technology[J]. Zhejiang Electric Power, 2021, 40(10): 42-50.
[6] 王锡凡, 卫晓辉, 宁联辉, 等. 海上风电并网与输送方案比较[J]. 中国电机工程学报, 2014, 34(31): 5459-5466. Wang Xifan, Wei Xiaohui, Ning Lianhui, et al. Integration techniques and transmission schemes for off-shore wind farms[J]. Proceedings of the CSEE, 2014, 34(31): 5459-5466.
[7] 李浩, 裴翔羽, 李泽文, 等. 具备故障电流限制能力的多端口直流断路器[J]. 电工技术学报, 2023, 38(10): 2818-2831. Li Hao, Pei Xiangyu, Li Zewen, et al. A multi-port DC circuit breaker with fault-current limiting capability [J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2818-2831.
[8] 束洪春, 邵宗学, 旷宇. 基于改进型限流混合式直流断路器的开断时序优化研究[J]. 电工技术学报, 2023, 38(22): 6176-6187. Shu Hongchun, Shao Zongxue, Kuang Yu. Research of opening timing optimization based on improved current-limiting hybrid DC circuit breaker[J]. Tran-sactions of China Electrotechnical Society, 2023, 38(22): 6176-6187.
[9] 朱海, 郝亮亮, 和敬涵, 等. HVDC送端交流系统故障引起换相失败的机理分析[J]. 电工技术学报, 2023, 38(16): 4465-4478. Zhu Hai, Hao Liangliang, He Jinghan, et al. Mechanism analysis of commutation failure caused by fault of HVDC sending end AC system[J]. Tran-sactions of China Electrotechnical Society, 2023, 38(16): 4465-4478.
[10] 王秀丽, 赵勃扬, 黄明煌, 等. 大规模深远海风电送出方式比较及集成设计关键技术研究[J]. 全球能源互联网, 2019, 2(2): 138-145. Wang Xiuli, Zhao Boyang, Huang Minghuang, et al. Research of integration methods comparison and key design technologies for large scale long distance offshore wind power[J]. Journal of Global Energy Interconnection, 2019, 2(2): 138-145.
[11] Tang Yingjie, Zhang Zheren, Xu Zheng. DRU based low frequency AC transmission scheme for offshore wind farm integration[J]. IEEE Transactions on Sustainable Energy, 2021, 12(3): 1512-1524.
[12] 段子越, 孟永庆, 宁联辉, 等. 柔性分频输电系统的构建规划及关键设备技术综述[J]. 电力系统自动化, 2023, 47(10): 205-215. Duan Ziyue, Meng Yongqing, Ning Lianhui, et al. Review on construction planning and key equipment technology of flexible fractional frequency tran-smission system[J]. Automation of Electric Power Systems, 2023, 47(10): 205-215.
[13] 段子越, 孟永庆, 宋博阳, 等. 基于模块化多电平矩阵换流器的柔性低频输电系统大信号稳定性分析[J]. 高电压技术, 2023, 49(9): 3745-3756. Duan Ziyue, Meng Yongqing, Song Boyang, et al. Large signal stability analysis of flexible low frequency transmission system based on modular multilevel matrix converter[J]. High Voltage Engineering, 2023, 49(9): 3745-3756.
[14] 王秀丽, 张海涛, 周嘉豪, 等. 远距离风电分频送出方式及大功率变频装置的研发[J]. 高电压技术, 2024, 50(5): 1978-1986. Wang Xiuli, Zhang Haitao, Zhou Jiahao, et al. Frequency converter development of fractional frequency transmission system in long-distance wind power integration[J]. High Voltage Engineering, 2024, 50(5): 1978-1986.
[15] Kammerer F, Kolb J, Braun M. A novel cascaded vector control scheme for the modular multilevel matrix converter[C]//IECON 2011-37th Annual Con-ference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 2011: 1097-1102.
[16] Kawamura W, Akagi H. Control of the modular multilevel cascade converter based on triple-star bridge-cells (MMCC-TSBC) for motor drives[C]// 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 2012: 3506-3513.
[17] Shang Shuonan, Meng Yongqing, Wang Jian, et al. Research on modeling and control strategy of modular multilevel matrix converter supplying passive networks[C]//2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, 2016: 1974-1978.
[18] 刘士利, 罗英楠, 刘宗烨, 等. 饱和多孔介质对流特性对高压交流海底电缆载流性能的影响[J]. 电工技术学报, 2023, 38(4): 1023-1031. Liu Shili, Luo Yingnan, Liu Zongye, et al. The influence of convective characteristics of saturated porous media on ampacity performance of submarine cable[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 1023-1031.
[19] Yu Zheyang, Zhang Zheren, Xu Zheng. Electromechanical transient modeling of the low-frequency AC system with modular multilevel matrix converter stations[J]. IEEE Transactions on Power Systems, 2024, 39(1): 921-933.
[20] 盛景, 陈聪, 向鑫, 等. 模块化多电平谐振变换器多自由度调压控制及子模块电容均压方法[J]. 电工技术学报, 2022, 37(24): 6216-6229. Sheng Jing, Chen Cong, Xiang Xin, et al. Multiple-degree-of-freedom control and capacitor voltage balancing method of modular multilevel resonant converter[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6216-6229.
[21] Liu Shenquan, Wang Xifan, Wang Biyang, et al. Comparison between back-to-back MMC and M3C as high power AC/AC converters[C]//2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 2016: 671-676.
[22] Kawamura W, Hagiwara M, Akagi H. Control and experiment of a modular multilevel cascade converter based on triple-star bridge cells[J]. IEEE Transactions on Industry Applications, 2014, 50(5): 3536-3548.
[23] Liu Shenquan, Wang Xifan, Meng Yongqing, et al. A decoupled control strategy of modular multilevel matrix converter for fractional frequency transmission system[J]. IEEE Transactions on Power Delivery, 2017, 32(4): 2111-2121.
[24] 程启明, 谢怡群, 马信乔, 等. 不平衡电网模块化多电平矩阵换流器的控制策略[J]. 高电压技术, 2023, 49(5): 1975-1984. Cheng Qiming, Xie Yiqun, Ma Xinqiao, et al. Control strategy of modular multilevel matrix converter under unbalanced grid conditions[J]. High Voltage Engine-ering, 2023, 49(5): 1975-1984.
[25] 郑涛, 宋伟男, 吕文轩. 基于M3C的低频输电系统不对称故障穿越控制策略[J]. 电力系统保护与控制, 2023, 51(8): 107-117. Zheng Tao, Song Weinan, Lü Wenxuan. Asymmetric fault ride-through control strategy for a low frequency AC transmission system based on a modular multi-level matrix converter[J]. Power System Protec-tion and Control, 2023, 51(8): 107-117.
[26] 高校平, 张晨浩, 宋国兵, 等. 海上风电低频输电系统低频侧不对称故障控制策略[J]. 电力自动化设备, 2023, 43(10): 160-166. Gao Xiaoping, Zhang Chenhao, Song Guobing, et al. Control strategies of offshore wind power low frequency transmission system under asymmetric fault of low-frequency side[J]. Electric Power Automation Equipment, 2023, 43(10): 160-166.
[27] Liu Yuchao, Li Guoqing, Wang He, et al. Research on AC line distance relay in the presence of modular multilevel converter based HVDC[C]//2016 IEEE PES Asia-Pacific Power and Energy Engineering Con-ference (APPEEC), Xi’an, China, 2016: 1622-1626.
[28] Shi Lei, Adam G P, Li Rui, et al. Control of offshore MMC during asymmetric offshore AC faults for wind power transmission[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1074-1083.
[29] 郑黎明, 贾科, 毕天姝, 等. 海上风电接入柔直系统交流侧故障特征及对保护的影响分析[J]. 电力系统保护与控制, 2021, 49(20): 20-32. Zheng Liming, Jia Ke, Bi Tianshu, et al. AC-side fault analysis of a VSC-HVDC transmission system connected to offshore wind farms and the impact on protection[J]. Power System Protection and Control, 2021, 49(20): 20-32.
[30] 郑涛, 康恒, 宋伟男. 可实现低频输电系统不对称故障穿越的M3C电容电压均衡控制策略[J]. 电力系统保护与控制, 2023, 51(23): 130-140. Zheng Tao, Kang Heng, Song Weinan. Asymmetric fault ride-through control strategy for low-frequency transmission systems realizing the capacitor voltage balance of modular multilevel matrix converters[J]. Power System Protection and Control, 2023, 51(23): 130-140.
[31] 赵勃扬, 王锡凡, 宁联辉, 等. 分频海上风电系统的不对称故障穿越控制[J]. 中国电机工程学报, 2023, 43(12): 4589-4599. Zhao Boyang, Wang Xifan, Ning Lianhui, et al. Ride-through control of fractional frequency offshore wind power system during unsymmetrical grid faults[J]. Proceedings of the CSEE, 2023, 43(12): 4589-4599.
[32] 张建坡, 李耐心, 田新成. 电网电压不平衡条件下模块化多电平换流器高压直流输电控制策略[J]. 电工技术学报, 2016, 31(22): 205-212. Zhang Jianpo, Li Naixin, Tian Xincheng. The control strategies of modular multilevel converter-high voltage direct current transmission under unbalanced grid voltage conditions[J]. Transactions of China Electrotechnical Society, 2016, 31(22): 205-212.
[33] 顾乔根, 张晓宇, 吕航, 等. 基于故障负序分量的低频变压器快速差动保护[J]. 电力系统自动化, 2023, 47(7): 184-192. Gu Qiaogen, Zhang Xiaoyu, Lü Hang, et al. Fast differential protection of low-frequency transformer based on fault negative sequence component[J]. Automation of Electric Power Systems, 2023, 47(7): 184-192.
Abstract Low frequency transmission technology enhances the transmission distance and capacity by reducing the transmission frequency, which is a new type of transmission technology taking into account the advantages of traditional AC and DC transmission, and has a good application prospect in the scenarios of medium and distant sea wind power transmission, new energy pooling and urban flexible interconnection.
Flexible low frequency transmission system is double-ended power electronics systems, when the low frequency transmission line occurs asymmetrical faults, M3C (modular multilevel matrix converter) will use the fault control strategy to achieve the corresponding control objectives, and the characteristics of the fault current will be affected by the control strategy, which in turn affects the performance of the traditional line protection. For this reason, this paper proposes a current differential protection performance improvement scheme for flexible low frequency transmission system based on control and protection synergy, which improves the action performance of current differential protection by actively regulating the magnitude of negative sequence current in the line through the M3C.
First, according to the power relationship during the asymmetrical fault on the low frequency side, the bridge arm active power imbalance component is theoretically deduced, the reasons for the M3C capacitor voltage imbalance are analysed, and for the problem that capacitor voltage balance through negative sequence current control limits the degree of freedom of the M3C negative sequence currents, a capacitor voltage balance strategy based on the M3C circulating current control is adopted, which realises the M3C capacitor voltage balance control with the mutual decoupling of negative sequence current control. Secondly, based on the action characteristics of the current differential protection, the influence of negative sequence current on the action performance of the current differential protection is analysed, and it is pointed out that the action performance of the current differential protection can be changed by regulating the negative sequence current in the line through the M3C to change the relationship between the action amount and the restraint amount. Finally, with the goal of improving the operational performance of the differential current protection, and under the constraint of ensuring that the M3C bridge arm doesn't overcurrent, the reference value of negative sequence current is theoretically calculated and selected.
In the simulation analysis, this paper establishes a flexible low frequency transmission system simulation model, through a large number of simulation experiments, in order to verify the feasibility and effectiveness of the proposed scheme. The simulation results in this paper show that: (1) The capacitor voltage balance strategy based on M3C circulating current control adopted in this paper is able to achieve the capacitor voltage balance of M3C during asymmetrical faults. (2) The negative sequence current reference value selected in this paper can ensure that the line fault current does not exceed the safe range and avoid the overcurrent problem of M3C bridge arm. (3) By comparing the action performance of current differential protection under different negative sequence currents, it is verified that the negative sequence current reference value selected in this paper effectively improves the action performance of current differential protection, and makes the current differential protection act correctly under various fault conditions.
keywords:Flexible low frequency transmission system, modular multilevel matrix converter, negative sequence currents control, capacitor voltage balance, differential current protection
DOI: 10.19595/j.cnki.1000-6753.tces.240202
中图分类号:TM77
国家自然科学基金联合基金资助项目(U2166205)。
收稿日期 2024-01-30
改稿日期 2024-03-11
郑 涛 男,1975年生,教授,博士生导师,研究方向为电力系统自动化及继电保护。E-mail:zhengtao_sf@126.com
康 恒 男,2000年生,硕士研究生,研究方向为柔性低频输电系统。E-mail:khengwork@163.com(通信作者)
(编辑 赫 蕾)