
图1 一体化系统运行模式
Fig.1 The operation model of integrated system
摘要 新能源富集和负荷集中地区建设源网荷储一体化系统是推动新能源大规模就地消纳的有效方式。然而,100%新能源场景下,一体化系统缺乏同步惯量支撑,频率稳定面临极大挑战。为深度挖掘“源-网-荷-储”各环节调频潜力,首先对跟网型和构网型新能源场站,以及需求侧响应的频率支撑能力进行研究,并根据系统实际运行状态和预想故障场景设置合理的虚拟惯性时间常数,建立一体化系统频率响应模型;其次,在100%新能源场景下的储能配置模型中,提出考虑各调频资源协同运行的储能优化配置方法,并利用时域仿真将频率安全稳定约束嵌入配置模型;最后,基于西南某地区待建设的源网荷储一体化试点工程进行算例验证,结果表明,该文提出的配置方法能够有效提升一体化系统频率稳定性。
关键词:源网荷储一体化系统 跟网型 构网型 频率稳定 储能优化配置
为实现“碳达峰、碳中和”目标,我国正逐步推动以新能源为主体的新型电力系统建设。在可再生能源富集型城市的工业园区建设“源网荷储一体化”系统(以下简称一体化系统)是推动区域能源结构转型的有效途径[1]。然而,100%新能源场景下,由于缺乏常规电源惯量支撑,频率稳定问题日益凸显[2]。储能电站具备功率双向调节、短时充放电速度快、调节能力强等特点,在一体化系统提供快速频率调节和惯量支撑方面具有显著优势[3-4]。储能的合理配置、源侧跟/构策略选型及需求侧响应等多类型、多资源调频措施的协调灵活配合,在提高消纳新能源发电能力、提升区域电网安全运行水平、增强一体化系统的频率稳定等方面具有重要意义。
针对一体化系统中各个环节调频能力的研究,目前主要聚焦在源侧跟/构网型控制策略、储能的快速频率响应(Fast Frequency Response, FFR)及其配置和负荷侧参与调频等方面。在发电侧新能源机组的跟/构网型控制策略方面,通过在新能源机组并网逆变器施加跟网型(Grid Following, GFL)和构网型(Grid Forming, GFM)控制策略,使其具备主动支撑能力[5-7],主要表现形式为虚拟同步机(Virtual Synchronous Generators, VSG)技术,并在工程中实际应用[8-9]。文献[10]梳理了现有的控制技术,并对跟网型控制和构网型控制策略及其相关应用进行分析。文献[11]分析了两种控制方式下风电机组的惯量响应特性,并探讨了风电机组提供的虚拟惯量对系统频率的影响,证实了VSG对降低最大频率变化率,提高频率最低点的作用。然而,现有关于多种类型VSG的频率支撑能力的研究,大多未考虑新能源设备的实际运行状态和预想故障场景对控制参数的影响,通常将惯性或者虚拟惯性时间常数设置为固定值,没有充分发挥VSG的灵活性,同时现有的规划研究也未计及新能源场站的构网型、跟网型控制策略对系统频率响应和储能配置的影响。在储能的快速频率响应及配置方面,近年来有学者针对无常规电源支撑的新能源基地和海岛微电网群的储能配置方法进行了研究。文献[12]对含直流运行方式的新能源基地进行储能优化配置,指出构网型场站能够提升基地的频率稳定能力;文献[13]通过不同功能类型的海岛微电网群协调控制,实现全部由绿色能源为海岛群负荷供电的目标。然而,鲜有学者针对100%新能源场景下一体化系统的储能配置方案展开研究。此外在负荷侧,利用需求侧响应参与系统的频率调节,亦能有效增强系统的频率稳定性[14-15]。文献[16]设计了需求侧响应参与频率控制的方法,并探讨了负荷的有功-电压耦合特性对频率稳定的影响。上述研究主要面向各灵活性资源的频率支撑能力,尚未考虑无常规电源支撑场景下,源网荷储各环节协同运行对一体化系统频率稳定运行及构网型储能场站配置的影响。
除此之外,频率稳定相关约束具有强非线性,导致储能优化配置模型求解困难。针对该问题,现有文献通常采用简化模型的方式和凸松弛技术进行处理。文献[17]建立了平均系统频率(Average System Frequency, ASF)模型,采用多个一阶惯性环节模拟动态过程,将系统频率响应曲线近似为直线;文献[18]采用综合惯性控制推导风电机组的传递函数,构建了含多等值机的扩展系统频率响应(System Frequency Response, SFR)模型,提高频率主动支撑能力。文献[19-20]基于序列建模思想,采用分段离散化处理各调频设备的暂态出力。上述处理频率响应曲线的方法使频率稳定指标更加乐观,导致储能配置结果存在一定的保守性。
以上研究对于提升一体化系统的调频能力和储能配置具有一定的指导意义,但在以下几个方面还需深入研究:①100%新能源场景下,综合考虑新能源场站的构网型和跟网型控制策略、储能的快速频率响应、需求侧响应各环节协调运行对储能配置的影响;②基于新能源出力特性和预想故障场景,构建合理的新能源场站虚拟惯性时间常数,保障新能源场站VSG的响应速度和有功输出平稳性;③考虑一体化系统频率响应特性,提出计及不同控制策略的储能配置方法。鉴于此,本文针对100%新能源场景下一体化系统的储能配置需求,建立了计及频率稳定约束和各调频资源协同运行的一体化系统储能优化配置模型。本文首先分析了风电、储能虚拟惯量能量来源和运行特性,根据一体化系统实际运行状态和预想故障场景,设计合理的虚拟惯性时间常数;其次,量化了新能源场站的跟网型和构网型控制策略对系统频率支撑的贡献度,构建了涵盖不同控制策略的新能源场站VSG和需求响应的一体化系统频率响应模型;进而,建立一体化系统在非计划脱网故障场景下保持频率稳定的储能配置模型,将系统频率响应模型内嵌至优化问题中;最后,依据西南某地区“源网荷储一体化试点工程”设置算例,验证本文所提方法的有效性,并分析了构网型及跟网型控制策略、需求侧响应等因素对储能配置的影响。
新型工业园区一体化系统由新能源场站、储能电站及工业负荷组成。系统实行“自发自用、余量存储、主网支撑”的运行机制。一体化系统配备大量的数据采集与监视控制系统和相量测量装置,能够实时监测系统的频率、电压及功率等信息。作为一体化系统的“神经中枢”,调度中心根据监测的电气量信息进行判断和下发动作指令,实现对系统内所有灵活性可控资源的优化调度,其运行模式如图1所示。

图1 一体化系统运行模式
Fig.1 The operation model of integrated system
100%新能源场景下,一体化系统在稳态运行时采用单馈入模式,仅在负荷高峰时段通过交流联络线向上级电网购电,新能源高发时段不反向输送电能,通过协调调度实现新能源就地消纳。相较于传统的一体化运行模式,100%新能源场景下新型工业园区一体化系统缺乏同步惯量支撑,在面对非计划脱网、负荷波动等有功扰动故障下容易出现频率失稳的风险。通过对一体化系统中新能源场机组并网逆变器进行构网型控制改进,提升场站的惯量和频率支撑能力,结合储能电站的快速频率响应以及需求侧响应参与调频,充分挖掘一体化系统源荷储各环节频率支撑潜力,形成多类型灵活性资源协调运行机制,能够有效提升系统的频率稳定能力。
本节分析了新能源场站虚拟惯量和需求侧响应频率支撑能力,并根据系统实际运行状态和预想故障场景合理地设置新能源场站的虚拟惯性时间常数。
风电机组的虚拟惯量由风机转子动能的辅助频率控制策略决定[21],风电机组的机械功率可表示为
 (1)
(1)
式中,Pm为风机的机械功率;ρ、Cp、λ、β、ωw、vw、Rw分别为空气密度、风能利用系数、叶尖速比、桨角距、叶轮半径、转速和叶片半径。
考虑到风机从最大功率点减小转速来提供有功支撑的运行模式在退出调频后会造成频率二次跌落的风险,本文根据国标GB/T 19963.1—2021《风电场接入电力系统技术规定第1部分:陆上风电》相关要求,采用减载运行方式来提供频率支撑[22]。减载工况下风机的输出功率 为
为
 (2)
(2)
式中,kd和d分别为减载功率跟踪系数和减载率;Cpd为减载风能利用系数;Cpmax为最佳风能利用系数。
忽略风机转速变化导致的机械能损失,支撑风电机组惯性的能量来自于超速运行储存在风机叶片中的动能[23]。风机允许的转速变化范围为0.7(pu)~1.2(pu),根据风速将风机的运行状态分为三个区间:d1[vmin,vd1)、d2[vd1,vd2)、d3[vd2,vwn)。
 (3)
(3)
式中,wwmax、wwmin分别为风电机组转速上、下限;vmin为风电机组减载运行的起始风速;vd1为风电机组达到最大功率点跟踪(Maximum Power Point Tracking, MPPT)点对应的风速;vd2为风电机组减载运行的最大风速;λopt为风电机组最佳叶尖速比。
当风速位于区间d1和d2时,风电机组采用超速控制进行减速,从而释放转子动能;当风速位于区间d3时,风电机组采用超速控制和变桨控制进行减速,进一步释放动能直至额定风速。根据不同的风速区间,风电机组可释放的动能为
 (4)
(4)
式中,Ek为风电机组k存储的动能;vwn为额定风速; 为转速变化量;J为风机转子固有惯量。
为转速变化量;J为风机转子固有惯量。
类比同步机的惯性时间常数定义,采用等值模型[24]计算一体化系统中风电场的虚拟惯性时间常数,有
 (5)
(5)
式中,Hk,t为t时刻风机k的虚拟惯性时间常数;PwN为风电场w的装机容量;Hw,t为t时刻风电场w的虚拟惯性时间常数;PN为风机额定容量;K为风电场集合。
光伏电站的实际输出功率受日照、季节和温度等因素的影响,具有较高的随机性。此外,由于光伏板不具备机械旋转部件,其等效惯量为零,需要通过减载备用或额外配置储能模块参与频率调节。为减少一体化系统的运行成本,光伏电站以最大功率输出模式运行,并采用光储一体化运行模式提供惯量支撑[3],其惯量支撑能力可等效为储能电站。
电化学储能具备短时充放电速度快、双向调节功率等优势,能够在功率扰动事故发生后提供快速功率支撑,提高系统的稳定性,还可以与光伏场站协同运行提供惯量支撑。根据GB/T 36547—2018《电化学储能系统接入电网技术规定》[25],储能惯性时间常数取值为4~12 s。在一体化系统实际运行中,负荷高峰时段联络线传输功率较大,此时联络线断开产生的功率缺额会对系统的频率稳定产生较大的影响。因此本文将一体化系统非计划脱网运行视为预想故障场景,设定储能的虚拟惯性时间常数与联络线功率成比例,有
 (6)
(6)
式中,He,t为t时段储能电站e的虚拟惯性时间常数;Ptran,t为t时段联络线传输功率;Pmax tran为联络线最大传输功率;Hmax和Hmin分别为储能场站虚拟惯性时间常数的上、下限。
在传统的一体化运行模式中,需求侧响应作为一种灵活的电力资源,通过实施碳交易机制直接影响能源的价格和供应结构,用户可以在碳交易市场中售卖碳配额,在获取收益的同时促进新能源的消纳。在100%新能源场景下,一体化系统内部无常规电源支撑,能够从源侧实现系统的零碳排放,因此本文在后续建模过程中不计及碳交易机制。同时工业负荷作为一体化系统的主要负荷类型,具有响应速度快、可控性强等特点。对负荷进行有效聚合,并通过调度中心进行统一管理,可实现负荷的柔性调节。将负荷需求响应和主动切负荷措施纳入频率调控体系,以保障系统的频率稳定。
本文考虑可中断负荷需求响应(Demand Response, DR)运行特性,一体化调度中心通过与用户签订激励合同的方式确定相应的可调用容量和成本。负荷需求响应运行特性如图2所示,当联络线断开后,一体化系统基于监测的频率变化信息,通过DR控制模块进行判断。如果系统频率达到DR动作阈值,调度中心对可中断负荷下达调整指令,参与系统调频,同时返回功率调整量。为了避免DR频繁动作从而降低用户满意度,负荷需求响应量由预设比例、动作阈值时的频率变化率和系统虚拟惯性时间常数决定。

图2 负荷需求响应运行特性
Fig.2 Load demand response operational characteristics
负荷高峰时段联络线功率较大,系统出现断线故障,系统难以保持频率稳定。如果采取上述调频措施仍存在不平衡功率,系统将根据负荷的重要程度和供电可靠性需求进行主动切负荷,直至系统可以支撑剩余负荷运行。主动切负荷措施是一体化系统频率安全稳定的“最后一道防线”。
本节首先分析了一体化系统的频率响应过程;然后分析了新能源场站VSG的控制策略;最后建立了包含构网型及跟网型风电场、构网型储能电站和需求侧响应环节的频率响应模型。
一体化系统的频率与实时有功功率平衡有关,图3描述了t0时刻发生功率缺额扰动后系统的频率响应过程。t0~tdb为惯量响应阶段,由于一次调频存在死区fdb,扰动瞬间系统的初始频率变化率值最大;tdb~tNF时段由惯量响应和一次调频共同作用向系统提供有功功率,经过调频死区后一次调频动作,当一次调频增发的功率等于功率缺额时,系统频率达到最低点fnadir;tNF~t1时段仅由一次调频提供功率支撑,系统频率逐步恢复至准稳态频率fss。

图3 频率响应过程
Fig.3 Frequency response process
本文在新能源场站中引入VSG技术,使其具备频率支撑能力。现有研究根据控制类型将VSG分为跟网型和构网型两大类[26-28]。控制原理如图4所示。
图4a描述了GFL控制原理,由锁相环(Phase Locked Loops, PLL)和电流控制构成,PLL用于追踪电压的相位,不具有组网能力,本质上为电流源。图4b描述了GFM控制原理,有功回路模拟发电机转子摇摆方程,无功回路采用无功-电压下垂控制,具有自组网能力,本质上为电压源[29-30]。


图4 GFL和GFM控制策略
Fig.4 The control strategy of GFL and GFM
本节建立了100%新能源场景下一体化系统的频率响应模型,以充分发挥源、储、荷三部分的频率支撑能力。对于“源”和“储”而言,通过在电源并网逆变器附加控制策略,新能源场站VSG可通过调节自身的输出功率来响应系统频率的变化;对于“荷”而言,主要考虑负荷需求响应和主动切负荷措施。图5给出了一体化系统中构网型场站、跟网型场站和需求侧响应协同运行的频率响应模型。

图5 一体化系统频率响应模型
Fig.5 Frequency response model of integrated system
2.3.1 一体化系统惯量需求
一体化系统惯量需求应满足最大频率变化率的指标要求,避免在有功扰动下触发继电保护装置动作,进而导致系统出现严重故障。在运行过程中一体化系统应满足最小惯量需求,即
 (7)
(7)
式中,Emin sys,t为t时段系统的最小惯量需求;DPloss,t为t时段预想功率扰动;RoCoFmax为系统最大频率变化率;f0为基准频率。
2.3.2 跟网型风电场
在传统跟网型风机基础上,对图4a中的锁相环施加额外的控制环节,为系统提供虚拟惯量支撑和一次调频支撑,分别响应系统频率变化率和频率偏差。由于GFL控制存在固有延时,并未改变扰动初始时刻系统频率变化率 ,而是以考虑延时的快速频率响应作用于系统上[31]。本文引入一阶惯性环节模拟其响应滞后性,跟网型风电场频率响应模型如下所示:
,而是以考虑延时的快速频率响应作用于系统上[31]。本文引入一阶惯性环节模拟其响应滞后性,跟网型风电场频率响应模型如下所示:
一次调频和延时环节为
 (8)
(8)
限幅环节为
 (9)
(9)
惯量响应环节为
 (10)
(10)
有功功率总调节量为
 (11)
(11)
式中,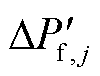 、Kf,j、Tf,j分别为跟网型风电场j经过一阶惯性环节的出力、一次调频系数以及一阶惯性环节时间常数;
、Kf,j、Tf,j分别为跟网型风电场j经过一阶惯性环节的出力、一次调频系数以及一阶惯性环节时间常数; 为经过固有延时后的频率偏差;DP1 f,j、Pf,j,max分别为跟网型风电场j参与一次调频的实际输出功率,以及参与一次调频的功率上限,该上限由风机的备用容量决定;DP2 f,j、KHf,j、THf,j分别为跟网型风电场j的惯量响应的输出功率、惯性环节比例系数、输出一阶惯性时间常数;DPf,j为最终的跟网型风电场输出功率。
为经过固有延时后的频率偏差;DP1 f,j、Pf,j,max分别为跟网型风电场j参与一次调频的实际输出功率,以及参与一次调频的功率上限,该上限由风机的备用容量决定;DP2 f,j、KHf,j、THf,j分别为跟网型风电场j的惯量响应的输出功率、惯性环节比例系数、输出一阶惯性时间常数;DPf,j为最终的跟网型风电场输出功率。
2.3.3 构网型风电场
通过在并网逆变器施加虚拟惯性控制策略,模拟同步机转子运动方程[32],理想工况下,构网型VSG与同步机组的动态特性几乎相同。构网型风电场经过调频死区后参与一次调频,如图5所示,频率响应模型由比例环节、限幅环节和一阶惯性环节串联表示。
一次调频环节为
 (12)
(12)
限幅环节为
 (13)
(13)
式中,Df为系统频率偏差; 、KF,i、TF,i分别为构网型风电场i经过一阶惯性环节的出力、一次调频系数、一阶惯性环节时间常数;DPF,i、PF,i,max分别为构网型风电场参与一次调频的实际输出功率和功率上限,该上限由风机的备用容量决定。
、KF,i、TF,i分别为构网型风电场i经过一阶惯性环节的出力、一次调频系数、一阶惯性环节时间常数;DPF,i、PF,i,max分别为构网型风电场参与一次调频的实际输出功率和功率上限,该上限由风机的备用容量决定。
2.3.4 构网型储能电站
与构网型风电场运行特性相似,构网型储能电站的频率响应模型由比例环节、一阶惯性环节和限幅环节组成[33],频率响应模型如下所示。
一次调频和限幅环节为
 (14)
(14)
输出限幅环节为
 (15)
(15)
式中, 、KE,m和TE,m分别为构网型储能电站经过一阶惯性环节的出力、一次调频系数、一阶惯性环节时间常数;DPE,m、RFFR ess分别为构网型储能参与一次调频的实际输出功率、快速频率响应功率,由储能的稳态出力和放电倍率决定。
、KE,m和TE,m分别为构网型储能电站经过一阶惯性环节的出力、一次调频系数、一阶惯性环节时间常数;DPE,m、RFFR ess分别为构网型储能参与一次调频的实际输出功率、快速频率响应功率,由储能的稳态出力和放电倍率决定。
2.3.5 需求侧响应
1)负荷需求响应
由图2可知,当调度中心监测到频率达到动作阈值时,系统将根据预案自动调整负荷,参与系统调频。DR调整量为
 (16)
(16)
 (17)
(17)
式中,fDR为负荷需求响应的低频触发阈值;tDR为低频触发阈值对应的时刻;KDR为负荷需求响应控制模块预设的比例系数;Ht为惯性时间常数;DPL、PL,max分别为负荷需求响应的实际输出功率、输出功率的上限;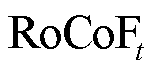 为系统频率变化率。
为系统频率变化率。
2)主动切负荷
当联络线功率较大导致维持系统频率稳定难度较大时,经过秒级延时后,允许系统切除一定量的负荷用来维持频率不越限。
 (18)
(18)
式中,DPcut,t、tcut和Pcut分别为发生联络线缺额后随时间变化的切负荷功率、切负荷的固有延时和切负荷动作阈值。
本节建立了考虑新能源场站和需求侧响应协同运行的储能优化配置模型,并将频率安全稳定约束嵌入模型中。模型目标主要考虑了储能的投资成本、维护成本、稳态运行成本以及预想故障场景下系统的需求侧响应成本等。约束条件主要包括基准运行场景约束、暂态频率约束和需求侧响应约束。
一体化系统储能的配置目标为最小化规划期间系统的总成本,如式(19)所示,包括稳态配置成本式(20)和需求侧响应成本式(21)。其中稳态配置成本包括储能日均投资成本式(22)、储能维护成本式(23)、系统运行成本式(24)。
 (19)
(19)
 (20)
(20)
 (21)
(21)
 (22)
(22)
 (23)
(23)
 (24)
(24)
其中
 (25)
(25)
式中,Cstable为储能的稳态配置成本;Cfault为预想故障下系统的需求侧响应成本;Cinv为储能日平均投资成本;Com为储能的日均维护成本;Cop为典型日场景下系统的运行成本,其中运行成本包括风电机组减载备用成本Creserve和向上级电网购电成本Ctran;CDR和Ccut分别为预想故障场景下系统的负荷需求响应成本和切负荷惩罚成本;y、te分别为储能设备的投资折现系数和设计使用寿命;cp、ce、com、creserve、ctran、cDR、ccut分别为储能系统单位功率投资成本、单位容量投资成本、维护成本、风机减载备用成本、联络线传输功率成本、负荷需求响应成本和切负荷惩罚成本的系数;Pn、En分别为储能系统配置的额定功率和额定容量;Rwi,t、PDR,t、Pcut,t分别为t时刻风电机组的备用容量、负荷需求响应量和切负荷量。
1)功率平衡约束
 (26)
(26)
式中,Pw,i,t为t时刻风电场i的出力;Pv,i,t为t时刻光伏场站i的出力;Nw和Nv分别为系统中风电场站和光伏场站的个数;Pess,ch,t和Pess,dis,t分别为t时段储能的充、放电功率。
2)联络线功率约束
 (27)
(27)
联络线工作在单馈入运行模式,即仅在负荷高峰期向上级电网购电,负荷低谷时不反向输送功率。
3)新能源场站出力约束
式(28)~式(30)分别为风电场和光伏电站的稳态出力约束。当风电出力高于额定功率的20%时需要参与调频,光伏场站采用MPPT模式并网运行。
 (28)
(28)
 (29)
(29)
 (30)
(30)
式中,Pavail w,i,t、Pactualw,i,t、Pactual v,i,t分别为风电机组可用最大出力、风机实际出力和光伏场站实际出力; 为风电场备用率。
为风电场备用率。
4)储能电站运行约束
储能运行约束包括储能充/放电功率约束式(31)~式(33);式(33)限制储能设备不能同时进行充电和放电;储能各时段容量约束式(34)~式(37);式(37)保障储能运行末时段的容量不低于初始时段。
 (31)
(31)
 (32)
(32)
 (33)
(33)
 (34)
(34)
 (35)
(35)
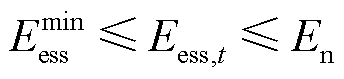 (36)
(36)
 (37)
(37)
式中,Uess,dis,t、Uess,ch,t分别为储能放、充电状态变量;Eess,t为t时段储能的容量;ηch、ηdis分别为储能充、放电效率;E0、Eess,T和Emin ess分别为储能初始容量、末时段容量及储能允许配置的最小容量;En为待优化储能容量。
本文通过最大频率变化率、频率偏差极值、准稳态频率偏差三个指标评估系统的频率稳定性。系统频率变化率极值通常出现在扰动事故发生的瞬间,根据转子运动方程式(38),得到系统的最大频率变化率式(39)及对应的约束式(40)。
 (38)
(38)
 (39)
(39)
 (40)
(40)
式中,Dsys为负荷阻尼系数;Nwi为构网型风电场数量;Nwj为跟网型风电场数量; 为频率变化量;
为频率变化量; 为系统总的惯性时间常数。
为系统总的惯性时间常数。
根据图5中各控制环节的频率响应模型,通过时域仿真方法得到扰动后的系统最大频率偏差值和准稳态频率偏差值,需要满足相应的系统暂态频率约束,表达式为
 (41)
(41)
 (42)
(42)
式中,Dfmax为最大频率偏差上限值; 为准稳态频率偏差上限值。
为准稳态频率偏差上限值。
构网型储能电站在经过调频死区后提供秒级的快速频率响应(FFR)功率。式(43)~式(45)分别为储能场站提供的FFR功率约束和容量约束。
 (43)
(43)
 (44)
(44)
 (45)
(45)
式中,Cmax ess为储能最大充放电倍率;RFFR ess,t为t时段储能的FFR功率;Dt为储能的快速频率响应时间;DEFFR ess,t为储能提供FFR的容量变化。
需求侧响应主要包含预想故障场景下系统的负荷需求响应(DR)和主动切负荷两种调频方法。式(46)、式(47)分别表示DR约束和切负荷约束。
 (46)
(46)
 (47)
(47)
式中,DPmin DR、DPmax DR分别为t时段可响应负荷的最大下调量和上调量;DPmax cut为t时段系统允许的最大负荷切除量。
鉴于频率响应模型存在大量的非线性控制环节,频率解析式表达困难,为了准确地获取系统时域频率响应动态曲线,采用时域仿真求解系统的频率响应模型得到频率稳定性指标结果。遗传算法对于优化问题中约束条件及目标函数的表达方式具有较高的宽容度,能够较为方便地与仿真模块相结合。因此,本文采用改进遗传算法内嵌仿真模块的方式求解储能的最优配置问题。求解流程如图6所示。
(1)输入系统的控制参数、经济参数和典型日新能源场站和负荷出力等数据。初始化种群,iter=0。
(2)将个体信息(En、Pn)传递至稳态配置模型中,将Pcut传递至频率响应模型中。调用CPLEX求解稳态配置成本式(19),约束条件包括式(26)~式(37)、式(43)~式(45),将求解得到的Ptran,t和 传递至步骤(3)。
传递至步骤(3)。
(3)根据式(5)、式(6)得到Hw和He,结合步骤(2)中传递的参数,建立一体化系统频率响应模型,并调用时域仿真软件得到频率响应曲线;校验系统是否满足暂态频率稳定约束式(40)~式(42)中的频率安全稳定指标。若满足频率要求,保留适应度值;若不满足,赋予适应度一个极大值。

图6 一体化系统储能优化配置求解流程
Fig.6 Flow chart of solution flow for optimizing energy storage configuration in integrated system
(4)更新适应度,交叉变异,得到子代信息。
(5)采用精英保留策略得到新父代。
(6)判断是否达到最大迭代次数,如果大于则通过解码最佳个体信息,输出适应度值包括储能配置、需求侧响应结果;反之,iter=iter+1,跳转至步骤(2)。循环迭代,直至迭代结束。
根据西南某地区源网荷储一体化系统试点工程设置算例,以验证本文所提方法的有效性。源网荷储一体化系统地理接线示意图如图7所示,一体化系统规划建设5个总装机容量为990 MW的风电场和3个总装机容量为510 MW的光伏场站,其中构网型风机与跟网型风机比例为4:1,风机和储能的控制参数见文献[4]。
选取该地区的典型日场景,以24 h为调度周期,以1 h为调度时段,新能源出力和负荷曲线如图8所示。模型中涉及的成本系数设置如下(单位:万元/ (MW·h)):cp=30、ce=15、com=0.002、creserve=0.003、ctran=0.0035、cDR=20、ccut=100。基准频率为50 Hz,调频死区为0.033 Hz。暂态频率稳定性指标:RoCoFmax=1 Hz/s、Dfmax=0.5 Hz、Dfmaxss=0.2 Hz。

图7 源网荷储一体化系统地理接线示意图
Fig 7 Schematic diagram of the geographic wiring of the source-grid-load-storage integration system

图8 新能源出力和总负荷
Fig.8 Load profile and renewable scenarios
采用本文提出的方法对上述待规划建设的一体化系统进行求解,得到储能配置方案、需求侧响应量及各成本结果见表1。
表1 储能配置结果
Tab.1 Energy storge configuration results

额定功率/MW额定容量/(MW·h)需求侧响应量/MW成本/万元 日均投资减载备用上级电网购电 234.98880.01285.965.692.3110.45
从优化配置结果可得,待配置的储能额定功率为234.98 MW,约占新能源总装机容量的15.7%,待配置的储能额定容量为880.01 MW·h,满足“一体化系统试点方案”中配置10%~20%储能,运行时间3~4 h的要求。日均总成本18.45万元,其中向上级电网购电成本占比约57%,可以看出一体化系统运行受上级电网影响较大。
5.2.1 系统惯量需求
虚拟惯量作为新能源场站的固有属性,其数值大小与实际运行状态相关,具有时变特性,如图9所示。由于考虑联络线非计划脱网为预想故障场景,因此在负荷低谷时段系统的惯量需求为零;在负荷高发时段,系统所需最低惯量最大可达7 500 MW·s,是风电所能提供的虚拟惯量的1.96倍,系统频率失稳的风险更高。

图9 一体化系统惯量需求
Fig.9 The inertia requirement of integrated system
5.2.2 一体化系统稳态运行分析
一体化系统运行曲线如图10所示。其中新能源出力和负荷具有明显的峰谷差,负荷高峰时段(10:00—20:00)的功率需求明显高于新能源出力总和,系统向上级电网购电。在负荷低谷时段(1:00—9:00, 21:00—24:00),负荷的电力需求小于风电场的发电功率,可以通过储能电站消纳风电机组的剩余功率,提高系统稳态运行时的能源利用率。

图10 一体化系统运行曲线
Fig 10 Operation curves of integrated system
结合表1配置结果和图8运行曲线,可得如下结论:
(1)一体化系统负荷高峰时段新能源发电总量仅为负荷的65%,缺额部分需要联络线功率和储能放电功率共同支撑。
(2)储能的稳态实际出力最大值为214.19 MW,为额定功率的91%,额定功率的剩余部分为预想故障场景下储能提供的功率支撑。由此可知,储能配置的额定功率由快速频率响应提供的功率和稳态运行功率共同决定。
(3)由于系统储能的调频时间为min级,主要表现为短时快速充放电保证系统的功率平衡而非电量平衡,因此储能容量配置受频率稳定约束影响较小,主要由稳态运行工况决定。
5.2.3 一体化系统暂态运行分析
基于上述储能配置和运行结果,得到各时刻预想故障场景(非计划脱网)的各时段的功率扰动量曲线如图11所示。

图11 各时段预想故障功率扰动量
Fig.11 Estimated power disturbance at each period
非计划脱网运行故障下,一体化系统在各时刻的最大频率偏差、频率变化率、准稳态频率偏差曲线如图12所示。在整个运行周期内,系统的最大频率偏差为0.39 Hz,最大准稳态频率偏差为0.19 Hz,最大频率变化率为0.89 Hz/s,均满足系统的频率稳定性指标要求。其中,16:00—18:00时段系统的准稳态频率偏差接近约束边界。由此可知,在该场景下准稳态频率偏差是限制一体化系统储能配置的主要因素。

图12 一体化系统频率指标
Fig.12 Frequency indicators for integrated system
为进一步验证本文所提方法在解决储能优化配置问题中的有效性,本文从是否考虑频率安全约束、需求侧响应、新能源场站VSG运行特性等方面对三种配置模型进行比较。模型对比场景见表2。
表2 模型对比场景
Tab.2 Model comparison cases

场景频率安全稳定约束需求侧响应约束储能参与频率支撑新能源场站VSG 1×PPP 2P×PP 3PPPP
对表2中的算例进行求解,得到各场景下一体化系统的储能配置结果见表3。图13为各场景对应的频率指标分布。场景1中负荷高峰时段系统的Δfss超过最大可容许范围,系统频率失稳。通过对比场景1和场景3可知,本文提出的考虑频率稳定约束的配置方法虽然成本增加了3 697.81元,但各调度时段频率指标均处于频率安全域内。相较于场景3,场景2未考虑需求侧响应,其配置的功率和成本较高,同时负荷高峰时刻的Δfss接近极限值,安全裕度较低,增加了系统频率失稳的风险。综上所述,考虑频率安全稳定约束、需求侧响应和新能源场站VSG运行特性的储能配置方案能够在提高一体化系统储能配置的投资经济性的同时有效地保证规划期内系统的频率稳定性,验证了本文所提储能优化配置方法的有效性。
表3 模型对比场景结果
Tab.3 Model comparison cases results

场景额定功率/MW额定容量/(MW·h)需求侧响应量/MW配置成本/元 1214.19826.85349.20185 563.99 2308.23889.80—197 208.71 3234.98889.43285.96189 261.80

图13 不同场景下频率指标分布
Fig.13 Comparison of frequency indicators in different cases
100%新能源场景下,风机在传统的跟网型控制下无法提供足量的惯量支撑,而构网型控制能够模拟同步机运行特性参与频率响应。为此,本文设置了构网和跟网比例分别为2:3、3:2、4:1以及全部为构网型场站共四种场景,其对储能配置的影响见表4。同时对Δfnadir、 和Δfss三个指标进行仿真,以说明构网型风机比例不同对储能配置的影响,具体仿真结果如图14所示。
和Δfss三个指标进行仿真,以说明构网型风机比例不同对储能配置的影响,具体仿真结果如图14所示。
表4 不同构网、跟网型风电场站比例对储能配置的影响
Tab.4 The impact of different proportion GFM and GFL wind stations on energy storage planning

构网:跟网额定功率/MW额定容量/(MW·h)需求侧响应量/MW配置成本/元 2:3448.84977.46214.37213 723.49 3:2370.61880.39238.17203 835.60 4:1234.98889.43285.96189 261.80 全部为构网268.77884.25240.90192 561.78
由图14a可以看出,所有场景下系统的Δfnadir均处于频率稳定域内,同时留有20%~30%的安全裕度,说明Δfnadir不是影响系统储能配置的主要因素。从图14b可以看出,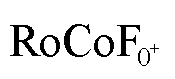 随构网型控制比例的增加而减小,这是由于跟网型控制存在固有延时并未改善系统的
随构网型控制比例的增加而减小,这是由于跟网型控制存在固有延时并未改善系统的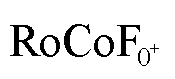 ,而构网型控制模拟同步及运行特性提供虚拟惯量支撑,能够有效改善系统的
,而构网型控制模拟同步及运行特性提供虚拟惯量支撑,能够有效改善系统的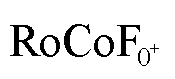 。当构网型占比低于4:1时,负荷高峰时段系统的
。当构网型占比低于4:1时,负荷高峰时段系统的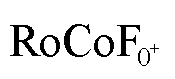 处于频率安全域边界,此时
处于频率安全域边界,此时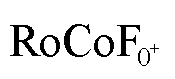 为影响储能配置的主要因素。构网型和跟网型场站比例为4:1的运行场景能够兼顾系统的稳定性和经济性,同时进一步验证了一体化试点工程中新能源场站控制策略的比例参数设置的合理性。
为影响储能配置的主要因素。构网型和跟网型场站比例为4:1的运行场景能够兼顾系统的稳定性和经济性,同时进一步验证了一体化试点工程中新能源场站控制策略的比例参数设置的合理性。


图14 构网型和跟网型比例对频率指标的影响
Fig.14 Impact of the proportion of GFM and GFL on frequency indicators
通过图14c和表4可以得到如下结论:当构网型风机占比不低于4:1时,储能配置成本随构网比例增加而增加,此时负荷高峰时段的Δfss处于稳定安全域边界。这是由于全部为构网型风机时,系统的惯量较大,此时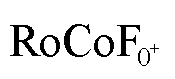 不再是影响储能配置的主要因素,根据式(15),全部为构网型场站时的频率变化率指标较小,导致系统的需求侧响应参与度较低,提供的一次调频功率不足,进而影响系统的Δfnadir和Δfss。为了保证上述两个指标处于频率安全稳定阈值内,将会增加系统的储能功率配置。
不再是影响储能配置的主要因素,根据式(15),全部为构网型场站时的频率变化率指标较小,导致系统的需求侧响应参与度较低,提供的一次调频功率不足,进而影响系统的Δfnadir和Δfss。为了保证上述两个指标处于频率安全稳定阈值内,将会增加系统的储能功率配置。
综上所述,构网型风机能够有效提升系统的惯量支撑水平从而改善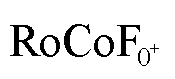 ,但同时影响需求侧响应的参与度。通过合理地设置构网型新能源场站控制比例和需求侧响应控制参数,可以实现源、储、荷的调频资源协同运行,使得一体化系统兼具频率稳定性和储能优化配置的经济性。
,但同时影响需求侧响应的参与度。通过合理地设置构网型新能源场站控制比例和需求侧响应控制参数,可以实现源、储、荷的调频资源协同运行,使得一体化系统兼具频率稳定性和储能优化配置的经济性。
从实际工况来看,新能源场站的控制参数以及各时段出力可以通过调度中心实时调整,而用户侧信息不确定性相对较大。因此,本节从负荷需求响应控制参数和负荷走势两个方面分析储能配置对需求侧响应控制参数变化的敏感程度。
5.5.1 负荷需求响应控制参数对储能配置的影响
基于5.3节中场景3,在动作阈值为0.2 Hz条件下,分别设置负荷需求响应比例系数K1为0、1.2和2;负荷需求响应比例系数K1=1.2的条件下,分别设置动作阈值为0.15、0.2、0.25 Hz。模拟六个不同运行场景,表5给出了优化配置结果。分析可知:通过增加比例系数和降低动作阈值,能够有效地增加负荷需求响应调节量,激发需求侧响应的参与度,减少储能配置成本。
表5 负荷需求响应控制参数对储能配置的影响
Tab.5 The impact of load demand response control parameters on energy storage planning

控制参数额定功率/MW额定容量/(MW·h)负荷需求响应量/MW配置成本/元 比例系数K10307.85882.13—197 056.75 1.2234.98889.43285.96189 261.80 2222.73875.93503.66187 737.80 动作阈值/Hz0.15234.98889.44285.96189 261.80 0.2267.89880.01197.38192 693.57 0.25284.43880.01129.94194 495.67
5.5.2 负荷变化趋势对储能配置的影响
本节在负荷总量保持不变的前提下,将部分高峰时段负荷平移至新能源高发时段,研究负荷走势对一体化系统储能配置的影响。将高峰时段(16:00—20:00)的负荷按照10%比例平移至低谷时段(1:00—5:00, 20:00—24:00),负荷变化趋势对储能配置的影响见表6。
表6 负荷变化趋势对储能配置的影响
Tab.6 The impact of trend of load change on energy storage planning

额定功率/MW额定容量/(MW·h)需求侧响应量/MW成本/万元 日均投资日均运行上级电网购电 237.15414.44242.303.7211.689.31
与场景3对比可知,将部分高峰时段负荷平移至新能源高发时段能够显著降低储能的容量配置、运行成本和向上级主网购电成本。额定功率配置结果基本不变,进一步说明储能的额定功率和额定容量分别由暂态频率约束和稳态运行状态决定。
本文针对100%新能源场景,提出了计及频率安全稳定约束和一体化系统各环节调频资源协同运行的储能优化配置方法,通过算例验证了本文所提方法的有效性,主要结论如下:
1)由于缺少同步电源的支撑,传统储能优化配置方案的频率越限风险突出,因此挖掘“源网荷储”各环节的有功资源的调频潜力是有必要的。本文所提方法充分考虑了新能源场站、储能电站与需求侧响应的频率支撑能力,能够实现多种调频资源的协同互补,在保证一体化系统频率安全稳定的同时提高了储能配置的经济性。
2)在新能源场站中引入VSG技术可以为一体化系统提供虚拟惯量支撑。本文根据实际运行工况及预想故障场景,设计了风电场和储能电站的虚拟惯性时间常数,利用风机中存储的转子动能和储能电站的快速频率响应为系统提供惯量支撑。
3)100%新能源场景下,构网型场站占比会影响储能配置。算例分析表明,构网和跟网型场站比例为4:1时一体化系统配置成本最低,相较于其他场景最大可减少11.4%的配置成本。完全由构网型场站组成的系统会影响需求侧响应的参与度,从而导致系统的储能配置功率提高14.3%,此时准稳态频率偏差将成为影响系统储能配置的主要因素。
4)需求侧响应会影响储能配置。算例分析表明,在保障用户满意度的基础上,设置合理的需求侧响应控制参数最大可降低23.8%的储能规划功率。将负荷高峰时段10%负荷平移至低谷时段可降低53%的储能配置容量。
本文提出了计及频率安全稳定和经济性的储能优化配置方法,考虑了“源储荷”协调运行对一体化系统频率稳定的影响,为解决100%新能源场景下一体化系统规划问题提供了新思路。
参考文献
[1] 孙惠, 翟海保, 吴鑫. 源网荷储多元协调控制系统的研究及应用[J]. 电工技术学报, 2021, 36(15): 3264-3271. Sun Hui, Zhai Haibao, Wu Xin. Research and application of multi-energy coordinated control of generation, network, load and storage[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3264-3271.
[2] 葛晓琳, 刘亚, 符杨, 等. 考虑惯量支撑及频率调节全过程的分布鲁棒机组组合[J]. 中国电机工程学报, 2021, 41(12): 4043-4058. Ge Xiaolin, Liu Ya, Fu Yang, et al. Distributed robust unit commitment considering the whole process of inertia support and frequency regulations[J]. Procee-dings of the CSEE, 2021, 41(12): 4043-4058.
[3] 赵冬梅, 徐辰宇, 陶然, 等. 多元分布式储能在新型电力系统配电侧的灵活调控研究综述[J]. 中国电机工程学报, 2023, 43(5): 1776-1799. Zhao Dongmei, Xu Chenyu, Tao Ran, et al. Review on flexible regulation of multiple distributed energy storage in distribution side of new power system[J]. Proceedings of the CSEE, 2023, 43(5): 1776-1799.
[4] 张智, 周明, 武昭原, 等. 考虑动态频率支撑的储能选址定容规划方法[J]. 中国电机工程学报, 2023, 43(7): 2708-2721. Zhang Zhi, Zhou Ming, Wu Zhaoyuan, et al. Energy storage location and capacity planning method considering dynamic frequency support[J]. Proceedings of the CSEE, 2023, 43(7): 2708-2721.
[5] 滕贤亮, 谈超, 昌力, 等. 高比例新能源电力系统有功功率与频率控制研究综述及展望[J]. 电力系统自动化, 2023, 47(15): 12-35. Teng Xianliang, Tan Chao, Chang Li, et al. Review and prospect of research on active power and frequency control in power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2023, 47(15): 12-35.
[6] 李欣然, 崔曦文, 黄际元, 等. 电池储能电源参与电网一次调频的自适应控制策略[J]. 电工技术学报, 2019, 34(18): 3897-3908. Li Xinran, Cui Xiwen, Huang Jiyuan, et al. The self-adaption control strategy of energy storage batteries participating in the primary frequency regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3897-3908.
[7] 张祥宇, 胡剑峰, 付媛, 等. 风储联合系统的虚拟惯量需求与协同支撑[J]. 电工技术学报, 2024, 39(3): 672-685. Zhang Xiangyu, Hu Jianfeng, Fu Yuan, et al. Virtual inertia demand and collaborative support of wind power and energy storage system[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 672-685.
[8] 曹炜, 钦焕乘, 陆建忠, 等. 新型电力系统下虚拟同步机的定位和应用前景展望[J]. 电力系统自动化, 2023, 47(4): 190-207. Cao Wei, Qin Huancheng, Lu Jianzhong, et al. Orientation and application prospect of virtual synchronous generator in new power system[J]. Automation of Electric Power Systems, 2023, 47(4): 190-207.
[9] 张崇, 李博, 李笑宇, 等. 基于虚拟同步机控制参数自适应调节的储能系统调频方法[J]. 发电技术, 2024, 45(4): 772-780. Zhang Chong, Li Bo, Li Xiaoyu, et al. A frequency regulation method of energy storage system based on adaptive adjustment of virtual synchronous generator control parameters[J]. Power Generation Technology, 2024, 45(4): 772-780.
[10] Kheshti M, Lin Shuyue, Zhao Xiaowei, et al. Gaussian distribution-based inertial control of wind turbine generators for fast frequency response in low inertia systems[J]. IEEE Transactions on Sustainable Energy, 2022, 13(3): 1641-1653.
[11] 张冠锋, 杨俊友, 孙峰, 等. 基于虚拟惯量和频率下垂控制的双馈风电机组一次调频策略[J]. 电工技术学报, 2017, 32(22): 225-232. Zhang Guanfeng, Yang Junyou, Sun Feng, et al. Primary frequency regulation strategy of DFIG based on virtual inertia and frequency droop control[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 225-232.
[12] 赵冬梅, 徐辰宇, 杜泽航, 等. 就地无常规电源支撑下考虑新能源基地频率稳定的储能优化配置方法[J]. 中国电机工程学报, 2024, 44(24): 9691-9706. Zhao Dongmei, Xu Chenyu, Du Zehang, et al. Optimization configuration Method for Energy storage considering frequency stability of new energy bases without conventional power supply support on site[J]. Proceedings of the CSEE, 2024, 44(24): 9691-9706.
[13] 赵波, 李得民, 吴在军, 等. 基于100%绿色能源供电目标的海岛微电网群容量优化配置[J]. 中国电机工程学报, 2021, 41(3): 932-945. Zhao Bo, Li Demin, Wu Zaijun, et al. Capacity optimal sizing of island microgrid clusters based on the target of 100% green energy power supply[J]. Proceedings of the CSEE, 2021, 41(3): 932-945.
[14] Tian Guanyu, Sun Qunzhou. A stochastic controller for primary frequency regulation using on/off demand side resources[J]. IEEE Transactions on Smart Grid, 2023, 14(5): 4141-4144.
[15] Cetinkaya U, Bayindir R. Impact of increasing renewable energy sources on power system stability and determine optimum demand response capacity for frequency control[C]//2022 10th International Conference on Smart Grid, Istanbul, Turkey, 2022: 396-400.
[16] 杨森, 杜文娟, 王旭斌, 等. 风火-需求侧响应协调频率控制方法[J]. 电网技术, 2017, 41(3): 845-853. Yang Sen, Du Wenjuan, Wang Xubin, et al. Coordinated frequency control method of wind/ thermal/demand response[J]. Power System Technology, 2017, 41(3): 845-853.
[17] 王宝财, 孙华东, 李文锋, 等. 考虑动态频率约束的电力系统最小惯量评估[J]. 中国电机工程学报, 2022, 42(1): 114-127. Wang Baocai, Sun Huadong, Li Wenfeng, et al. Minimum inertia estimation of power system considering dynamic frequency constraints[J]. Proceedings of the CSEE, 2022, 42(1): 114-127.
[18] Chu Zhongda, Zhang Ning, Teng Fei. Frequency-constrained resilient scheduling of microgrid: a distributionally robust approach[J]. IEEE Transactions on Smart Grid, 2021, 12(6): 4914-4925.
[19] 周海强, 鲁锦文, 薛峰, 等. 计及风电综合惯性控制的电力系统扩展频率响应模型[J]. 电力系统自动化, 2023, 47(8): 198-205. Zhou Haiqiang, Lu Jinwen, Xue Feng, et al. Extended frequency response model for power system considering wind power synthetic inertia control[J]. Automation of Electric Power Systems, 2023, 47(8): 198-205.
[20] 文云峰, 林晓煌. 孤岛与并网模式下微电网最低惯量需求评估[J]. 中国电机工程学报, 2021, 41(6): 2040-2053. Wen Yunfeng, Lin Xiaohuang. Minimum inertia requirement assessment of microgrids in islanded and grid-connected modes[J]. Proceedings of the CSEE, 2021, 41(6): 2040-2053.
[21] 聂永辉, 刘家僮, 孙斌, 等. 基于转子动能释放的风电并网系统非线性频率控制策略研究[J]. 中国电机工程学报, 2023, 43(23): 9127-9136. Nie Yonghui, Liu Jiatong, Sun Bin, et al. Research on nonlinear frequency control strategy of wind power grid connected system based on rotor kinetic energy release[J]. Proceedings of the CSEE, 2023, 43(23): 9127-9136.
[22] 国家市场监督管理总局, 中国国家标准化管理委员会. 风电场接入电力系统技术规定第1部分:陆上风电: GB/T 19963.1—2021[S]. 北京: 中国标准出版社, 2021.
[23] 王科, 秦文萍, 张宇, 等. 双馈风机等效惯量控制比例系数对系统功角首摆稳定的影响机理分析[J]. 电工技术学报, 2023, 38(3): 741-753. Wang Ke, Qin Wenping, Zhang Yu, et al. Mechanism analysis of effect of equivalent proportional coefficient of inertia control of DFIG on stability of first swing of power angle[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 741-753.
[24] Nakiganda A M, Dehghan S, Markovic U, et al. A stochastic-robust approach for resilient microgrid investment planning under static and transient islanding security constraints[J]. IEEE Transactions on Smart Grid, 2022, 13(3): 1774-1788.
[25] 国家市场监督管理总局, 中国国家标准化管理委员会. 电化学储能系统接入电网技术规定: GB/T36547—2018[S]. 北京: 中国标准出版社, 2019.
[26] 刘钊汛, 秦亮, 杨诗琦, 等. 面向新型电力系统的电力电子变流器虚拟同步控制方法评述[J]. 电网技术, 2023, 47(1): 1-16. Liu Zhaoxun, Qin Liang, Yang Shiqi, et al. Review on virtual synchronous generator control technology of power electronic converter in power system based on new energy[J]. Power System Technology, 2023, 47(1): 1-16.
[27] 余光正, 胡越, 刘晨曦, 等. 含跟网/构网型混联多馈入系统协调优化配置方法研究[J/OL]. 中国电机工程学报, 2023: 1-15. http://kns.cnki.net/kcms/ detail/11.2107.tm.20231220.1539.010.html. Yu Guangzheng, Hu Yue, Liu Chenxi, et al. Research on the coordinated optimization configuration method for hybrid multi-infeed systems with grid-following or grid-forming[J/OL]. Proceedings of the CSEE, 2023: 1-15.http://kns.cnki.net/kcms/detail/11.2107.tm.20231220. 1539.010.html.
[28] 葛俊, 宋鹏, 刘汉民, 等. 新能源场站虚拟同步发电机技术研究及示范应用[J]. 全球能源互联网, 2018, 1(1): 39-47. Ge Jun, Song Peng, Liu Hanmin, et al. Research and demonstration application of virtual synchronous generator technology in renewable energy power station[J]. Journal of Global Energy Interconnection, 2018, 1(1): 39-47.
[29] Zhang Haobo, Xiang Wang, Lin Weixing, et al. Grid forming converters in renewable energy sources dominated power grid: control strategy, stability, application, and challenges[J]. Journal of Modern Power Systems and Clean Energy, 2021, 9(6): 1239-1256.
[30] Pan Donghua, Wang Xiongfei, Liu Fangcheng, et al. Transient stability of voltage-source converters with grid-forming control: a design-oriented study[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(2): 1019-1033.
[31] 颜湘武, 王德胜, 杨琳琳, 等. 直驱风机惯量支撑与一次调频协调控制策略[J]. 电工技术学报, 2021, 36(15): 3282-3292. Yan Xiangwu, Wang Desheng, Yang Linlin, et al. Coordinated control strategy of inertia support and primary frequency regulation of PMSG[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3282-3292.
[32] 谢震, 杨曙昕, 代鹏程, 等. 构网型全功率风电机组网侧变流器耦合分析及抑制策略[J]. 电工技术学报, 2023, 38(14): 3745-3758, 3768. Xie Zhen, Yang Shuxin, Dai Pengcheng, et al. Grid-side coupling analysis and suppression strategy of grid-forming full-power wind turbines[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3745-3758, 3768.
[33] 梁紫雯, 牟龙华, 何楚璇. 微能源网互联系统的频率调节和消纳能力研究[J]. 电工技术学报, 2022, 37(增刊1): 74-82. Liang Ziwen, Mu Longhua, He Chuxuan. Research on frequency modulation and accommodation capability of interconnected system of micro-energy network[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 74-82.
Abstract It is an effective means to promote large-scale local consumption of new energy to construct an integrated source-grid-load-storage system in areas with abundant new energy and concentrated loads. However, the frequency stability problem is becoming increasingly prominent due to the lack of conventional power supply inertia support in the 100% new energy scenario. To address these issues, the potential of frequency modulation resources on the source, energy storage and load sides is fully explored in this paper, establishing an integrated system energy storage optimization configuration model considering frequency stability and the coordinated operation of various frequency modulation resources, realizing the coordinated operation of flexible adjustment resources and ensuring the frequency stability of the system.
Firstly, the virtual inertia time constant is reasonably set according to the actual operating state of the system and the expected fault scenario, which is based on the safety constraint of rate of change of frequency. Secondly, the influence of the control strategy and demand-side response on the frequency response of grid forming (GFM) and grid following (GFL) were explored, which improves the frequency regulation ability of new energy stations in all aspects. Finally, a frequency response model considering the dynamic frequency response constraints and the operation characteristics of frequency modulation resources in each link of the integrated system is established, so as to effectively avoid the frequency out-of-limit problem.
Simulation analysis of the proposed optimal configuration model for energy storage has a positive effect on improving the inertia level of the system and ensuring the frequency stability of the system. The frequency safety of the power system can be improved while improving economic benefits considering the frequency characteristics of new energy units, energy storage power stations and demand-side response under the framework of energy storage allocation optimization. The rotor kinetic energy stored in the wind turbine and the fast frequency response of the energy storage power station are used to provide inertia support for the system. Compared with the existing research, the proposed configuration method can effectively ensure that the frequency security and stability indicators are within the stability threshold. The system composed entirely of GFM will affect the participation of the demand-side response resulting in a 14.3% increase in the energy storage configuration power of the system. Additionally, it can reduce the planned energy storage power by up to 23.8% setting reasonable demand-side response control parameters.
Simulation analysis of the proposed configuration model of energy storage considering frequency stability constraints shows that the following conclusions: (1) Virtual synchronous generators technology is introduced into the new energy station to provide virtual inertia support for the integrated system. According to the actual operating conditions and expected fault scenarios, the virtual inertia time constants of the wind farm and the energy storage power station are designed. (2) The GFM control can effectively reduce  . However, it will affect the participation of demand-side response when the number of network-based stations is higher than a certain percentage. (3) The analysis of the demand side response will affect the energy storage configuration, and the case analysis shows that on the basis of ensuring user satisfaction, setting reasonable demand side response control parameters can effectively reduce the energy storage configuration cost of the integrated system.
. However, it will affect the participation of demand-side response when the number of network-based stations is higher than a certain percentage. (3) The analysis of the demand side response will affect the energy storage configuration, and the case analysis shows that on the basis of ensuring user satisfaction, setting reasonable demand side response control parameters can effectively reduce the energy storage configuration cost of the integrated system.
keywords:Source-grid-load-storage integrated system, grid following (GFL), grid forming (GFM), frequency stability, optimal configuration of energy storage
DOI: 10.19595/j.cnki.1000-6753.tces.240444
中图分类号:TM712
国家重点研发计划资助项目(2022YFB2402700)。
收稿日期 2024-03-20
改稿日期 2024-05-21
赵冬梅 女,1965年生,教授,博士生导师,研究方向为电力系统分析与控制、新能源发电与智能电网等。E-mail:zhao-dm@ncepu.edu.cn(通信作者)
宋晨铭 男,1996年生,博士研究生,研究方向电力系统优化运行和稳定性评估。E-mail:songchenming@ncepu.edu.cn
(编辑 赫 蕾)