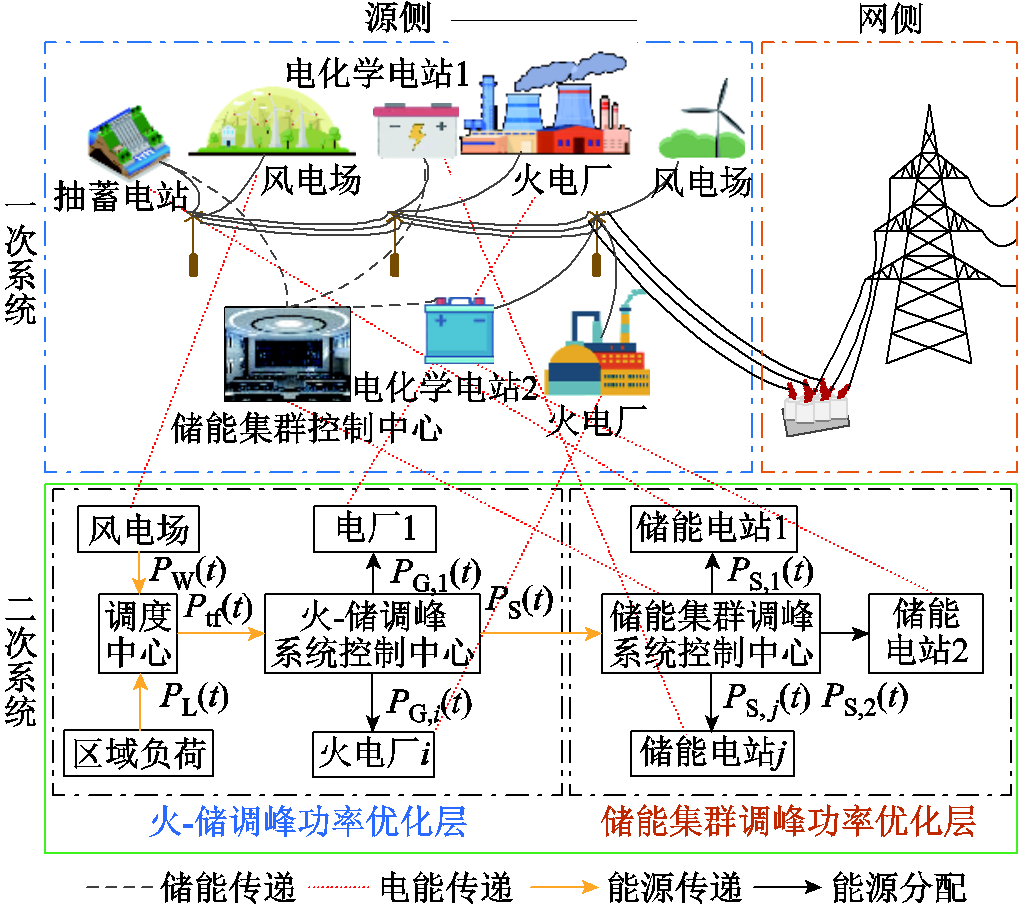
图1 储能集群辅助火电机组调峰系统示意图
Fig.1 Schematic diagram of the thermal power unit peaking system assisted by energy storage clusters
摘要 为应对大规模风电能源并网给电力系统调峰带来的严峻挑战,提出一种储能集群辅助火电机组调峰的分层优化控制策略。在火-储调控层,提出基于储能集群调峰盈余系数的火储调峰优化控制策略,通过引入储能调峰盈余系数,合理预留储能调峰出力空间,提高整体调峰效果;在储能集群内部调控层,为减缓储能电站老化提出多目标约束下各储能电站优化控制策略,考虑网络潮流约束、调控一致性约束、出力公平性约束等技术经济性约束条件,兼顾储能寿命、节点负荷率平衡度及运行成本等多目标模型,利用遗传算法计算得到各储能电站出力初值,与上层调峰任务分配中储能所需出力修正迭代,最终确定各储能电站最优出力。通过算例仿真得出,在高峰时段该文所提策略能实现调峰需求下降87.40 MW,在满足新能源完全消纳前提下,总运行成本下降3.62%,且各储能电站循环寿命次数都有不同程度的增加,其中锂电池储能电站增加了4.38%,从经济性和调峰技术性两方面验证了该文所提策略的有效性。
关键词:储能集群 电力系统调峰 电池寿命 双层优化控制策略
加快构建适应新能源占比逐渐提高的新型电力系统是达成“碳达峰、碳中和”目标的必由之路。然而,由于风电出力的不确定性,其大规模并网必将导致系统的净负荷峰谷差大幅增加[1-2]。为在维持系统源-荷功率平衡的前提下尽可能地提升新能源消纳水平,电力系统中对调峰资源的需求与日俱增[3-4]。随着电池成本的下降,储能作为一种快速响应的灵活性调节资源,能有效地辅助火电机组参与系统调峰,为系统提供灵活性,缓解系统调峰压力[5-7],随着电力系统中风电场的大量投运,以及各项储能利好政策的提出,近两年电力系统中储能电站爆发式增长,我国多个地区已形成储能集群态势,但存在利用率低、收益差的问题,储能集群的调控策略成为关键[8]。
储能辅助火电机组调峰的作用体现在两个方面:一方面是调峰资源的供给;另一方面是系统灵活性的补充。关于储能辅助火电机组调峰的调度模型与经济性已有许多相关研究。文献[9]通过深度强化学习与发电预测,在高比例新能源场景下实现考虑尖峰光伏发电并预留充足的储能资源。文献[10]提出将日前优化调度分为两阶段进行的集中调度与发电集团自主调度相协调的日前调度模型。文献[11]提出了火电机组利用储能资源参与电力系统调峰的配置和调度方案,实现调峰经济性的提高及风电消纳率的优化。文献[12]提出一种储能辅助火电机组深度调峰的分层优化调度方案,在经济性目标的驱动下优化储能及火电机组出力。文献[13]针对历史场景构建了风-火-储协同调峰模型,通过对调度预案的滚动修正来应对风电的不确定性,实现调峰经济性调度。文献[14-15]综合考虑需求响应和电池储能调度提出了联合优化策略,优化系统调峰效果及整体运行的经济性。然而,上述文献仅将储能作为调峰资源参与电力系统调度,忽略了储能的灵活性补给功能。
关于储能系统对于电力系统灵活性贡献的相关研究也有很多。文献[16]提出了考虑长周期供需不平衡风险的新型电力系统规划方法,能有效地提升电力系统的长周期平衡能力。文献[17]通过开展深度调峰改造联合配置储能的方式,提高系统灵活性,提升火电的调峰能力和运行经济性。文献[18]考虑各类灵活性主体利益驱动性,运用主从博弈的思想,实现灵活性供需优化和灵活性价值的合理补偿。文献[19]通过分析不同时间尺度下系统的运行特性,综合考虑储能成本、调节灵活性、新能源不确定性,建立电力系统储能容量规划模型。文献[20]提出一种考虑多灵活性资源协调调度的配电网新能源消纳策略。
上述文献主要聚焦于单一类型的储能技术。然而,随着新型电力系统的发展,区域电网中涌现出多样化和多元化的多类型储能技术。鉴于此,深入探讨多种储能技术如何共同辅助火电机组进行调峰,对于电力系统的稳定运行和高效调度具有重要的意义。
目前,对于区域电网中多个储能共同参与电力系统调峰的问题,仍然需要更加有效的调控手段。文献[21]以跟踪负荷曲线作为平抑目标函数,对抽水蓄能机组、蓄电池和超级电容设备进行功率分配。文献[22]将超级电容和蓄电池混合储能作为储能子网连接在直流母线上,提出以储能荷电状态(State of Charge, SOC)来划分五种工作模式的控制策略。文献[23]提出一种同时考虑电量型和功率型储能资源的日前-日内协同滚动调度策略,避免该储能资源因过度参与削峰填谷而导致能量不足。文献[24]针对混合储能系统的电动公交车提出了一种“车-网”互联实现混合储能的分层能源管理策略,实现了储能功率优化分配,延缓电池寿命退化。上述文献普遍将多个储能电站视为互不相连的独立实体,忽略了它们作为一个整体进行协同调控的潜力;在储能集群中,对于各储能单元间的负载均衡度以及寿命衰减相关约束考虑不足,可能导致特定储能电站的荷电状态过高或过低,以致该电站过早地丧失其调峰的能力。
针对现有研究中的不足之处,本文提出了一种双层控制策略,其主要贡献在于:①在上层策略中,通过引入储能调峰盈余系数,有效地延长了储能参与系统调峰的运行时间。与火电机组协同作用,达到了更优的调峰效果,显著提升了系统的调峰能力。②构建了一个考虑风电不确定性的火-储调峰功率经济分配模型,针对不同的调峰运行状态,利用储能调峰盈余系数对火-储间的出力任务进行调节,实现削峰填谷和系统灵活性的提升,同时满足了经济运行的要求。③在下层策略中,综合考虑不同储能电站间调峰特性的差异,通过多目标函数在储能集群内对调峰资源进行公平分配,并利用ε-约束算法对模型进行求解,降低了储能电站寿命的衰减速度、改善了负载率均衡度并且经济性也得到提升。
本文首先对含有储能集群的区域电网中的调峰运行状态进行分析和建模;然后提出储能集群辅助火电机组调峰的双层优化策略及模型;最后通过改进的IEEE 39节点系统验证了本策略的有效性,为实际应用提供了有力的支持。
本文所研究的系统中主要包含传统火电厂以及含多类型储能的储能集群和风电场。储能集群辅助火电机组调峰系统示意图如图1所示。图1中,上方为含储能集群的区域电网一次系统,左侧为电力系统源侧,各类型储能电站由储能集群控制中心统一控制,所发电力经由变压器送至右边网侧;下方为二次系统,主要包括火-储间调峰功率的优化以及储能集群内各储能电站调峰功率的优化。

图1 储能集群辅助火电机组调峰系统示意图
Fig.1 Schematic diagram of the thermal power unit peaking system assisted by energy storage clusters
本文主要研究:①高比例风电系统中储能集群辅助传统火电机组参与电网调峰调度问题;②针对含有储能集群的电力系统,如何分配储能与火电的功率以达到储能电站利用率高且调峰效果和经济性最优;③对于储能集群内部储能电站功率分配问题,不同储能电站间物理特性不同,如何充分发挥各储能电站优势达到技术性和经济性最优。
下面针对高比例风电系统中调峰运行状态进行分析,基于数据驱动对储能辅助火电机组调峰系统运行状态进行建模。
在高比例风电系统中,火电机组作为单一调峰资源,无法满足系统调峰需求。系统中火电机组出力为小时级(h级),h级的调节尺度无法满足现实的等效负荷波动。火电机组调峰示意图如图2所示。首先通过发电厂日前计划得出火电机组起停计划,得知各时段火电机组出力范围(灰色阴影区域);再通过历史数据对系统中的不确定性进行建模,通过模型更迭得出日前15 min级较为精确的等效负荷数据(红色曲线);重新制定15 min级火电机组出力计划(如图中黑色曲线),单一火电机组由于上/下爬坡率及出力上/下限的限制,使得不能完全跟踪等效负荷进行出力,于是出现调峰缺额(彩色部分所示)。

图2 火电机组调峰示意图
Fig.2 Schematic diagram of thermal power unit peaking
图2中,在[t1, t2]火电机组满足调峰需求;在[t2, t3]由于风电变化速度快,火电机组最大爬坡无法跟踪负荷,产生上调灵活性需求;在[t3, t4]火电机组容量不足,产生上调峰需求;[t5, t6]风力发电量锐减,火电机组调节速度较慢,产生下调灵活性需求;[t6, t7]等效负荷曲线低于火电机组最小出力,产生下调峰需求。
基于储能电站在实际运行过程中受到的功率约束、容量约束,构建储能集群调节能力模型为
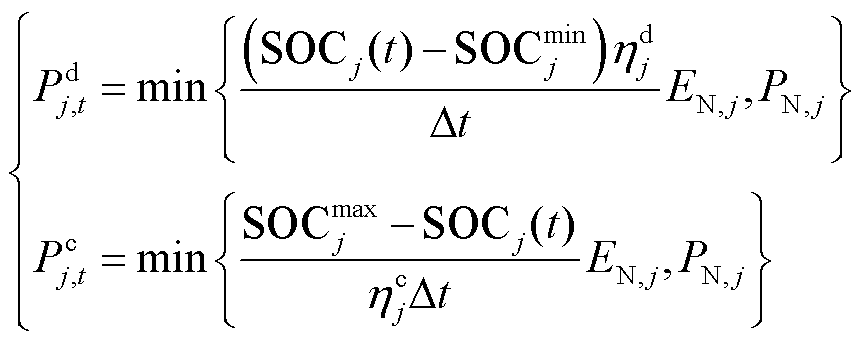 (1)
(1)
式中, 、
、 分别为
分别为 时刻储能电站
时刻储能电站 放电功率和充电功率;
放电功率和充电功率; 、
、 、
、 分别为储能电站
分别为储能电站 在
在 时刻的SOC实际值、SOC下限和SOC上限;
时刻的SOC实际值、SOC下限和SOC上限; 为储能电站
为储能电站 额定容量;
额定容量; 为储能电站
为储能电站 额定充放电功率;
额定充放电功率; 、
、 分别为储能电站
分别为储能电站 放电效率和充电效率。
放电效率和充电效率。
将上述单一储能电站出力推广至多类型储能集群的调节能力模型为
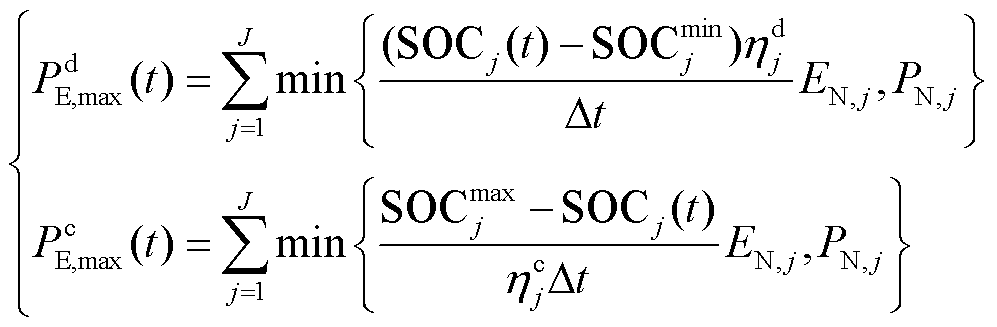 (2)
(2)
式中, 、
、 分别为区域内储能集群
分别为区域内储能集群 时刻充、放电功率最大值。
时刻充、放电功率最大值。
储能系统在调峰过程中能体现调峰资源提供者和系统灵活性提供者双重身份。日前机组出力计划以h级为时间尺度,系统灵活性为15 min级的时间尺度,对储能辅助火电机组调峰系统进行分析,存在以下六种情况。储能辅助火电机组调峰示意图如图3所示。

图3 储能辅助火电机组调峰示意图
Fig.3 Schematic diagram of thermal power unit peaking assisted by energy storage
1)储能不动作
 (3)
(3)
式中, 、
、 分别为储能集群充、放电功率。在[t1, t2]区间,火电机组能满足等效负荷需求,储能不动作。
分别为储能集群充、放电功率。在[t1, t2]区间,火电机组能满足等效负荷需求,储能不动作。
2)储能提供上调灵活性
 (4)
(4)
式中, 为上爬坡需求;
为上爬坡需求; 为火电机组上爬坡能力;
为火电机组上爬坡能力;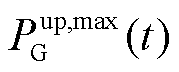 为火电机组上爬坡最大值;
为火电机组上爬坡最大值; 为火电机组出力上限。在t2时刻,火电机组由于机组起停,火电最大爬坡不足,导致在[t2, t3]区间系统上调灵活性不够,此时储能集群放电满足上调灵活性需求。
为火电机组出力上限。在t2时刻,火电机组由于机组起停,火电最大爬坡不足,导致在[t2, t3]区间系统上调灵活性不够,此时储能集群放电满足上调灵活性需求。
3)储能提供上调峰资源
 (5)
(5)
式中, 为储能电站应补充的上调峰资源;
为储能电站应补充的上调峰资源; 为总上调峰需求;
为总上调峰需求; 为火电机组上调峰出力。
为火电机组上调峰出力。
在[t3, t4]区间,火电机组难以满足调峰需求,储能为满足等效负荷运行提供上调峰资源。
4)火电对储能系统充电
 (6)
(6)
式中, 为系统火电机组可为储能电站提供的充电功率;
为系统火电机组可为储能电站提供的充电功率; 为时间间隔。
为时间间隔。
在[t4, t5]区间,火电机组能跟踪等效负荷,但由预测得到下一时刻存在较大的调峰资源需求,因此在该时段利用过剩的火电资源对储能集群进行充电,应对下一时段[t5, t7]电源需求。
5)储能提供下调灵活性
 (7)
(7)
式中, 为下爬坡需求;
为下爬坡需求; 为火电机组下爬坡能力;
为火电机组下爬坡能力; 为火电机组下爬坡最大值;
为火电机组下爬坡最大值; 为火电机组出力下限。在[t7, t8]区间内火电机组下爬坡能力不满足需求,此时储能通过吸收多余的风电,提高系统下调灵活性。
为火电机组出力下限。在[t7, t8]区间内火电机组下爬坡能力不满足需求,此时储能通过吸收多余的风电,提高系统下调灵活性。
6)储能提供下调峰资源
 (8)
(8)
式中, 为储能电站应补充的下调峰资源;
为储能电站应补充的下调峰资源; 为总下调峰需求。
为总下调峰需求。
在[t8, t9]区间火电机组下调峰能力不足,无法跟踪等效负荷,储能电站对下调峰资源进行补充。
由上述分析可知,在传统储能电站辅助火电机组调峰时不会存在情况4)传统火电机组为储能电站充电的状态,也就是在区域[t5, t8]内储能无法满足所有的调峰需求,产生失负荷现象,将影响系统安全运行。接下来就储能集群辅助火电机组调峰的运行状态进行详细的分析建模。
基于分布式控制的多个储能电站平滑风电功率波动可能导致储能电站充电和放电产生能量抵消,称为“抵消效应”;且多储能电站间由于电池特性不一致,其运行效率及成本存在差异。电力系统调峰用储能电池的特性见表1。为对多个储能电站间进行合理配合以达到经济性和技术性最优,需要对区域内储能电站进行集群控制,参考文献[26],基于技术特性、成本效益以及调峰需求等多个维度,本文将抽蓄储能、铅碳电池、锂电池、钠硫电池四类储能电站组成储能集群,应用于所研究系统的调峰。
表1 电力系统调峰用储能电池的特性
Tab.1 Characteristics of storage batteries for peaking in power system

性能指标数值 铅碳磷酸铁锂全钒液流锌溴液流钠硫 功率上限10 MW级MW级100 MW级100 MW级10 MW级 充放电效率(%)80~9090~9565~8065~80>90 系统效率(%)75~8585~9060~7060~70>80 成本/[元/(kW·h)]0.45~0.70.5~0.90.7~1.00.8~1.20.9~1.2 循环寿命/次500~3 0002 500~5 000>16 0002 500~5 0002 000~4 500
对储能集群内部出力分配方式对调峰效果及运行经济性的影响进行分析,不同配合方案示意图如图4所示。图4a、图4d表示不同方式下储能集群的运行时长。方式1为火电机组按最小出力运行,储能弥补剩余调峰需求;而方式2充分利用火电机组存在的富余的调峰能力,增加火电机组出力,储能电站出力时长由原来的[t1, t2]延长为[t1, t3],利用火电机组剩余调峰能力增大储能集群响应能力,从而提高系统调峰性能。

图4 不同配合方案示意图
Fig.4 Schematic diagrams of different fit options
图4b和图4e表示储能集群内部储能电站间出力的分配。由图4c看出,方式2较方式1运行成本下降;由图4f看出,运行方式2下储能集群内各储能电站总衰减程度小于方式1。
由上述分析得出,储能电站不同运行方式对系统的经济性和技术性都有直接影响,因此需要多储能电站间协调分配的优化策略,使其既能满足调峰运行经济性且能兼顾技术要求。
现对系统中可能出现的所有运行状态进行说明,将各运行状态通过矩阵表达,最后利用历史数据构建概率分布模糊集,以对不确定性进行定量分析。将火-储联合调峰可能出现的情况进行分类,风-火-储系统运行状态见表2。
表2 风-火-储系统运行状态
Tab.2 Operational status of the wind-fire-storage system

序号上爬坡不足下爬坡不足上调峰需求下调峰需求 1√ 2√ 3√√ 4√ 5√ 6√√ 7
对于系统来说,下一时刻出现的运行状态有 (m=7)种可能,出现场景集合为Q,0为满足要求,1为不满足要求。从左至右分别为上调峰需求、下调峰需求、上爬坡不足、下爬坡不足,上述七种情况转换为矩阵如式(9)所示。
(m=7)种可能,出现场景集合为Q,0为满足要求,1为不满足要求。从左至右分别为上调峰需求、下调峰需求、上爬坡不足、下爬坡不足,上述七种情况转换为矩阵如式(9)所示。
 (9)
(9)
基于大量历史数据获取各时段各场景出现的概率信息,进而构建场景出现概率分布模糊集 。出现概率分布模糊集相较于概率分布常用变量,在考虑风电负荷等因素下的计算复杂度更小,对噪声的敏感度更低,适合本文系统实际运行状况。
。出现概率分布模糊集相较于概率分布常用变量,在考虑风电负荷等因素下的计算复杂度更小,对噪声的敏感度更低,适合本文系统实际运行状况。
 (10)
(10)
式中, 为第
为第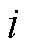 个不确定集合;
个不确定集合; 为所有不确定集合总和;
为所有不确定集合总和; 为数学期望;
为数学期望; 为变量
为变量 的数学期望;
的数学期望; 为下一时刻处于第
为下一时刻处于第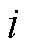 个不确定场景的概率;
个不确定场景的概率; 为场景变量
为场景变量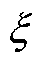 的概率分布;
的概率分布; 为
为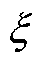 基于
基于 的全部概率分布集合。
的全部概率分布集合。
根据上述场景概率模型能得出各运行状态出现的概率,利用所得结果可求出各时刻下储能调峰盈余系数 为
为
 (11)
(11)
储能电站盈余系数 为储能电站为下一时刻调峰需求不足预留电量的需求,利用历史数据分析得到的系统存在上爬坡和上调峰需求场景分别为
为储能电站为下一时刻调峰需求不足预留电量的需求,利用历史数据分析得到的系统存在上爬坡和上调峰需求场景分别为 、
、 、
、 ,两场景响应存在概率为
,两场景响应存在概率为 、
、 、
、 ;同理,存在下爬坡和下调峰需求的场景和概率分别为
;同理,存在下爬坡和下调峰需求的场景和概率分别为 、
、 、
、 和
和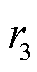 、
、 、
、 ;
; 和
和 分别为火电机组满足调峰需求及系统灵活性时场景和发生概率。上/下/无调节需求集合分别为Ru={r1, r2, r6}、Rd={r3, r4, r5}、Rb={r7},内部元素分别用
分别为火电机组满足调峰需求及系统灵活性时场景和发生概率。上/下/无调节需求集合分别为Ru={r1, r2, r6}、Rd={r3, r4, r5}、Rb={r7},内部元素分别用 、
、 、
、 表示,元素总数分别为un、dn、bn。
表示,元素总数分别为un、dn、bn。
根据第1节对系统调峰任务分配问题的分析,本文提出了高比例风电系统中储能集群辅助火电机组调峰分层优化策略,包括基于储能集群调峰盈余系数的火储调峰优化控制层和多目标约束下各储能电站优化控制层,其整体框架如图5所示。

图5 双层调控策略整体框架
Fig.5 Overall framework of the two-layer regulatory strategy
(1)基于储能集群调峰盈余系数的火储调峰优化控制层:对系统运行状态进行分析,根据历史数据对系统调峰运行场景进行建模,通过引入各时段储能调峰盈余系数对储能集群辅助系统调峰和提高系统灵活性的功率进行调控,构建了考虑风电不确定性的火-储调峰功率经济分配模型,在满足经济性目标函数的前提下完成储能集群与火电机组间调峰资源的最优分配。
(2)多目标约束下各储能电站优化控制层:提出考虑电池寿命的储能集群内部多目标储能电站间调峰功率优化模型,根据上层得到的储能集群调峰需求功率在下层多类型储能电站间进行分配。在考虑网络潮流约束、系统调峰资源供需平衡下以储能循环寿命系数、储能电站节点负载率均衡度及储能电站运行成本作为多目标函数,以实现多类型储能电站间的最优调峰出力分配。
本文所提双层优化模型既能充分发挥火电机组和储能集群各自的调峰优势,又能实现减缓储能电站循环寿命的衰减,保证区域电网整体的调峰质量和经济性。
本节介绍上层策略的功能,首先提出基于储能集群调峰盈余系数的火储调峰优化控制策略,然后构建火-储调峰功率经济分配模型,得出调峰任务在火-储间分配的初值。
在火电机组满足等效负荷阶段,依据历史负荷高峰波动概率值,通过储能调峰盈余系数与其作用区间( 为调峰盈余系数作用区间上/下界)的关系对火-储间调峰任务进行分配。
为调峰盈余系数作用区间上/下界)的关系对火-储间调峰任务进行分配。
当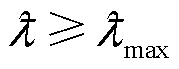 时,火电机组调整出力,使得储能电站SOC保持与储能盈余系数相同的水平;当
时,火电机组调整出力,使得储能电站SOC保持与储能盈余系数相同的水平;当
 时,将储能电站SOC调整至储能SOC预备需求中值
时,将储能电站SOC调整至储能SOC预备需求中值 ,能保证储能电站能发出最大功率;当
,能保证储能电站能发出最大功率;当 时,火电机组跟踪等效负荷,储能电站不参与。
时,火电机组跟踪等效负荷,储能电站不参与。
为简化公式,将上下需求等双向约束仅用一个公式表示, 为
为 时刻调峰需求;
时刻调峰需求; 为
为 时刻剩余调峰需求;
时刻剩余调峰需求; 为
为 时刻储能电站供给的调峰功率;
时刻储能电站供给的调峰功率; 为火电机组爬坡约束;
为火电机组爬坡约束; 为
为 时刻系统灵活性需求;
时刻系统灵活性需求; 为
为 时刻储能电站电量;
时刻储能电站电量; 为储能
为储能 预备需求值;
预备需求值; 为储能电站额定容量;
为储能电站额定容量; 为储能电站出力。系统运行状态示意图如图6所示。
为储能电站出力。系统运行状态示意图如图6所示。

图6 系统运行状态示意图
Fig.6 Schematic diagram of system operation status
各运行情况具体分析如下:
1) :
: ,
,
当火电机组上爬坡能力得到满足,上调峰容量小于等效负荷需求时,剩余调峰需求由储能系统补给。
 (12)
(12)
2) :
: ,
,
当火电机组上爬坡能力不足,上调峰容量充足时,储能电站对该时刻的上调灵活性进行补充。
 (13)
(13)
3) :
: ,
,
当火电机组下爬坡能力不足且下调峰容量小于等效负荷需求时,剩余调峰需求由储能系统补给。
 (14)
(14)
4) :
: ,
,
当火电机组下爬坡能力得到满足,下调峰容量小于等效负荷需求时,剩余下调峰资源由储能系统补给 。
。
 (15)
(15)
5) :
: ,
,
当火电机组下爬坡能力不足,下调峰容量满足等效负荷需求时,储能电站对该时刻的下调灵活性进行补充。
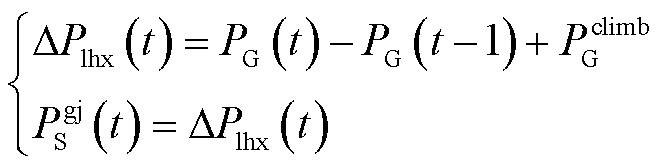 (16)
(16)
6) :
: ,
,
当火电机组上爬坡能力不足,上调峰容量小于等效负荷需求时,储能电站对该时刻的下调灵活性进行补充。
 (17)
(17)
7)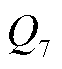 :
: ,
,
当火电机组爬坡能力得到满足,调峰容量满足等效负荷需求时,可利用储能调峰盈余系数对火电机组出力进行调节。
(1) :当储能调峰盈余系数
:当储能调峰盈余系数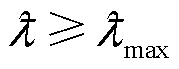 时,利用火电机组为储能系统充电,使得储能系统满足
时,利用火电机组为储能系统充电,使得储能系统满足 ,有一定的上调灵活性。如若该时刻储能电站
,有一定的上调灵活性。如若该时刻储能电站 ,则
,则 ;否则
;否则
 (18)
(18)
式中, 为火电机组在t时刻的实际出力。
为火电机组在t时刻的实际出力。
(2)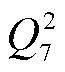 :当
:当 时,存在一定的上调不足概率,为避免浪费资源,储能电站无需与上调系数持平,满足
时,存在一定的上调不足概率,为避免浪费资源,储能电站无需与上调系数持平,满足 。如若该时刻储能电站
。如若该时刻储能电站 ,则
,则 ;否则
;否则
 (19)
(19)
(3) :当
:当 时,下一时刻下调能力不足,此时储能电站不动作,
时,下一时刻下调能力不足,此时储能电站不动作, ,以火电机组出力为主。
,以火电机组出力为主。
 (20)
(20)
4.2.1 目标函数
该目标函数旨在最小化系统的整体运行成本,其中包括火力发电机组的运行成本以及因弃风和失负荷导致的惩罚成本,具体为

 (21)
(21)
式中, 为系统总运行成本;
为系统总运行成本; 为火电机组运行成本;
为火电机组运行成本; 为弃风和失负荷引起的惩罚成本。
为弃风和失负荷引起的惩罚成本。
 (22)
(22)
式中, 为发电机组
为发电机组 的起动成本;
的起动成本; 为发电机组
为发电机组 的固定运行成本;
的固定运行成本; 、
、 为火电机组
为火电机组 的煤耗系数;
的煤耗系数; 为火电机组
为火电机组 在
在 时刻的出力;
时刻的出力; 为区域内火电机组总数量;
为区域内火电机组总数量; 为总时间尺度;
为总时间尺度; 为发电机组起停的决策变量,
为发电机组起停的决策变量, 表示开机,
表示开机, 表示不开机;
表示不开机; 为发电机组状态的决策变量,
为发电机组状态的决策变量,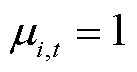 时表示运行,
时表示运行, 时表示停机。
时表示停机。
 (23)
(23)
式中, 为弃风惩罚系数;
为弃风惩罚系数; 为
为 时刻的弃风量;
时刻的弃风量; 为失负荷惩罚系数;
为失负荷惩罚系数; 为
为 时刻的失负荷量。
时刻的失负荷量。
 (24)
(24)
 (25)
(25)
式中,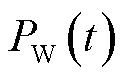 为风电场
为风电场 时刻发出的风电;
时刻发出的风电; 为
为 时刻上网风电;
时刻上网风电;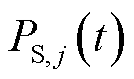 为储能电站
为储能电站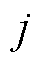 在
在 时刻出力;
时刻出力; 为
为 时刻需满足的电网负荷;
时刻需满足的电网负荷; 为区域内储能电站总数量。
为区域内储能电站总数量。
4.2.2 约束条件
1)功率平衡约束
 (26)
(26)
2)火电机组约束
火电机组出力上下限约束为
 (27)
(27)
火电机组爬坡约束为
 (28)
(28)
火电机组起停机约束为
 (29)
(29)
式中, 、
、 分别为火电机组
分别为火电机组 最小、最大出力;
最小、最大出力; 为火电机组
为火电机组 爬坡极限;
爬坡极限; 为火电机组
为火电机组 在
在 时刻的起停状态,1、0分别为起动、停机;
时刻的起停状态,1、0分别为起动、停机; 为最小开机时间;
为最小开机时间; 为最小关停时间。
为最小关停时间。
3)储能约束
储能电站SOC为
 (30)
(30)
式中, 为储能电站j在t时刻的能量;
为储能电站j在t时刻的能量;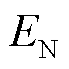 为储能集群额定容量。
为储能集群额定容量。
 (31)
(31)
储能电站充放电上下限约束为
 (32)
(32)
 (33)
(33)
储能电站首末功率一致约束为
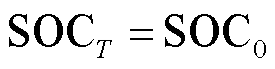 (34)
(34)
式中, 为储能集群在初始时刻的SOC值;
为储能集群在初始时刻的SOC值; 为放电终端的SOC值,令
为放电终端的SOC值,令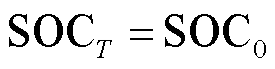 保证储能系统稳定运行。
保证储能系统稳定运行。
4)弃风约束
 (35)
(35)
式中, 为弃风上界。
为弃风上界。
5)网络运行约束
因本文研究电力系统的调峰调度策略,需考虑输电线路有功功率约束。
 (36)
(36)
式中, 为线路ab传输有功功率的上限;
为线路ab传输有功功率的上限; 为线路ab在
为线路ab在 时刻由节点a流向节点b的有功功率,计算方法为
时刻由节点a流向节点b的有功功率,计算方法为
 (37)
(37)
式中, 、
、 、
、 、
、 为网络拓扑的节点阻抗矩阵元素;
为网络拓扑的节点阻抗矩阵元素; 、
、 分别为线路
分别为线路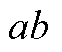 在节点
在节点 和节点
和节点 处的电抗值;
处的电抗值; 为t时刻电源节点n的有功功率;
为t时刻电源节点n的有功功率; 为负荷节点
为负荷节点 的有功功率;
的有功功率; 、
、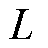 分别为节点及线路的集合。
分别为节点及线路的集合。
本节对储能集群内部功率分配模型进行介绍。首先为得到各储能电站循环寿命情况,利用雨流计数法得出储能电站循环寿命与放电深度的关系;然后提出包括储能电站循环寿命指数、节点负载率均衡度及储能运行经济性的多目标函数和相关约束;最后利用基于Pareto最优集合和 约束法算法对本文所提模型进行求解。
约束法算法对本文所提模型进行求解。
5.1.1 目标函数
储能集群内部储能电站间调峰资源分配需要关注其运行经济性及技术效果。对于经济性需要考虑电池循环寿命及系统运行成本,对于技术效果要考虑电站储能电站间的负载率。为此以下将对几个元素进行分析。
1)储能循环寿命
综合考虑全部因素分析电池寿命比较复杂,本文忽略温度以及充放电倍率对电池寿命的影响,只考虑充放电深度及循环次数对电池寿命的影响。根据多类型电池储能(磷酸铁锂电池、铅碳电池和钠硫电池)工程测试得到深度放电(Depth of Discharge, DOD)和循环次数N [25-26]的关系,采用5阶函数拟合关系如图7所示。运用雨流计数法,可根据电池SOC曲线得到电池工作DOD的 次循环DODj(u),则电池寿命衰减率可表示为
次循环DODj(u),则电池寿命衰减率可表示为

图7 电池循环次数与放电深度的关系
Fig.7 Relationship between the number of battery cycles and the depth of discharge
 (38)
(38)
式中, 为储能电站
为储能电站 第u次放电深度对应的电池循环寿命(次数);
第u次放电深度对应的电池循环寿命(次数); 为总放电次数。
为总放电次数。
2)负载率
为了最大化储能电站资源的有效利用,将发电机组在每个时间点的出力以及各储能电站的出力纳入多储能电站协同调峰优化运行模型作为决策变量,为准确地评估各储能电站的出力水平,引入“节点负载率”。
负载率是描述变压器实际承载的负荷与其最大容量之间比例的指标,负载率均衡度的数值越小,表明负载分配越均衡。节点负载率均衡度的计算公式为
 (39)
(39)
式中, 为第
为第 个储能电站在
个储能电站在 时刻的负载率;
时刻的负载率; 为此变电站所承担的负荷;
为此变电站所承担的负荷; 为多个储能电站在
为多个储能电站在 时刻的平均负载率。
时刻的平均负载率。
3)储能运行成本
为了显著提升储能电站的经济运行效率,构建储能电站运行成本模型,助力储能电站实现经济效益的最大化。
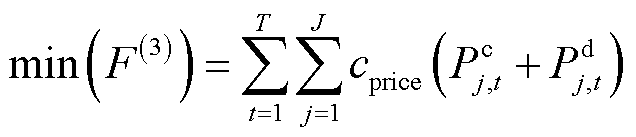 (40)
(40)
式中, 为储能运行价格。
为储能运行价格。
5.1.2 约束条件
1)荷电状态约束为
 (41)
(41)
式中,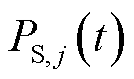 为储能电站
为储能电站 在
在 时刻出力;
时刻出力; 为储能集群的总功率需求。
为储能集群的总功率需求。
2)储能运行约束如式(32)、式(33)所示。
3)网络运行约束如式(36)、式(37)所示。
4)调控一致性约束
为保证各储能电站间同时充同时放,即调控一致性,储能电站电量不能存在反向增减的情况。
 (42)
(42)
式中, 为储能电站
为储能电站 在t时刻容量变化量;
在t时刻容量变化量; 为储能电站
为储能电站 在t时容量;
在t时容量; 为储能集群在
为储能集群在 时刻容量变化量;
时刻容量变化量; 为储能集群在t时刻容量;
为储能集群在t时刻容量; 为储能集群在
为储能集群在 时刻容量。
时刻容量。
5)出力公平性约束
为避免较为经济的储能电站一直处于运作状态,而经济性较差的储能电站利用率一直不高,造成能源浪费,在此引入储能电站剩余容量一致性约束。先将各储能电站的实时SOC进行标幺化,得到储能电站在各个时刻的剩余容量 ,提出
,提出 ,表示储能电站
,表示储能电站 的剩余容量与各电站
的剩余容量与各电站 时刻平均值
时刻平均值 的偏差,有
的偏差,有
 (43)
(43)
 (44)
(44)
式中, 为储能电站
为储能电站 在
在 时刻的剩余容量变化量;
时刻的剩余容量变化量; 为储能电站
为储能电站 在
在 时刻SOC变化量。
时刻SOC变化量。
因此出力公平性约束为
 (45)
(45)
式中,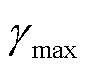 为系统允许总偏差最大值。
为系统允许总偏差最大值。
由3.1节,该优化模型共有三个目标函数,求解多目标优化问题时要在满足约束条件的基础上,在储能所接变电站负载率均衡度、电站寿命评价函数以及运行成本三个目标函数之间找到一个均衡解。
5.2.1 Pareto最优
在多目标优化问题中,所有可能的Pareto最优解构成了所谓的Pareto前沿。Pareto最优性的概念旨在提供一系列可接受的折中方案,供决策者从中选择。这些集合包含了所有无法被其他解所支配的最优解,由它们组成了Pareto前沿。设想面对一个最小化问题,涉及两个互相冲突的目标;在这种情况下,探讨以下三目标优化问题。
(1)对于属于同一Pareto前沿的每两个解,式(46)成立。
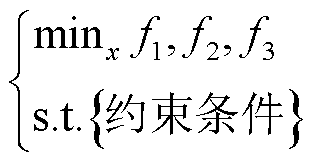 (46)
(46)
对于每一个属于Pareto前沿S的解xi,至少存在一个解xj,它至少在一个目标函数(这里称为fn)中优于xi。换言之,在考虑所有目标函数的集合中,Pareto前沿没有最优解。
 (47)
(47)
(2)对于属于较高Pareto前沿 和较低Pareto前沿S的每个解决方案,式(48)成立。
和较低Pareto前沿S的每个解决方案,式(48)成立。
 (48)
(48)
对于每个属于较高Pareto前沿 的解
的解 ,在较低Pareto前沿
,在较低Pareto前沿 中至少存在一个在任何目标函数中都不劣而在至少一个目标函数中更优的解
中至少存在一个在任何目标函数中都不劣而在至少一个目标函数中更优的解 。
。
5.2.2 多目标优化求解算法
本文采用ε-约束法对4.1节中多目标优化问题进行求解,相较于其他多目标求解方法能简化问题、更具有直观性、能减少计算负担且能满足本文系统实际运行需求。在求解最小优化问题时,它将原始目标函数之一最小化,而将其他目标函数转换为约束。本文中的三个目标函数只有一个被保留,另两个目标函数在约束阈值 的约束下变换,
的约束下变换, 转换为约束问题,有
转换为约束问题,有
 (49)
(49)
前文所描述的火-储调峰功率双层优化分配策略流程如图8所示。
1)储能电站间SOC均衡度

图8 双层优化控制策略流程
Fig.8 Flow chart of two-layer optimised control strategy
 (50)
(50)
式中, 为各储能集群间的SOC均值;
为各储能集群间的SOC均值; 为储能集群内各电站间的SOC均衡度,利用
为储能集群内各电站间的SOC均衡度,利用 得出各储能电站间SOC均衡程度和运行公平性,
得出各储能电站间SOC均衡程度和运行公平性, 越小表明公平性越好。
越小表明公平性越好。
2)调峰跟踪度
 (51)
(51)
式中, 为总电源出力;
为总电源出力; 为系统电源对负荷的跟踪程度,
为系统电源对负荷的跟踪程度, 越小表明策略跟踪度越好。
越小表明策略跟踪度越好。
3)单位能耗成本
 (52)
(52)
式中, 为总能耗成本;
为总能耗成本; 为总能源用量,其中包括火电储能及风电;
为总能源用量,其中包括火电储能及风电; 为总调度期内单位能耗成本,其值越小表示能源利用率越高。
为总调度期内单位能耗成本,其值越小表示能源利用率越高。
本文采用经过改进的IEEE 39节点网络作为实验基础,以验证所提方法的实际效果。选取一天 24 h作为调控周期,设置优化步长为15 min,确保调控策略的精确性和实时性。系统的拓扑结构如图9所示,涵盖了6台火电机组、5个风电机组以及5个储能电站。相关的火电机组与储能电站参数详见表3、表4。
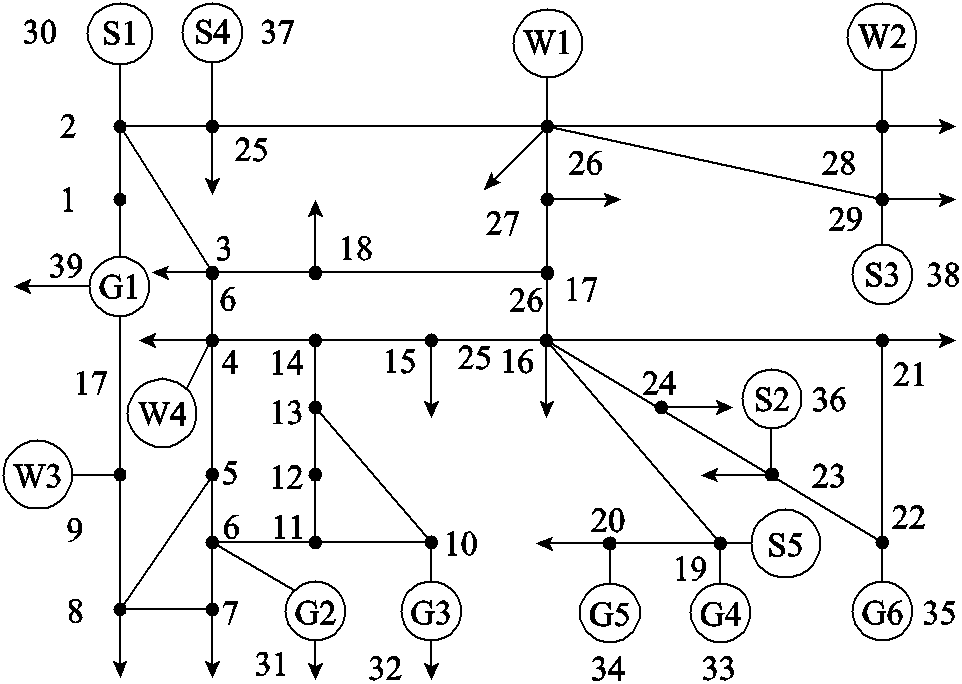
图9 改进IEEE 39节点网架结构
Fig.9 Improved IEEE 39 node mesh structure
表3 火电机组参数
Tab.3 Parameters of thermal power units

机组编号最大出力/MW最小出力/MW成本参数/(元/MW2), (元/MW), 元起停时间/h爬坡/[MW/(15 min)] G1150500.0375, 20, 372.5172 G2150500.0375, 20, 372.5172 G360150.625, 10, 316.5130 G450100.083 4, 32.5, 329.2130 G540100.25, 30, 276.4118 G645120.25, 30, 232.2124
表4 储能电站参数
Tab.4 Parameters of the energy storage plant

参数数值 储能电站1储能电站2储能电站3储能电站4储能电站5 位置/节点49192628 额定功率/MW101010515 额定容量/(MW·h)1616151043
(续)

参数数值 储能电站1储能电站2储能电站3储能电站4储能电站5 运维成本/(元/MW)400400500500300 充放电效率0.950.950.950.900.75 SOC限值(下限/上限)0.1/0.90.1/0.90.1/0.90.1/0.90.1/0.85 初始SOC0.50.50.50.50.5
火电装机容量为495 MW,风电装机容量为 600 MW,按照风电配储原则储能装机容量为 50 MW/100 MW·h。每个风电场都配备了相应的储能电站,以提升能源利用效率。风机的功率因数为0.95,弃风成本设定为0.3元/(kW·h),失负荷成本 8元/(kW·h)。
本文的仿真环境为Matlab 2022b,由于下层为多目标函数,存在非线性约束,在此利用YALMIP调用Gurobi求解器,结合多目标遗传算法进行求解。
6.2.1 火-储联合调峰性能及经济性分析
本节首先对历史数据进行分析得出火电机组各时段在各运行状态的概率;然后通过式(11)得出储能调峰盈余系数;最后通过传统策略与本策略在调峰效果和运行经济性方面的对比证明本文所提策略的有效性。
火电机组h级出力如图10所示。可以看出在2:00—4:00存在火电机组下调问题,需进行储能电站充电或弃风操作;而在16:00—22:00存在火电机组上调问题,在该时段需要储能集群进行充电。

图10 火电机组h级出力
Fig.10 Hourly thermal unit output
火电机组起停状态如图11所示。由图11得出,单一火电参与调峰,由于机组起停时间的限制,以及火电机组下调峰不足,存在不满足调峰需求的时段,例如13:00—14:00时段存在上调峰不足,而4:00前后存在下调不足。

图11 火电机组起停状态
Fig.11 Thermal power unit start-stop status
为强化储能资源在系统调节中的作用,本文对历史数据进行分析。火电调峰状态分析如图12所示。图12中的黄色色块表示存在调节需求的时间区间,绿色色块则表示火电机组满足系统的调节需求。通过观察图12a的净负荷历史数据热力图,发现每天10:00—20:00的区间内色彩最为鲜明,这代表用电高峰时段,等效负荷持续处于高位。进一步地,结合图10和图11所提供的信息,能够掌握每天各时段火电机组的起停状态及其出力的上下限。基于这些数据,分析了各时段的爬坡不足(如图12b所示)、调峰能力不足(如图12c和图12d所示)的情况,从而确定了储能电站需要提供预备出力的具体时段。
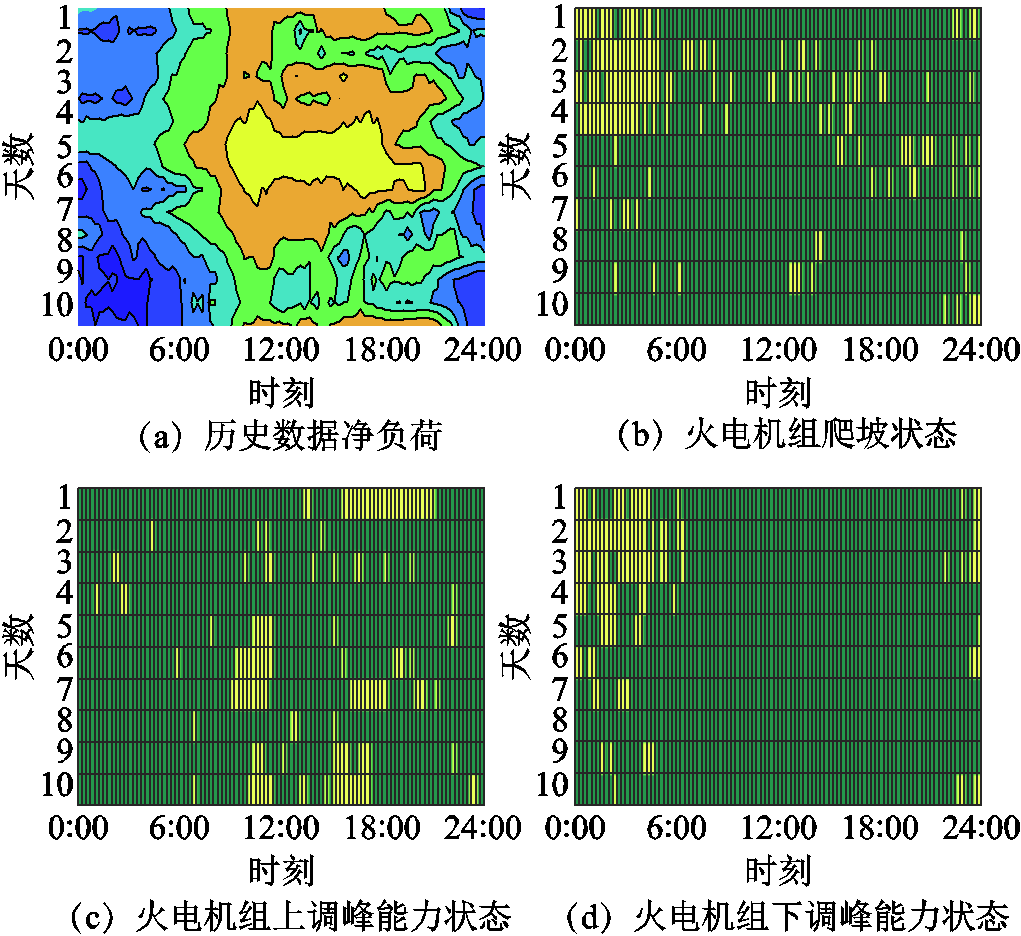
图12 火电调峰状态分析
Fig.12 Thermal power peaking state analysis
在0:00—1:00区间,火电机组爬坡不足和系统下调峰资源不足可能性较高,在该段时间内储能进行充电动作,提供下调灵活性;上调峰不足主要集中在8:00—21:00,处于用电高峰期,也属于等效负荷高峰期,同样也存在火电机组爬坡不足的情况,也就是在该时段为火电机组上爬坡不足且存在大概率的上调峰资源不足,储能在该时段需要进行放电,提供上调灵活性;当向上调峰需求与向下调峰需求可能性较为接近时,储能电站保持不变。
在储能集群参与调峰系统中,经济性及技术性的双重约束使得储能电站对调峰资源上调缺额及系统向上调节灵活性的灵敏度较调峰资源下调缺额及系统向下调节灵活性高得多。因此,本文主要分析系统向上调节能力。
根据所提研究策略,由上述历史数据的分析得出各时段下储能电站盈余需求系数如图13所示。可看出,系数较大值主要集中在8:00—21:00,这与前文的分析一致,即在该时段内需对存在需求的前一正常运行时段进行机组出力调整。

图13 储能电站盈余需求系数
Fig.13 Surplus demand factor for energy storage plants
为直观地看出所提策略的有效性,现与传统储能辅助火电机组调峰策略进行对比。各时段调峰运行如图14所示,其中策略1为传统火-储调峰分配策略,策略2为本文所提策略。
由图14可以看出,策略1下在持续高等效负荷阶段中由于储能电量不足,无法一直出力,导致在20:00前后出现失负荷的情况,而对于策略2在该时段并未出现失负荷,在15:00—16:00及18:00前后火电机组能满足调峰需求,且存在剩余可调节资源为储能进行充电操作,于是在储能调峰盈余系数的调节下,火电机组为储能充电,预留调峰资源。


图14 各时段调峰运行
Fig.14 Peaking operation at all times
策略2在储能调峰盈余系数的调节下,延长了储能参与调峰时间,从策略1下在19:30失去上调能力到策略2的22:00,延长了80%的运行时间,能满足区域全时段上调需求。
图15为不同策略调节下的剩余调峰需求。由图15可知,两种策略均能实现风电资源完全消纳。这是由于储能电站容量较大,能消纳系统无法使用的风电资源。对于失负荷,策略1下18:00—22:00期间存在大量的上调峰不足即失负荷现象,这对于系统安全运行是不利的,且经济性损失严重;而策略2在整个调峰周期内不存在上调峰需求,有效地保证电网的安全运行,达到了削峰填谷的目标。

图15 剩余调峰需求
Fig.15 Remaining peak demand
图16为不同策略下储能系统SOC变化情况。由图16可知,策略1下基本为全充全放,如在7:00时储能电站充满,随后便处于放电或不动作阶段;在19:00时完全放电,之后便又为充电或不动作。这种充放电模式对电化学储能电站循环寿命的损耗大。
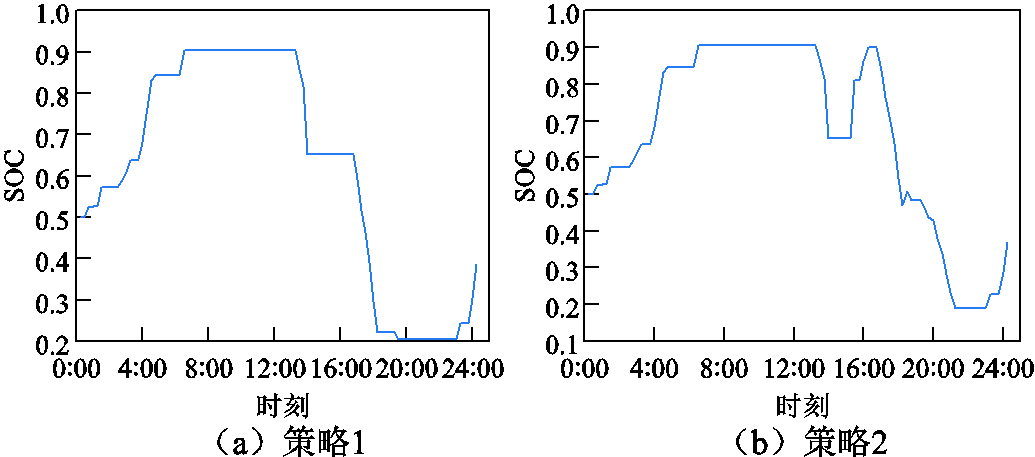
图16 储能系统SOC变化情况
Fig.16 Changes in SOC of energy storage systems
对于策略2,储能电站并未一直处于满充满放状态。策略2下,在7:00时储能电站充满,在13:00放电,而在15:00又发生充电动作。这是由于在储能调峰盈余系数指导下利用可调的火电资源对储能进行充电,为后续调峰作准备。随后在策略1下的放电阶段,策略2也存在小幅度的充电,对于电力系统来说,失负荷极其不利于安全稳定运行,换言之,在调峰资源高需求阶段,任何调峰资源的积累都是极为重要的。
策略技术性分析:本文提出的策略通过增加储能电站的充放电量来提高系统调节灵活性,由图15可以观察出,策略1由于储能容量不足,存在87.40 MW的上调峰需求,而策略2通过在火电机组满足调峰需求时为储能充电,保证储能电站在下一时段调峰需求高峰期间有足够多应对需求的电量。因此在策略1下存在上调峰需求的20:00时段,策略2不存在调峰问题。
策略经济性分析:调峰运行指标见表5。所提策略2相较于策略1,火电机组运行成本高0.22%,储能电站利用率较高,储能运行成本由365.78元增至427.68元;随即由弃风成本和失负荷成本构成的惩罚成本由原先策略1下的1.75×105元降至0元,策略2下不存在弃风及失负荷情况;策略2总运行成本比策略1减少1.70×105元,减少3.62%的运行成本。
表5 调峰运行指标
Tab.5 Peak operating indicator

指标策略1策略2增幅(%) 火电运行成本/元4.52×1064.53×1060.22 储能运行成本/元365.78427.6816.92 惩罚成本/元1.75×1050-100 总运行成本/元4.70×1064.53×106-3.62 调峰跟踪度1.908 30-100 单位能耗成本/(元/kW)0.109 60.106 1-3.19
综上所述,本文所提策略通过高效利用储能资源的调节灵活性,在技术性和经济性上相较于传统策略都有明显的提高。接下来验证本文提出的多储能电站间功率分配策略对减缓储能电站寿命衰减的有效性。
6.2.2 多储能电站SOC及寿命衰减分析
本文提出下层策略中将电站寿命评价函数作为多目标之一,相较于传统的策略1来说,增加了对储能寿命的考虑。为验证两个策略下储能寿命衰减程度,作如下分析。
图17为不同策略下各储能电站出力情况。储能电站1~5分别为锂离子电池储能电站1、锂离子电池储能电站2、铅碳电池储能电站、钠硫电池储能电站和抽蓄电站。抽蓄电站容量大,在大部分时间承担主要的调峰任务,由于在目标函数中增加了节点负载率均衡度以及储能电站循环寿命指数,未因为抽蓄价格较低就持续对抽蓄进行充电,使得每个储能电站都保留一定的调峰能力及灵活性,避免下一时段在储能功率约束下出现“有电未发”的现象。

图17 各储能电站出力
Fig.17 Output of each energy storage plant
图18为两个策略下各储能电站SOC对比情况。由于在储能循环寿命约束下,抽蓄电站有固定循环寿命,不受充放电深度的影响,策略2相较于策略1对抽蓄电站的消耗量要大得多,充放电频率也更大,对于电化学储能电站实施浅充浅放方式,在满足调峰效果的同时减缓储能寿命衰减。在节点负载率平衡的目标下,策略2储能电站之间的一致性指数为0.008 2,相较于策略1各储能电站SOC均衡度高26.79%,体现了策略对于各电站的公平性。

图18 各储能电站SOC
Fig.18 SOC of each energy storage plant
不同策略下储能寿命衰减对比见表6。策略2通过在模型中增加储能电站寿命损耗,使得循环老化成本低的抽蓄电站多出力,各电化学电站少出力。策略2中锂电池储能电站1的放电深度相较于策略1低5.38%,循环寿命次数增加了188次,锂电池储能电站2的循环寿命次数增加了4.62%,铅碳电池储能电站的循环寿命次数增加了5.42%,钠硫储能电站增加了28.64%。
表6 不同策略下储能寿命衰减对比
Tab.6 Comparison of energy storage life decay under different strategies

参数数值 策略电站1电站2电站3电站4电站5 放电深度10.0930.1150.1440.1600.184 20.0880.1040.1250.1180.263 循环次数18 2307 5143 3773 579— 28 4187 8613 5604 604—
不同策略下储能循环寿命如图19所示。可见,各类型电化学储能电站通过降低放电深度,在循环寿命次数方面都有一定的增加。前三个储能电站间增加幅度相差不大,而钠硫电池储能电站循环寿命变化更大,因为其在0.2放电深度之前,电池循环寿命对放电深度变化敏感度较另外两类要大得多。

图19 不同策略下储能循环寿命
Fig.19 Cycle life of energy storage under different strategies
6.2.3 SOCtj和 对策略的影响
对策略的影响
文中提出的储能SOC预备需求值( )及储能调峰盈余系数(
)及储能调峰盈余系数( )对于所提策略的调峰效果及储能循环寿命都有一定的影响,接下来对
)对于所提策略的调峰效果及储能循环寿命都有一定的影响,接下来对 和
和 进行分析。
进行分析。
调峰需求随SOCtj和 的变化如图20所示。由图20可知,调峰需求随两类系数的增加而减少。对于储能SOC预备需求值而言,SOCtj的增加会提高储能电站容量,提高应对高峰负荷的能力,调峰需求减少;而储能调峰盈余系数
的变化如图20所示。由图20可知,调峰需求随两类系数的增加而减少。对于储能SOC预备需求值而言,SOCtj的增加会提高储能电站容量,提高应对高峰负荷的能力,调峰需求减少;而储能调峰盈余系数 的增加会减少储能电站充电机会,从而增加调峰需求。
的增加会减少储能电站充电机会,从而增加调峰需求。

图20 调峰需求随 和
和 变化
变化
Fig.20 Peaking demand varies with  and
and
图21为系统运行成本与SOCtj和 上限的关系,基本趋势皆为先下降再上升。对于SOCtj来说,较高阶段可能出现储能充电但并未完全利用的情况,引起运行成本增加,后续则是储能调峰资源不够,引起失负荷、弃风等惩罚成本。
上限的关系,基本趋势皆为先下降再上升。对于SOCtj来说,较高阶段可能出现储能充电但并未完全利用的情况,引起运行成本增加,后续则是储能调峰资源不够,引起失负荷、弃风等惩罚成本。

图21 运行成本随SOCtj和 变化
变化
Fig.21 Variation of operating costs with SOCtj and
储能调峰盈余系数 较小时,会增加系统运行成本且调峰效果并未得到更好的改善;而该系数较高时,则会因预测误差而导致未在需求期间进行充电操作,导致惩罚成本增加。
较小时,会增加系统运行成本且调峰效果并未得到更好的改善;而该系数较高时,则会因预测误差而导致未在需求期间进行充电操作,导致惩罚成本增加。
储能电站循环寿命随SOCtj和储能调峰盈余系数变化情况如图22所示。可以看出,储能电站类型不同,对参数灵敏度以及反应结果各不相同:火电机组可调上限越大表示火电机组能为储能充电的功率越大,储能电站循环寿命随SOCtj的减小而减小,这是因为在SOCtj减小,火电为储能充电的概率更大,即储能更容易提前到达SOCmin,影响循环寿命,当其为0.65和0.60时由于其接近储能的初始运行状态,储能大多处于浅充浅放,循环次数有一定程度的增加;盈余系数为0.1表示储能大多时刻都保持SOCtj状态,一直浅充浅放,对寿命影响小,随着盈余系数增加,储能充放电量逐渐增加,循环寿命次数随之减少,当盈余系数为0.5、0.6即表示下一时段高峰负荷出现概率较高储能电站才动作,而这种概率是极小的,即储能电站动作次数很少,从而减缓循环寿命衰减,因此当盈余系数为0.5和0.6时循环寿命次数有一定程度的上升。

图22 储能循环寿命随SOCtj和 变化
变化
Fig.22 Energy storage cycle life varies with SOCtj and
综上所述,对于储能SOC预备需求值SOCtj而言,数值越大对系统调峰运行越有利,但基于系统运行成本及储能电站循环寿命衰减的约束,本文取值为0.88;对于储能调峰盈余系数调峰 而言,数值越小对系统调峰及储能循环寿命衰减越好,但基于区域运行成本约束,本文取值为0.3。通过上述分析得出本文对两系数取值的合理性。
而言,数值越小对系统调峰及储能循环寿命衰减越好,但基于区域运行成本约束,本文取值为0.3。通过上述分析得出本文对两系数取值的合理性。
本文提出了高比例风电系统中储能集群辅助火电机组调峰的双层优化调控策略。上层为基于各储能调峰盈余系数的火储调峰优化控制策略,得出各时段下储能集群与火电机组间调峰资源和系统灵活性的最优分配;下层为考虑储能寿命的多目标约束下各储能电站优化控制策略,在三重目标下求得各储能电站的最优出力。通过算例验证本文得出的主要结论如下:
1)本策略通过有效地利用火电机组的剩余可调容量对储能电站进行充电,显著减少了上调峰需求,实现了风电的全额消纳。这种优化配置不仅提高了能源利用效率,还促进了可再生能源的融入,实现资源优化配置;通过优化火电和储能的运行策略,本方法有助于促进环境的可持续发展。
2)尽管火电机组的运行成本略有增加,但通过减少上调峰需求和延长储能运行时间,总运行成本相比传统策略下降了3.62%。通过改变储能调峰盈余系数,得出了运行成本与调峰需求的最优关系。当选取SOCtj为0.88、储能调峰盈余系数为0.3时,达到了最优的经济性和调峰效果。本策略实施后,系统不存在弃风及失负荷的情况,极大地提升了电力系统的稳定性和可靠性。
3)在下层模型中增加储能电站寿命损耗成本,使得循环老化成本低的抽蓄电站多出力,而电化学电站则少出力,有效地平衡了负载率,并延长了各类储能设备的循环寿命,具有显著的经济效益。本策略不仅适用于当前的研究场景,其核心思想和方法论也可推广到其他电力系统中。
综上所述,本文提出的高比例风电系统中储能集群辅助火电机组调峰分层优化控制策略在资源优化配置、经济效益提升、储能寿命管理、调峰效果优化等方面均有积极意义。随着储能价格的下降,下一步将利用储能集群联合调峰调频,在不同时间尺度上实现储能资源的有效利用。
参考文献
[1] 国家能源局. 2023年全国电力工业统计数据[EB/OL]. [2024-01-26]. https://www.nea.gov.cn/2024-01/26/c1310762246.htm.
[2] 鲁宗相, 林弋莎, 乔颖, 等. 极高比例可再生能源电力系统的灵活性供需平衡[J]. 电力系统自动化, 2022, 46(16): 3-16. Lu Zongxiang, Lin Yisha, Qiao Ying, et al. Flexibility supply-demand balance in power system with ultra-high proportion of renewable energy[J]. Automation of Electric Power Systems, 2022, 46(16): 3-16.
[3] 中国储能网. 浅析国内电源侧储能利用率问题[EB/OL]. [2023-11-11]. https://www.escn.com.cn/20231111/ 47f4149732c5421e8c34bf25dad6f5b7/c.html.
[4] 李军徽, 安晨宇, 李翠萍, 等. 计及调峰市场交易的储能-新能源-火电多目标优化调度[J]. 电工技术学报, 2023, 38(23): 6391-6406. Li Junhui, An Chenyu, Li Cuiping, et al. Multi-objective optimization scheduling method considering peak regulating market transactions for energy storage-new energy-thermal power[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6391-6406.
[5] 李军徽, 陈国航, 马腾, 等. 高风电渗透率下液流电池储能系统调峰优化控制策略[J]. 发电技术, 2024, 45(3): 434-447. Li Junhui, Chen Guohang, Ma Teng, et al. Optimal control strategy of peak shaving of flow battery energy storage system under high wind power permeability[J]. Power Generation Technology, 2024, 45(3): 434-447.
[6] 李建林, 牛萌, 周喜超, 等. 能源互联网中微能源系统储能容量规划及投资效益分析[J]. 电工技术学报, 2020, 35(4): 874-884. Li Jianlin, Niu Meng, Zhou Xichao, et al. Energy storage capacity planning and investment benefit analysis of micro-energy system in energy intercom-nection[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 874-884.
[7] 孔昱凯, 温步瀛, 唐雨晨. 考虑辅助服务含储能区域电网运行优化[J]. 电气技术, 2021, 22(4): 26-32, 77. Kong Yukai, Wen Buying, Tang Yuchen. Operation optimization for regional grid containing energy storage considering auxiliary service[J]. Electrical Engineering, 2021, 22(4): 26-32, 77.
[8] 段潇涵, 孙丹, 赵琛, 等. 计及调频能力和经济效益的储能集群多状态区间优化策略[J]. 电力系统自动化, 2024, 48(5): 58-67. Duan Xiaohan, Sun Dan, Zhao Chen, et al. Multi-state interval optimization strategy for energy storage clusters considering frequency regulation ability and economic benefits[J]. Automation of Electric Power Systems, 2024, 48(5): 58-67.
[9] 陈明昊, 朱月瑶, 孙毅, 等. 计及高渗透率光伏消纳与深度强化学习的综合能源系统预测调控方法[J].电工技术学报, 2024, 39(19): 6054-6071. Chen Minghao, Zhu Yueyao, Sun Yi, et al. The predictive-control optimization method for park integrated energy system considering the high penetration of photovoltaics and deep reinforcement learning[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6054-6071.
[10] 麻秀范, 王戈, 朱思嘉, 等. 计及风电消纳与发电集团利益的日前协调优化调度[J]. 电工技术学报, 2021, 36(3): 579-587. Ma Xiufan, Wang Ge, Zhu Sijia, et al. Coordinated day-ahead optimal dispatch considering wind power consumption and the benefits of power generation group[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 579-587.
[11] 李军徽, 张嘉辉, 李翠萍, 等. 参与调峰的储能系统配置方案及经济性分析[J]. 电工技术学报, 2021, 36(19): 4148-4160. Li Junhui, Zhang Jiahui, Li Cuiping, et al. Configuration scheme and economic analysis of energy storage system participating in grid peak shaving[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4148-4160.
[12] 李军徽, 张嘉辉, 穆钢, 等. 储能辅助火电机组深度调峰的分层优化调度[J]. 电网技术, 2019, 43(11): 3961-3970. Li Junhui, Zhang Jiahui, Mu Gang, et al. Hierarchical optimization scheduling of deep peak shaving for energy-storage auxiliary thermal power generating units[J]. Power System Technology, 2019, 43(11): 3961-3970.
[13] 郝文波, 景菲, 颜庆宇, 等. 数据驱动下基于风电场景的多时间尺度调峰调度研究[J]. 电力系统保护与控制, 2023, 51(16): 115-126. Hao Wenbo, Jing Fei, Yan Qingyu, et al. A multi-time scale peak shaving scheduling strategy based on wind power scenario using a data-driven method[J]. Power System Protection and Control, 2023, 51(16): 115-126.
[14] 时瑞廷, 杨贺钧, 马英浩, 等. 计及峰谷平滑效益的需求响应和电池储能系统调度联合优化策略[J]. 电力自动化设备, 2023, 43(8): 49-55. Shi Ruiting, Yang Hejun, Ma Yinghao, et al. Joint optimization strategy of demand response and battery energy storage system dispatch considering peak-valley smoothing benefit[J]. Electric Power Automation Equipment, 2023, 43(8): 49-55.
[15] 赵东元, 胡楠, 傅靖, 等. 提升新能源电力系统灵活性的中国实践及发展路径研究[J]. 电力系统保护与控制, 2020, 48(24): 1-8. Zhao Dongyuan, Hu Nan, Fu Jing, et al. Research on the practice and road map of enhancing the flexibility of a new generation power system in China[J]. Power System Protection and Control, 2020, 48(24): 1-8.
[16] 姜海洋, 杜尔顺, 马佳豪, 等. 考虑长周期供需不平衡风险的新型电力系统规划方法[J]. 中国电机工程学报, 2024, 44(15): 5845-5858. Jiang Haiyang, Du Ershun, Ma Jiahao, et al. Power system optimal planning method considering long-term lmbalance risk[J]. Proceedings of the CSEE, 2024, 44(15): 5845-5858.
[17] 郑林烽, 缪源诚, 滕晓毕, 等. 考虑配储的火电机组灵活性改造模型与方法[J/OL]. 中国电机工程学报, 2024: 1-14. https://doi.org/10.13334/j.0258-8013.pcsee.231566. Zheng Linfeng, Liao Yuanchng, Teng Xiaobi, et al. Model and method for flexible retrofit of thermal power units considering energy storage configuration [J]. Proceedings of the CSEE, 2024: 1-14. https:// doi.org/10.13334/j.0258-8013.pcsee.231566.
[18] 潘郑楠, 邓长虹, 徐慧慧, 等. 考虑灵活性补偿的高比例风电与多元灵活性资源博弈优化调度[J]. 电工技术学报, 2023, 38(增刊1): 56-69. Pan Zhengnan, Deng Changhong, Xu Huihui, et al. Game optimization scheduling of high proportion wind power and multiple flexible resources considering flexibility compensation[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 56-69.
[19] 朱晓荣, 山雨琦. 考虑灵活性的储能容量多阶段分布鲁棒规划[J]. 电力自动化设备, 2023, 43(6): 152-159, 167. Zhu Xiaorong, Shan Yuqi. Multi-stage distributionally robust planning of energy storage capacity consi-dering flexibility[J]. Electric Power Automation Equipment, 2023, 43(6): 152-159, 167.
[20] 姜云鹏, 任洲洋, 李秋燕, 等. 考虑多灵活性资源协调调度的配电网新能源消纳策略[J]. 电工技术学报, 2022, 37(7): 1820-1835. Jiang Yunpeng, Ren Zhouyang, Li Qiuyan, et al. An accommodation strategy for renewable energy in distribution network considering coordinated dispatching of multi-flexible resources[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1820-1835.
[21] 林墨涵, 刘佳, 唐早, 等. 考虑多能耦合共享储能的微网多智能体混合博弈协调优化[J]. 电力系统自动化, 2024, 48(4): 132-141. Lin Mohan, Liu Jia, Tang Zao, et al. Coordinated optimization of mixed microgrid multi-agent game considering multi-energy coupled shared energy storage[J]. Automation of Electric Power Systems, 2024, 48(4): 132-141.
[22] 王力, 胡佳成, 曾祥君, 等. 基于混合储能的交直流混联微电网功率分级协调控制策略[J]. 电工技术学报, 2024, 39(8): 2311-2324. Wang Li, Hu Jiacheng, Zeng Xiangjun, et al.Hierarchical coordinated power control strategy for AC-DC hybrid microgrid with hybrid energy storage [J]. Transactions of China Electrotechnical Society, 2024, 2024, 39(8): 2311-2324.
[23] 吴永飞, 包宇庆. 电能型-功率型混合储能日前-日内协同滚动调度策略[J]. 电力系统自动化, 2024, 48(1): 77-87. Wu Yongfei, Bao Yuqing. Coordinated day-ahead and intra-day rolling scheduling strategy for electricity-power hybrid energy storage[J]. Automation of Electric Power Systems, 2024, 48(1): 77-87.
[24] Hou Jun, Song Ziyou. A hierarchical energy management strategy for hybrid energy storage via vehicle-to-cloud connectivity[J]. Applied Energy, 2020, 257: 113900.
[25] Alharbi H, Bhattacharya K. Stochastic optimal planning of battery energy storage systems for isolated microgrids[J]. IEEE Transactions on Sustainable Energy, 2018, 9(1): 211-227.
[26] 韩晓娟, 程成, 籍天明, 等. 计及电池使用寿命的混合储能系统容量优化模型[J]. 中国电机工程学报, 2013, 33(34): 91-97, 16. Han Xiaojuan, Cheng Cheng, Ji Tianming, et al. Capacity optimal modeling of hybrid energy storage systems considering battery life[J]. Proceedings of the CSEE, 2013, 33(34): 91-97, 16.
Abstract To address the challenges associated with integrating large-scale wind power into the power grid, we propose a layered optimization control strategy. This strategy employs energy storage clusters to support thermal power unit peaking. In the fire-storage control layer, an optimization control strategy is introduced based on the peak-regulating surplus coefficient of the energy storage cluster. The goal of this strategy is to reserve space for energy storage peak-regulating output by introducing the storage peak-regulating surplus coefficient, thereby enhancing the overall peak-regulating effect. In the internal control layer of the storage cluster, a multi-objective constraint optimization control strategy is proposed to mitigate the aging of the storage power station. This strategy considers various technical and economic constraints such as network tidal current constraints, regulation consistency constraints, output constraints, and fairness constraints. To determine the optimal power output of each energy storage power station, a multi-objective model is employed that takes into account factors such as slow decay of storage life, low node load rate balance, and low operating costs. The initial value of power output for each storage power station is obtained using genetic algorithms and iterated with the corrected power output of storage energy in the upper layer of the peak regulation task assignment. Through simulation, the proposed strategy can achieve a peak demand reduction of 87.40 MW, while also reducing the total operating cost by 3.62%. Additionally, the number of cycle lives for each energy storage power station increases to varying degrees, including a 4.38% increase for lithium battery storage plants. The effectiveness of the proposed strategy is verified from both an economic and technical standpoint.
In order to verify the effectiveness of the above control strategies, this paper takes an actual wind power and load data from a certain location in China for simulation analysis. The specific conclusions are as follows:
The peak optimization control strategy predicated on the surplus coefficient diminishes the peak shifting demand by 87.40MW in comparison to traditional methods, achieving a 100% wind power consumption rate. Utilizing the residual adjustable capacity of thermal power units to charge the energy storage stations leads to a 0.22% increment in their operating costs (from 365.78 ¥ to 427.68 ¥). However, this results in an 80% extension in the operation time of the energy storage, with no wind abandonment or load loss, culminating in a total operational cost reduction of 1.70×105 ¥ or 3.62% relative to traditional strategies.
By elevating the life loss cost of the energy storage stations within the lower model, while ensuring equitable load rate equalization, pumped storage stations with lower cycle aging costs are empowered, with the converse true for various electrochemical stations. Computational outcomes indicate that the depth of discharge for Lithium Battery Station 1 is reduced by 5.38% under the proposed strategy, increasing its cycle life by 188 times, and for Lithium Battery Station 2 by 4.62%.
Varying the surplus coefficient of energy storage peaking reveals its relationship with operational costs and peaking demands. Optimal economy and peaking effects are achieved when selecting a State of Charge (SOCtj) of 0.88 and a surplus coefficient of 0.3.
Keywords:Energy storage cluster, power system peaking, remaining useful life, two-layer optimal control strategy
DOI: 10.19595/j.cnki.1000-6753.tces.240545
中图分类号:TM614
国家电网有限公司科技项目资助(5108-202299257A-1-0-ZB)。
收稿日期 2024-04-07
改稿日期 2024-09-05
李军徽 男,1976年生,博士,教授,研究方向为新能源发电联网运行关键技术和储能技术的应用等。E-mail:lijunhui@neepu.edu.cn
李翠萍 女,1982年生,副教授,硕士生导师,研究方向为储能技术在电力系统中的应用。E-mail:licuipingabc@163.com(通信作者)
(编辑 赫 蕾)