
图1 离网型梯级水-风-光-蓄互补系统
Fig.1 Off-grid cascaded pumped-hydro-wind-photovoltaic complementary system
摘要 为了解决偏远地区的离网型系统供电可靠性问题,依托现有梯级水电改造混合式抽水蓄能成为一种有效手段,而变速抽水蓄能因其抽水能力可调使得相较于定速抽蓄更具运行灵活性。在此背景下,变速抽水蓄能改造梯级水电联合风光资源组成区域性100%清洁能源离网系统,可以在满足区域供电可靠性的前提下,促进水风光资源的消纳。基于此,构建了基于数据驱动的离网型抽水蓄能改造梯级水电联合配置风光资源的容量优化配置模型。首先,以等年值综合成本最小为目标,考虑水电-风电-光伏发电-抽水蓄能(水-风-光-蓄)系统运行、供电可靠性等约束,构建水-风-光-蓄多能互补的容量优化配置模型;然后,通过McCormick线性化方法,将原始混合整数非线性模型转换为混合整数线性优化模型;最后,考虑负荷、风电、光伏与水电来水量的随机性,综合1-范数和∞-范数构建基于数据驱动的分布鲁棒优化模型,并采用列与约束生成算法进行求解,验证模型的可行性。
关键词:混合式抽蓄改造 水-风-光-蓄 供电可靠性 分布鲁棒 列与约束生成
近年来,随着我国能源结构的转型升级,微电网将发挥其因地制宜、自给自足的独特优势,尤其是在我国以水电为主的偏远地区,其既是电网终端的重要支柱,又是中小型偏远地区的重要电能来源[1-2]。受自然条件影响,偏远地区微电网常配置一定比例新能源以实现离网运行[3]。以风电与光伏出力的不确定性为代表的新能源发电出力的不确定性,增加了离网型微电网可靠供电的难度[4-5]。
配置多类型电源进行互补运行是实现微电网可靠供电的有效手段。目前国内外已有相关学者研究了以火电为主的风-光-柴-储源偏远地区微电网的容量配置问题。文献[6]在考虑供电可靠性和可再生能源利用率的前提下,构建源荷交替迭代模型,通过求解得到风光柴储多能系统综合成本最小化的最优配置;文献[7]构建以总成本最小、CO2排放量最少为目标的离岸微型综合能源系统的电-热-CO2耦合模型,以此实现兼顾经济效益与环境效益的离岸微型综合能源系统多目标规划;文献[8]基于分布式电源的特征,构建了多种运行工况下的典型独立型风光柴储微电网,进而提出最优容量配置方法;文献[9]在考虑微电网稳定性、经济性、环保性的前提下,构建了以运行成本最低、稳定性最优为目标的风光柴储微电网最优配置模型。
然而,上述研究均包含常规燃料机组,无法真正实现完全由可再生能源供应负荷需求,实现由高污染、高耗能发电形式向清洁环保发电形式的转变。在水资源丰富、以水电为主要电源的偏远微电网,依托现有水电开发条件发展混合式抽水蓄能,可以提高原有水电的调节性能,进而提高偏远地区微电网供电的可靠性[10-12]。同时,传统抽蓄机组在抽水工况下功率难以调节,相比之下,变速抽蓄机组具有效率高、抽水工况入力可调优势,在偏远地区微电网的离网运行中进一步提升了调节灵活性[13-14]。当前已有部分研究探索了含梯级水电的水-风-光-储离网型100%清洁能源微电网容量优化配置。文献[15]在考虑输电需求和梯级水电综合特性前提下,以最小化波动为目标构建了基于互补保证率和累积时间比例的大型水-风-光-电混合系统模型和方法;文献[16]在充分考虑含小水电微电网的功率、能量的平衡特性后,提出一种基于功率能量特性的含小水电微电网储能优化配置方法;文献[17]针对可再生能源发电短期波动大、随机性强等问题,提出了一种水-风-光-储能多能源互补微网模型。然而,上述研究以电化学储能作为微电网调节资源,而依托现有梯级水电进行混合式抽蓄改造的研究集中于并网型大规模梯级水电系统优化运行调度[18-19],对于现有梯级水电进行抽蓄改造的容量配置问题研究仍然较少。
准确发刻画新能源出力的不确定性特征是制定离网型水-风-光-蓄互补系统容量配置方案的关键。随机优化(Stochastic Optimization, SO)通过构建一个基于不确定性概率分布的典型情景集合进行优化。文献[20]以蒙特卡洛抽样法为基础生成典型场景,基于两阶段SO法开展多能互补系统的调度优化研究,构建典型情景下的多能互补协同规划模型。实际运行中,随机变量实际概率分布往往未知,导致SO结果出现“样本外表现”较差问题。同时SO选取大规模场景计算模拟随机变量,导致计算效率较低。鲁棒优化(Robust Optimization, RO)利用不确定度集来描述随机变量的变动幅度,从而避免了对概率分布的假定。文献[21]基于准确概率分布的鲁棒理论,在考虑源网储综合出力约束基础上构建了考虑随机变量极端偏差条件下的鲁棒优化配置模型。但RO忽略了有价值的概率信息,得到考虑最差情况下的优化配置结果,使得系统的配置方案过于保守。
相比而言,分布鲁棒优化(Distributionally Robust Optimization, DRO)采用一种基于概率分布的模糊集合来刻画不确定性,寻求最劣概率分布下的最优解[22]。相比于RO和SO,DRO能够考虑随机变量的概率信息,也兼顾了结果的鲁棒性[23]。然而,分布鲁棒优化方法在离网型水-风-光-蓄优化配置的应用研究中尚未见报道。
在此背景下,本文以离网型梯级水电-风电-光伏-抽水蓄能系统作为研究目标,研究考虑梯级水电混合式抽蓄改造的风电、光伏、抽蓄容量优化配置问题。首先,在风光出力特性分析的基础上,构建基于1-范数和∞-范数的概率分布模糊集;然后,以实现100%清洁能源供电为目标,考虑梯级水力耦合、供电可靠性等约束,综合考虑各类电源的投资成本,建立离网型梯级水-风-光-蓄系统的分布鲁棒容量优化配置模型,提出以等年值综合成本最小化为目标的容量优化配置策略和相应的求解方法;最后,采用列与约束生成(Column and Constraint Generation, C&CG)算法求解离网型混合式抽蓄改造下的水-风-光-蓄系统分布鲁棒优化配置模型,并基于算例分析梯级水电混合式抽蓄改造在离网型微网对于供电可靠性和新能源消纳的作用,以及变速抽蓄机组的优势。
针对传统梯级水电站内的常规水电机组缺乏一定的储能能力,无法解决离网型系统的供电可靠性问题,构建离网型梯级水-风-光-蓄互补系统,旨在因地制宜地通过抽蓄改造梯级水电实现混合式抽蓄系统,并结合风电与光伏电站,组成100%清洁能源系统,以实现当地的绿色清洁能源可靠供电。
离网型梯级水-风-光-蓄互补系统如图1所示。为了实现离网形式下的高效联合运行,系统中主要包括梯级水电、风力发电、光伏发电和抽水蓄能。风电与光伏实现清洁能源供电,梯级水电-抽蓄系统通过扩建抽水蓄能机组组成梯级混合式抽水蓄能电站作为可调度电源,同时具备径流发电与抽水储能能力,以此补偿风电与光伏发电的波动性与随机性。与常规梯级水电站相比,梯级混合式抽水蓄能电站增加了抽水储能能力,此外,相较于传统纯抽水蓄能电站,梯级混合式电站具有天然径流来水,不再受上水库与下水库之间水量耦合限制进行发电,调节能力大幅提升。

图1 离网型梯级水-风-光-蓄互补系统
Fig.1 Off-grid cascaded pumped-hydro-wind-photovoltaic complementary system
本文以抽水蓄能机组、风电机组、光伏机组的等年值投资成本与系统运行时产生的等年值弃电惩罚成本之和最小为目标进行水-风-光-蓄互补系统容量优化配置。目标函数为
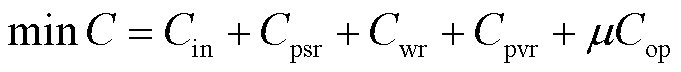 (1)
(1)
 (2)
(2)

 (4)
(4)
 (5)
(5)
 (6)
(6)
式中,C为等年值综合成本; 为抽水蓄能机组、风电机组、光伏机组的等年值投资成本之和;
为抽水蓄能机组、风电机组、光伏机组的等年值投资成本之和; 为弃电惩罚成本之和;
为弃电惩罚成本之和; 为等年值投资成本与运行成本间的等值系数,m =365;
为等年值投资成本与运行成本间的等值系数,m =365; 、
、 与
与 分别为抽水蓄能机组、风电机组与光伏机组的等年值投资成本;T为时间周期;I为梯级水电站的总级数;
分别为抽水蓄能机组、风电机组与光伏机组的等年值投资成本;T为时间周期;I为梯级水电站的总级数; 、
、 与
与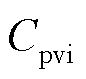 分别为抽水蓄能机组、风电机组与光伏机组的单位容量投资成本;
分别为抽水蓄能机组、风电机组与光伏机组的单位容量投资成本; 、
、 与
与 分别为抽水蓄能机组、风电机组与光伏机组的配置容量;
分别为抽水蓄能机组、风电机组与光伏机组的配置容量; 、
、 与
与 分别为抽水蓄能机组、风电机组与光伏机组的每年维护成本;r为资金折现率;L、H与J分别为抽水蓄能机组、风电机组与光伏机组的使用年限;
分别为抽水蓄能机组、风电机组与光伏机组的每年维护成本;r为资金折现率;L、H与J分别为抽水蓄能机组、风电机组与光伏机组的使用年限; 、
、 与
与 分别为单位弃风、弃光与弃水惩罚成本;
分别为单位弃风、弃光与弃水惩罚成本; 与
与 分别为第t时段风电与光伏机组的预测出力;
分别为第t时段风电与光伏机组的预测出力;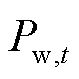 与
与 分别为第t时段风电与光伏机组的发电功率;
分别为第t时段风电与光伏机组的发电功率; 为第t时段第i级水电站的弃水流量;
为第t时段第i级水电站的弃水流量; 为第i级水电站水电机组的发电效率。
为第i级水电站水电机组的发电效率。
1.3.1 投资决策约束
1)风电与光伏电站装机容量约束
 (7)
(7)
式中, 与
与 分别为风电场最小与最大装机容量;
分别为风电场最小与最大装机容量; 与
与 分别为光伏电站最小与最大装机容量。
分别为光伏电站最小与最大装机容量。
2)抽水蓄能机组装机容量约束
 (8)
(8)
式中, 与
与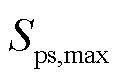 分别为抽水蓄能机组最小与最大装机容量。
分别为抽水蓄能机组最小与最大装机容量。
1.3.2 运行约束
1)系统功率平衡约束
 (9)
(9)
式中, 为第t时段第i级水电站水电机组的发电功率;
为第t时段第i级水电站水电机组的发电功率; 与
与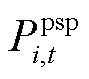 分别为第t时段第i级水电站抽水蓄能机组的发电功率与抽水功率;
分别为第t时段第i级水电站抽水蓄能机组的发电功率与抽水功率; 为第t时段负荷需求与系统联合出力间的功率缺额;
为第t时段负荷需求与系统联合出力间的功率缺额; 为第t时段的负荷。
为第t时段的负荷。
2)系统供电可靠性约束
在离网型清洁微网中,需满足系统供电可靠的前提条件,即
 (10)
(10)
式中, 为系统的最大切负荷率,取95%。
为系统的最大切负荷率,取95%。
3)风电与光伏电站出力约束
 (11)
(11)
 (12)
(12)
式中, 与
与 分别为第t时段风电与光伏机组的预测出力标幺值。
分别为第t时段风电与光伏机组的预测出力标幺值。
4)梯级混合式抽蓄电站水量平衡约束
常规梯级水电站需满足附录中式(A1)~式(A7)所示的运行约束。相较于常规梯级水电站,梯级混合式抽水蓄能电站调节灵活性更强,既有仅能发电的常规水电机组,又有同时兼备发电与抽水能力的抽水蓄能机组。因此,梯级混合式抽蓄电站除了需满足常规梯级水电站的运行约束外,在水量平衡与运行工况等方面仍需满足以下约束:
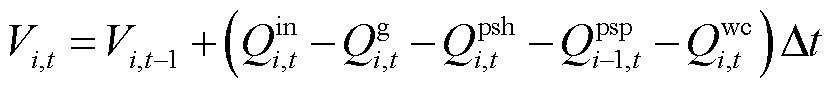 (13)
(13)
 (14)
(14)
式中, 为第t时段第i级水电站的水库库容;
为第t时段第i级水电站的水库库容; 与
与 分别为第t时段第i级水电站的入库流量与区间流量;
分别为第t时段第i级水电站的入库流量与区间流量; 与
与 分别为第t时段第i级水电站水电机组的发电流量与弃水流量;
分别为第t时段第i级水电站水电机组的发电流量与弃水流量; 与
与 分别为第t时段第i级水电站抽水蓄能机组的发电流量与抽水流量;
分别为第t时段第i级水电站抽水蓄能机组的发电流量与抽水流量; 为第i-1级水电站到第i级水电站之间的水流时滞;
为第i-1级水电站到第i级水电站之间的水流时滞; 为时间步长。
为时间步长。
5)抽水蓄能机组运行约束
抽蓄机组在发电工况下,运行特性与水电机组类似。在抽水工况下,变速抽水蓄能机组能够调节转速,从而实现抽水功率入力可调,可以更好地适应风电光伏出力的不确定性。故而,变速抽蓄的运行约束为
 (15)
(15)
 (16)
(16)
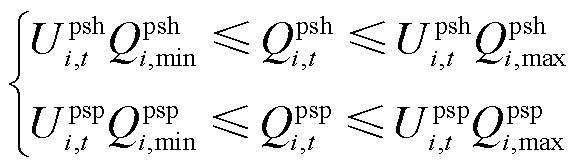 (17)
(17)
 (18)
(18)
 (19)
(19)
式中, 、
、 分别为变速抽蓄机组抽水功率下限与装机容量转换系数、变速抽蓄机组抽水功率上限与装机容量转换系数;
分别为变速抽蓄机组抽水功率下限与装机容量转换系数、变速抽蓄机组抽水功率上限与装机容量转换系数; 、
、 分别为变速抽蓄机组发电功率下限与装机容量转换系数、变速抽蓄机组发电功率上限与装机容量转换系数;
分别为变速抽蓄机组发电功率下限与装机容量转换系数、变速抽蓄机组发电功率上限与装机容量转换系数; 与
与 分别为第t时段第i级水电站抽水蓄能机组发电工况下的最小与最大发电流量;
分别为第t时段第i级水电站抽水蓄能机组发电工况下的最小与最大发电流量; 与
与 分别为第t时段第i级水电站抽水蓄能机组抽水工况下的最小与最大抽水流量;
分别为第t时段第i级水电站抽水蓄能机组抽水工况下的最小与最大抽水流量; 与
与 分别为第t时段第i级水电站抽水蓄能机组发电工况与抽水工况的开停机运行状态变量;
分别为第t时段第i级水电站抽水蓄能机组发电工况与抽水工况的开停机运行状态变量; 与
与 分别为第i级水电站抽水蓄能机组的发电效率与抽水效率;
分别为第i级水电站抽水蓄能机组的发电效率与抽水效率; 与
与 分别为第i级水电站抽水蓄能机组发电工况下的最小与最大发电功率;
分别为第i级水电站抽水蓄能机组发电工况下的最小与最大发电功率; 与
与 分别为抽水蓄能机组抽水工况下的最小与最大抽水功率。
分别为抽水蓄能机组抽水工况下的最小与最大抽水功率。
相比之下,在抽水工况下,定速抽水蓄能机组为恒定抽水功率,调节能力受限。故而定速抽蓄机组运行约束在发电工况下与变速抽蓄类似,在抽水工况下定速机组运行约束可以表示为
 (20)
(20)
 (21)
(21)
6)水电机组与抽水蓄能机组的运行状态互斥约束
 (22)
(22)
式中, 为第t时段第i级水电站水电机组的开停机运行状态变量。
为第t时段第i级水电站水电机组的开停机运行状态变量。
1.3.3 基于McCormick包络的非线性约束转换
针对离网型梯级水-风-光-蓄互补系统模型中的双线性项,McCormick包络方法的优势在于通过将双线性项转换为一组线性约束,降低了求解问题的计算难度[24-25]。McCormick包络方法示意图如图2所示。该方法可以将混合整数非线性规划问题松弛为混合整数线性规划问题,便于快速求解[26-28]。式(19)所示的变速抽水蓄能机组运行约束,由于需要配置变速抽蓄机组的装机容量,而变速抽蓄机组的装机容量又与 、
、 、
、 、
、 这四个连续变量有关,且与运行状态0-1变量如
这四个连续变量有关,且与运行状态0-1变量如 、
、 相乘后形成非线性约束。本文采用McCormick包络方法处理该0-1变量与连续变量相乘的双线性约束,则式(19)可以转换为式(23)、式(24)。
相乘后形成非线性约束。本文采用McCormick包络方法处理该0-1变量与连续变量相乘的双线性约束,则式(19)可以转换为式(23)、式(24)。
 (23)
(23)
 (24)
(24)
式中, 与
与 为转换后的线性变量;
为转换后的线性变量; 与
与 分别为单台变速抽蓄机组的最小装机容量、最大装机容量。
分别为单台变速抽蓄机组的最小装机容量、最大装机容量。

图2 McCormick包络方法示意图
Fig.2 Schematic diagram of the McCormick envelope method
针对风电和光伏发电的不确定性特性,本文建立了综合考虑1-范数与∞-范数的概率分布模糊集合。并以此为基础构建了一种基于数据驱动的两阶段分布鲁棒模型。第一阶段为投资决策问题,优化抽水蓄能机组与风电、光伏发电机组的配置容量;第二阶段为运行优化问题,以离网型梯级水-风-光-蓄互补系统的弃电最小为目标。因此,基于数据驱动的两阶段分布鲁棒容量优化配置模型的矩阵形式表示为
 (25)
(25)
s.t.
 (26)
(26)
 (27)
(27)
 (28)
(28)
 (29)
(29)
式中,x为第一阶段的决策变量,包括抽水蓄能机组与风电、光伏发电机组的配置容量;X为抽水蓄能与风电光伏的投资决策变量的可行域;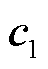 与
与 分别为单位容量投资成本与惩罚成本系数矩阵;
分别为单位容量投资成本与惩罚成本系数矩阵; 为第s个典型场景的实际概率;Ω为典型出力场景的混合概率分布模糊集;
为第s个典型场景的实际概率;Ω为典型出力场景的混合概率分布模糊集;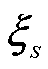 为将负荷、风电光伏与梯级水电来水的历史场景数据聚类后得到的第s个典型场景;
为将负荷、风电光伏与梯级水电来水的历史场景数据聚类后得到的第s个典型场景; 为第一阶段投资决策变量给定时,水电、风电与光伏出力典型场景下的系统运行决策变量,包括水电机组发电功率,风电与光伏发电机组发电功率,抽水蓄能机组发电功率等;Y为式(27)~式(29)组成的可行域;
为第一阶段投资决策变量给定时,水电、风电与光伏出力典型场景下的系统运行决策变量,包括水电机组发电功率,风电与光伏发电机组发电功率,抽水蓄能机组发电功率等;Y为式(27)~式(29)组成的可行域; 为抽水蓄能机组与风电光伏机组的等年值投资成本;
为抽水蓄能机组与风电光伏机组的等年值投资成本; 为概率分布模糊集内最恶劣情况下的的运行成本期望值,包括弃电的惩罚成本;K为典型场景的个数;A、b、C、g、D、E、d、M、N、e为相应的系数矩阵。此外,式(26)为第一阶段投资阶段决策的相关约束;式(27)与式(29)为第二阶段运行阶段决策的相关约束;式(28)为第一阶段决策变量与第二阶段决策变量相交叉的耦合约束。
为概率分布模糊集内最恶劣情况下的的运行成本期望值,包括弃电的惩罚成本;K为典型场景的个数;A、b、C、g、D、E、d、M、N、e为相应的系数矩阵。此外,式(26)为第一阶段投资阶段决策的相关约束;式(27)与式(29)为第二阶段运行阶段决策的相关约束;式(28)为第一阶段决策变量与第二阶段决策变量相交叉的耦合约束。
为了保证系统对于各种不确定性因素的保守性,提出一种基于混合范数模糊集的风电与光伏出力不确定性模型[29]。假定Z个历史场景通过K-means算法聚类得到K个离散的典型场景,则所有典型场景的初始概率为 ,第s个典型场景的初始概率为
,第s个典型场景的初始概率为 。同时,历史场景聚类后所得到的实际概率分布与初始概率分布存在差异[30]。本文基于1-范数和∞-范数建立不同置信度取值下的置信集合,有
。同时,历史场景聚类后所得到的实际概率分布与初始概率分布存在差异[30]。本文基于1-范数和∞-范数建立不同置信度取值下的置信集合,有
 (30)
(30)
式中, 与
与 分别为1-范数与∞-范数约束下的典型场景概率偏差极限值。
分别为1-范数与∞-范数约束下的典型场景概率偏差极限值。
由文献[31],通过给定的历史数据规模与置信度来构造置信集,即
 (31)
(31)
式中, 为括号内不等式成立的概率;
为括号内不等式成立的概率; 、
、 分别为1-范数与∞-范数概率分布不等式的置信度。
分别为1-范数与∞-范数概率分布不等式的置信度。
令 、
、 ,从而可以得到
,从而可以得到
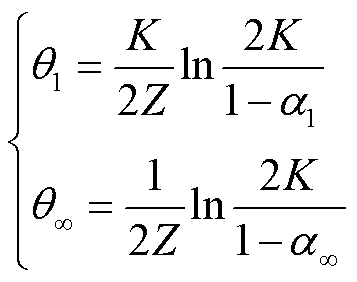 (32)
(32)
由式(32)可知,当历史数据规模Z增大时, 值变小,可见随着Z增大到∞时,
值变小,可见随着Z增大到∞时, 与
与 的值将无限趋近于0,此时的概率分布趋近于实际概率分布。
的值将无限趋近于0,此时的概率分布趋近于实际概率分布。
本文构建的基于数据驱动的离网型梯级水-风-光-蓄互补系统的两阶段分布鲁棒优化配置模型是一个min-max-min三层鲁棒优化模型,所建模型的max-min内层优化问题具有可并行求解的特殊性,同时C&CG算法无需进行对偶转换,且能避免出现复杂的非线性项[32]。因此本文采用可并行求解的C&CG算法进行求解,C&CG算法具体求解过程如下所示。
将原本的min-max-min三层优化问题分解为混合整数线性规划主问题与可并行求解的子问题,主问题为
 (33)
(33)
s.t.
 (34)
(34)
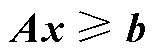 (35)
(35)
 (36)
(36)
 (37)
(37)
 (38)
(38)
式中, 为子问题最优割平面;
为子问题最优割平面; 为第m次迭代第s个典型场景的实际概率;
为第m次迭代第s个典型场景的实际概率; 为第m次迭代第s个典型场景下的运行决策变量;n为迭代次数。
为第m次迭代第s个典型场景下的运行决策变量;n为迭代次数。
当第一阶段投资决策变量 给定后,子问题进行并行求解,有
给定后,子问题进行并行求解,有
 (39)
(39)
由于子问题中第二阶段运行变量与典型场景不确定性概率之间相互独立,故可将子问题分为两步求解[33]。第一步先并行求解子问题中内层目标最小值问题;第二步再求解子问题中外层典型场景概率更新问题。
基于列与约束生成算法的分布鲁棒模型求解流程如图3所示。

图3 基于列与约束生成算法的模型求解流程
Fig.3 Flowchart of solving model based on C&CG algorithm
本文基于含有梯级水电站的离网型某偏远地区系统为算例进行仿真分析,系统中的梯级水电站共有三级,仅一二级水电站有较小的库容,第三级为径流式水电站。梯级水电站的基础参数见表1。每一级水电站均配置一台水电机组。抽水蓄能机组安装在第一级水电站,抽水蓄能机组的发电效率为0.9,平均抽水效率为1.2。抽水蓄能机组的投资成本为300万元/MW;风力发电机组的投资成本为800万元/MW;光伏发电机组的投资成本为500万元/MW;抽水蓄能机组与风电光伏发电机组的每年维护成本均为投资成本的1%。设置资金折现率为8%,抽水蓄能机组的设备使用年限为50年,风电机组与光伏机组的设备使用年限均为20年。单位弃风、弃光与弃水的惩罚费用分别为4 500、1 500、50 000元/(MW·h)。
表1 梯级水电站基础参数
Tab.1 Basic parameters of HPP

参数梯级水电站 一级二级三级 水库初时刻库容/(104 m3)3045— 水库末时刻库容/(104 m3)30,15,30,4545,30,45,60— 水库最小库容/(104 m3)00— 水库最大库容/(104 m3)6090— 水流时滞/h12— 水电机组最大发电功率/MW608048 水电机组最小发电功率/MW151812 水电机组发电效率1.158 21.77860.767 7
基于数据驱动的分布鲁棒优化模型所采用的1-范数与∞-范数置信度取值为 ,设置典型场景数K=4,历史数据规模Z=150。采用Matlab编写模型程序,调用GUROBI求解器运行求解。
,设置典型场景数K=4,历史数据规模Z=150。采用Matlab编写模型程序,调用GUROBI求解器运行求解。
为了验证本文所提出的分布鲁棒配置方法的可行性与优越性,将DRO的结果与SO、RO所得结果进行对比分析。原有历史数据经聚类后得到的典型场景的负荷需求曲线、风电与光伏出力特性曲线,以及梯级水电来水量如附录中第2节所示,四个典型场景所对应的概率分别为0.334 2、0.246 6、0.328 8、0.090 4。使用不同优化方法得到的抽蓄、风电、光伏配置容量结果对比见表2。不同优化方法的综合成本对比见表3。
表2 不同优化方法关于容量配置结果优化结果的对比
Tab.2 Comparison of the results of different optimization methods on configuration capacities

优化方法抽蓄机组配置容量/MW风电机组配置容量/MW光伏机组配置容量/MW SO2680139 DRO2475140 RO2476197
由表2与表3可以看出,随机优化算法是在给定的风电与光伏出力场景下进行决策,并未考虑实际概率分布与初始概率分布之间的偏差,从而得到了经济性较好但保守性较弱的配置方案;传统鲁棒优化算法只根据风电与光伏出力波动最恶劣的场景数据进行决策,因此传统鲁棒优化算法得到了保守性较强但经济性较差的配置方案。而分布鲁棒优化算法则能够在考虑最坏的概率分布下做出决策,又与仅考虑风电光伏出力波动最恶劣场景下进行决策的传统鲁棒优化方法有所不同。这是由于分布鲁棒优化算法可以通过修改置信度与历史数据规模调节概率偏差极限值,并能兼顾风电与光伏出力的随机性,使其在概率分布模糊集中具备一定的鲁棒性。因此,本文提出的离网型梯级水-风-光-蓄互补系统分布鲁棒容量优化配置模型可以同时兼顾经济性与保守性做出投资决策。
表3 不同优化方法关于综合成本优化结果的对比
Tab.3 Comparison of the results of different optimization methods on consolidated costs

优化方法配置成本/万元运行成本/万元年综合成本/万元 SO14 516.313 947.1118 504.04 DRO14 528.834 964.3619 493.19 RO17 531.313 789.4621 320.77
为了减少风电和光伏弃电量,离网型系统中仅有梯级水电难以满足系统对于风电与光伏机组出力的调节需求。因此,混合式抽蓄改造梯级水电相较于不改造后关于抽蓄与风电光伏机组配置容量的优化结果有着一定的影响,优化结果对比见表4。
表4 有无抽蓄机组时抽蓄与风电光伏机组配置容量的对比
Tab.4 Comparison of the capacity optimization of pumped storage units and wind-photovoltaic units with and without pumped storage units

抽蓄机组抽蓄机组配置容量/MW风电机组配置容量/MW光伏机组配置容量/MW 有2475140 无090151
由表4可知,为了满足离网型梯级水-风-光-蓄互补系统运行时供电可靠性的约束条件,当系统中没有抽蓄机组时,风电与光伏资源将增加配置容量以满足相应的负荷需求,与此同时整个系统对于新能源的消纳难度提高,弃电率增加;当系统中具备抽蓄机组时,依靠抽蓄机组的可调节能力,风光资源的配置容量有一定的减少,相应的弃电量也有所减低,对比分析有无抽蓄改造的典型场景弃电率见表5。由表5可知,在没有抽蓄机组的情况下,仅有梯级水电一级与二级较小的水库无法消纳大规模风电光伏机组的装机。因此,采用抽蓄机组改造梯级水电后,使得离网型梯级水-风-光-蓄互补系统通过抽蓄机组与水风光资源间的相互配合,调节水风光资源的出力波动,在改善系统调节灵活性的基础上,获得较好的运行经济性,减少弃风弃光惩罚成本。由表5可以看出,抽蓄机组的作用在负荷需求偏低、而风光预测出力较高的场景四中体现得尤为明显,该场景弃电率减少了近40%。从而说明了在离网型梯级水-风-光-蓄互补系统中保证供电可靠性的前提下,配置抽蓄机组改造梯级水电协同配置风光资源相较于定速抽蓄机组可以大大提高系统对于新能源的消纳能力,减少运行过程中产生的弃电成本。
表5 有无抽蓄机组时典型场景弃电率的对比
Tab.5 Comparison of electricity abandonment rates in typical scenarios with and without pumped storage units (%)

抽蓄机组弃电率 场景一场景二场景三场景四 有00026 无5.7903.9341.6
有无抽蓄机组时系统综合成本对比见表6。在满足供电可靠性的前提下,混合式抽蓄改造后的系统配置成本虽然有所增加,但具备抽蓄机组后离网型梯级水-风-光-蓄互补系统运行阶段的灵活调节能力更强,使得弃电成本大幅度降低,最终等年值综合成本减少。
表6 有无抽蓄机组时系统综合成本对比
Tab.6 Comparison of the system integrated costs with and without pumped storage units

抽蓄机组配置成本/万元运行成本/万元年综合成本/万元 有14 528.834 964.3619 493.19 无15 697.5613 772.9129 470.47
为了比较变速抽蓄相较于定速抽蓄在离网型梯级水-风-光-蓄互补系统中的作用,分别计算配置变速和定速抽蓄的配置成本、运行成本与等年值综合成本。其中,变速抽蓄机组的投资成本为300万元/ MW;定速抽蓄机组的投资成本为200万元/MW;变速抽蓄机组与定速抽蓄机组的每年维护成本均为投资成本的1%,设置资金折现率为8%,变速与定速抽蓄机组的设备使用年限均为50年。
相较于传统的定速抽蓄机组,变速抽蓄机组因其抽水工况入力可调优势且效率高,使得定速抽蓄机组既有的抽水储能、放水发电的调节能力大大增强。采用变速抽蓄机组和定速抽蓄机组关于配置容量与等年值综合成本优化结果的对比见表7,单一场景下变速抽蓄机组与定速抽蓄机组关于运行工况的对比如图4所示。
表7 定变速抽水蓄能机组对优化结果影响对比
Tab.7 Comparison of variable-speed and fixed-speed pumped storage units

抽蓄机组配置成本/万元运行成本/万元年综合成本/万元 变速14 528.834 964.3619 493.19 定速14 397.795 568.0819 965.87

图4 变速抽蓄机组与定速抽蓄机组运行工况
Fig.4 Operating conditions of variable-speed pumped storage units and fixed-speed pumped storage units
由表7可以看出,整个离网型系统在采用定速抽蓄机组改造梯级水电时,系统的配置成本略有降低,运行成本与年综合成本均有所升高。由图4可以看出,变速抽蓄机组的运行状态更为灵活,向下抽水量自由可控,发电工况与抽水工况下输出功率更大。这是因为定速抽水蓄能机组相较于变速抽水蓄能机组缺少了抽水工况下抽水量的可调节能力,使得系统在某一时刻水电、风电、光伏出力较多产生弃电时,无法与变速抽蓄机组一样,自由控制通过从下水库往上水库抽水进行储能时所需要的抽水量,从而消纳系统运行过程中这一时刻多发的电能。因此导致了系统运行阶段时所产生的弃电量提高,运行成本增多,年综合成本增加。
根据上述梯级水电站、风电场、光伏电站等机组的基础参数与数据,优化运行后得到四个典型场景下的负荷需求与系统各机组联合出力,以弃电率最高、运行成本最高的典型场景四为例,负荷与系统联合出力对比如图5所示。场景一~四各机组联合出力对比如附图5~附图7所示。

图5 典型场景四的负荷与系统联合出力对比
Fig.5 Comparison chart of load and system combined output for typical scenario 4
由图5可知,对于四个典型场景而言,离网型梯级水-风-光-蓄互补系统联合出力可以较好地满足当地的负荷需求,有一定可靠的供电能力。当场景中某一时刻系统的整体出力较大,超出负荷需求时,抽水蓄能机组从下水库向上水库进行抽水储能,消纳多余的水电、风电与光伏出力,减少弃电量,提高运行经济性;反之,当场景中某一时刻系统的整体出力较小,不满足负荷需求时,抽水蓄能机组从上水库向下水库进行放水发电,增加系统整体出力,降低功率缺额,提高供电可靠性。同时,四个典型场景的日内运行阶段均满足供电可靠性约束,实时联合出力达到了每一时刻负荷需求量的95%,因此,离网型混合式变速抽水蓄能改造梯级水电协同风电光伏资源组成水-风-光-蓄互补系统能够较好地满足离网型系统的供电可靠性。
为了对同时采用1-范数和∞-范数与只采用单一1-范数所得的年综合成本进行对比,取 、
、 进行求解,所得的优化结果对比见表8。
进行求解,所得的优化结果对比见表8。
表8 混合范数与单一1-范数的优化结果对比
Tab.8 Comparison of optimization results between mixed norms and single norm-1

年综合成本/万元 单一1-范数混合范数 0.619 605.3519 605.3518 947.1518 989.49 0.7 0.819 605.3519 048.99 0.919 605.3519 150.82
由表8可知,当只采用单一1-范数模型时,优化结果年综合成本相较于采用混合范数模型时的年综合成本高。
为了将同时采用1-范数和∞-范数与只采用单一∞-范数所得的年综合成本进行对比,设置 、
、 ,所得的优化结果见表9。
,所得的优化结果见表9。
表9 混合范数与单一无穷-范数的优化结果对比
Tab.9 Comparison of optimization results between mixed norms and single norm-∞

年综合成本/万元 单一∞-范数混合范数 0.519 493.1919 493.1919 323.1719 375.22 0.6 0.719 493.1919 473.12 0.9919 493.1919 493.19
由表9可知,当只采用单一∞-范数模型时,优化结果年综合成本也比采用混合范数模型时的年综合成本高。因此,采用综合考虑混合范数模型与仅采用单一范数模型相比,能够减少决策的保守性,获得更优的经济效益。
为了考虑历史场景数据的规模对于优化结果的影响,在置信度 、
、 与典型场景数K不变的前提下,改变历史数据规模Z的值,设置
与典型场景数K不变的前提下,改变历史数据规模Z的值,设置
 ,K=4,比较优化后所得的等年值综合成本,优化结果见表10。
,K=4,比较优化后所得的等年值综合成本,优化结果见表10。
表10 不同历史数据规模关于优化结果的对比
Tab.10 Comparison of optimization results for different historical data scales

历史数据规模1503006001 200 年综合成本/万元19 493.1918 995.9918 754.5818 630.44
由表10可知,随着历史数据规模的增大,年综合成本不断降低,这是因为由式(32)可知,当典型场景数K与置信度 、
、 保持不变时,随着历史数据规模Z的不断增大,概率偏差极限值
保持不变时,随着历史数据规模Z的不断增大,概率偏差极限值 、
、 降低,导致整个系统模型的保守度降低,因此最终的优化结果等年值综合成本减少。
降低,导致整个系统模型的保守度降低,因此最终的优化结果等年值综合成本减少。
本文构建的基于综合范数的水-风-光-蓄清洁能源微网优化配置模型,可以表示为一个两阶段优化问题。在处理该问题方面,已有研究证明了C&CG算法的优越性[34],即C&CG算法可以在较少次数迭代内完成收敛。为了体现在不同置信度下C&CG算法的求解效率区别,令 ,分别进行不同置信度下的模型优化求解,记录迭代的次数与上下界值,不同置信度关于算法计算效率的对比见表11。
,分别进行不同置信度下的模型优化求解,记录迭代的次数与上下界值,不同置信度关于算法计算效率的对比见表11。
表11 不同置信度关于算法计算效率的对比
Tab.11 Comparison of algorithm efficiency for different confidence intervals

置信度迭代次数下界值/元上界值/元 0.81185 075 075190 489 120 2190 489 120190 489 120 0.951185 075 075192 523 995 2192 523 995192 523 995 0.991185 075 075194 931 900 2194 931 900194 931 900
由表11可知,本文构建的离网型梯级水-风-光-蓄互补系统模型所使用的C&CG算法在不同置信度下均只需2次迭代即可满足收敛性要求,可见可并行求解的C&CG算法其计算效率更高。
本文针对风电与光伏出力的不确定性,构建了综合考虑1-范数与∞-范数的混合概率模糊集合,提出了一种离网型混合式变速抽蓄改造梯级水电从而构成梯级水-风-光-蓄互补系统的容量优化配置模型。综合考虑经济性与鲁棒性,得到最恶劣概率分布情况下抽蓄机组、风电与光伏机组的最优配置容量,并引入基于数据驱动的两阶段分布鲁棒优化方法,采用可并行求解的C&CG算法求解,得出如下结论:
1)随着规模性风电与光伏机组的装机,为了更好地消纳系统运行时产生的弃电,采用基于数据驱动的分布鲁棒优化方法相较于传统的随机优化方法能够更好地消纳水风光资源,减少弃电率,降低系统的运行成本。
2)本文所建立的容量优化配置模型在准确度与求解效率等方面具有较好的运行性能。能够综合负荷需求曲线与风电光伏出力的历史场景数据进行投资决策,求得的等年值综合成本虽略高于传统的随机优化方法求解结果,但保守度更低,更能够综合考虑极端恶劣场景对于系统供电可靠性的影响,因此离网型系统的供电可靠性得到了提高。同时考虑到风电光伏出力场景的随机性,相较于只考虑单一范数,采用混合范数可以使得准确度更高。此外,采用可并行求解的列与约束生成算法进行求解,无需进行对偶转换与双线性项计算,计算效率更高。
3)由于原有的梯级水电站水库容量较小,调节能力不足,本文建立了离网型混合式变速抽蓄改造的模型。相较于梯级水电配置风电和光伏发电,通过协同变速抽蓄机组与风电和光伏发电配置,可以明显降低运行阶段的弃电率。因此可以看出变速抽蓄机组改造后的混合式梯级水电的灵活调节能力得到了较大的提升,可以更好地消纳风电与光伏资源。
4)此外,本文所采用的变速抽蓄机组改造梯级水电构建的优化模型相较于采用传统定速抽蓄机组求解得到的等年值综合成本更低,消纳的弃电量更多,调节效果更强。
附 录
1. 常规梯级水电站约束
1)水力联系约束
 (A1)
(A1)
 (A2)
(A2)
2)库容控制约束
 (A3)
(A3)
式中,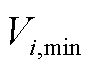 、
、 分别为第i级水电站的最小、最大库容;
分别为第i级水电站的最小、最大库容; 、
、 分别为第i级水电站的初时刻、末时刻库容。
分别为第i级水电站的初时刻、末时刻库容。
3)水电机组发电与弃水流量限制约束
 (A4)
(A4)
 (A5)
(A5)
式中, 、
、 分别为第t时段第i级水电站水电机组的最小、最大发电流量;
分别为第t时段第i级水电站水电机组的最小、最大发电流量; 、
、 分别为第t时段第i级水电站的最小、最大弃水流量。
分别为第t时段第i级水电站的最小、最大弃水流量。
4)水电机组出力特性约束
 (A6)
(A6)
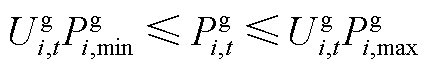 (A7)
(A7)
式中, 、
、 分别为第t时段第i级水电站水电机组的最小、最大发电功率。
分别为第t时段第i级水电站水电机组的最小、最大发电功率。
2. 历史数据聚类后的典型场景数据
基于一年的负荷需求,以及风电、光伏、来水量的历史数据,采用K-means聚类的方法,削减得到四个典型日的负荷需求、风电预测出力、光伏预测出力、来水量数据,以24 h为一个调度周期,作为四个典型场景进行优化配置。
本文中的梯级水电站一年中的来水量设置如下:由于配置周期是年时间尺度,因此考虑一年中包含枯水期、平水期以及丰水期,枯水期一天24 h的来水量统一设置为10×104 m3/h,平水期一天24 h的来水量统一设置为15×104 m3/h,丰水期一天24 h的来水量统一设置为20×104 m3/h。将一年的来水量数据与负荷历史数据、风电光伏历史数据组合,通过K-means聚类方法获得一个4行、96列的数值矩阵,4行分别代表四个典型场景,96列分别由负荷、风电、光伏、来水量一天的24 h数据组合而成。
典型场景中负荷需求曲线、光伏与风电预测出力特性曲线、来水量柱状图如附图1~附图4所示。场景概率分别为0.334 2、0.246 6、0.328 8、0.090 4。由附图1~附图4可知,场景一为平水期且多光少风场景,负荷需求中等;场景二为丰水期且少光少风场景,负荷需求较高;场景三为平水期且少光少风场景,负荷需求中等;场景四为枯水期且多光多风场景,负荷需求较低。

附图1 四个典型场景的负荷
App.Fig.1 Load per-unit value of four typical scenarios

附图2 四个典型场景的光伏预测出力标幺值
App.Fig.2 Predicted photovoltaic output per-unit value of four typical scenarios

附图3 四个典型场景的风电预测出力标幺值
App.Fig.3 Predicted wind output per-unit value of four typical scenarios

附图4 四个典型场景的来水量
App.Fig.4 Inflow of four typical scenarios
3. 典型场景各机组联合出力对比

附图5 典型场景一的负荷与系统联合出力对比
App.Fig.5 Comparison chart of load and system combined output for typical scenario 1

附图6 典型场景二的负荷与系统联合出力对比
App.Fig.6 Comparison chart of load and system combined output for typical scenario 2

附图7 典型场景三的负荷与系统联合出力对比
App.Fig.7 Comparison chart of load and system combined output for typical scenario 3
参考文献
[1] 王朋朋, 杜璇, 张桐博, 等. 基于小水电的某乡镇10 kV微电网规划研究[J]. 电力与能源, 2023, 44(4): 385-390. Wang Pengpeng, Du Xuan, Zhang Tongbo, et al. Research on 10 kV microgrid planning in a township based on small hydropower[J]. Power & Energy, 2023, 44(4): 385-390.
[2] Li Jie, Liu Yikui, Wu Lei. Optimal operation for community-based multi-party microgrid in grid-connected and islanded modes[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 756-765.
[3] Xu Xiao, Hu Weihao, Cao Di, et al. Optimized sizing of a standalone PV-wind-hydropower station with pumped-storage installation hybrid energy system[J]. Renewable Energy, 2020, 147: 1418-1431.
[4] 顾雪平, 白岩松, 李少岩, 等. 考虑风电不确定性的电力系统恢复全过程两阶段鲁棒优化方法[J]. 电工技术学报, 2022, 37(21): 5462-5477. Gu Xueping, Bai Yansong, Li Shaoyan, et al. Two stage robust optimization method for the whole-process power system restoration considering wind power uncertainty[J]. Transactions of China Electro-technical Society, 2022, 37(21): 5462-5477.
[5] 韩晓言, 丁理杰, 陈刚, 等. 梯级水光蓄互补联合发电关键技术与研究展望[J]. 电工技术学报, 2020, 35(13): 2711-2722. Han Xiaoyan, Ding Lijie, Chen Gang, et al. Key technologies and research prospects for cascaded hydro-photovoltaic-pumped storage hybrid power generation system[J]. Transactions of China Electro-technical Society, 2020, 35(13): 2711-2722.
[6] 邵志芳, 赵强, 张玉琼. 独立型微电网源荷协调配置优化[J]. 电网技术, 2021, 45(10): 3935-3946. Shao Zhifang, Zhao Qiang, Zhang Yuqiong. Source side and load side coordinated configuration optimization for stand-alone micro-grid[J]. Power System Technology, 2021, 45(10): 3935-3946.
[7] 张安安, 张红, 吴建中, 等. 离岸微型综合能源系统多目标随机规划[J]. 电力系统自动化, 2019, 43(7): 129-135, 173. Zhang An’an, Zhang Hong, Wu Jianzhong, et al. Multi-objective stochastic planning for offshore micro integrated energy systems[J]. Automation of Electric Power Systems, 2019, 43(7): 129-135, 173.
[8] Liu Huiwen, Wang Shengtie, Liu Guangchen, et al. SARAP algorithm of multi-objective optimal capacity configuration for WT-PV-DE-BES stand-alone micro-grid[J]. IEEE Access, 2020, 8: 126825-126838.
[9] Xing Yongchen, Duan Qing, Zhang Guobao, et al. Differential evolution algorithm based on entropy weight method to determine the weight to optimize the configuration of wind, solar, and diesel microgrid[J]. Journal of Physics: Conference Series, 2021, 1871(1): 012034.
[10] 国家能源局. 抽水蓄能中长期发展规划(2021-2035年)[R]. 北京: 国家能源局, 2021.
[11] 郭怿, 明波, 黄强, 等. 考虑输电功率平稳性的水-风-光-储多能互补日前鲁棒优化调度[J]. 电工技术学报, 2023, 38(9): 2350-2363. Guo Yi, Ming Bo, Huang Qiang, et al. Day-ahead robust optimal scheduling of hydro-wind-PV-storage complementary system considering the steadiness of power delivery[J]. Transactions of China Electro-technical Society, 2023, 38(9): 2350-2363.
[12] 康俊杰, 赵春阳, 周国鹏, 等. 风光水火储多能互补示范项目发展现状及实施路径研究[J]. 发电技术, 2023, 44(3): 407-416. Kang Junjie, Zhao Chunyang, Zhou Guopeng, et al. Research on development status and implementation path of wind-solar-water-thermal-energy storage multi-energy complementary demonstration project[J]. Power Generation Technology, 2023, 44(3): 407-416.
[13] 鲜于虎成, 黄显峰, 张艳青, 等. 考虑短期波动与弃电风险的水光互补系统中长期双层嵌套优化调度[J]. 电工技术学报, 2023, 38(21): 5781-5793. Xianyu Hucheng, Huang Xianfeng, Zhang Yanqing, et al. Medium-and long-term double-layer nested optimal scheduling of hydro-PV complementary system considering short-term power fluctuation and curtailment risk[J]. Transactions of China Electro-technical Society, 2023, 38(21): 5781-5793.
[14] Feng Chen, Zheng Yuan, Li Chaoshun, et al. Cost advantage of adjustable-speed pumped storage unit for daily operation in distributed hybrid system[J]. Renewable Energy, 2021, 176: 1-10.
[15] Zhang Yusheng, Lian Jijian, Ma Chao, et al. Optimal sizing of the grid-connected hybrid system integrating hydropower, photovoltaic, and wind considering cascade reservoir connection and photovoltaic-wind complementarity[J]. Journal of Cleaner Production, 2020, 274: 123100.
[16] 李进, 蔡泽祥, 岑伯维, 等. 基于功率能量特性的含小水电微电网储能容量配置方法[J]. 电力建设, 2024, 45(4): 123-133. Li Jin, Cai Zexiang, Cen Bowei, et al. Energy storage capacity configuration method for microgrids con-taining small hydropower based on power-energy characteristics[J]. Electric Power Construction, 2024, 45(4): 123-133.
[17] Gao Yang, Liu Bin, He Jinyu, et al. Capacity configuration optimization and analysis for multi-energy complementary microgrid in hydropower station considering the renewable energy accommodation[J]. Journal of Physics: Conference Series, 2021, 2108(1): 012064.
[18] 谭晶, 何川, 陈保瑞, 等. 考虑水光蓄互补和直流外送的电力系统分布鲁棒优化调度方法[J]. 中国电机工程学报, 2024, 44(15): 5947-5960. Tan Jing, He Chuan, Chen Baorui, et al. Distr-ibutionally robust optimal scheduling method of power system considering hydropower-photovoltaic-pumped storage complementarity and DC transmission[J]. Proceedings of the CSEE, 2024, 44(15): 5947-5960.
[19] Zhang Shuai, Yang Jingxian, Gao Hongjun, et al. Probabilistic chronological production simulation-based coordinated dispatching for cascaded hydro-PV-PSH combined power generation system[J]. Mathematical Problems in Engineering, 2020, 2020: 6677301.
[20] 左逢源, 张玉琼, 赵强, 等. 计及源荷不确定性的综合能源生产单元运行调度与容量配置两阶段随机优化[J]. 中国电机工程学报, 2022, 42(22): 8205-8215. Zuo Fengyuan, Zhang Yuqiong, Zhao Qiang, et al. Two-stage stochastic optimization for operation scheduling and capacity allocation of integrated energy production unit considering supply and demand uncertainty[J]. Proceedings of the CSEE, 2022, 42(22): 8205-8215.
[21] 吴孟雪, 房方. 计及风光不确定性的电-热-氢综合能源系统分布鲁棒优化[J]. 电工技术学报, 2023, 38(13): 3473-3485. Wu Mengxue, Fang Fang. Distributionally robust optimization of electricity-heat-hydrogen integrated energy system with wind and solar uncertainties[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3473-3485.
[22] 郑晓东, 陈皓勇, 段声志, 等. 基于场景概率驱动的输电网和储能分布鲁棒规划[J]. 电力自动化设备, 2022, 42(6): 170-178.Zheng Xiaodong, Chen Haoyong, Duan Shengzhi, et al. Distributionally robust planning of transmission network and energy storage based on scenario probability-driven[J]. Electric Power Automation Equipment, 2022, 42(6): 170-178.
[23] 孙旭, 邱晓燕, 张志荣, 等. 基于数据驱动的交直流配电网分布鲁棒优化调度[J]. 电网技术, 2021, 45(12): 4768-4778. Sun Xu, Qiu Xiaoyan, Zhang Zhirong, et al. Dis-tributed robust optimal dispatching of AC/DC distribution network based on data driven mode[J]. Power System Technology, 2021, 45(12): 4768-4778.
[24] Bo Yaolong, Xia Yanghong, Wei Wei, et al. Hyperfine optimal dispatch for integrated energy microgrid considering uncertainty[J]. Applied Energy, 2023, 334: 120637.
[25] Castro M P. Tightening piecewise McCormick relaxations for bilinear problems[J]. Computers and Chemical Engineering, 2015, 72: 300-311.
[26] 徐小圣, 徐昌睿, 李梦诗, 等. 考虑风电消纳的电热联合系统优化调度模型[J]. 南方电网技术, 2024, 18(11): 106-118. Xu Xiaosheng, Xu Changrui, Li Mengshi, et al. Optimization dispatching model of the combined heat and power system considering wind power consumption [J]. Southern Power System Technology, 2024, 18(11): 106-118.
[27] 井浩然, 赵红生, 姚伟, 等. 含分布式变速抽水蓄能的新能源发电系统灵活性资源规划[J]. 电力自动化设备, 2023, 43(11): 117-123, 173. Jing Haoran, Zhao Hongsheng, Yao Wei, et al. Flexible resource planning of renewable generation systems with distributed variable speed pumped storages[J]. Electric Power Automation Equipment, 2023, 43(11): 117-123, 173.
[28] Castillo P A, Castro P M, Mahalec V. Global optimization of MIQCPs with dynamic piecewise relaxations[J]. Journal of Global Optimization, 2018, 71(4): 691-716.
[29] 张帅, 汪子涵, 张蜀程, 等. 基于数据驱动分布鲁棒优化的梯级水光蓄联合优化调度[J]. 工程科学与技术, 2023, 55(2): 128-140. Zhang Shuai, Wang Zihan, Zhang Shucheng, et al. Data-driven distributionally robust optimization based coordinated dispatching for cascaded hydro-PV-PSH combined system[J]. Advanced Engineering Sciences, 2023, 55(2): 128-140.
[30] 王波, 王蔚, 马恒瑞, 等. 基于Wasserstein两阶段分布鲁棒的多主体多能微网合作博弈优化调度[J/OL]. 电工技术学报, 2024: 1-18[2024-11-02]. http://kns.cnki.net/kcms/detail/11.2188.tm.20241025.1338.002.html. Wang Bo, Wang Wei, Ma Hengrui, et al. Multi-Agent multi-energy microgrid cooperative game scheduling based on wasserstein two stage robust optimization [J/OL].Transactions of China Electro-technical Society, 2024: 1-18[2024-11-02]. http://kns.cnki.net/ kcms/detail/11.2188.tm.20241025.1338.002.html.
[31] Ding Tao, Yang Qingrun, Liu Xiyuan, et al. Duality-free decomposition based data-driven stochastic security-constrained unit commitment[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 82-93.
[32] 江一航, 赵书强, 王慧, 等. 计及风电、调相机支撑特性的频率安全约束分布鲁棒机组组合调度方法[J]. 电工技术学报, 2025: 40(1): 80-95. Jiang Yihang, Zhao Shuqiang, Wang Hui, et al. Distributionally robust frequency constrained unit commitment with frequency support of wind power and synchronous condenser[J]. Transactions of China Electrotechnical Society, 2025: 40(1): 80-95
[33] 李运鸿, 徐潇源, 严正. 基于生成对抗网络的独立微电网光-储容量分布鲁棒优化配置[J]. 电力系统自动化, 2023, 47(7): 51-62.Li Yunhong, Xu Xiaoyuan, Yan Zheng. Distributionally robust optimal allocation for capacity distribution of photovoltaic and energy storage units in standalone microgrid based on generative adversarial network[J]. Automation of Electric Power Systems, 2023, 47(7): 51-62.
[34] Zeng Bo, Zhao Long. Solving two-stage robust optimization problems using a column-and-constraint generation method[J]. Operations Research Letters, 2013, 41(5): 457-461.
Abstract To address the reliability issues of off-grid power systems in remote areas, retrofitting existing cascade hydropower with pumped storage has been regarded as a novel effective solution. The variable-speed pumped storage, due to its adjustable pumping capacity, is found to be more advantageous compared to fixed-speed systems. Consequently, the formation of a regional 100% clean energy off-grid system through the integration of variable-speed pumped storage with wind and photovoltaic re-sources is enabled. In this context, a data-driven capacity optimization model for off-grid cascaded hydro-wind-photovoltaic complementary system considering pumped-storage retrofitting is developed in this paper. Firstly, with the minimum comprehensive cost on an equivalent year as the objective, the optimal capacity configuration is achieved by considering the operation of the pumped-hydro-wind-photovoltaic system, power supply reliability, and various constraints. Secondly, using the McCormick linearization method, the original mixed-integer nonlinear model is transformed into a mixed-integer linear optimization model. Moreover, to handle uncertainties of load, wind, photo-voltaic, and inflow, a data-driven two-stage distributionally robust optimization configuration model for capacity optimization is presented based on both 1-norm and ∞-norm. The column and constraint generation (C&CG) algorithm is used to solve the proposed model. Finally, the feasibility is verified.
The following conclusions can be drawn from the simulation analysis: (1) With the scale-up of wind power and photovoltaic units, in order to better accommodate the curtailed electricity generated during system operation, the use of data-driven distributed robust optimization methods compared to traditional stochastic optimization methods can better integrate water, wind, and solar resources, reduce curtailment rates, and lower system operating costs. (2) The capacity optimization configuration model established in this paper has good operational performance in terms of accuracy and solution efficiency. It can make investment decisions by considering load demand curves and historical scenario data of wind and photovoltaic output, resulting in a slightly higher equivalent annual cost compared to traditional stochastic optimization methods but with lower conservatism. It can better consider the impact of extreme adverse scenarios on system power supply reliability, thus improving the reliability of off-grid systems. Additionally, considering the stochastic nature of wind and photovoltaic output scenarios, using a mixed norm instead of a single norm can improve accuracy. Moreover, using a parallelizable column and constraint generation algorithm for solving avoids dual transformation and bilinear term computations, leading to higher computational efficiency. (3) Due to the limited reservoir capacity and inadequate regulation capacity of existing cascade hydropower stations, a model for off-grid hybrid variable-speed pumped storage retrofit has been established in this paper. Compared to only adding wind and photovoltaic resources on top of cascade hydropower stations with limited regulation capacity, the retrofit with optimal capacity variable-speed pumped storage units significantly reduces curtailment rates during operation. This reflects a substantial improvement in the flexible regulation capacity of hybrid cascade hydropower after the variable-speed pumped storage retrofit, enabling better integration of wind and photovoltaic resources. (4) Furthermore, the optimization model constructed by retrofitting variable-speed pumped storage units into cascade hydropower stations used in this paper results in lower equivalent annual costs and more curtailed electricity absorption compared to using traditional fixed-speed pumped storage units, demonstrating stronger regulation effects.
keywords:Hybrid pumped storage retrofitting, hydro-wind-photovoltaic-storage, power supply reliability, distributinally robust, column and constraint generation
DOI: 10.19595/j.cnki.1000-6753.tces.240571
中图分类号:TM732
收稿日期 2024-04-11
改稿日期 2024-11-10
王海伦 男, 2000年生, 硕士研究生, 研究方向为新能源优化配置。E-mail:221606030051@hhu.edu.cn
李 杨 男, 1992年生, 副教授, 博士, 硕士研究生导师, 研究方向为多能互补优化。E-mail:eeliyang@hhu.edu.cn(通信作者)
(编辑 赫 蕾)