、无功功率
表达式[14]分别为摘要 可控电压源-电流源型混合直流输电系统是一种适用于大规模清洁能源送出场景的新型直流系统。针对可控电压源-电流源型混合直流输电系统暂态工况下运行特性提升问题，该文建立了可控电压源-电流源型混合直流输电系统数学模型，以刻画混合直流系统暂稳态工况下直流电压、电流和功率运行特性；分析了可控电流源型换流器无功功率与相位差和直流电流的变化关系，进而提出受端交流故障下提升混合直流系统无功支撑能力的实现方法；通过引入故障检测判据并考虑送受端通信延时，提出一种附加有功电流和无功功率控制模块的协调控制策略。仿真结果表明，所提控制策略在受端弱电网场景中，有效地减少了故障期间交流电压跌落量，实现了对受端电网的无功支撑，并且降低了故障期间直流电压跌落和线路过负荷水平，进而提升了混合直流系统的运行性能。
关键词：混合直流系统 协调控制 暂态工况 故障特性
2023年10月22日—24日，第二十五届中国科学技术协会年会在安徽省合肥市举办。会上，“如何在沙漠戈壁荒漠地区构建千万千瓦级新能源基地并实现安全稳定送出”被纳入2023年科技领域29个重大问题难题清单。为实现“双碳”目标和保证沙戈荒地区新能源高效外送，我国加快推进特高压电力输送通道建设工作，一大批特高压工程正在安排部署和持续推进中[1-2]。
可控电压源-电流源型混合直流送出方案，不但能提供频率基准和电压支撑，而且成本低、损耗小、可靠性高、不存在换相失败问题，因此更适用于运行工况复杂多变的大规模清洁能源送出场景[3-6]。其中，可控电压源型换流器（Voltage Source Converter, VSC）是指采用全控型器件——绝缘栅双极晶体管（Insulated Gate Bipolar Transistor, IGBT），直流电压极性保持不变，只能通过改变电流极性来改变功率流向的换流器，在本文中特指模块化多电平换流器（Modular Multilevel Converter, MMC）。可控电流源型换流器（Current Source Converter, CSC）是指采用全控型器件——逆阻型集成门极换流晶闸管（Reverse Blocking-Integrated Gate Commutated Thyristor, RB-IGCT），直流电流极性不变，改变潮流方向需改变电压极性的换流器。
近年来，国内外学者针对新能源基地远距离混合直流送出场景已开展了初步的研究工作，对其运行特性和协调控制策略进行了一定的探索。针对MMC的控制策略问题，文献[3]将传统VSC常用的矢量控制策略应用于MMC，但存在桥臂环流和损耗大的问题。针对这一问题，文献[4]进而建立了MMC内部环流控制器数学模型，并提出一种内部环流抑制控制策略。在协调控制策略方面，文献[5]提出送端采用基于晶闸管的电网换相换流器（Line Commuted Converter, LCC）、受端采用MMC的混合高压直流输电系统，并设计了系统稳态及启动策略。文献[6]提出送端采用LCC、受端采用CSC的混合直流输电系统，推导了电流源型换流器在dq旋转坐标系下的低频和稳态模型，分析并设计了稳态、启动、潮流反转以及故障穿越的控制策略，验证了该系统在远距离大容量输电领域的可行性。进一步地，为了实现CSC单位功率因数运行，文献[7]针对CSC换流器提出了一种最大功率因数控制策略，可以实现交直流故障穿越。文献[8]对桥臂电流和电容电压d、q分量进行解耦，提出了电流源型换流器内环和外环控制策略，能够实现有功、无功功率的解耦控制，从而实现定直流电压控制下的单位功率因数运行。为了降低器件的开关频率，文献[9-11]针对电流源型换流器提出基频调制策略，设计了外环功率控制器和内环电流控制器，并研究了功率运行范围。文献[10-13]建立了可控电流源型换流器稳态模型，设计了系统交直流侧关键参数，分析对比了传统调制、基波调制和特定载波调制等三种典型调制策略，提出一种可以消除桥臂直通现象的协调控制策略，并且扩大了功率运行范围。
综上所述，针对可控电压源、电流源换流器及混合直流系统协调控制已有一定的研究，然而对于送端采用MMC、受端采用CSC的混合直流系统，目前尚无相关参考文献。可控电压源-电流源型混合直流输电系统不存在换相失败问题，但是如何在发生交直流故障后，提升送受端换流器的主动支撑能力，保证清洁能源高效可靠送出和系统安全稳定运行依旧是亟待解决的难点问题。
为此，本文针对可控电压源-电流源型混合直流输电系统暂态工况下运行特性提升问题进行了深入的分析和研究。首先建立了可控电压源-电流源型混合直流输电系统的数学模型，基于混合直流系统送受端换流器的运行特性，分析了系统受端交流故障下的交流电压跌落和直流线路过电流的产生机理；然后基于可控电压源-电流源型混合直流系统动态特性，提出一种附加有功电流和无功功率控制模块的协调控制策略，有效地减少了故障期间交流电压跌落，降低了故障期间受端直流电压跌落和线路过负荷水平，从而降低电网安全风险事故发生的概率；最后，通过电磁暂态仿真软件PSCAD/ EMTDC进行仿真，验证了所提控制策略的正确性和有效性。
可控电压源-电流源型混合直流输电系统拓扑结构如图1所示，送端由四组MMC换流器并联组成，受端采用两组双移相串联型CSC换流器。图1中，PR、PI分别为送、受端换流器与交流系统间交换的有功功率；QR、QI分别为送、受端换流器与交流系统间交换的无功功率；UsR、UcR分别为送端网侧、换流器侧的交流电压幅值；UsI、UcI分别为受端网侧、换流器侧的交流电压幅值；XR、XI分别为送、受端换流变压器与相电抗器的等效电抗；UdcR、UdcI分别为单极系统送、受端直流线路电压；δR、δI分别为送、受端网侧与换流器侧电压矢量的移相角；Idc为线路的直流电流；RL为线路的等效电阻；XL为线路的等效电抗。不考虑换流器的损耗和电容电流，送端MMC换流器的有功功率、无功功率表达式[14]分别为
（1）
（2）
受端CSC换流器有功功率
、无功功率
表达式分别为
（3）
（4）
图1 可控电压源-电流源混合直流输电系统拓扑结构
Fig.1 Controllable voltage source-current source hybrid DC transmission system topology
当忽略换流器损耗时，送端MMC、受端CSC换流器的外特性方程式可分别表示为[12,15]
（5）
（6）
式中，Usm为MMC交流侧相电压幅值；Ivd为MMC交流侧电流d轴分量；udiffm为上、下桥臂连接处的基波相电压幅值；Er为基波线电压有效值；m为MMC的调制比；Um为CSC连接变压器阀侧相电压幅值；Id为CSC阀侧出口交流电流d轴分量；L、C分别为CSC中滤波器电感和电容；
为工作角频率；
为CSC中滤波电容电压q轴分量；
为网侧电压d轴分量。
联立式（5）和式（6），可得直流电流表达式为
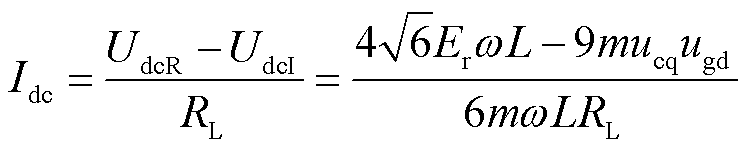（7）
当受端电网发生交流故障时，将导致交流母线电压下降，根据式（1）可知，网侧电压d轴分量减小，直接导致受端CSC侧直流电压降低，进而造成送端MMC侧直流电压也会随之降低。由于受端交流故障期间同时伴随着MMC子模块电容放电过程，送端直流电压降低导致子模块电容电压平均值降低。当交流调制波的幅值在(0,1]范围内调节时，可通过调节MMC输出调制比m使得交流电压不变。由式（1）可得，当送端直流电压降低后，MMC输出的调制比增大。当受端交流系统发生接地故障时，MMC交流侧电路主要为三相间的环流且幅值较小，可忽略不计。单相子模块电容放电等效电路如图2所示。
图2 单相子模块电容放电等效电路
Fig.2 Single-phase submodule capacitive discharge equivalent circuit
结合二阶RLC电路零输入响应理论，可得受端交流系统发生故障后的等效电路电容两端电压
和线路电流i(t)表达式[16]分别为
（8）
（9）
式中，RΣ为等效电路的等值电阻（上下桥臂电阻的串联，即2R0，R0为桥臂电阻）；LΣ为等效电路的等值电抗（上下桥臂电抗的串联，即2L0，L0为桥臂电感）；CΣ为等效电路的等值电容（送端换流站每相桥臂中处于充、放电状态的串联子模块数量相同，其容值均为C0/N，C0为子模块电容。受MMC子模块电容均压策略的控制，这些电容存在十分短暂的交替投切的过程，可以等效为两组电容并联持续放电，因此等效电容值为2C0/N；Udc0和Idc0分别为送端MMC稳态直流电压和直流电流。
将受端功率传输模型进行等效，对abc三相静止坐标系下的CSC换流器模型进行坐标变换，可以得到CSC在dq旋转坐标系下的低频模型。不计线路电阻和有功损耗，当取交流母线电压空间矢量Us方向为d轴正方向，从逆变器流向交流系统的功率为正方向，交流母线电压d轴分量usd=|Us|，q轴分量usq=0。则网侧有功功率Pac、无功功率Qac表达式分别为
（10）
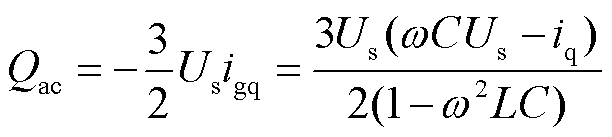（11）
式中，id、iq分别为换流阀出口电流在两相静止坐标系下的d、q分量，igd、igq分别表示受端馈入交流系统三相电流在两相静止坐标系下的d、q分量。
稳态运行时，直流系统从交流系统吸收的无功功率基本不变。由于短路故障，会导致交流母线电压发生扰动，在ms级的时间尺度下，直流电压、直流电流均会变化，随之带来的是换流器无功功率需求的改变。交流母线上并联的无功补偿装置投切时间在s级，无法实时跟踪换流器的无功变化，进而会破坏换流站与交流系统无功交换的动态平衡状态。因此，与换流器相连的交流系统和换流器之间的无功交互会对电压稳定产生巨大影响。
为进一步描述CSC与交流系统交互关系，针对CSC吸收无功功率（Q＞0）、单位功率因数运行（Q=0）、发出无功功率（Q＜0）三种典型工况，绘制CSC电气矢量图，如图3所示。其中，
为电容电流；
为电容电压；
为电容电压相位；
为桥臂电流；
为交流电网电流；
为交流电网电压，当系统采用电网电压定向控制时，方向为d轴正方向；δ为交流电网电流相位；
为滤波电感两端电压。
图3 CSC电气矢量图
Fig.3 CSC Electrical parameters vector diagram
由图3a可知，当电网交流电压超前交流电流时，CSC从电网吸收无功功率，电容电压和电网电压关系为
（12）
由图3c可知，当电网交流电压滞后交流电流时，CSC向电网发出无功功率，电容电压和电网电压关系为
（13）
根据文献[12]和式（11），CSC连接变压器阀侧的无功功率可进一步表示为
（14）
式中，
为网侧电压相位；
为调制函数相位。
稳态工况下，CSC侧变压器阀侧电压Us保持不变，影响CSC发出的无功功率Qac的因素主要为调制比m和调制函数相位φm。为了明确两个物理量对Qac的影响关系，分别对φm和m求偏导，可得
（15）
（16）
为保证换流阀电压相对稳定，相位差宜控制在±p/4以内。因此，
始终大于0，Qac随着φm的增大而增大。而当φg—φm∈(-p/4,0)时，
＞0，Qac随着m的增大而增大；当φg—φm∈(0,p/4)时，＜0，Qac随着m的增大而减小。
为进一步明确两个物理量对Qac的影响大小，令
（17）
显然，当CSC采用基波频率调制策略时，调制比m＞1，当tan(φg—φm)＜1时，k＞1恒成立，此时调制函数相角φm对无功功率的影响更大。
当系统处于额定运行工况时，线路直流电流为5 kA，根据式（14），可绘制受端CSC无功功率与相位差的关系曲线如图4所示。
图4 受端CSC无功功率与相位差的关系曲线
Fig.4 Relation curve of CSC at the receiving end reactive power and phase angle difference
由图4可知，当直流电流一定时，受端CSC所发出无功功率的大小随相位差的增大而减小，并且当相位差增大到0.36 rad（≈20.6°）时，受端CSC由发出无功功率转变为吸收无功功率的状态。
在滤波电容和滤波电感及阀侧电压固定的情况下，受端CSC的无功功率与相位差φg—φm、直流电流密切相关。其特性曲线如图5所示。
图5 受端无功功率与相位差、直流电流的关系
Fig.5 Relation diagram of reactive power at the receiving end versus phase angle difference and DC current
由图5可知，当相位差
时，直流电流、相位差的减小都有助于无功功率的增大；当相位差
时，尽可能地减小相位差、适当地增大线路过负荷水平有利于CSC增发无功功率。相比直流电流，相位差的改变对无功功率的影响效果更为明显。
因此，根据式（14），并结合上述分析可知，当受端电网发生交流故障时，可以通过减小故障期间的相位差或适当地调节线路负荷水平，进而增大CSC换流器发出无功功率，保证CSC无功支撑能力维持在较高水平，从而能够有效抑制故障期间交流母线的电压降落，降低电网安全风险事故发生的概率。
可控电压源-电流源型混合直流输电系统中作为主站的受端换流站承担着控制整个直流系统的直流电压的作用，而送端换流站作为从站，采用定交流功率控制来保证功率按需送出。
混合直流输电系统送端MMC换流器基本控制策略如图6所示。该策略采用直接电流控制，包含锁相环控制器、内环控制器、外环控制器、环流抑制控制器和触发脉冲生成器。锁相环控制器的作用是输出相位信号，为内环控制器和环流抑制控制器提供基准电压相位。触发脉冲生成器是根据最近电平逼近调制方式，实时控制上下桥臂投入的子模块数量，将MMC输出电压和调制波电压偏差控制在子模块电容电压一半的范围内。图6中，usj（j=a,b,c）表示交流系统的各相电压；isj（j=a,b,c）表示换流器交流出口处的各相电流；icirj（j=a,b,c）表示各相桥臂的环流；usd、usq分别表示交流系统的等效电势d、q轴分量；ivd、ivq分别表示换流器交流出口处电流的d、q轴分量；
、
分别表示各相上、下桥臂电压参考值；
、
分别表示各相上下桥臂差模电压、共模电压参考值；
、
分别表示上下桥臂差模电压、共模电压d、q轴分量参考值；icirdq表示桥臂环流d、q轴分量参考值；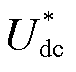
、
分别为直流侧电压、交流侧电压有效值的指令值；
、
分别为交流侧有功功率、无功功率的指令值。
图6 混合直流输电系统送端MMC基本控制策略
Fig.6 Basic control strategy of MMC at the sending end of hybrid DC transmission system
混合直流输电系统受端CSC的基本控制策略如图7所示。该策略本身只有一个控制自由度，即相位，在交流系统稳态运行情况下，受端CSC换流器根据需要控制电气量实际值与参考值，通过比例积分调节器直接输出调制函数相位差，作用于基波频率调制策略的正弦脉宽调制策略，然后输入触发脉冲发生器，生成逆阻型IGCT器件的脉冲触发信号，实现可控电流源型换流器的控制环节。图7中，Tm为采样周期；φ1为网侧电压的相位；φ2为换流器调制函数的相位。
本文所提出的协调控制策略在传统控制策略的基础上对系统送受端换流器控制策略均进行了改进，附加控制模块后的协调控制策略如图8所示。其中，一阶惯性环节的作用是模拟直流电压和直流电流的测量过程。PMMC、PMMC_ref分别为送端MMC交流有功功率测量值、参考值；ivd、ivdmax和ivdmin分别为内环电流控制器的d轴分量及其上下限幅值；Id、Idref分别为线路直流电流的测量值、参考值；UCSC、Uref分别为受端CSC直流电压的测量值、参考值；QCSC、Qref分别为受端CSC发出无功功率的测量值、参考值；TD为受端发生交流故障后，将信号传递到送端控制器所需的通信延时[17]。
图7 混合直流输电系统受端CSC基本控制策略
Fig.7 Basic control strategy of CSC at the receiving end of hybrid DC transmission system
图8 附加控制模块后的混合直流系统协调控制策略
Fig.8 Optimized coordinated control strategy for hybrid DC systems with additional control modules
故障检测包括不对称故障检测和三相故障检测。不对称故障检测是通过实时测量换流母线三相电压瞬时值的代数和（3U0）来实现的，其意义是表示电压的畸变程度。当受端交流系统发生不对称故障时，交流母线电压包含零序分量，即此时abc三相电压代数和不等于零。若3U0超过预设的阈值Vdiff，系统判定为检测到不对称故障，使能控制模块。
（18）
而三相故障检测是通过将换流母线三相电压变换至静止坐标系下的Uαβ分量来实现的，其意义是反映电压的跌落程度。当受端交流系统发生三相故障时，交流电压通过Clarke变换得到两相静止坐标系下α、β分量，求取α、β分量平方根可得电压合成矢量大小Uαβ。若Uαβ超过预设的阈值Vabz时，系统判定为检测到三相故障，启动控制模块。
（19）
（20）
当受端电网发生交流故障时，通过引入本文所提出的附加无功功率模块，进而改变CSC侧输出的相位差，以增大CSC发出的无功功率，提升故障期间受端换流器的无功支撑能力。
受端CSC换流站有功和无功电流不应超过最大允许的交流电流限制，即满足约束[18]
（21）
式中，iCSC_d、iCSC_q分别为CSC换流站交流电流的有功分量和无功分量；K为CSC换流站最大允许交流电流系数，考虑换流器的过负荷能力为1.3(pu)，即K取1.3；ICSC_N为CSC换流站交流电流额定值。根据瞬时功率理论，考虑电网电压定向原则，可得最大允许交流电流限制下的受端换流站有功和无功功率可行域，即
（22）
式中，
为受端电网电压有效值。
当系统检测到受端发生交流故障后，会先在受端控制器中产生触发信号，直接使能受端附加无功功率控制模块，再经TD信号延时，使能送端附加有功电流分量控制模块。
当受端交流母线发生故障时，送端MMC输出的有功功率会随之发生变化。当送端MMC有功功率变化量高于某一整定值时，通过减小内环电流控制器输出的d轴分量即有功电流ivd整定值，抑制直流线路负荷水平，等到送端MMC有功功率恢复后，又重新恢复有功电流控制器的整定值。本文所提附加有功电流控制模块引入斜率控制，可根据故障严重程度和MMC有功功率的变化趋势，动态调整ivd整定值，以达到最佳的控制效果。
有功电流变化量与输出有功功率变化量之间的关系式为
（23）
式中，Divd为送端MMC换流器有功电流参考值变化量；DP为送端MMC换流器输出有功功率参考值与实际测量值之差，即DP=PMMC_ref -PMMC；Imin为有功电流参考值变化量的最小值；Imax为有功电流参考值变化量的最大值；Pmin为输出有功功率参考值与实际测量值之差的最小值；Pmax为输出有功功率参考值与实际测量值之差的最大值；P0为当有功电流参考值变化量达到最大时，输出有功功率参考值与实际测量值之差的最小值。
由式（23）可以看出，附加有功电流控制模块输出的有功电流变化量指令Δivd与控制参数Imin、Imax、Pmin、P0和Pmax五个量有关。其对直流系统的恢复有着重要的影响。为此，需要对这些参数进行灵敏度分析，以便能以不同的权重区别各变量对系统恢复特性的影响，找出附加有功电流控制模块的最有效控制敏感点。对式（23）中Pmin＜ΔP≤P0所对应分段函数求偏导数。
（24）
（25）
（26）
（27）
由于
和
的值均大于0，在保持控制参数P0、Pmin不变的情况下，附加有功电流控制模块输出的电流指令变化量随着Imax和Imin的增大而增大。这意味着在输出有功功率较大时便将电流指令变化量设为最小值，使得动态过程中直流系统对受端交流系统无功功率的需求不会过高，有利于交流母线电压的恢复和稳定；但此时直流系统的传输有功功率会降低，不利于快速缓解送、受端交流系统内的功率失衡和功角稳定。Imax和Imin减小时控制效果相反。由于
和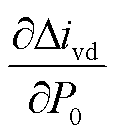
的值均小于0，在保持
控制参数Imax和Imin不变的情况下，附加有功电流控制模块输出的电流指令变化量随着P0和Pmin的增大而减小。由图8可知，直流线路的输送有功功率会随之增大，有利于缓解送、受端交流系统内的有功功率失衡和保持系统的功角稳定，但此时直流系统对受端交流系统的无功需求也相应增加，在某些情况下不利于动态过程中交流电压的恢复和电压稳定。P0、Pmin减小时控制效果相反[19]。
当直流输电受端交流系统发生三相短路故障，导致换流器交流侧母线电压大幅跌落时，附加有功电流控制模块强制性地降低有功电流分量指令值以控制系统功率的传输，达到降低线路负荷水平的目的，直至系统故障切除。避免换流阀由于长时间电流过大而缩短其使用寿命。
为验证所提协调控制策略在可控电压源-电流源型混合直流输电系统中的有效性，在PSCAD/ EMTDC平台搭建了如图1所示的额定电压为800 kV、额定电流为5 kA的混合直流输电系统仿真模型。系统的关键参数见表1。系统仿真模型中线路为频变模型，设置单回输电线路全长2 206.3 km，线路参数见表2。由于所提出的协调控制策略需要站间通信，仿真模型的线路长度为2 206.3 km，光信号在光缆中的传输速度一般为2c/3（c代表光速），根据直流线路输电长度，可粗略计算送受端通信延时。同时考虑信号收发等过程的影响，实际的延时一般会更长。实际工程中的通信延时可以通过试验获得，参考某±800 kV直流输电工程，输电线路全长2518 km，总通信延时约为18 ms[20]。因此本文仿真算例中的总通信延时设置为15 ms。仿真算例中，受端交流电网结构示意图如图9所示，受端交流电网关键参数见表3。
表1 可控电压源-电流源型混合直流系统参数
Tab.1 Parameters of controllable voltage source-current source type hybrid DC system
关键参数数值 送端受端 直流电压/kV800750 变压器电压比/(kV/kV)530/210525/110 变压器漏抗(pu)0.20.19 传输信号延时TD/ms15 单桥臂子模块数200 MMC侧桥臂电感/mH60 MMC侧直流电容/mF18 CSC侧滤波电容/μF35 CSC侧滤波电感/mH40
表2 直流输电线路参数
Tab.2 Parameters of DC transmission line
关键参数类型或具体数值 输电线路长度/km2 206.3 输电线路导线类型输电线路分裂间距/m六分裂0.5 输电线路间距/m22 输电线路离地高度/m48 单位长度电阻/(Ω/km)0.028 66 单位长度电感/(mH/km)0.885 5 单位长度电容/(μF/km)0.013 18 大地电阻率/(Ω·m)1 000
表3 受端交流电网关键参数表
Tab.3 Table of key parameters of the AC grid at the receiving end
参数数值 R1/Ω1.481 2 R2/Ω49.62 R3/Ω1.481 2 L1/H0.073 L2/H0.073
根据图9和表3计算可得受端电网短路比为
（28）
图9 受端交流电网示意图
Fig.9 Structure of the AC grid at the receiving end
式中，
为受端电网电压额定值；
为受端有功功率额定值；Z为受端交流电网总阻抗。
仿真算例中受端交流系统的短路比KSCR＜3，属于弱交流系统。
送端清洁能源基地额定电压等级为530 kV，受端直流馈入电网额定电压等级为525 kV。送端换流站包含四组并联的MMC阀组，然后各自级联到送端交流系统。并且MMC阀组的交直流侧均无需配置滤波器。受端换流站由两组十二脉动CSC阀组构成，十二脉动电路包括两组交流电压相位相差30°的六脉动逆变电路，每个六脉动电路在交流侧并联、直流侧串联。MMC采用最近电平逼近调制，CSC采用基波频率调制，载波频率为450 Hz，换流器动作频率为50 Hz。
图10a为MMC子模块电容电压平均值。图10b为MMC换流器A相上桥臂载波mau和下桥臂载波mal。由图10a可以看出，额定运行工况下MMC子模块电容电压额定值为2 kV，电容电压波动率控制在10%左右，符合工程实际要求。由图10b可以看出，上、下桥臂载波幅值控制在0～2之间，不存在过调制现象。
图10 MMC子模块电容电压上、下桥臂载波仿真波形
Fig.10 Simulated waveforms of MMC side submodule capacitance voltage, upper and lower bridge arm carrier voltage amplitude
图11a为受端交流电网三相电压，网侧电压波形质量较好；图11b为受端交流电网三相电流；图11c、图11d分别为额定工况下送受端直流电压Udc、线路直流电流Idc仿真波形，可以看出：送端直流电压实际仿真值为800 kV，由于直流线路存在压降作用，因此受端直流电压稳定在750 kV附近，与理论值保持一致。
图11 额定运行特性仿真波形
Fig.11 Simulation waveforms of rated operating characteristic
图11e为额定工况下送端输入的有功功率PacR、输出的无功功率QacR，从图中可以看出：有功功率稳定在4 000 MW，输出的无功功率为0 Mvar。图11f为额定工况下受端输出的有功功率PacI、输出的无功功率QacI，可以看出：两者实际仿真值分别为 3 700 MW、220 Mvar。图11g、图11h分别为额定工况下受端CSC换流器桥臂电压应力Ufa、电流应力Ipa，由于传统控制策略采用的是只有一个控制自由度的基频载波调制方法，因此换流器的动作频率为50 Hz。
当受端电网发生交流故障时，将导致交流母线电压下降，网侧电压d轴分量减小，直接导致受端CSC侧直流电压降低，进而造成送端MMC侧直流电压也会随之降低。由于受端交流故障期间同时伴随着MMC子模块电容放电过程，送端直流电压降低导致子模块电容电压平均值降低，MMC输出的调制比增大。
由于MMC三相上下桥臂具有对称性，这里以A相上桥臂子模块电容电压平均值和调制比为例，对上述描述开展定量分析和电磁暂态仿真验证，仿真波形如图12所示。仿真结果表明，稳态工况下MMC子模块电容电压额定值为2 kV，电容电压波动率控制在10%以内，而上桥臂调制比为0.79。设置当t=2.5 s时，受端交流系统发生两相经电阻接地短路故障，故障持续时间0.1 s。故障期间，子模块电容电压值不断降低，电压谷值为1.3 kV，即验证了故障期间桥臂子模块电容存在持续放电过程。故障发生后，故障期间上桥臂调制比不断增大，最大调制比可达0.857，但不会出现过调制现象。仿真结果验证了受端电网故障MMC输出的调制比增大这一结论的正确性。
图12 MMC上桥臂子模块电容电压平均值和调制比
Fig.12 MMC upper bridge arm submodule capacitor voltage averages and modulation ratio
4.2.1 混合直流系统受端两相短路故障
交流故障包括单相接地故障、两相接地故障、三相接地故障和相间故障，下面针对不对称故障和对称故障各取一种进行仿真分析。
本节对比分析了受端电网发生两相经接地电阻短路故障后，采用本文所提出的改进控制策略前后系统故障特性的差异。当t=2.5 s时，受端CSC交流母线发生两相短路故障，故障持续时间Δt=0.1 s。传统控制策略送端MMC采用定有功功率和无功功率控制，受端CSC采用定直流电压控制，而不施加其他附加控制。改进后，受端CSC附加无功功率控制模块，送端MMC不附加有功电流分量控制模块。受端电网两相短路故障有功、无功功率仿真波形仿真结果如图13所示。
图13 受端电网两相短路故障有功、无功功率仿真波形
Fig.13 Simulated waveforms of active and reactive power with two-phase short-circuit fault in the receiving end grid
图13a、图13c分别为两相短路故障下送端有功、无功功率波形，若采用无附加控制模块的传统控制策略，当t=2.5 s时，由于受端交流母线发生两相接地故障，MMC输出的有功功率迅速上升，最大值可达到5280 MW。与此同时，MMC输出的无功功率先上升到80 Mvar，随后跌落到-110 Mvar。当t=2.6 s时，即故障清除后，在定有功功率控制器的作用下，交流系统输出功率下降，回落到2 510 MW附近。若采用附加控制模块后的协调控制策略，故障起始阶段送端MMC输出有功功率最大值为 4 590 MW，送端MMC输出无功功率最大值为 75 Mvar，切除故障后的有功、无功最小值分别为 2 820 MW和-80 Mvar。仿真结果表明，在MMC暂态输出功率方面，采用附加控制策略故障前后仿真波形的变化趋势大致相同，但是故障起始阶段和切除后的功率波动量均明显小于传统控制策略的数值。并且，故障期间有功过负荷水平明显降低。
图13b、图13d分别为两相短路故障受端有功、无功功率波形。在t=2.5～2.6 s内，由于受端交流母线电压迅速降落，交流系统线电动势相比交流母线间的差值减小，因此在故障初期有功功率传输量有所降低，若采用传统控制策略，最小值为2 560 MW。故障后期及故障切除后的恢复阶段在受端定直流电压控制作用下，直流电压逐渐恢复，CSC传输的有功功率也逐渐升高，受控制器超调的影响，有功功率经过振荡过程最后恢复额定运行。
图14a～图14c分别为两相短路故障受端直流电压、直流电流和受端A相交流电流瞬时值波形。采用传统控制策略下的故障期间直流电流峰值为7.6 kA，采用附加控制策略后，峰值降低为6.1 kA。由此可见，采用附加控制策略有助于受端交流电网电压抬升，进而提高故障期间受端直流电压，并有效抑制受端发生两相短路故障时的直流过电流。
图14 受端电网两相短路故障直流电压、电流仿真波形
Fig.14 Simulated waveforms of DC voltage and current with two-phase short-circuit fault in the receiving end grid
图15a为CSC阀侧无功功率波形。采用传统控制策略时，故障发生后由交流母线馈入受端电网的无功功率不断减少，当t=2.52 s，CSC发出的无功功率跌落到50 Mvar。故障期间的无功输出量始终高于故障前的无功水平，最大无功发出量为3 250 Mvar。而采用附加控制策略后，故障期间受端CSC阀侧无功功率发出量明显增多，最大可达4 200 Mvar。图15b为受端交流母线故障相电压波形。由于弱受端电网交流故障穿越能力弱，无功支撑能力不足，导致交流母线故障相瞬时电压幅值跌落达55%，影响电网安全稳定运行。若采用附加控制策略，CSC始终可以向系统发出无功功率，并且在故障初期无功功率输出阶跃大，可以有效地抑制前期暂态低电压的跌落，相比采用传统控制策略下的跌落量可减少30.7%。
图15 受端电网两相短路故障CSC阀侧无功功率、A相交流电压仿真波形
Fig.15 Simulated waveforms of reactive power and A-phase AC voltage at valve side of CSC with two-phase short-circuit fault in the receiving end grid
仿真结果表明，采用附加控制策略提高了受端发生两相故障后的无功响应速度，保证CSC发出的无功功率维持在较高水平，进一步抑制故障期间交流母线的电压降落和线路过负荷水平，从而降低电网安全风险事故发生的概率。
4.2.2 混合直流系统受端三相短路故障
本节验证了当受端CSC所连交流系统发生三相经接地电阻短路故障时混合直流系统在不同协调控制策略下的动态响应性能。设置CSC交流侧在t=2.5 s时发生三相短路故障，故障持续时间Δt=0.1 s，故障过渡电阻为20 Ω。受端电网三相短路故障有功、无功功率仿真波形如图16所示。
图16a、图16c为送端MMC故障期间交流侧有功、无功功率仿真波形。两种控制策略下的仿真波形曲线走势与两相短路故障下的大致相同，但是故障期间波动量相比两相短路更大。采用传统控制策略的送端MMC侧暂态有功功率最大值为5 800 MW，最小值为2 400 MW，送端MMC侧暂态无功功率最大值为120 Mvar，最小值为 -150 Mvar。采用附加控制策略后送端MMC侧暂态有功功率最大值为4 500 MW，最小值为2 900 MW，送端MMC侧暂态无功功率最大值为100 Mvar，最小值为-110 Mvar。
图16b、图16d为受端CSC侧故障期间交流侧有功、无功功率仿真波形。两种控制策略下的故障期间有功功率输出量均有所下降，采用传统控制策略的CSC故障期间发出无功，故障恢复期间转为吸收无功，而采用附加控制策略的无功始终大于0，说明此阶段受端交流母线始终向交流电网发出无功功率。
图16 受端电网三相短路故障有功、无功功率仿真波形
Fig.16 Simulated waveforms of active and reactive power with three-phase short-circuit fault in the receiving end grid
受端电网三相短路故障直流电压、电流仿真波形如图17所示。与传统控制策略相比，采用附加控制后的受端直流电压故障期间跌落的谷值均有所抬升，避免故障期间直流电压跌落导致IGBT器件无法驱动，保证清洁能源灵活高效送出。传统控制策略下直流线路电流在故障期间的峰值为8.6 kA。而附加控制策略下直流线路电流峰值为7.1 kA，从而避免线路故障期间IGCT器件一直主动关断大电流，降低器件关断的热应力，削弱对器件的威胁，以延长器件的使用寿命，保障交流故障期间IGCT器件安全可靠关断。
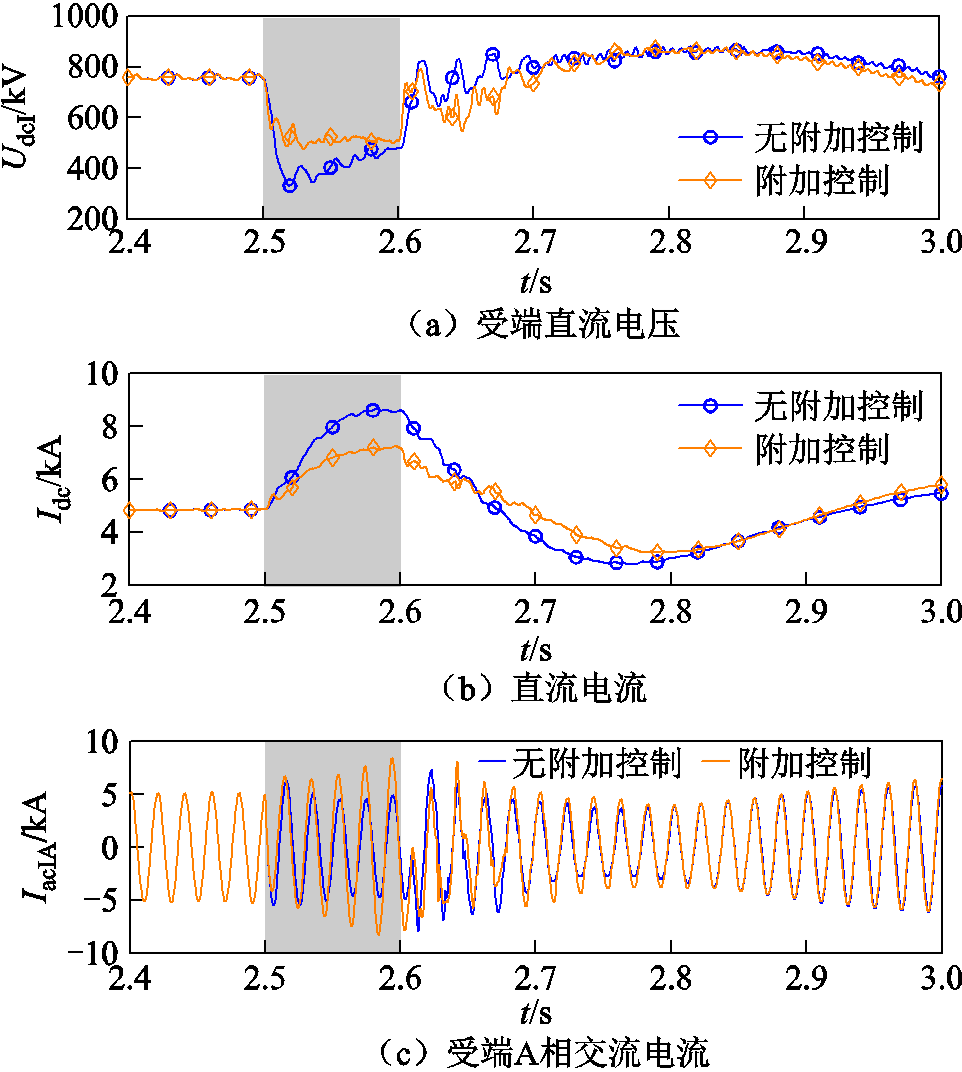
图17 受端电网三相短路故障直流电压、电流仿真波形
Fig.17 Simulated waveforms of DC voltage and current with three-phase short-circuit fault in the receiving end grid
受端电网三相短路故障CSC阀侧无功功率、A相交流电压仿真波形如图18所示。由图18可以看出，采用附加控制策略故障期间受端CSC阀侧发出无功功率明显增多，并且采用传统控制策略时，CSC侧交流母线相电压瞬时值峰值由450 kV下降至165 kV，而采用附加控制策略时，最低降落到240 kV，相比传统控制的瞬时值提升45.5%，有利于充分发挥受端换流器主动支撑受端电网电压的作用。
图18 受端电网三相短路故障CSC阀侧无功功率、A相交流电压仿真波形
Fig.18 Simulated waveforms of reactive power and A-phase AC voltage at valve side of CSC with three-phase short-circuit fault in the receiving end grid
针对大规模新能源基地远距离电力输送需求，目前典型的直流系统拓扑包括送端LCC-受端LCC常规直流系统、送端MMC-受端MMC柔性直流系统、送端LCC-受端CSC混合直流系统、送端LCC-受端MMC混合直流系统等。其中，LCC-LCC系统成本和损耗相对较低，但受端存在换相失败问题。LCC-MMC、LCC-CSC混合直流系统受端不存在换相失败问题，但送端弱电网接入能力较差。随着新能源比例不断增加，送端电网强度不断变弱，若仍采用LCC，在弱交流电网接入条件下，直流系统与电网的交互影响易引起复杂的次同步振荡问题，恶化直流送出系统的稳定性，严重时将会造成打捆外送系统产生振荡，引发大规模停电事故。系统惯量水平不断降低，外送直流系统受端交流故障期间在送端产生的不平衡功率会引发新能源场站虚拟惯性响应，进一步加剧送端暂态过电压。而MMC对交流电网强度要求低，不依赖送端交流系统运行，无需交流系统提供换相电压，无换相失败问题，具备提供紧急功率支援的能力。相比两电平和三电平VSC，MMC具有开关频率和功率损耗低等优势，并且紧凑和模块化的设计使得其易于安装、调试、维护和扩展。
另一方面，由于新能源出力具有波动性和随机性，这对换流器控制响应速度提出更高的要求。若送端换流器依然采用LCC，考虑到LCC-HVDC系统定电流控制环节的带宽通常处于10～30 Hz范围内[21-22]，因此LCC定电流控制响应时间通常为数ms级。而MMC器件等效开关频率可达kHz级别，电流内环控制系统响应时间可小于1 ms，阀基控制器（包括环流抑制控制和子模块电容电压均衡控制）响应周期为百μs级[23]，对新能源出力波动的响应控制能力更强，并且无需配置额外的无功补偿装置，即可为新能源场站提供无功支撑[24-25]。
另外，相比双端柔性直流系统，送端MMC-受端CSC混合直流送出方案在技术性能和经济效益上展现出一定的优势：不仅具有对送端弱电网的友好接入特性，还彻底消除了换相失败的风险，可实现送受端交直流故障的全穿越，并通过精简电容配置与减少器件数量，显著减小了换流站的体积和质量，从而降低了造价成本和运行损耗，为项目的长期经济运行奠定了坚实基础。但需要指出的是，本文所提出的混合直流系统拓扑存在一定的局限性，如不易实现潮流反转等。
将本文混合直流系统拓扑结构的优缺点与其他典型的直流系统进行对比总结，结果见表4。
为了对比分析MMC-CSC直流系统与LCC-CSC直流系统的稳态性能和暂态性能，在PSCAD/ EMTDC仿真平台中搭建了额定电压为800 kV、额定电流为5 kA的送端LCC-受端CSC直流输电单极系统仿真模型。其中，LCC-CSC系统整流侧采用带最小触发延迟角控制的定电流控制，逆变侧采用定直流电压控制。保证受端换流器主回路参数和系统初始条件一致，分别对上述两种直流系统的稳态响应特性进行仿真分析，LCC-CSC与MMC-CSC系统启动及额定运行仿真结果如图19所示。由仿真波形可知，LCC-CSC与MMC-CSC系统稳态工况下均能够实现功率稳定传输。但LCC有且仅有一个控制自由度，通过控制触发延迟角来决定输出直流电流的大小，进而调节输出有功功率的大小，而其输出的无功功率不可控。并且LCC换流器运行时需要从交流系统中吸收大量无功功率，同时换流装置在运行时会在交流侧产生大量谐波，因此需加装额外的交流滤波器和无功补偿装置。而MMC具有两个控制自由度，可以实现有功功率和无功功率解耦控制，无需配置交流滤波器，即可实现单位功率因数运行。并且MMC-CSC系统启动过程不存在明显的过电压和过电流冲击，能够有效地保证混合直流输电系统的安全稳定启动和单位功率因数运行。
表4 五种典型系统拓扑结构对比总结
Tab.4 Comparison of different delivery schemes
拓扑结构优点缺点 LCC-LCC拓扑结构简单，造价成本和运行损耗低，可以潮流反转送端弱电网接入能力差，受端容易发生换相失败 MMC-MMC弱电网接入能力强，无换相失败问题，可以潮流反转成本和损耗高，功率密度低，占地面积、体积质量大 LCC-MMC受端不存在换相失败问题，成本和损耗适中送端弱电网接入能力差，潮流反转不易实现 MMC-CSC弱电网接入能力强，无换相失败问题，成本和损耗适中不同源换流器耦合机理相对复杂，潮流反转不易实现
图19 LCC-CSC与MMC-CSC系统启动及额定运行仿真结果
Fig.19 LCC-CSC and MMC-CSC system startup and rated operation simulation results
为了进一步说明两种直流系统的暂态特性，对受端交流系统故障响应特性进行对比分析。两种直流系统受端均接入一个相同的交流系统，设定系统在2.5 s时发生CSC交流侧三相短路故障，2.6 s切除故障，LCC-CSC与MMC-CSC系统受端交流故障仿真结果如图20所示。
图20 LCC-CSC与MMC-CSC系统受端交流故障仿真结果
Fig.20 LCC-CSC and MMC-CSC system startup and rated operation simulation results
图20a～图20d分别为送、受端直流电压和有功功率波形。故障发生后，LCC-CSC系统由于受端采用全控器件，因此不会发生换相失败及功率传输中断现象，但是由于送端LCC换流器通过增大触发角来降低送端直流电压，因此由故障引起的功率损失较大，进而导致故障期间有功功率传输存在严重受限。并且2.6 s切除故障后，由于直流电压迅速恢复，而送端LCC控制器在2.8～3.8 s内始终处于定最小触发角状态，当t =4.2 s时，LCC-CSC系统恢复到额定运行状态，整个故障恢复过程持续时间较长。MMC-CSC系统交流故障发生后，三相交流电压瞬时值迅速跌落，在送端MMC换流站定有功功率的控制下，送端有功功率始终维持在2 000 MW以上。当t=3.5 s时送端有功功率恢复至额定运行状态，并且直流电压降落幅度明显减小。由图20f可知，相比LCC-CSC系统，故障期间MMC-CSC系统受端发出无功功率明显更多，这有助于进一步发挥受端换流器对受端电网的主动支撑能力。图20e、图20h分别为送端无功功率及送端交流电压有效值波形。由于LCC-CSC系统送端配置大量的无功补偿和交流滤波器装置，故障期间无功功率波动较大，送端交流电压有效值最大值接近1.2(pu)。并且直流系统受端交流故障期间在送端产生的不平衡功率会引发新能源场站虚拟惯性响应，进一步加剧送端暂态过电压现象，导致LCC-CSC系统送端大规模新能源机组存在脱网风险。而采用MMC-CSC系统，送端MMC换流器可以动态调节送端无功功率收发水平，提供交流电压和频率支撑，使得送端暂态过电压水平可降低为1.1(pu)，后续还可通过优化现有控制策略，继续开展前瞻性研究，进一步抑制送端暂态过电压。由图20g可知，由于送端MMC换流器故障期间子模块电容存在放电过程，受端交流故障会导致直流系统向短路点馈入功率，在故障及恢复期间故障电流较高，其峰值为9 kA。考虑IGCT器件的最大关断能力为2(pu)，该值在器件的关断能力范围之内。
综上所述，在故障期间，两种直流系统的直流电压均会出现明显的跌落现象，进而导致送受端功率传输受阻，但故障期间MMC-CSC系统电压跌落幅度和功率受阻程度相比LCC-CSC系统明显降低；并且MMC-CSC系统在故障清除后的恢复特性也要优于LCC-CSC系统，送端暂态过电压水平降低，受端交流故障的影响范围缩小，故障恢复时间进一步缩短。
通过对送端采用MMC、受端采用CSC构成的可控电压源-电流源型混合直流输电系统及协调控制策略进行研究，得到相关结论如下：
1）基于混合直流系统送受端换流器外特性分析，建立了混合直流系统交流故障期间的直流电压、电流和功率特性方程，进一步分析了受端CSC无功功率与相位差、直流电流的关系，得出可以通过减小故障期间的相位差或适当地调节线路负荷水平，增大受端CSC换流器发出无功功率的结论。
2）在弱受端电网场景中，所提出的附加有功电流和无功功率控制模块的协调控制策略，通过在送端引入基于Δivd-ΔP斜率控制的附加有功电流控制模块，在受端附加无功功率控制模块，有效地降低了受端交流故障工况下的线路过负荷水平，故障期间受端直流侧电压跌落实现了对受端电网的无功支撑，进而提高了混合直流系统的运行性能。
3）针对受端交流系统两相短路故障，可以减少30.7%的交流电压跌落；而在三相短路故障下，交流电压瞬时值相比传统控制策略可提升45.5%，进一步提高了受端换流器的主动支撑能力。
4）结合LCC、MMC两种类型换流器与送端电网交互特性分析及暂稳态性能仿真验证可知，相比于LCC-CSC系统，本文所研究的可控电压源-电流源型混合直流输电系统具有较强的弱系统接入能力，并且故障及故障恢复特性更优，可作为大规模清洁能源经特高压直流系统送出拓扑方案。
利用PSCAD/EMTDC进行了仿真验证，结果表明：所提出的控制策略在故障工况下能够主动支撑受端交直流侧电压，实现了对受端电网的无功功率支撑，从而保证清洁能源安全可靠地通过混合直流系统送出。
参考文献
[1] 舒印彪, 陈国平, 贺静波, 等. 构建以新能源为主体的新型电力系统框架研究[J]. 中国工程科学, 2021, 23(6): 61-69. Shu Yinbiao, Chen Guoping, He Jingbo, et al. Building a new electric power system based on new energy sources[J]. Strategic Study of CAE, 2021, 23(6): 61-69.
[2] 汤广福, 周静, 庞辉, 等. 能源安全格局下新型电力系统发展战略框架[J]. 中国工程科学, 2023, 25(2): 79-88. Tang Guangfu, Zhou Jing, Pang Hui, et al. Strategic framework for new electric power system develop-pment under the energy security pattern[J]. Strategic Study of CAE, 2023, 25(2): 79-88.
[3] 管敏渊, 徐政, 屠卿瑞, 等. 模块化多电平换流器型直流输电的调制策略[J]. 电力系统自动化, 2010, 34(2): 48-52. Guan Minyuan, Xu Zheng, Tu Qingrui, et al. Modeling and control of modular multilevel converter in HVDC transmission[J]. Automation of Electric Power Systems, 2010, 34(2): 48-52.
[4] Tu Qingrui, Xu Zheng, Xu Lie. Reduced switching-frequency modulation and circulating current sup-pression for modular multilevel converters[J]. IEEE Transactions on Power Delivery, 2011, 26(3): 2009-2017.
[5] 唐庚, 徐政, 薛英林. LCC-MMC混合高压直流输电系统[J]. 电工技术学报, 2013, 28(10): 301-310. Tang Geng, Xu Zheng, Xue Yinglin. A LCC-MMC hybrid HVDC transmission system[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 301-310.
[6] 薛英林, 徐政, 潘武略, 等. 电流源型混合直流输电系统建模与仿真[J]. 电力系统自动化, 2012, 36(9): 98-103. Xue Yinglin, Xu Zheng, Pan Wulue, et al. Modeling and simulation for a hybrid current source converter high voltage direct current transmission system[J]. Automation of Electric Power Systems, 2012, 36(9): 98-103.
[7] Xia Bing, Li Yaohua, Li Zixin, et al. Dual phase shift PWM-CSCs based hybrid HVDC transmission system[C]//2018 IEEE 27th International Symposium on Industrial Electronics (ISIE), Cairns, QLD, Australia, 2018: 378-383.
[8] 陈龙龙, 魏晓光, 张闻闻, 等. 可控电流源型换流器功率解耦控制策略[J]. 中国电机工程学报, 2024, 44(9): 3619-3632. ChenLonglong, Wei Xiaoguang, ZhangWenwen, et al. Power decoupling control strategy of controllable current source converter[J]. Proceedings of the CSEE, 2024, 44(9): 3619-3632.
[9] Luan Kedong, Li Yaohua, Li Zixin, et al. Research on unit power factor operation control stratage of actively commutation converter with switching frequency of 50Hz[C]//2020 4th International Conference on HVDC (HVDC), Xi’an, China, 2020: 175-178.
[10] 夏嘉航, 王晨欣, 展瑞琦, 等. 基于电流源换流器的混合型海上风电直流输电系统[J]. 电力系统自动化, 2021, 45(21): 129-138. XiaJiahang, WangChenxin, Zhan Ruiqi, et al. Hybrid DC transmission system for offshore wind power based on current source converter[J]. Automation of Electric Power Systems, 2021, 45(21): 129-138.
[11] Zhao Chengyong, Xia Jiahang, Guo Chunyi, et al. An improved control strategy for current source converter-based HVDC using fundamental frequency modulation[J]. International Journal of Electrical Power & Energy Systems, 2021, 133: 107265.
[12] 张闻闻, 陈龙龙, 魏晓光, 等. 基于可控关断的电流源型直流输电系统设计及运行方式[J]. 中国电机工程学报, 2022, 42(7): 2532-2541, 10.Zhang Wenwen, Chen Longlong, Wei Xiaoguang, et al.Design and operation mode of based on controllable currentsource converter HVDC system[J]. Proceedings of the CSEE, 2022, 42(7): 2532-2541, 10.
[13] Zhang Wenwen, Chen Longlong, Wei Xiaoguang, et al. Comparisons and improvements of key operating characteristics of current source converter applied in HVDC system[J]. CSEE Journal of Power and Energy Systems, 2023, 9(5): 1601-1612.
[14] Tian Xinshou, Chi Yongning, Li Longxue, et al. Review of the configuration and transient stability of large-scale renewable energy generation through hybrid DC transmission[J]. CES Transactions on Electrical Machines and Systems, 2024, 8(2): 115-126.
[15] 徐政. 柔性直流输电系统[M]. 2版. 北京: 机械工业出版社, 2017.
[16] 夏天, 夏向阳, 刘代飞, 等. 柔性直流系统的交流侧故障穿越优化控制策略[J]. 电气工程学报, 2021, 16(4): 196-204. Xia Tian, Xia Xiangyang, Liu Daifei, et al. AC-side fault crossing optimization control strategy for VSC-HVDC[J]. Journal of Electrical Engineering, 2021, 16(4): 196-204.
[17] 李佳, 夏勇军, 姚伟, 等. 采用VSC-HVDC改善LCC-HVDC直流侧暂态特性的无功协调控制[J]. 电网技术, 2022, 46(1): 101-110. Li Jia, Xia Yongjun, Yao Wei, et al. Reactive power coordinated control for improving transient charac-teristics of DC side of LCC-HVDC using parallel VSC-HVDC[J]. Power System Technology, 2022, 46(1): 101-110.
[18] 欧阳金鑫, 陈纪宇, 李昂, 等. 兼顾直流电压安全与无功支撑的柔性直流输电故障穿越控制[J]. 电工技术学报, 2024, 39(19): 6129-6144. Ouyang Jinxin, Chen Jiyu, Li Ang, et al. Fault ride-through control method for VSC-HVDC balancing between DC voltage security and reactive power support[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 6129-6144.
[19] 张彪, 王渝红, 李兴源. 改善直流系统恢复特性的VDCOL控制策略研究综述[J]. 华东电力, 2014, 42(5): 826-832. Zhang Biao, Wang Yuhong, Li Xingyuan. Overview on VDCOL, control strategy for improving DC system recovery characteristics[J]. East China Electric Power, 2014, 42(5): 826-832.
[20] 刘云. 我国特高压直流输电通信技术的巴西工程本地化通道设计方案[J]. 电网技术, 2018, 42(3): 973-980. Liu Yun. Research on localized channel design in Brazil Utilizing Chinese UHVDC telecommunication technologies[J]. Power System Technology, 2018, 42(3): 973-980.
[21] 傅闯, 叶运铭, 汪娟娟, 等. 基于D分割法的LCC-HVDC系统控制器参数整定方法[J]. 电力系统自动化, 2022, 46(13): 139-150. Fu Chuang, Ye Yunming, Wang Juanjuan, et al. D-partition method based controller parameter setting method for LCC-HVDC system[J]. Automation of Electric Power Systems, 2022, 46(13): 139-150.
[22] 陶瑜. 直流输电控制保护系统分析及应用[M]. 北京: 中国电力出版社, 2015.
[23] 贺之渊, 刘栋, 庞辉. 柔性直流与直流电网仿真技术研究[J]. 电网技术, 2018, 42(1): 1-11. He Zhiyuan, Liu Dong, Pang Hui. Research of Simulation technologies of VSC-HVDC and DC grids[J]. Power System Technology, 2018, 42(1): 1-11.
[24] 马富艺龙, 辛焕海, 刘晨曦, 等. 新能源基地柔性直流送出系统小扰动电压支撑强度评估[J]. 电工技术学报, 2023, 38(21): 5758-5770, 5938. Ma Fuyilong, Xin Huanhai, Liu Chenxi, et al. Small-disturbance system voltage support strength assessment method for renewables VSC-HVDC delivery system [J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5758-5770, 5938.
[25] 张祥宇, 胡剑峰, 付媛, 等. 风储联合系统的虚拟惯量需求与协同支撑[J].电工技术学报, 2024, 39(3): 672-685. Zhang Xiangyu, Hu Jianfeng, Fu Yuan, et al. Virtual inertia demand and synergistic support of wind storage hybrid system[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 672-685.
Abstract To ensure the efficient transmission of new energy from the desert and gobi Regions, China has accelerated the construction of ultra-high voltage direct current (UHVDC) transmission corridors. A large number of UHVDC projects are being arranged, deployed and continuously promoted. The controllable voltage source-current source type hybrid DC delivery scheme not only provides frequency reference and voltage support, but also has low cost, low loss, high reliability, and no phase change failure problem, so it is more suitable for large-scale clean energy delivery scenarios with complex and changing operating conditions. However, how to improve the active support capability of the converter at the sending and receiving ends after an AC fault occurs in the hybrid DC system to ensure efficient and reliable clean energy delivery and safe and stable operation of the system is still a difficult problem that needs to be solved urgently.
Firstly, a mathematical model of controllable voltage-current source hybrid DC transmission system is established to depict the DC voltage, current and power operation characteristics of the hybrid DC system under the transient steady state condition.Secondly, the reactive power of the controllable current source converter is analyzed in relation to the phase angle difference and the direct current, and then a method is proposed to improve the reactive power support capability of the hybrid DC system under the AC fault at the receiving end. Thirdly, by introducing an additional active current control module based on Δivd-ΔP slope control and an additional reactive power control module, the line overload level under the AC fault condition and the voltage drop during the fault period are effectively reduced, and the reactive power support to the receiving end grid is realized, which improves the operational performance of the hybrid DC system. Finally, the correctness and effectiveness of the proposed control strategy are verified by simulation with electromagnetic transient simulation software PSCAD/EMTDC. The proposed control strategy for two-phase short-circuit faults in the AC system at the receiving end can reduce the AC voltage dips by 30.7%, while under three-phase short-circuit faults, the instantaneous value of the AC voltage can be improved by 45.5% compared with the traditional control strategy, which improves the active support capability of the converter at the receiving end, and then reduces the probability of the occurrence of the safety risk accidents of the power grid.
The following conclusions can be drawn: (1) The reactive power emitted by the CSC converter at the receiving end is increased by reducing the phase angle difference during the fault period or by appropriately adjusting the line load level. (2) The proposed control strategy can actively support the AC and DC side voltages of the receiving end under the fault condition, realizing the reactive power support to the receiving end power grid. (3) Compared with the LCC-CSC system, the controllable voltage source-current source hybrid DC transmission system has strong weak-system access capability,better fault and fault recovery characteristics, which can be used as a topology scheme for large-scale clean energy transmission via UHVDC system.
keywords：Hybrid HVDC transmission system, coordinated control, transient conditions, fault characteristics
DOI: 10.19595/j.cnki.1000-6753.tces.240566
中图分类号：TM721
国家重点研发计划资助项目（2023YFB2405900）。
收稿日期 2024-04-10
改稿日期 2024-11-20
熊 耀 男，1999年生，博士研究生，研究方向为高压直流输电。Email：xy991111@163.com
魏晓光 男，1976年生，博士，教授级高级工程师，博士生导师，研究方向为高压直流输电系统拓扑及控制、核心直流换流装备设计与研发、大容量功率半导体器件研制与应用等。Email：weixiaoguang@neps.hrl.ac.cn（通信作者）
（编辑 郭丽军）