及等效内阻抗
组成，并联部分为一个受控电流源。图1中，
、
分别为t时段流入RPFC的i端的有功、无功功率，以流入为正，流出为负；
、
分别为t时段流入RPFC的j端的有功、无功功率；
为t时段线路ij配置的RPFC的功率损耗。摘要 新能源高比例接入会导致配电台区出现网架结构薄弱、局部负荷分配不均等承载力不足问题，通过台区柔性互联可解决上述问题，但电力电子式互联装置过高的投资及运维成本限制了其广泛应用。为此，该文提出一种面向配电台区经济性及综合承载力提升的旋转潮流控制器（RPFC）双层规划模型。首先，建立RPFC的稳态潮流模型，提出含RPFC的配电台区柔性互联结构；其次，构建含RPFC的配电台区双层规划模型，上层为RPFC选址定容层，以配电台区总投资成本最小为目标确定RPFC最优容量与位置，下层为运行优化层，构建考虑安全性、经济性、灵活性的综合承载力指标体系，并以综合承载力最高为目标优化RPFC运行功率；然后，为提高寻优速度和精度，提出一种改进引力场结合二阶锥规划的混合优化算法求解该双层规划模型；最后，将所提模型与其他规划模型进行对比，结果表明所提模型在降低配电台区总投资成本的同时提高了配电台区综合承载力。
关键词：配电台区 综合承载力 旋转潮流控制器 改进引力场算法 双层规划
随着以光伏和风机为代表的新能源发电渗透率的快速增长，传统配电台区采用单变压器、单线路的供电方式将无法有效地适应新能源发电的间歇性和波动性[1]，使得传统配电台区网架结构日趋薄弱[2]。此外，由于不同台区负荷性质及用电方式的差异，开环运行难以共享台区变压器的剩余容量[3]，导致相邻台区出现负荷不均衡，台区主变压器（简称主变）负载率差异过大[4]，降低了配电台区运行的经济性和可靠性，也增加了配电台区对承载能力的需求[5]。
柔性互联装置（Flexible Interconnection Device, FID）是一类能够将配电网互联且具有潮流灵活控制能力的配电设备[6]，通过连续精准地调节各端口的输出功率[7]，能够有效均衡负荷，改善潮流分布[8]，从而提高配电台区的承载力[9]。电力电子式FID如智能软开关（Soft Open Point, SOP）和柔性多状态开关（Flexible Multi-state Switch, FMS）凭借其良好的潮流控制能力和快速响应能力[10-12]，成为当前实现台区间柔性互联的主要装置。目前许多学者已对电力电子式FID在配电网中的规划问题开展研究。文献[13]提出基于改进灵敏度分析的有源配电网SOP优化配置方法，表明对SOP进行优化配置可有效降低配电网年综合运行成本，改善系统电压。文献[14]考虑了分布式电源不确定性对柔性互联配电网承载力的影响，提出了计及SOP和网络重构的分布式电源鲁棒承载能力评估模型。文献[15]从改善配电网馈线负荷不均衡问题入手，提出一种基于FMS的配电网双层负荷均衡方法，改善了负荷均衡程度，有效地减少了配电网网损，也改善了电压分布。文献[10-15]中的电力电子式FID的优势在于响应速度快，可以实现连续实时控制，但由于采用电力电子器件构成功率控制电路，存在投资及运行维护成本高，故障承受能力弱等问题[16-17]，成为目前制约电力电子式FID广泛应用的重要因素之一。
为降低FID投资成本，有学者提出一种基于旋转潮流控制器（Rotary Power Flow Controller, RPFC）的电磁式FID[18]，其采用旋转移相变压器（Rotary Phase Shifting Transformer, RPST）的转子协调旋转及电磁感应原理柔性调节线路潮流[19]，是一条与传统电力电子式FID并行且更具经济性的技术路线。目前已有文献研究RPFC在配电网中的规划配置应用。文献[20]提出RPFC可用于电压越限、柔性合环及潮流控制这三个典型场景，但未涉及RPFC的具体规划方法。在文献[20]的基础上，文献[21]对RPFC与无功补偿装置进行了协调规划，并与接入SOP及无功补偿方案对比，验证了RPFC更具经济性优势，但忽略了配电台区的承载力。文献[22]计及配电网新能源承载力，提出一种考虑RPFC和需求响应的配电网新能源承载力评估方法，表明接入RPFC能够提升配电网的新能源承载力，但未对RPFC的容量进行规划。因此，现有大部分研究在综合考虑经济性及承载力的RPFC的选址定容规划方面仍需进一步完善。
在对FID规划问题的求解方面，文献[23]将模拟退火和二阶锥规划算法相结合，具有一定的全局搜索能力，但该算法过程复杂，计算时间过长。文献[24]采用主从并行遗传算法和锥规划的混合算法，提高了求解效率，降低了计算时间，但该算法对参数设置较敏感，主从节点间存在通信延迟等问题[25]。文献[26]采用引力场算法（Gravitation Field Algorithm, GFA），它将变量集合抽象为宇宙尘埃系统，通过初始化尘埃群体，并设计分解算子、移动算子及吸附算子来实现尘埃之间的相互吸引和聚集，最终形成行星的过程视为得到最优解。该方法模型参数少、搜索效率高[27]，能够弥补上述算法的不足，但尘埃的初始位置容易影响求解准确度[28]。如何在提高GFA全局搜索能力的同时，避免初始位置设置不合理的问题，是求解RPFC规划问题的关键。
综上所述，为提高配电台区经济性，缓解配电台区承载能力不足的问题，本文提出一种面向配电台区经济性及综合承载力提升的旋转潮流控制器双层规划模型。首先，建立RPFC的模型并介绍含RPFC的柔性互联配电台区结构；其次，构建含RPFC的配电台区双层规划模型，分别为RPFC选址定容层及运行优化层；然后，采用改进引力场结合二阶锥规划（ImprovedGravitation Field Algorithm-Second Order Cone Programming, IGFA-SOCP）的混合优化算法对双层模型分层求解；最后，通过算例对本文提出的双层规划模型及优化算法进行验证。结果表明，所提双层规划模型与其他方案相比，可在降低配电台区总投资成本的同时有效提高综合承载力水平，所提优化算法提高了寻优精度，减少了迭代次数与求解时间。
旋转潮流控制器利用两台RPST分别在定子侧生成一个幅值不变、相位四象限变化的定子电压相量[29]，然后两组定子电压相量经过叠加合成一个幅值和相位均可调节的串联电压。RPFC单相简化电路如图1所示，其串联部分由一个受控理想电压源及等效内阻抗组成，并联部分为一个受控电流源。图1中，、分别为t时段流入RPFC的i端的有功、无功功率，以流入为正，流出为负；、分别为t时段流入RPFC的j端的有功、无功功率；为t时段线路ij配置的RPFC的功率损耗。
图1 RPFC单相简化电路
Fig.1 Single-phase simplified circuit of RPFC
本文采用文献[30]中的恒定有功/无功控制策略，并通过改变RPFC转子角的角度控制，从而实现对线路功率的连续调节，得到RPFC稳态潮流模型为
（1）
（2）
（3）
（4）
（5）
式中，
为t时段线路ij配置的RPFC电流；
为RPFC的等效电阻；
为RPFC的内部铁心损耗；
为线路ij配置的RPFC容量。
RPFC与电力电子式FID如统一潮流控制器（Unified Power Flow Controller, UPFC）、SOP在规划期间的主要区别体现在装置的经济性和可靠性方面。RPFC的经济性优势主要体现在生产成本、运行损耗和运维成本系数三个方面，而其可靠性优势则表现为较强的过载能力和更长的使用寿命。本文重点分析了RPFC的生产成本、运行损耗、运维成本系数及使用寿命四个特性，表1总结了三种装置在规划期间的差异性[19,29-32]。表中，“√”表示此特性小或弱，“√√”表示此特性中等，“√√√”表示此特性大或强。
表1 RPFC与电力电子式FID在规划期间差异性对比
Tab.1 Comparison of the differences between RPFC and power electronic FID during planning
特性UPFCSOPRPFC 生产成本√√√√√√ 运行损耗√√√√√√ 运维成本系数√√√√√ 过载能力√√√√√√ 使用寿命√√√√√√√
含RPFC的多馈线配电台区柔性互联结构如图2所示。该区域共包含3条馈线，在配置RPFC前，馈线1、馈线3接入光伏和风电机组的比例较高，本地消纳能力不足，常出现新能源机组功率倒送至台区主变压器的情况；而馈线2为重载线路，其负荷比例高于新能源机组，台区主变压器长期面临负载率过高的问题，影响了台区主变的安全稳定运行。当相邻台区通过柔性互联后，多馈线台区柔性闭环运行，风光过剩功率可直接通过互联装置供给至负荷侧，在实现台区内功率互济的同时也提高了末端高比例新能源的消纳率。
图2 含RPFC的配电台区柔性互联结构
Fig.2 Flexible interconnection structure of distribution station area containing RPFC
考虑到RPFC的规划与运行相结合的问题属于大规模非线性混合整数规划问题，直接使用传统求解器难以高效求解[33]。此外，该问题的结构与上下层优化模型的逻辑相符，采用分层优化方法进行处理能更好地解决该问题。因此，本文将RPFC的规划配置与运行优化分层处理，提出一种面向配电台区经济性及综合承载力提升的RPFC双层协调规划框架，分别为RPFC选址定容层及运行优化层。双层规划框架如图3所示。
图3 双层规划框架
Fig.3 Bi-level programming framework
上层为RPFC选址定容层。该层首先基于Kantorovich距离的场景缩减方法得到典型场景，以配电台区总投资成本最小为优化目标，同时在满足RPFC功率约束及容量约束的条件下，生成RPFC当前最优位置和容量；然后将RPFC选址定容方案传递至下层。
下层为运行优化层，优化目标为配电台区综合承载力最高。该层首先基于上层配置方案，求解得到各场景下RPFC的最优运行功率；然后将RPFC传输功率及支路潮流等优化结果反馈至上层；最后双层模型相互迭代优化，得到最优配置规划及运行优化方案。
根据RPFC双层规划框架，建立RPFC双层规划模型，分别为RPFC选址定容层模型及运行优化层模型。
2.2.1 RPFC选址定容层模型
RPFC选址定容层模型以配电台区总投资成本F1最小为目标函数，包括配电台区网络损耗成本、RPFC生产建设成本及运维成本，计算公式为
（6）
式中，
为配电台区网络损耗成本；
为RPFC的生产建设成本；
为RPFC的运维成本；
为电网分时电价；
为第m个场景t时段下馈线n的线路损耗；M为总场景数；N为配电台区的总馈线数；T为总时段数；
为第m个场景对应的概率；μ为贴现率；yRPFC为RPFC的经济使用年限；
为RPFC的安装节点集合；
为单位容量RPFC的设备投资成本；
为单位容量RPFC的土建安装成本；
为单位容量RPFC的运行维护成本系数；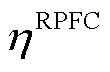
为RPFC的损耗成本系数；
为第m个场景t时段下RPFC的功率损耗。
RPFC选址定容层模型需满足RPFC容量约束及功率约束，具体为
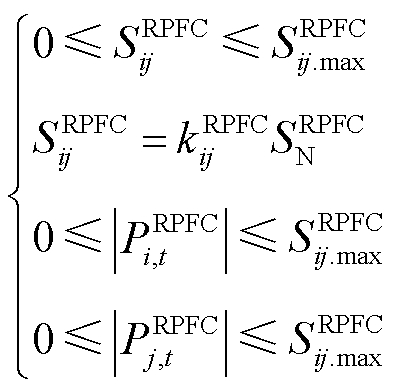（7）
式中，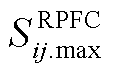
为线路ij配置的RPFC最大容量值；
为线路ij配置的RPFC单位容量值；
为一非负整数，代表线路ij配置单位容量RPFC的数量。
2.2.2 运行优化层模型
当前，配电网承载力通常是指其能够承载的最大新能源容量。例如，文献[34]通过新能源的最大装机容量来衡量配电网在接入新能源时的承载能力；文献[35-36]进一步将其定义为在满足安全运行约束条件下，配电网可接入的最大分布式电源容量；文献[14]则提出了分布式电源的鲁棒承载力，是指能够适应配电网任意位置接入的最大容量。然而，这些定义未充分考虑在柔性互联后，配电台区的网络结构变化及台区负载率等关键因素。因此，若直接将这些定义用于互联配电台区的规划，将无法全面反映实际的运行需求和状态。为此，亟须建立能够综合评估配电台区承载力的指标体系。
综上所述，本文提出一种在面对新能源高渗透率接入时，利用各种调控手段改善潮流分布，协调优化各类可调节资源功率，从而确保配电台区安全、经济、灵活运行的综合承载力指标体系。它在安全性方面主要体现在配电线路应对负荷波动，以及应对新能源在不同馈线间不均衡接入所带来的影响。通过提升台区潮流分布的均衡度，能够有效缓解因功率波动引发的连锁故障[15,37]。在经济性方面主要体现在通过各种调控手段优化源荷的时空特性，最大限度地减少网损费用，确保在新能源高渗透接入的情况下，台区仍能保持经济高效的电能传输。在灵活性方面则要求配电线路具有充足的容量裕度[38]，能够利用不同网架结构中的电能转移通道，灵活转移新能源过剩功率以平衡负荷功率。
因此，运行优化层以配电台区综合承载力指标F2最高为目标函数，包括互联均衡度指标FB、网损率指标FL、线路容量充裕度指标FC。
（8）
式中，
、
分别为第m个场景t时段下注入馈线1和馈线2的视在功率；
、
分别为馈线1和2连接的主变压器的额定容量。需要说明的是，当配电台区馈线数为2时，可直接利用式（8）计算；若馈线数大于2，则需对不同馈线进行
次排列组合，分别代入式（8）中计算FB后取平均值。
（9）
式中，
为配电台区的馈线节点集合；
为第m个场景t时段下线路ij的有功损耗；L为配电台区总支路数。
（10）
式中，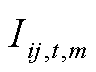
为第m个场景t时段下流过线路ij的电流；
为线路ij的电流最大值。
由于各指标的方向及量纲有所不同，为建立统一的指标评价体系，需要将逆向指标正向化。采用min-max标准化将各指标进行转换，如式（11）和式（12）所示。
（11）
（12）
式中，
、
分别为正向指标和逆向指标原值；
、
分别为指标的最大值、最小值；
为正向指标归一化值。为保证多指标赋权的科学公正，利用层次分析-熵权法[39]对各指标进行主客观的组合赋权。层次分析法的判断矩阵见附表1、最终确定配电台区综合承载力指标F2为
（13）
运行优化层模型需满足的约束条件包括RPFC运行约束及配电网运行安全约束。其中，RPFC运行约束见式（1）～式（5），配电网运行安全约束包括潮流约束、功率平衡约束及电压电流约束，如式（14）～式（19）所示。
（14）
（15）
（16）
（17）
（18）
（19）
式中，
、
分别为线路ij在t时段从节点i流向节点j的有功和无功功率；
、
分别为t时段流入节点j的净有功和无功功率；
、
分别为t时段光伏、风机的有功功率；
、
分别为t时段负荷的有功和无功功率；
、
分别为t时段节点i、j的电压；
、
分别为线路ij的电阻和电抗；
和
分别为节点i的电压下限值和上限值；
为t时段线路ij的电流。
由于式（16）和式（17）为非凸形式，采用二阶锥规划方法将上述非凸约束转换为二阶锥约束[40]，定义新优化变量——节点电压幅值的二次方Vi和支路电流幅值的二次方Lij，如式（20）所示。
（20）
式中，
、
分别为节点i的电压幅值、线路ij的电流幅值。
在满足目标函数是Lij的严格增函数条件下，可将式（20）中Lij变形为
（21）
再将式（21）等价转换为标准的二阶锥形式，有
（22）
此外，RPFC运行约束中式（4）、式（5）也为非凸形式，因此将式（4）、式（5）转换为式（23）及式（24）所示的旋转二阶锥形式[23]。
（23）
（24）
场景缩减技术可将生成的大量初始场景中的相似场景简化为有限的典型场景，从而能够在保证模型准确度的同时大幅降低计算量。目前场景缩减技术有多种实现方法，关键在于概率距离的选取[41]。利用Kantorovich距离的同步回代消除方法对初始场景进行缩减，能够较好地保留初始场景的概率分布特性，且在初始场景数规模较大时收敛较快[42]。为此，本文基于蒙特卡洛模拟方法[43]生成大量服从概率分布的风光随机出力场景，并采用Kantorovich距离对大量风光场景进行削减，流程如图4所示。
Kantorovich距离定义为
式中，m和
分别为场景集合Ci和
中的场景；pm和
分别为各场景概率；
为场景m和的欧氏距离；
为场景之间的概率乘积。
图4 多场景建模流程
Fig.4 Multi-scenario modeling flow chart
基于Kantorovich的场景缩减方法步骤如下：
（1）场景初始化：设置Mi为原始场景集合中保留场景集合Ci的总数，
为删除场景集合
的总数。确定集合C中的保留场景初始概率为1/M，集合C中的删除场景初始概率为1/。
（2）确定削减场景：根据Kantorovich距离计算所有场景之间的距离与其概率乘积的最小值，如式（26）所示，并将场景归入中。
（26）
（3）更新场景数量：将初始场景数Mi更新为Mi-1，删除场景数=+1。
（4）更新场景概率：通过式（27）选择距离场景最近的场景m，更新与被剔除场景最近的场景m的概率
，使得保留的场景集合C中所有场景概率和为1。然后更新删除场景集合中各场景概率为1/。
（27）
（5）转至步骤（2）重复迭代，直到场景集合
中的场景数量削减到所设定的数量M为止。
本文采用改进引力场算法-二阶锥规划的混合优化算法对所提双层模型进行求解。
改进引力场算法（IGFA）用于获取上层RPFC最优位置和容量，并将结果传递到下层。下层采用二阶锥规划（SOCP）方法，将复杂的非线性非凸模型转换为混合整数二阶锥模型，以求解各场景下的最优运行方案。其中，IGFA是通过在GFA中引入Tent混沌映射得到，增强了初始种群的随机性及遍历性[44]，改善了种群分布，从而提高全局搜索能力及收敛速度[45]。SOCP算法作为一种成熟的凸优化方法，通过松弛化原非凸约束，能够实现对原非凸模型的高效求解[46]。IGFA结合SOCP的混合算法不仅加速了优化算法的收敛过程，同时提高了整体求解的计算精度和稳定性。双层规划求解流程如图5所示，IGFA的算法流程如附图1所示，Tent混沌映射分布如附图2所示。
图5 双层规划流程
Fig.5 Bi-level programming flow chart
本文选择10 kV三馈线配电台区进行算例分析，其拓扑结构如图6所示。RPFC待安装位置为图中S1～S5处。台区共接入三组风机机组（WT）和三组光伏机组（PV），接入位置及容量见表2。基于Kantorovich距离的场景缩减方法得到五个典型场景的风光功率曲线如附图3和附图4所示，得到各场景概率分别为0.163、0.152、0.241、0.268、0.176。风电和光伏机组功率计算方法及参数见附录中式（A1）～式（A3）及附表2，蒙特卡洛模拟次数设为500次。本文采用的分时电价如附图5所示，节点及负荷参数见附表3，算例中其他参数见附表4。
图6 三馈线配电台区拓扑结构
Fig.6 Three-feeder distribution station area topology diagram
表2 新能源机组接入位置及容量
Tab.2 Location and capacity of new energy units
机组类型接入节点号每台机组额定功率/kW数量/台 PV12、15、1620020、20、20 WT6、7、1450010、20、10
本文所提的混合优化方法整体利用Matlab 2018b软件计算。其中，IGFA在Matlab软件直接运行，SOCP采用YALMIP框架调用GUROBI求解器，硬件为CPU型号为Intel Core i7-12700H，主频为2.30 GHz，RAM为16 GB的计算机。
为验证本文所提的RPFC双层规划模型对配电台区经济性及承载力的提升作用，设置了四种规划方案。方案1：未配置柔性互联装置；方案2：利用SOP柔性互联，采用文献[23]中双层规划模型进行选址定容及运行优化；方案3：利用RPFC柔性互联，采用文献[23]中双层规划模型进行选址定容及运行优化；方案4：利用RPFC柔性互联，并采用本文所提双层规划模型进行选址定容及运行优化。
4.2.1 选址定容规划结果分析
不同方案下柔性互联装置配置结果见表3。方案2～4均在S2和S3处配置RPFC，这是因为馈线2中9和12节点负荷功率较大，通过S2和S3提供潮流传输通道以就近消纳7和14节点处风机输出功率。方案2中SOP的容量低于方案3和方案4中配置电磁式RPFC的容量，这是因为单位容量SOP的交/直流换流器成本较高，为降低互联装置投资成本而减少了SOP的容量。方案3与方案4分别采用不同的规划模型，方案3仅以经济性最高为目标进行规划，而方案4采用本文所提综合考虑经济性和承载力的双层规划模型，为提升配电台区综合承载力而增加了0.2 MV·A互联装置容量，对承载力提升效果分析详见4.3.2节。
表3 各方案下柔性互联装置配置结果
Tab.3 Configuration results of flexible interconnection devices under each scheme
方案互联装置类型配置位置容量/(MV·A) 1——— 2SOPS2、S30.2、1.2 3RPFCS2、S30.9、3.1 4RPFCS2、S31.0、3.2
4.2.2 选址定容层经济性分析
不同规划方案的经济性对比见表4。结合表3和表4分析可得，方案1不进行互联时网损成本过高，方案2～4中配置柔性互联装置可以显著降低配电网的网损成本。方案2对SOP进行选址定容后，在降低网损的同时也减少了SOP装置的投资成本，使得总投资成本比方案1减少了4.16万元。方案3和方案4中，由于单位容量RPFC投资成本低于SOP，互联设备生产建设及运维成本之和比方案2分别减少了3.83万元和3.17万元，并且方案3和方案4的配置容量更大，降低的网损成本更多，最终方案3和方案4的总投资成本分别比方案2降低27.1%和26.8%。方案4的配电台区总投资成本比方案3多了0.22万元，虽然增加了总投资成本，但能有效提升配电台区的综合承载力。综上所述，与电力电子式互联装置SOP相比，RPFC能够减少装置自身的投资成本，进而降低配电台区总投资成本。
表4 不同规划方案的经济性对比
Tab.4 Economic comparison of different planning schemes （单位：万元）
方案互联设备生产建设成本互联设备运维成本网损成本配电台区总投资成本 10084.2284.22 215.691.4062.9780.06 312.510.7545.0958.35 413.130.7944.6558.57
4.3.1 运行优化结果分析
图7为方案2～4中柔性互联装置运行优化结果，结合图6对潮流传输方向进行分析。图7a中方案2的S2处RPFC的有功潮流为负，表明潮流从14节点流向10节点，S3处RPFC的有功潮流为正，表明潮流从7节点流向12节点，这是由于馈线2为重载线路，馈线1和3分别利用RPFC向其提供有功功率，降低馈线2的线路损耗及主变负载率。图7b和图7c中，方案4为尽可能地提升经济性和承载力，通过S3处的RPFC传输了更多的有功潮流，同时也将7节点和14节点接入的风机功率通过RPFC装置就近转移至负荷侧，实现了新能源机组的高效消纳。
图7 方案2～4互联装置运行优化结果
Fig.7 Optimization results of interconnected device operation of Scheme 2～4
4.3.2 配电台区综合承载力结果分析
不同规划方案的综合承载力指标对比情况见表5。方案1中由于未配置互联装置，馈线2为重载线路，线路容量充裕度不足，而馈线1和3新能源功率过剩但无法对馈线2进行潮流支援，造成配电台区总体潮流分布不均衡，且线路容量充裕度指标较低。表5 不同规划方案的综合承载力对比
Tab.5 Comparison of the comprehensive carrying capacity of different planning schemes
方案互联均衡度网损率线路容量充裕度综合承载力 10.5980.7680.7440.687 20.7270.7960.7940.765 30.9430.8190.8610.884 40.9500.8220.8720.891
对方案2～4中综合承载力对比结果可见，配置RPFC或SOP均能提高配电台区的承载力，方案2和方案3分别对SOP和RPFC装置进行选址定容及运行优化的目标函数只考虑经济性，而方案4在运行优化层从承载力提升的角度进行功率控制和潮流分配，因此方案4的承载力提升效果更优。对方案2～4中衡量承载力水平的三个具体指标进行分析，通过配置互联装置可降低配电台区的网损，网损率标准化指标均获得了一定的提高；方案4中互联均衡度和线路容量充裕度高于方案2的原因在于综合考虑经济性和承载能力后，上层规划的SOP换流器的高成本制约了方案2的安装容量，能够调控的潮流量减少，最终影响了配电台区的综合承载力。
由表5可见，方案3和方案4与方案2的综合承载力结果差距较大，表明容量配置的大小确实对综合承载力有显著影响。为进一步分析综合承载力结果与优化策略之间的关系，本文在方案2和方案3的基础上新增方案5和方案6。方案5：与方案2中配置SOP的位置和容量相同，但在运行优化期间采用本文所提综合承载力模型；方案6：与方案3中配置RPFC的位置和容量相同，但在运行优化期间采用本文所提综合承载力模型。这两种方案分别采用与方案2和方案3相同的互联装置配置容量，但在下层优化运行模型中引入本文所提综合承载力模型，以探讨不同优化策略对综合承载力的影响。
方案5和方案6的综合承载力分析结果见表6。对比表5和表6可见，与方案2和方案3相比，方案5和方案6的互联均衡度和线路容量充裕度均有所提升，但其经济性指标（即网损率）略低。这表明，在运行优化阶段，本文提出的综合承载力模型更侧重于增强配电台区系统的承载能力，因此方案5和方案6的综合承载力稍高于方案2和方案3。此外，表6也进一步表明，综合承载力并不完全由配置的互联装置容量大小决定，即在相同容量条件下，采用不同的优化策略求解，仍然会导致承载力结果存在差异。
表6 方案5和方案6的综合承载力结果
Tab.6 Comprehensive carrying capacity results of Scheme 5 and 6
方案互联均衡度网损率线路容量充裕度综合承载力 50.7300.7940.7980.767 60.9470.8160.8660.887
对不同规划方案的经济性及承载力进行综合对比结果如图8所示。相较于方案1，方案2～4均取得了不同程度的提升。其中，方案2引入SOP进行柔性互联，在经济性和承载力方面均有所改善。而方案3和方案4采用RPFC，相较于方案2在经济性和综合承载力上均有进一步提升。
图8 不同规划方案下经济性及承载力的综合对比
Fig.8 Comprehensive comparison of economics and carrying capacity under different planning schemes
方案3和方案4在经济性和承载力方面各具优势。方案3的RPFC双层规划模型均以经济性优化为核心，优化目标是投资和运行成本的最小化，因此在经济性方面略有优势。相较之下，方案4将经济性与承载力的协调优化作为双层模型的核心目标，为提升承载能力而增加了投资成本，导致经济性稍差。而在综合承载力方面，方案4在选址定容及运行优化过程中，不仅考虑了经济性，还充分考虑了配电台区负荷均衡、线路损耗及线路容量裕度的综合因素，实现了综合承载力的最大化。这种综合优化使得方案4在实际运行中能够更好地满足配电台区在安全性、经济性和灵活性等方面的需求，提高配电台区整体运行性能，而不仅局限于成本效益的优化。
综上所述，本文所提方案4的优势在于通过兼顾经济性和承载力，为高比例新能源接入配电台区提供了一种更为均衡的优化方案，有助于配电台区的长期稳定运行。
本文提出的双层规划采用IGFA-SOCP的混合优化算法进行求解，其中上层采用IGFA算法，将其与粒子群优化（Particle Swarm Optimization，PSO）算法和GFA算法均用于求解方案4，收敛结果如图9所示。由图9可见，IGFA迭代至第17次便已收敛至全局最优值58.57万元，GFA在第29次迭代时才完成收敛，而PSO在第83次迭代陷入了局部最优值60.05万元，表明所提IGFA的收敛速度更快，寻优精度更佳。
图9 不同算法下RPFC选址定容层收敛情况
Fig.9 Convergence of RPFC site selection and capacity determination layer under different algorithms
采用不同算法下双层模型求解情况的对比见表7。由表7可见，本文所提IGFA-SOCP混合优化算法具有更快的寻优速度，与GFA-SOCP算法相比，减少了12次迭代，求解时间减少了1 291.6 s。PSO-SOCP求解时间过长，且收敛效果也不如GFA-SOCP算法。只采用SOCP在计算5 h后仍未得出结果，这是由于决策变量维数过高且含有较多整数变量和0-1变量，迭代次数多，仅用SOCP求解难以收敛。而本文提出的IGFA-SOCP混合优化算法，通过IGFA对RPFC容量和位置进行预规划，降低双层模型的求解难度，提高了寻优速度和精度。图9与表7相结合验证了所提混合优化算法的收敛性与有效性。
表7 双层模型求解情况对比
Tab.7 Comparison of solutions for the bi-level model
方案求解算法迭代次数求解时间 4SOCP—＞5 h PSO-SOCP836 417.3 s GFA-SOCP292 685.8 s IGFA-SOCP171 394.2 s
本文选择一条与传统电力电子式柔性互联装置并行且更具经济性的技术路线，提出一种面向配电台区经济性及综合承载力提升的RPFC双层规划模型，并采用IGFA-SOCP混合优化算法进行求解。通过算例分析，得到以下结论：
1）与电力电子式互联装置相比，RPFC凭借更低的生产和运维成本，有效地减少了柔性互联装置的投资成本，进而降低配电台区总投资成本，为提升配电台区的承载力提供了更具经济效益的解决方案。
2）所提RPFC双层规划模型，上层为RPFC选址定容层，下层为运行优化层。其中，RPFC选址定容层模型以配电台区总投资成本最小为目标，协调运行优化层以配电台区综合承载力最高为目标，并从安全性、经济性、灵活性三个方面进行全面衡量。相比于SOP的双层规划，RPFC在提升配电台区互联均衡度、降低网损率及提高线路容量充裕度方面更具优势。
3）所提IGFA-SOCP混合求解算法通过将Tent混沌映射融入GFA中并结合SOCP，在提高全局搜索能力的同时降低双层模型的求解难度，进而优化了模型整体的求解流程，提高寻优速度和精度。
本文面向配电台区经济性及综合承载力提升开展RPFC的配置规划工作。研究表明，RPFC在提高配电台区经济性和承载能力方面具有理论上的潜在优势，但在功率控制精度、响应速度等方面仍不及电力电子式柔性互联装置。目前该装置仍处于创新性研究阶段，国内的示范和实际工程应用较为有限，本团队已研制一台10 kV/1 MV·A的RPFC装置并在河北涿州开展示范应用[47]，未来将继续探索如何克服市场认知度和技术成熟度等挑战，逐步扩大RPFC的应用范围。
附 录
附表1 层次分析法的判断矩阵
App.Tab.1 Judgment matrix of analytic hierarchy process
综合承载力指标互联均衡度网损率线路容量充裕度 互联均衡度123 网损率1/212 线路容量充裕度1/31/21
光伏发电机组输出功率主要受光照强度影响，一般认为光照强度服从Beta分布[48]，描述为
（A1）
式中，r和rmax分别为该时段的太阳实际辐照度和最大辐照度；
(·)为Gamma函数；
和
均为Beta分布的形状参数，取=2.8，=1.2。
由于光伏发电功率与光照强度近似成正比，因此，得到光伏发电功率服从Beta分布的概率密度分布函数为
（A2）
式中，PPV为光伏机组实际运行功率；PPV.N为光伏机组额定功率。结合附表2中光伏机组某日实际运行功率便可得到其概率密度分布。
附表2 光伏机组某日实际运行功率
App.Tab.2 Actual operating power of the photovoltaic unit on a certain day
时间/h有功功率/kW时间/h有功功率/kW 1013187.76 2014172.11 3015165.10 4016158.22 501785.31 658.38180 796.77190 8115.36200 9160.75210 10193.89220 11191.02230 12194.51240
风机出力的不确定性取决于风能的不确定性，风速一般认为服从两参数Weibull分布[49]，其概率密度函数为
（A3）
式中，v为实际风速；c为尺度系数，表征风速分布离散程度；s为形状系数。本文引用文献[50]中的参数，取c=1.9，s=5.78 m/s。
风机的输出功率与风速的关系为
（A4）
式中，PWT为风机输出功率；Pr为风机额定最大功率；vr为额定风速；vci为启动风速；vco为截止风速。本文引用文献[51]中的参数，取vr=11 m/s，vci=3 m/s，vco=20 m/s。式（A4）与式（A3）相结合可得到风机输出功率及其概率密度分布。
附图1 改进引力场算法流程
App.Fig.1 Improved gravitation field algorithm flow chart
附图2 Tent混沌映射分布
App.Fig.2 Tent chaos map distribution
附图3 风机典型场景
App.Fig.3 Typical scenarios of wind turbines
附图4 光伏典型场景
App.Fig.4 Typical scenarios of photovoltaics
附图5 分时电价
App.Fig.5 Time-of-use electricity price
附表3 配电台区节点及负荷参数
App.Tab.3 Node and load parameters of the distribution station area
首节点末节点电阻(pu)电抗(pu)末端有功功率/MW末端无功功率/Mvar 140.0750.102.01.6 450.080.113.01.5 460.090.182.00.8 670.040.041.51.2 280.110.114.02.7 890.080.115.03.0 8100.110.111.00.9 9110.110.110.60.1 9120.080.114.52.0 3130.110.111.00.9 13140.090.121.00.7 13150.080.111.00.9 15160.040.042.11.0
附表4 仿真算例其他参数
App.Tab.4 Other parameters of the simulation example
参数数值 贴现率0.08 RPFC经济使用年限/年25 单位容量RPFC设备成本/[元/(kV·A)]233.8 单位容量RPFC建设成本/[元/(kV·A)]100 单位容量RPFC运行维护成本系数0.008 配置RPFC最大容量值/(MV·A)5 配置RPFC单位容量值/(MV·A)0.1 RPFC等效电阻(pu)0.025 SOP经济使用年限/年20 单位容量SOP设备成本/[元/(kV·A)]1 000 单位容量SOP建设成本/[元/(kV·A)]100 单位容量SOP运行维护成本系数0.01 配置SOP最大容量值/(MV·A)5 配置SOP单位容量值/(MV·A)0.1 馈线1主变额定容量/(MV·A)20 馈线2主变额定容量/(MV·A)20 馈线3主变额定容量/(MV·A)10 电压下限值/kV9.3 电压上限值/kV10.7
参考文献
[1] 徐玉韬, 冯起辉, 谈竹奎, 等. 考虑转供与重构协同的多端柔性互联配电网供电恢复策略[J]. 电工技术学报, 2024, 39(9): 2696-2709. Xu Yutao, Feng Qihui, Tan Zhukui, et al. Optimal power restoration strategy for multi-terminal flexible interconnected distribution networks based on flexible interconnection device and network reconfiguration [J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2696-2709.
[2] 徐旖旎, 刘海涛, 熊雄, 等. 低压配电台区柔性互联关键技术与发展模式[J]. 中国电机工程学报, 2022, 42(11): 3986-4001. Xu Yini, Liu Haitao, Xiong Xiong, et al. Key technologies and development modes of flexible interconnection of low-voltage distribution station area[J]. Proceedings of the CSEE, 2022, 42(11): 3986-4001.
[3] 曹昉, 郑金钊, 郑怡馨. 基于VSC的优质光伏资源区配电台区柔性互联规划方法[J]. 南方电网技术, 2023, 17(1): 14-25. Cao Fang, Zheng Jinzhao, Zheng Yixin. VSC-based flexible interconnection planning method for distri-bution station areas of high-quality photovoltaic resource[J]. Southern Power System Technology, 2023, 17(1): 14-25.
[4] 朱建昆, 高红均, 贺帅佳, 等. 考虑供电能力提升的低压配电网柔性互联规划[J]. 高电压技术, 2024, 50(8): 3545-3554. Zhu Jiankun, Gao Hongjun, He Shuaijia, et al. Flexible interconnection planning of low-voltage station area distribution network considering power supply capacity improvement[J]. High Voltage Engineering, 2024, 50(8): 3545-3554.
[5] 王婷, 陈晨, 谢海鹏. 配电网对分布式电源和电动汽车的承载力评估及提升方法综述[J]. 电力建设, 2022, 43(9): 12-24. Wang Ting, Chen Chen, Xie Haipeng. Review on evaluation and promotion methods of carrying capacity for distributed generation and electric vehicles in distribution network[J]. Electric Power Construction, 2022, 43(9): 12-24.
[6] 王书征, 赵洋, 李沛林, 等. 考虑电压-无功调节的台区互联装置规划方法[J]. 电力工程技术, 2024, 43(3): 111-120. Wang Shuzheng, Zhao Yang, Li Peilin, et al. Planning method of station area interconnection device considering voltage-reactive power regulation[J]. Electric Power Engineering Technology, 2024, 43(3): 111-120.
[7] 王皓靖, 郭佩乾, 时珊珊, 等. 中压配电网多台区柔性互联技术应用现状与展望[J]. 电力系统自动化, 2025, 49(5): 13-23. Wang Haojing, Guo Peiqian, Shi Shanshan, et al. Application status and prospects of multi-substation flexible interconnection technology in medium-voltage distribution networks[J]. Automation of Electric Power Systems, 2025, 49(5): 13-23.
[8] 李勇, 凌锋, 乔学博, 等. 基于网侧资源协调的自储能柔性互联配电系统日前-日内优化[J]. 电工技术学报, 2024, 39(3): 758-773, 923. Li Yong, Ling Feng, Qiao Xuebo, et al. Day-ahead and intra-day optimization of flexible interconnected distribution system with self-energy storage based on the grid-side resource coordination[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 758-773, 923.
[9] Zhang Shenxi, Fang Yichen, Zhang Heng, et al. Maximum hosting capacity of photovoltaic generation in SOP-based power distribution network integrated with electric vehicles[J]. IEEE Transactions on Indus-trial Informatics, 2022, 18(11): 8213-8224.
[10] 杨剑锋, 李婷, 杨爱民, 等. 含电能路由器的光伏配电网电压越限问题潮流优化研究[J]. 发电技术, 2025, 46(1): 113-125. Yang Jianfeng, Li Ting, Yang Aimin, et al. Research on tidal optimization of voltage overrun problem in photovoltaic distribution network with electrical energy router [J]. Power Generation Technology, 2025, 46(1): 113-125.
[11] 祁琪, 姜齐荣, 许彦平. 智能配电网柔性互联研究现状及发展趋势[J]. 电网技术, 2020, 44(12): 4664-4676. Qi Qi, Jiang Qirong, Xu Yanping. Research status and development prospect of flexible interconnection for smart distribution networks[J]. Power System Technology, 2020, 44(12): 4664-4676.
[12] 张沈习, 王浩宇, 李然, 等. 考虑智能软开关接入的主动配电网扩展规划方法[J]. 中国电机工程学报, 2023, 43(1): 48-61. Zhang Shenxi, Wang Haoyu, Li Ran, et al. Active distribution network expansion planning method considering the integration of soft open point[J]. Proceedings of the CSEE, 2023, 43(1): 48-61.
[13] 熊正勇, 陈天华, 杜磊, 等. 基于改进灵敏度分析的有源配电网智能软开关优化配置[J]. 电力系统自动化, 2021, 45(8): 129-137. Xiong Zhengyong, Chen Tianhua, Du Lei, et al. Optimal allocation of soft open point in active distribution network based on improved sensitivity analysis[J]. Automation of Electric Power Systems, 2021, 45(8): 129-137.
[14] 葛少云, 侯亭玉, 吴鸣, 等. 柔性互联配电网分布式电源承载能力分布鲁棒优化模型[J]. 电力系统自动化, 2023, 47(13): 140-148. Ge Shaoyun, Hou Tingyu, Wu Ming, et al. Dis-tributionally robust optimization model of hosting capability for distributed generators in flexible inter-connected distribution network[J]. Automation of Electric Power Systems, 2023, 47(13): 140-148.
[15] 王灿, 吴耀文, 孙建军, 等. 基于柔性多状态开关的主动配电网双层负荷均衡方法[J]. 电力系统自动化, 2021, 45(8): 77-85. Wang Can, Wu Yaowen, Sun Jianjun, et al. Bi-layer load balancing method in active distribution network based on flexible multi-state switch[J]. Automation of Electric Power Systems, 2021, 45(8): 77-85.
[16] Yan Xiangwu, Peng Weifeng, Wang Yang, et al. Flexible loop closing control method for an active distribution network based on dual rotary phase shifting transformers[J]. IET Generation, Transmission & Distribution, 2022, 16(20): 4204-4214.
[17] 邵晨, 颜湘武, 贾焦心, 等. 面向“花瓣型”配电网的旋转潮流控制器两阶段转速功率控制策略[J].电工技术学报, 2025, 40(1): 52-63. Shao Chen, Yan Xiangwu, Jia Jiaoxin, et al. Two-stage speed-power control strategy for rotating power flow controller in "petal-shaped" distribution networks[J]. Transactions of China Electrotechnical Society, 2025, 40(1): 52-63.
[18] Ba A O, Peng Tao, Lefebvre S. Rotary power-flow controller for dynamic performance evaluation: Part I: RPFC modeling[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1406-1416.
[19] 颜湘武, 彭维锋, 贾焦心, 等. 基于转速自适应控制的旋转潮流控制器功率调节方法研究[J]. 中国电机工程学报, 2023, 43(13): 4971-4987. Yan Xiangwu, Peng Weifeng, Jia Jiaoxin, et al. Research on power regulation method of rotary power flow controller based on speed adaptive control[J]. Proceedings of the CSEE, 2023, 43(13): 4971-4987.
[20] 颜湘武, 邵晨, 吴鸣, 等. 基于电磁式旋转潮流控制器的有源配电网多场景控制[J]. 电工技术学报, 2023, 38(增刊1): 44-55. Yan Xiangwu, Shao Chen, Wu Ming, et al. Multi-scene control method of active distribution network based on electromagnetic rotating power flow controller[J]. Transactions of China Electrotechnical Society, 2023, 38(S1): 44-55.
[21] 李铁成, 李晓军, 杨鹏, 等. 基于柔性互联的有源配电网协调优化降损方法[J/OL]. 华北电力大学学报(自然科学版), 2024: 1-10. http://kns.cnki.net/ kcms/detail/13.1212.TM.20240111.1446.002.html. Li Tiecheng, Li Xiaojun, Yang Peng, et al. Coordinated optimal loss reduction method of active distribution network based on flexible interconnection [J/OL]. Journal of North China Electric Power University, 2024: 1-10. http://kns.cnki.net/kcms/ detail/ 13.1212.TM.20240111.1446.002.html.
[22] 颜湘武, 李洋洋, 卢俊达, 等. 考虑旋转潮流控制器和需求响应的配电网新能源承载力评估方法[J/OL]. 电力系统及其自动化学报, 1-10[2024-09-26]. https://doi.org/10.19635/j.cnki.csu-epsa.001490. Yan Xiangwu, Li Yangyang, Lu Junda, et al. Asses-sment method of new energy hosting capacity in distribution grid considering rotary power flow controllers and demand response[J/OL]. Proceedings of the CSU-EPSA, 1-10[2024-09-26]. https://doi.org/ 10.19635/j.cnki.csu-epsa.001490.
[23] 王成山, 宋关羽, 李鹏, 等. 考虑分布式电源运行特性的有源配电网智能软开关SOP规划方法[J]. 中国电机工程学报, 2017, 37(7): 1889-1897. Wang Chengshan, Song Guanyu, Li Peng, et al. Optimal configuration of soft open point for active distribution network considering the characteristics of distributed generation[J]. Proceedings of the CSEE, 2017, 37(7): 1889-1897.
[24] 马丽, 薛飞, 石季英, 等. 有源配电网分布式电源与智能软开关三层协调规划模型[J]. 电力系统自动化, 2018, 42(11): 86-93. Ma Li, Xue Fei, Shi Jiying, et al. Tri-level coordinated planning model of distributed generator and intelligent soft open point for active distribution network[J]. Automation of Electric Power Systems, 2018, 42(11): 86-93.
[25] 冯智莉, 易国洪, 李普山, 等. 并行化遗传算法研究综述[J]. 计算机应用与软件, 2018, 35(11): 1-7, 80. Feng Zhili, Yi Guohong, Li Pushan, et al. Review of parallel genetic algorithm[J]. Computer Applications and Software, 2018, 35(11): 1-7, 80.
[26] Huang Lan, Hu Xuemei, Wang Yan, et al. Gravitation field algorithm with optimal detection for unconstrained optimization[C]//2017 4th International Conference on Systems and Informatics (ICSAI), Hangzhou, China, 2017: 1411-1416.
[27] 陈世明, 刘俊恺, 肖娟. 基于引力场优化的Unscented FastSLAM2.0算法[J]. 控制理论与应用, 2018, 35(8): 1186-1193. Chen Shiming, Liu Junkai, Xiao Juan. Unscented Fast SLAM2.0 algorithm based on gravitational field optimization[J]. Control Theory & Applications, 2018, 35(8): 1186-1193.
[28] 胡雪梅. 爆炸引力场算法及其应用研究[D]. 长春: 吉林大学, 2023. Hu Xuemei. Research on explosion gravitation field algorithm and its application[D]. Changchun: Jilin University, 2023.
[29] 贾焦心, 彭维锋, 颜湘武, 等. 基于余弦定理的旋转潮流控制器功率解耦控制方法[J]. 电工技术学报, 2023, 38(13): 3425-3435. Jia Jiaoxin, Peng Weifeng, Yan Xiangwu, et al. Research on power decoupling control method rotary power flow controller based on cosine law[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3425-3435.
[30] 颜湘武, 邵晨, 彭维锋, 等. 基于旋转式潮流控制器的有源配电网柔性合环及紧急功率控制方法[J]. 中国电机工程学报, 2023, 43(16): 6192-6204. Yan Xiangwu, Shao Chen, Peng Weifeng, et al. Flexible loop closing and emergency power control method for active distribution network based on the rotary power flow controller[J]. Proceedings of the CSEE, 2023, 43(16): 6192-6204.
[31] 谭振龙, 张春朋, 姜齐荣, 等. 旋转潮流控制器与统一潮流控制器和Sen Transformer的对比[J]. 电网技术, 2016, 40(3): 868-874. Tan Zhenlong, Zhang Chunpeng, Jiang Qirong, et al. Comparative research on rotary power flow controller, unified power flow controller and Sen transformer[J]. Power System Technology, 2016, 40(3): 868-874.
[32] 陈柏超, 刘雷, 余梦泽, 等. 电磁混合式潮流控制器本体优化及控制[J]. 高电压技术, 2017, 43(4): 1086-1094. Chen Baichao, Liu Lei, Yu Mengze, et al. Ontology optimization and control strategy of electromagnetic hybrid power flow controller[J]. High Voltage Engineering, 2017, 43(4): 1086-1094.
[33] 刘一兵, 吴文传, 张伯明, 等. 基于混合整数二阶锥规划的主动配电网有功–无功协调多时段优化运行[J]. 中国电机工程学报, 2014, 34(16): 2575-2583. Liu Yibing, Wu Wenchuan, Zhang Boming, et al. A mixed integer second-order cone programming based active and reactive power coordinated multi-period optimization for active distribution network[J]. Proceedings of the CSEE, 2014, 34(16): 2575-2583.
[34] 杨志淳, 朱炳兆, 操燕春, 等. 提高配电网承载力的分布式光伏双层规划方法[J]. 华中科技大学学报(自然科学版), 2024, 52(7): 69-75. Yang Zhichun, Zhu Bingzhao, Cao Yanchun, et al. Distributed photovoltaic bilevel programming method for improving carrying capacity of distribution net-works[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2024, 52(7): 69-75.
[35] 刘洪, 曹睿智, 韩俊, 等. 配电网的分布式发电承载能力评估研究现状与未来展望[J/OL]. 电力系统自动化, 2024: 1-13. http://kns.cnki.net/kcms/detail/ 32.1180.TP.20240802.1559.004.html. Liu Hong, Cao Ruizhi, Han Jun, et al. Research status and future prospect of distributed generation hosting capacity assessment of distribution network [J/OL]. Automation of Electric Power Systems, 2024: 1-13. http://kns.cnki.net/kcms/detail/32.1180.TP.20240802.1559.004.html.
[36] 王强强, 姚良忠, 盛万兴, 等. 基于机会约束规划的配电网分布式光伏承载力提升方法[J]. 电力系统自动化, 2023, 47(18): 132-141. Wang Qiangqiang, Yao Liangzhong, Sheng Wanxing, et al. Enhancement method for distributed photovoltaic hosting capacity of distribution network based on chance-constrained programming[J]. Automation of Electric Power Systems, 2023, 47(18): 132-141.
[37] 戴松灵, 王晞, 刘方, 等. 考虑综合承载力的主动配电网优化调度与运行[J]. 电力建设, 2020, 41(2): 67-75. Dai Songling, Wang Xi, Liu Fang, et al. Optimal scheduling and operating of active distribution network considering comprehensive carrying capacity[J]. Electric Power Construction, 2020, 41(2): 67-75.
[38] 何叶, 杨晓东, 吴红斌, 等. 面向新型配电系统灵活性提升的智能软开关与储能系统协调规划[J]. 电力系统自动化, 2023, 47(18): 142-150. He Ye, Yang Xiaodong, Wu Hongbin, et al. Coordinated planning of soft open point and energy storage system for flexibility enhancement of new distribution system[J]. Automation of Electric Power Systems, 2023, 47(18): 142-150.
[39] 郝文斌, 孟志高, 张勇, 等. 新型电力系统下多分布式电源接入配电网承载力评估方法研究[J]. 电力系统保护与控制, 2023, 51(14): 23-33. Hao Wenbin, Meng Zhigao, Zhang Yong, et al. Carrying capacity evaluation of multiple distributed power supply access to the distribution network with the background of a new power system[J]. Power System Protection and Control, 2023, 51(14): 23-33.
[40] Farivar M, Low S H. Branch flow model: relaxations and convexification: part I[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2554-2564.
[41] 娄素华, 胡斌, 吴耀武, 等. 碳交易环境下含大规模光伏电源的电力系统优化调度[J]. 电力系统自动化, 2014, 38(17): 91-97. Lou Suhua, Hu Bin, Wu Yaowu, et al. Optimal dispatch of power system integrated with large scale photovoltaic generation under carbon trading environment[J]. Automation of Electric Power Systems, 2014, 38(17): 91-97.
[42] 赵书强, 要金铭, 李志伟. 基于改进K-means聚类和SBR算法的风电场景缩减方法研究[J]. 电网技术, 2021, 45(10): 3947-3954. Zhao Shuqiang, Yao Jinming, Li Zhiwei. Wind power scenario reduction based on improved K-means clustering and SBR algorithm[J]. Power System Technology, 2021, 45(10): 3947-3954.
[43] 鲜杏, 范传光, 文闪闪, 等. 考虑可再生能源随机性的孤岛微网容量优化配置方法[J]. 武汉大学学报(工学版), 2016, 49(1): 100-104, 125. Xian Xing, Fan Chuanguang, Wen Shanshan, et al. Optimal deployment for island microgrid considering probabilistic factors of renewable energy generations [J]. Engineering Journal of Wuhan University, 2016, 49(1): 100-104, 125.
[44] 李宏玉, 张孝民, 姜晨辉, 等. 基于改进飞蛾扑火算法的电动汽车充电站选址[J]. 电气自动化, 2023, 45(5): 113-114, 118. Li Hongyu, Zhang Xiaomin, Jiang Chenhui, et al. Location selection of electric vehicle charging station based on improved moth-flame algorithm[J]. Electrical Automation, 2023, 45(5): 113-114, 118.
[45] 夏雨烁, 张新生, 王明虎. 基于ISSA-NESN的可再生能源电力需求预测研究[J]. 电网与清洁能源, 2023, 39(6): 136-143. Xia Yushuo, Zhang Xinsheng, Wang Minghu. A study on renewable energy power demand forecast based on ISSA-NESN[J]. Power System and Clean Energy, 2023, 39(6): 136-143.
[46] 郭清元, 吴杰康, 莫超, 等. 基于混合整数二阶锥规划的新能源配电网电压无功协同优化模型[J]. 中国电机工程学报, 2018, 38(5): 1385-1396. Guo Qingyuan, Wu Jiekang, Mo Chao, et al. A model for multi-objective coordination optimization of voltage and reactive power in distribution networks based on mixed integer second-order cone programming [J]. Proceedings of the CSEE, 2018, 38(5): 1385-1396.
[47] 国内首台旋转移相潮流调控装置投用[J]. 电子质量, 2024(7): 105. The first rotating phase power flow control device in China is put into use[J]. Electronics Quality, 2024(7): 105.
[48] 刘方, 杨秀, 时珊珊, 等. 基于序列运算的微网经济优化调度[J]. 电工技术学报, 2015, 30(20): 227-237. Liu Fang, Yang Xiu, Shi Shanshan, et al. Economic operation of micro-grid based on sequence operation [J]. Transactions of China Electrotechnical Society, 2015, 30(20): 227-237.
[49] 颜湘武, 徐韵, 李若瑾, 等. 基于模型预测控制含可再生分布式电源参与调控的配电网多时间尺度无功动态优化[J]. 电工技术学报, 2019, 34(10): 2022-2037. Yan Xiangwu, Xu Yun, Li Ruojin, et al. Multi-time scale reactive power optimization of distribution grid based on model predictive control and including RDG regulation[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2022-2037.
[50] 许昌, 杨建川, 李辰奇, 等. 复杂地形风电场微观选址优化[J]. 中国电机工程学报, 2013, 33(31): 58-64, 7. Xu Chang, Yang Jianchuan, Li Chenqi, et al. Optimization of wind farm layout in complex terrain [J]. Proceedings of the CSEE, 2013, 33(31): 58-64, 7.
[51] 颜湘武, 卢俊达, 贾焦心, 等. 含循环换电负荷及充电站的微电网多目标优化调度[J]. 华北电力大学学报(自然科学版), 2024, 51(2): 1-12. Yan Xiangwu, Lu Junda, Jia Jiaoxin, et al. A multi-objective optimal dispatch of microgrid with cyclic swapping loads and charging stations[J]. Journal of North China Electric Power University (Natural Science Edition), 2024, 51(2): 1-12.
Abstract As a vital component of the power system, the power supply capacity within distribution station areas exerts a direct influence on urban economic development and the enhancement of residents' living standards. With the escalating integration of renewable energy sources, electric vehicles, and diversified load connections, these areas are confronted with significant challenges, including weak grid structures, uneven local load distribution, and inadequate carrying capacities. While the power electronic flexible interconnection device offers a potential solution to these issues, its high investment and operational costs hinder widespread adoption. In contrast, the rotary power flow controller (RPFC), an electromagnetic device, presents advantages such as cost-effectiveness and resilience to impacts. By enabling spatial regulation of line power flow, the RPFC can effectively bolster the bearing capacity of distribution areas, thereby enhancing their overall carrying capacity.
Firstly, the steady-state power flow model of the RPFC is established. The RPFC is a flexible interconnection device that regulates power flow based on the rotary phase shifting transformer (RPST) principle. Adjusting both the amplitude and phase of the series voltage allows for precise control of power flow along the line. Based on this, a flexible interconnection structure of the distribution station area containing RPFC is proposed.
Secondly, a bi-level programming framework for RPFC is proposed for improving the economy and comprehensive carrying capacity of the distribution station area, which includes the RPFC site selection and capacity determination layer and the operation optimization layer. The upper layer is the RPFC site selection and capacity determination layer. This layer obtains typical scenarios based on the scenario reduction method of Kantorovich distance. The optimization goal is to minimize the total investment cost of the distribution station area. At the same time, under the condition of satisfying the RPFC power constraint and capacity constraint, the current optimal location and capacity of RPFC are generated, and then the RPFC determination scheme is passed to the lower layer. The lower layer is the operation optimization layer. The optimization goal is to maximize the comprehensive carrying capacity of the distribution station area. Based on the upper layer configuration scheme, this layer solves the optimal operating power of RPFC under each scenario, and then feeds back the optimization results such as RPFC transmission power and branch power flow to the upper layer. The layers optimize each other to obtain the optimal configuration planning and operation optimization scheme.
Then, a bi-level programming model of the distribution station area containing RPFC is constructed based on the proposed bi-level programming framework. To improve the optimization speed and accuracy, an improved gravitational field algorithm is proposed, combined with second-order cone planning to form a hybrid optimization algorithm to solve the proposed bi-level programming model.
Finally, the proposed model and algorithm are validated through simulation examples. The simulation results indicate that the proposed IGFA-SOCP hybrid optimization algorithm enhances global search capability while reducing the difficulty of solving multi-layer models, thereby optimizing the overall model-solving process and reducing solution time. This verifies the correctness and effectiveness of the proposed model and solution algorithm.
keywords：Distribution station area, comprehensive carrying capacity, rotary power flow controller, improved gravitation field algorithm, bi-level programming
DOI: 10.19595/j.cnki.1000-6753.tces.L11059
中图分类号：TM732
国家电网有限公司总部科技项目资助（5108-202218280A-2-227-XG）。
收稿日期 2024-10-16
改稿日期 2024-11-21
颜湘武 男，1965年生，教授，博士生导师，研究方向为新能源电力系分析与控制、现代电力与变换、新型储能与节能等。E-mail：xiangwuy@ncepu.edu.cn
卢俊达 男，1998年生，博士研究生，研究方向为新能源发电与智能微电网，配电网优化调度等。E-mail：lujd777@163.com（通信作者）
（编辑 赫 蕾）