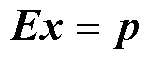（1）摘要 大型电气设备在进行有限元分析时，会遇到大规模数值计算问题。代数方程组阶数巨大导致计算时间长，计算效率低，有时甚至无法求解。该文研究有限元代数方程组的降阶求解，推导了分块迭代算法、正交降阶分解算法（OORDA），将禁忌搜索算法引入高斯消元法形成改进的高斯消元法（IGEM），提出了分块迭代算法分别与OORDA和IGEM相结合的方程组混合降阶算法，并通过编程实现。将OORDA、IGEM和两种混合降阶算法分别应用于长直载流导体的磁场有限元计算中，计算结果与解析解的对比验证了算法的正确性。将四种算法应用到单相变压器的磁场有限元计算中，两种混合降阶算法能够快速大幅降低方程组阶数，提高计算效率。该文提出的降阶算法可应用于电工装备物理场的大规模数值计算中，能显著提高复杂模型的有限元计算效率。
关键词：有限元分析 代数方程组 降阶算法 大规模数值计算 计算效率
电气设备、系统数字孪生技术的发展需要进行大量计算[1-4]。当研究对象庞大、模型复杂时，为保证计算和仿真的实时、快速和准确性[5-7]，常常需要进行降阶处理[8-9]，包括系统模型降阶[10-12]、控制策略降阶[13]、代数方程组降阶[14]等。
大型电气设备在进行有限元分析时，为保证计算精度，剖分网格数量庞大，从而导致有限元代数方程组阶数巨大，方程组求解十分困难[15-16]。大量内存的占用使得计算时间极长，计算效率低，有时甚至无法求解。方程组求解的计算量与阶数的三次方成正比，计算时间则随方程组阶数的增大呈指数级的增长。对方程组进行降阶处理，计算量将大幅减少，对大规模数值计算问题的解决具有重要意义。
针对代数方程组降阶的研究，常用的方法有正交降阶分解算法（Orthogonal Order-Reduced Decompo-sition Algorithm, OORDA）[17]、低秩近似[18]、分组降阶算法[19]、广义特征分解方法（Proper Generalized Decomposition, PGD）[20]和分块迭代算法[21]等。OORDA是基于正交分解法提出的，能够通过正交化逐层降低系数矩阵阶数，通过回代求出方程组的解，在电磁、机械领域工程中使用较多。与高斯消去法相比，它能更好地保持数值的稳定性，但是内存占用没有明显的改善，而且逐层的降阶效率较低。低秩近似不适用于满秩矩阵，分组降阶算法与传统算法相比，运算量有所增加。广义特征分解方法在减少计算量的同时，保持了算法的拟最优性。但是对于某些矩阵精度较差，迭代次数不易确定，需要选择合适的参数。
分块迭代算法将系数矩阵、未知量向量和右端向量进行分块，将每一个子块视为一个元素，按照点迭代进行降阶，进行一次可以将方程组阶数降为原来的一半。用于方程组降阶的分块迭代算法研究主要集中在数学领域，且分块过程未有详细的数学模型，分块迭代算法在工程领域的研究和应用较少。
本文详细推导了分块迭代算法，提出了用于原始矩阵变换的分块对角化和用于实现矩阵分块的分块左乘法。此外，本文还推导了OORDA，将禁忌搜索算法引入高斯消元法形成改进的高斯消元法（Improving Gaussian Elimination Method, IGEM）[22]，提出了分块迭代算法分别与OORDA和IGEM相结合的方程组混合降阶算法。针对磁场有限元分析形成的刚度矩阵，应用分块迭代算法进行降阶。降阶后的方程组可以采用OORDA求解，既能大幅降低原刚度矩阵的阶数，又能保证数值稳定性。也可以采用IGEM，计算效率更高，内存占用更少。将两种混合降阶算法、OORDA和IGEM分别应用于长直载流导体的磁场有限元计算中，计算结果与解析解的对比验证了算法的正确性。将四种算法应用于单相变压器的磁场有限元计算中，并对计算结果进行分析。
分块迭代算法通过矩阵变换将系数矩阵进行分块重组。原系数矩阵数据信息在分块过程中通过算法进行留存，分块的过程即为降阶的过程，每进行一次分块，阶数可以降低一半，而且可以重复降阶。
对于n阶的线性代数方程组，有
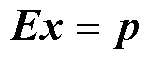（1）
若E为分块矩阵，有
（2）
x、p为分块向量，有
（3）
式中，I11为r×r的单位矩阵；I22为(n-r)×(n-r)的单位矩阵。
式（1）可以表述为
（4）
由式（4）可得
（5）
将式（5）代入式（4）可得
（6）
式（6）为r×r的方程组，求解x1，代入式（5），可计算得到x2。
因此，n×n阶的线性代数方程组的求解就降阶为求解r×r阶的线性代数方程组。
根据麦克斯韦方程，电工装备的电磁场可表示为椭圆形偏微分方程定解问题。采用有限元法求解时，可得到与离散单元相关的代数方程组。若电工装备尺寸庞大，为保证计算精度，需要大量的离散单元，导致代数方程组的阶数很高，求解时需要大量的计算资源和计算时间，有时甚至无法求解。对方程组进行降阶处理，能够显著提高计算效率。
对于有限元分析得到的n阶线性代数方程组，有
（7）
若要进行降阶，将原始刚度矩阵K转换为如式（2）所示的分块矩阵的过程包含两个阶段。
阶段1：将原始刚度矩阵K转换为对角矩阵A1。
（8）
式中，A1为对角线形式的矩阵；Ii为ni×ni的单位阵；Zi和Yi分别为可以进行规则移动的子矩阵块，Zi的转置与Yi形式相同，但数据不同，并非转置关系。对角线中单位矩阵的阶数由数据分布确定。当单位阵Ii的阶数确定后，Zi和Yi的阶数即可确定。例如Z2的列数与I2相同，Z2的行数与I3相同，Y2的列数与I3相同，Y3的行数与I2相同。
如何由K转换为A1，未见有文献给出，本文提出分块对角化的方法来实现此转换，推导如下。
（1）首先将矩阵K的对角线元素变为1。
（2）根据矩阵中的数据分布，在对角线处构造单位矩阵，将I1设置为一阶单位阵，I2～Im-1为二阶或二阶以上的单位阵，Im为一阶或任意阶的单位阵，设置时以尽可能保留原矩阵数据为原则。当单位阵Ii的阶数确定后，对应的行列元素形成相应的Zi和Yi，即可确定A1。
（3）为保障式（7）的恒等性，对角形式矩阵A1可表示为有限元刚度矩阵K左乘变化矩阵R1，即
（9）
其中
（10）
则变化矩阵R1为
（11）
式（9）转换为
（12）
阶段2：将对角矩阵A1转换为分块矩阵。
将A1进行分块组合（设m为偶数），变成A(1)的形式为
（13）
将矩阵A1中的子矩阵块进行分块移动，这个运算过程文献[21]提出通过寻找置换矩阵，再进行矩阵运算，但并未给出具体模型。本文提出了一种更为直观的分块左乘法，通过求解方程直接得到未知量。分别建立了这两种方法的数学模型，并通过编程实现。
1）置换矩阵法
对于矩阵A1存在一个置换矩阵P，使得
（14）
式（12）两端左乘置换矩阵P，得到
（15）
设
（16）
代入式（15），有
（17）
2）分块左乘法
矩阵A1左乘一个矩阵R2，转换为A(1)，即
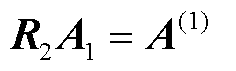（18）
则矩阵R2为
（19）
式（12）的两端左乘矩阵R2得到
（20）
即
（21）
需要注意的是，式（17）和式（21）中A(1)为相同的分块矩阵，可以进行降阶计算。但是由式（21）可以直接计算得到x，而式（17）计算得到的是y，需进一步由式（16）计算得到x。
两种方法都需要进行C++编程，从实现过程来看，置换矩阵法更为直观，左乘矩阵法在矩阵推导、程序编制方面的难度更大一些。
降阶算法的计算时间包含三个部分：方程组降阶、计算r阶方程组、代入计算n-r个未知数。其中第三部分代入计算消耗的时间很少。方程组阶数较低时，直接求解n阶方程组更快，采用降阶算法反而耗时较长。当方程组阶数高时，直接求解n阶方程组的计算时间迅速增加，方程组降阶及计算降阶后的r阶方程组所需的时间少于直接求解，故降阶算法的计算效率高于直接求解。当研究对象尺寸庞大、模型复杂时，有限元方程组阶数巨大，无法进行直接求解，降阶算法通过降阶使得超大型方程组的计算成为可能，这也是本文研究降阶算法的意义。
下面引用一个经典的推导有限元法计算过程的矩形槽算例[23]对分块迭代算法的降阶过程做一个说明。本文仅对单元分析和总体合成得到的刚度矩阵进行降阶计算，不讨论算例的实际计算结果。
矩形槽的三角形单元剖分如图1所示，矩形槽的磁场计算区域为
，采用三角形单元进行剖分，用φm求解磁场时满足的拉普拉斯方程边值问题为
图1 矩形槽的三角形单元剖分
Fig.1 Rectangular slot triangular meshing
（22）
式中，
为未知函数；s1为第一类边界；s2为第二类边界。
剖分后有8个单元和10个节点，每个直角三角形单元的直角边长均为1。通过有限元分析的单元分析和总体合成，得到代数方程组的刚度矩阵为
（23）
下面对K进行降阶运算。
1）阶段1：将矩阵K转换为对角矩阵A1。
首先将矩阵K的对角线元素变为1，每行元素均除以对角线元素，K变为
。
（24）
由于算例较为简单，对角线处已呈现单位对角阵，矩阵即为对角矩阵，=A1。写成式（25）分块矩阵的形式，可直接进行分块重组。
（25）
式（25）中的子矩阵块与式（24）中划分的子矩阵块一一对应。由于本算例单元少且剖分规整，有限元总体合成得到的刚度矩阵K经过将对角线元素变为1即可转换为A1。对于形状复杂、剖分单元多的模型，则需使用本文提出的分块对角化算法实现这一转换。本算例的二次降阶亦需使用这一算法，算法在二次降阶过程中有详细推导。
2）阶段2：将矩阵A1转换为分块矩阵A(1)。
下面对矩阵A1进行分块运算，将矩阵中的子矩阵块进行移动，转换成A(1)的形式，有
（26）
（27）
（28）
（29）
上述分块的过程可以通过推导置换矩阵，再进行矩阵运算实现，也可以通过本文提出的左乘矩阵法实现。因为本文提出的方法求解方程能够直接得到x，而置换矩阵的方法不能直接求得x（前面讨论过），所以后面的推导和计算过程均采用本文提出的方法。矩阵分块之后，方程组可写为
（30）
即
（31）
由式（31）可得到
（32）
（33）
令
（34）
求解式（33）的5阶代数方程组，可得
，代入式（32），可得
。于是求解有限元分析得到的10阶代数方程组就降为求解5阶代数方程组，计算量大幅降低。
式（33）的系数矩阵可继续进行降阶，直到降为一阶或二阶的方程组，即可完成求解。
第二次降阶的过程如下。
式（33）可以被表述为
（35）
针对K1，采用本文提出的分块对角化算法确定A2，找到矩阵
，对式（35）两端左乘矩阵，以保证未知量的计算结果不变。K1变为A2的分块对角化过程如下。
1）将K1的对角线元素变为1，K1变为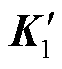
。
（36）
2）根据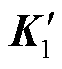中的数据分布，在对角线处构造单位矩阵，即将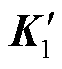对角线附近的某些元素置零，置零时以尽可能多地保留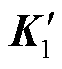中的数据为原则，于是得到对角矩阵A2。
为保证式（35）的恒等性，K1到A2的转换可表示为式（35）左乘矩阵，即
（38）
其中
（39）
确定K1与A2后，矩阵R1(2)为
（40）
式（38）即为
（41）
对矩阵A2进行分块操作，转换为矩阵A(2)的形式，有
（43）
（44）
（45）
（46）
此时，只需要计算一个三阶方程组（45），计算出的未知量为x1(2)=[ζ1 ζ2 ζ3]T，代入式（46），计算出
=[ζ4 ζ5]T，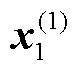
=[ζ1 ζ2 ζ3 ζ4 ζ5]T。将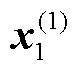代入式（32），计算出
=[ζ6 ζ7 ζ8 ζ9 ζ10]T，即可求解全部未知量x=[ζ1 ζ2 ζ3 ζ4 ζ5 ζ6 ζ7 ζ8 ζ9 ζ10]T。
从上面的推导过程可以看出，一个10阶的方程组，经过两次降阶处理，转换成三阶的方程组，一次分块阶数就降了一半，计算量大幅降低。当方程组阶数很高时，降阶效果尤为显著。
如果使用分块迭代算法单独求解，可以将方程组降为一阶或两阶，再反代回去，即可完成求解。但方程组阶数不高时，反复进行分块会消耗较长的计算时间，反而降低了降阶效果。因此，考虑使用其他方法与之结合，进行求解。
正交降阶分解算法基于Schur补定理将原系数矩阵的其他列向量分别与第一列正交化，一次降低一阶，重复此操作，直到降为一阶为止，最后进行反代，即可完成求解。
针对式（7）的系数矩阵K，根据Schur补定理，若矩阵K为非奇异矩阵，去掉矩阵K的第一列中第一个非零元素所在的行和列，剩下的n-1阶矩阵仍然为非奇异矩阵。
将矩阵K的每一列表示为一个列向量vi，即
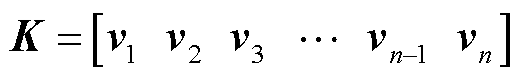（47）
将矩阵K的后n-1列分别与第一列进行正交化运算，有
（48）
式中，(v1,v2)表示v1与v2的内积。
于是矩阵K被转换为
（49）
（50）
式中，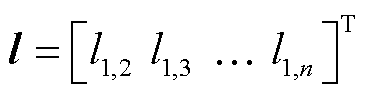
；I为n-1阶单位矩阵。
（51）
则线性方程组（7）变为
（52）
于是
（53）
（54）
式中，
。
式（53）两边左乘以
，得到
（55）
其中
（56）
（57）
求解可得
，未知量减少一个，由n个方程降为n-1个方程，有
（58）
上述过程可以使矩阵的任意列与其他列正交化。删除矩阵的第i行和第j列中的元素，矩阵将减少1阶。对降阶之后的矩阵重复上述操作，最后可将其降至1阶。在每一次正交降阶的过程中，
都能被解出。
（59）
当k=n时，yn=xn。
设
（60）
x与y之间的关系为
（61）
最后，通过回代法计算出x。
OORDA不需要计算逆矩阵，计算量比Gram Schmidt正交化QR法和双对角化方法小。它具有良好的数值稳定性，对病态问题更可靠。
高斯消元法属于直接求解方程组的方法，包括消元和回代两个过程。算法简单，但运算量大，计算时间长，占用内存多。当方程组达到一定阶数时，高斯消元法很难求解，因此高斯消元法很少在有限元法中使用。有限元分析得到的刚度矩阵是稀疏矩阵，里面含有大量的0元素，将禁忌搜索算法的思想引入高斯消元法中，形成IGEM。
此算法包含消元、建立信息表、回代三个过程。消元时检索系数矩阵第一列中的零元素，零元素所在行不参与运算，第一次消元完成后，同理进行下一行的消元，直到系数矩阵变为上三角矩阵。消元过程完成后，检索得到的上三角矩阵的非零元素，建立非零元素的位置信息表。回代时，代入信息表中相应位置的非零元素进行运算。综上所述，IGEM在消元与回代过程中，消除0元素对内存的占用以及相应增加的计算量，对于稀疏矩阵将大大降低高斯消元法的运算次数和计算量。
与禁忌搜索算法相结合的改进高斯消元法数学模型见表1。
表1 改进高斯消元法的数学模型
Tab.1 The mathematical model of the improving Gaussian elimination method
IGEM 消元for Kx=b for k=1 to n，i,e=k to n do if K [i] [k]≠0 then b [i]=b[i]- b [k] ×K [i] [k]÷K [k] [k] K [i] [e]=K [i] [e]- K [k] [e]×K [i] [k]÷K [k] [k] end if end for end for 建立信息表for j=1 to n , m=j to n do if K [j] [m]≠0 save j, m→C end if end for 回代for j, m∈C do x[j] = x[j]+ K [j][m] × x[m] x[j] =- x[j] ÷K [j][j] end for
将IGEM与普通的高斯消元法应用于不同阶数方程组的求解，方程组是本文算例单相变压器在不同网格剖分下由有限元分析得到的1 000、5 000、10 000阶稀疏矩阵。计算时间及误差见表2，误差是与用Matlab自带算法直接求解得到的结果比较得到。
可以看出，两种算法均具有很高的计算精度，IGEM求解不同阶数方程组的时间均明显小于普通的高斯消元法。同时，当方程组达到10 000阶时，普通高斯消元法的求解变得异常困难，很长时间未得到结果，而IGEM对于超过10 000阶的方程组在一定的时间内可以得到计算结果。
表2 高斯消元法计算时间对比
Tab.2 Comparison of calculation time using Gaussian elimination method
阶数普通的高斯消元法改进的高斯消元法 时间/s误差(%)时间/s误差(%) 1 0002.12.008×10-120.952.035×10-12 5 0004041.498×10-11341.501×10-11 10 000＞7 200—1418.734 372×10-8
由于OORDA与高斯消元法占用的内存很大，而分块迭代算法可以对方程组进行大幅降阶，正好弥补了两种算法这一缺点。将分块迭代算法分别与OORDA和改进高斯消元法相结合来求解大型方程组，不仅使数值更加稳定，而且内存的占用也不会很大。
由于OORDA和高斯消元法都有显著的内存需求，而分块迭代算法可以大幅度降低方程组的阶数，同时分块迭代算法在方程组阶数低时不适用于单独求解。因此，将分块迭代算法与两种算法相结合是较好的选择。本文提出了将分块迭代算法与OORDA相结合的混合算法1（HA1），将分块迭代算法与IGEM相结合的混合算法2（HA2）。对于高阶方程，采用分块迭代算法对方程组进行降阶，通过OORDA或IGEM求解降阶方程组。将混合降阶算法应用于求解大型方程组，不仅使数值解更稳定，而且大大降低了内存消耗。
本文将OORDA、IGEM、HA1和HA2四种算法分别应用于磁场的有限元计算，求解了不同网格数量下的磁场分布，考察了不同计算规模下算法的计算精度和计算效率。
本文研究对象的网格剖分、有限元计算中的单元分析与刚度矩阵合成均通过Ansys APDL命令流编程完成，提取单元和节点数据以及总体刚度矩阵的信息，通过C++编程还原总体刚度矩阵及其右端项，将本文研究的算法应用于方程组的求解。本文的算法通过C++编程实现，程序的运行环境为2.90GHz锐龙R7-4800H处理器和16 GB内存。
为了验证算法和程序的准确性，计算并讨论不同网格划分下电流为1 kA的长直载流导体的磁场分布。模型中，导线截面半径为0.01 m，计算场域是半径为0.3 m的圆形区域，计算场域最外层为边界。根据毕奥-萨伐尔定律，无限长直载流导体的磁感应强度为
（62）
式中，μ0为真空磁导率；I为流过长直载流导体的电流；r为采样点到导体的距离。
将本文提出的四种降阶算法应用于长直载流导体磁场有限元分析，并在场域中选取三个采样点，采样点位置信息及磁通密度解析解见表3。将三个采样点的计算结果与解析解进行比较，结果见表4，长直载流导体磁力线分布如图2所示。
表3 采样点的解析解
Tab.3 Analytical solution for sampling points
数据采样点 P1P2P3 (0.3,0)(0.1,0.17)(0.095,0.034) 到导线圆心(0,0)的距离/m0.30.20.1 磁通密度解析解/T6.67×10-40.0010.002
表4 降阶算法的验证
Tab.4 Verification of order-reduced algorithms
剖分规模算法相对误差(%) P1P2P3 剖分1OORDA3.527.709.99 IGEM2.568.1910.55 HA13.508.3810.87 HA23.268.969.05 剖分2OORDA1.897.619.03 IGEM1.598.099.54 HA11.846.517.29 HA21.867.799.78
图2 长直载流导体磁力线分布
Fig.2 Distribution of magnetic field lines produced by long straight wire carrying current
剖分1：节点数为1 096，单元数为2 146；剖分2：节点数为5 416，单元数为10 369。
从表4可以看出，降阶算法的计算结果与解析解吻合较好，验证了算法和程序的准确性。对于不同的网格划分，网格生成越细，计算精度越高。对于不同位置的取样点，离导体较近的点（P3）误差较大，离导体较远的点精度较高，符合毕奥-萨伐尔定律适用于离导体较远的点。
将上述算法和程序应用于一台单相变压器的磁场计算，DSP-241000/500型变压器参数见表5。
表5 单相变压器参数
Tab.5 Parameters of single-phase transformer
参数数值 额定容量/(MV·A)241 额定电压(kV/kV)550/18 高压绕组匝数635 低压绕组匝数36
单相变压器的网格剖分如图3所示，由Ansys APDL计算的磁通密度和磁力线分布如图4、图5所示。
图3 单相变压器剖分图
Fig.3 The meshes of single-phase transformer
图4 单相变压器磁通密度分布（Ansys）
Fig.4 Magnetic field distribution of single-phase transformer (Ansys)
图5 单相变压器磁力线分布（Ansys）
Fig.5 Distribution of magnetic field lines in single-phase transformers (Ansys)
图6和图7分别为使用混合算法2计算得到的磁通密度分布和磁力线分布。
图6 单相变压器磁通密度分布（自编程）
Fig.6 Magnetic field distribution of single phase transformer (self programming)
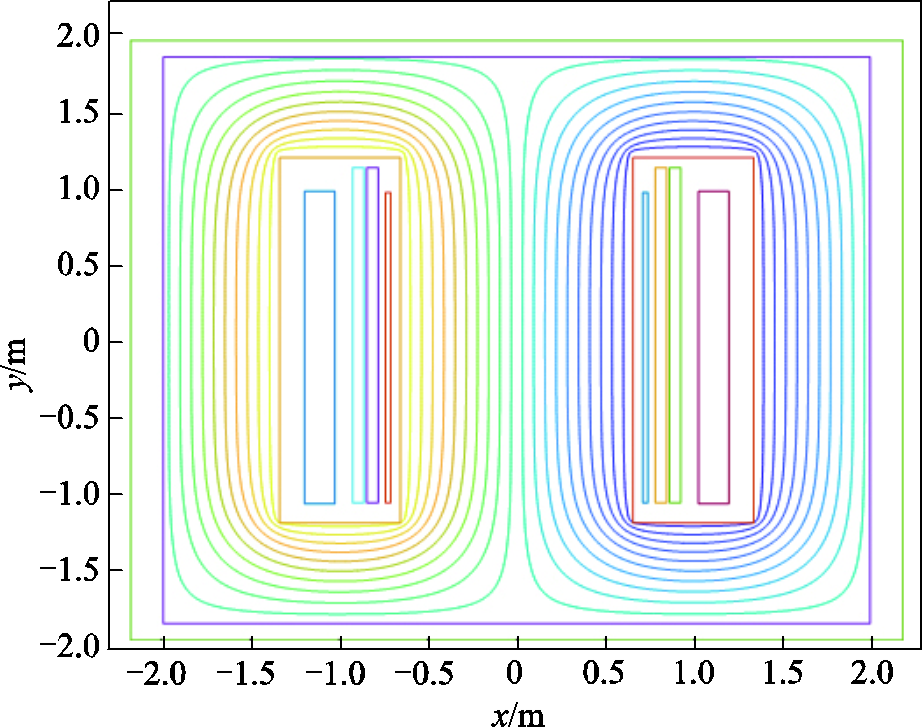
图7 单相变压器磁力线分布（自编程）
Fig.7 Distribution of magnetic field lines in single-phase transformers (self programming)
为考察算法在不同计算规模下的计算精度和计算效率，将变压器进行不同网格数量的剖分，四种算法的计算时间和计算精度分别见表6、表7，其相对误差是与Ansys APDL计算结果的比较而获得。
表6 单相变压器不同计算规模计算时间
Tab.6 Calculation time for single-phase transformer under different calculation scales
节点数单元数时间/s OORDAIGEMHA1HA2 7 97915 6241 31668183.814.6 12 34224 2702 967279835.149 20 68540 81611 4732 3084434251
表7 单相变压器不同计算规模计算精度
Tab.7 Calculation accuracy of single-phase transformers with different calculation scales
节点数单元数相对误差(%) OORDAIGEMHA1HA2 7 97915 6245×10-66.6×10-64×10-43×10-8 12 34224 2708×10-34.1×10-46×10-32×10-5 20 68540 8164×10-31.7×10-41×10-43×10-4
从表6和表7中可以看出，四种算法的计算结果与Ansys软件的有限元计算结果非常一致。随着计算规模的增大、方程组阶数的增加，OORDA和IGEM的计算时间急剧增加，导致计算效率降低，尤其是OORDA。过长的计算时间使得OORDA不适合单独求解。不过OORDA在求解的过程中不用计算逆矩阵，对于不便求逆的矩阵，这也不失为一种可行的选择。采用分块迭代算法降低方程组的阶数，然后采用OORDA或IGEM求解，大大提高了这两种算法的计算效率，计算规模越大，影响越显著。
分块迭代算法与改进高斯消元法相结合的混合降阶算法2计算效率的最高。可见分块迭代算法的降阶效果是十分显著的，对于方程组阶数巨大的大规模计算，可以使用分块迭代算法将方程组多次降阶，再进行求解，不仅能够大幅提升计算效率，也将使原本无法求解的计算可以进行成为可能。
本文研究有限元代数方程组的降阶和求解，将OORDA、IGEM以及分块迭代算法分别与OORDA、IGEM相结合的混合降阶算法应用于电工装备的磁场有限元计算中。结果表明，对于有限元分析得到的稀疏对称方程组，四种算法均具有较高的计算精度，分块迭代算法与IGEM相结合的混合降阶算法2的计算效率最高。分块迭代算法能够大幅降低方程组的阶数，分块迭代算法与OORDA、IGEM相结合能够显著提高这两种算法的计算效率。OORDA的计算时间较长，但对不便求逆的方程组具有较高的适用性。
有限元分析的计算时间与模型的大小和复杂程度密切相关，而降阶算法只与方程组的阶数相关。对于具有大物理尺寸、复杂模型的电工装备有限元分析遇到的大规模数值计算问题，本文研究的降阶算法能够为求解超大型代数方程组提供一种求解途径和参考。
参考文献
[1] 董华军, 温超阳, 孙鹏, 等. 基于正交实验新型真空灭弧室触头磁场仿真与参数优化设计[J]. 电工技术学报, 2022, 37(21): 5598-5606. Dong Huajun, Wen Chaoyang, Sun Peng, et al. Simulation and optimization of the contact magnetic field of a new type of vacuum interrupter based on orthogonal experiment[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5598-5606.
[2] 刘云飞, 张炳义, 宗鸣, 等. 基于非线性混合模型的模块组合式永磁电机磁场解析[J]. 电工技术学报, 2022, 37(18): 4593-4603. Liu Yunfei, Zhang Bingyi, Zong Ming, et al. Analytical prediction of magnetic field in modular combined permanent magnet motor by a nonlinear hybrid model[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4593-4603.
[3] 邱浩, 王曙鸿, 孙凤举, 等. 基于时域有限积分技术的四级串联快脉冲直线型变压器驱动源电磁特性[J]. 电工技术学报, 2022, 37(4): 816-826. Qiu Hao, Wang Shuhong, Sun Fengju, et al. The electromagnetic characteristics of the four-stage series-connected fast linear transformer driver based on time-domain finite integration technique[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 816-826.
[4] 黄天超, 王泽忠, 李宇妍. 换流变压器直流偏磁对油箱涡流损耗的影响[J]. 电工技术学报, 2023, 38(8): 2004-2014. Huang Tianchao, Wang Zezhong, Li Yuyan. The influence of converter transformer DC bias on eddy current loss of tank[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2004-2014.
[5] Guo Ze, Wang Shuhong, Tang Zuqi, et al. Fast time-domain solution of dynamic electromagnetic problems based on sinc interpolation[J]. IEEE Transactions on Magnetics, 2021, 57(6): 7200704.
[6] 赵志刚, 王丽美, 陈天缘, 等. 基于等效复数磁导率的利兹线绕组损耗计算模型[J]. 电工技术学报, 2024, 39(4): 948-955. Zhao Zhigang, Wang Limei, Chen Tianyuan, et al. Calculation model of winding loss of Litz-wire based on equivalent complex permeability[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 948-955.
[7] 龚天勇, 马光同, 任刚. 跑道型高温超导磁体的磁场解析计算模型[J]. 电工技术学报, 2023, 38(8): 1991-2003. Gong Tianyong, Ma Guangtong, Ren Gang. Analytical models for the magnetic field calculation of racetrack high-temperature superconducting magnet[J]. Transac-tions of China Electrotechnical Society, 2023, 38(8): 1991-2003.
[8] 刘刚, 胡万君, 郝世缘, 等. 油浸式变压器绕组瞬态温升降阶快速计算方法[J]. 电工技术学报, 2024, 39(3): 643-657. Liu Gang, Hu Wanjun, Hao Shiyuan, et al. Reduced order calculation method of steady temperature rise of oil immersed power transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 643-657.
[9] 刘刚, 郝世缘, 朱章宸, 等. 基于DMD-ATS油浸式电力变压器绕组瞬态温升快速计算方法研究[J]. 电工技术学报, 1-12[2025-04-02]. https://doi.org/10. 19595/j.cnki.1000-6753.tces.230465.Liu Gang, Hao Shiyuan, Zhu Zhangchen, et al. Research on rapid calculation method of transient temperature rise of winding of DMD-ATS oil-immersed power transformer[J]. Transactions of China Electro-technical Society, 1-12[2025-04-02].https://doi.org/ 10.19595/j.cnki.1000-6753. tces.230465
[10] 康军, 马凡, 胡健, 等. 一种多时间尺度线性系统模型降阶的误差预测方法[J]. 电工技术学报, 2017, 32(3): 56-64. Kang Jun, Ma Fan, Hu Jian, et al. An error prediction method of model order reduction for multi-time scale linear system[J]. Transactions of China Electro-technical Society, 2017, 32(3): 56-64.
[11] 许建成, 孙建军, 钟佩军, 等. 基于平衡实现理论的变流器并网系统降阶模型[J]. 电工技术学报, 2021, 36(增刊1): 255-264. Xu Jiancheng, Sun Jianjun, Zhong Peijun, et al. Reduced-order model of grid-connected converter system based on balanced realization theory[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 255-264.
[12] 陈鹏伟, 戚陈陈, 陈新, 等. 附加频率控制双馈风电场频率响应特性建模与参数辨识[J]. 电工技术学报, 2021, 36(15): 3293-3307.Chen Pengwei, Qi Chenchen, Chen Xin, et al. Frequency response modeling and parameter identification of doubly-fed wind farm with additional frequency control[J]. Transactions of China Electrotechnical Society, 2021, 36(15): 3293-3307.
[13] 顾理成, 陈前, 赵文祥, 等. 五相永磁容错电机的相间短路容错控制[J]. 电工技术学报, 2022, 37(8): 1972-1981. Gu Licheng, Chen Qian, Zhao Wenxiang, et al. Inter-phase short-circuit fault-tolerant control for five-phase permanent magnet fault-tolerant motors[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 1972-1981.
[14] 马益平, 姚艳, 汪雅静, 等. 配电网电压稳定的分布式评估方法[J]. 电测与仪表, 2021, 58(3): 28-33. Ma Yiping, Yao Yan, Wang Yajing, et al. Distributed evolution method of voltage stability in radial distribution networks[J]. Electrical Measurement & Instrumentation, 2021, 58(3): 28-33.
[15] Liu Zhaocheng, Cui Xiang, Li Xuebao, et al. Interface finite element method with lower calculation amount for step size-varying electro-quasistatic field prob-lem[J]. CSEE Journal of Power and Energy Systems, 2023, 9(5): 1710-1719.
[16] Qiu Hao, Wang Shuhong, Zhang Naming, et al. Field-circuit coupling and electromagnetic-thermal-mechanical coupling analysis of the single-stage fast linear transformer driver using time-domain finite integration technique[J]. IEEE Transactions on Magnetics, 2021, 57(6): 8401205.
[17] 李胜利, 王川龙, 温瑞萍. 求解非奇异线性方程组的正交降阶法[J]. 中北大学学报(自然科学版), 2014, 35(3): 248-251, 257. Li Shengli, Wang Chuanlong, Wen Ruiping. Ortho-gonal reduced-order method for solving nonsingular linear systems[J]. Journal of North University of China (Natural Science Edition), 2014, 35(3): 248-251, 257.
[18] 王芙蓉, 杨帆, 张亚, 等. 基于奇异值分解的矩阵低秩近似量子算法[J]. 物理学报, 2021, 70(15): 7-14. Wang Furong, Yang Fan, Zhang Ya, et al. Matrix low-rank approximate quantum algorithm based on singular value decomposition[J]. Acta Physica Sinica, 2021, 70(15): 7-14.
[19] 李文强, 刘晓. 循环三对角Toeplitz线性方程组的分组降阶算法[J]. 科技导报, 2012, 30(5): 43-48. Li Wenqiang, Liu Xiao. Grouping and order reducing algorithm for solving Toeplitz type circular tri-diagonal liner algebraic equation systems[J]. Science & Technology Review, 2012, 30(5): 43-48.
[20] Sabariego R V, Vanbroekhoven B, Gyselinck J, et al. RL-ladder circuit models for eddy-current problems with translational movement[J]. IEEE Transactions on Magnetics, 2022, 58(9): 6301304.
[21] 尹松柱, 谭领. 解某些线代数方程组的降阶方法[J]. 东北师大学报(自然科学版), 1965(2): 17-24. Ing Shungzhu, Tan Ling. A lowering order method for solving certain system of linear equations[J]. Journal of Northeast Normal University, 1965(2): 17-24.
[22] 刘长河. 大型稀疏线性方程组的数值解法[J]. 北京建筑大学学报, 2023, 39(1): 103-108. Liu Changhe. Numerical methods for solving the large-scale sparse linear equations[J]. Journal of Beijing University of Civil Engineering and Archi-tecture, 2023, 39(1): 103-108.
[23] 胡之光. 电机电磁场的分析与计算[M]. 北京: 机械工业出版社, 1982.
Abstract The development of digital twin technology for electrical equipment requires extensive calculation. For the electrical equipment with large physical dimension or complicated structure, a large number of meshing grids are needed to analyze its physical field accurately using finite element method(FEM), which leads to a huge order of algebraic equations and makes the solution very difficult, and sometimes it cannot be solved. For sparse symmetric equations obtained by finite element analysis, this paper researches effective order-reduced algorithms.
Firstly, the block iterative algorithm is derived and explored in detail, in which the block diagonalization method is proposed to transform the finite element stiffness matrix into the diagonal matrix. The diagonal matrix is the matrix with unit matrix at diagonal, and the matrix is divided into sub-matrix blocks according to the unit matrix. Next, the block left multiplication method is proposed to realize the movement of sub-matrix blocks and block reorganization, and the permutation matrix method is also derived to realize the process. The block reorganization can reduce the order of the equations to half of its original order, and can reduce the order repeatedly. Taking the finite element analysis of the magnetic field of the open slot of the motor as an example, the block iterative algorithm is used twice to reduce the order of the equations, and the original 10th-order stiffness matrix is reduced to 3rd order.
Next, the mathematical model of orthogonal order-reduced decomposition algorithm(OORDA) is also derived. OORDA is to orthogonalize any column of the matrix with other column vectors, removes elements from corresponding row and column, and the matrix will be reduced by one order. This operation is repeated until the matrix is reduced to first-order, and then substitute the result back to complete the solution. Aiming at the characteristics of sparsity of finite element stiffness matrix, the taboo search algorithm is introduced into the Gaussian elimination method to form an improved Gaussian elimination method(IGEM).The information of non-zero elements is extracted and recorded in the taboo information table, so as to eliminate the memory occupation and computation increase caused by zero elements during elimination and back-substitution processes, which will greatly reduce the number of operations and computational cost of Gaussian Elimination method.
Due to the notable memory requirements of both OORDA and Gaussian elimination method, and the fact that the block iterative algorithm can substantially reduce the order of the equations, the Hybrid Algorithm 1 (HA1) that combine the block iterative algorithm with OORDA and Hybrid Algorithm 2 (HA2) that combine the block iterative algorithm with IGEM are proposed in this paper. The four algorithms, OORDA, IGEM, HA1 and HA2 are applied to the finite element analysis of the magnetic field produced by a long straight wire carrying current, the correctness of the algorithms have been verified by comparing the calculation results with the analytical solution. The four algorithms are applied to calculate the magnetic field distribution of a single-phase transformer under different meshes. The results show that using the block iterative algorithm to reduce the order of the equations, and then employing the OORDA or IGEM to solve them can greatly improve the computational efficiency. The larger the calculation scale, the more significant the effect. The HA2 shows the highest computational efficiency. The OORDA is not suitable for solving high-order equations alone, but it is a feasible choice for matrices that are inconvenient to inverse.
All the algorithms in this paper are realized by programming in C++, and the order reduction algorithms can provide a solution approach and reference for large-scale numerical calculation.
keywords：Finite elementanalysis, algebraic equations, order-reduced algorithm, large scale numerical calculation, calculation efficiency
DOI: 10.19595/j.cnki.1000-6753.tces.240498
中图分类号：TM154
国家自然科学基金项目（52277015）和辽宁省研究生教育教学改革研究项目（LNYJG2022060）资助。
收稿日期 2024-03-29
改稿日期 2024-06-04
金 军 男，1998年生，硕士研究生，研究方向为方程组降阶算法及其在电工装备数值计算中的应用。E-mail：2806576727@qq.com
阎秀恪 女，1973年生，教授，博士生导师，研究方向为电气设备电磁场工程、优化设计理论与应用、并行计算算法的研究与应用。E-mail：yanxke@126.com（通信作者）
（编辑 赫 蕾）