
图1 洛伦兹力驱动冲压成形系统结构
Fig.1 Diagram of the Lorentz force-driven stamping system
摘要 洛伦兹力驱动冲压成形技术是一种在传统冲压成形中引入电磁成形技术的先进制造技术,其成形速度远大于传统冲压成形,能够有效提高板件的成形极限。然而,现有针对洛伦兹力驱动冲压成形技术的研究主要对成形的可行性进行验证,成形形状多为轴对称结构,且未对成形效果进行分析,难以满足工业中差异化的需求。因此,该文提出一种多边形金属板件洛伦兹力驱动冲压成形方案,建立有限元模型对动态过程和成形效果进行了分析,并对成形效果进行了优化。结果表明:该方案成功实现了成形深度为35 mm的多边形金属板件成形,最大成形速度为19.10 m/s,远大于传统冲压成形。最终板件贴模质量良好、等效应变较小、最大减薄率为20.13%。进一步针对最大减薄率进行参数优化,优化后板件最大减薄率为8.31%,相较于优化前提升了58.71%。该研究将拓展电磁成形技术的应用场景,实现差异化的零件加工成形。
关键词:电磁成形 洛伦兹力 板件 成形效果 减薄率
洛伦兹力驱动(Lorentz-Force-Driven, LFD)冲压成形技术是一种将传统准静态冲压成形技术和电磁成形技术相结合的新型板件成形技术,得益于其较高的成形速率,能有效提高板件的成形极限[1]。
现有板件成形多使用传统准静态冲压技术,然而,使用此技术成形时成形板件易出现撕裂、起皱等问题,难以对板件实现深冲成形[2]。研究表明,高速率成形可以有效提高工件的成形极限[3-4],电磁成形技术是一种典型的高速率成形技术,它利用洛伦兹力使得金属板件高速变形[5]。与传统的准静态成形工艺相比,具有提高成形极限和减少回弹的优势[6],因此广泛地应用于金属板件成形[7-8]。然而,在板件电磁成形中,成形线圈通常使用螺旋线圈,洛伦兹力主要作用在成形线圈正对的区域,在板件上并非均匀分布[9-10]。板件中心区域在惯性的作用下变形较大,板件成形形状主要为圆锥形或椭球形[11-12]。在需要形状控制的情况下使用电磁成形技术具有一定的局限性。
为了解决这个问题,诸多学者提出了电磁成形技术与传统准静态冲压技术相结合的洛伦兹力驱动冲压成形技术。Feng Fei等[13]将电磁成形和传统冲压成形相结合,发现较高的惯性力和接触压力延缓了塑性失效的产生,由于利用了锥形模具,使得板件的成形极限提高了100%。Cao Quanliang等[1]提出了洛伦兹力驱动板件高速冲压成形方法,并将其应用于5052-O铝合金圆柱杯成形中,通过两次放电实验实现拉伸比为2的5052铝合金圆柱形零件的变形,成形深度达到66.4 mm。G. A. Taber等[14]研制了一种简单的洛伦兹力驱动冲压装置,可用于板件成形。此项研究发现,与传统压力机相比,洛伦兹力驱动冲压下无缺陷的变形板件的最大速度为10 m/s,最大成形深度提高了30%。Fang Jinxiu等[15]提出了5052铝合金的电磁脉冲辅助增量拉伸,成形的圆柱杯高度是常规拉伸的2.42倍。Shang Jianhui等[16]采用电磁辅助板件冲压成形非对称面板,完成了平底锅状板件成形。在成形过程中冲头逐渐向下推进,冲压成形结束后,电磁力用于拉伸工件底部区域。结果表明,使用电磁辅助冲压成形工艺,成形深度从44.0 mm增加到63.5 mm。
上述研究表明,洛伦兹力驱动冲压成形技术的变形方式与传统准静态冲压一致,为拉伸变形。但是,洛伦兹力驱动冲压成形构件的拉伸比优于传统准静态成形方式,能够有效地提高板件成形极限,改善成形效果。不过,学者们主要对洛伦兹力驱动成形应用的可行性进行了研究,而未对成形板件的形状控制及成形质量进行深入探讨,成形结果通常局限于圆柱状或杯状结构。因此现有的洛伦兹力驱动冲压方法在实际工业应用中还有较大的局限性。然而,工业生产中对各类多边形板件的需求复杂,对各类板件的成形质量要求较高。
基于此,本文提出了一种多边形金属板件洛伦兹力驱动冲压成形方案。首先对成形系统的结构及成形原理进行介绍;然后使用有限元方法对洛伦兹力驱动冲压成形方法的动态过程进行了分析,并针对贴模质量、等效应变及减薄率三个参数分析成形效果;最后针对最大减薄率对成形效果进行了优化。本研究将大大拓展电磁成形技术的应用场景,通过更换不同类型的冲头实现差异化的零件成形。
洛伦兹力驱动冲压成形方法结合了准静态冲压和电磁成形两者的优势,成形过程能够在极短的时间内完成。一方面成形速率高可以改善板件的成形性能,另一方面通过冲头与模具配合可以控制成形板件的形状。
图1所示为洛伦兹力驱动冲压成形系统结构。该系统中包括成形线圈、驱动片、压边块和模具等。驱动装置由驱动片和冲头刚性连接而成。驱动片由导电性能良好的铜制成,可以产生足够的洛伦兹力。冲头主要用于控制板件的形状,冲头在碰撞过程中将承受巨大的反冲力,因此需要选择高强度材料,本文选用SS304不锈钢作为冲头的材料。驱动片和冲头刚性连接可以防止两者之间发生碰撞,使得放电能量尽可能多地转化为板件成形的塑性能。上述驱动结构其驱动部分刚性较强,可以重复成形板件。
成形过程为:首先将脉冲电流通入成形线圈,在空间产生脉冲磁场,脉冲磁场与驱动片中的感应涡流共同作用产生洛伦兹力;随后驱动装置在洛伦兹力的驱动下向下运动;最后驱使板件与模具碰撞成形为多边形板件。在该系统中冲头与模具都进行倒角处理保证板件良好贴模,同时对压边块设置合适的压边力及摩擦系数,以抑制工件起皱、破裂等问题。

图1 洛伦兹力驱动冲压成形系统结构
Fig.1 Diagram of the Lorentz force-driven stamping system
图2所示为洛伦兹力驱动冲压成形系统主要零部件尺寸。其中驱动线圈由30匝截面形状为 4 mm×2 mm的矩形导线组成,分为10层,在建立仿真模型中对结构进行了简化。待成形板件的厚度为2 mm。为了达到更好的成形效果,板件在两边相对于冲头和模具均缩进3 mm。同时对冲头和模具进行倒角处理,倒角半径均为3 mm。

图2 系统主要零部件尺寸
Fig.2 Parameter structure diagram of the main components of the system
在本文所设计的洛伦兹力驱动冲压成形系统中,驱动装置的重量会影响冲压成形的速度,进而影响成形质量。因此需要在保证足够刚度的情况下尽可能多地降低驱动装置的重量。驱动装置的质量主要由冲头决定,所设计的冲头壁厚需要保证冲头在冲压过程中不发生破裂,故冲头的材料选择和体积比设计尤为重要。Cao Quanliang等[1]研究发现使用304不锈钢作为冲头材料,并且将体积比设计为0.68时,会有较好的成形效果。故本文在校验之后也采用相同的体积比对冲头进行设计。
驱动片采用高电导率的铜制成,但驱动片的厚度会影响驱动装置的质量。为了获得较高的材料利用率,本文通过趋肤效应对驱动片的厚度进行设计。S. V. Desai等[17]研究表明,铝制驱动板的最佳厚度为0.83δ,而铜制驱动器的厚度等于趋肤深度![]() 。其中趋肤深度定义为
。其中趋肤深度定义为
![]() (1)
(1)
式中,f为电流频率;σ和μ分别为驱动片材料的电导率和磁导率。本文中电流频率、电导率和磁导率分别为170 Hz、5.98×107 S/m、1.26×10-6 H/m,经计算驱动板的厚度选择为5 mm。
洛伦兹力驱动冲压成形工艺主要使用排斥式电磁力,系统等效电路如图3所示。采用电容器组放电,由于成形过程主要发生在放电电流第一个半波的上升沿,因此在原来的RLC电路中引入续流回路,从而使电流不发生振荡,同时能够显著降低驱动线圈的焦耳热损耗,增加线圈的使用寿命[18]。

图3 系统等效电路
Fig.3 System equivalent circuit
由图3可知,在含续流回路的洛伦兹力驱动冲压成形系统等效电路中,将线圈和驱动片都等效为电阻和电感,列写微分方程进行求解,利用基尔霍夫电流定律可以求得线圈中的电流Icoil。包含续流回路的电路方程为
![]() (3)
(3)
 (4)
(4)
式中,Rs为线圈电阻;Ls为线圈电感;Rc、Lc分别为成形线圈的等效电阻与等效电感;Rw、Lw分别为工件的等效电阻与等效电感;Ic为流过成形线圈的放电电流;Iw为驱动片中的感应电流;U0为电容电源初始电压;UC为电容器电源放电电压;C为电容器的电容值;M为成形线圈与板件之间的互感系数(M是个动态且连续变化的量);Id为流过续流回路的电流;Rds为续流电阻。
电磁场求解可由MaxWell方程组表示为
![]() (5)
(5)
![]() (7)
(7)
![]() (8)
(8)
式中,H为磁场强度;J为感应涡流密度;B为磁感应强度;![]() 为电场强度;
为电场强度;![]() 为成形线圈的电导率;S为每一匝线圈的横截面积;v为介质的运动速度。其中驱动片上的感应涡流密度Je可表示为
为成形线圈的电导率;S为每一匝线圈的横截面积;v为介质的运动速度。其中驱动片上的感应涡流密度Je可表示为
![]() (9)
(9)
式中,N为成形线圈的匝数;A为磁矢势。这里引入磁矢势A以便更容易地求解MaxWell方程中的计算变量Je及B。
洛伦兹力驱动冲压成形系统中感应涡流和磁场共同作用产生洛伦兹力作用于驱动片,驱动片带动冲头向下运动从而使板件发生塑性形变,其过程可用以下平衡方程表示为
式中,![]() 为板件材料密度;u为板件的矢量位移,初始状态下u=0;
为板件材料密度;u为板件的矢量位移,初始状态下u=0;![]() 为板件的应力张量。本文采用厚度为2 mm的铝合金板件(AA-6063)进行仿真模拟。由于成形速度较高,需要考虑高应变率的影响,因此采用Cowper-Symonds本构方程,其表达式为
为板件的应力张量。本文采用厚度为2 mm的铝合金板件(AA-6063)进行仿真模拟。由于成形速度较高,需要考虑高应变率的影响,因此采用Cowper-Symonds本构方程,其表达式为
 (11)
(11)
式中,sy为屈服应力;![]() 为塑性应变速率;P为黏性参数;m为应变率硬化参数。对于AA-6063铝合金材料,P和m通常分别取6 500 s-1和0.25。图4为AA-6063铝合金的应力-应变曲线[19]。
为塑性应变速率;P为黏性参数;m为应变率硬化参数。对于AA-6063铝合金材料,P和m通常分别取6 500 s-1和0.25。图4为AA-6063铝合金的应力-应变曲线[19]。

图4 AA-6063铝合金应力-应变曲线
Fig.4 Stress-strain curves of AA-6063 aluminum alloy
与准静态冲压相比,洛伦兹力驱动冲压成形涉及的物理过程更加复杂。原因在于放电电流、电磁场以及机械场强耦合且是动态变化的。在这个物理过程中,线圈电流、驱动片上的洛伦兹力和板件的变形是三个重要参数。要准确得到这三个量,需要解决电路、电磁场和机械场之间的耦合问题。Du Limeng等[20]基于COMSOL Multiphysics 和LS-DYNA提出了一种迭代耦合法,相较于非迭代模型,采用该方法能够准确地模拟洛伦兹力驱动冲压成形的动态过程。因此本文基于此方法建立仿真模型,图5是迭代耦合法的流程示意图。

图5 迭代耦合法流程示意图
Fig.5 Schematic diagram of the iterative coupling process
图6所示为LS-DYNA建立的系统有限元模型。由于在实际实验中,成形线圈、压边块和模具均受到液压机的约束,因此在有限元中设置成形线圈、压边块和模具在三个方向上均约束。驱动片和冲头在x和y两个方向上约束。有限元模型相关电路参数和材料属性参数见表1、表2。

图6 LS-DYNA建立的系统有限元模型
Fig.6 The finite element model of the system established by LS-DYNA
表1 电路参数
Tab.1 Discharge parameters of the circuit

参数数值 放电电压U0/kV12 放电电容960 线路电阻10 线路电感5 续流电阻100
表2 材料属性参数
Tab.2 Material property parameters

参数数值 铜(线圈、驱动板)电导率5.98×107 杨氏模量118 泊松比0.35 密度8 900 金属板件电导率2.93×107 杨氏模量70 泊松比0.33 密度2 740 不锈钢(冲头、模具)杨氏模量195 泊松比0.35 密度7 930
板件使用LS-DYNA材料库中的*MAT_ PIECEWISE_ LINEAR_PLASTICITY材料模型。此模型可以用来模拟材料在复杂加载条件下的非线性行为,尤其是在动态加载、高速冲击等情况下。这种模型比简单的线弹性模型更为精确,因为它能够考虑材料的屈服、强化和塑性变形等非线性特性。其余部分采用*MAT_RIGID材料模型。由于在LS-DYNA中采用边界元法求解导体间的相互作用,因此不需要绘制空气网格,可以避免由于空气网格畸变造成的收敛性问题。
电磁场和机械场计算均采用相同的时间步长进行耦合。涉及电磁场的仿真,采用关键字*EM_CIRCUIT直接将在COMSOL计算出的电流波形加载至成形线圈中。涉及机械场的仿真,考虑实际中冲头、压片块、板件以及模具之间存在摩擦,采用关键字*CONTACT_SURFACE_TO_SURF-ACE对每个接触面进行定义,这里将接触面之间的摩擦系数μ设置为0.15。对于压边力,采用*LOAD_RIGID_BODY在压边块上方设置垂直方向150 kN的体积力。
在有限元仿真中,网格划分质量会影响计算结果的精度以及计算速率。其中,由于模具和冲头存在倒角区,不便于使用六面体网格(Hex)进行划分,故采用四面体网格(Tet)进行划分,其余部分采用六面体网格划分[21]。考虑每个组件在成形过程中对精度的影响程度,对各部分采用的网格剖分精度不同,各组件网格划分参数见表3。
表3 网格参数
Tab.3 Grid parameters

部位网格类型网格尺寸网格数量 成形线圈Hex101 059 驱动片Hex512 756 冲头Tet15778 压边块Hex1548 板件Hex138 250 模具Tet15850
本文根据Du Limeng等[20]的研究建立了仿真模型,该研究依托脉冲强磁场设备进行[22]。在进行仿真之前,需要对其准确性进行分析。依据该文中的数据,取放电电压为8 kV,续流回路电阻为50 mW,进行相应的仿真。对实验与仿真中工件的成形深度、成形轮廓进行对比,来证明该研究的准确性。
图7为实验和仿真中获得的工件横截面轮廓。实验中获得的工件最大成形深度为22.25 mm,仿真中获得的工件最大成形深度为22.31 mm,仿真结果与实验结果相比误差较小,两种结果的成形轮廓具有良好的一致性。这表明这种仿真方案可以用于预测洛伦兹力冲压成形过程,也证明了本文模型的准确性。

图7 实验和仿真中获得的工件横截面轮廓
Fig.7 Cross-sectional profile of the workpiece obtained in experiments and simulations
采用前文所述的放电参数进行仿真计算,成形线圈的放电电流波形如图8所示。由图8可知,脉冲电流具有陡峭的上升沿,在0.26 ms达到峰值,最大电流为50.12 kA。随后电流在2.50 ms基本趋于零,整个放电过程十分迅速。成形过程主要运用电流的上升沿,在该时段电流变化率大,因此可以产生足够大的洛伦兹力驱动冲头向下运动成形工件。

图8 放电电流波形
Fig.8 Discharge current waveform
为了分析成形的动态过程,将成形板件中点向下运动的坐标变化定义为成形深度,对成形深度和驱动片所受的洛伦兹力进行分析,如图9所示。由图9可知,洛伦兹力达到峰值时刻与电流峰值时刻相同,但在0.75 ms基本趋近于零,相较于电流波形有所提前。造成这样的差异是由于驱动板受洛伦兹力作用迅速远离成形线圈导致的。而在0.75 ms后,尽管洛伦兹力较小,但板件的成形深度持续增加。这是由于驱动装置的惯性作用,在洛伦兹力为零后仍驱动工件成形,在2.40 ms时板件达到最大成形深度35.20 mm。但在短时间内产生了回弹,在2.50 ms成形结束时最终成形深度为35.00 mm。因此该种成形方式具有显著的惯性成形特点。

图9 洛伦兹力和工件成形深度
Fig.9 Lorentz force and workpiece forming depth
进一步地,对成形过程中冲头的运动状态进行分析,图10所示为冲头位移和速度变化。由图10可知,在0.75 ms以前,成形线圈与驱动片之间的距离较小,线圈放电的能量一直作用在驱动片上。冲头在洛伦兹力的作用下做加速运动,冲头的最大速度达到19.10 m/s,而此时板件的成形深度仅为 9.20 mm。然后冲头开始做减速运动,而板件在冲头惯性运动下继续成形。2.40 ms时冲头速度减小为零,此时冲头不再驱动板件发生进一步变形,而在反冲速度的作用下冲头开始反向运动。板件的成形过程到2.50 ms时刻结束,冲头位移小于35.00 mm。

图10 冲头位移和速度变化
Fig.10 Punch displacement and velocity variation
与传统低速率成形方法相比,利用洛伦兹力冲压成形的方法成形板件时,当成形速度大于10 m/s即可提高板件的成形极限[14]。图10中冲头的最大速度达到19.10 m/s,虽然工件的成形速度低于传统的电磁成形方法,但其仍远高于传统准静态下的冲压成形方法。
根据成形过程中冲头的速度将洛伦兹力驱动冲压成形过程总结为以下三个阶段,不同阶段板件成形状态如图11所示。
(1)加速阶段(0 ms<t≤0.75 ms):驱动片在脉冲磁场和自身感应涡流作用下产生巨大的洛伦兹力驱动冲头运动,冲头处于加速状态。随着驱动片和线圈之间距离的增大,洛伦兹力迅速衰减。当t=0.75 ms时,洛伦兹力衰减为零,此时冲头速度达到最大值19.10 m/s。

图11 不同阶段板件成形状态
Fig.11 Forming state at different times
(2)惯性阶段(0.75 ms<t≤2.40 ms):驱动片和冲头在自身运动惯性的作用下继续驱动板件变形,两者在这个过程中均做减速运动,直至两者的速度减小为0,此时板件成形深度达到最大值。
(3)回弹阶段(2.40 ms<t≤2.50 ms):当冲头的运动速度减小为零时,不再具有驱动板件变形的作用。此时板件因自身应力作用发生回弹,对冲头产生反作用力,冲头在此力作用下产生反向速度,向上运动与板件分离。
板件在上述三个阶段结束时的成形深度分别为9.20 mm、35.20 mm和35.00 mm,在惯性阶段工件的成形深度增加了26.00 mm。由此可见,本文提出的洛伦兹力冲压成形方案主要在惯性阶段成形。与传统电磁成形技术相比都具有惯性成形特征,但在传统电磁成形方法中,工件是在自身惯性的作用下继续成形,而本文方法中工件则是在冲头运动惯性的作用下成形。由于冲头在惯性作用下的持续冲压,可以保证成形质量且控制成形形状。
图12为不同阶段板件上应力分布情况。对比图11和图12,在加速阶段时,由于冲头先接触板件中间区域,因此中间区域的应力率先增大。同时,由于冲头作用,板件向模具内运动,在模具倒角处发生巨大形变,故此处应力也逐步增大,其他位置受到牵连应力依次增大,观察图12a可得最大应力为265.6 MPa。在惯性阶段时,随着冲头速度的减小,冲头施加的压力也逐渐减小,板件应力增速减缓,观察图12b可得,在此阶段结束时刻,板件上最大应力为363.2 MPa,其增速远小于加速阶段,同时最大应力分布在板件变形最大的区域即板件侧壁区域。在回弹阶段时,冲头与板件完全贴合,变形基本完成,因此,应力值不会发生过大变化,观察图12c可知,最大应力为368.9 MPa,且最大应力也分布于板件侧壁区域。

图12 不同阶段下板件应力分布
Fig.12 Stress distribution of plates at different times
多边形板件最终成形效果如图13所示。由图可知,整个多边形板件成形质量良好,并未出现起皱、破裂等问题,达到了预期的成形效果。在后文中将进一步对板件成形效果的贴模质量、等效应变及减薄率进行分析。

图13 多边形板件最终成形效果
Fig.13 The final forming effect of the polygonal sheet
3.2.1 贴模质量分析
在t =0.75 ms之后,驱动片所受洛伦兹力衰减为零,冲头在惯性的作用下持续驱动板件发生塑性变形。图14所示为板件贴模顺序示意图,可以将板件贴模顺序分为三个阶段:第一步板件与模具侧壁接触完成贴合;第二步板件与模具底部贴合;第三步板件与模具的侧底部贴合。板件与模具侧底部的接触较为滞后,在成形最后阶段此处仍存在较小的贴模间隙。因此该区域的贴模对整个板件的贴膜质量十分重要。

图14 板件贴模顺序示意图
Fig.14 Schematic diagram of sheet sticking sequence
在贴模的第三步由于板件存在残余速度,侧底部区域会继续发生塑性形变,残余速度的大小和分布会影响此区域的变形,从而影响板件成形的贴模质量[23]。由图15a可以得到,在t=2.40 ms时,此区域板件最大变形速度为14.94 m/s,剩余动能使得板件与模具侧底端区域继续产生碰撞,使得贴模间隙减小。t=2.50 ms时刻,冲头与板件分离,由图15b可知板件整体速度反向且大幅减小,最大变形速度为5.386 m/s。因此反弹效果不明显,对板件贴模质量影响较小。


图15 不同时刻板件部分速度矢量分布
Fig.15 Velocity vector distribution of sheet parts at different times
图16为不同时刻下板件成形轮廓,最终时刻下板件成形深度为35.00 mm,且高度分布均匀,与最大成形深度仅有0.2 mm的差值。最终贴模状态如图17所示,板件与模具贴合良好。因此在洛伦兹力驱动冲压成形中,板件的回弹量处于一个较低的水平,对最终成形效果影响较小。
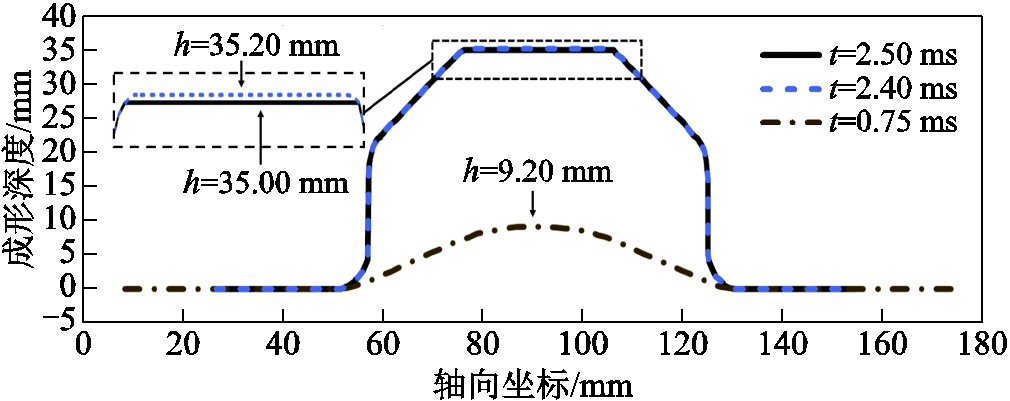
图16 不同时刻板件成形轮廓
Fig.16 Outline of the plate at different times

图17 最终贴模状态
Fig.17 Final mold state
3.2.2 等效应变分析
板件的等效应变能够反映工件内部受外力作用产生变形的情况,若成形结束后等效应变越大则板件性能越差,因此可以将最终成形状态板件的等效应变作为一个重要分析指标[24]。图18所示为最终成形状态板件的等效应变分布。由图18可知,板件两侧压边区域等效应变分布均匀,且水平低于其他区域,这是由于此处变形量小。板件主要变形区即板件底部的等效应变分布相对均匀,且等效应变值小于最大等效应变,这表示此处的变形更加均匀。板件的侧壁及倒角处均产生了较大的应变,该区域由于发生了大角度的弯折,是变形量最大的区域,因而等效应变最大。在冲压成形过程中,侧壁同时受到冲头向下的压力和弯曲应力的作用。而倒角处则是由于该部位被拉伸导致,过大的拉应力使其应变变大。

图18 最终成形状态板件的等效应变分布
Fig.18 The equivalent strain distribution diagram of the sheet in the final forming state
为了与准静态冲压成形板件等效应变进行对比,本文根据王涌纲等[25]的研究,设计了一组冲压速度为400 mm/s的准静态冲压成形仿真。图19为准静态冲压成形后的等效应变分布。对比图18与图19可以发现,相较于准静态冲压方式,通过洛伦兹力驱动冲压成形的板件底部、侧壁部及侧壁主要变形区域的等效应变分布更加均匀,这代表板件变形更加均匀,等效应变值也得到改善。洛伦兹力驱动冲压成形金属板成形方法具有显著优势。

图19 准静态冲压后成形板件的等效应变分布
Fig.19 Equivalence distribution of a quasi-static stamped form
3.2.3 减薄率分析
在冲压成形工艺中,若减薄较大容易出现起皱、破裂等问题。板件厚度分布越均匀,壁厚减薄率越低,零件的成形质量越好[26]。因此,可将板件的减薄率作为评价成形质量的重要指标。
图20所示为最终成形状态板件的减薄分布云图。由图20可知,板件的最大减薄率为20.13%,位于边沿处。板件整体边沿部分减薄分布不均匀,减薄率过大存在破裂的风险,需要对成形参数进行进一步的优化。

图20 最终成形状态板件的减薄分布
Fig.20 Thinning distribution of the sheet in the final form state
现有研究通过正交实验得出影响最大减薄率的各工艺参数分别为:压边力>摩擦系数>冲压速度[25]。在本文所述的成形系统中,冲压速度由驱动电路放电电压决定。实际生产中,材料应变速率对材料性能影响不明显,模具之间的间隙调整范围有限。后续将从压边力、摩擦系数、放电电压三个参数在现有模型的基础上通过多组仿真实验结果对比,优化冲压成形参数。
在实际成形实验中,若压边力设置过小,板件无法抵制过大的切向应力,从而在切向变形,失去稳定形成皱折。若压边力设置过大,会导致材料在成形过程中流动不充分,造成零件破裂[27]。
设置电路放电电压为12 kV,摩擦系数为0.15,压边力在50~250 kN范围内每隔50 kN取5组数据,压边力与板件厚度变化率关系如图21所示。采用减薄率和增厚率来评价板件的成形质量,选择两者的交叉点视为最优取值[28]。由图21可知,随着压边力取值的增加,减薄率数值不断上升,而增厚率的数值不断下降。压边力对减薄率的影响要大于增厚率,当压边力从50 kN到250 kN变化时,板件的减薄率从10.64%增加至33.25%,增厚率从14.89%减小至6.71%。且压边力从200 kN变化到250 kN后,减薄率的增加量明显提高,从24.7%增加至33.25%。这表示随着压边力的增加,板件减薄率的变化也会更加明显。在放电电压和摩擦系数不变的情况下,可以认为81.95 kN为压边力最优取值。

图21 压边力与板件厚度变化率关系
Fig.21 Relationship between blank holding force and sheet thickness
摩擦系数也会影响工件在压边区域的流动性,摩擦系数过小会使板件受力不均导致成形不充分,且会发生自由运动,从而产生皱折。摩擦系数过大则阻力高,进而造成板件减薄,在极端工况下会导致板件的破裂[29],故需要对摩擦系数进行优化。
摩擦系数与板件厚度变化率关系如图22所示,设置放电电压为12 kV,压边力取上述最优值81.95 kN,摩擦系数在0.05~0.25范围内每隔0.05取5组数据,通过减薄率和增厚率的变化确定最优摩擦系数。由图22可知,随着摩擦系数的增大,减薄率不断上升,而增厚率不断下降,两者交叉于一点。同样地,摩擦系数对减薄率的影响也大于增厚率,当摩擦系数从0.05增加至0.25时,减薄率从9.5%增加至21.36%,增厚率从16.06%减小至10.06%;且当摩擦系数从0.20增加至0.25时,减薄率也得到了大幅增加,从13.71%增加至21.36%。不过,对比图21与图22,可以发现,摩擦系数对厚度变化的影响要小于压边力。在放电电压和压边力不变的情况下,可以认为0.171为摩擦系数最优取值。

图22 摩擦系数与板件厚度变化率的关系
Fig.22 Relationship between friction coefficient and sheet thickness
冲压速度是成形效果的关键因素之一,成形的冲压速度由放电电压决定。冲压速度过高会导致板件无法完全贴合模具,影响成形的精度和质量;冲压速度过小则会导致板件形变过度,产生裂纹和毛刺。故需要对放电电压进行优化。
在压边力、摩擦系数分别取上述最优取值81.95 kN和0.171情况下,将放电电压在11~13 kV范围每隔0.5 kV取5组数据,通过减薄率和增厚率的变化确定最优放电电压。放电电压与板件厚度关系如图23所示。由图23可知,随着放电电压的不断增加,减薄率呈现不断下降趋势,而增厚率呈现上升趋势。当放电电压从11 kV增加至13 kV时,减薄率从8.63%增加至13.16%,增厚率从11.71%减小至7.94%。对比压边力和摩擦系数的影响可以发现,减薄率和增厚率的变化量更为接近,且变化量也更小。这说明,这三种参数对厚度变化的影响程度为:压边力>摩擦系数>放电电压。选择两者的交叉点作为最优取值。在压边力和摩擦系数不变的情况下,可以认为11.74 kV为驱动电路放电电压最优取值。

图23 放电电压与板件厚度变化率关系
Fig.23 Relationship between discharge voltage and sheet thickness
由上述仿真分析可得,冲压最优工艺参数为压边力为81.95 kN,摩擦系数为0.171,驱动电路放电电压为11.74 kV。对优化后的参数进行仿真分析,图24为最优参数下板件减薄分布。此时最大减薄率为8.311%,相较于优化前最大减薄率提升了58.71%。最大减薄率下降明显,边沿部分厚度分布均匀。

图24 最优参数下成形板件减薄分布
Fig.24 Thinning distribution of formed sheet under optimal parameters
本文在仿真研究的基础上提出了一种多边形金属板件洛伦兹力驱动冲压成形方案。在对成形原理进行理论分析的基础上,利用有限元模型深入探究了其成形动态过程及成形质量相关特性,并开展了相关优化工作。主要结论如下:
1)本方案在设定参数下实现了成形深度为35 mm的多边形金属板件成形,所得最大成形速度为 19.10 m/s,此速度远高于传统准静态成形方法。板件贴模质量表现良好,等效应变分布相比于传统冲压成形方法更为均匀,且等效应变值得到改善,最大减薄率为20.13%。最终成形效果良好,未出现起皱、破裂等情况。
2)本方案结合了电磁成形与传统冲压成形的特点。从仿真结果及理论分析可知,成形过程十分迅速,仅需 2.50 ms 即可完成,且呈现惯性形成的特点。通过冲头与模具配合实现了对成形板件形状的控制。
3)进一步针对最大减薄率这一关键指标进行了仿真优化分析,选择摩擦系数、压边力和放电电压为优化参数。经仿真计算,优化后得到的最佳参数组合为摩擦系数为0.171、压边力为81.95 kN、驱动电路放电电压为11.74 kV。得出的板件最大减薄率为8.311%,相较于优化前的结果提升了 58.71%。
参考文献
[1] Cao Quanliang, Du Limeng, Li Zhenhao, et al. Investigation of the Lorentz-force-driven sheet metal stamping process for cylindrical cup forming[J]. Journal of Materials Processing Technology, 2019, 271: 532-541.
[2] Ghosh S K. Principally on sheet metal forming defects as described in the eleventh biennial congress of the international deep drawing research group (IDDRG)[J]. International Journal of Mechanical Sciences, 1981, 23(4): 195-211.
[3] Balanethiram V S, Daehn G S. Hyperplasticity: increased forming limits a high workpiece velocity[J]. Scripta Metallurgica et Materialia, 1994, 30(4): 515-520.
[4] 熊奇, 邱爽, 李彦昕, 等. 组合式电磁成形技术研究进展[J]. 电工技术学报, 2024, 39(9): 2710-2729. Xiong Qi, Qiu Shuang, Li Yanxin, et al. Research progress of combined electromagnetic forming technology[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2710-2729.
[5] 熊奇, 朱鑫辉, 赵翔, 等. AZ31镁合金管件电磁吸引式成形动态特性研究[J]. 电工技术学报, 2023, 38(10): 2577-2588, 2636. Xiong Qi, Zhu Xinhui, Zhao Xiang, et al. Research of dynamic characteristics in electromagnetic attraction forming of AZ31 magnesium alloy tube[J]. Tran-sactions of China Electrotechnical Society, 2023, 38(10): 2577-2588, 2636.
[6] Dong Pengxin, Li Zhangzhe, Feng Sheng, et al. Fabrication of titanium bipolar plates for proton exchange membrane fuel cells by uniform pressure electromagnetic forming[J]. International journal of hydrogen energy, 2021, 46(78): 38768-38781.
[7] 邱立, 李彦涛, 苏攀, 等. 电磁成形中电磁技术问题研究进展[J]. 电工技术学报, 2019, 34(11): 2247-2259. Qiu Li, Li Yantao, Su Pan, et al. Research on electromagnetic problems in electromagnetic forming process[J]. Transactions of China Electro-technical Society, 2019, 34(11): 2247-2259.
[8] 熊奇, 杨猛, 周丽君, 等. 双线圈吸引式板件电磁成形过程中的涡流竞争问题[J]. 电工技术学报, 2021, 36 (10): 2007-2017. Xiong Qi, Yang Meng, Zhou Lijun, et al. Eddy current competition in electromagnetic forming process of double coil suction plate[J]. Transactions of China Electrotechnical Society, 2021, 36 (10): 2007-2017.
[9] Wu Zelin, Cao Quanliang, Fu Junyu, et al. An inner-field uniform pressure actuator with high performance and its application to titanium bipolar plate forming [J]. International Journal of Machine Tools and Manufacture, 2020, 155: 103570.
[10] 邵子豪, 吴伟业, 汪晨鑫, 等. 基于双层凹型集磁器的管件电磁胀形电磁力特性及变形行为研究 [J]. 电工技术学报, 2024, 39(5): 1245-1255. Shao Zihao, Wu Weiye, Wang Chenxin, et al. Electromagnetic force and formability analysis of tube electromagnetic bulging based on double-layer concave magnetic field shaper[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1245-1255.
[11] Lai Zhipeng, Han Xiaotao, Cao Quanliang, et al. The electromagnetic flanging of a large-scale sheet workpiece[J]. IEEE Transactions on applied superco-nductivity, 2013, 24(3): 1-5.
[12] Xiong Qi, Cao Quanliang, Han Xiaotao, et al. Axially movable electromagnetic forming system for large-scale metallic sheet[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 1-4.
[13] Feng Fei, Li Jianjun, Huang Liang, et al. Formability enhancement of 5052 aluminium alloy sheet in electromagnetic impaction forming[J]. The International Journal of Advanced Manufacturing Technology, 2021, 112: 2639-2655.
[14] Taber G A, Kabert B A, Washburn A T, et al. An electromagnetically driven metalworking press[C]// Proceedings of the 5th International Conference on High Speed Forming, Dortmund, Germany, 2012: 125-134.
[15] Fang Jinxiu, Mo Jianhua, Li Jianjun. Microstructure difference of 5052 aluminum alloys under conventional drawing and electromagnetic pulse assisted incremental drawing[J]. Materials Characterization, 2017, 129: 88-97.
[16] Shang Jianhui, Daehn G. Electromagnetically assisted sheet metal stamping[J]. Journal of Materials Processing Technology, 2011, 211(5): 868-874.
[17] Desai S V, Kumar S, Satyamurthy P, et al. improvement of performance of electromagnetic welding process by use of driver materials[J]. International Journal of Applied Electromagnetics and Mechanics, 2011, 35(2): 113-121.
[18] Cao Quanliang, Han Xiaotao, Lai Zhipeng, et al. Analysis and reduction of coil temperature rise in electromagnetic forming[J]. Journal of Materials Processing Technology, 2015, 225: 185-194.
[19] 张骁. 脉冲强磁场作用下管件胀拉成形数值模拟与实验研究[D]. 武汉: 华中科技大学, 2017. Zhang Xiao. Numerical simulation and experimental study of bulging drawing forming under pulsed high magnetic fields[D]. Wuhan: Huazhong University of Science and Technology, 2017.
[20] Du Limeng, Li Xian, Xia Liangyu, et al. Numerical and experimental verification of an iterative coupling method for analyzing the Lorentz-force-driven sheet metal stamping process[J]. The International Journal of Advanced Manufacturing Technology, 2021, 115(7): 2161-2173.
[21] 刘晓杰, 金康宁, 单斌, 等. 织构化冲压模具的应力数值模拟分析[J]. 表面技术, 2019, 48(8): 9-15. Liu Xiaojie, Jin Kangning, Shan Bin, et al. Numerical simulation analysis of stress in textured stamping die[J]. Surface Technology, 2019, 48(8): 9-15
[22] Xie Jianfeng, Zhang Shaozhe, Shi Jiangtao, et al. Realization of the reconfigurable pulsed high magnetic field facility and its scientific application at Wuhan National Pulsed High Magnetic Field Centre[J]. High Voltage, 2023, 8(5): 898-906.
[23] 陈盟. 基于轴-径双向脉冲洛伦兹力加载的铝合金筒形件变形行为及其控制研究[D]. 武汉: 华中科技大学, 2020. Chen Meng. Research on deformation behavior and control strategy of aluminum cylindrical parts under axial-radial pulsed Lorentz forces[D]. Wuhan: Hua-zhong University of Science and Technology, 2020.
[24] 刘俭辉, 赵贺, 冉勇, 等. 基于临界面理论的多轴等效应变疲劳寿命预估模型[J]. 中国机械工程, 2022, 33(15): 1821-1827. Liu Jianhui, Zhao He, Ran Yong, et al. Multiaxial equivalent strain fatigue life prediction model based on critical plane theory[J]. China Mechanical Engineering, 2022, 33(15): 1821-1827.
[25] 王涌纲, 何仕荣, 顾猛, 等. 金属双极板冲压成形数值分析及回弹补偿[J]. 塑性工程学报, 2024, 31(2): 43-50. Wang Yonggang, He Shirong, Gu Meng, et al. Numerical analysis and springback compensation of metal bipolar plate stamping forming[J]. Journal of Plasticity Engineering, 2019, 31(2): 43-50.
[26] 陈一哲, 范宏德, 王祎纯, 等. 车用纤维金属层板构件冲压变形行为研究[J]. 汽车工程, 2023, 45(3): 517-525. Chen Yizhe, Fan Hongde, Wang Yichun, et al. Research on stamping deformation behavior of automotive fiber metal laminates[J]. Automotive Engineering, 2023, 45(3): 517-525.
[27] 秦泗吉, 李学洋, 潘自给, 等. 压边力控制技术研究现状[J]. 塑性工程学报, 2022, 29(10): 1-11. Qin Siji, Li Xueyang, Pan Zizi, et al. Research status of crimping force control technology[J]. Journal of Plasticity Engineering, 2022, 29 (10): 1-11.
[28] 李奇涵, 邢继刚, 高嵩, 等. 5052铝合金方盒件冲压成形变压边力技术[J]. 锻压技术, 2020, 45(9): 51-56. Li Qihan, Xing Jigang, Gao Song, et al. Deformation holding force technology of 5052 aluminum alloy square box parts[J]. Forging Technology, 2020, 45(9): 51-56.
[29] 刘强, 俞国燕, 梅端. 基于Dynaform与RBF-NSGA-II算法的冲压成形工艺参数多目标优化[J]. 塑性工程学报, 2020, 27(3): 16-25. Liu Qiang, Yu Guoyan, Mei Duan. Multi-objective optimization of stamping process parameters based on dynaform and RBF-NSGA-II algorithm[J]. Journal of Plasticity Engineering, 2019, 27(3): 16-25.
Abstract Comparison with the conventional quasi-static stamping technology, the utilization of Lorentz force-driven stamping technology has the potential to significantly enhance the forming limit of sheet metal. Nevertheless, the extant research merely corroborated the viability of this approach, yet did not investigate the ultimate forming quality, which is challenging to align with the diverse requirements of the industry. Consequently, a Lorentz force stamping scheme for polygonal sheet metal is put forth in this paper. A finite element model is constructed to examine the dynamic process and forming effect, and the forming effect is optimized.
Firstly, the basic model of the stamping system is established, and the most important parts of the system driver and punch are designed, and the circuit with continuous flow circuit is used to generate repulsive force to drive the forming. Secondly, because the forming process is very fast, a simulation model must le established to study the forming dynamic process and the final forming effect in detail. Finally, a fully coupled electromagnetic and mechanical field model is established to verify the feasibility of the proposed scheme.
The simulation results demonstrate that the forming process of this scheme can be divided into three distinct stages: the acceleration stage, the inertia stage, and the rebound stage. The maximum forming depth achieved was 35.00 mm, with the plate exhibiting smooth sticking. The equivalent strain level was low, with a maximum thinning rate of 20.13%. The shaped plate exhibited an effective forming effect. The maximum thinning rate was optimized by manipulating the holding force, friction coefficient and discharge voltage. The maximum thinning rate was reduced to 8.31% under the optimal parameter combination.
The conclusions are as follows: (1) The scheme is capable of forming polygonal sheet metal at a significantly higher speed than the traditional quasi-static forming method, while also enhancing the forming limits of sheet metal. The final forming effect is satisfactory. (2) The method exhibits characteristics of both electromagnetic forming and traditional quasi-static forming. The forming process is completed within 2.50 ms, which is a relatively short time. The forming dynamic process is divided into three stages according to the speed change of the driving device: accelerating dynamic stage, inertia stage and rebound stage. The principal forming stage is the inertial movement stage, which ensures the subsequent forming effect. (3) The friction coefficient, the blank holding force, and the discharge voltage have been selected to further optimize the maximum thinning rate. Following the optimization process, the optimal parameter combination was identified as a friction coefficient of 0.171, a blank holding force of 81.95 kN, and a discharge voltage of 11.74 kV for the drive circuit. At this juncture, the maximum thinning rate of the plate is 8.31%, which represents a 58.71% increase over the preceding baseline.
Keywords:Electromagnetic forming, Lorentz force, sheet metals, forming effect, reduction rate
DOI: 10.19595/j.cnki.1000-6753.tces.240556
中图分类号:TM154
武汉强磁场学科交叉基金资助项目(WHMF202121)。
收稿日期 2024-04-08
改稿日期 2024-09-27
熊 奇 男,1990年生,博士,副教授,博士生导师,研究方向为电磁成形、多场耦合分析及储能技术。E-mail:pandaqi0218@gmail.com
阎 诺 男,1997年生,硕士研究生,研究方向为电磁成形、电磁场分析及应用。E-mail:mamba1021@126.com(通信作者)
(编辑 郭丽军)