 (1)
(1)
摘要 数值积分是求解电路微分方程的经典方法之一,但传统数值积分形式固定、积分精度不可调节,且精度、计算量与积分的定量关系不明确。针对此问题,该文提出一种基于任意代数精度的显隐式数值积分算法。首先,给出显隐式数值积分的构造方法,以任意代数精度为条件确定积分系数,并分析证明所提积分算法的精度与稳定性;其次,定义单位时间计算量,补充传统数值积分评价指标,并研究单位时间计算量随方程维度、积分精度等因素的变化规律;最后,通过实时仿真验证所提积分算法与指标的有效性。仿真结果表明,与传统高阶积分相比,所提积分算法的准确度可提高33%~72%,计算量可减小9%~42%,单位时间计算量可减小16%~61%,且单位时间计算量能够定量描述精度、计算量与积分的关系,对数值积分的选择具有指导意义。
关键词:电路微分方程 数值积分 代数精度 计算量
从电路原理分析到电力系统工程应用,从拓扑结构设计到机电系统建模仿真[1-3],电路微分方程贯穿电气工程学科的各个领域。但随着电力系统规模的日益增大以及高频[4-6]半导体开关在电力系统中的广泛应用,快速准确地求解电路微分方程的难度越来越大。
根据不同的组织规则,电路方程分为节点方程和状态空间方程。虽然两种方程形式不同,但均属于常系数微分方程,求解方法具有同一性。
常见的电路微分方程[7]求解方法有:解析求解法[8]、数值积分法[9]、零极点匹配法[10]、指数函数求解法[11]等。其中,数值积分法具有简单高效、适用范围广、灵活性强等显著优点,在实际应用中占据重要地位。目前应用于电路微分方程求解的数值积分大致分为以下四类。
1)显隐式数值积分。如前后向欧拉积分、梯形积分、阻尼梯形积分等。欧拉积分精度较低,稳定性较强[12]。梯形积分精度较高,但在电路非状态量突变时易发生数值振荡[13]。阻尼梯形积分则通过加权系数动态调节积分精度与稳定性。显隐式数值积分结构简单、计算效率高,应用最为广泛,但精度普遍较低。
2)高阶积分。如龙格库塔积分[14]、Gear积分[15-16]、向后微分公式(Backward Differentiation Formula, BDF)积分[17]、Adams积分[17]等。龙格库塔积分的显式4阶积分形式最为经典,具备4阶精度,但计算量也是欧拉积分的4倍,且稳定域较小。Gear积分、BDF积分、Adams积分形式略有不同,但均属于线性多步积分[18]。线性多步积分采用更多积分节点参与计算,在提高积分精度的同时会导致计算量急剧增加。相较于显隐式积分,高阶积分具备明显的精度优势,但积分结构复杂、计算量大、计算效率低。
3)预测校正[19]积分。该积分采用任意一种显式积分作为预测公式、任意一种隐式积分作为校正公式。预测公式解决了部分隐式积分不可解的问题,而预测校正公式的分离计算使得该积分被广泛应用于并行系统设计。但两种积分的组合使用会导致误差累积、积分精度较差、计算量成倍增加,制约该积分的应用。
4)各类新型积分。如泰勒级数法、矩阵指数法、配点法等。泰勒级数法[20-21]是对微分方程进行有限项的泰勒级数展开,得到具有高阶截断误差的积分表达式,但此法稳定性较差。矩阵指数法采用Duhamel积分[22]形式将微分方程拆解为线性部分与非线性部分。线性部分借助矩阵指数进行解析求解,非线性部分以高次多项式拟合求解。配点法[23-25]则是将方程未知解展开为包含一组可调参数的实验函数,通过可调参数的反复试验,使得实验函数逼近解析解。
新型积分精度极高,其中矩阵指数法的精度接近数学解析法,但计算流程复杂。如泰勒级数法需计算函数的高阶导数,矩阵指数法非线性拟合环节需划分间隔较小的时间区段,配点法则需进行大量重复试验。因此新型积分的计算效率较低。此外,有关新型积分精度与稳定性的理论依据尚未完善,仍处于数学研究阶段,实际应用有限。
综上所述,目前广泛应用于电路微分方程求解的数值积分主要是显隐式数值积分和各类高阶积分,但这两类积分无法同时兼顾精度优势和计算优势。且各类显隐式积分与高阶积分的积分结构固定,积分系数无法调节,导致只能使用现有积分而无法自主构造新积分。如何优化积分结构及系数,在保留显隐式积分计算效率优势的同时提高积分精度有待研究。
另外,目前多采用稳定性、精度、计算量等传统指标评价数值积分。在电力系统实时仿真[26-27]等实际应用中,上述三种指标的定性关系为:积分阶数越高,稳定性越强,精度越高,计算量越大。但由于精度与计算量互为矛盾,且二者的定量关系不明确,在实际应用中选择数值积分时,传统指标的指导意义有限。如何提出一种定量指标明确精度与计算量的相对关系有待研究。
因此,本文提出一种任意阶数与任意精度的显式或隐式积分算法。首先,通过自主选择差分项及阶数构造新积分,保证积分结构及计算效率优势,根据任意代数精度确定积分系数,保证积分精度;其次,定义单位时间计算量,明确积分精度、积分步长、电路规模、计算量之间的定量关系;最后,通过理论分析与仿真实验,验证所提积分算法与单位时间计算量的有效性。
传统多步积分的一般表达式为
 (1)
(1)
式中,y为积分项;f为积分映射关系;a、b为积分系数;h为积分步长;t为积分时刻;n为积分阶数;m为积分步数;i、j为步数的计数。
不同的多步积分对应的积分系数的确定依据不同,如BDF积分系数是由拉格朗日插值确定,Adams积分系数是由泰勒级数展开法确定等。
但无论使用何种系数确定方法,多步积分只能使用等步长连续差分项,且各阶积分系数为定值,不可调整。积分结构与积分系数一旦确定,则各阶积分的精度不可调整。前4阶Adams显隐式积分的系数及精度详见附表1和附表2。
因此,为提高计算效率,应优化传统多步积分结构;为提高积分精度,应优化积分系数确定方法。
数值积分的本质是借助“以直代曲”思想,对曲边梯形进行近似求解。精度高低取决于积分对曲边梯形的拟合程度。由于任意曲线均可表示为高次多项式,故对曲边梯形拟合程度的高低等价于数值积分求解高次多项式准确度的高低。由此可得以下充要条件。
对解析积分
 (2)
(2)
其n阶数值积分 具有m次代数精度的充要条件是:当f(x)分别为
具有m次代数精度的充要条件是:当f(x)分别为 时,
时, 。
。
用于电路微分方程求解的数值积分的结构及参数具备实际物理意义。积分节点为系统观测时刻,差分项为各时刻系统状态值。由此可知:
(1)若某数值积分包含n项差分项,则称该积分为n阶数值积分。
(2)当某数值积分求解k时刻系统的解时,若其差分项不包含k时刻系统状态值,则称该数值积分为显式积分;否则为隐式积分。
显然,对式(2)解析积分,其显式数值积分最高为n阶。由于隐式积分包含当前时刻系统状态值,故其隐式数值积分最高为n+1阶。
以显隐式积分结构为基础,以代数精度为充要条件确定积分系数,提出一种任意阶数任意代数精度的显隐式数值积分,具体如下。
(1)n阶显式积分表达式(上标e表示显式)为
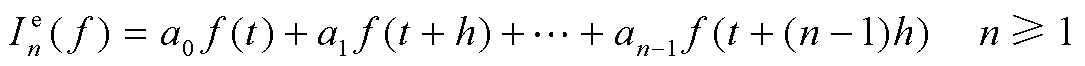 (3)
(3)
式中,a0~an-1为显式积分系数。
(2)n+1阶隐式积分表达式(上标i表示隐式)为
 (4)
(4)
式中,b0~bn为隐式积分系数。
(3)根据m(m≤n)次代数精度联立方程,求解待定参数。
 (5)
(5)
 (6)
(6)
由式(3)和式(4)可知,与传统多步法等高阶积分相比,所提积分算法结构更简单,计算效率更高。而基于高阶代数精度的系数确定方法,使得积分精度高于传统显隐式积分。
由式(5)和式(6)可知,各阶积分的最高代数精度m等于积分阶数n。在满足m≤n的条件下,可在同阶积分结构下获得不同代数精度的积分,克服了显隐式积分与高阶积分精度固定的缺陷。
为方便后续验证,本文仅以前4阶显隐式积分为例进行分析。并以m=n为条件确定积分系数,此时积分代数精度等于积分阶数。
以二阶隐式积分为例,其表达式为
 (7)
(7)
则由
 (8)
(8)
可得
 (9)
(9)
同理可得前四阶显隐式积分表达式见表1。
由表1可知,当积分阶数为1和2时,本文隐式积分等价于后向欧拉积分与梯形积分。
表1 前四阶显隐式积分公式
Tab.1 The first four orders integration formula

积分类型差分项及系数 f(t)f(t+h)f(t+2h)f(t+3h) 一阶显式h——— 一阶隐式0h—— 二阶显式02h—— 二阶隐式h/2h/2—— 三阶显式3h/409h/4— 三阶隐式h/34h/3h/3— 四阶显式08h/3-4h/38h/3 四阶隐式3h/89h/89h/83h/8
数学中比较积分精度的标准系统模型为
 (10)
(10)
式中,y为状态量;y0为状态量初值;t0为初始时刻;l为系统模型系数。
以二阶隐式积分为例,其局部截断误差[28]ln+1为

截断误差首项的数量级O称为准确度阶数,首项系数称为误差常数。准确度阶数越高、误差常数越小,则积分精度越高。
同理可得前四阶显隐式积分的准确度阶数与误差常数见表2。
表2 前四阶积分精度比较
Tab.2 Accuracy comparison of the first four orders integration

积分类型误差首项准确度阶数误差常数 一阶显式O(h2)/211/2 一阶隐式-O(h2)/21-1/2 二阶显式O(h3)/321/3 二阶隐式-O(h3)/122-1/12 三阶显式3O(h4)/833/8 三阶隐式-O(h4)/453-1/45 四阶显式14O(h5)/45414/45 四阶隐式-O(h5)/404-1/40
由表2可知,所提积分算法阶数越高,准确度阶数越高,精度越高。且隐式积分误差常数通常小于同阶显式积分,即隐式积分精度高于显式积分。
稳定性[12]要求数值积分具备收敛性,不会放大系统扰动误差,即当系统出现扰动时,数值积分受扰动的影响不大于原解析积分受扰动的影响,其定义为:使用某种数值积分时,若在节点tn上的函数近似值存在扰动dn,由它在后续各节点上引起的误差dm(m>n)均不超过dn,即|dm|≤|dn|(m>n),则称该方法是稳定的。
对式(2)解析积分而言,所提数值积分表达式可统一为
 (12)
(12)
式中,ck为积分系数。
假设扰动后的被积函数为 ,则扰动
,则扰动 可记为
可记为
 (13)
(13)
扰动对原未知积分的影响为
 (14)
(14)
而扰动对数值积分的影响为
 (15)
(15)
任意数值积分的精度至少为一次代数精度,即当f(x)=1时,In(f)=I(f)恒成立,则有
 (16)
(16)
由式(15)、式(16)可知,当ck≥0时,有
 (17)
(17)
即原未知解析积分与数值积分受系统扰动的影响一致。故ck≥0为数值积分具有稳定性的充分不必要条件。
由表1可知,隐式积分系数均为正数,积分稳定性强。部分高阶显式积分出现负系数,根据上述分析可知显式积分稳定性弱于隐式积分。
数值积分的传统评价指标主要是稳定性、精度和计算量。稳定性作为数值积分成立的前提,可独立验证。但精度与计算量对同一数值积分的评价结果一般互为矛盾。如高阶积分精度高,但计算量大;低阶积分精度低,但计算量小。
作为互为矛盾的两种评价指标,优先保证积分精度,则需以牺牲计算效率为代价;优先保证计算效率,则需以牺牲精度为代价。此外,由于精度、计算量与数值积分的定量关系不明确,导致牺牲精度或计算效率引发的负面影响不可估计。
对数值积分而言,步长越小则精度越高。以精度为前提,则可确定不同数值积分达到该精度所需的临界步长。而计算量是电路方程进行单次积分求解对应的乘加运算之和,步长则是进行单次积分求解所能允许的最大时间。因此,精度与计算量可借助步长建立定量关系。
综合考虑精度、计算量、步长等因素,提出一种积分评价新指标——单位时间计算量,其定义式为
 (18)
(18)
式中, 为精度为h时对应的最大积分步长;cp,q为维度为p,q的电路微分方程进行一次积分求解时的总运算量;c1、c2分别为乘法运算量和加法运算量;
为精度为h时对应的最大积分步长;cp,q为维度为p,q的电路微分方程进行一次积分求解时的总运算量;c1、c2分别为乘法运算量和加法运算量; 、
、 为乘加运算的加权系数。
为乘加运算的加权系数。
若将该指标用于数值积分理论分析,则加权系数k1、k2取值为1即可。若将该指标用于实际软硬件平台中数值积分算法的评价,则加权系数k1、k2取值由式(19)确定。
 (19)
(19)
式中,t1、t2分别为软硬件平台执行单次乘加运算所需的实际耗时。
由式(18)可知,单位时间计算量刻画了积分精度与计算量的定量关系,反映的是数值积分在不同精度下单个步长内瞬时计算量的大小。该指标可同时表征不同数值积分精度与计算量的定量变化规律,对积分性能的评价更全面,更适用于指导数值积分算法的选择。
由于隐式积分具备更高的精度及稳定性,故以本文前四阶隐式积分为例进行理论分析,分别记为I1、I2、I3、I4。同时选取二阶隐式Gear积分[15]、三阶隐式BDF积分[17]、四阶隐式Adams积分[17]为对比,分别记为G2、B3、A4。
假设电路微分方程规模为
 (20)
(20)
式中,A为状态转移矩阵;x为状态量;B为输入矩阵;v为输入量。
理论分析时,取k1=k2=1。若对式(20)进行单次积分求解,则上述七类积分算法的理论运算量见表3。
表3 理论运算量
Tab.3 Theoretical calculation quantity

积分类型乘法运算加法运算运算量之和 I1q2+qpq2+qp-q2q2+2qp-q I2q2+qp+2pq2+qp+p-q2q2+2qp+3p-q I32q2+qp+3p2q2+qp+2p-q4q2+2qp+5p-q I43q2+qp+4p3q2+qp+3p-q6q2+2qp+7p-q G22q2+qp2q2+qp-q4q2+2qp-q B33q2+qp3q2+qp-q6q2+2qp-q A43q2+qp+4p3q2+qp+3p-q6q2+2qp+7p-q
另一方面,由式(11)可知,精度与积分步长的定量关系隐藏在局部截断误差中。由于高阶误差余项可忽略,故取误差主项作近似处理,可得精度与积分步长的对应关系。
以二阶隐式积分为例,其误差主项可近似为
 (21)
(21)
忽略误差正负,则有
 (22)
(22)
同理可得其余积分在不同精度下对应的最大理论步长。结合理论运算量,可得单位时间计算量的理论计算结果见表4。
由表4可知,单位时间计算量与电路方程规模p,q及精度h息息相关。其中参数h存在高次开方项,参数q存在二次项,故参数h、q对单位时间计算量的影响高于参数p。
表4 单位时间计算量理论值
Tab.4 Theoretical value of computational effort per unit time

积分类型 I1 I2 I3 I4 G2 B3 A4
为直观比较不同积分算法的单位时间计算量,以表4理论计算结果为基础,简要分析单位时间计算量随各类因素的变化规律。
以本文一阶隐式积分I1与传统三阶隐式BDF积分B3为例,在积分精度为0.01时,比较微分方程维度对单位时间计算量的影响,结果如图1所示。

图1 微分方程维度的影响
Fig.1 The influence of differential equation dimension
由图1可知,方程维度越大,单位时间计算量越大。与方程输入向量维度p相比,方程阶数q对单位时间计算量的影响更大,此现象与表4理论分析结论一致。而图1所示两种积分所得曲面的变化程度不同,说明不同积分的单位时间计算量受方程维度变化的影响程度不同。
当微分方程维度分别为p=2、q=6与p=6、q=3时,研究积分精度h对单位时间计算量的影响,结果如图2所示。

图2 积分精度的影响
Fig.2 The influence of integration accuracy
由图2可知,积分精度越高,单位时间计算量越大,但不同积分算法受精度的影响程度不同。且当方程维度不同时,各类积分算法单位时间计算量的变化趋势及相对大小顺序不同,进一步说明方程维度对单位时间计算量的影响不同。此外,当积分阶数相同时,本文积分算法I2、I3、I4的单位时间计算量普遍低于传统高阶积分算法G2、B3、A4,具有明显的效率优势。
单位时间计算量的意义在于:指导不同应用场景中数值积分算法的选择。因此给出积分精度h=0.01时,不同方程维度下单位时间计算量最小的积分算法分布,结果如图3所示。

图3 单位时间计算量最小的积分分布
Fig.3 Integral distribution with the minimum computational effort per unit time
由图3可知,当积分精度为0.01时,对上述七类隐式积分算法而言,本文二阶隐式积分I2适合高阶电路方程求解;传统三阶隐式BDF积分B3适合多输入电路方程求解;而当电路输入量与方程阶数均较高时,本文三阶隐式积分I3的求解效率最佳。
由本节分析可知,单位时间计算量受微分方程规模与精度等因素的影响均呈现规律性变化。在对不同拓扑结构的电力系统进行微分方程求解时,单位时间计算量能同时定量比较精度与计算量,为数值积分算法的选择提供更加准确、全面的指导。
数值积分的本质是对电路方程中微分项的近似求解,而微分项均源自电容与电感。电路方程中的电容电感主要有两种:①电路中真实存在的电容和电感;②采用L/C恒导纳模型[29]替代半导体开关时的等效电容和电感。
因此,分别以经典RLC电路与两电平变换器为实验对象,验证所提积分算法求解电路微分方程的有效性。实验电路如图4和图5所示,其电路参数见表5和表6。

图4 RLC电路模型
Fig.4 RLC circuit model

图5 两电平变换器
Fig.5 Two-level converter
表5 RLC电路参数
Tab.5 Parameters of RLC circuit

参数数值 电阻R/Ω0.2 电容C/F1 电感L/H0.25 电压源10sin(10pt) 电容电压初值1 电感电流初值2
表6 两电平变换器参数
Tab.6 Parameters of two-level converter

参数数值参数数值 直流电压源Udc/V20负载电阻R/Ω10 串联电阻r/ mΩ1 负载电感L/mH2 电容C1, C2/mF4 调制波频率/Hz50 开关等效导纳Gs/S0.302 三角波频率/kHz5
为实验电路搭建的实时仿真硬件平台如图6所示。为便于对仿真波形进行细节放大等处理,将示波器波形数据导入Matlab进行处理。

图6 实时仿真硬件平台
Fig.6 Hardware platform for the real-time simulation
对比积分选用本文隐式积分I1、I2、I3、I4与传统高阶隐式积分G2、B3、A4,比较七类积分算法在精度、计算量、单位时间计算量等方面的性能差异。
分别计算上述七类积分算法的准确度阶数和误差常数,结果见表7。
由表7可知,随着积分阶数增加,所提积分算法的准确度阶数越高、误差常数越小、精度越高,符合数值积分阶数越高、精度越高的一般规律。当积分阶数相同时,与传统高阶积分相比,所提积分算法的准确度阶数相同,但误差常数更小,即积分I2、I3、I4的理论精度高于传统高阶积分G2、B3、A4。
表7 不同积分精度比较
Tab.7 Accuracy comparison of different integration

积分类型准确度阶数误差常数 I11-1/2 I22-1/12 I33-1/45 I44-1/40 G22-2/9 B33-3/22 A44-19/720
以RLC电路中的电容电压为例,比较积分精度。由电路易得电容电压解析解uE为
 (23)
(23)
式中, w为输入电压源频率,w =10p。
各类积分所得电容电压波形如图7所示。各类积分数值解与解析解的最大绝对误差见表8。
表8 不同积分最大绝对误差
Tab.8 Maximum absolute error of different integration

积分类型最大绝对误差积分类型最大绝对误差 I10.155 12—— I20.022 76G20.083 59 I30.004 76B30.011 37 I40.000 82A40.001 22


图7 电容电压波形
Fig.7 Capacitor voltage waveforms
由图7和表8可知,与低阶积分相比,高阶积分具备绝对的精度优势。积分阶数提高一阶,最大绝对误差缩小一个数量级,与表7所得“阶数越高、准确度阶数越高”的理论分析结果一致。此外,本文积分算法I2、I3、I4的最大绝对误差比同阶积分算法G2、B3、A4分别减小72%、58%、33%,与表7所得“本文积分误差常数小于同阶积分”的理论分析结果一致。
随着积分阶数的提高,本文积分算法的精度优势逐渐减弱,但与传统高阶积分相比,本文积分的精度优势仍十分明显。
L/C恒导纳开关模型一般采用后向欧拉(I1)积分作为模型离散方法,此处仅以同阶积分B3、I3为例比较积分精度与稳定性。以精度更高的双值电阻开关模型为参考,两电平变换器的上桥臂开关电流波形如图8所示。

图8 上桥臂开关电流波形
Fig.8 Current waveform of upper bridge arm switch
由图8可知,高阶积分具有更高的精度与稳定性,采用高阶积分离散恒导纳模型,可有效抑制数值振荡,提高开关模型的仿真精度。积分I3对模型的改进效果明显优于积分B3,说明本文积分I3的精度与稳定性均高于传统同阶积分B3。
表3已给出各类积分算法的理论计算量。由表3可知,除四阶积分I4与A4计算量相同外,本文积分I2、I3的理论计算量低于传统积分G2、B3,计算效率更高。
以RLC电路为例,记录仿真100 000步各类积分算法的实际耗时,不同积分耗时比较见表9。
表9 不同积分耗时比较
Tab.9 Comparison of time consumption with different integration

积分理论运算量实际耗时/s I1100.103 I2130.110 I3230.218 I4330.297 G2180.190 B3260.239 A4330.299
由表9可知,积分I4和A4的计算量与实际耗时大致相等。而本文积分I2、I3的实际耗时比同阶积分G2、B3分别减小42%、9%,与理论分析结论一致。与传统高阶积分相比,本文采用的显隐式积分结构更简单,能有效减小积分计算量,提高计算效率。
以两电平变换器为例比较单位时间计算量。由式(18)的定义式可知,单位时间计算量由不同精度下的最大仿真步长与加权乘加运算量确定。
分别在仿真精度为0.01、0.001时进行重复试验,记录满足不同精度要求时各类积分算法的最大仿真步长。
以基于Xilinx的乘法器IP核(Multiplier)官方数据为例,在速度优先策略下,两个单精度数相乘的最优流水线长度为5个周期,相加则为1个周期。则由式(19)可得乘加运算加权系数k1、k2的取值为
 (24)
(24)
不考虑分压电容与负载电感,两电平变换器的电路方程维度为p=1、q=2,由此可得实际电路的加权乘加运算量。
根据最大仿真步长与实际运算量计算单位时间计算量,结果见表10和表11。
表10 精度h = 0.01时单位时间计算量对比
Tab.10 Comparison of computational effort per unit time with h = 0.01

积分类型/s/103 I15.70.003 801.500 I27.50.014 040.534 I312.50.021 900.571 I417.50.040 500.432 G29.70.011 350.854 B313.70.018 000.761 A417.50.023 560.742
表11 精度h = 0.001时单位时间计算量对比
Tab.11 Comparison of computational effort per unit time with h = 0.001

积分类型/s/103 I15.70.000 3815.000 I27.50.007 001.071 I312.50.009 301.344 I417.50.021 000.833 G29.70.003 502.771 B313.70.008 601.593 A417.50.015 801.107
由表10和表11可知,积分精度越高,所需的仿真步长越小,单位时间计算量越大。
与传统高阶积分G2、B3、A4相比,当精度为0.01时,同阶积分I2、I3、I4的单位时间计算量分别减少37%、25%、41%。当精度为0.001时,积分I2、I3、I4的单位时间计算量分别减少61%、16%、25%。说明在相同精度的前提下,本文积分算法的计算效率远远高于传统同阶积分算法。
整体而言,高阶积分的单位时间计算量更小。但对比积分I2、I3可知,积分I2的单位时间计算量更小,计算效率高于积分I3。虽然高阶积分精度高,但计算量大,而单位时间计算量是同时对精度与计算量进行定量比较的指标,故单位时间计算量与积分阶数无必然联系。因此,在相同精度条件下,以单位时间计算量为指标,可确定计算效率最高的积分算法。
本文提出一种基于任意代数精度的显式或隐式数值积分,理论证明了所提积分算法的精度与稳定性,并定义单位时间计算量来补充传统积分评价指标。通过理论分析与仿真实验,验证所提积分算法与指标的有效性。具体结论如下:
1)所提积分算法采用显隐式积分结构,与传统高阶积分相比,积分结构更简单,计算效率更高,实际仿真耗时可比同阶积分减小9%~42%。
2)基于任意代数精度的参数确定方法,可大幅提高积分精度。积分阶数相同时,与传统高阶积分相比,所提积分算法精度可提高33%~72%。
3)定义单位时间计算量,明确精度、计算量与积分的定量关系。给出理论计算方法,并研究其随电路方程规模、精度等因素的变化规律。在相同精度条件下,与传统高阶积分相比,所提积分算法的单位时间计算量可减小16%~61%。
针对本文提出的基于代数精度的显隐式数值积分以及评价指标单位时间计算量,应用前景与未来研究方向主要有以下几个方面:
1)除电路微分方程求解外,所提数值积分算法还可用于弱电信号的频谱分析、电力系统的暂态及稳态响应分析、器件建模与电磁暂态仿真等领域。
2)单位时间计算量能定量比较积分精度与计算量,可用于开关模型离散方法的确定、实时仿真或大规模仿真中积分算法的选择、以资源优先或速度优先的FPGA设计等领域。
3)所提积分算法为定步长积分,即差分项之间的积分步长相等。如何确定变步长积分的积分系数有待进一步研究。
4)作为积分评价新指标,单位时间计算量的实际应用有待进一步推广。
附 录
附表1 Adams显式积分
App.Tab.1 Adams explicit integration

积分阶数准确度阶数误差常数 一阶1———11/2 二阶3/2-1/2——25/12 三阶23/12-16/125/12—33/8 四阶55/24-59/2437/24-9/244251/720
附表2 Adams隐式积分
App.Tab.2 Adams implicit integration

积分阶数准确度阶数误差常数 一阶1———1-1/2 二阶1/21/2——2-1/12 三阶5/128/12-1/12—3-1/24 四阶9/2419/24-5/241/244-19/720
参考文献
[1] Wunderlich A S, Santi E. Closed-form implicit models for efficient simulation of power electronics[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(2): 1568-1577.
[2] 易新强, 王东, 刘海涛, 等. 考虑原动机调速特性的中压直流发电机组动态仿真模型[J]. 电工技术学报, 2024, 39(10): 2974-2983. Yi Xinqiang, Wang Dong, Liu Haitao, et al. Dynamic simulation model of MVDC generating set consi-dering the speed regulation characteristics of prime movers[J]. Transactions of China Electro-technical Society, 2024, 39(10): 2974-2983.
[3] 虞竹珺, 赵争鸣, 施博辰, 等. 基于刚性检测的电力电子系统自适应仿真算法[J]. 电工技术学报, 2023, 38(12): 3208-3220, 3247. Yu Zhujun, Zhao Zhengming, Shi Bochen, et al. An adaptive simulation method for power electronics systems based on stiffness detection[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3208-3220, 3247.
[4] Bai Hao, Huang Gang, Liu Chen, et al. A controller HIL testing approach of high switching frequency power converter via slower-than-real-time simulation [J]. IEEE Transactions on Industrial Electronics, 2024, 71(8): 8690-8702.
[5] Chalangar H, Ould-Bachir T, Sheshyekani K, et al. Methods for the accurate real-time simulation of high-frequency power converters[J]. IEEE Transactions on Industrial Electronics, 2022, 69(9): 9613-9623.
[6] 管乐诗, 程怡, 施震宇, 等. 一种10 MHz高频DC-DC功率变换器及其同步整流技术[J]. 电工技术学报, 2023, 38(18): 5029-5038. Guan Yueshi, Cheng Yi, Shi Zhenyu, et al. A 10 MHz high frequency DC-DC power converter and its synchronous rectification technology[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 5029-5038.
[7] Gray W S, Verriest E I. Linear operator differential equations with applications to linear time-varying systems[C]//2023 59th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2023: 1-7.
[8] Baiburin V B, Karabutov M V. Method for accelerated numerical solution of nonlinear differential equations [C]//2023 IEEE XVI International Scientific and Technical Conference Actual Problems of Electronic Instrument Engineering (APEIE), Novosibirsk, Russian Federation, 2023: 1190-1193.
[9] 何绍民, 张喆, 卢倚平, 等. 基于计算前沿面的实时仿真数值积分并行构造及其数值模型解耦加速方法[J]. 电工技术学报, 2023, 38(16): 4246-4262. He Shaomin, Zhang Zhe, Lu Yiping, et al. Numerical model decoupling acceleration method with numerical integration parallelism construction based on com-putation front in real-time simulation[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4246-4262.
[10] Watson N, Arrillaga J. Power systems electromagnetic transients simulation[M]. 2nd ed. Stevenage: IET, 2018.
[11] Clitan I, Colosi T, Unguresan M L, et al. Prospects of algebraization of deformable exponential functions through ordinary differential equations and partial differential equations[C]//2020 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 2020: 1-5.
[12] Tzounas G, Dassios I, Milano F. Small-signal stability analysis of numerical integration methods[J]. IEEE Transactions on Power Systems, 2022, 37(6): 4796-4806.
[13] Bai Hao, Liu Chen, Majstorovic D, et al. Real-time simulation technology for modern power electronics [M]. Singapore: Academic Press, 2023.
[14] Boldo S, Faissole F, Chapoutot A. Round-off error and exceptional behavior analysis of explicit Runge-Kutta methods[J]. IEEE Transactions on Computers, 2020, 69(12): 1745-1756.
[15] Lebedka S M, Petrovskyi M V, Veprik Y N. Discrete models of the electric grid elements, obtained with using the second-order formula of implicit gear method[C]//2017 IEEE First Ukraine Conference on Electrical and Computer Engineering (UKRCON), Kyiv, UKraine, 2017: 584-588.
[16] Song Xinli, Tang Yong, Zhong Wuzhi, et al. New mixed integral algorithm for unified dynamic power system simulations of transient, medium-term and long-term stabilities[C]//2011 IEEE/PES Power Sys-tems Conference and Exposition, Phoenix, AZ, USA, 2011: 1-7.
[17] Yushkova M, Sanchez A, de Castro A. The necessity of resetting memory in Adams–bashforth method for real-time simulation of switching converters[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6175-6178.
[18] Aghahassani M, Castronuovo E D, Ledesma P, et al. Application of linear multi-step methods to a transient stability constrained optimal power flow model[C]// 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I& CPS Europe), Madrid, Spain, 2020: 1-6.
[19] Zhao Zhengming, Yuan Liqiang, Bai Hua, et al. Electromagnetic transients of power electronics sys-tems[M]. Singapore: Singapore Springer, 2019.
[20] Veigend P, Nečasová G, Šátek V. Solving linear and nonlinear problems using Taylor series method[J]. Open Computer Science, 2024, 14(1): 302-309.
[21] Wang Bin, Xu Xin, Sun Kai. Power system transient stability analysis using high-order Taylor expansion systems[C]//2019 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 2019: 1-5.
[22] Trotsenko Y, Brzhezitsky V, Protsenko O, et al. Calculation of high voltage divider accuracy using Duhamel’s integral[C]//2018 IEEE 17th International Conference on Mathematical Methods in Electro-magnetic Theory (MMET), Kyiv, UKraine, 2018: 213-216.
[23] Sevastianov L A, Lovetskiy K P, Kulyabov D S. Multistage collocation pseudo-spectral method for the solution of the first order linear ODE[C]//2022 Ⅷ International Conference on Information Technology and Nanotechnology (ITNT), Samara, Russian Federation, 2022: 1-6.
[24] Yaghoobnia A, Kazemi M. A collocation method for the numerical solution of a class of linear stochastic integral equations based on Legendre polynomials [C]//2022 Second International Conference on Distributed Computing and High Performance Computing (DCHPC), Qom, Iran, 2022: 26-30.
[25] Conte D, D’Ambrosio R, D’Arienzo M P, et al. Singly diagonally implicit multivalue collocation methods[C]// 2020 International Conference on Mathematics and Computers in Science and Engineering (MACISE), Madrid, Spain, 2020: 65-68.
[26] 周斌, 汪光森, 李卫超, 等. 基于FPGA的电力电子系统电磁暂态实时仿真通用解算器[J]. 电工技术学报, 2023, 38(14): 3862-3874. Zhou Bin, Wang Guangsen, Li Weichao, et al. An FPGA-based general solver for electromagnetic transient real-time simulation of power electronic systems[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3862-3874.
[27] 付浩, 李鹏, 富晓鹏, 等. 面向多FPGA实时仿真器的资源优化配置方法[J]. 电力系统自动化, 2023, 47(11): 88-100. Fu Hao, Li Peng, Fu Xiaopeng, et al. Optimal resource allocation method for real-time simulator based on multiple field programmable gate arrays[J]. Automation of Electric Power Systems, 2023, 47(11): 88-100.
[28] Boldo S, Faissole F, Chapoutot A. Round-off error analysis of explicit one-step numerical integration methods[C]//2017 IEEE 24th Symposium on Computer Arithmetic (ARITH), London, UK, 2017: 82-89.
[29] 王钦盛, 王灿, 潘学伟, 等. 基于FPGA的电力电子恒导纳开关模型修正算法及实时仿真架构[J]. 电力系统自动化, 2024, 48(1): 150-159. Wang Qinsheng, Wang Can, Pan Xuewei, et al. Fixed-admittance switch model correction algorithm and real-time simulation architecture of power electronics based on field programmable gate array[J]. Auto-mation of Electric Power Systems, 2024, 48(1): 150-159.
Abstract The circuit differential equation is the foundation of electrical engineering, spanning various fields such as circuit principle analysis, topology design, and power system engineering applications. However, with the increasing scale of the power system and the widespread application of high-frequency semiconductor switches, solving circuit differential equations quickly and accurately has become increasingly challenging. Numerical integration is one of the classic methods for solving circuit differential equations, but traditional numerical integration methods are fixed in form, with non-adjustable integration accuracy, and the relationship between accuracy, computation effort, and integration is not well-defined. Moreover, traditional indicators such as stability, accuracy, and calculation effort only allow for qualitative comparisons of numerical integration, making it difficult to accurately evaluate integration accuracy and computation efficiency. To address these problems, an explicit or implicit numerical integration algorithm based on arbitrary algebraic precision is proposed. Meanwhile, the computational effort per unit time is defined to supplement the traditional integral evaluation indicators.
Firstly, the construction method of explicit and implicit numerical integration is given. By independently selecting the differentiation items and their orders to construct a new type of integration, the structure of the integration is simplified, thereby enhancing the efficiency of the integration calculation. Secondly, a method for determining integral parameters based on arbitrary algebraic precision is proposed to improve integration accuracy, and the accuracy and stability of the proposed algorithm are proved. Finally, computational effort per unit time is defined to clarify the quantitative relationship between accuracy, computational effort, and numerical integration. And the patterns of variation with respect to the scale of circuit equations and factors like accuracy are investigated.
Using classic RLC circuits and a two-level converter as experimental objects, a real-time simulation hardware platform is built to verify the effectiveness of the proposed integration algorithm and evaluation indicator. The simulation results indicate that compared to low-order integrations, high-order integrations have an absolute advantage in accuracy. Increasing the integral order by one reduces the maximum absolute error by an order of magnitude. When the integral order is the same, compared to traditional high-order integration, the accuracy of the proposed integration algorithm can be improved by 33% to 72%, the computational effort can be reduced by 9% to 42%, and computational effort per unit time can be reduced by 16% to 61%. Furthermore, the proposed integration algorithm has higher stability and stronger ability to suppress numerical oscillations compared to traditional numerical integration.
The following conclusions can be drawn from the simulation analysis: (1) Compared to traditional numerical integration, the proposed integration structure is simpler and more computationally efficient. The parameter determination method based on algebraic precision makes the integration more accurate, more stable, and better at suppressing numerical oscillations. (2) The computational effort per unit time can simultaneously characterize the quantitative relationship between accuracy, calculation effort, and numerical integration, allowing for accurate assessment of integration performance. For the proposed numerical integration algorithm and evaluation indicator, the main aspects of application prospects and future research directions are as follows: (1) The proposed integration algorithm can be used in power system transient response analysis, device modeling and electromagnetic transient simulation. (2) The computational effort per unit time can be used to determine the discrete method in switch model and to select the integration algorithm in real-time simulation. (3) The structure and accuracy of variable-step numerical integration need to be further studied.
keywords:Circuit differential equation, numerical integration, algebraic precision, calculation effort
DOI: 10.19595/j.cnki.1000-6753.tces.240572
中图分类号:TM133
国家自然科学基金面上项目资助(51477179)。
收稿日期 2024-04-11
改稿日期 2024-09-21
杜金鹏 男,1995年生,博士研究生,研究方向为数值积分、电力电子系统建模与仿真。E-mail:jpdu_1409@163.com
王 康 男,1991年生,博士,助理研究员,研究方向为电力电子系统实时仿真。E-mail:25729819@qq.com(通信作者)
(编辑 赫 蕾)