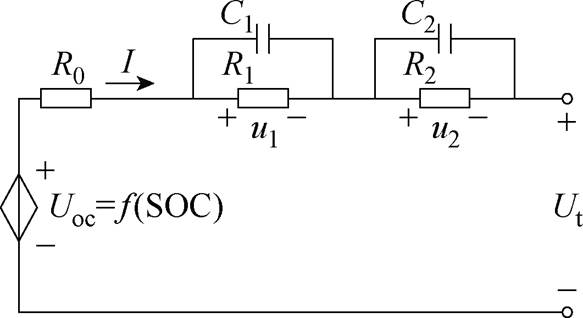
图1 DP等效电路模型
Fig.1 DP equivalent circuit model
摘要 锂电池荷电状态(SOC)的精确估计对于提高电池能量利用率、保障电池安全运行具有重要意义。针对模型不确定性导致基于卡尔曼滤波(KF)的SOC估计方法精度低的问题,提出一种联合改进型滑模观测器(ISMO)的自适应扩展卡尔曼滤波(AEKF)算法,以实现SOC高精度估计。首先,基于双极化(DP)等效电路模型建立融合饱和函数的ISMO,以降低传统滑模观测器的抖振。其次,设计一种新型自适应衰减因子,以降低过往陈旧测量数据对扩展卡尔曼滤波估计结果的影响,并基于融合饱和函数的ISMO,实现联合ISMO的AEKF估计方法设计。最后,基于自主实验平台获取实测模拟工况数据搭建仿真模型,验证了所提ISMO_AEKF算法在不同工况下,相比于AEKF、ISMO_EKF和其他同类型联合算法,具有更高的估计精度及鲁棒性。
关键词:荷电状态 饱和函数 滑模观测器 自适应衰减因子 卡尔曼滤波
锂电池因具有使用寿命长、功率特性好等特点,在新能源汽车领域得到了广泛应用[1]。荷电状态(State of Charge, SOC)是锂电池剩余电量的关键指标,准确的SOC对于确保锂电池的安全性能和能量高效利用至关重要[2-3]。锂电池作为典型的非线性系统,其SOC无法直接测量,只能依赖数学方法进行估计,本文将针对锂电池SOC估计展开研究。
当前常用的SOC估计方法[4-8]有开路电压法、库仑计数法、数据驱动法和模型法。其中,开路电压法需要电池长时间静置才能通过测量开路电压以估计SOC,该方法不能实现SOC的实时在线估计;库仑计数法是工程上获取电池SOC最简单通用的方法,但其估计误差会随着时间累计逐渐增大,同时对电流测量精度要求较高;数据驱动法主要是指神经网络[9-11],其以电池循环充放电电流、电压和温度等参数作为模型输入,通过建立输入参数与SOC的非线性映射关系以估计SOC,此类算法估计精度高,但需要大量数据离线训练,耗时长,不便于SOC的即时估计。
模型法通常基于等效电路模型或电化学模型,并结合不同的滤波器或观测器进行SOC估计。目前,由于其闭环控制、高估算精度和强鲁棒性等优点,基于模型法的SOC估计受到了众多学者的青睐。常见模型法[12-15]包括卡尔曼滤波、H∞滤波(H-Infinity Filter, HIF)、粒子滤波以及滑模观测器等。HIF通过构建基于博弈论的代价函数寻求最优估计,估计结果具有很强的鲁棒性,但其未对模型不确定性和噪声做任何假设,不利于估计精度的提高。粒子滤波(Particle Filter, PF)同样不受系统模型约束,并且不受白噪声假设与线性化误差影响。但此方法存在典型的粒子退化问题,不适合长时间尺度系统的状态估计。滑模观测器(Sliding Mode Observer, SMO)是一种低计算需求并且兼有良好鲁棒性的非线性观测器,其开关函数会根据所观测系统状态实时切换,使系统状态在滑模面上逐渐收敛至平衡点。但其离散的开关特性会造成系统抖振,尤其是出现高频噪声时,抖振现象会进一步加剧。
卡尔曼滤波是一种最优化自回归数据处理算法,当其应用于强非线性系统时,常见形式有扩展卡尔曼滤波(Extended Kalman Filter, EKF)[16]、无迹卡尔曼滤波(Unscented Kalman Filter, UKF)[17]以及容积卡尔曼滤波(Cubature Kalman Filter, CKF)[18]等。锂电池系统属于强非线性系统,且存在极为复杂的运行噪声和外界干扰,这些系统噪声分布规律和统计特性尚不明确。现有卡尔曼滤波方法在模型参数确定、系统噪声满足均值和方差已知的Gaussian分布时,能够实现最小方均误差意义下的最优状态估计,但在系统模型参数不确定、噪声统计特性不满足高斯分布或未知时,估计精度下降甚至使滤波发散。
由以上分析可知,不同类型的模型法虽然从不同角度提高了SOC估计的精度及鲁棒性,但也均存在各自的不足。为解决单一类型算法的局限性,较多文献建立了联合算法用以估计SOC。
文献[19]将扩展卡尔曼滤波算法和BP神经网络联合,利用神经网络补偿EKF的过程噪声协方差,得益于闭环误差校正,其表现出较高的SOC估计精度。但该算法以神经网络进行噪声补偿,不可避免地存在时延问题,影响了SOC估计的实时性,实用价值有待进一步研究。文献[20]基于数据驱动调整无迹卡尔曼滤波的噪声协方差矩阵。文献[21]将深度学习与卡尔曼滤波联合,利用神经网络捕获输入信号的空间和时间特性以消除瞬态信号振荡的影响。文献[20-21]与文献[19]类似,均以复杂耗时的数据处理过程为代价克服了卡尔曼滤波器将噪声干扰视为高斯白噪声对估计精度的影响。文献[22]基于电热模型建立了CKF和HIF联合算法,该算法能在考虑噪声和温度变化的同时降低计算成本,但基于卡尔曼滤波建立估计算法的过程忽略了过往测量数据对估计误差的影响,造成估计精度降低。文献[23]设计了一种基于SMO的HIF算法,降低了模型不确定性及随机噪声对估计结果的扰动,提高了算法的鲁棒性。但该算法完全忽略噪声也是不切实际的。文献[24]设计一种基于EKF的SMO算法,此算法在EKF的状态更新方程中引入防抖函数以克服SMO因噪声干扰而导致的抖振现象,并实时更新滑模参数。该算法具有良好的估计性能和鲁棒性,但与文献[22]相似,未考虑历史数据对估计结果的影响,随着时间累积,估计精度会逐渐降低,甚至会导致滤波发散问题。
基于上述分析,较多学者提出联合算法用以估计SOC,相较于单一估计算法,精度高且鲁棒性强,但仍然存在以下问题:
(1)SMO能够有效克服模型不确定性和随机噪声对估计结果的影响,但其离散的开关函数会导致估计结果的抖振[12, 16, 19, 24]。
(2)卡尔曼滤波算法依赖所有过往测量数据用以估计下一时刻的状态变量,忽略了当前测量数据的比重,没有充分考虑新息占比[17-18, 20-22],造成卡尔曼滤波稳态条件下跟踪能力弱、估计精度低的问题。
基于上述问题,本文提出一种联合改进滑模观测器的自适应扩展卡尔曼滤波(Improved Sliding Mode Observer_Adaptive Extended Kalman Filter, ISMO_AEKF)SOC估计方法,实现SOC的高精度、强鲁棒估计。具体创新点体现在:
(1)基于饱和函数可以在边界层外进行实时切换控制,而在边界层内,可实施线性化的反馈控制,从而减少系统抖动的优点,基于饱和函数改进传统SMO的符号函数,从而降低传统SMO的系统抖动现象。
(2)基于EKF引入一种新型自适应衰减因子,在弱化过往测量数据对当前估计结果不利影响的同时,充分强化现时观测数据的作用,从而提升EKF算法的跟踪性能和估计精度。
为实现基于模型的SOC高精度估计,必须建立精确且计算量小的等效电路模型来表征锂电池的电气特性。双极化(Dual Polarization, DP)模型能够较好地平衡计算复杂度和估算精度[5],本文选用如图1所示的双极化模型进行SOC估计研究。图1中,Uoc为开路电压(Open Circuit Voltage, OCV),其为关于SOC的函数,I为回路电流,R0为欧姆内阻,R1、R2为极化电阻,C1、C2为极化电容,u1、u2分别为电阻R1、R2电压,Ut为电池端电压。

图1 DP等效电路模型
Fig.1 DP equivalent circuit model
根据元件特性及基尔霍夫电压电流定律,DP等效电路模型离散化状态方程可表示为
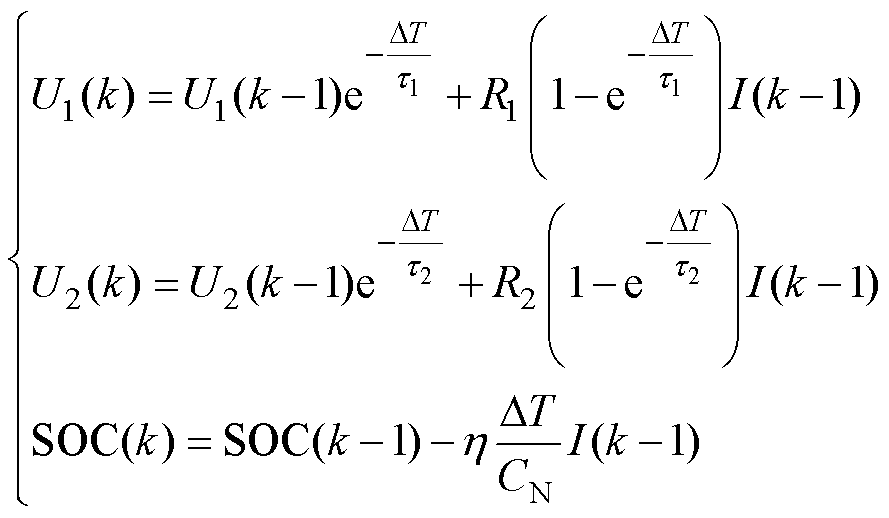 (1)
(1)
 (2)
(2)
式中,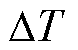 为采样周期;
为采样周期;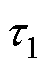 =R1C1,
=R1C1,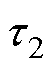 =R2C2为两个RC并联回路的时间常数;CN为电池的额定容量;
=R2C2为两个RC并联回路的时间常数;CN为电池的额定容量;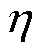 为库仑效率。基于DP模型,考虑如下系统
为库仑效率。基于DP模型,考虑如下系统
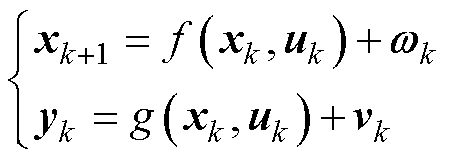 (3)
(3)
式中,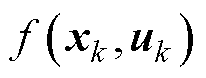 与
与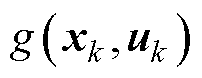 分别为转移函数与测量函数;xk为系统在k时刻的状态变量;uk与yk分别为k时刻的输入、输出;
分别为转移函数与测量函数;xk为系统在k时刻的状态变量;uk与yk分别为k时刻的输入、输出;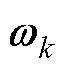 与vk分别为状态方程的过程噪声和观测噪声。令式(3)所示系统稳定,SMO的标准形式为
与vk分别为状态方程的过程噪声和观测噪声。令式(3)所示系统稳定,SMO的标准形式为
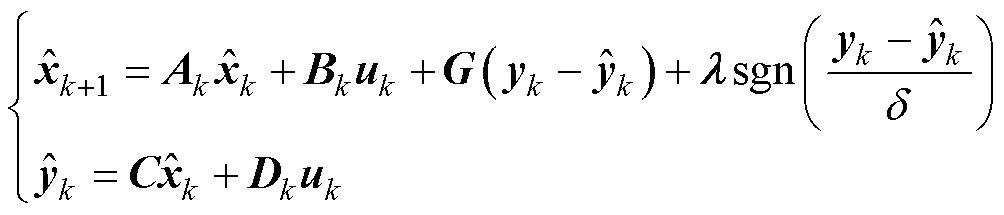 (4)
(4)
式中,Ak为系统矩阵;Bk为输入矩阵;Ck为输出矩阵;Dk为前馈矩阵;sgn( · )为符号函数;G为输出反馈增益矩阵;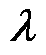 为饱和函数增益;
为饱和函数增益;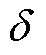 为边界层。在没有外界干扰和高频噪声的理想状态下,符号函数能使SMO在切换面上形成理想的滑动模态直至收敛至平衡点,但实际情况存在不可避免的干扰或噪声,符号函数会使SMO出现抖振现象。饱和函数具有在边界层之外进行实时切换控制的优点,而在边界层内部,其可实施线性化的反馈控制,从而显著减少系统的抖动现象。为降低传统SMO抖动问题,本文设计饱和函数
为边界层。在没有外界干扰和高频噪声的理想状态下,符号函数能使SMO在切换面上形成理想的滑动模态直至收敛至平衡点,但实际情况存在不可避免的干扰或噪声,符号函数会使SMO出现抖振现象。饱和函数具有在边界层之外进行实时切换控制的优点,而在边界层内部,其可实施线性化的反馈控制,从而显著减少系统的抖动现象。为降低传统SMO抖动问题,本文设计饱和函数 取代符号函数以改进SMO,即
取代符号函数以改进SMO,即
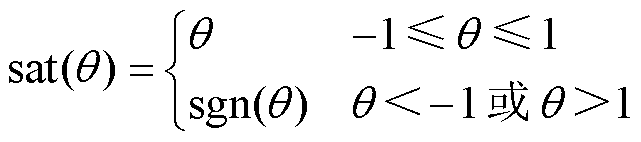 (5)
(5)
改进后的SMO离散空间方程为
 (6)
(6)
状态估计的动态误差为
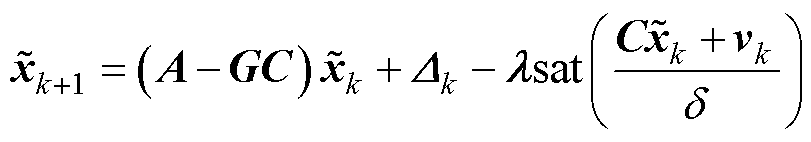 (7)
(7)
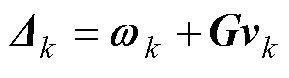 (8)
(8)
对于式(3)所示系统,设定合适的滑模参数,使得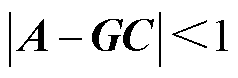 成立[15],则有:动态误差在边界层
成立[15],则有:动态误差在边界层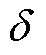 外时,SMO为准滑动模态,且动态误差逐渐趋于
外时,SMO为准滑动模态,且动态误差逐渐趋于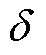 ;动态误差在边界层
;动态误差在边界层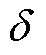 内时,SMO稳定,且当k趋于无穷大时,动态误差有界。具体而言,选取边界层
内时,SMO稳定,且当k趋于无穷大时,动态误差有界。具体而言,选取边界层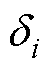 、输出反馈增益矩阵G和饱和函数增益
、输出反馈增益矩阵G和饱和函数增益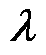 ,设
,设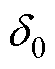 为系统最小边界层,选取相同的输出反馈增益和饱和函数增益,若
为系统最小边界层,选取相同的输出反馈增益和饱和函数增益,若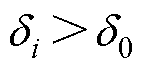 ,则有:动态误差超出边界层
,则有:动态误差超出边界层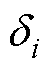 的情况下,SMO为准滑动模态,且其滑动路径穿过边界层
的情况下,SMO为准滑动模态,且其滑动路径穿过边界层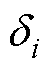 并在边界层内部振荡;当动态误差位于边界层
并在边界层内部振荡;当动态误差位于边界层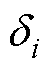 之内,其滑动路径将逐渐趋于稳定直到收敛直至边界层
之内,其滑动路径将逐渐趋于稳定直到收敛直至边界层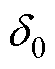 范围之内。
范围之内。
EKF以卡尔曼滤波为基础,其核心在于:对于非线性系统,运用泰勒级数在采样点将其状态方程展开,通过舍去高阶项,实现非线性系统的线性化。
对于式(3)所示系统,在采样点将转移函数和测量函数泰勒展开,仅保留一阶项与常数项。可得线性化空间模型为
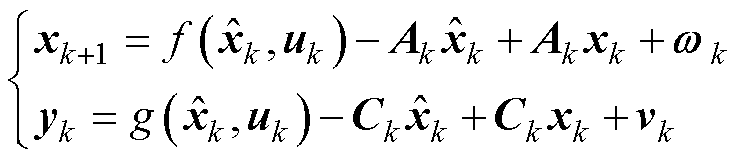 (9)
(9)
系统矩阵Ak和输出矩阵Ck分别表示为
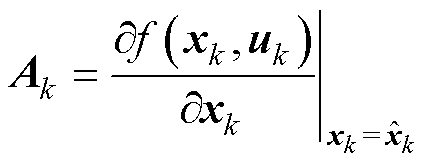 (10)
(10)
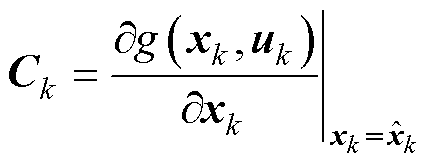 (11)
(11)
本文通过设计一种新型自适应衰减因子以减少滤波器存储的过往数据,确保滤波器充分利用现时测量数据,减小陈旧测量数据对当前状态估计的不利影响,以提高算法估计精度。设新息为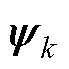 ,表示为
,表示为
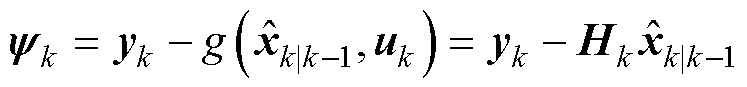 (12)
(12)
式中,Hk为测量矩阵,新息协方差矩阵理论值可由卡尔曼滤波器的理论标称值得到,即
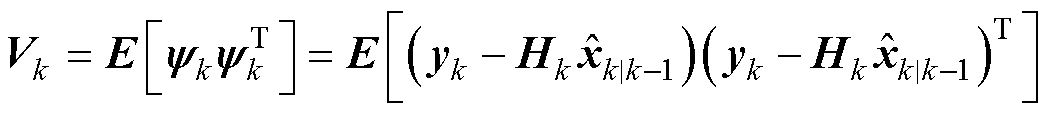
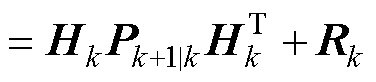 (13)
(13)
式中,Pk+1|k为误差协方差;Rk为测量噪声协方差。根据新息历史数据定义实时估计协方差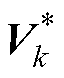 为
为
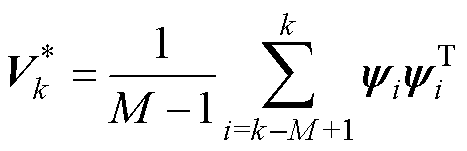 (14)
(14)
式中,参数M表示开窗的大小,即新息历史数据的个数,开窗的大小选择与SOC估计精度密切相关[13, 25],本文设定M=6。为满足AEKF的强跟踪性质,该算法必须满足正交定理。EKF的最优增益矩阵K必须满足
 (15)
(15)
式中,j=1, 2, 3,…。EKF需要误差协方差Pk取最优值,新息矩阵则恒定正交。
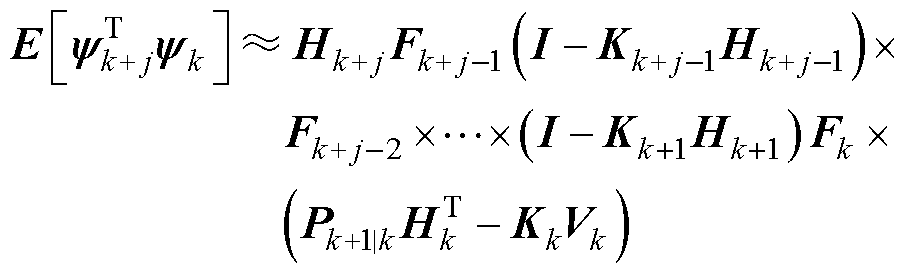 (16)
(16)
式中,Fk为系统状态矩阵。由上述推导可知,对每一个j值都存在
 (17)
(17)
新息序列会因系统参数扰动而出现估计误差。为确保AEKF受到系统摄动的情况下依然具有强跟踪性,需确保新息序列数据自相关函数始终为零,进而实时迭代增益矩阵Kk,保证新息序列数据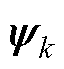 正交。EKF在采样点泰勒展开过程中省略了二阶及以上的各项,不可避免地引入线性化误差,因此新息序列很难为白噪声,但当Sk近似为零时,新息序列就会具有类似高斯白噪声的性质,有助于增强算法的鲁棒性和估计精度。
正交。EKF在采样点泰勒展开过程中省略了二阶及以上的各项,不可避免地引入线性化误差,因此新息序列很难为白噪声,但当Sk近似为零时,新息序列就会具有类似高斯白噪声的性质,有助于增强算法的鲁棒性和估计精度。
基于等效电路模型进行SOC估计时,当估计电压随时间推移逐步与电压真实值产生偏差时,表明新息响应偏高。为使式(16)成立,需令式(17)等于零,从而使EKF具备出色的跟踪能力。但在式(17)中,Hk保持不变,而系统建模误差会造成新息协方差矩阵的理论值Vk与真实值有所偏差。为解决此问题,引入估计新息协方差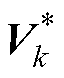 用以替代Vk, 则有
用以替代Vk, 则有
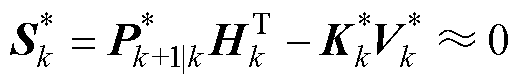 (18)
(18)
如式(18)所示,令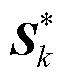 近似为零,从而使系统具有强跟踪性质。其中
近似为零,从而使系统具有强跟踪性质。其中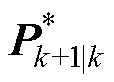 和
和 是经过加权处理的误差协方差矩阵和最优增益。为确保式(18)成立,引入自适应衰减因子
是经过加权处理的误差协方差矩阵和最优增益。为确保式(18)成立,引入自适应衰减因子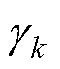 ,取其与误差协方差Pk+1|k的乘积。若
,取其与误差协方差Pk+1|k的乘积。若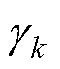 >1,则增益Kk权重提高,不仅增加了新息占比,同时也增强了系统的鲁棒性。加权后的误差协方差为
>1,则增益Kk权重提高,不仅增加了新息占比,同时也增强了系统的鲁棒性。加权后的误差协方差为
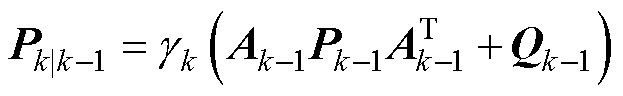 (19)
(19)
为简化衰减因子,定义
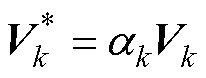 (20)
(20)
其中
 (21)
(21)
式中,tr表示矩阵取迹运算。
新增益 根据
根据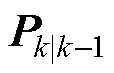 与
与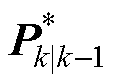 的关系可得
的关系可得
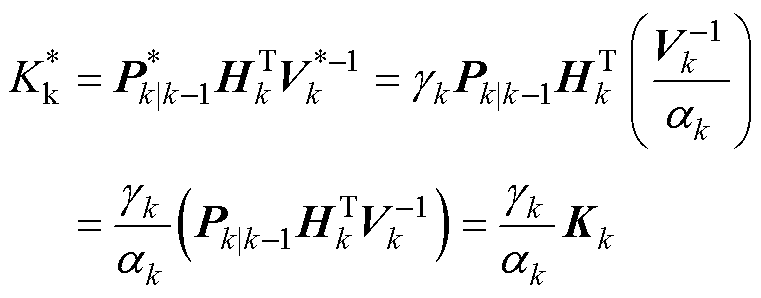 (22)
(22)
式(22)展开可得
 (23)
(23)
假设 满秩,则式(23)可化简为
满秩,则式(23)可化简为
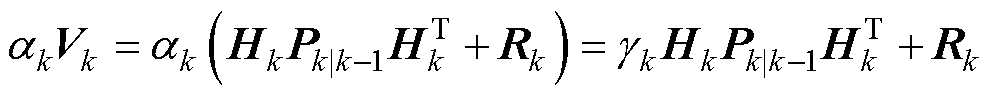 (24)
(24)
由式(24)可得,利用系数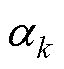 加权新息协方差矩阵Vk依赖衰减因子
加权新息协方差矩阵Vk依赖衰减因子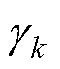 加权误差协方差矩阵Pk|k−1来实现。由式(21)可求得新息协方差系数
加权误差协方差矩阵Pk|k−1来实现。由式(21)可求得新息协方差系数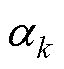 ,衰减因子可由式(24)得到。为避免求逆运算,在式(24)取矩阵的迹(trace),式(24)可转换为
,衰减因子可由式(24)得到。为避免求逆运算,在式(24)取矩阵的迹(trace),式(24)可转换为
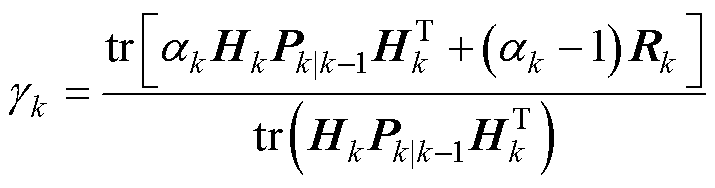 (25)
(25)
式(25)需满足 满秩,但实际情况下难以实现,对式(24)变形可得
满秩,但实际情况下难以实现,对式(24)变形可得
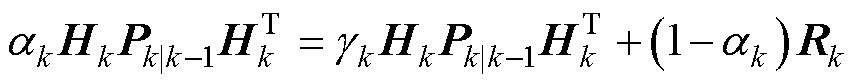 (26)
(26)
由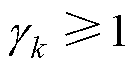 可得
可得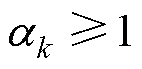 。EKF量测方程中所有参数均可通过建模求得,依靠预测误差协方差矩阵Pk|k−1进行权重计算,与量测噪声Rk无关,式(26)中将量测噪声矩阵Rk忽略并假设
。EKF量测方程中所有参数均可通过建模求得,依靠预测误差协方差矩阵Pk|k−1进行权重计算,与量测噪声Rk无关,式(26)中将量测噪声矩阵Rk忽略并假设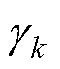 =
=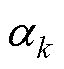 ,通过式(21)计算求得
,通过式(21)计算求得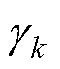 。
。
综上所述,AEKF中的自适应衰减因子仅需计算新息协方差矩阵和其矩阵的迹,易于实现,提高了算法的跟踪性能及估计精度。AEKF算法流程如图2所示。
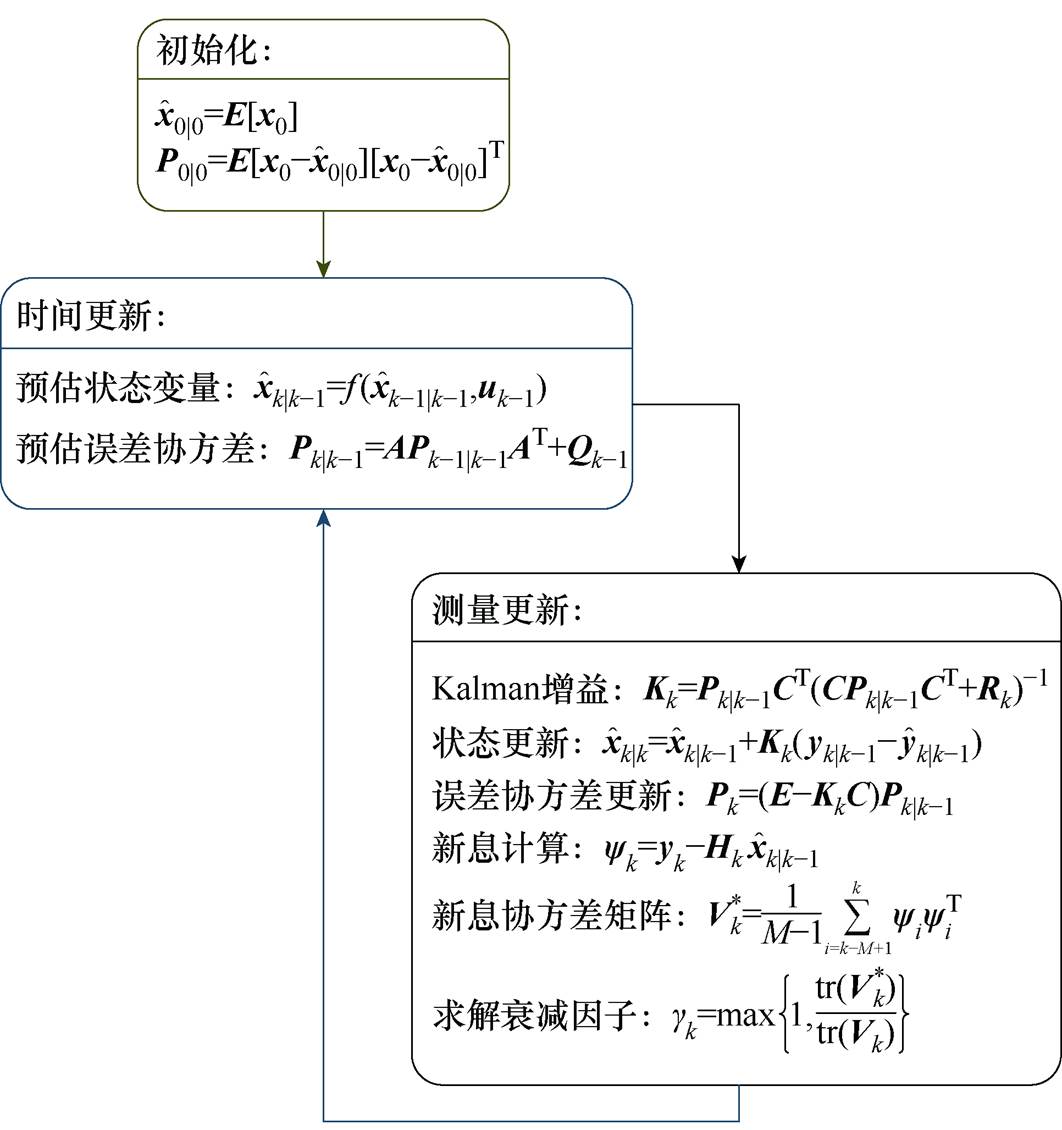
图2 AEKF算法流程
Fig.2 Algorithm flowchart of AEKF
SMO为非线性状态观测器且对模型参数扰动具有较强的鲁棒性,在一定程度上能降低系统参数变化和外界扰动的影响[15, 23-24],本文联合算法利用改进滑模观测器作为输入端估计系统的状态变量,ISMO对建模误差鲁棒性较强,一定程度上降低了系统参数变化和外界扰动的影响,基于ISMO的AEKF算法可以减小建模误差造成的滤波发散问题。联合ISMO的AEKF算法迭代过程如下所述。
1)时间更新
预估状态变量
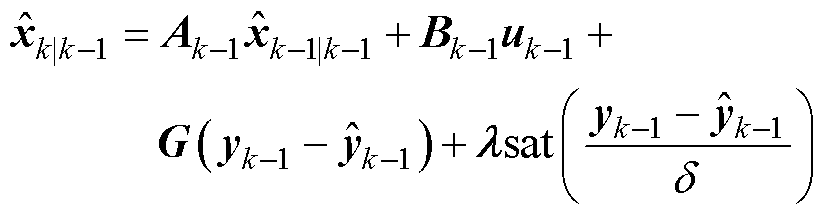 (27)
(27)
预估误差协方差
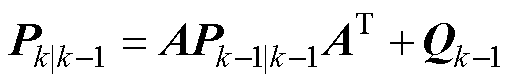 (28)
(28)
2)测量更新
Kalman最优增益
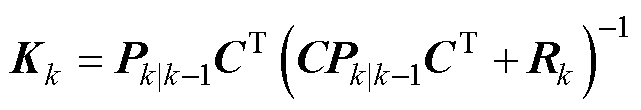 (29)
(29)
状态更新
 (30)
(30)
误差协方差更新
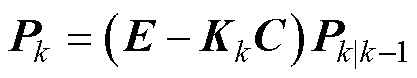 (31)
(31)
新息计算
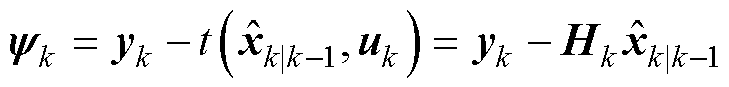 (32)
(32)
求解衰减因子
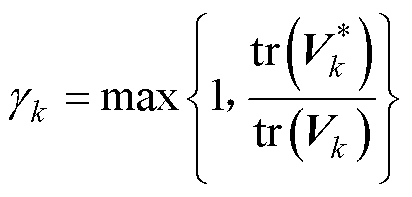 (33)
(33)
至此,ISMO_AEKF设计完成,具体算法流程如图3所示。
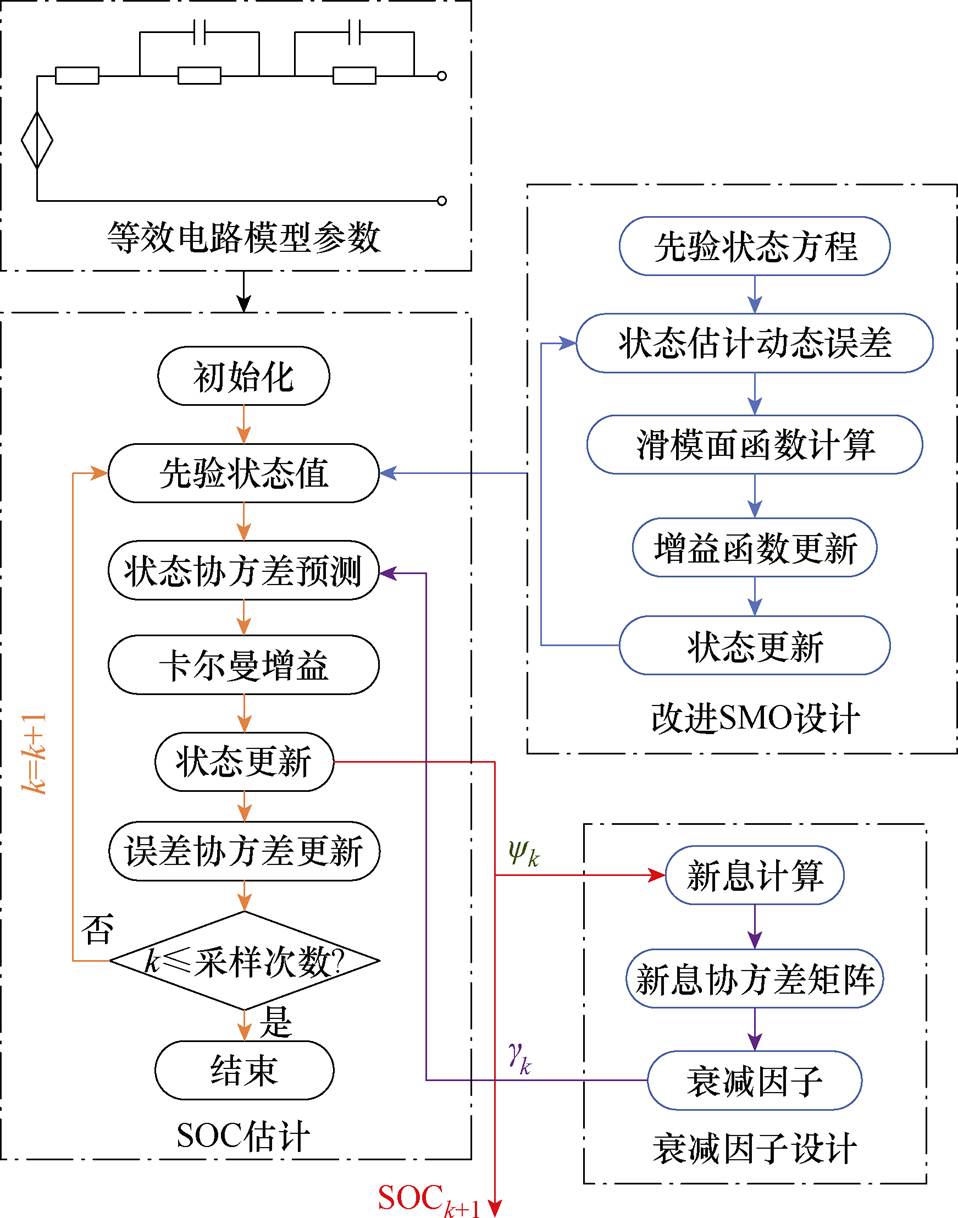
图3 ISMO_AEKF算法流程
Fig.3 Algorithm flowchart of ISMO_AEKF
本文以三洋NCR18650GA型3.5A·h三元锂电池作为实验对象,表1为锂电池主要参数。本文电池测试系统如图4所示。电池测试系统由锂离子电池、上位机、中位机、Neware可编程电子负载与BPH- 060A型高低温试验箱构成。电池测试设备型号为CT-4008T-5V6A-S1,测试误差小于1%,最大电流上升时间为1 ms,本实验设置采样频率为2 Hz。高低温试验箱保障电池工作在稳定的温度。
表1 锂电池主要参数
Tab.1 Lithium battery main parameters

参 数数 值 充电截止电压/V4.2 放电截止电压/V2.5 额定电压/V3.7 额定容量/(A·h)3.5

图4 电池测试系统
Fig.4 Battery test system
本文实验过程基于美国典型的动态压力测试(Dynamic Stress Test, DST)工况和世界轻型汽车测试循环(World Light vehicle Test Cycle, WLTC)工况进行适当比例缩小用以模拟实际电池的运行工况。模型输入工况如图5所示。工况中电流大于零表示放电,小于零表示充电,等于零则表示搁置,两种模拟工况都包括了锂电池充放电和搁置运行状态。
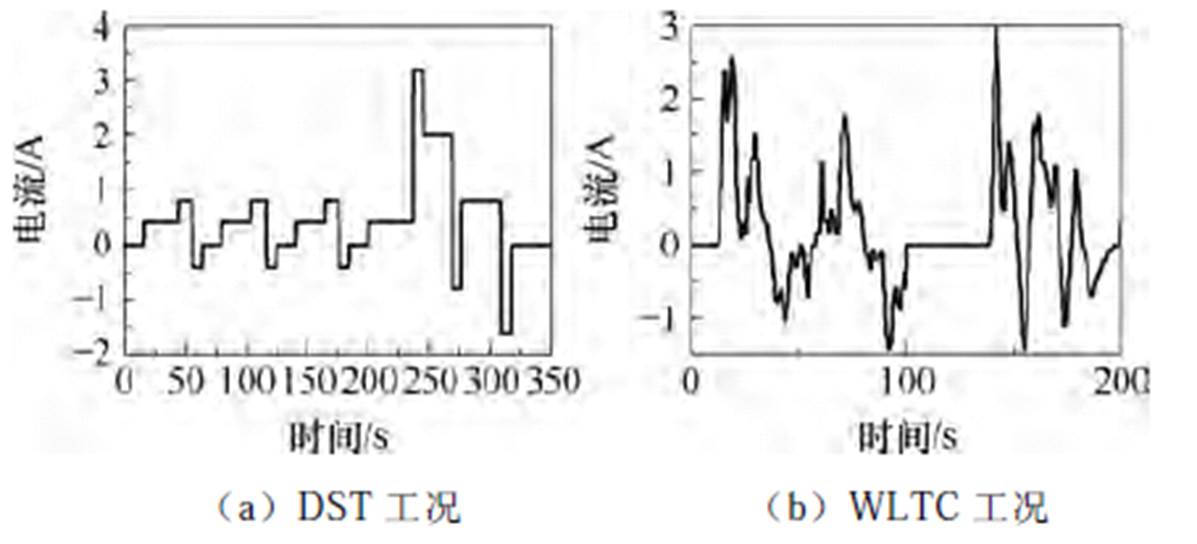
图5 模型输入工况
Fig.5 Model input conditions
实验数据获取过程首先在装有Neware BTS 8.0程序的上位机中设置模拟工况,然后使用Neware可编程电子负载控制电池充放电,并采样数据。
本节对新型联合估计算法精度和鲁棒性进行讨论,以检验本文联合算法的先进性。
4.2.1 估计精度分析
将新型ISMO_AEKF算法与第2节中设计的AEKF算法、文献[24]中联合EKF的SMO算法(SMO_EKF)以及联合ISMO的普通EKF算法(ISMO_ EKF)进行对比,以讨论本文所提算法的估计精度。对比研究基于实测数据在MatlabR2023b/ Simulink中完成,模型参数设置见表2。
表2 各状态参数初始值
Tab.2 Initial value of each state parameter
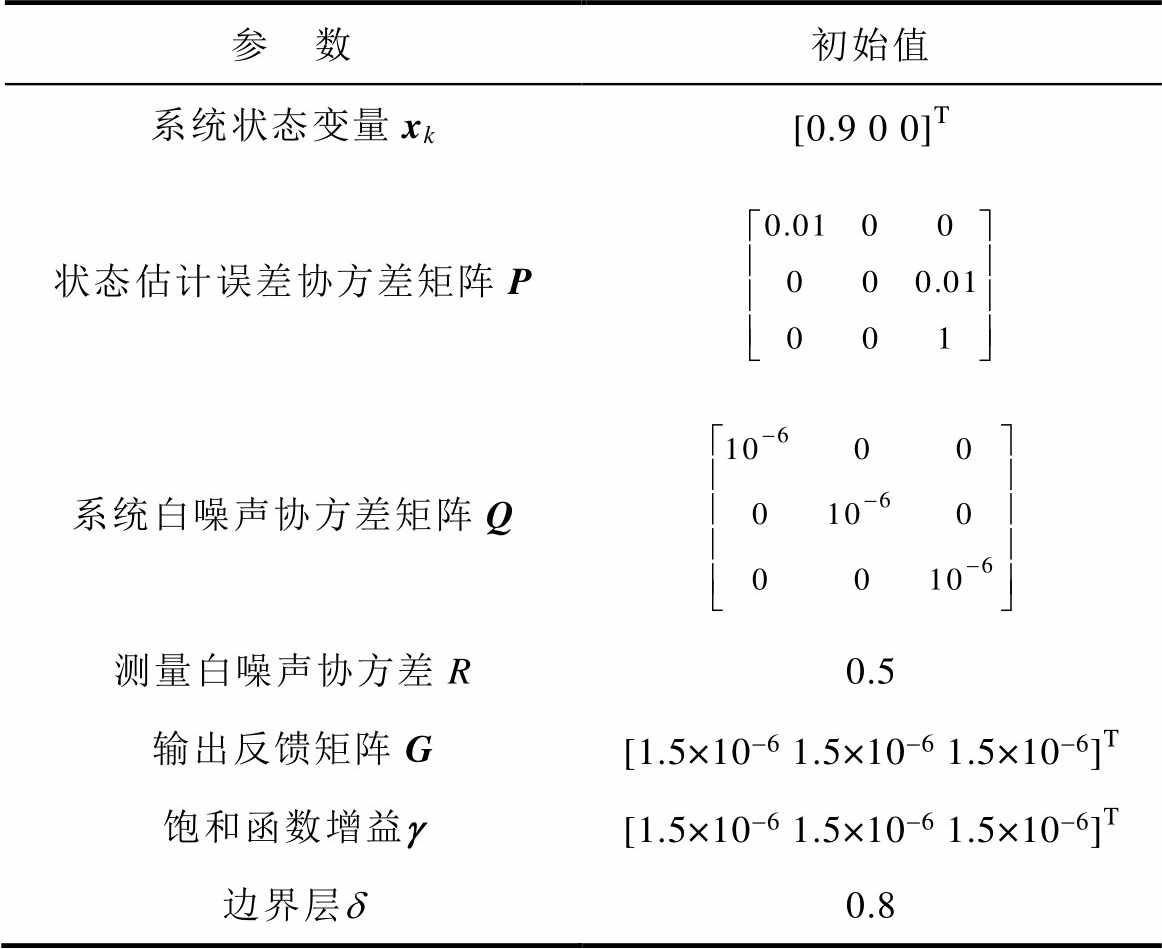
参 数初始值 系统状态变量xk[0.9 0 0]T 状态估计误差协方差矩阵P 系统白噪声协方差矩阵Q 测量白噪声协方差R0.5 输出反馈矩阵G[1.5×10-6 1.5×10-6 1.5×10-6]T 饱和函数增益g[1.5×10-6 1.5×10-6 1.5×10-6]T 边界层d0.8
由于仿真过程中没有量测误差,SOC真实值可由库仑计数法求得。在两种模拟工况下,ISMO_ AEKF与其余三种方法仿真结果如图6、图7所示。不同模拟工况下估计结果的平均绝对误差(Mean Absolute Error, MAE)与方均根误差(Root Mean Square Error, RMSE)见表3。

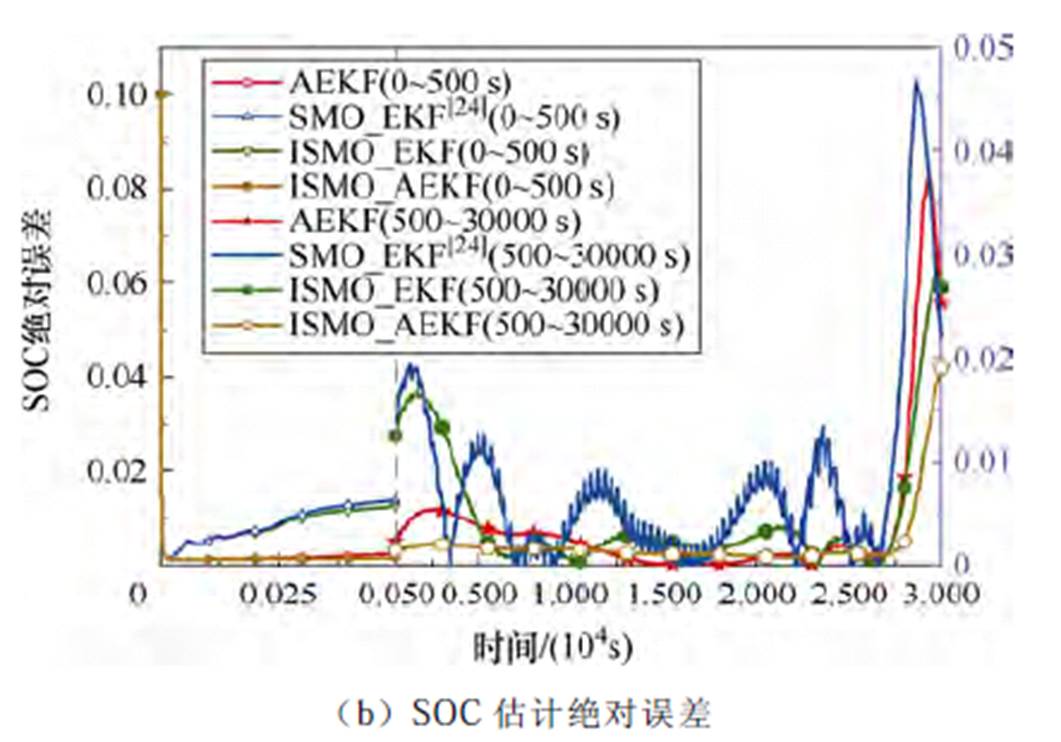
图6 DST工况SOC估计结果
Fig.6 SOC estimation results under DST condition
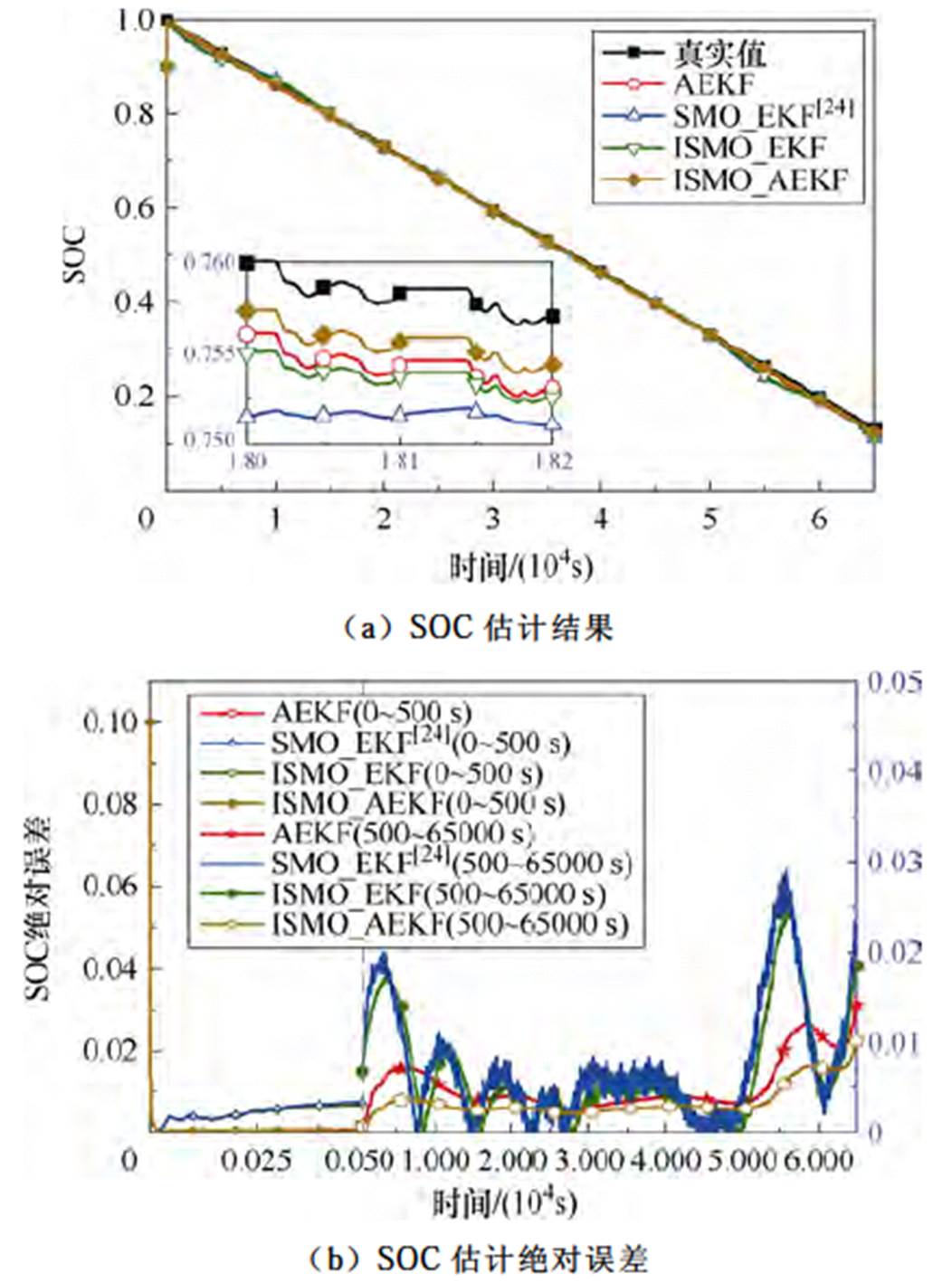
图7 WLTC工况SOC估计结果
Fig.7 SOC estimation results under WLTC condition
由图6、图7和表3可得,本文所提ISMO_AEKF算法相比于单独的AEKF算法、文献[24]中联合EKF的SMO算法(SMO_EKF)和联合ISMO的普通EKF算法(ISMO_EKF)在DST、WLTC工况下均具有更好的估计精度。这是由于本文所提AEKF算法在传统扩展卡尔曼滤波算法中引入一种自适应衰减因子,衰减因子仅需加权计算新息协方差矩阵和新息协方差矩阵的迹,没有大幅增加计算量的同时充分强化了现时观测数据的作用,提高了估值精度和算法跟踪性能,但此类滤波算法仍然没有克服卡尔曼滤波对建模误差敏感,建模不精确会导致估计精度大幅降低甚至造成滤波器发散的问题。文献[24]所提SMO_EKF联合算法兼具EKF对系统噪声良好的滤波性能和SMO对建模误差扰动鲁棒性强的优点,但估计过程中SMO离散的开关特性不可避免地会造成估计结果的抖振。ISMO_EKF算法在文献[24]的基础上用饱和函数代替传统SMO的符号函数有效地降低了系统抖振,提高了估计的过程稳定性,但EKF未考虑历史陈旧测量数据对估计结果的影响,随着时间累积估计结果会逐渐降低。具体而言,ISMO_AEKF算法与其余三种算法相比,在DST工况下,MAE分别下降了16.8%、59.3%、28.9%,RMSE分别下降了45.1%、87.3%、44.2%;在WLTC工况下,MAE分别下降了16.8%、41.0%、31.8%,RMSE分别下降了19.8%、60.3%、49.7%,验证了ISMO_AEKF具有更高的估计精度。
表3 不同工况MAE和RMSE
Tab.3 MAE and RMSE under different conditions
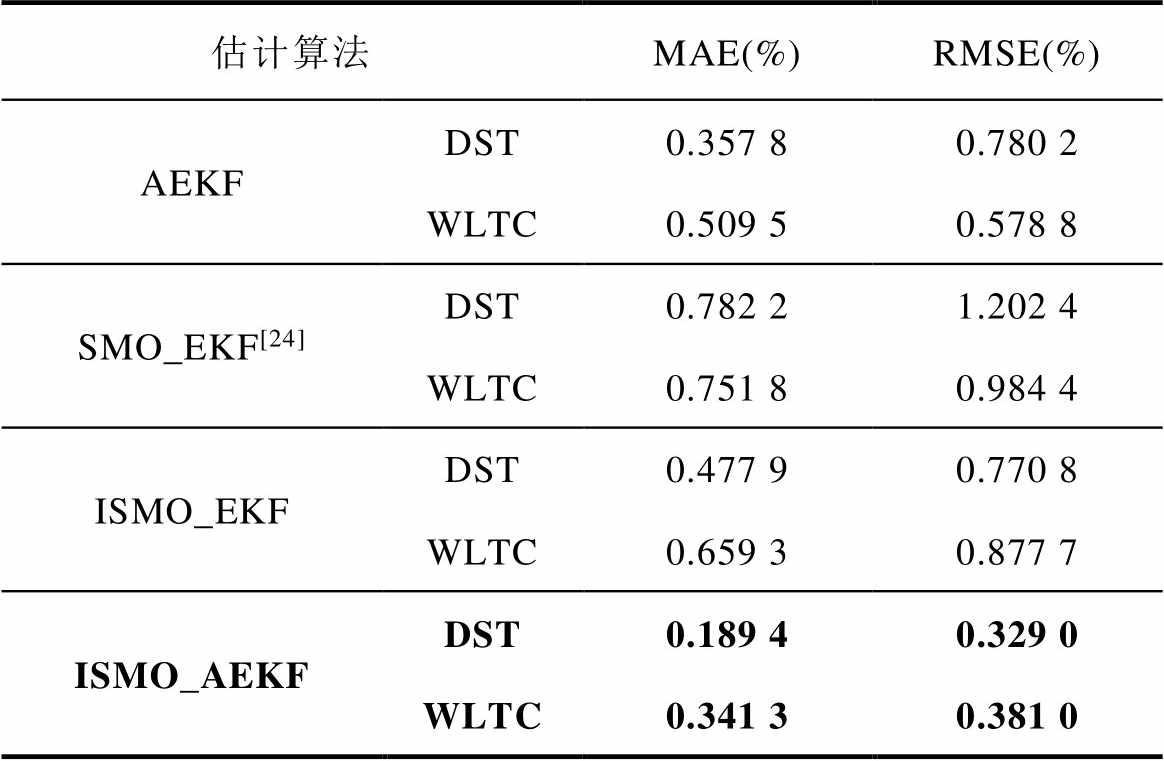
估计算法MAE(%)RMSE(%) AEKFDST0.357 80.780 2 WLTC0.509 50.578 8 SMO_EKF[24]DST0.782 21.202 4 WLTC0.751 80.984 4 ISMO_EKFDST0.477 90.770 8 WLTC0.659 30.877 7 ISMO_AEKFDST0.189 40.329 0 WLTC0.341 30.381 0
4.2.2 鲁棒性分析
为验证本文所提算法在受到参数扰动时的鲁棒性,本节基于额定容量CN设计一个均值为零,方差为0.1且服从高斯分布的随机扰动信号。因DST工况和WLTC工况单个周期时间不同,为比较扰动发生频率对各滤波算法的影响,设置模拟工况间隔20个工况周期使额定容量接收一次扰动信号。两种工况条件以及不同扰动信号采样周期条件下,ISMO_AEKF算法与其他算法估计结果如图8、图9所示,估计结果的MAE与RMSE见表4。
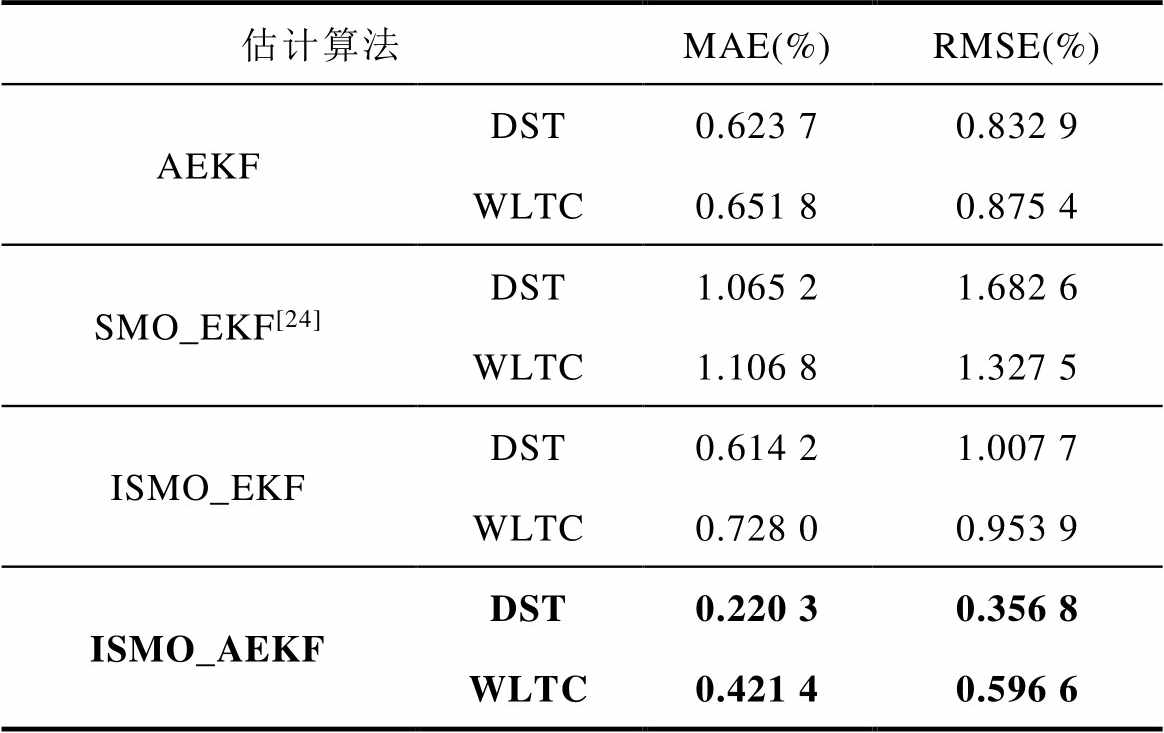
由图8、图9和表4可得,在加入随机参数扰动的情况下,本文所提ISMO_AEKF算法相比于AEKF算法和同类型联合算法,在DST和WLTC工况下均具有更好的估计精度,验证了ISMO_AEKF算法具有良好的鲁棒性。在DST工况下,MAE分别下降了0.403 4%、0.844 9%、0.393 9%,RMSE分别下降了0.476 1%、1.325 8%、0.650 9%;在WLTC工况下,MAE分别下降了0.230 4%、0.685 4%、0.306 6%,RMSE分别下降了0.278 8%、0.730 9%、0.357 3%,验证了ISMO_AEKF算法在参数扰动下仍具有较高的估计精度。

图8 参数扰动下DST工况SOC估计结果
Fig.8 SOC estimation results for DST condition under parameter perturbation
本文所提ISMO_AEKF算法鲁棒性优于AEKF算法和同类型联合算法的原因在于:AEKF对建模误差敏感,建模的不精确会导致估计误差增大甚至滤波器发散;文献[24]中引入滑模观测器解决了建模误差造成的滤波发散问题,但传统SMO又会造成系统抖振;ISMO_EKF算法联合了ISMO,有效地克服了系统的抖振问题,但没有考虑过往量测数据对估计结果的不利影响,使滤波器吸收大量陈旧数据,导致滤波器在稳态条件下跟踪性能弱,甚至造成滤波发散从而降低SOC估计精度。综上分析,ISMO_AEKF算法相比于AEKF和同类型联合估计算法具有更高的估计准确性和更好的鲁棒性。
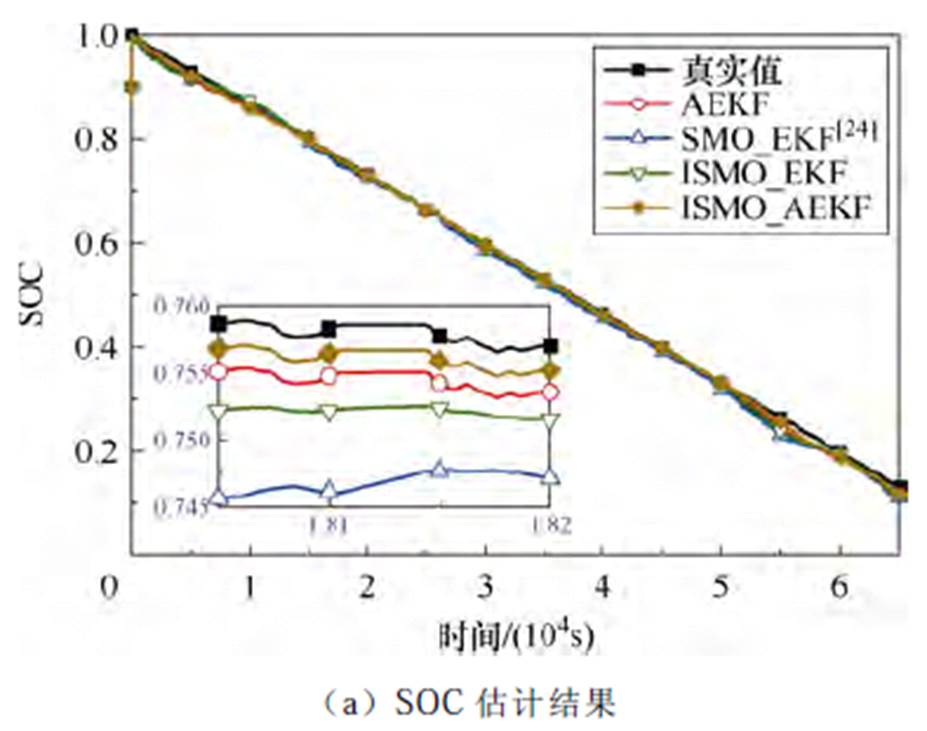
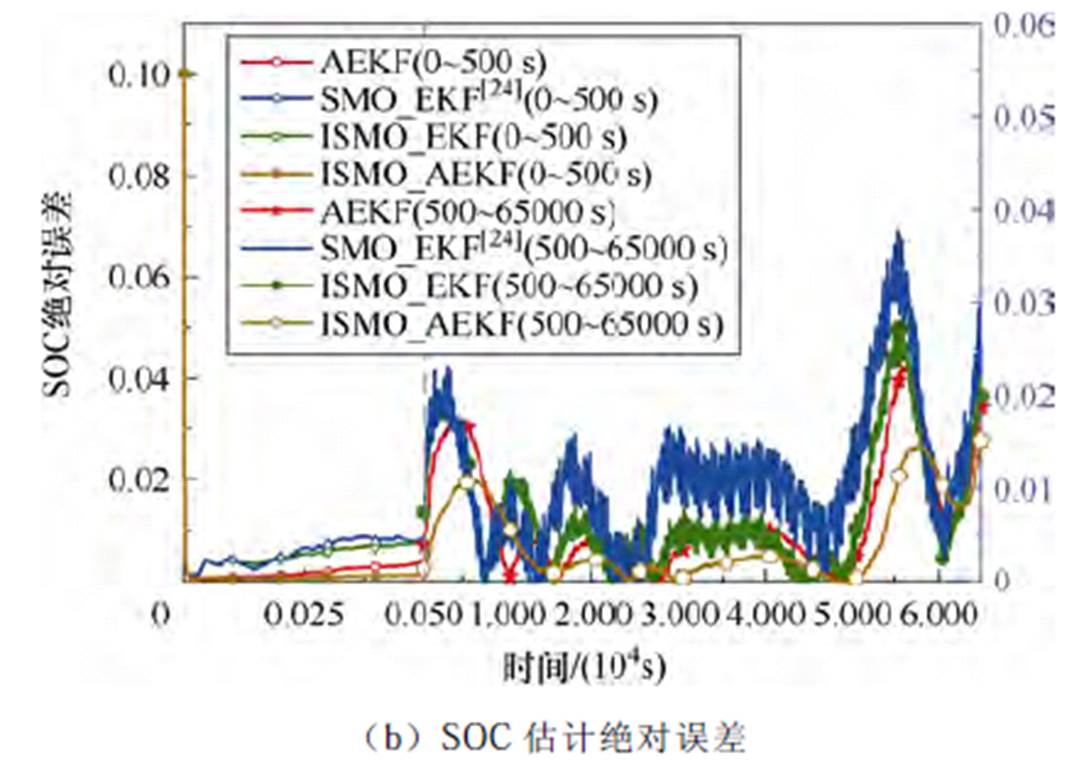
图9 参数扰动下WLTC工况SOC估计结果
Fig.9 SOC estimation results for WLTC condition under parameter perturbation
表4 参数扰动下不同工况MAE和RMSE
Tab.4 MAE and RMSE for different conditions under parameter perturbation
估计算法MAE(%)RMSE(%) AEKFDST0.623 70.832 9 WLTC0.651 80.875 4 SMO_EKF[24]DST1.065 21.682 6 WLTC1.106 81.327 5 ISMO_EKFDST0.614 21.007 7 WLTC0.728 00.953 9 ISMO_AEKFDST0.220 30.356 8 WLTC0.421 40.596 6
SOC高精度估计是保障锂电池安全运行和能源高效利用的重要举措。本文基于双极化等效电路模型提出了一种联合改进滑模观测器的自适应扩展卡尔曼滤波算法,以提高SOC估计的精度及鲁棒性。首先,考虑到卡尔曼滤波对建模误差鲁棒性较差,联合带饱和函数的滑模观测器估计系统的状态变量和观测量的一步预估,有效地克服了建模不精确导致的滤波发散问题,同时饱和函数可以降低传统滑模观测器因离散的开关特性引起的系统抖振现象。其次,设计一种新型自适应衰减因子,充分强化现时观测数据的作用,提高了扩展卡尔曼滤波的动态跟踪性能和估计精度。再次,利用自主实验平台测试数据验证了ISMO_AEKF算法相比于自适应扩展卡尔曼滤波算法和同类型联合算法具有更高的估计精度和更强的鲁棒性。最后,本文在验证新型估计方法先进性时,以锂电池单体为实验对象,未来的研究将考虑把新型估计方法应用于锂电池组,以进一步提高新型估计方法的实用性。
参考文献
[1] Khan F M N U, Rasul M G, Sayem A S M, et al. Design and optimization of lithium-ion battery as an efficient energy storage device for electric vehicles: a comprehensive review[J]. Journal of Energy Storage, 2023, 71: 108033.
[2] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207.
Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of lithium-ion battery and their application scenarios[J]. Automation of Electric Power Systems, 2022, 46(14): 193-207.
[3] Selvaraj V, Vairavasundaram I. A comprehensive review of state of charge estimation in lithium-ion batteries used in electric vehicles[J]. Journal of Energy Storage, 2023, 72: 108777.
[4] Yu Quanqing, Huang Yukun, Tang Aihua, et al. OCV- SOC-temperature relationship construction and state of charge estimation for a series-parallel lithium-ion battery pack[J]. IEEE Transactions on Intelligent Transportation Systems, 2023, 24(6): 6362-6371.
[5] 刘萍, 李泽文, 蔡雨思, 等. 基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法[J]. 电工技术学报, 2024, 39(10): 3232-3243.
Liu Ping, Li Zewen, Cai Yusi, et al. Joint estimation method of SOC and SOH based on the fusion of equivalent circuit model and data-driven model[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3232-3243.
[6] Wang Chao, Zhang Xin, Yun Xiang, et al. A novel hybrid machine learning coulomb counting technique for state of charge estimation of lithium-ion batteries[J]. Journal of Energy Storage, 2023, 63: 107081.
[7] 黄凯, 孙恺, 郭永芳, 等. 基于观测方程重构滤波算法的锂离子电池荷电状态估计[J]. 电工技术学报, 2024, 39(7): 2214-2224.
Huang Kai, Sun Kai, Guo Yongfang, et al. State of charge estimation of lithium-ion battery based on observation equation reconstruction filtering algo- rithm[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2214-2224.
[8] Duan Linchao, Zhang Xugang, Jiang Zhigang, et al. State of charge estimation of lithium-ion batteries based on second-order adaptive extended Kalman filter with correspondence analysis[J]. Energy, 2023, 280: 128159.
[9] Wang Qiao, Ye Min, Wei Meng, et al. Deep con- volutional neural network based closed-loop SOC estimation for lithium-ion batteries in hierarchical scenarios[J]. Energy, 2023, 263: 125718.
[10] 刘素贞, 陈云龙, 张闯, 等. 融合多维超声时频域特征的锂离子电池荷电状态估计[J]. 电工技术学报, 2023, 38(17): 4539-4550, 4563.
Liu Suzhen, Chen Yunlong, Zhang Chuang, et al. State of charge estimation of lithium-ion batteries fused with multi-dimensional ultrasonic time- frequency domain features[J]. Transactions of China Electrotechnical Society, 2023, 38(17): 4539-4550, 4563.
[11] Guo Shanshan, Ma Liang. A comparative study of different deep learning algorithms for lithium-ion batteries on state-of-charge estimation[J]. Energy, 2023, 263: 125872.
[12] Liu Zheng, Zhao Zhenhua, Qiu Yuan, et al. Enhanced state of charge estimation for Li-ion batteries through adaptive maximum correntropy Kalman filter with open circuit voltage correction[J]. Energy, 2023, 283: 128738.
[13] Shu Xing, Chen Zheng, Shen Jiangwei, et al. State of charge estimation for lithium-ion battery based on hybrid compensation modeling and adaptive H- infinity filter[J]. IEEE Transactions on Transportation Electrification, 2023, 9(1): 945-957.
[14] 刘旖琦, 雷万钧, 刘茜, 等. 基于双自适应扩展粒子滤波器的锂离子电池状态联合估计[J]. 电工技术学报, 2024, 39(2): 607-616.
Liu Yiqi, Lei Wanjun, Liu Qian, et al. Joint estimation of lithium-ion battery state based on double adaptive extended particle filter[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(2): 607-616.
[15] 孙冬, 陈息坤. 基于离散滑模观测器的锂电池荷电状态估计[J]. 中国电机工程学报, 2015, 35(1): 185- 191.
Sun Dong, Chen Xikun. Charge state estimation of Li-ion batteries based on discrete-time sliding mode observers[J]. Proceedings of the CSEE, 2015, 35(1): 185-191.
[16] Shi Na, Chen Zewang, Niu Mu, et al. State-of-charge estimation for the lithium-ion battery based on adaptive extended Kalman filter using improved parameter identification[J]. Journal of Energy Storage, 2022, 45: 103518.
[17] Miao Yue, Gao Zhe, Xiao Shasha, et al. Initial value compensation of an adaptive fractional-order unscented Kalman filter for estimating the state of charge of lithium-ion batteries[J]. Journal of Energy Storage, 2023, 70: 107857.
[18] Chen Lin, Yu Wentao, Cheng Guoyang, et al. State- of-charge estimation of lithium-ion batteries based on fractional-order modeling and adaptive square-root cubature Kalman filter[J]. Energy, 2023, 271: 127007.
[19] Liu Xingtao, Li Qiule, Wang Li, et al. Data-driven state of charge estimation for power battery with improved extended Kalman filter[J]. IEEE Transa- ctions on Instrumentation and Measurement, 2023, 72: 1500910.
[20] Lee K J, Lee W H, Kim K K K. Battery state- of-charge estimation using data-driven Gaussian process Kalman filters[J]. Journal of Energy Storage, 2023, 72: 108392.
[21] Li Menghan, Li Chaoran, Zhang Qiang, et al. State of charge estimation of Li-ion batteries based on deep learning methods and particle-swarm-optimized Kalman filter[J]. Journal of Energy Storage, 2023, 64: 107191.
[22] Li Kangqun, Zhou Fei, Chen Xing, et al. State- of-charge estimation combination algorithm for lithium-ion batteries with Frobenius-norm-based QR decomposition modified adaptive cubature Kalman filter and H-infinity filter based on electro-thermal model[J]. Energy, 2023, 263: 125763.
[23] Yao Jianxin, Ding Jie, Cheng Yanyun, et al. Sliding mode-based H-infinity filter for SOC estimation of lithium-ion batteries[J]. Ionics, 2021, 27(12): 5147- 5157.
[24] 周娟, 孙啸, 刘凯, 等. 联合扩展卡尔曼滤波的滑模观测器SOC估算算法研究[J]. 中国电机工程学报, 2021, 41(2): 692-702.
Zhou Juan, Sun Xiao, Liu Kai, et al. Research on the SOC estimation algorithm of combining sliding mode observer with extended Kalman filter[J]. Proceedings of the CSEE, 2021, 41(2): 692-702.
[25] Liu Yuyang, Wang Shunli, Xie Yanxin, et al. A novel adaptive H-infinity filtering method for the accurate SOC estimation of lithium-ion batteries based on optimal forgetting factor selection[J]. International Journal of Circuit Theory and Applications, 2022, 50(10): 3372-3386.
Abstract Accurate estimation of a lithium battery’s state of charge (SOC) is of great significance for improving energy utilization efficiency and ensuring a safe operation. This paper addresses the study of SOC estimation based on the Kalman filter (KF). The traditional KF algorithms rely on all past measurements to estimate the state variables at the next moment, ignoring the weight of current measurements, resulting in weak tracking ability and low estimation accuracy under steady-state conditions of KF. This paper proposes an adaptive extended Kalman filter (AEKF) algorithm with a jointly improved sliding mode observer (ISMO) to improve SOC estimation accuracy and robustness.
First, an improved sliding mode observer incorporating the saturation function is built based on a dual-polarization (DP) equivalent circuit model that can balance estimation accuracy and computational complexity. The saturation function can switch the control outside the boundary layer in real-time and implement the linearized feedback control inside the boundary layer, significantly reducing the chattering of the traditional sliding mode observer. Second, a novel adaptive fading factor is introduced based on the extended Kalman filter (EKF), which strengthens the role of the present observation data while weakening the unfavorable influence of the stale measurements. Thus, the EKF algorithm’s tracking performance and estimation accuracy are enhanced. Finally, the robustness of the improved sliding mode observer system is utilized to predict the state vectors of the system and alleviate the problem of filter dispersion caused by modeling inaccuracies. Accordingly, an adaptive extended Kalman filter with the improved sliding mode observer (ISMO_AEKF) algorithm is established, which combines the advantages of AEKF and ISMO.
Based on the self-built experimental platform, the Sanyo NCR18650GA 3.5 A·h lithium ternary battery is taken as the experimental object to obtain the measured simulated working condition data. The estimation accuracy and robustness of the joint algorithm are verified by the simulation models.
The results show that the mean absolute error (MAE) and the root mean square error (RMSE) of the joint algorithm ISMO_AEKF are both less than 0.35% for SOC under the dynamic stress test (DST) condition and less than 0.4% under the world light vehicle test cycle (WLTC) condition. The estimation accuracy is improved compared to the traditional KF and other joint algorithms.
A random perturbation signal with zero mean and 0.1 variance and obeying Gaussian distribution is chosen to be added to the rated capacity. Under this perturbation signal, the MAE and RMSE of the joint algorithm are both less than 0.4% for SOC in the DST condition and less than 0.6% for the WLTC condition. The proposed ISMO_AEKF algorithm has better estimation accuracy under DST and WLTC conditions, verifying that the ISMO_AEKF algorithm has good robustness.
Future research mainly focuses on applying novel algorithms to the battery management system of new energy vehicles to further improve its practicality.
keywords:State of charge, saturation function, sliding mode observer, adaptive fading factor, Kalman filter
中图分类号:TM912
DOI: 10.19595/j.cnki.1000-6753.tces.240373
国家自然科学基金项目(62373137)、河南省高校基本科研业务费项目(NSFRF210332, NSFRF230604)资助。
收稿日期 2024-03-07
改稿日期2024-04-26
钱 伟 男,1978年生,博士,教授,博士生导师,研究方向为非线性系统状态估计、鲁棒控制、智能控制等。E-mail: qwei@hpu.edu.cn(通信作者)
王浩宇 男,2000年生,硕士研究生,研究方向为锂电池状态估计。E-mail: 3044432663@qq.com
(编辑 陈 诚)