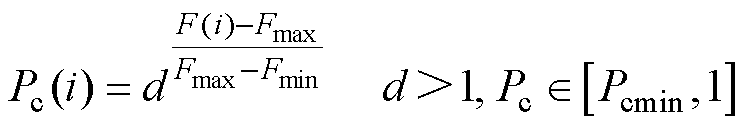（1）
摘要 基于噪声协方差匹配方法的自适应无迹卡尔曼滤波（AUKF）算法，其固定长度的时间窗影响算法噪声统计量。且AUKF中匹配窗口长度常由经验法确定，在复杂工作条件下容易引起噪声协方差估算的不确定。为了进一步提高算法的噪声协方差估算精度，提出一种由自适应遗传算法（AGA）确定初始窗口长度的变窗口自适应无迹卡尔曼滤波（VAUKF）。并引入Allan方差分析法识别误差序列的波动，再基于更新规则适当调整窗口长度，提高VAUKF对时变噪声的抗干扰能力。通过FUDS、US06工况验证所提出的VAUKF算法可行性。仿真结果表明，VAUKF相比AUKF在不同工况下都实现了荷电状态（SOC）预测精度和鲁棒性的提高。
关键词：SOC预测 自适应无迹卡尔曼 变窗口自适应无迹卡尔曼
锂离子电池被广泛应用于新能源汽车[1]和电池储能系统[2]，其具有能量密度大、输出电压高等优点。准确掌握锂电池的荷电状态（State of Charge, SOC）有利于电池的管理和控制，影响锂电池的安全和使用寿命。与数据驱动方法[3-4]相比，卡尔曼滤波算法不需要依赖大量的数据集训练，能够借助观测数据预测状态量，最终得到系统的最优估计。
卡尔曼滤波算法在非线性系统的预测应用出现了扩展卡尔曼滤波（Extended Kalman Filter, EKF）[5]、无迹卡尔曼滤波（ptive Untraceable Kalman Filtering, UKF）[6]，其中UKF相较EKF不需要进行雅可比矩阵的运算，且能达到二阶以上的逼近精度。对于锂电池非线性时变系统，算法取得固定噪声协方差容易导致预测误差[7]。以往研究通过对UKF做噪声自适应提高算法的时变跟踪能力。自适应无迹卡尔曼滤波（Adaptive Untraceable Kalman Filtering, AUKF）的噪声协方差自适应方法有协方差匹配法、贝叶斯法、极大似然法等[8]。其中，基于噪声协方差匹配法的AUKF自适应公式简单，且能获得较高的预测精度[9]。
基于噪声协方差匹配法的AUKF需要对误差新息序列在选择的时间窗长度下进行噪声统计，进而更新测量、状态噪声协方差。其时间窗长度由经验法获得，实际工程应用中锂电池工作条件复杂，容易影响噪声协方差的估算精度。且受到模型误差、充放电倍率的影响，误差新息序列的幅值分布会发生变化[10]。在误差新息序列分布出现变化时，AUKF取固定的噪声协方差匹配时间窗长度影响算法的噪声统计量。
目前，部分研究通过Allan方差法分析噪声特性。文献[11]通过Allan方差建立噪声模型，分析噪声对无迹粒子滤波的影响。文献[12]将Allan方差与Sage-Husa滤波器结合用于解决自适应卡尔曼滤波的滤波耦合问题，提高算法抗干扰能力。文献[13]通过Allan方差计算自适应卡尔曼滤波算法的观测噪声，降低算法滤波发散问题。文献[14]利用Allan方差辨识传感器噪声，并用于改进扩展卡尔曼的算法估计，减小有色噪声对算法预测性能的影响。
以往研究证明了遗传算法（Genetic Algorithm, GA）具有良好的参数寻优能力[15]。而自适应遗传算法（Adaptive Genetic Algorithm, AGA）在避免局部最优和算法收敛速度上被证明取得了良好的参数计算能力[16]。文献[17]通过AGA估计模型参数，提高中心差分卡尔曼的算法精度。将AGA用于确定AUKF时间窗长度，有利于避免窗口长度选值不当导致的预测误差。为了加快寻优效率，本文对GA交叉和变异概率做自适应调整，设计了新的自适应遗传算法（AGA）。针对窗口固定长度影响算法噪声统计量的问题，本文提出一种变窗口自适应无迹卡尔曼滤波（Variable-window Adaptive Untraceable Kalman Filtering, VAUKF）。提出的VAUKF通过AGA来获得最优的时间窗长度，并引入交叠式分组Allan方差分析法识别误差序列的波动，迭代过程对窗口长度进行适当调整。
本文基于二阶RC锂离子电池等效电路模型，在美国联邦城市运行工况（Federal Urban Driving Schedule, FUDS）和US06高速循环工况（US06）数据下进行仿真建模。仿真分析将VAUKF与AUKF进行对比，探讨算法在不同工况下的预测性能表现。通过Allan方差获取算法预测过程的噪声水平，确定算法变窗口调整规则的基数，并分析噪声波动对算法预测性能的影响。然后，针对噪声匹配窗口更新规则探讨不同倍率下VAUKF的SOC预测表现，为VAUKF提供较为合理的参数条件。仿真结果表明，VAUKF能有效改善算法对时变噪声的抗干扰能力，提高了SOC预测的精度和鲁棒性。
遗传算法（GA）具有智能性及良好的全局寻优能力。GA是一种优胜劣汰的智能方法，通过在选择操作过程中，经过淘汰劣势个体保留优势个体，并进一步执行交叉、变异，最终找到最适应当前条件的种群个体，得到最优解。以往AUKF噪声协方差匹配窗口长度由经验法确定，当面对复杂工况时容易出现不确定性，将GA用于AUKF窗口长度的确定，相比以往的经验法更智能。为了加快算法寻优效率，在文献[16-17]的自适应规则基础上，针对本文噪声匹配窗口的寻优问题，对交叉、变异概率设计新的自适应公式。
劣势个体在较大的交叉概率上加以扰动，加快算法收敛；优势个体取较小的交叉概率避免个体丢失，提高算法精度。交叉概率自适应公式为
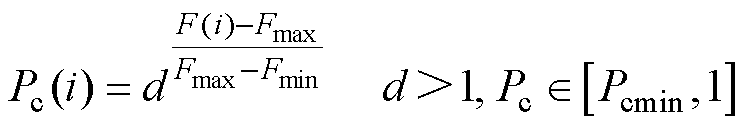（1）
式中，i为第i个个体；Fmax、Fmin分别为适应度函数最大、最小值；Pcmin为交叉概率最小值。F(i)越接近最小值，Pc越小，相对地，F(i)越接近最大值，Pc越接近1。
在AGA迭代计算中，较大变异概率能增强算法搜索能力，避免陷入局部收敛；较小变异概率有利于减小算法波动，特别是算法后期保留优势个体参数，逐渐缩小寻优区间，并对劣势个体取较大变异概率加快算法收敛。变异概率自适应公式为
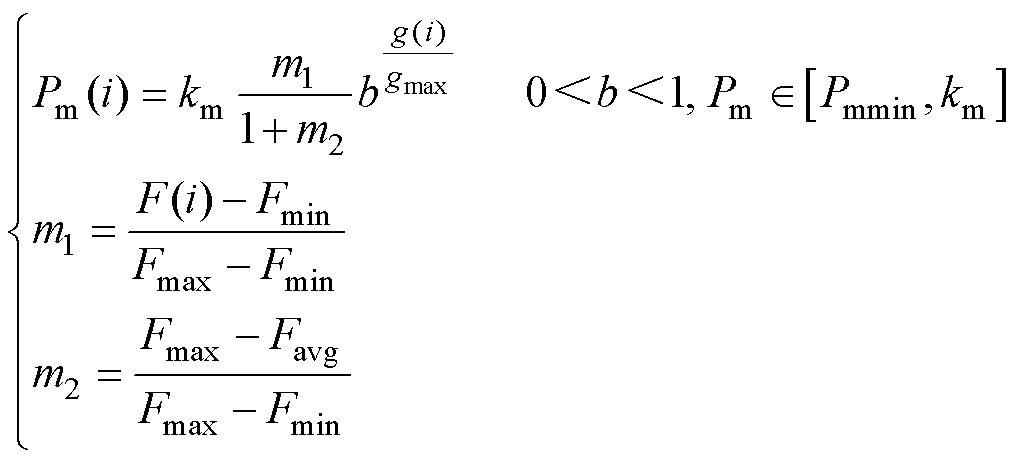（2）
式中，Pmmin、km分别为变异概率最小、最大取值；g(i)为当前算法迭代次数；gmax为终止代数。
AGA选择操作为轮盘赌法和最佳保留策略相结合，对最佳个体进行保留避免丢失，通过轮盘赌法淘汰劣势个体。考虑到时间窗长度为整数，选择实数编码，避免频繁的编码解码过程。AGA将取得电压预测值yi(k)和电压测量值y(k)均方差最小值为目标，适应度函数为
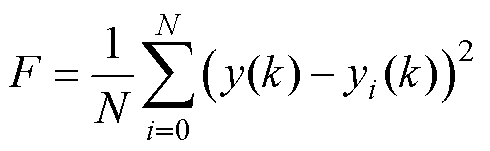（3）
式中，N为算法迭代次数。
UKF通过无迹变换（Unscented Tansform, UT）变换构造新点集，以新点集的均值和协方差代替非线性点集参与状态估计。UT变换首先对n维状态向量进行对称采样，构造2n+1个Sigma点，公式为
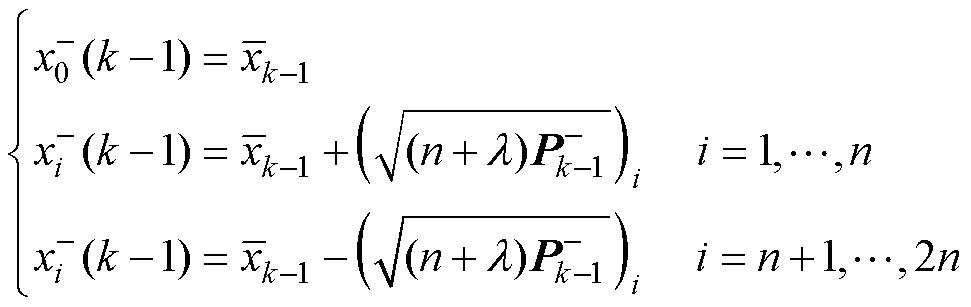（4）
其中
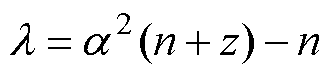
式中，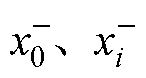
为选取状态量，用其均值代替非线性状态量；
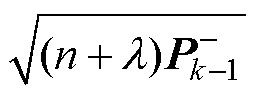为二次方根矩阵；下标i为矩阵第i列；a 为尺度参数，取值在0～1之间；z为比例因子，一般取0。相应的点集权重为
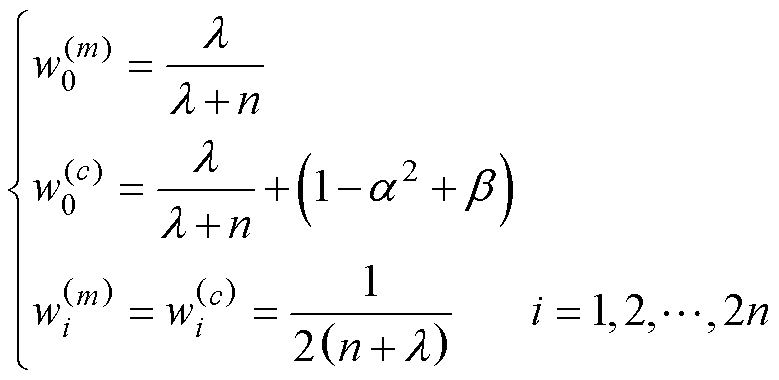（5）
式中，
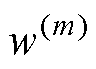和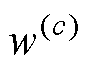
分别为均值和协方差权重；b 在参数为单变量时取0，在高斯分布下取2。
UKF算法计算步骤如下：
（1）初始化。
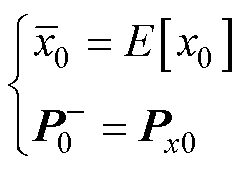（6）
式中，
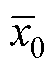和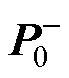
分别为原状态分布的均值和方差。
（2）同理按照式（4）所选择的采样策略，构造Sigma点。
（3）由式（5）计算采样点权重。
（4）计算状态预测值。
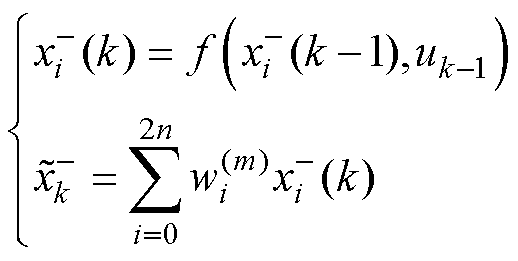（7）
式中，uk-1为k-1时刻的系统输入信号。
（5）计算误差协方差预测值。
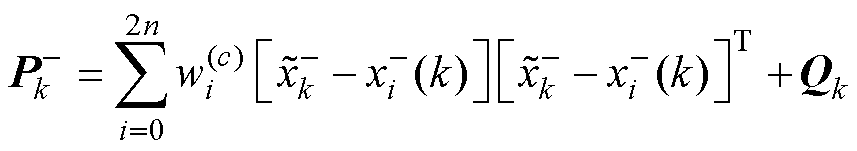（8）
式中，Qk为k时刻的过程噪声协方差。
（6）计算观测预测值。
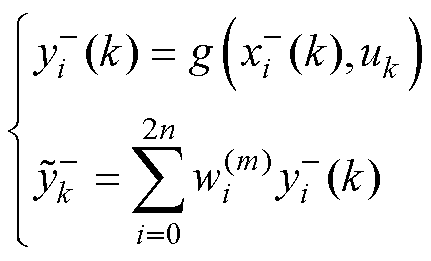（9）
（7）计算观测协方差和互协方差预测值。
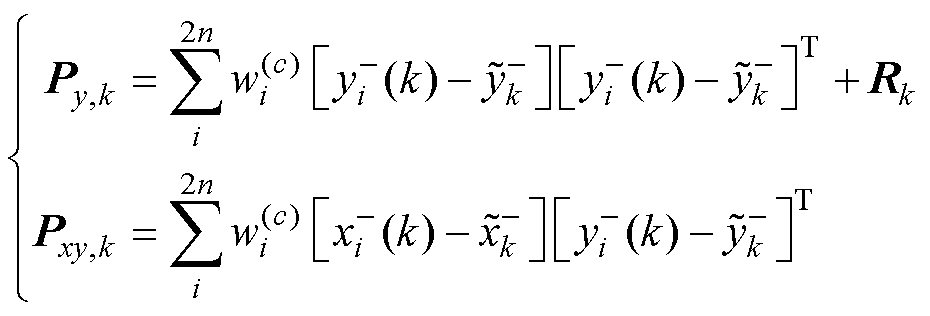（10）
式中，Rk为k时刻的观测噪声协方差。
（8）计算卡尔曼增益。
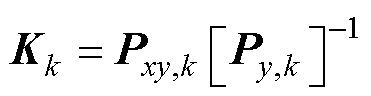（11）
（9）更新状态预测值。
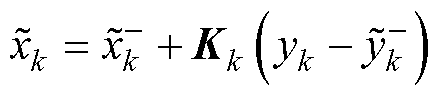（12）
（10）计算误差协方差矩阵。
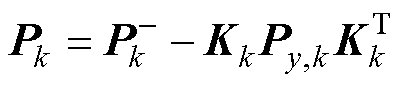（13）
（11）令k=k+1，返回步骤（2）直至SOC预测结束。
在UKF的基础上，AUKF[9]基于噪声协方差匹配（Covariance Matching, CM）方法，通过自适应规律对过程噪声协方差Q、观测噪声协方差R进行自适应更新。其状态噪声协方差Q和测量噪声协方差R自适应公式为
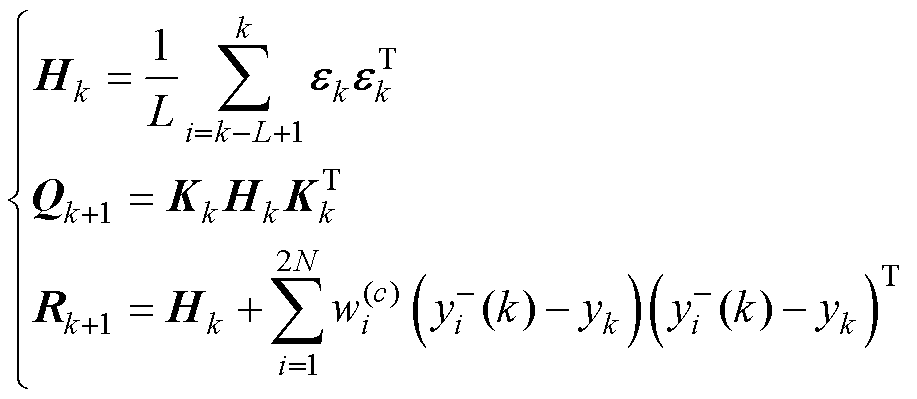（14）
其中
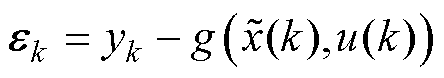
E=[1 2 … k]
式中，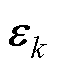
为误差新息；E为误差新息序列；Hk为新息协方差矩；L为窗口长度，通过自适应遗传算法（AGA）进行确认。AGA可通过历史数据训练得到L参数，也可以通过在线测量，取前50组数据进行训练，其中构造种群随机个体L取值范围为[3, 30]。
受到模型精度、电压电流动态特性影响，固定窗口长度下噪声统计量受到影响，导致预测误差。在AUKF的基础上，变窗口的自适应无迹卡尔曼滤波（VAUKF）通过更新误差新息序列，并基于Allan方差法识别序列波动。通过分析误差新息序列的分布变化来调整窗口长度，提高噪声匹配的准确性。
Allan方差分析可用于分析误差序列的波动，其将序列按时间尺度进行特征提取，能获取指定时间尺度内的误差波动情况。考虑高斯噪声影响的系统中，非线性时变系统的噪声不一定服从标准正态分布。系统时变噪声方差能反映误差序列的分布变化。对E序列进行分析，识别数据波动，并按照设定规则进行VAUKF中窗口长度的调整。基于交叠式分组Allan方差法识别序列波动计算方差基值s0，有
（15）
式中，l为时间尺度；t为第t个时间节点；t 为采样时长；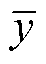
为电压均值；s 为方差；分组k=G/l，G为待分析数据的大小；j为分组后每一组从j开始统计。
算法智能确定L并返回L值的过程中，将误差新息序列进行Allan方差分析，计算当前数据s。为了简化当前数据的Allan方差计算，改为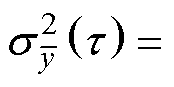
。
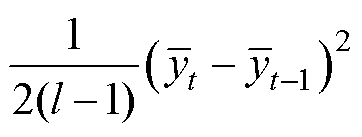计算后的方差s 与s0做对比，按照以下更新规则进行L的更新。
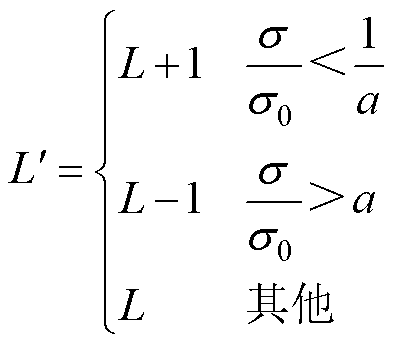（16）
式中，a为倍数，取正数。
基于VAUKF算法的SOC预测流程如图1所示。首先将AGA、自适应遗忘因子最小二乘（Adaptive Forgetting Factor Recursive Least Squares, AFFRLS）、AUKF算法参数初始化，此时将L设为0；第二步通过AFFRLS[18]估算二阶RC等效电路模型参数，并更新状态方程；第三步计算AGA种群中个体适应度值，并进行AGA选择、交叉、变异操作，更新种群个体，循环迭代直至满足终止条件并退出AGA算法迭代；第四步计算参数s0，然后将得到的L窗口和s0更新到VAUKF。L窗口通过实时采集数据进行计算得到L最优参数，考虑到算法计算负担可以通过历史数据离线完成；第五步判断VAUKF算法是否满足运行条件，满足则开始VAUKF的SOC预测迭代，此时AFFRLS更新的模型参数将用于VAUKF的迭代预测。在VAUKF预测过程中将通过Allan方差法识别误差新息序列波动，满足窗口更新规则时更新窗口长度，并将新的窗口L用于状态和测量噪声协方差的计算。VAUKF中状态和测量噪声协方差随时间变化，计算公式与AUKF一致，但L在更新规则下进行调整。
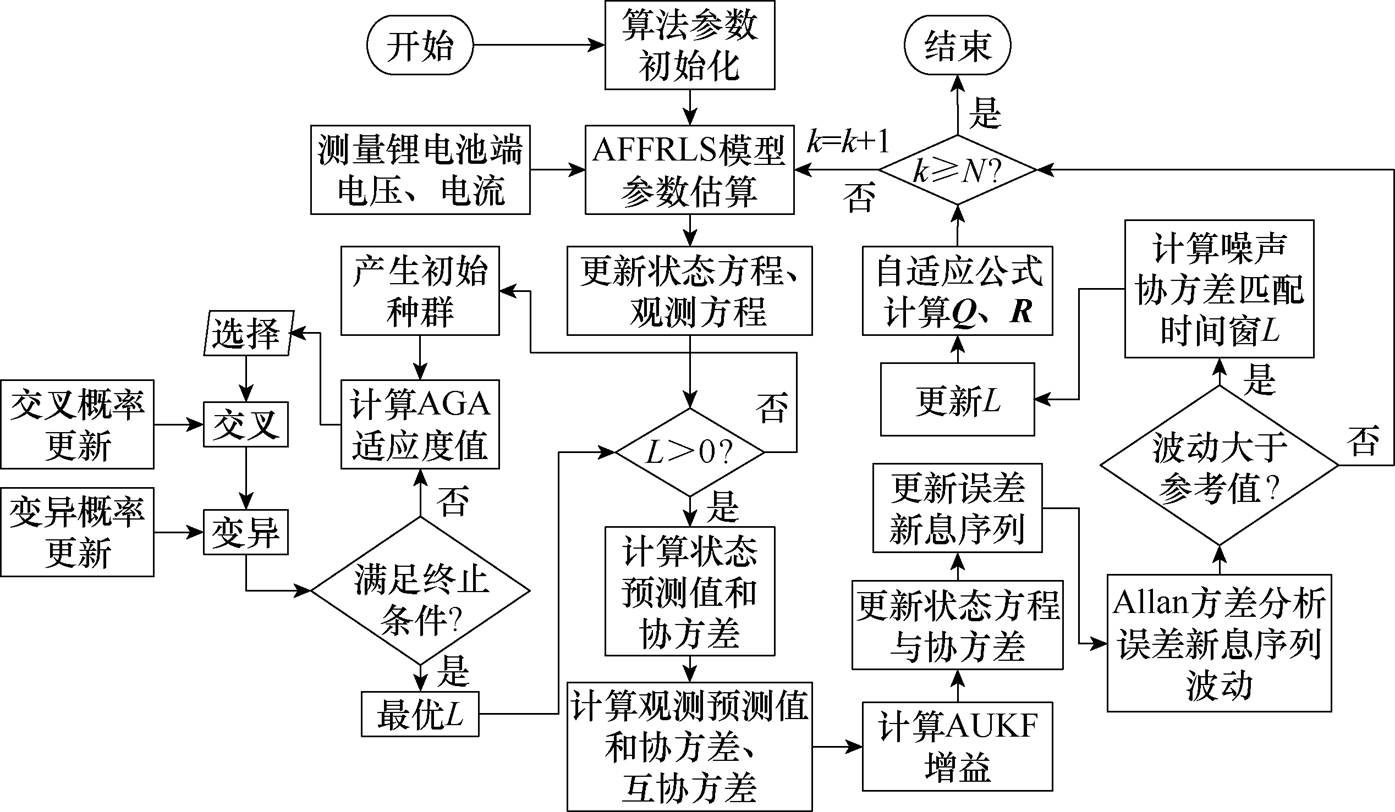
图1 基于VAUKF算法的SOC预测流程
Fig.1 SOC prediction flow chart based on VAUKF algorithm
选取锂电池FUDS、US06工况进行SOC预测分析。测试系统为新威公司的CT-4008Tn设备，规格为5 V、6 A，如图2所示。锂电池为18650型，额定容量2 A·h，额定电压3.7 V，最大放电电流3C，内阻小于或等于65 mW，工作温度-20～60℃，测试环境为室温20℃。
图2 锂离子电池试验平台
Fig.2 Lithium-ion battery experimental platform
AUKF、VAUKF参数初值见表1，FUDS和US06工况为相同的算法初值。VAUKF窗口长度由AGA算法确定，窗口长度取值设置在区间[3, 50]。经过仿真调试，AGA参数初值设置见表2。
表1 AUKF、VAUKF参数初值
Tab.1 Initial parameter values of the AUKF and VAUKF
参 数取 值 SOC初值1 Q初值(1×10-6, 1×10-6, 1×10-6) R初值1×10-2 P初值(1×10-4, 1×10-4, 1×10-4)
表2 AGA参数初值
Tab.2 Initial parameter values of the AGA
参 数取 值 种群大小20 交叉概率最小值0.5 变异概率最小值0.01 变异概率最大值0.1
锂电池二阶RC等效电路模型参数由AFFRLS算法进行估计，参数结果如图3所示。模型参数动态变化反映了参数在工况条件下电池输出的时变特性，得到的模型参数结果将用于后续SOC预测的仿真分析。
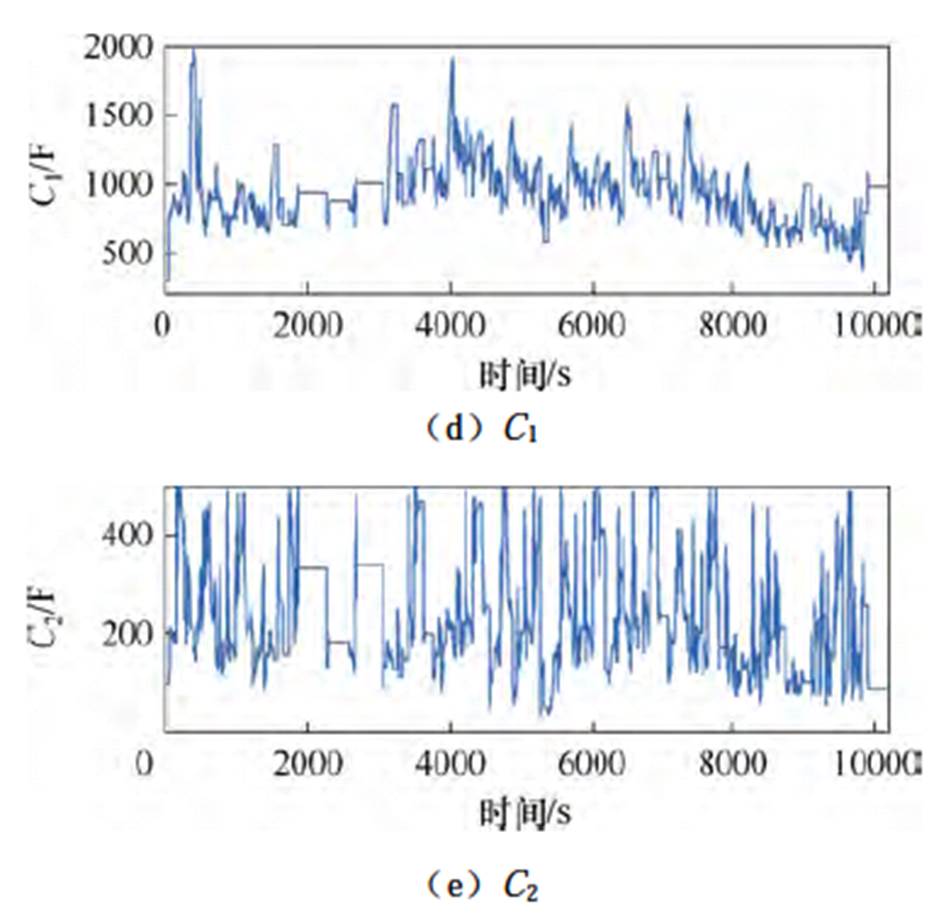
图3 北京动态应力工况的锂电池二阶RC等效电路模型参数
Fig.3 Parameters of second-order RC equivalent circuit model for lithium battery via Beijing dynamic stress test
AGA循环过程中误差新息序列的Allan方差分析过程如图4所示。由图4可知，t 处于40、80点曲线近似水平，此时方差值为3.207 7×10-4、3.024 0× 10-4，取其平均得s0=3.115 9×10-4。得到s0按照设定规则与s 进行判断更新窗口L长度。
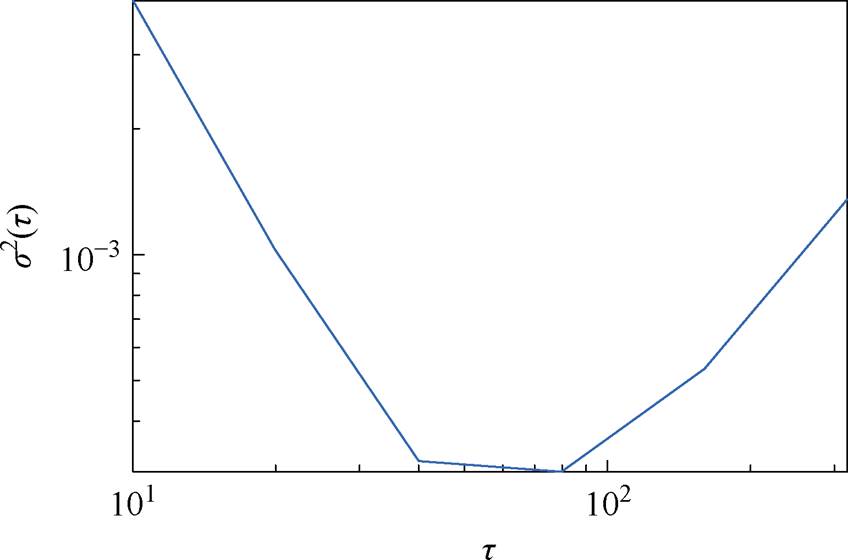
图4 FUDS工况的Allan方差
Fig.4 Allan variance of FUDS condition
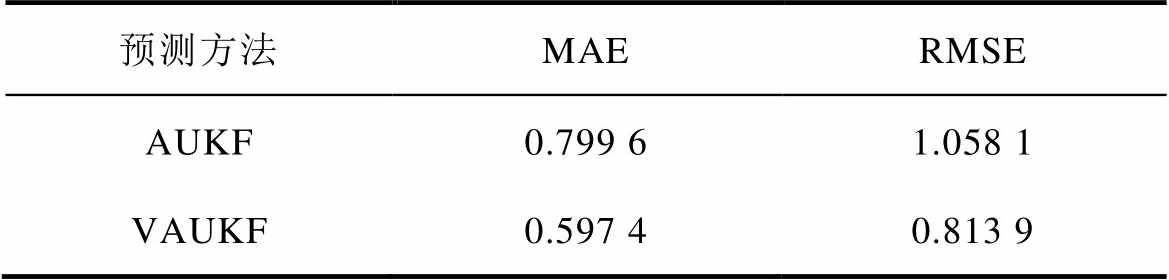
通过自主实验测量锂电池FUDS工况数据，基于AUKF和VAUKF的SOC预测结果如图5所示，相应的预测误差见表3。由图5可知，整体上VAUKF估算精度更高。受到模型精度影响，在200～3 500 s、5 800～7 600 s期间，AUKF算法出现了较大的预测误差，最大超过2%。而VAUKF通过对窗口的调整，提高了算法对非线性系统的跟踪能力，取得更好的预测表现。另外由表3可知，VAUKF较AUKF在均方误差（Mean Absolute Error, MAE）提升了25.3%，在方均根误差（Root Mean Square Error, RMSE）提升了24.4%。可见，VAUKF鲁棒性和精度优于AUKF。
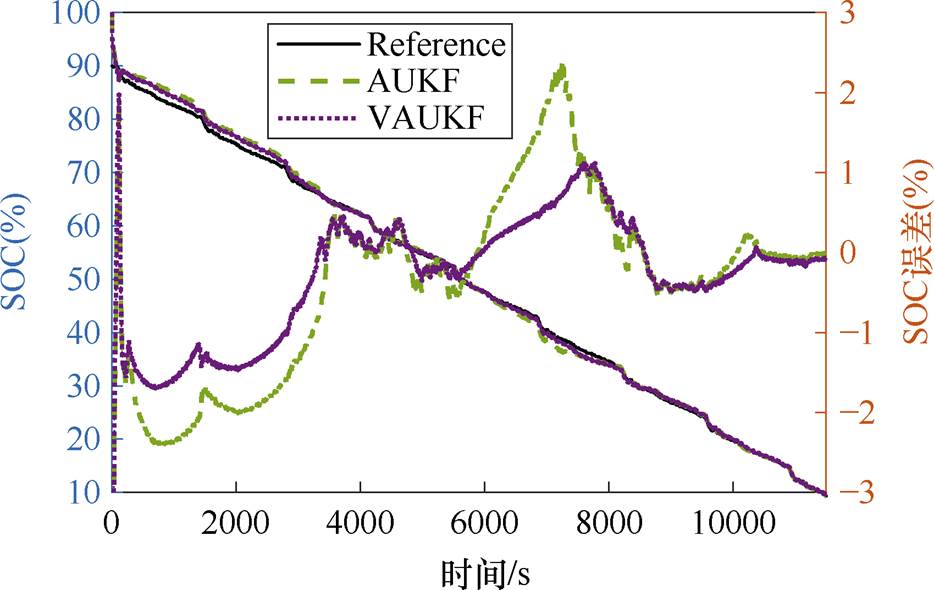
图5 FUDS工况的SOC预测结果
Fig.5 SOC estimation results via FUDS
表3 FUDS工况的SOC预测误差
Tab.3 SOC estimation error of FUDS condition （%）
预测方法MAERMSE AUKF0.799 61.058 1 VAUKF0.597 40.813 9
图6为VAUKF在FUDS工况下的s 和窗口长度变化。在图6a中s 变化显示，算法在不同时间段都出现方差波动较大的情况，前期和后期最明显。固定的窗口长度下，AUKF无法更充分地统计噪声变化，导致噪声协方差的不准确性。由图6b可知窗口长度的变化，可见算法前期和后期，算法通过减小窗口长度提高新的误差新息在Hk中的比重，进而获得更准确的噪声协方差。在算法中期窗口长度随误差新息序列的分布变化围绕窗口基数上下调整。VAUKF借助窗口长度的调整，改变噪声统计量，比固定窗口长度的AUKF具有更好的预测表现。
图6 VAUKF的s 和窗口长度变化
Fig.6 Variation of s and window length for VAUKF
US06工况的Allan方差如图7所示。由图7可知，t 处于160、320点曲线近似水平，此时方差值为1.479 3×10-4、1.695 6×10-4，取其平均得s0= 1.587 5×10-4。
图7 US06工况的Allan方差
Fig.7 Allan variance of US06 condition
图8为US06工况下的SOC预测结果，表4为相应的预测误差。从图8可以看出，算法前期VAUKF的SOC曲线更接近参考线，其误差曲线更靠近0参考点，说明此时VAUKF的预测精度更高。在260～2 800 s、5 100～7 100 s中VAUKF的预测误差更小。由表4可知，VAUKF较AUKF在MAE提升了21.4%，在RMSE提升了20.2%。
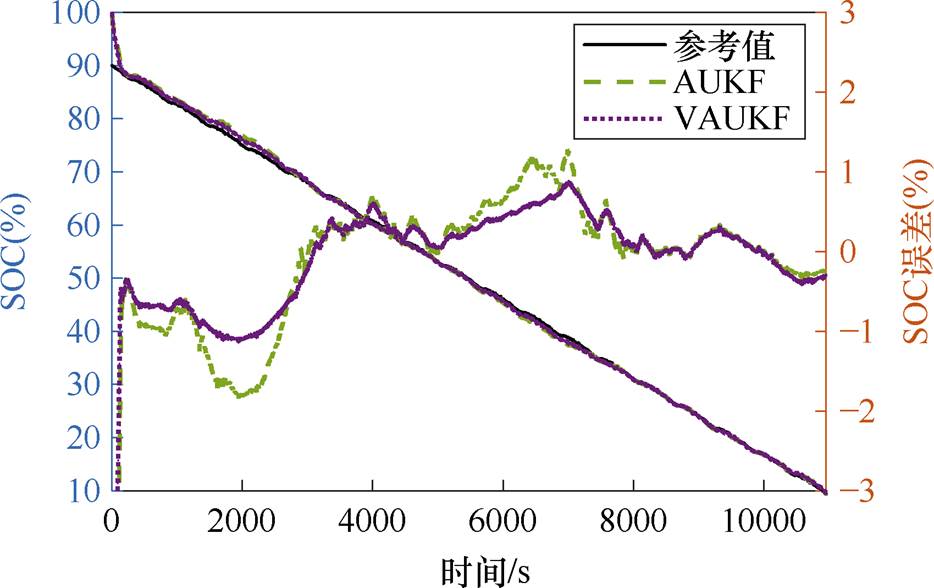
图8 US06工况的SOC预测结果
Fig.8 SOC estimation results via US06
从图8和图5来看，在AUKF出现误差明显增大的时间段，VAUKF有效地减小了预测误差，且误差波动小于AUKF，可见VAUKF提高了算法的鲁棒性。在AUKF预测精度较接近0参考线的时间段，VAUKF与AUKF预测结果较为接近。说明VAUKF对窗口微调有利于改善AUKF预测过程出现的误差突然增大的情况。
表4 US06工况的SOC预测误差
Tab.4 SOC estimation error of US06 condition （%）
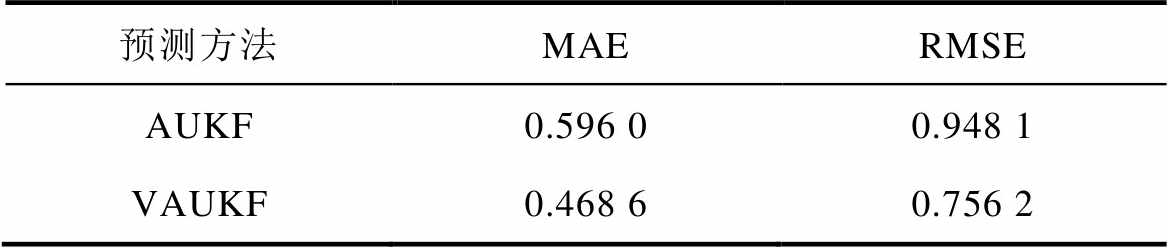
预测方法MAERMSE AUKF0.596 00.948 1 VAUKF0.468 60.756 2
仿真数据集在室温开放环境下进行，更好地模拟了实际工程中锂电池的工作环境，此时锂电池建模和OCV-SOC拟合曲线不可避免存在误差。模型误差的存在会造成AUKF在预测过程中的误差增大现象，为了提高算法预测精度，可以适当调节算法的窗口长度。但窗口长度调节幅度较大时反而容易引起算法的不稳定，因此，VAUKF基于窗口长度进行±1微调。
US06工况下VAUKF的s 和窗口长度变化如图9所示。与FUDS工况一致，US06工况预测过程中s 随时间变化而时刻变化。图9b与图6b对比可知，在US06工况下窗口变化更频繁，这是由于Allen分析取得的s0比FUDS工况小。从两种工况的误差预测情况来看，VAUKF都在AUKF误差增大较明显的时间段内做到了优化。受到算法初值影响，FUDS工况下算法前期误差波动比US06大。
VAUKF算法中方差倍率a取值影响SOC预测结果，本节基于FUDS工况进行不同a值的仿真分析，结果如图10所示。
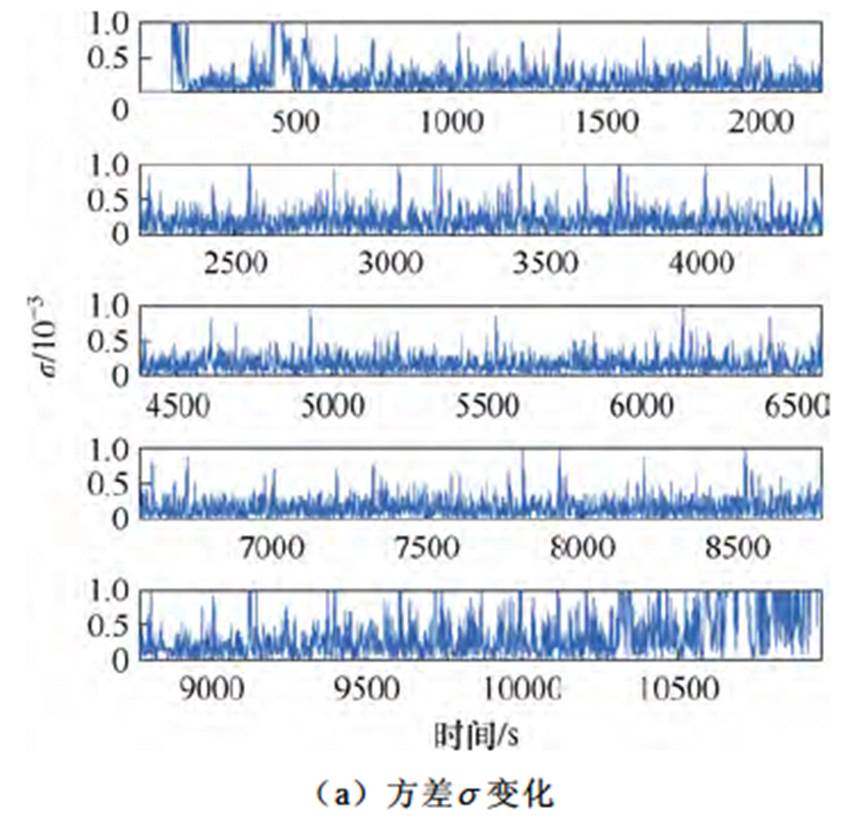
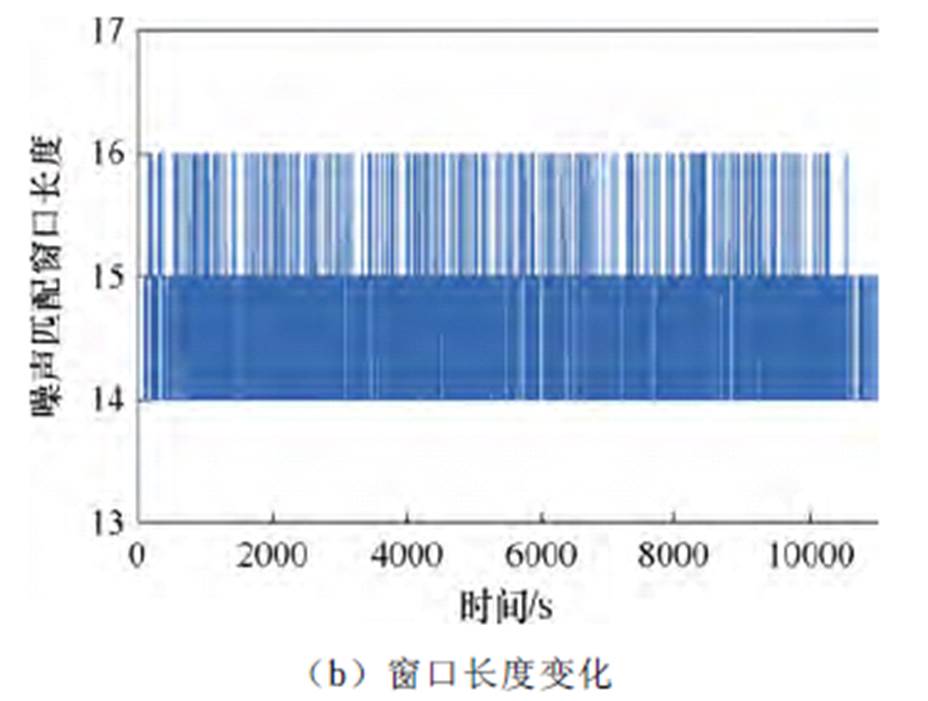
图9 VAUKF的s 和窗口长度变化
Fig.9 Variation of s and window length for VAUKF
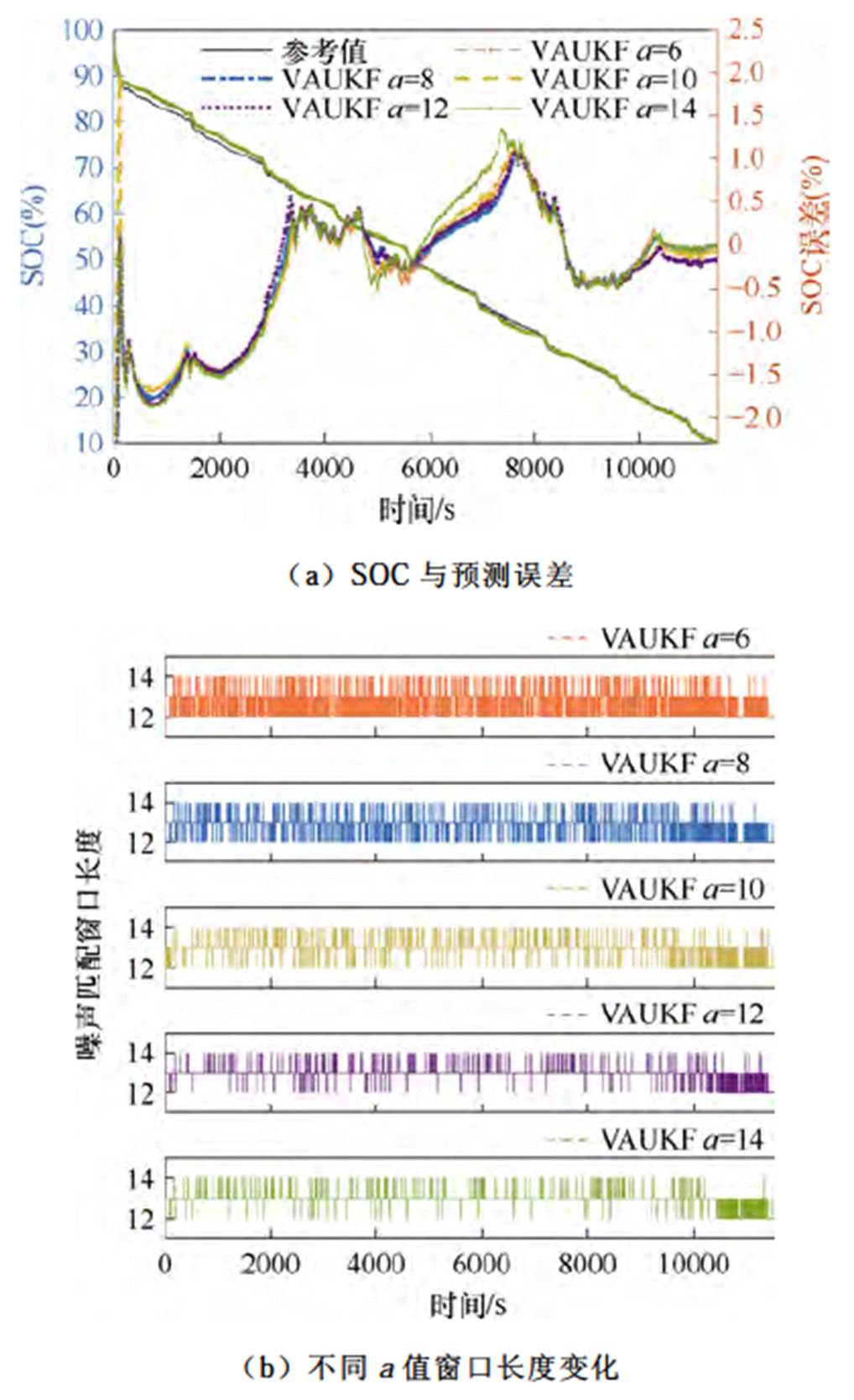
图10 FUDS工况下不同a值的SOC预测结果
Fig.10 SOC estimation results with different a values under FUDS condition
图10a中SOC误差曲线，a=14时预测误差大于其他曲线，整体上其他方差倍率曲线较为接近。图10b可以看到窗口长度的变化，a值越小窗口长度调整越频繁，在a取值为14时，算法前中期窗口长度几乎没有进行调整；另外可以看出，在算法后期误差新息序列波动较为明显。不同的a值整体预测结果较为接近，主要差距体现在算法误差波动较大的时间段。
FUDS下不同a值的SOC预测误差见表5。从表5可知，不同的a值下算法预测的RMSE有所变化，但不超过0.1%。a=10取得RMSE最小，a=14时RMSE基本接近AUKF。当a=14时算法窗口小幅度，基本以L=13参与算法运算，与取固定窗口长度的AUKF方法预测表现接近。a=6时，算法对序列幅值分布变化更为敏感，反而影响算法精度。因此，在FUDS工况下，综合考虑算法精度和鲁棒性，a取值为10较为合适。
表5 FUDS下不同a值的SOC预测误差
Tab.5 SOC estimation error of different a values under FUDS condition （%）
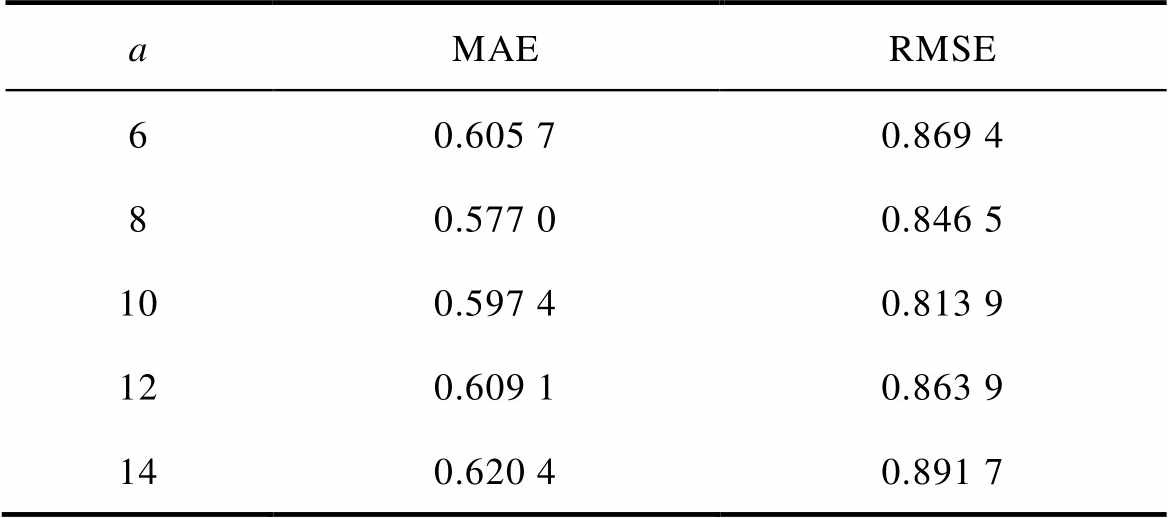
aMAERMSE 60.605 70.869 4 80.577 00.846 5 100.597 40.813 9 120.609 10.863 9 140.620 40.891 7
固定长度的协方差匹配窗口影响AUKF的预测性能，为了进一步提高SOC预测精度，本文提出一种VAUKF算法。且为了避免噪声协方差匹配窗口长度选值不当容易引起预测不确定性，提出VAUKF由AGA确定初始窗口长度。基于FUDS和US06工况数据进行锂电池SOC预测，结果验证了VAUKF算法的可行性。
仿真结果表明，FUDS工况下，VAUKF较AUKF在MAE提升了25.3%，在RMSE提升了24.4%；US06工况下，VAUKF较AUKF在MAE提升了21.4%，在RMSE提升了20.2%。在VAUKF取不同方差倍率时，FDUS工况下仍能获得优于AUKF的预测结果，倍率取10表现最好。因此，所提出的VAUKF比固定噪声协方差匹配时间窗的AUKF有更好的预测性能。
提出的VAUKF方法通过Allan有效辨识方差波动，并基于更新规则调整噪声匹配窗口，实现算法噪声的自适应更新。VAUKF算法对时变噪声抗干扰能力得到提升，进而提高了算法的噪声估计精度。本文研究可为后续UKF优化算法在锂电池SOC预测中的应用提供理论参考。未来可开发供算法实验验证的BMS系统，以便进一步验证算法在硬件系统中的可行性。
参考文献
[1] How D N T, Hannan M A, Hossain Lipu M S, et al. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: a review[J]. IEEE Access, 2019, 7: 136116-136136.
[2] Hannan M A, Wali S B, Ker P J, et al. Battery energy-storage system: a review of technologies, optimization objectives, constraints, approaches, and outstanding issues[J]. Journal of Energy Storage, 2021, 42: 103023.
[3] 刘萍, 李泽文, 蔡雨思, 等. 基于等效电路模型和数据驱动模型融合的SOC和SOH联合估计方法[J]. 电工技术学报, 2024, 39(10): 3232-3243.
Liu Ping, Li Zewen, Cai Yusi, et al. Joint estimation method of SOC and SOH based on fusion of equivalent circuit model and data-driven model[J]. Transactions of China Electrotechnical Society, 2024, 39(10): 3232-3243.
[4] Chen Kui, Zhou Shuyuan, Liu Kai, et al. State of charge estimation for lithium-ion battery based on whale optimization algorithm and multi-kernel relevance vector machine[J]. The Journal of Chemical Physics, 2023, DOI：10.1063/5.0139376.
[5] 黄凯, 孙恺, 郭永芳, 等. 基于观测方程重构滤波算法的锂离子电池荷电状态估计[J]. 电工技术学报, 2024, 39(7): 2214-2224.
Huang Kai, Sun Kai, Guo Yongfang, et al. State of charge estimation of lithium-ion battery based on observation equation reconstruction filtering algo- rithm[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2214-2224.
[6] 颜湘武, 邓浩然, 郭琪, 等. 基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J]. 电工技术学报, 2019, 34(18): 3937-3948.
Yan Xiangwu, Deng Haoran, Guo Qi, et al. Study on the state of health detection of power batteries based on adaptive unscented Kalman filters and the battery echelon utilization[J]. Transactions of China Elec- trotechnical Society, 2019, 34(18): 3937-3948.
[7] 孙金磊, 唐传雨, 李磊, 等. 基于状态与模型参数联合估计的老化电池可充入电量估计方法[J]. 电工技术学报, 2022, 37(22): 5886-5898.
Sun Jinlei, Tang Chuanyu, Li Lei, et al. An estimation method of rechargeable electric quantity for aging battery based on joint estimation of state and model parameters[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5886-5898.
[8] Chen Zewang, Yang Liwen, Zhao Xiaobing, et al. Online state of charge estimation of Li-ion battery based on an improved unscented Kalman filter approach[J]. Applied Mathematical Modelling, 2019, 70: 532-544.
[9] Zhang Shuzhi, Zhang Chen, Jiang Shiyong, et al. A comparative study of different adaptive extended/ unscented Kalman filters for lithium-ion battery state- of-charge estimation[J]. Energy, 2022, 246: 123423.
[10] Sun Daoming, Yu Xiaoli, Wang Chongming, et al. State of charge estimation for lithium-ion battery based on an Intelligent Adaptive Extended Kalman Filter with improved noise estimator[J]. Energy, 2021, 214: 119025.
[11] 李岩松, 欧阳进, 刘君, 等. 基于Allan方差的磁光玻璃型光学电流互感器噪声分析[J]. 电力系统自动化, 2015, 39(12): 126-129, 137.
Li Yansong, Ouyang Jin, Liu Jun, et al. Analysis on noise of magneto-optical glass type optical current transformer based on Allan variance[J]. Automation of Electric Power Systems, 2015, 39(12): 126-129, 137.
[12] 胡杰, 程向红, 朱倚娴. 基于Allan方差解耦自适应滤波的旋转SINS精对准方法[J]. 中国惯性技术学报, 2017, 25(2): 156-160, 165.
Hu Jie, Cheng Xianghong, Zhu Yixian. Refined alignment in rotary SINS based on Allan variance decoupling adaptive filter[J]. Journal of Chinese Inertial Technology, 2017, 25(2): 156-160, 165.
[13] 李醒飞, 韩佳辰, 刘帆. 基于Allan方差解耦自适应滤波的MHD/MEMS信号融合方法[J]. 中国惯性技术学报, 2020, 28(2): 237-241.
Li Xingfei, Han Jiachen, Liu Fan. Signal fusion method of MHD-MEMS based on Allan variance decoupling adaptive filter[J]. Journal of Chinese Inertial Technology, 2020, 28(2): 237-241.
[14] 欧阳晓凤, 曾芳玲, 吕大千, 等. 升空平台相对测量误差对定位精度的影响及定位算法[J]. 北京航空航天大学学报, 2024, 50(1): 187-197.
Ouyang Xiaofeng, Zeng Fangling, Lü Daqian, et al. Positioning accuracy and localization algorithm with relative measurement errors in blast-off platforms[J]. Journal of Beijing University of Aeronautics and Astronautics, 2024, 50(1): 187-197.
[15] 苏玉刚, 陈龙, 吴学颖, 等. 基于遗传算法的SS型磁耦合WPT系统负载与互感识别方法[J]. 电工技术学报, 2018, 33(18): 4199-4206.
Su Yugang, Chen Long, Wu Xueying, et al. Load and mutual inductance identification method of SS-type magnetically-coupled WPT system based on genetic algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4199-4206.
[16] Zhang Shumei, Qiang Jiaxi, Yang Lin, et al. Prior- knowledge-independent equalization to improve battery uniformity with energy efficiency and time efficiency for lithium-ion battery[J]. Energy, 2016, 94: 1-12.
[17] He Lin, Wang Yangyang, Wei Yujiang, et al. An adaptive central difference Kalman filter approach for state of charge estimation by fractional order model of lithium-ion battery[J]. Energy, 2022, 244: 122627.
[18] 范兴明, 封浩, 张鑫. 最小二乘算法优化及其在锂离子电池参数辨识中的应用[J]. 电工技术学报, 2024, 39(5): 1577-1588.
Fan Xingming, Feng Hao, Zhang Xin. Optimization of least squares method and its application in parameter identification of lithium-ion battery model[J]. Transa- ctions of China Electrotechnical Society, 2024, 39(5): 1577-1588.
Abstract In the lithium-battery charge state prediction, the Kalman filter algorithm is independent of a large number of dataset training. It can predict the state quantities with the observed data to obtain the optimal estimation of the system in the form of extended Kalman (extended Kalman filter (EKF)), untraceable Kalman filter (UKF), and other extended forms. However, the Kalman filtering algorithm and its extended forms for lithium battery nonlinear time-varying system obtain a fixed noise covariance, easily leading to the prediction error. Therefore, this paper proposes a variable-window adaptive untraceable Kalman (VAUKF) to determine the adaptive untraceable Kalman time window length, avoiding the prediction error caused by improper window length selection. The adaptive genetic algorithm (AGA) has been proven to achieve good parameter computation ability in avoiding local optimization and convergence speed problems. Thus, AGA calculates the optimal time window length, the overlapping grouped Allan ANOVA identifies the error sequence fluctuation, and the iterative process adjusts the window length appropriately. The VAUKF improves the SOC’s prediction accuracy and robustness compared to the AUKF.
First, based on the second-order RC lithium-ion battery equivalent circuit model, simulation modeling is carried out under the Federal Urban Driving Schedule (FUDS) and US06 high-speed cycling condition (US06) data. The noise level of the prediction process is obtained through the Allan variance, the variable window adjustment rule is determined, and the impact of noise fluctuations on prediction performance is analyzed. Then, the SOC prediction performance of VAUKF under different multiplicities is explored for the noise-matching window update rule, which provides more reasonable parameter conditions for VAUKF. Finally, the tracking ability and convergence speed of VAUKF and AUFK under different working conditions are analyzed, and the simulation results are discussed.
Compared with AUKF, the VAUKF decreases MAE by 25.3% and RMSE by 24.4% in RMSE under the FUDS condition. MAE and RMSE are decreased by 21.4% and 20.2% under the US06 condition. When the VAUKF takes different variance multiplicities, the FDUS condition still obtains better prediction results than AUKF, with the best performance when the multiplier is 10. The proposed VAUKF has better prediction performance than the AUKF with a fixed noise covariance matching time window. It can improve the anti-interference ability against time-varying noise the accuracy and robustness of SOC predictions.
keywords：State of charge (SOC) estimation, adaptive unscented Kalman filter, variable window adaptive unscented Kalman filter
中图分类号：TM912
DOI: 10.19595/j.cnki.1000-6753.tces.240442
国家自然科学基金（61741126）、广西自然科学基金（2022GXNSFAA035533）资助项目。
收稿日期2024-03-20
改稿日期2024-04-30
范兴明 男，1978年生，教授，博士生导师，研究方向为智能化电器和高电压新技术。E-mail: fanxm_627@163.com
张 鑫 女，1976年生，硕士，高级实验师，研究方向为智能化电器。E-mail: zhangxin_wt@163.com（通信作者）
（编辑 崔文静）