图1 混合风电场结构
Fig.1 The structure of hybrid wind farm
摘要 基于匹配控制策略的构网型直驱风电场部分替代跟网型直驱风电场后，匹配构网型风机对形成的混合风电场次同步振荡（SSO）影响机理尚不明确。该文针对混合风电场中跟网型风机引发SSO的场景，建立混合风电场并网系统的小信号模型，基于特征值分析法分析混合风电场中的主导SSO模态及其参与因子，采用阻尼转矩法揭示匹配构网型风机占比对混合风电场SSO的振荡影响机理。结果表明：匹配构网型风机在主导SSO模式下可以改善混合风电场的阻尼特性，对跟网型风电场引发的SSO起到抑制效果；虽然匹配构网型风机占比增加会降低混合风电场的SSO的发生风险，但是其参数几乎不参与此主导SSO模态，跟网型风电场内部参数是主导的参与因子；典型占比下，通过增大直流母线电容参数、减小锁相环比例系数、增大电流内环的积分系数，可降低SSO的发生风险，基于PSCAD/EMTDC仿真平台验证了理论分析的可靠性。
关键词：匹配控制 混合风电场 次同步振荡 占比
随着“双碳”目标的提出，新能源机组在电力系统中的渗透率逐年增高[1]。电力系统呈现“双高”特征，出现较多风电场发生的振荡事故[2]，例如，2015年新疆哈密地区的跟网型直驱风电场出现20～40 Hz的次同步振荡（Subsynchronous Oscillation, SSO）现象[3]。相较于跟网型控制，构网型控制具备良好的电压、频率支撑能力[4-5]。因此，风能可通过两种控制共存的混合风电场外送，此场景的小干扰振荡稳定性问题研究亟须开展。
构网型控制的本质可等效为电压源，克服了跟网型控制低惯量、弱阻尼的缺点，可分为匹配控制、虚拟同步发电机（Virtual Synchronous Generator, VSG）控制等[6]。其中匹配控制又称为惯性同步控制，通过直流母线电压同步并间接控制功率，对电网表现出更强的鲁棒性[7-10]。文献[8]将匹配控制应用在直驱风机，通过特征值分析多机系统的模态及阻尼比，结果表明系统中存在低频振荡风险。文献[9-10]将匹配控制应用在直流输电系统，研究表明直流电压与风电场存在的动态耦合影响系统稳定。除此之外，较多研究针对其他构网控制类型展开，模型解析结果表明，构网控制下系统的主导振荡模式集中在2 Hz以下[11-12]。文献[12-13]针对双馈风机，分别从特征值及阻抗解析的角度，研究功率同步及VSG控制下的弱电网并网稳定性问题，结果表明：负阻尼、负阻抗效应是系统稳定性弱的原因。同时，强电网下多构网VSG直驱机组并联、微电网下的多VSG并联等场景均存在低频振荡风险[14-16]。以上研究表明构网型控制对振荡的影响集中在低频段，尚缺乏对次同步频段的影响分析。
有关文献针对构网型机组衍生的混合系统展开一些振荡问题研究，但主要围绕VSG控制，缺乏针对匹配控制的研究。文献[17]研究VSG换流器与双馈风电场并联系统的小信号稳定性问题，结果表明：VSG电压控制与双馈风机电流控制存在环路开环模态谐振现象。基于特征值分析法，文献[18-19]研究VSG控制的直驱风机对跟网型新能源的影响，结果表明VSG控制可以降低跟网型新能源的SSO风险，但是缺乏物理层面的解释。储能可以根据电网反馈调节自身运行状况，能够用来抑制新能源场站的SSO[20]。文献[21-22]分别将VSG控制、下垂控制应用在储能系统，能够有限地改善新能源场站的负阻尼特性，降低SSO的发生风险。综上所述，由于匹配控制和VSG控制存在差异，且受到工程青睐，因此有必要研究匹配控制下的直驱风机对跟网型新能源场站的SSO影响。
新能源电力系统SSO的主要分析方法包括时域的特征值分析法以及频域的阻抗分析法[23]。前者建模严谨，能够提供振荡模态并定位参与的参数；后者具备一定的物理意义支撑。有研究提供采取多种方法研究SSO问题的思路[24]，以解决某一种方法无法兼顾所有优点的问题。阻尼转矩法针对主导元件的动态过程[25-27]，参考Heffron-Phillips模型[28-29]进行小信号模型的重构，借助等效阻尼系数从物理层面解释SSO问题。因此，本文采用特征值分析法、阻尼转矩法，研究混合风电场中基于匹配控制的构网直驱风机对跟网直驱风机振荡的影响。
本文针对构网/跟网型混合风电场的SSO问题，首先介绍所采用的匹配构网型控制、跟网型控制以及待研混合风电场拓扑。其次，基于混合风电场并网系统数学模型，采用模块化建模的方法，在Matlab/ Simulink仿真平台中构建待研系统的小信号模型。然后，解析混合风电场并网系统小信号模型，从风机占比角度分析主导SSO模态及其参与因子，并从阻尼的角度阐释匹配构网型风机对SSO的影响机理。最后，从根轨迹和电磁暂态时域响应两个角度，分析系统不同运行参数下SSO特性的变化情况。
混合风电场由跟网型直驱风电场和匹配控制的构网型直驱风电场组成，分别由单台额定容量5 MW的风机采用单机聚合等效[30]构成。单台风机由单质量块轴系、直驱永磁同步电机、滤波器、控制系统等部分构成。
混合风电场结构如图1所示。混合风电场中共N台风机，额定风速为10 m/s。单机聚合等效后的风电场经一级箱变升压至公共耦合点（Point of Common Coupling, PCC），最后经二级变压器升压将电能汇入戴维南等效的交流电网。跟网型网侧换流器控制（Grid-Side Converter Control, GSC）采用直流电容电压外环、电流内环（对偶处PI参数设置相同）的传统双环控制；构网型GSC基于匹配控制思路，采用电压外环（对偶处PI参数设置相同）、与跟网型一致的电流内环（对偶处PI参数设置相同），并引入无功下垂控制提供系统扰动期间需要的惯性[31]。跟网型、匹配构网型机侧换流器控制（Machine-Side Inverter Control, MSC）均采用转速外环、电流内环的控制策略[32]，跟网型风电场改造为匹配构网型风电场时，机侧可保留最大功率追踪特性。
图1 混合风电场结构
Fig.1 The structure of hybrid wind farm
图1混合风电场拓扑中各变量定义如下：k1为箱变的电压比；iL、iM分别为单台跟网型、匹配构网型风机的汇入电流；N1为跟网型风电场风机数量，N2为匹配构网型风电场风机数量；RS、XS分别为单个聚合风电场35 kV线路阻抗；k2为二级变压器的电压比；RT、XT为戴维南等效后的345 kV线路阻抗；CQ为无功补偿电容。系统拓扑的主要参数详见附表1，部分相同参数仅于跟网型风电场列出。
图1混合风电场控制中各变量定义如下：CDC、uDC1, uDC2分别为直流母线电容、电压；Lt1, Lt2、Lg1, Lg2、Cf1, Cf2、Rd1, Rd2分别为考虑无源阻尼的LCL型滤波器参数，包括滤波电感、滤波电容、阻尼电阻，L为Lt1与Lg1之和；it1, it2、ig1, ig2分别为GSC和滤波器出口电流；Ut1, Ut2、Uf1, Uf2、Ug1, Ug2为滤波器上电压；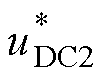
为
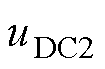对额定值的标幺值，稳态时为1；w0为额定角速度；qpll、q 为滤波器出口处相位；Qf为Uf2测量点无功功率；下标“ref”、“dq”用于表示参考值、dq坐标下的参数；RV、XV为虚拟阻抗；un为并网点相电压幅值。控制器参数详见附表2。
考虑混合风电场部分构成存在高度相似的特点，本节基于系统的数学模型建立更灵活的模块化小信号模型。首先基于电气连接关系划分模块；然后将数学模型转化成确定输入输出关系的子模块状态空间模型；最后连接各子模块，得到闭环系统小信号模型。
如图1所示，混合风电场中跟网型风机和匹配构网型风机的区别主要在于GSC，即GSC控制器数学模型不同。两类风机的轴系模块、发电机模块、MSC模块、直流电容模块、受控源聚合等效模块数学模型形式相同。由于篇幅限制，仅针对匹配构网型风机GSC进行数学模型介绍，风机各子模块数学模型及交流电网数学模型详见文献[32]。
基于匹配控制思想的匹配构网风机由直流母线电容积分生成相位，即
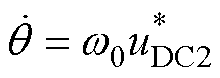（1）
式（1）中，q 用于abc和dq的坐标变换，是匹配构网GSC的双环控制电压信号构建的基础，双环控制的数学模型为
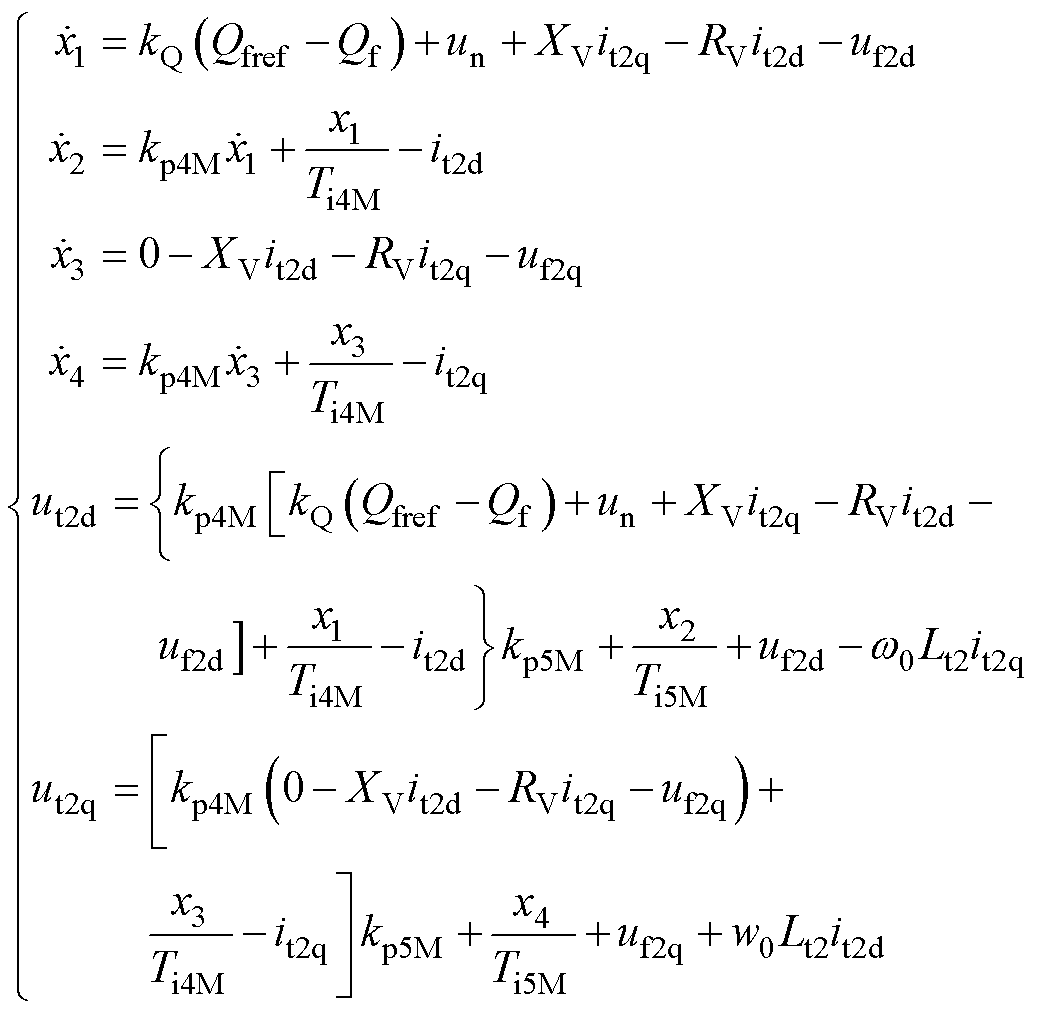（2）
式中，x1、x2、x3、x4为引入的中间变量；it2d、it2q为it2的d、q分量；ut2d、ut2q为ut2的d、q分量；uf2d、uf2q为uf2的d、q分量；kp4M、Ti4M分别为匹配构网GSC外环比例、积分系数；kp5M、Ti5M分别为匹配构网GSC内环比例、积分系数；dq控制链路因对偶设置相同；其他参数与图1一致。
2.2.1 子模块建模
小信号模型的本质是将系统的微分方程组在潮流稳态工作点处进行线性化。模块化建模的关键在于将子模块重复线性化的过程，得到高移植性的子模块小信号模型，在不同系统拓扑中根据相应的电气关系连接子模块小信号模型，得到待研系统的闭环小信号模型。其中，子模块小信号模型的线性化数学形式为
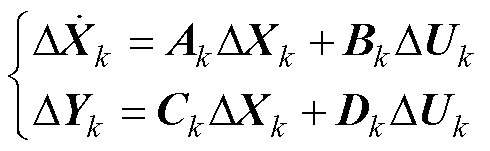（3）
式中，D为线性化变量；Xk为子模块k的状态量构成的矩阵；Uk为子模块k的输入量构成的矩阵；Yk为子模块k的输出量构成的矩阵；Ak为子模块k的状态矩阵；Bk为子模块k的输入矩阵；Ck为子模块k的输出矩阵；Dk为子模块k的传递矩阵。各子模块的相应矩阵，由某一相同的潮流稳态工作点求得。
以匹配构网GSC的双环控制为例（将其定义为子模块k），线性化式（2）得到形如式（3）的线性化数学形式，即
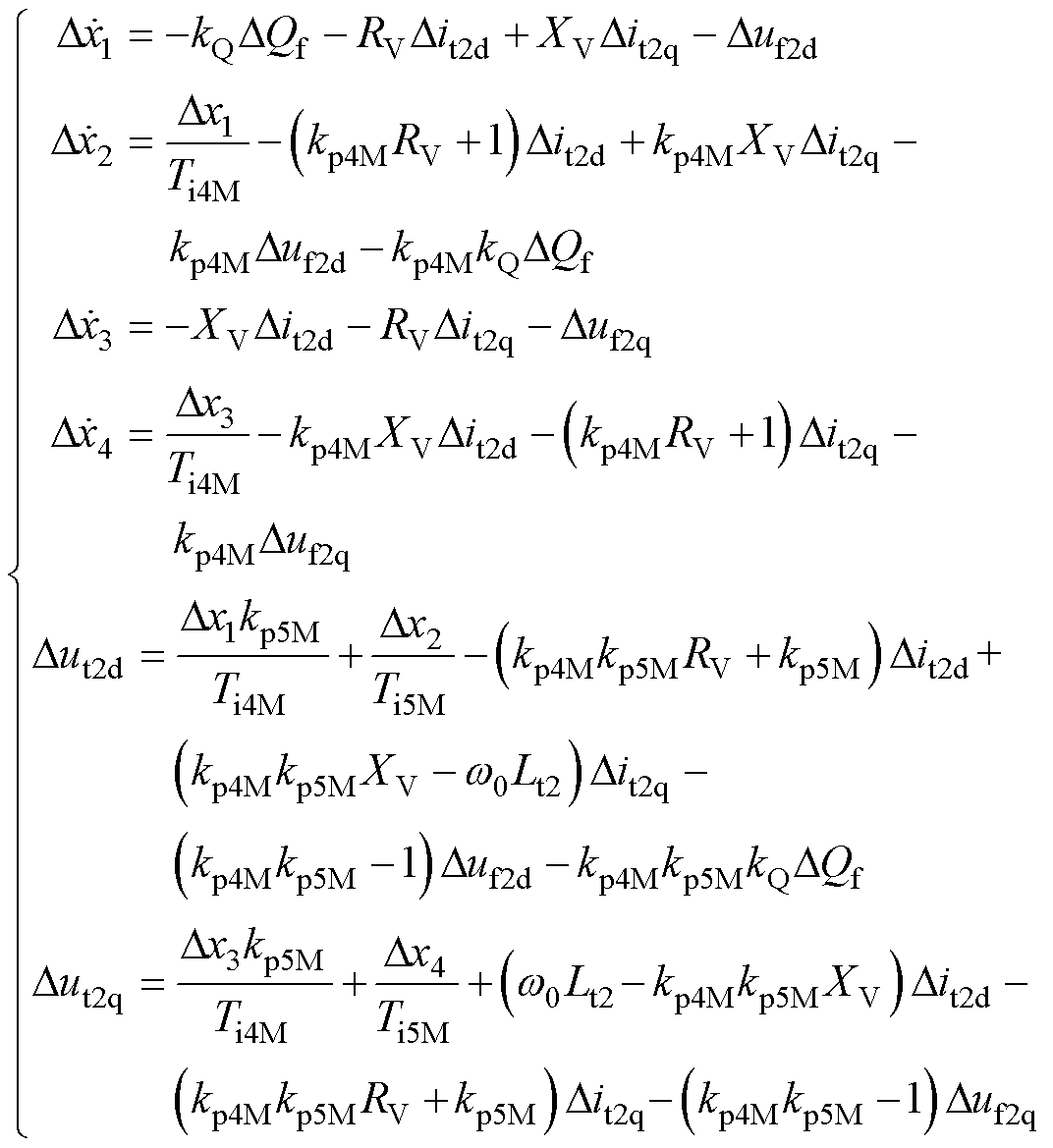（4）
式中，控制给定量等常数线性化后为0，不在公式中体现；按照式（3）的形式，则Xk=[x1x2x3x4]T，Uk=[it2dit2quf2duf2qQf]T，Yk=[ut2dut2q]T；Ak、Bk、Ck、Dk分别为
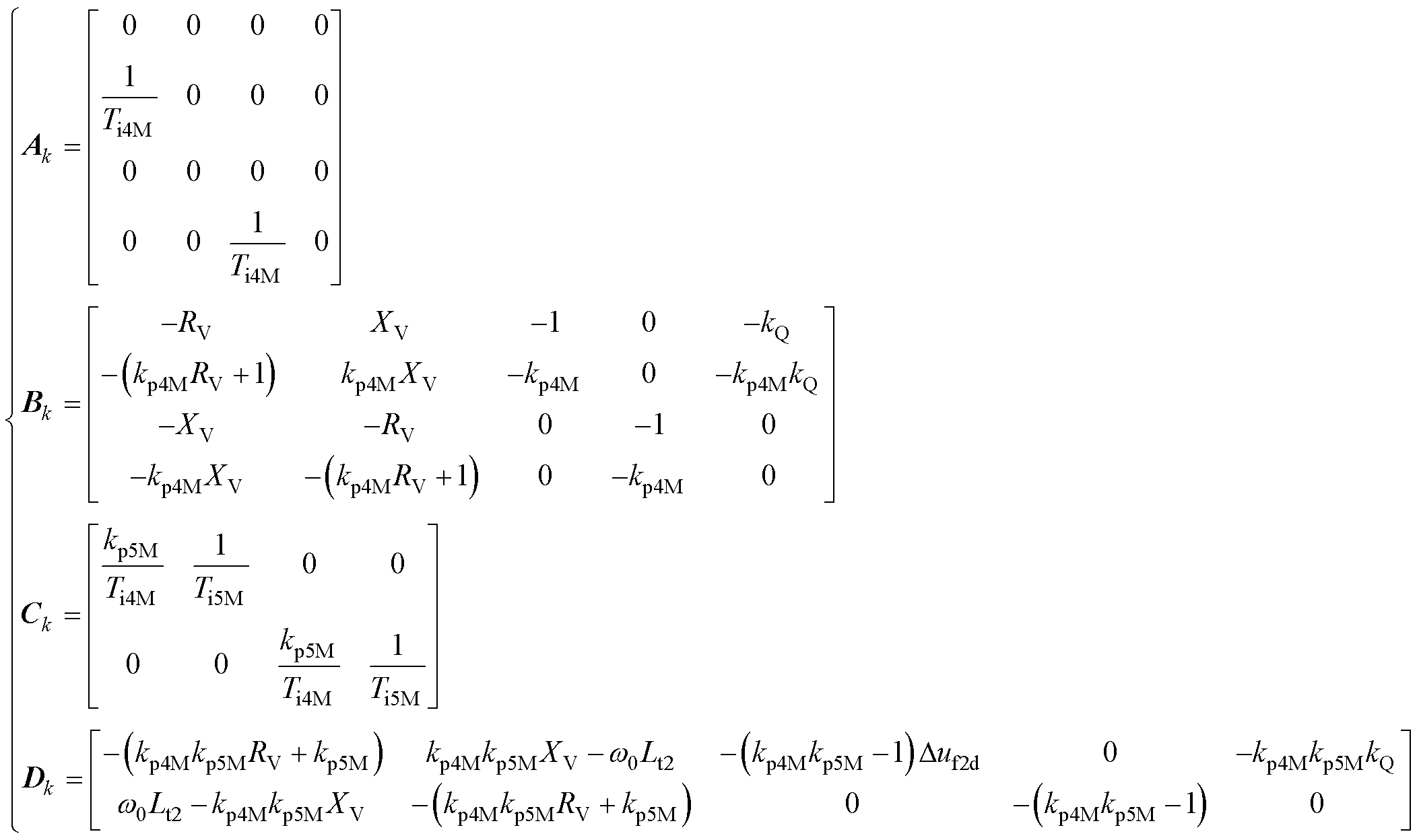（5）
2.2.2 闭环小信号模型
混合风电场中，跟网型风电场和匹配构网型风电场分别位于各自的dq坐标系下，输电线路位于xy坐标系下，涉及坐标耦合。因此，闭环小信号模型中需要引入如式（6）所示的坐标变换，将不同变量统一坐标系建模。
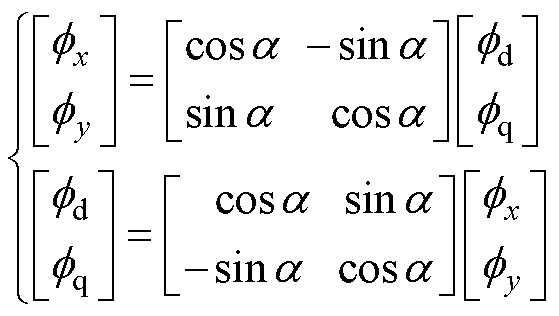（6）
式中，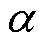
为dq与xy坐标系的角度偏差；
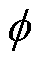为任意变量；下标dq、xy为相关坐标系下变量。
基于Matlab/Simulink仿真平台，根据图1的结构及参数，构建如式（3）的各子模块状态空间模型，连接各子模块输入、输出接口，得到混合风电场闭环小信号模型，即
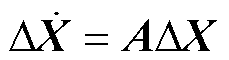（7）
式中，A、X分别为闭环系统状态矩阵、状态变量矩阵。将X中的状态变量按照所属子模块进行划分，结果见表1。
表1 状态变量划分结果
Tab.1 The results of state variables division
子系统组别子模块组别状态变量编号 跟网型风电场轴系Xmass11 PMSGXG12、3 MSC控制XMSC14～6 直流电容XDC17 GSC控制XGSC18～10 PLL控制XP111、12 滤波器XLCL113～18 匹配构网型风电场轴系Xmass219 PMSGXG220、21 MSC控制XMSC222～24 直流电容XDC225 GSC控制XGSC226～29 匹配控制XP230 滤波电感XL31、32 滤波电容XC33、34 35 kV线路XS235、36 交流电网无功电容XQ37、38 345 kV线路XT39、40
混合风电场各子模块的具体接口关系如图2所示，其中单机聚合模型与二级变压器模型没有单独构建子模块，即风电场台数、电压比关系附在相关子模块的Ak、Bk、Ck、Dk矩阵中。
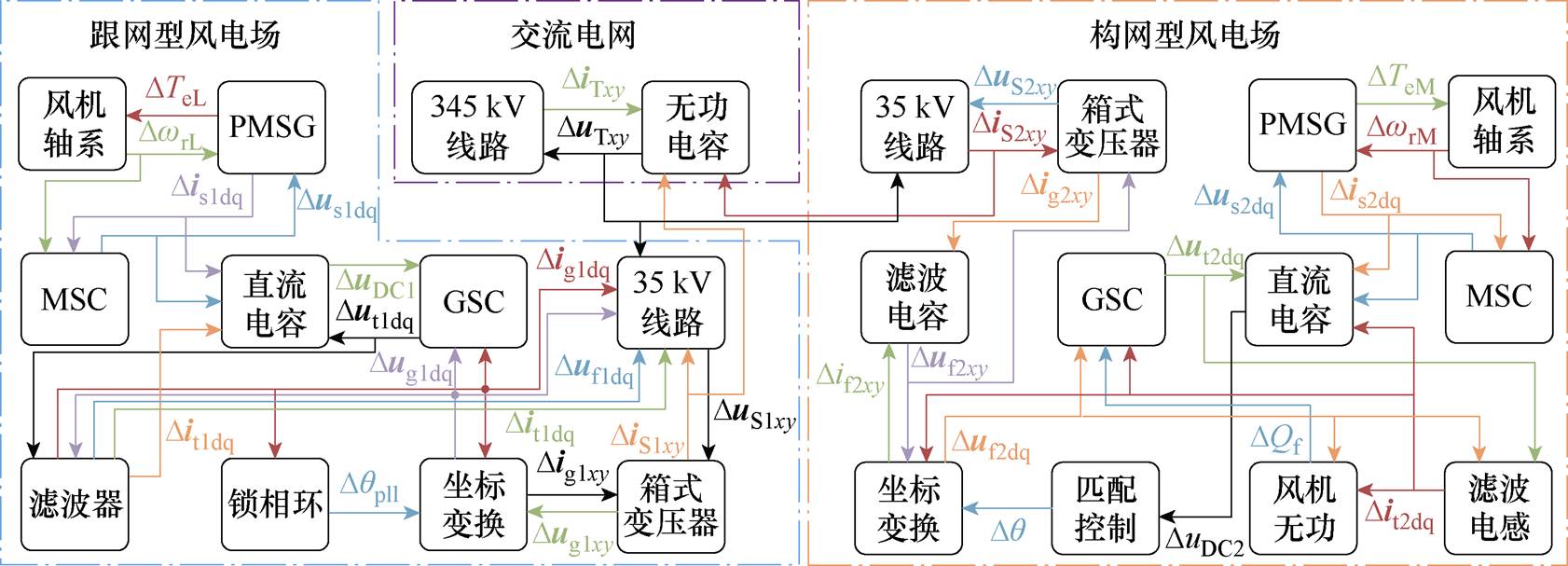
图2 混合风电场小信号模型
Fig.2 The small-signal model of hybrid wind farm
如图2及表1所示，混合风电场闭环小信号模型划分为24个子模块，共40阶。其中，跟网型风电场子系统分为风机轴系模块、锁相环模块等10个模块；交流电网子系统分为345 kV线路模块、无功电容2个模块；构网型风电场子系统分为风机轴系模块、匹配控制模块等12个模块。
本节旨在研究混合风电场中，匹配构网型风机比例对跟网型风电场SSO的影响。首先，基于混合风电场小信号模型，从模态参与因子角度出发，研究混合风电场并网系统的SSO特性。其次，采用阻尼转矩法，分析混合风电场并网系统的阻尼特性，揭示跟网型风电场引发SSO后，匹配构网型风机占比对SSO的影响机理。最后，结合时域仿真验证以上分析结果的正确性。
3.1.1 系统主导振荡模态
基于第2节建立的闭环小信号模型，按照附表1、附表2所列参数，计算并筛选出混合风电场并网系统主导振荡模态。保证混合风电场中风机总数不变，以1为步长，逐渐增加匹配构网型风机台数，使匹配构网型风机占比从0%逐渐增至90%，主导振荡模态的根轨迹见附表1。其中选取6个工况，具体工况设置工况见表2。
如表2所示，通过减小跟网型风机台数N1、增大匹配构网型风机台数N2，提高匹配构网型风机占比，同时保持混合风电场中风机总台数为60。其中：工况1条件下，混合风电场中只存在跟网型风机，为跟网型风电场，场站短路比为1.8，系统运行于弱电网；工况2～6下，仅改变N1、N2，系统各电压等级下输电线路参数与工况1保持一致。工况1～6的主导振荡模态见表3。
表2 模态设置工况
Tab.2 The setting conditions of modal
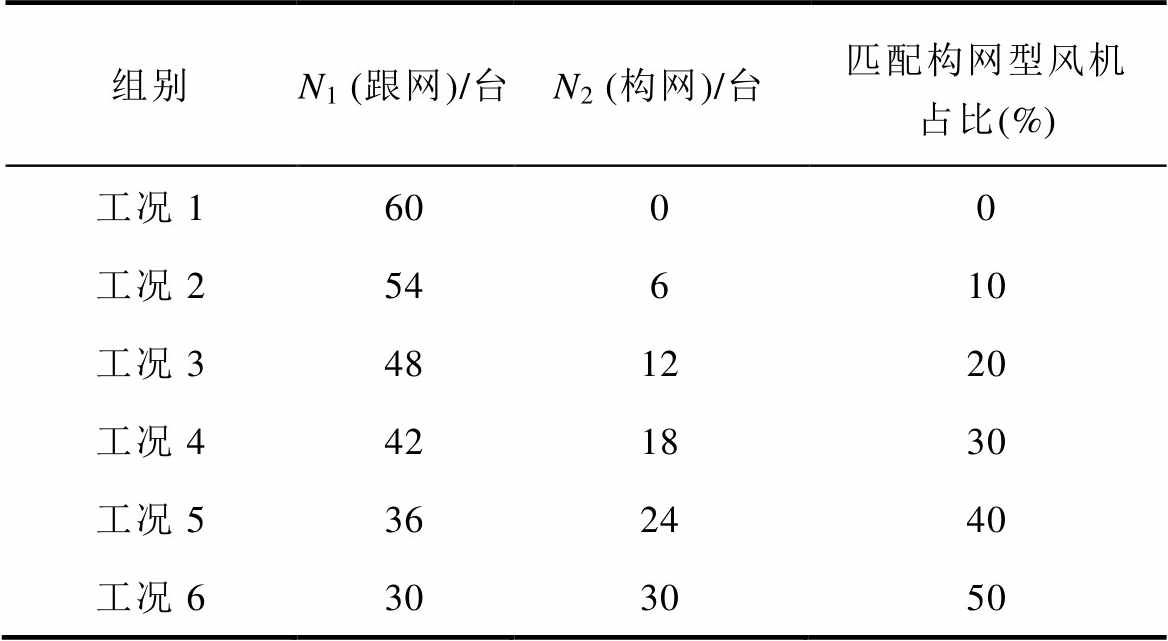
组别N1 (跟网)/台N2 (构网)/台匹配构网型风机占比(%) 工况16000 工况254610 工况3481220 工况4421830 工况5362440 工况6303050
表3 各工况主导振荡模态
Tab.3 The main oscillation mode of each condition
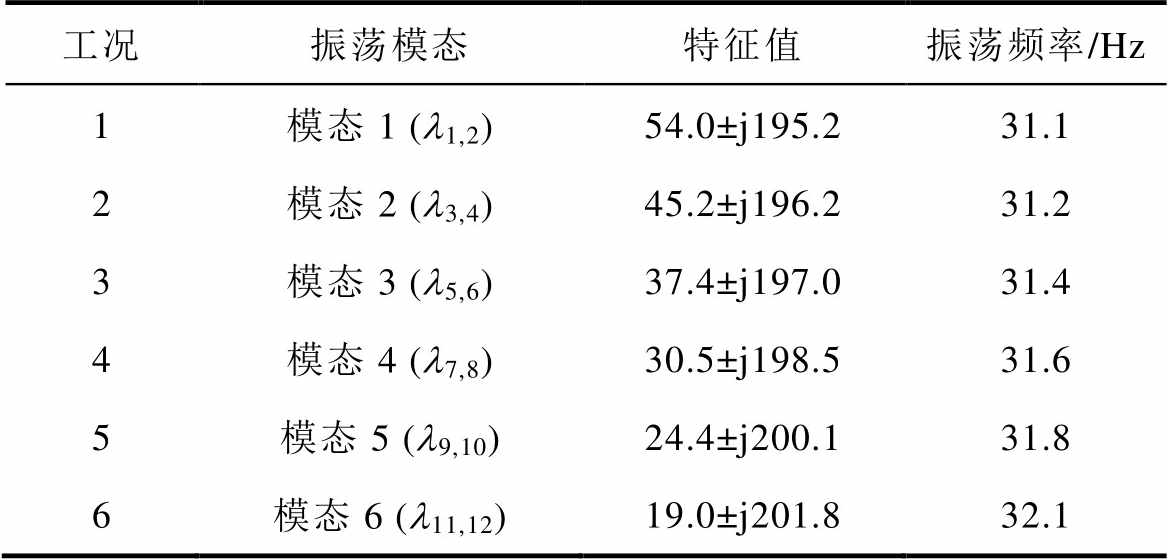
工况振荡模态特征值振荡频率/Hz 1模态1 (l1,2)54.0±j195.231.1 2模态2 (l3,4)45.2±j196.231.2 3模态3 (l5,6)37.4±j197.031.4 4模态4 (l7,8)30.5±j198.531.6 5模态5 (l9,10)24.4±j200.131.8 6模态6 (l11,12)19.0±j201.832.1
如表3所示，六种工况下均存在一个主导的振荡模态，其频率在31～32 Hz附近，处于SSO频段，称之为主导SSO模态。六种工况下主导SSO模态的特征根实部均为正，表示混合风电场在六个工况下均有发生31 Hz左右SSO的风险。模态的特征根实部及频率趋势详如图3所示。
图3表明，工况1～6（匹配构网型风机占比0%～50%）的主导SSO模态的特征根实部逐渐降低，振荡频率从31.1 Hz升至32.1 Hz。这表明：随着匹配构网型风机占比增加，混合风电场发生SSO的风险逐渐降低，振荡频率逐渐升高。
图3 不同占比的主导SSO模态关键量
Fig.3 Different proportions of the dominant SSO modal key quantities
3.1.2 主导振荡模态参与因子
参与因子大小反映参量对振荡模态的参与度强弱，一般参与度越强的参量对振荡影响越明显。本节将参与因子做归一化处理，状态参量的参与因子所占比例越高，该参量对SSO的参与度越大。
基于混合风电场小信号模型，将3.1.1节描述的工况1～6分别进行参与因子分析，得到主导SSO模态的参与因子结果，如图4所示。
图4中，状态变量符号与表1保持一致，XDC1、XGSC1、XP1、XLCL1主要状态变量占比值从左到右分别呈现，并将各工况参与因子占比在表4中列出。XDC1与CDC参数相关；XGSC1依次与跟网型风机控制PI1L、PI2L、PI3L参数相关；XP1依次与锁相环（Phase Locked Loop, PLL）PI、积分器参数相关；XLCL1依次与Lt1、Cf1、Lg1参数相关。部分参数的参与度极低（例如交流电网中XT占比不到0.4%）时，则不在图4体现。
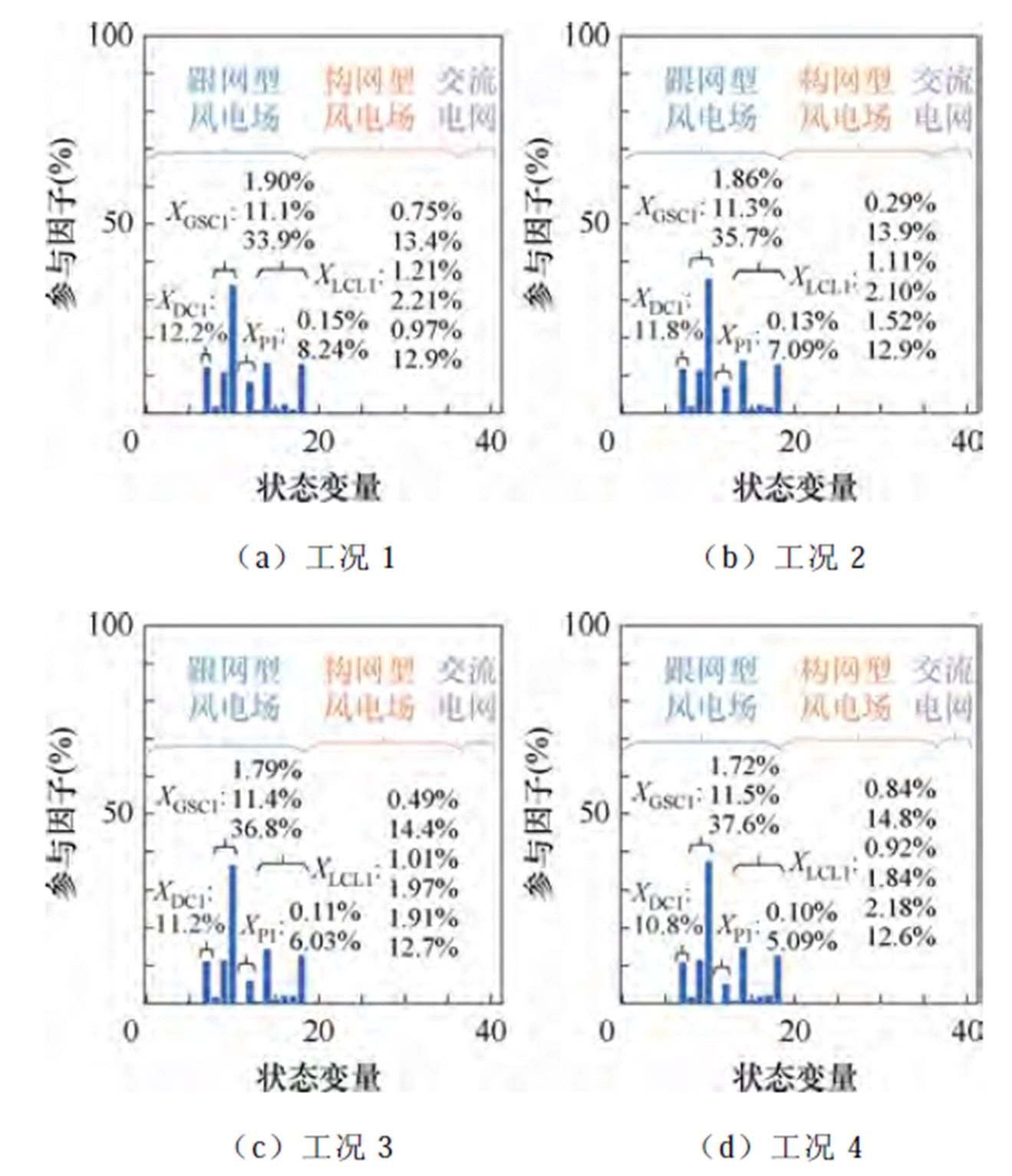
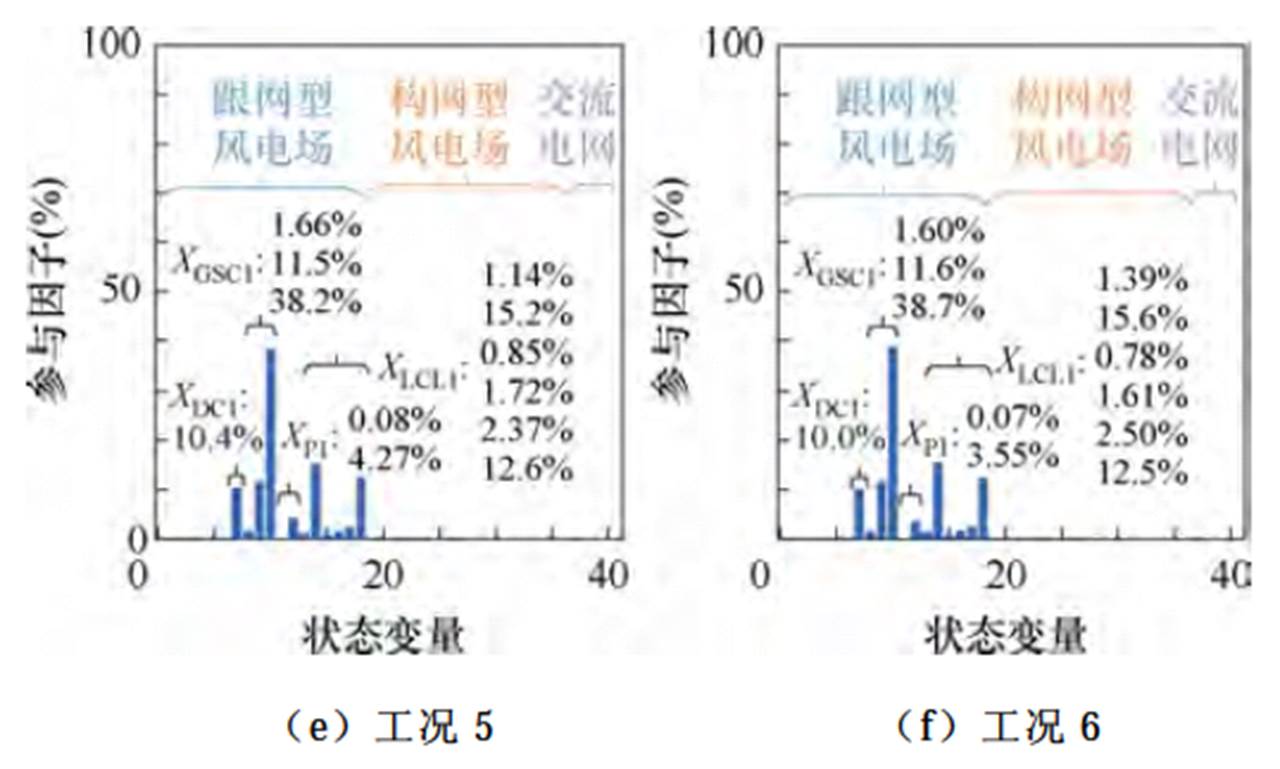
图4 主导SSO模态参与因子
Fig.4 Participation factors of the main SSO mode
表4 各工况参与因子占比
Tab.4 Proportion of participating factors in each working condition
状态变量占比(%)趋势 工况1工况2工况3工况4工况5工况6 XDC112.211.811.210.810.410.0递减 XGSC11.901.861.791.721.661.60递减 11.111.311.411.511.511.6递增 33.935.736.837.638.238.7递增 XP10.150.130.110.100.080.07递减 8.247.096.035.094.273.55递减 XLCL10.750.290.490.841.141.39无 13.413.914.414.815.215.6递增 1.211.111.010.920.850.78递减 2.212.101.971.841.721.61递减 0.971.521.912.182.372.50递增 12.912.912.712.612.612.5递减
参与因子结果表明，混合风电场发生由跟网型风电场引发的SSO后，主导SSO模式由跟网型风电场参数主要参与，匹配构网型风电场和交流电网参数相较下参与度有限。随着混合风电场中匹配构网型风机占比增加，这种参与情况基本不变，仍由XDC1、XGSC1、XP1、XLCL1四类参数主要参与。但是随着匹配构网型风机占比增加，四类参数的参与度存在不同变化。
如图4及表4所示，匹配构网型风机占比在0%～ 50%变化时，XDC1的参与度从12.2%降至10.0%，参与度较低且总体保持不变；XGSC1的参与度由高到低依次为PI3L、PI2L、PI1L对应状态变量，PI3L参与度由33.9%升至38.7%，PI2L参与度由11.1%升至11.6%，PI1L参与度由1.90%降至1.60%；XP1参与度主要体现在PLL积分器状态变量上，由8.24%降至3.55%；XLCL1的参与度分别介于0.29%～1.39%、13.4%～15.6%、0.78%～1.21%、1.61%～2.21%、0.97%～2.50%、12.5%～12.9%，其中，第一项非单调变化，第二、五项递增，第三、四、六项递减。
综上所述，该主导SSO模态由跟网型风电场的直流电容、GSC控制、PLL控制、滤波器主要参与。GSC控制中PI3L参数的参与度最高，且随着混合风电场中匹配构网型风机占比的增加而增加。本待研场景下，当混合风电场中引发振荡后，匹配构网型风机占比增加将降低系统发生SSO的风险，但不会改变影响SSO的参与参数分布情况。
阻尼转矩法根据待研系统的动态元件，得到类Heffron-Phillips模型，从阻尼系数的角度分析系统的小干扰稳定性，得到物理层面的结论。3.1节参与因子结果表明，XP1的PLL积分器状态变量参与度较高，本节从PLL动态过程出发，推导混合风电场并网系统的类Heffron-Phillips模型。
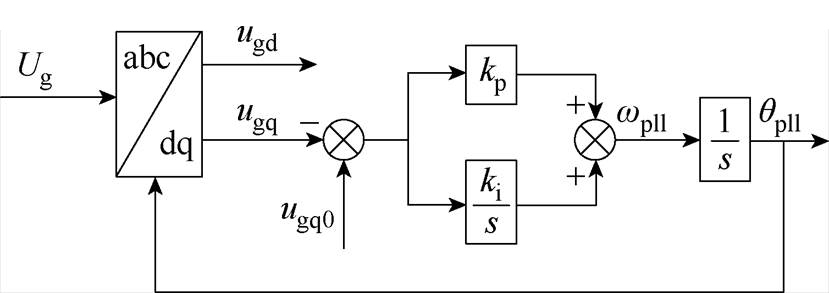
图5 PLL动态过程
Fig.5 The dynamic process of PLL
图5中，wpll为PLL输出角频率，kp、ki分别为PLL的PI比例、积分系数，ugq0为常数0，其他参数与图1保持一致。PLL的动态方程可以表示为
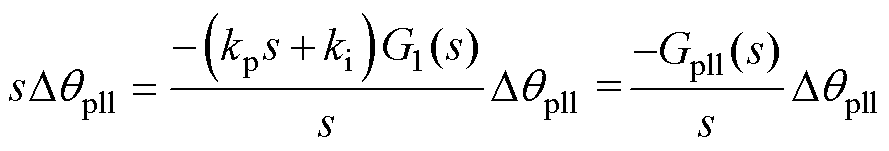（8）
式中，G1(s)为Dqpll到Dugq的开环传递函数。算子s=s+jw 在主导SSO模式下，s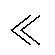
w。因此存在s≈jw，可将式（8）推导为二阶运动方程形式，即为
（9）
图6为并网同步发电机的Heffron-Phillips模型框图，D、J、K分别为等效的阻尼系数、惯性系数、同步系数。系数D的正、负分别表征系统稳定、不稳定，D越小，系统所具有的阻尼越小，系统失稳的风险越大。
图6 Heffron-Phillips模型框图
Fig.6 The block diagram of Heffron-Phillips mode
将式（9）类比图6，可得到基于PLL动态过程的混合风电场类Heffron-Phillips模型。此时，D类比为Im[Gpll(s)]/w（称为DP）；J类比为1/(kps+ki)；K类比为Re[Gpll(s)]；Dw 类比为Dwpll；DTm类比为Dugq0；DTe1+DTe2类比为Dugq。
针对混合风电场的主导SSO模态，当跟网型风电场中并网点Ug受到扰动，Dugq与常数0不平衡，PLL输出相位Dqpll偏离稳态工作点，进而通过Park变换影响Dugq，最终可能引发振荡。参考图6中Heffron-Phillips模型中阻尼系数的物理意义，选取基于PLL动态过程类Heffron-Phillips模型的阻尼系数DP，为评估系数。当DP为正时，混合风电场并网系统对主导SSO模式表现正阻尼，系统没有失稳的风险；反之DP为负时，系统可能因阻尼不足发生振荡，且在阻尼极小值附近频率处的振荡风险最大。
同3.1节，选取工况1～6，求解出混合风电场中匹配构网风机在0%～50%变化时的DP频率特性如图7所示。图7给出DP在SSO频段附近的频率特性曲线，随着匹配构网风机比例分别在0%～50%升高，DP在各个频率处均表现为阻尼增大。浅黄透明区域表明：随着匹配构网型风机占比增加，阻尼极小值处的频率逐渐升高，与表3结果保持一致。各DP频率特性在31～33 Hz范围附近达到阻尼极小值，混合风电场在此频率范围内发生SSO风险最大。
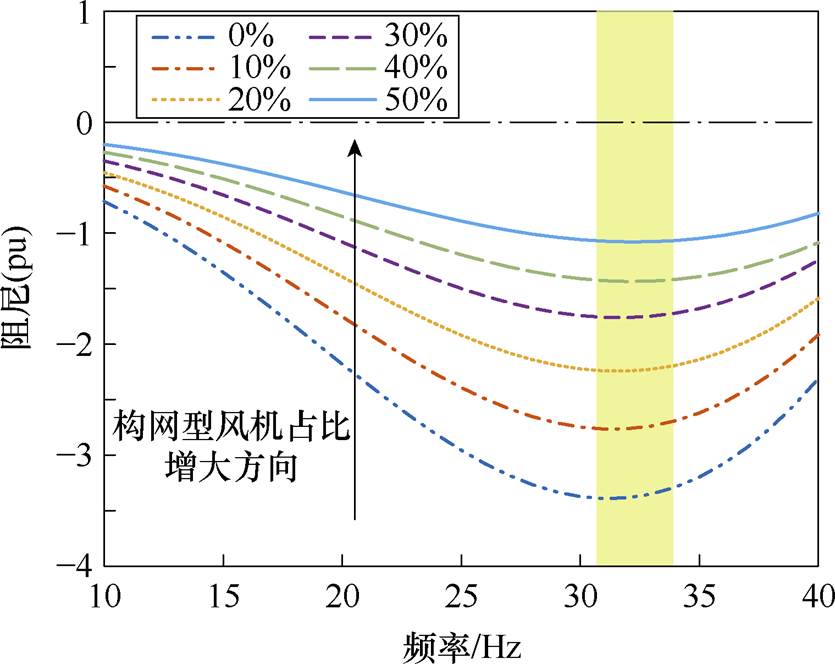
图7 DP频率特性
Fig.7 The frequency characteristics of DP
由图7分析可得，匹配构网型风机在混合风电场中将改善系统的阻尼特性，降低跟网型风电场引发的SSO风险。随着匹配构网型风机增加，DP频率特性曲线逐渐上移但间隔变小，这表明：匹配构网型风机对阻尼的改善作用将一直存在，但效果将会减弱。
3.3.1 混合风电场SSO特性
由3.1节模态分析结果可知，工况1～6不同匹配构网风机占比下的混合风电场内，均存在1个31～32 Hz的主导SSO模态。本节以工况1为例，通过基于PSCAD/EMTDC电磁暂态仿真验证系统的SSO特性，其他工况的SSO特性比对结果将在3.3.2节给出。设工况1下共仿真3 s，2 s时将跟网型风电场内Kp2L、Kp3L参数同时由5阶跃至1，以激发跟网型风电场内风机均发生SSO。系统发生的SSO将通过电压、电流、功率等电气量表现[1]，本文选取35 kV线路电压有效值US为观测量。
图8a、图8b分别给出US的SSO波形、频谱特性分析结果。系统受到扰动后，US虽然存在较多模态的振荡，但31 Hz处的振荡幅值明显高于其他频段，对应表3中的主导SSO模态。表3中工况1的特征值实部为正、虚部对应频率为31.1 Hz，与电磁暂态仿真结果保持一致，验证了基于混合风电场小信号模型的模态分析的正确性。其他工况结论与工况1保持一致，限于篇幅，不再赘述。
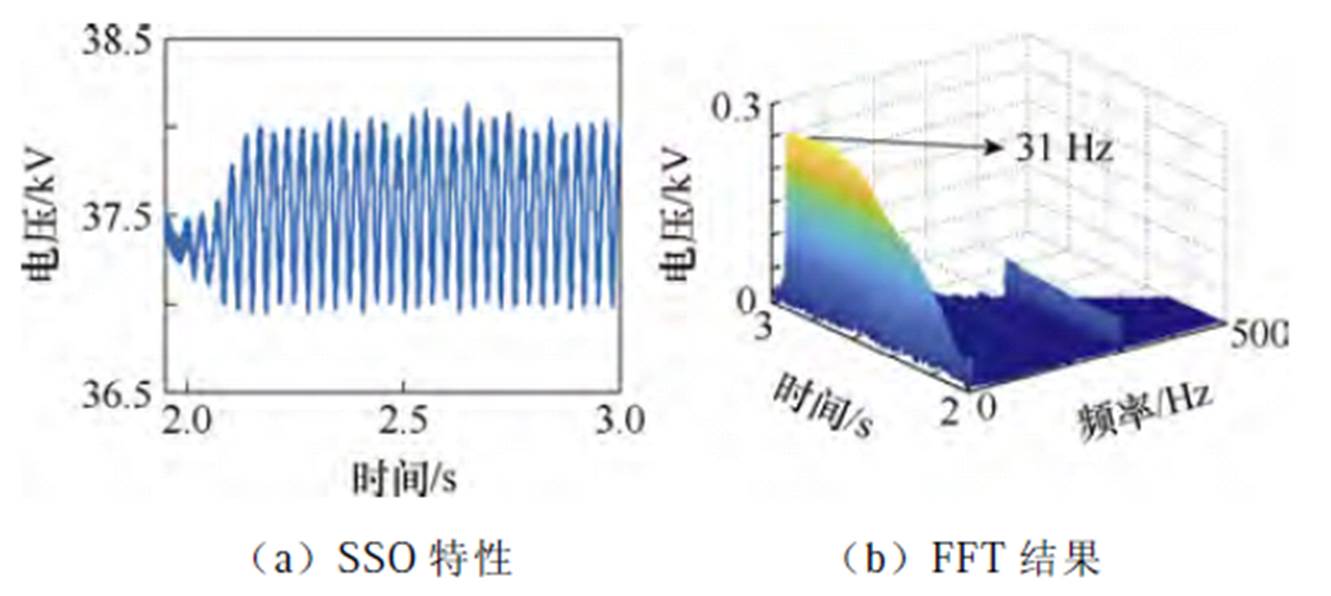
图8 工况1的US特性
Fig.8 The US characteristics of Case 1
3.3.2 匹配构网型风机占比对SSO特性的影响
3.1节的结果表明，随着匹配构网型风机占比增加，混合风电场的主导SSO模态特征值实部减小，发生SSO的风险将会降低。3.2节借助阻尼系数的物理意义，从阻尼的角度解释机理，表明匹配构网型风机会通过改善系统的阻尼，从而抑制SSO。
为验证混合风电场中匹配构网型风机的占比对跟网型风电场SSO特性的影响。本节对工况1～5在PSCAD/EMTDC中，进行同3.3.1节激发SSO的电磁暂态仿真。为进一步验证匹配构网型风机占比对混合风电场SSO抑制的效果，补充工况7～11的电磁暂态仿真，保持跟网型风机振荡台数N1为60不变，改变N2的匹配构网型、跟网型风机构成，N2内跟网型风机不激发振荡，并与工况1～5匹配构网型风机比例保持一致，具体设置见表5。
表5 补充工况设置
Tab.5 Supplemental setting conditions
组别N1/台N2(构网+跟网)/台匹配构网型风机占比(%) 工况7600+600 工况86012+4810 工况96024+3620 工况106036+2430 工况116048+1240
为进一步分析混合风电场并网系统的主导SSO特性，在PSCAD/EMTDC中采用带通滤波器提取次同步分量，并以37 kV为基准值对US取标幺值，以SSO波形达到幅值为原则截取2～2.5 s的仿真结果。图9给出随着匹配构网型风机占比变化，混合风电场的SSO特性。其中，图9a对应风机总台数N1+N2恒为60的工况，图9b对应振荡的跟网型风机台数N1恒为60的工况。
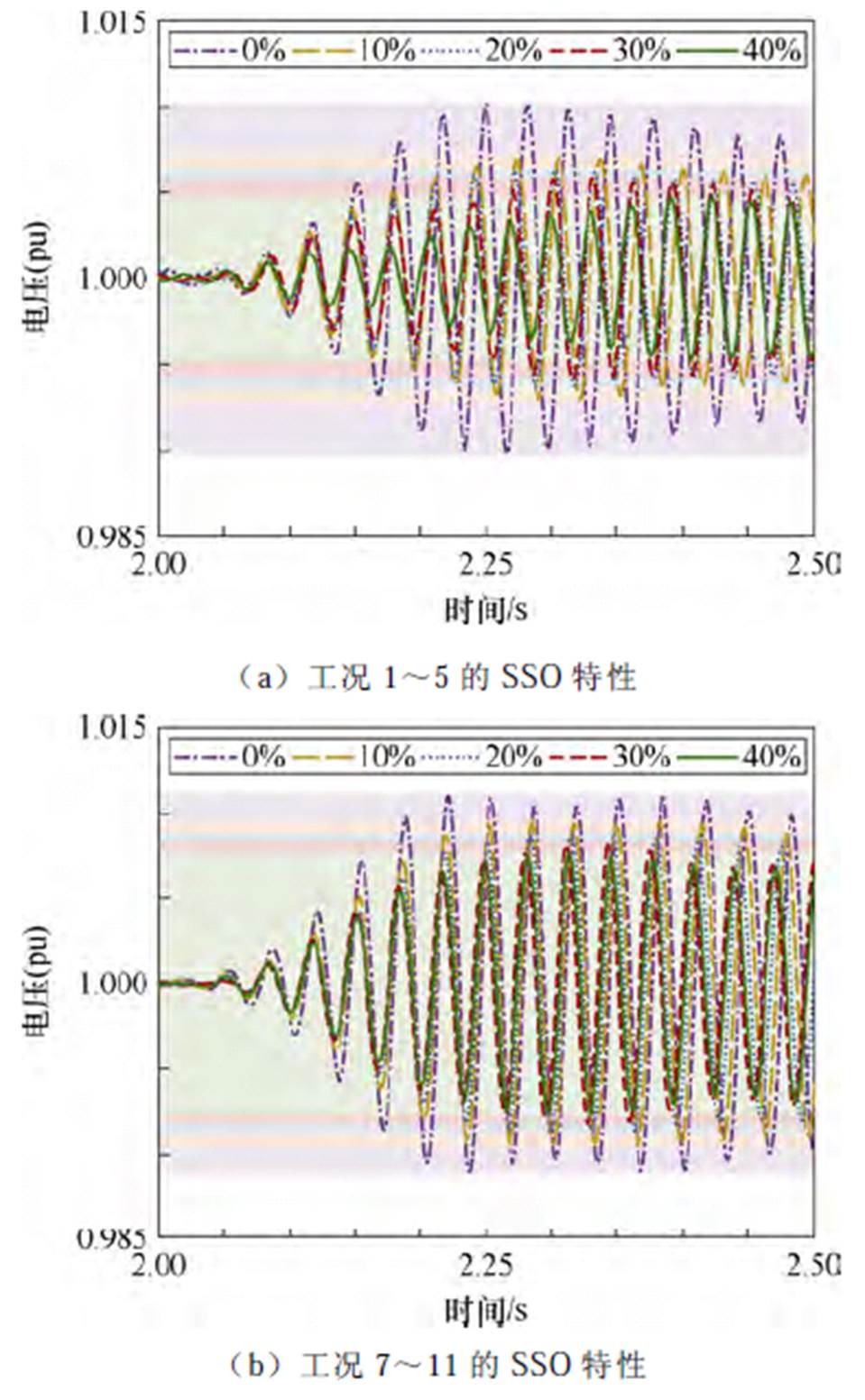
图9 US仿真波形
Fig.9 Simulated waveforms of US
如图9所示，随着匹配构网型风机占比增加，SSO的幅值将逐渐降低，表明混合风电场并网系统的阻尼逐渐增大，发生SSO的风险降低，验证了特征值分析及阻尼特性分析结果。图9b相较于图9a，保证了跟网风机振荡数量不变，进一步验证了占比对阻尼特性的影响。仿真结果表明，匹配构网型风机占比在20%～40%的SSO幅值削弱程度，明显低于占比在0%～20%的SSO幅值削弱程度，考虑跟网型风机改造为匹配构网型风机的成本，因此本文认为在本算例下，混合风电场中匹配构网风机比例在20%较为合适。
由第3节分析可知，本算例下选取20%为匹配构网风机典型占比。因此本节基于工况3，分析混合风电场中参数对SSO的影响。基于参与因子分析结果，采用根轨迹分析与时域仿真结合的方法，对跟网风电场中的直流母线电容、锁相环比例系数、电流环积分系数进行影响因素分析，并提出基于参数优化的混合风电场SSO抑制措施。
以120 mF为步长，改变跟网型风电场内直流电容CDC参数从12 mF增至18 mF，即从1.0(pu)增至1.5(pu)，工况3的其他参数与附表1、附表2保持一致。从状态变量参与度和模态根轨迹两个角度，观测主导SSO模态特性，结果如图10所示。
由图10可知，CDC由1.0(pu)逐渐增加到1.5(pu)时，XDC1参与度约在1%范围内增大，始终对主导SSO模态保持一定的参与度。主导SSO模态的特征根沿正半轴向虚轴的方向运动，频率略微降低，混合风电场并网系统在该模式下的稳定性增强。
基于PSCAD/EMTDC验证：在工况3中，仅改变跟网型风机中的CDC，分别选取CDC=12 mF、CDC= 5 mF、CDC=18 mF三组仿真。设置相同的SSO激发条件并同样以US为观测对象，次同步分量提取后的标幺电磁暂态仿真波形如图11所示。
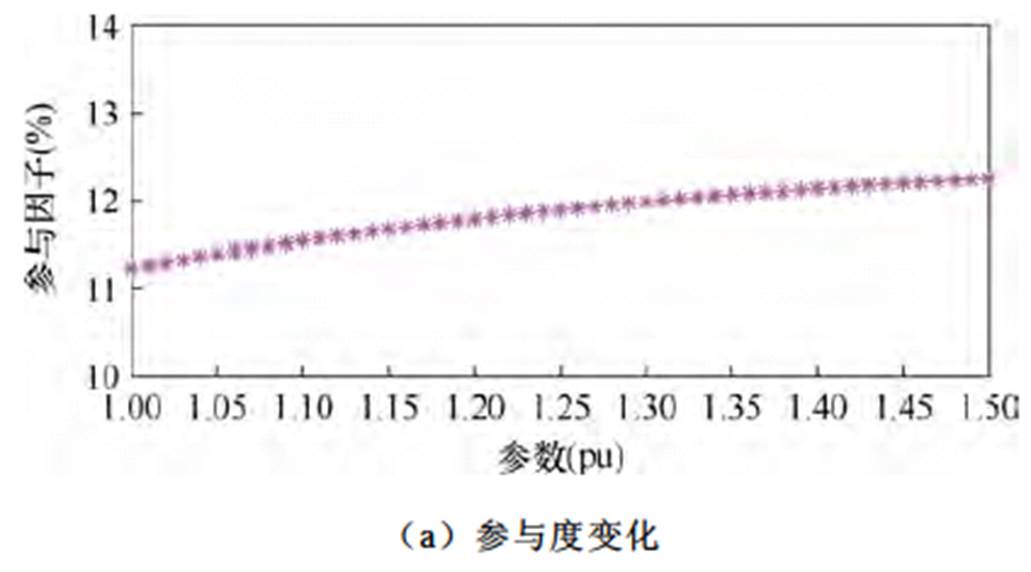
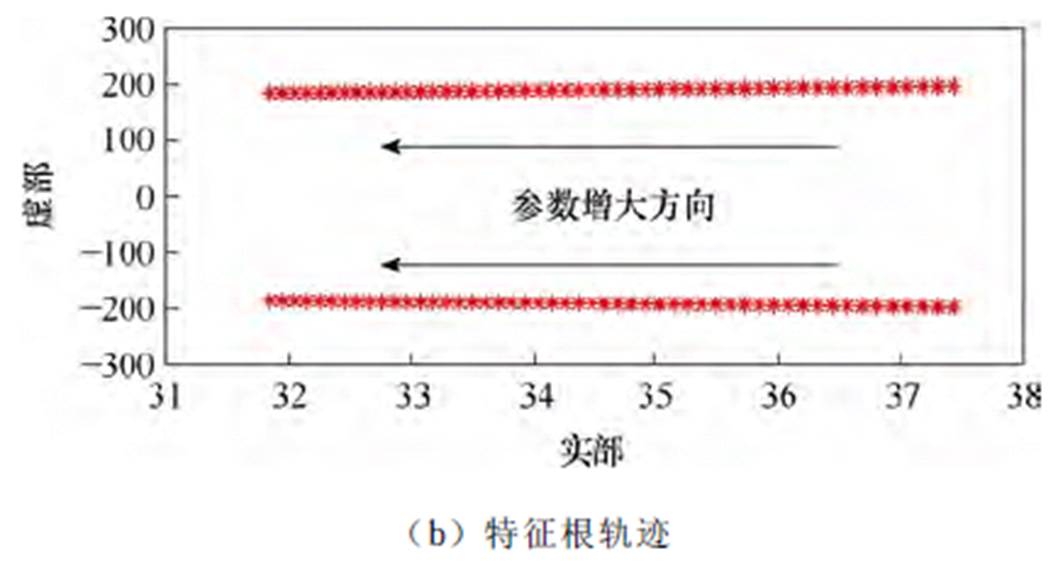
图10 CDC变化后SSO模态特性
Fig.10 SSO modal characteristics after CDC changes
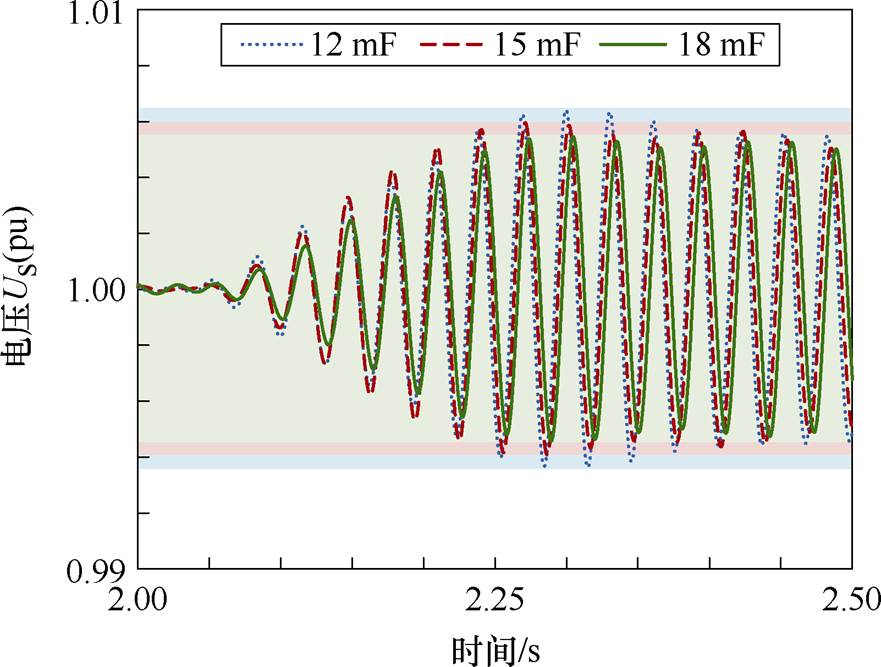
图11 US仿真波形
Fig.11 Simulated waveforms of US
由图11可知，随着跟网型风电场内CDC增大，US的振幅逐渐降低、相邻波峰时间变长，对应主导SSO模态实部下降、频率降低。混合风电场内阻尼增强，与图10的理论分析结果一致。因此，通过增大跟网型风电场内CDC参数，将进一步降低混合风电场发生SSO的风险。
参与因子分析表明：PLL的积分器主要参与主导SSO模态，而PLL的PI环节参与度极低。由图5可知，PI中的比例系数与PLL的积分器以串联形式关联，因此选取Kppll参数进行影响因素分析。以1.2为步长，仅改变工况3中的Kppll参数由120减小至60，即从1.0(pu)减小至0.5(pu)。观测XP1中积分器状态变量的参与度及主导SSO模态的根轨迹，结果如图12所示。
由图12所知，Kppll由1.0(pu)逐渐减小到0.5(pu)时，XP1中积分器的参与度约在3%的范围降低，且参与度处在较低的水平。主导SSO模态的根轨迹由正半轴向虚轴运动，且频率基本保持不变。此时，混合风电场并网系统在该模式下的稳定性增强。
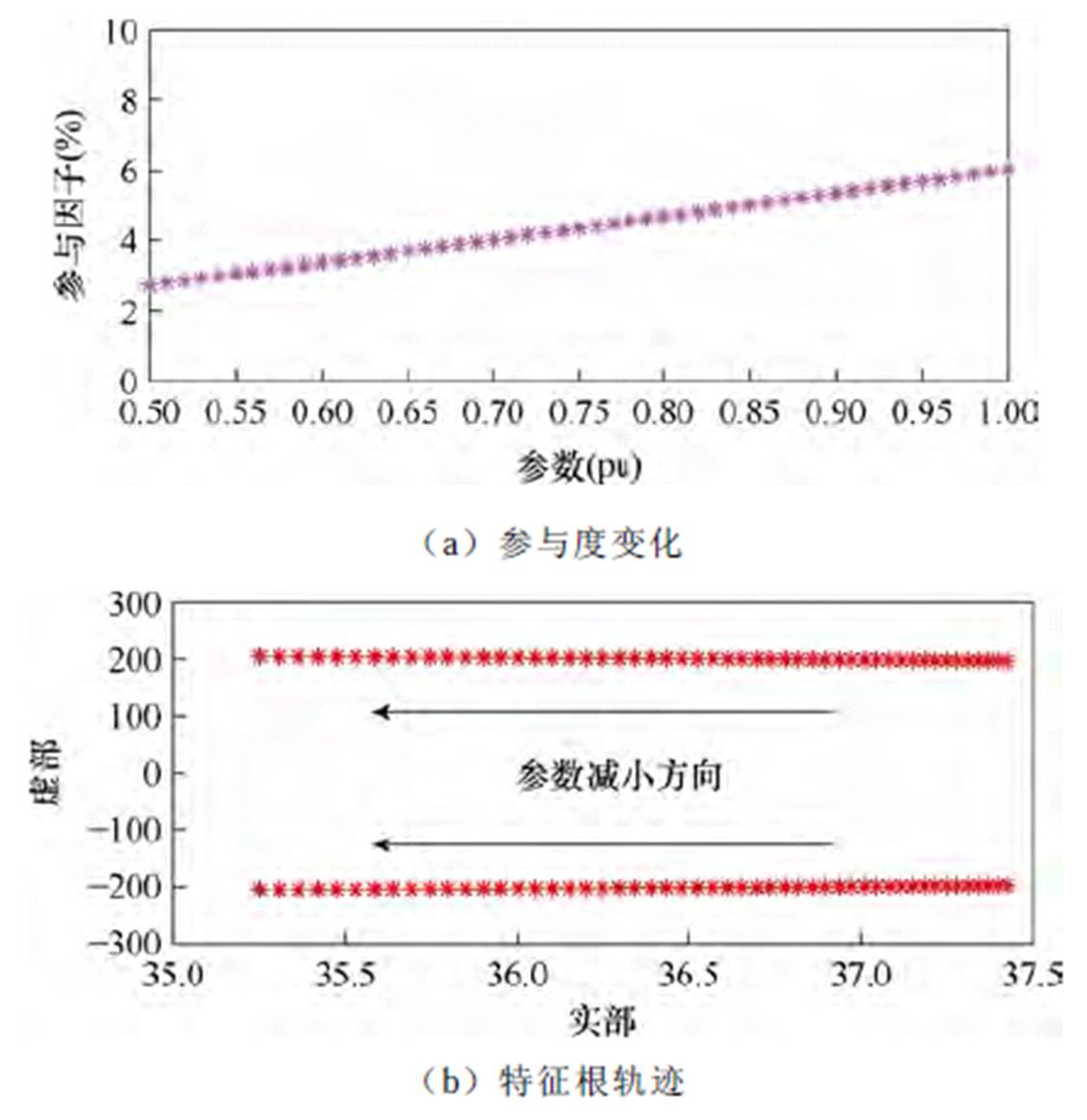
图12 Kppll变化后SSO模态特性
Fig.12 SSO modal characteristics after Kppll changes
基于PSCAD/EMTDC验证：在工况3中，仅改变跟网型风机中的Kppll，保证其他仿真参数不变，且设置相同的SSO激发条件并同样以US为观测对象。分别选取Kppll=120、Kppll=90、Kppll=60三组仿真，次同步分量提取后的标幺电磁暂态波形如图13所示。
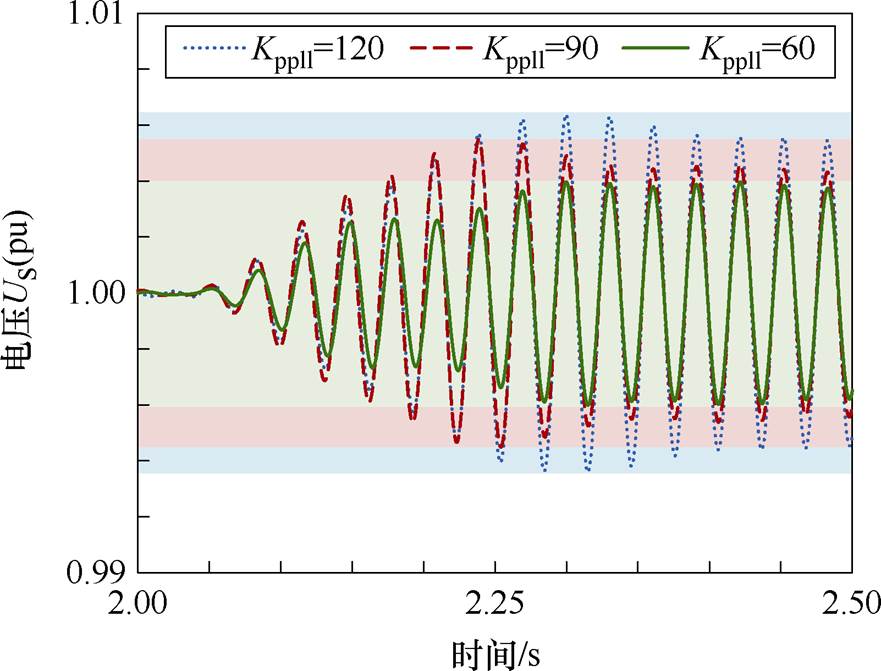
图13 US仿真波形
Fig.13 Simulated waveforms of US
由图13可知，随着Kppll参数的减小，US的振幅逐渐降低，表明主导SSO模态实部减小，混合风电场阻尼增大而稳定性增强。时域仿真结果与图12的模态分析结果一致，验证了特征值分析的准确性。因此，通过降低PLL的Kppll参数，将进一步降低混合风电场发生SSO的风险。
XGSC1中的PI3L参与度最高，本节将分析PI3L所对应的电流环积分系数Ti3L。以(5/9) s为步长，保证工况3中其他参数同附表1和附表2，仅改变Ti3L由(1/0.018) s增加至(1/0.012) s，即从1.0(pu)增至1.5(pu)。观测XGSC1中PI3L的状态变量的参与度及主导SSO模态的根轨迹，结果如图14所示。
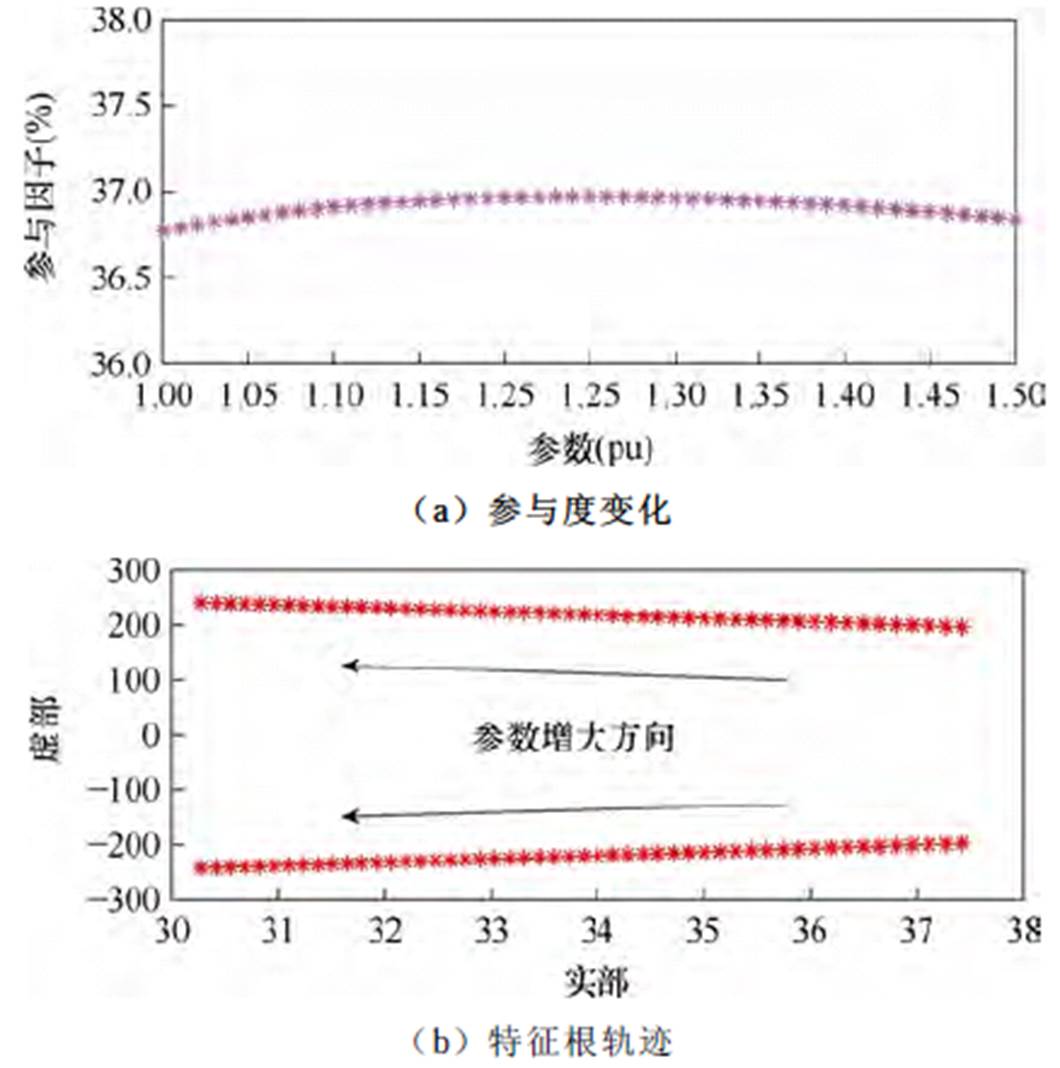
图14 Ti3L变化后SSO模态特性
Fig.14 SSO modal characteristics after Ti3L changes
由图14可知，Ti3L由1.00(pu)逐渐增加到1.50(pu)时，XGSC1中的PI3L参与度始终保持在36.8%左右的高比例状态。主导SSO模态的特征值实部逐渐降低、虚部逐渐升高，表明对应SSO的幅值将会减小、振荡频率将会增大。此时，混合风电场并网系统在该模式下的稳定性增强。
基于PSCAD/EMTDC验证：保证工况3的其他仿真环境不变，仅改变跟网型风机中的Ti3L参数，设置相同的SSO激发条件并同样以US为观测对象。分别选取Ti3L=(1/0.001 8) s、Ti3L=(1/0.001 6) s、Ti3L= (1/0.001 4) s三组仿真，次同步分量提取后的标幺电磁暂态波形如图15所示。
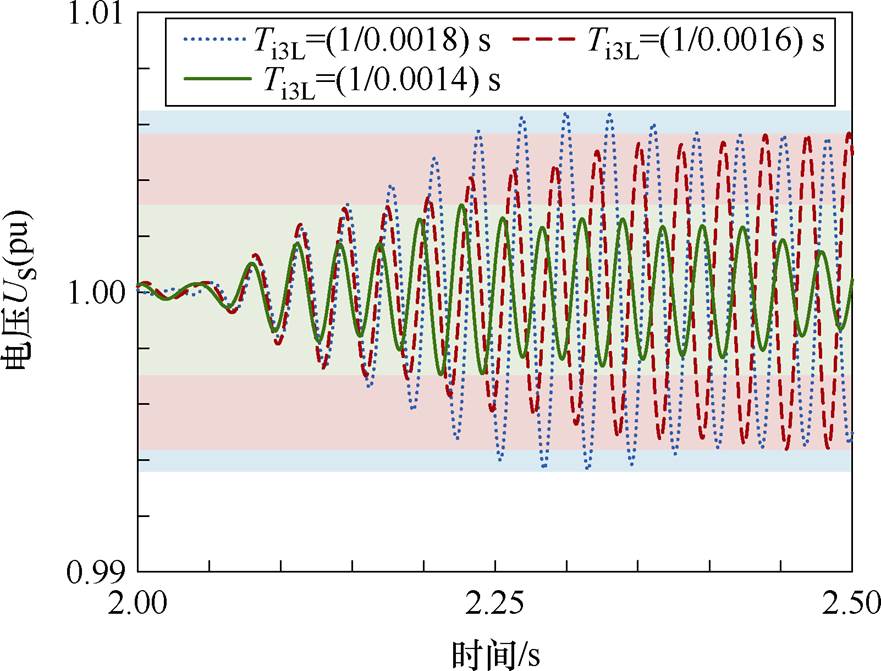
图15 US仿真波形
Fig.15 Simulated waveforms of US
由图15可知，随着Ti3L参数的增加，US的振幅逐渐降低而频率逐渐增大，表明主导SSO模态实部减小而虚部增大，混合风电场稳定性增强。时域仿真结果与图14的模态分析结果一致，验证了理论分析的正确性。因此，通过增大电流环积分系数Ti3L，将进一步降低混合风电场发生SSO的风险。
本文针对由基于匹配控制策略的构网型风机、传统跟网型风机构成的混合风电场并网系统，通过特征值分析法研究系统的主导SSO模态，采用阻尼转矩法分析了匹配构网型风机占比对跟网型风机引发SSO的影响机理。针对匹配构网型风机占比为20%的典型情况，提出参数优化方案，主要结论如下：
1）混合风电场内发生跟网型风机引发的SSO时，这种SSO模式主要与跟网型风电场参数有关，匹配构网型风电场参数对此SSO模式几乎不参与。
2）匹配构网型风机在混合风电场中，能够改善系统的阻尼。当混合风电场中跟网型风机发生SSO时，匹配构网型风机能够发挥抑制作用。匹配构网型风机占比增加，抑制作用也随之增加但效果减弱，本算例下匹配构网型风机占比在20%较为合适。
3）匹配构网型风机仅在占比增加的情况下，会对跟网型风机的SSO产生明显抑制。要进一步降低混合风电场发生SSO的风险，可以基于跟网型风电场进行参数优化：在一定范围内，增大直流母线电容参数CDC、减小PLL比例系数，增大电流内环PI3L的积分系数Ti3L。
本文考虑混合风电场中跟网型风机引发的SSO问题，所得结论对工程存在一定的指导意义。
附 录
附表1 主拓扑参数
App.Tab.1 Main topology parameters
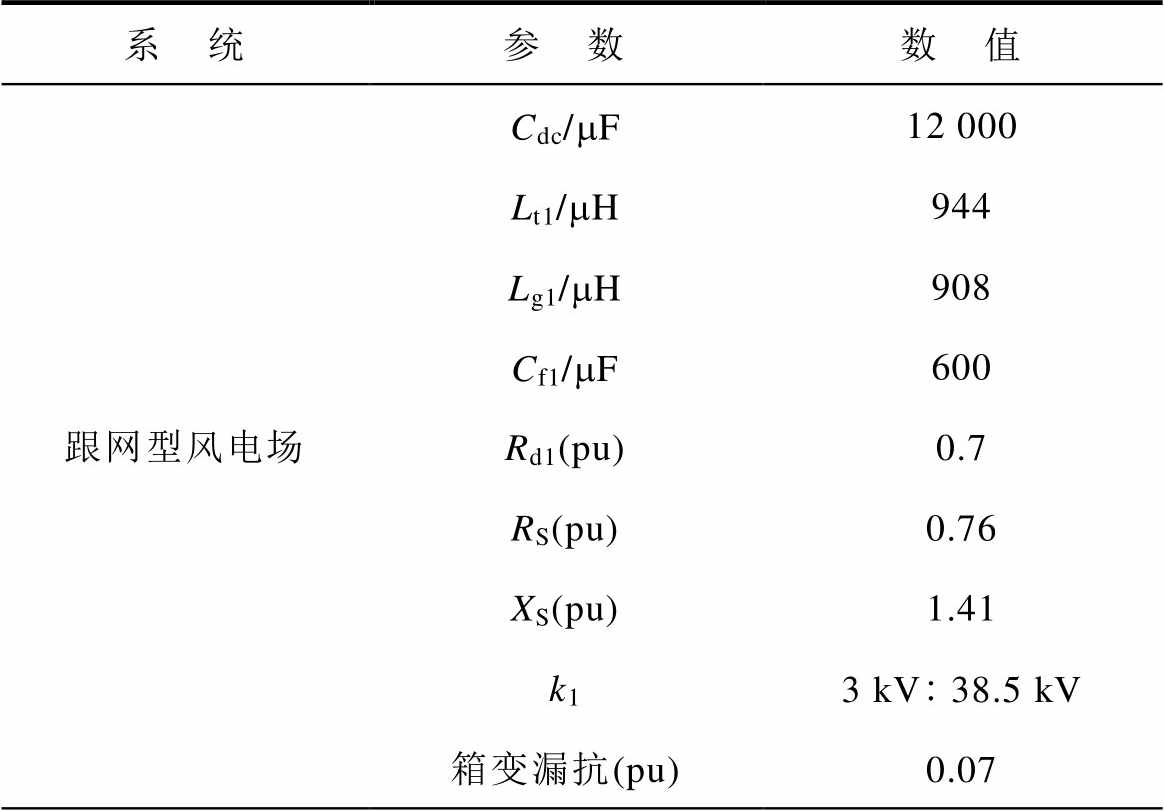
系 统参 数数 值 跟网型风电场Cdc/mF12 000 Lt1/mH944 Lg1/mH908 Cf1/mF600 Rd1(pu)0.7 RS(pu)0.76 XS(pu)1.41 k13 kV38.5 kV 箱变漏抗(pu)0.07
（续）
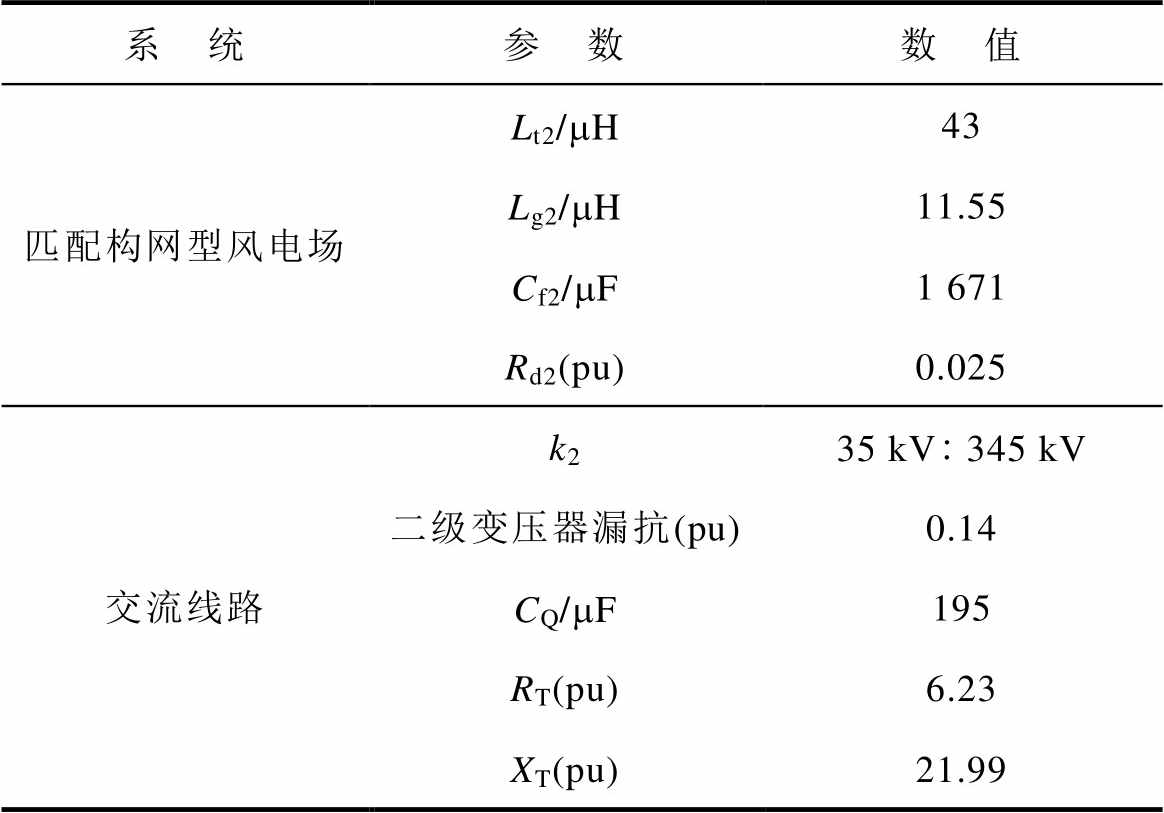
系 统参 数数 值 匹配构网型风电场Lt2/mH43 Lg2/mH11.55 Cf2/mF1 671 Rd2(pu)0.025 交流线路k235 kV345 kV 二级变压器漏抗(pu)0.14 CQ/mF195 RT(pu)6.23 XT(pu)21.99
附表2 控制器参数
App.Tab.2 Controller parameters
系 统参 数数 值 跟网型PLL比例系数Kppll120 PLL积分系数Kipll/s-1700 无功外环比例系数Kp1L10 无功外环积分系数Ti1L/s0.003 电流内环比例系数Kp2L, Kp3L5 振荡激发后Kp2L, Kp3L1 电流内环积分系数Ti2L, Ti3L/s0.0018 直流电压给定udc1/kV5 角速度额定值w0/(rad/s)100p 匹配构网型电压外环比例系数Kp4M10 电压外环积分系数Ti4M/s0.1 电流内环比例系数Kp5M0.2 电流内环积分系数Ti5M/s0.2 虚拟感抗(pu)6.0×10-3 虚拟感抗(pu)1.4×10-2 无功给定Qfref0 下垂系数kQ0.01
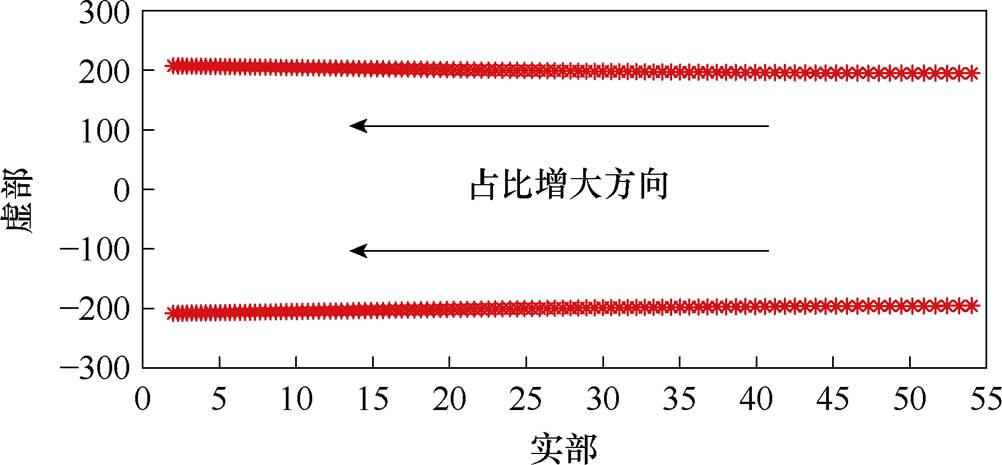
附图1 特征根轨迹
App.Fig.1 The trajectories offeature root
参考文献
[1] 黄萌, 凌扬坚, 耿华, 等. 功率同步控制的构网型变流器多机交互分析与稳定控制研究综述[J]. 高电压技术, 2023, 49(11): 4571-4583.
Huang Meng, Ling Yangjian, Geng Hua, et al. Review on multi-machine interaction analysis and stability control of grid converter with power synchronization control[J]. High Voltage Engineering, 2023, 49(11): 4571-4583.
[2] 孙秋野, 隋政麒, 王睿, 等. “双高”电力系统非经典稳定性分析[J]. 中国电机工程学报, 2023, 43(增刊1): 1-13.
Sun Qiuye, Sui Zhengqi, Wang Rui, et al. Non- classical stability analysis of “double-high” power system[J]. Proceedings of the CSEE, 2023, 43(S1): 1-13.
[3] 李景一, 毕天姝, 于钊, 等. 直驱风机变流控制系统对次同步频率分量的响应机理研究[J]. 电网技术, 2017, 41(6): 1734-1740.
Li Jingyi, Bi Tianshu, Yu Zhao, et al. Study on response characteristics of grid converter control system of permanent magnet synchronous generators (PMSG) to subsynchronous frequency component[J]. Power System Technology, 2017, 41(6): 1734-1740.
[4] 周琰. 构网型换流器同步频率振荡特性分析及抑制策略研究[D]. 北京: 华北电力大学, 2023.
Zhou Yan. Analysis of synchronous frequency oscillation characteristics and research on suppression strategy of reticulated converter[D]. Beijing: North China Electric Power University, 2023.
[5] 孙正龙, 郝舒宇, 李明达, 等. 含构网型双馈风电的电力系统低频振荡能量结构分析方法[J/OL]. 电工技术学报, 1-16.
Sun Zhenglong, Hao Shuyu, Li Mingda, et al. low frequency oscillation analysis method for grid- forming doubly-fed wind power systems based on energy structures[J/OL]. Transactions of China Electrotechnical Society, 1-16.
[6] 迟永宁, 江炳蔚, 胡家兵, 等. 构网型变流器: 物理本质与特征[J/OL]. 高电压技术, 1-15[2024-01-23].
Chi Yongning, Jiang Bingwei, Hu Jiabing, et al. Reticulated converters: physical nature and characte- ristics[J/OL]. High Voltage Technology, 1-15 [2024- 01-23].
[7] Yang Renxin, Shi Gang, Cai Xu, et al. Voltage source control of offshore all-DC wind farm[J]. The Journal of Engineering, 2019, 2019(18): 4718-4722.
[8] 袁枭添, 杜正春, 李宇骏, 等. 基于直流电压同步的构网型直驱风机两阶段主动阻尼支撑控制策略[J]. 电网技术, 2023, 47(12): 4995-5007.
Yuan Xiaotian, Du Zhengchun, Li Yujun, et al. Two- stage control of DC voltage-synchronized directly- driven wind turbine for active damping support[J]. Power System Technology, 2023, 47(12): 4995- 5007.
[9] 桑顺, 徐婷, 齐琛, 等. 惯性同步构网型变换器定量感知电网频率的机理及抗干扰控制策略[J]. 电网技术, 2023, 47(4): 1395-1406.
Sang Shun, Xu Ting, Qi Chen, et al. Mechanism of quantitatively sensing grid frequency and anti- disturbance control strategy for the grid-forming converter[J]. Power System Technology, 2023, 47(4): 1395-1406.
[10] Yang Renxin, Shi Gang, Cai Xu, et al. Autonomous synchronizing and frequency response control of multi-terminal DC systems with wind farm inte- gration[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2504-2514.
[11] Wang Weiyu, Jiang Lin, Cao Yijia, et al. A parameter alternating VSG controller of VSC-MTDC systems for low frequency oscillation damping[J]. IEEE Transa- ctions on Power Systems, 2020, 35(6): 4609-4621.
[12] 谢震, 高翔, 张悬光, 等. 弱电网下功率同步构网型DFIG的阻尼分析及转矩振荡抑制[J]. 电力系统自动化, 2023, 47(11): 29-38.
Xie Zhen, Gao Xiang, Zhang Xuanguang, et al. Damping analysis and torque oscillation suppression of power synchronized grid-forming doubly-fed induction generator in weak grid[J]. Automation of Electric Power Systems, 2023, 47(11): 29-38.
[13] 李辉, 王坤, 胡玉, 等. 双馈风电系统虚拟同步控制的阻抗建模及稳定性分析[J]. 中国电机工程学报, 2019, 39(12): 3434-3443.
Li Hui, Wang Kun, Hu Yu, et al. Impedance modeling and stability analysis of virtual synchronous control based on doubly-fed wind generation systems[J]. Proceedings of the CSEE, 2019, 39(12): 3434-3443.
[14] 王玉坤, 张慕婕, 李壮, 等. 构网型直驱风电机组间控制相互作用研究[J/OL]. 电力自动化设备: 1-10.
Wang Yukun, Zhang Mujie, Li Zhuang, et al. Research on control interaction between grid-based direct-drive wind turbines[J/OL]. Electric Power Automation Equipment, 1-10 [2024-01-23].
[15] 薛翼程, 张哲任, 徐政, 等. 构网型变流器对交流系统低频振荡的影响分析与阻尼控制[J]. 电力系统自动化, 2023, 47(16): 103-113.
Xue Yicheng, Zhang Zheren, Xu Zheng, et al. Impact analysis and damping control of grid-forming con- verter for low-frequency oscillation of AC system[J]. Automation of Electric Power Systems, 2023, 47(16): 103-113.
[16] Fu Siqi, Sun Yao, Li Lang, et al. Power oscillation suppression of multi-VSG grid via decentralized mutual damping control[J]. IEEE Transactions on Industrial Electronics, 2022, 69(10): 10202-10214.
[17] Sun Peng, Xu Hao, Yao Jun, et al. Dynamic interaction analysis and damping control strategy of hybrid system with grid-forming and grid-following control modes[J]. IEEE Transactions on Energy Con- version, 2023, 38(3): 1639-1649.
[18] 罗澍忻, 韩应生, 余浩, 等. 构网型控制在提升高比例新能源并网系统振荡稳定性中的应用[J]. 南方电网技术, 2023, 17(5): 39-48.
Luo Shuxin, Han Yingsheng, Yu Hao, et al. Appli- cation of grid-forming control in improving the oscillation stability of power systems with high proportion renewable energy integration[J]. Southern Power System Technology, 2023, 17(5): 39-48.
[19] 王东泽, 孙海顺, 黄碧月, 等. 基于虚拟同步控制的电压源型直驱风电机组并网稳定性分析[J]. 高电压技术, 2022, 48(8): 3282-3294.
Wang Dongze, Sun Haishun, Huang Biyue, et al. Analysis of grid-connected stability of voltage- source-type PMSG-based wind turbine based on virtual synchronous control[J]. High Voltage Engin- eering, 2022, 48(8): 3282-3294.
[20] 张祥宇, 罗程远, 付媛, 等. 风储锁相弹性耦合下的系统次同步振荡抑制技术[J]. 中国电机工程学报, 2024, 44(16): 6507-6518.
Zhang Xiangyu, Luo Chengyuan, Fu Yuan, et al. Subsynchronous oscillation suppression technology of the system under the elastic coupling of wind-storage lock-in[J]. Proceedings of the CSEE, 2024, 44(16): 6507-6518.
[21] 伍双喜, 王晰, 刘洋, 等. 基于构网型储能的风电场-弱电网次同步振荡抑制方法[J]. 电力建设, 2024, 45(4): 147-155.
Wu Shuangxi, Wang Xi, Liu Yang, et al. Subsyn- chronous damping control of grid-forming BESS in wind farms connected to a weak AC grid[J]. Electric Power Construction, 2024, 45(4): 147-155.
[22] 吴家杰, 陈新, 张东辉, 等. 构网型储能变换器在新能源接入场景下并网稳定性分析及提升策略[J/OL]. 中国电机工程学报: 1-14 [2024-01-23].
Wu Jiajie, Chen Xin, Zhang Donghui, et al. Grid- connected stability analysis and improvement strategy of grid-based energy storage converter in new energy access scenario[J/OL]. Proceedings of the CSEE, 1-14[2024-01-23].
[23] 陈露洁, 徐式蕴, 孙华东, 等. 高比例电力电子电力系统宽频带振荡研究综述[J]. 中国电机工程学报, 2021, 41(7): 2297-2310.
Chen Lujie, Xu Shiyun, Sun Huadong, et al. A review of the research on broadband oscillation of power systems with high proportion of power electronics[J]. Proceedings of the CSEE, 2021, 41(7): 2297-2310.
[24] 高本锋, 邓鹏程, 孙大卫, 等. 基于匹配控制的构网型直驱风电场次同步振荡机理与特性研究[J]. 电工技术学报, 2024, 39(9): 2755-2770.
Gao Benfeng, Deng Pengcheng, David Sun, et al. mechanism and characteristics of subsynchronous oscillation of grid forming direct-drive wind farm based on matching control[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2755-2770.
[25] Yuan Hao, Yuan Xiaoming, Hu Jiabing. Modeling of grid-connected VSCs for power system small-signal stability analysis in DC-link voltage control time- scale[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3981-3991.
[26] Lu Jun, Yuan Xiaoming, Hu Jiabing, et al. Motion equation modeling of LCC-HVDC stations for analyzing DC and AC network interactions[J]. IEEE Transactions on Power Delivery, 2020, 35(3): 1563- 1574.
[27] Huang Yunhui, Zhai Xuebing, Hu Jiabing, et al. Modeling and stability analysis of VSC internal voltage in DC-link voltage control timescale[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(1): 16-28.
[28] 高本锋, 王义, 范辉, 等. 基于阻尼路径的新能源经LCC-HVDC送出系统次同步交互作用分析方法[J]. 电工技术学报, 2023, 38(20): 5572-5589.
Gao Benfeng, Wang Yi, Fan Hui, et al. A sub- synchronous interaction analysis method of renewable energy generations integrated with LCC-HVDC system based on damping path[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5572- 5589.
[29] Hu Jiabing, Yuan Hao, Yuan Xiaoming. Modeling of DFIG-based WTs for small-signal stability analysis in DVC timescale in power electronized power systems[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1151-1165.
[30] 李龙源, 付瑞清, 吕晓琴, 等. 接入弱电网的同型机直驱风电场单机等值建模[J]. 电工技术学报, 2023, 38(3): 712-725.
Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al. Single machine equivalent modeling of weak grid connected wind farm with same type PMSGs[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 712-725.
[31] Li Yujun, Yuan Xiaotian, Li Jiapeng, et al. Novel grid-forming control of PMSG-based wind turbine for integrating weak AC grid without sacrificing maximum power point tracking[J]. IET Generation, Transmi- ssion & Distribution, 2021, 15(10): 1613-1625.
[32] 高本锋, 刘培鑫, 刘王锋, 等. 直驱风电场并网对火电机组次同步谐振影响[J/OL]. 电工技术学报, 1-16 [2024-01-23].
Gao Benfeng, Liu Peixin, Liu Wangfeng, et al. influence of grid connected direct drive wind farm on subsynchronous resonance of thermal power units[J/OL]. Transactions of China Electrotechnical Society, 1-16 [2024-01-23].
Abstract With the increasing penetration rate of new energy units, the power system has more oscillation accidents with grid-following direct-drive wind farms. Compared with the grid-following control, the grid- forming control has suitable voltage and frequency support capabilities, and wind energy can be transmitted through the hybrid wind farm where the two controls coexist. After the grid-forming direct-drive wind farm based on the matching control strategy partially replaces the grid-following one, the influence mechanism of the hybrid wind farm subsynchronous oscillation (SSO) formed by the match-grid-forming wind turbine needs to beclarified.
This paper first introduces the match-grid-forming control, the grid-following control, and the topology of the hybrid wind farm. Based on the mathematical model of the grid-connected system, the small signal model of the system is constructed in Matlab/Simulink simulation using the modular modeling method. Then, the small signal model of the grid-connected system is analyzed, the dominant SSO mode and its participating factors areanalyzed from the wind turbine proportion perspective, and the influence of match-grid-forming wind turbines on SSO is explained from the damping perspective. Finally, regarding root trajectory and electromagnetic transient time-domain response, the changes in SSO characteristics under different operating parameters are analyzed.
After the SSO triggered by the grid-following wind farm occurs in the hybrid wind farm, the parameters of the grid-following wind farm are mainly involved in the dominant SSO mode, and the participation of the match-grid-forming wind farm and the AC grid parameters is limited. With the increase of match-grid-forming wind turbines in the hybrid wind farm, the eigenroots of the dominant SSO mode gradually decrease, and the oscillation frequency in creases in the range of about 1 Hz. Moreover, the damping of hybrid wind farms increases in the subsynchronous frequency band. There is a damping minimum in the damping frequency characteristic curve, and the risk of SSO at this frequency is the greatest in the system.
The conclusions are as follows. (1) The SSO caused by the grid-following wind turbine in the hybrid wind farm is mainly related to the parameters of the grid-following wind farm, which are rarely involved in the SSO mode. (2) Match-grid-forming wind turbines can improve the system’s damping in hybrid wind farms. When SSO occurs in a hybrid wind farm, the match-grid-forming wind turbine can play a restraining role. The proportion of match-grid-forming fans increases, and the inhibition effect also increases. However, the effect is weakened, and the proportion of match-grid-forming fans is appropriate at 20%. (3) Only when the proportion of match- grid-forming fans increases, can the SSO of grid-following fans be inhibited significantly. The parameters can be optimized based on the grid-following wind farms: within a specific range, increase the DC bus capacitance parameter CDC, decrease the phase-locked loop proportionality factor, and increase the integration coefficient of PI3L in the current inner loop Ti3L.
keywords：Matching control, hybrid wind farms, subsynchronous oscillation (SSO), percentage
中图分类号：TM712
DOI: 10.19595/j.cnki.1000-6753.tces.240359
华北电力科学研究院有限责任公司科技项目资助（KJZ2023123）。
收稿日期 2024-03-06
改稿日期2024-12-30
高本锋 男，1981年生，副教授，研究方向为高压直流输电和电力系统次同步振荡。E-mail: gaobenfeng@126.com
刘培鑫 男，2000年生，硕士研究生，研究方向为电力系统次同步振荡。E-mail: liupeixin2022@126.com（通信作者）
（编辑 郭丽军）