图1 PL-ESS系统等效简化电路
Fig.1 Equivalent simplified circuit of PL-ESS
摘要 带脉冲负载的储能系统（PL-ESS）是一类典型的独立电力系统，“负阻抗”和周期脉冲特性极易造成系统不稳定。该文面向PL-ESS稳定性和较高的性能要求，在传统无源控制算法设计的基础上，提出注入虚拟储能的无源控制（VESI-PBC）算法，通过提高能量函数的收敛速度，使直流母线电压快速稳定以适应脉冲负载中高频模态切换工况。该文阐述VESI-PBC控制器的设计过程，对其控制系统稳定性进行根轨迹分析，同时深入剖析VESI-PBC算法的控制机理，指出该算法控制目标并非内环电流跟踪，而是超前响应外环电压的动态变化，其实质是快速响应负载脉冲电流的瞬态变化，有效提高DC-DC变换器输出电流（源端输出电流）的快速响应能力，同时降低了电容电流，从而增强了母线电压抗负载快速扰动的鲁棒性。通过仿真与实际平台试验，设置了较小容感比参数，验证了VESI-PBC算法的可行性与有效性，可满足PL-ESS系统中高频工况下瞬时脉冲电流的需求。VESI-PBC算法简单灵活，可适用于含脉冲恒功率负载的、稳定性较弱（容感比较小）、脉冲频率覆盖范围广、非线性较强的独立电力系统。
关键词：脉冲恒功率负载 储能系统 无源控制 能量函数 系统稳定性
随着储能技术和电能变换技术的发展，以及雷达、电磁弹射、电磁炮[1-2]等高功率脉冲武器系统在国防军事中的广泛应用，直流储能系统逐渐成为脉冲负载类设备的常用供电方式之一[3-4]，尤其是考虑军事装备的静默需求和闲时耗能特性。带脉冲负载储能系统（Energy Storage System with Pulsed Load, PL-ESS）是一类典型的独立供电系统[5]，由于源端容量有限、源载功率相当、惯性系数小，极易受到负载动态变化的影响[6]。
作为系统关重件，脉冲负载设备往往配备恒压控制器与直流母线连接，即使母线电压动态波动，其输出脉冲峰值功率也不会受到影响，因而呈现出脉冲“恒功率”负载状态。目前已有大量文献[7-12]指出，恒功率负载的“负阻抗”特性会放大母线电压扰动信号，进而导致系统不稳定现象。而脉冲恒功率负载具有典型的周期性脉冲用电特性，动态变化强烈[5-6, 13]，而设备端还要求高质量的直流供电：一方面要求限制直流母线电压波动率，如目前新型雷达设备要求供电系统直流母线电压最大波动率必须限制在一定范围内[14]；另一方面为满足瞬时峰值恒功率，还要求在中高频（fPL=100 Hz～1 kHz）工况下，源端能够快速满足脉冲负载瞬时电流需求。
平抑母线电压波动，最简单常用的方法是增大母线电容，该方法虽可有效降低母线电压波动，但同时也降低了负载电流的响应速度，无法满足脉冲负载瞬时电流需求。目前已有大量文献针对带恒功率负载的直流微电网系统进行稳定性分析和控制[7-12]。文献[10]针对恒功率负载稳定性问题提出一种基于并联虚拟电阻的有源阻尼控制方法。文献[11]也提出类似虚拟电阻的有源阻尼控制策略补偿下垂系数来提高含恒功率负载系统稳定裕度。文献[12]提出基于平方和规划算法来对带恒功率负载的直流微电网进行大信号稳定性分析。文献[15]针对脉冲负载周期性功率突变，提出一种自适应阻尼比控制方法，使电压响应性能可直接通过阻尼比精确调节，不依赖于控制参数，并通过附加占空比调节实现输出电流均衡。上述有源阻尼方法可增强系统稳定性，但并未明显提高系统抗负载扰动的刚度和快速性；文献[15]对输入电压扰动具有抑制作用，但未关注瞬时电流的快速响应。
无源控制（Passivity Based Control, PBC）[16-20]由于控制结构简单、高效和易实现等优点，被广泛应用于DC-DC变换器控制中，在实现对期望点快速跟踪的同时，还能保证直流微电网的大扰动稳定性。PBC与其他算法的融合性较强，大量文献基于PBC在外环加入PI控制[16]、滑模[17]、虚拟电机[18]、虚拟阻尼[19]、高增益状态观测器[20]等算法，有效提高了直流电压抗扰动能力。文献[17]提出无源滑模控制策略，将基于欧拉模型的无源控制器应用到内环电流，并引入滑模控制，使控制器具有更强的抗干扰能力和更快的响应速度。文献[18]用虚拟直流电机补偿控制改进互联和阻尼分配的无源控制方法，为DC-DC变换器提供额外的惯性和阻尼，增强大信号扰动的鲁棒性，提升了无源控制器的适应性。该方法具有电压超调小、调节速度快的优点，但实现较为复杂。文献[21]采用卡尔曼动态状态估计方法来提高脉冲负载直流微电网的鲁棒性，但实现也较为复杂，响应快速性也有待讨论。
综上所述，PL-ESS系统具有较强的非线性和恒功率特性，该类设备还在保证系统稳定性的前提下，要求直流母线电压具备较强的刚度（抗负载扰动鲁棒性），同时还要具备瞬时脉冲电流的快速响应。PBC基于Lyapunov函数构造，以系统稳定收敛为前提设计控制器[16-20]，适用于稳定性较弱的PL-ESS系统。本文针对脉冲恒功率负载对母线电压较低波动率和瞬时电流快速响应的要求，在现有PBC方法[16, 19]的基础上，提出了注入虚拟储能的无源控制（Virtual Energy Storage Injection-PBC, VESI-PBC），通过提高能量函数收敛速度，来提高系统抗脉冲负载扰动能力。
PL-ESS系统主电路拓扑结构[4-5, 13-14]如图1所示。图中，储能单元用直流电压源表示，通过DC-DC变换器Boost升压接入直流母线。us为源端输入电压，rs为电源内阻，L、C分别为变换器的输入电感和输出电容，VD1为二极管，S1为IGBT开关；Rc为常规负载的等效阻值；负载的脉冲特性由开关SPL控制。为保证脉冲负载设备脉冲峰值功率的有效性，一般采用控制器保证脉冲功率峰值的恒定，因此，脉冲负载表现为“脉冲恒功率负载”。为简化分析，设元器件均为理想元器件。
图1 PL-ESS系统等效简化电路
Fig.1 Equivalent simplified circuit of PL-ESS
取电感电流iL和电容电压uC为系统状态变量，列出其状态方程为
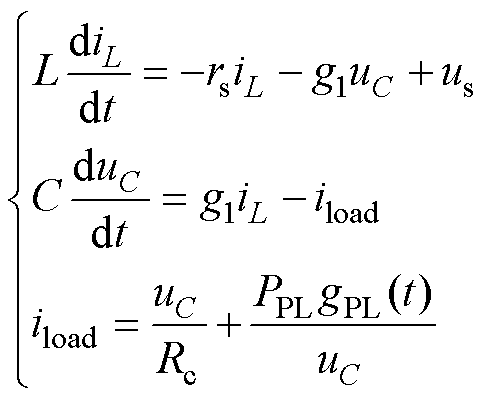（1）
式中，g1为DC-DC变换器开关S1的开关函数；gPL(t)为开关SPL脉冲控制信号，gPL=1为加载模态，gPL=0为减载模态；iload为负载电流；PPL为脉冲负载的峰值功率。由式（1）可见，以“恒功率”出现的脉冲负载，不仅在脉冲动态特性上表现为开关非线性，其静态特性也为非线性。先对其进行处理，在稳态点泰勒展开为
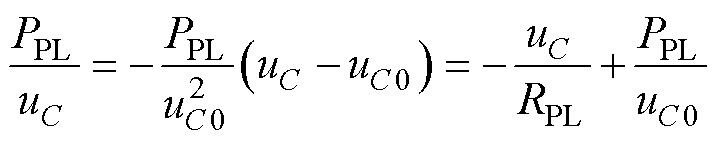
其中，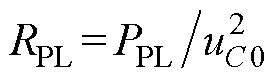
，进一步得
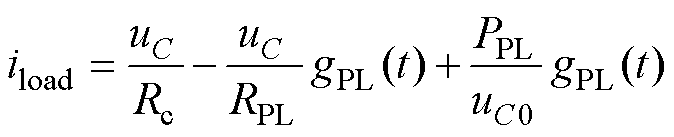（2）
式中，uC0为母线稳态电压。依据无源控制理论，将式（2）代入式（1），令x=[iL uC]，将其对应写成Euler-Lagrange（EL）模型为
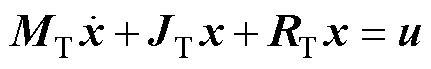（3）
式中，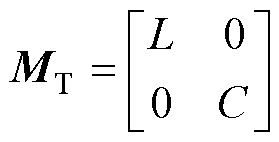
为正定对角矩阵（储能矩阵），代表系统中的无源储能器件；
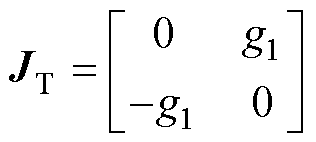为反对称矩阵（
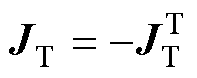，互联矩阵）；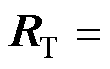
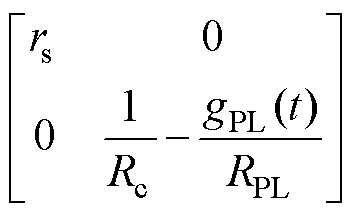为对称正定矩阵（耗散矩阵）；
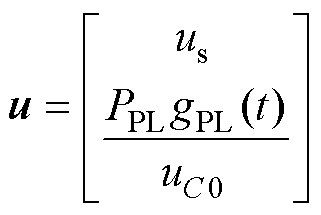表示系统与外部（电网/电源）能量交换；脉冲负载工作期间在加载模态（gPL=1）和减载模态（gPL=0）间切换。耗散矩阵RT表明：gPL=1加载模态时，脉冲负载呈现为“负阻抗”特性。
取PL-ESS系统存储能量函数为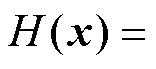
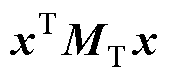，已知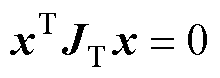
，得其导数dH(x)/dt为
（4）
令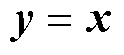
、
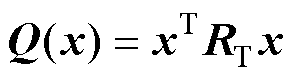，则系统满足耗散不等式为
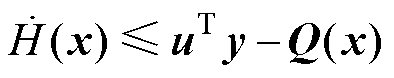（5）
即可判定该系统式（3）为“严格无源”，可进行无源控制器设计。
无源控制器设计的核心在于控制误差能量函数快速收敛至稳态，虚拟阻尼注入的无源控制（Virtual Damping Injection-PBC, VDI-PBC）算法比传统无源控制算法有更快的收敛速度，具体为：设计虚拟阻尼Ra＞0（正定），即
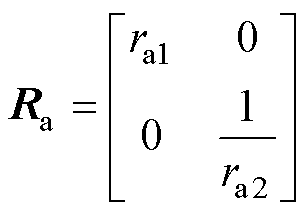（6）
得到注入虚拟阻尼的耗散项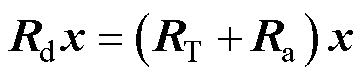
。令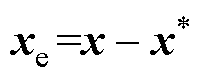
（
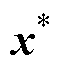为x的期望值），代入式（3）得
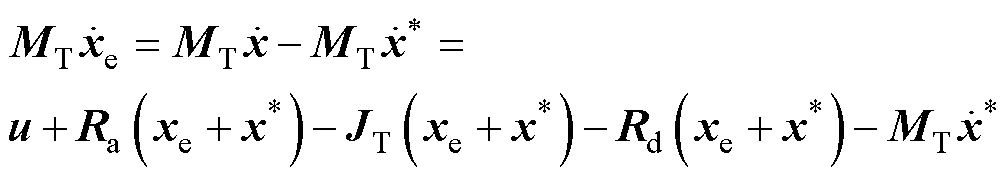（7）
取误差能量函数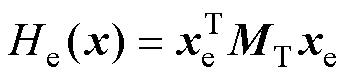
，取其导数dHe(x)/dt，并将式（7）代入得
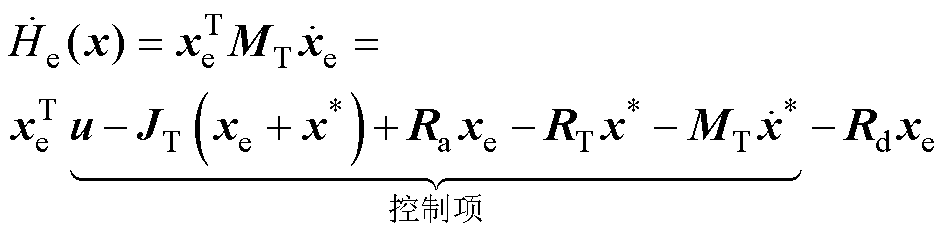（8）
若能将式（8）控制项控制为0，则有
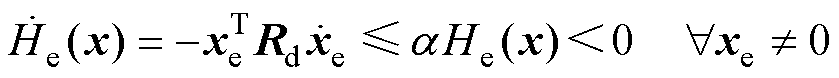（9）
可见能量函数He(x)呈指数渐近稳定，且其收敛速度由耗散项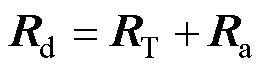
决定，已知RT项内阻rs很小，因此主要由虚拟阻尼矩阵Ra的ra决定。且ra值越大，He(x)收敛速度越快。
令式（8）控制项为0，且
，得控制律为
（10）
将参数代入式（10），展开得到VDI-PBC算法下，PL-ESS系统DC-DC控制器g1的指令电压 VVDI为
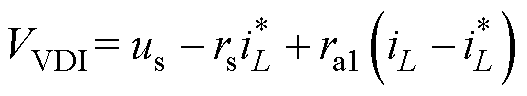（11）
式中，取ra1=ra。式（9）表明：ra值越大，误差能量函数He(x)收敛速度越快。但ra值过大会使系统出现超调现象[16-20]。
为增强系统抗脉冲负载冲击的能力，需进一步提高系统收敛的快速性，本文在VDI-PBC的基础上，提出注入虚拟储能的无源控制算法。
设定虚拟电感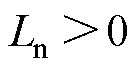
，虚拟电容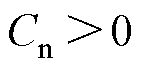
，构造虚拟储能矩阵如下
（12）
可见MN＞0（正定），得到注入虚拟储能的储能项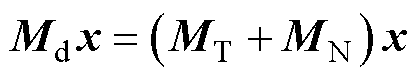
，代入式（3）得
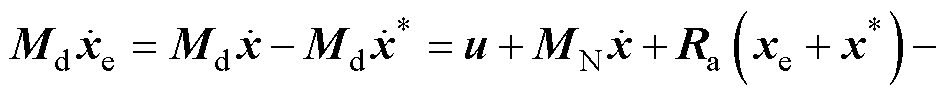
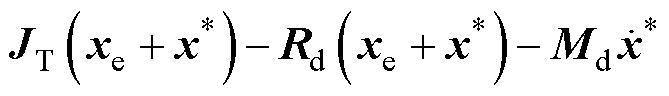（13）
取同样误差能量函数He(x)，取其导数dHe(x)/dt，并将式（13）代入得
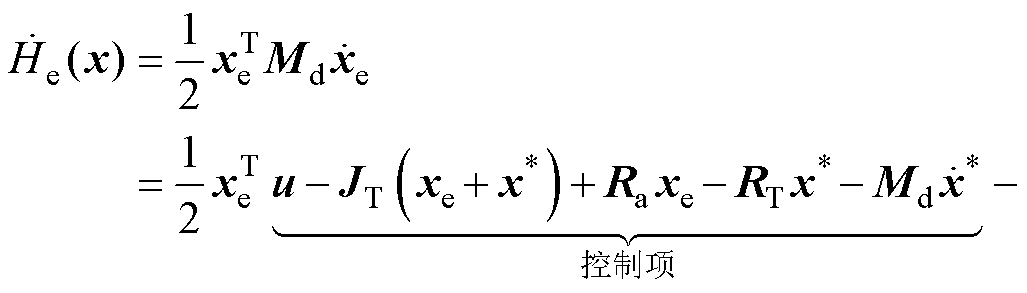
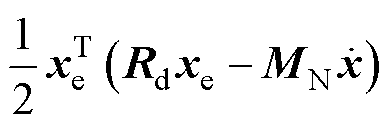（14）
将式（14）控制项控制为0，则有
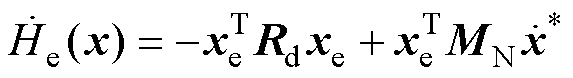（15）
已知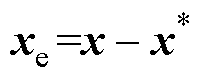
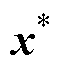，是x的指令，
代表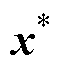的变化率。多数控制器设计中指令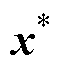一般取恒定值，此处为内环电流控制器设计，指令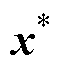来源于电压外环控制输出，因此
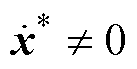，依据指令对误差的控制规律，有：当
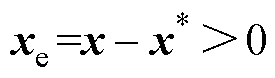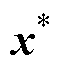时，将产生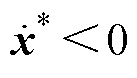
，引导x变小；反之，
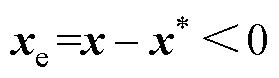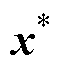时，产生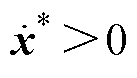
，引导x变大；故无论
取何值，都有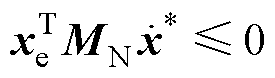
（详细证明过程见附录），由此证得
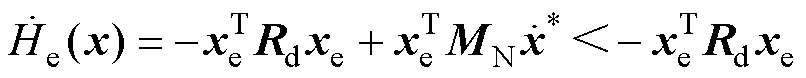（16）
可见，能量函数导数dHe(x)/dt负定，系统稳定；式（16）也表明：He(x)呈指数渐近稳定，且其收敛速度高于VDI-PBC，同时由Rd和MN决定。
展开式（14）控制项，得到虚拟储能注入的无源控制器（VESI-PBC）控制律为
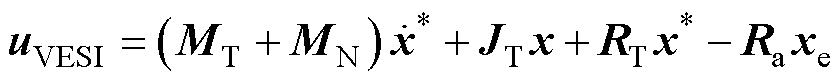（17）
与VDI-PBC控制律uVDI相比，MN注入储能器件矩阵，储能矩阵系数L修改为L+Ln，C修改为C+Cn，Ln、Cn分别为虚拟电感和虚拟电容。将式（3）参数代入式（17），展开可得VESI-PBC算法下，PL-ESS系统DC-DC控制器指令电压VVESI为
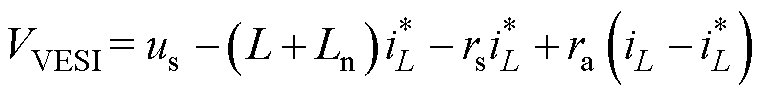（18）
实际设备DC-DC变换器电感L取值较小，一般为10-6～10-3 H，而虚拟电感Ln取值为1～10 H，因此可以认为L+Ln≈Ln。式（15）表明，较之VDI-PBC，VESI-PBC算法中增大Ln，可进一步提高系统能量函数He(x)收敛的快速性。但注入储能函数及Ln值对母线电压波动率的抑制效果，将进一步通过与其他算法的比较来进行说明。
式（11）和式（18）分别给出了VDI-PBC和VESI-PBC算法下DC-DC控制器的指令电压，常用的PI控制电流内环指令电压VPI为
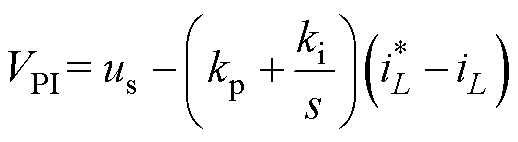（19）
可以看出，三种控制算法都采用电感电流iL反馈控制，且都需要加上电源支撑us。去除支撑部分，三种电流内环控制结构分别如图2a～图2c所示。可以看出，图2b和图2c可以用图2c同时表示：Ln=0时为VDI-PBC；Ln≠0时为VESI-PBC。
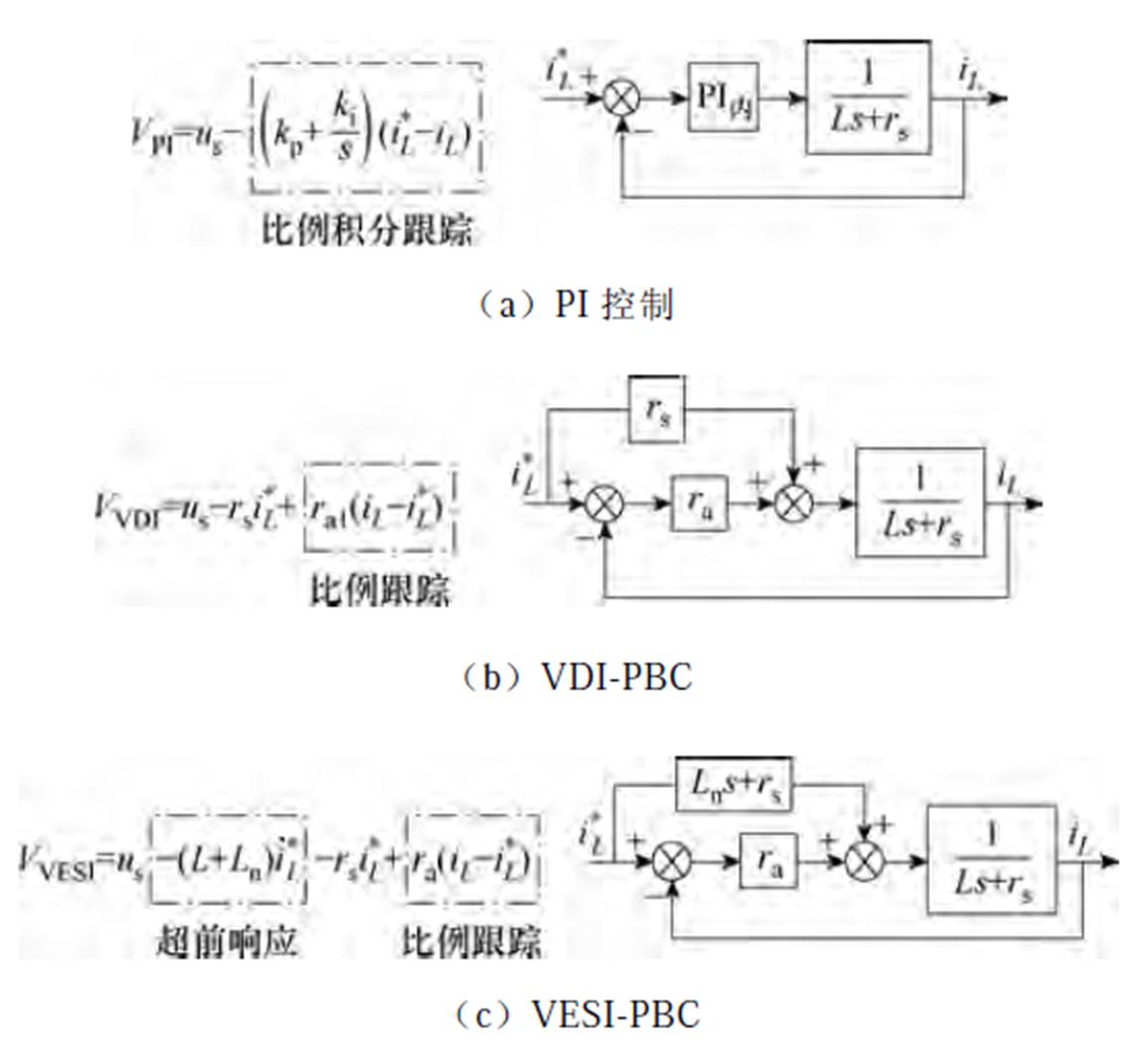
图2 三种电流内环控制算法
Fig 2 Three kinds of current inner loop control algorithms
“电压外环+电流内环”双闭环结构是DC-DC控制最常见的控制策略[22]。VESI-PBC算法是针对内环电流iL的控制器，还需与外环电压uC控制相结合电容电压uC（也是直流母线电压udc）反馈，通
过外环PI控制器为电流内环Gi(s)产生电流指令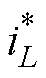
，得到PL-ESS系统的双闭环控制结构如图3所示。
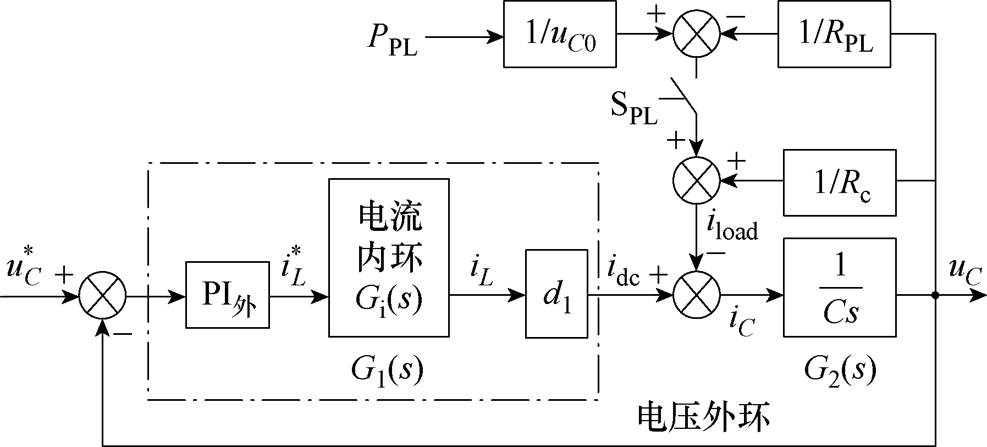
图3 PL-ESS系统的双闭环控制结构
Fig.3 Control structure diagram of PL-ESS
图3中，d1=1-d，d为DC-DC变换器驱动信号g1的占空比；负载电流iload结构依据式（2）构造。由此得到基于VESI-PBC算法的PL-ESS系统整体控制策略如图4所示。
需要特别说明之处：①us为电源输出电压，rs为电源内阻，iL既为电感电流，又为电源输出电流is；②在
后进行限幅，否则将产生较大或不可控的毛刺。
VESI-PBC算法推导过程表明，以提高目标能量函数的收敛速度为目标来设计控制器，理论上可提高系统在加减载模态切换时状态变量x=[iL uC]收敛至期望值的速度，但算法控制机理、控制效果随Ln的变化规律并不明确。下面分析VESI-PBC算法的实质控制机理。
图4 基于VESI-PBC的PL-ESS系统整体控制策略
Fig.4 Control strategy of PL-ESS based on VESI-PBC
PL-ESS设备性能要求在抑制直流母线电压uC波动的同时，提高DC-DC变换器输出电流idc和源端输出电流is响应脉冲负载电流iload的快速性。由图3可得上述参量的关联关系为
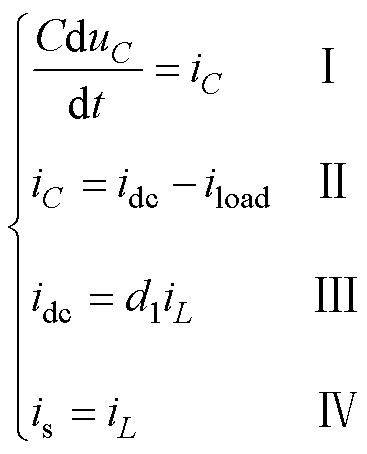（20）
式（20）中，Ⅰ表明，电流iC引起uC波动，减小DuC为控制目标，故期望iC→0；Ⅱ表明，要求iC→0，则期望idc→iload；由Ⅲ可知，同理期望iL→iload/d1；Ⅳ表明，如果iL能快速响应iload，则源端电流输出is响应速度也将随之提高。因此，负载脉冲特性导致iload呈现为周期脉冲波形，则理想控制效果下，电流内环控制量iL也应该为周期脉冲波形。
依据上述期望控制效果，对比图2三种内环控制结构及式（11）、式（18）、式（19）可得：
（1）内环PI控制对象为误差变量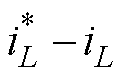
，其控制效果仅在于iL对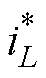的跟踪，因此双PI控制对uC的控制仅依赖外环PI。由于电容C的作用，uC的动态变化滞后于负载电流iload，因而响应速度受限。
（2）VDI-PBC控制除了对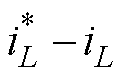有比例跟踪项外，式（11）还将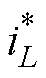引入内环控制，因此，对来自于外环uC的动态变化有一定的响应速度。
（3）VESI-PBC控制在VDI-PBC基础上引入了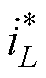
。式（18）表明，受控量VVESI第4项实现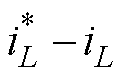的比例跟踪，第3项响应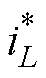的动态变化，第2项
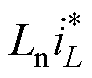超前响应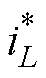的变化趋势，其实质是超前响应uC的动态变化趋势，即负载电流iload产生的瞬时冲击扰动。可知Ln值越大，超前响应速度越快。
（4）与PI控制相比，VDI-PBC控制可快速响应电压uC的动态变化，而VESI-PBC更是超前响应uC，对负载电流iload扰动有更快的响应速度。
由此总结出VESI-PBC的控制机理：该算法内环控制的目的并不只是控制iL跟踪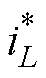，其实质是通过引入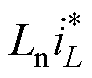，超前控制idc快速跟踪iload，从而提高电流响应速度，减小电压波动，达到抗负载扰动的目的。理论上，Ln值越大，DC-DC变换器输出电流idc越接近于iload，母线电压uC波动率越小。
下面基于控制理论，进一步讨论VESI-PBC算法的稳定性，以及虚拟电感Ln值对PL-ESS系统稳定性的影响规律。
依据图3，脉冲负载呈现出“负阻抗”特性，“恒峰值功率”PPL需视为独立于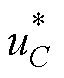
的输入。令G1(s)= 
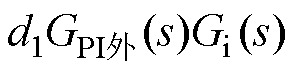，G2(s)=1/(Cs)，其中PBC的电流内环传递函数（Ln=0为VDI-PBC）为
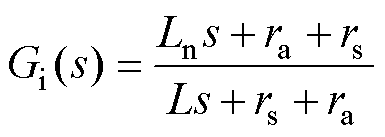（21）
以母线电压UC(s)为输出，写出2个输入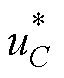（和PPL）与UC(s)的关系式为
（22）
令
，用于表征负载载重，负载越大，载重越重。取式（22）的特征根方程，可得参数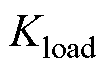
的根轨迹函数为
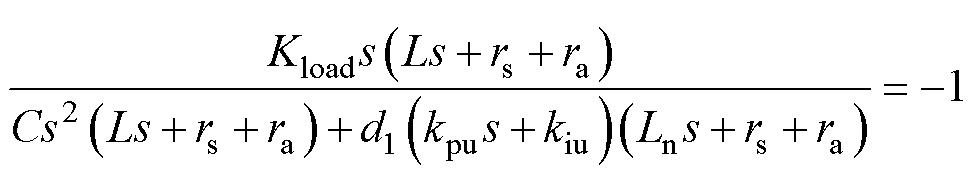（23）
式中，kpu、kiu为电压外环PI参数。由于脉冲负载存在“负阻抗”特性，即存在Kload＜0的情况。式（23）无法直接讨论参数小于0时根轨迹的走向，故需分情况讨论：
1）Kload≥0
减载模态Kload0=1/Rc＞0；加载模态RPL≥Rc时，Kload1=1/Rc-1/RPL≥0。取第4.1节仿真参数，其中d1=2/3，基于式（23）绘制系统根轨迹如图5a所示。分析可知：
（1）Kload＞0，零极点始终位于左半平面，系统处于稳定状态。随着Kload的增大，p1向z1（零点）靠近，稳定裕度降低，表明载重越重，系统稳定裕度越低。
（2）对比Ln=0和Ln=1 H，即零极点位置，两者主极点p1不变，次极点p2增大（-729→-46），也就是说，较之VDI-PBC，VESI-PBC算法的稳定裕度略有降低。
（3）Ln=0时Kload在某范围内，根轨迹偏离横轴，系统进入欠阻尼状态；Ln=1 H时，根轨迹均位于横轴，系统一直处于过阻尼状态。表明注入虚拟电感Ln可提高系统的刚度和抗干扰性。
2）Kload＜0
加载模态中RPL＜Rc时，Kload1＜0。
对式（23），令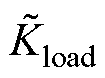
=-Kload＞0，将式（23）乘以-1得
（24）
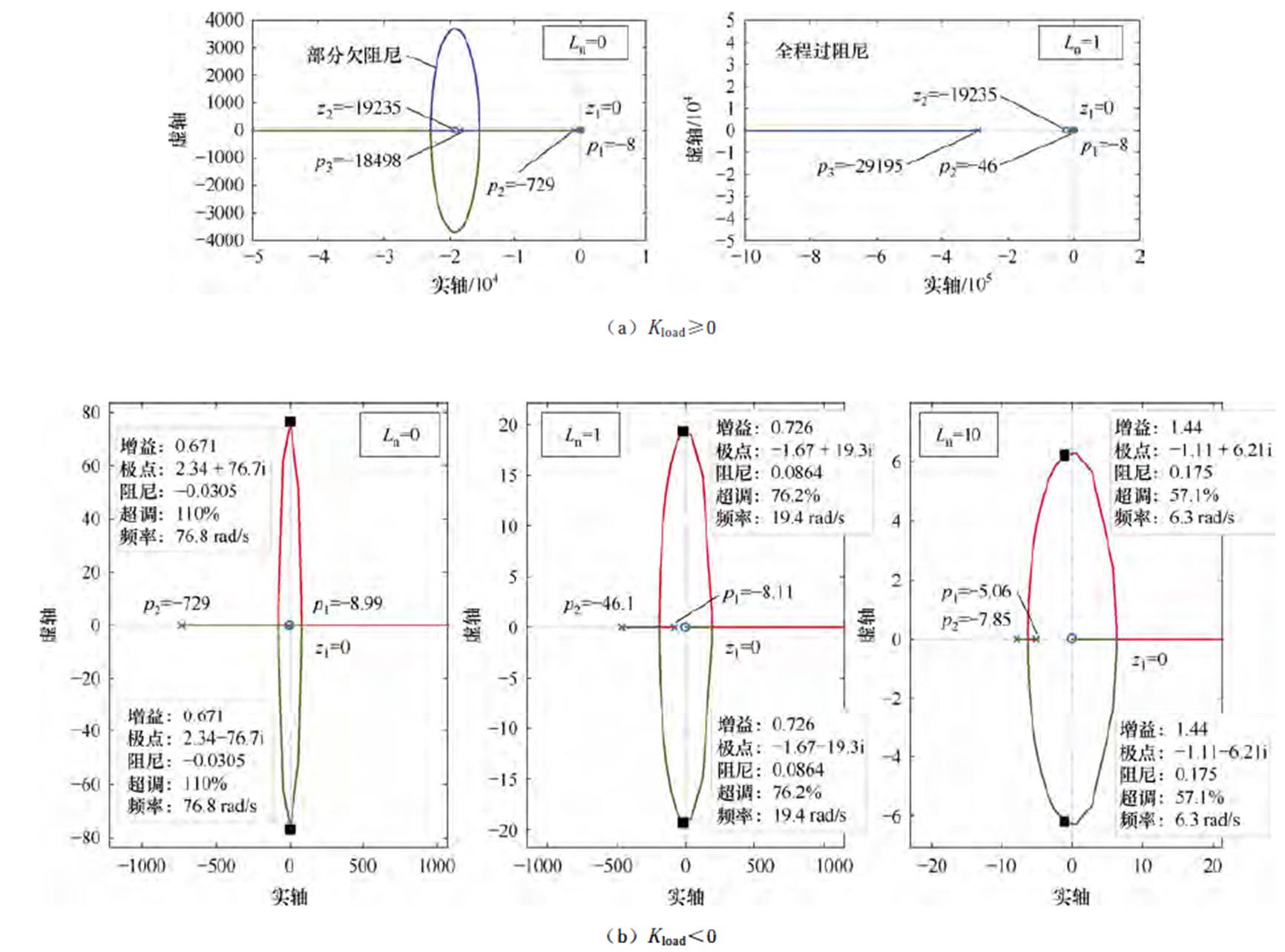
图5 系统函数的参数根轨迹图
Fig.5 Parameter root locus analysis of system function
取同样的参数，基于式（24）分别取Ln=0, 1, 10 H，绘制关于参数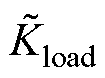=0→∞（相当于Kload=0→-∞）的根轨迹如图5b所示。由于控制系统根轨迹所示稳定性主要由靠近y轴的主极点值及其增益来决定，故只显示了y轴附近的局部图。
可知Kload=0→-∞，当负值过大时，极点将进入右半平面，控制系统将进入“不稳定”状态，故取轨迹与y轴的交点临界处，如图5b中的游标处显示了临界点的动态性能参数，同时获取主极点和次极点的值，列于表1中。
表1 系统参数根轨迹性能
Tab.1 System parameter root trajectory performance
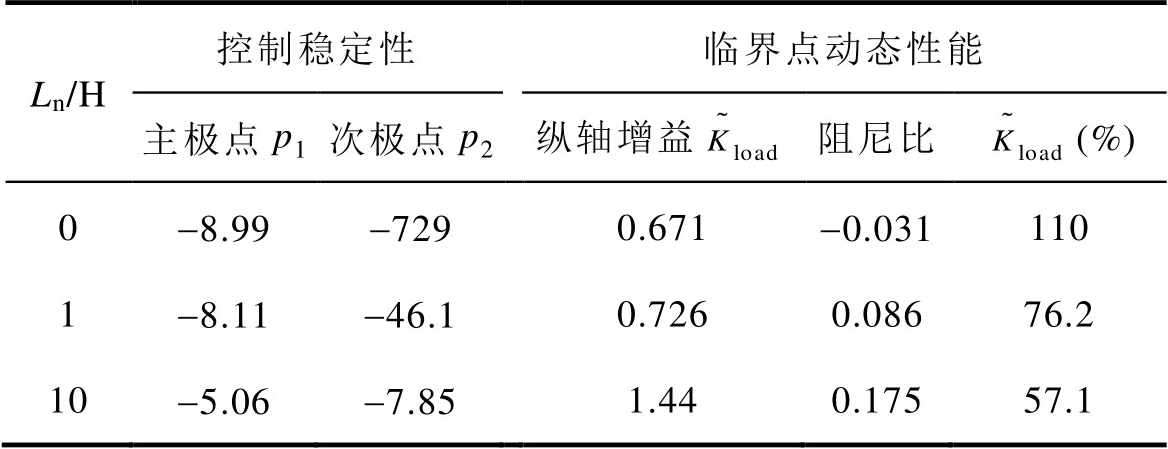
Ln/H控制稳定性临界点动态性能 主极点p1次极点p2纵轴增益阻尼比(%) 0-8.99-7290.671-0.031110 1-8.11-46.10.7260.08676.2 10-5.06-7.851.440.17557.1
分析图5b和表1可以得出以下结论：
（1）Ln取值越大，主极点p1和次极点p2都更向虚轴靠近，p1靠近速度较慢，p2靠近速度较快。再次表明：较之VDI-PBC（Ln=0），VESI-PBC算法的稳定裕度略有降低，且Ln越大，稳定裕度越小。
（2）对比临界点的动态性能。VDI-PBC（Ln=0）为负阻尼；而Ln＞0时，阻尼为正，为过阻尼状态，且阻尼值随着Ln值的增大而增大；与之对应的超调量，则随着Ln值的增大而减小，可见注入虚拟电感Ln可提高系统的刚度和抗干扰性。
（3）对比临界点增益。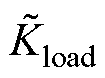
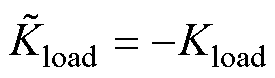，得
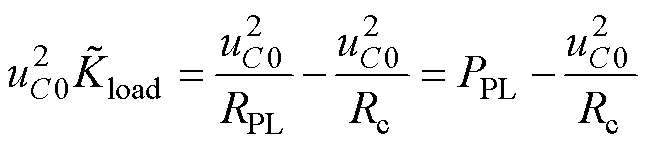（25）
表1表明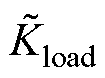，临界值随着Ln的增大而增大，也就是，PPL临界值随着Ln的增大而增大。可见增大Ln，有利于提高PL-ESS系统的最大可承受脉冲峰值功率。
依据图1中PL-ESS系统电路结构，以及图4控制策略，搭建PL-ESS系统Matlab/Simulink模型，参数设置见表2。为与VDI-PBC比较，设置PI参数kpi=1和kii=50。
为验证算法对不同频率脉冲功率的适用性，取脉冲频率fPL=0.5 Hz→1 Hz→5 Hz→10 Hz→50 Hz→ 100 Hz→300 Hz→500 Hz→1 000 Hz。新型雷达设备要求直流电压最大波动率|dmax|≤5%[2]。分别设置三种电流内环控制算法参数（见表2），得到母线电压uC波形如图6所示。
表2 试验平台参数/Simulink仿真模型参数
Tab.2 Parameters of test platform/Simulink models
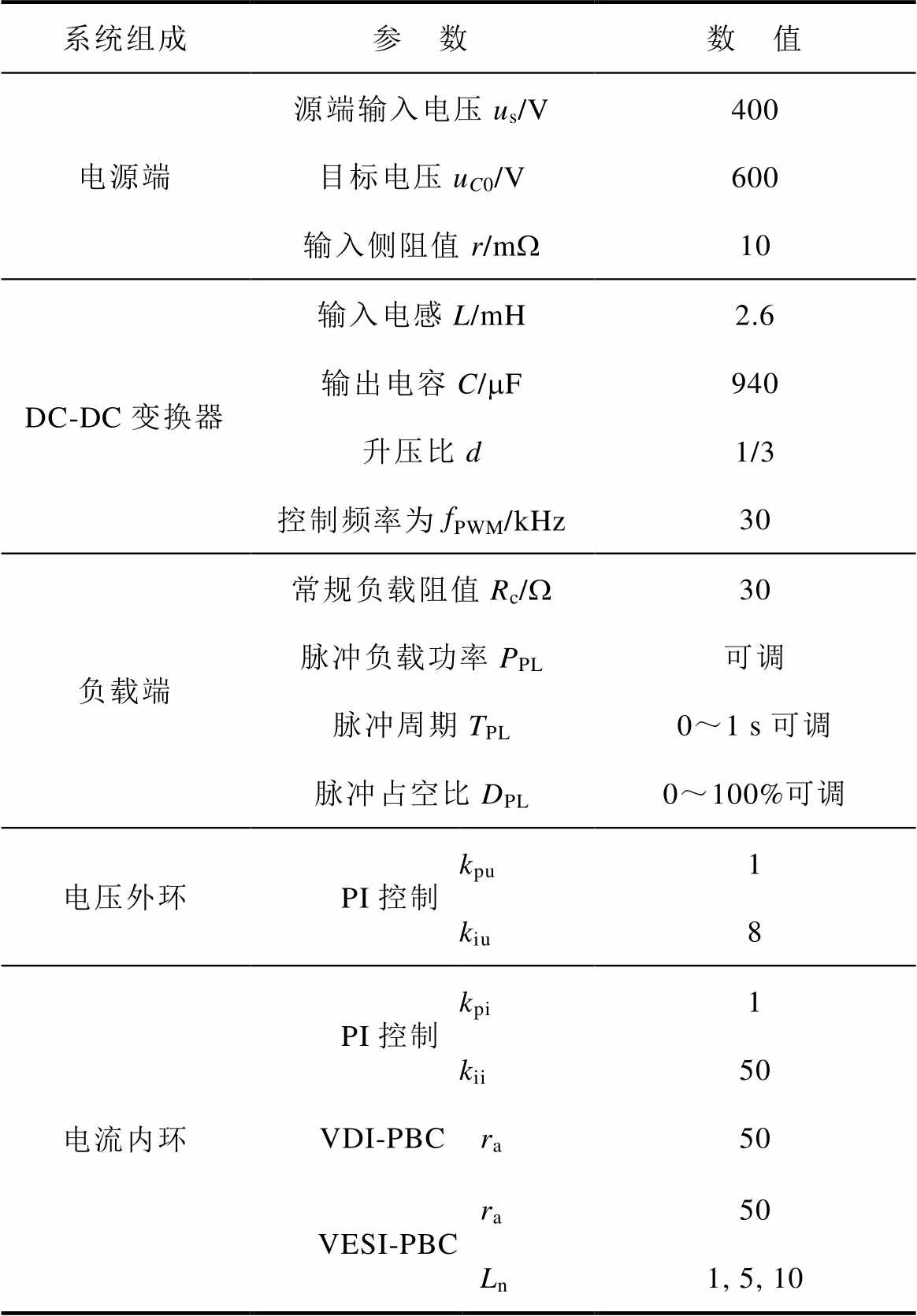
系统组成参 数数 值 电源端源端输入电压us/V400 目标电压uC0/V600 输入侧阻值r/mW10 DC-DC变换器输入电感L/mH2.6 输出电容C/mF940 升压比d1/3 控制频率为fPWM/kHz30 负载端常规负载阻值Rc/W30 脉冲负载功率PPL可调 脉冲周期TPL0～1 s可调 脉冲占空比DPL0～100%可调 电压外环PI控制kpu1 kiu8 电流内环PI控制kpi1 kii50 VDI-PBC ra50 VESI-PBCra50 Ln1, 5, 10
图7绘制了脉冲频率fPL=5 Hz/50 Hz时，内环电流iL与指令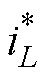
、DC-DC输出电流idc与负载电流iload，以及电容电流iC的仿真波形（各参量测点已在图4红圈处标出）。
uC最大波动率±dmax测算公式为
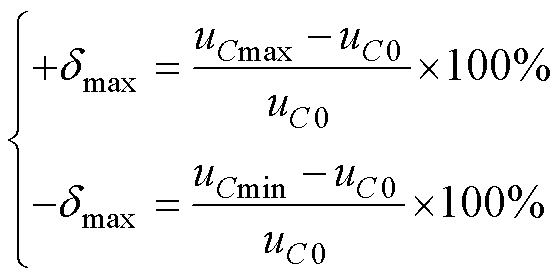（26）
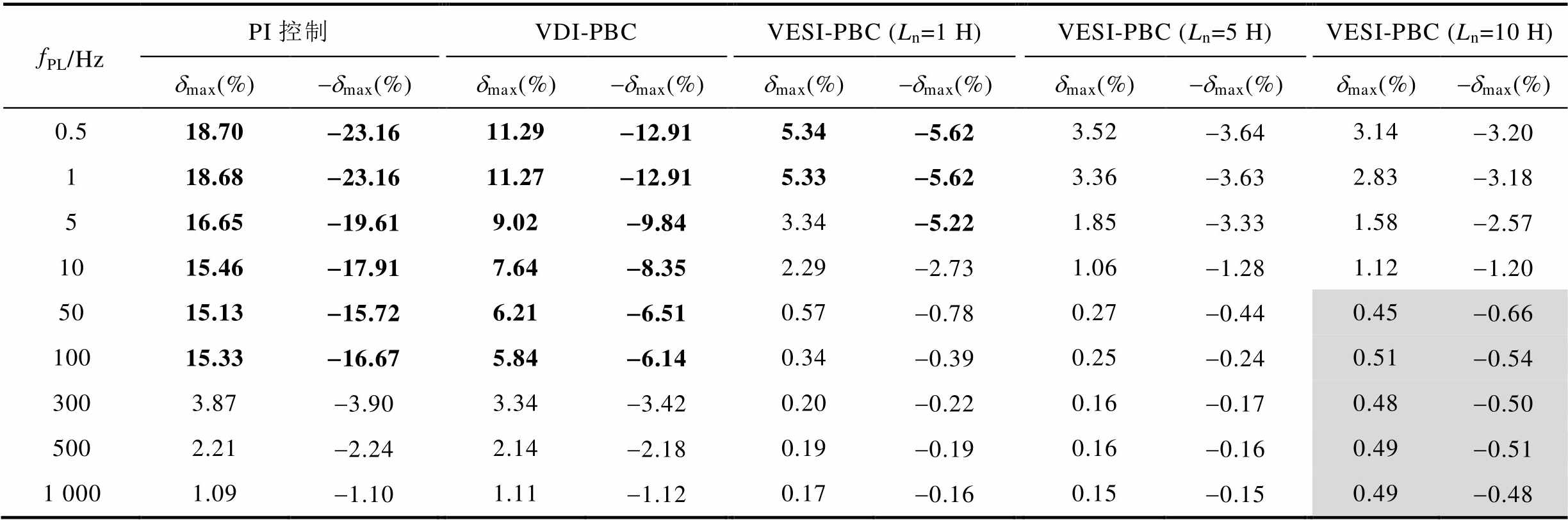
测算结果见表3，其中Ⅰ～Ⅴ分别对应PI、VDI- PBC、VESI-PBC（Ln=1 H、5 H、10 H）算法，加粗部分为不满足性能指标的波动率。
依据图6、图7波形和表3可得出以下结论：
图6 不同脉冲频率fPL下直流母线电压uC波形
Fig.6 Waveforms of DC bus voltage uCunder different pulse frequencies fPL
图7 三种控制算法下不同参量波形对比
Fig.7 Comparison of waveforms of three types of algorithm
表3 直流母线电压uC最大波动率
Tab.3 Maximum fluctuation rate of DC bus voltage uC
fPL/HzPI控制VDI-PBCVESI-PBC (Ln=1 H)VESI-PBC (Ln=5 H)VESI-PBC (Ln=10 H) dmax(%)-dmax(%)dmax(%)-dmax(%)dmax(%)-dmax(%)dmax(%)-dmax(%)dmax(%)-dmax(%) 0.518.70-23.1611.29-12.915.34-5.623.52-3.643.14-3.20 118.68-23.1611.27-12.915.33-5.623.36-3.632.83-3.18 516.65-19.619.02-9.843.34-5.221.85-3.331.58-2.57 1015.46-17.917.64-8.352.29-2.731.06-1.281.12-1.20 5015.13-15.726.21-6.510.57-0.780.27-0.440.45-0.66 10015.33-16.675.84-6.140.34-0.390.25-0.240.51-0.54 3003.87-3.903.34-3.420.20-0.220.16-0.170.48-0.50 5002.21-2.242.14-2.180.19-0.190.16-0.160.49-0.51 1 0001.09-1.101.11-1.120.17-0.160.15-0.150.49-0.48
注：灰色底纹部分数据为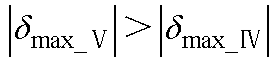
。
1）图6和表3显示，相同负载下，母线电压最大波动率dmax随脉冲频率fPL的增大而减小，符合脉冲负载电力系统暂态特性规律。
2）由图6和表3可知，对比三种控制算法，VESI-PBC可有效降低母线电压uC的最大波动率dmax，且Ln取值越大，dmax越小，系统抗负载扰动能力越强。与2.3节分析结论一致。
3）通过图7观察系统内部各参量运行规律，进一步剖析验证VESI-PBC算法在PL-ESS系统中实质控制机理：
（1）内环电流跟踪性能。内环电流控制本身目的在于控制电流iL对指令电流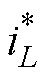的跟踪。由图7a所示，PI控制和VDI-PBC的iL紧跟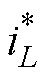，尤其后者几乎完全跟随了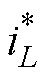。而VESI-PBC下的iL几乎没有跟随对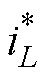，而是超前于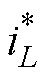，且Ln越大，iL越接近方波。
（2）负载电流跟踪性能。负载电流跟踪性能是指DC-DC变换器输出电流idc对负载电流iload的跟随特性。图7b所示，VESI-PBC最佳，VDI-PBC次之，PI控制最差；对比图7b、图7c可知，脉冲频率fPL越高，后两者的跟踪效果就越差。这是因为这2个控制器电流响应速度太慢，无法跟踪较高频率下的负载脉冲电流的瞬时变化，而VESI-PBC电流则可快速响应。由图3可知，idc=d1iL，正是因为VESI-PBC的iL超前于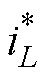，才使其控制下的idc快速跟随iload，且Ln越大，idc越接近iload。
（3）母线电压波动。由2.3节分析可知，uC波动来自电容电流iC的积分。对比图7d和图7e，由于VESI-PBC的idc紧密跟随iload，产生了较小的iC，从而有效降低了母线电压uC的波动；且Ln越大，iC越小，DuC越小。而PI控制和VDI-PBC下的iC较大，因而引起uC较大的波动幅度。
4）但VESI-PBC算法存在的问题是，虽然DuC随着Ln的增大减小，但Ln过大，各参量会产生较多高频毛刺。这是因为VESI-PBC的指令电压中，
如式（18）所示，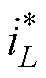
不仅引入了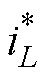的正常动态变化，还放大了其他干扰电流，产生额外的毛刺，且Ln越大，毛刺越多。从图6还可以看出，fPL越高，脉冲负载动态变化越剧烈，则毛刺也越多。
可见VESI-PBC既减小了母线电压uC的波动，还快速响应了瞬时脉冲负载电流iload，比单纯增大储能电容C具有更快速的响应性能。且Ln值越大，电压电流控制性能就越好。但随着fPL增大，尤其是高频工况时，Ln过大会引入毛刺，故需选取合适的值。或者在直流侧加入LC滤波器也可有效滤除这些高频毛刺。
基于实际试验平台对VESI-PBC效果进行验证。PL-ESS系统试验平台如图8所示，由三大部分组成：①源端参数：采用储能单元（磷酸铁锂电池模块/DC 390 V/42.6 kW·h），用于输出稳定的400 V直流电压us。②DC-DC变换器参数：输入滤波电感L=2.6 mH，输出电容C=940 mF（可知系统“容感比”C/L=0.36较小，已知较大的“容感比”可使系统具有更好的稳定性，则所选试验系统稳定度较差）；基于Boost升压结构，目标电压uC0=600 V，PWM控制脉冲频率fPWM=30 kHz。③载端参数：直流侧常规负载Rc=30 W（静态功率为12 kW），脉冲负载峰值功率PPL=30 kW，是常规负载的2.5倍，脉冲占空比DPL、脉冲频率fPL均可调。
图8 PL-ESS试验系统平台
Fig.8 Test Platform of PL-ESS
实测电压、电流数据采用YOKOGAWA示波记录仪DL850E获取。分别取fPL=2、50、200、500 Hz，DPL=50%；控制参数：电压外环PI控制参数：kpu=1，kiu=8；电流内环分别采用PI控制（kpi=2，kii=6，参数已优化）；VDI-PBC取ra=10试验最优，ra再增大会出现超调；VESI-PBC采用Ln=3 H即可满足全频率段|dmax|≤5%的性能要求。
图9对比显示了三种算法在不同脉冲频率下的母线电压uC（蓝色）、电源电压us（绿色）、DC-DC输出电流idc，以及电容电流iC波形。标号（①～-）与图10所示uC/idc相域图对应。
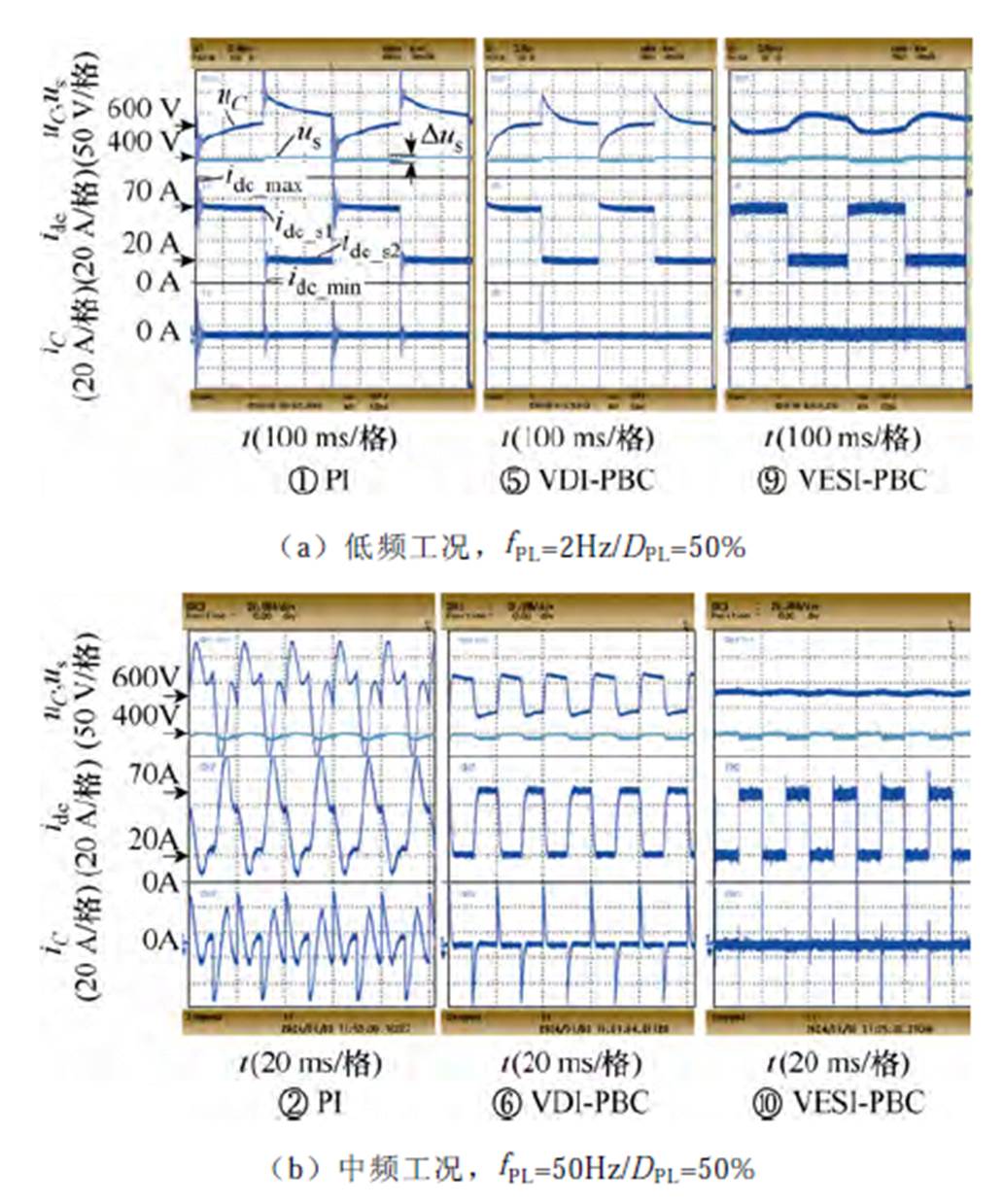
图9 不同工况下试验波形
Fig.9 Waveforms under different working conditions
测算出指标数值见表4，Ⅰ～Ⅲ分别对应PI、VDI-PBC和VESI-PBC三种算法。其中，±dmax为母线电压uC的波动率，具体见式（26）；idc_s1和idc_s2分别对应加载模态和减载模态idc的稳态值；idc_max和idc_min分别为idc最大值和最小值（由于毛刺原因，idc_s1≠idc_max，idc_s2≠idc_min，测算值具体区别如图9a中①所示），Dus为电源电压us的波动值。
图10 uC-idc相域图
Fig.10 Time-domian of uC-idc
表4 实际试验测算值
Tab.4 Index values of actual test
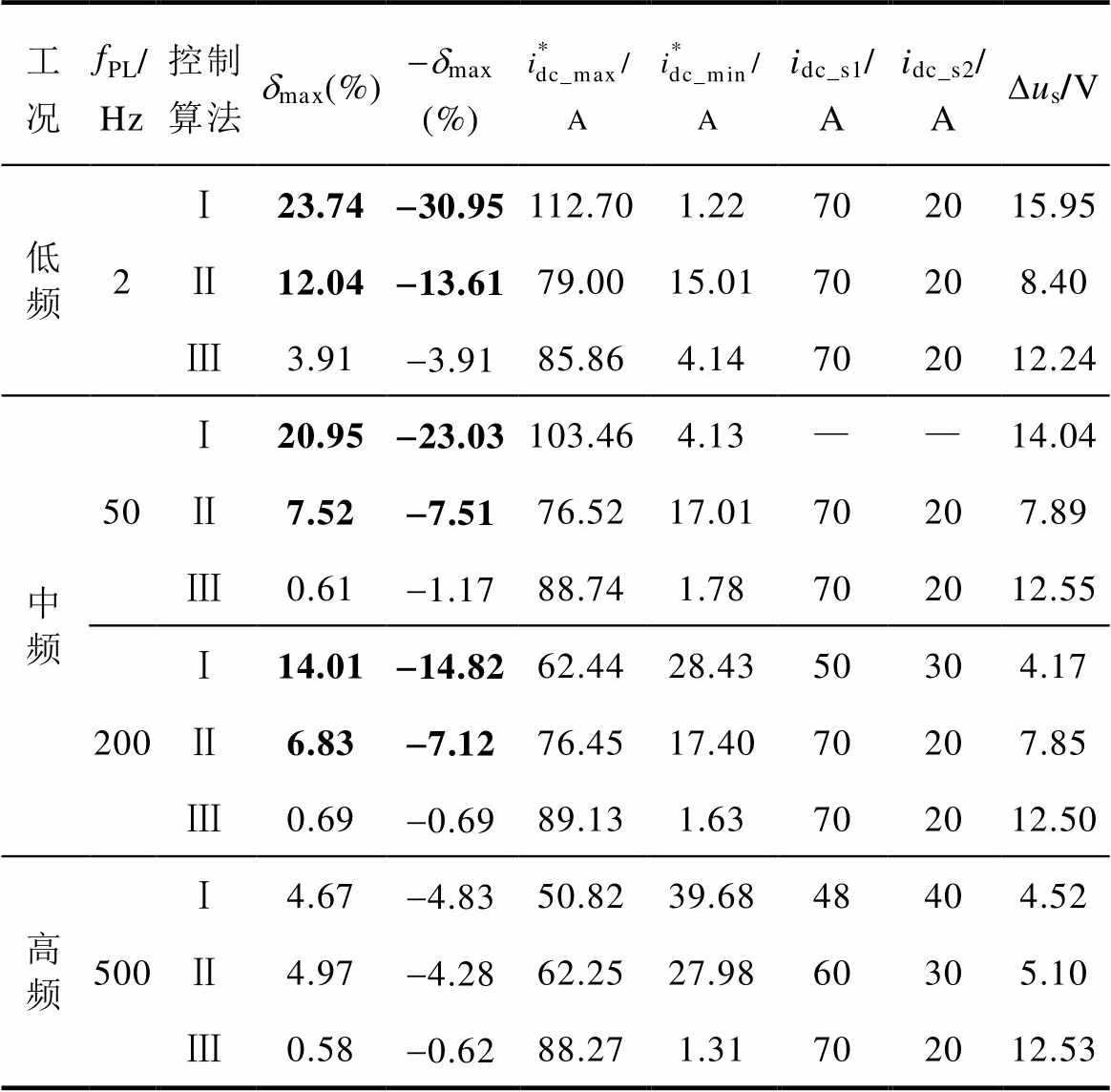
工况fPL/Hz控制算法dmax(%)-dmax(%)idc_s1/Aidc_s2/ADus/V 低频2Ⅰ23.74-30.95112.701.22702015.95 Ⅱ12.04-13.6179.0015.0170208.40 Ⅲ3.91-3.9185.864.14702012.24 中频50Ⅰ20.95-23.03103.464.13——14.04 Ⅱ7.52-7.5176.5217.0170207.89 Ⅲ0.61-1.1788.741.78702012.55 200Ⅰ14.01-14.8262.4428.4350304.17 Ⅱ6.83-7.1276.4517.4070207.85 Ⅲ0.69-0.6989.131.63702012.50 高频500Ⅰ4.67-4.8350.8239.6848404.52 Ⅱ4.97-4.2862.2527.9860305.10 Ⅲ0.58-0.6288.271.31702012.53
注：*由于毛刺影响，VESI-PBC所测idc_max和idc_min数据为毛刺尖端。
依据图9波形和表4，可得出以下结论：
（1）|dmax|为PL-ESS设备的重要性能指标。VESI-PBC算法可有效降低母线电压uC的波动率，本试验参数下，取Ln=3 H即可满足全频率段|dmax|＜5%的性能要求；而VDI-PBC和PI控制仅在高频工况（fPL＞200 Hz）下满足电压性能要求，相比而言，VDI-PBC要优于PI。
（2）DC-DC控制输出电流idc是另一个需要关注的性能参数。前文分析可知，系统加减载2个模
态的稳态电流期望值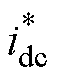
=iload，依据试验系统参数可计算得
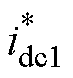=20 A，
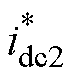=70 A。实测波形可以看出：①中低频状态下，三种算法都能将输出电流idc控制在期望值附近；②高频状态下，PI和VDI-PBC都由于响应速度太慢，而无法保证idc运行在期望点。VESI-PBC则因为
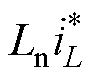超前项提高了电流响应速度，即使在高频状态下仍能保证idc可以快速稳定至期望值。
输出电压uC和DC-DC输出电流idc用于表征PL-ESS系统的输出能力，将实测波形数据绘制uC/idc相域图如图10所示。分析图10，可以继续得出以下结论：
（1）控制目标idc→iload，以便减轻母线电容C承担的瞬时冲击电流iC，因此，uC/idc相域图的理想期望输出状态应该是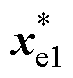
=[20 A 600 V]，
= [70 A 600 V]，在相域图上应该为一条以600 V平行于x轴，并在20 A和70 A来回切换的线段。可见，VESI-PBC不同工况下的时域波形最接近期望状态，VDI-PBC次之，PI几乎不能完成期望需求。
（2）低频状态下（fPL≤50 Hz），PI和VDI-PBC虽然电流可达至期望值，但电压超调太高，如图10中①②⑤所示；而中高频（fPL≥200 Hz），电压波动幅值有所降低，但两者电流动态性能不足以跟随脉冲负载的高频切换，导致输出电流idc无法达到期望值（20 A和70 A），如图10中③④⑧所示。尤其当fPL=500 Hz时，PI控制的uC和idc都无法快速响应，导致uC和idc波动极小，在相域图中逐渐缩小为一点，如图10中④所示。
图10相域图充分体现了VESI-PBC算法应用于PL-ESS系统的优越性：母线电压uC全频率段波动率|dmax|＜5%；输出电流idc全频率段满足期望值输出；VESI-PBC算法以满足Lyapunov稳定性为前提进行设计，保证了系统运行过程的稳定性。而VDI- PBC和PI都无法同时满足PL-ESS设备对电压电流的性能要求。
（3）在部分工况下VESI-PBC的源端电压波动Dus略大于VDI-PBC和PI，这是由于源端输出电流is快速响应负载电流，而引起的电压波动。
综上所述，VESI-PBC既增强了母线电压的刚度，提高了PL-ESS系统抗脉冲负载快速扰动的能力，又增强了DC-DC输出电流的快速响应能力，满足中高频工况下瞬时负载电流需求。且所选试验系统容感比较小（稳定性较弱），VESI-PBC控制仍能满足设备对电压电流的性能需求。
本文以脉冲负载电池储能系统（PL-ESS）为研究对象，面向脉冲恒功率负载系统稳定性和电压电流性能需求，在无源控制算法设计的基础上，提出了注入虚拟储能的无源控制（VESI-PBC）算法。在保证系统稳定性的前提下，同时提高了直流母线电压抗脉冲负载扰动的鲁棒性和输出电流响应脉冲瞬时电流的快速性，满足PL-ESS系统高质量的直流供电性能需求。研究结论如下：
1）VESI-PBC算法以提高能量函数收敛速度为目标设计控制器，首先保证了PL-ESS系统稳定性。控制系统根轨迹法分析结论表明，该算法在“恒功率”特性下依然能保证系统的稳定性。
2）VESI-PBC控制机理研究表明，其控制目标是通过引入储能电感导数项，超前响应外环电压的动态变化，其实质是快速响应负载脉冲电流的瞬态变化，分担了输出电容C的缓冲功能，从而同时满足增强母线电压刚度，在全频率段满足|dmax|＜5%和提高输出电流响应快速性的双重性能需求。
3）VESI-PBC效果与Ln值有关，Ln越大，控制性能越好；但过大的Ln会在PL-ESS系统高频工况下引入毛刺，故需选取合适值。
4）VESI-PBC算法比单纯增大储能电容C有更快速的响应性能，即便是在“容感比”较小的系统也可以实施，因而适用于稳定性较弱（容感比较小）、脉冲频率覆盖范围广、非线性动态特性强烈的含脉冲负载的独立电力系统中。
附 录
需证明
，其公式如下
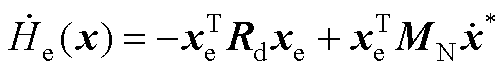（A1）
现以文中控制对象为例对其进行证明：
文中控制对象为“电压外环+电流内环”控制结构，如附图1所示，所设计的电流内环输入指令
即为电压外环输出，因此并非为一个恒定值，即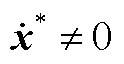
。本文中电压外环采用PI控制器，设其控制参数为kp和ki，得
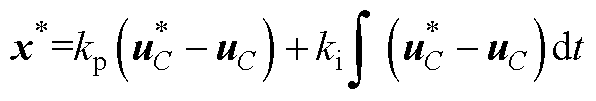（A2）
式（A2）求导得
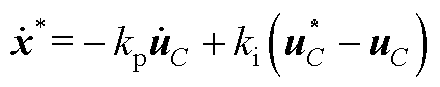（A3）
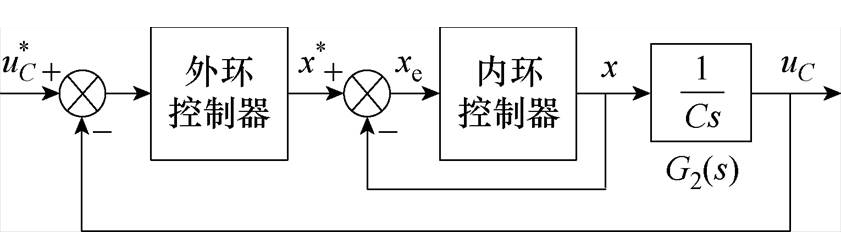
附图1 双闭环控制结构
App.Fig.1 Double closed loop control structure diagram
如附图1所示，x为电流内环被控参量，内环控制器正是被设计的内容。假设采用最简单的比例控制（设比例系数为kpi），因此有
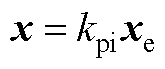（A4）
内环电流x输出后经由电容C输出电容电压uC，如附图1所示，得
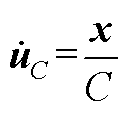（A5）
将式（A4）代入式（A5）得
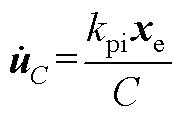（A6）
将式（A6）代入式（A3）得
（A7）
对比式（A7）前后项系数，C取值一般为10-6～10-3，而kp、kpi和ki取值一般为1～10，可见第一项系数远大于第二项系数。令K=kpkpi/C，式（A7）可写为
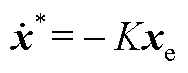（A8）
将式（A8）代入式（A1）得
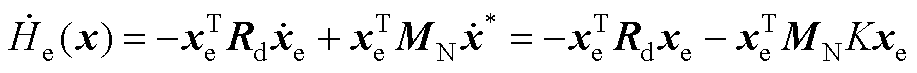（A9）
故有，得证。
参考文献
[1] Zhang Bao, Kou Yong, Jin Ke, et al. Dynamic response of electromagnetic railgun under time- dependent electromagnetic moving loads[J]. Journal of Sound and Vibration, 2020, 483: 115451.
[2] Tu Zhenghong, Fan Bo, Zhang Wei, et al. Optimal state-constrained control of DC shipboard power systems for online pulsed power load accommo- dation[J]. IEEE Transactions on Smart Grid, 2022, 13(1): 96-105.
[3] 高雪平, 付立军, 纪锋, 等. 含脉冲负载的综合电力系统储能优化配置研究[J]. 国防科技大学学报, 2022, 44(6): 81-88.
Gao Xueping, Fu Lijun, Ji Feng, et al. Research on optimal configuration of energy storage in integrated power system with pulse load[J]. Journal of National University of Defense Technology, 2022, 44(6): 81-88.
[4] 王勇, 刘正春, 刘金宁, 等. 带脉冲负载电池储能系统的源载耦合建模[J]. 陆军工程大学学报, 2023, 2(2): 23-30.
Wang Yong, Liu Zhengchun, Liu Jinning, et al. Source-load coupled modeling of battery energy storage system with pulse load[J]. Journal of Army Engineering University of PLA, 2023, 2(2): 23-30.
[5] 孙国亮, 高路, 周鋆玲, 等. 脉冲负载对独立电力系统运行特性影响[J]. 舰船科学技术, 2023, 45(2): 135-140.
Sun Guoliang, Gao Lu, Zhou Junling, et al. Influence of pulse load on operation characteristics of independent power system[J]. Ship Science and Technology, 2023, 45(2): 135-140.
[6] 樊靖轩, 施佳楠, 徐子梁, 等. 基于GaN的开关线性复合高速随动脉冲负载直流变换器[J]. 电工技术学报, 2024, 39(6): 1818-1829.
Fan Jingxuan, Shi Jianan, Xu Ziliang, et al. GaN-based switched linear composite high-speed follow-up pulse load DC converter[J]. Transactions of China Electrotechnical Society, 2024, 39(6): 1818- 1829.
[7] 张泽华, 宋桂英, 张晓璐, 等. 考虑恒功率负载的直流微电网稳定性与鲁棒性控制策略[J]. 电工技术学报, 2023, 38(16): 4391-4405.
Zhang Zehua, Song Guiying, Zhang Xiaolu, et al. Stability and robustness control strategy of DC microgrid considering constant power load[J]. Transactions of China Electrotechnical Society, 2023, 38(16): 4391-4405.
[8] 李欣, 邹俊南, 刘金辉. 带恒功率负载的直流微电网稳定性控制研究综述(英文)[J/OL]. Journal of Measurement Science and Instrumentation, 2023, https://link.cnki.net/urlid/14.1357.TH.20231219.1630. 002.2023.
[9] 吴家荣, 卢振坤, 文春明. 带恒功率负载多电平 Buck变换器逆解耦自适应滑模控制[J/OL]. 电机与控制学报, 2023, https://kns.cnki.net/kcms2/detail/ 23.1408.TM.20230530.0946.002.html
[10] 游逍遥, 刘和平, 苗轶如, 等. 带恒功率负载的双极性直流系统稳定性分析及其有源阻尼方法[J]. 电工技术学报, 2022, 37(4): 918-930.
You Xiaoyao, Liu Heping, Miao Yiru, et al. Stability analysis and active damping method of the bipolar DC system with constant power loads[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 918-930.
[11] 郑长明, 董萱萱, 肖子语, 等. 基于虚拟电阻有源阻尼的LC滤波型永磁同步电机系统预测电流控制[J]. 电工技术学报, 2023, 38(22): 6059-6069.
Zheng Changming, Dong Xuanxuan, Xiao Ziyu, et al. Virtual resistance active damping based predictive current control of LC-filtered permanent magnet synchronous motor system[J]. Transactions of China Electrotechnical Society, 2023, 38(22): 6059-6069.
[12] 魏威, 郑华俊, 袁旭峰, 等. 基于平方和规划的带恒功率负载的直流微电网大信号稳定性分析[J]. 电网与清洁能源, 2023, 39(8): 27-35.
Wei Wei, Zheng Huajun, Yuan Xufeng, et al. An analysis of large signal stability of the DC microgrid with constant power load based on sum of squares programming[J]. Power System and Clean Energy, 2023, 39(8): 27-35.
[13] 严鋆, 王金全, 陈颖, 等. 基于开关函数的脉冲功率负载大信号模型研究[J]. 电工技术学报, 2020, 35(16): 3509-3517.
Yan Jun, Wang Jinquan, Chen Ying, et al. Study on large-signal model for pulsed power load based on switching functions[J]. Transactions of China Elec- trotechnical Society, 2020, 35(16): 3509-3517.
[14] 孙勇, 林松. 相控阵雷达发射单元供电建模及特性研究[J]. 现代雷达, 2020, 42(9): 80-85.
Sun Yong, Lin Song. A study on power supply model and characteristic of phased array radar transmitting unit[J]. Modern Radar, 2020, 42(9): 80-85.
[15] 林周宏, 黄文焘, 邰能灵, 等. 舰船脉冲功率负载Buck变换器自适应阻尼比控制方法[J/OL]. 中国电机工程学报, 2023, https://doi.org/10.13334/j.0258- 8013.pcsee.230717.
[16] 王久和. 电能变换器及其无源控制[M]. 北京: 科学出版社, 2014.
[17] 程启明, 李剑辉, 赖宇生, 等. 非理想条件下基于MMC的电力电子变压器的无源滑模控制策略[J]. 高电压技术, 2023, 49(4): 1556-1566.
Cheng Qiming, Li Jianhui, Lai Yusheng, et al. Passivity-based sliding-mode control strategy for power electronic transformer based on MMC under non-ideal conditions[J]. High Voltage Engineering, 2023, 49(4): 1556-1566.
[18] 王勉, 唐芬, 陈麒宇, 等. DC-DC变换器并联系统无源控制及大信号稳定性研究[J]. 中国电机工程学报, 2022, 42(18): 6789-6802.
Wang Mian, Tang Fen, Chen Qiyu, et al. Passivity- based control and large signal stability of DC-DC converter parallel system[J]. Proceedings of the CSEE, 2022, 42(18): 6789-6802.
[19] 李萍, 王久和. 基于无源与自抗扰的Vienna整流器控制策略研究[J]. 电网技术, 2022, 46(4): 1575- 1584.
Li Ping, Wang Jiuhe. Control strategy of Vienna rectifier based on passivity-based and active disturbance rejection controller[J]. Power System Technology, 2022, 46(4): 1575-1584.
[20] 敖文杰, 陈家伟, 陈杰, 等. 燃料电池-锂电池混合供电系统的无源控制策略及参数设计方法[J]. 电工技术学报, 2024, 39(2): 580-594.
Ao Wenjie, Chen Jiawei, Chen Jie, et al. Passive control strategy and parameter design method of fuel cell-lithium battery hybrid power supply system[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 580-594.
[21] 肖润龙, 王刚, 徐晨, 等. 含脉冲负载的中压直流综合电力系统的无迹卡尔曼动态状态估计方法[J]. 中国电机工程学报, 2020, 40(23): 7555-7565.
Xiao Runlong, Wang Gang, Xu Chen, et al. An unscented Kalman filter based dynamic state estimation for the medium-voltage DC integrated power system with pulse load[J]. Proceedings of the CSEE, 2020, 40(23): 7555-7565.
[22] 尹英龙, 刘宝泉. 闭环控制DC/DC变换器带恒功率负载的稳定性研究[J]. 重庆理工大学学报(自然科学), 2021, 35(2): 198-204, 233.
Yin Yinglong, Liu Baoquan. Research on the stability of closed-loop Buck converter with constant power load[J]. Journal of Chongqing University of Tech- nology (Natural Science), 2021, 35(2): 198-204, 233.
Abstract An energy storage system with pulsed load (PL-ESS) is a typical isolated power system with limited source capacity, small coefficient inertia, and weak stability. In recent years, pulse load devices have been equipped with power controllers to ensure the performance of pulse power emission, which presents a state of pulse ‘constant power’ load. The negative impedance characteristic of constant power loads is known to amplify the bus voltage disturbance and exacerbate instability. Methods have been presented to achieve stability control of power systems with constant power loads. However, most of them focus on suppressing the fluctuation of bus voltage without simultaneously satisfying the fast response of instantaneous load current. This paper proposes a Virtual Energy Storage Injection-Passive Based Control (VESI-PBC) method based on the traditional PBC. By improving the convergence speed of the energy function, the dc-bus voltage can be quickly stabilized to adapt to the switching conditions of pulse loads in medium or high-frequency mode.
Firstly, based on the topology structure of ESS with pulse constant power load, an Euler-Lagrange mathematical model is established to judge whether the system is strictly passive. Secondly, a virtual energy storage matrix is constructed, and the virtual inductance Ln is superimposed on the energy-storage inductance L to accelerate the convergence speed of the energy error function He(x) and ensure the system stability. Thirdly, by designing control terms, the VESI-PBC control is obtained. Compared with PI and VDI-PBC control, VESI-PBC
control includes terms of (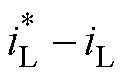
) and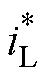 
and introduces 
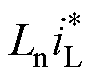, which leads the response to the dynamic changes
in bus voltage uC. Finally, a dual closed-loop control strategy based on the VESI-PBC algorithm is proposed for the PL-ESS main circuit structure. Taking system stability as the precondition, the VESI-PBC method is designed to ensure stability. The controller can converge more quickly to the steady state when PL-ESS switches between pulse power loading and unloading modes, responding to the fast performance requirements of medium or high-frequency working conditions in PL-ESS.
The stability analysis of the PL-ESS control model based on the root locus method shows that the VESI-PBC algorithm still ensures a certain stability margin of the system with “constant power” characteristics. The introduction of Ln improves the system damping ratio, i.e., enhances the robustness of the bus voltage disturbance resistance. Simulation and actual test results show that the VESI-PBC algorithm effectively reduces the bus voltage fluctuation rate while ensuring the maximum fluctuation rate of dc-bus voltage |dmax|≤5% on the test platform. It can meet the voltage performance requirements of new radar devices and the instantaneous pulse current performance requirements of constant power pulse loads under medium and high-frequency operating conditions (fPL=100 Hz～1 kHz). Compared with PI and VDI-PBC algorithms, the VESI-PBC algorithm can rapidly respond to the load current by advanced response to the dynamic changes of the outer loop voltage and track the inner loop current. The larger the Ln value, the greater the fluctuation rate of bus voltage |dmax|, and the faster the response speed of the controller's output current idc to the pulse current. However, the high-frequency interference current is amplified, causing additional spikes in the waveform. In experiments, small Capacitance-to-Lnductance ratios (weak stability) are selected, and phase-domain and time-domain waveforms of two key parameters, |dmax| and idc, are plotted. Compared with PI and VDI-PBC, the VESI-PBC algorithm can simultaneously meet the voltage and current performance requirements from low-frequency to high-frequency operating conditions, which can be applied to weakly stable PL-ESS systems.
The following conclusions can be drawn. (1) The VESI-PBC algorithm ensures the stability of the PL-ESS with constant power characteristics, aiming to improve the convergence speed of the energy function. (2) VESI-PBC control effect is related to the Ln, and the larger the Ln. However, excessive Ln introduces burrs under high-frequency operating conditions in PL-ESS. An appropriate value needs to be selected. (3) The VESI-PBC algorithm can also be implemented in systems with small capacitance-to-inductance ratios, making it suitable for isolated power systems containing pulse loads with weak stability, wide pulse frequency coverage, and nonlinear dynamic characteristics.
keywords：Pulse constant power load, energy storage system, passivity control, energy function, system stability
中图分类号：TM711
DOI: 10.19595/j.cnki.1000-6753.tces.240410
国家自然科学基金面上资助项目（62373039）。
收稿日期 2024-03-15
改稿日期2024-04-02
王 勇 男，1984年生，博士研究生，讲师，研究方向为微电网储能与负荷建模特性。E-mail: ja9q520@163.com
王谱宇 男，1989年生，博士，副教授，硕士生导师，研究方向为交直流混合电力系统的分析、控制与保护，非侵入式负荷辨识。E-mail: puyu.wang@hotmail.com（通信作者）
（编辑 陈 诚）