 )和TR的基本关系。由此,变换器获得了优化的提前导通时间(TR_op)及相应的优化效率(hop)。为验证理论分析的有效性,基于LCLC谐振变换器,该文搭建一台500 W的实验样机。相比传统控制方法,采用该文效率优化分析方法后,轻载(20%负载)运行效率提升2%以上(93.757%~95.821%)。
)和TR的基本关系。由此,变换器获得了优化的提前导通时间(TR_op)及相应的优化效率(hop)。为验证理论分析的有效性,基于LCLC谐振变换器,该文搭建一台500 W的实验样机。相比传统控制方法,采用该文效率优化分析方法后,轻载(20%负载)运行效率提升2%以上(93.757%~95.821%)。摘要 针对移相调制轻载零电压软开关(ZVS)缺失效率低下的问题,该文提出一种应用于移相调制同步整流型谐振变换器的轻载效率优化分析方法。该方法采用同步整流管提前导通的方式,通过调节同步整流管的开通时序,实现了部分能量从二次侧到一次侧的回馈。在同步整流开关管提前导通的过程中,降低的损耗(一次侧滞后桥臂开关管开通损耗和输出电容损耗)和增加的损耗(一次侧滞后桥臂开关管关断损耗和回路导通损耗)之间形成动态博弈,这对变换器的综合效率具有重要影响。通过构建受控变量(同步整流开关管提前导通时间TR)与损耗(Ploss)之间的数学模型,该文总结得出不同工作条件下损耗导数( )和TR的基本关系。由此,变换器获得了优化的提前导通时间(TR_op)及相应的优化效率(hop)。为验证理论分析的有效性,基于LCLC谐振变换器,该文搭建一台500 W的实验样机。相比传统控制方法,采用该文效率优化分析方法后,轻载(20%负载)运行效率提升2%以上(93.757%~95.821%)。
)和TR的基本关系。由此,变换器获得了优化的提前导通时间(TR_op)及相应的优化效率(hop)。为验证理论分析的有效性,基于LCLC谐振变换器,该文搭建一台500 W的实验样机。相比传统控制方法,采用该文效率优化分析方法后,轻载(20%负载)运行效率提升2%以上(93.757%~95.821%)。
关键词:移相调制 效率优化 多谐振直流变换器 同步整流 软开关
新型电力系统下提升用电生态效能是实现降碳减排,推进能源革新的必由之路。当前用户光伏、储能、电子产品等直流设备接入系统容量快速上升,系统源荷直流特征愈发明显[1-3]。
DC-DC变换器作为接口电路,具有连接不同电压等级和不同类型用电设备与用电网关键环节的作用。相较于PWM型变换器,谐振型变换器具有高频、高效率、高功率密度以及低电磁干扰等优点,可广泛应用于光伏系统、直流微电网、直流用电适配、电动汽车等领域[4-6]。
经典LLC谐振直流变换器具有结构简单、软开关性能良好的特点[7-10]。传统脉冲频率调制(Pulse Frequency Modulation,PFM)下,受结构固有限制,变换器在过谐振区域(fs>fr)时电压增益曲线平缓,难以适应宽输出电压应用场合[11]。为此,一些学者倾向于采用PFM和移相调制(Phase Shift Modu- lation, PSM)相结合的混合调制方式拓宽电压增益范围[12-14],即以谐振频率点的电压增益为标准增益,PFM应用于升压区域,PSM应用于降压区域。但是,PSM模式下,轻载运行时逆变单元滞后桥臂开关管开通时,谐振腔电流较小,无法为死区时间内开关管输出电容Coss充放电提供充足的能量,造成零电压软开关(Zero Voltage Switching, ZVS)缺失。由此产生了轻载效率低下的问题[15-17]。
为解决上述问题,众多学者从拓扑创新和控制改善两个方面进行了相关研究。拓扑创新方面,文献[18]提出了一种改进的电容钳位型LLC变换器,在此基础上采用定频移相调制方法,改善了传统移相LLC变换器软开关缺失的问题,拓宽了软开关实现范围,提升运行效率。但是此方法需额外引入辅助变压器和整流单元,增加了拓扑复杂性。文献[19]提出了使用电感值能在大范围内逐渐变化的非线性电感并采用自适应导通时间控制技术来提高DC- DC变换器的轻载效率。控制改善方面,文献[20]采用PFM和PSM同时进行的控制方法,在轻载时减小占空比,减小变压器的交流磁通密度,进而优化轻载效率。文献[21]提出了一种结合占空比调节的扩展移相调制方法,进而延展软开关实现范围。文献[22]提出了一种同步整流管提前导通的控制方式,将二次侧能量向一次侧进行部分反馈,进而实现了完全的ZVS。但是,同步整流管提前导通的过程本身也是一个损耗变化的博弈过程,这对变换器综合效率具有重要影响。所以,完全实现ZVS提升轻载运行效率只是效率优化的一种特定情况,不同参数不同运行工况下完全实现ZVS下的损耗博弈结果不一定使得运行效率达到优化效果。上述研究在提升轻载效率方面取得了一定的效果,但是不断探索宽增益、高效率运行的分析方法仍然是谐振型变换器的研究热点。
本文提出了一种应用于移相调制同步整流型谐振变换器的轻载效率优化分析方法(a Light Load Efficiency Optimal Analysis Method applied to phase- shift-modulation synchronous rectification resonant converters, LLEOAM)。在同步整流管提前导通的基础上,不同于直接设定同步整流提前导通时间为实现完全ZVS的时间[22],本文以获得不同运行条件最优效率为目标,构建了受控变量(同步整流开关管提前开通时间TR)与损耗Ploss间的数学模型,提出并总结了不同工作条件下损耗导数 和TR的基本关系。由此,变换器获得了优化的提前导通时间TR_op及相应的优化效率hop。
和TR的基本关系。由此,变换器获得了优化的提前导通时间TR_op及相应的优化效率hop。
最后,基于同步整流LCLC谐振变换器,本文搭建了一台500 W的实验样机并进行了相关实验验证。
图1给出了LCLC多谐振直流变换器的拓扑结构。其总体分为三个部分:逆变单元、谐振腔单元和整流单元。逆变单元由4个MOSFET开关管组成的全桥结构,主要功能为将输入直流电变换为方波信号;谐振腔单元由2个电感L1和Lm、2个电容C1和Cm及1个高频变压器T组成;整流单元应用同步整流技术,采用全桥结构,将谐振腔输出的交流电变换为直流电以供后级负载使用。
与传统LLC相似,图中L1和C1分别为谐振电感与谐振电容,T为高频变压器,Vin为输入电压源,Co为输出电容,Ro为负载;S1~S4为一次侧逆变全桥开关管,S5~S8为二次侧整流全桥开关管;与LLC不同的是,LCLC的关键之处在于在励磁电感Lm上串联了一个附加励磁电容Cm,构成一个新的等效励磁电感结构LM。同样采用PFM时,LCLC变换器获得快速升压调节能力。LM的表达式为

图1 LCLC变换器拓扑结构
Fig.1 Topology structure of LCLCDC-DC converter
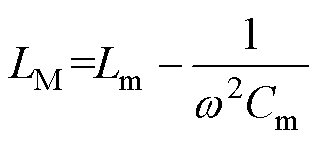 (1)
(1)
式中,w 为角频率,w=2πfs,fs为开关频率。
此外,其主谐振频率fr表达式为
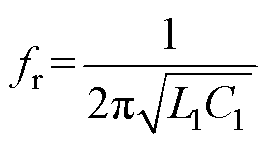 (2)
(2)
本文采用PFM和PSM相结合的混合调制方法来实现高效率和宽电压增益。以主谐振频率fr下的电压增益为标准增益,PFM应用于高电压增益区域。得益于Lm和Cm的串联变励磁结构,变换器获得快速升压调节能力。PSM应用于低电压增益区域。此阶段内,变换器工作频率固定在fr,通过调节移相角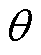 调节输出电压,这样可以有效拓宽增益范围。此外,PSM下,S1和S3是超前桥臂开关管,S2和S4是滞后桥臂开关管。
调节输出电压,这样可以有效拓宽增益范围。此外,PSM下,S1和S3是超前桥臂开关管,S2和S4是滞后桥臂开关管。
同时,传统PSM方式,在轻载工况下面临滞后桥臂软开关缺失、效率低下的问题。对此,文献[22]提出了一种同步整流管提前导通控制(Synchronous Rectification Advance On-Time control, SRAOT)方法,通过能量从二次侧向一次侧回馈的方式实现完全ZVS。
图2给出了PSM下不采用SRAOT和采用SRAOT同步整流LCLC变换器的对比仿真波形[22]。图中,VDS_S2为S2的漏极-源极电压;VGS_SX为开关管SX的驱动信号(X=1, 2, 3, 4, 5, 6, 7, 8);iL1为流过L1的电流;iLM为流过等效励磁电感LM的电流;iS6为流过S6的电流;TD为死区时间;TF为额外的提前导通时间,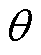 为移相角。所以,同步整流管总的提前导通时间TR表示为
为移相角。所以,同步整流管总的提前导通时间TR表示为
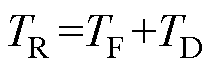 (3)
(3)
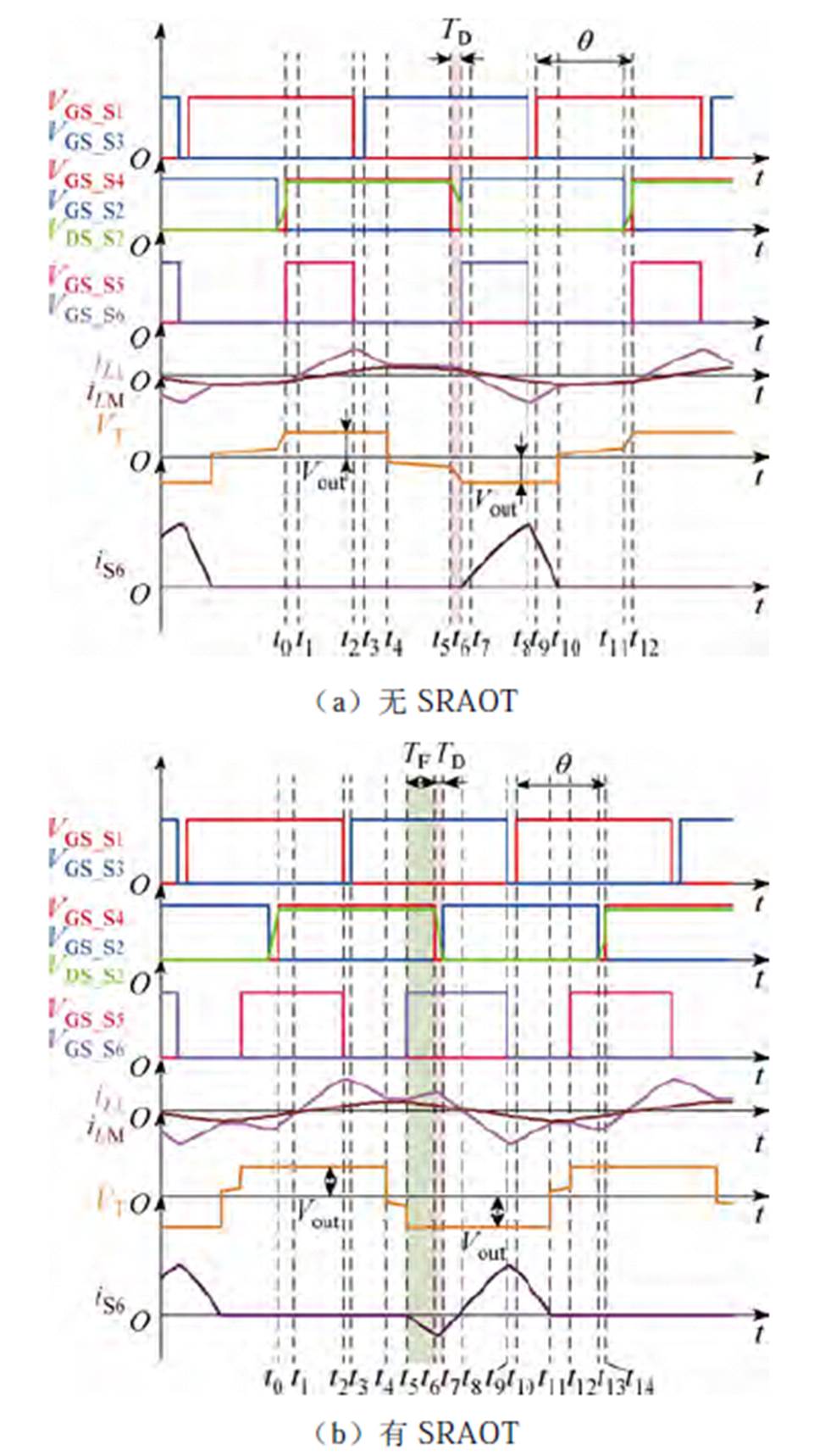
图2 同步整流LCLC变换器PSM波形
Fig.2 Waveforms of synchronous rectification LCLC converter under PSM
值得注意的是,iS6在TR的作用下负向流动,如图2b所示。这意味着iS6从二次侧回馈到了一次侧。这使得逆变单元中滞后桥臂开关管的关断电流增加。因此,滞后桥臂开关管有足够的能量在死区时间内完成充放电过程,并成功地完全实现了ZVS。但是,完全实现ZVS提升轻载运行效率只是效率优化的一种特定情况,不同参数不同运行工况下完全实现ZVS时运行效率不一定有所提升。
造成这一现象的主要原因如下:在同步整流开关管提前导通的过程中,一次侧滞后桥臂开关管开通损耗和输出电容损耗降低,同时一次侧滞后桥臂开关管的关断损耗和回路导通损耗增加。由此,降低的损耗与增加的损耗之间形成博弈折中操作,这对变换器综合效率具有重要影响。所以,完全实现ZVS提升轻载运行效率只是效率优化分析的一种特定情况,不同参数不同运行工况下完全实现ZVS下的损耗博弈结果不一定使得运行效率达到最优。
因此,本文提出了一种应用于同步整流型谐振变换器的轻载效率优化分析方法(LLEOAM)。在同步整流管提前导通控制的基础上,不同于直接设置TR=TZVS的方式[22],本文以获得不同运行条件为最优效率为目标,得到了优化的提前导通时间TR_op及相应的优化效率hop。
此处,Tzvs是确保逆变单元滞后桥臂开关管实现ZVS时同步整流管提前导通的最小时间。为确定其取值大小,需进行软开关实现条件分析,详细过程如下。
软开关实现过程是通过对开关管输出电容Coss电荷进行放电完成的。电容的放电公式为
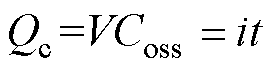 (4)
(4)
式中,Qc为电容中的电荷量;V为电容电压;i和t分别为放电电流和放电时间。分析式(4)可知,电容的放电过程与放电电流大小和放电时间有关。要想实现开关管的ZVS,有两个思路:①提升开关管开通前谐振腔电流;②增加死区时间。本文中,死区时间固定,采用提升开关管开通前谐振腔电流的方式实现ZVS。
传统不采用SRAOT时(见图2a),iL1(t6)与iL1(t5)及实现ZVS的条件关系如式(5)所示,无额外补充的电流能量,无法实现滞后桥臂开关管的ZVS。
 (5)
(5)
式中,iL1(t6)与iL1(t5)分别为图2a中t5和t6时刻的iL1值;Vin为输入电压。
采用SRAOT后(见图2b),为充分说明滞后桥臂开关管ZVS的实现过程,此处以滞后桥臂S2的ZVS实现为例,进行详细的分析。
对t6~t7中S2开通前的换流过程进行分析,可得
 (6)
(6)
因此,滞后桥臂开关管实现ZVS的条件为
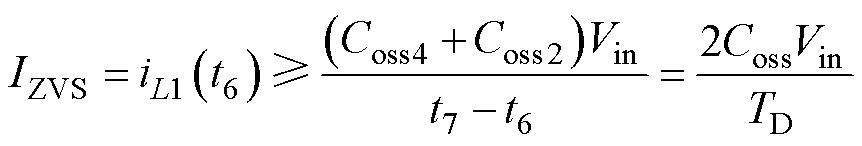 (7)
(7)
此处,IZVS为滞后桥臂开关管实现ZVS的边界条件,Coss2=Coss4=Coss。
与无SRAOT相比,有SRAOT调节下通过提前开通同步整流管实现一次侧谐振电流提升的部分为
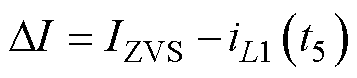 (8)
(8)
将式(7)代入式(8)得
 (9)
(9)
由于死区时间极短,图2b中的iL1(t7)和iL1(t6)数值上近似等效相等。结合文献[22]中的模态分析式(15)和本文中的式(9),得到TFmin表达式为
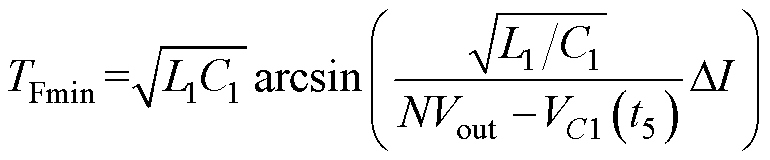 (10)
(10)
进一步地,将式(9)和式(10)结合,可解得提前开通时间最小值TRmin的值。这是滞后桥臂开关管实现ZVS条件下,同步整流管提前开通时间的最小值,即有
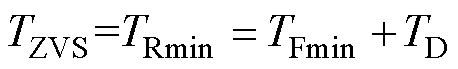 (11)
(11)
在增加同步整流管提前导通时间TR的过程中,降低的损耗和增加的损耗之间存在博弈,这对整体效率有重要影响。因此,调整TR可以实现效率优化。本节首先构建了受控变量(同步整流开关管提前开通时间TR)与损耗Ploss间的数学模型。并分析了轻载效率优化分析方法(LLEOAM)的工作原理,提出并总结了不同工作条件下损耗导数 和TR的基本关系。由此,变换器获得了优化的提前导通时间TR_op及相应的优化效率hop。
和TR的基本关系。由此,变换器获得了优化的提前导通时间TR_op及相应的优化效率hop。
TR变化过程中,主要受影响的损耗为一次侧滞后桥臂开关管开通损耗,输出电容损耗,一次侧滞后桥臂开关管关断损耗,回路导通损耗。此外,随着TR的增加,前两种损耗逐渐降低,后两种损耗逐渐增加。损耗模型的建立可以为LLEOAM提供依据,详细过程如下。
3.1.1 开通损耗
超前桥臂开关管S1和S3可实现ZVS,开通损耗Pturnon,13=0;滞后桥臂开关管S2、S4未实现ZVS时有开通损耗Pturnon,S24,表示为
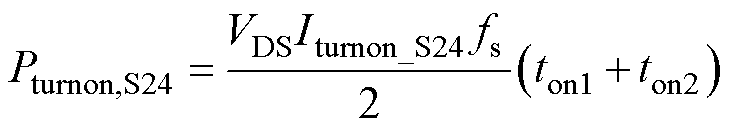 (12)
(12)
式中,Pturnon,S24为滞后桥臂开关管S2或S4的开通损耗;Iturnon_S24为开通电流。
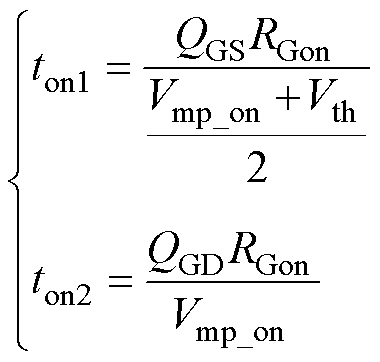 (13)
(13)
式中,QGS为栅极与源极之间的存储电荷量;RG_on为开通过程中开关管栅极回路等效阻抗;Vmp_on为开通过程米勒平台电压;Vth为门极阈值电压。
开关管漏-源极电压VDS可表示为
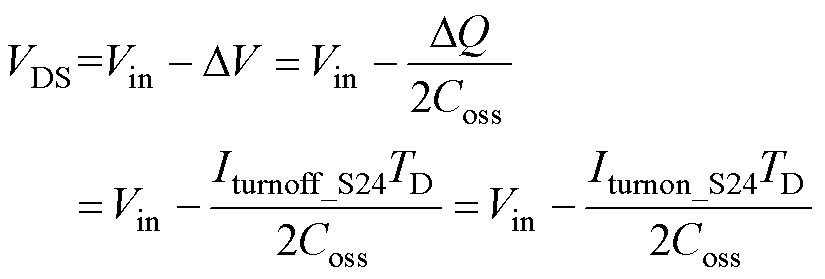 (14)
(14)
式中,Vin为输入电压;Iturnoff_S24为关断电流。
将式(14)代入式(12)可得
 (15)
(15)
值得说明的是,由于死区时间极短,Iturnon_S24和Iturnoff_S24在数值上近似等效相等,如图2a中的iL1(t6)和iL1(t5),或者图2b中的iL1(t7)和iL1(t6)。Iturnon_S24表达式为
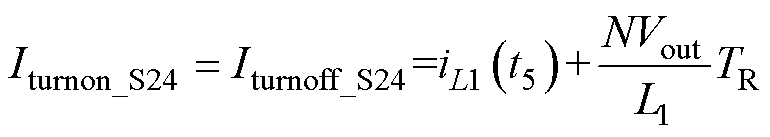 (16)
(16)
式中,iL1(t5)为t5时刻流过L1的电流;N为匝比;Vout为输出电压。
进一步地,将式(16)代入式(15),可以得到滞后桥臂开关管开通损耗与TR的关系式为
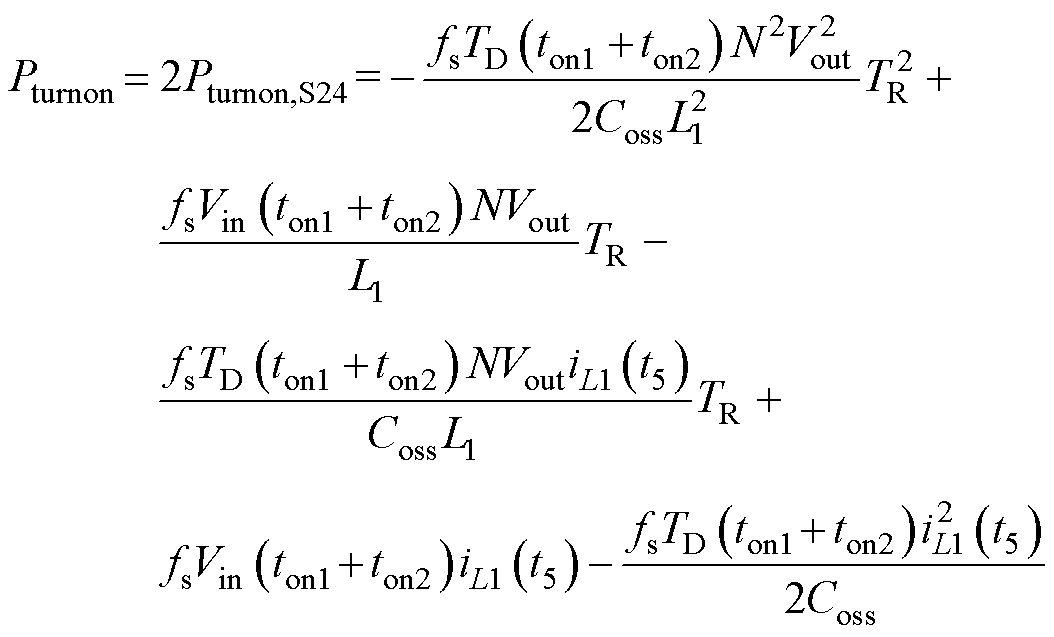 (17)
(17)
式中,Pturnon为滞后桥臂开关管总开通损耗。
3.1.2 输出电容损耗
ZVS未实现的情况下,死区时间内输出电容Coss充放电过程没有完成。故开关管开通时VDS无法降低至0,如图2a所示。这意味着Coss中仍然保有部分剩余的能量,产生了输出电容损耗。此处,由于只有滞后桥臂开关管S2、S4未实现ZVS,故输出电容损耗只与S2和S4有关。其表达式为
 (18)
(18)
将式(18)代入式(16)可得
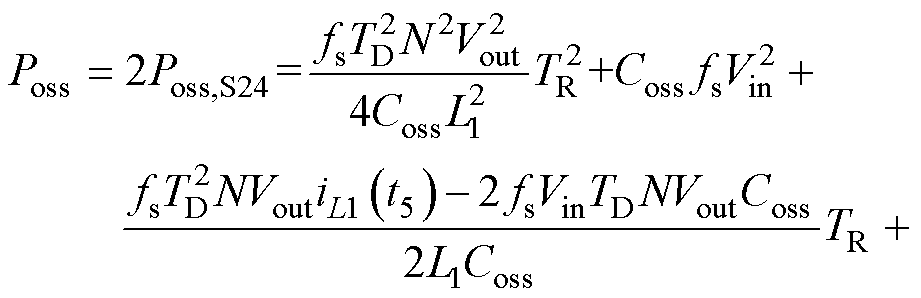
 (19)
(19)
在TR不断增加的过程中,部分种类的损耗降低;同时,也有部分种类的损耗增加,即关断损耗和导通损耗。这两种增加的损耗的模型构建过程如下。
3.1.3 关断损耗
关断损耗的增加主要是由关断电流的增加引起的,这主要涉及S2和S4。其表达式为

 (20)
(20)
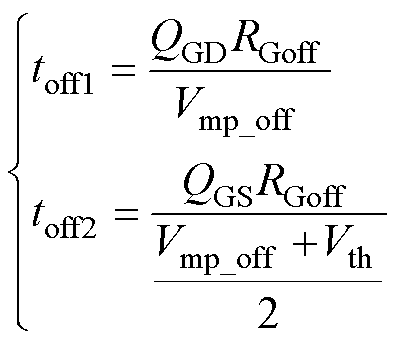 (21)
(21)
式中,RGoff为关断过程中开关管栅极回路等效阻抗;Vmp_off为关断过程米勒平台电压。
3.1.4 导通损耗
变换器中导通损耗主要涉及一次侧开关管、谐振电感、谐振电容、变压器以及二次侧开关管。
一次侧开关管导通损耗为
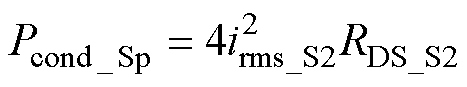 (22)
(22)
电感L1导通损耗为
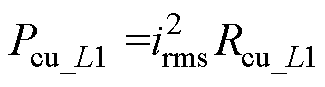 (23)
(23)
电容C1导通损耗为
 (24)
(24)
变压器导通损耗为
 (25)
(25)
二次侧开关管导通损耗为
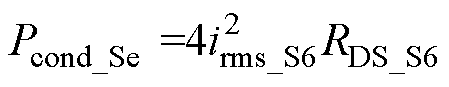 (26)
(26)
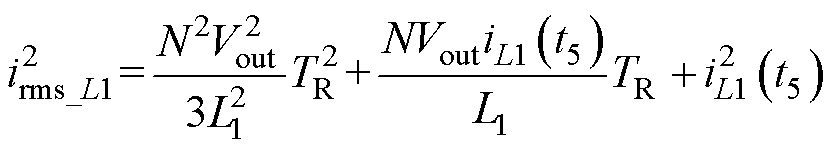 (27)
(27)
 (28)
(28)
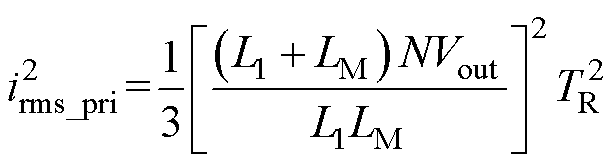 (29)
(29)
 (30)
(30)
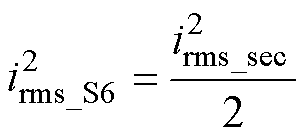 (31)
(31)
式中,irms_L1为谐振电流有效值;irms_pri和irms_sec分别为变压器一次和二次绕组电流有效值;irms_S2和irms_S6分别为开关管S2和S6的电流有效值,即代表一次侧和二次侧开关管电流有效值;Rcu_L1为L1的等效电阻;RC1为C1的等效电阻;Rcu_T_pri和Rcu_T_sec分别为变压器一次绕组和二次绕组的等效电阻;RDS_S2和RDS_S6分别为一次侧开关管和二次侧开关管的导通电阻。
因此,变换器总体导通损耗为
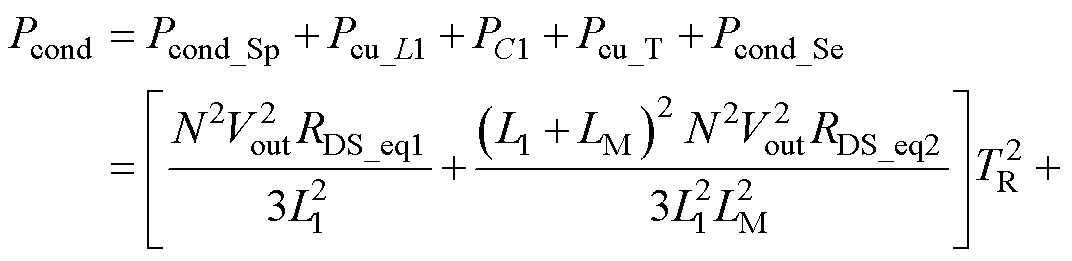
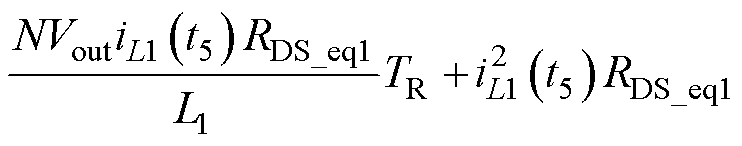 (32)
(32)
其中
 (33)
(33)
根据上述分析,在TR的变化过程中,四种受影响的损耗差值与受控变量TR的关系式为
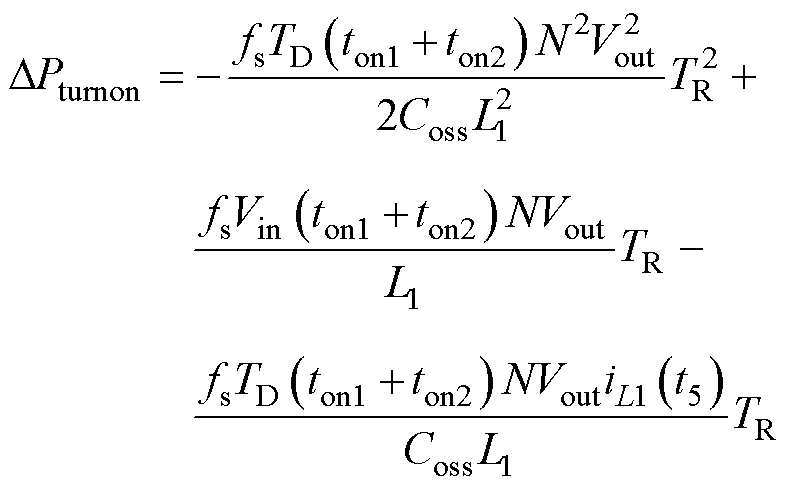 (34)
(34)
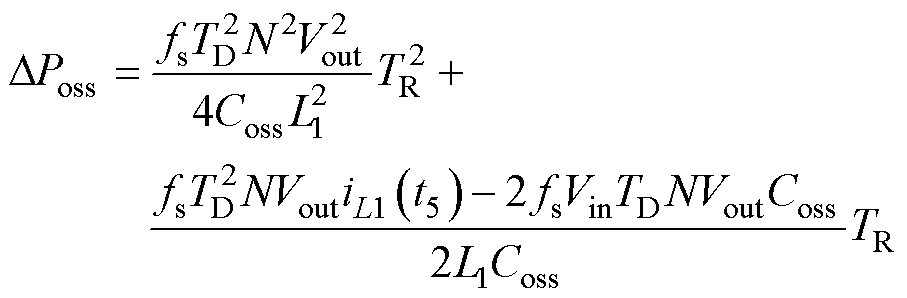 (35)
(35)
 (36)
(36)
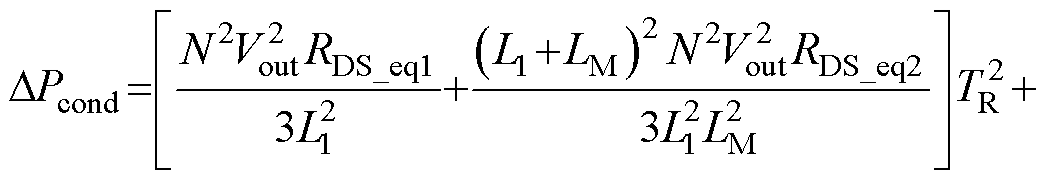
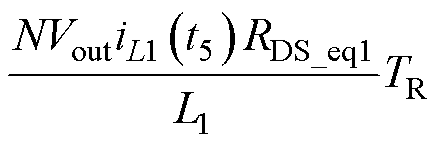 (37)
(37)
式中,ΔPturnon为降低的开通损耗;ΔPoss为降低的输出电容损耗;ΔPturnoff为增加的关断损耗;ΔPcond为增加的导通损耗。
综上所述,Pturnon和Poss与TR呈负相关,而Pturnoff和Pcond与TR呈正相关。所以,在降低的损耗(开通损耗和输出电容损耗)和增加的损耗(关断损耗和导通损耗)间形成动态博弈,进而引入了综合损耗最小的折中优化问题。基于此博弈,本节详细阐述了效率优化分析方法的原理。损耗差值之和Ploss与TR关系式为
 (38)
(38)
本文所提的轻载效率优化分析方法(LLEOAM)的核心思想分别为对Ploss求取一阶导数 和二阶导数
和二阶导数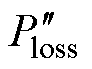 ,即
,即
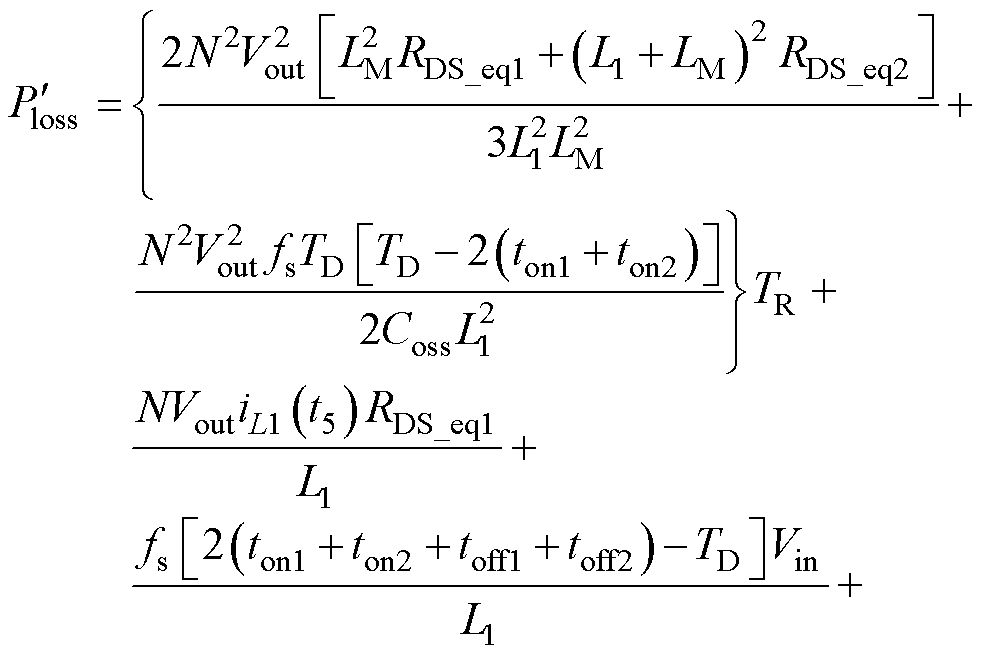
 (39)
(39)
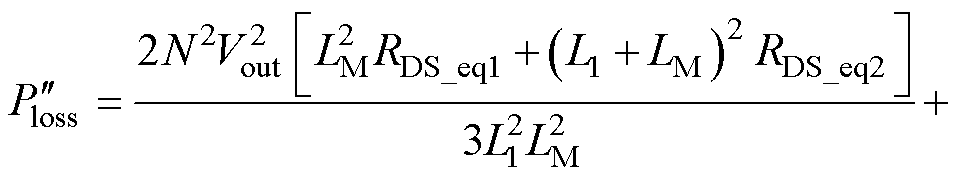
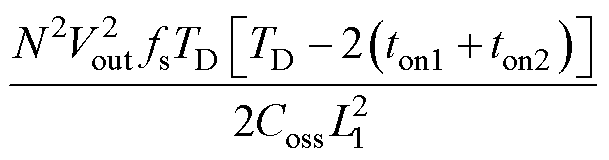 (40)
(40)
(1)当一阶导数 =0时,解得函数极值点,对应
=0时,解得函数极值点,对应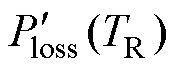 的过零点(TR=Tcross)。
的过零点(TR=Tcross)。
(2)当二阶导数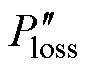 >0时,
>0时,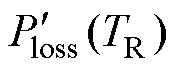 为单调递增的直线,Tcross为函数的极小值点(Plossmin(TR_exmin)),由于
为单调递增的直线,Tcross为函数的极小值点(Plossmin(TR_exmin)),由于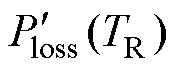 为一阶函数,所以在全域范围内极小值点即为最小值点。此时,损耗最小值点即对应效率最优点。相反地,若二阶导数
为一阶函数,所以在全域范围内极小值点即为最小值点。此时,损耗最小值点即对应效率最优点。相反地,若二阶导数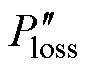 <0,
<0,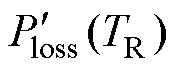 为单调递减的直线,Tcross为函数的极大值点(Plossmax(TR_exmax)),同样由于
为单调递减的直线,Tcross为函数的极大值点(Plossmax(TR_exmax)),同样由于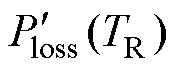 为一阶函数,全域范围内极大值点即为最大值点。此时,损耗最大值点即对应着效率最小值点,若想获得优化的运行效率则需要比较TR取值边界的效率点,进而获得最优效率。
为一阶函数,全域范围内极大值点即为最大值点。此时,损耗最大值点即对应着效率最小值点,若想获得优化的运行效率则需要比较TR取值边界的效率点,进而获得最优效率。
(3)对于过零点Tcross<0的情况,这代表着极值点出现在同步整流管滞后开通的情况。此时,无法构建回馈电流通路,ZVS并未得到改善。式(34)~式(36)为0,式(37)发生变化,使得本文建模式(38)并不完全适用。但显而易见的是,与同步整流管提前开通的情况相比,本工况相当于二次侧同步整流导通时间减小。这样本应流过二次侧同步整流管沟道的电流经由同步整流管的二极管完成电流闭合回路。这样反而会增加变换器的损耗,所以在实际应用中此种同步整流管滞后导通的工况并不可取。故同步整流管提前导通时间不能为负数,其取值左边界TR=0。
(4)对于过零点Tcross>TZVS的情况,这代表着极值点出现在滞后桥臂开关管已经实现ZVS后,同步整流管仍然继续提前导通的情况。此时,降低的损耗(开通损耗和输出电容损耗)已经降为0、无法继续优化;但是,同步整流管继续提前导通仍然会使得增加的损耗(关断损耗和导通损耗)继续增加,这样反而会增加变换器的损耗,对变换器运行不利。所以在实际应用中此种工况并不可取。同步整流管提前导通时间不能超过TZVS,其取值右侧边界为TR=TZVS。
因此,针对全负载工况,基于本文建模方法与边界分析,使得损耗最小的同步整流管提前导通时间TR_op只出现在[0, TZVS]区间内,进而获得最优效率hop。
具体根据 和Tcross在不同工作条件下的区别,
和Tcross在不同工作条件下的区别, 总共可以呈现六种结果,如图3所示。分析图3可知,TR_op的影响因素有两个:①
总共可以呈现六种结果,如图3所示。分析图3可知,TR_op的影响因素有两个:①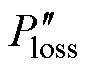 的正负方向,决定了
的正负方向,决定了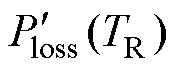 的增减关系;②0、Tcross和Tzvs之间的位置关系,影响了TR_op的选择。
的增减关系;②0、Tcross和Tzvs之间的位置关系,影响了TR_op的选择。

(a)>0且Tcross<0(b)>0且 0≤Tcross≤TZVS(c)>0且Tcross>TZVS

(d)<0且Tcross<0(e)<0且 0≤Tcross≤TZVS(f)<0且Tcross>TZVS
图3 不同参数下 的波形
的波形
Fig.3 The waveforms of based on different parameters
based on different parameters
进一步地,TR_op具体值的选取规则提炼如下。
(1)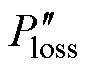 >0且Tcross<0:当TR≥0时,
>0且Tcross<0:当TR≥0时,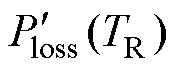 >0且单调递增。这意味着Ploss随着TR的增加而增加,对应的效率逐渐降低。因此,TR_op=0,以获得最佳效率,如图3a所示。
>0且单调递增。这意味着Ploss随着TR的增加而增加,对应的效率逐渐降低。因此,TR_op=0,以获得最佳效率,如图3a所示。
(2)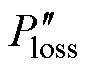 >0和0≤Tcross≤TZVS:当0≤TR≤Tcross时,
>0和0≤Tcross≤TZVS:当0≤TR≤Tcross时,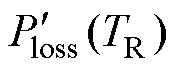 <0且单调递增,这表示Ploss在该区间内随着TR的增加而减小。而当Tcross<TR≤TZVS时,
<0且单调递增,这表示Ploss在该区间内随着TR的增加而减小。而当Tcross<TR≤TZVS时,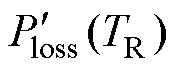 >0且单调递增,表明Ploss随TR的增加而增加。因此,Tcross是极小值点,其对应最低的损耗和最高的效率。因此,TR_op=Tcross,如图3b所示。
>0且单调递增,表明Ploss随TR的增加而增加。因此,Tcross是极小值点,其对应最低的损耗和最高的效率。因此,TR_op=Tcross,如图3b所示。
(3)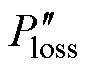 >0且Tcross>TZVS:当0≤TR≤TZVS时,
>0且Tcross>TZVS:当0≤TR≤TZVS时,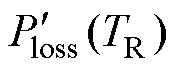 <0且单调递增。这意味着Ploss随着TR的增加而减小,对应的效率逐渐增加。因此,TR_op=TZVS,以获得最佳效率,如图3c所示。
<0且单调递增。这意味着Ploss随着TR的增加而减小,对应的效率逐渐增加。因此,TR_op=TZVS,以获得最佳效率,如图3c所示。
(4)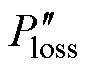 <0且Tcross<0:当TR≥0时,
<0且Tcross<0:当TR≥0时,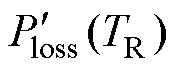 <0且单调递减。这意味着Ploss随着TR的增加而减小,对应的效率逐渐增加。因此,TR_op=TZVS以获得最佳效率,如图3d所示。
<0且单调递减。这意味着Ploss随着TR的增加而减小,对应的效率逐渐增加。因此,TR_op=TZVS以获得最佳效率,如图3d所示。
(5)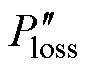 <0且0≤Tcross≤TZVS:当0≤TR≤Tcross时,
<0且0≤Tcross≤TZVS:当0≤TR≤Tcross时,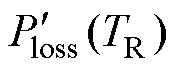 >0且单调递减,这表示Ploss在该区间内随着TR的增加而增加。而当Tcross<TR≤TZVS时,
>0且单调递减,这表示Ploss在该区间内随着TR的增加而增加。而当Tcross<TR≤TZVS时,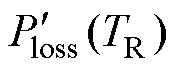 <0且单调递减,这表明在该区间Ploss随TR的增大而减小。因此,Tcross是极大值点,其对应于最高的损耗和最低的效率。因此,TR_op=0或TZVS,如图3e所示。
<0且单调递减,这表明在该区间Ploss随TR的增大而减小。因此,Tcross是极大值点,其对应于最高的损耗和最低的效率。因此,TR_op=0或TZVS,如图3e所示。
(6)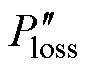 <0且Tcross>TZVS:当0≤TR≤TZVS时,
<0且Tcross>TZVS:当0≤TR≤TZVS时,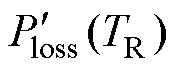 >0且单调递减。这意味着Ploss随着TR的增加而增加,这对应着效率的逐渐降低。因此,TR_op=0以获得最佳效率,如图3f所示。
>0且单调递减。这意味着Ploss随着TR的增加而增加,这对应着效率的逐渐降低。因此,TR_op=0以获得最佳效率,如图3f所示。
通过上述分析方法,变换器可以获得最小的损耗,进而获得最佳的运行效率hop。
图4给出了具体的轻载效率优化方法(LLEOAM)的实施流程。
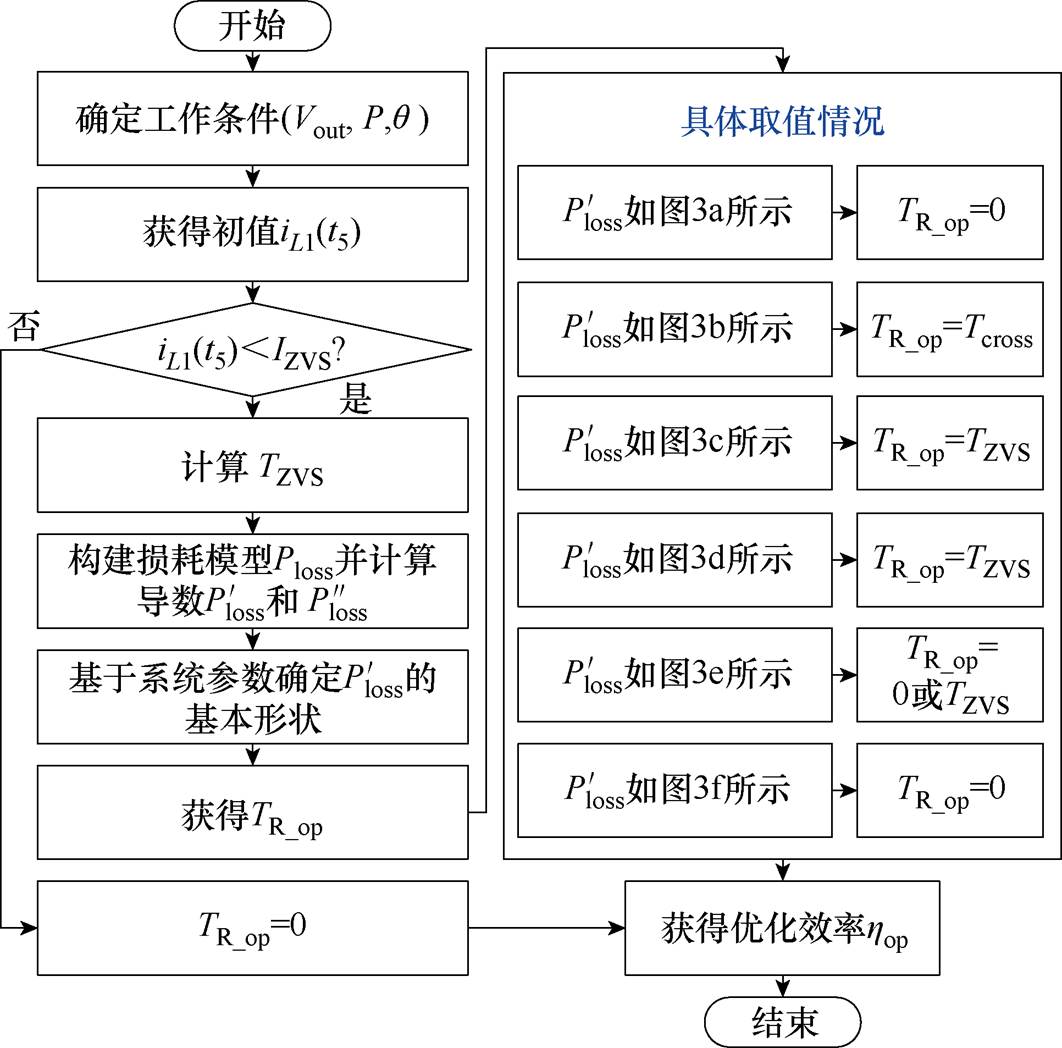
图4 轻载效率优化方法流程
Fig.4 The overall flowchart of LLEOAM
具体实施流程如下:
(1)确定变换器的工作状态,如输出电压Vout、功率等级P和移相角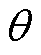 。
。
(2)获得了图2a中iL1(t5)的初始值。
(3)获得滞后桥臂开关管实现ZVS所需的电流IZVS。然后,比较iL1(t5)和IZVS的大小,确定滞后桥臂开关管在没有同步整流管提前导通的情况下是否能够实现ZVS。如果iL1(t5)>IZVS,意味着滞后桥臂开关管可以在没有同步整流管提前导通的情况下实现ZVS。此时,TR_op=0。相反地,如果iL1(t5)<IZVS,则意味着滞后桥臂开关管在没有同步整流管提前导通的情况下无法实现ZVS。然后,求解使得逆变单元滞后桥臂开关管实现ZVS所需的最小同步整流开关管提前导通时间Tzvs。
(4)针对iL1(t5)<IZVS的情况,在计算TZVS后,建立损耗模型Ploss,并计算损耗一次导数 及二次导数
及二次导数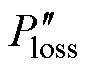 。
。
(5)将参数代入 和
和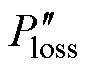 ,确定
,确定 的基本形状。
的基本形状。
(6)根据图3中 的不同结果,确定TR_op的具体值。
的不同结果,确定TR_op的具体值。
(7)根据TR_op得到该状态下的优化效率hop。
基于上述分析,本文搭建了PSIM仿真模型,相关参数及说明见表1。此外,本文也搭建了一台500 W的LCLC变换器实验样机,以进一步验证理论分析的可行性和合理性。实验样机如图5所示。
表1 变换器相关参数及说明
Tab.1 The specification and the parameters

参 数数值 (型号) L1/mH80 C1/nF24 Lm/mH420 Cm/nF47 N181 输入电压/V375 额定功率/W500 额定频率/kHz115 开关频率工作范围/kHz80~115 一次侧开关管型号C3M0065090D 二次侧开关管型号IXFP110N15T2
对于本文样机,其参数刚好可以满足图3b中的条件。这意味着TR_op=Tcross以获得优化的运行效率。对于图3b而言,Tcross是一个介于0~TZVS之间的值,这里称为不完全ZVS效率优化。
为了更好地比较分析,在相同的输出电压和轻载条件下进行了三组不同TR取值的实验验证,并提出了不完全ZVS效率优化概念,如图6所示。

图5 实验样机图片
Fig.5 The photo of the prototype
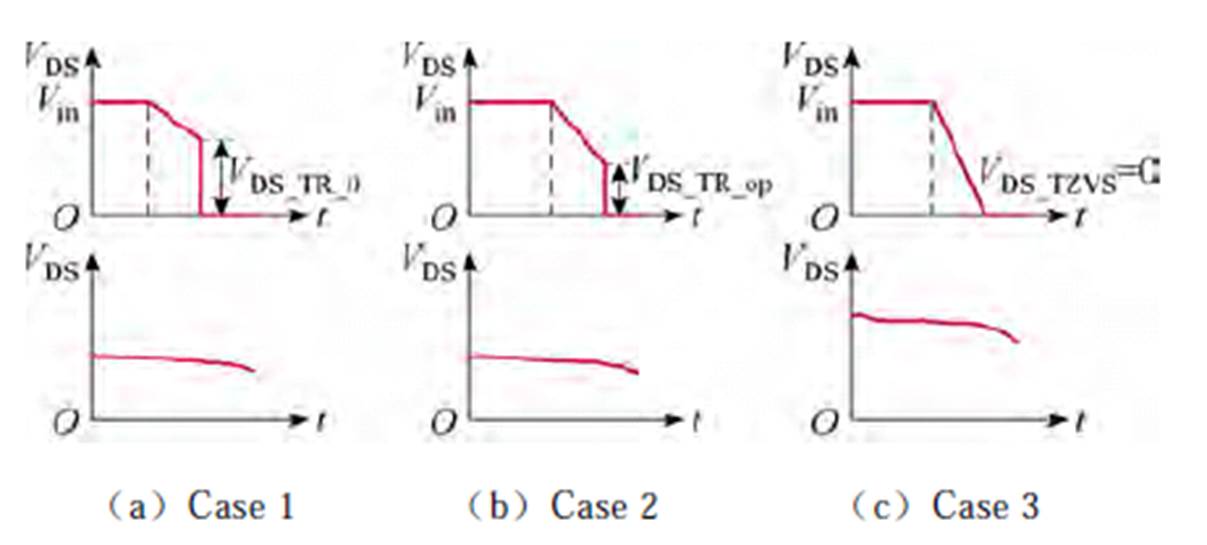
图6 不完全ZVS概念
Fig.6 The concept of incomplete ZVS efficiency optimization
根据TR的值,可以得到以下三种情况。
(1)Case 1:TR=0。同步整流开关管未提前导通。这种情况下由于iL1较低,逆变器单元滞后桥臂开关管ZVS丢失。与滞后桥臂开关的开通时刻相对应的VDS=VDS_TR_0,这个值相对较高。变换器工作在硬开关模式,如图6a所示。
(2)Case 2:TR=TR_op=Tcross。同步整流开关管提前导通。此外,提前导通时间TR_op=Tcross是以得到优化效率为博弈目标而获得的。此种情况下,逆变器单元滞后桥臂开关管ZVS条件没有完全实现,但与Case 1相比有所改善。此处称为不完全ZVS模式,如图6b所示。
(3)Case 3:TR=TZVS。同步整流开关管提前导通。此外,提前导通时间TR=TZVS是以获得逆变器单元滞后桥臂开关管ZVS为目标获得。这种情况下,由于iL1明显增加,与滞后桥臂开关的开通时刻相对应的VDS减小至0。变换器工作在完全ZVS模式。此时,尽管变换器已经实现了ZVS(变换器的开通损耗和输出电容损耗降低到0),但由于电流有效值的过度增加,关断损耗和导通损耗显著增加。这导致整体效率的下降。此处称为完全ZVS模式,如图6c所示。
针对这三种不同的情况,本文进行了对比仿真验证。对于不同情况下的仿真有一些相同的条件:①变换器在断续模式下以PSM方法工作;②输入电压Vin=375 V,标准输出电压Vout_nom=35 V,标准功率P=100 W,工作频率fs=115 kHz,移相角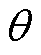 =114°。图7给出了P=100 W时三种不同Case下的仿真波形。图中,VGS_S1、VGS_S4和VDS_S4分别为一次侧开关管S1、S4和二次侧开关管S5的驱动信号,VDS_S4为一次侧开关管S4的漏源级电压,iL1为流过电感L1的电流,Vout为输出电压,Ts为工作周期(Ts= 8.69 ms)。
=114°。图7给出了P=100 W时三种不同Case下的仿真波形。图中,VGS_S1、VGS_S4和VDS_S4分别为一次侧开关管S1、S4和二次侧开关管S5的驱动信号,VDS_S4为一次侧开关管S4的漏源级电压,iL1为流过电感L1的电流,Vout为输出电压,Ts为工作周期(Ts= 8.69 ms)。
图7a为Case 1时P=100 W的仿真波形。滞后桥臂开关管S4和同步整流管S5同时开通,即TR=0。由iL1波形可知,滞后桥臂开关管S4在开通前的谐振电流相对较小,难以为充放电过程提供足够的能量。观察VDS_S4波形可知,S4开通时,VDS_S4=161.9 V,未能实现完全ZVS。此时,输出电压为35.0 V。变换器工作在为硬开关模式。
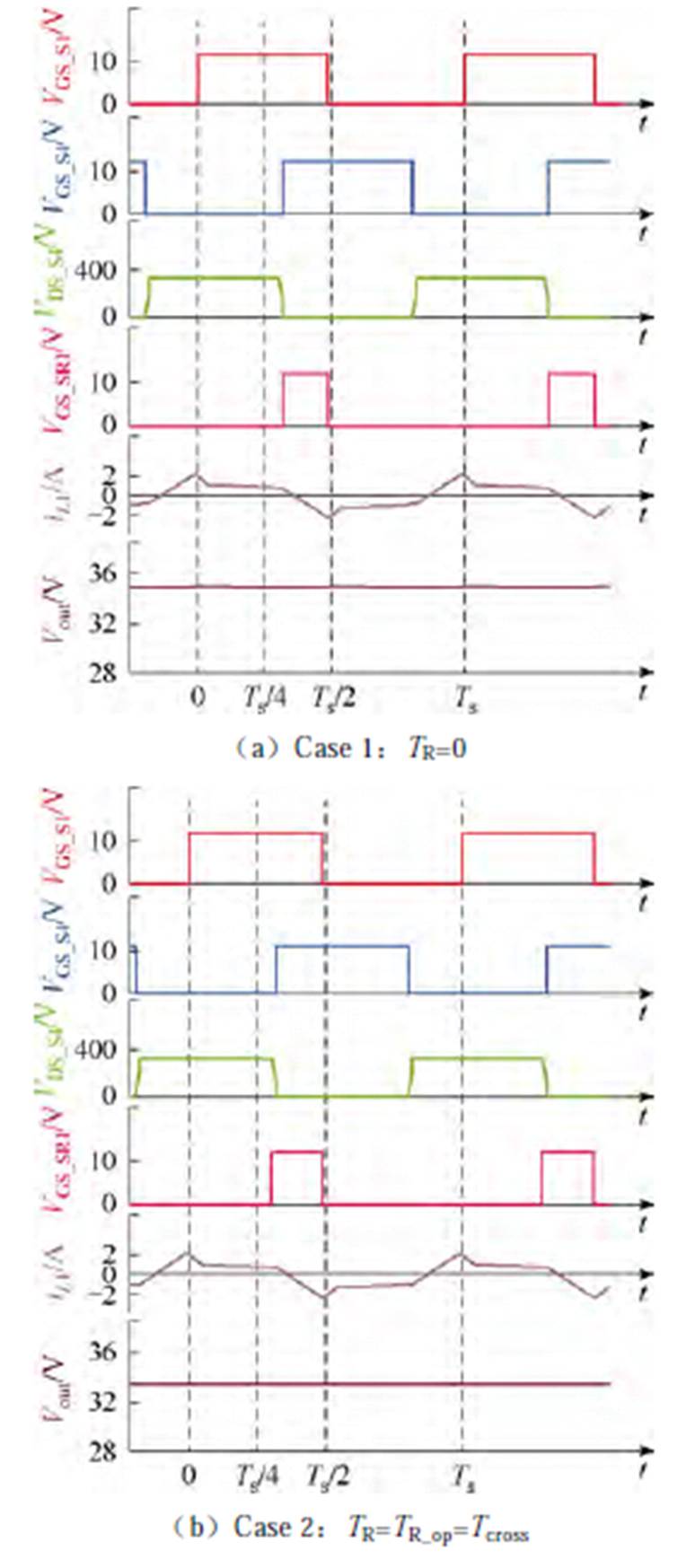
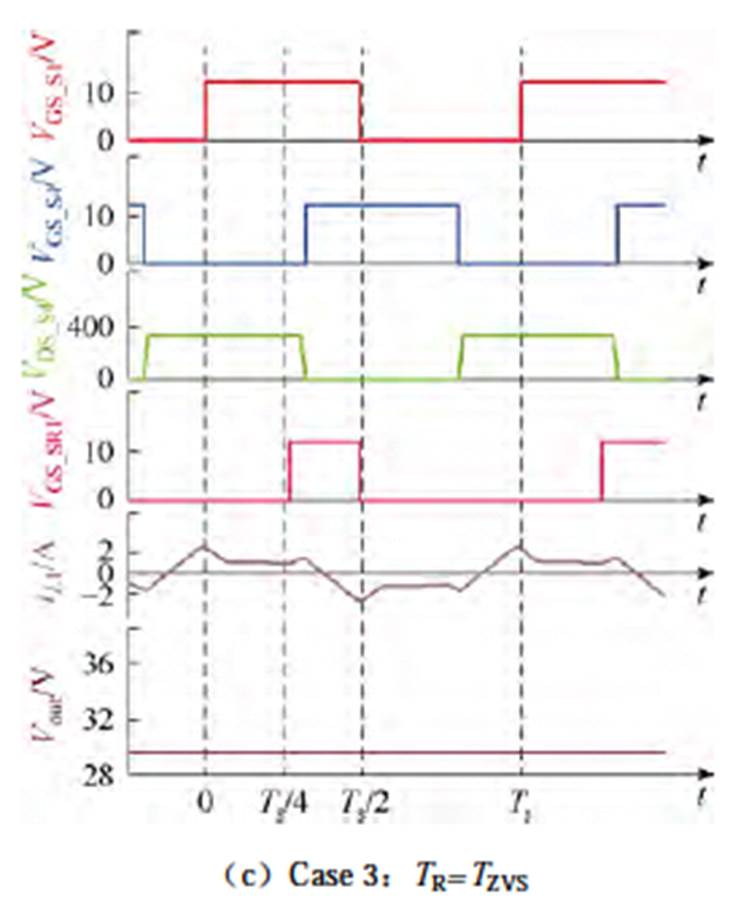
图7 P=100 W时三种Case下的实仿真波形
Fig.7 Simulation waveforms of P=100 W under three Cases
图7b为Case 2时P=100 W的仿真波形。此时,滞后桥臂开关管S4比同步整流管S5提前开通,TR= TR_op=Tcross。与图7a相比,滞后桥臂开关管S4在开通前的谐振电流iL1变化较小,该部分能量反馈会对滞后桥臂开关管的换流过程产生一定影响。所以,此工况下S4开通时,VDS_S4为有所减小,为128.7 V。在关断损耗和导通损耗几乎不变的前提下,可有效降低开通损耗和输出电容损耗。因此,此工况提升了变换器的整体工作效率。此时,输出电压为33.3 V。变换器工作在为不完全ZVS模式。
图7c为Case 3时P=100 W的仿真波形。此时,滞后桥臂开关管S4比同步整流管S5提前开通,TR= TZVS>Tcross。与图7a和图7b相比,滞后桥臂开关管开通前的谐振电流显著增加,这为开关管充放电过程提供了足够的能量。此外,S4开通时,VDS_S4= 0 V。但是,能量回馈过多,输出电压大幅下降,输出电压为29.6 V。系统增加的损耗将大于减少的损耗,造成整体损耗大幅增加,导致整体运行效率的降低。变换器工作在为完全ZVS模式。
为了进一步验证理论分析和仿真结果的正确性,本文基于实验样机进行了相关验证。实验波形如下所示。对于不同情况下的实验有一些相同的条件:①变换器在断续模式下以PSM方法工作;②输入电压Vin=375 V,标准输出电压Vout_nom=35 V,标准功率P=100 W,工作频率fs=115 kHz,移相角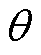 =117°。
=117°。
4.2.1 Case 1:TR=0 ns
图8给出了Case 1时P=100 W的实验波形。VGS_S5为二次侧开关管S5的驱动信号,图8a为一次侧波形,图8b为图8a的放大波形。此时,输入电压为375 V,工作频率为115 kHz,输出电压为34.7 V。从图8c可以看出,S4和S5同时开启(TR=0 ns)。此外,由图8b可知,滞后桥臂开关管S4在开通前的谐振电流相对较小,难以为充放电过程提供足够的能量,未能实现ZVS。此外,当VGS_S4被使能时,S4的漏极-源极电压(VDS_S4)约为163 V。这表明变换器工作在Case 1下(硬开关模式)。
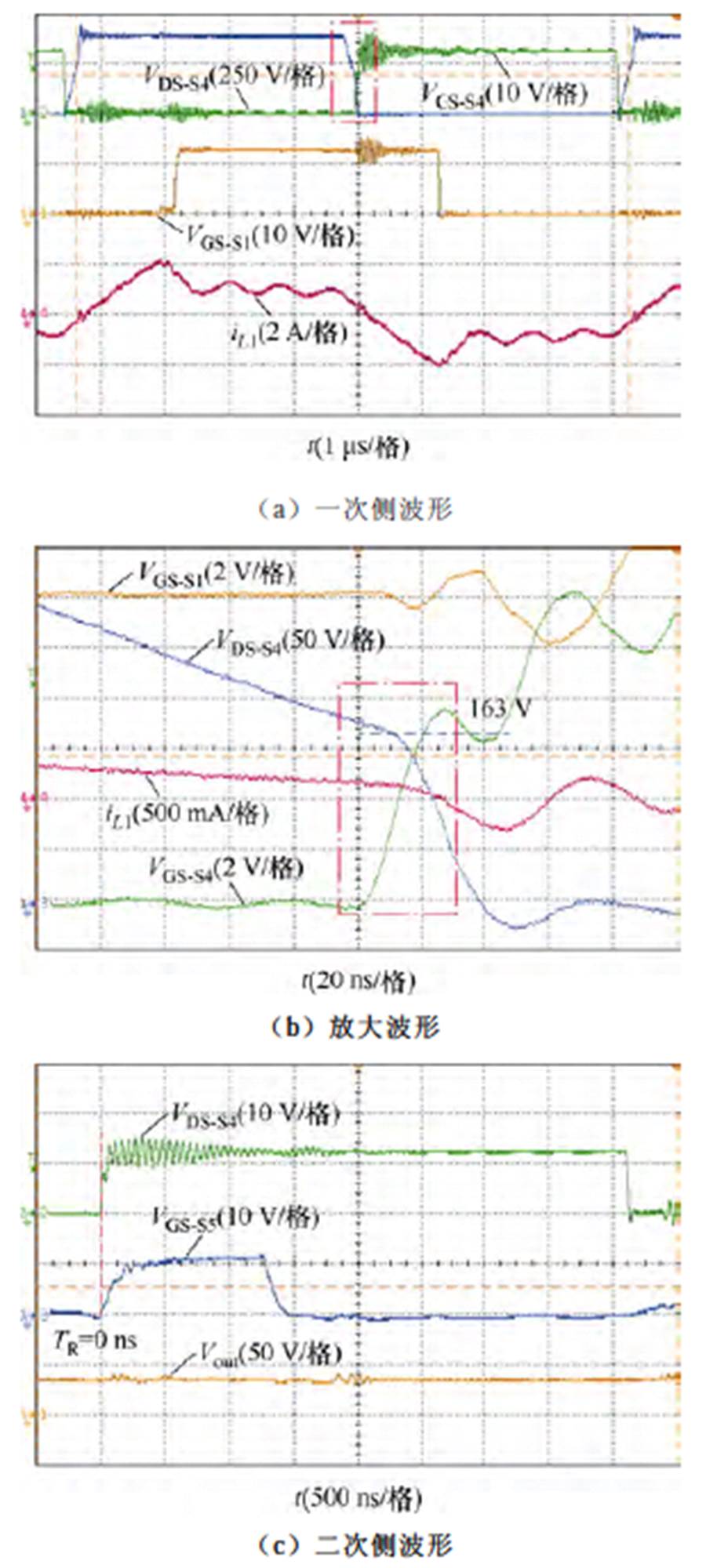
图8 Case 1时P=100 W的实验波形
Fig.8 Experimental waveforms of P=100 W in Case 1
4.2.2 Case 2:TR=TR_op=Tcross
图9给出了Case 2时P=100 W的实验波形。图9b为图9a的放大波形。各变量定义与图8相同。此时,输入电压为375 V,工作频率为115 kHz,输出电压为33.7 V。从图9c观察可知,S5比S4更早开通,且提前导通时间TR=TR_op=Tcross=90 ns。分析图9b可知,与图8b相比,采用不完全ZVS效率最优控制,滞后桥臂开关管导通前谐振电流增加非常小,该部分能量反馈对滞后桥臂开关管的换流过程有一定影响。所以,相比于图8b,使能VGS_S4时,VDS_S4减小。在关断损耗和导通损耗几乎不变的前提下,有效地降低了开通损耗和输出电容损耗。因此,提升了变换器的整体工作效率,变换器工作在不完全ZVS模式(Case 2)。
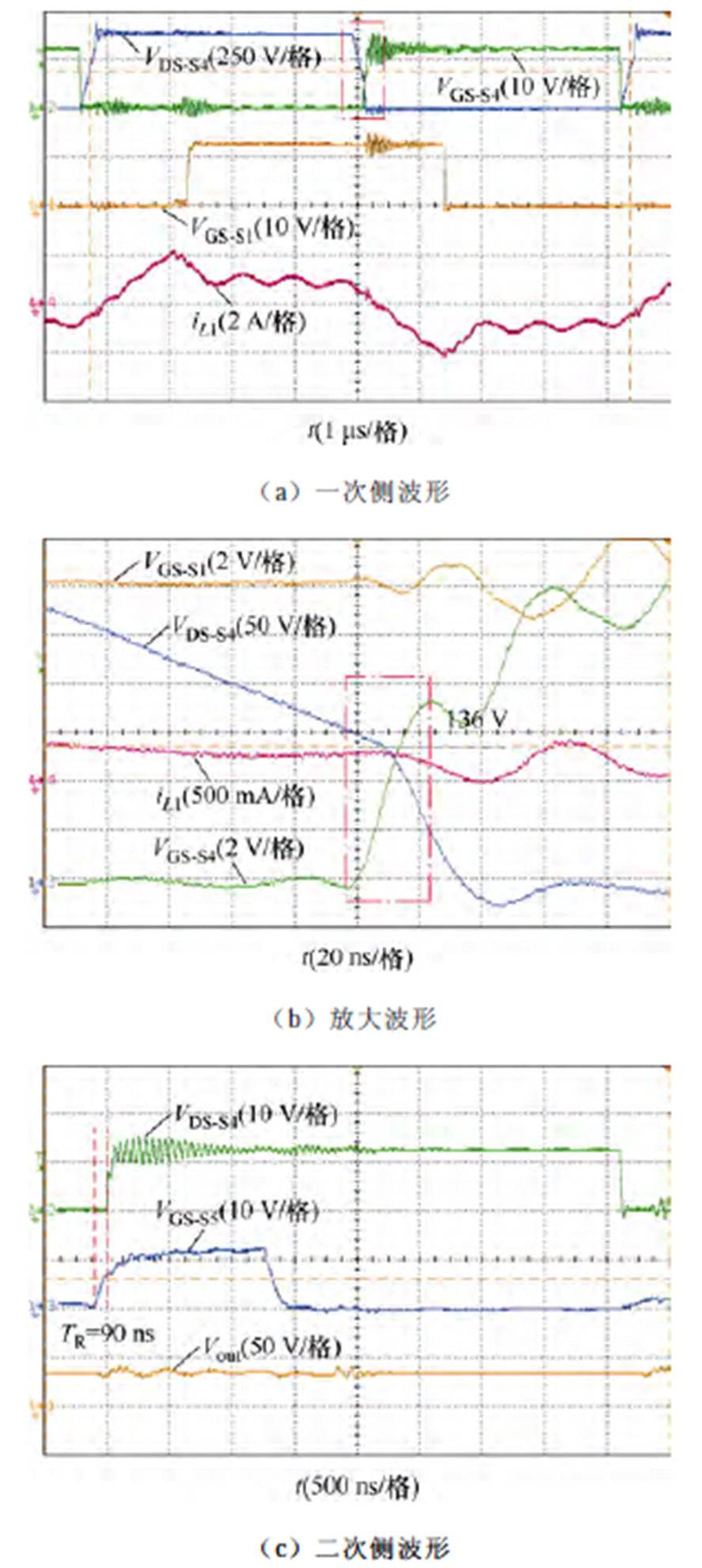
图9 Case 2时P=100 W的实验波形
Fig.9 Experimental waveforms of P=100 W in Case 2
4.2.3 Case 3:TR=TZVS
图10为Case 3时P=100 W的实验波形。图10b是图10a的放大波形。各变量定义与图8定义相同。由于回流能量过大,输出电压大幅下降,为29.9 V。从图10c观察可知,S5比S4更早开通,并且提前导通时间TR=TZVS=245 ns。此外,分析图10b可得,与图8b和图9b相比,滞后桥臂开关管开通前的谐振电流显著增加,这为开关管充放电过程提供了足够的能量,变换器实现了完全的ZVS。然而,由于大量的能量回馈,使得系统增加的损耗大于减少的损耗,系统整体损耗大幅增加,导致整体运行效率的降低。

图10 Case 3时P=100 W的实验波形
Fig.10 Experimental waveforms of P=100 W in Case 3
基于横河WT3000功率分析仪,本文给出了变换器在额定输出电压不同功率下的效率曲线,如图11所示。变换器额定频率、额定输出电压、393 W工况下获得了最高运行效率97.81%,这足以满足一般应用场合的效率需求。
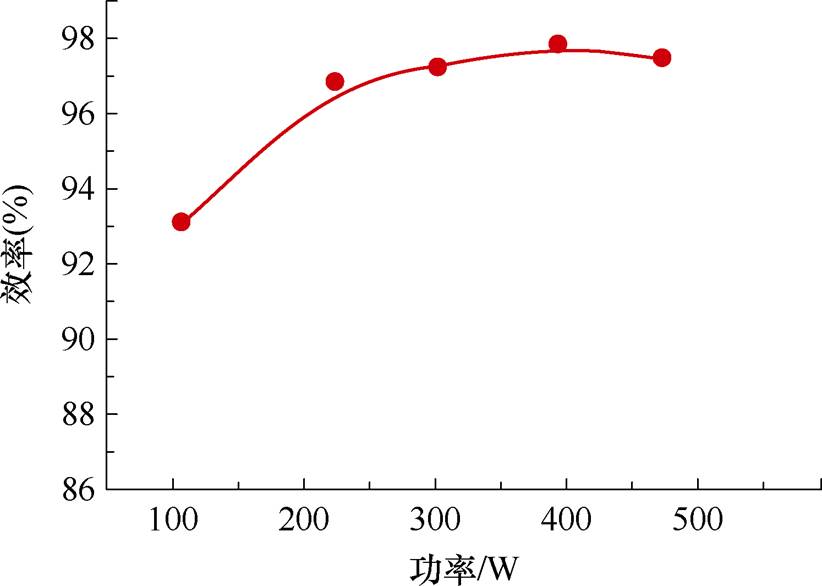
图11 额定输出电压(Vout=46.5 V)下不同功率效率曲线
Fig.11 Efficiency curve under different power of therated output voltage (Vout=46.5 V)
此外,针对本文的研究重点,即提高轻载运行效率,本文给出了变换器Vout=35 V时P=100 W的损耗分析及效率曲线,如图12所示。图中,降低的损耗是开通损耗和输出电容损耗,增加的损耗是关断损耗和导通损耗。可以观察到,在同一种运行工况的三种Case下,随着TR的增加(TR [0, TZVS],变换器总体运行效率与受影响的损耗的增减变化趋势相对应,符合理论分析。即受影响的损耗先减小后增大,同时效率曲线先增大后减小。
[0, TZVS],变换器总体运行效率与受影响的损耗的增减变化趋势相对应,符合理论分析。即受影响的损耗先减小后增大,同时效率曲线先增大后减小。
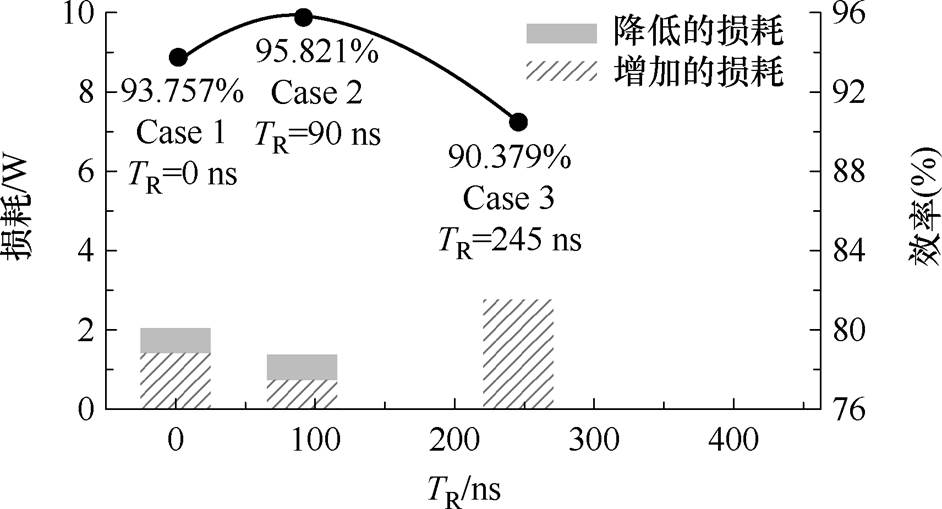
图12 Vout=35 V时P=100 W的损耗分析及效率曲线
Fig.12 Loss analysis and efficiency curves under the condition of P=100 W and Vout=35 V
主要原因是当TR相对较小时(在Case 1和Case 2之间),回馈能量相对有限,这对电路中电流变化影响很小。因此,增加的损耗增量也非常小;然而,在这个阶段,降低的损耗会显著减少,使得总损耗减小。直到Case 2,变换器损耗达到最小,并且相对应的效率达到最大。之后,随着TR继续增加(在Case 2和Case 3之间),回馈能量继续逐渐增强。降低的损耗被完全消除,变换器实现了完全ZVS。但是,由于过多的能量回馈导致了增加的损耗大幅上升,使得整体效率反而降低。在P=100 W的条件下,效率提升的效果明显。与不采用LLEOAM的传统方法(Case 1:TR=0)相比,采用LLEOAM(Case 2:TR=90ns)的效率提高了2%以上(从93.757%提高到95.821%)。
表2给出了不同控制方法的性能对比。相较于其他文献,本文提出的LLEOAM方法在改善轻载效率方面有良好效果,效率达95.821%(20%负载)。此外,变换器峰值效率达97.81%,具有一定的优势,变换器在全负载范围内均获得了良好的效率。
表2 不同控制方法的性能对比
Tab.2 Performance comparison among different methods

文献文献[23]文献[24]文献[25]本文LLEOAM 输入电压/V330~400320~385390375 输出电压/V12485646.5 功率等级/W300720350500 调制方式PFM+BurstPFM+PSM+PWMPFMPFM+PSM+ LLEOAM 峰值效率(%)9696.295.0097.81 轻载效率(%)93(20)95.2(20)91.09(20)95.821(20)
本文提出了一种应用于移相调制同步整流型谐振变换器的轻载效率优化分析方法(LLEOAM)。在同步整流管提前导通控制的基础上,以获得不同运行条件最优效率为目标,构建了受控变量(同步
整流开关管提前开通时间TR)与损耗(Ploss)间的数学模型,提出并总结了不同工作条件下损耗导数(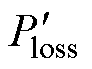 )和TR的基本关系,有效提升变换器的运行效率。最后,基于同步整流LCLC谐振变换器,本文搭建了一台500 W的实验样机并进行了相关实验验证。相比于传统无LLEOAM的方法,本文提出的LLEOAM使得变换器轻载运行效率(20%负载)提升2%以上(93.757%~95.821%)。此外,在谐振频率下变换器最高运行效率达97.81%,可满足一般应用场合。
)和TR的基本关系,有效提升变换器的运行效率。最后,基于同步整流LCLC谐振变换器,本文搭建了一台500 W的实验样机并进行了相关实验验证。相比于传统无LLEOAM的方法,本文提出的LLEOAM使得变换器轻载运行效率(20%负载)提升2%以上(93.757%~95.821%)。此外,在谐振频率下变换器最高运行效率达97.81%,可满足一般应用场合。
参考文献
[1] 曾嵘, 赵宇明, 赵彪, 等. 直流配用电关键技术研究与应用展望[J]. 中国电机工程学报, 2018, 38(23): 6791-6801, 7114.
Zeng Rong, Zhao Yuming, Zhao Biao, et al. A prospective look on research and application of DC power distribution technology[J]. Proceedings of the CSEE, 2018, 38(23): 6791-6801, 7114.
[2] 李海波, 赵宇明, 刘国伟, 等. 基于时序仿真的商业楼宇交流与直流配电系统能效对比[J]. 电工技术学报, 2020, 35(19): 4194-4206.
Li Haibo, Zhao Yuming, Liu Guowei, et al. The time sequential simulation based energy efficiency com- parison of AC and DC distribution power system in commercial buildings[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4194-4206.
[3] 熊雄, 季宇, 李蕊, 等. 直流配用电系统关键技术及应用示范综述[J]. 中国电机工程学报, 2018, 38(23): 6802-6813, 7115.
Xiong Xiong, Ji Yu, Li Rui, et al. An overview of key technology and demonstration application of DC distribution and consumption system[J]. Proceedings of the CSEE, 2018, 38(23): 6802-6813, 7115.
[4] 周国华, 邱森林, 张小兵. 宽增益高效率级联式四开关Buck-Boost LLC变换器[J]. 电工技术学报, 2024, 39(4): 1103-1115.
Zhou Guohua, Qiu Senlin, Zhang Xiaobing. Cascaded four-switch Buck-Boost LLC converter with wide gain range and high efficiency[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1103- 1115.
[5] 李加明, 任小永, 周治成, 等. 基于谐振网络优化的双向LLC-DCX多模块并联系统均流优化研究[J]. 电工技术学报, 2023, 38(10): 2720-2730, 2756.
Li Jiaming, Ren Xiaoyong, Zhou Zhicheng, et al. Research on current sharing optimization of bidirectional LLC-DCX multi-module parallel system based on resonant network optimization[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(10): 2720-2730, 2756.
[6] 徐菁涛, 许国, 孙尧, 等. 耦合电感集成型谐振变换器及其自适应频率控制[J]. 电工技术学报, 2023, 38(4): 998-1009.
Xu Jingtao, Xu Guo, Sun Yao, et al. Coupled inductor integrated resonant converter with adaptive frequency control[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 998-1009.
[7] 李彬彬, 王志远, 张丙旭, 等. 采用辅助变压器的可调压谐振零电压零电流开关变换器[J]. 电力系统自动化, 2022, 46(7): 160-169.
Li Binbin, Wang Zhiyuan, Zhang Bingxu, et al. Voltage-regulatable resonant zero-voltage zero- current switching converter with auxiliary trans- former[J]. Automation of Electric Power Systems, 2022, 46(7): 160-169.
[8] 周子航, 高祎韩, 刘懿静,等. 基于平面磁元件的 LLC变换器相关参数的整体优化设计方法[J/OL]. 电工技术学报, https://doi.org/10.19595/j.cnki.1000- 6753.tces.230778.
Zhou Zihang, Gao Yihan, Liu Yijing, et al. Para- meters flobal optimization design method for LLC converter with planar magnetic[J/OL]. Transa- ctions of China Electrotechnical Society, https://doi.org/ 10.19595/j.cnki.1000-6753.tces.230778.
[9] 荣振帅, 迟迎超, 孙战, 等. 基于氮化镓的高频LLC变换器研究[J]. 电气传动, 2023, 53(2): 3-9.
Rong Zhenshuai, Chi Yingchao, Sun Zhan, et al. Research on high frequency LLC converter based on GaN[J]. Electric Drive, 2023, 53(2): 3-9.
[10] 陈天锦, 曹亚, 曹智慧, 等. 基于复合控制的LLC谐振变换器轻载纹波优化[J]. 电气传动, 2021, 51(8): 34-39.
Chen Tianjin, Cao Ya, Cao Zhihui, et al. LLC resonant converter light ripple optimization based on composite control[J]. Electric Drive, 2021, 51(8): 34-39.
[11] 朱天宇, 纪延超, 王建赜. 一种高效率的宽输出电压范围 LLSC 谐振变换器及其控制方法[J]. 电工技术学报, 2022, 37(18): 4697-4706.
Zhu Tianyu, Ji Yanchao, Wang Jianze. A high efficiency and wide gain range LLSC resonant converter and its control method[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4697- 4706.
[12] Wu Hongfei, Zhan Xiaohai, Xing Yan. Interleaved LLC resonant converter with hybrid rectifier and variable-frequency plus phase-shift control for wide output voltage range applications[J]. IEEE Transa- ctions on Power Electronics, 2017, 32(6): 4246-4257.
[13] Xue Bo, Wang Haoyu, Liang Junrui, et al. Phase-shift modulated interleaved LLC converter with ultrawide output voltage range[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 493-503.
[14] Mumtahina U, Wolfs P J. Multimode optimization of the phase-shifted LLC series resonant converter[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10478-10489.
[15] Yeon C O, Kim J W, Park M H, et al. Improving the light-load regulation capability of LLC series resonant converter using impedance analysis[J]. IEEE Transactions on Power Electronics, 2017, 32(9): 7056-7067.
[16] 吕正, 颜湘武, 孙磊. 基于变频-移相混合控制的L-LLC谐振双向DC-DC变换器[J]. 电工技术学报, 2017, 32(4): 12-24.
Lü Zheng, Yan Xiangwu, Sun Lei. A L-LLC resonant bidirectional DC-DC converter based on hybrid control of variable frequency and phase shift[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 12-24.
[17] Shi Lin, Liu Bangyin, Duan Shanxu. Burst-mode and phase-shift hybrid control method of LLC converters for wide output range applications[J]. IEEE Transa- ctions on Industrial Electronics, 2020, 67(2): 1013- 1023.
[18] Wu Jiayang, Li Sinan, Tan S C, et al. Fixed-frequency phase-shift modulated capacitor-clamped LLC resonant converter for EV charging[J]. IEEE Transactions on Power Electronics, 2022, 37(11): 13730-13742.
[19] 王来利, 裴云庆, 秦洋, 等. 使用平面非线性电感提高高频DC-DC变换器轻载效率[J]. 电工技术学报, 2012, 27(2): 10-17, 32.
Wang Laili, Pei Yunqing, Qin Yang, et al. Improving light load efficiency of high frequency DC-DC converters with planar nonlinear inductors[J]. Transactions of China Electrotechnical Society, 2012, 27(2): 10-17, 32.
[20] Kim J H, Kim C E, Lee J B, et al. A simple control scheme for improving light-load efficiency in a full-bridge LLC resonant converter[C]//2014 Inter- national Power Electronics Conference (IPEC- Hiroshima 2014-ECCE ASIA), Hiroshima, Japan, 2014: 1743-1747.
[21] Zhao Biao, Yu Qingguang, Sun Weixin. Extended- phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4667-4680.
[22] Lin Jingyuan, Yueh H Y, Lin Yifeng, et al. Variable- frequency and phase-shift with synchronous recti- fication advance on-time hybrid control of LLC resonant converter for electric vehicles charger[J]. IEEE Journal of Emerging and Selected Topics in Industrial Electronics, 2023, 4(1): 348-356.
[23] 李志军, 徐铎, 孙乐, 等. 基于可变拓扑结构LLC变换器的新型混合调制策略[J]. 太阳能学报, 2021, 42(2): 338-345.
Li Zhijun, Xu Duo, Sun Le, et al. Novel hybrid modulation strategy based on variable topology LLC converter[J]. Acta Energiae Solaris Sinica, 2021, 42(2): 338-345.
[24] Kim J H, Kim C E, Kim J K, et al. Analysis on load-adaptive phase-shift control for high efficiency full-bridge LLC resonant converter under light-load conditions[J]. IEEE Transactions on Power Elec- tronics, 2016, 31(7): 4942-4955.
[25] Jeong Y, Lee Minsu, Park J D, et al. Hold-up time compensation circuit of half-bridge LLC resonant converter for high light-load efficiency[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13126-13135.
Abstract The characteristics of high efficiency and wide gain are the key indicators of the operational performance of resonant converters. Traditionally, pulse frequency modulation (PFM) is used to adjust the voltage gain of resonant converters. However, due to inherent structural limitations, the classical resonant converter has a flat voltage gain curve in the over-resonant region (fs>fr), which makes it difficult to adapt to wide output voltage applications, such as the LLC and LCLC resonant converters. Therefore, phase shift modulation (PSM) can be employed. It can effectively widen the voltage gain range. Unfortunately, the traditional PSM control method faces the problem of missing soft switching in the lagging bridge arm under light load conditions. Thus, this paper proposes a light load efficiency optimal analysis method for phase-shift- modulated synchronous rectification resonant converters (LLEOAM).
Firstly, the idea that the synchronous rectifier is conducted in advance is adopted in the LLEOAM. By adjusting the advance conduction time of the synchronous rectifier, some energy is fed back from the secondary side to the primary side. Interestingly, in the process of increasing the advance conduction time of the synchronous rectifier, there is a dynamic game between the reduced loss (turning on loss and output capacitance loss of the primary lagging bridge arm switch) and the increased loss (turning off loss of the primary lagging bridge arm switch and loop conduction loss), which has an important impact on the overall efficiency. Secondly, by constructing the mathematical model between the controlled variable (the synchronous rectifier advance conduction time TR) and the loss (Ploss), the basic relationship diagram between the loss derivative (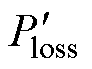 ) and TR under different working conditions is put forward and summarized. Finally, the optimized advance conduction time (TR_op) and the corresponding optimization efficiency (hop) are obtained. Overall, LLEOAM adopts the idea of a loss game to propose a general and universal TR calculation method instead of simply and roughly setting a TR that makes the lagging bridge arm switching tube realize ZVS.
) and TR under different working conditions is put forward and summarized. Finally, the optimized advance conduction time (TR_op) and the corresponding optimization efficiency (hop) are obtained. Overall, LLEOAM adopts the idea of a loss game to propose a general and universal TR calculation method instead of simply and roughly setting a TR that makes the lagging bridge arm switching tube realize ZVS.
A 500 W experimental prototype is built based on an LCLC resonant converter. Simulation analysis and power experiments are conducted. Besides, a concept of incomplete ZVS efficiency optimization is proposed. According to the value of TR, three cases can be obtained: Case 1 (TR=0), Case 2 (TR=TR_op=Tcoss), and Case 3 (TR=TZVS). The test results show that in the condition of P=100 W and Vout=35 V, the efficiency of the three different cases is 93.757%, 95.821%, and 90.379%, respectively. Compared with traditional PSM control (Case 1), the efficiency of light load (20% load) is improved by more than 2% (93.757% to 95.821%) by using the efficiency optimization analysis method. Compared with traditional synchronous rectification advanced on-time control (Case 3), the efficiency of light load (20% load) is improved by more than 5% (90.379% to 95.821%).
The following conclusions can be drawn. (1) Regarding low efficiency under light load conditions, a light load efficiency optimal analysis method is proposed for LLEOAM. (2) Instead of traditional synchronous rectification advanced on-time control’s setting TR=TZVS, LLEOAM adopts the idea of loss tradeoff to propose a universal and effective calculation method of TR. (3) It can be extended to all synchronous rectification resonant converters and has good universality.
keywords:Phase shift modulation, efficiency optimization, multi-resonant DC-DC converter, synchronous rectification, soft switching
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.240420
国家自然科学基金青年基金——建筑/户用兆赫兹千瓦级储能双向直流变换技术及其控制方法研究(52307216)和基于宽禁带器件的高效率无隔离变低压柔性互联关键技术研究(5400- 202418174A-1-1-ZN)资助项目。
收稿日期 2024-03-18
改稿日期2024-04-22
陈梦颖 女,1993年生,博士研究生,研究方向为谐振型软开关直流变换器及其控制。E-mail: cmying@tju.edu.cn
陈 博 男,1989年生,博士,副研究员,研究方向为多谐振直流变换器等。E-mail: cb92614@tju.edu.cn(通信作者)
(编辑 陈 诚)