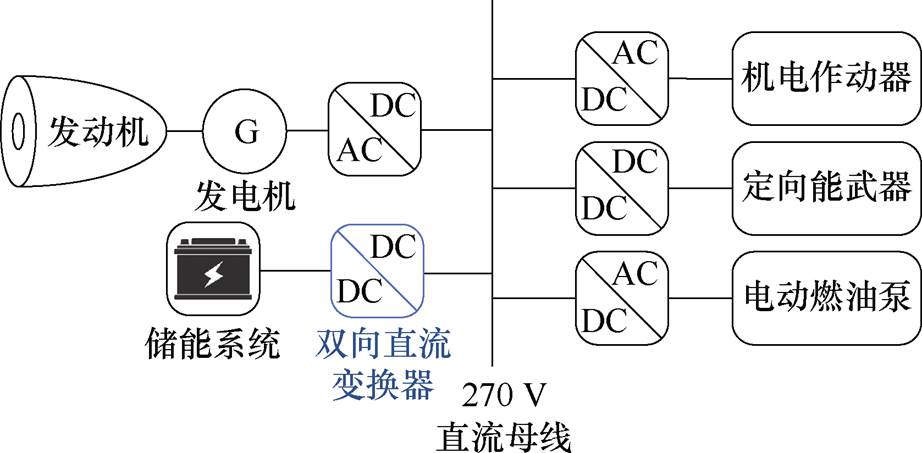
图1 多电飞机电源架构框图
Fig.1 Power architecture of more electric aircraft
摘要 电流模式控制是实现双有源桥变换器(DAB)高动态功率调控的有效手段。但在高频高功率密度应用场合,现有的电流模式控制方案仍存在电流传感器带宽不足、“模拟+数字”混合控制器实现复杂的问题。基于“比较触发”机制,该文提出一种适用于高频DAB变换器(百kHz开关频率)的电流模式控制及实现方法,通过罗氏线圈实现高频电感电流的精确感知,并设计基于单一微控制器的模数混合电流模式控制器,简化了控制系统结构、降低了系统成本。采用该文提出的控制方案,可实现高频DAB变换器电感电流的高动态控制,进而实现变换器的快速功率调控和逐周期限流保护。实验结果表明:所提方法实现了200 kHz DAB变换器的电流模式控制,电感电流的动态响应时间仅为2.5 ms,开关频率水平和动态响应远高于并优于已有研究成果。
关键词:双有源桥变换器 电流模式控制 罗氏线圈 动态响应
多电化、全电化是当前飞机发展的主要方向之一,是实现飞机轻量化、降低燃油消耗、提高系统可靠性和维护性的重要手段。与交流电源系统相比,270 V高压直流电源系统具有损耗低、质量轻、可靠性高等优点,已在我国空军主力机型中获得成功应用,并成为多电飞机电源系统的主要架构之一[1]。图1为多电飞机电源系统及其负载的简化结构框图,主要包括发电单元和负载两大部分。270 V高压直流母线电压由与飞机引擎机械耦合的发电机和整流器所建立。出于可靠性的考虑,发电单元的输出侧一般采用非电解电容器,使得直流母线呈现低惯量的特性[2]。而机电作动器、电动燃油泵、定向能武器等高动态负载的运行,均以短时(数十至数百ms之间)大功率消耗为前提,会对直流母线造成高频度、高强度的瞬态功率扰动[3-4],进而引发以下两大问题:①直流母线电压动态调节困难,易导致母线电压剧烈波动,甚至触发欠电压、过电压故障报警,严重影响母线上其他负荷的正常运行[5];②发电机转矩发生突变,造成与其机械耦合的飞机引擎非推进功率占比增大,增加发生喘振的风险,威胁飞机的安全、可靠运行[2]。

图1 多电飞机电源架构框图
Fig.1 Power architecture of more electric aircraft
将动态响应时间尺度为ms级的超级电容集成于飞机的电源系统,对高动态负载的瞬态功率进行快速补偿,可有效抑制母线电压波动、平滑发电机转矩[6],如图1所示。而双向直流变换器作为超级电容与直流母线的能量交互接口,其动态性能的优劣将直接影响瞬态功率补偿的效果。
双有源桥(Dual Active Bridge, DAB)变换器可实现双向功率传输,且具有电气隔离、升降压变换、软开关运行等优点[7-11],在多电飞机电源系统瞬态功率补偿应用中具有潜在的应用前景,其电路拓扑如图2所示[12]。图2中,变换器的电路拓扑由一次侧和二次侧两个全桥电路组成,两者的桥臂中点通过匝比为nt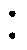 1的高频变压器和电感L相连接,电感电流记为iL。V1和V2分别为直流母线和储能单元的电压,i1和i2分别为输入电流和输出电流,va和vb分别为一次侧和二次侧全桥的输出电压,Q1~Q8为功率开关器件,C1和C2分别为输入、输出滤波电容。
1的高频变压器和电感L相连接,电感电流记为iL。V1和V2分别为直流母线和储能单元的电压,i1和i2分别为输入电流和输出电流,va和vb分别为一次侧和二次侧全桥的输出电压,Q1~Q8为功率开关器件,C1和C2分别为输入、输出滤波电容。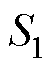 、
、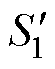 和
和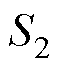 、
、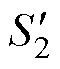 分别为一次侧和二次侧开关器件的控制信号,且
分别为一次侧和二次侧开关器件的控制信号,且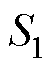 与
与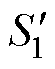 互补、
互补、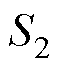 与
与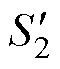 互补,占空比均为50%。DAB变换器常用的调制方式为移相调制,通过调节
互补,占空比均为50%。DAB变换器常用的调制方式为移相调制,通过调节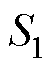 和
和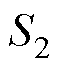 的相位,实现对传输功率的控制。
的相位,实现对传输功率的控制。
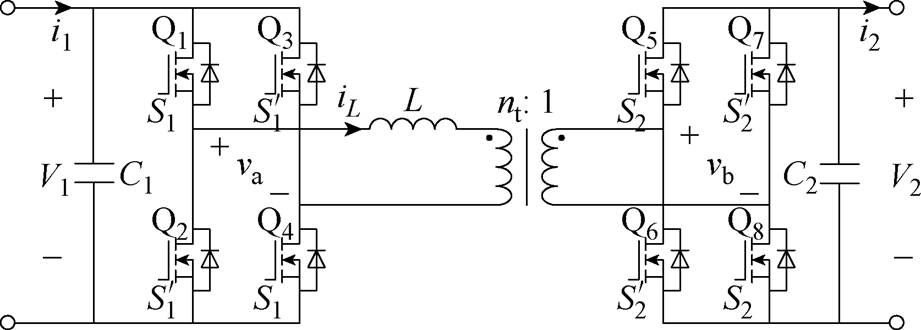
图2 双有源桥变换器的电路拓扑
Fig.2 Topology of DAB converters
但在基于移相控制建立的DAB变换器控制系统中,受到电感电流iL的高频动态特性影响,DAB变换器的小信号幅频特性曲线在开关频率处呈现二阶谐振特征,导致传统单环控制方法受系统幅值裕度约束,存在环路增益不足、穿越频率低的问题,难以实现高动态性能(带宽仅为百Hz级别)。有学者提出采用负载电流前馈控制来提升DAB变换器的动态响应,但由于缺乏对漏感电流的直接调控,在强瞬态过程(如传输功率突变)中会引入直流偏置,增加开关器件的电流应力和变压器饱和的风险[13]。
通过建立电感电流内环,使其对外近似等效为受控电流源,以消除传统单环控制中谐振特性的影响,是大幅提升系统动态性能的重要途径。国内外学者为此提出了多种基于模型预测的电感电流控制方法。为消除动态过程中电感电流的直流分量,有学者提出了无电感电流反馈的动态控制方法[14-17],但由于缺乏对实际电流的感知,难以补偿通态损耗、死区时间等因素造成的影响,同时也缺少过电流保护能力。还有学者提出了预测电流模式控制方法[18-19],但由于依赖于电感参数,需采取额外的补偿措施[18]。此外,基于变换器的状态平面轨迹,还有学者提出了DAB变换器的边界控制方法[20-22],但由于采样和控制频率必须远高于开关频率,因此不适用于高频场合。总的来讲,基于模型预测的电感电流控制方法,在参数敏感性、算法计算量、限流保护等方面存在不足,由于涉及逐周期电流采样和复杂计算,在高频应用场合中实现较为困难。现有文献报道的实验结果开关频率一般处于10~25 kHz的水平。
文献[23-24]借鉴PWM直流变换器中峰值电流模式控制的思想,提出了基于“比较触发”机制的DAB变换器电流模式控制方法。该电流模式控制器由模拟比较器和数字触发器构成,与基于模型预测的电流控制方法相比,其优点包括:①无需对电感电流连续采样和复杂运算,适用于高开关频率场合;②具备限流保护能力,且在负载突变、功率方向切换等动态过程自动实现零直流偏置;③对电感等参数变化不敏感。但文献[23-24]中仅给出了“比较触发”机制的理论分析和仿真结果,并未给出实验验证。基于相同的原理,文献[25]采用运算放大器、比较器和FPGA实现了DAB变换器的电流模式控制,其中变换器的开关频率为25 kHz。虽然电流模式控制在提升DAB变换器动态性能方面具备诸多优点,但在实际应用中,特别是高频高密度应用场合,仍面临以下两方面的挑战:
(1)电感电流的精确感知面临困难。电流模式控制依赖电感电流的精确感知,当DAB变换器的开关频率达到百kHz时,要求电流传感器的带宽达到数MHz。但目前常见的霍尔电流传感器的带宽普遍处于百kHz的水平,难以满足电流模式控制的需求。
(2)“模拟+数字”控制器的实现较为复杂。基于“比较触发”机制的电流模式控制器依赖模拟比较器和数字触发器,与传统移相控制相比,其控制系统所涉及的元件更多、控制逻辑更复杂。如何简化控制器的结构、降低系统成本值得进一步研究。
针对上述问题,本文提出一种基于罗氏线圈的高频DAB变换器电流模式控制及实现方案。一方面,将罗氏线圈电流传感器应用于百kHz开关频率DAB变换器,实现对高频电感电流的精确感知,为电流模式控制奠定基础;另一方面,设计基于单一微控制器(Microcontroller Unit, MCU)的模数混合电流模式控制器,将电流模式控制器的比较、触发等环节由1片MCU集成,简化控制系统结构、降低系统成本。采用本文提出的控制方案,可实现百kHz开关频率DAB变换器电感电流的高动态控制,进而实现DAB变换器的快速功率调控和逐周期限流保护。
本文提出的DAB变换器的模数混合电流模式控制框图如图3所示。模数混合电流模式控制器采用MCU实现,其主要包括两个比较器和一个RS触发器。当功率正向传输(由V1侧传输至V2侧)时,一次侧全桥电路产生占空比为50%的高频方波电压。控制器将电感电流iL与电流参考值±iref进行比较,在比较点处对二次侧的开关管进行触发控制。
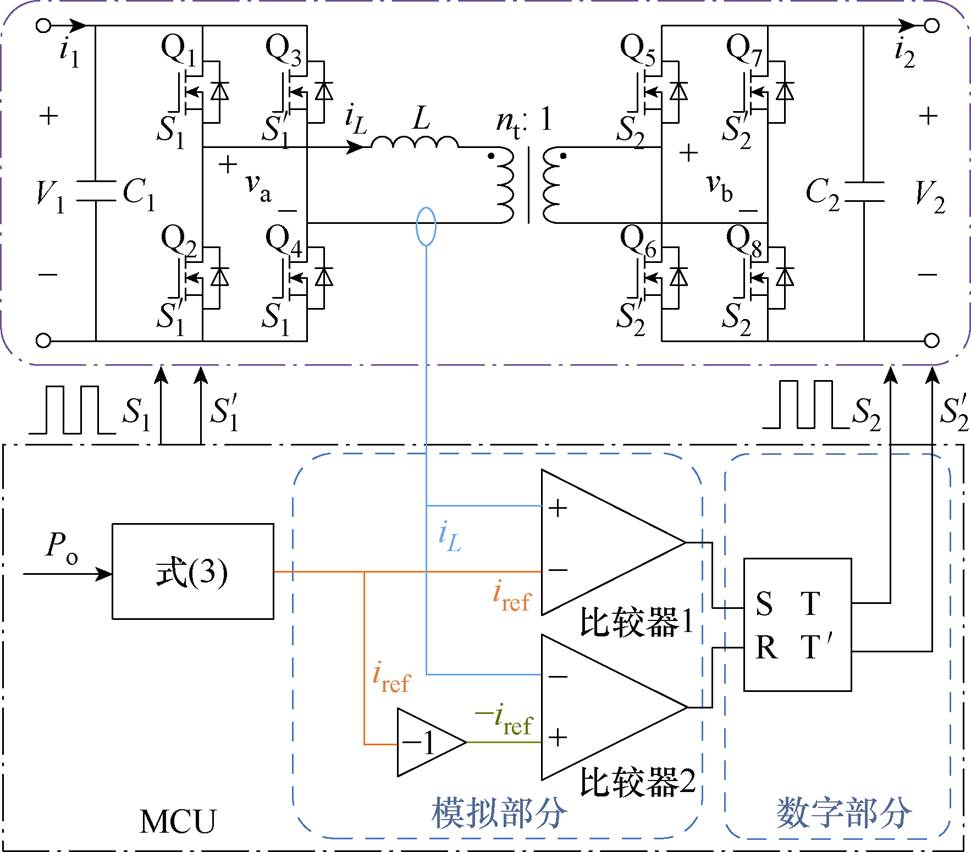
图3 DAB变换器模数混合电流模式控制框图
Fig.3 Block diagram of DAB converters with analog-digital hybrid current mode control
图4给出了在该控制方法下,DAB变换器的电感电流、RS触发器的输入输出信号和全桥电路输出电压va和vb的波形。
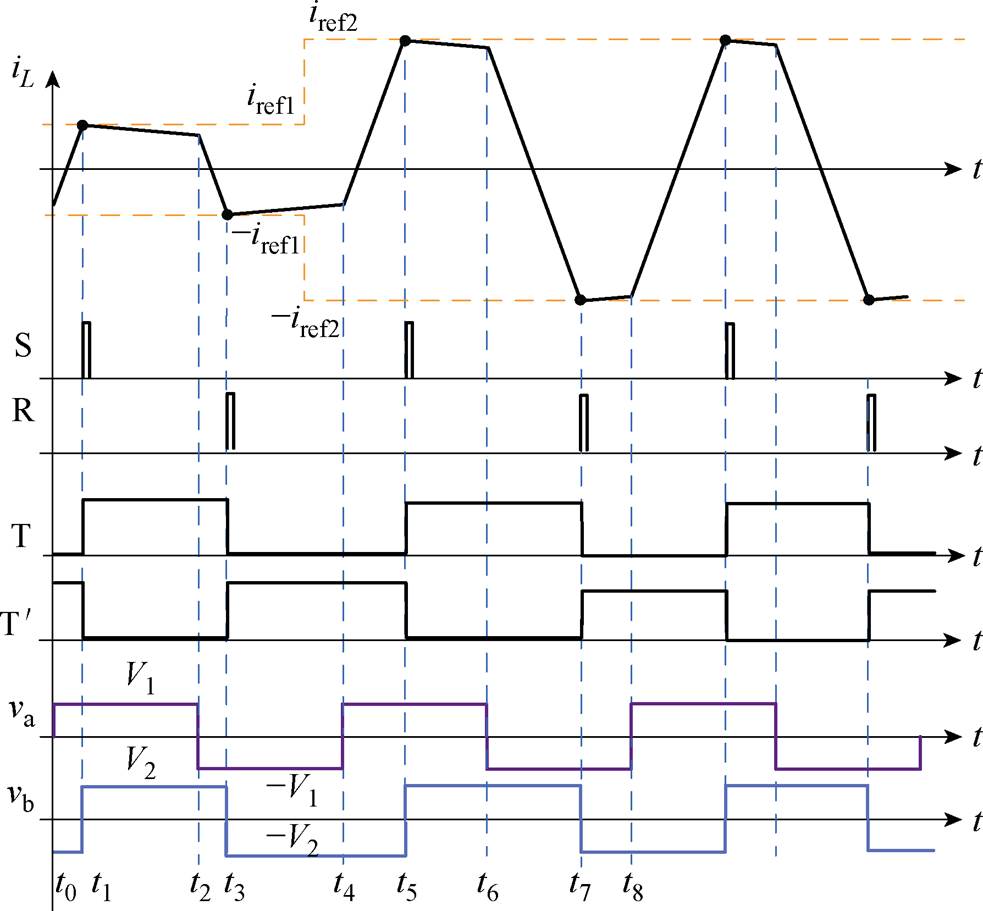
图4 模数混合电流模式控制下DAB变换器的波形
Fig.4 Waveforms of DAB converter with analog-digital hybrid current mode control
在t0~t1时间内,va电压为V1,vb电压为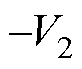 ,电感电流以斜率
,电感电流以斜率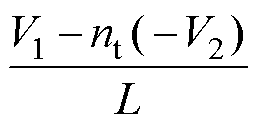 上升。
上升。
在t1时刻,电感电流iL达到正比较点iref,图3比较器1的输出由低置高,触发器置位引脚S接收到该上升边沿后,其输出T为高电平,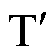 为低电平,因此,二次侧Q5和Q8导通、Q6和Q7关断,二次侧桥臂中点vb电压由-V2变为V2。电感电流在t1~t2时间内以斜率
为低电平,因此,二次侧Q5和Q8导通、Q6和Q7关断,二次侧桥臂中点vb电压由-V2变为V2。电感电流在t1~t2时间内以斜率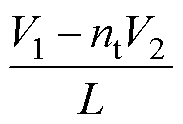 变化。
变化。
在t2时刻,一次侧桥臂中点电压va由V1变为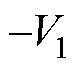 ,vb维持V2不变。电感电流iL在t2~t3时间内以斜率
,vb维持V2不变。电感电流iL在t2~t3时间内以斜率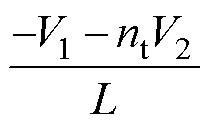 减小。
减小。
在t3时刻,电感电流iL下降到负比较点-iref,比较器2的输出由低置为高,触发器复位引脚R接收到该上升边沿后,其输出T为低电平,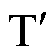 为高电平,因此,二次侧Q5和Q8关断、Q6和Q7导通,二次侧桥臂中点vb电压由V2变为
为高电平,因此,二次侧Q5和Q8关断、Q6和Q7导通,二次侧桥臂中点vb电压由V2变为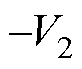 。电感电流在t3~t4时间内以斜率
。电感电流在t3~t4时间内以斜率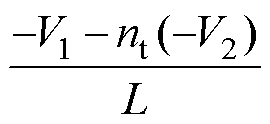 变化。
变化。
在t4时刻之后,va电压为V1,vb电压为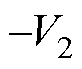 ,电感电流重新以0~t1时间内的斜率
,电感电流重新以0~t1时间内的斜率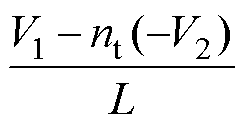 增大,进入下一个周期。
增大,进入下一个周期。
从图4可以看出,稳态时,DAB变换器在模数混合电流模式控制下的电感电流波形、全桥电路输出电压波形与传统移相控制一致。因此,就传输功率、软开关范围等稳态特性而言,二者完全相同。但需要注意的是,模数混合电流模式控制是基于“比较触发”事件对开关器件进行控制的,在控制机制上存在本质的不同。
图4还给出了在该控制方式下变换器的动态响应波形。在t3~t4时间段,电流参考值由iref1突变至iref2,则在t4~t5时间段内电感电流持续增加直至到达新的参考值iref2。自此,电感电流进入新的稳态。从以上分析可知,模数混合电流模式控制使电感电流具备了极高的动态响应速度和逐周期限流能力,其暂态过程仅需半个开关周期即可完成。因此,在该控制方式下变换器具备极高的功率控制响应能力,能够满足多电飞机瞬态功率补偿的应用需求。
还需要说明的是,当变换器反向(从V2侧传递至V1侧)传输功率时,需控制二次侧全桥(Q5~Q8)产生占空比为50%的高频方波电压,控制器将电感电流iL与电流参考值±iref进行比较,在比较点处对一次侧的开关管进行触发控制。
从图4可以看出,电流参考值iref与DAB变换器的传输功率密切相关。iref越大,则传输功率越大。在实际应用中,电流参考值±iref由变换器传输功率Po计算得到。以功率正向传输为例,忽略变换器寄生电阻和变压器励磁电感,给出iref关于Po的函数关系。
在稳态情况下,DAB变换器的传输功率Po的表达式[26]为
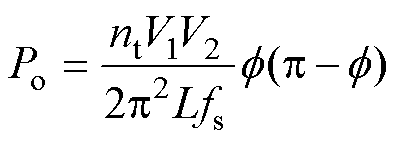 (1)
(1)
式中,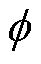 为方波电压va和vb的相位差;fs为开关频率。
为方波电压va和vb的相位差;fs为开关频率。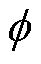 与iref的函数关系可以推导[25]为
与iref的函数关系可以推导[25]为
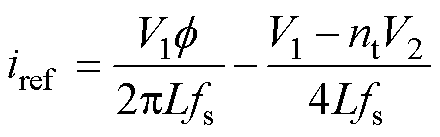 (2)
(2)
联立式(1)和式(2),可得
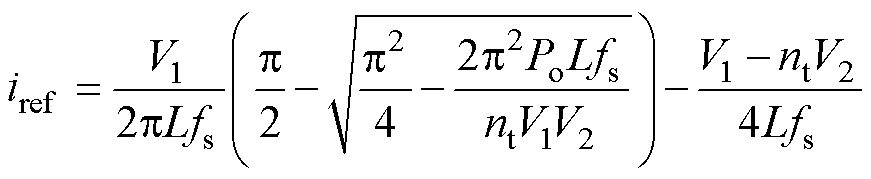 (3)
(3)
式(3)描述了电感电流参考值iref与传输功率Po之间的函数关系。如果已知变换器要达到的传输功率,则通过式(3)就可以计算出参考电流iref的取值。
实现DAB变换器的电流模式控制,依赖于对电感电流的精准感知。在多电飞机等高功率密度应用场合,DAB变换器的开关频率不断提升。当开关频率达到数百kHz时,要求电流传感器的带宽达到数MHz以准确捕获电感电流的基波和谐波信息(至少6次)[27]。
然而,当前电力电子装置中普遍采用霍尔型电流传感器时,其带宽一般处于几百kHz的水平,不足以支撑对高频电感电流的准确测量;而电阻分流器对变换器主电路造成一定的侵入,导致功耗增加,且难以与主电路之间实现电气隔离。电流互感器和罗氏线圈是两种常见的隔离高频电流传感器,其带宽可以达到数MHz至数十MHz。电流互感器通常选用标准化的环形磁心,与之相比,罗氏线圈的骨架采用非导磁材料,其设计更加灵活。例如,采用3D打印技术,可以制作出任意尺寸、任意形状、多种材质的线圈骨架,特别适用于高密度电力电子装置中在异形狭小空间下的电流感知。此外,罗氏线圈还可以采用印制电路板(Printed circuit board, PCB)作为骨架,利用PCB走线和过孔作为绕组,将电流传感器集成在电路板上,不仅使线圈的寄生参数精确可控,还可以实现电流传感器的高密度集成。因此,本文选用罗氏线圈电流传感器对高频DAB变换器的电感电流进行感知。
罗氏线圈电流传感器由罗氏线圈和积分器两部分构成,如图5a所示。由于非磁性骨架不产生聚磁效应,因此线圈仅检测被骨架空间占据的这一部分交变磁场。根据楞次定律,该交变磁场在线圈的两个端口之间感应出电动势e(t),该电动势为所测电流的微分信号,在经过积分器积分后即可重现被测电流。
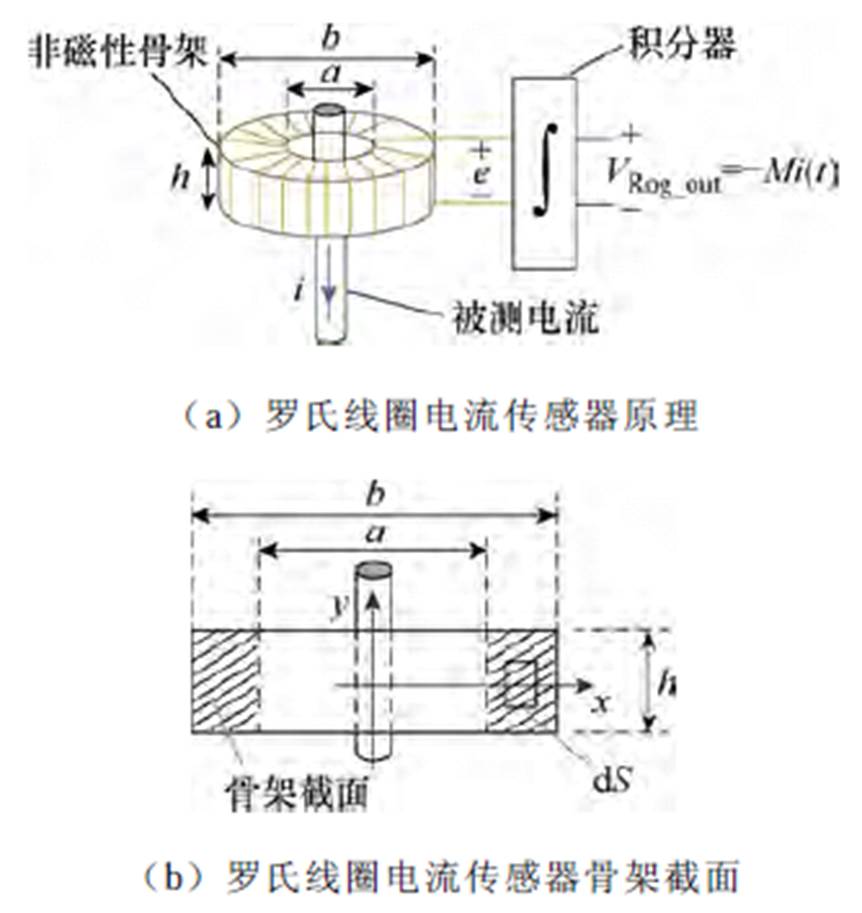
图5 罗氏线圈电流传感器原理和骨架截面
Fig.5 Rogowski coil current sensor schematic and cross-sectional view
由毕奥-萨伐尔定律可知,通过电流为i(t)的无限长直导线在距离其为c的任意一点的磁感应强度B满足
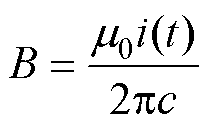 (4)
(4)
式中,m0为空气磁导率,m0=4p×10-7 H/m。对于内径为a、外径为b、骨架高度为h、截面为矩形的环形骨架,建立如图5b所示的坐标系。取面积微元dS,则穿过该面积微元的磁通量为
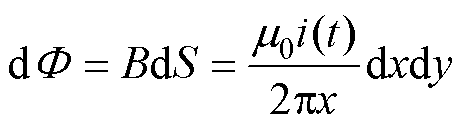 (5)
(5)
则每匝线圈所包围的磁通为
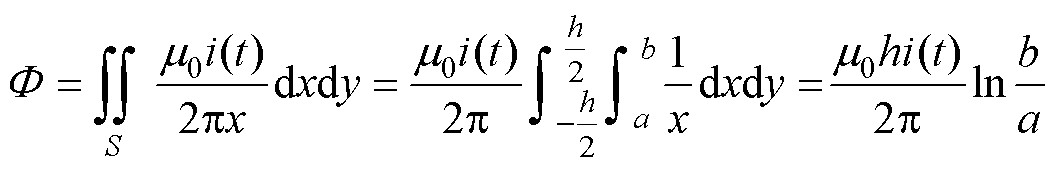 (6)
(6)
故罗氏线圈的感应电动势为
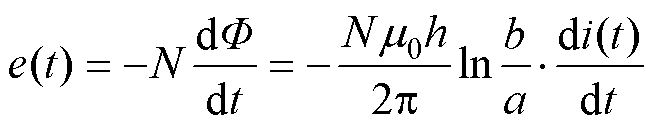 (7)
(7)
式中,N为线圈匝数。
通过一个积分器对e(t)进行积分,即可得到输出电压VRog_out(t)的表达式为
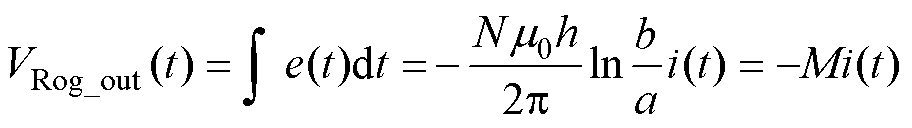 (8)
(8)
式中,M为被测导体与罗氏线圈之间的互感。
从式(8)可以看到,感生电动势e(t)经过积分器后得到的电压信号VRog_out(t)与被测电流i(t)成正比,可用于反映被测电流的信息。
罗氏线圈的传输特性表征了被测电流与积分器输出电压随频率变化的传递关系,是用来描述电流传感器带宽、灵敏度的重要途径。以下对积分器输出电压VRog_out(s)和被测电流I(s)在频域下的传递函数进行推导。罗氏线圈的集总参数等效电路模型和积分器电路如图6所示。对于集总参数等效电路列写KCL和KVL方程,可得
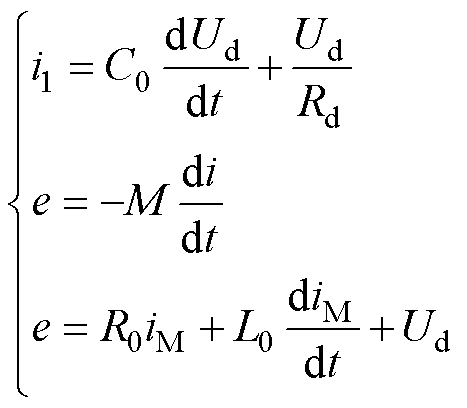 (9)
(9)
式中,R0、L0、C0分别为线圈的内阻、自感、分布电容;Rd为线圈的终端电阻;Ud为线圈的终端电压;iM为罗氏线圈感应电流。
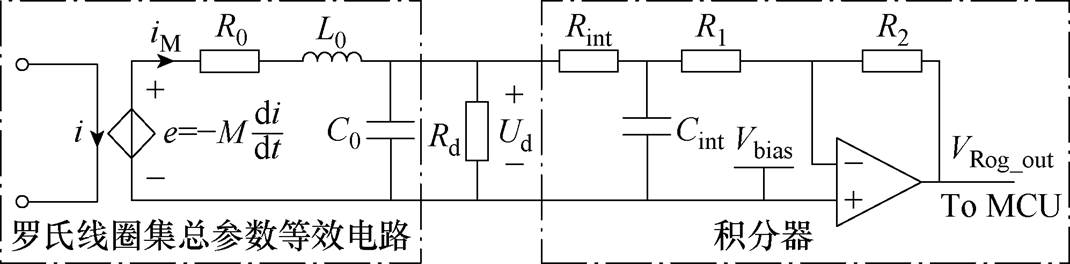
图6 罗氏线圈电流传感器
Fig.6 Rogowski coil current sensor
对式(9)进行拉普拉斯变换,整理得到罗氏线圈的传递函数Gcoil(s)为
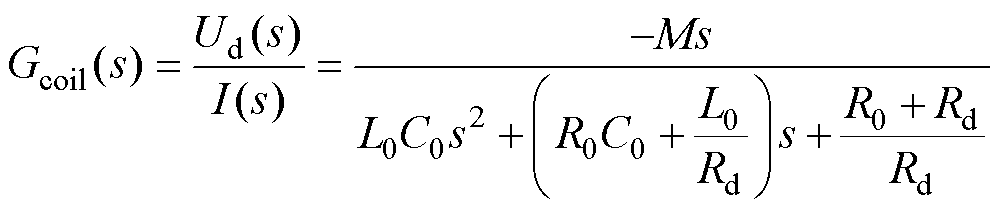 (10)
(10)
式(10)描述了罗氏线圈终端电压与被测电流之间的频率关系。本文使用RC无源积分器对罗氏线圈的终端电压进行积分,并使用反相比例放大电路放大积分得到的信号。反相比例放大电路也用于将Gcoil(s)的反相信号变为正相信号。此外,无源积分器需要满足其转折频率远小于开关频率,以工作在积分状态为例。
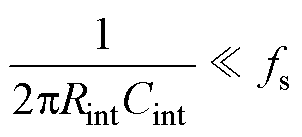 (11)
(11)
式中,Rint和Cint分别为积分电阻和积分电容。对于图6中的积分电路,其传递函数可以表示为
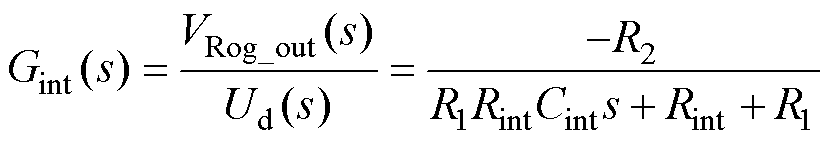 (12)
(12)
因此,罗氏线圈电流传感器传输特性表达式为
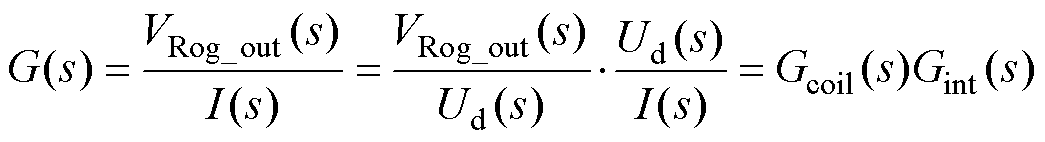 (13)
(13)
本文针对开关频率200 kHz、电感电流峰值最大15 A的DAB变换器,设计了罗氏线圈电流传感器,其带宽为30 kHz~3 MHz,灵敏度为150 mV/A,测量量程为(-15 A, 15 A)输出电压范围为(0 V,3 V)。所设计的罗氏线圈骨架由3D打印制作,其实物照片如图7所示。罗氏线圈的尺寸参数和积分处理电路的参数分别见表1和表2。

图7 制作的罗氏线圈实物
Fig.7 The picture of the Rogowski coil
表1 罗氏线圈尺寸参数
Tab.1 Dimensions parameters of Rogowski coil

参 数数 值 线圈内径a/mm9 线圈外径b/mm18 线圈高度h/mm4 漆包线线径p/mm0.3 线圈匝数N50
表2 罗氏线圈积分处理电路参数
Tab.2 Integral processing circuit parameters of Rogowski coil

参 数数 值 R1/kW1 R2/kW16 Rd/kW1 Rint/kW5.1 Cint/nF2.2
为了对罗氏线圈电流传感器的性能进行验证,本文采用Bode100矢量网络分析仪对其传输特性进行了测试,测试原理如图8a所示。通过Bode100的扰动源信号端口输出10 kHz~10 MHz频率的信号,并作为输入信号接入测量通道CH1。Ra=10 W 精度为0.1%的高精度无感电阻,用于产生幅值为1/10扰动源端口电压,且相位与之相同的电流信号i(t)。将积分器输出信号VRog_out(t)接入CH2。测试得到的传输特性如图8所示。从图8中可以看出,Bode100测量得到的罗氏线圈电流传感器的带宽约为30 kHz~3.2 MHz,带宽能够覆盖被测电感电流6次谐波以内的分量,满足对电感电流的准确感知需求。200 kHz处所对应的幅值为-15 dB,对应的灵敏度为179 mV/A,与理论设计基本相符。
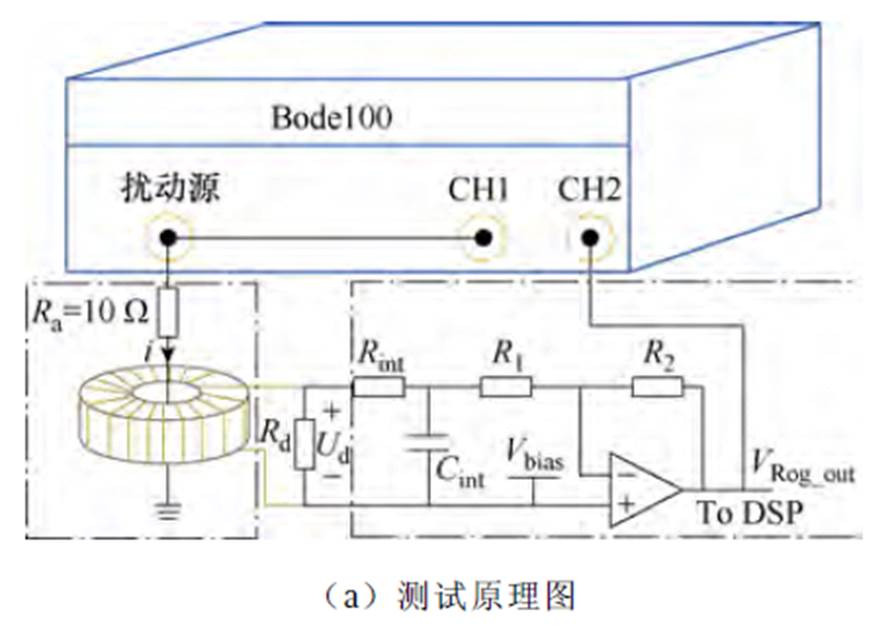
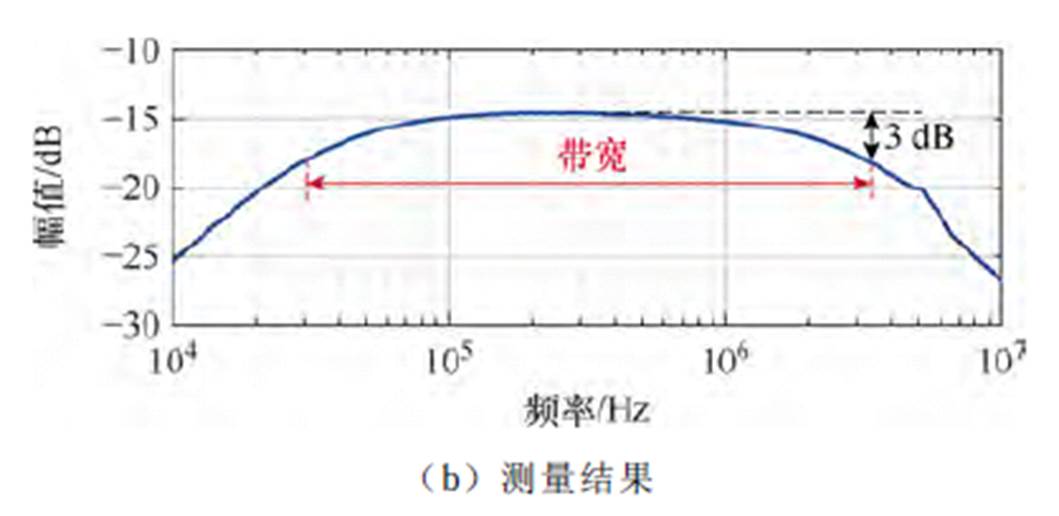
图8 罗氏线圈电流传感器传输特性测试原理及结果
Fig.8 Rogowski coil current senser transfer characteristic testing schematic and results
本文以德州仪器公司的微控制器TMS320F28379D作为主控芯片,将模数混合电流模式控制中的模拟比较器和数字触发器集成于单一微控制器中,以实现简化控制系统结构、降低系统成本的目的。
模数混合电流模式控制器的MCU实现框图如图9所示。利用MCU的比较器模块(Comparator Subsystem, CMPSS)将罗氏线圈电流传感器的输出信号VRog_out(t)与软件所设定的参考电流iref进行比较。其中,参考电流iref需折算为与VRog_out(t)同量纲的电压信号,并通过CMPSS模块内部的数模转换器(DAC)产生。该MCU的每个CMPSS模块包含两个比较器,其输出信号分别定义为CTRIPH和CTRIPL,用于指示比较结果,其输出逻辑为

图9 基于MCU的模数混合电流模式实现框图
Fig.9 Implementation diagram of the analog-digital hybrid current mode control based on the MCU
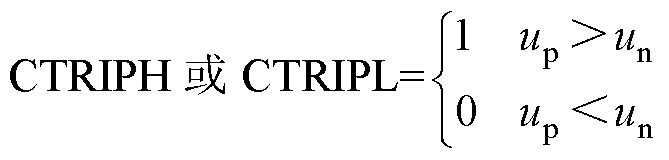 (14)
(14)
式中,up为比较器输入的正端电压;un为负端电压。CMPSS模块的输出信号CTRIPH和CTRIPL通过MCU的交叉开关(X-BAR)传递至ePWM模块,即图9中所示的TRIP4和TRIP5两路信号。
在ePWM模块中,利用数字比较(Digital Compare, DC)子模块和动作限定(Action Qualifier, AQ)子模块来实现图3中RS触发器的功能。DC子模块接收TRIP4、TRIP5信号,将其转换为事件触发信号DCAEVT1和DCBEVT1并进一步输送给AQ模块。AQ模块则依据触发信号的状态,通过配置AQCTL2寄存器控制功率管驱动信号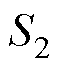 、
、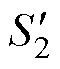 。此外,每个开关周期都通过DCAEVT1触发一次中断服务子程序,进行电流参考值的更新以及变换器端口电压和电流的监测。
。此外,每个开关周期都通过DCAEVT1触发一次中断服务子程序,进行电流参考值的更新以及变换器端口电压和电流的监测。
CMPSS输出信号、X-BAR输出信号、事件触发信号DCAEVT1和DCBEVT1和功率管控制信号,相对于电感电流波形的控制逻辑时序,如图10所示。当iL>iref时,CMPSS模块的比较器1输出CTRIPH由0置1,与之对应的信号传输链路中的TRIP4、DCAEVT1也由0置1,AQ子模块控制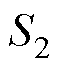 置高、
置高、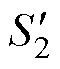 置低,使得DAB进入下一模态,电感电流斜率发生变化。
置低,使得DAB进入下一模态,电感电流斜率发生变化。
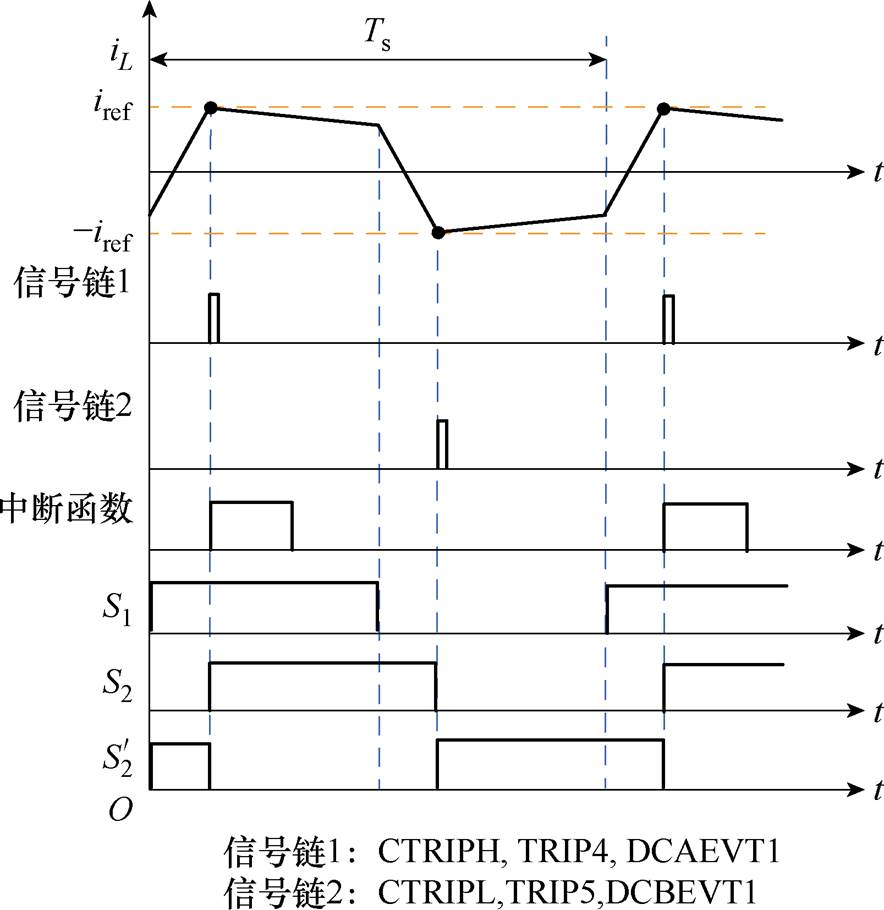
图10 MCU中电流模式控制时序
Fig.10 Timing diagram of the current mode control in MCU
当iL<-iref时,CMPSS模块的比较器2输出CTRIPL由0置1,与之对应的信号传输链路中的TRIP5、DCBEVT1也由0置1,AQ子模块控制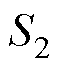 置低、
置低、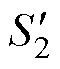 置高,使得DAB进入下一模态,电感电流斜率发生改变。
置高,使得DAB进入下一模态,电感电流斜率发生改变。
本文搭建了一台150 V输入、150 V输出,开关频率为200 kHz,最大传输功率为1.4 kW的DAB变换器样机,对本文提出的基于罗氏线圈的模数混合电流模式控制及实现方法进行验证。原理样机的实物照片如图11所示,样机的参数见表3。
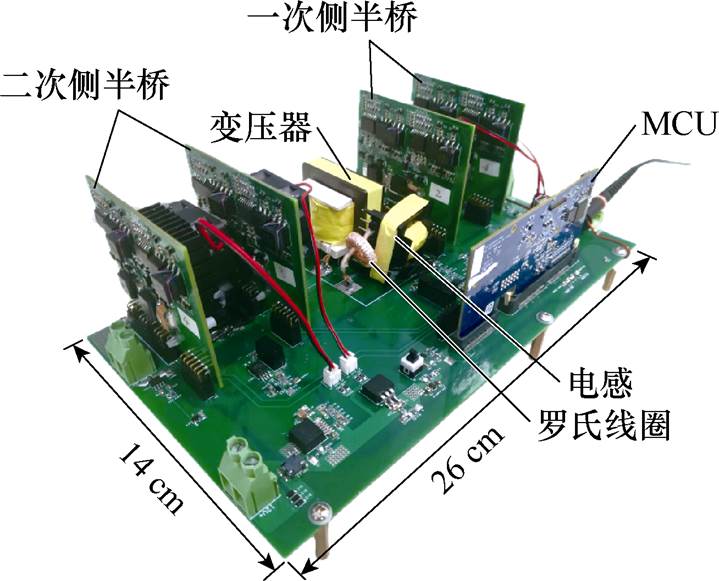
图11 DAB变换器样机实物照片
Fig.11 The picture of the DAB converter prototype
表3 原理样机的电路参数
Tab.3 Parameters of the converter prototype
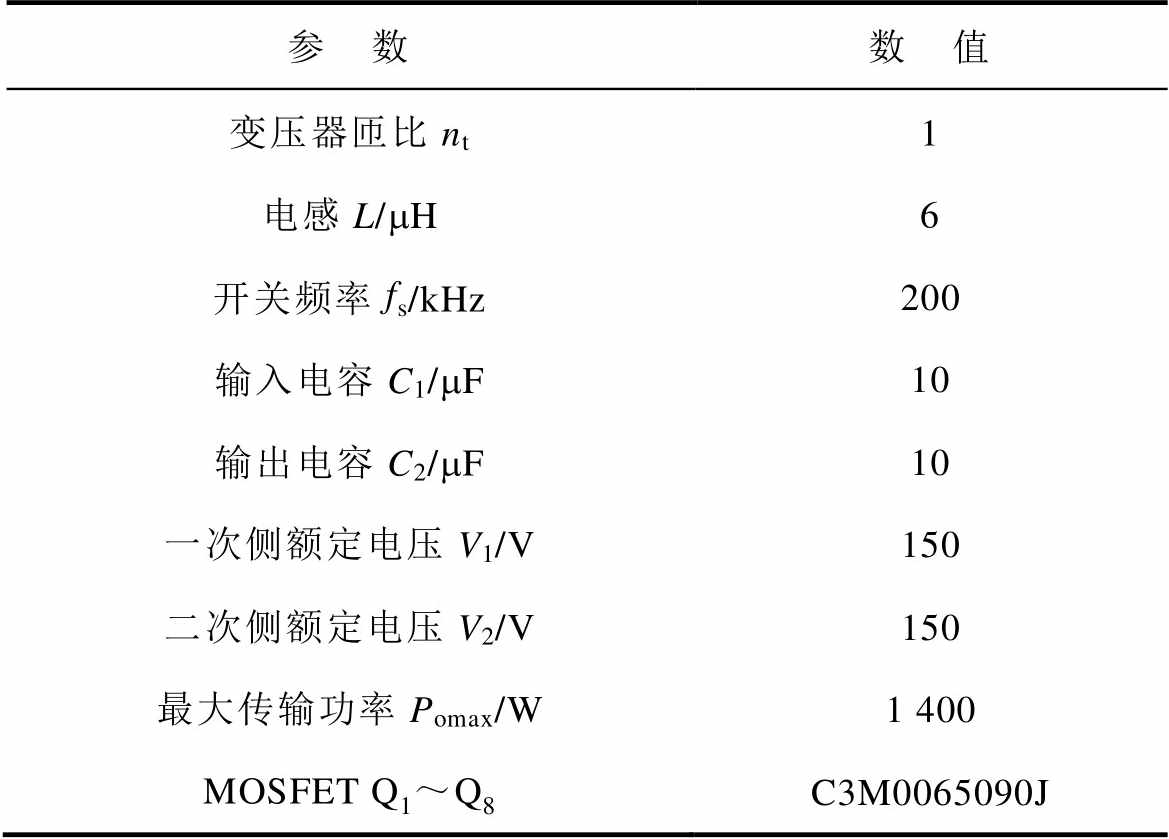
参 数数 值 变压器匝比nt1 电感L/mH6 开关频率fs/kHz200 输入电容C1/mF10 输出电容C2/mF10 一次侧额定电压V1/V150 二次侧额定电压V2/V150 最大传输功率Pomax/W1 400 MOSFET Q1~Q8C3M0065090J
首先,对所设计的罗氏线圈电流传感器的性能进行了验证。DAB变换器工作于传统的移相控制方式,输入电压150 V,输出电压150 V,传输功率700 W。分别采用罗氏线圈电流传感器、霍尔电流传感器(ACS730KLCTR-40AB-T,带宽1 MHz)对DAB变换器的电感电流进行测量,并与高频电流探头(TCP0030A,带宽120 MHz)的测量结果进行对比,实验波形对比如图12所示。图中,iL_Tek为电流探头所测得的电感电流波形,作为参考基准;iL_Rog为罗氏线圈电流传感器测得的电感电流波形;iL_Hall为霍尔电流传感器ACS730测得的电感电流波形。
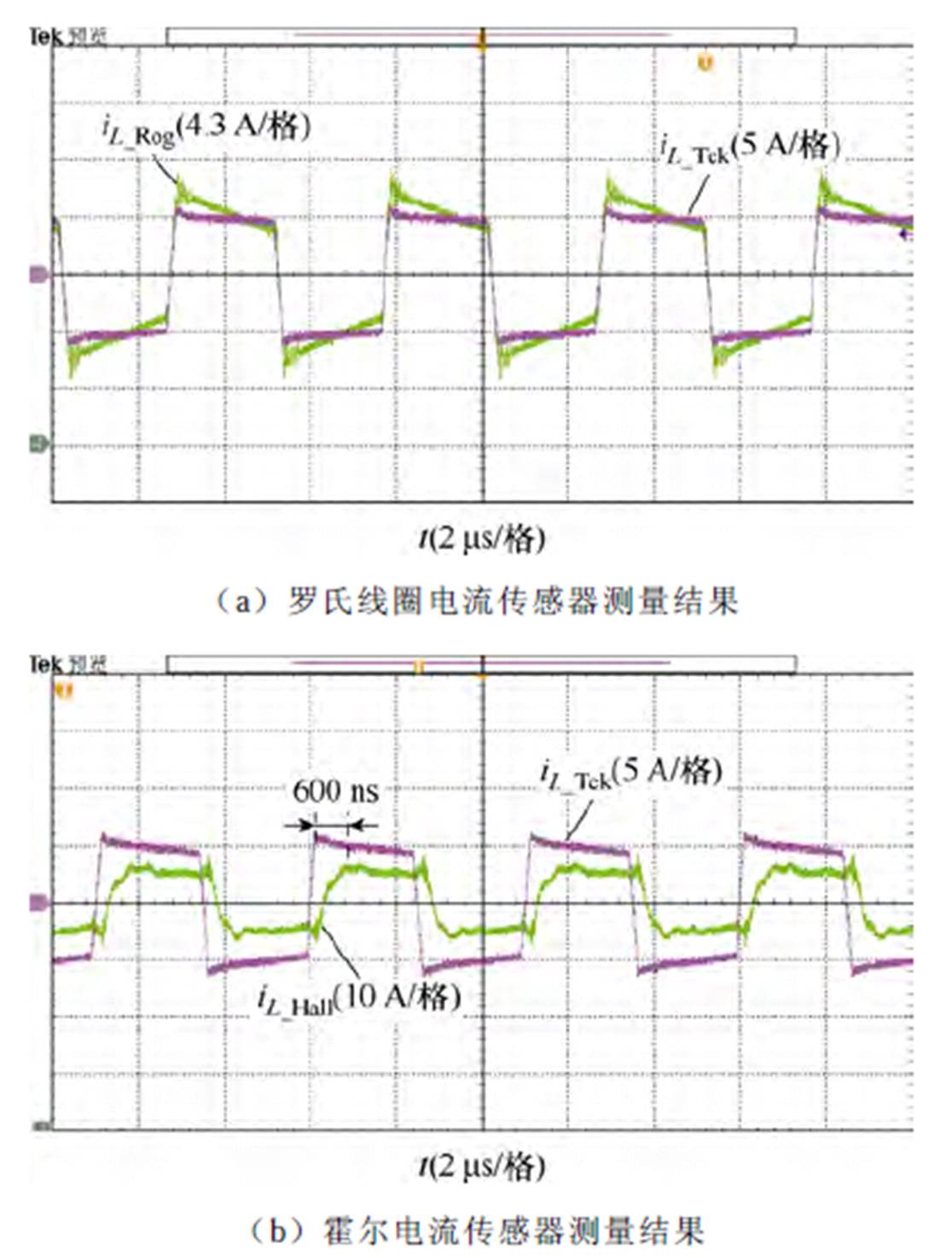
图12 电流传感器测量结果对比
Fig.12 Comparison of current senser measurement results
从图12a所示的实验结果可以看出,在电感电流的快速上升和快速下降阶段(上升/下降时间约200 ns),罗氏线圈电流传感器的测量结果与高频电流探头的测量结果基本重合,几乎没有延迟,展现出优异的高频性能。在电感电流的“平台”阶段,罗氏线圈电流传感器的测量结果存在下垂现象。但由于电流模式控制中电感电流的比较点发生在电流快速上升和快速下降阶段,因此“平台”阶段的下垂现象对控制系统的性能并不会产生影响。
相比较而言,图12b所示的实验波形表明,霍尔电流传感器的测量结果上升缓慢,与实际电感电流波形之间存在明显的延迟,电感电流峰值对应的延迟时间达600 ns,难以实现对电感电流的准确跟踪。可以预测,若采用该霍尔电流传感器进行电流模式控制,将引入额外的43.2°的相移偏差。因此,霍尔电流传感器对于高频DAB变换器的电流模式控制并不适用。
采用所设计的罗氏线圈电流传感器和本文提出的模数混合电流模式控制实现方法,对DAB变换器的传输功率进行控制。实验平台框图如图13所示。变换器的一次电压V1和二次电压V2均使用直流电源进行电压钳位,并分别并联电阻负载Ri和Ro来吸收变换器传输的功率。为防止异常情况下电流反灌造成直流电源损坏,在电源输出端分别串联了防电流反灌二极管。
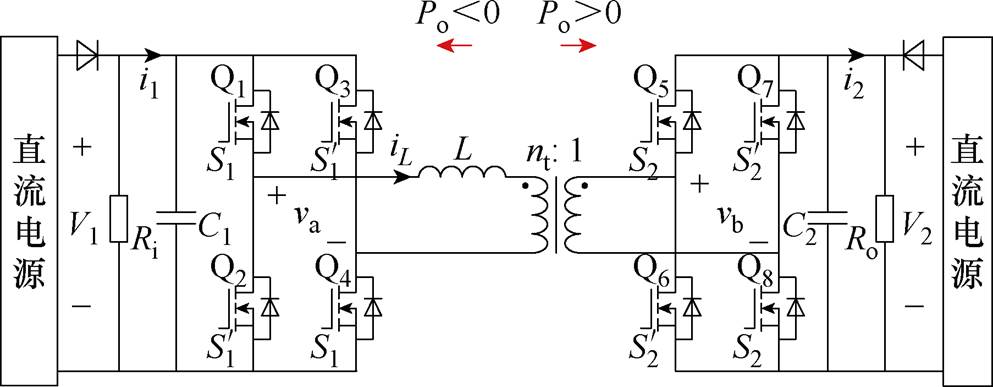
图13 实验平台框图
Fig.13 Diagram of the experimental platform
DAB变换器起动时的波形如图14所示。图14中,电感电流分别采用电流探头和罗氏线圈电流传感器测得。变换器的输入电压为140 V,输出电压为150 V,电流参考值为10 A,对应传输功率为1 000 W。从实验波形可以看出,电感电流的动态响应时间小于半个开关周期,且被牢牢限制在所设定的电流参考±iref范围内。同时,在起动时电感电流不存在传统移相控制由于移相角突变所造成的电流过冲和直流偏置。实验结果表明,采用本文提出的模数混合电流模式控制策略,DAB变换器能够实现平滑快速起动。从实验结果还可以看出,变换器的输出电流i2上升时间约为12 ms,变换器展现出极高的传输功率响应速度。
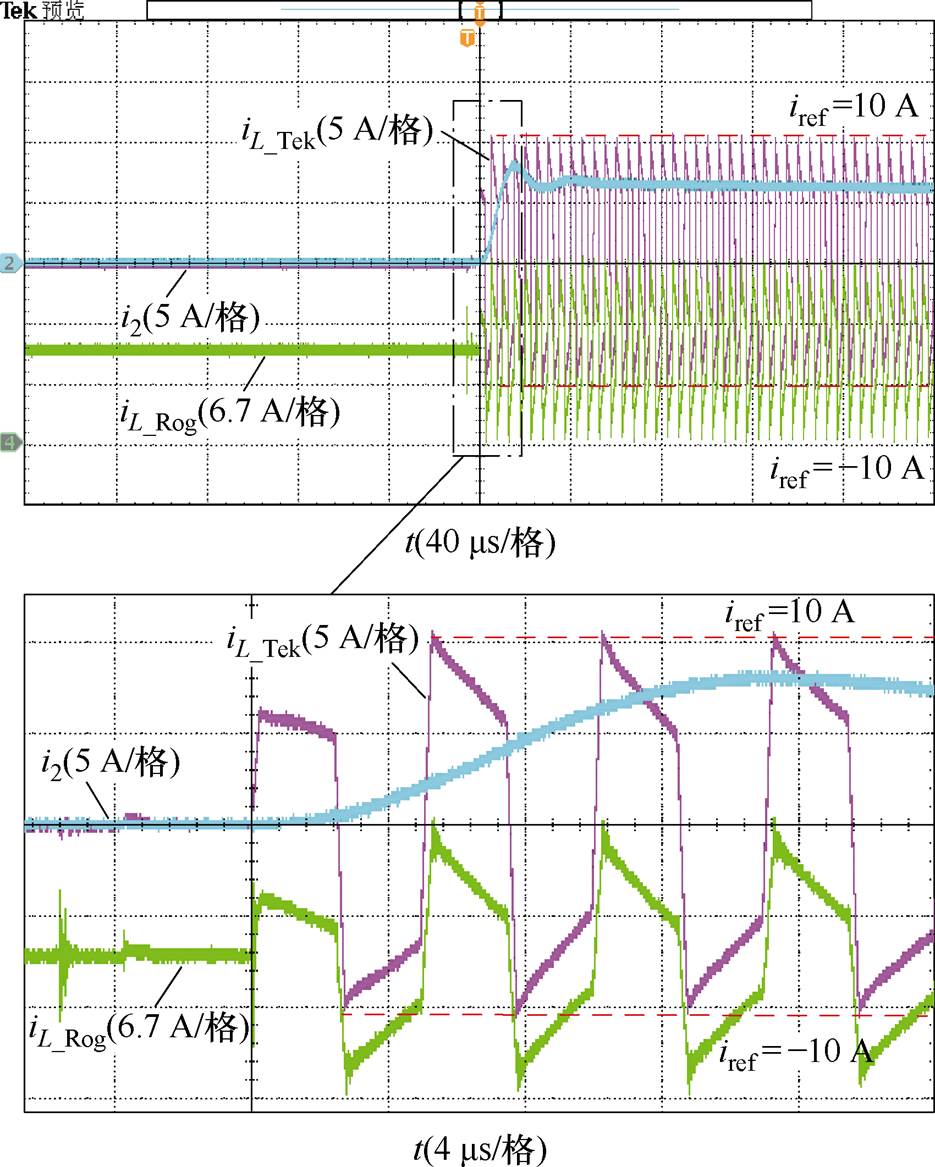
图14 DAB变换器起动时的波形
Fig.14 Waveforms of the DAB converter during start-up
图15为电流参考值从10 A(对应传输功率1 000 W)阶跃增加至14 A(传输功率1 400 W),再阶跃降低为10 A时,变换器的暂态响应波形。变换器的输入电压为140 V,输出电压为150 V。与起动过程类似,不管是功率突增还是功率突减,电感电流的动态响应时间均小于半个开关周期且过渡平滑,但被牢牢控制在所设定的电流参考±iref1和±iref2范围内。变换器输出电流i2的上升时间和下降时间约为12 ms。该实验结果表明,采用本文提出的模数混合电流模式控制策略,DAB变换器能够实现对功率指令的快速跟踪。
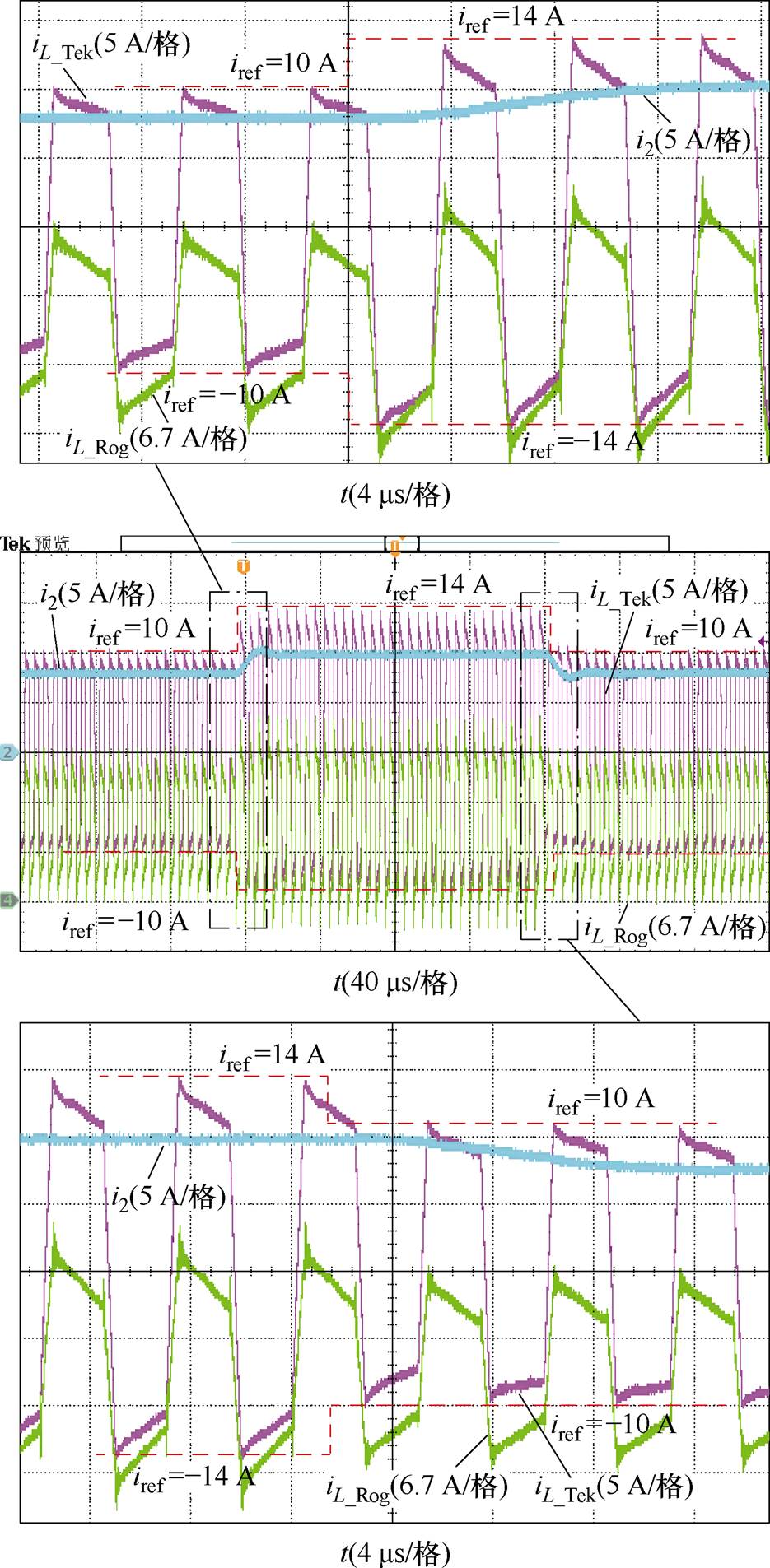
图15 DAB变换器功率突增、突减时的波形
Fig.15 Waveforms of the DAB converter during power step-up and step-down
表4从变换器开关频率、动态响应、传输功率和直流偏置等方面,将本文提出的方法与现有电流模式控制的研究成果进行了对比。
表4 与已有研究成果的对比
Tab.4 Comparison with existing works
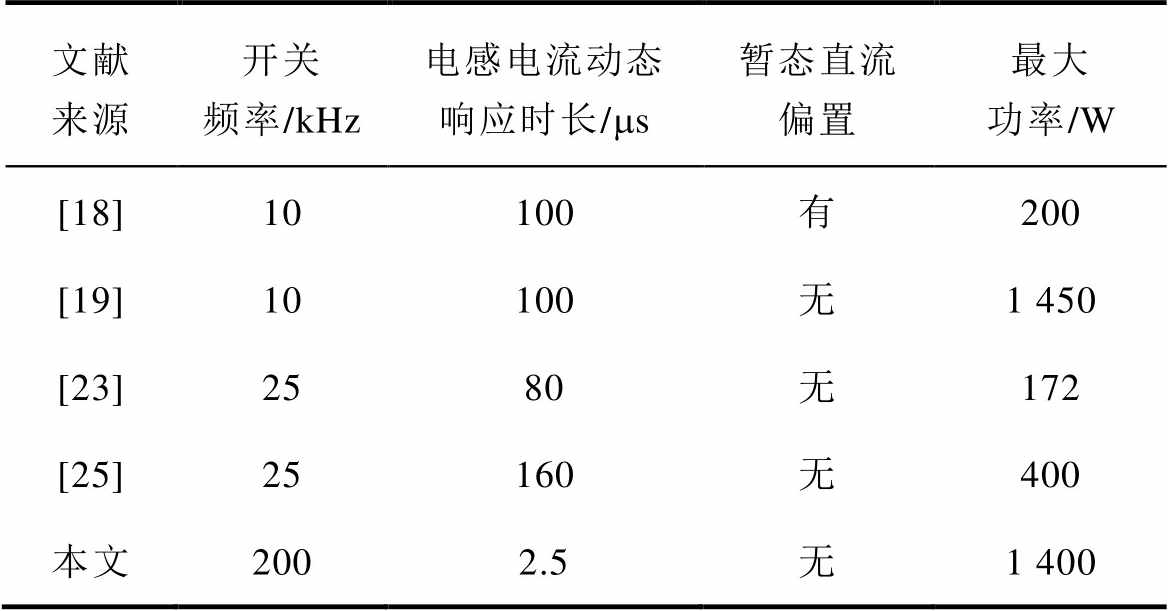
文献来源开关频率/kHz电感电流动态响应时长/ms暂态直流偏置最大功率/W [18]10100有200 [19]10100无1 450 [23]2580无172 [25]25160无400 本文2002.5无1 400
从开关频率看,本研究的开关频率200 kHz是已有研究报道的8~20倍,采用本文提出的方法,可将电流模式控制拓展至百kHz的DAB变换器。也正得益于此,本文的研究结果展现出了极高的动态响应特性,电感电流动态响应时间为2.5 ms,仅为已有研究的1/64~1/32。
针对高频DAB变换器电流模式控制中,电感电流精确感知困难和“模拟+数字”混合控制器实现复杂的问题,本文提出一种基于罗氏线圈的高频DAB变换器电流模式控制及实现方案。得到如下结论:
1)设计了30 kHz~3.2 MHz的高带宽罗氏线圈电流传感器,并将其应用于百kHz开关频率的DAB变换器,实现了对高频电感电流的精确感知。
2)设计了基于单一微控制器的模数混合电流模式控制方案,将电流模式控制器的比较、触发等环节由MCU集成,简化了控制系统结构,降低了系统软硬件复杂程度,减小系统成本。
实验结果表明,采用所提方法,实现了开关频率200 kHz、传输功率1.4 kW原理样机的电流模式控制,电感电流的动态响应迅速,响应时间仅为2.5 ms,进而实现了变换器的快速功率调控和逐周期限流保护。
参考文献
[1] 李永东, 章玄, 许烈. 多电飞机高压直流供电系统稳定性研究综述[J]. 电源学报, 2017, 15(2): 2-11.
Li Yongdong, Zhang Xuan, Xu Lie. A survey on stability analysis for HVDC power system in MEA[J]. Journal of Power Supply, 2017, 15(2): 2-11.
[2] Todd R, Wu D, dos Santos Girio J A, et al. Supercapacitor-based energy management for future aircraft systems[C]//2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Expo- sition (APEC), Palm Springs, CA, USA, 2010: 1306- 1312.
[3] Tariq M, Maswood A I, Gajanayake C J, et al. Modeling and integration of a lithium-ion battery energy storage system with the more electric aircraft 270 V DC power distribution architecture[J]. IEEE Access, 2018, 6: 41785-41802.
[4] Turpin C, Morin B, Bru E, et al. Power for aircraft emergencies: a hybrid proton-exchange membrane H2/O2 fuel cell and ultracapacitor system[J]. IEEE Electrification Magazine, 2017, 5(4): 72-85.
[5] 王成山, 李微, 王议锋, 等. 直流微电网母线电压波动分类及抑制方法综述[J]. 中国电机工程学报, 2017, 37(1): 84-98.
Wang Chengshan, Li Wei, Wang Yifeng, et al. DC bus voltage fluctuation classification and restraint methods review for DC microgrid[J]. Proceedings of the CSEE, 2017, 37(1): 84-98.
[6] 宋清超, 陈家伟, 蔡坤城, 等. 多电飞机用燃料电池-蓄电池-超级电容混合供电系统的高可靠动态功率分配技术[J]. 电工技术学报, 2022, 37(2): 445- 458.
Song Qingchao, Chen Jiawei, Cai Kuncheng, et al. A highly reliable power allocation technology for the fuel cell-battery-supercapacitor hybrid power supply system of a more electric aircraft[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 445-458.
[7] 康薇, 肖飞, 任强, 等. 双有源桥DC-DC变换器三移相调制及其死区效应分析和补偿[J]. 电工技术学报, 2024, 39(6): 1907-1922.
Kang Wei, Xiao Fei, Ren Qiang, et al. Three-phase shift modulation of DC-DC converter with dual active bridges and its dead-time effect analysis and compensation[J]. Transactions of China Electro- technical Society, 2024, 39(6): 1907-1922.
[8] 刘子薇, 孙兆龙, 刘宝龙, 等. 基于直接功率控制的双有源桥暂态直流偏置抑制策略[J]. 电工技术学报, 2023, 38(12): 3234-3247.
Liu Ziwei, Sun Zhaolong, Liu Baolong, et al. Transient DC bias suppression strategy of dual active bridge based on direct power control[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3234-3247.
[9] 李林柘, 邹旻洋, 吴京驰, 等. 基于周期组合序列调制的三电平双有源桥均压策略[J]. 电工技术学报, 2024, 39(2): 514-524, 540.
Li Linzhe, Zou Minyang, Wu Jingchi, et al. Voltage sharing strategy of three-level dual active bridges based on periodic combined sequence modulation[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 514-524, 540.
[10] 江凌峰, 龚邻骁, 金新宇, 等. 基于遗传算法的多模块IPOP双有源全桥DC-DC变换器总电流有效值优化策略[J]. 电工技术学报, 2023, 38(24): 6782- 6797.
Jiang Lingfeng, Gong Linxiao, Jin Xinyu, et al. Total root mean square current optimization of IPOP dual active bridge DC-DC converter based on genetic algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6782-6797.
[11] 高晨祥, 林丹颖, 韩林洁, 等. 双有源桥型电力电子变压器电磁暂态实时低耗等效模型[J]. 电力系统自动化, 2024, 48(8): 195-206.
Gao Chenxiang, Lin Danying, Han Linjie, et al. Real-time low-consumption equivalent model of electromagnetic transient of double active bridge power electronic transformer[J]. Automation of Electric Power Systems, 2024, 48(8): 195-206.
[12] Swaminathan N, Cao Yue. An overview of high- conversion high-voltage DC-DC converters for electrified aviation power distribution system[J]. IEEE Transactions on Transportation Electrification, 2020, 6(4): 1740-1754.
[13] Segaran D, Holmes D G, McGrath B P. Enhanced load step response for a bidirectional DC-DC converter[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 371-379.
[14] Li Xiaodong, Li Yifan. An optimized phase-shift modulation for fast transient response in a dual- active-bridge converter[J]. IEEE Transactions on Power Electronics, 2014, 29(6): 2661-2665.
[15] Hu Jingxin, Cui Shenghui, von den Hoff D, et al. Generic dynamic phase-shift control for bidirectional dual-active bridge converters[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6197-6202.
[16] Bu Qinglei, Wen Huiqing, Wen Jiacheng, et al. Transient DC bias elimination of dual-active-bridge DC-DC converter with improved triple-phase-shift control[J]. IEEE Transactions on Industrial Elec- tronics, 2020, 67(10): 8587-8598.
[17] Zhao Biao, Song Qiang, Liu Wenhua, et al. Transient DC bias and current impact effects of high- frequency-isolated bidirectional DC-DC converter in practice[J]. IEEE Transactions on Power Electronics, 2016, 31(4): 3203-3216.
[18] Dutta S, Hazra S, Bhattacharya S. A digital predictive current-mode controller for a single-phase high- frequency transformer-isolated dual-active bridge DC-to-DC converter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(9): 5943-5952.
[19] Wei Shusheng, Zhao Zhengming, Li Kai, et al. Deadbeat current controller for bidirectional dual- active-bridge converter using an enhanced SPS modulation method[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 1274-1279.
[20] Oggier G G, Ordonez M, Galvez J M, et al. Fast transient boundary control and steady-state operation of the dual active bridge converter using the natural switching surface[J]. IEEE Transactions on Power Electronics, 2014, 29(2): 946-957.
[21] Duan Renzhi, Yuan Liqiang, Gu Qing, et al. Finite- state-machine model of boundary control for dual- active-bridge converter[C]//2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 2017: 1-6.
[22] Shi Haochen, Wen Huiqing, Cao Zhenyan, et al. Minimum-current-stress boundary control using multiple-phase-shift-based switching surfaces[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 8718-8729.
[23] Shan Zhenyu, Jatskevich J. Digital and analog implementations of nonlinear-feedforward controller for a dual-active-bridge converter[C]//2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 2015: 4337-4342.
[24] Shan Zhenyu, Jatskevich J, Cho E, et al. A feed- forward control method of dual-active-bridge DC/DC converter to achieve fast dynamic response[C]//2014 IEEE 36th International Telecommunications Energy Conference (INTELEC), Vancouver, BC, Canada, 2014: 1-6.
[25] Vazquez N, Liserre M. Peak current control and feed-forward compensation of a DAB converter[J]. IEEE Transactions on Industrial Electronics, 2020, 67(10): 8381-8391.
[26] 杨敏. PWM加移相控制双有源全桥双向DC-DC变换器的研究[D]. 南京: 南京航空航天大学, 2013.
Yang Min. Research on dual active full-bridge bidirectional DC-DC converter controlled by PWM plus phase shift[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013.
[27] Niklaus P S, Bortis D, Kolar J W. High-bandwidth high-CMRR current measurement for a 4.8 MHz multi-level GaN inverter AC power source[C]//2021 IEEE Applied Power Electronics Conference and Exposition (APEC), Phoenix, AZ, USA, 2021: 200- 207.
Abstract The current mode control effectively achieves high dynamic response for dual active bridge (DAB) converters. However, for high-frequency and high-power-density applications, the existing control methods still face some limitations. On the one hand, the bandwidth of the commonly used current sensors, e.g., Hall-effect sensors, is not high enough to capture the complete information of the high-frequency inductor current. On the other hand, the existing implementation methods rely on analog comparators and digital triggers, which involve more discrete components and complex control logic than the traditional phase shift control. This paper proposes an analog-digital hybrid current mode control for high-frequency (hundreds of kHz) DAB converters. A high bandwidth (30 kHz~3 MHz) Rogowski current sensor is designed to accurately capture the inductor current, while the analog-digital hybrid current mode controller is implemented using a sole microcontroller, reducing system cost, complexity, and PCB layout area.
Firstly, the operating principle of the analog-digital hybrid current mode control for DAB converters is detailed, and the inductor current reference value ±iref as a function of transmission power is derived. The theoretical analysis shows that the steady-state performance with the current mode control is equivalent to traditional phase shift control, and the inductor current shows an extremely fast dynamic response. Secondly, the feasibility and advantages of the Rogowski coil for sensing high-frequency inductor current are illustrated. Its operating principle, together with transfer characteristics, is analyzed. A Rogowski coil current sensor is fabricated to capture at least six harmonics of the inductor current of a 200 kHz DAB converter prototype. The bandwidth of the Rogowski coil current sensor is measured as 3.2 MHz using a vector network analyzer, which is sufficient for current mode control. An experimental comparison shows that Rogowski coil current sensors achieve higher accurate measurements of high-frequency inductor current than commercial Hall current sensors (ACS730). In addition, the implementation scheme of the analog-digital hybrid current mode control in a digital controller platform is described. The analog comparison and digital trigger functions are integrated using one microcontroller unit (MCU), which reduces system complexity and cost. Taking TMS320F28379D from Texas Instruments as an example, the implementation flow and register configuration are elaborated.
A DAB converter prototype is designed with 1.4 kW-200 kHz, 150 V input, and 150 V output. The experimental results show that the inductor current of the DAB converter exhibits a swift dynamic response. The dynamic response time of the inductor current for the transient process, such as start-up, power step-up, and power step-down, is less than half of the switching period (2.5 ms). The response time is only 1/64 to 1/32 of the existing research. In addition, the inductor current is firmly restricted to current reference ±iref, which can be dynamically adjusted in the digital controller. Therefore, a cycle-by-cycle current limiting capability is simultaneously achieved.
The following conclusions can be drawn. (1) The designed Rogowski coil current sensor can accurately capture the information of high-frequency inductor current, which is a prerequisite for current mode control. (2) The analog comparison and digital trigger functions are successfully integrated into a digital control to reduce system complexity and cost. (3) The DAB converter shows excellent dynamic performance using the proposed analog-digital hybrid current mode control method and implementation strategy.
keywords:Dual active bridge converter, current mode control, Rogowski coil, dynamic response
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.240386
国家自然科学基金项目(52407201)和河北省高等学校科学研究项目(QN2023105)资助。
收稿日期 2024-03-08
改稿日期2024-04-25
朱博阳 男,1999年生,硕士研究生,研究方向为隔离型DC-DC变换器。E-mail: 202121401037@stu.hebut.edu.cn
韩伟健 男,1989年生,讲师,研究方向为双向DC-DC变换器建模与控制。E-mail: weijian.han@hebut.edu.cn(通信作者)
(编辑 陈 诚)