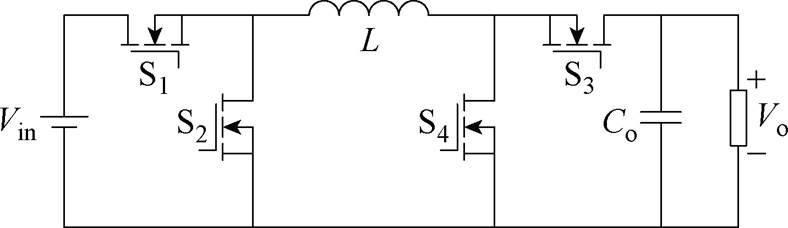
图1 四管Buck-Boost变换器
Fig.1 Four-switch Buck-Boost converter
摘要 四管Buck-Boost变换器(FSBB)具有输入电压范围宽、输入输出同极性、控制自由度高等优势,非常适合在直流微电网中对光伏电池或储能电池起到能量管理的作用。对于FSBB的研究主要集中在效率的提升和多模式控制的平滑切换两个方面。该文针对FSBB的多模式控制方法,分析不同的控制模式对于FSBB效率的具体影响,并提出一种可以减小电感电流纹波的交错双沿调制方式;在此基础上提出一种变频控制策略,当变换器输入电压接近输出电压时能够降低开关频率以提高变换效率。在实验室搭建了一台输入8~35 V、输出28 V、满载600 W的原理样机,验证了所提变频控制策略的有效性。
关键词:四管Buck-Boost变换器 交错双沿调制 变频控制 模式平滑切换
四管Buck-Boost(Four-Switch Buck-Boost, FSBB)变换器因其具有升降压变换能力,且结构完全对称、功率可双向流通,而广泛应用于光储一体直流微电网系统,以应对系统电压变化范围宽的特性[1-4],其电路拓扑如图1所示。图1中,Vin为输入电压,Vo为输出电压,S1~S4为开关管,L为电感,Co为输出滤波电容。

图1 四管Buck-Boost变换器
Fig.1 Four-switch Buck-Boost converter
由于FSBB存在两个控制自由度,即其实现给定电压增益可能存在多个占空比以及相位组合。工作于单模式控制时,FSBB类似传统Buck-Boost变换器,即两个主控管同时开通、关断,依靠电感储能实现电压变换。文献[5-6]研究表明,电路中S1与S3同时开通的时间占比越大,直接传输的功率比重就越高,相应的变换效率也就越高。显然,FSBB工作于单模式时完全不存在直接功率通路,因而变换器的效率优化较为困难。
两模式控制时,变换器某个时刻等效为Buck或Boost变换器[7-8],Buck模式主控管S4常关闭,Boost模式主控管S1常导通,此时开关次数减少一半,效率提升显著,但在输入、输出电压相接近时,FSBB中主控管的理论占空比会出现接近0或1的情况,这会影响到开关管的可靠工作[9-11]。对于这种情况,文献[12-13]提出通过工作模式区间的合理划分并辅以一些补偿策略以避免脉冲丢失,从而实现模式的平滑过渡。
为解决上述问题,在两模式控制基础上引入中间过渡模式,从而构建了三模式控制,在过渡模式中,通过固定S1占空比为最大值dmax,调节S4占空比实现升降压变换。除了占空比的优化外,文献[14]讨论了调制方式对FSBB的影响,结果表明,交错调制方式有利于减小FSBB电感电流的脉动及有效值,以达到改善效率的目的。并提出在过渡模式下降低开关频率,使得整体损耗下降,有效地提高了过渡模式的效率。
在上述基础上,四模式控制将中间过渡模式分为拓展降压(Extend-Buck, E-Buck)和拓展升压(Extend-Boost, E-Boost)两种模式[15-16],E-Buck模式中固定S4占空比为最小值,调整S1占空比;E-Boost模式中固定S1占空比为最大值,调整S4占空比。该控制模式下模式切换时占空比突变有所减小,因而切换过程更平滑,但由于工作模式较多,控制复杂程度增加。
为改善上述控制策略的不足,本文将从控制模式和调制方式两个角度对FSBB的效率进行优化。首先,分析不同控制模式对电感电流的影响,进而选取一种高效率的多模式控制;其次,分析调制方式对电感电流纹波的影响,提出交错对称载波方式,有效降低电感电流纹波。最后,提出一种FSBB倍频的变频控制策略并进行了实验验证。
为了便于分析,按照功能定义FSBB的电感左、右两侧的桥臂分别为Buck单元和Boost单元,其中S1、S4是主控管,S2、S3是同步整流管,d1、d2分别为Buck单元和Boost单元的占空比,则变换器的增益M为
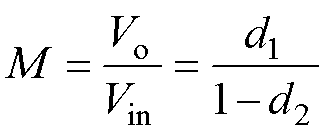 (1)
(1)
与变换器导通损耗直接相关的是电感电流有效值。为简化分析过程,利用平均值替代有效值进行损耗分析是可行的[17]。在电感电流平均值相同时,其纹波越大,有效值就越大。为了定性分析不同控制模式下的效率表现,本节将对不同控制模式下的电感电流纹波与平均值进行分析和比较。
两模式控制时,电感电流纹波与平均值分别与Buck变换器和Boost变换器的表达式是一样的,电感电流纹波Irip_2与平均值Iavg_2分别为
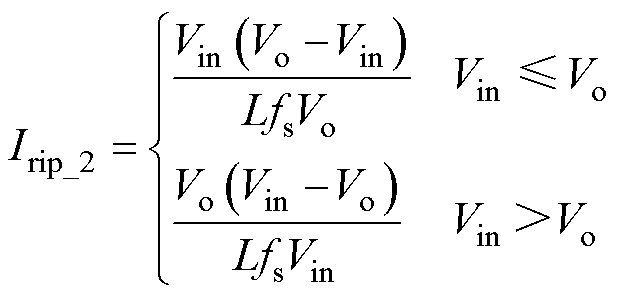 (2)
(2)
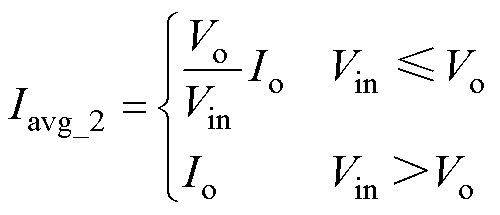 (3)
(3)
式中,fs为开关频率;Io为输出电流。
三模式控制时,中间过渡模式存在一个固定不变的占空比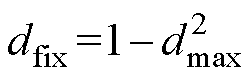 ,在升压与降压的不同情况下,电感电流纹波也是不同的。可以得到电感电流纹波Irip_3与平均值Iavg_3分别为
,在升压与降压的不同情况下,电感电流纹波也是不同的。可以得到电感电流纹波Irip_3与平均值Iavg_3分别为
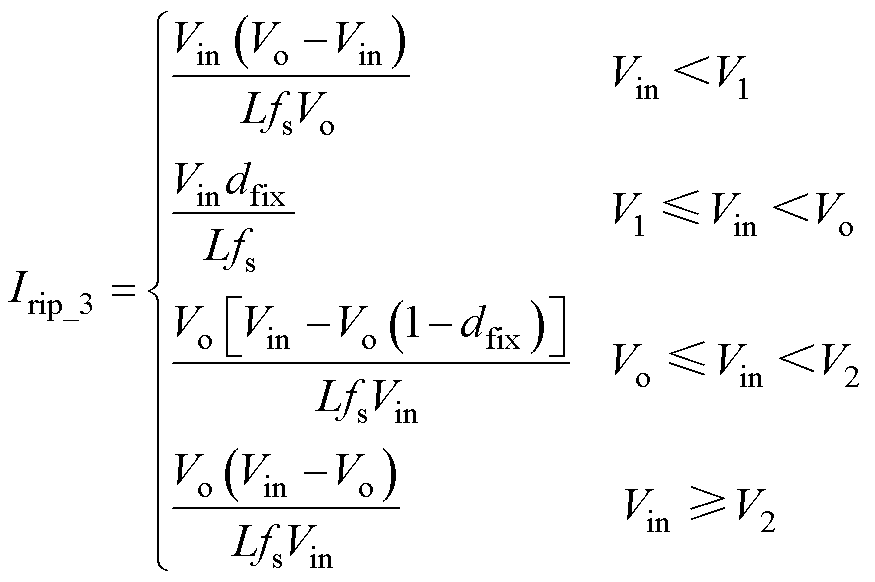 (4)
(4)
 (5)
(5)
式中, ;
;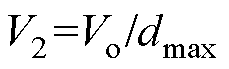 ;
;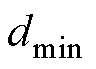 =0.1;
=0.1;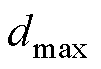 =0.9。
=0.9。
四模式控制时,中间过渡模式分为两段。E- Boost模式中d1固定为最大值dmax,E-Buck模式中d2固定为最小值dmin。可以得到电感电流纹波Irip_4与平均值Iavg_4分别为
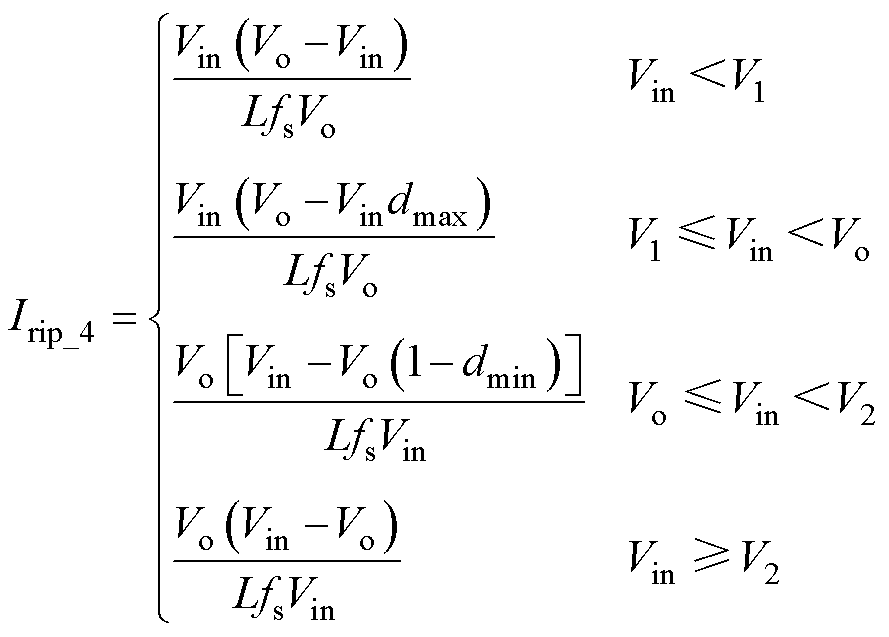 (6)
(6)
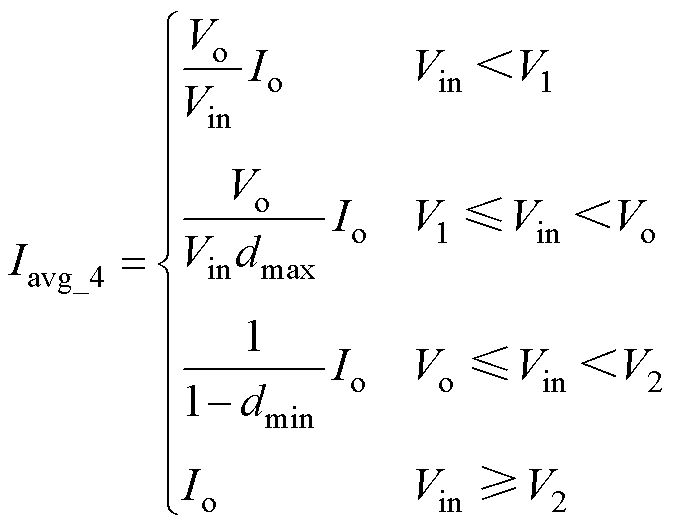 (7)
(7)
为比较不同控制模式下的电感电流纹波及平均值,以单模式工况输入输出电压相等时的电感电流纹波Irip_ref及平均值Iavg_ref为基准对电感电流进行归一化处理,得到不同控制模式下的电感电流纹波及平均值的对比如图2与图3所示。可以看出,两模式控制在输入输出电压接近时的电感电流纹波和平均值均最小,因此其效率表现最优。
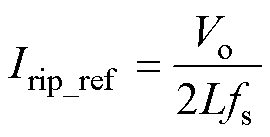 (8)
(8)
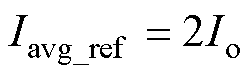 (9)
(9)
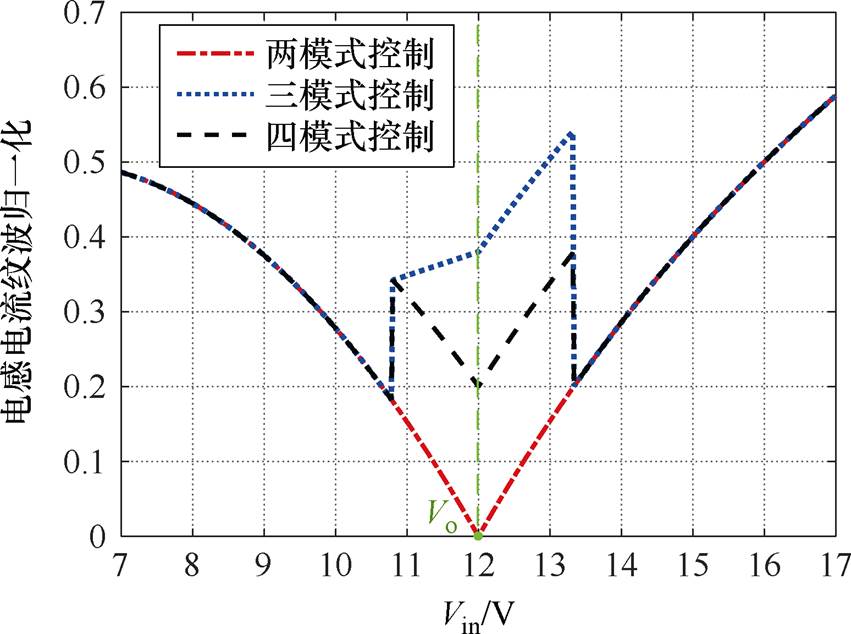
图2 不同控制模式的电感电流纹波对比
Fig.2 Comparison of the inductor current ripple of different control modes
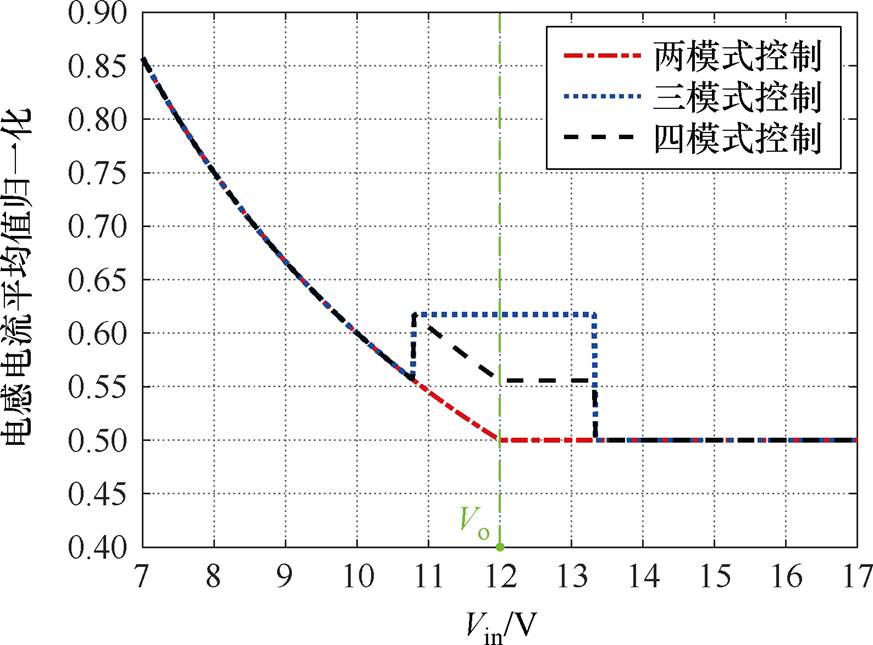
图3 不同控制模式的电感电流平均值对比
Fig.3 Comparison of the average inductor current of different control modes
FSBB的电感电流的平均值IL_avg是由占空比d2的大小决定的,即
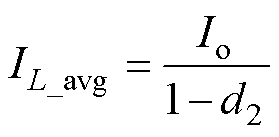 (10)
(10)
由式(10)可知,在相同增益下,减小d2有利于减小电感电流的平均值,因此,两模式控制的电感电流纹波和平均值均最小,但在输入输出相等时,两模式控制存在可靠性问题,故需要采取在保证多模式平滑可靠切换的条件下降低多模式控制时d2大小的方式。
除此之外,占空比d2相同的条件下,减少或避免S1与S4同时导通,可增加直接功率通路的占比,从而降低电感电流纹波,进一步提高变换器效率。
为最大程度地避免S1与S4同时导通,本文提出采用交错双沿三角波代替传统锯齿波作为控制载波,交错双沿三角载波调制如图4所示。此时,驱动的载波是两个相位差为180°的三角波。通过对两个载波附加不同的电压偏置实现不同工作模式的区分:当控制信号低于Boost载波的最小值时,即d2=0,Boost桥臂的主控管S4不开通,变换器工作在Buck模式;当控制信号高于Buck载波的最大值时,即d1=1,Buck桥臂的主控管S1恒开通,变换器工作在Boost模式;当控制信号与两个载波同时交截时,变换器工作在Buck-Boost模式。在这种载波形式下,S1与S4的开通与关断时间都会随着控制信号电平的改变而改变。由于两个载波幅值差异和相位的交错,保证了S1与S4可以最大程度地避免同时导通,从而提升变换器的效率。
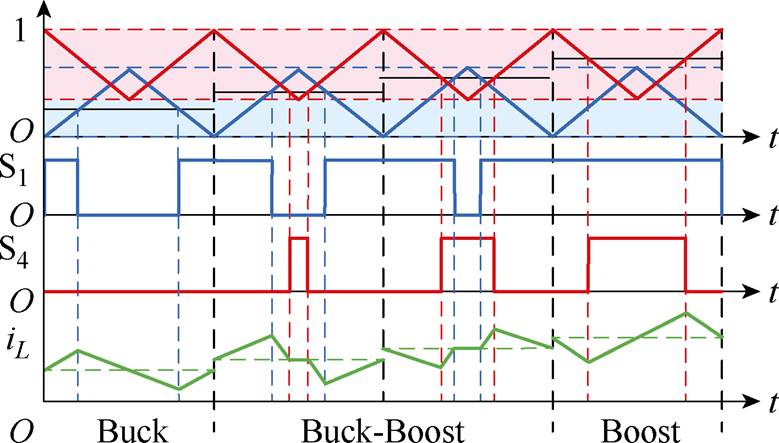
图4 交错双沿三角载波调制
Fig.4 Interleaved dual-edge triangular carrier modulation
此外,传统前后沿调制下每个开关周期始末位置的电感电流大小并非电感电流平均值,前后沿调制如图5所示,此时切换模式易造成输出电压的波动。而交错双沿调制下每个开关周期始末位置的电感电流大小恰为电感电流平均值(见图4),此时切换模式便可以实现变换器工作状态的平稳过渡。
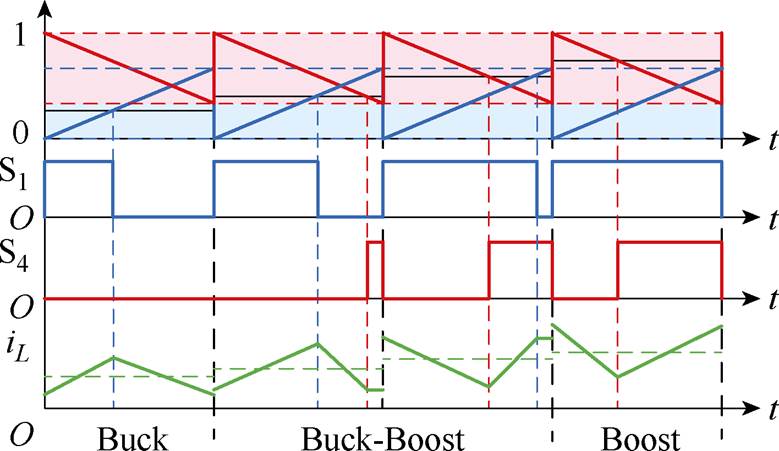
图5 前后沿调制
Fig.5 Front and back edge modulation
由图2可知,在输入、输出电压接近时,两模式控制可以有效降低电感电流纹波。在两模式控制下,当变换器增益接近于1时,电流纹波接近于0。多管开关工作,开关损耗占比增加,由于此时电流纹波小,为降低开关损耗提供了便利。基于这一点,本文提出一种变频多模式的控制策略,在此策略之下,FSBB电感两侧的半桥被分为高频桥臂与低频桥臂,且在不同的输入电压下会调整开关频率以实现最优的变换效率。
考虑到变换器中桥臂结构采用了自举的驱动方式,需要不定期开通下管为上管驱动补充供电能量,因此上管完全开通的工作状态无法实现,实际采用的是E-Buck与E-Boost结合的两模式控制方式。在采用交错双沿调制时,变频过程如图6所示。两个桥臂开关频率均与一个频率为fbase的同步信号SYNC进行同步,每当同步信号上升沿到来时,都会将PWM计数器置零以实现驱动信号的同步。频率以及占空比的变化也需要与这个SYNC信号同步,由于交错双沿载波形成的电感电流使得每个开关周期始末位置(即SYNC信号到来的位置)的值正是电感电流的平均值,此时修改计数器以及比较值就可以实现变换器的频率无缝切换,如图6中实现了S1驱动频率翻倍而不带来输出电压的波动。
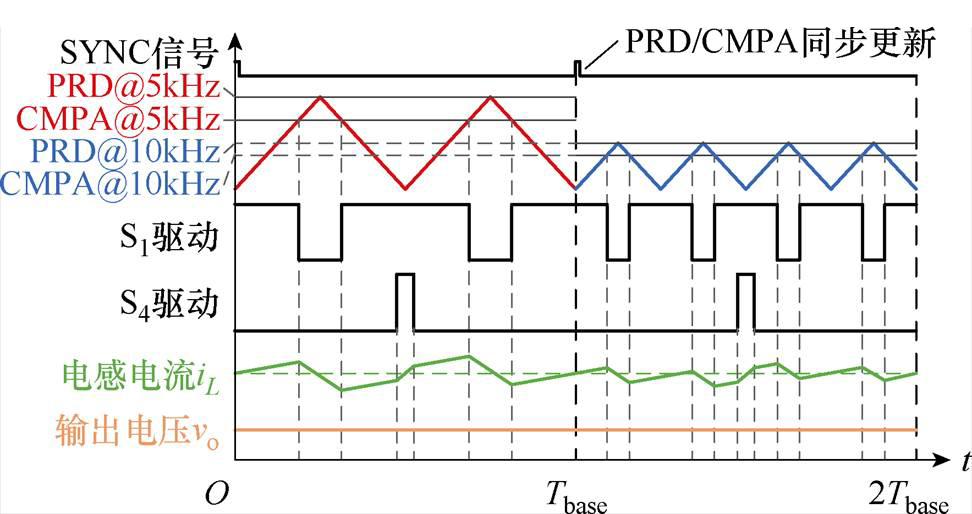
图6 交错双沿载波的变频过程
Fig.6 The frequency conversion process of interleaved dual-edge carrier
考虑到数字控制的离散性,这里采取的变频是整数倍频的方式,可以保证两个半桥驱动的同步。变频多模式控制策略的频率切换过程如图7所示。图7中的输入、输出电压比值接近1的工作点,由于这时输入、输出电压相差较小,虽然开关频率较低,但是其电感电流纹波仍可控制在较低水平。
随着输入电压偏离输出电压值,电感电流纹波随之增大。以两模式控制在对应中间过渡模式时的最大电感电流纹波DIL_max为上限,此时为了保证电感电流纹波不超过DIL_max,需要提高开关频率以降低电感电流纹波。若输入电压升高,则在减小Buck占空比的同时提高Buck桥臂的频率。这是因为出于效率考虑,这时的Boost占空比是一个固定的最小值,如提高Boost频率则会使得开关管开通时间减少,由于本文使用的开关管为低成本的Si管,开关速度较慢,可能会导致其无法可靠导通。相应地,若输入电压降低,则在增加Boost占空比的同时提高其开关频率,就可以得到变频多模式控制策略。图7描述了变换器工作状态的频率切换过程。
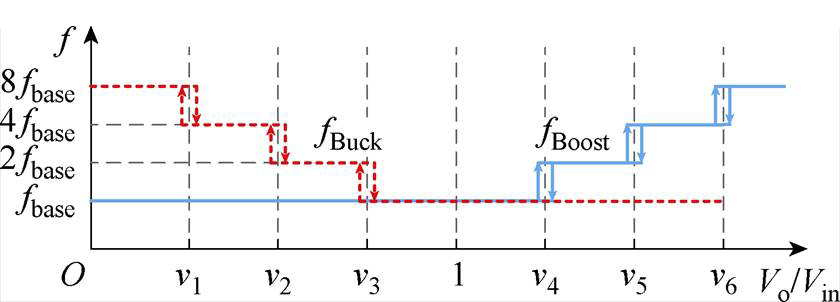
图7 变频多模式控制策略的频率切换过程
Fig.7 Frequency switching process of variable frequency multi-mode control strategy
因此,在不同的输入条件下,通过改变频率就可以在满足电感电流纹波小于DIL_max的前提下尽可能地减小开关损耗。接下来具体讨论频率变化的分界点,首先需要找出电感电流纹波与不同频率的工作模式之间的关系,通过理论推导得到在不同模式下的电感电流纹波DIL为
(1)fBuck=fBoost(Vin<Vo
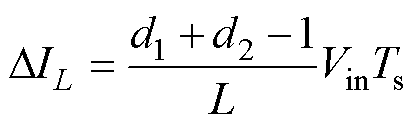 (11)
(11)
(2)2fBuck=fBoost
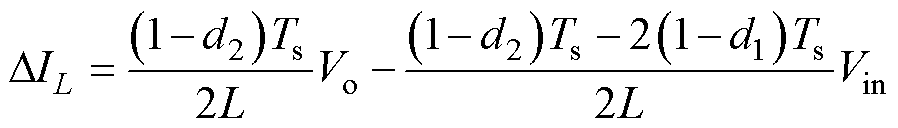 (12)
(12)
(3)4fBuck=fBoost
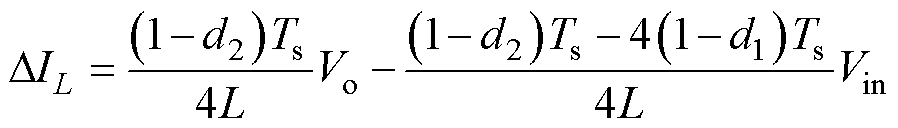 (13)
(13)
(4)8fBuck=fBoost
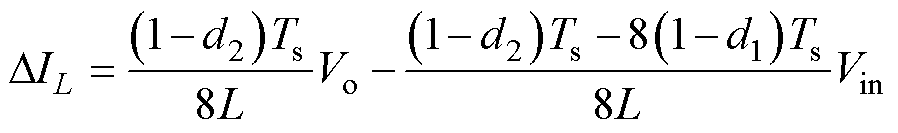 (14)
(14)
(5)fBuck=fBoost(Vin>Vo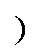
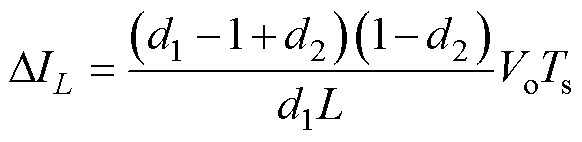 (15)
(15)
(6)fBuck=2fBoost
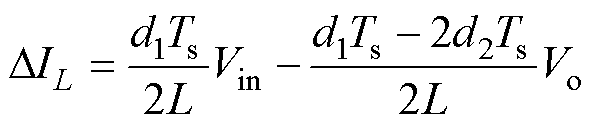 (16)
(16)
(7)fBuck=4fBoost
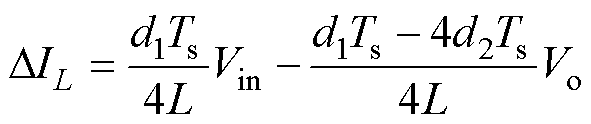 (17)
(17)
(8)fBuck=8fBoost
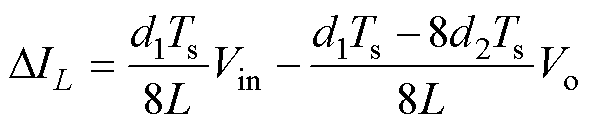 (18)
(18)
式中,Ts为开关周期。
综合上述表达式(11)~式(18),可以得到FSBB不同频率下电感电流纹归一化对比如图8所示。图中模式1代表开关频率fBuck=fBoost的模式;模式2代表开关频率fBuck=2fBoost或2fBuck=fBoost的模式;模式3代表开关频率fBuck=4fBoost或4fBuck=fBoost的模式;模式4代表开关频率fBuck=8fBoost或8fBuck= fBoost的模式。
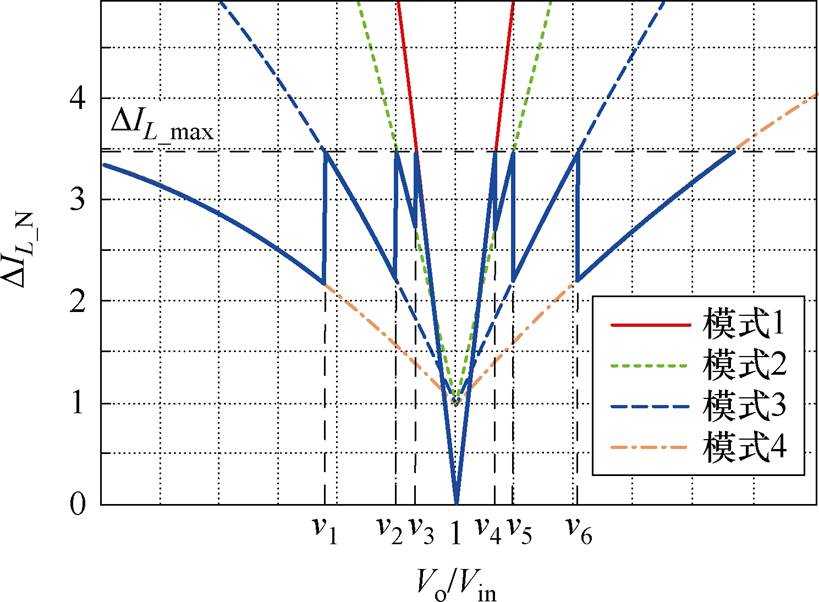
图8 FSBB不同频率的电感电流纹波归一化对比
Fig.8 The normalized comparison of inductor current ripple at different frequencies of FSBB
理论计算的结果表明在输入、输出电压接近的工作点附近,即使采用较低的开关频率,也可以将电感电流纹波控制在一定范围内。以最大电感电流纹波DIL_max为界限,交截后得到模式切换的分界点为v1=0.845, v2=0.921, v3=0.957, v4=1.043, v5=1.087,v6=1.143。模式切换过程如图8中(蓝色)加粗实线所示。
在不同的频率选取下,变换器的驱动以及电感电流波形如图9所示。
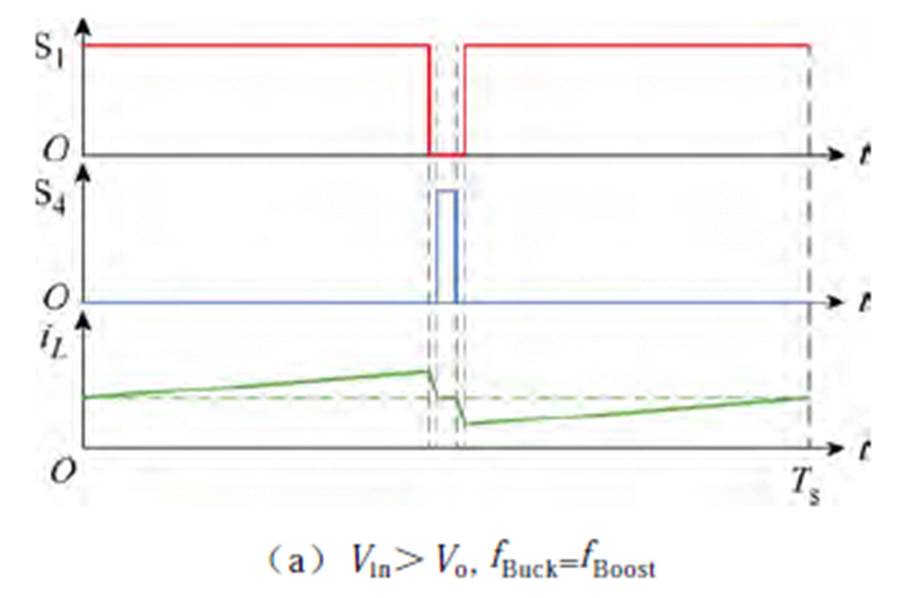
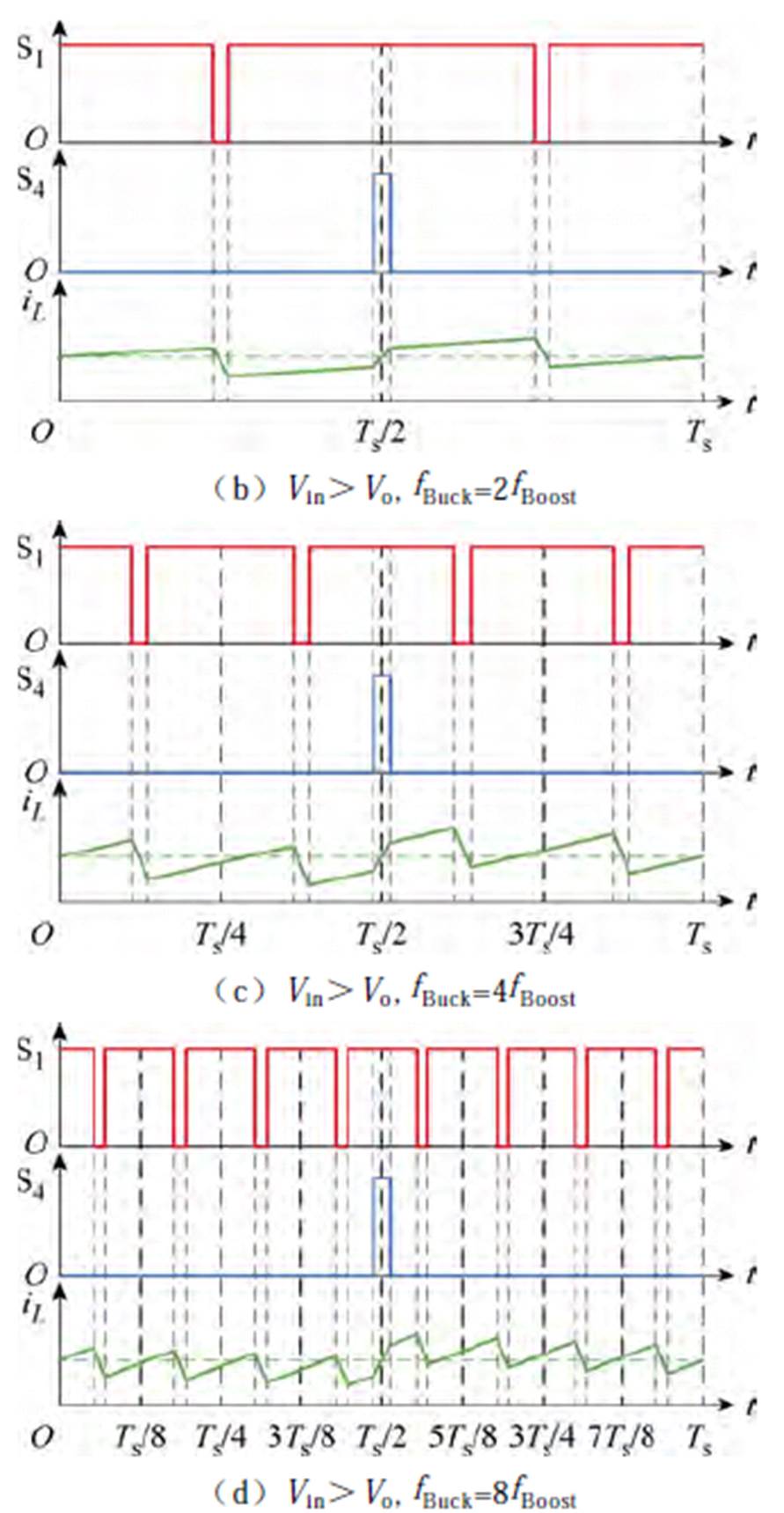
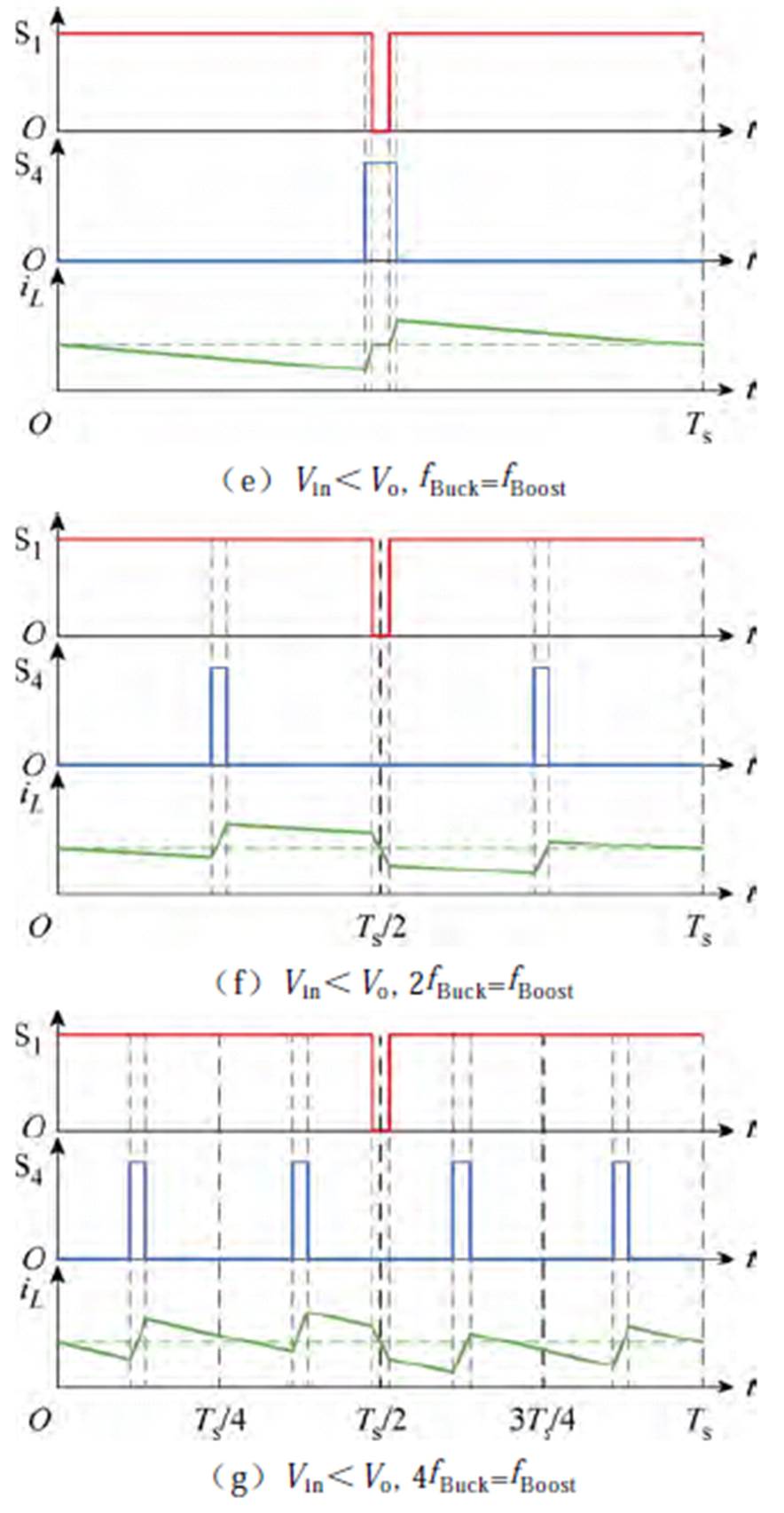

图9 FSBB驱动与电感电流波形的关系
Fig.9 The relationship between the drive of FSBB and the waveform of inductor current
为验证所提出模式切换的改进策略,搭建了一台用于光伏电池充电的原理样机。在体积允许的情况下,降低开关频率,可以有效提升变换器的效率。样机的输入电压为8~35 V、输出电压为28 V、满载功率600 W,样机主要参数见表1,原理样机如图10所示。
表1 样机主要参数
Tab.1 The main parameters of the prototype
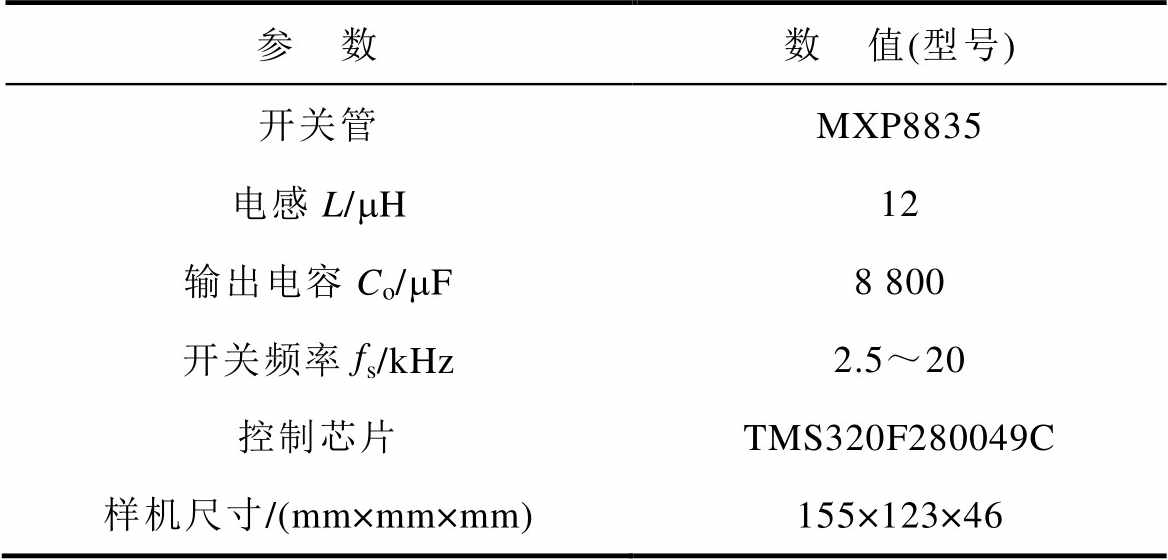
参 数数 值(型号) 开关管MXP8835 电感L/mH12 输出电容Co/mF8 800 开关频率fs/kHz2.5~20 控制芯片TMS320F280049C 样机尺寸/(mm×mm×mm)155×123×46

图10 原理样机
Fig.10 Principle prototype diagram
实验样机与SolarEdge公司的光伏电池充电器OPJ300-LV所使用的开关管的成本比较见表2。可以看出,在满载功率大一倍的情况下,本实验样机开关管的成本仍相对较低。虽然MXP8835的开通时间和关断时间较长,但由于本文的开关频率较低,开关管仍能实现可靠的导通。
表2 开关管成本对比
Tab.2 Cost comparison of switches
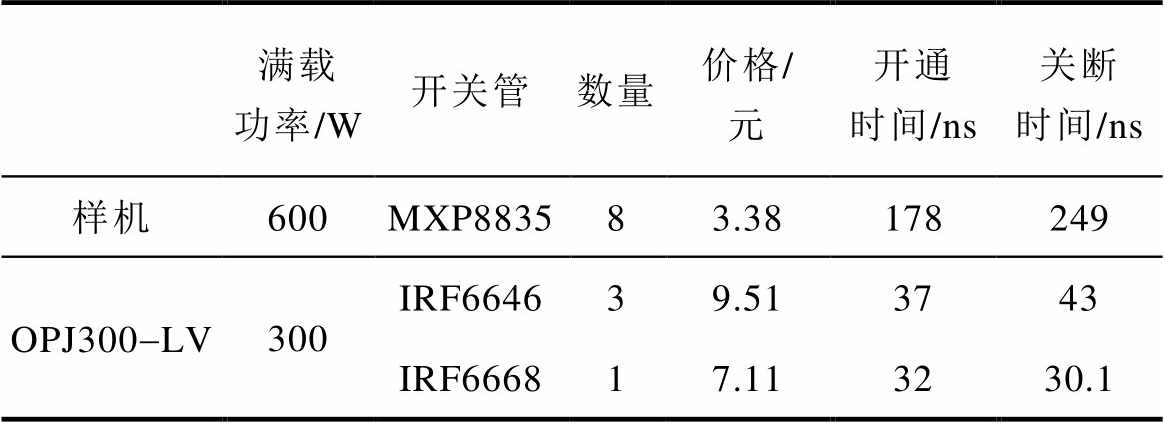
满载功率/W开关管数量价格/元开通时间/ns关断时间/ns 样机600MXP883583.38178249 OPJ300-LV300IRF664639.513743 IRF666817.113230.1
实验得到变换器在几个典型输入下的稳态工作波形如图11所示。由实验波形可见,变换器在一个比较宽的输入电压范围内都可以实现输出电压的闭环稳定控制,图11a和11e给出了变换器的输入、输出电压相接近的工作状态,这时两个桥臂的开关频率都是最低的,为fbase(2.5 kHz)。当输入电压升高(降低)时,变换器会进入到如图11b(图11f)所示的工作状态,这时的Buck桥臂(Boost桥臂)的频率提高。实验波形表明变换器能够在不同模式下实现升降压变换。
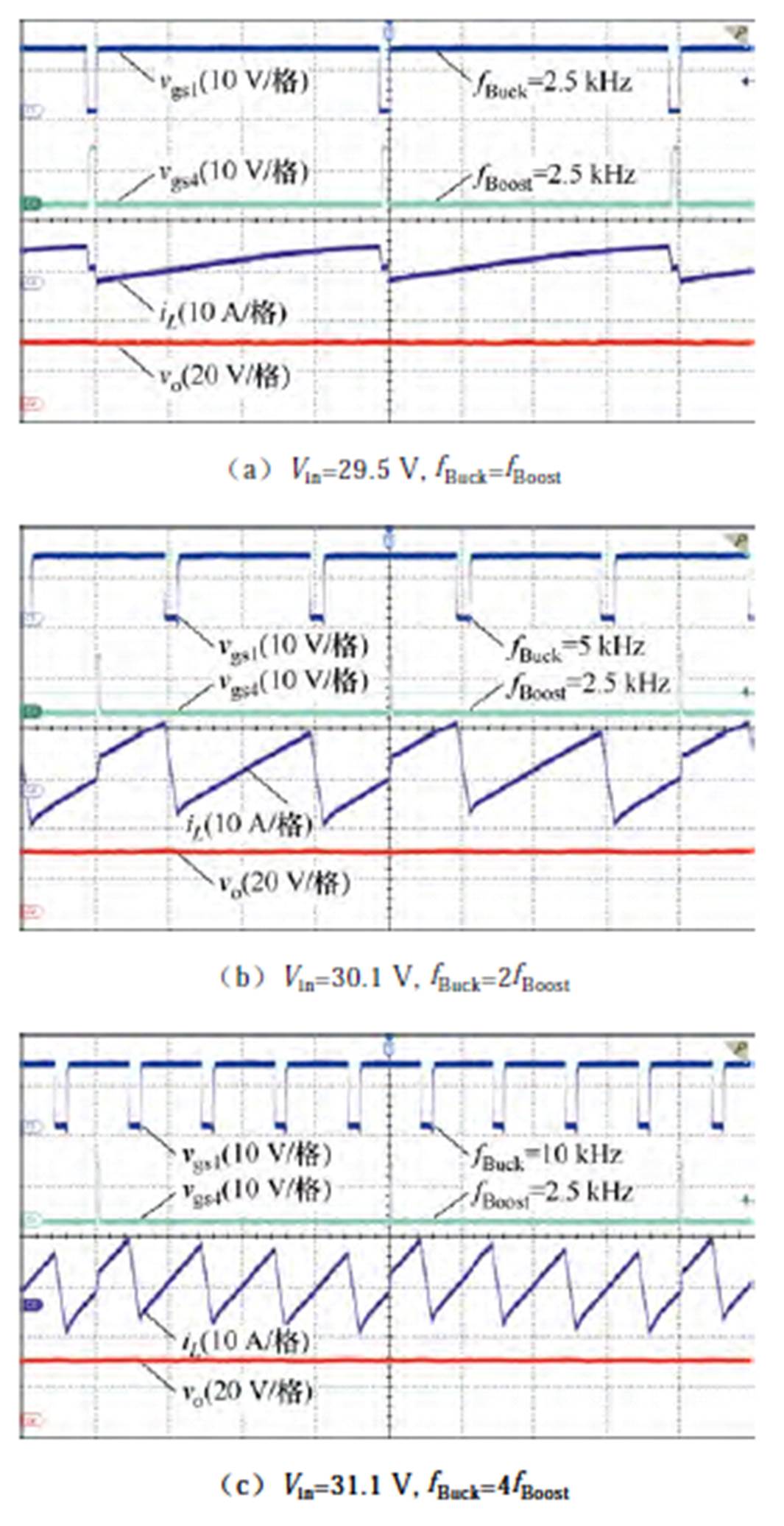
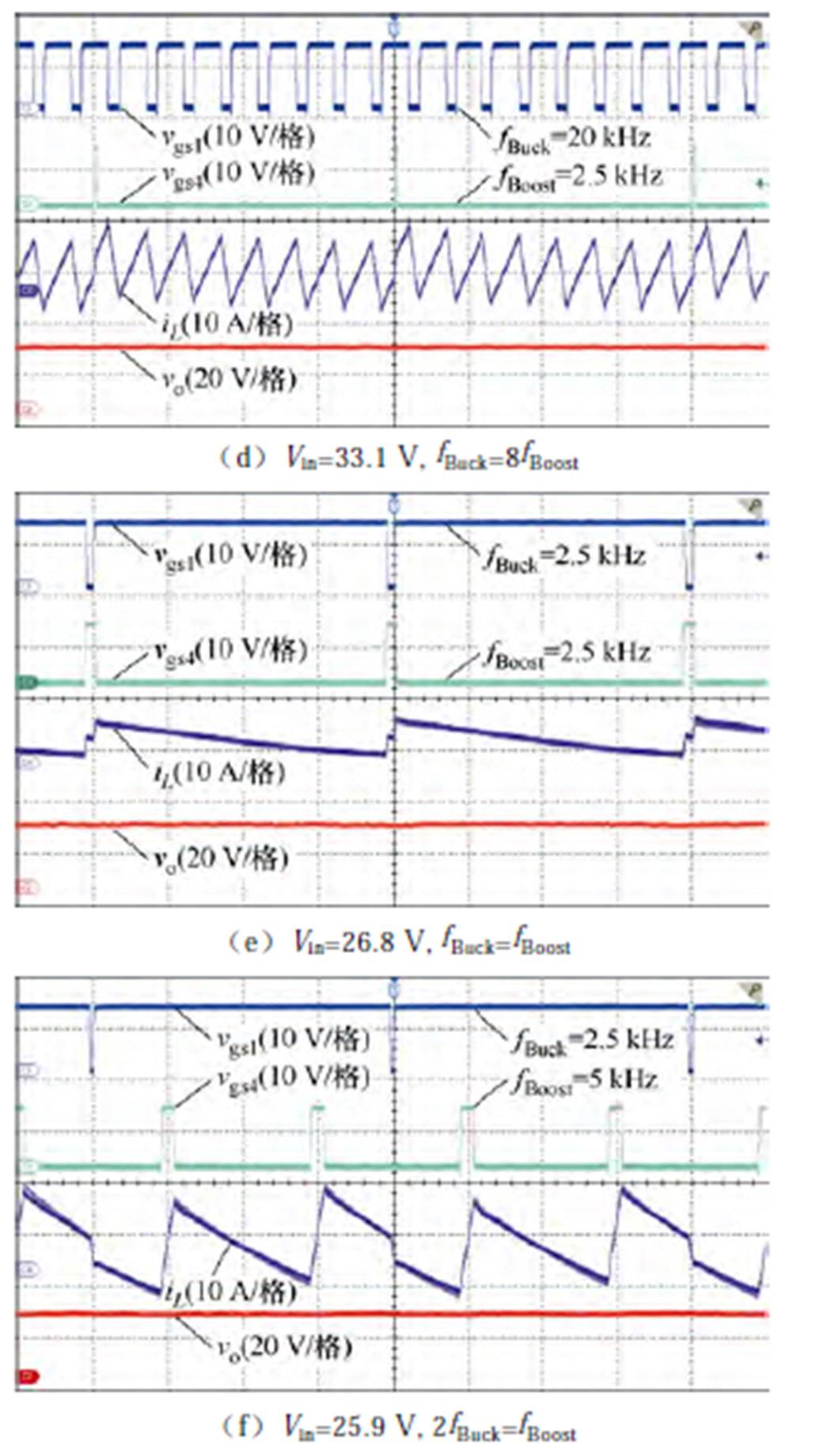
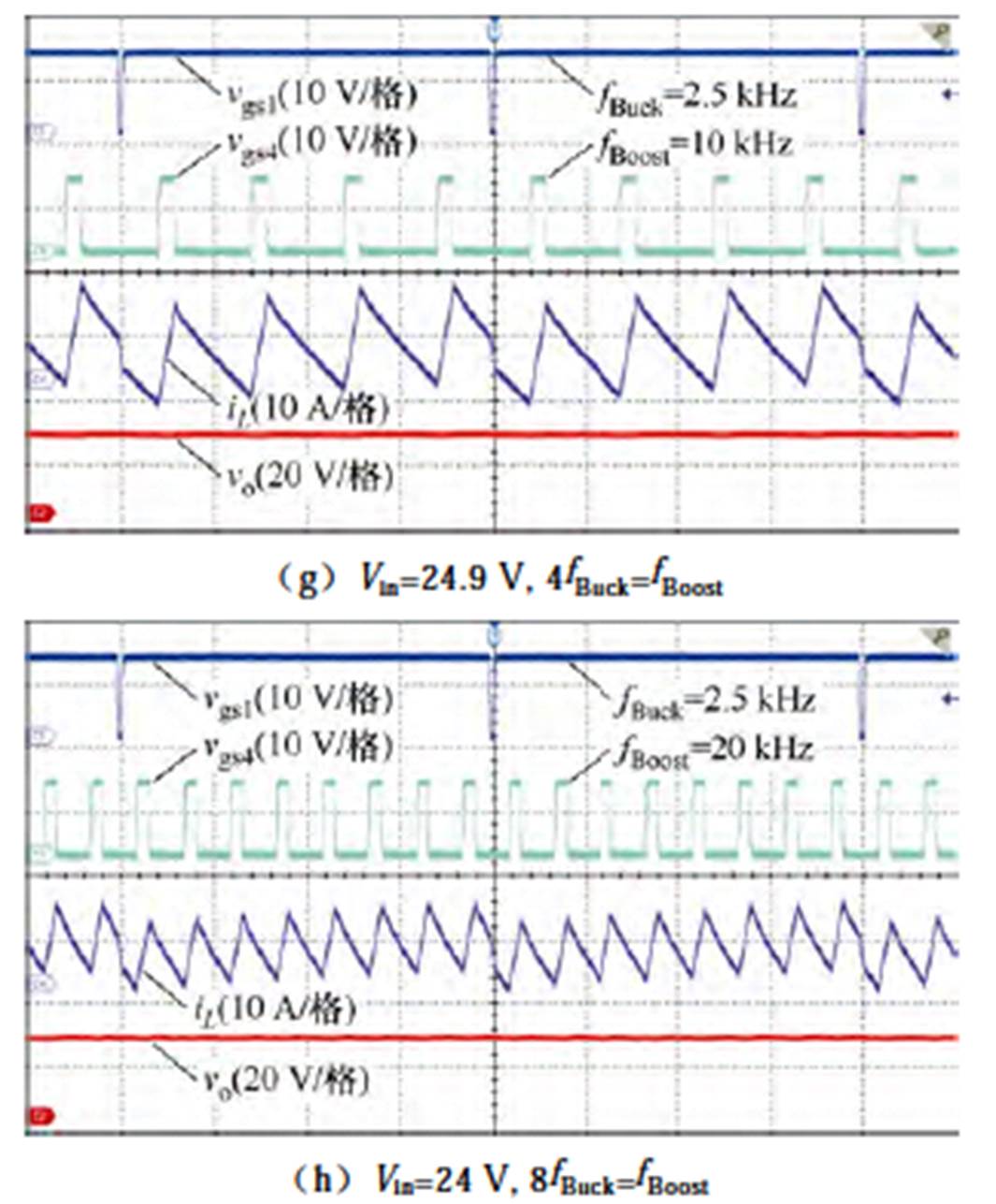
图11 不同输入下的稳态工作波形(Vo=28 V)
Fig.11 Steady-state operating waveforms under different inputs (Vo=28 V)
为验证所提FSBB变频控制策略在效率上的优势,图12所示为在额定工作点28 V/500 W输出时,分别采用传统定频(20 kHz)两模式控制和本文所提的变频两模式控制所测得的效率曲线。当采用所提变频两模式控制策略时,由于开关频率降低使得开关损耗显著减小,虽然电感电流纹波的增大使得导通损耗增大,但是整体损耗是减小的,因此效率得以提升。当输入电压接近输出电压时,两个桥臂开关频率均降为最低的fbase(2.5 kHz),此时所提出的变频控制策略的效率优势就越明显。
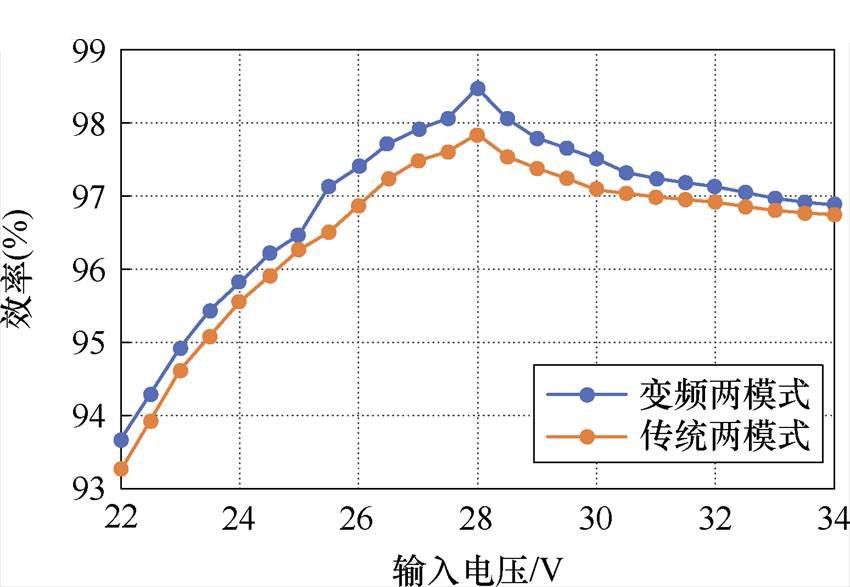
图12 效率曲线对比
Fig.12 Efficiency curves comparison
图13给出了变换器在升压、降压以及升降压情况下的损耗分布。可以看出,所提变频控制策略使得开关损耗显著减小,虽然电感电流纹波的增加使得导通损耗有所增加,但是整体的变换效率得到了提升,尤其是在输入、输出电压接近的工作点附近,变换器的效率得到了显著提升。

图13 不同输入下的变换器损耗分布对比
Fig.13 Comparison chart of converter loss distribution under different inputs
最后,对所提出的变频控制策略在模式切换过程中的稳定性进行了验证。FSBB变频控制策略的模式切换过程如图14所示,当输入电压以一个固定的斜率变化时,可以看到,该策略能够自动地调整频率以提高变换效率,调整开关频率时电感电流纹波随之改变,在模式切换过程中变换器始终能保持输出电压的稳定。
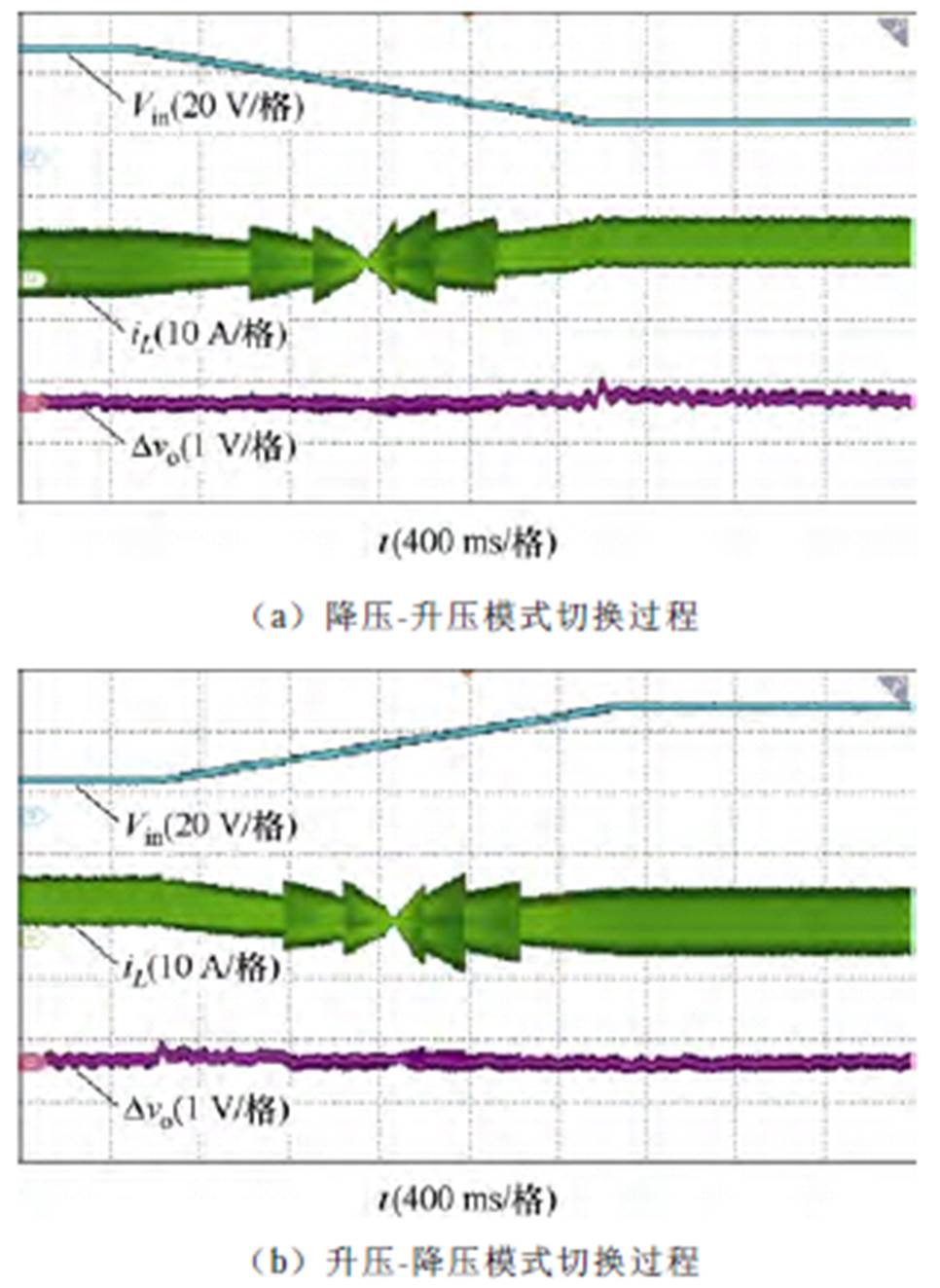
图14 FSBB变频控制策略的模式切换过程
Fig.14 Mode switch procedure of FSBB frequency conversion control strategy
具体切换过程的放大波形如图15所示。由于模式切换过程的原理都是一样的,所以这里只给出了一例频率切换的波形。图中给出了Buck桥臂频率切换而Boost桥臂频率不变的情况,在所提出的交错双沿载波下,频率切换处电感电流大小恰好是其平均值。由此时的频率变化过程中变换器的输出电压始终保持稳定,从一个稳态直接切换到另一个稳态,不存在调整时间,证明了交错双沿载波可以实现频率的无缝切换。
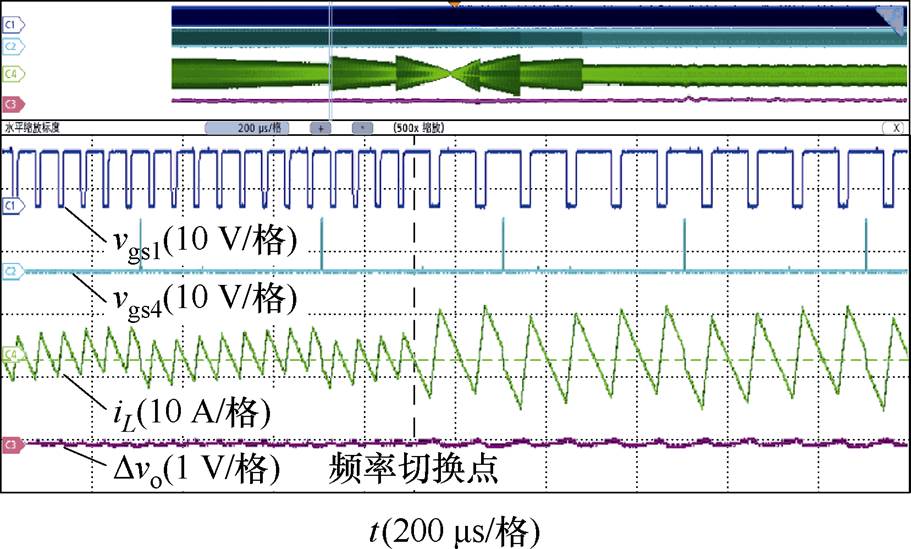
图15 变频多模式的模式切换放大波形
Fig.15 Variable frequency multi-mode mode switch amplification waveforms
针对FSBB变换器,本文首先分析了不同控制模式对电感电流的影响,进而选取一种高效率的多模式控制方式。其次讨论了载波形式对变换器电感电流纹波的影响,提出了交错双沿调制策略,具有较小的电感电流纹波以及模式切换过程速度快的优势。最后提出了一种倍频的变频控制策略,通过定量计算电感电流纹波,在输入、输出电压接近时降低变换器开关频率,以此来减小开关损耗,尽管导通损耗有所增大,但变换器整体的效率得以提升。实验证明,所提出的变频控制策略不仅提高了变换器的效率,而且能够实现平滑的模式切换,在输入改变时输出电压始终保持稳定。
参考文献
[1] 赵书强, 王慧, 田娜, 等. 基于模型预测控制的直流微电网虚拟惯性优化方法[J]. 电工技术学报, 2023, 38(12): 3264-3276.
Zhao Shuqiang, Wang Hui, Tian Na, et al. Model predictive control based DC microgrid virtual inertia optimal method[J]. Transactions of China Elec- trotechnical Society, 2023, 38(12): 3264-3276.
[2] 张昊, 李昱, 尹亚飞, 等. 直流微电网集成式高品质协同控制策略[J]. 电工技术学报, 2023, 38(23): 6345-6358.
Zhang Hao, Li Yu, Yin Yafei, et al. An integrated high-quality cooperative control strategy of DC microgrids[J]. Transactions of China Electrotechnical Society, 2023, 38(23): 6345-6358.
[3] 高圣伟, 祝庆同. 一种独立光储发电系统用宽输入范围非隔离三端口变换器[J]. 电工技术学报, 2023, 38(4): 970-982.
Gao Shengwei, Zhu Qingtong. A wide input range non-isolated three-port converter for stand-alone PV storage power generation system[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 970-982.
[4] 任小永, 唐钊, 阮新波, 等. 一种新颖的四开关Buck-Boost变换器[J]. 中国电机工程学报, 2008, 28(21): 15-19.
Ren Xiaoyong, Tang Zhao, Ruan Xinbo, et al. A novel four switch Buck-Boost converter[J]. Proceedings of the CSEE, 2008, 28(21): 15-19.
[5] 方天治, 王愿, 张惠丽, 等. 四管Buck-Boost变换器的改进型三模式变频软开关控制策略[J]. 电工技术学报, 2021, 36(21): 4544-4557.
Fang Tianzhi, Wang Yuan, Zhang Huili, et al. An improved three-mode variable frequency control strategy based on four-switch Buck-Boost con- verter[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4544-4557.
[6] Guo Zhiqiang, Mao Tianhao. Efficiency optimization and control strategy of four-switch Buck-Boost con- verter for wide conversion ratio[J]. IEEE Transactions on Power Electronics, 2023, 38(9): 10702-10715.
[7] Ahmad H J, Hagiwara M. A compact high-power noninverting bidirectional Buck-Boost chopper for onboard battery energy storage systems[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 1722-1735.
[8] 周国华, 邱森林, 张小兵. 宽增益高效率级联式四开关Buck-Boost LLC变换器[J]. 电工技术学报, 2024, 39(4): 1103-1115.
Zhou Guohua, Qiu Senlin, Zhang Xiaobing. Wide gain and high efficiency cascaded four-switch Buck-Boost LLC converter[J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1103-1115.
[9] 吴岩, 王玮, 曾国宏, 等. 四开关Buck-Boost变换器的多模式模型预测控制策略[J]. 电工技术学报, 2022, 37(10): 2572-2583.
Wu Yan, Wang Wei, Zeng Guohong, et al. Multi- mode model predictive control strategy for the four- switch Buck-Boost converter[J]. Transactions of ChinaElectrotechnical Society, 2022, 37(10): 2572-2583.
[10] Díaz V, Barrado A, Lázaro A, et al. Comparison of several modulation strategies for the Four Switch Buck-Boost converter[C]//2023 IEEE 17th Inter- national Conference on Compatibility, Power Elec- tronics and Power Engineering (CPE-POWERENG), Tallinn, Estonia, 2023: 1-6.
[11] Bai Yuning, Hu Sideng, Yang Zhi, et al. Model predictive control for four-switch Buck-Boost converter based on tuning-free cost function with smooth mode transition[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(6): 6607-6618.
[12] Ma Jianjun, Zhu Miao, Pan Chunyang, et al. Multimode operation of non-inverting Buck-Boost converter for energy storage system[C]//2021 IEEE 30th International Symposium on Industrial Elec- tronics (ISIE), Kyoto, Japan, 2021: 1-5.
[13] 戴瑞然, 马运东, 王鹏, 等. 一种基于多谐振开关槽与Buck-Boost电路的准并联变换器[J/OL]. 电工技术学报, 2024: 1-19. DOI: 10.19595/j.cnki.1000- 6753.tces.230918.
Dai Ruiran, Ma Yundong, Wang Peng, et al. A quasi parallel converter based on multi resonant switched tank and Buck-Boost circuit[J/OL]. Transactions of China Electrotechnical Society, 2024: 1-19. DOI: 10.19595/j.cnki.1000-6753.tces.230918.
[14] 任小永, 阮新波, 李明秋, 等. 双沿调制的四开关Buck-Boost变换器[J]. 中国电机工程学报, 2009, 29(12): 16-23.
Ren Xiaoyong, Ruan Xinbo, Li Mingqiu, et al. Dual edge modulated four-switch Buck-Boost converter[J]. Proceedings of the CSEE, 2009, 29(12): 16-23.
[15] 任林涛, 汪飞, 肖杨婷, 等. 四开关Buck-Boost变换器研究综述[J]. 电气工程学报, 2023, 18(2): 52-69.
Ren Lintao, Wang Fei, Xiao Yangting, et al. Review research on the four-switch Buck-Boost converter[J]. Journal of Electrical Engineering, 2023, 18(2): 52-69.
[16] 曹以龙, 吴丹, 朱冬冬, 等. 一种基于四开关Buck- Boost变换器的四模式控制策略[J]. 电源学报, 2022, 20(5): 111-118.
Cao Yilong, Wu Dan, Zhu Dongdong, et al. Four- mode control strategy based on four-switch Buck- Boost converter[J]. Journal of Power Supply, 2022, 20(5): 111-118.
[17] Wani R, Patil S L, Shinde P. Modeling and simulation of average current-mode controlled bidirectional multiphase DC-DC converters used in hybrid vehicles[C]//2021 6th International Conference for Convergence in Technology (I2CT), Maharashtra, India, 2021: 1-7.
Abstract The four-switch Buck-Boost converter (FSBB) has the advantages of a wide input voltage range, input and output polarity, and high control degree of freedom, which is suitable for charging photovoltaic cells in a DC microgrid. At present, research on FSBB mainly focuses on the smooth switching of multi-mode control and efficiency improvement. After discussing the influence of multi-mode control and modulation mode on FSBB efficiency, this paper proposes a variable frequency control strategy that considers efficiency improvement and smooth mode switching.
Through the analysis of the inductor current under multi-mode control, it can be concluded that the inductor current ripple and average value of the two-mode control are the smallest when the input and output voltages are close, and its efficiency performance is optimal. Under the same gain, reducing d2 can reduce the average value of inductance current. In addition, under the same duty cycle d2, reducing or avoiding the simultaneous conduction of S1 and S4 can reduce the ripple of the inductor current. Both are beneficial in improving the efficiency of the converter. Then, this paper proposes an interleaved dual-edge modulation method, which avoids the simultaneous conduction of S1 and S4 while ensuring that d2 is a small value.
Under the two-mode control, when the converter gain is close to 1, the inductor current ripple is close to 0. The multi-switch switch works, and the switching loss ratio increases. Because the current ripple is small at this time, reducing the switching loss is convenient. The average value of the inductor current formed by the interleaved dual-edge modulation is exactly the starting and ending position values of each switching cycle. Thus, the frequency can be modified to achieve a smooth transition of the converter operating mode. A variable frequency multi-mode control strategy is proposed. Then, the half-bridge on both sides of the inductor of FSBB is divided into high-frequency and low-frequency bridges. When the input and output voltages are close, the frequency of the two bridges is the lowest fbase. When the input voltage increases (decreases), ensuring the inductor current ripple does not exceed DIL_max, the Buck duty cycle is reduced, and the frequency of the Buck bridge is increased (the Boost duty cycle and the frequency of the Boost bridge are increased).
A 600 W FSBB prototype is built to verify the proposed variable frequency control strategy. The experimental results show that the converter can achieve Buck-Boost conversion in different modes. When the input voltage changes, the strategy can automatically adjust the frequency to improve the conversion efficiency. When the switching frequency is adjusted, the inductor current ripple changes, and the converter can always maintain the stability of the output voltage during the mode-switching process. Compared with the fixed- frequency two-mode control, the proposed frequency conversion significantly reduces the switching loss due to the decrease of the switching frequency. Although the increase in the inductor current ripple increases the conduction loss, the overall loss is reduced, thereby improving the efficiency. Especially near the operating point when the input and output voltages are close, the converter’s efficiency is significantly improved.
keywords:Four-switch Buck-Boost converter, interleaved dual-edge modulation, variable frequency control, smooth mode switch
中图分类号:TM461
DOI: 10.19595/j.cnki.1000-6753.tces.240409
国家自然科学基金资助项目(52177181)。
收稿日期 2024-03-15
改稿日期2024-04-27
罗利江 男,1999年生,硕士研究生,研究方向为功率电力电子变换技术。E-mail: luolijiang@nuaa.edu.cn
林聪智 男,1979年生,硕士,讲师,研究方向为电力电子变换技术、电力系统自动化。E-mail: lincongzhi@jmu.edu.cn(通信作者)
(编辑 陈 诚)