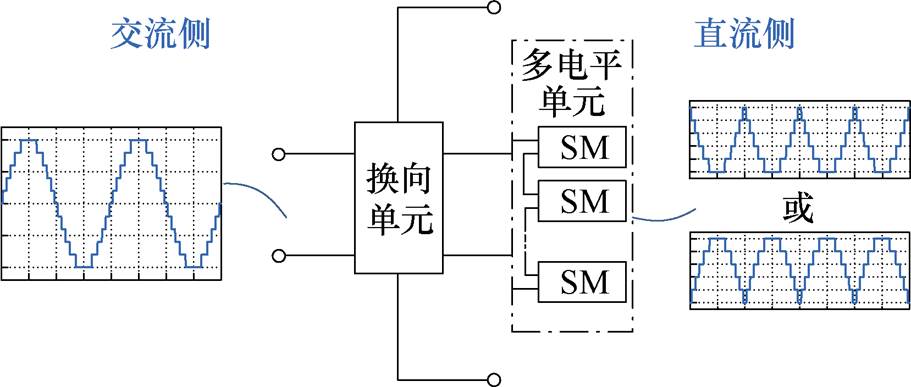
图1 HWS-MMC拓扑概念
Fig.1 Topology concept of HWS-MMC
摘要 半波整形模块化多电平换流器（HWS-MMC）是一种新型融合两电平拓扑和模块化多电平拓扑优点的轻型化混合多电平换流器，其利用低频换向开关配合，将多电平单元调制生成的正弦半波翻转为完整正弦波形输出，实现交直流功率变换。该文在分析HWS-MMC基本原理和多电平单元能量平衡机理的基础上，建立反映模块电容电压和直流母线电容电压动态的数学模型，并基于多尺度开关周期平均化方法获得HWS-MMC不含高频和基频开关特性的全平均值动态模型，进而提出考虑并网电流控制、两级直流电压控制以及多电平单元电容相间和相内电压均衡控制的多目标控制策略。最后通过RT-Lab控制硬件在环实时仿真验证了动态模型和控制策略的有效性。
关键词：半波整形模块化多电平换流器 动态模型 能量平衡 电压均衡 多目标控制
模块化多电平换流器（Modular Multilevel Con- verter, MMC）具备输出电能质量高、模块化易拓展等优势[1-2]，已成为高压大容量交直流功率变换装备的主要方案，广泛应用于柔性直流输电等工程领域。传统MMC面临设备体积、质量大，造价成本高等方面的挑战[3-6]，其轻量化研究是长期以来的关注热点。
现有MMC轻量化研究存在两种技术路线：一种是通过降容控制或子模块拓扑改进，降低传统MMC子模块电容容值或用量[7]；另一种是融合两电平拓扑和模块化多电平拓扑优点构成所谓的混合模块化多电平换流器（Hybrid Multilevel Converter, HMC）[8-13]。传统MMC每相上、下桥臂均需要调制生成完整正弦波形，仅有一半子模块处于投入状态，子模块数量多、利用率低。而HMC减少了多电平调制所需的子模块数量，轻量化效果明显，是MMC轻量化研究的重要方向之一。
交替桥臂换流器（Alternate Arm Converter, AAC）为最早提出的HMC拓扑[8]，多电平单元只需调制出正弦半波，降低了子模块数量需求，但AAC每相仍需要两个多电平单元（桥臂），子模块总量仍较多。混合级联多电平换流器（Hybrid Cascaded Multilevel Converter, HCMC）在两电平拓扑交流侧串联多电平单元，每相只需一个能够输出交流峰峰值的全桥多电平单元，子模块数量大幅减 少[9]，但直流侧串联开关需承受直流电压，所需器件总数相对较多。直流侧并联多电平单元的HMC（DC side Parallel-HMC, DCP-HMC）[10]和直流侧串联多电平单元的HMC（DC side Series-HMC, DCS- HMC）[11]均能减少子模块数量，但需要在每个相单元的交流出口装设变压器以提供电气隔离。基于桥臂复用思想，桥臂复用型MMC（Arm Multiplexing MMC, AM-MMC）[12-13]利用切换开关实现了中间桥臂分时参与上、下桥臂调制，而三相复用桥臂MMC（Three Phase Multiplexing Arm-MMC, TPMA- MMC）[14]通过两电平拓扑实现了桥臂三相间复用，均提升了换流器的功率密度。T型桥臂交替多电平换流器（T-type Alternate Arm Multilevel Converter, T-AAMC）[15]结合了HCMC和AAC的特点，在电容总容量相当的前提下获得了运行灵活性和效率的提升。混合串联换流器（Hybrid Series Converter, HSC）[16]可视为HCMC和DCP-HMC的融合，子模块数和器件总数介于二者之间。基于桥臂交替和分时复用思想，一种新型HMC被提出[17-18]，文献[17]称为半波交替MMC（Half-wave Alternating MMC, HA-MMC），文献[18]称为分时复用MMC（Time- Sharing principle-based MMC, TS-MMC），该拓扑进一步提升了子模块利用率，相对已有HMC子模块数量和器件电压应力降低。
在上述混合模块化多电平换流器（HMC）中，DCP-HMC、DCS-HMC以及HA-MMC（TS-MMC），每相均可看成由一个多电平整形单元和一个换向单元构成，其中多电平单元进行半波整形，只需调制生成多电平正弦半波，三相所需子模块数最低，可降至传统MMC的25%。基于此半波整形思想，本文将新型HMC称为半波整形MMC（Half-Wave Shaping based MMC, HWS-MMC），从波形调制角度凸显拓扑特点。
文献[17-18]在详细论述HWS-MMC工作原理的基础上，针对桥臂能量平衡问题，分别提出了移相调制和三次谐波注入方法，实现宽范围下子模块能量平衡和电容电压稳定；但现有研究均以直流侧理想电压源逆变工况为例，对拓扑原理和桥臂能量平衡进行说明，尚未涉及HWS-MMC动态建模、直流母线电压控制以及模块电容动态能量平衡控制等详细多目标控制的设计研究。
鉴于此，本文针对HWS-MMC的动态模型及多目标控制策略进行研究。首先，从半波整形角度阐述HWS-MMC的拓扑构建思路，介绍其工作原理、能量平衡问题和移相宽范围调制方法。其次，建立了反映子模块电容电压和直流母线电压动态的数学模型；在此基础上采用多尺度开关周期平均化方法获得换流器不含高频和基频开关特性的全平均值动态模型。然后，基于动态模型，系统地建立以换流器并网电流控制、两级直流电容电压控制以及相间和相内模块均压控制为目标的整体控制策略，并进行控制器设计。最后，在RT-Lab实时仿真平台搭建HWS-MMC系统模型，验证所提控制策略的有效性。
基于半波整形思想的HWS-MMC相单元拓扑基本概念如图1所示，由多电平单元和换向单元构成。多电平单元进行正弦半波调制，换向单元连接交流侧和直流侧，在完成交直流变换的同时将正弦半波翻转为完整正弦波；多电平单元仅需配置半波调制所需的子模块数，相对于全波调制，子模块数可减半，且每相只需一个多电平桥臂，故所需子模块数理论上可降至传统MMC的25%。
图1 HWS-MMC拓扑概念
Fig.1 Topology concept of HWS-MMC
根据换向单元和多电平单元的不同连接方式，HWS-MMC相单元可有不同的元结构形式，典型元结构如图2所示。图2a为多电平单元与换向单元并联型的HWS-MMC，图2b为二者串联型HWS- MMC，图2c为多电平单元嵌入换向单元的HWS- MMC。其中换向开关均为多个IGBT或IGCT串联构成，按基频周期通断。并联型HWS-MMC不具备交流调压能力（交流电压峰值即为直流母线电压值），串联型HWS-MMC的4个换向开关均承受直流母线电压，而嵌入型HWS-MMC交流侧换向开关仅承受0.5倍直流母线电压，所需串联开关器件数量少。本文以嵌入型HWS-MMC作为对象，对其动态模型及多目标控制策略进行深入研究，后文直接将其称为HWS-MMC。
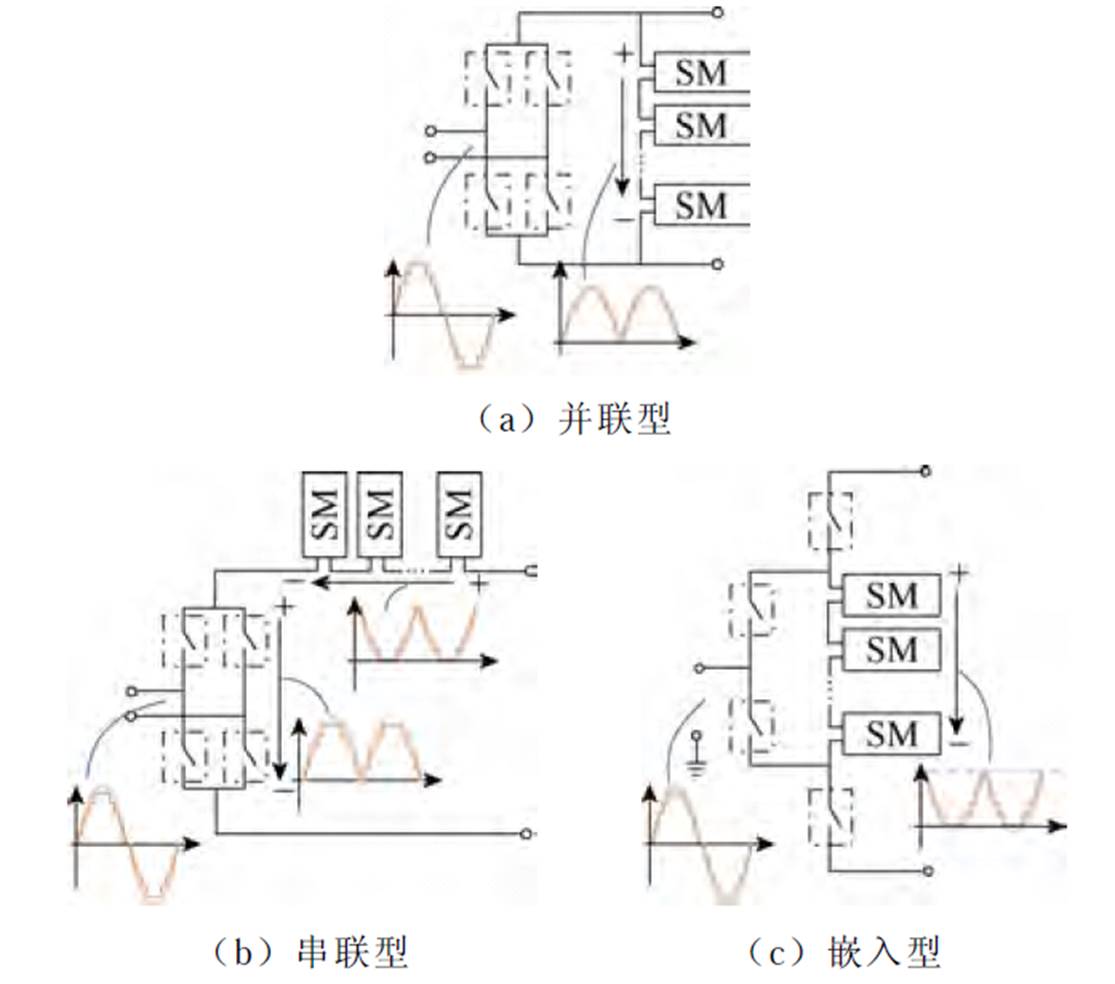
图2 HWS-MMC典型元结构
Fig.2 Typical basic structure of HWS-MMC
嵌入型HWS-MMC拓扑和工作原理如图3所示，其中交流侧换向开关采用IGBT正反向串联形式，多电平单元可采用半、全桥模块混合配置。以a相为例：多电平单元生成含直流偏置的半波多电平电压umc；换向单元将正弦半波极性翻转为完整正弦波。图中Cdc为直流母线电容。
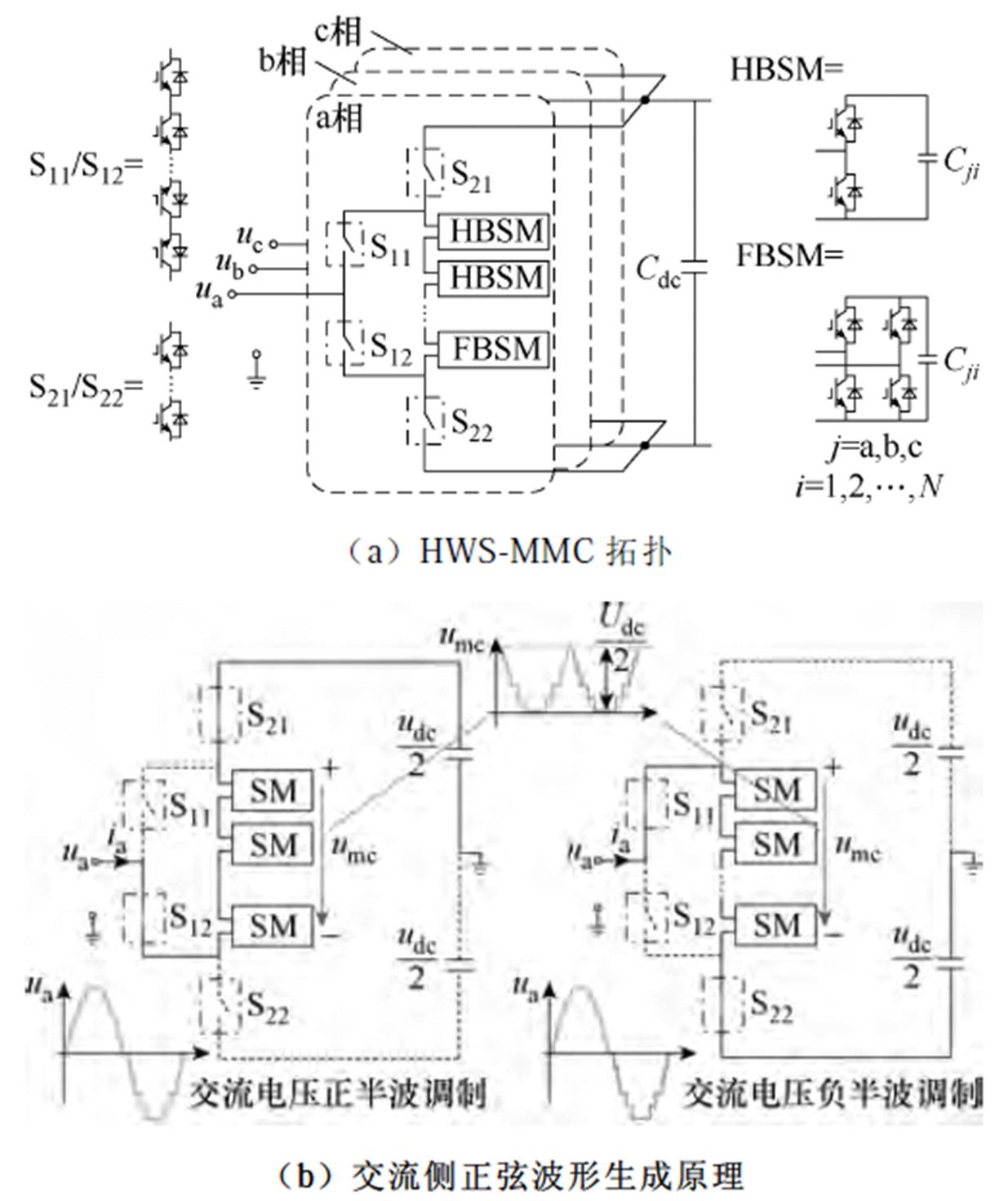
图3 HWS-MMC拓扑和工作原理
Fig.3 Topology and principle of HWS-MMC
忽略开关谐波，设a相交流端口电压和电流为
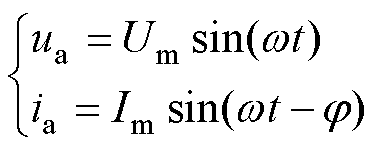（1）
式中，Um、Im分别为相电压和电流幅值；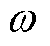
为交流电网角频率；
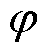为ia滞后ua的角度，即功率因数角。
根据ua的正负半周，换向单元两组开关交替导通以实现波形翻转，定义a相换向单元开关函数为
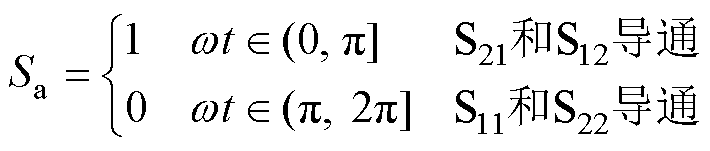（2）
根据图3及式（1）、式（2），多电平单元电压umc、电流imc可表示为
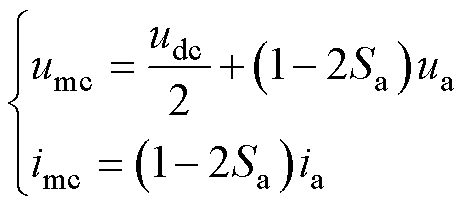（3）
式中，udc为直流母线电容电压。
根据式（1）～式（3），可得HWS-MMC多电平单元在调制周期内的累积能量随时间变化的表达式为
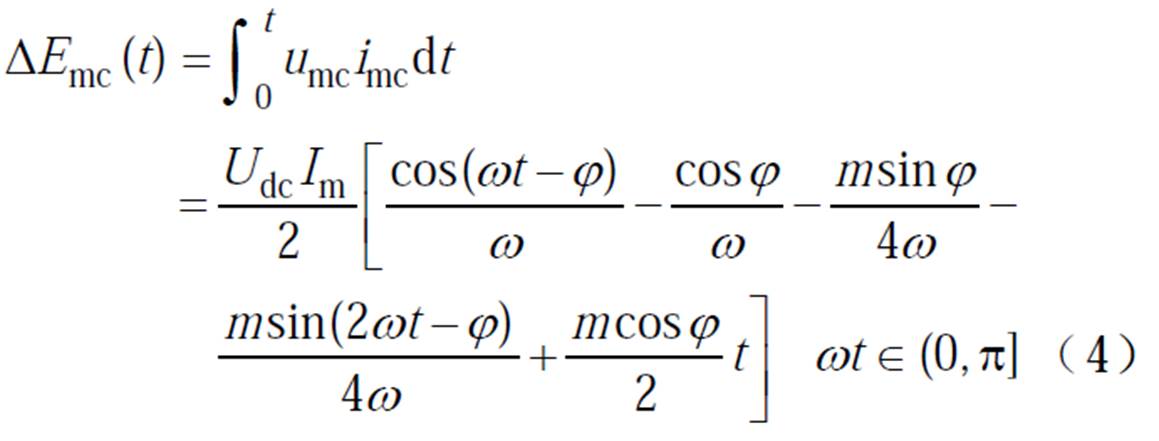
式中，m为调制比，m=Um/(Udc/2)，Udc为直流母线电容电压udc稳态值。令式（4）中t=p/w，得到半波周期多电平单元累积能量值为
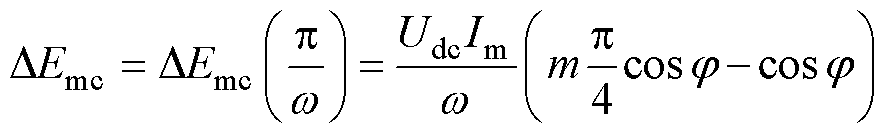（5）
由式（5）可见，任意j 时，只有当m=4/p 时，才能保证桥臂在半波周期内累积能量为0，换流器才能工作于稳态。但在实际应用中，换流器端口交流电压需实现宽范围调节，以满足系统运行工况变化要求。对此本文采用换向单元移相调制方法[17]，引入新的控制自由度，以突破特定调制比的约束。
移相调制策略令换向单元切换点滞后于端口电压基波ua（或参考电压）过零点q 角度，则式（2）中换向单元开关函数修改为
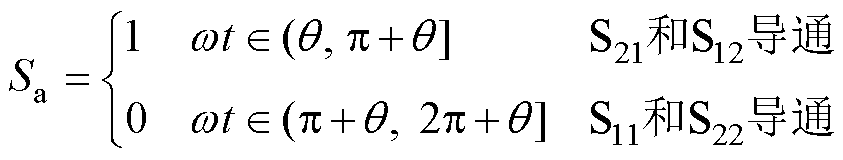（6）
根据式（6），重新计算HWS-MMC多电平单元在半波周期内的能量累积表达式为
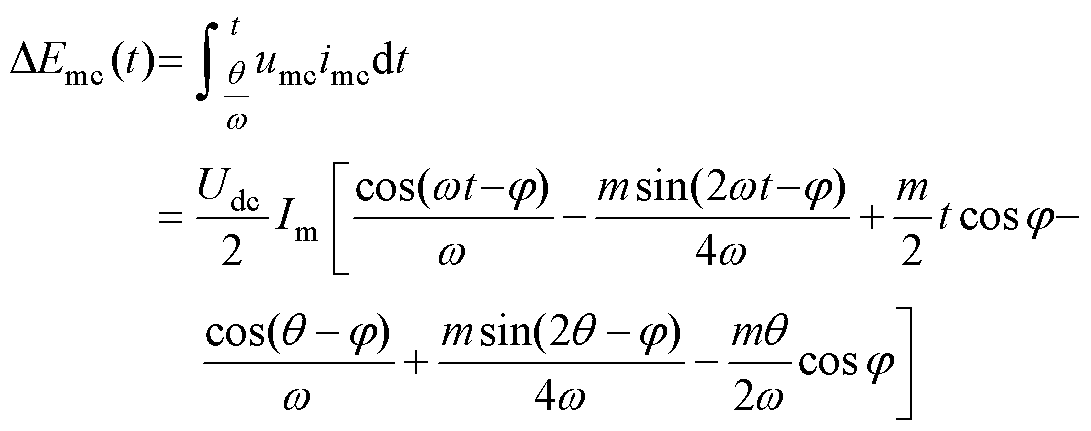
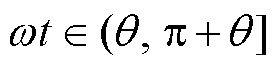（7）
由式（7）可得半波周期多电平单元累积能量值为
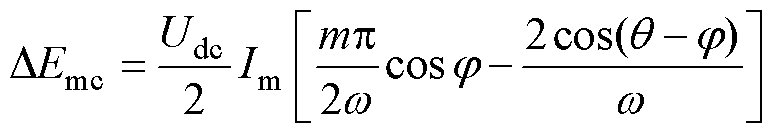（8）
由式（8）可知，当采用移相控制时，可通过调整q，使DEmc保持为0，突破对特定调制比的限制。
令式（8）DEmc=0可解得移相角q ，因随着q 绝对值增大，多电平单元电压的最大值增大，需要的子模块数量增多，因此q 应取绝对值较小的值，为
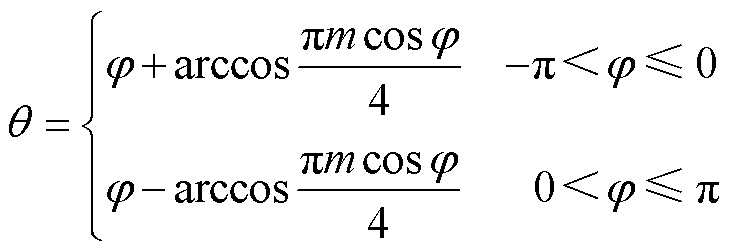（9）
根据式（9），可以画出q 随j 和m的变化规律如图4所示，可知当m在[0, 4/p]，q 随j 分别在[-p, 0]和 (0, p) 区间单调变化，q 的变化范围为[-p/2, p/2]。
图4 移相角随功率因数角和调制比变化规律
Fig.4 The variation of phase shifting angel with power factor angel and modulation index
进一步根据式（4）、式（7）及式（9），图5绘出了不同工况下多电平桥臂累积能量的理论曲线，绘图参数为Udc=100 V，Im=20 A。由图5可见，当换向开关采用过零同步控制时，只有当m=4/p，才能保证桥臂累积能量平衡；而当调制比m=0.9或0.5时，DEmc(t)将发散，桥臂能量不能平衡，无法稳定工作；而采用移相调制时，根据式（9）计算移相角，无论调制比如何变化，均可保证在不同功率因数下的能量平衡，HWS-MMC可实现宽范围运行（限于篇幅，图中仅给出m=0.9和m=0.5两种情况）。
图5 HWS-MMC多电平单元累积能量理论波形
Fig.5 Theoretical waveforms of the accumulated energy of HWS-MMC multilevel unit
由图3可知，与传统MMC直流母线电压即为每相投入的子模块电容电压之和不同，HWS-MMC多电平单元模块电容总电压uC与直流母线电容电压udc相互独立，需实现两级直流电压的稳定控制。本节以图6所示的等效电路及变量定义，建立数学模型。
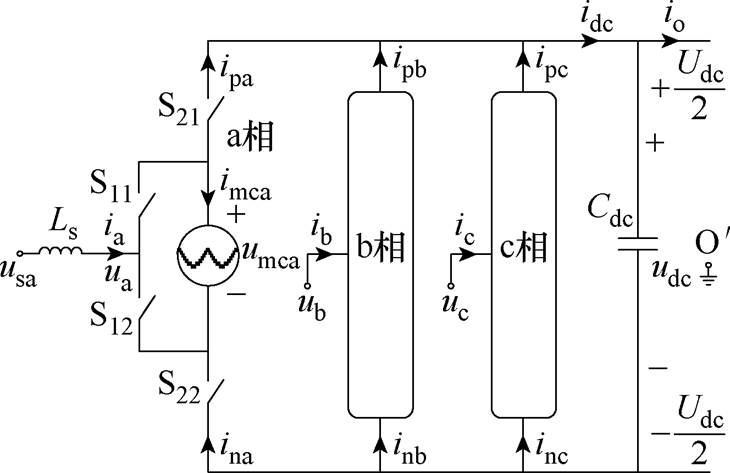
图6 HWS-MMC等效电路
Fig.6 HWS-MMC equivalent circuit
多电平单元桥臂由全桥（或半桥）子模块级联而成，假设每相各子模块电容电压均衡，三相桥臂模块电容总电压分别为uCa、uCb、uCc，则可将每相多电平单元用一个模块等效，等效模块电容为Ce，根据多电平调制原理，各相多电平单元桥臂电压为
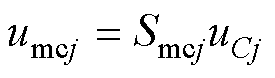（10）
式中，umcj为每相多电平单元桥臂端口电压，下标j=a, b, c表示abc三相，下文同；Smcj为多电平单元的等效平均开关函数。
三相正弦调制函数hj为
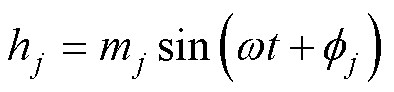（11）
式中，mj为各相幅值调制比，稳态时ma=mb=mc= Um/(Udc/2)；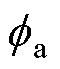
=0°，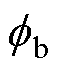
=-120°，
=120°为三相初相位；则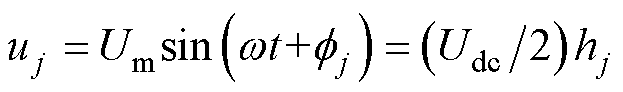
。
结合式（10）、式（11）及半波换向原理式（3），可推导得到多电平单元平均开关函数与正弦调制函数满足关系
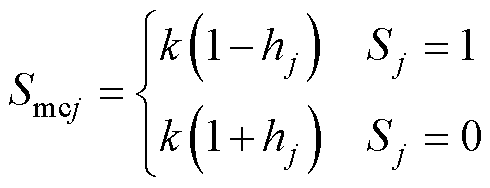（12）
式中，k为1/2直流母线电压与多电平桥臂电容总电压两者的稳态值之比，即k=(Udc/2)/UC；Sj为j相换向单元开关函数。
由式（3）可得三相多电平单元桥臂电流为
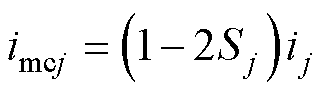（13）
式中，ij（j=a, b, c）为三相交流电流。
根据多电平单元交流侧和直流侧功率平衡，以及式（10）、式（13），可得模块电容充电电流为
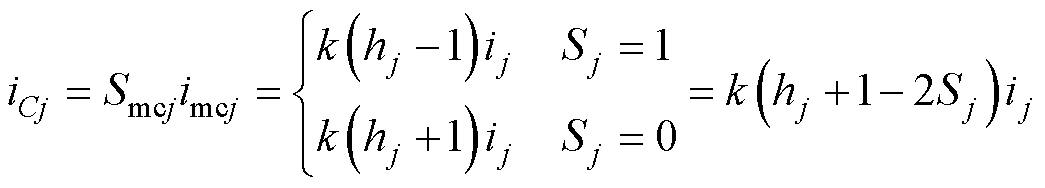（14）
进而可得桥臂等效模块电容电压动态方程为
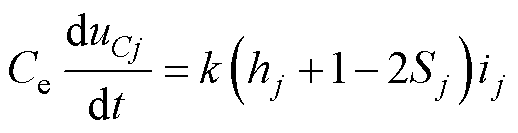（15）
当交流侧采用电感作为滤波元件时，根据基尔霍夫电压定律（KVL），换流器交流网侧电流动态方程可表示为
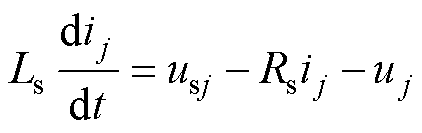（16）
式中，usj为三相网侧电压；Ls为交流滤波电感；Rs为其等效电阻。
则根据半波换向原理，各相交流端口电压uj为
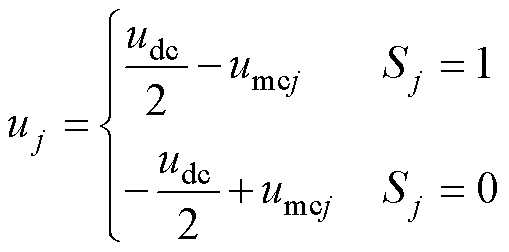（17）
将式（10）、式（12）代入式（17），可得
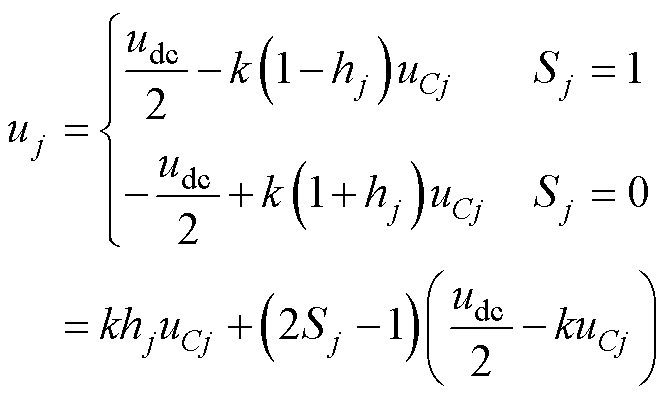（18）
对于直流母线侧动态建模，由于换向开关通断切换，使HWS-MMC相电流分段分时注入正负直流母线，引起直流侧电流脉动。考虑三相对称，结合基尔霍夫电流定律（KCL），可得HWS-MMC流入直流母线的电流为
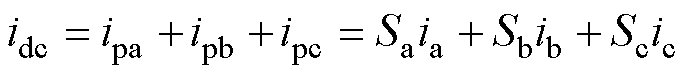（19）
则换流器直流母线电容电压动态方程为
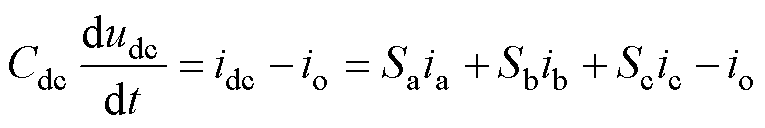（20）
式中，io为换流器直流母线侧输出电流。
为了依据经典线性控制理论进行HWS-MMC控制策略的设计，需要得到HWS-MMC不含开关特性的平均值线性动态模型。
根据第2.1节和2.2节分析可知，式（15）、式（16）、式（18）、式（20）即为HWS-MMC的动态数学模型，因模型中多电平单元开关函数用平均值Smcj表征，该模型已对高频开关特性进行了平均化，此处称为准平均值模型，结合图6所示电路拓扑，可得三相HWS-MMC准平均值电路模型如图7所示。
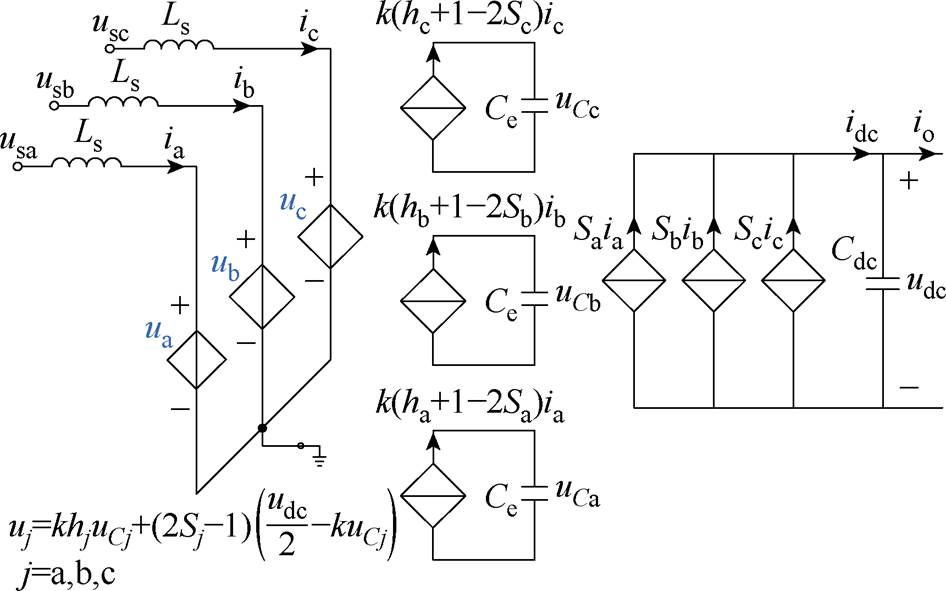
图7 HWS-MMC准平均值模型等效电路
Fig.7 Quasi-average model of HWS-MMC
由图7可见，HWS-MMC交流侧特性与传统电压源型换流器（Voltage Source Converter, VSC）类似，内部多电平单元电容特性与MMC类似，直流输出侧电容特性与六脉动整流电路类似；虽然该模型已不含高频开关函数，但仍含有基频开关函数、状态量与控制量乘积等非线性环节，为进行多目标控制设计，还需进一步平均化和线性化。
对于电流微分方程中基频开关函数的影响，如式（16）和式（18），根据控制环路时间尺度分离特性，在交流电流控制时间尺度，直流电容电压可认为是慢变量。假设在直流电压控制器的作用下，直流母线电容电压保持为其稳态值Udc，模块电容电压保持为其稳态值UCj，则由式（16）、式（18），交流电流微分方程可表示为
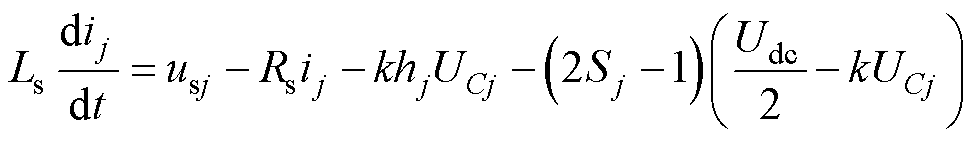（21）
而由式（12）中k=(Udc/2)/UC，代入式（21），可消除基频开关函数项的影响，交流电流动态方程可转换为与传统VSC并网换流器的线性方程相同的方程式
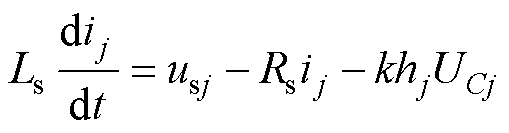（22）
对于电容电压动态方程中基频开关函数的影响，如式（15）、式（20），可采用低频周期平均化方法。
根据HWS-MMC工作原理，其多电平单元以基频半周为工作周期，则对式（15）在一个基频半波内取平均值，即
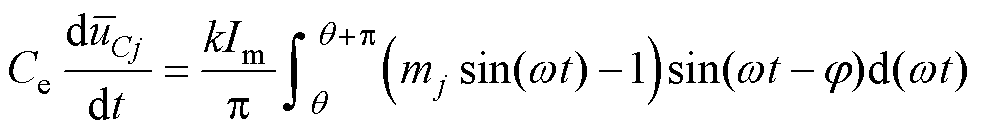
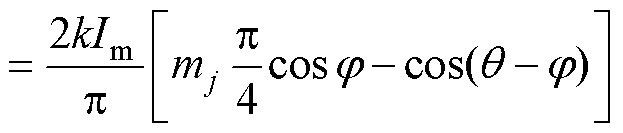（23）
对式（19）进行推导分析可知，idc在一个工频周期内脉动6次，周期为p/3，对其在p/3周期内求平均值得
（24）
代入式（20），得直流母线电压平均动态方程为
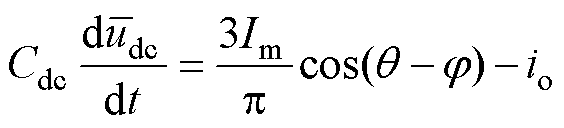（25）
综上所述，可得HWS-MMC变换器不含高频、基频开关特性的全平均值动态模型，如式（22）、式（23）、式（25）。
在通过换向开关移相调制保证模块电容稳态能量平衡的前提下，依据2.3节中动态数学模型，进行HWS-MMC换流器整体控制策略设计，其控制目标主要包括：①交流侧并网电流正弦波形及功率因数控制；②直流母线电容电压稳定在参考值；③多电平单元模块电容电压平均值稳定在参考值，同时确保其相间和相内子模块电压均衡。
在采用时间尺度分离、慢变量稳态假设的方法消除电流微分方程中基频开关函数的影响后，HWS- MMC交流电流动态方程已简化为式（22），与传统级联H桥换流器类似，可沿用传统级联H桥网侧电流的控制方法[20]。
对式（22）进行Park变换，可得网侧电流基于dq坐标系的动态方程为
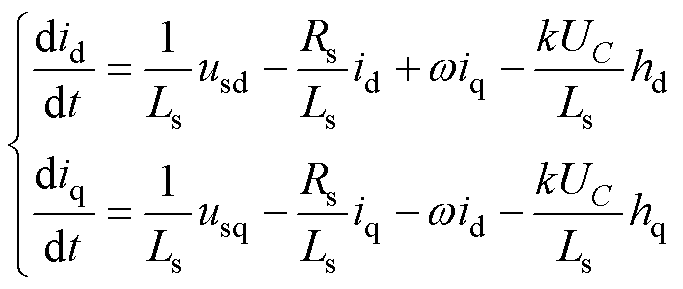（26）
式中，usd、id、hd和usq、iq、hq分别为d轴和q轴的电网电压、电流及调制信号。
设新的控制量v=[vd vq]T，令式（26）等号右端等于v，可得到电流环的反馈控制律为
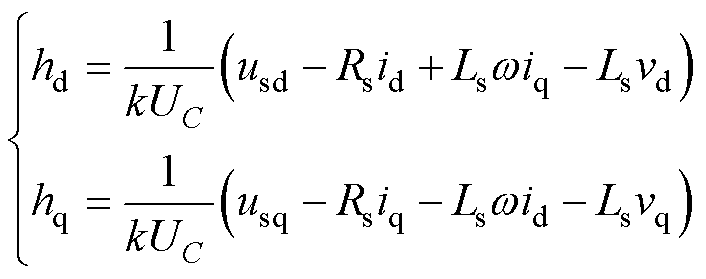（27）
新控制量可采用比例-积分（PI）控制，即
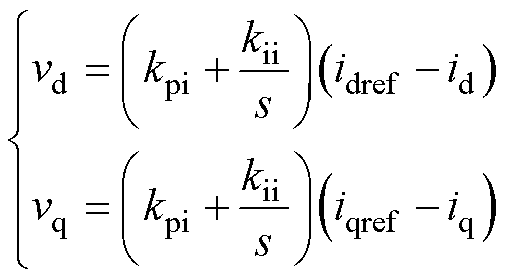（28）
式中，idref、iqref为电流参考值；kpi、kii为电流环PI控制器参数，可根据典型二阶线性系统控制设计方法进行整定[21]。
将式（27）、式（28）代入式（26），网侧电流闭环传递函数可写成如下典型二阶线性系统形式
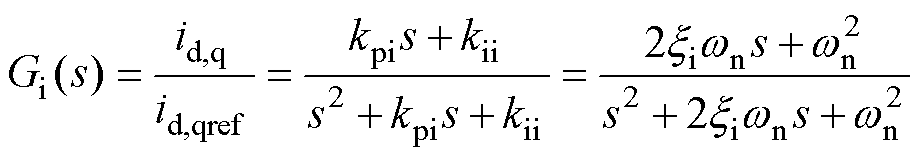（29）
式中，xi为阻尼比；wn为自然角频率。根据该典型二阶系统带宽、阻尼比与PI参数的关系，有
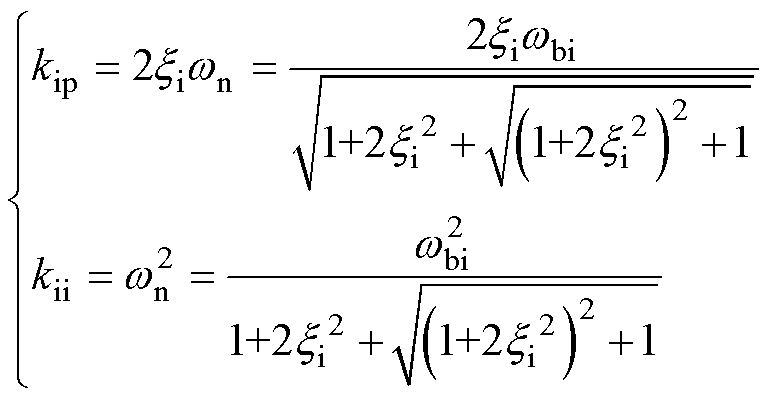（30）
式中，wbi=2p fbi，fbi为环路控制带宽。因此，根据选定的带宽和阻尼比，即可通过式（30）计算出相应控制器的PI参数。如取电流环带宽fbi=370 Hz，阻尼比xi=0.707，有kpi=1 600，kii=1.28×106（下文其他环路控制参数设计方法与此相同）。
综上所述，可得电流环控制框图如图8所示，由电流控制生成dq轴调制信号hd、hq，经旋转/静止坐标变换产生三相正弦调制波ha、hb、hc。
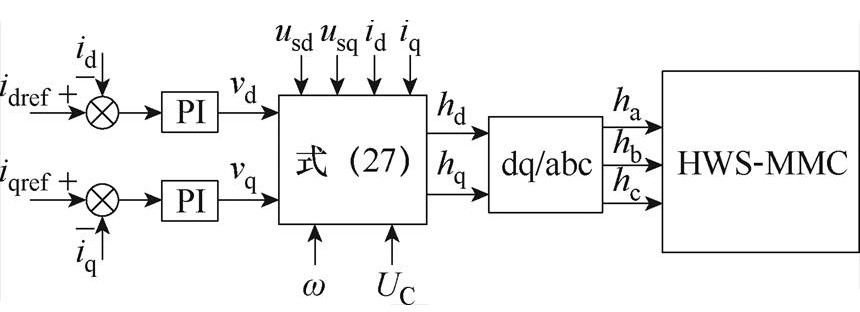
图8 电流内环控制框图
Fig.8 Inner current loop control block diagram
HWS-MMC直流侧包含直流母线电容电压以及多电平桥臂模块电容电压两级直流电压动态，二者相互独立，均需要控制。当采用d轴矢量定向进行Park变换时，有id=Im，且在电压控制时间尺度，可认为电流已跟踪其参考指令idref，即id=idref=Im，则根据式（25）和式（23），两级直流电压动态方程可重写为
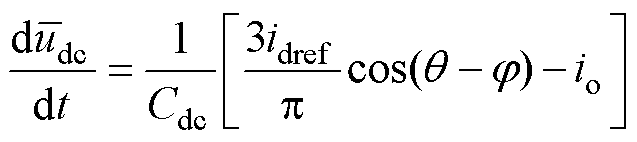（31）
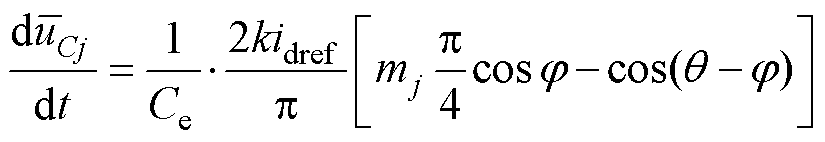（32）
根据式（31）、式（32），可知直流母线电压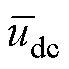
与模块电容总电压
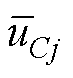为被控状态量，二者需要两个独立的控制量予以控制。本文选择idref为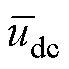的控制量。对于模块电容电压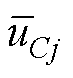，其动态与调制比mj和移相角q 均有关，由1.3节可知，由于能量平衡约束q 和m之间存在关系（式（9）），即二者只存在一个控制自由度，因此结合1.3节中稳态能量平衡控制，选移相角q 作为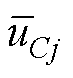的控制量，在由稳态能量平衡控制计算得到q0的基础上，利用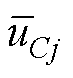控制环生成移相角增量，以消除动态过程中累积能量造成的电容电压偏差，因此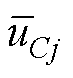控制环实际上为模块电容动态能量平衡控制。
1）对于直流母线电压控制
令直流母线电压动态方程式（31）等号右端等于新控制量vu_dc，可得直流电压控制律为
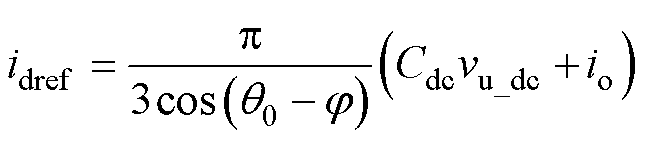（33）
新控制量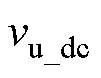
采用比例-积分（PI）控制，即
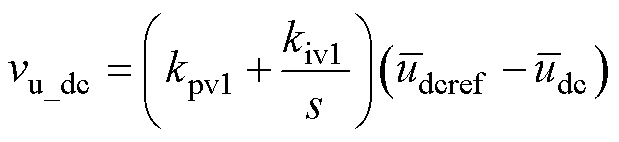（34）
式中，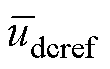
为直流母线电压参考值；kpv1、kiv1为直流母线电压环PI控制器参数。
结合式（33）、式（34）和式（31），可知直流母线电压闭环传递函数也可表示成如电流环式（29）所示的典型二阶线性系统形式。因此，PI参数kpv1和kiv1可根据典型二阶系统控制设计方法，通过选定合适的带宽和阻尼比进行整定。此外，实际控制中，式（33）中系数项cos(q0-j)可用其稳态值代替，以避免其动态波动对控制产生不利影响。
2）对于模块电容电压控制
模块电容电压动态方程式（32）中控制量q 项呈现为余弦函数形式，且与m存在约束关系，需进行线性化处理。基于小信号分析，可将q 余弦项用二阶泰勒级数代替，即cos(q-j)=1-(q-j)2/2，有
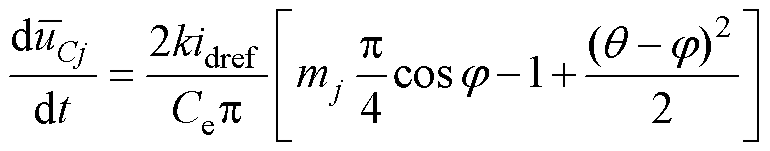（35）
将式（35）中变量用稳态量叠加小扰动量表 示为
（36）
代入式（35），消去稳态量及二阶以上小扰动量，可得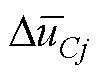
与
之间满足的线性关系为
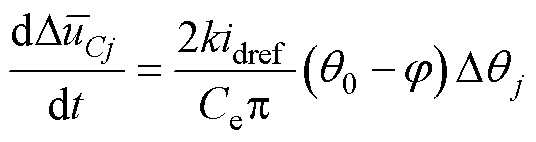（37）
由于模块电容电压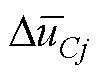包含三相变量，此处考虑各相不均衡差异，各相移相角以
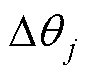（j=a, b, c）表示。
式（37）中，当q0与j 关系不同时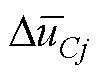，随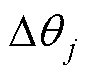的变化方向不同，当q0＞j，随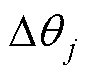增大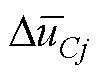，增大，反之减小，因此式（37）可改写为
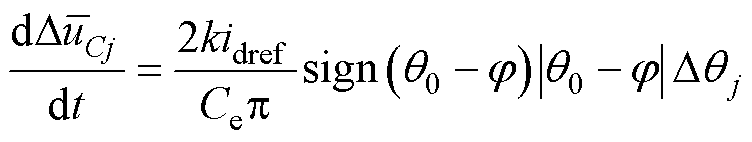（38）
令式（38）等号右端等于新控制量vcj，可得模块电容电压控制律为
（39）
新控制量vcj采用比例-积分（PI）控制，即
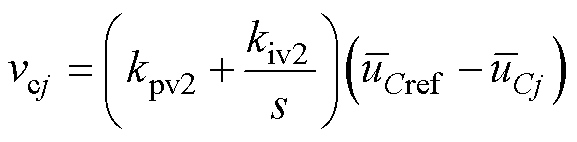（40）
式中，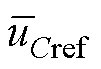
为模块电容电压参考值；kpv2、kiv2为模块电容电压环PI控制器参数。
将式（39）、式（40）代入式（38），可知模块电容电压闭环传递函数也可表示成如式（29）所示的典型二阶线性系统形式。因此参数kpv2和kiv2也可根据二阶系统选定合适的带宽和阻尼比进行整定。此外，实际控制中，式（39）中分母项|q0-j |可用其稳态值代替，以避免其动态波动对控制产生不利影响。
根据式（33）、式（34），可得直流母线电压控制策略如图9a所示。根据式（39）、式（40），结合1.3节稳态能量平衡控制，得三相多电平单元模块电容电压控制框图如图9b所示，通过该控制，消除了动态过程中累积能量造成的电容电压偏差，实现了动态能量平衡，且因跟踪同一参考值，三相模块电容电压可实现相间均衡。
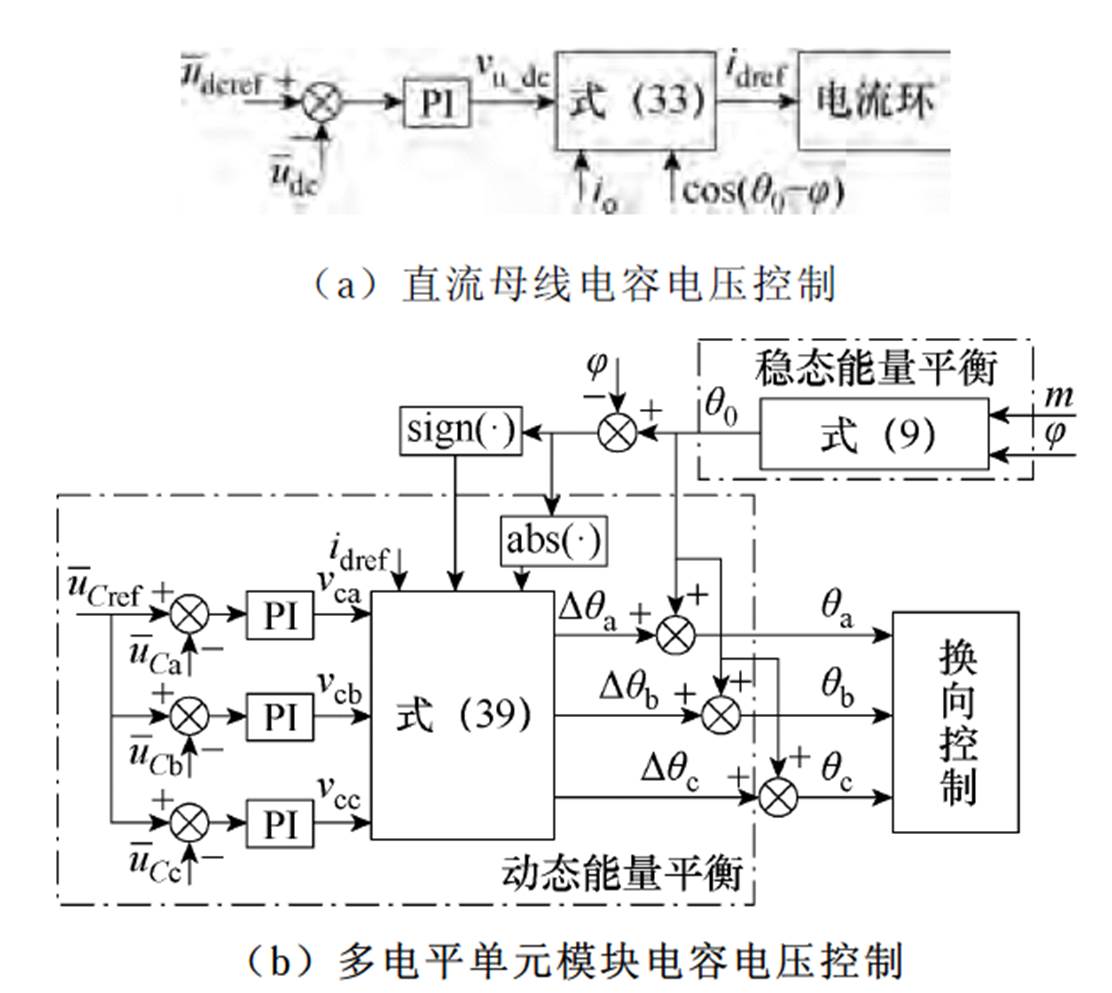
图9 HWS-MMC两级直流电容电压控制
Fig.9 Two-stage DC voltage control of HWS-MMC
在根据图9、图8中两级直流电压环、电流环控制得到三相换向单元的移相角qj以及多电平单元的正弦调制波hj后，通过换向控制逻辑及子模块均压控制，得到HWS-MMC换向单元的开关信号以及多电平单元的开关信号，具体如下。
3.3.1 换向控制逻辑
根据式（6）、式（12），可绘制采用移相调制的半波换向原理如图10所示。
为方便实现移相算法，设比较变量
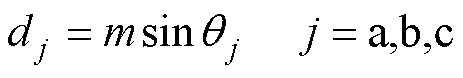（41）
以a相为例进行分析，为适用一般工况，设ha= msin(w t-j0)，j0为其初相位，图10中j0=0。
图10 移相调制的半波换向原理
Fig.10 Diagram of half wave commutation with phase shift modulation
在ha上升段，其微分dha/dt=mwcos(w t-j0)＞0时，将调制波ha与da比较，当ha＞da时，Sa=1，否则Sa=0；在ha下降段，其微分dha/dt=mwcos(wt-j0)＜0时，将调制波ha与-da比较，当ha＜-da时，Sa=0，否则Sa=1。b相和c相换向函数Sb、Sc计算方法与a相相同，由此可得到三相换向开关函数。
在确定Sj（j=a, b, c）的基础上，可按式（6）生成各相换向单元的开关信号S11j、S12j、S21j、S22j；基于上述分析，移相换向控制框图如图11上部分所示。
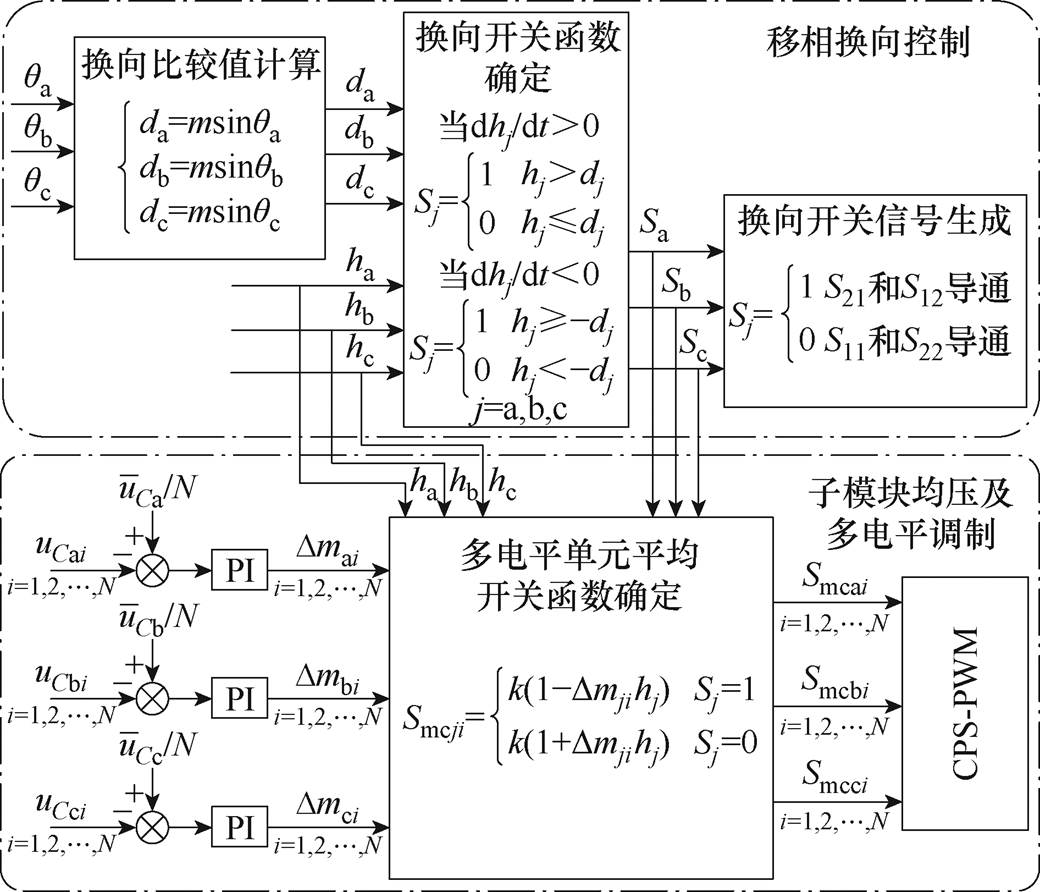
图11 移相换向及子模块均压控制框图
Fig.11 Block diagram of phase shift commutation and submodule voltage balancing control
3.3.2 子模块均压控制及多电平调制
通过图9b控制可将各相多电平桥臂模块电容总电压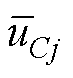控制在参考值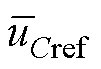，在此基础上，还需确保桥臂中各子模块电容电压均衡，才能实现理想的多电平输出波形。根据不同的调制策略，多电平换流器中子模块均压方法通常有两种，当采用最近电平逼近调制（Nearest Level Modulation, NLM）时，可采用电压排序的均衡方法[22-23]；当采用载波移相（Carrier Phase Shifting, CPS）PWM方法时，可通过对各模块调制比的修正实现均压，本文采用后者。
设每相多电平单元有N个子模块，各子模块电容电压为uCji（j=a, b, c; i=1,×××, N），当不考虑子模块均衡控制时，j相各模块采用相同的调制波Smcj（见式（12）），当考虑子模块均衡控制时，子模块调制波修正为
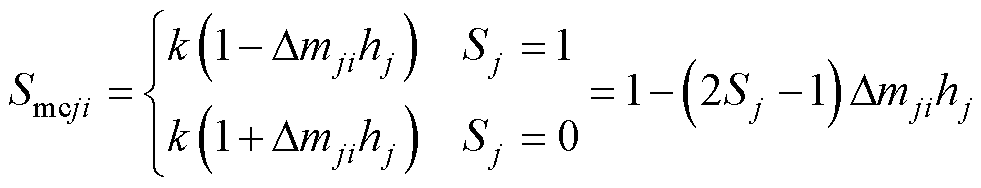（42）
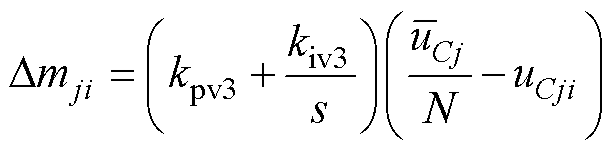j=a, b, c; i=1,…, N（43）
式中，kpv3、kiv3为子模块电压均衡控制PI控制器参数。
根据式（42）、式（43），考虑子模块均压的多电平单元调制框图如图11下面部分所示。综合各部分控制设计，HWS-MMC系统整体控制框图如图12所示。
图12 HWS-MMC整体控制策略
Fig.12 The overall control strategy of HWS-MMC
本文基于RT-Lab控制硬件在环实时仿真平台搭建了如图13所示的HWS-MMC系统，以验证拓扑建模和控制策略的有效性。系统仿真参数见表1，根据系统参数可计算得两级直流电压稳态值之比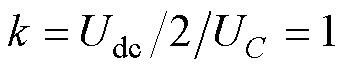
。
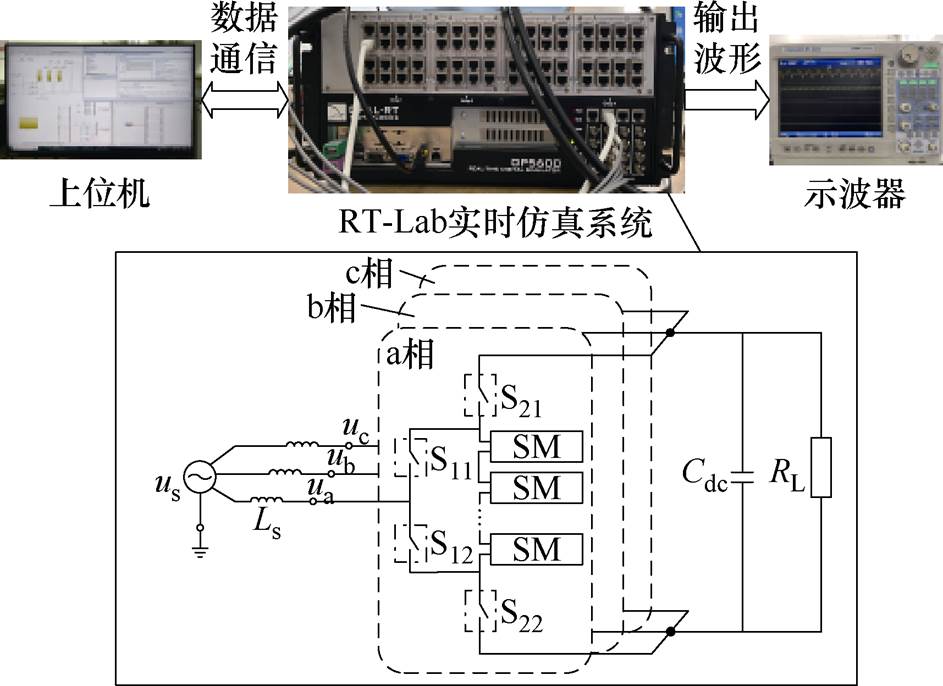
图13 HWS-MMC RT-Lab仿真平台
Fig.13 RT-Lab simulation platform of HWS-MMC
表1 HWS-MMC仿真参数
Tab.1 HWS-MMC simulation parameters
参 数数 值 额定容量/MW16 电网线电压有效值us/kV10 子模块数量N5 子模块电容C/mF20 子模块电容电压uCji/kV2 直流母线电容Cdc/mF10 直流母线电压udc/kV20 电网电感Ls/mH15 电流控制带宽fbi/Hz370 阻尼比xi0.707 直流电压控制带宽fbdc/Hz13 阻尼比xdc0.707 模块电容电压控制带宽fbe/Hz77 阻尼比xe3.67 子模块均压控制带宽fbm/Hz56 阻尼比xm2.04
控制参数也在表1中列出，考虑到本拓扑直流母线电压环为外层整体控制，模块电容电压环为中间层能量平衡控制，电流环为内层控制，控制带宽由外层到内层依次增加；根据二阶系统最优控制，电流环和直流母线电压环阻尼比均设置为0.707，而考虑调节q 对系统影响较敏感，为减小模块电容电压响应的振荡与超调，将其阻尼比设定为过阻尼。
图14为HWS-MMC在电网电压扰动和负载扰动下的运行结果。t1时刻电网电压跌落50%，t2时刻电网电压恢复，t3时刻负载降低50%，t4时刻恢复。由图14b可见，在上述扰动下，通过本文移相调制及多环路控制，系统直流母线电压和多电平单元模块电容电压维持稳定，且三相模块电容电压相间均衡；图14c展示了a相子模块电容电压实现了相内均衡。图14d中功率波形显示了HWS-MMC与传统MMC类似的有功功率和无功功率解耦控制特性，能够实现有功无功独立控制。图14e为系统运行过程中调制比m和平均移相角q0随系统扰动变化的波形（根据实时仿真数据绘制）。结果表明，在本文多目标控制策略下，通过移相控制能够实现HWS-MMC宽电压范围稳定运行的目标。
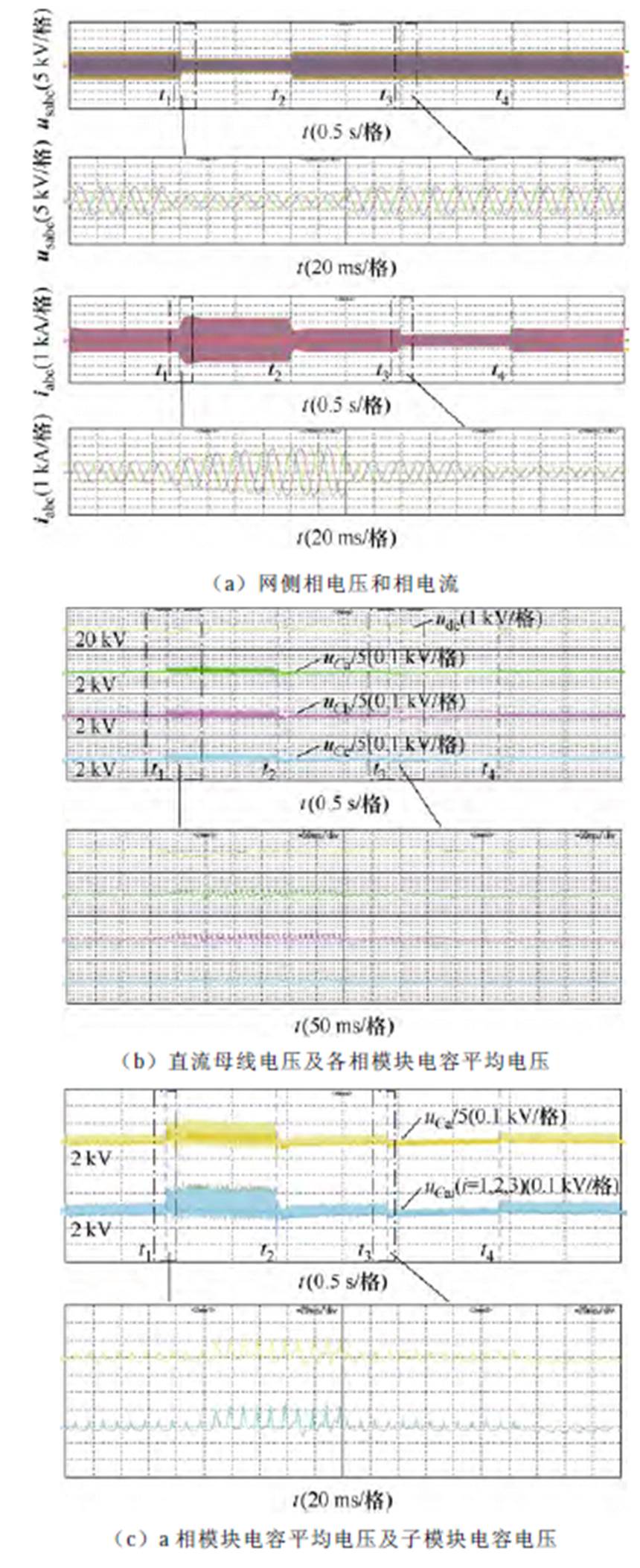
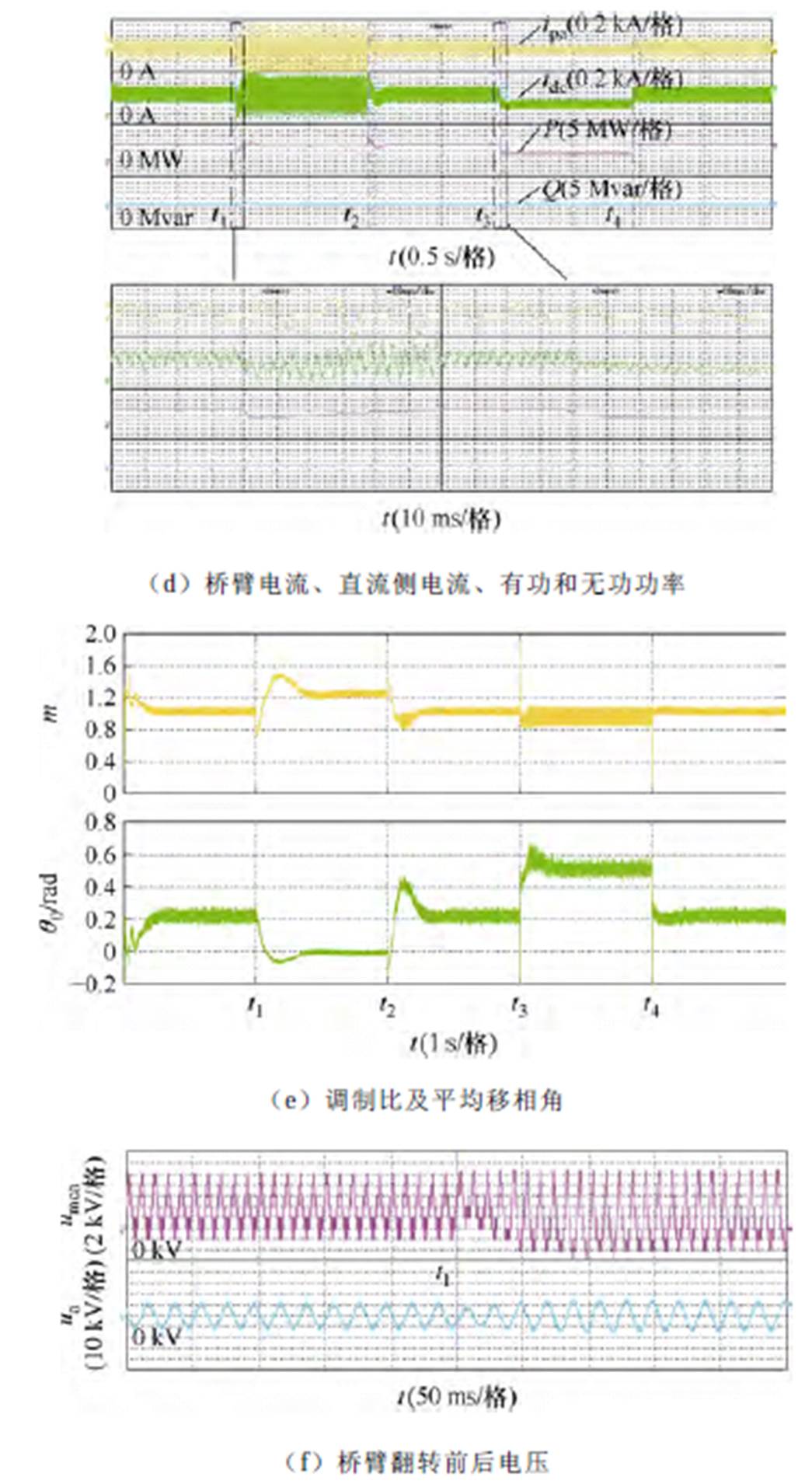
图14 电网电压和负载扰动下HWS-MMC波形结果
Fig.14 HWS-MMC waveforms under grid voltage and load disturbances
图14a～图14d各图中下半部分以及图14f中给出了扰动时刻附近的HWS-MMC各波形细节。图14d中显示了直流母线电流呈六脉动，与理论分析一致；由图14f可见，多电平单元生成的半正弦多电平电压在换向开关调控下实现了阀侧完整正弦波形输出。
图15为HWS-MMC在大范围无功功率调节时的波形结果。由动态模型及能量平衡机理可知，HWS-MMC移相角q 的选取与换流器阀侧交流电压、电流相位差j 密切相关，而j 受系统运行无功功率状态的影响更显著，故本文对系统无功功率大幅变化时的控制策略有效性进行进一步验证。t1时刻无功功率由0变化至-8 Mvar，t2时刻恢复至单位功率因数，t3时刻变化至8 Mvar，t4时刻恢复。实验结果表明，在系统无功功率大范围调节时，多目标控制策略仍然能够很好地实现并网电流、直流母线电压以及模块电容电压相间相内均衡等控制目标，进一步验证了理论建模和控制策略的有效性。
图15 无功功率调节下HWS-MMC波形结果
Fig.15 HWS-MMC waveform under reactive power regulations
本文针对半波整形MMC建立了完整的动态模型，并提出考虑并网电流控制、两级直流电容电压控制以及多电平单元相间和相内模块电容电压均衡控制的多目标控制策略，通过RT-Lab实时仿真平台验证了建模和控制策略的有效性，结论如下：
1）HWS-MMC交流侧特性与传统VSC类似，内部多电平单元电容特性与MMC类似，直流输出侧电容特性与六脉动整流电路类似。多电平单元平均开关函数与正弦调制函数之间的关系除受半波换向拓扑约束决定外，还与多电平模块电容电压与直流母线电容电压的稳态值之比有关；在文中所提关系下，可消除基频开关函数的影响，使交流电流动态方程转化为与传统VSC并网换流器相同的动态方程。
2）不同于传统MMC，HWS-MMC直流母线电容电压和多电平模块电容电压两级直流动态相互独立，需分别设计电压控制器，实现直流母线电容以及桥臂模块电容的能量平衡；通过附加移相控制可在实现各相模块电容电压稳定控制的同时，达到相间电压均衡。
3）结合移相调制换向逻辑，采用子模块调制波修正，可在多电平单元电容电压相间均衡的基础上实现相内子模块电压均衡。
本文仅就HWS-MMC的动态模型和控制设计展开研究，后续将结合实际柔性直流输电场景开展HWS-MMC拓扑优化和涉网适用性研究。
参考文献
[1] 杨晓峰, 林智钦, 郑琼林, 等. 模块组合多电平变换器的研究综述[J]. 中国电机工程学报, 2013, 33(6): 1-14.
Yang Xiaofeng, Lin Zhiqin, Zheng Qionglin, et al. A review of modular multilevel converters[J]. Pro- ceedings of the CSEE, 2013, 33(6): 1-14.
[2] 侯玉超, 郭祺, 涂春鸣, 等. 面向输出性能优化的高低频混合型模块化多电平变换器及其调控策略[J]. 电工技术学报, 2024, 39(14):4467-4479.
Hou Yuchao, Guo Qi, Tu Chunming, et al. A high and low frequency hybrid modular multilevel converter for output performance optimization and its control strategy[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4467-4479.
[3] 蔡旭, 杨仁炘, 周剑桥, 等. 海上风电直流送出与并网技术综述[J]. 电力系统自动化, 2021, 45(21): 2-22.
Cai Xu, Yang Renxin, Zhou Jianqiao, et al. Review on offshore wind power integration via DC trans- mission[J]. Automation of Electric Power Systems, 2021, 45(21): 2-22.
[4] 李子欣, 徐飞, 赵成勇, 等. 面向高压直流输电的电流源型主动换相换流器研究综述[J]. 中国电机工程学报, 2021, 41(3): 1053-1068.
Li Zixin, Xu Fei, Zhao Chengyong, et al. Research review of current-source type actively commutated converter for high voltage direct current transmission systems[J]. Proceedings of the CSEE, 2021, 41(3): 1053-1068.
[5] 樊强, 俞永杰, 夏嘉航, 等. 低容值半桥型模块化多电平变换器直流故障辅助清除策略[J]. 电工技术学报, 2022, 37(14): 3713-3722.
Fan Qiang, Yu Yongjie, Xia Jiahang, et al. Auxiliary strategy for DC fault clearing of low capacitance half-bridge modular multilevel converter[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(14): 3713-3722.
[6] 任鹏, 涂春鸣, 侯玉超, 等. 基于Si和SiC器件的混合型级联多电平变换器及其调控优化方法[J]. 电工技术学报, 2023, 38(18): 5017-5028.
Ren Peng, Tu Chunming, Hou Yuchao, et al. Research on a hybrid cascaded multilevel converter based on Si and SiC device and its control optimization method[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 5017-5028.
[7] 许建中, 李钰, 陆锋, 等. 降低MMC子模块电容电压纹波幅值的方法综述[J]. 中国电机工程学报, 2019, 39(2): 571-584.
Xu Jianzhong, Li Yu, Lu Feng, et al. A review of suppression methods for sub-module capacitor voltage ripple amplitudes in modular multilevel converters[J]. Proceedings of the CSEE, 2019, 39(2): 571-584.
[8] Merlin M M C, Green T C, Mitcheson P D, et al. A new hybrid multi-level voltage-source converter with DC fault blocking capability[C]//9th IET International Conference on AC and DC Power Transmission (ACDC 2010), London, 2010: 1-5.
[9] Adam G P, Finney S J, Williams B W, et al. Network fault tolerant voltage-source-converters for high- voltage applications[C]//9th IET International Con- ference on AC and DC Power Transmission (ACDC 2010), London, 2010: 1-5.
[10] Feldman R, Tomasini M, Amankwah E, et al. A hybrid modular multilevel voltage source converter for HVDC power transmission[J]. IEEE Transactions on Industry Applications, 2013, 49(4): 1577-1588.
[11] Adam G P, Abdelsalam I A, Ahmed K H, et al. Hybrid multilevel converter with cascaded H-bridge cells for HVDC applications: operating principle and scala- bility[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 65-77.
[12] 王琛, 陶建业, 王毅, 等. 桥臂复用型模块化多电平换流器的拓扑及控制研究[J]. 中国电机工程学报, 2022, 42(9): 3373-3384.
Wang Chen, Tao Jianye, Wang Yi, et al. Research on topology and control of arm multiplexing modular multilevel converter[J]. Proceedings of the CSEE, 2022, 42(9): 3373-3384.
[13] 李宇薇, 王毅, 高玉华, 等. 桥臂复用模块化多电平变流器单极接地故障无闭锁穿越及能量均衡[J]. 电工技术学报, 2025, 40(1): 190-202.
Li Yuwei, Wang Yi, Gao Yuhua,et al. Pole-to-ground fault riding-through and energy balance of arm- multiplexing modular multilevel converter[J]. Transa- ctions of China Electrotechnical Society, 2025, 40(1): 190-202.
[14] Lan Jianxi, Chen Wu, Li Xin, et al. A three-phase multiplexing arm modular multilevel converter with high power density and small volume[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 14587-14600.
[15] Fan Shiyuan, Chen Cong, Yang Heya, et al. A cost- effective and DC-fault tolerant alternate arm con- verter with wide range voltage adaptability[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(6): 6673-6686.
[16] Patro S K, Shukla A, Ghat M B. Hybrid series converter: a DC fault-tolerant HVDC converter with wide operating range[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(1): 765-779.
[17] 高玉华, 王琛, 王毅, 等. 基于半波交替的轻型化MMC拓扑及控制策略[J]. 电力系统自动化, 2023, 47(17): 149-159.
Gao Yuhua, Wang Chen, Wang Yi, et al. Topology and control strategy of light-weight modular multi- level converter with half-wave alternating[J]. Auto- mation of Electric Power Systems, 2023, 47(17): 149-159.
[18] Huang Ming, Li Weilin, Zou Jianlong, et al. Analysis and design of a novel hybrid modular multilevel converter with time-sharing alternative arm con- verter[J]. IEEE Transactions on Industrial Electronics, 2024, 71(1): 14-26.
[19] Merlin M M C, Green T C. Cell capacitor sizing in multilevel converters: cases of the modular multilevel converter and alternate arm converter[J]. IET Power Electronics, 2015, 8(3): 350-360.
[20] 孙玉巍, 李永刚, 刘教民, 等. 级联式电力电子变压器协调控制策略[J]. 中国电机工程学报, 2018, 38(5): 1290-1300.
Sun Yuwei, Li Yonggang, Liu Jiaomin, et al. Coor- dinative control strategy for cascaded power elec- tronic transformer[J]. Proceedings of the CSEE, 2018, 38(5): 1290-1300.
[21] (美) Richard C. Dorf, (美) Robert H. Bishop著. 谢红卫. 现代控制系统[M]. 2版. 北京: 电子工业出版社, 2015.
[22] 武鸿, 王跃, 薛英林, 等. 适用多功率的最近电平调制下MMC子模块开路故障诊断策略[J]. 电工技术学报, 2024, 39(1): 233-245, 302.
Wu Hong, Wang Yue, Xue Yinglin, et al. A diagnosis strategy for open-circuit submodule faults in MMCs under nearst level modulation suitable for different powers[J]. Transactions of China Electrotechnical Society, 2024, 39(1): 233-245,302.
[23] 徐政. 柔性直流输电系统[M]. 2版. 北京: 机械工业出版社, 2017.
Abstract The traditional modular multilevel converter (MMC) has drawbacks such as many submodules, large volume and weight, and high cost. The lightweight MMC topologies have become a research hotspot. Half-Wave Shaping MMC (HWS-MMC) is a new lightweight hybrid multilevel converter that integrates the merits of the two-level topology and the MMC topology. The HWS-MMC can reduce the module numbers and voltage stress since the multilevel arm only needs to modulate part of the sinusoidal waveform. In existing studies, phase-shift modulation and third-order harmonic injection methods for energy balance issues of the wide-range operation of HWS-MMC are based on the inverter operation with supply ideal DC voltages supply, and no detailed multi-objective control design has been conducted. Therefore, this paper studies the dynamic model and multi-objective control strategy of HWS-MMC.
Firstly, the topology and working principle of HWS-MMC are introduced, and the energy balance mechanism and phase-shift wide-range modulation method are clarified by deriving the arm energy accumulation expression. The mathematical models of internal and external variables are established for HWS-MMC, including grid current dynamics, submodule capacitor voltages, and DC bus capacitor voltage. Then, a fully averaged dynamic model without switching characteristics is obtained and linearized using the multi-scale switching period averaging technique. An overall control strategy is systematically established with the objectives of grid current control, two-stage DC voltage control, and energy balancing control between phases and within an arm. The design method of the multi-loop controllers and commutation control logic are also given.
An HWS-MMC system is built on the RT-Lab platform. Experiments are conducted under the grid voltage disturbance, load disturbance, and reactive power regulations. The waveforms, including the AC voltage and current, the DC bus and submodule capacitor voltages, the modulation coefficient and phase-shift angle, and the active and reactive power, are given. The results show that the modulation coefficient and phase-shift angle are adjusted accordingly through the multi-loop control, ensuring the stability of the DC bus voltage and the submodule capacitor voltages. In addition, voltage balancing between and within phases is achieved. The half-sinusoidal multilevel waveform and six-pulsation DC bus current are consistent with the theoretical analysis.
The following conclusions can be drawn. (1) The AC side characteristics of HWS-MMC are similar to traditional VSC, the characteristics of the internal module capacitors are similar to MMC, and the DC bus characteristics are similar to the six-pulsation rectifier. (2) The dynamics of the DC bus capacitor voltage and submodule capacitor voltage are independent. (3) The multi-control objectives are achieved with additional phase-shifting control and the submodule modulating wave correction.
keywords：Half-wave shaping based modular multilevel converter (MMC), dynamic model, energy balancing, voltage balancing, multi-objective control
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.240462
国家自然科学基金（52077079）和中央高校基本科研业务费专项资金（2022MS072）资助项目。
收稿日期 2024-03-22
改稿日期2024-05-21
孙玉巍 女，1987年生，讲师，研究方向为新能源电力系统的新型电力变换拓扑、建模及控制技术。E-mail: sunyuwei@ncepu.edu.cn
付 超 男，1979年生，讲师，研究方向为风力发电、光伏发电、储能、交直流混合电力系统控制等。E-mail: fuchao@ncepu.edu.cn（通信作者）
（编辑 郭丽军）