图1 传统DAB模型预测控制框图
Fig.1 Diagram of conventional MPC for DAB
摘要 传统的双有源桥(DAB)变换器模型预测控制(MPC)依赖于系统参数的准确性,针对该问题,该文提出一种DAB移动离散控制集无模型预测电压控制(MDCS-MFPVC)策略,消除了系统参数对DAB变换器电压控制的影响。首先,分析参数失配对传统MPC的影响。其次,建立DAB变换器离散数据模型,替代传统的数学模型,提高了预测电压控制的鲁棒性。再次,通过数据模型误差反馈和多输入变量的设置,结合最小二乘法对离散数据模型进行实时辨识;结合系统采样和数据模型辨识结果,实现未来时刻的电压无模型预测,并通过价值函数评估最优移相角,应用在下一个控制周期。该方法可以实时辨识DAB系统数据模型,消除了参数失配对MPC的影响,保证了输出电压的鲁棒性。最后,通过搭建DAB变换器仿真和实验系统,验证了所提方法的有效性。
关键词:双有源桥变换器 无模型预测 电压控制 离散移动控制集 参数鲁棒性
随着可再生能源的快速发展,直流微电网的规模与应用范围也不断扩大[1]。为了实现直流微电网中可再生能源的灵活配置和优化利用,DC-DC变换器的应用得到了推广,为直流微电网的发展提供了支持与保障[2]。其中,双有源电桥(Dual Active Bridge, DAB)变换器因其具有双向电能传输、宽电压转换范围和零电压软开关等能力而受到广泛的关注[3-5]。当DAB变换器应用于直流微电网时,必须有效应对负载突变、电压突变等运行工况。因此,控制系统的鲁棒性和动态性能是DAB变换器高效控制的重要指标。
近年来,模型预测控制(Model Predictive Control, MPC)因其动态响应迅速、控制原理简单以及多目标控制能力强等优点,在DAB变换器中得到了广泛应用,实现了DAB变换器稳定且高效的输出电压控制[6-10]。MPC利用DAB变换器的离散模式实现未来时刻的输出电压预测。然而,MPC的控制性能依赖于系统精确的离散模型,在DAB变换器系统实际的运行过程中,电感和电容的实际参数会随着温度、硬件老化和运行条件的改变而发生变化,导致其实际参数与模型参数存在误差,进而造成DAB变换器性能降低[11-12]。
为了提高DAB变换器MPC输出电压控制的参数鲁棒性,研究人员已经提出多种基于参数辨识的MPC方法[13-16]。文献[13]中,研究人员提出了一种基于梯度下降法的MPC,实现了电感参数的在线计算。文献[14]中,研究人员提出了一种基于卡尔曼滤波的电感辨识方法。文献[15-16]中,研究人员使用递归最小二乘法在线辨识DAB电感参数,提高了MPC的参数鲁棒性。然而,在上述参数辨识方法实施前,仍需建立较为准确的系统模型,进而得到系统辨识变量与输入输出变量的关系。同时,上述参数辨识方法忽略了寄生参数的影响,当辨识误差存在时,仍然会影响DAB变换器的输出电压性能。
针对上述问题,本文提出了一种DAB变换器移动离散控制集无模型预测控制(Moving-Discrete- Control-Set Model-Free Predictive Voltage Control, MDCS-MFPVC)方法。首先,分析了DAB变换器中电感和电容发生参数失配时的输出电压预测误差;其次,建立了DAB变换器数据模型,并基于递归最小二乘法实现数据模型辨识,有效替代传统数学模型;最后,建立了DAB变换器移动离散控制集,结合价值函数评估,实现无模型预测电压控制。所提MDCS-MFPVC方法的主要贡献如下:①与传统MPC方法[6-10]相比,所提MDCS-MFPVC无需建立系统准确的数学模型,提高了预测控制的参数鲁棒性;②与基于参数辨识的MPC方法[13-16]相比,所提MDCS-MFPVC无需辨识电感和电容参数。
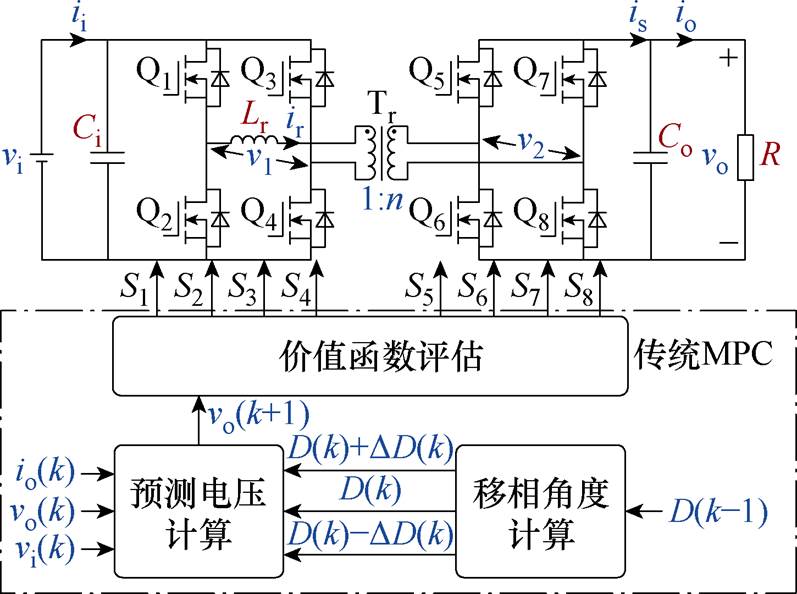
图1为单相DAB变换器电路拓扑结构,其由两个H桥、一个变压器组成。图1中,Q1~Q4为一次侧H桥开关管,其由控制信号S1~S4驱动;Q5~Q8为二次侧H桥开关管,其由控制信号S5~S8驱动;Tr为变压器,n为变压器的匝数比,Lr为变压器漏感,ir为漏感电流。vi为一次侧直流电源,Ci为一次侧输入电容,ii为一次侧输入电流,vo为二次侧输出电压,Co为二次侧输出电容,is为二次侧H桥输出电流,io为负载电流,R为负载电阻,v1为变压器一次电压,v2为变压器二次电压。

图1 传统DAB模型预测控制框图
Fig.1 Diagram of conventional MPC for DAB
如图1所示,传统的MPC主要包括移相角计算部分、预测电压计算部分和价值函数评估[13]。其中,单向功率传输的DAB移相角范围离散形式可以表示为{0, DD, 2DD,…, 0.5},移相角计算得到了每个控制周期的移相角范围DD。在得到移相角范围后,可将其代入预测电压公式中,计算每个移相角对应的预测电压vo(k+1),并将其代入价值函数中,计算每个移相角对应的预测电压误差,选择误差最小的移相角作为最优移相角,进而基于单重移相(Single- Phase-Shift, SPS)调制原理实现开关管控制。
SPS调制策略通过改变一次、二次侧开关器件驱动信号的移相角,从而控制二次侧输出电流与输出电压波形。在实施基于SPS的MPC方法时,一次侧和二次侧H桥均施加50%的占空比。其中,输入侧H桥开关管Q1、Q4的控制信号S1、S4保持一致,其与开关管Q2、Q3的控制信号S2、S3保持互补。同理,输出侧H桥开关管Q5、Q8的控制信号S5、S8保持一致,其与开关管Q6、Q7的控制信号S6、S7保持互补。基于SPS调制策略,DAB一次侧、二次侧开关信号以及电压和电流波形如图2所示[13]。图中,Ts为控制周期,D为v1和v2间的移相角。在基于SPS的MPC方法下,DAB的传输功率P[9]为
 (1)
(1)
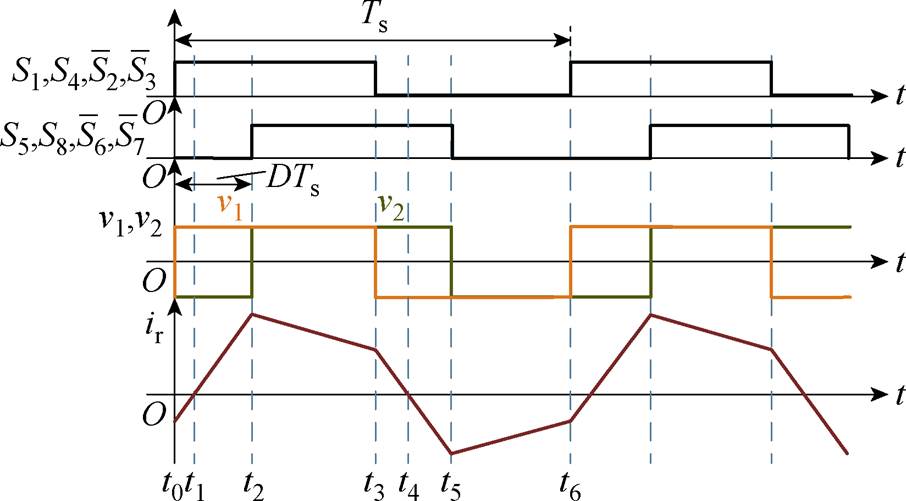
图2 SPS下DAB开关信号及电压电流波形
Fig.2 Waveforms of switching signers, voltage and current under SPS-based DAB
根据式(1),可以得到输出侧H桥的平均输出电流Is表示为
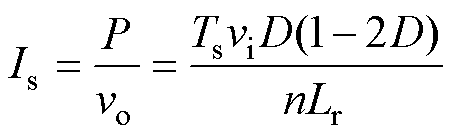 (2)
(2)
如图1所示,二次侧输出电压vo可以表示为
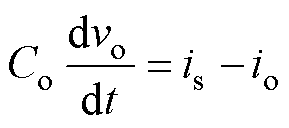 (3)
(3)
将式(2)所示的输出侧H桥的平均输出电流Is代入式(3),可以得到平均输出电压Vo为
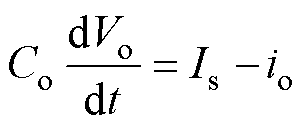 (4)
(4)
根据前向欧拉法,对式(4)离散化,得
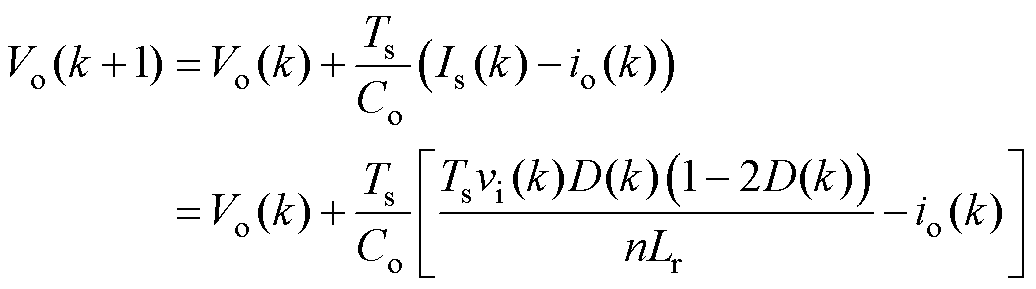 (5)
(5)
根据式(5)可知,k+1时刻的输出电压vo(k+1)由Lr和Co决定。当MPC中变压器漏感模型参数Lr0以及输出电容模型参数Co0与其实际参数Lr和Co不匹配时,会导致vo(k+1)的预测精度降低。图3显示了Lr0和Co0与Lr和Co不匹配时的预测电压误差voerr,参数误差系数m=Lr0/Lr=Co0/Co。根据图3可知,当Lr0和Co0与Lr和Co的误差增加时,预测电压误差voerr随之增加,导致DAB输出功率及效率降低。
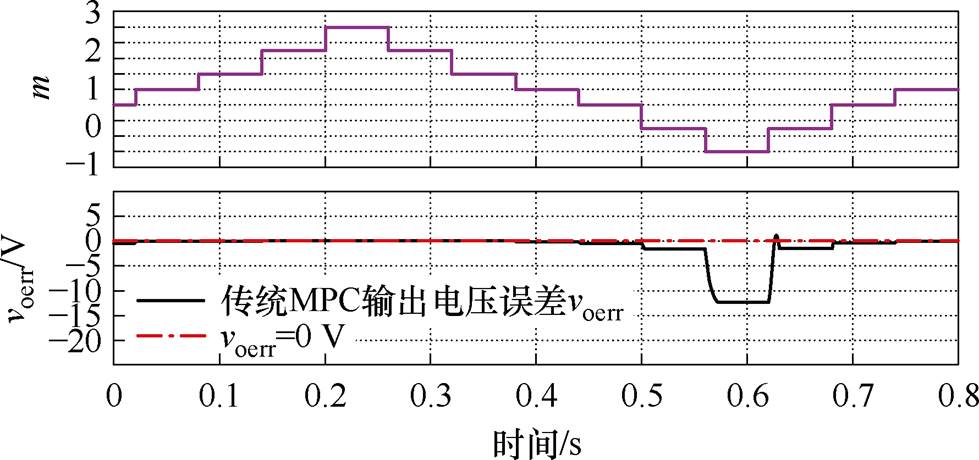
图3 参数失配时传统MPC预测电压误差
Fig.3 Prediction voltage error of conventional MPC under parameter mismatch
为了消除参数失配对预测控制的影响,本文针对DAB提出一种MDCS-MFPVC方法,其控制框图如图4所示,主要由数据模型辨识、无模型预测电压计算、移相角计算以及价值函数评估四部分组成。
根据式(5)所示DAB变换器离散数学模型,本文建立了DAB变换器离散数据模型为
 (6)
(6)
其中
 (7)
(7)
式中,A(k)、B(k)均为系统已知项、未知项以及扰动的集合,其将通过辨识方法得到,无需根据系统数学模型计算,从而消除了参数的影响。
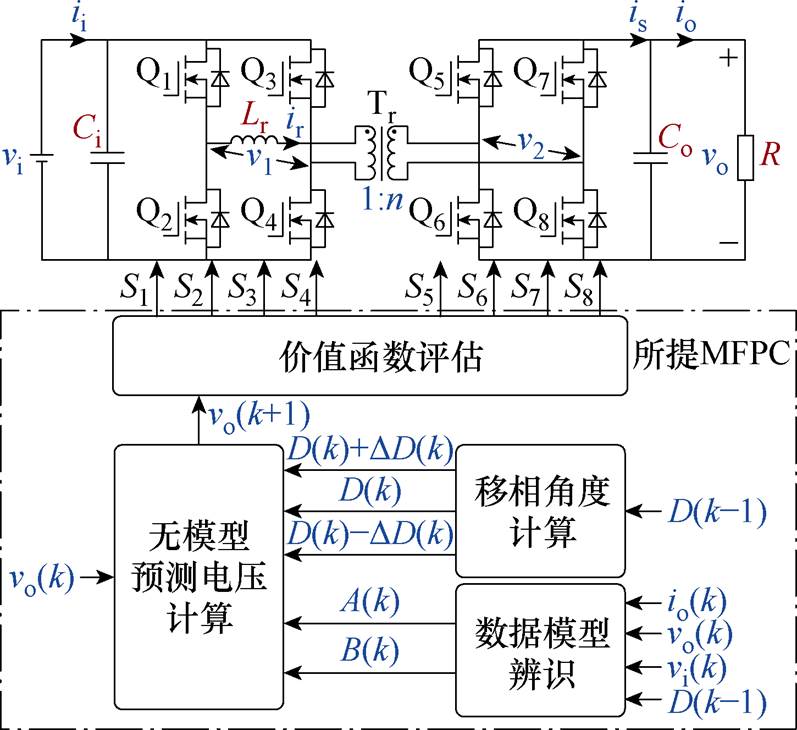
图4 所提MDCS-MFPVC框图
Fig.4 Diagram of proposed MDCS-MFPVC
式(6)的矩阵形式可以表示为
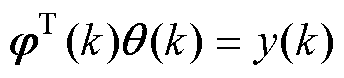 (8)
(8)
其中
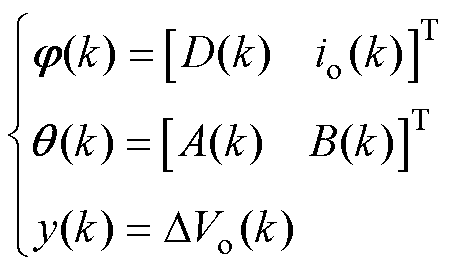 (9)
(9)
根据式(8),所提数据模型识别过程可表示为
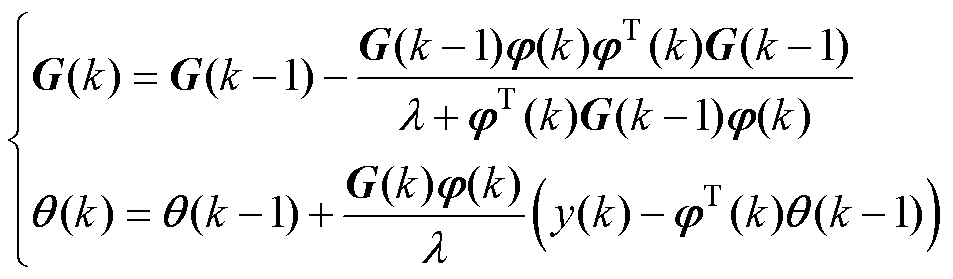 (10)
(10)
式中,G为递归计算的中间矩阵;l 为遗忘因子,其取值范围一般为[0.9, 1]。q 和G的初值可由式(11)计算或根据经验设定。
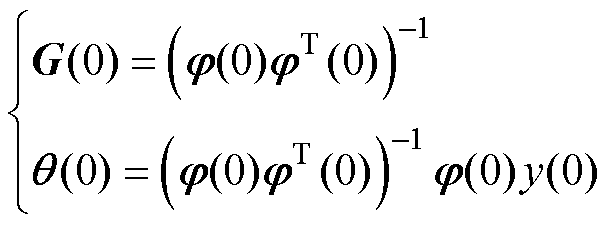 (11)
(11)
在单向功率传输的DAB变换器系统中,移相角范围为0~0.5,其离散形式可以表示为{0, DD, 2DD,…, 0.5}。其中,DD表示[9]为
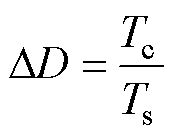 (12)
(12)
式中,Tc为DSP处理器的时钟周期。
在传统的MPC中,需要将{0, DD, 2DD,…, 0.5}中所有的移相角代入预测电压进行误差计算,为了降低MPC实施过程中的计算量,可将移相角范围设置为{D(k)-DDa(k), D(k), D(k)+DDa(k)}。其中,D(k)为上一控制周期的最优移相角,DDa(k)为自适应移相角,其可表示为
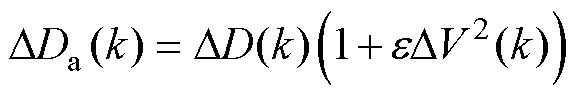 (13)
(13)
其中
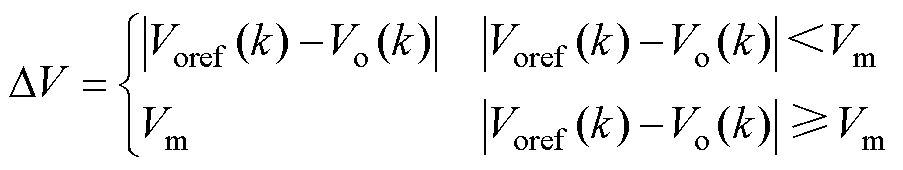 (14)
(14)
式中,Voref为输出电压参考值;Vm为最大电压误差;e 为调整系数。
图5所示为所提DAB无模型预测电压控制示意图,在第k-1个控制周期中,通过应用移相角D(k-1)使输出电压由vo(k-1)变为vo(k)。
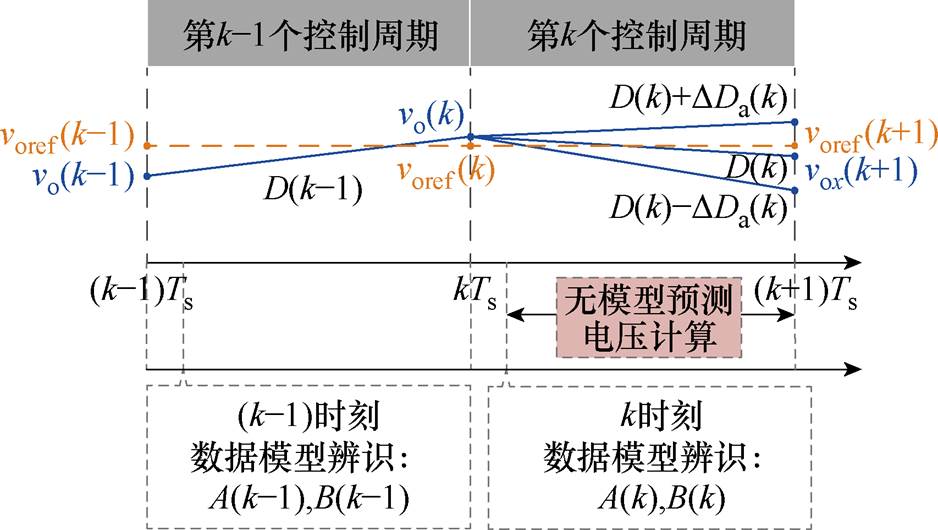
图5 所提DAB无模型预测电压控制示意图
Fig.5 Schematic diagram of proposed MFPC for DAB
为了实现无模型预测电压控制,k时刻的数据模型A(k)和B(k)在第k个控制周期开始后实现辨识。通过计算移相角范围及其对应的预测电压,并根据价值函数评价预测误差,实现无模型预测电压控制。具体实现过程如下所示。
基于2.1节获得的数据模型A(k)和B(k)以及2.2节得到的移相角D(k)-DDa(k), D(k), D(k)+DDa(k),可以得到不同移相角对应的电压差分别为
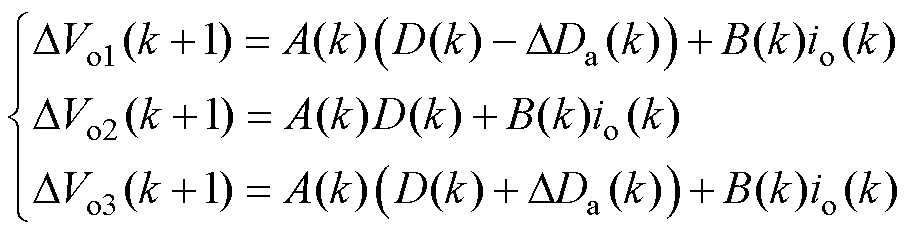 (15)
(15)
式中,DVo1(k+1)、DVo2(k+1)、DVo3(k+1)分别为移相角D(k)-DDa(k)、D(k)、D(k)+DDa(k)对应的电压差分。结合k时刻输出电压采样Vo(k)以及电压差分DVox(k+1),可得到k+1时刻的输出电压Vox(k+1)为
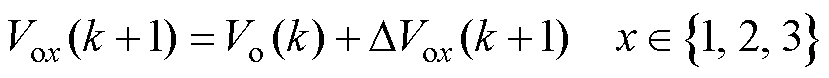 (16)
(16)
如式(15)、式(16)所示,所提DAB预测电压计算无需使用任何DAB模型参数,便可实现无模型预测电压控制,提高了预测控制的参数鲁棒性。
为了在D-DDa, D, D+DDa三个移相角中选择最优的移相角并应用在下一控制周期,本节定义价值函数[13]为
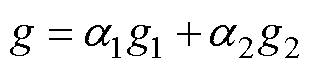 (17)
(17)
其中
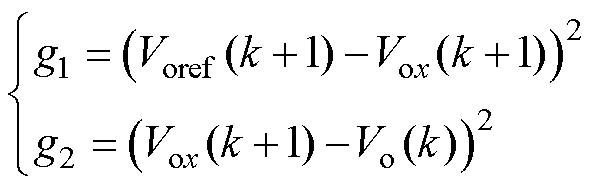 (18)
(18)
式中,g1为参考电压跟踪的价值函数;g2为保证DAB稳态性能的价值函数;a1和a2分别为g1和g2的权重因子。
图6为所提DAB变换器MDCS-MFPVC的方法流程。首先,通过采样获得vo(k)和io(k),将其代入式(10)计算A(k)和B(k)。其次,根据式(13)、式(14)得到自适应移相角DDa(k),结合上一控制周期最优移相角,获得当前控制周期移相角集合{D(k)+DDa(k), D(k), D(k)-DDa(k)},并将其代入式(15)、式(16)计算获得每个移相角对应的Vox(k+1)。最后,根据式(17)所示的价值函数评估Vox(k+1)选择价值函数最低的移相角作为最优移相角应用在下一个控制周期。
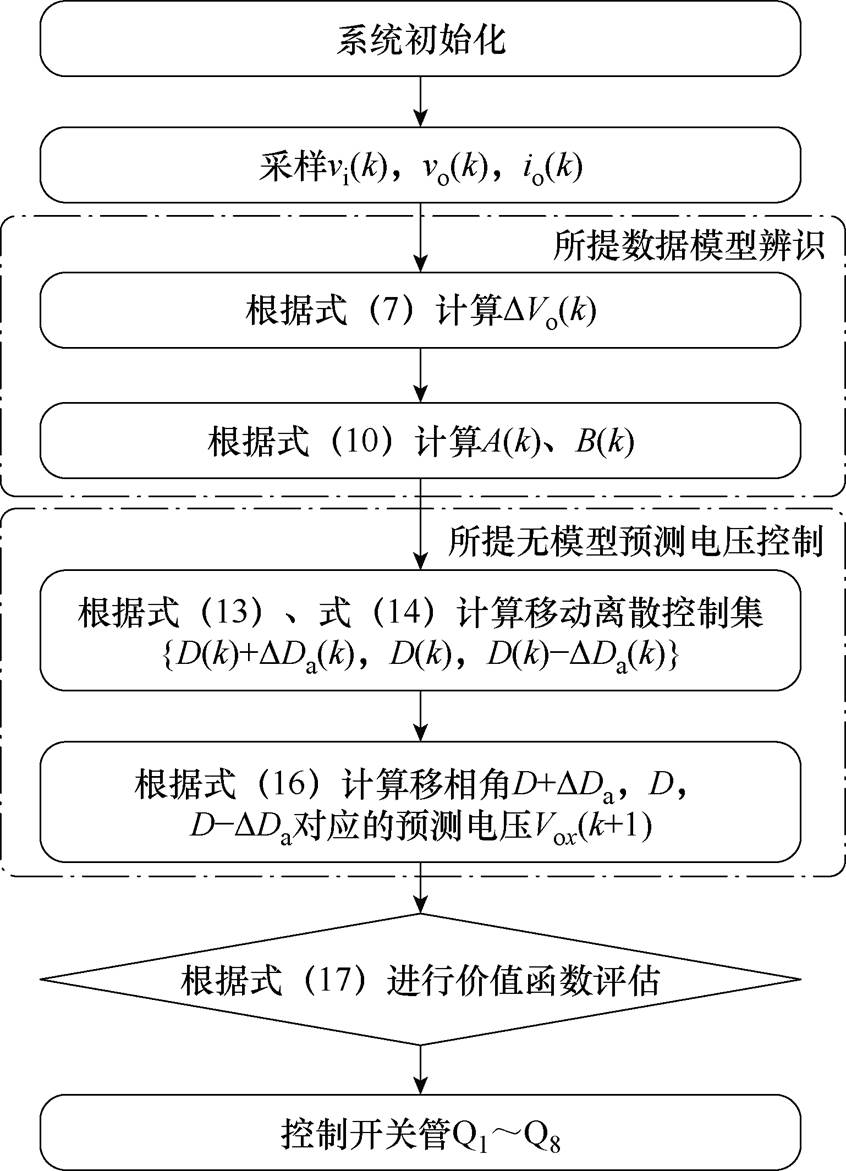
图6 所提DAB变换器MDCS-MFPVC方法流程
Fig.6 Flow chart of proposed MDCS-MFPVC method for DAB converter
为了验证所提MDCS-MFPVC方法的有效性,本节通过Matlab/Simulink搭建了DAB仿真平台,比较了传统MPC方法与所提MDCS-MFPVC方法的输出电压性能。DAB变换器系统参数见表1。
表1 DAB变换器系统及控制参数
Tab.1 System and control parameter of DAB converter
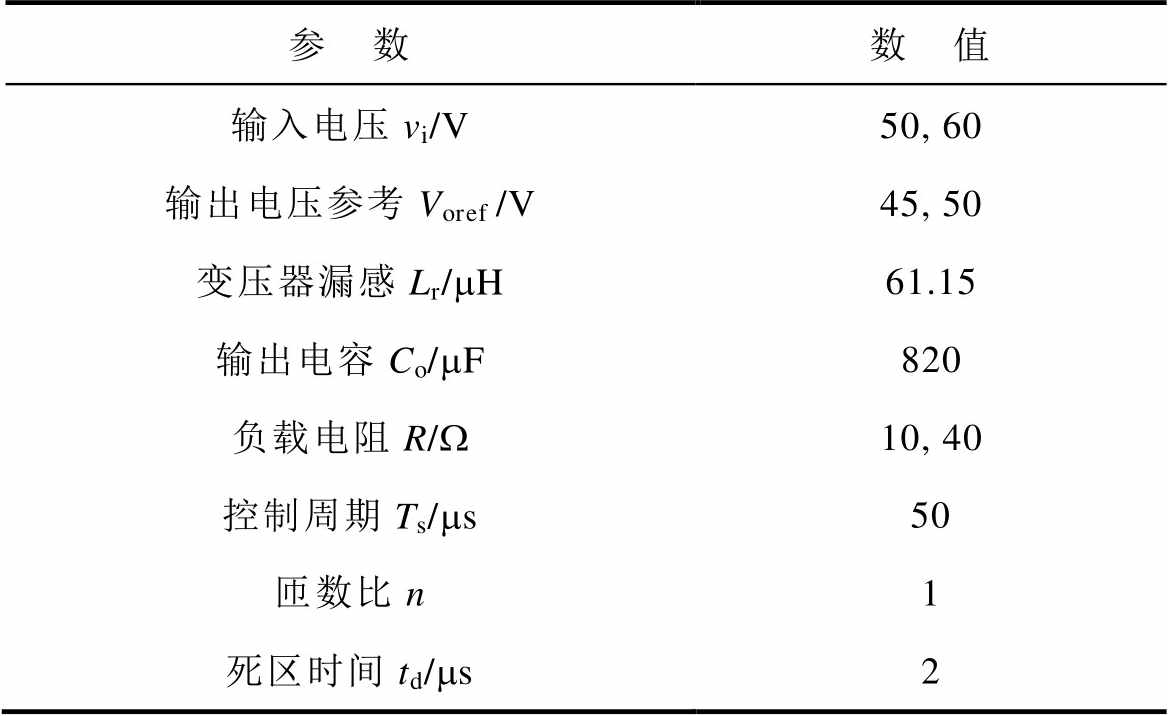
参 数数 值 输入电压vi/V50, 60 输出电压参考Voref /V45, 50 变压器漏感Lr/mH61.15 输出电容Co/mF820 负载电阻R/W10, 40 控制周期Ts/ms50 匝数比n1 死区时间td/ms2
图7比较了DAB变换器漏感模型参数Lr0与其实际参数Lr失配、输出电容模型参数Co0与其实际参数Co失配时,所提MDCS-MFPVC方法与传统MPC方法的输出电压性能。其中,输出电压参考值Voref=50 V。

图7 参数失配时稳态性能仿真比较(Voref=50 V)
Fig.7 Simulation comparison of steady-state performance under mismatched parameter (Voref=50 V)
如图7所示,当应用传统MPC方法时,由于其依赖于准确的模型参数,参数失配导致较大的输出电压误差。在50%参数误差时,输出电压误差达到14 V。当应用所提MDCS-MFPVC方法时,其通过数据模型对输出电压进行预测,保证输出电压性能不受参数失配影响。
图8比较了参数失配时传统MPC方法与所提MDCS-MFPVC方法的输出电压误差,输出参考电压Voref=50 V。当误差系数m=1时,所提MDCS- MFPVC方法输出电压误差为0.11 V,传统MPC方法的输出电压误差为0.081 V。当误差系数m=1.8时,传统MPC方法的输出电压误差为0.19 V,所提MDCS-MFPVC方法输出电压误差仍为0.11 V。当误差系数m=0.2时,传统MPC方法的输出电压误差达到14 V,比所提方法输出电压误差增加13.89 V。
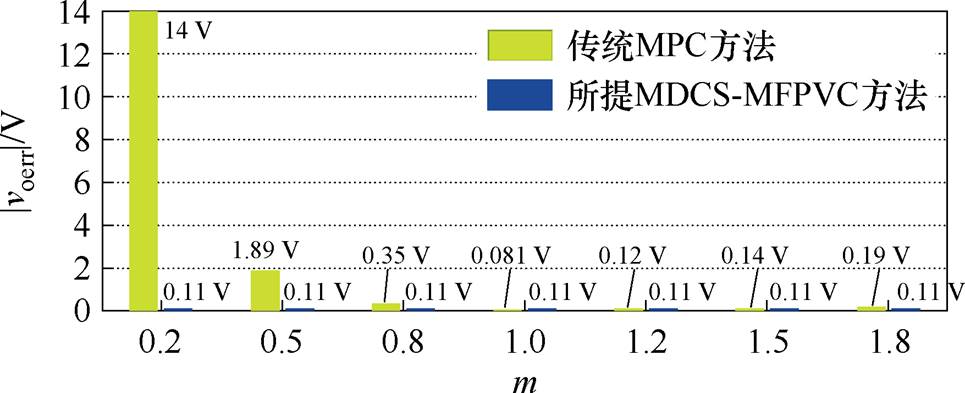
图8 参数失配时稳态误差仿真比较(Voref=50 V)
Fig.8 Simulation comparison of steady-state error under mismatched parameter (Voref=50 V)
图9比较了DAB变换器漏感模型参数Lr0与其实际参数Lr失配、输出电容模型参数Co0与其实际参数Co失配时,所提MDCS-MFPVC方法与传统MPC方法的输出电压性能。其中,输出电压参考值Voref=45 V。
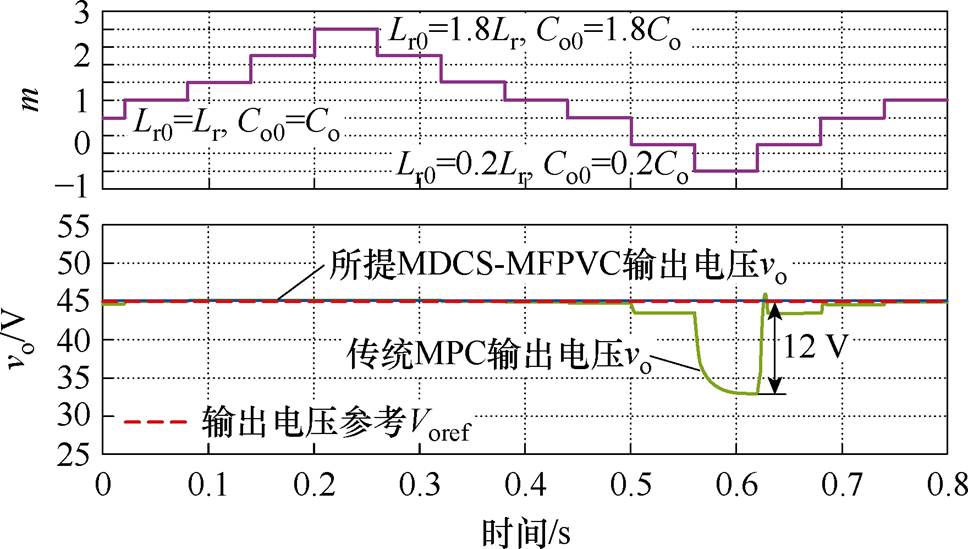
图9 参数失配时稳态性能仿真比较(Voref=45 V)
Fig.9 Simulation comparison of steady-state performance under mismatched parameter(Voref=45 V)
如图9所示,当应用传统MPC方法时,由于其依赖于准确的模型参数,参数失配导致了较大的输出电压误差。在50%参数误差时,输出电压误差达到12 V。当应用所提MDCS-MFPVC方法时,其通过数据模型对输出电压进行预测,保证输出电压性能不受参数失配影响。
图10比较了参数失配时传统MPC方法与所提MDCS-MFPVC方法的输出电压误差,输出参考电压Voref=45 V。当误差系数m=1时,所提MDCS- MFPVC方法输出电压误差为0.098 V,传统MPC方法的输出电压误差0.095 V。当误差系数m=1.8时,传统MPC方法的输出电压误差0.22 V,所提MDCS-MFPVC方法输出电压误差仍为0.098 V。当误差系数m=0.2时,传统MPC方法的输出电压误差达到12 V,比所提方法输出电压误差增加11.902 V。
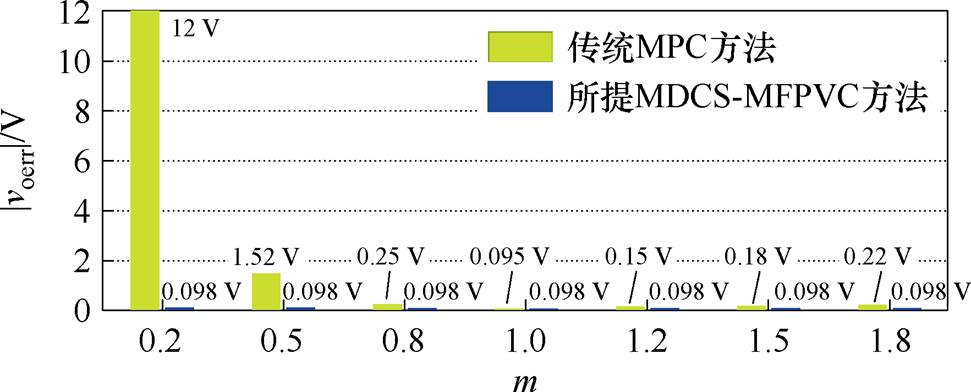
图10 参数失配时稳态误差仿真比较(Voref=45 V)
Fig.10 Simulation comparison of steady-state error under mismatched parameter (Voref=45 V)
3.2.1 参考电压突变
图11比较了参考电压突变时,所提MDCS- MFPVC方法与传统MPC方法的动态性能。
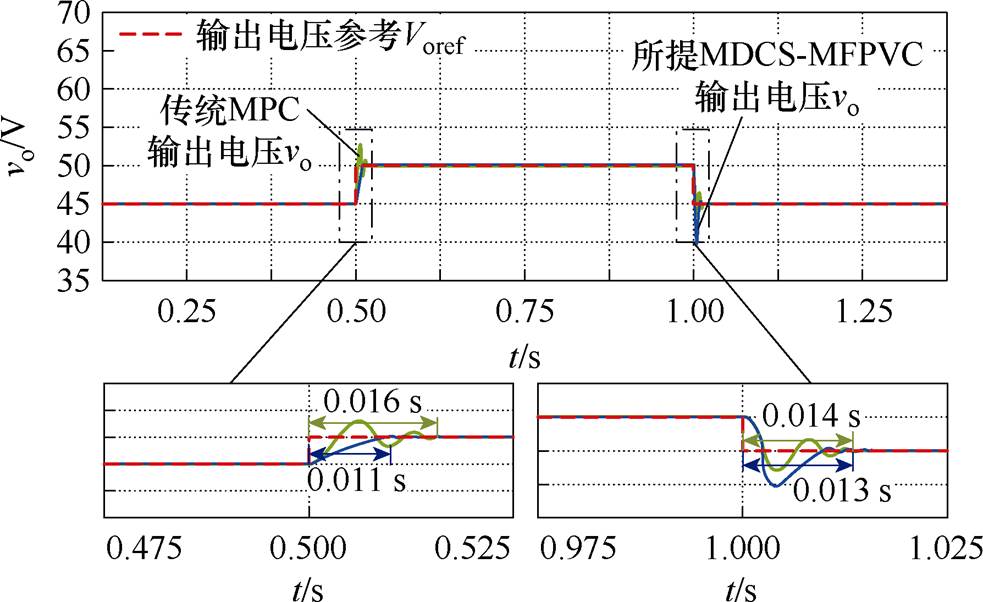
图11 参考电压突变时动态性能仿真比较
Fig.11 Simulation comparison of dynamic-state performance under changed reference voltage
如图11所示,当应用传统MPC方法时,在参考电压由45 V突增为50 V时,其响应速度为0.016 s;在参考电压由50 V突减为45 V时,其响应速度为0.014 s;当应用所提MDCS-MFPVC方法时,在参考电压由45 V突增为50 V时,其响应速度为0.011 s,在参考电压由50 V突减为45 V时,其响应速度为0.013 s,与传统MPC方法相比分别减少0.005 s、0.001 s。
3.2.2 负载电阻突变
图12比较了负载电阻突变时,所提MDCS- MFPVC方法与传统MPC方法的动态性能。
如图12所示,在负载电阻由40 W 突减为10 W 时,所提MDCS-MFPVC方法与传统MPC方法的动态性能相近,为0.016 s;在负载电阻由10 W 突增为40 W 时,所提MDCS-MFPVC方法与传统MPC方法的动态性能仍然相近,为0.007 5 s。验证参数准确时,所提MDCS-MFPVC方法在负载电阻突变时与传统MPC拥有相近的动态性能。
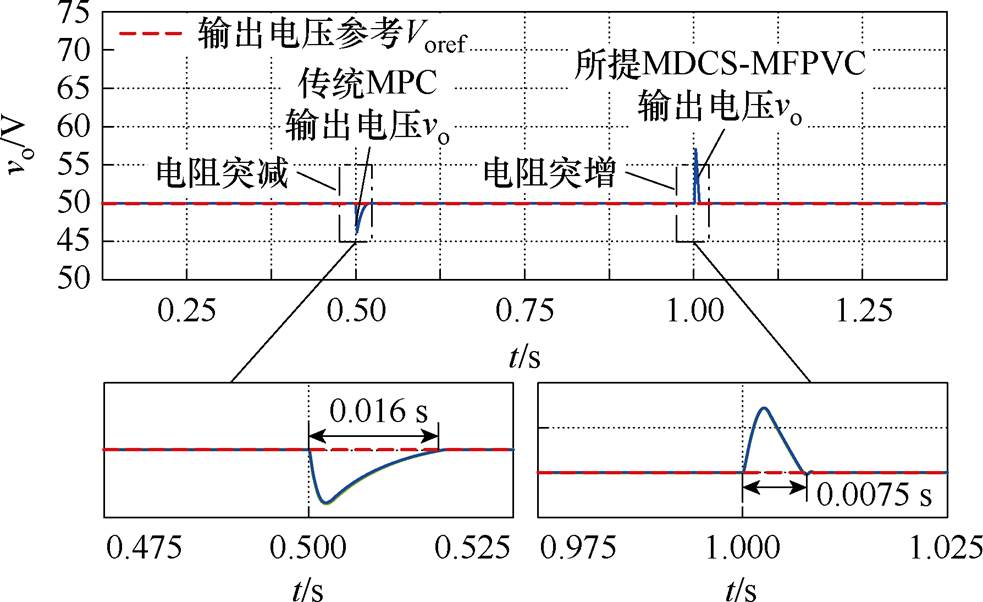
图12 负载电阻突变时动态性能仿真比较
Fig.12 Simulation comparison of dynamic-state performance under changed load resistance
3.2.3 输入电压突变
图13比较了输入电压突变时,所提MDCS- MFPVC方法与传统MPC方法的动态性能。

图13 输入电压突变时动态性能仿真比较
Fig.13 Simulation comparison of dynamic-state performance under changed input voltage
如图13所示,在输入电压由50 V突增为60 V时,所提MDCS-MFPVC方法与传统MPC方法的动态性能相近;在输入电压由60 V突减为50 V时,所提MDCS-MFPVC方法与传统MPC方法的动态性能仍然相近。验证参数准确时,所提MDCS- MFPVC方法在负载电阻突变时与传统MPC拥有相近的动态性能。
为了验证所提MDCS-MFPVC方法的有效性,本节搭建了如图14所示的DAB变换器实验平台,比较了传统MPC方法与所提MDCS-MFPVC方法的输出电压性能。实验平台采用模块化设计,一个H桥作为一个模块,两个H桥通过变压器相连接,这样设计可以提高系统的灵活性和可扩展性,同时有助于简化复杂系统的维护和升级。实验平台系统及控制参数见表1。其中,根据式(1)并综合考虑系统输入电压vi、输出电压vo、变压器匝数比n、变压器漏感Lr、算法计算负担等,系统控制周期Ts=20 kHz。
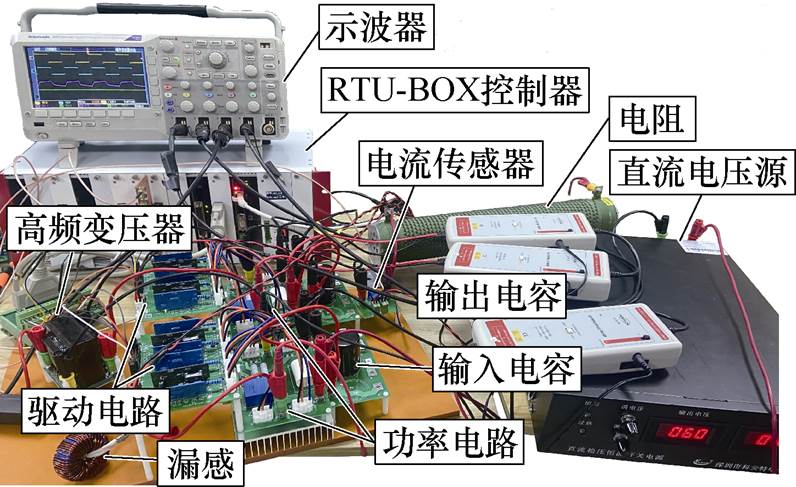
图14 DAB变换器实验平台
Fig.14 Experimental platform of DAB converter
在图14所示的DAB实验平台中,控制器采用RTU-BOX,其主处理器采用32位浮点型处理器TMS320C28346,在实验中,可以实现传统MPC算法及所提MFPC算法的实施。
4.1.1 寄生参数下鲁棒性能对比
图15比较了寄生参数存在时,所提MDCS- MFPVC方法与传统MPC方法的稳态性能。在图15中,输出电压参考Voref=45 V。
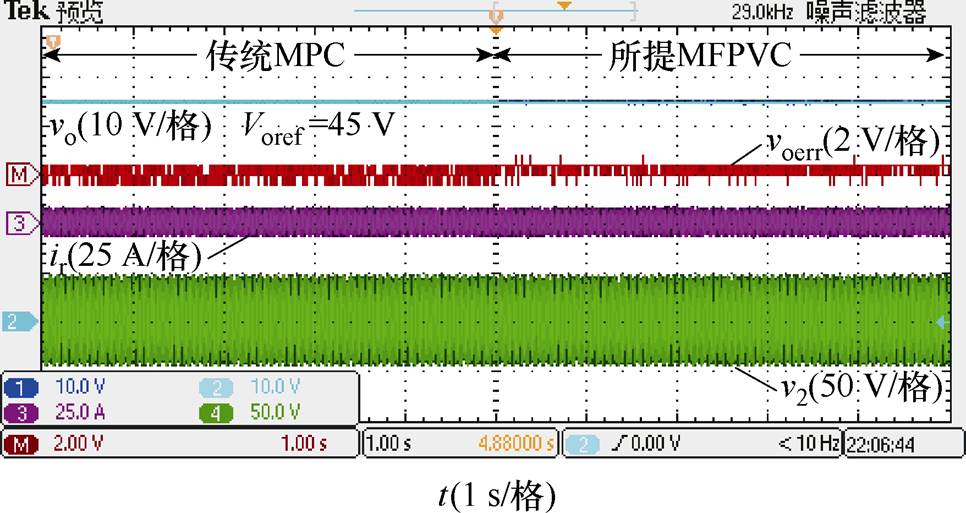
图15 寄生参数存在时稳态性能实验比较
Fig.15 Experimental comparison of steady-state performance in the presence of parasitic parameters
如图15所示,当应用传统MPC方法时,由于其依赖于准确的模型参数,寄生参数的存在导致输出电压误差增大。当控制算法切换为所提MDCS- MFPVC方法时,可以利用数据模型替代传统的预测模型,消除了寄生参数对输出电压控制的影响。
4.1.2 参数失配下鲁棒性能对比
图16比较了漏感模型参数Lr0与其实际参数Lr失配、输出电容模型参数Co0与其实际参数Co失配时,所提MDCS-MFPVC方法与传统MPC方法的稳态性能。在图16a、图16b中,输出电压参考Voref =50 V;在图16c、图16d中,输出电压参考Voref =45 V。
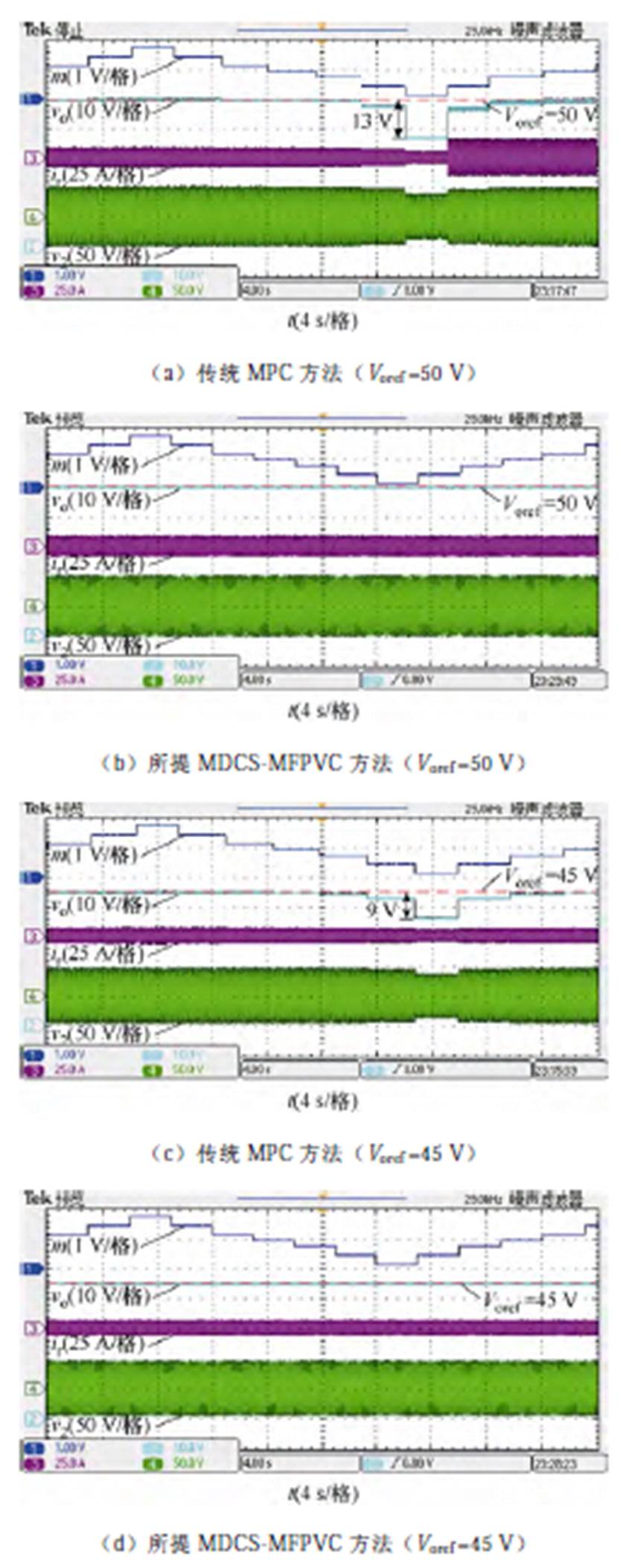
图16 参数失配时稳态性能实验比较
Fig.16 Experimental comparison of steady-state performance under mismatched parameter
如图16a所示,当应用传统MPC方法时,由于其依赖于准确的模型参数,参数失配导致输出电压误差增大,在50%参数误差时,输出电压误差达到13 V,同时导致效率降低。如图16b所示,当应用所提MDCS-MFPVC方法时,可以利用数据模型替代传统的预测模型,消除了参数失配对输出电压控制的影响,保证了系统运行效率。
如图16c所示,当应用传统MPC方法时,在50%参数误差时,输出电压误差达到9 V。如图16d所示,当应用所提MDCS-MFPVC方法时,输出电压性能不受参数失配影响,拥有良好的鲁棒性。
4.2.1 参考电压突变
图17比较了参考电压突变时,所提MDCS- MFPVC方法与传统MPC方法的动态性能。
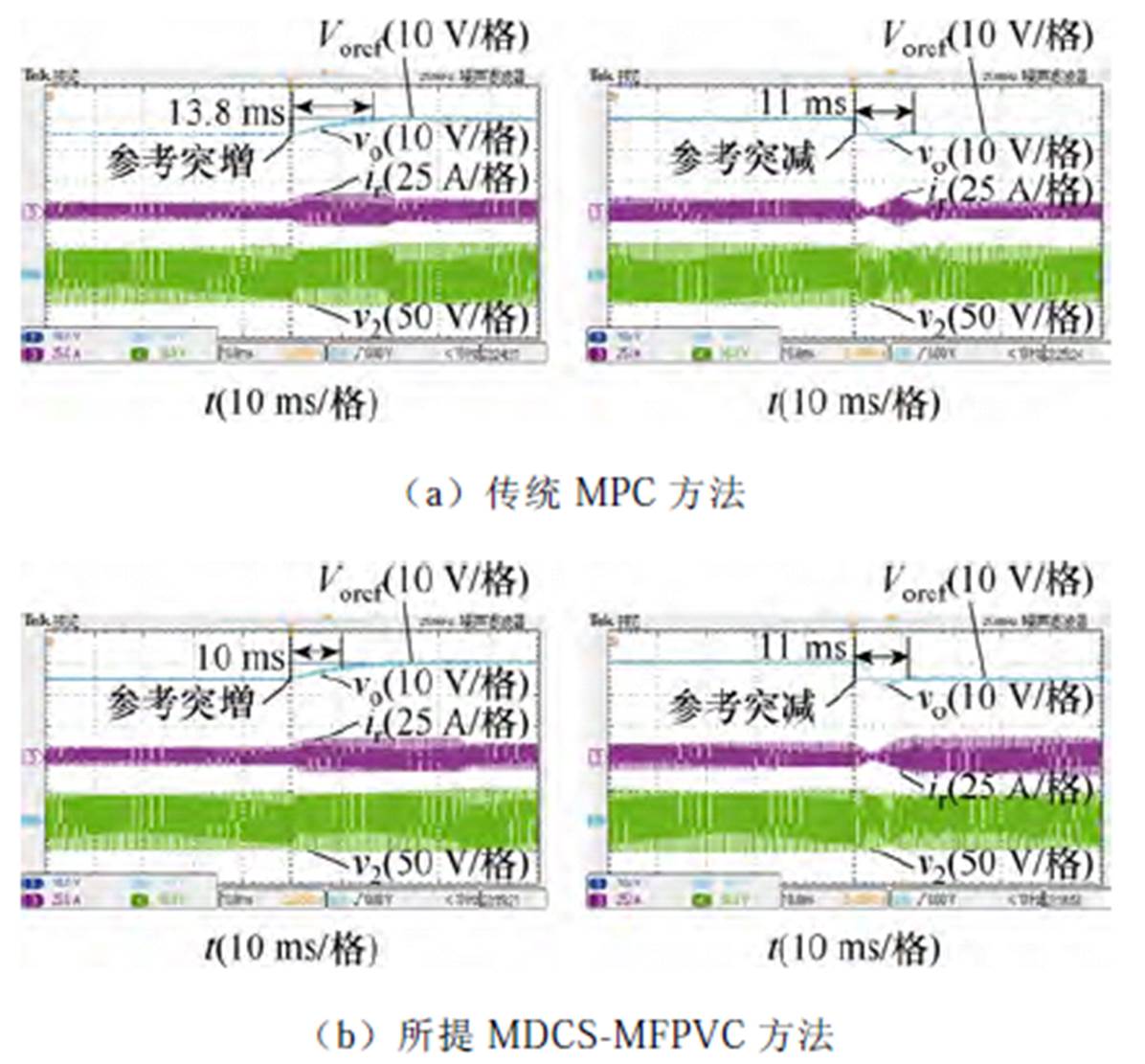
图17 参考电压突变时动态性能实验比较
Fig.17 Experimental comparison of dynamic-state performance under changed reference voltage
如图17a所示,当应用传统MPC方法时,在参考电压由45 V突增为50 V时,其响应时间为13.8 ms;在参考电压由50 V突减为45 V时,其响应时间为11 ms。如图17b所示,当应用所提MDCS-MFPVC方法,在参考电压突增时响应时间为10 ms,参考电压突减时响应时间为11 ms,与传统MPC方法相比分别减少3.8 ms、0 ms。
4.2.2 负载电阻突变
图18比较了负载电阻突变时,所提MDCS- MFPVC方法与传统MPC方法的动态性能。
如图18a所示,当应用传统MPC方法时,在负载由10 W 突增为40 W 时,输出功率由满载突减为轻载,其响应时间为6.9 ms;在负载由40 W 突减为10 W 时,输出功率由轻载突增为满载,其响应时间为16.5 ms。如图18b所示,当应用所提MDCS- MFPVC方法,在负载突增和突减时,其仍可以快速跟踪参考电压,响应速度与传统MPC方法相近,验证了所提方法的有效性。


图18 负载突变时动态性能实验比较
Fig.18 Experimental comparison of dynamic-state performance under changed load
4.2.3 输入电压突变
图19比较了输入电压突变时,所提MDCS- MFPVC方法与传统MPC方法的动态性能。

图19 输入电压突变时动态性能实验比较
Fig.19 Experimental comparison of dynamic-state performance under changed input voltage
如图19a所示,当应用传统MPC方法时,在输入电压由50 V突增为60 V时,其可以快速跟踪参考电压;在输入电压由60 V突减为50 V时,其响应时间为6 ms。如图19b所示,当应用所提MDCS- MFPVC方法,在输入电压突增和突减时,其响应速度与MPC方法相近,可以快速跟踪参考电压,验证了所提方法的有效性。
表2比较了传统PI方法、传统MPC方法以及所提MDCS-MFPVC方法在不同工况下的电压误差、响应速度等性能。
表2 多工况下控制方法性能对比
Tab.2 Performance comparison of control methods under multiple operating conditions
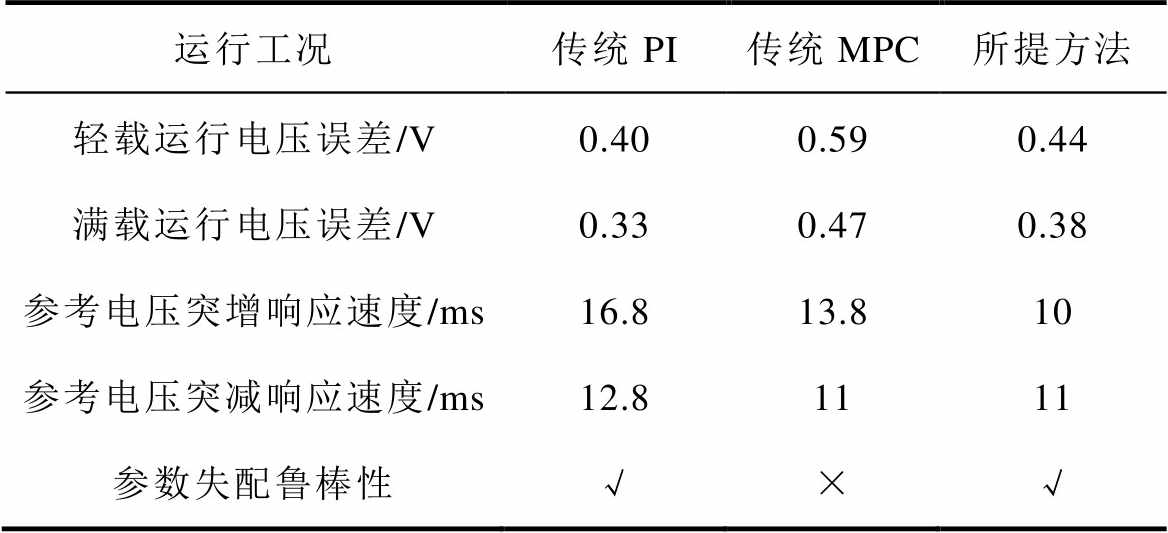
运行工况传统PI传统MPC所提方法 轻载运行电压误差/V0.400.590.44 满载运行电压误差/V0.330.470.38 参考电压突增响应速度/ms16.813.810 参考电压突减响应速度/ms12.81111 参数失配鲁棒性√×√
注:√表示性能较好;×表示性能较差。
表2中,在轻载、满载运行时,传统PI方法、传统MPC方法及所提MDCS-MFPVC方法的电压误差相近。当系统运行在参考电压突变模式时,传统PI方法响应时间最慢,所提MDCS-MFPVC方法响应速度率高于传统MPC方法。此外,当系统运行在参数失配条件下时,传统MPC方法将引起较大的电压误差,而传统PI方法和所提MDCS- MFPVC方法均不受参数失配的影响,拥有良好的鲁棒性能。
本文针对DAB变换器提出了一种移动离散控制集无模型预测电压控制。该方法利用数据模型替代传统的数学模型,并结合最小二乘法在每个控制周期在线辨识DAB系统数据模型,消除了参数对预测控制的影响;通过设计自适应移相范围,实现无模型预测电压控制,提高了预测控制的鲁棒性。仿真和实验结果说明了,当参数准确时,与传统MPC方法相比,所提方法拥有相近的稳态性能和响应能力。当参数失配时,与传统MPC方法相比,所提方法拥有优越的鲁棒性。
参考文献
[1] 曹善康, 魏繁荣, 林湘宁, 等. 网侧电压跌落下计及无功支撑效能的直流微电网多目标优化策略[J]. 中国电机工程学报, 2023, 43(15): 5759-5772.
Cao Shankang, Wei Fanrong, Lin Xiangning, et al. Multi-objective optimization strategy of DC micro- grid based on reactive power support efficiency during voltage sag[J]. Proceedings of the CSEE, 2023, 43(15): 5759-5772.
[2] Dragičević T, Lu Xiaonan, Vasquez J C, et al. DC microgrids: part II: a review of power architectures, applications, and standardization issues[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3528-3549.
[3] Shao Shuai, Chen Linglin, Shan Zhenyu, et al. Modeling and advanced control of dual-active-bridge DC-DC converters: a review[J]. IEEE Transactions on Power Electronics, 2022, 37(2): 1524-1547.
[4] 刘子薇, 孙兆龙, 刘宝龙, 等. 基于直接功率控制的双有源桥暂态直流偏置抑制策略[J]. 电工技术学报, 2023, 38(12): 3234-3247.
Liu Ziwei, Sun Zhaolong, Liu Baolong, et al. Transient DC bias suppression strategy of dual active bridge based on direct power control[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3234-3247.
[5] 杨向真, 王锦秀, 孔令浩, 等. 电压不匹配运行条件下双有源桥变换器的效率优化方法[J]. 电工技术学报, 2022, 37(24): 6239-6251.
Yang Xiangzhen, Wang Jinxiu, Kong Linghao, et al. Efficiency optimization method of DAB converters under wide-voltage operating conditions[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(24): 6239-6251.
[6] 安峰, 宋文胜, 杨柯欣. 电力电子变压器的双有源全桥DC-DC变换器模型预测控制及其功率均衡方法[J]. 中国电机工程学报, 2018, 38(13): 3921-3929, 4034.
An Feng, Song Wensheng, Yang Kexin. Model predictive control and power balance scheme of dual-active-bridge DC-DC converters in power electronic transformer[J]. Proceedings of the CSEE, 2018, 38(13): 3921-3929, 4034.
[7] Chen Linglin, Shao Shuai, Xiao Qian, et al. Model predictive control for dual-active-bridge converters supplying pulsed power loads in naval DC micro- grids[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1957-1966.
[8] Chen Linglin, Lin Lüyi, Shao Shuai, et al. Moving discretized control set model-predictive control for dual-active bridge with the triple-phase shift[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8624-8637.
[9] Tarisciotti L, Chen Linglin, Shao Shuai, et al. Finite control set model predictive control for dual active bridge converter[J]. IEEE Transactions on Industry Applications, 2022, 58(2): 2155-2165.
[10] Deng Yaru, Song Wensheng, Yin Shuai, et al. A model predictive control scheme without current sensor of dual active bridge DC-DC converters: improving dynamic performance and reducing hardware cost[J]. IEEE Transactions on Trans- portation Electrification, 2023, 9(2): 2916-2928.
[11] 尹政, 胡存刚, 芮涛, 等. LC滤波型电压源逆变器无模型预测电压控制策略[J]. 电工技术学报, 2023, 38(14): 3723-3732.
Yin Zheng, Hu Cungang, Rui Tao, et al. Model-free predictive voltage control strategy for LC-filtered voltage source inverter[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3723-3732.
[12] 芮涛, 尹政, 汪凤翔, 等. 基于双矢量的并网逆变器无模型预测电流控制策略[J]. 电工技术学报, 2023, 38(14): 3759-3768.
Rui Tao, Yin Zheng, Wang Fengxiang, et al. Model- free predictive current control strategy of grid- connected inverter based on double-vector[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(14): 3759-3768.
[13] Zhu Yi, Yang Yong, Wen Huiqing, et al. Model predictive control with a novel parameter identi- fication scheme for dual-active-bridge converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2023, 11(5): 4704-4713.
[14] Li Yuan, Sahoo S, Dragičević T, et al. A model predictive control based power sharing control of dual active bridge converter with parameters estimation[C]// IECON 2022-48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 2022: 1-6.
[15] Guo Zhiqiang, Luo Yong, Sun Kai. Parameter identification of the series inductance in DAB con- verters[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7395-7399.
[16] Li Xuming, Dong Zheng, Cao Yan, et al. Model- predictive control with parameter identification for multi-dual-active-bridge converters achieving accurate power balancing[J]. IEEE Transactions on Power Electronics, 2023, 38(9): 10880-10894.
Abstract In power electronics, the dual active bridge (DAB) converter stands as a pivotal component in various applications, from electric vehicle charging stations to renewable energy systems. The conventional model predictive control (MPC) strategies for the DAB converter are inherently tethered to the precision of system parameters. Any deviation or uncertainty in these parameters can lead to suboptimal performance or instability in the voltage control loop. Based on a moving-discrete control set, this paper proposes a free predictive voltage control (MDCS-MFPVC) strategy to eliminate the influence of system parameters on the voltage control of the DAB converter.
Firstly, the influence of parameter mismatch on conventional MPC is analyzed. Then, the discrete data model of the DAB converter is established to replace the conventional mathematical model and improve the robustness of predictive voltage control. Then, through the error feedback of the data model and the setting of multiple input variables, the discrete data model is identified in real time with the least square method. Combined with system sampling and data model identification results, model-free predictive of voltage at a future time is realized, and the optimal phase shift angle is evaluated by cost function and applied to the next control period. This method can identify the system data model of the DAB converter in real time, eliminating the influence of parameter mismatch on MPC, and ensuring the robustness of output voltage. Finally, the simulation and experiment system of the DAB converter is set up to verify the effectiveness of the proposed method.
Parameter robustness simulation shows that when the output voltage reference is 50 V, the maximum output voltage error of the proposed MDCS-MFPVC method is 0.11 V, 13.89 V lower than the conventional MPC method. When the output voltage reference is 45 V, the maximum output voltage error of the conventional MPC and the proposed MDCS-MFPVC is 12 V and 0.098 V, respectively. The parameter robustness experiment shows that the proposed MDCS-MFPVC method cannot be affected by any changed parameters, verifying the effectiveness of the proposed method. Dynamic performance simulation and experiment show that the proposed MDCS-MFPVC has a dynamic performance similar to the conventional MPC under changed output voltage reference, load resistance, and input voltage.
The following conclusions can be drawn. (1) The proposed MDCS-MFPVC method has good parameter robustness. When the parameters are mismatched, the output voltage error of the DAB is significantly reduced, and the voltage quality is improved. When the parameters are accurate, the voltage performance of the proposed MDCS-MFPVC is similar to that of the conventional MPC. (2) The proposed MDCS-MFPVC method has a similar dynamic performance when the output voltage reference, load resistance, and input voltage change.
In future studies, the proposed method can be extended and applied to the multi-active bridge converter system to further study the power distribution and parameter robustness of the system.
keywords:Dual active bridge converter, model-free predictive, voltage control, moving-discrete control set, parameter robustness
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.240357
国家重点研发计划“政府间国际科技创新合作”重点专项资助项目(2022YFE0196300)。
收稿日期 2024-03-06
改稿日期2024-05-07
尹 政 男,1996年生,博士研究生,研究方向为新能源变换器预测控制。E-mail: zyin@seu.edu.cn
邓富金 男,1983年生,教授,博士生导师,研究方向为模块化多电平变流器。E-mail: fdeng@ seu.edu.cn(通信作者)
(编辑 陈 诚)