摘要 该文提出一类元件复用型单相无桥倍压式功率因数校正（PFC）电路拓扑，在Sepic、Cuk、Zeta型双变换单元无桥PFC拓扑的基础上，通过重构电流路径以实现双变换单元的合并，使元件利用率得以提高，同时交流侧的高功率因数特性以及相同输出电压下开关管的低电压应力优势被完全保留。该文详尽分析中间储能单元的换流过程以及电路结构的推衍过程，并进行拓扑的性能比较。考虑到电路工作原理分析过程的类似性，以Sepic型单相无桥倍压式PFC变换器为例，对其进行开关周期的模态分析，推导变换器的输入电流特性、稳态电压增益以及器件应力，并对相关电路参数进行设计。最后，搭建实验样机，实验结果验证了该拓扑推衍方案的可行性以及理论分析与参数设计的正确性。
关键词：无桥功率因数校正（PFC）变换器 拓扑推衍 元件复用 倍压式结构
在航空中频电源系统中，为了给后级用电设备供电，需要将交流发电机输出的400 Hz交流电经过前级功率因数校正（Power Factor Correction, PFC）变换器二次变换转化为直流电[1]。交流电系统的基波频率（400 Hz）是工频系统（50 Hz）的8倍，这就要求PFC变换器具有快速的电流跟踪能力，高功率因数和高效率是其重要的技术特征要求[2-4]。考虑到电路拓扑是PFC技术研究的基础，拓扑结构的优化可以从源头上改善和提升PFC变换器性能，国内外学者不断提出新型PFC电路拓扑以适应其高性能需求[5-6]。
基本型无桥Boost PFC变换器于1983年由美国罗克韦尔公司率先提出，相比于有桥形式拓扑，其电流通路上减少了一个低速二极管，变换器效率得以有效提高[7]。此后，无桥PFC拓扑得到越来越多的关注与研究，图腾柱PFC[8]、Dual-Boost无桥PFC[9]、三电平无桥PFC[10]及其衍生拓扑被相继提出。文献[11]采用开关-电容网络对传统三电平拓扑进行重新构造，提出了一类新型三电平无桥PFC电路，可控器件数量减少一半且部分开关管电压应力减半，损耗较传统三电平明显减小。文献[12]融合了Dual-Boost无桥PFC与三电平无桥PFC的优点，提出了一类三电平伪图腾柱PFC电路，降低了部分半导体器件的电压应力，提高了电路的输出电压等级。
与此同时，无桥结构的设计思想也可以应用于Sepic、Cuk及Zeta型PFC电路中，由此推衍得到的PFC电路具有断续导通模式（Discontinuous Con- duction Mode, DCM）下自动实现功率因数校正的特点，更适合应用于航空中频400 Hz电源系统中[13]。基于传统桥式电路，文献[14-16]分别给出了Dual- Sepic、Dual-Cuk与Dual-Zeta无桥PFC电路，该类电路采用双变换单元分别处理交流输入电压的正、负半周。文献[17]在文献[14-15]基础上，将双变换单元中的储能电感与输出二极管进行合并，电路结构得以简化。文献[18-19]将开关电感网络引入到Sepic型无桥拓扑中，有效地拓宽了变换器的电压增益范围。文献[20-21]对Cuk型无桥拓扑的中间储能单元进行结构优化，实现了在无需附加反相放大器电路的情况下变换器直流输出电压为正。文献[22-24]将倍压式输出结构引入到Sepic、Cuk、Zeta型无桥拓扑中，提出了一类基于双变换单元的无桥倍压式PFC电路，该类电路具有同等级直流输出电压下低电压应力的优势，但由于使用的储能元件和开关器件较多，电路具有进一步优化的空间。
考虑到电路结构的对称性，元件复用被认为是简化多变换单元拓扑的有效途径[25]。本文将元件复用的概念延伸到Sepic、Cuk、Zeta型双变换单元无桥PFC电路中，提出一类基于元件复用的单相无桥倍压式PFC电路拓扑，适用于航空中频电源系统等输入频率较高的应用场合。利用双向开关管与输出侧半桥结构对中间储能单元的电流路径进行重构，以实现双变换单元的有效合并。详尽分析电路结构优化的推衍过程，并进行电路性能比较。考虑到电路原理分析过程的类似性，以Sepic型无桥倍压式PFC变换器为例，具体分析电路的工作原理与电路特性，并给出相关电路参数的设计过程，最后搭建实验样机进行实验验证。
基于双变换单元的Sepic、Cuk型无桥PFC变换器拓扑如图1所示，其中间储能单元为具有对称结构的两个Sepic、Cuk变换单元。
DCM下，Sepic、Cuk型双变换单元无桥PFC电路的中间储能单元在开关周期内的换流过程如图2与图3所示。可以看到，两个Sepic、Cuk变换单元工作独立且互不影响。储能电容C1、储能电感L2，二极管VD1、VD4、VD5工作在正半周期；储能电容C2、储能电感L3，二极管VD2、VD3、VD6工作在负半周期。正、负半周内电路的工作过程完全相同，电流路径具有结构上的对称性。从电路自身元器件数量来看，中间储能单元使用2个储能电感、2个储能电容和7个半导体器件；从电流流经元器件数量来看，中间储能单元有1个储能电感、1个储能电容和最多3个半导体器件工作；从电压应力来看，开关管S两端电压峰值为输入电压峰值与1/2直流输出电压之和。
图1 基于双变换单元的单相无桥倍压式PFC变换器
Fig.1 Single-phase bridgeless voltage-doubler PFC converters based on dual-converter cells
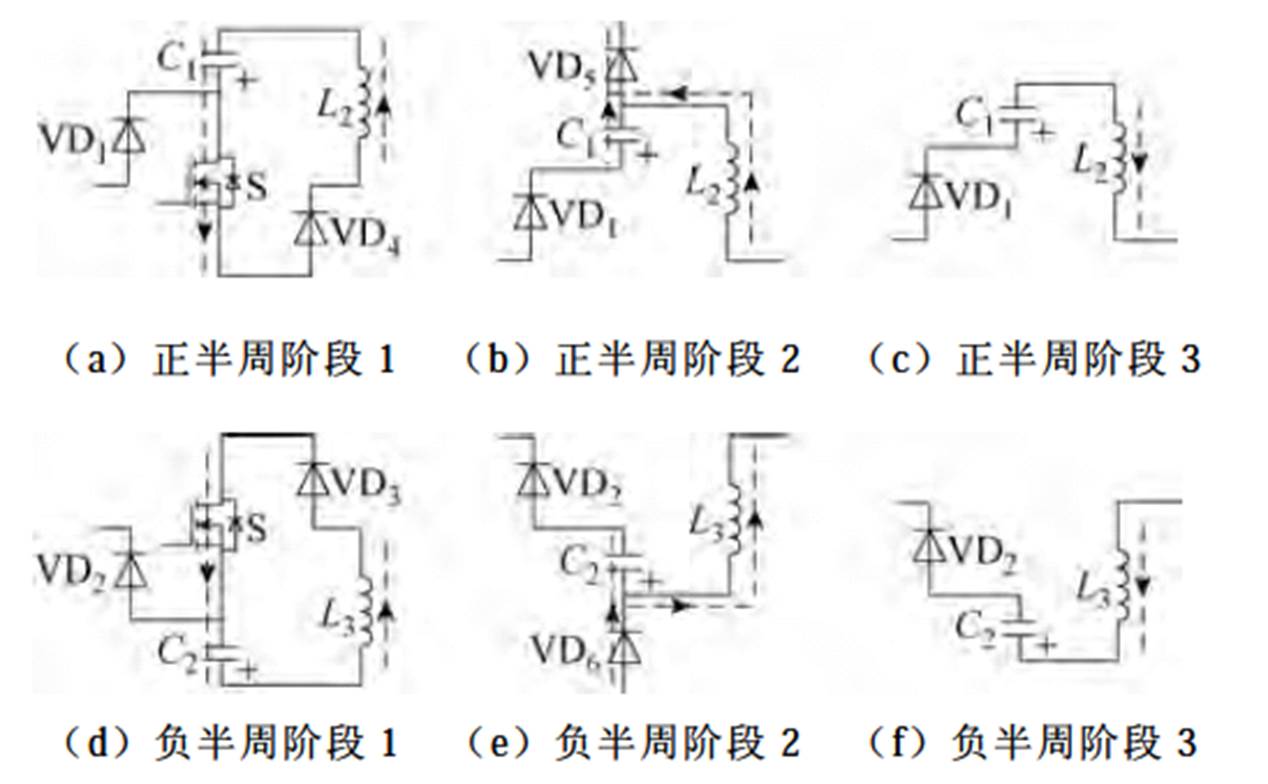
图2 Sepic型双变换单元中间储能单元换流路径
Fig.2 Commutation paths of Sepic intermediate-storage unit based on dual-converter cells
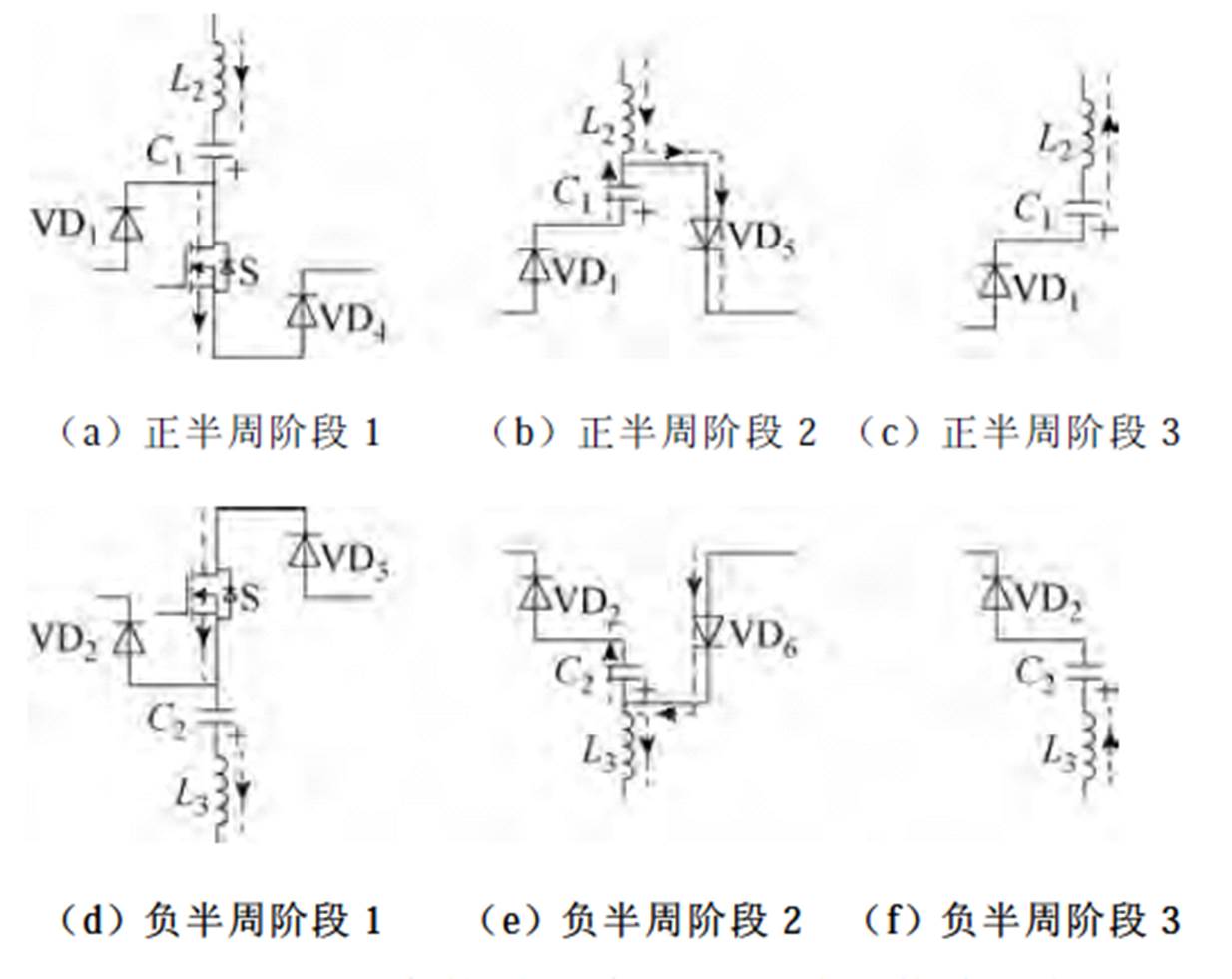
图3 Cuk型双变换单元中间储能单元换流路径
Fig.3 Commutation paths of Cuk intermediate-storage unit based on dual-converter cells
基于以上分析，Sepic型双变换单元无桥PFC电路的中间储能单元采用结构对称的两个Sepic电路分别工作在交流输入电压的正、负半周，元器件利用率较低。考虑到两个Sepic电路工作电流的对称特性，本文利用双向开关管与二极管半桥结构对中间储能单元的电流路径进行重构，以实现储能电容与储能电感的元件复用、双Sepic变换单元的有效合并，元件复用过程如图4所示。可以看到，输入侧低速二极管被完全移除，两组储能电容与储能电感（C1与L2、C2与L3）复用为一组（Cs与Ls），储能电容Cs与储能电感Ls同时工作于交流输入电压的正、负半周，Cs两端电压呈交流变化。
图4 Sepic型双变换单元无桥PFC电路的元件复用过程
Fig.4 Component-multi-used process of Sepic bridgeless PFC circuit based on dual-converter cells
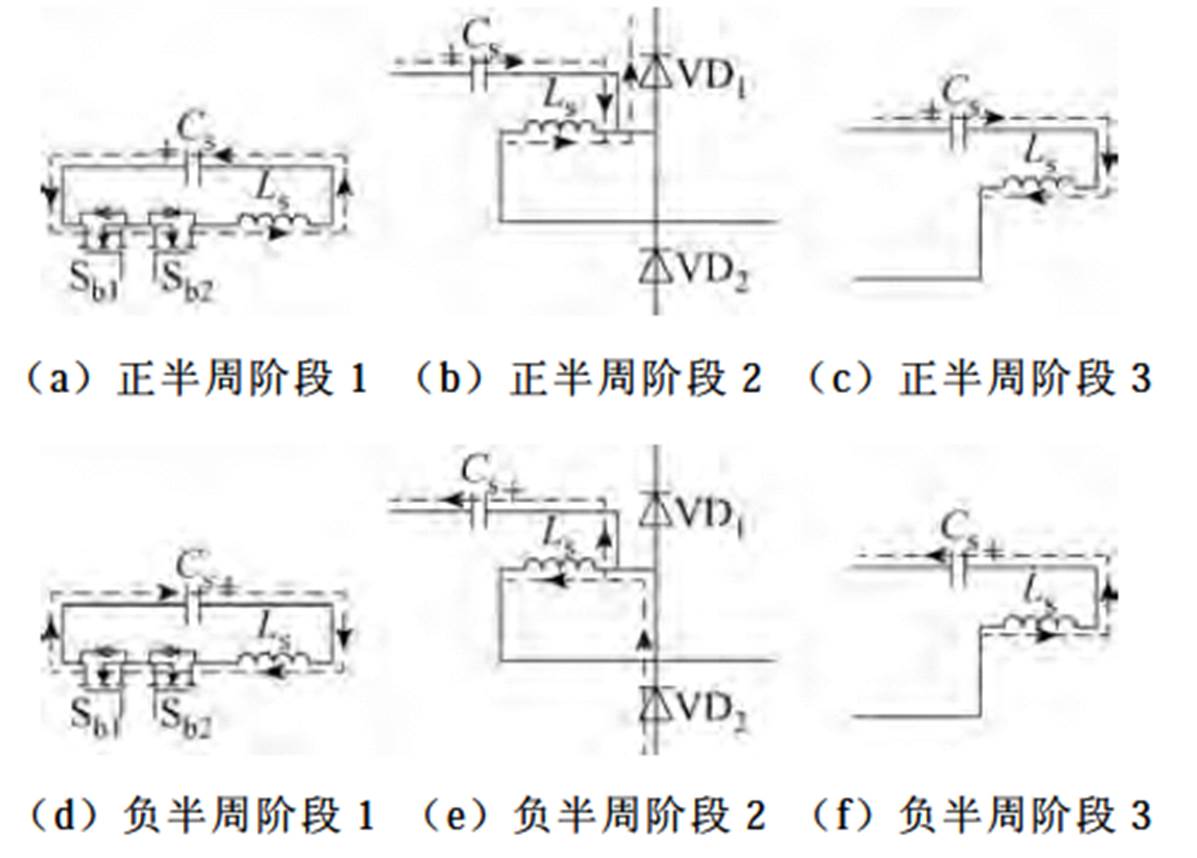
元件复用后电路中间储能单元在一个开关周期内的换流路径如图5所示。对比图2与图5可知，元件复用后电路的工作原理并没有发生变化，储能电感Ls在一个开关周期内仍然具有充电、放电与续流三个工作阶段，但工作电流的路径发生了重构。使用双向开关管Sb1与Sb2为储能电感Ls提供双向充电电流通路；使用二极管VD1与VD2构成的半桥结构保证输出电流的单向性，在正半周内VD1工作，负半周内VD2工作，电流通路上半导体数量最多为2个。
3
图5 基于元件复用的Sepic型中间储能单元换流路径
Fig.5 Commutation paths of Sepic intermediate-storage unit with shared components
不同于Sepic变换单元，Cuk变换单元的储能电感位于输出侧，与输出滤波电容直接相连，在一个开关周期内其电流具有双向性。为实现储能电容电感的元件复用，在使用双向开关管的基础上，将半桥结构中的二极管替换为开关管，Cuk型双变换单元无桥PFC电路的元件复用过程如图6所示。
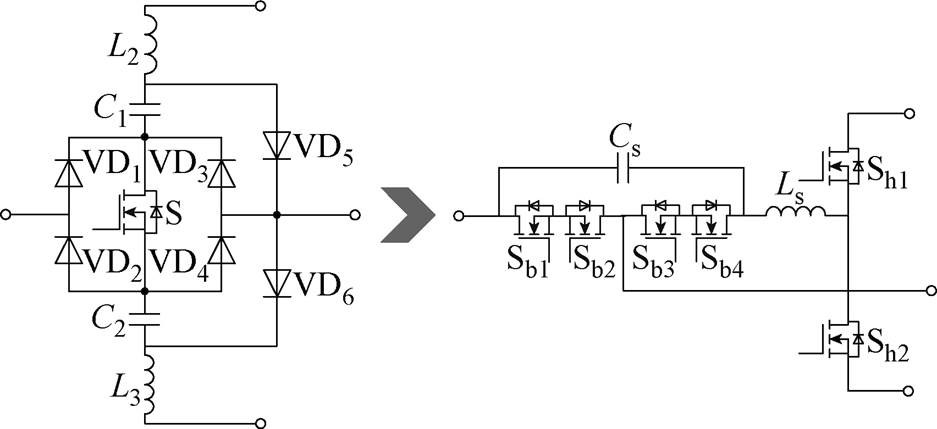
图6 Cuk型双变换单元无桥PFC电路的元件复用过程
Fig.6 Component-multi-used process of Cuk bridgeless PFC circuit based on dual-converter cells
如图6所示，两组储能元件（C1与L1、C2与L3）复用为一组（Cs与Ls）。电路使用了两组双向开关管Sb1、Sb2与Sb3、Sb4；Sb1、Sb2用于形成储能电感Ls的充电回路；Sb3、Sb4用于形成储能电感Ls的放电回路。
元件复用后电路中间储能单元在一个开关周期内的换流路径如图7所示。对比图3与图7可知，元件复用后Cuk型电路的工作原理没有发生变化，仅是电流的工作路径发生了重构。使用双向开关管Sb1与Sb2为储能电感Ls提供双向充电电流通路；使用双向开关管Sb3与Sb4为储能电感Ls提供双向放电电流通路；使用开关管Sh1与Sh2构成的半桥结构保证输出电流的双向性，在正半周内Sh2工作，负半周内Sh1工作，电流通路上半导体数量最多为3个。
图7 基于元件复用的Cuk型中间储能单元换流路径
Fig.7 Commutation paths of the Cuk intermediate-storage unit with shared components
以元件复用为目标，基于双向开关管与半桥结构，重构中间储能单元电流路径，由此推衍得到如图8与图9所示的基于元件复用的无桥倍压式Sepic与Cuk型PFC优化拓扑。其中，半桥结构使用的半导体器件由其流过的电流极性决定，当流经电流为双向电流时，使用开关管，如Cuk型优化拓扑；当流经电流为单向电流时，使用二极管以简化控制，如Sepic型优化拓扑、工作于临界导通模式（Critical Conduction Mode, CRM）的Cuk型优化拓扑。
图8 基于元件复用的无桥倍压式Sepic型PFC变换器
Fig.8 Bridgeless voltage-doubler Sepic PFC converter with shared components
图9 基于元件复用的无桥倍压式Cuk型PFC变换器
Fig.9 Bridgeless voltage-doubler Cuk PFC converter with shared components
对比Cuk型无桥拓扑优化前后中间储能单元的工作电流路径可知，此种电流路径重构方式不仅实现了储能电感与电容的元件复用，还将电路的直流输出电压极性由负变为正。同时基于此种拓扑推衍方法，得到基于元件复用的无桥倍压式Zeta型PFC变换器电路，如图10所示。可以看到，Zeta型推衍拓扑的半桥结构使用了二极管，这是因为电路较大的滤波电感Lf一般置于输出侧以减小输出电流纹波，输出电流具有单向性。
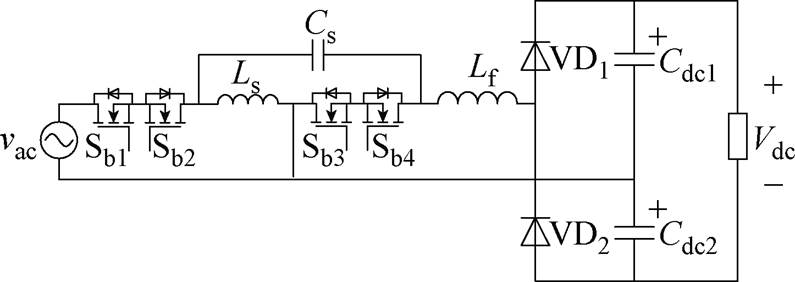
图10 基于元件复用的无桥倍压式Zeta型PFC变换器
Fig.10 Bridgeless voltage-doubler Zeta PFC converter with shared components
将提出的元件复用无桥倍压式PFC拓扑与其他已有无桥PFC拓扑在电感电容使用数量、半导体器件使用数量、开关管电压应力以及直流输出电压极性上进行性能比较，见表1。可以看到，相比其他无桥PFC拓扑，所提出元件复用电路拓扑的中间储能单元实现了有效合并，滤波电感、储能电感与储能电容的使用数量达到最少，元件利用率得以提高；采用倍压式输出结构，开关管的电压应力得以有效降低；Cuk型拓扑的直流输出电压极性为正，电路性能得到改善。
表1 拓扑性能比较
Tab.1 Topology performance comparison
无桥PFC拓扑参考文献输入滤波电感数量中间储能单元数量半导体器件数量开关管电压应力输出电压极性 CLSVD Dual-Sepic无桥PFC[14]22224Vm+Vdc+Vdc Sepic无桥优化拓扑[17]22123Vm+Vdc+Vdc Sepic无桥优化拓扑[18]22224Vm+2Vdc+Vdc Sepic无桥优化拓扑[19]22216Vm+Vdc+Vdc Sepic无桥优化拓扑[22]12216Vm+Vdc/2+Vdc Sepic元件复用型优化拓扑本文11122Vm+Vdc/2+Vdc Dual-Cuk无桥PFC[15]22224Vm+Vdc-Vdc Cuk无桥优化拓扑[17]22123Vm+Vdc-Vdc Cuk无桥优化拓扑[20]22115Vm+Vdc+Vdc Cuk无桥优化拓扑[21]21115Vm+Vdc+Vdc Cuk无桥优化拓扑[23]12216Vm+Vdc/2-Vdc Cuk元件复用型优化拓扑本文11160Vm+Vdc/2+Vdc Dual-Zeta无桥PFC[16]22224Vm+Vdc+Vdc Zeta无桥优化拓扑[24]22224Vm+Vdc/2+Vdc Zeta元件复用型优化拓扑本文11160Vm+Vdc/2+Vdc
注：Vm为输入电压峰值；Vdc为直流输出电压。
基于得到的元件复用型优化拓扑，考虑到工作原理分析过程的类似性，以Sepic型无桥倍压式PFC变换器为例，对其开关周期工作模态、稳态特性以及控制方案进行具体分析。类似的分析过程可扩展到其他元件复用无桥拓扑中。
Sepic型无桥倍压式PFC变换器的电路结构如图8所示，包括输入滤波电感Lf、储能电感Ls、储能电容Cs、双向开关管Sb1与Sb2、二极管VD1与VD2以及输出滤波电容Cdc1与Cdc2。
分析前，做出如下说明：①电路工作于DCM；②使用的半导体器件、电感和电容均为理想元器件，Cdc1与Cdc2的电容值相等，均为Cdc。考虑到正负半周内电路工作的类似性，仅对正半周的一个开关周期内电路的工作模态进行分析。电路稳态时一个交流周波内的主要工作波形和正半周内一个开关周期的主要电流波形如图11所示。正半周一个开关周期内的三个工作模态如图12所示。
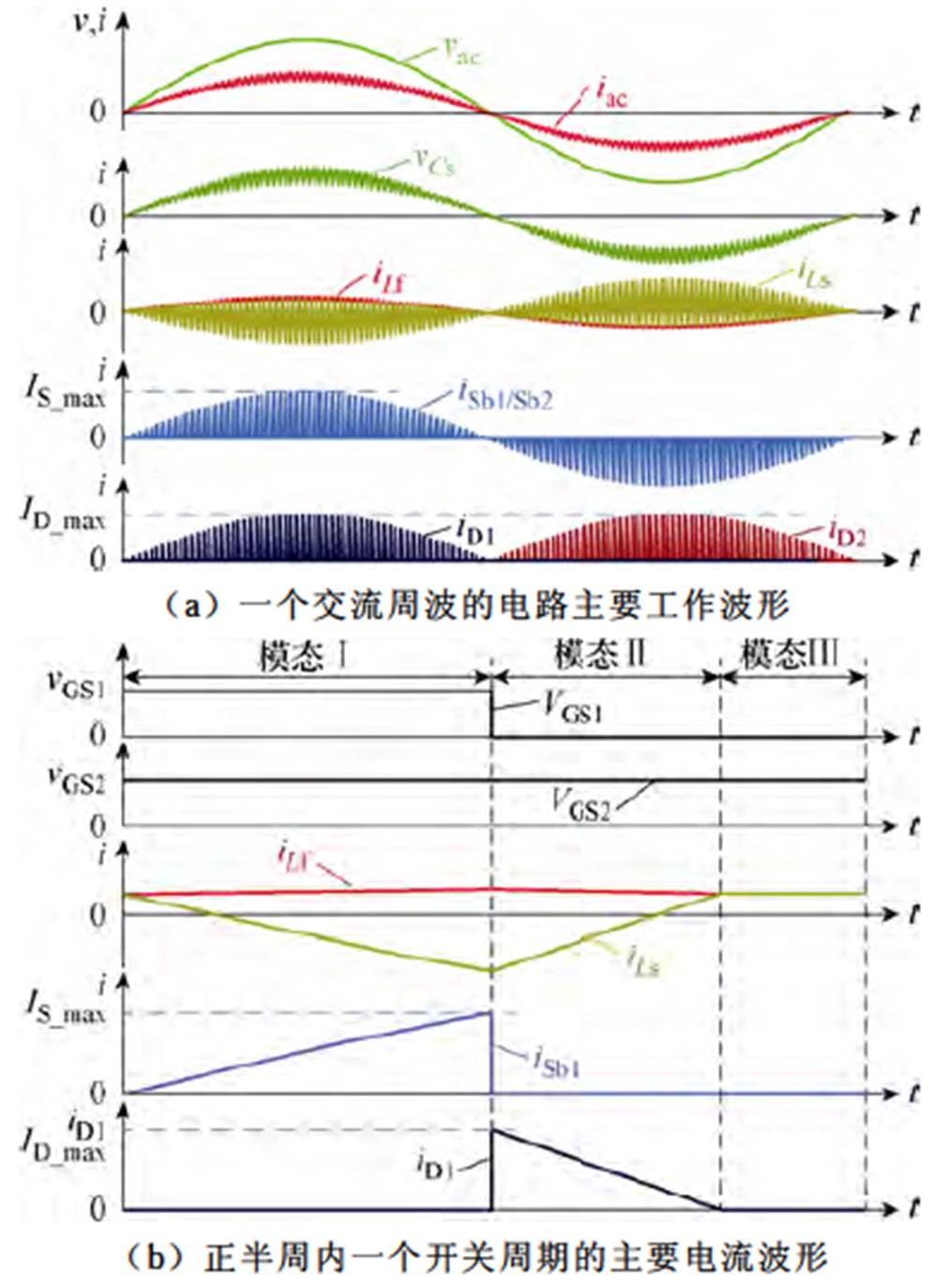
图11 电路稳态工作波形
Fig.11 Steady-state operating waveforms of the circuit
图12 正半周一个开关周期内的三个工作模态
Fig.12 Diagram of three operating modes in a switching period for positive cycle
模态Ⅰ：如图12a所示，双向开关管Sb1与Sb2导通，输入滤波电感Lf与储能电感Ls两端电压分别为输入电压|vac|和储能电容电压|vCs|，Lf与Ls的电流iLf、iLs线性上升。同时二极管VD1与VD2处于关断状态，负载由输出滤波电容Cdc1与Cdc2提供能量。电路状态方程为
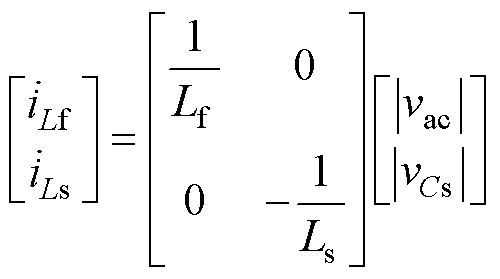（1）
模态Ⅱ：如图12b所示，开关管Sb1关断，二极管VD1导通，电感Lf与Ls经过VD1一同向输出滤波电容Cdc1以及负载释放能量。Lf与Ls的电流开始呈线性下降，VD1的电流也由峰值开始呈线性下降。电路状态方程为
（2）
模态Ⅲ：如图12c所示，二极管VD1电流下降为0而关断，电感Lf通过储能电容Cs与电感Ls形成续流回路。此时负载由输出滤波电容Cdc1与Cdc2提供能量。电路状态方程为
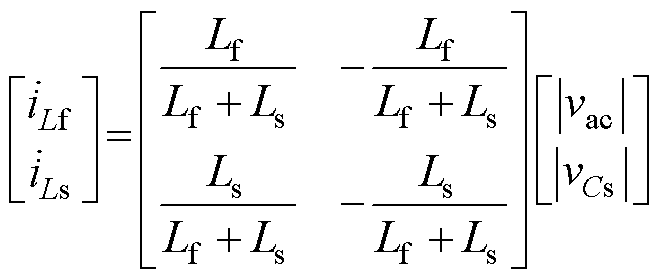（3）
2.2.1 输入电流特性
依据伏秒平衡原理，输入滤波电感Lf与储能电感Ls在一个开关周期内的平均电压为0，从而有
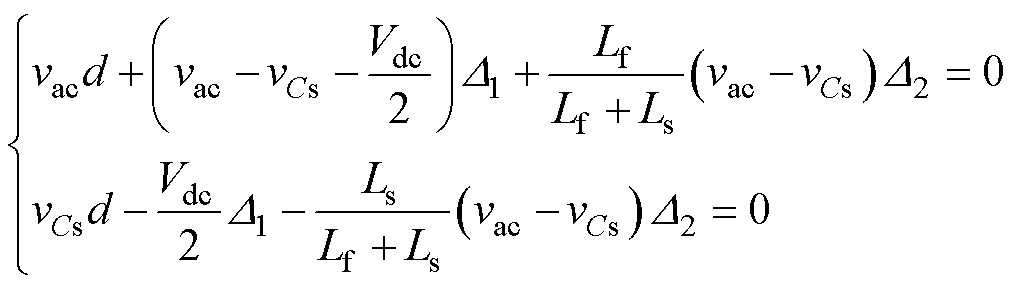（4）
式中，vac为交流输入电压；vCs为储能电容两端电压；Vdc为直流输出电压；d为占空比；D1为模态Ⅱ时间占比；D2为模态Ⅲ时间占比。
对式（4）化简可得
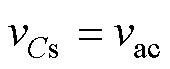（5）
式（5）表明，储能电容两端电压vCs跟随输入电压vac呈正弦交流变化。由模态切换过程可知，模态Ⅱ开始时刻，输出侧二极管电流达到峰值iD_max，表示为
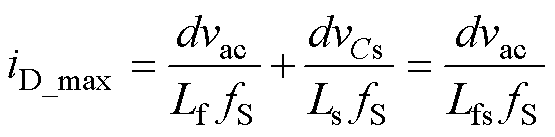（6）
式中，fS为开关频率；Lfs为输入滤波电感Lf与储能电感Ls的并联电感，Lfs=LfLs/(Lf+Ls)。
在模态Ⅱ期间，输出侧二极管电流由峰值开始线性下降，电流波形呈三角形，其面积与开关周期的比值即为一个开关周期内变换器输出电流的平均值iD_avg。结合式（4）与式（6），iD_avg可表示为
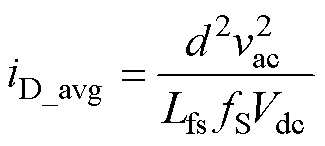（7）
依据输入输出瞬时功率守恒，得到变换器输入电流iac的表达式为
（8）
由式（8）可知，在开关频率fS、占空比d以及并联电感Lfs一定时，变换器的输入电流与输入电压同相位变化，输入侧功率因数理论上为1。
2.2.2 电压增益特性
基于式（8），稳态工作下变换器输入侧的平均功率Pin可表示为
（9）
式中，Vac_rms为交流输入电压的有效值。同时，变换器直流侧输出功率Pout可表示为
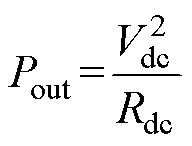（10）
式中，Rdc为直流负载。定义变换器电压增益M为直流输出电压与交流输入电压有效值的比值。根据平均功率守恒，联立式（9）与式（10），推导出变换器电压增益M的表达式为
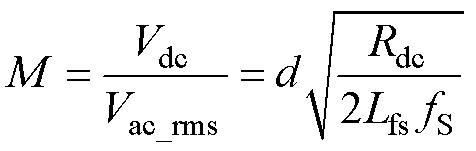（11）
观察式（11）可知，在开关频率fS、并联电感Lfs以及直流负载Rdc一定时，输出电压的大小可通过调节占空比d的大小进行灵活调节。
2.2.3 器件应力分析
在开关管导通阶段（模态Ⅰ），流经开关管Sb1、Sb2的电流为输入滤波电感Lf与储能电感Ls的电流之和，由此开关管Sb1、Sb2电流应力最大值表示为
（12）
在开关管关断阶段（模态Ⅱ），开关管Sb1、Sb2两端承受储能电容Cs电压与输出滤波电容Cdc1、Cdc2电压之和，由此得到开关管Sb1、Sb2电压应力最大值表示为
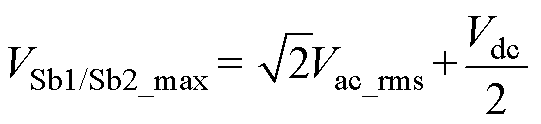（13）
由式（13）可知，变换器保留了倍压式输出结构在相同输出电压下开关管电压应力较低的优点。
此外，在模态Ⅱ期间，输出侧两个二极管一个导通、一个关断。关断的二极管承受反压，反压大小等于输出电压；导通的二极管电流由峰值呈线性下降，由此得到二极管VD1、VD2电压、电流应力最大值分别为
（14）
观察如式（8）所示的电流表达式可知，DCM下变换器的输入电流具有自然跟踪输入电压呈正弦规律变化的能力。占空比d可通过输出电压的电压闭环获得，具体的控制方案如图13所示。
图13 控制方案
Fig.13 Control scheme
由输出侧电流关系可得
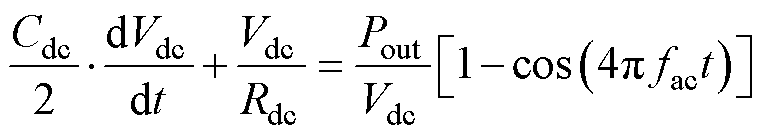（15）
式中，fac为交流输入电源频率。变换器稳态工作时，输出电压微分项的直流分量为0，从而得到输出电压纹波的表达式为
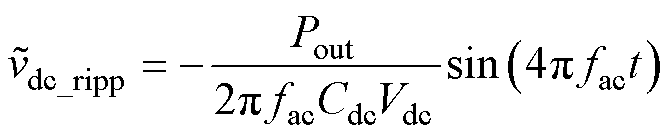（16）
由式（16）可知，输出电压中存在二倍于输入电源频率的低频电压纹波，因此设计PI控制器的带宽远低于二倍交流输入电源频率，以减小电压纹波对控制环路的影响。为进一步减少开关损耗，对双向开关管驱动信号vGS1、vGS2进行发波控制，驱动波形如图14所示。
图14 发波控制波形
Fig.14 Waveforms of control diagram
可以看到，在输入电压正半周内对Sb1施加占空比控制信号，Sb2施加持续导通信号；在输入电压过零的发波切换过渡阶段，对Sb1与Sb2同时施加相同的占空比信号；在输入电压负半周内对Sb2施加占空比控制信号，Sb1施加持续导通信号。
为保证电路能够一直工作在断续状态，需要在对电路参数设计前对DCM临界条件进行确定。
DCM临界状态下，在一个开关周期内续流阶段（模态Ⅲ）的时间占比趋近于0，占空比d需满足
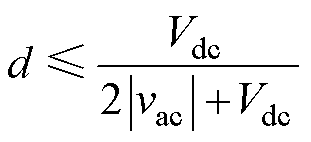（17）
考虑极端情况|vac|=
Vac_rms，得到最大占空比dmax的表达式为
（18）
观察式（18）可知，系统的最大占空比由输入输出电压决定。当交流输入电压有效值与直流输出电压确定时，最大占空比dmax也随之确定。
变换器电感参数的设计包括并联电感Lfs、输入滤波电感Lf以及储能电感Ls的设计。
对式（9）变形可得并联电感Lfs的表达式为
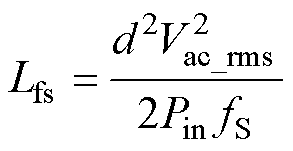（19）
式（19）表明，当输入电压有效值、输入功率以及开关频率确定时，并联电感Lfs的取值与系统占空比直接相关。Lfs过大时，由式（19）计算得到的占空比将超过式（18）确定的最大占空比dmax，此时电路无法在整个交流周波内工作于DCM。因此，dmax限制了Lfs最大取值，Lfs的设计公式为
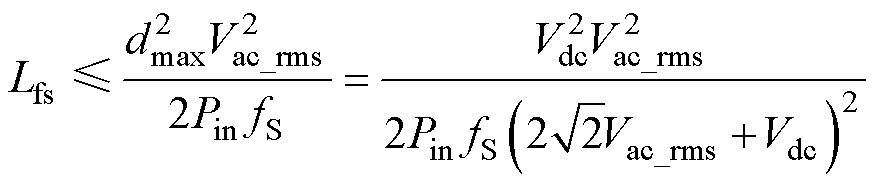（20）
输入滤波电感Lf电流工作于连续状态，其电流纹波DiLf可表示为
（21）
由式（21）可以看出，当占空比、开关频率以及储能电感一定时，DiLf在交流输入电压峰值处达到最大。为满足纹波要求，选择输入电压峰值处对电感Lf进行设计。结合式（18），电感Lf的设计公式为
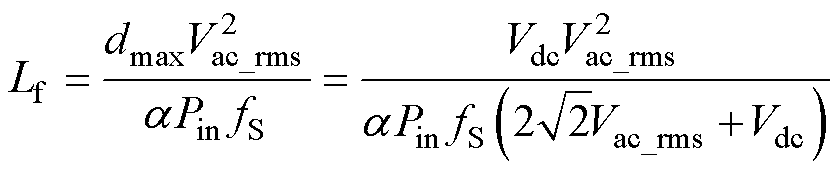（22）
式中，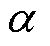
为输入电流纹波系数。
基于并联电感Lfs与输入滤波电感Lf的设计公式，结合并联电感公式，即可得到储能电感Ls为
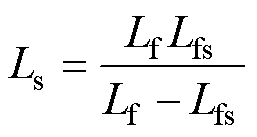（23）
变换器电容参数的设计包括储能电容Cs与输出滤波电容Cdc1、Cdc2。
由式（5）可知，储能电容电压理论上等于交流输入电压，开关周期内电容电压可视为定值。因此，储能电容不能设计过大以充分保证其两端电压的跟随性；与此同时，储能电容也不能设计过小以防止其与电路电感产生高频振荡。储能电容Cs一般根据电路电感参数进行设计，使其产生的谐振频率wr远高于交流输入电源频率，且远低于开关频率，Cs的设计公式为
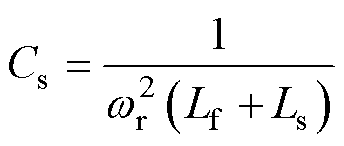（24）
式中，wr取开关角频率的5%～10%。
输出滤波电容用于平衡时变输入功率和恒定负载功率之间的差异，稳定直流输出电压。基于式（16），得到输出电压纹波脉动量Dvdc_ripp为
（25）
由此得到输出滤波电容Cdc1、Cdc2为
（26）
在理论分析的基础上，为进一步验证所提变换器拓扑的可行性，搭建一台如图15所示的基于元件复用的无桥倍压式Sepic型PFC变换器实验样机，样机主要参数见表2。
图15 实验样机
Fig.15 Experimental prototype
表2 样机主要参数
Tab.2 Component parameters of the prototype
参 数数 值 (型号) 交流输入电压有效值Vac_rms/V115±10% 交流输入电压频率fac/Hz400 直流输出电压Vdc/V400 输出功率Pdc/W300 开关频率fS/kHz50 输入滤波电感Lf/mH1500 储能电感Ls/mH85 储能电容Cs/mF1 输出滤波电容Cdc1, Cdc2/mF220×4 开关管Sb1, Sb2IPW60R017C7 二极管VD1, VD2HFA15TB60PBF DSPTMS320F280049C
以航空中频电源115Vrms/400 Hz参数作为交流输入，变换器稳态下输入侧交流电压、电流以及输出侧直流电压、电流的实验波形分别如图16、图17所示。观察输入电压、电流波形可知，该变换器的输入电流能够很好地保持与输入电压同相位变化，使用电能质量分析仪测得输入电流的总谐波畸变率（Total Harmonic Distortion, THD）为3.5%。观察输出侧电压、电流波形可知，直流输出电压稳定在400 V，两个输出滤波电容电压平衡，均为200 V。
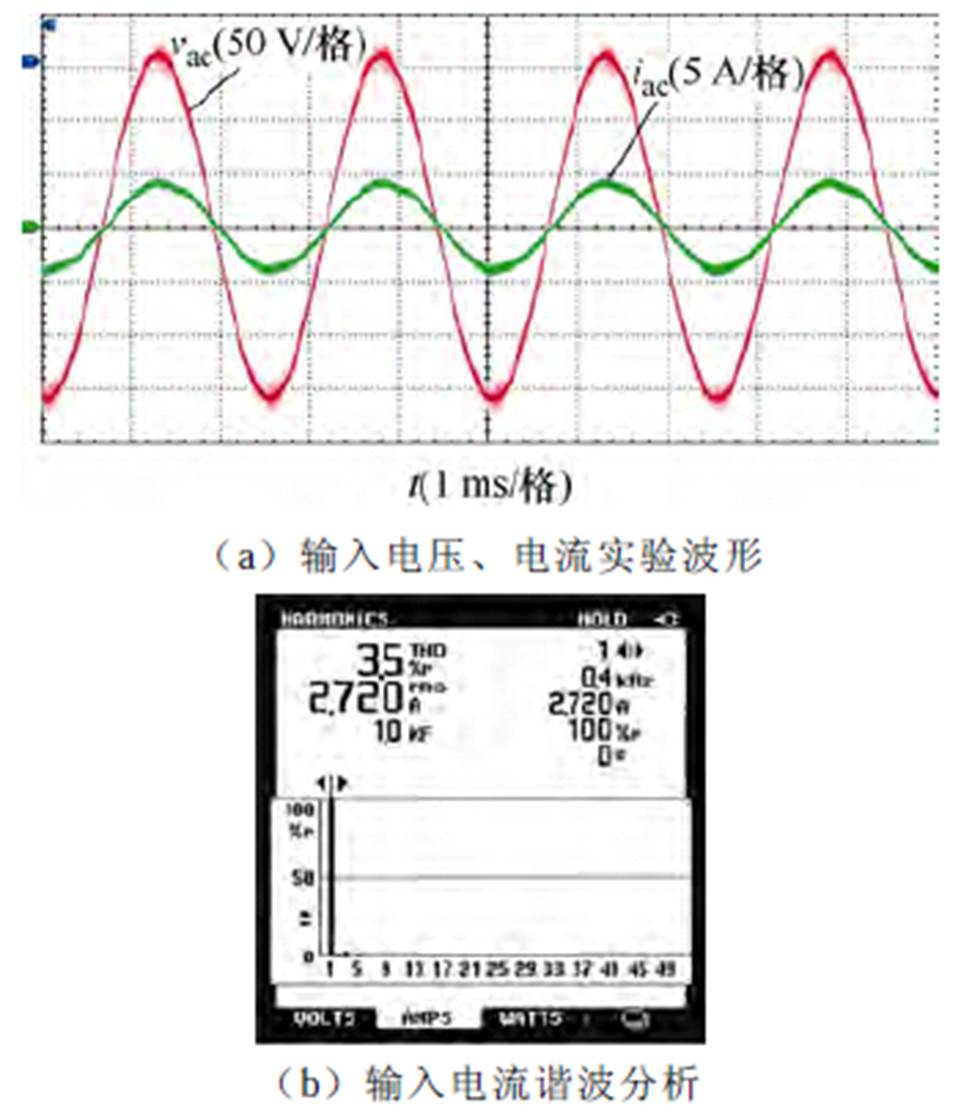
图16 输入侧电压、电流实验波形及电流谐波分析
Fig.16 Measured input voltage and current waveforms and input current harmonic analysis
储能电容两端电压与交流输入电压的波形比较如图18所示，可以看到，储能电容电压跟随输入电压呈正弦规律变化。
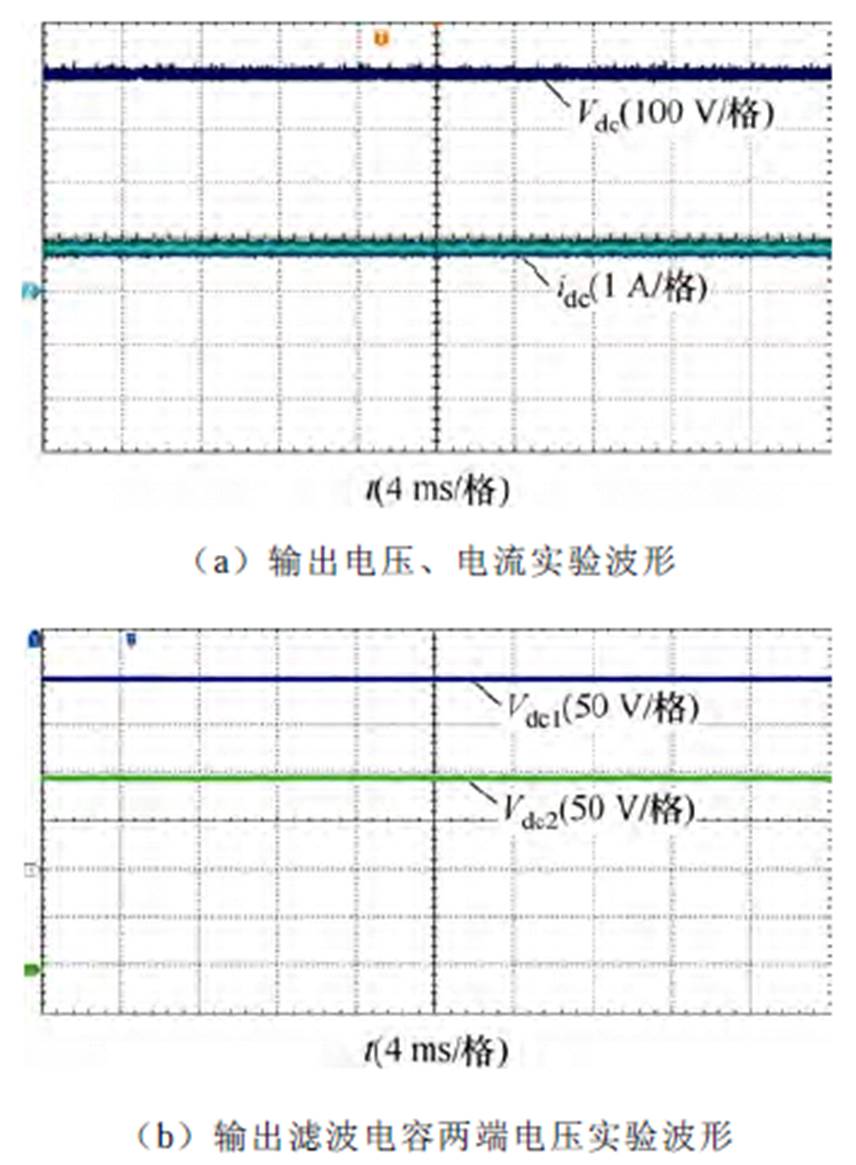
图17 输出侧电压、电流实验波形
Fig.17 Measured output voltage and current waveforms
图18 储能电容电压与输入电压实验波形
Fig.18 Measured voltage waveforms of the energy- storage capacitor and the input
开关管Sb1与Sb2两端的电压实验波形如图19所示，可以看到，Sb1与Sb2分别为半周期开关工作、半周期持续导通的工作状态，开关周期内开关管存在三个工作模态，由于开关管结电容的实际存在，续流阶段开关管两端电压出现振荡。测得开关管两端的最大电压为364 V，基本等于理论值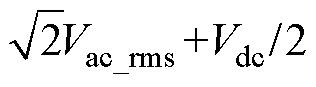
。
二极管VD1与VD2两端的电压波形如图20所示，可以看到，二者电压波形在一个交流周波呈对称关系，开关周期内二极管存在三个工作模态，由于开关管结电容的存在，续流阶段二极管两端电压出现振荡。测得二极管承受的最大反压为400 V，等于理论值Vdc。
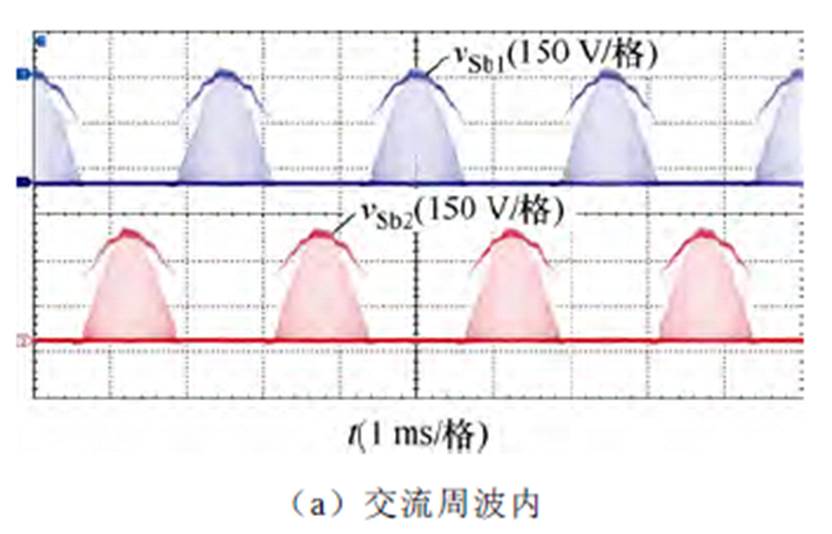
图19 开关管电压实验波形
Fig.19 Measured voltage waveforms of the switches
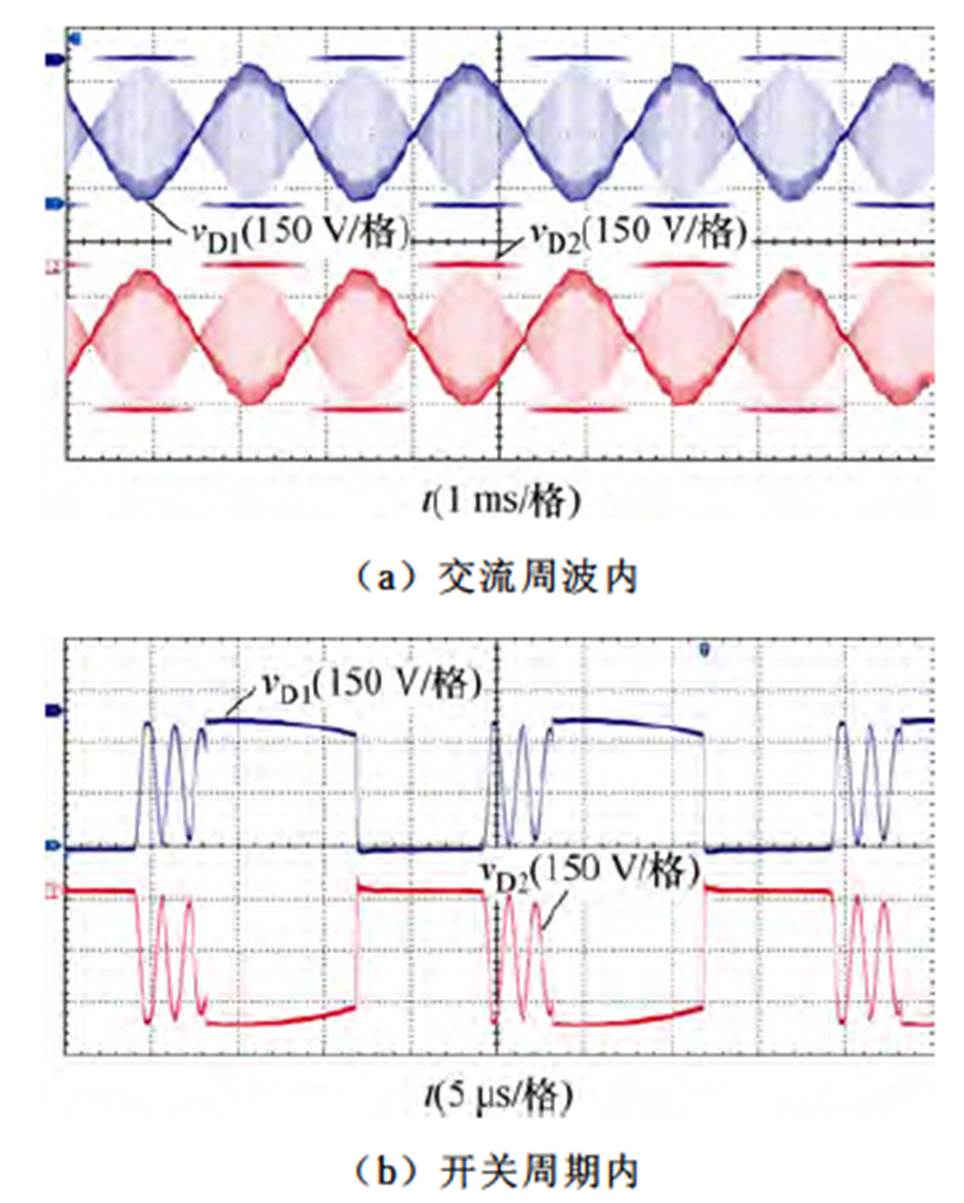
图20 二极管电压实验波形
Fig.20 Measured voltage waveforms of the diodes
电路的动态响应测试波形如图21所示，可以看到，当负载由半载切到满载时，输出电压能够在闭环控制下保持稳定，验证了控制方案的有效性。
图22为变换器效率、功率因数（Power Factor, PF）、THD随负载功率的变化曲线。可以看到，变换器在较宽的负载范围内具有较高的功率因数、转换效率以及较低的输入电流THD。输入侧PF始终大于0.99，输入电流THD在5%以内，额定功率下的最高效率为95.9%。考虑到小功率下电路损耗占比较大，适当增大负载功率并对电路参数进行优化，变换器效率可得到进一步提高。
图21 动态响应测试波形
Fig.21 Dynamic performance experimental waveforms
图22 变换器效率、PF与THD随负载功率变化曲线
Fig.22 Measured efficiency/PF/THD versus load power
本文提出了一类基于元件复用的单相无桥倍压式PFC变换器拓扑，具有元器件利用率高、控制简单等优点，适用于航空400 Hz电源系统等输入频率较高的应用场合。相关理论分析与实验结果验证了所提拓扑的可行性，主要研究结果如下：
1）提出一类基于元件复用的无桥倍压式Sepic、Cuk、Zeta型PFC拓扑，相较于双变换单元无桥PFC拓扑，中间储能单元实现了有效合并，电路自身使用的元器件数量得以减少，电路结构得到了简化。同时，DCM下自动实现PFC、控制简单、可靠性高、相同输出电压下开关管电压应力较低的优势被完全保留。
2）所提基于元件复用的无桥倍压式PFC变换器使用双向开关管与半桥结构，重构中间储能单元的电流路径，实现一组储能电感与电容同时工作于交流输入电压的正、负半周。半桥结构使用的半导体器件由其流过的电流极性决定，当流经电流为双向电流时，使用开关管以提供双向通路；当流经电流为单向电流时，使用二极管以简化控制。
3）在所提出的电流路径重构方式下，Sepic、Cuk、Zeta PFC电路原本的工作原理并没有发生变化，同时使得原本负输出电压的电路输出正极性的输出电压，电路性能得到改善。该种电流路径重构方式具有一定的研究价值，可以推广到其他拓扑推衍过程中。
参考文献
[1] 石健将, 陆熙, 王宝臣, 等. 航空400Hz三相高功率因数PWM整流器的零静差矢量控制[J]. 电工技术学报, 2010, 25(2): 80-85.
Shi Jianjiang, Lu Xi, Wang Baochen, et al. 400Hz aeronautical three-phase PWM rectifier based on vector control with zero-static-error compensation[J]. Transactions of China Electrotechnical Society, 2010, 25(2): 80-85.
[2] 倪靖猛, 方宇, 邢岩, 等. 基于优化负载电流前馈控制的400Hz三相PWM航空整流器[J]. 电工技术学报, 2011, 26(2): 141-146, 164.
Ni Jingmeng, Fang Yu, Xing Yan, et al. Three-phase 400Hz PWM rectifier based on optimized feedforward control for aeronautical application[J]. Transactions of China Electrotechnical Society, 2011, 26(2): 141- 146, 164.
[3] 郝振洋, 徐子梁, 陈宇, 等. 航空Vienna整流器故障诊断与容错控制[J]. 电工技术学报, 2020, 35(24): 5152-5163.
Hao Zhenyang, Xu Ziliang, Chen Yu, et al. Fault diagnosis and fault tolerant control for aviation Vienna rectifier[J]. Transactions of China Electro- technical Society, 2020, 35(24): 5152-5163.
[4] 徐子梁, 任小永, 吴玲燕, 等. 航空Vienna整流器缺相控制方法[J]. 电工技术学报, 2023, 38(20): 5560-5571.
Xu Ziliang, Ren Xiaoyong, Wu Lingyan, et al. A lack phase control strategy for aircraft Vienna rectifier[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5560-5571.
[5] 王立乔, 臧朔, 李翀, 等. 一种基于对称半桥功率解耦拓扑的单相电流型变换器[J/OL]. 电工技术学报, 2024, https://doi.org/10.19595/j.cnki.1000-6753. tces.231924.
Wang Liqiao, Zang Shuo, Li Chong, et al. A single- phase current-source converter based on the sym- metrical half-bridge power decoupling topology[J/OL]. Transactions of China Electrotechnical Society, 2024, https://doi.org/10.19595/j.cnki.1000-6753.tces.231924.
[6] 陈正格, 陈健, 许多, 等. 单相无桥功率因数校正变换器拓扑族推演回顾与性能分类总结[J]. 中国电机工程学报, 2024, 44(7): 2786-2801.
Chen Zhengge, Chen Jian, Xu Duo, et al. Rethinking of single-phase bridgeless power factor converter topology synthesis and performance summary based on topology structures[J]. Proceedings of the CSEE, 2024, 44(7): 2786-2801.
[7] Martinez R, Enjeti P N. A high-performance single- phase rectifier with input power factor correction[J]. IEEE Transactions on Power Electronics, 1996, 11(2): 311-317.
[8] 黄帆, 任小永, 陈乾宏, 等. 临界电流模式图腾柱无桥功率因数校正换相谐振抑制[J]. 电工技术学报, 2024, 39(12): 3816-3826.
Huang Fan, Ren Xiaoyong, Chen Qianhong, et al. Suppression of commutation resonance for totem- pole bridgeless power factor correction in critical current model[J]. Transactions of China Electro- technical Society, 2024, 39(12): 3816-3826.
[9] 马辉, 郑凯通, 卢云, 等. 一族电感耦合式Dual- Boost无桥三电平整流器[J]. 中国电机工程学报, 2021, 41(16): 5705-5714.
Ma Hui, Zheng Kaitong, Lu Yun, et al. A family of Dual-Boost bridgeless three-level rectifiers with common-core inductors[J]. Proceedings of the CSEE, 2021, 41(16): 5705-5714.
[10] 徐鑫雨, 吴红飞, 贾益行, 等. 基于三端口无桥PFC的两级式隔离型双输出AC-DC变换器[J]. 中国电机工程学报, 2020, 40(22): 7431-7440.
Xu Xinyu, Wu Hongfei, Jia Yihang, et al. A two-stage isolated dual-output AC-DC converter based on three- port bridgeless PFC[J]. Proceedings of the CSEE, 2020, 40(22): 7431-7440.
[11] 马辉, 鲁海鹏, 郑凯通, 等. 基于开关-电容网络的单相三电平PFC电路研究[J]. 中国电机工程学报, 2020, 40(22): 7398-7408.
Ma Hui, Lu Haipeng, Zheng Kaitong, et al. Research on three-level PFC circuit topology based on Switch- diode-capacitor network[J]. Proceedings of the CSEE, 2020, 40(22): 7398-7408.
[12] 马辉, 徐甜川, 范李平, 等. 一类三电平伪图腾柱无桥PFC变换器[J]. 中国电机工程学报, 2024, 44(2): 691-703.
Ma Hui, Xu Tianchuan, Fan Liping, et al. A family of three-level pseudo totem-pole power factor correction circuit[J]. Proceedings of the CSEE, 2024, 44(2): 691-703.
[13] Athalye P, Maksimovic D, Erickson R. High- performance front-end converter for avionics appli- cations aircraft power systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(2): 462-470.
[14] Ma Hongbo, Li Yuan, Lai J S, et al. An improved bridgeless SEPIC converter without circulating losses and input-voltage sensing[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(3): 1447-1455.
[15] Fardoun A A, Ismail E H, Sabzali A J, et al. New efficient bridgeless Cuk rectifiers for PFC appli- cations[J]. IEEE Transactions on Power Electronics, 2012, 27(7): 3292-3301.
[16] Jha A, Singh B. Bridgeless ZETA PFC converter for low voltage high current LED driver[C]//2017 6th International Conference on Computer Applications In Electrical Engineering-Recent Advances (CERA), Roorkee, India, 2017: 539-544.
[17] Sabzali A J, Ismail E H, Al-Saffar M A, et al. New bridgeless DCM Sepic and Cuk PFC rectifiers with low conduction and switching losses[J]. IEEE Transactions on Industry Applications, 2011, 47(2): 873-881.
[18] Babaei M, Monfared M. High step-down bridgeless Sepic/Cuk PFC rectifiers with improved efficiency and reduced current stress[J]. IEEE Transactions on Industrial Electronics, 2022, 69(10): 9984-9991.
[19] Kumar A D, Gupta J, Singh B. A reduced switch high step down gain bridgeless coupled switched inductor Sepic HPF AC-DC converter for LVEVs charging applications[J]. IEEE Transactions on Industry Appli- cations, 2024, 60(1): 633-644.
[20] Yang H T, Chiang H W, Chen C Y. Implementation of bridgeless Cuk power factor corrector with positive output voltage[J]. IEEE Transactions on Industry Applications, 2015, 51(4): 3325-3333.
[21] 皇甫宜耿, 王爱本, 赵犇, 等. 一种具有正输出电压的无桥Cuk PFC变换器[J]. 西北工业大学学报, 2021, 39(3): 611-616.
Huangfu Yigeng, Wang Aiben, Zhao Ben, et al. A bridgeless Cuk PFC converter with positive output voltage[J]. Journal of Northwestern Polytechnical University, 2021, 39(3): 611-616.
[22] Costa P J S, Illa Font C H, Lazzarin T B. A family of single-phase voltage-doubler high-power-factor Sepic rectifiers operating in DCM[J]. IEEE Transactions on Power Electronics, 2017, 32(6): 4279-4290.
[23] Rahul P, Saravana P P. A bridge less Cuk-derived voltage doubler based power factor correction rectifier[C]//2022 IEEE 1st Industrial Electronics Society Annual On-Line Conference (ONCON), kharagpur, India, 2022: 1-6.
[24] Ratil P R, Saravana S P. A bridge-less IPOS PFC zeta converter fed BLDC motor drive for home appli- ances[C]//2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 2022: 1-6.
[25] 刘雪山, 许建平, 王楠, 等. 断续模式单电感双输出Buck功率因数校正变换器[J]. 电工技术学报, 2015, 30(22): 62-70.
Liu Xueshan, Xu Jianping, Wang Nan, et al. Single- inductor dual output Buck power factor correction converter operating in discontinuous conduction mode[J]. Transactions of China Electrotechnical Society, 2015, 30(22): 62-70.
Abstract Power factor and efficiencyare important technical requirements for the front-end power factor correction (PFC) converters in avionic power systems with 400 Hz line frequency. Optimizing the topology structure can fundamentally improve and enhance the performance of the PFC converter. As a consequence, this paper proposes a family of single-phase bridgeless voltage-doubler PFC topologies to achieve the component sharing of dual-converter cells.
Based on the Sepic/Cuk/Zeta-type dual-converter bridgeless PFC topologies, the current path of the intermediate-storage unit is reconstructed by adopting the bidirectional switches and half-bridge output structure. Hence, the combination of dual-converter cells is achieved. Among them, the semiconductor type of half-bridge structure is determined by the current polarity. The switches are utilized when the flowing current is bidirectional, and the diodes simplify the control scheme when the flowing current is unidirectional. The working principle of the circuit remains unchanged after sharing the components, and the merits of high power factor and low voltage stress are fully retained. Compared with other bridgeless Sepic/Cuk/Zeta-type PFC topologies, the number of filter inductors, energy-storage inductors, and energy-storage capacitors is minimized, improving the component utilization. The voltage stresses of the switches are greatly reduced by adopting the voltage-doubler output structure. Moreover, the DC output voltage polarity of the Cuk-type topology is positive, thus improving the performance of the circuit.
Considering the similarity of principle analysis, the proposed Sepic-type bridgeless voltage-doubler PFC converter is analyzed as an example. Similarly, the other converters of the proposed family can be analyzed. The energy-storage inductor processes three working stages during a switching cycle, and the common set of the energy-storage capacitor and inductor operates for both positive and negative half-line cycles. The expression of input current can be obtained based on the input-output instantaneous power balance. It is worth noting that the input current is naturally in phase with the input voltage in discontinuous conduction mode (DCM) when the parallel inductance, duty cycle, and switching frequency are fixed. The static gain of the proposed converter is defined by the ratio between the DC output voltage and the root-mean-square (rms) value of the input voltage, which can be regulated flexibly by adjusting the duty cycle. Thus, the proposed converter only requires a control loop for the output voltage. The crossover frequency of the voltagecompensatoris designed well below twice the line frequency to attenuate excessive second-harmonic injection from output voltage into the duty cycle. The pulse width modulation (PWM) signal modulator generates control signals to drive the bidirectional switches. During the positive or negative half-line cycle of the AC input voltage, the duty cycle control signal is applied to the main switch, and the other switch is always turned on to reduce its loss.
ASepic-type experimental prototype has been constructed to verify the proposed topology. The proposed converter with 400 Hz input voltage has a maximum efficiency of 95.9% and a current THD of 3.5% with an almost unity power factor.
keywords：Bridgeless power factor correction (PFC) converter, topological derivation, components sharing, voltage-doubler structure
中图分类号：TM461
DOI: 10.19595/j.cnki.1000-6753.tces.240304
国家自然科学基金资助项目（51377036）。
收稿日期 2024-02-27
改稿日期2024-04-29
丁明远 男，1995年生，博士研究生，研究方向为有源功率因数校正、软开关技术、非线性数字控制技术。E-mail: myding95@163.com
李浩昱 男，1974年生，教授，博士生导师，研究方向为电力电子系统控制技术、极端环境电能变换与控制技术等。E-mail: lihy@hit.edu.cn（通信作者）
（编辑 陈 诚）