 (1)
(1)
摘要 针对平面变压器印制电路板(PCB)绕组每层绕线温度分布不均与损耗大的问题,该文提出一种电流密度均匀分布的平面变压器绕线宽度优化方法。首先,详细讨论了PCB绕组电流密度有效值的时不变性与计算方法,分析了交直流电阻的数学关系。然后,推导了环形绕组直流电阻的表达式,利用数学归纳法详细证明了电流密度分布均匀时环形绕组内外径之比的约束条件,并给出了考虑绕组间隙的绕组宽度修正公式,揭示了电流密度有效值与绕组损耗同时最优的内在联系。最后,基于六路绕组输出反激变换器的标准型号磁心,采用两种绕组宽度排布方法对变压器的电流密度、绕组损耗和发热情况进行对比分析,通过有限元仿真与实验验证了所提的绕组电流密度分布均匀时PCB绕组宽度设计方法的正确性与普适性。
关键词:平面变压器 绕组内外径等比 电流密度 数学归纳法
变压器作为现代小功率开关电源的重要组成元件,对系统效率和体积有着较大的影响,因此,高度低和漏感低的平面变压器[1]备受国内外学者的关注。然而,高频下的趋肤效应与邻近效应[2-3]使得变压器绕组电流在其横截面上分布不均,尤其对于应用广泛的反激(Flyback)变压器而言,一次侧匝数较多使其邻近效应变得更加明显,进一步加剧了绕组电流密度分布的不均匀性,容易产生变压器绕组局部高温热点。因此,实现变压器绕组电流密度分布的均匀化与绕组损耗最小化,成为平面变压器印制电路板(Printed Circuit Board, PCB)绕组优化设计的关键问题之一。
国内外诸多学者对绕组设计的相关问题进行了深入研究。在绕组结构方面,文献[4-7]对各类分数匝形式进行了论述,当一、二次侧匝比偏大时,分数匝结构可显著减少绕组匝数,绕组长度的调整也更加灵活,有利于减小高功率、大电压变换场合的绕组损耗。文献[7-9]对应用于LLC拓扑和单开关双升压拓扑的变压器绕线宽度进行了设计,针对减小变压器绕组阻抗进行分析并提出了绕组宽度的优化方法,控制同一层内各匝绕线的内径与外径满足等比例关系,重点在于实现绕组交直流阻抗及其损耗的最小化,可有效提升变压器效率,但文献[7-8]未验证该方法对任意匝绕组的适用性;此外,由文献[7]中绕组电流密度分布图可知绕组存在电流拥挤的现象,文献[8-9]未对绕组电流密度分布情况进行进一步分析。在寄生参数方面,文献[10-12]对PCB的寄生电容进行了分析,此类杂散参数是造成变压器电磁噪声的主要原因,可采用绕线相对位置交错或优化一、二次侧噪声路径的方法进行改善。在大电流并联输出的均流方面,文献[13-14]对变压器的多绕组耦合问题进行了探讨,主要解决思路有:优化绕线的排列与连接方式、矩阵式磁件的设计、耦合系数的优化等。文献[15]分析了PCB绕线与变换器其他元器件之间出现电流拥挤现象的原因,通过将绕组与终端元器件并联连接,调节各层绕线排布顺序,以改善绕组的电流拥挤现象,同时减小其传导损耗。在绕线设计方面,文献[16]提出了一种自动化绕线排布技术,能够在有限的磁心窗口内利用算法筛选出绕组损耗最小且磁心窗口利用率最高的排布方案,但此方法对电流拥挤现象的改善不明显。文献[17]提出了一种绕线解耦方法,将同一磁心中无耦合关系的绕线垂直放置,利用几何位置对其进一步解耦,消除二者间的邻近效应影响,但对于各绕线间耦合程度要求较高的场合则不宜直接参考。文献[18-19]研究了大电流变压器中PCB过孔带来的绕组损耗,采用一种3D的PCB绕线来扩大横截面积,在不改变磁心规格的情况下减小了绕组交直流阻抗。文献[20-23]研究的磁件集成与文献[24]提出的绕组等效电路模型也为绕组结构改善与变压器效率提高提供了新的思路。上述文献成果更多是集中在变压器绕组总损耗或寄生参数优化设计上展开的研究,鲜有针对因电流密度分布不均带来的绕组局部高温热点问题的讨论。
本文在上述研究基础上,以多路输出反激拓扑为研究对象,提出了一种电流密度均匀分布的平面变压器绕线优化方法,在兼顾绕线损耗最小的同时,最大限度地提升变压器整体效率与散热性能。首先,对变压器损耗与电流密度的量化方法进行了介绍,重点在于实现绕组电流密度的最均匀分布,并将该方法推广至任意匝数以验证普适性,全面精细地阐述其理论基础。其次,探讨了高频下绕线交直流电阻模型之间的关联,从理论上揭示了电流密度与绕线损耗相互影响的内在机理。然后,以六路输出Flyback变压器为对象,设计了绕线排布方式和绕线宽度,并通过有限元仿真分析了绕组的电流密度与损耗特性。最后,通过实验验证了PCB环形绕线内外径优化方法的有效性。
绕组设计的主要目标是提升变压器的效率并改善绕组电流密度的分布特性,故首先对其损耗与电流密度的影响因素进行分析。
变压器损耗可分为磁心损耗与绕组损耗两部分,其中,磁心损耗Pcore可由Steinmetz公式计算[25]。计算式为
 (1)
(1)
式中,f为变换器开关频率;Bmax为磁感应强度峰值;T为磁心工作温度;a、b 为磁性材料损耗系数;Cm、Ct2、Ct1、Ct为磁性材料温度系数。
当铜导体工作在直流或低频条件下,且忽略温度变化所带来的微小影响时,其阻值不随工作状态变化而改变,可视为一个常数,此时导体在电路中产生的损耗即为直流损耗;当铜导体工作在高频条件下,电磁感应作用所产生的涡流会使得导体导电有效横截面积缩小,以致导体阻值增大,阻值增大后导体所产生的损耗增大部分即为交流损耗。绕组损耗由直流损耗和交流损耗两部分组成,有
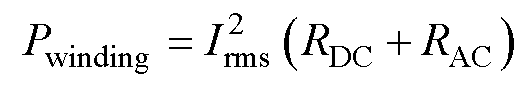 (2)
(2)
式中,Irms为绕组电流有效值;RDC为绕组直流电阻;RAC为绕组交流电阻。RDC是指绕组固有的电阻物理特性,直流或低频工作条件下,只存在RDC对应产生的直流损耗;RAC为表征高频趋肤效应和邻近效应带来的交流损耗对应的电阻值,可由Dowell一维定理计算,RAC=FRRDC,其中FR为交流电阻系数。对于本文研究的反激变压器,工作时RDC与RAC同时存在,对应损耗分别为直流偏置电流产生的固有损耗与电流纹波产生的交流损耗。
当变压器一、二次电流达到一个开关周期内的最大值时,对应的绕组电流密度同时达到该开关周期内的峰值。但由于一、二次侧电感不属于纯电阻元件,在一个开关周期内对绕组两端施加恒定电压时,其绕组电流与电流密度随时间呈线性变化,无法直接使用欧姆定律计算。
然而,衡量绕组损耗与发热的直接因素为绕组电流的有效值,而非瞬时值,且在一个开关周期内,绕组电流有效值保持不变,故从损耗角度出发,可近似认为在一个开关周期内,施加在变压器一、二次绕组两侧的电压有效值与电感电流有效值满足线性关系,可使用欧姆定律进行计算。
假设一个开关周期内施加在绕组两端的电压有效值为Urms,则该周期内绕组电流密度有效值为
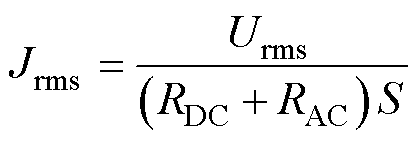 (3)
(3)
式中,S为绕组截面积。
结合式(2)、式(3)可知,当磁心型号确定时,绕组损耗与电流密度均受到绕组电流有效值、交直流电阻及横截面积的影响,且二者存在较强的相关性,可通过单开关周期内有效值的形式进行量化计算。
平面变压器磁心参数确定后,PCB绕组的优化和排布成为关键。本节深入分析绕组电流密度与绕线几何参数间的数学关联,推导了电流密度分布均匀时的绕线内外径比值的计算方法,并总结了电流密度与绕组损耗间的内在联系,以供下文分析和验证。
基于上述讨论,影响绕组电流密度分布的因素较多,为降低分析复杂度,首先对绕组交直流电阻的数值关系进行推导。其中,交流电阻可由Dowell一维定理计算[26-27],有
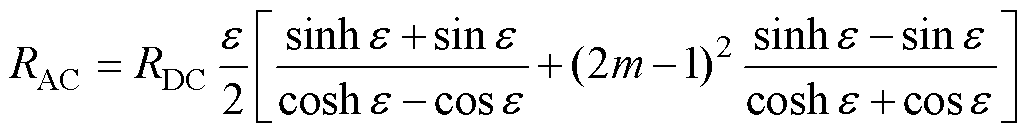 (4)
(4)
式中,m为单层绕线磁动势终值与其磁动势变化量的比值,由一、二次侧绕线排布方式决定; 为垂直磁场方向导线厚度与趋肤深度的比值。变压器高频工作时产生的趋肤效应、邻近效应与边缘效应是影响趋肤深度的主要因素,而矩形截面导体的曲率效应使得电荷更易聚集在尖端,也会影响绕组的趋肤深度大小。若变换器开关频率与其他电气参数一定,上述效应的影响也随之确定,故
为垂直磁场方向导线厚度与趋肤深度的比值。变压器高频工作时产生的趋肤效应、邻近效应与边缘效应是影响趋肤深度的主要因素,而矩形截面导体的曲率效应使得电荷更易聚集在尖端,也会影响绕组的趋肤深度大小。若变换器开关频率与其他电气参数一定,上述效应的影响也随之确定,故 可视为常量,即可将交流电阻表达式简化为
可视为常量,即可将交流电阻表达式简化为
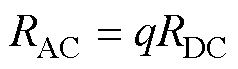 (5)
(5)
式中,q在绕组设计过程中可视为常量。
分析式(5)可知,交流电阻RAC与直流电阻RDC的数值成正比,因此仅需分析直流电阻数值对绕组电流密度的影响即可。
采用微元法对环形绕组直流电阻进行计算,圆环绕组结构如图1所示。
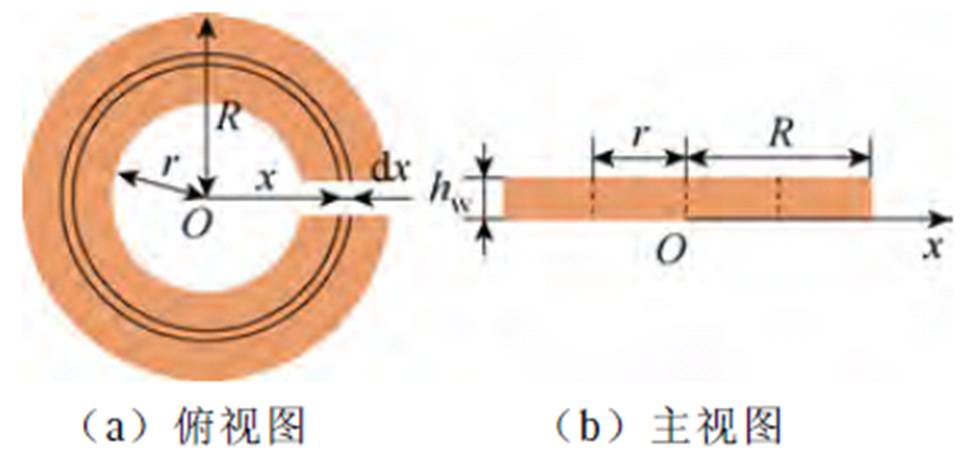
图1 环形绕组结构示意图
Fig.1 Schematic diagram of the annular winding structure
图1中,r为圆环内半径,R为圆环外半径,hw为绕线厚度。以圆心为原点,沿半径方向将该圆环划分为无数个半径为x,宽度为dx的环形导体微元,并对每个导体微元的直流电阻dRDC进行积分,即可得到此环形绕线的直流电阻RDC为
 (6)
(6)
式中,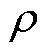 为导体材料电阻率。
为导体材料电阻率。
在准确计算环形绕组交直流电阻数值的基础上,可对绕组电流密度的均匀程度进行量化分析。
传统骨架式变压器多为漆包线绕制,其结构的高度封闭性使得绕组散热困难,故工程设计时往往控制每匝绕线的电流密度小于8 A/mm2,改善散热特性的同时也缓解了高频涡流效应对电流密度分布的不利影响。不同于传统变压器,平面变压器的散热特性更佳,故其每匝绕线的电流密度设计值通常较大,使得高频下趋肤效应与邻近效应的影响更加明显,加剧了其电流密度分布的不均匀性。
然而,绕组电流有效值由变换器工况决定[28],无法改变,故应从优化绕组几何参数的角度改善此问题。由前述分析可知,绕组电流密度可在单开关周期内以有效值的形式量化,因此,可对PCB同一层上每匝绕线的电流密度有效值进行计算,以对绕线参数进行分析和改进。
基于以下三个假设:①假设PCB同一层上相邻绕线的间隙宽度相对于每匝绕线的宽度可忽略不计;②假设PCB同一层上每匝绕线为同心圆电流路径;③假设同一绕线在PCB不同层间连接处的阻抗可忽略不计。本文通过数学归纳法对绕组电流密度均匀分布条件进行推导。
图2所示为PCB同一层上绕线匝数分别为2和N时的环形绕线结构示意图。
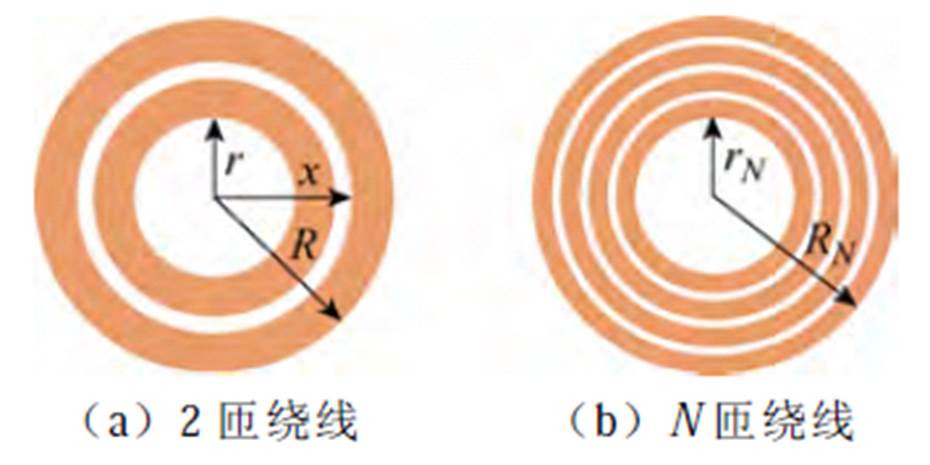
图2 环形绕线结构示意图
Fig.2 Schematic diagram of the annular winding structure
2.2.1 2匝绕线
当同一层绕线匝数为2时,如图2a所示,以最靠近中柱的绕线为最内侧绕线,设其内半径为r,电流密度有效值为J1。以最靠近边柱的绕线为最外侧绕线,设其外半径为R,电流密度有效值为J2。内侧绕线的外半径等于相邻外侧绕线内半径,均为x,且每匝绕线上的电压降有效值均为DU。
在式(3)、式(6)的基础上,分别列出两匝绕线的电流密度有效值表达式为
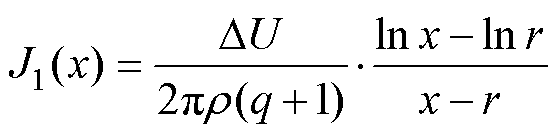 (7)
(7)
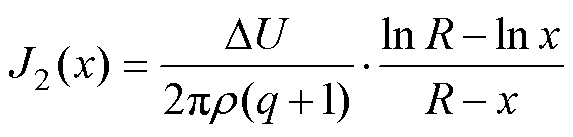 (8)
(8)
为衡量绕线电流密度分布的均匀程度,对J1、J2作方差处理,有
 (9)
(9)
该方差取值即可用于衡量每匝绕线上的电流密度偏离平均电流密度的程度,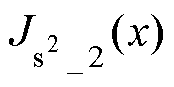 越小,该层PCB上电流分布越均匀。
越小,该层PCB上电流分布越均匀。
分析式(9)可知,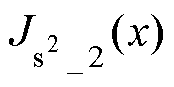 在x∈(0,+∞)上连续且二阶可导,写出
在x∈(0,+∞)上连续且二阶可导,写出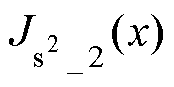 在x∈(0,+∞)上的一、二阶导数,有
在x∈(0,+∞)上的一、二阶导数,有
 (10)
(10)
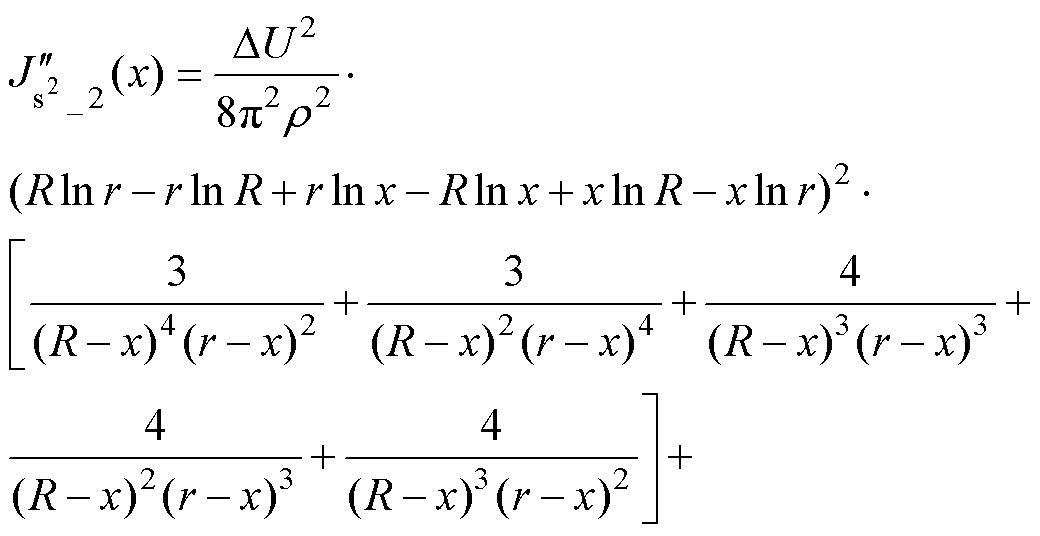
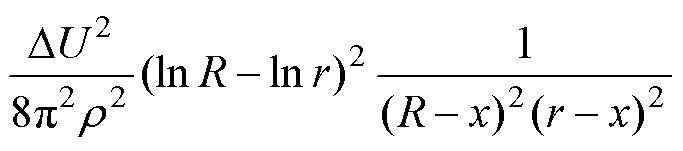 (11)
(11)
由于 时,
时,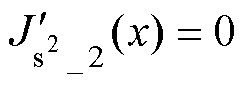 ,故
,故 为函数
为函数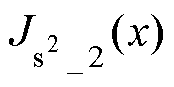 的一个驻点,且
的一个驻点,且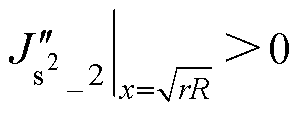 ,根据极值定理,
,根据极值定理, 为
为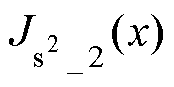 的极小值点。
的极小值点。
因此,当 时,两匝绕线的电流密度有效值方差
时,两匝绕线的电流密度有效值方差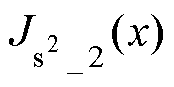 最小,最小值为
最小,最小值为
 (12)
(12)
此时两匝绕线各自外径与内径的比值k2_min(半径比)均满足
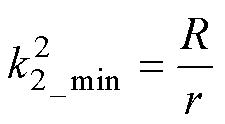 (13)
(13)
2.2.2 N匝绕线
当同一层绕线匝数为N时,如图2b所示,设最内侧绕线的内半径为rN,最外侧绕线的外半径为RN,由中柱指向边柱第n匝绕线的内半径为rn,列写第n匝绕线的电流密度有效值为
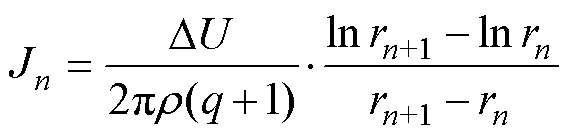 (14)
(14)
则N匝绕线电流密度有效值JN的平均值为
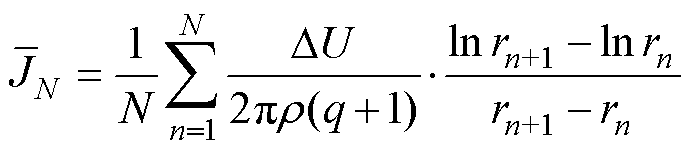 (15)
(15)
对PCB同一层上绕线的Jn作方差处理,有
 (16)
(16)
假设当每匝绕线外径与内径的比值kN_min均满足关系式(17)时,N匝绕线的电流密度有效值方差最小,且最小值如式(18)所示。
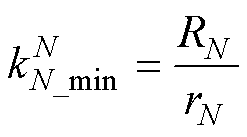 (17)
(17)

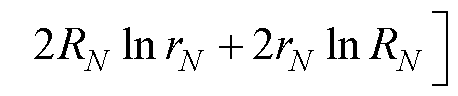 (18)
(18)
此时该层PCB上各匝绕线的电流密度分布最均匀。
2.2.3 N+1匝绕线
当同一层绕线匝数为N+1时,设其最内侧绕线的内半径为rN+1,最外侧绕线的外半径为RN+1,第N圈绕线的外半径为RN。
基于N匝绕线的假设结论,即可推导N+1匝绕线的最小电流密度有效值方差为

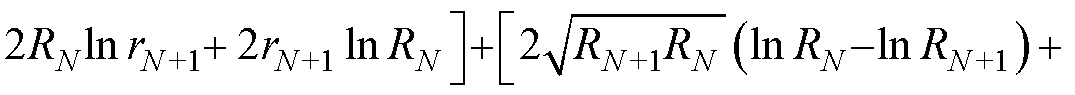
 (19)
(19)
同理,求得函数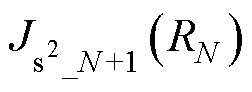 的极小值点为
的极小值点为
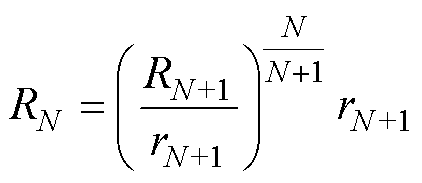 (20)
(20)
则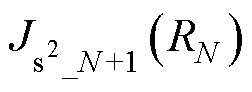 最小值可简化为
最小值可简化为
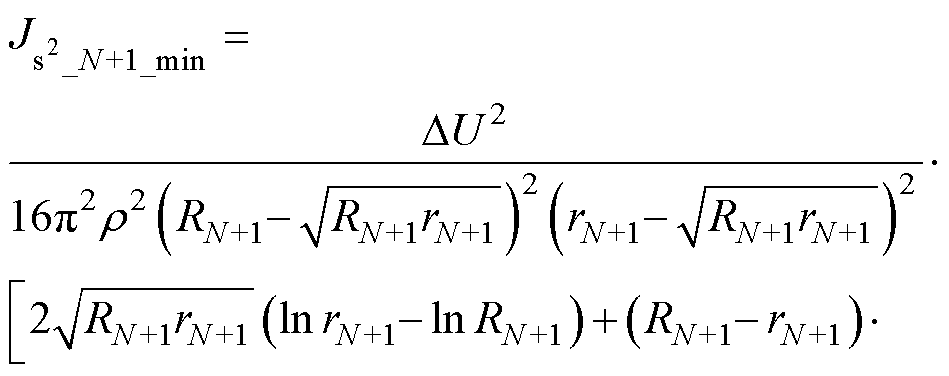
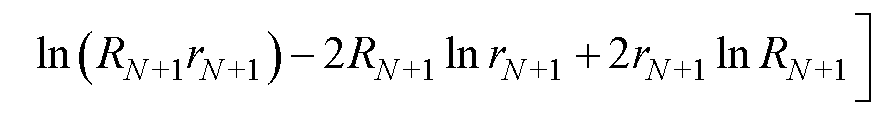 (21)
(21)
且此时每匝绕线的半径比均满足
 (22)
(22)
根据数学归纳法,类比同一层PCB上绕组匝数分别为2、N、N+1时的最优电流密度方差结果可知,若同一层PCB上绕组匝数为N,且每匝绕线的内外半径比均满足式(17)所示约束关系,则该层绕线的电流密度分布最均匀。
基于上述推导,分析同一层绕线电流密度分布不均的根本原因。
常规绕组设计中,通常不考虑其内外径比值,仅以通流能力为标准选取相等的宽度值,故每匝绕线的横截面积也随之相等。然而,平面变压器的扁平化特点使其磁心窗口宽度较大,外侧绕线半径远大于内侧,导致内外侧阻抗分布不均,进而导致各匝绕线的电流密度分布不均。
等比化设计绕线内外径即可通过适当减小内侧绕线横截面积,增大外侧绕线横截面积,以电流密度为首要优化目标,从绕组内外侧绕线电流密度均匀的角度出发,寻求绕线宽度优化的设计方案,以补偿因周长不一致而导致的阻抗不均,从而解决阻抗不均导致的电流拥挤问题。在环形绕组匝数相同时,以铜导体的载流能力与绕线磁柱尺寸确定最内侧绕线内半径和最外侧绕线外半径,这样即确定了绕组区域所占总面积。等宽度的环形绕组在该环形面积内对绕组宽度进行平均分配,而上述内外径等比的绕组宽度在同样的环形面积内根据结论半径比分配绕组宽度,保证了绕组优化前后所占PCB面积相等。
为确定此方法对绕组损耗的改善效果,对比文献[7, 9]所提出的改变绕线宽度以提高变压器效率的设计思路,该方法以效率为首要优化目标,寻求绕组阻抗最小时的宽度设计方案。文献[7]所得绕组最小阻抗下对应的最优宽度约束条件与上述内外径等比结论相似,而文献[9]中结论与上述结论一致,说明本文在对绕组各匝绕线电流密度的优化过程中得到的结论,同时也达到了减小绕组损耗的效果,在一定程度上表明了电流密度与绕组损耗存在内在联系。
分析一个开关周期内,绕组电流密度有效值Jrms与其绕组损耗Pwinding的数学关系,有
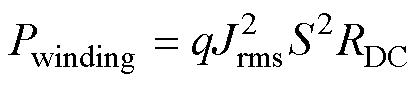 (23)
(23)
式(23)显示,当绕组电流确定时,影响绕组损耗的根本因素为其直流阻抗取值。若同一层PCB内外侧阻抗不均,使其交直流总阻抗偏大,则会同时增大绕组损耗,降低变压器效率。
因此,同一层绕线电流密度分布不均与绕线损耗偏大的内在机理一致,均可通过内外径等比化设计进行改善。
前述假设中,在不影响结论有效性的前提下,忽略了绕线间隙宽度以简化模型。但在实际绕线中,绕线间隙宽度相比于绕线宽度往往数量级相差并不大,故该间隙宽度不能忽略。为使模型精度更接近实际情况,需要在计算过程中考虑相邻绕线的间隙宽度,并使用前述结论对绕线间隙进行计算分析,磁心窗口实际使用情况示意图如图3所示。
图3中,rcore为磁心中柱半径,Rcore为磁心边柱内径,Dx为相邻绕线间隙宽度。最内侧绕线内半径为rcore+Dx,最外侧绕线外半径为Rcore-Dx,列写出工程实际中考虑PCB同一层上绕线间隙的内外半径比kN_real的修正数学模型为

图3 磁心窗口实际使用情况示意图
Fig.3 Schematic diagram of the actual usage of the core window
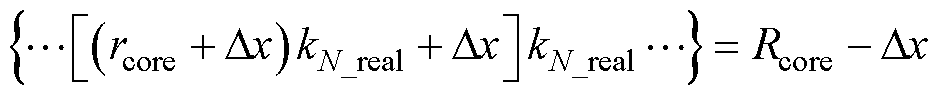 (24)
(24)
进而可以化简为类似式(17)的形式,有
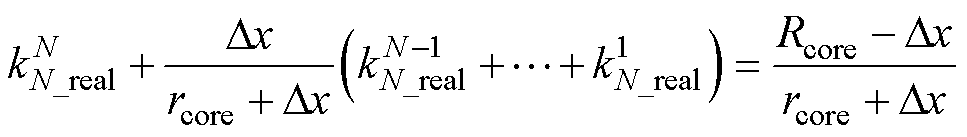 (25)
(25)
综上所述,在满足三个假设的前提下,对于任意正整数匝数N,当N匝绕线内外径比均满足式(25)所示约束关系时,该层绕线的电流密度分布最均匀,且绕组损耗最小。
为验证绕线内外径等比排列下的损耗特性与电流密度分布特性,以30 W六路输出Flyback变换器的变压器为对象,搭建Ansys有限元仿真模型,观察并分析仿真结果。
六路输出Flyback主电路结构如图4所示。图4中,Lp为变压器的一次侧电感,Lm为变压器的励磁电感,Ls1~Ls6为变压器第1~6路输出绕组的二次侧电感,Lk为变压器的一次侧漏感,np 1为变压器一次侧与第一路二次绕组的匝数比。S1为一次侧开关管,VD1~VD6为二次侧整流二极管,Cin为输入滤波电容,Cout为输出滤波电容,R1~R6为第1~6路输出回路的负载电阻。Vin为变换器的输入电压,Vout1~Vout6为变换器第1~6路输出电压。
1为变压器一次侧与第一路二次绕组的匝数比。S1为一次侧开关管,VD1~VD6为二次侧整流二极管,Cin为输入滤波电容,Cout为输出滤波电容,R1~R6为第1~6路输出回路的负载电阻。Vin为变换器的输入电压,Vout1~Vout6为变换器第1~6路输出电压。

图4 反激变换器主电路
Fig.4 Flyback converter main circuit diagram
变换器设计指标要求见表1。
表1 变换器设计指标
Tab.1 Converter design indicators

项 目指 标 输入电压范围Vin/VDC 110~240 输出回路1 Vout1/V24 Iout1/A0.4 输出回路2 Vout2/V+12 Iout2/A0.5 输出回路3 Vout3/V-12 Iout3/A0.5 输出回路4 Vout4/V5 Iout4/A0.1 输出回路5 Vout5/V18 Iout5/A0.1 输出回路6 Vout6/V18 Iout6/A0.2 回路1输出电压精度s1(%)≤3 回路1~5输出电压精度sm(%)≤18 交叉调整率Sm(%)≤20 效率h(%)>88
由于变换器包含六路输出,而实际情况中,变压器各路绕组的漏感难以严格按照匝比二次方关系分布,因此系统易出现交叉调节问题。若要求六路输出电压精度均较高,则需对每一路增设反馈机制,但此方法会明显增大设备体积。因此,根据各路输出的性能要求,仅选择精度要求最高的回路1参与输出电压反馈,其他回路则利用各绕组间的耦合关系完成闭环调节。
以东磁标准磁心ECW32C为例,对各路绕组排布方式进行设计,对应绕组匝数见表2。
由于一次绕组匝数较多,无法全部绕制于一层PCB上,故根据磁心窗口宽度将其分为三层,每层六匝绕线。各路二次绕组均单独绕制于一层,再根据连接需求设置两层PCB用于走线,一层PCB用于屏蔽共模干扰,共计使用12层PCB。
表2 变压器绕组设计指标
Tab.2 Transformer winding design index

绕 组匝 数 Lp18 Ls14 Ls22 Ls32 Ls41 Ls53 Ls63
为提升绕组的整体散热性,应合理分配各层PCB的相对位置。首先,采用一、二次侧绕线完全交错的形式提高变压器耦合系数。其次,将电流较大发热相对明显的绕线层排列在PCB外层,增加其与绝缘介质的接触程度,提高该层PCB的散热性能。最后,确定12层PCB的排列方式如图5所示。

图5 12层PCB相对排列位置示意图
Fig.5 Schematic diagram of the relative arrangement of the 12-layer PCB
各层绕线排布方式设计完成后,即可对各匝绕线的宽度进行计算。单层PCB所排列的绕组匝数有四种,分别为N=2、3、4、6,结合输入侧电压等级与PCB安全间距要求,根据式(25)求得各层绕线最优内外径之比kN_real,见表3。其中,最优内外径之比kN_real受绕线间隙宽度Dx、绕线匝数N、磁心中柱半径rcore、磁心边柱内径Rcore影响,故对于不同绕线间隙宽度或不同磁心尺寸的情况,需要根据式(25)重新计算最优内外径之比kN_real。
进而可求出每匝绕线的最优宽度,称最靠近磁心中柱的绕线为匝1,最靠近磁心边柱的绕线为匝6,得到各绕线宽度数据见表4。
表3 单层PCB不同匝数所对应绕线最优内外径比
Tab.3 The optimal radius ratio of the windings corresponding to the different turns of the single-layer PCB

NkN_real 21.440 31.257 41.174 61.097
表4 内外径等比时不同匝数对应绕线最优宽度
Tab.4 Optimal width of each winding corresponding to different turns of single-layer PCB (单位: mm)
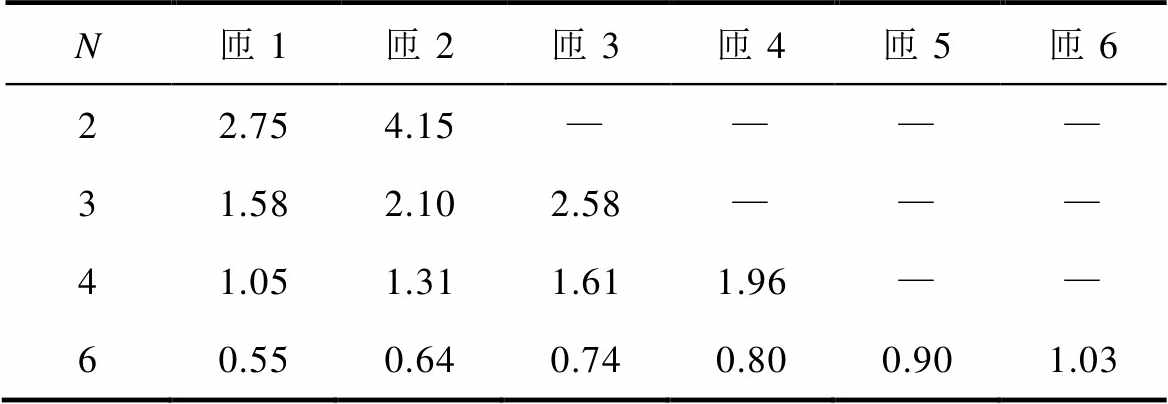
N匝1匝2匝3匝4匝5匝6 22.754.15———— 31.582.102.58——— 41.051.311.611.96—— 60.550.640.740.800.901.03
为对比不同设计方案下的损耗特性与电流密度分布特性,保持磁心尺寸不变,按照PCB同一层上绕线宽度恒定的方式计算各层绕线宽度,所得数据见表5。
表5 宽度恒定时不同匝数对应绕线宽度
Tab.5 Winding width corresponding to different turns when the width is constant (单位: mm)
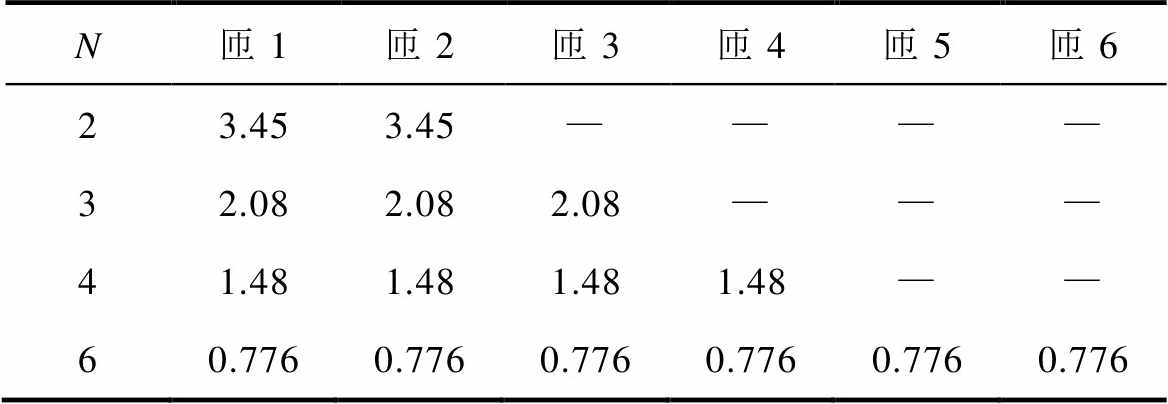
N匝1匝2匝3匝4匝5匝6 23.453.45———— 32.082.082.08——— 41.481.481.481.48—— 60.7760.7760.7760.7760.7760.776
通过仿真对两种设计方案下的绕组损耗与电流密度分布情况进行对比分析。
以Ansys为平台在PCB同一层上绕线内外径等比排列、绕线宽度恒定排列两种情况下搭建有限元仿真模型,分别观察各模型的绕组电流密度分布与交直流损耗情况。
3.3.1 电流密度仿真对比
在两种仿真模型中添加相同电流激励,激励是有效值为0.338 A的正弦激励,频率为300 kHz,在该高频激励下,分别对其绕组电流密度分布情况进行仿真,当单层PCB绕线匝数N=2时,得到不同设计方法下的绕线电流密度分布,如图6所示。

图6 N=2时绕组电流密度分布
Fig.6 Winding current density distribution at N=2
分析图6所示绕组电流密度分布可知,当一层PCB排列两匝绕线时,内外径等比排列情况下的绕组改善了宽度恒定排列绕组的边缘电流密度较高的现象,同时绕组中间部分的电流密度分布更均匀。
同理,分别作出N=3, 4, 6时不同宽度设计方法的绕组电流密度分布,如图7~图9所示。

图7 N=3时绕线电流密度分布
Fig.7 Winding current density distribution at N=3

图8 N=4时绕线电流密度分布
Fig.8 Winding current density distribution at N=4
图9 N=6时绕线电流密度分布
Fig.9 Winding current density distribution at N=6
通过观察图6~图9所示电流密度分布情况可知,对于任意正整数匝数N,PCB同一层上绕线内外径等比排列情况下的电流密度都是最均匀的。
3.3.2 绕组损耗仿真对比
在两种仿真模型中添加相同电流激励,分别观察不同设计方法所对应的交流阻抗与绕组损耗仿真数据,并绘制柱状图,如图10所示。观察图10所示仿真数据可知,对于不同设计方法,绕线内外径等比排列下的交直流总损耗更低,且相比于常规的宽度恒定设计,此方法可使绕组损耗减小13.1%,从仿真上验证了PCB绕线内外径等比设计理论的正确性。同时,单层PCB绕线匝数N的取值范围不受理论约束,说明此方法具有普适性。
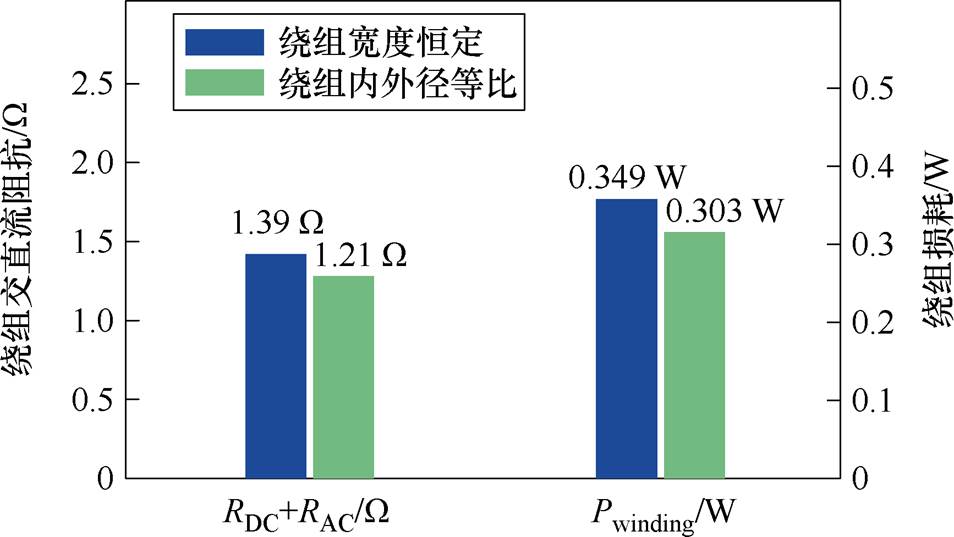
图10 不同设计方法对应的交直流阻抗与绕组损耗
Fig.10 AC and DC impedance & winding losses corresponding to different width design methods
根据上述指标,分别在PCB同一层上绕线内外径等比排列、绕线宽度恒定排列两种情况下设计并绘制PCB绕组,搭建两台30 W六路输出Flyback变换器样机,其中输出电压Vout1~Vout6分别对应图4所示变压器绕组Ls1~Ls6,且仅输出电压Vout1参与信号反馈,实验平台如图11所示,其中,对比图11b和图11c可知,绕组优化前后变压器的尺寸不变,因此变压器功率密度也不变。

图11 30 W六路输出Flyback变换器及变压器样机
Fig.11 Prototype of 30 W six-channel output flyback converter and transformer
为验证变压器各绕组带载能力,保持最低输入电压Vin=100 V,维持回路2满载,同时对输出回路1在满载与轻载之间进行切载,测试输出电压Vout1与Vout2变化情况,如图12所示。分析如图12所示电压波形,负载切换过程中,回路1输出电压始终保持Vout1=24.7 V,输出精度s1=2.9%,满足指标要求,说明系统稳定性与准确性良好。当输出回路1满载时,回路2输出电压Vout2_max=12.7 V,输出回路1轻载时,回路2输出电压Vout2_min=11.9 V,故回路2输出电压交叉调整率S2=6.7%,满足指标要求S2<20%。
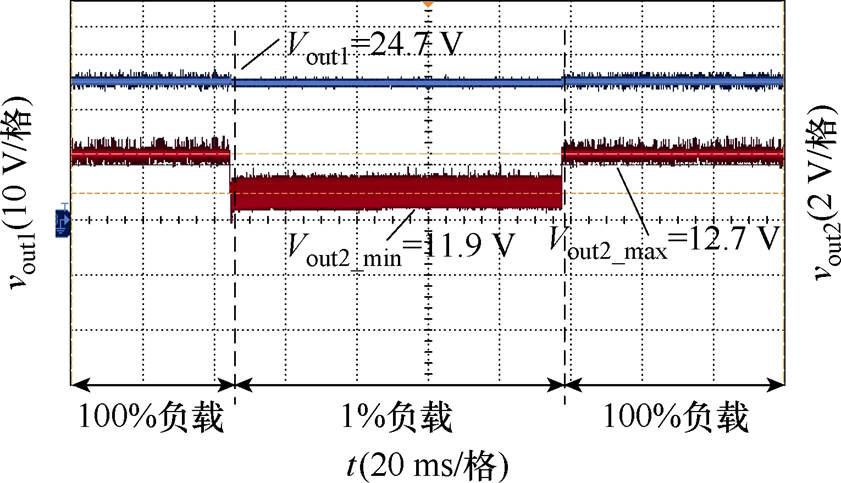
图12 回路1切载时Vout1、Vout2输出电压波形
Fig.12 Waveforms of the output voltages of Vout1 and Vout2 during the load cut-off of loop 1
在相同工况下对其他各回路的输出电压精度及交叉调整率均进行测试与计算,确保30 W实验平台对应的变压器,满足输出电压和负载能力的指标要求。为对比变压器绕组损耗及电流密度分布,验证变压器的散热性能,不增设外置散热器,在环境温度25℃、最低输入电压Vin=100 V、输出功率Pout=30 W(满载)条件下对两台样机进行测试,此时流经变压器一次绕组的电流最大,待电路稳定运行一段时间且各器件温升稳定后,分别记录两台变换器的工作温度,如图13所示。
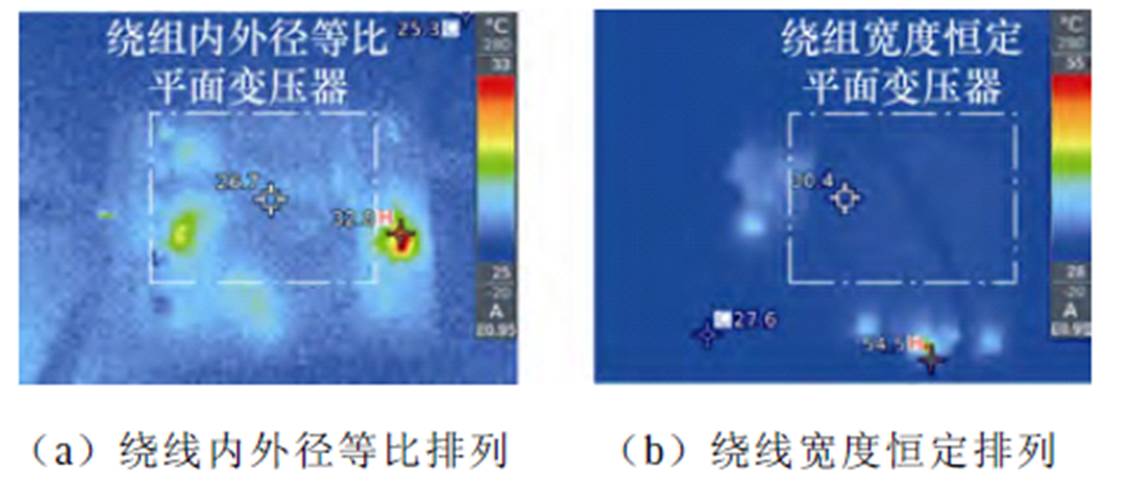
图13 变换器满载运行温度变化情况
Fig.13 Temperature change of converter at full load
对比图13两种不同设计方案下的变换器温升情况可知,在环境温度25℃且满载的工况下,PCB同一层上绕线内外径等比排列下的变压器工作温升较低,仅为1.1℃,较绕线宽度恒定设计下的变压器温升降低了3.7℃,从而也验证了优化后损耗降低的正确性。由于两变压器磁心型号及工作条件完全一致,故说明内外径等比排列方案更有利于提升变压器的散热性能。
保持最低输入电压Vin=100 V,分别在50%、60%、80%及100%负载下测量两台变换器的效率,并绘制效率曲线如图14所示。
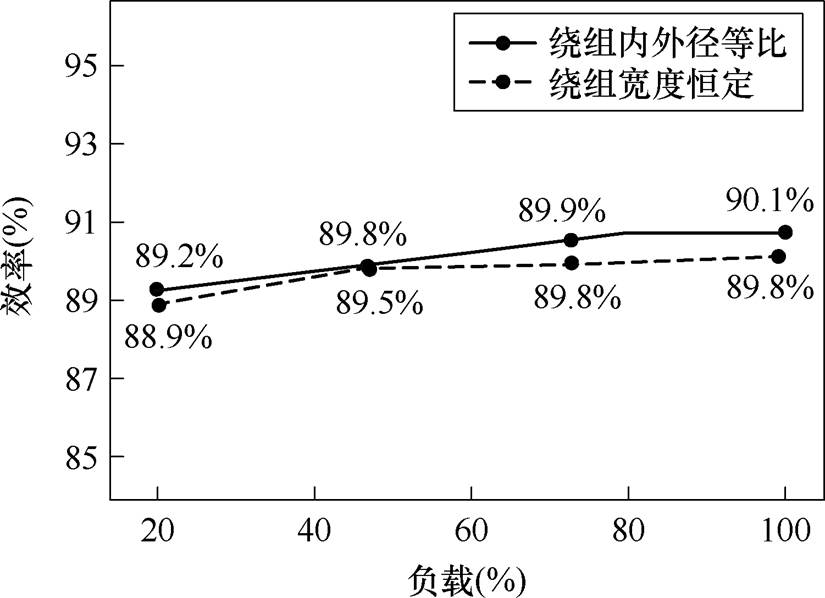
图14 两台变换器效率曲线对比
Fig.14 Converter efficiency curves under different loads
观察图14所示效率曲线可知,在全负载范围内,绕线内外径等比设计下的变换器效率均大于绕线宽度恒定设计,且可在50%负载下达到88.9%,满载时可达90.1%,说明内外径等比设计能够有效降低绕组损耗,提高变压器效率。
综上所述,在不影响多路输出变换器交叉调节特性的前提下,绕线内外径等比设计能够使得变压器绕组电流密度分布最均匀,且绕组损耗最小,满足变压器的散热与高效率需求,优化前后变换器在整体损耗与发热情况方面均有改善,变压器尺寸保持不变,该方法在不牺牲变压器损耗、尺寸和温升的前提下,改善了绕组电流密度分布情况,验证了内外径等比化设计的可行性与正确性。考虑到绕组电流密度有效值的计算不受变换器工作条件影响,因此这一方法适用于各种电力电子拓扑下的变压器,具有较强的实用性与普适性。
本文针对平面变压器的PCB绕组电流密度分布问题进行了深入研究。阐述了绕组电流密度分布与交直流阻抗取值有关,通过数学分析确定在单开关周期内绕组电流密度可通过有效值的形式量化计算。利用数学归纳法推导了同一层绕线电流密度均匀分布的条件是控制每匝绕线的外径与内径比值相等,并得出电流密度分布不均与绕组损耗偏大内在机理一致的结论。通过适当调整各层绕组的相对位置,将发热明显的绕线层排布于PCB相对外侧,使得变压器内部发热呈现均匀特征,避免了绕组上高温热点的存在。有限元仿真结果显示,本文所采用的绕线内外半径等比排布策略有效地改善了绕组电流密度分布的均匀性,降低了绕组损耗。30 W的工程测试样机实验结果表明,在满足各个绕组输出电压精度和交叉调整率指标要求的基础上,该优化设计显著改善了变压器的损耗和散热特性,整机效率可达90.1%,验证了设计方法是可行的。
参考文献
[1] 赵志刚, 张学增. LLC平面变压器绕组损耗与漏感改进有限元计算方法[J]. 电工技术学报, 2022, 37(24): 6204-6215.
Zhao Zhigang, Zhang Xuezeng. Improved finite element method of winding loss and leakage inductance for planar transformer used in LLC converter[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6204-6215.
[2] 高璐, 徐策, 董光冬, 等. 基于电磁仿真软件的平面变压器共模电磁干扰建模方法及其应用[J]. 电工技术学报, 2020, 35(24): 5057-5063.
Gao Lu, Xu Ce, Dong Guangdong, et al. Common mode electro-magnetic interference modeling method of planar transformers based on CST software and its application[J]. Transactions of China Electrotechnical Society, 2020, 35(24): 5057-5063.
[3] 刘越, 吴红飞, 邹军, 等. CRM-PFC矩阵式低高度平面电感优化设计[J]. 中国电机工程学报, 2021, 41(19): 6760-6769.
Liu Yue, Wu Hongfei, Zou Jun, et al. Optimal design of CRM-PFC matrix low-height planar inductor[J]. Proceedings of the CSEE, 2021, 41(19): 6760-6769.
[4] Li Siqi, Rong Enguo, Min Qingyun, et al. A half-turn transformer with symmetry magnetic flux for high- frequency-isolated DC/DC converters[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(8): 6467-6470.
[5] Liu Yuchen, Chen Chen, Chen Kaide, et al. Design and implementation of a planar transformer with fractional turns for high power density LLC resonant converters[J]. IEEE Transactions on Power Elec- tronics, 2021, 36(5): 5191-5203.
[6] Liu Yuchen, Chen Kaide, Chen Chen, et al. Quarter- turn transformer design and optimization for high power density 1-MHz LLC resonant converter[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 1580-1591.
[7] Wang Shuo, Wu Hongfei, Lee F C, et al. Integrated matrix transformer with optimized PCB winding for high-efficiency high-power-density LLC resonant converter[C]//2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 2019: 6621-6627.
[8] Fei Chao, Lee F C, Li Qiang. High-efficiency high- power-density 380V/12V DC/DC converter with a novel matrix transformer[C]//2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 2017: 2428-2435.
[9] Guan Yueshi, Wang Yijie, Wang Wei, et al. Analysis and design of a 1-MHz single-switch DC-DC converter with small winding resistance[J]. IEEE Transactions on Industrial Electronics, 2018, 65(10): 7805-7817.
[10] Zhang Zhengda, Liu Chunhui, Wang Mengzhi, et al. High-efficiency high-power-density CLLC resonant converter with low-stray-capacitance and well-heat- dissipated planar transformer for EV on-board charger[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 10831-10851.
[11] Ostergaard C, Kjeldsen C S, Nymand M. Calculation of planar transformer capacitance based on the applied terminal voltages[C]//2020 IEEE 21st Work- shop on Control and Modeling for Power Electronics (COMPEL), Aalborg, Denmark, 2020: 1-7.
[12] Ansari S A, Davidson J N, Foster M P, et al. Design and analysis of a fully-integrated planar transformer for LCLC resonant converters[C]//2021 23rd European Conference on Power Electronics and Applications, Ghent, Belgium, 2021: 1-8.
[13] Liu Yue, Wu Hongfei, Wang Yunfei, et al. Automatic current sharing of paralleled windings for LLC resonant converter with secondary-side resonant inductors[J]. IEEE Transactions on Power Electronics, 2023, 38(11): 13594-13598.
[14] Chen Wei, Yan Yipeng, Hu Yuequan, et al. Model and design of PCB parallel winding for planar transformer[J]. IEEE Transactions on Magnetics, 2003, 39(5): 3202-3204.
[15] Ahmed M H, Nabih A, Lee F C, et al. Low-loss integrated inductor and transformer structure and application in regulated LLC converter for 48-V bus converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1): 589-600.
[16] Thummala P, Schneider H, Zhang Zhe, et al. Efficiency optimization by considering the high- voltage flyback transformer parasitics using an auto- matic winding layout technique[J]. IEEE Transactions on Power Electronics, 2015, 30(10): 5755-5768.
[17] Dou Yi, Ouyang Ziwei, Andersen M A E. Design the high-frequency DC-DC converter with integrated coupled inductor and current-balancing-transformer[C]// 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 2020: 2610-2616.
[18] Ahmed M, Fei Chao, Lee F C, et al. High efficiency two-stage 48V VRM with PCB winding matrix trans- former[C]//2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 2016: 1-8.
[19] Yu Ruiyang, Chen Tianxiang, Liu Pengkun, et al. A 3-D winding structure for planar transformers and its applications to LLC resonant converters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(5): 6232-6247.
[20] Liu Yue, Wu Hongfei, Tai Yu, et al. Optimal design of GaN and PCB-winding based transformer-inductor- integrated magnetics for CLL resonant converter[C]// 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 2020: 5430-5435.
[21] 倪硕, 吴红飞, 陈君雨, 等. 交错并联临界导通模式Buck电感高密度集成与优化[J]. 电工技术学报, 2022, 37(18): 4688-4696.
Ni Shuo, Wu Hongfei, Chen Junyu, et al. Integration and optimization of a high power density inductor for an interleaved critical conduction mode buck con- verter[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4688-4696.
[22] 李紫薇, 吴学智, 王静, 等. 谐振开关电容变换器磁集成电感设计[J]. 电工技术学报, 2022, 37(24): 6230-6238.
Li Ziwei, Wu Xuezhi, Wang Jing, et al. Design of magnetic integrated inductor for resonant switched capacitor converter[J]. Transactions of China Electro- technical Society, 2022, 37(24): 6230-6238.
[23] 程鹤, 徐恺, 李朋圣, 等. 三相CLLC谐振变换器磁集成平面变压器设计与优化[J]. 电工技术学报, 2024, 39(12): 3774-3786.
Cheng He, Xu Kai, Li Pengsheng, et al. Design and optimization of three-phase CLLC resonant converter with magnetic integrated planar transformer[J]. Transactions of China Electrotechnical Society, 2024, 39(12): 3774-3786.
[24] 杨思莹, 王松, 陈志豪, 等. 基于优化算法的变压器绕组等效电路建模[J]. 电气技术, 2023, 24(8): 29-36, 49.
Yang Siying, Wang Song, Chen Zhihao, et al. Equivalent circuit modeling of transformer winding based on optimization algorithms[J]. Electrical Engin- eering, 2023, 24(8): 29-36, 49.
[25] 康丽, 张艳丽, 唐伟, 等. 基于变系数Steinmetz公式的直流偏磁下铁心损耗计算[J]. 电工技术学报, 2019, 34(增刊1): 1-6.
Kang Li, Zhang Yanli, Tang Wei, et al. Calculation of core loss under DC bias based on Steinmetz formula with variable coefficient[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 1-6.
[26] 桑汐坤, 王懿杰, 徐殿国. 基于输入并联输出串联的高效高升压比DC-DC变换器[J]. 电工技术学报, 2023, 38(20): 5488-5502.
Sang Xikun, Wang Yijie, Xu Dianguo. High-efficiency high voltage gain DC-DC converter based on input parallel and output series connection[J]. Transactions of China Electrotechnical Society, 2023, 38(20): 5488-5502.
[27] 王瑞田, 肖飞, 赵治华, 等. 基于辅助绕组的中频变压器绕组交流电阻测量方法[J]. 电工技术学报, 2019, 34(2): 245-254.
Wang Ruitian, Xiao Fei, Zhao Zhihua, et al. Investigation on measurement method of transformer winding AC resistance by using auxiliary winding[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 245-254.
[28] 刘树林, 沈一君, 刘旭, 等. 正-反激变换拓扑的功率传输分配特性及设计考虑[J]. 电工技术学报, 2023, 38(18): 5006-5016.
Liu Shulin, Shen Yijun, Liu Xu, et al. Power transmission distribution characteristics and design considerations of forward-flyback conversion topology[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 5006-5016.
Abstract In recent years, with the continuous expansion of the market demand for consumer electronic products, various types of small and medium-power switch-mode power supplies have emerged. Particularly in modern small-power switch-mode power supplies, topologies represented by flyback converters play a crucial role in practical applications. In such power systems, the transformer, as one of the core components, significantly affects the overall system efficiency and power density. Planar transformers have attracted considerable attention due to their low height and leakage inductance characteristics.
When the transformer operates under high-frequency conditions, the skin effect and proximity effect prevent the current from distributing uniformly across its cross-section. In flyback converters, the primary winding has a large number of turns, and the intensified proximity effect further exacerbates the uneven distribution of current density in each winding, concurrently reducing the efficiency of the transformer. This paper proposes a winding-width optimization method for planar transformers to achieve uniform distribution of current density.
First, a quantitative method for measuring the current density of windings is discussed. The root mean square (RMS) value of the winding current density within a single switching cycle is time-invariant, which leads to the use of Ohm's Law to calculate its RMS value. Subsequently, through theoretical analysis, it is determined that when the operating conditions of the transformer are constant, the main factors affecting the winding current density are its geometric parameters. The constraints on the inner and outer diameters of the winding are derived to achieve the most uniform current density distribution. Considering the inevitable presence of winding clearances in practical engineering, the formula is adjusted to calculate the optimal inner-to-outer diameter ratio. Furthermore, an in-depth analysis explores the inherent relationship between winding current density distribution and winding losses. A comparison with the literature reveals that the constraints on winding width for uniform current density distribution and minimal losses are consistent. It is indicated that the influencing mechanisms for factors are related to the uniformity of impedance values for AC and DC components.
Taking the Hengdian Group DMEGC Magnetics standard core ECW32C as an example, the widths of individual windings on the same PCB layer are calculated using two methods: winding width in proportion and constant winding width. Under the same excitation conditions, a comparative analysis of current density and winding losses is conducted through finite element simulation. The results indicate that the design with proportional distribution of inner and outer winding radius leads to a more uniform current density distribution and minimized winding losses. Two prototypes of 30 W flyback converters are constructed, and experimental results confirm that the proportional distribution of inner and outer winding radius is more conducive to improving the transformer's heat dissipation characteristics. Since the calculation of winding current density effective value is not affected by the working conditions of the transformer, this method is practical under various power electronic topologies.
keywords:Planar transformer, proportional winding radius, current density, mathematical induction
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.240240
收稿日期2024-02-06
改稿日期2024-07-02
安少亮 男,1983年生,副教授,硕士生导师,研究方向为高效率、高功率密度电力电子变换器与控制技术。E-mail: shaoliang.an@xaut.edu.cn(通信作者)
吴 庆 女,1999年生,硕士研究生,研究方向为磁集成反激变换器。E-mail: 1378478148@qq.com
(编辑 崔文静)