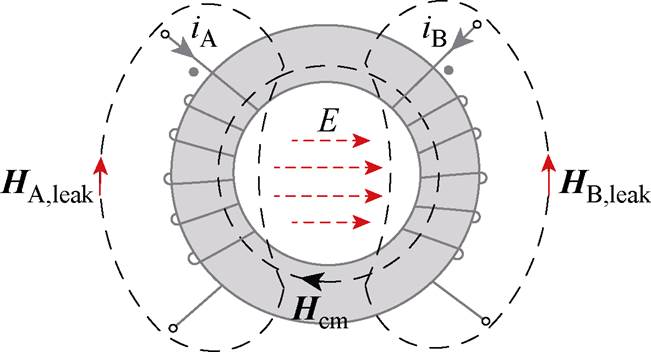
图1 CMC内部的电磁场示意图
Fig.1 Electric and magnetic fields inside a CMC
摘要 在电磁干扰（EMI）滤波器的设计和功率变换器的EMI噪声预测中，共模扼流圈的精确建模至关重要。然而，在高频下受共模扼流圈寄生参数的影响，现有模型难以准确表征其滤波特性。该文分析现有模型的缺点在于无法完整反映共模扼流圈的内部电场特性，因此根据共模扼流圈差模分量在高频下的插入损耗谐振点特性提出一种新的高频模型，该模型通过综合考虑端部和绕组中间寄生电容的影响从而完整表征差模分量的电场特性，并解析新模型电路结构给出模型中寄生参数的提取流程。实验结果表明，新模型在150 kHz～30 MHz下具有良好的拟合精度，证明了该模型的准确性。
关键词：电磁干扰 滤波器 共模电感 寄生参数提取 建模
目前，随着功率变换器开关频率的提高和功率密度的增加，电磁干扰（Electromagnetic Interference, EMI）已经成为一个日益重要的问题[1-2]。随着电力电子器件向高功率密度发展，EMI滤波器常被用于抑制电力电子装置的传导EMI[3-4]。因此准确地表征宽频段下滤波器的性能，并且合理地设计滤波器的尺寸和质量可以极大地帮助抑制功率电子装置传导EMI噪声[5-7]。
共模扼流圈（Common-Mode Choke, CMC）是EMI滤波器的重要组成部分，高磁导率的磁心使得其可以有效地抑制共模（Common Mode, CM）电流，并且其泄漏的电感在一定程度上可以用于抑制差模（Differential Mode, DM）电流。然而共模扼流圈的高频特性极大地影响高频段EMI滤波器的滤波性能。因此，CMC的建模与设计工作尤为重要，文献[8-11]通过采用不同的磁心结构或绝缘介质对CMC进行平面磁集成以进一步减小滤波器的体积。然而高频下由于寄生参数的存在，往往难以预测CMC的特性[12]。如果仅仅采用模型，那么在数百kHz到几MHz以后衰减性能相较于预期值差距很大，很大程度上会影响高频下滤波器性能的准确预测。因此，考虑CMC的寄生参数并建立准确的高频CMC模型对于更好地设计EMI滤波器以及预测其滤波性能有着重大意义。
已经有许多研究关注滤波器组件的3D建模[13-15]，文献[16]在此基础上利用场分析的理论结合复数磁导率建立了一个3D全波CMC模型，可以较为准确地提取CMC内部寄生参数，并且缩短仿真时间。文献[17-18]根据CMC的几何形状以及材料参数提出了一种CMC内部寄生电容的计算方法，在此基础上得到了基于CMC结构参数的寄生参数计算模型[19]。
基于测量得到的阻抗特性来描述CMC高频特性是最普遍、高效的[20-22]。文献[23]通过多种不同的连接方式进行阻抗测量得到了一个准确的CMC模型，文献[24]在此基础上利用数值计算对其进行简化。文献[25-26]将CMC等效为一个四端口器件进行分析，并利用遗传算法对寄生参数进行提取。然而上述文献的缺陷在于仅进行阻抗测量难以得到能够真正表征CMC高频特性曲线的参数，并且仅仅将绕组间电容归算至两侧难以表征出CMC高频下完整的电场特性。传统插入损耗测量的测量方式不符合GB/T 7341及EN55017的测量标准，而两种插入损耗在10 MHz以上的高频部分相差很大，因此即使能拟合传统插入损耗测试也并不代表可以表征CMC高频下真正的滤波特性。
本文基于阻抗测量与标准差模插入损耗测量方式相结合提出了一种新的CMC的高频模型及其参数提取方法。首先，对CMC的高频模型进行简单分析并介绍了传统CMC模型建模方法以及常用的CMC测试连接方式。其次，介绍了传统建模方式的局限性，分析了两种测量方式的差异，并根据CMC物理模型提出了一个新的等效电路模型，该模型可拟合多谐振点的插入损耗曲线。再次，介绍了模型中寄生参数的提取方法，最终经过实验验证模型在100 kHz～30 MHz的传导频率范围内取得了良好的结果。最后，验证了所提模型的准确性。
滤波器中CMC的电磁场示意图如图1所示，它由磁心与两个相同的绕组构成一个对称的结构，因此CMC的等效电路模型也应该是对称的。此外它由磁心内部的主磁通（Hcm）产生共模分量，空气中的漏磁通（HA,leak和HB,leak）产生CMC的差模分量以抑制差模电流。因此其高频模型不仅要能够描述CMC在高频下磁场响应以及电场响应（E），还应准确表征其共模与差模分量。
图1 CMC内部的电磁场示意图
Fig.1 Electric and magnetic fields inside a CMC
CMC常利用共模电感与漏感集成在一起，其漏感可视为DM电感。因此往往将其共模分量与差模分量分开建模。共模部分结构较为简单，本文主要针对差模部分进行优化。
图2为常用的CMC的高频电路模型，其包含了CMC中的共模分量与差模分量并且分开对不同分量进行建模。图2中，LCM为绕组主磁通所产生的共模电感；CCM为共模分量的寄生电容；RDM为共模电感磁心损耗等效电阻；LDM为绕组泄漏磁通所产生的漏感，等效为差模电感；CDM为绕组漏电容；RDM为差模电感磁心损耗等效电阻；Cw为两个绕组之间的寄生电容。
传统CMC模型结构简单，根据几次不同的阻抗测量与数据拟合即可得到其模型中的寄生参数。为区分不同的测试方式，本文将阻抗测试方式称为Z配置，散射参数的测试方式称为S配置。传统的阻抗测量示意图如图3所示，Z1配置等效电路如图4所示。图3a为Z1配置，Z1配置将1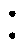
1的变压器分量抵消，其得到的差模分量阻抗曲线ZL1如图5所示；图3b为Z2配置，Z2配置将CMC的输出端口开路，测量集总的绕组间寄生参数，得到的阻抗曲线ZC2如图6所示。
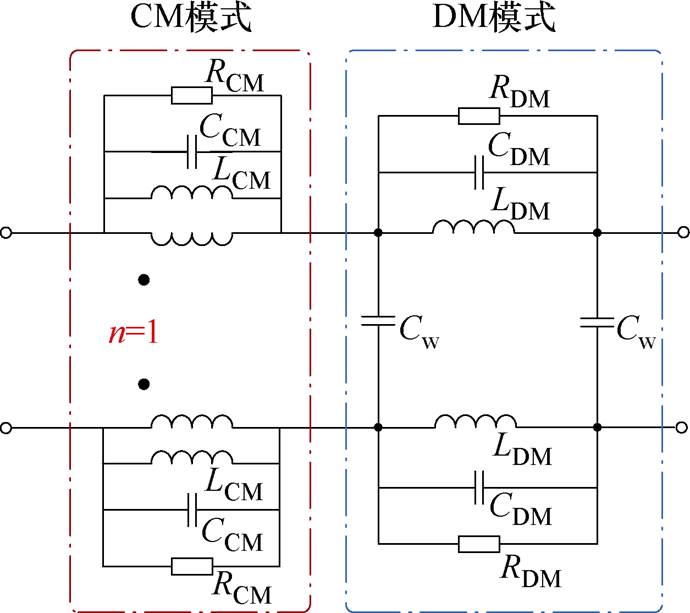
图2 传统CMC模型
Fig.2 Traditional CMC model
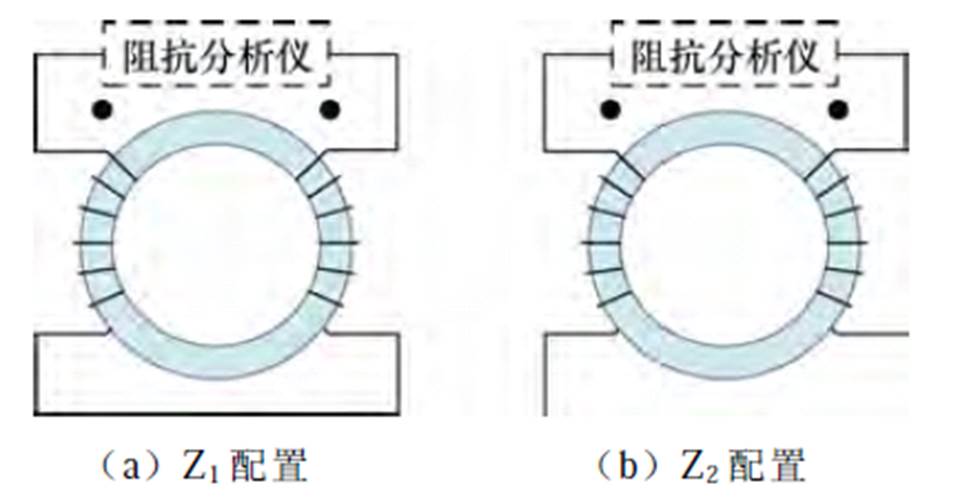
图3 阻抗测量示意图
Fig.3 Schematic diagram of impedance measurement
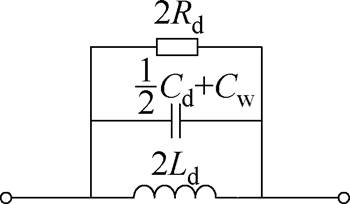
图4 Z1配置等效电路
Fig.4 Equivalent circuit for Z1
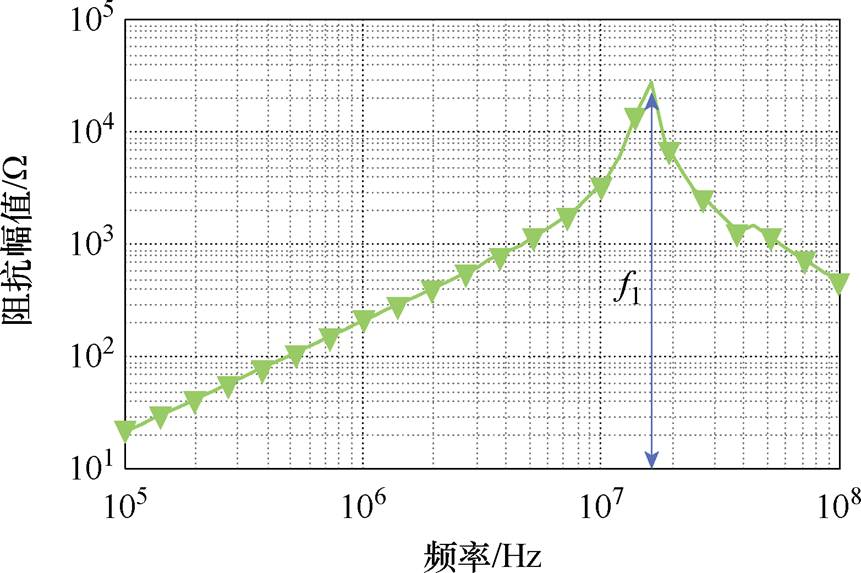
图5 ZL1测试阻抗特性曲线
Fig.5 ZL1 test impedance characteristic curve
图6 ZC2测试阻抗特性曲线
Fig.6 ZC2 test impedance characteristic curve
如图2所示，Z1配置下CMC的共模分量抵消，此配置下仅存在差模分量阻抗ZL1，Z1与Z2配置共同提取绕组寄生电容Cw。
传统的CMC模型在Z2配置下，于低频段（电感线性段）可以得到
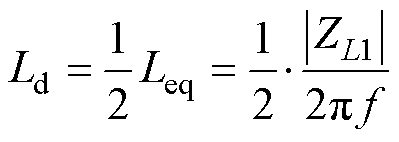（1）
式中，差模电感Ld为测量得到的等效电感Leq的一半。
由Z1配置下谐振点的频率f1及幅值ZL1( f1)可以得到绕组漏电容Cd和差模分量磁心损耗等效电阻Rd分别为
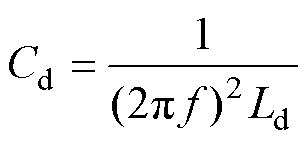（2）
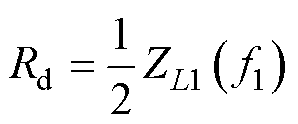（3）
由于Cw的数值较小，ZC2配置下阻抗测量结果在较低频率下表现为容性特征，而阻抗测量值近似为两个Cw的并联阻抗，因此
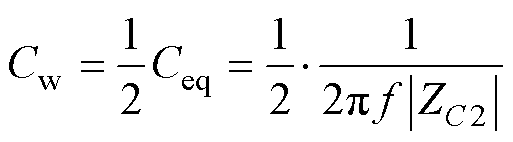（4）
根据式（1）～式（4）可以得到传统CMC模型下的所有寄生参数，将模型代入Saber电路仿真软件并与图7所示的插入损耗测试方法进行对比，图7中，RS和R0为50 W 的源阻抗，Vs为矢量网络分析仪的小信号源，测试中使用了射频变压器作为共地的隔离。传统方法的实测与模型计算结果对比如图8所示。
根据CMC的对称性，在S1配置下节点1和2处输入近似相等的电流，以此模拟共模电流。在S2配置下，将通过这些节点流经相位为+180°的等效电流来模拟CMC的差模模式。而S3配置则展示了CMC的一个绕组连接在矢量网络分析仪中的测试信号发生器（Tracking Generator, TG）和射频信号接收器（Radio Frequency, RF）之间，而另一个绕组保持开路，本文将称此配置为开路配置，这种工作模式下既包含了共模分量，又包含了差模分量[24]。
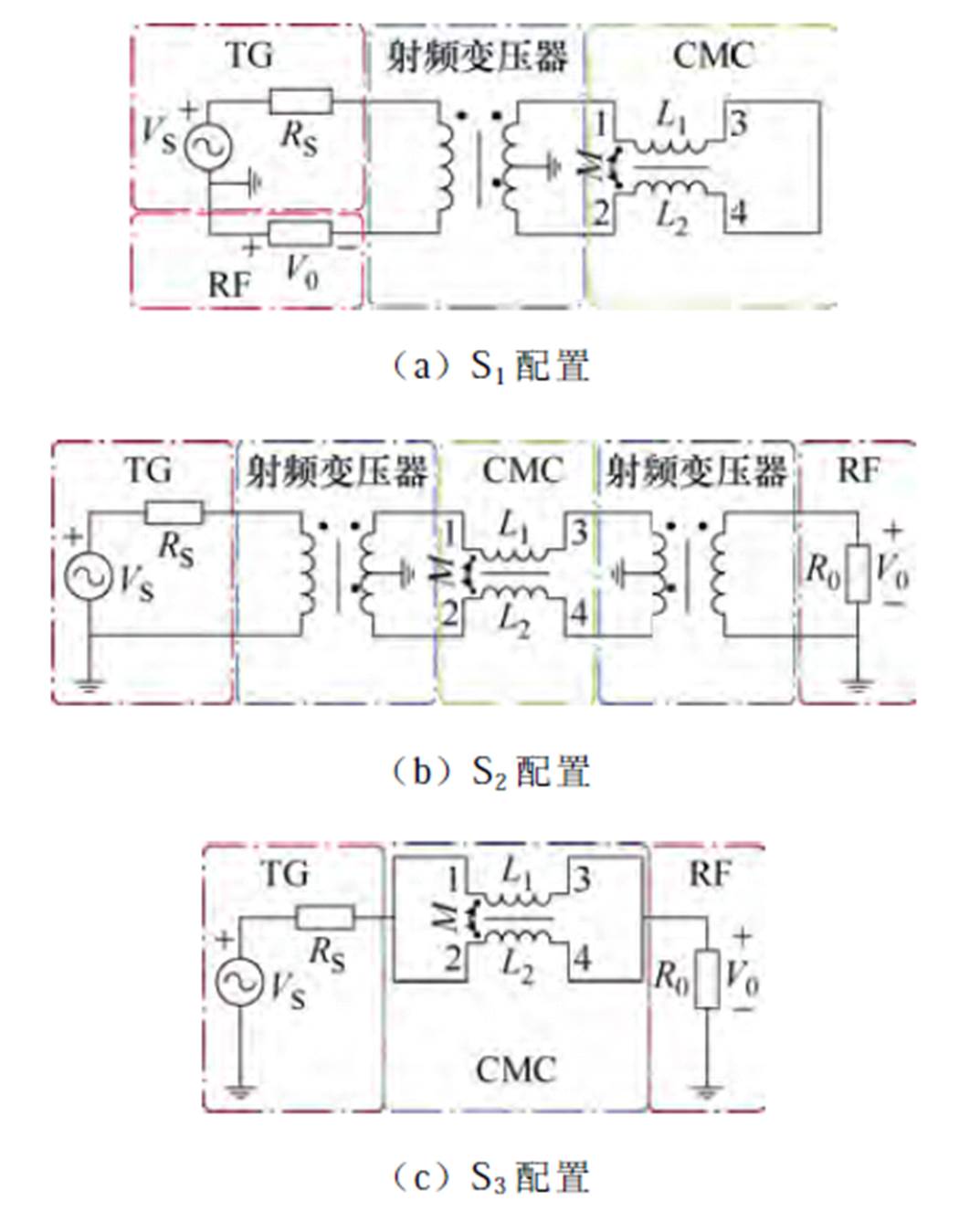
图7 插入损耗测试配置
Fig.7 Insertion loss test configuration
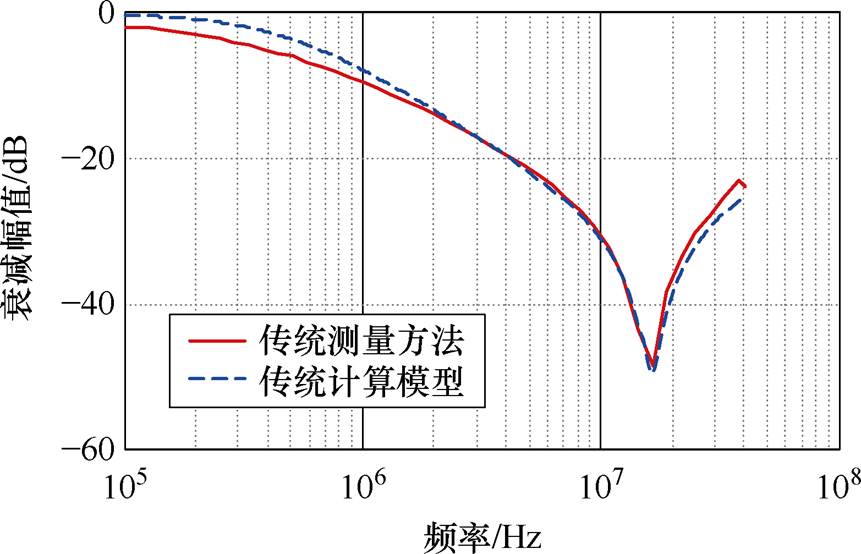
图8 传统方法的实测与模型计算结果对比
Fig.8 The traditional method's actual measurements compared with model calculation results
根据图8所示，传统的CMC等效电路模型与传统的插入损耗测试方法在100 kHz～30 MHz范围内呈现良好的拟合效果。然而，这并不能代表其准确性，根据最新的GB/T 7341和EN55017规范中所规定的差模插入损耗测试方法（见图7b），两者在低频下的插入损耗测试波形相符，但在高频段却呈现完全不一致的趋势。为了更好地展现两者在高频时特性的差异，将插入损耗特性的测量范围扩展至更高频率段（40 MHz），如图9所示。
图9 S1（传统）与S2（国标）测试结果对比
Fig.9 Comparison of S1 (traditional) and S2 (GB) test results
本文认为导致图9中二者在高频段插入损耗趋势不同的主要原因在于CMC模型中的电容分量。低频时，主要由Ld的磁场响应主导；而高频时，以电容Cw与Cd的电场响应为主。
S1与S2两种测量方式的区别在于是否将输出端口Port2短路。当输出端口短路时，模型右侧的Cw短路，导致两者的噪声路径不一致。低频下，Cw的容值较小，导致其阻抗较大，与50 W 并联几乎不起作用，因此两者在低频段几乎一致。然而高频时，Cw的阻抗较小，与50 W 并联后对插入损耗测试产生较大影响。
此外，S2所示的插入损耗测试方法更能准确地反映实际噪声电流的流向。因此，仅基于阻抗值（S1配置类似）所建立的传统CMC高频模型并不能真实反映出实际CMC寄生电容的高频特性。
CMC高频模型原理如图10所示。根据图1中的CMC电磁场分布可知，两个绕组之间的电场耦合应被视为绕组整体之间的耦合（见图10中红线）。然而，目前所有的模型都将电容简单地归算至两个端口，将绕组间的电容归算至两个绕口，在很多情况下并不能准确地拟合复杂的多谐振点的CMC模型。
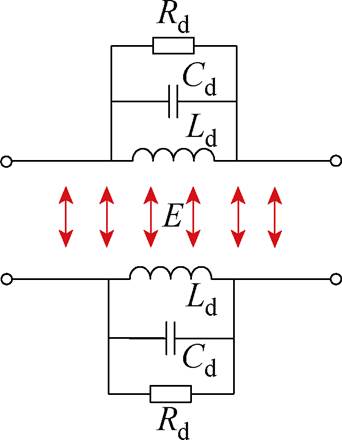
图10 CMC高频模型原理
Fig.10 CMC high frequency model schematic
本文提出的新模型的集总等效电路如图11所示，根据CMC磁通的共模与差模分量将CMC模型分为共模模型与差模模型，其中共模模型为一个1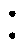1的变压器模型，差模模型为k=-1的耦合电感模型。
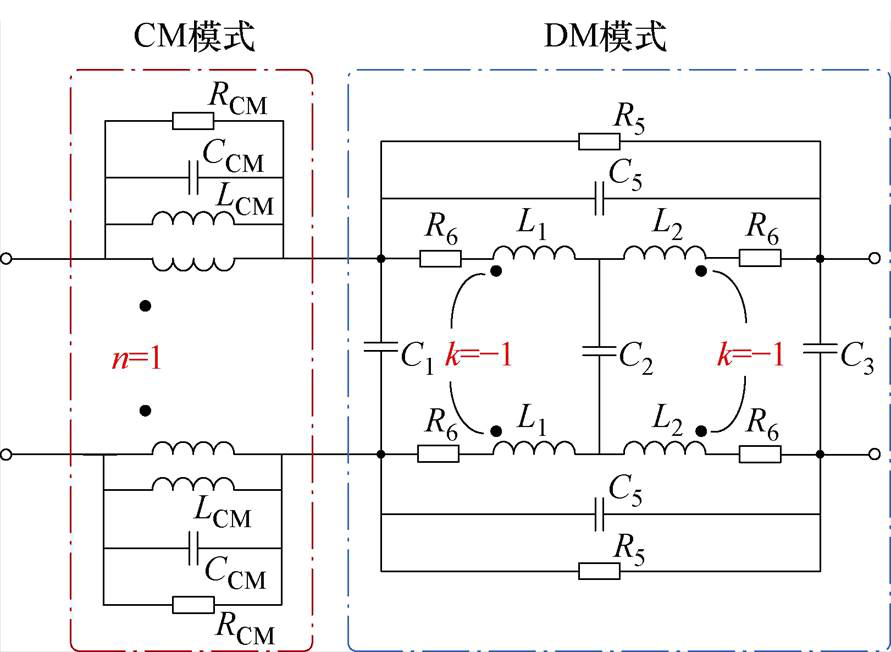
图11 优化的CMC高频电路模型
Fig.11 Improved CMC high-frequency circuit model
本文提出优化的差模模型相较于传统模型，将差模感量Ld分解为大小相等的两个电感L1与L2，并添加中间电容C2以将绕组间的电容分摊至整体。
由于CMC共模分量的磁通仅在磁心中流通，而差模分量的磁通仅在空气中流通。因此，共模分量为1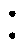1的变压器同时需要将分段的差模电感设置成耦合系数k=-1的耦合电感，以确保共模电流不受差模分量的影响[21]。
本文提出的CMC模型的差模分量模型如图12a所示，由于两绕组通过的差模电流大小相等、方向相反，通过将耦合电感解耦，简化后的等效电路如图12b所示，该模型的寄生参数提取更为复杂。由于绕组损耗电阻相对较小，较高频段时以磁场响应或电场响应为主，因此最后对R6进行提取。
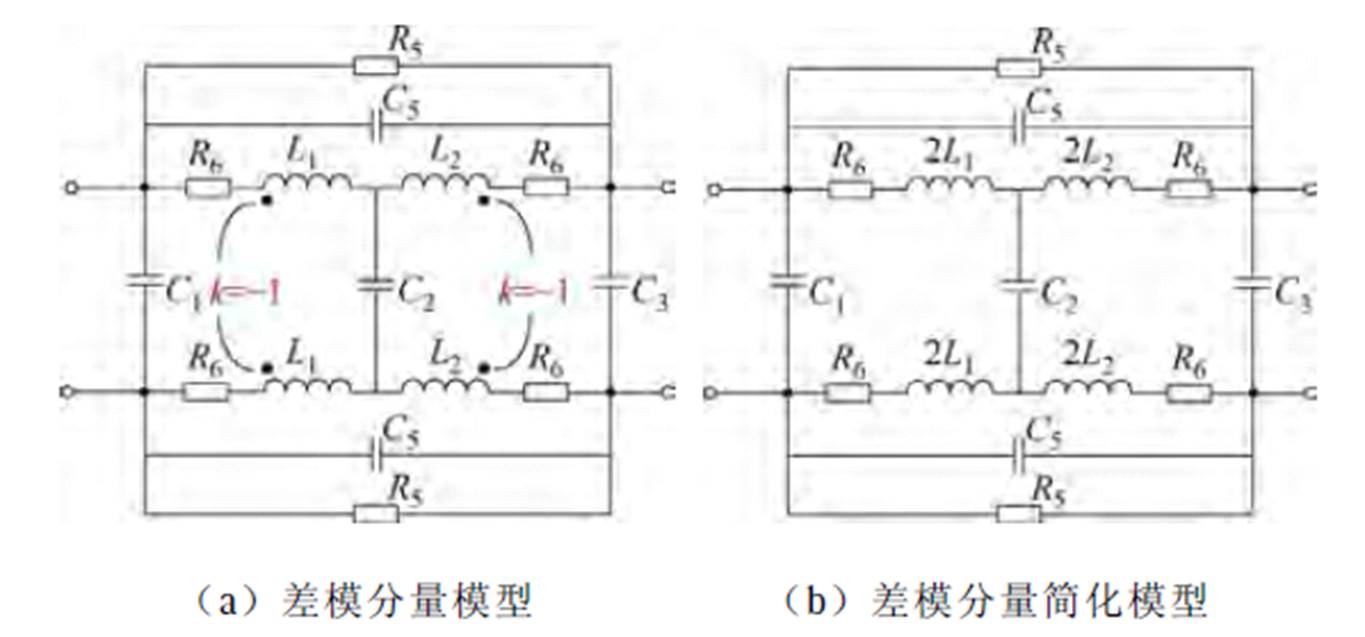
图12 差模分量高频电路模型
Fig.12 Differential mode high-frequency circuit model
商用CMC的两个绕组间以及绕组的两个端子间结构往往具有良好的对称性，且k=-1的耦合电感模型在差模电流激励下可以化简为双倍的差模电感，如图12b所示。故可以对图12b中的参数做出如下假设
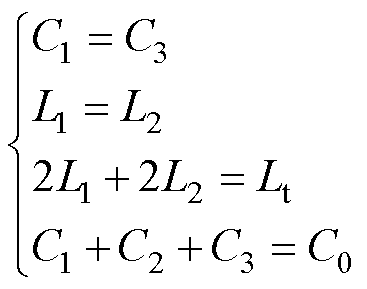（5）
式中，Lt为低频下（f1之前）总的泄漏电感；C0为绕组之间总的寄生电容。
对图12b中R5与C5并联部分进行星形-三角形变换，化简后的等效电路如图13所示，其中集总参数定义在式（6）中给出。
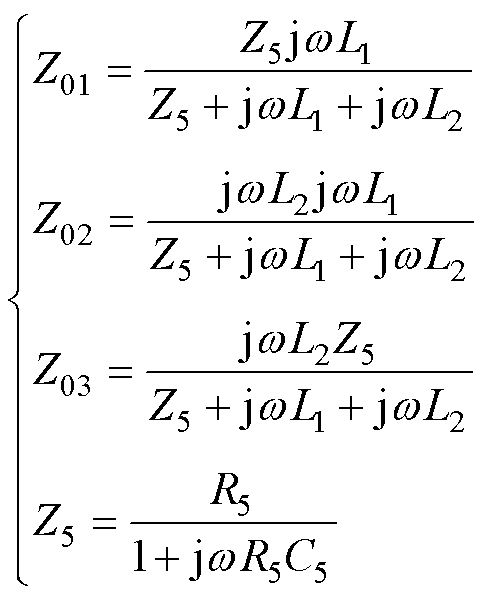（6）
式中，Z01、Z02、Z03对应星形-三角形变换后的阻抗。
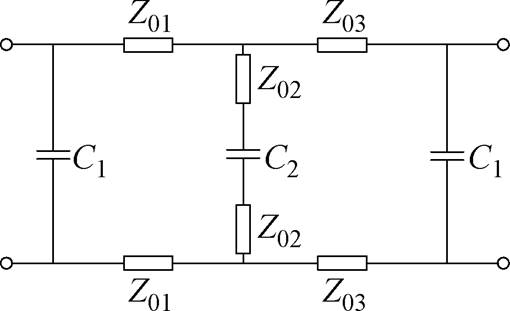
图13 高频模型简化示意图
Fig.13 Simplified schematic diagram of the high-frequency model
模型在Z1与Z2配置对应的等效电路如图14所示。由于在频率较低时Z5
jwL1，由Z1等效电路模型可以在低频时计算L1、L2为
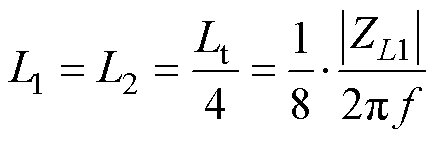（7）
图14 Z1、Z2配置的等效电路
Fig.14 Equivalent circuit diagram for Z1, Z2 setup
星形-三角形变换后插入损耗测试原理如图15所示，图中，Zs为2Z02与C2串联后的阻抗，其表达式如式（8）所示。电容值C0由在Z2配置中测量的泄漏阻抗确定，然而它是由三个电容并联，因此还需要额外的两个方程方能确定全部的容值。
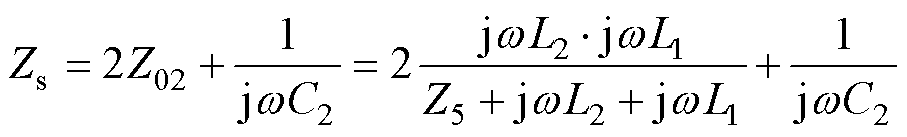（8）
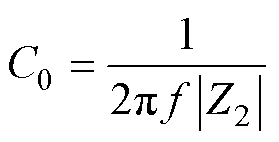（9）
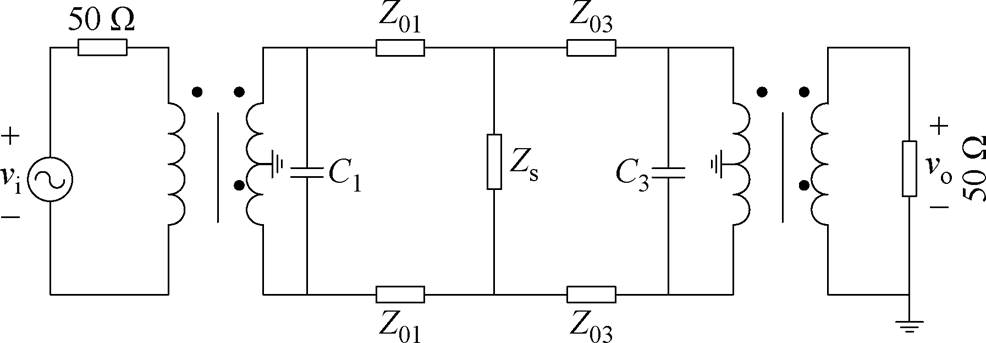
图15 S2配置的测试等效电路
Fig.15 Test equivalent circuit diagram for S2 configuration
由图9的标准插入损耗曲线可观察到在高频段存在两个幅值相近的谐振点f2与f3，故最后两个方程可从图15所示的配置中获得。易知当阻抗Zs达到最小值0时，插入损耗也为最小值，由于R5与C5并联，高频下C5的阻抗远小于R5，因此可以忽略R5以简化式（8），即
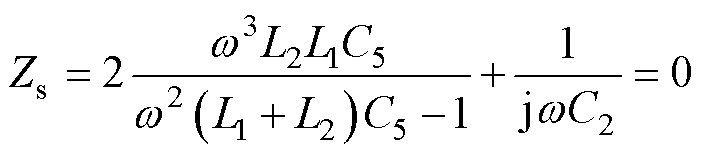（10）
根据式（10）的等式左右同时乘以w，可以得到关于w的一元方程，因此可得谐振点频率f2与f3与模型中各寄生参数之间的关系为
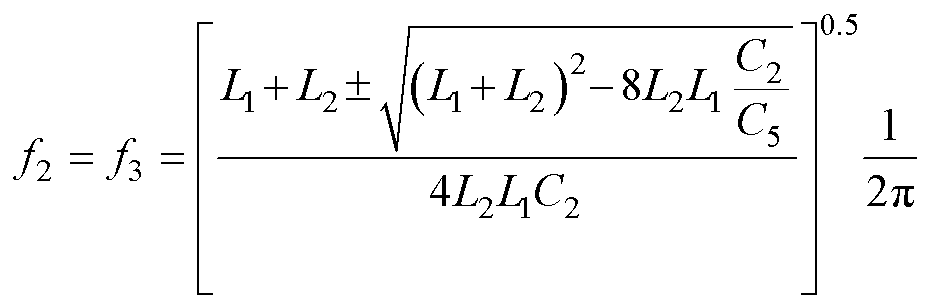（11）
由f2与f3二次方后相加减，约掉C5之后即可得到C2的表达式如式（12）所示，此时f2、f3与C2已经通过观察且由式（12）得到，因此只需代入式（11）即可得到C5的表达式。
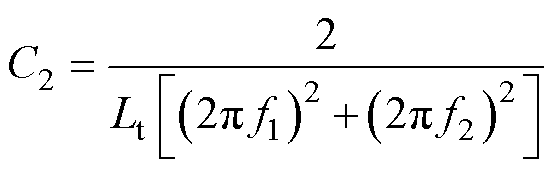（12）
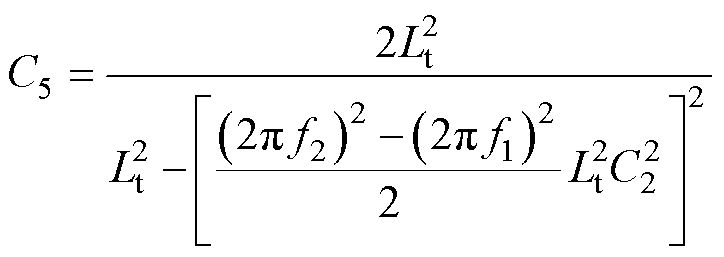（13）
联合式（5）、式（11）、式（13）易得C1与C3，表1列出了绕组间寄生电容的参数值。
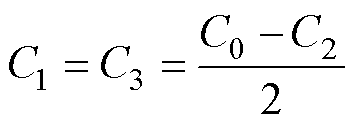（14）
表1 绕组间寄生电容容值
Tab.1 The value of the parasitic capacitance between the windings （单位: pF）
参 数数 值 C11.287 C21.326 C31.287
图16所示的S4配置为2、4端子的绕组开路，仅对1、3端子绕组进行测量，此配置下用于测量绕组间的寄生电容。
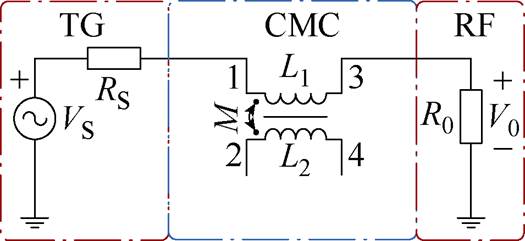
图16 单绕组插入损耗测试（S4配置）
Fig.16 Single-winding insertion loss test (S4 setup)
由于两个绕组中存在电场耦合，即使绕组开路仍然会有部分差模电流流过，因此该配置中既包含了共模分量，又包含了差模分量。根据电桥平衡原理，S4配置下的等效电路模型如图17所示。
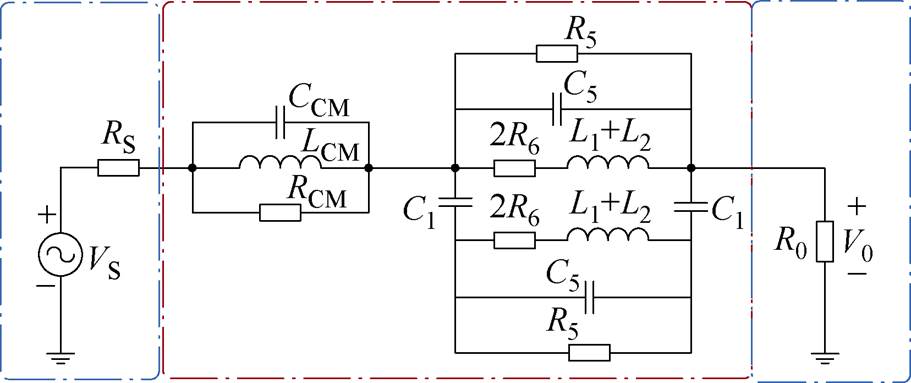
图17 S4配置下的等效电路模型
Fig.17 Equivalent circuit model of S4 setup
假设红框内电路结构的开路阻抗为Zoc，则图17所示的S参数可由式（15）进行计算，S4配置下S21曲线如图18所示。
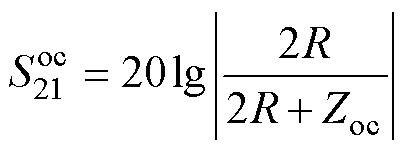（15）
式中，R=RS=R0=50 W。
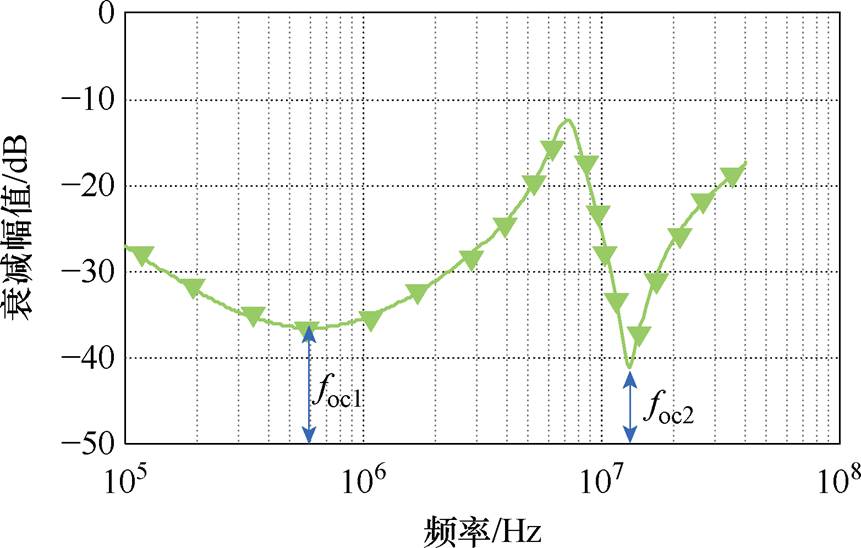
图18 S4配置下的S21曲线
Fig.18 S21 curve for S4 configuration
结合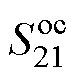
曲线与文献[24]中分析可知，S4设置下的第一个谐振点foc1即为共模分量谐振点，而第二个谐振点foc2应小于差模分量谐振点f2，即
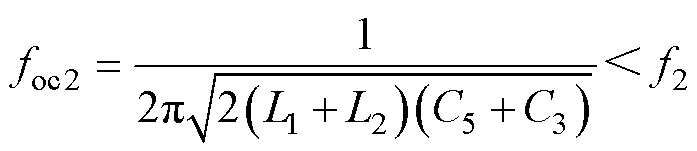（16）
由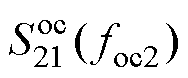
可以得到绕组损耗电阻R5为
（17）
在低频（100 kHz附近）下，差模感量阻抗较小，此时的插入损耗（Insertion Loss, IL）主要由磁心损耗电阻R6引起，忽略差模模型电感感量，则
（18）
根据式（18）易得R6为
（19）
通过上述步骤，可以得到模型的所有差模分量寄生参数，表2列出了CMC的泄漏参数。
表2 CMC泄漏参数
Tab.2 CMC leakage parameters （单位: pF）
参 数数 值 C11.287 C21.326 C31.287
对CMC的CM分量建模时，不考虑其差模分量。CM分量本质上由绕在磁心的两个相同绕组产生，可以等效为一个匝比n=1
1的变压器。共模分量测试配置如图19所示，其等效电路如图20所示，由等效电路可以看出在共模配置ZL3下，差模分量被抵消，此时仅剩下共模分量。
图19 共模阻抗测量示意图（ZL3配置）
Fig.19 Common mode impedance measurement diagram (ZL3 setup)
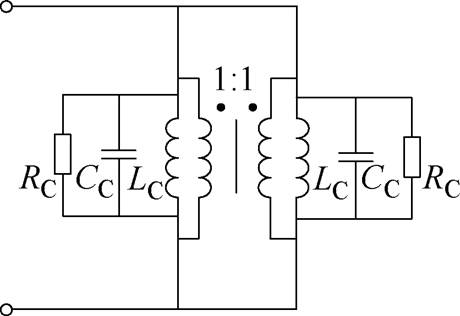
图20 ZL3配置的等效电路模型
Fig.20 Equivalent circuit model for ZL3 configuration
由ZL3测试得到的阻抗曲线如图21所示，由阻抗曲线可以进一步提取共模分量寄生参数。
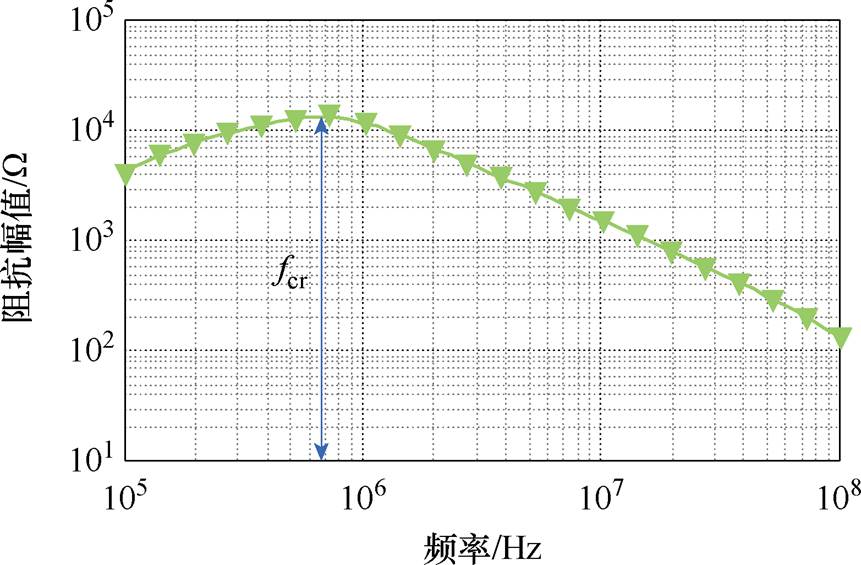
图21 Z3测试阻抗特性曲线
Fig.21 Z3 test impedance characteristic curve
根据图20，可以写出其等效阻抗的表达式为
（20）
式中，LC为CM感量；CC为绕组的寄生电容；RC为磁心损耗电阻。
频率较低时，共模阻抗以为主，即
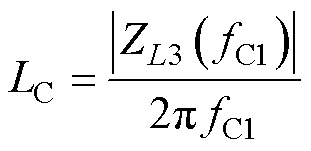（21）
根据阻抗特性曲线的谐振点fcr可以得到寄生 电容为
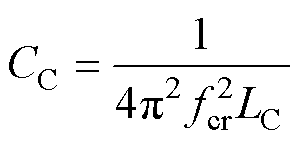（22）
最后，根据谐振点处的幅值可以得到绕组损耗电阻RC为
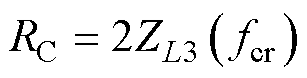（23）
表3列出了CMC共模分量的寄生参数。
表3 CMC共模分量寄生参数
Tab.3 CMC parasitic parameter of common mode component
参 数数 值 LC/mH7.22 CC/pF9.74 RC/W13 200
为了验证所提出的模型，本节通过二端口测量对模型进行测试。测试的CMC样品如图22所示，实验所使用的阻抗分析仪型号为WK 65120B，矢量网络分析仪型号为KEYSIGHT E5072A。
图22 实验用CMC示意图
Fig.22 Schematic diagram of CMC for experimental use
在实验中采用了两种配置，共模S3配置及差模S2配置。采用表1与表2中提取得到的寄生参数并在Saber电路仿真软件中搭建S2配置等效电路后仿真得到的S21幅值对比如图23所示。
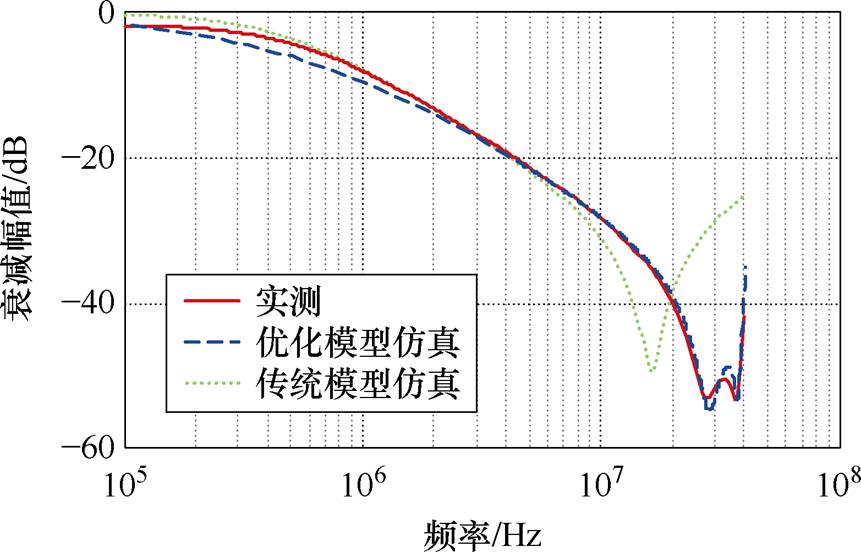
图23 差模分量S21幅值对比
Fig.23 Comparison of amplitudes of differential-mode component S21
图23为差模插入损耗的测量结果与仿真结果的比较，在100 kHz～30 MHz频率范围内测量与优化模型仿真结果一致性良好，而传统模型在10 MHz以上显示出完全不同的趋势，验证了本文所提出的优化的CMC的模型的有效性。
根据表3所示的共模参数搭建电路仿真模型并与实测S3配置进行对比，图24为共模分量的实测与仿真结果对比，由图24可知，CMC共模模型在100 kHz～30 MHz内具有较好的一致性，证明本文所提出的CMC高频模型的有效性。
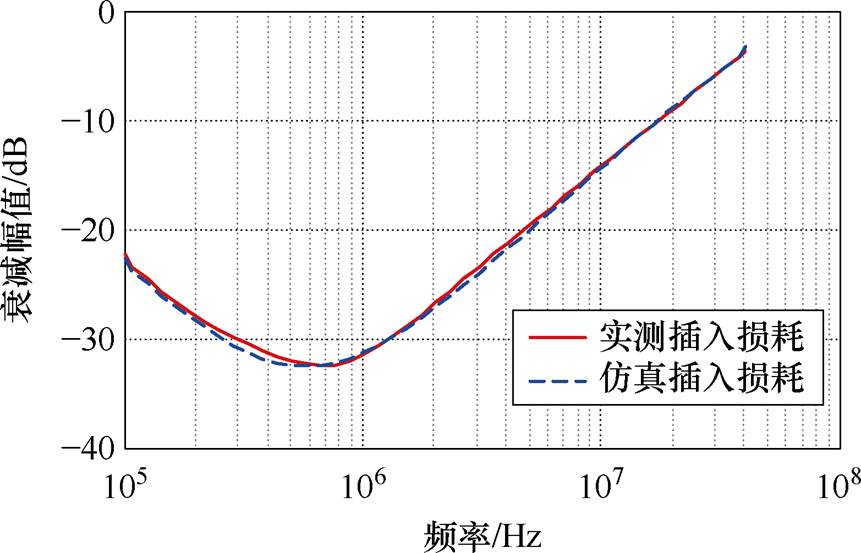
图24 共模分量S21幅值对比
Fig.24 Comparison of amplitudes of common-mode component S21
此外，如本文第2节所述，理想的差模模型应对共模电流没有衰减作用，即差模模型的共模抑制比（Common-Mode Rejection Ratio, CMRR）（dB）应为0。为了验证这一分析，本文在Saber电路仿真软件中对图12所示的差模模型在S3配置（共模配置）下进行仿真，并将k=0进行对比，得到的仿真波形如图25所示。
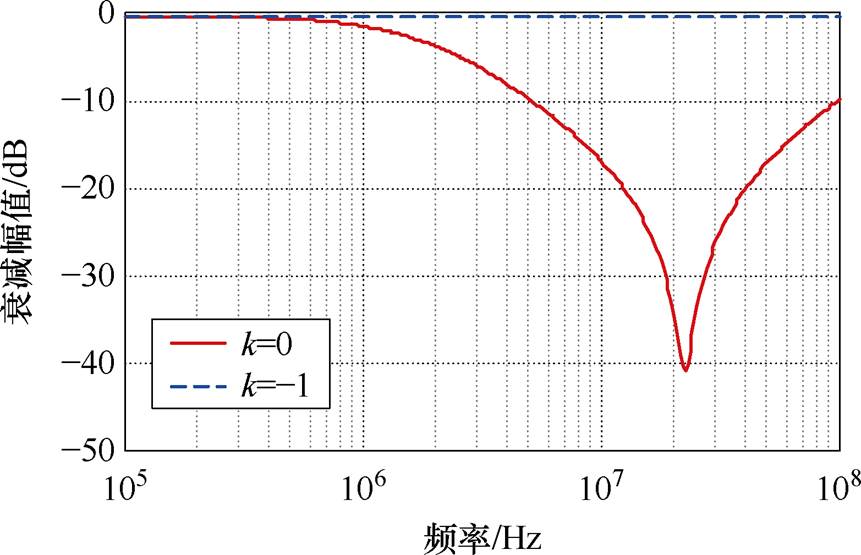
图25 两种电感设置下的S21对比
Fig.25 S21 comparison for two inductance settings
由图25的仿真波形可见，本文将差模电感量分为两部分，并将两个绕组中的四个电感对应设置为k=-1的耦合电感，对共模电流并无衰减作用，因此并不影响CMC共模分量模型，验证了第2节分析以及模型的正确性。
EMI滤波器等效电路中，将绕组间的电容归算至两个端口在很多情况下无法准确地表示复杂的多谐振点的CMC模型。为了提高模型的准确性，需要考虑其完整电场特性，本文通过分析CMC高频下的多谐振点特性，提出了一种新的CMC高频模型，该模型将差模分量电感分为两部分，在原有端部电容的基础上通过引入中间段电容分支对绕组间寄生电容进行完整建模。并通过电路原理对新模型在不同测量方式下的等效电路进行化简，进而实现模型中各寄生参数的提取，实验结果表明，新模型在150 kHz～30 MHz具有良好的拟合精度。
参考文献
[1] 彭金融, 毛行奎, 崔文玲, 等. 基于插入无源二端口网络的噪声源阻抗提取方法研究[J]. 电工技术学报, 2023, 38(2): 523-532.
Peng Jinrong, Mao Xingkui, Cui Wenling, et al. Research on noise soure impedance extraction method based on inserting passive two-port network[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 523-532.
[2] 何杰, 刘钰山, 毕大强, 等. 开关变换器传导干扰抑制策略综述[J]. 电工技术学报, 2022, 37(6): 1455-1472.
He Jie, Liu Yushan, Bi Daqiang, et al. Review of conducted electromagnetic interference suppression strategies for switching converters[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1455- 1472.
[3] 丁凯, 查晓明, 陈允平. 有源滤波器非线性行为分析及其电磁干扰的抑制[J]. 电力系统自动化, 2006, 30(15): 48-50, 69.
Ding Kai, Zha Xiaoming, Chen Yunping. Analysis of nonlinear dynamical behaviors of active power filter and its capability for suppressing EMI[J]. Automation of Electric Power Systems, 2006, 30(15): 48-50, 69.
[4] 谢静逸, 陈为, 陈庆彬, 等. 考虑电磁场耦合的磁性元件近场耦合模型[J]. 中国电机工程学报, 2022, 42(13): 4652-4664.
Xie Jingyi, Chen Wei, Chen Qingbin, et al. Magnetic components near field coupling model considering electromagnetic field coupling[J]. Proceedings of the CSEE, 2022, 42(13): 4652-4664.
[5] Shin D, Jeong S, Baek Y, et al. A balanced feed- forward current-sense current-compensation active EMI filter for common-mode noise reduction[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(2): 386-397.
[6] 王安宇, 周阳, 郑峰, 等. 应用于三相PWM逆变器的EMI滤波器元件不对称度研究[J]. 中国电机工程学报, 2022, 42(7): 2681-2691, 25.
Wang Anyu, Zhou Yang, Zheng Feng, et al. Investigation of the asymmetry of EMI filter components applied to three-phase PWM inverter[J]. Proceedings of the CSEE, 2022, 42(7): 2681-2691, 25.
[7] Goswami R, Wang Shuo. Investigation and modeling of combined feedforward and feedback control schemes to improve the performance of differential mode active EMI filters in AC-DC power con- verters[J]. IEEE Transactions on Industrial Electro- nics, 2019, 66(8): 6538-6548.
[8] 杨玉岗, 陈晓静, 靳明智. 椭圆形平面无源集成EMI滤波器的特性研究[J]. 电源学报, 2017, 15(3): 44-49.
Yang Yugang, Chen Xiaojing, Jin Mingzhi. Chara- cteristics research for elliptic planar passive integrated EMI filter[J]. Journal of Power Supply, 2017, 15(3): 44-49.
[9] 江师齐, 王卫, 王盼宝, 等. 一种结构对称型电磁集成电磁干扰滤波器分析与设计[J]. 电工技术学报, 2022, 37(22): 5826-5835.
Jiang Shiqi, Wang Wei, Wang Panbao, et al. Analysis and prototyping of the electromagnetic integration of a structure-symmetrical electromagnetic interference filter[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5826-5835.
[10] 杨玉岗, 那欣, 王长华, 等. 基于积木式交错并联的平面全集成EMI滤波器[J]. 电工技术学报, 2012, 27(3): 181-187.
Yang Yugang, Na Xin, Wang Changhua, et al. Planar completely integrated EMI filter based on stacked- type interleaved connection[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 181-187.
[11] 陆子健, 叶鑫, 刘艺涛. 基于交错多地层结构的平面磁集成EMI滤波器设计[J]. 中国电机工程学报, 2022, 42(13): 4706-4717.
Lu Zijian, Ye Xin, Liu Yitao. Design of planar magnetic integrated EMI filter with multi-GND-layer structure[J]. Proceedings of the CSEE, 2022, 42(13): 4706-4717.
[12] Kovacic M, Hanic Z, Stipetic S, et al. Analytical wideband model of a common-mode choke[J]. IEEE Transactions on Power Electronics, 2012, 27(7): 3173-3185.
[13] Moonen N, Buesink F, Leferink F. Optimizing capacitor placement in EMI-filter using back annotation of 3D field coupling parameters in circuit models[C]//2016 International Symposium on Elec- tromagnetic Compatibility-EMC EUROPE, Wroclaw, Poland, 2016: 576-580.
[14] Moonen N, Buesink F, Leferink F. Enhanced circuit simulation using mutual coupling parameters obtained via 3D field extraction[C]//2016 Asia-Pacific Inter- national Symposium on Electromagnetic Com- patibility (APEMC), Shenzhen, China, 2016: 181- 183.
[15] Asmanis G, Stepins D, Asmanis A, et al. Mutual couplings between EMI filter components[C]//2015 IEEE International Symposium on Electromagnetic Compatibility (EMC), Dresden, Germany, 2015: 908- 913.
[16] Moonen N, Vogt-Ardatjew R, Roc’h A, et al. 3-D full-wave high frequency common mode choke modeling[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(3): 707-714.
[17] Pasko S W, Kazimierczuk M K, Grzesik B. Self- capacitance of coupled toroidal inductors for EMI filters[J]. IEEE Transactions on Electromagnetic Compatibility, 2015, 57(2): 216-223.
[18] Ayachit A, Kazimierczuk M K. Self-capacitance of single-layer inductors with separation between conductor turns[J]. IEEE Transactions on Electro- magnetic Compatibility, 2017, 59(5): 1642-1645.
[19] Heldwein M L, Dalessandro L, Kolar J W. The three-phase common-mode inductor: modeling and design issues[J]. IEEE Transactions on Industrial Electronics, 2011, 58(8): 3264-3274.
[20] Sánchez A M, Pérez A, Regué J R, et al. A modal model of common-mode chokes for conducted inter- ference prediction[J]. IEEE Transactions on Elec- tromagnetic Compatibility, 2010, 52(3): 749-752.
[21] 陈恒林, 陈玮, 冯利民, 等. 基于阻抗测量的共模扼流圈高频建模[J]. 电工技术学报, 2007, 22(4): 8-12.
Chen Henglin, Chen Wei, Feng Limin, et al. High frequency modeling for common mode chokes based on impedance measurement[J]. Transactions of China Electrotechnical Society, 2007, 22(4): 8-12.
[22] Skibin S, Stevanović I. Behavioral circuit modeling of chokes with multi-resonances using genetic algo- rithm[C]//2011 IEEE International Symposium on Electromagnetic Compatibility, Long Beach, CA, USA, 2011: 454-458.
[23] Kotny J L, Margueron X, Idir N. High-frequency model of the coupled inductors used in EMI filters[J]. IEEE Transactions on Power Electronics, 2012, 27(6): 2805-2812.
[24] Tan Wenhua, Cuellar C, Margueron X, et al. A high frequency equivalent circuit and parameter extraction procedure for common mode choke in the EMI filter[J]. IEEE Transactions on Power Electronics, 2013, 28(3): 1157-1166.
[25] Domínguez-Palacios C, Bernal J, Prats M M. Characterization of common mode chokes at high frequencies with simple measurements[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 3975-3987.
[26] Ojeda-Rodríguez Á, Bernal-Méndez J, Martín-Prats M A. Modal theory and approach for accurate characterization of common-mode chokes[J]. IEEE Transactions on Power Electronics, 2023, 38(9): 10516-10529.
Abstract As power electronic power converters move towards higher frequencies, it exacerbates the electromagnetic interference (EMI) issues in power electronic systems. Accurate modeling of common-mode chokes is crucial in designing EMI filters and predicting EMI noise in power converter systems. However, existing models struggle to represent the complex parasitic parameter structure inside common-mode chokes accurately. It leads to significant discrepancies between the actual filtering characteristics of common-mode chokes operating at high frequencies and their ideal designs. Particularly concerning are the insertion loss characteristics at multiple resonance points, where existing models struggle to fit the multi-resonance characteristics of common-mode chokes and exhibit entirely different insertion loss trends at high frequencies.
Common-mode chokes can be divided into common-mode and differential-mode components based on the flow path of their magnetic flux. This paper primarily focuses on the analysis and modeling of the differential-mode component. The impedance testing method of traditional common-mode choke differential- mode models does not comply with the EN55017 testing standard. The main difference is that traditional impedance testing typically involves shorting one port of the common-mode choke to measure the differential- mode component. However, shorting the port alters the actual path of the differential-mode current, thereby failing to accurately characterize the complete inter-winding capacitance distribution of common-mode chokes, resulting in different trends between the two testing methods above 10 MHz. Additionally, the traditional common-mode choke differential-mode model assumes ideal inductance. However, when connected in series with the common-mode component at high frequencies, this idealization alters the filtering characteristics of the model's common-mode component. Therefore, the proposed differential-mode model should not exhibit a counteracting effect on common-mode current.
Firstly, by analyzing the electromagnetic field distribution inside common-mode chokes, a new high-frequency model is proposed. This new model, when considering inter-winding capacitance, divides the inductance of the differential-mode component of one winding into two equal parts based on existing terminal capacitance. Furthermore, a new inter-winding parasitic capacitance branch is added between the two parts of the inductance, in conjunction with the existing terminal capacitance branch, to simulate the complete inter-winding electric field characteristics. Setting the differential-mode inductance as a coupled inductance with a coupling coefficient of -1 can fully counteract its influence on the common-mode component. This proposed model accurately fits the insertion loss characteristics of the differential-mode component of common-mode chokes under the EN55017 testing standard's multiple resonance points. Secondly, an equivalent circuit model is established under different insertion loss tests. Utilizing principles such as star-to-delta transformation and the Wheatstone bridge balance principle, the equivalent circuit is simplified, and circuit expressions are derived. Then, a comprehensive process for extracting parasitic parameters within the new model is proposed.
Experimental conclusions are as follows. (1) Setting the inductance model of the differential-mode component as a coupled inductance with k=-1 does not attenuate common-mode current. (2) Compared with traditional models, the proposed new model exhibits good fitting accuracy within the frequency range of 150 kHz to 30 MHz and effectively represents the multi-resonance characteristics of common-mode chokes.
keywords：Electromagnetic interference, filter, common-mode chokes, extraction of parasitic parameters, modeling
中图分类号：TM614
DOI: 10.19595/j.cnki.1000-6753.tces.240297
国家自然科学基金（51777036）和《台达电力电子科教发展计划》资助项目。
收稿日期 2024-02-23
改稿日期2024-03-18
兰宇杰 男，1998年生，博士研究生，主要从事电磁兼容诊断与抑制方面的研究工作。E-mail: lyj9810@foxmail.com
陈庆彬 男，1985年生，教授，博士生导师，主要从事无线电能传输技术和电磁兼容诊断与抑制方面的研究工作。E-mail: cqb@fzu.edu.cn （通信作者）
（编辑 陈 诚）