图1 12/10极电励磁双凸极发电机结构
Fig.1 The structure of a 12/10 pole DSEG
摘要 可控整流发电是提高电励磁双凸极发电机（DSEG）输出功率的有效途径。针对桥式半控正弦化DSEG系统，该文提出了一种基于电流梯度的无位置传感器控制策略。基于桥式半控DSEG工作模态，发现负向换相区间这一特殊位置区域正弦化DSEG感应电动势与电流梯度的特别对应关系，并提出据此进行转子位置估计；在此基础上，为抑制实际DSEG系统脉冲宽度调制（PWM）斩波导致电流梯度难以计算的问题，提出一种基于脉冲触发的电流梯度获取方法以实现负向换相区间这一特殊区间内的绕组感应电动势信息提取；进一步地，为避免续流电流反向增大易造成误触发的问题，提出一种基于非导通相判定的触发信息约束方法；最后，基于脉冲触发估计获得的三个基准位置，对DSEG转速估计进而获得全周期转子位置估计角，实现DSEG桥式半控整流发电的无位置传感器运行。所提方法无需额外增加硬件电路，实验验证了所提控制方法的正确性与有效性。
关键词：正弦化电励磁双凸极发电机 桥式半控整流发电 无位置传感器控制 电流梯度
电励磁双凸极发电机（Doubly Salient Electro- magnetic Machine, DSEM）具有结构简单、可靠性高、磁场调节灵活、故障时易于灭磁等优点，在航空电源、风电等领域具有较大的应用前景[1-4]。传统电励磁双凸极发电机（Doubly Salient Electromagnetic Generator, DSEG）常采用不控整流发电（Bridge Uncontrolled Rectifier, BUCR）方式，通过调节励磁电流实现输出电压控制，无需转子位置信息，但该发电方式的输出功率受限[5-7]。
可控整流发电是提升DSEG发电性能的有效途径，不少学者对其展开了研究[8-9]。文献[8]通过对比分析DSEG全控整流与半控整流发电方法，揭示了DSEG可控整流发电提高系统输出功率密度的机理。针对桥式全控DSEG发电，文献[9]提出了一种DSEG最大输出功率点选取方法，并将提前角度控制与“三相九拍”控制结合，抑制系统损耗，进一步优化系统性能。与不控整流发电相比，可控整流发电需要转子位置信息，一定程度上削弱了其优势，因此，DSEG可控整流发电工况下的无位置传感器技术具有重要研究价值。
在电励磁双凸极电机（Doubly Salient Electro- magnetic Machine, DSEM）无位置传感器控制方面，已有相关学者展开研究，所采用控制方法主要包括电感法[10-11]、反电动势法[12]、磁链法[13-14]等。文献[10]通过向电枢绕组注入一定数量的检测电压脉冲，根据响应电流判断电感关系，从而提取转子位置信息。根据端电压中基波分量的过零点与换相点对应这一特性，文献[11]提出了基于端电压变换的DSEM无位置传感器控制，并优化了滤波器截止频率的选择方法。考虑到DSEM非导通相相电压即励磁电动势，其大小在同一位置下仅与励磁电流和转速相关，文献[12]通过设置与励磁电流和转速相关的线反电动势参考阈值得到换相位置。DSEM线磁链的负向过零点也包含位置信息，文献[13-14]提出将换相点处的自感作为等效自感计算磁链，解决了全周期自感难以测量的问题，降低实施难度并保证了换相点的估计准确性。
尽管上述方法实现了DSEM的无位置传感器运行，但上述研究多针对电动工况。DSEM发电运行特性与电动存在明显区别，导致上述无位置传感器控制方法中的脉冲注入、反电动势提取等方面不能直接应用。DSEG可控整流发电工况的无位置传感器控制策略研究尚处于起步阶段，文献[15]提出了适用于三相H桥半控型变换器的无位置传感器控制方法，通过非导通相电流的自注入估计感应电动势正向过零点获取特殊位置，但该方法依赖于相互解耦的三相电枢电流，无法应用到采用桥式变换器的DSEG可控整流发电系统。DSEG的电机结构、工作原理与开关磁阻发电机（Switched Reluctance Generator, SRG）相似，其无位置传感器控制技术有重要的参考价值。SRG的位置估计方法常基于电感-位置角的对应关系实现[16-17]，文献[16]通过最小均方方法计算相电流斜率估算电感，再根据离线建立的非线性电感-角度映射模型估计换相位置，不受磁路饱和影响，但其存在算法复杂、数据需求量大、训练时间长等不足。文献[17]对SRG非导通相绕组进行滞环控制以注入电流脉冲，通过检测开关管的导通时间判断转子是否到达特殊位置，但该方法需提前存储特殊位置处的电流上升时间，且受转速工况影响。
针对桥式半控整流（Bridge Semi-controlled Rectifier, BSR）正弦化DSEG系统，本文提出一种基于相电流梯度的无位置传感器控制策略。首先基于BSR-DSEG发电特性分析，发现了在负向换相区间，三相绕组电压被钳位至零，其包含转子位置信息的反电动势仅与相电流梯度相关，因此提出一种基于电流梯度的负向换相区间基准位置估计策略；在此基础上，为抑制实际系统脉冲宽度调制（Pulse Width Modulation, PWM）斩波带来电流梯度难以计算的问题，本文提出一种基于脉冲注入的相电流梯度计算方法，为避免换相电流方向增大可能造成脉冲误触发，提出通过增加非导通相绕组判定以提升电流梯度计算准确度；基于估计获得的三个负向换相区间基准位置及估计转速便可获得全角度周期转子位置估计角，进而实现BSR-DSEG的无位置传感器运行。最后，在一台12/10极正弦化DSEG样机上对本文所提方法进行了实验研究，结果验证了所提控制策略的正确性与有效性。
图1给出了本文研究的12/10极正弦化DSEG的结构，其定转子均为凸极结构，转子上无绕组与永磁体，通过定子上的集中式励磁绕组进行励磁，该电机通过转子多段斜极实现电机反电动势正弦以解决传统方波DSEG转矩脉动大的问题[18]。
图1 12/10极电励磁双凸极发电机结构
Fig.1 The structure of a 12/10 pole DSEG
本文以A相绕组感应电动势反向过零点作为转子位置0°，DSEG感应电动势与互感对应关系如图2所示。图中，Lp（p=a, b, c）为A、B、C相电枢绕组自感；Lpf为p相电枢绕组与励磁绕组间的互感；ep为感应电动势，以发电机运行惯例建立其方程，有
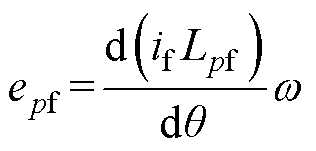（1）
式中，epf为励磁感应电动势；if为励磁电流；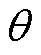
为电机转子电角度；
为电机电角速度。DSEG运行时一般将励磁电流控制在一恒定值，因此，反电动势表达式可化简为
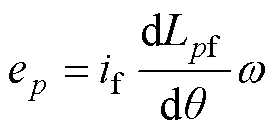（2）
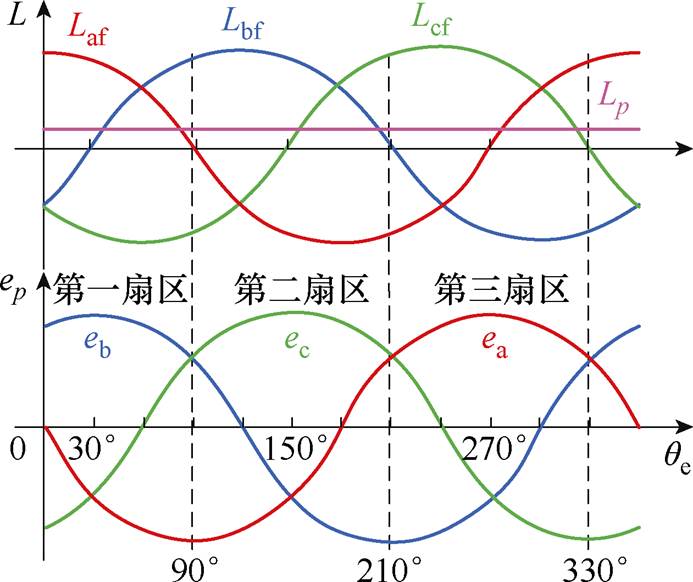
图2 DSEM感应电动势与互感示意图
Fig.2 The schematic diagram of induced EMF
p相绕组的电压为
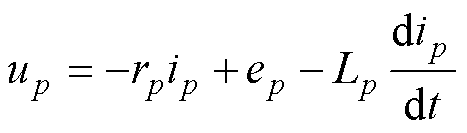（3）
式中，rp为p相绕组内阻；ip为p相电流。
传统DSEG常采用不控整流发电，系统拓扑如图3所示，励磁绕组电流通过不对称半桥控制。该发电方式控制简单、无需位置传感器，但其发电输出功率密度受限[19]。
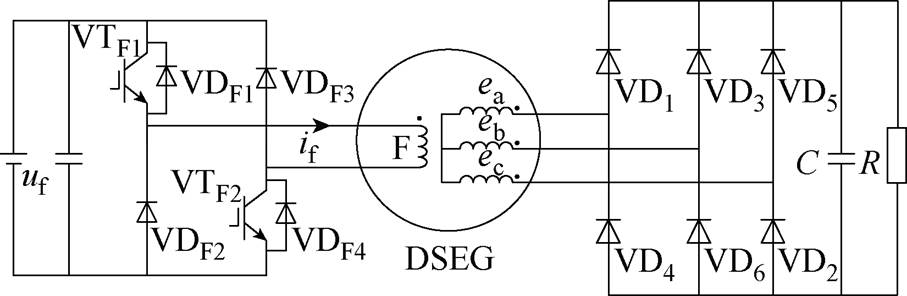
图3 BUCR-DSEG发电系统拓扑
Fig.3 BUCR-DSEG power generation system topology
本文选取BSR构成DSEG可控整流发电系统，拓扑如图4所示，其将不控整流桥下桥臂二极管替换为IGBT，增加绕组储能模态，提高电枢绕组电流变化率，以达到提升DSEG发电功率密度的目的。另外，与全控整流电路相比，其具有控制简单、硬件成本低的优势[20-21]。
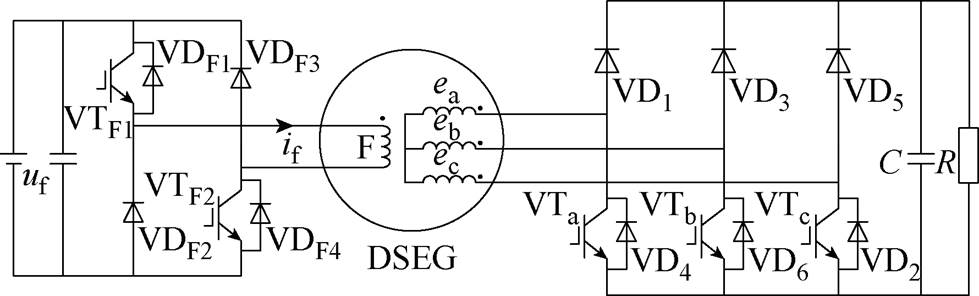
图4 BSR-DSEG发电系统拓扑
Fig.4 BSR-DSEG power generation system topology
图5给出了BSR-DSEG电流斩波控制示意图。图中，gp为相应开关管的驱动信号。如图5所示，根据DSEG感应电动势变化特性，将一个电角度周期划分为三个扇区，以第一扇区（330°～360°+ 30°）为例说明BSR系统工作模态，（330°～360°）区间内，VTb导通（on）时B+C-短路储能，直流侧电容向负载供电，如图6a所示；VTb关断（off）时，B、C两相绕组通过VD3、VD2构成B+C-发电回路，如图6b所示。
图5 BSR-DSEG电流斩波控制示意图
Fig.5 CCC control diagram of BSR-DSEG
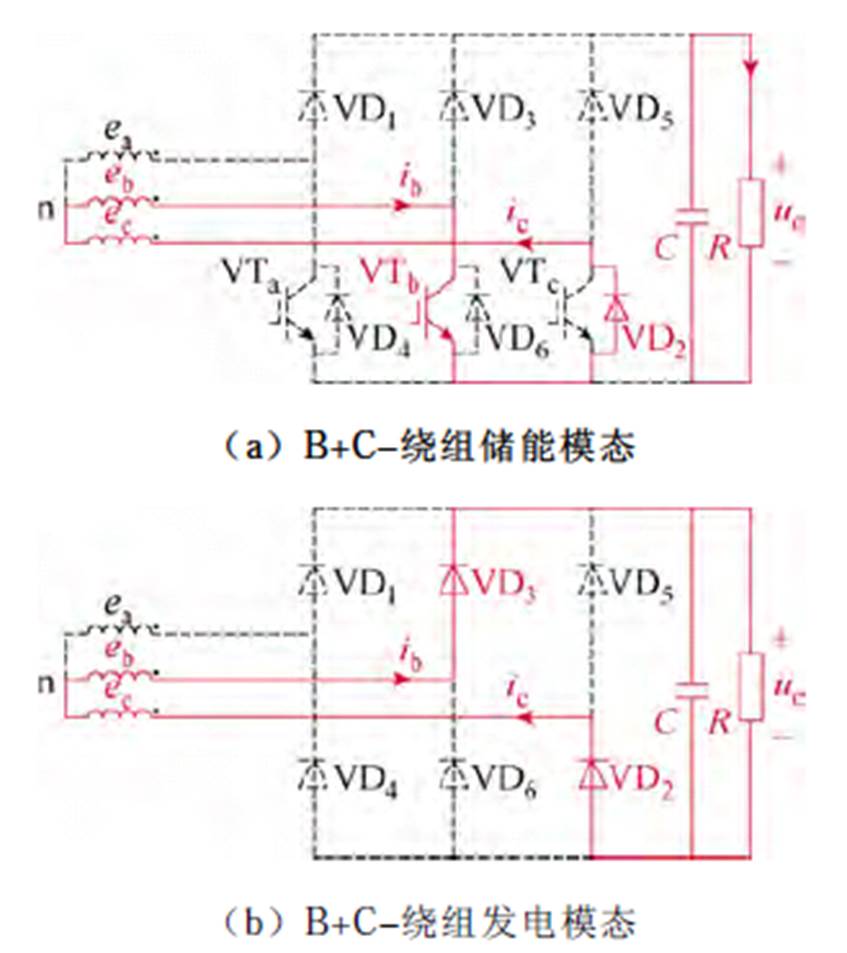
图6 第一扇区BSR-DSEG工作模态示意图
Fig.6 The schematic diagram of BSR-DSEG in sector 1
如图6所示，第一扇区电机中点电压un=-uc，因此有
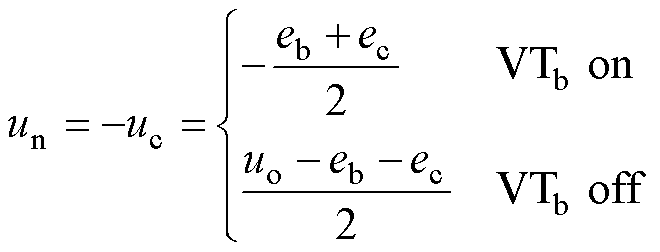（4）
不同开关状态下，中性点电压变化导致绕组端电压发生改变，以A相为例，有
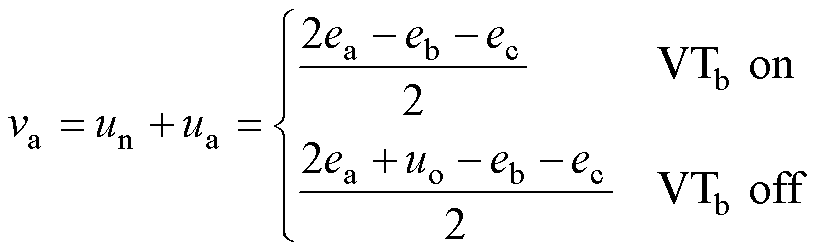（5）
根据该扇区内三相反电动势关系，VTb导通时有va＜0，因此VD4导通，A相绕组出现负向增大的非导通相电流，如图7a所示；VTb关断时va＞0，该电流衰减，系统工作模态如图7b所示。
BSR可控整流发电可以较大地提高系统发电性能，但其需要转子位置信息。DSEM发电运行时转速相对较高，可通过反电动势进行转子位置估计。由第2节分析可知，BSR仅对正向电流斩波控制，在负向换相区间内，相应开关管导通时，三相电压钳位至0，忽略绕组内阻压降，相电流梯度只与自感、感应电动势相关。根据此特性，本文提出根据负向换相区间这一特殊位置的相电流梯度与转子角度（反电动势）的映射关系，实现DSEG转子位置的估计。
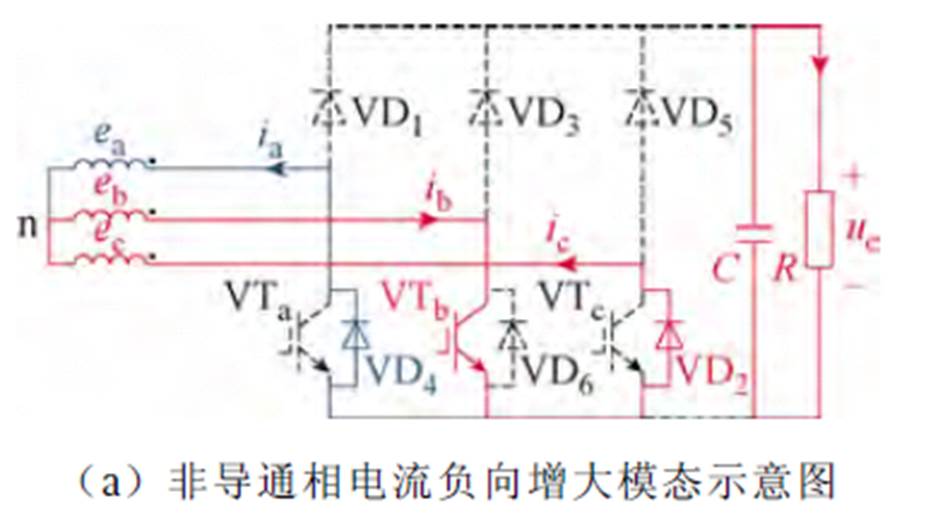
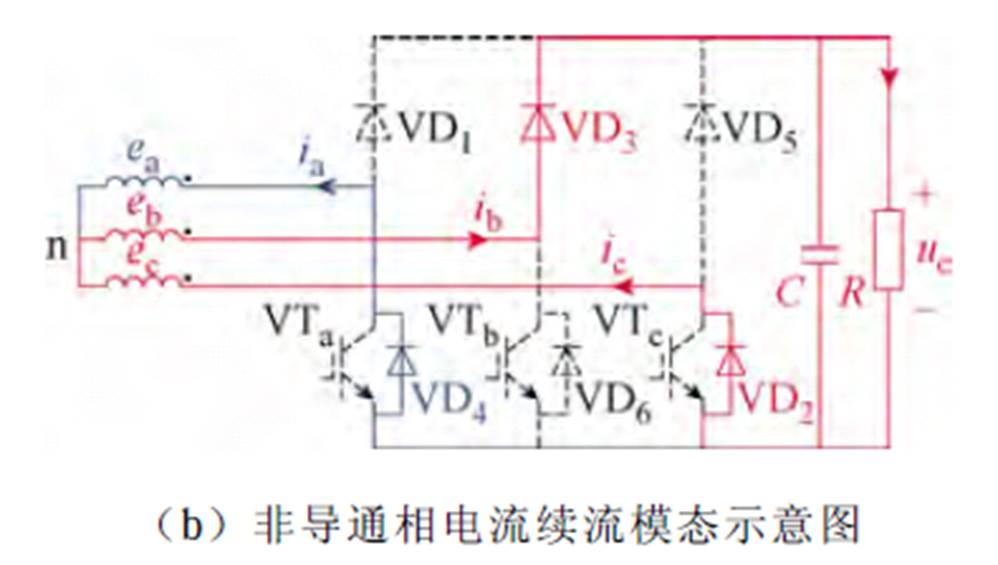
图7 A相非导通相电流路径示意图
Fig.7 Circuit of non-conductive phase current path in A-phase
仍以第一扇区为例，该区间内三相电流示意图如图8所示，该区间内VTb斩波以维持ib在电流参考值iref。
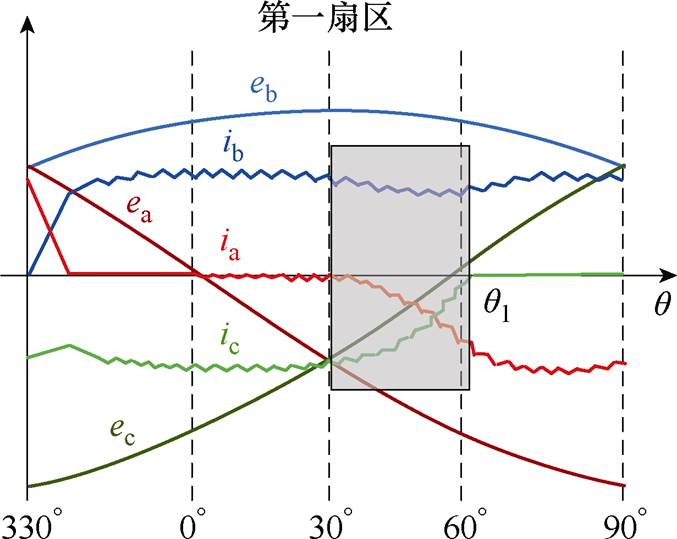
图8 第一扇区三相电流示意图
Fig.8 Three phase currents in sector 1
转子到30°后，A相负向感应电动势最大，负向换相开始，30°～q1区间内，ia反向增大至-iref，由于相电感的存在，ic逐渐衰减至0。本文定义该区间为第一扇区负向换相区间，换相过程中VTb导通时，系统工作模态如图9a所示。
由KVL得
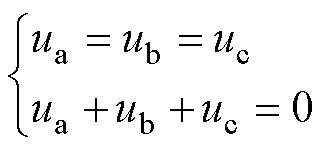（6）
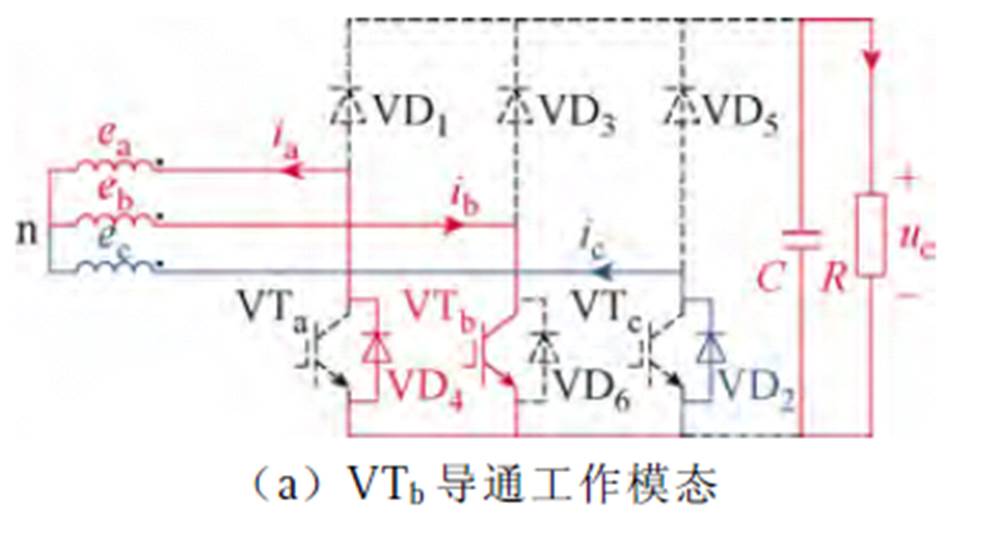
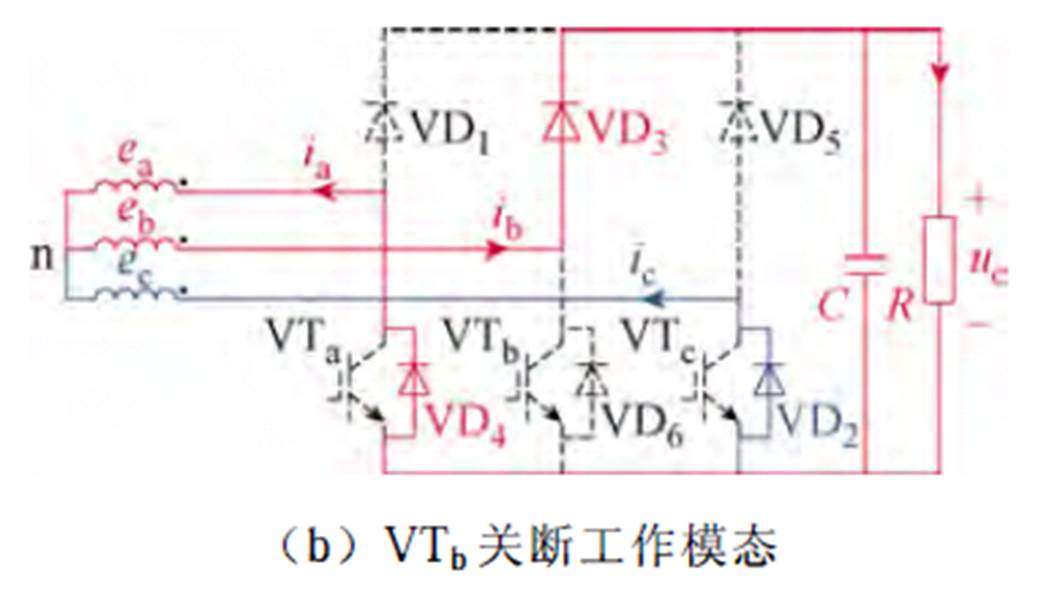
图9 第一扇区负向换相区间工作模态
Fig.9 The operating mode of negative commutation process in sector 1
可知该工作模态下绕组相电压被钳位于0，若忽略绕组内阻，由式（3）得p相电流梯度表示为
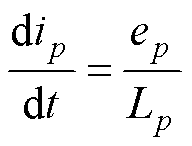（7）
因此，第一扇区的负向换相区间内，开关管VTb导通时，相电流梯度与绕组感应电动势呈正相关。VTb关断时，A、B相绕组相负载供电同时给直流侧电容充电，ic通过VD2续流，电路模态如图9b所示，由KVL可知，此模态下三相电压表达式为
（8）
进一步地，结合式（3），可得该模态下三相相电流梯度表达式为
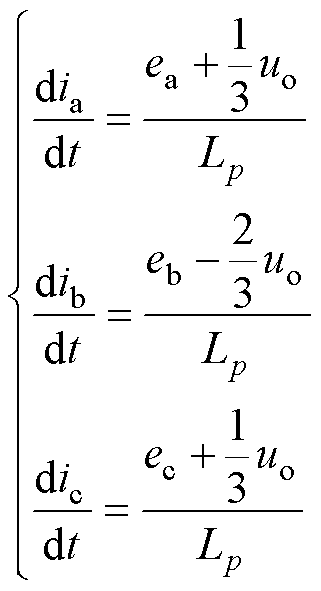（9）
结合式（7）及感应电动势关系，在第一扇区的负向换相区间内，ia梯度为负，ic梯度随VTb通/断状态负/正交替变化。
综上所述，在负向换相区间内，相应开关管导通时，电流梯度包含绕组反电动势信息，开关管关断会导致续流相电流负向增大。
根据3.1节分析，在负向换相区间，基于三相电流梯度获取绕组反电动势信息便可实现该区间内一基准位置qp的估计，进一步结合估计转速实现可控整流发电无位置传感器运行。
如图2所示，本文研究正弦化DSEG三相绕组感应电动势表达式为
（10）
式中，k为互感Lpf对转子角度导数的峰值。因此，第一扇区负向换相区间转子位置qa表达式为
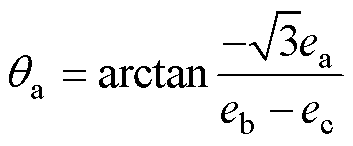（11）
进一步地，结合式（7），有
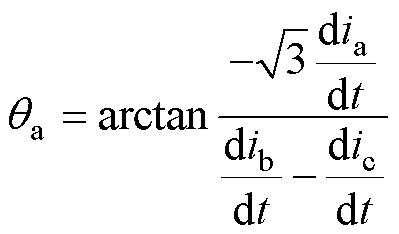（12）
其他两个扇区基准位置qb、qc的估计亦有类似方法，有
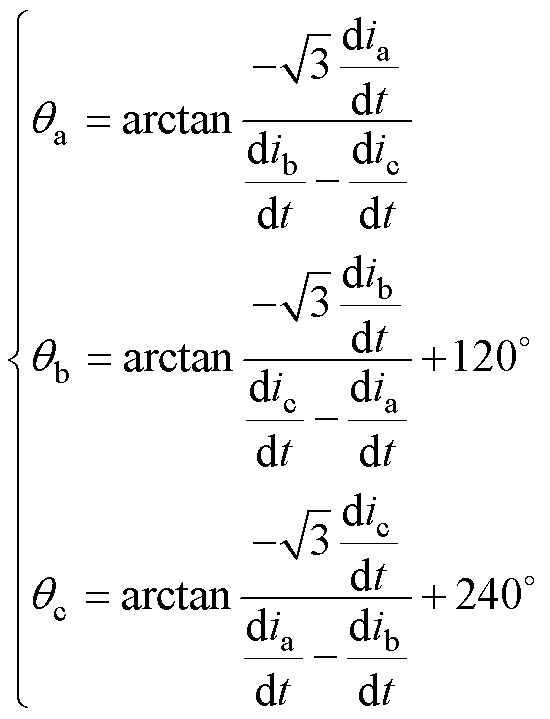（13）
实际BSR DSEG系统中相电流呈高频斩波状、电流梯度正负交变，第一扇区负向换相区间三相电流示意图如图10所示。考虑到系统中采样频率与开关频率一致，即一个控制周期仅进行一次电流采样，这给电流梯度的获取带来较大难度。为此，本文提出一种基于触发函数的电流梯度获取策略：通过控制相应开关管导通两个控制周期，向三相绕组注入电流，使相电流单调变化两个采样周期来准确获取电流梯度。
为确保系统在注入电流时工作于负向换相区间，避免非导通相绕组无法注入电流的问题，本文提出通过设置电流阈值ion-ref与过阈值触发函数hitp来确定电流注入时刻。当负向换相区间内的反向增大电流越过ion-ref时触发函数hitp=1，表明转子位于负向换相区间。在之后的两个控制周期内，开通相应开关管注入电流，在此过程中进行电流梯度辨识并估计基准位置。基于触发函数的电流注入方法如图11所示，以A相为例，ia在负向换相区间增大越过ion-ref，开通B相开关管VTb，驱动信号为gb-inject，在此区间注入电流并估计基准位置qa。
图10 第一扇区负向换相区间三相电流示意图
Fig.10 Schematic diagram of three-phase current in the negative commutation of the first sector
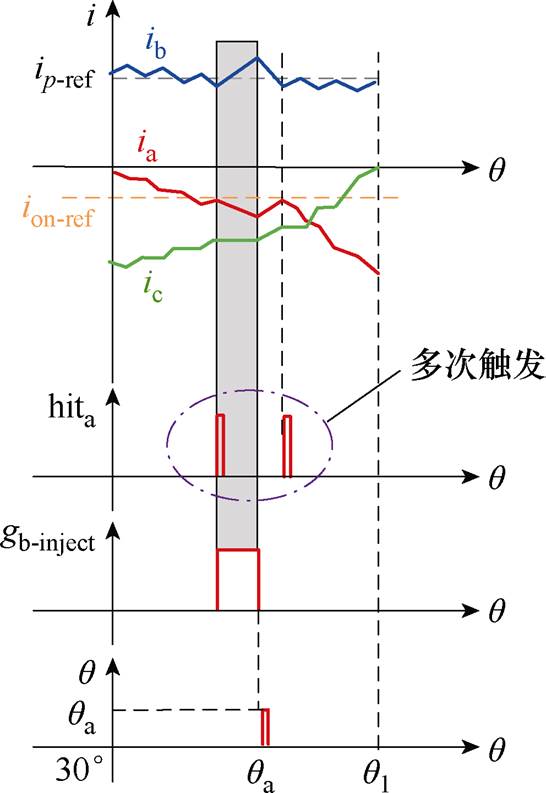
图11 基于触发函数的电流注入方法
Fig.11 The current injection method based on trigger function
为避免电流梯度辨识结束后出现如图11所示多次越过ion-ref使得算法重复执行，导致电流脉动增大的问题，设置对触发函数值累加，如式（14）所示。当且仅当累加函数Jp=1后的两个控制周期内执行位置估计算法，获取当前扇区内的基准位置后重置前扇区对应累加函数。
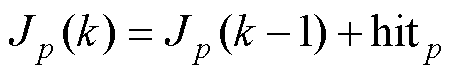（14）
式中，Jp(k)与Jp(k-1)分别为当前计算周期和上一计算周期函数值。
另外，上述方法需负换相区间内的反向增大电流触发实现，为避免3.1节分析的续流电流反向增大造成的误触发问题，提出增加基于非导通相判定的触发电流约束条件。由图5可知，不同扇区的负向换相开始时导通相绕组不同，电流路径存在区别，在换相过程中存在相似特性，可根据电流正负判断非导通相以选取触发电流。以第一扇区为例，负向换相结束前持续存在B+C-电流，定义此区间中A相绕组为非导通相Anon，在此区间内仅以ia作为触发电流，消除续流电流ic的影响。其余两个扇区亦有类似方法，基于非导通相判定的触发电流约束条件见表1。
表1 基于非导通相判定的触发电流约束条件
Tab.1 Constraint based on non-conductive phase judgment of trigger current
电流模态非导通相Pnon触发电流ip B+C-Anonia C+A-Bnonib A+B-Cnonic
在电流阈值选取方面，若电流阈值设置过小，非导通相反电动势较小，导致电流梯度较小，影响基准位置估计准确度；若电流阈值设置过大，电流梯度较大，开关管导通时电流脉动增大，影响系统性能。综合考虑，本文根据当前电枢电流参考值设置电流阈值ion-ref为
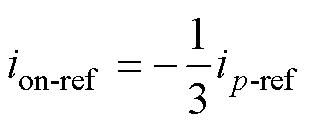（15）
式中，ip-ref为电枢电流给定值。
以第一扇区基准位置qa的估计过程为例说明本节所提控制方法。基于触发函数的基准位置qa获取方法如图12所示，第一扇区负向换相开始前为B+C-工作模态，由表1可得此时为Anon区间，以ia作为触发电流，其反向增大越过ion-ref时hita=1，在之后的两个控制周期内控制开关管VTb导通两个控制周期以获取电流梯度，驱动信号如图12中gb-inject所示，在此区间内三相电流如图12灰色区域所示，gb-inject结束后输出基准位置qa，之后第一扇区不再执行算法，第二扇区对应基准位置qb估计结束后清零Ja。
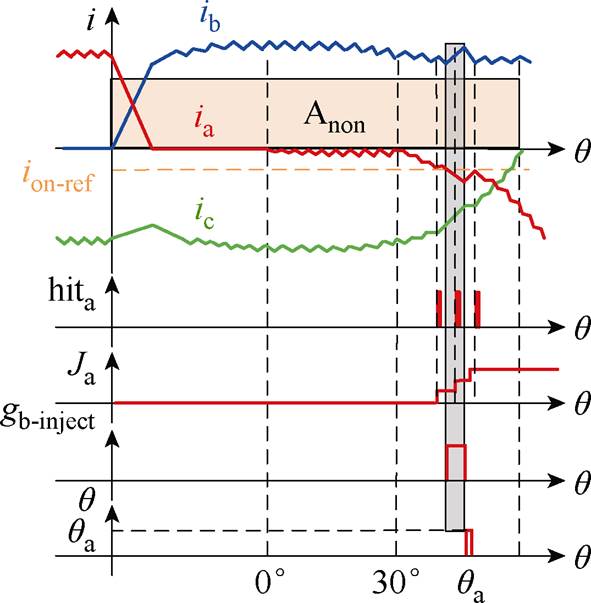
图12 基于触发函数的基准位置qa获取方法
Fig.12 The method for obtaining qa based on trigger function
在估计获得三个基准位置qa、qb、qc后，通过相邻两个基准位置之间的角度差Dq 与时间间隔DT即可估计角速度west，有
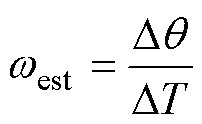（16）
进一步地，便可得到全周期转子位置角，有
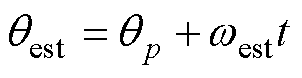（17）
式中，t为距离最近一次基准位置的时间；qp为最近一次的基准位置。转子位置估计流程如图13所示，图中Jp*为上一扇区对应累加函数。
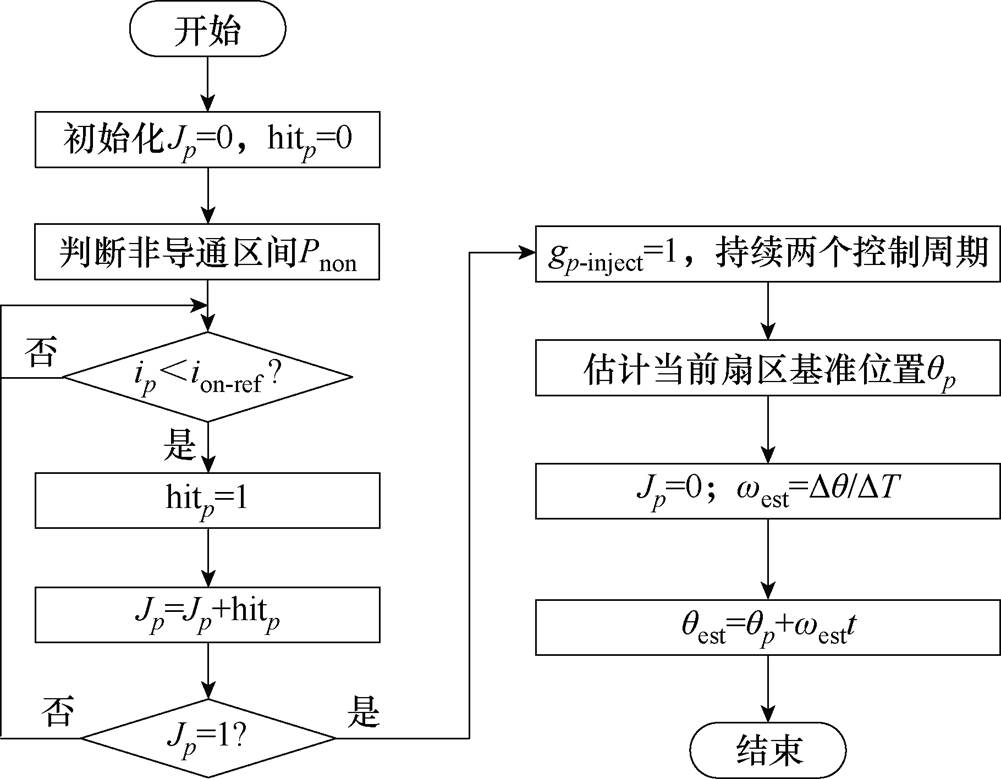
图13 位置估计方法实施流程
Fig.13 Position estimation method flowchart
图14给出了DSEG BSR无位置传感器可控整流发电控制框图，励磁电流控制在额定值if-ref，系统发电采用经典电压外环、电流内环双闭环控制模式，斩波所需转子位置信息由3.3节所提估计方法获得。
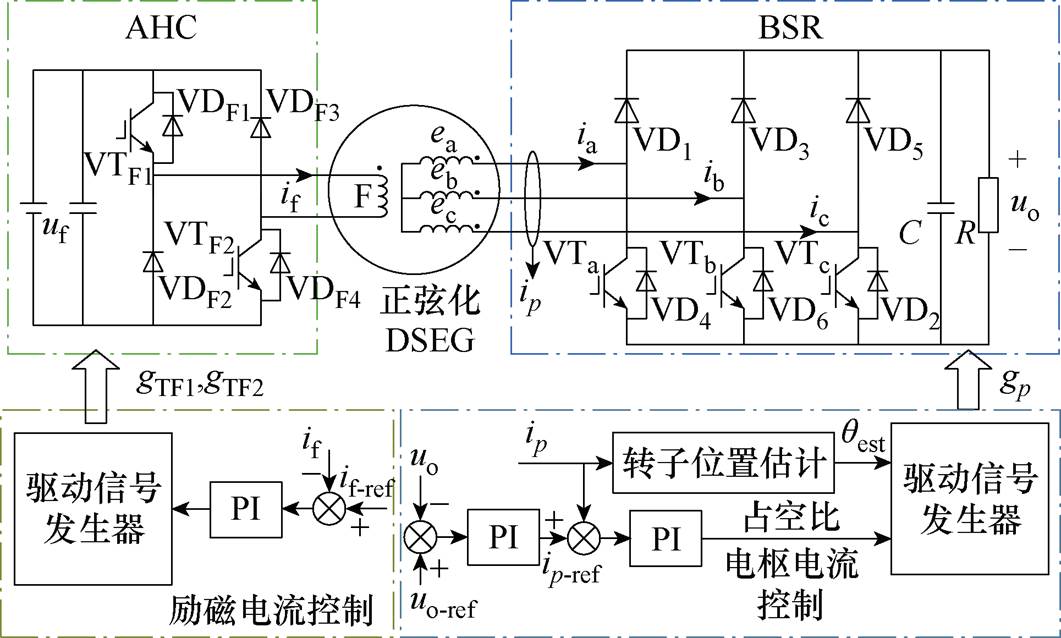
图14 BSR DSEG无位置传感器控制框图
Fig.14 Position sensorless control block diagram for BSR DSEG
图15给出了DSEG实验平台示意图，主要包括一12/10极正弦化DSEG、与之同轴连接的永磁同步电机、功率电路、采样调理电路、驱动电路、可调电阻负载箱等。DSEG主要参数见表2。
图15 实验平台示意图
Fig.15 Schematic diagram of the experimental platform
表2 DSEG主要参数
Tab.2 Main parameters of DSEG
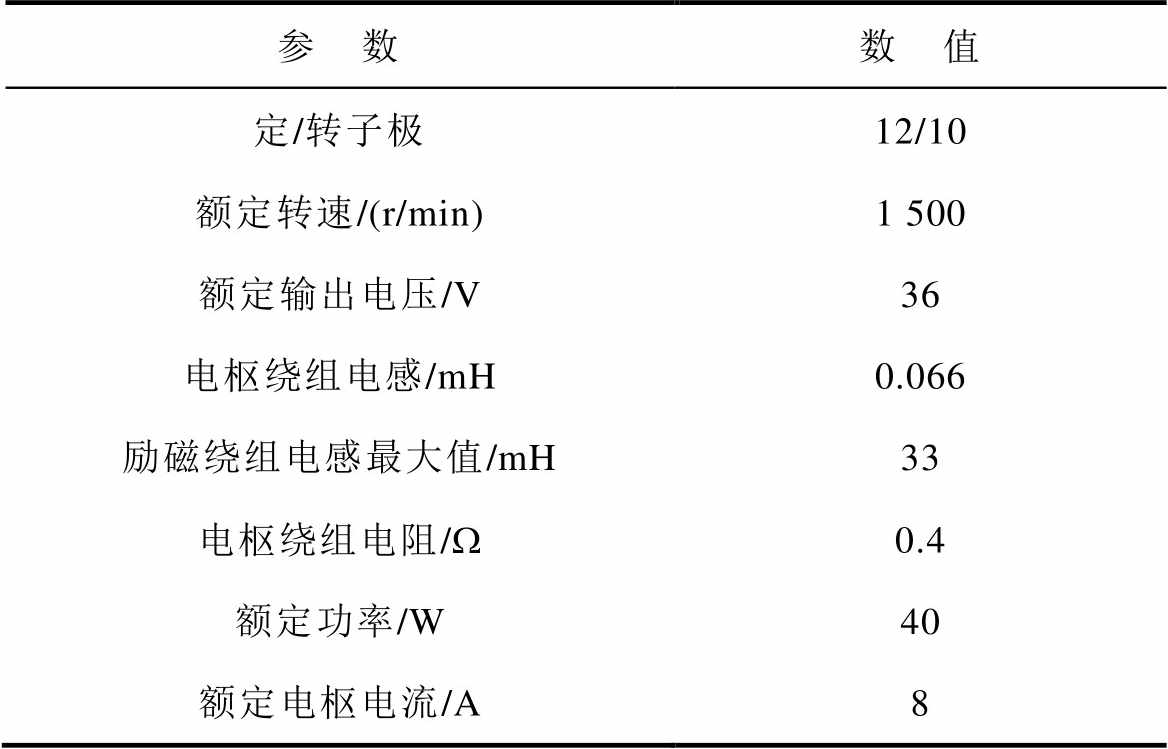
参 数数 值 定/转子极12/10 额定转速/(r/min)1 500 额定输出电压/V36 电枢绕组电感/mH0.066 励磁绕组电感最大值/mH33 电枢绕组电阻/W0.4 额定功率/W40 额定电枢电流/A8
图16给出了额定工况下样机的感应电动势波形。可以看出，样机感应电动势正弦且三相对称，验证了新型样机设计的正确性，同时为本文研究无位置传感器控制方法奠定了基础。
然后对BSR DSEG可控整流发电进行实验验证。图17给出了不同工况下有位置传感器的实验结果，可以看出，电流波形与第2节分析一致，系统输出电压稳定于给定值36 V，验证了BSR DSEG可控整流发电的有效性。
图16 样机三相感应电动势
Fig.16 The three-phase induced electromotive force of the experimental prototype
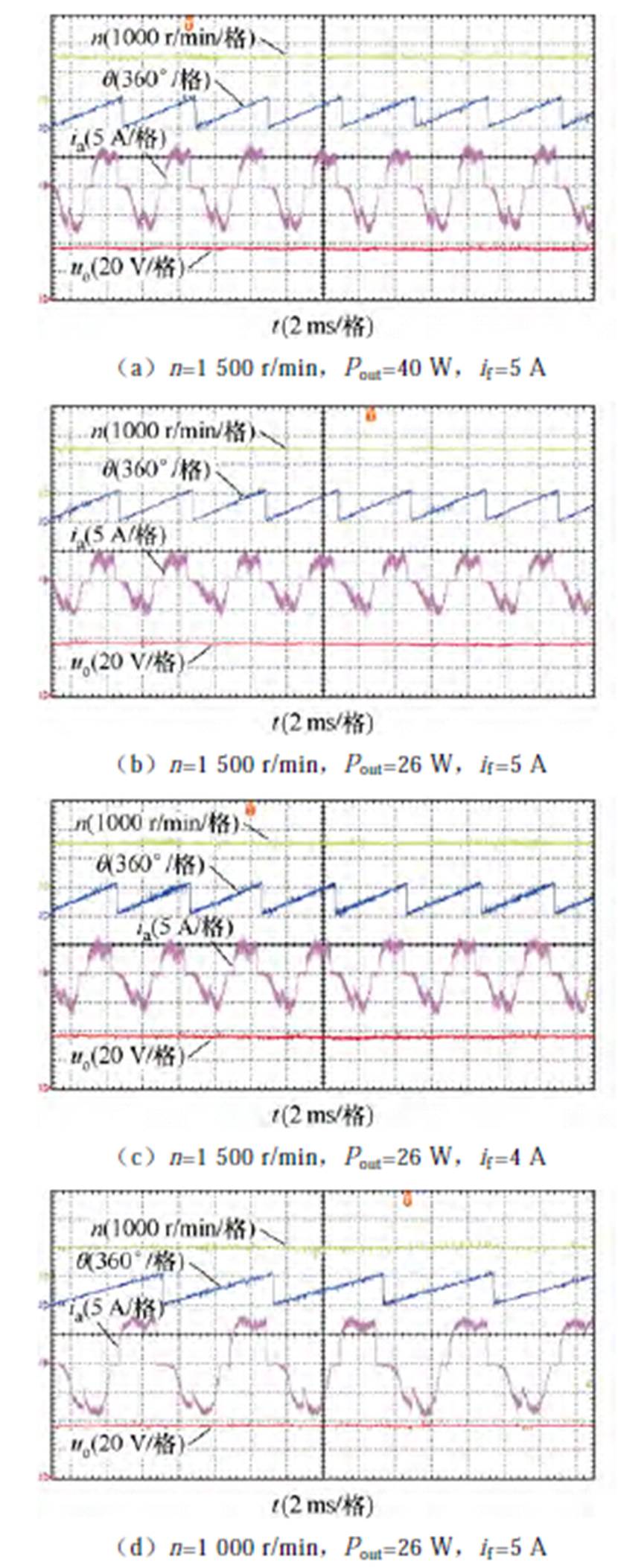
图17 桥式半控整流发电实验波形
Fig.17 BSR power generation experimental waveforms
在此基础上，对本文所提BSR DSEG转子位置估计方法进行实验验证。综合考虑非导通相电流幅值对采样精度及转子位置估计的影响，实验设置ion-ref=-1/3iref。图18a给出了基于电流触发函数的脉冲注入细节波形，可以看出，在该区间内，当ia负向增大越过ion-ref时，触发函数hita=1，在接下来两个控制周期100 ms内开通B相功率管，在导通区间内进行电流梯度计算及基准位置qa估计。需要说明的是，由于该区间内系统处于短路储能模态，输出基准位置后VTb依然导通一段时间，导致ia仍反向增大。一个电角度周期内三个基准位置的估计结果如图18b所示，可以看出，本文所提方法能够实现三个基准位置及转速的估计。
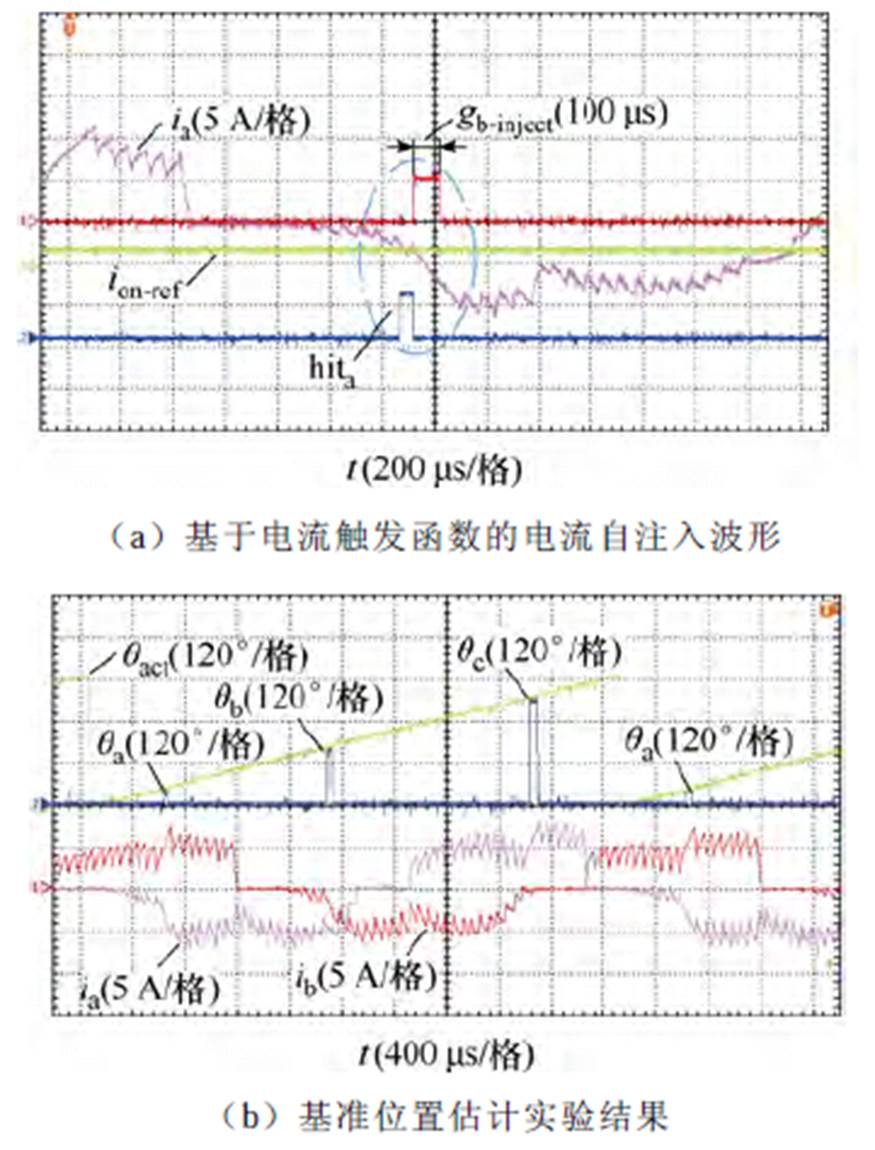
图18 基于电流触发函数的基准位置估计实验结果
Fig.18 Experimental results of qp estimation based on current triggering function
在上述实验基础上，对BSR DSEG无位置传感器控制进行了实验研究，图19给出了稳态实验结果。可以看出，在宽转速、负载工况下，所提方法能够在全角度周期准确估计转子位置，不同工况下iref的差异导致阈值ion-ref的不同，因此基准位置估计区间呈现差别，但所提方法均能在负向换相区间实现基准位置估计，实现了BSR DSEG无位置传感器可控整流发电的稳定运行。
接着对所提方法的动态性能进行实验，在额定励磁if =5 A条件下进行了以下加减速（1 000 r/min至1 500 r/min）、加卸载（26 W至40 W）动态实验，结果如图20所示。可以看出，在转速、负载变化工况下，所提方法依然能够准确地进行转子位置估计，经一定动态调节时间后，输出电压稳定于给定电压，BSR DSEG系统能够稳定发电运行，验证了所提方法的正确性及可行性。
图19 稳态实验结果
Fig.19 Experimental results of steady state
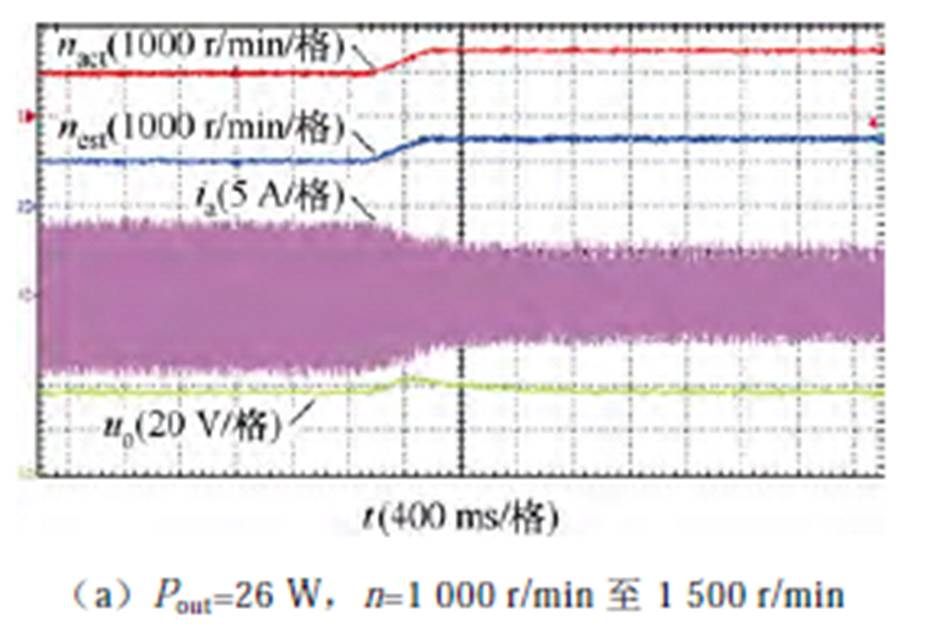
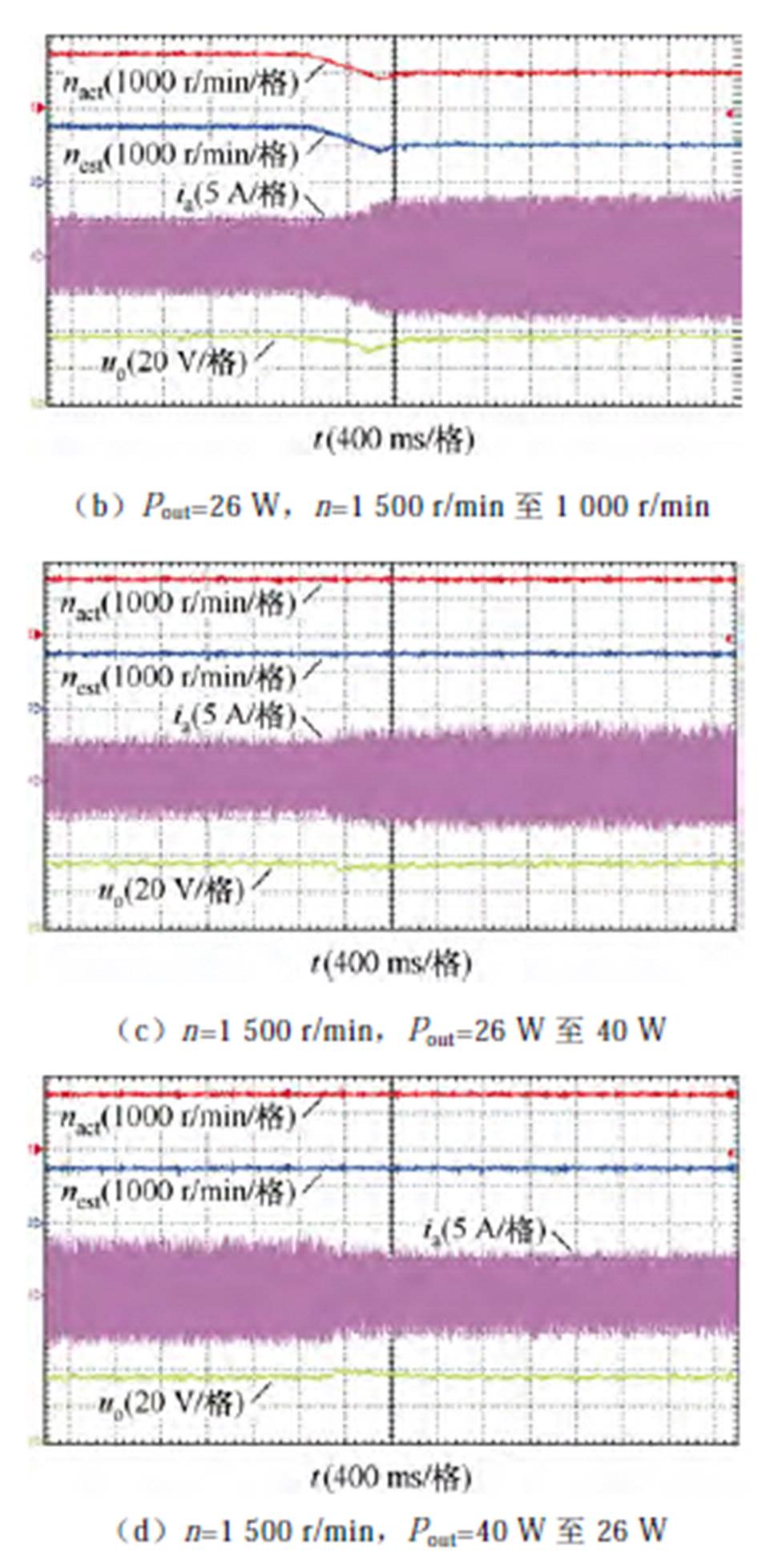
图20 动态实验结果
Fig.20 Experimental results of dynamic state
图21给出了1 000 r/min至1 500 r/min加速、36.7 W至40.1 W加载动态过程的实验结果，并给出了全过程转子位置估计曲线，结果表明，本文所提无位置传感器控制策略在加速、加载动态过程中依然能够进行转子位置估计，系统能够稳定运行。
图21 动态过程估计角度与实际角度对比结果
Fig.21 Comparison results between estimated angles and actual angles in dynamic processes
图22给出了动态过程位置估计误差曲线，由于估计转速更新存在一定滞后，且本文进行转子位置估计时基于两个基准位置间（1/3电角度周期）电机转速恒定，导致转子位置估计相较于稳态过程误差增大，加速、加载过程误差在±10°左右，系统运行稳定，考虑到这是系统相对很短暂的动态运行过程，可认为这个估计误差对整个DSEG发电系统来说是可以接受的。
为提高DSEG-BSR系统功率密度及可靠性，基于系统发电模态分析，本文提出一种基于电流梯度的无位置传感器控制方法，为提高所提方法准确性及可实施性，进一步构建了基于脉冲触发的相电流梯度计算方法。实验结果表明：
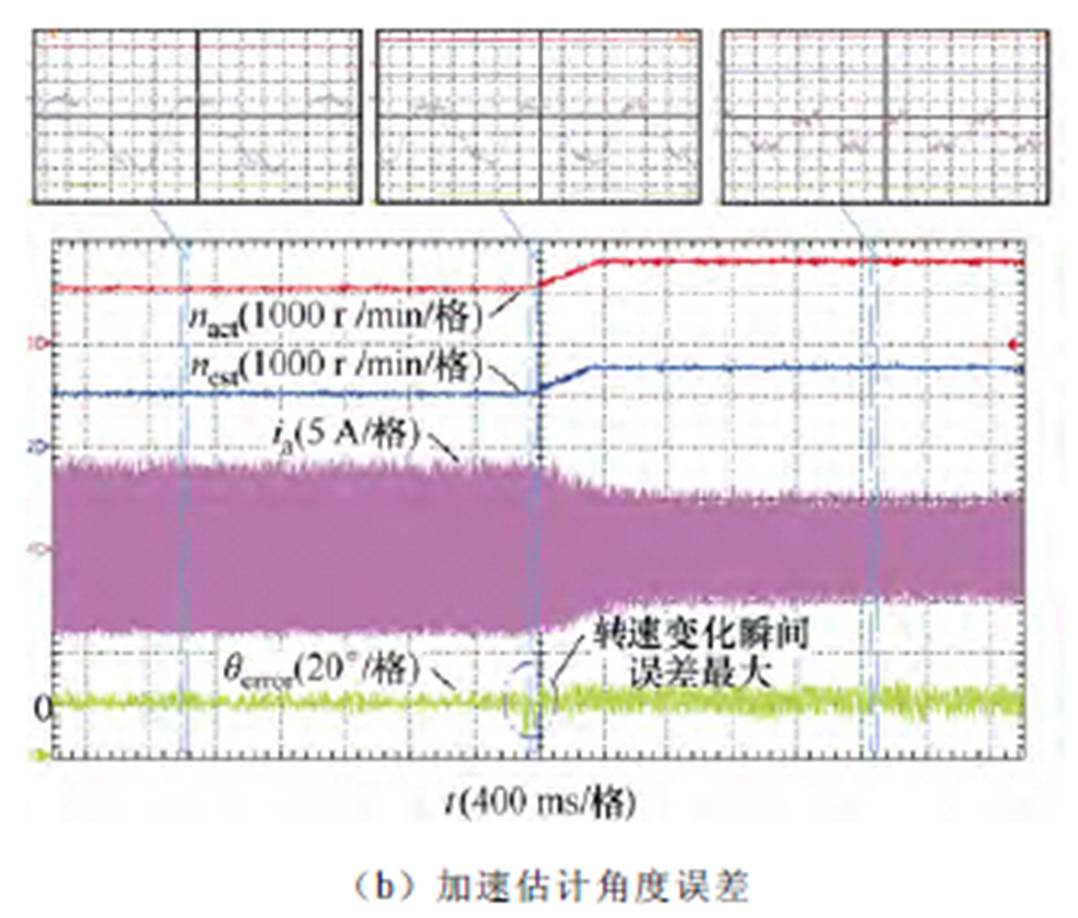
图22 动态过程估计角度误差
Fig.22 Comparison results between estimated angles and actual angles in dynamic processes
1）本文所提脉冲触发方法能够实现负换相区间三相电流梯度的准确辨识，实现了负向换相这一特殊区间的基准位置估计。
2）本文所提方法能够在宽转速、负载及稳态、动态工况下进行转子位置准确估计，实现了BSR DSEG的无位置传感器运行。
3）本文所提方法无需预知系统参数、无需额外增加硬件，具有较强的适应性，亦可推广应用于其他DSEG发电系统中。
鉴于本方法所获得转子位置基于三个扇区基准位置估计精度及基准位置间转速不变的假设，在转速变化动态过程产生一定误差，后期可采用基于转子加速度不变的方法估计转子位置信息以进一步提升系统动态过程位置估计精度；另外，本方法基于三相正弦反电动势进行转子位置估计，应用于传统方波DSEM中，需要进一步根据特殊的非正弦反电动势特性进行相应改进。
参考文献
[1] Sarlioglu B, Morris C T. More electric aircraft: review, challenges, and opportunities for commercial transport aircraft[J]. IEEE Transactions on Trans- portation Electrification, 2015, 1(1): 54-64.
[2] 赵耀, 沈翀, 李东东, 等. 极端条件下基于特征层面信号融合的电励磁双凸极电机匝间短路故障诊断[J]. 电工技术学报, 2023, 38(10): 2661-2674.
Zhao Yao, Shen Chong, Li Dongdong, et al. Inter-turn short circuit diagnosis of wound-field doubly salient machine based on multi-signal fusion on feature level under extreme conditions[J]. Transactions of China Electrotechnical Society, 2023, 38(10): 2661-2674.
[3] 陈旭, 张卓然, 于立, 等. 基于改进型准比例谐振控制的电励磁双凸极电机电流谐波抑制方法[J]. 电工技术学报, 2023, 38(14): 3836-3848, 3861.
Chen Xu, Zhang Zhuoran, Yu Li, et al. Current harmonic suppression method of doubly salient electro-magnetic machine based on improved quasi proportional resonant control[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3836- 3848, 3861.
[4] 赵耀, 陆佳煜, 李东东, 等. 基于机电信号融合的电励磁双凸极电机绕组匝间短路故障诊断[J]. 电工技术学报, 2023, 38(1): 204-219.
Zhao Yao, Lu Jiayu, Li Dongdong, et al. A fault diagnosis strategy for winding inter-turn short-circuit fault in doubly salient electro-magnetic machine based on mechanical and electrical signal fusion[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 204-219.
[5] Zhao Yao, Wang Huizhen, Li Dongdong, et al. Comparative research of a wound-field doubly salient generator with different rectifiers[J]. IEEE Transa- ctions on Industrial Informatics, 2018, 14(11): 4851- 4863.
[6] 温腾翔, 周波, 周兴伟, 等. 电励磁双凸极发电机励磁故障容错控制策略[J]. 中国电机工程学报, 2019, 39(10): 3047-3055.
Wen Tengxiang, Zhou Bo, Zhou Xingwei, et al. Fault-tolerant control of doubly salient electro- magnetic generators under excitation fault con- ditions[J]. Proceedings of the CSEE, 2019, 39(10): 3047-3055.
[7] 许涵, 赵争鸣, 施博辰, 等. 基于离散状态事件驱动的电励磁同步电机系统建模解算方法[J]. 电工技术学报, 2023, 38(10): 2602-2612.
Xu Han, Zhao Zhengming, Shi Bochen, et al. Modeling and simulation of electrically excited synchronous machine based on discrete state event- driven approach[J]. Transactions of China Electro- technical Society, 2023, 38(10): 2602-2612.
[8] Wang Kaimiao, Zhou Bo, Zhou Xingwei. Com- parative researches on doubly salient electro-magnetic generator with semi-controlled and full-controlled rectification methods[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-6.
[9] Chen Liang, Xu Yanwu, Ding Shuye, et al. Output performance model and three-phase nine-state control for doubly salient electromagnetic generator[J]. IEEE Transactions on Power Electronics, 2023, 38(12): 16022-16033.
[10] Zhou Xingwei, Zhou Bo, Wang Kaimiao, et al. Two-step rotor position estimation method for doubly salient electromagnetic starter-generator over zero and low speeds range[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(3): 2664-2673.
[11] Liu Weifeng, Wang Huizhen, Wang Yongjie, et al. Position sensorless control for doubly salient electro- magnetic motor based on the terminal voltage[J]. IET Electric Power Applications, 2019, 13(12): 2070- 2078.
[12] Zhou Xingwei, Zhou Bo, Wang Kaimiao. Position sensorless control for doubly salient electromagnetic machine with improved startup performance[J]. IEEE Transactions on Industrial Electronics, 2020, 67(3): 1782-1791.
[13] Liu Weifeng, Wang Huizhen, Wang Yongjie, et al. Sensorless control strategy for doubly salient electro- magnetic machine based on the line-to-line excitation flux linkage[J]. IET Electric Power Applications, 2019, 13(12): 1911-1920.
[14] 付康壮, 刘计龙, 麦志勤, 等. 改进型IF控制结合有效磁链法的永磁同步电机全速域无位置传感器控制策略[J]. 电工技术学报, 2022, 37(22): 5704-5716.
Fu Kangzhuang, Liu Jilong, Mai Zhiqin, et al. A full-speed domain sensorless control strategy for permanent magnet synchronous motor based on improved IF control and effective flux method[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5704-5716.
[15] Wang Kaimiao, Zhou Bo, Zhou Xingwei, et al. A current self-injection based position sensorless control for DSEG with controlled rectification[J]. IEEE Transactions on Power Electronics, 2022, 37(3): 3308-3320.
[16] Echenique E, Dixon J, Cardenas R, et al. Sensorless control for a switched reluctance wind generator, based on current slopes and neural networks[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 817-825.
[17] Chen Hao, Nie Rui, Gu J, et al. Efficiency opti- mization strategy for switched reluctance generator system with position sensorless control[J]. IEEE/ ASME Transactions on Mechatronics, 2021, 26(1): 469-479.
[18] 蒋思远, 周波, 黄旭珍, 等. 不同励磁方式的电励磁双凸极电机正弦化设计与分析[J]. 中国电机工程学报, 2023, 43(4): 1598-1611.
Jiang Siyuan, Zhou Bo, Huang Xuzhen, et al. Sinusoidal design and analysis of doubly salient electro-magnetic machine with two different exci- tation modes[J]. Proceedings of the CSEE, 2023, 43(4): 1598-1611.
[19] 陈冉, 陈志辉, 毛志鑫, 等. 一种用于电励磁双凸极发电机的新型半控整流拓扑研究[J]. 中国电机工程学报, 2012, 32(36): 117-122.
Chen Ran, Chen Zhihui, Mao Zhixin, et al. A novel rectifier topology for doubly salient electro-magnetic generators[J]. Proceedings of the CSEE, 2012, 32(36): 117-122.
[20] Wang Kaimiao, Zhou Bo, Zhou Xingwei, et al. Minimum field current increment control for doubly salient electro-magnetic generator with improved dynamic performance[J]. IEEE Transactions on Indu- strial Electronics, 2022, 69(5): 4566-4575.
[21] 殷生晶, 王晓琳, 张艳. 基于扰动观测器补偿的高速永磁同步发电机稳压控制策略[J]. 电工技术学报, 2023, 38(14): 3800-3811.
Yin Shengjing, Wang Xiaolin, Zhang Yan. Voltage stabilization control strategy of high-speed permanent magnet synchronous generator based on disturbance observer compensation[J]. Transactions of China Electrotechnical Society, 2023, 38(14): 3800-3811.
Abstract The doubly salient electromagnetic machine (DSEM) features a simple structure, high reliability, flexible magnetic field regulation, and easy demagnetization in case of failure. It is promising for applications in aviation power supplies and wind power generation. Traditional doubly salient electromagnetic generator (DSEG) often employs uncontrolled rectification generation methods. The output voltage is regulated by adjusting the field current, but this method limits the output power improvement. Compared to the uncontrolled rectification generation, the controlled rectification generation can enhance the output power by adding the armature current regulation. However, the rotor position information is required. Thus, sensorless control for the DSEM with a controlled rectifier is of great research value. Taking the DSEM with a bridge semi-controlled rectifier (BSR) sinusoidal DSEG system as an example, this paper proposes a novel sensorless control strategy based on the current gradient.
Firstly, by analyzing the operating mode of the DSEG with BSR, the corresponding relationship between sinusoidal DSEG inductive electromotive force (EMF) and the current gradient is explored in the negative commutation region. A current gradient acquisition method based on pulse triggering is proposed to extract the back EMF information. Furthermore, a triggering information constraint method based on non-conductive phase judgment is proposed to avoid the error trigging caused by the reverse freewheeling. Finally, the estimated rotor position through the electrical cycle can be obtained according to the three reference angular positions and the estimated angular velocity.
The current waveforms aligned with previous analyses, and the system's output voltage stabilized at the command value of 36 V, confirming the effectiveness of the controlled rectification generation for the BSR DSEG. Tests on sensorless control for the BSR DSEG were conducted. Under wide speed and load conditions, the proposed method accurately estimated the rotor position throughout the angular cycle, achieving stable sensorless controlled rectification generation for the BSR DSEG. Furthermore, dynamic performance experiments were conducted under rated excitation conditions, including acceleration, deceleration, loading, and unloading tests. The results demonstrated that the proposed method consistently provided accurate rotor position estimation under varying speed and load conditions, ensuring stable power generation operation.
Conclusions can be drawn as follows. (1) The proposed pulse triggering method can accurately identify the three-phase current gradient in the negative commutation interval, achieving benchmark position estimation in this particular interval. (2) The proposed method enables accurate rotor position estimation under wide speed, load, and steady-state and dynamic conditions, facilitating the sensorless operation of the BSR DSEG. (3) The proposed method does not require prior knowledge of system parameters or additional hardware, demonstrating strong adaptability and potential for application in other DSEG generation systems.
keywords：Sinusoidal doubly salient electromagnetic generator, bridge semi-controlled rectifier (BSR), position sensorless control, current gradient
中图分类号：TM352
DOI: 10.19595/j.cnki.1000-6753.tces.240341
国家自然科学基金（52377046）和江苏省自然科学基金（BK20242051）资助项目。
收稿日期2024-03-04
改稿日期2024-05-29
周兴伟 男，1990年生，博士，副教授，研究方向为电机驱动控制、新能源发电。E-mail: zhxw@hhu.edu.cn（通信作者）
郭耀武 男，1999年生，硕士研究生，研究方向为电机驱动控制。E-mail: ywguo@hhu.edu.cn
（编辑 崔文静）