
图1 高速直线感应电机拓扑及等效电路
Fig.1 The topology and equivalent circuit of linear induction motor with segmented stator
摘要 高速直线感应电机在跨声速运行时,激波非定常特性引发的抖振现象易导致电机动子速度测量受到强烈不确定扰动,推力控制失稳、跨声速运行失败。该文首先建立了高速直线感应电机自学习数学模型,由历史实验数据学习电机模型参数,依据数学模型对直线感应电机动子速度进行高精度多步预测。其次由预测速度与传感器量测速度构建滚动预测矩阵,提出基于矩阵列向量变异程度的量测速度可信度计算方法。最后依据预测速度、量测数据及可信度值加权运算,提出不确定扰动下高速直线感应电机自学习抗扰控制策略。仿真结果验证了自学习抗扰控制策略对短时不确定扰动有较好的抑制效果,在跨声速时修正速度与实际速度误差小于0.7%,有效解决了不确定扰动导致的电流分量偏离和推力失稳问题,原理样机实验结果验证了控制策略对不确定扰动抑制的有效性。
关键词:不确定扰动 直线感应电机 抗扰控制 自学习模型
高速直线感应电机(High-Speed Linear Induction Motor, HS-LIM)具有动子质量轻、结构简单、可靠性高等优势,适用于地面高速电磁推进实验设施(电磁橇)和电磁发射等领域[1-2]。然而,高速直线感应电机在跨声速运行时,激波非定常气动特性会使动子产生强烈抖振[3-4],导致直线电机动子位置速度测量及电磁机构受到强烈不确定扰动。该扰动具有短时、高动态、突发及不可预测性,易引起直线感应电机转差率控制异常、推力控制失稳、跨声速运行失败,是制约系统超声速运行的瓶颈问题。
针对高速电机高性能控制,目前研究主要集中在无速度传感器控制、自抗干扰控制、自学习控制等方面。高速电机无速度传感器控制主要有高频信号注入法和模型观测法两大类。其中,高频信号注入法常用的有旋转高频电压信号注入法和脉动高频电压信号注入法。文献[5]提出一种基于高频信号注入的永磁同步直线电机速度观测方法,并对位置角误差进行了补偿。文献[6]采用拓展卡尔曼滤波器配合高频注入法,提高了参数变化时动子速度估计精度。高频信号注入法不依赖电机的基波反电动势,在低速时能够取得良好的位置和速度估计性能。但是,高速时该方法性能易受到高频噪声、系统带宽、逆变器最大输出电压等因素影响[7]。相比于高频信号注入方法,基于电机数学模型的转速估计方法不需要额外的信号注入,其动态性能较好[8-9],主要包括全阶观测器、模型参考自适应系统(Model ReferenceAdaptive System, MRAS)[10-11]与滑模观测器(Sliding Mode Observer, SMO)[12-14]等。MRAS方法是基于稳定理论的辨识方法,具有较好的渐近收敛和动态性能,方法简单、易于实现,但与SMO相比,其对电机参数的依赖性较大且抗干扰能力弱。SMO降低了对电机模型精度的依赖,鲁棒性较强,文献[13]中提出一种迭代超螺旋滑模控制方法,利用超螺旋滑模控制抑制不确定性因素的影响,增强系统的鲁棒性。文献[14]提出一种负载变化下滑模无传感器控制感应电机主动零频穿越及脉动抑制策略,将转速观测范围扩展到定子电流近零频低速工况。文献[15]将滑模变结构控制与MRAS相结合,既保留了MRAS自身的优点,又具有滑模控制对参数不敏感的特性。基于模型的无速度传感器控制方法对电机数学模型精度依然有要求,难以适用于参数快速时变、非线性强耦合、高动态特点的高速直线感应电机。
为了解决基于模型的无速度传感器控制方法抗扰性弱、鲁棒性低的缺点,文献[16-17]将自抗扰控制(Active Disturbance Rejection Control, ADRC)技术应用于电机无速度传感器控制中,补偿了系统中存在的非线性扰动,提高了速度观测的精度与干扰下的快速响应能力。与传统PI控制技术相比,自抗扰控制技术在无速度传感器控制中表现出较好的控制效果[18-21],但也存在ADRC参数难以整定的问题。为此,文献[22-23]将遗传算法和人工智能技术应用在自抗扰电机控制系统中,将深度强化学习(Deep Reinforcement Learning, DRL)方法参与自抗扰控制器参数自动调优,有效降低了计算量,提高了参数的灵敏度。ADRC能够有效地消除电机系统持续性内外部扰动影响,但对于短时突发性不确定扰动抑制效果不明显,跨声速时快速时变电机参数可能会造成扩张状态观测器发散,进而导致推力控制失稳。自学习控制方法通常以数据驱动为核心,不需要依赖先验性的模型知识,克服了基于模型的抗干扰控制方法参数依赖性强和鲁棒性差等缺点[24-25]。文献[24]针对动车组的速度跟踪控制问题,将改进的多输入多输出偏格式动态线性化无模型自适应控制(Partial Form Dynamic Linearization-improved Model-Free Adaptive Control, PFDL-iM-FAC)引入动车组自动驾驶系统中,优化了动车组速度的跟踪精度。文献[26]针对精密定位的音圈电机易受到内外扰动从而影响系统最终定位精度问题,在建立音圈电机数学模型的基础上,利用历史数据自学习算法对非线性控制器增益系数进行实时调整,提高了位置估计的精度与抗扰性能。以上方法大多数针对旋转电机或低速直线电机扰动特性进行抑制,然而跨声速直线电机激波影响具有强烈不确定扰动和非定常特性,现有方法无法满足。
本文针对高速直线感应电机在跨声速时推力控制易失稳问题,提出不确定扰动下高速直线感应电机自学习抗扰控制策略。相比于依赖电机参数的无速度传感器控制方法,研究直线感应电机自学习数学模型弱化对电机参数依赖,降低电机参数非线性快速时变对速度观测的影响。相比于传统自抗扰控制方法,本文研究基于滚动预测速度、量测数据及可信度值三者加权运算的抗扰控制方法,提高对突发性不确定扰动的抑制能力。
高速直线感应电机拓扑及等效电路如图1所示,图1a为高速直线感应电机拓扑,包括直线电机分段定子、动子、变频器和测量控制设备,通过采集动子的速度位置和定子电流实现直线感应电机推力的闭环控制。图1b为高速直线感应电机等效电路,图中当动子高速运动时电机定子的互感快速变化,an为动子覆盖第n个定子段的比例系数。

图1 高速直线感应电机拓扑及等效电路
Fig.1 The topology and equivalent circuit of linear induction motor with segmented stator
本文研究对象为长定子直线感应电机,控制策略为间接磁场定向,当各个定子段供电电流相等时,从动子角度看直线感应电机互感和磁链未发生变化,因此采用虚拟动子磁链为状态变量,直线感应电机第n个定子段的状态方程[27]为
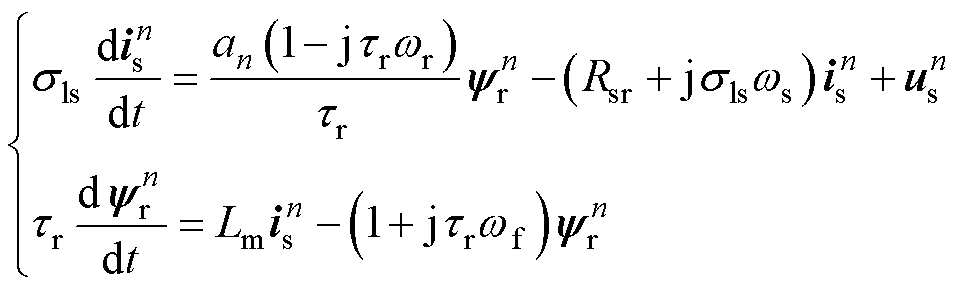 (1)
(1)
其中
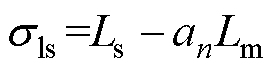
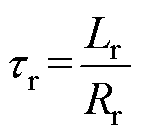
式中,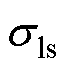 为电感解耦时变参数;Rsr为电阻解耦时变参数;
为电感解耦时变参数;Rsr为电阻解耦时变参数;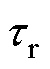 为时间常数;Ls为定子电感;Lm为励磁电感;Lr为动子电感;Rr为动子电阻;
为时间常数;Ls为定子电感;Lm为励磁电感;Lr为动子电感;Rr为动子电阻;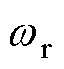 为动子角频率;
为动子角频率;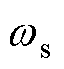 为定子角频率;
为定子角频率;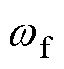 为转差频率;
为转差频率;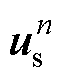 、
、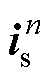 分别为第n个定子段电压、电流;
分别为第n个定子段电压、电流;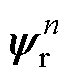 为第n个定子段虚拟动子磁链。
为第n个定子段虚拟动子磁链。
由虚拟动子磁链、定子电流和动子覆盖比例可得到直线感应电机动子所受的总电磁推力为所有定子段推力之和,m个定子段产生的推力为
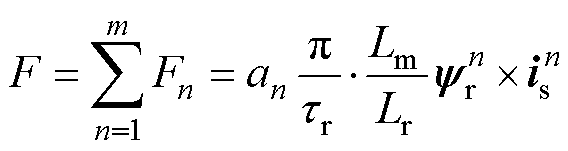 (2)
(2)
直线感应电机动子速度v为
 (3)
(3)
式中,mg为动子质量;k0为静摩擦力;k1为一阶风阻系数;k2为二阶风阻系数。动子阻力主要包括静摩擦力k0、一阶风阻k1v和二阶风阻k2v2。
直线感应电机采用间接磁场定向控制策略,当动子磁场定向正确时,q轴磁链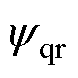 =0。当所有定子段电流都相等时,电机各定子段覆盖比例an相加为常数,电机推力由式(2)可简化为
=0。当所有定子段电流都相等时,电机各定子段覆盖比例an相加为常数,电机推力由式(2)可简化为
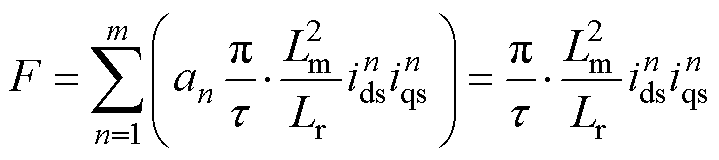 (4)
(4)
式中,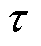 为直线电机极距长度;
为直线电机极距长度;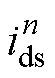 、
、 分别为第n个定子段磁场定向后d、q轴电流[28]。
分别为第n个定子段磁场定向后d、q轴电流[28]。
直线感应电机在跨声速运行时,速度量测值受到不确定扰动,磁场定向角频率为速度测量值与转差率之和,导致电机磁场定向角度会受到严重干扰。错误的角频率会导致定子电流is在dq轴分量偏离预设理想值,从而导致推力失稳。不确定扰动下直线感应电机磁场定向偏差影响如图2所示,受扰后坐标系与正常坐标系分别以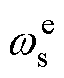 和
和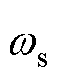 的角速度旋转,两坐标系夹角
的角速度旋转,两坐标系夹角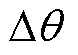 不断变化,定子电流矢量is在dq轴分量
不断变化,定子电流矢量is在dq轴分量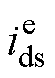 、
、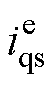 偏离预设理想值ids、iqs。
偏离预设理想值ids、iqs。
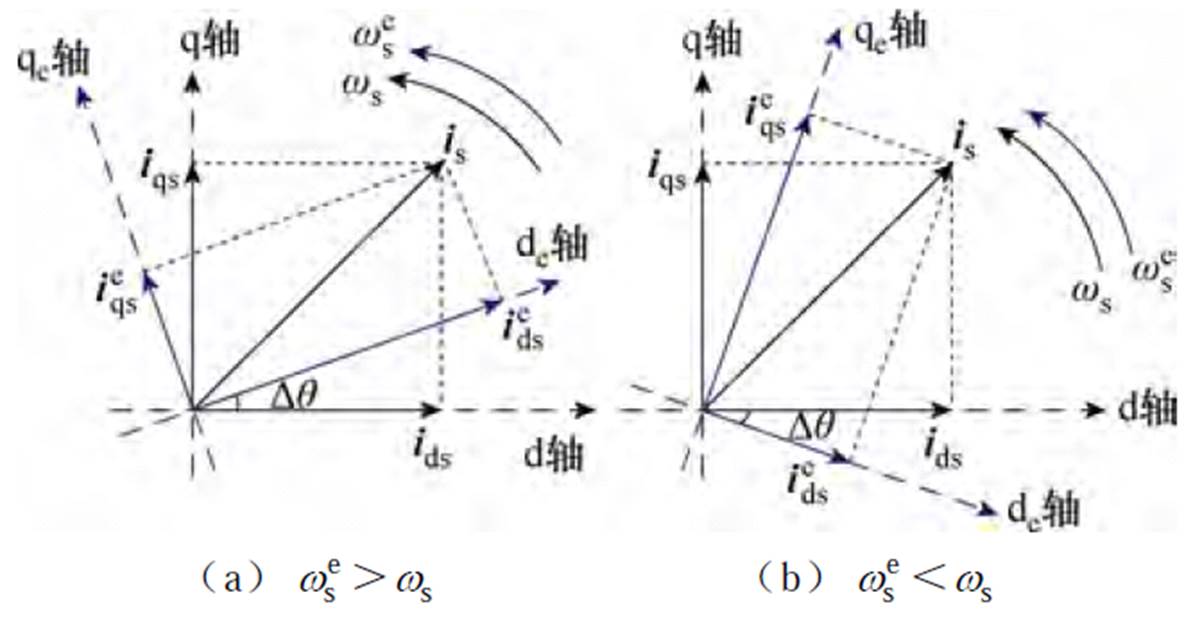
图2 不确定扰动下直线感应电机磁场定向偏差影响
Fig.2 Field orientation deviation of linear induction motor under uncertain disturbance
以直线感应电机动子角频率百分比表示速度不确定扰动系数e,速度测量值受扰后速度和转差率角频率偏差为
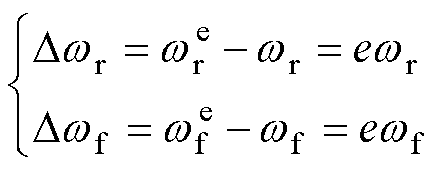 (5)
(5)
式中,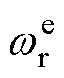 为量测装置受扰后测量的动子角频率;
为量测装置受扰后测量的动子角频率;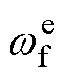 为受扰后的转差率。
为受扰后的转差率。
受扰后电机实际推力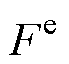 与电机理想推力F存在误差
与电机理想推力F存在误差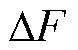 ,有
,有
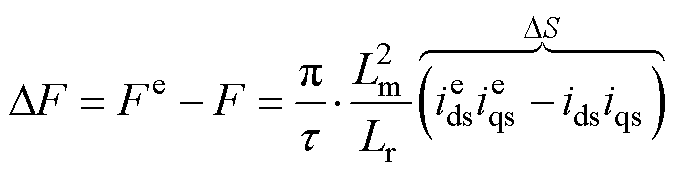 (6)
(6)
由直线感应电机转差率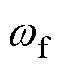 与定子dq轴电流的关系可得到不确定扰动系数e对直线感应电机推力影响规律为
与定子dq轴电流的关系可得到不确定扰动系数e对直线感应电机推力影响规律为
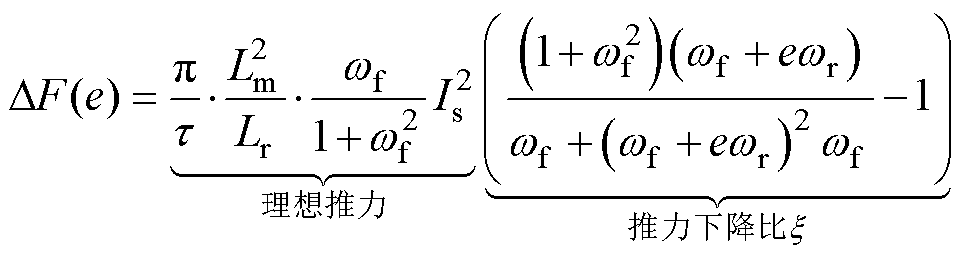 (7)
(7)
式中,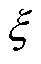 为推力下降比;
为推力下降比;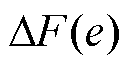 为推力下降量;Is为定子段电流的幅值。
为推力下降量;Is为定子段电流的幅值。
当动子以不同速度v运行(v=100, 200, 300, 400, 500 m/s)时,随着不确定扰动系数e改变,电机系统推力下降比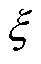 变化曲线如图3所示。不确定扰动系数e=0时
变化曲线如图3所示。不确定扰动系数e=0时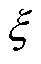 =0,推力保持理想输出,e在-0.2~0.2范围变化时推力下降明显。当动子速度v越高,推力下降比
=0,推力保持理想输出,e在-0.2~0.2范围变化时推力下降明显。当动子速度v越高,推力下降比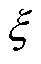 对e也越敏感,此时较小的不确定扰动也可能会导致推力快速下降,如图3中局部放大图所示。不确定扰动系数e改变0.1,电机在100 m/s速度时推力下降比仅0.1左右,而在500 m/s速度时其推力下降比高达约1.5。
对e也越敏感,此时较小的不确定扰动也可能会导致推力快速下降,如图3中局部放大图所示。不确定扰动系数e改变0.1,电机在100 m/s速度时推力下降比仅0.1左右,而在500 m/s速度时其推力下降比高达约1.5。

图3 不确定扰动系数、动子速度对推力影响曲线
Fig.3 Thrust curves of uncertain perturbation coefficient and mover velocity
由式(2)和式(3)可得到直线感应电机不确定扰动下单个定子段实际推力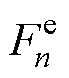 和速度v的数学表达式为
和速度v的数学表达式为
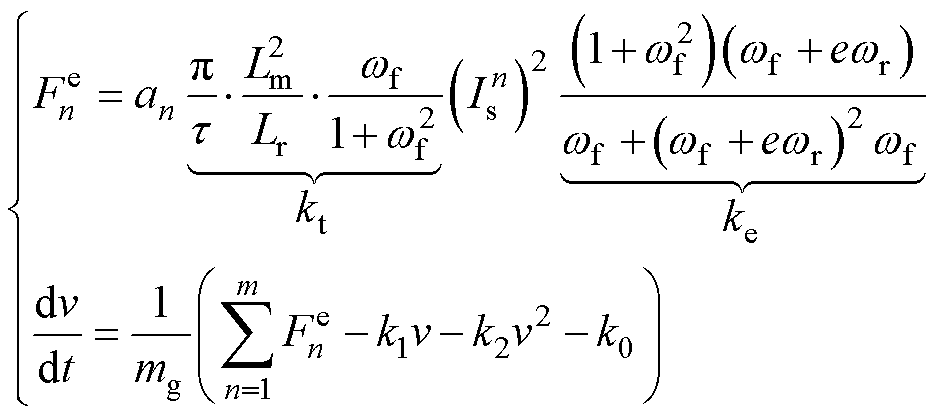 (8)
(8)
式中,kt为推力系数;ke为推力扰动系数;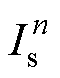 为第n段定子电流的幅值。
为第n段定子电流的幅值。
简化式(8)可得自学习模型为
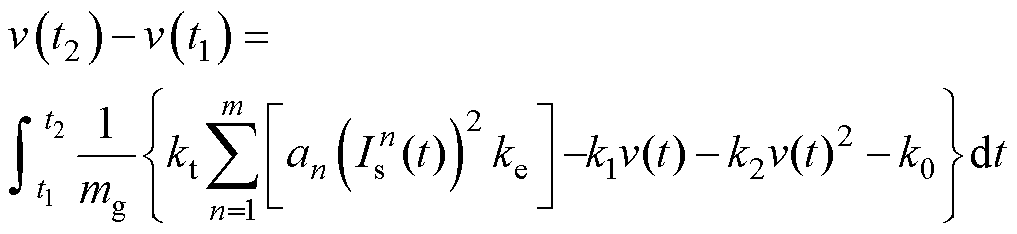 (9)
(9)
由于温度、风力、风向、湿度等因素影响,超声速运行前需通过亚音速实验数据自学习模型各参数。
在超声速运行前直线感应电机受到扰动概率较小,因此扰动系数ke设置为常数1,自学习参数采用最小二乘法如式(10)~式(12)所示。
 (10)
(10)
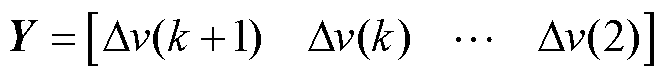 (11)
(11)
 (12)
(12)
其中
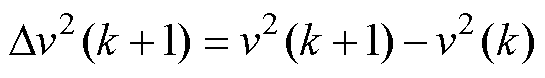
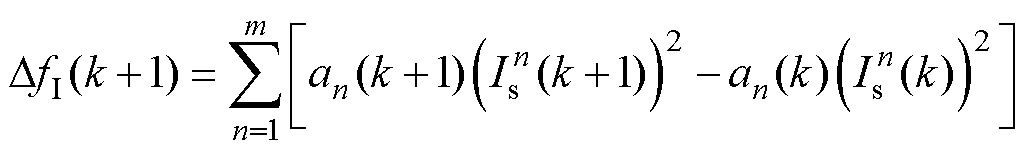
式中,X为速度变化估计矩阵;Y为速度变化实测矩阵; 为参数学习矩阵;k为第k次采样或计算结果;Ts为离散化计算步长;
为参数学习矩阵;k为第k次采样或计算结果;Ts为离散化计算步长;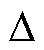 为变化量;
为变化量;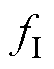 为电流产生推力的增量。
为电流产生推力的增量。
直线感应电机离线化自学习模型如式(13)所示,可较为准确地反映系统运行特性。
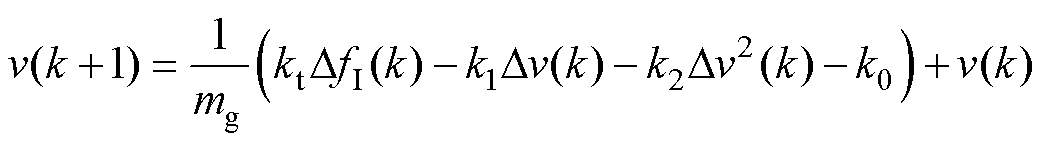 (13)
(13)
由直线感应电机自学习模型可实现速度的模型预测,假设在跨声速时电机控制给定电流和转差率不发生改变,可短时预测未来速度值为
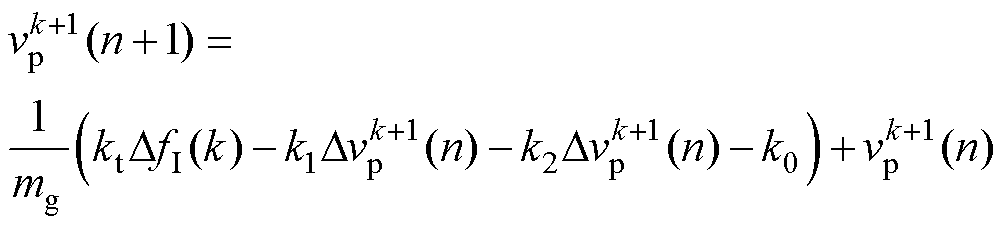 (14)
(14)
本文对于每个实际测量数据依据式(14)预测未来5个计算步长的速度,将实际测量值和预测值构建5×5滚动预测矩阵,如图4所示。正常状态下,滚动预测矩阵列向量元素与均值的偏差为零,而当速度量测值受到不确定扰动时会导致速度量测不准,若不加以修正,错误速度量测值加入滚动预测矩阵会使列向量发生变异。

图4 直线电机5×5滚动预测矩阵
Fig.4 5×5 rolling prediction matrix
本文采用式(15)计算矩阵列向量速度基准值,式(16)计算速度偏差S(i, j),衡量滚动预测矩阵的变异程度。
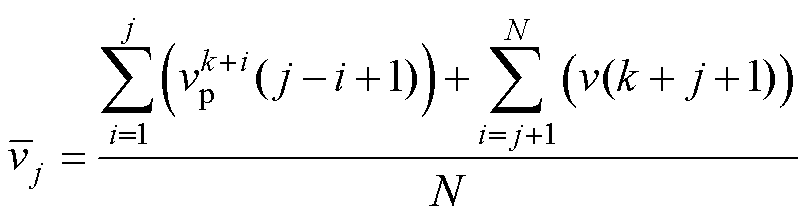 (15)
(15)
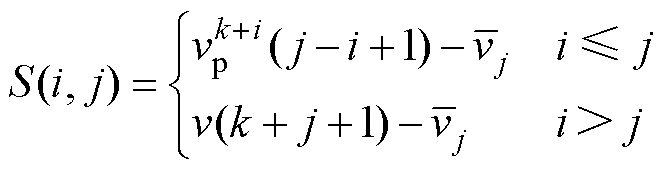 (16)
(16)
式中,N为矩阵阶数;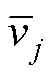 为滚动预测矩阵第j列向量的均值;i为滚动预测矩阵行数;j为滚动预测矩阵列数。
为滚动预测矩阵第j列向量的均值;i为滚动预测矩阵行数;j为滚动预测矩阵列数。
以初始速度v=300 m/s、不确定扰动系数e=0.2为例对滚动预测矩阵特性进行分析,在无速度修正时5个控制周期滚动预测矩阵的变异程度如图5所示,预测与实际值误差可达到40 m/s。
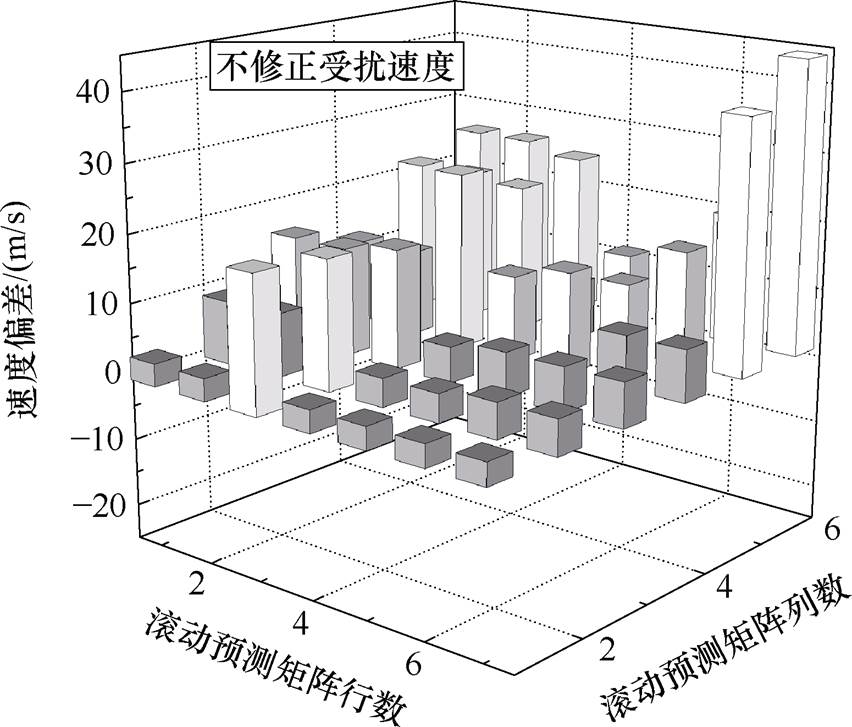
图5 无速度修正时滚动预测矩阵的变异程度
Fig.5 Degree of variation of the rolling prediction matrix without speed correction
本文依据滚动预测矩阵提出了一种基于可信度判定的速度不确定扰动修正方法,通过实时修正速度量测值并将修正后的量测值加入滚动预测矩阵与磁场定向控制系统,确保速度信息准确可靠。在第k+N+1个周期,速度量测值v(k+N+1)的可信度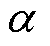 计算方法为
计算方法为
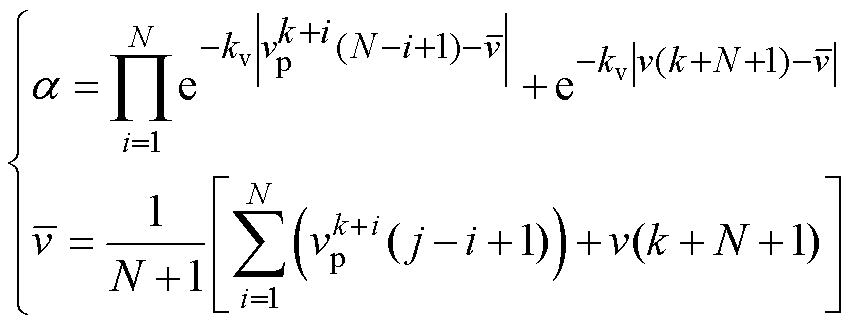 (17)
(17)
式中,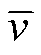 为修正向量的均值;kv为噪声调节系数,与传感器量测噪声有效值g 相关。
为修正向量的均值;kv为噪声调节系数,与传感器量测噪声有效值g 相关。
传感器噪声会对滚动预测矩阵带来扰动,影响式(17)中可信度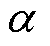 判定准确性,因此本文引入噪声调节系数kv。在噪声较小工况下,提高kv值可提高方法的修正速度和准确性。在噪声较大工况下,通过计算传感器量测信号噪声有效值g 调节kv值,可在可信度判定的响应速度和准确性之间取折中,提高不确定扰动抑制能力。以测速范围0~400 m/s,噪声有效值小于3 m/s为例,kv值计算方法为
判定准确性,因此本文引入噪声调节系数kv。在噪声较小工况下,提高kv值可提高方法的修正速度和准确性。在噪声较大工况下,通过计算传感器量测信号噪声有效值g 调节kv值,可在可信度判定的响应速度和准确性之间取折中,提高不确定扰动抑制能力。以测速范围0~400 m/s,噪声有效值小于3 m/s为例,kv值计算方法为
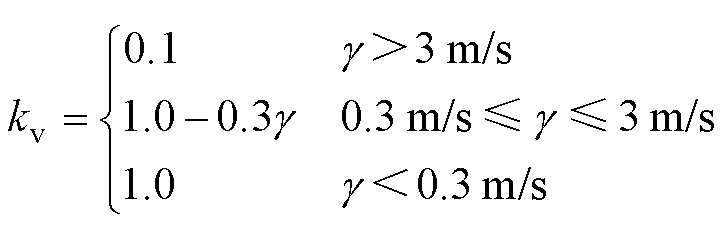 (18)
(18)
速度修正值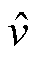 (k+N+1)的计算方法为
(k+N+1)的计算方法为
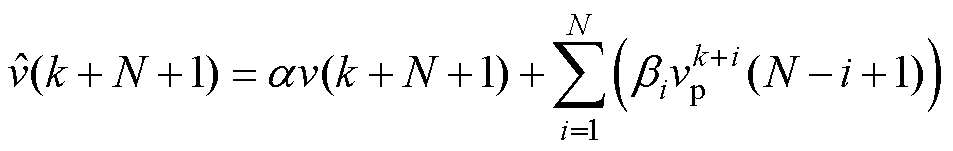 (19)
(19)
其中
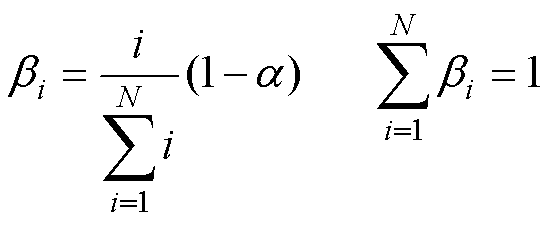
式中,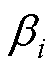 为不同周期预测速度的可信度占比。可知,离当前所在周期越近且i越大,其速度预测值的可信度占比
为不同周期预测速度的可信度占比。可知,离当前所在周期越近且i越大,其速度预测值的可信度占比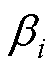 越大,修正速度越重要。
越大,修正速度越重要。
同样以初始速度v=300 m/s、不确定扰动系数e=0.2为例,经过速度修正后5个控制周期滚动预测矩阵的变异程度如图6所示,图中矩阵变异得到较好的改善,预测与实际值误差不超过5 m/s,有效且快速地阻断了扰动传播对速度测量的影响。

图6 速度修正后滚动预测矩阵的变异程度
Fig.6 Degree of variation of the rolling prediction matrix with speed correction
以直线感应电机自学习模型与可信度计算为基础,本文提出了高速直线感应电机自学习抗扰控制策略,如图7所示。直线电机每个定子段采用间接磁场定向控制策略,通过控制恒定转差率和定子侧电流幅值实现推力大小闭环控制。首先由位置s通过查表得到直线电机预定推力曲线,同时计算出转差率给定值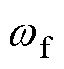 和电流给定值
和电流给定值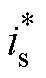 ,由
,由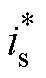 和
和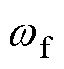 依据感应电机稳态方程可计算出定子dq轴给定电流
依据感应电机稳态方程可计算出定子dq轴给定电流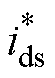 和
和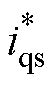 。由当前动子运动角速度
。由当前动子运动角速度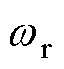 及转差角速度
及转差角速度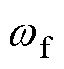 可计算出参考电流角速度
可计算出参考电流角速度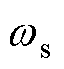 ,对
,对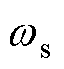 进行积分可得间接磁场定向中动子磁链角度
进行积分可得间接磁场定向中动子磁链角度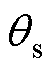 ,由定子测量电流iabc可得到dq轴电流的反馈值ids和iqs,再经PI反馈控制器和电压前馈控制器可得到参考电压ud和uq。控制器输出的参考电压经坐标变换后经变流器调制,调制后的三相电压为直线感应电机提供电能。
,由定子测量电流iabc可得到dq轴电流的反馈值ids和iqs,再经PI反馈控制器和电压前馈控制器可得到参考电压ud和uq。控制器输出的参考电压经坐标变换后经变流器调制,调制后的三相电压为直线感应电机提供电能。

图7 高速直线感应电机自学习抗扰控制策略框图
Fig.7 Block diagram of self-learning anti-disturbance control strategy for HS-LIM
高速直线感应电机在跨声速时速度量测值易受不确定扰动影响,动子角速度存在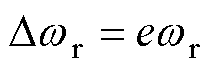 误差,导致间接磁场定向中动子磁链角度
误差,导致间接磁场定向中动子磁链角度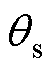 偏离理论值,直线感应电机推力输出F下降,严重时会引起跨声速失败。本文提出的速度自抗扰修正方法如下:
偏离理论值,直线感应电机推力输出F下降,严重时会引起跨声速失败。本文提出的速度自抗扰修正方法如下:
(1)跨声速实验开始前进行亚声速实验,根据亚声速实验电流和速度历史数据及直线感应电机自学习模型式(13)计算出模型参数,如推力系数、阻力系数k0、k1、k2等。
(2)跨声速实验时,由模型预测式(14)及实际测量的速度和电流值多步预测未来速度,依据量测时间向量和预测时间向量构建滚动预测矩阵。
(3)由当前量测数据和滚动预测矩阵可根据式(17)和式(18)得到量测数据可信度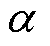 和噪声调节系数kv。
和噪声调节系数kv。
(4)由量测值、预测值及可信度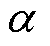 通过式(19)自抗扰修正可得到速度最优估计值
通过式(19)自抗扰修正可得到速度最优估计值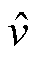 。
。
(5)将最优估计值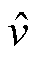 代替传感器速度量测值进入滚动预测矩阵中,实现了高速直线感应电机速度的高精度多步预测,阻断扰动传播过程。
代替传感器速度量测值进入滚动预测矩阵中,实现了高速直线感应电机速度的高精度多步预测,阻断扰动传播过程。
(6)将最优估计值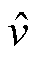 代替传感器速度量测值进入滚动预测矩阵与磁场定向控制,实现了高速直线感应电机自学习抗扰控制。
代替传感器速度量测值进入滚动预测矩阵与磁场定向控制,实现了高速直线感应电机自学习抗扰控制。
为了验证本文提出的高速直线电机抗扰控制策略方法的有效性,搭建了Matlab/Simulink仿真平台,包括直线感应电机控制模块和电机模型数字仿真模块。首先将多次离线仿真数据代入自学习模型相关参数,验证自学习模型的准确性,仿真验证结果见表1。表中参考模型参数kt、k0~k2为设定数值,自学习模型参数kt、k0~k2为基于多次离线仿真数据的自学习结果,自学习模型参数初始值为多次离线数据参数学习的平均值。由表1可知,自学习模型参数与参考模型参数差别较小,验证了本文提出的自学习模型可较好地学习高速直线感应电机电磁暂态特性,有效地缓解了自学习抗扰控制对系统参数准确性的依赖。
表1 高速直线感应电机自学习模型参数仿真结果
Tab.1 The parameter simulation results of HS-LIM self-leaning model

参 数数 值 参考模型自学习模型 kt/(N/A2)1.00.992 k1/(N·s2/m2)0.150.147 k2/(N·s/m)0.020.018 k0/N1 0001052
为了模拟高速直线感应电机动子在声速附近的激波扰动,在直线电机动子速度达到声速附近(约340 m/s)时对速度量测值施加e=-0.2的不确定扰动。图8为不确定扰动下高速直线电机跨声速仿真结果,图8a和图8b分别为无抗扰控制和自学习抗扰控制策略仿真结果对比。由图8a可知,当直线感应电机动子速度达到声速附近时,量测速度的不确定扰动会导致直线感应电机定子电流在间接磁场定向下dq轴电流有较大扰动,引起直线感应电机推力失稳,跨声速失败。图8b中提出的自学习抗扰控制策略有效地抑制了声速附近的不确定扰动,dq轴电流和直线电机推力在跨声速时平稳,动子突破了音障,达到364 m/s。

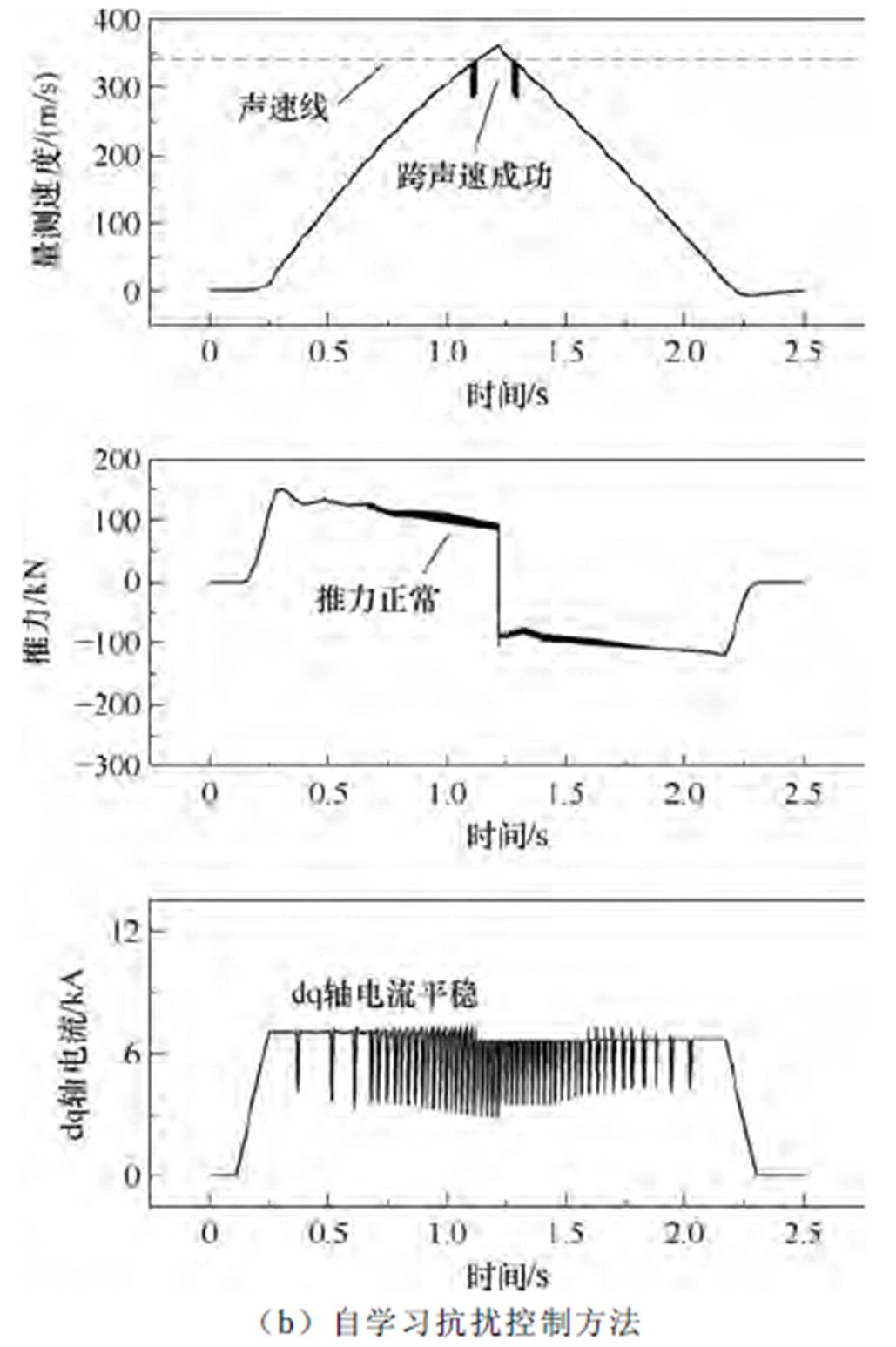
图8 不确定扰动下高速直线感应电机跨声速仿真实验结果
Fig.8 Simulation results of transonic velocity under uncertain disturbance for HS-LIM
自学习抗扰控制方法的细节波形如图9所示,图9a为跨声速时受扰动量测速度,图9b为量测速度可信度实时计算结果。对比图9a和图9b可知,量测速度一旦受扰,根据滚动矩阵计算出的量测速度可信度会快速下降至零线附近,表明此时传感器量测速度近乎不可用,实现了不确定扰动严重程度的快速评估。图9c为根据可信度与多个周期速度预测结果对量测速度进行抗扰修正后的速度,图9d为抗扰修正速度与实际速度的误差。由图9可知,经过自学习抗扰修正后速度误差值不超过2.5 m/s,以声速340 m/s为基准值,速度抗扰后仿真的修正速度与实际速度的最大误差小于0.7%,对直线感应电机转差率和推力影响较小,实现了系统跨声速稳定运行。由于高速直线感应电机采用自学习数学模型,抗扰控制策略对电机参数非线性快速时变特性不敏感,具有较好的鲁棒性。
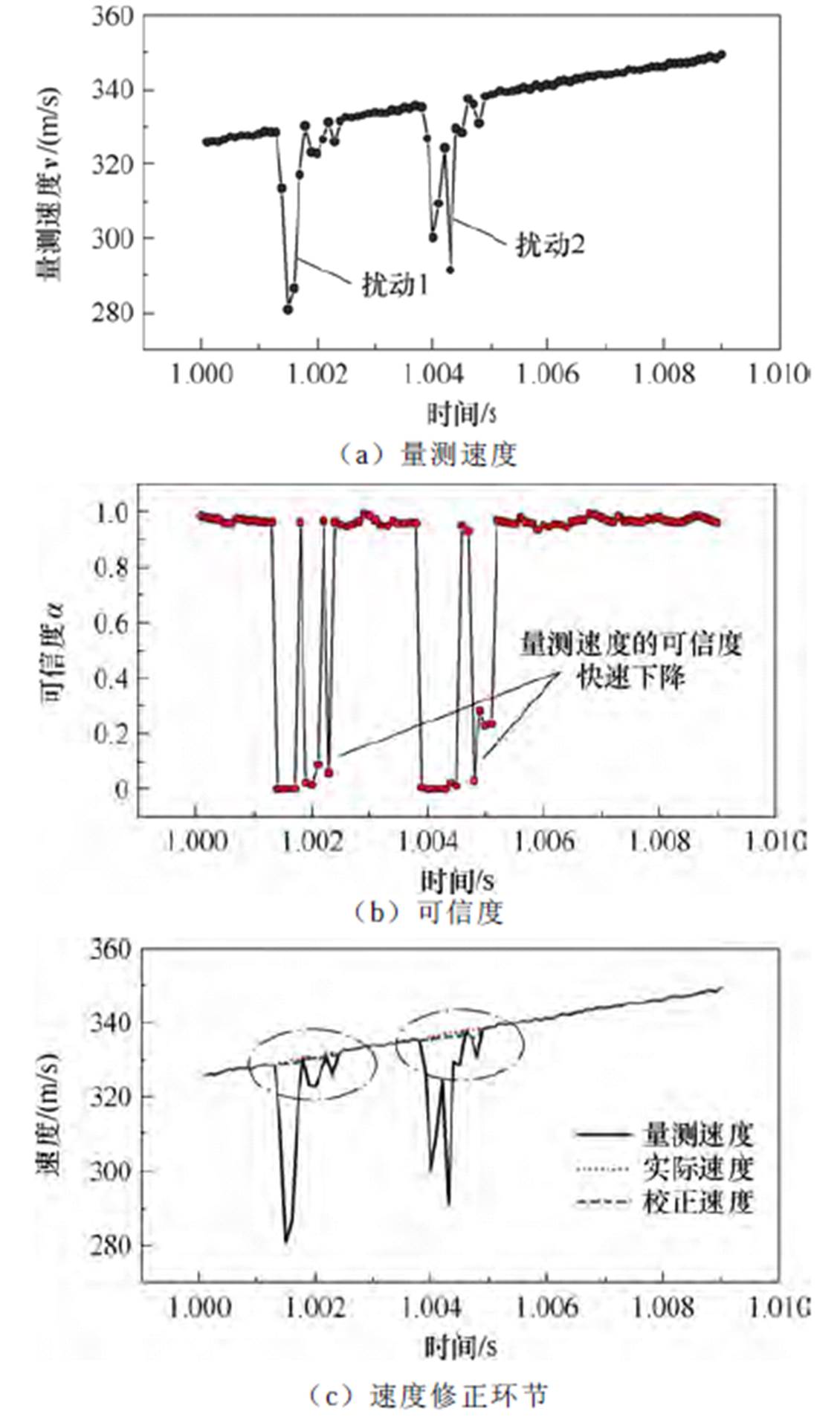

图9 高速直线感应电机速度抗扰控制的波形细节图
Fig.9 The detailed velocity and reliability waveform of the disturbance rejection method of HS-LIM
为验证该方法在更大不确定扰动下的有效性,本文在直线电机动子速度达到声速(约340 m/s)附近对速度量测值施加e=-0.5不确定扰动,图10为高速直线电机跨声速时自学习抗扰控制仿真结果。
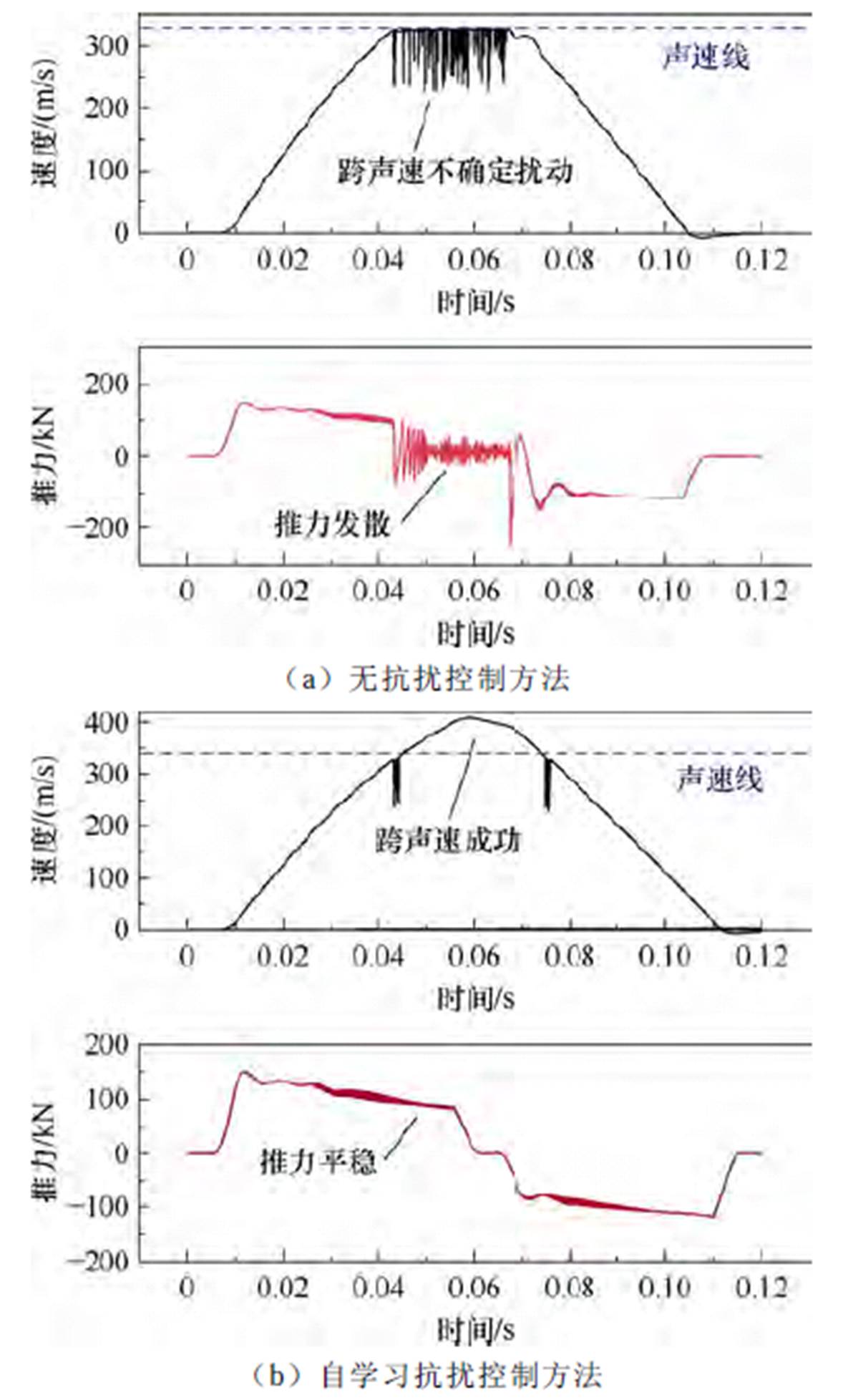
图10 不确定扰动下高速直线电机跨声速仿真实验
Fig.10 Simulation results of transonic velocity under uncertain disturbance for HS-LIM
由图10a可知,量测速度的不确定扰动会引起直线感应电机推力失稳,跨声速失败。图10b采取自学习抗扰控制策略后,在e=-0.5的不确定扰动下电机推力输出稳定,动子突破音速最高达到400 m/s。
高速直线电机速度测量噪声会降低速度修正精度,将本文提出的方法与不考虑噪声抑制方法进行仿真对比分析,仿真结果如图11所示。假设不确定扰动系数e=-0.2,传感器噪声有效值分别为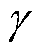 =0和
=0和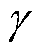 =2 m/s,图11a为无噪声影响且不考虑噪声抑制的仿真结果,此时kv=1,
=2 m/s,图11a为无噪声影响且不考虑噪声抑制的仿真结果,此时kv=1,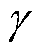 =0。图11b为噪声影响有效值
=0。图11b为噪声影响有效值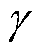 =2 m/s,且不考虑噪声抑制方法的仿真结果,此时kv=1。图11c为噪声有效值为
=2 m/s,且不考虑噪声抑制方法的仿真结果,此时kv=1。图11c为噪声有效值为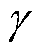 =2 m/s时,采用考虑噪声抑制方法的仿真结果,此时kv=0.4。对比图11a和图11b可知,在无噪声影响时kv=1具有较好的速度修正效果,但在
=2 m/s时,采用考虑噪声抑制方法的仿真结果,此时kv=0.4。对比图11a和图11b可知,在无噪声影响时kv=1具有较好的速度修正效果,但在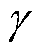 =2 m/s噪声影响时会严重降低速度修正精度。对比图11b和图11c可知,本文提出的方法由式(18)和
=2 m/s噪声影响时会严重降低速度修正精度。对比图11b和图11c可知,本文提出的方法由式(18)和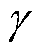 =2 m/s计算出噪声调节系数kv=0.4,修正速度的精度明显优于图11b不考虑噪声抑制方法,验证了本文方法具有较好的传感器噪声抑制效果。
=2 m/s计算出噪声调节系数kv=0.4,修正速度的精度明显优于图11b不考虑噪声抑制方法,验证了本文方法具有较好的传感器噪声抑制效果。

图11 考虑噪声抑制的自学习抗扰方法仿真结果
Fig.11 Simulation results of self-learning anti-disturbance control strategy with noise suppression
为了验证本文提出的自学习抗扰控制策略的有效性,搭建了直线感应电机推进系统原理样机实验平台如图12所示,包括定子、动子、分段供电开关、位置速度测量等设备。实验平台参数见表2,由24个定子段组成,控制算法与仿真一致,定子电流幅值为8 A,转差频率为10 Hz,直流电压为100 V,供电切换时定子内无动子覆盖。

图12 直线感应电机推进系统原理样机
Fig.12 The prototype experiment platform of HS-LIM
表2 原理样机实验平台参数
Tab.2 The parameters of the prototype experiment platform

参 数数 值 定子个数N24 定子长度Ss/mm240 动子长度Sm/mm360 气隙宽度hs/mm10 动子厚度hm/mm6
直线感应电机自学习模型实验结果如图13所示,图13a和图13b分别为加速和减速阶段实验结果。由图可知,自学习模型式(13)计算结果与实验结果基本一致。加速过程学习速度与实际速度的误差不超过5%,减速过程学习速度与实际速度的误差不超过6%,实验结果验证了自学习模型的有效性和准确性。根据对实验数据的分析,提出实验误差主要来源于两方面:①在动子加减速运动全程,实验平台各处摩擦阻力变化不均匀,影响了速度趋势的学习,导致自学习模型与实际速度产生误差;②直线感应电机动子速度测量值由位置传感器测量数据求导得出,测量误差和噪声导致自学习模型与实际速度产生差别。
量测速度可信度计算与速度抗扰修正实验结果如图14所示,在动子速度达到5 m/s时,对传感器量测速度施加扰动系数e=0.2的不确定扰动。图14a中直线感应电机动子量测速度受扰后,通过滚动预测矩阵计算出的可信度在0.15 s时间内快速下降到零附近,实现了不确定扰动严重程度的快速评估。图14b中可信度修正后的量测速度与实际速度的误差小于1%。修正后量测速度与实际速度的误差来源主要有两方面:①修正速度由预测速度与实际速度通过可信度加权运算后得到,自学习模型误差影响预测速度的准确性;②噪声抑制的延时特性会给修正速度准确性带来影响。
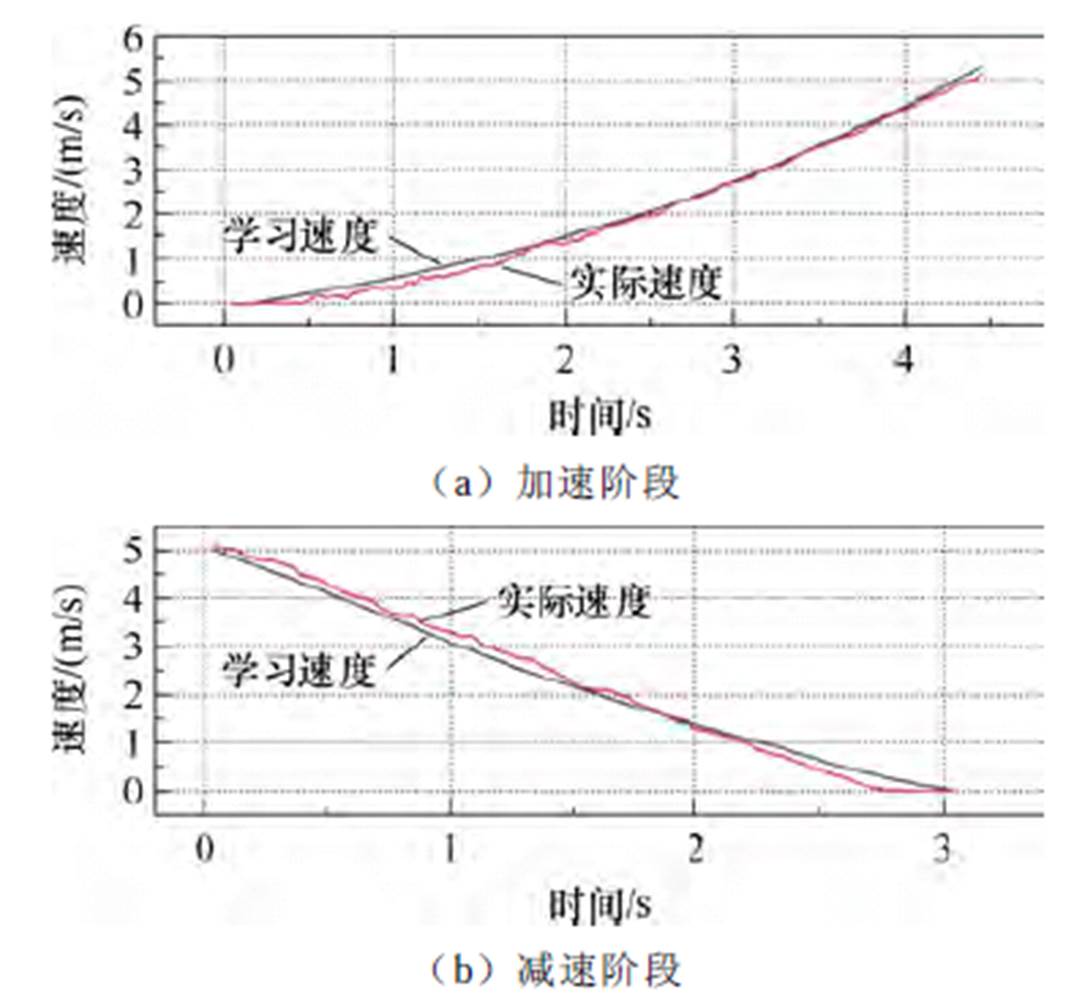
图13 直线感应电机自学习模型实验结果
Fig.13 Experimental results of self-learning model
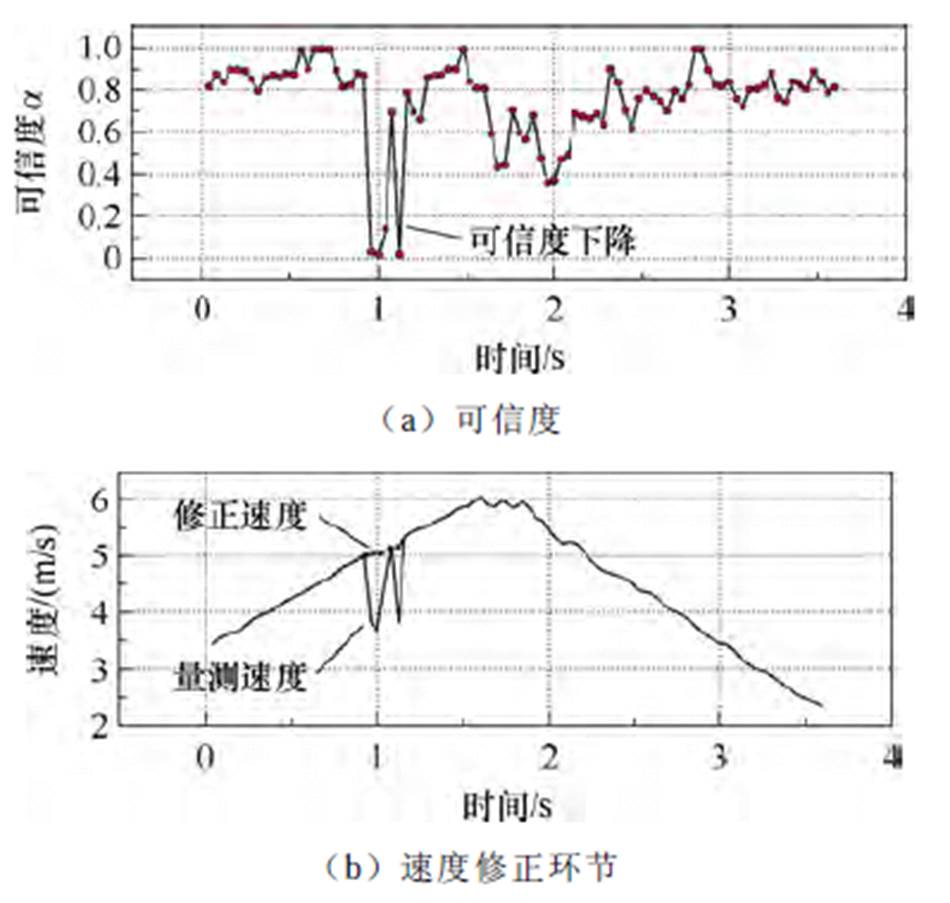
图14 量测速度可信度与修正速度实验结果
Fig.14 Experimental verification results of reliability and correction speed
图15为对速度量测值施加e=-0.2的不确定扰动,不确定扰动下抗扰控制实验结果。当速度达到5 m/s时,图15a和图15b分别为无抗扰控制与自学习抗扰控制的对比实验结果。由图15a可知,若不采取抗扰控制策略,dq轴电流会偏离给定值,导致推力输出下降,动子速度无法突破预设速度。由图15b可知,自学习抗扰控制方法可减少不确定扰动对dq轴电流分量的影响,动子突破预设速度,实现稳定的抗扰控制。

图15 直线感应电机自学习抗扰控制策略原理样机实验结果
Fig.15 Experiment results of self-learning anti-disturbance control strategy for HS-LIM
为了验证自学习抗扰控制策略在不同速度下的抑制扰动能力,本文在动子速度达到12 m/s时,对传感器量测速度施加扰动,自学习抗扰控制方法实验结果如图16所示,图16a为无抗扰控制的实验结果,动子速度无法突破预设速度,图16b为自学习抗扰控制方法后,动子成功突破预设速度,实验验证了本文所提出方法的有效性。
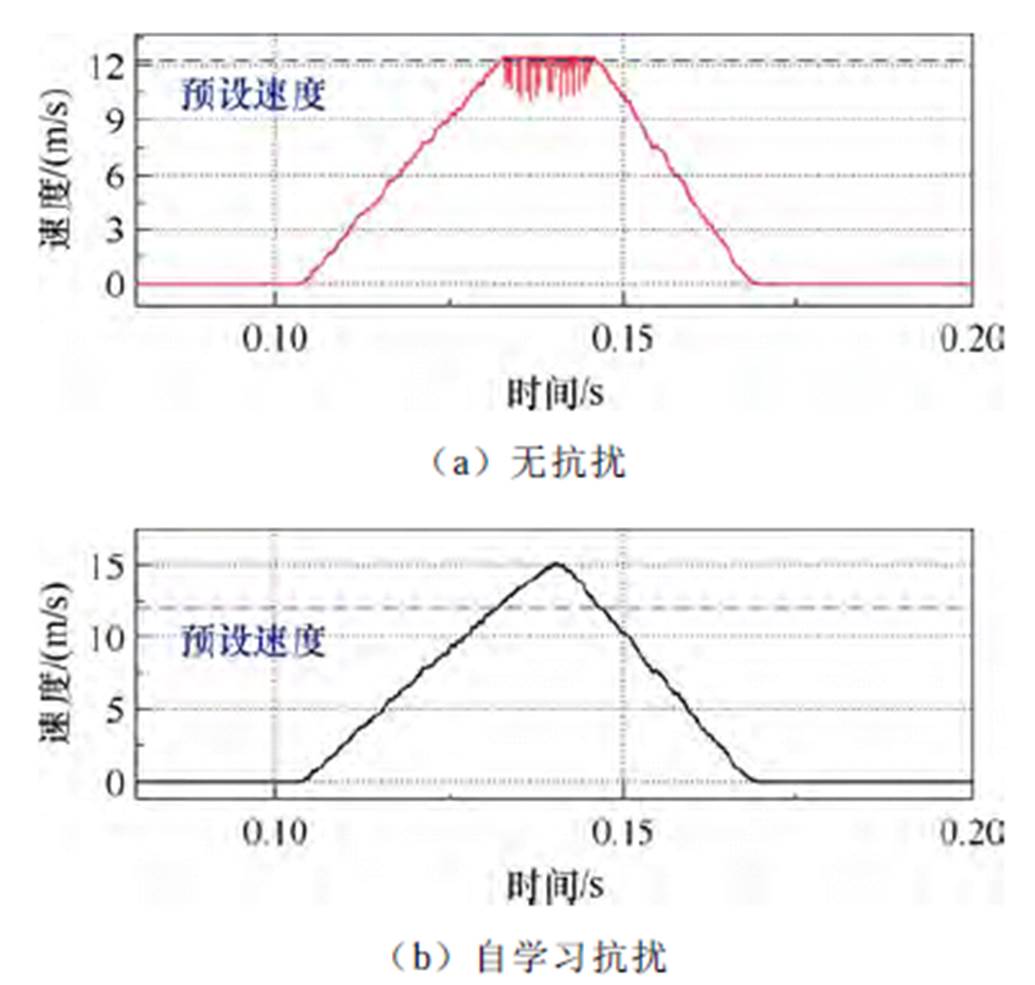
图16 自学习抗扰控制策略原理样机实验结果
Fig.16 Experiment results of self-learning anti-disturbance control strategy
本文提出了高速直线感应电机自学习抗扰控制策略,经仿真和实验验证得出如下结论:
1)提出的高速直线电机自学习数学模型可以实现直线电机动子速度高精度多步快速预测。
2)基于滚动预测矩阵列向量变异程度的速度修正方法可阻断不确定扰动的传播,实现不确定扰动的准确抑制,直线电机动子速度仿真误差小于0.7%,实验误差小于1%。,且具有较好的噪声抑制能力。
3)在e=-0.2和e=-0.5的不确定扰动下,提出的自学习抗扰控制策略可抑制不确定扰动,实现直线电机dq轴电流与推力稳定控制。
本文研究成果可应用于高速直线感应电机推进系统,对跨声速激波不确定扰动进行有效抑制,实现系统跨声速稳定运行。
参考文献
[1] Ma Weiming, Lu Junyong, Liu Yingquan. Research progress of electromagnetic launch technology[J]. IEEE Transactions on Plasma Science, 2019, 47(5): 2197-2205.
[2] 鲁军勇, 柳应全. 电磁发射用直线电机及其控制技术综述[J]. 电工技术学报, 2024, 39(19): 5899-5913.
Lu Junyong, Liu Yingquan. Review on linear motor for electromagnetic launch and its control tech- nology[J]. Transactions of China Electrotechnical Society, 2024, 39(19): 5899-5913.
[3] 马启悦, 高传强, 孙健. 基于神经网络的激波抖振特征提取与始发预测[J]. 航空科学技术, 2024, 35(7): 49-55.
Ma Qiyue, Gao Chuanqiang, Sun Jian. Shock buffet feature extraction and onset prediction based on neural network[J]. Aeronautical Science & Tech- nology, 2024, 35(7): 49-55.
[4] 高传强, 张伟伟. 机翼跨声速抖振数值模拟及模态分析[J]. 航空学报, 2019, 40(7): 122597.
Gao Chuanqiang, Zhang Weiwei. Numerical simu- lation and modal analysis of transonic buffet flow over wings[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(7): 122597.
[5] Cupertino F, Pellegrino G, Giangrande P, et al. Sensorless position control of permanent-magnet motors with pulsating current injection and com- pensation of motor end effects[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1371-1379.
[6] 杨春雨, 马婷婷, 周林娜, 等. 永磁同步直线电机低速域无位置传感器控制[J]. 微特电机, 2018, 46(9): 59-62, 67.
Yang Chunyu, Ma Tingting, Zhou Linna, et al. Sensorless control for permanent magnet synchronous linear motor at low speed[J]. Small & Special Elec- trical Machines, 2018, 46(9): 59-62, 67.
[7] 王天擎, 王勃, 于泳, 等. 基于二阶变增益滑模的感应电机电压模型磁链观测器[J]. 中国电机工程学报, 2024, 44(11): 4490-4500.
Wang Tianqing, Wang Bo, Yu Yong, et al. Voltage model rotor flux observer of induction motor based on second-order variable gain sliding mode[J]. Pro- ceedings of the CSEE, 2024, 44(11): 4490-4500.
[8] 于林鑫, 袁昕, 丁国华, 等. 基于模型预测锁相环的永磁同步电机转子位置估计方法[J]. 电气技术, 2024, 25(8): 18-26, 52.
Yu Linxin, Yuan Xin, Ding Guohua, et al. Research on sensorless control of permanent magnet syn- chronous motor based on model predictive method based phase locked loop[J]. Electrical Engineering, 2024, 25(8): 18-26, 52.
[9] 王震宇, 孙伟, 蒋栋. 基于虚拟电压注入的闭环磁链观测器的感应电机无速度传感器矢量控制系统[J]. 电工技术学报, 2022, 37(2): 332-343.
Wang Zhenyu, Sun Wei, Jiang Dong. Induction motor speed sensorless vector control system based on closed-loop flux observer with virtual voltage injection[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 332-343.
[10] 蒋林, 刘梁鸿, 李坤, 等. 基于滑模控制的异步电机全阶观测器研究[J]. 电气传动, 2019, 49(4): 19-22.
Jiang Lin, Liu Lianghong, Li Kun, et al. Study on full order observer based on sliding mode control for asynchronous motor[J]. Electric Drive, 2019, 49(4): 19-22.
[11] 邹甲, 张健侨, 吉程椿. 基于BP双层神经网络MRAS下PMSM的转速辨识研究[J]. 电气传动, 2023, 53(6): 8-13.
Zou Jia, Zhang Jianqiao, Ji Chengchun. Speed identification of permanent magnet synchronous motor based on BP double-layer neural network MRAS[J]. Electric Drive, 2023, 53(6): 8-13.
[12] 陈玥轩, 葛兴来, 左运, 等. 一种感应电机无速度传感器系统的电流传感器容错控制策略[J]. 中国电机工程学报, 2022, 42(6): 2346-2356.
Chen Yuexuan, Ge Xinglai, Zuo Yun, et al. A current sensor fault-tolerant control strategy for speed- sensorless induction motor system[J]. Proceedings of the CSEE, 2022, 42(6): 2346-2356.
[13] 贺玉晓, 王丽梅. 永磁直线同步电动机迭代超螺旋滑模控制[J]. 电气技术, 2022, 23(6): 24-29.
He Yuxiao, Wang Limei. Iterative super-twisting sliding mode control for permanent magnet linear synchronous motor[J]. Electrical Engineering, 2022, 23(6): 24-29.
[14] 杨凯, 李孺涵, 罗成, 等. 负载变化下无传感器感应电机主动零频穿越及脉动抑制策略[J]. 电工技术学报, 2023, 38(18): 4910-4920.
Yang Kai, Li Ruhan, Luo Cheng, et al. Proactive low-frequency ride-through method and its ripple reduction for sensorless induction motor drives under load variations[J]. Transactions of China Electro- technical Society, 2023, 38(18): 4910-4920.
[15] 涂炜, 江卫华, 胡为兵, 等. 基于自适应算法的IPMSM无速度传感器研究[J]. 自动化与仪表, 2020, 35(3): 82-87.
Tu Wei, Jiang Weihua, Hu Weibing, et al. Research on IPMSM speed sensorless based on adaptive algorithm[J]. Automation & Instrumentation, 2020, 35(3): 82-87.
[16] Lu Wenqi, Li Qiang, Lu Kaiyuan, et al. Load adaptive PMSM drive system based on an improved ADRC for manipulator joint[J]. IEEE Access, 2021, 9: 33369- 33384.
[17] 王建渊, 王海啸, 尹忠刚, 等. 基于一阶线性自抗扰控制器的同步磁阻电机无速度传感器控制[J]. 电工技术学报, 2024, 39(14): 4405-4421.
Wang Jianyuan, Wang Haixiao, Yin Zhonggang, et al. Sensorless control of synchronous reluctance motor based on first order linear active disturbance rejection controller[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4405-4421.
[18] Lin Shiyu, Cao Yanfei, Li Chen, et al. Two-degree- of-freedom active disturbance rejection current control for permanent magnet synchronous motors[J]. IEEE Transactions on Power Electronics, 2023, 38(3): 3640-3652.
[19] 蒋毅, 廖看秋, 朱跃欧, 等. 基于粒子群优化算法的磁浮列车自抗扰悬浮控制器研究[J]. 电气技术, 2024, 25(7): 39-44, 49.
Jiang Yi, Liao Kanqiu, Zhu Yueou, et al. Research on active disturbance rejection suspension controller of maglev train based on particle swarm optimization[J]. Electrical Engineering, 2024, 25(7): 39-44, 49.
[20] Wang Bo, Tian Minghe, Yu Yong, et al. Enhanced ADRC with quasi-resonant control for PMSM speed regulation considering aperiodic and periodic dis- turbances[J]. IEEE Transactions on Transportation Electrification, 2022, 8(3): 3568-3577.
[21] 方圣龙, 樊继东. 一种基于自抗扰的永磁同步电机复合控制策略[J]. 电机与控制应用, 2023, 50(10): 62-69.
Fang Shenglong, Fan Jidong. A composite control strategy of permanent magnet synchronous motor based on active disturbance rejection[J]. Electric Machines & Control Application, 2023, 50(10): 62-69.
[22] 高云雷, 王玉彬, 黄瑛. 基于自抗扰迭代学习控制的双定子磁场调制电机转矩脉动抑制策略[J]. 电机与控制应用, 2021, 48(6): 10-16.
Gao Yunlei, Wang Yubin, Huang Ying. Torque ripple suppression strategy of field-modulation double-stator motor based on ILC-ADRC[J]. Electric Machines & Control Application, 2021, 48(6): 10-16.
[23] Wang Yicheng, Fang Shuhua, Hu Jianxiong. Active disturbance rejection control based on deep reinforcement learning of PMSM for more electric aircraft[J]. IEEE Transactions on Power Electronics, 2023, 38(1): 406-416.
[24] 李中奇, 周靓, 杨辉. 高速动车组数据驱动无模型自适应控制方法[J]. 自动化学报, 2023, 49(2): 437-447.
Li Zhongqi, Zhou Liang, Yang Hui. Data-driven model-free adaptive control method for high-speed electric multiple unit[J]. Acta Automatica Sinica, 2023, 49(2): 437-447.
[25] 郑鑫鑫, 张大海, 曹荣敏, 等. 改进无模型自适应迭代学习的直线电机滑模控制[J]. 电机与控制学报, 2024, 28(7): 120-130.
Zheng Xinxin, Zhang Dahai, Cao Rongmin, et al. Improved model free adaptive iterative learning control for linear motor sliding mode control[J]. Electric Machines and Control, 2024, 28(7): 120-130.
[26] 程苗苗, 翟朋辉, 张英杰, 等. 基于自学习非线性PID的音圈电机精密定位系统[J]. 电工技术学报, 2023, 38(6): 1519-1530.
Cheng Miaomiao, Zhai Penghui, Zhang Yingjie, et al. A voice coil motor-driven precision positioning system based on self-learning nonlinear PID[J]. Transactions of China Electrotechnical Society, 2023, 38(6): 1519-1530.
[27] 徐飞, 李子欣, 孔甘霖, 等. 变长分段直线感应电机数学建模[J]. 中国电机工程学报, 2024, 44(13): 5338-5348.
Xu Fei, Li Zixin, Kong Ganlin, et al. Mathematical model of variable-length segmented linear induction motor[J]. Proceedings of the CSEE, 2024, 44(13): 5338-5348.
[28] 张明远, 史黎明, 范满义, 等. 长初级双边直线感应电动机分段推力协同控制和测速算法[J]. 电工技术学报, 2023, 38(3): 659-669.
Zhang Mingyuan, Shi Liming, Fan Manyi, et al. Thrust cooperative control and speed measurement algorithm of segmented long primary double-sided linear induction motor[J]. Transactions of China Elec- trotechnical Society, 2023, 38(3): 659-669.
Abstract High-speed linear induction motors have the advantages of light rotor mass, simple structure, and high reliability, which are suitable for ground ultra-high-speed test facilities and electromagnetic launch fields. However, when high-speed linear induction motors run at transonic speeds, the unsteady aerodynamic characteristics of shock waves will cause strong vibrations in the rotor, resulting in strong uncertain disturbances in the position and speed measurement of the linear motor rotor and the electromagnetic mechanism. This uncertain disturbance is short-term, highly dynamic, sudden, and unpredictable. Consequently, slip control of the linear induction motor is abnormal, thrust control is unstable, and the transonic operation fails, seriously restricting the system speed improvement.
This paper establishes a self-learning mathematical model of a high-speed linear induction motor. The parameters of the motor model are learned through historical experimental data to realize high-precision multi-step prediction of the mover speed. The prediction speed constructs the rolling prediction matrix, the sensor measurement speed is calculated, and a method for reliability evaluation of the measurement speed is proposed based on the variation degree of the matrix column vector. Finally, according to the weighting of the prediction velocity, the measurement data, and the credibility value, a self-learning anti-disturbance control strategy for a high-speed linear induction motor under uncertain disturbance is proposed to realize the anti-disturbance control under transonic speed conditions.
The simulation and experimental results show that the proposed model can realize linear motor rotors’ high-precision multi-step rapid speed prediction. The speed correction method blocks the propagation of uncertain disturbances and accurately suppresses uncertain disturbances. The rotor speed’s simulation error is less than 0.7%, and the experimental error is less than 1%. Under the uncertain disturbance of e=0.2, the proposed self-learning anti-disturbance control strategy can realize the stable control of dq axis current and thrust with good uncertain disturbance suppression capability. The research results can be applied to high-speed linear induction motor propulsion systems.
keywords:Uncertain disturbance, linear induction motor, anti-disturbance control, self-learning model
中图分类号:TM346
DOI: 10.19595/j.cnki.1000-6753.tces.241634
中国科学院稳定支持基础研究领域青年团队计划资助项目(YSBR-045)。
收稿日期2024-09-14
改稿日期2024-10-29
徐 飞 男,1983年生,博士,副研究员,硕士生导师,研究方向为高速直线电磁驱动系统数学建模及控制保护。E-mail: xufei@mail.iee.ac.cn
李子欣 男,1981年生,博士,研究员,博士生导师,研究方向为大功率电力电子变换器和高速直线电磁驱动。E-mail: lzx@mail.iee.ac.cn(通信作者)
(编辑 崔文静)