图1 偏心情况示意图
Fig.1 Schematic diagram of eccentricity
摘要 心室辅助系统、心脏泵对其薄片电机的悬浮性能要求较高，不平衡磁拉力对薄片电机的悬浮性能有很大的影响。已有研究忽略了定子的开槽对不平衡磁拉力的影响，模型精确度较低，补偿效果一般。该文利用气隙磁导比来衡量定子开槽对气隙的影响，与传统的不平衡磁拉力模型相结合，提出一种考虑开槽影响的电机偏心气隙磁场解析式，从磁场调制的角度分析偏心时不平衡磁拉力的产生机理，并计算开槽影响的电机偏心不平衡磁拉力。最后通过补偿实验验证了理论分析的正确性与必要性。
关键词：薄片电机 偏心不平衡磁拉力 磁场调制效应 不平衡磁拉力产生机理
无轴承永磁薄片电机的转子一般为圆环形的永磁体[1-2]，没有轴承且轴向长度较短，具有高转速、高功率密度、无机械磨损等特点，因此特别适用于人工心脏泵等对超洁净运输有极高要求的场合[3]。近年来，由于新冠疫情的大面积爆发，心肺衰竭的患者数量急剧上升，人工心脏泵作为能够在心肺衰竭手术中为患者提供体外血液循环的关键器械，受到了广泛关注[4]。
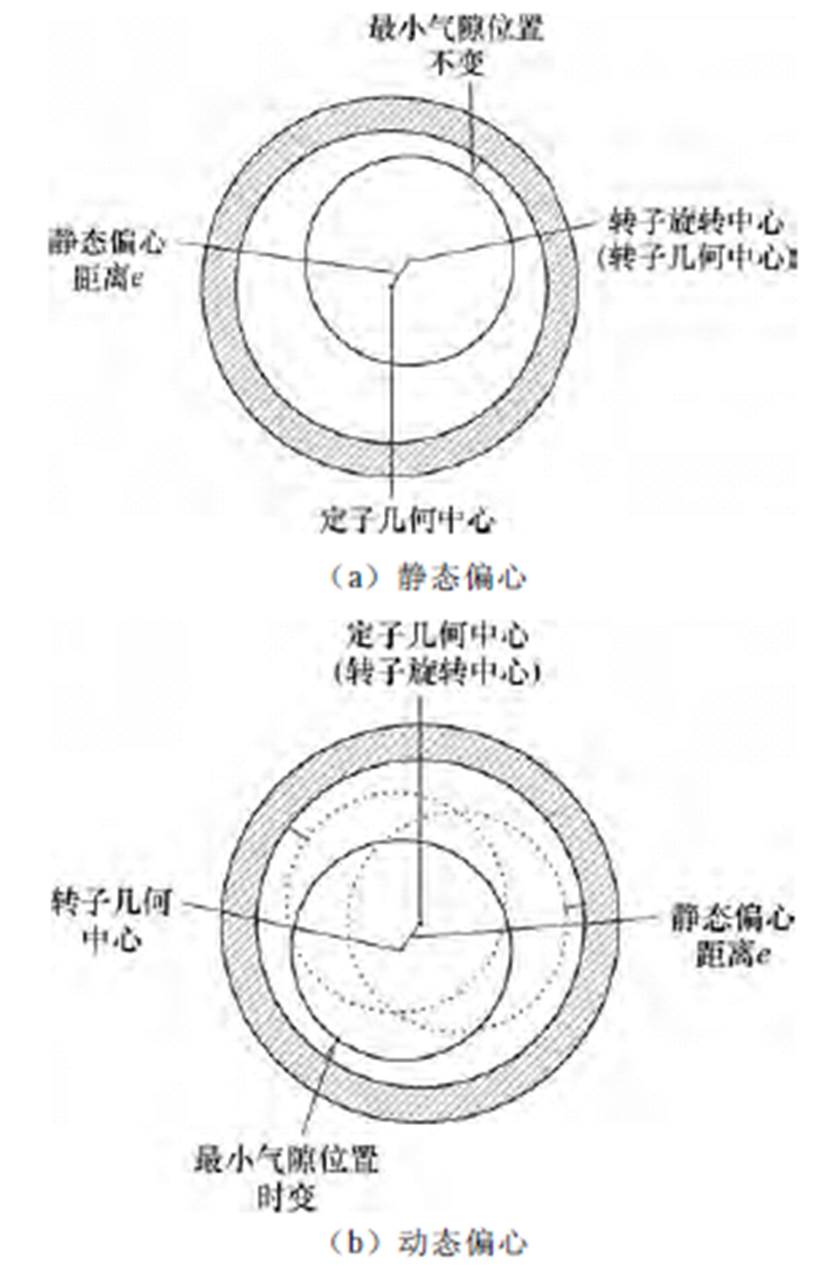
心脏泵运行时对血液的剪切力和挤压力将直接影响患者的生命安全，这两种力和无轴承永磁薄片电机悬浮时转子的偏心情况相关，因此无轴承永磁薄片电机转子悬浮时的偏心大小将直接影响电机的工作性能[5]。无轴承永磁薄片电机的任意一种偏心情况均可以看成两种基本偏心类型的组合：一种称为静态偏心，该类型中转子绕着自己的几何中心旋转，与定子不同心，其结构如图1a所示，可以看出，由偏心导致的最小气隙位置不随时间变化；另一种称为动态偏心，该类型中转子绕着定子的几何中心旋转，与定子同心，其结构如图1b所示，可以看出，该结构由偏心导致的最小气隙位置会随着时间变化。
图1 偏心情况示意图
Fig.1 Schematic diagram of eccentricity
由于电机没有轴承这一结构，所以如何将转子稳定且没有偏心地浮在电机的定子几何中心就成了无轴承永磁薄片电机的控制重点[6]。然而，不平衡磁拉力会使得电机转子在径向上产生较大的振动，这一振动会极大地影响薄片电机的悬浮性能。因此，精确解析无轴承永磁薄片电机的偏心不平衡磁拉力并对其进行补偿显得尤为重要[7-9]。
无轴承永磁薄片电机的转子在悬浮时的径向位移不为零，这一特点使得转子的几何中心与定子几何中心不同心，产生偏心现象。转子偏心后使得原本正弦分布的气隙磁场畸变，产生谐波，这些谐波与基波相互作用，成为薄片电机中不平衡磁拉力的主要来源。除此之外，加工误差、传感器位置安装不对称等因素也会产生少量不平衡磁拉力，但由于其含量较小，本文不做考虑。因此，如何精确解析偏心下的气隙磁场是精准分析无轴承永磁薄片电机不平衡磁拉力的关键[10]。
文献[11-12]以一维解析法为基础，通过建立转子的磁动势模型，并与气隙磁导率模型相结合，简单直观地得到了偏心时永磁电机的磁场分布情况，但是，对于如静态偏心和动态偏心等不同转子偏心类型没有进行区分，只可做不平衡磁拉力的定性分析。文献[13]推导了区分永磁电机的动、静偏心情况下的不平衡磁拉力模型，提升了模型精度，但其重点分析了不平衡磁拉力的谐波特性，而忽略了不平衡磁拉力的高精度定量分析。上述文献分析都建立在一维解析的基础之上，模型精度不够高，只适用于对不平衡磁拉力进行定性分析，用于分析不平衡磁拉力的大小时，误差较大[14]。
此外，Z. Q. Zhu等学者在文献[15-16]中，以子域法为基础，建立了永磁电机的二维磁场分布解析模型，实现了电机解析从一维到二维的转变。Li Yanxin、Z. Q. Zhu等在文献[17-18]中，利用子域叠加法，将偏心磁场等效成多个同心磁场的叠加，但没有给出具体的解析式。随后，U. Kim、Zhou Yu、仇志坚等学者，将一阶摄动法与子域法结合，建立了表贴式永磁电机、插入式永磁电机的偏心磁场解析模型，提升了解析精度[19-21]。为了便于分析，上述模型都没有考虑定子开槽的影响，对传统有轴承这类偏心情况较简单的电机进行定量分析时，精度尚可，但用于偏心情况复杂多变的无轴承薄片电机时，开槽影响所带来的误差难以忽略。
目前，对永磁电机的不平衡力磁拉力补偿的研究主要集中在有轴承类永磁电机上，对无轴承的永磁薄片电机的相关研究较少。文献[22]研究了交替极无轴承永磁电机的偏心磁场，建立了基于二维解析法的数学模型。文献[23]建立了一对极永磁薄片电机的偏心磁场解析模型，并基于此模型对不平衡磁拉力进行补偿。上述文献将已有的有轴承永磁电机偏心磁场模型拓展到永磁薄片电机，但依然存在忽略开槽影响、模型精度不够高、误差相对较大的问题。
已有分析模型对比见表1，现有的有轴承永磁电机偏心不平衡磁拉力分析模型并不适用于对模型精度有较高要求的无轴承永磁薄片电机，已有的关于无轴承永磁薄片电机的偏心不平衡磁拉力分析模型没有考虑定子开槽影响，模型精度亦不够高。因此，需要建立一种考虑开槽影响的高精度解析模型来对无轴承薄片电机的不平衡磁拉力进行精确解析。
表1 已有分析模型对比
Tab.1 Comparison of existing analysis models
类型优点缺点 模型一[11-12]计算简单没有区分偏心类型，精度较低 模型二[13]区分了偏心类型没有对不平衡磁拉力进行定量分析 模型三[15-16]以子域法为基础进行建模，提升了模型精度计算较为复杂，没有考虑开槽影响 模型四[17-18]利用子域叠加法进行建模，提升了模型精度没有给出不平衡磁拉力的具体表达式，没有考虑开槽影响 模型五[19-21]结合子域法与一阶摄动法，提升了模型精度计算较为复杂，没有考虑开槽影响 模型六[22-23]针对无轴承电机的不平衡磁拉力进行建模，提升了模型精度计算较为复杂，没有考虑开槽影响
近年来，随着磁场调制理论的不断丰富，许多电机问题都可以用磁场调制原理来解释[24-25]，为了更好地研究不平衡磁拉力，本文将从磁场调制的角度去分析不平衡磁拉力产生的机理，并优化其数学模型。
本文将一维与二维解析法相结合，提出了一种基于磁场调制理论的考虑定子开槽影响的无轴承薄片电机偏心气隙磁场解析方法。首先，利用气隙磁导比来衡量开槽对电机偏心磁场的影响，对偏心不平衡磁拉力进行精确解析。其次，基于磁场调制理论，重新分析了不平衡磁拉力产生的内在机理。然后，通过将考虑开槽前后的不平衡磁拉力的值与仿真数值进行对比，证明本文所建模型精度高、计算简单，适用于无轴承永磁薄片电机偏心不平衡磁拉力的精确解析。最后，通过不平衡磁拉力的精确补偿实验，验证了精确补偿不平衡磁拉力能较大程度地提高薄片电机的悬浮性能，证实了理论分析的准确性和有效性。
本文选取一对极的永磁环作为电机转子。考虑到建模复杂程度与计算难度，忽略定子铁心磁化非线性及饱和的问题。由电机的简化模型图2可知，电机被分成了永磁体和气隙两个子域。图中，Rs、Rm、Rr分别为定子内径、转子外径与转子内径。
图2 电机简化模型
Fig.2 Simplified model of motor
根据子域法和一阶摄动法，可以得到一对极圆环形永磁转子偏心后的气隙磁通密度分别为
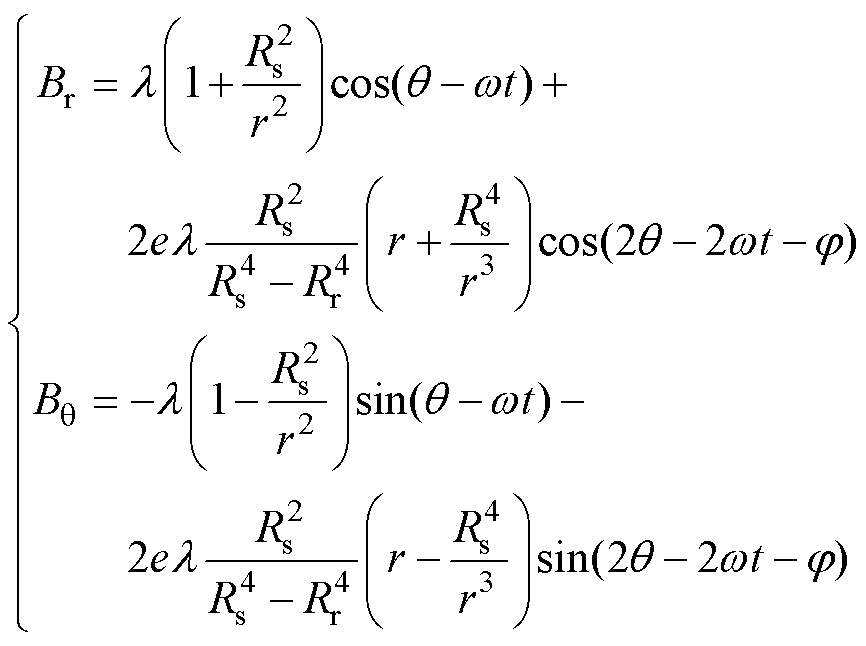（1）
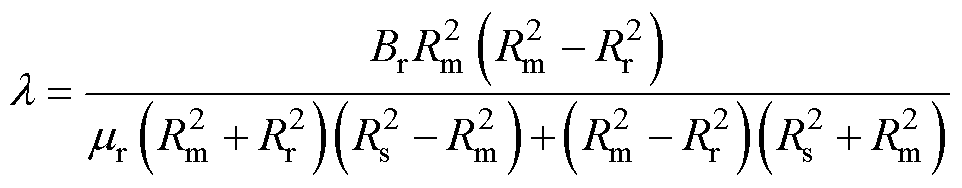（2）
式中，q 为转子的旋转角度；l 为磁通密度系数；r为气隙半径；Br和Bq 分别为气隙磁通密度的径向与切向分量；e、w、j、mr分别为转子偏心距离、转子转速、转子偏心角度与永磁体的相对磁导率。根据麦克斯韦应力张量法，定转子在x、y方向上所受的不平衡磁拉力分别为
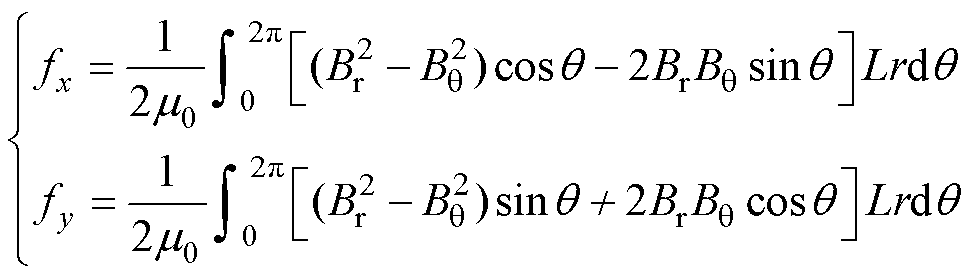（3）
式中，L为转子的轴向长度。将式（1）、式（2）代入式（3）中，化简得
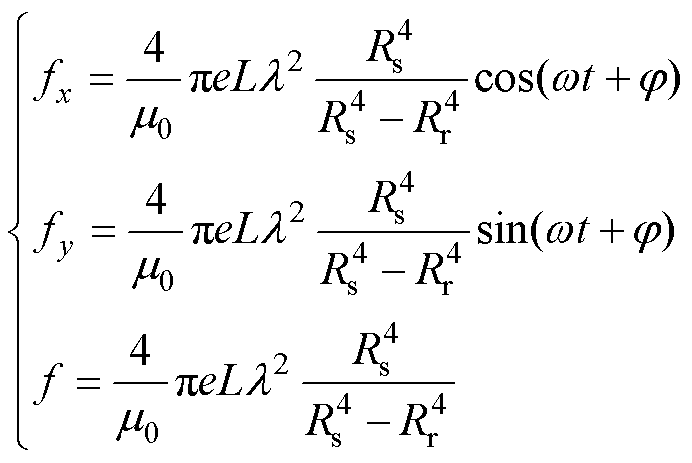（4）
式中，f为定转子所受的不平衡磁拉力的合力。
本节以忽略开槽的电机不平衡磁拉力数学模型为基础，用气隙磁导比[26]来衡量开槽对不平衡磁拉力的影响。
建立如图3所示的简化解析模型。图中，R1为定子内径，R2为转子外径，a1为定子槽宽，a2为定子槽口宽。
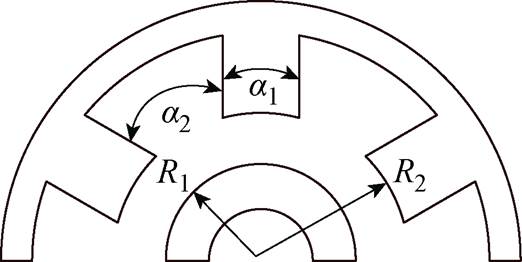
图3 简化解析模型
Fig.3 Simplified analytical model
设电机开槽前后的气隙磁通密度分别为Bslotloss和Bslot，均为复数形式，其表达式分别为
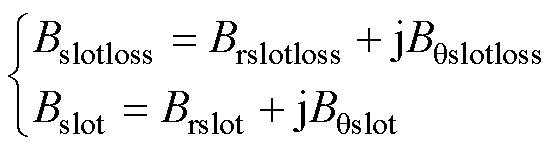（5）
式中，Brslotloss和Bqslotloss分别为开槽前的径向与切向磁通密度；Brslot和Bqslot分别为开槽后的径向与切向磁通密度。定义气隙磁导比x(r, q) 来描述任意位置处定子开槽对气隙磁通密度的影响，记为x，其表达式为
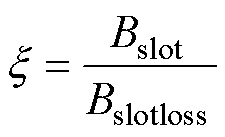（6）
气隙磁导比的具体表达式为
（7）
式中，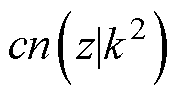
、
、
、
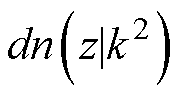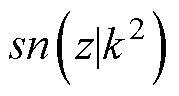分别为三种雅可比椭圆函数和第一类完全椭圆积分。z、k和w的值可通过式（8）和式（9）来确认。
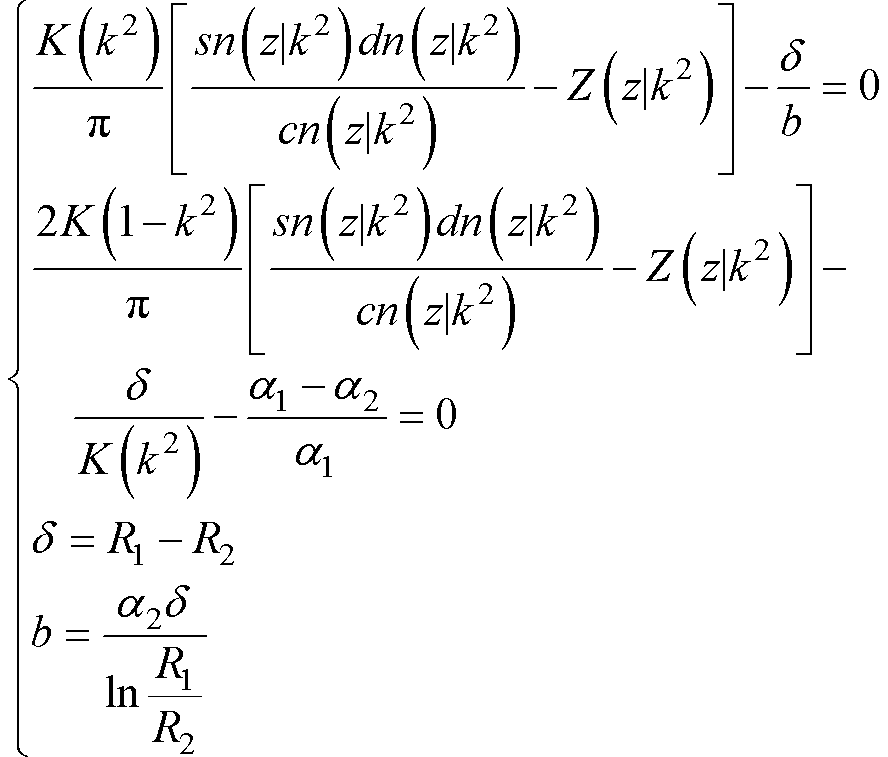（8）
（9）
式中，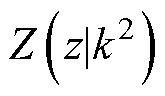
为雅可比Zeta函数；
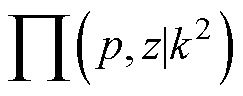为雅可比函数的反函数；p为其函数变量。
根据气隙磁导比的定义，考虑了开槽影响的偏心气隙磁通密度分别为
（10）
进一步地，根据式（10）可以得到考虑了开槽影响的偏心不平衡磁拉力为
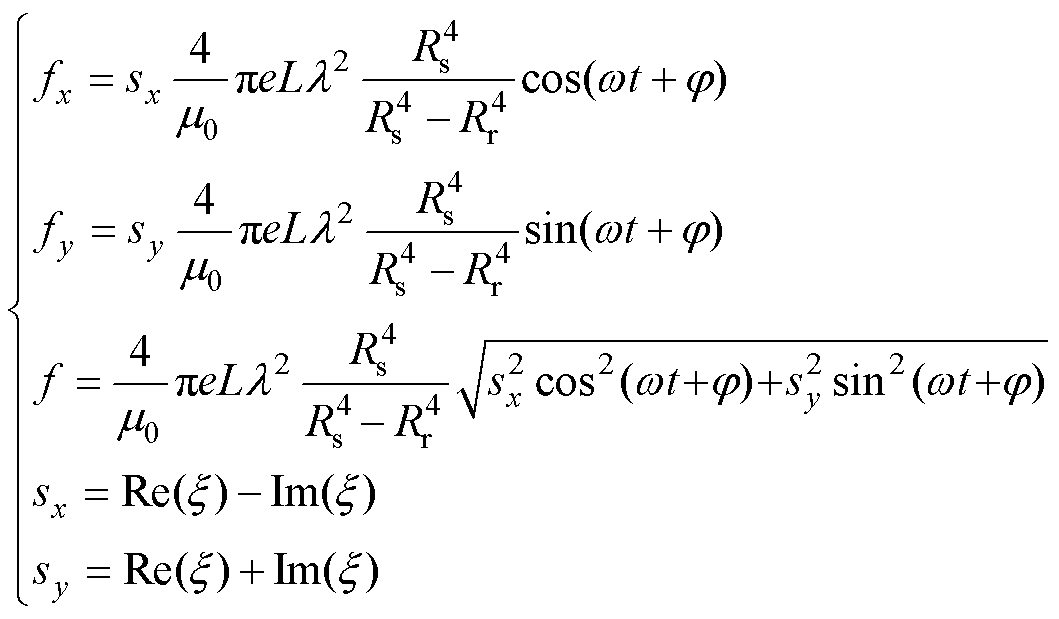（11）
式中，sx、sy分别为定子开槽对不平衡磁拉力x轴、y轴分量fx、fy的影响系数。
为便于说明作用机理，下面以忽略开槽情况下的fx为例，从磁场调制的角度分析不平衡磁拉力的产生原理。
观察式（10）可以发现，转子不偏心，即e=0时，气隙均匀分布，此时永磁磁场在气隙中均匀分布，形成一对极磁通密度；转子偏心后，气隙分布不再均匀，永磁磁场产生类似定子齿的调制效果，将原本均匀分布的一对极磁场调制出二对极的谐波磁场。至此，原本只有基波磁场的气隙中开始出现二对极的谐波磁场。
当电机参数及偏心状况确定时，三角函数的系数项均为常数，所以式（10）可以改写为
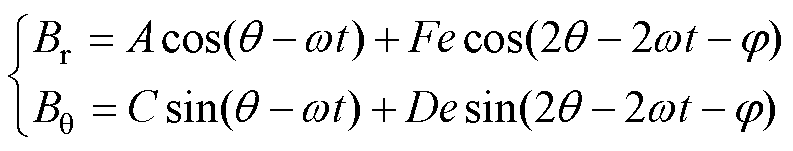（12）
式中，A、F、C、D为电机参数及偏心状况确定时式（10）中各三角函数的系数。
将式（11）代入式（10）的fx表达式，可得
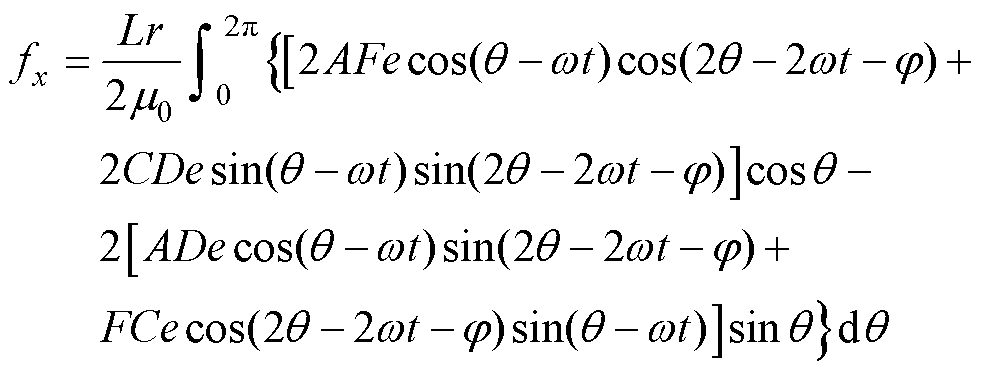（13）
由三角函数与积分的性质可知，若要使fx的值不为0，那么积分项只能保留如式（13）所示的这些项，也只有这些项所代表的磁通密度才可以产生不平衡磁拉力，本文称之为有效磁通密度。
为进一步说明有效磁通密度的产生与作用机理，现对式（12）进一步改写，即
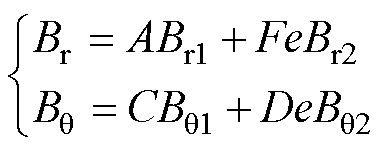（14）
其中
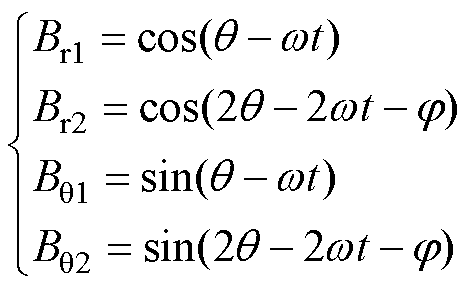（15）
式中，Br1与Bq1分别为一对极永磁体的径向与切向磁通密度；Br2与Bq2分别为由不均匀气隙调制出的谐波磁场的径向与切向磁通密度。于是式（13）可以改写为
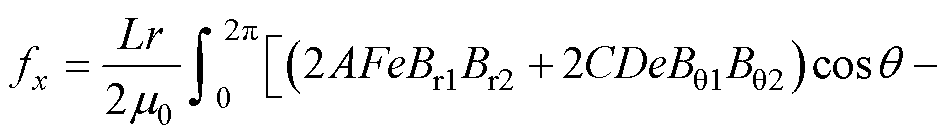
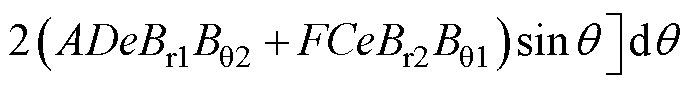（16）
分析式（16）可知，基波磁场的径向与切向磁通密度分别与不均匀气隙调制出的谐波磁场的径向与切向磁通密度相互作用，产生了不平衡磁拉力。当电机参数固定时，不平衡磁拉力的大小仅与转子偏心距离e的大小有关，且力的方向始终指向气隙最小处。
为验证模型的精准性，本文以一台永磁薄片电机为例，其转子为一对极的圆环形永磁体，转子逆时针45°偏心，偏心距离e的大小为0.3mm。电机参数见表2。
表2 电机参数
Tab.2 Motor parameters
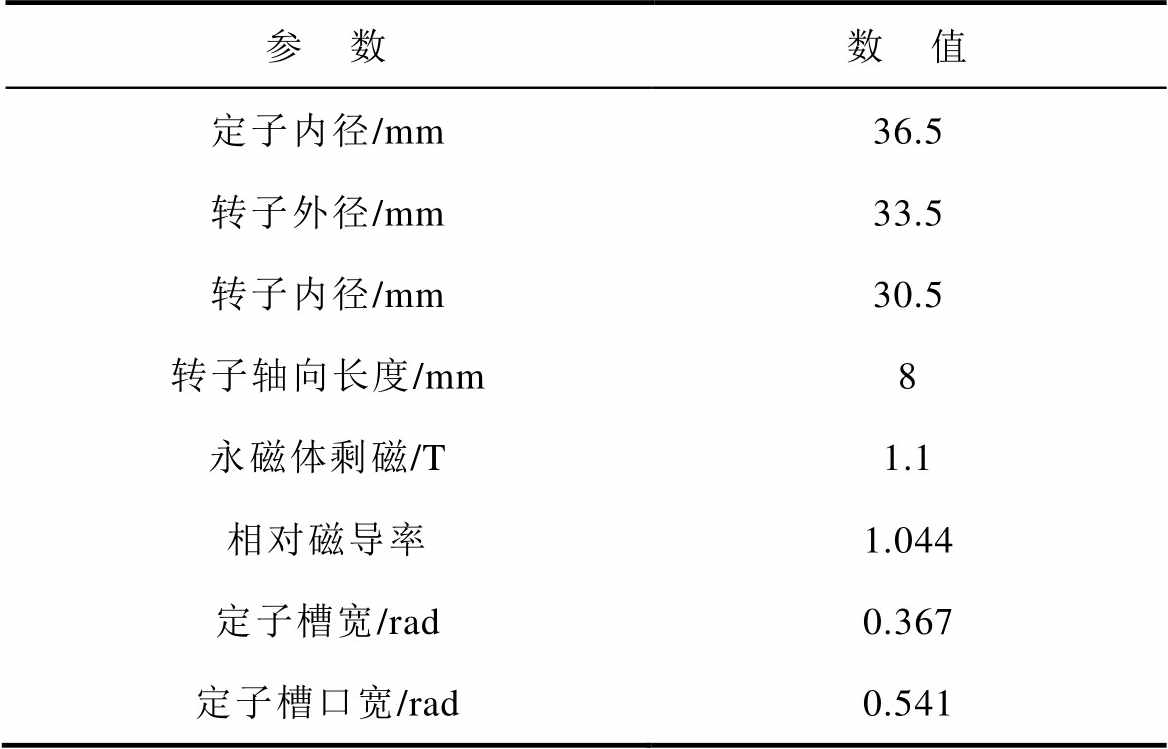
参 数数 值 定子内径/mm36.5 转子外径/mm33.5 转子内径/mm30.5 转子轴向长度/mm8 永磁体剩磁/T1.1 相对磁导率1.044 定子槽宽/rad0.367 定子槽口宽/rad0.541
经计算，气隙磁导比的关键参数z、k、雅可比函数的值见表3。
表3 气隙磁导比关键参数
Tab.3 Key parameters of air gap magnetic permeability ratio
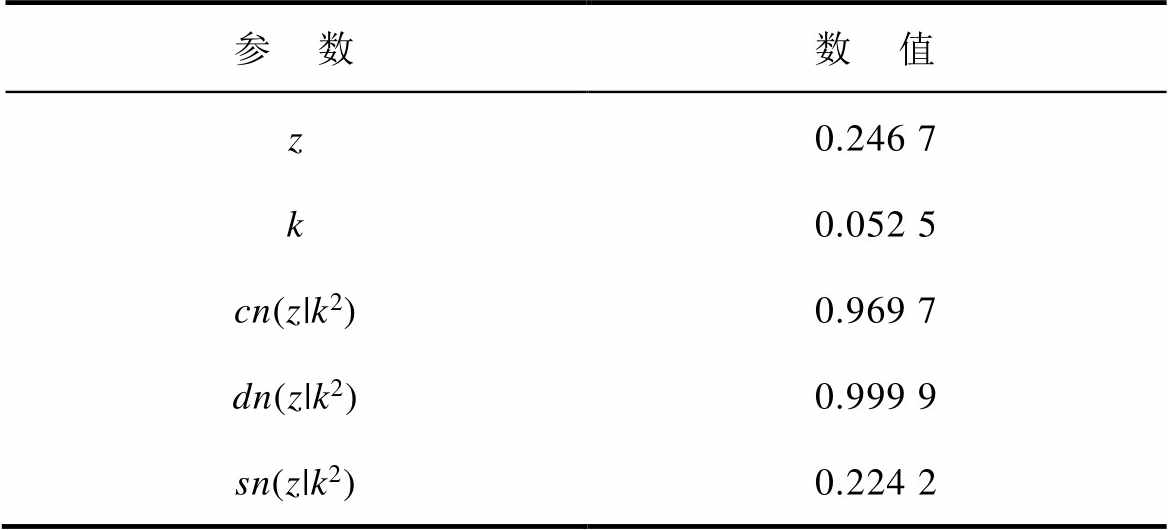
参 数数 值 z0.246 7 k0.052 5 cn(z|k2)0.969 7 dn(z|k2)0.999 9 sn(z|k2)0.224 2
分别计算考虑开槽的本文模型、基于一维解析法的不考虑开槽的模型一和基于二维解析法的不考虑开槽的模型六的不平衡磁拉力，并与有限元仿真结果进行对比，结果如图4所示。
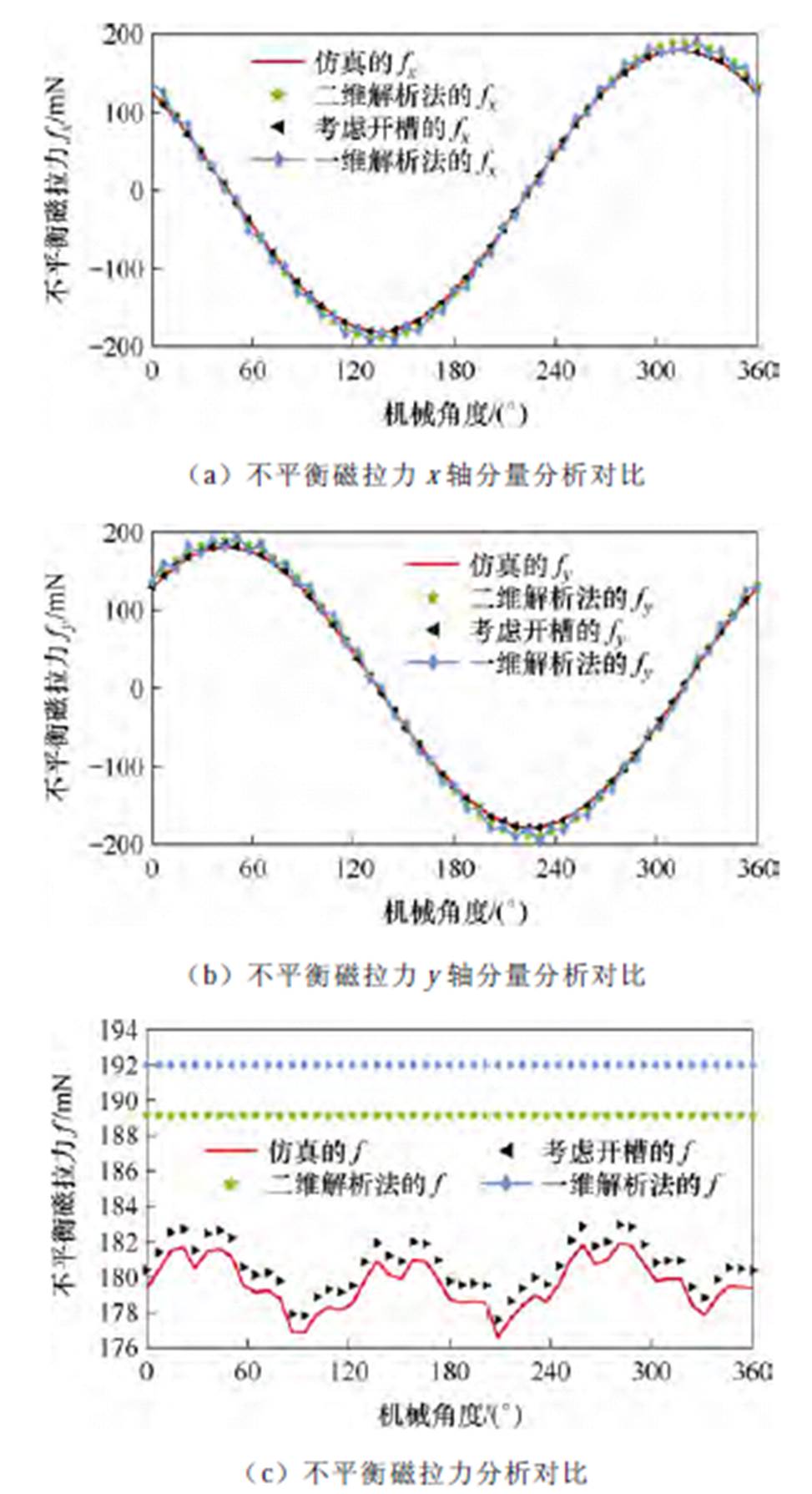
图4 不平衡磁拉力仿真对比
Fig.4 Simulation comparison of unbalanced magnetic pulling force
结合图4、式（3）、式（10）可以发现：不平衡磁拉力x、y轴分量的仿真值与理论推导值基本吻合，验证了所建模型的正确性。
（1）忽略开槽影响的模型六的不平衡磁拉力理论值偏大，比仿真值大5.2%左右。
（2）忽略开槽影响的模型一的不平衡磁拉力理论值最大，达到了6.7%左右。
（3）考虑了开槽影响的不平衡磁拉力理论值最接近仿真值，比仿真值大0.5%左右。
（4）有槽薄片电机的偏心不平衡磁拉力并非恒定值，忽略开槽影响的不平衡磁拉力理论值为一恒定值，而考虑了开槽影响的不平衡磁拉力理论值体现了这一点，数值分布与仿真数据基本一致。
综上所述，相比于已有的忽略开槽影响的不平衡磁拉力模型，本文提出的考虑了开槽影响的不平衡磁拉力模型将误差从6.7%下降到0.5%左右，模型精度大幅提高，更加适合于对悬浮精度有极高要求的心脏泵用薄片电机。
为了验证所建模型的补偿效果，在Matlab的Simulink中搭建如图5所示的薄片电机简化悬浮模型，以x轴补偿为例，结合推导的数学模型可知，通过改变不平衡磁拉力补偿的数值，即可验证不加补偿、施加基于一维解析法的不考虑开槽的模型一的补偿、施加基于二维解析法的不考虑开槽的模型六的补偿和本文补偿四种情况下的位移效果。各情况补偿效果如图6所示。
结合图6，分析补偿效果，可以发现：
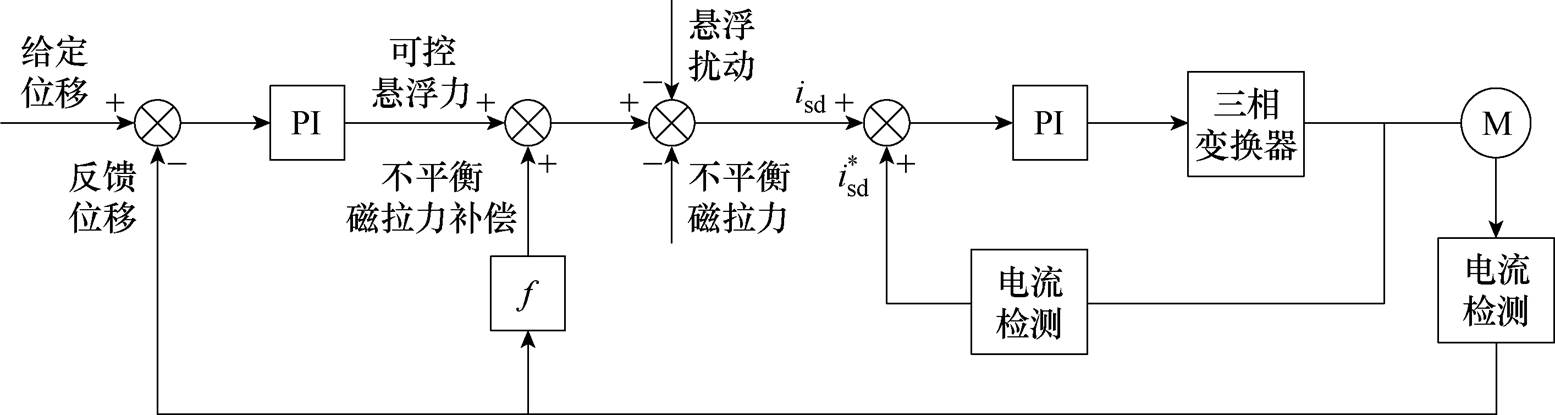
图5 简化补偿控制框图
Fig.5 Simplified compensation control block diagram
（1）无轴承薄片电机的不平衡磁拉力对位移的影响不可忽略。
（2）未加不平衡磁拉力的补偿时，位移收敛相对缓慢，位移波动的幅值相对较大，严重影响电机的悬浮性能。
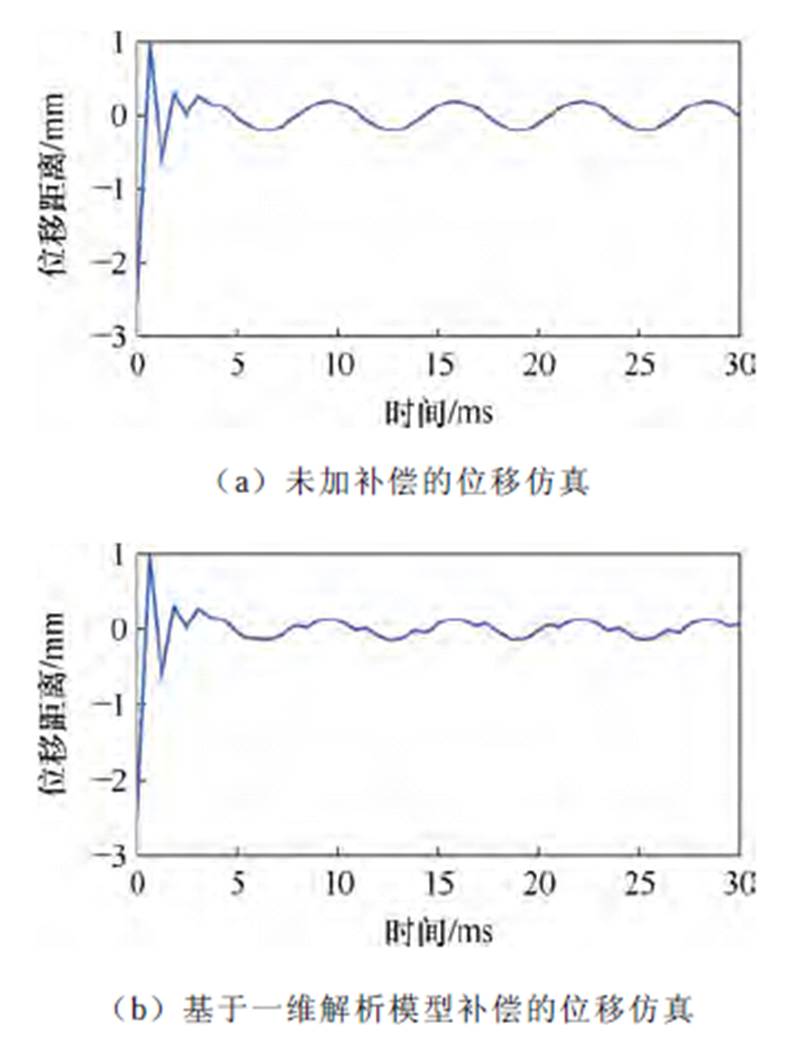
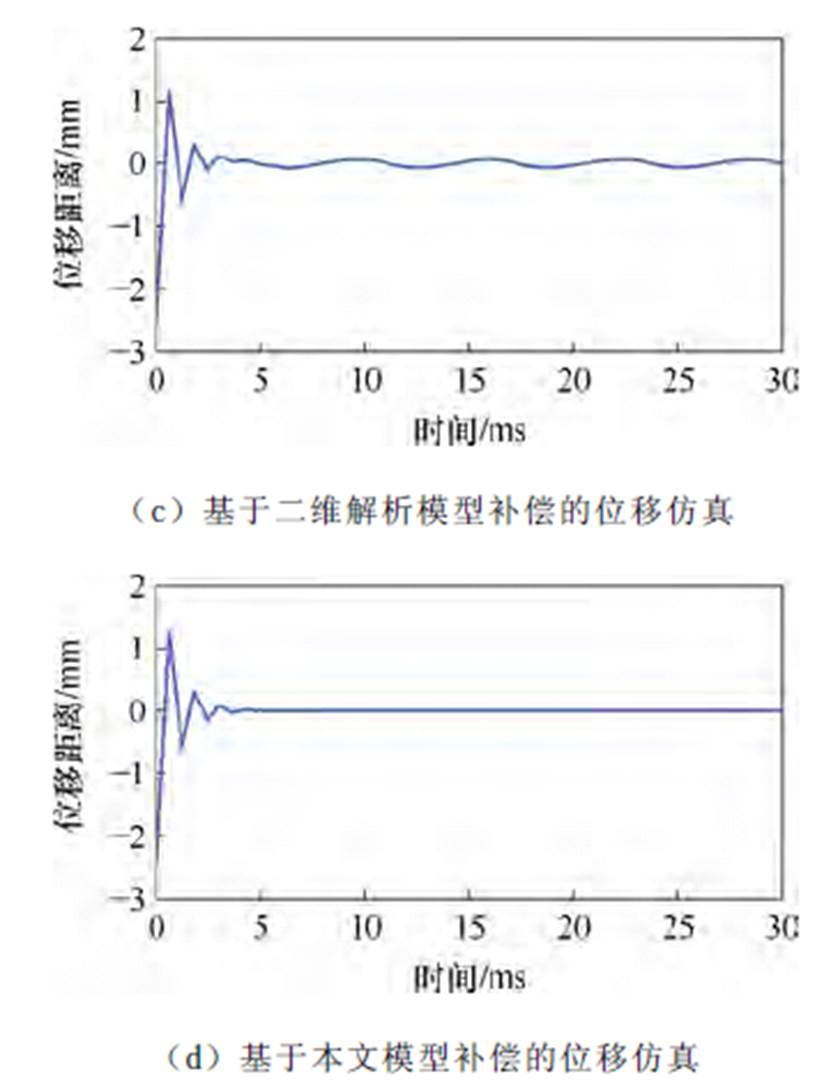
图6 各补偿方案下的位移仿真
Fig.6 Displacement simulation diagram under various compensation schemes
（3）加入基于模型一和模型六的不平衡磁拉力补偿后，位移收敛加快，位移波动的幅值相对于不加补偿而言明显降低，但波动依然存在，对电机悬浮性能的影响仍然不可忽略。
（4）加入本文模型的不平衡磁拉力补偿后，位移收敛更快，位移波动近乎完全消除，在理想情况下，不平衡磁拉力对电机悬浮性能的影响可忽略不计。
综上所述，对薄片电机而言，相较于传统有轴承电机，由于没有轴承的特殊结构，使得不平衡磁拉力严重影响其悬浮性能。基于已有的不平衡磁拉力数学模型，虽然可以在一定程度上减小不平衡磁拉力对电机悬浮性能的影响，但并不能完全消除这个影响，而基于本文考虑了开槽影响的不平衡磁拉力数学模型的补偿，由于模型的精度相对已有模型而言大幅提高，在理想情况下，已经可以完全消除不平衡磁拉力对电机悬浮性能的影响，极大地提高了电机的悬浮性能，更加适合于对悬浮精度有极高要求的心脏泵用薄片电机。
为验证本文提出的考虑了开槽影响的不平衡磁拉力模型特别适用于薄片电机，实验室搭建了如图7所示的实验平台，包括薄片电机、基于DSP28335的控制板等。电机系统的整体控制框图如图8所示，图中，fx和fy分别为x、y方向的不平衡磁拉力的补偿值，不同补偿方法得到的补偿值均不相同。
静止悬浮时的补偿效果如图9所示。以x轴位移为例，当不加不平衡磁拉力补偿时，位移在±100 mm左右，幅值相对较大，证明不平衡磁拉力对悬浮的影响相对较大；当加入基于模型一和模型六的补偿后，电机悬浮情况有所好转，位移分别在±60 mm、±30 mm左右，不平衡磁拉力对悬浮的影响相对较小，但依然不可忽略；当加入基于本文考虑了开槽影响的不平衡磁拉力数学模型的补偿后，电机悬浮情况最好，位移在±5 mm左右，不平衡磁拉力对电机悬浮性能的影响已经可以忽略不计，证明了本文提出的数学模型精确度显著提高，电机在静止悬浮时的补偿效果相对较好。
图7 实验平台
Fig.7 Experimental platform
图8 系统整体控制框图
Fig.8 Overall system control block diagram
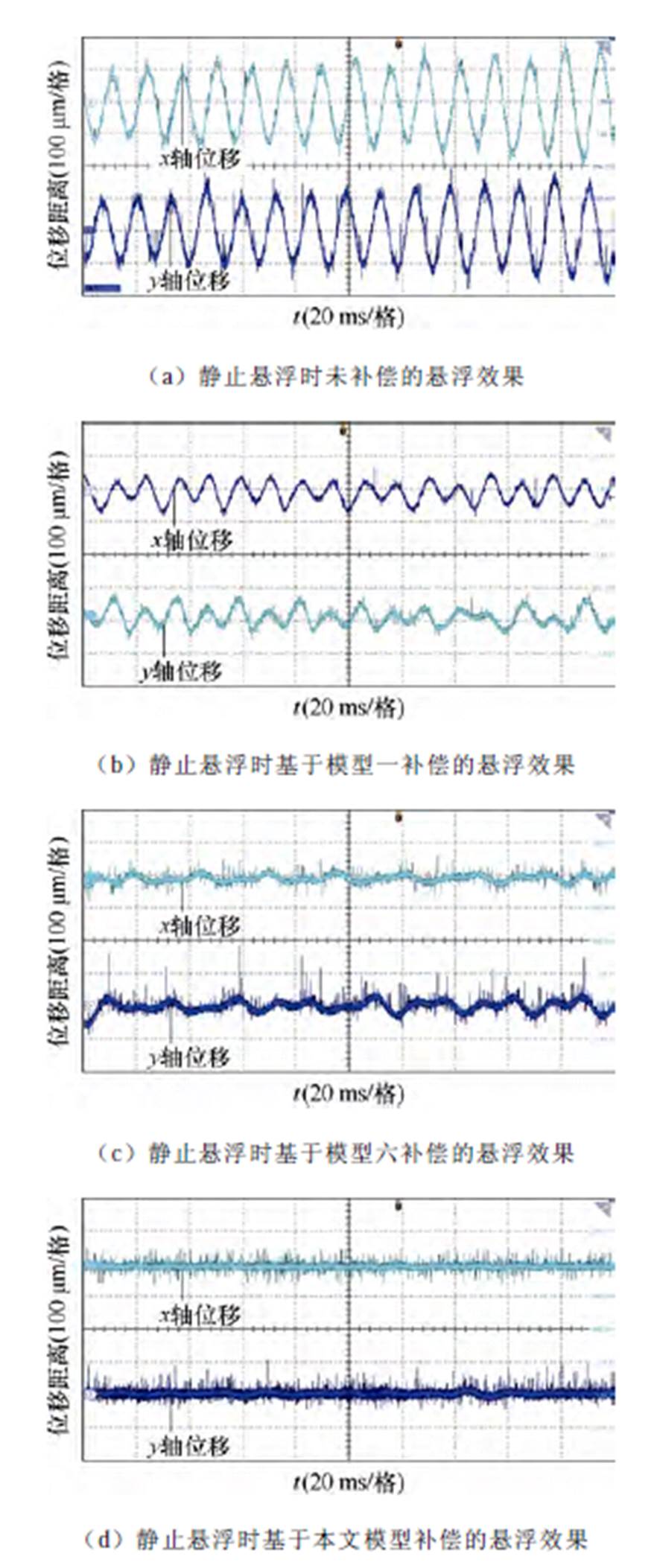
图9 静止悬浮时各补偿方案下的悬浮效果
Fig.9 Suspension effects under various compensation schemes during static suspension
电机转速在3 000 r/min时，不同补偿方案的效果如图10所示。以x轴位移为例，当不加不平衡磁拉力补偿时，位移在±90 mm左右，幅值相对较大，证明当薄片电机旋转工作时，不平衡磁拉力对悬浮的影响相对较大；当加入基于模型一和模型六的补偿后，电机悬浮情况有所好转，位移分别在±55 mm、±40 mm左右，不平衡磁拉力对悬浮的影响相对较小，但依然不可忽略；当加入基于本文考虑了开槽影响的不平衡磁拉力数学模型的补偿后，电机悬浮情况最好，位移在±20 mm左右，此时位移波动依旧存在，结合电机静止时的补偿实验结果，可以认为此时的波动是由转子旋转、外加扰动增大等引起，与不平衡磁拉力基本无关，证明了本文提出的数学模型准确度显著提高，电机在3 000 r/min下的补偿效果依然相对较好。
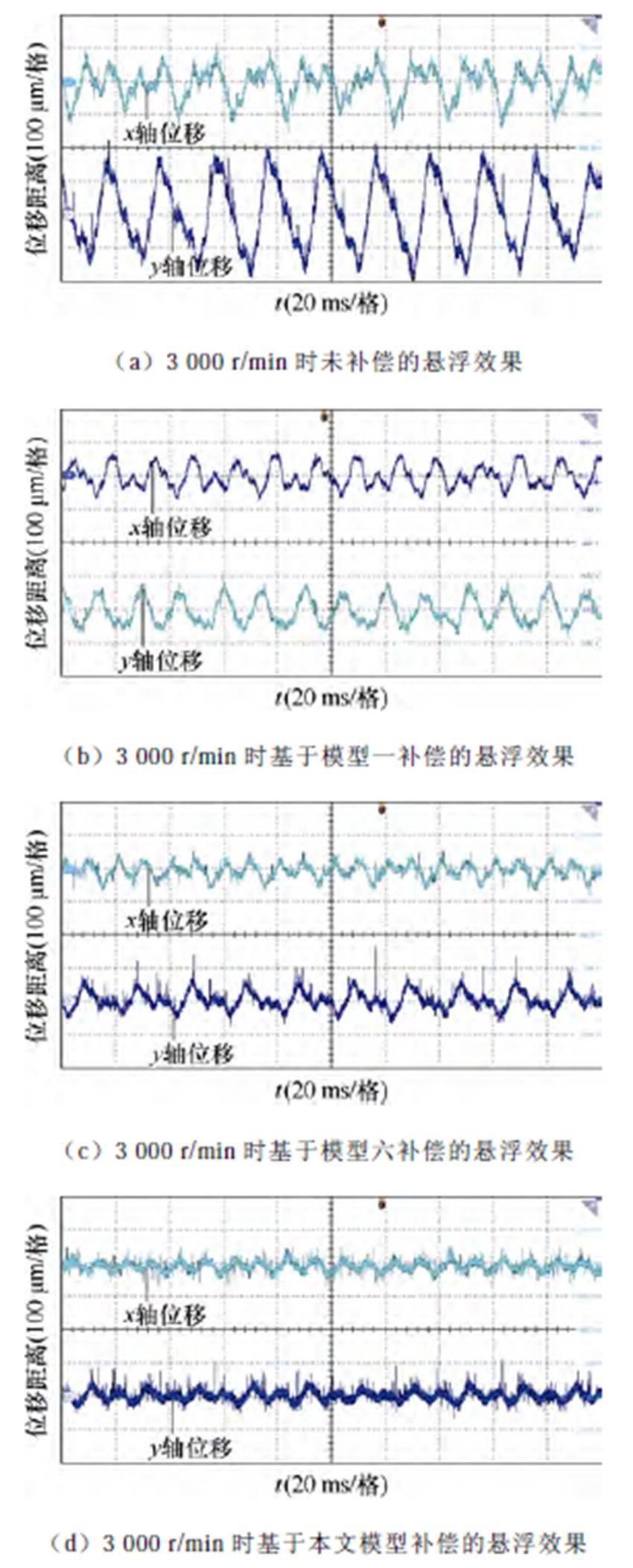
图10 3 000 r/min时各补偿方案下的悬浮效果
Fig.10 Suspension effect under various compensation schemes at 3 000 r/min
上述实验结果的综合对比如图11所示，可以看出，相比之下，基于本文模型补偿的悬浮效果最好，极大地提高了永磁薄片电机的悬浮性能。
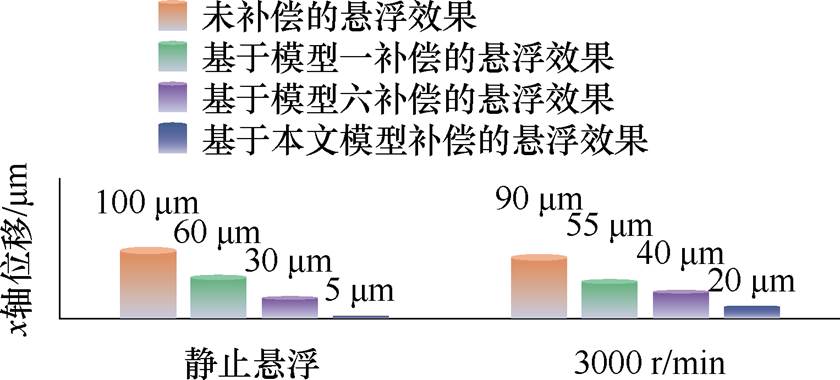
图11 不同转速下的不同补偿方案效果对比
Fig.11 Comparison of the effects of different compensation schemes at different speeds
本文针对永磁薄片电机的不平衡磁拉力提出一种考虑了定子开槽影响的不平衡磁拉力数学模型，得到以下结论：
1）相比于传统有轴承电机，永磁薄片电机因为没有机械轴承，当不考虑不平衡磁拉力补偿时，电机的悬浮性能相对较差，位移在90～100 mm左右。
2）已有的不考虑开槽影响的不平衡磁拉力模型在仿真中的误差为5.2%～6.7%左右，基于此模型对永磁薄片电机进行不平衡磁拉力补偿时，由于模型精度不够，虽然能够提升电机的悬浮性能，将位移降低到30～40 mm左右，但用于对悬浮性能有极高要求的心脏泵用薄片电机时，悬浮位移仍然偏大。
3）本文提出的考虑了开槽影响的不平衡磁拉力模型在仿真中的误差为0.5%左右，显著提高了模型精度，基于此模型对薄片电机进行不平衡磁拉力补偿时，能够显著提升电机的悬浮性能，将位移降低到15 mm以下，适用于对悬浮性能有极高要求的心脏泵用永磁薄片电机。
参考文献
[1] 王晓琳, 石滕瑞, 鲍旭聪. 基于频域拟合的无轴承永磁薄片电机径向悬浮力建模分析[J]. 电工技术学报, 2023, 38(2): 317-329.
Wang Xiaolin, Shi Tengrui, Bao Xucong. Accurate mathematical modeling of radial suspension force on bearingless permanent magnet slice motors based on frequency domain fitting[J]. Transactions of China Electrotechnical Society, 2023, 38(2): 317-329.
[2] 赵士豪, 陈进华, 张驰, 等. 不均匀气隙表贴式永磁同步电机磁场解析计算[J]. 电工技术学报, 2022, 37(14): 3502-3513.
Zhao Shihao, Chen Jinhua, Zhang Chi, et al. Analytical calculation of magnetic field of permanent magnet synchronous motor with uneven air gap structure[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3502-3513.
[3] Martin N, Natale B, Reto S. Bearinless centrifugal pump for highly pure chemicals[C]//8th International Symposium on Magentic Bearing, Mito, Japan, 2002: 283-288.
[4] 胡炳全, 陈盛奎, 潘俞丹. 体外膜肺氧合在高危重症冠心病患者介入治疗中的应用进展[J]. 现代医学与健康研究电子杂志, 2021, 7(24): 136-138.
Hu Bingquan, Chen Shengkui, Pan Yudan, et al. Pro- gress in the application of extracorporeal membrane oxygenation in interventional treatment of critically ill coronary heart disease patients[J]. Modern Medicine and Health Research, 2021, 7(24): 136-138.
[5] 张艺, 王宇, 张成糕. 基于霍尔负序解调法的无轴承永磁薄片电机径向位移检测方法[J]. 中国电机工程学报, 2023, 43(19): 7659-7668.
Zhang Yi, Wang Yu, Zhang Chenggao. Radical displacement detection method based on negative sequence demodulation method on hall signals of bearingless permanent magnet slice motor[J]. Pro- ceedings of the CSEE, 2023, 43(19): 7659-7668.
[6] Gerada D, Mebarki A, Brown N L, et al. High-speed electrical machines: technologies, trends, and developments[J]. IEEE Transactions on Industrial Electronics, 2014, 61(6): 2946-2959.
[7] 于丰源, 陈昊, 闫文举, 等. 宽窄定子极轴向磁通开关磁阻电机的设计与分析[J]. 电工技术学报, 2023, 38(5): 1261-1274.
Yu Fengyuan, Chen Hao, Yan Wenju, et al. Design and characteristic analysis of a wide-narrow stator poles axial flux switched reluctance machine[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1261-1274.
[8] 孙德博, 胡艳芳, 牛峰, 等. 开关磁阻电机调速系统故障诊断和容错控制方法研究现状及展望[J]. 电工技术学报, 2022, 37(9): 2211-2229.
Sun Debo, Hu Yanfang, Niu Feng, et al. Status and prospect of fault diagnosis and tolerant control methods for switched reluctance motor drive system[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2211-2229.
[9] 张业成, 刘国海, 陈前. 基于电流波动特征的永磁同步电机匝间短路与局部退磁故障分类诊断研究[J]. 电工技术学报, 2022, 37(7): 1634-1643, 1653.
Zhang Yecheng, Liu Guohai, Chen Qian. Dis- crimination of interturn short-circuit and local demagnetization in permanent magnet synchronous motor based on current fluctuation characteristics[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1634-1643, 1653.
[10] 邓文哲, 左曙光, 林福, 等. 偏心条件下轴向磁通轮毂电机不平衡弯矩建模与分析[J]. 电工技术学报, 2017, 32(13): 153-161.
Deng Wenzhe, Zuo Shuguang, Lin Fu, et al. Modeling and analysis of unbalanced moment for an axial-flux in-wheel motor with eccentricity[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 153- 161.
[11] Smith A C, Dorrell D G. Calculation and measure- ment of unbalanced magnetic pull in cage induction motors with eccentric rotors. part 1: analytical model[J]. IEE Proceedings-Electric Power Appli- cations, 1996, 143(3): 193.
[12] Dorrell D G, Hsieh M F, Guo Youguang. Unbalanced magnet pull in large brushless rare-earth permanent magnet motors with rotor eccentricity[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4586-4589.
[13] Song J Y, Kang K J, Kang C H, et al. Cogging torque and unbalanced magnetic pull due to simultaneous existence of dynamic and static eccentricities and uneven magnetization in permanent magnet motors[J]. IEEE Transactions on Magnetics, 2017, 53(3): 8200609.
[14] Zhu Z Q, Wu L J, Xia Z P. An accurate subdomain model for magnetic field computation in slotted surface-mounted permanent-magnet machines[J]. IEEE Transactions on Magnetics, 2010, 46(4): 1100-1115.
[15] Zhu Z Q, Howe D, Bolte E, et al. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. I. open-circuit field[J]. IEEE Transactions on Magnetics, 1993, 29(1): 124-135.
[16] Wu L J, Zhu Z Q, Staton D, et al. Subdomain model for predicting armature reaction field of surface- mounted permanent-magnet machines accounting for tooth-tips[J]. IEEE Transactions on Magnetics, 2011, 47(4): 812-822.
[17] Li Yanxin, Lu Qinfen, Zhu Ziqiang. Unbalanced magnetic force prediction in permanent magnet machines with rotor eccentricity by improved super- position method[J]. IET Electric Power Applications, 2017, 11(6): 1095-1104.
[18] Zhu Z Q, Wu L J, Mohd Jamil M L. Influence of pole and slot number combinations on cogging torque in permanent magnet machines with static and rotating eccentricities[C]//IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 2013: 2834-2841.
[19] Kim U, Lieu D K. Magnetic field calculation in permanent magnet motors with rotor eccentricity: with slotting effect considered[J]. IEEE Transactions on Magnetics, 1998, 34(4): 2253-2266.
[20] Zhou Yu, Li Huaishu, Meng Guangwei, et al. Analytical calculation of magnetic field and cogging torque in surface-mounted permanent-magnet machines accounting for any eccentric rotor shape[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3438-3447.
[21] 仇志坚, 李琛, 周晓燕, 等. 表贴式永磁电机转子偏心空载气隙磁场解析[J]. 电工技术学报, 2013, 28(3): 114-121.
Qiu Zhijian, Li Chen, Zhou Xiaoyan, et al. Analytical calculation of no-load air-gap magnetic field in surface-mounted permanent magnet motors with rotor eccentricity[J]. Transactions of China Electro- technical Society, 2013, 28(3): 114-121.
[22] 周晓燕, 李琛, 仇志坚, 等. 基于摄动法的交替极永磁电机偏心磁场解析计算[J]. 电工技术学报, 2013, 28(9): 321-331.
Zhou Xiaoyan, Li Chen, Qiu Zhijian, et al. Magnetic field calculation for consequent-pole motor with rotor eccentricity based on perturbation method[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 321-331.
[23] 吴海同. 磁悬浮高速永磁电机偏心不平衡分析与补偿研究[D]. 南京: 南京航空航天大学, 2020.
Wu Haitong. Analysis and compensation research on eccentricity and unbalance of magnetic suspension high speed permanent magnet motors[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2020.
[24] Cheng Ming, Han Peng, Hua Wei. General airgap field modulation theory for electrical machines[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6063-6074.
[25] Cheng Ming, Wen Honghui, Han Peng, et al. Analysis of airgap field modulation principle of simple salient poles[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 2628-2638.
[26] 于吉坤, 李立毅, 张江鹏, 等. 定子开槽永磁同步电机气隙比磁导解析计算[J]. 电工技术学报, 2016, 31(增刊1): 45-52.
Yu Jikun, Li Liyi, Zhang Jiangpeng, et al. Analytical calculation of air-gap relative permeance in slotted permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(S1): 45-52.
Abstract Unbalanced magnetic pulling force significantly impacts the suspension performance of bearingless slice motors. Previous studies have overlooked the influence of stator slotting on an unbalanced magnetic pulling force, resulting in low model accuracy and average compensation effect. In addition, the existing models for analyzing the eccentric unbalanced magnetic pulling force of permanent magnet motors are unsuitable for bearingless permanent slice film motors that require high model accuracy. The existing models for bearingless permanent slice film motors do not consider the influence of stator slots, and the model accuracy is not high enough. Therefore, it is necessary to establish a high-precision analytical model that takes into account the influence of slotting to accurately analyze the unbalanced magnetic pulling force.
The radial displacement of the rotor of a bearingless permanent magnet slice film motor during suspension is not zero. The geometric center of the rotor fails to be concentric with the geometric center of the stator, resulting in eccentricity. Such eccentricity distorts the originally sinusoidal air gap magnetic field and produces harmonics, which become the main source of unbalanced magnetic pulling force in thin film motors. A small amount of unbalanced magnetic pulling force generated from machining errors and asymmetric sensor installation is neglected. Therefore, accurately analyzing the air gap magnetic field under eccentricity is the key to accurately analyzing the unbalanced magnetic pulling force of bearingless permanent magnet slice motors.
Combined with one-dimensional and two-dimensional analytical methods, this paper proposes an eccentric air gap magnetic field analysis method for bearingless slice film motors based on magnetic field modulation theory, considering the influence of stator slotting. The air gap magnetic permeability ratio measures the effect of slotting on the eccentric magnetic field of the motor, and the eccentric unbalanced magnetic pulling force is analyzed. Then, based on the theory of magnetic field modulation, the underlying mechanism of unbalanced magnetic pulling force is reanalyzed. It is proven that the model constructed in this paper has high accuracy and simple calculation. Finally, compensation experiments verify that precise compensation of unbalanced magnetic pulling force can greatly improve the suspension performance of bearingless slice motors.
The proposed unbalanced magnetic tension model has an error of about 0.5% in simulation, significantly improving the accuracy. When compensating for the unbalanced magnetic tension of a thin film motor, it can significantly improve the suspension performance of the motor and reduce displacement to 15 mm, suitable for heart pump thin film motors with extremely high suspension performance requirements.
keywords：Bearingless slice motor, eccentric unbalanced magnetic pull, magnetic field modulation effect, the mechanism of unbalanced magnetic pull
中图分类号：TM461
DOI: 10.19595/j.cnki.1000-6753.tces.240321
国家自然科学基金（51977107, U2141227, 52377058）和航空科学基金（2020HKZ0001）资助项目。
收稿日期2024-03-01
改稿日期2024-04-23
王 锁 男，1996年生，硕士研究生，主要研究方向为永磁电机本体及其控制。E-mail: 1453518901@qq.com
王 宇 男，1982年生，工学博士，副教授，主要研究方向为交流电机本体及其控制。E-mail: wanghaohao@nuaa.edu.cn（通信作者）
（编辑 崔文静）