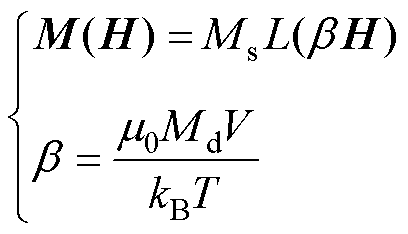（1）
摘要 磁粒子成像（MPI）利用检测装置感应可视场内不同位置处磁纳米粒子（MNPs）的非线性磁化响应，并基于所获得的检测信号重建MNPs浓度分布。该文基于激励与接收线圈磁场强度对检测信号的影响，论证了X-space和投影重建成像算法中MPI检测装置磁场均匀性的重要性，继而提出一种由具有较高磁场均匀性的正方形亥姆霍兹线圈所构成的改进开放式检测装置。此外，在零磁场点和零磁场线扫描移动两种情况下，基于不同装置下均匀分布MNPs所获得的检测信号，评估了两种传统开放式检测装置和所提改进装置的检测效果。研究结果表明，所提改进开放式装置的检测结果相比两种传统开放式装置显著接近理想情况，进而也证实了检测装置磁场均匀性的重要性。此外，该文还发现在改进装置基础上采用二次谐波检测方法相较于三次谐波检测，可获得更佳的检测效果。
关键词：磁粒子成像 开放式检测装置 检测信号 磁场均匀性 正方形亥姆霍兹线圈
磁粒子成像（Magnetic Particle Imaging, MPI）作为新兴医学成像技术已广泛应用于显像造影、磁纳米热疗、细胞追踪等生物医学领域[1-2]。它利用接收线圈感知磁纳米粒子（Magnetic Nanoparticles, MNPs）在交变激励磁场作用下的非线性磁化响应，并通过算法将感应电压还原为浓度，实现定量检测可视场（Field of View, FOV）内MNPs浓度分布[3-4]。在X-space和投影重建（Projection Reconstruction, PR）等成像算法中，接收线圈检测磁化信号所产生的感应电压（检测信号）用于表征MNPs浓度，其值越高，MNPs浓度越大[4-7]。检测信号取决于诸多影响因素，而检测装置磁场属性则是其中重要的决定因素之一，其又进一步包括激励线圈磁场强度、频率和接收线圈磁场灵敏度等因素[4-5, 8-9]。因此，激励线圈磁场强度和接收线圈磁场灵敏度需在FOV内近乎一致，以使检测信号能够精确表征MNPs浓度而不受其他因素影响。否则，不佳的磁场均匀度将可能导致检测到的MNPs浓度混淆[5, 9-10]、只能进行一维或二维检测而无法对分布在整个FOV的MNPs进行浓度检测[4, 7]等问题。虽然系统矩阵成像算法无需考虑检测装置的磁场均匀性，但其需要长时间校准且开销较大[8]。此外，在X-space和PR成像算法中，额外的校正算法能够纠正磁场不均匀造成的误差，但实现较为复杂[11]。因此，对MPI装置端进行改进优化，即优化检测装置中激励与接收线圈的磁场均匀性，从而提供一种适用于X-space和PR成像算法且精度较高的检测装置是有必要的。
尽管现有文献从不同的角度对MPI检测装置进行了研究，但尚未有文献关注检测信号大小受检测装置（即激励和接收线圈）的磁场均匀性的影响并进一步改进。文献[12-13]虽有提及MPI检测装置磁场均匀性的重要性，但均仅对所提线圈装置本身的磁场均匀性进行了研究，未进一步应用于MPI检测装置并分析检测信号大小受磁场均匀性的影响。文献[14-15]采用螺线管线圈组成检测装置，分析了MNPs尺寸对检测信号大小的影响并实现了MNPs位置的检测。螺线管线圈在装置中心区域有着较好的磁场均匀性，然而其磁场分布并不完全均匀，特别是在装置边缘区域[9]。同时，MNPs位置检测对检测装置磁场均匀性的要求并不高，文献[14-15]也同样未分析磁场均匀性对检测信号的影响。此外，螺线管线圈所组成的检测装置为封闭式结构，这种结构目前使用最为广泛，但其成像物状态不易被观察且与其他医疗设备兼容性较差[16]。针对螺线管边缘区域均匀性较低的问题，文献[17]增添了两个校正线圈，有效地优化了螺线管边缘的磁场均匀性，然而该研究并未将优化后线圈用于MPI检测研究中且该改进线圈仍为封闭式结构。进一步地，虽然开放式MPI检测装置目前较为少见，但其可以有效地克服上述封闭式结构装置的缺点。文献[4, 12]采用单面激励与接收线圈组成了开放式的检测装置，且其因单面结构有着相较于其他开放式装置更大的自由度。然而，单面结构也造成了装置磁场的不均匀，进而导致检测深度和范围受限。文献[18-19]则采用双面圆形线圈作为激励磁场产生装置，可有效地解决检测深度受限问题且仍然保持开放式结构。然而，所提双面圆形线圈并未采用亥姆霍兹线圈配置，这将会导致其所产生的磁场均匀性未达最优[20]。
本文通过讨论检测信号与激励场峰值强度和接收场灵敏度关系分析了X-space和PR成像算法中MPI检测装置的磁场均匀性的重要性，并以此为基础提出了一种基于正方形亥姆霍兹线圈的改进开放式检测装置。同时，本研究将所提改进装置与两种传统开放式检测装置在FOV内不同平面上的检测效果进行了对比分析，包括零磁场点（Field Free Point, FFP）和零磁场线（Field Free Line, FFL）扫描移动两种情况。其中，MNPs呈均匀分布时，理想的检测应是FOV内所有平面上的检测信号均一致。此外，本研究还讨论、对比了奇次与偶次谐波检测的结果，以便进一步降低检测误差、提高检测精度。
MNPs的非线性磁化特性是MPI技术的基础，其可以通过朗之万函数L(a)=coth(a)-1/a进行描述[8, 21-22]
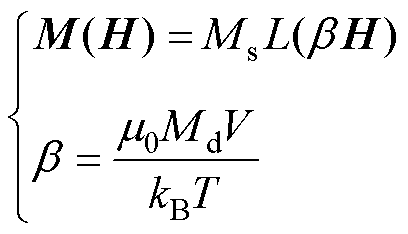（1）
式中，M为MNPs的磁化强度；H为作用于MNPs的磁场强度；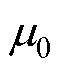
为真空磁导率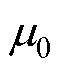，=4p×10-7 H/m；kB为玻耳兹曼常数，kB=1.380 6×10-23 J/K；T为MNPs的温度；V为MNPs的体积，V=4/3×pR3，R为MNPs的半径；Ms为饱和磁化强度，其与MNPs体积分数f 和磁畴磁化强度Md=446 kA/m相关，其值可表示为Ms=fMd[21-22]。值得一提的是，体积分数f 与MNPs浓度C之间可以相互转换[23-24]，即
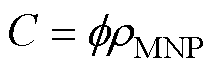（2）
式中，rMNP为MNPs的密度。
基于上述独特的磁化特性，MNPs在外加交变激励磁场作用下将产生连续非线性变化的磁化响应，从而导致磁通量发生变化，进而反映在接收线圈的电压变化上，如图1a所示。根据法拉第电磁感应定律[25-26]和互易定理，接收线圈感应电压可表示为
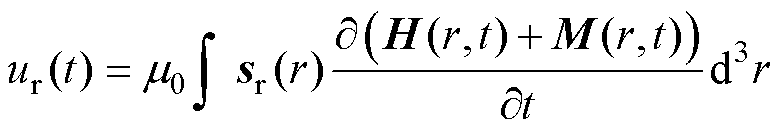（3）
式中，H(r,t)和M(r,t)分别为空间位置r处t时刻的激励磁场强度和MNPs磁化强度；sr(r)为空间位置r处接收线圈的磁场灵敏度，定义为线圈通过单位电流时所产生的磁场强度，其可表示为
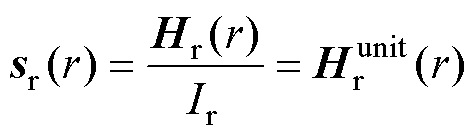（4）
式中，Hr(r)为线圈通过电流Ir时在空间r处产生的磁场强度；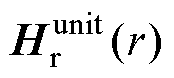
为通过单位电流在空间r处产生的磁场强度，其与sr(r)等价。
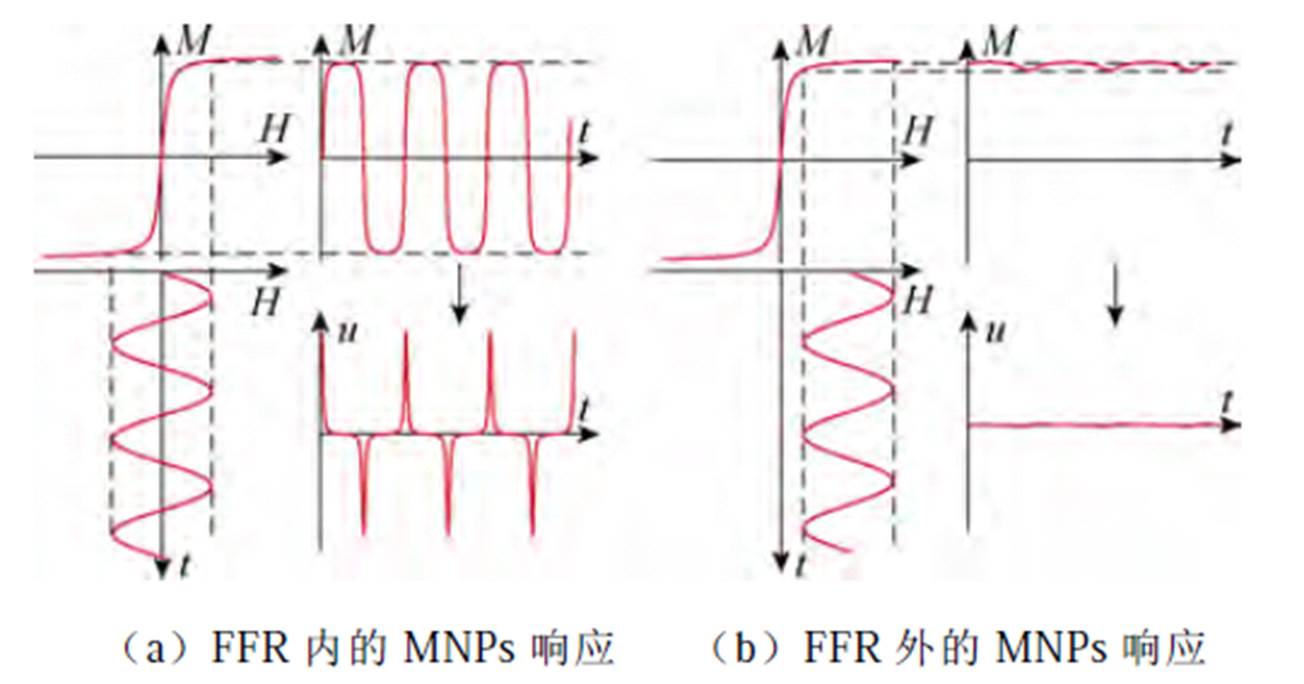
图1 不同磁场作用下的MNPs响应
Fig.1 MNPs responses under different magnetic fields
由式（3）可知，接收线圈感应电压所反映的信号包含了激励磁场信号，因此消去激励磁场信号以精确地检测MNPs磁化信号是必要的。消去法是目前常用的去除激励磁场信号的方法，其是将有无MNPs存在时接收线圈的感应电压相减以达到消去激励信号的目的[3, 5]。无MNPs存在时，接收线圈感应电压表示为
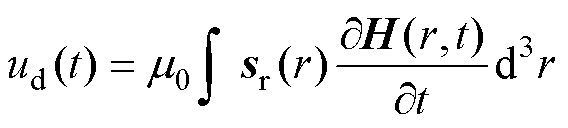（5）
将式（3）与式（5）相减并联合式（1）与式（2）即可得接收线圈检测MNPs磁化信号所产生的感应电压（检测信号）为
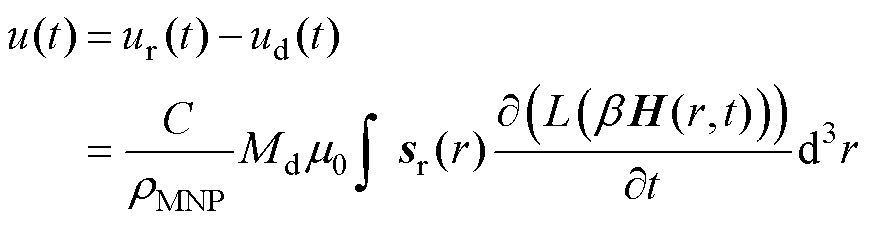（6）
由式（6）可知，检测信号大小可以直接反映MNPs的浓度C。这为X-space和PR等成像算法提供了理论支撑，它们将检测信号用于表征MNPs浓度[4-7]。
此外，X-space和PR等成像算法可在频域上将检测信号还原为浓度[4-5, 7, 27]。当施加正弦交变激励磁场作用于MNPs时，根据多倍角公式和式（7）所示郎之万函数的泰勒级数展开式，可将式（6）中空间r处L(βH(t))展开为式（8）所示的形式。
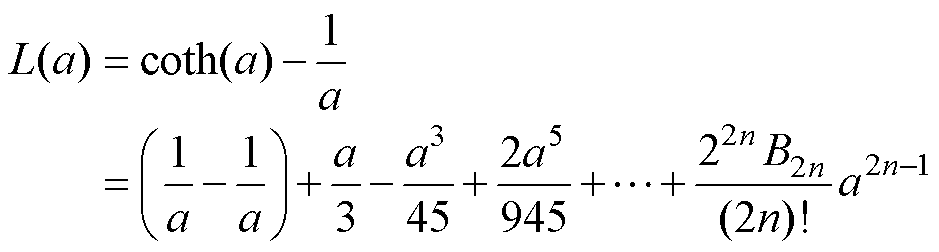（7）
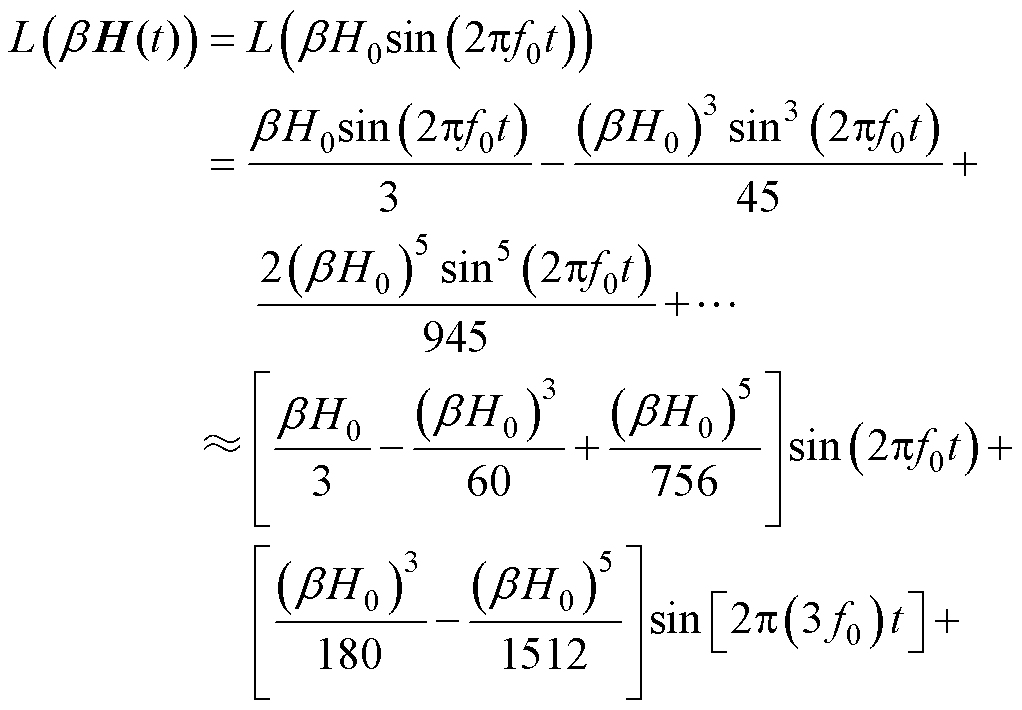
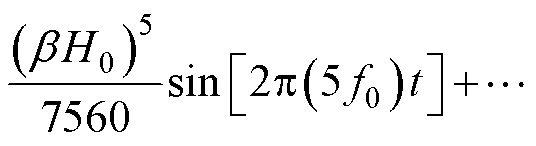（8）
式中，H0和f0分别为正弦激励磁场的幅值和频率。由此可知，当激励磁场为正弦形式时，检测信号仅存在于奇次谐波中，且各奇次谐波大小同样均可对MNPs浓度（体积分数）进行表征。其中，三次谐波不但不易被激励信号干扰而且大于其他奇次谐波分量，因此其在以往研究中被广泛用于代表检测信号并表征MNPs浓度[4, 5, 7, 11]。本文后续也将默认使用三次谐波信号进行检测。
当FOV内仅有交变激励磁场作用时，所有MNPs均将被激发并产生磁化信号，进而导致检测信号无法表征具体位置的MNPs浓度。为了实现整个FOV内不同位置MNPs浓度的检测，空间编码是必要的步骤。空间编码需要在交变激励磁场的基础上施加一个含有零磁场区域（Field Free Region, FFR）的静态选择场，FFR的形式包括FFP和FFL，如图2所示[3, 9, 28]。FFR内的MNPs仅受到激励磁场作用，将会产生磁化信号并被接收线圈检测，如图1a所示；而FFR外的MNPs在静态磁场的作用下将处于饱和磁化状态，无法被激励磁场激发因而无法产生磁化信号，如图1b所示[1, 11, 29]。因此，通过在FOV内扫描移动FFR便可以选择不同位置的MNPs产生磁化信号，从而对不同位置的MNPs浓度进行检测，进而最终获得MNPs浓度的空间分布。
图2 FFR示意图
Fig.2 FFR diagrams
联立式（6）与式（8）可获得检测信号三次谐波大小与激励磁场强度峰值和接收磁场灵敏度的关系，如图3所示。其中，MNPs粒径设置为30 nm，体积分数为0.033（即浓度为171 mg/mL）[23-24]；激励磁场强度幅值范围设置为10 kA/m（12.6 mT/m0）上下浮动50%，该激励峰值能够使MNPs饱和磁化并满足MPI激励强度限制[2, 30]；接收磁场灵敏度范围设置为600 A/m上下浮动50%。此外，图3对三次谐波信号大小进行了归一化处理，以更直观地展现检测装置磁场对检测信号大小的影响。由图3可知，在不同激励磁场强度峰值和接收磁场灵敏度大小的情况下，同一浓度的MNPs将会导致不同大小的检测信号。因此，在X-space和PR等成像算法中，如果FOV内不同位置的激励磁场强度和接收磁场灵敏度存在差异，MNPs浓度的空间分布将无法被准确获取。
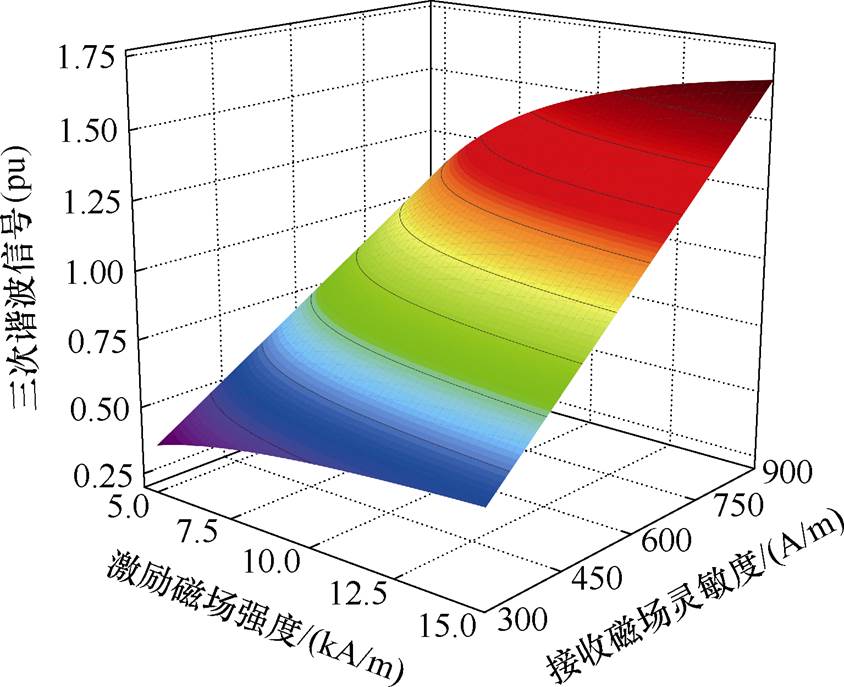
图3 不同激励磁场幅值和接收磁场灵敏度对三次谐波检测信号大小的影响
Fig.3 Effect of different excitation magnetic field amplitudes and receiving magnetic field sensitivities on the third harmonic detection signal
综上所述，为使不同位置的MNPs浓度能够被检测信号精确表征，优化检测装置（激励线圈和接收线圈）的磁场均匀性使激励线圈磁场强度和接收线圈磁场灵敏度在FOV内近乎一致是十分重要的，这为本文后续检测装置的改进与分析提供了理论依据。
鉴于检测装置磁场均匀性在MNPs浓度精确检测中的重要性，本文提出了一种基于正方形亥姆霍兹线圈的开放式检测装置。正方形亥姆霍兹线圈在保持开放式结构的同时，相较于传统圆形亥姆霍兹线圈具有更高的磁场均匀性[31]。以往文献与本文所提出的开放式检测装置如图4所示。图4a中的装置模型基于文献[4, 12, 29]构建，该装置为单面结构的开放式检测装置，其激励线圈与接收线圈均为单面圆形线圈；图4b中装置模型则基于文献[18-19]构建，并根据文献建议将接收线圈的数量增加至5个，同时采用双面圆形线圈作为激励线圈；图4c则为本文所提出的改进开放式检测装置，其激励线圈与接收线圈均为正方形亥姆霍兹线圈，以提供良好的激励和接收磁场均匀性。为方便叙述，本文将图4中装置依次命名为：传统装置1、传统装置2和改进装置。
同时，本文根据以往研究中FOV的常见形 状[3, 7-11, 15, 18]设置FOV为(50×50×50) mm3的矩体，如图4所示，该尺寸可以满足文献[22-24]中瘤内MNPs浓度分布检测的需求。表1根据该FOV尺寸统一设置了图4中不同检测装置的线圈尺寸，以便对不同装置的检测效果进行对比。
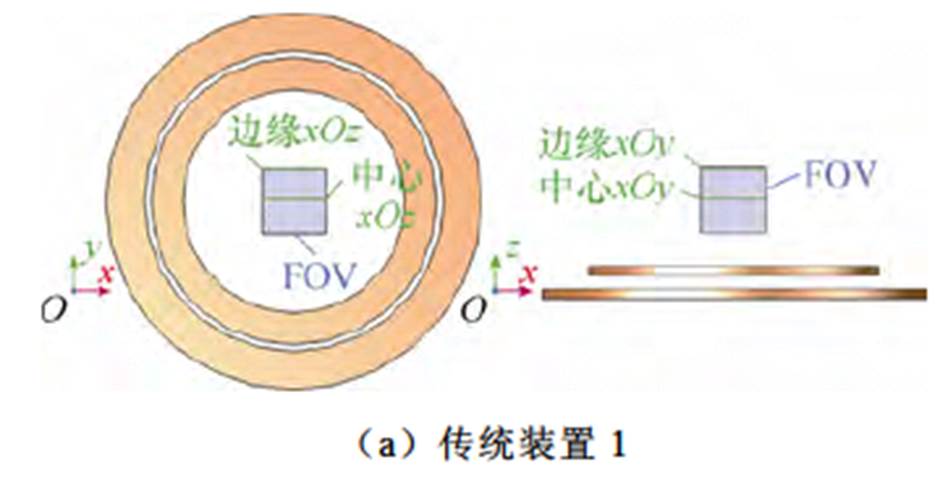
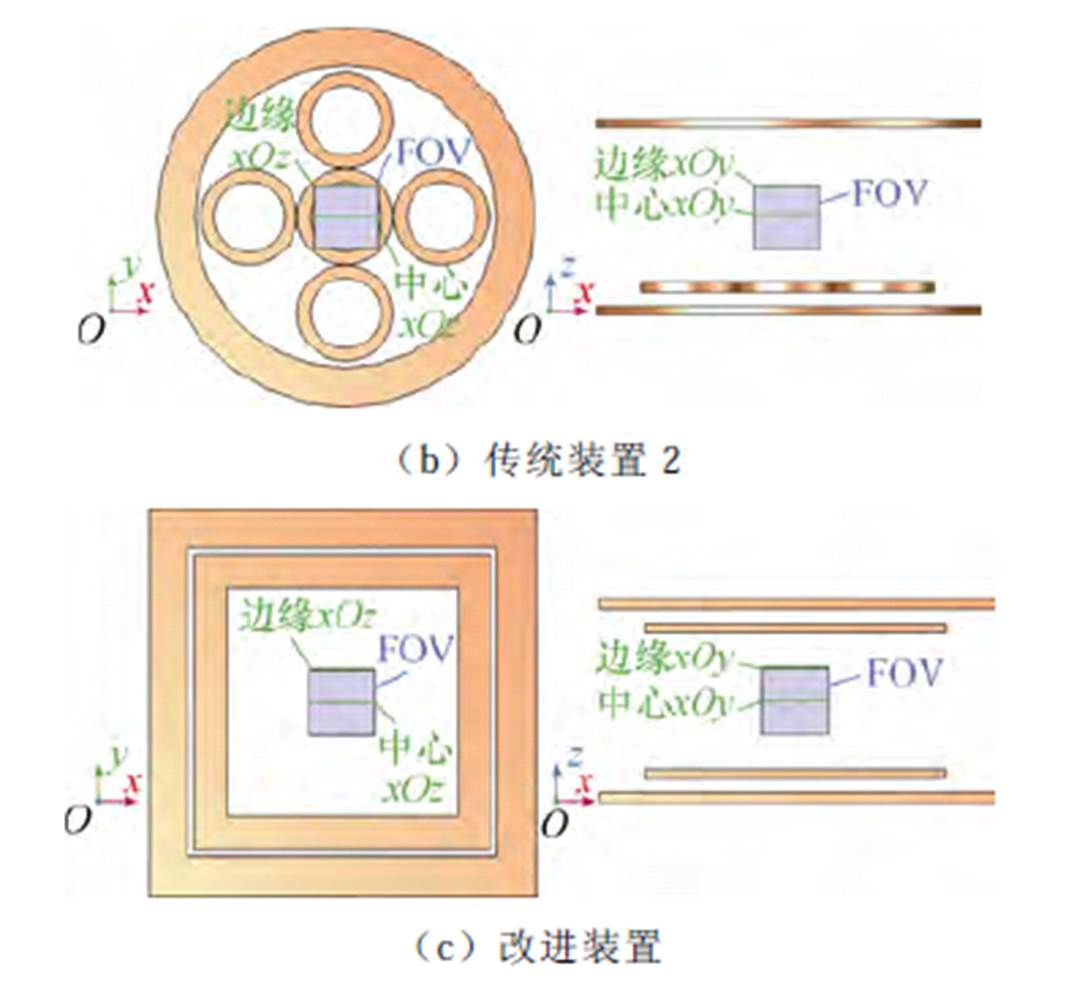
图4 开放式检测装置几何模型
Fig.4 Geometric models of open detection devices
表1 检测装置尺寸参数
Tab.1 Size parameters of detection devices
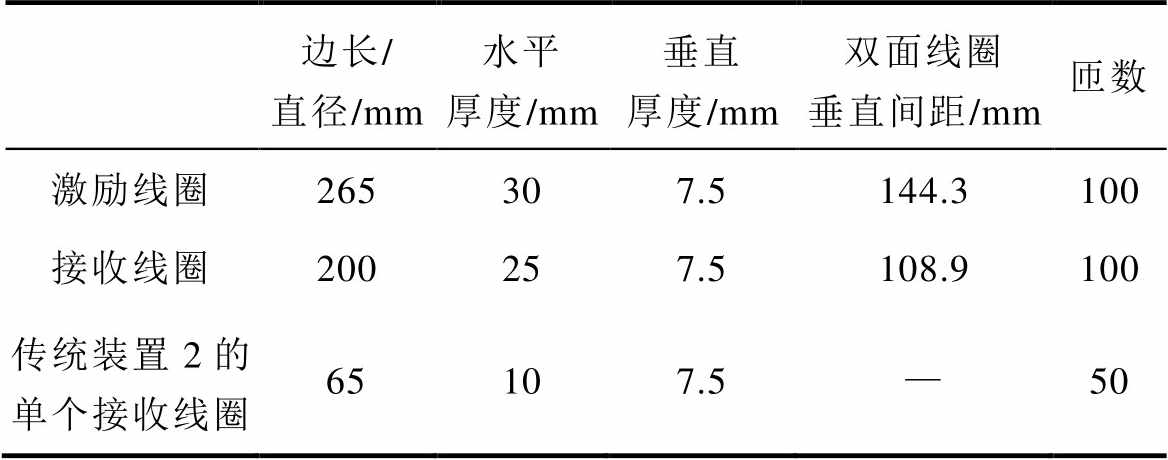
边长/直径/mm水平厚度/mm垂直厚度/mm双面线圈垂直间距/mm匝数 激励线圈265307.5144.3100 接收线圈200257.5108.9100 传统装置2的单个接收线圈65107.5—50
开放式MPI系统中的FFP通常采用永磁体或麦克斯韦线圈[15, 30, 32]产生，其为椭球体形状且长轴是短轴的两倍，如图2a所示；FFL则常为采用多个矩形线圈产生[7, 18, 33]的圆柱体形状，如图2b所示。为简化计算过程并聚焦于检测装置的效果分析，本研究忽略产生FFR的线圈装置，并分别构建了体积分数为0.033的椭圆体MNPs和圆柱体MNPs模型，两个模型分别称为FFP-MNPs和FFL-MNPs。同时，本研究以2.5 mm分辨率为标准，对MNPs模型的尺寸进行设置：FFP-MNPs的短轴长度为2.5 mm（z轴）、长轴为5 mm（x、y轴），FFL-MNPs的直径为2.5 mm、高为50 mm（x方向FFL）。其中，分辨率主要与磁场梯度有关[6, 8, 33]，现有FFR线圈装置已足以产生能够实现2.5 mm分辨率的磁场梯度[3, 7, 33]。
将所构建的MNPs模型在FOV内进行移动即可模拟FFR在具有MNPs均匀分布的FOV内的扫描移动。本研究将分别对所构建的FFP-MNPs和FFL-MNPs模型在FOV内不同位置受激励线圈所产生的激励场激发时接收线圈的检测信号进行分析，以评估检测装置的检测效果。理想情况下，即激励和接收线圈所产生的磁场完全均匀时，因MNPs在FOV内均匀分布，MNPs模型处于不同位置时的检测信号应完全一致。
此外，本研究设置激励磁场频率为以往研究常用的20 kHz[1-2, 15]，并向激励线圈通以合适大小的电流使FOV中心点的磁场强度为满足检测需求的10 kA/m（12.6 mT/m0）[2, 30]。此外，本文检测信号通过有限元软件COMSOL Multiphysics[34-35]实现麦克斯韦偏微分方程的求解，而其仿真物理环境为具有16 GB RAM的Intel(R) Core(TM) i7-9700处理器。
根据3.1节中所述FFP-MNPs模型的尺寸参数，FFP的移动扫描点（xp, yp, zp）需满足式（9），从而通过移动覆盖FOV以对MNPs浓度分布进行检测。
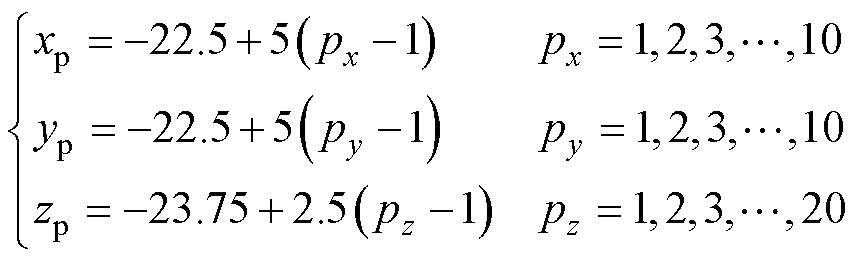（9）
图5描述了FFP扫描移动情况下两种传统开放式检测装置和本文所提改进开放式检测装置在FOV中心平面上的三次谐波检测信号大小，其中第一列代表中心xOy平面，第二列代表中心xOz平面，第一、第二、第三行依次代表传统装置1、传统装置2和改进装置。根据式（9）所描述的FFP移动位置，xOy中心平面为z=1.25 mm，xOz中心平面为y=2.5 mm，如图4所示。为简化分析，本文应用磁场对称性对图5中的数据进行了求解。为更加直观地对比不同装置的检测效果，图5中的三次谐波信号均以FFP-MNPs模型位于FOV中心点（0, 0, 0）时的检测信号为基准进行归一化处理。此外，本节后续的检测信号也均进行了与图5相同的处理。
由图5a、图5c可知，两种传统装置在xOy中心平面上的检测效果与理想情况有一定差距，且传统装置2的检测信号大小变化范围比传统装置1更大、更加不理想。由图5b、图5d可知，两种传统装置在xOz中心平面上的检测效果均相较于xOy中心平面更加恶化，靠近线圈一侧的三次谐波信号远大于远离线圈一侧的信号，这与单面线圈靠近线圈一侧的磁场强度更大的特性相符。与xOy中心平面不同的是，在xOz中心平面上，传统装置2的检测效果虽然仍与FFP-MNPs位于不同位置处时检测信号完全一致的理想检测有着较大的差距，但其相较于传统装置1的检测效果有所改善，变化范围减小。造成这一现象的原因是激励线圈和接收线圈磁场均匀性对检测结果的共同作用以及不同平面上装置磁场均匀性的不一致。
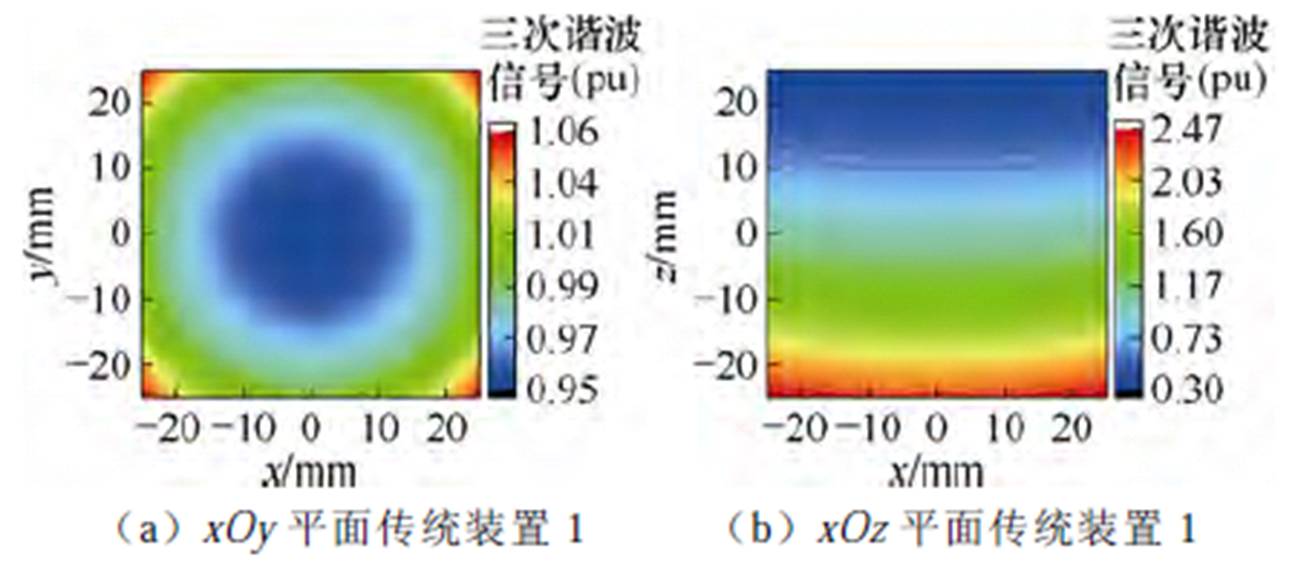
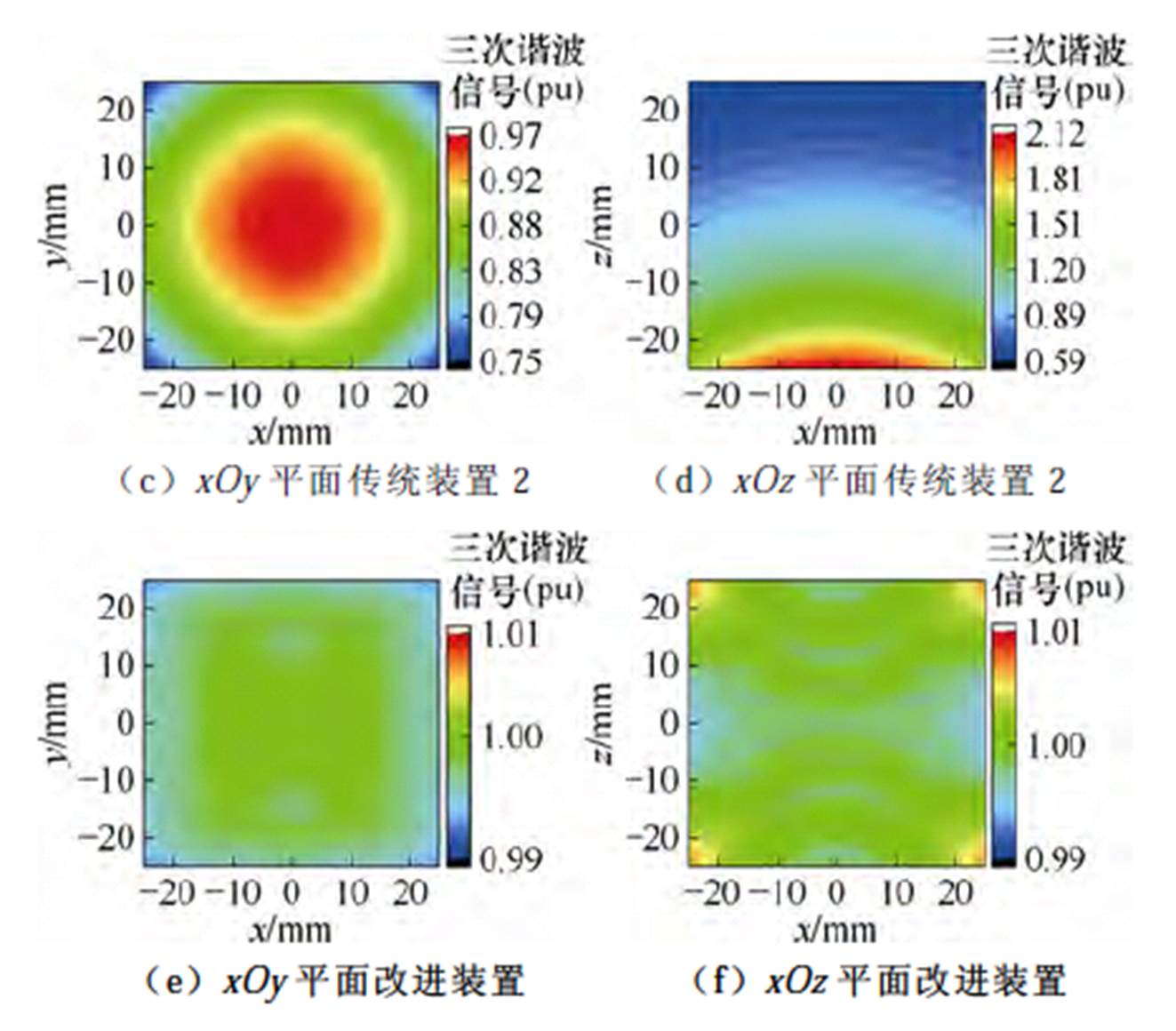
图5 FFP扫描下不同装置在FOV中心平面上的三次谐波检测信号
Fig.5 Third harmonic detection signals on the FOV center planes by different devices under FFP scanning
图6根据文献[20]所提均匀性评估指标有效百分比F=Seff/Stotal，分别描述了三种开放式检测装置的激励和接收线圈在FOV范围内不同中心平面上的磁场均匀性，其中Seff表示平面上磁场强度H满足0.997Hcenter≤H≤1.003Hcenter部分的面积，Hcenter为平面中心的磁场强度，Stotal为FOV上中心平面的面积。由图6可知，在xOy中心平面上，传统装置1的激励和接收线圈的磁场均匀性均远优于传统装置2的接收线圈的均匀性（1个数量级以上）；而在xOz中心平面上，传统装置1中激励和接收线圈与传统装置2中接收线圈三者的磁场均匀性均较低且近似，但传统装置2的激励磁场均匀性相比传统装置1的磁场均匀性提升了50倍左右。这导致传统装置2在xOz中心平面上的检测效果虽与理想情况有一定差距，但仍较优于传统装置1，而在xOy中心平面上两者的检测效果呈现了相反的结果。上述讨论进一步说明了式（6）～式（8）与图（3）所示检测装置磁场均匀性对于获得精确检测信号从而正确表征MNPs浓度的重要性。
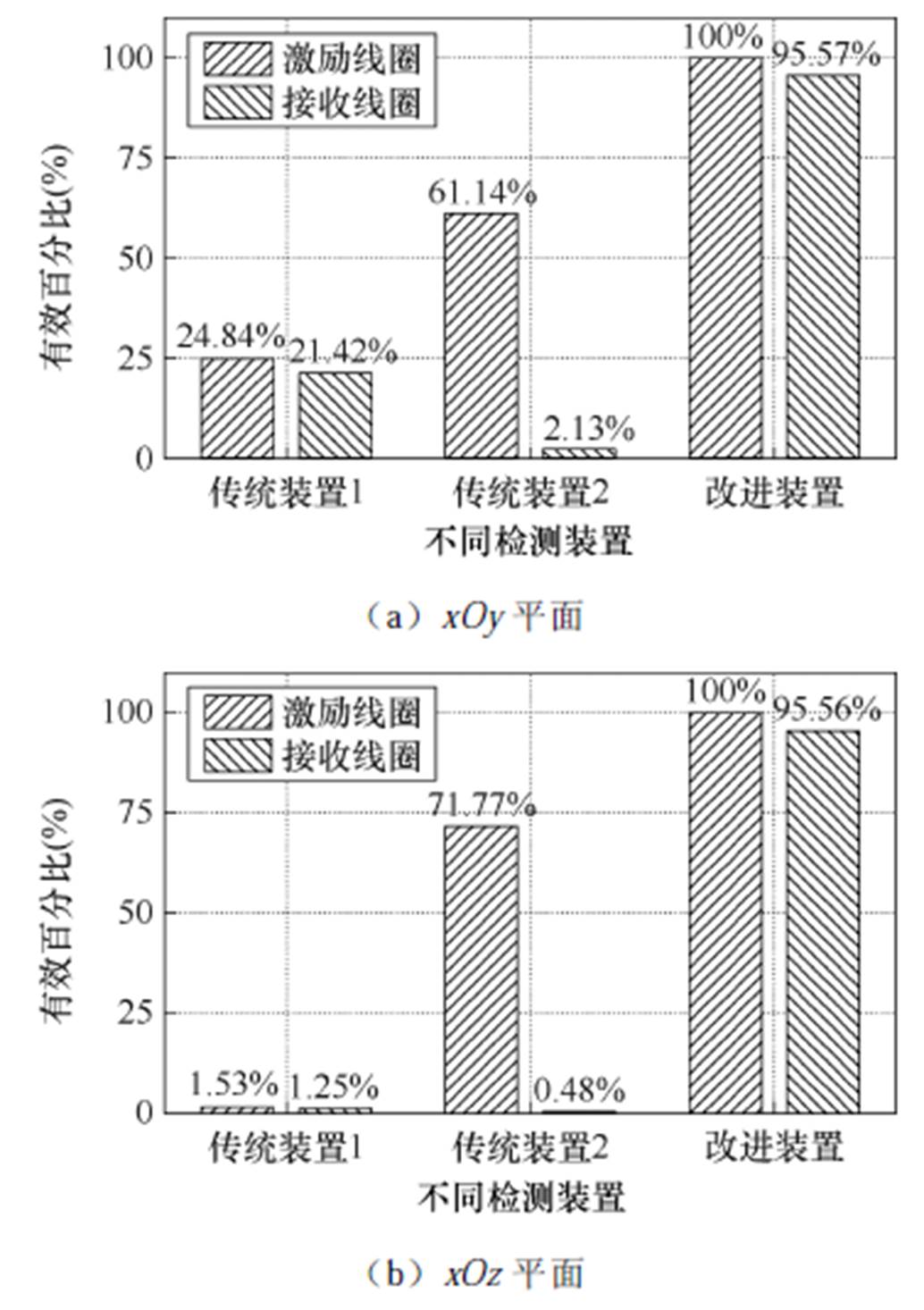
图6 不同检测装置在FOV中心平面上的磁场均匀性
Fig.6 Magnetic field uniformity of different detection devices on the FOV center planes
由图6亦可知，本研究基于正方形亥姆霍兹线圈的改进开放式检测装置的激励与接收线圈磁场均匀性均显著优于两种传统装置，故改进装置具有远优于两种传统装置的检测效果。如图5e、图5f所示，无论是中心xOy平面还是中心xOz平面，FFP-MNPs模型位于不同位置时的检测信号均几乎一致，接近理想效果。此外，本文将图5e、图5f中色度条颜色所对应的最大、最小信号分别设置为1.01(pu)和0.99(pu)，以更清晰地体现本文所提改进装置的优越性。
同时，不同检测装置在FOV中心平面上以理想检测效果为基准的三次谐波最大检测误差见表2。表2清晰地体现了本研究所提改进装置相较于两种传统装置具有更加优异的检测效果。
为更全面地分析所提改进装置在整个FOV空间检测的优势，本文对FOV边缘平面上的检测信号大小进行了求解。根据式（9）所描述的FFP移动位置，xOy边缘平面为z=23.75 mm，xOz边缘平面为y=22.5 mm，如图4所示。边缘平面的检测信号变化趋势与中心平面几乎一致，因此，图7仅描述了不同装置检测信号的大小范围。比较图7和图5所示信号变化范围可知，改进装置的边缘与中心平面差异远小于两种传统装置，这体现了改进装置在FOV空间的三维检测效果最为优异。同时，改进装置的边缘平面检测效果相较于中心平面虽有恶化且检测信号大小变化范围增大，但仍十分接近于理想情况。
表2 FFP扫描下不同装置在FOV中心平面上的三次谐波检测最大误差
Tab.2 Maximum errors of third harmonic detection on the FOV center planes by different devices under FFP scanning
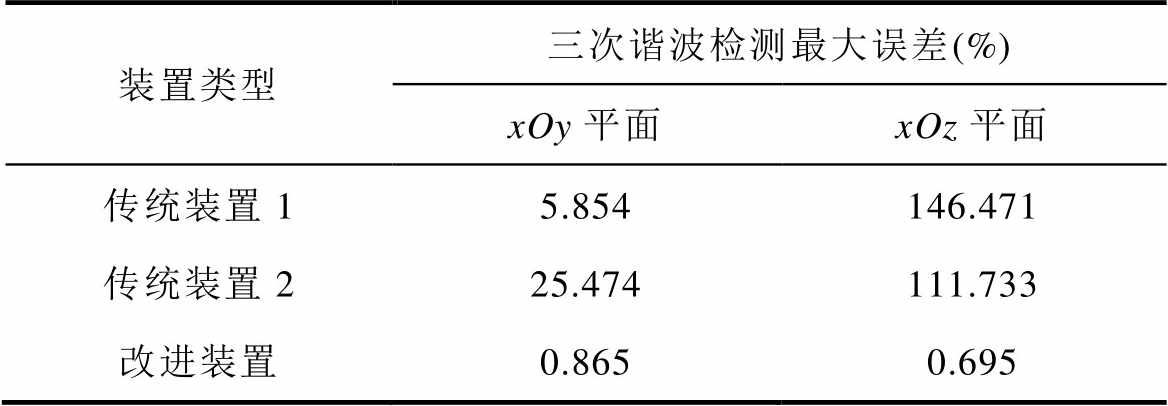
装置类型三次谐波检测最大误差(%) xOy平面xOz平面 传统装置15.854146.471 传统装置225.474111.733 改进装置0.8650.695
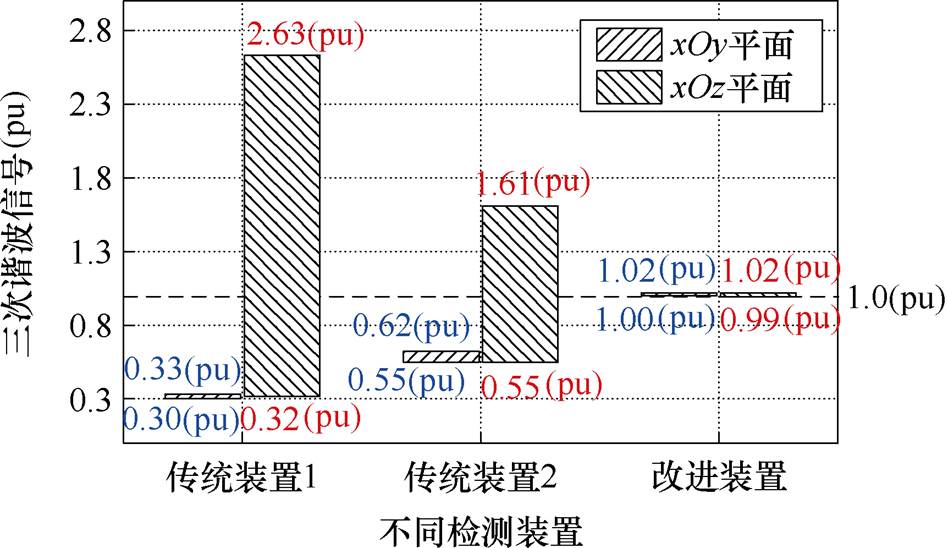
图7 FFP扫描下不同装置在FOV边缘平面上的三次谐波检测信号大小范围
Fig.7 Third harmonic detection signal ranges on the FOV edge planes by different devices under FFP scanning
表3列出了不同检测装置在FOV边缘平面上相较于理想情况的三次谐波最大检测误差。由表3可知，改进装置在边缘xOy平面和边缘xOz平面的最大检测误差均为1.977%。该误差值也即为FOV空间内的最大检测误差，虽然其相较于中心平面上的最大误差有所上升，但仍然显著优于两种传统装置，与理想的检测效果非常接近。
表3 FFP扫描下不同装置在FOV边缘平面上的三次谐波检测最大误差
Tab.3 Maximum errors of third harmonic detection on the FOV edge planes by different devices under FFP scanning
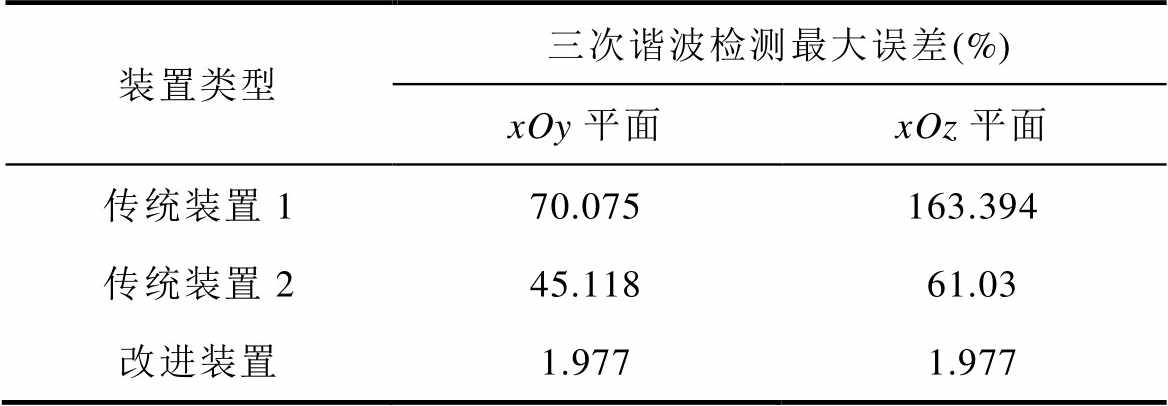
装置类型三次谐波检测最大误差(%) xOy平面xOz平面 传统装置170.075163.394 传统装置245.11861.03 改进装置1.9771.977
为进一步降低检测误差并提高检测精度，本研究还分析了改进装置的二次谐波检测效果。通过在正弦激励磁场的基础上叠加一个与磁场峰值大小相同的直流磁场，即
=H0sin(2pf0t)+H0，可以激发MNPs产生以二次谐波为主的偶次谐波[14-15]。图8a、图8b分别描述了FFP-MNPs模型位于各个xOy和xOz平面最边缘点时的改进装置检测的三次与二次谐波信号变化趋势。由图8可知，三次与二次谐波的变化趋势几乎完全一致，且二次谐波更加接近于理想检测情况。此外，二次谐波检测在FOV内的最大误差为1.247%，同样优于三次谐波检测的1.977%。因此，在所提改进开放式检测装置的基础上采用二次谐波检测方法能够进一步提升对MNPs磁化信号的检测精度。
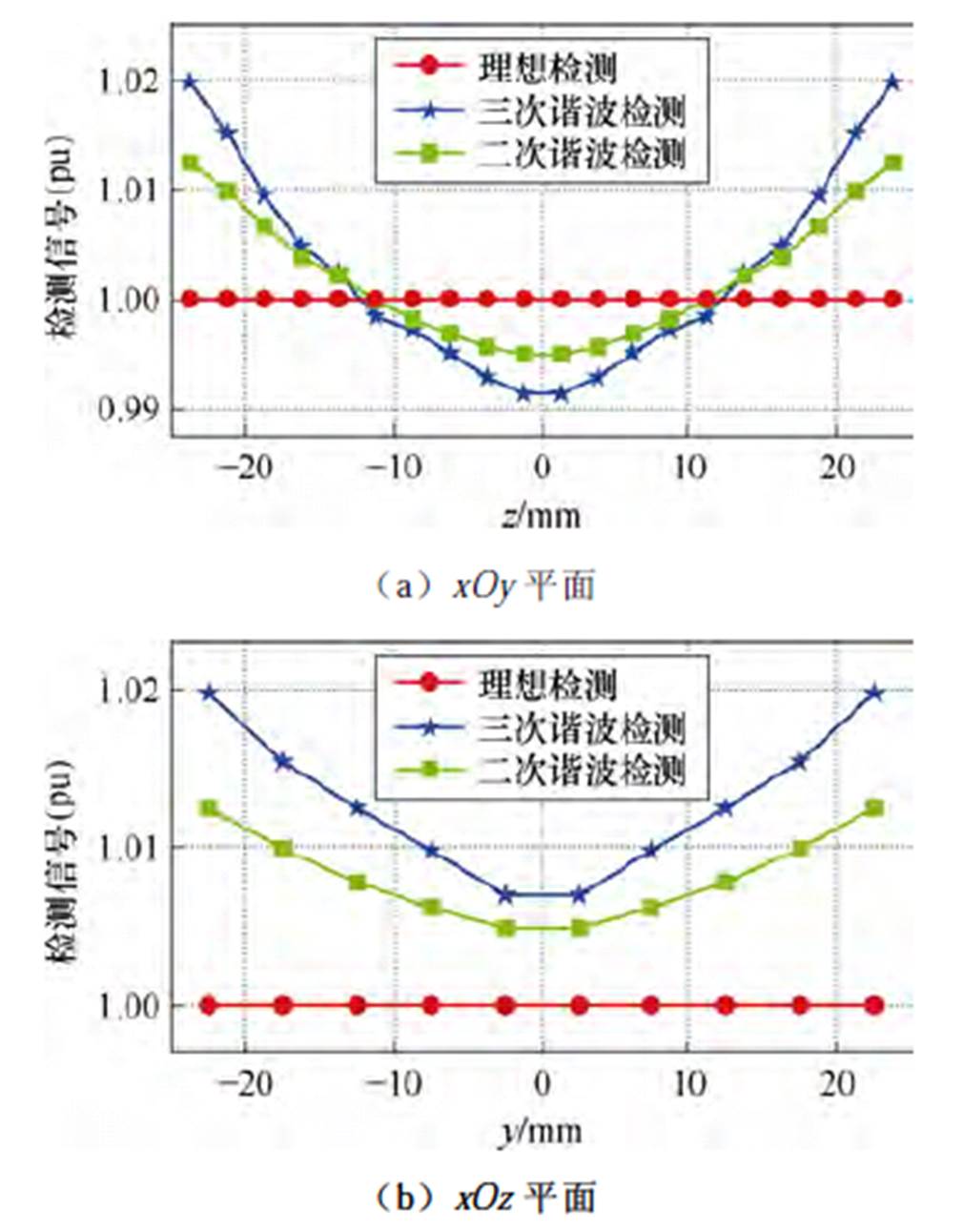
图8 改进装置下平面边缘点处FFP-MNPs模型的谐波检测信号
Fig.8 Harmonic detection signals of FFP-MNPs model for planar edge points under the improved device
FFL是MPI中另一种常见的FFR，为此本文还研究了在FFL扫描移动情况下不同检测装置的检测效果。据3.1节中所述FFL-MNPs模型的尺寸参数，FFL（x方向）的移动扫描点（yp, zp）需满足式（10），从而可通过移动覆盖FOV以对MNPs浓度分布进行检测。
（10）
图9、图10分别描述了FFL扫描移动情况下三种检测装置在FOV中心和边缘平面上的三次谐波检测信号大小。根据式（10）所描述的FFL扫描移动的位置，xOy中心平面为z=1.25 mm，xOz中心平面为y=1.25 mm，xOy边缘平面则为z=23.75 mm，xOz边缘平面为y=23.75 mm，如图4所示。为更加直观地对比不同检测装置的检测效果，对图9、图10中的三次谐波信号进行了与3.2节中同样的处理，即应用磁场对称性进行求解分析并以FFL- MNPs模型位于FOV中心位置（0, 0）时的检测信号为基准进行了归一化处理。
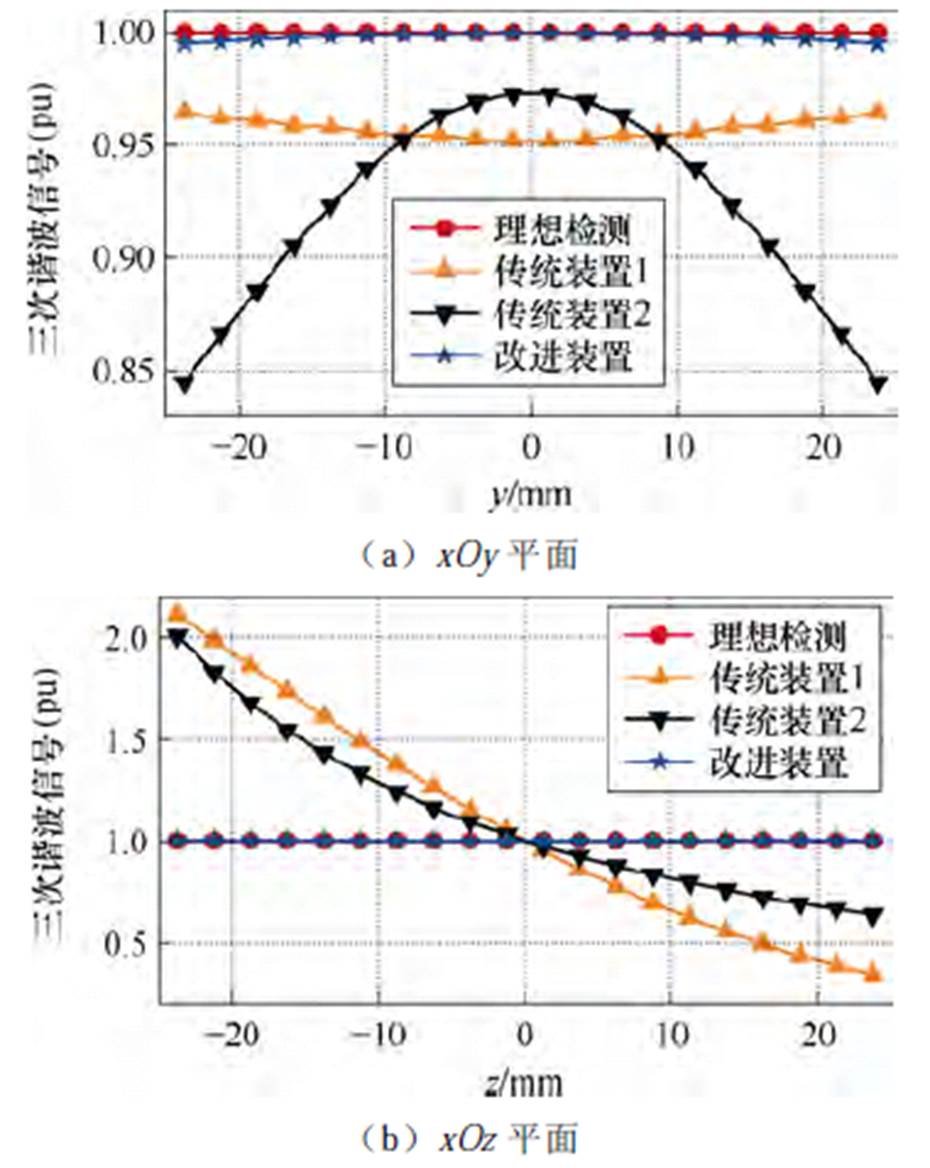
图9 FFL扫描下不同装置在FOV中心平面上的三次谐波检测信号
Fig.9 Third harmonic detection signals on the FOV center planes by different devices under FFL scanning
由图9、图10可知，基于FFL的检测结果与基于FFP的结果近似。其中，在xOz平面上，由图9b、图10b可知，无论是中心还是边缘平面，靠近线圈一侧信号明显更大，且随着FFL位置逐渐远离线圈，信号迅速减小。同时，传统装置1的检测信号下降速度更快，其变化范围也更大，有着相较于传统装置2更大的检测误差，这与图5b、图5d所展现的结果一致。由图9a、图10a可知，与xOz平面所体现的结果相反，在xOy平面上，无论是中心还是边缘平面，传统装置1的检测信号变化范围相较于传统装置2均更小。传统装置1（单面激励与接收线圈）在xOy平面上变化范围较小的特性使其在二维平面检测上的精度较高，与文献[4, 7]的结果一致，但其在xOz平面上所展现的不佳检测效果使其无法适用于FOV三维空间的检测。与两种传统装置不同，本文所提的改进装置能够获得十分接近于理想的检测效果，在FOV空间的信号检测上显著优于两种传统装置，如图9、图10所示。
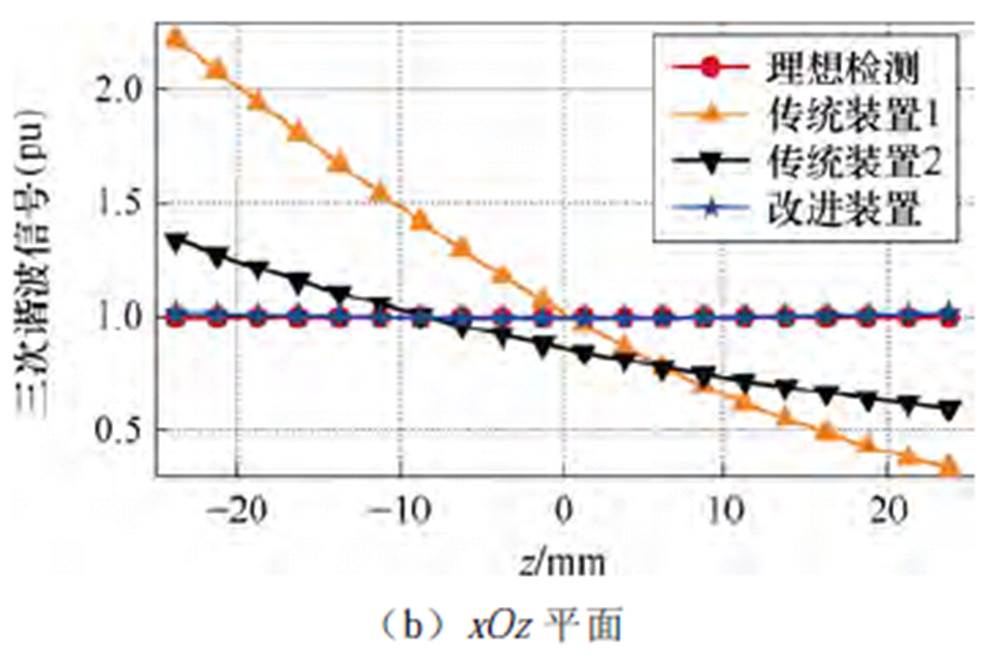
图10 FFL扫描下不同装置在FOV边缘平面上的三次谐波检测信号
Fig.10 Third harmonic detection signals on the FOV edge planes by different devices under FFL scanning
此外，与3.2节基于FFP的信号检测结果的分析类似，本研究同样分析并比较了基于FFL的改进装置的二次与三次谐波检测效果，如图11所示。图11描述了FFL扫描移动情况下改进装置在不同平面上三次和二次谐波检测的最大误差，其中边缘平面上的最大检测误差即为在FOV空间内的最大检测误差。由图11可知，与对FFP-MNPs进行检测的结果相同，二次谐波检测的精度优于三次谐波检测。
图11 FFL扫描下改进装置在不同平面上不同谐波检测的最大误差
Fig.11 Maximum errors of different harmonics detection on different planes by the improved device under FFL scanning
本研究根据X-space和PR成像算法中MPI检测装置磁场均匀性的重要性提出了一种基于正方形亥姆霍兹线圈的改进开放式检测装置，其中装置线圈可在提供较高均匀度磁场的同时保持检测装置的开放性。改进装置的检测效果以FOV内不同平面上的检测信号精度为评估指标，与两种传统开放式检测装置进行比较。研究结果表明，无论是FFP还是FFL扫描移动情况，改进装置均能取得显著优于两种传统装置的检测效果，更加适用于X-space和PR成像算法并提供优异的检测精度。改进装置在两种扫描移动情况下的检测信号最大误差分别为1.977%与1.51%，非常接近于理想的检测情况。同时，本研究还发现，在改进装置的基础上使用二次谐波检测方法能够获得相较于三次谐波检测更高的检测精度，其在FFP与FFL扫描移动情况下的检测信号最大误差分别降低至1.247%与0.98%。本文所提改进开放式检测装置可为后续研究工作提供支持，其可与X-space和PR成像算法、FFP或FFL选择场装置相结合从而搭建完整的成像系统并实现浓度图像重建。
参考文献
[1] Healy S, Bakuzis A F, Goodwill P W, et al. Clinical magnetic hyperthermia requires integrated magnetic particle imaging[J]. WIREs Nanomedicine and Nanobiotechnology, 2022, 14(3): e1779.
[2] Lei Siao, He Jie, Gao Pengli, et al. Magnetic particle imaging-guided hyperthermia for precise treatment of cancer: review, challenges, and prospects[J]. Molecular Imaging and Biology, 2023, 25(6): 1020-1033.
[3] Le T A, Bui M P, Yoon J. Development of small- rabbit-scale three-dimensional magnetic particle imaging system with amplitude-modulation-based reconstruction[J]. IEEE Transactions on Industrial Electronics, 2023, 70(3): 3167-3177.
[4] Mcdonough C, Newey D, Tonyushkin A. 1-D imaging of a superparamagnetic iron oxide nanoparticle dis- tribution by a single-sided FFL magnetic particle imaging scanner[J]. IEEE Transactions on Magnetics, 2022, 58(8): 1-5.
[5] Murase K, Hiratsuka S, Song Ruixiao, et al. Development of a system for magnetic particle imaging using neodymium magnets and gradio- meter[J]. Japanese Journal of Applied Physics, 2014, 53(6): 067001.
[6] Goodwill P W, Conolly S M. The x-space formulation of the magnetic particle imaging process: 1-D signal, resolution, bandwidth, SNR, SAR, and magneto- stimulation[J]. IEEE Transactions on Medical Imaging, 2010, 29(11): 1851-1859.
[7] Chinchilla C, Mcdonough C, Negash A, et al. 2D projection image reconstruction for field free line single-sided magnetic particle imaging scanner: simu lation studies[J]. International Journal on Magnetic Particle Imaging, 2021, 7(1): 2104001.
[8] Rahmer J, Weizenecker J, Gleich B, et al. Signal encoding in magnetic particle imaging: properties of the system function[J]. BMC Medical Imaging, 2009, 9(1): 4.
[9] Goodwill P W, Konkle J J, Zheng Bo, et al. Projection x-space magnetic particle imaging[J]. IEEE Transa- ctions on Medical Imaging, 2012, 31(5): 1076-1085.
[10] Medimagh H, Weissert P, Bringout G, et al. Artifacts in field free line magnetic particle imaging in the presence of inhomogeneous and nonlinear magnetic fields[J]. Current Directions in Biomedical Engineering, 2015, 1(1): 245-248.
[11] Murase K. Three-dimensional image reconstruction in projection-based magnetic particle imaging[J]. Japanese Journal of Applied Physics, 2021, 60(8): 088001.
[12] Othman N B, Birahim M F S, Zakaria W N W, et al. A simulation study of excitation coil design in single- sided MPI scanner for human body application[J]. Bulletin of Electrical Engineering and Informatics, 2019, 8: 1279-1288.
[13] Wojtczyk H, Bringout G, Tenner W, et al. Toward the optimization of D-shaped coils for the use in an open magnetic particle imaging scanner[J]. IEEE Transa- ctions on Magnetics, 2014, 50(7): 1-7.
[14] Tanaka S, Suzuki T, Kobayashi K, et al. Analysis of magnetic nanoparticles using second harmonic responses[J]. Journal of Magnetism and Magnetic Materials, 2017, 440: 189-191.
[15] Tanaka S, Murata H, Oishi T, et al. 2D magnetic nanoparticle imaging using magnetization response second harmonic[J]. Journal of Magnetism and Magnetic Materials, 2015, 383: 170-174.
[16] Kim C, Nan J, Kim J, et al. Open-structure magnetic particle spectroscopy (OMPS): feasibility study[J]. IEEE Magnetics Letters, 2022, 13: 1-5.
[17] Tang Yundong, Jin Tao, Flesch R C C, et al. Improvement of solenoid magnetic field and its influence on therapeutic effect during magnetic hyperthermia[J]. Journal of Physics D: Applied Physics, 2020, 53(30): 305003.
[18] Sasayama T, Tsujita Y, Morishita M, et al. Three- dimensional magnetic nanoparticle imaging using small field gradient and multiple pickup coils[J]. Journal of Magnetism and Magnetic Materials, 2017, 427: 144-150.
[19] 祖婉妮, 柯丽, 杜强, 等. 基于迭代补偿的纳米粒子磁化信号检测方法研究[J]. 仪器仪表学报, 2022, 43(1): 136-144.
Zu Wanni, Ke Li, Du Qiang, et al. A detection method of magnetization signal of nanoparticles based on iterative compensation[J]. Chinese Journal of Scientific Instrument, 2022, 43(1): 136-144.
[20] Tang Yundong, Ding Yubin, Jin Tao, et al. Improvement for magnetic field uniformity of Helmholtz coils and its influence on magnetic hyper- thermia[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 1-8.
[21] Rosensweig R E. Heating magnetic fluid with alternating magnetic field[J]. Journal of Magnetism and Magnetic Materials, 2002, 252: 370-374.
[22] Tang Yundong, Flesch R C C, Jin Tao. Numerical analysis of temperature field improvement with nanoparticles designed to achieve critical power dissipation in magnetic hyperthermia[J]. Journal of Applied Physics, 2017, 122(3): 034702.
[23] Astefanoaei I, Dumitru I, Chiriac H, et al. Thermofluid analysis in magnetic hyperthermia using low Curie temperature particles[J]. IEEE Transactions on Magnetics, 2016, 52(7): 1-5.
[24] Tang Yundong, Flesch R C C, Jin Tao, et al. Com- putational evaluation of malignant tissue apoptosis in magnetic hyperthermia considering intratumoral injection strategy[J]. International Journal of Heat and Mass Transfer, 2021, 178: 121609.
[25] 李海毅, 李明明, 刘亚南, 等. 宽温域磁致伸缩位移传感器输出电压模型及特性分析[J]. 电工技术学报, 2023, 38(20): 5343-5353.
Li Haiyi, Li Mingming, Liu Yanan, et al. Output voltage model and characteristic analysis of mag- netostrictive displacement sensor for wide operating temperature[J]. Transactions of China Electrotech- nical Society, 2023, 38(20): 5343-5353.
[26] 黄文美, 陶铮, 郭萍萍, 等. 变压应力条件下铁镓合金棒材高频磁特性测试与模型构建[J]. 电工技术学报, 2023, 38(14): 3769-3778.
Huang Wenmei, Tao Zheng, Guo Pingping, et al. Analysis and modeling of high frequency magnetic properties of rod gallium iron alloy under variable compressive stress[J]. Transactions of China Elec- trotechnical Society, 2023, 38(14): 3769-3778.
[27] Knopp T, Biederer S, Sattel T F, et al. Prediction of the spatial resolution of magnetic particle imaging using the modulation transfer function of the imaging process[J]. IEEE Transactions on Medical Imaging, 2011, 30(6): 1284-1292.
[28] 杨丹, 王雨忱, 李天兆, 等. 一种基于线性零磁场的动脉血管扫描成像方法仿真[J]. 电工技术学报, 2024, 39(2): 343-355.
Yang Dan, Wang Yuchen, Li Tianzhao, et al. Simulation of an arterial scanning imaging method based on linear zero magnetic field[J]. Transactions of China Electrotechnical Society, 2024, 39(2): 343-355.
[29] Sattel T F, Knopp T, Biederer S, et al. Single-sided device for magnetic particle imaging[J]. Journal of Physics D: Applied Physics, 2009 42(2): 022001.
[30] Pablico-Lansigan M H, Situ S F, Samia A C S. Magnetic particle imaging: advancements and perspectives for real-time in vivo monitoring and image-guided therapy[J]. Nanoscale, 2013, 5(10): 4040-4055.
[31] Ghaly S M A, Khan M O. Design, simulation, modeling, and implementation of a square Helmholtz coil in contrast with a circular coil for MRI applications[J]. Engineering, Technology & Applied Science Research, 2019, 9: 4990-4995.
[32] 闫孝姮, 李政兴, 潘也, 等. 相同极性永磁体对感应式磁声磁粒子浓度成像过程影响的仿真[J]. 电工技术学报, 2022, 37(8): 1926-1937.
Yan Xiaoheng, Li Zhengxing, Pan Ye, et al. Simulation of the influence of permanent magnets of the same polarity on the magneto-acoustic concentration tomography of magnetic nanoparticles with magnetic induction process[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 1926- 1937.
[33] 刘洋洋, 杜强, 柯丽, 等. 磁性粒子成像线型零磁场设计及性能分析[J]. 电工技术学报, 2020, 35(10): 2088-2097.
Liu Yangyang, Du Qiang, Ke Li, et al. Design and analysis of magnetic field-free line in magnetic particle imaging[J]. Transactions of China Electro- technical Society, 2020, 35(10): 2088-2097.
[34] 程书灿, 赵彦普, 张军飞, 等. 电力设备多物理场仿真技术及软件发展现状[J]. 电力系统自动化, 2022, 46(10): 121-137.
Cheng Shucan, Zhao Yanpu, Zhang Junfei, et al. State of the art of multiphysics simulation technology and software development for power equipment[J]. Automation of Electric Power Systems, 2022, 46(10): 121-137.
[35] 徐海松, 张大宁, 胡冉, 等. 基于谐波分量的配电电缆绝缘劣化状态带电检测技术[J]. 电工技术学报, 2024, 39(7): 2161-2173.
Xu Haisong, Zhang Daning, Hu Ran, et al. A live detection technology of distribution network cable insulation deterioration state based on harmonic components[J]. Transactions of China Electrotech- nical Society, 2024, 39(7): 2161-2173.
Abstract The magnetic field strength of magnetic particle imaging (MPI) detection devices (excite and receive coils) has a direct impact on the detection signal of magnetic nano particle (MNPs) magnetization response. The non-uniformity of the magnetic field makes reconstructing MNP concentration challenging by detection signals in the reconstruction algorithms such as x-space and projection reconstruction (PR). Although the system matrix imaging algorithm or additional correction algorithm can correct the error caused by the non-uniform magnetic field of detection devices, it is complex and costly. Therefore, it is necessary to design a detection device with a highly uniform magnetic field.
This study investigated the importance of magnetic field uniformity of MPI detection devices in x-space and PR imaging algorithms after revealing the relationship between the detection signal, the peak intensity of the excitation magnetic field, and the sensitivity of the receiving magnetic field. A modified open detection device with square Helmholtz coils was proposed. The square Helmholtz coil provides a uniform magnetic field while maintaining the detection device’s openness. The detection performance of the proposed and two traditional open detection devices were evaluated in two scenarios: field free point (FFP) and field free line (FFL) scanning movement .It is noted that the ideal detection signals should be consistent within the field of view (FOV) due to the uniform distribution of MNPs. In addition, the results of second-harmonic and third-harmonic detection were compared.
Simulation results show that: (1) In the case of FFP scanning movement, the maximum detection errors of the proposed improved open detection device are 0.865% and 1.977% on the center and edge planes, respectively, which are closer to the ideal detection effect than the two traditional ones. (2) The FFL scanning movement shows similar results to the FFP scanning movement, and the detection accuracy of the proposed device is more excellent than the two traditional devices under the same condition, with maximum detection errors of 0.51% and 1.51% on the center and edge planes. (3) The maximum detection errors of FFP and FFL scanning movement cases can be reduced from 1.977% and 1.51% of the third harmonic detection to 1.247% and 0.98% of the second harmonic detection.
The following conclusions can be drawn. (1) In FFP or FFL scanning movement, the detection performance of the proposed device is closer to the ideal detection than the two traditional open detection devices, which is suitable for the X-space and PR imaging algorithms. (2) When the proposed device is considered for the image reconstruction, the second harmonic detection helps to reduce the detection errors and improve detection results compared to the third harmonic detection.
keywords：Magnetic particle imaging, open detection device, detection signal, magnetic field uniformity, square Helmholtz coil
中图分类号：TM154.1
DOI: 10.19595/j.cnki.1000-6753.tces.240394
国家自然科学基金（62071124, 62471144）和巴西国家科学技术发展委员会（309244/2018-8）资助项目。
收稿日期 2024-03-11
改稿日期2024-04-01
汤云东 男，1981年生，博士，副教授，博士生导师，研究方向为生物医学电子信息技术及相关交叉学科。E-mail: tangyundong@fzu.edu.cn（通信作者）
丁宇彬 男，2000年生，硕士研究生，研究方向为生物医学电子信息技术。E-mail: 221120102@fzu.edu.cn
（编辑 郭丽军）