图1 感应滤波变压器拓扑
Fig.1 Inductive filter transformer topology
摘要 大电流、低电压的工业整流系统存在电磁环境差、能耗高等问题，该文以感应滤波整流变压器为对象，提出了一种考虑阻抗匹配的变压器损耗分层优化设计方法，利用Sobol灵敏度算法对变压器参数进行了分层处理，旨在降低优化维度，提升寻优能力。首先，介绍感应滤波变压器绕组排布及接入外部系统方式，建立了考虑负载谐波影响的感应滤波变压器电流传递关系模型，获得了实施谐波抑制的阻抗匹配条件；其次，根据感应滤波变压器设计规范，确定了变压器损耗优化的约束条件与优化参数；然后，通过对优化参数进行Sobol灵敏度分析，确立了分层架构；最后，给定设计参数进行案例分析与仿真验证。结果表明：所提的分层优化方法得到的解最优值和平均值都优于未分层优化结果，具有更好的寻优能力和稳定性，分层优化后变压器总损耗降低11.3%，实施感应滤波后谐波畸变率从8.84%降至4.29%，滤波性能良好，验证了该文方法的有效性。
关键词：整流变压器 灵敏度分析 阻抗匹配 分层优化设计
工业整流系统承担交直流电能变换的任务，其直流耗能大，直流输出电流多为kA级别，电气运行环境具有大功率、大电流、低电压特点，且存在严重的谐波污染和电能损耗问题[1]。其中，变压器损耗在工业整流系统损耗中占比高达40%，变压器的节能降损是工业整流系统运行环境治理的重点工作。
变压器损耗主要包括磁心损耗与绕组损耗。磁心损耗是变压器磁心工作时磁滞和涡流现象引起的损耗，其大小与磁心工作频率、磁通密度和材料特性相关[2-3]。绕组损耗是绕组线圈通过电流时产生的损耗，其大小与线圈导线材料和工作电流相关[4-5]。因此，变压器节能降损主要从以下几个方面开展研究：
（1）变压器材料工艺改进。变压器磁心材料改进主要考虑高导磁性、低磁滞性、低涡流损耗等方面，包括非晶态合金[6-7]、铁氧体[8-9]等新型软磁材料的应用及改进。文献[7]应用Finemet FT-3 M和Vitroperm 500F纳米晶合金材料，相较于传统硅钢片磁心材料，最高实现了73.53%和89.22%的损耗降低。文献[10]开发了带凹槽的晶粒取向硅钢，有效降低了变压器的噪声和损耗。
（2）变压器物理结构优化。合理选择变压器结构参数，能避免过度设计，有效降低变压器运行损耗。变压器优化设计以智能算法为主[11]，文献[12]以变压器铁心尺寸参数为变量，利用改进型广义差分进化算法对损耗及成本进行多目标优化，实现了总损耗和制造成本双重降低。文献[13]以铁心厚度、绕组匝数、绕组截面积为优化变量，结合效率和成本约束对变压器总损耗进行优化，并对比评估了差分进化算法、遗传算法及改进的非支配排序遗传算法的优化性能。文献[14]利用有限元状态空间模型与人工神经网络计算变压器的性能特征，结合粒子群算法对变压器进行了优化设计。随着优化参数和优化约束的增加，变压器优化设计维度和寻优空间复杂度不断提高，优化有可能会陷入“维度陷阱”，算法寻优能力下降。
（3）变压器电磁环境治理。接入整流系统时，整流侧大量谐波流窜至变压器，引起变压器磁心损耗增加，谐波抑制是整流变压器降损必不可少的一环。文献[15]提出一种使用直流侧混合脉波倍增技术的串联36脉波整流器，有效降低了系统的主要低阶谐波，削弱纹波和失真，但随之而来的是成本和复杂度的提高。文献[16]提出的晶闸管控制的LC耦合混合有源滤波器，可以同时提供无功、谐波和不平衡功率补偿。然而，该类混合滤波装置应用于工业整流系统时，独特的大电流电气环境对器件的耐电流能力和装置容量提出了极高的要求，因而使得滤波装置不具备性价比优势。文献[17]提出感应滤波变压器，通过增设特殊滤波绕组及阻抗匹配设计，在整流侧和供电侧间增添了一道“屏蔽门”，将谐波感应至滤波侧进行有效抑制。其额外的滤波绕组给谐波提供了新通路，且其可外接无源滤波装置，保有了无源滤波低成本、高可靠性的优点，还进一步提升了其滤波性能[18]。感应滤波技术在工业整流系统谐波抑制上有巨大的潜力。当前感应滤波变压器相关研究中较少涉及零阻抗匹配设计和性能优化的问题。
因此，本文针对大电流、低电压的工业整流系统，以感应滤波变压器为研究对象，考虑其特殊阻抗匹配条件，提出了一种损耗最小化的变压器分层设计方法。该方法考虑变压器结构参数和运行条件约束，选定了变压器优化模型，以保障整体优化设计；应用Sobol灵敏度分析方法对优化参数进行了分层处理，降低了层级优化维度。进一步结合改进差分进化算法和分层架构对感应滤波变压器进行优化设计，在算法收敛后，利用降维分层优化跳出收敛，进一步探寻搜索空间，有效提升寻优能力。最后结合有限元方法验证了变压器设计参数的可行性。
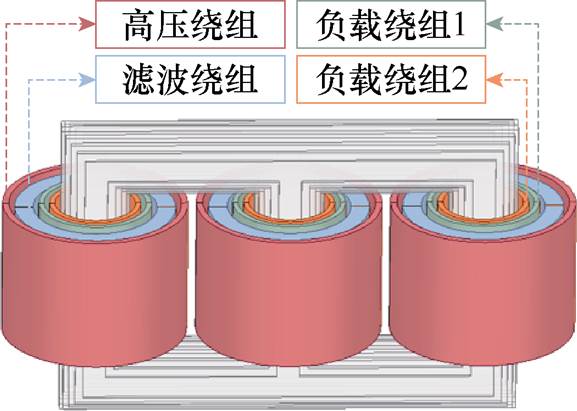
图1给出了感应滤波变压器（Inductive Filter Transformer, IFT）的拓扑，该变压器采用三相四绕组结构，最外侧高压绕组（W1）连接电网；相邻的是滤波绕组（W2），承担谐波抑制和无功补偿的主要功能，连接滤波装置；内侧分别是负载绕组1（W4）与负载绕组2（W3），连接整流负载。
图1 感应滤波变压器拓扑
Fig.1 Inductive filter transformer topology
将整流负载等效为电流源，电网等效为电压源串联阻抗，得到由感应滤波变压器构成的感应滤波整流系统单相等效电路如图2所示。图中，U1～U4为各绕组端电压，I1～I4为各绕组端电流，Us为高压侧供电电压，I3L、I4L为负载等效电流源，Zs为系统等效阻抗，Zf为滤波装置等效阻抗。所有参数均已折算至高压侧。
图2 感应滤波整流系统单相等效电路
Fig.2 Equal circuit of inductive filter rectifier system
由图2可得感应滤波整流系统的电压电流关系为
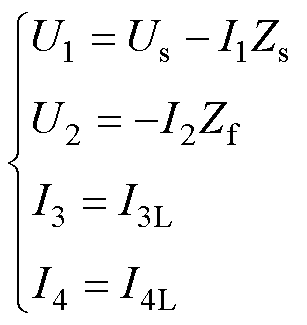（1）
根据多绕组电压传递理论得IFT各绕组端口电压关系式为
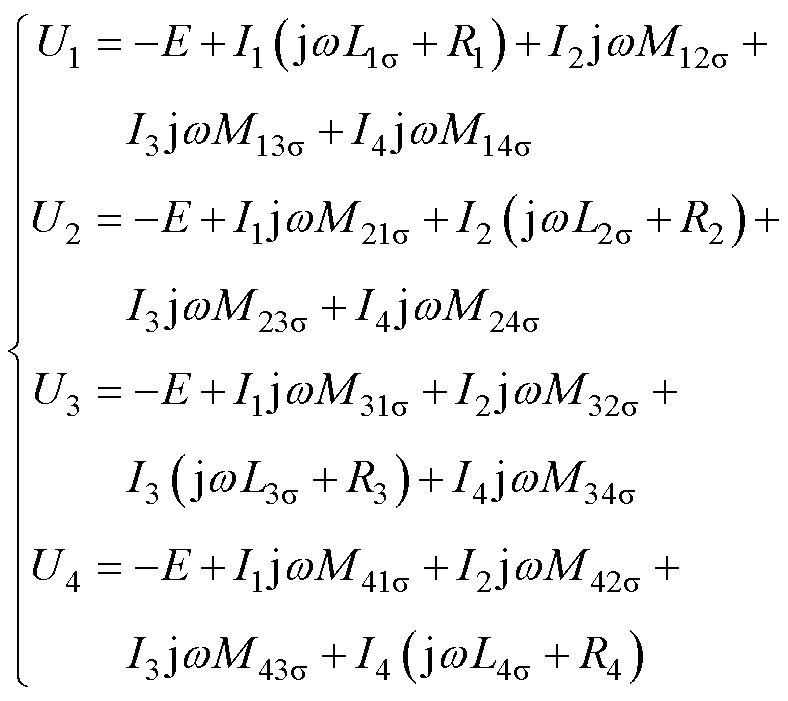（2）
式中，w 为工频角频率；U1～U4为各绕组端电压；I1～I4为各绕组端电流；E为主磁通感应电动势；Mxys 为绕组x和绕组y之间的漏磁互感（x, y=1, 2, 3, 4；x≠ y）；L1s～L4s 为各绕组的漏磁自感；R1～R4为各绕组的电阻。
由安匝平衡原理可得各绕组端电流为
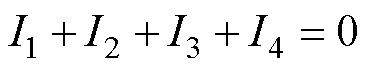（3）
联合式（2）和式（3）可以得到绕组电压差为
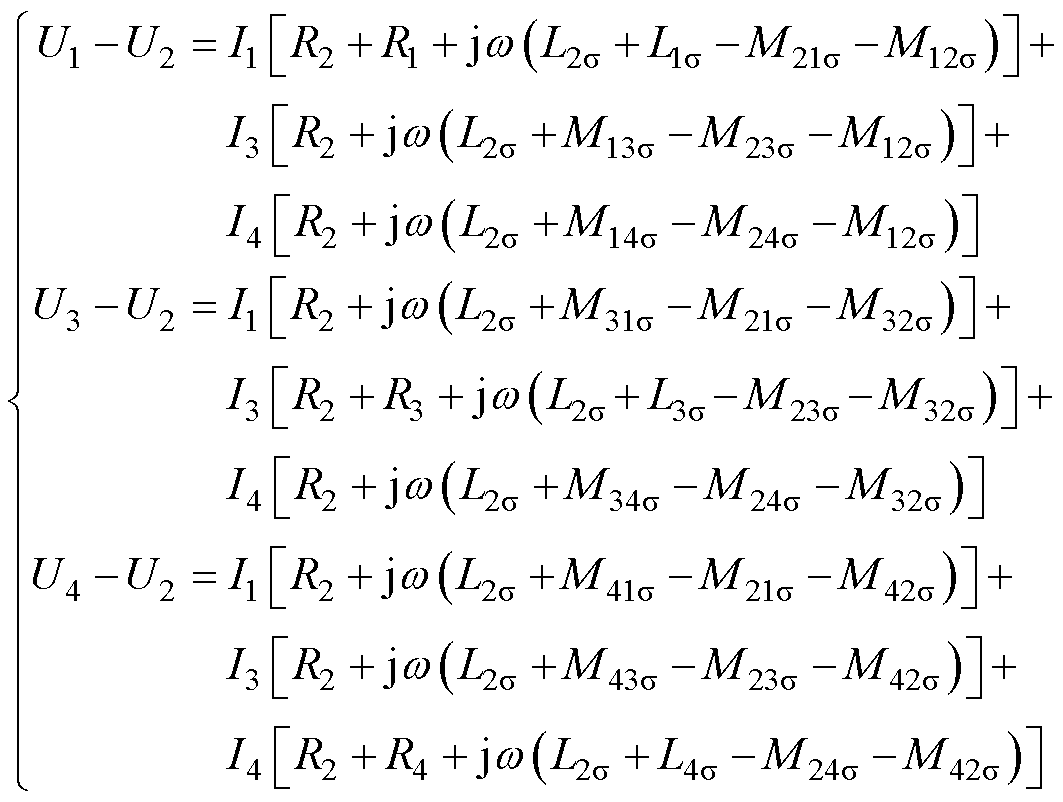（4）
其中
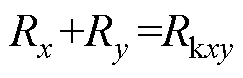
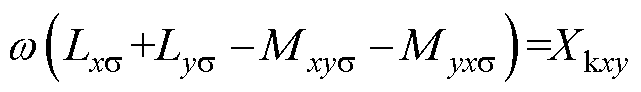
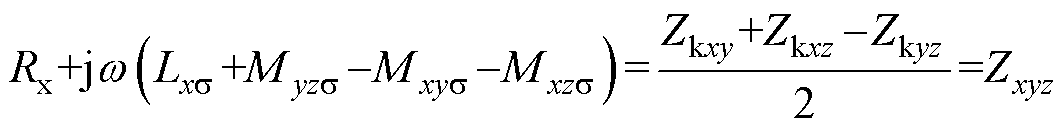
式中，Rkxy为绕组x和绕组y之间的短路电阻，Xkxy为绕组x和绕组y之间的短路电抗，则绕组x和绕组y之间的短路阻抗Zkxy=Rkxy+jXkxy；Zxyz为绕组x的等值漏阻抗，且存在Zkxy=Zkyx、Zxyz=Zxzy（x, y, z=1, 2, 3, 4；x≠y≠z）。根据上述分析可以将式（4）可进一步变换为
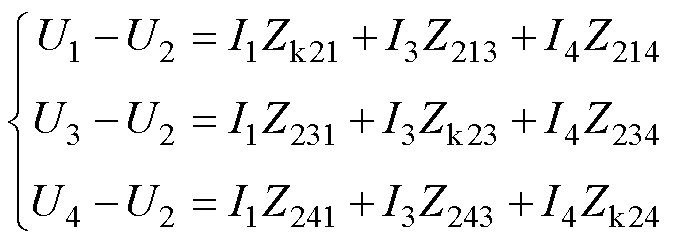（5）
将式（1）代入式（5）可得高压侧电流为
（6）
进一步得到h次谐波环境下高压侧电流为
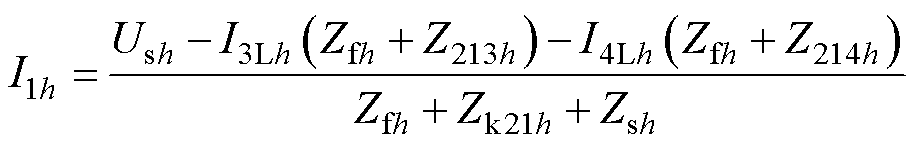（7）
滤波器理想调谐频域下，有Zfh=0，忽略网侧谐波电压影响（Ush=0），若变压器绕组设计满足滤波绕组的等值漏阻抗为0，即Z213h=Z214h=0，此时高压侧电流不含谐波成分，即负载侧的谐波被滤波器组滤除，高压侧不受谐波侵扰。
如何实现滤波绕组的零等值漏阻抗，是感应滤波变压器设计上的关键问题。绕组的等值漏阻抗通过短路阻抗计算而来，滤波绕组对应的等值漏阻抗计算为
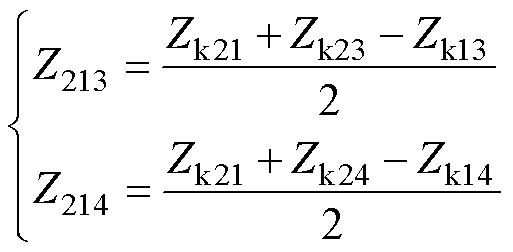（8）
而短路阻抗的计算与变压器的绕组排列及尺寸紧密关联，图3给出了四绕组感应滤波变压器的绕组排设，图中，r0为铁心半径，r1～r4为各绕组与铁心的中心距，r34、r42和r21为铁心和气隙之间的中心距，a1～a4为绕组幅向宽度，a03、a34、a42、a21为绕组间绝缘间隙，H1为绕组轴向高度。
图3 感应滤波变压器绕组排设
Fig.3 Winding layout of inductive filter transformer
变压器短路阻抗主要由短路电抗计算而来，任意绕组x、y间的短路阻抗为
（9）
式中，f为基波频率；N1为高压绕组匝数；rxy为绕组x、y间洛氏系数；KX为附加电抗系数；
为绕组x和y之间的漏磁面积；et为每匝电压；Hxy为绕组x和y的平均轴向高度。
滤波绕组等值漏阻抗计算所需洛氏系数和漏磁面积表达式分别为
（10）
（11）
由式（8）～式（11）可知，绕组轴向高度、绕组横向宽度、绕组间绝缘间隙等设计参数都对变压器短路阻抗有影响。图4a给出了滤波绕组等值漏阻抗随绕组轴向高度、绕组辐向宽度变化时的零取值面，同时调节高度和宽度参数，可以实现等值漏阻抗为0，但是对应的绕组辐向宽度趋于0。图4b给出了绕组间隙变化时的绕组等值漏阻抗零取值面，仅调节绕组间绝缘间隙参数可以影响等值漏阻抗的取值，但是受限于其他参数影响，无法达到等值漏阻抗为0的条件，且观察曲面发现在绕组间绝缘间隙a34取值靠近0时，两零取值面呈现相交的趋势。
综上所述，通过调节尺寸参数可以实现滤波绕组对应等值漏阻抗为0，即Z213=Z214=0，但对应绕组辐向宽度及绝缘间隙需要趋于0。在实际工程应用中，绕组轴向高度、绕组辐向宽度、绕组绝缘间隙这些参数还影响着系统其他性能特征，其存在一定的范围约束，无法任意调节。因此，在实际设计中多采用近似零等值漏阻抗设计。
图4 等值漏阻抗零取值面
Fig.4 Equivalent impedance zero value surface
四绕组变压器两负载绕组通常移相接入12脉波整流器，由此，可以得到两负载绕组电流为
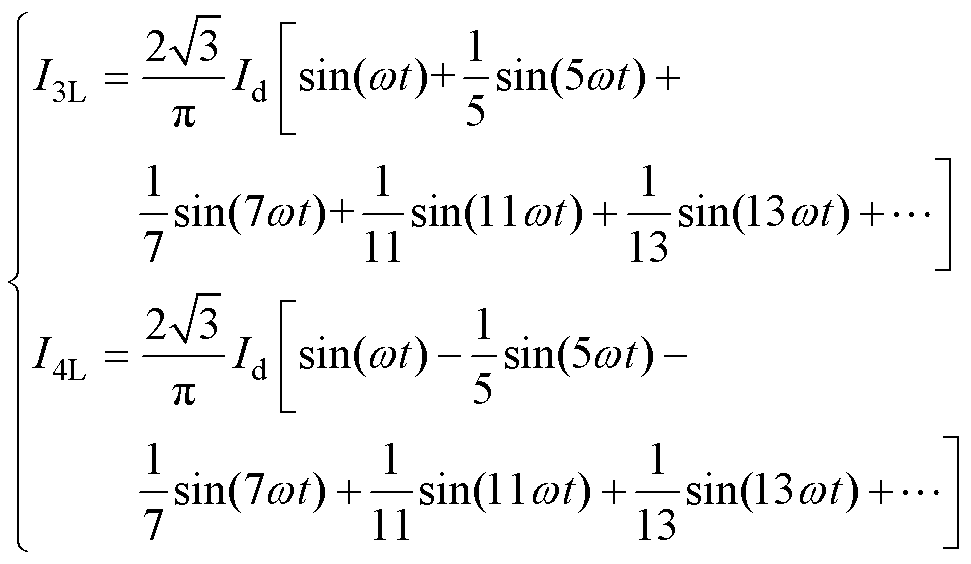（12）
式中，Id为整流器直流输出电流。
对于h=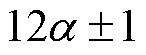
（
=1, 2, …）次谐波，有I3Lh= I4Lh。忽略电网的背景谐波，式（7）可以进一步表示为
（13）
根据式（13）可以给出感应滤波整流系统的h次谐波滤除率的表达式为
（14）
当外接滤波装置为调谐滤波器时，Zfh远小于其他参数，可忽略。其他参数转化为标幺值，假定Zk21h=k%，Zs=r%+jg%，其中，k%为h次谐波下短路阻抗标幺值，r%为网侧阻抗电阻标幺值，g%为网侧阻抗电抗标幺值，Z213h和Z214h的变化范围为 [-u%, u%]，则可以得到不同滤除率bmin对应的近似零等值漏阻抗范围。
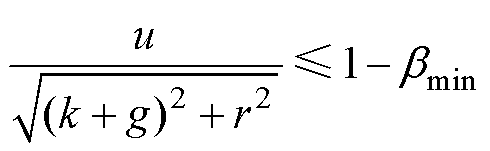（15）
由于两负载绕组的匝比取整偏差及绕组漏感的影响，其移相角无法精确等于30°，可能存在I3Lh≠I4Lh的情况，因此式（13）中的表达式可能存在一定偏差，本文取bmin±5%的范围进行验证。
感应滤波变压器优化设计考虑损耗的最小化，因此优化目标选取为变压器的总损耗，其包括空载损耗P0和负载损耗PL两大部分，有
（16）
2.1.1 空载损耗P0
空载损耗又称铁损，由铁心磁滞损耗、涡流损耗构成，工程应用下铁损计算模型为
（17）
式中，Pc为铁心材料单位损耗（W/kg）；Kp为工艺系数，与铁心材料及制造工艺相关，取1.44；Gacross为铁心磁通拐角部分的质量；Galong为铁心磁通非拐角部分质量。
Pc计算式为
（18）
式中，Kh为基于磁心材料类型的磁滞损耗系数；Ke为基于磁心材料类型的涡流损耗系数；Bm为最大磁通密度。本文优化设计铁心材料选型为宝钢30Q120，其对应Kh=6.27×10-3，Ke=3.87×10-5。
铁心质量相关计算式为
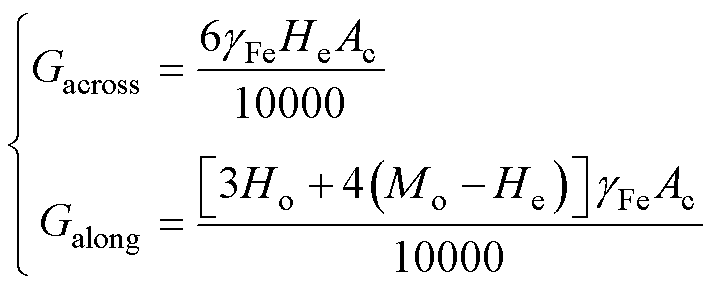（19）
式中，Ac为铁心截面积；He为铁轭高；Ho为铁心柱窗高；Mo为铁心柱中心距；
为硅钢片的比重。
2.1.2 负载损耗PL
负载损耗主要是变压器运行过程中绕组产生的损耗，包括由绕组内阻产生的焦耳热损耗Pdc、绕组中的涡流损耗Ped及结构件中由于泄漏磁通产生的杂散损耗Pst。
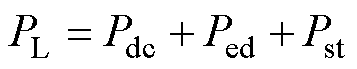（20）
其中
（21）
式中，I为绕组额定电流；R75为75℃条件时的绕组电阻。
整流变压器工作在谐波环境下，相较于常规变压器，其绕组涡流损耗和杂散损耗的计算要考虑谐波影响。涡流损耗Ped计算式为
（22）
式中，Hh-ed为绕组涡流谐波影响因子；Fed为涡流损耗占焦耳热损耗百分比计算值。
Fed计算式为
（23）
式中，N为绕组匝数；m为导体轴向高度；H为绕组电抗高度；J为绕组导线电流密度。
Hh-ed计算式为
（24）
式中，hmax为最高有效谐波次数；Ihrms为h次谐波对应电流有效值；I1rms为基波电流有效值。
杂散损耗主要是泄漏磁通变压器构件中引起的损耗，参照IEEE Std C57.110[19]，无谐波环境下，油浸式变压器涡流损耗和杂散损耗比例约为1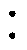
0.67。所以杂散损耗简化计算为
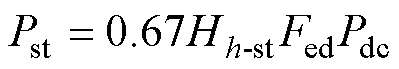（25）
其中
（26）
式中，Hh-st为杂散谐波影响因子。
变压器的优化设计必须符合国家标准的热、电和机械限制[20]，针对感应滤波变压器，主要有以下约束：
（1）阻抗电压约束。阻抗电压U对短路电流大小、电压质量高低、系统运行性能都有影响。因此，国标对不同等级标准的短路阻抗做了范围规定。
（27）
（2）近似等值漏阻抗约束。参照式（15），假定网侧等效电阻为0.5 W，网侧等效电感为0.5 mH，预设最小谐波滤除率为90%，可以得到对应的等值漏阻抗范围为
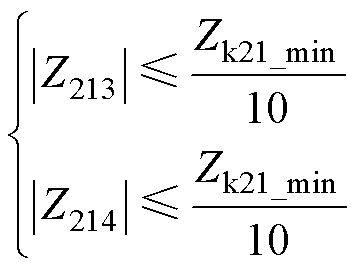（28）
式中，Zk21_min为最小谐波滤除率为90%对应的短路阻抗最小值。
（3）温升约束。变压器温升Tw应小于所使用绝缘材料的工作温度极限。
（29）
（4）电流密度约束。电流密度J与导线成本成反比关系，与负载损耗成正比关系，变压器铜导线的电流密度约束为
（30）
（5）导线宽厚比约束。导线宽厚比l满足
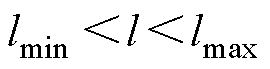（31）
（6）绕组高度比约束。为了保障磁动势平衡，减少漏磁泄漏，各绕组的高度比Hr应该控制在一定 范围。
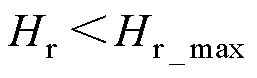（32）
（7）窗高约束
（33）
式中，D为铁心直径。
感应滤波变压器在设计过程中考虑的参数很多，选择关键的优化变量对提高优化效率和准确率至关重要。图5为感应滤波变压器结构。
图5 感应滤波变压器结构
Fig.5 Structure of the inductive filter transformer
由1.2节分析可知，影响感应滤波效果的关键等值漏阻抗参数与绕组辐向宽度、轴向高度、绕组间隙相关。变压器绕组是由导线绕制而成，绕组辐向宽度、轴向高度参数受导线尺寸影响，其中负载绕组匝数较少，通常采用特殊双饼连续式并联，其并联饼数也是影响绕组轴向高度的重要参数。而损耗参数与铁心、绕组尺寸及最大磁通密度相关。选定绕组间隙（a03、a34、a42、a21）、导线尺寸（m1×n1、m2×n2、m3×n3、m4×n4）、导线并绕数（t1×p1、t2×p2、t3×p3、t4×p4）、负载绕组并联饼数（Ml3、Ml4）、最大磁通密度（Bm）为优化变量。m1～m4为各绕组导线轴向高度，n1～n4为各绕组导线辐向宽度，p1～p4为各绕组导线轴向并绕数，t1～t4为各绕组导线辐向并绕数。
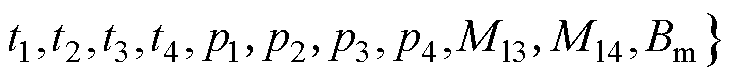（34）
在确定优化目标、优化约束、优化变量后，进一步评估优化变量相关灵敏度，探寻影响优化目标及约束性能的变量设计权衡，从而通过分层优化降低优化维度。
Sobol算法是一种基于方差的全局灵敏度分析法，应用模型分解思想和蒙特卡洛抽样方法[21]，可以有效评价系统单参独立敏感度和多参相互作用敏感度。变压器的设计会涉及多个输入参数，并且参数之间存在交互效应，Sobol算法能够同时考虑参数之间的主效应和交互效应，并且提供较为准确的灵敏度指标，易于理解和解释[22-23]。
该算法定义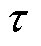
维单元体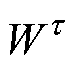
作为输入空间域，表示为
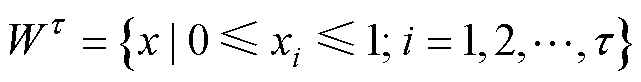（35）
进一步地，基于多重积分将目标函数唯一分解成参数间相互作用子项，有
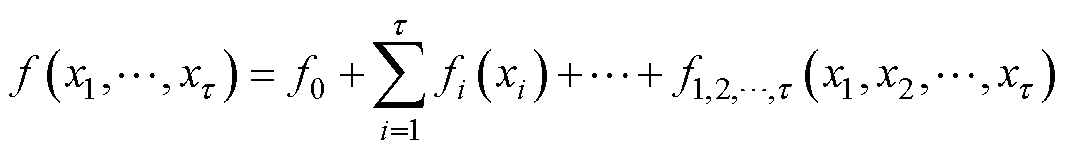（36）
式中，各参数满足以下特点：
（1）f0为常数项，各子项对包含参数的积分为0。
（37）
（2）各子项间均正交。
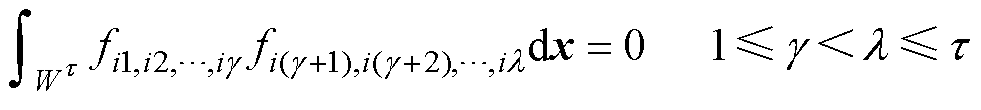（38）
（3）各子项表达式由多重积分可得
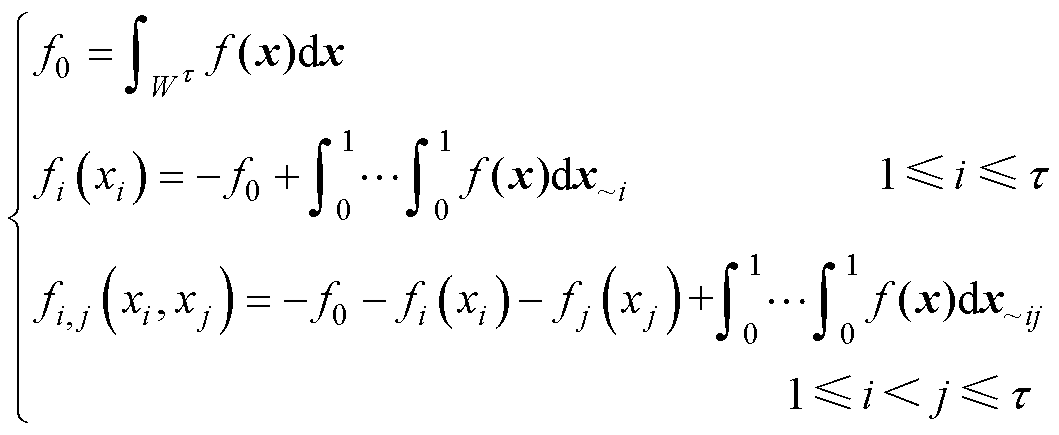（39）
式中，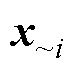
为除xi外的其他输入参数；
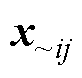为除xi和xj外的其他输入参数。
因此，目标函数的总方差可表示为
（40）
将各子项的方差定义为偏方差，有
（41）
各阶偏方差与总方差的比值对应各阶灵敏度系数，q阶灵敏度系数定义为
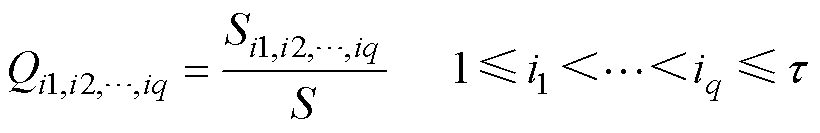（42）
式中，
为q阶灵敏度系数，表示q个参数交互对目标函数的影响。当q=1时，Qi1为参数xi1的一阶灵敏度系数，表征xi1对目标输出的影响。
灵敏度分析参数变化区间为优化变量优化区间，利用蒙特卡洛采样构造8 000×23变量矩阵，通过变压器设计解析式得到8 000×1优化目标矩阵。进一步地进行Sobol灵敏度分析，得到图6所示的感应滤波变压器损耗相关优化参数一阶灵敏度分析结果。
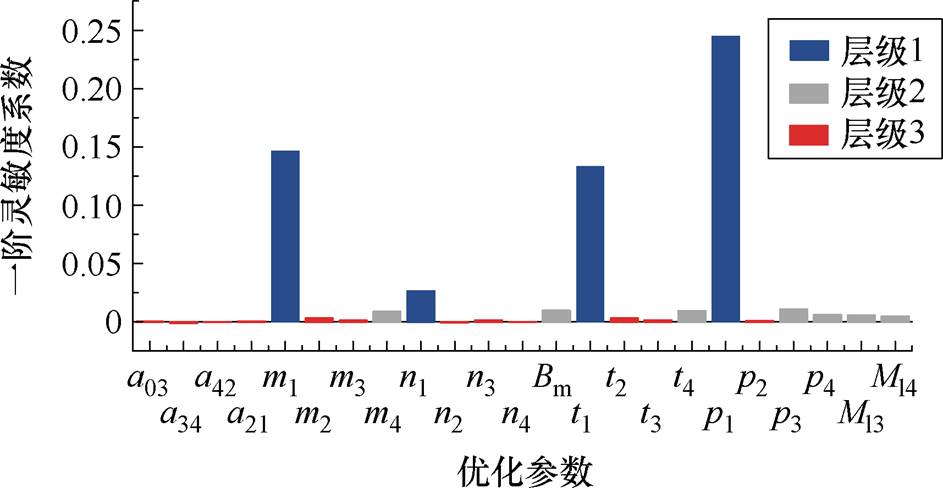
图6 损耗灵敏度分析结果
Fig.6 Results of loss sensitivity analysis
灵敏度越大，参数对目标函数的影响越大，m1、m4、n1、Bm、t1、t4、p1、p3这几个参数的灵敏度系数较大，划分为第一层级，其他参数a03、a34、a42、a21、m2、m3、n2、n3、n4、t2、t3、p2、p4、Ml3、Ml4划分为第二层级。基于划分的优化层级，选取合适的优化算法，首先对所有优化参数进行全局优化，所得优化值作为局部优化中未优化参数的初始值。然后依次优化各层级参数，上一层级优化值都用于更新下一层级优化参数，图7给出了分层优化的流程。
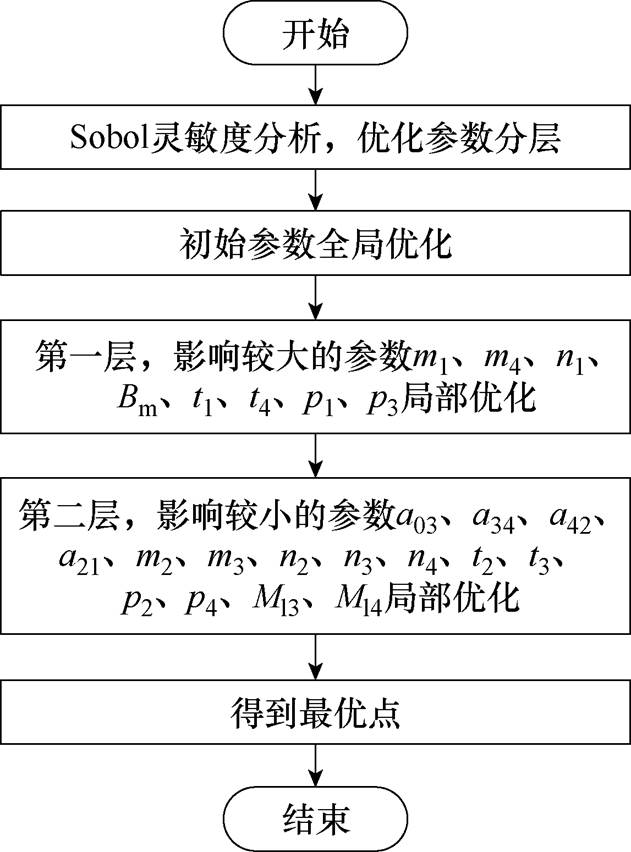
图7 分层优化流程
Fig.7 Hierarchical optimization process
根据感应滤波变压器设计规范，给定油浸式感应滤波变压器基本设计参数见表1。变压器运行在额定工况，负载绕组连接两组6脉波整流负载，构成12脉波整流系统。考虑31次以下谐波作为有效谐波进行谐波负载损耗计算，参照式（24）和式（26）计算得负载绕组的Hh-ed=10.12，Hh-st=1.367。
表1 感应滤波变压器基本设计参数
Tab.1 Design parameters of inductive filter transformer
参数高压绕组滤波绕组负载绕组1负载绕组2 额定容量/(kV·A)6 3001 6003 1503 150 额定电压/kV35100.40.4 优化约束范围取值-0.6%＜Z213＜0.6%; -0.6%＜Z214＜0.6%; Uk21_min=6%; Uk21_max=8%; Uk42_min=4%; Uk42_max=6%; Uk34_min=3%; Uk34_max=4%; Tw_max=20 K; Jmin=1.5 A/mm2; Jmax=3 A/mm2; lmin=1.4; lmax=8; Hr_max=1.05; 700 mm＜Ho＜1 400 mm 优化变量范围取值a03, a34, a42, a21: [15 mm, 40 mm]; m1, m2, m3, m4: [2 mm, 5 mm]; n1, n2, n3, n4: [5 mm, 16 mm]; t1, t2, t3, t4: [1, 12]; p1,p2,p3,p4: [1, 12]; Ml3, Ml4: [15, 50]; Bm: [1.6 T, 1.7 T]
根据2.4节中所提分层架构，选取改进差分进化算法进行优化测试[24]，初始优化迭代次数为2 000（D0），第一层迭代次数为400（D1），第二层迭代次数为600（D2），设置一组对照优化（D_con），其不采取分层优化，与初始优化具有相同的随机数种子，迭代次数为初始优化和各层优化迭代次数之和，取3 000。
图8为各层优化迭代曲线，图9为50次分层优化和对照优化的随机优化结果。分层优化中各层能在上层优化的基础上进一步优化目标函数，在算法收敛后，分层优化能够降维跳出收敛，寻到更优解，且在相同迭代次数下，分层优化得到的总损耗目标均值为44.88 kW，优化最小值为42.37 kW，对照优化均值为47.21 kW，最小值为47.15 kW。分层优化的最优值和优化均值都优于对照优化，其寻优能力和稳定得到了有效提升。
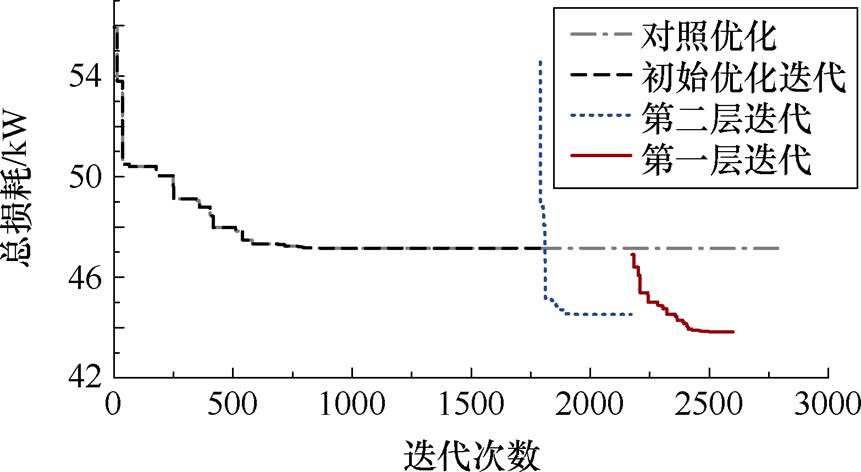
图8 优化迭代曲线
Fig.8 Optimization iterative curves
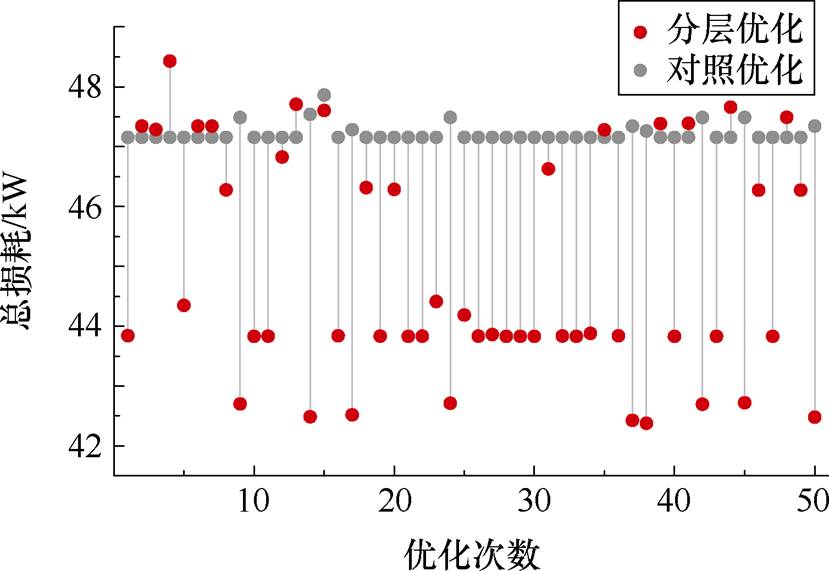
图9 随机优化结果
Fig.9 Random optimization results
选取50次中最优值为最优变压器个体，表2为对应的对照优化和分层优化最优变压器个体设计参数及损耗。
通过有限元仿真方法对优化前后的变压器进行仿真分析，验证滤波性能、运行损耗等关键参数优化结果的有效性。仿真软件为Ansys2022，采用Maxwell 3D计算模块，求解器设置为Magnetic Transient。为了提高有限元仿真速率，对变压器做以下处理：忽略垫块、绝缘纸对磁场影响，仅仿真铁心及绕组对磁场的影响，其他结构件忽略，绕组近似看作圆环形导体。有限元模型如图1所示，外电路如图10所示。有限元仿真步长为10 ms，仿真总长为80 ms。
表2 优化设计结果
Tab.2 Optimization design results
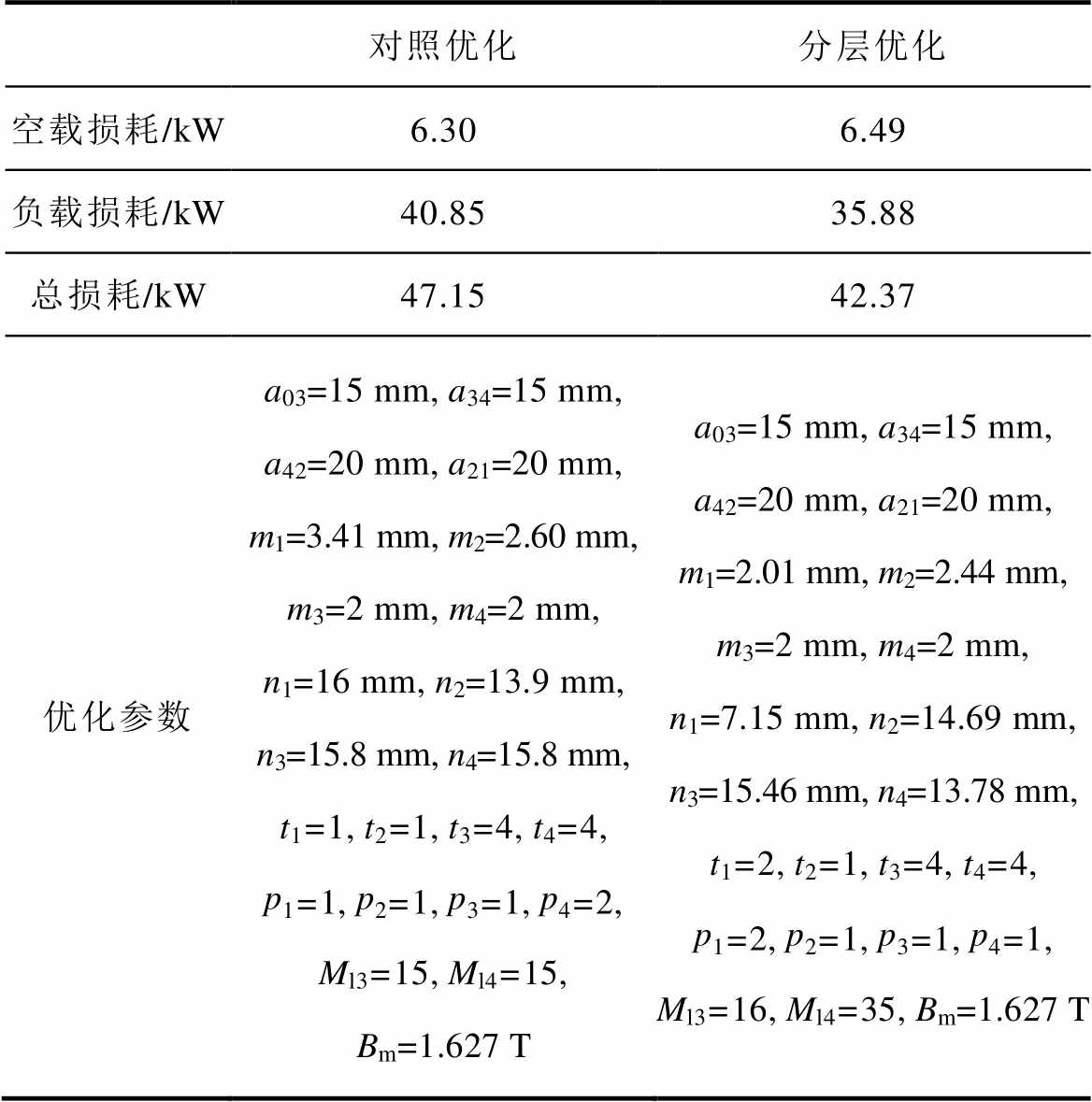
对照优化分层优化 空载损耗/kW6.306.49 负载损耗/kW40.8535.88 总损耗/kW47.1542.37 优化参数a03=15 mm, a34=15 mm, a42=20 mm, a21=20 mm, m1=3.41 mm, m2=2.60 mm, m3=2 mm, m4=2 mm, n1=16 mm, n2=13.9 mm, n3=15.8 mm, n4=15.8 mm, t1=1, t2=1, t3=4, t4=4, p1=1,p2=1,p3=1,p4=2, Ml3=15, Ml4=15, Bm=1.627 Ta03=15 mm, a34=15 mm, a42=20 mm, a21=20 mm, m1=2.01 mm, m2=2.44 mm, m3=2 mm, m4=2 mm, n1=7.15 mm, n2=14.69 mm, n3=15.46 mm, n4=13.78 mm,t1=2, t2=1, t3=4, t4=4, p1=2,p2=1,p3=1,p4=1, Ml3=16, Ml4=35, Bm=1.627 T
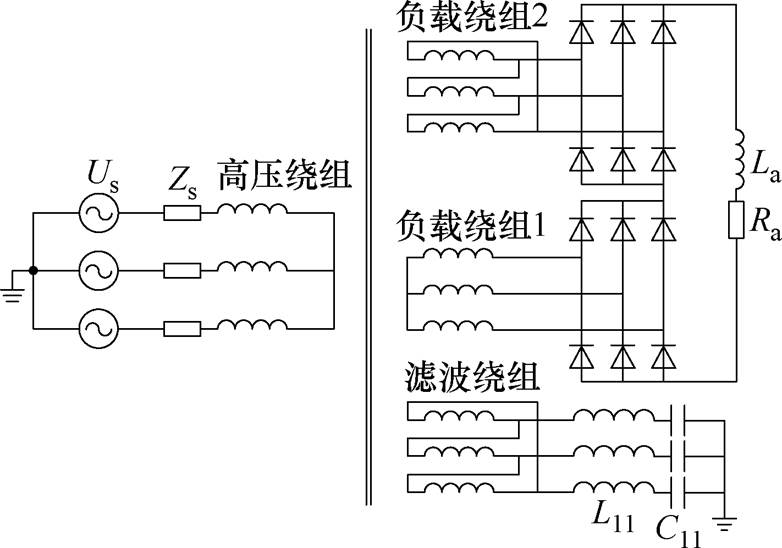
图10 外部激励电路
Fig.10 External excitation circuit
1）感应滤波性能
测试整流工作环境下，优化后感应滤波变压器的感应滤波性能。图10给出了外部激励电路，表3给出了电路相关参数。两负载绕组移相等效为12脉波整流，网侧电流中11、13次谐波含量较高，滤波绕组接入11次单调谐滤波器进行滤波。参照2.2节分析，谐波滤除率理想性能为90%±5%。
图11、图12分别为接入滤波器前后的高压侧电流波形及频谱图，优化设计后的感应滤波变压器展现了良好的感应滤波效果，高压侧谐波畸变率从8.84%降至4.29%，11次谐波电流从5.86 A下降至0.704 A，谐波滤除率达到87.9%，满足预设的感应滤波性能。
表3 激励电路参数
Tab.3 Excitation circuit parameters
参 数取 值 网侧阻抗Zs/(W/mH)0.5 负载电流Ra/W0.2 负载电感La/mH0.2 网侧电压Us/kV20.207 单调谐滤波器电容C11/mF10.077 单调谐滤波器电感L11/mH8.304
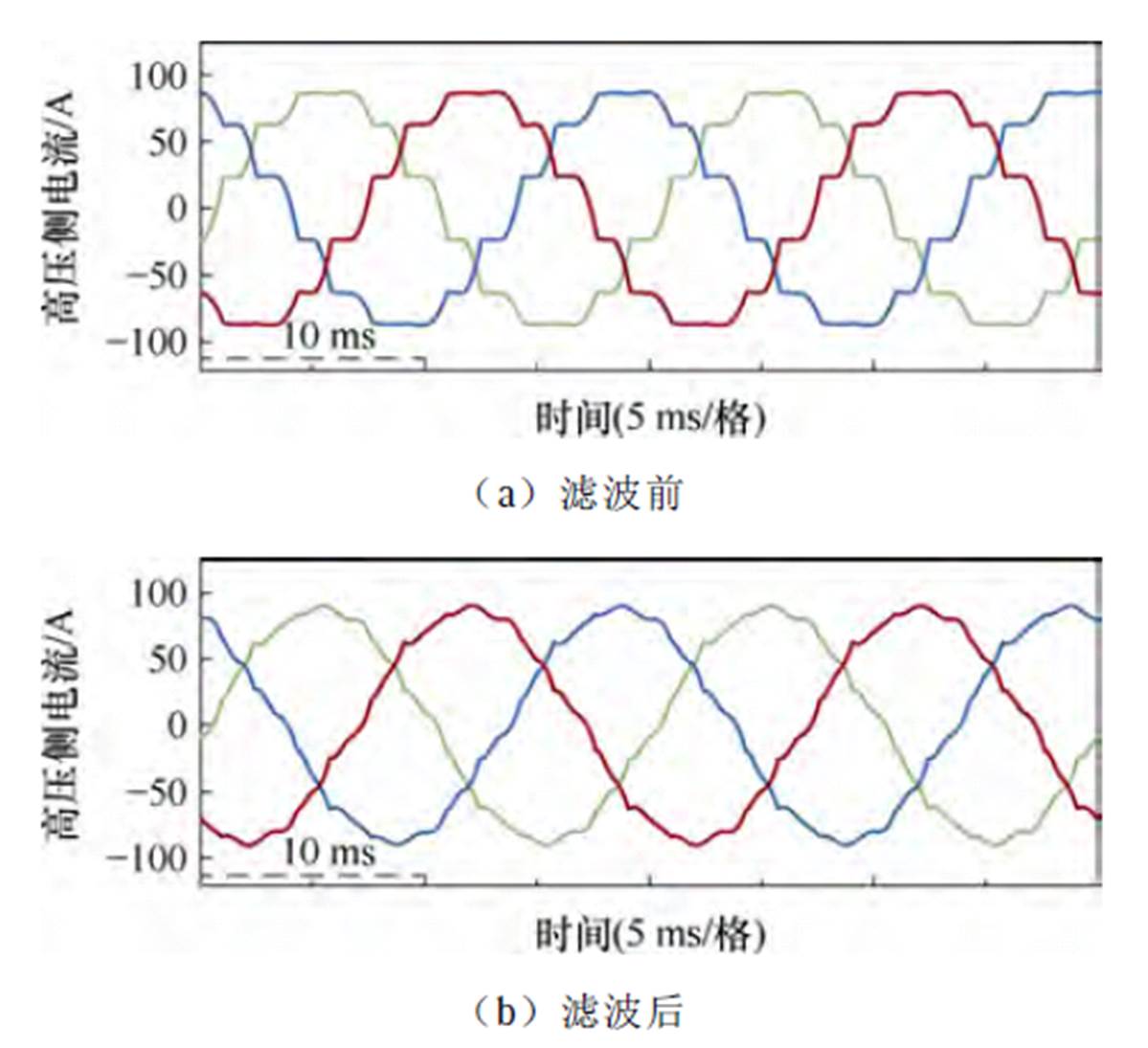
图11 高压绕组电流
Fig.11 High voltage winding current waveforms
图12 电流频谱图
Fig.12 Current spectrogram
2）损耗对比分析
图13为采用对照优化和分层优化变压器损耗对比结果。为了提高有限元仿真速率，对变压器模型进行了简化，导致仿真值与计算值之间存在一定的偏差。采用分层优化相比于对照优化总损耗计算值降低10.10%，通过仿真分析可知，采用分层优化相比于对照优化总损耗降低11.30%，验证了优化设计的可行性。
图13 损耗对比分析
Fig.13 Comparison analysis of loss
本文提出一种感应滤波变压器损耗最小化的结构参数分层优化设计方法。该优化方法在保证滤波效果的同时，能有效降低变压器的损耗，达到节能降损的目的。相较于全局优化方法，该方法能使变压器损耗进一步降低11.30%，网侧电流谐波畸变率从8.84%降至4.29%。总结如下：
1）探究了感应滤波变压器的滤波机理，分析了滤波性能与阻抗匹配条件的关联关系，建立了谐波滤除率与阻抗匹配之间的数学模型，获得了不同滤除率对应的近似零等值漏阻抗范围。
2）运用Sobol灵敏度方法对变量进行分层，降低优化维度，充分探寻搜索空间，提升寻优能力和稳定性，解决了感应滤波变压器的结构参数维度较高且存在交互效应的问题。
3）提出基于改进差分进化算法的分层优化设计方法，在算法陷入局部收敛时降维跳出收敛，寻到更优解，在保证感应滤波性能良好的同时降低变压器的损耗。
参考文献
[1] Keddar M, Zhang Zhifeng, Periasamy C, et al. Power quality improvement for 20 MW PEM water elec- trolysis system[J]. International Journal of Hydrogen Energy, 2022, 47(95): 40184-40195.
[2] 孙鹤, 李永建, 刘欢, 等. 非正弦激励下纳米晶铁心损耗的计算方法与实验验证[J]. 电工技术学报, 2022, 37(4): 827-836.
Sun He, Li Yongjian, Liu Huan, et al. The calculation method of nanocrystalline core loss under non- sinusoidal excitation and experimental verification[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 827-836.
[3] 刘欢, 李永建, 张长庚, 等. 非正弦激励下纳米晶材料高频磁心损耗的计算方法改进与验证[J]. 电工技术学报, 2023, 38(5): 1217-1227.
Liu Huan, Li Yongjian, Zhang Changgeng, et al. Calculation and experimental verification of core loss in high frequency transformer under non-sinusoidal excitation[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1217-1227.
[4] 谭又博, 余小玲, 臧英, 等. 谐波电流对换流变压器绕组损耗及温度分布特性的影响[J]. 电工技术学报, 2023, 38(2): 542-553.
Tan Youbo, Yu Xiaoling, Zang Ying, et al. The influence of harmonic current on the loss and temperature distribution characteristics of a converter transformer winding[J]. Transactions of China Elec- trotechnical Society, 2023, 38(2): 542-553.
[5] 潘希, 黄永红, 沈耀明. 大容量三相自耦变压器的杂散损耗研究[J]. 电气工程学报, 2024, DOI: 10. 1289.TM.20240227.1418.010.
Pan Xi, Huang Yonghong, Shen Yanming. Research of stray loss in three phase auto transformer with large capacity[J]. Journal of Electrical Engineering, 2024, DOI: 10.1289.TM.20240227.1418.010.
[6] 赵燕春, 王博, 李泽锋, 等. 铁基非晶复合材料的磁学性能研究[J]. 兰州理工大学学报, 2021, 47(2): 1-6.
Zhao Yanchun, Wang Bo, Li Zefeng, et al. Study on magnetic properties of Fe-based amorphous com- posites[J]. Journal of Lanzhou University of Tech- nology, 2021, 47(2): 1-6.
[7] Taghikhani Z, Ali Taghikhani M, Gharehpetian G B. Comprehensive comparative analysis of Metal-Oxide nanoadditives impacts on oil-filled finemet and vitroperm alloy core transformers HST concerning nanofluid thermophysical properties accurate esti- mation[J]. Energy Conversion and Management, 2022, 260: 115594.
[8] Peng Xin, Peng Kun, Huang Jianping. Synthesis and magnetic properties of core-shell structured finemet/ NiZn ferrite soft nanocomposites by co-precipitation[J]. Journal of Alloys and Compounds, 2017, 691: 165- 170.
[9] Mori S, Mitsuoka T, Sugimura K, et al. Core-shell structured Mn-Zn-Fe ferrite/Fe-Si-Cr particles for magnetic composite cores with low loss[J]. Advanced Powder Technology, 2018, 29(6): 1481-1486.
[10] Takajo S, Ito T, Omura T, et al. Loss and noise analysis of transformer comprising grooved grain- oriented silicon steel[J]. IEEE Transactions on Magnetics, 2017, 53(9): 2001606.
[11] 赵志刚, 白若南, 陈天缘, 等. 基于智能优化算法的高频变压器电磁结构优化设计[J]. 电工技术学报, 2024, 39(18): 5610-5625.
Zhao Zhigang, Bai Ruonan, Chen Tianyuan, et al. Optimization design of electromagnetic structure of high frequency transformer based on intelligent optimization algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(18): 5610-5625.
[12] 杨新生, 张云鹏, 徐桂芝, 等. 基于T-y 有限元法的多目标函数变压器优化设计[J]. 电工技术学报, 2021, 36(增刊1):75-83.
Yang Xinsheng, Zhang Yunpeng, Xu Guizhi, et al. Based on T-y multi objective function transformer optimization design using finite element method[J] Transactions of China Electrotechnical Society, 2021, 36(S1): 75-83
[13] Mohammed M S, Vural R A. NSGA-II FEM based loss optimization of three-phase transformer[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 7417-7425.
[14] Arkadan A A, Gutierrez-McCoy M A. Power transformer characterization and design optimization environment[J]. IEEE Transactions on Magnetics, 2023, 59(5): 8400305.
[15] 王英, 王亚兰, 陈小强, 等. 基于直流侧混合电压谐波注入的低谐波串联36脉波整流器[J]. 电工技术学报, 2023, 38(19): 5288-5303.
Wang Ying, Wang Yalan, Chen Xiaoqiang, et al. A series 36-pulse rectifier operating in low harmonic state based on hybrid voltage harmonic injection at DC side[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5288-5303.
[16] Sou W K, Chao Chiwa, Gong Cheng, et al. Analysis, design, and implementation of multi-quasi- proportional-resonant controller for thyristor- controlled LC-coupling hybrid active power filter (TCLC-HAPF)[J]. IEEE Transactions on Industrial Electronics, 2022, 69(1): 29-40.
[17] 李勇, 刘珮瑶, 胡斯佳, 等. 基于感应滤波的光伏电站谐波谐振抑制方法[J]. 电工技术学报, 2022, 37(15): 3781-3793.
Li Yong, Liu Peiyao, Hu Sijia, et al. Harmonic resonance damping method of photovoltaic power station based on inductive filtering[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3781- 3793.
[18] 王灿, 宁志毫, 张可人, 等. 电解铝用高效感应滤波整流供电系统分析[J]. 电机与控制学报, 2017, 21(7): 78-86.
Wang Can, Ning Zhihao, Zhang Keren, et al. Analysis on efficient rectifier power supply system for electrolytic aluminium based on inductive filtering method[J]. Electric Machines and Control, 2017, 21(7): 78-86.
[19] IEEE recommended practice for establishing liquid immersed and dry-type power and distribution transformer capability when supplying nonsinusoidal load currents: IEEE Std C57.110-2018[S]. 2018.
[20] 国家市场监督管理总局, 国家标准化管理委员会. 电力变压器 第11部分: 干式变压器: GB/T 1094.11—2022[S]. 北京: 中国标准出版社, 2022.
[21] 王丰华, 王劭菁, 苏磊, 等. 采用Sobol’算法分析变电站接地网关键参数的灵敏度[J]. 高电压技术, 2017, 43(1): 300-306.
Wang Fenghua, Wang Shaojing, Su Lei, et al. Sensitivity analysis of substation grounding grid parameters based on Sobol’ method[J]. High Voltage Engineering, 2017, 43(1): 300-306.
[22] Feng Feng, Xue Jianguo, Zhang Jianan, et al. Concise and compatible MOR-based self-adjoint EM sen- sitivity analysis for fast frequency sweep[J]. IEEE Transactions on Microwave Theory and Techniques, 2023, 71(9): 3829-3840.
[23] 陈彬, 陈健, 唐波, 等. 高频变压器漏电感参数灵敏度分析及其半经验模型[J]. 电机与控制学报, 2021, 25(10): 97-111.
Chen Bin, Chen Jian, Tang Bo, et al. Sensitivity analysis and semiempirical model of leakage inductance parameters of high frequency trans- former[J]. Electric Machines and Control, 2021, 25(10): 97-111.
[24] Das S, Suganthan P N. Differential evolution: a survey of the state-of-the-art[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 4-31.
Abstract The industrial rectifier system is responsible for converting AC and DC electrical energy, and the electrical operating environment is characterized by high power, high current, and low voltage. It faces significant challenges, such as severe harmonic pollution and power loss. Transformer loss contributes to 40% of the total loss in the industrial rectifier system. Therefore, reducing transformer loss is key to managing the operational environment of the industrial rectifier system. In recent years, the research on the reduction of transformer loss has primarily focused on three areas: improving the material process, optimizing the physical structure, and managing the electromagnetic environment. Previous literature has rarely researched the zero-impedance matching design and performance optimization of inductive filtering transformers.
This paper aims to develop a new hierarchical optimization strategy for the multi-objective optimization of the inductive filtering rectifier transformer, considering winding impedance matching. The transformer’s structural parameters reduce operational loss by establishing hierarchical architecture through Sobol sensitivity analysis of parameters. Firstly, the filtering mechanism is revealed based on the topological structure of the inductive filtering rectifier transformer. According to the relationship between voltage and current, impedance-matching conditions for implementing inductive filtering technology are obtained. The correlation between harmonic filtering performance and matching conditions is analyzed. A harmonic filtering rate is proposed, and a constraint of approximately zero equivalent leakage impedance is given for different harmonic filtering rates. Secondly, regarding the high dimension of the transformer structure parameters and the strong interaction effect between the parameters, the Sobol sensitivity analysis algorithm is used to stratify the optimization transformer parameters. Finally, a hierarchical optimization design method is proposed based on an improved differential evolution algorithm. The optimized parameters are used as the initial values of the unoptimized parameters in the local optimization. Then, the parameters of each level are optimized successively, which updates the optimization parameters of the next level. It can jump out of local convergence by reducing dimensions to find a better solution. This optimization method ensures a good induction filtering effect and reduces the operating loss of the transformer.
Through case analysis, it can be seen that under the same number of iterations, the target average of total loss obtained by hierarchical optimization is 44.88 kW, and the optimal value is 42.37 kW. The target average of total loss obtained by control optimization is 47.21 kW, and the optimal value is 47.15 kW. The optimal and mean values of hierarchical optimization are better than control optimization. Compared with control optimization, hierarchical optimization can effectively improve the optimization ability and stability. The finite element simulation results show that the current harmonic distortion rate at the high voltage network side is reduced from 8.84% to 4.29%, which meets the design requirements of filtering performance. Compared with the global optimization method, the hierarchical optimization method can further reduce the transformer loss by 11.3%, which verifies the feasibility of the optimal design.
keywords：Rectifier transformer, sensitivity analysis, impedance matching, hierarchical optimization design
中图分类号：TM41
DOI: 10.19595/j.cnki.1000-6753.tces.240349
国家自然科学基金（52207146）、湖南省重点领域研发计划（2023GK2007）和江苏省能源动力高端装备工程研究中心开放课题基金（JSNYDL-202401）资助项目。
收稿日期2024-03-05
改稿日期2024-05-15
刘乾易 男，1992年生，博士，讲师，硕士生导师，主要研究方向为电能质量优化与控制。E-mail: liu7y@foxmail.com
刘 芳 女，1982年生，博士，教授，博士生导师，主要研究方向为智能电网技术、电力系统稳定与控制、新能源发电等。E-mail: csuliufang@csu.edu.cn（通信作者）
（编辑 崔文静）