图1 电枢测速实验平台
Fig.1 The velocity measurement platform of armature
摘要 枢轨间的动态摩擦力是影响轨道式直线推进电磁能装备运动特性的重要因素之一。但在极端电磁热力冲击工作条件下，摩擦因数的实时原位测量极具挑战，因此目前研究中枢轨间的摩擦因数大多采用定常值。为了提高数值模型的计算精度，该文提出基于动态摩擦因数反演的直线推进电磁能装备运动特性研究方法。首先，根据电磁推进实验可观测数据与电枢动力学正演模型，建立基于改进动态粒子群优化算法（DPSO）的枢轨间摩擦因数与轨道电感梯度的反演模型，得到其时空特性。然后，在此基础上建立枢轨瞬态电磁热力耦合有限元模型，分析动态摩擦因数对装备运动特性的影响。最后，通过实验验证该文考虑动态摩擦因数的方法可大大提高有限元模型的计算精度，为进一步对电磁能装备可靠性预测和结构优化设计提供理论参考，并为极端工况下材料特性实时原位测量提供新的解决思路。
关键词：直线推进电磁能装备 动态摩擦因数 参数反演 动态粒子群优化算法 运动特性
在现代电磁动力学应用领域，轨道式直线推进电磁能装备因其能够快速、高效地将电磁能转化为机械动能而备受关注[1-2]。电枢在运动过程中除了受电磁力、空气阻力、机械预紧力等的影响[3]，由高速滑动而产生的摩擦力也是影响发射性能的重要因素，它不仅决定了枢轨能量转换的效率，而且影响着整个装备的工作稳定性和可靠性。
轨道式直线推进电磁能装备的工作过程受高功率脉冲电流激励，出口速度极快，枢轨材料的电磁热力特性会发生剧烈变化[4-6]，因此在分析装备电磁综合性能时需考虑材料的实际服役条件。高速滑动电接触条件下，接触面间的摩擦因数受接触材料、载荷、滑动速度等影响而呈动态变化[7-8]，但在电枢高速运动的极端工况下实现对枢轨摩擦特性的实时原位测量是非常困难的。
目前，对直线推进电磁能装备摩擦特性的研究中，枢轨间的动态摩擦因数及对运动特性的影响是传统建模中大多忽视的关键方面。文献[9]建立了电磁推进过程中的多场耦合动力学模型，分析了接触电阻的压阻效应和接触界面的摩擦效应等非理想因素对电磁推进的影响。文献[10]对轨道进行分段并建立瞬态温度场计算模型，得到了电阻焦耳热与摩擦热为热载荷共同作用下的轨道温升时空分布特性。文献[11]建立电磁推进系统的能量平衡方程，通过仿真计算出摩擦和空气阻力作为不可逆因素引起的能量损失。文献[12]将整个滑动电接触过程分为干摩擦接触、液化层接触和高速不稳定接触三个阶段，并采用层次分析法从解析角度对枢轨滑动电接触过程不同阶段的状态和机理进行了评估。
受极端电磁热力冲击工作条件的影响，很难实现对枢轨间摩擦因数的实时原位测量，目前考虑枢轨间摩擦力对系统运动特性影响的研究中摩擦因数大多采用固定经验值，定常的摩擦模型无法准确地描述电枢的实际运动特性。因此，本文提出一种基于动态摩擦因数反演的直线推进电磁能装备运动特性的研究方法，首先，根据电磁推进实验可观测数据与电枢动力学正演模型建立基于改进的动态粒子群优化算法（Dynamic Particle Swarm Optimization, DPSO）的枢轨间摩擦因数与轨道电感梯度的反演模型，利用电枢实测速度对正演模型计算速度进行实时修正以得到其时空特性。然后，在此基础上建立枢轨系统瞬态电磁热力耦合模型，利用有限元法对比分析摩擦因数为动态值与固定值时装备的运动特性。最后，通过实验验证了理论分析的正确性。本文考虑动态摩擦因数的方法可大大提高有限元模型计算精度，为进一步对电磁能装备可靠性预测和结构优化设计提供了理论参考，并为极端工况下对材料特性的实时原位测量问题的解决提供了新思路。
为得到电枢在整个过程中的实际运动速度，搭建基于B探针测速的直线推进电磁能装备实验平台，如图1所示。
图1 电枢测速实验平台
Fig.1 The velocity measurement platform of armature
激励电源由6个脉冲电容放电提供，并通过电流传感器对脉冲放电电流进行采集。B探针是由单根铜导线缠绕多匝而制成的线圈环。内轨道全长2.1 m，将10个自制的B探针均匀紧贴于上下轨道之间的绝缘材料上，当带有电流的电枢经过时，在电枢磁场作用下线圈内产生感应信号并通过采集系统输出。通过对各B探针信号的过零点时刻与位置进行拟合，得到电枢的位移和速度随时间的变化曲线如图2所示。膛口电压与轨道电流随时间的变化曲线如图3所示。
根据图3可知，膛口电压波形平稳并没有发生突变性的升高，由此可知，电枢在整个运动过程中枢轨接触良好并没有发生转捩。
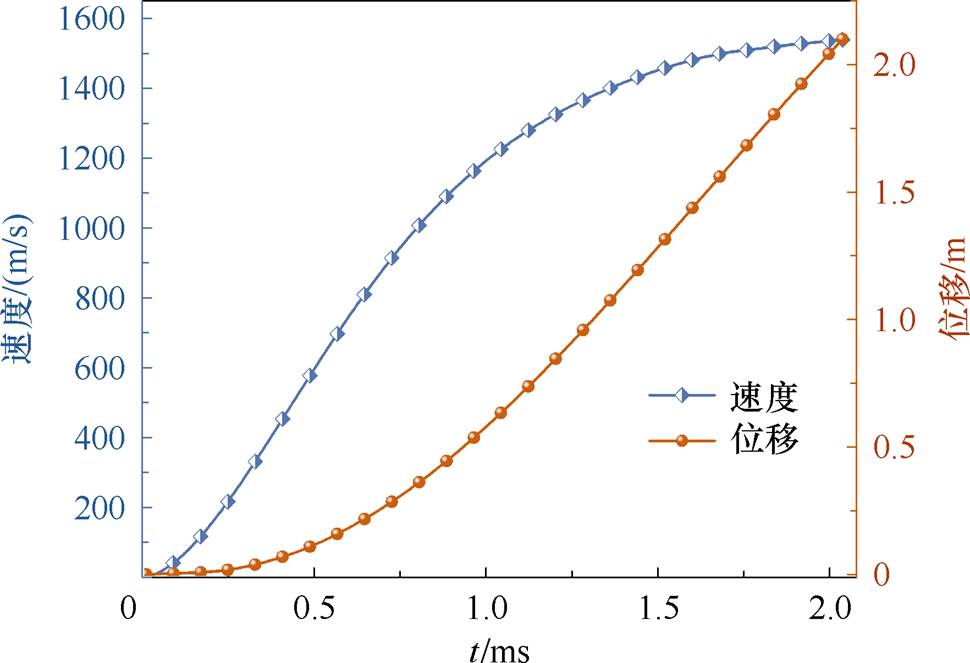
图2 电枢的位移和速度随时间的变化曲线
Fig.2 The displacement and velocity curves of the armature with time
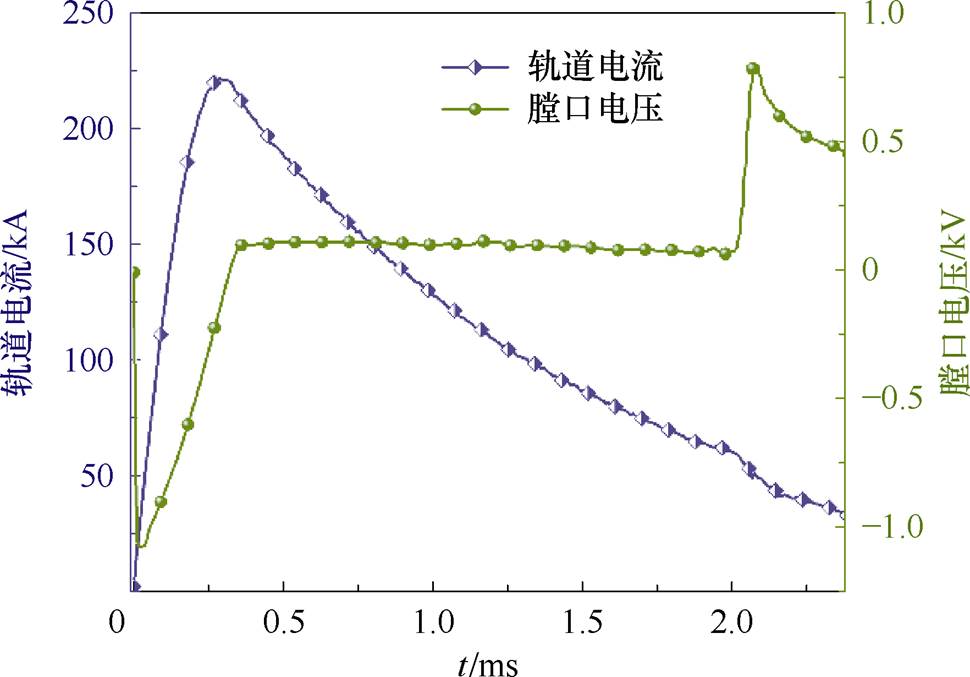
图3 膛口电压和轨道电流随时间的变化曲线
Fig.3 The muzzle voltage and rail current curves with time
电枢在运动过程中，除了电磁力，摩擦力也是影响电枢运动速度的重要因素。直线推进电磁能装备的原理如图4所示。
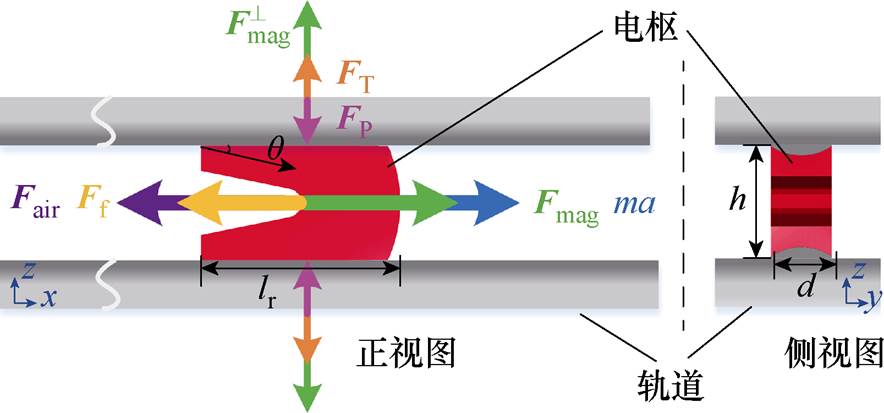
图4 直线推进电磁能装备的原理
Fig.4 The schematic diagram of linear propulsion electromagnetic energy equipment
电枢运动的瞬态过程中，轨道的电感梯度受电流扩散程度和趋肤效应的影响而使其随电流和磁场动态变化，若将电感梯度取常数值会影响电枢的计算速度，因此在计算电枢速度时不仅要考虑摩擦因数的动态变化还需要考虑轨道电感梯度的动态变化。根据电枢动力学方程可知，电枢在运动方向上的受力关系为
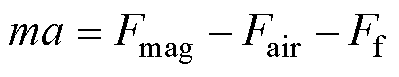（1）
式中，m为电枢质量；a为电枢加速度；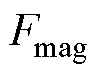
为电磁推力；
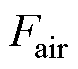为空气阻力；
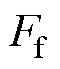为摩擦力。
电枢所受电磁推力为
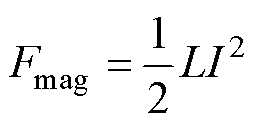（2）
式中，L为轨道电感梯度；I为激励电流。
在电枢低速运动阶段，电枢所受的阻力主要是摩擦力，但电枢在高速运动时会产生冲击波进而产生空气阻力，空气阻力大小与电枢的运动速度和其气动力外形有关，有
（3）
式中，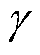
、
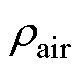分别为空气阻力系数和空气密度；
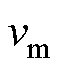、x分别为电枢的实际运动速度、位移；d、h分别为电枢的宽和高；
为黏滞摩擦因数。
枢轨间为“固-固”接触，接触压力为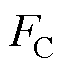
，则电枢沿轨道滑动受到的摩擦力为
（4）
式中，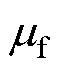
为枢轨间的摩擦因数。考虑电枢沿垂向的电磁力
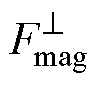、枢轨间过盈配合所受的机械预紧力
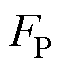、电枢作用于轨道的热膨胀力
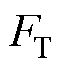，则枢轨间的接触压力为
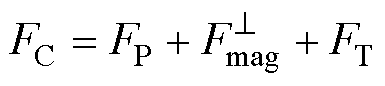（5）
垂向电磁力为
（6）
式中，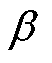
为电枢壁受到的电磁力垂直于轨道方向的分量转化为对轨道挤压力的系数；
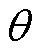为电枢尾翼的角度。
假设电流在电枢区域内均匀分布，由于充电时间非常短，忽略电枢运动过程中温度的改变，取电枢垂向的平均温度来计算电枢作用于轨道的热膨胀力[13]，有
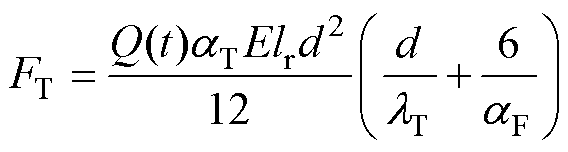（7）
式中，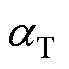
、
、
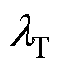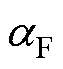分别为电枢材料的热膨胀系数、热导率、热交换系数；E为电枢材料的杨氏模量；lr为电枢的长度；Q(t)为电枢的热源功率。当电流流经电枢时，电枢的温升热源主要包括电阻焦耳热和电枢高速滑动时，枢轨间摩擦产生的热量，由于热膨胀力相对于电磁力和预紧力较小，所以在此处计算摩擦热时不考虑热膨胀力的影响，则
（8）
式中，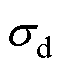
为电枢材料的电导率。
综合各式可知电枢计算速度为
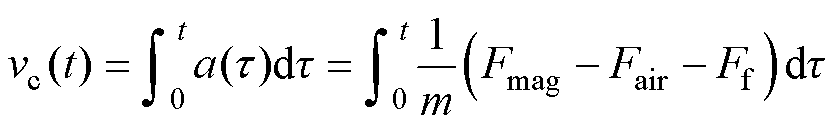（9）
根据式（1）～式（9）即可初步建立在电枢运动过程中速度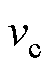
和枢轨间的摩擦因数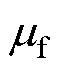、轨道电感梯度L之间的非线性映射关系
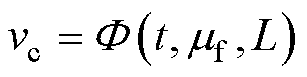。但在实际的发射过程中，由于系统内极端电磁热力冲击环境使枢轨间摩擦因数与轨道电感梯度均随时间而动态变化，而这种含多动态参数的正演模型很难直接反推出其每个动态参数，因此本文通过在多维空间搜索，反演出在整个推进过程中最接近电枢实时状态的动态参数组合。
数据反演计算为复杂模型特性参数的确定提供了新思路，该方法已在岩土工程、地球物理、医学成像等领域得到广泛的应用。针对电磁推进过程中由于极端条件而形成的非线性系统，数据反演并不仅仅依赖于理论公式，而是从实验数据入手通过优化过程来适应实测数据以确定最接近电枢运动过程中实时状态的模型参数。因此根据第1节分析，可通过最小化理论模型计算速度与实测速度之间的差距来实现动态摩擦因数与电感梯度值的反演。由于电枢速度是时间的函数，因此需要在每个时刻都找到目标函数最小时对应的摩擦因数与电感梯度值，则目标函数为
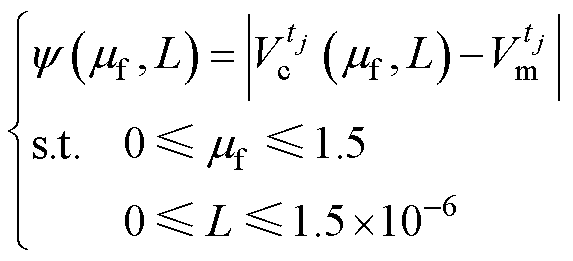（10）
式中，
、
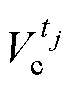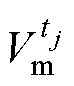分别为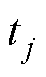
时刻的理论模型计算速度和实测速度。
粒子群优化（Particle Swarm Optimization, PSO）算法是通过群体中个体之间的协作和信息共享来寻找最优解，由于其结构简单、参数少、容易实现、收敛速度较快的优点而被广泛应用[14]。PSO的核心在于个体与种群之间的信息交流，即速度的更新与位置的更新。在求解过程中，速度的更新实际是粒子下一次迭代需要移动的距离和方向，是一个位置向量，包括记忆项、自身认知项、群体认知项。速度和位置更新公式为
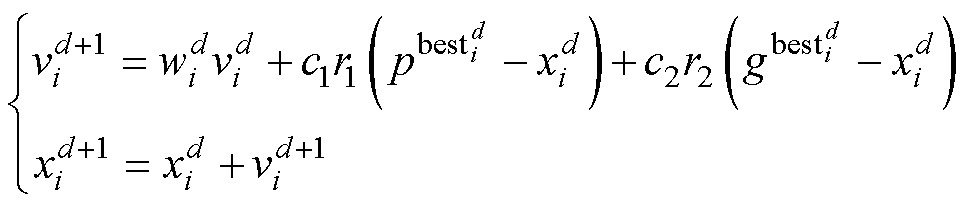（11）
式中，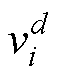
、
分别为第d轮迭代时第i个粒子的速度和位置；
、
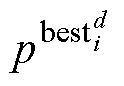分别为第d轮迭代后粒子i搜索到的个体最优解和整个粒子群的最优解；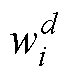
为速度惯性权重；
、
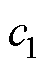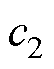分别为个体学习因子、社会学习因子；
。
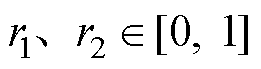惯性权重是PSO算法的重要参数，起到平衡全局搜索能力和局部搜索能力的作用，恰当的惯性权重可以提高寻优能力，减少迭代次数[15]。因此，本文采用自适应权值策略在粒子搜索过程中动态调整惯性权重。惯性权重w满足
（12）
其中
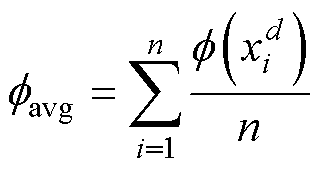
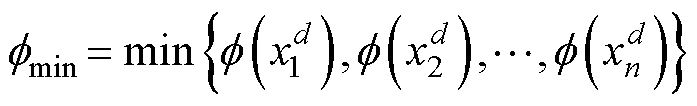
式中，
为第d轮迭代时当前粒子的目标函数值；
、
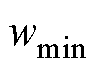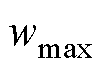分别为给定的最小惯性权重和最大惯性权重，取0.4和0.9；
、
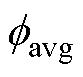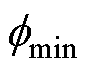分别为第d轮迭代时所有粒子的平均目标函数值和最小目标函数值。
为了防止粒子速度在搜索空间中移动过快而错过潜在的最优解陷入局部最优解，本文提出通过引入边界条件限制粒子速度，当粒子速度超出预设的最大速度时，将超速的粒子在速度边界内随机分布，以保证粒子的多样性和合适的搜索能力，超速粒子通过式（13）调整。
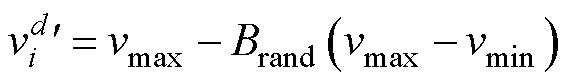（13）
式中，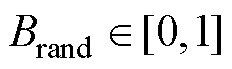
；
、
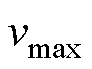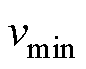分别为搜索速度的上、下边界。
为了实现循环寻优，在每个时刻都找到使目标函数最小时对应的最优解，需要考虑不同时刻带来的动态环境的改变。在环境变化前使用记忆机制来存储上一时刻的最优位置信息，当检测到环境变化时，使用记忆库中的解来初始化粒子的位置，则在t时刻的粒子位置和速度可初始化为
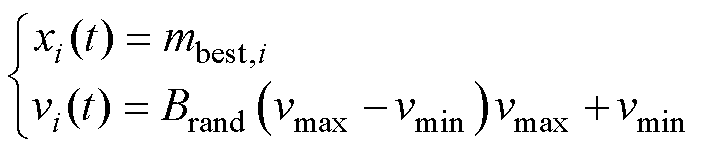（14）
式中，
为记忆库中存储的最优位置。当检测到环境变化时，使用记忆库中的解来初始化粒子位置，并为粒子提供随机化的新速度，使得粒子立即跳转到已知的有前景的区域进行搜索，既可以提高算法的适应性，又可以增加粒子搜索新环境的灵活性。基于DPSO的参数反演流程如图5所示。
图5 参数反演流程
Fig.5 The flowchart for parameter inversion
每一时刻对应的目标函数值随迭代次数的变化曲线如图6所示，得到修正后的电枢计算速度与实测速度的对比曲线如图7所示。
由图7可知，根据反演模型得到修正前后的计算速度与实测速度吻合度较高，整体误差为1.53%。根据反演模型计算得到的枢轨间摩擦因数与轨道电感梯度随实测速度与时间的变化曲线如图8所示。
根据图8可知，在电枢运动过程中，枢轨间的摩擦因数随着电枢速度的增大从0.63开始迅速下降，0.3 ms后下降趋势减缓并逐渐趋向稳定值0.24。出现这种现象的原因是：在电枢刚开始运动时摩擦因数较高主要是由于枢轨表面间的粘附力所致，但在脉冲大电流的激励下电枢迅速产生焦耳热使得枢轨界面出现熔化液态铝，致使枢轨接触面由干滑动摩擦向流体润滑滑动摩擦转变，此时枢轨间摩擦因数不断降低。在较短时间内，枢轨接触面上熔化铝产生充分，使其进入完全流体润滑摩擦阶段，随着电枢速度的增大，单位时间内润滑层中由流体黏滞力引起的剪切变形量增大，进而导致润滑层的厚度减小，从而增大了摩擦因数，但摩擦因数增大引起的摩擦热量的增加使液态铝黏度降低又会引起摩擦因数的减小，因此最终摩擦因数逐渐趋于稳定饱和值。从整体来看，枢轨间的摩擦因数相对较高，这是由于与电枢接触的内轨道是耐磨钢材料，耐磨钢较硬，会使电枢接触表面在运动过程中出现一定的磨损而增大摩擦因数；经过多次发射，轨道表面会出现微裂纹和表面损伤而使表面粗糙度增加，从而导致摩擦因数增大。
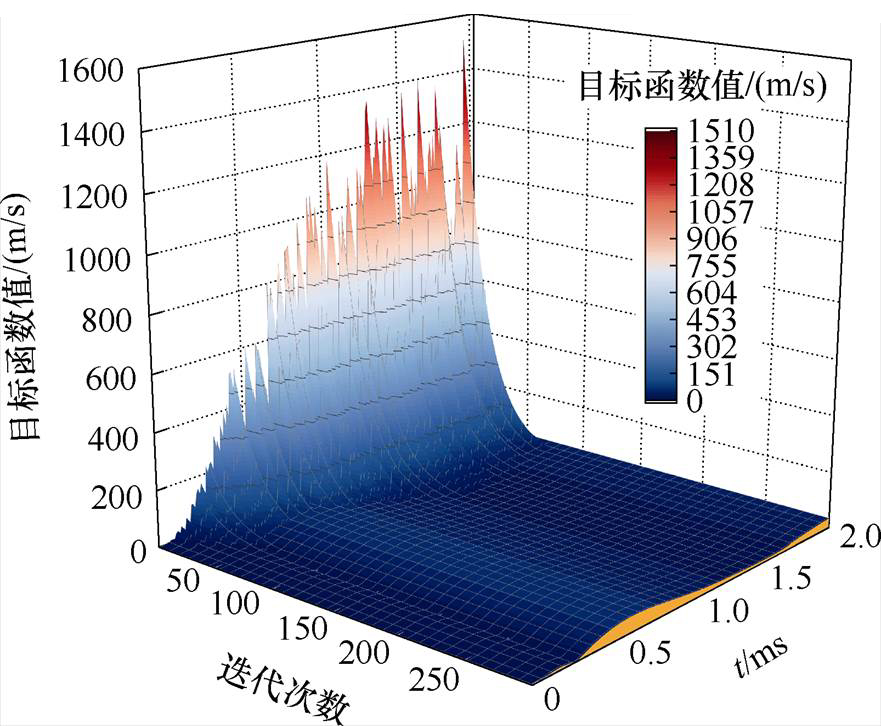
图6 不同时刻目标函数值随迭代次数的变化曲线
Fig.6 The variation curves of the objective function values with iteration numbers at different time
图7 修正前后的电枢速度曲线
Fig.7 The armature velocity curves before and after correction
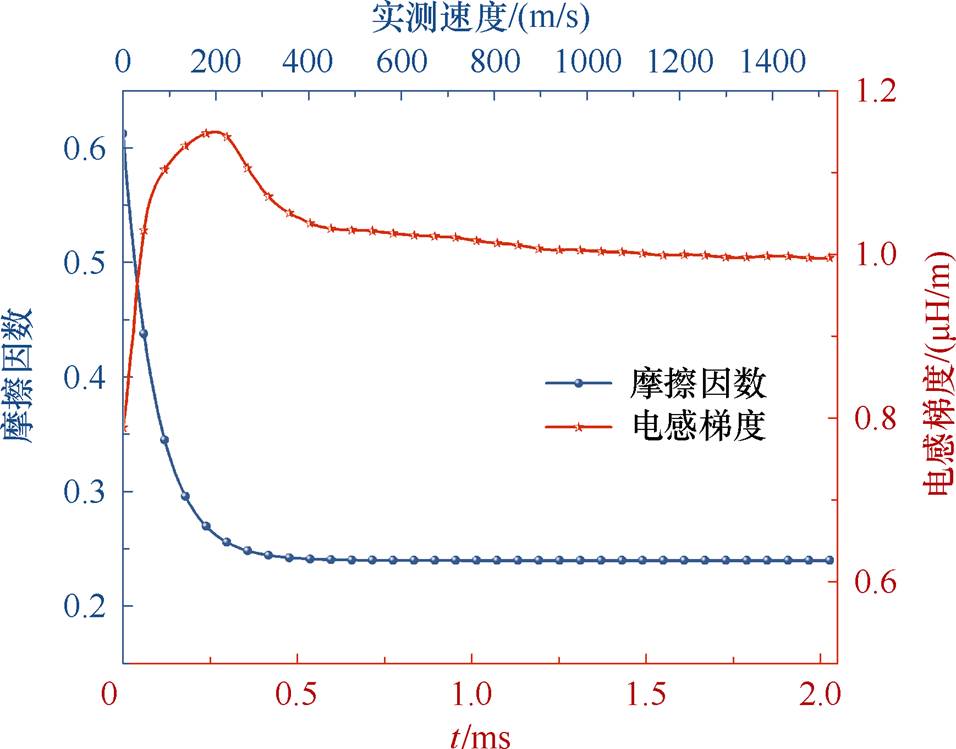
图8 反演参数随时间与实测速度的变化曲线
Fig.8 The curves of inversion parameters with time and measured velocity
电感梯度在电流峰值时刻达到最大值，为1.15 mH/m，随后逐渐减小至1 mH/m。在电流峰值时刻之前，受电流的扩散影响使得电感梯度逐渐增大；随着电枢速度的增大，受速度趋肤效应的影响，电流集中在轨道内表面而使得电感梯度逐渐减小并趋于稳定。
为了提高直线推进电磁能装备运动特性的数值计算精度和准确计算考虑枢轨间动态摩擦因数对电枢运动特性的影响，本文基于上述反演得到的动态摩擦建立枢轨系统的电磁热力耦合模型，根据有限元法对电枢运动特性进行分析。枢轨的结构、几何尺寸、材料特性确定后，轨道电感梯度的变化间接受电流分布和磁场分布的影响，所以在有限元计算时，轨道电感梯度的动态变化已经考虑在内了。
枢轨导体为高电导的金属材料，忽略磁导率的各向异性，则枢轨区域的三维瞬态电磁场为
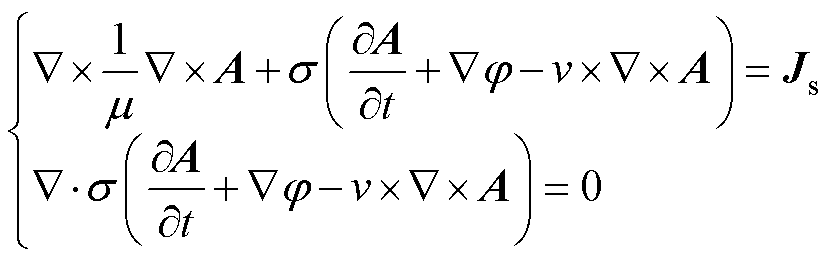（15）
式中，
为介质磁导率；A为矢量磁位；
为介质的电导率；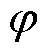
为标量电位；v为电枢速度；
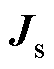为激励电流。枢轨中传导电流密度由轨道流入电枢的电流密度和由于电枢运动而产生的运动感应项对电流的影响两部分构成，若直接进行有限元求解会引起离散后的系数矩阵不对称，因为1.1节实测的轨道电流中已经包含了这一部分的叠加效果，所以本文为避免计算电枢运动项，激励电流采用实际发射过程中测量的电流。则进一步可得枢轨电磁力为
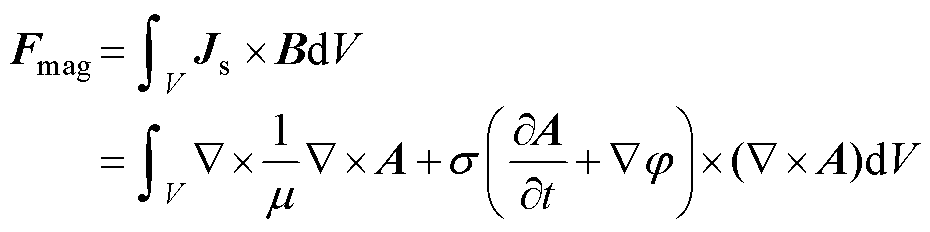（16）
式中，B为磁感应强度；V为电磁力分析域。
在电枢运动过程中，电流通过枢轨时产生的电阻焦耳热和枢轨间高速滑动产生的摩擦热是枢轨系统中的主要热量来源。则考虑动态摩擦因数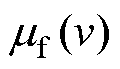
的枢轨的温度场控制方程为
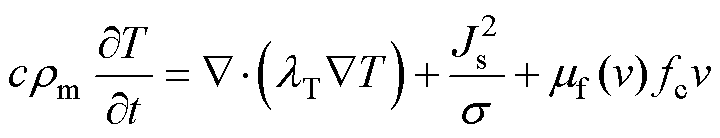（17）
式中，c为材料的比热容；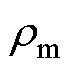
为材料密度；T为温度；
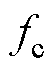为枢轨接触面处的压强。
根据反演得到的摩擦因数随速度的变化曲线，可建立摩擦因数模型为
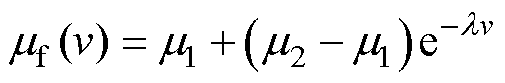（18）
式中，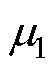
、
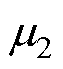分别为摩擦因数随速度变化的初始值和稳定值；
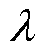为衰减系数。
为了更准确地反映摩擦因数随速度的变化趋势，本文将枢轨间的摩擦因数按照速度进行分段，并利用非线性最小二乘拟合方法来确定各个速度段内摩擦因数模型的参数，其目标函数为
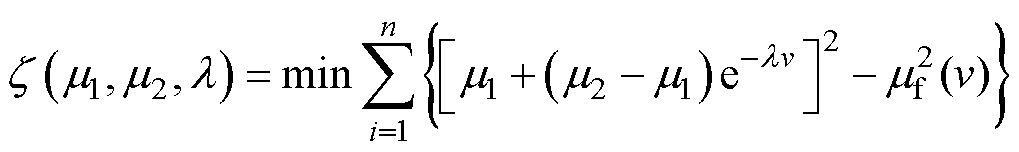（19）
计算可得各分段参数为
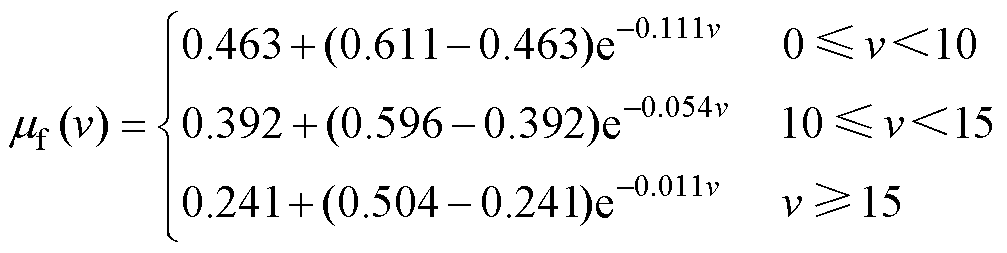（20）
建立枢轨系统的几何模型，本文采用凹弧电枢和凸弧轨道配合形式的枢轨模型，轨道全长2.1 m，几何剖分模型如图9所示，图10为电枢部位示意图。
图9 枢轨几何剖分图
Fig.9 Geometric sectional diagram of the armature rail
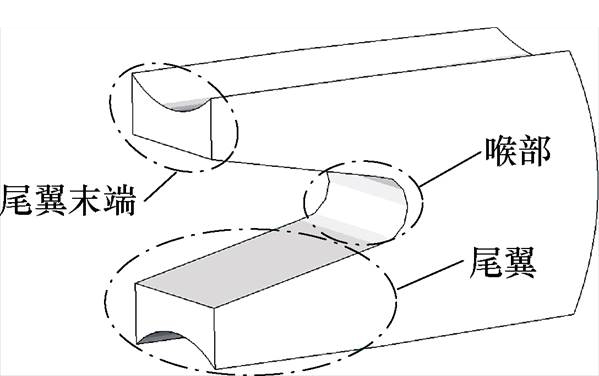
图10 电枢部位示意图
Fig.10 Schematic diagram of armature parts
按照实测速度对应的位移将轨道分段，根据式（20）对各段接触面摩擦特性进行模拟。电枢运动特性与其电流密度和磁场分布密切相关，经计算可得动态摩擦因数（Dynamic Friction Coefficient, DFC）和摩擦因数为固定值（Fixed Friction Coefficient, FFC）0.24情况下电枢速度为370 m/s时对应电枢电流密度和磁通密度分布分别如图11、图12所示。
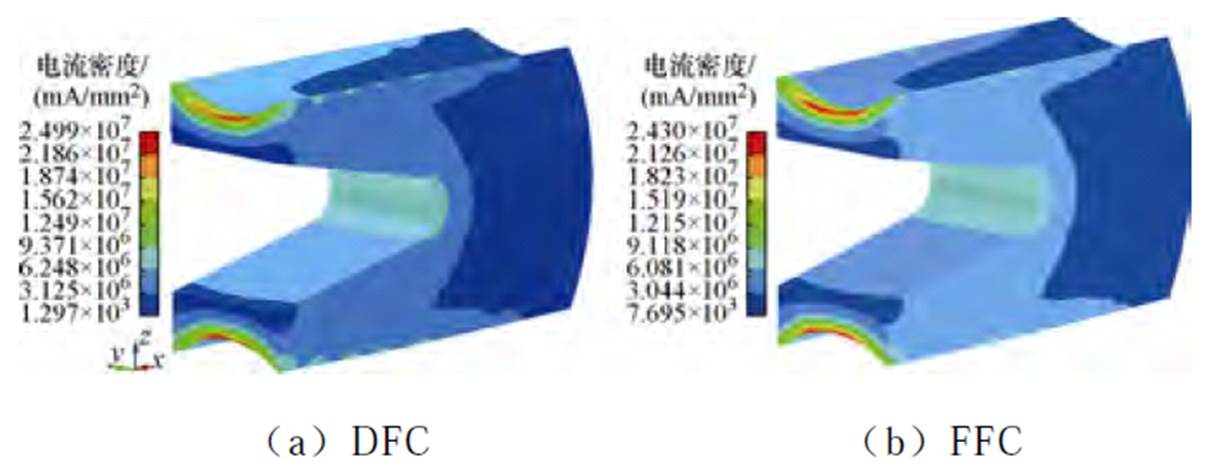
图11 电流密度分布
Fig.11 Distribution of current density
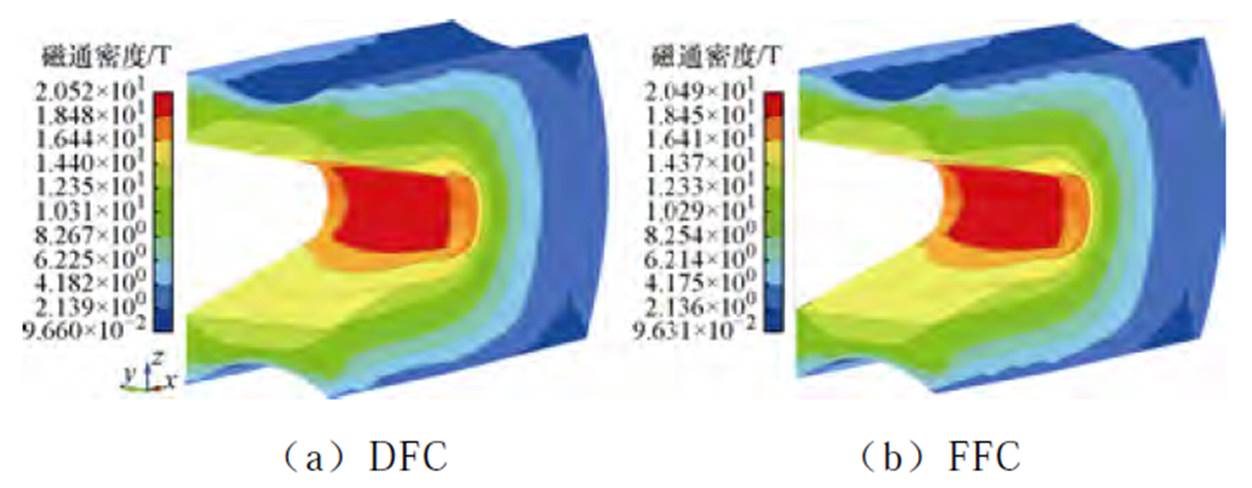
图12 磁通密度分布
Fig.12 Distribution of magnetic field strength
根据图11、图12可知，电流密度和磁通密度在电枢喉部和尾翼两端处分布较为集中，在尾翼末端处电流密度最大为2.50×1010 A/m2，在喉部位置的磁通密度最大为20.52 T，电流密度与磁通密度DFC情况下要比FFC时大，这主要是因为在电枢运动前期，摩擦因数前期的动态变化过程使得电枢受到的摩擦力较大，需要更高的电流密度和磁感应强度来产生足够的洛伦兹力以克服摩擦，使电枢加速到与FFC时相同的速度。
电枢温度是影响其运动特性的关键因素，电枢在速度为370 m/s和1 120 m/s时的温度分布分别如图13、图14所示。
电枢温度主要由电阻焦耳热和摩擦热引起，根据图13、图14可知，电枢温度在速度较低时主要集中在电枢尾翼末端和喉部位置，这是因为在电枢运动初期电流迅速增大，焦耳热分布受电流密度分布影响而迅速增大，随着电枢速度的增大，摩擦热也逐渐增大致使枢轨接触面处的温度分布越来越集中。电枢速度在1 120 m/s时的温度最高可达2 643℃，且比FFC时要高，这主要是因为电阻焦耳热和摩擦热的生成是一个累积过程，摩擦因数的动态变化使得枢轨接触面处的摩擦热比FFC时高，而且由于电流密度和磁通密度较FFC时大使得焦耳热也较高，因此随着电枢速度的增大，两种情况下的温度差逐渐增大。为了更直观地看出考虑动态摩擦因数对电枢温度的影响，对枢轨接触面上的摩擦能密度分布和温度较为集中的电枢上的A、B、C三个采集点的温度随时间的变化曲线做进一步分析，三点位置如图14b所示。图15为摩擦能密度分布，图16为各采集点的温度随时间的变化曲线。
图13 电枢速度为370 m/s时的温度分布
Fig.13 The temperature distribution at armature velocity of 370 m/s
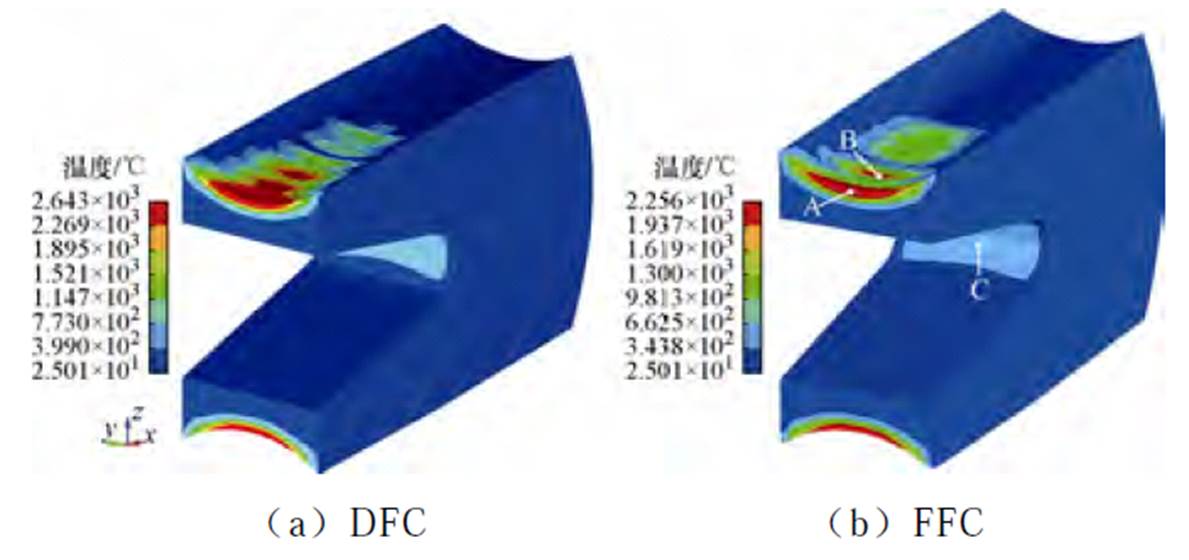
图14 电枢速度为1 120 m/s时的温度分布
Fig.14 The temperature distribution at armature velocity of 1 120 m/s
根据图15可知，摩擦引起的能量密度受接触压力影响主要集中在电枢两翼靠近尾翼的位置，且电枢速度较低时DFC与FFC两种情况下的差异已经很明显了。
从图16可知，枢轨接触面上A、B点的温度先迅速增大后减小，产生这一现象的主要原因是枢轨间摩擦热受接触压力、动态摩擦因数及电枢运动速度影响。在电枢运动初期，激励电流迅速增大使电枢焦耳热引起的温度迅速升高，同时电枢尾翼受到的洛伦兹力也迅速增大，导致枢轨间接触压力增大，进而滑动摩擦引起的温度也迅速升高。在电枢运动后期，激励电流减小，枢轨间接触压力逐渐减小，虽然电枢速度增大但相较于接触压力的变化却较小，因此从整体看接触面上焦耳热和摩擦热导致的温升都逐渐减小。摩擦因数的动态变化对枢轨接触面上采集点的温度影响较大，在0.75 ms时DFC与FFC两种情况下A点温差可达522℃。电枢喉部的C点温度主要受焦耳热影响，受摩擦热影响较小，使得两种情况下该点的温差较小。
图15 电枢速度为370 m/s时的摩擦能密度分布
Fig.15 The friction energy density distribution at armature velocity of 370 m/s
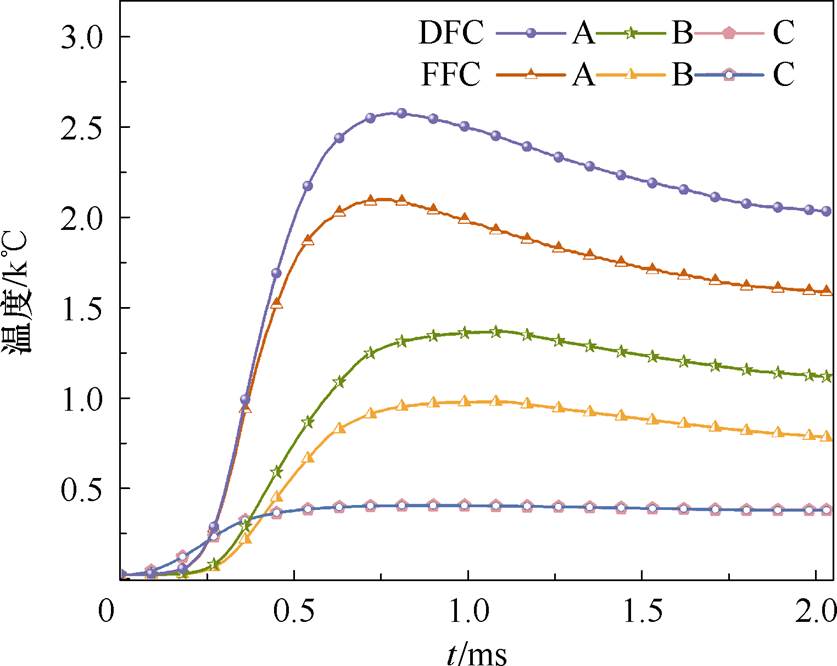
图16 各采集点的温度随时间的变化曲线
Fig.16 The temperature curves of the collection point with time
为了验证理论分析的正确性，搭建直线推进电磁能装备的实验平台（与1.1节电枢速度测试为同一次实验）如图17所示。
根据第3节的模型计算可得DFC与FFC时电枢的运动速度，与电枢实测速度进行对比，结果如图18所示。同时利用高斯计测得下轨道中内轨中间预留孔位置x方向的磁感应强度曲线并与DFC、FFC时模型计算结果进行对比，如图19所示。
图17 直线推进电磁能装备的实验平台
Fig.17 The experimental platform for linear propulsion electromagnetic energy equipment
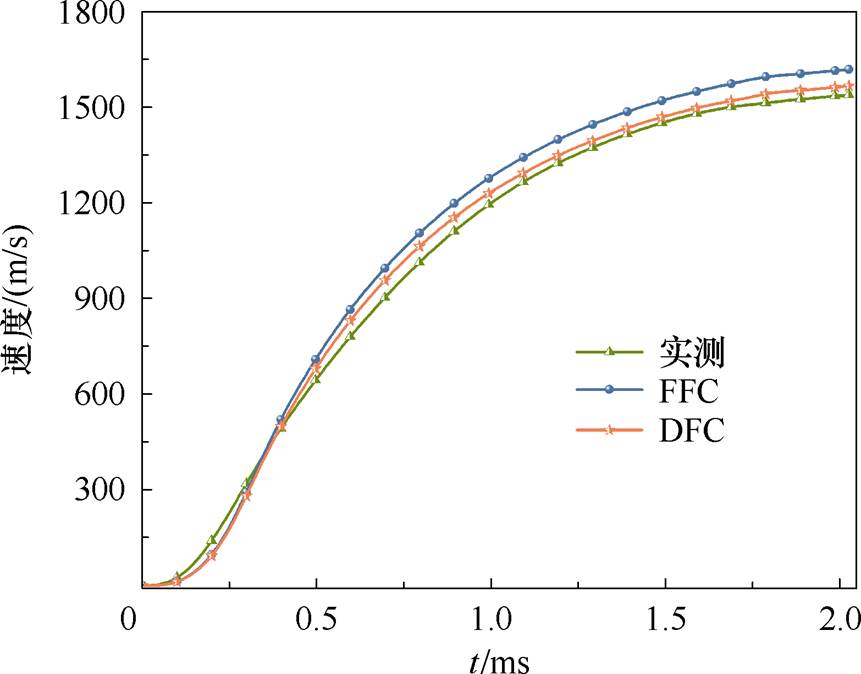
图18 电枢速度曲线
Fig.18 The curves of armature velocity
图19 轨道上采集点的磁感应强度曲线
Fig.19 The magnetic field strength curves at collection points on the rail
由图18可知，DFC时电枢的速度曲线比FFC时与实测速度曲线的拟合程度更高，考虑固定摩擦系数和动态摩擦因数时的出口速度计算值分别为1 635 m/s和1 567 m/s，相较于1 539 m/s的实测值误差分别为96 m/s和28 m/s，这说明考虑动态摩擦因数的有限元模型计算精度大大提高。由图19可以看出，采集点处磁感应强度曲线与理论计算结果整体波形趋势基本一致，且DFC时与实测结果更接近，这也验证了理论分析的正确性。根据反演计算得到的动态摩擦因数修正后的有限元模型可以更好地预测直线推进电磁能装备的运动特性。
实测磁感应强度幅值小于理论计算值，这主要是因为实际的电枢运动环境要复杂的多，仿真中未考虑枢轨材料磁特性受极端条件的影响，同时高斯计探头并不能完全地深入轨道内部，只能紧贴于轨道外侧面，这也会对实验测试结果造成一定误差。
为提高轨道式直线推进电磁能装备运动特性的数值计算精度，本文提出了基于动态摩擦因数反演的运动特性研究方法，得出以下结论：
1）反演得到的枢轨间摩擦因数随着电枢速度的增大从0.63开始迅速下降，0.3 ms后下降趋势减缓，最终趋向稳定值0.24。
2）同一速度下，考虑摩擦因数动态变化与固定摩擦因数时的计算相比，电枢电流密度、磁通密度和温度均有增大，其中对枢轨接触面温度影响更大，特别是在0.75 ms时，A点温差可达522℃。
3）考虑固定摩擦因数和动态摩擦因数时的出口速度计算值分别为1 635 m/s和1 567 m/s，相较于1 539 m/s的实测值误差分别为96 m/s和28 m/s。实测的磁感应强度曲线与考虑动态摩擦因数时的计算结果也更接近。
参考文献
[1] 马伟明. 关于电工学科前沿技术发展的若干思考[J]. 电工技术学报, 2021, 36(22): 4627-4636.
Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.
[2] 李兵, 李卫超, 荆从凯. 电磁发射系统研究现状及应用展望[J]. 兵器装备工程学报, 2023, 44(10): 173-181.
Li Bing, Li Weichao, Jing Congkai. Research status and application prospects of electromagnetic launch system[J]. Journal of Ordnance Equipment Engin- eering, 2023, 44(10): 173-181.
[3] 杜佩佩, 鲁军勇, 冯军红, 等. 电磁轨道发射器电磁结构耦合动态发射过程数值模拟[J]. 电工技术学报, 2020, 35(18): 3802-3810.
Du Peipei, Lu Junyong, Feng Junhong, et al. Numerical simulation of dynamic launching process of electromagnetic rail launcher with electromagnetic and structural coupling[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3802-3810.
[4] 马伟明, 鲁军勇. 电磁发射技术的研究现状与挑战[J]. 电工技术学报, 2023, 38(15): 3943-3959.
Ma Weiming, Lu Junyong. Research progress and challenges of electromagnetic launch technology[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 3943-3959.
[5] 高博, 邱群先, 郄文静, 等. 电磁轨道炮电枢多场耦合分析与试验研究[J]. 电工技术学报, 2020, 35(增刊2): 341-345.
Gao Bo, Qiu Qunxian, Qie Wenjing, et al. Multi-field coupling analysis and experimental research on armature of electromagnetic railgun[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 341-345.
[6] Liu Shaowei, Du Xiangyu, Guan Jiao, et al. Research on transient contact characteristics of the hyperbolic rail augmented quadrupole launcher[J]. IEEE Transa- ctions on Plasma Science, 2022, 50(10): 3794-3801.
[7] Lin Y, Li J Z, Pan J, et al. Current-carrying wear behavior and the interface evolution of the Cu/Al tribological pair[J]. Engineering Failure Analysis, 2023, 153: 107549.
[8] Brown L, Xu D, Ravi-Chandar K, et al. Coefficient of friction measurement in the presence of high current density[J]. IEEE Transactions on Magnetics, 2007, 43(1): 334-337.
[9] Dai Keren, Yang Yuxin, Yin Qiang, et al. Theoretical model and analysis on the locally concentrated current and heat during electromagnetic propulsion[J]. IEEE Access, 2019, 7: 164856-164866.
[10] 范薇, 苏子舟, 张涛, 等. 增强型电磁轨道炮瞬态温升时空分布[J]. 高电压技术, 2021, 47(9): 3346-3354.
Fan Wei, Su Zizhou, Zhang Tao, et al. Spatial- temporal distribution of transient temperature rise in augmented electromagnetic railgun[J]. High Voltage Engineering, 2021, 47(9): 3346-3354.
[11] Zhou Pengfei, Li Baoming. Exergy analysis of the electromagnetic railgun[J]. IEEE Transactions on Plasma Science, 2021, 49(12): 3980-3987.
[12] Li Shizhong, Li Jun, Xia Shengguo, et al. Phase division and critical point definition of electro- magnetic railgun sliding contact state[J]. IEEE Transa- ctions on Plasma Science, 2019, 47(5): 2399-2403.
[13] Cao Bin, Ge Xia, Guo Wei, et al. Analysis of rail dynamic deformation during electromagnetic launch[J]. IEEE Transactions on Plasma Science, 2017, 45(7): 1269-1273.
[14] 李婕, 杨淑英, 谢震, 等. 基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识[J]. 电工技术学报, 2022, 37(18): 4604-4613.
Li Jie, Yang Shuying, Xie Zhen, et al. Online parameter identification of permanent magnet synchronous motor based on fast particle swarm optimization algorithm with effective information iterated[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4604-4613.
[15] 周嗣理, 李国丽, 王群京, 等. 基于改进粒子群优化算法的永磁球形电机驱动策略研究[J]. 电工技术学报, 2023, 38(1): 166-176, 189.
Zhou Sili, Li Guoli, Wang Qunjing, et al. Improved particle swarm optimization algorithm based driving strategy research for permanent magnet spherical motor[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 166-176, 189.
Abstract In the working process of linear propulsion electromagnetic energy equipment, friction between the armature and rail due to high-speed sliding is one of the important factors affecting its motion characteristics. However, realizing real-time and in-situ friction coefficient measurement is challenging under extreme electromagnetic, thermal, and mechanical shock conditions. Therefore, the friction coefficient between the armature and rails is fixed as the empirical value in the current research. The actual motion characteristics of the armature fail to be accurately captured because the potential impact of its dynamic changes on the performance of the system is ignored. This paper proposes a method based on the dynamic friction coefficient inversion of motion characteristics.
Firstly, a nonlinear mapping relationship between the armature velocity with the armature-rail friction coefficient and the rail inductance gradient during the armature motion is deduced from the observable data measured by the electromagnetic propulsion experiment and the armature kinetics forward model. Then, the inversion model for the armature-rail friction coefficient and rail inductance gradient is established using the improved dynamic particle swarm optimization (DPSO). The computational velocity is corrected in real-time by the measured velocity of the armature to obtain the spatiotemporal characteristics. The friction coefficient between the armature and rails starts to decrease rapidly with increasing armature velocity, then the decreasing trend slows down and finally tends to a stable value.
Then, the model for transient electromagnetic, thermal, and mechanical coupling is established. Motion characteristics of the equipment are analyzed when the friction coefficient is dynamic (DFC) and constant (FFC). Herein, the friction coefficient between the armature and rails is segmented according to velocity, and the parameters of each velocity segment are determined using the nonlinear least squares fitting method. The results show that the dynamic change of the friction coefficient increases the armature current density, magnetic density, and temperature at the same velocity, which greatly affects the temperature of the armature-rail contact surface. A high current density and magnetic induction are necessary to produce enough Lorentz force to overcome the increased friction caused by the dynamic changes in the friction coefficient. Therefore, the simultaneous increase of friction heat and resistance heat causes the temperature difference on the contact surface of the armature rail to increase gradually under DFC and FFC conditions. The temperature difference reaches 522℃ at 0.75 ms.
Finally, an experimental platform for the linear propulsion electromagnetic energy equipment is built to measure the armature velocity and the magnetic induction strength at the rail. Considering the dynamic friction coefficient, the armature velocity and the magnetic induction intensity are close to the measured values, and the calculation accuracy of the model is high, verifying the correctness of the theoretical analysis.
keywords：Linear propulsion electromagnetic energy equipment, dynamic friction coefficient, parameter inversion, dynamic particle swarm optimization, motion characteristics
中图分类号：TM359.4
DOI: 10.19595/j.cnki.1000-6753.tces.240277
国家自然科学基金重大研究计划重点项目（92066206）和河北省省级科技计划项目（225676163GH）资助。
收稿日期2024-02-19
改稿日期2024-03-11
赵文月 女，1991年生，博士研究生，研究方向为工程电磁场与磁技术。E-mail: 1205887741@qq.com
闫荣格 女，1969年生，教授，博士生导师，研究方向为工程电磁场与磁技术。E-mail: yanrg@hebut.edu.cn（通信作者）
（编辑 崔文静）