
图1 FOMe原理示意图
Fig.1 Schematic diagram of FOMe
摘要 随着电池循环充放电,电极颗粒膨胀收缩会导致电极颗粒表面出现裂纹甚至导致电极颗粒破裂,进一步引发电极活性材料损失和锂离子损失,加剧锂离子电池老化。为准确地表征和预测电极颗粒应变及裂纹生长过程,该文提出一种考虑电化学扩散和材料形变的锂离子电池电极颗粒裂纹生长模型。该模型根据锂离子在电极颗粒中的扩散过程计算电极颗粒固相扩散诱导应力,并根据电极颗粒所受应力预测电极颗粒裂纹生长速度。最终,所提模型实现了颗粒裂纹生长与锂离子扩散的双向耦合。实验和仿真结果表明,所提模型能准确地预测电极颗粒所受应力、颗粒裂纹生长趋势和电极活性材料损失。
关键词:锂离子电池 裂纹生长 活性材料损失 电化学模型 应力
为应对全球变暖,减少化石能源的使用,锂离子电池由于其能量密度高、循环寿命长、自放电率低等优点被广泛应用于智能终端设备、电动汽车以及大型储能设备中[1]。随着锂离子电池循环充放电,锂离子电池不断老化,其主要特征表现在:电池充放电容量下降,内阻增加[2-3];老化电池不仅充放电性能大幅下降,还可能引发热失控[4],危及人民生命财产安全。因此,锂离子电池老化状态估计对保障电池安全运行,最大化电池使用寿命具有重要意义[5-6]。虽然锂离子电池老化的外在表现特征相同,但其内部老化机理复杂,各个电池内部的老化路径差异巨大[7-8]。
电极活性材料损失是导致电池老化的主要原因之一[9],电极颗粒破裂又是导致电极活性材料损失的主要原因。锂离子电池在循环充放电过程中,由于锂离子在电极颗粒中的扩散效应,锂离子浓度在电极颗粒中分布不均匀,电极颗粒会受到固相扩散诱导应力[10],从而导致电极颗粒产生裂纹,并不断生长。电极颗粒裂纹生长不仅会使得电极颗粒内部活性材料直接暴露在电解液中与电解液发生副反应,生成新的固体电解质界面(Solid Electrolyte Interphase, SEI)膜[11],导致电池中活性锂离子损失和电解液损失,还可能会诱发电极颗粒破裂,导致电极中导电剂、粘结剂失效,电极活性材料损失[12-13]。因此,分析电极颗粒应力变化及裂纹生长对探究锂离子电池内部老化机理,研究电池老化路径具有重要意义[14]。
近年来,已有许多学者针对由于应力引起的电极颗粒活性材料失效原理进行了研究。Li Xuemin等[15]通过观测电极颗粒形态,分析电极颗粒元素,发现负极颗粒裂纹生长会导致SEI膜增厚,负极颗粒之间接触面积减小;正极颗粒裂纹生长会导致正极活性材料损失,正极颗粒之间接触面积减小,阻抗增大。Ai Weilong等[16]根据基于耦合扩散机理的伪二维(Pseudo 2-Dimensional, P2D)模型研究了电极颗粒中的应力变化,结果表明,应力大小由锂离子浓度梯度决定。在高倍率充放电时,电极-隔膜界面处产生了很大的应力,导致隔膜附近电极颗粒破裂,局部电极活性材料损失。M. Klinsmann等[17-18]利用断裂相场法,根据锂离子在电极颗粒中嵌入/脱出的物理机理建立电极颗粒裂纹生长模型,所提模型能同时预测电极颗粒中锂离子浓度和裂纹的演变,而不受裂纹路径的几何形状、尺寸等预设限制的影响。然而,现有的电极颗粒裂纹生长模型均较为复杂,耦合参数过多,难以应用在实时电池管理系统中。
为准确预测电极颗粒内部状态,分析由固相扩散诱导应力引起的电极颗粒老化机理,本文提出一种基于简化电化学模型的电极颗粒裂纹生长模型。该模型首先根据考虑液相极化的分数阶模型(Fractional-Order Model with electrolyte, FOMe)计算电极颗粒内部锂离子浓度分布,再根据电极颗粒内部锂离子浓度分布得到电极颗粒所受应力。最终,结合电极颗粒材料特性完成电极颗粒裂纹生长的仿真预测。
FOMe是基于单颗粒(Single Particle, SP)模型的锂离子电池简化电化学模型。该模型假设电流在电极中均匀分布,并且将整个电极视为一个电极颗粒。FOMe原理示意图如图1所示。为简化锂离子在固液相中扩散的计算过程,FOMe利用分数阶Padé近似方法简化锂离子在固相中的扩散,利用二状态系统简化锂离子在液相中的扩散。

图1 FOMe原理示意图
Fig.1 Schematic diagram of FOMe
定义放电电流为负,充电电流为正,则流入电极颗粒的电流为正,流出电极颗粒的电流为负。根据菲克第二定律及其边界条件,去极点后的电极颗粒表面锂离子浓度变化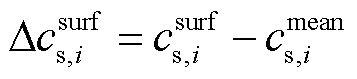 与电流
与电流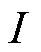 之间的关系可表示为
之间的关系可表示为
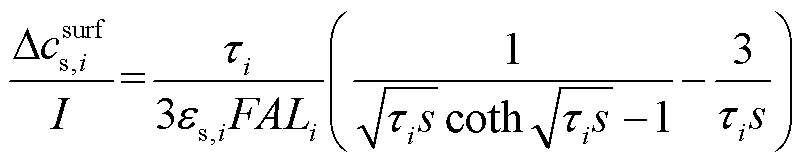 (1)
(1)
式中,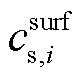 和
和 分别为电极颗粒表面锂离子浓度和平均锂离子浓度,
分别为电极颗粒表面锂离子浓度和平均锂离子浓度,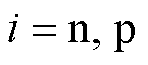 分别代表正、负电极;
分别代表正、负电极;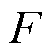 为法拉第常数;
为法拉第常数;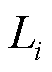 为电极厚度;
为电极厚度;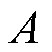 为电极表面积;
为电极表面积;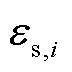 为固相体积分数;
为固相体积分数;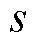 为微分算子;
为微分算子;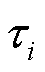 为固相扩散时间常数,其被定义为
为固相扩散时间常数,其被定义为
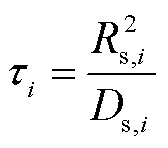 (2)
(2)
式中,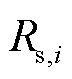 为电极颗粒粒子半径;
为电极颗粒粒子半径;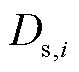 为电极固相扩散系数。
为电极固相扩散系数。
由于式(1)是一个超越函数,精确求解去极点后的电极颗粒表面锂离子浓度计算十分复杂。分数阶Padé近似方法是一种利用有理多项式近似方法,其常被用于简化复杂系统和求解分数阶方程[19]。利用分数阶Padé近似方法简化式(1)可得
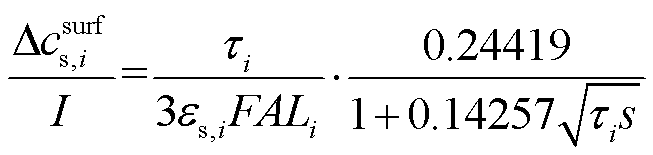 (3)
(3)
根据式(3),电极颗粒表面锂离子浓度可由式(4)计算获得。
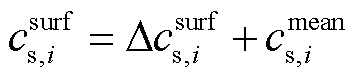 (4)
(4)
由此可得电池电动势UE为
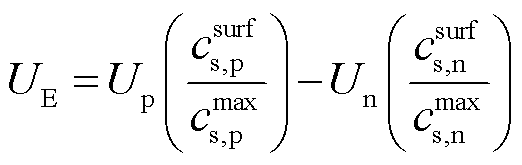 (5)
(5)
式中,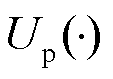 、
、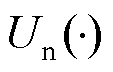 分别为正、负极平衡电位,其值与电极颗粒表面锂离子浓度相关;
分别为正、负极平衡电位,其值与电极颗粒表面锂离子浓度相关;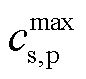 、
、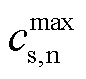 分别为正、负极活性材料最大锂离子浓度。
分别为正、负极活性材料最大锂离子浓度。
锂离子电池液相极化过电势是由于液相锂离子浓度分布不均导致的,为简化锂离子在液相扩散的计算过程,本文提出二状态方程液相近似方法。
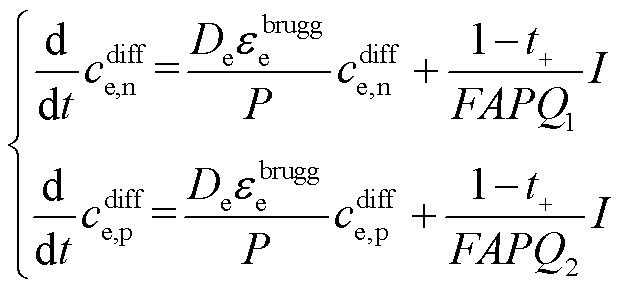 (6)
(6)
式中,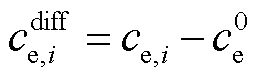 ,即
,即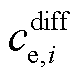 为靠近集电极处液相锂离子浓度
为靠近集电极处液相锂离子浓度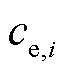 与液相初始锂离子浓度
与液相初始锂离子浓度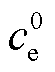 之差;
之差;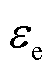 为液相体积分数;
为液相体积分数;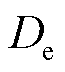 为液相扩散系数;上标brugg为Bruggman系数;
为液相扩散系数;上标brugg为Bruggman系数;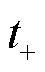 为液相锂离子迁移数;P、Q1、Q2可由式(7)计算获得。
为液相锂离子迁移数;P、Q1、Q2可由式(7)计算获得。
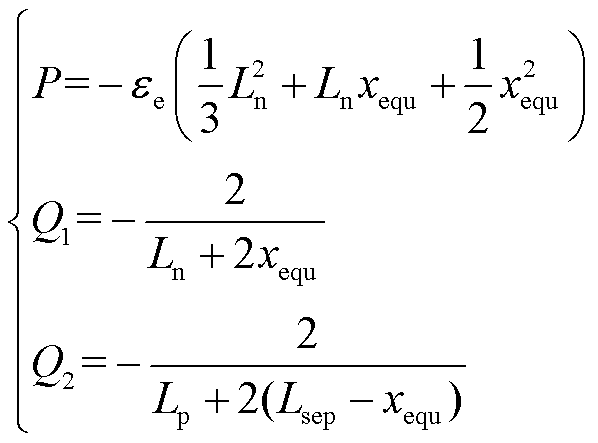 (7)
(7)
式中,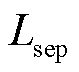 为隔膜厚度;xequ表达式为
为隔膜厚度;xequ表达式为
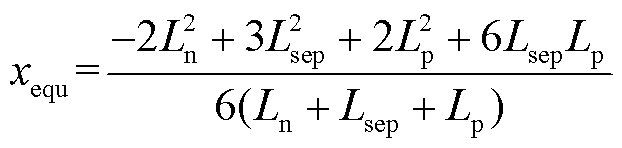 (8)
(8)
靠近集电极处的液相锂离子浓度直接影响电池液相极化过电势的大小,电池液相极化过电势为
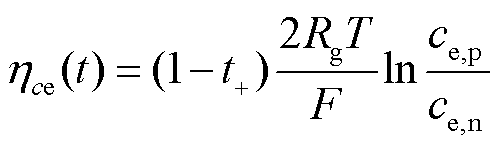 (9)
(9)
式中,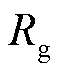 为理想气体常数;
为理想气体常数;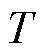 为电池温度。
为电池温度。
最终,锂离子电池端电压可由电池电动势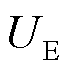 、液相极化过电势
、液相极化过电势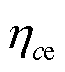 和欧姆极化过电势
和欧姆极化过电势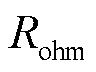 I计算获得,即
I计算获得,即
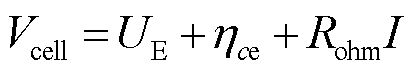 (10)
(10)
式中,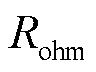 为电池欧姆内阻。
为电池欧姆内阻。
电极颗粒在脱锂/嵌锂过程中,电极颗粒体积不断发生变化,其体积变化大小与电极颗粒平均嵌锂量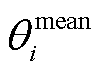 有关[20]。因此,将电极颗粒半径膨胀比
有关[20]。因此,将电极颗粒半径膨胀比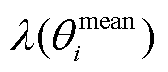 定义为
定义为
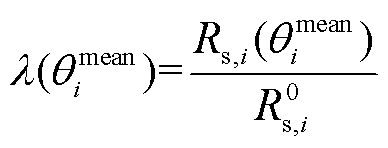 (11)
(11)
式中,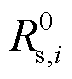 和
和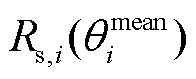 分别为电极颗粒在零嵌锂量状态下和
分别为电极颗粒在零嵌锂量状态下和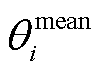 嵌锂量状态下的粒子半径。电极颗粒平均嵌锂量
嵌锂量状态下的粒子半径。电极颗粒平均嵌锂量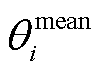 表达式为
表达式为
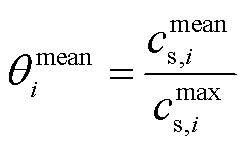 (12)
(12)
在电极颗粒物质的量不变的情况下,电极颗粒所能容纳的锂离子总量不变。随着电极颗粒膨胀收缩,电极颗粒的体积在变化,其理论最大锂离子浓度也在变化[21]。电极颗粒理论最大锂离子浓度随嵌锂量的变化可通过式(13)计算获得。
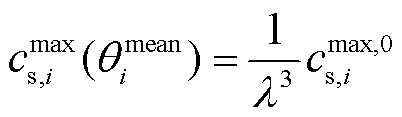 (13)
(13)
式中,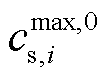 和
和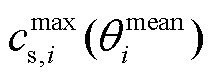 分别为电极颗粒在零嵌锂量状态下和
分别为电极颗粒在零嵌锂量状态下和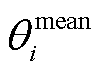 嵌锂量状态下的理论最大锂离子浓度。
嵌锂量状态下的理论最大锂离子浓度。
锂离子电池在循环充放电过程中,由于锂离子在电极颗粒中的扩散效应,导致锂离子浓度在电极颗粒中分布不均匀,从而导致电极颗粒内部应力分布不均匀[22]。假设电极颗粒为膨胀/收缩各向同性的线弹性球体,则在球坐标系中表示半径为R的球形粒子内由固相扩散引起的应力应变关系的径向和切向分量分见式(14)和式(15),在球坐标系中表示的电极球形颗粒示意图如图2所示。
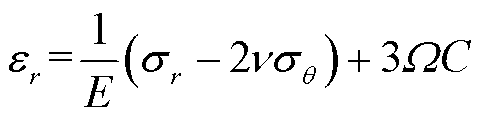 (14)
(14)
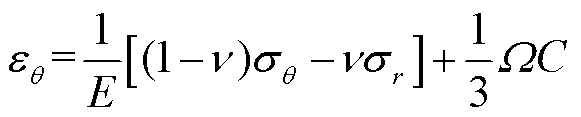 (15)
(15)
式中,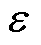 和
和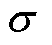 分别为电极颗粒应变和应力;
分别为电极颗粒应变和应力;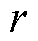 为球坐标系下的半径;
为球坐标系下的半径;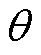 为球面上任一点与xOy平面开域的夹角;
为球面上任一点与xOy平面开域的夹角;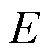 为杨氏模量;
为杨氏模量;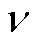 为泊松比;C为摩尔浓度;W为溶液偏摩尔体积。
为泊松比;C为摩尔浓度;W为溶液偏摩尔体积。
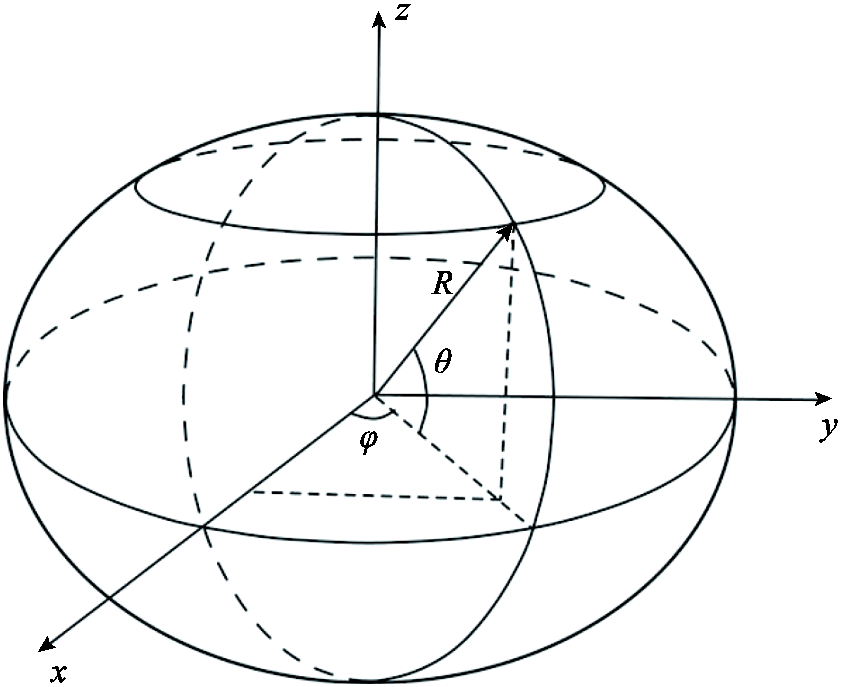
图2 球形电极颗粒示意图
Fig.2 Schematic diagram of spherical paritcles
由于球体的对称性,径向应变和切向应变的微分方程可表示为
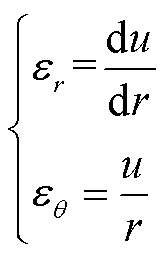 (16)
(16)
式中,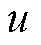 为径向位移。由于锂离子在电极颗粒中扩散的速度比电极颗粒的弹性形变速度慢得多,电极颗粒中建立力学平衡的速度比建立物质平衡的速度快得多,因此,电极颗粒中的力学平衡问题被视为静态平衡问题。在没有额外力的作用下,文献[23]给出了球体的静态力学平衡方程,即
为径向位移。由于锂离子在电极颗粒中扩散的速度比电极颗粒的弹性形变速度慢得多,电极颗粒中建立力学平衡的速度比建立物质平衡的速度快得多,因此,电极颗粒中的力学平衡问题被视为静态平衡问题。在没有额外力的作用下,文献[23]给出了球体的静态力学平衡方程,即
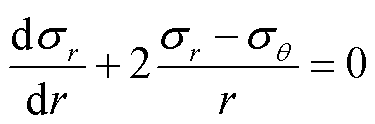 (17)
(17)
结合球形颗粒的边界条件,球体外表面径向应力为0,即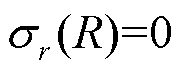 ,径向值边界r=0,球体的径向应力和切向应力可解得
,径向值边界r=0,球体的径向应力和切向应力可解得
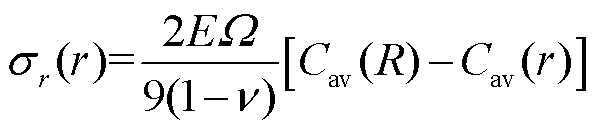 (18)
(18)
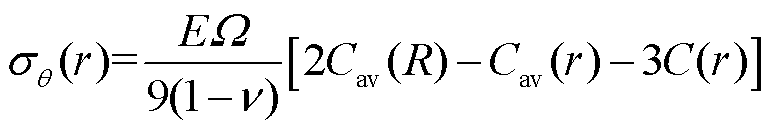 (19)
(19)
式中,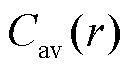 是半径为R的电极颗粒内的半径为r的球形体积中的平均锂离子浓度,
是半径为R的电极颗粒内的半径为r的球形体积中的平均锂离子浓度,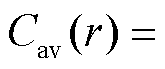
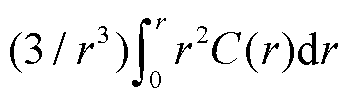 。由于在电极颗粒中心锂离子浓度变化为0,即
。由于在电极颗粒中心锂离子浓度变化为0,即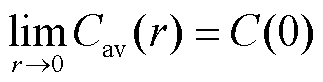 ,电极颗粒中心的压力为纯静水压力[24],即
,电极颗粒中心的压力为纯静水压力[24],即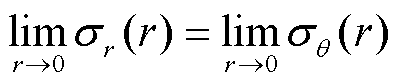 。又由于
。又由于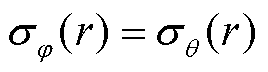 ,电极颗粒所受平均应力可被定义为
,电极颗粒所受平均应力可被定义为
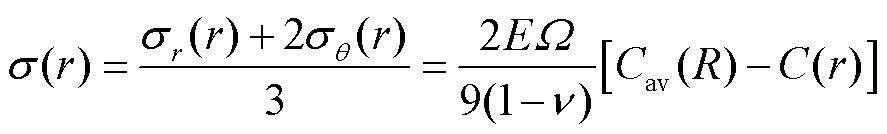 (20)
(20)
锂离子电池在循环充放电过程中,锂离子在电极颗粒中嵌入/脱出会导致电极颗粒体积发生变化。电极颗粒体积变化会影响电极固相扩散弛豫时间,也会影响电极电化学反应速度,从而影响固相锂离子浓度分布和电极颗粒应力变化,最终影响电池的充放电性能。本文提出考虑电极颗粒应力影响的FOMe(FOMe considering Stress, FOMeS)。当输入电流给FOMe时,FOMe能计算出电极颗粒的平均嵌锂量,根据电极平均嵌锂量可计算出当前电极颗粒膨胀比,从而获得当前电极颗粒粒子半径。由于当前时刻存储在电极颗粒中的锂离子数量不变,电极颗粒体积变化会导致电极颗粒中锂离子浓度变化。电极颗粒粒子半径和锂离子浓度的改变同时影响电极颗粒中锂离子浓度的分布,进而影响电极颗粒内部应力变化。以镍钴铝酸锂电池为例,其正极材料为镍钴铝酸(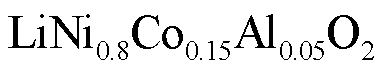 , NCA),负极材料为石墨。假设该电池正极颗粒半径膨胀比为1.05,负极颗粒半径膨胀比为1.1。满电状态下的NCA电池,以1C(2.8 A)电流恒流放电3 600 s,则考虑应力变化的FOMe与不考虑应力变化的FOMe仿真获得的正极和负极固相表面锂浓度差如图3所示。
, NCA),负极材料为石墨。假设该电池正极颗粒半径膨胀比为1.05,负极颗粒半径膨胀比为1.1。满电状态下的NCA电池,以1C(2.8 A)电流恒流放电3 600 s,则考虑应力变化的FOMe与不考虑应力变化的FOMe仿真获得的正极和负极固相表面锂浓度差如图3所示。
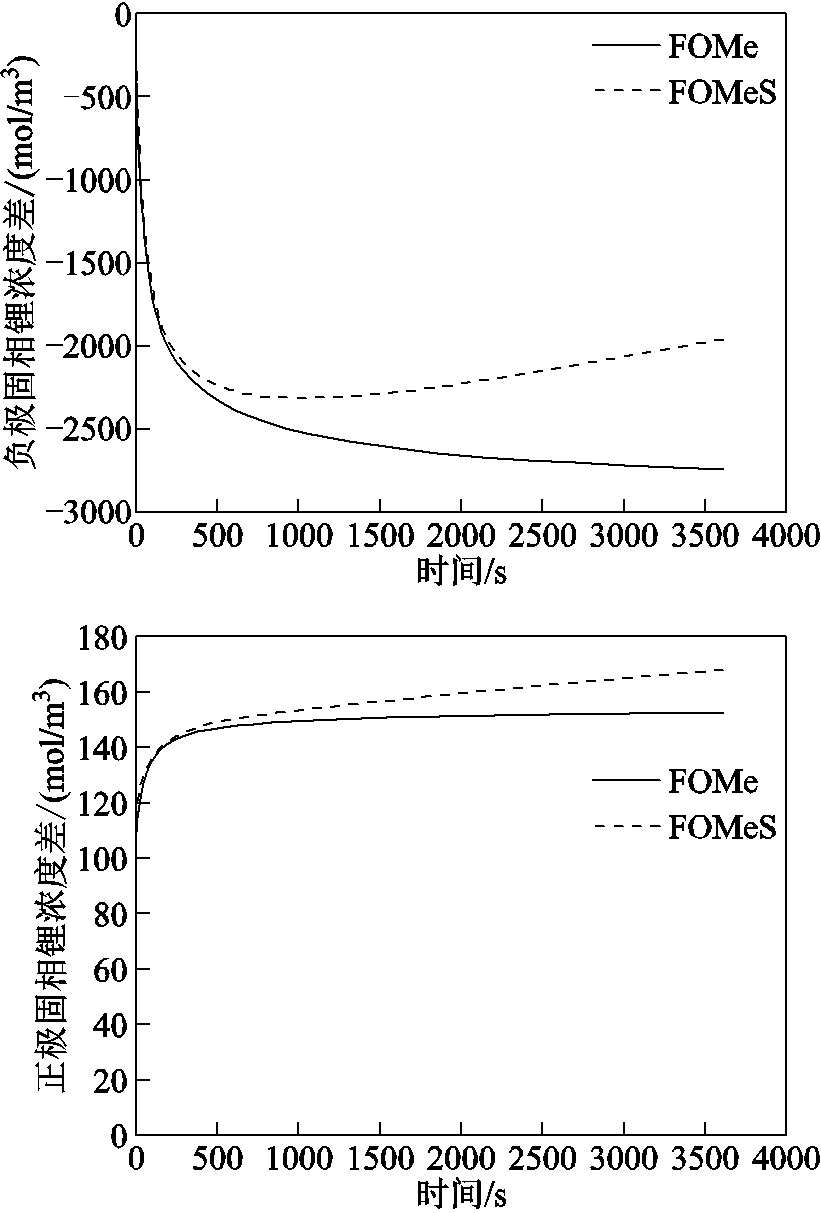
图3 正极和负极固相表面锂浓度差
Fig.3 The lithium ion concentration difference on the surface of electrode particles
在恒流放电过程中,负极颗粒表面锂浓度差不断减小。恒流放电负极颗粒平均嵌锂量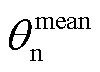 不断减小,负极颗粒体积不断缩小,导致在低嵌锂量区间的负极固相扩散时间常数比在高嵌锂量区间的负极固相扩散时间常数更小。因此,在负极低嵌锂量区间时,FOMeS的负极固相表面锂浓度差幅值比FOMe的负极固相表面锂浓度差幅值更小。在恒流放电过程中,正极颗粒表面锂浓度差不断增大。恒流放电正极颗粒平均嵌锂量
不断减小,负极颗粒体积不断缩小,导致在低嵌锂量区间的负极固相扩散时间常数比在高嵌锂量区间的负极固相扩散时间常数更小。因此,在负极低嵌锂量区间时,FOMeS的负极固相表面锂浓度差幅值比FOMe的负极固相表面锂浓度差幅值更小。在恒流放电过程中,正极颗粒表面锂浓度差不断增大。恒流放电正极颗粒平均嵌锂量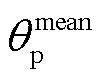 不断增加,电极颗粒体积也不断膨胀,从而导致正极固相扩散时间常数不断增加。因此,在正极高嵌锂区间时,FOMeS的正极固相表面锂浓度差比FOMe的正极固相表面锂浓度差更大。由于负极颗粒的粒子半径更大,且负极固相扩散系数更小,在恒流放电过程中,负极固相表面锂浓度差的幅值比正极更大。
不断增加,电极颗粒体积也不断膨胀,从而导致正极固相扩散时间常数不断增加。因此,在正极高嵌锂区间时,FOMeS的正极固相表面锂浓度差比FOMe的正极固相表面锂浓度差更大。由于负极颗粒的粒子半径更大,且负极固相扩散系数更小,在恒流放电过程中,负极固相表面锂浓度差的幅值比正极更大。
为简化电极颗粒应力生长模型,使得模型可分析计算,本文所提电极颗粒裂纹生长模型仅考虑由固相扩散诱导应力引起的电极颗粒裂纹生长,暂不考虑由电极颗粒相互挤压等其他外力引起的电极颗粒裂纹生长。锂离子电池电极颗粒裂纹生长是多物理场相互耦合作用的结果,其中包括物质迁移场、机械应力场、机械应变场[25]。当给电池施加电流时,锂离子从电极颗粒表面嵌入/脱出,由于扩散作用造成电极颗粒内部锂离子分布不均,使得电极颗粒受到固相扩散诱导应力,应力值大小可由FOMeS计算得出。根据FOMeS计算得到的固相扩散诱导应力值的大小,结合电极颗粒材料属性,计算获得电极颗粒裂纹生长速度并仿真电极颗粒裂纹生长形状。电极颗粒裂纹生长模型基本原理如图4所示。
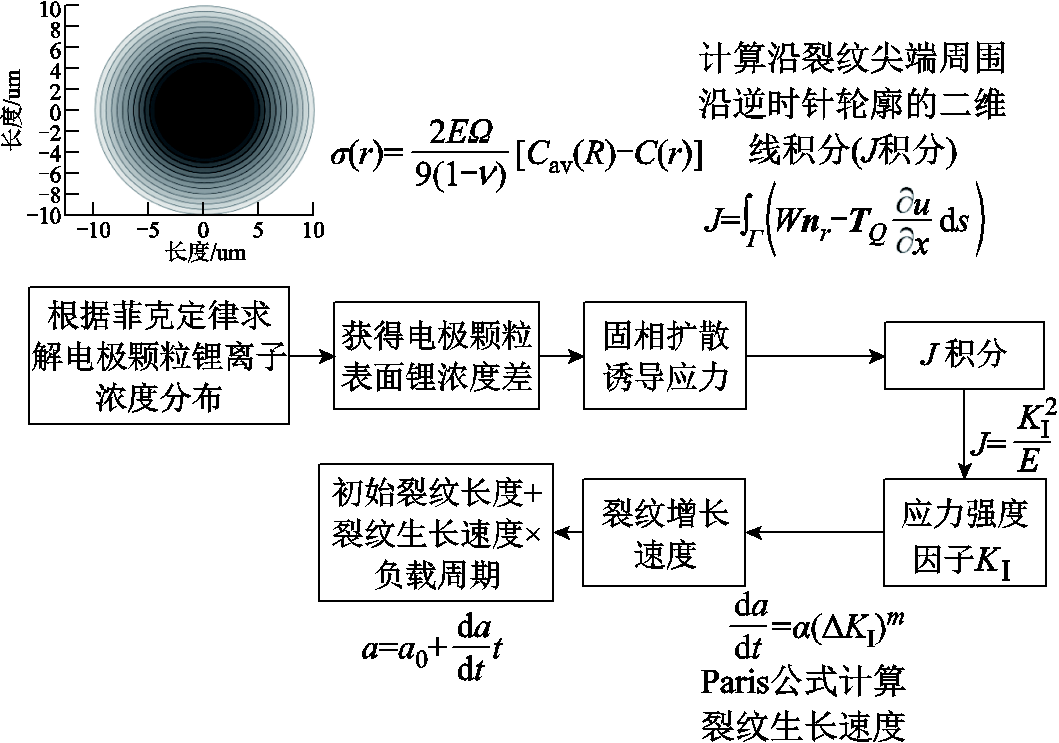
图4 电极颗粒裂纹生长模型基本原理
Fig.4 Schematic diagram of the electrode particle crack growth model
当给电池施加电流时,锂离子嵌入/脱出电极颗粒表面,造成电极颗粒内部锂离子分布不均,电极颗粒表面锂浓度差可以根据FOMe计算得出。锂离子在电极颗粒中分布不均,使得电极颗粒受到固相扩散诱导应力,应力值大小可由FOMeS计算得出。最后,根据FOMeS计算得到的固相扩散诱导应力值的大小,结合电极颗粒材料属性,计算获得电极颗粒裂纹生长速度并仿真电极颗粒裂纹生长形状。
根据电极颗粒所受固相扩散诱导应力大小和电极颗粒的形状,可计算出该电极颗粒的J积分。J积分被定义为裂纹尖端周围沿逆时针轮廓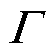 的二维独立路径线积分,即
的二维独立路径线积分,即
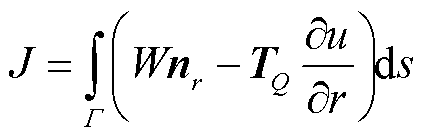 (21)
(21)
式中,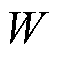 为应变能密度;
为应变能密度;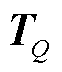 为牵引力矢量;
为牵引力矢量;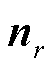 为径向法矢分量。
为径向法矢分量。
根据J积分确定固相扩散诱导应力强度因子KI,J积分与模式Ⅰ下的固相扩散诱导应力强度因子关系为
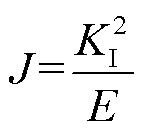 (22)
(22)
当锂离子电池电极颗粒承受固相扩散诱导应力时,电极颗粒有向内生长的趋势,裂纹生长速度可以根据Paris公式计算获得,其形式为
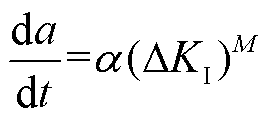 (23)
(23)
式中,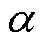 和M为电极颗粒材料参数;DKI为应力强度因子的范围。假设应力负荷在0~50 MPa之间时,设DKI=KI。
和M为电极颗粒材料参数;DKI为应力强度因子的范围。假设应力负荷在0~50 MPa之间时,设DKI=KI。
最终,电极颗粒裂纹生长长度a根据初始电极颗粒裂纹长度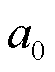 加上裂纹生长速度
加上裂纹生长速度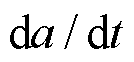 与负载周期t的乘积求得,即
与负载周期t的乘积求得,即
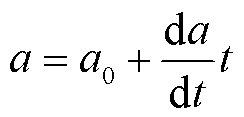 (24)
(24)
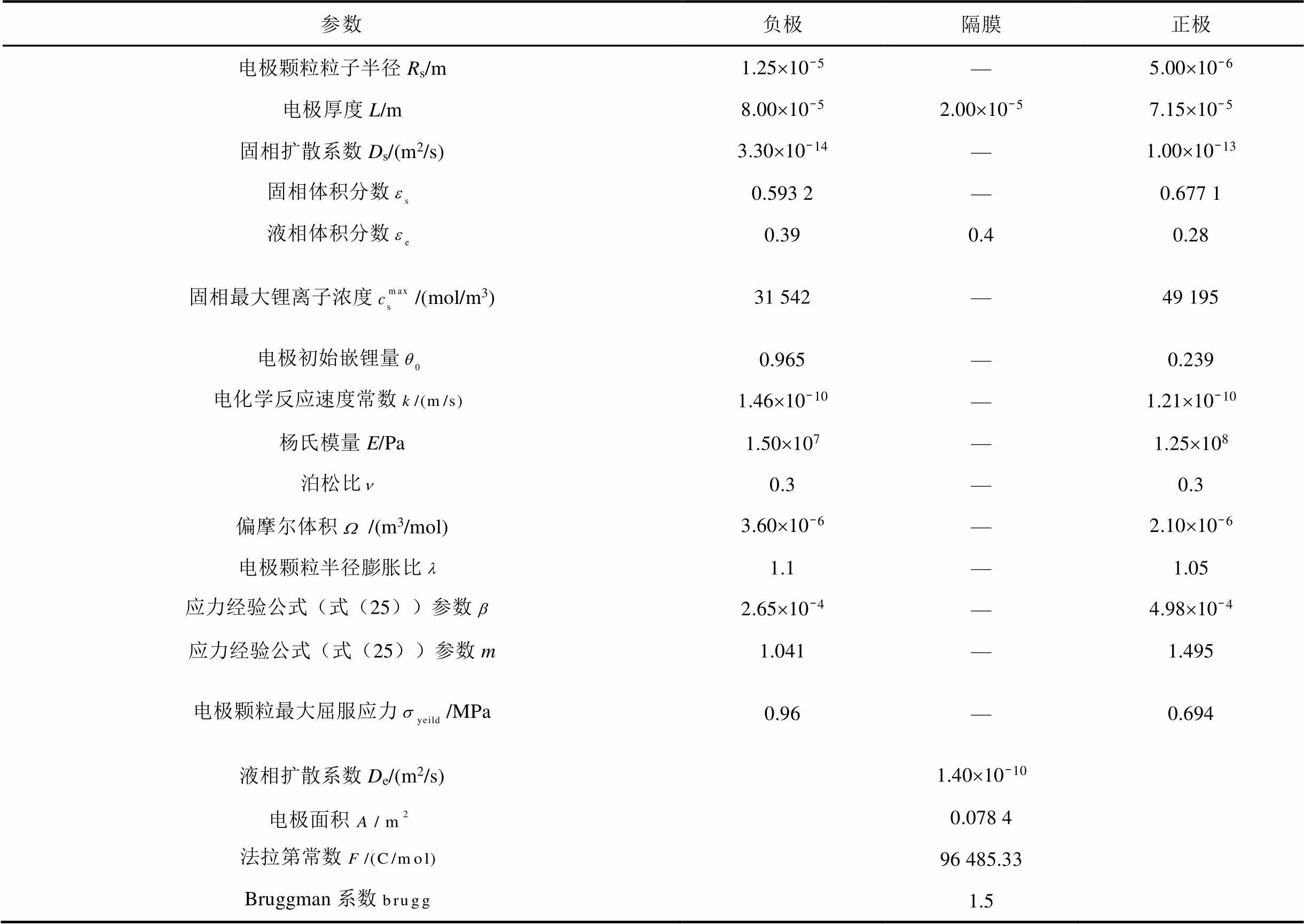
以2 800 mA·h镍钴铝酸锂电池为研究对象,对 NCA电池进行仿真实验,以验证所提电极颗粒裂纹生长模型的有效性。仿真与实验所用NCA电池对应的电化学参数见表1。
表1 NCA电池电化学参数
Tab.1 Electrochemical parameters of NCA battery
参数负极隔膜正极 电极颗粒粒子半径Rs/m1.25´10-5—5.00´10-6 电极厚度L/m8.00´10-52.00´10-57.15´10-5 固相扩散系数Ds/(m2/s)3.30´10-14—1.00´10-13 固相体积分数0.593 2—0.677 1 液相体积分数0.390.40.28 固相最大锂离子浓度/(mol/m3)31 542—49 195 电极初始嵌锂量0.965—0.239 电化学反应速度常数1.46´10-10—1.21´10-10 杨氏模量E/Pa1.50´107—1.25´108 泊松比0.3—0.3 偏摩尔体积/(m3/mol)3.60´10-6—2.10´10-6 电极颗粒半径膨胀比1.1—1.05 应力经验公式(式(25))参数2.65´10-4—4.98´10-4 应力经验公式(式(25))参数m1.041—1.495 电极颗粒最大屈服应力/MPa0.96—0.694 液相扩散系数De/(m2/s)1.40´10-10 电极面积0.078 4 法拉第常数96 485.33 Bruggman系数1.5
(续)

参数负极隔膜正极 理想气体常数Rg/[J/(K·mol)]8.314 472 初始液相锂离子浓度ce,0/(mol/m3)1 000 液相锂离子迁移数0.38 电池温度T/K298
在4.2 V满电状态下,NCA电池以1C(2.8 A)电流恒流放电3 600 s,根据表1中NCA电池电化学参数计算得到放电过程中正负极颗粒固相扩散诱导应力如图5所示。
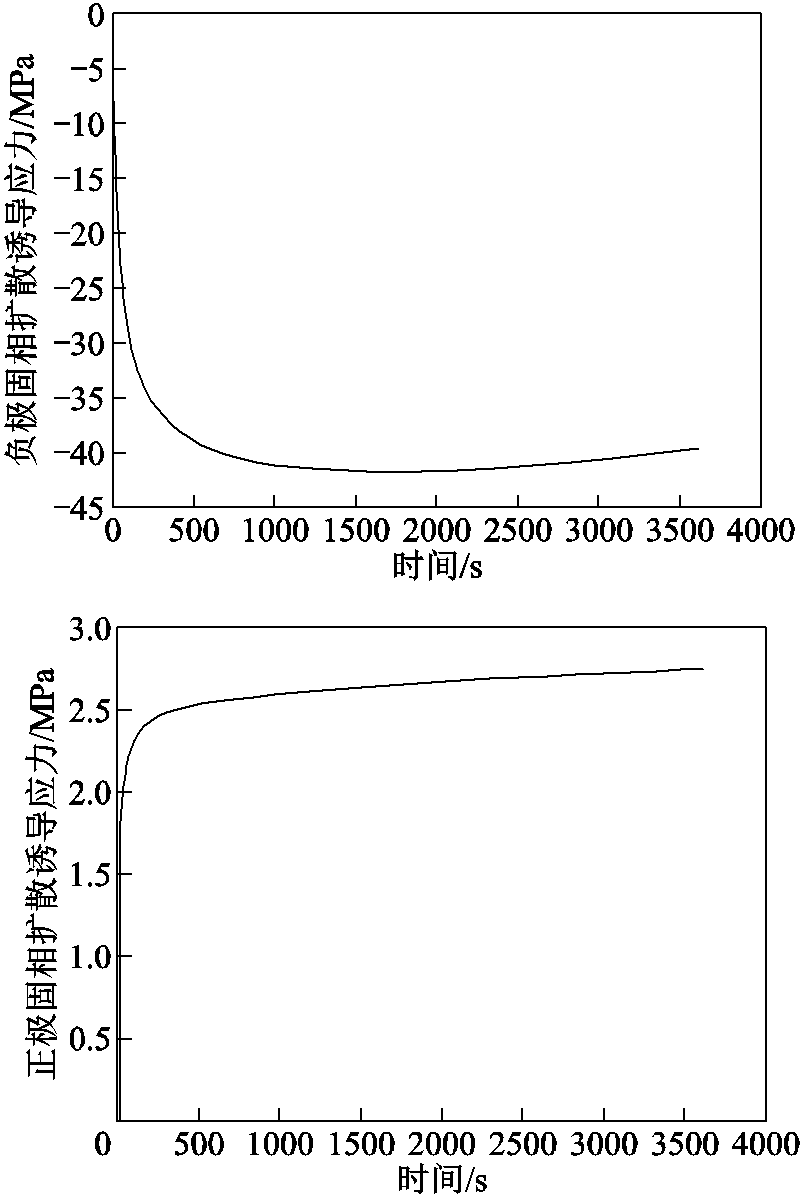
图5 NCA电池正负极颗粒固相扩散诱导应力
Fig.5 Solid phase diffusion-induced stress of positive and negative electrode particles in NCA cells
从图5中可以看出,随着NCA电池放电时间的增加,NCA电池负极固相扩散诱导应力先快速增大再缓慢减小。电池在恒流放电过程中,锂离子从负极颗粒表面流出,负极固相表面锂离子浓度差幅值迅速增大,负极固相扩散诱导应力也迅速增大。由于在恒流放电过程中负极颗粒粒子半径逐渐减小,负极扩散时间常数逐渐减小,导致负极颗粒内部锂离子浓度不均匀程度减小,从而导致负极颗粒固相扩散诱导应力有所减小。在恒流放电过程中,锂离子嵌入正极颗粒中,导致正极颗粒体积逐渐增大,正极扩散时间常数增大,锂离子浓度在正极颗粒的不均匀性增大,最终致使正极固相扩散诱导应力在放电过程中逐渐增大。由于负极颗粒粒子半径比正极颗粒粒子半径大,且负极固相扩散系数比正极扩散系数小,导致负极颗粒内部锂离子浓度分布不均匀性比正极大,所以负极颗粒所受固相扩散诱导应力幅值更大。
电池在充放电过程中,电极颗粒长期受到固相扩散诱导应力的影响,导致电极颗粒出现破裂,粘结剂、导电剂失效,从而造成电池活性材料损失,导致电池老化。电极活性材料损失与固相扩散诱导应力具有强相关性,文献[26]给出了电极容量损失与电极颗粒所受应力之间的关系,即
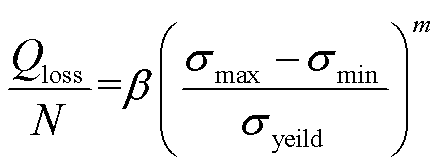 (25)
(25)
式中,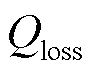 为电极损失容量;N为电池循环周次;
为电极损失容量;N为电池循环周次;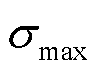 和
和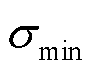 分别为电极颗粒所受最大和最小应力;
分别为电极颗粒所受最大和最小应力;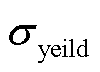 为电极颗粒最大屈服强度;
为电极颗粒最大屈服强度;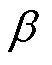 、m和
、m和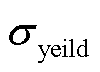 均为经验公式(25)待拟合参数。
均为经验公式(25)待拟合参数。
由于电极颗粒所受应力难以实际测得,为验证所提FOMeS的有效性,设计NCA电池老化实验。设置NCA电池截止电压上限为4.2 V,截止电压下限为2.5 V,循环老化实验步骤如下。
(1)以C/30电流对NCA电池进行恒流充放电,静置1 h。
(2)以1C电流对NCA电池进行恒流恒压充电,恒流恒压充电的截止电流为50 mA,静置1 h,以1C电流对NCA电池放电,再静置1 h,NCA电池循环充放电49次。
(3)循环重复步骤(1)和步骤(2),直至电池循环周次达到250次。
根据NCA电池循环老化实验中的C/30恒流充放电数据,利用双水箱模型辨识正负极电极容量[27]。同时,根据FOMeS计算正负极固相扩散诱导应力,结合式(25)计算电极容量随电池老化的损失。最终,根据老化实验辨识所得正负极电极容量验证所提模型的有效性。老化实验验证FOMeS基本原理如图6所示。
不同循环周次下NCA电池放电电压如图7所示。从图7中可以看出,随着电池循环老化,电池的放电时间不断减小,放电容量不断减小,电池内阻不断增加。前100周老化电池电压曲线间隔较大,后150周电池电压曲线间隔逐渐减小,说明该电池老化速度先快后慢。该电池容量相关的健康状态(State of Health, SOH)随循环周次的变化如图8所示。
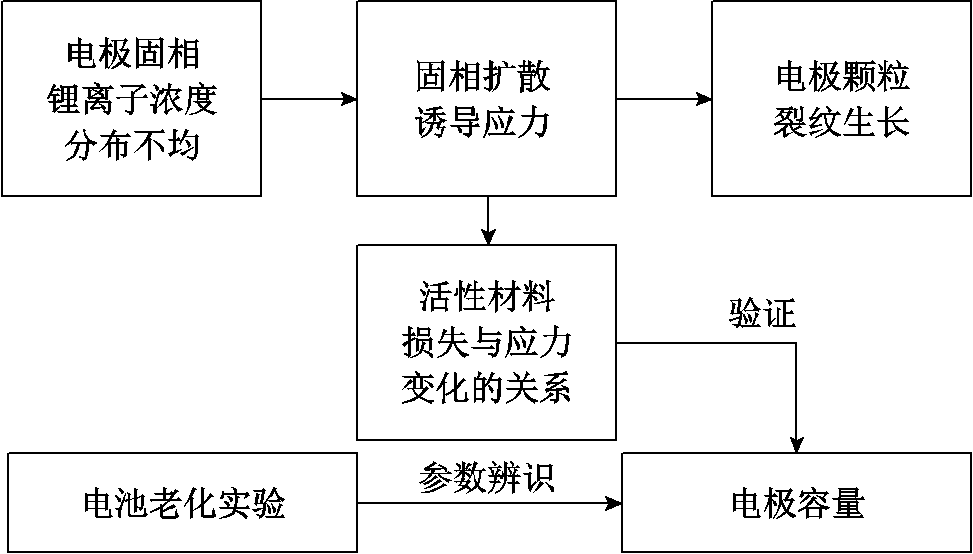
图6 FOMeS有效性验证原理
Fig.6 Schematic diagram of FOMeS verification
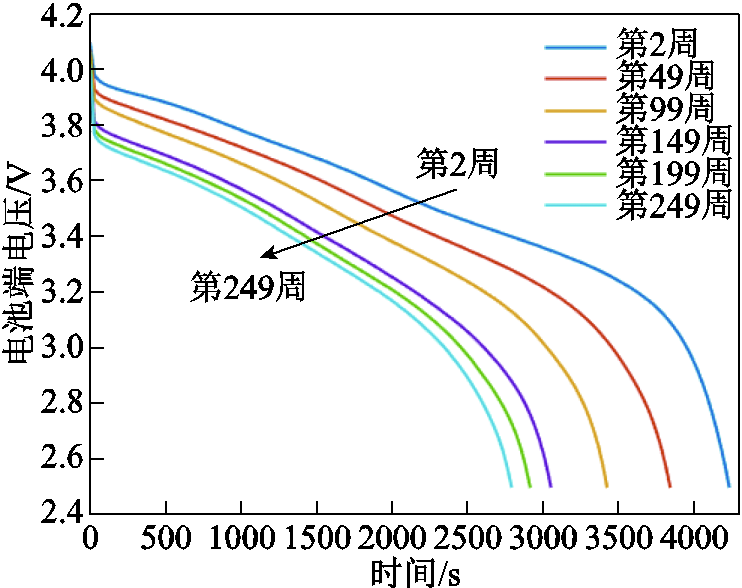
图7 不同循环周次NCA电池恒流放电电压对比
Fig.7 Constant current discharge voltages comparison of NCA cells in different cycles
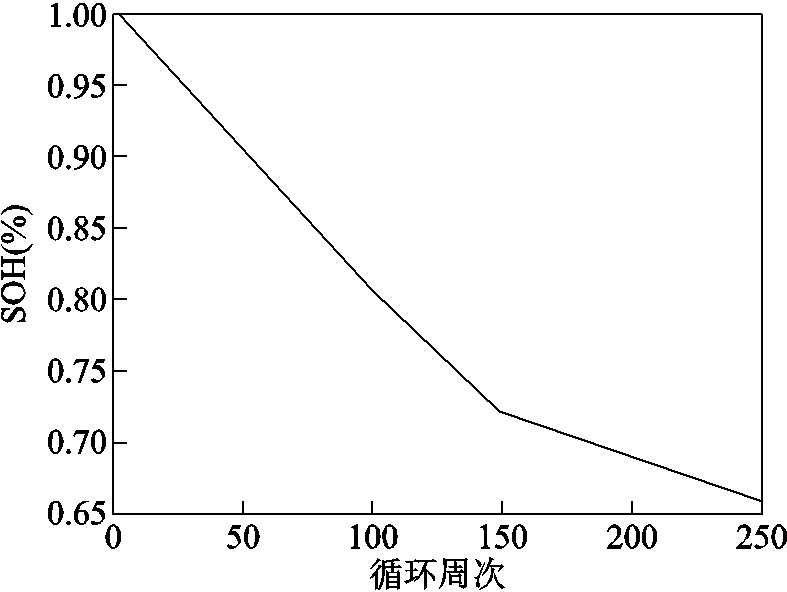
图8 NCA电池容量相关SOH
Fig.8 Capacity-dependent SOH of NCA
NCA电池内部导致电池老化的原因错综复杂,主要可以分为两类:锂离子损失和活性材料损失。导致锂离子损失的主要原因为SEI膜生长副反应,SEI膜生长副反应消耗锂离子和电解液导致电极嵌锂区间收窄。活性材料损失的关键在于应力所引发的颗粒破裂,以及粘结剂和导电剂的失效,从而导致部分电极材料被孤立,引发电极活性材料损失。电极活性材料损失主要体现在电极容量减小。
为获取不同循环周次的NCA电池电极容量,根据电池C/30恒流放电电压和双水箱模型,利用粒子群算法(Particle Swarm Optimization, PSO)辨识不同老化阶段NCA电池的热力学参数,包括正极初始嵌锂量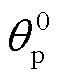 、负极初始嵌锂量
、负极初始嵌锂量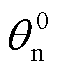 、正极容量
、正极容量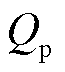 、负极容量
、负极容量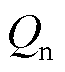 。不同老化阶段NCA电池热力学参数辨识结果见表2,在不同循环周次下,NCA电池热力学参数变化趋势如图9所示。
。不同老化阶段NCA电池热力学参数辨识结果见表2,在不同循环周次下,NCA电池热力学参数变化趋势如图9所示。
表2 FOMeS热力学参数辨识
Tab.2 Thermodynamic parameters identification of FOMeS
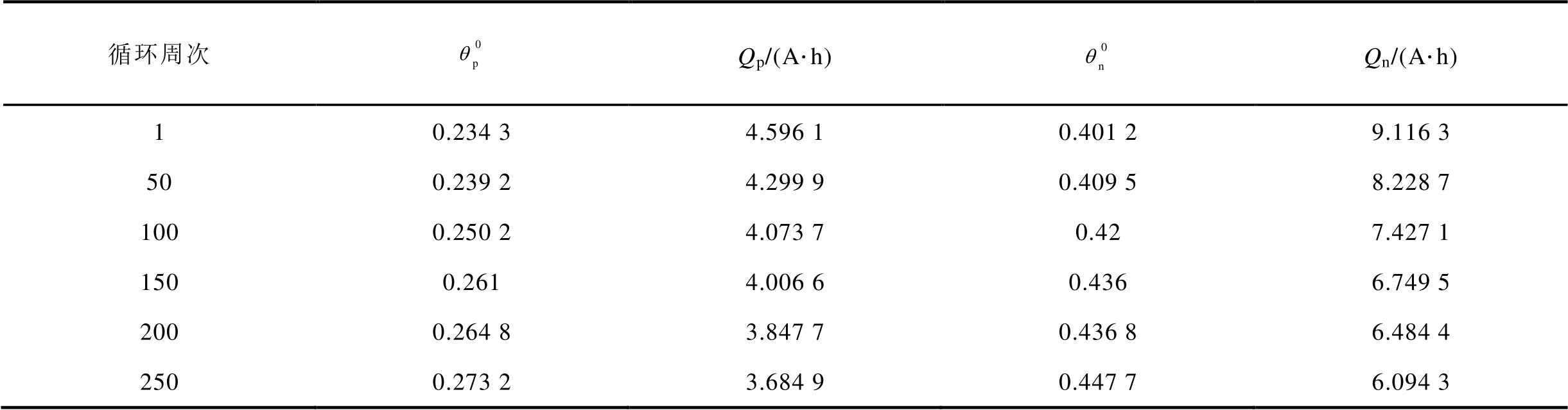
循环周次Qp/(A·h)Qn/(A·h) 10.234 34.596 10.401 29.116 3 500.239 24.299 90.409 58.228 7 1000.250 24.073 70.427.427 1 1500.2614.006 60.4366.749 5 2000.264 83.847 70.436 86.484 4 2500.273 23.684 90.447 76.094 3
从表2和图9中可以看出,随着电池循环老化,满电时正负极初始嵌锂量都在上升,表明在电池内部发生了锂离子损失,电池内阻不断增加。在电池充放电过程中,电池提前达到截止电压上、下限,致使电极嵌锂区间发生漂移。电池正负极容量都随着循环周次的增加而减小,表明在循环老化过程中正负极活性材料损失,导致正负极容量下降。
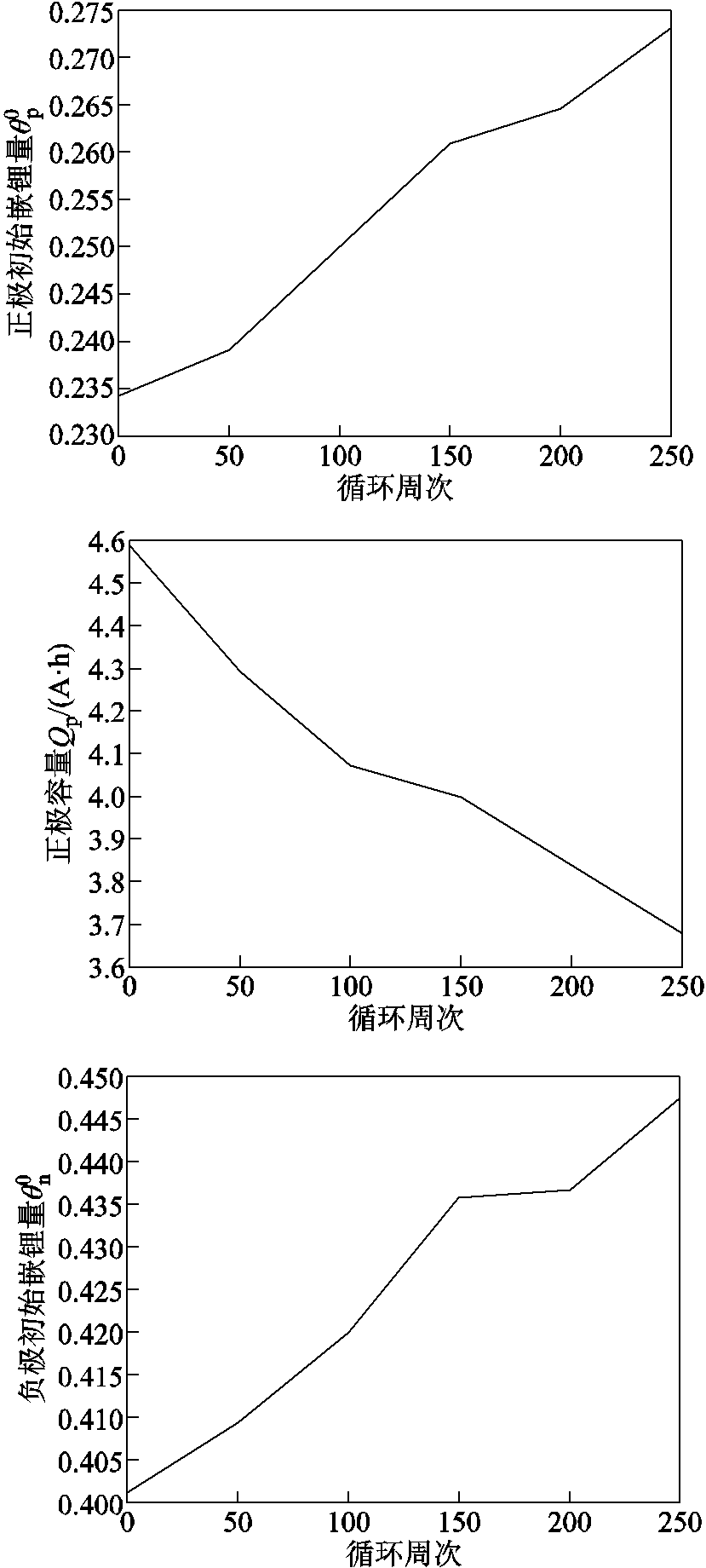
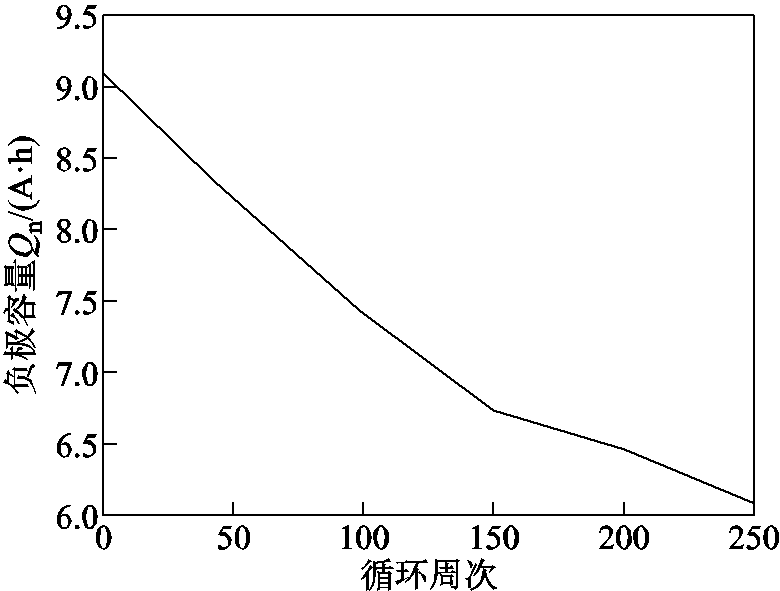
图9 NCA电池热力学参数随循环周次变化
Fig.9 Thermodynamic parameters in NCA battery change with cycle number
在不同循环周次下,NCA电池C/30恒流放电实测电压与双水箱模型仿真电压对比如图10所示,电压误差对比见表3。
从图10和表3中可以看出,在所有老化阶段下的双水箱模型C/30恒流放电仿真电压曲线都与NCA电池实测电压曲线贴合,且最大电压方均根误差(Root Mean Square Error, RMSE)不超过33 mV,最大电压平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)不超过0.63%。双水箱模型仿真电压与实测电压误差分析结果表明,利用PSO算法结合C/30恒流放电曲线能准确辨识NCA电池的正极初始嵌锂量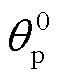 、负极初始嵌锂量
、负极初始嵌锂量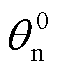 、正极容量
、正极容量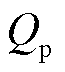 、负极容量
、负极容量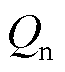 。
。
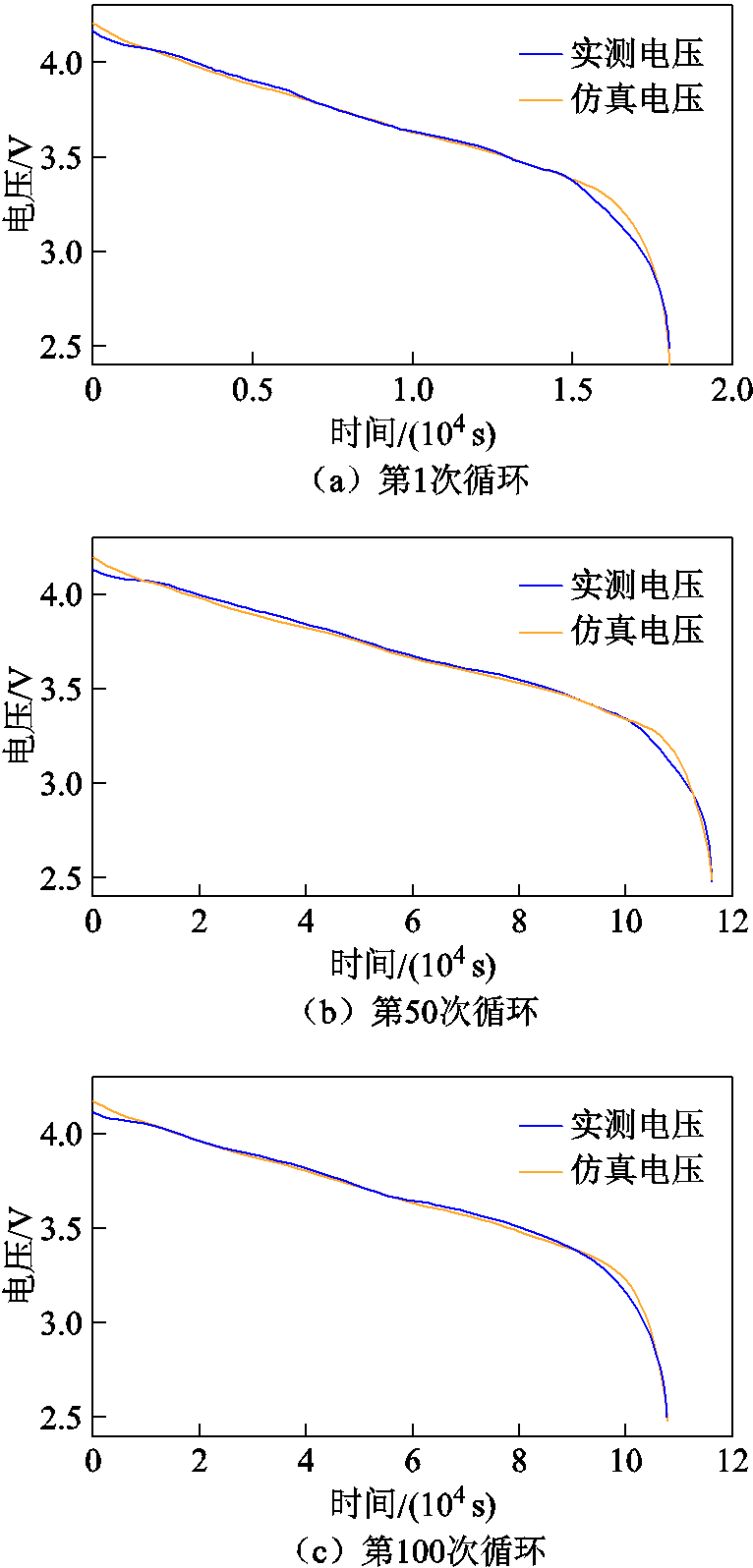
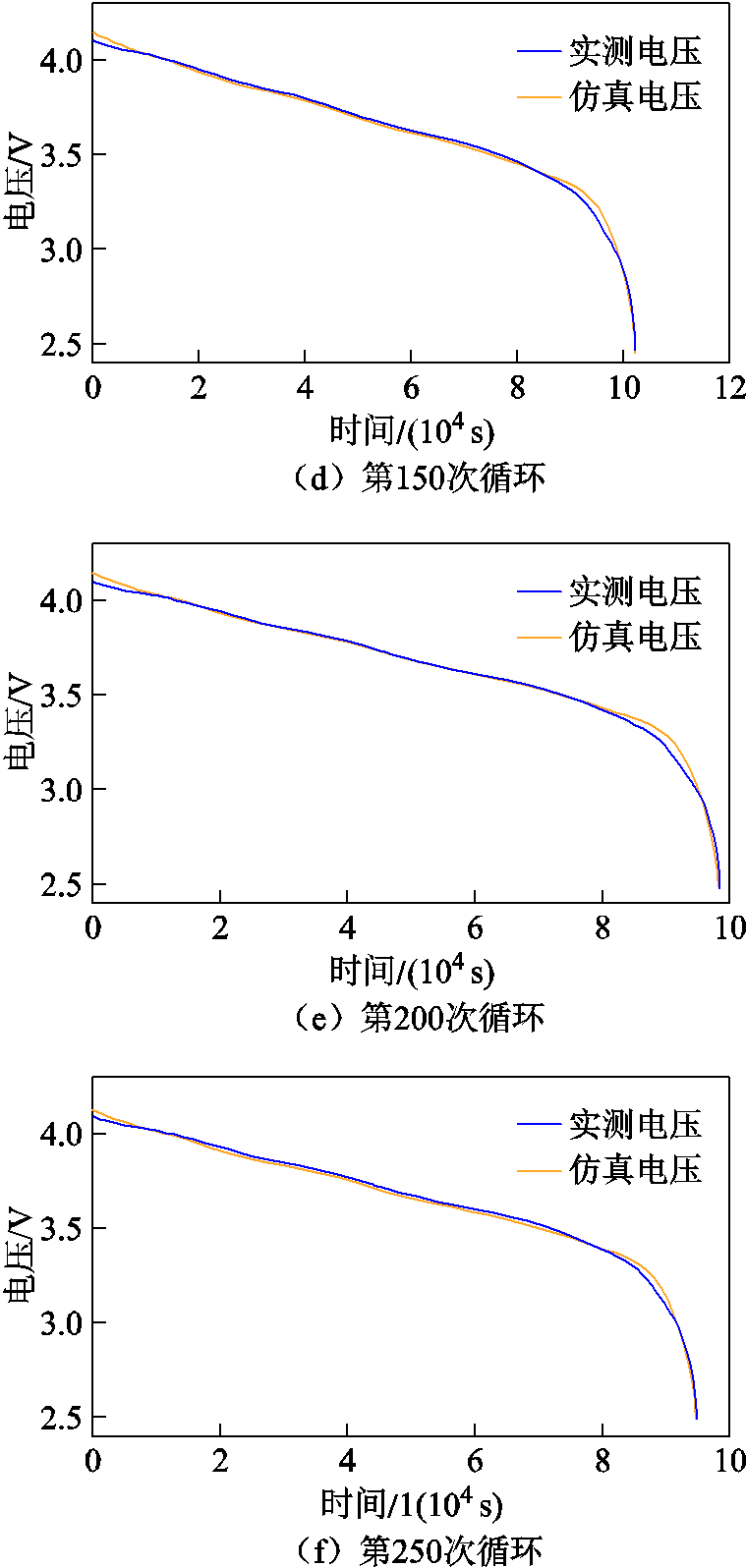
图10 不同循环周次下1/30C双水箱模型仿真电压
Fig.10 Voltage of double tank model at 1/30C current in different cycles
表3 C/30恒流放电双水箱模型电压误差
Tab.3 Voltage errors of double tank model at C/30 constant current discharge
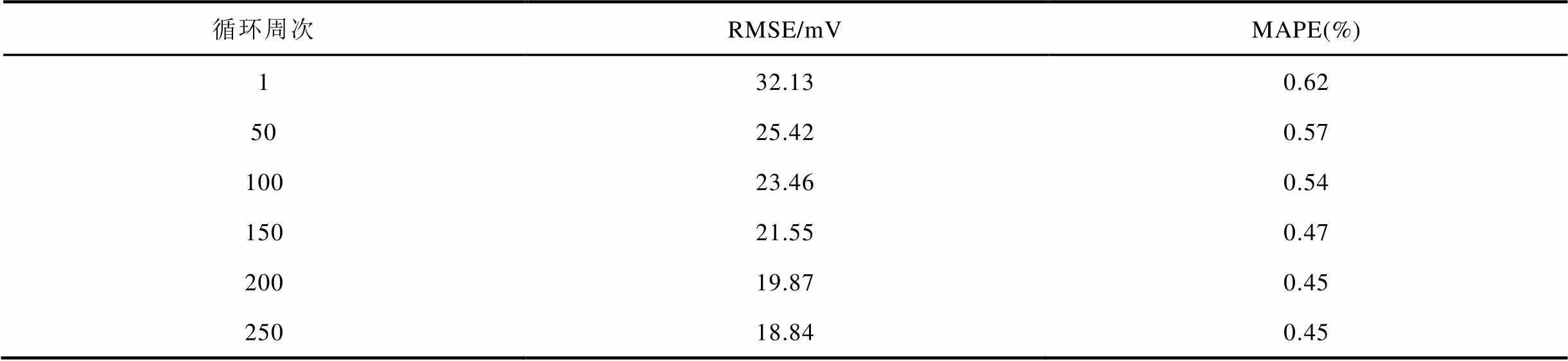
循环周次RMSE/mVMAPE(%) 132.130.62 5025.420.57 10023.460.54 15021.550.47 20019.870.45 25018.840.45
由于电极颗粒内部应力难以测量,为验证所提FOMeS应力预测的准确性。利用不同老化阶段1/30C恒流放电数据辨识正负极容量,并与电极容量应力相关经验公式(25)计算所得电极容量进行对比结果如图11所示。
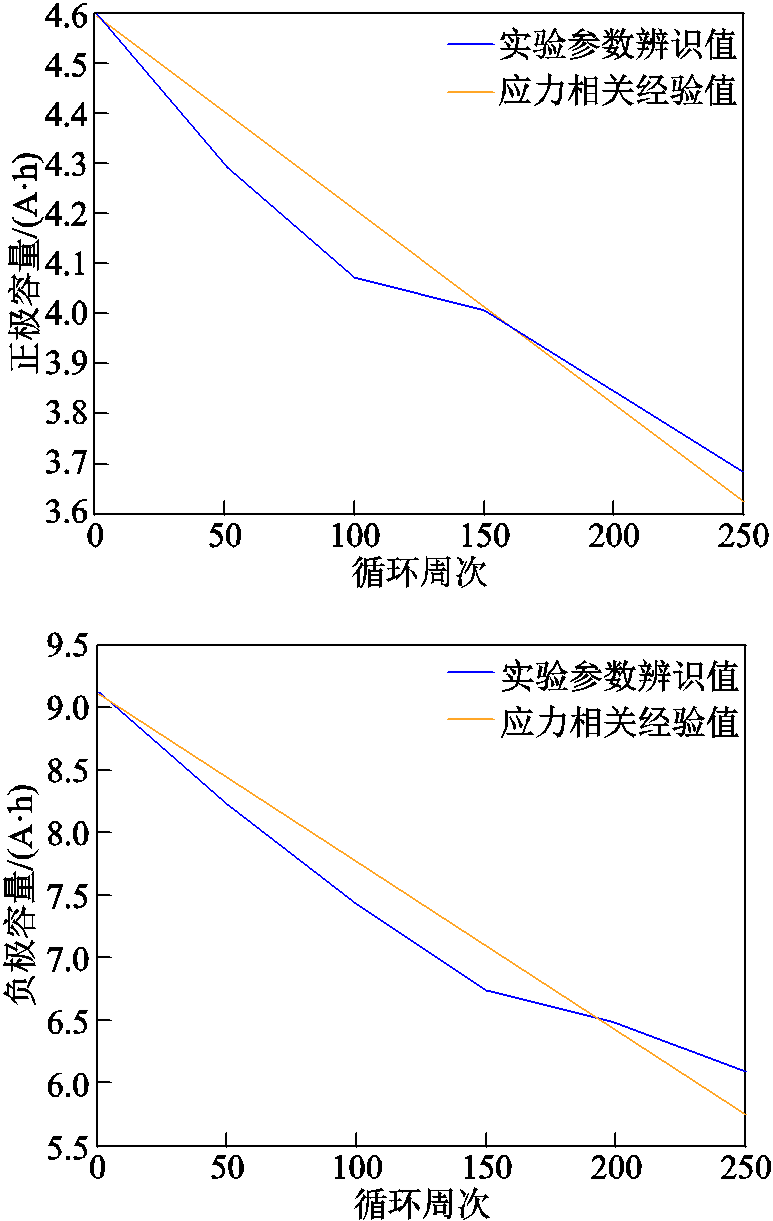
图11 老化实验参数辨识值与应力经验公式计算值对比
Fig. 11 Comparison between the identified value of aging experiment and stress empirical equation
从图11中可以看出,老化实验参数辨识所得的正负极容量随循环周次变化曲线与根据应力相关经验公式计算获得的正负极容量随循环周次变化曲线十分接近。以老化实验参数辨识所得的电池正负极容量为真值,根据电极颗粒固相扩散诱导应力计算获得的电池正负极容量对比老化实验参数辨识所得的电池正负极容量的误差见表4。
表4 由应力计算获得的电极容量误差
Tab.4 Errors of electrode capacity calculated by stress

误差正极负极 RMSE/(A·h)0.073 90.260 2 MAPE(%)1.373 43.178 5
由电极颗粒固相扩散诱导应力计算出的正极容量RMSE仅为0.073 9 A·h,MAPE仅为1.373 4%。负极容量预测误差则稍大,负极容量RMSE为 0.260 2 A·h,MAPE为3.178 5%。实验结果表明,所提FOMeS能较为准确地反映电极颗粒内部锂离子浓度分布,预测电极颗粒固相扩散诱导应力。
以1C电流对2.8 A·h NCA电池进行恒流充电仿真。首先根据FOMeS计算电极颗粒中锂离子浓度分布,再根据固相锂离子浓度分布计算电极颗粒所受固相扩散诱导应力,将应力数据输入电极颗粒裂纹生长模型。最终,根据电极颗粒所受固相扩散诱导应力,结合电极颗粒材料属性,完成电极颗粒受力分析,计算电极颗粒裂纹生长速度。设置负极颗粒初始裂纹长度为0.2Rs,n(2.5´10-6 m),仿真得到负极颗粒形变状态及其内部应力分布如图12所示。
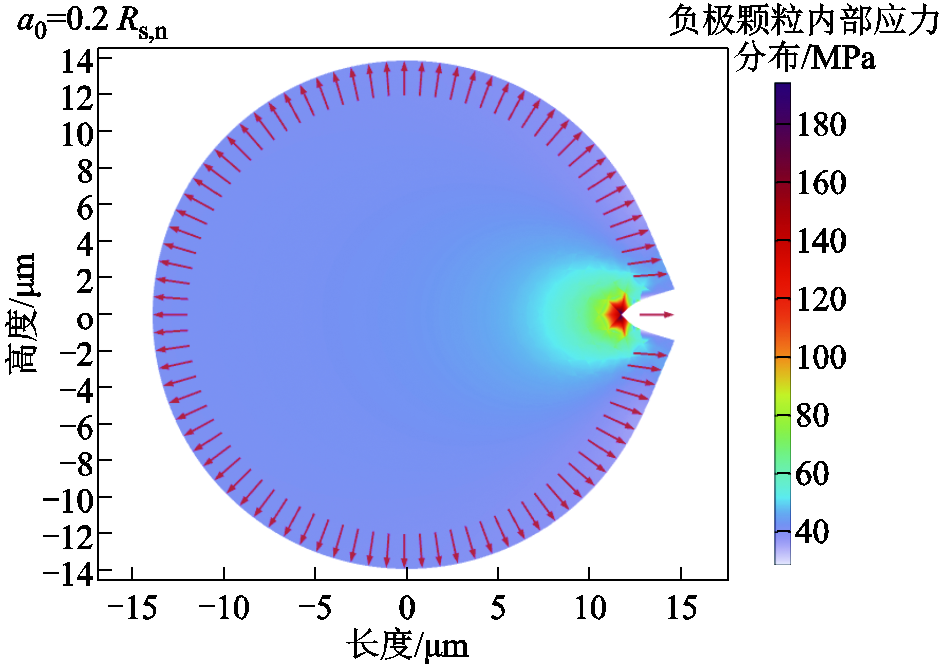
图12 负极颗粒形变及其内部应力分布
Fig.12 Deformation and stress distribution of negative particles
电池在充电过程中,锂离子嵌入负极颗粒,颗粒外层锂离子浓度高于颗粒中心锂离子浓度,负极颗粒受到向外膨胀的应力。从图12中可以看出,在裂纹端点处,负极颗粒所受应力最大,且裂纹有继续向内生长的趋势。
在充电过程中,锂离子从正极颗粒中脱出,导致电极颗粒中心锂离子浓度高,颗粒外层锂离子浓度低,从而致使正极颗粒受到向内收缩的应力。在1C恒流充电工况下,设置正极颗粒初始裂纹长度为0.2Rs,p(1´10-6 m),则仿真得到正极颗粒形变状态及其应力分布如图13所示。
从图13中可以看出,正极颗粒所受最大应力也是在裂纹端点处,且该裂纹有向内部生长的趋势。由于正极颗粒离子半径更小,正极固相扩散系数更大,导致正极颗粒内部锂离子分布不均匀性更小,正极颗粒所受到的固相扩散诱导应力更小。此外,负极石墨颗粒比正极NCA颗粒更为柔软,负极颗粒杨氏模量比正极颗粒杨氏模量小了一个数量级。在相同的应力作用下,负极颗粒也更易发生形变。
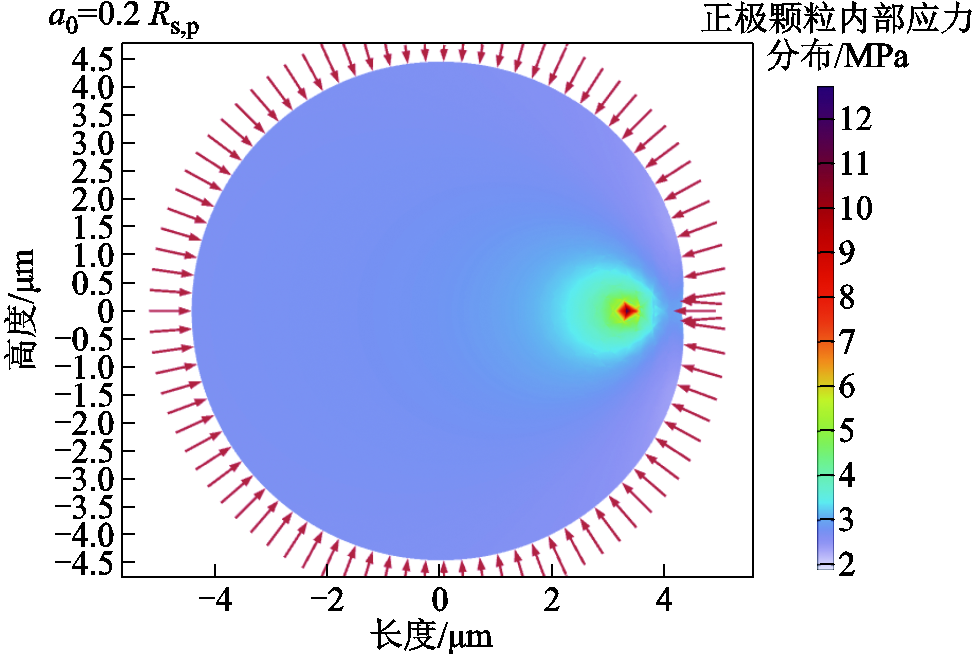
图13 正极颗粒形变及其内部应力分布
Fig.13 Deformation and stress distribution of positive particles
电极颗粒裂纹生长速度与电极颗粒裂纹端点处所受应力直接相关,而电极颗粒裂纹端点处所受应力不仅受电极颗粒所受平均应力大小影响,还受电极颗粒裂纹长度的影响。图14绘制了在1C恒流充电工况下正负极颗粒裂纹生长速度与颗粒裂纹长度之间的关系。
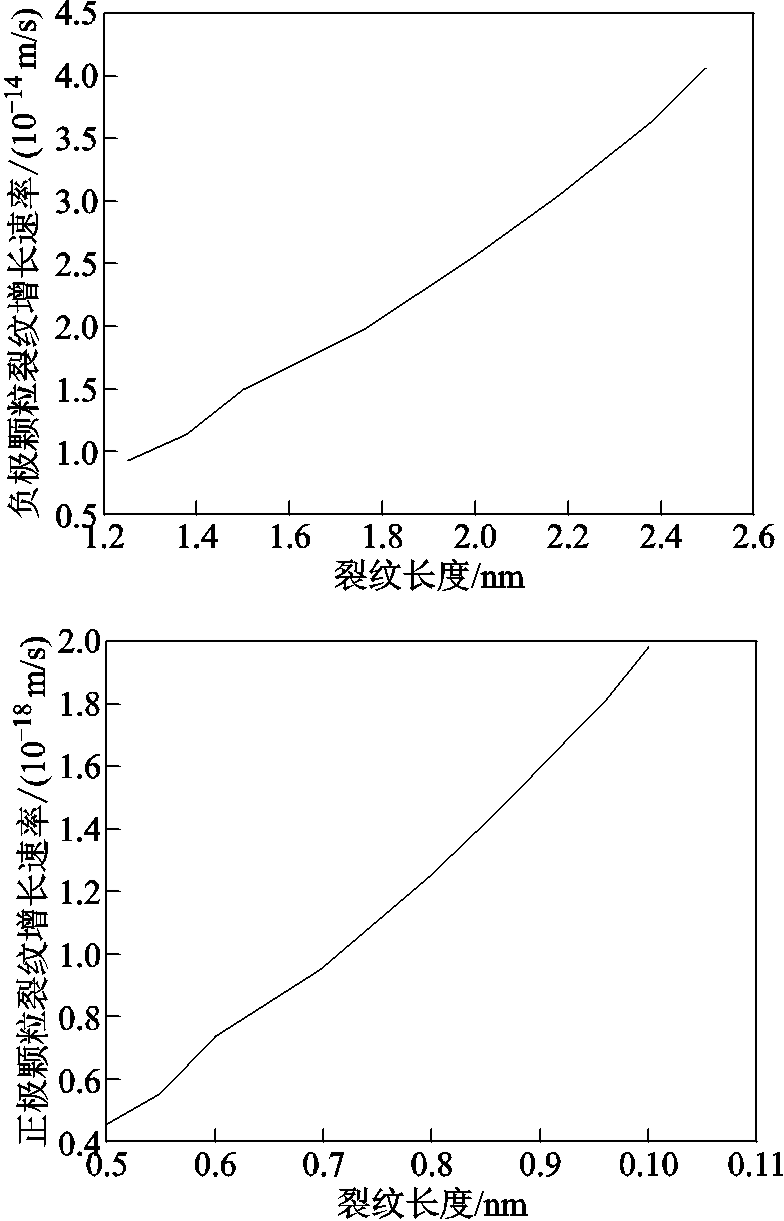
图14 电极颗粒裂纹生长速度与裂纹长度之间的关系
Fig.14 Relationship between electrode particles crack growth rate and crack length
从图14中可以看出,随着电极颗粒裂纹长度的加深,电极颗粒裂纹生长速度也逐渐加快。电极颗粒裂纹越长导致电极颗粒内部锂离子浓度和应力分布不均匀性加剧,电极颗粒裂纹端点处应力增大,最终导致电极颗粒裂纹加速生长。由于负极颗粒粒子半径更大,负极固相扩散系数更小,导致负极颗粒内部锂离子浓度分布更不均匀,负极颗粒所受固相扩散诱导应力更大。负极材料杨氏模量更小,更易发生形变。因此,负极颗粒裂纹生长速度比正极颗粒裂纹生长速度快得多。
为揭示电池老化特性,探究电池电极活性材料的损失机理,本文提出一种考虑固相扩散诱导应力的电极颗粒裂纹生长模型,该模型耦合了电极颗粒中锂离子扩散、应力以及形变过程。为分析电极固液相锂离子浓度分布,提出FOMe简化计算锂离子在固液相中的扩散过程。在FOMe的基础上,根据电极颗粒应力应变原理,建立电极固相表面锂浓度差与电极颗粒固相扩散诱导应力之间的关系,提出FOMeS用于计算电极颗粒所受固相扩散诱导应力。为验证所提FOMeS的有效性,提出利用电池老化实验数据辨识的正负极容量与FOMeS根据应力经验公式计算出的正负极容量进行对比分析方法。电池老化实验结果表明,所提FOMeS能较为准确地预测电极固相扩散诱导应力和老化电池电极正负极容量变化趋势。最后,根据电极颗粒所受应力,结合电极颗粒材料属性,仿真分析电极颗粒内部应力分布及其形变趋势,根据Paris公式计算电极颗粒裂纹生长速度,预测电极颗粒裂纹生长深度及趋势。
参考文献
[1] ZhuGuorong, Kong Chun, Wang J V, et al. A fractional-order model of lithium-ion battery considering polarization in electrolyte and thermal effect[J]. Electrochimica Acta, 2023, 438: 141461.
[2] 顾菊平, 蒋凌, 张新松, 等. 基于特征提取的锂离子电池健康状态评估及影响因素分析[J]. 电工技术学报, 2023, 38(19): 5330-5342. Gu Juping, Jiang Ling, Zhang Xinsong, et al. Estimation and influencing factor analysis of lithium-ion batteries state of health based on features extraction[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5330-5342.
[3] Liu Zhen, Cai Rui, Chen Bingbing, et al. Effect of electrochemical reaction on diffusion-induced stress in hollow spherical lithium-ion battery electrode[J]. Ionics, 2017, 23(3): 617-625.
[4] 陈猛,王军,王雯雯,等. 应用支持向量机的锂电池不可逆析锂检测研究 [J/OL]. 电工技术学报, 1-10. Chen Meng, Wang Jun, Wang Wenwen, et al. Research on irreversible lithium plating detection in lithium-ion batteries using support vector machine[J]. Transactions of China Electrotechnical Society, 1-10.
[5] 董明, 范文杰, 刘王泽宇, 等. 基于特征频率阻抗的锂离子电池健康状态评估[J]. 中国电机工程学报, 2022, 42(24): 9094-9104. Dong Ming, Fan Wenjie, Liu Wangzeyu, et al. Health assessment of lithium-ion batteries based on characteristic frequency impedance[J]. Proceedings of the CSEE, 2022, 42(24): 9094-9104.
[6] 余佩雯, 郁亚娟, 常泽宇, 等. 相关向量机预测锂离子电池剩余有效寿命[J]. 电气技术, 2023, 24(2): 1-5. Yu Peiwen, Yu Yajuan, Chang Zeyu, et al. Remain useful life prediction of lithium-ion battery based on relevance vector machine[J]. Electrical Engineering, 2023, 24(2): 1-5.
[7] 李弈, 张金龙, 漆汉宏, 等. 基于VaDE-WGANGP的锂离子电池老化特性建模[J]. 电工技术学报, 2024, 39(13): 4226-4239. Li Yi, Zhang Jinlong, Qi Hanhong, et al. Ageing performance modeling of Li-ion batteries based on VaDE-WGANGP[J]. Transactions of China Electro-technical Society, 2024, 39(13): 4226-4239.
[8] Reniers J M, Mulder G, Howey D A. Review and performance comparison of mechanical-chemical degradation models for lithium-ion batteries[J]. Journal of the Electrochemical Society, 2019, 166(14): A3189-A3200.
[9] Wang Xiaofei, Tong Qi. Peridynamic modeling of delayed fracture in electrodes during lithiation[J]. Computer Methods in Applied Mechanics and Engineering, 2023, 404: 115774.
[10] Zhang Yang, Zhu Zhenxing. Diffusion stress modeling of micro hollow spherical shell electrode[J]. The International Journal of Advanced Manufacturing Technology, 2020, 108(1): 499-504.
[11] Zhu Guorong, Kong Chun, Wang J V, et al. A fractional-order electrochemical lithium-ion batteries model considering electrolyte polarization and aging mechanism for state of health estimation[J]. Journal of Energy Storage, 2023, 72: 108649.
[12] Du Yating, Fujita K, Shironita S, et al. Capacity fade characteristics of nickel-based lithium-ion secondary battery after calendar deterioration at 80 ℃[J]. Journal of Power Sources, 2021, 501: 230005.
[13] Weisenberger C, Meir B, Röhler S, et al. A post-mortem study of commercial 18650 lithium-ion cells with LiNi0.5Co0.2Mn0.3O2// Graphite chemistry after prolonged cycling (>7000 cycles) with low C-rates[J]. Electrochimica Acta, 2021, 379: 138145.
[14] 王绥军, 胡晨, 孙召琴, 等. 电流过载工况下三元锂离子电池性能衰退机制[J]. 中国电机工程学报, 2023, 43(20): 7940-7947. Wang Suijun, Hu Chen, Sun Zhaoqin, et al. Performance degradation mechanism of ternary lithium batteries under current overload[J]. Proceedings of the CSEE, 2023, 43(20): 7940-7947.
[15] Li Xuemin, Colclasure A M, Finegan D P, et al. Degradation mechanisms of high capacity 18650 cells containing Si-graphite anode and nickel-rich NMC cathode[J]. Electrochimica Acta, 2019, 297: 1109-1120.
[16] Ai Weilong, Kraft L, Sturm J, et al. Electrochemical thermal-mechanical modelling of stress inhomo-geneity in lithium-ion pouch cells[J]. Journal of the Electrochemical Society, 2020, 167(1): 013512.
[17] Klinsmann M, Rosato D, Kamlah M, et al. Modeling crack growth during Li extraction in storage particles using a fracture phase field approach[J]. Journal of the Electrochemical Society, 2015, 163(2): A102-A118.
[18] Klinsmann M, Rosato D, Kamlah M, et al. Modeling crack growth during Li insertion in storage particles using a fracture phase field approach[J]. Journal of the Mechanics and Physics of Solids, 2016, 92: 313-344.
[19] Basdevant J L. The padé approximation and its physical applications[J]. Fortschritte Der Physik, 1972, 20(5): 283-331.
[20] Bhattacharya S, Riahi A R, Alpas A T. A transmission electron microscopy study of crack formation and propagation in electrochemically cycled graphite electrode in lithium-ion cells[J]. Journal of Power Sources, 2011, 196(20): 8719-8727.
[21] Li Xueyan, Zhang Zhiyuan, Gong Lili, et al. Revealing the mechanism of stress rebound during discharging in lithium-ion batteries[J]. Journal of Energy Storage, 2023, 58: 106454.
[22] Cheng Y T, Verbrugge M W. Evolution of stress within a spherical insertion electrode particle under potentiostatic and galvanostatic operation[J]. Journal of Power Sources, 2009, 190(2): 453-460.
[23] Timoshenko Stephen P, Goodier James Norman. Theory of elasticity[M]. Engineering Societies Monographs, NewYork: McGyaw-Hill, 1970.
[24] Bezaeva N S, Gattacceca J, Rochette P, et al. Demagnetization of ordinary chondrites under hydrostatic pressure up to 1.8 GPa[J]. Geochemistry International, 2022, 60(5): 421-429.
[25] 吴建营, 洪屹峰. 基于统一相场理论的锂电池电极颗粒断裂模拟研究[J]. 力学学报, 2022, 54(9): 2472-2488. Wu Jianying, Hong Yifeng. Phase-field cohesive modeling of fracture in storage particles of lithium-ion batteries[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(9): 2472-2488.
[26] Laresgoiti I, Käbitz S, Ecker M, et al. Modeling mechanical degradation in lithium ion batteries during cycling: solid electrolyte interphase fracture[J]. Journal of Power Sources, 2015, 300: 112-122.
[27] 韩雪冰. 车用锂离子电池机理模型与状态估计研究[D]. 北京: 清华大学, 2014. Han Xuebing. Study on li-ion battery mechanism model and state estimation for electric vehicles[D]. Beijing: Tsinghua University, 2014.
Abstract Loss of electrode active material in lithium-ion batteries is one of the main causes of lithium-ion battery degradation, and electrode particle rupture is in turn the main mechanism leading to electrode active material loss.However, it is difficult to directly observe the state of electrode particles during charge and discharge. Therefore, this paper proposes a fractional-order model with electrolyte considering stress (FOMeS) to observe the lithium-ion concentration and stress changes in electrode particles. Furthermore, the electrode particle cracking model is proposed based on FOMeS and the material properties of the electrode particles. The accuracy of the proposed model is indirectly verified through NCA (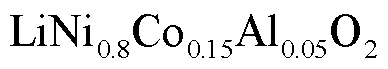 ) battery cycling aging experiments.
) battery cycling aging experiments.
Firstly, to achieve accurate internal state observation in lithium-ion batteries, a fractional-order model with electrolyte (FOMe) is proposed. FOMe is a simplified electrochemical lithium-ion batteries model based on single particle model, which simplifies solid-phase lithium-ion diffusion with fractional-order Padé approximation, and simplifies electrolyte-phase lithium-ion diffusion with two state-space systems. FOMe achieves accurate lithium-ion concentration prediction in solid phase and electrolyte phase with low computational complex.
Secondly, the lithium-ion concentration distribution in electrode particles affects the solid-phase diffusion-induced stresses, and the strain of electrode particles affects the solid-phase lithium-ion concentration distribution. To establish the relationship between the stress, the strain and the lithium-ion concentration in electrode particles, a fractional-order model with electrolyte considering stress (FOMeS) is proposed. To verify the effectiveness of FOMeS, a NCA lithium-ion battery aging experiment is designed. The 1/30C constant current discharge voltage data is used to identify the thermodynamic parameters of NCA batteries in different aging stages with particle swarm optimization. The positive and negative electrodecapacitiesidentified from the experiment are highly consistent with the positive and negative electrode capacities predicted from FOMeS. The positive electrode capacity RMSE and MAPE of FOMeS are 0.073 9 A·h and 1.373 4%, respectively. The negative electrode capacity RMSE and MAPE of FOMeS are 0.260 2 A·h and 3.178 5%, respectively. The experiment result shows that FOMeS achieves accurate lithium-ion concentration and solid phase diffusion-induced stress prediction.
Finally, to further investigate the effect of solid-phase diffusion-induced stress on the crack growth trend of electrode particles, the electrode particle cracking model is proposed. The proposed model combines the solid phase diffusion-induced stress based on FOMeS with the material properties of the electrode particles, the crack growth rate of the electrode particles can be calculated by the Paris equation. The stress and strain of electrode particles are simulated at 1C rate constant current charge and discharge. The simulation results show that the crack growth rate of electrode particles accelerates with the deepening of the crack length of electrode particles. For the NCA battery used in the experiment, the radius of negative electrode particles is larger than that of positive electrode particles, the solid-phase diffusion coefficient of negative electrode particles is smaller than that of positive electrode particles, and the Young’s modulus of negative electrode particles is smaller than that of positive electrode particles. Therefore, the growth rate of crack propagation in negative electrode particles is faster than that in positive electrode particles.
There are some conclusions can be made: (1) Compared with FOMe, FOMeS provides a more realistic response to the effect of electrode particle strain on lithium-ion concentration in electrode particles. (2) The aging battery experiments show that FOMeS accurately describes the stress trend of electrode particles and the loss of electrode capacity. (3) The electrode cracking model achieves the electrode particle crack growth simulation and predict the electrode particle crack growth trend.
keywords:Lithium-ion batteries, crack growth, loss of active material, electrochemical model, stress
DOI: 10.19595/j.cnki.1000-6753.tces.240314
中图分类号:TM911
国家自然科学基金资助项目(52277224, 51977163)。
收稿日期 2024-02-28
改稿日期 2024-05-06
孔 纯 男,1994年生,博士研究生,研究方向为锂离子电池建模与控制。E-mail:kongchun@whut.edu.cn
王 菁 女,1991年生,博士,讲师,研究方向为锂离子电池建模与健康管理。E-mail:jingvwang@whut.edu.cn(通信作者)
(编辑 郭丽军)