基于简支绕组横梁算法的变压器绕组形变矢量化监测模型
范晓舟1 袁洁平1 薛 峰2 王湘女2 律方成1 耿江海1
(1. 华北电力大学河北省输变电设备安全防御重点实验室 保定 071003 2. 广东电网有限责任公司东莞供电局 东莞 523000)
摘要 变压器绕组状态监测非常重要,为精确地监测变压器绕组变形方向与变形程度,该文结合简支横梁原理与布里渊光时域分析技术,提出了针对变压器绕组的形变矢量化监测算法。基于材料力学理论推导,建立了布里渊频移量与绕组形变轴向、径向分量关系式,利用布里渊光时域分析技术建立了变压器绕组形变矢量化监测模型。通过对光纤复合导线和内置光纤的35 kV绕组施加轴向形变和径向形变,借助布里渊光时域反射技术完成了形变监测,验证了监测模型的准确性。结果表明,复合导线实验中轴向形变测量平均误差为6.60%,径向形变测量平均误差为5.88%;内置光纤的35 kV绕组实验中轴向形变平均误差为9.63%,径向形变平均误差为5.18%。实验结果验证了绕组形变矢量化监测模型可实现绕组形变方向和形变程度的监测,有效地提高绕组形变程度的监测精度。
关键词:绕组形变 矢量化监测 光纤传感 简支绕组横梁
0 引言
电力行业是国民经济发展的重要组成部分,电力系统的稳定运行关系社会各行各业的发展[1]。变压器作为电力系统中的关键设备,其稳定性对电网安全运行有着至关重要的作用[2]。变压器运行时受到短路冲击会发生不同类型的形变,如鼓包、塌陷等,进而导致绕组磁场畸变,可能会使变压器局部受力急剧增大,造成变压器停运,严重情况下变压器存在燃爆的可能[3-4]。因此,监测变压器绕组形变具有重大意义。
目前,频率响应法、低压脉冲法和短路电抗法等传统绕组变形检测方法已经被广泛接受,但传统绕组形变检测方法具有一定的局限性:频率响应法需变压器停运后进行实验[4-5];低压脉冲法具有对首端响应不明显的问题[6];短路电抗法对潜伏性故障的灵敏性不高[7]。诸多学者基于传统检测方法进行了改进,如文献[8]利用振动和电抗信息综合诊断绕组形变故障,建立电抗信息和振动的数学方程和求解模型,研究绕组故障后的信号变化规律;文献[9]提出一种基于振动信号多特征值的变压器故障检测方法,提出了两端式故障诊断流程,完成了变压器的横向诊断。但改进后的传统检测方法大多属于间接测量,无法直接获得绕组形变信息,也较难反映绕组形变的真实情况和方向。
分布式光纤传感(Distributed Fiber Optic Sensing, DFOS)以光纤作为传感介质,利用不同散射机制的光波实现对温度、应变、振动等物理量的长距离连续测量[10]。并且光纤纤芯成分为石英,具有耐腐蚀、绝缘且不受强电磁干扰的特性,在变压器绕组在线监测中具有广泛的应用前景[11]。文献[12]根据布里渊散射频谱的互相关拟合辨识变压器绕组变形的特征,结果表明光纤对绕组形变的监测效果更好,且监测与反馈时间更短,但该研究未能实现绕组形变程度的判断。文献[13]将布拉格光纤光栅布设在110 kV变压器绕组上,对其进行短路冲击实验,通过光-力理论转换方程得到实际应变。但光纤光栅仅测量局部应变点,无法实现对绕组整体形变的全面监测。文献[14]利用布里渊光时域反射计测量光纤形变程度,并通过极限学习机对检测信号进行模式识别以实现变压器绕组变形的检测。文献[15]利用布里渊-拉曼联合测量方法,提取有效的光纤温度和应变信息,实现光纤温度和应变解调,并完成局部热点和变形定位。文献[16]通过固体力学仿真与实验得到光纤应变与挠度呈二次函数关系,并可实现光纤径向形变的定位与监测。
传统分布式光纤传感技术在变压器中运用时,使用单根光纤来监测变压器的径向形变。但绕组形变并非单一方向,不同方向的形变矢量叠加会造成单根光纤形变的监测误差增大。在变压器实际运行过程中,轴向形变和径向形变均会对变压器造成不同程度和类型的伤害,因此实现绕组轴向和径向形变监测,进一步提高分布式光纤形变的监测精度是十分必要的。
为解决轴向形变和径向形变难以监测的问题,本文提出了一种基于简支绕饼横梁解调算法的变压器绕组形变矢量化监测模型。首先基于材料力学和布里渊光时域反射分析技术(Brillouin Optical Time Domain Analysis, BOTDA)推导和建模,获得形变布里渊频移量及其轴向、径向分量的关系式;其次,设计矢量化光纤传感器并布设在铝条上模拟绕组导线,对其施加不同方向和程度的形变,通过BOTDA实验平台完成对形变布里渊的传感;最后,试制35 kV载纤绕组,开展不同形变下的布里渊频移测试,实现绕组矢量化形变监测。
1 BOTDA测量原理
布里渊散射现象是由注入的光波场与光纤中的弹性声波场间相互耦合作用而产生的一种非线性光散射现象,它的频率和强度相对入射光均会发生变化。布里渊散射相对于入射光频率的变化量称为布里渊频移[17-18]。因此在光纤的一端注入固定频率为f的脉冲光,即可获得一个中心频率为f-Df的背向布里渊散射信号,对这个信号进行收集和处理后,便可以实现自发布里渊散射的频域或者强度对应变和温度的检测[19-20]。布里渊频移与温度和应变均呈线性关系,其关系式为
2 绕组形变矢量化监测模型
在物理层面,根据应力方向的不同,可将应力分为正切力和切应力,正切力与应变方向平行,而切应力则垂直于应变方向。当变压器突发短路时,绕组会受到巨大的轴向或径向电磁力。当绕组导线的弯曲应力与压拉应力的合应力超过导线材料的屈服强度时,绕组导线就会在所在平面内发生轴向或径向形变。由于受电磁力作用或绕组匝间短路、夹件松动等其他因素的随机性的影响,绕组形变常是多方向且不规则的[22]。现有研究大多使用单根光纤监测应变,无法区分轴向应变和径向应变。为进一步提高形变监测精度,本文结合BOTDA与简支横梁原理,提出形变矢量化监测模型。
2.1 轴向形变与布里渊频移变化量关系
在变压器内部,为保证轴向压紧力,使用垫块将线圈等弧长地分成n段,可看成n段绕组绕段基本单元,进而可看成简支梁。基于材料力学,绕组截面上的内力有剪力和弯矩两种,其中,弯曲正应力与弯矩有关(轴向形变),而弯曲切应力与剪力有关(径向形变)。当该截面段的宽长之比大于5时,可将其看成纵向纤维互不挤压。此时,绕组截面上的点为单向应力状态。在静力学中,轴力是指作用在结构元件上的内力,是与杆件轴线相重合的内力。基于静力学,可知其轴力公式为
式中,FN为截面所受的正应力;E为弹性模量,是一个常数;ρ0为中性层曲率,当轴向应变一定时为常数;y为中性轴到受力点的距离;A为绕组的横截面积;Sz为截面对中性轴(受到弯折后长度不变的轴)的静矩。由于绕组截面只受剪力和弯矩影响,中性轴静矩Sz=0,可推出中性轴通过截面形心,且中性轴垂直于对称轴,因此在绕组截面中可确定中性轴位置。
将光纤布设在绕组线圈两边,取其微段示例,如图2所示。其中光纤纤芯到中性轴的距离称为中性轴距,设为d。
由图2可知,当绕组微段弯曲后,微段弯曲外侧被拉伸,长度变长,但其弯曲内侧受到挤压力作用,长度变短。光纤弯曲弧长为
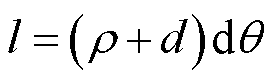 (3)
(3)
式中,l为光纤弯曲后的弧长;ρ为中性轴弧长所对应的半径;dθ为微段弯曲后所对应的圆心夹角。由弯曲前后中性轴长度不变可得
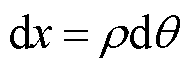 (4)
(4)
式中,dx为初始光纤微段长度,也为弯曲前后的中性轴微段长度。由应变定义式可得
式中,ε为光纤所受应变值;Dl为光纤形变前后的弧长差。即轴向形变一定时,简支绕饼横梁的曲率半径与中性轴距成正比。结合布里渊频移与温度、应变呈线性关系,当温度不敏感且假设初始应变为0时,可得
 (6)
(6)
式中,Dv为应变布里渊频移变化量。式(5)为简支绕饼横梁曲率与应变关系,联立式(5)和式(6)可得
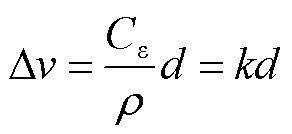 (7)
(7)
式中,k为应变布里渊曲率系数,k = Cε /ρ。由此可看出布里渊频移变化量与光纤到中性轴的距离呈线性关系。
2.2 径向形变与布里渊频移变化量关系
当简支绕饼横梁受到垂直轴向的均匀挤压时,绕组会沿直径发生径向应变,布设在绕组外表面的光纤被一同拉伸,中性轴距和轴向半径不发生改变。此时,多根光纤的径向应变及其布里渊频移变化量相等,即
式中, Dvxn为第n根光纤所测的径向应变布里渊频移变化量。根据布里渊频移变化量与应变呈线性关系可知,其径向应变在受力均匀状态下同样相等,即
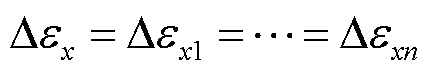 (9)
(9)
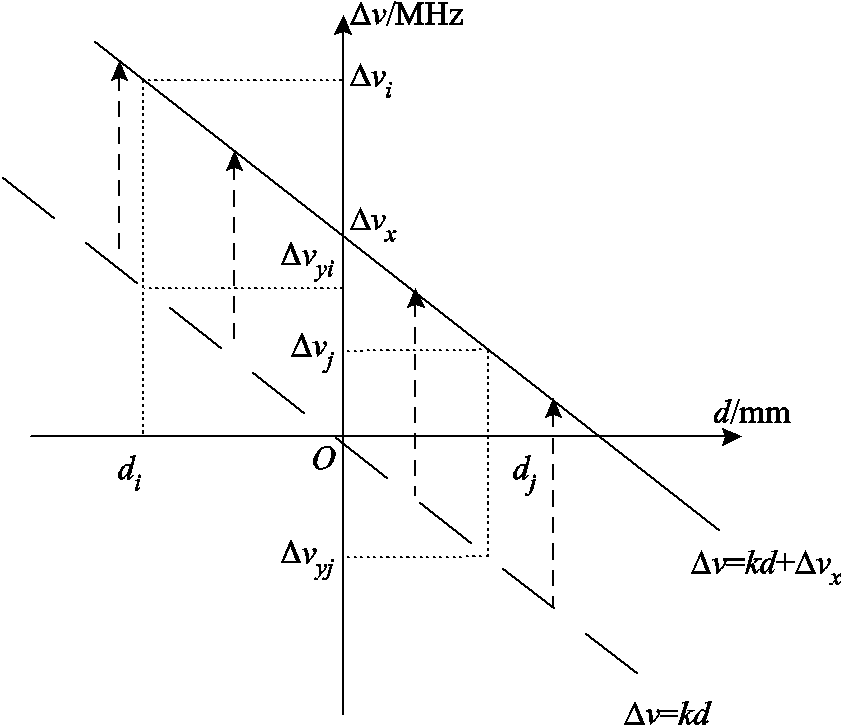
式中,Dεx为光纤的径向应变;Dεxn为第n根的光纤径向应变。当温度一定时,形变布里渊频移变化量与轴向、径向分量关系如图3所示,可知布里渊频移变化量为轴向应变布里渊频移变化量和径向应变布里渊频移变化量之和,且轴向应变布里渊频移变化量与中性轴距成正比,由此可得光纤的布里渊频移变化量为
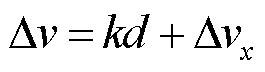 (10)
(10)
在实际工程应变中,绕饼横梁所受剪力不可能完全均匀,多根光纤的径向应变也应有细微差距。
2.3 形变矢量化解调
使用布里渊光时域分析技术,结合布里渊频移变化量与其分量关系式,提出了形变矢量化模型。若在绕组上布设n根光纤,使用BOTDA测得n根光纤的总布里渊频移值为
式中,v为总布里渊频移;vn为第n根光纤的布里渊频移。总形变可划分为径向形变和轴向形变,设n根光纤径向形变的总布里渊频移变化量为
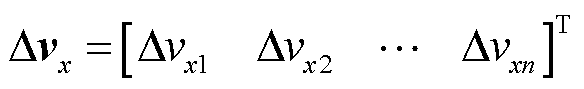 (12)
(12)
式中,Dvxn为第n根光纤所测的径向应变布里渊频移变化量。当变压器仅受到径向应变时,总布里渊频移变化量等于径向布里渊频移变化量,即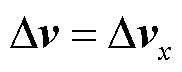 。设多根光纤的轴向应变布里渊频移变化量为
。设多根光纤的轴向应变布里渊频移变化量为
式中,Dvyn为第n根光纤所测的轴向应变布里渊频移变化量。当变压器受到轴向应变时,若多根光纤中性轴距相等,其轴向形变总和为0;若中性轴距不等,则通过布里渊频移变化量可得其轴向形变。总布里渊频移为轴向、径向分频移之和,由此可得各根光纤所监测形变的布里渊频移分量公式为
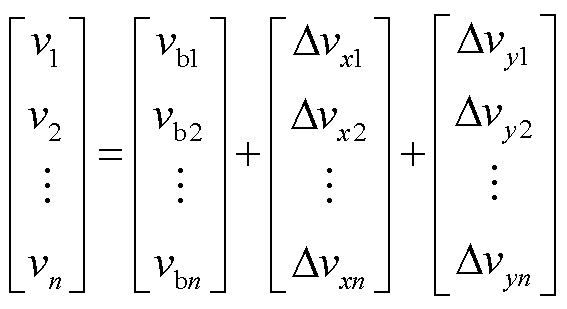 (14)
(14)
式中,vbn为各根光纤在形变点的初始布里渊频移量。至此可建立n根光纤布里渊频移的综合矩阵,其中径向形变的布里渊频移变化量相等;而对于初始布里渊频移数据,因室温恒定且暂无形变,温度不敏感,即其初始布里渊频移量也相等。基于此特性对上述矩阵两两做差,即得两根光纤的应变差值,表示为
式中,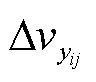 为两根光纤布里渊频移差值;vi和vj分别为第i根和第j根光纤监测的布里渊频移量;Dvyi和Dvyj分别为第i根和第j根光纤监测的轴向布里渊频移变化量。由于轴向应变与光纤偏移量具有线性关系,应变与中性轴距呈线性关系,可得
为两根光纤布里渊频移差值;vi和vj分别为第i根和第j根光纤监测的布里渊频移量;Dvyi和Dvyj分别为第i根和第j根光纤监测的轴向布里渊频移变化量。由于轴向应变与光纤偏移量具有线性关系,应变与中性轴距呈线性关系,可得
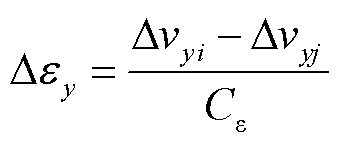 (16)
(16)
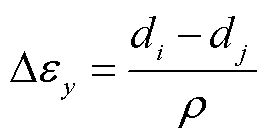 (17)
(17)
式中,Dεy为光纤所受轴向应变值;di和dj分别为第i根和第j根光纤的中性轴距。首先,联立式(16)与式(17)可得轴向布里渊频移与中性轴距具有线性关系,进而可得到应变布里渊曲率系数k;然后测量光纤中性轴距,标定光纤获得应变系数;最后结合计算所得的应变布里渊曲率系数即可获得轴向方向的应变,即
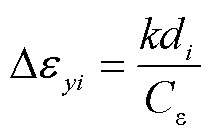 (18)
(18)
式中,Dεyi为第i根光纤所受的轴向应变。由总应变布里渊频移变化量减去轴向布里渊频移变化量即得径向布里渊频移变化量,再结合应变系数可求得径向方向应变为
联合径向应变与轴向应变即可得到最终的形变程度和方向,表示为
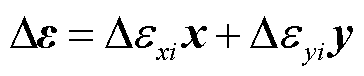 (20)
(20)
式中,Dε为变压器最终的形变矢量;x为径向形变方向;y为轴向形变方向。形变方向和大小最终构成绕组形变矢量化监测模型。
3 光纤复合导线实验与分析
3.1 光纤复合导线实验
由形变矢量化监测模型可知,当布设的光纤相对导线中性轴有一定距离时,通过两根光纤制成矢量化光纤传感器可完成轴向与径向形变的解调。
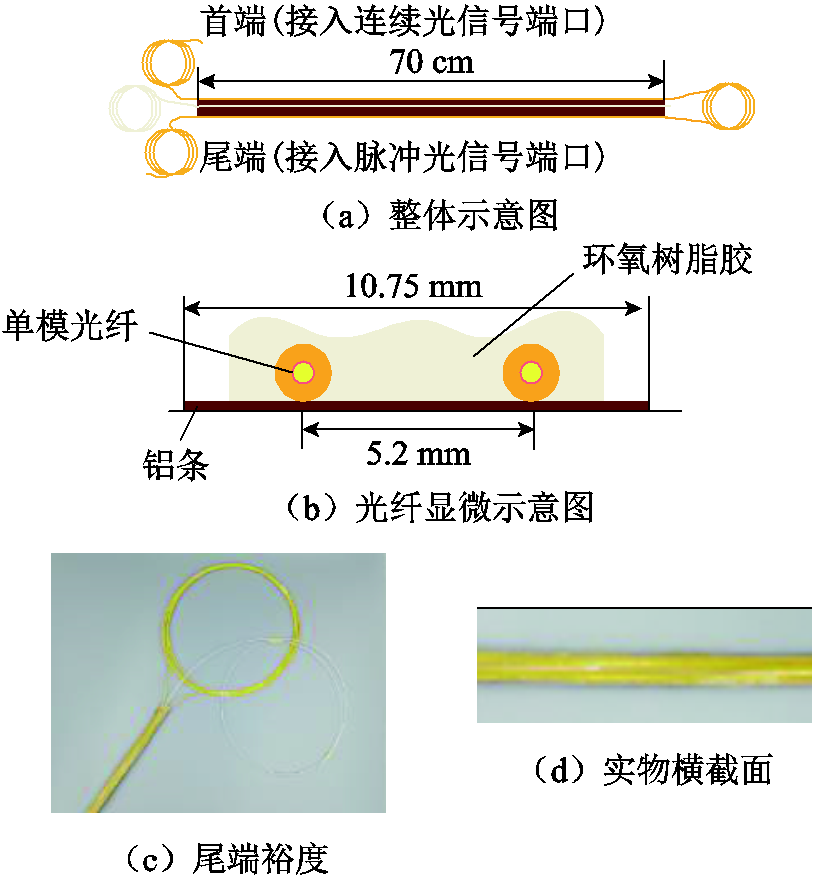
本实验使用一根长为72 cm、宽为10.75 mm、厚为5.52 mm的铝条导线。由于环氧树脂胶固化后不发脆,易弯曲,使用少许变压器用环氧树脂将光纤固定在铝条导线两边,可有效地防止绕组通电后光纤受电磁力振动而产生偏移。所选用光纤直径为0.9 mm,护套为Hytrel。Hytrel是一种热塑聚酯弹性体嵌段共聚物(Thermoplastic Polyester-Ether Elastomer, PTFE),因其电老化和热老化参数优于油浸绝缘纸,能够在干式变压器和油浸式变压器中稳定运用[23]。每根光纤粘贴长度为70 cm,同时在两根光纤间预留一定长度的松弛光纤以便定位,控制形变区域光纤总长为9 m,如图4所示。以接入连续光信号端口的光纤为首端光纤,接入脉冲光信号端口的光纤为尾端光纤。
应变为形变量与原始尺寸的比值,其定义式为
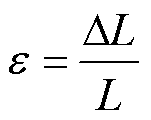 (21)
(21)
式中,DL为形变长度变化量;L为初始长度;ε为应变,无量纲,通常由百分数表示。由于某些形变量很小,通常为μm级,因此使用微应变με来表述微小的形变,即1ε=106με。
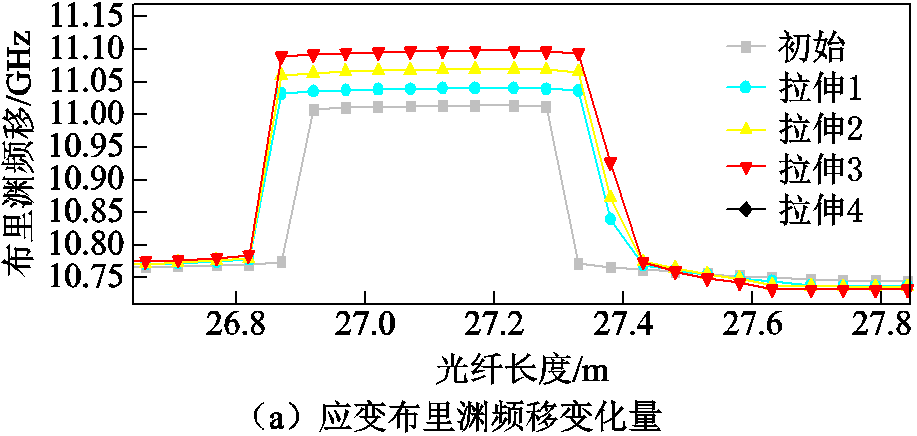
由于光纤应变系数受护套类型、出厂批次等多因素影响,为减小误差,标定光纤获得光纤应变系数。使用高精度位移拉力机,控制拉力机夹具间的光纤初始长度为352.66 mm,以步进为0.2 mm拉伸光纤获得应变值,通过BOTDA获得应变布里渊频移变化量,如图5所示。由式(21)计算拟合得到光纤系数为0.049 MHz/mε,拟合方差为0.999,拟合情况较好。
光纤相对铝条中性轴总距离为5.2 mm,单边光纤与中性轴距离分别为3.65 mm与1.55 mm。使用全自动拉/压力试验机施加形变,虎台钳固定铝条两端模拟垫块,有效地防止拉力机施加形变时导线偏移,通过空间分辨率为20 cm的BOTDA采集布里渊频移量,实验装置如图6所示。
使用BOTDA对铝条初始状态测量两次布里渊频移值。考虑施加形变后,铝条无法恢复原样,为控制变量以便后续验证,先使用拉力试验机对光纤施加径向形变,控制压力使得径向挠度变化至 5 mm,静止5 min以稳定拉力机所施加压力与形变,测量径向布里渊频移变化量作为后续检验数据。翻转铝条,使其轴向朝上施加压力并监测,每组实验改变压力后静置5 min使形变稳定,而后采集形变布里渊频移值。
3.2 实验数据处理
布里渊频移量与温度、应变均呈线性关系,光纤温度系数单位为MHz/℃,光纤应变系数单位为MHz/με。在室温环境下,温度稳定,变化量小于0.5℃,鉴于典型温度系数为1.1 MHz/℃,可得频移变化小于0.55 MHz;典型应变系数为0.05 MHz/ με[24],由于光纤应变为0~20 000 με,所对应的布里渊频移为1 000 MHz,因此在室温环境下实验时对温度不敏感。而在实际运行过程中,可在矢量光纤传感器中间并排布设多模光纤,完成对温度的解调,进而解调应变与其频移大小,同样可实现对温度不敏感。光纤复合导线实验结果如图7所示。
使用综合形变后的布里渊频移量减去初始状态布里渊频移量,取其最大形变布里渊频移变化量,结果见表1。而正负应变叠加时,其频移值逐渐减小,侧面验证了不同形变矢量叠加导致单根光纤存在监测误差大甚至监测不出的问题。
表1 综合应变布里渊频移变化量
Tab.1 Synthetic strain brillouin frequency shift
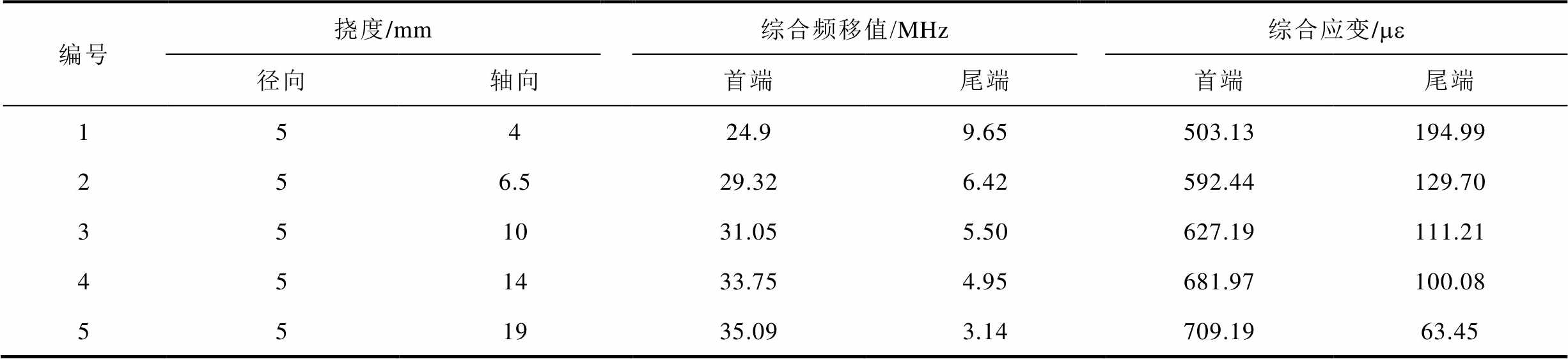
编号挠度/mm综合频移值/MHz综合应变/me 径向轴向首端尾端首端尾端 15424.99.65503.13194.99 256.529.326.42592.44129.70 351031.055.50627.19111.21 451433.754.95681.97100.08 551935.093.14709.1963.45
取首端与尾端光纤所测布里渊频移量与中性轴距建立坐标系,得到应变布里渊曲率系数见表2。
表2 应变布里渊曲率系数
Tab.2 Strain Brillouin frequency shift coefficient
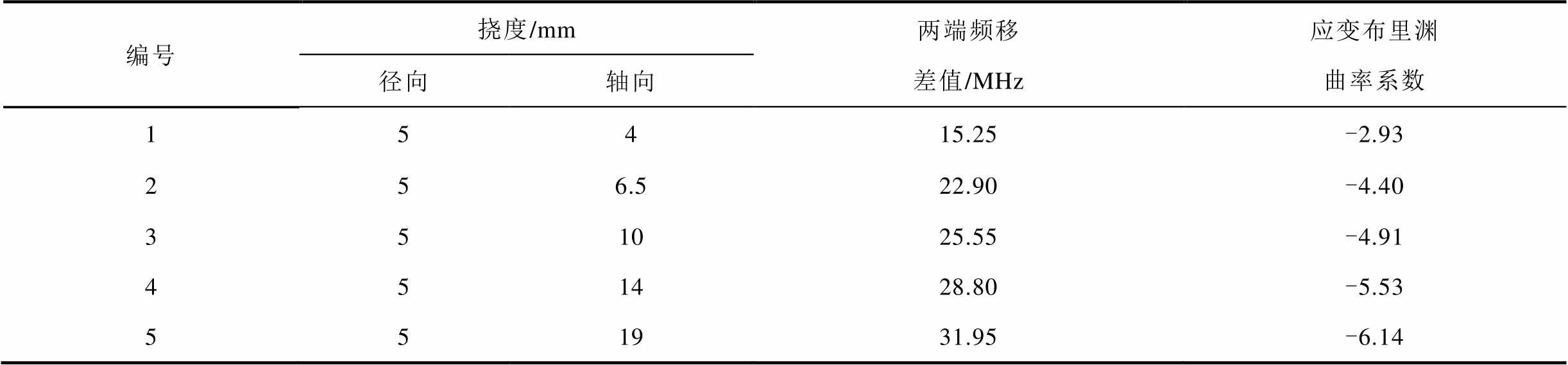
编号挠度/mm两端频移差值/MHz应变布里渊曲率系数 径向轴向 15415.25-2.93 256.522.90-4.40 351025.55-4.91 451428.80-5.53 551931.95-6.14
表2中数据验证了当施加形变与中性轴距一定时,应变布里渊系数的绝对值随着铝条应变的增大而增大。由应变布里渊系数与两端光纤中性轴距相乘得出两端光纤的轴向形变数据频移值,除以应变系数得到轴向微应变,见表3。
表3 轴向应变值
Tab.3 Axial strain values
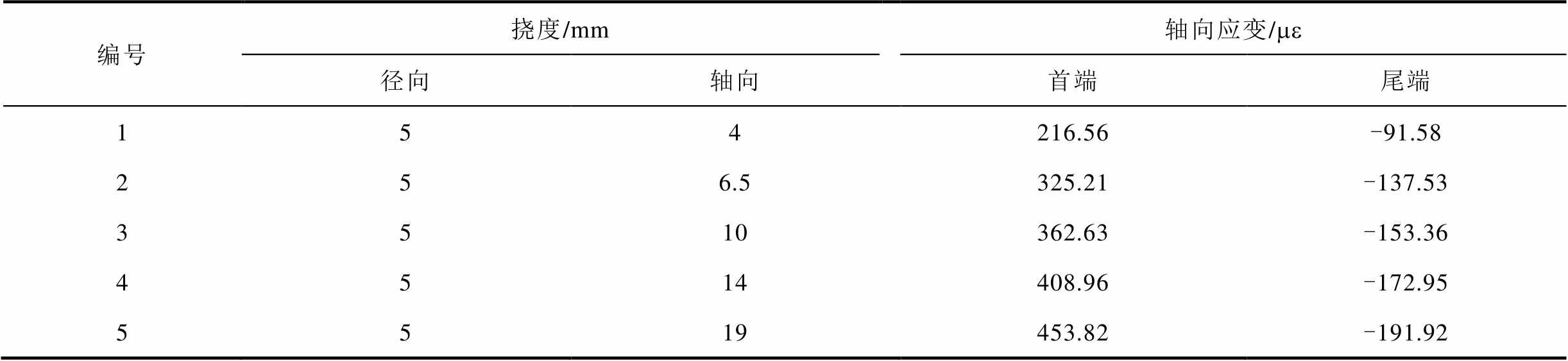
编号挠度/mm轴向应变/me 径向轴向首端尾端 154216.56-91.58 256.5325.21-137.53 3510362.63-153.36 4514408.96-172.95 5519453.82-191.92
由表3可知,首端光纤监测结果为正应变,尾端光纤监测结果为负应变。由布里渊频移量减去轴向形变布里渊频移量即可得到其径向形变布里渊频移量,进而由应变系数求得其径向应变值,见表4。
表4 径向应变值
Tab.4 Radial strain values
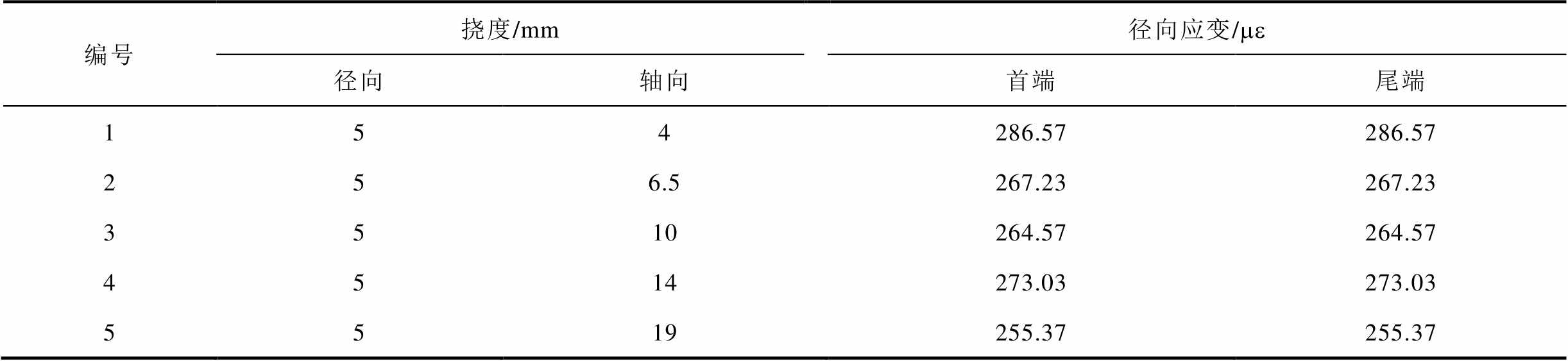
编号挠度/mm径向应变/me 径向轴向首端尾端 154286.57286.57 256.5267.23267.23 3510264.57264.57 4514273.03273.03 5519255.37255.37
由表4可知,径向应变均为正应变,结合轴向形变与径向形变及其方向可以获得其矢量化形变值(见式(20))。本实验矢量化监测结果见表5。
表5 矢量化形变值
Tab.5 Vectorization
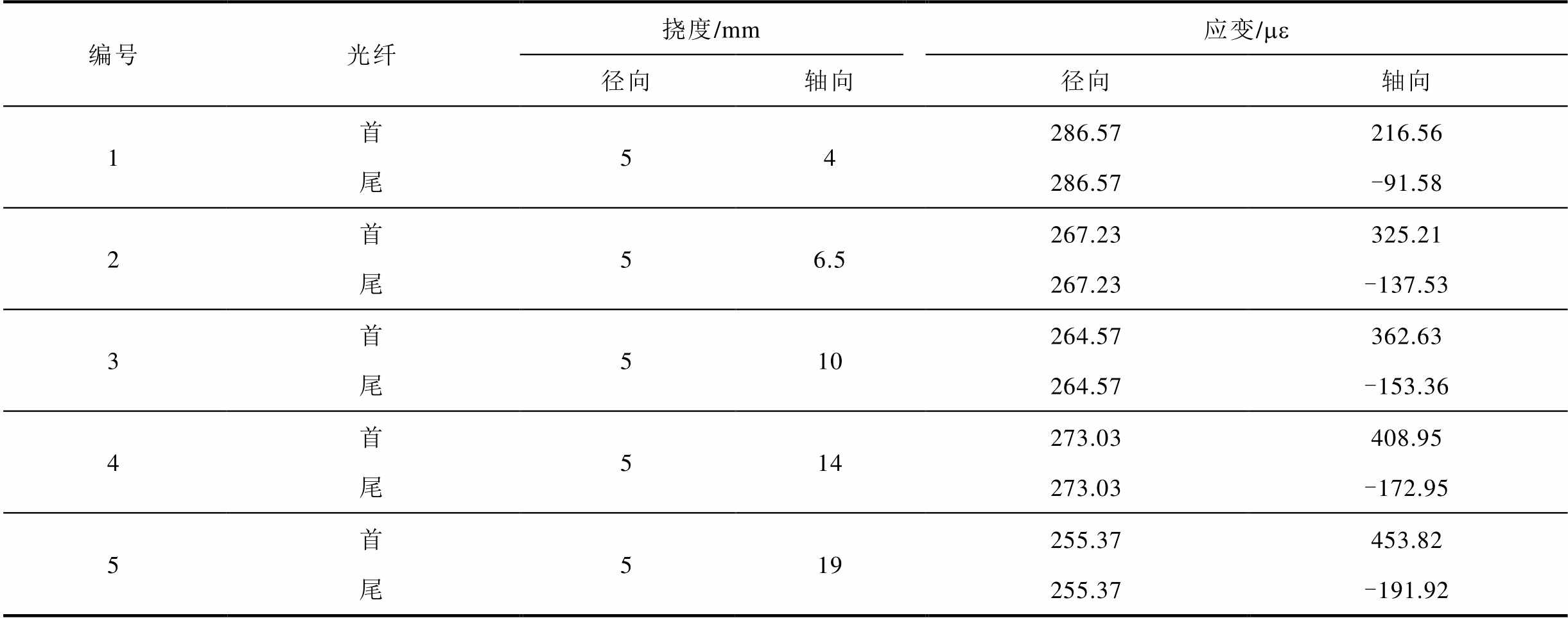
编号光纤挠度/mm应变/me 径向轴向径向轴向 1首54286.57216.56 尾286.57-91.58 2首56.5267.23325.21 尾267.23-137.53 3首510264.57362.63 尾264.57-153.36 4首514273.03408.95 尾273.03-172.95 5首519255.37453.82 尾255.37-191.92
3.3 矢量化数据分析
3.3.1 矢量化方向判定
基于光纤应变原理可知,光纤受到拉伸时,其应变为正应变;反之,光纤收到挤压时,其相对弧长缩短,应变为负应变。针对该原理特点,当明确光纤端口时,可通过应变结果判断其形变方向。
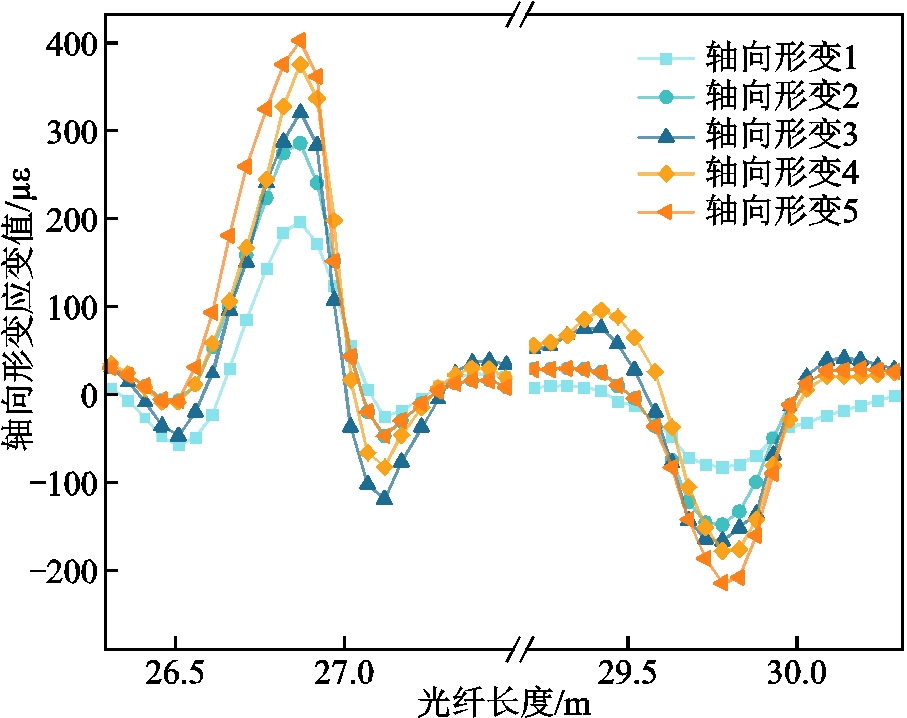
对铝条依次施加挠度为4、6.5、10、14、19 mm的轴向形变,并使用BOTDA完成监测,不同轴向挠度下的轴向形变应变值如图8所示。此时铝条向下偏移,首端光纤受拉伸作用发生正应变,尾端光纤受挤压发生负应变,符合规律。若施加向上位移,则其结果相反。由此可判定轴向形变方向。
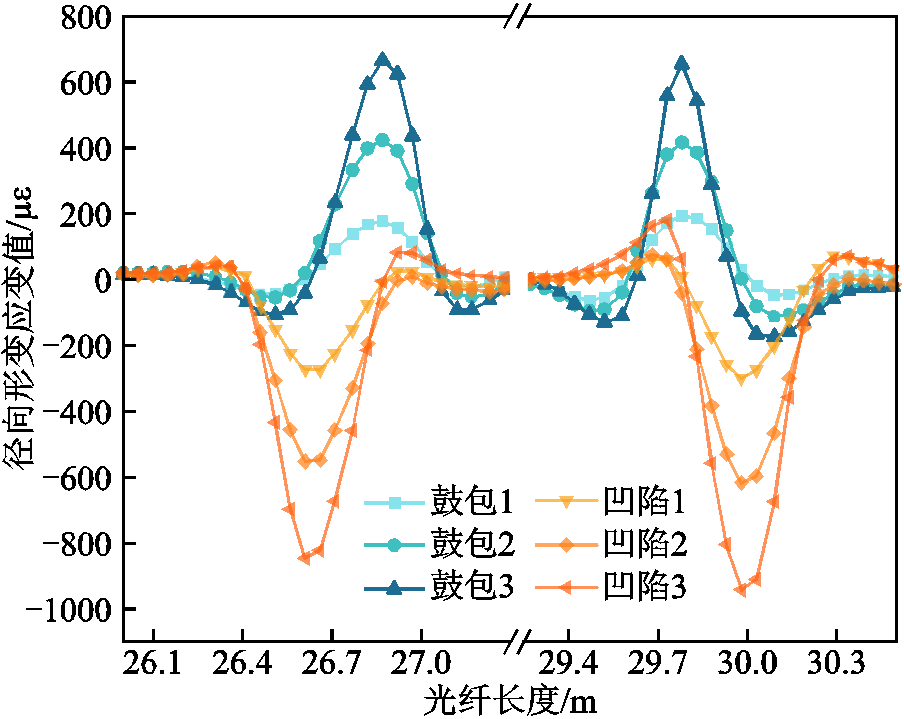
不同径向挠度实测情况如图9所示,当导线受径向拉伸形成鼓包时,其形变布里渊频移量为正数,即发生正应变,符合规律;当光纤受到挤压凹陷时,发生负应变,其值为负,由此可判定光纤径向形变方向。
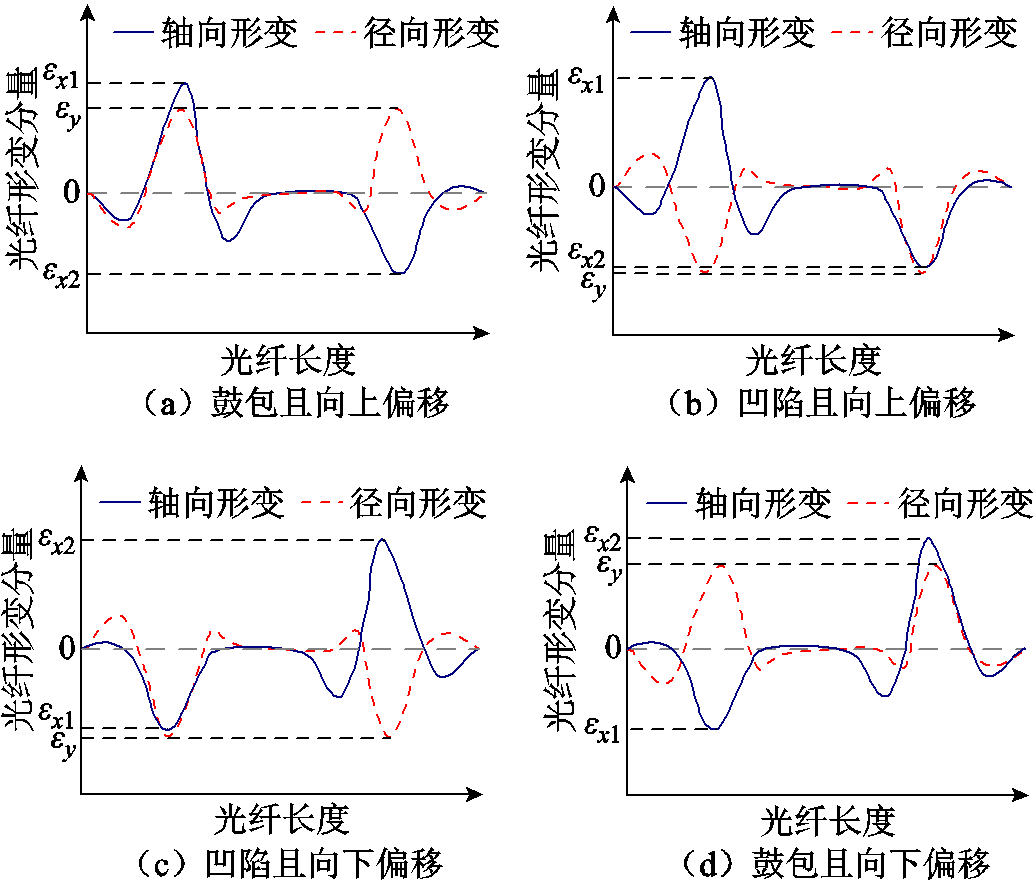
基于轴向与径向形变方向的特点,以首端光纤的应变分量正负值作为形变方向的判断依据,首端轴向形变为正值表示绕组发生向上偏移的形变;轴向形变为负值表示绕组发生向下偏移的形变。当首端径向形变为正值时,绕组发生鼓包;径向形变为负值时,绕组发生凹陷,四种情况示意图如图10所示,至此可通过矢量化形变方向判断其具体形变方向。由铝条实验可知其形变方向为鼓包且向上偏移。
3.3.2 轴向数据分析
使用实测轴向形变值与解调出的轴向形变值进行误差分析,评估其解调准确性。轴向形变检验量见表6。
表6 轴向形变检验量
Tab.6 Axial deformation test quantity
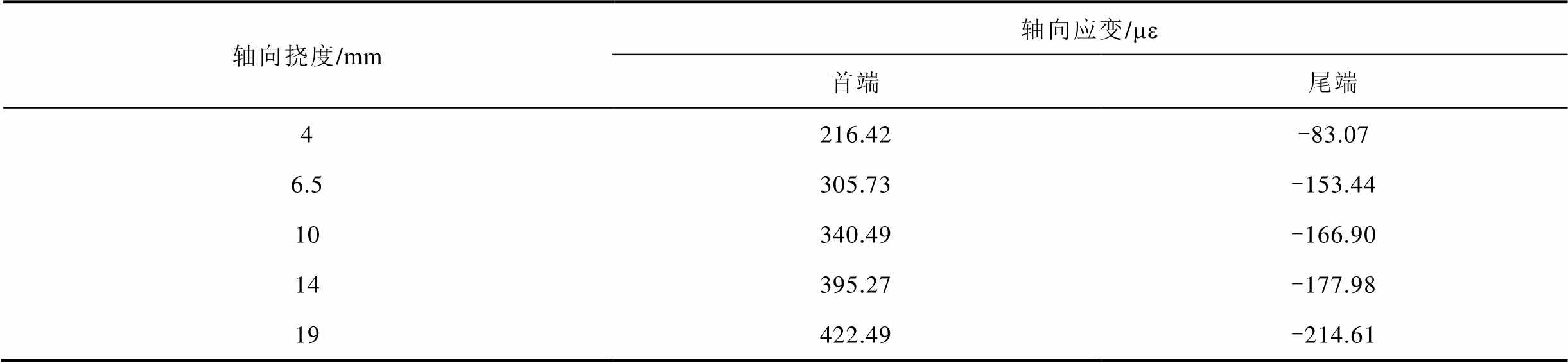
轴向挠度/mm轴向应变/me 首端尾端 4216.42-83.07 6.5305.73-153.44 10340.49-166.90 14395.27-177.98 19422.49-214.61
为定量评判实验的准确性,根据式(22)求其相对误差,并取每组数据误差均值,其结果见表7。
式中,Deryp为第p次实际应变监测值;Deyp为第p次解调应变值;m为实验次数。
由表7可得其轴向形变解调平均误差为6.60%,这是由于实验过程中,径向形变并不相等,径向形变差值也并入轴向形变差值中造成误差。此外,在布设光纤过程中环氧树脂胶涂抹不均导致光纤表面胶厚度不一致,受力不均使得其误差增大,但总体解调情况良好。
表7 轴向形变误差
Tab.7 Axial deformation error

轴向挠度/mm轴向形变误差(%) 45.16 6.58.37 107.31 143.15 198.99 平均值6.60
3.3.3 径向数据分析
在铝条实验中,施加挠度为5 mm的径向形变,测量其布里渊频移变化值与应变值可得其首端频移变化量为15.18 MHz,应变值为286.71με;其尾端频移变化量为13.76 MHz/με,应变值为278.06με。理想情况下光纤所测的径向应变相等,因此使用其均值代表径向挠度为5 mm的频移变化量与应变值。求得其应变均值为282.38με。依据式(22)对其求误差并取平均值,解得径向形变平均误差为5.88%。其误差主要由实际施加轴向形变时可能造成径向形变变化,且压力机压力轻微变动导致受力不均造成。
4 35 kV载纤绕组模型实验
为验证载纤绕组模型形变监测的可行性,检验实际应用有效性,本文选用某35 kV绕组作为布设对象,并对其随机施加形变,测量其相关数值并解调出矢量化形变量。
4.1 绕组实验
本文选用某35 kV绕组为监测对象,绕组模型直径为49.5 cm,共40饼,导线宽度为10.61 mm。表面布设方式因其分布式光纤预应变较小且不改变绕组原有结构的特性,最适合用于光纤布设[25]。基于此,在绕组外表面进行螺旋回绕式布设光纤。布设过程中,先通过导引装置将绕组导线包裹绝缘纸,避免光纤直接接触导线。回绕时,在光纤尾部预留一段光纤以便光纤定位,将光纤通过特定夹具固定在绕组宽面,保证光纤间距一致。先使用少许变压器用环氧树脂将光纤固定在导线宽面两边,再使用白布条斜向进行缠绕包裹固定。这种方式不会改变变压器原有的绝缘结构,同时能保证光纤和导线同步变形,且不受变压器油流和振动的影响,可满足干式变压器和油浸式变压器运行要求。
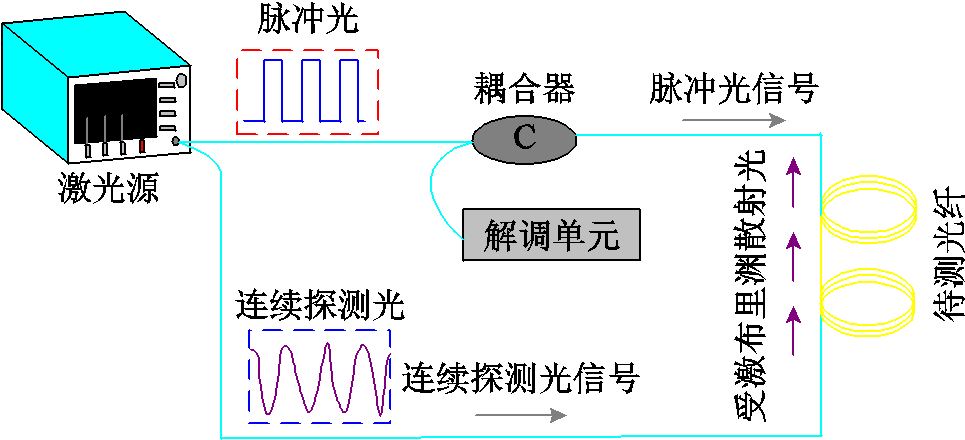
本实验中为观察绕组形变时光纤的形变状态,未在绕组布设光纤时使用白布条包裹,但缺少该步骤不会对实验结果造成影响。此外,为验证不同中轴距情况下模型的解调效果,在最外侧绕饼中的上段和中段选取2段线圈布设不同间距的光纤。考虑实际工程中温度与应变解调的问题,在两根光纤中间布设1条多模光纤,以实现变压器运行时对温度不敏感。测量线圈1布设光纤间距为1.68 mm与3.72 mm,线圈2布设光纤间距为1.34 mm与 3.06 mm。绕组光纤两端分别接入两盘光纤盘,以防端面反射。最终将光纤首尾两端接入BOTDA系统。实验设备连接示意图如图11所示。
在室温情况下测量两组初始状态布里渊频移量。利用垫块对其施加鼓包形变,单个垫块厚度为1.9 mm,计算总的垫块厚度得出轴向挠度。稳定后施加外力使得绕饼向下或向上偏移,如图12所示。使用BOTDA测量两组形变后的数值,并用卷尺与游标卡尺测量其挠度。
4.2 绕组实验数据处理
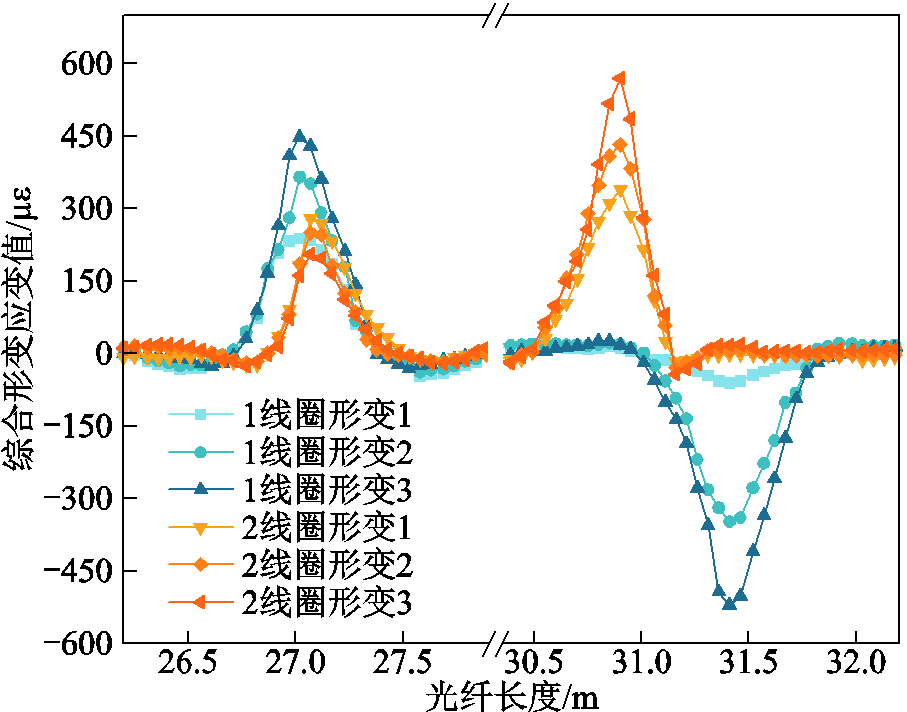
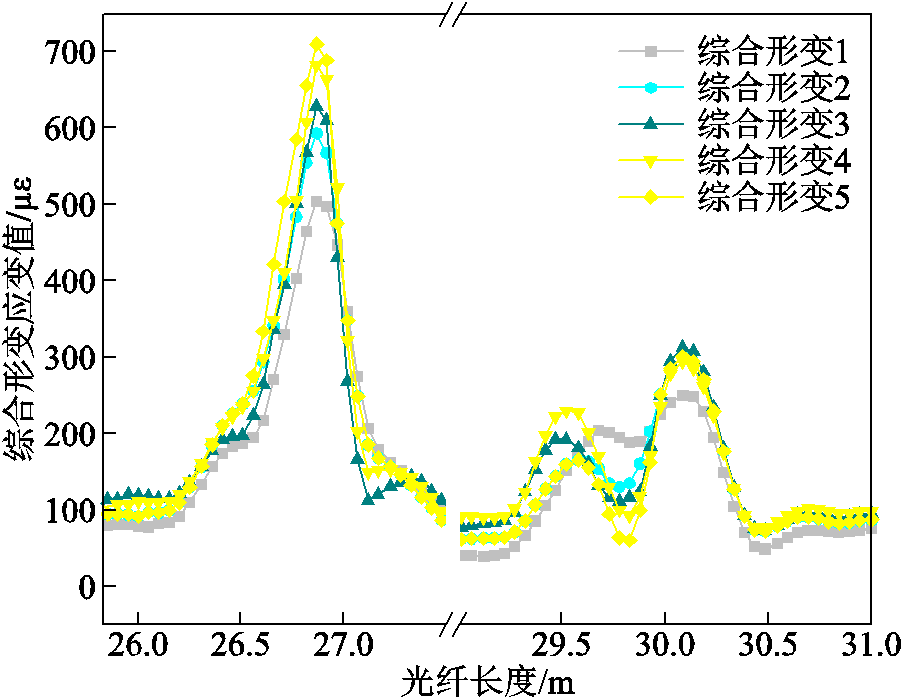
分别在线圈1施加微小的径向形变与不同程度的轴向形变3处,在线圈2施加较大的径向形变与不同程度的轴向形变3处,测量得到综合形变应变值如图13所示。在室温环境下施加形变并测量,由于环境相对温差小且矢量化光纤传感器处于同一区域,二者频移值相减可去除温度影响。
依据矢量化形变解调算法,先求解光纤形变频移与应变差值见表8。表中,编号1~3为线圈1形变,编号4~6为线圈2形变。
表8 绕组综合形变
Tab.8 Composite winding deformation
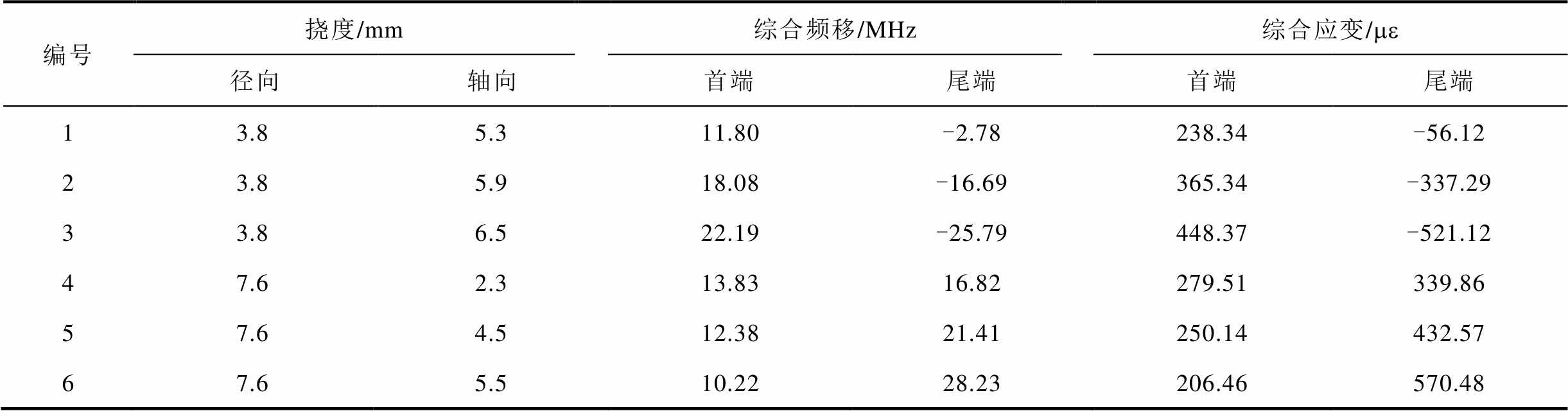
编号挠度/mm综合频移/MHz综合应变/me 径向轴向首端尾端首端尾端 13.85.311.80-2.78238.34-56.12 23.85.918.08-16.69365.34-337.29 33.86.522.19-25.79448.37-521.12 47.62.313.8316.82279.51339.86 57.64.512.3821.41250.14432.57 67.65.510.2228.23206.46570.48
取频移变化值与各自中性轴距建立坐标系,求取应变布里渊曲率系数见表9。绕组1为施加向上轴向形变,其应变布里渊曲率系数为负数;绕组2为施加向下轴向形变,其系数为正。当BOTDA的输入接口与光纤输入端保持一致时,系数正负反映轴向频移方向。
表9 绕组应变布里渊曲率系数
Tab.9 Brillouin curvature coefficient of winding strain
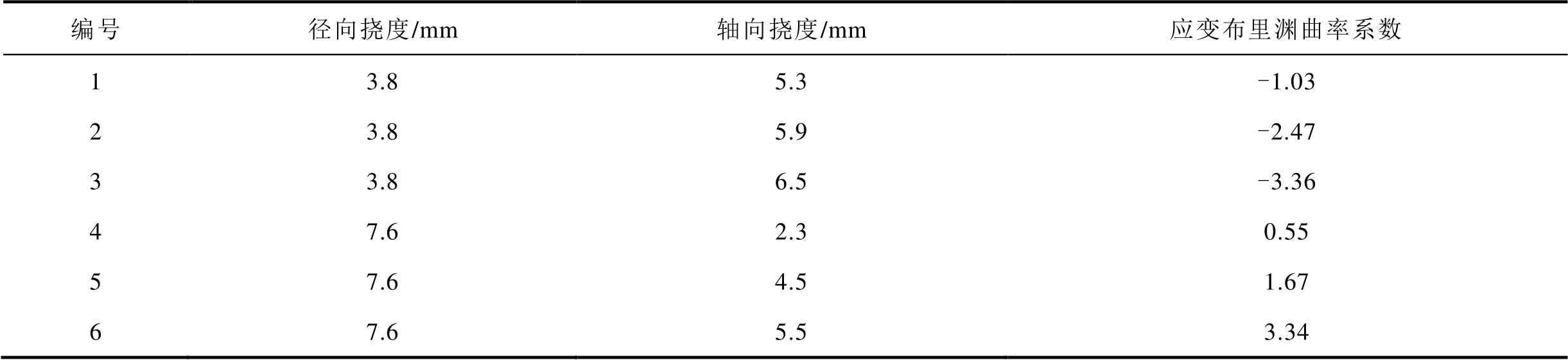
编号径向挠度/mm轴向挠度/mm应变布里渊曲率系数 13.85.3-1.03 23.85.9-2.47 33.86.5-3.36 47.62.30.55 57.64.51.67 67.65.53.34
由应变布里渊曲率系数乘以各根光纤中性轴距求得轴向应变频移,再乘以应变系数得出绕组轴向应变值,见表10。
表10 绕组轴向形变
Tab.10 Axial deformation of winding
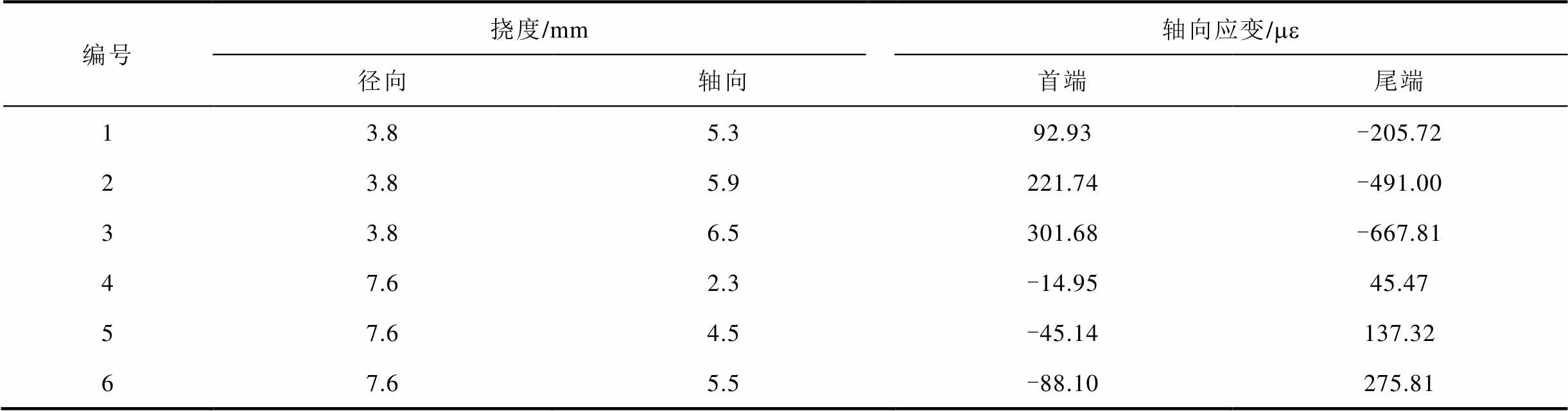
编号挠度/mm轴向应变/me 径向轴向首端尾端 13.85.392.93-205.72 23.85.9221.74-491.00 33.86.5301.68-667.81 47.62.3-14.9545.47 57.64.5-45.14137.32 67.65.5-88.10275.81
总布里渊频移值减去轴向频移值得到径向布里渊频移值,再除以应变系数得径向应变值,具体结果见表11。
表11 绕组径向形变
Tab.11 Winding radial deformation
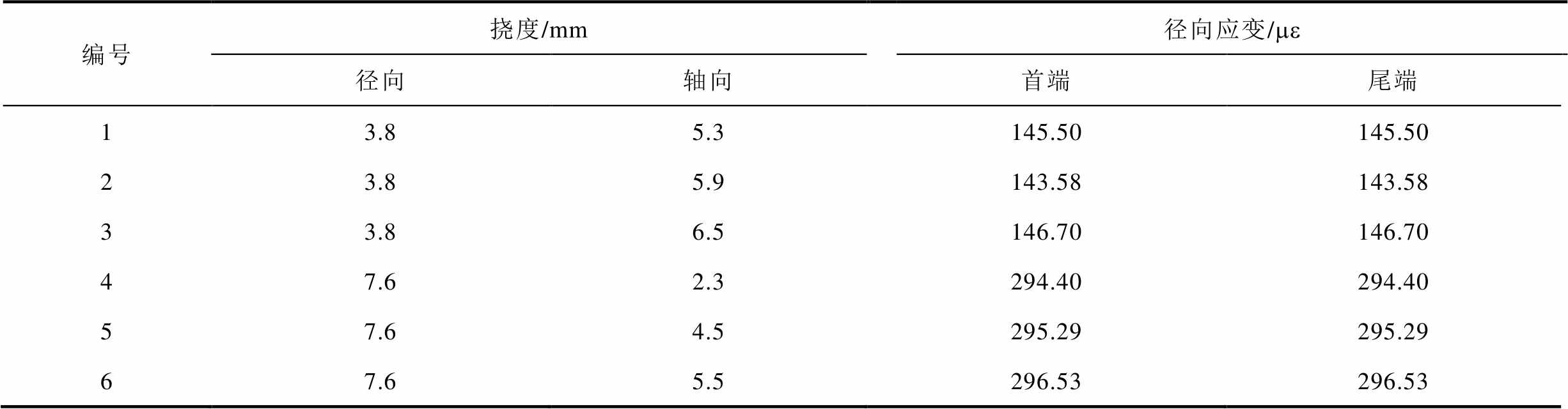
编号挠度/mm径向应变/me 径向轴向首端尾端 13.85.3145.50145.50 23.85.9143.58143.58 33.86.5146.70146.70 47.62.3294.40294.40 57.64.5295.29295.29 67.65.5296.53296.53
解调方向与结果见表12。由结果象限可知,形变1~3为鼓包上移,形变4~6为不同程度的鼓包下移。与解调结论相符,印证了矢量化形变理论,可实现实际工程运用。
表12 绕组形变结果
Tab.12 Winding deformation result
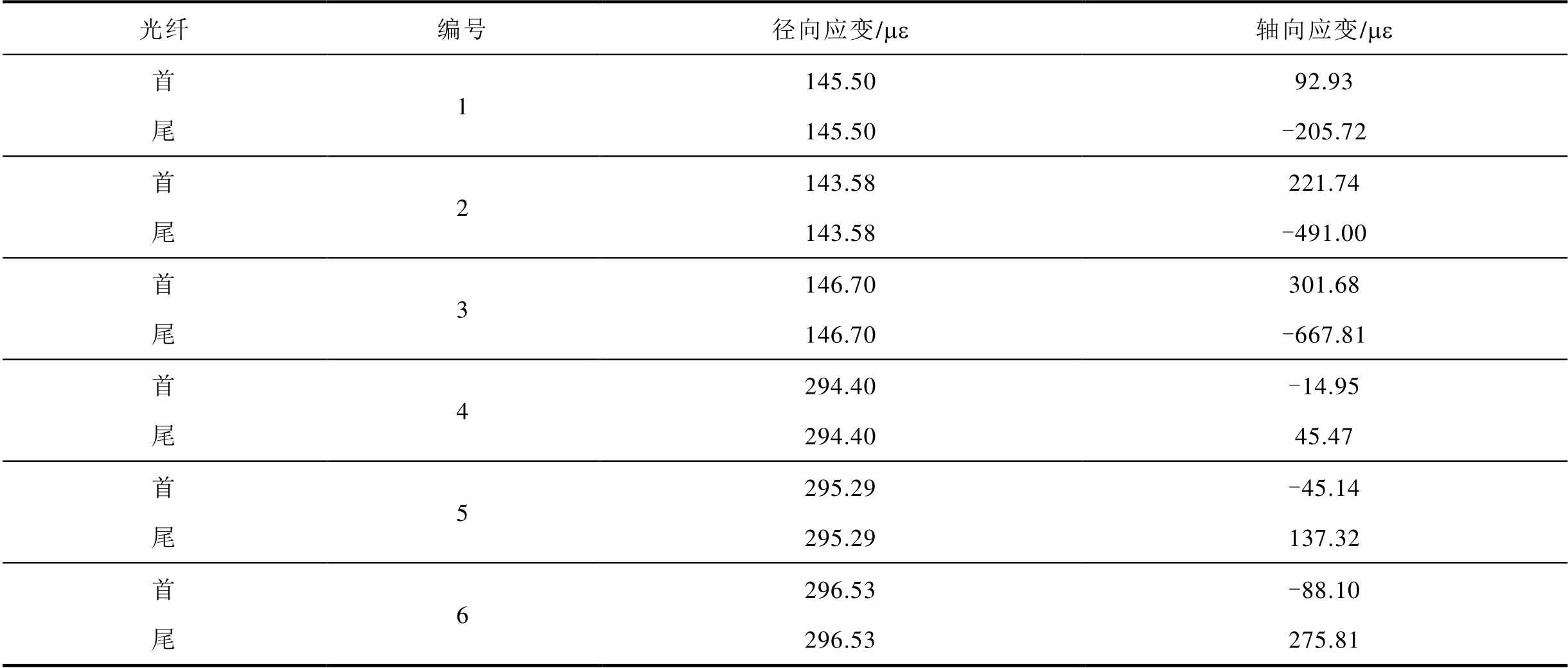
光纤编号径向应变/me轴向应变/me 首1145.5092.93 尾145.50-205.72 首2143.58221.74 尾143.58-491.00 首3146.70301.68 尾146.70-667.81 首4294.40-14.95 尾294.4045.47 首5295.29-45.14 尾295.29137.32 首6296.53-88.10 尾296.53275.81
4.3 误差分析
为定量分析绕组形变解调误差,以光纤实测应变值为理想值,对解调数据进行误差分析,实测应变值见表13。表中形变方向的正负值与解调结果正负值一致,因此验证了形变1~3为鼓包上移,形变4~6为鼓包下移。
表13 绕组实测形变结果
Tab.13 The measured deformation result of winding
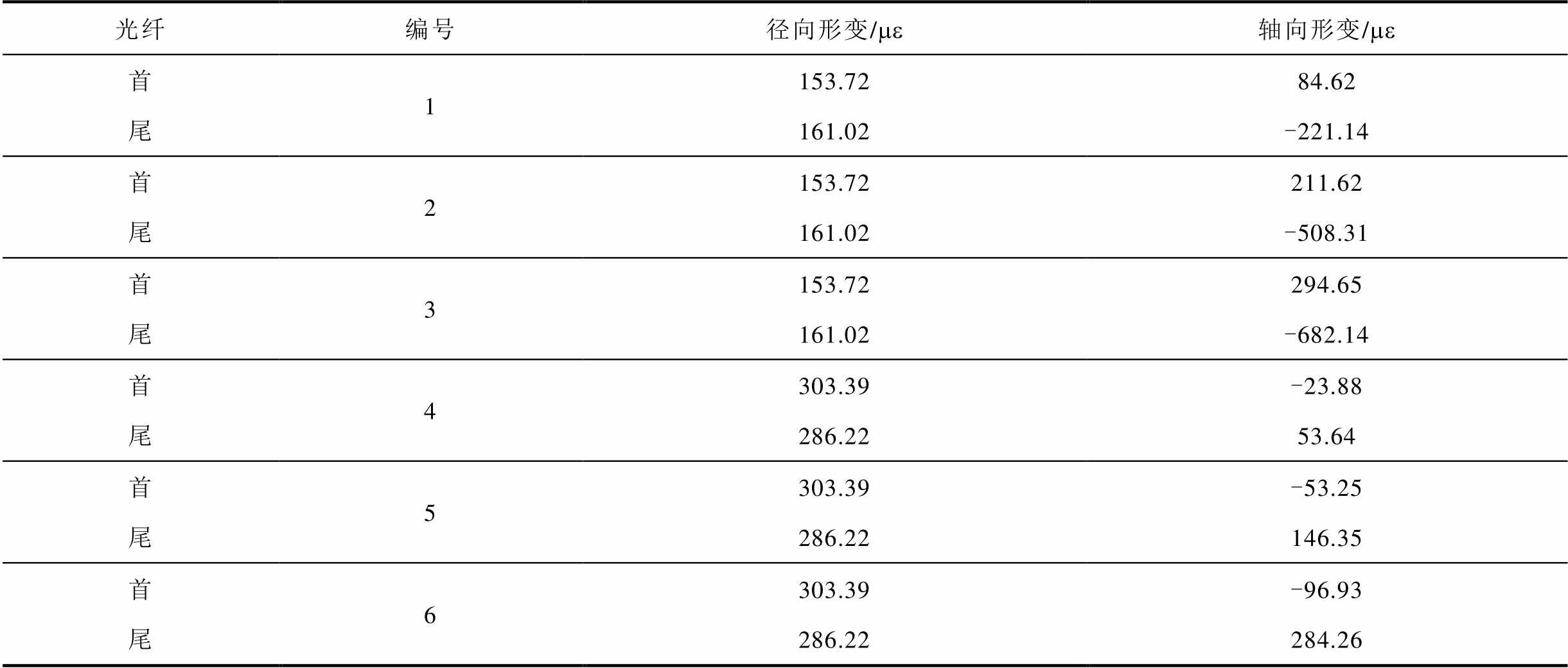
光纤编号径向形变/me轴向形变/me 首1153.7284.62 尾161.02-221.14 首2153.72211.62 尾161.02-508.31 首3153.72294.65 尾161.02-682.14 首4303.39-23.88 尾286.2253.64 首5303.39-53.25 尾286.22146.35 首6303.39-96.93 尾286.22284.26
以式(22)定量计算其绕组实验误差,结果见表14。由表14可看出,轴向平均误差为9.63%,这是由于AB胶涂抹不均导致径向形变挠度与监测所得应变值有微小差异,且其径向应变差值也算入轴向形变中所导致。此外,监测过程中还受设备采集误差影响,但解调效果良好。径向平均误差为5.18%,这主要由施加压力不均且胶面厚度不均导致。
表14 绕组形变误差
Tab.14 Winding deformation error
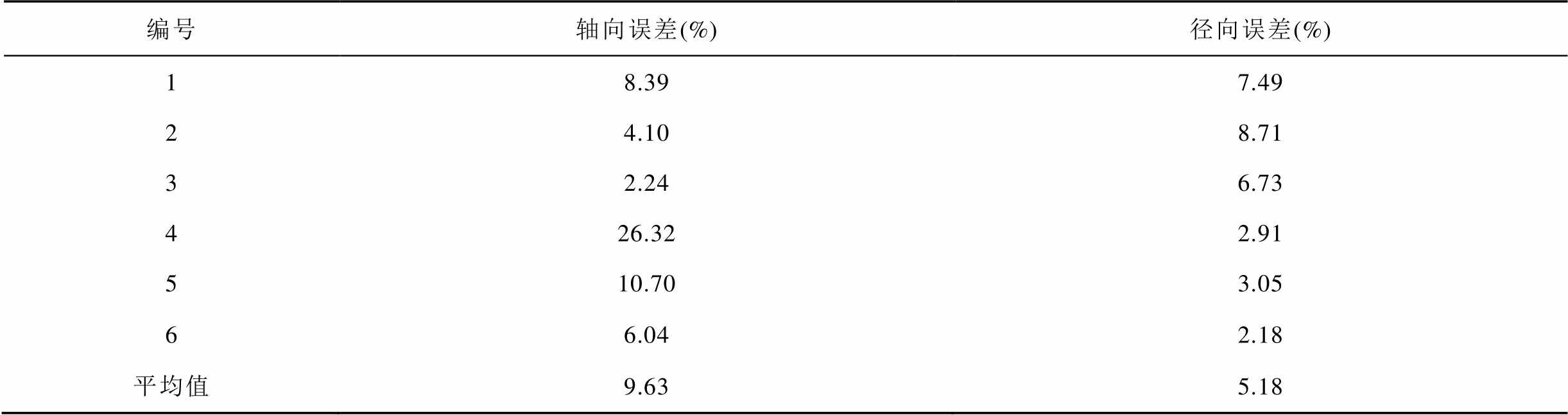
编号轴向误差(%)径向误差(%) 18.397.49 24.108.71 32.246.73 426.322.91 510.703.05 66.042.18 平均值9.635.18
5 结论
采用传统单根光纤监测形变时,因光纤布设位置不同存在无法监测轴向形变或监测形变较实际形变偏小等问题。为实现绕组轴向形变和径向形变的精细化监测,本文提出了一种基于简支绕饼横梁解调算法的变压器绕组形变矢量化监测模型,并通过光纤复合导线实验和35 kV载纤绕组模型实验数据分析,证明了该模型的有效性,得出以下结论:
1)绕组线圈可简化为简支绕饼横梁,结合材料力学得出轴向形变时光纤的中性轴与应变布里渊频移量呈线性关系,径向形变时2根光纤应变布里渊频移量几乎相等,可得应变布里渊频移量与其轴向、径向分量的关系式,推导出光纤矢量化形变解调模型。
2)在光纤复合导线实验中设计了矢量化光纤传感器,并将其布设在铝条上模拟绕组导线,完成了对轴向形变和径向形变的监测,且验证了导线鼓包和向上偏移为正应变,凹陷和向下偏移为负应变,对监测结果的正负判定可明确其内部形变方向,结果所得导线轴向形变平均误差为6.60%,径向形变平均误差为5.88%。
3)在不改变变压器绝缘结构的前提下对35 kV绕组完成了光纤布设,进行了内置光纤的35 kV绕组形变监测实验,得到其轴向形变平均误差为9.63%,径向形变平均误差为5.18%,主要由受力不均与设备采集误差导致,但总体误差较小,且在形变增大后趋于稳定,验证了绕组形变矢量化监测模型的可行性,实现了绕组形变具体方向和大小解调,可进一步提高绕组形变程度的监测精度。
参考文献
[1] 刘道生, 周春华, 丁金, 等. 变压器纳米改性油纸复合绝缘研究综述[J]. 电工技术学报, 2023, 38(9): 2464-2479, 2490. Liu Daosheng, Zhou Chunhua, Ding Jin, et al. Research overview of oil-paper composite insulation modified by nano particles for transformer[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2464-2479, 2490.
[2] 律方成, 汪鑫宇, 王平, 等. 基于振动偏离及加权熵的多次短路冲击下变压器绕组机械形变辨识[J]. 电工技术学报, 2023, 38(11): 3022-3032. Lü Fangcheng, Wang Xinyu, Wang Ping, et al. Mechanical deformation identification of transformer winding under multiple short-circuit impacts based on vibration deviation and weighted entropy[J]. Transactions of China Electrotechnical Society, 2023, 38(11): 3022-3032.
[3] Bagheri M, Naderi M S, Blackburn T. Advanced transformer winding deformation diagnosis: moving from off-line to on-line[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2012, 19(6): 1860-1870,
[4] 吴立增, 朱永利, 苑津莎. 基于贝叶斯网络分类器的变压器综合故障诊断方法[J]. 电工技术学报, 2005, 20(4): 45-51. Wu Lizeng, Zhu Yongli, Yuan Jinsha. Novel method for transformer faults integrated diagnosis based on Bayesian network classifier[J]. Transactions of China Electrotechnical Society, 2005, 20(4): 45-51.
[5] Nosratian Ahour J, Seyedtabaie S, Gharehpetian G B. Modified transformer winding ladder network model to assess non-dominant frequencies[J]. IET Electric Power Applications, 2017, 11(4): 578-585.
[6] Narayana G S, Badgujar K P, Kulkarni S V. Factorisation-based transfer function estimation technique for deformation diagnostics of windings in transformers[J]. IET Electric Power Applications, 2013, 7(1): 39-46.
[7] Rahbarimagham H, Esmaeili S, Gharehpetian G B. Determination of transformer HV winding axial displacement occurrence, direction, and extent using time-domain analysis of UWB signals[J]. IET Science, Measurement & Technology, 2018, 12(4): 514-520.
[8] 曹辰, 徐博文, 李辉. 基于振动与电抗信息的变压器绕组形变状态综合监测方法[J]. 高电压技术, 2022, 48(4): 1518-1530. Cao Chen, Xu Bowen, Li Hui. Composite monitoring method for the state of transformer winding deformation based on vibration and reactance information[J]. High Voltage Engineering, 2022, 48(4): 1518-1530.
[9] 杜厚贤, 刘昊, 雷龙武, 等. 基于振动信号多特征值的电力变压器故障检测研究[J]. 电工技术学报, 2023, 38(1): 83-94. Du Houxian, Liu Hao, Lei Longwu, et al. Power transformer fault detection based on multi-eigenvalues of vibration signal[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 83-94.
[10] 陈起超, 张伟超, 白仕光, 等. 非本征光纤法-珀传感器局部放电检测研究进展[J]. 电工技术学报, 2022, 37(5): 1305-1320. Chen Qichao, Zhang Weichao, Bai Shiguang, et al. Research progress of extrinsic fiber fabry-perot interferometer sensor in partial discharge detection[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1305-1320.
[11] Luo Jianbin, Hao Yanpeng, Ye Qing, et al. Development of optical fiber sensors based on Brillouin scattering and FBG for on-line monitoring in overhead transmission lines[J]. Journal of Lightwave Technology, 2013, 31(10): 1559-1565.
[12] 秦数棋. 基于光纤传感的电力变压器运行状态监测方法[J]. 自动化应用, 2022(10): 1-3, 7. Qin Shuqi. Monitoring method of power transformer running state based on optical fiber sensing[J]. Automation Application, 2022(10): 1-3, 7.
[13] 刘宏亮, 高树国, 孙路, 等. 基于布拉格光纤传感的变压器绕组多次短路冲击应变[J]. 科学技术与工程, 2022, 22(35): 15631-15640. Liu Hongliang, Gao Shuguo, Sun Lu, et al. Impact strain of transformer winding multiple short circuit based on Bragg fiber sensor[J]. Science Technology and Engineering, 2022, 22(35): 15631-15640.
[14] 刘云鹏, 步雅楠, 田源, 等. 基于分布式光纤传感的变压器绕组变形检测与故障识别可行性研究[J]. 高电压技术, 2019, 45(5): 1483-1489. Liu Yunpeng, Bu Yanan, Tian Yuan, et al. Feasibility study on transformer winding deformation detection and fault identification based on distributed optical fiber sensing[J]. High Voltage Engineering, 2019, 45(5): 1483-1489.
[15] 刘云鹏, 李欢, 高树国, 等. 分布式光纤传感在大型变压器温度和绕组变形监测中的应用研究[J]. 中国电机工程学报, 2022, 42(16): 6126-6135, 6186. Liu Yunpeng, Li Huan, Gao Shuguo, et al. Research on application of distributed optical fiber sensing in monitoring of temperature and winding deformation of large transformer[J]. Proceedings of the CSEE, 2022, 42(16): 6126-6135, 6186.
[16] 刘云鹏, 李欢, 田源, 等. 基于分布式光纤传感的绕组变形程度检测[J]. 电工技术学报, 2021, 36(7): 1347-1355. Liu Yunpeng, Li Huan, Tian Yuan, et al. Winding deformation detection based on distributed optical fiber sensing[J]. Transactions of China Electro-technical Society, 2021, 36(7): 1347-1355.
[17] 杨志, 黄雯利, 赵丽娟. 光纤传感技术在油浸式电力变压器状态监测应用的研究进展[J]. 高压电器, 2023, 59(6): 137-146. Yang Zhi, Huang Wenli, Zhao Lijuan. Research progress of fiber-optic sensing technology in condition monitoring and application in oil-immersed power transformer[J]. High Voltage Apparatus, 2023, 59(6): 137-146.
[18] 肖海, 刘云鹏, 庄新宇, 等. 光纤复合型110 kV油纸套管研制及内部温度分布特性[J]. 高电压技术, 2023, 49(9): 3946-3955. Xiao Hai, Liu Yunpeng, Zhuang Xinyu, et al. Development and internal temperature distribution characteristics of 110 kV optical fibers composite oil-impregnated paper bushing[J]. High Voltage Engineering, 2023, 49(9): 3946-3955.
[19] Susa D, Nordman H. A simple model for calculating transformer hot-spot temperature[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1257-1265.
[20] Horiguchi T, Tateda M. BOTDA-nondestructive measurement of single-mode optical fiber attenuation characteristics using Brillouin interaction: theory[J]. Journal of Lightwave Technology, 1989, 7(8): 1170-1176.
[21] 闫晨光, 张芃, 徐雅, 等. 换流变压器有载分接开关级间短路故障差动保护动作特性[J]. 电工技术学报, 2023, 38(21): 5878-5888, 5912. Yan Chenguang, Zhang Peng, Xu Ya, et al. Differential protection performance for converter transformer intertap short-circuit faults in on-load tap changers[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5878-5888, 5912.
[22] 薛博. 基于布里渊散射效应的分布式光纤测温系统研究[D]. 太原: 太原理工大学, 2019. Xue Bo. Research on distributed optical fiber temperature measurement system based on Brillouin scatering efect[D]. Taiyuan: Taiyuan University of Technology, 2019.
[23] 刘云鹏, 田源, 王博闻, 等. 光纤护套材料在变压器油中的电老化特性研究[J]. 绝缘材料, 2019, 52(2): 52-57. Liu Yunpeng, Tian Yuan, Wang Bowen, et al. Study on electrical ageing characteristics of optical fiber sheath material in transformer oil[J]. Insulating Materials, 2019, 52(2): 52-57.
[24] Hong Chengyu, Zhang Yifan, Li Guowei, et al. Recent progress of using Brillouin distributed fiber optic sensors for geotechnical health monitoring[J]. Sensors and Actuators A: Physical, 2017, 258: 131-145.
[25] 高树国, 刘云鹏, 贺鹏, 等. 不同敷设方式对分布式光纤监测变压器绕组变形的影响研究[J]. 高压电器, 2018, 54(11): 253-259. Gao Shuguo, Liu Yunpeng, He Peng, et al. Research on the influence of different laying modes on transformer winding deformation of distributed optical fiber monitoring[J]. High Voltage Apparatus, 2018, 54(11): 253-259.
Vectorization Monitoring Model of Transformer Winding Deformation Based on Simply Supported Winding Beam Algorithm
Fan Xiaozhou1 Yuan Jieping1 Xue Feng2 Wang Xiangnü2 Lü Fancheng1 GengJianghai1
(1. Hebei Provincial Key Laboratory of Power Transmission Equipment Security Denfense North China Electric Power University Baoding 071003 China 2. Guangdong Power Grid Limited Liability Company Dongguan Power Supply Bureau Dongguan 523000 China)
Abstract Winding deformation is one of the important causes of transformer failure and is the focus of transformer condition monitoring. To achieve accurate monitoring of the direction and degree of transformer winding deformation, this paper combines the principle of a simple beam with the Brillouin optical time-domain analysis technique and proposes a vectorized monitoring algorithm for transformer winding deformation.
Firstly, based on the theoretical derivation of material mechanics, the Brillouin frequency shift of axial deformation is proportional to the distance from the optical fiber to the neutral axis, and the Brillouin frequency shift of radial deformation is equal to the law, and the relationship between the Brillouin frequency shift and its axial and radial components is established, and the Brillouin optical time-domain analysis is combined to establish a vectorized monitoring model of the deformation of transformer windings that can be used in actual operation.
The vectorized fiber optic sensors are designed, and the fiber optic composite conductor model is built on a single conductor. 5 sets of axial and radial deformations of different degrees are applied by a high-precision tensile machine, and the deformation monitoring is completed with the help of the Brillouin optical time-domain reflection technology, and the result verifies that the conductor is subjected to the bulging and upward deviation as the positive strain, and the depression and downward deviation as the negative strain, and the coordinate system of the direction of deformation is constructed, and the deformation direction determination can be achieved by the demodulation result. The deformation direction can be determined by the demodulation results, calculating the experimental error of the conductor axial deformation monitoring error average value of 6.60%, radial deformation monitoring error average value of 5.88%, the analysis of the error caused by the high-precision press slight jitter and uneven application of the epoxy resin adhesive, but demodulation effect is generally good, to achieve the deformation of the fiber optic composite conductor direction and degree of monitoring.
To effectively prevent the fiber optic offset caused by vibration when the transformer is running without changing the internal insulation structure of the transformer, the fiber optic is fixed on the coil by using epoxy resin and insulating paper specially designed for transformers, and the 35 kV winding model with built-in vectorized fiber optic sensor is successfully tested, and the deformation monitoring of the windings is completed by applying six groups of axial and radial deformation of different degrees by human beings, and by using the time-domain reflection technology of Brillouin light. The deformation of the winding is monitored by Brillouin's optical time-domain reflection technique. The experimental results show that the mean value of the monitoring error of axial deformation is 9.63%, and the monitoring error of radial deformation is 5.18%, which is mainly caused by the uneven force when applying the force as well as the equipment acquisition error, and the error tends to be stabilized after the deformation is increased, and the experimental results effectively verified the feasibility of the vectorized monitoring model of the winding deformation, and realized the direction of the deformation of the transformer and the degree of demodulation of the deformation, which further improves the monitoring accuracy of the winding deformation. The monitoring accuracy of winding deformation is further improved.
keywords:Winding deformation, vectorized monitoring, optical fiber sensing, simply supported winding beam
DOI: 10.19595/j.cnki.1000-6753.tces.240264
中图分类号:TM41
中央高校基本科研业务费专项资金(2023MS106)和南方电网公司科技项目(031900KK52220012)资助。
收稿日期 2024-02-17
改稿日期 2024-03-21
作者简介
范晓舟 男,1990年生,工程师,研究方向为电气设备在线监测及故障诊断。E-mail:fxz@ncepu.edu.cn(通信作者)
袁洁平 女,1999年生,硕士研究生,研究方向为电气设备在线监测及故障诊断。E-mail:3300871720@qq.com
(编辑 李 冰)
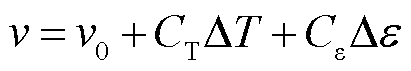 (1)
(1)
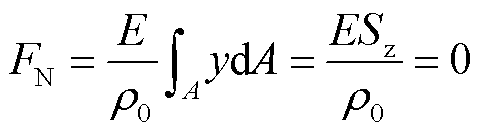 (2)
(2)

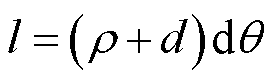 (3)
(3)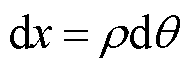 (4)
(4)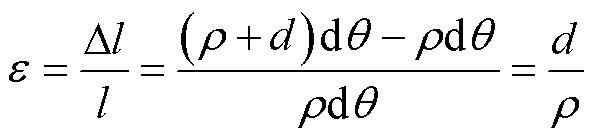 (5)
(5)
 (6)
(6)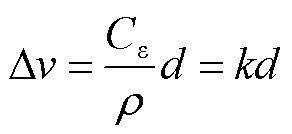 (7)
(7)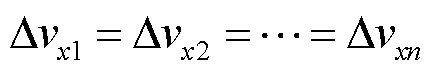 (8)
(8)
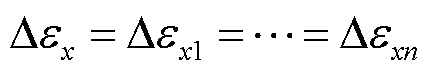 (9)
(9)
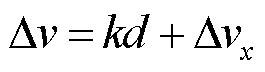 (10)
(10)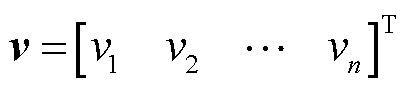 (11)
(11)
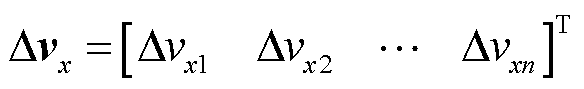 (12)
(12)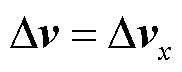 。设多根光纤的轴向应变布里渊频移变化量为
。设多根光纤的轴向应变布里渊频移变化量为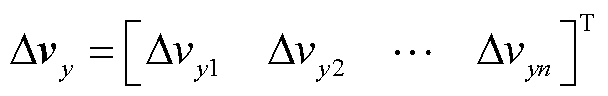 (13)
(13)
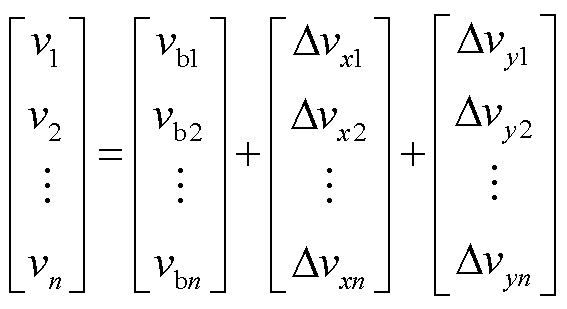 (14)
(14)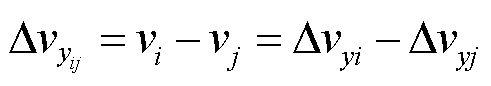 (15)
(15)
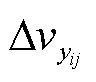 为两根光纤布里渊频移差值;v
为两根光纤布里渊频移差值;v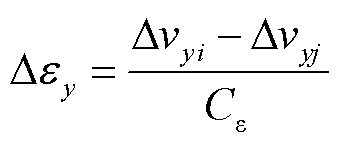 (16)
(16)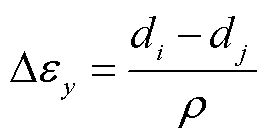 (17)
(17)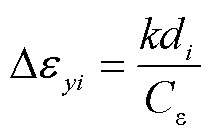 (18)
(18)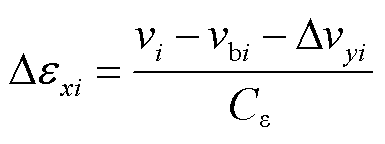 (19)
(19)
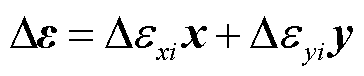 (20)
(20)
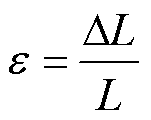 (21)
(21)







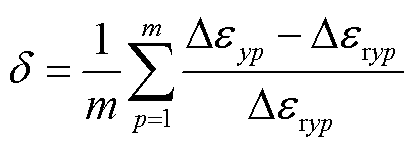 (22)
(22)