Tab.1 Distribution of defect types by manufacturer A self-check

破坏种类占试验瓷件百分比(%)占剔除瓷件百分比(%) 顶部裂纹0.8020.72 侧面裂纹0.6216.11 杂质0.7419.18 原因不明1.7043.99
摘要 随着交直流特高压输电工程的发展,420 kN和550 kN大吨位圆柱头瓷绝缘子凭借其头部尺寸小、质量轻、便于标准化生产等优点,正逐步取代圆锥头产品。为保证圆柱头瓷绝缘子整体的机械和电气性能,电力行业标准规定瓷件在胶装前需要逐只进行内水压试验,以剔除瓷件中的缺陷,但标准中并未明确规定关键试验参数(水压载荷),制造企业多依据自身经验进行试验,试验参数的设置缺乏科学依据。该文首先对内水压试验后破损瓷件中典型缺陷的类型及分布位置进行统计;然后针对内水压试验对不同类型、位置杂质的剔除灵敏性进行研究;最后获得了内水压试验中杂质大小、弹性模量、形状参数以及应力边界条件等因素对瓷件内部应力的影响规律。研究成果可以为规范内水压试验方法及参数、提高大吨位圆柱头瓷绝缘子产品质量提供理论依据。
关键词:圆柱头绝缘子 内水压试验 有限元仿真 夹杂应力
瓷绝缘子具有良好的化学稳定性,能够耐受不利的环境条件,具有良好的绝缘性能、耐热性和抗老化性,被广泛地应用于国内各电压等级输电线路上[1]。我国特高压工程的推进建设,对悬式瓷绝缘子提出了更高的机械性能和电气性能方面的要求。传统的盘形悬式瓷绝缘子产品多为圆锥头结构,相较于圆锥头结构,圆柱头结构产品头部尺寸更小、质量更轻、更适用于大吨位产品使用,且圆柱头产品更容易实现自动化生产,能够保证产品质量的一致性[2-3]。
目前国内绝缘子制造厂家正积极推动420 kN和550 kN大吨位圆柱头盘形悬式瓷绝缘子的制造工艺优化和质量提升工作,已经取得一定的进展,但仍缺乏圆柱头绝缘子的质量管控和现场运行经验。如何进一步提升圆柱头瓷绝缘子的质量给制造厂家提出了极大的挑战[3]。
绝缘子瓷件一般由石英或铝矾土/高温氧化铝及黏土、长石等无机矿物按照配比烧制而成。生产过程中,由于原材料、窑炉中存在杂质,或瓷质烧制不均匀等因素,烧成后的瓷件内部存在若干小的孔洞、杂质等缺陷。在输电线路运行时,瓷绝缘子在外部环境作用下,受到电-热-机械应力的共同作用,绝缘子瓷件内部原本存在的微裂纹、微小气孔等缺陷进一步发展,最终导致整体机械性能和电气性能大幅下降[4-12]。
因此,为了能够在绝缘子出厂前剔除劣质瓷件,提升绝缘子的整体质量,厂家需要在出厂前对绝缘子的机械性能和电气性能进行有效的检测,对瓷件进行逐只内水压试验就是提升瓷件质量的有效手段之一。日本NGK公司在20世纪90年代便将内水压试验作为绝缘子出厂的例行检测项目[13-14],其经验表明内水压试验能够有效剔除瓷件中存在的缺陷,避免后续金具胶装成本的浪费。内水压试验的原理是通过对瓷件头部注水加压,使得瓷件整体受到高应力作用,当瓷件中存在不规则形状气孔、杂质和微裂纹缺陷时,缺陷处会出现明显的应力集中,一旦超过瓷材料的断裂强度,瓷件会发生损坏。
为了保证我国大吨位瓷绝缘子的整体机械性能和电气性能,电力行业标准DL/T 1000.1—2018《标称电压高于1 000 V架空线路绝缘子使用导则第1部分:交流系统用瓷或玻璃绝缘子》等规定,瓷件在胶装前需要逐只进行内水压试验,但标准中并未明确规定关键试验参数如水压载荷等,制造企业多依据自身经验进行试验,对水压载荷的设置仅考虑瓷件剔除率这一单一因素。例如,目前420 kN和550 kN产品瓷件的试验水压载荷之所以设置为 36 MPa,是为了将剔除率控制在3%左右,可见该试验参数的设置缺乏科学依据[15]。为了确定合理的绝缘子内水压试验的水压载荷,保证试验能够剔除存在缺陷的瓷件,同时不损坏完好瓷件,亟须进一步优化大吨位瓷绝缘子的内水压试验方法,并针对不同型号、不同尺寸的绝缘子给出合理的水压值。
为实现这一目标,亟须明确烧制后绝缘子瓷件内部存在的缺陷类型、形貌、尺寸等因素,并且明确内水压试验对不同类型、位置缺陷的剔除灵敏性。在此基础上,研究优化内水压试验程序及参数,为大吨位圆柱头瓷绝缘子的出厂检验方法提供理论依据。考虑到内水压试验属于破坏性试验,而单片绝缘子的造价较高,并且烧成后瓷件内部缺陷存在随机性,进行大量试验研究较为困难,因此,对内水压试验中瓷件内部的应力分布进行仿真计算尤为重要。
王黎明等通过有限元仿真计算了长棒形悬式绝缘子在集中力、均布力、扭转力等不同载荷下的应力分布情况[16];杨海涛等通过有限元仿真计算了不同载荷下支柱绝缘子的应力分布,并结合强度理论提出了断裂判据[17];张廼龙等通过有限元仿真计算了不同结构悬式绝缘子应力分布的区别,并以应力大小为依据对绝缘子进行了结构优化[18]。有限元仿真是计算材料内部应力分布、电场分布等的有效手段[19-25],但是目前少有学者针对瓷绝缘子内部微小缺陷导致应力变化的情况进行分析计算,可以参考学者对岩土材料夹杂应力分布的有限元计算和解析计算的方法进行研究[26-29]。付云伟等基于相互作用直推估计法建立了考虑含夹杂相互作用的夹杂界面裂纹开裂模型,并通过有限元计算验证了其方法的可靠性[26];杨万科等建立了在远场三轴应力作用下的椭球形空洞洞壁上应力状态的解析解,并与有限元计算得到的应力解进行对比验证其解析解的可靠性[28]。
基于上述考虑,本文对国内某厂家某批次550 kN特高压大吨位瓷绝缘子内水压试验中导致瓷件破坏的缺陷进行分析并总结归类。针对铁点、杂质等缺陷搭建有限元仿真模型,通过仿真手段获得内水压试验中瓷件内部杂质尺寸、弹性模量、形状以及应力边界条件等因素对瓷件内部应力的影响规律,分析内水压试验对不同缺陷的剔除灵敏性。研究成果可以为规范内水压试验方法及参数、提高大吨位圆柱头瓷绝缘子产品质量提供理论依据。
对国内大吨位盘形悬式瓷绝缘子生产厂家内水压试验情况的调研结果表明,目前多数厂家均对550 kN产品瓷件进行36 MPa水压载荷的内水压试验。对两厂家(分别记为A和B)某批次试验结果进行统计,厂家A共计试验10 145片,剔除388片,剔除率为3.82%;厂家B共计试验48 830片,剔除1 743片,剔除率为3.57%,厂家自查缺陷类型分布情况见表1和表2。
表1 厂家A自查缺陷类型分布情况
Tab.1 Distribution of defect types by manufacturer A self-check

破坏种类占试验瓷件百分比(%)占剔除瓷件百分比(%) 顶部裂纹0.8020.72 侧面裂纹0.6216.11 杂质0.7419.18 原因不明1.7043.99
表2 厂家B自查缺陷类型分布情况
Tab.2 Distribution of defect types by manufacturer B self-check
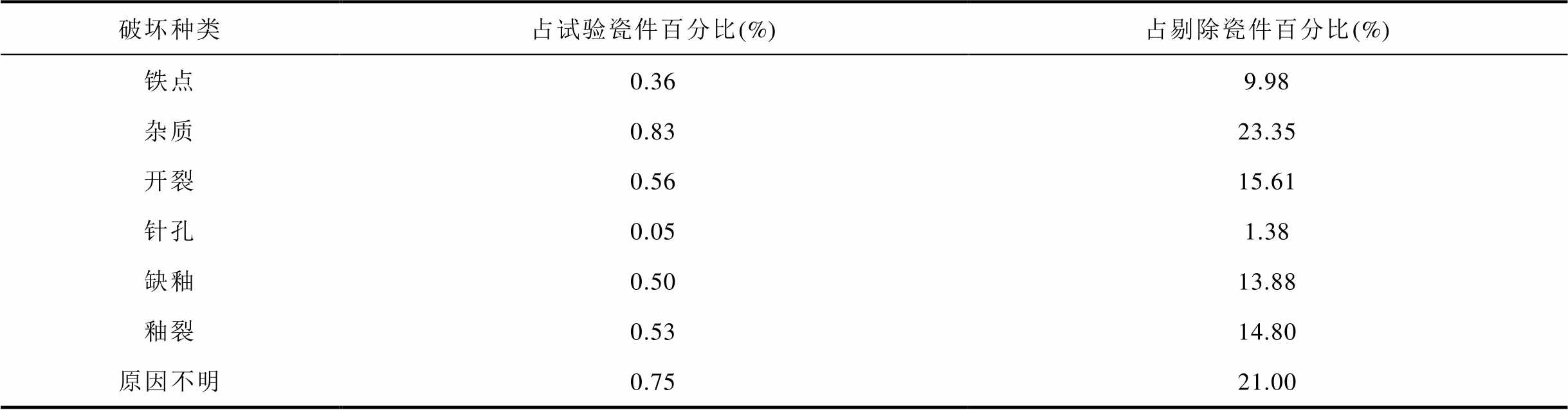
破坏种类占试验瓷件百分比(%)占剔除瓷件百分比(%) 铁点0.369.98 杂质0.8323.35 开裂0.5615.61 针孔0.051.38 缺釉0.5013.88 釉裂0.5314.80 原因不明0.7521.00
目前部分厂家也在进行调整内水压试验水压载荷的相关试验研究,如前文提到的厂家B,曾采用多个水压载荷等级分别进行试验,各水压等级试验数量均为20片,各水压载荷等级剔除率见表3。厂家B统计得到,38 MPa以上水压载荷试验中,破坏瓷件均未发现明显缺陷,但由于试验样品数量过少,其计算得到概率的可靠性存疑。另有厂家C采用45 MPa水压载荷对550 kN产品进行内水压试验,共计试验1 102片,剔除19片,剔除率为1.72%,破坏原因分类见表4。
表3 厂家B各水压载荷等级剔除率
Tab.3 Removal rate of each water pressure load class by manufacturer B
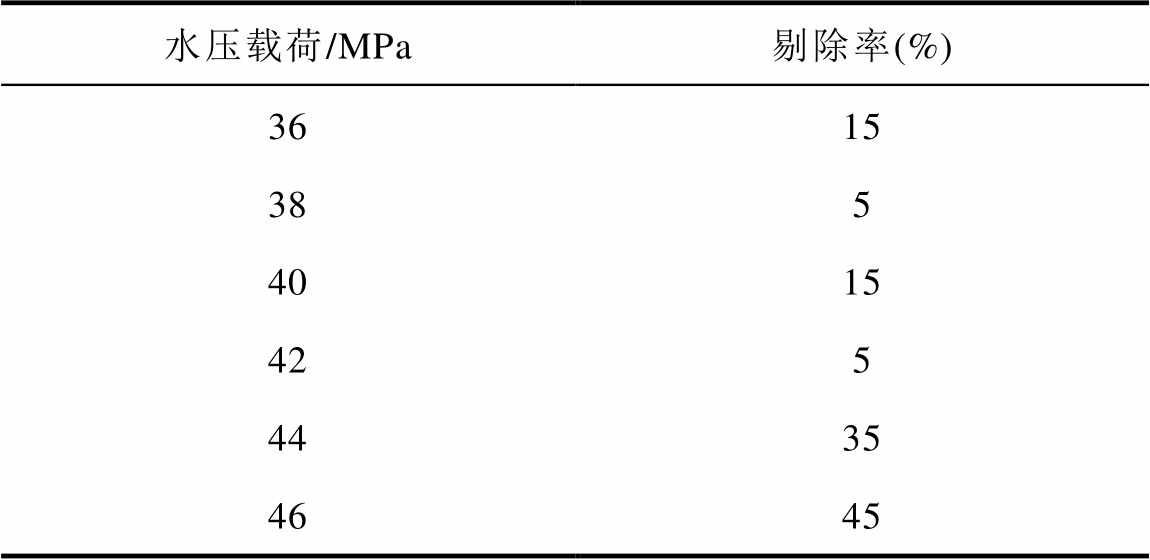
水压载荷/MPa剔除率(%) 3615 385 4015 425 4435 4645
表4 厂家C自查缺陷类型分布情况
Tab.4 Distribution of defect types by manufacturer C self-check

破坏种类占剔除瓷件百分比(%) 铁点47.37 内裂10.53 杂质5.26 底眼缩釉5.26 颈部釉面气孔5.26 头部拐角内侧开裂5.26 原因不明21.05
1.1节中指出不同厂家对各自内水压试验中破坏产品的缺陷分类不尽相同,且均存在相当数量的原因不明的剔除产品,于是本团队在国内某厂家进行内水压试验,记录某批次产品进行内水压试验的情况,对缺陷进行归类,并注重分析厂家提到的未发现明显缺陷的破坏瓷件。试验中550 kN产品共计1 414片,破坏数量为53片,剔除率约为3.75%。该厂家内水压试验机布置图如图1所示。需要说明的是,上述统计均针对某次试验中一定数量瓷件的统计数据,与整体批次进行内水压试验的最终统计剔除率有所差异。试验后对破坏瓷件进行逐只缺陷查找,分析导致瓷件破坏的主要原因。本文所提到的未发现明显缺陷的原因不明瓷件,被认为是由于设备密封胶圈与瓷件之间接触力过大导致瓷件发生破坏。
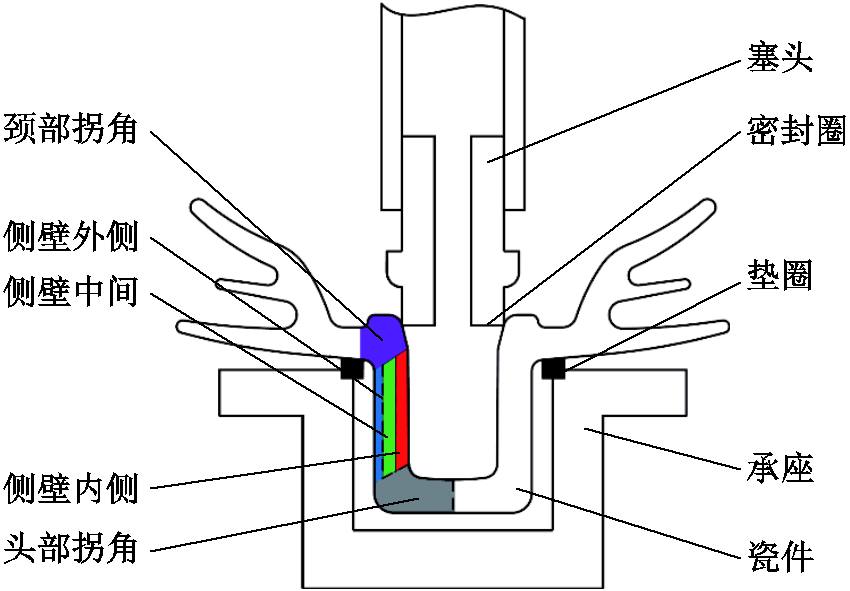
图1 内水压试验机布置图
Fig.1 Layout drawing of hydraulic test
内水压试验中破坏瓷件的缺陷可以分为铁点、微裂纹开裂、杂质以及黄芯四种主要类型,对试验中破坏瓷件缺陷类型与位置进行数量统计,结果如图2a、图2b所示,其典型形貌如图3所示,具体分析说明如下。
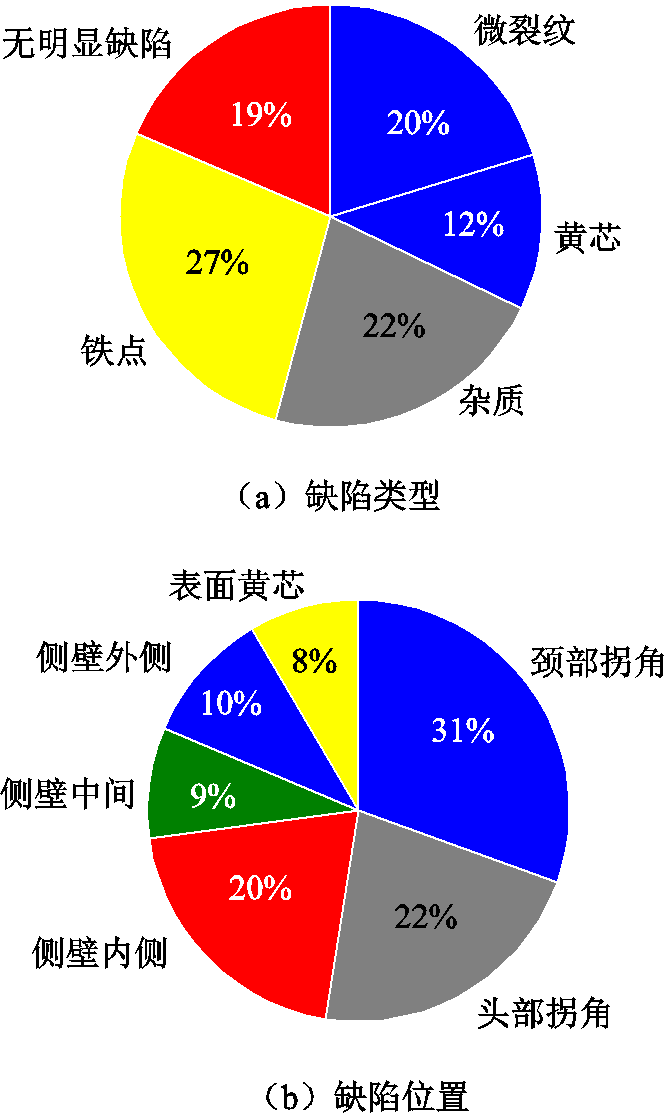
图2 缺陷类型与位置
Fig.2 Type and direction of defects
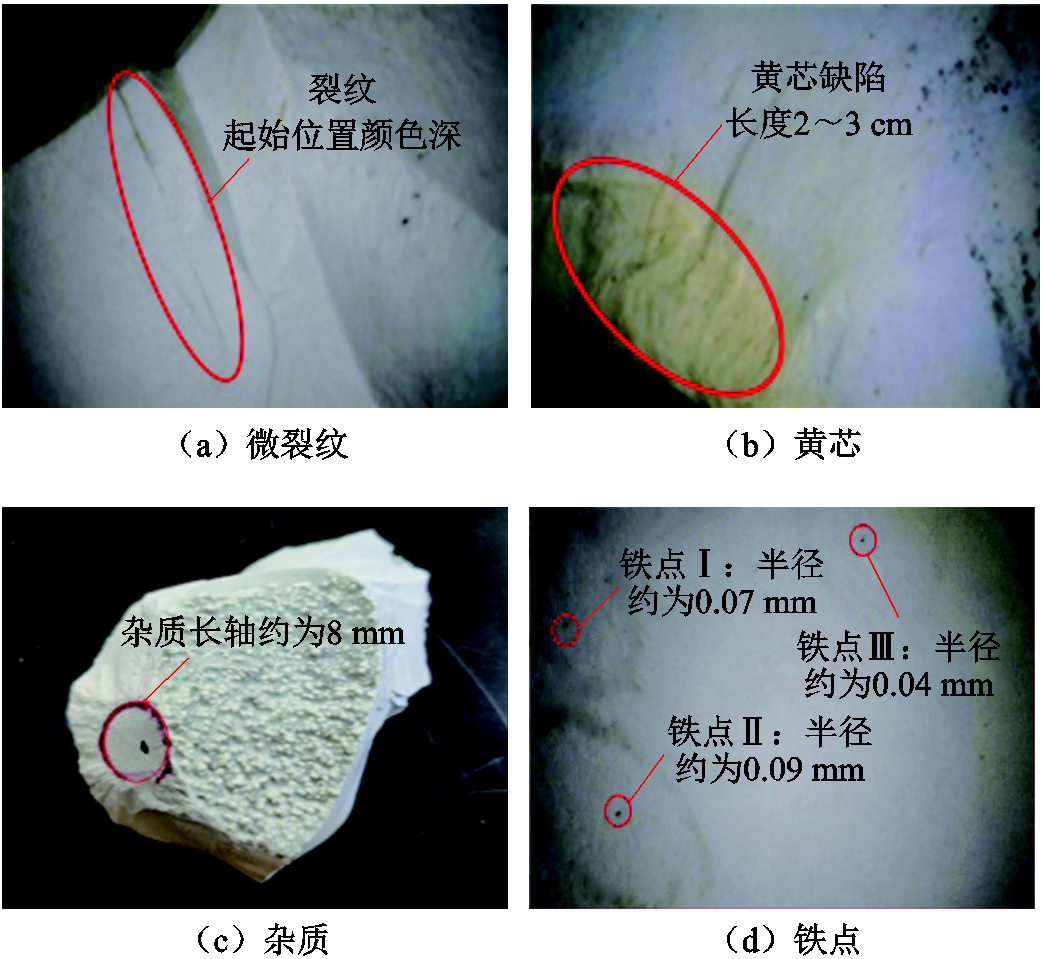
图3 绝缘子的典型缺陷形貌
Fig.3 Typical defects of insulator
1)微裂纹:微裂纹缺陷被认为是瓷件本身存在的微小裂纹,在水压作用下扩展,当尺寸扩展到一定程度时引起瓷件整体发生断裂。观察收集到的破坏瓷件,其中裂纹长度约为3~4 cm。需要指出的是,本文认为瓷件碎片中观察到的裂纹应为原始裂纹在内水压试验作用后扩展形成的,裂纹原始长度、宽度无法予以准确统计。
2)黄芯:黄芯是指在断面上发现的颜色形貌明显异于良好瓷质的区域,此类区域本身抗拉强度低于烧结良好的瓷件,在水压作用下应力大于其破坏强度导致断裂。在内水压试验中收集到的剔除黄芯缺陷均为宽度为1~2 cm、长度为2~3 cm的显著缺陷。
3)杂质:杂质缺陷是指在瓷件中存在的尺寸较大的缺陷异物,水压作用下在杂质附近造成应力异常集中导致此处成为开裂源,该类杂质的长轴尺寸为8~10 mm。
4)铁点:铁点的尺寸过小,通过肉眼难以分辨,在显微镜下拍摄确定其尺寸均小于0.1 mm。
由于与其他几种缺陷相比,铁点的尺寸较小,为研究内水压试验对此种缺陷的剔除效果,下文中通过对小尺寸缺陷在内水压作用下的应力仿真计算,验证内水压试验对该种缺陷的剔除灵敏性。
本文将铁点等杂质简化为球体和椭球体两种形状。为计算杂质对瓷件应力分布的影响,可以采用子模型法计算杂质处的应力集中系数,即以杂质为中心向外建立正方体的子模型区域,并以杂质中心为坐标原点,以垂直正方体边界面的方向设置x-y-z三轴。通过对该正方体域设置边界条件,单独计算杂质处的应力情况。有限元计算杂质处的应力集中系数具体流程如图4所示。首先对内水压试验中完好瓷件的应力分布进行仿真计算,在瓷件内不同位置截取正方体计算其中的平均第一、第二、第三主应力作为子模型计算时的x-y-z三向边界应力条件;然后建立子模型域,加入杂质在子模型内进行杂质附近应力计算。
相较于在完整瓷件内直接加入杂质进行仿真,子模型法大大简化了计算步骤,其理论基础是杂质的存在仅会对杂质附近区域应力造成影响,不会导致远场应力发生变化。在瓷件内头部拐角应力集中区域Ⅰ、内壁应力集中区域Ⅱ以及颈部应力集中区域Ⅲ选取三个位置,分别采用子模型法和在完整瓷件中加入杂质直接计算的方法进行仿真。结果表明,当正方体域边长大于杂质尺寸的3倍以上时,有无杂质引起边界上的应力变化不会超过0.52%,两种方法计算得到的杂质附近应力结果差异最大不超过3.5%。考虑本文的主要目的是对比不同应力条件下,尤其是主应力与杂质不同夹角方向对应力集中情况的影响,采用子模型法进行计算,不仅满足分析要求,而且更容易总结对不同杂质剔除灵敏度的归一性规律。
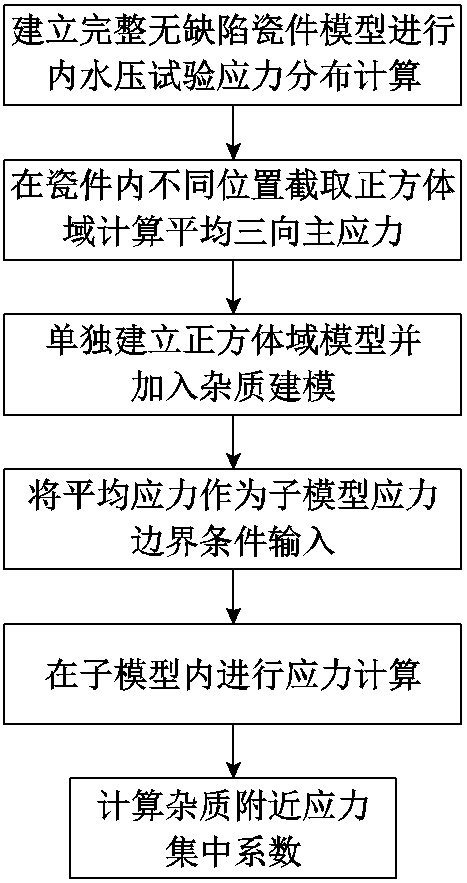
图4 有限元计算杂质处应力集中系数流程
Fig.4 Flow chart of finite element calculation of stress concentration coefficient at defect
日本NGK公司曾对内水压试验中瓷件内部应力分布情况进行理论分析,简化试验条件,认为瓷件仅在头部内壁受到均匀水压载荷的压力作用。因此,将问题简化为材料力学中典型厚壁圆筒问题,根据拉美公式,计算瓷件内部的三向应力为[30]
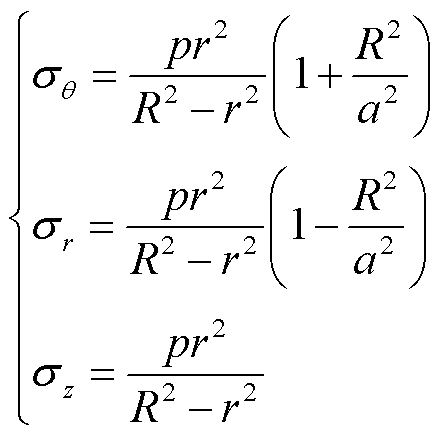 (1)
(1)
式中,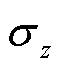 、
、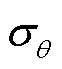 和
和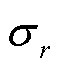 分别为轴向应力、环向应力和径向应力,三向应力彼此垂直;r和R分别为绝缘子瓷件圆柱体头部的内径和外径;a为计算位置距中心轴线的距离;p为内水压试验的水压载荷。
分别为轴向应力、环向应力和径向应力,三向应力彼此垂直;r和R分别为绝缘子瓷件圆柱体头部的内径和外径;a为计算位置距中心轴线的距离;p为内水压试验的水压载荷。
从式(1)可知,瓷件各处受到的最大拉应力为环向应力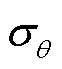 ,且最大值在头部内壁处,在考虑瓷件破坏判据时应该重点关注环向应力大小。通过水压载荷值计算瓷件内部环向应力大小,可建立内水压载荷与瓷件本征强度之间的关联。
,且最大值在头部内壁处,在考虑瓷件破坏判据时应该重点关注环向应力大小。通过水压载荷值计算瓷件内部环向应力大小,可建立内水压载荷与瓷件本征强度之间的关联。
实际内水压试验中瓷件上的受力情况更加复杂,除水压载荷外,试验装置对瓷件的支撑作用、密封圈与瓷件的接触压力等均会对瓷件应力分布情况造成影响,难以通过解析法计算获得精确的应力解。因此,本文采用有限元仿真对应力分布情况进行计算。计算时首先假定瓷件完好无缺陷且为连续线性弹性体,采用线性弹性力学理论进行计算,其本构方程为
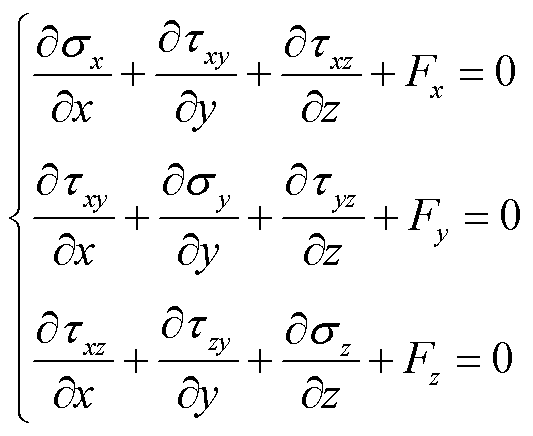 (2)
(2)
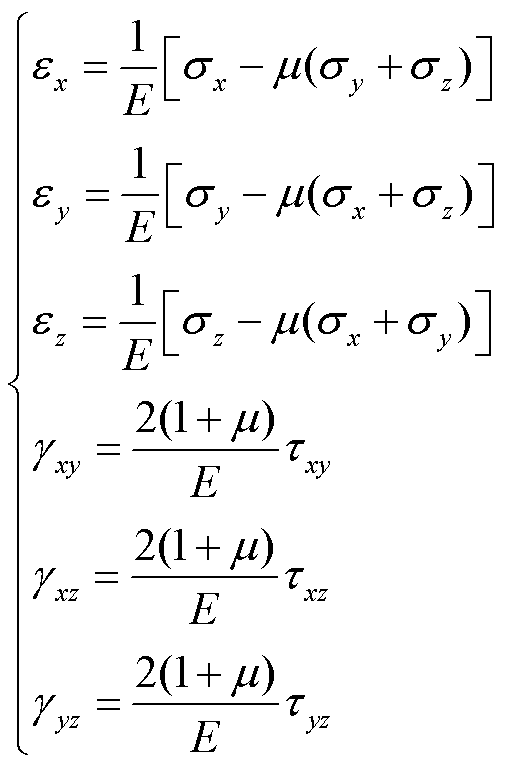 (3)
(3)
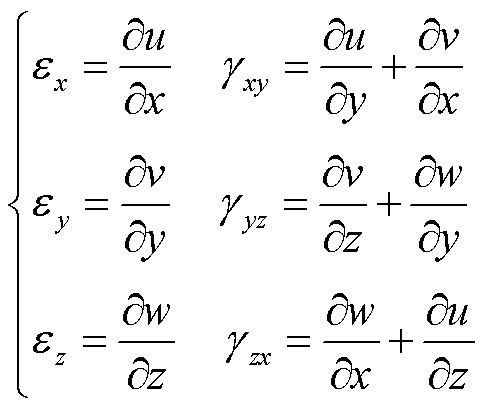 (4)
(4)
式中,下标x、y、z分别表示坐标轴对应方向;F为施加载荷;σ为正应力;τ为切应力;ε为正应变;γ为切应变;u、v、w分别为x、y、z方向的位移;E为材料弹性模量;μ为材料泊松比。
在颈部拐角外放置垫片施加固定约束,并在内壁边上施加360 MPa水压载荷,可以计算得到瓷件上第一主应力分布如图5所示。瓷件头顶拐角位置(区域Ⅰ)、内壁靠下位置(区域Ⅱ)以及颈部拐角位置(区域Ⅲ)存在三处应力集中。在这三个区域中,区域Ⅲ的第一主应力最大,区域Ⅰ次之,区域Ⅱ最小。当采用第一强度理论作为瓷件破坏判据时,应比较第一主应力与抗拉强度的大小关系,通过有限元计算的第一主应力的方向与圆柱坐标系下的环向应力方向相似,且大小大致相同,内壁上高度为65 mm水平位置上的第一主应力大小随着距中心轴线的距离变化曲线的有限元仿真结果和式(1)的解析解的规律基本相同,如图6所示。瓷件各位置应力可以为后文中计算缺陷附近的应力提供边界条件。
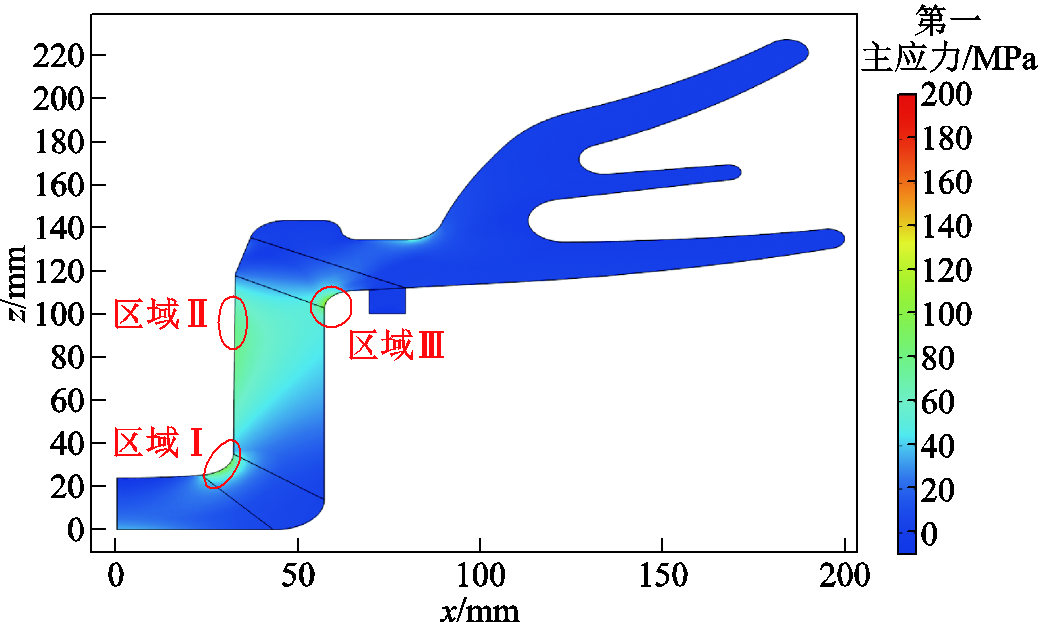
图5 36 MPa内水压试验有限元仿真应力云图
Fig.5 Stress cloud image for finite element simulation of 36 MPa internal water pressure test
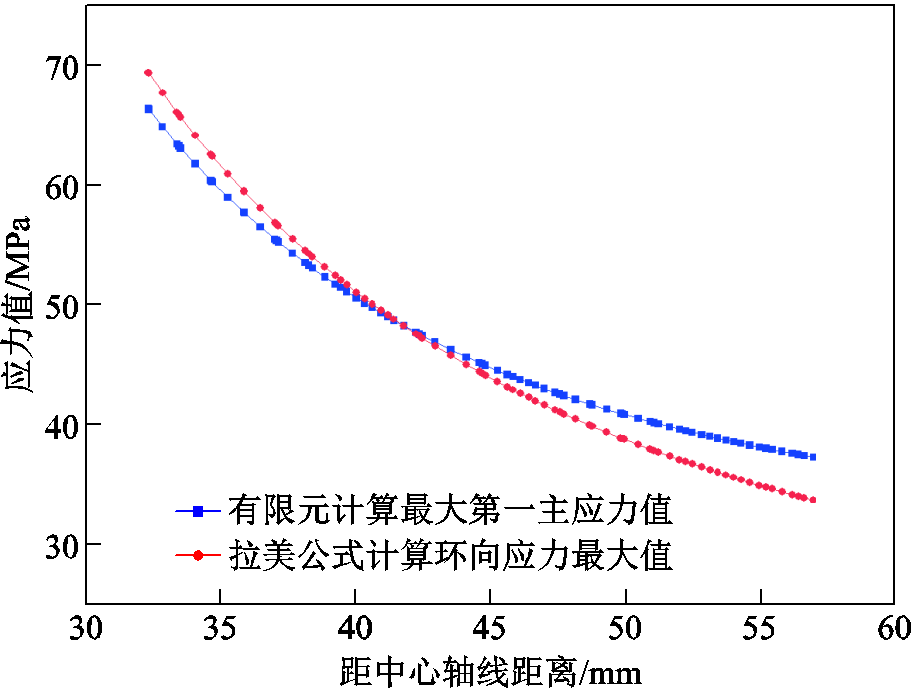
图6 不同位置处内壁最大主应力解析解和仿真结果
Fig.6 Analytical solution and simulation results of the change of the maximum principal stress of inner wall with the size of the radius
内水压试验对缺陷的剔除效果最终由水压作用下缺陷附近的最大第一主应力值决定[31]。因此,本文定义杂质附近瓷件上最大第一主应力与杂质附近区域边界应力之比为杂质引起的瓷件应力集中系数k,用于表征不同杂质引起的瓷件的应力集中情况,表示为
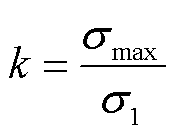 (5)
(5)
式中,σmax为杂质附近最大第一主应力;σ1为子模型边界应力。
由于系统线性,当子模型的边界条件线性增加时,如果杂质参数不变,边界条件中的第一主应力与杂质附近的最大第一主应力呈线性关系,即应力集中系数保持不变。
影响应力集中系数的主要因素可以分为杂质本身参数和边界应力条件两类。第3节将从杂质弹性模量、杂质大小、杂质形状、杂质与主应力的角度以及边界三向应力之间的比例关系等方面对应力集中系数的影响进行讨论。在仿真中对杂质设置不同参数进行参数化扫描,以明确内水压试验对不同类型缺陷的剔除灵敏性。不同扫描参数物理意义见表5。由于陶瓷材料的弹性模量对除气孔以外的其他显微结构特征都不敏感,为简化计算,在有限元计算时认为杂质附近陶瓷基体的弹性模量参数不发生改变。本文参考岩土力学中处理夹杂杂质的方法,将杂质形状设置为椭球体,用于模拟杂质形状尖锐的情况,设置的椭球体缺陷仅考虑存在一条长轴、另两条短轴长度相等的情况。在设置子模型边界应力条件时,子模型边界应力z方向设置为完好瓷件仿真结果的第一主应力σ1,x方向设置为第二主应力σ2,y方向设置为第三主应力σ3,子模型仿真示意图如图7所示,计算得到杂质附近截面应力云图如图8所示。
表5 扫描参数物理意义
Tab.5 Physical meaning of scanning parameters

参数名称物理意义单位 Eimpurity杂质弹性模量GPa rimpurity球体杂质半径mm aimpurity椭球体杂质短轴长mm ksize椭球体杂质长短轴比 q杂质长轴与坐标轴夹角° ksp2第二主应力与第一主应力的比值 ksp3第三主应力与第一主应力的比值
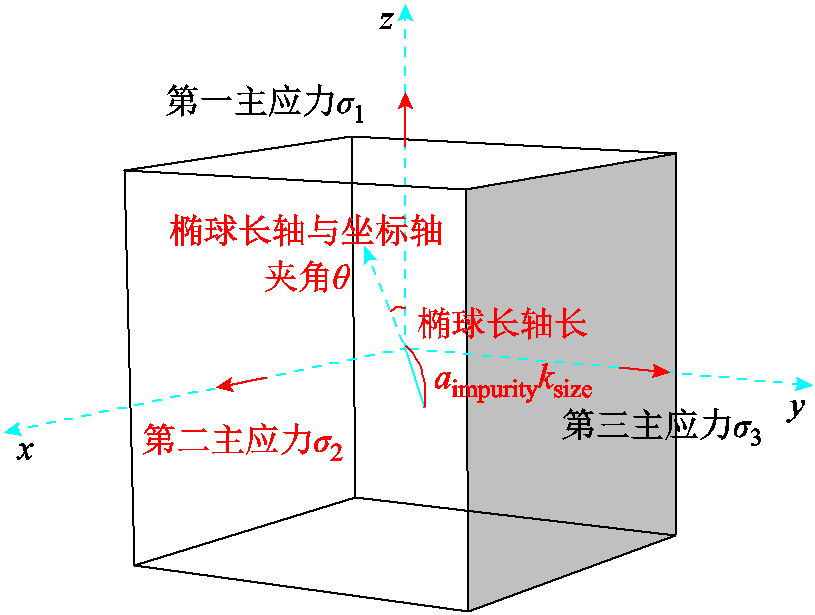
图7 子模型杂质示意图
Fig.7 Submodule impurity diagram
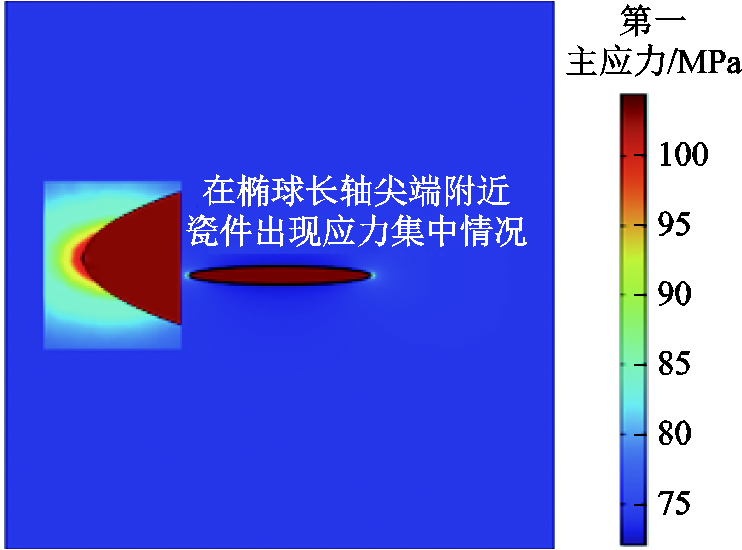
图8 杂质处截面应力云图
Fig.8 Stress nephogram of cross section at impurity
为分析杂质不同参数对应力集中系数的影响,总结归一化结论,本节及后文中选取内壁区域Ⅱ上某点,将其第一、第二、第三主应力74 MPa、4 MPa和-24 MPa分别设置为子模型三向边界应力。氧化铝陶瓷烧结过程中可能存在硅、铁、钙、镁等元素形成的杂质[32],如铁铝氧化物弹性模量通常在100~200 GPa之间变化,所以在建立仿真模型时,设置基体弹性模量为100 GPa,杂质弹性模量Eimpurity从0~200 GPa变化,计算不同弹性模量的球形杂质附近的应力集中系数,结果如图9所示。
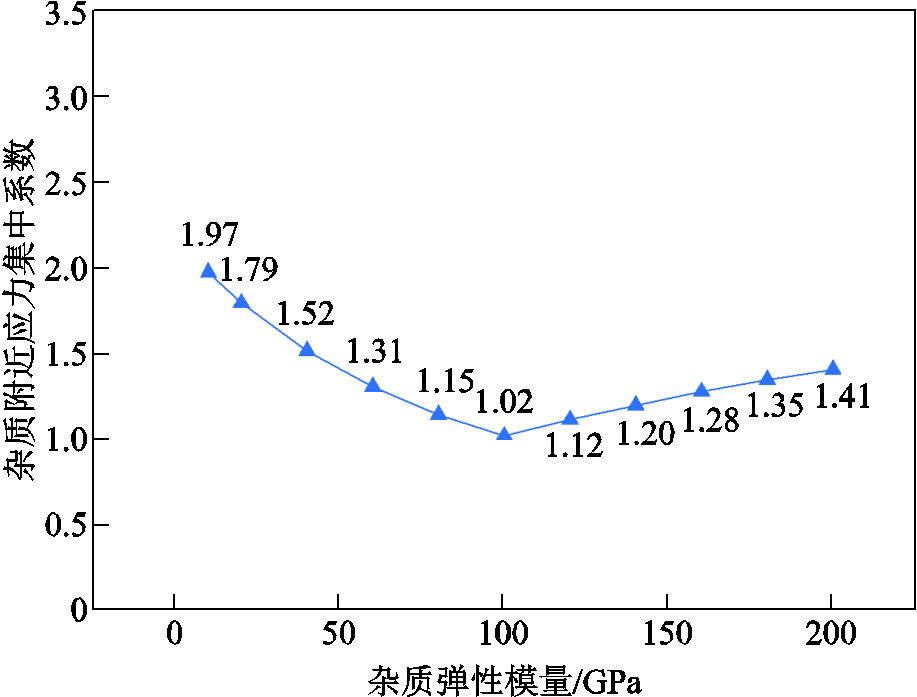
图9 杂质附近应力集中系数随杂质弹性模量变化关系
Fig.9 The relation between the stress concentration factor near the impurity and young's modulus of the impurity
从图9中可以看出,杂质附近的最大第一主应力与杂质和基体弹性模量的差值呈正相关,两者弹性模量相差越大,杂质附近瓷件内的最大第一主应力值越大。以半径rimpurity=0.05 mm的球形杂质为例,当杂质弹性模量从10 GPa增加到100 GPa时,应力集中系数k从1.97减小至1.02,随后当杂质弹性模量从100 GPa增加到200 GPa时,应力集中系数k又逐渐增加至1.41。当杂质弹性模量小于基体弹性模量时,应力集中系数随弹性模量差值的变化相较于杂质弹性模量大于基体弹性模量的情况更快。
为分析杂质本身大小及杂质形状对应力集中情况的影响,设置椭球体杂质的短轴长aimpurity和长短轴之比ksize作为扫描参数,分别设置aimpurity为0.01、0.02、0.04、0.06、0.08、0.10 mm,ksize为1、2、4、6、8、10进行计算,其中长短轴比值越大,说明椭球体杂质形状越尖锐。根据瓷件内壁上的应力,设置子模型三向应力边界大小为74 MPa、4 MPa和-24 MPa不变,杂质长轴与第一主应力平行和垂直两种条件下的试验结果如图10所示。需要说明的是,杂质长轴绕不同方向旋转至与第一主应力垂直时计算得到的应力集中系数大致相同,为节约篇幅,本节仅展示一种情况下应力集中系数的变化,图10b中展示的是杂质长轴与第二主应力方向相同的情况。
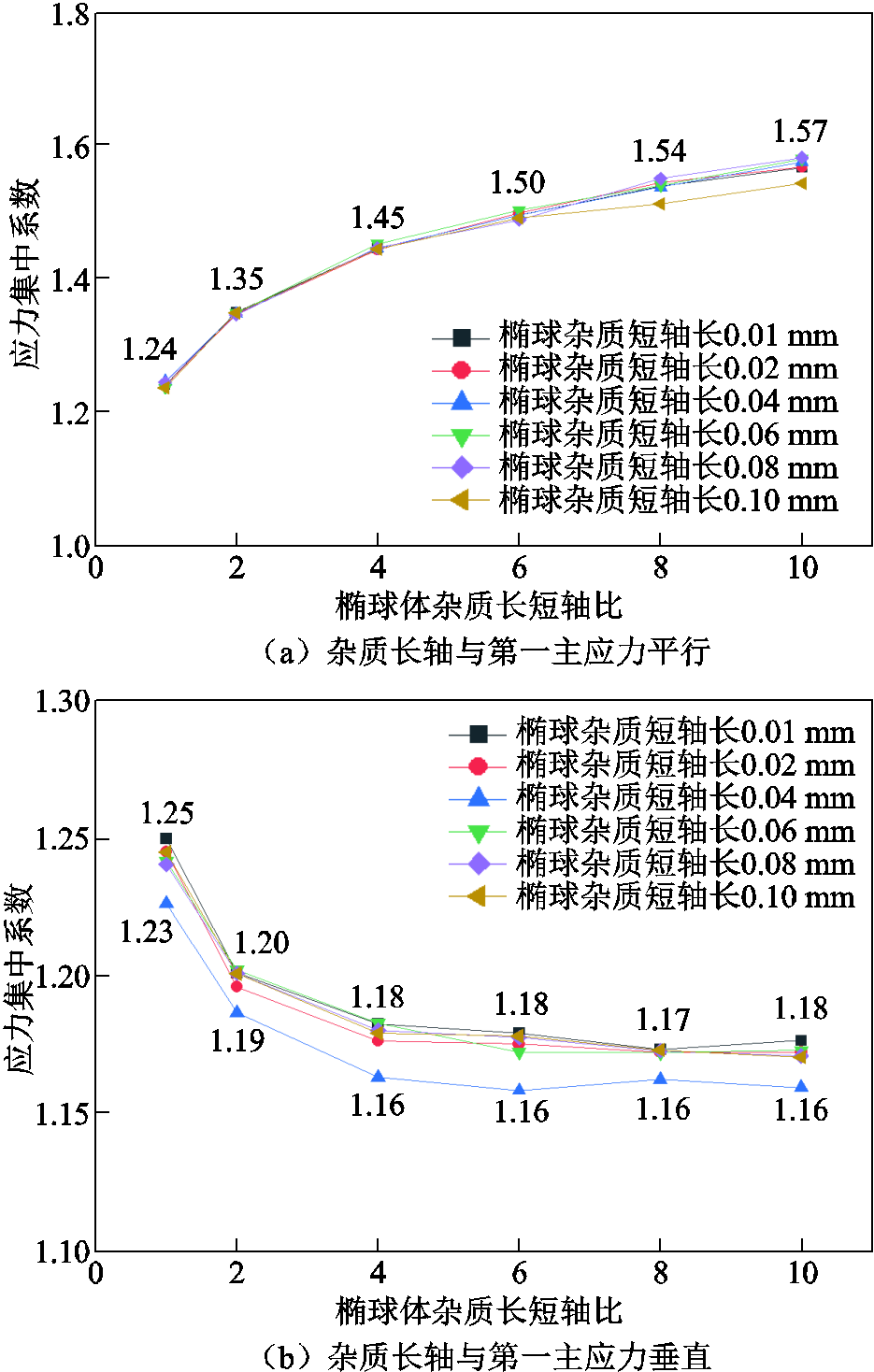
图10 集中系数随椭球杂质大小形状的变化
Fig.10 The change of stress concentration factor with the size and shape of the impurity in the ellipsoid
如图10所示,当杂质长轴方向与第一主应力方向平行时,杂质形状的改变会显著影响应力集中情况,杂质形状越尖锐,应力集中系数越大。当椭球体短轴长和球体半径相同时,长短轴比ksize=10时的应力集中系数比球体杂质的高26.6%。杂质长轴方向与第一主应力方向垂直时,该影响程度稍弱。在不同椭球杂质短轴长度的条件下,应力集中系数k随椭球体长短轴比ksize的变化规律近似。
然而,对于长短轴比相同的椭球杂质,在一定尺寸范围内改变椭球大小,并不会明显影响应力集中系数,即杂质尺寸对应力集中系数的影响有限。以长短轴比均为4的椭球杂质为例,当短轴长从0.01 mm到0.10 mm变化时,应力集中系数相差不超过0.15%。
根据上述分析,当杂质形状比较尖锐,且长轴方向与第一主应力方向夹角在合适值时,即使杂质尺寸较小,也可能引起较大的应力集中系数变化。因此,内水压试验可以剔除瓷件内部尺寸较小但形状尖锐的杂质缺陷。
3.3.1 杂质与边界第一主应力夹角的影响
对比椭球体杂质长轴与第一主应力方向平行(图10a)和垂直(图10b)两种情况,应力集中系数随杂质长短轴之比的变化趋势不同,当杂质形状较为尖锐时,边界主应力与椭球杂质之间的夹角方向会显著影响杂质附近应力集中系数。保持边界主应力方向不变,子模型三向边界应力大小分别设置为74 MPa、4 MPa和-24 MPa,椭球杂质长轴和短轴长分别为0.5 mm和0.05 mm,改变椭球杂质长轴与第一主应力之间的夹角,计算获得杂质附近瓷件内最大第一主应力、应力集中系数与角度,如图11所示。
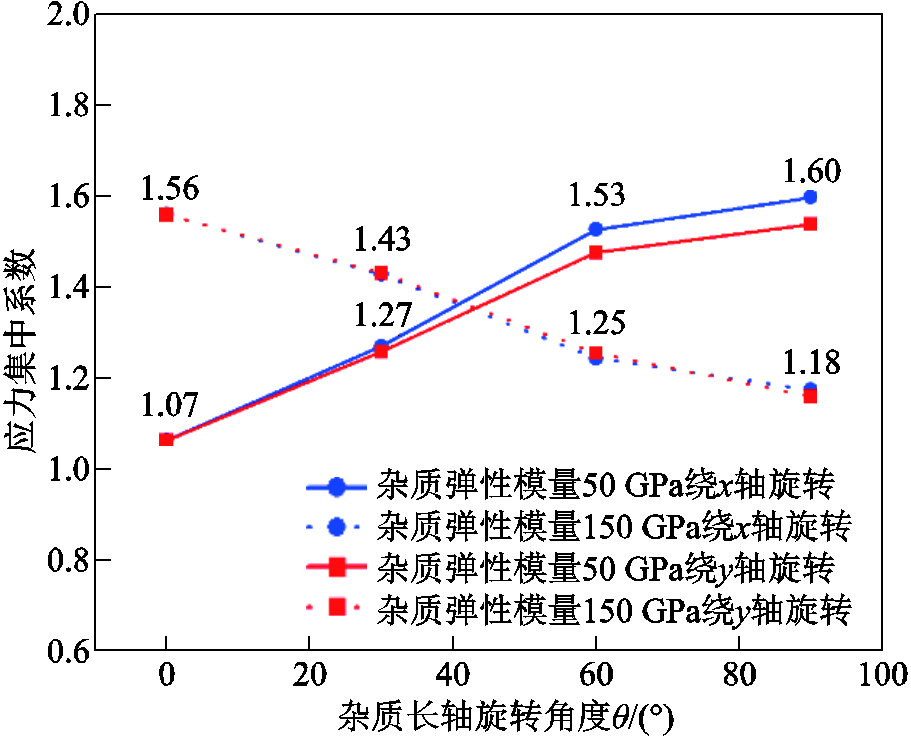
图11 杂质应力集中系数随长轴与第一主应力方向夹角的变化曲线
Fig.11 The change of stress concentration factor with angle between the major axis and the first principal stress
从图11可以看出,椭球形杂质长轴与第一主应力方向之间的夹角会显著影响杂质附近瓷件的应力集中情况,且当杂质与基体弹性模量大小关系不同时,最大应力值随角度的变化趋势不同:
1)当杂质弹性模量大于基体弹性模量时,应力集中系数随杂质长轴与第一主应力方向夹角的增大而减小。以弹性模量为150 GPa的杂质为例,长轴与第一主应力方向一致时的应力集中系数为长轴与第一主应力夹角为90°情况下的1.32倍。
2)当杂质弹性模量小于基体弹性模量时,应力集中系数变化趋势相反,应力集中系数随长轴与第一主应力方向夹角的增大而增大。以弹性模量为 50 GPa的杂质为例,长轴方向与第一主应力方向一致时的应力集中系数是长轴与第一主应力夹角为90°时的67%。
不同弹性模量杂质的应力集中系数随应力方向夹角的变化趋势大致相同。图12为不同弹性模量杂质下,杂质长轴同应力方向相同时与杂质长轴同应力方向成90°情况的应力集中系数比值随杂质弹性模量变化的曲线。考虑到铁点杂质弹性模量应大于瓷件基体弹性模量,故当铁点杂质长轴与第一主应力方向一致时,应力集中系数最大,内水压试验对此种情况下缺陷的剔除效果最明显。
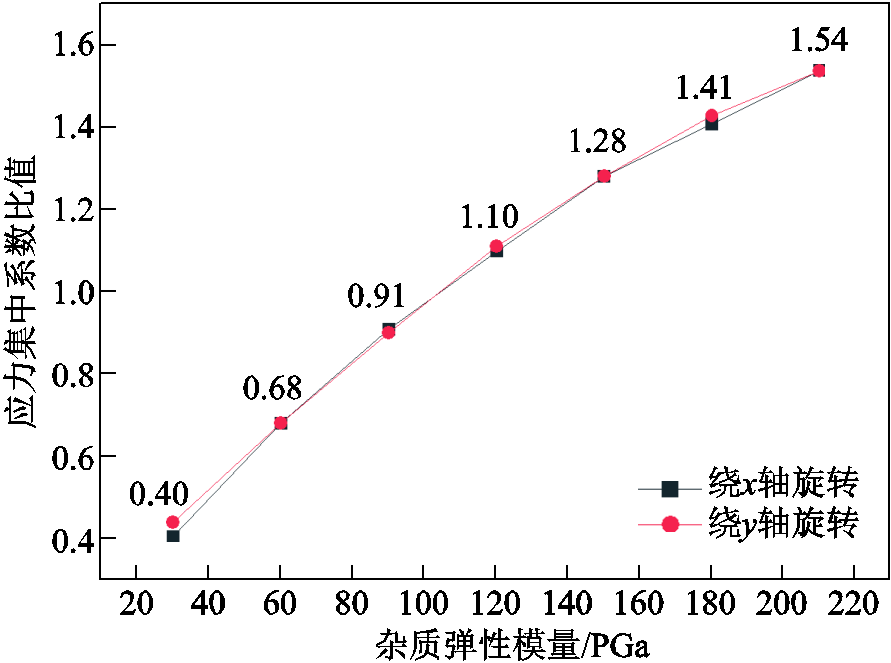
图12 应力集中系数比值随杂质弹性模量变化曲线
Fig.12 The ratio of stress concentration coefficient varies with elastic modulus of impurities
3.3.2 三向主应力之间比例关系的影响
在内水压试验中,瓷件上不同位置的第二、第三主应力与第一主应力的比值有所不同,三向主应力的不同比例关系可能会影响杂质处的应力集中系数。为研究三向应力不同比例关系下应力集中系数的变化,根据2.1节计算得到的内水压试验时完好瓷件内壁上的应力分布,简化边界条件,设置第一主应力σ1=80 MPa,将第二主应力与第一主应力的比值记为ksp2,第三主应力与第一主应力的比值记为ksp3。本节中固定仿真杂质弹性模量Eimpurity均为150 GPa。
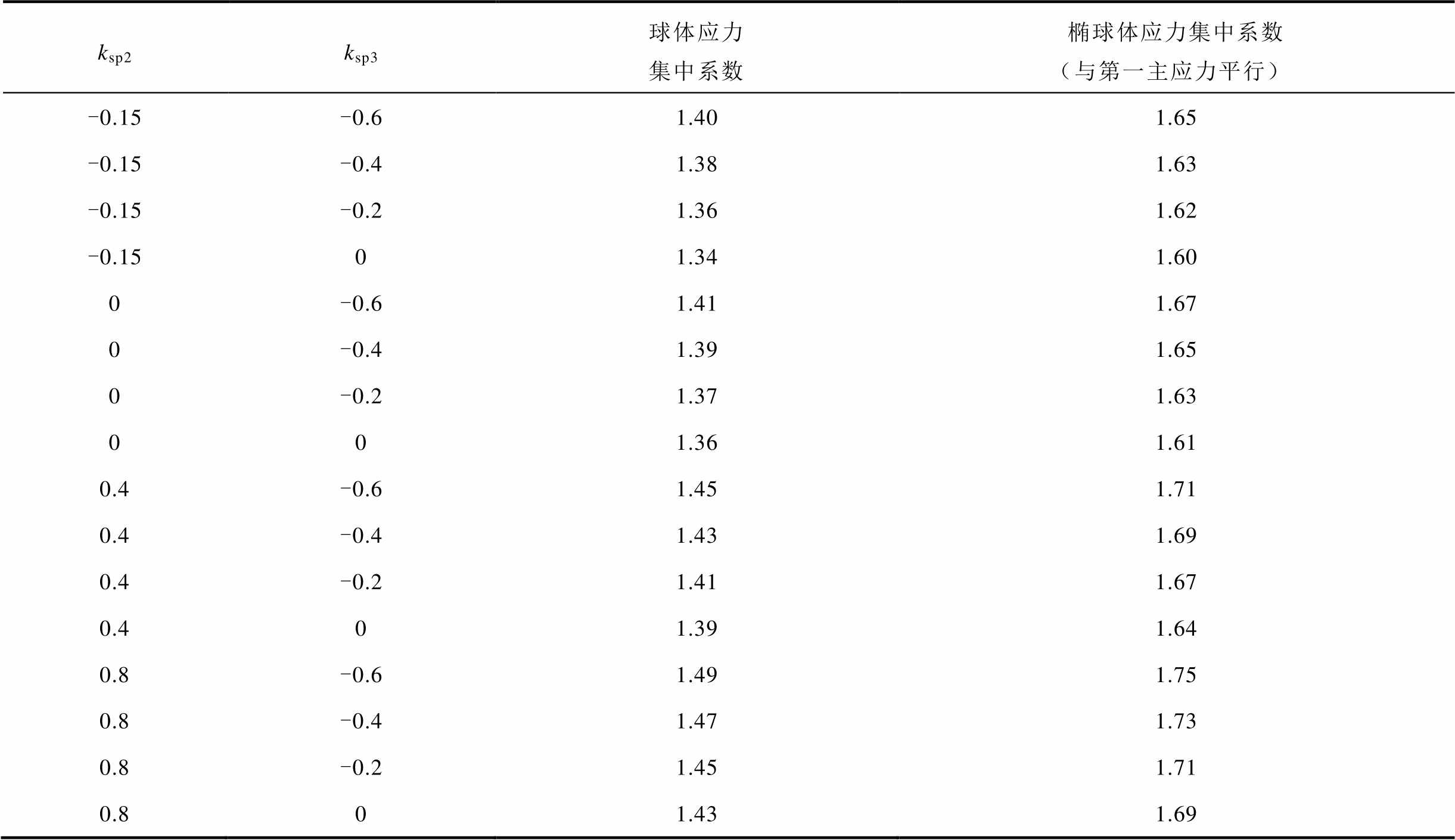
由于球体杂质应力集中系数不受杂质与主应力夹角的影响,首先对球体杂质在不同三向应力比例下的应力集中系数变化进行分析。设置球体杂质半径rimpurity=0.05 mm,分析完整瓷件进行内水压试验时的应力情况,依据仿真结果中第二、第三主应力与第一主应力的比例范围,设置ksp2在-0.15~0.8之间变化,ksp3在-0.6~0之间变化,应力集中系数变化见表6。固定第一主应力和第二主应力不变,减小第三主应力绝对值,球体杂质应力集中系数减小;固定第一主应力和第三主应力大小不变,增大第二主应力大小,球体杂质应力集中系数增大。对于球形杂质,当固定第一主应力不变,改变第二主应力和第三主应力与第一主应力之比时,应力集中系数最大值与最小值差异仅约为6.7%。
表6 应力集中系数随第二、第三主应力与第一主应力比值变化结果
Tab.6 The stress concentration coefficient varies with the ratio of the second and third principal stresses to the first principal stresses
ksp2ksp3球体应力集中系数椭球体应力集中系数(与第一主应力平行) -0.15-0.61.401.65 -0.15-0.41.381.63 -0.15-0.21.361.62 -0.1501.341.60 0-0.61.411.67 0-0.41.391.65 0-0.21.371.63 001.361.61 0.4-0.61.451.71 0.4-0.41.431.69 0.4-0.21.411.67 0.401.391.64 0.8-0.61.491.75 0.8-0.41.471.73 0.8-0.21.451.71 0.801.431.69
结合3.2节的分析,对于椭球体杂质而言,椭球体杂质长轴与应力方向的夹角会影响应力集中系数大小,且当长轴方向与主应力方向平行时,应力集中系数最大,故分别分析椭球长轴与x-y-z三向应力方向一致时的情况。设置椭球体杂质短轴长aimpurity=0.05 mm,长短轴比ksize=10,ksp2在-0.15~0.8之间变化,ksp3在-0.6~0之间变化,此时应力集中系数变化也列于表6中。固定第一主应力和第二主应力不变,减小第三主应力绝对值,椭球体附近应力集中系数减小;固定第一主应力和第三主应力大小不变,增大第二主应力大小,椭球体杂质应力集中系数增大。椭球长轴与三向应力分别平行时,应力集中系数的变化情况均一致,且与球体变化情况一致,为节约篇幅,这里不再列出具体数据。长轴方向与x-y-z三向应力平行时,应力集中系数最大值与最小值的差异分别约为9.38%、13.39%和9.44%。因此,可以得出结论:三向主应力的比例对于应力集中系数的影响并不显著,估算杂质应力集中系数时可以重点关注杂质与第一主应力之间的夹角方向。
绝缘子瓷件属于脆性材料,且其抗压强度远高于抗拉强度,可以采用第一强度理论作为材料破坏判据,由第一主应力σ1与抗拉强度[σ]的大小关系判断材料在应力作用下是否发生破坏。利用三点弯曲试验测量某批次瓷件的抗拉强度约为182 MPa,正态分布标准差为8.8 MPa。依据本文2.1节计算结果,550 kN瓷件在36 MPa水压载荷下,瓷件内出现三处应力集中区域,其应力最大值分别约为区域Ⅱ内壁处的80 MPa、区域Ⅰ头部拐角处的100 MPa和区域Ⅲ颈部拐角处的120 MPa,三者均小于瓷件抗拉强度,可以认为完好瓷件进行36 MPa水压试验时被破坏的概率极低。
而当瓷件中出现铁点等杂质缺陷时,会引起杂质附近瓷件区域中出现应力集中情况。当杂质为形状尖锐的椭球体时,应力集中系数最高可达到1.5~1.6。按照完好瓷件中主应力大小进行计算,区域Ⅰ头部拐角出现该种杂质时,最大应力将会达到150~160 MPa,区域Ⅲ颈部拐角处最大应力会达到180~190 MPa,36 MPa水压载荷下对此处区域杂质缺陷剔除效果良好。但是对于内壁等其余位置可能会存在漏检问题,可以进一步酌情提升水压载荷。但是要注意避免区域Ⅲ和区域Ⅰ位置应力过大,导致完好瓷件在试验中发生破坏。各厂家内水压试验条件设置各有不同,需根据各厂条件分别判断水压载荷设置。
应力集中区域最大第一主应力值随水压载荷变化情况如图13所示。有限元计算结果表明,内水压试验中增加水压载荷会进一步增大完好瓷件内部应力,完好瓷件在内水压试验中被破坏的风险增加,导致部分满足运行条件的瓷件发生破损,降低了绝缘子生产的全过程合格率,增加了生产成本,同时还可能导致瓷件内部新缺陷的产生。因此,理论上瓷件进行内水压试验时的试验效果应该呈一倒“U形”曲线,内水压试验剔除率及试验效果随压强变化示意图如图14所示。当试验压强值较小时,随试验压强升高,试验效果变好;超过一定压强值后,进一步提升压强会导致试验效果变差。因此,内水压试验压强值应存在最优区间,在确保影响运行的缺陷全部被剔除的同时,保证良好瓷件不会在内水压试验中被损坏。寻找该区间水压载荷的上、下限值,需要进一步进行仿真及试验研究。
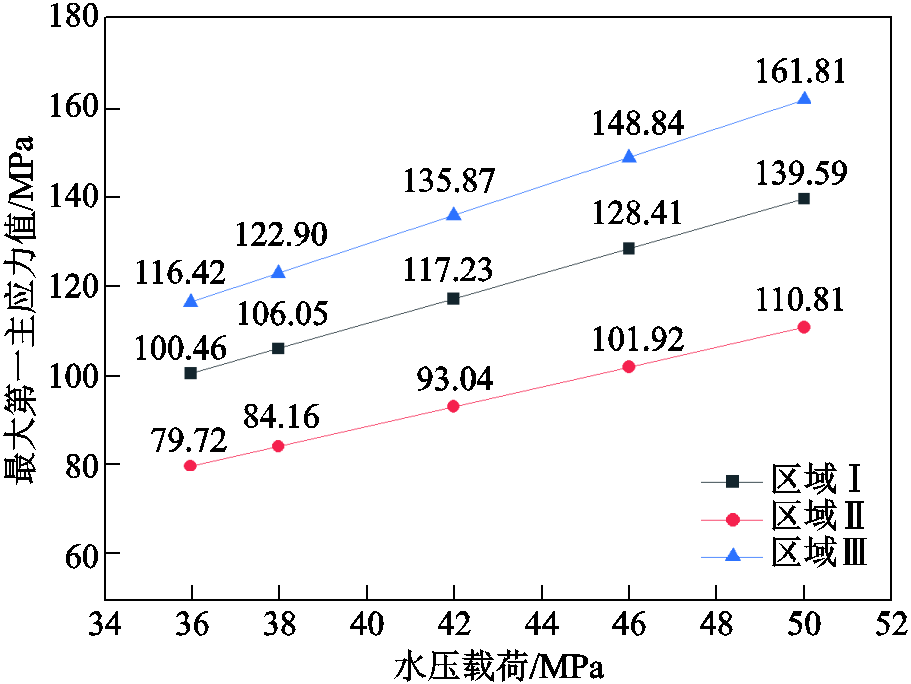
图13 应力集中区域最大第一主应力值随水压载荷变化
Fig.13 The maximum first principal stress in stress concentration area varies with water pressure load
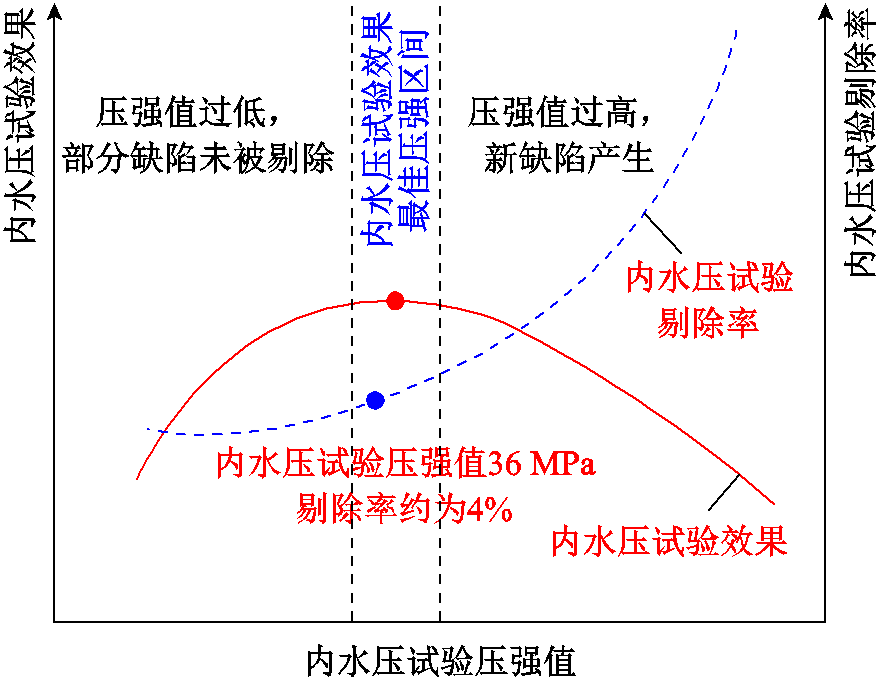
图14 内水压试验剔除率及试验效果随压强变化示意图
Fig.14 The change of internal water pressure test rejection rate and test effect with pressure
根据G. R. Irwin等提出的断裂力学理论,含有裂纹体的材料发生断裂并失稳扩展,最终发生断裂的条件为
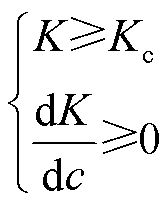 (6)
(6)
式中,K为应力强度因子,是关于外加应力和裂纹尺寸c的函数,其决定了裂纹位置局部场的强度;Kc为裂纹系统的临界应力场强度。
内水压试验剔除杂质等缺陷的过程可以归结为陶瓷材料夹杂物导致微裂纹诱发开裂的过程。在内水压试验过程中,杂质附近形成的应力场会诱发夹杂物/基体界面形成微裂纹,杂质的形状尺寸会影响夹杂物附近的应力场分布,并影响诱发的裂纹尺寸。包含杂质与微裂纹的系统可以近似看作椭球体周围环绕微裂纹带的情况,如图15所示[33-34]。裂纹尖端的应力场强度近似计算式为
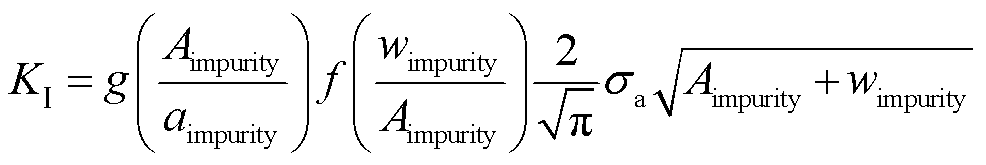 (7)
(7)
式中,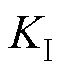 为裂纹尖端的应力强度因子;g(·)和f(·)分别为考虑杂质的修正因子和几何形状的修正系数,均为其自变量的增函数;
为裂纹尖端的应力强度因子;g(·)和f(·)分别为考虑杂质的修正因子和几何形状的修正系数,均为其自变量的增函数;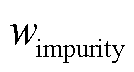 为杂质外微裂纹带的宽度;
为杂质外微裂纹带的宽度;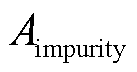 为杂质长轴长;
为杂质长轴长;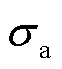 为裂纹处应力大小。式(7)表明,杂质形状越尖锐,杂质与微裂纹带形成的应力强度因子越大,越容易发生断裂,试验中剔除效果越好。然而杂质附近形成微裂纹带的原理目前尚不清晰,式(7)也仅能对不同形状的杂质引起开裂的趋势进行大致分析,后续仍需进一步研究[28]。
为裂纹处应力大小。式(7)表明,杂质形状越尖锐,杂质与微裂纹带形成的应力强度因子越大,越容易发生断裂,试验中剔除效果越好。然而杂质附近形成微裂纹带的原理目前尚不清晰,式(7)也仅能对不同形状的杂质引起开裂的趋势进行大致分析,后续仍需进一步研究[28]。
图15 杂质微裂纹系统示意图
Fig.15 Schematic diagram of impurity microcrack system
1)厂家内水压试验结果表明,对于大吨位瓷绝缘子,在36 MPa内水压试验中可以有效地剔除瓷件中较为明显的缺陷,例如在水压作用下扩展的尺寸较大的裂纹、尺寸较大的杂质以及本征强度较低的黄芯部分。少数断面上存在只能在显微镜下观察到的尺寸较小的铁点杂质。
2)内水压试验对缺陷的剔除效果应主要通过缺陷附近瓷件上的最大第一主应力值进行判断,该值主要受到杂质附近边界主应力的大小以及杂质上应力集中系数的影响。瓷件进行36 MPa内水压试验时,瓷件内壁上第一主应力在40~80 MPa,头部位置第一主应力从10~110 MPa变化。因此,内水压试验对绝缘子头部拐角及侧壁靠内位置的微小杂质剔除效果最佳。
3)杂质附近瓷件内应力集中系数主要受杂质的弹性模量、杂质形状、杂质长轴方向与主应力之间夹角的影响:杂质附近区域的应力集中系数与杂质和基体弹性模量差值呈正相关;杂质形状越尖锐,杂质附近区域应力集中系数越大,且杂质形状对应力集中系数的影响比杂质大小的影响更大;形状尖锐的杂质等缺陷附近的应力集中系数受杂质与边界应力方向夹角的影响明显;三向边界应力之间的比例关系对应力集中系数的影响并不显著。
4)本文建立椭球体杂质来表征在试验中发现的形状尖锐的杂质缺陷,根据本文计算结果,形状尖锐的杂质处的应力集中情况对于杂质与第一主应力的夹角方向更为敏感,尖锐杂质与边界应力方向的夹角显著影响剔除效果。
为了保证瓷件质量,后续将研究瓷件缺陷对绝缘子电气性能的影响规律,明确运行条件下瓷件内部不同缺陷的发展规律,进一步确定内水压试验的合理水压载荷值。
参考文献
[1] 关志成. 绝缘子及输变电设备外绝缘[M]. 北京: 清华大学出版社, 2006.
[2] 周兆禹. 盘形悬式绝缘子的结构分析与优化[D]. 包头: 内蒙古科技大学, 2012. Zhou Zhaoyu. Structure analysis and optimization of the cap and pin insulator[D]. Baotou: Inner Mongolia University of Science & Technology, 2012.
[3] 周学明, 尹骏刚, 胡丹晖, 等. 圆柱头盘形悬式瓷绝缘子钢脚结构优化分析[J]. 电瓷避雷器, 2022(2): 159-166. Zhou Xueming, Yin Jungang, Hu Danhui, et al. Pin structure optimization of cylindrical head suspension porcelain insulator[J]. Insulators and Surge Arresters, 2022(2): 159-166.
[4] 刘洪吉, 耿三平, 王军, 等. 特高压交流输电线路瓷绝缘子劣化分析[J]. 电瓷避雷器, 2022(6): 159-164. Liu Hongji, Geng Sanping, Wang Jun, et al. Aging analysis of porcelain insulators used in UHV AC transmission line[J]. Insulators and Surge Arresters, 2022(6): 159-164.
[5] 王博, 张丹丹, 闫振华, 等. 温度对瓷支柱绝缘子机械性能影响仿真研究[J]. 高压电器, 2020, 56(4): 74-79. Wang Bo, Zhang Dandan, Yan Zhenhua, et al. Simulation study on the influence of temperature on the mechanical properties of porcelain post insulator[J]. High Voltage Apparatus, 2020, 56(4): 74-79.
[6] 高博, 闫振华, 赵禹来, 等. 瓷件微观结构对悬式瓷绝缘子机械性能和抗温度变化性能的影响研究[J]. 电瓷避雷器, 2019(5): 255-261. Gao Bo, Yan Zhenhua, Zhao Yulai, et al. Study on the effect of ceramic microstructure on mechanical properties and temperature resistance of suspended porcelain insulators[J]. Insulators and Surge Arresters, 2019(5): 255-261.
[7] Cherney E A, Baker A C, Kuffel J, et al. Evaluation of and replacement strategies for aged high voltage porcelain suspension-type insulators[J]. IEEE Transactions on Power Delivery, 2014, 29(1): 275-282.
[8] 宿志一, 车文俊. 电网运行中绝缘子的损坏原因及检测[J]. 电力设备, 2005(3): 10-13. Su Zhiyi, Che Wenjun. Damage reason and detection of insulator in power network operation[J]. Electrical Equipment, 2005(3): 10-13.
[9] 陈国宏, 高嵩, 黄瑞平, 等. 机械振动疲劳条件下装配缺陷盘形悬式瓷绝缘子串元件劣化试验研究[J]. 电瓷避雷器, 2021(4): 203-208. Chen Guohong, Gao Song, Huang Ruiping, et al. Experimental investigation on degradation of the high-voltage porcelain insulator string units containing assembly defects during mechanical vibration fatigue[J]. Insulators and Surge Arresters, 2021(4): 203-208.
[10] 宋治波, 杨昊, 申巍, 等. 交流电压下伞型结构对染污绝缘子电弧路径及绝缘性能的影响[J]. 电工技术学报, 2024, 39(13): 4116-4126. Song Zhibo, Yang Hao, Shen Wei, et al. Influence of umbrella structure on the arc path and insulating properties of contaminated insulators under AC voltage[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 4116-4126.
[11] 余颖, 刘亚东, 李维, 等. 配电线路针式绝缘子早期故障动态特性研究[J]. 电工技术学报, 2023, 38(1): 71-82. Yu Ying, Liu Yadong, Li Wei, et al. Simulation and experimental research on pin insulator incipient fault dynamic characteristic in the distribution network[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 71-82.
[12] 裴少通, 马子儒, 刘云鹏, 等. 500 kV输电线路劣化瓷绝缘子非线性发热特性的红外分析[J]. 高压电器, 2024, 60(1): 33-40. Pei Shaotong, Ma Ziru, Liu Yunpeng, et al. Infrared analysis of nonlinear heating characteristics of deteriorated porcelain insulator of 500 kV transmission lines[J]. High Voltage Apparatus, 2024, 60(1): 33-40.
[13] Okada T, Kimoto I. Improvement of suspension insulator reliability by porcelain proof testing [C]//1968 8th Electrical Insulation Conference, Los Angeles, CA, USA, 1968: 173-176.
[14] Fujimura T. The evolution of porcelain insulator technology in Japan[J]. IEEE Electrical Insulation Magazine, 1995, 11(3): 26-36.
[15] 国家能源局. 标称电压高于1000V架空线路绝缘子使用导则第1部分:交流系统用瓷或玻璃绝缘子: DL/T 1000.1—2018[S]. 北京: 中国电力出版社, 2019.
[16] 王黎明, 汪创, 袁田, 等. 高压直流输电线路耐张串用长棒形悬式瓷绝缘子的机械特性[J]. 高电压技术, 2012, 38(3): 655-662. Wang Liming, Wang Chuang, Yuan Tian, et al. Mechanical characteristics of porcelain long rod suspension insulators for tension strings on HVDC transmission lines[J]. High Voltage Engineering, 2012, 38(3): 655-662.
[17] 杨海涛, 陈庆涛, 丁国成, 等. 高压支柱瓷绝缘子力学特性分析及断裂机理研究[J]. 电瓷避雷器, 2017(4): 178-183. Yang Haitao, Chen Qingtao, Ding Guocheng, et al. Mechanical properties analysis and fracture mechanism study of high voltage post porcelain insulator[J]. Insulators and Surge Arresters, 2017(4): 178-183.
[18] 张廼龙, 刘洋, 高嵩, 等. 盘型悬式绝缘子瓷件的应力分析和结构优化[J]. 哈尔滨工业大学学报, 2021, 53(2): 98-103. Zhang Nailong, Liu Yang, Gao Song, et al. Stress analysis and structural optimization of porcelain for disc suspension insulator[J]. Journal of Harbin Institute of Technology, 2021, 53(2): 98-103.
[19] 徐鹏飞, 田金涛, 孙明道, 等. 252 kV三相共箱盆式绝缘子应力测试与分析[J]. 高压电器, 2021, 57(10): 120-126. Xu Pengfei, Tian Jintao, Sun Mingdao, et al. Stress test and analysis of 252 kV three-phase insulating spacer[J]. High Voltage Apparatus, 2021, 57(10): 120-126.
[20] 郭子豪, 王浩然, 李禾, 等. 特高压盆式绝缘子水压试验中应力应变分布的仿真计算与光纤测量[J]. 高电压技术, 2018, 44(3): 993-1002. Guo Zihao, Wang Haoran, Li He, et al. Calculation and experimental study on strain and stress distribution of UHV GIS spacer during hydrostatic test[J]. High Voltage Engineering, 2018, 44(3): 993-1002.
[21] Wang Haoran, Guo Zihao, Feng Hua, et al. Simulation and experimental study on mechanical performance of UHV GIS spacer in hydrostatic test[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(5): 3122-3131.
[22] 施毅舟, 张欣, 李西育, 等. 基于应力应变分析的盆式绝缘子破裂趋势判断方法研究[J]. 电瓷避雷器, 2015(2): 19-22, 30. Shi Yizhou, Zhang Xin, Li Xiyu, et al. Judgment method of basin insulator rupture process based on the analysis of stress and strain[J]. Insulators and Surge Arresters, 2015(2): 19-22, 30.
[23] 张语桐, 吴泽华, 徐家忠, 等. 特高压GIS用单支撑绝缘子绝缘结构优化设计[J]. 电工技术学报, 2023, 38(1): 258-269. Zhang Yutong, Wu Zehua, Xu Jiazhong, et al. Optimization design of insulation structure for post insulator in UHVAC GIS[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 258-269.
[24] 王超, 李文栋, 陈泰然, 等. 550k V GIS盆式绝缘子小型化设计(一): 几何形状优化[J]. 电工技术学报, 2022, 37(7): 1847-1855. Wang Chao, Li Wendong, Chen Tairan, et al. Compact design of 550 kV basin-type spacer in gas insulated switchgear (part I)—structure optimization[J]. Tran-sactions of China Electrotechnical Society, 2022, 37(7): 1847-1855.
[25] 李群, 高嵩, 杨生哲, 等. 国产特高压大吨位悬式瓷绝缘子机电性能提升与工艺优化方法[J]. 电工技术学报, 2023, 38(19): 5304-5315. Li Qun, Gao Song, Yang Shengzhe, et al. Mechanical and electrical performance improvement and process optimization of domestic UHV large tonnage suspension porcelain insulator[J]. Transactions of China Electrotechnical Society, 2023, 38(19): 5304-5315.
[26] 付云伟, 张龙, 倪新华, 等. 考虑夹杂相互作用的复合陶瓷夹杂界面的断裂分析[J]. 力学学报, 2016, 48(1): 154-162. Fu Yunwei, Zhang Long, Ni Xinhua, et al. Interface cracking analysis with inclusions interaction in composite ceramic[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(1): 154-162.
[27] 尹光志, 刘超, 李铭辉, 等. 椭圆形钻孔应力场解析解及水力压裂特性[J]. 煤炭学报, 2019, 44(增刊1): 61-73. Yin Guangzhi, Liu Chao, Li Minghui, et al. Analytical solution of stress field on elliptical borehole and its hydraulic fracturing characteristics[J]. Journal of China Coal Society, 2019, 44(S1): 61-73.
[28] 杨万科, 王启智, 廖丽萍, 等. 远场三轴应力作用下一般椭球洞的应力分布[J]. 地下空间与工程学报, 2011, 7(3): 435-443. Yang Wanke, Wang Qizhi, Liao Liping, et al. Stress distribution of the general ellipsoidal cavity in infinite body subjected to triaxial compressive stresses[J]. Chinese Journal of Underground Space and Engineering, 2011, 7(3): 435-443.
[29] 廖丽萍, 杨万科, 王启智. 椭球形空洞地基稳定性分析[J]. 岩土力学, 2010, 31(增刊2): 138-148. Liao Liping, Yang Wanke, Wang Qizhi. Stability analysis of an ellipsoidal cavity in foundation[J]. Rock and Soil Mechanics, 2010, 31(S2): 138-148.
[30] 邹德仕, 于清波. 圆柱头瓷绝缘子生产过程中内水压值的确定方法[J]. 电工材料, 2022(2): 65-67. Zou Deshi, Yu Qingbo. Method for determining the value of hydraulic inner pressure test in cylindrical head suspension porcelain[J]. Electrical Engineering Materials, 2022(2): 65-67.
[31] 邵仕超. 圆柱头盘形悬式瓷绝缘子设计研究[D]. 北京: 清华大学, 2021. Shao Shichao. Study on the design of disc porcelain suspension insulator with cylindrical head[D]. Beijing: Tsinghua University, 2021.
[32] 李玉书, 吴落义, 李瑛. 电瓷工艺与技术[M]. 北京: 化学工业出版社, 2007.
[33] Danzer R, Lube T, Supancic P, et al. Fracture of ceramics[J]. Advanced Engineering Materials, 2008, 10(4): 275-298.
[34] 龚江宏. 陶瓷材料断裂力学[M]. 北京: 清华大学出版社, 2001.
Abstract Porcelain parts of insulator are generally made of calcined alumina and inorganic minerals such as clay and feldspar in accordance with the ratio of firing. Due to impurities in raw materials and kilns in the production process, there may be defects such as impurities and pores in porcelain parts. In the actual operating environment, the insulator is subjected to electrical, thermal and mechanical stress, as a result of which internal defects of porcelain parts may be further expanded, resulting in a significant decline in the overall mechanical and electrical properties of the insulator. In order to improve the overall quality of insulators, DL/T 1001.1 stipulates that porcelain parts need to carry out hydraulic test one by one before adhesive assembly to remove the defects in porcelain parts, but the standard doesn’t clearly specify the key test parameter (water pressure), manufacturing enterprises set the pressure based on experience, the test parameters lack scientific basis. In order to scientifically guide the setting of the test conditions of the internal hydraulic test, the types and distribution positions of the removal defects by internal hydraulic test were statistically analyzed, and different factors affecting the sensitivity of the removal of impurities in the internal hydraulic test were analyzed.
First of all, the hydraulic test of domestic porcelain insulator manufacturers was investigated, and it was found that the manufacturers didn’t carry out detail statistics of the position and type of defects removed by the hydraulic test. The author went to a domestic insulator manufacturer to track a batch of products, collect the porcelain pieces destroyed in the hydraulic test, and classify the defects on the section, which are mainly divided into yellow core, micro-cracks, impurities and so on.
Secondly, the article has analyzed the internal stress distribution of intact porcelain parts in the hydraulic test by finite element simulation. On this basis, according to different types of defects, the stress calculation is carried out by setting up defect model. The stress distribution in the hydraulic test is taken as the boundary stress condition of the calculation of submodel, and different defects are set in the submodel to calculate the local stress. The sensitivity of internal hydraulic test to remove different defects is analyzed by calculating the stress concentration coefficient at the defect. According to the results, the influence of elastic modulus, size and shape of impurities and different stress boundary conditions on the stress concentration coefficient at the defect is analyzed.
Finally, the article analyzed the reasonableness of the current hydraulic test conditions in the manufacturers based on the first principal theory. The subsequent work will further optimize the setting of internal water pressure test conditions based on the statistical accumulation of defect removal data from the manufacturer's internal water pressure test and the actual operation of the large-tonnage porcelain insulators produced by the manufacturer in the line.
Keywords: Cylindrical head insulator, hydraulic inner pressure test, finite element simulation, stress of inclusions
DOI: 10.19595/j.cnki.1000-6753.tces.240299
中图分类号:TM216
国家自然科学基金资助项目(51977117)。
收稿日期 2024-02-26
改稿日期 2024-04-15
仪明哲 男,1995年生,硕士研究生,研究方向为瓷绝缘子力学性能。E-mail:m17703646290@163.com
曹 彬 男,1993年生,博士,研究方向为高压外绝缘。E-mail:huhu0512@126.com(通信作者)
(编辑 李 冰)