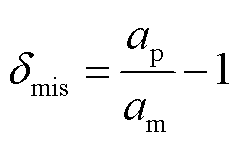（1）摘要 纳米颗粒分散性是影响纳米电介质绝缘性能的关键因素。为实现分散性的无损表征，该文首先建立了表征纳米颗粒团聚程度的团聚界面失配模型，并推导了纳米电介质非线性响应本构关系；然后利用数值模拟方法对纳米电介质非线性响应本构关系进行验证，并基于仿真结果确定了最优的实验激励信号参数；最后制备了不同分散性的纳米二氧化硅掺杂环氧样品，对其进行非线性超声（NLUS）测试，结合界面失配模型实现了等效粒径的定量反演。NLUS粒径反演结果与大量扫描电子显微镜（SEM）统计结果误差在2.75%～5.2%之间，表明所提出的非线性声学方法可实现颗粒团聚程度的准确定量评估。
关键词：纳米改性材料 纳米分散性评估 非线性超声 无损检测
纳米电介质是指将纳米级的无机填料较为均匀地分散到聚合物电介质基体中而形成的一种复合体系。研究表明，向纳米电介质中添加纳米颗粒可以在一定程度上提高材料的击穿场强、体积电阻率，进而有效地提高材料的绝缘性能[1-3]。但在实验中也出现了添加纳米颗粒后的材料绝缘性能下降的情况[4-5]。目前学者们普遍认为纳米颗粒在基体中发生的团聚现象是导致纳米电介质绝缘性能下降的主要因素[6-11]。因此，检测纳米电介质中纳米颗粒的团聚程度对评估材料的改性效果意义重大。
环氧树脂（Epoxy Resin, EP）是常见的纳米电介质基体，目前存在的环氧绝缘件缺陷无损检测方法包括基于电学特性的脉冲电流法、感应电荷层析成像法，以及X射线检测法、微波检测法、超声脉冲反射法、相控阵超声法、非线性超声（Nonlinear Ultrasonic, NLUS）法等[12]，但上述方法均未用于材料中的纳米颗粒分散性检测。目前主要采用微观成像法[13-15]实现纳米颗粒分散性检测，即通过扫描电子显微镜（Scanning Electron Microscope, SEM）、透射电子显微镜（Transmission Electron Microscope, TEM）及原子力显微镜（Atomic Force Microscopy, AFM）等设备，直接观察固体材料内部纳米颗粒的分散状态。这种方法的优点在于能直观地观测区域内纳米颗粒的分散情况，但其单次测量时间较长，费用较高，并且观测区域极其有限，仅能说明材料中局部区域颗粒的分散情况，不能反映材料整体的分散性。同时该方法需要截取小段原材料进行处理，流程较复杂且破坏待测材料，测试后的材料无法继续使用[16-18]。因此，需要研究无损、快速、整体的纳米电介质颗粒分散性评估方法。
有别于传统超声方法，非线性超声主要通过检测声波在材料中传播时产生的高阶畸变来实现对材料内部细微缺陷的检测[19]。当材料内部存在微纳尺度缺陷时，缺陷处的应力-应变关系不再满足胡克定律，由线性关系转变为非线性关系[20]。对材料施加高频高能超声波激励后，非线性应力-应变关系导致声波中出现高次谐波[21-22]，通过观察高次谐波分量的幅值，即可定量描述波形畸变情况。非线性声学方法在金属材料评估中起步较早[19]，主要用于金属疲劳损伤、蠕变损伤、微纳缺陷检测[19, 23-24]。近年来，非线性超声的应用领域逐渐向非金属材料延伸。对环氧固化过程中的研究显示[25-26]，非线性超声可以灵敏地反映非金属材料的固化程度，随着固化过程中材料力学性能的改变，其二次、三次谐波分量也将改变。对物理老化以及热老化高聚物的研究则表明，超声的非线性畸变可以反映材料的早期老化[23-24]。本课题组前期已通过试验证实可通过非线性超声手段有效检测出0.76～9.85 mm的弱粘接缺陷[27-28]，之后于2021年首次提出了利用非线性超声技术评估纳米颗粒分散性[29]，结果表明填料团聚粒径与非线性超声系数大致呈线性关系。但由于建模较为粗糙，未能建立非线性波形特征参数与等效粒径间的定量关系，同时对于试验参数的选取等也缺乏理论支撑。
本文首先通过类比建立表征纳米颗粒团聚程度的团聚界面失配模型，进而获得纳米电介质非线性响应本构模型；然后，结合数值模拟对纳米电介质非线性响应本构模型进行验证，并根据数值仿真结果优化非线性超声实验激励信号参数；最后，制备不同分散性的SiO2颗粒改性环氧树脂样品，对样品进行SEM、AFM及NLUS测试，实现了等效粒径的定量反演工作，进一步验证了非线性响应本构模型的有效性与颗粒分散性检测的准确性。
晶格失配导致不同物相之间的应力-应变关系出现非线性变化。金属材料领域中的晶格失配程度通常使用晶格失配系数δmis表示[30-31]，有
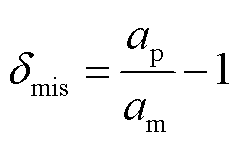（1）
式中，ap和am分别为金属析出相和金属基体相的晶格空间尺寸，即晶格常数。
将金属基体中的晶格失配现象类比推演至纳米电介质领域，使用团聚界面失配系数表示界面失配程度，即纳米颗粒团聚程度，分别讨论分散状态和团聚状态下的界面失配系数计算公式。
直径为DNP的均匀分散的纳米颗粒模型如图1a所示。当纳米颗粒稳定分散时，其与有机基体之间会产生一定的界面物相距离dIF。完全分散的纳米颗粒在基体中的分布可类比于在直径为DNP的孔洞中心放置了一个直径为DNP+2dIF的球体。由文献[32-34]可知，纳米电介质中颗粒与基体的界面物相距离dIF不足0.2 nm，对于本文DNP在100 nm及以上的研究对象而言，界面物相距离dIF可以忽略，因此分散界面的界面失配系数δNP表达式为
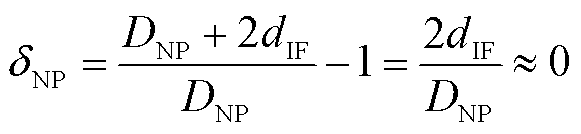（2）
式（2）表明分散状态的纳米颗粒与基体之间的界面失配效应近似为0。
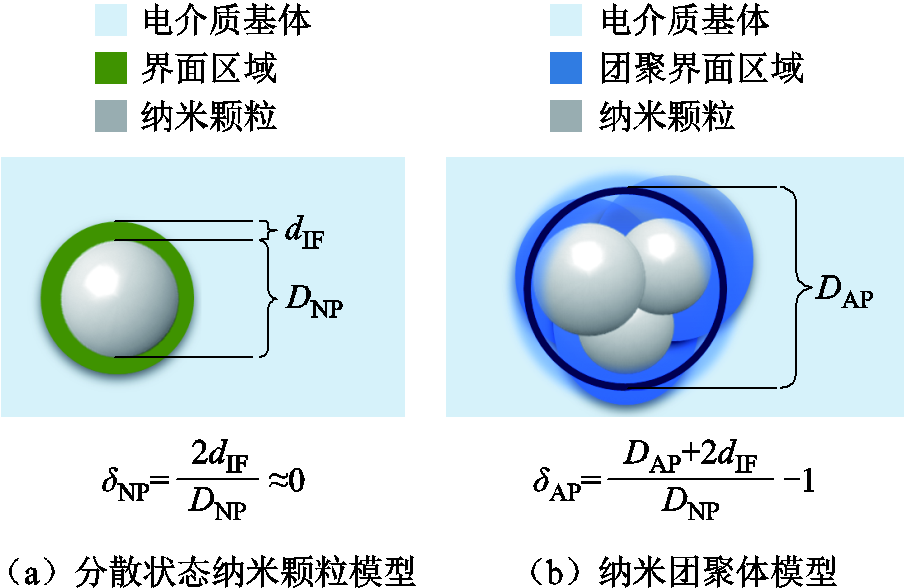
图1 不同状态界面失配系数示意图
Fig.1 Schematic diagram of interface mismatch coefficients in different states
团聚状态的纳米颗粒模型如图1b所示，设纳米团聚体的等效粒径为DAP，则团聚状态的纳米颗粒在基体中的分布可类比于在直径为DNP的孔洞中心放置了一个直径为DAP+2dIF的球体，团聚界面的界面失配系数δAP表达式为
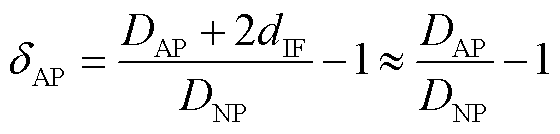（3）
由式（3）可知，团聚状态下的界面失配系数大于0。界面失配可反映纳米颗粒对基体局部结构产生的挤压扭曲作用，会造成界面结构的扭曲与内聚性应变，是纳米电介质体系中非线性的主要来源。对于EP、交联聚乙烯（Cross-Linked Polyethylene, XLPE）等多种基体纳米电介质材料，当掺杂的纳米颗粒出现团聚时，通过检测团聚界面产生的非线性响应，理论上可实现材料分散性的快速、无损检测。
基于纳米电介质团聚界面失配模型，定量求解非线性响应本构模型。取纳米电介质内部一微小体积元DV进行分析，当超声波在固体中传播时，DV产生形变并出现微小位移u，声波沿x方向传播的波动方程为[35]
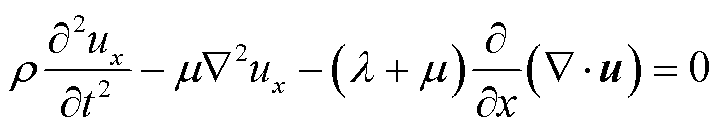（4）
式中，ρ为固体材料密度；λ、μ为固体拉梅常数；拉普拉斯算子表示为
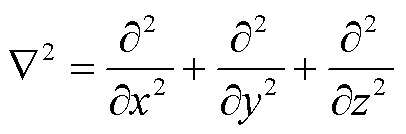（5）
只考虑纵波沿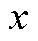
方向的传播时，可得到一维纵波在固体中传播的波动方程为[3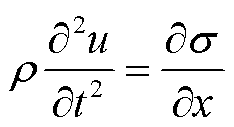6]
（6）
式中，t为传播时间；σ为界面应变。
微纳缺陷导致材料内部局部区域应力-应变关系变为非线性，展开至二阶的非线性应力-应变关系满足[20-22,3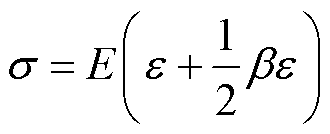7]
（7）
式中，E为杨氏模量；ε为界面应力；β为二阶非线性系数，可定量表示声波畸变程度。将式（7）代入式（6）可得
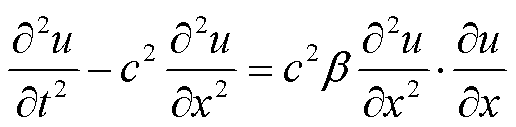（8）
式中，c为光速。采用微扰法求解式（8），设基频激励信号为一束幅值为A1、波数为k、角频率为ω的正弦纵波，得到波动解为
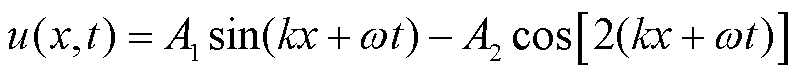（9）
其中,二次谐波分量幅值A2满足
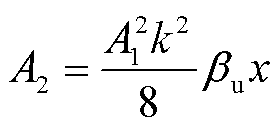（10）
二阶非线性系数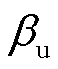
满足
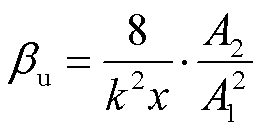（11）
为充分考虑界面失配效应对基体局部结构的力学作用，认为在各向同性的固体介质中，界面失配效应既非膨胀也非流体静力学[38]，纳米颗粒周围微区域的平均位移场可表示为
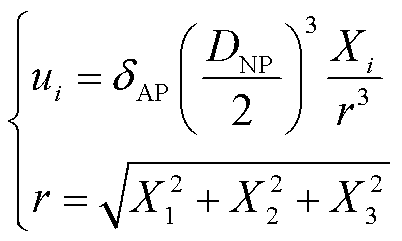（12）
式中，ui为纳米颗粒位移向量在i方向的笛卡尔分量，i=1, 2, 3分别对应x, y, z方向；Xi为拉格朗日坐标向量在i方向的分量；r为质点位置到颗粒中心的径向距离。
假设纳米颗粒掺杂浓度较低时，颗粒的分布间距L远大于颗粒尺寸DAP、DNP，且分布间距的变化不影响总体的失配效应，即将L视为均一化的等效值，从而有
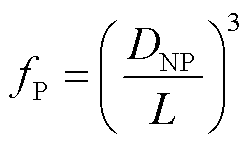（13）
式中，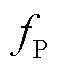
为掺杂纳米填料的体积分数。利用球形颗粒的径向对称性，取简化对称条件为
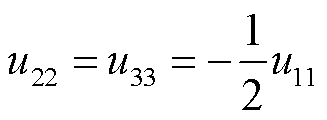（14）
联立式（12）～式（14），获得检测区域内的平均应变为
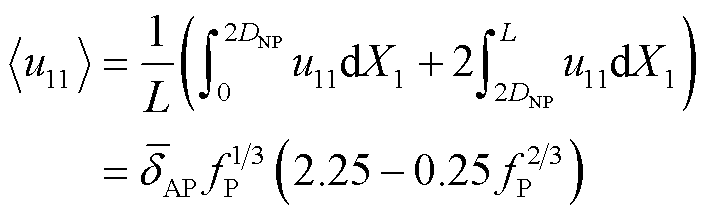(15)
式中，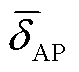
为检测区域内的平均团聚界面失配系数。
将式（6）中波动方程的应变σ展开为高阶张量形式[34,37]为
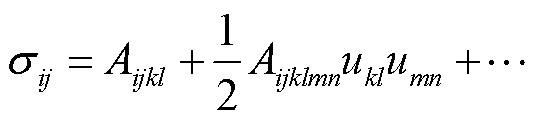（16）
式中，Aijkl和Aijklmn分别为二阶和三阶Huang氏系数（下标i、j、k、l、m、n为张量维数的一般表示形式），与高阶Brugger弹性常数Cijkl和Cijklmn有关，分别表示为
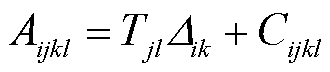（17）
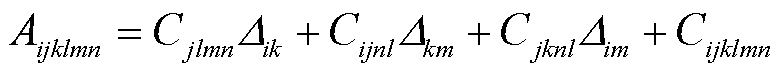（18）
式中，Tjl为初始应力；Dik为Kronecker增量，故可得相应形式的波动方程为
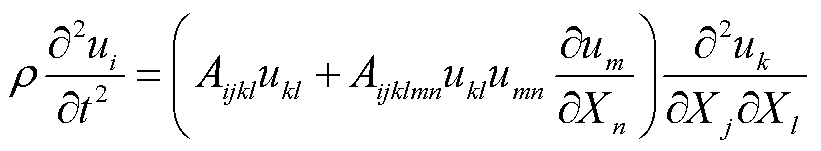（19）
采用微扰法对式（19）展开求解，代入式（14）的径向对称条件，可得高阶张量形式的非线性系数增量Dβ为
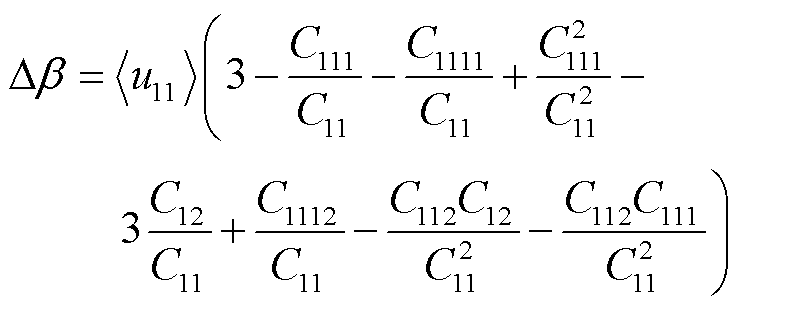(20)
由式（15）和（20）可得
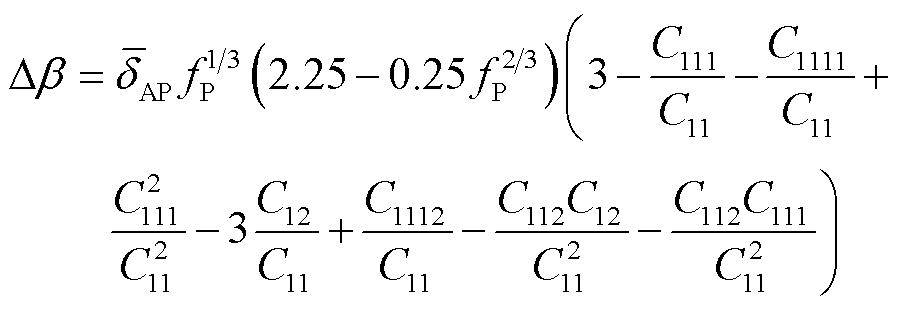(21)
利用Hiki-Granato关系式[39]对式（21）进行简化，可得
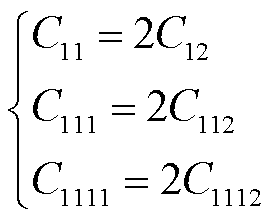（22）
将式（22）代入式（21），获得基于团聚界面失配效应的纳米电介质非线性系数的解析表达式为
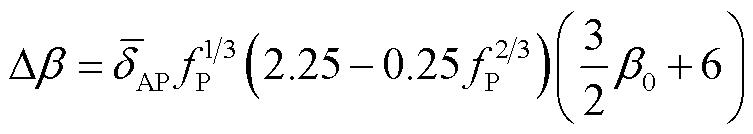（23）
式中，β0为材料固有非线性系数，本文在计算过程中取β0=1。
结合式（7）、式（23）对式（4）经典波动方程中的源项进行修正，获得纳米电介质内波动场控制方程在颗粒区域的边界条件为
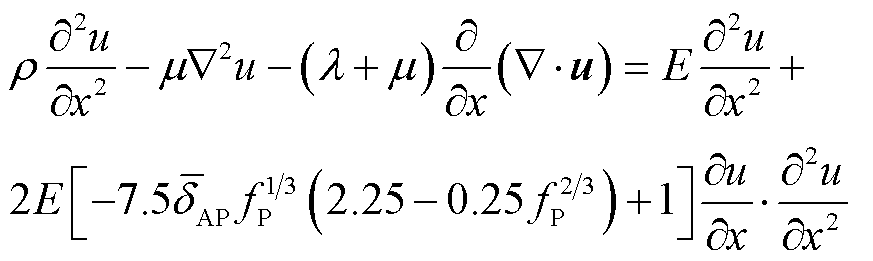(24)
式（24）描述了超声波在纳米电介质基体/纳米团聚体区域的传播过程，据此建立几何模型进行数值模拟，验证非线性响应本构模型的正确性。
利用COMSOL Multiphysics软件搭建SiO2/EP纳米电介质简化模型，使用偏微分模块波动方程接口构建物理场。SiO2、EP材料参数设置见表1。
表1 材料参数设置
Tab.1 Settings of material parameter
材料密度ρ/(kg/m3)杨氏模量E/GPa泊松比 EP基体1 2005.60.38 SiO2颗粒2 20070.20.3
实验中，沿着超声波激励信号施加方向的回波中携带的团聚界面区域信息较多，因此为了降低模型复杂度，缩短仿真时间，将实际三维纳米电介质模型简化为二维xOy平面。EP基体二维简化模型为边长为4 mm的正方形。分散状态SiO2颗粒二维简化模型为直径相同的圆形，当颗粒发生团聚时，圆形的直径随着团聚程度的增大而增加。不同团聚程度的SiO2颗粒随机分布在纳米电介质区域内部，并且在同一模型中，不同团聚程度颗粒数量呈现Weibull分布。本文搭建了不掺杂纳米颗粒（纯基体）、掺杂粒径为100 nm的分散状态纳米颗粒（δ=0）、纳米团聚体平均粒径130 nm（δ=0.3）、纳米团聚体平均粒径150 nm（δ=0.5）四种模型。其中，纳米团聚体平均粒径130 nm（δ=0.3）、纳米团聚体平均粒径150 nm（δ=0.5）模型中颗粒数量分布如图2所示。由图2可知，两种模型中不同团聚程度颗粒数量均满足Weibull分布。
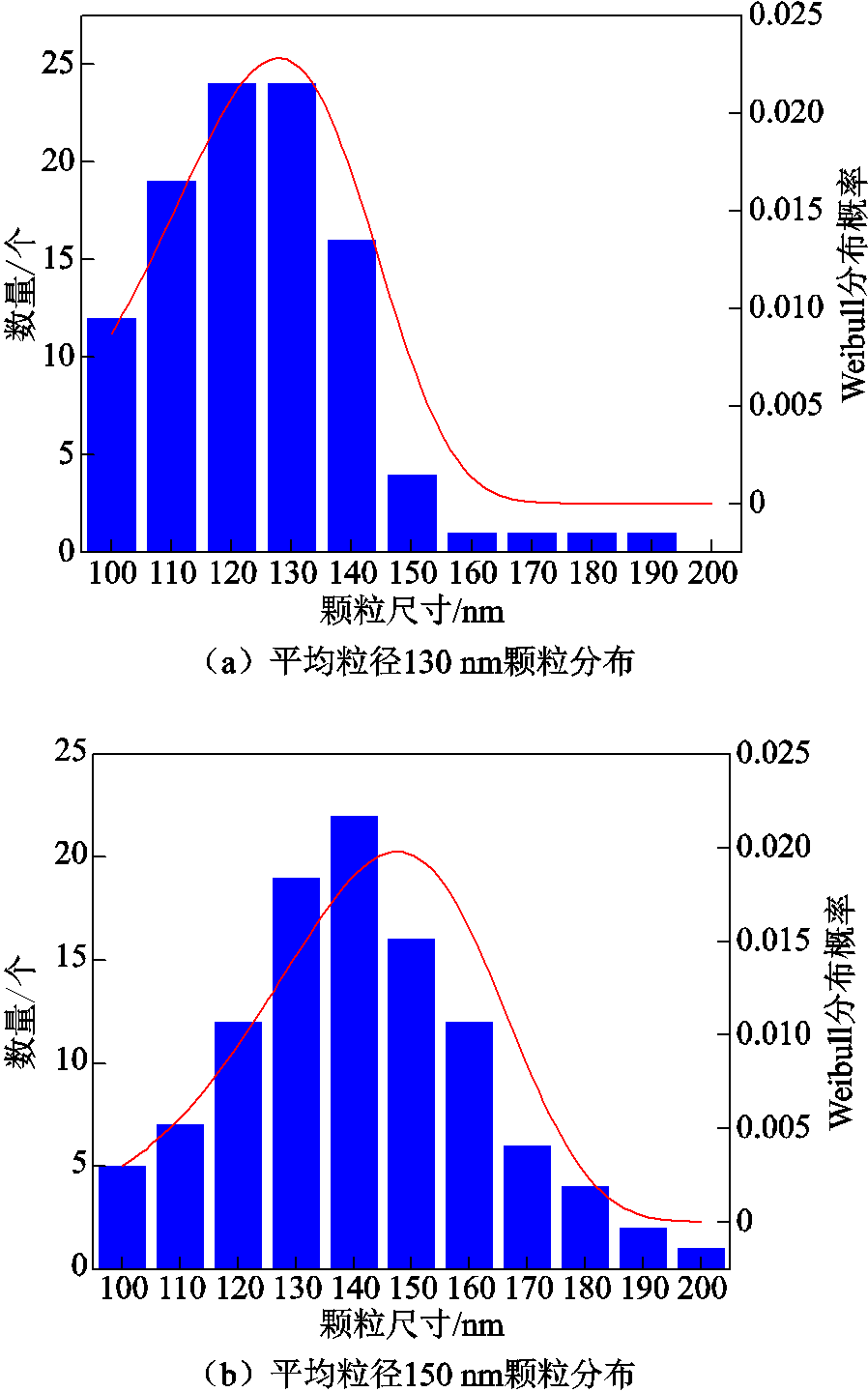
图2 纳米颗粒分布
Fig.2 The distribution of nanoparticles
使用频率为1 MHz、幅值为50 nm的正弦波作为激励信号，仿真时长为一个周期T，时间变量步长为0.01T，四种模型在t=0.01T时刻的二维声场分布如图3所示。图3中，不同直径的圆形代表不同团聚程度的纳米颗粒，随机分布在边长为4 mm的二维xOy平面内；各颜色数值表示二维声场内各处的相对超声强度。由同一时刻模型的相对超声强度不同可知，式（24）可以反映超声波在纳米电介质内的传播状态。
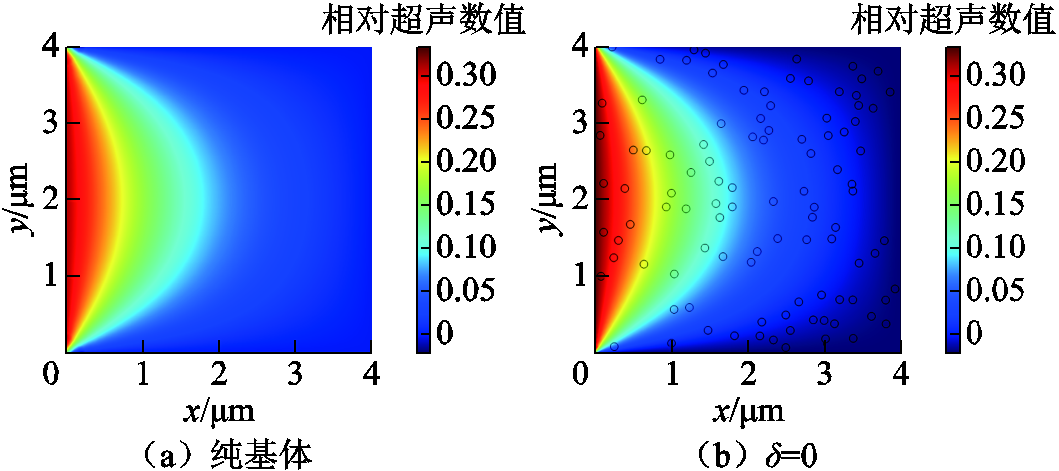
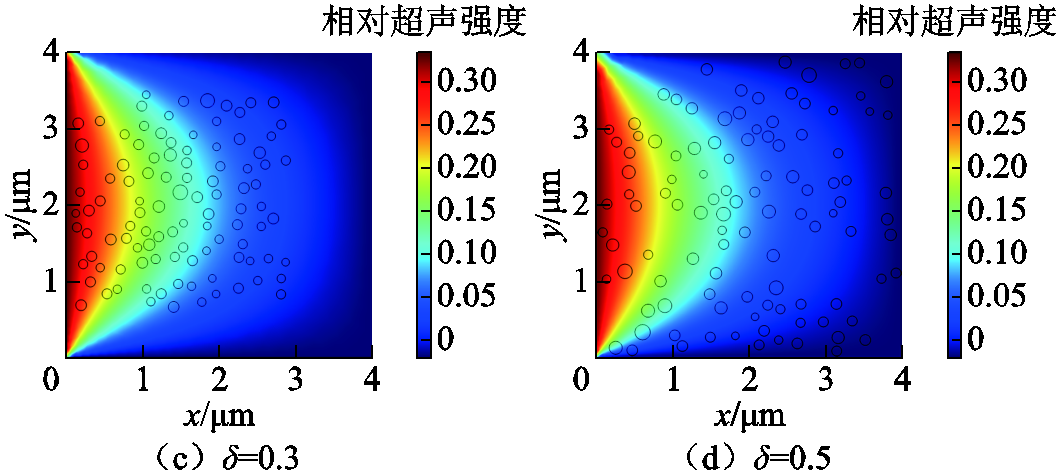
图3 t=0.01T时刻二维声场分布
Fig.3 2D sound field distribution when t=0.01T
激励信号经过四种模型后的时域波形如图4所示。由图4可知，随着失配系数δ的增大，时域波形出现微小形变，但幅值基本不变。为了详细分析波形的畸变程度，对时域波形信号进行快速傅里叶变换（Fast Fourier Transform, FFT）分析，获得四种模型的信号频谱如图5所示。由图5可知，超声波在经过四种模型区域后均产生了高阶畸变，且随着δ增加，高阶畸变增加。其中分散状态颗粒也有高阶畸变产生，这是由于在式（23）中取材料固有非线性系数β0=1所导致。同时由于有限元仿真过程中网格剖分会引入非线性，纯基体模型也有高阶畸变产生。但纯基体模型中的高阶畸变含量远小于其他模型，因此后续分析中可对非线性系数进行正则化处理，只分析由团聚界面引入的非线性响应的大小。
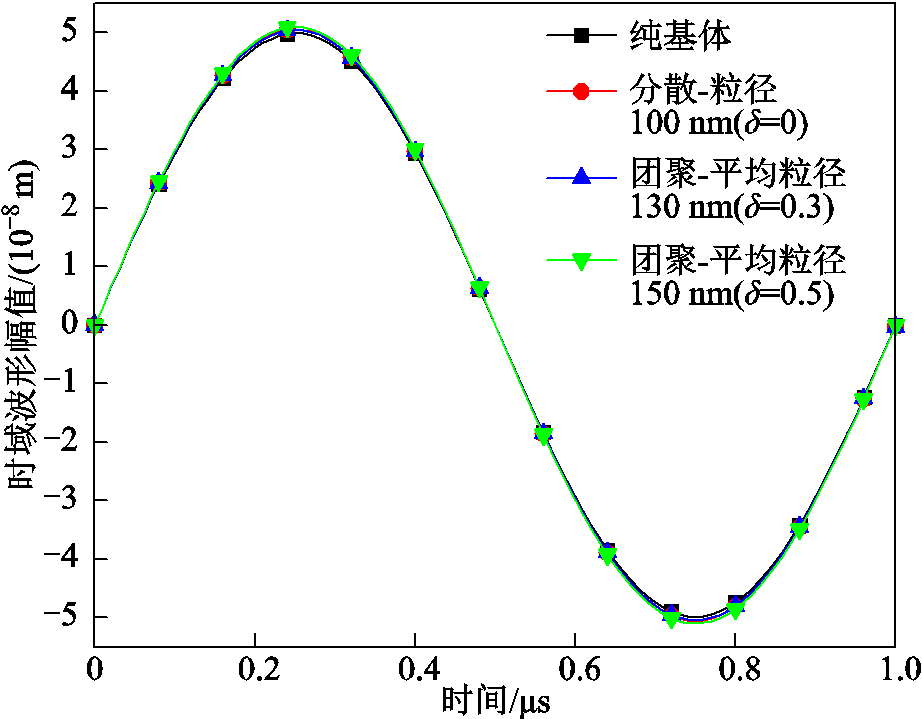
图4 1 MHz四种模型的时域波形
Fig.4 Time-domain waveforms of four models when f=1 MHz
从频谱图中提取基波幅值A1、二次谐波幅值A2，由式（11）计算各模型非线性系数如图6所示。可以看出，随着团聚程度的增加，模型的非线性系数也增加，数值模拟验证了纳米电介质非线性响应本构模型的正确性。
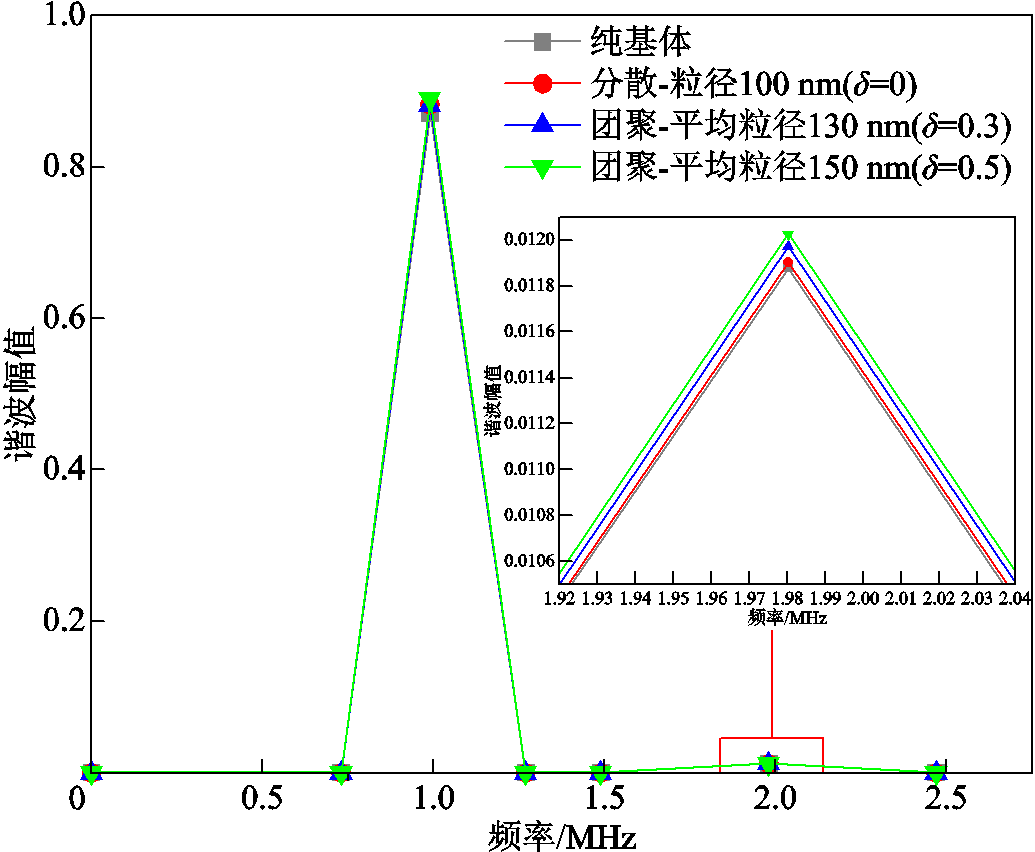
图5 四种模型的信号频谱
Fig.5 The signal spectrograms of four models
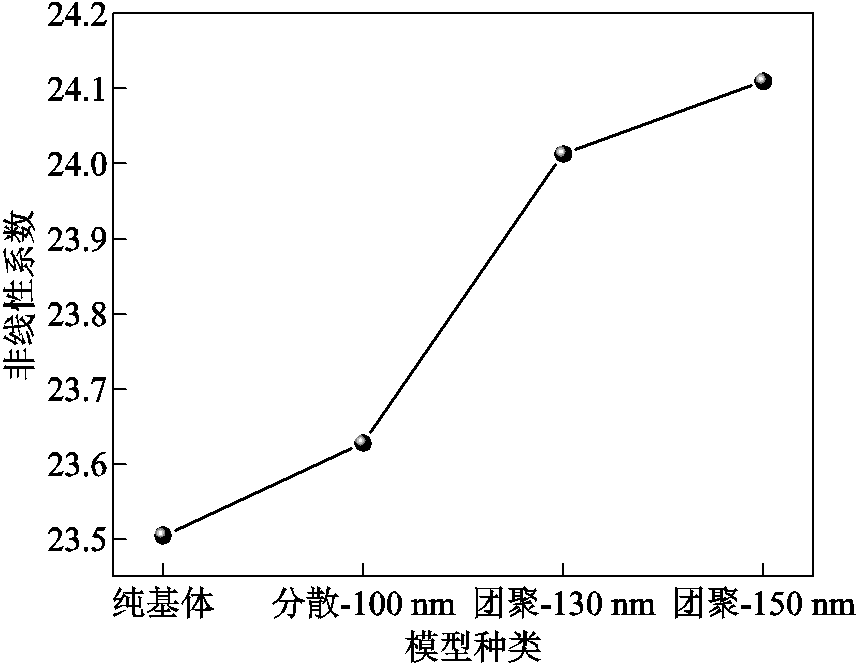
图6 各模型非线性系数变化
Fig.6 The changes in nonlinear coefficients of each model
现有的非线性声学实验激励信号中心频率大多集中在0.1～10 MHz[40-44]，因此本文在该频率范围内探究适用于颗粒分散性检测的激励信号最优频率参数。按照2.1节建模方法对团聚体系（δ=0.3）和分散体系（δ=0）进行建模仿真。为了对比分析不同频率非线性响应的大小，对非线性系数进行归一化处理，不同频率下分散体系与团聚体系归一化非线性系数如图7所示。由图7可知，在0.1～10 MHz频率范围内，通过归一化非线性系数可以明显地区分分散体系与团聚体系。在分散体系与团聚体系内，非线性响应对频率变化并不敏感；当激励信号频率大于5 MHz时，纳米电介质团聚体系非线性响应有所下降，主要是由于波形发生重叠现象，对频谱的分析产生影响。因此，初步确定频率参数设置区间为0.1～5 MHz，在平台搭建阶段将根据超声探头宽频带的幅频增益参数，进一步优化频率设定，确保能够同时采集到二阶和三阶响应信号。
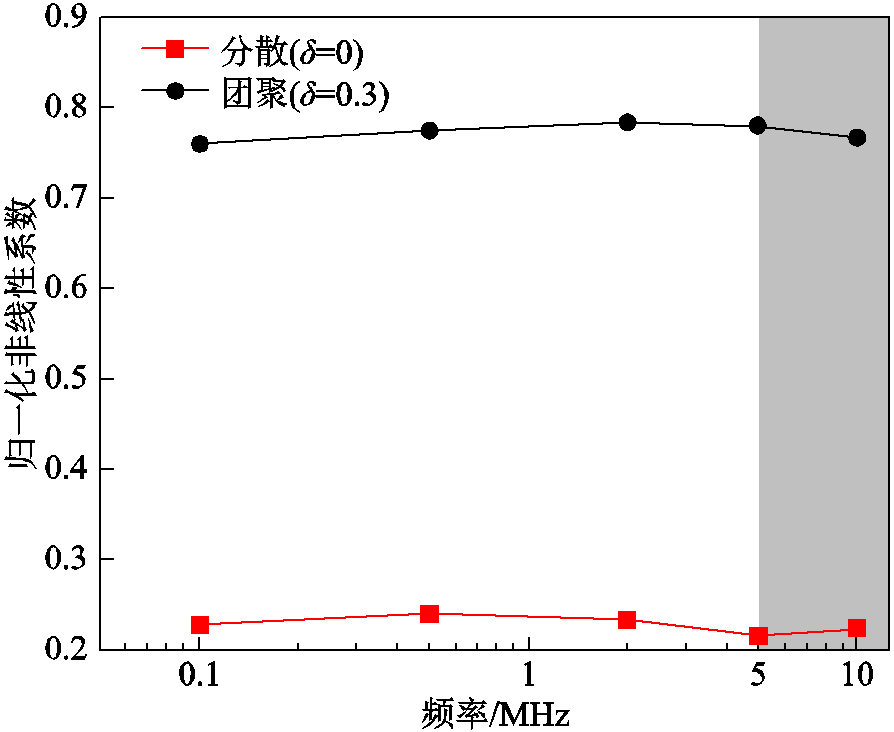
图7 不同频率下归一化非线性系数
Fig.7 The normalized nonlinear coefficients at different frequencies
改变激励信号的幅值，在分散体系和团聚体系模型中进行仿真模拟，得到不同幅值下归一化非线性系数如图8所示。由仿真结果可知，分散体系内非线性响应与激励信号幅值的大小无关，属于材料固有非线性系数。而在团聚体系内，归一化非线性系数随着激励幅值的增加呈现出先增大后减小的趋势，这可能是由于激励信号幅值过大时，团聚界面的应变情况更为复杂。为了尽可能地提升声学信号在不同团聚程度体系内的区分度，根据仿真结果选取最佳激励幅值为70 nm。在后续的测试平台搭建过程中，将结合超声探头的压电系数，以及信号增益情况，共同调制激励信号接近最优区间。
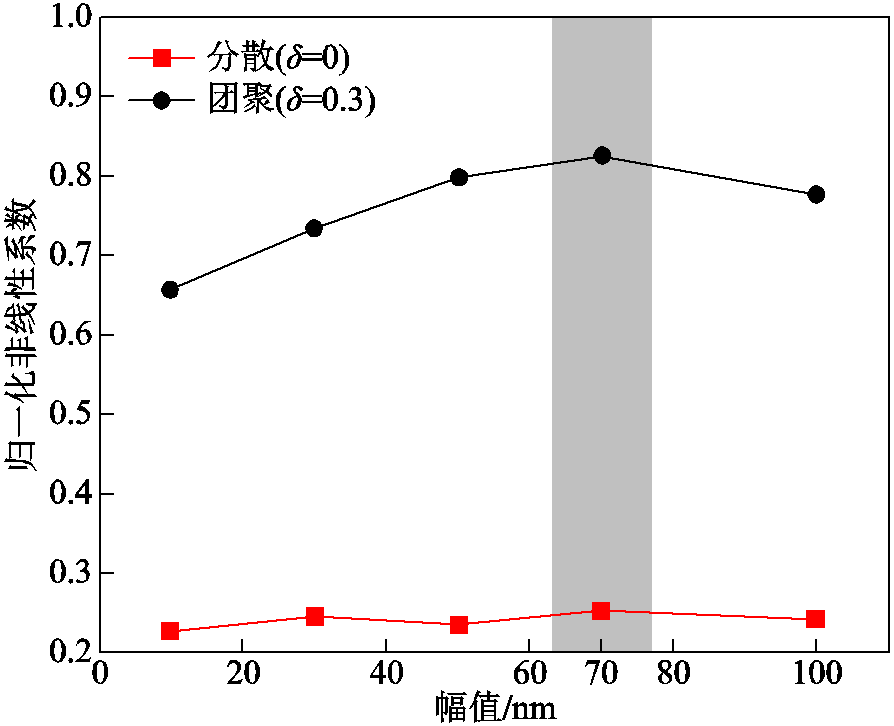
图8 不同幅值下归一化非线性系数
Fig.8 The normalized nonlinear coefficients at different amplitudes
为了验证理论分析的结果，本文制备了二氧化硅颗粒改性环氧树脂样品（SiO2/EP），并利用AFM、SEM表征其微观结构。搭建非线性超声实验平台，研究二阶非线性系数与颗粒团聚程度的关系。
实验样品基体为双酚A型环氧树脂E-51，分别制备掺杂两种粒径（50 nm、100 nm）的SiO2样品。为了提高SiO2颗粒的分散性，使用硅烷偶联剂3-氨丙基三乙氧基硅烷（KH550）对SiO2颗粒进行表面改性，使用纯度≥80%的甲基四氢邻苯二甲酸酐作为固化剂，纯度为99%的邻苯二甲酸二甲酯作为增韧剂，纯度为98%的1,2-二甲基咪唑作为促进剂。SiO2/EP样品制备流程如图9所示。
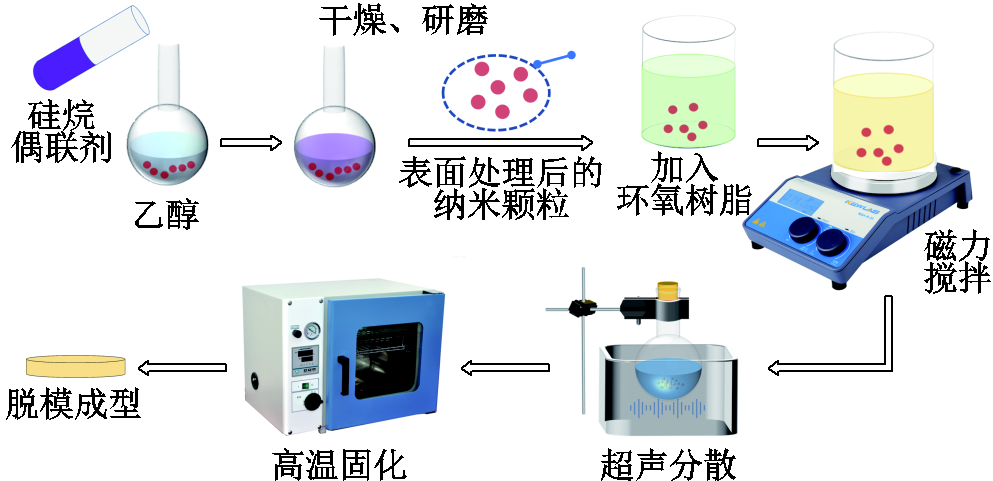
图9 SiO2/EP样品制备流程
Fig.9 The flow-process of SiO2/EP sample preparation
首先，将纳米SiO2颗粒置于真空干燥箱中，设置温度为100℃，干燥24 h。将干燥后的纳米颗粒转入烧瓶中，加入适量无水乙醇并超声分散1 h，获得混合液A。按照体积比1:1:18分别量取KH550、去离子水、无水乙醇三种试剂于烧瓶中进行水解反应，获得溶液B。然后取适量的溶液B加入混合液A中，获得混合液C。在120℃恒温下加热搅拌混合液C，冷凝回流，反应10 h后，将所得悬浊液在60℃下真空干燥，并将干燥后的表面改性颗粒用球磨机研磨12 h。接着将纳米颗粒加入环氧树脂中，并在50℃下搅拌1 h，按照100:80:10:1的质量比混合环氧树脂、固化剂、增韧剂、促进剂，在50℃下轮流进行恒温搅拌与超声分散的操作。在超声分散过程中，本文通过改变超声分散时间来获得不同分散程度的样品，设置超声分散时间分别为1 h、2 h、6 h，获得三种不同分散程度的样品，分别记为SiO2/EP-1h、SiO2/EP-2h、SiO2/EP-6h。分散结束后，将混合液倒入金属模具，真空脱泡处理，再置于恒温箱中，在90℃下高温固化2 h，最后冷却脱模获得样品。
本文使用原子力显微镜（Bruker Dimension Icon）搭载的力谱分析模组对样品界面进行原位界面观察，采样频率为1 kHz，纳米探针曲率半径为 8 nm。在探针与样品表面从接触、压紧到回弹及分离过程中，采集力-位移曲线。在测试过程中多次移动探针位置并对颗粒附近的界面区域进行多次扫描，以获取所有测量点的原位数据。
为了观察SiO2纳米颗粒在基体内的分散情况，本文使用场发射扫描电镜（Quattro SEM）进行样品观测。测试前，将样品进行液氮脆断和喷金处理。
非线性超声测试平台由信号发生单元、信号处理单元、信号接收单元以及测样单元组成，系统结构如图10所示。非线性超声测试系统主机（RITEC RAM-5000 SNAP）可输出固定频率、幅值、周波数的脉冲串。
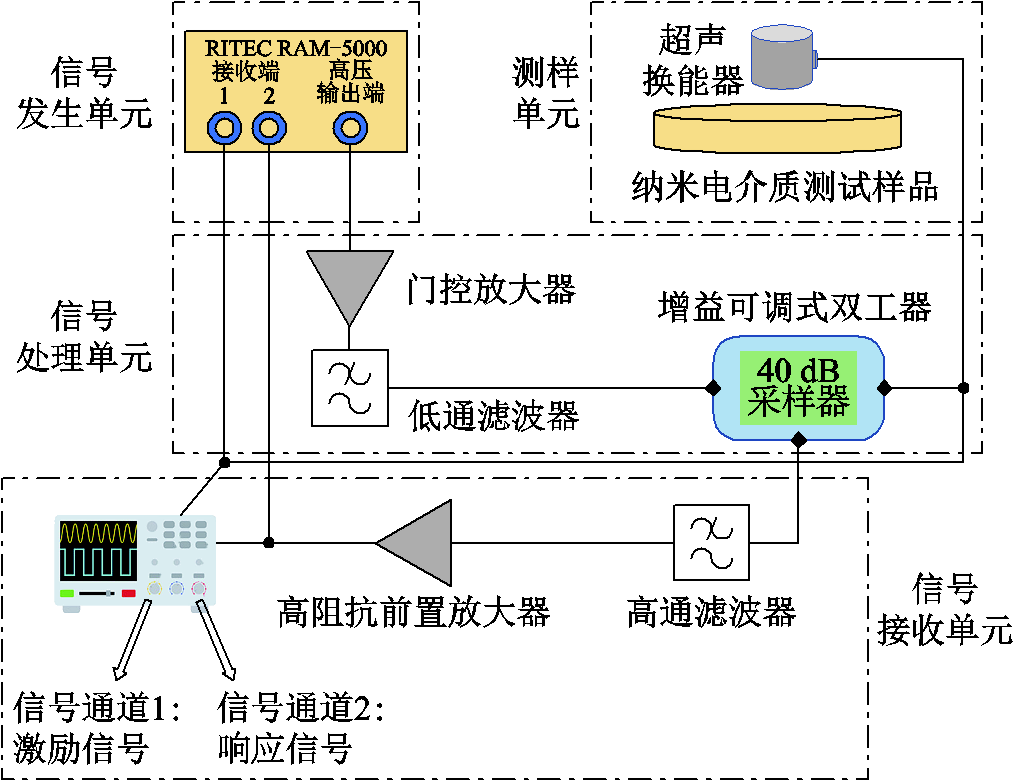
图10 非线性超声测试平台系统结构
Fig.10 The systemic structure of nonlinear ultrasonic testing platform
实验前需结合实际测试系统对激励信号参数进行进一步优化。2.2节仿真结果初步确定了激励信号频率参数设置范围为0.1～5 MHz，本节在确定激励信号频率时主要考虑宽频带范围内的幅频增益情况。奥林巴斯公司生产的三类主流非线性超声换能器V106、V154和V182的中心频率以及最高增益50%以上区间见表2。由表2可知，在同时满足二阶和三阶非线性系数测量的前提下，V182探头的有效增益频带较宽，因此采用V182探头作为超声换能器，将激励信号基频设置为1.5 MHz，实现二倍频3.0 MHz与三倍频4.5 MHz的高增益检测。对于激励信号幅值参数，仿真结果显示70 nm对应最优的非线性声学响应，因此在实验过程中设置声学信号源输出电压Uout=120 V，声学探头的压电系数d33=600 pm/V，根据Au=d33Uout计算得出激励信号幅值Au近似为72 nm，接近于理论仿真的最优幅值。设置激励信号脉冲串周波数为3，同时为了避免在换能器与样品表面之间引入额外非线性，使用丙三醇作为耦合剂均匀涂抹在二者表面。
表2 典型非线性超声换能器的宽频响应范围
Tab.2 The wide frequency response range of typical nonlinear ultrasonic transducers
探头型号中心频率/MHz-3 dB带宽范围/MHz V1062.251.3～3.4 V154V1822.253.51.2～3.01.4～4.6
分散状态SiO2颗粒微观形貌如图11a所示，其中SiO2粒径为50 nm，灰度值表示纳米颗粒及其相邻表面的实际高度。根据探针与样品表面接触、压紧到回弹及分离这一动态过程的力-位移（F-Δl）曲线，可以提取颗粒-基体界面的应力-应变（σ-ε）曲线，计算公式为
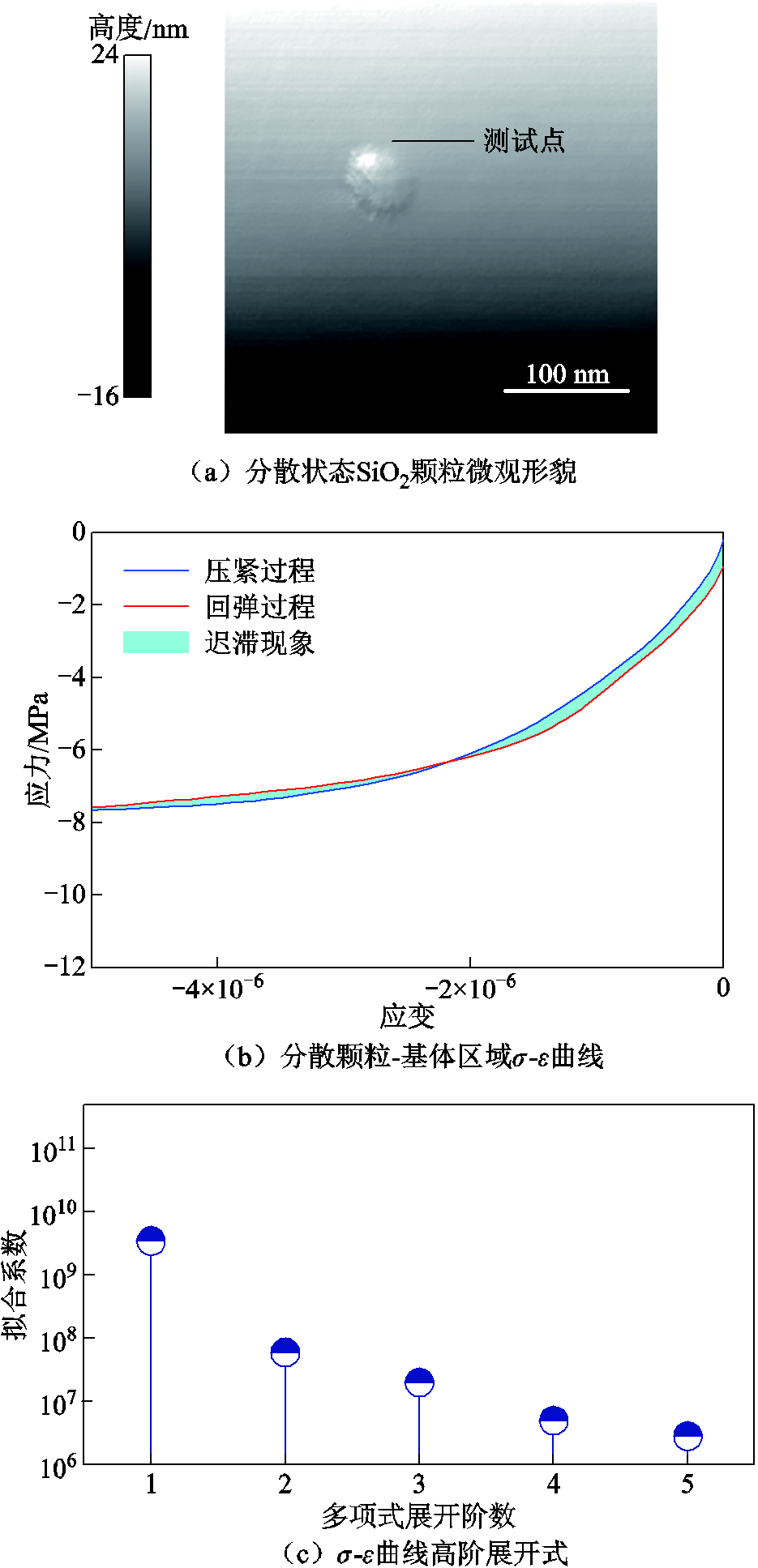
图11 分散状态颗粒-基体界面AFM测试结果
Fig.11 The AFM test results of dispersed particle-matrix interface
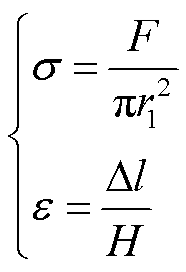（25）
式中，F为纳米探针尖端所受的力；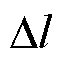
为探针尖端位移；r1为纳米探针半径；H为被测样品厚度。本实验中r1=8 nm，H=50 mm。
在分散纳米颗粒-基体界面区域（图11a中橙色标记点）进行AFM单点测试，获得的σ-ε曲线如图11b所示。在压紧与回弹过程中，σ-ε曲线的迟滞现象可以忽略。由于电介质基体存在高阶模量，因此σ-ε曲线并未呈现严格线性关系。利用Levenberg-Marquardt算法对图11b中的σ-ε本构关系进行高阶拟合，得到本构关系高阶展开式如图11c所示。原位单点力学分析表明，分散纳米颗粒与基体之间的界面区域本构关系畸变低，与线性成分相比，高阶畸变项的衰减率超过1/100。在AFM力谱中对图11a中所有像素点进行分析，结合式（7）计算二阶非线性参数β，获得β扫描图如图11d所示。由于无机纳米颗粒结构有序性优于有机基体，因此SiO2颗粒区域β值较低。图11d中橙色虚线框标记区域为探针从基体向颗粒中心移动的过程，该过程β变化曲线如图11e所示。当探针从基体相移动到颗粒相时，β由2平滑下降至0.2。测试结果表明，分散状态颗粒-基体界面区域力学本构关系没有明显的界面效应。图11反映了式（2）中模型假设的有效性。
纳米团聚体微观形貌如图12a所示。使用相同的方法对纳米团聚体-基体界面AFM测试结果进行分析，结果如图12b～图12e所示。对比图12b和图11b可知，团聚体界面处本构关系的迟滞现象不可忽略，非线性变化更为显著。图12c为团聚界面处σ-ε曲线的高阶分量，其中线性分量不再像图11c中占主导地位。图12d中橙色虚线框标记区域为探针从基体-团聚体-基体的移动过程，该区域β变化曲线如图12e所示。对比图12e和图11e可知，纳米团聚体周围区域的β出现明显上升，峰值为8.76。结合图12a中材料相的高度连续性，可以推测团聚界面是纳米电介质非线性的主要来源，并且团聚界面处的结构失配并不局限于纳米颗粒周围的局部区域dIF，而是会扩展到围绕团聚体约30 nm的区域。
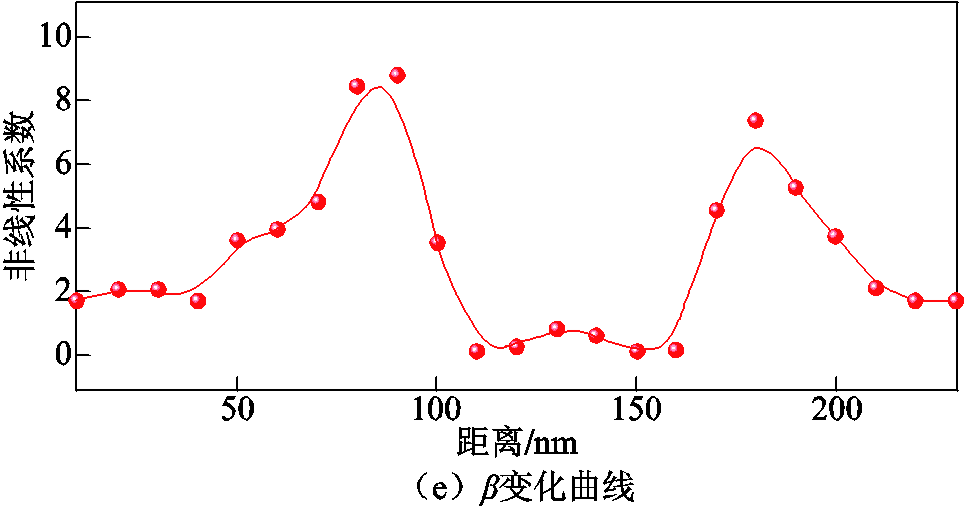
图12 团聚状态颗粒-基体界面AFM测试结果
Fig.12 The AFM test results of agglomerated particle- matrix interface
三种不同分散性SiO2/EP样品微观形貌及其粒径统计信息如图13所示，根据SEM结果求出三种样品平均粒径分别为137 nm、130 nm、109 nm。代入式（3）求出平均界面失配程度分别为0.37、0.30、0.09。当超声分散时间较短时，样品中存在多个颗粒团聚形成的纳米团聚体；随着超声分散处理时间的增加，颗粒团聚程度降低，以分散状态纳米颗粒为主。
图13 不同分散处理时间的SiO2/EP样品微观形貌与粒径统计
Fig.13 The microscopic morphology and particle size statistics of SiO2/EP samples with different dispersion processing times
对三种不同分散性样品以及EP纯基体样品进行非线性超声测试。在同一样品表面取20个测试点进行测试，将接收的反射波时域波形进行FFT分析，计算样品各位置β的平均值，绘制出四种样品以及其团聚程度如图14所示。由图14可知，随着超声分散处理时间增加，颗粒团聚程度减小，同时β减小。未掺杂纳米颗粒的EP纯基体也具有非线性，但其β远小于掺杂纳米颗粒的情况，表明由颗粒团聚界面失配引发的非线性响应可以有效地反映在声频畸变中，与仿真结果一致。
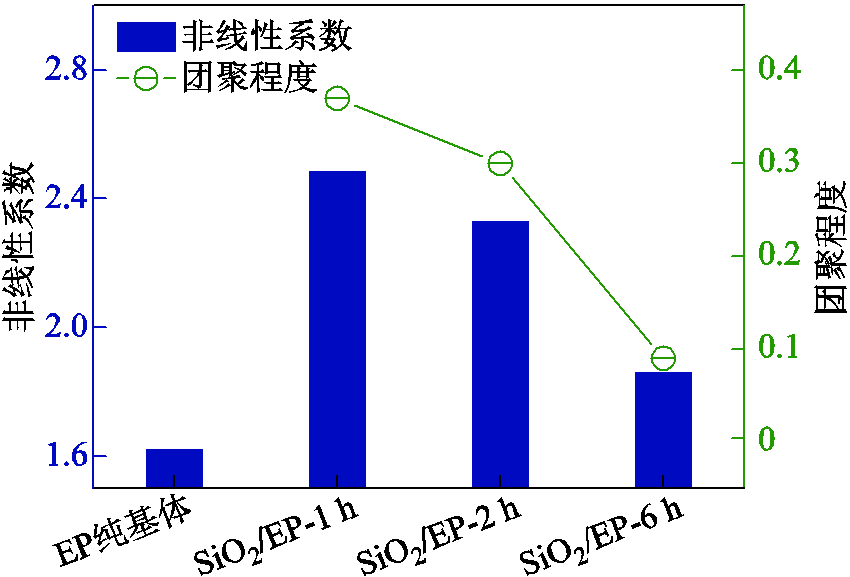
图14 基体与三种样品的非线性系数和团聚程度
Fig.14 The nonlinear coefficients and degree of aggregation between the matrix and three samples
由于同种基体的固有非线性系数为定值，为便于对比分析实验结果与理论计算结果，对非线性系数进行正则化处理。实验和理论计算得到的正则化非线性系数∆β/β0的比较如图15所示。由图15可知，实验和理论计算得到的正则化非线性系数均随着团聚程度的增大而增大。当团聚程度较小时，二者的误差较小；随着团聚程度的增加，二者的误差增大。该误差与电介质制备过程中纳米颗粒-基体界面内聚应变增加的有限性有关。在实际的有机介质成型过程中，热固化/冷却过程会在基质内提供有限的应变松弛，从而保持界面的结构完整性[45]。因此，尽管纳米团聚体附近的界面内聚应变会增加，但实际增加值可能略低于式（15）中的理论计算值，这也是模型误差的主要来源。当团聚程度较低时，内聚应变减小，因此理论模型与实际情况的误差较小。正则化非线性系数的对比结果表明，理论模型与实际模型的误差在3%～11%之间，可根据理论模型反演纳米团聚体的等效粒径，实现对纳米颗粒团聚程度的定量评估。
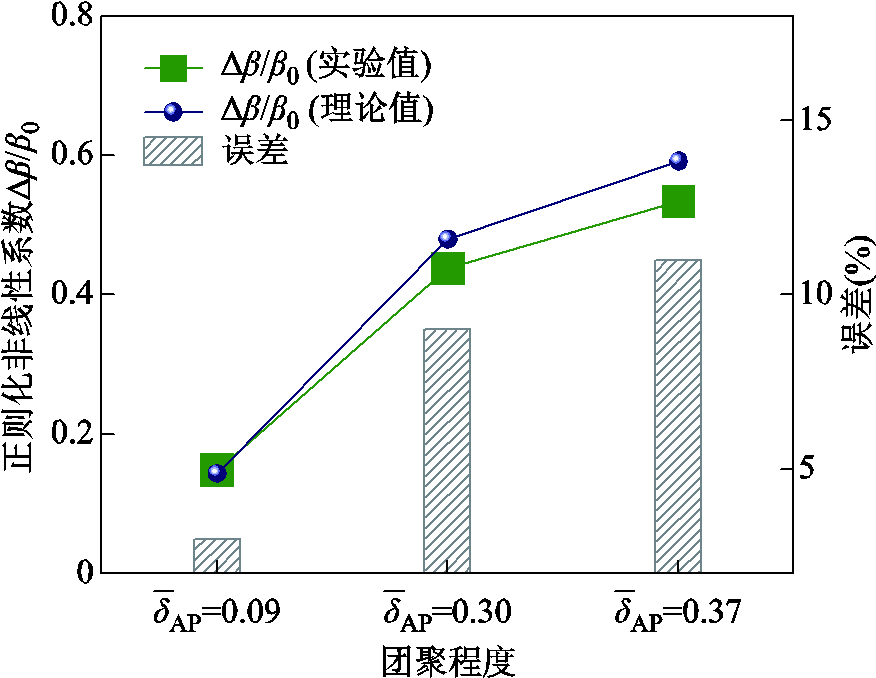
图15 复合样品非线性超声特征的实验值与理论值对比
Fig.15 The comparison between experimental and theoretical values of nonlinear ultrasonic characteristics of composite samples
根据式（23）的理论模型，纳米团聚体的等效粒径可表示为
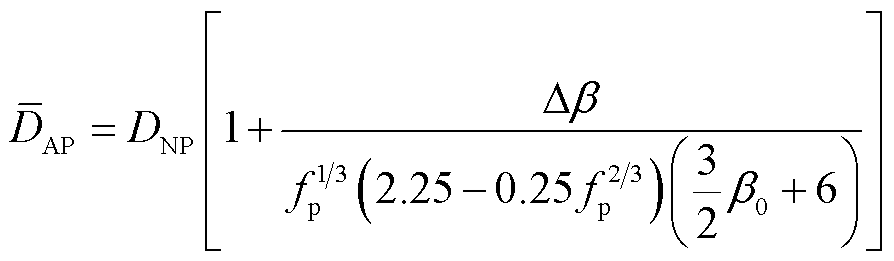（26）
式（26）中，分散状态粒径DNP以及掺杂含量fp可通过材料制备过程查询，材料非线性系数∆β以及基体固有非线性系数β0可通过NLUS测量，利用式（26）可实现纳米团聚体粒径的反演。对制备的三组不同分散性的SiO2/EP样品进行粒径反演，并结合SEM统计结果进行交叉检验，对比结果如图16所示。由图16可知，NLUS粒径反演结果与SEM粒径统计结果整体误差在2.75%～5.2%之间，表明NLUS测试可以实现粒径的定量反演。同时NLUS在测试过程中具有快速、无损、整体检测的优点，适用于大体积纳米电介质的分散性评估。
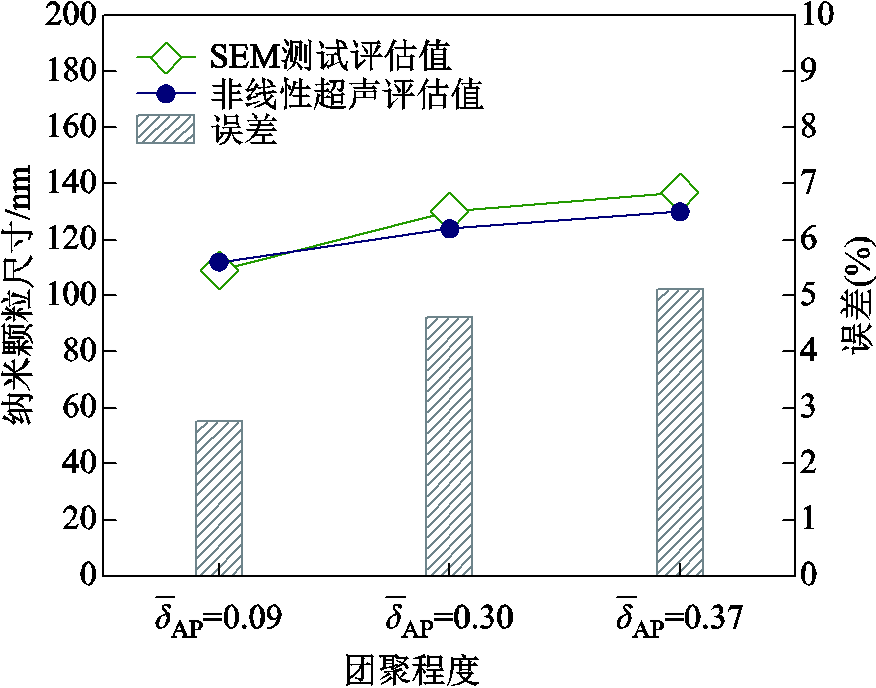
图16 NLUS与SEM测试结果对比
Fig.16 The comparison between NLUS and SEM destructive characteristics of composite samples
纳米颗粒分散性影响纳米电介质改性效果，但现有分散性检测方法无法满足无损、快速、整体检测的要求。本文首先建立了纳米电介质团聚界面失配模型，并推导了纳米电介质非线性响应本构模型；其次，利用数值模拟验证了纳米电介质非线性响应本构模型的正确性，并确定了激励参数最优区间；最后，制备了纳米改性材料并对其进行了AFM、SEM、NLUS测试。测试结果揭示了纳米电介质非线性的来源，表明NLUS结合纳米电介质非线性响应本构模型可实现纳米团聚体等效粒径的反演。总体而言，本文得出以下结论：
1）纳米电介质内由颗粒团聚导致的界面失配是引起声频响应畸变的主要原因，而分散状态颗粒与基体界面对声频响应畸变的贡献可忽略。
2）超声波在纳米电介质内部传播过程中出现的声频响应畸变的程度与材料内部纳米颗粒团聚程度有关，颗粒团聚程度越高，输出信号的非线性系数越大，可通过该现象实现对材料团聚程度的整体无损评估。
3）结合NLUS测试结果与理论模型可实现纳米团聚体等效粒径的反演。实验结果表明，NLUS反演结果与SEM统计结果误差在2.75%～5.2%之间，同时NLUS具有快速、无损、整体检测的优点。
参考文献
[1] 程子霞, 邢威威, 张云霄, 等. 纳米MgO/环氧树脂复合材料的陷阱特性及对电树枝特性的影响研究[J]. 电工技术学报, 2022, 37(21): 5562-5569. Cheng Zixia, Xing Weiwei, Zhang Yunxiao, et al. Study on trap properties of nano-MgO/epoxy resin composites and its influence on electrical tree properties[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5562-5569.
[2] 戴超, 朱光宇, 丁曼, 等. 高温阶梯式升压下等离子体处理纳米颗粒对环氧树脂复合材料的电荷动力学特性影响[J]. 电工技术学报, 2023, 38(21): 5712-5724. Dai Chao, Zhu Guangyu, Ding Man, et al. Influence of plasma treated nanoparticles on charge dynamics of epoxy based nanocomposites under stepped boost at high temperature[J]. Transactions of China Electro-technical Society, 2023, 38(21): 5712-5724.
[3] 曹春诚, 李文博, 程显, 等. 纳米Al2O3/环氧树脂复合材料微秒脉冲沿面闪络特性研究[J]. 高压电器, 2023, 59(6): 111-119. Cao Chuncheng, Li Wenbo, Cheng Xian, et al. Study on surface flashover characteristic of nano-Al2O3/ epoxy resin composites in microsecond pulse[J]. High Voltage Apparatus, 2023, 59(6): 111-119.
[4] Wang Sijiao, Zha Junwei, Wu Yunhui, et al. Preparation, microstructure and properties of polyethylene/alumina nanocomposites for HVDC insulation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(6): 3350-3356.
[5] 王霞, 王陈诚, 朱有玉, 等. 高压直流塑料电缆绝缘用纳米改性交联聚乙烯中的空间电荷特性[J]. 高电压技术, 2015, 41(4): 1096-1103. Wang Xia, Wang Chencheng, Zhu Youyu, et al. Space charge profiles in XLPE nano dielectrics used for HVDC plastic cable insulation[J]. High Voltage Engineering, 2015, 41(4): 1096-1103.
[6] Peng Zhongchuan, Li Qian, Li Huayi, et al. Polyethylene-modified nano silica and its fine dispersion in polyethylene[J]. Industrial & Engineering Chemistry Research, 2017, 56(20): 5892-5898.
[7] Balzer C, Armstrong M, Shan Bohan, et al. Modeling nanoparticle dispersion in electrospun nanofibers[J]. Langmuir, 2018, 34(4): 1340-1346.
[8] 何金良, 彭思敏, 周垚, 等. 聚合物纳米复合材料的界面特性[J]. 中国电机工程学报, 2016, 36(24): 6596-6605, 6911. He Jinliang, Peng Simin, Zhou Yao, et al. Interface properties of polymer nanocomposites[J]. Proceedings of the CSEE, 2016, 36(24): 6596-6605, 6911.
[9] Roy M, Nelson J K, MacCrone R K, et al. Polymer nanocomposite dielectrics - the role of the interface[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2005, 12(4): 629-643.
[10] 姜楠, 李志阳, 彭邦发, 等. 等离子体羟基化改性纳米SiO2粒子对绝缘纸绝缘特性的影响[J]. 电工技术学报, 2023, 38(24): 6817-6827. Jiang Nan, Li Zhiyang, Peng Bangfa, et al. Effect of plasmas hydroxylation modified nano-SiO2 particles on insulation characteristics of insulating papers[J]. Transactions of China Electrotechnical Society, 2023, 38(24): 6817-6827.
[11] 刘道生, 周春华, 丁金, 等. 变压器纳米改性油纸复合绝缘研究综述[J]. 电工技术学报, 2023, 38(9): 2464-2479, 2490. Liu Daosheng, Zhou Chunhua, Ding Jin, et al. Research overview of oil-paper composite insulation modified by nano particles for transformer[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2464-2479, 2490.
[12] 李进, 赵仁勇, 杜伯学, 等. 电工环氧绝缘件缺陷无损检测方法研究进展[J]. 电工技术学报, 2021, 36(21): 4598-4607. Li Jin, Zhao Renyong, Du Boxue, et al. Research progress of nondestructive detection methods for defects of electrical epoxy insulators[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4598-4607.
[13] Chen Lianyi, Xu Jiaquan, Choi H, et al. Processing and properties of magnesium containing a dense uniform dispersion of nanoparticles[J]. Nature, 2015, 528(7583): 539-543.
[14] Wang Fei, Ma Jinzhu, Xin Shaohui, et al. Resolving the puzzle of single-atom silver dispersion on nanosized γ-Al2O3 surface for high catalytic performance[J]. Nature Communications, 2020, 11(1): 529.
[15] Wetteland C L, Liu Huinan. Optical and biological properties of polymer-based nanocomposites with improved dispersion of ceramic nanoparticles[J]. Journal of Biomedical Materials Research Part A, 2018, 106(10): 2692-2707.
[16] 谭及兰. 改性的纳米氧化铝杂化三层复合PI薄膜的结构与介电性能[D]. 哈尔滨: 哈尔滨理工大学, 2014. Tan Jilan. Structure and dielectric properties of modified nano-alumina hybrid three-layer PI composite films[D]. Harbin: Harbin University of Science and Technology, 2014.
[17] Zhang Naiyin, Xu Changlu, Azer A, et al. Dispersibility and characterization of polyvinyl alcohol–coated magnetic nanoparticles in poly(glycerol sebacate) for biomedical applications[J]. Journal of Nanoparticle Research, 2019, 21(12): 275.
[18] 付翔. 定量评价纳米粒子在基体中的分散性[D]. 杭州: 浙江理工大学, 2014. Fu Xiang. Quantitative evaluation of dispersion of nanoparticles in the matrix[D]. Hangzhou: Zhejiang Sci-Tech University, 2014.
[19] Buck O. Harmonic generation for measurement of internal stresses as produced by dislocations[J]. IEEE Transactions on Sonics and Ultrasonics, 1976, 23(5): 346-350.
[20] Gedroits A A, Krasil’Nikov V A. Finite-amplitude elastic waves in solids and deviations from Hooke’s Law[J]. Soviet Journal of Experimental and Theoretical Physics, 1963, 16(5): 1122-1126.
[21] Nagy P B. Fatigue damage assessment by nonlinear ultrasonic materials characterization[J]. Ultrasonics, 1998, 36(1/2/3/4/5): 375-381.
[22] Cantrell J, Yost W. Acoustic harmonic generation from fatigue-induced dislocation dipoles[J]. Philosophical Magazine, Part A, 1994, 69(2): 315-326.
[23] Demčenko A, Koissin V, Korneev V A. Noncollinear wave mixing for measurement of dynamic processes in polymers: physical ageing in thermoplastics and epoxy cure[J]. Ultrasonics, 2014, 54(2): 684-693.
[24] 焦敬品, 李亮, 何存富, 等. 有机材料热老化损伤非线性超声检测试验研究[J]. 北京工业大学学报, 2016, 42(1): 24-29. Jiao Jingpin, Li Liang, He Cunfu, et al. Experimental investigation of thermal aging of organic polymer materials with nonlinear ultrasonic method[J]. Journal of Beijing University of Technology, 2016, 42(1): 24-29.
[25] 张剑锋, 轩福贞, 项延训. 材料损伤的非线性超声评价研究进展[J]. 科学通报, 2016, 61(14): 1536-1550. Zhang Jianfeng, Xuan Fuzhen, Xiang Yanxun. Evaluation of material damage using nonlinear ultrasonic wave[J]. Chinese Science Bulletin, 2016, 61(14): 1536-1550.
[26] Koissin V, Demčenko A, Korneev V A. Isothermal epoxy-cure monitoring using nonlinear ultrasonics[J]. International Journal of Adhesion and Adhesives, 2014, 52: 11-18.
[27] 王汉卿, 成立, 廖瑞金, 等. 复合绝缘子交界面非线性力学模型及弱粘接缺陷无损检测方法[J]. 中国电机工程学报, 2019, 39(3): 895-905, 968. Wang Hanqing, Cheng Li, Liao Ruijin, et al. Nonlinear mechanical model of composite insulator interface and nondestructive testing method for weak bonding defects [J]. Proceedings of the CSEE, 2019, 39(3): 895-905, 968.
[28] Wang Hanqing, Cheng Li, Liao Ruijin, et al. Nonlinear ultrasonic nondestructive detection and modelling of kissing defects in high voltage composite insulators[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2020, 27(3): 924-931.
[29] 成立, 方伟, 王汉卿, 等. 基于非线性声学的纳米复合电介质分散性整体无损评估方法[J]. 中国电机工程学报, 2021, 41(15): 5401-5411. Cheng Li, Fang Wei, Wang Hanqing, et al. Overall nondestructive evaluation method for the dispersion of nanocomposite dielectrics based on nonlinear acoustics[J]. Proceedings of the CSEE, 2021, 41(15): 5401-5411.
[30] Punnose S, Mukhopadhyay A, Sarkar R, et al. Characterisation of microstructural damage evolution during tensile deformation of a near-α titanium alloy: Effects of microtexture[J]. Materials Science and Engineering: A, 2014, 607: 476-481.
[31] Xiang Yanxun, Deng Mingxi, Xuan Fuzhen. Thermal degradation evaluation of HP40Nb alloy steel after long term service using a nonlinear ultrasonic technique[J]. Journal of Nondestructive Evaluation, 2014, 33(2): 279-287.
[32] Zhao Junhua, Lu Lixin, Zhang Zhiliang, et al. Continuum modeling of the cohesive energy for the interfaces between films, spheres, coats and substrates [J]. Computational Materials Science, 2015, 96: 432-438.
[33] Ben Sudong, Zhao Junhua, Rabczuk T. A theoretical analysis of interface debonding for coated sphere with functionally graded interphase[J]. Composite Structures, 2014, 117: 288-297.
[34] Hossain D, Tschopp M A, Ward D K, et al. Molecular dynamics simulations of deformation mechanisms of amorphous polyethylene[J]. Polymer, 2010, 51(25): 6071-6083.
[35] 张发友. 基于非线性超声的材料损伤检测研究[D]. 郑州: 郑州大学, 2019. Zhang Fayou. Study on damage detection of materials based on nonlinear ultrasonic[D]. Zhengzhou: Zhengzhou University, 2019.
[36] Richardson J M. Harmonic generation at an unbonded interface-I. planar interface between semi-infinite elastic media[J]. International Journal of Engineering Science, 1979, 17(1): 73-85.
[37] Cantrell J H, Yost W T. Acoustic nonlinearity and cumulative plastic shear strain in cyclically loaded metals[J]. Journal of Applied Physics, 2013, 113(15): 153506.
[38] Cantrell J H, Zhang X G. Nonlinear acoustic response from precipitate-matrix misfit in a dislocation network [J]. Journal of Applied Physics, 1998, 84(10): 5469-5472.
[39] Hiki Y, Granato A V. Anharmonicity in noble metals; higher order elastic constants[J]. Physical Review, 1966, 144(2): 411-419.
[40] 江念. 金属非金属粘接强度非线性超声检测信号处理方法研究[D]. 太原: 中北大学, 2015. Jiang Nian. Research of signal processing method for nonlinear ultrasonic testing of adhesive strength between metal and nonmetal components[D]. Taiyuan: North University of China, 2015.
[41] 李秋锋, 李建慧, 卢超, 等. 搅拌摩擦加工CNTs/Al复合材料超声非线性评价[J]. 焊接学报, 2017, 38(11): 87-92, 133. Li Qiufeng, Li Jianhui, Lu Chao, et al. Ultrasonic nonlinear evaluation for carbon-nanotubes reinforced aluminum matrix composites processed by friction stir processing method[J]. Transactions of the China Welding Institution, 2017, 38(11): 87-92, 133.
[42] Hong Xiaobin, Lin Xiaohui, Yang Bo, et al. Crack detection in plastic pipe using piezoelectric transducers based on nonlinear ultrasonic modulation[J]. Smart Materials and Structures, 2017, 26(10): 104012.
[43] Alston J, Croxford A, Potter J, et al. Development of a nonlinear ultrasonic NDE technique for detection of kissing bonds in composites[C]//SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Portland, Oregon, USA, 2017: 101691J.
[44] 陆铭慧, 刘磨, 张雪松, 等. RTM玻璃纤维/E51环氧树脂复合材料孔隙含量对超声特征参数的影响[J]. 复合材料学报, 2018, 35(2): 291-297. Lu Minghui, Liu Mo, Zhang Xuesong, et al. Effect of void content on ultrasonic characteristic parameters of RTM glass fiber/epoxy composites[J]. Acta Materiae Compositae Sinica, 2018, 35(2): 291-297.
[45] Wang Chuang, Zhou Gang, Sun Qing, et al. Numerical simulation of the interfacial stress between epoxy resin and metal conductor of power equipment during epoxy curing[J]. High Voltage, 2022, 7(5): 903-915.
Abstract Doped nanoparticles can effectively enhance the electrical properties of nanodielectrics; however, the degree of agglomeration of particles in the matrix significantly influences the modification effect. At present, microscopic imaging is predominantly employed to evaluate the degree of nanodielectric particle agglomeration; however, this method is time-consuming and costly for a single measurement, offers a highly limited observation area, and may damage the material under investigation. Nonlinear ultrasound enables the detection of micro- and nano-defects in materials by detecting nonlinear changes in stress-strain and is a potential technique for assessing the degree of particle agglomeration. This paper investigates the origin of the nonlinear response of nanodielectrics and employ nonlinear ultrasound technology for assessing nanodielectric particle dispersion. The findings indicate that the equivalent particle size inversion results obtained through nonlinear ultrasound technology exhibit an error margin of 3%～6% compared to the particle size statistical results from the scanning electron microscope (SEM). Furthermore, nonlinear ultrasound technology facilitates a rapid, comprehensive, and nondestructive evaluation of the degree of nanodielectric particle agglomeration.
An agglomerated interfacial mismatch model was initially developed, employing the interfacial mismatch coefficient δ to analogously describe the degree of particle agglomeration. On this basis, an ontological model of the nonlinear response of nanodielectrics is derived by combining the nonlinear ultrasonic wave motion equation to quantitatively solve the nonlinear response of nanodielectrics introduced due to the particle agglomeration interface. Subsequently, a simplified two-dimensional acoustic model for SiO2/epoxy resin (EP) featuring varying degrees of agglomeration was created using COMSOL software's partial differential equation module, to validate the nanodielectric nonlinear response model, and the simulation results demonstrate that the second-order nonlinear coefficient β escalates with the degree of particle agglomeration. Combined with the simulation model, the optimal interval of ultrasonic excitation signal frequency parameter is 0.1～5 MHz, and the optimal amplitude parameter is 70 nm, which provides a theoretical basis for the construction of the subsequent experimental platform. Ultimately, three SiO2/EP samples with different dispersibility were prepared by controlling the ultrasonic dispersion treatment time. The nonlinear ultrasound experimental setup was established, and the samples underwent testing using in atomic force microscopy (AFM), SEM, and nonlinear ultrasound.
The AFM test results indicate that the stress-strain hysteresis in the dispersed particle-substrate interface region is negligible, with no additional nonlinearity introduced. In the agglomerated particle-substrate interface region, the stress-strain hysteresis is significant, with a notable increase in the nonlinear coefficient, highlighting the agglomeration interface as the primary source of nonlinearity in nanodielectrics. SEM and nonlinear ultrasound test outcomes reveal that the degree of agglomeration in the three samples escalates as the ultrasonic dispersion treatment time decreases, with a concurrent increase in the nonlinear coefficient. Utilizing the nonlinear coefficient and in conjunction with the nanodielectrics' nonlinear response model, the equivalent particle size of agglomerates can be quantitatively determined. The test outcomes demonstrate that the equivalent particle size determined by nonlinear ultrasound technology exhibits an error margin of 2.75% to 5.2% compared to SEM particle size statistics. Furthermore, this method offers the benefits of speed, comprehensiveness, and non-destructive evaluation, presenting a novel approach for assessing nanodielectric dispersion.
Keywords：Nano-modified materials, evaluation of nano-dispersibility, nonlinear ultrasound, non-destructive testing
DOI: 10.19595/j.cnki.1000-6753.tces.240133
中图分类号：TB553；TM215.92
国家自然科学基金（52077013）和重庆市自然科学基金面上项目（cstc2021jcyj-msxmX0489）资助。
收稿日期 2024-01-19
改稿日期 2024-02-20
邱勇霖 男，1997年生，硕士研究生，研究方向为高电压绝缘技术、无损评估等。E-mail：202011021029@cqu.edu.cn
成 立 男，1989年生，副教授，博士生导师，研究方向为高电压试验技术、复合绝缘材料老化机理和无损评估等。E-mail：cheng116@cqu.edu.com（通信作者）
（编辑 李 冰）