（1）
摘要 为研究温度对油纸绝缘频域介电谱的影响，并探索高效的频温归一化策略以消除不同环境因素带来的测试温度误差，该文提出了基于极化复电容实部一阶微分解谱的多弛豫分解方法。首先，利用微分图谱特征划分出低频弛豫、中低频多弛豫、高频弛豫三类不同弛豫区间进行频温介电机理推演，发现各弛豫过程温度特性差异显著；其次，以Arrhenius衍生方程计算不同弛豫的活化能，基于该频温特性参量提取介质中多类贡献分量的频温频移因子，还原标准温度下的介电图谱；最后，利用不同温度及不同老化程度的试样验证该方法。实验分析表明，该方法很好地解决了传统频温归一法所存在的偏差，且对于不同老化程度的介质具有较好的适用性，可为现场测试提供可靠的理论支撑。
关键词：油纸绝缘 微分解谱 弛豫活化能 频域介电法 频温归一化
电力变压器作为电力系统输配电中的重要设备，其工况对推进“双碳”背景下电力系统的安全稳定运行具有重要意义[1]。油纸绝缘作为变压器绝缘系统中的主绝缘部分，针对其绝缘状态进行评估是判定电力变压器工况的重要环节[2-3]。现今针对油纸绝缘状态评估的测试手段已由传统吊芯方法转变为多类无损测试方法，并且诸如频域介电法（Frequency Domain Spectroscopy, FDS）、回复电压法、极化/去极化电流法、油中溶解气体法等多种测试技术日益成熟。其中，FDS因具备强抗干扰性、较低施加电压且有望实现在线监测的特性成为国内外研究的热点[4]。
FDS的测试研究主要面向油纸绝缘的老化与受潮状态展开，近年来国内外学者已通过分频段提取tanδ积分值、频谱斜率方均根以及Havriliak-Negami（H-N）模型参量等不同方式搭建了基于FDS测试图谱的特征模型，并融合算法用于评估绝缘状态[5-7]。受制于实验室测试环境过于理想、地域气候特征不同、检修前负载状态差异等因素的影响，FDS测试过程中的温度环境无法保持统一。而相关研究与各类实测数据均表明测试图谱的态势往往与环境温度高度相关，温度变化会导致包含水分和酸在内的老化副产品在油和纸板中迁移[8]，这将令标准温度下所建立的特征评估模型无法准确地判别不同温度下的介质绝缘工况。故在此背景下探讨一种高效合理的温度归一化策略是精准诊断油纸绝缘状态的必要前提。
在早期的研究中，学者们主导以“主曲线”（master curve）法对所测量结果进行归一化处理，即利用统一活化能提取频移因子对整体图谱进行归一化处理[9]。文献[10]通过活化能计算的方式验证了其可行性，然而该处理方法在高低频段所造成的误差容易被忽略。文献[11]指出在某些情况下，FDS图谱中有不止一种机制负责分散，它们通常具有不同的温度依赖性。针对这一现象，D. Linhjell与J. Liu等通过严格的实验测试提出了平均活化能的概念并进行温度归一化，但该方法仍无法避免介质中复杂耦合的多弛豫带来的频移偏差[12-13]。高岩峰等以高温硫化硅橡胶的介电响应为例分析了介质内部的电荷扩散过程、低频弥散过程、弛豫峰型介电响应过程的不同活化能导致的“主曲线”法的误差[14]。谢佳成等采用复介电常数实部微分结合H-N模型的分频段方法对“主曲线”法进行优化，但针对低频弛豫区域的较大偏差以及中低频段多弛豫的活化能分析研究尚存空白[15]。I. Fofana等通过研究低温状态下的FDS测试图谱发现，介质中几何电容的贡献并不受温度影响[16]，故频温归一化应探究复合弛豫与电导分量在频移过程中的状态变更。而油纸绝缘系统中存在多弛豫过程，具有不同势垒高度的单一弛豫在结合时将产生复合反应，从而表现出多个松弛弛豫区域之间的耦合态[17]。
综上所述，提出一类消除传统频移方法所带来误差的频温归一化策略对油纸绝缘的现场诊断具有重要意义。因此，本文首先以宽频带上不同弛豫的频温机理分析为侧重点，通过微分谱线特征划分低频、中低频、高频段三类弛豫区间，并从机理层面解释宏观图谱现象，对弛豫特征值进行定量分析；其次，针对复电容实虚部的成分进行剖析，提出利用极化复电容实部微分谱线特征分离中低频段的多个弛豫；最后，基于不同弛豫活化能提取相应的频温平移因子对谱线进行频温归一化。本文所提策略包含以实验支撑的机理分析，并在实验验证中对比不同老化状态下该策略与传统策略归一化后与实测值的拟合成效，结果表明其拟合优度均有较大提升，故可提高工程应用精度。
油纸绝缘系统是由绝缘油与绝缘纸组合而成的无序电介质，加入外施电场后，无序电介质中的微观粒子将通过能量交换的方式达到最终的平衡状态，这一过程即为弛豫过程[18]。在外施交流电场作用下，系统内部将发生电子位移极化、离子位移极化、偶极子转向极化、界面极化等多类极化过程，已有多项研究证实Arrhenius方程可很好地用于表征多项极化弛豫的频温表现[10-13]。油纸复合绝缘介质在外加电场作用下的弛豫状态往往复杂多变，以高频偶极子极化为例，温度升高会使得分子热运动加剧，导致偶极子极化过程减弱，整体幅值降低，同时弛豫时间增大，在双对数曲线上有向左下方移动的趋势，这也是导致“主曲线”法在高频段产生误差的原因。综上所述，需探究不同频段不同极化过程的频温特性差异，方可修正误差。
油纸绝缘介质不同组成成分的特性影响了FDS测试在不同温度下的测试结果。线性响应理论指出，材料中表现出的多弛豫特征可以视作多个单一弛豫叠加的结果，并且每个单一弛豫均具有独立的活化能[19]。单一弛豫的Arrihenius方程可表示为[20]
（1）
式中，τ为单一弛豫的极化弛豫时间；A0为该方程的系数；u为活化能值；k为玻耳兹曼常数，k=1.380 7× 10-23 J/K；T为弛豫过程中的温度。
复电容虚部主曲线频温平移结果如图1所示。采用“主曲线”法进行温度归一化时将导致高频段区域出现严重差异，同时低频区域出现分岔。以上现象表明，绝缘介质所包含的不同弛豫间的活化能差异显著，导致采用单一活化能进行频温平移的“主曲线”法将造成较大误差。另外，在油纸绝缘介质中，电导部分主要由固体绝缘纸与液体绝缘油共同构成，且电导过程存在其独立活化能[15]。除跳跃电导外，油纸绝缘系统中还包含交流电导过程。上述电导过程在介质中表现出的频率与温度依赖性高度相似，在交流电场作用下电导率与温度间的关系可表述为
（2）
式中，
为交流电导在不同活化能作用下的特征时间常数；α为分子系数；
为交流电导对应的独立活化能。
图1 复电容虚部主曲线频温平移结果
Fig.1 Complex capacitance imaginary part of the main curves frequency temperature shift result
综上分析可知，当外施电场进行测试时，若介质中仅包含单一弛豫过程，其弛豫时间常数与电导特征时间常数均与温度呈指数幂关系，均具有固定活化能。但绝缘介质中包含复杂多样的弛豫过程，固定活化能的分析也不成立，故如何分离多弛豫并对应其弛豫活化能是解决问题的关键。
介质中除弛豫分量外往往存在极化无关分量的贡献，如复电容实部
中包含了频率无关电容
的贡献，复电容虚部
中包含了电导过程G的贡献。故在区分多弛豫之前需先剔除二者的影响。
由于介质复极化率实部与虚部由同一响应函数
变换而来，故二者之间存在明确的关联，满足Kramers-Kronig（K-K）变换关系[21]，表示为
（3）
（4）
式中，
为角频率；
为柯西主值积分；
和
分别为单一弛豫过程a的复极化率实部和虚部。由于复电容实部与虚部分别包含极化无关分量与G，故复电容实部与虚部无法完全实现K-K变换，即将复电容实部与虚部分别进行K-K变换后，与G的值均为0，利用这一特性可通过K-K变换分离出这两个分量，分别表示为
（5）
（6）
式中，
和
分别为单一弛豫过程a的复电容实部和虚部。
图2为未老化试样在不同温度下的复电容虚部通过上述K-K变换分离出的电导贡献经拟合后的分布情况，结合式（5）与式（6）可得
（7）
式中，
为复电容虚部中的电导贡献分量。根据式（7）可得电导贡献分量在双对数坐标系下的横坐标为ln ω，故此时电导分量为斜率为-1的直线，其截距则为电导的对数值ln G。图2中通过最小二乘法拟合所得各温度平均电导贡献斜率为-1.019，与分析结论相对应。同时可观察到随着温度的上升，电导贡献也向高频方向移动。
图2 不同温度下复电容虚部中的电导贡献
Fig.2 Conductance contributions in the imaginary part of the complex capacitance at various temperatures
根据扩展德拜模型理论，复合绝缘介质等效为由数量为N的不同弛豫支路以及几何等效电路组成。若令弛豫分量i的时间常数为τi，且其特征电阻与特征电容值分别为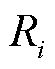
与
，则扩展德拜模型等效电路如图3所示[22]。通过复合介质扩展德拜等效电路的等效导纳Y(ω)计算，可得介质复电容实、虚部的表达式分别为
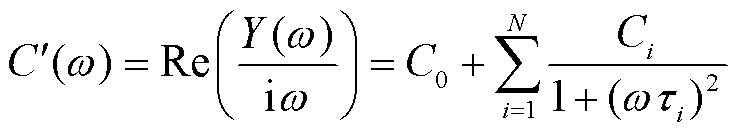（8）
（9）
图3 扩展德拜模型等效电路
Fig.3 Extend Debye model equivalent circuit
结合式（8）、式（9）以及上述分析可知，通过对复电容实虚部进行K-K变换可剔除极化无关分量与G，从而定量地得到仅表征弛豫的极化分量
与
为
（10）
（11）
经过2.1节极化无关分量的分离，可得到仅与弛豫相关的极化复电容实虚部分量，但如何将极化分量中的多弛豫分离，进而分析不同弛豫间活化能的差异是开展研究的重要前提。由于多弛豫之间的耦合作用较强，叠加后状态复杂，故本节提出基于极化复电容实部谱线微分的多弛豫分离方法。
为了探究极化复电容谱线蕴含的弛豫特征，首先将其角频率部分进行对数坐标变换，即令
，并对实部极化分量进行微分，表示为
（12）
可以发现，实部谱线的一阶微分具备极大值峰值点，其坐标为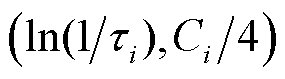
，以图4中实测数据的极化复电容实部微分谱线为例，其峰值点坐标可取为第一弛豫特征。为发掘剩余微分谱线蕴含的弛豫特征，计算第一弛豫过程所贡献的微分谱线分量如图4中蓝色虚线所示，剔除该分量获得剩余谱线，可观察到剩余谱线特征峰值点，第二弛豫过程特征表现突出，同样记录其坐标并求解对应弛豫分量。以此类推可将谱线中叠加的多弛豫分离。
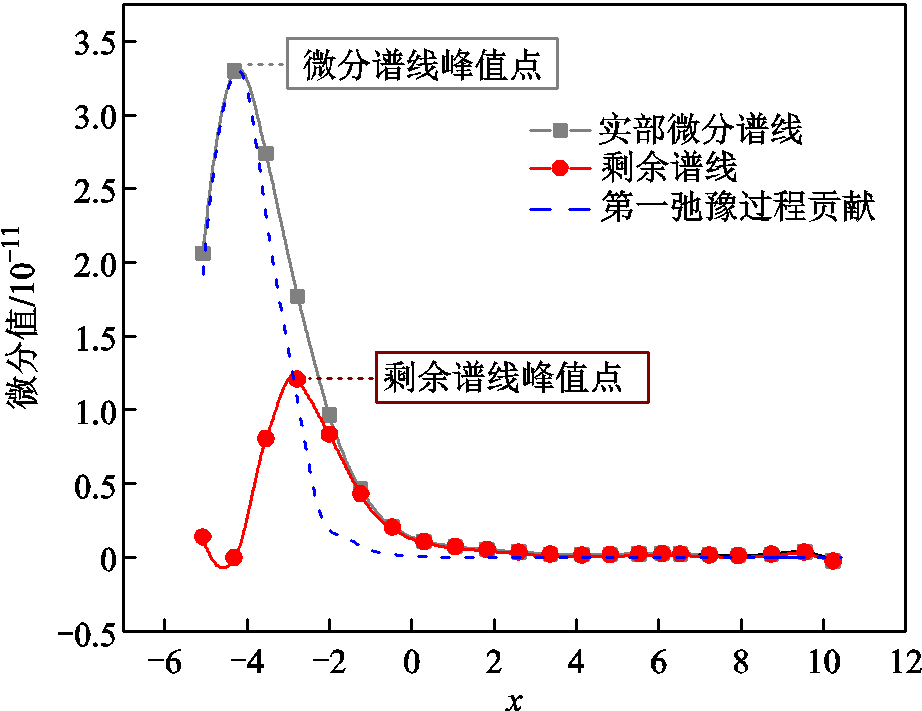
图4 弛豫分离过程
Fig.4 Multi-relaxation separation process
经上述分析，各独立弛豫对应的弛豫时间常数与特征电容计算式为
（13）
式中，
为第i个弛豫对应峰值点的角频率；
和
分别为求解第i个弛豫时对应峰值点的横、纵坐标。
为验证本文所提方法应对不同老化状态的通用性，本文制备了四类不同老化程度的油纸绝缘试样。绝缘油选取克拉玛依25号环烷烃矿物油进行测试，同时将T4变压器纸板裁剪为9 cm×9 cm的正方形以保证与三电极装置金属板贴合。将各组绝缘纸板充分浸泡于矿物油中24 h后，放入130℃高温的真空烘箱分别进行0、10、20、30 d的加速老化，并对其进行FDS谱线测量。
在测试方面，选用奥地利Omicron公司所研发的DIRANA频域介电响应测量装置进行测试。实验中采用可有效减少泄漏电流影响的三电极测量装置，并将其放入装备温度及压力表盘的密封烘箱中加热至待测温度，静置1 h保证整体介质充分加热完毕。设定频率区间为10-3～5×103 Hz，将仪器连接至计算机端，调整输出峰值电压为200 V，对整体介质进行加压测量，分别测量各种状态试样在35、45、55、65、75℃下的FDS谱线，具体接线示意图如图5所示。
图5 FDS测试接线示意图
Fig.5 FDS test wiring schematic diagram
在130℃加速老化下，不同试样老化天数与纸板聚合度（Degree of Polymerization, DP）之间的关系见表1。
表1 不同试样老化天数与聚合度的关系
Tab.1 The relationship between the aging days and DP of different samples
老化天数/dDP 01 179 10798 20659 30539
本节基于前文分析，以未老化试样数据为例进行频温机理分析与归一化策略研究。FDS实测该试样的复电容实部与虚部分别如图6a与图6b所示。实部在低频段快速下降且斜率发生改变，随着温度的升高曲线逐渐向高频段移动；而该曲线在高频段由于受形状系数的影响较大，不同温度下均出现频率越高，实部电容值越贴近的现象。该现象的宏观解释为：高频区域由介质偶极子转向弛豫主导，当频率升高时，弛豫时间减小，相较无穷分量而言偶极子转向弛豫占比微小，故曲线贴近无穷分量。
图6 未老化试样复电容实虚部曲线
Fig.6 Complex capacitance real-virtual part curves of unaged specimen
通过观察复电容虚部曲线可以看出，随着温度的升高，复电容虚部值同样趋于向高频段方向移动。而电导主导的中低频段曲线在温度升高的过程中并没有呈现显著的电导斜率，反而随着温度的升高于中频段出现了明显的弛豫峰。这是由于中低频区域以油纸绝缘介质的界面极化过程为主导，区别于单一材质的介质系统，油纸绝缘试样由纤维素纸板与矿物油混合组成，其中纸板纤维素为长链大分子有机物，这一结构使矿物油更易浸入，从而在微观层面上形成界面极化层并发生界面极化，出现多弛豫相互耦合的情况，而参与贡献的多弛豫环节之间的活化能差异导致升温后贡献值变化程度不一，在温度升高的过程中各弛豫依照各自活化能等级改变频域状态，导致叠加态弛豫峰的出现。这一现象更加表明在宽频范围内不同弛豫所蕴含的活化能差异很大程度地影响不同温度状态下的虚部谱线。
此外虚部曲线在103 Hz以上的高频段均出现了上翘现象。该频率区间主要由偶极子转向弛豫主导，而界面极化分量、电导分量占比均降至极低[23]。在温度作用下其贡献分量同样趋向往更高频段移动，偶极子极化在高温下表现不明显，在低温下表现明显，并且会导致FDS曲线在高频段出现明显的上翘。因此，虚部在高频处的分量需单独分析。
不同温度下极化复电容实部微分谱线如图7所示，可见未老化试样在不同温度下，其极化复电容实部微分谱线均表现出明显的峰值点。通过分析该谱线峰值点所在频率的左侧区间可知，随着实验温度的升高，式（13）的计算结果呈明显下降趋势，该区间内的主要现象被称为低频弥散现象，其主要弛豫特征发生在更低频段[24]。
图7 不同温度下极化复电容实部微分谱线
Fig.7 Differential spectra of the real part of the polarized complex capacitance at various temperatures
故微分谱线峰值出现的具体原因可归结如下：低频段的弛豫活化能与中低频相比偏差较大，导致其并不能够掩盖交界处贡献弛豫的峰值表现。因此分析可知，式（13）所提的定量关系对于弛豫活化能差异导致的突出峰值十分敏感。
随着温度上升，微分谱线总体呈现向高频段区域移动的趋势，宏观表现为频率特性右移导致弛豫时间常数下降，低频区域的部分弛豫将随着温度的升高进入测试频段内。观察曲线末端发现，高频区出现了几乎不随温度发生移动的峰值点，即活化能近乎为0的温度无关弛豫现象，其原因为：偶极子极化随温度的变化体现在幅值方面，且本身具备的极化活化能也较小，在图7中无法明确体现频移[25]。
综上分析，由低频段、中低频段以及偶极子极化弛豫过程主导的频温特性均不相同，故可首先将微分峰值点所在频率作为基准划分低频与中低频区域，独立分析低频段的频温特性；其次令偶极子极化主导的近乎温度无关峰值点处的频率作为解谱分界节点，划分中低频多弛豫与高频弛豫，即宽频段内可划分出三类弛豫区间：低频弛豫区间、中低频弛豫区间、高频弛豫区间。
为分离中低频段内处于叠加隐藏状态的各弛豫，首先通过式（5）、式（6）分离出实、虚部中的极化无关电容及电导分量，并将极化复电容实部按式（12）进行一阶微分，获得第一个微分峰值点及其特征量；然后计算出对应弛豫贡献以及剩余微分谱线，以此类推，解谱直至出现温度无关弛豫后停止。为更好地体现宽频段内的解谱过程，以45℃测试结果为例进行弛豫分离，结果如图8所示。由图8可知，在4.1节中所划定的中低频多弛豫解谱频段范围内，通过微分解谱的方法可将中低频分离出如图8所示的6个主要弛豫，并记录解谱过程中的各个弛豫分量数据。根据第1节基于Arrhenius方程的频温分析可知，将主曲线通过本文所提的多频段划分以及中低频多弛豫分离方法分离出多个弛豫后，各弛豫在不同温度下的表现互相独立且不同，各自的弛豫活化能表现也不尽相同，故需将不同频段内各部分弛豫过程进行单独计算与分析。
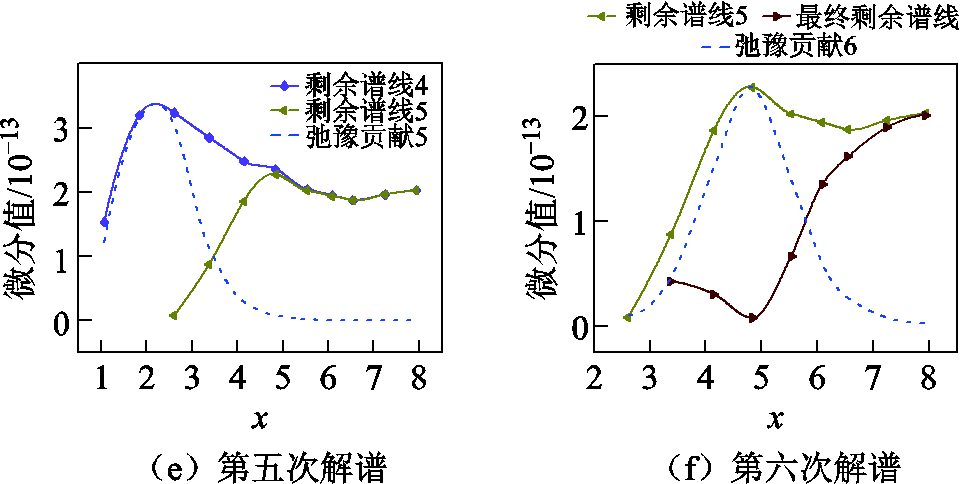
图8 多弛豫分离过程
Fig.8 Multi-relaxation separation process
此外，为拟合与分析高频段偶极子主导的弛豫活化能分量，此处将极化复电容虚部的中低频弛豫分量剔除，即可得到各温度下高频弛豫分量如图9所示，根据该分量可计算对应高频弛豫的独立活化能与频移因子。通过低频弛豫分析、中低频微分解谱以及高频弛豫分解得到不同温度下各弛豫特征参量见表2。
图9 不同温度下复电容虚部中的高频弛豫分量
Fig.9 High-frequency relaxation components in the imaginary part of a complex capacitor at various temperatures
表2 不同温度下各弛豫特征参量
Tab.2 The parameters of each relaxation feature at different temperatures
弛豫分量特征弛豫时间τ/s弛豫活化能u/eV 35℃45℃55℃65℃75℃ 低频812.4298.9109.940.514.90.962 中低频1890.7163.133.17.49.01.431 中低频2147.226.95.51.20.31.428
（续）
弛豫过程特征弛豫时间τ/s弛豫活化能u/eV 35℃45℃55℃65℃75℃ 中低频336.36.71.40.30.11.425 中低频48.11.40.30.070.021.433 中低频50.2890.1110.0450.0190.0080.812 中低频60.017×10-34×10-33×10-32×10-30.444 高频0.0018×10-55×10-54×10-52×10-50.245 电导159.1658.0321.167.712.780.993
为提出使试样介电图谱高效归一化的策略，本节结合2.1节中的电导分离过程、图8的解谱过程、图9的高频弛豫分量与表2数据进行分析，可得到如下结论：
1）对于低频段而言，用
表示低频段内不同温度下的特征弛豫时间，对应弛豫的活化能以
表征，可观察到该数值与解谱后的中低频活化能
间有较大差距。在温度升高过程中，低频弛豫区间右移程度不及中低频段各弛豫，故导致对应图6b中温度升高后复电容虚部出现弛豫峰现象。
2）对于中低频段而言，将主曲线通过特定方式分离为多个弛豫后，以τ1～τ6表征不同过程的弛豫时间常数。部分弛豫在不同温度下的表现并不相同。中低频弛豫过程1～4的弛豫活化能表现相近，均约为1.43 eV，相近的弛豫活化能会导致弛豫表现出的实部分量相互掩盖峰值。当频率升高时，曲线末端的弛豫活化能大幅降低，谱线峰值点不再被掩盖，从而可观察到如图8a所标注出的谱线隆起与峰值。
3）
用于表征高频极化弛豫部分的特征弛豫时间，对应弛豫活化能以
表征。相关文献表明，高频损耗峰约出现于103～105 Hz数量级[24]，故根据4.1节中所提中低频与高频区间划分基准，可单独计算相应高频段弛豫活化能的贡献。
将解谱所获得的第i个弛豫的弛豫活化能ui作为中低频段内各弛豫温度归一化的核心特征，通过设定频温平移因子
进行特征平移，令每一贡献量均由待调整温度转换至标准温度
状态（弛豫时间常数
）；同理计算低频弛豫、高频弛豫、电导过程的频移因子并实现归一化，最终组合平移后的所有分量构建标准温度下的介电图谱。其中，为衡量各弛豫随温度移动的幅度，对中低频段内解谱后各分量分别定义其频温平移因子
，将低频分量、高频极化分量、电导贡献对应频温平移因子定义为
、
、
，具体表示为
（14）
（15）
试样介电图谱由55℃归一化至35℃过程中各弛豫分量的频温频移因子计算结果见表3。依照对应因子进行频温平移，并于基准温度下叠加所有贡献分量，即可还原基准温度下的复电容虚部曲线。未老化试样自55℃归一化至标准温度35℃时的分解过程如图10所示，归一化后虚部极化分量与实际测试曲线间的拟合优度
达98.3%。
表3 各分量频温频移因子（55℃→35℃）
Tab.3 Frequency shift factor for each component frequency temperature（55℃→35℃）
弛豫分量频移因子弛豫过程频移因子 低频9.05中低频424.78 中低频126.89中低频56.43 中低频226.94中低频62.8 中低频326.91高频1.73
图10 归一化策略与测量数据的对比（55℃→35℃）
Fig.10 Comparison of the normalized strategies to the measured data（55℃→35℃）
由图10可知，在测试频段范围内，35℃试样的微分谱线并未观察到低频段分量。为了测试低频段独立活化能
的平移效果，选取55℃试样与75℃试样进行归一化验证，将55℃试样归至75℃下并与该温度下的测试数据进行比较，如图11所示，虚部极化分量拟合优度
达98.6%。
图11 归一化策略与测量数据的对比（55℃→75℃）
Fig.11 Comparison of the normalized strategies to the measured data（55℃→75℃）
结合前文研究，基于谱线微分与弛豫活化能的频温归一化流程可总结如下：
1）实际工程应用中应先确定平移系数方能确定绝缘状况。由式（15）可知，本文所提策略是针对同一样品的，在未知老化状态下仅需测试两组不同温度的数据即可进行各温度下的数据归一化。测试过程中应设置尽量多的测试点对待测试样进行FDS谱线测量，得到相应复电容实虚部曲线数据。
2）针对实虚部数据进行K-K变换计算，归算并拟合出不同温度下的极化无关电容值及电导贡献分量。
3）分别以微分谱线峰值处的频率、高频偶极子极化主导的近乎温度无关峰值处的频率为基准，划分低频弛豫、中低频多弛豫与高频弛豫区间，将中低频区间内的极化复电容实部微分谱线按2.2节所提方法进行逐一解谱，划分不同弛豫并由式（13）计算不同弛豫特征参量
，同时计算电导特征时间常数
、低频特征时间常数
与高频极化特征时间常数
。
4）根据不同温度下多弛豫数据计算出各弛豫对应活化能
，同时计算低频弛豫活化能、电导分量活化能
及高频弛豫活化能
。
5）根据不同活化能等级计算不同的频温平移因子，频移不同分量，叠加还原标准温度下的FDS介电图谱。
由上述研究发现，本文所提出的频温归一化策略能够很好地适配未老化试样在各温度下的表现。为了探究多弛豫频温归一化策略在不同老化程度试样上的通用性，本节通过“主曲线”法与本文所提方法分别对所有老化状态样品进行归一化分析。为便于更直观地展现不同频段内的频移差异性，选取由65℃归至45℃的过程进行分析。所有老化状态样本在两种方法下的拟合优度对比见表4。
表4 所有老化试样在两种方法下的拟合优度对比
Tab.4 Comparison of the goodness of fit of all aging specimens using both methods
DP传统法(%)本文方法(%) 1 17984.598.1 79884.797.9 65982.698.7 53981.997.2
限于篇幅，本节主要展示老化20 d样本的结果，如图12所示，各分量频移因子计算结果见表5。其中采用“主曲线”法的归一化曲线与实际曲线拟合优度为82.6%；而采用本文归一化策略后虚部极化分量与实际测试曲线拟合优度达98.7%。综上分析可以看出，本文所提策略更贴近实际情况，且对不同老化状态具有通用性。
图12 老化20 d试样归一化策略与主曲线法的对比
Fig.12 Comparison between the normalization strategy and the master curve method for aging 20-day specimens
表5 老化20 d试样各分量频移因子（65℃→45℃）
Tab.5 Frequency shift factor for each component of 20 days aging specimen（65℃→45℃）
弛豫分量频移因子弛豫分量频移因子 低频9.05中低频424.8 中低频126.9中低频56.43 中低频226.9中低频62.75 中低频326.9高频1.73
由图12中可明显观察到“主曲线”法在中频段区域的拟合误差较小，但在低频及高频区域均出现了较大偏差，对此分析如下：
1）中低频段乃至更低频率范围内，“主曲线”法计算结果均出现较大分岔，其本质为：低频-中低频弛豫分解区间存在多个弛豫活化能差异，故该频段内不同弛豫在区域交界处将表现出图谱频移差异，而“主曲线”法的统一频移因子观念导致多个弛豫未能以相应的活化能进行频移，从而产生偏差。
2）在角频率坐标系下拟合程度较好的中频区域由电导分量主导，而“主曲线法”所测统一活化能一般由该频段选取，通过前文分析可知，该频段内部各弛豫活化能数值相近，故该频段误差较为轻微，拟合状态良好。
3）高频段内弛豫时间极短，经计算该频段内偶极子转向弛豫主导的弛豫活化能值相较中-低频段而言较小，导致以中频段主导活化能进行频移的“主曲线”法在高频段将原图谱向低频方向偏差移动，使图谱上翘现象提早出现，产生较大误差。
通过对不同程度的老化样品进行分析，还发现了以下值得注意的现象：一方面，老化20 d试样在各区间范围内的弛豫活化能均低于未老化试样，这是由于绝缘纸板是天然的纤维素聚合物，随着老化程度的加深，其纤维素长链会越来越短，将产生更多的水溶性有机酸和水分等老化副产品，助力分子间的势垒迁移行为，导致宏观弛豫活化能降低[26-27]；另一方面，未老化试样低频区的弛豫活化能低于中低频弛豫解谱区的活化能，然而老化20 d试样则与之相反，这一现象表明相较于电导分量而言，主导中低频段的界面极化对应的弛豫活化能对老化程度的变化更为敏感，即弛豫活化能下降幅度更大。
针对传统方法进行温度归一化会产生较大拟合偏差的问题，本文充分地分析各弛豫的频温响应机理，提出了一种基于微分谱线解谱，提取多弛豫频移因子的温度归一化策略。通过实验证明了该方法的有效性，并得出以下结论：
1）区别于传统方法，本文所提频温归一化策略具有严谨的频温机理解释，以多弛豫活化能差异性分析为基础的归一化策略是达到高精度修正图谱的有效路径。
2）低频弛豫区、中低频弛豫区与高频弛豫区的活化能差异明显。其中，中低频段各弛豫间的活化能亦有区别，呈现随频率升高而逐渐降低的趋势。
3）本文所提策略对于不同绝缘老化状态样品具备良好的适用性。同时发现随着老化程度的加深，各区间弛豫活化能均出现程度不一的下降，即不同弛豫过程对老化状况的敏感程度并不一致，可为后续绝缘老化诊断的相关研究提供可靠的理论支撑。
参考文献
[1] 邹阳, 林锦煌, 何津, 等. 基于频谱解构法的油纸绝缘扩展德拜模型参数辨识[J]. 电工技术学报, 2023, 38(3): 622-632. Zou Yang, Lin Jinhuang, He Jin, et al. Parameter identification of oil paper insulation extended Debye model based on spectrum deconstruction method[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 622-632.
[2] 梁一霖, 张明泽, 刘骥, 等. 复杂运行条件下非均匀老化油纸绝缘典型电场变化特性[J]. 高电压技术, 2024, 50(4): 1731-1741. Liang Yilin, Zhang Mingze, Liu Ji, et al. Variation characteristics of typical electric field of non-uniform aging oil-paper insulation under complex operating conditions[J]. High Voltage Engineering, 2024, 50(4): 1731-1741.
[3] 赵洪山, 常杰英, 曲岳晗, 等. 基于二元非线性Wiener随机过程的变压器油纸绝缘剩余寿命预测方法[J]. 电工技术学报, 2023, 38(15): 4040-4049. Zhao Hongshan, Chang Jieying, Qu Yuehan, et al. Residual life prediction method of transformer oil-paper insulation based on binary nonlinear Wiener random process[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4040-4049.
[4] 姚欢民, 穆海宝, 张大宁, 等. 时变温度下油纸绝缘频域介电谱曲线校正方法研究[J]. 电工技术学报, 2023, 38(1): 246-257. Yao Huanmin, Mu Haibao, Zhang Daning, et al. Study on the frequency domain spectroscopy curves correction method of oil-paper insulation at time-varying temperature[J]. Transactions of China Electrotechnical Society, 2023, 38(1): 246-257.
[5] 黄猛, 李怡然, 吴延宇, 等. 计及界面电荷和极性效应的油纸复合绝缘非线性电路等效模型[J]. 电工技术学报, 2024, 39(11): 3422-3432. Huang Meng, Li Yiran, Wu Yanyu, et al. Equivalent nonlinear circuit model with interface charge and polarity effect for oil-paper composite insulation[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3422-3432.
[6] 刘道生, 周春华, 丁金, 等. 变压器纳米改性油纸复合绝缘研究综述[J]. 电工技术学报, 2023, 38(9): 2464-2479, 2490. Liu Daosheng, Zhou Chunhua, Ding Jin, et al. Research overview of oil-paper composite insulation modified by nano particles for transformer[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2464-2479, 2490.
[7] Xu Qingchuan, Wang Shengkang, Lin Fuchang, et al. Extracting frequency spectroscopy of oil-immersed paper based on havriliak–negami model without known insulation structure of transformer[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 1-12.
[8] 张国治, 闫伟阳, 王堃, 等. 流动绝缘油中纤维杂质颗粒运动特性仿真研究[J]. 电工技术学报, 2023, 38(9): 2500-2509. Zhang Guozhi, Yan Weiyang, Wang Kun, et al. Simulation research on movement characteristics of fiber impurity particles in flowing insulating oil[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2500-2509.
[9] Liao Ruijin, Liu Jiefeng, Yang Lijun, et al. Quantitative analysis of insulation condition of oil-paper insulation based on frequency domain spectroscopy[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(1): 322-334.
[10] Zhang Yiyi, Liu Jiefeng, Zheng Hanbo, et al. Feasibility of a universal approach for temperature correction in frequency domain spectroscopy of transformer insulation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(5): 1766-1773.
[11] 高竣, 王有元, 齐超亮, 等. 温度改变方式对应用频域介电谱法评估油纸绝缘状态的影响[J]. 电工技术学报, 2015, 30(24): 255-261. Gao Jun, Wang Youyuan, Qi Chaoliang, et al. Effect of temperature change mode on condition assessment of oil-paper insulation based on frequency-domain dielectric spectroscopy method[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 255-261.
[12] Linhjell D, Lundgaard L, Gafvert U. Dielectric response of mineral oil impregnated cellulose and the impact of aging[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2007, 14(1): 156-169.
[13] Liu J, Fan X, Zheng H, et al. Aging condition assessment of transformer oil-immersed cellulosic insulation based upon the average activation energy method[J]. Cellulose, 2019, 26(6): 3891-3908.
[14] 高岩峰, 梁曦东, 仵超, 等. 介电响应分析中温度归一化获得标准曲线的方法、意义及应用[J]. 中国电机工程学报, 2017, 37(15): 4530-4537. Gao Yanfeng, Liang Xidong, Wu Chao, et al. Application and significance of the master curve obtained by temperature normalization method in the analysis of dielectric response[J]. Proceedings of the CSEE, 2017, 37(15): 4530-4537.
[15] 谢佳成, 夏昌杰, 董明, 等. 频域介电谱温度归一化微观机理及优化策略研究[J]. 高电压技术, 2021, 47(7): 2416-2424. Xie Jiacheng, Xia Changjie, Dong Ming, et al. Microscopic mechanism and optimized strategy for temperature normalization process of frequency domain spectroscopy[J]. High Voltage Engineering, 2021, 47(7): 2416-2424.
[16] Fofana I, Hemmatjou H, Meghnefi F, et al. On the frequency domain dielectric response of oil-paper insulation at low temperatures[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2010, 17(3): 799-807.
[17] Varakantham S R, Kliem H. Dielectric relaxational phenomena in interacting composite structures[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2021, 28(3): 845-852.
[18] 殷之文. 电介质物理学[M]. 2版. 北京: 科学出版社, 2003.
[19] Hoffmann G, Poliszko S. Temperature-frequency transformation in dielectric thermal analysis (DETA) of wood relaxation properties[J]. Journal of Applied Polymer Science, 1996, 59(2): 269-275.
[20] 杨丽君, 齐超亮, 邓帮飞, 等. 采用修正Cole-Cole模型提取油纸绝缘频域介电谱的特征参量方法[J]. 高电压技术, 2013, 39(2): 310-317. Yang Lijun, Qi Chaoliang, Deng Bangfei, et al. Application of modified Cole-Cole model to extract characteristics of frequency dielectric spectroscopy of oil-paper insulation[J]. High Voltage Engineering, 2013, 39(2): 310-317.
[21] 高岩峰, 卢毅, 梁曦东, 等. Kramers-Kronig变换在介电响应分析中的数值计算方法、意义及应用[J]. 中国电机工程学报, 2020, 40(1): 318-329. Gao Yanfeng, Lu Yi, Liang Xidong, et al. Numerical computational method, application and significance of the Kramers-Kronig transform in the analysis of dielectric response[J]. Proceedings of the CSEE, 2020, 40(1): 318-329.
[22] 张璐, 李洋, 穆海宝, 等. 冲击电压激励下变压器套管介电响应快速测量方法[J]. 高压电器, 2023, 59(6): 147-153. Zhang Lu, Li Yang, Mu Haibao, et al. Fast measurement method of dielectric response of transformer bushing under impulse voltage excitation [J]. High Voltage Apparatus, 2023, 59(6): 147-153.
[23] 吴广宁, 钟鑫, 包健康. 温度对油纸绝缘介电频谱特性的影响[J]. 高电压技术, 2015, 41(12): 4081-4088. Wu Guangning, Zhong Xin, Bao Jiankang. Effect of temperature on dielectric spectrum characteristic of oil-paper insulation[J]. High Voltage Engineering, 2015, 41(12): 4081-4088.
[24] Dissado L A, Hill R M. A cluster approach to the structure of imperfect materials and their relaxation spectroscopy[J]. Proceedings of the Royal Society of London Series A, 1983, 390(1798): 131-180.
[25] Xie Jiacheng, Dong Ming, Hu Yizhuo, et al. Modeling oil-paper insulation frequency domain spectroscopy based on its microscopic dielectric processes[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2019, 26(6): 1788-1796.
[26] 王世强, 魏建林, 杨双锁, 等. 油纸绝缘加速热老化的频域介电谱特性[J]. 中国电机工程学报, 2010, 30(34): 125-131. Wang Shiqiang, Wei Jianlin, Yang Shuangsuo, et al. Frequency domain dielectric spectroscopy characteristics of oil-paper insulation under accelerated thermal aging[J]. Proceedings of the CSEE, 2010, 30(34): 125-131.
[27] 杨丽君, 邓帮飞, 廖瑞金, 等. 应用时–温–水分叠加方法改进油纸绝缘热老化寿命模型[J]. 中国电机工程学报, 2011, 31(31): 196-203. Yang Lijun, Deng Bangfei, Liao Ruijin, et al. Improvement of lifetime model on thermal aging of oil-paper insulation by time-temperature-moisture superposition method[J]. Proceedings of the CSEE, 2011, 31(31): 196-203.
Abstract In order to investigate the impact of temperature on the frequency domain dielectric spectrum of oil-paper insulation and to develop an effective frequency-temperature normalization method to mitigate test temperature errors induced by various environmental factors, this study employs a first-order differential mapping of the real part of the complex capacitance to categorize three types of relaxation intervals. It integrates the Kramers-Kronig(K-K) transform and the derivative equations of the Arrhenius model to examine the mechanism of multiple relaxation frequencies and temperature. Additionally, it proposes a frequency-temperature normalization approach to restore dielectric mapping at standard temperature.
Aiming at the frequency domain dielectric testing of oil-paper insulation in the frequency domain of the mechanism is not clear, the insulation medium contains different relaxation between the activation energy difference is significant, resulting in the use of a single activation energy for the frequency and temperature shifting of the "master curve" method will cause a large error and other issues, this paper carries out the oil-paper insulation frequency and temperature mechanism and the study of the normalization. The following operations are carried out for the frequency domain dielectric data measured at two different temperatures, firstly, the K-K transformation is carried out on the real and imaginary parts of the complex capacitance data, and the geometric capacitance and conductivity contributions at different temperatures are normalized and fitted, and then, by means of the first-order differentiation of the real part of the polarized complex capacitance, the frequency point at the peak of the differentiation spectral line, the frequency point at the nearly temperature-independent peak dominated by high-frequency dipole polarization, are taken out as benchmarks to divide the low-frequency frequency and the high-frequency frequency. The low and middle frequency bands are then deconvolved to separate the different relaxations and calculate their relaxation time constants and relaxation activation energies. Finally, the characteristic quantities of the two sets of test data are brought into the Arrhenius derivative equation to obtain the frequency-temperature shift factor of each component, and then the frequency shift is performed to restore the frequency-domain dielectric spectra at the standard temperature.
Through the analysis of actual experimental data, the effectiveness of the method is proven, leading to the following conclusions: (1) Unlike the traditional "master curve" method, the temperature normalization strategy proposed in this paper provides a rigorous explanation of the frequency-temperature mechanism. The normalization strategy, based on the analysis of the variability of multi-relaxation activation energies, is an effective approach to achieve high-precision correction of the maps. (2) The activation energies of the low-frequency relaxation region, the middle-low-frequency region, and the high-frequency relaxation region are obviously different. Among them, the activation energies of the middle and low-frequency relaxation regions also differ, showing a trend of gradually decreasing with increasing frequency. (3) The strategy proposed in this paper has good applicability to samples with different insulation aging states. At the same time, it is found that the activation energy for relaxation decreases with the degree of aging. This indicates that the sensitivity of various relaxation processes to aging conditions is not uniform, providing a solid theoretical foundation for future studies on diagnosing insulation aging.
keywords：Oil paper insulation, microdisintegration spectrum, relaxation activation energy, frequency domain dielectric method, frequency-temperature normalization
DOI: 10.19595/j.cnki.1000-6753.tces.240328
中图分类号：TM85; TM411
国家自然科学基金资助项目（92266110, 52377088）。
收稿日期 2024-03-03
改稿日期 2024-04-26
邹 阳 男，1980年生，博士，副教授，研究方向为电气系统智能化故障诊断。E-mail：240017444@qq.com
黄 煜 男，1999年生，硕士研究生，研究方向为电气系统智能化故障诊断。E-mail：1051266256@qq.com（通信作者）
（编辑 李 冰）