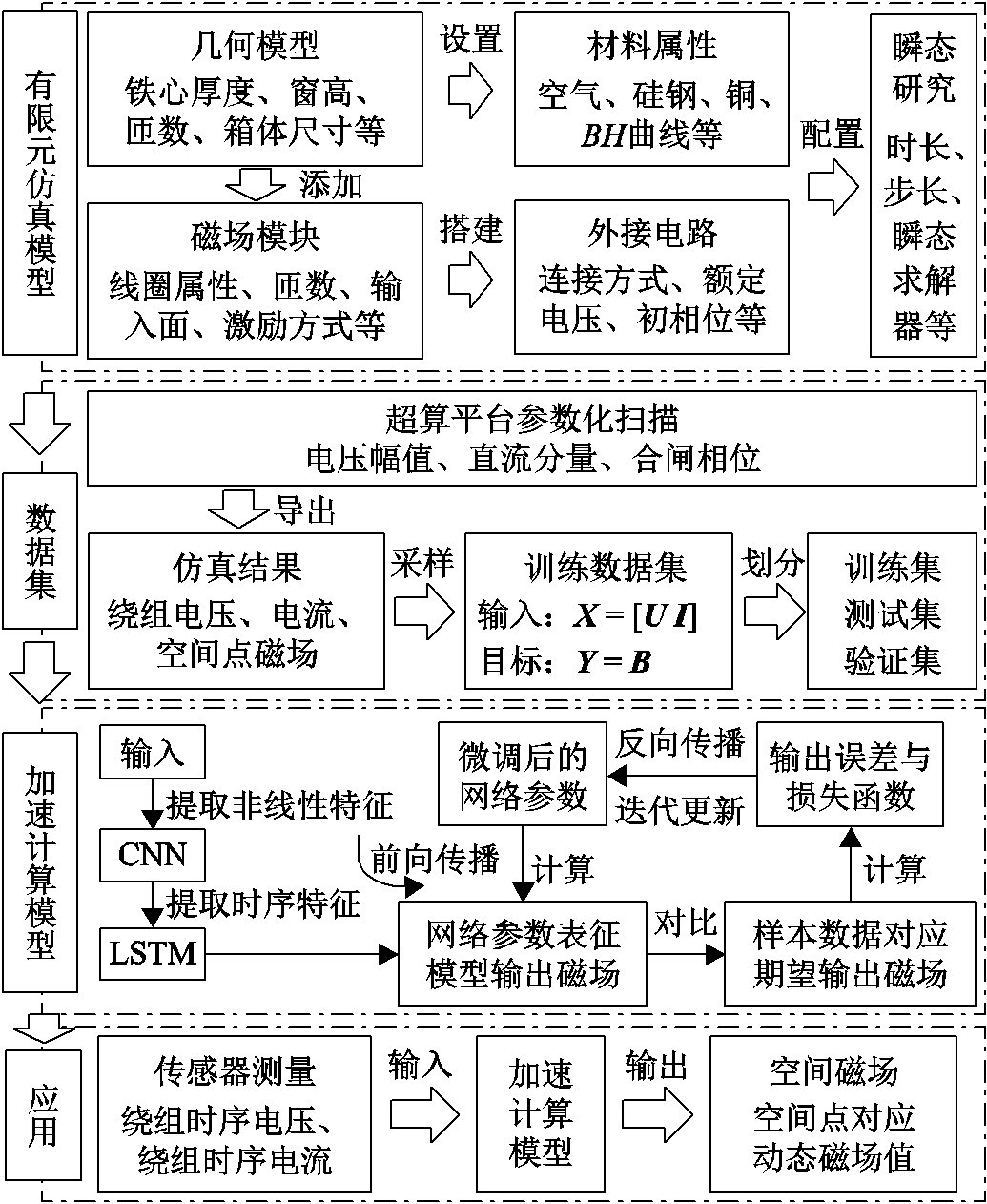
图1 工作流程
Fig.1 Work flow chart
摘要 快速获得变压器空间磁场动态分布是构建变压器数字孪生体的基础之一,然而现有快速计算方法难以快速、准确地获得铁心饱和工况下的磁场分布特性。因此,该文提出了计及铁心非线性的变压器空间动态磁场加速计算方法。首先,构建变压器电磁场路耦合仿真模型,对关键变量进行参数化扫描,仿真获得不同非线性工况下的大量磁场数据,构建涉及铁心非线性工况的主磁通和漏磁通数据集;其次,提出融合卷积神经网络(CNN)和长短期记忆网络(LSTM)的双分支深度学习模型,训练提取磁场数据的空间和时间特征,解决主、漏磁通差异大造成的模型训练难题;最后,利用模型获得输入电压、电流与内部空间磁场分布的非线性映射关系,实现空间动态磁场的加速计算,为变压器数字孪生体的构建提供了快速获得磁场数据的方法。
关键词:非线性 卷积神经网络 长短期记忆网络 磁场 加速计算
“双碳”目标下我国正处于能源与数字革命融合发展的时期,电力系统数字化转型已迫在眉睫[1],而数字孪生是构建电力装备及系统数字化的重要途径[2]。变压器是电力系统的核心装备之一,构建变压器数字孪生体是电力系统数字化在装备层的重要任务[3],能够实现变压器运行状态的实时感知和预测,为状态评估和快速决策提供实时数据。
变压器的磁场分布是决定变压器性能和运行状态的关键物理场之一。变压器正常运行时漏磁场的分布具有对称性,可利用绕组漏磁分布特征量对变压器早期故障进行研究[4],也可以通过磁场测量实现变压器绕组形变的在线监测以及对形变类型的判定[5]。主磁通可以反映变压器铁心的运行状态,掌握主磁通的分布,能够支撑铁心形状和尺寸的优化设计[6-7],降低磁通损耗,提高变压器的效率和技术经济性等[8]。
目前变压器磁场的主要获取方法可以分为三类:传感器测量、有限元仿真、算法反演。传感器测量主要基于磁通门、电磁感应线圈、霍尔效应等原理测量交流或直流磁场[9],但是磁场传感器测量存在灵敏度低、成本高以及测量位置不灵活的局限性[10],只能获得测量点的磁场值而非整个空间的磁场分布。有限元仿真能够描述变压器内部复杂的磁场分布特性,采用Ansys、COMSOL等成熟商业软件仿真的结果与实际测量结果具有较高的一致性,其准确性已被实际测量和理论分析所验证[11]。然而,电力变压器体积大、结构复杂,且内部组件存在多尺度特性,造成有限元仿真耗时以小时计[12],部分三维仿真耗时数天[13],难以满足变压器物理场数字孪生快速、高效的需求。
近年来,随着数据量的增加,人们进入大数据时代,研究统一于理论、实验和模拟,以数据驱动的第四范式成为主流[14],人们使用机器学习(Machine Learning, ML)方法来分析数据,寻找规律,并进行预测。Ansys开发了针对多物理场的快速仿真模块[15],基于Twin Builder可训练获得变压器磁场各降阶模块[16]。COMSOL公司发布的最新版本增加了数据驱动代理模型,为数字孪生模型提供了强大的支持[17]。深度学习算法在变压器领域的研究主要集中在磁场和温度计算[18-21]等方面,例如,基于深度信念网络(Deep Belief Network, DBN)和变压器漏磁场信息快速识别变压器的故障类型[22];通过多状态解析模型输出的漏磁场信息与物理实测信息之间的差异快速识别并定位绕组早期故障[23];采用支持向量机(Support Vector Machine, SVM)[5]实现对变压器绕组形变的准确分类以及形变严重程度的判定;本征正交分解(Proper Orthogonal Decomposition, POD)法和深度神经网络(Deep Neural Network, DNN)可以用于有限元仿真的加速;利用深度学习(Deep Learning, DL)可预测电磁器件中的场分布[24];朴素贝叶斯算法[25]可用于评估预测静电放电的磁场和电场;基于U-net网络可实现物理场的快速计算[26]。以上加速计算与预测方法均能用于磁场的快速计算,但研究中忽略了铁磁材料的非线性特性以及空间磁场的差异化分布等特点。
综上所述,变压器的磁场计算主要考虑的是铁心工作在线性区的工况,而在实际运行中,常见的工频过电压、直流偏磁和励磁涌流工况都会使励磁电流增大、铁心饱和,使变压器铁心工作在非线性区。变压器内部磁场分布特征的改变会造成现有快速计算方法性能劣化:①随着铁心饱和程度加深,空间磁场的非线性变化特性越发凸显,现有计算过程未计及变压器铁心的非线性特性,铁心饱和与未饱和时的磁场分布在数值上无法线性互推,因此难以实时掌握铁心饱和时的磁场分布情况;②主磁通与漏磁通的数值差异较大,在深度学习网络的训练过程中会产生误导性的交互影响,造成局部磁场计算误差较大。对于特定的非线性运行工况,只能通过数以小时计的有限元仿真获取其磁场分布,计算速度难以满足构筑数字孪生体的要求,因此需构建计及铁心非线性特性的空间磁场快速计算模型。
针对变压器铁心的非线性特性以及磁场的分布特征,本文提出一种融合卷积神经网络(Convolutional Neural Network, CNN)[27]和长短时记忆(Long Short-Term Memory, LSTM)[28]网络的双分支训练的加速计算模型:利用CNN强非线性表征能力提取变压器端口电压、电流与内部空间磁场的非线性映射关系;采用LSTM网络传递和表达电压、电流、磁场时间序列中的动态信息并且保留历史特征;通过双分支结构分别训练主、漏磁通与输入电压和电流的非线性关系,解决主、漏磁通数值差异大造成信息之间相互干扰的问题,实现变压器空间磁场从小时级到秒级的快速计算,支撑变压器数字孪生模型构建与空间磁场近实时可视化。
本文提出了一种基于大量仿真数据驱动的空间磁场加速计算模型,具体工作流程如图1所示。

图1 工作流程
Fig.1 Work flow chart
1)搭建有限元仿真模型:获取变压器的几何参数和电气参数后,根据参数在有限元仿真软件中建立几何模型、设置外电路激励、配置瞬态求解器,输出正常工况下变压器三维磁场的有限元仿真模型。
2)超算平台参数化扫描获取数据:基于步骤1)中建立的有限元仿真模型,借助超算平台对模型中外电路设置的电压幅值、直流分量和合闸相位进行参数化扫描,获取大量非线性工况下的仿真结果,导出时序的绕组电压、电流作为输入数据集以及磁场点云数据作为目标数据集。
3)训练加速计算模型:将步骤2)中的数据集进行预处理与划分,作为加速计算模型训练的数据基础,融合CNN与LSTM构建双分支训练网络,确定合适的迭代次数、批量数据大小、学习率等网络超参数,训练主、漏磁通与电压、电流的映射关系,输出包含网络参数的模型文件。
4)应用加速计算模型:调用步骤3)输出的模型文件,计算指定绕组电压、电流输入对应的空间磁场输出,并在时间与空间尺度上对比模型的输出值与有限元仿真值或实测值之间的误差。
在变压器磁场的相关研究中,基于有限元的变压器“场-路”耦合模型已经被试验证明为准确的磁场分析方法[29],因此本文以有限元仿真的计算结果作为研究的数据基础。
以一台SFSZ20-20000/110-NX2三相三绕组电力变压器为研究对象,其额定容量为20 MV·A,连结组别为YNyn0d11,主要结构参数见表1,电气参数见表2。
表1 电力变压器的结构参数
Tab.1 Structural parameters of power transformer
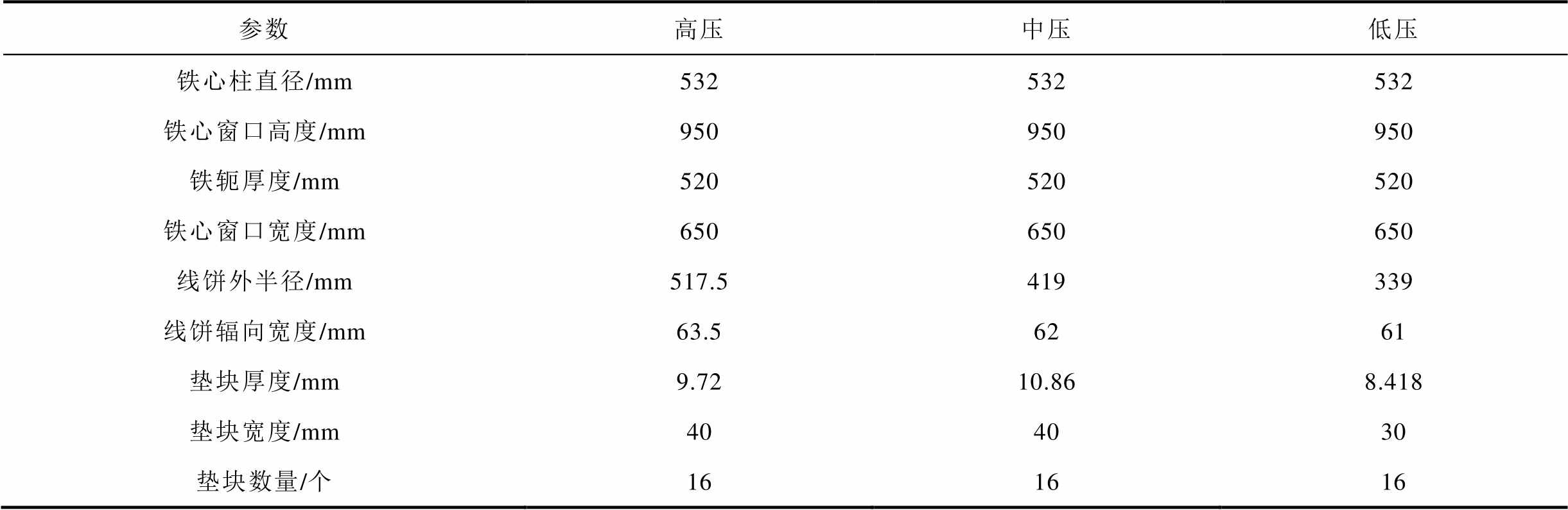
参数高压中压低压 铁心柱直径/mm532532532 铁心窗口高度/mm950950950 铁轭厚度/mm520520520 铁心窗口宽度/mm650650650 线饼外半径/mm517.5419339 线饼辐向宽度/mm63.56261 垫块厚度/mm9.7210.868.418 垫块宽度/mm404030 垫块数量/个161616
表2 电力变压器的电气参数
Tab.2 Electrical parameters of power transformer

参数高压中压低压 额定电压/kV11038.510.5 额定电流/A104.97299.91 099.71 绕组匝数/匝798279132 额定容量/(MV·A)202020
为了减少有限元仿真的计算量,根据变压器的对称性建立模型,忽略影响磁场分布的次要因素,对有限元模型做以下简化[30]:
1)忽略变压器的铁心拉板、上下夹件、箱壁磁屏蔽、箱盖电屏蔽等结构件的影响。
2)忽略变压器绕组垫块、压板、夹件、撑条以及线饼与线饼的间隙,将绕组等效为空心的圆柱体。
3)由于叠片之间的距离相对于铁心的整体尺寸非常小,忽略铁心叠片结构不影响计算精度且能降低计算复杂度,因此将其建模为一个整体。
根据电力变压器的结构参数建立的三维有限元仿真模型如图2所示,其主要结构包括铁心和绕组,绕组分为高压绕组、中压绕组和低压绕组(由外到内),同心绕在铁心的三个心柱上。
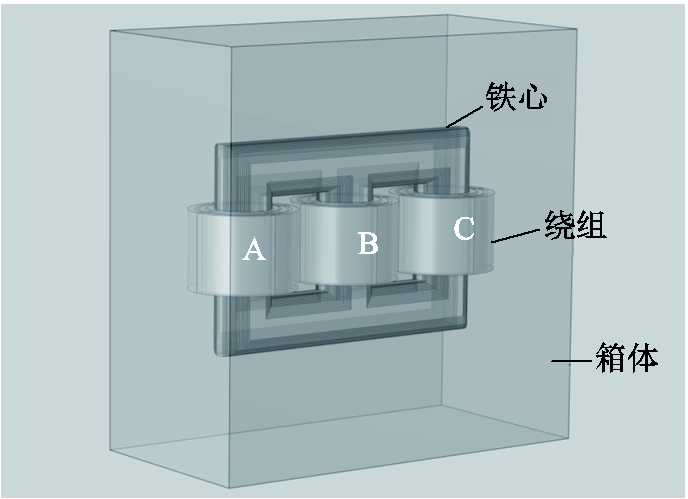
图2 变压器有限元仿真模型
Fig.2 Finite element simulation model of transformer
本文基于实际变压器参数定义了额定电压、电流和匝数等电气参数,设置变压器各部分材料,并导入如图3所示的铁心硅钢片材料的磁通密度-磁场强度曲线。
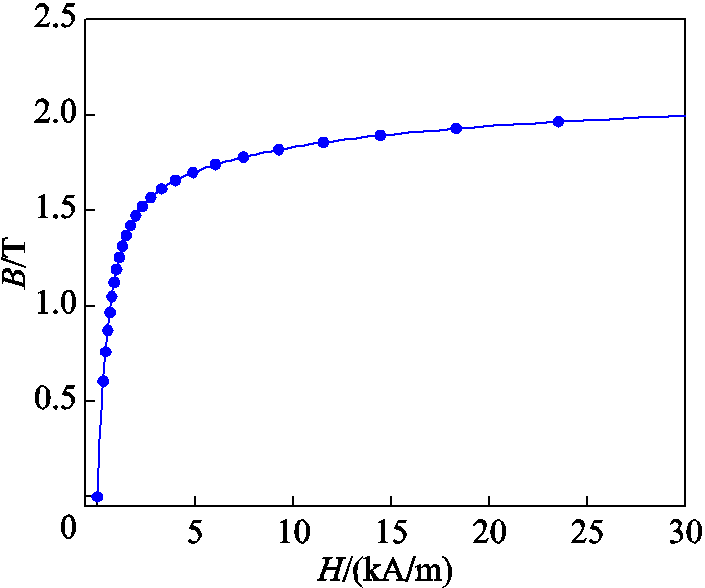
图3 变压器铁心磁通密度-磁场强度曲线
Fig.3 Magnetic induction intensity-magnetic field intensity curve of transformer core
对建立的几何模型进行网格剖分如图4所示。网格质量越接近1表明网格质量越好,由图4可知本文的有限元仿真模型网格质量较好。

图4 网格质量
Fig.4 Mesh quality
搭建外接电路作为外部激励进行联合仿真,外电路连接示意图如图5所示。图中,Is为中性点注入的直流偏置量,A相电源电压表达式为
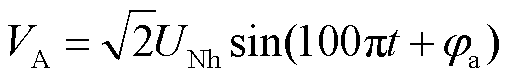 (1)
(1)
式中,UNh为A相交流电源电压的有效值;φa为其初相位,在本文仿真中φa=0°,B、C相的初相位分别设置为φb=120°,φc=-120°。
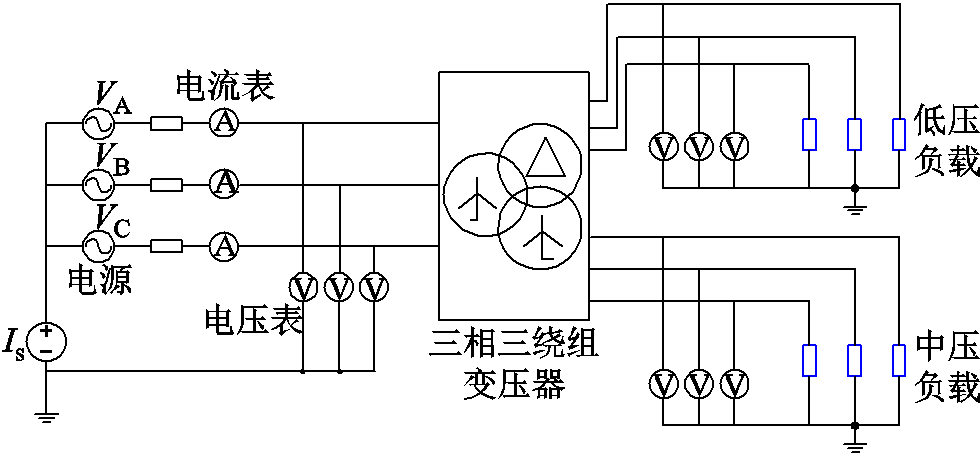
图5 外电路连接示意图
Fig.5 External circuit connection schematic
配置瞬态求解器求解空间磁场,图6为中压负载低压空载时,某时刻有限元仿真得到的铁心及绕组的磁场分布情况。由于铁心具有非线性特性以及三相固有的相位差异,心柱的饱和程度存在差异。基于此模型更改运行参数,可获得多工况有限元仿真数据。
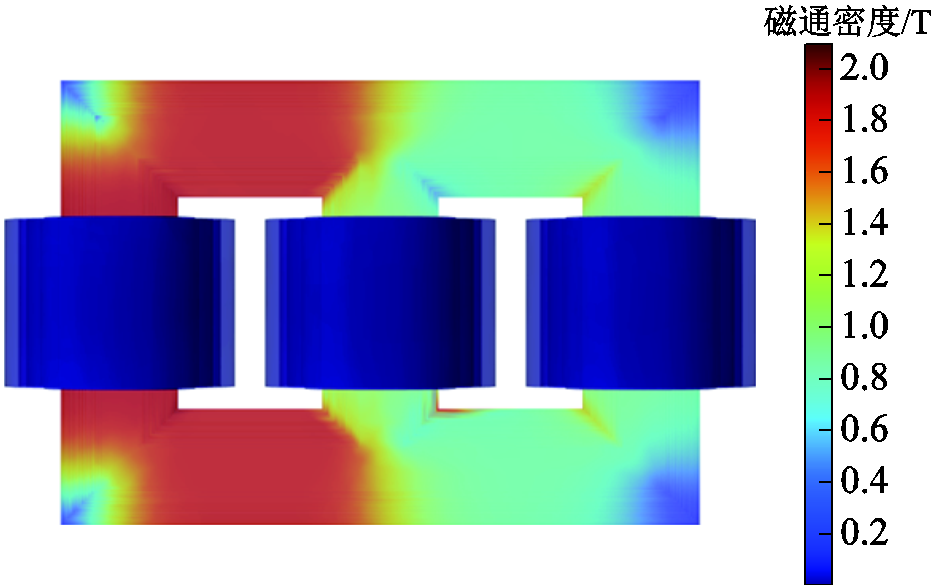
图6 有限元仿真结果
Fig.6 Finite element simulation results
实际运行中涉及变压器铁心非线性的工况主要包括工频过电压工况、直流偏磁工况及励磁涌流工况。这些工况都会使铁心饱和,显著影响变压器磁场的空间分布特性。
根据标准DL/T 1848—2018《220 kV和110 kV变压器中性点过电压保护技术规范》,中性点绝缘电压等级为110 kV的变压器其工频耐受电压为170 kV。基于正常工况下的变压器有限元仿真,对激励电源的幅值UNh进行参数化扫描,扫描范围从额定电压1.0(pu)(110 kV)到1.6(pu)(176 kV),扫描步长为0.02(pu),共获得62个过电压工况仿真结果。
根据标准DL/T 1799—2018《电力变压器直流偏磁耐受能力试验方法》,直流偏磁最大为变压器空载电流峰值的2.6倍。基于有限元仿真测得空载时励磁电流峰值为14 A,对变压器中性点连接的直流源Is从2~50 A进行参数化扫描,扫描步长为2 A,共获得50个直流偏磁工况仿真结果。而直流偏磁工况仿真结果是由瞬态到稳态的瞬变过程,在导出结果时仅导出达到稳态的数据。
基于额定电压下中、低压空载的变压器有限元仿真模型,对电压源的初相位φ从0°~120°进行参数化扫描,扫描步长为5°,共获得25个励磁涌流工况仿真结果。
三个典型非线性类型仿真工况总结见表3,基于超算平台辅助计算并导出仿真结果构造数据集,用于第3节加速计算模型的训练、验证及测试。
表3 数据库中仿真工况总结
Tab.3 Summary of simulation conditions in the database

非线性类型带载情况参数化扫描数据类型工况数(组) 中压低压范围步长 工频过电压负载空载1.0(pu)~1.6(pu)0.02(pu)稳态31 空载负载31 直流偏磁负载空载2~50 A2 A稳态25 空载负载25 励磁涌流空载空载0°~120°5°暂态25 总工况数(组)137
工频过电压工况下的电流与磁场有限元仿真结果如图7所示。当绕组电压为1.1倍额定电压时,变压器铁心工作在非线性区,正弦变化的主磁通密度产生的尖顶励磁电流叠加到高压绕组电流,使得高压绕组电流畸变。当电压增加,即饱和程度加深时,主磁通密度随着时间正弦变化且幅值增大,而漏磁通密度受绕组电流影响,会产生不同程度的畸变。
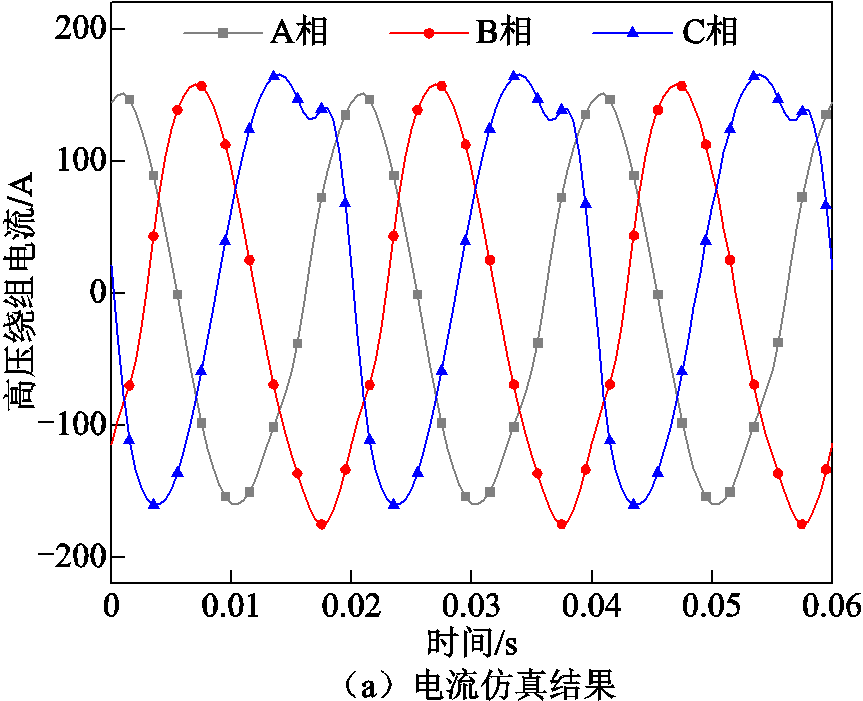
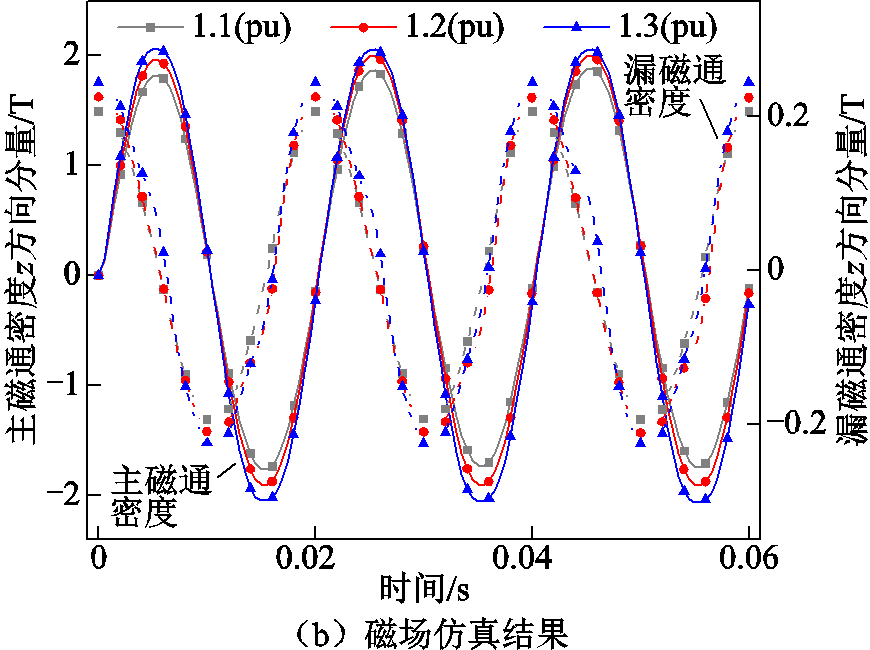
图7 电流与磁场有限元仿真结果(工频过电压)
Fig.7 Finite element simulation results of current and magnetic field (power frequency overvoltage)
直流偏磁工况下的电流与磁场有限元仿真结果如图8所示,此时设置绕组中性点流入的直流偏置量为20 A,使得铁心的工作点沿B-H曲线上移到非线性区,因此高压绕组电流波形在发生整体偏移的同时还发生了畸变,主磁通密度保持正弦变化但受电流偏移的影响而发生偏移,漏磁通密度受绕组电流畸变的影响而产生畸变。
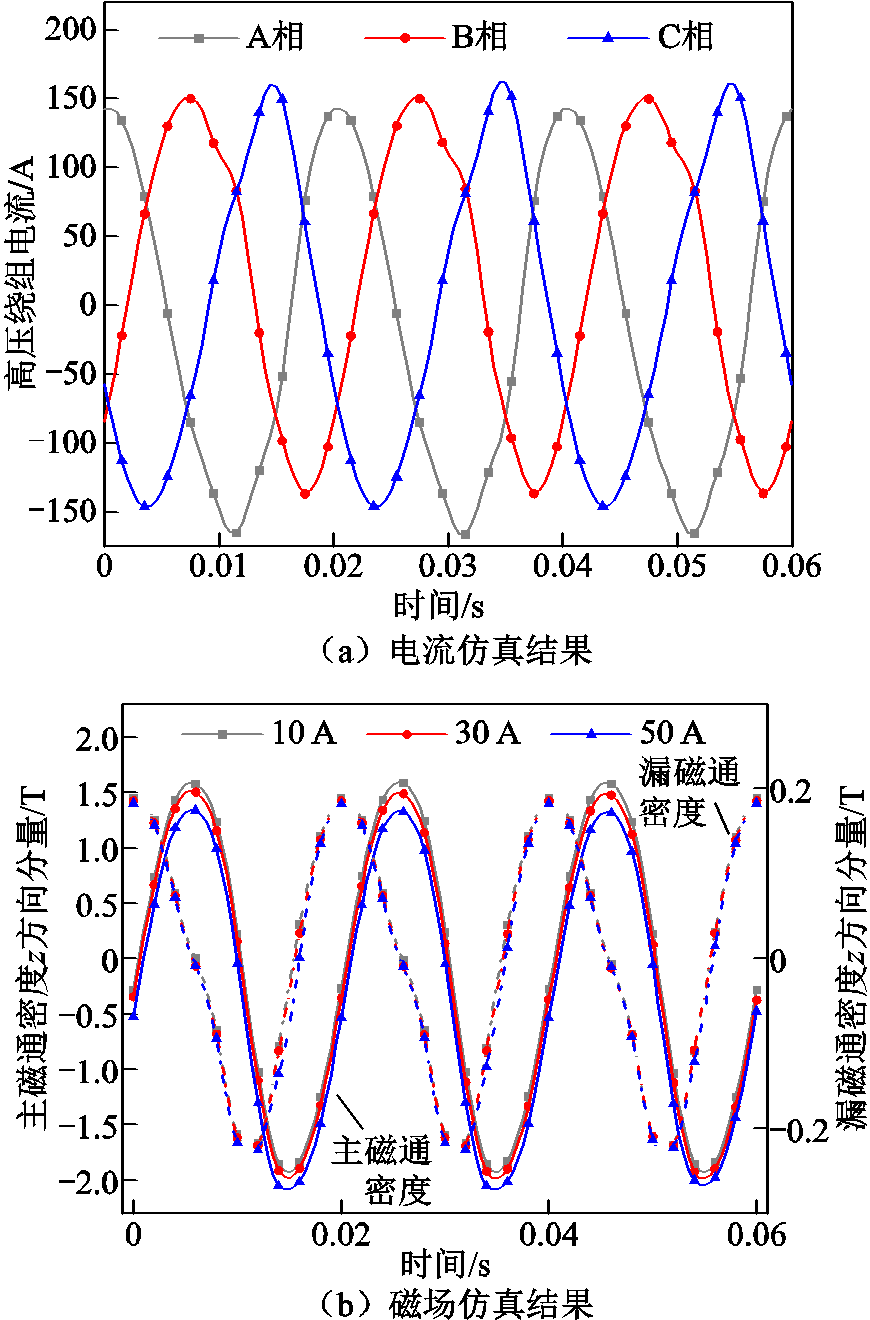
图8 电流与磁场有限元仿真结果(直流偏磁)
Fig.8 Finite element simulation results of current and magnetic field (DC bias)
励磁涌流工况下的电流与磁场有限元仿真结果如图9所示,此时A相绕组电压的初相位为0°,励磁电流幅值激增然后随时间衰减。当初相位不相同时,同一位置的主磁通密度波形会发生位置与相位的偏移,而漏磁通密度受绕组电流影响与绕组电流变化规律相似。
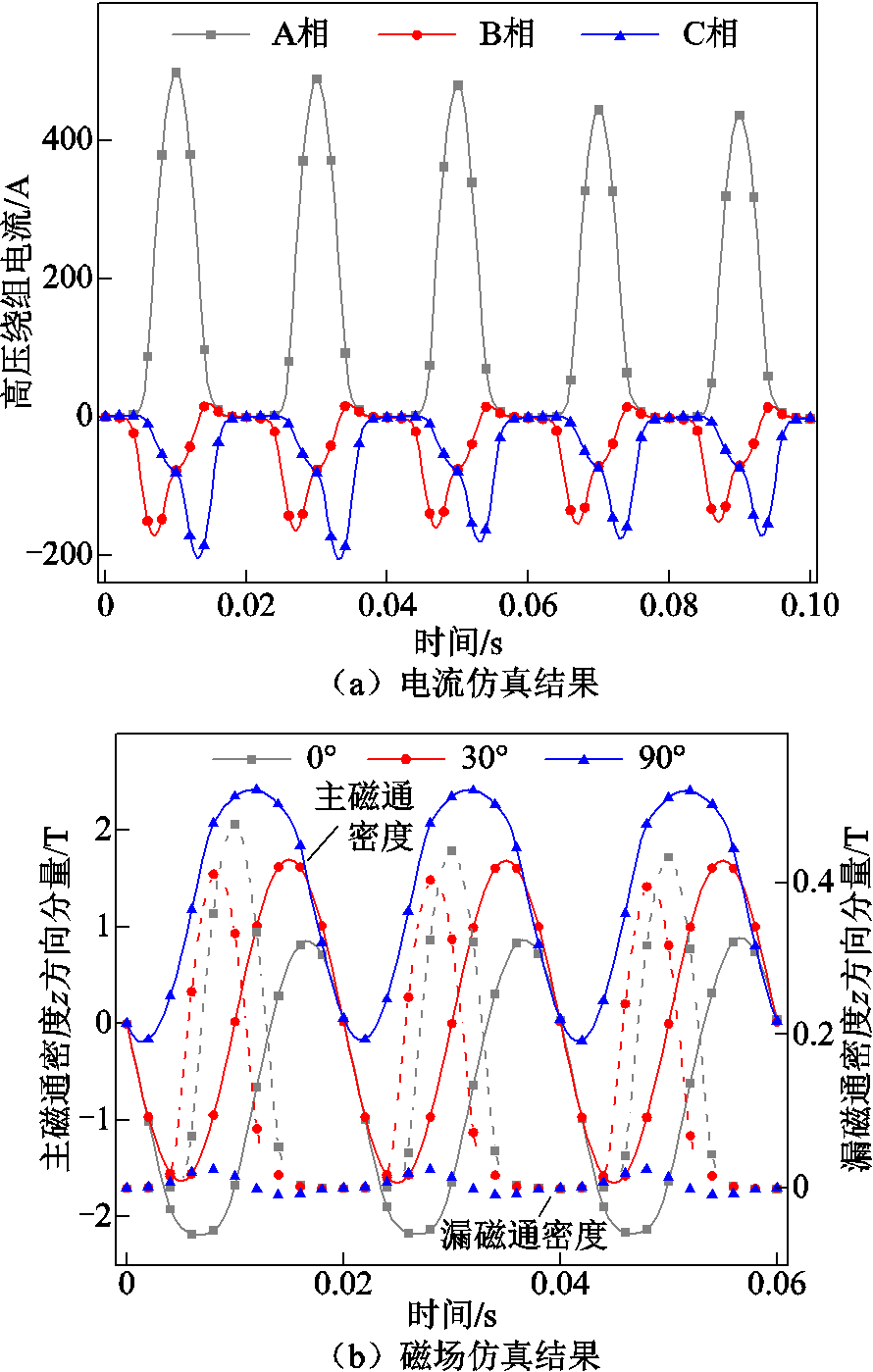
图9 电流与磁场有限元仿真结果(励磁涌流)
Fig.9 Finite element simulation results of current and magnetic field (inrush current)
考虑到电压和电流是变压器运行时的基本物理量且是容易测量获得的数据,因此使用这两个物理量作为模型的输入具有实际可行性。导出有限元仿真结果构建数据集可用于深度学习网络的训练,数据中包含绕组端口电压与电流时间序列数据U、I,空间坐标x、y、z矩阵D,以及对应坐标下的磁场时间序列数据B,其中磁场数据B可为x、y、z任一方向分量或模值。构造端口输入电压和电流时间序列矩阵,表示为
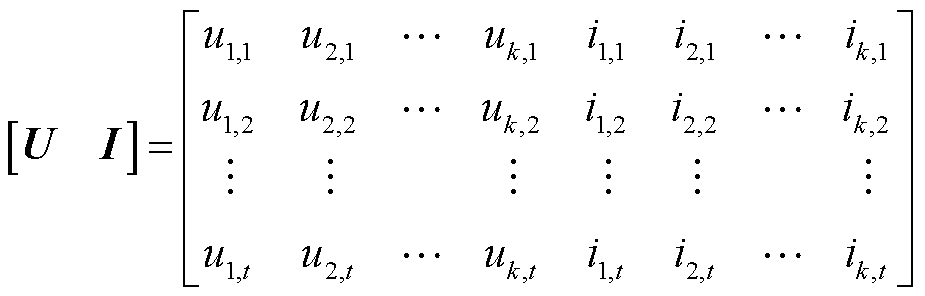 (2)
(2)
式中,uj和ij(j=1, 2,…, k)分别表示绕组j电压、电流;k为绕组的数量;t为时间序列数据长度。
考虑到空间主磁通密度和漏磁通密度差异较大,因此将空间区域分为两部分,构造场点矩阵为
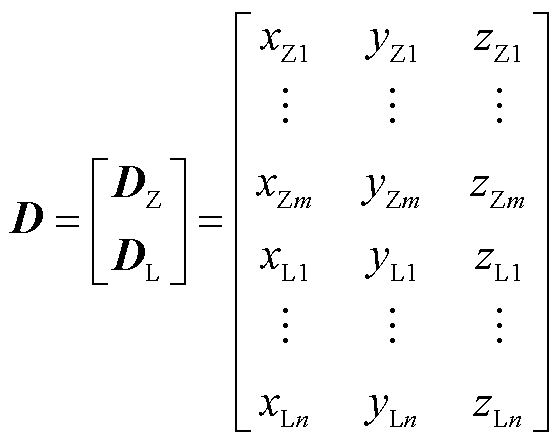 (3)
(3)
式中,下标“Z”和“L”分别代表主磁通密度和漏磁通密度对应变量;x、y、z为空间点的三向坐标;m和n分别为主磁通密度和漏磁通密度导出的对应坐标点数量。
将场点对应的磁通密度导出作为主磁通密度矩阵BZ和漏磁通密度矩阵BL,构造场量矩阵为
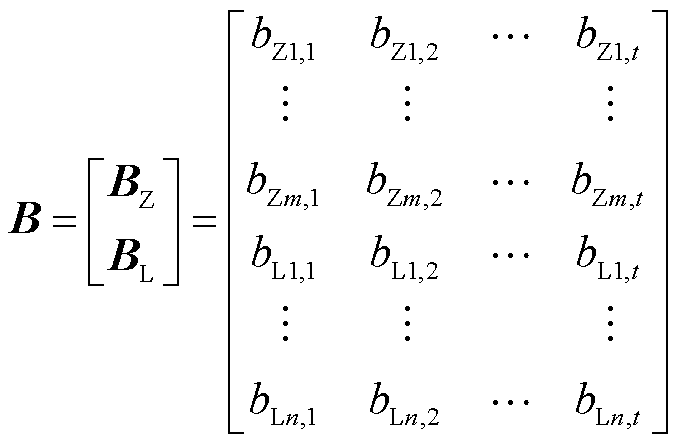 (4)
(4)
在2.4节构建的数据集中,以时间序列矩阵U、I作为输入数据Praw,空间磁通密度矩阵BZ和BL作为输出数据Qraw,分别表示为
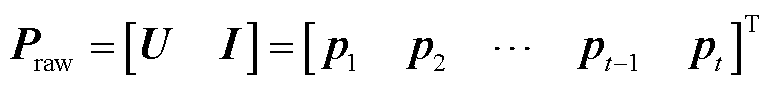 (5)
(5)
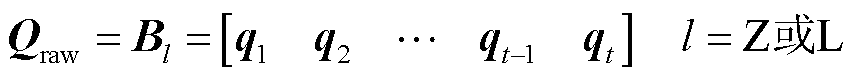 (6)
(6)
对于使用探头或传感器测量的实际数据,现场环境会对其产生随机干扰。为削弱测量数据中噪声的影响,采用中值滤波Med{·}对数据进行滤波处理,如式(7)所示,通过滤波可消除孤立的噪声点,从而得到接近原始值的数据。
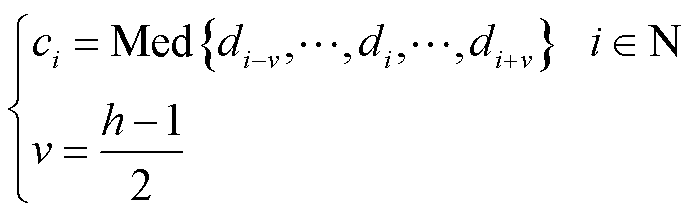 (7)
(7)
式中,ci为滤波后序列数据中的第i个数据;di为滤波前序列数据中的第i个数据;h为滤波的窗口长度,且h为奇数。
为了消除各维度特征之间数量级的差异而带来的训练权重偏向,使模型更容易学习特征之间的关系,提高模型的训练效果和泛化性能。本文使用零均值(zero-score)归一化方法对原始数据进行预处理,Praw、Qraw分别经过式(8)和式(9)的运算得到PG和QG。
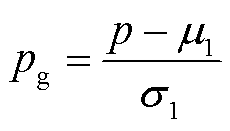 (8)
(8)
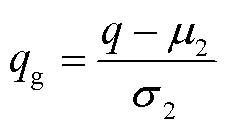 (9)
(9)
式中,pg、qg为归一化后的值;p、q分别为输入(电压/电流)、输出(磁通密度)数据;μ1、μ2分别为输入、输出样本数据的均值;σ1、σ2分别为输入、输出样本数据的标准差。
为确保在模型训练过程中有足够的数据用于学习,同时也有足够的数据用于验证模型的性能,以及评估其在未见过的数据上的泛化能力,将总的数据集PG和QG按7:2:1的比例划分为训练集{Ptrain, Qtrain}、测试集{Ptest, Qtest}和验证集{Pval, Qval}。
对于三相三绕组变压器,式(2)中k=9,式(4)中m=19 487,n=19 656。每个有限元仿真结果导出0.04 s的数据(时间间隔为0.5 ms),共81个时刻。基于参数化扫描结果,可获得5 022个工频过电压时序数据、4 050个直流偏磁时序数据、2 025个励磁涌流时序数据,共11 097个时序数据,因此在式(2)中t=11 097。
为准确地获取变压器端口电压、电流与内部空间磁场的非线性映射关系以及时间序列的动态特征,基于主、漏磁通密度分布差异化的显著特征,本节基于CNN和LSTM搭建了双分支的深度学习模型,训练网络结构如图10所示。归一化后的电压电流矩阵PG分别输入主磁通密度和漏磁通密度的训练分支,同时经过CNN网络映射到高维提取空间特征。考虑到加入池化操作可能会丢失时序数据中一些重要的时间顺序信息,从而影响时序数据的拟合精度,因此CNN的输出矩阵经过变换直接输入LSTM网络中提取其时间维度的前后依赖关系,最后分别经过一个全连接层,进行解码后线性映射输出空间主、漏磁通密度Q2、Q1,将二者结果进行拼接,即得到最终加速计算模型完整的计算结果。具体方法如下。

图10 CNN-LSTM网络结构
Fig.10 Structure of CNN-LSTM network
式(5)定义的输入电压电流矩阵Praw经过式(8)归一化后得到输入矩阵PG。对PG的t-1时刻的数据pt-1进行卷积提取特征,卷积后的输出分别进行加权偏置计算,加和后得到ut,再通过激活函数ReLU得到全连接层的输出pt,表示为
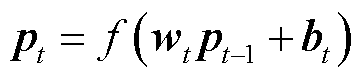 (10)
(10)
式中,f为激活函数;wt为权重系数;bt为偏置。
CNN的输出pt和LSTM网络在t−1时刻的隐藏状态ht-1作为LSTM网络t时刻的输入。LSTM处理输入数据包括三个步骤。
1)遗忘门,输入数据经过加权偏置计算后,再激活函数σ得到遗忘信息ft,表达式如式(11)所示,其中激活函数的输出为[0,1]之间的任意数值。
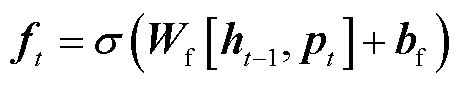 (11)
(11)
式中,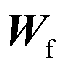 为
为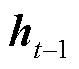 与
与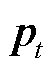 到遗忘门激活函数
到遗忘门激活函数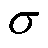 的权重矩阵;
的权重矩阵;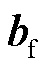 为对应偏置。
为对应偏置。
2)输入门,输入数据分别经过新的加权偏置计算后,再分别经过激活函数σ和tanh层得到中间输入it和中间细胞状态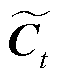 。计算式为
。计算式为
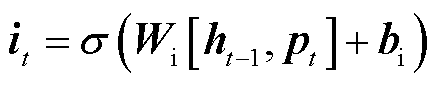 (12)
(12)
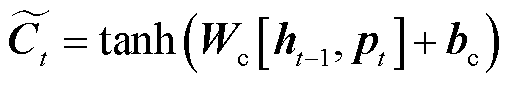 (13)
(13)
式中,Wi、Wc分别为ht-1与pt到输入门激活函数σ与tanh层的权重矩阵;bi、bc为对应偏置。
将遗忘信息ft与t-1时刻的细胞状态Ct-1中的对应元素相乘,中间输入it和中间细胞状态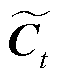 中的对应元素相乘,二者加和之后得到t时刻的细胞状态Ct,计算式为
中的对应元素相乘,二者加和之后得到t时刻的细胞状态Ct,计算式为
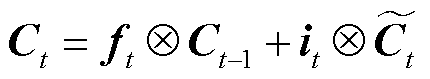 (14)
(14)
式中,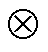 为哈达玛积算子,表示两个矩阵的对应元素相乘。
为哈达玛积算子,表示两个矩阵的对应元素相乘。
3)输出门,输入经过再一次加权偏置计算后,通过激活函数σ得到输出门的输出信息ot,计算式如式(15)所示。t时刻的细胞状态Ct再通过tanh层处理后,与ot对应元素相乘,得到t时刻隐含层的输出ht,计算式如式(16)所示。
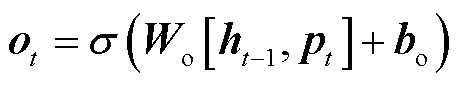 (15)
(15)
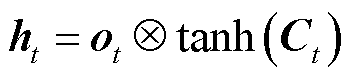 (16)
(16)
式中,Wo为ht-1与pt到输出门激活函数σ的权重矩阵;bo为对应偏置。
批量大小是每次迭代训练时所使用的样本数量,较大的批量大小可以加速训练过程,但会占用更多内存。学习率是用于控制模型参数更新步长或速度的超参数,较大的学习率会导致训练过程不稳定,可能无法收敛。优化器是用于调整模型参数以最小化损失函数的算法,影响模型的收敛速度和性能。因此批量大小、学习率和优化器的选择影响深度学习网络的收敛时间和计算效率。在网络训练时,三个参数分别设置不同数值进行测试,以均方误差作为训练过程中的损失函数。
不同批量大小、学习率和优化器下的误差对比曲线分别如图11、图12及图13所示,可确定批量大小、学习率分别设置为64、0.01,选用优化器Adam时损失函数值最小,即误差最小。
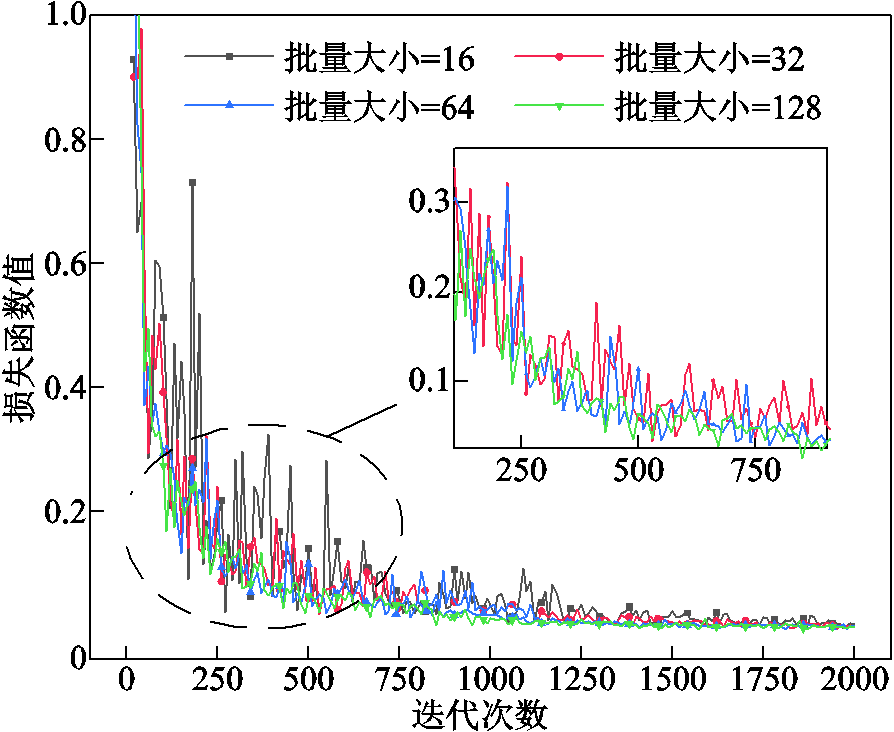
图11 不同批量大小的误差对比曲线
Fig.11 Error comparison curves of different batch sizes
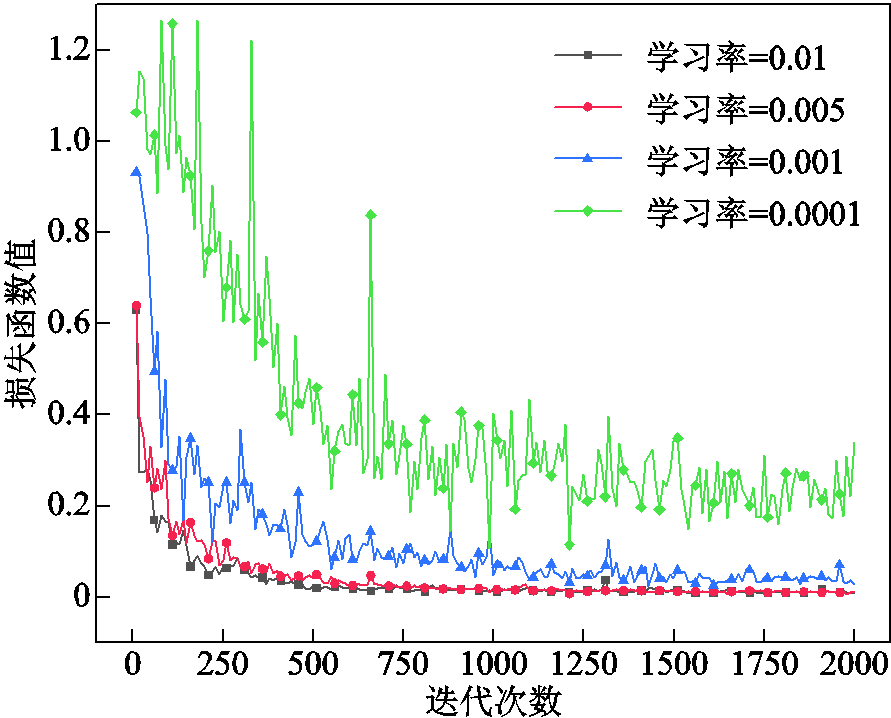
图12 不同学习率的误差对比曲线
Fig.12 Error comparison curves of different learning rates
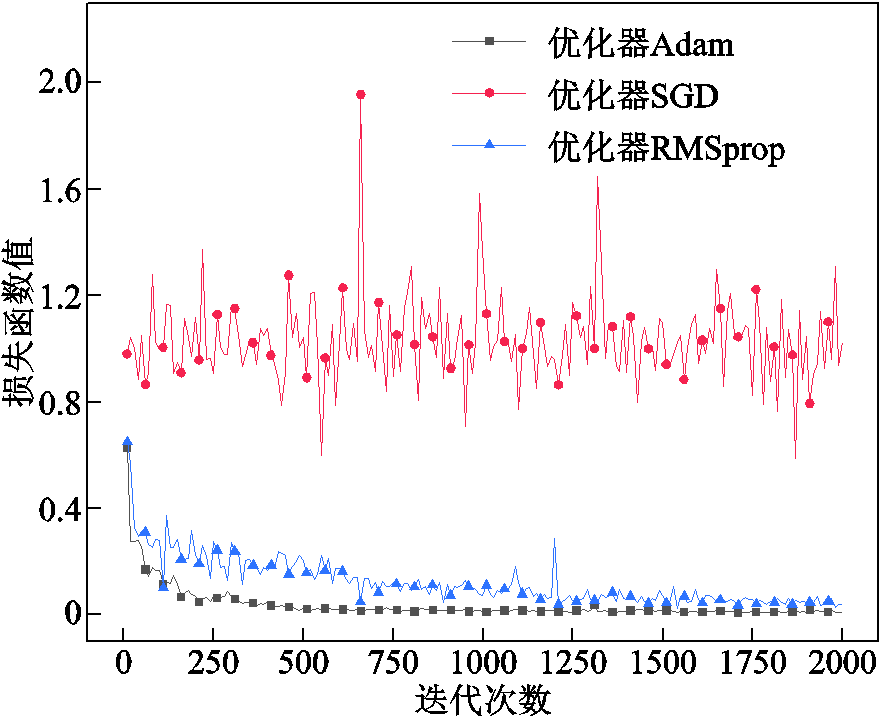
图13 不同优化器的误差对比曲线
Fig.13 Error comparison curves of different optimizers
输入矩阵中包含高、中、低压绕组的电压与电流数据,卷积核大小设为3×1。在进行卷积时可以同时覆盖三个电压等级的绕组电压或电流,从而更好地提取数据特征。输入特征维度与输出维度差异较大,中间神经元个数的设计呈现逐层递增的特点,使得网络中有足够的参数对中间特征进行有效的组合和转换,最后输出目标值。因此,根据网络结构和数据特点确定了CNN-LSTM的结构参数,见表4。
表4 CNN-LSTM模型结构参数
Tab.4 Structural parameters of CNN-LSTM model

训练层类型参数结构训练层类型参数结构 卷积层权重32×1×3LSTM层偏置2256 卷积偏置32全连接层1权重19 487×1 024 LSTM层权重1256×32全连接层1偏置19 487 LSTM层权重2256×64全连接层2权重19 656×1 024 LSTM层偏置1256全连接层2偏置19 656
将归一化后的数据输入CNN的卷积层,输入通道为1,输出通道为32,卷积核尺寸为3×1;将卷积后的输出作为LSTM层的输入,输入大小为32的特征序列,隐藏状态大小为64,LSTM层的层数为1;全连接层将LSTM层的输出进行线性变换,将其映射到大小分别为19 487和19 656的输出空间,将输出进行组合即可得到整体的计算结果。
模型训练过程耗时2 h 13 min左右,训练后的模型计算单个时刻的输出耗时约为0.04 s,训练过程中的总参数超过4 000万,其中包括卷积层、LSTM层和全连接层的权重和偏差,占用内存约为160 MB,因此计算设备需要满足至少有200 MB的可用RAM,同时支持Pytorch框架的指令集和每秒数十亿次的浮点运算能力,此外需要高速内存加载模型的输入和输出。
本次仿真基于PyTorch框架的Python语言实现,硬件平台设置为:CPU为Intel i5-10400 2.90 GHz,GPU为NVIDIA GeForce GTX 1080 Ti 11 G,内存RAM为16 GB。本节对提出的基于CNN-LSTM的加速计算模型的准确性进行了验证。
4.1.1 稳态测试结果
基于加速计算模型计算某一个时刻的磁场分布情况并进行可视化,同时可视化相同条件下有限元仿真的计算结果,以及二者的计算差值,如图14所示。可以看出,模型的计算结果与仿真呈现同样的铁心饱和程度不同的特点,二者空间磁场分布基本一致。
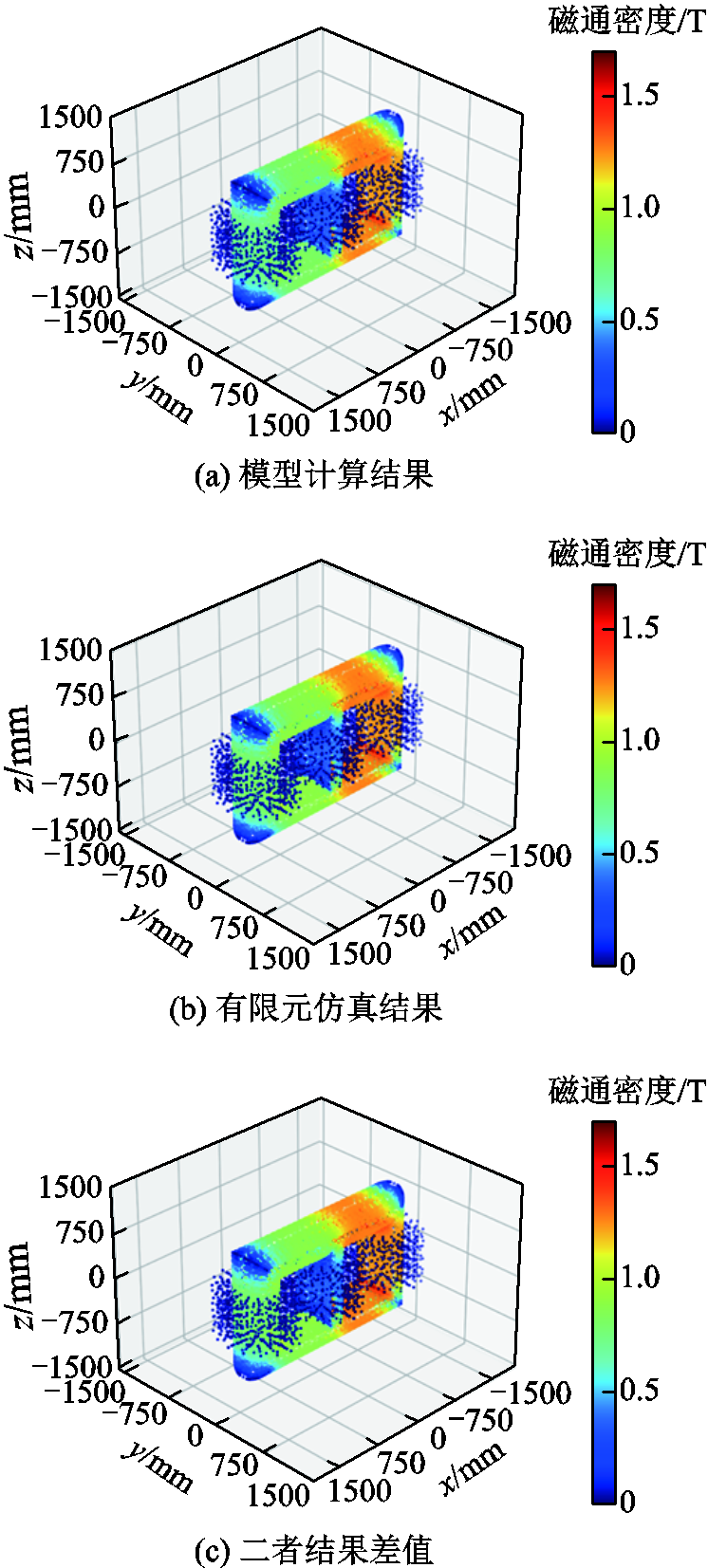
图14 计算结果可视化
Fig.14 visualization of calculation results
为进一步验证加速计算模型计算主磁通密度的准确性,选取如图15所示六个磁通路径,以测试集中的一组计算结果为例,对不同轴线上磁通密度的有限元仿真值和本文提出的加速计算模型计算值进行对比,结果如图16所示。从图16可知,两者曲线几乎一致,误差较小。绕组间漏磁及铁心轴线上的磁通分布都呈现中部高、两端低时的特征,端部漏磁几乎为零,而同一时刻铁轭左右两边铁心饱和程度不相同,存在差值。此外,从图16中可知,绕组间主、漏磁通空间分布数值存在明显的差异。

图15 磁通对比路径
Fig.15 Magnetic flux comparison path
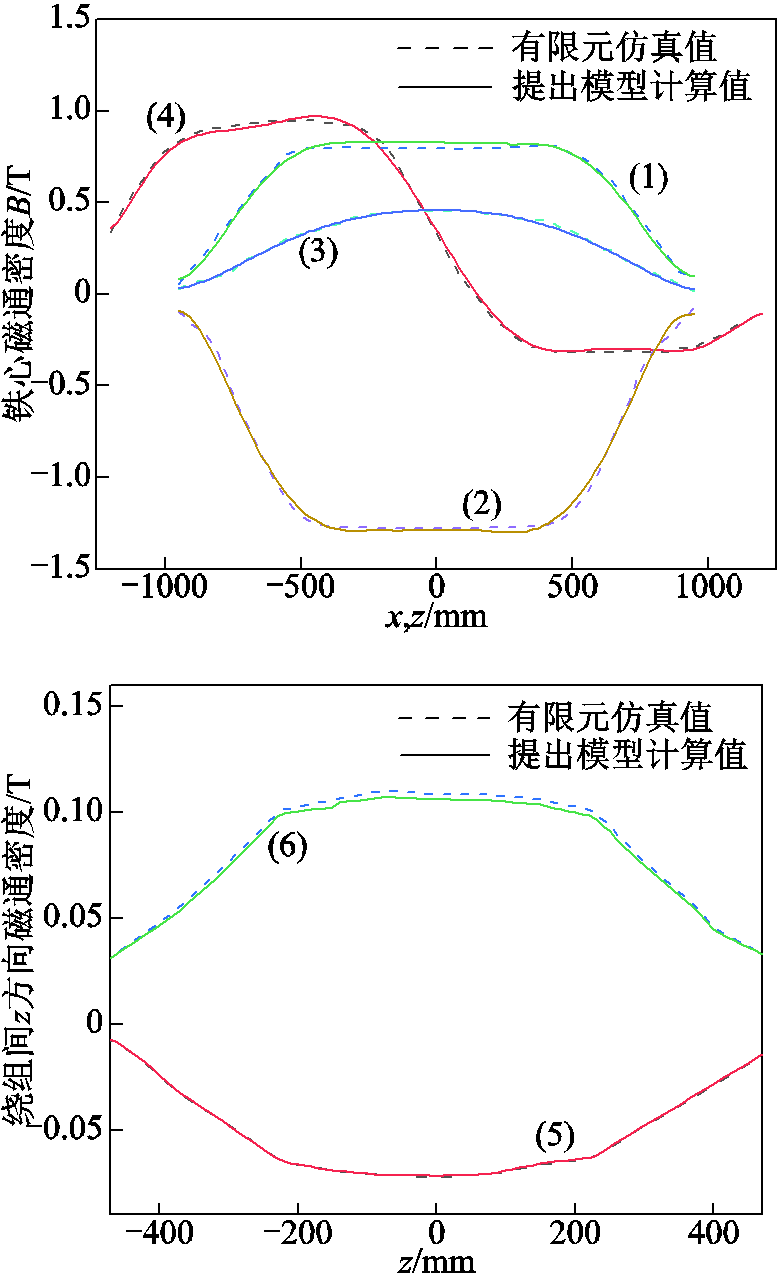
图16 不同位置磁场的仿真值与计算值对比曲线
Fig.16 Comparison curves of magnetic field simulation value and calculated value at different positions
4.1.2 动态测试结果
为分析加速计算模型的动态计算能力,选取如图17所示的两个点为对比点,在不同工况下,对两个位置上连续0.04 s内磁通密度的模型计算值和仿真值进行对比。其中,M点为B相心柱的几何中心,N点为A相心柱左边高、中压绕组间主通道的中点。
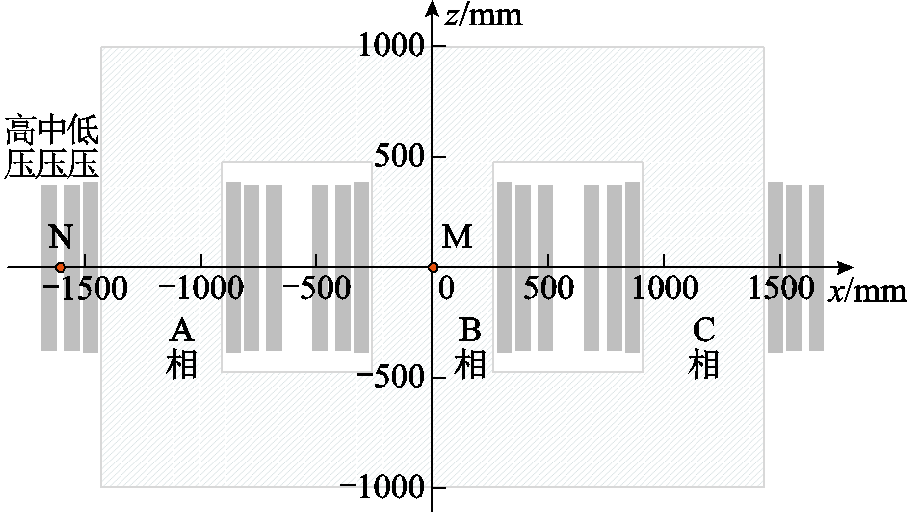
图17 时序对比点
Fig.17 Time sequence comparison points
图18为不同工况下有限元仿真值与本文方法的计算值的对比曲线。其中图18a为1.12倍额定电压下的工频过电压工况,图18b为中性点流入15 A直流电流时的直流偏磁工况,图18c为A相绕组电压的初相位为45°的励磁涌流工况。
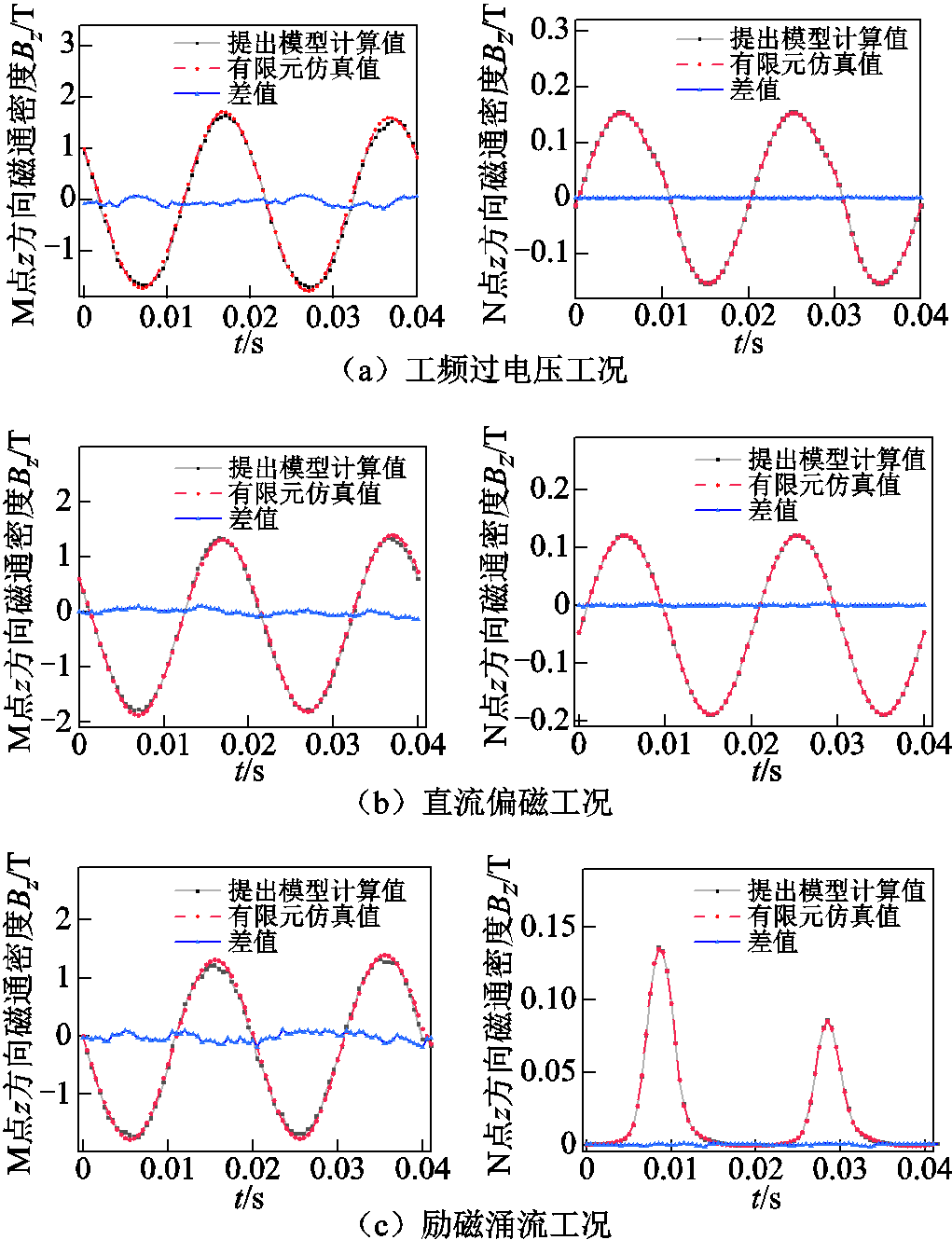
图18 不同位置磁场计算值和仿真值随时间的对比曲线
Fig.18 Comparison curves of the calculated and simulated value of the magnetic field at different positions with time
从图18中可以看出,本文提出的模型计算值与有限元仿真值具有一致性。当保持外电路的激励电压为正弦电压时,M点主磁通密度波形保持为正弦波形,而由于直流偏磁工况中存在直流分量,使得工作点沿B-H曲线上移到非线性段,因此M点主磁通密度出现上下偏移的情况,励磁涌流工况也因为励磁电流的激增而偏移。N点磁通密度波形受绕组电流影响,出现一定程度的畸变,励磁涌流工况下的影响尤为明显。
4.2.1 训练效果评价指标
本文采用平均绝对误差(Mean Absolute Error, MAE)、均方误差(Mean Square Error, MSE)、拟合优度(R-Square, R2)作为评价指标对模型的准确性进行评估。各指标的表达式分别为
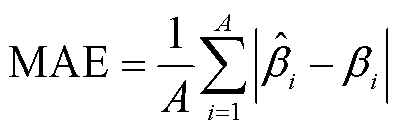 (17)
(17)
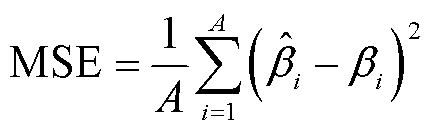 (18)
(18)
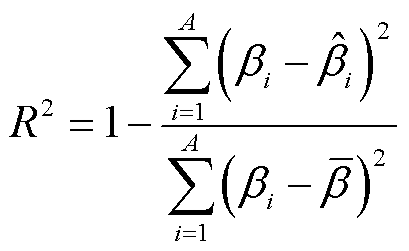 (19)
(19)
式中,A为有限元仿真导出的数据中测试集的样本数;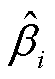 为模型计算的第i个值;
为模型计算的第i个值;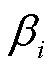 为测试集的第i个真实值即有限元计算值;
为测试集的第i个真实值即有限元计算值;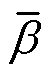 为测试集的有限元计算值的平均值。
为测试集的有限元计算值的平均值。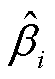 、
、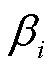 、
、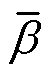 均经过归一化处理。
均经过归一化处理。
4.2.2 不同网络性能对比
采用网格搜索法获取不同网络的最佳超参数组合,将提出的模型与LSTM、CNN以及多层感知机(Multilayer Perceptron, MLP)的不同指标进行对比,如图19所示。可见,本文模型的MAE和MSE最小,R2最接近于1,因此本文提出的CNN-LSTM模型综合效果更优。由于主磁通在铁心转角处的仿真结果出现局部极值,因此主磁通的计算误差略大于漏磁通。
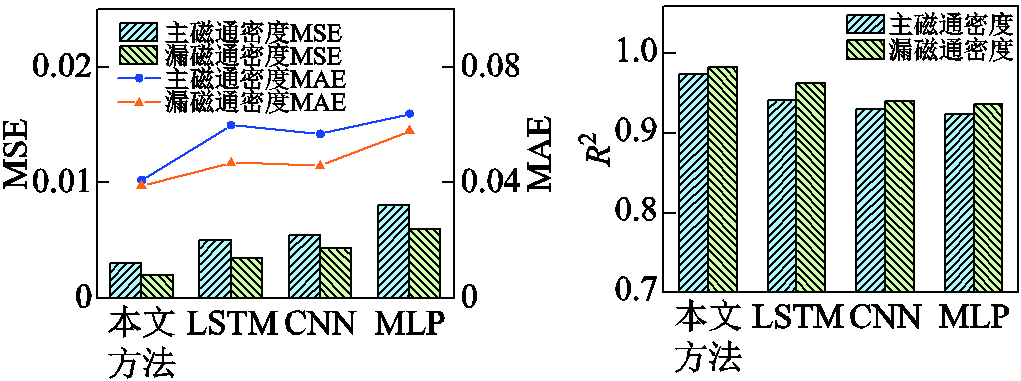
图19 不同算法的评价指标对比
Fig.19 Comparison histogram of evaluation indexes of different algorithms
根据MSE绘制训练过程中的损失函数变化,如图20所示。在前500次迭代中,损失值快速下降,2 000次迭代后趋于稳定,损失值稳定在0.01附近。对模型计算时间进行记录,得到单个时步计算时间为0.04 s左右,达到了快速计算的效果。
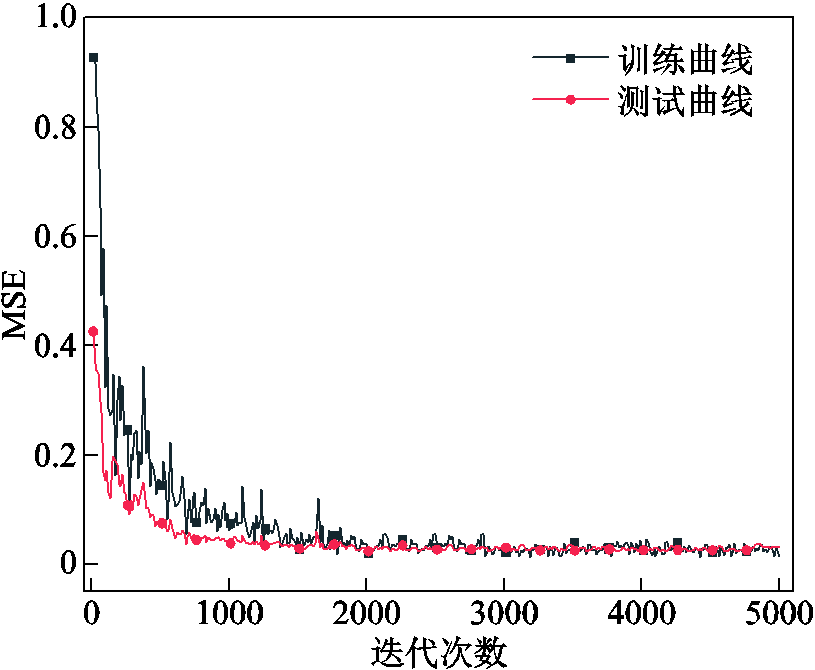
图20 训练与测试损失函数曲线
Fig.20 Training and testing loss function curve
4.2.3 数据集规模与噪声水平对准确度的影响
在学习率、迭代周期和优化器固定不变的情况下,通过改变扫描步长来调整训练数据集的规模,共设置如表5所示五种情况。表5中,Δu、ΔI、Δφ分别为工频过电压、直流偏磁、励磁涌流有限元仿真的参数化扫描步长,步长越大数据集规模越小。
表5 不同数据集规模
Tab.5 Different dataset sizes

编号Δu(pu)ΔI/AΔφ/(°)数据集规模/组 10.022511 097 20.044105 751 30.066153 969 40.088202 997 50.1010252 592
针对本文的变压器模型,采用不同深度学习网络训练不同规模数据集的拟合优度R2如图21所示。在数据较多的情况下(如表5数据集1),所有网络的R2的值都在0.9以上,而不同网络对数据集规模变化的敏感程度不同,在数据集规模较小的情况下,本文方法仍具有一定优势。以R2>0.95作为网络计算准确度的要求,按表5中数据集2的步长进行参数化扫描可满足要求,此时有限元仿真数据集的数量为5 751组。不同型号尺寸的变压器只影响磁场数据集中点的数量,可采用相同步长配置构建数据集。
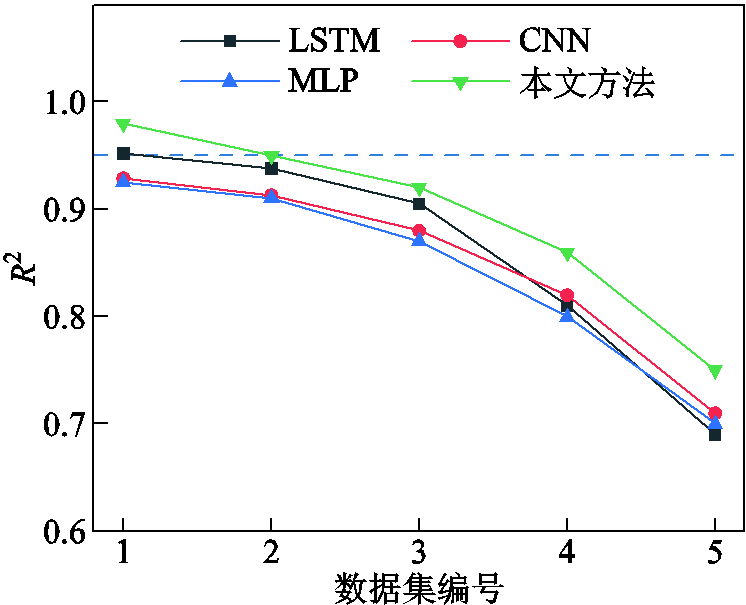
图21 不同网络的拟合优度随数据集规模的变化曲线
Fig.21 Curves of R2 of different networks with the size of the data sets
为了验证所提方法在抗噪方面的性能,对数据集添加了信噪比为60、50、40 dB的噪声数据。使用不同方法训练含不同噪声等级的数据集的准确度,结果见表6,可见相较于其他方法,所提方法具有较高的抗噪性。
表6 不同噪声水平下训练准确度
Tab.6 Training accuracy under different noise levels

噪声/dBMLPLSTMCNN本文方法 无噪声0.9250.9520.9290.974 600.9120.9330.9100.972 500.8980.9170.8970.969 400.8890.8920.8870.966
本节考虑了MAE、MSE和R2三个性能指标以及损失函数曲线的收敛性,综合比较了CNN、LSTM、MLP和本文所提CNN-LSTM的计算性能,并对比了数据集规模变化后的训练效果。
结果表明,所提模型在三个评价指标上的综合表现最佳,单独的CNN模型在MAE和MSE指标上表现略差,这说明CNN模型在图像处理领域具有较好的特性,但在处理时间序列数据时可能受限于其局部感知能力。LSTM模型在时间序列数据建模方面具有一定的优势,MLP模型在一般的线性任务中表现良好。随着迭代次数的增加,MSE呈现逐渐减小的趋势,表明所提方法可靠性较高,且其计算速度快,基本满足近实时需求。此外,所提模型在训练过程中的损失值曲线收敛速度较快,并且表现出较低的过拟合风险。这表明该模型能够更好地学习数据的特征,并具有较好的泛化能力。在不同数据量的训练中,当数据集规模较大时,所提模型计算准确度较高且上升空间较小,在满足精度需求的条件下,通过选择合适大小的数据集,能在获得较好的模型的同时避免占用太多计算资源。
为了能够通过实测数据验证所提方法的优越性,基于实验室现有条件,本节以一台50 V·A的单相双绕组变压器为研究对象验证提出的加速计算模型,试验平台如图22所示。
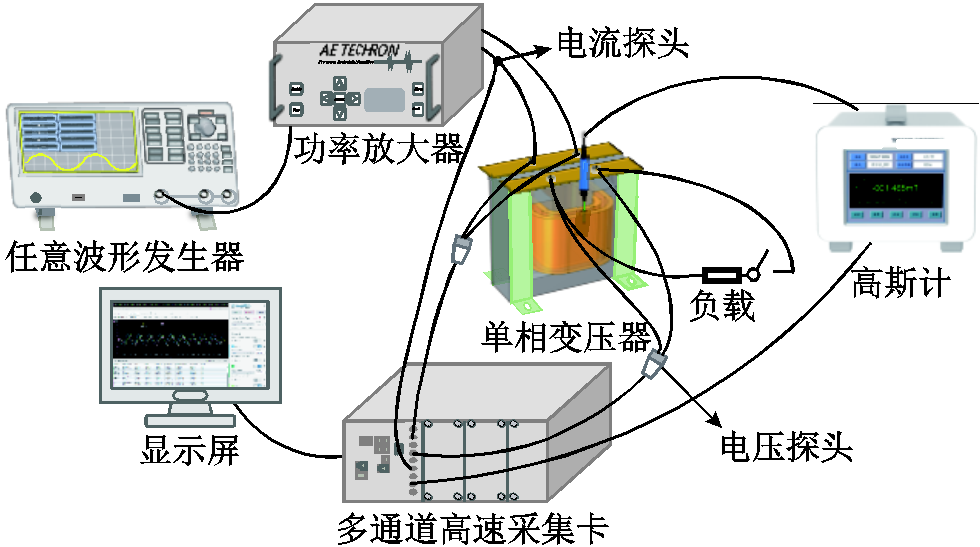
图22 试验平台
Fig.22 Test platform
任意波形发生器(AFG 31000 SERIES)与功率放大器(AE TECHRON 7548)组合作为电源激励连接变压器的一次绕组,二次绕组空载,电压探头测量一、二次绕组的电压,电流探头测量一次绕组电流,高斯计(TM6160B)测量空间的漏磁。测量信号通过多通道高速采集卡同时采集,在显示屏上实时显示波形。
基于试验平台开展工频过电压、直流偏磁和励磁涌流试验,处理变压器铁心饱和工况下的试验数据,获得试验变压器的B-H曲线。本文采用Jiles-Atheron(J-A)磁滞模型描述铁心的磁滞效应,基于粒子群优化(Particle Swarm Optimization, PSO)算法求解变压器的B-H曲线,并与试验获得的B-H曲线进行对比,如图23所示,求解所得的J-A模型参数见表7。
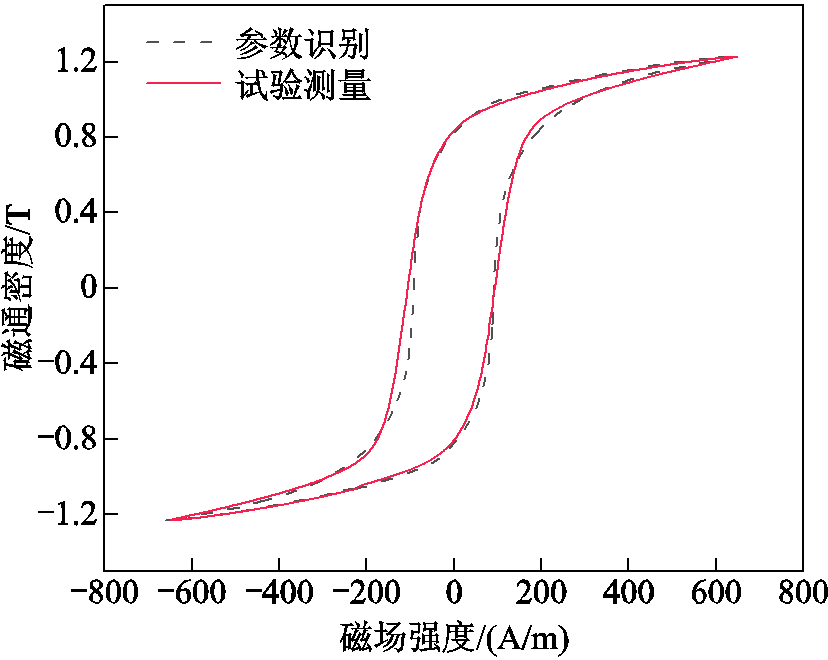
图23 J-A模型参数辨识
Fig.23 Parameter identification of J-A model
表7 J-A模型参数
Tab.7 Parameters of J-A model

参数数值 磁化饱和强度Ms/(A/m)1.216 6×106 钉扎损耗k/(A/m)68.626 磁化可逆性c0.030 7 域间耦合α3.027×10-4 域壁密度a/(A/m)134.7
根据表7的J-A模型参数以及表8的试验变压器几何与电气参数,搭建了试验变压器的有限元仿真模型如图24所示。
表8 试验变压器相关参数
Tab.8 Test transformer related parameters

参数数值参数数值 额定容量/(V·A)50匝数比55:55 额定电压/V50铁心材料DQ151-φ0.35 心柱宽度/mm60窗口高度/mm124 铁心厚度/mm60窗口宽度/mm36 旁柱宽度/mm30绕组高度/mm90

图24 试验变压器有限元仿真模型
Fig.24 Finite element simulation model of test transformer
额定电压下,试验与仿真所得的一次绕组电压与电流曲线的对比如图25所示,验证了有限元模型的准确性。
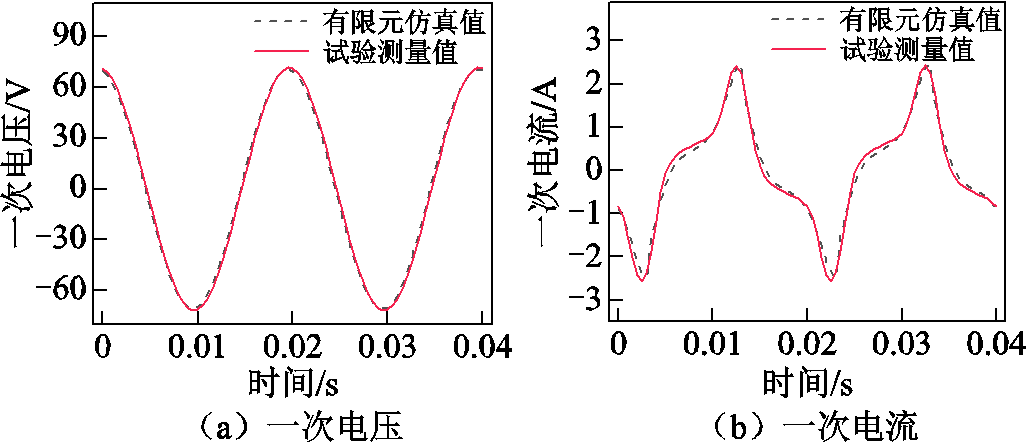
图25 试验与仿真的电压与电流曲线对比
Fig.25 Comparison of voltage and current curves between test and simulation
对有限元仿真模型进行参数化扫描,获取试验变压器不同饱和程度下的运行数据集,其中包含绕组的电压、电流以及空间磁场数据,并基于本文所提方法对其进行训练,获得试验变压器的加速计算模型。采用加速计算模型计算空间点漏磁通密度,计算点位置如图26a所示,计算结果随时间的变化曲线与实测波形对比如图26b、图26c所示。结果表明,计算值与实测值最大误差在0.07 mT左右,本文所提方法具有较高的准确度。
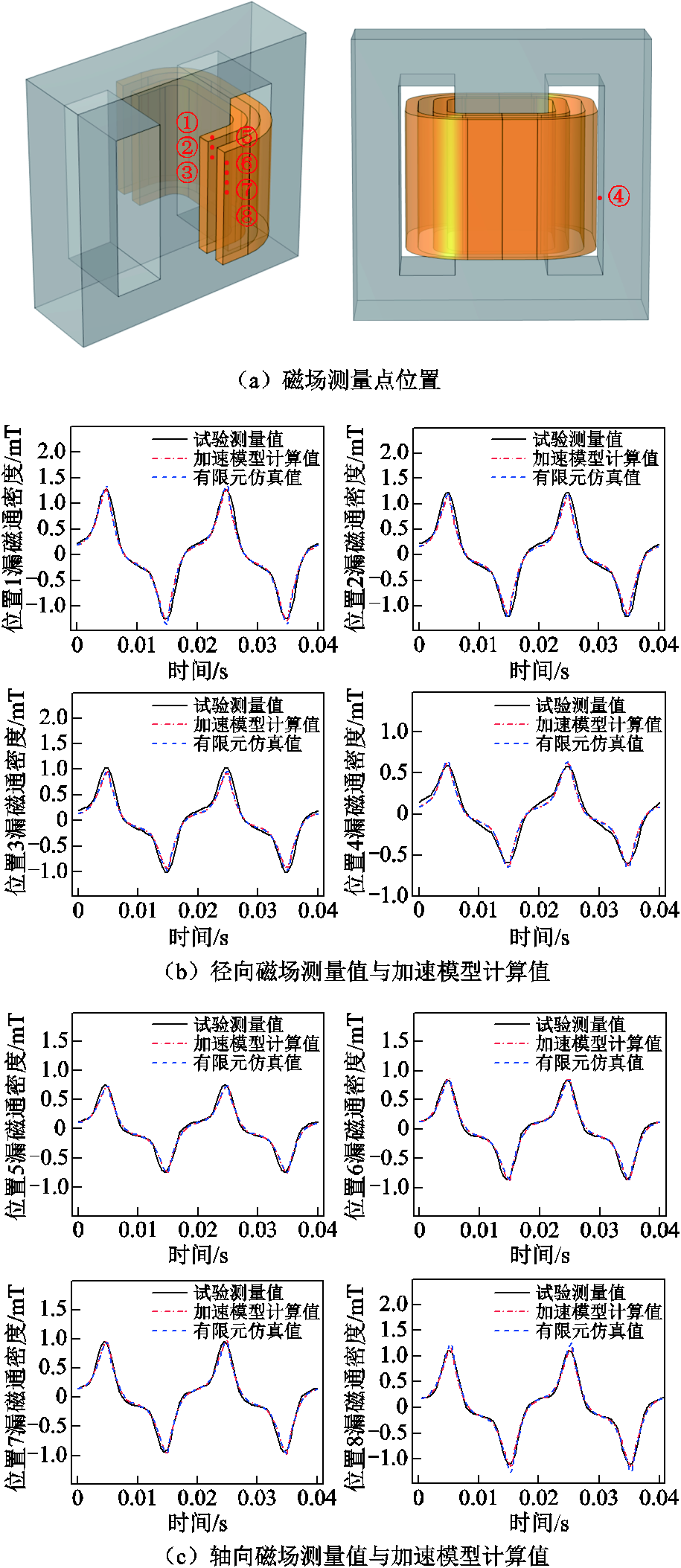
图26 漏磁计算值与试验测量值对比曲线
Fig.26 The comparison curve between the calculated and actual measured value of magnetic flux leakage
本文提出了一种基于有限元仿真和CNN-LSTM的变压器空间动态磁场快速计算模型,该模型首先基于主、漏磁通差异性设计了双输出结构,分别基于CNN多层映射编码,提取电压、电流到空间磁场的映射关系,再利用双向LSTM提取电场与磁场之间时间维度的前后依赖关系,最后进行解码线性映射,输出模型计算的空间主磁通密度和漏磁通密度。通过仿真分析、算法对比与试验验证,得出以下结论:
1)模型设计了基于CNN-LSTM的双分支空间动态磁场快速计算模型,将空间磁场求解任务分为两个子问题,避免了主、漏磁通差异引起的拟合偏差,具有一定的可解释性和准确性。
2)模型的构建基于计及铁心非线性特性的多工况有限元仿真,重点聚焦于学习和映射铁心非线性特性影响磁场分布的行为,从而在数字孪生的框架下实现更高效和准确的磁场分布的快速计算。
3)在不同位置与时间段内,基于模型计算的磁场值与有限元仿真值以及试验测量值均具有较好的一致性,表明加速计算模型的计算性能较好。模型计算单个时步变压器的磁场分布用时在0.04 s左右,相对有限元仿真在时间上大大缩短。与其他算法相比本文的方法也具有一定的优势。
在工程实践中,可以通过传感器实时采集电压和电流时序数据,并将其输入模型中进行预测,以获取对应时刻的磁场分布,从而实现对变压器空间磁场分布的近实时观测,可对变压器运行状态进行连续监测,并估计其运行情况,从而为变压器的辅助故障分析、实时监测保护以及电力装备数字孪生研究提供支撑。
参考文献
[1] Arrano-Vargas F, Konstantinou G. Modular design and real-time simulators toward power system digital twins implementation[J]. IEEE Transactions on Industrial Informatics, 2023, 19(1): 52-61.
[2] 杨帆, 郝翰学, 王鹏博, 等. 电力装备多物理场数值计算发展现状[J]. 高电压技术, 2023, 49(6): 2348-2364. Yang Fan, Hao Hanxue, Wang Pengbo, et al. State of the art of multiphysics simulation technology for power equipment[J]. High Voltage Engineering, 2023, 49(6): 2348-2364.
[3] Moutis P, Alizadeh-Mousavi O. Digital twin of distribution power transformer for real-time monitoring of medium voltage from low voltage measurements[J]. IEEE Transactions on Power Delivery, 2021, 36(4): 1952-1963.
[4] 邓祥力, 朱宏业, 严康, 等. 基于光纤漏磁场测量的变压器磁平衡保护研究[J]. 电工技术学报, 2024, 39(3): 628-642. Deng Xiangli, Zhu Hongye, Yan Kang, et al. Magnetic balance protection of transformers based on optical fiber leakage magnetic field measurement[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 628-642.
[5] 周院超, 王雪. 基于磁场测量的变压器绕组形变在线监测方法[J]. 电测与仪表, 2017, 54(17): 58-63, 87. Zhou Yuanchao, Wang Xue. The on-line monitoring method of transformer winding deformation based on magnetic field measurement[J]. Electrical Measurement & Instrumentation, 2017, 54(17): 58-63, 87.
[6] 张陈擎宇, 周利军, 李沃阳, 等. 考虑边界磁密分级的节能型卷铁芯损耗计算方法[J]. 高电压技术, 2023, 49(9): 3940-3948. Zhang Chenqingyu, Zhou Lijun, Li Woyang, et al. Core loss computation of energy-saving wound core considering divided grades on boundary magnetic flux density[J]. High Voltage Engineering, 2023, 49(9): 3940-3948.
[7] 汲胜昌, 何国阳, 李丽, 等. 不同叠片接缝形式的换流变压器铁心电磁与振动特性分析[J]. 高压电器, 2023, 59(10): 110-119, 128. Ji Shengchang, He Guoyang, Li Li, et al. Analysis of electromagnetic and vibration characteristics of converter transformer core with different lamination joint forms[J]. High Voltage Apparatus, 2023, 59(10): 110-119, 128.
[8] Stulov A, Tikhonov A, Snitko I. Fundamentals of artificial intelligence in power transformers smart design[C]//2020 International Ural Conference on Electrical Power Engineering (UralCon), Chelyabinsk, Russia, 2020: 22-24.
[9] 潘启军, 马伟明, 赵治华, 等. 磁场测量方法的发展及应用[J]. 电工技术学报, 2005, 20(3): 7-13. Pan Qijun, Ma Weiming, Zhao Zhihua, et al. Development and application of measurement method for magnetic field[J]. Transactions of China Electrotechnical Society, 2005, 20(3): 7-13.
[10] 万宝睿. 变压器局部放电油箱接缝处电磁波磁场分量检测方法研究[D]. 北京: 华北电力大学, 2022. Wan Baorui. Research on detecting PD method of magnetic field component at the gap of transformer oil tank[D]. Beijing: North China Electric Power University, 2022.
[11] Taher A, Sudhoff S, Pekarek S. Calculation of a tape-wound transformer leakage inductance using the MEC model[J]. IEEE Transactions on Energy Conversion, 2015, 30(2): 541-549.
[12] 赵玉顺, 戴义贤, 庄加才, 等. 基于热固耦合的中频变压器绝缘材料性能参数优化配合方法[J]. 电工技术学报, 2023, 38(4): 1051-1063. Zhao Yushun, Dai Yixian, Zhuang Jiacai, et al. Optimization of insulation material performance parameters for medium frequency transformers based on thermosolid coupling[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 1051-1063.
[13] 闫晨光, 郝治国, 张保会, 等. 电力变压器油箱形变破裂建模及仿真[J]. 电工技术学报, 2016, 31(3): 180-187. Yan Chenguang, Hao Zhiguo, Zhang Baohui, et al. Modeling and simulation of power transformer tank deformation and rupture[J]. Transactions of China Electrotechnical Society, 2016, 31(3): 180-187.
[14] 北京大数据研究院. 2022科学智能峰会: 发生在当下的科技革命[EB/OL]. [2024-05-06]. http://www. bibdr.org/nd.jsp?id=264.
[15] ANSYS. Ansys Twin Builder[EB/OL]. [2024-05-06]. https://www.ansys.com/zh-cn/products/digital-twin/ ansys-twin-builder.
[16] 张重远, 刘迪程, 高成龙, 等. 基于Twin Builder的110kV油浸式变压器3维磁场降阶模型及损耗分析[J]. 高电压技术, 2024, 50(3): 941-951. Zhang Zhongyuan, Liu Dicheng, Gao Chenglong, et al. Three-dimensional magnetic field model order reduction and loss analysis of 110kV oil-immersed transformer based on twin builder[J]. High Voltage Engineering, 2024, 50(3): 941-951.
[17] COMSOL. COMSOL Multiphysics®6.2发布亮点[EB/OL]. [2024-05-06]. https://cn.comsol.com/ release/ 6.2.
[18] 刘云鹏, 黎晏霖, 李欢, 等. 基于布里渊光时域峰值边沿分析的变压器绕组局部热点检测[J]. 电工技术学报, 2024, 39(11): 3486-3498. Liu Yunpeng, Li Yanlin, Li Huan, et al. Local hot spot detection of transformer windings based on Brillouin optical time domain peak edge analysis[J]. Transactions of China Electrotechnical Society, 2024, 39(11): 3486-3498.
[19] Taheri A A, Abdali A, Rabiee A. A novel model for thermal behavior prediction of oil-immersed distribution transformers with consideration of solar radiation[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1634-1646.
[20] 王山, 高萌, 卓然, 等. 变压器温度耦合仿真模型的高效降阶算法研究[J]. 高压电器, 2023, 59(8): 115-126. Wang Shan, Gao Meng, Zhuo Ran, et al. Research on high efficient order reduction algorithm for temperature coupling simulation model of transformer[J]. High Voltage Apparatus, 2023, 59(8): 115-126.
[21] 刘刚, 郝世缘, 胡万君, 等. 基于子循环自适应串行交错时间匹配算法的油浸式变压器绕组瞬态温升计算[J]. 电工技术学报, 2024, 39(4): 1185-1197. Liu Gang, Hao Shiyuan, Hu Wanjun, et al. Transient temperature rise calculation of oil immersed transformer winding based on sub cyclic adaptive staggered time matching algorithm [J]. Transactions of China Electrotechnical Society, 2024, 39(4): 1185-1197.
[22] 邓祥力, 吴文强, 杨梅, 等. 基于漏磁场和深度信念网络的变压器绕组变形诊断研究[J]. 变压器, 2021, 58(8): 42-48. Deng Xiangli, Wu Wenqiang, Yang Mei, et al. Research on transformer winding deformation diagnosis based on leakage magnetic field and deep belief network[J]. Transformer, 2021, 58(8): 42-48.
[23] 邓祥力, 严康, 朱宏业, 等. 基于变压器绕组电路-漏磁场多状态解析模型的早期故障保护[J]. 电网技术, 2023, 47(9): 3808-3821. Deng Xiangli, Yan Kang, Zhu Hongye, et al. Transformer winding early fault protection based on circuit-magnetic leakage field multi-state analytical model[J]. Power System Technology, 2023, 47(9): 3808-3821.
[24] Khan A, Ghorbanian V, Lowther D. Deep learning for magnetic field estimation[J]. IEEE Transactions on Magnetics, 2019, 55(6): 2899304.
[25] Fotis G, Vita V, Ekonomou L. Machine learning techniques for the prediction of the magnetic and electric field of electrostatic discharges[J]. Electronics, 2022, 11(12): 1858.
[26] 张宇娇, 赵志涛, 徐斌, 等. 基于U-net卷积神经网络的电磁场快速计算方法[J]. 电工技术学报, 2024, 39(9): 2730-2742. Zhang Yujiao, Zhao Zhitao, Xu Bin, et al. Fast calculation method of electromagnetic field based on U-net convolutional neural network[J]. Transactions of China Electrotechnical Society, 2024, 39(9): 2730-2742.
[27] 李平, 胡根铭. 基于数据增强型一维改进卷积神经网络的变压器故障诊断方法[J]. 电网技术, 2023, 47(7): 2957-2967. Li Ping, Hu Genming. Transformer fault diagnosis based on data enhanced one-dimensional improved convolutional neural network[J]. Power System Technology, 2023, 47(7): 2957-2967.
[28] 范志远, 杜江. 基于相关变分模态分解和CNN-LSTM的变压器油中溶解气体体积分数预测[J]. 高电压技术, 2024, 50(1): 263-273. Fan Zhiyuan, Du Jiang. Prediction of dissolved gas volume fraction in transformer oil based on correlation variational mode decomposition and CNN-LSTM[J]. High Voltage Engineering, 2024, 50(1): 263-273.
[29] 郝艳, 咸日常, 胡玉耀, 等. 基于场-路耦合有限元法的干式变压器匝间短路暂态特性研究[J]. 南方电网技术, 2023, 17(6): 90-98. Hao Yan, Xian Richang, Hu Yuyao, et al. Research on transient characteristics of interturn short circuit of drytype transformer based on field-circuit coupled finite element method[J]. Southern Power System Technology, 2023, 17(6): 90-98.
[30] 潘超, 安景革, 刘闯, 等. 变压器偏磁效应噪声特性的多场耦合分析与抑制[J]. 电工技术学报, 2023, 38(18): 5077-5088. Pan Chao, An Jingge, Liu Chuang, et al. Multi-field coupling analysis and suppression for biased magnetic noise in transformer[J]. Transactions of China Electrotechnical Society, 2023, 38(18): 5077-5088.
Abstract The magnetic field is one of the key physical fields that reflects the operating state of the transformer. Quickly obtaining the dynamic distribution of the spatial magnetic field of the transformer is one of the foundations for constructing the digital twin of the transformer. The main acquisition methods of transformer magnetic field can be divided into sensor measurement, finite element simulation and algorithm inversion. The installation position of the magnetic field sensors are not flexible, and can only obtain the magnetic field at the measurement points; the finite element simulation can calculate the magnetic field at any positions, but it takes a long time and cannot meet the requirement of digital twin second-level simulation. The deep learning algorithm and structure must be selected and designed according to the characteristics of training data. The existing fast calculation methods are difficult to accurately obtain the magnetic field distribution under core saturation conditions.
Based on the nonlinear characteristics of the transformer core and the differential distribution of the main and leakage magnetic flux, this paper proposed a magnetic field accelerated calculation method considering the nonlinearity of the core. Firstly, the field-circuit coupling simulation model of three-phase transformer was constructed, and the key variables were parametrically scanned. A large number of magnetic field data under different nonlinear working conditions were obtained by simulation, and the main flux and leakage flux data sets related to the nonlinear working conditions of the core were constructed. Secondly, a two-branch deep learning model combining convolutional neural network and long short-term memory network was proposed to train and extract the spatial and temporal characteristics of magnetic field data, and solved the model training problem caused by the obvious difference between the main and leakage magnetic flux. Finally, the nonlinear mapping relationship between the input voltage, current and the internal space magnetic field distribution was obtained by using the model, and the accelerated calculation of the spatial dynamic magnetic field was realized, which provided a fast method for obtaining magnetic field data for the construction of transformer digital twin.
Considering three typical nonlinear working conditions of power frequency overvoltage, DC bias and inrush current, the magnetic field acceleration calculation model of three-phase transformer and test transformer was trained. It takes about 0.04s to calculate the magnetic field distribution of a single time step, which is greatly shortened compared with the finite element simulation. The results showed that for the three-phase transformer, comparing the calculated values of the magnetic field acceleration calculation model with the finite element simulation, the average absolute errors of the main magnetic flux and the leakage magnetic flux are 0.04 T and 0.9mT, respectively, and the relative error is less than 5%. For the single-phase test transformer, the root mean square error of the radial and axial leakage flux are about 0.1 mT and 0.05 mT, respectively, and the ratio to the peak is within 10%. Therefore, the magnetic field acceleration calculation model proposed can quickly and accurately calculates the spatial magnetic field distribution of the transformer, and provides a method for quickly obtaining magnetic field data for the construction of transformer digital twins.
keywords:Nonlinear, convolutional neural network, long short-term memory network, magnetic field, acceleration calculation
DOI: 10.19595/j.cnki.1000-6753.tces.240281
中图分类号:TM41
国家自然科学基金资助项目(51977018)。
收稿日期 2024-02-20
改稿日期 2024-04-10
司马文霞 女,1965年生,教授,博士生导师,教育部“长江学者”特聘教授,研究方向为电磁暂态感知、建模、分析与防护,电网雷电致灾机理与接地防护技术,电力装备绝缘失效机制与防御技术。E-mail:cqsmwx@cqu.edu.cn
杨 鸣 男,1987年生,教授,博士生导师,研究方向为交直流电网电磁暂态特性分析与防护,变压器类装备电磁暂态建模与应用,新型直流装备电磁暂态建模与应用。E-mail:cqucee@cqu.edu.cn(通信作者)
(编辑 李 冰)