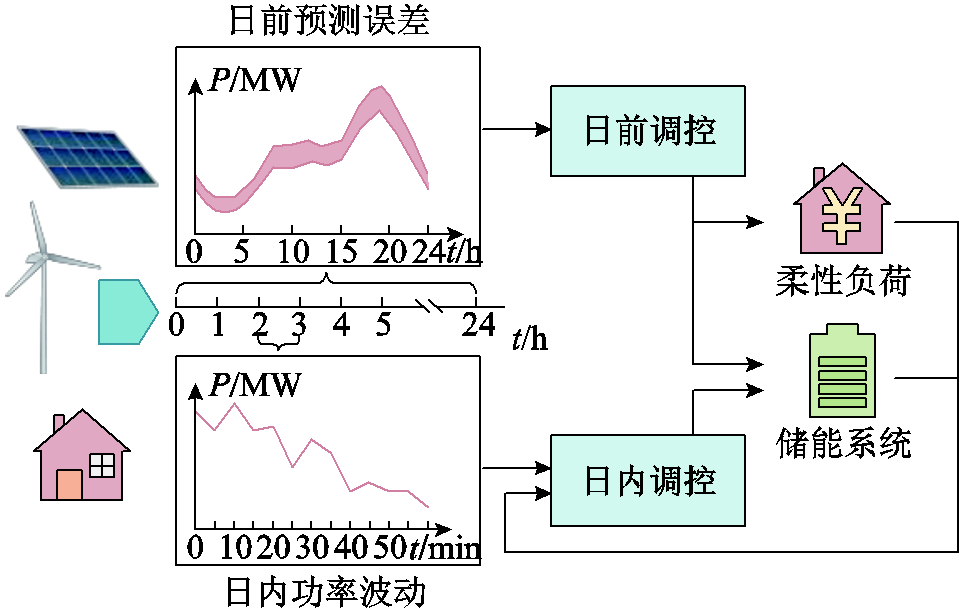
图1 多时间尺度优化调控策略框架
Fig.1 The multi-timescale optimal scheduling frame work
摘要 构建以新能源为主体的新型电力系统是实现“双碳”目标的重要举措,配电网源荷储协同是促进高比例风光能源消纳的有力措施。基于数据驱动的人工智能方法具有无模型、自适应等特点,可以自主学习风光能源及负荷的复杂不确定性,对有源配电网优化调控具有良好的支撑作用。该文考虑源荷功率预测精度特点和设备运行调控特性,提出基于深度强化学习算法的有源配电网多时间尺度智能优化调控方法。其中,日前阶段制定储能系统和柔性负荷的调控计划,以实现配电网的经济运行,减小对上级电网造成的调峰压力,并针对多节点多时段状态空间设计相应的特征提取方法;日内阶段将优化调度问题转换为马尔科夫决策过程,设计表征联络线功率波动平抑和灵活性资源日前计划跟踪效果的奖励函数,实现了对全调控时段内的功率波动平抑及跟踪日前计划效果的统筹优化。最后通过修改后的IEEE 33算例系统验证了所提方法的有效性与优越性。
关键词:有源配电网 优化调控 源荷储协同 深度强化学习
构建以新能源为主体的新型电力系统是实现“双碳”目标的必由之路,而促进以风能、太阳能为代表的可再生能源并网消纳将成为完成这一目标的关键[1]。推动有源配电网等新形态电网建设可满足新能源分布式发电和新型交互式用能设备的大量接入,对新能源的开发利用起到了支撑作用[2]。但风、光等新能源发电出力具有波动性、随机性和不可控性,其装机容量的增加将提高配电网的不确定性和调控难度,配电网的安全经济运行正面临严峻挑战。合理地利用储能系统[3]、柔性负荷[4]等灵活性资源对能量进行跨时调度和波动平抑,可促进新能源消纳,减小其对上级电网造成的调峰压力,已成为国内外关注的热点[5-6]。在此背景下,有源配电网源荷储协同优化对解决上述问题具有重要价值。
为提高配电网运行的经济性和安全性,在配电网优化调控时需考虑风、光能源的复杂不确定性[7]。对于不确定性优化问题,常用的方法有模糊优化[8]、随机优化[9]、区间优化[10]、鲁棒优化[11]等。其中,模糊优化使用模糊隶属度函数假定随机变量分布,易受主观因素的影响[12];随机优化通常假设随机变量服从某一概率分布模型,其依赖于参数假设,往往难以准确地描述不确定量的实际分布[13];区间优化使用区间变量代替点变量,适用于波动范围较小的情况[14];鲁棒优化只需不确定量的变化范围,其通常针对不确定集中的最坏情况进行优化,给出的调度结果一般偏保守[14]。
在实际运行时,由于源荷预测精度随着时间尺度的减小而不断提高,并且考虑到电网不同时间尺度的调控需求和设备响应特性的差异[15],许多学者采用多时间尺度的调控框架以降低预测误差对调控效果的影响[16-18]。文献[19]和文献[20]分别采用线性优化和近似动态规划实现了多时间尺度调度,但仅以波动功率平抑或经济运行作为单目标,对多目标协同的考虑不够充分;文献[21]在日内采用随机模型预测控制的方法实现了对功率波动平抑和运营成本的综合优化,但其整体优化效果受预测窗大小限制,且较为依赖预测信息。此外,日内阶段对部分快速响应设备进行再调控易使其运行状态大幅偏离日前计划,进而会对其调控能力及全时段调控效果造成影响。因此,需要对提高全时段调控效果的优化方法进行进一步研究。
上述文献大多采用传统方法,其求解速度和精度受限于问题规模、变量维数以及物理模型的准确程度,难以应对配电网中设备种类日益增长、运行特性复杂多样和系统参数不明确等挑战。而基于数据驱动的人工智能方法具有无模型和自适应等特点,其不依赖精确的物理建模,在求解高维非线性问题时具有一定优势,为上述问题的解决提供了一种有效途径[22-25]。
人工智能技术可有效地支撑源网荷储的协同运行[26],而深度强化学习将具有感知能力的深度学习和具有决策能力的强化学习相结合,已经在仿真分析[27]、智能调度[28]、无功优化[29]等方面得到了较多应用,其在电力系统中的作用已得到充分体现。文献[30]阐述了深度强化学习相较于传统方法的优势,其可以处理更大量的数据,且具有实时性和较好的鲁棒性;文献[31]在不假设数据集中不确定性分布的情况下,在优化过程中通过深度强化学习方法捕获和利用历史及当前数据中包含的多个不确定性;文献[32]针对不同响应速度的设备建立了两时间尺度控制策略,并在长时间尺度上通过深度强化学习算法提高其在整体调控时段内的调控效果。现有研究大多将深度强化学习方法用于实时或滚动优化,往往采用单时段或一定前瞻时段内的变量作为状态空间,而日前调度状态空间具有多节点、多时段的特点,若不对高维变量造成的信息冗余问题进行处理,将会对优化效果造成一定影响。
鉴于此,为实现配电网中灵活性资源的合理利用,在统筹考虑源荷不确定性和各可调控设备运行特性的基础上,本文提出了一种基于深度强化学习的有源配电网多时间尺度多目标协同优化调控策略。与已有的研究工作相比,本文的创新和贡献如下:
1)建立有源配电网多时间尺度智能优化调控模型,通过数据驱动的深度强化学习方法自主学习源荷不确定性,在保证配电网经济稳定运行的同时实现对风、光等间歇性不可控分布式电源的消纳。
2)考虑有源配电网多时段状态空间中存在的信息冗余,根据其时空耦合特性构造状态矩阵,并重新设计特征提取方法,可有效地提高深度强化学习方法的优化效果和收敛性。
3)分析源荷不确定性影响配电网运行的不同表现形式,将优化调控问题转换为马尔科夫决策过程(Markov Decision Process, MDP),利用深度强化学习方法实现对全时段内的功率波动平抑及日前计划跟踪效果的优化。
配电网中因风/光等不可控电源而产生的源荷不匹配问题将加重上级电网的调峰压力,其出力的不确定性也将影响配电网的稳定经济运行。因此,需要在考虑源荷不确定性的情况下,通过综合调控储能系统、柔性负荷等灵活性资源提高对新能源的消纳能力。配电网中常采用电化学等储能设备,其具有较短的响应时间,可对功率波动进行实时平抑。此外,为维持储能系统的可持续运行,一般需要保证其在一个调控周期内的能量守恒。对于柔性负荷,本文考虑其日前市场机制[33],在日前阶段给出其调控计划。
风、光能源及负荷的不确定性对配电网日内运行造成的影响主要体现为两种形式:①风、光能源及负荷受环境等因素影响,其功率本身随时间不断波动,不同设备所产生的同向波动通过配电网进行传递,并叠加至配电网与上级电网的联络线上,将对配电网本身以及上级电力系统的稳定运行造成影响;②若利用储能等可调控设备对一段时间内功率波动的累计偏差进行平抑,其实际运行状态将与日前计划产生偏差,会对其未来的调控能力造成影响。本文在日内阶段主要考虑对联络线功率波动和储能系统荷电状态(State of Charge, SOC)与日前计划的偏差进行优化。
因此,本文采用多时间尺度协调优化调控的方法,在日前以1 h为时间尺度,考虑源荷不确定性,以配电网日运行成本最低、配电网与上级电网联络线功率最平滑为目标,制定柔性负荷和储能系统的调控计划,且具有一定的鲁棒性;在日内以5 min为时间尺度,根据源荷的高精度预测,在日前计划的基础上对储能系统充放电功率进行调整,在跟踪日前调控计划的同时,减小配电网与上级电网联络线上因负荷及风、光发电的随机性导致的实时功率波动。本文所提多时间尺度优化调控策略框架如图1所示。

图1 多时间尺度优化调控策略框架
Fig.1 The multi-timescale optimal scheduling frame work
如果一个系统在下一时刻的状态只与当前时刻的状态相关,则这个系统可称为马尔科夫过程(Markov Process, MP)。强化学习的基本思想是最大化智能体从环境中获得的回报以学习最优策略,可用马尔科夫决策过程(MDP)对强化学习问题进行建模。MDP通常由状态空间S、动作空间A、奖赏函数ρ、状态转移函数f等组成[34],其中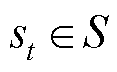 表示智能体在t时刻所处的状态,
表示智能体在t时刻所处的状态,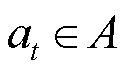 表示智能体在t时刻做出的动作,
表示智能体在t时刻做出的动作,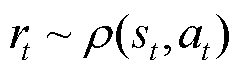 表示智能体在状态
表示智能体在状态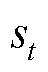 下执行动作
下执行动作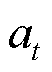 获得的奖励值。
获得的奖励值。
深度确定性策略梯度(Deep Deterministic Policy Gradient, DDPG)是一种基于演员-评论家(Actor-Critic)方法的深度强化学习算法,其吸收了深度Q网络(Deep Q-Network, DQN)和确定策略梯度(Deterministic Policy Gradient, DPG)算法的优点,对连续控制任务可获得良好的决策效果。DDPG主要由策略网络、价值网络、经验回放池等部分组成,其中,策略网络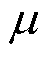 根据状态生成动作,价值网络Q则根据状态和动作输出一个反映动作好坏的实数。策略网络与价值网络又分为当前网络与目标网络,将当前策略网络、目标策略网络、当前价值网络和目标价值网络分别表示为
根据状态生成动作,价值网络Q则根据状态和动作输出一个反映动作好坏的实数。策略网络与价值网络又分为当前网络与目标网络,将当前策略网络、目标策略网络、当前价值网络和目标价值网络分别表示为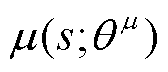 、
、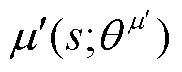 、
、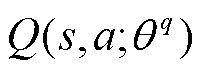 和
和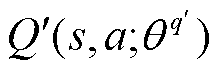 ,其网络参数分别为
,其网络参数分别为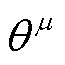 、
、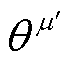 、
、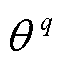 和
和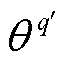 ,目标网络的结构和初始参数与当前网络相同。在生成样本数据时,DDPG将从环境中探索得到的数据以一个状态转换序列
,目标网络的结构和初始参数与当前网络相同。在生成样本数据时,DDPG将从环境中探索得到的数据以一个状态转换序列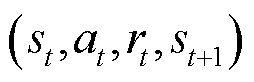 为单元存放在记忆库中。当记忆库充满数据时,则对最旧的样本数据进行替换,以保证记忆库中存放序列的及时更新。
为单元存放在记忆库中。当记忆库充满数据时,则对最旧的样本数据进行替换,以保证记忆库中存放序列的及时更新。
训练时,从经验回放池中抽取m条样本,将价值网络的时间差分误差(Temporal Difference error, TD error)作为其损失函数,表示为
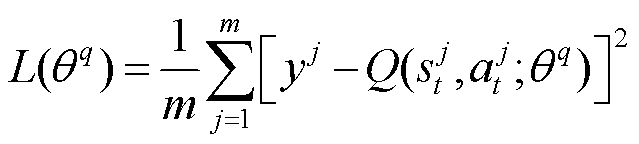 (1)
(1)
其中
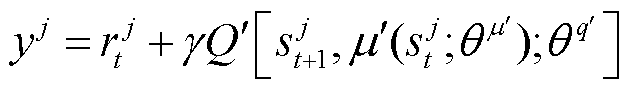 (2)
(2)
式中,m为批训练样本条数;j为样本序号;y为时间差分目标(TD target);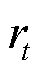 为当前奖励值;
为当前奖励值;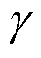 为折扣因子;
为折扣因子;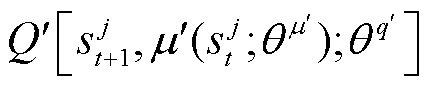 为目标价值网络对下一时刻状态
为目标价值网络对下一时刻状态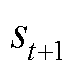 和目标策略网络对当前状态输出动作
和目标策略网络对当前状态输出动作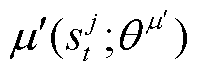 的打分;
的打分;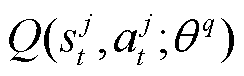 为当前价值网络对当前状态
为当前价值网络对当前状态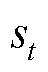 和当前动作
和当前动作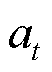 的打分。
的打分。
为使得面对任意状态S时,策略网络都能做出良好的动作,令策略网络的目标函数为价值网络打分的期望,表示为
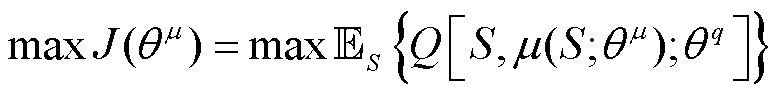 (3)
(3)
式中,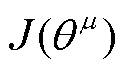 为当前策略网络的目标函数;
为当前策略网络的目标函数;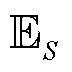 {·}为状态空间S内当前价值网络对当前策略网络做出动作的打分期望。
{·}为状态空间S内当前价值网络对当前策略网络做出动作的打分期望。
以批训练的方式对价值网络打分期望进行近似,即将批训练使用的m条样本对应的价值网络打分作为策略网络优化目标值的近似,并遵循确定性策略,通过梯度下降法对策略网络的参数进行更新。
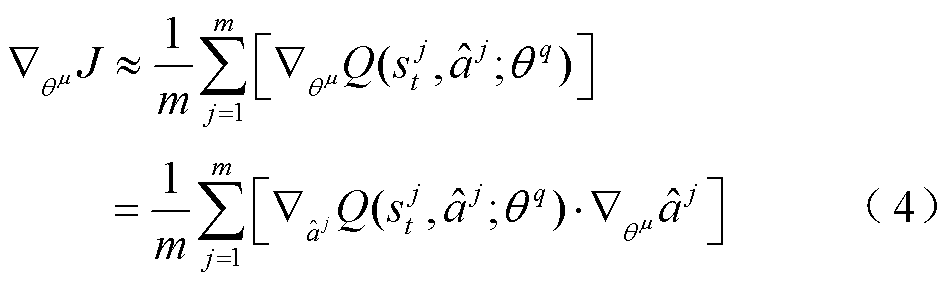
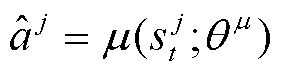 (5)
(5)
式中,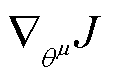 为策略网络目标函数对策略网络参数的梯度,将m条批训练样本对策略网络参数的梯度作为其近似;
为策略网络目标函数对策略网络参数的梯度,将m条批训练样本对策略网络参数的梯度作为其近似;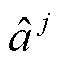 即
即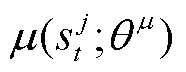 ,为当前策略网络对当前状态输出的动作。
,为当前策略网络对当前状态输出的动作。
最后,采用滑动平均的方式,按照一定的比例使用当前网络的参数对目标网络进行更新。
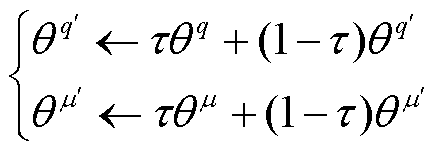 (6)
(6)
式中,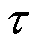 为软更新系数。
为软更新系数。
在日前和日内阶段,均采用DDPG算法对智能体进行训练,以得到合理的有源配电网优化调控策略。根据选择的状态空间选取部分配电网运行信息作为智能体的状态输入,将智能体动作输出映射为调控指令,并根据奖励函数计算奖励值,采用DDPG算法对日前和日内智能体进行训练,以得到合理的有源配电网优化调控策略。其中,日前智能体所需的配电网运行信息包括每一调控时段内每一节点的净负荷预测功率,其变量维数由配电网节点数量和日前调控时段数共同决定;日内智能体所需的运行信息包括当前调控时段、各节点的短期预测功率与其日前预测功率的差值,以及储能实际荷电状态与参考荷电状态的差值。智能体可根据历史数据和在线运行数据进行离线训练,其总体框架如图2所示。
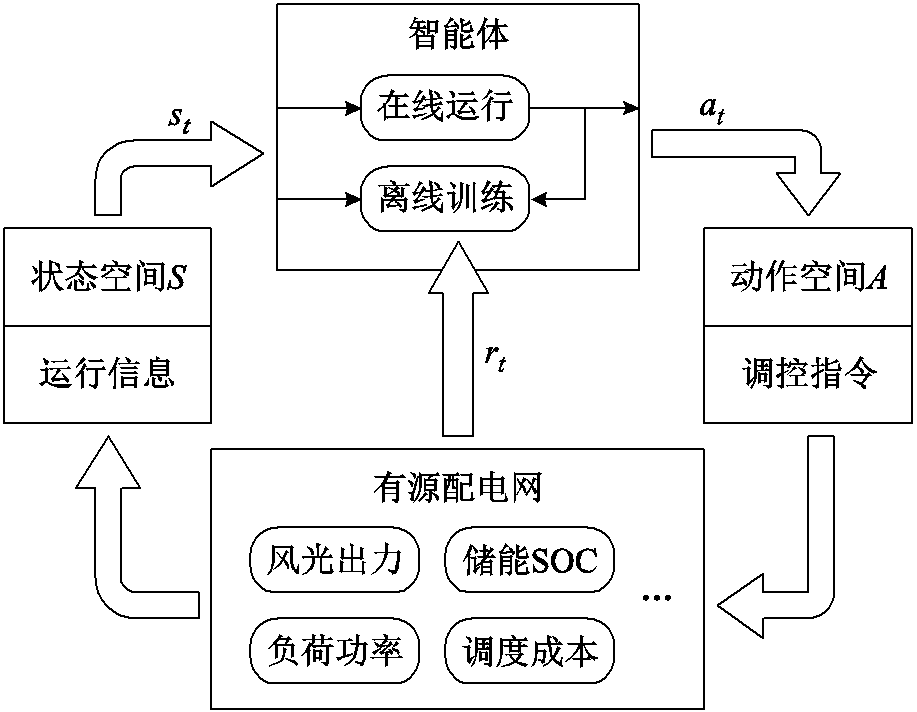
图2 智能优化调控框架
Fig.2 Intelligent optimization scheduling frame work
随着风、光发电容量的不断增长,电力系统负荷曲线发生了较大变化,且风力发电呈现逆调峰特性,加剧了电网运行调度的难度。在配电网接入大量分布式风、光电源后,可能会发生功率倒送的现象,危害上级电网的安全运行。储能系统可以在低负荷时吸收电能,在高负荷时释放电能,起到“削峰填谷”的作用,但运行时其使用寿命会消耗,具有一定的运行成本。
为保证配电网的经济运行,同时降低配电网中风、光发电对上级电网造成的调峰压力,本文日前调控以配电网日运行成本最低、联络线功率最平滑为优化目标。
2.1.1 配电网日运行成本最低
以对风、光发电的全部消纳为前提,配电网的日运行成本为
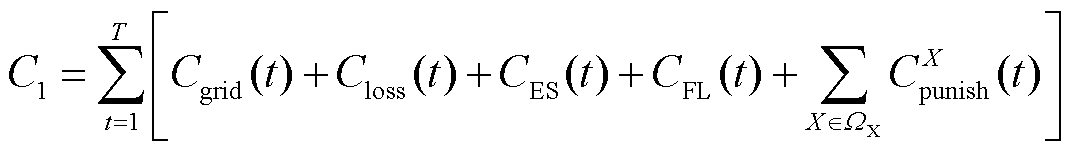 (7)
(7)
式中,T为调控周期内调控时段数;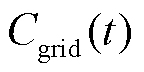 、
、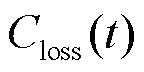 、
、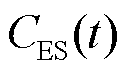 、
、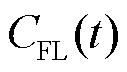 和
和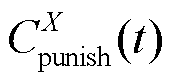 分别为t时刻配电网购售电成本、配电网有功损耗成本、储能系统调控成本[35]、柔性负荷调控成本[36]和体现约束条件X的惩罚成本;
分别为t时刻配电网购售电成本、配电网有功损耗成本、储能系统调控成本[35]、柔性负荷调控成本[36]和体现约束条件X的惩罚成本;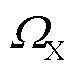 为约束条件集合,包括储能荷电状态约束、线路功率约束等约束条件。式(7)中各成本变量的具体计算式为
为约束条件集合,包括储能荷电状态约束、线路功率约束等约束条件。式(7)中各成本变量的具体计算式为
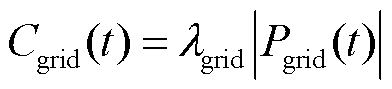 (8)
(8)
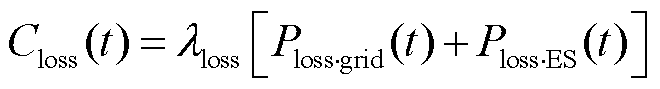 (9)
(9)
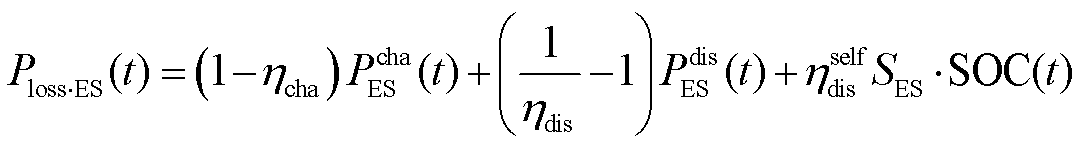 (10)
(10)
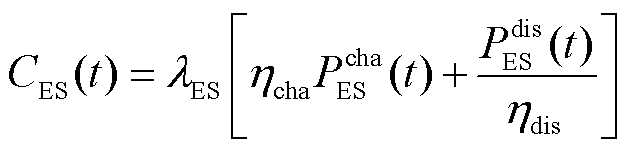 (11)
(11)
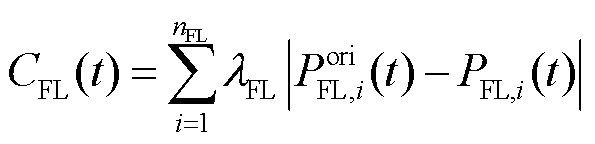 (12)
(12)
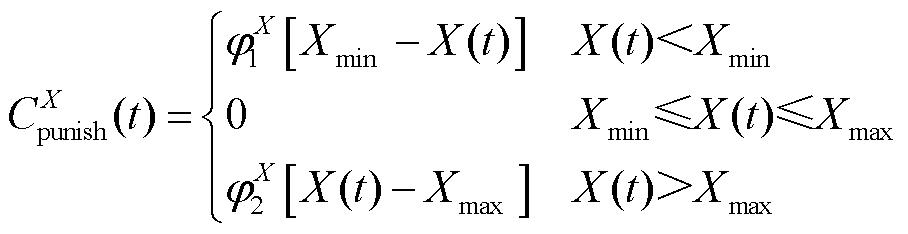 (13)
(13)
式中,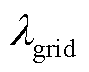 、
、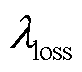 、
、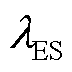 和
和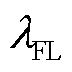 分别为单位电价、损耗成本系数、储能调控成本系数和柔性负荷调控成本系数;
分别为单位电价、损耗成本系数、储能调控成本系数和柔性负荷调控成本系数;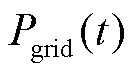 、
、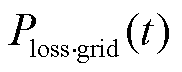 、
、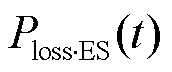 、
、 、
、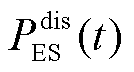 、
、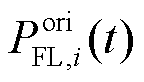 和
和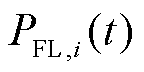 分别为t时刻的配电网与上级电网交换功率、配电网有功网损、储能有功损耗、储能充电功率、储能放电功率、第i类柔性负荷原始功率和第i类柔性负荷调控后功率;
分别为t时刻的配电网与上级电网交换功率、配电网有功网损、储能有功损耗、储能充电功率、储能放电功率、第i类柔性负荷原始功率和第i类柔性负荷调控后功率;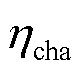 、
、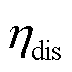 和
和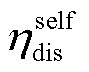 分别为储能系统的充电效率、放电效率和自放电率;
分别为储能系统的充电效率、放电效率和自放电率; 为储能系统总容量;SOC(t)为储能系统在t时刻的荷电状态;
为储能系统总容量;SOC(t)为储能系统在t时刻的荷电状态;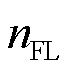 为柔性负荷总数;
为柔性负荷总数;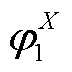 和
和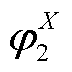 为约束条件X的惩罚系数,通常取较大值;
为约束条件X的惩罚系数,通常取较大值;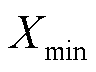 和
和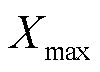 分别为约束条件X的下限和上限。
分别为约束条件X的下限和上限。
2.1.2 联络线功率最平滑
可用功率均方差表征联络线功率的平滑程度[8],其计算公式为
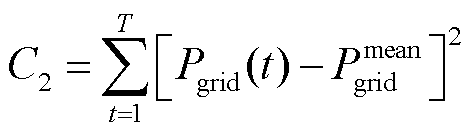 (14)
(14)
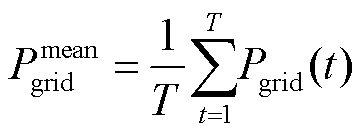 (15)
(15)
式中,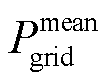 为调控周期内联络线功率的平均值。
为调控周期内联络线功率的平均值。
上述两个目标函数相互影响,且量纲不同,对其分别进行归一化后采用线性加权和作为最终的目标函数,具体计算式为
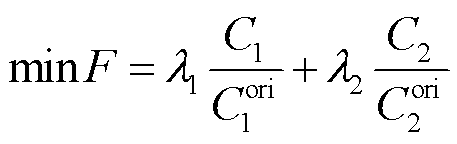 (16)
(16)
式中,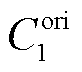 和
和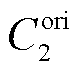 分别为调控前的日运行成本和联络线功率均方差;
分别为调控前的日运行成本和联络线功率均方差;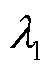 和
和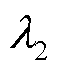 分别为两个目标函数的权重系数,其和为1。
分别为两个目标函数的权重系数,其和为1。
除传统潮流方程约束、电量平衡约束、线路功率约束、节点电压约束等约束条件外,在调控周期内,配电网运行还需要满足储能系统及柔性负荷的有关约束条件。
2.2.1 储能系统
在任意时刻,储能只能处于充电或放电状态,且充放电功率有最大值,约束条件表示为
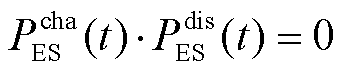 (17)
(17)
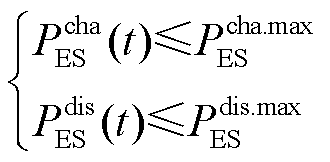 (18)
(18)
式中,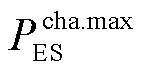 和
和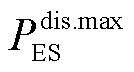 分别为储能系统允许的最大充电和放电功率。
分别为储能系统允许的最大充电和放电功率。
为保护储能使用寿命,防止过充过放,储能系统需考虑自身荷电状态约束,表示为
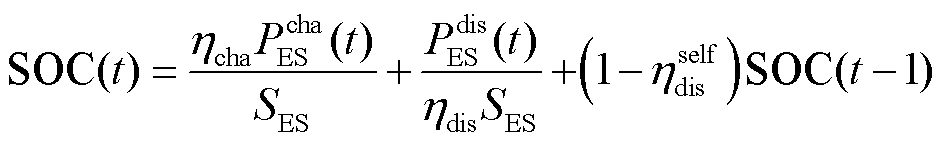 (19)
(19)
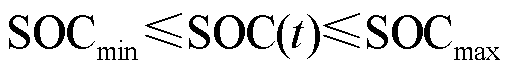 (20)
(20)
式中, 和
和 分别为储能系统荷电状态的下限和上限。
分别为储能系统荷电状态的下限和上限。
将对储能系统荷电状态的约束转换为罚函数的形式作为其惩罚成本[28],具体计算式如式(13)所示。
为维持储能系统的持续运行,需保证其在一个调控周期内的能量守恒,即在一个调控周期内初、末SOC相等,表示为
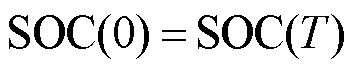 (21)
(21)
式中,SOC(0)和SOC(T)分别为储能系统在调控周期初、末的荷电状态。
2.2.2 柔性负荷
用户侧具有多种形式的柔性负荷[37],其中可中断负荷可以作为一种虚拟电源,其调控策略可与分布式电源同等考虑[38];而可平移负荷可以视作一种特殊的可转移负荷,故本文以可转移负荷为例,探寻配电网中柔性负荷的调控模式,其约束条件为调控周期内负荷总量保持不变,即
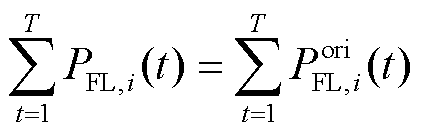 (22)
(22)
此外,在每个调控时段内可转移负荷的调节能力受到一定限制,即可转移负荷的功率存在上下限。
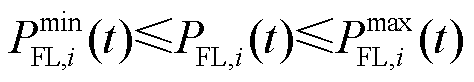 (23)
(23)
式中,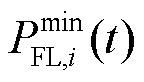 和
和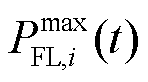 分别为t时刻第i类柔性负荷的功率下限和上限。
分别为t时刻第i类柔性负荷的功率下限和上限。
上述包含不确定性源荷功率的优化模型是一个不确定优化模型,其求解过程通常需要将不确定量确定化,如采用分布函数等方式描述不确定量的分布情况,并利用其可信度区间或鲁棒边界进行优化求解,或使用场景生成和削减方法生成典型场景并进行优化求解,但这些确定化方法可能会导致对源荷不确定性的描述不够准确。而基于数据驱动的深度强化学习方法无需对源荷不确定量的分布进行假设,数据集中的源荷不确定性将在训练过程中体现,并通过强化学习过程被智能体捕捉。因此,将有源配电网不确定性优化调控问题转换为深度强化学习任务进行求解具有一定优势。
在日前阶段,智能体的每一回合只有一次交互,即智能体根据状态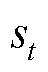 做出动作
做出动作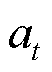 并获得奖赏
并获得奖赏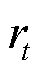 ,因此,价值网络的损失函数从时间差分误差退化为预测误差,即式(1)变为
,因此,价值网络的损失函数从时间差分误差退化为预测误差,即式(1)变为
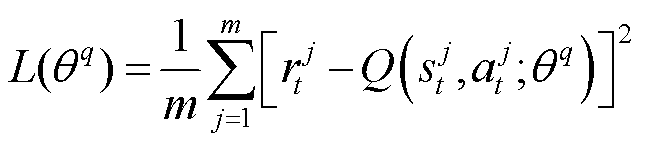 (24)
(24)
日前调控所用的深度强化学习任务相关设定如下。
1)状态空间
日前调控的目标与配电网的运行状态信息在时间和空间上均具有相关性。一方面,由于配电网中存在参数缺失或不准确的情况,需要从配电网运行状态中提取如网损等优化目标的信息;另一方面,日前调控模型是对配电网在整个调控周期内的各项目标进行优化,需要综合配电网在各个时段内的状态信息。因此,本文日前调控所用DDPG的状态空间为
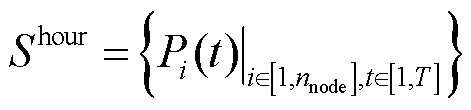 (25)
(25)
式中,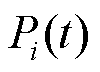 为
为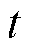 时刻第
时刻第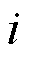 个节点的净负荷功率;
个节点的净负荷功率;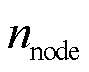 为配电网中节点数。
为配电网中节点数。
2)动作空间
日前调控的控制对象为储能系统及柔性负荷,故其动作空间为
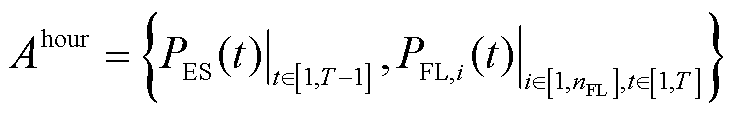 (26)
(26)
3)奖励函数
DDPG中的策略网络会学习如何最大化奖励,因此,为最小化目标函数,将奖励值设置为负的目标函数,即
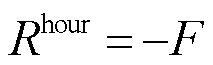 (27)
(27)
4)网络结构
考虑到状态空间中存在多时段多节点数据,其变量维数较高,且存在一定程度的信息冗余,因此需要通过特征提取网络对其进行特征提取。深度学习中常用的特征提取网络有全连接网络和卷积神经网络。其中,全连接网络将相邻两层隐藏层中的所有神经元全部连接,通过训练使智能体学习输入与输出之间的非线性映射关系;卷积神经网络类似于生物视觉神经结构,常用于识别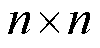 方形范围内的特征信息。上述两种特征提取网络的效果已在许多领域中得到了验证,但其特征提取方式并未考虑配电网多时段状态空间中变量的时空关系。
方形范围内的特征信息。上述两种特征提取网络的效果已在许多领域中得到了验证,但其特征提取方式并未考虑配电网多时段状态空间中变量的时空关系。
考虑状态空间中各状态信息的时空耦合特性,将其中各变量以行为节点序号、列为时间的方式进行排列,转换为 维的状态矩阵形式。由于如网损等受配电网参数不明确影响的优化目标只与当前时间截面的配电网状态有关,因此采用
维的状态矩阵形式。由于如网损等受配电网参数不明确影响的优化目标只与当前时间截面的配电网状态有关,因此采用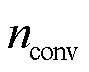 个
个 的一维卷积网络对每一时间截面上节点状态信息的空间特征进行提取,并保留所提取空间特征的时序关系,得到
的一维卷积网络对每一时间截面上节点状态信息的空间特征进行提取,并保留所提取空间特征的时序关系,得到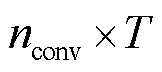 维的空间特征时序矩阵。将提取到的空间特征时序矩阵展平后送入全连接网络,通过训练使智能体学习其时间关系,最终生成相应控制动作。在策略网络及价值网络中均采用上述对状态空间的处理方法,得到日前调控DDPG网络结构如图3所示。
维的空间特征时序矩阵。将提取到的空间特征时序矩阵展平后送入全连接网络,通过训练使智能体学习其时间关系,最终生成相应控制动作。在策略网络及价值网络中均采用上述对状态空间的处理方法,得到日前调控DDPG网络结构如图3所示。
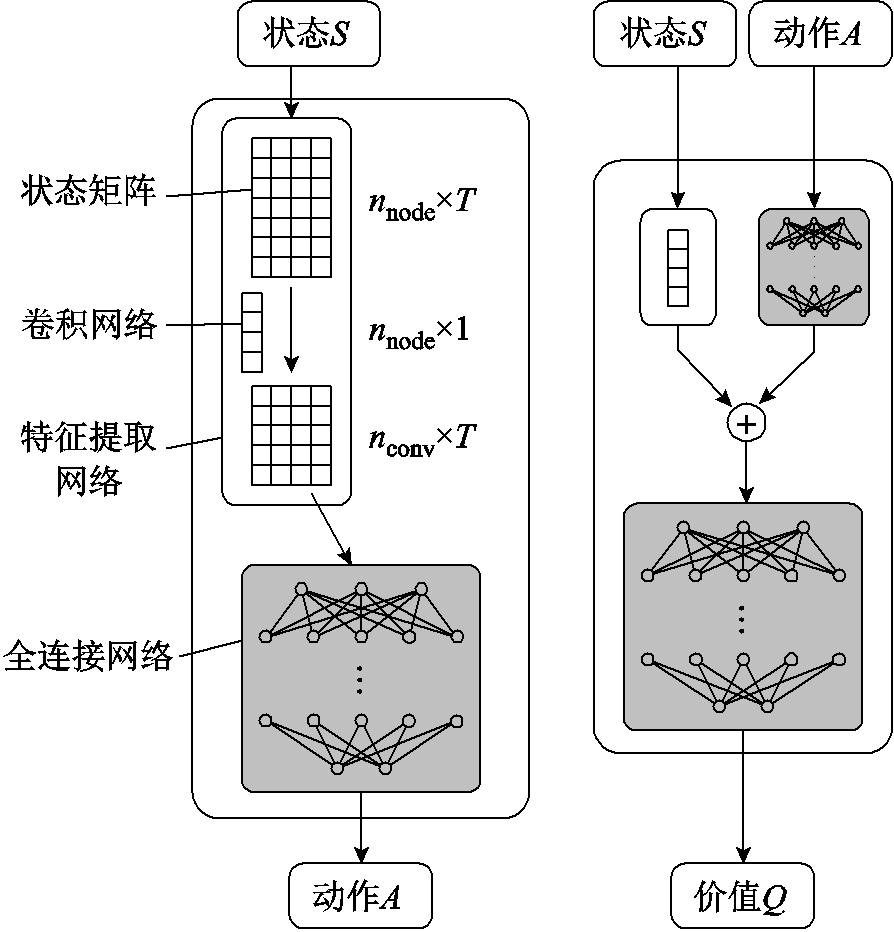
图3 采用改进特征提取网络的日前调控DDPG网络结构
Fig.3 Structure of DDPG network with improved feature extraction network in day-ahead stage
为弥补日前调控模型中各预测量精度不足的问题,及时平抑因风、光能源及负荷产生的联络线功率波动,在日内根据超短期预测进行实时优化。日内功率波动示意图如图4所示。源荷波动具有一定的随机性,其日内实际功率并不均匀分布于日前预测值的两侧。若以联络线功率跟踪日前计划值为目标进行全额平抑[21],这种源荷波动导致的联络线功率整体偏移将会使储能系统实际运行状态大幅偏离日前计划值,进而影响综合调控的经济性和鲁棒性,甚至违背相关约束条件。
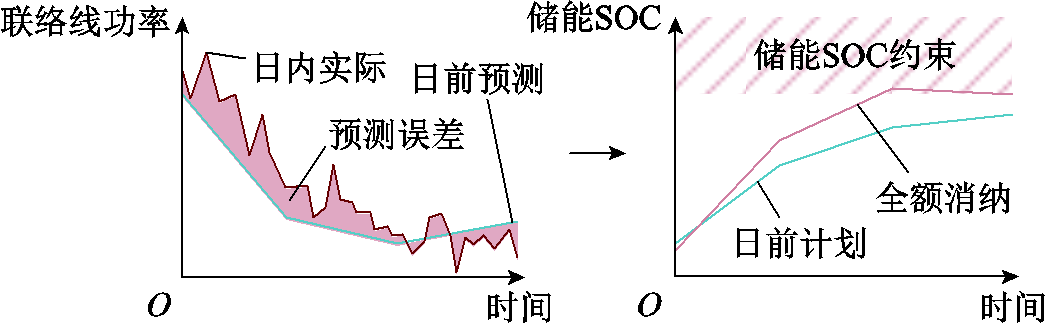
图4 日内功率波动示意图
Fig.4 Schematic diagram of intraday power fluctuation
通过设计合理反映联络线功率偏离和储能SOC偏离的奖励函数,可训练智能体以得到综合评价上述两者在全调控时段内偏离情况的价值网络,以及使得累计偏离最小的动作网络,从而实现日内调控的目标。
在每一个时刻,智能体根据超短期预测计算联络线功率偏差值及储能荷电状态偏离量,并依此确定储能系统出力的修正量,这一过程为经典的强化学习模型,其相关设定如下。
1)状态空间
在日内调控中,智能体需在跟踪日前计划的同时,平抑源荷产生的不确定性功率波动,因此,本文日内调控所用DDPG的状态空间为
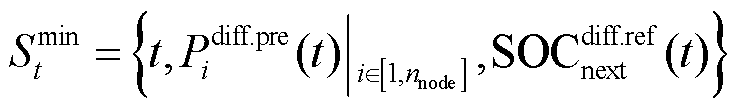 (28)
(28)
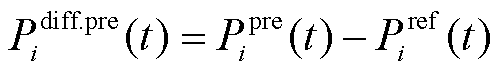 (29)
(29)
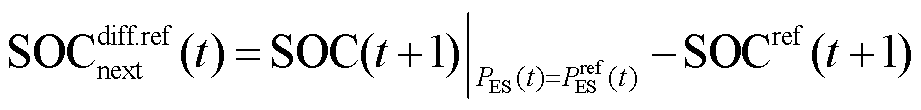 (30)
(30)
式中,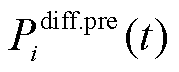 为t时刻第i个节点短期预测功率
为t时刻第i个节点短期预测功率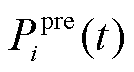 与日前预测功率
与日前预测功率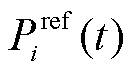 的差值;
的差值;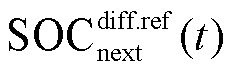 为t时刻储能按照日前计划出力时,其在t +1时刻的SOC偏差量;
为t时刻储能按照日前计划出力时,其在t +1时刻的SOC偏差量;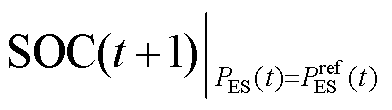 为储能在t时刻SOC的基础上按照日前计划出力后在t+1时刻的SOC;
为储能在t时刻SOC的基础上按照日前计划出力后在t+1时刻的SOC;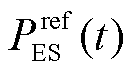 为t时刻储能的日前计划出力;
为t时刻储能的日前计划出力;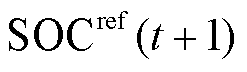 为储能在t +1时刻的SOC日前计划值。
为储能在t +1时刻的SOC日前计划值。
2)动作空间
智能体在日前计划值的基础上对储能功率进行修正,其动作空间为
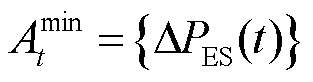 (31)
(31)
式中,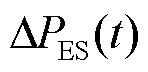 为对储能功率的修正量。
为对储能功率的修正量。
3)奖励函数
为降低联络线功率波动、减小储能系统荷电状态与日前计划的偏差,实现日内调控目标,需设计能够合理评价智能体动作合理性的奖励函数,其主要由跟踪日前计划和平抑功率波动两部分组成。
智能体动作跟踪日前计划的效果可由两方面体现:一方面为对储能SOC的修正量,反映当前时刻该动作的直接效果;另一方面为储能SOC的偏差量,反映历史动作的累积控制效果。对上述两者进行线性加权可得
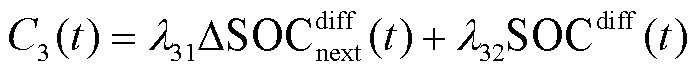 (32)
(32)
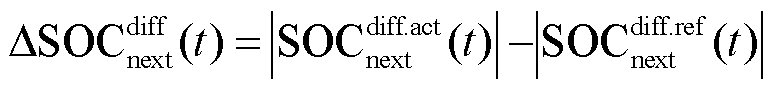 (33)
(33)
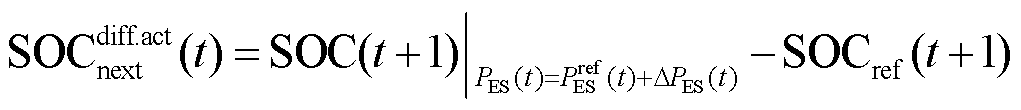 (34)
(34)
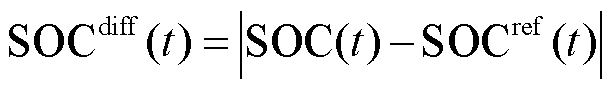 (35)
(35)
式中,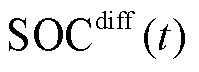 为t时刻储能SOC偏差量;
为t时刻储能SOC偏差量;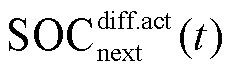 为t时刻储能按照当前调控动作修正出力时,其在
为t时刻储能按照当前调控动作修正出力时,其在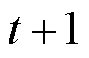 时刻的SOC偏差量;
时刻的SOC偏差量;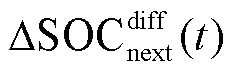 体现了当前调控动作对储能SOC的修正效果;
体现了当前调控动作对储能SOC的修正效果;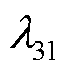 和
和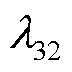 为权重系数。
为权重系数。
另外,可通过调控前后联络线功率偏离的差值[39]评价当前时刻动作平抑功率波动的效果。
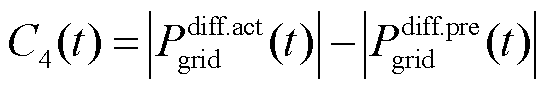 (36)
(36)
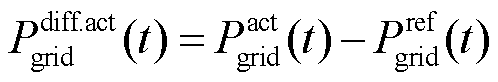 (37)
(37)
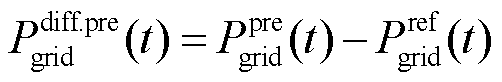 (38)
(38)
式中,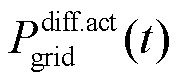 和
和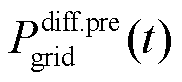 分别为t时刻联络线上调控后功率与日前预测功率的差值和短期预测功率与日前预测功率的差值;
分别为t时刻联络线上调控后功率与日前预测功率的差值和短期预测功率与日前预测功率的差值;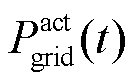 、
、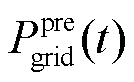 和
和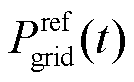 分别为t时刻对储能功率进行修正后的联络线功率、联络线短期预测功率和联络线日前预测功率。
分别为t时刻对储能功率进行修正后的联络线功率、联络线短期预测功率和联络线日前预测功率。
对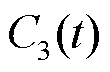 和
和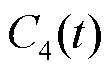 进行线性加权并取反,最终构建奖励函数为
进行线性加权并取反,最终构建奖励函数为
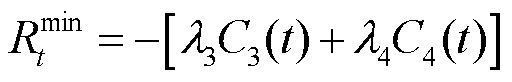 (39)
(39)
式中,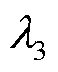 和
和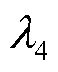 分别为两目标的权重系数。
分别为两目标的权重系数。
4)网络结构
由于日内DDPG的状态空间和动作空间均较为简单,故采取全连接网络作为其策略网络和价值网络,具体参数见后文4.2节。
本文仿真计算基于Python 3.9环境下的TensorFlow 2.10平台和Keras 2.10框架,硬件配置为AMD Ryzen 5 5600H处理器和NVIDIA GTX 1650计算卡。
针对上述有源配电网多目标优化调控方法,本文采用IEEE 33节点拓展系统进行仿真验证。该配电网电压基准值为12.66 kV,其结构如图5所示。
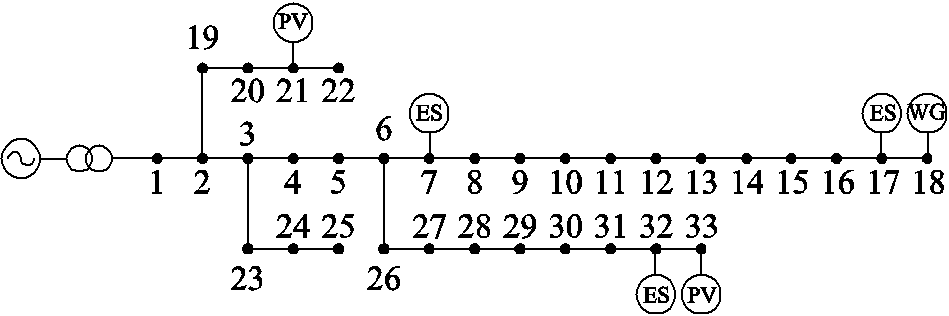
图5 修改后的IEEE 33算例系统
Fig.5 Modified IEEE 33-bus distribution network
在保持原有线路参数不变的基础上,在节点18接入容量为1 MW的风电场;在节点33、21分别接入容量为0.6、0.3 MW的光伏机组;在节点7、17、32分别接入最大功率为0.4、0.2、0.2 MW,容量为1.2、0.6、0.6 MW·h的储能装置;接入负荷总有功容量为2 MW,其分布保持原有参数不变;此外,每个节点均存在分布时段和可调度时段不同的两类柔性负荷,其分布与负荷分布相同,参数见表1[40]。相关电源及负荷均视为恒功率因数。优化调控成本和储能系统等参数[11,36]见附表1、附表2。
表1 柔性负荷参数
Tab.1 Parameters of flexible load

原负荷时段/h功率分布/MW可调度时段/h 16, 17, 180.1, 0.2, 0.110~20 18, 19, 200.1, 0.2, 0.112~23
采用蒙特卡洛法构造配电网500天运行数据集[12],针对典型日内负荷曲线、风电出力曲线和光伏出力曲线,假设其预测误差均服从正态分布,以1 h和5 min为时间尺度添加噪声,以模拟较长时间尺度下的功率预测误差和短时功率波动,并按照8:2的比例将上述数据集划分为训练集和测试集。图6为源荷日前h级尺度的不确定范围及某天实际情况;图7为日内某天min级尺度的源荷随机波动情况,以及其导致的联络线功率波动情况。

图6 日前不确定范围
Fig.6 Uncertain scope in day-ahead stage

图7 日内功率波动
Fig.7 Power fluctuation in intraday stage
深度强化学习算法的效果与其网络参数相关,本文所用网络结构和超参数见表2。对于本文仿真算例,为平衡所提取空间特征的质量和降维效果,日前调控特征提取网络中卷积网络数量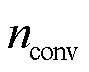 = 8。
= 8。
表2 网络结构及超参数
Tab.2 Structure and parameters of network
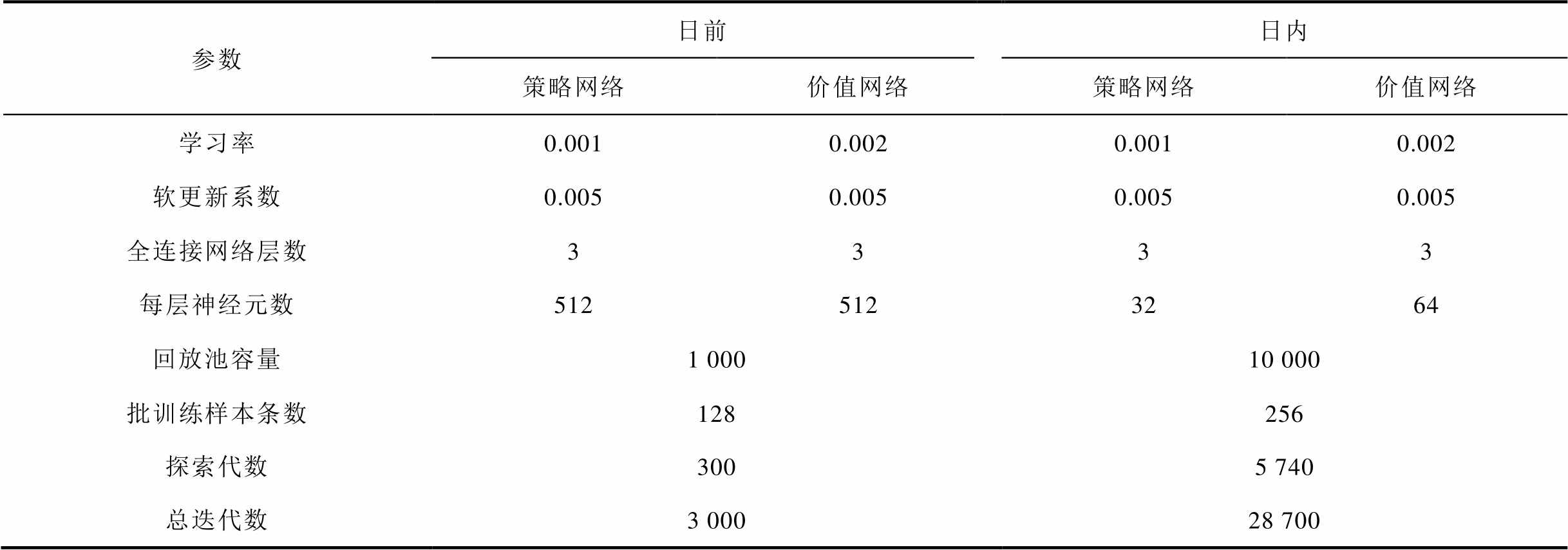
参数日前日内 策略网络价值网络策略网络价值网络 学习率0.0010.0020.0010.002 软更新系数0.0050.0050.0050.005 全连接网络层数3333 每层神经元数5125123264 回放池容量1 00010 000 批训练样本条数128256 探索代数3005 740 总迭代数3 00028 700
通过训练过程中智能体获得奖励值的变化以评估深度强化学习算法的训练效果。其中,日运行成本系数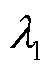 和联络线功率平滑度系数
和联络线功率平滑度系数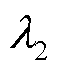 的比例、储能日前计划跟踪系数
的比例、储能日前计划跟踪系数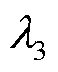 和功率波动平抑系数
和功率波动平抑系数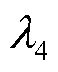 的比例分别控制日前和日内调控中对不同优化目标的偏向,在运行过程中可根据实际需求选取;储能SOC修正系数
的比例分别控制日前和日内调控中对不同优化目标的偏向,在运行过程中可根据实际需求选取;储能SOC修正系数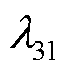 和储能SOC偏差系数
和储能SOC偏差系数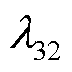 的比例主要影响智能体对储能SOC偏离的容忍程度,过大的
的比例主要影响智能体对储能SOC偏离的容忍程度,过大的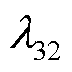 会使智能体对储能功率的再调控过于保守,最终选取的各多目标权重系数见附表3。为排除随机性干扰,使用不同的随机数种子重复进行十次实验,得到日前和日内阶段收敛情况分别如图8和图9所示,其中浅色部分为十次训练的奖励值波动范围,深色线条为平均奖励值曲线。训练过程中奖励值在一定区间内波动,并逐渐收敛至某一数值附近,可见在经过设定迭代次数的训练后,日前和日内智能体均能有效收敛。由于环境状态存在的不确定性,其奖励值也在一定范围内波动。
会使智能体对储能功率的再调控过于保守,最终选取的各多目标权重系数见附表3。为排除随机性干扰,使用不同的随机数种子重复进行十次实验,得到日前和日内阶段收敛情况分别如图8和图9所示,其中浅色部分为十次训练的奖励值波动范围,深色线条为平均奖励值曲线。训练过程中奖励值在一定区间内波动,并逐渐收敛至某一数值附近,可见在经过设定迭代次数的训练后,日前和日内智能体均能有效收敛。由于环境状态存在的不确定性,其奖励值也在一定范围内波动。

图8 日前阶段收敛情况
Fig.8 Convergence case in day-ahead stage

图9 日内阶段收敛情况
Fig.9 Convergence case in intraday stage
为验证本文所提特征提取网络的有效性,将直接采用全连接网络[41]和采用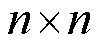 卷积网络[12]作为特征提取网络的网络结构与本文所提网络结构进行对比,其收敛情况如对比图10所示。直接采用全连接网络时,由于配电网状态矩阵中存在较多的信息冗余,网络拟合效果较差,导致智能体不能较好地学习数据特征,其收敛曲线存在一定的振荡现象,优化效果也较差;采用
卷积网络[12]作为特征提取网络的网络结构与本文所提网络结构进行对比,其收敛情况如对比图10所示。直接采用全连接网络时,由于配电网状态矩阵中存在较多的信息冗余,网络拟合效果较差,导致智能体不能较好地学习数据特征,其收敛曲线存在一定的振荡现象,优化效果也较差;采用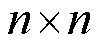 卷积网络作为特征提取网络时,配电网状态矩阵中的信息能在一定程度上被提取出来,但该网络结构并未针对多阶段状态空间中变量的时空关系进行相应改进,因此其收敛情况和优化效果虽较采用全连接网络时有所提高,但每次实验的收敛曲线仍有较大差异,说明其优化效果具有一定的随机性,且总体优化效果仍不及本文方法;采用本文方法时,收敛曲线快速接近最终迭代值,且独立实验之间最终的优化值差异更小,优化效果更好且更稳定。因此,本文所提特征提取网络可以有效地提高算法的收敛性和收敛效果。
卷积网络作为特征提取网络时,配电网状态矩阵中的信息能在一定程度上被提取出来,但该网络结构并未针对多阶段状态空间中变量的时空关系进行相应改进,因此其收敛情况和优化效果虽较采用全连接网络时有所提高,但每次实验的收敛曲线仍有较大差异,说明其优化效果具有一定的随机性,且总体优化效果仍不及本文方法;采用本文方法时,收敛曲线快速接近最终迭代值,且独立实验之间最终的优化值差异更小,优化效果更好且更稳定。因此,本文所提特征提取网络可以有效地提高算法的收敛性和收敛效果。

图10 不同特征提取网络收敛情况对比
Fig.10 Comparison of convergence of different feature extraction networks
为验证本文方法优化调控效果和本文所提特征提取网络的有效性和优越性,将本文方法与其他方法进行对比。其中,方法1通过场景法考虑源荷不确定性,并采用遗传算法进行求解;方法2采用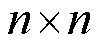 卷积网络作为特征提取网络,其余部分与本文方法相同。在十次重复实验内,方法1包括场景生成、缩减、求解在内的平均计算时间为273 min,方法2及本文方法训练时间分别为93 min及91 min,生成策略耗时均在0.1 s以内,因此本文使用的人工智能方法在计算速度方面更具优势。十次重复实验在测试集上的优化结果平均值如图11所示,其中方法1优化结果整体偏高,且分布较为离散,说明其优化效果具有一定的随机性;方法2优化效果整体较好,但仍有部分实验结果较差;而本文方法优化效果最好,且不同独立实验的优化结果更为接近,具有较好的稳定性。
卷积网络作为特征提取网络,其余部分与本文方法相同。在十次重复实验内,方法1包括场景生成、缩减、求解在内的平均计算时间为273 min,方法2及本文方法训练时间分别为93 min及91 min,生成策略耗时均在0.1 s以内,因此本文使用的人工智能方法在计算速度方面更具优势。十次重复实验在测试集上的优化结果平均值如图11所示,其中方法1优化结果整体偏高,且分布较为离散,说明其优化效果具有一定的随机性;方法2优化效果整体较好,但仍有部分实验结果较差;而本文方法优化效果最好,且不同独立实验的优化结果更为接近,具有较好的稳定性。
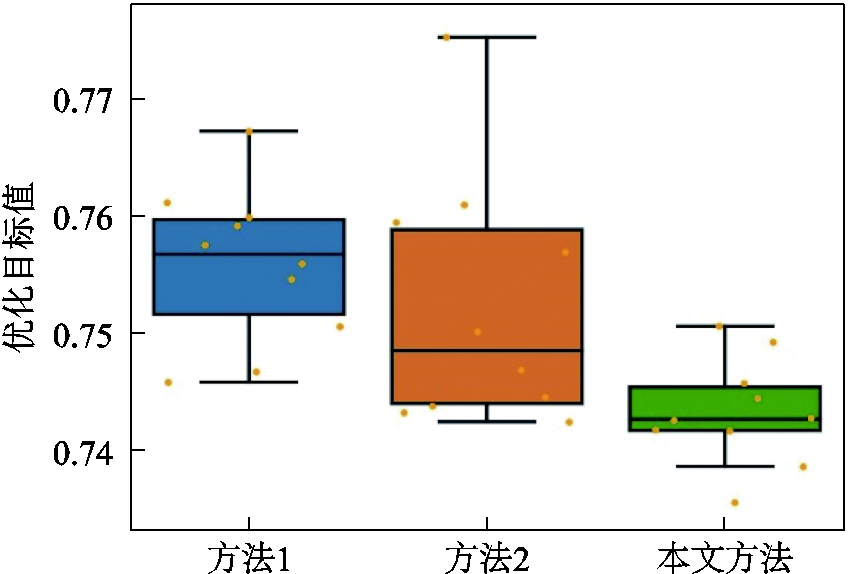
图11 日前重复实验结果对比
Fig.11 Comparison of repeated experimental results in day-ahead stage
为验证本文方法在不确定环境下优化调控效果的有效性和优越性,计算测试集数据中本文方法、方法1和方法3调控方案的优化目标值,其中方法3未考虑源荷不确定性,直接通过遗传算法对日前确定性优化模型进行求解。三种方法的优化结果如图12所示。由图12可见,方法3优化值分布不规则,部分优化值分布于某一数值附近,且分布较为离散,说明其优化效果受源荷功率不确定性影响较大;方法1通过场景法考虑源荷不确定性,针对整体调控效果进行优化,使优化值分布更为集中,但仍呈现多个集中点叠加的分布规律,说明通过场景缩减技术得到的典型场景所表征的源荷不确定性可能与其实际概率分布仍有差异;而本文方法所得优化值分布与方法1相似,但分布更为集中,说明通过数据驱动的深度强化学习方法可以使智能体有效学习数据集中的源荷不确定性,在面对复杂不确定场景时将更具优势。

图12 日前不确定性影响对比
Fig.12 Comparison of impacts of uncertainty in day-ahead stage
在日前调控结果的基础上,日内以min级尺度对储能功率进行实时修正以实现对功率波动的平抑。为验证本文方法全时段调控效果的有效性和优越性,将本文方法与其他方法进行对比。其中,方法4为全额平抑,即利用储能系统将有源配电网中的源荷波动功率全部平抑;方法5为单步优化,在每个调度时段内以本文奖励函数最大为目标并采用粒子群算法进行优化。十次重复实验在测试集上的优化结果如图13所示,图中虚线为方法4在一天之中获得的累计奖励值。由图13可知,方法5在每一调控时段内对平抑波动功率和跟踪储能日前计划的优化目标进行了统筹考虑,从而在一定程度上提高了奖励值,而本文方法在此基础上考虑了当前时段调控指令对全时段内整体优化效果的影响,从而大幅提高了累计奖励值。本文方法累计奖励值分布较方法5更为分散的原因主要在于:方法5仅对当前调控时段进行优化,其解空间较为简单,对整体优化效果的影响也较小;而本文方法关注全时段整体优化效果,因此解空间更为复杂,受训练过程中不确定环境影响,得到的智能体参数存在一定差异,导致最终的优化结果在一定范围内变化。
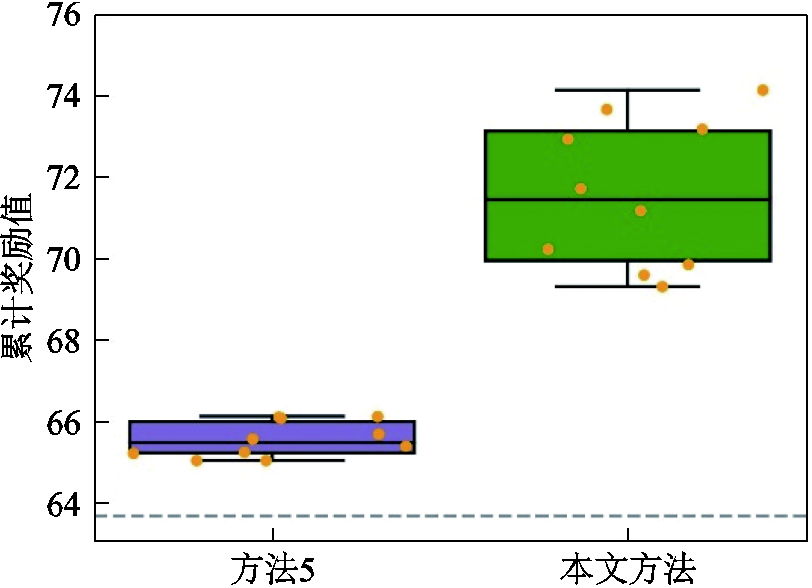
图13 日内重复实验结果对比
Fig.13 Comparison of repeated experimental results in intraday stage
为验证本文方法多目标优化的通用性,以日前调度为例,取不同权重因子并进行训练后,从测试集中随机选取一天数据计算各优化目标值,得到调控前及不同权重因子下各优化目标值见表3。可见日前调控后综合运行成本有所增加,其主要成本仍为购电成本,但储能调控成本占比提高较多,这主要是因为储能设备单位调控成本目前仍在较高水平。当 取值增加时,联络线功率均方差逐渐减小,表明调峰效果变好,此时储能调控成本有所增加,导致综合运行成本增加;而柔性负荷调控成本并无明显变化趋势,说明当前调控成本下通过柔性负荷进行调峰具有较好的性价比。日前调控通过合理调整全天配电网潮流以降低网络损耗,当权重因子
取值增加时,联络线功率均方差逐渐减小,表明调峰效果变好,此时储能调控成本有所增加,导致综合运行成本增加;而柔性负荷调控成本并无明显变化趋势,说明当前调控成本下通过柔性负荷进行调峰具有较好的性价比。日前调控通过合理调整全天配电网潮流以降低网络损耗,当权重因子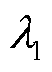 和
和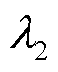 分别取0.3和0.7时,有功网损成本降低了37.97%,联络线功率均方差降低了62.57%。
分别取0.3和0.7时,有功网损成本降低了37.97%,联络线功率均方差降低了62.57%。
表3 日前调控优化目标值
Tab.3 Target value of day-ahead scheduling
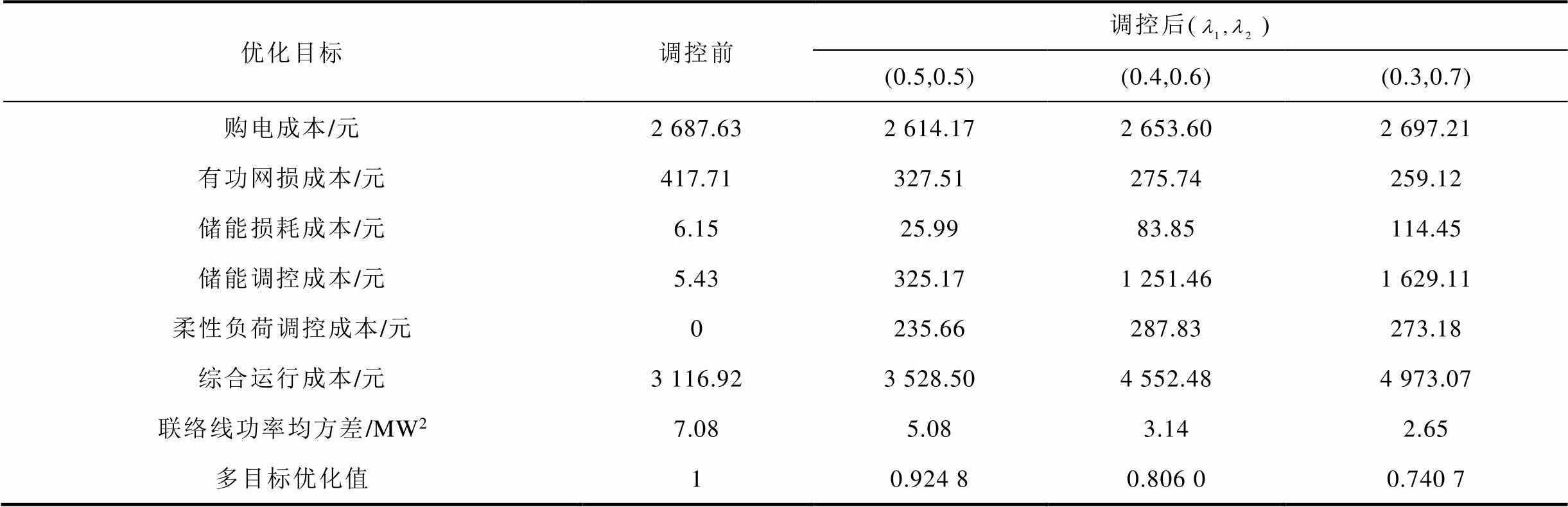
优化目标调控前调控后() (0.5,0.5)(0.4,0.6)(0.3,0.7) 购电成本/元2 687.632 614.172 653.602 697.21 有功网损成本/元417.71327.51275.74259.12 储能损耗成本/元6.1525.9983.85114.45 储能调控成本/元5.43325.171 251.461 629.11 柔性负荷调控成本/元0235.66287.83273.18 综合运行成本/元3 116.923 528.504 552.484 973.07 联络线功率均方差/MW27.085.083.142.65 多目标优化值10.924 80.806 00.740 7
日前调控前后联络线功率如图14所示,可见在0~6 h时,配电网向上级电网倒送功率有所降低,这是因为储能系统在此时处于充电状态,吸收了风机的大部分出力;在16~22 h时,配电网的负荷高峰得到了有效削减,此时储能和柔性负荷共同作用,减小了配电网的需求功率。其中在柔性负荷可调度时段的限制下,智能体将原本分布在16~20 h的部分柔性负荷重新分配至10~15 h和22~23 h以实现削峰填谷。通过日前调控,配电网总体功率波动得到了有效平抑,其对上级电网造成的调峰压力也随之减小。在实际运行中,可根据配电网及上级电网的要求合理调整各目标权重以实现多目标最优。

图14 日前调控结果
Fig.14 Results of day-ahead scheduling
图15为方法4全额平抑、方法5单步优化和本文方法日内调控前后的联络线功率。图16为三种方法的储能日前计划出力、日内实际出力、日前参考SOC和日内实际SOC结果。由图16可见,在大部分时段内,本文方法和方法5对储能系统功率的调控方案与方法4基本相同,说明两者均对功率波动进行了有效平抑。在功率波动较大时,本文方法和方法5均减小了对联络线功率波动的平抑程度,以避免对储能系统SOC造成较大影响。本文方法和对比方法的区别主要体现在6~7 h和19~21 h。其中,在6~7 h时,联络线功率实际值与日前预测存在偏差,因此方法4和方法5通过调控储能系统使联络线功率维持日前计划值,而导致储能系统SOC发生了偏离;本文方法考虑了当前时段调控命令对后续时段的影响,主动减小了对联络线功率的跟踪,减小了储能SOC的偏离,从而保留了一定的调控能力。在19~21 h时,联络线功率也产生了较大偏差,本文方法和方法5均在平抑功率波动和跟踪储能日前计划之间做出了一定取舍,但方法5针对单一时段进行优化,未能对储能SOC偏离值进行主动修正,因此储能SOC仍有较大偏离,且调控结束时储能SOC较初始值有一定的偏差;而本文方法通过考虑全时段的优化效果,使得调控时段内储能SOC偏离值始终维持在一定范围内,并且大幅降低了储能SOC初末状态偏差。为及时平抑源荷造成的随机波动,部分时段储能功率出现频繁过零的现象,这一调控指令可由一定策略分配至不同的储能系统及单元组[42],本文暂不对其进行讨论。

图15 日内联络线功率调控结果
Fig.15 Results of tie-line power in intraday stage

图16 日内储能实际运行结果
Fig.16 Actual operation of energy storage in intraday stage
三种方法的日内调控指标对比见表4,其中,调控前指储能系统完全按照日前计划运行,其储能SOC实际偏差为0,功率波动即为源荷功率在联络线上的实际波动;方法4对联络线功率波动进行了全额平抑,因此储能系统SOC产生了较大的偏差,从而降低了累积奖励值;方法5在每一时间截面上进行单步优化,在功率波动平抑和储能跟踪日前计划之间进行了一定取舍,从而提高了奖励值;本文方法则不仅权衡了两目标的优化效果,还考虑了当前时段动作对未来的影响,从而提高了整个调控时段内的累积奖励值。在实际运行中,可根据配电网及储能的要求合理选择各目标权重以实现综合优化调控。
表4 不同方法日内调控指标对比
Tab.4 Comparison of intra-day scheduling indicators using different methods

调控指标调控前方法4方法5本文方法 累计功率偏差/MW2.4800.390.75 累计SOC偏差01.471.020.39 累计奖励值063.6265.5372.97
本文考虑源荷在多时间尺度上的不确定性,提出了一种基于深度强化学习的有源配电网源荷储多时间尺度优化调控策略,并通过算例验证了该方法的有效性和优越性,主要结论如下:
1)采用基于数据驱动的深度强化学习方法,不依赖于概率分布假设,可自主学习数据集中不确定量的概率信息;根据多时段状态空间变量时空耦合特性设计的特征提取网络可以有效地提高深度学习方法的优化效果和收敛性。
2)日前调控以1 h为时间尺度,在不假设源荷不确定量概率分布的情况下,实现了配电网日运行成本最低和联络线功率最平滑的多目标优化,当权重因子取一定值时,有功网损成本降低了37.97%,联络线功率均方差降低了62.57%。
3)日内调控以5 min为时间尺度,以短期预测为基础,储能功率修正量为控制对象,考虑源荷实际功率与日前预测功率的持续偏移问题,在跟踪日前计划的基础上实现了对风、光能源及负荷功率波动的实时平抑。
后续工作将考虑电网在不同时间尺度上的其他调控需求,以及不同种类新型储能对调控策略的具体影响,以完善本文所提方法。
附 录
附表1 优化调控成本参数
App.Tab.1 Cost parameters of optimal scheduling

参数数值 单位电价/[元/(kW·h)]0.36 损耗成本系数/[元/(kW·h)]0.68 储能调控成本系数/[元/(kW·h)]0.6 柔性负荷调控成本系数/[元/(kW·h)]0.4 储能SOC约束惩罚系数/元1 000 线路功率约束惩罚系数/(元/kW)10
附表2 储能系统参数
App.Tab.2 Parameters of energy storage systems

参数数值 充电效率0.95 放电效率0.95 自放电率/h-10.000 5 初始SOC0.3 SOC下限0.1 SOC上限0.9
附表3 多目标权重系数
App.Tab.3 Multi objective weight coefficient

权重系数数值 日运行成本系数0.3 联络线功率平滑度系数0.7 储能SOC修正系数0.3 储能SOC偏差系数0.7 储能日前计划跟踪系数30 功率波动平抑系数10
参考文献
[1] 张智刚, 康重庆. 碳中和目标下构建新型电力系统的挑战与展望[J]. 中国电机工程学报, 2022, 42(8): 2806-2819. Zhang Zhigang, Kang Chongqing. Challenges and prospects for constructing the new-type power system towards a carbon neutrality future[J]. Proceedings of the CSEE, 2022, 42(8): 2806-2819.
[2] 辛保安, 单葆国, 李琼慧, 等. “双碳”目标下“能源三要素”再思考[J]. 中国电机工程学报, 2022, 42(9): 3117-3126. Xin Baoan, Shan Baoguo, Li Qionghui, et al. Rethinking of the “three elements of energy” toward carbon peak and carbon neutrality[J]. Proceedings of the CSEE, 2022, 42(9): 3117-3126.
[3] Boicea V A. Energy storage technologies: the past and the present[J]. Proceedings of the IEEE, 2014, 102(11): 1777-1794.
[4] 王珂, 姚建国, 姚良忠, 等. 电力柔性负荷调度研究综述[J]. 电力系统自动化, 2014, 38(20): 127-135. Wang Ke, Yao Jianguo, Yao Liangzhong, et al. Survey of research on flexible loads scheduling technologies [J]. Automation of Electric Power Systems, 2014, 38(20): 127-135.
[5] Gill S, Kockar I, Ault G W. Dynamic optimal power flow for active distribution networks[J]. IEEE Transactions on Power Systems, 2014, 29(1): 121-131.
[6] 尤毅, 刘东, 钟清, 等. 主动配电网优化调度策略研究[J]. 电力系统自动化, 2014, 38(9): 177-183. You Yi, Liu Dong, Zhong Qing, et al. Research on optimal schedule strategy for active distribution network[J]. Automation of Electric Power Systems, 2014, 38(9): 177-183.
[7] Chen Xiaoshuang, Lin Jin, Liu Feng, et al. Optimal control of DERs in ADN under spatial and temporal correlated uncertainties[J]. IEEE Transactions on Smart Grid, 2020, 11(2): 1216-1228.
[8] 金国彬, 潘狄, 陈庆, 等. 考虑源荷不确定性的直流配电网模糊随机日前优化调度[J]. 电工技术学报, 2021, 36(21): 4517-4528. Jin Guobin, Pan Di, Chen Qing, et al. Fuzzy random day-ahead optimal dispatch of DC distribution network considering the uncertainty of source-load[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4517-4528.
[9] 徐崇博, 杨晓东, 张有兵, 等. 考虑风险管控的含智能软开关主动配电网随机运行优化方法[J]. 电力系统自动化, 2021, 45(11): 68-76. Xu Chongbo, Yang Xiaodong, Zhang Youbing, et al. Stochastic operation optimization method for active distribution networks with soft open point considering risk management and control[J]. Automation of Electric Power Systems, 2021, 45(11): 68-76.
[10] 李鹏, 王加浩, 黎灿兵, 等. 计及源荷不确定性与设备变工况特性的园区综合能源系统协同优化运行方法[J]. 中国电机工程学报, 2023, 43(20): 7802-7812. Li Peng, Wang Jiahao, Li Canbing, et al. Collaborative optimal scheduling of the community integrated energy system considering source-load uncertainty and equipment off-design performance[J]. Proceedings of the CSEE, 2023, 43(20): 7802-7812.
[11] 梁俊文, 林舜江, 刘明波, 等. 主动配电网分布式鲁棒优化调度方法[J]. 电网技术, 2019, 43(4): 1336-1344. Liang Junwen, Lin Shunjiang, Liu Mingbo, et al. Distributed robust optimal dispatch in active distribution networks[J]. Power System Technology, 2019, 43(4): 1336-1344.
[12] 李鹏, 姜磊, 王加浩, 等. 基于深度强化学习的新能源配电网双时间尺度无功电压优化[J]. 中国电机工程学报, 2023, 43(16): 6255-6266. Li Peng, Jiang Lei, Wang Jiahao, et al. Optimization of dual-time scale reactive voltage for distribution network with renewable energy based on deep reinforcement learning[J]. Proceedings of the CSEE, 2023, 43(16): 6255-6266.
[13] Li Yunyi, Wan Can, Chen Dawei, et al. Nonparametric probabilistic optimal power flow[J]. IEEE Transactions on Power Systems, 2022, 37(4): 2758-2770.
[14] 王骞, 张学广, 徐殿国. 考虑内–外生双重不确定性的风储系统联合规划方法[J]. 中国电机工程学报, 2023, 43(1): 169-181. Wang Qian, Zhang Xueguang, Xu Dianguo. A joint planning method of wind-storage system considering endogenous and exogenous uncertainty[J]. Proceedings of the CSEE, 2023, 43(1): 169-181.
[15] Lopez-Ramos L M, Kekatos V, Marques A G, et al. Two-timescale stochastic dispatch of smart distribution grids[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 4282-4292.
[16] Li Peng, Wang Zixuan, Wang Jiahao, et al. A multi-time-space scale optimal operation strategy for a distributed integrated energy system[J]. Applied Energy, 2021, 289: 116698.
[17] 陈明昊, 孙毅, 谢志远. 基于双层深度强化学习的园区综合能源系统多时间尺度优化管理[J]. 电工技术学报, 2023, 38(7): 1864-1881. Chen Minghao, Sun Yi, Xie Zhiyuan. The multi-time-scale management optimization method for park integrated energy system based on the Bi-layer deep reinforcement learning[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1864-1881.
[18] 李勇, 凌锋, 乔学博, 等. 基于网侧资源协调的自储能柔性互联配电系统日前-日内优化[J]. 电工技术学报, 2024, 39(3): 758-773, 923. Li Yong, Ling Feng, Qiao Xuebo, et al. Day-ahead and intra-day optimization of flexible interconnected distribution system with self-energy storage based on the grid-side resource coordination[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 758-773, 923.
[19] Kalantar-Neyestanaki M, Cherkaoui R. Coordinating distributed energy resources and utility-scale battery energy storage system for power flexibility provision under uncertainty[J]. IEEE Transactions on Sustainable Energy, 2021, 12(4): 1853-1863.
[20] Zhu Jianquan, Chen Jiajun, Zhuo Yelin, et al. Stochastic energy management of active distribution network based on improved approximate dynamic programming[J]. IEEE Transactions on Smart Grid, 2022, 13(1): 406-416.
[21] Wang Kang, Wang Chengfu, Zhang Zhenwei, et al. Multi-timescale active distribution network optimal dispatching based on SMPC[J]. IEEE Transactions on Industry Applications, 2022, 58(2): 1644-1653.
[22] Kamruzzaman M, Duan Jiajun, Shi Di, et al. A deep reinforcement learning-based multi-agent framework to enhance power system resilience using shunt resources[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5525-5536.
[23] 顾雪平, 刘彤, 李少岩, 等. 基于改进双延迟深度确定性策略梯度算法的电网有功安全校正控制[J]. 电工技术学报, 2023, 38(8): 2162-2177. Gu Xueping, Liu Tong, Li Shaoyan, et al. Active power correction control of power grid based on improved twin delayed deep deterministic policy gradient algorithm[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2162-2177.
[24] 董雷, 杨子民, 乔骥, 等. 基于分层约束强化学习的综合能源多微网系统优化调度[J]. 电工技术学报, 2024, 39(5): 1436-1453. Dong Lei, Yang Zimin, Qiao Ji, et al. Optimal scheduling of integrated energy multi-microgrid system based on hierarchical constraint reinforcement learning[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1436-1453.
[25] 胡维昊, 曹迪, 黄琦, 等. 深度强化学习在配电网优化运行中的应用[J]. 电力系统自动化, 2023, 47(14): 174-191. Hu Weihao, Cao Di, Huang Qi, et al. Application of deep reinforcement learning in optimal operation of distribution network[J]. Automation of Electric Power Systems, 2023, 47(14): 174-191.
[26] 王继业. 人工智能赋能源网荷储协同互动的应用及展望[J]. 中国电机工程学报, 2022, 42(21): 7667-7682. Wang Jiye. Application and prospect of Source-grid-load-storage coordination enabled by artificial intelligence[J]. Proceedings of the CSEE, 2022, 42(21): 7667-7682.
[27] 汤涌, 姚伟, 王宏志, 等. 电网仿真分析与决策的人工智能方法[J]. 中国电机工程学报, 2022, 42(15): 5384-5406. Tang Yong, Yao Wei, Wang Hongzhi, et al. Artificial intelligence techniques for power grid simulation analysis and decision making[J]. Proceedings of the CSEE, 2022, 42(15): 5384-5406.
[28] 李涛, 胡维昊, 李坚, 等. 基于深度强化学习算法的光伏-抽蓄互补系统智能调度[J]. 电工技术学报, 2020, 35(13): 2757-2768. Li Tao, Hu Weihao, Li Jian, et al. Intelligent economic dispatch for PV-PHS integrated system: a deep reinforcement learning-based approach[J]. Transactions of China Electrotechnical Society, 2020, 35(13): 2757-2768.
[29] 张剑, 崔明建, 何怡刚. 结合数据驱动与物理模型的主动配电网双时间尺度电压协调优化控制[J]. 电工技术学报, 2024, 39(5): 1327-1339. Zhang Jian, Cui Mingjian, He Yigang. Dual timescales coordinated and optimal voltages control in distribution systems using data-driven and physical optimization[J]. Transactions of China Electrotechnical Society, 2024, 39(5): 1327-1339.
[30] 张自东, 邱才明, 张东霞, 等. 基于深度强化学习的微电网复合储能协调控制方法[J]. 电网技术, 2019, 43(6): 1914-1921. Zhang Zidong, Qiu Caiming, Zhang Dongxia, et al. A coordinated control method for hybrid energy storage system in microgrid based on deep reinforcement learning[J]. Power System Technology, 2019, 43(6): 1914-1921.
[31] Huang Shiying, Li Peng, Yang Ming, et al. A control strategy based on deep reinforcement learning under the combined wind-solar storage system[J]. IEEE Transactions on Industry Applications, 2021, 57(6): 6547-6558.
[32] Yang Qiuling, Wang Gang, Sadeghi A, et al. Two-timescale voltage control in distribution grids using deep reinforcement learning[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2313-2323.
[33] Wu Hongyu, Shahidehpour M, Alabdulwahab A, et al. Demand response exchange in the stochastic day-ahead scheduling with variable renewable generation [J]. IEEE Transactions on Sustainable Energy, 2015, 6(2): 516-525.
[34] 刘全, 翟建伟, 章宗长, 等. 深度强化学习综述[J]. 计算机学报, 2018, 41(1): 1-27. Liu Quan, Zhai Jianwei, Zhang Zongchang, et al. A survey on deep reinforcement learning[J]. Chinese Journal of Computers, 2018, 41(1): 1-27.
[35] 董雷, 陈卉, 蒲天骄, 等. 基于模型预测控制的主动配电网多时间尺度动态优化调度[J]. 中国电机工程学报, 2016, 36(17): 4609-4617. Dong Lei, Chen Hui, Pu Tianjiao, et al. Multi-time scale dynamic optimal dispatch in active distribution network based on model predictive control[J]. Proceedings of the CSEE, 2016, 36(17): 4609-4617.
[36] 姜云鹏, 任洲洋, 李秋燕, 等. 考虑多灵活性资源协调调度的配电网新能源消纳策略[J]. 电工技术学报, 2022, 37(7): 1820-1835. Jiang Yunpeng, Ren Zhouyang, Li Qiuyan, et al. An accommodation strategy for renewable energy in distribution network considering coordinated dispatching of multi-flexible resources[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1820-1835.
[37] Li Peng, Wang Zixuan, Liu Haitao, et al. Bi-level optimal configuration strategy of community integrated energy system with coordinated planning and operation[J]. Energy, 2021, 236: 121539.
[38] 朱兰, 周雪莹, 唐陇军, 等. 计及可中断负荷的微电网多目标优化运行[J]. 电网技术, 2017, 41(6): 1847-1854. Zhu Lan, Zhou Xueying, Tang Longjun, et al. Multi-objective optimal operation for microgrid considering interruptible loads[J]. Power System Technology, 2017, 41(6): 1847-1854.
[39] Sheng Hongzhang, Wang Chengfu, Li Bowen, et al. Multi-timescale active distribution network scheduling considering demand response and user comprehensive satisfaction[J]. IEEE Transactions on Industry Applications, 2021, 57(3): 1995-2005.
[40] 刘俊峰, 罗燕, 侯媛媛, 等. 考虑广义储能的微电网主动能量管理优化算法研究[J]. 电网技术, 2023, 47(1): 245-255. Liu Junfeng, Luo Yan, Hou Yuanyuan, et al. Research on optimization algorithm of active microgrid energy management considering generalized energy storage[J]. Power System Technology, 2023, 47(1): 245-255.
[41] 王珂, 姚建国, 余佩遥, 等. 基于深度强化学习的电网前瞻调度智能决策架构及关键技术初探[J]. 中国电机工程学报, 2022, 42(15): 5430-5439. Wang Ke, Yao Jianguo, Yu Peiyao, et al. Architecture and key technologies of intelligent decision-making of power grid look-ahead dispatch based on deep reinforcement learning[J]. Proceedings of the CSEE, 2022, 42(15): 5430-5439.
[42] 李相俊, 马锐. 考虑电池组健康状态的储能系统能量管理方法[J]. 电网技术, 2020, 44(11): 4210-4217. Li Xiangjun, Ma Rui. Energy management method of energy storage system considering the SOH of battery pack[J]. Power System Technology, 2020, 44(11): 4210-4217.
Abstract The stochastic, volatile, and uncontrollable nature of renewable energy generation such as wind and solar leads to increased uncertainty and difficulty in regulation with the expansion of installed capacity. Consequently, the safe, economical, and stable operation of distribution networks faces formidable challenges. The data-driven artificial intelligence method has the characteristics of model-free and self-adaptation. It can independently learn the complex uncertainty of wind and solar energy and load, and has a good supporting role for the optimal regulation of active distribution network. Consider the problem of high dimensional variable information redundancy in day-ahead scheduling and the dilemma of stabilizing fluctuating power and tracking day ahead scheduling in intraday scheduling, this paper proposes a multi-timescale intelligent optimal regulation method for active distribution network based on deep reinforcement learning algorithm.
Firstly, a multi time scale framework for active distribution networks (AND) was constructed based on the operational characteristics and regulatory requirements of the equipment, and the corresponding state inputs and action outputs of deep reinforcement learning (DRL) agents at different time scales were described. In the day-ahead stage, this paper takes the lowest daily operation cost of ADN and the smoothest tie line power as the optimization objective. In order to reduce the influence of high-dimensional variable information redundancy in the day ahead state space on the optimization effect, an improved feature extraction method considering the spatio-temporal coupling characteristics of the day-ahead state information is proposed. In the intraday stage, considering the full absorption of uncertain power will cause deviations from the pre-scheduled operating status of controllable equipment as energy storage system (ESS), this paper designs a reward function that reasonably reflects the tie line power deviation and state of charge (SOC) deviation of ESS, and realizes the optimization in the whole scheduling period through the deep reinforcement learning method.
Simulation results show that agents on both time scales can converge effectively. In the day ahead stage, while controlling the daily comprehensive operation cost of ADN, the peak value on the tie line is smoothed. The active power loss and the mean square deviation of tie line power is reduced. Compared with using fully connected network and n×n convolutional network as feature extraction network, the proposed feature extraction method has improved the convergence and convergence speed of DRL agent. In the intraday stage, the proposed method realizes the adaptive stabilization of fluctuating power while tracking the day ahead plan of scheduling equipment. The optimization effect of the proposed method in the whole scheduling period is better than that of the full consumption and single-step optimization.
The following conclusions can be drawn from the simulation analysis: (1) Using the data-driven deep reinforcement learning method, the probability information of uncertainty in the data set can be learned autonomously. The feature extraction network designed according to the spatio-temporal coupling characteristics of multi period state space variables can effectively improve the optimization effect and convergence of the deep learning method. (2) Without assuming the probability distribution of source and load uncertainty, the day-ahead dispatch realizes the multi-objective optimization of the ADN with the lowest daily operation cost and the smoothest tie line power. (3) The intraday dispatch takes into account the offset between the actual power and the day ahead forecast power of the source and load, and realizes the real-time stabilization of the fluctuation of uncertain power while tracking the day-ahead plan.
keywords:Active distribution network, optimal dispatch, source-load-storage coordination, deep reinforcement learning
DOI: 10.19595/j.cnki.1000-6753.tces.240316
中图分类号:TM73
国家电网公司科技项目资助(4000-202316071A-1-1-ZN)。
收稿日期 2024-02-29
改稿日期 2024-05-06
李 鹏 男,1965年生,教授,博士生导师,研究方向为新能源电力系统、综合能源系统与微网、储能技术应用、人工智能在智慧能源中的应用等。E-mail:ncepulp@ncepu.edu.cn
钟瀚明 男,1999年生,硕士研究生,研究方向为人工智能在电网优化运行方面的应用。E-mail:ncepuzhm@ncepu.edu.cn(通信作者)
(编辑 李 冰)