图1 基于分层模型预测控制的电力系统在线决策恢复框架
Fig.1 Online decision-making framework for system restoration based on hierarchical model predictive control
摘要 在“双碳”背景下,电力系统的风电渗透率不断提升,风电机组对大停电后系统恢复过程的影响日益显著。为应对风电出力不确定性对恢复过程的影响,该文提出了一种基于分层模型预测控制的电力系统恢复在线决策方法。首先,为满足不同的恢复决策需求,引入分层控制结构,将恢复任务解耦,以动态更新的风电预测信息为基础,提出基于两种滚动机制的双层滚动优化策略:上层考虑元件恢复次序的后效性,采用前瞻到底滚动机制进行元件恢复次序决策;下层考虑风电预测精度近高远低的实际,采用滑动时间窗口滚动机制进行发电机组出力计划和负荷恢复计划决策。然后,在反馈校正环节,根据实测风电数据,建立储能等灵活性资源的实时调度模型并修正风电功率预测。最后,通过修改的新英格兰39节点系统和实际系统算例验证所提方法的有效性与实用性。
关键词:模型预测控制 大停电 风电不确定性 滚动机制 在线恢复 实时校正
随着以新能源为主体的新型电力系统的快速发展,风电装机占比迅速提高,系统运行特性更加复杂多变[1]。同时,在新能源不确定性、极端天气、设备故障等因素的共同影响下,电力系统发生大停电事故的风险呈现增大趋势[2]。近年来,世界范围内发生了多起大停电事故,例如,2016年澳大利亚“9·28”大停电[3]、2018年巴西“3·21”大停电[4]、2021年美国得州“2·15”大停电[5]等。因此,研究如何制定含风电的电力系统大停电后的安全、高效系统恢复方案对于提升系统保底安全性和减小停电损失具有重要意义。
风电机组具有启动功率小、爬坡速率快等优点,在系统恢复过程中快速恢复风电机组可有效地加快系统恢复进程,及早恢复重要负荷以减小停电损失[6]。但是,由于风速的随机性和波动性,相比于传统机组,风电机组具有出力不确定、抗扰能力弱等特点,将给系统恢复带来更多不确定性因素[7]。关于风电参与系统恢复过程的研究已取得一定的成果[8-10]:文献[11]论证了储能型风电场作为黑启动电源的可行性;文献[12]以风储系统作为黑启动电源,进一步考虑经济性和储能运行策略,提出一种储能容量配置方法;文献[13]采用生产可能性边界方法,将含风电电力系统的网架重构问题转换为启动功率分配的多目标优化问题;文献[14]综合考虑恢复策略的风险和收益,建立考虑风电出力不确定性的负荷恢复线性优化模型。以上文献主要集中于风电参与系统恢复的局部问题,没有对风电参与的系统恢复方案进行全过程统筹优化。
针对规模风电参与的电力系统恢复的全过程决策问题,已有研究多基于恢复初期的风电预测结果和预测误差制定离线恢复预案。文献[15]基于风电典型场景,采用随机优化方法刻画风电出力不确定性,提出一种离线全过程恢复方法;文献[16]考虑预测误差分布的时空特性,采用多面体鲁棒不确定集描述风电出力的不确定性,通过求解两阶段问题得到全过程恢复方案。由于风电功率预测精度远低于传统负荷预测,且预测误差随预测超前时间增加而增大,因此风电出力呈现强不确定性[17]。考虑到系统恢复过程中的网架强度较低,以及可调用的灵活性资源较少,随机优化方法对极端场景的抵御能力弱,容易导致二次停电,延误恢复过程;鲁棒优化虽然能较好地应对风电极端出力场景,但是采用鲁棒优化对恢复全过程进行长时间尺度决策会导致制定的恢复方案过于保守,降低系统恢复效率,增大停电损失。综上所述,基于恢复初期预测数据的离线优化方法不能保证恢复方案对实时工况的可用性,从而无法有效地满足风电高占比系统的恢复决策需求。因此,研究在线跟踪风电出力超短时预测的电力系统恢复在线决策方法具有重要意义。
模型预测控制(Model Predictive Control, MPC)在电力系统功率调度中已有一定的应用[18-19]。MPC基于动态更新的预测数据,采用滚动优化-单步执行的控制策略,同时利用实测信息反馈校正,能够有效地克服多重不确定性的影响[20],为规模风电接入后的电力系统恢复决策问题提供了一种解决思路。文献[21]基于模型预测控制思想,提出一种风光储联合参与黑启动过程的组合电源控制策略;文献[22]考虑微电网不确定性,采用鲁棒模型预测控制方法,建立配电网恢复滚动优化模型。然而,基于传统MPC的系统恢复决策方法以有限时域滚动机制进行滚动优化,决策过程只着眼于短期优化时域内的恢复收益而不能兼顾后续恢复,容易导致决策结果陷入局部最优,缺乏对长过程系统恢复全局最优性的考量[23]。
在以往工作的基础上,本文提出了一种基于分层模型预测控制的电力系统恢复在线决策方法,并通过修改的新英格兰39节点系统和某实际系统作为算例验证了所提方法的有效性。其主要贡献为:①考虑风电预测精度构建了动态风电不确定集合,反映预测超前时间对风电预测误差的影响;②将恢复任务进行解耦,提出了前瞻到底和滑动时间窗口两种滚动机制相结合的双层滚动策略进行恢复方案的序贯决策,既利用了全时段风电预测数据增强模型的前瞻性,又避免了远端预测误差对功率调度方案造成直接影响;③根据风功率实际测量值,建立储能等灵活性资源的实时调度模型,通过对灵活性资源的有效调配,最大化利用风电资源。本文方法的优势是通过在线滚动决策有效地提高恢复方案对风电出力不确定性的适应能力,从而保障系统恢复过程的安全高效执行。
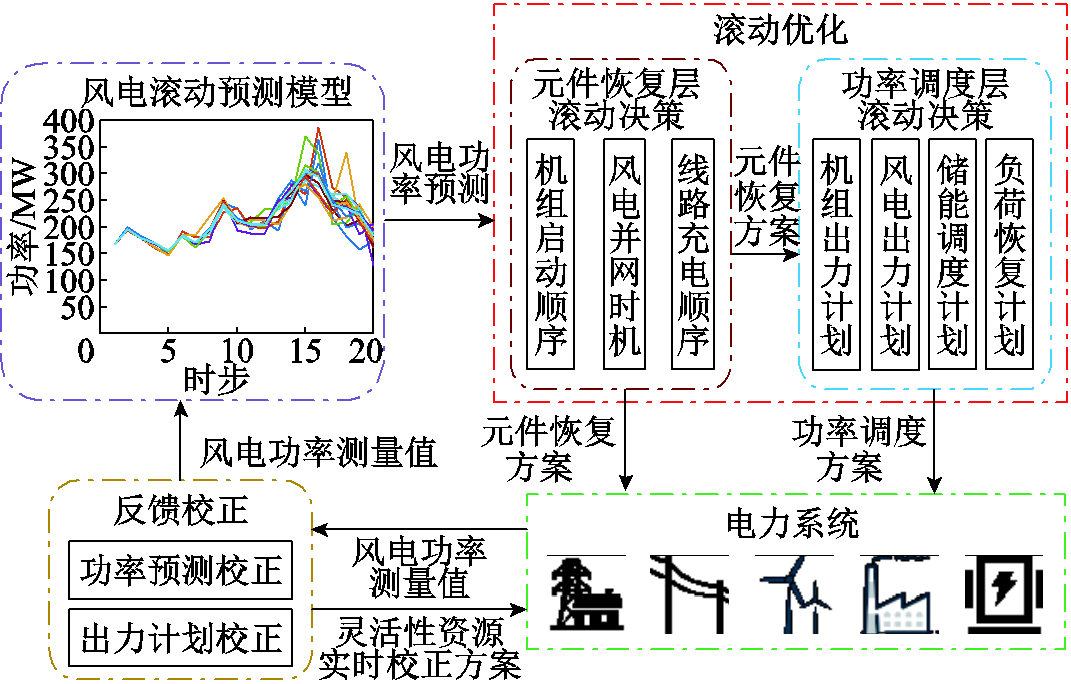
针对风电出力不确定性等问题,本文提出了基于分层模型预测控制的电力系统恢复在线决策整体框架。在该框架中风电场有功功率预测、恢复决策滚动优化、预测误差反馈校正等环节相互配合以实现恢复方案的在线优化。基于分层模型预测控制的电力系统在线决策恢复框架如图1所示。

图1 基于分层模型预测控制的电力系统在线决策恢复框架
Fig.1 Online decision-making framework for system restoration based on hierarchical model predictive control
根据相关规程要求,实际风电场超短期预测应至少每15 min滚动执行一次并自动向电力调度中心上报未来一段时间的风电场有功功率预测结果[24],这为后续滚动优化和反馈校正提供了数据基础。
滚动优化过程中的优化时域长度直接影响决策结果的优劣。在电力系统恢复过程中,受到元件恢复时间、时步内最大操作数和线路充电无功功率的限制,每一时步能恢复的元件数量有限[25]。由于连通性约束,先前恢复的元件决定了当前可恢复的元件集合,元件恢复次序的选择具有较强的后效性,不同的元件恢复次序对恢复效果的影响体现在一个较长时间的积累过程。因此,在决策元件恢复顺序时,需要较长的滚动优化时域以保证模型的前瞻性。同时,如果优化时域过大,优化时域远端预测精度明显降低,过早地预留较多备用资源意义不大且可能导致恢复效率降低,同时也会带来过大的计算负担,求解速度可能无法满足在线恢复的要求。
传统的模型预测控制的滚动优化环节为单层结构,很难协调恢复过程中的多种要求[26]。为了兼顾恢复效率、恢复安全和求解速度等多方面的需求,本文引入分层控制结构,提出一种适应含风电电力系统恢复的双层滚动优化策略,将电力系统恢复方案分为元件恢复层和功率调度层两层进行滚动优化。
电力系统恢复属于短期调度,其全段风电预测数据均可作为衡量风电功率支撑能力的重要指标,远端预测误差对于元件恢复次序决策的影响较小,且可以通过后续滚动优化进行修正。因此,元件恢复层考虑元件恢复的后效性,以全局恢复效率为目标,采用前瞻到底的滚动机制,将当前时步至恢复结束作为优化时域,对恢复决策时域内的所有恢复时段中的元件恢复操作进行统一优化,以便各恢复主体能够提前协调并做好恢复前的准备工作。
功率调度层基于元件恢复层确定的元件恢复次序,考虑风电远端预测误差增大对功率调度造成的影响,采用滑动时间窗口的滚动机制,将后续有限时步作为优化时域以保证决策域内预测信息的准确性,求解各时步发电机出力计划以及母线负荷恢复计划,由各恢复主体执行优化时域内第1时步的恢复计划。
针对系统恢复过程中的风电预测误差,在元件恢复层采用非参数核密度估计法刻画风电不确定性,将满足一定置信水平的风电功率预测作为风电计划出力上限,在大概率风电场景下优化元件恢复方案的同时简化了模型、加快了求解速度;而功率调度层则采用鲁棒优化方法保证恢复方案在极端风电场景下的可行性。另外,考虑到大型发电机组的启动需要一定的准备时间,频繁变更的元件启动计划不利于机组启动进行,元件恢复层可以根据系统实际情况每隔几个时步启动一次。以元件恢复层每隔2个时步启动一次为例,令ST为恢复总时步数,分层滚动优化策略示意图如图2所示。
恢复框架包括两个反馈校正环节。一方面,与功率调度层相互配合,在功率调度层执行的仍是基于预测的超前控制。由于风电预测存在偏差,功率调度层的风电计划出力与风电实际可利用出力之间依旧存在偏差,在反馈校正环节以储能作为主要的灵活性资源来平抑风电出力波动,最小化风电不确定性对恢复过程的影响。同时,恢复过程中电网可调节资源趋于紧张,时间上超前的功率调度层能够根据风电预测结果提前安排恢复计划,预留调整空间,而时间上滞后的反馈校正层不具备这种前瞻能力,反馈校正层功能的顺利执行依赖与功率调度层的动态协调,因此,需要在功率调度层优化的过程中,为反馈校正预留足够的灵活性资源。另一方面,将当前时刻的风电功率实际测量值加入新一轮滚动优化的预测环节,更新预测模型输入数据从而对风功率预测进行修正,减小下一时刻的风电预测误差。
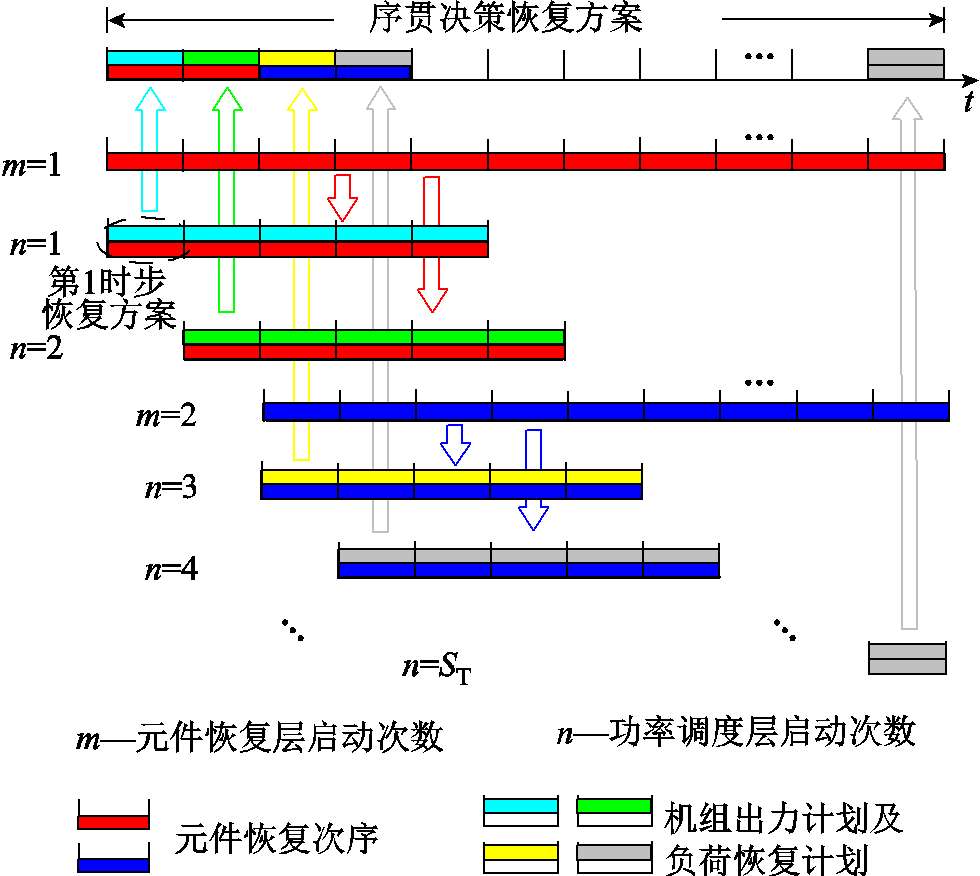
图2 分层滚动优化策略示意图
Fig.2 Schematic diagram of hierarchical scrolling optimization strategy
根据相关规程要求,风电场的功率预测系统应具备超短期预测能力[24]。本文以时序预测为例,给出风功率预测模型的基本形式,作为后续滚动优化的基础。
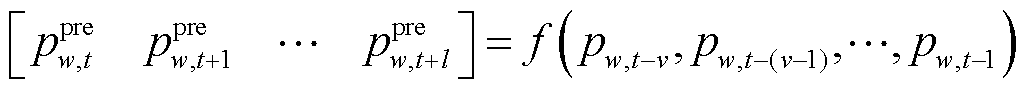 (1)
(1)
式中,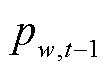 为风电场w在
为风电场w在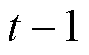 时刻的历史风功率数据;
时刻的历史风功率数据;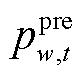 为风电场w在
为风电场w在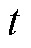 时刻的预测风功率数据;v、l分别为预测模型中所需历史数据和预测数据个数;
时刻的预测风功率数据;v、l分别为预测模型中所需历史数据和预测数据个数;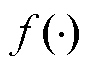 为递推预测函数。
为递推预测函数。
值得注意的是,MPC对预测模型的具体形式并没有特别的要求。随着气象观测和风功率预测技术的发展,可以采用更精确的风功率预测模型。
2.2.1 目标函数
在电力系统恢复过程中,应在恢复系统主要网架的同时尽快向停电负荷供电[27]。元件恢复层采用前瞻到底的滚动机制,每一时段的元件恢复操作决策考虑其对于后续恢复时段的影响,将恢复全过程加权负荷恢复量最大和恢复网架规模最大定为恢复目标,则元件恢复决策层的目标函数可描述为
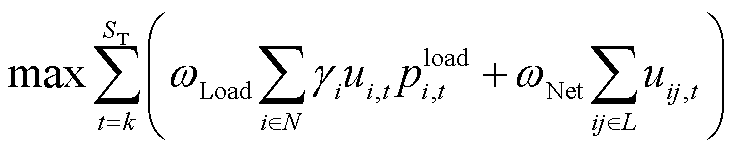 (2)
(2)
式中,k为当前滚动优化时域的起始时步;N、L分别为系统母线、线路集合;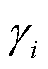 为母线i处负荷的重要性系数;ui,t、uij,t为二元决策变量,分别表示
为母线i处负荷的重要性系数;ui,t、uij,t为二元决策变量,分别表示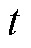 时步母线
时步母线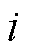 和线路
和线路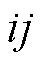 是否被恢复;
是否被恢复;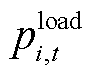 为
为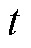 时步母线
时步母线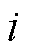 恢复的有功负荷量;
恢复的有功负荷量;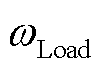 、
、 分别为负荷恢复量和网架规模两个指标的权重系数。
分别为负荷恢复量和网架规模两个指标的权重系数。
2.2.2 约束条件
系统恢复决策过程中面临系统安全要求、恢复操作逻辑、恢复主体电气特性等限制[28]。因此,本文在元件恢复优化决策模型中计及元件恢复顺序约束、线路潮流约束、电压及相位约束、机组出力约束、负荷约束、储能电站运行约束和系统频率约束等约束条件。
1)元件恢复顺序约束
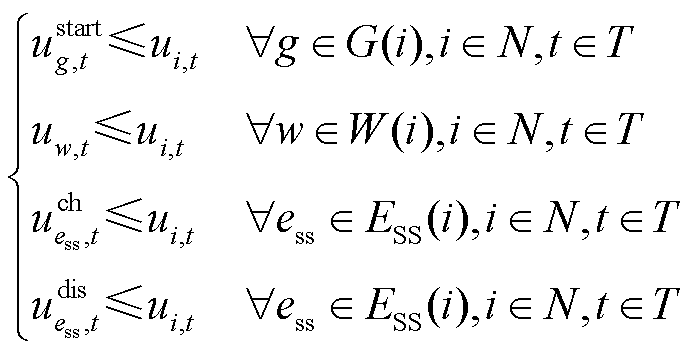 (3)
(3)
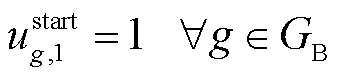 (4)
(4)
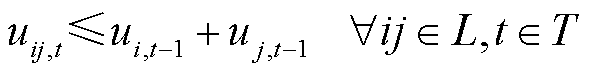 (5)
(5)
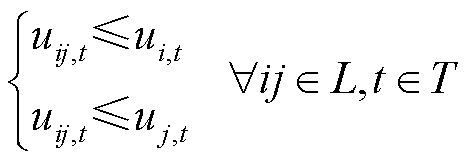 (6)
(6)
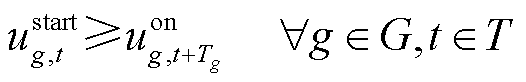 (7)
(7)
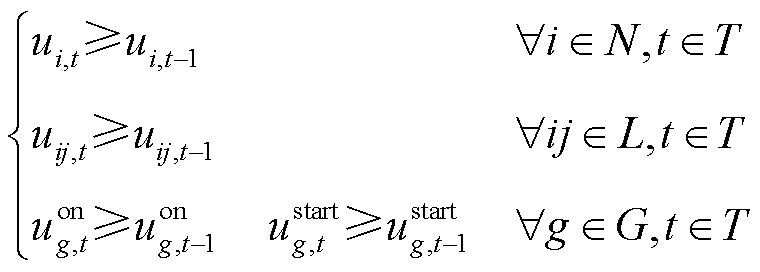 (8)
(8)
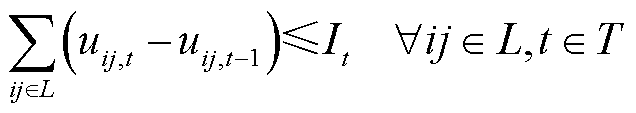 (9)
(9)
式中,G(i)、W(i)、ESS(i)分别为与母线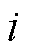 相连的常规发电机组、风电场和储能集合;GB、
相连的常规发电机组、风电场和储能集合;GB、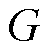 、T分别为黑启动机组、常规发电机组和当前滚动优化时域内的恢复时步集合;
、T分别为黑启动机组、常规发电机组和当前滚动优化时域内的恢复时步集合;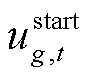 、
、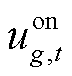 分别为表征机组g在时步t是否被恢复和是否并网出力的二元变量;
分别为表征机组g在时步t是否被恢复和是否并网出力的二元变量;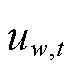 为表征风电场w在时步t是否被恢复的二元变量;
为表征风电场w在时步t是否被恢复的二元变量;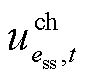 、
、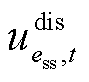 为表征储能运行状态的二元变量,
为表征储能运行状态的二元变量,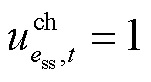 表示储能处于充电状态,
表示储能处于充电状态,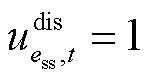 表示储能处于放电状态;Tg为机组g并网所需最短时步数;It为t时步最多恢复线路条数。式(3)表示所在母线被恢复之后,相连的非黑启动机组(包括风电)、储能才能被恢复;式(4)表示黑启动机组具有自启动能力,在恢复开始时刻已启动;式(5)表示线路在一端母线充电后才能被恢复;式(6)表示若某条线路已被恢复,则线路两端母线均已带电;式(7)表示机组
表示储能处于放电状态;Tg为机组g并网所需最短时步数;It为t时步最多恢复线路条数。式(3)表示所在母线被恢复之后,相连的非黑启动机组(包括风电)、储能才能被恢复;式(4)表示黑启动机组具有自启动能力,在恢复开始时刻已启动;式(5)表示线路在一端母线充电后才能被恢复;式(6)表示若某条线路已被恢复,则线路两端母线均已带电;式(7)表示机组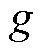 启动后至少经过Tg时步才能并网出力;式(8)表示母线、线路以及发电机组恢复后不再失电;式(9)表示由于受操作资源限制,t时步最多允许恢复It条线路。
启动后至少经过Tg时步才能并网出力;式(8)表示母线、线路以及发电机组恢复后不再失电;式(9)表示由于受操作资源限制,t时步最多允许恢复It条线路。
2)线路潮流约束
为了提高模型的计算效率,适应在线快速决策的需求,采用文献[29]中线性化方法对交流潮流约束进行线性化处理,如式(10)~式(12)所示。当线路未被恢复,uij=0,式(10)和式(11)被松弛,式(12)约束线路潮流为0;当线路ij已被恢复,uij=1,式(10)和式(11)分别为线路有功和无功潮流约束,式(12)为线路传输功率极限约束。
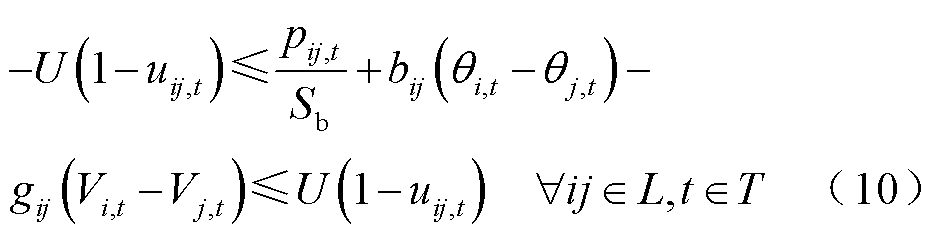
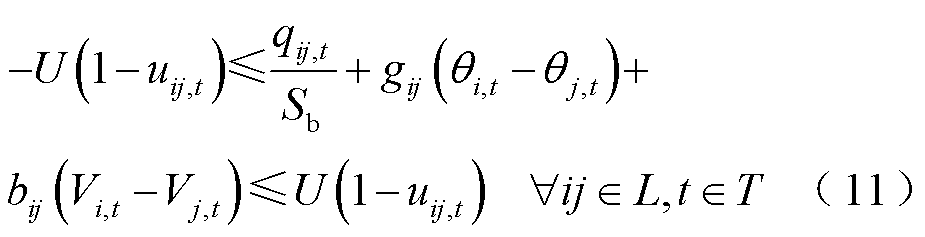
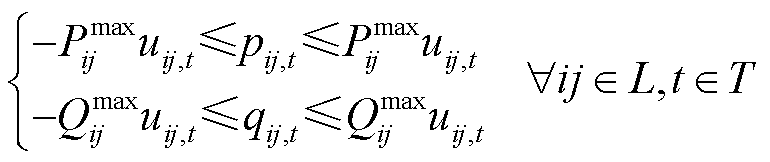 (12)
(12)
式中,pij,t、qij,t分别为在时步t流过线路ij的有功、无功功率;Sb为基准功率;U为足够大的正数;bij、gij分别为线路ij的电纳与电导;θi,t、Vi,t分别为母线i在时步t的相位和电压幅值;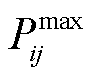 、
、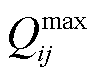 分别为线路ij允许流过有功、无功功率的最大值。
分别为线路ij允许流过有功、无功功率的最大值。
3)电压及相位约束
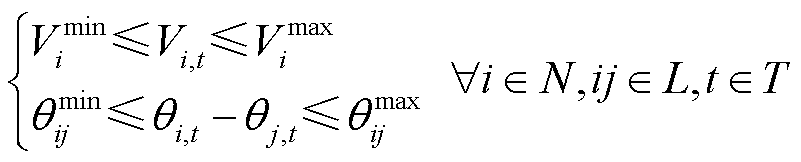 (13)
(13)
式中,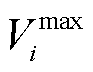 、
、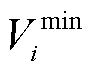 分别为母线
分别为母线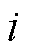 电压幅值允许的最大、最小值;
电压幅值允许的最大、最小值;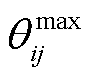 、
、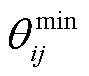 分别为母线i、j之间相位差允许的最大、最小值。式(13)表示母线电压、线路相位差应维持在系统安全运行允许范围内。
分别为母线i、j之间相位差允许的最大、最小值。式(13)表示母线电压、线路相位差应维持在系统安全运行允许范围内。
4)常规机组出力约束
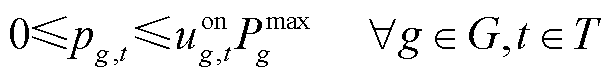 (14)
(14)
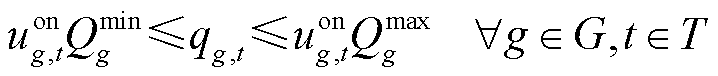 (15)
(15)
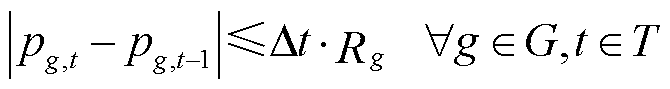 (16)
(16)
式中,pg,t、qg,t分别为机组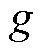 在时步
在时步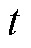 的有功、无功出力;
的有功、无功出力;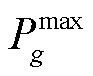 为机组g的最大有功出力;
为机组g的最大有功出力;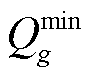 、
、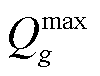 分别为机组
分别为机组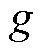 最大吸收无功和最大发出无功;
最大吸收无功和最大发出无功;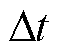 为恢复时步长;Rg为机组g的最大爬坡速率。式(14)和式(15)分别表示火电机组有功、无功出力不超过其上、下限;式(16)为机组爬坡约束。
为恢复时步长;Rg为机组g的最大爬坡速率。式(14)和式(15)分别表示火电机组有功、无功出力不超过其上、下限;式(16)为机组爬坡约束。
5)风电场出力约束
采用非参数核密度估计法刻画元件恢复决策面临的风电出力不确定性,假设e1, e2,…, eq,…, er为r个历史风电预测误差样本数据,则风电预测误差概率密度函数表示[30]为
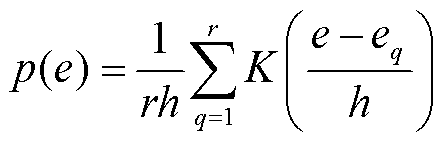 (17)
(17)
式中,h为带宽;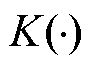 为核函数,本文采用高斯核函数
为核函数,本文采用高斯核函数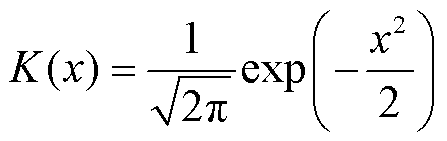 ;e为风电预测误差。由于不同预测超前时间的风电预测精度不同,其风电预测误差概率亦不相同,通过对不同预测超前时步数tp的多组历史数据样本采用非参数核密度估计可以得到对应的风电预测误差概率密度函数p(e, tp)。
;e为风电预测误差。由于不同预测超前时间的风电预测精度不同,其风电预测误差概率亦不相同,通过对不同预测超前时步数tp的多组历史数据样本采用非参数核密度估计可以得到对应的风电预测误差概率密度函数p(e, tp)。
针对预测误差“近小远大”的特点,分段设定置信水平应对元件恢复决策面临的风电不确定性问题如式(18)所示。
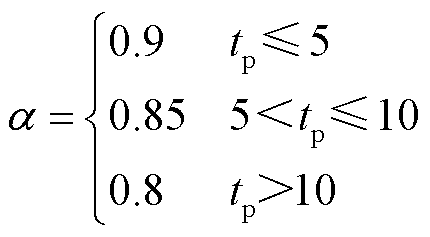 (18)
(18)
式中,α为风电预测误差置信水平。在优化时域近端的预测精度较高区间,严格要求置信水平,以提高当前元件恢复操作对后续风电场景的适应能力;在优化时域远端,适当地放松置信水平要求,避免由于远端极端预测误差场景导致低估风电出力水平,降低模型的前瞻性。随着时间推移,预测模型会为后续元件恢复决策的调整提供更准确的风电预测信息。
根据风电预测误差概率密度函数可以确定给定置信水平下的最大风电预测误差,并给出元件恢复层风电场出力约束为
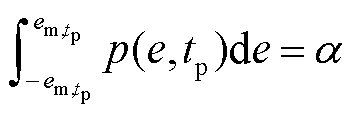 (19)
(19)
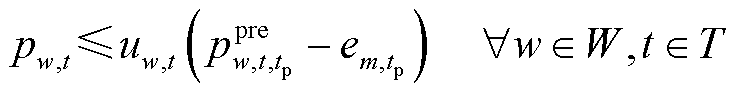 (20)
(20)
式中,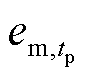 为置信水平α下超前tp时步的最大风电预测误差;W为风电场集合;pw,t、
为置信水平α下超前tp时步的最大风电预测误差;W为风电场集合;pw,t、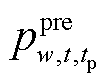 分别为风电场w在时步t的计划出力和超前tp时步的风功率预测值。
分别为风电场w在时步t的计划出力和超前tp时步的风功率预测值。
6)负荷约束
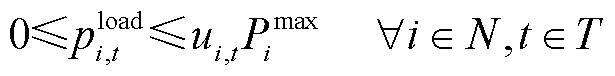 (21)
(21)
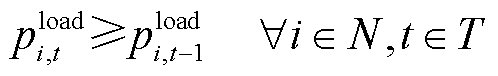 (22)
(22)
式中,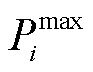 为母线
为母线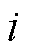 上的待恢复负荷总量。式(21)表示母线i负荷恢复量小于该母线总停电负荷;式(22)表示负荷恢复后不再失电。
上的待恢复负荷总量。式(21)表示母线i负荷恢复量小于该母线总停电负荷;式(22)表示负荷恢复后不再失电。
7)储能电站运行约束
储能电站具有响应速度快、双向充放电能力等特点[31-32],在恢复过程中可以同时作为恢复功率源和灵活性资源。考虑储能电站的电气特性,其运行约束可表示为
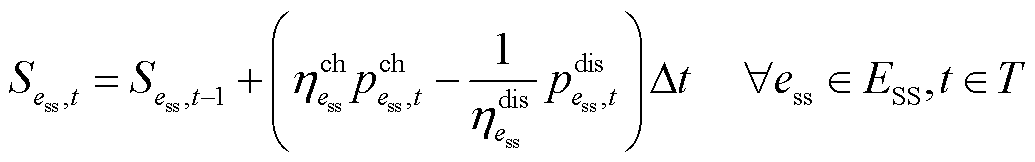 (23)
(23)
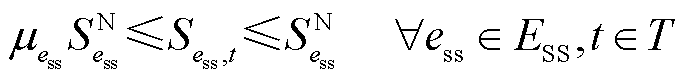 (24)
(24)
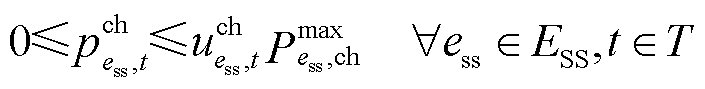 (25)
(25)
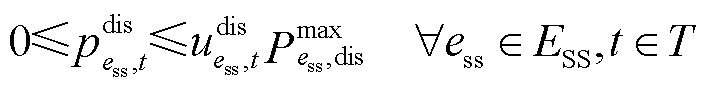 (26)
(26)
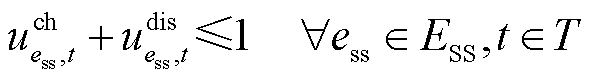 (27)
(27)
式中,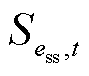 为储能ess在时步
为储能ess在时步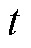 的荷电状态;
的荷电状态;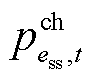 、
、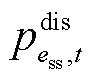 分别为储能ess在时步
分别为储能ess在时步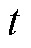 的充、放电功率;
的充、放电功率;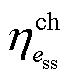 、
、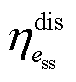 分别为储能ess的充、放电效率;
分别为储能ess的充、放电效率;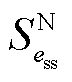 为储能ess的额定容量;
为储能ess的额定容量;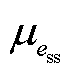 为储能ess的最低荷电水平;
为储能ess的最低荷电水平;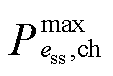 、
、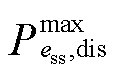 分别为储能ess最大充、放电功率。式(23)为表示储能荷电状态变化的状态方程;式(24)表示储能荷电状态的运行范围;式(25)、式(26)分别表示储能充、放电功率不超过上限;式(27)表示储能充、放电过程不能同时进行。
分别为储能ess最大充、放电功率。式(23)为表示储能荷电状态变化的状态方程;式(24)表示储能荷电状态的运行范围;式(25)、式(26)分别表示储能充、放电功率不超过上限;式(27)表示储能充、放电过程不能同时进行。
8)功率平衡约束
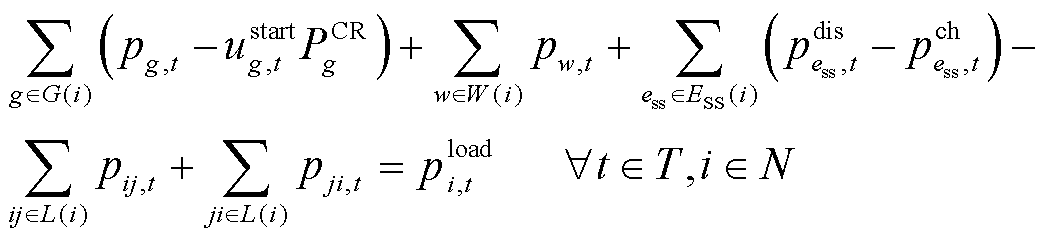 (28)
(28)
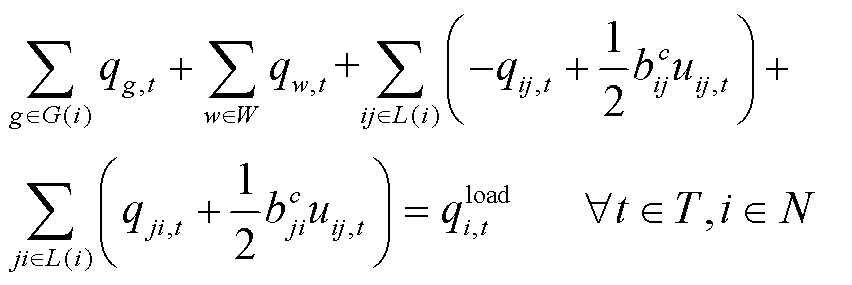 (29)
(29)
式中,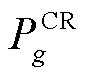 为机组
为机组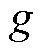 的启动功率;L(i)为与节点i相连的线路集合;
的启动功率;L(i)为与节点i相连的线路集合;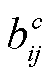 为线路ij的并联电抗;
为线路ij的并联电抗;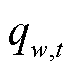 为风电机组w在时步t的无功出力;
为风电机组w在时步t的无功出力;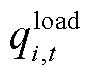 为母线i在t时步已恢复的无功负荷。式(28)和式(29)分别表示任意时步所有已恢复节点均满足有功、无功功率平衡。
为母线i在t时步已恢复的无功负荷。式(28)和式(29)分别表示任意时步所有已恢复节点均满足有功、无功功率平衡。
9)频率约束
考虑机组的频率响应特性,单时步负荷投入量应不超过频率约束允许的上限[33]。因此频率约束表示为
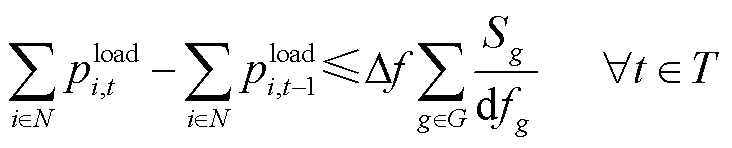 (30)
(30)
式中,Δf为系统频率下降允许的最大值;Sg为机组g的额定容量;dfg为机组g的频率响应率。
依据已建立的恢复决策框架,功率调度层在元件恢复层的决策基础上,采用滑动时间窗口滚动机制优化源荷协调的功率调度方案。相较于元件恢复层,功率调度层侧重于考虑在优化时间窗内如何充分利用已有源网侧资源,在保证系统安全的前提下最大化时域内的恢复效益,同时为反馈校正层留有足够的调度空间。基于以上恢复要求,建立功率调度层鲁棒优化双层模型为
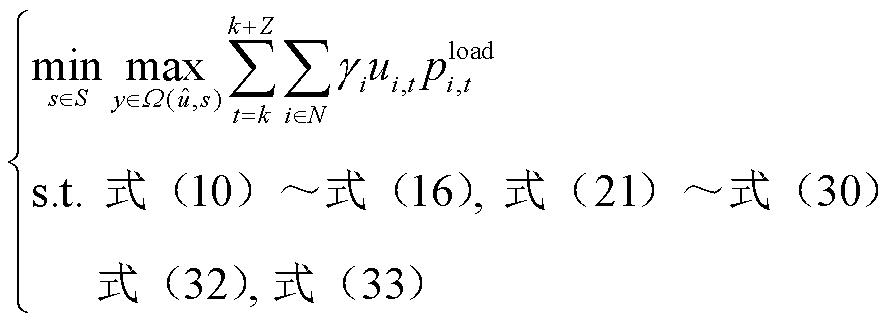 (31)
(31)
式中,s和S分别为风电场出力场景和出力场景不确定集合;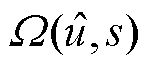 为功率调度层决策变量集合,与元件恢复层滚动优化结果
为功率调度层决策变量集合,与元件恢复层滚动优化结果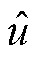 和风电场出力场景s有关;Z为功率调度层采用滑动时间窗口的宽度;y为功率调度层决策变量,主要包括已恢复机组出力和各母线负荷恢复量。上层min问题旨在寻找风电出力不确定集合中对恢复目标影响最恶劣的风电场景;下层max问题则在上层问题求得的最恶劣场景下优化场站出力及负荷投入计划以最大化恢复目标,所建双层模型可以保证恢复方案在极端风电场景下的可行性。min-max问题的求解将在3.1节详细解释。
和风电场出力场景s有关;Z为功率调度层采用滑动时间窗口的宽度;y为功率调度层决策变量,主要包括已恢复机组出力和各母线负荷恢复量。上层min问题旨在寻找风电出力不确定集合中对恢复目标影响最恶劣的风电场景;下层max问题则在上层问题求得的最恶劣场景下优化场站出力及负荷投入计划以最大化恢复目标,所建双层模型可以保证恢复方案在极端风电场景下的可行性。min-max问题的求解将在3.1节详细解释。
功率调度层的约束条件与机组启动层的约束条件大致相同,区别在于表征元件是否启动的二元变量不再作为决策变量,而是由元件恢复层决策结果传入。
区别于传统固定风电不确定集[34],本文基于鲁棒优化思想考虑风电预测精度和地理分散效应构建动态风电不确定集合。考虑超前预测时间后,对时间轴上某固定时刻进行风电预测的不确定集如图3所示,随着恢复进行,预测超前时间减小,预测精度上升,集合中心跟踪最新功率预测产生偏移,不确定集合也随之整体收缩。更新风电场出力约束为
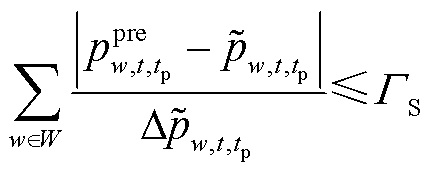 (32)
(32)
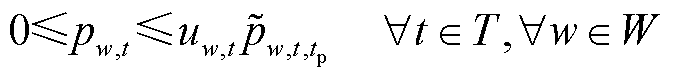 (33)
(33)
式中,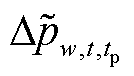 为超前tp时步对风电场w在t时步的风功率最大预测误差;
为超前tp时步对风电场w在t时步的风功率最大预测误差;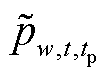 为可能的风电实际可利用出力;
为可能的风电实际可利用出力;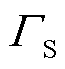 为风电不确定预算。式(32)表示动态风电不确定性集合,当
为风电不确定预算。式(32)表示动态风电不确定性集合,当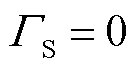 时,认为风电场预测准确,相应模型退化为确定性模型,随着
时,认为风电场预测准确,相应模型退化为确定性模型,随着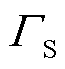 逐渐增大,风电不确定集合也逐渐扩大,
逐渐增大,风电不确定集合也逐渐扩大,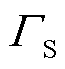 的取值应由风电场地理位置分布和预测模型精度等要素共同决定。
的取值应由风电场地理位置分布和预测模型精度等要素共同决定。
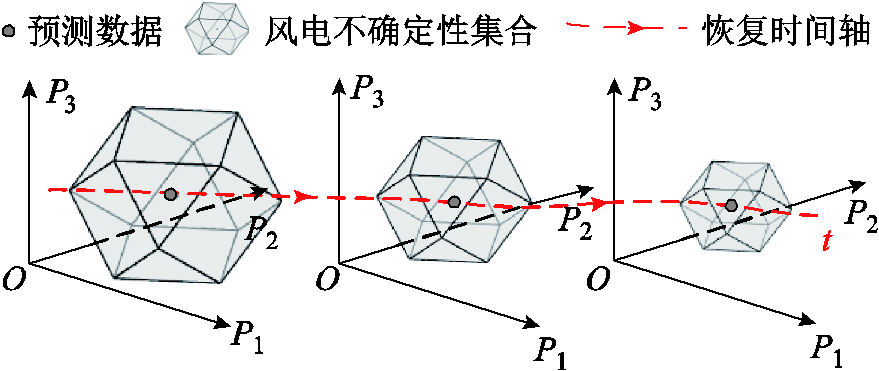
图3 考虑预测超前时间的动态风电不确定集
Fig.3 Dynamic wind power uncertainty set considering leading time
2.4.1 功率平衡校正
在功率平衡校正环节中,由于风功率预测值和实际测量值仍存在偏差,需要利用灵活性资源以平抑风电出力的不确定性,确保在恢复过程中功率平衡的同时最大化利用风电资源。本文以储能电站作为灵活性资源,建立功率平衡校正环节优化模型。
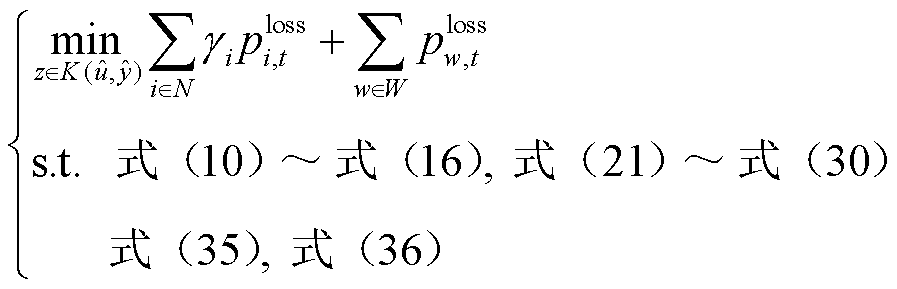 (34)
(34)
式中,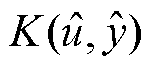 为反馈校正层决策变量集合,与元件恢复层滚动优化结果
为反馈校正层决策变量集合,与元件恢复层滚动优化结果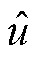 和功率调度层滚动优化结果
和功率调度层滚动优化结果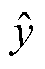 有关;z为反馈校正层决策变量,相比于功率调度层,由于响应时间的限制,校正层可以利用的调度资源进一步减少,决策变量主要包括储能充放电功率、负荷紧急切除量
有关;z为反馈校正层决策变量,相比于功率调度层,由于响应时间的限制,校正层可以利用的调度资源进一步减少,决策变量主要包括储能充放电功率、负荷紧急切除量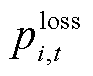 和风电场弃风量
和风电场弃风量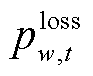 。
。
在反馈校正环节中,各风电场测量装置向恢复控制中心上传当前时步实际风电出力能力。当风电实际出力能力大于计划出力时,应通过储能储存多余的风电,若储能出力下调空间不足,则需要进行弃风,表示为
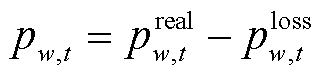 (35)
(35)
式中,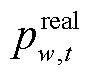 为风电场w在t时步的实际出力上限测量值。
为风电场w在t时步的实际出力上限测量值。
当风电实际出力能力小于计划出力时,应增大储能出力,若储能出力上调空间不足,则需要紧急切除部分负荷,表示为
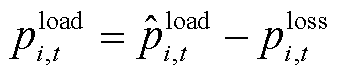 (36)
(36)
式中,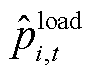 为母线i在t时步功率调度层安排的负荷恢复量。
为母线i在t时步功率调度层安排的负荷恢复量。
2.4.2 预测数据校正
在预测数据校正环节,将新得到的实际风电测量数据加入预测模型中,更新下一次滚动优化时域内的风电预测数据,即
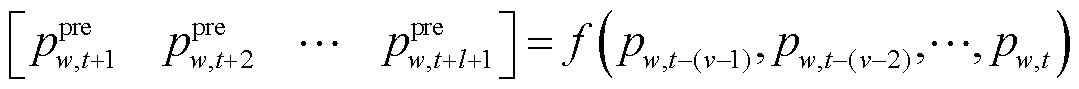 (37)
(37)
根据本文提出的基于分层模型预测控制的系统恢复在线决策方法,逐时步滚动求解元件恢复层、功率平衡层、反馈校正层恢复方案。第2节建立的系统恢复模型可表达为一个多时段四层优化模型,其中第k时段优化模型写成紧凑的数学表达式为
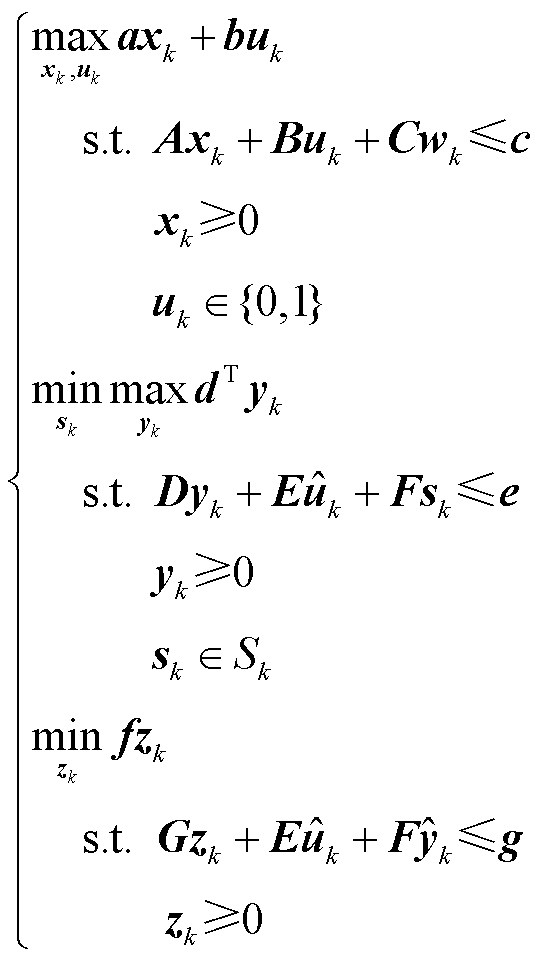 (38)
(38)
式中,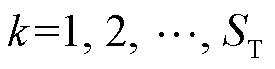 ;uk为元件恢复层决策变量;xk为元件恢复层场站出力向量;
;uk为元件恢复层决策变量;xk为元件恢复层场站出力向量;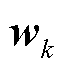 为风电功率预测向量;A, B, C, D, E, F, a, b, c, d, e, f, g为对应系数矩阵或向量。
为风电功率预测向量;A, B, C, D, E, F, a, b, c, d, e, f, g为对应系数矩阵或向量。
功率调度层的min-max双层优化问题无法直接求解,采用强对偶理论将min-max双层优化问题转换为min单层问题,表示为
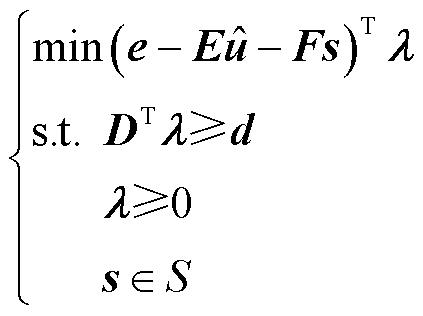 (39)
(39)
式中,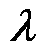 为y的对偶变量。
为y的对偶变量。
模型求解流程如图4所示,具体流程如下。
1)建立风电功率预测模型。
2)获取待恢复电力系统信息,设置时步计数器t=1。
3)根据预测模型预测后续时步风电出力。
4)判断当前时步元件恢复层优化是否启动。若启动,则确定元件恢复层优化时域,求解模型得到元件恢复次序;若不启动,则进入步骤5)。
5)确定下层决策窗口,基于上层决策所得元件恢复次序,求解下层问题的对偶问题,确定最恶劣风电场景,进而得到当前时步功率调度方案。
6)交流潮流校验。若通过则执行当前时步恢复方案;若不通过,则添加不可行割,返回步骤5)。
7)获取当前时步风电功率实际测量值,求解功率平衡校正优化模型,得到当前时步的灵活性资源校正方案。
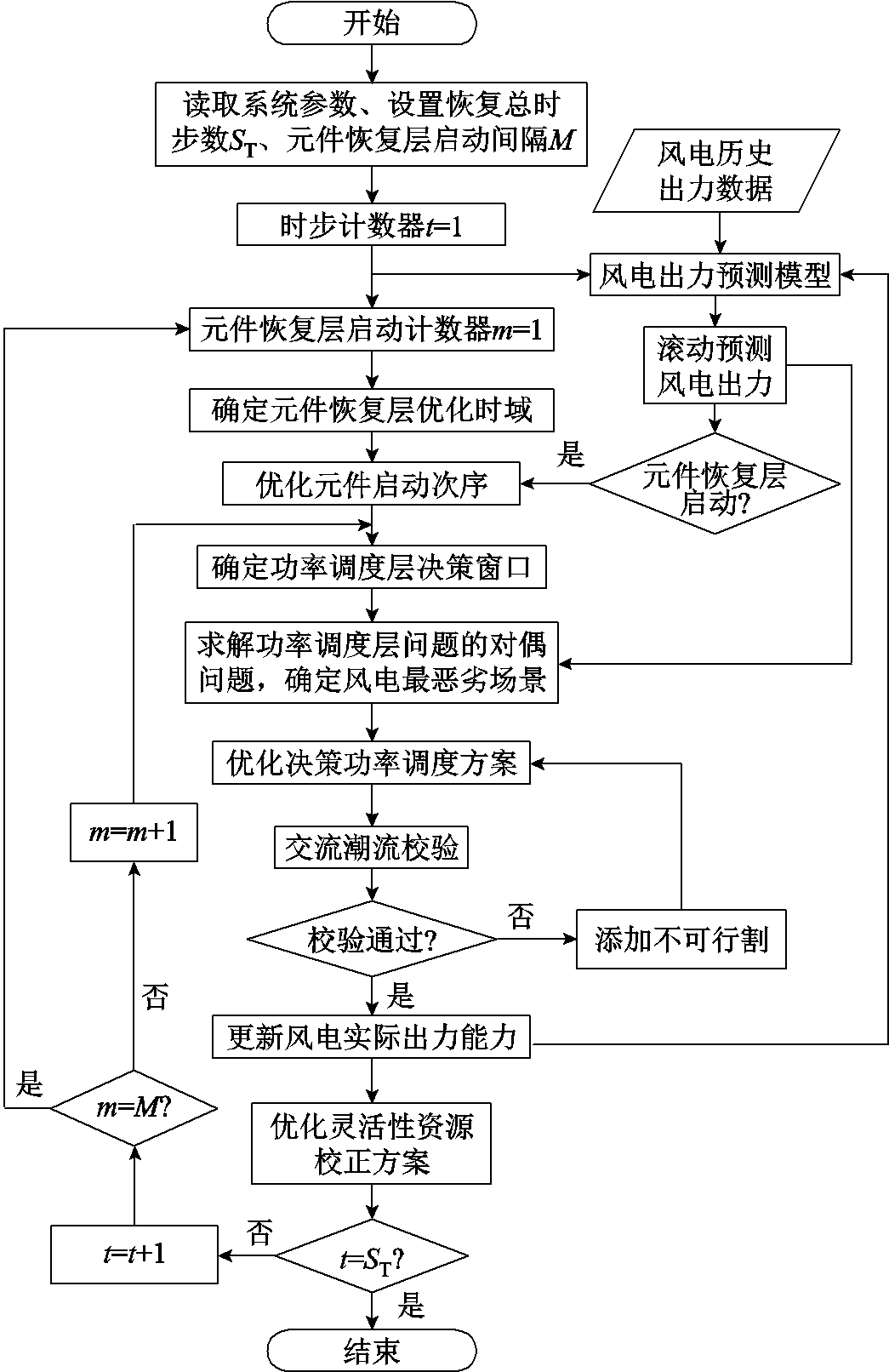
图4 基于分层模型预测控制的系统恢复方案求解流程
Fig.4 Flow chart for system restoration scheme solution based on hierarchical model predictive control
8)判断是否已完成所有恢复时步决策,如已完成,则优化结束;如未完成,令t=t+1,转回步骤3)。
本文以修改的新英格兰39节点系统和某省级电网的局部系统为算例,对所提方法的可行性与有效性进行验证。模型在Matlab平台上搭建,通过Yamlip工具箱调用Gurobi求解器求解,计算机配置为Intel(R) i5-8265U CPU,安装内存为8 GB。
4.1.1 参数设置
采用修改的新英格兰39节点系统作为算例1进行测试,系统共有10台常规发电机组、3座风电场、2个储能电站、39个节点、46条线路,系统接线图如图5所示。假设大停电事故发生后系统处于全停状态;系统内所有机组、母线和线路等未遭到物理破坏,均具备可恢复能力;节点30接入的发电机组G1为黑启动机组,并且在第1时步自启动成功,其余机组不具备自启动能力,发电机参数见附表1;节点3、7、21各设有一座风电场,风电滚动预测数据如附图1~附图3所示;节点3、19各设有一座储能电站,规模为25 MW/50 MW·h,充放电效率为0.95,储能电站最低运行荷电状态为10%;负荷权重系数设为0.8~1,系统待恢复负荷总量为5 061 MW;根据待恢复系统规模设定恢复总时步数为20,恢复步长为15 min,每时步最大恢复线路数量为4条;元件恢复层决策每时步启动一次,功率调度层滚动决策窗口长度为5个时步。
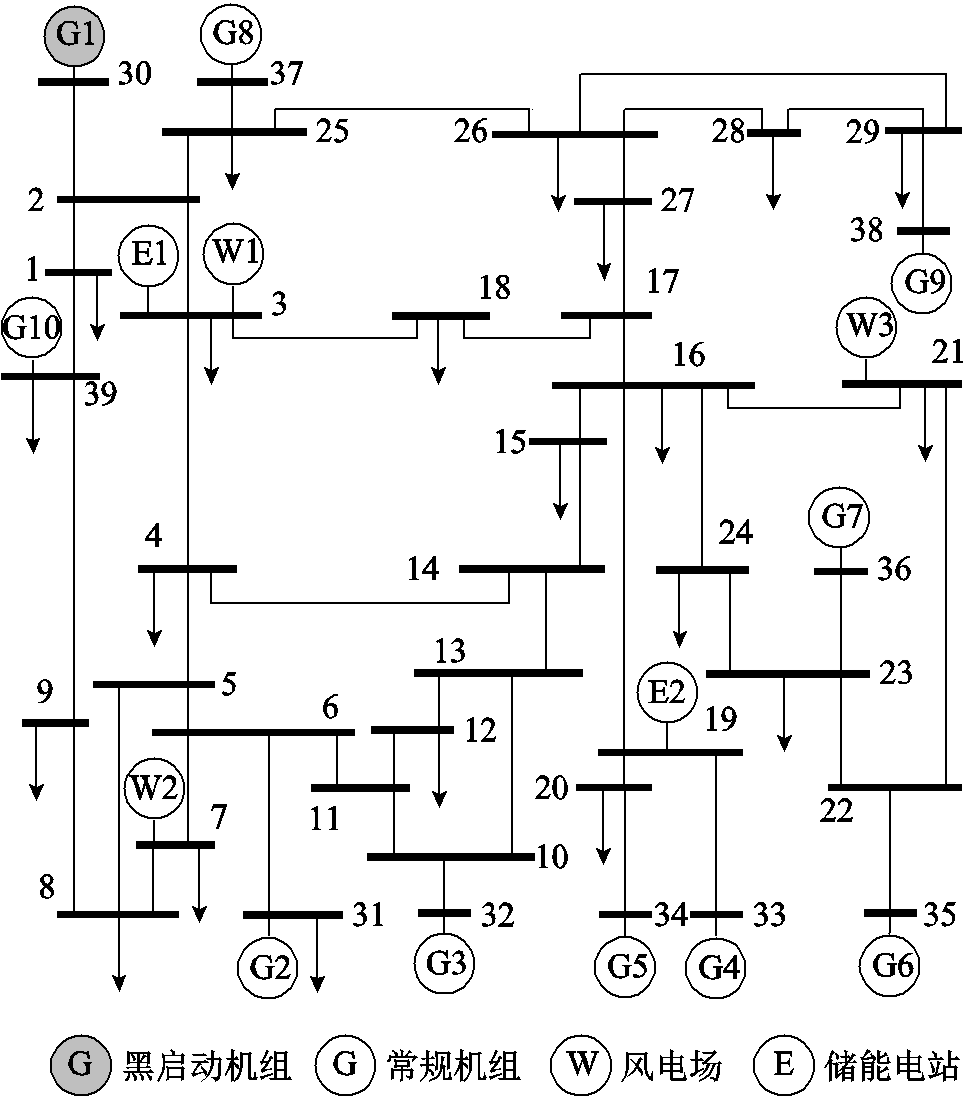
图5 算例1系统接线图
Fig.5 Wiring diagram of Case 1
4.1.2 优化结果与分析
采用本文提出的基于分层模型预测控制的电力系统恢复在线决策方法可得到修改的新英格兰39节点系统大停电后的恢复方案。
为分析滚动优化对元件恢复次序决策的影响,对比基于恢复初期预测数据离线优化和本文所提在线滚动优化两种决策方式下得到的元件恢复次序,见表1。
表1 算例1的元件恢复次序
Tab.1 Component restoration sequence in Case 1

时步恢复机组编号恢复线路编号 离线优化滚动优化离线优化滚动优化 1———— 2G1G155 3W1W11,3,41,3,4 4——2,6,7,402,6,7,41
(续)

时步恢复机组编号恢复线路编号 离线优化滚动优化离线优化滚动优化 5——8,30,41,448,9,30,40 6——10,26,4610,11,23,26 7W2W312,14,27,2814,19,27,28 8W3W213,32,33,3515,20,33,35 9——18,34,36,3722,36,37,44 10G4, G10G4, G8, G109,20,29,3912,32,39,46 11G8—19,23,24,3817,31,34,43 12G9—11,15,21,2213,18,24,25 13G2G216,42,43,4516,29,38,42 14—G317,25,3121,45 15G5, G6G6—— 16G3, G7G7, G9—— 17—G5——
从表1可以看出,两种决策方式下得到的元件恢复次序存在明显区别。通过分析风电预测数据可以发现,第1时步对风电出力做出的预测,低估了W3的有功出力水平,高估了W2的有功出力水平,因此,选择在第7时步恢复W2,在第8时步恢复W3。虽然对于恢复初期的预测数据,所得到的元件恢复次序是最优解,但是由于风电预测误差,此时的最优在时序上是相对的。在滚动优化过程中,基于修正后误差更小的预测数据,在第7时步优先恢复W3,对恢复路径和传统机组启动时间也进行了调整,推迟了G5、G9的启动时间,提前了G3、G8的启动时间。由此可以说明,相较于基于恢复初期的风电预测结果制定离线恢复预案,本文所提方法采用滚动优化决策可以弱化风电出力不确定性的影响,跟随不断更新、精度变高的风电预测数据,动态地调整元件恢复方案以取得更好的恢复效果。
负荷恢复量是衡量系统恢复效率的重要指标,选择两种系统恢复决策方法对比说明本文所提方法在恢复负荷效率时的优越性。为便于对比,将采用本文所提基于分层模型预测控制的在线决策方法确定的恢复方案命名为方案1。方案2和方案3为对比方案,其中方案2为采用传统模型预测控制[22]、基于有限时域窗口滚动策略优化的恢复方案;方案3为基于恢复初始时刻预测数据、采用鲁棒优化方法得到的恢复方案。图6和表2分别对比了三个方案各时步的负荷恢复总量和全过程总恢复电量。
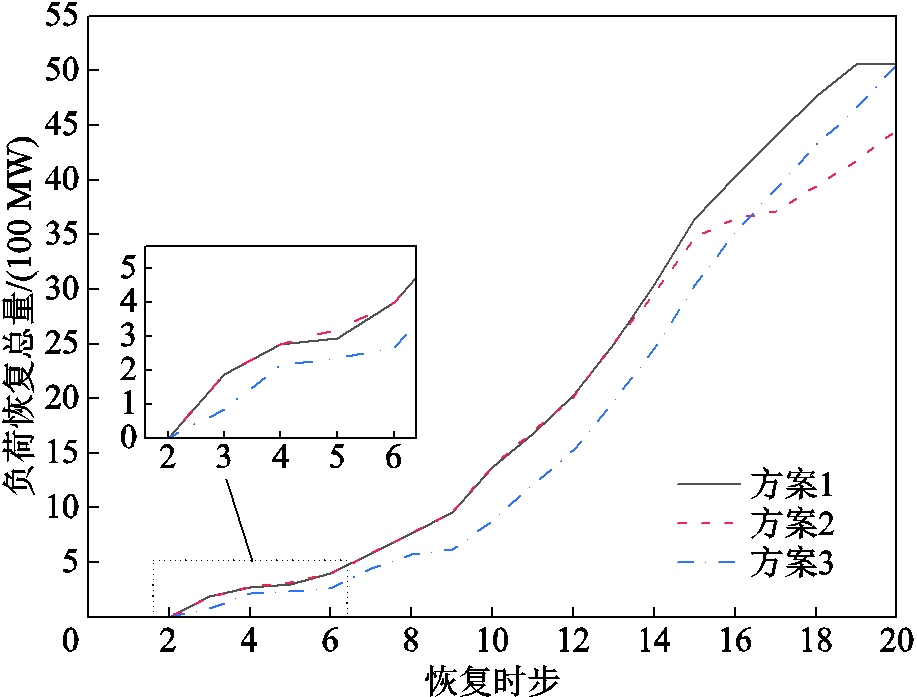
图6 算例1的负荷恢复总量
Fig.6 Total load restoration amount in Case 1
表2 算例1的总恢复电量对比
Tab.2 Comparison of total eletric quantity in Case 1

恢复方案总恢复电量/(GW·h) 方案110.27 方案29.37 方案38.75
由图6和表2可以看出,方案1在第19时步末时,5 061 MW停电负荷已全部恢复,全过程恢复电量达到10.27 GW·h。方案2与方案1同为基于模型预测控制的恢复方案,但方案2采用有限时域窗口滚动策略,模型的前瞻性不足,在前期恢复决策中追求当前优化时域内局部最优,未考虑方案对滚动窗口后续恢复的影响,因此,虽然方案2在恢复初期的几个时步内的负荷恢复量略大于方案1,但后续恢复效率远低于方案1,第19时步累计恢复负荷仅有4 177 MW,第20时步时仍未完成系统恢复,总恢复电量为9.37 GW·h。方案3对恢复全过程统一决策,但由于恢复初始时刻预测远端的预测误差较大,为保证方案的鲁棒性,制定的恢复方案相对保守,大量灵活性资源被用作备用,第19时步累计恢复负荷4 655 MW,整体恢复效果也劣于方案1。对比可知,本文所提方法在负荷恢复效率方面具有一定的优势。
功率调度层的鲁棒恢复模型包含风电不确定预算。表3展示了调节风电不确定预算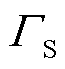 对结果的影响。从表3可以看出,当
对结果的影响。从表3可以看出,当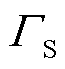 较小时,功率调度层制定的恢复方案鲁棒性较差,若实际风电出力能力不足,则会导致已恢复负荷再次被强制切除,增加停电损失。随着
较小时,功率调度层制定的恢复方案鲁棒性较差,若实际风电出力能力不足,则会导致已恢复负荷再次被强制切除,增加停电损失。随着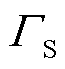 增加,恢复方案逐渐偏向保守,总恢复电量降低,被迫切负荷减小,反馈校正环节则需要更多的储能调度空间以吸纳计划外的风电资源。因此,在恢复决策过程中应根据实际风电预测误差情况选择合适的
增加,恢复方案逐渐偏向保守,总恢复电量降低,被迫切负荷减小,反馈校正环节则需要更多的储能调度空间以吸纳计划外的风电资源。因此,在恢复决策过程中应根据实际风电预测误差情况选择合适的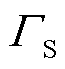 ,以取得更优的恢复效果。
,以取得更优的恢复效果。
表3 风电不确定预算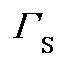 对恢复结果的影响
对恢复结果的影响
Tab.3 Influence of wind uncertain budget on restoration result

总恢复电量/(GW·h)被迫切负荷/MW校正环节累计储能调度量/MW 010.27525.1143.51 110.2685.4677.43 210.2660118.56 310.2600155.63
图7、图8分别展示了恢复过程中各个时步风电场和储能电站的出力情况。观察图7可以发现,风电场在第3、7、8时步依次接入电网。风电并网初期,由于系统恢复过程中转动惯量不足,在频率约束的限制下,无法完全用于恢复负荷,储能也不具备吸收所有剩余风电的能力,造成一定量的弃风;从第10时步开始,在充足的灵活性资源支撑下,风电均能以最大功率出力,未发生明显的弃风情况。观察图8可以发现,一方面,作为有初始荷电水平的有源场站,储能在大部分时步以放电状态运行为系统恢复提供功率支持;另一方面,作为灵活性资源,储能在风电接入初期以充电状态运行吸收多余功率,并在每个时步根据风电实际测量值实时调整充放电功率以实现功率平衡,恢复全过程未发生被迫切负荷的情况。以上结果可以说明,通过本文提出的滚动机制和反馈校正环节,可以减小风电出力不确定性对恢复方案的影响,进而降低对预留灵活性资源的需求,最大化风电和储能出力,加快系统恢复进程。
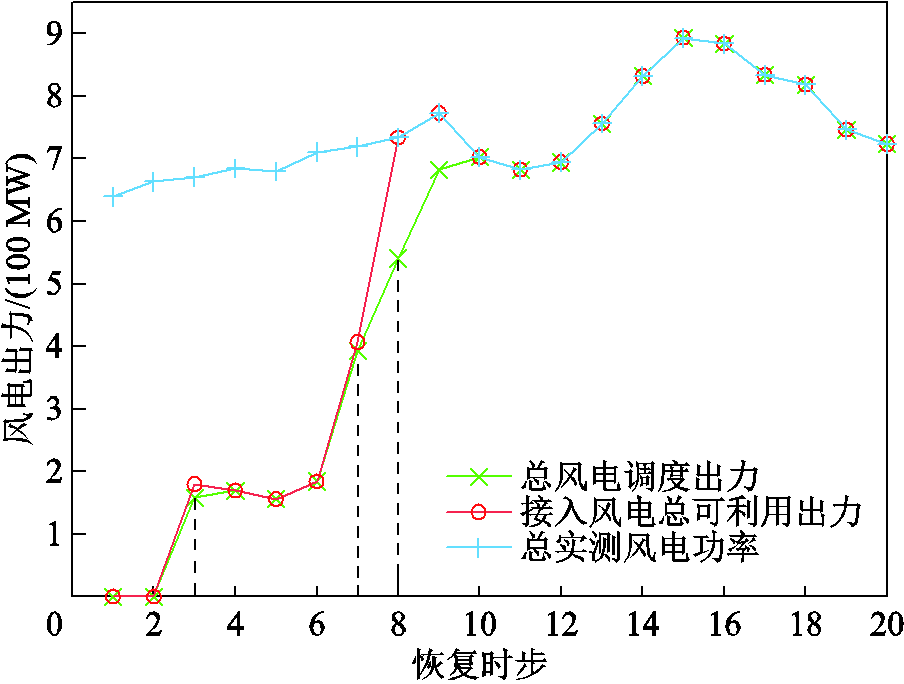
图7 算例1的风电场出力
Fig.7 Wind power output in Case 1
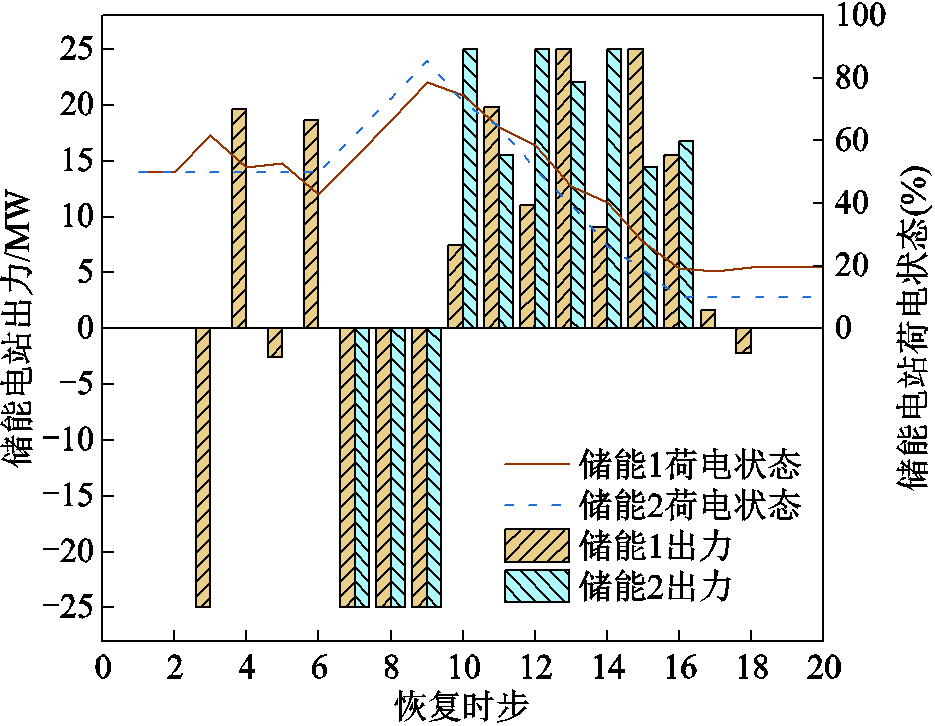
图8 算例1的储能电站状态
Fig.8 State of energy storage power station in Case 1
在模型求解速度方面,统计Gurobi求解器给出的求解时间,单次元件恢复层模型最长求解时间为53 s,单次功率调度层模型求解时间均小于1 s,单次反馈校正层模型求解时间均小于0.2 s,模型计算速度满足在线决策的要求。
4.2.1 参数设置
本文采用某省级电网的局部系统进行测试,进一步验证所提方法的有效性和实用性。该系统包含7台发电机组、62个节点、75条线路、5个风电场、2个储能电站,电网拓扑如附图4所示。假设大停电事故发生后系统处于全停状态;系统内所有机组、母线和线路等未遭到物理破坏,均具备可恢复能力。其中,JDC和JXT为黑启动机组,其他机组不具备黑启动能力,负荷权重均设为1,待恢复负荷总量为5 836 MW,设定恢复总时步数为20,恢复步长为15 min,每时步最大恢复线路数量为6条;元件恢复层决策每时步启动一次,功率调度层滚动决策窗口长度为5个时步。
4.2.2 优化结果与分析
采用本文提出的基于分层模型预测控制的电力系统恢复在线决策方法可得到实际系统大停电后的恢复方案。考虑风电预测数据更新滚动优化得到的元件恢复次序见表4。
表4 算例2的元件恢复次序
Tab.4 Component restoration sequence in Case 2

时步恢复机组恢复线路 1—— 2JXT, JDCJXT-JXT, JDC-JQY 3—JQY-JGD, JQY-JSC, JQY-JDC, JXT-JYF, JXT-JTH, JQY-JSB 4JGYJGD-JKY, JSC-JLQ, JSC-JGY, JDC-JGY, JYF-JSM, JTH-JSM
(续)

时步恢复机组恢复线路 5JSJJKY-JDC1, JGD-JCJ, JLQ-JNJ, JLQ-JQR, JSM-JSJ, JSM-JDC 6JXLJCJ-JDD, JCJ-JXL, JSB-JXG, JBY-JGY, JDC-JLY, JDC-JBZ 7JDC1JGD-JNJ, JCJ-JDT, JSB-JDT, JLY-JNG, JBZ-JGY, JSB-JXJ 8JQR, JLDJXJ-JDS, JXJ-JLF, JNG-JLD, JXJ-JLZ, JGY-JPC, JGY-JXN, 9—JCJ-JTH, JXL-JBJ, JLZ-JXJ, JLF-JZY, JPC-JGE, JLZ-JXB 10JGQJXG-JZQ22, JSC-JBY, JXJ-JLC, JNG-JXQ, JGY-JSZ, JGE-JGQ 11JXNJXG-JXL, JXG-JZQ21, JXJ-JLF, JDS-JGD, JNG-JJZ, JPC-JZH 12JXBJSC-JFC, JDS-JHF, JZY-JSL, JSZ-JJZ, JXQ-JHG, JLZ-JPC 13JLCJXJ-JGD, JHF-JYY, JLZ-JYY, JYF-JXC, JHG-JHY, JBX-JZH 14—JGY-JYD, JHY-JNJ, JPC-JHY, JNJ-JBX, JPC-JBX, JZH-JGE 15—JYY-JWZ
从表4可以看出,在第4~6、8、10时步,风电机组陆续并网出力;在第7、8、11~13时步,常规机组陆续开始爬坡出力;在第12时步,恢复JLZ-JPC线路,两个黑启动子系统并列运行;在第15时步,系统网架全部被恢复。
图9和图10展示了实际系统算例的负荷恢复总量和风电出力情况。可以看出,风电均能以较高的出力水平参与系统恢复过程,在第19时步时,5 836 MW停电负荷全部被恢复。
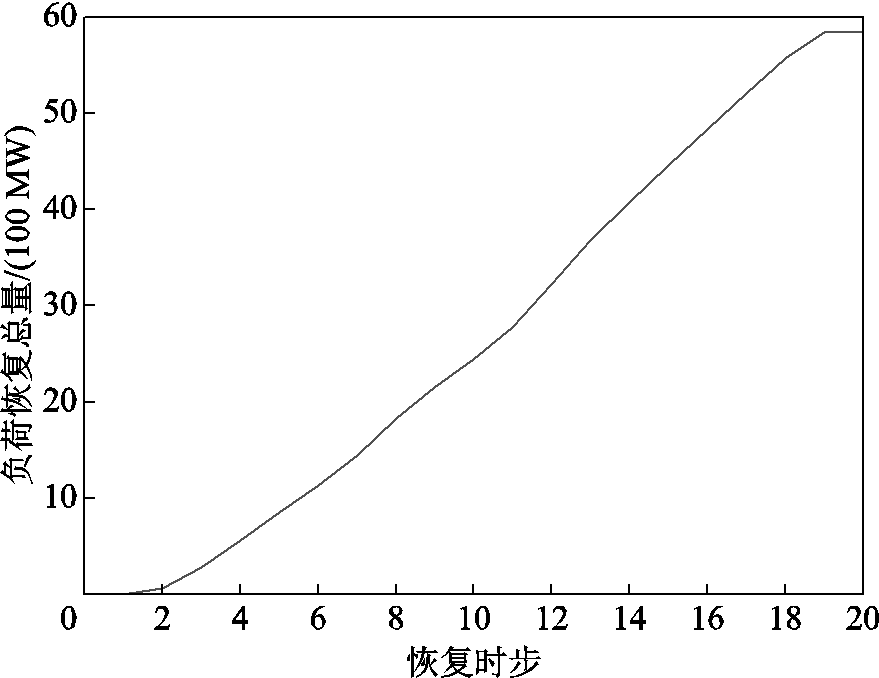
图9 算例2的负荷恢复总量
Fig.9 Total load restoration amount in Case 2
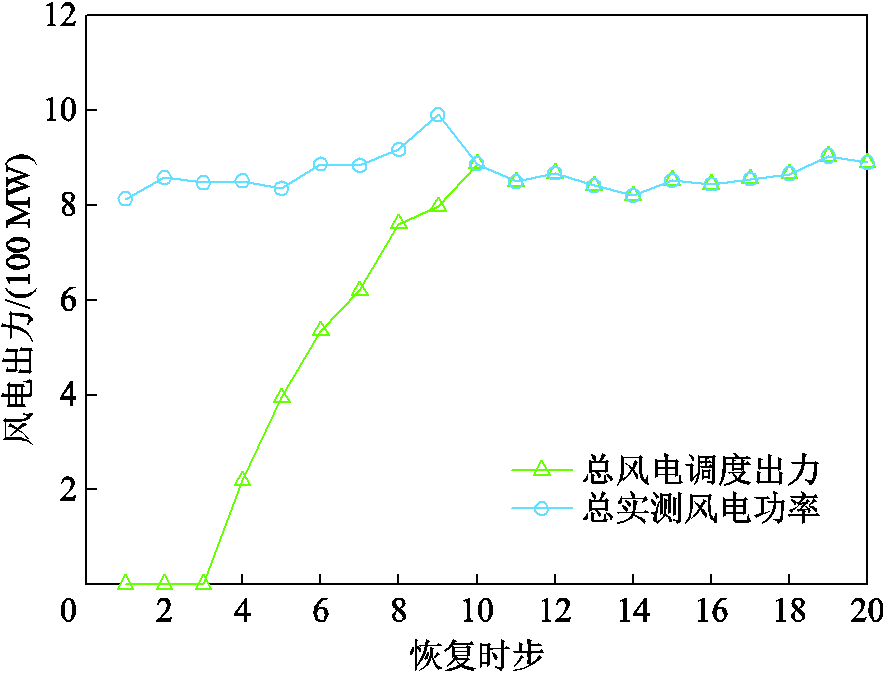
图10 算例2的风电出力
Fig.10 Wind power output in Case 2
在模型求解速度方面,单次元件恢复层最长求解时间为86 s,单次功率调度层最长求解时间均小于1 s,单次反馈校正层最长求解时间均小于0.2 s,模型求解速度满足实际系统在线决策的要求。
以上结果验证了所提方法支持含风电实际系统多黑启动电源并行协调恢复的可行性。
电力系统大停电事故发生后,合理地利用风电资源,跟踪风电预测数据在线制定恢复计划,对快速恢复系统运行以减少停电损失具有重要意义。本文提出了一种基于分层模型预测控制的含风电电力系统恢复在线决策方法。综合考虑全局恢复效率和模型求解速度,设计了分层滚动优化机制,建立了含风电电力系统恢复滚动优化模型。基于修改的新英格兰39节点系统和某实际系统的算例结果表明,本文所提方法能够为电力系统制定安全高效的恢复方案,与传统方法相比具有明显优势。基于本文研究可以得出以下结论:
1)在线滚动优化决策可以有效地应对风电出力的不确定性,跟踪不断更新、精度变高的风电预测数据,动态地调整元件恢复次序、机组出力计划和负荷恢复方案。
2)与传统模型预测控制追求局部最优相比,本文提出的分层模型预测控制采用上层前瞻到底、下层滑动时间窗口的双层滚动优化策略,能够在保证计算速度的同时兼顾恢复安全和全局恢复效率。
3)所提灵活性资源实时调度模型能充分发挥灵活性资源响应时间短的优势,在确保恢复过程系统功率平衡的同时最大化利用风电资源。
附录 仿真系统参数
附表1 修改的新英格兰39节点常规发电机组参数
App.Tab.1 Generator parameters of modified New England 39-bus
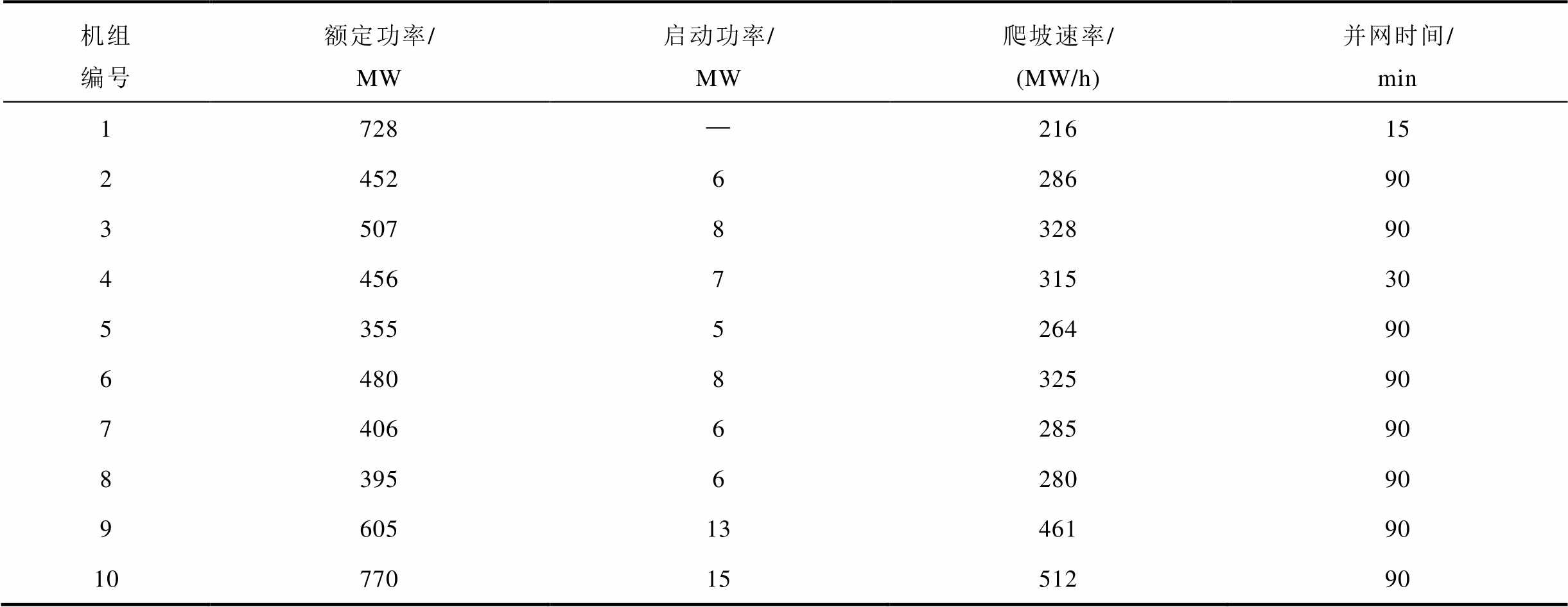
机组编号额定功率/MW启动功率/MW爬坡速率/(MW/h)并网时间/min 1728—21615 2452628690 3507832890 4456731530 5355526490 6480832590 7406628590 8395628090 96051346190 107701551290
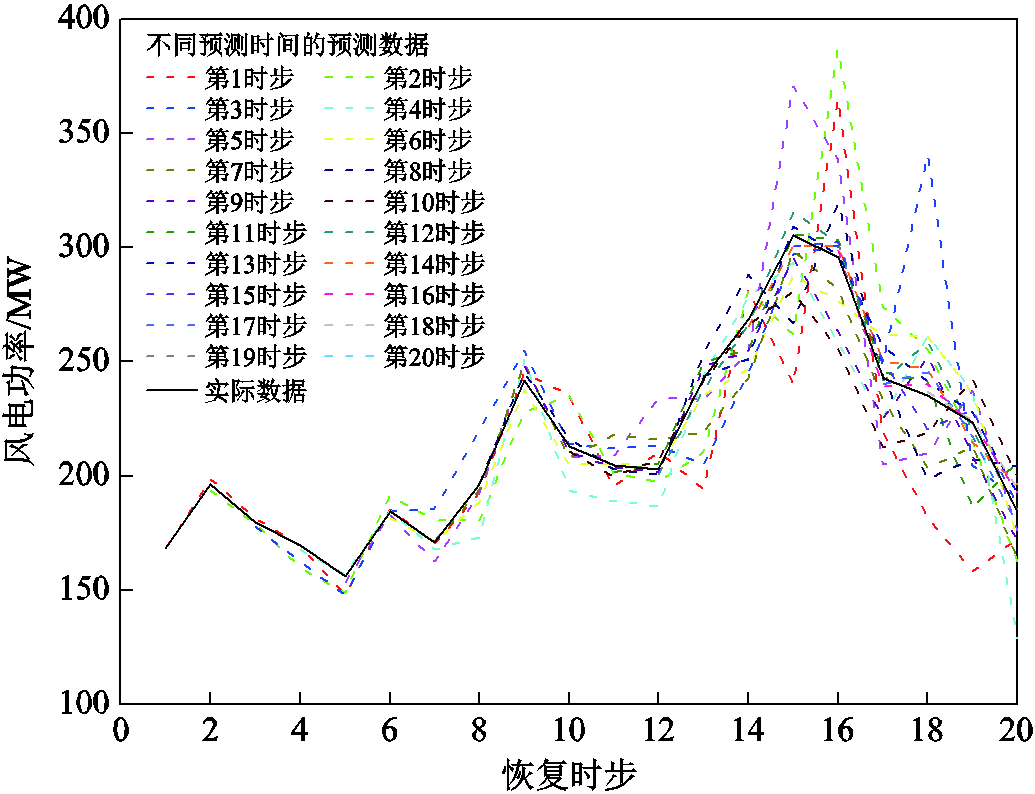
附图1 风电场1的滚动预测数据
App.Fig.1 Rolling forecast data of wind farm 1
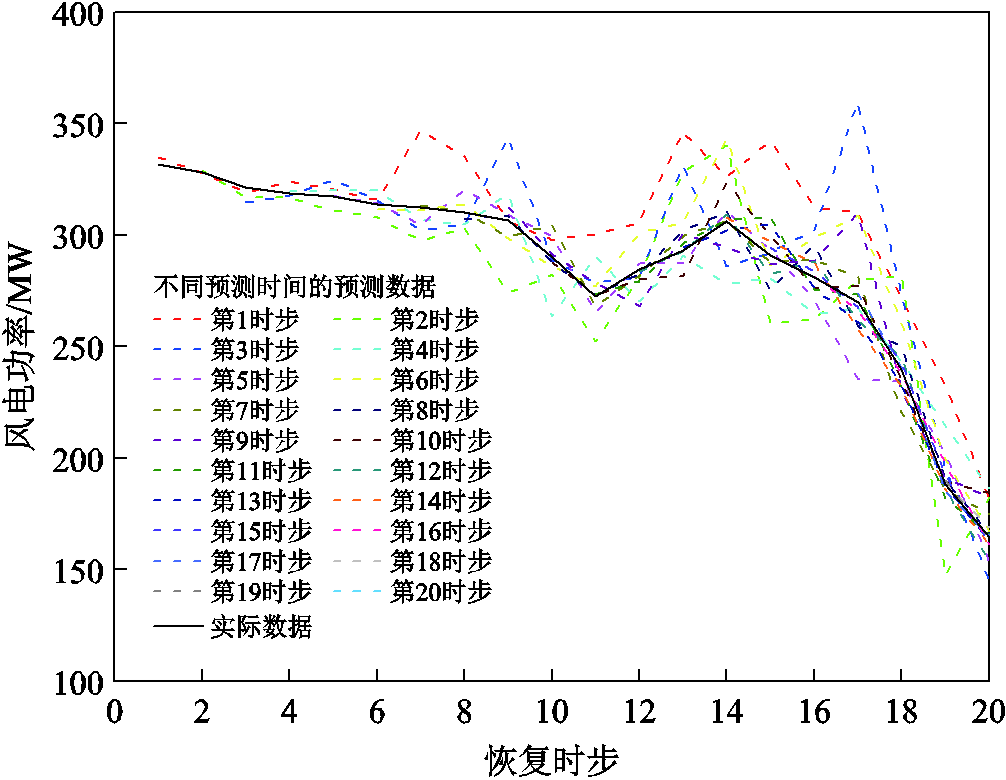
附图2 风电场2的滚动预测数据
App.Fig.2 Rolling forecast data of wind farm 2
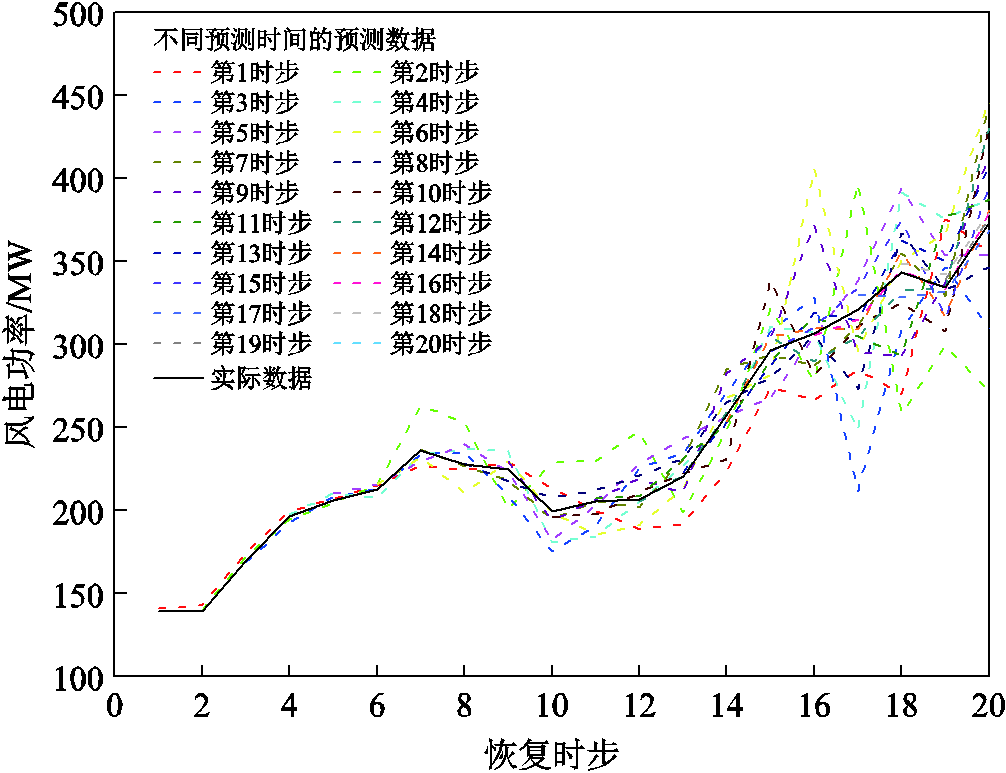
附图3 风电场3的滚动预测数据
App.Fig.3 Rolling forecast data of wind farm 3
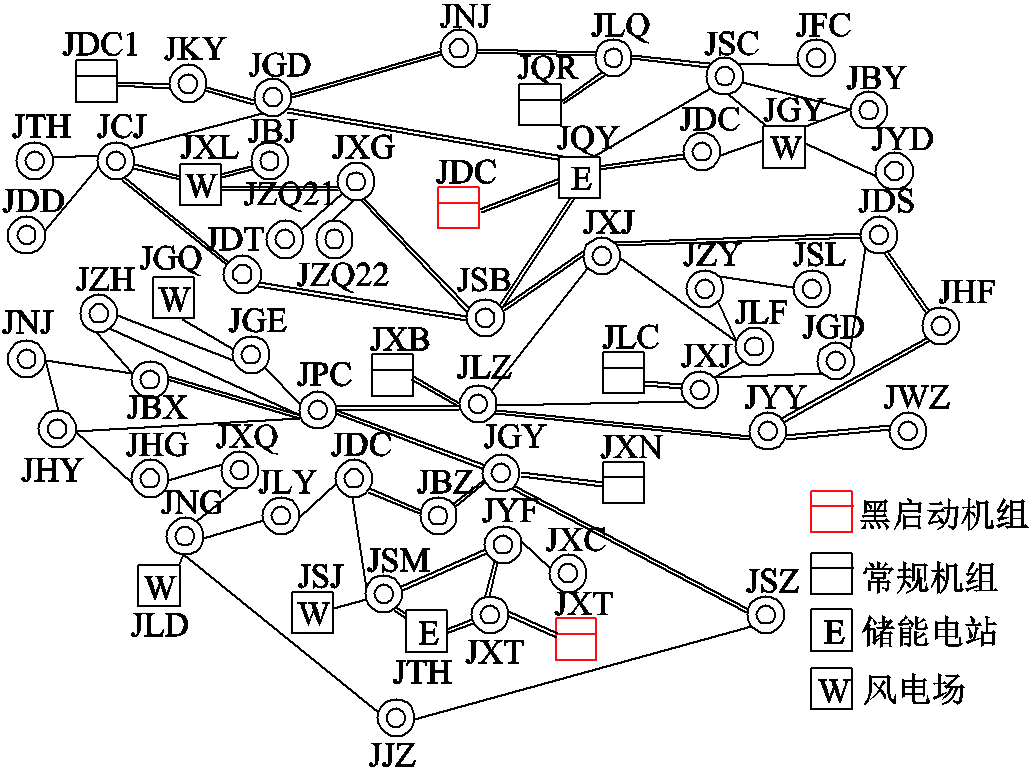
附图4 实际系统拓扑
App.Fig.4 Actual system topology
参考文献
[1] 辛保安, 李明节, 贺静波, 等. 新型电力系统安全防御体系探究[J]. 中国电机工程学报, 2023, 43(15): 5723-5731. Xin Baoan, Li Mingjie, He Jingbo, et al. Research on security defense system of new power system[J]. Proceedings of the CSEE, 2023, 43(15): 5723-5731.
[2] 孟荣涛, 李少岩, 顾雪平, 等. 光热电站作为黑启动电源时计及机组恢复效益的运行优化[J]. 电工技术学报, 2023, 38(13): 3486-3498. Meng Rongtao, Li Shaoyan, Gu Xueping, et al. Operation optimization considering unit recovery effect when concentrating solar power station acts as black-start power source[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3486-3498.
[3] 曾辉, 孙峰, 李铁, 等. 澳大利亚“9·28”大停电事故分析及对中国启示[J]. 电力系统自动化, 2017, 41(13): 1-6. Zeng Hui, Sun Feng, Li Tie, et al. Analysis of “9·28” blackout in South Australia and its enlightenment to China[J]. Automation of Electric Power Systems, 2017, 41(13): 1-6.
[4] 易俊, 卜广全, 郭强, 等. 巴西“3·21”大停电事故分析及对中国电网的启示[J]. 电力系统自动化, 2019, 43(2): 1-6. Yi Jun, Bu Guangquan, Guo Qiang, et al. Analysis on blackout in Brazilian power grid on March 21, 2018 and its enlightenment to power grid in China[J]. Automation of Electric Power Systems, 2019, 43(2): 1-6.
[5] 严道波, 文劲宇, 杜治, 等. 2021年得州大停电事故分析及其对电网规划管理的启示[J]. 电力系统保护与控制, 2021, 49(9): 121-128. Yan Daobo, Wen Jinyu, Du Zhi, et al. Analysis of Texas blackout in 2021 and its enlightenment to power system planning management[J]. Power System Protection and Control, 2021, 49(9): 121-128.
[6] 叶茂, 刘艳, 顾雪平, 等. 基于动态风电穿透功率极限的黑启动方案制定[J]. 中国电机工程学报, 2018, 38(3): 744-752. Ye Mao, Liu Yan, Gu Xueping, et al. Black start scheme formation considering dynamic wind power penetration limit[J]. Proceedings of the CSEE, 2018, 38(3): 744-752.
[7] 顾雪平, 白岩松, 李少岩, 等. 电力系统黑启动恢复问题的研究评述[J]. 电工技术学报, 2022, 37(13): 3183-3200. Gu Xueping, Bai Yansong, Li Shaoyan, et al. Research review of power system black-start restoration[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3183-3200.
[8] 张璨, 孙磊, 林振智, 等. 含风电场的电力系统最优网络重构策略[J]. 电力系统及其自动化学报, 2016, 28(2): 22-29. Zhang Can, Sun Lei, Lin Zhenzhi, et al. Optimal network reconfiguration strategy for power systems with integrated wind farms[J]. Proceedings of the CSU-EPSA, 2016, 28(2): 22-29.
[9] 荣俊杰, 周明, 李庚银. 考虑动态频率安全的风电参与负荷恢复优化调度[J]. 电网技术, 2022, 46(4): 1335-1345. Rong Junjie, Zhou Ming, Li Gengyin. Optimal dispatch of wind power participating in load restoration considering dynamic frequency security[J]. Power System Technology, 2022, 46(4): 1335-1345.
[10] 韩讴竹, 陈志铭, 丁涛, 等. 计及风电不确定性的电力系统黑启动恢复模型[J]. 电网技术, 2023, 47(8): 3289-3301. Han Ouzhu, Chen Zhiming, Ding Tao, et al. Power system black-start restoration model considering wind power uncertainties[J]. Power System Technology, 2023, 47(8): 3289-3301.
[11] 刘力卿, 杜平, 万玉良, 等. 储能型风电场作为局域电网黑启动电源的可行性探讨[J]. 电力系统自动化, 2016, 40(21): 210-216. Liu Liqing, Du Ping, Wan Yuliang, et al. Feasibility discussion on using storage-based wind farm as black-start power source in local power grid[J]. Automation of Electric Power Systems, 2016, 40(21): 210-216.
[12] 闫来清, 曹丽源, 薛太林, 等. 风电场黑启动储能容量优化配置: 一种考虑储能运行策略的方法[J]. 电力系统保护与控制, 2022, 50(16): 131-139. Yan Laiqing, Cao Liyuan, Xue Tailin, et al. Optimal configuration of wind farm black start energy storage capacity: a method considering energy storage operation strategy[J]. Power System Protection and Control, 2022, 50(16): 131-139.
[13] 刘艳, 季晨阳, 马艺瑄, 等. 基于生产可能性边界的含规模风电电力系统网架重构策略[J]. 电网技术, 2022, 46(8): 2986-2995. Liu Yan, Ji Chenyang, Ma Yixuan, et al. Production-possibility frontier-based network reconfiguration strategy for power system integrated with scaled wind farm[J]. Power System Technology, 2022, 46(8): 2986-2995.
[14] 赵瑾, 王洪涛, 曹曦. 计及风电条件风险价值的负荷恢复双层优化[J]. 中国电机工程学报, 2017, 37(18): 5275-5285. Zhao Jin, Wang Hongtao, Cao Xi. Bi-level optimization of load restoration considering the conditional value at risk of wind power[J]. Proceedings of the CSEE, 2017, 37(18): 5275-5285.
[15] Golshani A, Sun Wei, Zhou Qun, et al. Incorporating wind energy in power system restoration planning[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 16-28.
[16] 顾雪平, 白岩松, 李少岩, 等. 考虑风电不确定性的电力系统恢复全过程两阶段鲁棒优化方法[J]. 电工技术学报, 2022, 37(21): 5462-5477. Gu Xueping, Bai Yansong, Li Shaoyan, et al. Two stage robust optimization method for the whole-process power system restoration considering wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5462-5477.
[17] 王扬, 赵书强, 徐岩, 等. 基于机会约束目标规划的风火储系统滚动调度[J]. 电网技术, 2017, 41(1): 192-199. Wang Yang, Zhao Shuqiang, Xu Yan, et al. Rolling dispatch of wind/thermal/storage system based on chance constrained goal programming[J]. Power System Technology, 2017, 41(1): 192-199.
[18] 叶林, 李智, 孙舶皓, 等. 基于随机预测控制理论和功率波动相关性的风电集群优化调度[J]. 中国电机工程学报, 2018, 38(11): 3172-3183. Ye Lin, Li Zhi, Sun Bohao, et al. Optimal dispatch of system integrated wind farm clusters based on stochastic model predictive control considering temporal correlation of wind power[J]. Proceedings of the CSEE, 2018, 38(11): 3172-3183.
[19] 刘立阳, 吴军基, 孟绍良. 基于预测控制的含风电滚动优化调度[J]. 电工技术学报, 2017, 32(17): 75-83. Liu Liyang, Wu Junji, Meng Shaoliang. A rolling dispatch model for wind power integrated power system based on predictive control[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 75-83.
[20] 叶林, 路朋, 赵永宁, 等. 含风电电力系统有功功率模型预测控制方法综述[J]. 中国电机工程学报, 2021, 41(18): 6181-6197. Ye Lin, Lu Peng, Zhao Yongning, et al. Review of model predictive control for power system with large-scale wind power grid-connected[J]. Proceedings of the CSEE, 2021, 41(18): 6181-6197.
[21] 李军徽, 尤宏飞, 李翠萍, 等. 基于模型预测控制的风光储黑启动功率协调策略[J]. 电网技术, 2020, 44(10): 3700-3708. Li Junhui, You Hongfei, Li Cuiping, et al. Power coordination strategy based on model predictive control for black start with PV-wind-battery system[J]. Power System Technology, 2020, 44(10): 3700-3708.
[22] 谢云云, 杨正婷, 蔡胜, 等. 基于鲁棒模型预测控制的配电网供电恢复策略[J]. 电力系统自动化, 2021, 45(23): 123-131. Xie Yunyun, Yang Zhengting, Cai Sheng, et al. Power supply restoration strategy for distribution network based on robust model prediction control[J]. Automation of Electric Power Systems, 2021, 45(23): 123-131.
[23] 李少岩, 曹珂, 顾雪平, 等. 多直流馈入受端系统与直流联络线协调恢复的一体化建模与求解[J]. 电工技术学报, 2023, 38(21): 5862-5877. Li Shaoyan, Cao Ke, Gu Xueping, et al. Integrated modeling and solution for coordinated restoration of multi-infeed receiving-end systems and HVDC Tie lines[J]. Transactions of China Electrotechnical Society, 2023, 38(21): 5862-5877.
[24] 国家能源局. 风电功率预测技术规定: NB/T 10205—2019[S]. 北京: 中国电力出版社, 2020.
[25] 刘玉田, 王洪涛, 叶华. 电力系统恢复理论与技术[M]. 北京: 科学出版社, 2014.
[26] 张伯明, 陈建华, 吴文传. 大规模风电接入电网的有功分层模型预测控制方法[J]. 电力系统自动化, 2014, 38(9): 6-14. Zhang Boming, Chen Jianhua, Wu Wenchuan. A hierarchical model predictive control method of active power for accommodating large-scale wind power integration[J]. Automation of Electric Power Systems, 2014, 38(9): 6-14.
[27] 伊昆明, 孙磊, 丁江, 等. 基于凸包理论的含风电电力系统负荷恢复方案优化[J]. 电力系统自动化, 2024, 48(5): 77-87. Yi Kunming, Sun Lei, Ding Jiang, et al. Load restoration scheme optimization for power system with wind power based on convex hull theory[J]. Automation of Electric Power Systems, 2024, 48(5): 77-87.
[28] Patsakis G, Rajan D, Aravena I, et al. Optimal black start allocation for power system restoration[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6766-6776.
[29] Yang Jingwei, Zhang Ning, Kang Chongqing, et al. A state-independent linear power flow model with accurate estimation of voltage magnitude[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3607-3617.
[30] 徐询, 谢丽蓉, 梁武星, 等. 考虑风电预测误差时序性及风电可信度的双层优化模型[J]. 电工技术学报, 2023, 38(6): 1620-1632, 1661. Xu Xun, Xie Lirong, Liang Wuxing, et al. Bi-level optimization model considering time series characteristic of wind power forecast error and wind power reliability[J]. Transactions of China Electro-technical Society, 2023, 38(6): 1620-1632, 1661.
[31] 林莉, 林雨露, 谭惠丹, 等. 计及SOC自恢复的混合储能平抑风电功率波动控制[J]. 电工技术学报, 2024, 39(3): 658-671. Lin Li, Lin Yulu, Tan Huidan, et al. Hybrid energy storage control with SOC self-recovery to smooth out wind power fluctuations[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 658-671.
[32] 李翠萍, 司文博, 李军徽, 等. 基于集合经验模态分解和多目标遗传算法的火-多储系统调频功率双层优化[J]. 电工技术学报, 2024, 39(7): 2017-2032. Li Cuiping, Si Wenbo, Li Junhui, et al. Two-layer optimization of frequency modulated power of thermal generation and multi-storage system based on ensemble empirical mode decomposition and multi-objective genetic algorithm[J]. Transactions of China Electrotechnical Society, 2024, 39(7): 2017-2032.
[33] Gu Xueping, Bai Yansong, Li Shaoyan, et al. An optimisation method of whole-process restoration decision-making of power systems considering disturbance-resisting ability of the restored network[J]. IET Generation, Transmission & Distribution, 2023, 17(7): 1638-1651.
[34] Wei Wei, Liu Feng, Mei Shengwei, et al. Two-level unit commitment and reserve level adjustment considering large-scale wind power integration[J]. International Transactions on Electrical Energy Systems, 2014, 24(12): 1726-1746.
Abstract Under the background of 'carbon peaking and carbon neutrality', the wind power penetration rate in the power system is constantly increasing, and the impact of wind turbine units on the power system restoration process after blackout is becoming more and more significant. Reasonably utilizing wind power resources can effectively accelerate the restoration process and reduce the blackout losses. However, the traditional power system restoration optimization methods only depend on the prediction data at the initial restoration stage, which have weak applicability to real-time conditions and are not suitable for the restoration scenario of high wind power proportion. To address the impact of wind power output uncertainty on the restoration process, this paper proposes an online rolling optimization method for power system restoration based on a hierarchical model predictive control framework.
Firstly, to meet various restoration decision-making requirements, a hierarchical control structure is employed to formulate the restoration task as a two-layer optimization model, where a rolling optimization strategy with two different rolling mechanisms is proposed based on dynamically updated wind power forecast information, to coordinate the foresight and information accuracy in rolling optimization for different decision objectives. Considering the aftereffect of the component restoration decision-making, the upper layer adopts the forward-to-the-end rolling mechanism to optimize the component restoration sequence within the entire restoration process. With the aim of maximizing the overall restoration efficiency, this layer utilizes the full-time wind power prediction data to determine the component restoration sequence. At the lower layer, based on the component restoration sequence determined by the upper layer, taking into account the practical scenario where the accuracy of wind power forecasts decreases with increase of the lead time, a sliding time window rolling mechanism is employed for decision-making in both generator output planning and load restoration planning. It takes the subsequent finite time step as the optimization domain to ensure the accuracy of the prediction information within the decision domain, avoiding direct impact of the remote prediction errors on power scheduling schemes. Meanwhile, this layer reserves enough adjustment space for feedback correction link. Then, in the feedback correction link, based on the measured wind power data, a real-time scheduling model of flexible resources such as energy storage is established and the wind power prediction is corrected. Finally, the proposed method is verified in the modified New England 39-bus system and a real power system.
The results indicate that the method can formulate a safe and efficient restoration scheme for the wind power integrated power system. The following conclusions can be drawn from the simulation analysis: (1) The online rolling optimization decision can track the continuously updated wind power forecast data with increasing accuracy to adjust the component restoration sequence, generator output plans, and load restoration schemes dynamically. (2) Compared to the traditional model predictive control, the hierarchical model predictive control which employs the rolling optimization strategy in this paper, can improve the restoration efficiency of the whole process while ensuring the calculation speed and restoration safety. (3) The real-time scheduling models of the flexible resources can not only fully leverage the rapid response advantage of the flexible resources to ensure system power balance during the restoration process but also improve the utilization rate of the wind power resources.
Keywords:Model predictive control, blackout, wind power uncertainty, rolling mechanism, online restoration, real-time correction
DOI: 10.19595/j.cnki.1000-6753.tces.240331
中图分类号:TM732
国家自然科学基金资助项目(U22B2099)。
收稿日期 2024-03-03
改稿日期 2024-05-07
顾雪平 男,1964年生,教授,博士生导师,研究方向为电力系统安全稳定评估与控制、电力系统安全防御与恢复控制、智能技术在电力系统中的应用等。E-mail:xpgu@ncepu.edu.cn
李少岩 男,1989年生,副教授,硕士生导师,研究方向为电力系统安全防御和恢复控制、电力系统韧性评估与主动提升、人工智能及规划数学在电力系统中的应用等。E-mail:shaoyan.li@ncepu.edu.cn(通信作者)
(编辑 李 冰)