为配置在换流站出口处的限流电抗器，M、N、P、Q为线路各端的直流母线；l1～l4为直流输电线路长度，R1～R8为配置于线路两端的保护装置。f1～f4为线路上的故障位置，其中f1为区内前半段故障；f2为区内后半段故障；f3为正向区外故障；f4为反向区外故障。规定正方向为母线指向线路。摘要 对于多端柔性直流电网而言，当限流电抗器集中配置在换流站出口时，基于边界元件特性的暂态量保护方案难以适用。针对此问题，该文首先通过分析故障电流行波的传输特性，构造了兼具幅值与方向特征的复合暂态能量；其次，通过定性分析不同位置故障时线路两端故障电流波形特征，明确了区内外故障时线路两端复合暂态能量的差异；在此基础上，为进一步提高区内故障时保护的灵敏性以及区外故障时保护的可靠性，通过构造校正函数自适应调整制动量幅值，提出了一种基于复合暂态能量的多端柔性直流电网自适应差动保护方案；最后， PSCAD /EMTDC仿真结果表明，所提自适应差动保护方案在不同故障条件下均能可靠地识别区内外故障，且其具有较好的耐受过渡电阻以及抗噪声干扰能力。
关键词：多端柔性直流电网 电流行波 复合暂态能量 制动量校正函数 自适应差动保护
近年来，基于模块化多电平换流器（Modular Multilevel Converter, MMC）的柔性直流输电技术得到了快速发展[1-2]。柔性直流输电具有控制灵活、电能质量好、无需滤波装置等优势[3]，是目前的研究热点之一。然而相较于传统的高压直流输电系统，柔性直流输电系统阻尼小，系统发生故障后，直流侧故障电流迅速上升，其在几ms内可能达到换流器电力电子器件的耐受上限[4]，这对故障的快速识别提出了更高的要求。
暂态量保护动作速度快，能够满足柔性直流输电系统对于保护速动性的要求。按照是否依赖边界元件进行划分，现有柔性直流输电线路保护方法可分为两类。在基于边界元件的保护原理中，文献[5]利用限流电抗器对高频分量的阻滞作用，构造了基于高频暂态能量的单端量保护方案，然而该方案耐过渡电阻能力较弱。对此，文献[6-7]分别提出了利用高低频能量比、极波信息熵构造暂态量保护方案，提高了方案的可靠性。文献[8]提出了基于限流电抗器两端暂态电压比值的纵联方向保护，能够保护线路全长。上述保护原理只适用于限流电抗器配置在线路两端的拓扑结构，但从提升经济性角度出发，限流电抗器集中配置在换流站出口更具优势[9]，因此需要研究不依赖边界元件的保护方案。
在不依赖边界元件的保护原理中，文献[10]根据零模行波与线模行波到达保护安装处的时间差构造了测距式单端保护方案，然而该方案在区内末端存在死区。文献[11]通过分析区内外故障时前行波与反行波波形差异，构造了基于波形相关系数的纵联保护方案，然而该方案计算较为复杂。文献[12]依据行波的传输不变性构造了行波差动保护方案，然而行波差动保护需实时传输每一个采样时刻的电压量与电流量，对系统的通信要求高。文献[13]提出基于电流行波的极性比较式保护方案，然而该方案依赖首波头的准确捕获，当噪声干扰较强时，数据波动较大，首波头极性容易误判。
针对上述问题，本文首先通过分析故障电流行波的传输特性，构造兼具幅值与方向特征的复合暂态能量；其次，通过定量分析不同位置故障时线路两端故障电流的波形特征，明确了区内外故障时线路两端复合暂态能量的差异；在此基础上，利用校正函数自适应调整制动量幅值，进而提出了基于复合暂态能量的柔性直流输电线路自适应差动保护方案；最后，大量的PSCAD/EMTDC的仿真结果表明，本文所提自适应差动保护方案在不同故障条件下均能可靠地识别故障区段，具有较高的灵敏度。
限流电抗器集中配置在换流站出口的多端柔性直流电网的拓扑结构如图1所示。图中，为配置在换流站出口处的限流电抗器，M、N、P、Q为线路各端的直流母线；l1～l4为直流输电线路长度，R1～R8为配置于线路两端的保护装置。f1～f4为线路上的故障位置，其中f1为区内前半段故障；f2为区内后半段故障；f3为正向区外故障；f4为反向区外故障。规定正方向为母线指向线路。
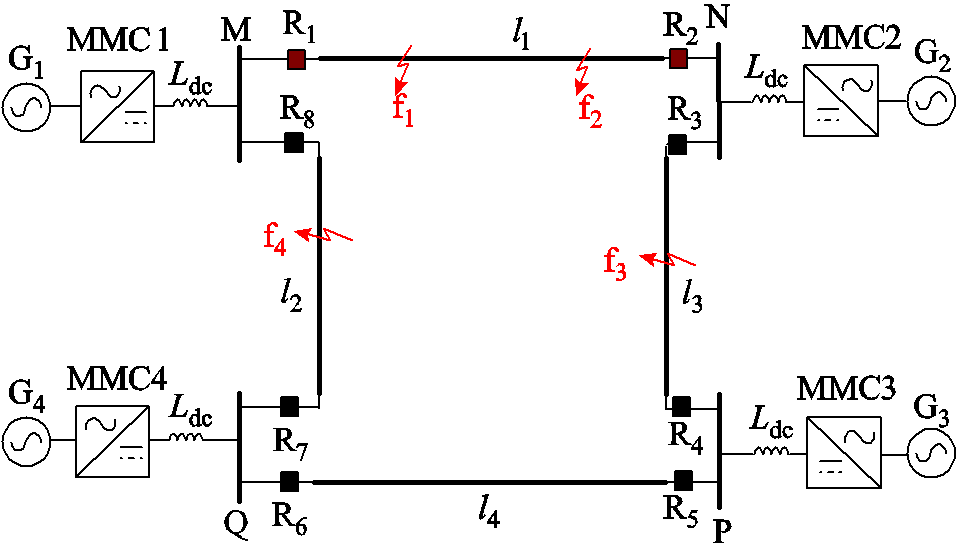
图1 多端柔性直流电网拓扑结构
Fig.1 Topological structure diagram of multi-terminal flexible DC power grid
由于行波仅与故障分量网络有关，因此下文分析仅在故障分量网络展开。考虑到直流输电线路正负极间存在耦合，可利用凯伦贝尔变换[14]对其进行解耦，解耦公式为
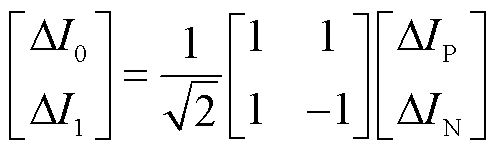（1）
式中，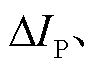
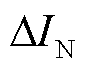分别为线路正负极对应的故障电流分量；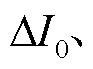
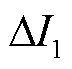分别为解耦后得到的零模电流与线模电流。由于线模分量受频率变化影响小，衰减较为微弱，因此本文选取线模分量作为分析对象。
故障初始阶段，MMC换流站的控制策略未发生改变，因此故障网络可看成一个线性系统[15]。由叠加定理可知，输电线路发生故障后，故障点处相当于施加了一个等效电压源，由其产生的故障行波沿线路向两端传输[16]。区内故障时的故障附加网络如图2所示。
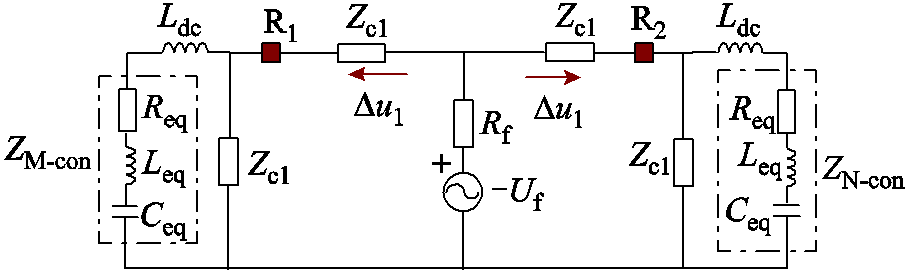
图2 区内故障时故障附加网络
Fig.2 Fault additional network of internal fault
图2中，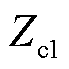
为线路线模波阻抗，
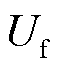为故障前故障点处额定电压，
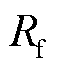为过渡电阻，
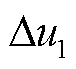为故障点处的初始电压行波，
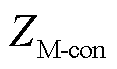与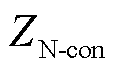
分别为M侧与N侧MMC的等效阻抗[17]，
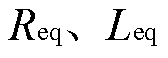和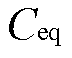
分别为MMC在子模块闭锁前的等效电阻、等效电感和等效电容。
以正极接地故障为例，故障点处线模初始电压行波的表达式[18]为
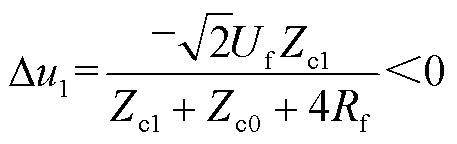（2）
式中，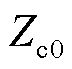
为线路的零模波阻抗。
行波为高频暂态信号，因此MMC的等效阻抗呈感性[19]，此时可忽略MMC等效电阻与电容的影响。根据彼得逊法则可知，母线M处行波折反射系数及其取值范围为
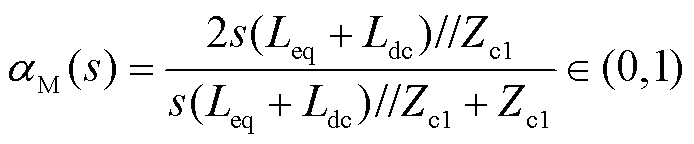（3）
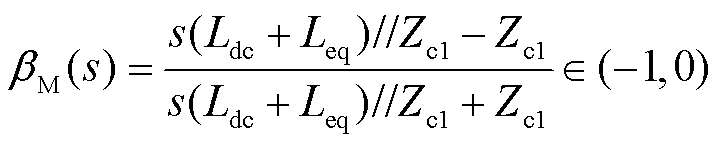（4）
鉴于多端柔性直流电网拓扑结构的对称性，其他母线处的折反射系数如式（3）、式（4）所示。同理，以单极接地故障为例，故障点处行波折反射系数及其取值范围[20]为
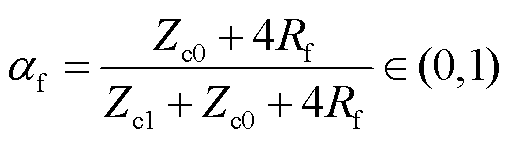（5）
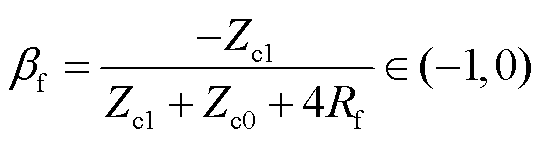（6）
现有暂态量保护方案主要利用不同频率分量经线路边界的幅值衰减差异[5-8]来构造保护判据，然而当限流电抗器集中配置在换流站出口时，本线与邻线间不存在明显的边界，此时区内外故障特征量的差异显著降低，基于故障分量幅值信息的保护方案可能存在不适用情况。
故障暂态信号中蕴含着丰富的故障信息，为解决利用单一幅值信息在无边界电网结构中适用性显著降低的问题，本文构造一种兼具幅值与方向特征的复合暂态能量，其定义为
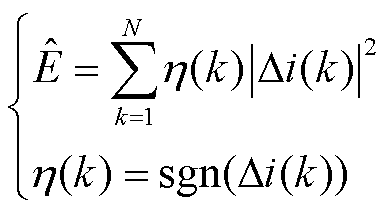（7）
式中，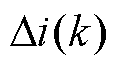
为线路故障电流分量；N为采样点数；
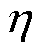为单个采样时刻故障电流极性；
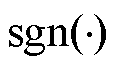为符号函数。
对于柔性直流电网，线路两端故障电流极性在区内外故障时存在显著差异。在此基础上，以正负极性作为方向特征的纵联保护被提出，但其存在一定的缺陷[21]。从波过程角度来看，故障电流可以看成首行波以及后续折反射波按一定时序的叠加[22]。由于行波折反射过程受故障位置与系统拓扑结构影响而呈现较为复杂的变化规律，因此暂态电流的波动特征也具有随机性，考虑到高阻或高噪的影响，直接根据正负值识别故障区域较为困难。
相较于直接利用电流方向特征，本文通过构造式（7）所示复合暂态能量对故障后线路两侧暂态电流幅值以及方向特征进行统一描述，其本质上均由故障行波的折反射过程决定。为了进一步明确复合暂态能量幅值以及方向特征随行波传输的变化规律，下文将定性分析不同位置故障时复合暂态能量特征差异，为构造保护新原理提供理论依据。
2.2.1 区内故障
区内故障时行波折反射过程如图3所示。图中，x1与x2分别为故障点与M、N两端的距离；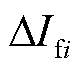
、
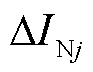分别为第i个来自故障点与第j个来自对端母线N的反射波；以首行波到达保护R1处的时间为零时刻，
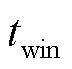为选定的时窗，分别考察上述不同行波信号作用下保护R1处故障电流的变化情况。考虑到线模分量的传输衰减较为微弱，为简化分析，下文分析过程中不考虑线路传输函数的影响。
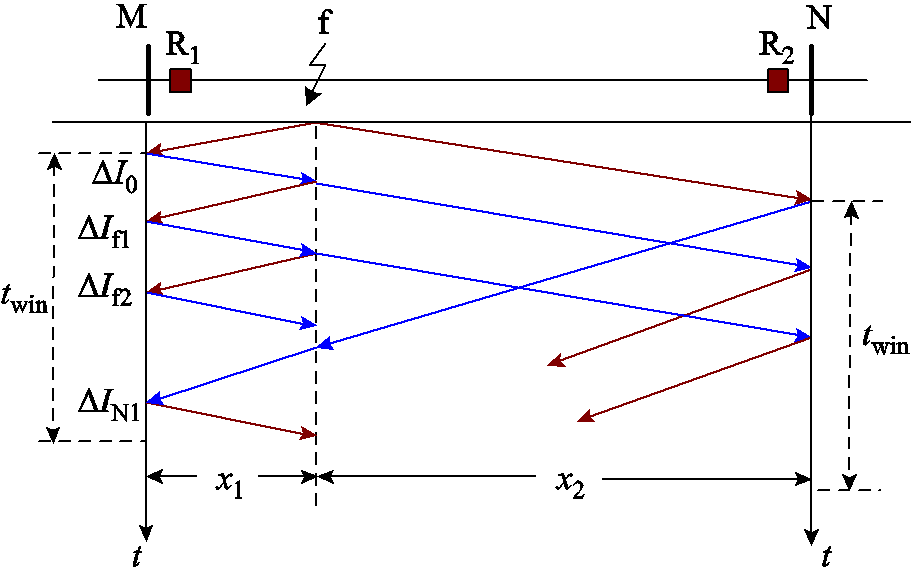
图3 区内故障时行波折反射过程
Fig.3 Refractive reflection process of traveling wave in case of internal fault
1）首行波
区内故障时保护R1检测到的首行波频域表达式如式（8）所示，对其进行拉氏反变换求得区内故障时首行波时域解析表达式如式（9）所示。考察其单调性，易知此时故障电流单调递增且恒大于零。
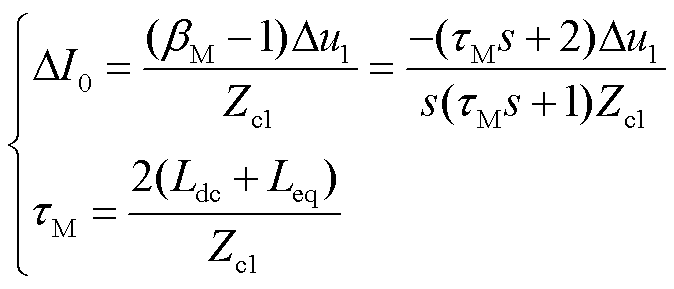（8）
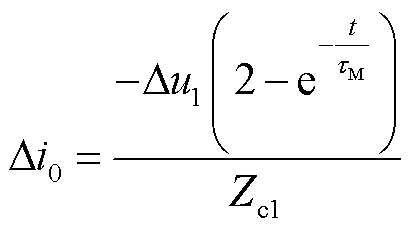（9）
2）故障点反射波
以首个来自故障点的反射波(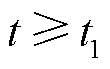
)为例进行分析，其频域表达式为
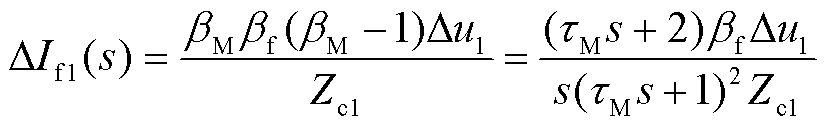（10）
对式（10）进行拉氏反变换，得到其时域表达式为
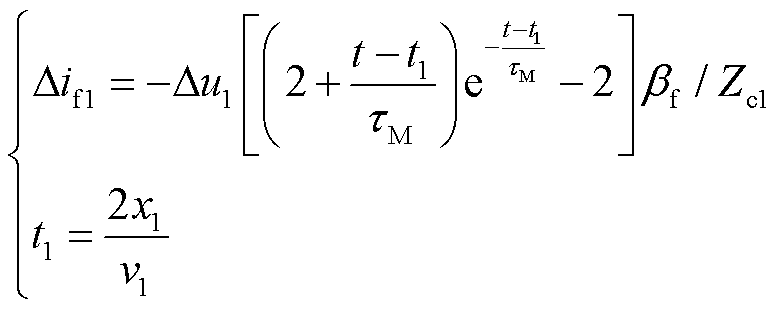（11）
式中，v1为线模行波在线路上的波速。
考察式（11）函数单调性，易知其在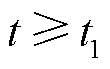时为增函数，因此在首个故障点反射波作用下，保护R1处故障电流持续增大。
3）对端母线N反射波
以首个来自对端母线N的反射波(
)为例进行分析，其频域表达式为
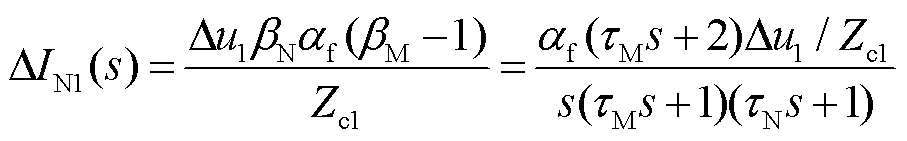（12）
考虑到线路结构具有对称性，故
。对式（12）进行拉式反变换，可得到其时域表达式为
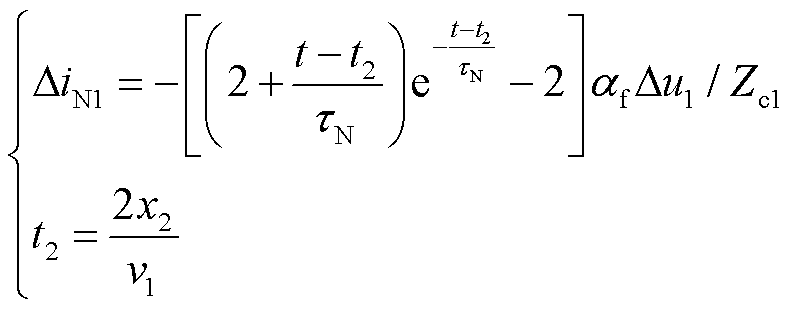（13）
考察式（13）单调特性，易知其在时为减函数，因此在首个来自对端母线N反射波作用下，保护R1处故障电流持续降低。
同理，当后续的故障点反射波与对端母线N反射波作用于保护R1时，可采用相同的方法进行分析，且首个故障点或对端母线反射波作用为主因。综上所述，来自故障点反射波将使保护R1处的故障电流增大，而来自对端母线反射波将使保护R1处的故障电流减小。观察图3行波折反射过程可知，随着故障距离增大，保护R1检测到的故障电流受到来自对端母线反射波影响逐渐加深，因此下文将以最严重情况，即区内末端故障为例进行讨论。
区内末端故障时行波的折反射过程如图4所示。考察此时保护R1处故障电流的极性特征。
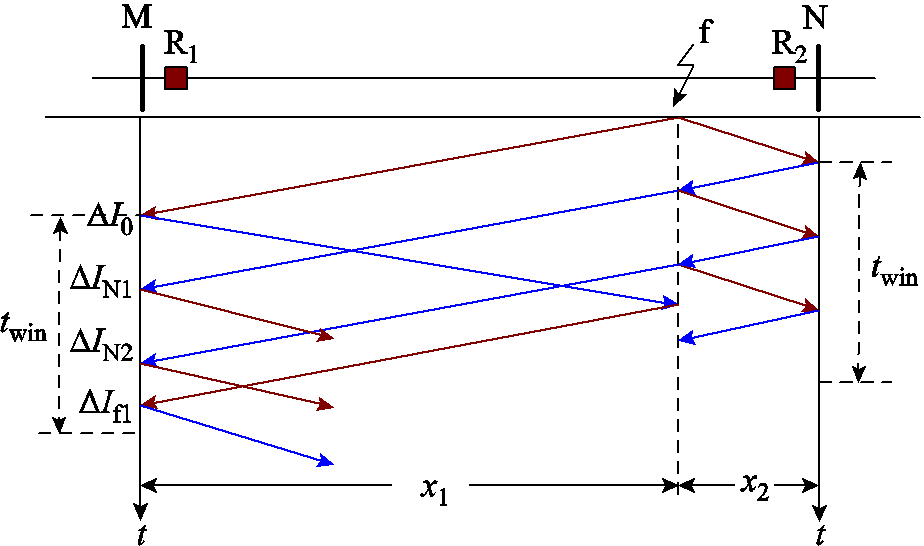
图4 区内末段故障时行波折反射过程
Fig.4 Refractive reflection process of traveling wave in case of remote-end internal fault
对于区内末端故障，行波在故障点与母线N间频繁折反射，此时保护R1处故障电流主要受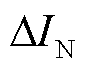作用，其在复频域下的表达式
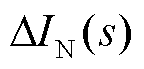可以表示为
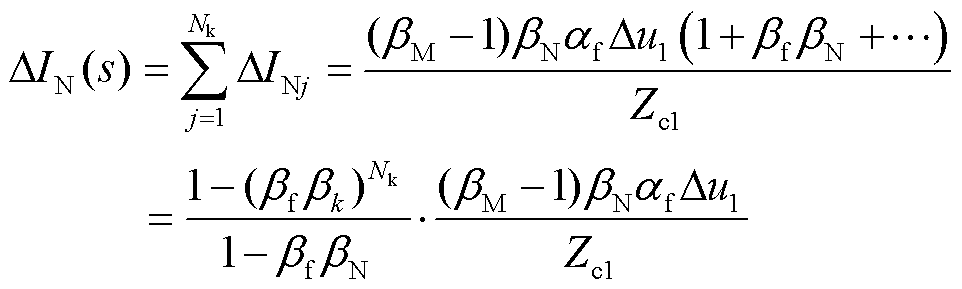（14）
式中，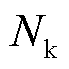
为对端母线反射波个数。将式（4）代入式（14）中，根据终值定理[23]求得在对端母线N反射波作用下故障电流的近似时域量为
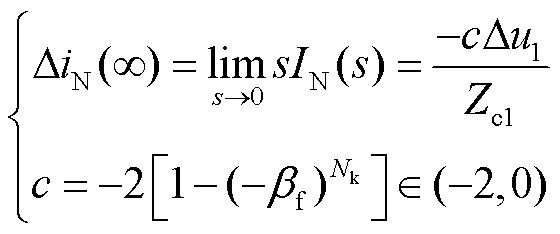（15）
观察式（9）可知，由于首行波在t趋向于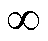
时的终值近似为
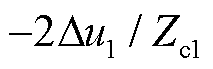，因此末端故障时对端母线N反射波作用下的故障电流终值可能出现接近于零的情况，但考虑到上文的假定条件为对端母线N反射波作用时间无限长，且忽略了行波在线路上的传输损耗，因此末端故障时，实际观测到的故障电流始终大于零。
当区内其他位置发生故障时，在有限时窗内，保护R1观测到的来自母线N反射波减少，而来自故障点的反射波增多，因此保护R1观测到的故障电流最小值必然大于区内末端故障时的最小值，由此可得出以下结论：当被保护线路内部发生故障时，故障电流始终为正极性，然而随着故障距离增大，对端母线反射波作用增强，保护R1处暂态电流幅值也相应较低。
需要注意的是，根据式（3）～式（6）行波折反射系数取值范围可知，来自母线Q或母线P的反射波与首行波极性相反。对于最为不利的区内末端高阻故障，当相邻线路末端反射波到达后，保护R1端观测到的故障电流可能会出现极性为负的情况，因此所选时间窗需排除该反射波干扰。
2.2.2 区外故障
正向区外故障时行波折反射过程如图5所示。在不考虑母线P反射波的影响下，分别对保护R1观测到的首行波以及故障点反射波的时域解析式进行分析。
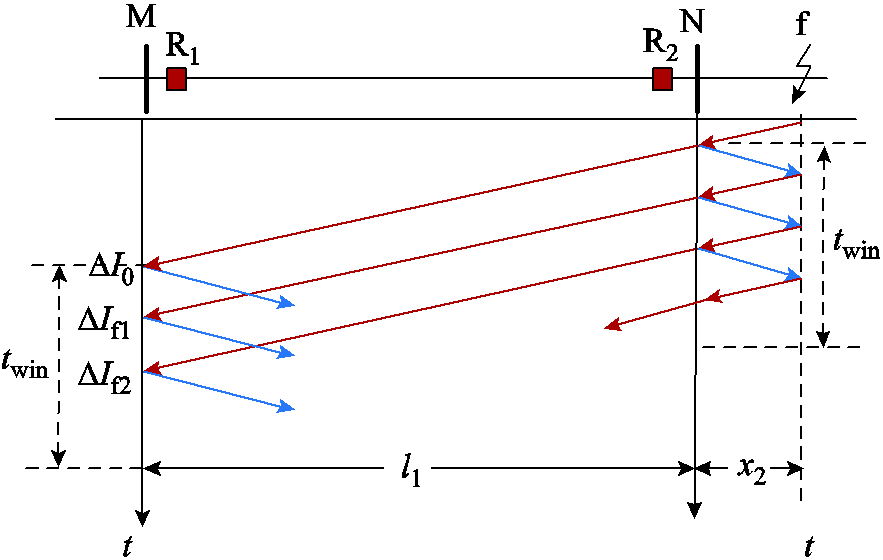
图5 正向区外故障行波折反射过程
Fig.5 Refractive reflection process of traveling wave in case of forward external fault
正向区外故障时，保护R1处观测到的首行波为N端母线的折射波，其频域表达式为
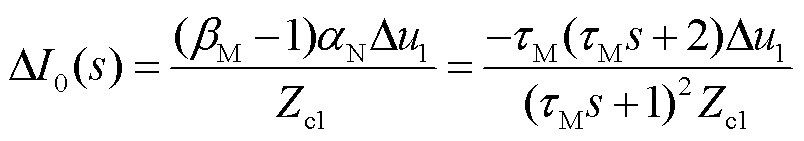（16）
对式（16）进行拉氏反变换，得到首行波的时域解析式为
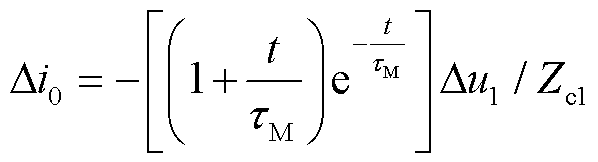（17）
由式（17）可知，保护R1处的故障电流呈单调递减特征，但故障电流始终为一正值。
正向区外故障时，以首个来自故障点的反射波为例，其频域表达式为
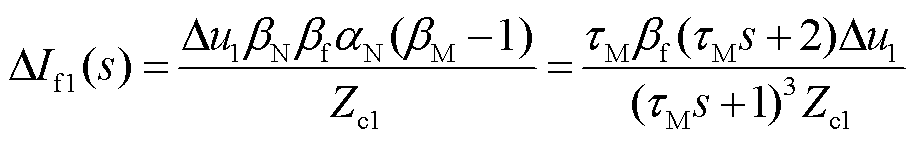（18）
对式（18）进行拉氏反变换，得到其时域解析式为
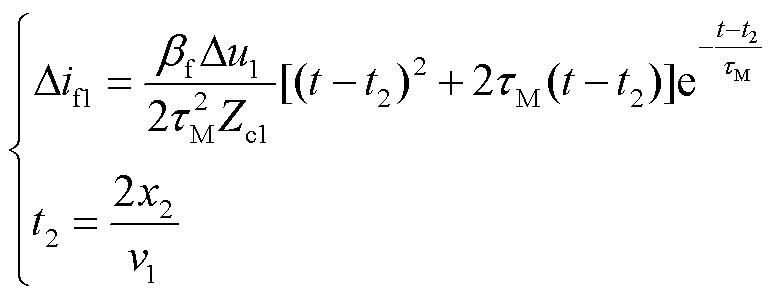（19）
根据式（19）可知，其存在极小值点，且大于零，因此故障点反射波持续时间内保护R1处的故障电流始终为一正值。以此类推，后续故障点反射波与首行波极性相同，故障电流始终为正极性。
当保护R1反方向发生故障时，结合上述分析可知，保护R1处观测到的故障电流始终为一负值。
综上所述，正方向发生故障时，保护R1处观测到的故障电流始终为正极性；反方向发生故障时，保护R1处观测到的故障电流始终为负极性，由于线路结构具有对称性，保护R2处同样满足上述结论。由此可知，本文所构造的复合暂态能量在选定时间窗内具有明确的方向属性。
为了更加直观地反映区内外故障时线路两端复合暂态能量的特征差异，绘制不同位置故障时复合暂态能量随时间变化曲线如图6、图7所示。结合上述分析，本文构建的复合暂态能量满足以下特征：区内故障时线路两端复合暂态能量同方向，且线路近端或远端发生故障时，其幅值差异最大，而当线路中点附近发生故障时，其幅值差异最小；区外故障时线路两端复合暂态能量方向相反，且其幅值差异较小。
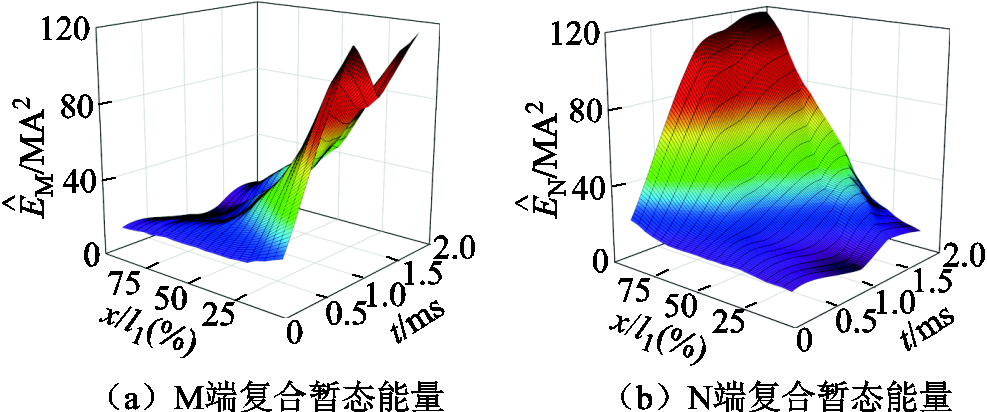
图6 区内故障时线路两端复合暂态能量变化曲线
Fig.6 Composite transient energy variation curves at both ends of the line during internal faults
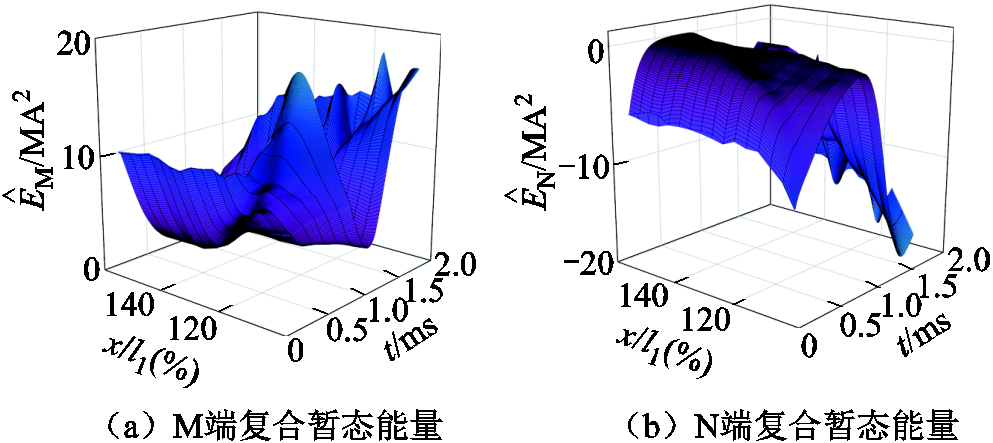
图7 区外故障时线路两端复合暂态能量变化曲线
Fig.7 Composite transient energy variation curve at both ends of the line during external faults
由2.2节分析可知，线路两端复合暂态能量在区内外故障时存在显著差异，据此可构造差动保护方案以有效识别故障区段。仿照传统比率制动式差动保护构造的保护判据为
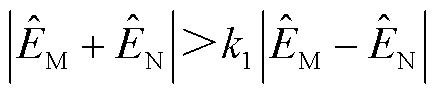（20）
式中，k1为制动系数。
根据式（20）可知，该保护判据的灵敏度系数ksen可表示为
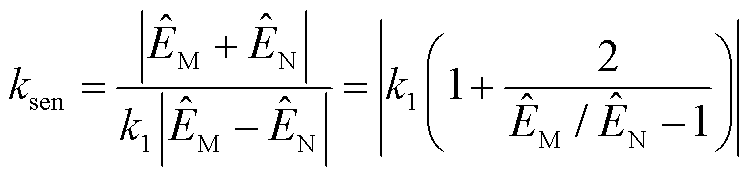（21）
根据图6可知，当线路中点附近故障时，线路两端复合暂态能量幅值相近，此时式（21）具有一定的灵敏度。然而当线路近端或末端故障时，考虑到该情况下线路两端复合暂态能量幅值差异较大，此时式（21）灵敏度较低。对此，本文在传统比率制动式差动保护基础上，通过引入自适应校正函数，构造了一种具有自适应能力的比率制动式差动保护。该方案能够显著提升区内故障时保护的灵敏性，并且兼顾区外故障时的可靠性，保护动作判据为
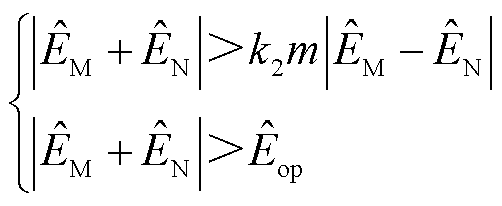（22）
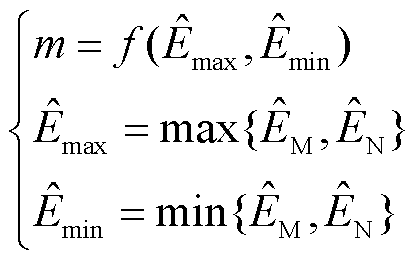（23）
式中，m为与
、
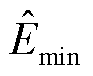有关的自适应制动量校正函数；
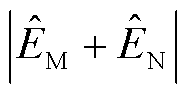为自适应差动保护动作量；
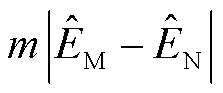为校正后的制动量；k2为自适应差动保护的制动系数；
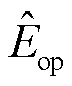为差动保护的动作门槛，用以避免正常运行或外部系统极弱情况下保护误动作。以系统正常运行时可能出现的最大不平衡电流为基准进行整定。
校正函数的设计需遵循以下原则：①对于区内故障，在不改变动作量的前提下，校正函数值应满足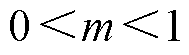
，且校正函数值应根据线路两侧复合暂态能量幅值比自适应调整。对于线路中点附近故障，校正函数取值应较大，而对于线路近端或末端故障，校正函数值应显著降低以提高保护灵敏性。②对于区外故障，为提高保护的安全性，校正函数值应满足
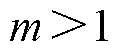，使得保护可靠不动作。③校正函数值需受过渡电阻变化影响小，使得保护方案适用于金属性故障或高阻故障等不同故障工况。
基于上述原则，本文设计的校正函数为
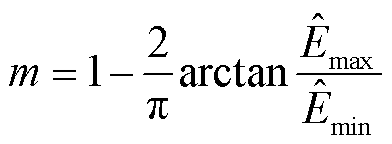（24）
自适应制动量校正函数的波形如图8所示。其中，校正函数值m位于阴影区段内。下文将对所设计的差动保护方案动作特性进行分析。
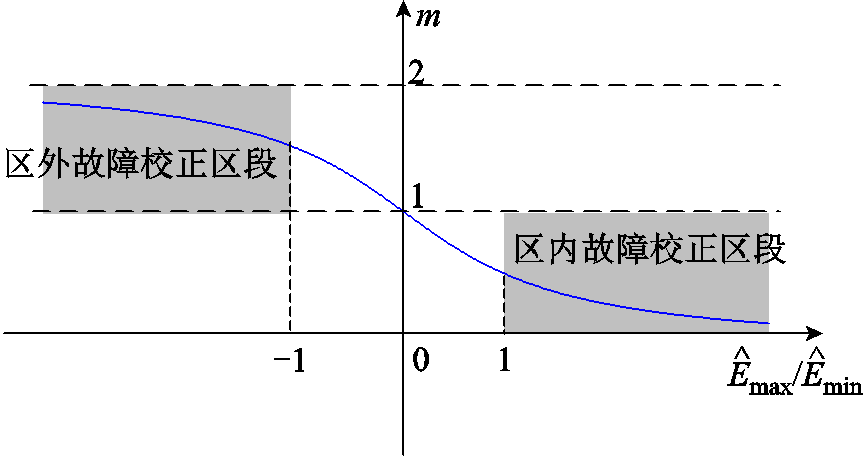
图8 自适应制动量校正函数波形
Fig.8 Adaptive restraining value correction function waveform
当系统正常运行时，故障附加网络中无能量流动，保护可靠不动作；观察图6a与图6b可知，发生区内故障时，线路两端复合暂态能量方向相同，然而当区内近端或末端发生故障时，线路两端复合暂态能量幅值差异较大；本文所构造的校正函数满足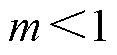
，且两端能量差值越大，校正函数值越低，可以有效地降低制动量幅值，提高区内故障时的灵敏性。当被保护线路外部发生故障时，由图7a与图7b可知，线路两端复合暂态能量方向相反，此时校正函数满足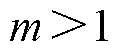，可以有效增大制动量，提升保护的可靠性。当外部系统较弱时，尽管此时故障暂态特征不明显，但本文所构造的复合暂态能量利用累加形式放大了单个采样时刻的方向以及幅值信息，因此本文所提保护方案对于弱系统仍具有较好的适应性。
对于式（22）中制动系数k2，参照传统比率制动式差动保护中制动系数的选取原则，通过故障仿真数据分析，本文选取k2=0.8。为方便对比分析，式（20）中制动系数k1也取为0.8。
线路发生故障后，线路两端检测到的故障电流发生突变，可利用其突变特征构造启动判据为
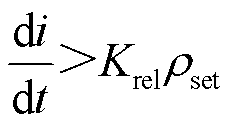（25）
式中，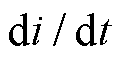
为电流变化率；
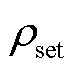为启动判据的门槛值，按照躲过区外高阻接地故障时的最大值进行整定；
为可靠系数，本文取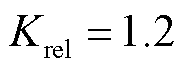
。
本文利用正负极电流故障分量能量比值实现故障选极[24-25]，其定义为
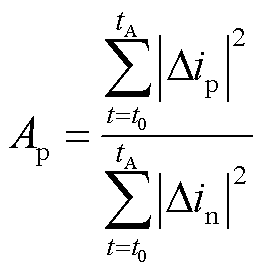（26）
式中，t0为保护启动时刻；tA为故障选极判据时间窗，本文选为0.2ms；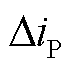
与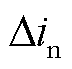
分别为正、负极故障电流，对应的选极判据为
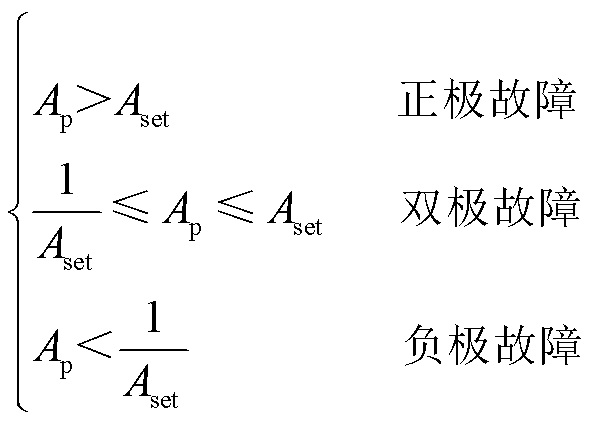（27）
式中，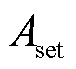
为设定的故障选极定值，考虑一定裕度，本文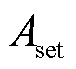=2。
3.4.1 雷击干扰问题
在实际的工程实践中，雷击干扰会对保护的可靠性产生影响。为防止雷击干扰造成的保护误动作，需构造雷击干扰识别判据。雷击干扰可以分为反击与绕击[26]。其中，反击为雷击杆塔或避雷线，而绕击为雷击输电线路。反击可通过线模分量的幅值进行区分[27]，本文主要针对雷电绕击的情况进行分析。
由文献[28]可知，雷击电流波在时域中表现为较窄的尖峰波，其幅值在达到波峰后不断衰减，若截取相同时间窗内前后两段电流波，则后半段时间窗内故障电流的能量远小于前半段时间窗内的能量。对于短路故障后的电流行波，其变化较为平缓，所以在μs级数据窗内，短路故障时的能量变化远不及雷击干扰剧烈。因此本文利用前后两段时间窗内复合暂态能量的比值作为雷击干扰识别判据。
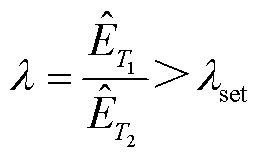（28）
式中，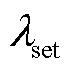
为雷击干扰的整定阈值，以区外末端故障为基准进行整定，T1=T2=50 μs。
3.4.2 时间窗选取
对于双端量保护而言，时间窗的选取需综合考虑信号通信延时以及换流器极限耐受时间。线路发生出口故障时，M端保护装置立即启动，而N端保护装置需等待初始行波传输延时才能感受到故障，保护的动作时序如图9所示，此时满足约束关系。
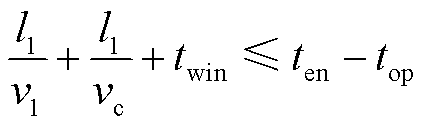（29）
式中，l1为柔直线路MN的长度；vc为信息在通道内的传输速度，v1=0.204 km/μs，vc=0.295 km/μs[29]；top为直流断路器动作时间，可取典型值2.5 ms；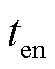
为换流器的极限耐受时间，工程中一般取6 ms。
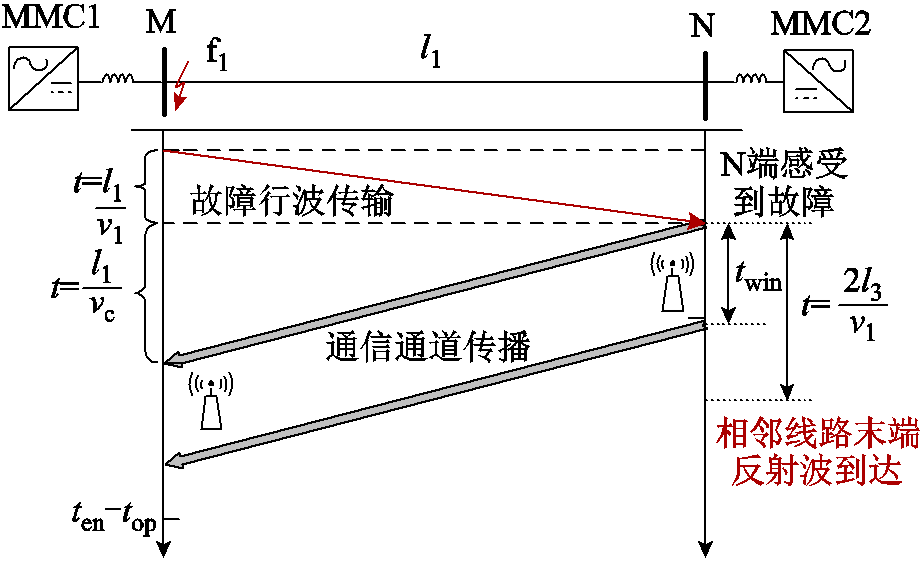
图9 线路出口故障动作时序
Fig.9 Action sequence diagram of fault at the line exit
结合2.2.1节分析可知，末端故障时相邻柔直线路反射波可能会对复合暂态能量方向特征产生影响，因此本文通过时间窗对其加以限制，结合上述分析，时间窗选取应同时满足
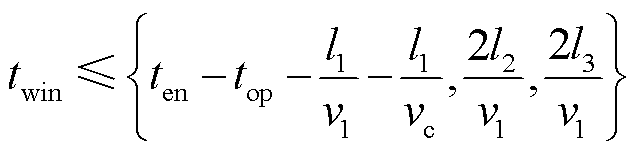（30）
根据式（30）约束关系，结合附表1中柔直线路参数，在考虑一定裕度的前提下，本文选取时间窗长为0.8 ms。
本文所提基于复合暂态能量的自适应差动保护方案流程如图10所示。保护启动后，分别计算T1与T2时间窗内的复合暂态能量比值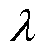
。当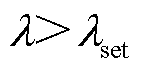
时，判断为雷击干扰；否则两端进行纵联通信，并且计算线路两端复合暂态能量差动量与制动量。若满足式（22）所示差动判据，则判断为区内故障，利用式（26）、式（27）进行故障选极，保护动作；否则判断为区外故障，保护不动作。
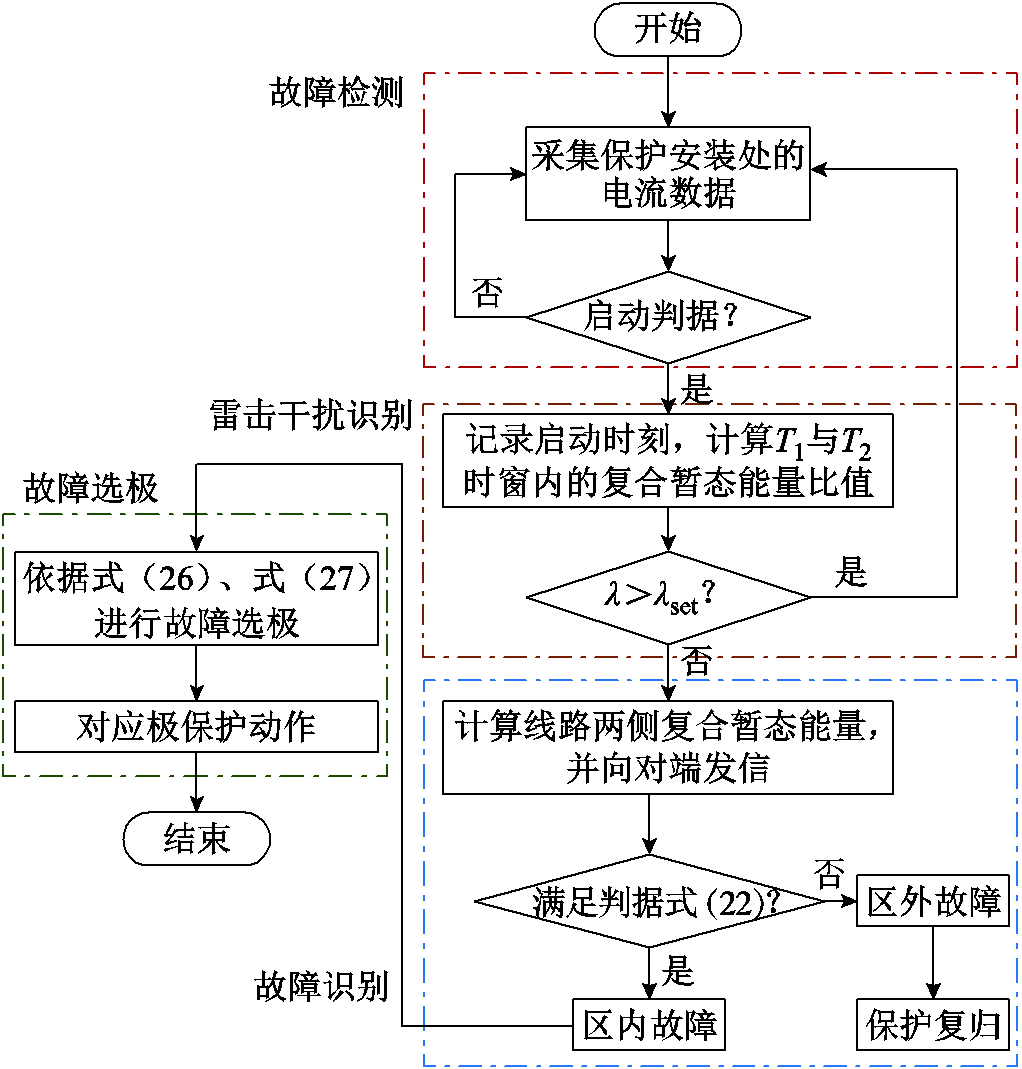
图10 保护方案流程
Fig.10 Flow chart of protection scheme
为验证本文所提基于复合暂态能量自适应差动保护方案的有效性，在 PSCAD/EMTDC仿真平台搭建图1所示的±400 kV四端柔性直流输电系统模型。所有换流站均采用半桥型MMC；柔性直流系统参数见附表1所示，线路采用频变参数模型，其杆塔结构如附图1所示。仿真采样率设置为50 kHz。
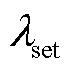整定为3.6 MA2，整定为2。
1）区内f1点故障
在被保护线路f1处设置过渡电阻为50 Ω的正极接地故障，故障点距离M端80 km，故障时刻为0.3 ms，绘制线路两端线模电流波形如图11所示。
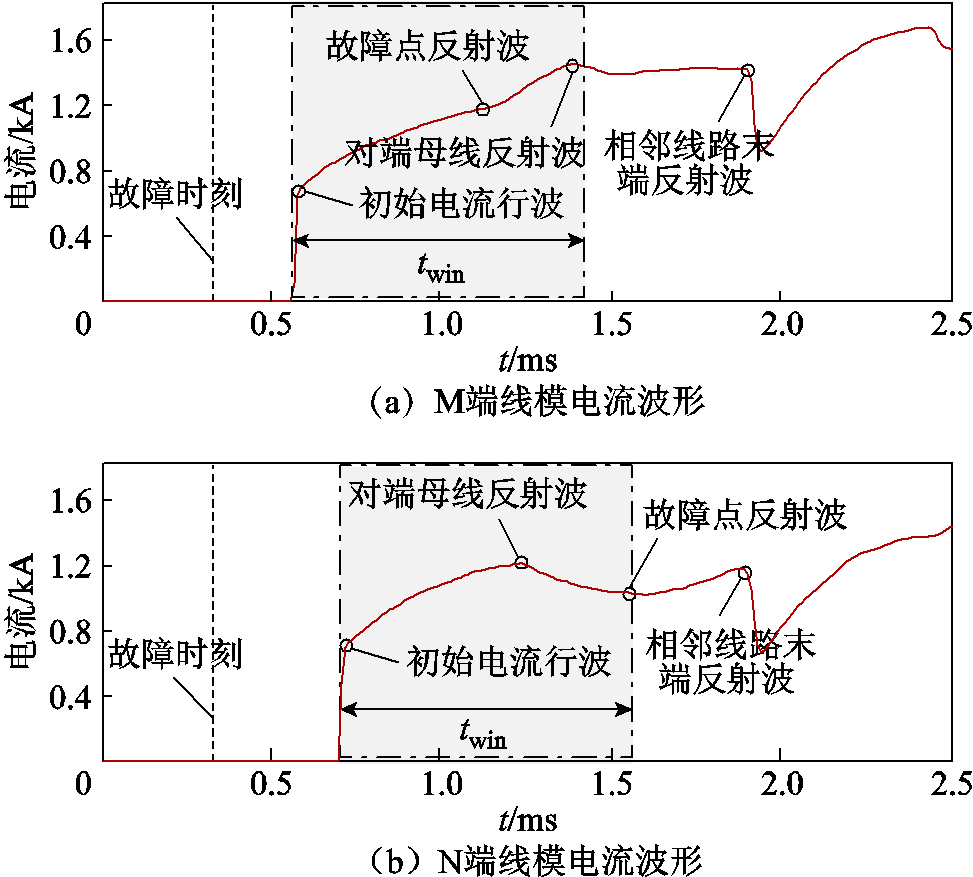
图11 区内f1故障时线路两端线模电流波形
Fig.11 Waveform of line mode current at both ends of the line during internal fault at f1
由图11a与图11b可知，故障发生后，电流行波分别经0.27 ms与0.4 ms传输至母线M与母线N，由于限流电抗器集中配置在MMC出口处，此时保护R1处故障电流会产生正的突变；随着时间的推移，流经MMC支路的行波能量逐渐增大，此时暂态电流缓慢上升。在故障点反射波作用下，M端故障电流单调递增；在对端母线反射波作用下，M端故障电流单调递减，故障电流波形变化趋势与2.2.1节理论分析相一致，且在选定的时间窗内，线路两端故障电流均为正极性。
为验证本文所提自适应差动保护方案的动作性能，依据式（23）、式（24）分别计算其动作量、制动量得到波形如图12a所示；绘制所提差动方案的灵敏度系数，得到其波形如图12b所示。
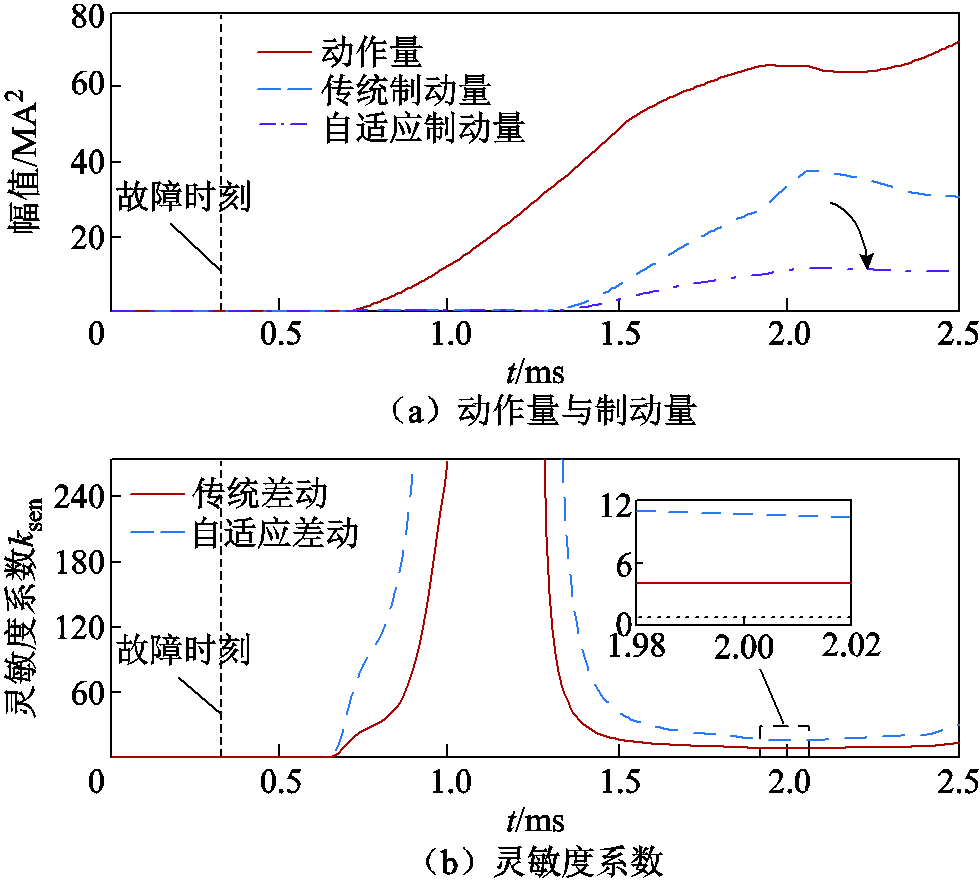
图12 区内f1故障时保护动作情况
Fig.12 Action situation during internal fault at f1
由图12a可知，区内故障时动作量都显著大于制动量，且本文所构造的自适应差动保护能有效降低制动量。观察图12b可知，传统差动保护制动系数和自适应差动制动系数尖峰均出现在M端故障点反射波到达时刻，这是由于首波头持续时间内，线路两端首行波波形与幅值相近；随着后续折反射波到达，线路两端故障电流的波形与幅值产生差异，此时的制动系数显著降低；对于本文所提自适应差动保护，自适应矫正函数m能够有效削弱制动量幅值，随着行波后续折反射过程变化，本文所提自适应差动保护灵敏性显著优于传统差动方案。
2）区内f2点故障
在被保护线路f2处设置过渡电阻为50 Ω的正极接地故障，故障点距离M端170 km，故障时刻为0.3 ms，绘制线路两端线模电流波形如图13所示。
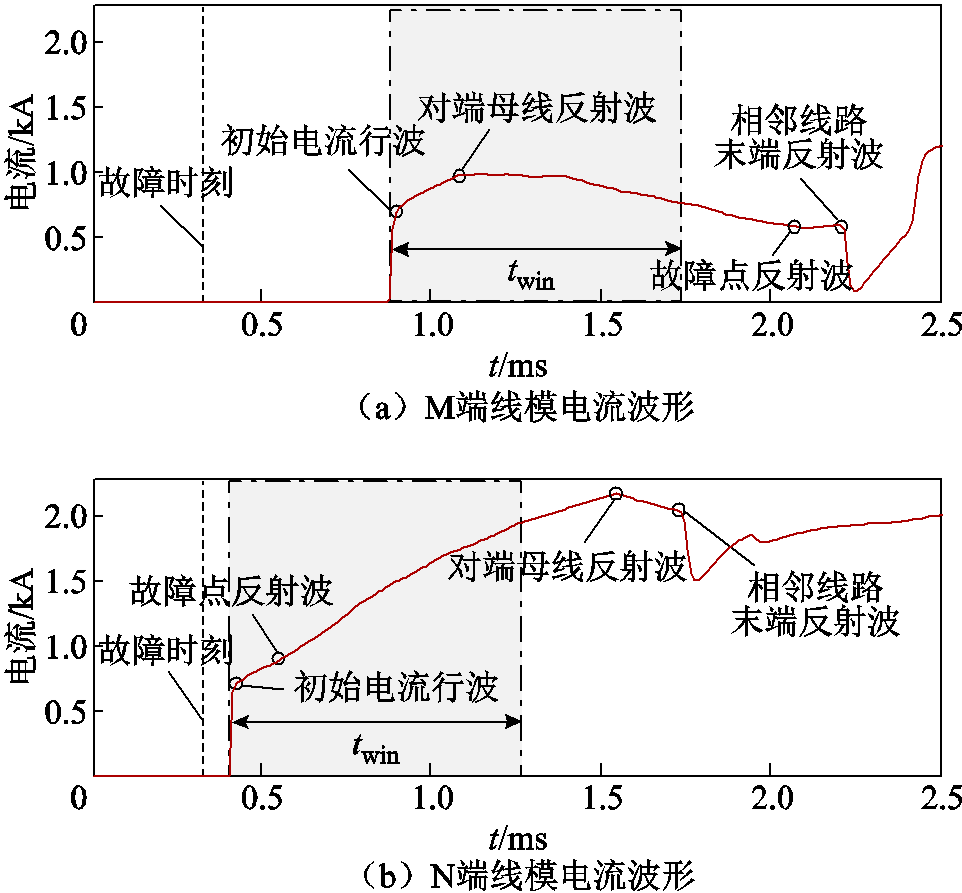
图13 区内f2故障时线路两端线模电流波形
Fig.13 Waveforms of line mode current at both ends of the line during internal fault at f2
观察图13a可知，故障发生后，电流行波经0.57 ms传输至M端母线，保护R1处的故障电流发生正的突变。对于区内后半段故障，来自对端母线的反射波起主要作用，因此保护R1处的故障电流持续降低，仿真结果与2.2.1节理论分析相一致。此外，当相邻线路末端反射波到达后，M端故障电流可能会出现极性为负的情况，本文通过限定时间窗排除了末端反射波的干扰，因此M段观测到的故障电流始终为正极性。由图13b可知，保护R处的故障电流受故障点反射波影响持续增大，在选定时间窗内，故障电流始终大于零。
图14为区内后半段故障时本文所提自适应差动保护方案的动作情况。由图14可知，区内后半段故障时，本文所构造的自适应校正函数能有效降低制动量；对于区内末端故障，线路两端观测到的行波折反射过程差异较大，故障电流波形也存在较大差异，此时参照传统差动方案计算得到的复合暂态能量制动系数较小，保护动作判据的灵敏度也较低，而本文所提自适应差动保护能有效提升末端故障时保护灵敏性，相较于传统差动方案优势明显。
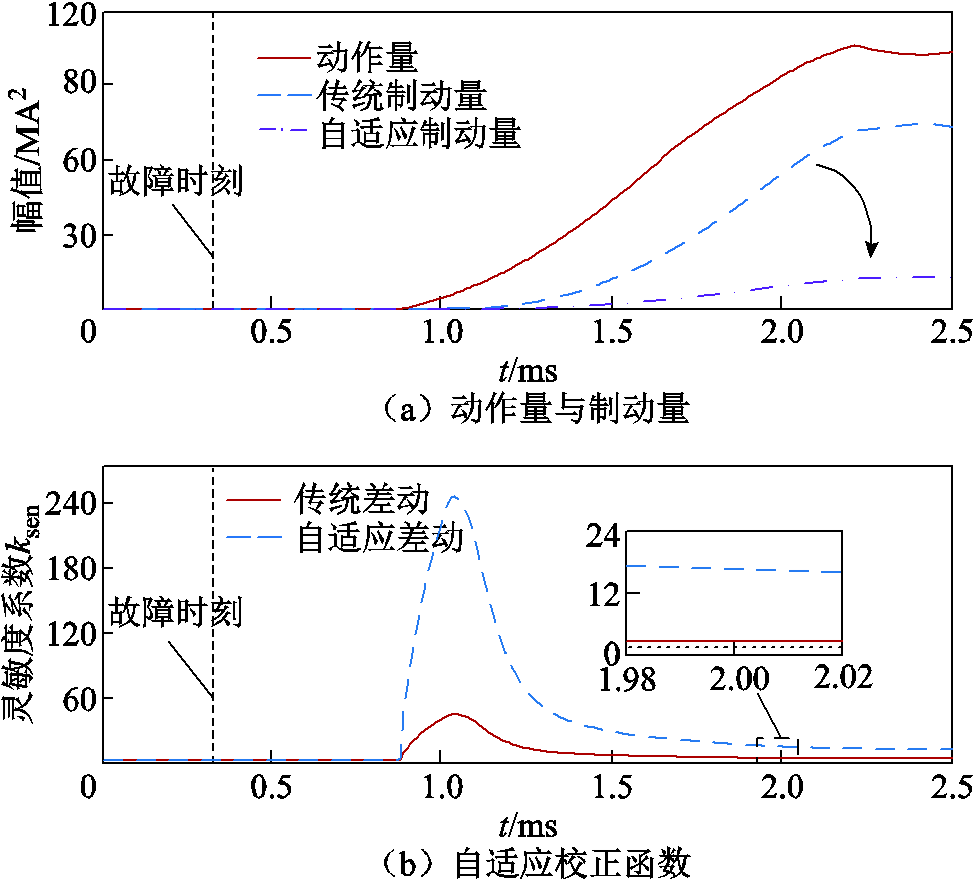
图14 区内f2故障时保护动作情况
Fig.14 Action situation during internal fault at f2
3）区外f3点故障
在f3处设置过渡电阻为50 Ω的正极接地故障，故障点距离N端40 km，故障时刻为0.3 ms，绘制线路两端线模电流波形如图15所示。
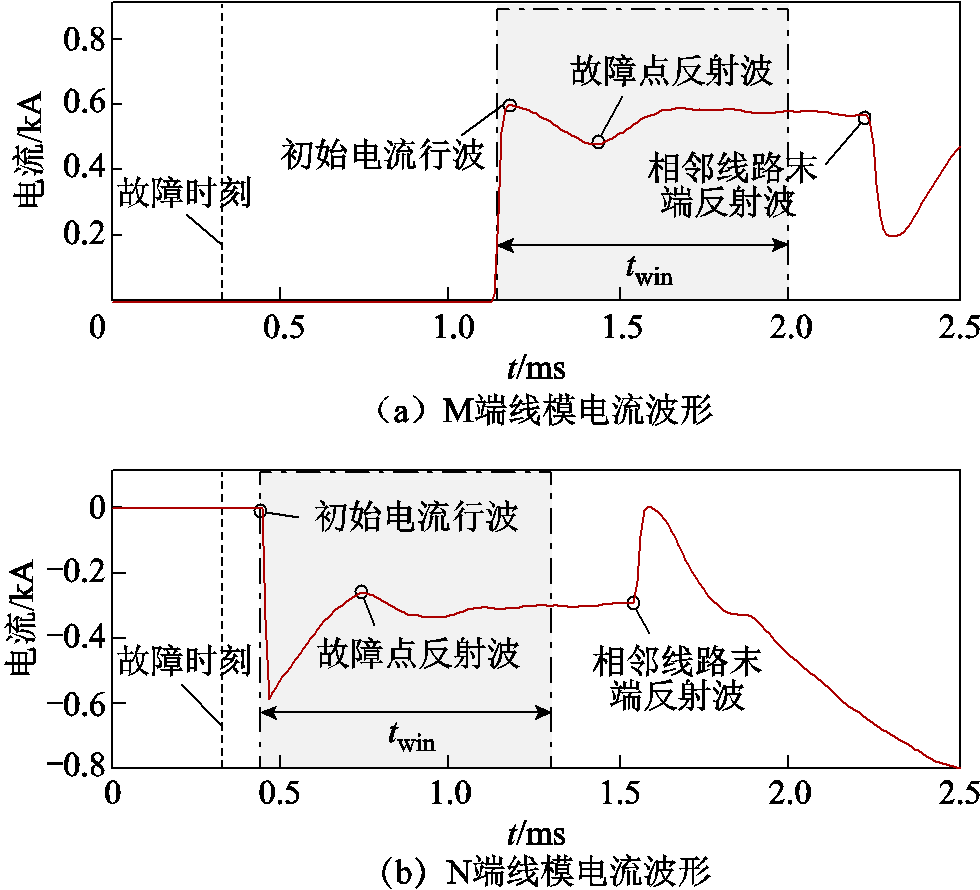
图15 区外f3故障时线路两端线模电流波形
Fig.15 Waveform of line mode current at both ends of the line during external fault at f3
观察图15a可知，故障发生后，电流行波经0.8 ms传输至M端母线，保护R1处的故障电流发生正的突变，随着时间的推移，MMC2换流器支路分流作用逐渐增强，此时故障电流呈现对数下降趋势；与此同时，故障点反射波与首行波同极性，因此当故障点反射波到达后，故障电流逐渐上升，仿真结果与2.2.2节理论分析一致。
图16为区外故障时本文所提自适应差动保护方案的动作情况。由图16a、图16b可知，本文构造的自适应差动保护能有效增大制动量，从而保证了区外故障时保护可靠不动作，提升了安全性。
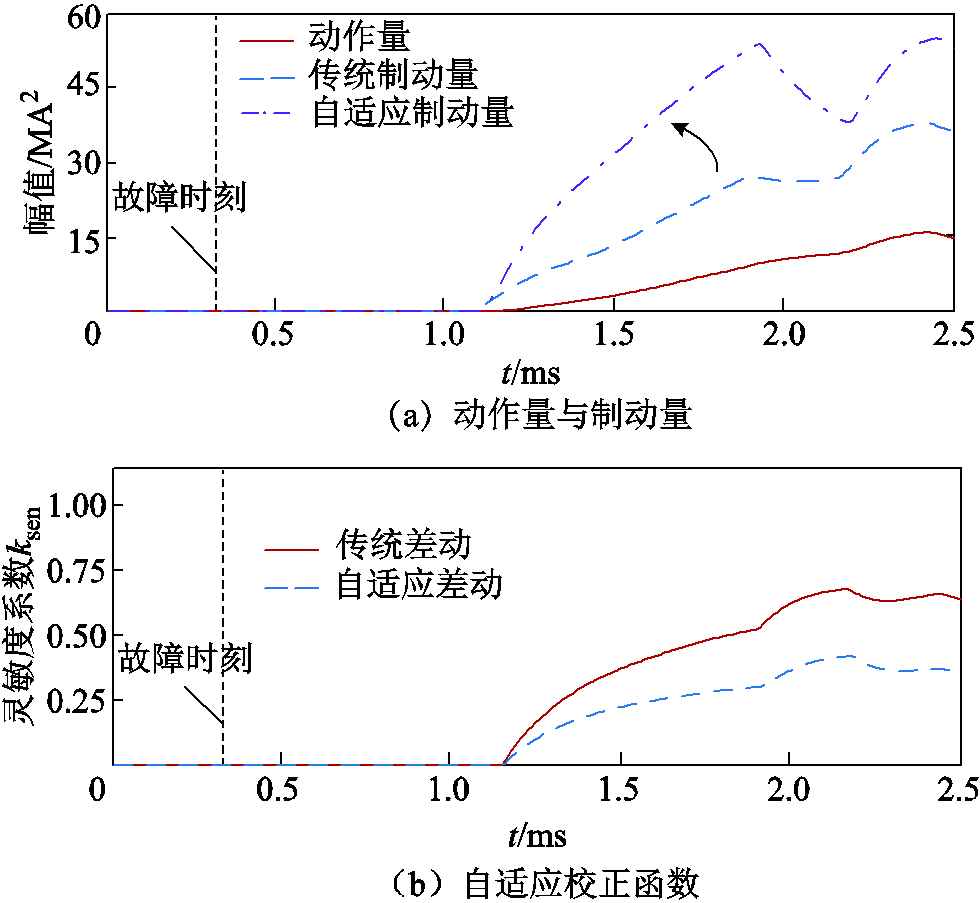
图16 区外f3故障时保护动作情况
Fig.16 Action situation during external fault atf3
为了测试本文所提保护方案的耐过渡电阻能力，在线路不同位置处设置故障点。其中，f1与f2分别为距离M端80 km与170 km的区内故障，f3为距离M端240 km的正向区外故障，f4为距离M端40 km的反向区外故障。分别考察两种差动方案在不同过渡电阻下的动作性能见表1。
表1 不同过渡电阻下仿真结果
Tab.1 Simulation results under different fault resistance
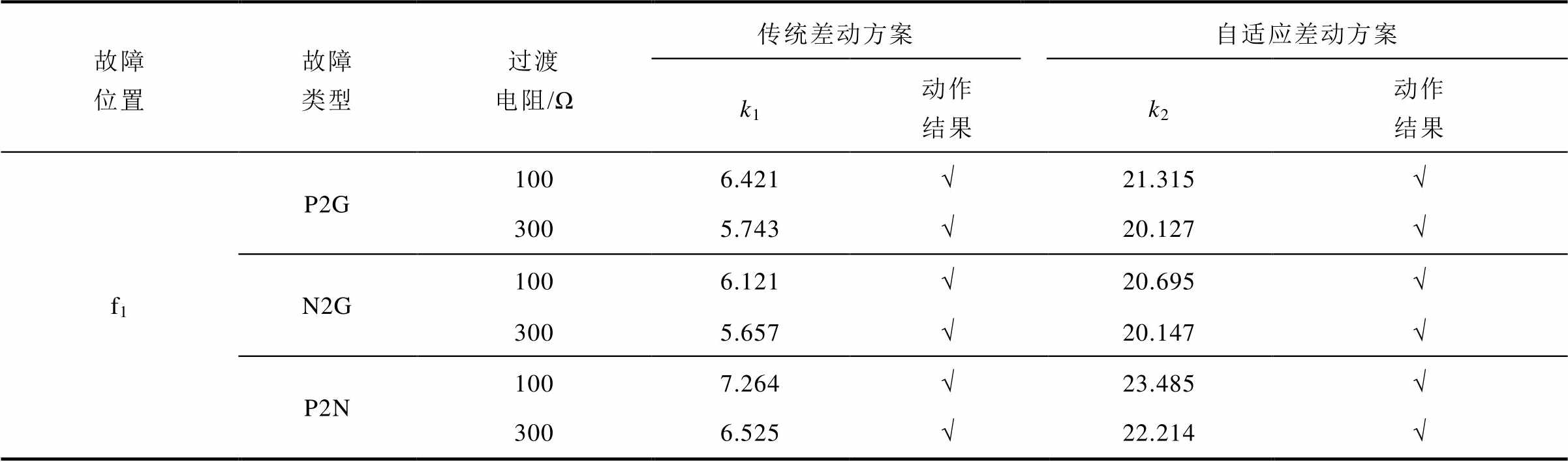
故障位置故障类型过渡电阻/Ω传统差动方案自适应差动方案 k1动作结果k2动作结果 f1P2G1006.421√21.315√ 3005.743√20.127√ N2G1006.121√20.695√ 3005.657√20.147√ P2N1007.264√23.485√ 3006.525√22.214√
（续）
故障位置故障类型过渡电阻/Ω传统差动方案自适应差动方案 k1动作结果k2动作结果 f2P2G1002.165√12.325√ 3001.454√11.734√ N2G1002.365√12.175√ 3001.476√11.692√ P2N1002.458√13.236√ 3001.627√12.579√ f3P2G1000.459×0.286× 3000.426×0.273× N2G1000.419×0.275× 3000.396×0.268× P2N1000.486×0.345× 3000.425×0.298× f4P2G1000.472×0.254× 3000.438×0.247× N2G1000.459×0.286× 3000.426×0.273× P2N1000.434×0.343× 3000.421×0.312×
由表1可知，区内故障时本文所提自适应差动保护方案能够显著提升保护的灵敏性。对于区内末端故障，随着过渡电阻的增大传统差动保护的灵敏性逐渐降低，这是由于故障点透射作用增强致使线路两端暂态电流波形差异增大，而本文所提自适应差动保护能够根据线路两端复合暂态能量差异自适应调整制动量幅值，其在高阻故障下的动作性能显著优于传统差动保护。区外故障时所提自适应差动保护能够一定程度上增大制动量，且其受过渡电阻影响较小，进一步保证了保护的可靠不动作。
4.3.1 噪声干扰问题
在实际的工程实践中，保护装置测得的电流信号易混有不同成分的噪声干扰，从而对保护判据产生影响。为验证所提方案抗噪声干扰能力，分别在线路不同位置处设置故障点，并在线路两端测得的仿真数据中叠加信噪比（Signal Noise Ratio, SNR）为20 dB与30 dB的高斯白噪声，得到仿真结果见表2。
由表2可知，复合暂态能量对噪声具有较好的抑制效果，对于不同故障位置以及故障类型，噪声干扰对保护的影响均较小，因此本文所提方案具有较好的抗噪声干扰能力。
表2 不同噪声干扰下的仿真结果
Tab.2 Simulation results under different noise interference
故障类型故障位置SNR/dBk2AP判别结果 单极接地故障f12022.54331.723区内/正极 3020.40736.345区内/正极 f22012.5430.013区内/负极 3012.3210.051区内/负极 f3200.353 区外 300.332区外 f4200.371区外 300.347区外 双极故障f12023.6521.173区内/双极 3023.5920.927区内/双极 f22016.4581.108区内/双极 3016.1270.943区内/双极 f3200.327区外 300.315区外 f4200.334区外 300.321区外
4.3.2 雷击干扰
为了验证本文所提雷击干扰判据的有效性，在被保护线路内部设置雷击干扰。雷电流幅值分别设置为10、20、30 kA，得到的仿真结果见表3。由表3可知，雷电干扰为高频脉冲波，其幅值衰减十分迅速，因此T1时段内的复合暂态能量远大于T2时段，比值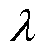
2；对于区内末端或区外末端故障，在μs级的数据窗内，其前后两段时窗内复合暂态能量差异不大，因此本文所提方案能正确排除雷击干扰的影响。
表3 雷击干扰识别判据仿真结果
Tab.3 Simulation results of lightning interference identification criteria
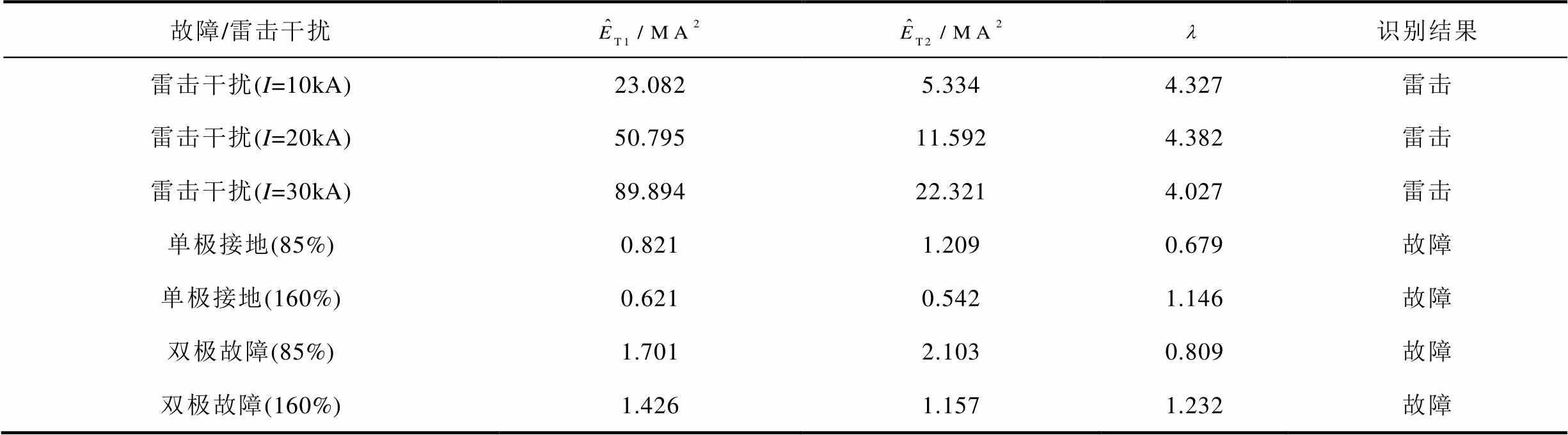
故障/雷击干扰识别结果 雷击干扰(I=10kA)23.0825.3344.327雷击 雷击干扰(I=20kA)50.79511.5924.382雷击 雷击干扰(I=30kA)89.89422.3214.027雷击 单极接地(85%)0.8211.2090.679故障 单极接地(160%)0.6210.5421.146故障 双极故障(85%)1.7012.1030.809故障 双极故障(160%)1.4261.1571.232故障
为验证保护方案对数据不同步的适应能力，在不同故障位置设置过渡电阻为50Ω的正极故障，以N端数据为基准对M端数据进行调整，设置多种同步误差，得到数据不同步对保护判据的影响仿真结果如图17所示。
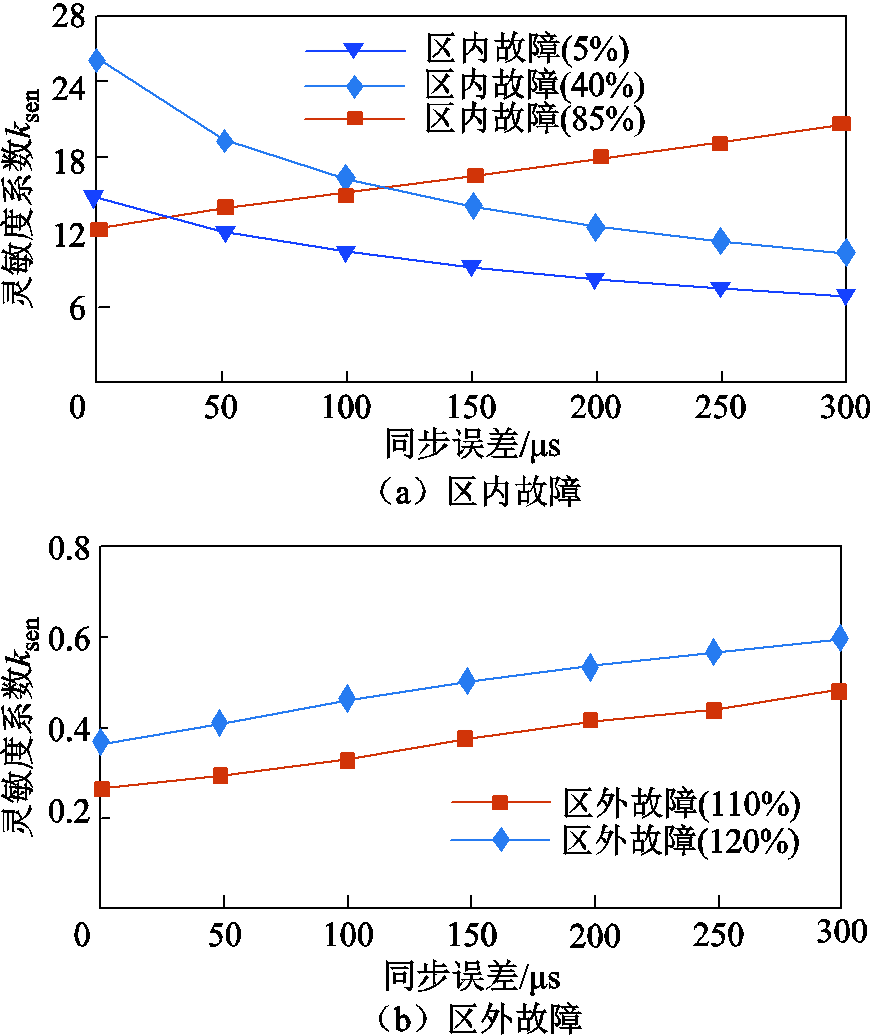
图17 数据不同步对保护判据的影响
Fig.17 The influence of asynchronous data on protection criteria
由图17可知，数据不同步对所提保护方案的动作性能会产生一定影响，但即使在较大同步误差下，所提保护判据仍可正确识别区内外故障，所提保护方案对数据同步要求较低。
针对限流电抗器集中配置在多端柔性直流电网换流站出口时，基于边界元件特性的暂态量保护方案难以适用的问题，提出了一种基于复合暂态能量的自适应差动保护方案，具体结论如下：
1）不同位置发生故障时，本文所构造的复合暂态能量均具有明确的方向性，具体表现为：区内故障时线路两端复合暂态能量方向相同；区外故障时线路两端复合暂态能量方向相反。
2）本文所提方案能够依据区内外故障时线路两端的复合暂态能量特征差异自适应校正制动量幅值，有效地提升了区内故障时保护的灵敏性以及区外故障时保护的安全性。
3）本文所提保护方案不依赖于线路边界，且无需进行阈值整定，具有较好的工程适用性；仿真结果表明，方案在不同故障位置以及不同故障类型下均能能够可靠识别区内外故障，且受过渡电阻和噪声干扰影响较小。
本文所提保护方案为双端量保护，考虑到通信中断等极端情况，后续需进一步开展与其相配合的单端量保护方案的研究。
附 录
附表1 柔性直流电网系统参数
App.Tab.1 Flexible DC power grid system parameters
参数数值 MMC额定容量/MW直流侧额定电压/kV桥臂电抗/mH子模块等效电容/mF限流电抗器/mH桥臂子模块数线路长度(l1～l4)/km换流变压器漏抗(%)750±400501510020020015
附图1 直流输电系统杆塔拓扑结构
App.Fig.1 Tower topology structure of DC transmission system
参考文献
[1] 雷顺广, 束洪春, 李志民. 基于桥臂功率特征的全-半混合型柔性直流输电线路保护[J]. 电工技术学报, 2023, 38(13): 3563-3575. Lei Shunguang, Shu Hongchun, Li Zhimin. Full-half bridge hybrid VSC-HVDC transmission line protection method based on power characteristics of bridge arms[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3563-3575.
[2] 饶宏, 周月宾, 李巍巍, 等. 柔性直流输电技术的工程应用和发展展望[J]. 电力系统自动化, 2023, 47(1): 1-11.Rao Hong, Zhou Yuebin, Li Weiwei, et al. Engineering application and development prospect of VSC-HVDC transmission technology[J]. Automation of Electric Power Systems, 2023, 47(1): 1-11.
[3] 刘海金, 李斌, 温伟杰, 等. 柔性直流系统的线路保护关键技术与展望[J]. 电网技术, 2021, 45(9): 3463-3477. Liu Haijin, Li Bin, Wen Weijie, et al. Review and prospect on transmission line protection in flexible DC system[J]. Power System Technology, 2021, 45(9): 3463-3477.
[4] 孙栩, 王华伟, 雷霄, 等. 架空线柔性直流电网的直流短路电流限制研究[J]. 电力自动化设备, 2017, 37(2): 219-223. Sun Xu, Wang Huawei, Lei Xiao, et al. Restriction of DC short circuit current for overhead lines of flexible DC grid[J]. Electric Power Automation Equipment, 2017, 37(2): 219-223.
[5] 李斌, 何佳伟, 李晔, 等. 基于边界特性的多端柔性直流配电系统单端量保护方案[J]. 中国电机工程学报, 2016, 36(21): 5741-5749. Li Bin, He Jiawei, Li Ye, et al. Single-ended protection scheme based on boundary characteristic for the multi-terminal VSC-based DC distribution system[J]. Proceedings of the CSEE, 2016, 36(21): 5741-5749.
[6] 束洪春, 刘可真, 朱盛强, 等. ±800kV特高压直流输电线路单端电气量暂态保护[J]. 中国电机工程学报, 2010, 30(31): 108-117. Shu Hongchun, Liu Kezhen, Zhu Shengqiang, et al. ±800kV UHVDC transmission line protection based on single end electrical transient signal[J]. Proceedings of the CSEE, 2010, 30(31): 108-117.
[7] 束洪春, 田鑫萃, 张广斌, 等. ±800kV直流输电线路的极波暂态量保护[J]. 中国电机工程学报, 2011, 31(22): 96-104. Shu Hongchun, Tian Xincui, Zhang Guangbin, et al. Protection for ±800 kV HVDC transmission lines using pole wave transients[J]. Proceedings of the CSEE, 2011, 31(22): 96-104.
[8] 何佳伟, 李斌, 李晔, 等. 多端柔性直流电网快速方向纵联保护方案[J]. 中国电机工程学报, 2017, 37(23): 6878-6887. He Jiawei, Li Bin, Li Ye, et al. A fast directional pilot protection scheme for the MMC-based MTDC grid[J]. Proceedings of the CSEE, 2017, 37(23): 6878-6887.
[9] 郑涛, 宋祥艳. 适用于多端直流电网的电压极性比较式行波保护方案[J]. 电网技术, 2022, 46(12): 4690-4698. Zheng Tao, Song Xiangyan. Traveling wave protection scheme of voltage polarity comparison formula for multi-terminal DC power network[J]. Power System Technology, 2022, 46(12): 4690-4698.
[10] 童宁, 林湘宁, 张雪松, 等. 不依赖于边界元件的架空型多端柔直电网就地测距式接地保护原理[J]. 中国电机工程学报, 2019, 39(7): 2049-2059. Tong Ning, Lin Xiangning, Zhang Xuesong, et al. Fault location based single-ended protection strategy for overhead VSC-MTDC independent on boundary component[J]. Proceedings of the CSEE, 2019, 39(7): 2049-2059.
[11] 林湘宁, 刘琦, 范理想, 等. 基于相关分析的多端直流电网线路纵联保护新原理[J]. 电力系统保护与控制, 2020, 48(13): 45-55. Lin Xiangning, Liu Qi, Fan Lixiang, et al. A novel pilot protection for VSC-MTDC based on correlation analysis[J]. Power System Protection and Control, 2020, 48(13): 45-55.
[12] 苏煜, 汤士明, 石勇. 直流输电线路差动保护新原理[J]. 电力系统及其自动化学报, 2022, 34(10): 152-158. Su Yu, Tang Shiming, Shi Yong. Novel differential protection principle for DC transmission lines[J]. Proceedings of the CSU-EPSA, 2022, 34(10): 152-158.
[13] 董杏丽, 董新洲, 张言苍, 等. 基于小波变换的行波极性比较式方向保护原理研究[J]. 电力系统自动化, 2000, 24(14): 11-15. Dong Xingli, Dong Xinzhou, Zhang Yancang, et al. Directional protective relaying based on polarity comparison of travelling wave by using wavelet transform[J]. Automation of Electric Power Systems, 2000, 24(14): 11-15.
[14] 李晔, 李斌, 刘晓明, 等. 基于反向行波幅值比的对称单极柔性直流系统行波方向保护[J]. 电工技术学报, 2023, 38(9): 2418-2434. Li Ye, Li Bin, Liu Xiaoming, et al. The direction protection based on the amplitude ratio of the backward traveling wave for the symmetrical monopole flexible DC system[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2418-2434.
[15] 刘佳硕, 李永丽, 陈晓龙, 等. 基于暂态电流比值的多端柔性直流电网保护[J]. 电网技术, 2023, 47(4): 1439-1449. Liu Jiashuo, Li Yongli, Chen Xiaolong, et al. Novel protection based on transient current ratio for MTDC grid[J]. Power System Technology, 2023, 47(4): 1439-1449.
[16] 束洪春, 刘力滔, 唐玉涛, 等. 基于行波暂态能量的半波长输电线路高灵敏增强型纵联保护方案[J]. 电工技术学报, 2022, 37(24): 6372-6387. Shu Hongchun, Liu Litao, Tang Yutao, et al. Highly sensitive enhanced pilot protection of half-wavelength transmission line based on directional traveling wave energy[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6372-6387.
[17] 徐政. 柔性直流输电系统[M]. 2版. 北京: 机械工业出版社, 2017.
[18] Dong Xinzhou. The theory of fault travel waves and its application[M]. Singapore: Springer Singapore, 2022.
[19] 陈淼, 贾科, 王康达, 等. 基于前行波波形特征的柔性直流输电线路单端行波保护[J]. 电网技术, 2022, 46(6): 2386-2392. Chen Miao, Jia Ke, Wang Kangda, et al. Single terminal traveling wave protection for flexible HVDC transmission lines based on forward wave shape information[J]. Power System Technology, 2022, 46(6): 2386-2392.
[20] 陈田田, 李银红. 基于电压折射波幅值正负差异的柔性直流电网两段式行波保护[J]. 电力系统自动化, 2022, 46(3): 129-136. Chen Tiantian, Li Yinhong. Two-section traveling wave protection for flexible DC grid based on positive and negative difference of voltage refractive wave amplitude[J]. Automation of Electric Power Systems, 2022, 46(3): 129-136.
[21] 王聪博, 贾科, 毕天姝, 等. 基于暂态电流波形相似度识别的柔性直流配电线路保护[J]. 电网技术, 2019, 43(10): 3823-3831. Wang Congbo, Jia Ke, Bi Tianshu, et al. Protection for flexible DC distribution system based on transient current waveform similarity identification[J]. Power System Technology, 2019, 43(10): 3823-3831.
[22] 邓丰, 徐帆, 曾哲, 等. 基于多源暂态信息融合的单端故障定位方法[J]. 电工技术学报, 2022, 37(13): 3201-3212. Deng Feng, Xu Fan, Zeng Zhe, et al. Single-ended fault location method based on multi-source transient information fusion[J]. Transactions of China Electro-technical Society, 2022, 37(13): 3201-3212.
[23] 贾科, 姚昆鹏, 刘子奕, 等. 基于故障行波差异性的柔性直流输电线路纵联保护[J]. 中国电机工程学报, 2024, 44(7): 2616-2628. Jia Ke, Yao Kunpeng, Liu Ziyi. Pilot protection for flexible HVDC transmission lines based on the difference of fault traveling waves [J]. Proceedings of the CSEE, 2024, 44(7): 2616-2628.
[24] 戴志辉, 刘自强, 刘雪燕, 等. 基于首行波曲率的柔性直流输电线路单端量保护[J]. 电工技术学报, 2021, 36(9): 1831-1841. Dai Zhihui, Liu Ziqiang, Liu Xueyan, et al. Single-ended protection for flexible DC transmission line based on curvature of initial traveling wave[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1831-1841.
[25] 杨亚宇, 邰能灵, 谢卫, 等. 利用单端边界能量的直流输电线路全线速动保护[J]. 电工技术学报, 2023, 38(9): 2403-2417. Yang Yayu, Tai Nengling, Xie Wei, et al. A whole-line fast protection scheme for HVDC transmission line based on single-ended boundary energy[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2403-2417.
[26] 吴通华, 黎钊, 李新东, 等. 适配柔直系统快速性及可靠性需求的雷击干扰识别方法[J]. 电力系统保护与控制, 2022, 50(24): 1-12. Wu Tonghua, Li Zhao, Li Xindong, et al. Lightning interference identification method for the speed and reliability of a flexible DC system[J]. Power System Protection and Control, 2022, 50(24): 1-12.
[27] 顾垚彬, 宋国兵, 郭安祥, 等. 针对直流线路行波保护的雷击识别方法研究[J]. 中国电机工程学报, 2018, 38(13): 3837-3845. Gu Yaobin, Song Guobing, Guo Anxiang, et al. A lightning recognition method for DC line travling-wave protection of HVDC[J]. Proceedings of the CSEE, 2018, 38(13): 3837-3845.
[28] 薛士敏, 陈硕, 顾诚, 等. 一种基于暂态量的柔性直流系统保护及雷击识别方法[J]. 电力系统保护与控制, 2022, 50(9): 45-53. Xue Shimin, Chen Shuo, Gu Cheng, et al. A method for protection and lightning identification in a flexible DC system based on transient quantities[J]. Power System Protection and Control, 2022, 50(9): 45-53.
[29] 童宁, 范理想, 林湘宁, 等. 不依赖边界元件及同步对时的多端柔直电网波形匹配式差动保护原理[J]. 中国电机工程学报, 2019, 39 (13): 3820-3833. Tong Ning, Fan Lixiang, Lin Xiangning, et al. Waveform matching based protection strategy for VSC-MTDC independent on synchronization and boundary component[J]. Proceedings of the CSEE, 2019, 39 (13): 3820-3833.
Abstract Flexible HVDC transmission systems offer significant advantages in solving the challenges of large-scale renewable energy integration and long-distance power transmission, indicating a major trajectory for the future transformation and growth of power systems. Compared to traditional HVDC systems, flexible HVDC systems are weakly damped, and their fault current rise rate is rapid. If faults are not cleared promptly, converter blockages may occur, demanding higher requirements for quick fault identification. Current engineering practices typically install current-limiting reactors at both ends of flexible HVDC lines. However, with the development of flexible DC grids, a single converter station may have multiple outgoing lines. In such cases, concentrating the current-limiting reactors at the converter station outlet can effectively reduce construction costs and improve economic efficiency.
Existing traveling wave protection schemes for multi-terminal flexible HVDC grids typically use the blocking effect of current-limiting reactors on high-frequency components to construct protection criteria. However, when current-limiting reactors are concentrated at the converter station outlet, there are no obvious boundary elements between adjacent lines, significantly reducing the adaptability of traditional protection schemes in boundary-less grid structures. Therefore, new protection schemes that do not rely on boundary elements need to be further investigated.
To address these issues, this paper first analyzes the transmission characteristics of fault current traveling waves and constructs a composite transient energy with both amplitude and directional features. To further clarify the variation patterns of the composite transient energy's amplitude and directional characteristics with wave transmission, the paper qualitatively analyzes the waveform characteristics of fault currents at both ends of the line for faults occurring at different locations. For internal faults, the composite transient energy at both ends of the line has the same direction, and the amplitude difference is the largest when the fault occurs at either the near end or remote end of the line, while it is the smallest when the fault occurs near the midpoint of the line. For external faults, the composite transient energy at both ends of the line has opposite directions, and the amplitude difference is minimal. Based on these conclusions, this paper introduces an adaptive restraint correction function into the traditional ratio differential protection criterion. For internal faults, without changing the operating quantity, the adaptive correction function can reduce the restraint quantity, and the greater the energy difference at both ends of the line, the lower the correction function value, effectively enhancing the sensitivity of the protection. For external faults, the proposed adaptive correction function can effectively increase the restraint quantity to ensure reliability.
Finally, extensive PSCAD/EMTDC simulation experiments verify the effectiveness of the proposed adaptive differential protection scheme based on composite transient energy for multi-terminal flexible HVDC grids. The simulation results show that the proposed scheme significantly improves the sensitivity of protection for near-end or remote-end internal faults compared to traditional differential protection and ensures reliability during external faults. The scheme does not rely on line boundaries and does not require threshold setting, offering good engineering applicability and being less affected by transition resistance and noise interference.
keywords：Multi terminal flexible DC power grid, current traveling wave, composite transient energy, restraining quantity correction function, adaptive differential protection
DOI: 10.19595/j.cnki.1000-6753.tces.240195
中图分类号：TM77
国家自然科学基金联合基金资助项目（U2166205）。
收稿日期 2024-01-29
改稿日期 2024-07-05
郑 涛 男，1975年生，教授，博士生导师，研究方向为电力系统自动化及继电保护。E-mail：zhengtao_sf@126.com
陈云飞 男，2000年生，硕士研究生，研究方向为新能源电力系统继电保护。E-mail：3369354137@qq.com（通信作者）
（编辑 赫 蕾）