摘要 构网型双馈风电机组并入系统具有主动支撑电网的作用。随着构网型双馈风电机组容量的增加，构网型双馈风电机组参与系统区间振荡的现象将逐步凸显。针对含构网型双馈风电机组电力系统的区间振荡问题，提出一种基于能量结构的电力系统区间振荡分析方法。首先，推导了同步发电机及构网型双馈风电机组的能量结构；其次，根据元件的能量结构，分析了元件动能与端口能量的交互关系，在时域方面，对元件实际动能分解，得到动能增量与模式动能，在特征值方面，通过对动能增量以及模式动能进行分析，阐述了利用动能增量以及模式动能可以分析各机组参与振荡程度及模态的理论基础；再次，利用动能增量及模式动能，建立了复合指标，该指标可用于评估系统区间振荡；最后，通过仿真分析验证了该方法的可行性。
关键词：低频振荡 构网型双馈风电机组 动能增量 模式动能
在大型长距离输电系统中，弱阻尼区间振荡现象时有发生。这一问题长期出现在电力系统中，给系统的安全与稳定带来巨大的挑战[1-3]。不同于同步发电机固有的功率同步机制，并网的风电机组的同步行为由变流器控制策略决定[4-5]。目前对于主流的双馈风电机组，其通过锁相环跟踪电网电压，通过功率解耦控制，实现风力发电机组向电网的功率注入，这类机组也称之为电网跟随型风电机组[6-8]。与跟网型风电机组不同，构网型风电机组无需通过锁相环构建输出电压和频率，通过相应控制方法即可使构网型风电机组自主同步运行[9-11]。在未来，构网型风电机组将成为主流的发展方向。针对构网型风电机组控制，当前主流的控制方法有虚拟同步发电机（Virtual Synchronous Generator, VSG）控制[12-13]、下垂控制[14]、功率同步控制[15]、直流电容惯性控制[16]、虚拟振荡器控制[17-19]等。本文中构网型双馈风电机组采用VSG控制。
VSG控制的基本原理是将传统同步发电机的转子运动方程及励磁控制方式引入风电机组控制器中，从而模拟同步发电机的物理特性[20]。当含有VSG控制的构网型风电机组接入电网中时，由于它与同步发电机具有相似的摇摆特性，也会引入与同步机相似的问题，含有VSG控制的新能源机组也会参与包含同步机的机电振荡模式中，从而与同步机产生相应的交互作用[21]。文献[22]利用复转矩分析法分析了含VSG控制变流器单机无穷大系统的小干扰稳定性，并扩展到多机系统，说明含VSG控制的变流器接入对系统主导低频振荡模式的影响。文献[23]研究了含VSG控制的变流器在交流电网中低频振荡的参与程度，并通过模态分析详细分析了多机系统下与同步发电机的交互过程。文献[24]研究发现采用VSG控制的光伏电站接入大电网后，系统的稳定性逐渐提升，但由于VSG控制与同步机存在相似的振荡特性，会产生新的振荡模态。而针对构网型双馈风电机组，其在机电尺度下的低频振荡的相关研究则刚刚起步[25-28]。文献[25]对构网型双馈风机的VSG控制环节展开研究，得到关于VSG控制环节的二阶闭环特征方程，将典型参数代入并对闭环特征方程解析，发现VSG控制的构网型双馈风机在低频段具有明显的弱阻尼特性。文献[26]提出一种结合系统主导振荡模式在线辨识和粒子群优化算法的双馈风电机组VSG控制器参数协调控制策略，利用Prony方法对含构网型双馈风电的电力系统主导模态进行辨识，结合粒子群优化算法对VSG参数进行动态控制，从而实现系统阻尼的调控，但其结果受辨识方法精度的限制。文献[27]提出了一种基于哈密顿原理的构网型双馈风电机组的非线性弹性耦合控制策略，利用该控制策略对在SVG控制运行方式下的双馈风电机组与同步发电机之间的振荡进行抑制，但受到信号的通信延迟的影响。文献[28]建立了构网型双馈风电机组的阻抗模型，研究电网强度和控制参数对系统稳定性的影响，但由于阻抗模型存在局限性，系统模态结果容易丢失。
随着风电机组渗透率的逐步提升，以及构网型双馈风电机组的推广，且构网型双馈风电机组的控制具有和同步发电机转子运动方程相似的动力学机制，处于网架结构末端的风电机组将会通过长距离输电线路与其他发电机组产生区间振荡现象。通过对系统区间振荡的基本特征分析，可以有助于识别区间振荡过程中交互的机组，并对相关机组实施相应的控制手段，以达到抑制区间振荡的目的。目前对区间振荡现象的分析方法主要有基于线性化模型的特征值分析方法[29-30]、基于量测数据的分析方法[31-34]、能量法[35-38]等。基于特征值的分析方法在物理意义上十分明确，但计算效率受到系统维数制约。基于量测数据的分析方法不依赖系统模型，但难以揭示系统低频振荡的物理本质。能量法是一种基于Lyapunov函数稳定理论的分析方法，对于所构建的能量函数具有清晰的物理意义，利用所构建的能量函数可以实现在线计算，达到即时量测即时辨别的目的。文献[39]首次提出利用能量方法来分析系统的区间振荡现象，分别对两机系统能量进行推导，利用能量的相位性质来区分系统是否发生区间振荡。文献[40]在频域下利用动能偏差对同步机主导的区间振荡进行区分。文献[41]基于暂态能量流，给出同步机能量表达式及动能与特征向量的关系，并定义了动能参与因子。总体来说，现有能量方法适用于对只含传统同步机组的电力系统进行分析，而针对含构网型双馈风电的电力系统的区间振荡问题亟须解决。
综上所述，针对构网型双馈风电机组会参与系统区间振荡问题，现有文献已有初步探索[25]，但仍然存在不足：①低频段下构网型双馈风电机组与同步机区间振荡现象尚未展开深入研究；②现有分析区间振荡的方法较为复杂，需构建发电机-变压器-线路-负荷及其他附加控制器的线性化模型，从而对整个系统进行建模分析[26-27]；③能量法在应用于传统同步发电机的过程中，其所对应的能量均具有实际的物理意义，而针对构网型双馈风电机组，需依据其内部控制结构厘清相应能量的物理意义。在此基础上，本文主要工作如下：首先，类比同步发电机能量结构，构建了构网型双馈风电机组的能量函数，并提出适用于分析构网型双馈风电机组的能量结构，另外借助能量结构体现了系统发生区间振荡时构网型双馈风电机组和同步发电机动能与暂态能量的交互过程，从能量的角度阐释了构网型双馈风电机组区间振荡过程中的物理过程；其次，从系统时域角度出发，将构网型双馈风电机组的虚拟动能进行分解，由于其动能增量无法区分振荡机群，从而提出模式动能的概念；再次，又结合特征值方法从特征值视角对构网型双馈风电机组及同步机的动能增量和模式动能进行分析，从而证明了利用动能增量及模式动能分析系统各机组参与区间振荡水平的可行性；最后，利用机组动能增量和模式动能构建机组间参与区间振荡的具体指标，该指标为机组参与振荡的程度及机群进行排序划分，为后续构网型双馈风电机组参与系统区间振荡的分析与控制提供了参考价值。
本节通过对电力系统元件能量结构进行构造，将系统能量依据能量转换形式分为注入能量、交互性质的暂态能量及耗散能量。依据设备的物理结构对同步发电机及构网型双馈风电机组的能量进行推导，并将元件各部分能量按所属的能量结构进行划分。最后对元件动能增量和注入网络的端口能量关系进行探究。
文献[37]给出系统能量流流入同步发电机节点的表达式为
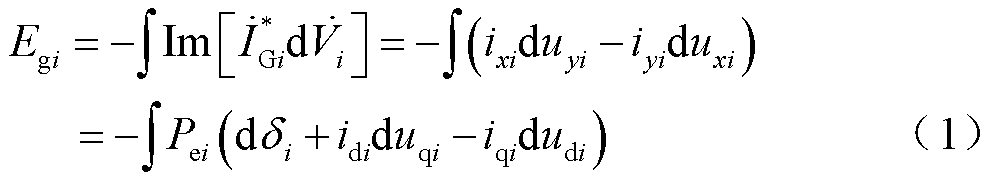
式中，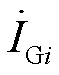
为第i台同步发电机流出的电流相量；*表示电流相量的共轭；
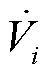为第i台同步发电机机端电压相量；
、
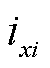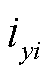分别为电流相量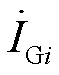在系统xy同步坐标系的电流分量；
、
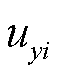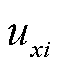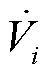为电压相量在系统xy同步坐标系的电压分量；
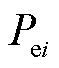为第i台同步发电机的电磁功率；
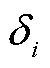为第i台同步发电机的转子角；
、
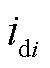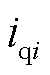分别为电流相量在dq坐标系的电流分量；
、
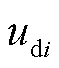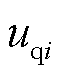分别为电压相量在dq坐标系的电压分量。
将同步发电机四阶微分方程[39]代入式（1）中，可以得到同步发电机能量结构为
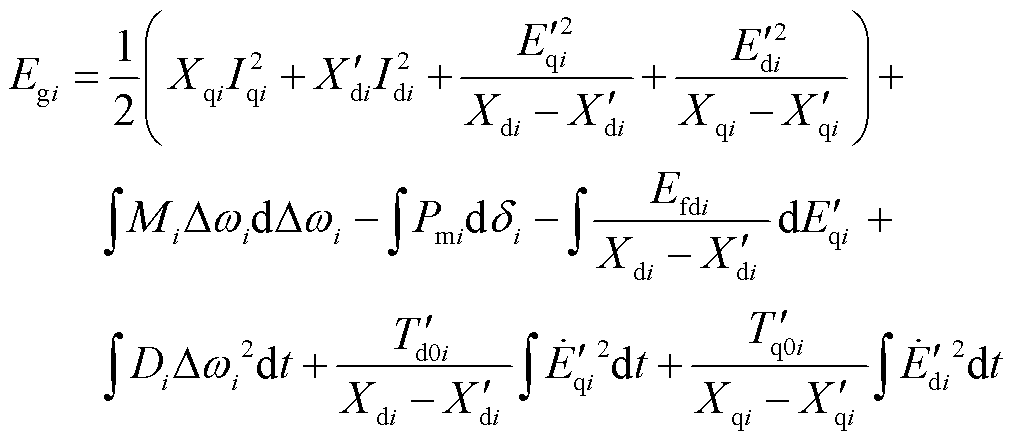（2）
式中，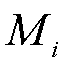
为同步发电机i的惯性时间常数；
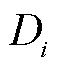为同步发电机i的机械阻尼系数；
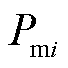为同步发电机i的机械功率；
、
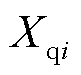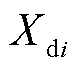分别为同步发电机i的q轴和d轴的同步电抗；
、
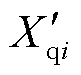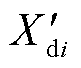分别为同步发电机i的q轴和d轴的次同步电抗；
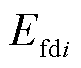为同步发电机i的励磁电动势；
、
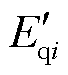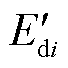分别为同步发电机i的q轴和d轴暂态电动势；
、
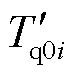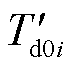分别为同步发电机i的q轴和d轴开路暂态时间常数。
式（2）描述了同步发电机向系统中注入能量，经过能量的交互以及耗散，最终流入电网的物理过程。
根据式（2）可以将上述能量分为同步发电机的注入能量、暂态能量、耗散能量。注入能量代表了发电机的具体能量来源；发电机的暂态能量体现了能量间的交互过程；发电机的耗散能量体现了能量的消耗过程。下面对这三部分能量进行展开。
1）发电机注入能量
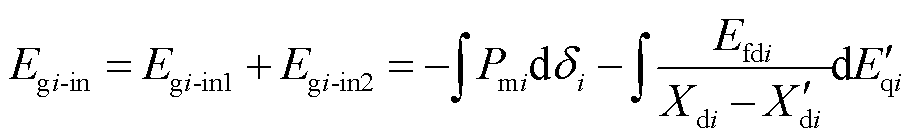（3）
式中，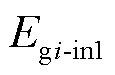
为同步发电机调速系统所注入的能量；
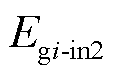为励磁系统所注入的能量。
2）发电机暂态能量
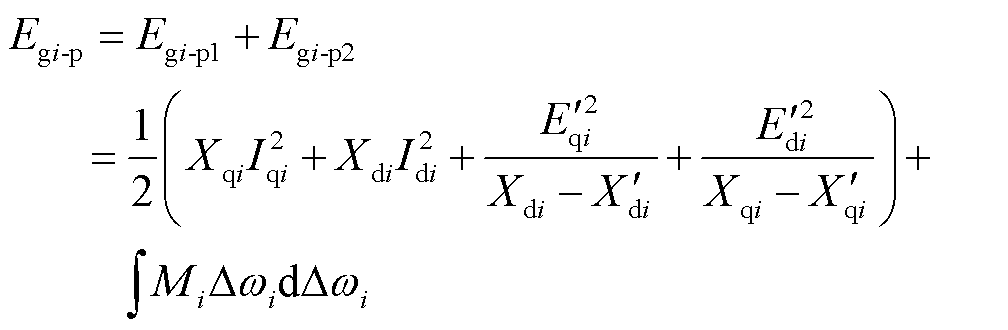(4)
式中，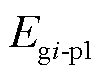
为发电机励磁绕组及定子绕组的暂态能量；
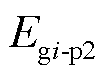为发电机轴系旋转所具有的暂态能量。
3）发电机耗散能量
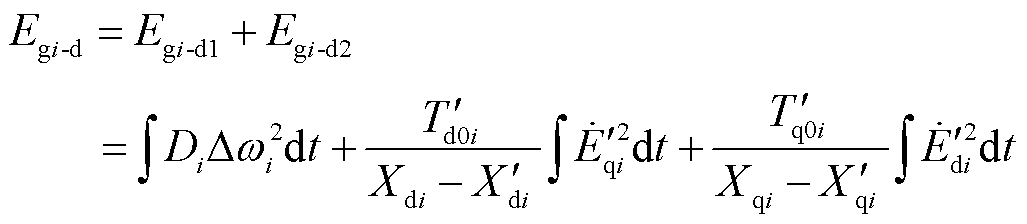（5）
式中，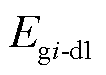
为同步发电机轴系产生的耗散能量；
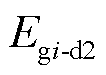为同步发电机励磁绕组的耗散能量。
综上所述，同步发电机能量结构关系式为
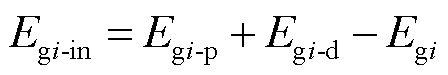（6）
同步发电机能量结构示意图如图1所示。同步发电机调速系统、励磁系统注入能量，经过发电机内部耗散结构的耗散，剩余能量供给暂态能量项和发电机端口。由于暂态能量作为具有交互性质及周期性质的能量，在能量交互过程中，端口能量和同步发电机的暂态能量之间发生交互作用，并且从元件端口经过系统网络和其他发电机组关联。
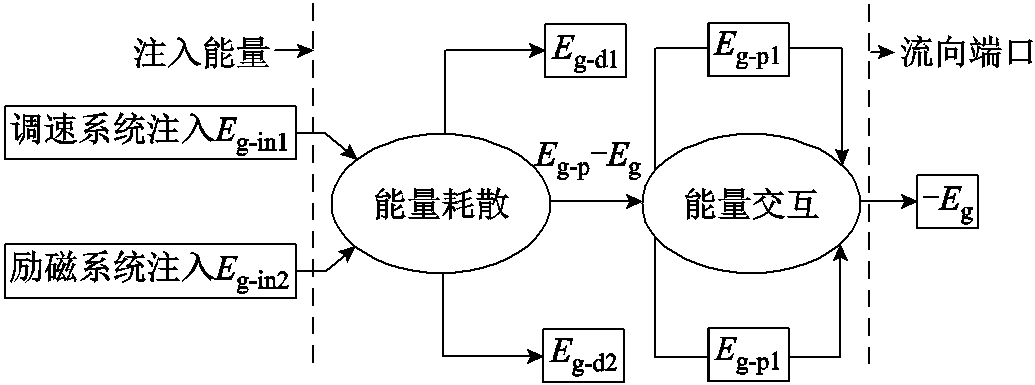
图1 同步发电机能量结构示意图
Fig.1 Energy structure diagram of synchronous generator
构网型双馈风电机组与跟网型双馈风电机组不同的是转子侧变流器的控制方式。构网型双馈风电机组将传统双馈风电机组转子侧变流器的定向矢量控制方式替换为调节电压幅值-相位的控制方式。本文中构网型双馈风电机组使用VSG控制[12-13]。
针对基于VSG控制的构网型双馈风电机组，图2给出了构网型双馈风电机组VSG控制示意图。
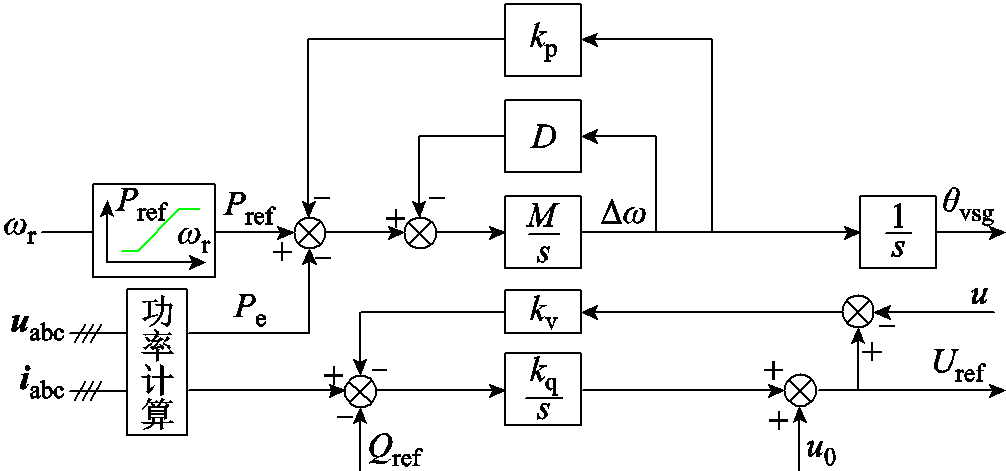
图2 构网型双馈风电机组VSG控制示意图
Fig.2 Structure diagram of VSG control of grid-forming doubly-fed wind turbine generator
构网型双馈风电机组的VSG控制表达式为
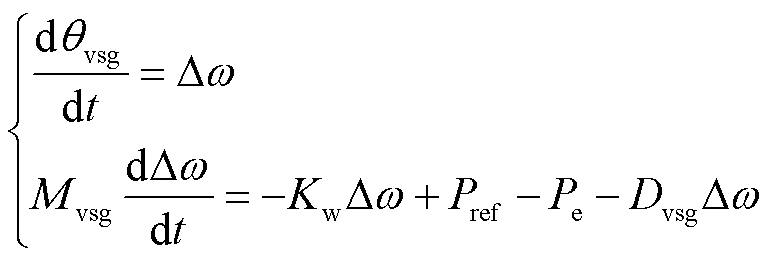（7）
式中，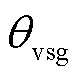
为VSG控制形成的虚拟转子角，同时也为构网型双馈风电机组的定子电压相位指令；
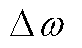为虚拟角频率偏差；
、
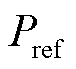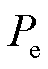分别为给定的功率参考值和构网型双馈风电机组的电磁功率；
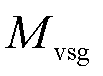为VSG控制所对应的虚拟惯量；
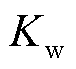和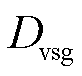
分别为VSG控制的虚拟调频系数及虚拟阻尼系数。
而对于双馈风电机组本身的电气模型，在此假设：忽略定子磁通暂态过程；定子和转子均采用电动机惯例，则双馈风电机组的转子、定子电压方程[42]为
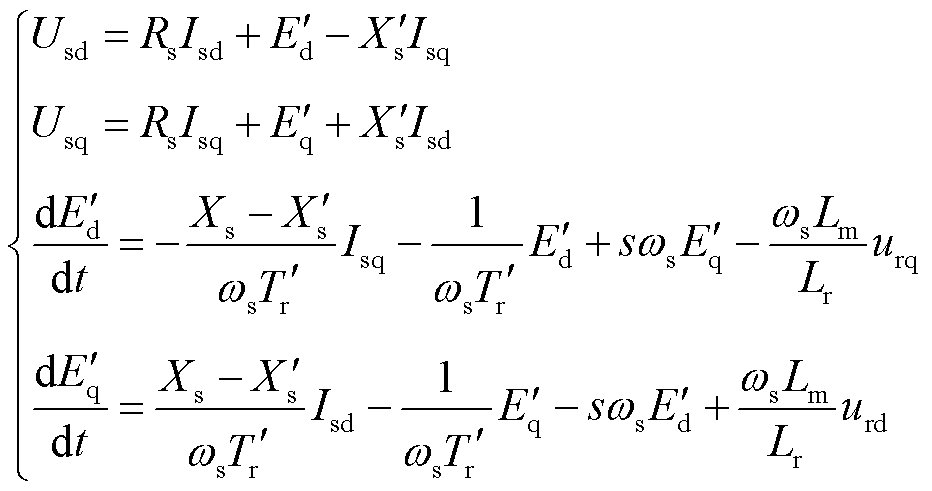（8）
式中，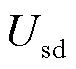
、
、
、
、
、
、
、
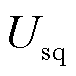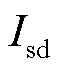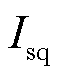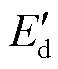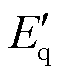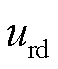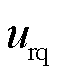分别为定子电压dq轴分量、定子电流dq轴分量、定子暂态电动势dq轴分量、转子电压dq轴分量；
、
、
、
、
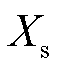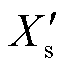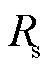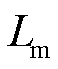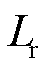分别为定子电抗、定子暂态电抗、定子电阻、定转子互感、转子自感；
、
、
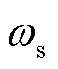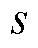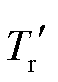分别为定子角速度、转差率、转子回路时间常数。
将式（7）、式（8）代入式（1）中，可以得到
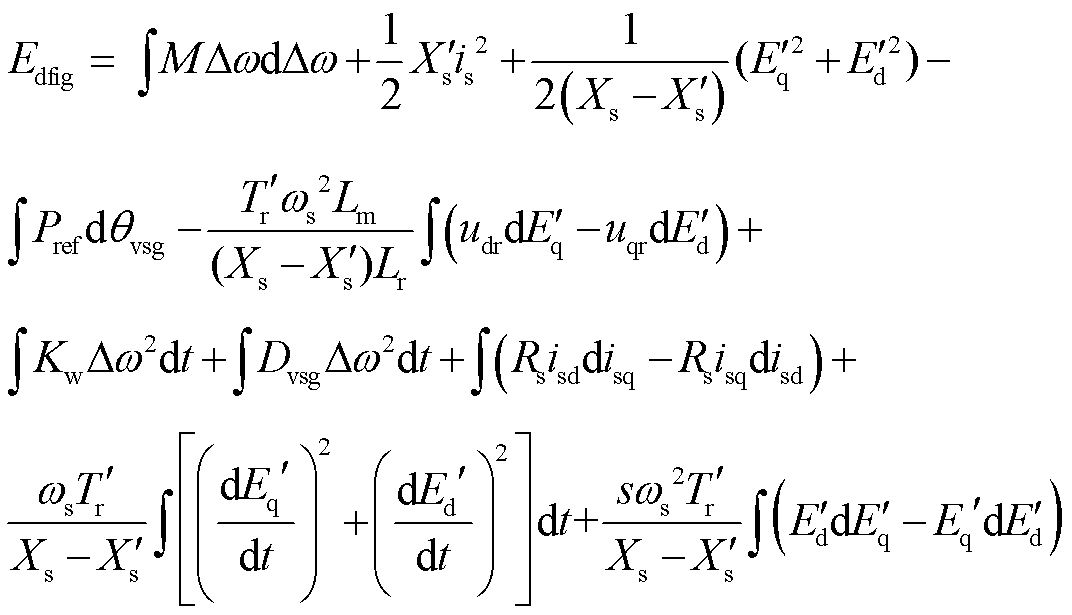（9）
通过式（9）可以得到构网型双馈风电机组的能量函数。依据能量形式，将其分为注入能量结构、耗散能量结构、交互能量结构。下面对这三部分能量结构进行分析。
1）构网型双馈风电机组注入能量
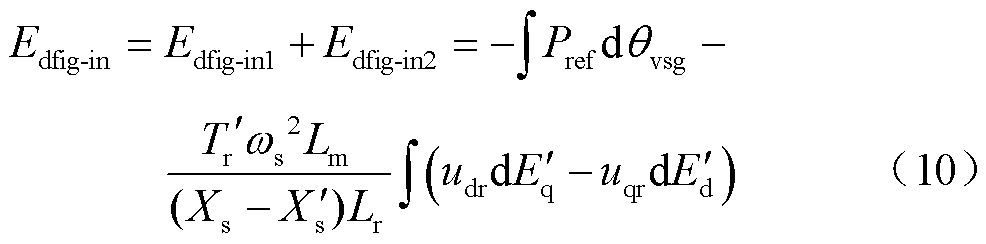
式中，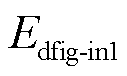
为构网型双馈风电机组轴系经VSG控制通道所注入的能量；
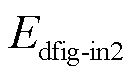为电压电流控制所注入的能量。
2）构网型双馈风电机组暂态能量
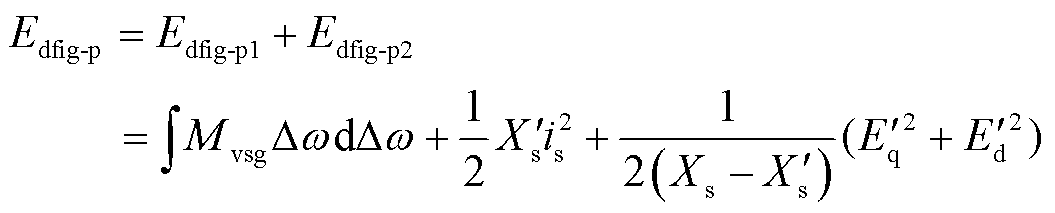（11）
式中，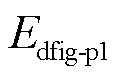
为VSG控制通道的暂态能量，又称作构网型双馈风电机组虚拟动能增量，与同步机实际转子动能不同，其从控制角度模拟了传统同步机的物理运行过程，体现了模拟同步机运行过程中相应的动能；
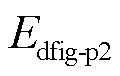为电压电流环控制通道的暂态能量，其中能量的第一项为定子电抗所对应的磁场势能，第二项为转子回路中转子电抗所对应的磁场势能。
3）构网型双馈风电机组耗散能量
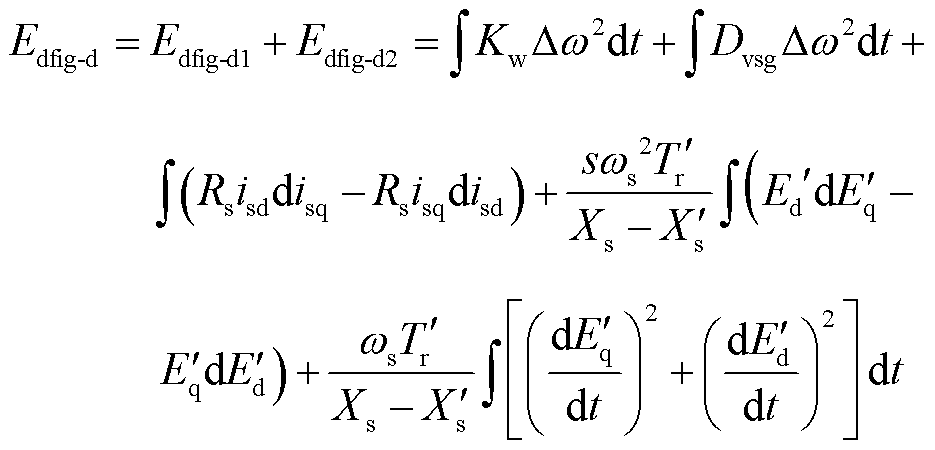（12）
式中，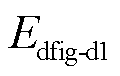
为VSG控制通道的耗散能量，其中能量的第一项为虚拟调频系数项产生的耗散能量，第二项为虚拟阻尼系数项产生的耗散能量；
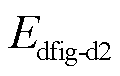为电压电流控制通道的耗散能量，其中第一项为定子电阻所产生的耗散能量，第二项为转子电阻所产生的耗散能量，第三项为转子磁通衰减过程中产生的耗散能量。
综上所述，构网型双馈风电机组能量结构关系式为
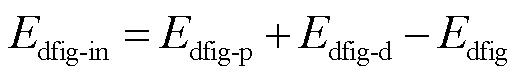（13）
构网型双馈风电机组能量结构示意图如图3所示。构网型双馈风电机组能量由风机轴系和电流电压控制产生，经过双馈风电机组控制及内部定转子回路相关元件的耗散，剩余能量供给暂态能量项和双馈风电机组端口，暂态能量作为具有交互性质及周期性质的能量，在能量交互过程中，端口能量和双馈风电机组的暂态能量之间将会发生交互作用，并且从元件端口经过系统网络和其他发电机组相关联。
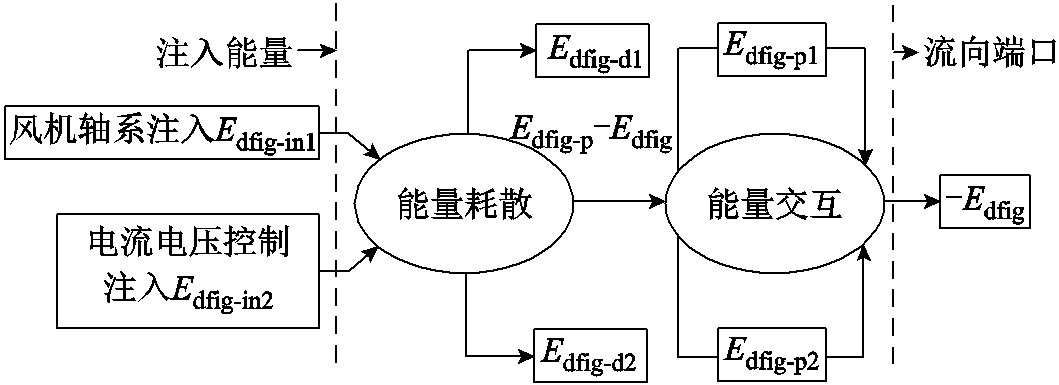
图3 构网型双馈风电机组能量结构示意图
Fig.3 Energy structure diagram of grid-forming doubly-fed wind turbine generator
同步发电机的转子运动方程为
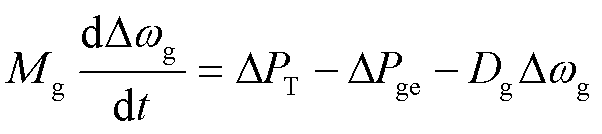（14）
式中，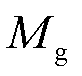
为同步发电机的惯性时间常数；
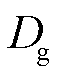为同步发电机的机械阻尼系数；
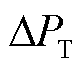为同步发电机的机械功率偏差；
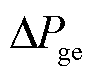为同步发电机的电磁功率偏差；
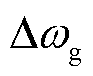为同步发电机的电角速度偏差。
忽略发电机调速系统的动态过程，令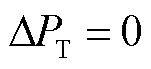
，并对等式两边同时乘以
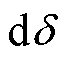进行积分，得到
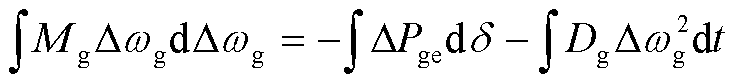（15）
式中包含三项，等式左边为同步发电机的动能增量；等式右边第一项为发电机端口能量项；等式右边第二项为发电机耗散能量项。由于耗散能量不属于周期性质的交互能量，通过式（15）可见，同步发电机转子偏差动能与发电机端口能量存在相应的交互过程。
图4为单机系统设置微小扰动下同步发电机端口能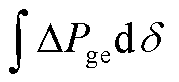量
和动能增量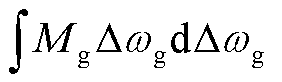
的时域曲线。从曲线中可以看出，同步发电机的端口能量曲线与动能增量曲线具有相反的相位，这印证了式（15），即在系统的振荡过程中同步发电机动能与其端口能量存在交互过程。而针对基于VSG控制的构网型双馈风电机组，同步发电机转子运动方程体现的是真实的物理同步结构。针对VSG控制，对式（7）进行线性化，并对等式两边同时乘以
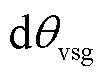进行积分，设
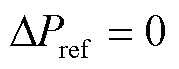，可以得到
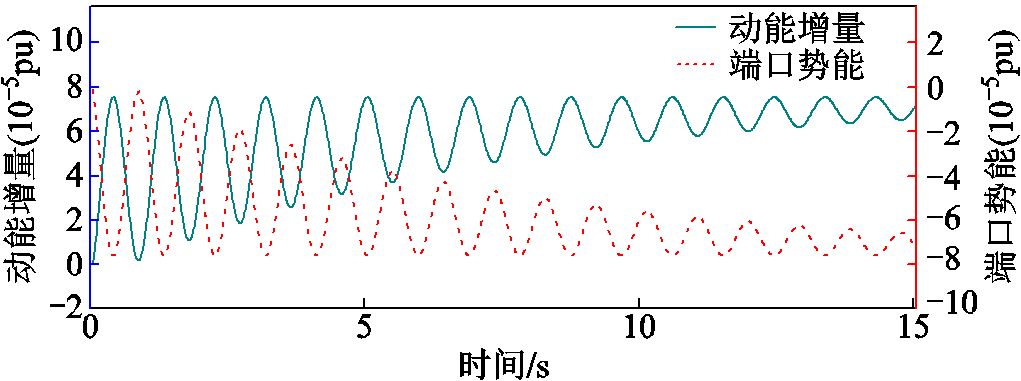
图4 同步机动能势能关系
Fig.4 Relationship of kinetic energy-potential energy of synchronous generator
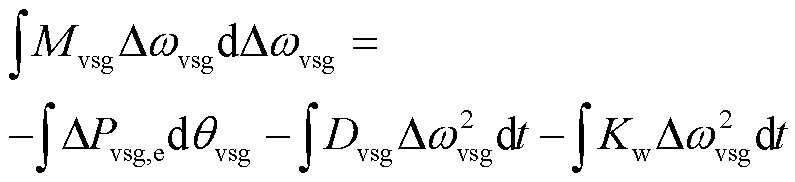(16)
式中，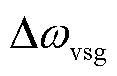
为虚拟角频率偏差；
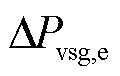为机组电磁功率偏差。
式（16）中等号左边为构网型双馈风电机组的虚拟动能增量，等式右侧第一项为构网型双馈风电机组端口能量项，等式右边第二项为虚拟调频系数和虚拟阻尼系数相关的耗散能量项。只考虑周期性能量的交互过程，可以看出构网型双馈风电机组的虚拟动能增量与端口能量存在交互过程。
图5为单机情况下构网型双馈风电机组端口能量项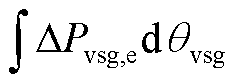
和虚拟动能增量
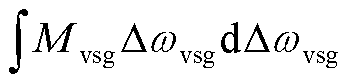的时域曲线，其端口势能与虚拟动能增量在振荡过程中存在交互作用。
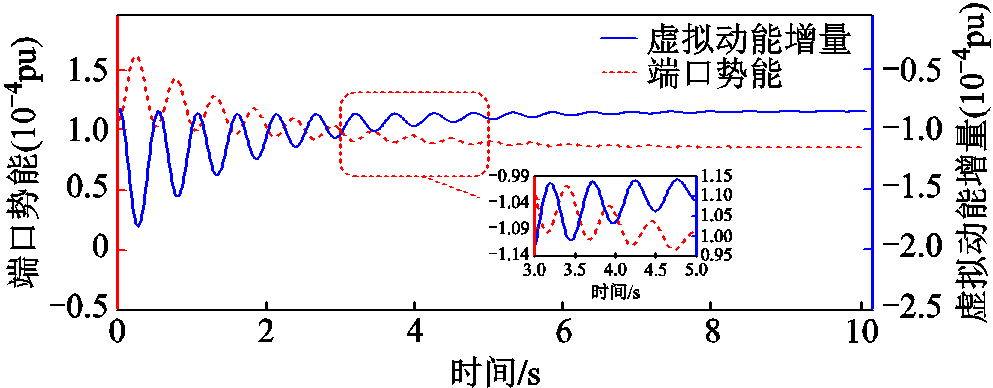
图5 构网型双馈风电机组动能势能关系
Fig.5 Relationship of kinetic energy-potential energy of grid-forming doubly-fed wind turbine generator
综上所述，在系统发生扰动时，同步发电机和构网型双馈风电机组的动能项与端口能量项相位相反，说明在系统发生振荡的过程中发电机内部动能与端口存在能量的交互过程，为后续利用动能相关项分析系统区间振荡提供了可行性。
含构网型双馈风电机组的电力系统的微分方程和代数方程为
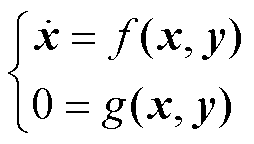（17）
式中，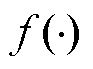
、
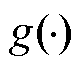分别为微分方程和代数方程所对应的函数映射关系；x为系统的状态变量；y为系统的输出变量，例如系统的电流、电压等电气量。
将式（17）线性化为
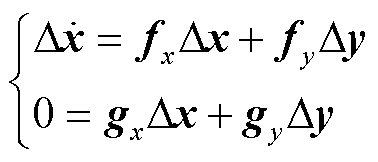（18）
式中，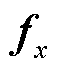
、
、
、
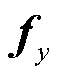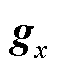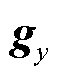为系统的雅克比矩阵。将式（18）中的变量
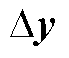消去，可以得到
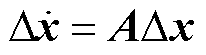（19）
式中，A为系统的状态空间矩阵，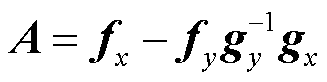
。式（19）中的状态变量
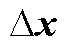可由列向量表示为
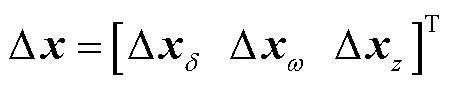（20）
式中，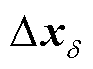
包括同步发电机转子角
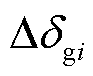及构网型双馈风电机组的虚拟转子角
；
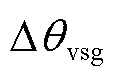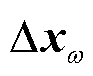包括同步发电机转速偏差
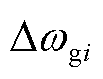及构网型双馈风电机组的虚拟转速偏差
；
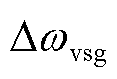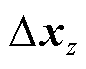包含系统中同步发电机以及构网型双馈风电机组等其他状态变量。
根据式（19），可以得到状态变量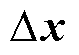
的时域表达式为
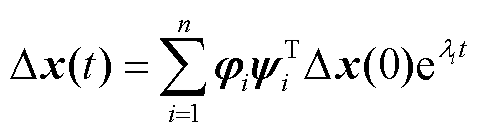（21）
式中，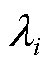
为系统第i个振荡模式的特征值；
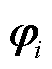为第i个振荡模式的右特征向量，反映了第i个模式中各个变量的相对振荡程度；
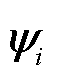为第i个振荡模式的左特征向量，反映了在第i个模式下各变量占比的主导大小；
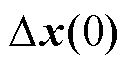为系统在t=0 s时状态变量的数值。
系统在运行过程中，同步发电机与构网型双馈风电机组的动能增量与端口能量均存在交互过程。这种交互过程在各电源之间进行，线路作为能量交互过程中的流通路径。针对各发电机之间交互以动能为主的物理过程。下面对各发电机以及构网型双馈风电机组的动能关系做出解释。
对于同步发电机，第i台同步发电机的实际动能可以写为
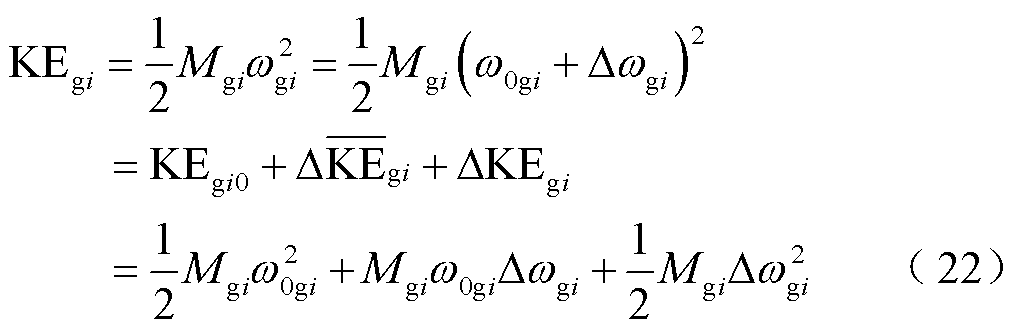
式中，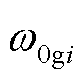
为第i台同步发电机的稳态角速度；
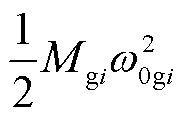为同步发电机初始动能，体现了发电机稳态时所储存的动能大小；
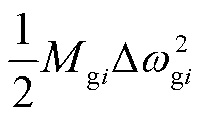为同步发电机动能增量，体现了发电机受扰后转子动能的变化情况；
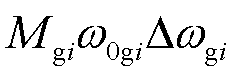为同步发电机的模式动能，体现了同步发电机在受到扰动后，相对于发电机稳态动能的动能变化情况。
对于构网型双馈风电机组，与同步发电机同理，其虚拟动能可以写为
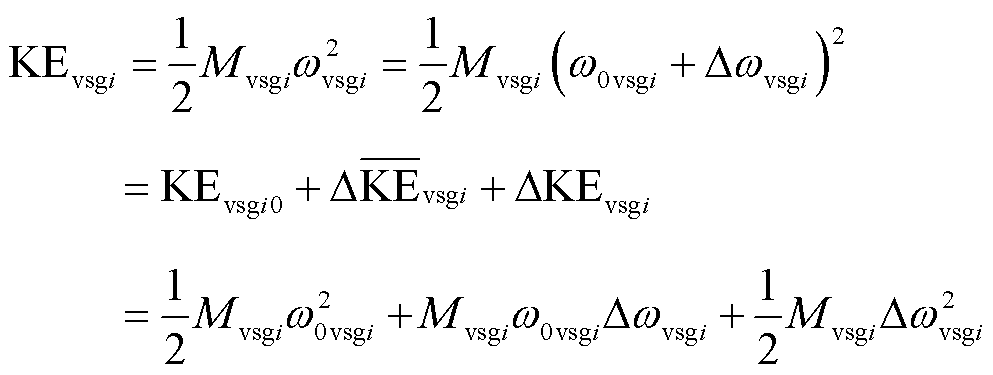（23）
式中，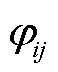
为右特征向量矩阵中第i行第j列元素；
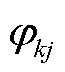为右特征向量矩阵中第k行第j列元素；
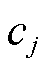为由初始条件引起的第j个模式被激励的幅值；
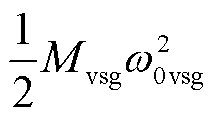为构网型双馈风电机组的初始虚拟动能；
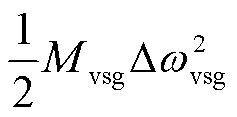为构网型双馈风电机组的虚拟动能增量；
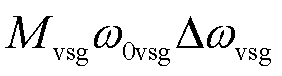为构网型双馈风电机组的虚拟模式动能。
第i台同步发电机和第k台构网型双馈风电机组的速度偏差分别为
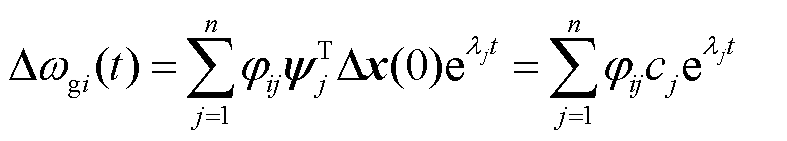（24）
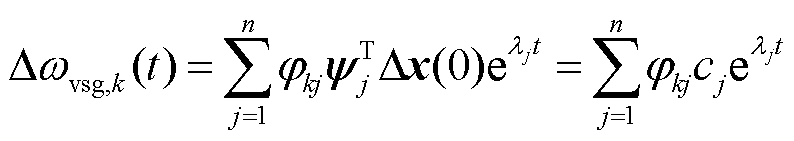（25）
式中，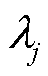
为系统第j个振荡模式的特征值，
；
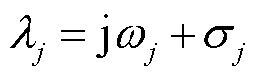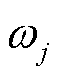和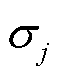
分别为第j个振荡模式的振荡频率及阻尼系数。由此可知，第i台发电机和构网型双馈风电机组的速度偏差由系统各振荡模式提供的速度偏差分量构成。
已知速度偏差可以推导出第i台发电机以及构网型双馈风电机组的动能增量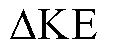
，假设初始条件
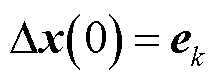，其中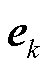
是第k个元素为1，其他元素为0的单位列向量，则
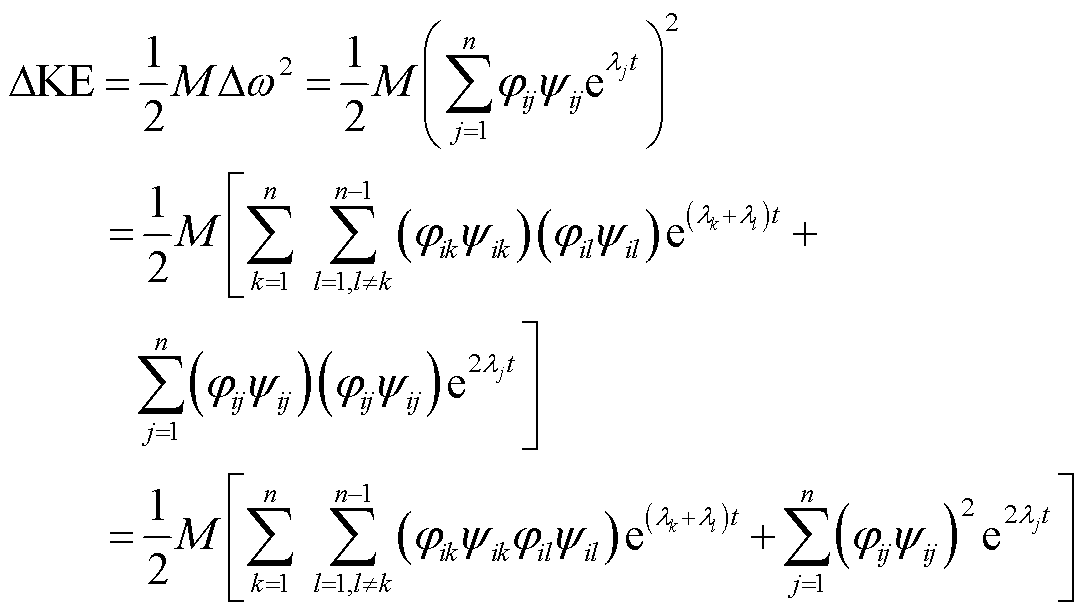（26）
式中，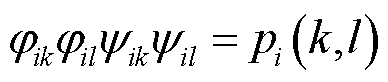
，
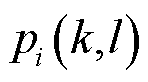为第i台发电机动能增量中模式k与模式l的动能参与因子；
，
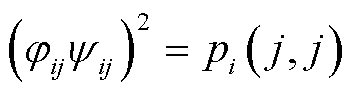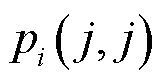为第i台发电机动能增量中模式j的动能参与因子。对于参与特征值为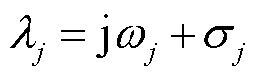主导振荡模式的发电机组，主要考虑在主导振荡模式下各发电机与构网型双馈风电机组之间的相互作用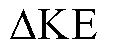，中包括了互模式能量以及主导模式能量，由于本文研究的是主导模式下的区间振荡过程，主导模式能量
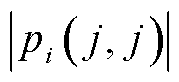与角速度增量参与因子二次方呈正相关。因此通过动能增量可以体现主导振荡模式中各发电机组的参与程度。
当机组之间发生区间振荡时，各机组状态变量的右特征向量的相位体现了机组区间振荡的物理现象。假设机群A与机群B发生区间振荡，机群A与B的右特征向量相位差约为180°，而对于主导模式能量而言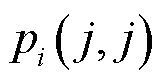，中的相位关系由
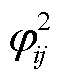体现，此时相对振荡的机群A、B在主导模式能量中将以同相位的形式出现；若存在不参与振荡的机群C，则机群C与其他机组相位呈现约为90°的关系，而在主导模式能量中，机群C的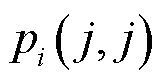相位将与机群A或机群B同相。综上所述，动能增量中的主导模式能量可以直观清晰地描述各机组参与振荡水平，而各机组区间振荡的相位关系难以厘清。后续将利用模式动能的概念对区间振荡现象进一步解释。
在系统主导振荡模式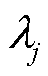下，将右特征向量
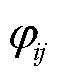以相量形式表示，记作
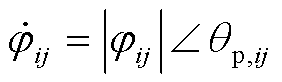；初始值
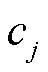记作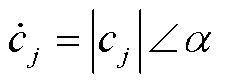
，其所在模式的模式动能为
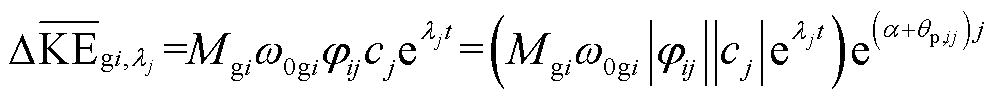（27）
针对同一主导振荡模式，其模式所在的模式动能相位受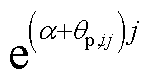
项影响，各机群振荡相位的相对关系只受
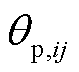影响，而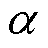
只受系统状态变量初始值影响，其值为常数。主导振荡模式所在的模式动能的相位可以体现出各机组区间振荡的相位关系及其能量的转换关系。
由第2节可知，当系统受扰后，元件的动能和势能存在相互转换过程。同步发电机的能量转换过程是同步发电机转子动能增量和网络势能的相互转换；而基于VSG控制的构网型双馈风电机组的能量转换过程是机组的虚拟动能增量和网络势能的相互转换。在能量转换的过程中体现了系统在各模式下各元件能量的分布状况。
通过前文对元件动能增量的分析，动能增量的振荡幅值水平可以作为衡量发电机参与振荡水平的评价指标。定义在主导振荡模式下各机组动能增量幅值的最大值为振荡参与度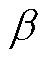
的幅值，即
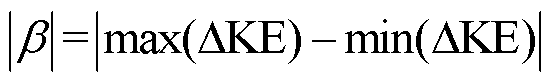（28）
通过对前文中模式动能进行分析，机组的相位信息可由各机组的模式动能相位表示。定义在主导振荡模式下各机组模式动能相位为振荡参与度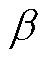的相位，即
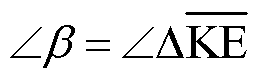（29）
由此可以得到振荡参与度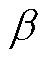为
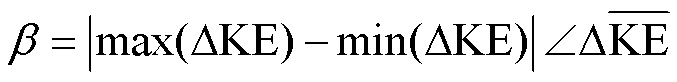（30）
通过求出各机组所的振荡参与度幅值并进行排序，可以得到各机组在振荡过程中对振荡的贡献程度；通过求出各机组振荡参与度的相位信息，可以对参与振荡的机组进行分群。机组A与机组B存在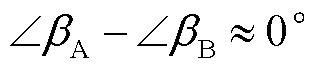
时，认为机组A与与机组B趋势相同，属于同一机群；当机组A与机组B存在
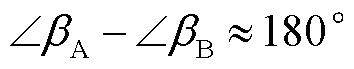时，认为机组A与与机组B趋势不同，属于不同机群。
综上所述，利用指标振荡参与度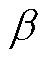可以从能量的角度清晰地反映当系统发生区间振荡时，各机组参与区间振荡的程度以及各机组的模态相位。为后续基于能量结构的区间振荡分析方法提供了切实有效的分析指标。
基于上述对指标的讨论，可以利用指标来区分含构网型双馈风电的电力系统发生区间振荡时，各机组参与区间振荡的水平以及各机组间模态相位关系。本节将提出一种基于能量结构的区间振荡分析方法，具体方法流程如图6所示。
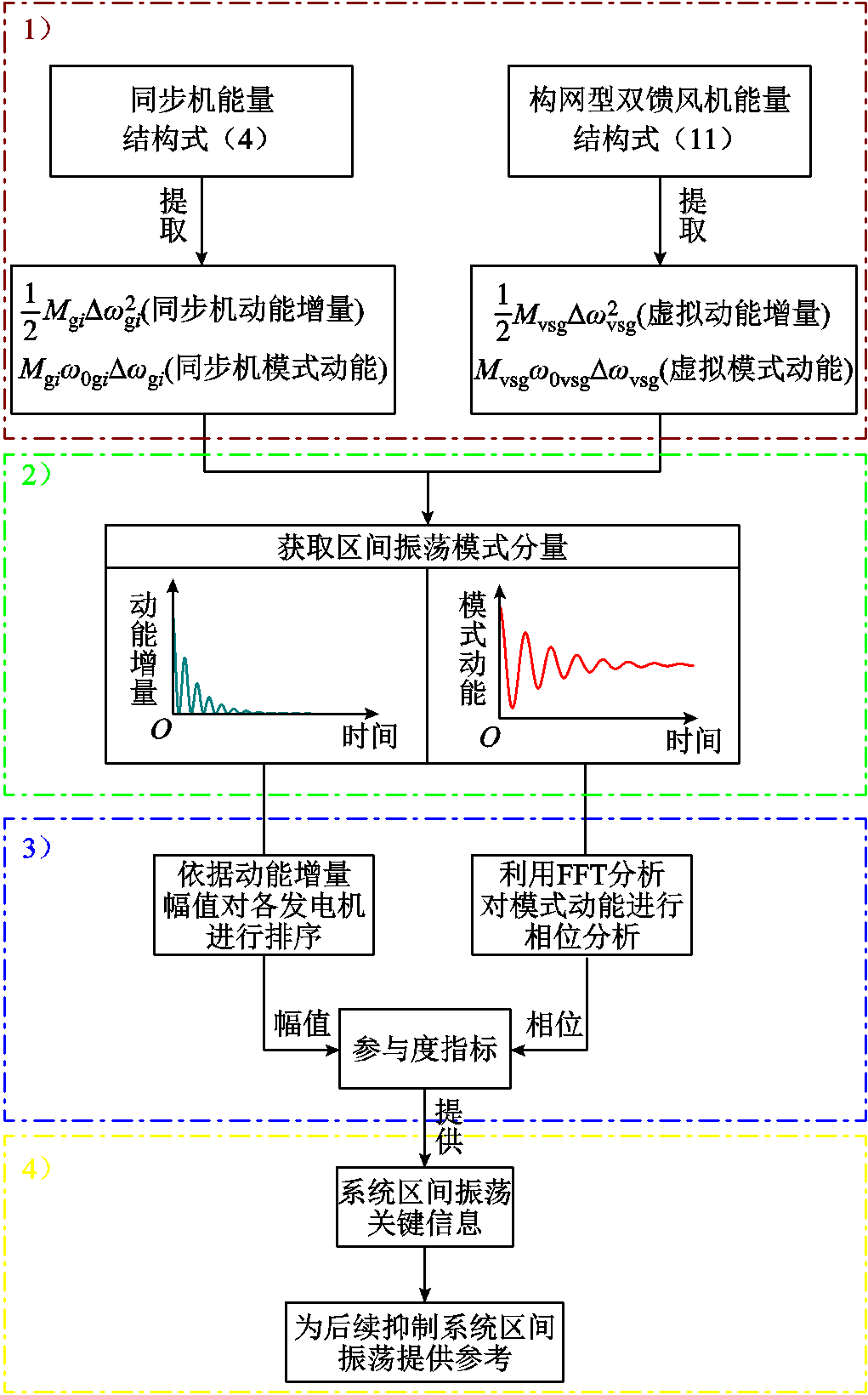
图6 方法流程
Fig.6 Method flow chart
1）根据式（4）与式（11）构建同步发电机以及基于VSG控制的构网型双馈风电机组的能量结构。根据所构建的能量结构，提取出与同步发电机相关的动能增量和模式动能，以及构网型双馈风电机组相关的虚拟动能增量及虚拟模式动能。
2）实时对系统低频振荡现象进行监测，当系统发生低频振荡时，应对各同步发电机的动能增量和模式动能及构网型双馈风电机组的虚拟动能增量和虚拟模式动能进行实时量测。并通过分解算法提取出各振荡模式下的动能增量和虚拟动能增量，以及模式动能和虚拟模式动能。通过信号分解算法提取出所重点关心的区间模式下的动能增量和模式动能及虚拟动能增量和虚拟模式动能。
3）根据提取出的动能增量及虚拟动能，针对所提取出的动能增量，将动能增量按幅值大小进行排序；另外将提取出的模式动能利用快速傅里叶变换（Fast Fourier Transformation, FFT）分析获取其相位信息。将各机组的动能增量幅值与虚拟动能提供的相位信息结合构成参与度指标。
4）根据步骤3）中各机组的参与度指标，按照幅值与相位进行排序及分群，从而得到参与振荡水平程度较高的机组，以及区间振荡过程中各机组机群的分布情况。获取到的区间振荡信息可以为后续抑制系统区间振荡提供参考。
为了验证本文所提方法的有效性，在Powerfactory/digsilent平台上搭建了如图7所示的四机两区仿真系统，其中将区域1中同步发电机G2替换为构网型双馈风电机组；同步发电机G1、G3、G4采用详细的六阶模型进行建模，励磁模型和调速器模型分别采用IEEET1[43]与TGOV1[44]；基于VSG控制的构网型双馈风电机组共计200台并入电网，详细参数见表1。
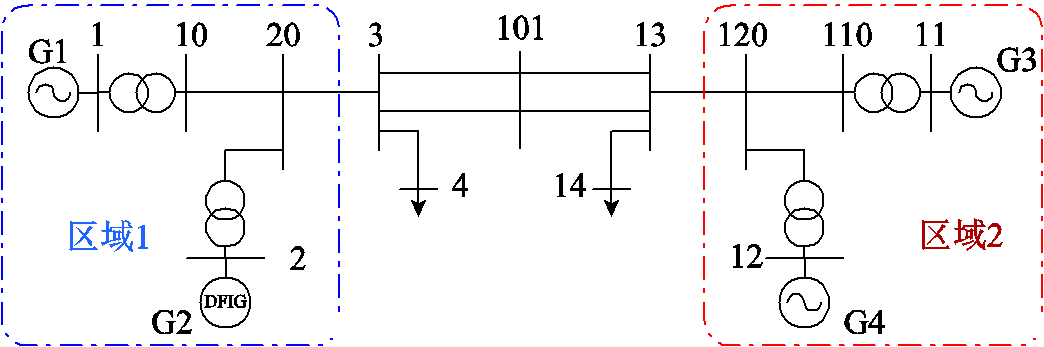
图7 四机两区域仿真系统
Fig.7 The diagram of four-generator two-area system
表1 构网型双馈风电机组参数
Tab.1 Parameters of grid-forming doubly-fed wind turbine generator
参数数值参数数值 额定功率/(MV·A)7Kq1 000 Qref/var0U0(pu)1 Kp2Rs(pu)0.01 Kv30Lm(pu)4 M/s10Lr(pu)0.1 D2Ls(pu)0.01
在母线101处施加三相短路故障，持续0.01 s，系统发生低频振荡现象，系统联络线功率如图8所示。对功率进行FFT分析，图9给出了联络线功率的FFT分析频谱。根据图9可以发现区域1与区域2之间存在区间振荡现象。
对系统进行模态分析，系统的机电振荡模式见表2。系统振荡模态图如图10所示，包含了两个本地振荡模式和一个区间振荡模式。与传统双馈风电机组不同，构网型双馈风电机组会主动参与系统的区间振荡。图10a展示了构网型双馈风电机组G2及同步机G1与其他同步机G3、G4的区间振荡过程。结合表2，模式1为系统的区间振荡模式，该模式的阻尼比远小于工程中所要求的5%，需重点关注该模式；图10b为振荡模式2的模态图，该模式为区域2中同步机G3相对于同步机G4振荡的本地振荡模式；图10c为振荡模式3的模态图，该模式为区域1中同步机G1相对于构网型双馈风电机组G2振荡的本地振荡模式。
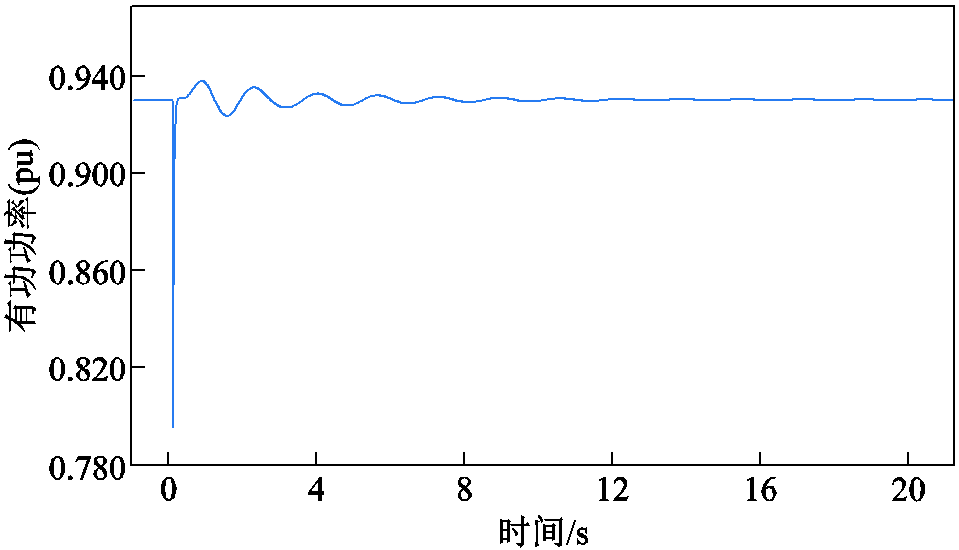
图8 系统联络线功率
Fig.8 Tie-line power of the power system
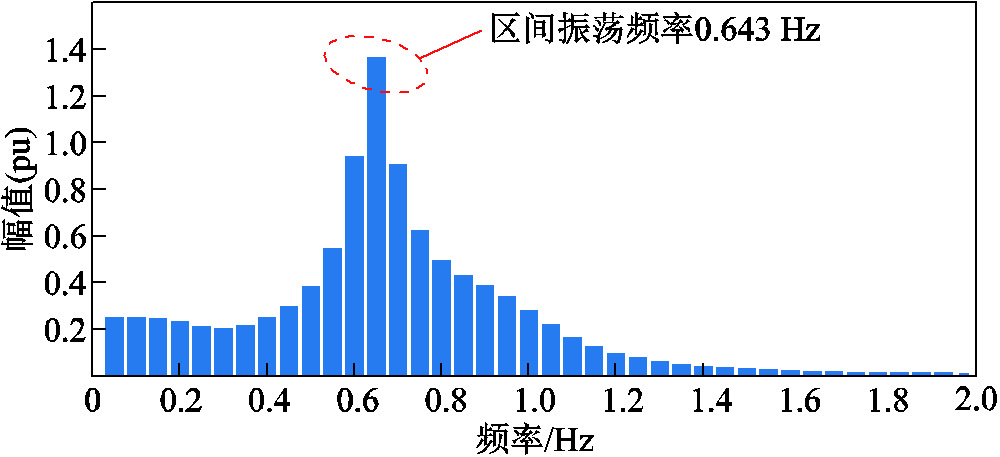
图9 系统联络线功率的频谱
Fig.9 Frequency spectrum of tie-line power of the power system
表2 系统机电振荡模式
Tab.2 Electromechanical oscillation mode of the power system
模式序号特征值频率f/Hz阻尼比ξ(%) 1-0.149±4.037j0.6433.669 2-1.039±6.072j0.96616.871 3-2.825±6.885j1.0937.956
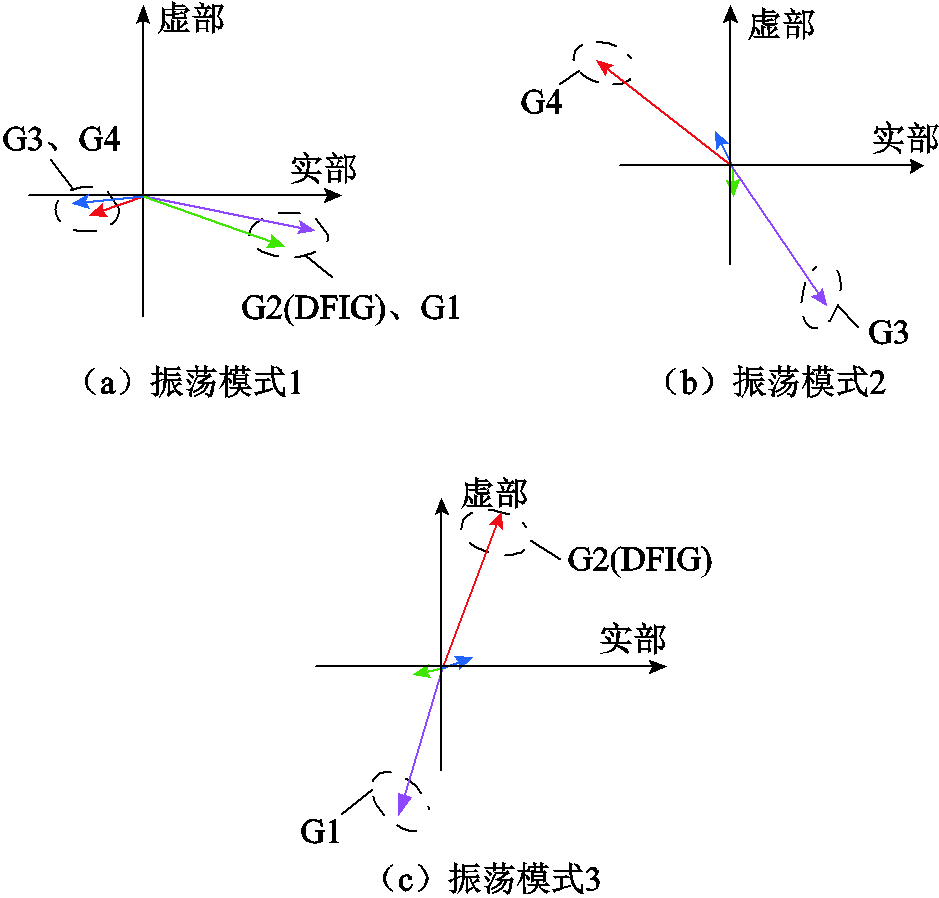
图10 系统振荡模态
Fig.10 Modal shapes of the power system
4.1.1 区间模式分析
针对系统区间振荡模式，获取区间振荡模式下各个发电机组的动能增量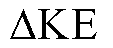
，附图1给出了各发电机的动能增量曲线。附图1中，在区间振荡模式下，各发电机动能增量曲线具有相同相位，但各发电机动能增量幅值不同，同步发电机G1与双馈风电机组G2的动能增量幅值远大于同步发电机G3、G4的动能增量幅值。
为了验证动能增量幅值是否能体现各发电机参与区间振荡的水平，图11给出了四台发电机组归一化后的参与因子，以及归一化后的动能增量幅值。根据图11，各发电机动能增量幅值相对大小趋势与各发电机参与因子相对大小趋势相同，说明利用发电机动能增量幅值可以近似表征机组参与振荡水平具有可行性。当电力系统发生低频振荡时，可以通过对动能增量幅值较大的机组施加相关控制，以抑制低频振荡。
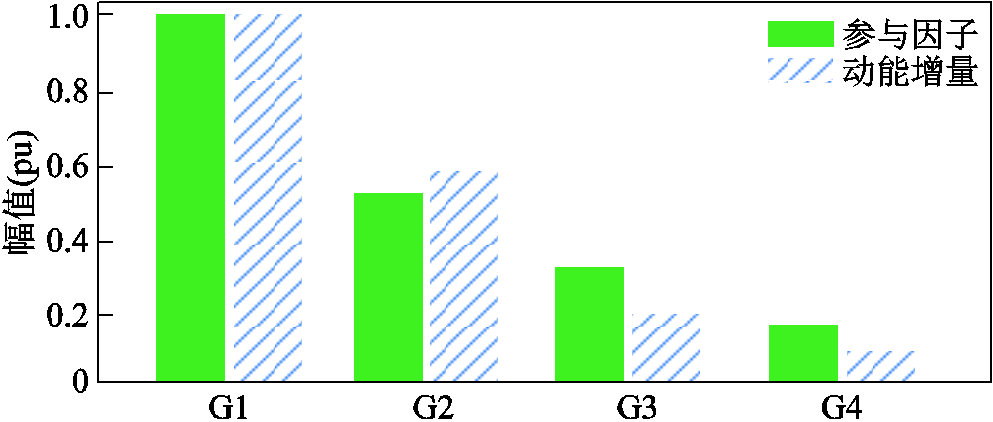
图11 动能增量及参与因子幅值对比
Fig.11 Amplitude comparison chart of increment of kinetic energy and participation factor
附图2给出了系统中各发电机在区间振荡模式下的模式动能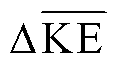
。针对附图2中各发电机的模式动能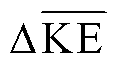，利用FFT进行相位分析，图12给出了各发电机模式动能在区间振荡模式下的矢量图。由图12可知，在区间振荡过程中，发电机G1、G2的模式动能相位与发电机G3、G4模式动能相位相反。
根据图12并结合图10a，图12中发电机G1、G2与发电机G3、G4在区间振荡过程中模式动能的相位相反，即在区间振荡过程中，发电机G1、G2的模式动能与发电机G3、G4的模式动能通过网络存在交换过程。与图10a中系统区间振荡模态图进行对比可以发现，利用各发电机的模式动能可以判断各发电机在区间振荡过程中的相对相位情况。当系统出现低频振荡现象时，结合系统潮流及各机组模式动能信息，可对机组振荡区域进行有效划分。
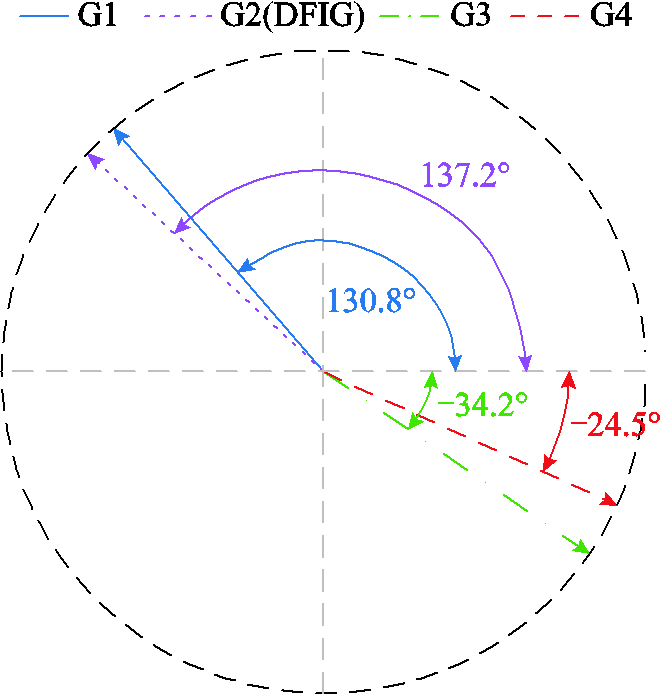
图12 模式动能矢量图
Fig.12 Vector diagram of modal kinetic energy
为了更加直观地反映各机组在区间振荡过程中的参与水平，利用各机组的动能增量幅值及模式动能相位构成振荡参与度指标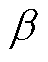
，参与度指标依据动能增量幅值从大到小进行排序。各机组的振荡参与度指标见表3。由表3可以发现，发电机G1、G2相对于发电机G3、G4发生摆动，且发电机G1、G2参与度幅值最大，依据所求得的参与度指标，应着重对G1、G2机组实施相应的控制措施来抑制系统的区间振荡。应用本文所提出的方法可以准确地提供各发电机参与振荡的水平及相对振荡机群，为后续振荡的抑制提供了参考和依据。
表3 区间振荡参与程度指标
Tab.3 Degree of oscillation participation
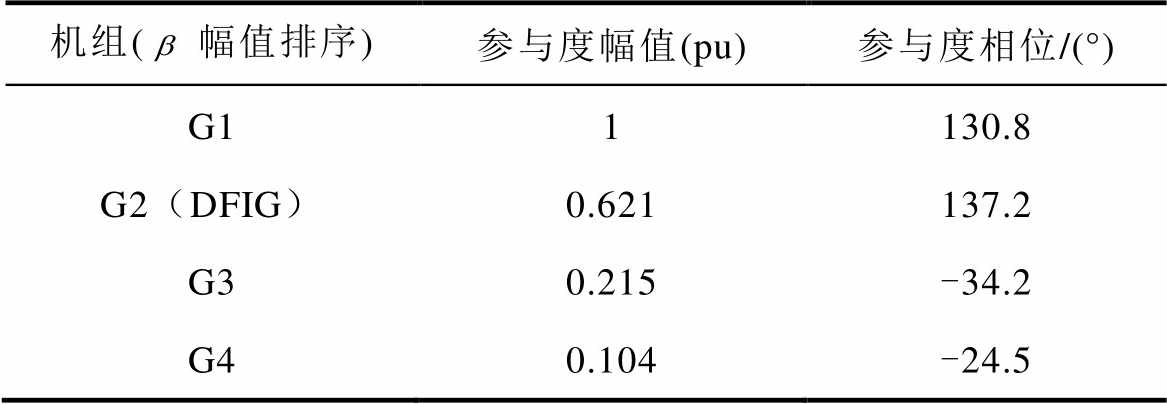
机组(幅值排序)参与度幅值(pu)参与度相位/(°) G11130.8 G2（DFIG）0.621137.2 G30.215-34.2 G40.104-24.5
4.1.2 G1-G2本地模式分析
针对G1相对于G2的本地振荡模式，获取G1、G2在本地振荡模式下的动能增量，给出了G1、G2的动能增量曲线，如附图3所示。
将G1、G2本地模式动能增量幅值进行归一化，与G1、G2本地振荡模式的参与因子进行对比，如图13所示。可以发现G1、G2动能增量幅值相对大小趋势与各发电机参与因子相对大小趋势相同。
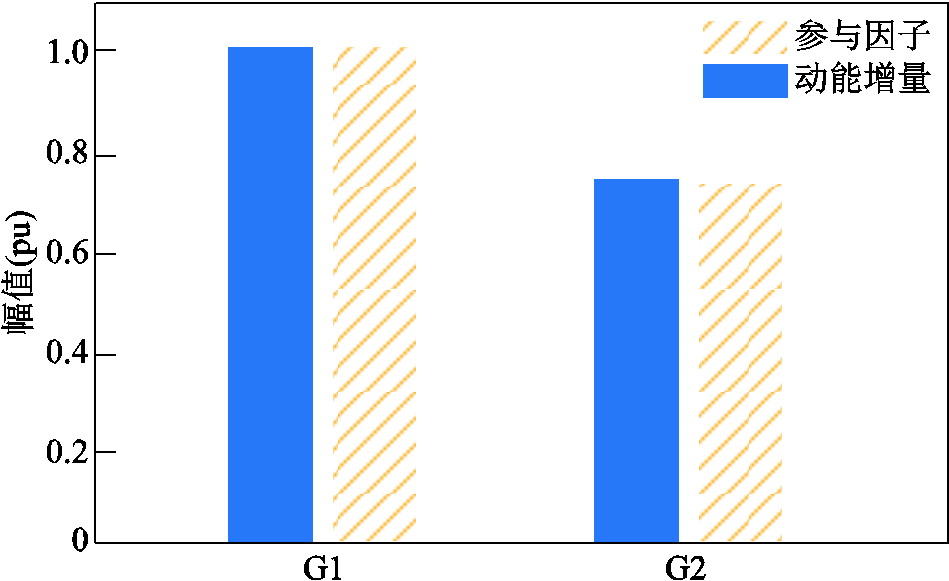
图13 动能增量及参与因子幅值对比
Fig.13 Amplitude comparison chart of increment of kinetic energy and participation factor
另外，附图4给出了G1、G2本地振荡模式的模式动能。由附图4可以发现，G1、G2模式动能具有相反的相位。与图10c相对应，说明在G1、G2之间发生相对振荡，即为G1、G2的本地振荡模式。
在仿真算例1的基础上，为了验证多构网型双馈风电机组接入系统后本文方法的可行性，在仿真算例1中120母线处并入构网型双馈风电机组，新场景下四机两区域结构接线图如图14所示。
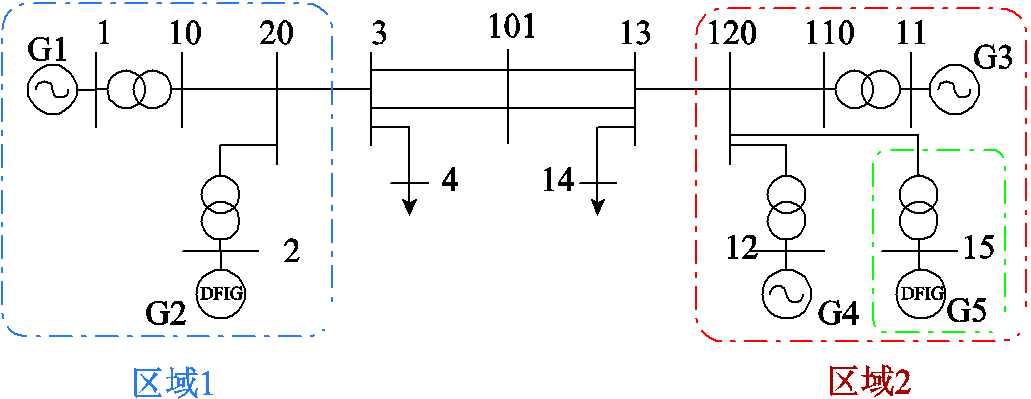
图14 新场景下四机两区域结构接线图
Fig.14 The diagram of four-generator two-area system in the new scenario
在母线101处施加0.01 s三相短路故障，激发系统振荡，对该系统联络线功率进行监测，并对联络线功率进行FFT分析，新场景下系统联络线功率频谱如图15所示。另外对上述系统进行模态分析，发现系统存在区域1与区域2之间的区间振荡模式，其振荡模态图如图16所示。其振荡频率f= 0.669 Hz，阻尼比ξ=2.579%。振荡频率与图15所分析的结果一致。
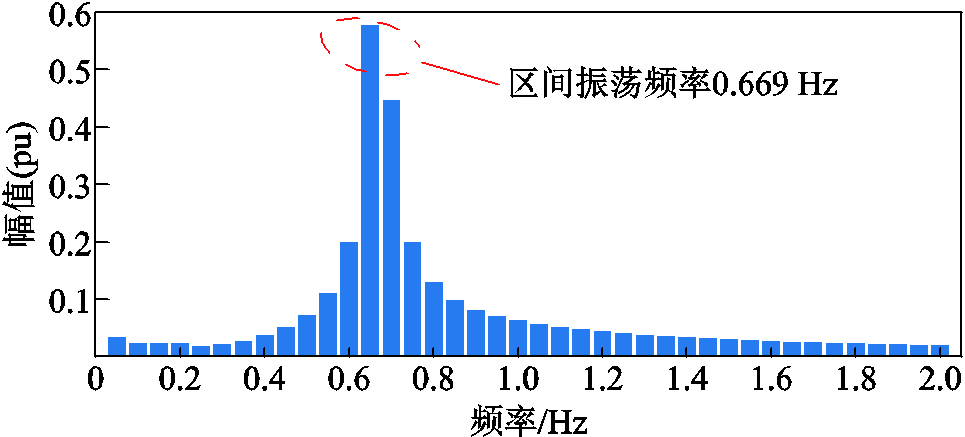
图15 新场景下系统联络线功率频谱
Fig.15 Frequency spectrum of tie-line power of the power system in the new scenario
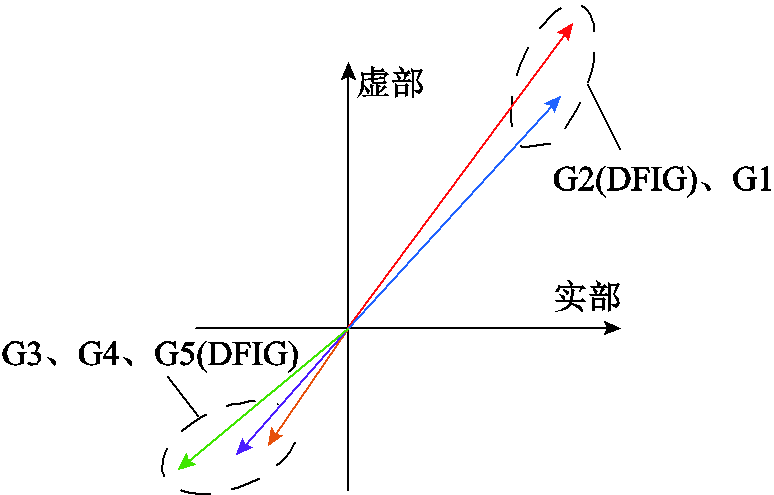
图16 新场景下系统区间模式模态
Fig.16 System interval mode in the new scenario
针对系统区间振荡模式，获取区间振荡模式下各个发电机组的动能增量。附图5给出了各发电机的动能增量曲线。图17给出了G1～G5归一化后的参与因子及动能增量幅值的柱状图。由图17可以看出，各发电机动能增量幅值相对大小趋势与各发电机参与因子相对大小趋势相同。
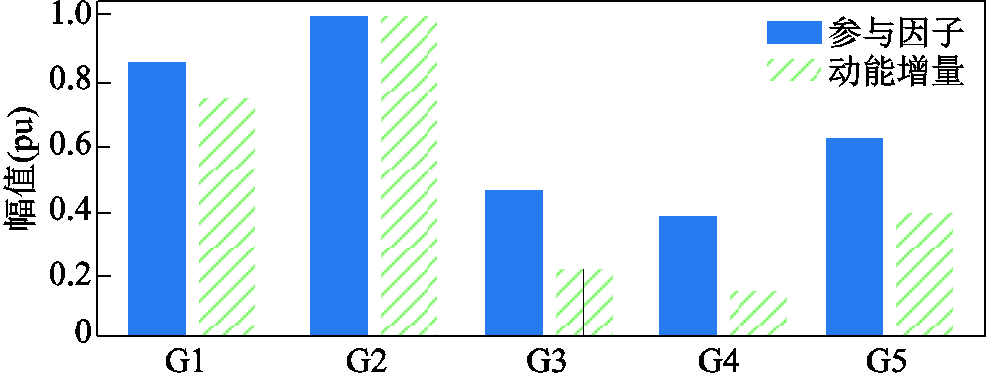
图17 新场景下动能增量及参与因子幅值对比
Fig.17 Amplitude comparison chart of increment of kinetic energy and participation factor in the new scenario
附图6给出了系统中各发电机在区间振荡模式下的模式动能。由附图6可知，在区间振荡过程中，发电机G1、G2的模式动能相位与发电机G3、G4、G5模式动能相位相反。针对附图6中各发电机的模式动能，利用FFT进行相位分析，图18给出了各发电机模式动能在区间振荡模式下的矢量图。
根据图18可以得到，发电机G1、G2与发电机G3、G4、G5在区间振荡过程中模式动能的相位相反，所以利用各发电机的模式动能可以判断各发电机在区间振荡过程中的相对相位情况。为了反映各机组在区间振荡过程中的参与水平，表4给出了各机组的振荡参与度指标。
由表4可以发现，发电机G1、G2相对于发电机G3、G4、G5发生相对摆动，在区域1中发电机G2参与度幅值最大，而对于区域2来说发电机G5参与度幅值最大。依据所求得的参与度指标，应着重对区域1中G1、G2机组以及区域2中的G5机组采取相应的控制措施来抑制系统的区间振荡。针对含多构网型双馈风电机组电力系统而言，应用本文所提出的方法仍可以准确地提供各发电机参与振荡的水平及相对振荡机群，为后续振荡的抑制提供参考和依据。
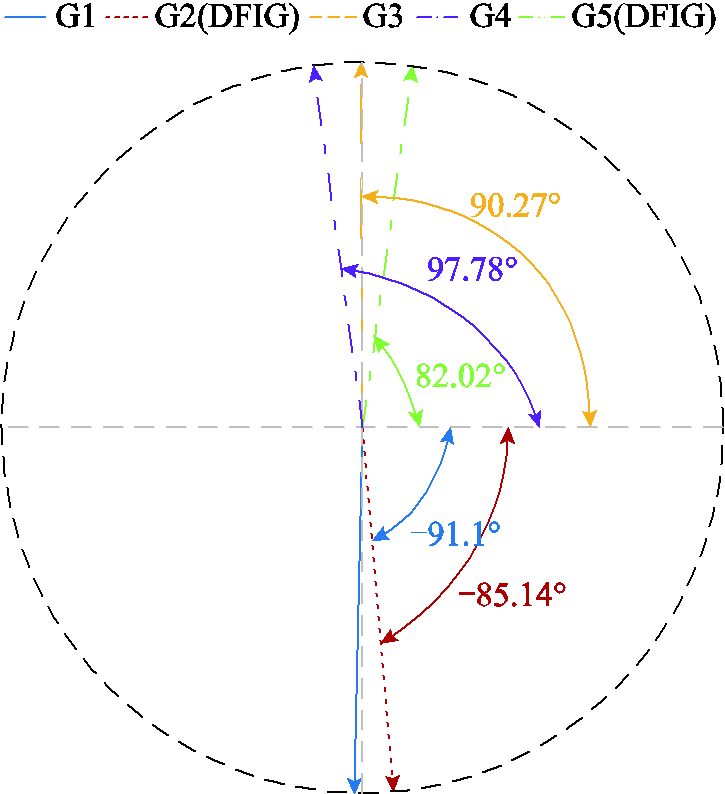
图18 新场景下模式动能矢量图
Fig.18 Vector diagram of modal kinetic energy in the new scenario
表4 新场景下区间振荡参与程度
Tab.4 Degree of Oscillation participation in the new scenario
机组（幅值排序）参与度幅值(pu)参与度相位/(°) G2（DFIG）1-85.14 G10.742-91.1 G5（DFIG）0.38182.02 G30.20790.27 G40.13897.78
本文提出一种含构网型双馈风电机组的电力系统区间振荡的分析方法。首先推导了构网型双馈风电机组与同步发电机的能量结构；然后对能量结构中的动能相关项结合特征值方法进行分析，并定义了模式动能概念，依据动能增量及模式动能构建振荡参与度指标来分析系统区间振荡过程；最后在四机两区系统中进行仿真，得到如下结论：
1）本文建立并推导了构网型双馈风电机组及传统同步机组的能量函数，依据能量的交互-耗散-传递过程构建相应的能量结构，提取出暂态能量的动能项，其中动能项与端口能量存在交互过程。
2）通过动能相关项与特征值方法的结合分析，证明了同步机及构网型双馈机组的动能增量幅值可以反映各机组参与区间振荡的程度；相应的模式动能的相位可以反映各机组的模态信息。
3）本文提出的方法可以对系统区间振荡进行在线分析，无需使用额外的电气量，仅需对各机组的动能相关项进行提取，结合当前广域测量系统即可实现对系统区间振荡模式中各机组参与程度及机群的划分。
后续可以在多构网型设备的新型电力系统中进行进一步研究，对本方法进行进一步完善。
附 录
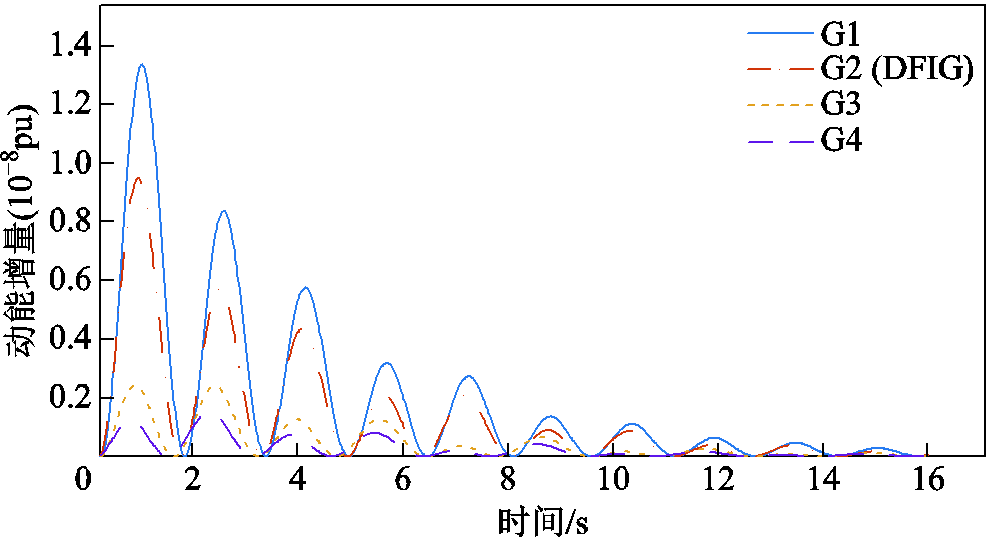
附图1 算例1（区间模式）中各发电机的动能增量
App.Fig.1 The increment of kinetic energy of each generator in Case 1(interval mode)
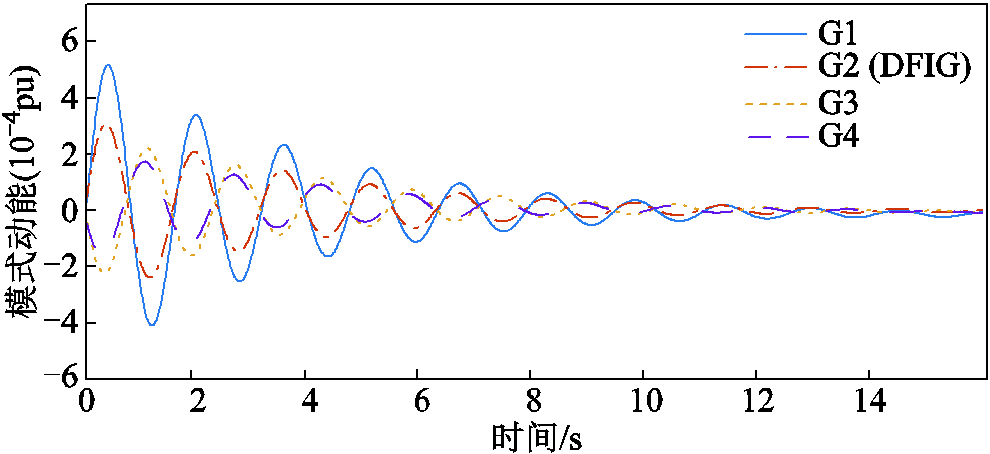
附图2 算例1（区间模式）中各发电机的模式动能
App.Fig.2 The modal kinetic energy of each generator in Case 1(interval mode)
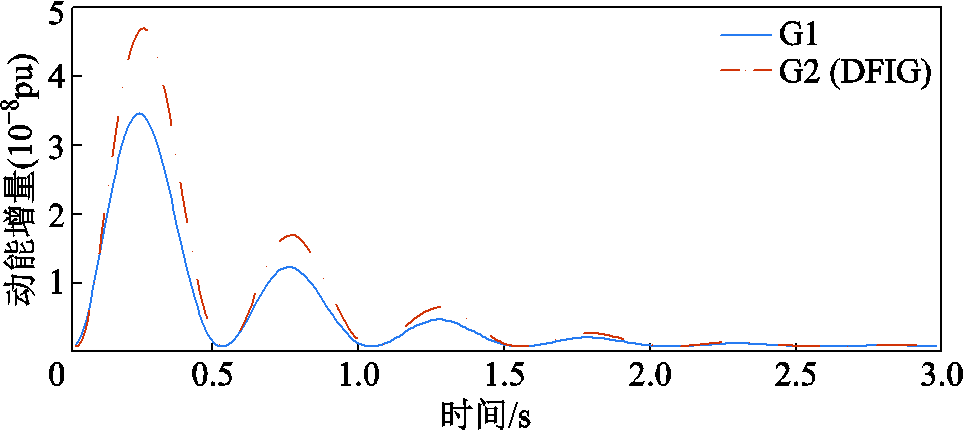
附图3 算例1（本地模式）中发电机G1、G2的动能增量
App.Fig.3 The increment of kinetic energy of generators G1 and G2 in Case 1 (local mode)
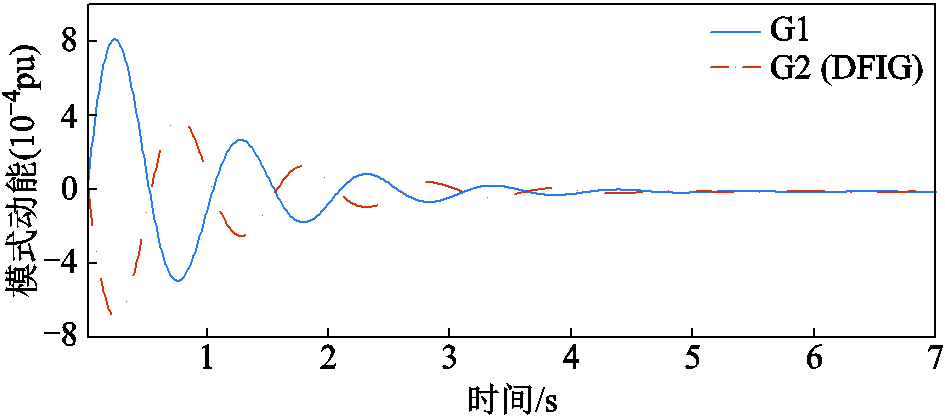
附图4 算例1（本地模式）中发电机G1、G2的模式动能
App.Fig.4 The modal kinetic energy of generators G1 and G2 in Case 1 (local mode)
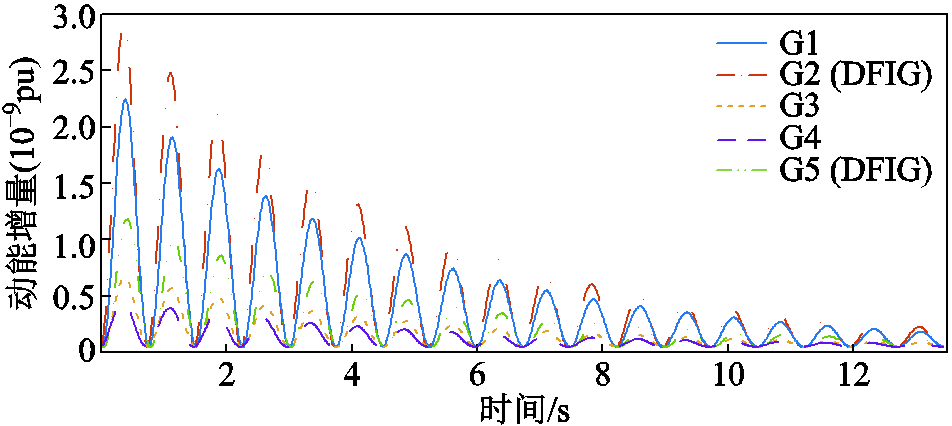
附图5 算例2（区间模式）中各发电机的动能增量
App.Fig.5 The increment of kinetic energy of each generator in Case 2(interval mode)
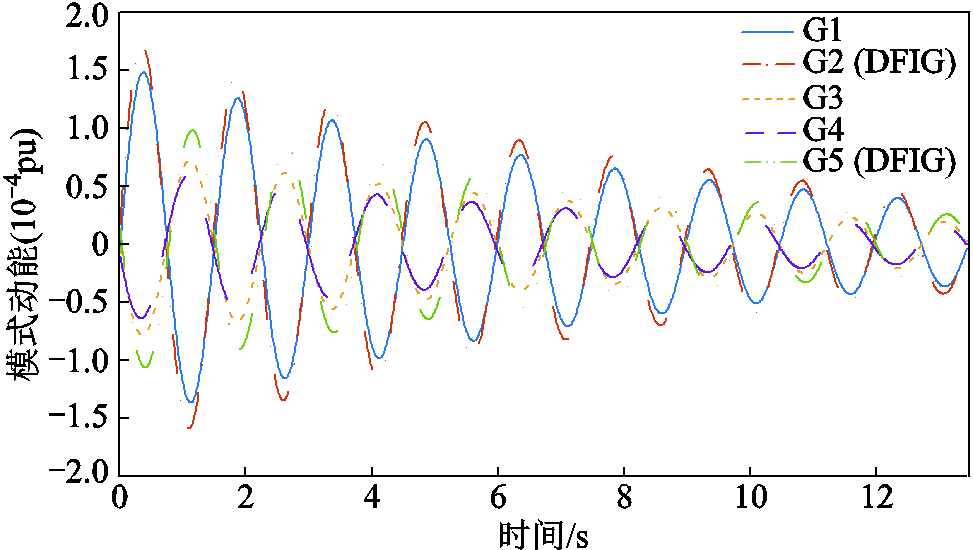
附图6 算例2（区间模式）中各发电机的模式动能
App.Fig.6 The modal kinetic energy of each generator in Case 2(interval mode)
参考文献
[1] 孙大卫, 刘辉, 李蕴红, 等. 风火/光火打捆系统中逆变电源调频与惯量控制对低频振荡的影响机理[J]. 中国电机工程学报, 2021, 41(17): 5947-5957. Sun Dawei, Liu Hui, Li Yunhong, et al. Effect mechanism of primary frequency and virtual inertia control of inverter power on low frequency oscillation in wind-thermal/solar-thermal bundled system[J]. Proceedings of the CSEE, 2021, 41(17): 5947-5957.
[2] 王海鑫, 刘铭崎, 董鹤楠, 等. 含高比例新能源的电力系统低频振荡分析与抑制综述[J]. 电力自动化设备, 2023, 43(9): 152-163. Wang Haixin, Liu Mingqi, Dong Henan, et al. Review on analysis and suppression of low-frequency oscillation in power system with high penetration of renewable energy sources[J]. Electric Power Automation Equipment, 2023, 43(9): 152-163.
[3] 张旭, 陈云龙, 岳帅, 等. 风电参与电力系统调频技术研究的回顾与展望[J]. 电网技术, 2018, 42(6): 1793-1803. Zhang Xu, Chen Yunlong, Yue Shuai, et al. Retrospect and prospect of research on frequency regulation technology of power system by wind power[J]. Power System Technology, 2018, 42(6): 1793-1803.
[4] Roscoe A, Knueppel T, Da Silva R, et al. Response of a grid forming wind farm to system events, and the impact of external and internal damping[J]. IET Renewable Power Generation, 2020, 14(19): 3908-3917.
[5] 谢震, 孟浩, 张兴, 等. 基于定子虚拟阻抗的双馈风电机组虚拟同步控制策略[J]. 电力系统自动化, 2018, 42(9): 157-163, 187. Xie Zhen, Meng Hao, Zhang Xing, et al. Virtual synchronous control strategy of DFIG-based wind turbines based on stator virtual impedance[J]. Automation of Electric Power Systems, 2018, 42(9): 157-163, 187.
[6] Bu Siqi, Du Wenjuan, Wang Haifeng. Model validation of DFIGs for power system oscillation stability analysis[J]. IET Renewable Power Generation, 2017, 11(6): 858-866.
[7] Du Wenjuan, Bi Jingtian, Cao Jun, et al. A method to examine the impact of grid connection of the DFIGs on power system electromechanical oscillation modes[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3775-3784.
[8] Du Wenjuan, Bi Jingtian, Wang H F. Small-signal angular stability of power system as affected by grid-connected variable speed wind generators-a survey of recent representative works[J]. CSEE Journal of Power and Energy Systems, 2017, 3(3): 223-231.
[9] 李辉, 王坤, 胡玉, 等. 双馈风电系统虚拟同步控制的阻抗建模及稳定性分析[J]. 中国电机工程学报, 2019, 39(12): 3434-3443. Li Hui, Wang Kun, Hu Yu, et al. Impedance modeling and stability analysis of virtual synchronous control based on doubly-fed wind generation systems[J]. Proceedings of the CSEE, 2019, 39(12): 3434-3443.
[10] 洪敏. 弱电网下双馈风机的同步控制动态特性及其协调控制策略研究[D]. 杭州: 浙江大学, 2017. Hong Min. Reseach on the dynamic behaviors of DFIG wind turbines in weak grids with synchronized control and its coordinated control strategy[D]. Hangzhou: Zhejiang University, 2017.
[11] 周鹏, 张新燕, 邸强, 等. 基于虚拟同步机控制的双馈风电机组预同步并网策略[J]. 电力系统自动化, 2020, 44(14): 71-78. Zhou Peng, Zhang Xinyan, Di Qiang, et al. Pre-synchronous grid-connection strategy of DFIG-based wind turbine with virtual synchronous generator control[J]. Automation of Electric Power Systems, 2020, 44(14): 71-78.
[12] Gao Fang, Iravani M R. A control strategy for a distributed generation unit in grid-connected and autonomous modes of operation[J]. IEEE Transactions on Power Delivery, 2008, 23(2): 850-859.
[13] Hou X, Sun Y, Zhang X, et al．Improvement of frequency regulation in VSG-based AC microgrid via adaptive virtual inertia[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1589-1602.
[14] Pogaku N, Prodanovic M, Green T C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid[J]. IEEE Transactions on Power Electronics, 2007, 22(2): 613-625.
[15] Zhang Lidong, Harnefors L, Nee H P. Power-synchronization control of grid-connected voltage-source converters[J]. IEEE Transactions on Power Systems, 2010, 25(2): 809-820.
[16] 张家玮, 张琛, 史先强, 等. 储能型静止无功发生装置及其自同步电压源控制[J]. 高电压技术, 2023, 49(1): 61-71. Zhang Jiawei, Zhang Chen, Shi Xianqiang, et al. Energy-storage-type static var generator and its autonomous-synchronization voltage source control[J]. High Voltage Engineering, 2023, 49(1): 61-71.
[17] Johnson B B, Dhople S V, Hamadeh A O, et al. Synchronization of parallel single-phase inverters with virtual oscillator control[J]. IEEE Transactions on Power Electronics, 2014, 29(11): 6124-6138.
[18] 屠勇, 苏建徽, 杨向真, 等. 虚拟振荡器控制的新型逆变器无线并联方案[J]. 中国电机工程学报, 2016, 36(15): 4184-4192. Tu Yong, Su Jianhui, Yang Xiangzhen, et al. A novel virtual oscillator control in wireless parallel connected inverters[J]. Proceedings of the CSEE, 2016, 36(15): 4184-4192.
[19] Groß D, Colombino M, Brouillon J S, et al. The effect of transmission-line dynamics on grid-forming dispatchable virtual oscillator control[J]. IEEE Transactions on Control of Network Systems, 2019, 6(3): 1148-1160.
[20] Zhong Qingchang, Weiss G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[21] Fu Siqi, Sun Yao, Liu Zhangjie, et al．Power oscillation suppression in multi-VSG grid with adaptive virtual inertia[J]．International Journal of Electrical Power & Energy Systems, 2022, 135: 107472.
[22] Huang Linbin, Xin Huanhai, Wang Zhen. Damping low-frequency oscillations through VSC-HVdc stations operated as virtual synchronous machines[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5803-5818.
[23] Wang Weiyu, Jiang Lin, Cao Yijia, et al. A parameter alternating VSG controller of VSC-MTDC systems for low frequency oscillation damping[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4609-4621.
[24] Zhou Xinyi, Cheng Shu, Wu Xun, et al. Influence of photovoltaic power plants based on VSG technology on low frequency oscillation of multi-machine power systems[J]. IEEE Transactions on Power Delivery, 2022, 37(6): 5376-5384.
[25] 韩应生, 孙海顺, 秦世耀, 等. 电压源型双馈风电并网系统小扰动低频稳定性分析[J]. 电工技术学报, 2023, 38(5): 1312-1324, 1374. Han Yingsheng, Sun Haishun, Qin Shiyao, et al. Low-frequency stability analysis of voltage-sourced doubly-fed wind power grid-connected system under small disturbance[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1312-1324, 1374.
[26] 杨涛, 廖勇. 含双馈风电场的互联电力系统虚拟惯量与虚拟阻尼协调控制方法[J]. 电力自动化设备, 2020, 40(11): 92-100. Yang Tao, Liao Yong. Coordinated control method of virtual inertia and virtual damping for interconnected power system with doubly-fed wind farm[J]. Electric Power Automation Equipment, 2020, 40(11): 92-100.
[27] 张祥宇, 黄泳漩, 付媛. 非线性弹性耦合下双馈风电机组的暂态能量转移与振荡特性分析[J]. 电工技术学报, 2024, 39(13): 3956-3974. Zhang Xiangyu, Huang Yongxuan, Fu Yuan. Transient energy transfer and oscillation characteristics analysis of doubly-fed wind turbine under nonlinear elastic couplin[J]. Transactions of China Electrotechnical Society, 2024, 39(13): 3956-3974.
[28] 谢震, 许可宝, 秦世耀, 等. 基于电压源型和电流源型双馈风电机组稳定性对比分析[J]. 电网技术, 2021, 45(5): 1724-1735. Xie Zhen, Xu Kebao, Qin Shiyao, et al. Comparative analysis of doubly-fed wind turbine stability based on voltage source and current source[J]. Power System Technology, 2021, 45(5): 1724-1735.
[29] Perez-arriaga I J, Verghese G C, Schweppe F C. Selective modal analysis with applications to electric power systems, PART I: heuristic introduction[J]. IEEE Transactions on Power Apparatus and Systems, 1982, PAS-101(9): 3117-3125.
[30] Byerly R, Bennon R, Sherman D. Eigenvalue analysis of synchronizing power flow oscillations in large electric power systems[J]. IEEE Transactions on Power Apparatus and Systems, 1982, PAS-101(1): 235-243.
[31] 李天云, 高磊, 赵妍. 基于HHT的电力系统低频振荡分析[J]. 中国电机工程学报, 2006, 26(14): 24-30. Li Tianyun, Gao Lei, Zhao Yan. Analysis of low frequency oscillations using HHT method[J]. Proceedings of the CSEE, 2006, 26(14): 24-30.
[32] 竺炜, 唐颖杰, 周有庆, 等. 基于改进Prony算法的电力系统低频振荡模式识别[J]. 电网技术, 2009, 33(5): 44-47, 53. Zhu Wei, Tang Yingjie, Zhou Youqing, et al. Identification of power system low frequency oscillation mode based on improved prony algorithm[J]. Power System Technology, 2009, 33(5): 44-47, 53.
[33] 李施, 丁仁杰. 一种基于信号相关性的低频振荡辨识方法[J]. 电力系统保护与控制, 2018, 46(11): 46-54. Li Shi, Ding Renjie. An identification method for low-frequency oscillation based on signal correlation[J]. Power System Protection and Control, 2018, 46(11): 46-54.
[34] 刘君, 肖辉, 曾林俊, 等. 基于RSSD和ICA算法的低频振荡模态参数辨识[J]. 电工技术学报, 2018, 33(21): 5051-5058. Liu Jun, Xiao Hui, Zeng Linjun, et al. Parameter identification of low frequency oscillation based on RSSD and ICA algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 5051-5058.
[35] Shen Yaqi, Ma Jing, Wang Letian. Study on DFIG dissipation energy model and low-frequency oscillation mechanism considering the effect of PLL[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 3348-3364.
[36] Sun Zhenglong, Cai Guowei, Yang Deyou, et al. A method for the evaluation of generator damping during low-frequency oscillations[J]. IEEE Transactions on Power Systems, 2019, 34(1): 109-119.
[37] 孙正龙, 王嘉琛, 潘超, 等. 基于支路模式振荡能量的低频振荡区域定位方法[J]. 中国电机工程学报, 2023, 43(17): 6589-6602. Sun Zhenglong, Wang Jiachen, Pan Chao, et al. Low-frequency oscillation area location method based on branch mode oscillation energy[J]. Proceedings of the CSEE, 2023, 43(17): 6589-6602.
[38] 姜涛, 高浛, 李筱静, 等. 基于小波耗散能量谱的电力系统强迫振荡源定位[J]. 电工技术学报, 2023, 38(7): 1737-1750. Jiang Tao, Gao Han, Li Xiaojing, et al. Forced oscillation source location in power system using wavelet dissipation energy spectrum[J]. Transactions of China Electrotechnical Society, 2023, 38(7): 1737-1750.
[39] Jing C, McCalley J D, Kommareddy M. An energy approach to analysis of interarea oscillations in power systems[J]. IEEE Transactions on Power Systems, 1996, 11(2): 734-740.
[40] Messina A R, Ochoa M, Barocio E. Use of energy and power concepts in the analysis of the inter-area mode phenomenon[J]. Electric Power Systems Research, 2001, 59(2): 111-119.
[41] Yu Yiping, Grijalva S, Thomas J J, et al. Oscillation energy analysis of inter-area low-frequency oscillations in power systems[J]. IEEE Transactions on Power Systems, 2016, 31(2): 1195-1203.
[42] 孙正龙, 姜权峰, 王嘉琛, 等. 含风电电力系统机电振荡局部阻尼评估方法[J]. 高电压技术, 2021, 47(10): 3452-3466. Sun Zhenglong, Jiang Quanfeng, Wang Jiachen, et al. Evaluation method of local damping of electrome-chanical oscillation of power systems containing wind turbines[J]. High Voltage Engineering, 2021, 47(10): 3452-3466.
[43] Board I S. IEEE recommended practice for excitation system models for power system stability studies[J]. 1992.
[44] Zheng Z, Xu Y, Mili L, et al. Observability analysis of a power system stochastic dynamic model using a derivative-free approach[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5834-5845.
Abstract In large long-distance transmission system,weakly damped oscillations sometimes occur.The integration of Grid-forming doubly-fed wind turbines into the system plays an active role in supporting the power grid. As the capacity of Grid-forming doubly-fed wind turbines increases, the phenomenon of Grid-forming doubly-fed wind turbines participating in system interval oscillations will gradually become prominent.
Firstly, the energy structure of synchronous generator and Grid-forming doubly-fed wind turbine is derived from the energy of component ports, and the energy properties of the energy structure are classified, and the interaction relationship between component kinetic energy and port energy is analyzed.Secondly, the actual kinetic energy of the component is decomposed in time domain, and the incremental kinetic energy and mode kinetic energy are obtained.Then, from the Angle of eigenvalue analysis, kinetic energy increment and mode kinetic energy are analyzed, and the theoretical basis for analyzing the vibration degree and mode of each unit in the power system of Grid-forming doubly-fed wind turbine is explained.In addition, by using kinetic energy increment and mode kinetic energy, a composite index is established, which evaluates the degree of oscillation participation of each unit and group division in the system interval oscillation from the perspective of amplitude and phase. This index provides a quantitative basis for the analysis of low-frequency oscillation of power system with Grid-forming doubly-fed wind turbine.
The mode kinetic energy and kinetic energy increment curves of the dominant oscillation modes of each generator set are given in the four-generator two-area system. The index of oscillation participation is obtained based on kinetic energy, and the results of the index are consistent with the traditional eigenvalue analysis.At the same time, in the scenario of multiple Grid-forming doubly-fed wind turbines, the method is still applicable and has certain feasibility.This method can provide guidance for the suppression of low frequency oscillations in power system.
The conclusions of this paper are given as follows: (1) This paper established the structure energy of Grid-forming doubly-fed wind turbine and synchronous generator , and based on the interaction energy dissipation - transfer process to build the corresponding energy structure, and extract the transient kinetic energy,There is an interaction process between kinetic energy term and port energy. (2) Through the combined analysis of kinetic energy correlation terms and eigenvalue method, it is proved that the incremental amplitude of kinetic energy of synchronous generator and Grid-forming doubly-fed wind turbine can reflect the participation degree of each unit in the interval oscillation;The phase of the corresponding modal kinetic energy can reflect the modal information of each unit. (3) The method proposed in this paper can analyze the system interval oscillation online, without the use of additional electric gas, only the kinetic energy related items of each unit are extracted, and combined with the WAMS , the participation degree of each unit and the division of the group in the system interval oscillation mode can be realized.
keywords：Low frequency oscillation, grid-forming doubly-fed wind turbine generators, incremental kinetic energy, modal kinetic energy
DOI: 10.19595/j.cnki.1000-6753.tces.240271
中图分类号：TM71
国家自然科学基金面上资助项目（52277084）。
收稿日期 2024-02-19
改稿日期 2024-04-23
孙正龙 男，1988年生，博士，副教授，研究方向为新能源电力系统稳定与控制，人工智能在电力系统应用。E-mail：nedusunzl@neepu.edu.cn（通信作者）
郝舒宇 男，1999年生，博士研究生，研究方向为电力系统稳定与控制。E-mail：haoshuyu666@126.com
（编辑 赫 蕾）